Smart Contract-Aided Attribute-Based Signature Algorithm with Non-Monotonic Access Structures

1  Introduction

With the growth of information technology, distributed file systems and information management have become essential components of modern data management. Systems like Git, vehicle networking, and the Internet of Things (IoT) require efficient data sharing and collaboration while ensuring information security and privacy. These systems face complex access control challenges. Traditional public key encryption, relying on certificates and key maintenance, is insufficient for addressing access control needs in distributed environments.

Attribute-based cryptography (ABC), including Attribute-Based Encryption (ABE) and Attribute-Based Signatures (ABS) [1], offers a novel solution for access control in distributed file systems by using attributes to define access policies. Xu et al. [2] proposed an access control scheme using ABE and ABS for read-write permissions on distributed version control systems. Hong et al. [3] proposed an attribute-based online/offline signature scheme for mobile crowdsensing scenarios. Li et al. [4] and Patil et al. [5] proposed an access control scheme based on ABC for electronic health records. In the above application scenarios, ABS is often used to verify or manage permissions, especially for writing. In this framework, users’ signing keys are linked to their attributes, and signatures are associated with specific access policies. Only entities whose attributes meet predefined conditions can generate valid signatures. This simplifies key distribution, reduces maintenance costs, and enhances flexibility, making it ideal for distributed environments.

In practical applications, several challenges hinder the effectiveness of existing solutions. Most ABS implementations rely on monotonic access structures, limiting their ability to express complex access control logic. Compared to traditional access control lists (ACL), ABS struggles to offer fine-grained revocation or permission adjustments at the individual attribute or user level. To better align with real-world needs, ABS must support non-monotonic access policies, such as AND, OR, NOT, and Threshold gates. These enhancements would improve policy expressiveness and enable more precise permission management, such as “Faculty AND Accounting AND (non-math department)”. However, extending monotonic ABS to non-monotonic schemes is challenging. In non-monotonic designs, user key attributes are often independent, allowing malicious users to forge signatures by concealing certain attributes(such as “math department”), which poses a security risk. We refer to this type of forgery as “attribute concealment.” Okamoto et al. propose an ABS supporting non-monotonic structures [6]. To avoid attribute concealment, the scheme requires that the key must contain information about all attributes in the attribute space, but its low verification efficiency makes it impractical.

This also highlights another critical challenge faced by ABS: ABS algorithms typically involve complex bilinear pairing operations, which pose significant challenges for resource-constrained devices. The introduction of non-monotonic access structures further increases this computational burden, conflicting with the lightweight computing demands of IoT devices. To address this, researchers have explored server-aided mechanisms [7–11] where remote servers take on most of the computational tasks. However, this approach raises new concerns about server trustworthiness. Although server assistance can reduce client-side computational load, it also introduces security and trust issues, as users must trust that servers will not leak sensitive information or tamper with computation results. Additionally, the trustworthiness of servers hinders the delegation of attribute-related computations in ABS. If the server is responsible for verifying the correctness of user attributes, it introduces the risk of compromising user attribute privacy, making challenges like attribute concealment difficult to address. Thus, the trust issue with external servers and the forgery risk of non-monotonic access structures present conflicting problems.

Therefore, developing ABS algorithms that support non-monotonic access policies while maintaining efficiency is an urgent research topic. This paper proposes a smart contract-aided ABS scheme (SC-ABS) that supports non-monotonic access policies, effectively addressing the conflict between server trust issues and attribute concealment. Our contributions are outlined below:

1.    We present a new attribute-based signature scheme that supports non-monotonic access structures on attributes. Our scheme can handle any access structure that can be represented by a boolean formula involving AND, OR, NOT, and threshold operations.

2.    Our scheme introduces a smart contract-aided computation mechanism in which the computation program is transparently recorded on the blockchain and automatically executed upon meeting predefined conditions. This ensures the security of intermediate results. Compared to traditional server-aided schemes, this approach is secure against collusion attacks and simultaneously reduces computational overhead for users.

3.    We implemented SC-ABS, then tested its computational overhead and compared it with other server-assisted ABS algorithms. Additionally, we conducted a comprehensive security analysis. SC-ABS is more suitable for data security protection and permission control in the distributed scenario of limited resources.

2  Related Works

2.1 Attribute-Based Signature

Attribute-based signatures (ABS), first proposed in [1], ensure that only entities whose attributes satisfy the access policy can generate valid signatures. The most widely used existing ABS schemes are monotonic access structures such as the schemes of Maji et al. [1,12]. Okamoto et al. [6] present a fully secure ABS scheme in the standard model that supports general non-monotonic predicates. However, this scheme requires a fixed classification for attributes, and users must possess all attribute types, resulting in low efficiency due to the need for multiple bilinear pairings, making it impractical.

The computational overhead of ABS is a significant barrier to its widespread use. To address this, several server-aided ABS schemes have been proposed. Cui et al. [7] introduced server-aided ABS, transferring the signature and verification work to the server to reduce overhead. However, Xiong et al. [13] demonstrated that Cui et al.’s scheme lacks collusion security, and their scheme had correctness issues. Huang et al. [8] proposed a secure server-aided ABS that meets stronger security definitions. Chen et al. [9] used an access tree structure and delegated verification to the server, while Li et al.’s scheme [10] only supports threshold-based access strategies. These server-aided ABS schemes typically face server trust issues and do not support non-monotonic access policies.

ABS supporting non-monotonic access structures offers more expressive access control strategies, but it also incurs high computational overhead and poses a risk of attribute concealment. Current server-aided ABS are limited by server trust and struggle to address attribute concealment. To address these challenges, this paper proposes a smart contract-based trusted aided ABS algorithm that incorporates a non-monotonic access structure.

2.2 Smart Contract

Smart contracts, introduced by Nick Szabo in 1994, are “computerized transaction protocols that execute the terms of a contract” [14]. They aim to fulfill common contractual conditions without the need for intermediaries [14,15]. Smart contracts are facilitated by blockchain platforms like Ethereum. The scheme presented in this paper leverages Ethereum [16] for the design and deployment of smart contracts aimed at assisted computing. As a widely deployed blockchain, Ethereum enables developers to create smart contracts using languages like Solidity and Vyper, compile them, and deploy them. To deploy a smart contract, the owner initiates a transaction, creating a contract account. Any Ethereum account interacts with the smart contract through the contract account. When an Ethereum account invokes a function to update data stored on the Ethereum network, it submits a corresponding transaction, which is recorded on the Ethereum network.

Advantages of Smart Contract Assistance. Smart contracts aided ABS is different from server-aided ABS, and blockchain-based smart contracts have more advantages than traditional third-party servers.

•   Distributed services: Smart contracts, deployed on the blockchain, provide distributed and decentralized services, mitigating the single point of failure risk faced by traditional third-party servers.

•   Reliability: Once issued, a smart contract cannot be tampered with. It is automatically executed when conditions are met, and no party can alter the result. Multiple independent nodes process and verify the contract logic, effectively preventing manipulation and ensuring timely execution according to specified terms. This makes smart contract results more reliable than those from traditional servers.

•   Security: Smart contracts function as digital protocols, with open and transparent logic that can be reviewed by all users. As long as the code logic is correct, the stored information cannot be maliciously exploited, and the contract cannot perform actions outside the agreement, such as colluding with malicious users. In comparison to traditional third-party servers, smart contracts offer greater security for aided services.

3  Preliminaries

First, we provide the definition of an access structure. Then we give background information on bilinear maps and our cryptographic assumption. Finally, we give some background on linear secret-sharing schemes.

Definition 1: Access Structure [17]: Let 𝒫={P1,…,Pn} be a set of parties. A collection A⊆2𝒫 is monotonic. For ∀B and C, if B∈A and B⊆C then C∈A. A monotonic access structure is a monotonic collection A for non-empty subsets of {P1,…,Pn}, namely A⊆2𝒫∖⧸0. The sets in A are considered authorized sets, while those not in A are unauthorized sets.

3.1 Bilinear Maps

The ABS algorithms use the idea of bilinear pairs based on elliptic curves. Let G0 be a cyclic group of prime order p generated by g. Let G1 be a group of order p. We can define e as a bilinear map, e:G0×G0→G1. The bilinear map e has the following properties:

1.    Bilinearity: e(ua,vb)=e(u,v)ab for all u,v∈G0 and a,b∈Zp.

2.    Non-degeneracy: e(g,g)≠1.

3.2 Security Model

The security model is defined as a game between a polynomial-time adversary A and a challenger C, where the challenger C interacts with a smart contract to perform its operations.

Setup: Adversary A allocates the target attribute set S∗ and forwards it to C. Challenger C generates public parameters PK and master key MSK, and then returns PK to A.

Query: The adversary A adaptively issues the following query to C.

•   Key extraction query: The adversary A selects the access policy Γ and additional attributes ϱ. The challenger C then executes the key generation algorithm to produce the corresponding partial signature key psk and the user signing key usk for A.

•   Signature query: The adversary A selects a message m and sends a request to the challenger C. The smart contract then generates a partial signature based on the attribute set S associated with A’s account. If the attribute set S satisfies the access policy, the smart contract completes the signature generation process, producing the final signature σ, which is returned to A.

•   User signature verification query: The adversary A has the signature σ of the message m under the attribute set S. After receiving the signature, C applies the signature extraction algorithm to produce a converted signature σ^, which is sent back to A. A computes an intermediate signature σ1~ and returns it to C. Finally, C performs the user signature verification and returns the verification result.

Signature forgery: A generates a forged signature σ∗ for a message m∗ under an attribute set S∗. A is considered successful if the following conditions are met:

•   A sends σ∗ to C. C generates a converted signature σ∗^ and returns it to A. A executes the aided signature verification algorithm to compute an intermediate signature σ∗~, which is sent to C, and C returns the verification correct.

•   Adversary A has never issued a signature query for message m∗ and attribute set S∗.

3.3 Linear Secret-Sharing Schemes

First, we introduce the design of a non-monotonic access policy based on the Linear Secret-Sharing Scheme (LSSS).

Definition 2: Linear Secret-Sharing Schemes [18]: Let 𝒫 be the set of all attributes, L be a matrix of l×m, and let π:{1,…,l}→𝒫 be a function that maps each row in the matrix to an attribute. A linear secret-sharing scheme (LSSS) on Zp is a secret-sharing scheme π on an access policy A based on the attribute set 𝒫. The linear secret-sharing scheme consists of two efficient algorithms:

ShareL,π: Input s∈Zp as the shared secret, choose s2,…,sm∈Zp, let s=(s,s2,…,sm). For each attribute π(i), compute its share λi=⟨Li⋅s⟩, where Li is the ith row of L. Finally, output l shares L⋅s.

ReconL,π: Input an authorization set S∈A, let I={i∣π(i)∈S}. The output is a set of constants (i,μi)i∈I, which satisfies the linear reconstruction property ∑i∈Iμiλi=s.

Non-Monotonic Access Structures. We refer to the method proposed by [18] to transform the monotonic access policy into a non-monotonic access policy. Assume a linear secret-sharing scheme family {∏A}A∈𝒜𝒮. For each access policy A∈𝒜𝒮, the attribute set 𝒫 covered by it has the following properties: There are two types of attribute names in 𝒫, positive attributes (such as “English department”, recorded as x) and negative attributes (such as “non-English department”, recorded as x′). If x∈𝒫, then x′∈𝒫, and vice versa. Positive attributes and negative attributes are conceptually related.

Definition 3: non-monotonic access policy family 𝒜𝒮: For each access policy A∈𝒜𝒮, the attribute set it covers is 𝒫. Define a possible non-monotonic access policy NM(A) where the attribute set it covers is 𝒫~, the set of all positive attributes in 𝒫. For each set S~⊂𝒫~, define N(S~)=S~∪{x′∣x∈𝒫~∖S~}. If and only if N(S~) is an authorized set in A, S~ is an authorized set in NM(A). For each authorization set X∈NM(A), there is a set in A that contains all attributes in X and all negative attributes not in X.

4  Scheme Construction

We designed a smart contract-aided attribute-based signature algorithm with non-monotonic access structures (SC-ABS). The algorithm involves three entities: attribute authorities, smart contracts, and users. As shown in Fig. 1, the attribute authority is responsible for key initialization and issuance, while the smart contract assists with calculations that users can sign and verify as needed. Compared to traditional ABS, our algorithm supports non-monotonic access strategies. Additionally, it introduces smart contracts as trusted, autonomous computing agents that execute programs automatically upon invocation, thereby eliminating the need for third-party involvement.

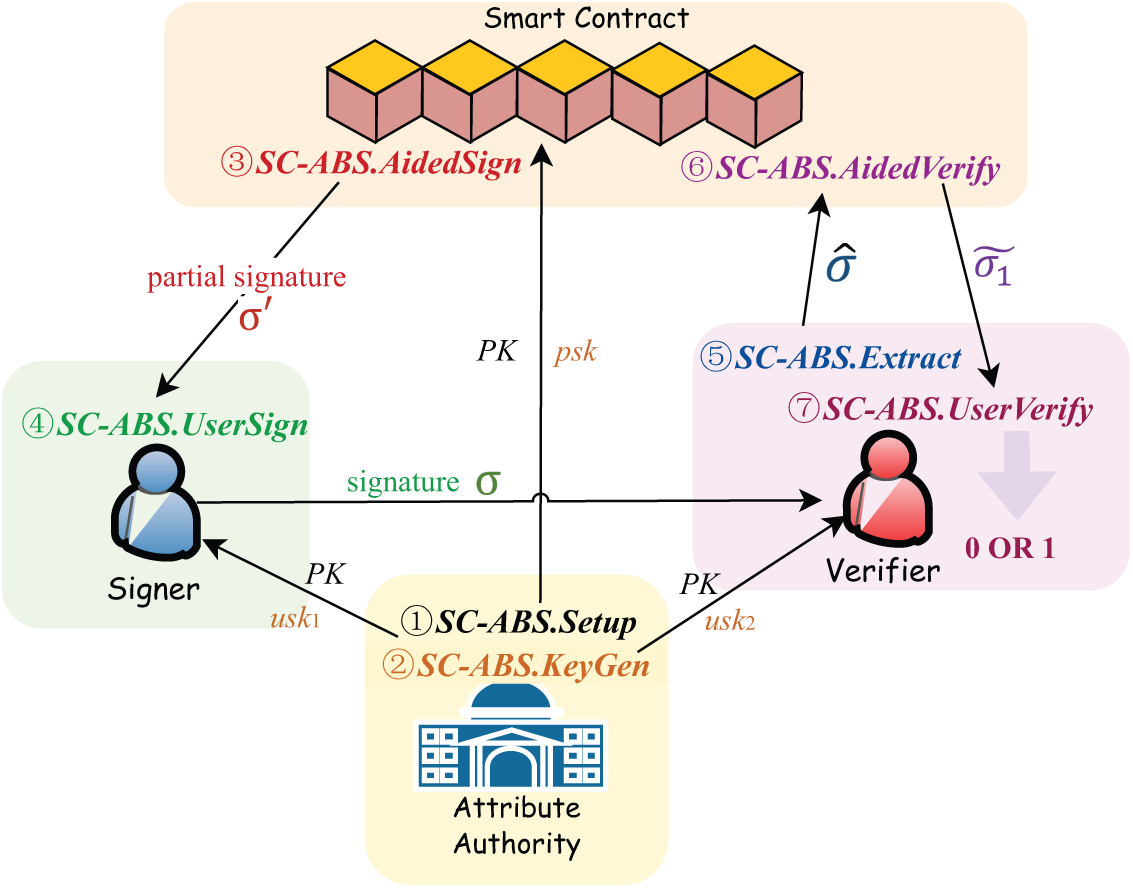
Figure 1: Algorithm framework of SC-ABS

4.1 Smart Contract Aided ABS

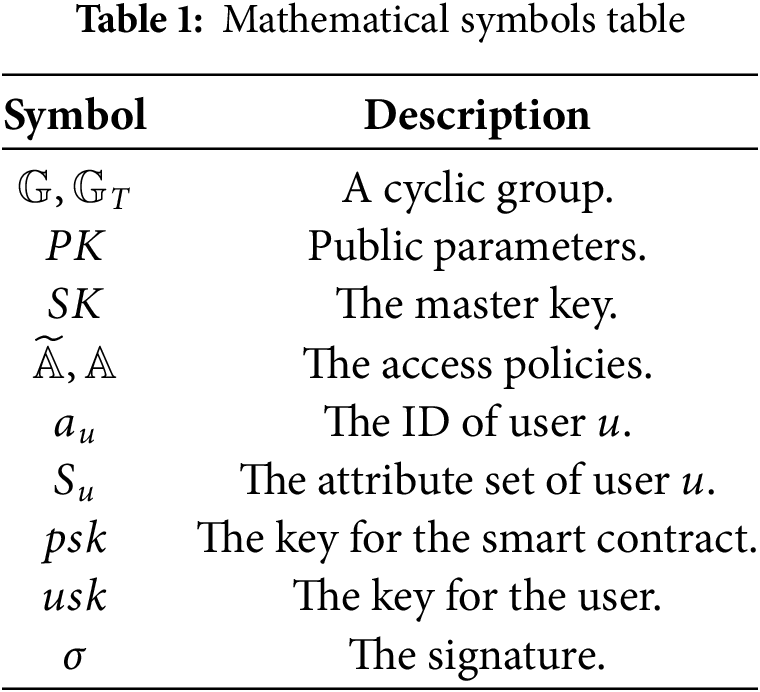
As shown in the Fig. 1, referring to Xiong et al., we designed the SC-ABS algorithm as follows, of which the meaning of symbols is shown in Table 1:

SC-ABS.Setup(λ): The algorithm, executed by the attribute authority, takes the security parameter λ as input and then generates the system parameters and the master key. Divided into four steps:

1.    Select the multiplicative cyclic group G,GT of prime order p>2λ, and define the bilinear pair e:G×G⟶GT.

2.    Randomly select r0,u0,u1,…,un∈G. Define the collision-resistant hash function H(m)=u0∏j=1nujm[j], where m[j] represents the message string The jth position of m.

3.    Set the attribute universe U=1,2,…,l, and for each attribute i∈U, randomly select ri∈G. Define an additional attribute ϱ and randomly select rϱ∈G.

4.    Randomly select α1,α2∈Zp and generator g∈G, and calculate Z=e(g,g)α1+α2.

Then, the system’s public parameters are denoted as PK={g,e,G,GT,H,Z,r0,{ri}i∈U∪ϱ,u0,…,un}, the master key is SK={α1,α2}. PK is published to both smart contracts and all users, and SK is protected by the attribute authority.

SC-ABS.KeyGen(PK,SK,A~,au,Su): The algorithm is executed by the attribute authority. It uses the public parameters PK, master key SK, access policy A~, user ID au, and its attribute set Su as inpu. Based on a linear secret-sharing scheme that supports non-monotonic access policies, the algorithm generates partial signature keys and user signature keys. The algorithm is divided into the following steps:

1.    The non-monotonic access policy A~ and a certain monotonic access policy A satisfy A~=NM(A). The non-monotonic access policy A~ covers the attribute set P⊆U, then the monotonic access policy A covers the attribute set 𝒫, 𝒫 contains the attributes in P and the corresponding negative attributes. A can be related to the linear secret-sharing scheme (L,π), where L is a matrix of l×m. For each row k∈[1,l] in L, π(k) maps to an attribute in 𝒫.

2.    Randomly select v2,v3,…,vm∈Zp, and define vector v→={α1,v2,…,vm}, calculate φπ(k)=Lk→⋅v→, where Lk→ represents the kth row of matrix L.

3.    For each row k∈[1,l] in L, randomly select xk∈Zp. The user has a unique ID value au. For the additional attribute ϱ, the user also selects a random value xϱ,au∈Zp. This random value xϱ,au is associated with the user ID and the attribute ϱ.

4.    Compute dk=gφπ(k)(r0⋅rπ(k))xk,dk′=gxk,dk′′={rixk}i∈U∪ϱ,i≠π(k).

5.    Similarly, calculate dau=gα2(r0∏i∈Su∪ϱri)xϱ,au,dau′=gxϱ,au.

Then, based on the linear secret-sharing scheme (L,π), the partial signature key psk={dk,dk′,dk′′}k∈[1,l] and Su is assigned to the smart contract, and the user signature key is usk={dau,dau′}. To protect the security of psk and Su, we use the eWEB scheme [19], which is a blockchain encryption scheme using dynamic active secret sharing. eWEB securely stores encoded secrets, relying on an honest majority of dynamic point sets and granting access only to authorized users meeting the creator’s criteria. This ensures secure storage of private information and prevents unauthorized access to smart contract data.

SC-ABS.AidedSign(H(m),psk,A~,au,Su): This algorithm will be executed by the smart contract when the user initiates an aided signature request. With message digest H(m), public parameters PK, access policy A~, signer ID au and its attribute set Su as input, the smart contract calculates the output partial signature. The algorithm is divided into the following steps:

1.    Confirm whether the attribute set Su of the signer au satisfies the access policy. If so, define K={k}π(k)∈Su and optionally a set of constants {ωk}∈Zp, satisfying ∑k∈Kωkφπ(k)=α1.

2.    Randomly select η,ζ,s∈Zp, based on the current time t, select β∈Zp for the time point in the same period, and calculate:

{σ0′=∏k∈K(dk⋅∏i∈Su∪ϱ,i≠π(k)dk,i′′)ωk⋅(r0∏i∈Su∪ϱri)η⋅H(m)ζ⋅H(t)au+s,σ1′=gη∏k∈K(dk′)ωk,σ2′=gζ,σ3′=gs,σ4′=(r0∏i∈Su∪ϱri⋅H(t))1β.(1)

Then the partial signature generated by the smart contract for the signer au based on the message m is σ′={σ0′,σ1′,σ2′,σ3′,σ4′,H(m)}.

SC-ABS.UserSign(usk,σ′,m,t): The algorithm will be executed by the user after he receives a partial signature returned by the smart contract. With the user signature key usk, partial signature σ′, message m, and time t as input, the user calculates the final signature. Firstly, the user randomly selects xϱ,au′,ζ′,s′∈Zp, and computes:

{σ0=σ0′⋅dau⋅(r0∏i∈Su∪ϱri)xϱ,au′⋅H(m)ζ′⋅H(t)s′,σ1=σ1′⋅gxϱ,au′⋅dau′,σ2=σ2′⋅gζ′,σ3=σ3′⋅gau+s′,σ4=σ4′.(2)

Finally, the user gets the signature of message m based on his own attribute set Su: σ={σ0,σ1,σ2,σ3,σ4,m,t}.

SC-ABS.Extract(σ): The algorithm is executed by the user verifying the signature. After extracting the signature, the result is sent to the smart contract for assisted verification. The user selects {σ0,σ1,σ3,σ4,t} in signature σ, randomly selects δ∈Zp, and calculates σ0^=σ0δ,σ1^=σ1δ,σ3^=σ3δ,σ^4=σ4δ as a result of extraction σ^={σ0^,σ1^,σ3^,σ^4,t}.

SC-ABS.AidedVerify(σ^): The smart contract accepts the extraction result σ^ and calls the algorithm to perform aided signature verification. The specific calculation is as follows:

e(σ0^,g)e(σ1^,(σ^4)βH(t))e(σ3^,H(t))=σ1~.(3)

The smart contract returns σ1~ to the user who needs to verify the signature.

SC-ABS.UserVerify(σ,σ1~): The user receives the verification result σ1~ provided by the smart contract and will perform the final calculation:

σ2~=e(σ2δ,H(m))⋅Zδ.(4)

Determine whether σ1~ is equal to σ2~. If they are equal, the signature verification is successful, and the system outputs 1. Otherwise, signature verification fails, and the system outputs 0.

In SC-ABS, the smart contract is responsible for the auxiliary calculation of signature and verification. After completing the local calculation, the user initiates a calculation request to the smart contract in the form of publishing a transaction, and the smart contract verifies the user identity, performs the calculation, and returns the calculation result.

4.2 Proof of Correctness

Theorem 1: SC-ABS is correct if for all λ∈N:

Pr[PK,SK←Setup(λ);psk,usk←KeyGen(PK,SK,A~,au,Su);σ′←AidedSign(H(m),psk,A~,au,Su)σ←UserSign(usk,σ′,m,t):UserVerify(σ,AidedVerify(Extract(σ)))=1]=1.(5)

Proof Proving the correctness of SC-ABS requires showing the equivalence between σ1~ and σ2~. In the signature extraction conversion process, the δ parameters can be effectively offset against each other. As a result, there is no need to include the δ exponent in subsequent derivations. We first derive the result of σ1~: Let ∑k∈Kωkφπ(k)=p1, ∑k∈Kωkxk=p2, r0∏i∈Su∪ϱri=R, η+xϱ,au+xϱ,au′=X, au+s+s′=S, obviously p1=α1.

{e(σ0,g)=e(gp1⋅(R)p2+X⋅H(m)ζ+ζ′⋅H(t)S⋅gα2,g)=e(gα1+α2,g)⋅e((R)p2+X,g)⋅e(H(m)ζ+ζ′,g)⋅e(H(t)S,g);e(σ1,(σ4)βH(t))=e(gp2+X,R⋅H(t)H(t))=e(g,(R)p2+X);e(σ3,H(t))=e(gS,H(t)).(6)

Therefore, we can deduce:

σ1~=e(σ0,g)e(σ1,(σ4)βH(t))e(σ3,H(t))=e(gα1+α2,g)⋅e((R)p2+X,g)⋅e(H(m)ζ+ζ′,g)⋅e(H(t)S,g)e(g,(R)p2+X)e(gS,H(t))=e(gα1+α2,g)e(H(m)ζ+ζ′,g).(7)

For σ2~, we can derive:

σ2~=e(σ2,H(m))⋅Z=e(gζ+ζ′,H(m))e(g,g)α1+α2.(8)

Therefore, σ1~ and σ2~ are equivalent. □

5  Security Analysis

This section is the analysis of SC-ABS security. We will analyze the security of the algorithm and smart contracts.

5.1 Unforgeability and Anonymity

We refer to Waters et al.’s [20] definitions and demonstrate in the appendix that SC-ABS satisfies unforgeability and anonymity under the random oracle model.

In SC-ABS, the smart contract manages aided signing and verification. During signing, the signer initiates a transaction, and the smart contract determines their attribute information based on the account, enhancing security. SC-ABS relies not only on the difficulty of bilinear pairing problems but also on the trustworthiness of the smart contract. During aided signing, when an adversary requests a signature, the challenger provides the attribute set and signature for the message. However, users cannot specify their attributes in the smart contract signing phase; it strictly adheres to the rules and uses the set linked to the user’s account. Therefore, as long as the user’s account is secure, attackers cannot query a signature for any attribute set.

5.2 Smart Contract Security

By introducing the smart contract, the computational process can be transparently displayed on the blockchain, and all user transactions are immutable. This ensures that the entire SC-ABS system is auditable and traceable. Additionally, implementing an audit penalty mechanism in practice can effectively raise the cost of malicious attacks.

This section will focus on analyzing the security of the data stored in the smart contract on the blockchain, specifically addressing the variables security, the intermediate results security, and collusion security.

Data Stored by Smart Contracts. The data stored by the smart contract on the blockchain can be classified into two categories:

1.    Variables in the Ethereum Virtual Machine (EVM) environment: public parameters PK, the partial signature key psk, and the user attribute set Su.

2.    Transactions on the blockchain: intermediate results generated by the smart contract, namely partial signature σ′ and aided verification result σ1~.

5.2.1 Variables Security

For the stored variables, PK is the public parameter, accessible to all participants as part of the system. Since PK does not introduce any privacy risks, it can be stored in plaintext without concerns for data security. In contrast, psk and Su involve key and user attribute information, which must be securely stored. By utilizing the eWEB scheme, we can securely encrypt and store psk and Su on the blockchain. Only the smart contract, when executing according to predefined logic, can access the relevant parameters. Even if a malicious user attempts to monitor the execution of the smart contract by tracking its memory, this memory data is temporary and not synced to the blockchain. Therefore, malicious users cannot monitor memory data from other nodes running the smart contract.

5.2.2 Intermediate Result Security

The intermediate result generated by the smart contract contains a partial signature σ′ and an aided verification result σ1~, which is stored in plaintext on the blockchain as part of the transaction. Concerns may arise about whether these intermediate results could lead to information leakage or facilitate collusion. Therefore, it is essential to analyze the security of these intermediate results, focusing on protection against man-in-the-middle attacks and replay attacks.

1.    Man-in-the-middle attack: Suppose there is a middleman au′ who obtains the intermediate result of the signature applied by other users au, but because the signature σ0′ contains the user’s unique ID information au, the middleman cannot generate σ3 that also contains au, so the intermediate result cannot be used.

2.    Replay attack: Assume that user ru once had written permission to the file, but after the permission was revoked later, it no longer satisfies the access policy. The access policy of the file has not changed, and then user ru attempts to use the signature intermediate results obtained in the past to generate a signature that satisfies the access policy. σ′ contains the time information H(t) of the aided signing and the corresponding value β of the time period. Suppose the user uses the intermediate result at time t to forge a signature at time t′, then when the smart contract verifies the signature, there is:

e(σ0^,g)e(σ1^,(σ4^)β′H(t′))e(σ3^,H(t′))

Since H(t) and β are used in σ0^ and σ4^, the aided signature verification result cannot pass SC-ABS. UserVerify. Therefore, signature forging cannot succeed.

5.2.3 Collusion Security Analysis

In SC-ABS, collusion attacks among multiple users occur when users with attribute sets that don’t satisfy the access policy try to generate valid signatures by combining their signature keys. Since the full signature is generated from partial signatures that contain attributes of the user, conspirators must merge their partial signatures. The σ0′ is tied not only to the user’s attribute set but also to their ID information au. Additionally, each user’s attribute set is randomized with different random numbers, and parameters related to the additional attribute ϱ vary across users. Therefore, users whose attribute sets do not meet the access policy cannot combine their partial signatures to generate valid ones, and α1 cannot be recovered.

In collusion attacks between signers and smart contracts, all transactions are stored on the blockchain, ensuring that intermediate signatures and aided verification results are auditable and non-repudiable. Smart contracts issued by trusted attribute authorities are deployed as open, transparent programs on the blockchain, executing automatically when specific conditions are met. Unlike third-party servers with opaque logic, participants can review the code’s logic and security, significantly reducing the risk of malicious behavior. A correct smart contract generates intermediate signatures only based on the attribute set associated with the user account that initiated the request. In the signature verification algorithm, the smart contract cannot access the message m, and any malicious attempt to upload a message will be rejected due to format non-compliance. As transparent, self-executing programs issued by trusted institutions, rather than third-party institutions or individuals, the smart contract is secure against collusion attacks.

In summary, the use of smart contracts for aided computation is secure against collusion attacks. Additionally, the information stored on the blockchain is secure under the design of this solution, effectively protecting against privacy threats.

6  Performance

In this section, we conduct a comprehensive evaluation of the SC-ABS scheme. This includes analyzing its storage, computing, and communication overhead; comparing its computing overhead with that of other server-assisted ABS algorithms; and performing a functional comparison with related algorithms.

We implemented the SC-ABS algorithm based on the PBC (Pairing-Based Cryptography) library, and our experiments were conducted using C on a system with an Intel Core CPU (1.60 GHz, 2 GB RAM). We tested the computing time overhead of the smart contract and the client respectively. We set the size of the attribute space to 10 and the number of attributes involved in the access policy to 5, for a total of 100 times. The average time of smart contract-aided signature is 0.0082 s, the average time of user signature is 0.0044 s, the average time of smart contract-aided verification is 0.0034 s, and the average time of user signature extraction and verification is 0.006 s, which the verification time is 0.0012 s.

Let d be the size of the default attribute set, a the user’s attribute set size, a′ the minimum attributes required for access, and l the number of attributes in the policy. In the SC-ABS scheme, we minimize client-side computational overhead. Specifically, the smart contract signature involves 2a′+7 exponentiations (EG) over the group G, while user signing requires only 6 exponentiations over G. The aided verification process entails merely 3 pairing operations (P) performed by the smart contract over G. Additionally, the user-end verification cost is relatively low, consisting of one EG, one exponentiation (EGT) over the group GT, and one P.

As shown in Table 2, we compare our SC-ABS scheme with other 5 server-aided attribute-based signature (SAABS) schemes [7–11]. Compared to other SAABS, SC-ABS features the shortest user secret key length and incurs the least user-end signing cost. The aided verification cost is also minimal, involving just one additional pairing operation compared to the two pairings of SA-ABSR [7]. Moreover, the user-end verification cost is comparable to that of most SAABS schemes. For aided signing costs, when l≥a′+4, SC-ABS exhibits the lowest computational cost, which is advantageous as access policies become increasingly complex. Moreover, the signature length of SC-ABS is shorter than that of ABSAVS [9], DABSAS [10], and SAABS-CR [11] but slightly longer than SA-ABSR and InSAABS. This is due to the introduction of time-dependent information to implement replay protection in distributed file systems. On the other hand, we also compare SC-ABS with another non-aided non-monotonic ABS [6]: while SC-ABS costs 4 pairing operations during verification, the latter algorithm costs l+3 pairing operations during verification. Thus SC-ABS proves to be efficient on algorithm and further more efficient with smart contract aiding.

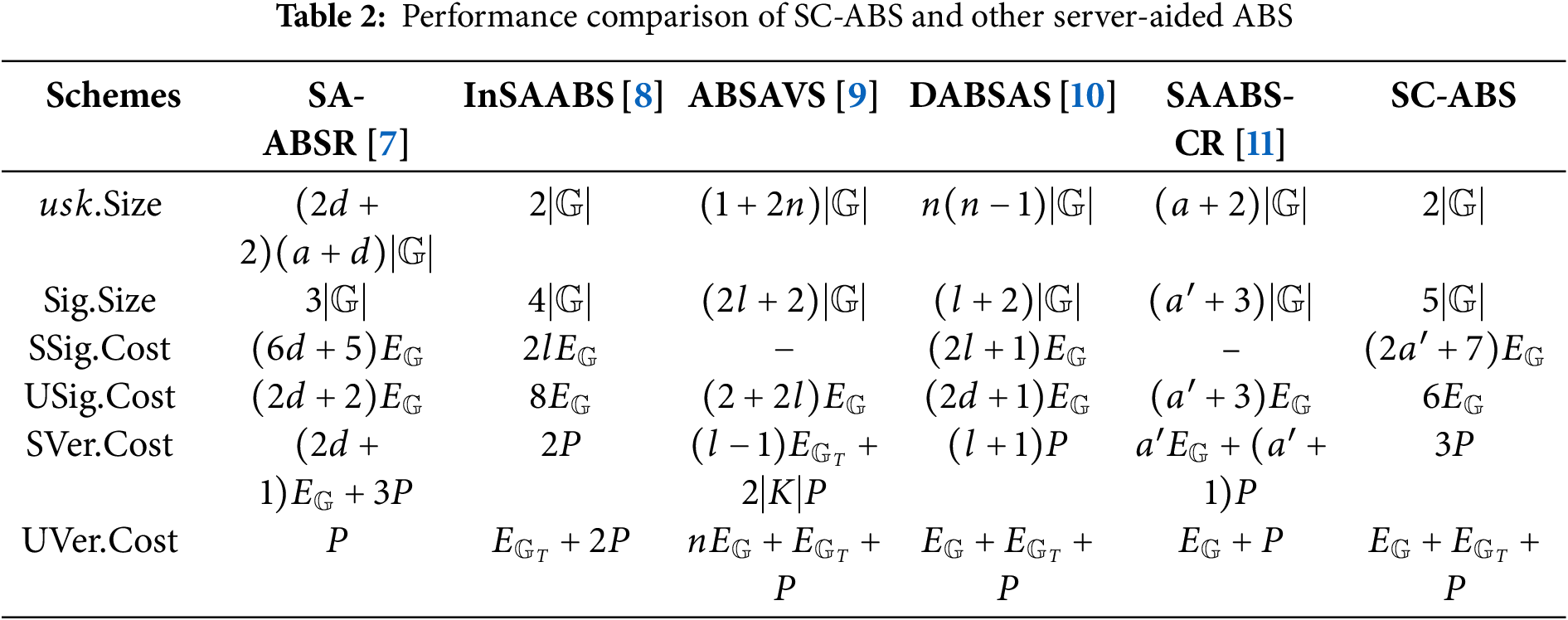
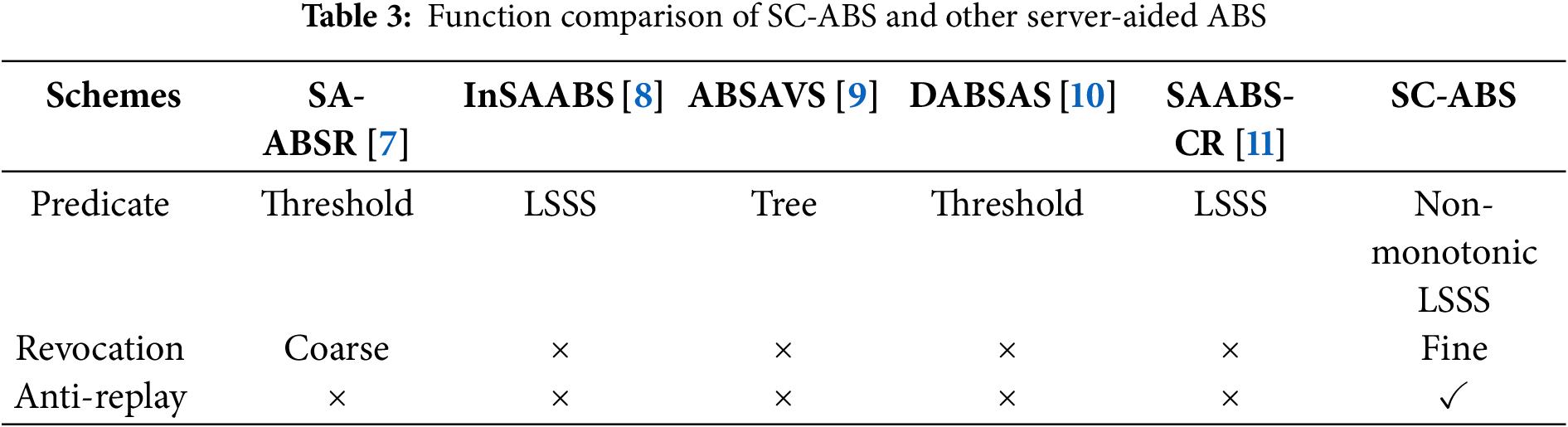
We also compared the security features of the above six schemes, as shown in Table 3. Only SC-ABS employs the most expressive non-monotonic LSSS access structure, which supports both fine-grained attribute revocation and replay resistance. While SA-ABSR supports coarse-grained attribute revocation, it is vulnerable to collusion attacks; InSAABS and SAABS-CR utilize more expressive LSSS access structures but do not support revocation functionality. The other five SAABS fail to protect against malicious user replay attacks on signatures in distributed systems (such as Git). Therefore, compared with other SAABS, SC-ABS supports a richer set of security features without increasing computational overhead, making it better suited for the requirements of distributed systems.

7  Conclusion

In this paper, we propose a smart contract-aided ABS scheme that supports a non-monotonic access structure. We use negative attributes to extend the monotonic access structure to the non-monotonic access structure. Based on the distributed and reliable characteristics of smart contracts, we perform auxiliary computations to reduce the computing cost of users and prevent users from forging signatures by attribute concealment. We prove that SC-ABS satisfies unforgeability and anonymity under a random oracle model, and evaluate its computational performance. Experimental results show that compared with other server-assisted schemes, our scheme can improve security and reduce the computing cost of the client.

In the future, we plan to apply this solution to popular distributed file systems such as Git and design fine-grained user permission granting and revocation schemes based on this approach. The proposed scheme will require users to have closer interactions with blockchain technology. However, it is also essential to consider whether the introduction of smart contracts might introduce additional security risks and overheads. Evaluating and mitigating these potential issues will be a key focus of our further research.

Acknowledgement: This work was supported by National Natural Science Foundation of China. The authors wish to thank anonymous reviewers for their valuable comments and suggestions that improved this paper.

Funding Statement: The specific funding Grant Number is No. 82090053.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Xin Xu, Zhen Yang; analysis and interpretation of results: Xin Xu; draft manuscript preparation: Xin Xu, Yongfeng Huang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Xin Xu, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Appendix A SC-ABS Security Proofs: We analyze the security of the SC-ABS algorithm. The security analysis of the ABS algorithm usually includes two points: unforgeability and anonymity.

Appendix A.1 Unforgeability

Unforgeability means that a valid signature can only be generated using a partial signing key and the corresponding user signing key.

Theorem A1: If there exists a polynomial-time adversary A that wins the above game with non-negligible probability ε under a chosen message attack, it means that a polynomial-time challenger C can be built, with non-negligible probability ε′≥εqs(n+1)) solves the q-DHE problem, where qs represents the number of allowed signature queries, and n represents the bit length of message m.

Proof: Assuming that under the polynomial time algorithm A can destroy the proposed solution with a non-negligible probability ε, then there is a polynomial time challenger C: given g,g1,…,gq,gq+2,…,g2q, the challenger can calculate gq+1=gaq+1 through the following steps.

Initialization: Challenger C manages an attribute domain U=1,2,…,q, and the adversary specifies a target attribute set S∗ and forwards it to C. C randomly selects α1′,α2′,a∈Zp, and defines Z=e(g1,gq)⋅e(g,g)α1′+α2′, implicitly defined α1=α1′+aq+1,α2=α2′, for simplicity, we set gi=gai here. C selects γ0,{γi}i∈U∈Zp, and calculates r0=gγ0∏i∈S∗ri−1 and ri=gγigq+1−i. Randomly select constants θ∈[1,n], x0,y0,{xj},{yj}∈Zp,j∈[1,n]. For each bit j∈[1,n] of message m, define u0=gaq(x0−2θqs)gy0,uj=gaqxjgyj. Finally, C selects the hash function H(⋅), and the system public parameters are PK={g,e,G,GT,H,Z,r0,{ri}i∈U,u0,…,un}.

According to the security proof of [20], we define the following function for each message:

J(m)=x0+∑j=1nxjm[j]−2θqs;K(m)=y0+∑j=1nyjm[j].(A1)

According to the above function, for a message m, there is:

H(m)=u0∏j=1nujm[j]=gqJ(m)gK(m).(A2)

where m[j] represents the jth position of the message string m.

Query: Adversary A issues the following query to challenger C:

•   Key extraction query: Suppose there is an access policy (L,π), where L is an LSSS matrix of l×m. Since the attribute set S∗ specified by adversary A does not satisfy the access policy (L,π), we define a set K, and the elements in K are matrix L that satisfy  pi(k)∈LinenumberkofS∗. Challenger C defines a vector ω→=(−1,ω2,…,ωm)∈Zpm−1, satisfying Lk→⋅ω→=0,k∈K and ω→⋅(1,0,…,0)=−1. The challenger defines a vector v′→=(0,v2′,…,vm′)∈Zpm−1 and calculate v→=−(α1′+aq+1)ω→+v′→.

–   If π(k)∈S∗, then Lk→⋅ω→=0, φπ(k)=Lk→⋅v→=−(α1′+aq+1)Lk→⋅ω→+Lk→⋅v′→=0+Lk→⋅v′→=Lk→⋅v′→. C chooses {xk}∈Zp and compute:

{dk=gφπ(k)(r0⋅rπ(k))xk=gL→kv→′(r0⋅rπ(k))xk,dk′=gxk,{dk′′=rixk}i∈U,i≠π(k).(A3)

–   If π(k)∉S∗, then Lk→⋅ω→≠0, φπ(k)=Lk→⋅v→=Lk→⋅(v′→−α1′ω→)−Lk→⋅ω→⋅aq+1=Lk→⋅(v′→−ω→(α1′+aq+1). C chooses {xk′}∈Zp and compute:

Dk={dk=gL→k⋅(v→′−α1′ω→)(r0rπ(k))xk′⋅(gπ(k)−(γ0+γπ(k))∏i∈S∗gπ(k)γigq+1−i+π(k))−L→kω→;dk′=gxk′gπ(k)L→k⋅ω→;{dk′′=rixk′⋅(gγigq−i+1)L→kω→aπ(k)}i∈U,i≠π(k).(A4)

Set xk=xk′+aπ(k)⋅Lk→⋅ω→, exists:

Dk={dk=gφπ(k)⋅(r0rπ(k))xk;dk′=gxk′gπ(k)Lkω→=gxk;{dk′′=rixk′⋅(gγigq−i+1)L→kω→aπ(k)=rixk}i∈U,i≠π(k).(A5)

For the additional attribute ϱ, C randomly selects xϱ∈Zp and calculates dϱ=gα2′(r0∏i∈S∗∪ϱri)xϱ,dϱ′=gxϱ. Finally, challenger C returns the following key: psk={Dk|k∈[1,l]},usk=(dϱ,dϱ′).

•   Signature query Adversary A selects message m and initiates a request to challenger C. The signature includes time t and the signer’s identity attribute to prevent replay attacks. Here we hide the calculation related to t and prove that without t, forging signatures is still impossible to achieve in polynomial time. Challengers follow the steps below to sign.

–   If J(m)=0, the challenger aborts the calculation.

–   If J(m)≠0, the challenger randomly selects xϱ′,η,ζ,ζ′,ζ¨∈Zp, and let ζ+ζ′=ζ¨−aJ(m). The signature is generated as follows:

{σ0=gα2′⋅(r0∏i∈S∗∪ϱri)xϱ⋅(r0∏i∈S∗∪ϱri)xϱ′⋅gα1′⋅(r0∏i∈S∗∪ϱri)η⋅(gqJ(m)gK(m))ζ¨⋅g1−K(m)J(m)=gα1+α2⋅(r0∏i∈S∗∪ϱri)xϱ+xϱ′+η⋅(gqJ(m)gK(m))ζ+ζ′;σ1=gη⋅gxϱ+xϱ′=gη+xϱ+xϱ′;σ2=gζ¨g1−1J(m)=gζ¨−aJ(m)=gζ+ζ′.(A6)

Finally, for the signature query of message m, challenger C will returnσ={σ0,σ1,σ2,m}.

•   User signature verification query: The adversary A has the signature σ of the message m under the attribute set S. After receiving the signature, C executes the signature extraction algorithm and randomly selects δ∈Zp, calculate σ0^=σ0δ,σ1^=σ1δ, and the converted signature σ^={σ0^,σ1^} is returned to A. A calculates the intermediate signature σ1~ and returns it to C. A executes the aided verification algorithm and calculates the following intermediate results:

e(σ0^,g)e(σ1^,r0∏i∈S∗∪ϱri)=σ1~.(A7)

The challenger computes σ2~=e(σ2δ,H(m))⋅Zδ and Determine whether σ1~ is equal to σ2~. If they are equal, the signature verification is successful, otherwise the signature verification fails.

Signature forgery: The adversary A forges the signature of the message m∗ under the attribute set S∗σ∗={σ0∗,σ1∗, sigma2∗,m∗}. A has never initiated a signature query for message m∗ under attribute set S∗. If J(m)≠0, challenger C interrupts the calculation. If J(m)=0, then there is:

σ0∗=gα2′⋅(r0∏i∈S∗∪ϱri)xϱ⋅(r0∏i∈S∗∪ϱri)xϱ′⋅gα1′⋅(r0∏i∈S∗ri)η⋅(gqJ(m∗)gK(m∗))ζ⋅g1−K(m∗)J(m∗)=gα1′⋅gaq+1⋅gα2′⋅(σ1∗)γ0⋅(σ2∗)K(m∗).(A8)

The challenger can then calculate:

gaq+1=σ0∗gα1′⋅gα2′⋅(σ1∗)γ0⋅(σ2∗)K(m∗).(A9)

If the challenger can calculate gaq+1, the following event is defined:

1.    Eμ: Random μth signature query for message m, J(m)≠0;

2.    E′: For the forged signature σ∗ of message m∗, there exists J(m∗)=0.

In addition, define an event E, indicating that C did not terminate the calculation during the above query process. Using the method in [20], the probability of event E is calculated as follows:

Pr⁡[E]=Pr⁡[⋂μ=1qsEμ⋂E′]≥14qs(n+1).(A10)

□

Appendix A.2 Anonymity

Anonymity refers to: assuming there are two signatures σA and σB that comply with the unified access policy, the user cannot distinguish between the two signatures. Let au+s+s′=S. We can analyze the structure of the signature:

{σ0=g∑k∈Kρπ(k)ωk+α2⋅(r0∏i∈Su∪ϱri)∑k∈Kxkωk+η+xϱ,au+xϱ,au′⋅H(m)ζ+ζ′⋅H(t)S,σ1=g∑k∈Kxkωk+η+xϱ,au+xϱ,au′,σ2=gζ+ζ′,σ3=gS,σ4=(r0∏i∈Su∪ϱriH(t))1/β.(A11)

Among them, there are xϱ,au and au parts of user-specific information, which only exist at the index position, and the random numbers η,xϱ,au′,s,s′∈Zp, which are also exponential, such that ∑k∈Kxkωk+η+xϱ,au+xϱ,au′ and au+s+s′ are random. The signature does not contain attribute information, so the user cannot confirm the identity of the signer from the signature, or distinguish between two signatures.

References

1. Maji H, Prabhakaran M, Rosulek M. Attribute-based signatures: achieving attribute-privacy and collusion-resistance. Cryptology ePrint Archive; 2008 [cited 2025 Feb 28]. Available from: http://eprint.iacr.org/2008/328. [Google Scholar]

2. Xu X, Cai Q, Lin J, Pan S, Ren L. Enforcing access control in distributed version control systems. In: 2019 IEEE International Conference on Multimedia and Expo (ICME) 2019; 2019 Jul 8–12; Shanghai, China. New York, NY, USA: IEEE. 2019. p. 772–7. doi:10.1109/ICME.2019.00138. [Google Scholar] [CrossRef]

3. Hong H, Hu B, Sun Z. An efficient and secure attribute-based online/offline signature scheme for mobile crowdsensing. Hum-Cent Comput Inf Sci. 2021;11:26. doi:10.22967/HCIS.2021.11.026. [Google Scholar] [CrossRef]

4. Li X, Wang H, Ma S, Xiao M, Huang Q. Revocable and verifiable weighted attribute-based encryption with collaborative access for electronic health record in cloud. Cybersecurity. 2024;7(1):1–19. doi:10.1186/s42400-024-00211-1. [Google Scholar] [CrossRef]

5. Patil RY. A secure privacy preserving and access control scheme for medical internet of things (MIoT) using attribute-based signcryption. Int J Inf Technol. 2024;16(1):181–91. doi:10.1007/s41870-023-01569-0. [Google Scholar] [CrossRef]

6. Okamoto T, Takashima K. Efficient attribute-based signatures for non-monotone predicates in the standard model. IEEE Trans Cloud Comput. 2014;2(4):409–21. doi:10.1109/TCC.2014.2353053. [Google Scholar] [CrossRef]

7. Cui H, Deng RH, Liu JK, Yi X, Li Y. Server-aided attribute-based signature with revocation for resource-constrained industrial-internet-of-things devices. IEEE Trans Industr Inform. 2018;14(8):3724–32. doi:10.1109/TII.2018.2813304. [Google Scholar] [CrossRef]

8. Huang Z, Lin Z. Secure server-aided attribute-based signature with perfect anonymity for cloud-assisted systems. J Inf Secur Appl. 2022;65(1):103066. doi:10.1016/j.jisa.2021.103066. [Google Scholar] [CrossRef]

9. Chen Y, Li J, Liu C, Han J, Zhang Y, Yi P. Efficient attribute based server-aided verification signature. IEEE Trans Serv Comput. 2022;15(6):3224–32. doi:10.1109/TSC.2021.3096420. [Google Scholar] [CrossRef]

10. Li J, Chen Y, Han J, Liu C, Zhang Y, Wang H. Decentralized attribute-based server-aid signature in the internet of things. IEEE Internet Things J. 2022;9(6):4573–83. doi:10.1109/JIOT.2021.3104585. [Google Scholar] [CrossRef]

11. Chen B, Xiang T, Li X, Zhang M, He D. Efficient attribute-based signature with collusion resistance for internet of vehicles. IEEE Trans Veh Technol. 2023;72(6):7844–56. doi:10.1109/TVT.2023.3240824. [Google Scholar] [CrossRef]

12. Maji HK, Prabhakaran M, Rosulek M. Attribute-based signatures. In: Cryptographers’ Track at the RSA Conference; 2011; Berlin, Germany: Springer. p. 376–92. [Google Scholar]

13. Xiong H, Bao Y, Nie X, Asoor YI. Server-aided attribute-based signature supporting expressive access structures for industrial internet of things. IEEE Trans Indust Inform. 2019;16(2):1013–23. doi:10.1109/TII.2019.2921516. [Google Scholar] [CrossRef]

14. SZABO N. Smart contracts; 1994 [cited 2024 Feb 29]. Available from: https://nakamotoinstitute.org/library/smart-contracts/. [Google Scholar]

15. Christidis K, Devetsikiotis M. Blockchains and smart contracts for the internet of things. IEEE Access. 2016;4:2292–303. doi:10.1109/ACCESS.2016.2566339. [Google Scholar] [CrossRef]

16. Wood G et al. Ethereum: a secure decentralised generalised transaction ledger. Ethereum Project Yellow Paper. 2014;151:1–32. [Google Scholar]

17. Bethencourt J, Sahai A, Waters B. Ciphertext-policy attribute-based encryption. In: 2007 IEEE Symposium on Security and Privacy (SP’07); 2007;Oakland, CA, USA. Washington, DC, USA: IEEE Computer Society. p. 321–34. doi:10.1109/SP.2007.11. [Google Scholar] [CrossRef]

18. Ostrovsky R, Sahai A, Waters B. Attribute-based encryption with non-monotonic access structures. In: Proceeding of the 2007 ACM Conference on Computer and Communications Security, CCS 2007; 2007 Oct 28–31; Alexandria, VA, USA. New York, NY, USA: ACM; 2007. p. 195–203. doi:10.1145/1315245.1315270. [Google Scholar] [CrossRef]

19. Goyal V, Kothapalli A, Masserova E, Parno B, Song Y. Storing and retrieving secrets on a blockchain. In: IACR International Conference on Public-Key Cryptography; 2022 Mar 8–11; Virtual Event. Cham, Switzerland: Springer; 2022. Vol. 13177, p. 252–82. doi:10.1007/978-3-030-97121-2_10. [Google Scholar] [CrossRef]

20. Waters B. Efficient identity-based encryption without random oracles. In: Annual International Conference on the Theory and Applications of Cryptographic Techniques; 2005 May 22–26; Aarhus, Denmark. Cham, Switzerland: Springer; 2005. Vol. 3494, p. 114–27. doi:10.1007/11426639_7. [Google Scholar] [CrossRef]