Dynamic Route Optimization for Multi-Vehicle Systems with Diverse Needs in Road Networks Based on Preference Games

1  Introduction

With the rising number of vehicles on the road networks, traffic congestion has become more frequent. Expanding roads and imposing vehicle restrictions are ineffective solutions to this issue [1,2]. In a vehicle-road collaborative environment, vehicle-road communication technology enables the real-time exchange of traffic status information between vehicles and the road infrastructure [3,4]. Consequently, transportation systems display key characteristics such as interconnectivity, personalization, and adaptability. These features not only enhance the intelligence of road traffic control but also significantly increase the complexity of traffic management challenges [5].

Intelligent collaborative decision-making technology for vehicle groups, which considers varying traffic needs, is seen as an effective solution for alleviating congestion and optimizing traffic. This is achieved through the transmission, fusion, and interaction of traffic information across both time and space [6–8]. Through dynamic vehicle route planning at the micro level, traffic performance at the macro level can be enhanced, addressing the needs of various vehicles and optimizing the use of road network resources [9–12].

Most existing studies on vehicle routing planning are static and can be classified into two categories: routing planning and centralized multi-vehicle routing planning [13–15]. Single-vehicle route selection planning identifies the most efficient path by analyzing the current road conditions and predicting future road states. Rosita et al. applied the Dijkstra algorithm with multi-criteria decision-making to optimize route assignment for individual vehicles [16]. Wang et al. introduced a comprehensive path optimization model that incorporates Kalman-filtered short-term predictions and an enhanced bootstrap-based Dijkstra algorithm to determine the optimal vehicle routes [17]. Chauhan et al. developed a path discovery model combining the Bellman-Ford algorithm with a Topology-Preserving Feature Network (TPFN), leveraging a deep Long Short-Term Memory (LSTM) classifier and Bellman-Ford pattern search optimization to compute the nearest optimal route for a single-vehicle [18]. While these methods offer the benefits of clarity and simplicity, they also have notable limitations. Besides involving complex computations and being prone to local optima, single-vehicle optimization methods overlook vehicle interaction. As a result, multiple vehicles may be directed onto the same route, and the planned paths may fail to adapt to emergencies or prioritize certain vehicles. Consequently, actual travel results often deviate from expectations, limiting their effectiveness in alleviating traffic congestion. Centralized multi-vehicle route selection planning reformulates the problem as a maximum-minimum optimization task, aiming to determine the globally optimal set of recommended routes for multi-vehicles [19,20]. Ebrahimi et al. introduced the Best Neighborhood Algorithm for Routing Traffic (BNART), a heuristic approach designed for centralized route guidance of autonomous vehicles [21]. Multi-vehicle centralized route planning methods can achieve a global benefit, but this often comes at the expense of some vehicles. Being static, these methods are ill-equipped to handle emergencies and may even lead to traffic congestion drifts. In contrast to static vehicle routing planning, vehicles in large-scale road networks with multiple intersections must navigate through diverse regions and interact with multiple vehicles and edge devices [22]. Therefore, there is a coupling between the trajectories of the same vehicle across different regions, as well as between the trajectories of different vehicles within the same region. Furthermore, the urgency for different vehicles to pass through certain areas varies significantly, posing a considerable challenge in solving the collaborative decision-making problem for vehicle path selection in road network scenarios. Conventional static vehicle path planning methods are no longer suitable for future cooperative vehicle path scenarios. Several researchers have conducted preliminary studies on the collaborative decision-making problem for multi-vehicle dynamic route selection in large-scale scenarios [23–25]. One approach integrates heuristic algorithms with conventional path optimization techniques. Jiang et al. combined ant colony and particle swarm algorithms with the A∗ method to develop an intelligent optimization algorithm featuring adaptive ant colony and particle swarm optimization. By employing different search strategies at various stages of the algorithm, they dynamically adjusted the vehicle routes [26]. Typaldos et al. developed a method for determining the quickest route using the A∗ algorithm [27]. While the single-vehicle dynamic path optimization method addresses the limitations of static path planning and enhances both performance and responsiveness, its reliance on individual decision-making prevents effective coordination of overall road network demands, making it challenging to prioritize the needs of high-priority vehicles. Another common approach is the decentralization strategy, where the large road network is segmented into smaller areas, with vehicles coordinating and performing path selection planning within their respective zones. Lu et al. designed a two-layer traffic coordination control system, where the claims of multiple vehicles were sent to the intersection’s edge for game control [28]. Similarly, Batista et al. created a path selection model and developed an optimization algorithm by dividing the traffic into sub-areas and limiting the search range [29]. Due to the independence of vehicle trajectories across different zones, the decentralized strategy fails to fully harness the benefits of vehicle group collaborative decision-making for optimal route selection, thereby increasing the uncertainty in traffic control performance. Current methods struggle to dynamically and effectively address the varying individual traffic needs and the overall traffic system control performance. Consequently, there is an urgent need for a new vehicle group collaborative route selection algorithm to effectively balance individual needs with the coordination performance of the road network. To address this, this study presents a collaborative routing algorithm for multiple vehicles at single intersections, grounded in preference games (ACRABPG). A collaborative decision-making model was developed for vehicles with varying traffic demands, based on micro-intersections, to address the challenge of multi-vehicle route selection in a large-scale transportation network. A comparative analysis was conducted with two alternative algorithms to assess the effect of changing the relative frequency of vehicles with different traffic demand profiles on the mean travel duration of automobiles. A comparative analysis was performed on the traffic control performance of the collaborative decision-making models for vehicles with varying traffic demands across different traffic scenarios.

This study is structured as follows: Section 2 presents the problem description, while Section 3 covers the development of a multi-vehicle dynamic route selection model based on game theory. Section 4 discusses the application of the multi-vehicle collaborative route selection algorithm in road networks using game theory principles. Section 5 presents a simulation analysis, and Section 6 summarizes the limitations of this study.

2  Problem Description

2.1 Scenario Description

Fig. 1 illustrates the scenario of vehicle group collaborative route selection decision-making in the vehicle-road collaborative environment examined in this study. The blue area represents the intersection conflict zone, where vehicles make specific path choices. The vehicles are categorized into two types: ordinary traffic demand vehicles, denoted as Cargeneral, do not have high traffic urgency, while priority vehicles, denoted as Carspecial, have urgent traffic demands. Carspecial prefers smooth road sections. The identification process for Carspecial involves two steps: vehicle initiation and confirmation by the roadside unit. In the vehicle-road collaborative environment, roadside units are classified into two types. The first type, known as the conventional roadside unit, includes an information collection module and a data distribution module, facilitating direct communication with vehicles and other roadside infrastructure. The second type, known as the game roadside unit, is positioned at intersections and comprises an information collection module, a game computation module, and a data distribution module. Its primary function is to optimize vehicle route planning within its designated control area. The game roadside unit operates within a defined control area. As shown in Fig. 1, the game roadside unit at intersection I1 manages a control area encompassing 9 intersections and 12 directed roads, delineated by the green dashed box. For clarity, this study is based on three key assumptions regarding the research scenario: In the road network setting, all vehicles are considered connected. In other words, vehicles are equipped with communication capabilities for vehicle-to-road interactions. This study assumes an ideal vehicle-to-road communication environment, disregarding factors such as delay and packet loss. In addition, vehicle lane-changing behavior on road segments was not considered.

Figure 1: Typical large-scale road network scenario

2.2 Scientific Issues

The objective of collaborative vehicle routing decision-making in large-scale road network scenarios is to use the vehicle-road collaboration platform to generate optimal routes based on real-time traffic conditions. This approach balances road network usage while accommodating the diverse requirements of individual vehicles. This study defines a relatively balanced road network from the vehicle’s perspective, assessing whether similar vehicles opt for a particular road despite the availability of potentially better alternatives. This metric is used to determine whether a road is experiencing excessive usage. The definition of a road being idle is determined by whether similar vehicles opt for alternative routes and whether selecting this road results in increased revenue. To accomplish the objectives of this research, the following two key scientific challenges must be addressed:

Problem 1: The collaboration of multiple vehicles at a single intersection is fundamentally a game-theoretic process, where the Nash equilibrium of the vehicles’ interest determines the optimal collaborative road choice for the groups of vehicles passing through the intersection. A Nash equilibrium is a game scenario in which each participant selects their optimal strategy independently of others’ choices, leading to a stable outcome for the entire game. At a single intersection, vehicles display varying levels of traffic urgency, and the number of vehicles can fluctuate. Consequently, identifying the right game model and selecting an algorithm to achieve equilibrium are key challenges. These factors add to the difficulty of achieving a Nash equilibrium in the multi-vehicle cooperative path selection problem at a single intersection.

Problem 2: A large-scale road network consists of numerous junctions and route segments, where overlapping control areas and restricted cognitive ranges between intersections pose a challenge. Furthermore, when developing a game model at a single intersection to assess the benefits of each strategy, the current road conditions were used to estimate the time required to reach the temporary terminus. However, when a vehicle arrives at the next game intersection, the actual road condition may differ to varying extents from the previously predicted state. The traffic conditions on unconnected roads may have changed significantly, potentially causing vehicles to receive conflicting routing outcomes at both the next and previous intersections. The routing recommendation provided to the vehicle at the yellow intersection I5 in Fig. 2 may differ from the recommendation given when driving to the green intersection I8. Consequently, coordinating vehicle routing decisions across multiple intersections within a road network to achieve traffic balance and maintain the continuity of traffic flow presents a significant challenge.

Figure 2: Large-scale road network

3  Construction of a Multi-Vehicle Dynamic Route Selection Model Based on Game Theory

3.1 Multi-Vehicle Collaborative Model at a Single Intersection

To address the challenges of model determination and Nash equilibrium solutions in multi-vehicle collaborative road selection at a single intersection, this study introduces a collaborative modeling approach. The proposed model facilitates a road selection game among vehicles with diverse requirements, ensuring efficient traffic management and optimal road resource allocation in single-intersection scenarios.

The scenario shown in Fig. 2 was selected, and the road model was represented using a directed weighted graph H=(I,L). In this context, I denotes the set of points in the graph, representing intersections. Each point Ii∈I corresponds to the i-th intersection within the set. L represents the set of edges in the graph, corresponding to the available paths. Each directed weighted edge lji∈L signifies the road segment connecting the intersection Ii to intersection Ij, with the edge weight indicating the actual physical distance of the road segment.

The road model was developed based on the Bureau of Public Roads (BPR) formula [30]. It represents a high-level, macroscopic road model. By evaluating the maximum load capacity of the road, the highest permissible driving speed, and the current quantity of vehicles on the road, the determination of the time required for vehicles to traverse a specific road section becomes possible. The BPR formula is expressed as follows:

t=tfree(1+α(ncap)β)(1)

In this context, t denotes the duration required for a vehicle to traverse the road section, while tfree represents the time needed for vehicles to navigate the section at their maximum speed, assuming unobstructed road conditions. Cap represents the maximum vehicular capacity of the road section, and n denotes the current number of vehicles present. α and β are constant parameters. This study adopts a simplified approach to intersection delays, where different actions incur varying time consumptions, but identical actions are assigned the same constant time value.

Given the large number of vehicles involved in road selection planning at intersections and their varying urgency levels, priority is assigned to vehicles with higher urgency. Consequently, vehicles with lower urgency must yield and take less congested road sections. However, it is equally important to consider the overall traffic efficiency of the vehicles. Therefore, a population game model incorporating altruistic preferences is established, with the game process defined as G=(S,A).

S represents a “society” comprising multiple “populations”. A “population” p∈S consists of several game individuals, and in this study, all vehicles requiring passage through an intersection within a given time frame are defined as game individuals within the population. A denotes the set of strategies available to all individual players in the game, referring to the actions vehicles can select at intersections, such as turning left, proceeding straight, making a U-turn, or turning right.

Each group of vehicles is defined as a “population” p, with the vehicles participating in the game being grouped based on two criteria: their temporary endpoint and their current location. The temporary endpoint is an intersection near the game intersection, determined by each vehicle’s final destination relative to the current intersection. Vehicles within the same group share both a temporary endpoint and a current road segment. For clarity, this study refers to the vehicle’s current road segment as its initial point. As a result, the number of populations in the model is the product of the number of temporary endpoints and the number of initial points.

For a “population” p consisting of multiple game individuals, its strategy set is defined as Ap=(a1,p,a2,p,…,am,p),where m∈◻+ represents the number of available actions at the intersection. This set constitutes a pure strategy set. The set of vehicles within this group is denoted as Vp, which includes two categories: Cargeneral and Carspecial. Each vehicle selects a specific pure strategy. At this stage, the state Xp of the “population” p can be understood as a set of different strategy proportions. To accommodate altruistic preferences, the action strategy selected by Carspecial aims to increase the proportion ρ, while Cargeneral select its action strategies by reducing the proportion of weight ϑ. At this point, the status of “population” p is represented as Xp=(xp1,xp2,…,xpm),where m∈◻+ denotes the number of available strategies. Here, xpk represents the proportion of individuals in the “population” p who selects the action ak,p∈Ap. The overall community state, consisting of all population states, is denoted as Δ(X)={Xp:p∈S}. The objective of the multi-vehicle collaboration is to develop a reasonable and effective traffic diversion method that ensures an optimal distribution of vehicles across different roads to prevent congestion or underutilization. This approach prioritizes the needs of high-priority vehicles while maximizing the benefits for all game participants. Consequently, in the game model G=(S,A), the optimization goal is to determine a community state Δ(X) in which no individual can identify a strategy that offers a better outcome than their currently selected one.

To achieve this objective, this study evaluates the benefits of each strategy based on the time required for a vehicle to reach its temporary endpoint. It aims to enhance the revenue of priority vehicles, Carspecial by increasing its selection strategy in proportion to its weight—specifically, increasing xpCarspecialk of Carspecial within “population” p. The driving time associated with the strategy ak,p on the road is denoted as dlink,k,p while dcross,k,p represents the time spent at the intersection by the strategy ak,p. A binary variable, Ri,jk,p is introduced to indicate whether the strategy ak,p involves traversing a road section lji, where a value of 1 signifies passage and 0 otherwise. Consequently, the formula and constraints governing the benefit ck,p of each action in “population” p as well as the average benefit c¯p of each strategy, are formulated as follows:

0≤xpk≤1,∀ak,p∈Ap,∀p∈S(2)

Vp={Carspecial,Cargeneral}(3)

xpk=xpCarspecialk⋅ρ+xpCargeneralk⋅ϑ(4)

ρ>1(5)

0<ϑ≤1(6)

∑k=1mxpk=1,∀p∈S(7)

ck,p=−(dcrass,k,p+dlink,k,p)(8)

dlink,k,p=∑lji∈LRi,jk,p⋅dlinki,j(9)

c¯p=∑ak,p∈Apxpk⋅ck,p(10)

The delay dlinki,j in section lji is computed using the BPR equation, given by the following formula:

dlinki,j=dfreei,j(1+α(njicapji)β)(11)

nji=∑p∈S∑ak,p∈Apxpk⋅|Vp|⋅Ri,jk,p+n0i,j(12)

here, dfreei,j represents the time required for vehicles to traverse the road section at maximum speed under unobstructed conditions. n0i,j and capji denote the current number of vehicles traveling on section lji and its load capacity, respectively. |Vp| represents the number of vehicles in the population p.

The objective of this study is to identify a community state Δ(X) where no individual in the game can adopt a strategy that outperforms their current choice. Accordingly, the Nash equilibrium point for the population game model G is determined and computed as follows:

NE(G)={Δ(X):cpi≥ck,p,∀ak,p∈Ap−{api},∀vpi∈Vp,∀p∈S}(13)

3.2 Collaborative Model between Multiple Intersections

When a vehicle leaves the game intersection following a recommended strategy, the recommendation results at the next game intersection may differ due to changes in the road network status. This study introduces a multi-vehicle collaborative model that integrates the recommended routing outcomes across multiple intersections, developing a routing game for vehicles with varying demands in multi-intersection scenarios. This approach ensures seamless traffic scheduling and optimal road resource allocation.

Given the large number of vehicles participating in road selection planning at multiple intersections and the different attributes of different vehicles, some vehicles have urgent traffic needs. Some vehicles follow the strategy recommended by the previous game intersection and prefer to ensure the continuity of traffic scheduling when reaching that intersection. Some are vehicles that have just entered the intersection of the game; some are vehicles that have completed the previous intersection recommendation strategy. Therefore, it is still necessary to classify these vehicles into three categories. One consists of priority vehicles Carspecial with urgent traffic needs. Priority vehicles prefer to pass on smooth road sections. The identification of Carspecial requires two steps. First, this process is initiated by the vehicle itself and subsequently confirmed by the roadside unit to be correct; a vehicle with a very clear road direction is defined as a directional traffic vehicle Cartoward. This article proposes that when following the strategy recommended by the game at the previous intersection, vehicles that prefer to ensure the continuity of traffic scheduling at that intersection have a very clear road direction; vehicles with low traffic urgency and those that completed the recommended strategy at the previous intersection (such vehicles do not have urgent traffic needs) are recognized as ordinary traffic demand vehicles Cargeneral.

To address the needs of Carspecial, ensure the continuity of Cartoward’s traffic scheduling, and achieve effective coordination among multiple intersections, Cartoward must not participate in the intersection game and must continue to follow the previous strategy, and Cargeneral must give way to a certain extent. Of course, considering the traffic efficiency of all game vehicles is even more important. Therefore, as in Section 2.1, the vehicles at these intersections, except for Cartoward, still conform to the characteristics of the population game, and the game process is represented by G=(S,A). “S” (society) refers to all vehicles in the road selection game that need to travel through the intersection within a unit of time. “S” (society) is composed of multiple “p” (populations); that is, p∈S. A is a set of optional actions for vehicles on the road of the game, such as left turns, straight motion, u-turns, and right turns.

The vehicles participating in the game are grouped according to their starting point and temporary endpoint near the intersection of the game. Vehicles within the same group have the same temporary endpoint and are currently driving on the same road segment. To make the description more concise, this article refers to the current section of a vehicle as the initial point of the vehicle. In this way, the population in the model, which is the number of vehicle groups, is equal to the product of the number of temporary endpoints and the number of initial points.

For a “population” p containing multiple game individuals, its strategy set is defined as Ap=(a1,p,a2,p,…,am,p),m∈◻+, where m is the number of optional actions at the intersection. As defined, this is a pure policy set. The set of vehicles belonging to this group is defined as Vp, which includes two categories: Cargeneral and Carspecial. A specific strategy is chosen for each vehicle, which is a pure strategy. At this point, the status of the population p is Xp=(xp1,xp2,…,xpm),m∈◻+. Here, xpk represents the proportion of people in the population p who choose action ak,p∈Ap. To satisfy altruistic preferences, this article increases the action strategy selected by Carspecial by the weight ratio γ, which means increasing the proportion of Carspecial to xpk in population p. Correspondingly, the action strategy chosen by Cargeneral is based on its weight τ to reduce the proportion; that is, the proportion of xpk to Cargeneral is reduced in population p. The community state composed of all population states is Δ(X)={Xp:p∈S}. The purpose of multivehicle collaboration is to find a reasonable and effective diversion method and allocate a reasonable number of vehicles to different roads so that no roads are overused or idle, which can meet the needs of priority vehicles and maximize the benefits of game participants. Therefore, for the game model G=(S,A), the optimization goal is transformed into finding a community state Δ(X) in which no individual in the game can find a strategy that is better than their current selected strategy.

This article evaluates the benefits of each strategy based on the time required for the vehicle to reach the temporary endpoint. We use dlink,k,p to represent the driving time of the strategy ak,p on the road and dcross,k,p to describe the time spent by the strategy ak,p at the intersection. We use a binary number Ri,jk,p to indicate whether the strategy ak,p is to pass through the section lji. If so, this value is 1; otherwise, it is 0. The formulas and constraints for calculating the benefits ck,p of actions in the population p and the average benefits c¯p of each strategy in the population p are as follows:

0≤xpk≤1,∀ak,p∈Ap,∀p∈S(14)

Vp={Carspecial,Cargeneral}(15)

xpk=xpCarspecialk⋅γ+xpCargeneralk⋅τ(16)

γ>1(17)

0<τ≤1(18)

∑k=1mxpk=1,∀p∈S(19)

ck,p=−(dcrass,k,p+dlink,k,p)(20)

dlink,k,p=∑lji∈LRi,jk,p⋅dlinki,j(21)

c¯p=∑ak,p∈Apxpk⋅ck,p(22)

The delay dlinki,j in section lji is calculated using the BPR equation, and the formula is:

dlinki,j=dfreei,j(1+α(njicapji)β)(23)

nji=∑p∈S∑ak,p∈Apxpk⋅|Vp|⋅Ri,jk,p+n0i,j+ntowardi,j(24)

here, dfreei,j represents the time required for vehicles to travel through the road section at the fastest speed when the road is unobstructed. n0i,j and capji describe the current number of vehicles driving on section lji and the load capacity of section lji, respectively, while ntowardi,j represents the number of Cartoward that will drive on section lji. |Vp| is the number of vehicles in the game among population p.

As the primary aim of this article is to identify a community state Δ(X) in which no individual participating in the game can discover a strategy superior to their current chosen strategy, our objective is to determine a Nash equilibrium point for the population game model G. This is calculated as follows: G, calculated as follows:

NE(G)={Δ(X):cpi≥ck,p,∀ak,p∈Ap−{api},∀vpi∈Vp,∀p∈S}(25)

4  Implementation of the Multi-Vehicle Collaborative Route Selection Algorithm in Road Networks Based on Game Theory

4.1 Single-Intersection, Multi-Vehicle Collaborative Road Selection Algorithm

The population game model is transformed into a replicator subdynamic model to determine the Nash equilibrium. During initialization, the control range and the temporary endpoint position of each game roadside unit are established. Vehicles assign driving routes based on each strategy, selecting roads at game intersections according to the strategic direction. In non-intersection segments, vehicles continue along the optimal route in terms of the physical distance to the temporary endpoint. When multiple shortest paths with equal physical distances exist, the selection is made proportionally. The strategic benefits are then computed, and the average sum of the benefits is determined for these road segments.

During vehicle operation, the assisted driving system registers an agent for each vehicle on the conventional roadside unit. This unit categorizes vehicles as Carspecial and Cargeneral according to their requests and strategy executions. As vehicles approach intersections equipped with game roadside units, conventional roadside units assess whether a vehicle will reach the intersection in the next period, considering its current position, speed, and acceleration. If a vehicle is unable to reach the intersection before the end of the next period, the conventional roadside unit continues to monitor its movements. If a vehicle cannot reach the intersection in the current period but can do so in the next period, the conventional roadside unit transmits vehicle information, such as type and endpoint location—to the game roadside unit at the intersection and registers an agent for the vehicle on this unit. After the current period, all vehicle agents on the roadside unit participate in the game. The game roadside unit initially assigns a temporary endpoint for the agents based on the final destination of the vehicle. These agents were then grouped according to their current road section (initial point) and temporary endpoint, with the number of agents in each group recorded. Furthermore, the game roadside unit collects data on the number of vehicles on each link within its control area. By computing the travel time for each strategy to reach the temporary endpoint, the benefits of each strategy are determined based on preferences. The evolutionary dynamic model is represented by an ordinary differential Eq. (26), which is solved using the fourth-order Runge-Kutta method (RK4), a numerical approach for solving the initial value problems of ordinary differential equations. RK4 is widely recognized for its high accuracy and stability, making it a standard tool in scientific and engineering applications.

dxpi=xpi(ci,p−c¯p),∀ai,p∈Ap,p∈S(26)

The fourth-order Runge–Kutta solution method is described as follows. For ordinary differential equations, the expression is given as follows:

dxpidt=f(t,xpi)(27)

Given the initial state xpi(0) and the iteration step size h, the value of xpi(h) after one iteration is obtained as follows:

dxpidt=f(t,xpi)(28)

F1=hf(0,xpi(0))(29)

F2=hf(h2,xpi(0)+F12)(30)

F3=hf(h2,xpi(0)+F22)(31)

F4=hf(h2,xpi(0)+F3)(32)

xpi(h)=xpi(0)+16(F1+2F2+2F3+F4)(33)

Through multiple iterations, the game converges dynamically to a stable point, representing the Nash equilibrium state for all vehicle agents on the current roadside unit. Subsequently, the game is played with roadside units, and the number of vehicles traveling in each direction is calculated for each agent group based on the Nash equilibrium state. For each group and travel direction, a corresponding number of vehicle agents is evenly selected according to their expected arrival time at the intersection, and their travel direction is determined. Upon receiving the recommended routing scheme, each agent communicates directly with the corresponding vehicle through the game’s roadside unit, relaying the routing scheme to the vehicle’s assisted driving system. The driver then follows the vehicle’s system guidance to implement the travel route. A vehicle agent that completes the game is removed from the game by the roadside unit. Vehicles that have passed through the intersection register their agents with the game’s roadside unit at the next intersection, obtaining new routes through another iteration of the game. Fig. 3 shows the primary process of the multi-vehicle cooperative route algorithm conducted on a single-game roadside unit. The corresponding algorithm is Algorithm 1.

Figure 3: Flowchart of the single intersection, multi-vehicle collaborative road selection algorithm

4.2 Multi-Vehicle Collaborative Route Selection Algorithm in a Road Network

Similar to the multi-vehicle collaborative road selection at a single intersection, the multi-vehicle collaborative road selection algorithm in the road network also converts the population game model into a replicator subdynamic model to compute the Nash equilibrium. The control range and temporary endpoint position for each game roadside unit are established at the start. For each strategy, the appropriate driving route is assigned, with the road selected based on the strategy’s direction at the game intersection. The vehicles then continue to the temporary endpoint in the non-intersection section, following the route that minimizes the physical distance. When multiple shortest paths with equal physical distances exist, these paths are selected based on their proportional lengths. The strategic benefits are calculated, and the average total benefits for these road segments are determined.

Throughout the vehicle’s journey, the assisted driving system assigns an agent to the vehicle on the conventional roadside unit. The conventional roadside unit categorizes vehicles into Carspecial, Cartoward, and Cargeneral depending on their request and the strategy execution of their strategies. As vehicles near intersections with game roadside units, conventional roadside units assess whether the vehicle will reach the intersection in the next period, based on its current position, speed, and acceleration. If the vehicle is unable to reach the intersection before the next period ends, the conventional roadside unit will continue tracking the vehicle’s movements. If a vehicle is unable to reach the intersection by the end of the current period but can arrive before the next period concludes, the conventional roadside unit will transmit the vehicle’s information, including its type and endpoint location, to the game roadside unit at the intersection and register an agent for the vehicle. At the end of the current period, as the system transitions into the next, all vehicle agents on the roadside unit engage in the game. Initially, the game roadside unit assigns a temporary endpoint to each agent based on the vehicle’s final destination. These agents were then grouped according to their current road section (initial point) and temporary endpoint, with the number of agents in each group recorded. In addition, the game roadside unit collects data on the number of vehicles on each link within its control area and the route selection plan for Cartoward. By computing the travel time for each strategy to the temporary endpoint, the benefits of each strategy are determined based on preferences. The ordinary differential Eq. (26) are derived from the evolutionary dynamic model, and the fourth-order Runge–Kutta method is used to solve this system (27)–(33). Fig. 4 shows the primary process of the multi-vehicle cooperative route algorithm conducted on a single-game roadside unit. The corresponding algorithm is Algorithm 2.

Figure 4: Flowchart of the single-intersection, multi-vehicle collaborative road selection algorithm

5  Simulation Analysis

5.1 Numerical Settings

To validate the effectiveness of the optimization method proposed in this study, a simulation scenario, as shown in Fig. 5, was employed. The analysis focuses on various performance indicators, such as average travel time, road network throughput, road load balance, and other metrics, across different vehicle types and traffic demand conditions. The road model in the scenario shown in Fig. 5a comprises 9 intersections and 24 bidirectional roads, with 10 starting points and 9 temporary endpoints defined within the model. Vehicles enter the network from the starting points and exit at the endpoints. Upon entry, there is an 80% probability that vehicles will select intersections with a diagonal direction as their destination, while 10% are designated as Cargeneral. Vehicle arrivals adhere to a Poisson distribution, and each vehicle begins with an initial speed of 20 m/s, which is the maximum speed. Once a vehicle enters a road, its speed is determined based on the BPR equation from the US Bureau of Engineering, considering the vehicle density on the current road. Assume that a single-game roadside unit is positioned at the central intersection, I1, and the vehicle density on the route is capped at 130 vehicles per kilometer. Roads within the control field range from 1.2 to 1.5 km in length, while those outside the field measure 0.2 km. The model roads were constructed using the BPR equation from the US Bureau of Engineering. All roads have a load capacity of 80 vehicles per kilometer, with parameters α, β, and ρ set at 0.8, 0.6, and 1.2, respectively. The algorithm uses a step size of 0.01 and runs for 1000 iterations. Intersection delays are fixed, with 25 s for u-turns, 15 s for left turns, 1 s for straight travel, and 5 s for right turns. The time interval between games in the single-intersection multi-vehicle collaborative routing algorithm was set at 30 s. The road network model in Fig. 5b comprises 25 intersections and 60 two-way roads, with 10 road starting points and 25 temporary ending points. The remaining road configurations are consistent with those used in the single-intersection multi-vehicle routing collaborative algorithm, with γ set to 1.2. Vehicles enter the road network based on a Poisson distribution and exit at the designated endpoints. Each intersection is equipped with a game roadside unit.

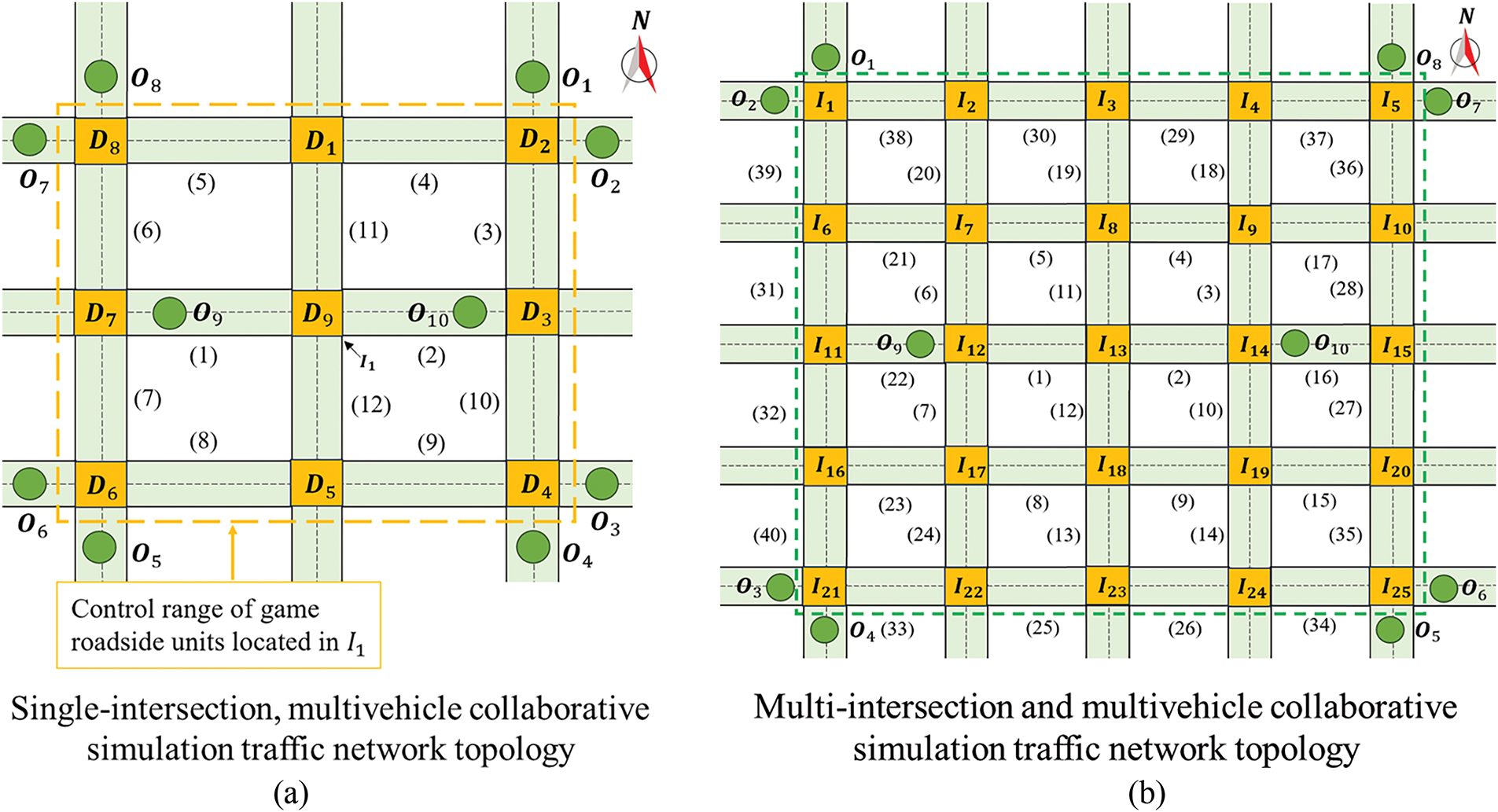
Figure 5: Two types of simulation scenarios

This study uses VISSIM 4.3 (PTVAG, 2008) for simulation, with the model implemented in Python 3.7.4. The experiments were conducted on a desktop computer featuring an Intel 3.6 GHz CPU and 16 GB of RAM. Each simulation run lasted for 1.5 h.

Several routing algorithms have been developed to address different aspects of vehicle navigation. The social routing algorithm [31] follows fair game principles but does not consider specific vehicle requirements. It uses social networks to group vehicles based on trajectory overlap, with all but the last vehicle in each group following historical routes. The last vehicle calculates the shortest path to its destination, considering the plans of the preceding vehicles. This algorithm clusters vehicles within a 30 s. The shortest path algorithm [32], a non-collaborative approach, directs each vehicle to follow the shortest physical route to its destination. The comprehensive path optimization model (CPOM) [17] incorporates Kalman filtering for short-term predictions and introduces a time dimension factor through a layered approach. It employs an enhanced Dijkstra algorithm for optimal route planning. The emergency vehicle timing collaborative evolution path optimization method (TCEPO) [33] introduces a second-level optimization objective, incorporating flexible time windows for intersection safety evaluation in uncertain environments. TCEPO aims to optimize rescue path risk coefficients using an improved ripple expansion algorithm.

5.2 Simulation Results and Analysis

This study first examines the multi-vehicle collaborative routing problem under varying traffic demands at a single intersection. The road network throughput and average vehicle travel time are the primary performance metrics used to evaluate traffic efficiency. The network throughput is quantified by recording the number of vehicles that reached their endpoint during the simulation. Since travel times for vehicles still en route remained undetermined, the average travel time was calculated based only on completed trips. To compare the performance of the multi-vehicle collaborative routing algorithms under different traffic conditions at single intersections, an average vehicle inflow of 10 veh/min was set as the starting point. For the starting points O9 and O10, the initial average inflow rate was set to 20 veh/min. The simulation recorded the number of vehicles reaching their destination within 1.5 h and the average travel times for different vehicle types. The initial proportion of priority vehicles was 10%. Subsequently, the inflow rates were gradually increased to 40, 60, and 80 veh/min, with simulations repeated at each stage to analyze the results. Fig. 6a presents the road throughput for each flow rate, while Fig. 6b shows the average vehicle travel times.

Figure 6: Road network throughput and average vehicle travel time under varying traffic flow conditions

The multi-vehicle collaborative optimization algorithm based on the preference game proposed in this study consistently achieves maximum or near-maximum throughput, regardless of traffic flow variations. Moreover, its effectiveness in improving the traffic throughput increases with higher traffic volumes. For example, when vehicle inflow at the starting points O9 and O10 reaches 60 veh/min, ACRABPG exceeds the social route algorithm by 10.12%, the shortest path algorithm by 64.15%, CPOM by 36.41%, and TCEPO by 79.62%. At 80 veh/min, its throughput exceeds the social routing algorithm by 60.15%, the shortest path algorithm by 92.97%, CPOM by 121.42%, and TCEPO by 155.58%. These results demonstrate that as traffic flow increases, the proposed algorithm effectively distributes vehicles, mitigating congestion and preventing excessive travel time. This highlights the advantages of the cooperative game theory in traffic management.

Compared to the four existing methods, the algorithm proposed in this study achieves the shortest average travel time across various traffic flow densities. Under all four traffic conditions, the average travel time using the proposed method remains below 225 s. When the vehicle inflow at the starting points O9 and O10 reaches 80 veh/min, the proposed method reduces the average travel time by 365, 520, 437, and 578 s compared to the Social routing algorithm, the shortest path algorithm, CPOM, and TCEPO, respectively. These results demonstrate that the proposed method effectively mitigates congestion and enhances traffic efficiency. For specific vehicle types, priority vehicles experience an average travel time reduction of 7% compared to other vehicles in the road network. Meanwhile, the average travel time of ordinary vehicles increases only slightly, by approximately 1%. This indicates that the proposed method effectively balances individual vehicle priorities with overall road network efficiency. In contrast, the other four methods struggle to achieve optimal results. While the shortest path algorithm performs well under low traffic conditions, it leads to congestion as the traffic volume increases. The social routing algorithm significantly reduces the average travel time compared to the shortest path algorithm, but fails to efficiently redistribute traffic under higher densities. CPOM, which employs Kalman filtering for short-term prediction, efficiently manages traffic under low-flow conditions but fails to prevent congestion as the volume increases. TCEPO, by prioritizing certain vehicles, significantly compromises the passage efficiency of ordinary vehicles under high traffic density. To further assess the algorithm’s ability to balance individual vehicle needs with overall road network coordination, priority vehicle proportions were set to 10%, 15%, 20%, 25%, and 30%. The vehicle inflow rates at the starting points O9 and O10 were fixed at 60 and 80 veh/min, respectively. The results of this analysis, illustrating the impact on the average vehicle travel time, are presented in Fig. 7.

Figure 7: Average travel time of vehicles in environments with varying proportions of priority vehicles

Fig. 7 demonstrates that regardless of variations in vehicle inflow rates and the proportion of priority vehicles among all simulated vehicles, the average travel time for priority vehicles remains significantly lower than that for ordinary vehicles, achieving a minimum time saving of 16 s. Notably, the travel time of ordinary vehicles is at most 8 s longer than the overall average. These results indicate that the proposed algorithm effectively balances individual requirements with road network coordination performance across environments with varying priority vehicle ratios. To further assess the algorithm’s efficacy in managing vehicle diversion, a statistical evaluation of traffic density was conducted within the control range of the game roadside unit. This evaluation took place every 15 min during each simulation process, under conditions where the average vehicle inflow rate at the starting points O9 and O10 was 80 veh/min with 10% of the vehicles being priority vehicles. Given the bidirectional traffic on the same road, the vehicle density in the forward direction (default: south to north and west to east) is represented as a positive value, while that in the reverse direction is represented as a negative value. Fig. 8 illustrates the vehicle density distributions for the five algorithms at each time step.

Figure 8: Vehicle density distributions of various algorithms at different time intervals

As shown in Fig. 8a,b, a significant diversion effect is demonstrated by the proposed method. Although higher vehicle densities in both directions are exhibited by Roads 1 and 2 compared to other roads, the overall distribution of vehicles is relatively balanced. The timely diversion of vehicles to less congested roads ensures that most routes do not experience high vehicle density or slow traffic. In contrast, dynamic routing adjustments based on road conditions are lacking in the shortest path algorithms illustrated in Fig. 8e,f, leading to uneven traffic distribution. Saturation is reached by some roads while others remain underutilized. As the simulation progressed, traffic congestion worsened, with an increase in the number of congested road sections. Initially, higher traffic densities are only known on Road 1 (positive direction) and Road 2 (reverse direction), but by the 90-min mark, saturation is reached on 14 roads, including both directions of Roads 1 and 2. High traffic density and congestion on certain roads are also exhibited by the social routing selection algorithms shown in Fig. 8c,d in the latter stages of the simulation. The CPOM method, shown in Fig. 8g,h, is employed to divert vehicles to less congested road sections using the predicted data. However, due to its inability to effectively prioritize certain vehicles, a gradual increase in the traffic flow density was observed after 60 min. The TCEPO method, shown in Fig. 8i,j, places so much emphasis on the passage rights of priority vehicles that it significantly compromises the passage rights of ordinary vehicles. As the simulation time advances, congestion begins to build on all roads. This highlights that improving traffic efficiency becomes a significant challenge without effectively balancing the competing interests of multiple vehicles.

The proposed ACRABPG method and the four other methods underwent simultaneous significance testing using the Origin software. Because the data did not follow a normal distribution, non-parametric testing was used for the significance analysis. The null hypothesis stated that ACRABPG does not differ significantly from the other four methods, with the significance level set at 0.05. Tables 1 and 2 present the simulation results, where a value of 0 indicates no significant difference between the two methods and 1 denotes a significant difference.

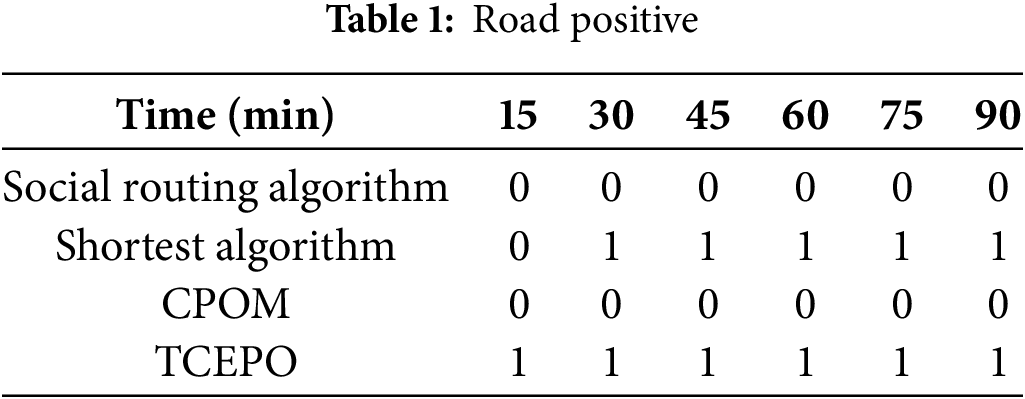
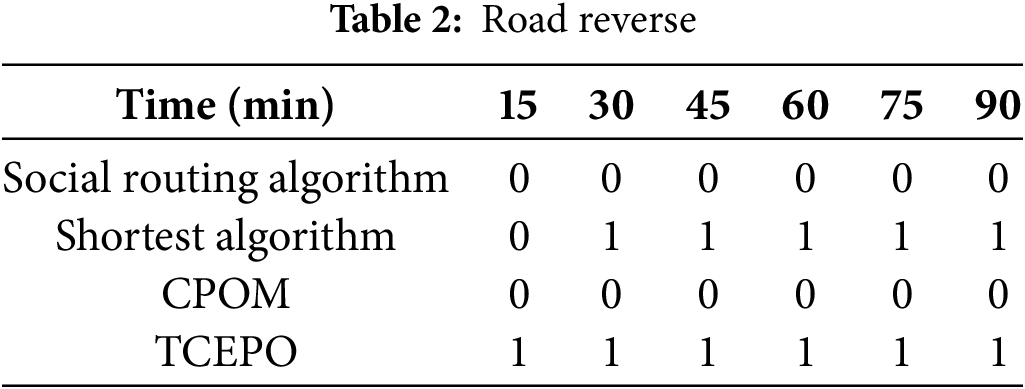
The results in Tables 1 and 2 show that the proposed method in this study exhibits no significant difference from the social routing and CPOM methods in terms of skewness. However, its mean is notably smaller—approximately 2.7 and 2.4 times lower than those of the social routing and CPOM methods, respectively. After 15 min of simulation, a significant difference emerged between the proposed method and both the shortest path and TCEPO methods, indicating distinct data biases among these approaches. The effectiveness of the proposed method lies in its ability to redirect vehicles to uncongested road sections while maintaining traffic efficiency, thereby preventing partial road congestion and low traffic flow on certain roads. This capability highlights the progressive nature of the proposed method.

To evaluate the ACRABPG proposed in this study for the multi-vehicle collaborative routing problem with varying traffic demands in road network scenarios, this study focuses on two key indicators: road throughput and average vehicle travel time. These metrics are similar to those used in the single-intersection scenarios. The initial game vehicle composition included 30% directional vehicles and 10% priority vehicles. The inflow rate from the starting points O1 to O8 was set at 20 veh/min, while that from O9 and O10 was also initially set at 20 veh/min. To assess the algorithm’s performance under high traffic flow conditions, the vehicle inflow rates at the starting points O9 and O10 were gradually increased to 40, 60, and 80 veh/min, with simulations conducted for each scenario. Figs. 9 and 10 illustrate the road network throughput during the simulation process and the average travel time of vehicles reaching their destinations, respectively.

Figure 9: Road network throughput and average vehicle travel time under varying traffic flow conditions

Figure 10: Average travel times of vehicles in environments with varying proportions of priority vehicles

Fig. 9 shows that the ACRABPG method consistently achieves the highest road network throughput, regardless of the vehicle inflow rates. Its advantage becomes more pronounced as the vehicle inflow rate increases. For example, when the inflow rate at O9 and O10 reaches 80 veh/min, the proposed method improves the throughput by 48.61%, 107.77%, 75.64%, and 114.97% compared to the social routing algorithm, the shortest path algorithm, CPOM, and TCEPO, respectively. The four comparison methods perform adequately when the vehicle flows at O9 and O10 is 40 veh/min, with road throughput only 1.00%, 2.75%, 2.00%, and 3.95% lower than ACRABPG. However, as the traffic flow increased to 60 and 80 veh/min, their throughputs diverged significantly. At 60 veh/min, the Social routing algorithm maintains a relatively high throughput (23,125 veh) compared to the shortest path algorithm, CPOM, and TCEPO. When the inflow rate reached 80 veh/min, all four methods experienced substantial performance deterioration, indicating their poor adaptability to increasing traffic demand. To further evaluate the proposed algorithm’s ability to balance individual needs and road network coordination under varying priority traffic vehicle ratios, additional tests were conducted. Initially, directional traffic vehicles comprised 30% of the game vehicles, while priority traffic proportions were set at 10%, 15%, 20%, 25%, and 30%. The vehicle inflow rates at O9 and O10 were set at 60 and 80 veh/min. The analysis of the average vehicle travel times yielded the results shown in Fig. 10.

Fig. 10 shows that regardless of variations in the vehicle inflow rate and the proportion of priority vehicles among all game vehicles, the average travel time for priority vehicles remains substantially lower than that of ordinary vehicles, with a minimum difference of 37 s. Meanwhile, the travel time for ordinary vehicles does not substantially exceed that of all game vehicles, with a maximum difference of only 19 s. This result indicates that the proposed algorithm effectively balances individual needs and road network coordination in scenarios with different priority vehicle ratios. To further evaluate the effectiveness of the proposed algorithm in vehicle diversion, a simulation was conducted under the following conditions: an average vehicle inflow rate of 80 veh/min at the starting points O9 and O10, an initial directional vehicle proportion of 30%, and a priority vehicle proportion of 10%. During each simulation, the traffic density within the game roadside unit’s control range was recorded every 15 min. Due to bidirectional traffic on the same road, the density of vehicles traveling in the positive direction is represented as a positive value, while that in the reverse direction is denoted as a negative value (with the default direction set as west to east and from south to north). Fig. 11 illustrates the vehicle density distributions of the three algorithms at each time step.

Figure 11: Vehicle density distributions of different algorithms at various time points

As shown in Fig. 11a,b, the proposed ACRABPG method effectively redirects vehicles to less congested roads, enabling them to exit the road network quickly. This approach prevents any road network from reaching saturation density, maintaining an average network traffic density of 34 vehicles, thereby demonstrating its strong traffic diversion capability. Fig. 11c,d shows that the social routing algorithm successfully distributes vehicles across less congested roads, promoting load balancing. However, after 60 min of simulation, it still results in high vehicle density and congestion on multiple roads, such as roads 17 to 20. Fig. 11e,f indicates that the shortest path algorithm, which prioritizes the shortest physical distance, leads to severe congestion on these routes while leaving alternative roads underutilized. For example, intersections 22 to 40 experience full congestion, whereas roads 3 to 14 accommodate fewer than 24 vehicles. As shown in Fig. 11g,h, the CPOM method effectively allocates vehicles to low-traffic road sections because of its predictive capability. Although it prevents road saturation, its limited prediction range hampers congestion reduction, resulting in an overall traffic density 1.6 times higher than that of ACRABPG. Finally, Fig. 11i,j demonstrates that the TCEPO method, which prioritizes certain vehicles, inevitably leads to congestion by compromising ordinary vehicles. This highlights the importance of balancing the needs of different participants to prevent worsening congestion.

Concurrently, the proposed ACRABPG method and the four alternative methods underwent significance testing using the Origin software. Because the data did not follow a normal distribution, this study employed a non-parametric test for significance analysis. The null hypothesis stated that ACRABPG does not differ significantly from the other four methods, with a significance level of 0.05. Tables 3 and 4 present the simulation results, where 0 indicates no significant difference between the two methods and 1 denotes a significant difference.

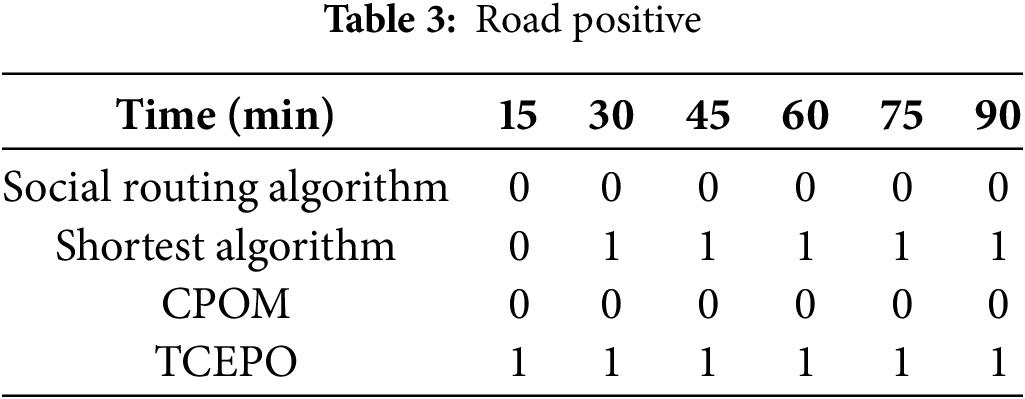
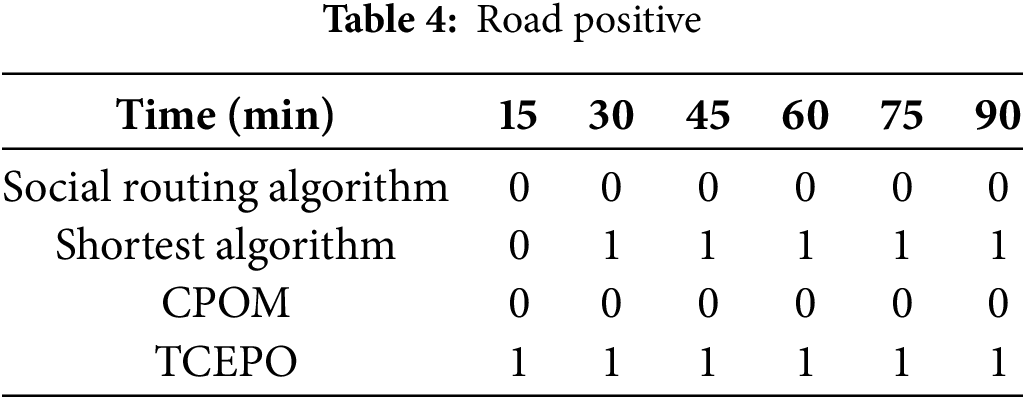
The results presented in Tables 3 and 4 demonstrate that the proposed method exhibits no significant difference in skewness from the social routing and CPOM methods. However, its mean value is notably smaller—approximately 2.8 and 3.1 times lower than the social routing and CPOM methods, respectively. After 15 min of simulation, significant differences emerged between the proposed method and both the shortest path and TCEPO methods, indicating distinct data biases among these approaches. The effectiveness of the proposed method lies in its ability to redirect vehicles to uncongested sections while maintaining traffic efficiency, thereby preventing partial road congestion and low traffic flow on certain roads. This capability underscores the progressive nature of the method introduced in this study.

6  Conclusion

This study proposes a dynamic multi-vehicle routing method for road networks with varying traffic demands based on preference games. The collaborative routing problem for vehicle groups in a large-scale road network scenario is transformed into a collaborative decision-making problem at a micro-scale intersection. This transformation effectively reduces the complexity of modeling and solving the collaborative routing decision-making problem for vehicle groups in large-scale scenarios. Vehicles participating in road selection decisions at intersections were modeled using a population game approach. By categorizing vehicle types and assigning corresponding weights, the model balances the road network to accommodate priority traffic demands while enhancing general applicability. A rapid algorithm for solving the population game model was designed for specific scenarios, ensuring benefits for both individual vehicle and multi-vehicle cooperative operations. As a result, the proposed method improves the performance in terms of the average vehicle travel time, road network throughput, and road load balancing.

The approach presented in this study can be extended in several significant directions. First, this study focuses exclusively on the routing problem for connected vehicles. Future research could explore integrating this approach with signalization control to enable collaborative decision-making that considers both vehicle routes and signalized rights of way. Second, while this study evaluates vehicle movement efficiency, it does not account for key factors such as vehicle energy consumption. Future work should incorporate multiple performance metrics to enhance the applicability. In addition, subsequent research should investigate the proposed control approach in more complex intersection scenarios, including intersections with multiple legs and lanes per leg. Finally, improving the overall traffic performance by coordinating various vehicle types such as buses and lorries presents another promising avenue for future studies.

Acknowledgement: The authors thank the laboratory of the School of Transportation Science and Engineering at Beihang University and the laboratory of the School of Electrical and Control Engineering at North China University of Technology for their support.

Funding Statement: This research was financially funded by the National Key Research and Development Program Project 2022YFB4300404.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Jixiang Wang; data collection: Jing Wei; analysis and interpretation of results: Siqi Chen; draft manuscript preparation: Haiyang Yu and Yilong Ren. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data used to support the findings of this study are available from the corresponding author upon request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Zheng X, Huang N, Bai YN, Zhang X. A traffic-fractal-element-based congestion model considering the uneven distribution of road traffic. Phys A Stat Mech Appl. 2023;632:129354. doi:10.1016/j.physa.2023.129354. [Google Scholar] [CrossRef]

2. Vishnoi SC, Ji J, Bahavarnia M, Zhang Y, Taha AF, Claudel CG, et al. CAV traffic control to mitigate the impact of congestion from bottlenecks: a linear quadratic regulator approach and microsimulation study. ACM J Auton Transport Syst. 2024;1(2):1–37. doi:10.1145/3636464. [Google Scholar] [CrossRef]

3. Hu J, Li X, Hu W, Xu Q, Kong D. A cooperative control methodology considering dynamic interaction for multiple connected and automated vehicles in the merging zone. IEEE Trans Intell Transp Syst. 2024;25(9):12669–81. doi:10.1109/TITS.2024.3386200. [Google Scholar] [CrossRef]

4. Deng J, Wu X, Wang F, Li S, Wang H. Analysis and classification of vehicle-road collaboration application scenarios. Procedia Comput Sci. 2022;208:111–7. doi:10.1016/j.procs.2022.10.018. [Google Scholar] [CrossRef]

5. Diderot CD, Bernice NWA, Tchappi I, Mualla Y, Najjar A, Galland S. Intelligent transportation systems in developing countries: challenges and prospects. Procedia Comput Sci. 2023;224:215–22. doi:10.1016/j.procs.2023.09.030. [Google Scholar] [CrossRef]

6. Shao C, Cheng F, Xiao J, Zhang K. Vehicular intelligent collaborative intersection driving decision algorithm in Internet of Vehicles. Future Gener Comput Syst. 2023;145:384–95. doi:10.1016/j.future.2023.03.038. [Google Scholar] [CrossRef]

7. Wang J, Yu H, Chen S, Ye Z, Ren Y. Heterogeneous traffic flow signal control and CAV trajectory optimization based on pre-signal lights and dedicated CAV lanes. Sustainability. 2023;15(21):15295. doi:10.3390/su152115295. [Google Scholar] [CrossRef]

8. Yu H, Wang J, Ren Y, Chen S, Dong C. Signal control study of oversaturated heterogeneous traffic flow based on a variable virtual waiting zone in dedicated CAV lanes. Appl Sci. 2023;13(5):3054. doi:10.3390/app13053054. [Google Scholar] [CrossRef]

9. Ishtiaque Mahbub AM, Malikopoulos AA. Conditions to provable system-wide optimal coordination of connected and automated vehicles. Automatica. 2021;131:109751. doi:10.1016/j.automatica.2021.109751. [Google Scholar] [CrossRef]

10. Xie Y, Lu G, Zheng F, Cao P, Liu X. A hierarchical approach for integrating merging sequencing and trajectory optimization for connected and automated vehicles. IEEE Trans Intell Transp Syst. 2024;25(7):7552–67. doi:10.1109/TITS.2024.3350708. [Google Scholar] [CrossRef]

11. Wu Q, Xia X, Song H, Zeng H, Xu X, Zhang Y, et al. A neighborhood comprehensive learning particle swarm optimization for the vehicle routing problem with time windows. Swarm Evol Comput. 2024;84:101425. doi:10.1016/j.swevo.2023.101425. [Google Scholar] [CrossRef]

12. Xu B, Li SE, Bian Y, Li S, Ban XJ, Wang J, et al. Distributed conflict-free cooperation for multiple connected vehicles at unsignalized intersections. Transp Res Part C Emerg Technol. 2018;93:322–34. doi:10.1016/j.trc.2018.06.004. [Google Scholar] [CrossRef]

13. Mak S, Xu L, Pearce T, Ostroumov M, Brintrup A. Fair collaborative vehicle routing: a deep multi-agent reinforcement learning approach. Transp Res Part C Emerg Technol. 2023;157:104376. doi:10.1016/j.trc.2023.104376. [Google Scholar] [CrossRef]

14. Ma K, Liao S, Niu Y. Connected vehicles’ dynamic route planning based on reinforcement learning. Future Gener Comput Syst. 2024;153:375–90. doi:10.1016/j.future.2023.11.037. [Google Scholar] [CrossRef]

15. Ahmed F, Huynh N, Ferrell W, Badyal V, Padmanabhan B. Vehicle re-routing under disruption in cross-dock network with time constraints. Expert Syst Appl. 2024;237:121517. doi:10.1016/j.eswa.2023.121517. [Google Scholar] [CrossRef]

16. Rosita YD, Rosyida EE, Rudiyanto MA. Implementation of dijkstra algorithm and multi-criteria decision-making for optimal route distribution. Procedia Comput Sci. 2019;161:378–85. doi:10.1016/j.procs.2019.11.136. [Google Scholar] [CrossRef]

17. Wang J, Niu H. A distributed dynamic route guidance approach based on short-term forecasts in cooperative infrastructure-vehicle systems. Transp Res Part D Transp Environ. 2019;66:23–34. doi:10.1016/j.trd.2018.05.005. [Google Scholar] [CrossRef]

18. Chauhan SS, Kumar D. Mode search optimization algorithm for traffic prediction and signal controlling using bellman-ford with TPFN path discovery model based on deep LSTM classifier. SN Comput Sci. 2023;4(5):686. doi:10.1007/s42979-023-02140-1. [Google Scholar] [CrossRef]

19. Xue D, Guo Y, Li N, Song X, He M. Cross-domain cooperative route planning for edge computing-enabled multi-connected vehicles. Comput Electr Eng. 2023;108:108668. doi:10.1016/j.compeleceng.2023.108668. [Google Scholar] [CrossRef]

20. Li T, Guo F, Krishnan R, Sivakumar A. An analysis of the value of optimal routing and signal timing control strategy with connected autonomous vehicles. J Intell Transp Syst. 2024;28(2):252–66. doi:10.1080/15472450.2022.2129021. [Google Scholar] [CrossRef]

21. Ebrahimi D, Sudarshan G, Alzhouri F. BNART: a novel centralized traffic management approach for autonomous vehicles. In: 2024 20th International Conference on the Design of Reliable Communication Networks (DRCN); 2024 May 6–9; Montreal, QC, Canada. doi: 10.1109/DRCN60692.2024.10539171. [Google Scholar] [CrossRef]

22. Zhang J, Pei H, Ban X, Li L. Analysis of cooperative driving strategies at road network level with macroscopic fundamental diagram. Transp Res Part C Emerg Technol. 2022;135:103503. doi:10.1016/j.trc.2021.103503. [Google Scholar] [CrossRef]

23. Wang Y, Cai P, Lu G. Cooperative autonomous traffic organization method for connected automated vehicles in multi-intersection road networks. Transp Res Part C Emerg Technol. 2020;111:458–76. doi:10.1016/j.trc.2019.12.018. [Google Scholar] [CrossRef]

24. Ishtiaque Mahbub AM, Malikopoulos AA, Zhao L. Decentralized optimal coordination of connected and automated vehicles for multiple traffic scenarios. Automatica. 2020;117:108958. doi:10.1016/j.automatica.2020.108958. [Google Scholar] [CrossRef]

25. Liu Y, Zhang K, Hou B, Li Q, Feng J, Nguyen TMT, et al. Real-time traffic impedance and priority based cooperative path planning mechanism for SOC-ITS: efficiency and equilibrium. Simul Model Pract Theory. 2023;122:102683. doi:10.1016/j.simpat.2022.102683. [Google Scholar] [CrossRef]

26. Jiang C, Fu J, Liu W. Research on vehicle routing planning based on adaptive ant colony and particle swarm optimization algorithm. Int J Intell Transp Syst Res. 2021;19(1):83–91. doi:10.1007/s13177-020-00224-3. [Google Scholar] [CrossRef]

27. Typaldos P, Papageorgiou M, Papamichail I. Optimization-based path-planning for connected and non-connected automated vehicles. Transp Res Part C Emerg Technol. 2022;134:103487. doi:10.1016/j.trc.2021.103487. [Google Scholar] [CrossRef]

28. Lu J, Li J, Yuan Q, Chen B. A multi-vehicle cooperative routing method based on evolutionary game theory. In: 2019 IEEE Intelligent Transportation Systems Conference (ITSC); 2019 Oct 27–30; Auckland, New Zealand. doi: 10.1109/itsc.2019.8917441. [Google Scholar] [CrossRef]

29. Batista SFA, Leclercq L, Menéndez M. Dynamic traffic assignment for regional networks with traffic-dependent trip lengths and regional paths. Transp Res Part C Emerg Technol. 2021;127:103076. doi:10.1016/j.trc.2021.103076. [Google Scholar] [CrossRef]

30. Gore N, Arkatkar S, Joshi G, Antoniou C. Modified bureau of public roads link function. Transp Res Rec. 2023;2677(5):966–90. doi:10.1177/03611981221138511. [Google Scholar] [CrossRef]

31. Lin K, Li C, Fortino G, Rodrigues JJPC. Vehicle route selection based on game evolution in social Internet of vehicles. IEEE Internet Things J. 2018;5(4):2423–30. doi:10.1109/JIOT.2018.2844215. [Google Scholar] [CrossRef]

32. Caprio DD, Ebrahimnejad A, Alrezaamiri H, Arteaga FJS. A novel ant colony algorithm for solving shortest path problems with fuzzy arc weights. Alex Eng J. 2022;61(5):3403–15. doi:10.1016/j.aej.2021.08.058. [Google Scholar] [CrossRef]

33. Wu J, Lin Y, Qi W. Timing co-evolutionary path optimisation method for emergency vehicles considering the safe passage. Transp A Transp Sci. 2023;25:1–33. doi:10.1080/23249935.2023.2253477. [Google Scholar] [CrossRef]