 Open Access
Open Access
ARTICLE
Sufficient and Necessary Conditions for Leader-Following Consensus of Second-Order Multi-Agent Systems via Intermittent Sampled Control
School of Science, Nanjing University of Posts and Telecommunications, Nanjing, 210023, China
* Corresponding Author: Yuanzhen Feng. Email:
Computers, Materials & Continua 2025, 83(3), 4835-4853. https://doi.org/10.32604/cmc.2025.063179
Received 07 January 2025; Accepted 04 March 2025; Issue published 19 May 2025
Abstract
Continuous control protocols are extensively utilized in traditional MASs, in which information needs to be transmitted among agents consecutively, therefore resulting in excessive consumption of limited resources. To decrease the control cost, based on ISC, several LFC problems are investigated for second-order MASs without and with time delay, respectively. Firstly, an intermittent sampled controller is designed, and a sufficient and necessary condition is derived, under which state errors between the leader and all the followers approach zero asymptotically. Considering that time delay is inevitable, a new protocol is proposed to deal with the time-delay situation. The error system’s stability is analyzed using the Schur stability theorem, and sufficient and necessary conditions for LFC are obtained, which are closely associated with the coupling gain, the system parameters, and the network structure. Furthermore, for the case where the current position and velocity information are not available, a distributed protocol is designed that depends only on the sampled position information. The sufficient and necessary conditions for LFC are also given. The results show that second-order MASs can achieve the LFC if and only if the system parameters satisfy the inequalities proposed in the paper. Finally, the correctness of the obtained results is verified by numerical simulations.Keywords
In recent years, MASs have always been at the forefront of control and network science research. The rapid development of MASs owes mainly to their widespread applications in formation control of UAVs [1], spacecraft attitude coordination control [2], distributed control in microgrids [3], and so on.
Serving as a basis for the control of MASs, studies on consensus are of great practical and theoretical significance. Up to now, many meaningful research results have been obtained. For example, studies [4] and [5] discussed the consensus in first-order MASs under switching and dynamically changing topologies, respectively. Since second-order dynamics is more usual than first-order in applications, consensus on second-order MASs has drawn the interest of an increasing number of researchers. Authors in [6] proposed several second-order algorithms to solve the consensus problems. The consensus of heterogeneous second-order nonlinear MASs was studied in [7–9], whereas studies [10] and [11] discussed the consensus problems for discrete-time MASs under directed information exchange.
Under the continuous control framework, communication between agents must always be maintained. The intermittent control strategy was proposed to overcome the excessive consumption of limited resources in continuous control. Using the intermittent control technique, studies [12] and [13] studied the consensus problems of linear and nonlinear MASs, respectively. Intermittent control was also used in [14–16] to study the second-order consensus of time-delay MASs. The distributed consensus problem for leader-following MASs was investigated in [17] via directed intermittent communication.
Although intermittent control can shorten the controller’s running time, the frequency of information transmission cannot be decreased. Sampled-based intermittent controllers were introduced to improve control efficiency and solve second-order consensus problems [18–20]. LFC in second-order MASs was analyzed in [18] by designing an intermittent controller based on a filter with relative state information. In particular, the topology graph in [18] is undirected; however, it is virtually impossible to guarantee bidirectional communication between agents. Therefore, studying MASs with directed topologies of one-way communication is more practical. Reference [19] discussed the consensus of directed second-order MASs by employing current and sampled information. For the containment control problem, the proof of consensus for MASs has been given in [20] under a directed communication topology. Studies [19] and [20] both used the current and sampled state information to design the intermittent communication control protocols.
Sampled data can be used to design control protocols when real-time information is unavailable. For second-order leaderless MASs, periodic intermittent control protocols using sampled information were designed in [21] and [22]. Study [21] considered a consensus protocol with sampled position and velocity information. A protocol with sampled and past sampled position information was proposed in [22] to overcome the dependence on velocity information. By analyzing the relationship of the system parameters, sufficient and necessary conditions have been obtained to ensure the consensus of MASs.
It should be pointed out that none of the above references explored the LFC problems for directed MASs by taking an intermittent sampled control strategy. Based on these analyses, it is valuable to delve deeply into the intermittent sampled LFC control problems for second-order MASs under weighted directed graphs.
The key contributions made by this paper are outlined below. Firstly, a distributed intermittent controller is proposed, which guarantees the second-order LFC and effectively reduces the energy loss of the MAS. Secondly, time delay is considered when designing the controller. Based on the relations of the communication bandwidth, the sampling period, and the time delay, sufficient and necessary conditions for LFC are derived by analyzing the error dynamics of the MAS. Furthermore, following the idea in [23], an intermittent controller based only on sampled position information is designed, under which LFC can still be reached if and only if control parameters, time delay, communication bandwidth, and sampling period satisfy certain conditions.
Before proceeding, we need to introduce some symbols: R,
This part will briefly introduce some necessary basics.
Basic graph theory is introduced by considering a MAS, which includes one leader and N followers.
If there is a node (defined as the root node) such that directed paths exist from this node to every other node in the graph, we say that the directed graph has a directed spanning tree. If
Lemma 1 ([24]): L + D is nonsingular if
Lemma 2 ([25]): Consider a block matrix
Lemma 3 ([26]): Consider a polynomial of order two with complex coefficients:
Lemma 4 ([27]): For a third-order complex coefficient polynomial:
Consider a second-order MAS, which includes N followers and one leader. The
where
where
Definition 1: For any
The following ISC protocol is introduced to reduce energy consumption:
where
Remark 1: Continuous control protocols, which are widely applied in the study of consensus-related problems of second-order MASs, will cause excessive consumption of limited resources. Controllers using current and sampled state information were designed in [18–20] to decrease the control cost. Reference [18] considered the LFC problems of undirected MASs; however, the obtained results do not apply to MASs under directed graphs. References [19] and [20] address the leaderless consensus of MASs in directed topologies. The controller (3) proposed in this paper only uses the sampled data to deal with the LFC problems of directed MASs.
3 Leader-Following Consensus without Time Delay
In this part, ISC protocol (3) is applied to study the LFC problem of MAS (1)–(2).
Let
Let
Eq. (5) can be further reworded to
where
For matrix H, there is a nonsingular matrix K such that
where
Before proceeding, the following assumption and proposition need to be given.
Assumption 1:
Proposition 1: When Assumption 1 holds, system (1)–(2) with protocol (3) can reach LFC if and only if
Proof of Proposition 1 (Necessity): If
(Sufficiency): If
Corollary 1: Under Assumption 1, MAS (1)–(2) can reach LFC if and only if the following N systems are asymptotically stable:
where
Proof of Corollary 1 (Necessity): If MAS (1)–(2) reaches LFC, it follows from Proposition 1 that
(Sufficiency): When the N systems in the (8) are asymptotically stable, then
Although Proposition 1 and Corollary 1 provide some conditions for ensuring LFC, they do not show how consensus behavior is affected by relevant parameters of the system. Therefore, the following theorem is given to show the relationship among them.
Theorem 1: With (3), MAS (1)–(2) can reach the LFC if and only if
where
Proof of Theorem 1: From (8), we can obtain
When
Solving the first equation of (10) and substituting its solution into the second equation of (10), it can be obtained that
where
Hence, we have
When
where
where
Corollary 2: When
where
Proof of Corollary 2: When
Undirected graphs can be considered unique directed graphs. For undirected graphs, the subsequent corollary can be derived.
Corollary 3: If the communication topology of all the followers is undirected, system (1)–(2) can reach the LFC if and only if
where
Proof of Corollary 3: When G is undirected, the eigenvalues
4 Leader-Following Consensus with Time Delay
It is widely known that time delay has always been present in actual systems and can not be ignored. For time delay situations, a kind of ISC algorithm is proposed.
where
Remark 2. Since time delay always exists in engineering applications, based on [18], we further consider the time-delay system and propose a time-delay controller that only uses the sampled information. Literature [13] and [14] considered the leaderless consensus of linear and nonlinear MASs, respectively, where intermittent control protocols were designed using sampled information. As a comparison, this paper discusses the ISC problem of second-order leader-following MASs. An ISC protocol (17) is designed for MAS (1)–(2) with time delay to achieve LFC.
With (17), by using procedures similar to those in Section 3, we obtain that
Let
Let
Theorem 2: When Assumption 1 holds, MAS (1)–(2) with the protocol (17) achieves the LFC if and only if one of the following conditions hold:
1)
where
2)
where
Proof of Theorem 2: Based on Eq. (20), we deduce that
Therefore,
where
Let
Case 1:
For
By letting
Therefore, for
Case 2: When
Let
For
Case 3:
Let
For
Case 4:
Let
For
If
For Cases 1 and 3, let
where
where
For Cases 2 and 4, let
where
where
Remark 3: In Theorem 2, sufficient and necessary conditions are provided under which system (1)–(2) achieves LFC with protocol (17). From the relationship of
Remark 4: The second-order LFC of MAS (1)–(2) with time delay can be reached if and only if (21) holds. In Case 1, we can first set the values of
Corollary 4: For the undirected topology, the second-order MAS (1)–(2) reaches the LFC if and only if one of the following is satisfied:
1)
where
2)
where
Proof of Corollary 4: For undirected graph G, we can easily get
5 Leader-Following Consensus Based Only on Position Information
Obtaining velocity information is difficult in engineering applications, so we propose the following ISC protocol based only on position information.
Remark 5: Velocity information was used in designing the controllers in [18,19] and [21]. However, it is usually hard to get the velocity information. When velocity is unavailable, systems need to rely on position data to reach consensus. This motivates us to explore whether LFC can still be reached when protocols are designed based only on position data. In fact, most studies regard the time delay as a detrimental factor due to its significant impact on system stability (examples include references [4,14–16], and [21]). When velocity information is absent, the LFC cannot be achieved by relying solely on position information. In such cases, incorporating time delay information can be beneficial for reaching consensus. Reference [23] proved that under some circumstances, time delay is beneficial to achieving the consensus of MASs, in which a continuous time-delay control algorithm was designed to reach second-order consensus. ISC protocol (31) employing the time-delay sampled position information is proposed in this paper for second-order MASs to achieve LFC, which can effectively reduce the energy loss of MASs and solve the problem that the velocity information is unavailable.
After similar calculations as in Theorem 2, we obtain that
where
Theorem 3: Suppose that Assumption 1 holds. MAS (1)–(2) with control protocol (31) reaches LFC if and only if one of the following holds:
1)
where
2)
where
Proof of Theorem 3: The steps of the proof for this part are akin to that of Theorem 2, so it will not be repeated here. □
Remark 6: By following the same line as in Remark 4, we can select proper parameters for (33) and (34) to be satisfied under which LFC in MAS (1)–(2) can still be reached.
Corollary 5: For undirected graphs, MAS (1)–(2) with the protocol (31) can achieve the LFC if and only if one of the following conditions is valid:
1)
where
2)
where
Proof of Corollary 5: A similar proof follows from Corollary 4. □
Remark 7: Both [19] and [20] used the current and sampled state information to design the control protocols, while this paper only uses the sampled information to improve the control efficiency further. In addition, considering that velocity information is difficult to obtain, this paper proposes an ISC protocol (31) that only utilizes the sampled position information, and the sufficient and necessary conditions for LFC are obtained. This approach can avoid the control cost resulting from the velocity measurement.
Consider a second-order MAS, which includes
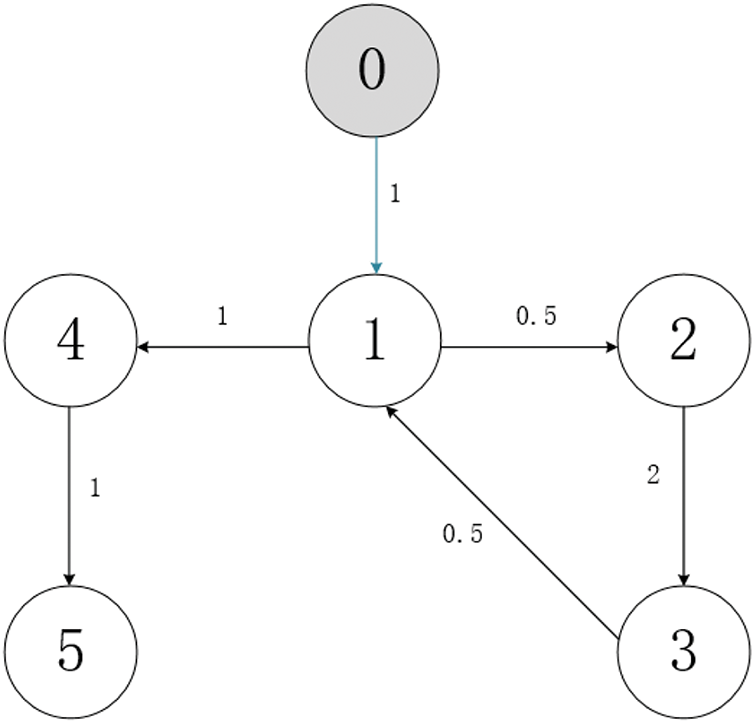
Figure 1: Communication graph of MAS (1)–(2)
Example 1: Consider system (1), (2) with protocol (3). According to Theorem 1, we choose

Figure 2: State errors between the followers and the leader when
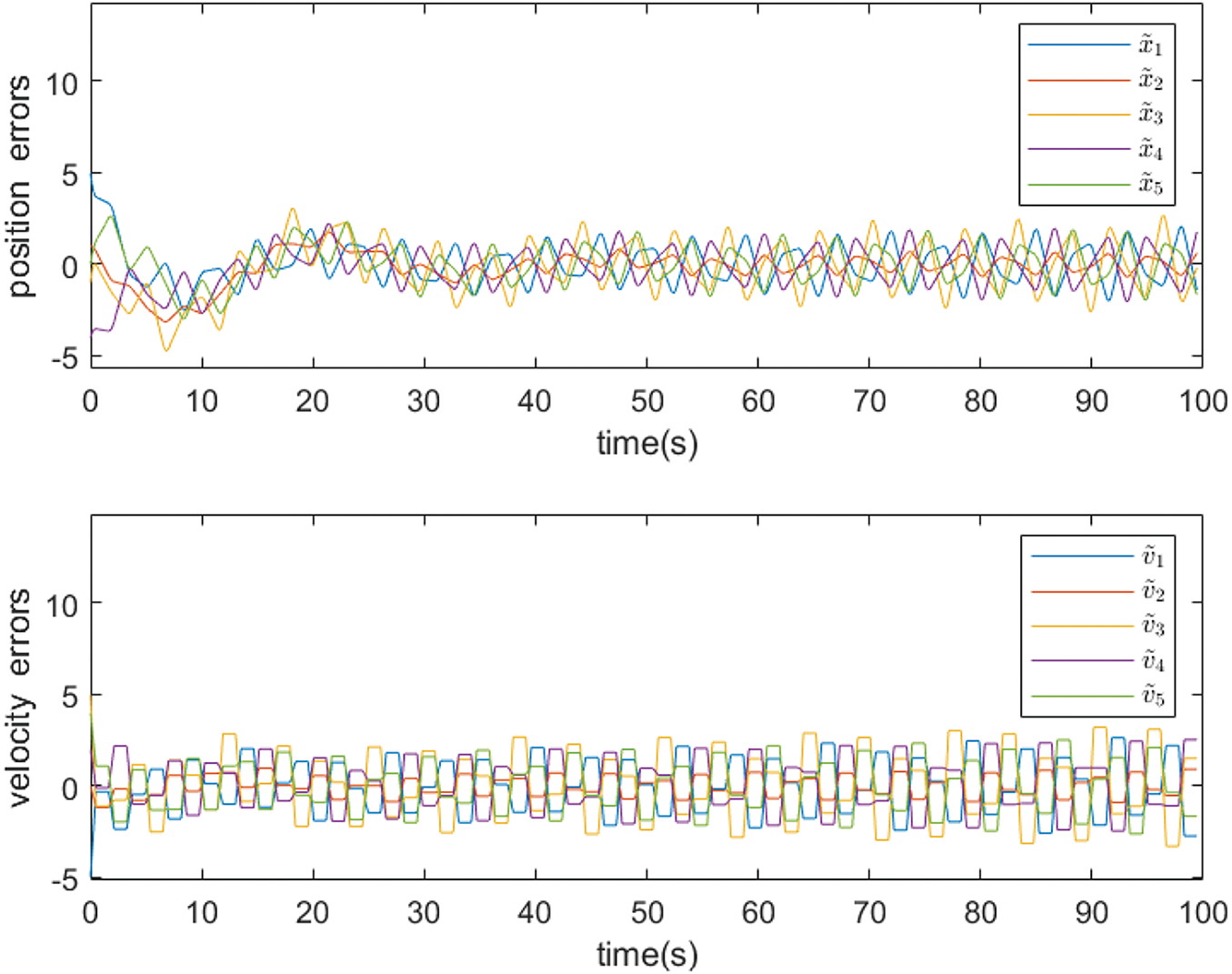
Figure 3: State errors between the followers and the leader when
Example 2: In this example, simulations in two different cases (Cases
When

Figure 4: The error trajectories of system (1)–(2) with protocol (17) in Case
When

Figure 5: The error trajectories of system (1)–(2) with protocol (17) in Case
Under protocol (17), the position and velocity errors between all the followers and the leader tend to
Example 3: The other two different cases (Cases
When

Figure 6: The error trajectories of system (1)–(2) with protocol (31) in Case
When

Figure 7: The error trajectories of system (1)–(2) with protocol (31) in Case
In these two cases, the state errors between all the followers and the leader converge to
Second-order LFC problems in MASs are investigated in this work. Firstly, a new ISC protocol is proposed, and consensus conditions are analyzed to ensure the LFC. A sufficient and necessary condition dependent on coupling gain, sampling period, communication bandwidth, and network structure is obtained. Besides, input delay is taken into account, and a time-delay protocol is proposed. According to the relationship of system parameters, four cases are discussed separately, and it is concluded that MAS can reach the LFC if and only if system parameters satisfy certain conditions. Furthermore, considering it is hard to get the velocity information, an intermittent sampled protocol only with position information is proposed. A sufficient and necessary condition is also acquired to guarantee the LFC. In the future, we will further investigate the second-order LFC of MASs with quantized communication or stochastic switching topologies, etc.
Acknowledgement: The authors are grateful to all the editors and anonymous reviewers for their comments and suggestions.
Funding Statement: This research was supported by the National Natural Science Foundation of China under Grants 62476138 and 42375016.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Ziyang Wang; draft manuscript preparation: Ziyang Wang and Yuanzhen Feng; funding acquisition and supervision: Zhengxin Wang and Yuanzhen Feng; review: Cong Zheng. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Not applicable.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
Abbreviations
| ISC | Intermittent sampled control |
| LFC | Leader-following consensus |
| MASs | Multi-agent systems |
References
1. Dong X, Yu B, Shi Z, Zhong Y. Time-varying formation control for unmanned aerial vehicles: theories and applications. IEEE Trans Control Syst Technol. 2014;23(1):340–8. doi:10.1109/TCST.2014.2314460. [Google Scholar] [CrossRef]
2. Zou A, Kumar KD, Hou Z. Attitude coordination control for a group of spacecraft without velocity measurements. IEEE Trans Control Syst Technol. 2011;20(5):1160–74. doi:10.1109/TCST.2011.2163312. [Google Scholar] [CrossRef]
3. Ning B, Han Q, Ding L. Distributed finite-time secondary frequency and voltage control for islanded microgrids with communication delays and switching topologies. IEEE Trans Power Syst. 2021;51(8):3988–99. doi:10.1109/TCYB.2020.3003690. [Google Scholar] [PubMed] [CrossRef]
4. Olfati-Saber R, Murray RM. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans Autom Control. 2004;49(9):1520–33. doi:10.1109/TAC.2004.834113. [Google Scholar] [CrossRef]
5. Ren W, Beard RW. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans on Autom Control. 2005;50(5):655–61. doi:10.1109/TAC.2005.846556. [Google Scholar] [CrossRef]
6. Ren W. On consensus algorithms for double-integrator dynamics. IEEE Trans Automat Contr. 2008;53(6):1503–9. doi:10.1109/TAC.2008.924961. [Google Scholar] [CrossRef]
7. Lu M, Wu J, Zhan X, Han T, Yan H. Consensus of second-order heterogeneous multi-agent systems with and without input saturation. ISA Trans. 2022;126(1):14–20. doi:10.1016/j.isatra.2021.08.001. [Google Scholar] [PubMed] [CrossRef]
8. Du H, Wen G, Wu D, Cheng Y, Lü J. Distributed fixed-time consensus for nonlinear heterogeneous multi-agent systems. Automatica. 2020;113(1):108797. doi:10.1016/j.automatica.2019.108797. [Google Scholar] [CrossRef]
9. Chen C, Han Y, Zhu S, Zeng Z. Neural network-based fixed-time tracking and containment control of second-order heterogeneous nonlinear multiagent systems. IEEE TNNLS. 2024;35(8):11565–79. doi:10.1109/TNNLS.2023.3262925. [Google Scholar] [PubMed] [CrossRef]
10. Liang S, Wang F, Liu Z, Chen Z. Necessary and sufficient conditions for leader-follower consensus of discrete-time multiagent systems with smart leader. IEEE Trans Syst Man Cybern: Syst. 2022;52(9):2779–88. doi:10.1109/TSMC.2021.3055578. [Google Scholar] [CrossRef]
11. Su H, Ye Y, Qiu Y, Cao Y, Chen M. Semi-global output consensus for discrete-time switching networked systems subject to input saturation and external disturbances. IEEE Trans Cybern. 2018;49(11):3934–45. doi:10.1109/TCYB.2018.2859436. [Google Scholar] [PubMed] [CrossRef]
12. Wen G, Duan Z, Ren W, Chen G. Distributed consensus of multi-agent systems with general linear node dynamics and intermittent communications. Int J Robust Nonlinear Control. 2014;24(16):2438–57. doi:10.1002/rnc.3001. [Google Scholar] [CrossRef]
13. Wen G, Duan Z, Li Z, Chen G. Consensus and its L2-gain performance of multi-agent systems with intermittent information transmissions. Int J Control. 2012;85(4):384–96. doi:10.1080/00207179.2011.654264. [Google Scholar] [CrossRef]
14. Wen G, Duan Z, Yu W, Chen G. Consensus of second-order multi-agent systems with delayed nonlinear dynamics and intermittent communications. Int J Control. 2013;86(2):322–31. doi:10.1080/00207179.2012.727473. [Google Scholar] [CrossRef]
15. Liu C, Liu L, Wu Z. Intermittent event-triggered optimal control for second-order delayed multiagent systems with input constraints. IEEE TSMC. 2024;54(5):2698–710. doi:10.1109/TSMC.2023.3346949. [Google Scholar] [CrossRef]
16. Yu Z, Jiang H, Hu C, Fan X. Consensus of second-order multi-agent systems with delayed nonlinear dynamics and aperiodically intermittent communications. Int J Control. 2017;90(5):909–22. doi:10.1080/00207179.2016.1187305. [Google Scholar] [CrossRef]
17. Huang N, Duan Z, Zhao Y. Leader-following consensus of second-order non-linear multi-agent systems with directed intermittent communication. IET Control Theory Appl. 2014;8(10):782–95. doi:10.1049/iet-cta.2013.0565. [Google Scholar] [CrossRef]
18. Chen T, Wang F, Xia C, Chen Z. Leader-following consensus of second-order multi-agent systems with intermittent communication via persistent-hold control. Neurocomputing. 2022;471(3):183–93. doi:10.1016/j.neucom.2021.10.111. [Google Scholar] [CrossRef]
19. Wang F, Liu Z, Chen Z. Sampled-hold-based consensus control for second-order multiagent systems under aperiodically intermittent communication. IEEE Trans Circuits Syst I: Reg Papers. 2022;69(9):3794–803. doi:10.1109/TCSI.2022.3176667. [Google Scholar] [CrossRef]
20. Chen T, Wang F, Xia C, Chen Z. Containment control for second-order multi-agent systems with intermittent sampled position data under directed topologies. Knowl Based Syst. 2022;257(2):109892. doi:10.1016/j.knosys.2022.109892. [Google Scholar] [CrossRef]
21. Yu Z, Jiang H, Hu C. Second-order consensus for multiagent systems via intermittent sampled data control. IEEE Trans Syst Man Cybern: Syst. 2018;48(11):1986–2002. doi:10.1109/TSMC.2017.2687944. [Google Scholar] [CrossRef]
22. Su H, Liu Y, Zeng Z. Second-order consensus for multiagent systems via intermittent sampled position data control. IEEE Trans Cybern. 2020;50(5):2063–72. doi:10.1109/TCYB.2018.2879327. [Google Scholar] [PubMed] [CrossRef]
23. Ma Q, Xu S. Intentional delay can benefit consensus of second-order multi-agent systems. Automatica. 2023;147(1):110750. doi:10.1016/j.automatica.2022.110750. [Google Scholar] [CrossRef]
24. Zhang H, Lewis FL. Adaptive cooperative tracking control of higher-order nonlinear systems with unknown dynamics. Automatica. 2012;48(7):1432–9. doi:10.1016/j.automatica.2012.05.008. [Google Scholar] [CrossRef]
25. Gantmakjer F. The theory of matrices. New York, NY, USA: Chelsea Publishing; 1960. [Google Scholar]
26. Parks PC, Hahn V. Stability theory. In: Englewood Cliffs. NJ, USA: Prentice-Hall; 1993. [Google Scholar]
27. Huang N, Duan Z, Chen G. Some necessary and sufficient conditions for consensus of second-order multi-agent systems with sampled position data. Automatica. 2016;63(9):148–55. doi:10.1016/j.automatica.2015.10.020. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools