Efficient Searchable Encryption Scheme Supporting Fuzzy Multi-Keyword Ranking Search on Blockchain

1  Introduction

As the volume of data increases, data owners are starting to host their data with cloud service providers. Considering the sensitivity and privacy of the data, these data are usually encrypted before transmission to the cloud. The existing encryption mechanism makes the data in the ciphertext state unable to be retrieved directly in plaintext, thus losing the data retrieval function. The traditional approach is to first download all the encrypted data on the server to the local area, then use the key to decrypt all these data into plaintext format, and finally perform the retrieval operation. This approach may trigger overburdening of the server while consuming a large amount of local computational resources and inefficient retrieval. Searchable encryption technology can achieve effective retrieval based on ciphertext data. However, most of the existing searchable encryption schemes are based on cloud servers, which have the problem of single point of failure of centralized devices and are not credible. In addition, the existing schemes only return files containing search keywords, and cannot sort the returned files according to the importance of keywords in the file. Most of them only support single keyword or precise search, which has defects in function.

Aiming at these problems, a ciphertext retrieval scheme supporting fuzzy multi-keyword sorted search on blockchain is proposed. The scheme uses blockchain and IPFS to store index and encrypted files in a distributed manner, respectively. The distributed ledger of blockchain is tamper-proof, which ensures the authenticity of the stored index data. The smart contract based on blockchain is responsible for performing data retrieval. Due to the decentralization and non-tampering characteristics of blockchain, the smart contract can avoid the problems of dishonest search that may occur in traditional centralized servers when performing retrieval operations, thus ensuring the reliability of data retrieval. Implement fuzzy multi-keyword search in ciphertext state using LSH and BF. A weighted statistical algorithm combining TF-IDF and RWS is proposed to calculate the similarity between files and trapdoors to realize the ranking of query results, and a balanced binary tree is introduced to construct an index structure to improve the efficiency of ciphertext retrieval. The contributions of this article are as follows:

(1)   Blockchain technology is introduced to store the index, smart contracts are utilized to carry out data search work, and ciphertext files are uploaded to IPFS for off-chain storage. It eliminates the problems of single point of failure and dishonest search that exist in traditional cloud servers and ensures the security of data and the reliability of data search.

(2)   Aiming at the functional limitations and low-performance problems of fuzzy multi-keyword searchable encryption schemes on the blockchain, the keywords are mapped into vectors by using the pairwise encoding function, and the fuzzy multi-keyword retrieval is realized with the help of locally sensitive hash and Bloom filter techniques. At the same time, the index vectors and query vectors are encrypted using the secure k-nearest neighbor algorithm. The relevance score is accurately calculated while avoiding privacy leakage.

(3)   Considering the importance of keywords in different regions of the file, this paper proposes a Region Weight Score weighting algorithm. The correlation between the two is measured by the position of the keyword in the file. Considering both word frequency and inverse document frequency, a weighted statistical algorithm combining TF-IDF and weight region score is proposed to calculate the similarity between the file and the trapdoor, so as to sort the query results. Improve the ranking quality and personalized experience of search results.

(4)   A balanced binary tree index structure was adopted, and a binary tree traversal strategy suitable for this scheme was designed to accurately return top – k files without traversing all index vectors during the search, further improving retrieval efficiency and reducing storage space and communication overhead.

2  Related Work

In recent years, Song et al. [1] first introduced symmetric searchable encryption (SSE). By symmetrically encrypting the keywords and uploading them to the cloud server for storage. However, SSE needs to perform global traversal operations when performing search, which has the problems of low efficiency and large computational overhead. Wu et al. [2] proposed a public key authenticated encryption and fast keyword search scheme that can well protect indexing and keyword privacy. However, it is currently impossible to extend the PAEFKS scheme to multi-keyword search scenarios. Curtmola et al. [3] proposed a keyword-based search strategy that utilizes an inverted indexing method, which makes it possible to perform searches without having to retrieve all the files. However, the strategy is limited to single-keyword searches.

Aiming at these problems, Golle et al. [4] introduced the method of multi-keyword search and constructed a secure framework for performing conjunctive keyword searches of encrypted data. However, in the face of scenes that require approximate matching, the scheme shows obvious limitations. Wang et al. [5] proposed a secure sorted keyword search method for encrypted cloud data, which represents indexes and trapdoors in vector format and achieves retrieval by performing computation on the vectors. However, the scheme only focuses on single keyword search and does not involve multi-keyword search. Xia et al. [6] proposed a secure multi-keyword sorting search method for encrypted cloud data, which realized multi-keyword sorting search results through a vector space model and TF-IDF algorithm. However, the scheme does not take into account the importance of the position of the keywords in the document, and cannot achieve a fuzzy search function. Chen et al. [7] proposed a multi-keyword ciphertext retrieval method based on hierarchical clustering, which can achieve linear computational complexity with an exponentially growing document set. However, this method cannot evaluate the importance of keywords in the document. And does not support a fuzzy search function. Zhu et al. [8] proposed an indexing structure based on hierarchical cohesive clustering to gather highly relevant files in clusters to improve the efficiency of text retrieval. However, only exact keyword search is supported.

To solve the problem of users not being able to obtain correct search results due to spelling errors, Li et al. [9] proposed for the first time a fuzzy keyword search technique executed in a cloud computing environment. However, the scheme does not consider the semantic privacy of keywords, and attackers may be able to crack. Vaanchig et al. [10] proposed a temporary fuzzy keyword search public key cryptography method combining fuzzy functions and cryptographic trees and achieved secure retrieval of time-related data. However, the search results cannot be sorted according to the degree of relevance to the search keywords. Wang et al. [11] implemented fuzzy multi-keyword ciphertext search using Bloom Filter (BF) and Locality-Sensitive Hashing (LSH) techniques to eliminate predefined dictionaries. However, it is necessary to traverse the global file when performing the search, which leads to low efficiency. Liu et al. [12] proposed a matrix-based multi-keyword fuzzy search strategy, which realizes the of keywords with the help of the incommensurable nature of prime numbers. However, the search time of this scheme will increase with the increase in the number of query keywords.

To address the above challenges, Miao et al. [13] proposed a verifiable searchable encryption scheme that features short ciphertext length, fast ciphertext conversion, and an accelerated search process of search results. However, the scheme does not involve fuzzy keyword search functions, and cannot achieve sorting of search results. The schemes proposed by Ge et al. [14] and Liu et al. [15] validate multi-keyword search results through public key cryptography. While these schemes can verify document validity and keyword inclusion, they cannot guarantee that all relevant files are retrieved. The searchable encryption schemes mentioned above are all based on cloud servers, but the centralized cloud servers are vulnerable to a single point of failure, and the data may have the risk of leakage or tampering. Using decentralized blockchain technology can perfectly solve the problem of a single point of failure. Hu et al. [16] constructed a decentralized privacy-preserving search system that replaces the role of a central server with smart contracts to ensure that data owners have reliable access to accurate search results. Similarly, Zhang et al. [17] proposed a blockchain-based stable keyword search architecture that supports two-party verification and direct fair transactions, eliminating the involvement of a third party. Han et al. [18] proposed a blockchain-assisted multi-keyword searchable encryption scheme to solve the single-point failure problem of centralized systems. However, the above schemes do not support the function of fuzzy search and cannot sort the search results. Yan et al. [19] proposed a verifiable fuzzy searchable encryption scheme with blockchain-assisted multi-user scenarios to achieve fine-grained access control in multi-user scenarios. However, the returned files cannot be sorted according to the importance of keywords in the file.

At present, the existing searchable encryption schemes have their advantages and limitations. The existing schemes have the problems of imperfect functions, low retrieval efficiency, inaccurate retrieval results, and centralized cloud servers that are vulnerable and untrustworthy. A ciphertext retrieval scheme supporting fuzzy multi-keyword ranking search on the blockchain is proposed to solve the above problems.

3  Preliminaries

3.1 TF-IDF Algorithm

TF-IDF technique is commonly used in information retrieval and text mining to evaluate the importance of a word for a particular document in a collection of files. The formula is shown below, Where TFfj,wi′ denotes the frequency of occurrence of keyword wi in the file fj, IDFwi′ denotes the frequency of occurrence of files containing the keyword wi in the total set of files, Nfj,wi denotes the number of keywords wi in the file fj, N denotes the total number of files, Nwi denotes the number of files containing keyword wi, see Eqs. (1) and (2).

TFfj,wi′=1+ln⁡Nfj,wi(1)

IDFwj′=ln⁡(1+N/Nwi)(2)

Normalize it to get Eqs. (3) and (4):

TFfj,wi=TFfj,wi′∑wi∈W(TFfj,wi′)2(3)

IDFwj=IDFwj′∑wj∈W(IDFwj′)2(4)

3.2 Regional Weighting Scores

Zfi,wj denotes the weight region score, suppose a file has φ regions, let the weight coefficients of these φ regions are g1, g2,…, gφ. Assume that the importance of these φ regions is decreasing. Their weight coefficients should satisfy (5)–(7) three conditions:

g1,g2,…,gφ∈[0,1](5)

∑x=1φgx=1(6)

g1≥g2≥…≥gφ(7)

If the keyword appears in region i then let Vi=1, otherwise 0. Derive the weighted region score Eq. (8):

Zfi,wj=∑x=1φgxVx(8)

3.3 Localized Sensitive Hashing

LSH [20] is an algorithm for similarity searching of high-dimensional data. It utilizes a hash function to map similar points in a high-dimensional space into the same bucket to quickly search for points that are similar to the query point. When two points in a high-dimensional space are close together, there is a higher probability that they will be mapped to the same hash value. Conversely, there is a lower probability that two points will be mapped to the same hash value when they are farther apart. If any two points s,t∈{0,1}k and h∈H satisfy (9) and (10):

d(s,t)≤r1:Pr[h(s)=h(t)]≥p1(9)

d(s,t)≥r2:Pr[h(s)=h(t)]≤p2(10)

Then the hash function family H is said to be sensitive, in the case of character input error is not big even if there is an input error that is easy to map in the near-neighborhood, constitutes a prerequisite for the realization of fuzzy retrieval. In this scheme, the p-stable distribution LSH function of the form of Eq. (11) is used to realize the effective dimensionality reduction of high-dimensional vectors.

ha,b(v)=⌊a⋅v+bω⌋(11)

3.4 Bloom Filter

The main use of BF is to determine whether an element belongs to a collection. It can be understood as a very long binary vector of 0 and 1 s, initially all 0 s by default. When an element is added, the element serves as input to the k hash function, whose output value corresponds to the subscript of the binary array, and the binary value corresponding to the subscript is changed from 0 to 1. When determining whether an element belongs to a set, it is again necessary to input the element into the K hash function and determine the position in the Bloom filter array based on the output hash value. If any of the corresponding binary bits is 0, the element is not in the set; if all bits are 1, the element can be considered to be in the set. As shown in Fig. 1, the BF has already stored the element set {a,b,c}. Now we want to query whether elements a and f are included in this set. Since element a, after being mapped by two hash functions h1 and h2, has all the values mapped to the BF as 1, it can be judged that a exists in the set. After element f is mapped by the two hash functions h1 and h2, there are 0 values among those mapped to the Bloom filter, so it can be judged that f does not exist in the set.

Figure 1: Bloom filter query

4  System Model

The scheme includes a total of four parts: Data Owner (DO), Data User (DU), Interplanetary File System (IPFS), and Blockchain (BC), and the specific modeling process is shown in Fig. 2.

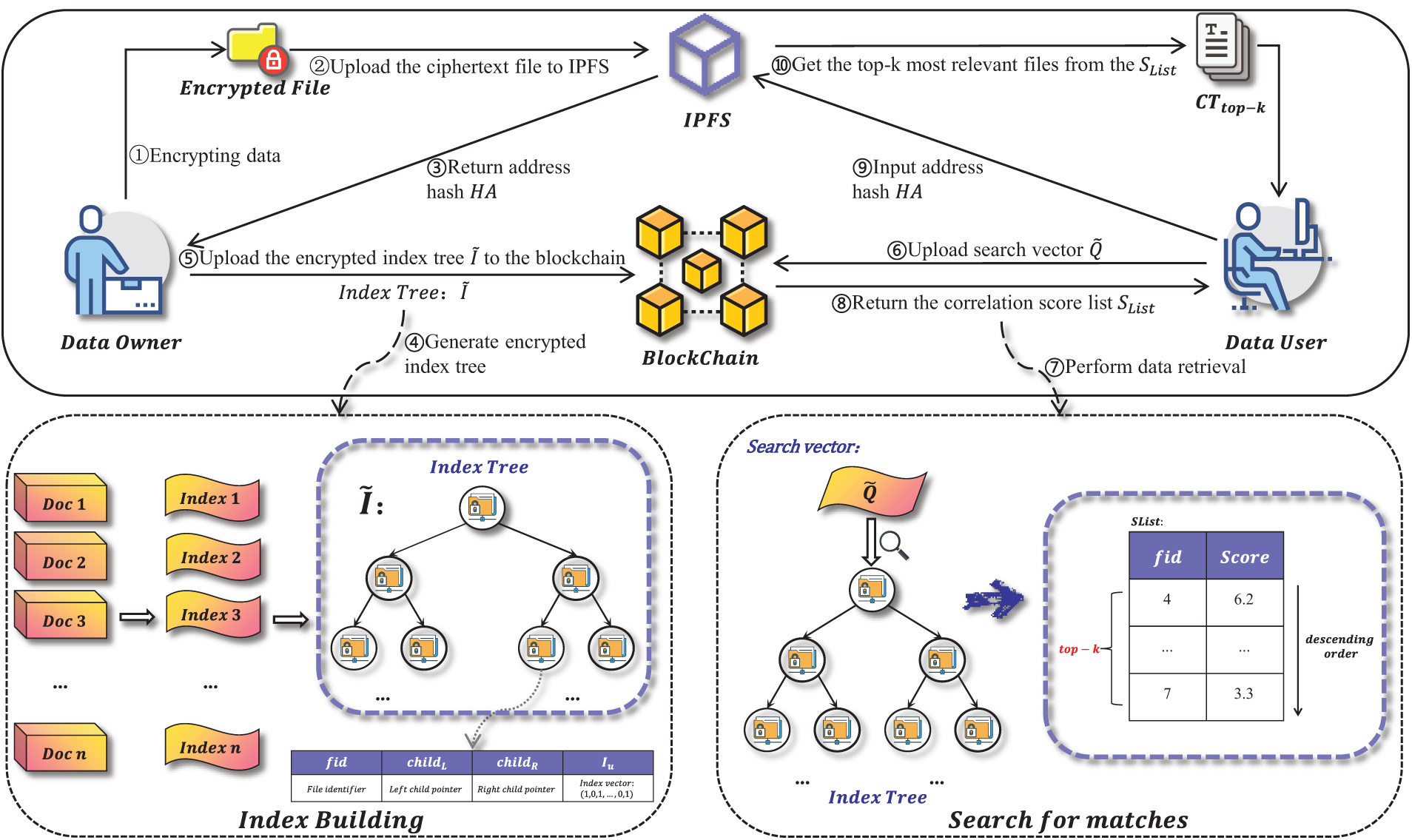
Figure 2: System model

Data Owner (DO): The DO extracts the keyword set W={w1,w2,…,wm} from the file set F={f1,f2,…,fn}. A Bloom filter BFi is generated for each file fi, and the keywords are transformed into vectors by pairwise encoding and then it is loaded into the Bloom filter BFi through the LSH as the index vector Ii of the file fi. Using file information as leaf nodes, construct an index tree I from bottom to top, and encrypt the index tree to obtain I~, and upload the encrypted index tree I~ to the blockchain. Encrypt the plaintext file to obtain an encrypted file C, and upload it to IPFS.

Data User (DU): After getting the authorization, the user generates the search vector Q based on the set of search keywords Wq. Upload the encrypted search vector Q~ to BC. After searching and matching to obtain the score list SList, DU accesses the IPFS to retrieve the top−k most relevant ciphertext files.

Blockchain (BC): The BC is mainly responsible for storing the encrypted index tree I~ and the search vector Q~. In addition, after receiving the search vector Q~ uploaded by the data user, the smart contract performs a search and matches through the index tree I~ to get the score list SList and sends it to the DU.

Interplanetary File System (IPFS): IPFS is a distributed file system that can store the encrypted files and generate a unique hash value for each stored file. The relevant algorithms are defined below:

(1)   SK←KeyGen(1λ): Key generation algorithm. The security parameter λ is input by the DO and the key set SK={k,S,M1,M2} is output, where k is a symmetric key, S is an m-dimensional binary vector, and M1 and M2 are m × m-dimensional invertible matrices.

(2)   C←Enc(k,F): symmetric encryption algorithm, which is performed by the DO. Input a collection of files F and a symmetric key k, output an encrypted file C, and upload C to IPFS.

(3)   I~←BuildIndex(SK,F): Index tree generation algorithm, which is executed by the DO. Input the key SK and the set of files F to generate the index vector Ii for each file fi, which constitutes the index tree I. The index tree is then encrypted to obtain I~, which is uploaded to the BC.

(4)   Q~←GenTrapdoor(SK,Wq): Trapdoor generation algorithm, executed by the DU. Input the key SK and the set of search keywords Wq to generate the search vector Q, which is then encrypted to obtain Q~, and upload Q~ into the BC system.

(5)   SList←ScoreSearch(I~,Q~): Search algorithms, executed by smart contracts. Input the encrypted index tree I~ and the search vector Q~, compute the corresponding inner products to obtain the relevance scores, and sort them to return the top−k encrypted files with the highest relevance scores.

(6)   F←Dec(k,C): Decryption algorithm, performed by the DU. After obtaining the ciphertext sorting result, the ciphertext is decrypted by inputting the symmetric key k to obtain the plaintext set F.

5  Fuzzy Multi-Keyword Sorted Ciphertext Retrieval Scheme

In the field of encrypted data retrieval, traditional methods have many limitations in function and performance, which seriously affect the security, accuracy, and efficiency of data retrieval. This chapter proposes a fuzzy multi-keyword ranked ciphertext retrieval scheme based on blockchain. Among them, Section 5.1 mainly analyzes the construction algorithm of index and trapdoor, which is the basis of ciphertext retrieval. Section 5.2 introduces the data retrieval algorithm, which realizes the data retrieval operation based on index and trapdoor. In Section 5.3, based on the above two algorithms, the specific ciphertext data retrieval scheme is elaborated in detail to form a complete ciphertext retrieval system.

5.1 Index and Trapdoor Construction

(1) Index construction

Keyword conversion: As shown in the keyword conversion section of Fig. 3, the keywords are converted into vector form using pairwise encoding, which is the use of two adjacent characters in a string to generate a two-character set BS. Assuming a character w1={s1,s2,…,sn}, a vector V1={x1,x2,…,xm} with m-dimensional values all 0, where m>>n. If Hash{si,si+1}=j, then xj=1.

Figure 3: Index and trapdoor generation process

BF generation: Inserting keywords into Bloom filters as shown in the index construction section of Fig. 3, an m-dimensional Bloom filter Ii is generated for each file fi and each bit is initialized to 0. For each keyword wj in fi, using BVj as the input of l LSH functions, the output value represents the subscript of Ii and the value corresponding to the position of the subscript is changed to TFfi,wj′×Zfi,wj, which is shown in Fig. 3, the vector weighting part. By using independent hash functions H={h1,h2,…,hl} to convert multiple binary m-dimensional vectors, utilizing the property of LSH, the same LSH function can map multiple similar keywords to the same position with high accuracy. The same keyword undergoes different LSH functions to achieve the final generalized word vector corresponding bits as similar or even the same. Eventually, the inner product of the index vector and the search vector represents the relevance of the document to the search keyword, as shown in the last step of Fig. 3.

Index tree construction: Create a node for each file as a leaf node of the tree. The internal nodes are then constructed based on the information from the child nodes Each node u contains information: u=<fid,childL,childR,Iu>, where fid denotes the file identifier, childL and childR denote the pointers to the left and right child nodes, and Iu denotes the index vector of the corresponding file of the node. For the leaf node, childL and childR are null. For the internal node, fid is null, Iu[i]=max{u.childL→Iu[i],u.childR→Iu[i]}. The specific steps are shown in Fig. 4 and Algorithm 1.

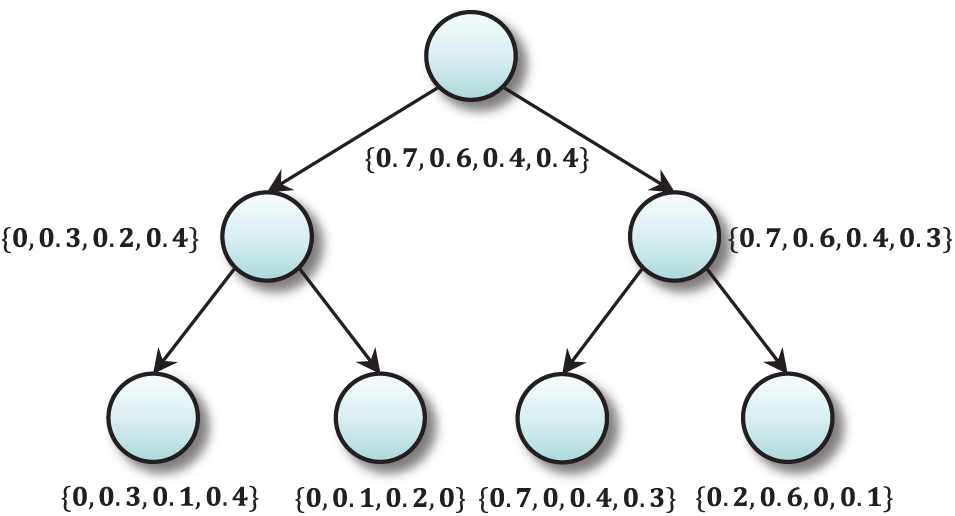
Figure 4: Index tree generation

(2) Trapdoor construction

Search vectors are constructed using the same principles as index vectors. The keywords are converted into vector form using pairwise encoding, which generates a two-character set BS′ using two adjacent characters in a string. Suppose a character w′={s1′,s2′,…,sn′}, a vector V′={x1′,x2′,…,xm′} with m-dimensional values all 0, where m>>n, and If Hash{si,si+1}=j, then xj=1. An m-dimensional Bloom filter Q with the initial state of all 0 is set up for the search trapdoor, and the binary vector transformed into the search keyword is used as the input to the l LSH functions and the output values represent the subscripts of Q. The values corresponding to the positions of the subscripts are changed to the IDF-weighted values of the keywords. The trapdoor generation process is shown in Fig. 3.

5.2 Data Retrieval

The data retrieval process is performed by the blockchain. The inner product between the index Ii and trapdoor Q is then expressed as the correlation between file fi and query keyword w.At the beginning of the search, an empty score list SList=<fid,score> is created, where fid denotes the file identifier and score denotes the score of the file associated with fid. Store the top−k files with the highest scores in the SList and sort them in descending order, where k is determined by the DU based on their actual needs. According to the index tree generation strategy, the internal node vector value takes the maximum value of its child node vector. When performing data retrieval, the inner product of the search vector and the internal node vector is calculated. When the inner product is less than the minimum value of the score list, it will not continue to traverse down. The retrieval algorithm is shown below, where u.score is the inner product of the index vector Iu in node u and the search vector Q, and SList_min is the score with the smallest correlation in the SList. Its data retrieval process is shown in Fig. 5. The specific algorithm for data retrieval is shown in Algorithm 2.

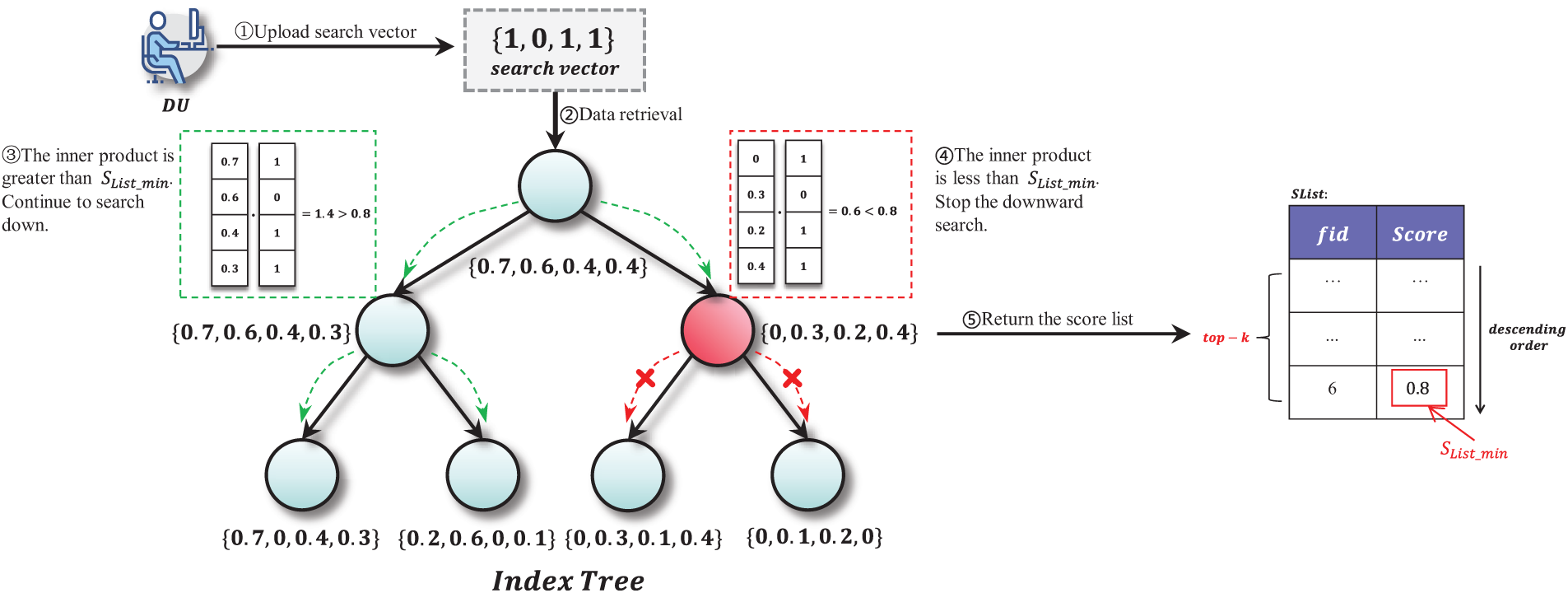
Figure 5: Data retrieval based on index tree

5.3 Program Description

The blockchain-based fuzzy multi-keyword searchable encryption scheme is shown below. Fig. 6 is the algorithm timing diagram of this scheme, and the algorithm of the specific scheme is shown in Algorithm 3.

Figure 6: Timing diagram of the algorithm

(1)   SK←KeyGen(1λ): The DO inputs the security parameter λ and outputs the key set SK={k,S,M1,M2}. Where k is a symmetric key that encrypts the file, S is an m-dimensional binary vector, and M1 and M2 are m × m-dimensional invertible matrices that serve to encrypt the index.

(2)   C←Enc(k,F): The DO encrypts F={f1,f2,…,fn} using the symmetric key k to obtain the encrypted file C={c1,c2,…,cn} and stores it in IPFS.

(3)   I~←BuildIndex(SK,F): The DO extracts the keyword Wi={w1,w2,…,wm} in fi. Generate an m-dimensional Bloom filter Ii for each file fi and initialize each bit to 0. For each keyword wj in fi, the keyword is transformed into a vector BVj by pairwise encoding, and utilizes BVj as the input of l LSH functions, and the output values represent the subscripts of Ii, and the values corresponding to the positions of the subscripts are changed to TFfi,wj′×Zfi,wj. The unencrypted index tree I is generated by the index tree construction algorithm, which is described in Section 5.1. Use S to split the index vector Iu in the node into two random vectors {Iu′,Iu′′}. The rules are as follows: If S[i]=1 then Iu′[i]+Iu′′[i]=Iu[i], and Iu′[i] and Iu′′[i] can take any value; If S[i]=0 then Iu′[i]=Iu′′[i]=Iu[i]. Obtain the encrypted index vector as I~u={M1TIu′,M2TIu′′}, and upload the encrypted index tree I~ to the blockchain.

(4)   Q~←GenTrapdoor(SK,Wq): The DU generates a Bloom filter Q based on the set of search keywords Wq and initializes each bit to 0. For each keyword wz, the keyword is transformed into a vector BVz by pairwise encoding, and utilizes BVz as the input of l LSH functions, the output value represents the subscript of Q, and the value corresponding to the position of the subscript is changed to IDFwz, the specific construction principle is shown in Section 5.1. Use S to split the search vector Q in the node into two random vectors {Q′,Q″}. The rules are as follows: If S[i]=1, then Q′[i]=Q′′[i]=Q[i]. If S[i]=0 then Q′[i]+Q′′[i]=Q[i]. Q′[i] and Q′′[i] can take any value. Obtain the encrypted search vector Q~={M1−1Q′,M2−1Q′′}, and upload the encrypted search vector Q~ to the blockchain.

(5)   SList←ScoreSearch(I~,Q~): After receiving the Q~ submitted by the DU, the blockchain executes the search matching through the smart contract. The process is described in Algorithm 2, in which the inner product (i.e., relevance score) of the encrypted index vector and the search vector is computed as Eq. (12):

SScore(Iu~,Q~)={M1TIu′,M2TIu′′}⋅{M1−1Q′,M2−1Q′′}=(M1TIu′)⋅(M1−1Q′)+(M2TIu′′)⋅(M2−1Q′′)=Iu′⋅Q′+Iu′′⋅Q′′=Iu⋅Q(12)

In Eq. (12), the result of making the inner product of vectors after encryption is the same as the result of making the inner product of plaintext vectors. After executing the query algorithm, the score list SList is returned and the corresponding ciphertext file is returned to the DU based on the fid in the list.

(6)   F←Dec(k,C): After the DU gets the returned ciphertext file, the file is decrypted using the symmetric key k to get the plaintext file.

5.4 Security Analysis

(1)   Document Privacy: The DO encrypts the collection of plaintext files before sending them to IPFS, and the DU gets the decryption key only after authorization, so only the DO and the authorized DU can get the plaintext files, and this scheme achieves document retrieval based on document identifiers, which has nothing to do with the content of the plaintext files and achieves the privacy of the files.

(2)   Confidentiality of encrypted index trees and search vector: This scheme utilizes the secure k-nearest neighbor algorithm to encrypt the index vectors Iu of nodes in the index tree. Since the generated binary vector S is random, the encrypted index vectors Iu~ can not be associated with the unencrypted index vectors Iu, and the generated encrypted vectors Iu~ are different even for the files that have the same keywords. Q~ is obtained by encrypting the search vector Q by the secure k-nearest neighbor algorithm, and even if the two sets of search keywords searched are the same, the obtained Q~ is not the same.

(3)   Unrelatedness of queries: In this scheme, the search vector Q achieves cryptographic uncertainty through the randomized decomposition of binary vectors. Even if the DU issues the same search request twice in a row, the vector Q obtained after decomposition encryption will be different, thus ensuring the uncorrelatedness between queries. However, even if the same search vector is encrypted to obtain different search vectors, the relevance score calculated by the inner product is still the same. It follows that when correlating the same search requests, the retrieval or access pattern is leaked under the known ciphertext model.

(4)   Security of data storage and reliability of retrieval: The solution utilizes blockchain technology to store encrypted index trees and search vectors, and the ciphertext files are stored in the IPFS distributed file system, which eliminates the single point of failure that exists in traditional cloud servers, provides higher reliability, and ensures file integrity. Utilizing smart contracts to perform data retrieval solves the problem of dishonest searches on traditional cloud servers and ensures the reliability of data retrieval.

In Table 1, we compare this scheme with other schemes in terms of the above security performance.

6  Performance

6.1 Performance of Time Complexity

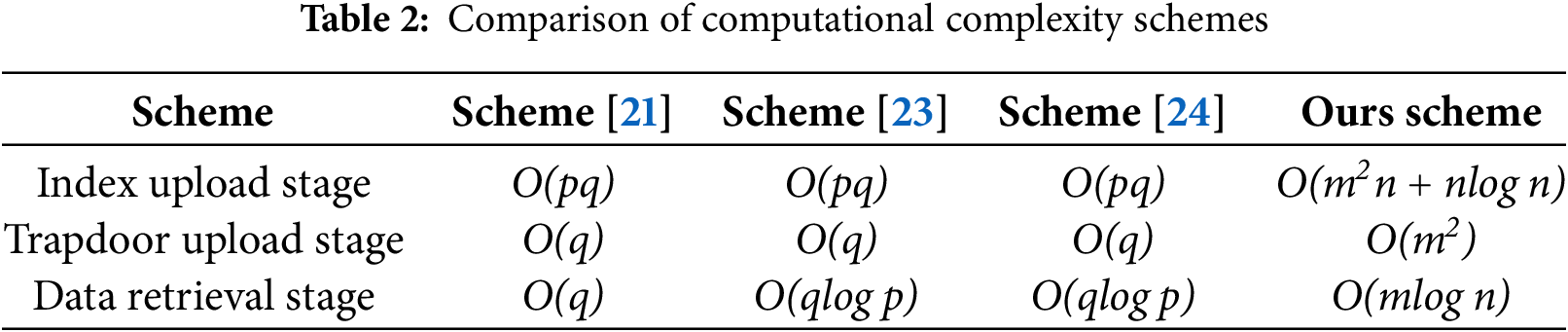
In this section, we analyze the communication complexity of the scheme from three key links: index upload stage, trapdoor upload stage, and data retrieval stage. And in Table 2 compared with the existing scheme. In the following analysis, n represents the number of files, m represents the dimension of the index or trapdoor, p is the number of exact keywords, and q is the maximum number of fuzzy keywords.

6.2 Performance Testing

The experimental environment in this study is a 64-bit Windows 10 operating system, with an Intel(R) Core(TM) i5-7300HQ CPU running at 2.50 GHz and 16 GB of RAM. The proposed solution is implemented by writing the smart contract in the Go language and using Fabric to set up a local blockchain network for deploying the smart contract. Terminal commands are then employed to interact with the deployed smart contract. We randomly selected 3000 files from the IEEE database as the dataset and extracted approximately 65,000 keywords from the dataset. The minimum number of keywords in a file is 107, while the maximum is 396. The number of LSH functions is set to l = 20, and the length of the Bloom filter is set to m = 5000. To demonstrate the fuzzy search capability of the data, we adopt a similar approach to the original method. We randomly select a keyword and then alter one of its characters to construct a fuzzy keyword. The experimental part mainly measures the time consumption of the index construction stage, trapdoor construction stage, and search matching stage.

6.2.1 Single File Index Generation

Fig. 7 shows how the time taken for index generation changes with the number of keywords. Literature [25] needs to perform encryption operations on each keyword to generate an index. Therefore, the time spent on generating the index increases with the increase in the number of keywords. In this scheme and reference [26], the increase in the number of keywords has almost no impact on the time required to generate indexes. This is because both this scheme and Literature [26] map all keywords to the Bloom filter, and the time consumed for index construction is more related to the number of Bloom filter bits and less related to the number of keywords. On this basis, the index construction efficiency of this scheme is better than that of Literature [26], because this scheme uses dual encoding functions to directly convert keywords into vectors, while Literature [26] needs first to convert keywords into lowercase and then extract the stem before converting them into vectors.

Figure 7: Time cost of index generation [25,26]

6.2.2 Trapdoor Generation

As shown in Fig. 8, the trapdoor generation time in [25] increases with the number of keywords. When the number of keywords is 10, the time consumption is about 110 ms, and the increase in the number of keywords has almost no effect on the time consumption of trapdoor generation in this scheme and Literature [26]. This is because both this scheme and Literature [26] map all keywords to the Bloom filter, and the time consumed by constructing trapdoors is more related to the number of Bloom filter bits and less related to the number of keywords. On this basis, the overall efficiency of trapdoor generation in this scheme is better than that of Literature [26]. When the number of keywords is 4, the time cost is about 10 ms, while the time cost of Literature [26] is about 43 ms. The reason is that this scheme utilizes dual encoding functions to directly convert keywords into vectors, which is more efficient compared to Literature [26].

Figure 8: Time cost of trapdoor generation [25,26]

6.2.3 Index Tree Construction

Fig. 9 illustrates how the time cost for generating the entire index tree varies with the number of files when the index tree is constructed based on all files. As shown in the figure, the time cost for index generation increases with the number of files. When the number of files reaches 3000, the indexing generation stage of this scheme takes 200 s, which is much lower than other schemes. This is because the index structure is different from other schemes. As shown in Fig. 7, the index generation time of this scheme is mainly related to the number of files, while the index generation time of other schemes is mainly related to the number of keywords contained in the files. Among them, Literature [24] has the highest time cost because it uses the RSA accumulator for verification.

Figure 9: Time cost of index building [21,23,24]

6.2.4 Search Matching

Since the comparative scheme only supports fuzzy searches for single keywords, we also conducted fuzzy single-keyword searches to enable a fair comparison. As shown in Fig. 10, the time consumed during the data retrieval phase increases approximately linearly with the number of files. When the number of files is 3000, the data retrieval time for the scheme in [22] is 3.2 s, while the retrieval times for the scheme in [21,23], and [24] are 5.1, 5.3, and 16 s, respectively. The time costs of Literature [21] and Literature [23] are similar, and when the number of files is 1000, the increased time consumption of both schemes is significantly reduced. Because both of these schemes are based on building an index for a single keyword, as the number of files increases, the growth rate of different keywords slows down, which is equivalent to the growth rate of different indexes slowing down, resulting in a slower growth rate of search time. As shown in the experimental figure, when the number of files is 3000, the data retrieval time for this scheme is only 0.6 s. Compared to the scheme in [22], this scheme demonstrates higher retrieval efficiency. This is because this scheme is based on an index tree to construct an index structure. By using the pruning technique of the index tree, the most relevant k files can be obtained without traversing all the index vectors. Literature [24] still has the highest search time overhead due to the use of the RSA accumulator.

Figure 10: Search time [21–24]

7  Conclusion

This paper proposes a blockchain-based fuzzy multi-keyword ranked ciphertext retrieval scheme to overcome the limitations of traditional searchable encryption schemes in terms of functionality, performance, and security. The scheme utilizes blockchain technology to store file indexes, IPFS to store encrypted files, and smart contracts to perform data retrieval tasks. It effectively addresses the issues of single point of failure and dishonest search associated with centralized servers, ensuring the security of data and the reliability of retrieval. By leveraging LSH and BF techniques, the scheme achieves fault tolerance for spelling errors and supports multi-keyword retrieval, thereby enhancing the accuracy and comprehensiveness of the search results. By combining the TF-IDF algorithm with RWS, the scheme more accurately evaluates the relevance between keywords and files, enabling ranking of the retrieval results and enhancing the user experience. The index structure is built using a balanced binary tree, coupled with pruning techniques, which significantly improves retrieval efficiency while reducing storage space and communication overhead. The experimental results show that this scheme is superior to existing schemes in terms of index construction efficiency, data retrieval efficiency, and security, providing new ideas and methods for the field of encrypted data retrieval. Future work could further explore how to apply this scheme to a broader range of application scenarios and investigate more efficient index structures and retrieval algorithms.

Acknowledgement: We would like to acknowledge the editors and reviewers for their comments.

Funding Statement: This research was funded by the Jilin Provincial Department of Education Scientific Research Project (Project No. JJKH20250872KJ). The funding body had no role in the design of the study, collection, analysis, and interpretation of data, or in writing the manuscript.

Author Contributions: The authors confirm their contribution to the paper as follows: Data curation, conceptualization, Hongliang Tian; methodology, writing—review, editing, writing—original draft preparation, software and validation, Zhong Fan; formal analysis, investigation and resources, Zhiyang Ruan; visualization and supervision, Aomen Zhao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Z. F. upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Abbreviations

References

1. Song DX, Wagner D, Perrig A. Practical techniques for searches on encrypted data. In: 2000 IEEE Symposium on Security & Privacy (IEEE S&P); 2000 May 14–17; Berkeley, CA, USA. p. 44–55. doi:10.1109/SECPRI.2000.848445. [Google Scholar] [CrossRef]

2. Wu M, Dong X, Cao Z, Shen J. A privacy preserving public-key searchable encryption scheme with fast keyword search. In: 2017 International Conference on Computer Technology, Electronics and Communication (ICCTEC); 2017 Dec 19–21; Dalian, China. p. 579–85. doi:10.1109/ICCTEC.2017.00131. [Google Scholar] [CrossRef]

3. Curtmola R, Garay J, Kamara S, Ostrovsky R. Searchable symmetric encryption: improved definitions and efficient constructions. J Comput Secur. 2011;19(5):895–934. doi:10.3233/JCS-2011-0426. [Google Scholar] [CrossRef]

4. Golle P, Staddon J, Waters BR. Secure conjunctive keyword search over encrypted data. In: 2004 Cryptography & Network Security Conference (ACNS); 2004 Jun 8–11; China: Yellow Mountain. p. 31–45. doi:10.1007/978-3-540-24852-1_3. [Google Scholar] [CrossRef]

5. Wang C, Cao N, Li J, Ren K, Lou W. Secure ranked keyword search over encrypted cloud data. In: 2010 IEEE 30th International Conference on Distributed Computing Systems (ICDCS); 2010 Jun 21–25; Genoa, Italy. p. 253–62. [Google Scholar]

6. Xia Z, Wang X, Sun X, Wang Q. A secure and dynamic multi-keyword ranked search scheme over encrypted cloud data. IEEE Trans Parallel Distrib Syst. 2016;27(2):340–52. doi:10.1109/TPDS.2015.2401003. [Google Scholar] [CrossRef]

7. Chen C, Zhu X, Shen P, Hu J, Guo S, Zahir T, et al. An efficient privacy-preserving ranked keyword search method. IEEE Trans Parallel Distrib Syst. 2016;27(4):951–63. doi:10.1109/TPDS.2015.2425407. [Google Scholar] [CrossRef]

8. Zhu X, Dai H, Yi X, Yang G, Li H. Muse: an efficient and accurate verifiable privacy-preserving multi-keyword text search over encrypted cloud data. Secur Commun Netw. 2017;2017:1–17. [Google Scholar]

9. Li J, Wang Q, Wang C, Cao N, Ren K, Lou W. Fuzzy keyword search over encrypted data in cloud computing. In: 2010 Proceedings IEEE International Conference on Computer Communications; 2010 Mar 14–19; San Diego, CA, USA. p. 1–5. [Google Scholar]

10. Vaanchig N, Qin Z. Public key encryption with temporary and fuzzy keyword search. Math Biosci Eng. 2019;16(5):3914–35. doi:10.3934/mbe.2019193. [Google Scholar] [PubMed] [CrossRef]

11. Wang B, Yu S, Lou W, Hou YT. Privacy-preserving multi-keyword fuzzy search over encrypted data in the cloud. In: 2014 Proceedings IEEE International Conference on Computer Communications; 2014 Apr 27–May 2; Toronto, ON, Canada. p. 2112–20. [Google Scholar]

12. Liu Q, Peng Y, Wu J, Wang T, Wang G. Secure multi-keyword fuzzy searches with enhanced service quality in cloud computing. IEEE Trans Netw Serv Manag. 2021;18(2):2046–62. doi:10.1109/TNSM.2020.3045467. [Google Scholar] [CrossRef]

13. Miao Y, Deng RH, Choo KKR, Liu X, Ning J, Li H. Optimized verifiable fine-grained keyword search in dynamic multi-owner settings. IEEE Trans Dependable Secur Comput. 2021;18(4):1804–20. [Google Scholar]

14. Ge X, Yu J, Chen F, Kong F, Wang H. Toward verifiable phrase search over encrypted cloud-based IoT data. IEEE Internet Things J. 2021;8(16):12902–18. doi:10.1109/JIOT.2021.3063855. [Google Scholar] [CrossRef]

15. Liu X, Yang X, Luo Y, Zhang Q. Verifiable multi-keyword search encryption scheme with anonymous key generation for medical internet of things. IEEE Internet Things J. 2022;9(22):22315–26. doi:10.1109/JIOT.2021.3056116. [Google Scholar] [CrossRef]

16. Hu S, Cai C, Wang Q, Wang C, Luo X, Ren K. Searching an encrypted cloud meets blockchain: a decentralized, reliable and fair realization. In: 2018 Proceedings IEEE International Conference on Computer Communications; 2018 Apr 16–19; Honolulu, HI, USA. p. 792–800. [Google Scholar]

17. Zhang Y, Deng RH, Shu J, Yang K, Zheng D. Tkse: trustworthy keyword search over encrypted data with two-side verifiability via blockchain. IEEE Access. 2018;6:31077–87. doi:10.1109/ACCESS.2018.2844400. [Google Scholar] [CrossRef]

18. Han H, Wang Z, Xu Z, Dong X, Tian W. Enhancing IoT security and efficiency: a blockchain-assisted multi-keyword searchable encryption scheme. IEEE Access. 2024;12:148677–92. doi:10.1109/ACCESS.2024.3472119. [Google Scholar] [CrossRef]

19. Yan X, Cheng P, Tang Y, Zhang J. Blockchain-assisted verifiable and multi-user fuzzy search encryption scheme. Appl Sci. 2024;14(24):11740. doi:10.3390/app142411740. [Google Scholar] [CrossRef]

20. Liu G, Yang G, Bai S, Zhou Q, Dai H. Fsse: an effective fuzzy semantic searchable encryption scheme over encrypted cloud data. IEEE Access. 2020;8:71893–906. doi:10.1109/ACCESS.2020.2966367. [Google Scholar] [CrossRef]

21. Ge X, Yu J, Hu C, Zhang H, Hao R. Enabling efficient verifiable fuzzy keyword search over encrypted data in cloud computing. IEEE Access. 2018;6:45725–39. doi:10.1109/ACCESS.2018.2866031. [Google Scholar] [CrossRef]

22. Li X, Tong Q, Zhao J, Miao Y, Ma S, Weng J, et al. Vrfms: verifiable ranked fuzzy multi-keyword search over encrypted data. IEEE Trans Serv Comput. 2023;16(1):698–710. doi:10.1109/TSC.2021.3140092. [Google Scholar] [CrossRef]

23. Wang J, Ma H, Tang Q, Li J, Zhu H, Ma S, et al. Efficient verifiable fuzzy keyword search over encrypted data in cloud computing. Comput Sci Inf Syst. 2013;10(2):667–84. doi:10.2298/CSIS121104028W. [Google Scholar] [CrossRef]

24. Huang R, Li Z, Wu G. A verifiable encryption scheme supporting fuzzy search. In: 2019 International Conference on Security, Privacy, and Anonymity in Computation, Communication, and Storage (SpaCCS); 2019 Jul 14–17; Atlanta, GA, USA. p. 397–411. [Google Scholar]

25. Shu J, Yang K, Jia X, Liu X, Wang C, Deng RH. Proxy-free privacy-preserving task matching with efficient revocation in crowdsourcing. IEEE Trans Dependable Secur Comput. 2021;18(1):117–30. doi:10.1109/TDSC.2018.2875682. [Google Scholar] [CrossRef]

26. Wang B, Fu S, Zhang X, Xie T, Lyu L, Luo Y. Reliable and privacy-preserving task matching in blockchain-based crowdsourcing. In: 2021 Proceedings of the 30th ACM International Conference on Information and Knowledge Management (CIKM); 2021 Nov 1–5; New York, NY, USA. p. 1879–88. doi:10.1145/3459637.3482385. [Google Scholar] [CrossRef]