Recent Advancement in Formation Control of Multi-Agent Systems: A Review

Abbreviations

1  Introduction

In recent years, cooperative control of distributed multi-agent systems (MASs) has received increasing attention from research scholars due to its widespread applications in practical missions such as surveillance [1], transportation [2], and search and rescue [3]. This field comprises consensus, output regulation, motion coordination, distributed optimization, formation, distributed estimation, and so on. Consensus is a fundamental issue in cooperative control that numerous researchers have addressed. Generally speaking, the consensus aims to design a proper control protocol to lead all the agents to achieve an agreement on states [4]. Within these topics, formation control is one of the most important problems in cooperative control of MASs, which has been investigated based on different autonomous platforms, such as unmanned aerial vehicles (UAVs) [5], mobile robots [6], and artificial satellites [7]. Motivated by these examples, the formation control problem (FCP) of MASs has been widely researched and applied in various areas, such as load transportation [8], cooperative localization [9], and target enclosing [10]. Generally, formation signifies that a group of agents cooperate based on local information while satisfying some specified positions as a geometric shape. Based on the interaction topology and sensing capability of MASs, results in formation control of MAS have been divided into position-based, distance-based, and displacement-based control [11]. The results in formation control can be categorized as time-invariant formation control (TIFC) [12] and time-varying formation control (TVFC) [13]. Under practical circumstances, the formation of MASs may change, and TVFC is required [14]. That is to say, the TVFC is more applicable than the TIFC [15]. More specifically, according to topology structures, formation control for MASs can be mainly divided into leaderless formation control [16] and leader-follower (L-F) or tracking formation control [17]. However, the leaderless formation techniques are not sufficient in some scenarios, such as enclosing the time-varying target [18]. Up to now, several methodologies and approaches/strategies have been developed to solve the FCP of MASs, such as the L-F approach [19], the behavioral approach [20], and the virtual approach [21–23]. Among these methods, the L-F control method is mostly applied in many applications because of its simplicity and scalability. Another attractive method to realize formation is via distributed consensus control laws. Inspired by the progress of consensus theory [24], there is an emerging trend to investigate consensus-based formation control based on local neighboring interactions. By extending the consensus protocols, FCPs of MASs with first and second-order dynamics were studied in [25,26]. FCPs for nonlinear MASs are investigated in [27,28]. Many consensus-based control techniques have recently been developed to deal with the FCP of MASs [29,30]. In recent years, scholars have increasingly adopted innovative research strategies and measurements to investigate the FCP of MASs. Many results have been obtained on formation control with first-order dynamics [31], second-order dynamics [32], high-order dynamics [33], and non-linear dynamics [34]. In many practical applications, such as target enclosing missions of UAV and mobile robots, the agents/systems with non-identical dynamics. Therefore, studying the FCP of heterogeneous multi-agent systems (HMASs) is significantly important [35]. Recently, there have been many interesting developments in the FCP of MASs from various perspectives. Results on the FCP of MASs with one leader/target have been addressed in [36,37]. However, in many practical applications, multiple leaders must be investigated, which is more challenging than a single leader. Many significant developments concerning the time-varying formation containment control (FCC) were achieved, such as [38,39]. To achieve distributed tasks, a group formation deals with the formation control of MASs having multiple subgroups, where every subgroup may have multiple leaders addressed in [40]. With the development of bipartite consensus, scholars developed control strategies to address the bipartite-formation control (BFC) problem [41,42]. To improve the convergence rate, many control strategies have been suggested to solve the finite-time (FT) FCPs [43]. Moreover, the event-triggered control (ETC) mechanism has been intensely investigated in formation control for its significant advantages [44,45]. The solution to the FCP under various communication constraints, such as actuator saturation [46], faults [47], and disturbances in system dynamics [48], has intense practical significance. Driven by the theoretical and practical importance of formation control in multi-agent systems (MASs), we review recent advancements and specific topics in this area. This review is mainly reported from a control perspective, seeking to provide the researchers with a comprehensive summary of theoretical and practical advancements in the formation control of MASs. First, we focus on the categorization of FCP and review the different measurements to solve this problem. Second, recent developments in formation control techniques, including the L-F technique, behavioral technique, and virtual structure technique, are reviewed. Third, a detailed analysis of FCC, group/cluster formation control, bipartite formation, FT formation, and event-trigged formation by providing different system models is the principal context of this paper. Finally, the solution of FCP under different network constraints, such as actuator saturations, actuator faults, and disturbances, is of intense significance concerning practical applications. In this paper, we present recent advances and approaches in the formation control of MASs. Our review of this advancing research trend aims to move the research further in this direction and identify future research areas. We review the recent advancement in the formation control of MASs that was not covered in the previous surveys. This review mainly aims to offer an up-to-date outlook on the formation control problem (FCP) in MASs and highlight recent developments that have not been systematically reviewed. More particularly, we study special topics in formation control, such as time-varying containment control (FCC), bipartite formation, group formation, event-triggered formation, formation through constrained dynamics, and finite-time (FT) formation. This emphasizes innovations and revised contributions beyond traditional approaches and thus sets our review apart from previous surveys. Even if some earlier breakfast-room questionnaires have discussed elementary understandings and methods, like leader-follower (L-F) methods, behaviorist approaches, and virtual structure strategies, they do not have thorough discussions related to modern discussions. We fill the gap by reviewing recent developments, including consensus-based formation control under nonlinear dynamics, formation control for heterogeneous MASs, and methods to deal with practical constraints like actuator saturation, faults, and disturbances. Moreover, we include a comprehensive study of recent methods for enhancing convergence rates and robustness of the system metrics, such as finite-time control and event-triggered techniques. This review aims to bring the latest developments in this area into perspective, with special attention to the recent advancements in formation control strategies. In contrast, similar surveys focus mainly on seminal works, and, as such, our survey aims to outline new methodologies, emerging trends, and under-explored domains within the field, paving the way to address critical research gaps that will provide insights on future research endeavors. This review addresses gaps in existing surveys and emphasizes the recent advances in the field to give researchers clear ideas of the current state of MAS formation control, inspiring innovations in this rapidly growing field. This review contributes in three ways:

1. We propose a new classification framework for formation control methodologies, which includes recent developments in FCC, bipartite formation, and constrained dynamic systems.

2. We systematically review recent advances in formation control techniques, including emerging methods such as group/cluster formation and event-triggered control, which remain underexplored in prior literature.

3. We analyze the solutions to FCP under real-world constraints, such as actuator limitations and external disturbances, and identify promising future research areas to guide subsequent studies in this domain.

The remainder of the paper is organized as follows. Section 2 reviews related work in formation control. Section 3 presents a bibliometric analysis of formation control research. Section 4 introduces the preliminaries and problem formulation for formation control. Section 5 discusses communication-based formation control, while Section 6 explores communication-free formation control. Section 7 focuses on the formation problem via model-based approaches. Section 8 presents simulation examples to demonstrate key concepts. Section 9 summarizes the applications of formation control. Finally, Section 10 concludes the paper and discusses future research directions. The organization of the paper is illustrated in Fig. 1.

Figure 1: Paper organization

2  Related Work

Recent advancements in formation and containment control for multi-agent systems (MAS) have brought significant progress, particularly with applying fuzzy logic, sliding mode techniques, and adaptive control strategies. An event-triggered optimal control method has been introduced for continuous-time switched nonlinear systems, enhancing control efficiency and stability [49]. Furthermore, passive formation and containment control in nonlinear autonomous ship systems have been further explored, where interval type-2 Takagi-Sugeno fuzzy models were used to account for external disturbances [50]. A predefined-time consensus method was developed for second-order nonlinear multi-agent systems in consensus algorithms, leveraging sliding mode techniques to improve convergence [51]. Similarly, a novel interval type-2 fuzzy sliding mode tracking approach has been proposed, addressing the formation and containment problem in nonlinear multi-agent systems while emphasizing robustness and precision [52]. Research into formation control has examined fixed and switching hierarchies in heterogeneous multi-agent systems, providing solutions that enhance coordination and allow for more adaptable system configurations [53]. Additionally, fuzzy steering control for multiple-ship systems was introduced, ensuring that formation and containment are achieved under complex, real-world conditions [54]. Moving on to multi-UAV systems, an adaptation of a neural-based framework for distributed formation control has been proposed to deal with unmodelled dynamics and uncertainties inherent in such systems [55]. Other contributions have targeted the area of nonholonomic wheeled robots, developing formation control techniques that increase stability in the presence of disturbances and enhance the applicability of the theoretical aspects to mobile robotic systems [56]. There are also other studies that dealt with formation and containment problems in nonlinear multi-boiler systems, which also use fuzzy interval type-2 Takagi-Sugeno descent models as a general approach to gain insight into bigger multi-agent systems [57]. Multi-agent systems have gained considerable interest over the past few years, particularly for their applications in domains such as robotics, autonomous vehicles, and sensor networks. Multi-agent systems are frequently used in situations that are significantly dynamic and uncertain, making it essential that agents can coordinate effectively with each other while also maintaining the desired formation for the mission. Surveys in recent years on consensus within multi-agent systems have elaborated on the progress achieved in establishing decentralized algorithms in a way that enemies are capable of selecting on the basis of local information whilst obtaining a global objective. Because each individual agent in a system can only communicate very little and has widely different computational abilities [58], such approaches are essential. One particularly powerful technique for controlling formations is spatial barycentric coordinates. This technique uses geometric relationships depending on their positions in the environment to maintain fixed relative positions between agents. The research indicates that the use of barycentric coordinates allows multi-agent systems to adjust their formation while complying with decentralized control rules continuously. It is scalable and robust, as agents can calculate their positions in relation to neighbours without global communication [59]. The changing interaction topologies for agents complicate the maintenance of consensus in dynamic systems. In practical situations, network communication links may change rapidly, leading to a transient or delayed exchange of state information between agents. Nonetheless, research has shown reliance on Lyapunov stability and graph theory to prove convergence. The ability to adapt to evolving network structures is an important feature of contemporary consensus protocols, allowing systems to maintain strong performance, even in real-time applications [60]. A lot of inspiration for the distributed formation control strategies is driven by nature, e.g., highly efficient decentralized coordination strategies like flocking, herding, and schooling. In these biological systems, individual agents follow simple local rules for maintaining alignment, proximity to others, and collision avoidance. These principles have also been reformulated as multi-agent systems, giving rise to natural, scalable, and fault-tolerant formation behaviours. In practical multi-agent scenarios, security threats such as denial-of-service (Dos) attacks may jeopardise communication, which hinders communication and harms systems’ performance. To alleviate these issues, they have proposed adaptive control approaches for heterogeneous schemes that control time-varying formation and maintain operability even in the existence of those attacks. Such strong strategies are for self-driving cars, where safety and continuous service are paramount [61]. With the evolution of multi-agent systems, privacy has emerged as a key consideration. Algorithms that preserve privacy, such as edge-event-triggered mechanisms, can create agreement among agents without exposing sensitive data. No sacrifices to agents’ privacy are needed as these methods provide guaranteed time within prescribed time bounds. A-MASE methods leveraging privacy-preserving techniques are essential to support the safe deployment of multi-agent systems within privacy-sensitive environments [62]. This considerable volume follows a few chapters reviewing different methods for dispersed development control. These figures underscore the critical need for scalable and adaptive algorithms capable of addressing the inherent complexities of multi-agent coordination. Such complexities include heterogeneous agent capabilities, communication constraints, and the management of uncertainty in dynamic environments [63]. Consequently, these works serve as valuable references that illuminate the field’s current state while identifying key challenges and promising directions for future research.

3  Bibliometric Analysis

A bibliometric analysis was performed to investigate trends in the research related to distributed and cooperative control in multi-agent systems (MAS) for the last two decades. The data set (2000 articles) was derived from the Scopus database and was processed with VOSviewer software (version 1.6.18). The analysis was based on words from article titles, abstracts, and indexed keywords. A total of 4663 different keywords were extracted, of which only 158 were mentioned more than five times in the dataset. The network was then generated based on the term co-occurrence data to identify 10 independent research clusters corresponding to major topics of interest under the general topic of MAS control. The clusters indicate several subfields in the topic, including formation control, consensus algorithms, distributed algorithms and coordination, and optimization methods. Given that the final network of terms produced 1033 links of link strength 1585, these results highlight MAS research topics’ overall depth and interconnectedness. Such findings show that this domain has matured as a cohesive and interlocked body of work, with important concepts continually interacting with and informing each other. The area of distributed optimization algorithms exhibited the weakest network strength in Cluster 8. This finding indicates that this field is still at the emerging level, or it could be overlooked in the context of the MAS-related works of literature. This may guide further work toward developing more holistic and interconnected approaches to decentralized control and communication in complex systems that manage computing workloads across various conditions. The analysis also underscores the dynamic nature of MAS research, with some areas enjoying sustained attention and development and others, such as distributed optimization, calling for additional exploration to fulfil the increasing demands of real-world applications. This study also reveals that several of the main topics uncovered are connected to timely technologies, thus highlighting the growing importance of interdisciplinary approaches in MAS research, including machine learning, network theory, and real-time data processing. A review of the current trends and gaps in the literature creates a cluster of opportunities for future research and inspires innovation in this rapidly changing field. The co-occurrence network of keywords provides a visual representation to identify the relationships between the research clusters that have been identified, giving a better understanding of the topics that are more important in research in MAS and in which they interconnect. The corresponding network provides a virtual map that enables researchers to orient themselves in the increasingly broad field distributed and cooperative control of multi-agent systems illustrated in Fig. 2. Table 1 summarizes the cluster analysis of control strategies, presenting key categories, the frequency of their occurrence, and related keywords, thereby providing a comprehensive overview of their distribution and relevance in the context of multi-agent systems.

Figure 2: Co-occurrence network of keywords

4  Preliminaries and Problem Formulation

4.1 Preliminaries

Notations: Throughout this paper, the notation is standard. Let Rn define the n-dimensional column vector. Rn×m denotes the n×m real matrix. ‖⋅‖F represents the Euclidean norm. The notation ‘T’ denotes the transpose of a matrix. In represents the n×n identity matrix. Denote by ⊗ the Kronecker product. sgn(⋅) indicates the signum function.

Interaction Topology: Communication between a group of agents can be described by a directed or undirected graph. The interaction graph could be static or dynamic. In a fixed communication graph, the edges stay invariant, while the edges in a dynamic communication graph are time-varying. Based on graph theory, G(V,E,𝒜) represents a graph, where V=1,2,…,n and E⊂V×V is the set of vertex/nodes and edges, respectively. An edge eij=(i,j)∈E signifies that the agent i sends information to the agent j. A=[aij]∈Rn×n is the weighted adjacency matrix of the graph G where aij=1 if eij∈E and aij=0 otherwise. The set of neighbours of the vertex i is represented by Ni={j∈V| eij∈E}. The graph G is undirected if aij=aji. The Laplacian matrix L∈Rn×n of a directed graph G can be defined as L = D − A, where D=diag(∑j∈Niaij), i=1,…,n. For further details on algebraic graph theory, refer to [64]. Table 2 provides a comprehensive list of symbols and their respective definitions used throughout the paper. It serves as a reference for understanding the key variables and mathematical notations associated with the discussed multi-agent systems and formation control techniques.

4.2 Problem Formulation

Leader-following strategies are widely employed in the formation control of multi-agent systems because of their simplicity, robustness, and scalability. Specifically, a leader agent gives a reference trajectory with followers controlling their distance from the leader and therefore desired formations. The approach is well-known in the literature as it can achieve stability and guarantee convergence on the squirrelly. Moreover, leader-following is a natural structure to build upon in order to design more general formation control strategies in which agents adjust according to both local and global information related to path-following, thus ensuring scalable coordination. We use this approach when the system needs to follow a moving target or maintain a certain geometric formation. Although other approaches, like pure consensus-based control, are possible, leader-following serves as a natural, intuitive, and computationally efficient framework from which we can explore the dynamics of the formations. Now, to formalize the formation control problem, we start with defining the agent i relative position error with respect to the leader. This is an important step to clarify the goal of the control law, i.e., how the follower agents converge to the achievable formation with respect to the leader.

limt→∞‖pi(t)−p0(t)−fi0‖=0,(1)

where pi(t) is the position of agent i, p0(t) is the position of the leader agent, and fi0 is the desired relative position of agent i with respect to the leader. We want the error between the position of the agent i and the desired relative position to the leader to go to zero. So we define the relative position error ei(t) for agent i:

ei(t)=pi(t)−p0(t)−fi0.(2)

Each agent i must adjust its position pi(t) to minimize ei(t). To ensure that ei(t) goes to zero as t→∞, a natural choice is a proportional control law for each agent, where the velocity of each agent depends on the relative error. To achieve the desired relative position, a proportional control law is typically chosen. This type of control law ensures that the relative position error ei(t) between each follower and the leader is minimized over time, driving the system towards the desired formation. The velocity of each agent is directly related to the error, ensuring convergence.

p˙i(t)=−Kiei(t),(3)

where Ki is a positive gain. This will make each agent i move towards its desired relative position with respect to the leader. Since agents are connected by a graph, we also want to ensure that the agents move together and follow the leader’s trajectory. In many cases, each agent can also adjust its position based on the relative positions of its neighbors. So, we use a consensus-based protocol, where each agent i communicates with its neighbors in the graph and adjusts its position accordingly. The control law for each agent can be generalized to:

p˙i(t)=−Ki∑j∈Ni(pi(t)−pj(t))−Ki(pi(t)−p0(t)−fi0),(4)

where ∑j∈Ni(pi(t)−pj(t)) represents the interaction between agent i and its neighbours (this encourages consensus), The control protocol for each agent i is given by:

p˙i(t)=−Ki(∑j∈Ni(pi(t)−pj(t))+(pi(t)−p0(t))−fi0),(5)

where Ki>0 is the gain for agent i, Ni is the set of neighbors of agent i, p0(t) is the position of the leader, and fi0 is the desired relative position of agent i with respect to the leader. This protocol ensures that, as t→∞, each agent i converges to its desired relative position concerning the leader. Specifically, we have:

limt→∞‖pi(t)−p0(t)−fi0‖=0.(6)

This control protocol employs a leader-follower structure alongside a consensus-driven approach to achieve the desired behavior. The Laplacian matrix and interactions within the neighborhood ensure that the agents move in a coordinated manner to attain the desired relative positions.

4.3 Categorization

The goal of formation control is to establish a suitable control rule that guarantees that the team of agents obtains a given, pre-specified, ordered spatial configuration while travelling along the preferred path. Generally, the formation control techniques MASS can be classified into centralised techniques [65] and decentralised techniques [66]. The basis for this classification comes from the control structure; this defines the way that agents communicate, share information, and make decisions. In centralized approaches, all agents seek a central controller for decision-making. Decentralized approaches enable the agents to make decisions using local observation and interactions. In particular, decentralised methods are more robust and flexible relative to centralised approaches. Because of the less demanding computation and communication costs, distributed control approaches are typically preferred to centralized approaches. Based on the time in terms of convergence, FCPS can be categorised into FT formation control [67] and fixed-time formation control [68]. Additionally, based on the coordinated variables used, the formation problem can be classified into state formation problems [69] and output formation problems [70]. In the output formation problem, only relative output information is available to each agent, and only the outputs of agents are required to realize the desired formations, making this problem more complex and challenging than the state formation problem. Formation control is designed to guide moving, interacting agents to maintain a specified shape or configuration for a coordinated objective. The system dynamics of each agent i in the multi-agent system (MAS) are defined by:

p˙i(t)=Api(t)+Bui(t),∀i∈{1,2,…,N}(7)

where A∈Rn×n and B∈Rm×m represent system matrices with appropriate sizes, pi(t)∈Rm and ui(t)∈Rn denote respectively the state and the control input of the agent i. The objective of formation control is to design the control input ui(t) so that the agents maintain a specified formation, i.e., the relative distances and orientations between the agents remain fixed. A common approach is to use the relative positions of neighboring agents to guide the control input. Let pi(t)−pj(t) represent the relative position vector between agents i and j. The control law for each agent is typically designed in the form:

ui(t)=−∑j∈Nikij(pi(t)−pj(t)),(8)

where Ni denotes the set of neighbors of agent i, kij is a positive constant gain, determining the strength of interaction between agents i and j, (pi(t)−pj(t)) is the relative position vector between agent i and agent j. The overall dynamics of the agents, incorporating the formation control law, are as follows:

p˙(t)=Ap(t)+Bu(t).(9)

Substituting the control law into this, we get:

p˙i(t)=Api(t)−B∑j∈Nikij(pi(t)−pj(t)).(10)

This system can be written in matrix form as:

p˙(t)=Ap(t)−BKLp(t),(11)

where p(t)=[p1(t),p2(t),…,pN(t)]T be the vector of all agent positions. The matrix K is a diagonal matrix of gains kij, and L is the Laplacian matrix. To ensure that the agents converge to the desired formation, we perform a Lyapunov stability analysis. We define a Lyapunov function V(p) as:

V(p)=∑i∈V∑j∈Nikij‖pi(t)−pj(t)‖2,(12)

where kij are positive constants. This Lyapunov function represents the total “energy” of the system or the sum of squared relative distances between neighboring agents. Next, we take the time derivative of V(p):

V˙(p)=−p(t)TLp(t).(13)

Since L is positive semi-definite and p(t)≠0, we conclude that V˙(p)≤0. This shows that the energy of the system is non-increasing, which implies that the agents are converging to a consensus state. Based on the interaction topology property, problems in the formation control of multi-agent systems (MASs) can be divided into two categories:

Leaderless Formation Control Protocol (FCP): All agents have a common role and jointly determine the swarm behavior through local interactions. The general leaderless FCP is to design a control protocol for multi-agents such that:

limt→∞‖pij(t)−fij‖=0,i=1,2,…,N,j∈Ni,(14)

where fij represents the desired relative position between agents i and j. Where pij(t) represents the position of agent i relative to agent j at time t, and fij is the desired final position between agents i and j. The control protocol typically involves a function that governs how each agent adjusts its position based on the relative positions of other agents in the system. To design such a protocol, one common approach is to use cooperative control strategies and concepts such as graph theory (where the agents form a graph G=(V,E)) and distributed control. One approach would be to define the relative distance between agents and apply a velocity control law to minimise the error between them. Here’s a simplified version of a potential control law: Define the relative position error between agent i and agent j as:

eij(t)=pi(t)−pj(t)−fij.(15)

The velocity of agent i can be adjusted by using a control law such as:

p˙i(t)=∑j∈NiKijeij(t),(16)

where Kij>0 is a positive gain, and Ni is the set of neighbors of agent i. The sum implies that each agent adjusts its position based on the error with respect to all its neighbours. The term Kij determines how strongly agent i should adjust its position relative to agent j. Holds for any preset bounded initial condition where pij(t)=pi(t)−pj(t) and fij=(fi−fj). The reference fij is the formation deviation between the ith agent and the jth agent. The agent i has to keep a formation deviation fij with the neighbour agent j. In [71], formation stabilisation for MASS was studied without the leader. An illustration of the FCP is presented in Fig. 3. The leader agent determines the predefined formation trajectories, and the follower agents are controlled to track the leader agent. The general L-FCP is to design a control protocol for MAS such that:

limt→∞‖pi(t)−fi0−p0(t)‖=0,(17)

where pi(t) is the position of agent i at time t, p0(t) is the position of the leader (agent 0), and fi0 is the desired relative position of agent I with respect to the leader 0. For any preset bounded initial condition where p0(t)∈Rm represents the desired trajectory and the reference fi0 represents the formation deviation with respect to p0(t). Note that when fi0 is dynamic, the FTP is extended to a TVFT problem. In a leader-follower framework, agent 0 (the leader) typically follows a predefined trajectory, and the followers (agents 1, 2,\ldots, N) adjust their positions relative to the leader and each other, based on the desired relative formation. The key idea is to design a control law for each follower such that their relative positions with respect to the leader converge to the desired values. Each follower agent adjusts its velocity based on the relative error ei(t). The control law for each follower i can be designed as:

p˙i(t)=−Kiei(t),(18)

where Ki>0 is a positive gain that determines the speed at which agent i corrects its position. This law ensures that each follower moves in a direction that reduces the position error relative to the leader. For the leader (agent 0), the position can evolve according to a predefined trajectory, p0(t). Typically, the leader’s motion is not influenced by the followers, as the leader is assumed to be independent. Its dynamics could be given by:

p˙0(t)=v0(t),(19)

where v0(t) is the velocity of the leader (which could be known or predefined). Thus, the control protocol for each follower i is:

p˙i(t)=−Ki(pi(t)−p0(t)−fi0),(20)

where Ki>0 is a gain that ensures the error decays, and p0(t) is the position of the leader. This protocol will ensure that as t→∞, each follower converges to its desired relative position with respect to the leader, satisfying the condition.

limt→∞‖pi(t)−fi0−p0(t)‖=0.(21)

Figure 3: Formation control problem (a) Leaderless formation problem (b) Formation tracking problem

Remark 1: If fi0=0, then limt→∞‖pi(t)−p0(t)‖=0 implies that the state consensus or point formation is achieved by all the agents. Thus, the consensus can be considered a special case of formation control.

The current findings in formation control can be categorized into two main types.

TIFC: It is also referred to as fixed formation control. TIFC signifies that the geometric formation created by a group of agents is time-invariant/fixed [72]. TIFC may have limitations in practical applications. In TIFT, all follower agents adhere to the same trajectory as the leader, while the formations among the follower agents remain fixed. Results on TIFC for MASs are addressed in [73,74].

TVFC: It is also called dynamic formation control. TVFC signifies that the agents can change their fixed formation configuration, which is more significant in many practical tasks and causes challenges in designing distributed control protocols [75]. An illustration of the time-varying formation is represented in Fig. 4. TVFC is particularly relevant in practical applications, such as target enclosing, where followers maintain a desired time-varying formation while following the leader’s time-varying path. Therefore, studying TVFC is significant. In the following section, we will define time-varying formation.

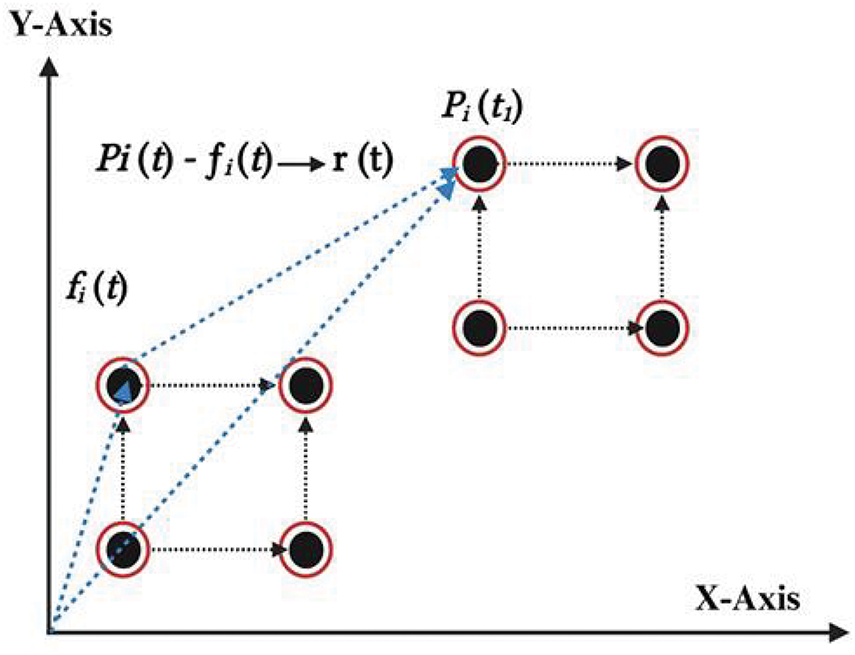
Figure 4: Illustration of time-varying formation in multi-agent system

Definition 1. MAS (1) is said to accomplish a time-varying formation if for any bounded initial conditions pi(0)∈Rn,i=1,…,N, the following equation:

limt→∞(pi(t)−fi(t)−r(t))=0,(22)

where f(t)=[f1T(t),f2T(t),…,fnT(t)]T specifies the desired time-varying formation vector with fiT(t) is a bounded piecewise differentiable vector and the function r(t) denotes the formation reference. Eq. (22) defines the condition for a Multi-Agent System (MAS) to achieve a time-varying formation. It specifically describes the desired relationship between the agents’ positions, the formation vector, and the reference trajectory over time.

pi(t) represents the position of agent i at time t, where each agent’s position is a vector in Rn, with i=1,…,N, and N is the total number of agents in the system. fi(t) refers to the desired time-varying formation vector for agent i, which is a bounded piecewise differentiable vector. This vector describes the desired relative position of agent i in the formation at time t relative to a predefined reference. The vector f(t)=[f1(t),f2(t),…,fn(t)]T contains the desired formation for all agents in the system. r(t) represents the formation reference, which could refer to an overall trajectory or a global reference point to which the entire formation is aligned. It’s important to note that r(t) is typically time-varying as well, indicating that the desired formation and positions are not static but evolve over time. The equation states that, as time progresses towards infinity (i.e., t→∞), the difference between the actual position of agent i (pi(t)), its desired formation position (fi(t)), and the formation reference (r(t)) must approach zero. Consider the following general MAS:

{p˙i(t)=Api(t)+Bui(t),yi(t)=Cpi(t),(23)

where yi(t)∈Rq denotes the output of agent i. The definition of the time-varying output formation is presented as follows.

Definition 2. The time-varying output formation characterised by the vector f(t) is said to be achieved for MAS if the following equation:

limt→∞(yi(t)−fi(t)−r(t))=0,(24)

holds for any preset bounded initial conditions.

Remark 2. Note from the equation, when C=In, the output formation problem reduces to a state formation problem. In TVFC, the formation information f(t) and its derivative will be introduced into the analysis and design of the TVFC protocols, making the TVFC problem more challenging.

4.4 Categorical Measurements in Formation Control

Formation control can be designed using various strategies, including position-based, bearing-based, displacement-based, and distance-based. Each strategy depends on the available sensing and control variables. The position-based strategy is the most commonly considered approach, where the full relative position information of neighbouring agents is available and can be used as feedback to achieve a desired formation pattern [76]. This strategy allows for precise control of agent positions within the formation and is often employed when complete positional data are available. In bearing-based formation control, the control input for each agent is determined by the relative bearings (angles) of its neighbouring agents [77]. This approach is particularly useful when only angular information can be measured, and it helps maintain the desired formation by aligning the relative bearings between agents. However, the lack of direct distance measurements introduces challenges in achieving precise distance-based control. The displacement-based strategy measures relative distances and relative orientations between agents for feedback, although relative positions cannot be directly measured. The control law is based on aligning agent orientations using consensus control, after which displacement-based formation control can be formulated by using relative distances like the position-based strategy. Only the relative distances between agents must be maintained in the distance-based strategy. This approach emphasises controlling the distance between neighbouring agents without requiring complete positional information [78]. It is especially useful when measuring distances is more feasible than determining exact positions or angles. Each of these strategies is designed for different operational environments, depending on the available sensors and the precision of control required. This enables the agents to attain a synchronised formation tailored to the precise objectives of the task.

5  Communication-Based Formation Control

Communication-based formation control is one of the important strategies for multi-agent systems (MAS). The core of this descriptor is a method of informing agents in a cluster with respect to each other so that they can share information in real-time and coordinate with each other, hardening dynamic and robust formulation patterns. By incorporating cooperation or communication, these agents can continually update their positions based on feedback provided by their neighboring agents, upholding the formation while the agents move and interact in their environment. In this section, we review communication-based formation control approaches and classify them into four strategies that include position-based, bearing-based, displacement-based, and distance-based strategies. Each strategy has it’s strengths and weaknesses in relation to the task, which is determined by both the available modalities for observation and the operation conditions. An example is position-based strategies, which require the knowledge of complete relative position information between all agents, enabling exact control of the formation shape. In contrast, bearing-based strategies rely on relative angular measurements to coordinate their actions, making them suitable for cases where positional information is absent. Assuming position information is available only in a local region, displacement-based strategies that rely on relative distances and relative orientations for feedback control can achieve maintenance of formation without the same positional measurement. In multi-agent systems, coordinating multiple agents to maintain a desired formation is challenging, especially in dynamic and uncertain environments. The primary issues encountered in formation control are scalability, communication constraints, leader-follower problems, decentralization, adaptability to dynamic environments, and robustness. Different control strategies aim to address these problems, each with strengths and weaknesses. Table 3 compares various control strategies used in multi-agent formation control, evaluating how each approach addresses key issues such as scalability, communication constraints, and decentralization. It highlights the advantages and limitations of each strategy, demonstrating which approach is more suitable for specific challenges like dynamic environments, leader-follower problems, and system robustness. The comparison helps identify the strengths and weaknesses of each strategy in handling complex multi-agent coordination tasks.

5.1 Leader-Follower Method

Under this approach, one agent is considered a leader, and the other agents are the followers. The leader agent moves along a trajectory, and the follower agents follow/track the leader agent [79]. Agents require following a trajectory to maintain the desired formation, where a virtual/actual leader generates the trajectory. The desired relative distances and bearing with a leader are anticipated to be maintained [80]. The L-F method has been widely applied in the formation control of MASs due to its practicability and simplicity. However, there is no feedback information between the followers and the leader. The formation tracking problem (FTP) for MASs with first-order dynamics is addressed in [81,82]. TVFT problems for second-order MASs with one leader under directed and switching topologies are addressed in [83,84], respectively, where necessary and sufficient conditions to achieve TVFT were proposed. A three-dimensional space L-F formation control scheme is exploited in [85] using the persistence of excitation of bearing vectors of the desired formation. In [86], a bearing-only formation control law is designed for single-integrator MASs with a moving leader at a constant velocity, where the follower agents are unaware of the leader’s velocity. The investigation focused on observer-based fixed-time formation control (FTP) for second-order multi-agent systems (MASs), considering both the presence and absence of communication delays. Additionally, the time-varying formation control problem (FCP) for high-order MASs, featuring a single leader with bounded unknown inputs and operating under switching communication topologies, was also addressed. Based on Riccati inequalities, a distributed adaptive formation protocol is designed to solve the time-varying FTP under fixed and switching topologies [87]. The proposed protocol could update the coupling weights based on the neighbour agents’ information. An FTP for discrete-time linear MASs is studied in [88] using a directed switching topology based on a reduced-order observer-based technique. For the FTP of nonlinear MASs, various control techniques have been developed to handle the nonlinearities. An L-F formation control technique is proposed for mobile robots without the direct use of position measurements. A position estimator is developed to ensure online position estimates of relative followers, thereby guaranteeing the stability of the entire formation system. Additionally, a novel observer-based formation control technique is proposed for multi-agent systems (MASs) with nonlinear dynamics and time-varying communication delays. Using neural network (NN) strategies, the formation tracking problem for second-order MASs with unknown nonlinear dynamics is addressed. Furthermore, an adaptive formation tracking problem is investigated for a class of nonholonomic MASS, utilising bearing-only measurements and velocity estimates. By using only adaptive output-feedback information, the TVFT problem for second-order nonlinear MASs under switching-directed topologies is investigated in [89,90]. In [91], a neuro-adaptive-based back-stepping control protocol that applies rigid graph theory is designed to investigate distance-based FTP for second-order nonlinear MASs with bounded time delay. Based on the distributed extended state observer, a practical TVFT protocol is designed in [92] for high-order nonlinear MASs by using only local neighboring output information. In [93], two kinds of L-F formation control problems were addressed for second-order autonomous unmanned systems with constant/time-varying velocities for the leader. Based on nearby information, a sliding mode control technique is presented for the TVFT of a multi-UAV with a dynamic leader [94]. A novel observer-based controller is developed to address the FTP for a group of nonholonomic agents [95]. The developed controller provides the possibility to adjust the desired trajectory to be followed such that the information about the new trajectory is not available to the followers, as shown in Fig. 5. TVOFTP for non-identical/different types of agents investigated in which the leader is assumed to be an active subject to cyber-attacks. TVFT scheme for linear HMASs is developed in [96] via an output regulation approach with a leader of nonzero inputs under directed topologies. A new distributed L-F formation control scheme for a class of heterogeneous planar underactuated vehicles is proposed in [97]. The proposed scheme does not necessitate any global position measurements of the followers. An adaptive TVOFTP of general linear HMASS with an unknown leader is exploited in [98], based on solving a time-varying L2 gain design.

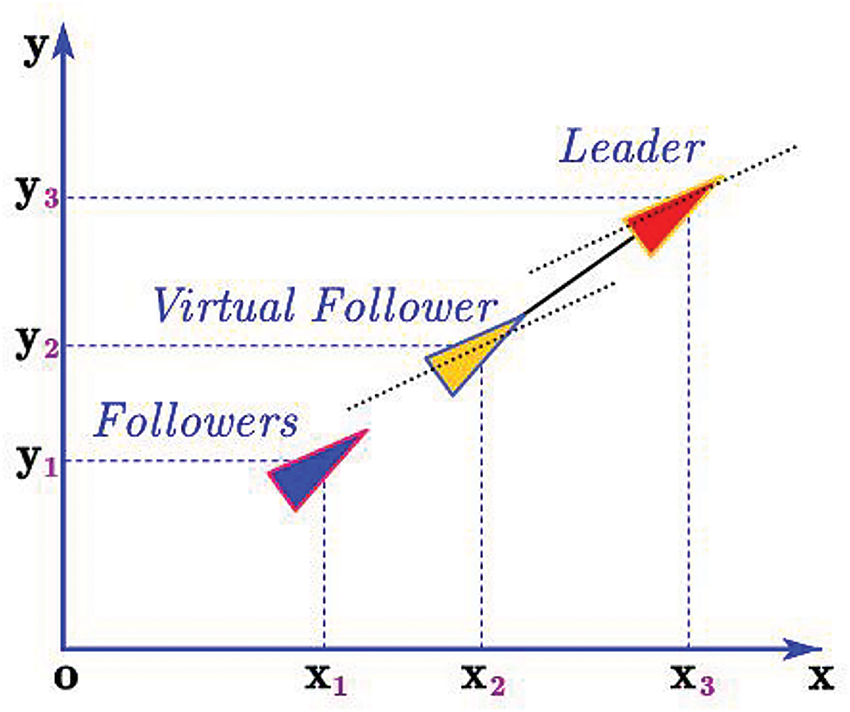
Figure 5: Basic model of the leader-follower method

Remark 3. Most of the existing results on L-F formation control necessitate the presence of orientations of the local coordinate system or the global reference frame. Such a necessity is unavailable in the GPS-denied environment. To address the FCP without any global reference frame, some control techniques have been designed based only on bearing or range measurements [99].

5.2 Behavior-Based Method

In this case, a group behaviour includes several tasks (subtasks) and is defined to achieve the desired global behaviour. A behaviour-based method defines some basic agents’ behaviours. The behaviour-based method defines some basic agent behaviours that are specified in advance, such as collision avoidance, formation keeping, trajectory following, obstacle avoidance, etc. [100]. It has clear formation feedback and can rapidly expand. However, it is difficult to express the behaviour mathematically, which does not ensure the stability of the formation control. Collision/obstacle avoidance is a fundamental requirement in forming a control protocol due to its practical implementation in some tasks, such as real-world flight. In comparison with obstacle avoidance, collision avoidance among agents is more challenging due to the moving agent’s unknown movement directions. Recently, many relevant techniques were developed to achieve the FCP with collision and obstacle avoidance. By using the graph Laplacian, a formation control technique is designed to achieve the formation control for second-order MASs with collision avoidance [101]. With a sliding control approach and repulsive potential function, an adaptive distributed L-F fixed-time FCP for second-order MASs with collision avoidance is investigated in [102]. Analysis of practical TVOFTP with obstacle dodging, collision avoidance, and connectivity maintenance is investigated for high-order MASs [103]. A TVFT for second-order MASs is studied in [104] with connectivity preservation and collision avoidance. Different from the relative velocity is presented in [105] to specify the risk of communication interruption and collision. Formation tracking control with collision avoidance was addressed for nonlinear multi-agent systems (MASs) by employing the artificial potential field (APF) approach combined with neural network (NN) techniques. In [106], an observer-based Leader-Follower (L-F) formation technique was proposed, enabling multi-robot systems to efficiently perform both obstacle avoidance and precise position tracking. A behaviour-based formation control scheme is adopted to solve the problem of autonomous navigation and formation in a dynamic environment for a group of mobile robots. The adopted scheme consists of four behaviors: target tracking, dynamic wall following, collision, and obstacle avoidance [107]. A novel control scheme based on neural networks is designed for a class of second-order nonlinear multi-agent systems to solve the formation control problem with multiple tasks, including obstacle avoidance, collision avoidance, and connectivity maintenance. A behaviour-based formation scheme is designed for a group of unicycles to simultaneously solve two tasks/behaviours, i.e., formation tracking and obstacle avoidance [108]. The behaviour-based approach is shown in Fig. 6.

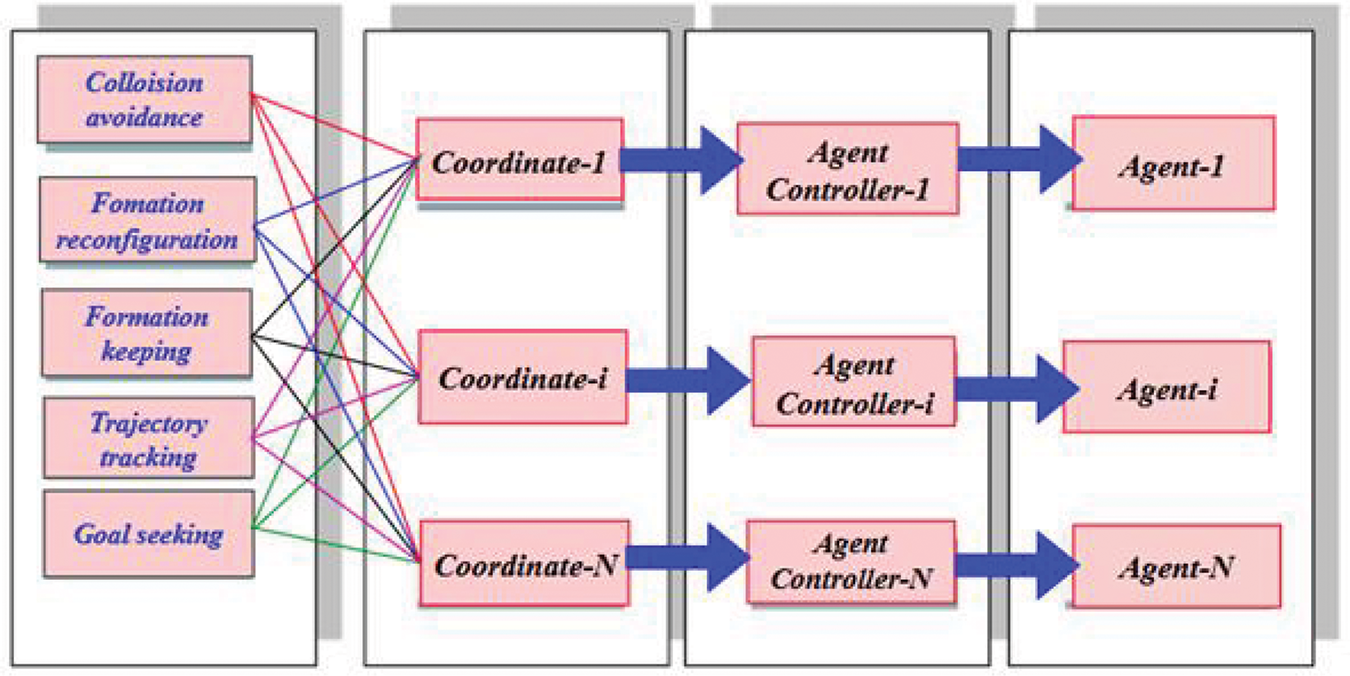
Figure 6: Behavior-based approaches

5.3 Artificial Potential Method

Artificial potential function (APF) is the commonly applied approach in developing control protocols for the formation control of MASs. The concept of the APF method is first proposed in [109]. Formation control with target tracking and navigation is studied based on the extremum-seeking control method and Artificial Potential Fields (APF). The main focus of the APF method is to consider the nearby agents or obstacles as high-potential fields. Then, if any agent enters the high-potential fields, a strong repulsive force will be produced to push it away from them, and thus the collision will be avoided. APF method has the advantage of good real-time performance due to its simple structure. The APF method is well-known as a collision avoidance technique as it demands less calculation, and thus, it is applicable for real-time applications [110]. Several artificial potential fields have recently been constructed to deal with FCPs with collision avoidance and obstacle avoidance for MASs. Based on a novel adaptive APF, a formation control protocol that simultaneously guarantees formation control with collision avoidance for linear MASs with first-order dynamics is presented in [111]. Bounded potential functions are developed to ensure collision avoidance and connectivity problems of second-order MASs in the formation [112]. Also, in [113], the authors use APF and repulsive forces to deal with the obstacle avoidance problem of the second-order MASS formation control problem. In [114], two APF functions are constructed for solving collision and obstacle avoidance problems for the formation control of second-order MASs. The repulsive forces supplied by the APF solve the collision avoidance between agents and avoid external obstacles.

In [115], a rotational potential field is developed to derive a formation control algorithm that allows a group of spacecraft to achieve a regular polygonal formation while avoiding collisions. An FTP for a class of nonlinear MASs with collision avoidance is solved based on the APF and the integration of a radial basis function neural network (RBF-NN) [116], as shown in Fig. 7. Based on an improved APF approach and a light transmission model, a novel formation control strategy with obstacle avoidance for UAVs is proposed [117]. An adaptive APF was employed to achieve the spacecraft formation reconfiguration with control uncertainties while avoiding multi-obstacle [118].

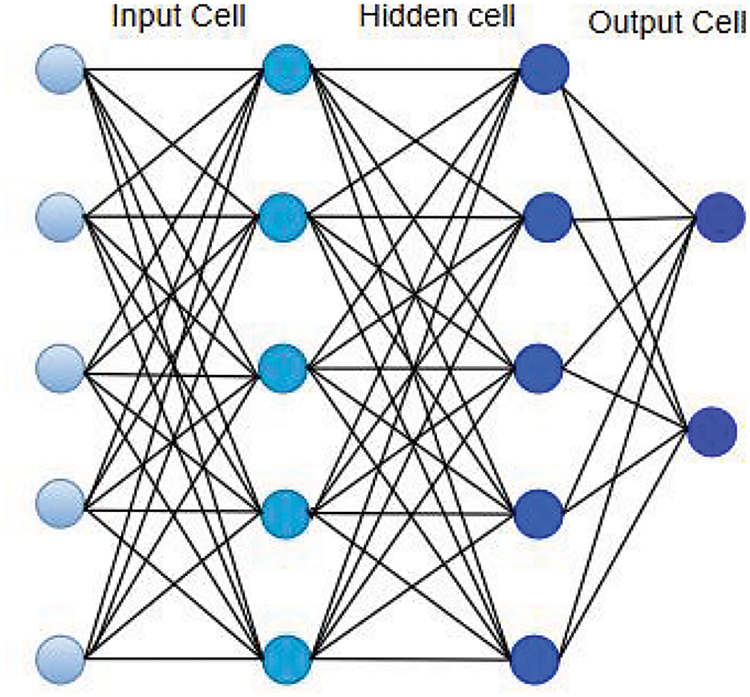
Figure 7: Neural network algorithms

5.4 Virtual Structure Method

The virtual structure method represents the entire formation system as a unified virtual rigid body, where each agent in the system is associated with a distinct virtual reference point on the structure. This virtual structure serves as a framework that dictates the spatial positions of all agents, and the desired formation is achieved as long as each agent adheres to its corresponding reference point on this virtual structure [119]. This is done by abstracting the single point of failure. The inherent robustness of the virtual structure method is one of its major advantages. The virtual structure method is markedly distinct from other formation control strategies, such as the leader-follower (L-F) way, which depends greatly on the introduced leader-agent behaviour. On the contrary, the virtual method preserves the geometrical integrity of formations based on the relative positions of agents with respect to each other. An elementary example of the system against all agents potentially failing or malfunctioning on any level. Through this method, every individual agent is guided by the same virtual reference point without necessarily imitating the motion of its neighbours, thus producing a global formation that remains stable in the presence of one or more agent failures [120]. Distilled from its robustness, the virtual framework scheme retains high precision in keeping the desired framework. This synchronisation of reference points allows for formation control of the agents whose positions are updated based on the reference points in the virtual space. However, one major drawback of this approach is that it is static/limited. For example, suppose in response to environmental changes such as adding obstacles or altering terrain, the formation needs to be reorganized (transformed). Fig. 8 illustrates the basic steps of the virtual structure method, depicting the transition from Step 1 to Step 4. In that case, the virtual structure method does not have an inbuilt mechanism to transform or reconfigure the structure of the formations. Such variations can be difficult to account for with fixed reference points resistant to redesign without outside modification or retraining. Even within this constraint, the virtual structure method has proved to be very successful in a variety of contexts, in particular within multi-agent systems. For example, a virtual structure control-based formation guidance method has been introduced for parafoil formations, where the desired configuration of the planned flight path can be maintained while simultaneously ensuring that the desired trajectory is followed. A virtual structure-based control scheme is also proposed to coordinate nonholonomic intelligent vehicles in robotics [121]. This method uses coordinate transforms to control the position and movement of vehicles to keep formation on the desired path. Also, a structure-based linear algebra method in virtual space has been used to form multi-robot structures, allowing the robots to cooperate to achieve tracking on a given trajectory and maintain a piece of specified information. This method is particularly valuable in dynamic settings where coordinated maneuvering is essential for accomplishing particular tasks. Moreover, a structured approach to robot formations is proposed for groups of robots with obstacle-avoidance capabilities in these systems. The virtual structure approach is widely implemented to achieve robust and accurate control performance; however, adapting to varying environmental conditions remains a challenge for future research efforts. In the future, this limitation could be addressed by incorporating adaptive features or real-time reconfiguration capabilities, making the formation remain agile and reactive in dynamic settings [122].

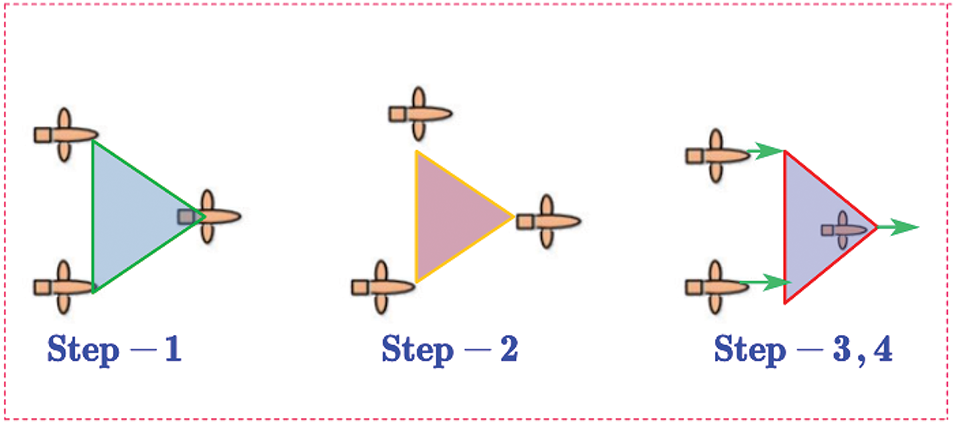
Figure 8: Basic illustration of virtual structure method

5.5 Consensus Based Method

Consensus algorithms are an effective approach to address agent formation control. Consensus control aims to drive the states of agents in a formation to an identical expectation [123]. Under different linear models, the classical consensus algorithms can be represented in different ways. Under the first-order linear integral model, the consensus protocol can be represented as:

uti=∑j∈Naij(xj−xi),(25)

when the first-order integral dynamic model is extended to the second-order dynamic model, the system consensus protocol can be formulated as follows:

uti=∑j∈Naij((xj−xi)+γ(vj−vi)),(26)

where g > 0 is a scaling factor. The exchange of information between agents in consensus algorithm-based formations is achieved through the communication topology. Formation consensus control has been shown to be achievable when the communication topology interacts frequently with the system. In some cases, the constraints on the weight factors in the information update scheme can be extended to more general scenarios. Additionally, the minimum requirements for achieving consensus control have been explored using graph theory and matrix theory, particularly in the context of directed graphs. Studies have also focused on achieving average consensus for topological graphs in strongly connected and balanced states, especially in the presence of communication delays, as shown in Fig. 9. In certain applications, the dynamic evolutionary consensus has been applied to the formation flight of multiple space-based interferometers. Consensus control, based on nonlinear contraction theory, has been utilized to address a variety of challenges, such as formation-keeping, attitude alignment, and obstacle avoidance in clusters. However, many studies in this area assume that the formation operates under a unidirectional information exchange topology, with some extending this work by providing the necessary conditions for achieving formation consensus in such topologies. The use of Lyapunov functions to design continuous time-invariant consensus protocols has been explored for first-order integral agents, facilitating finite-time control in undirected topological networks. Other studies have focused on dividing agent formation information into global and local components, creating nonlinear consensus protocols to implement formation control within a finite time. Furthermore, control laws have been proposed to achieve finite-time consensus with local information exchange. In the context of communication delays, several studies have implemented formation control within the same time delay framework. Recent advancements have expanded the interaction topology from undirected to directed, with further considerations of formation control under different communication delays. Additional approaches to consensus algorithms include Lagrangian-based controllers, decentralized adaptive output consensus protocols, and sliding mode tracking protocols. These techniques have been applied to heterogeneous linear systems with unknown parameters, and solutions have been developed to cope with perturbations, actuator failures, and disturbances in the formation control of multi-agent systems.

Figure 9: Flow chart of the load control process

5.6 Formation-Containment Based Method

Most existing results regarding Formation Tracking Problems (FTPs) focus on a single-leader scenario. However, in several practical applications, the need arises to address situations where multiple targets, considered as leaders, need to be tracked. This leads to the generalization of the FCP into the Formation Containment Control (FCC) problem. The objective of the FCC problem goes beyond merely guiding the followers to converge within the convex hull formed by the leaders; it also involves ensuring that the leaders maintain a predefined formation among themselves. The motivation behind exploring the FCC problem comes from numerous real-world applications where multiple leaders must be tracked or contained within a formation. A prominent example of such a scenario is the cooperative formation flying of multiple unmanned and manned combat aerial vehicles (CAVs). In this scope of study, the manned CAVs (connected and autonomous vehicles) can be taken as the leaders, while the unmanned CAVs are the followers who are supposed to come together and maintain a desired formation to provide coverage around the manned CAVs. Therefore, desired formation and movement. It should be noted that tracking the formation of several leaders is more complicated than when only a single leader is present in the mission. In a single-leader scenario, followers only have to monitor the motion of a single leader, but with multiple leaders, followers need to adjust their position with respect to each leader while keeping the overall formation. This implies that the agents have to continuously adjust to the shifting locations of several leaders, leading to complex control methods to preserve equilibrium and attraction ability into the specified formation. In many practical scenarios, this added complexity can be seen in coordinated aerial missions, robotic swarm formations, or multi-agent systems for search and rescue tasks. These interactions need to be properly handled due to the relative of the leader and because of the formation. As illustrated in Fig. 10, the formation containment problem in 2D shows a scenario in which followers are required to stay within a region (convex hull) spanned by several leaders while maintaining a particular formation. This can be generalized to higher-dimensional cases, where the agents must stay in line with the leader and each other, creating a more stable walking formation. A proper design or finding of solutions for the FCC problem is a basis for creating feedback control strategies in the dynamic interaction of followers and multiple leaders, which are ubiquitous in real-world models. These strategies should fulfil both the containment and formation objectives. This includes complex algorithms that consider communication latencies, uncertainties in the system, and the requirement for reliable coordination between the agents. An increase in leaders brings complexity to the proposed system, as it means that more computation power and control techniques are needed to ensure stability and reasonable performance for different scenarios. However, the problem with the existing formulation of FCC is its assumption about the leader-to-leader ratio.

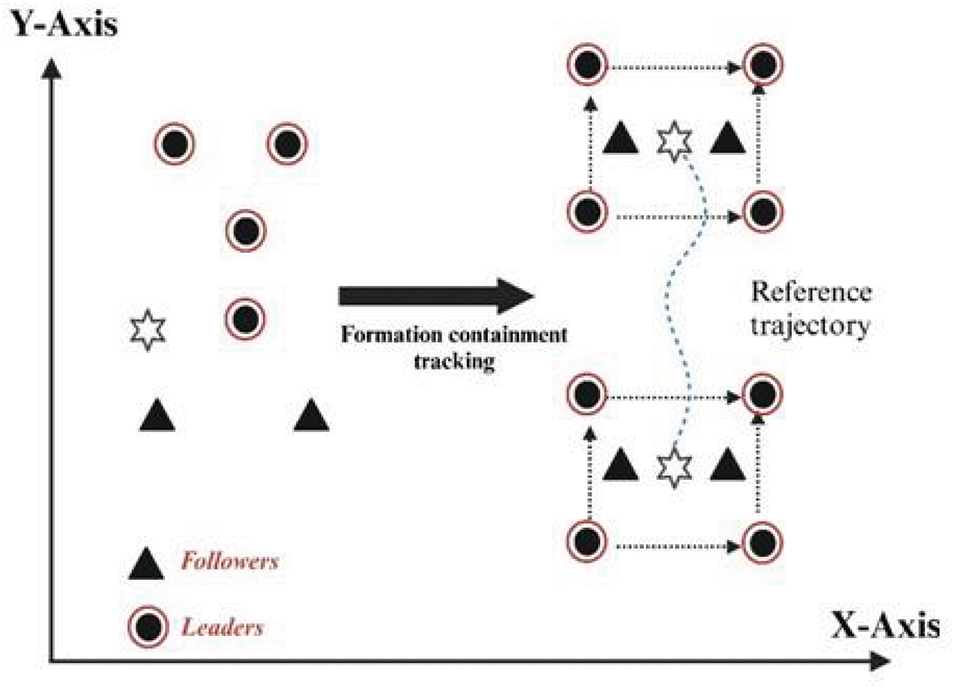
Figure 10: Formation containment framework

Assume that there are M (M < N) followers and N − M leaders. Let F={1,2,⋯,M} and L={M+1,M+2,⋯,N} be the followers and leaders subscript sets, respectively. Consider the desired TVF of leaders as fL(t)=[fM+1T(t),fM+2T(t),…,fNT(t)]T where fi(t) (i∈L) is piecewise and continuously differentiable. Under this setup, the MAS (1) is said to realize the formation-containment tracking if, for any given bounded initial states, there exists a vector-valued function r(t)∈Rn, and positive constants cj (j∈F) satisfying the equation ∑j=N+1N+Mcj=1 such that for any k∈F, j∈L, and the following hold simultaneously [124].

limt⟶∞(ρk(t)−∑j=M+1Ncjpj(t))=0.(27)

Remark 4. According to the definition of FCC, for fi=0, the FCC problem becomes a containment problem. If N=1, the definition of FCC is reduced to FTP with one leader, and when fi=0 and N=1, it is reduced to the consensus problem. Hence, the containment, formation tracking, and consensus problems can all be considered special cases of the formation containment problem. FCC of first-order MASs was studied in [125,126] under undirected and switching communication topologies. Sufficient conditions to achieve time-varying FCC for MASs with second-order dynamics with time-varying delays are proposed in [127,128]. Based on bearing measurements, a novel control protocol is designed to achieve the formation tracking for multiple moving leaders for second-order MASs [129]. In [130], a bearing-only control protocol is developed to investigate FCC for second-order MASs in a local reference frame, assuming that the leaders’ velocities are constant. The FCC is addressed under continuous communication, in which every agent instantly transmits its information from its neighboring agents at every instant of time. However, the continuous information transmission among agents consumes/wastes too much energy, and under some circumstances, it cannot be applied. Thus, FCC has been studied under-sampling communication to reduce communication consumption. For instance, based on sampled data, formation tracking of second-order MASs with multiple leaders is investigated on a fixed-directed communication topology [131]. The proposed control protocol is designed under the assumption that the leaders have no communication with each other and interaction between agents only occurs at discrete instants. FCC problem of second-order MASs with only sampled position data is investigated in [132], where sufficient conditions are established by using matrix theory and algebraic graph theory. Based on sampled-data control, the FCC of second-order MASs with sampling delays is studied in [133], where interactions among leaders were needed. In [134], formation-containment protocols were designed for second-order MASS under aperiodic intermittent communication, and the convergence conditions were established by constructing Lyapunov functions. Sufficient conditions to achieve a multi-UAV FCC over directed communication topologies are presented in [135]. Time-invariant formation-containment analysis for general linear swarm systems with a directed communication graph was studied in [136], where feasible conditions to achieve the desired formation are established. To achieve FCC, a control protocol is given as follows [137]:

{ui(t)=K1pi(t)+K2∑j∈Niwij(pi(t)−pj(t)),i∈ℱ,ui(t)=K1pi(t)+K3∑j∈Niwij((pi(t)−fi(t))−(pj(t)−fj(t))),i∈ℒ.(28)

where Ki∈Rm×n(i=1,2,3) are constant gain matrices. Note that the gain matrix k1 will be used to assign the motion modes of the state formation reference. k2K3 will be used to drive the state of the followers to converge to the convex hull formed by those of the leaders. The formation control of multi-agent systems (MASs) with high-order dynamics was examined under time-invariant communication topologies, considering the effects of communication delays. TVFT problem with multiple leaders was investigated in [138], where necessary and sufficient conditions to achieve TVFT were derived by applying the properties of the Laplacian matrix between followers and leaders. However, the leader’s control inputs were zero. Necessary and sufficient conditions of FCC of linear time-invariant (LTI) MASs are established in [139], where observer-based output feedback control laws are designed. Both communication delays and switching networks were taken into consideration for MASs to solve the predefined FCC. A novel control protocol is designed to achieve the output-FCC under switching interaction topologies with multiple leaders of unknown bounded inputs [140]. Under-sampling data, TVFT for general linear MASs with multiple leaders is investigated in [141] such that there is no communication between leaders. A stochastic sampling mechanism is proposed to achieve the TVFT with multiple leaders in the presence of communication delays. Novel adaptive TVOFT control protocols are proposed to realize stabilization and tracking of time-varying formation with no global information [142]. In [143], an output-FCC problem for general LTI MASs is considered, in which only outputs of agents are required to construct and achieve the formation-containment. Several strategies have been applied to handle the nonlinearities. NNs were applied to approximate the nonlinearities. Based on adaptive NNs, practical time-varying FTP for a class of second-order nonlinear MASs containing multiple leaders with time-varying disturbances is studied in [144]. Three-dimensional FCP is investigated in [145] for multiple UAVs under directed switching communication topologies. In [146], the authors investigated the FCC problem for high-order nonlinear MASs with multiple leaders with unknown control input under directed interaction topology. A distributed disturbance observer was employed to handle the nonlinearities and unknown control input of leaders. In [147], practical FCC protocols are developed based on extended state observers for the multiple ASV systems with multiple leaders, and the dynamics of the ASV system were simplified by applying the coordinate transformation approach. A hierarchical sliding control scheme is proposed to investigate the FCC problem of multiple under-actuated surface vessels (USVs) with sampling communication [148]. A stochastic sampling mechanism is proposed to address FCC for multi-robot systems [149]. The system is transformed into a linear system by applying the linearization analysis. The authors in [150] studied TVOFTP for general linear homogenous and heterogeneous MASs with multiple leaders. In [151], the TVOFTP of linear HMASs with multiple leaders under directed communication topology is investigated. Based on an output regulation method, the TVFT scheme is designed [152] for linear HMASs with multiple leaders under switching interaction topologies.

5.7 Bipartite Formation Base Method

The interdependence of agents may exhibit cooperation and antisocial behaviour in many real-world systems. For instance, in biological systems, members may be cooperators and also competitors as activators/inhibitors to chase scarce resources. Communication among agents is traditionally represented as a signed graph, where a positive edge translates into a cooperative interaction and a negative edge into a competing (i.e., antagonistic) one to model such networks. In [153], the notion of bipartite consensus is studied on signed graphs. Based on the outcomes of bipartite consensus tracking, researchers turned their attention to building a new type of pattern of formation known as a bipartite formation. The majority of research focuses on the formation control of Mas’s unsigned cooperative interaction. Additionally, the signed networks [154]. To explain the bipartite formation framework, a communication topology in the signed graph is suggested in Fig. 11. Considering the bipartite consensus problem, few works have been proposed to solve the bipartite formation control problem. In human-machine interaction, in a master-slave manner, the teleoperation template is one of the bipartite formation applications. There are master-slave interactions in robotics, wherein a master controller operates a robot (the slave) to perform complex tasks that could be hazardous or impractical for a human operator to perform directly. The bipartite formation framework leads to a clean separation of concerns in these systems: a subset of agents work together, and a second subset acts competitively or antagonistically to achieve the goals of the formed pairs. Alternative research focused on real-world applications of bipartite formation, such as in distributed sensor networks where nodes need to cooperate to cover a certain area and avoid causing interference to nodes owned by competitors. You are designed for the environment through bipartite formation. This type of system is important in application settings like environmental monitoring, where agents are dispersed across vast regions and need to share information to obtain information cooperatively and competitively. For instance, the bipartite formation in multi-agent systems (MASs) can control the locomotion of agents in territories that balance cooperation and competition. One possibility, in a swarm robotics scenario, is for a group of robots to explore unknown terrain. They work together to spread data but compete for limited resources, such as energy or data points they come across. Managing these paradoxical relationships while dictating the formation of such a swarm is the challenge that the bipartite formation model attempts to solve. Furthermore, there are some difficulties in the stability and convergence of the formation since the concept of bipartite consensus in signed networks. Because signed edges do not simply reflect cooperative interactions but also hostile ones, the agents’ ability to agree on both their position and action is dependent on cooperative and opposing interactions, respectively. This duality complicates ensuring that the system equilibrates in a stable and feasible configuration. While many works in the literature have investigated consensus problems on signed networks, bipartite formation control is a relatively new topic. In view of the above, ongoing research will lead to more advanced algorithms capable of managing dynamic agent-agent interactions and the evolution of network topologies and functionalities of agents. How to reach a consensus in signed networks when the information is not complete or the communication channels are noisy is still an open question. However, the potential applications of bipartite formation control are not limited to the scenarios highlighted above; for instance, in military operations, where agents of the same team (e.g., unmanned aerial vehicles) must coordinate their path while competing for limited resources or avoiding conflict.

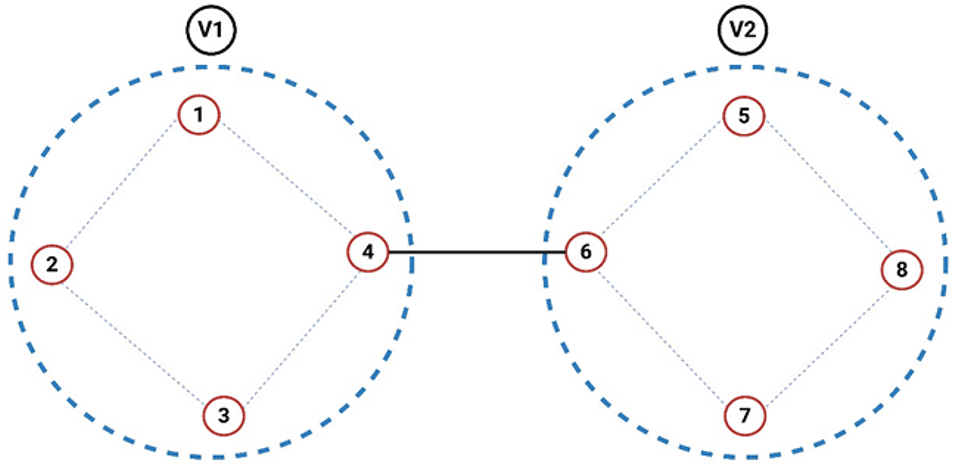
Figure 11: Signed communication topology illustrating cooperative and antagonistic interactions

Consider the MASs (5), consisting of N+1 agents, where N are follower agents, and one is a leader agent labeled 0. A bipartite formation is achieved for MASs (5) if, for any bounded initial conditions, the agents’ states satisfy the conditions.

limt→∞∥pi(t)−fi(t)−δip0(t)∥=0,∀i=1,2,…,N,(29)

where δi=1 if i∈V1, δi=−1 if i∈V2.

Remark 5. Note that the motivation of the BFC of MAS is to realize a general formation design composed of two groups. The physical significance of BFC is that the robots/agents in each group form a desired formation pattern and move in an opposite direction from an antagonist group. Based on the theories proposed, the analysis of the formation problem for first-order MASs over antagonistic interactions was investigated in [155,156]. The necessary and sufficient conditions were presented to achieve the desired antagonistic formation. Based on bipartite consensus, the formation tracking of second-order MASs with communication delays under the directed graph is investigated [157]. The problem was solved by designing a Laplacian matrix. An adaptive control law is designed to address the bipartite TVFT problem for linear MASs with a leader of unknown input under signed digraphs. The proposed protocol depends only on the relative output information and does not require eigenvalue information. The control protocol to achieve BFC with one leader for general linear MAS (5) is developed as follows:

{ui=K(si−σi)+ηi−εiβϕi(BTPϕ¯i),s˙0=As0+Bu0+F(Cs0−y0)=Asi+BK(si−σi)+F(Csi−yi+Cfi)−εiβϕi(BTPϕ¯i),σ˙i=Aσi+(ci+gi)FCωi−εiβBϕi(BTSω¯i),ϱ˙i=ω¯iTCTCω¯i.(30)

proved that the proposed adaptive control protocol solves the general linear bipartite TVFT problem. On the basics of Pontryagin’s principle, a distributed control protocol is developed to solve the prescribed-time bipartite consensus FCP [158]. The Bipartite Time-Varying Optimal Formation Tracking Problem (TVOFTP) for general linear multi-agent systems (MASs) with multiple leaders, subject to matched uncertainties, is studied, where the outputs of followers form two antagonistic time-varying sub-formations. Based on bipartite consensus, authors in [159] proposed a formation control scheme for high-order MASs under communication delays. Bipartite formation tracking of nonholonomic robots under the signed graph is investigated in [160]. Based on the event-trigged sampled-data mechanism, a guaranteed-cost bipartite FCP for second-order nonlinear MASs with antagonistic interactions is investigated in [161]. BFC for nonlinear discrete-time multi-input multi-output MASs under signed digraph where agents are considered completely unknown [162]. In [163], the bipartite fixed-time time-varying FCC was considered for linear HMASs. In [164] investigation of time-varying output bipartite FCP for linear HMASs by event-triggered communication over signed digraphs has been discussed. Bipartite TVFT for unknown nonlinear HMASs under undirected signed graphs is addressed in [165]. Based on nonlinear decomposition, a distributed adaptive control protocol is designed to guarantee the convergence of bipartite TVFT errors. In [166], bipartite output FTP for HMASs with multiple leaders under switching communication topology is investigated. To address this problem, a novel, fully distributed asynchronous dynamic edge-event-triggered control protocol is designed. Based on the ETC mechanism, bipartite TVOFTP is studied for homogeneous and heterogeneous MASs with a group of non-autonomous leaders over switching communication topology [167]. Based on the composite ETC transmission mechanism, an adaptive bipartite TVOFTP is investigated for linear HMASs under a signed digraph [168].

Remark 6. Traditional control methods often depend on global communication topology details, such as the non-zero eigenvalues of the Laplacian matrix. However, extracting these eigenvalues becomes increasingly difficult in large-scale networked systems. To overcome this challenge, adaptive formation control mechanisms have been developed that operate without relying on eigenvalue information.

Remark 7. A scheme with more than two agent groups exists in networks with antagonistic and cooperative interactions. In this scheme, agents within the same group are cooperative, while agents across different groups may be either cooperative or antagonistic/competitive. This results in a cluster/group formation problem, as discussed in the following subsection.

5.8 Group/Cluster Formation

All aforementioned works have been dedicated to a single prescribed formation control problem wherein the agents are instructed to preserve and create a single geometric pattern. In summary, all agents are anticipated to establish a common formation. This is a simplified way to think, and though it is helpful in some ways, it has limited application in more complicated, real-world situations. For example, in multi-agent systems (MAS) such as rescue missions, multi-target enclosing, or obstacle avoidance tasks, agents may need to form multiple formations or pursue different operational strategies concurrently. As single-formation problems do not account for what to do when diverse formation tasks appear in an ongoing operation, they fail to overcome both the temporal and spatial limits imposed by the assumptions and constraints. The results of existing work, as mentioned, only focus on single-formation scenarios, which makes their direct extension to solve real-world tasks with multiple-formation configurations increasingly limited by the complexity and diversity of real-world tasks. Thus, group FCPs, which offer the capability to flexibly and efficiently organize MASs into several sub-groups or clusters, each having its own specific function, are becoming increasingly essential to study and develop. In particular, formation control of multi-agent systems can be partitioned into several groups (or clusters), and each group aims to achieve a particular formation (usually to perform different tasks). Agents in each sub-group interact with each other to achieve one sub-formation, while cooperation and competition among groups can occur simultaneously. Such a framework enables the management of multiple formation assignments while assisting the sub-groups’ inefficient task allocation, which in turn improves the flexibility and capability of the MAS. In some cases, especially when MASs are assigned to distributed or cooperative missions, the system may need partitioning into different subgroups or clusters. These groups are, in fact, formation patterns per subgroup, having leaders who need to cooperate in a manner that will not compromise their formation, as this needs to work in parallel with a global goal. Important scenarios where agents must adjust to new conditions quickly deal with variable environmental parameters. There are several solutions for group formation control problems, such as group consensus-based strategies in which agents of each subgroup agree to the desired formation placement. Yet, consensus-based solutions alone cannot tackle the more complicated time-varying group formation (TVGF) control issues. The TVGF problem generalizes the group formation control by not only considering the group dynamics in the system but also the time-varying dynamics that change from time to time (e.g., leader positional dynamics, environmental dynamics, objectives dynamics, etc.), thereby requiring real-time adaptation of the dynamics by the followers according to their objectives. The difference between group consensus and group formation is in their goals. The goal of group consensus is to achieve agreement or alignment within a group, while the goal of group formation control is to control not only the formation of each group but also the formation of different groups, which must have different patterns and specs. Time-varying patterns, even through cooperation and competition between clusters. As a result, while considering cooperative and competitive behaviors between clusters. The ability to effectively form groups is of utmost importance in the study and implementation of MASs, as it significantly affects the system’s performance of sophisticated, real-time tasks with multiple agents having possibly conflicting goals. Whether maintaining a persistent team of resources, monitoring several targets, or performing complicated group efforts, formation control is of vital importance to successful multi-agent operations. The ability to divide the MAS into functional subgroups, each with its formation control and objectives, while ensuring coordination across groups significantly enhances the efficiency, robustness, and scalability of the overall system. The cluster/group formation framework is shown in Fig. 12. This concept of group formation control has far-reaching implications across various practical applications, including autonomous vehicle fleets, robotic swarms for environmental monitoring, and large-scale industrial processes where different agents must work together to complete distributed tasks while maintaining their operational integrity. Therefore, the study and development of effective group formation control protocols are critical for enabling MASs to tackle the complex and diverse challenges presented by real-world multi-agent missions [169]. For illustration, suppose, without loss of generality, that MAS (1) is divided into M(M∈N,M≥1) clusters/sub-groups. In other words, these M sub-groups 𝒱1,𝒱2,…,𝒱M satisfying 𝒱k≠∅, 𝒱=∪k=1M𝒱k, and 𝒱k∩𝒱s=∅(k,s∈{1,2,…,M},k≠s). Consider Λ the subscript of the cluster such that i∈Λ Moreover, let qΛ∈N denotes the number of agents in the cluster 𝒱Λ. The agent set of the sub-group Λ is indexed as 𝒱Λ={QΛ+1,QΛ+2,…,QΛ+qΛ} where QΛ=Σm=0Λ−1qm with q0=0.GΛ represents the underlying interaction topology associated with the sub-group 𝒱Λ, Λ∈{1,2,…,M}. For any sub-group Λ∈{1,2,…,M}, the expected time-varying sub-formation is specified/characterized by the vector f¯Λ(t)=[fQΛ+1T(t),fQΛ+2T(t),⋯,fQΛ+qΛT(t)]T∈RnqΛ. The formation vector of the entire MAS is described by:

{fF(t)=[f¯1T(t),f¯2T(t),⋯,f¯MT(t)]Tp¯Λ=[pQΛ+1T(t),pQΛ+2T(t),⋯,pQΛ+qΛT(t)]T.(31)

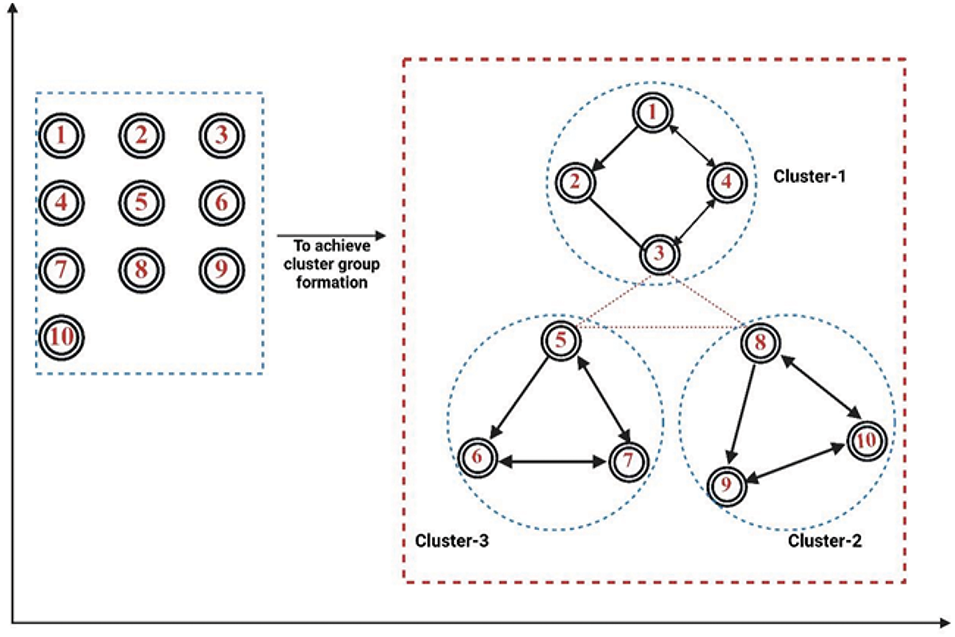
Figure 12: Cluster/group formation framework

Thus, the group/cluster formation definition is followed immediately [170].

Definition 3. MAS (1) achieves a time-varying group/cluster formation characterized by f(t) if, for any cluster/subgroup Λ∈{1,2,…,M}, there exists a vector-valued function rΛ(t)∈Rn such that the condition holds for any given bounded initial states. Here, rΛ(t) represents the reference vector of the formation for every agent in subgroup Λ. Additionally, f¯Λ(t) represents a relative offset vector to rΛ(t) for the agents in subgroup Λ, which corresponds to the desired time-varying sub-formation.

limt→∞(p¯Λ(t)−f¯Λ(t)−(In¯Λ⊗rΛ(t)))=0.(32)

Remark 8. Note that the definition of group formation provides a framework for realizing a time-varying group formation (TVGF) determined by vectors. Moreover, if only a single subgroup exists (i.e., M=1), then the presented definition of TVGF is reduced to a single (complete) formation. Furthermore, it can be observed that if f¯Λ(t)=0, then the above definition simplifies the group (or cluster) consensus formulation as presented in [171]. In this sense, the problem of group formation is more general and encompasses many classical research problems as special cases. In [172], a decentralized group formation containment framework is designed for a team of multiple robots modeled by single integrator dynamics having multiple fixed or time-varying targets. Considering switching topologies, authors in [173] proposed a control law for second-order MASs to achieve TVGF tracking. The study presented a technique to split the agents into subgroups and transform the FCP into an asymptotic stability problem. The TVGF tracking approach is developed for MAS with second-order dynamics under fixed topologies. Authors in [174] proposed a distributed control protocol for second-order MASs containing multiple leaders to address TVGF tracking with communication delays. Based on relative information, the TVGF tracking protocol for second-order MASs under switching topology is presented in [175]. In [176], an identifier-based control protocol is developed to solve the TVGF problem of second-order MASs in the presence of disturbances and model uncertainties. A distributed adaptive control protocol was introduced to address the time-varying group formation (TVGF) tracking problem in high-order multi-agent systems (MASs) involving multiple leaders. Notably, the approach does not require prior knowledge of the communication topology. By leveraging group or cluster consensus, the TVGF tracking problem is explored for general linear MASs. The group formation protocol is formulated using an algebraic Riccati-based method, and a corresponding control algorithm is developed to achieve effective TVGF tracking.

ui(t)=K∑j∈𝒩1wij[(pj(t)−fj(t))−(pi(t)−fi(t))]+vi(t),(33)

where i=1,⋯,N, K∈Rm×n is a constant gain matrix and vi(t)∈Rm represent the TVGF compensation signal dependent on fi(t). A novel TVGF tracking technique is developed to achieve A novel TVGF tracking technique is developed to achieve TVGF tracking under switching communication topologies, in which the agents are divided into a virtual leader, a group leader, and a group follower [177]. Based on the adaptive control technique, a TVGF tracking problem is further investigated under external disturbances and switching interaction topologies. Based on the observer approach, a distributed TVGF problem was investigated in [178] for linear MASs under the directed communication topology. The groups therein have a cyclic partition, which is more practical than the topology with the acyclic groups. Considering the communication delays, authors in [179] investigated the group FCP for networked linear MASs under aperiodic sampling. H∞ group formation scheme with a stochastic sampling technique for networked MASs is investigated in [180]. Note that, different from group FCP without sampling and aperiodic sampling, in group FCP with a stochastic sampling strategy, every agent will be sampled and transmitted stochastically. By using NN, an adaptive protocol is developed to achieve group formation for second-order nonlinear MASs. Based on an adaptive NN approximator, a distributed control protocol to solve a multi-group FTP for second-order nonlinear MASs with unknown dynamics and with and without communication delays [181]. In [182], an event-triggered sampling control technique is applied to deal with the group FCP of nonlinear MASs over a directed graph. Based on the LMI approach and Lyapunov theory, sufficient conditions are presented to solve the GFP for both fixed and switching topology. Moreover, an observer-based distributed control protocol is constructed using output information to solve the TVGF problem for linear HMASs under directed interaction topology with an acyclic partition [183].

6  Communication-Free Formation Control

6.1 Formation Control Based on Trigger Mechanism

In traditional continuous control settings, every agent is typically embedded with a limited number of microprocessors, onboard communication modules, and actuation modules and executed periodically, which drives extreme consumption of computation and communication resources. Most existing research on formation control relies on continuous communication among neighboring agents and regular controller updates. However, this approach is unrealistic in some practical applications, such as multi-quadrotor UAV systems, due to limitations in communication and control resources. To overcome this problem, researchers have proposed the ETC mechanism, which can greatly reduce the consumption of computation and communication resources. Research on ETC is active as a technique for reducing the frequency of updated control information. In practice, it is significant to deal with the formation control problem of MASs with the ETC mechanism. ETC-based formation problem for simple integrator MASs is studied in [184,185], where the control input is considered to be constant between two communications, as shown in Fig. 13. The threshold is considered constant in [186], which also presents the communication trigger condition with a time-varying threshold. Based on a complex-valued Laplacian, a novel distributed event-triggered control (ETC) scheme for first-order MASs is designed over an undirected graph for both continuous and discrete-time dynamics. It is shown that formation achieves a specific configuration globally, and the closed-loop system of the resulting Zeno/Zeno-like behaviour is excluded. In [187–189], event-triggered control (ETC) protocols are designed for first- or second-order multi-agent systems (MASs) to achieve formation control while preserving connectivity. A distributed formation control scheme was proposed based on a dynamic ETC communication mechanism for networked MASs with limited communication resources, where the threshold parameter is variable. Unlike existing ETC mechanisms with a fixed threshold parameter, the proposed ETC condition allows the threshold to vary over time based on a dynamic rule. The ETC formation protocol is provided as follows:

ui(t)=K∑j∈Niaij(yi(tkih)−yj(tk~jjh))+Hfi,(34)

where xj(tkik~j) represents the newly transmitted local measurement obtained from robot/agent i’s neighbors with k~j≡arg⁡mink{θ−tki∣θ>tk^i, k′∈𝒩}. h>0 is the sampling period, K and H denote the protocol gain matrix. In [190], an ETC-based TVFC problem under undirected communication topology is presented, where the technique involves an event condition for every agent relying on the agent’s state only. Practical fixed-time ETC strategies are developed to achieve the TVFT of MASs with multi-dimensional dynamics under directed graph topology [191]. In [192], a distributed ETC-based formation protocol is designed for discrete-time nth-order linear MASs with one virtual leader. Based on the ETC strategy and adaptive control technique, a novel distributed protocol is developed to solve the ETC-based TVFT problem [193].

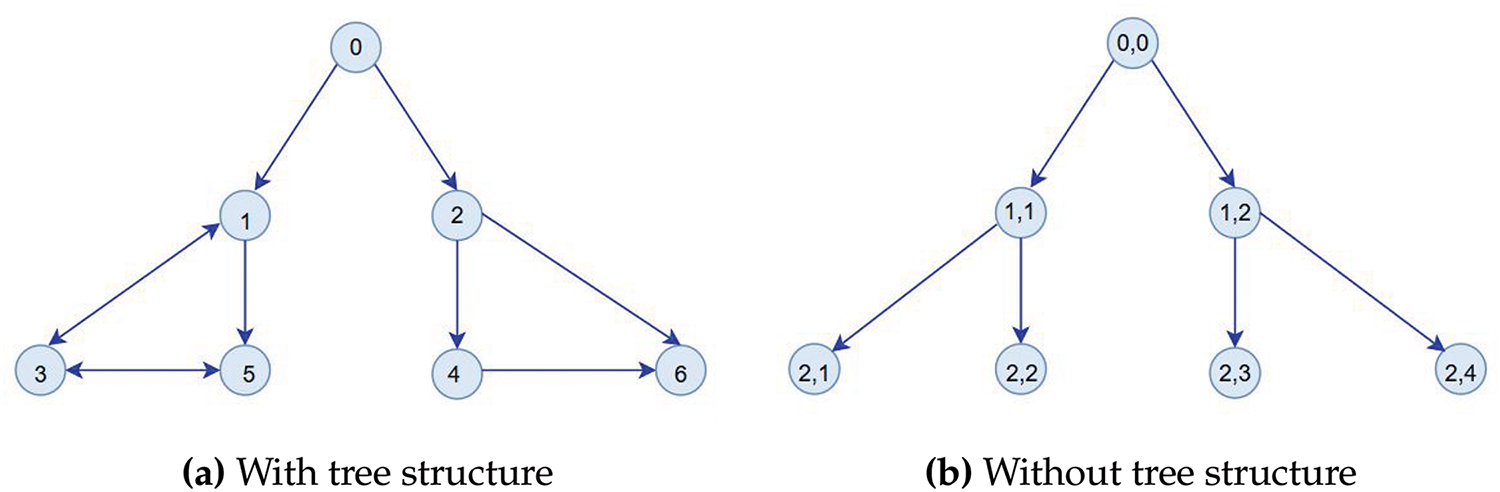
Figure 13: Communication topologies (a) with tree structure (b) without tree structure

Based on the ETC mechanism, a fixed-time ETC-based TVFT problem with multiple leaders is considered [194]. A distributed formation tracking problem using the ETC mechanism is investigated in [195], in which the problem is converted into a consensus-line problem. The dashed arrows in the figure represent communication connections that exist in the system but are ignored during topology layering. An ETC-based FTP of multiple robots is studied in a leader’s coordinate frame, which introduces a super-twisting sliding mode differentiator (without velocity measurements) [196]. For HMAS, a novel distributed adaptive ETC scheme is designed to solve the TVFC problem of unified non-linear HMASs with distinct orders and dynamics in the presence of disturbances and uncertainties. Fig. 14 indicates the case of dividing layers.

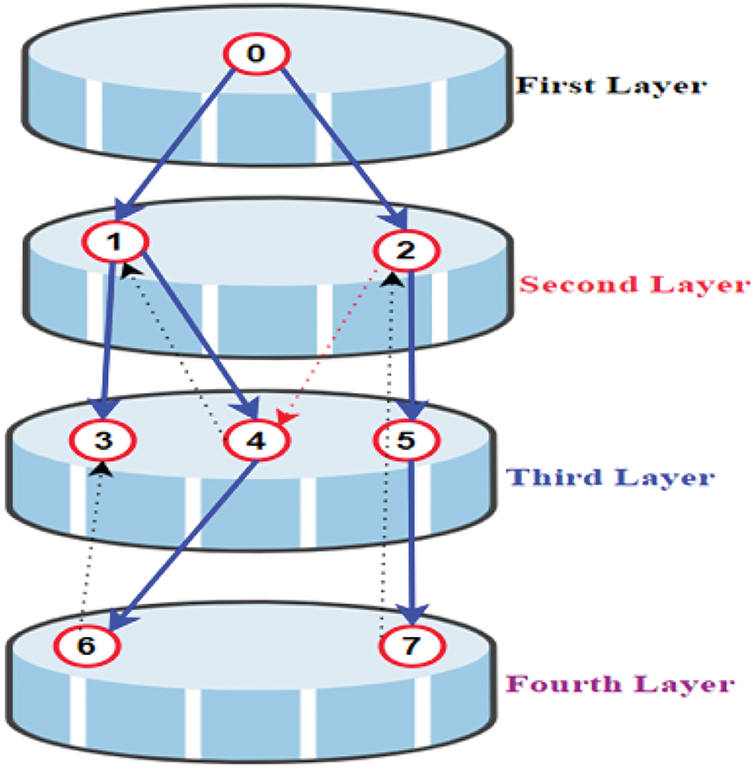
Figure 14: Layered system topology with omitted inter-layer communications

6.2 Finite-Time Formation Control

In the aforementioned works, the formation control algorithms are asymptotically convergent. However, many practical systems require that the formation can be achieved with a faster convergence rate. Thus, improving the convergence rate of formation control is significant and challenging. Unlike control laws with asymptotic convergence, FT control is more desirable in practical applications due to its fast convergence rate within FT.FT convergence means that the setting time is supposed to be bound for a given MAS [197]. To enhance the speed and ability of disturbance rejection, the FT control scheme has been applied to develop cooperative FT formation control protocols. Lyapunov-based strategies have been widely used to design distributed control laws in FT. FT control has been applied to deal with the time-invariant and TVFC problem of first-order MASs. The FT formation control was investigated for first-order MASs where the communication topology was considered undirected and connected. It was assumed that the global formation information is known by only a few agents. Based on relative orientation measurements, an FT bearing-only formation control technique for first-order MASs is presented in [198]. A fast terminal sliding mode control scheme is designed in [199] for second-order MASs to achieve the desired TVFT with FT convergence. In [200], an FT formation control design is developed for second-order MASs based on multi-virtual leaders (i.e., allowing every agent to follow its virtual leader). In [201], a formation control protocol is developed for second-order MASs under heterogeneous communication topology to achieve the desired formation in FT. Under the proposed control law, the connectivity of the velocity topology is not required. A robust technique based on integral sliding mode control was developed to ensure fixed-time (FT) formation tracking and connectivity preservation for second-order multi-agent systems (MASs), even in the presence of disturbances. The FT formation problem was also investigated with only output information for nominal second-order MASs [202]. Based on the Pontryagin maximum principle, the authors in [203] proposed an optimal formation control protocol for networked linear MASs to realize the desired formation in an FT. The basic mechanism of Finite-Time Formation Control is shown in Fig. 15. The fixed-time formation control problem (FT-FCP) was examined for a class of nonlinear second-order multi-agent systems (MASs) over a directed communication graph, where the formation was maintained as fixed. For nonholonomic mobile robots, the authors in [204] presented some FT formation control algorithms based on the FT control technique. Due to environmental disturbances, the velocity information of the agent is unavailable. To address this problem, FT output feedback [205] and the FT convergent observers are applied to achieve formation control in FT. Recently, based on the FT Lyapunov theorem, a distributed control technique is designed via dynamic gain control to solve the FT-FCP of nonlinear MASs [206]. FT-FCP for disturbed second-order HMASs with directed communication topologies is considered in [207] without global information (i.e., outer/inner neighbors’ state/input information, Laplacian spectrum). A signal generator-based FT formation control strategy is constructed for disturbed HMASs to complete the desired formation task in FT [208].

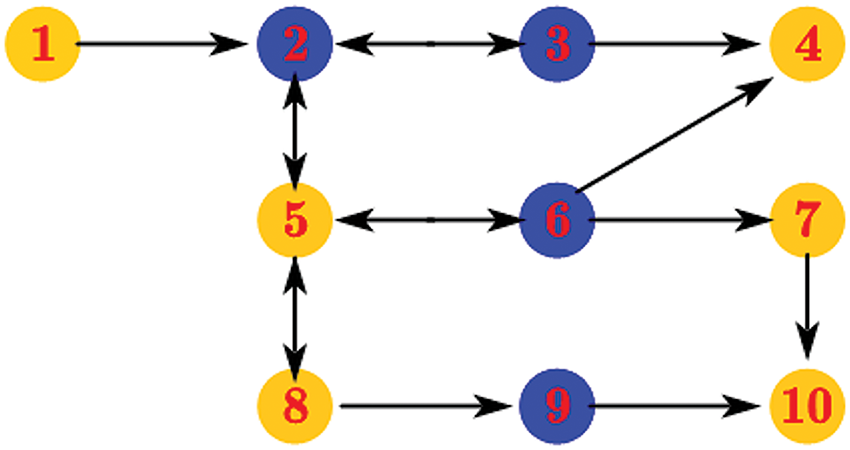
Figure 15: Finite-time formation control mechanism

7  Formation Problem via Model-Based

7.1 Formation With Actuator Saturation

In practical systems, actuator saturation is an inherent constraint, necessitating the adoption of effective control strategies. A low-gain feedback approach is widely recognized as an efficient technique to mitigate the adverse effects of input saturation constraints. Recent research has explored the integration of saturation constraints in the FCP of multi-agent systems (MASs) to enhance system stability and performance. Considering a MAS where each agent follows a predefined dynamic model, it is imperative to account for real-world limitations. From a practical standpoint, network constraints, including actuator saturation, actuator faults, and external disturbances, must be carefully addressed in the design and control of MASs. These factors play a crucial role in ensuring robust and reliable system operation, particularly in applications requiring high precision and adaptability.

p˙i(t)=Api(t)+Bσϖ(ui(t)),i=1,…,N,(35)

where A∈Rn×n,B∈Rn×m satisfies that rank(B)=m,pi(t)∈Rn and ui(t)∈Rm indicate the state and the control input of the ιth agent. For some constant ϖ>0,σϖ:Rm→Rm represents the saturation function given as:

σϖ(ui)=[σϖ(ui1),σϖ(ui2),⋯,σϖ(uim)]T,(36)

where σϖ(uij)= sgn(uij)min{|uij|,Δ}. Here, we denote the time-varying formation by:

f(t)=[f1T(t),f2T(t),…,fnT(t)]T,(37)

where ||fi(t)||≤c¯ for a positive scalar c¯. The TVFT problem of MASs subjected to input saturation is presented as follows. For MAS (12), the semi-global TVFT problem signifies that for any a priori preset bounded set χ∈Rn,pi(0)∈χ (i = 1,2,\ldots, N), to operate a control protocol ui(t) for every agent i, such that:

limt→∞‖pi(t)−fi(t)−p0(t)‖=0 for any i=1,…,N,(38)

where p0(t) denotes the leader dynamics. Based on the low-gain feedback technique, an algorithm is developed to solve the TVFT of second-order MASs subjected to saturation under switching interaction topologies. It was demonstrated that the proposed algorithm enables the achievement of semi-global TVFT, accompanied by the introduction of sufficient conditions for formation tracking. The implementation of three-layer NNs in FTP for first-order uncertain MASs subject to actuator saturation is addressed in [209]. Using the back-stepping approach and distributed extended state observer, a practical TVOFTP is solved for high-order nonlinear strict-feedback MASs subject to input saturation [210]. The output-feedback formation control for wheeled mobile robots subject to saturating actuators is studied in [211].

7.2 Formation in MASs with Faults

In practice, the probability of each agent suffering from faults is increasing due to the complexity of the systems. Faults in a single agent can affect the whole system’s stability and change the expected formation via the interaction topology/network. Thus, to guarantee the efficiency and reliability of team operations, distributed fault-tolerant control schemes for MASs are a crucial necessity. Several fault-tolerant control techniques are proposed to handle the FCP under actuator failures. The robust stability of first-order MASs moving to a desired rigid formation in the presence of actuator faults and unknown time-varying delays is analyzed in [212]. For MASs of n agents, an actuator fault is generally modeled as [213]:

uiF(t)=li(t)ui(t)+bi(t),(39)

where ui(t) denotes the healthy controller input of agent i, uiF(t) represents the actuator output of the agent i, li(t)∈[0,1] represents the healthy indicator factor (i.e., effectiveness factor), bi(t) denotes an additive fault (i.e., the bias fault), i=1,…,n. Based on an adaptive mechanism, a fully distributed fault-tolerant TVFT control protocol is designed to address the problem of fault-tolerant TVFT for second-order multi-agent systems (MASs) with actuator faults and a non-cooperative target. The design of a leader-following formation control for double integrator MASs in the presence of communication faults is presented in [214]. In [215], a fault-tolerant TVFC problem for multi-agent systems (MASs) with second-order dynamics is studied, subject to bias and loss of effectiveness faults under directed interaction topologies. A distributed fault-tolerant formation tracking control scheme was developed for second-order nonlinear uncertain MASs with a time-varying leader under bidirectional intercommunication topology. Adaptive formation tracking control protocols are designed based on diagnostic information to achieve formation tracking in the presence of faults. A distributed fault-tolerant formation tracking control framework is developed in [216] for a class of uncertain ground mobile robots in the presence of actuator faults, process faults, and modeling uncertainty over a bidirectional communication topology. The design of a novel adaptive distributed fault-tolerant formation control scheme for both the kinematics and dynamics of wheeled mobile robotics subject to actuator faults and unknown uncertainties is investigated in [217]. The adaptive fault-tolerant TVFT of nonlinear MASs containing multiple leaders subject to actuator faults is investigated [218]. In [219], the cooperative TVFC problem of HMASs subject to external disturbances and unknown actuator faults is investigated. In [220], a cooperative fault-tolerant FTP for HMASs subject to actuator faults under switching-directed communication topologies is investigated. A distributed fault-tolerant formation control protocol is developed using local neighborhood information to ensure the desired formation tracking of a dynamic leader.

7.3 Formation in MASs with Disturbances

In some practical scenes, MASs may be affected by external disturbances and noises due to the presence of environmental uncertainties, which can decrease the control protocol performance and drive the system to divergence. For example, atmospheric disturbances in the formation flight of UAVs can be considered additional forces, which may yield instabilities in system dynamics. Therefore, it is significant to investigate the disturbance rejection in FCPs such that MASs can achieve the disturbance rejection in the formation while preserving the stability of the closed-loop. Here, consider a MAS where every agent is governed by the following dynamics.

p˙i(t)=Api(t)+Bσϖ(ui(t)),i=1,…,N,(40)

where pi(t)∈Rn, ui(t)∈Rm, and wi(t)∈Rm denote the state, the control input, and unknown bounded disturbances of the agent i, respectively, A∈Rn×n, B∈Rn×m such that rank(B)=m. A distance-based controller is designed for minimally infinitesimally rigid formations of first- and second-order MASs subject to bounded unknown disturbances [221]. The designed control law drives the agents to achieve the desired formation and suppress the disturbances. By adopting an extended state observer technique, the compensation of the external disturbance is estimated. Based on the active disturbance rejection controller, a novel, robust TVFT protocol is constructed for second-order MASs to solve FTPs with disturbances [222]. Based on an integral sliding mode control scheme, a novel event-triggered controller was developed in [223] to solve the TVFC problem for higher-order MASs subject to external disturbances. The time-varying formation tracking (TVFT) problem in multi-agent systems (MASs) has been extensively explored under various challenging scenarios, including unknown external disturbances, input delays, nonlinear dynamics, and uncertainties in control directions. Recent advancements have introduced novel time-varying shape configurations and disturbance observers to manage such complexities in linear and high-order MASs. Finite-time control strategies have been developed to address mismatched disturbances and unknown leader inputs. At the same time, robust adaptive protocols have been proposed for uncertain nonlinear systems, incorporating mechanisms such as Nussbaum-type functions and compensating techniques to mitigate disturbance-induced errors. These contributions collectively enhance the resilience and adaptability of MASs operating in dynamic environments [224–227].

8  Simulation Examples

8.1 Formation Control with Different Time-Varying Delays

The field of formation control in multi-agent systems is much concerned with robotics and control theory. Such systems are quite sensitive to time-varying delays, which can prevent agents from timely synchronization and coordination. The lack of synchronization also causes inconsistencies in maintaining the formation. Indeed, in practical scenarios, it is generally unavoidable that adaptive formation control strategies are crucial to avoid topology switching leading to a disconnection of agents. Moreover, external interference can add some uncertainties and perturbations, which will make the desired formations hard to maintain. Modeling time delays is vital for realizing reliable and resilient formation control in practice. Throughout the years, researchers have come to realize the necessity of using more advanced techniques to deal with these delays in multi-agent systems. Some of these methods include distributed protocols, employing predictive control algorithms to mitigate delays, and decentralized control strategies to diminish their repercussions and information control. These methodologies help reach the desirable configurations, enabling multi-agent systems to operate according to specification despite adversarial conditions. Fig. 16 presents various perspectives on a multi-agent system’s position and velocity responses under the influence of different time-varying communication delays. In Fig. 16a,b, the x-axis and y-axis positions respectively exhibit distinct patterns across agents due to heterogeneous delays. The trajectories demonstrate periodic fluctuations with varying steady-state offsets, suggesting that time-varying delays significantly impact position synchronization and may prevent full convergence, especially when delays are non-uniform. Fig. 16c and d displays the corresponding velocity responses on the x-axis and y-axis. Here, despite initial disturbances and fluctuations, the agents’ velocities tend toward a bounded oscillatory regime. While full consensus is not achieved, the velocities stabilize into predictable patterns, indicating a level of coordination despite delay-induced disruption. This figure underscores the sensitivity of multi-agent dynamics to time-varying delays. While velocities show partial stabilization, positions remain dispersed, highlighting that such delays can impede consensus. Proper compensation or delay-tolerant control strategies are essential for robust performance in delayed networked systems.

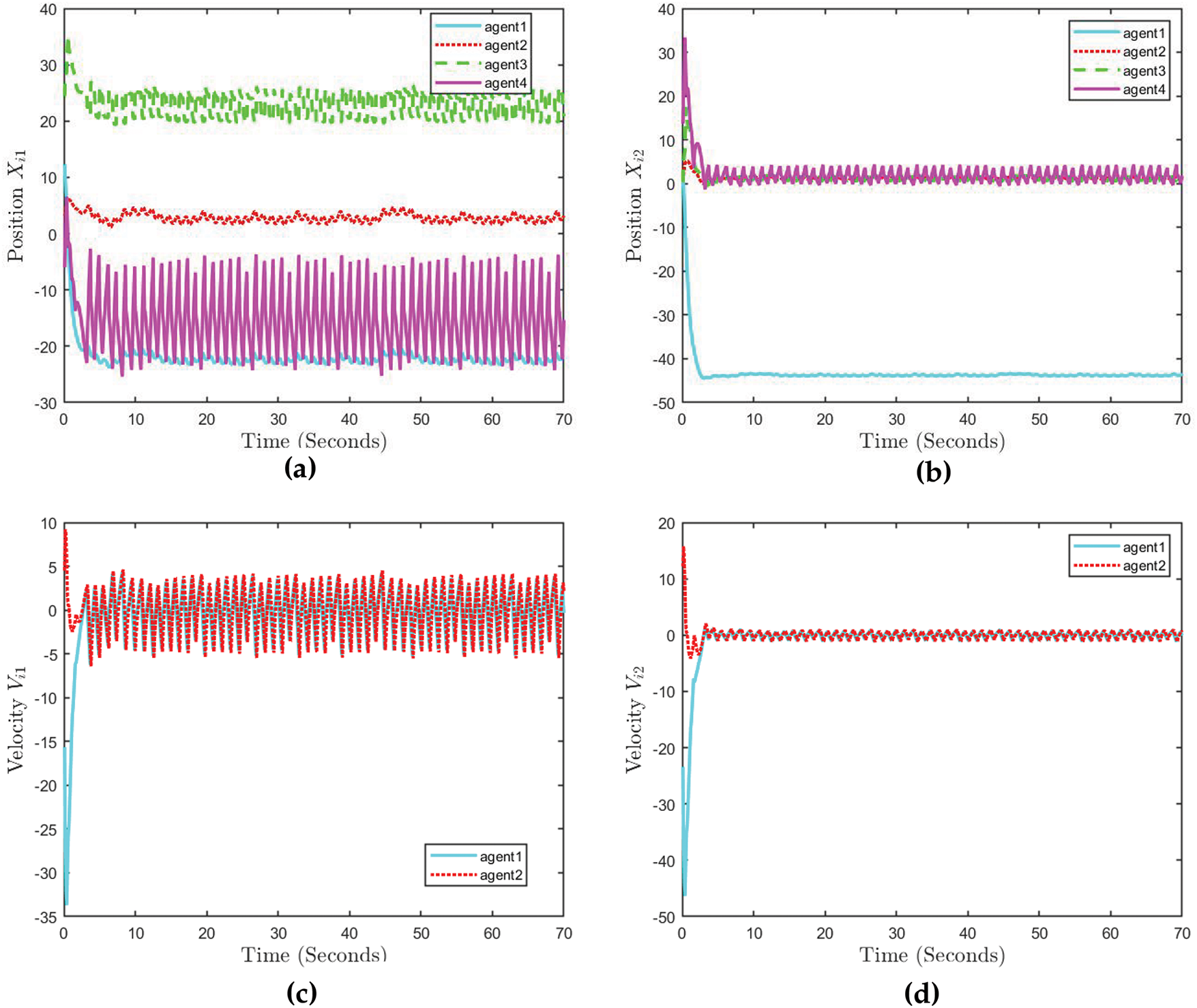
Figure 16: Different views of position and velocity of multi-agent on different time-varying delays

8.2 Formation Control under Switch Directed Topology

A heterogeneous multi-agent system is considered, comprising four agent nodes and a virtual leader. The system includes two first-order agents and two second-order agents, with agents 3 and 4 representing the second-order dynamics. The distinct dynamic models corresponding to the first- and second-order agents are formulated to reflect the system’s structural diversity. The governing equations are adopted from [53].

{s˙i(t)=vi(t),v˙i(t)=ui(t),i=1,2s˙i(t)=vi(t),i=3,4(41)

Fig. 17 illustrates the position trajectories of agents along the x-axis and y-axis in a fixed directed topology without control inputs. In Fig. 17a, agents exhibit sustained oscillations with increasing amplitude, indicating instability and a lack of convergence. Fig. 17b shows partial stabilization along the y-axis; however, significant divergence persists among agents. These results highlight the inadequacy of natural dynamics in achieving consensus under fixed topology without control mechanisms. Fig. 18 presents agent trajectories under a switching topology. In both Fig. 18a and b, agent positions along the x-axis and y-axis converge over time, demonstrating the stabilizing effect of dynamic topology. The adaptability and redundancy introduced by switching communication links enhance coordination and support robust consensus across the network. The sensor sampling period is set to h=0.1s. The communication delay is modeled as λ(t)=3|sin⁡(0.02πt)|(s), and the condition h(t)<0.945 is satisfied, with h(t)=0.5|sin⁡(0.1πt)|(s). Fig. 19 presents the velocity trajectories of agents on the x-axis and y-axis under a switching topology. In Fig. 19a, initial fluctuations in the x-axis velocities converge smoothly to equilibrium, demonstrating effective damping and synchronization over time. Fig. 19b exhibits similar behavior for y-axis velocities, where initial discrepancies are gradually reduced, and agents reach a stable velocity profile. This indicates that the switching topology facilitates velocity consensus despite initial disturbances or variations in agent states. Fig. 20 provides a 3D representation of agents’ position and velocity responses in time under a switch-directed topology. In Fig. 20a, the x−y position trajectories over time demonstrate convergence, with agents stabilizing into coordinated motion. Fig. 20b illustrates the corresponding velocity responses, revealing a smooth transition toward consensus. The integration of position and velocity responses in a switching framework confirms the effectiveness of dynamic topologies in ensuring both spatial alignment and velocity synchronization across multi-agent systems. Fig. 21 presents the velocity trajectories of agents on the x-axis and y-axis within a fixed directed topology without control inputs. In Fig. 21a, the x-axis velocities exhibit persistent oscillations with increasing amplitude, highlighting instability and divergence in agent behavior. Fig. 21b shows a relatively more stable y-axis response; however, discrepancies remain among agents, suggesting the absence of coordinated dynamics. These results indicate that fixed topologies without control fail to enforce velocity consensus, compromising system stability. Fig. 22 displays the position trajectories of agents under the same fixed topology. In Fig. 22a, agents along the x-axis exhibit growing divergence over time, with no evidence of convergence or synchronization. Similarly, Fig. 22b shows widening gaps in the y-axis positions, further emphasizing the system’s inability to reach position consensus. The increasing spread across both axes reflects the instability of the system dynamics and the critical need for control input or adaptive mechanisms in such configurations. These figures highlight the inherent instability of the system as the position and velocity of the agents evolve without any control inputs. This paper analyses the system behaviour design approach, with the simulation results providing valuable insights into the system’s performance. The results clearly show how control inputs affect the agents’ movement and how they maintain proximity to the formation, offering important information for researchers. The visual feedback helps to deepen the understanding of the effectiveness of the proposed design in controlling agent motion and ensuring their adherence to the formation. Moreover, the simulations demonstrate the advantages of the proposed design method, highlighting improvements in stability, optimal control strategies, and the overall performance of formation control in heterogeneous multi-agent systems operating under fixed-directed topologies. These findings underscore the proposed method’s potential to address significant challenges in the coordination and management of complex multi-agent systems [53].

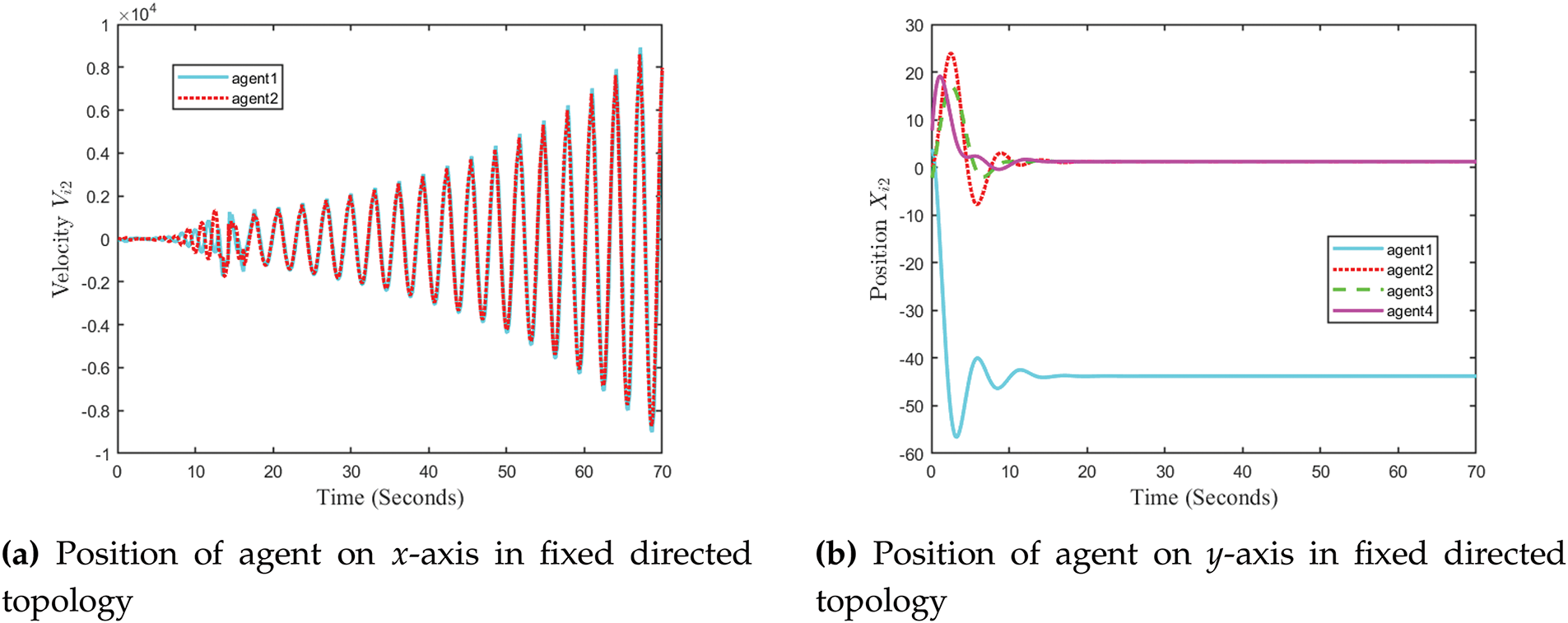
Figure 17: Positions of agent on x-axis and y-axis in fixed directed topology without control inputs

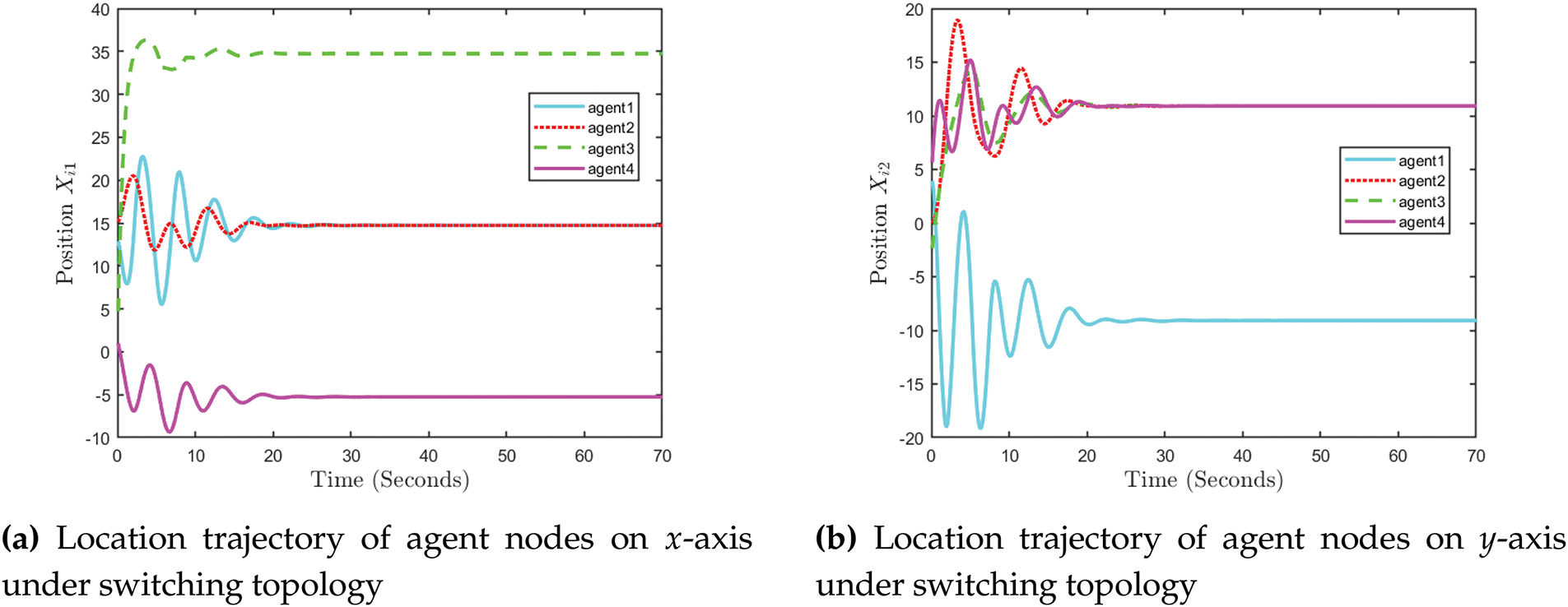
Figure 18: Location trajectory of agent nodes on the x-axis and y-axis under switching topology

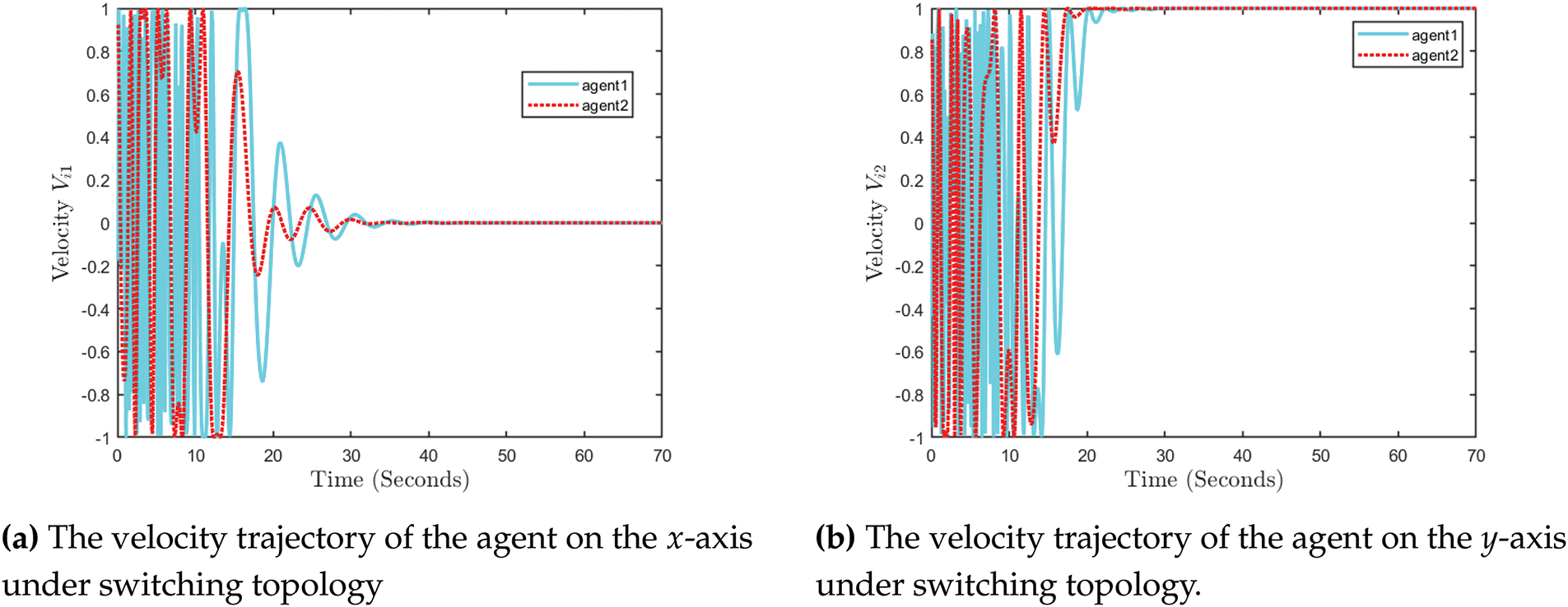
Figure 19: The velocity trajectory of the agent on the x-axis and y-axis under switching topology

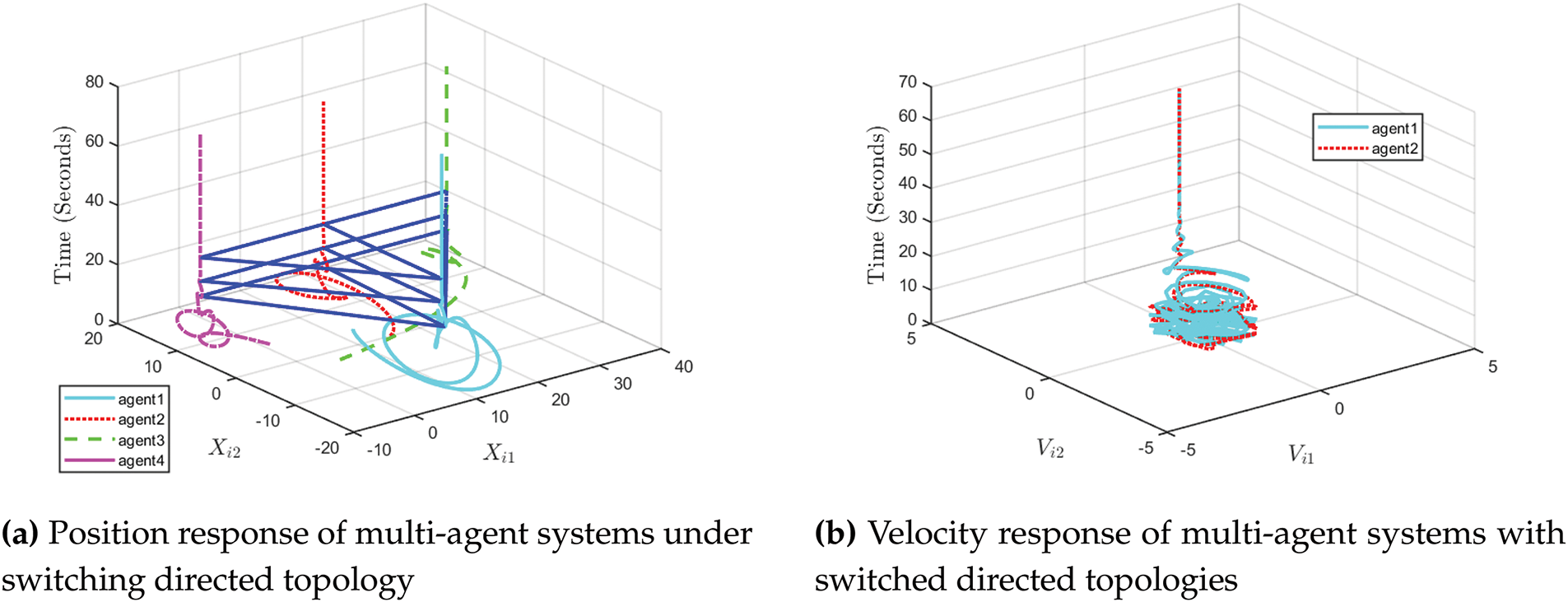
Figure 20: Position and velocity trajectory of the agent on the x-axis and y-axis under switch-directed topology

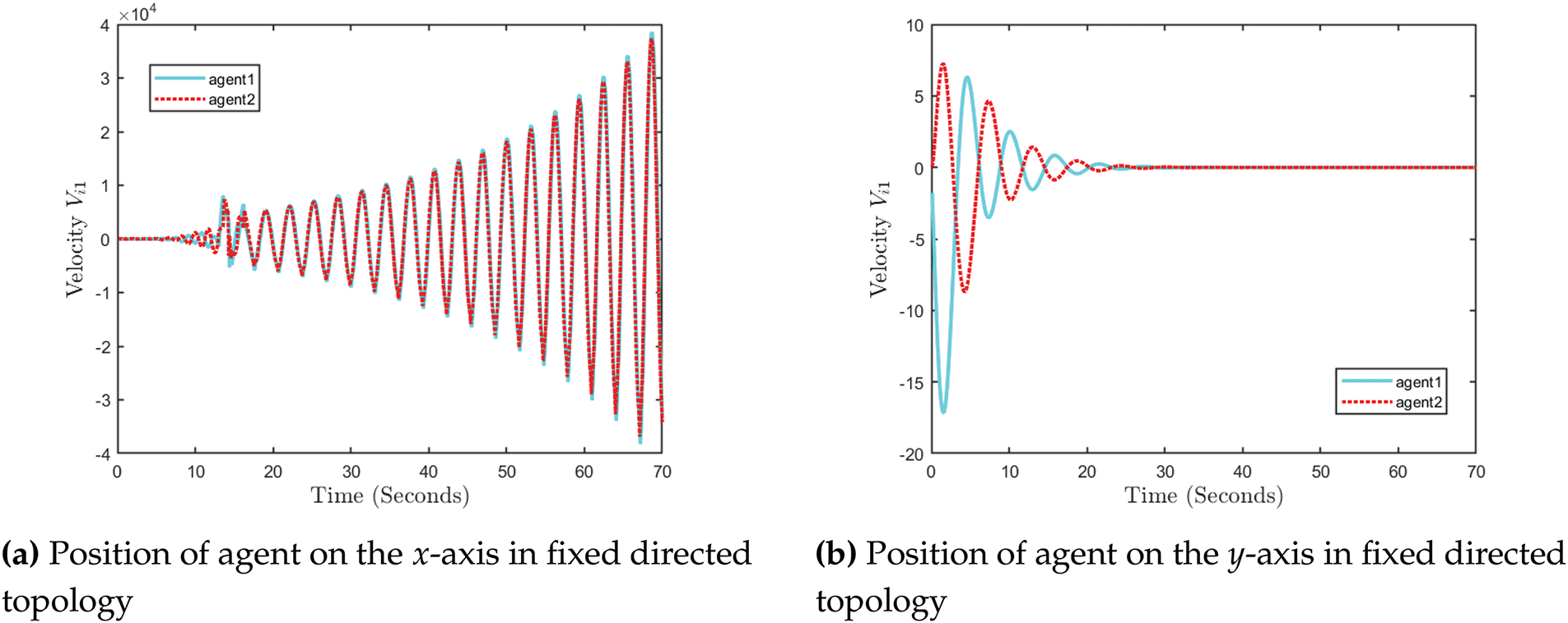
Figure 21: Positions of agent on x-axis and y-axis in fixed directed topology without control inputs

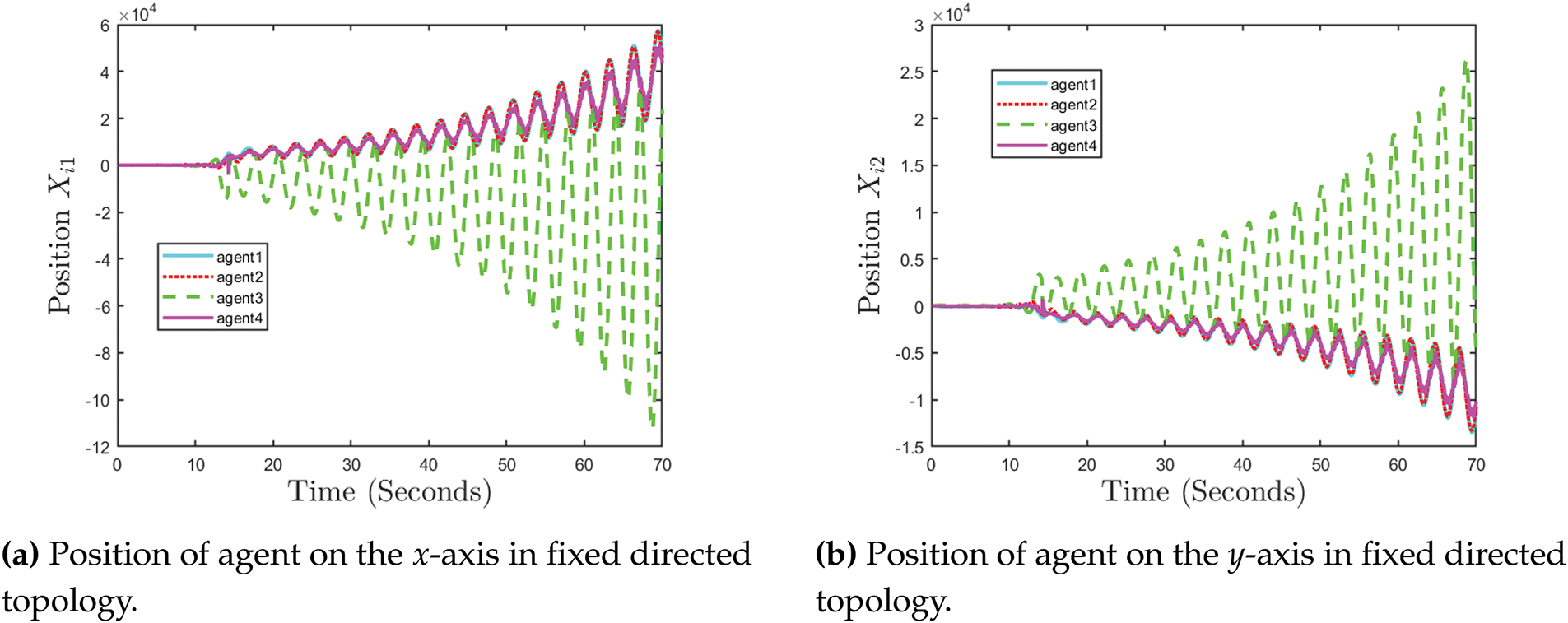
Figure 22: Agent positions on the x-axis and y-axis in fixed directed topology without control inputs

9  Applications of Formation Control

Formation control in Multi-Agent Systems (MAS) has emerged as a prominent research focus within the academic community, owing to its substantial applicability across industrial and defence sectors. In military operations, formation control enables a range of critical functions, including escort and convoy protection, autonomous security patrols, persistent surveillance, cooperative localization, and distributed mapping. This section provides a comprehensive overview of these applications, underscoring the strategic utility of coordinated agent behavior in complex, dynamic environments.

Formation control of UAV systems: The applications of UAVs involve search and rescue (SAR) tasks where a group of UAVs accomplishes a SAR task in the minimum possible time while retrieving survivors in natural disasters [228]. The work in [229] presented a hierarchical architecture to patrol geographical borders using a fleet of UAVs. The presented framework has been validated and demonstrated by experiments using three UAVs.

Formation control of satellites: Satellite formation flying is a pioneering technology for future space tasks/missions. Its main applications comprise deep space exploration missions and surveillance of the Earth and its nearby environment. A class of small satellite (CubeSat) formation flying tasks for different applications, including presentations on Earth science, astronomy, and planetary science, is shown in [230]. A navigation approach is proposed in [231] to perform satellite formation flying missions in low earth orbit.

Formation control of AUVs: The application of MAS formation control has received particular consideration, especially in AUVs. They have applications in target hunting, one of the challenging missions of multi-AUVs in underwater environments [232]. Applications in source search (i.e., source localization and detection missions) to locate the source by using a fleet of AUVs in the ocean [233]. The source search of AUVs is significant in monitoring pollution, drug detection, and the detection of leaky chemicals.

Formation control of UGVs: Unmanned Ground Vehicles (UGVs) are critical in various military operations, including security patrols, urban rescue missions, and combat support tasks. The persistent surveillance problem has been addressed in [234], where UGVs with detection capabilities are deployed to identify randomly occurring events across a road network. Beyond military applications, the scope of formation control in multi-agent systems (MASS) extends to various domains, including industrial automation, cooperative logistics, national defence, and healthcare systems. These diverse applications are illustrated in Fig. 23, highlighting the versatility and growing relevance of MASs formation control across sectors [235].

Figure 23: Applications of circular formation control: (a) a group of micro-satellites orbiting the earth (b) a group of UAVs performing surveillance and navigation missions [235]

10  Conclusions and Future Directions

This paper presents a comprehensive review of recent advancements in formation control for Multi-Agent Systems (MASs). It examines key methodologies and critical formation control problems (FCPs) such as L-F formation, FCC, BFC, ETC-based formations, and group formation with constrained dynamics. The paper highlights significant progress made in both the theoretical understanding and practical application of these techniques, addressing the challenges posed by complex and dynamic environments. While considerable progress has been achieved, several unresolved challenges remain that require further research to enhance the effectiveness and scalability of MASs in real-world applications. Future research should focus on the following areas:

1. Extending formation control methods to multi-UAV systems and realistic communication networks, tackling challenges like non-uniform time delays and unknown dynamics.

2. Expanding current FCP strategies to address the complexities of human-machine interaction in dynamic systems.

3. Integrating collision and obstacle avoidance directly into formation control strategies to ensure safety in practical engineering environments.

4. Developing methods for dynamic formations based on bearing-only measurements, an unresolved issue in current research.

5. Enhancing scalability and robustness of control algorithms, ensuring their adaptability in large-scale, real-world applications.

In conclusion, while MASs formation control has made significant progress, addressing these remaining challenges will fully unlock the potential of MASs, enabling their effective deployment in a wide range of practical, real-world applications.

Acknowledgement: We want to express our sincere appreciation to Nanjing University of Science and Technology, Nanjing, China, for continued support and providing the necessary resources that contributed to the successful completion of this research. The authors gratefully acknowledge Muhammad Hashim Bukhari from Saudi Aramco, 5130, Dhahran, Kingdom of Saudi Arabia (muhammadhashim.bukhari@aramco.com), for his valuable contributions and support throughout this research.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China under Grant 6237319, and in part by the Postgraduate Research and Practice Innovation Program of Jiangsu Province under Grant KYCX230479.

Author Contributions: The authors confirm contribution to the paper as follows: Study Conception and Design: Aamir Farooq and Zhengrong Xiang; Analysis and Interpretation of Results: Wen-Jer Chang; Software, Methodology: Muhammad Shamrooz Aslam; Writing, Review, and Editing: Aamir Farooq and Zhengrong Xiang; Supervision: Zhengrong Xiang and Wen-Jer Chang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: No specific data related to this article as it is a review article.

Ethics Approval: No applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Zhang RW, Song BF, Pei Y, Yun QJ. Improved method for subsystems performance trade-off in system-of-systems oriented design of UAV swarms. J Syst Eng Electron. 2019;30(4):720–37. doi:10.21629/JSEE.2019.04.10. [Google Scholar] [CrossRef]

2. Chen B, Cheng HH. A review of the applications of agent technology in traffic and transportation systems. IEEE Trans Intell Transp Syst. 2010;11(2):485–97. doi:10.1109/TITS.2010.2048313. [Google Scholar] [CrossRef]

3. Meng W, He Z, Rodney T, Su R, Xie L. Integrated multi-agent system framework: decentralised search, tasking and tracking. IET Control Theory Appl. 2015;9(3):493–502. doi:10.1049/iet-cta.2014.0469. [Google Scholar] [CrossRef]

4. Olfati-Saber R, Murray RM. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans Autom Control. 2004;49(9):1520–33. doi:10.1109/TAC.2004.834113. [Google Scholar] [CrossRef]

5. Dong X, Yu B, Shi Z, Zhong Y. Time-varying formation control for unmanned aerial vehicles: theories and applications. IEEE Trans Control Syst Technol. 2014;23(1):340–8. doi:10.1109/TCST.2014.2314460. [Google Scholar] [CrossRef]

6. Yoo SJ, Kim TH. Distributed formation tracking of networked mobile robots under unknown slippage effects. Automatica. 2015;54(10):100–6. doi:10.1016/j.automatica.2015.01.043. [Google Scholar] [CrossRef]

7. Zhang J, Hu Q, Xie W. Integral sliding mode-based attitude coordinated tracking for spacecraft formation with communication delays. Int J Syst Sci. 2017;48(15):3254–66. doi:10.1080/00207721.2017.1371359. [Google Scholar] [CrossRef]

8. Bai H, Wen JT. Cooperative load transport: a formation-control perspective. IEEE Trans Robot. 2010;26(4):742–50. doi:10.1109/TRO.2010.2052169. [Google Scholar] [CrossRef]

9. Yan W, Fang X, Li J. Formation optimization for AUV localization with range-dependent measurement noise. IEEE Commun Lett. 2014;18(9):1579–82. doi:10.1109/LCOMM.2014.2344033. [Google Scholar] [CrossRef]

10. Zhang M, Liu HHT. Cooperative tracking a moving target using multiple fixed-wing UAVs. J Intell Robot Syst. 2016;81(3):505–29. doi:10.1007/s10846-015-0236-9. [Google Scholar] [CrossRef]

11. Oh KK, Park MC, Ahn HS. A survey of multi-agent formation control. Automatica. 2015;53(9):424–40. doi:10.1016/j.automatica.2014.10.022. [Google Scholar] [CrossRef]

12. Tran VP, Garratt M, Petersen IR. Switching time-invariant formation control of a collaborative multi-agent system using negative imaginary systems theory. Control Eng Pract. 2020;95(1):104245. doi:10.1016/j.conengprac.2019.104245. [Google Scholar] [CrossRef]

13. Dong X, Li Y, Lu C, Hu G, Li Q, Ren Z. Time-varying formation tracking for UAV swarm systems with switching directed topologies. IEEE Trans Neural Netw Learn Syst. 2018;30(12):3674–85. doi:10.1109/TNNLS.2018.2873063. [Google Scholar] [PubMed] [CrossRef]

14. Brinón-Arranz L, Seuret A, Canudas-De-Wit C. Cooperative control design for time-varying formations of multi-agent systems. IEEE Trans Autom Control. 2014;59(8):2283–8. doi:10.1109/TAC.2014.2303213. [Google Scholar] [CrossRef]

15. Gong Y, Wen G, Peng Z, Huang T, Chen Y. Observer-based time-varying formation control of fractional-order multi-agent systems with general linear dynamics. IEEE Trans Circuits Syst II Express Briefs. 2019;67(1):82–6. doi:10.1109/TCSII.2019.2899063. [Google Scholar] [CrossRef]

16. Hua Y, Dong X, Li Q, Ren Z. Distributed fault-tolerant time-varying formation control for second-order multi-agent systems with actuator failures and directed topologies. IEEE Trans Circuits Syst II Express Briefs. 2017;65(6):774–8. doi:10.1109/TCSII.2017.2748967. [Google Scholar] [CrossRef]

17. Zhao W, Yu W, Zhang H. Observer-based formation tracking control for leader-follower multi-agent systems. IET Control Theory Appl. 2019;13(2):239–47. doi:10.1049/iet-cta.2018.5443. [Google Scholar] [CrossRef]

18. Dou L, Yu X, Liu L, Wang X, Feng G. Moving-target enclosing control for mobile agents with collision avoidance. IEEE Trans Control Netw Syst. 2021;8(4):1669–79. doi:10.1109/TCNS.2021.3078120. [Google Scholar] [CrossRef]

19. Wen G, Zhang C, Hu P, Cui Y. Adaptive neural network leader-follower formation control for a class of second-order nonlinear multi-agent systems with unknown dynamics. IEEE Access. 2020;8:148149–56. doi:10.1109/ACCESS.2020.3015957. [Google Scholar] [CrossRef]

20. Lee G, Chwa D. Decentralized behavior-based formation control of multiple robots considering obstacle avoidance. Intell Serv Robot. 2018;11(1):127–38. doi:10.1007/s11370-017-0240-y. [Google Scholar] [CrossRef]

21. Juan L, Xu Z, Honghan HZ, Xue D. Trajectory tracking control of multi-AUVs formation based on virtual leader. In: 2019 IEEE International Conference on Mechatronics and Automation (ICMA); 2019; Tianjin, China. p. 291–6. doi:10.1109/ICMA.2019.8816396. [Google Scholar] [CrossRef]

22. Zhou D, Wang Z, Schwager M. Agile coordination and assistive collision avoidance for quadrotor swarms using virtual structures. IEEE Trans Robot. 2018;34(4):916–23. doi:10.1109/TRO.2018.2857477. [Google Scholar] [CrossRef]

23. Li J, Li T, Liu C, Qin Q. Formation control of marine surface vessels based on sliding mode control and local state observer. In: 2018 Eighth International Conference on Information Science and Technology (ICIST); 2018. p. 8–14. doi:10.1109/ICIST.2018.8426147. [Google Scholar] [CrossRef]

24. Zou W, Shi P, Zhengrong X, Shi Y. Consensus tracking control of switched stochastic nonlinear multiagent systems via event-triggered strategy. IEEE Trans Neural Netw Learn Syst. 2019;31(3):1036–45. doi:10.1109/TNNLS.2019.2917137. [Google Scholar] [PubMed] [CrossRef]

25. Ren W. Consensus strategies for cooperative control of vehicle formations. IET Control Theory Appl. 2007;1(2):505–12. doi:10.1049/iet-cta:20050401. [Google Scholar] [CrossRef]

26. Liu C, Tian Y. Formation control of multi-agent systems with heterogeneous communication delays. Int J Syst Sci. 2009;40(6):627–36. doi:10.1080/00207720902755762. [Google Scholar] [CrossRef]

27. Mei J, Ren W, Ma G. Distributed coordination for second-order multi-agent systems with nonlinear dynamics using only relative position measurements. Automatica. 2013;49(5):1419–27. doi:10.1016/j.automatica.2013.01.058. [Google Scholar] [CrossRef]

28. Dong W. Robust formation control of multiple wheeled mobile robots. J Intell Robot Syst. 2011;62(3):547–65. doi:10.1007/s10846-010-9451-6. [Google Scholar] [CrossRef]

29. Bhowmick P, Ganguly A, Sawann S. A new consensus-based formation tracking scheme for a class of robotic systems using negative imaginary property. IFAC-PapersOnLine. 2022;55(1):685–90. doi:10.1016/j.ifacol.2022.04.112. [Google Scholar] [CrossRef]

30. He X, Geng Z. Consensus-based formation control for nonholonomic vehicles with parallel desired formations. Int J Control. 2019;94(2):507–20. doi:10.1080/00207179.2019.1598581. [Google Scholar] [CrossRef]

31. Lin Z, Wang L, Han Z, Fu M. A graph Laplacian approach to coordinate-free formation stabilization for directed networks. IEEE Trans Autom Control. 2016;61(5):1269–80. doi:10.1109/TAC.2015.2454711. [Google Scholar] [CrossRef]

32. Dong X, Zhou Y, Ren Z, Zhong Y. Time-varying formation control for unmanned aerial vehicles with switching interaction topologies. Control Eng Pract. 2016;46(11):26–36. doi:10.1016/j.conengprac.2015.10.001. [Google Scholar] [CrossRef]

33. Yu J, Dong X, Li Q, Ren Z. Time-varying formation tracking for high-order multi-agent systems with switching topologies and a leader of bounded unknown input. J Franklin Inst. 2018;355(5):2808–25. doi:10.1016/j.jfranklin.2018.01.017. [Google Scholar] [CrossRef]

34. Li X, Wen C, Fang X, Wang J. Adaptive bearing-only formation tracking control for nonholonomic multiagent systems. IEEE Trans Cybern. 2021;52(8):7552–62. doi:10.1109/TCYB.2020.3042491. [Google Scholar] [PubMed] [CrossRef]

35. Xia L, Li Q, Song R, Zhang Z. Leader-follower time-varying output formation control of heterogeneous systems under cyber attack with active leader. Inf Sci. 2022;585(2):24–40. doi:10.1016/j.ins.2021.11.026. [Google Scholar] [CrossRef]

36. Liang X, Liu YH, Wang H, Chen W, Xing K, Liu T. Leader-following formation tracking control of mobile robots without direct position measurements. IEEE Trans Autom Control. 2016;61(12):4131–7. doi:10.1109/TAC.2016.2547872. [Google Scholar] [CrossRef]

37. Wang M, Zhang T. Leader-following formation control of second-order nonlinear systems with time-varying communication delay. Int J Control Autom Syst. 2021;19(5):1729–39. doi:10.1007/s12555-019-0759-0. [Google Scholar] [CrossRef]

38. Su H, Zhang J, Chen X. A stochastic sampling mechanism for time-varying formation of multiagent systems with multiple leaders and communication delays. IEEE Trans Neural Netw Learn Syst. 2019;30(12):3699–707. doi:10.1109/TNNLS.2019.2891259. [Google Scholar] [PubMed] [CrossRef]

39. Jiang W, Rahmani A, Wen G. Fully distributed time-varying formation-containment control for large-scale nonholonomic vehicles with an unknown real leader. Int J Control. 2021;94(4):1020–32. doi:10.1080/00207179.2019.1626996. [Google Scholar] [CrossRef]

40. Hu J, Bhowmick P, Lanzon A. Distributed adaptive time-varying group formation tracking for multiagent systems with multiple leaders on directed graphs. IEEE Trans Control Netw Syst. 2019;7(1):140–50. doi:10.1109/TCNS.2019.2913619. [Google Scholar] [CrossRef]

41. Yan C, Zhang W, Su H, Li X. Adaptive bipartite time-varying output formation control for multiagent systems on signed directed graphs. IEEE Trans Cybern. 2021;52(9):8987–9000. doi:10.1109/TCYB.2021.3054648. [Google Scholar] [PubMed] [CrossRef]

42. Wang W, Huang C, Huang C, Cao J, Lu J, Wang L. Bipartite formation problem of second-order nonlinear multi-agent systems with hybrid impulses. Appl Math Comput. 2020;370(11):124926. doi:10.1016/j.amc.2019.124926. [Google Scholar] [CrossRef]

43. Wang Y, Song Y, Ren W. Distributed adaptive finite-time approach for formation-containment control of networked nonlinear systems under directed topology. IEEE Trans Neural Netw Learn Syst. 2017;29(7):3164–75. doi:10.1109/TNNLS.2017.2714187. [Google Scholar] [PubMed] [CrossRef]

44. Wu J, Ji Y, Sun X, Fu W, Zhao S. Anonymous flocking with obstacle avoidance via the position of obstacle boundary point. IEEE Internet Things J. 2025;12(2):2002–13. doi:10.1109/JIOT.2024.3465881. [Google Scholar] [CrossRef]

45. Ge X, Han QL. Distributed formation control of networked multi-agent systems using a dynamic event-triggered communication mechanism. IEEE Trans Ind Electron. 2017;64(10):8118–27. doi:10.1109/TIE.2017.2701778. [Google Scholar] [CrossRef]

46. Liu J, Fang J, Li Z, He G. Time-varying formation tracking for second-order multi-agent systems subjected to switching topology and input saturation. Int J Control Autom Syst. 2020;18(4):991–1001. doi:10.1007/s12555-019-0473-y. [Google Scholar] [CrossRef]

47. Khalili M, Zhang X, Cao Y, Polycarpou MM, Parisini T. Distributed adaptive fault-tolerant leader-following formation control of nonlinear uncertain second-order multi-agent systems. Int J Robust Nonlinear Control. 2018;28(15):4287–308. doi:10.1002/rnc.4232. [Google Scholar] [CrossRef]

48. Yang X, Fan X. Distributed formation control for multiagent systems in the presence of external disturbances. IEEE Access. 2019;7:80194–207. doi:10.1109/ACCESS.2019.2923852. [Google Scholar] [CrossRef]

49. Xiang Z, Li P, Zou W. Event-triggered optimal control for a class of continuous-time switched nonlinear systems. IEEE Trans Autom Sci Eng. 2024, 1–11. doi:10.1109/TASE.3368438. [Google Scholar] [CrossRef]

50. Chang WJ, Lin YH, Ku CC. Passive formation and containment control of multiple nonlinear autonomous ship systems with external disturbances based on interval type-2 T-S fuzzy model. Int J Fuzzy Syst. 2024;25(8):2505–17. doi:10.1007/s40815-024-01742-y. [Google Scholar] [CrossRef]

51. Jin D, Xiang Z. Predefined-time consensus for second-order nonlinear multi-agent systems via sliding mode technique. IEEE Trans Fuzzy Syst. 2024;32(8):4534–41. doi:10.1109/TFUZZ.2024.3402397. [Google Scholar] [CrossRef]

52. Chang YH, Lin YH, Lee YC, Ku CC. Investigating formation and containment problem for nonlinear multi-agent systems via interval type-2 fuzzy sliding mode tracking approach. IEEE Trans Fuzzy Syst. 2024;32(7):4163–77. doi:10.1109/TFUZZ.2024.3387045. [Google Scholar] [CrossRef]

53. Aslam MS, Bilal H, Chang WJ, Yahya A, Badruddin IA, Kamangar S, et al. Formation control of heterogeneous multi-agent systems under fixed and switching hierarchies. IEEE Access. 2024;12:97868–82. doi:10.1109/ACCESS.2024.3419815. [Google Scholar] [CrossRef]

54. Lin YH, Chang WJ, Pen CL. Fuzzy steering control for T-S fuzzy model-based multiple ship systems subject to formation and containment. Int J Fuzzy Syst. 2023;25(5):1782–94. doi:10.1007/s40815-023-01479-0. [Google Scholar] [CrossRef]

55. Yu Y, Guo J, Ahn CK, Xiang Z. Neural adaptive distributed formation control of nonlinear multi-UAVs with unmodeled dynamics. IEEE Trans Neural Netw Learn Syst. 2023;34(11):9555–61. doi:10.1109/TNNLS.2022.3157079. [Google Scholar] [PubMed] [CrossRef]

56. Gao X, Liu X, Chen C, Qiu X, Xiang Z. Formation control of multiple nonholonomic wheeled robots with disturbances. Proc Chin Intell Syst Conf. 2023;1089(8):625–34. doi:10.1007/978-981-99-6847-3. [Google Scholar] [CrossRef]

57. Lin H, Chang WJ, Ku CC. Solving formation and containment control problem of nonlinear multi-boiler systems based on interval type-2 Takagi-Sugeno fuzzy models. Processes. 2022;10(6):1216. doi:10.3390/pr10061216. [Google Scholar] [CrossRef]

58. Qin J, Ma Q, Shi Y, Wang L. Recent advances in consensus of multi-agent systems: a brief survey. IEEE Trans Ind Electron. 2017;64(6):4972–83. doi:10.1109/TIE.2016.2636810. [Google Scholar] [CrossRef]

59. Li F, Ning J, Liu H, Zhang Y, Liu Y. Spatial barycentric coordinates based distributed formation control for multi-agent systems. ISA Trans. 2025;156(7):333–43. doi:10.1016/j.isatra.2024.11.040. [Google Scholar] [PubMed] [CrossRef]

60. Wei R, Beard RW. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans Autom Control. 2005;50(5):655–61. doi:10.1109/TAC.2005.846556. [Google Scholar] [CrossRef]

61. Tang C, Ji L, Yang S, Guo X. Adaptive bipartite time-varying formation tracking control for heterogeneous multi-agent systems with DoS attacks. ISA Trans. 2025;157(4):56–67. doi:10.1016/j.isatra.2024.12.028. [Google Scholar] [PubMed] [CrossRef]

62. Ji L, Niu F, Guo X, Xie Y, Li H. Prescribed-time privacy-preserving bipartite consensus of multiagent systems via edge-event-triggered method. J Franklin Inst. 2025;362(1):107423. doi:10.1016/j.jfranklin.2024.107423. [Google Scholar] [CrossRef]

63. Liu Y, Liu J, He Z, Li Z, Zhang Q, Ding Z. A survey of multi-agent systems on distributed formation control. Unmanned Syst. 2023;12(5):913–26. doi:10.1142/S2301385024500274. [Google Scholar] [CrossRef]

64. Godsil C, Gordon FR. Algebraic graph theory. Springer Science and Business Media; 2001. doi:10.1007/978-1-4613-0163-9. [Google Scholar] [CrossRef]

65. Yang C, Cheng T. Leader-follower cooperative swinging by UAVs without interagent communication. Int J Control. 2022;95(1):104–13. doi:10.1080/00207179.2020.1779959. [Google Scholar] [CrossRef]

66. He W, Yan B, Wu C. Distributed cooperative formation control for multi-agent systems based on robust adaptive strategy. ICIC Express Lett. 2020;14(7):661–8. doi:10.24507/icicel.14.07.661. [Google Scholar] [CrossRef]

67. Xiao F, Wang L, Chen J, Gao Y. Finite-time formation control for multi-agent systems. Automatica. 2009;45(11):2605–11. doi:10.1016/j.automatica.2009.07.012. [Google Scholar] [CrossRef]

68. Xiong T, Gu Z. Observer-based adaptive fixed-time formation control for multi-agent systems with unknown uncertainties. Neurocomputing. 2021;423(2):506–17. doi:10.1016/j.neucom.2020.10.074. [Google Scholar] [CrossRef]

69. Dong X, Hu G. Time-varying formation control for general linear multi-agent systems with switching directed topologies. Automatica. 2016;73(2):47–55. doi:10.1016/j.automatica.2016.06.024. [Google Scholar] [CrossRef]

70. Dong X, Shi Z, Lu G, Zhong Y. Time-varying output formation control for high-order linear time-invariant swarm systems. Inf Sci. 2015;298(6):36–52. doi:10.1016/j.ins.2014.11.047. [Google Scholar] [CrossRef]

71. Zhao Y, Duan Q, Wen G, Zhang D, Wang B. Time-varying formation for general linear multiagent systems over directed topologies: fully distributed adaptive technique. IEEE Trans Syst Man Cybern Syst. 2018;51(1):532–41. doi:10.1109/TSMC.2018.2877818. [Google Scholar] [CrossRef]

72. Wang C, Hilton T, Zuo Z, Barry L, Ding Z. Fixed-time formation control of multi-robot systems: design and experiments. IEEE Trans Ind Electron. 2018;66(8):6292–301. doi:10.1109/TIE.2018.2870409. [Google Scholar] [CrossRef]

73. Wang P, Baocang BD. Distributed RHC for tracking and formation of non-holonomic multi-vehicle systems. IEEE Trans Autom Control. 2014;59(6):1439–53. doi:10.1109/TAC.2014.2304175. [Google Scholar] [CrossRef]

74. Li W, Chen Z, Liu Z. Formation control for nonlinear multi-agent systems by robust output regulation. Neurocomputing. 2014;140(9):114–20. doi:10.1016/j.neucom.2014.03.030. [Google Scholar] [CrossRef]

75. Li X, Xie L. Dynamic formation control over directed networks using graphical Laplacian approach. IEEE Trans Autom Control. 2018;63(11):3761–74. doi:10.1109/TAC.2018.2798808. [Google Scholar] [CrossRef]

76. Zhang D, Tang Y, Zhang W, Wu X. Hierarchical design for position-based formation control of rotorcraft-like aerial vehicles. IEEE Trans Control Netw Syst. 2020;7(4):1789–800. doi:10.1109/TCNS.2020.3000738. [Google Scholar] [CrossRef]

77. Wang J, Luo X, Li X, Guan X. Specified-time bearing-based formation control of multi-agent systems via a dynamic gain approach. J Franklin Inst. 2018;355(17):8619–41. doi:10.1016/j.jfranklin.2018.09.008. [Google Scholar] [CrossRef]

78. Mehdifar F, Bechlioulis CP, Hashemzadeh F, Baradarannia M. Prescribed performance distance-based formation control of multi-agent systems. Automatica. 2020;119(6):109086. doi:10.1016/j.automatica.2020.109086. [Google Scholar] [CrossRef]

79. Yang Z, Zhu S, Chen C, Feng G, Gu X. Leader-follower formation control of nonholonomic mobile robots with bearing-only measurements. J Franklin Inst. 2020;357(3):1628–43. doi:10.1016/j.jfranklin.2019.11.025. [Google Scholar] [CrossRef]

80. Lin Z, Ding W, Yan G, Yu C, Alessandro G. Leader-follower formation via complex Laplacian. Automatica. 2013;49(6):1900–6. doi:10.1016/j.automatica.2013.02.055. [Google Scholar] [CrossRef]

81. Mylvaganam T, Alessandro A. A differential game approach to formation control for a team of agents with one leader. In: 2015 American Control Conference (ACC); 2015. p. 1469–74. doi:10.1109/ACC.2015.7170940. [Google Scholar] [CrossRef]

82. Dong X, Xiang J, Han L, Li Q, Ren Z. Distributed time-varying formation tracking analysis and design for second-order multi-agent systems. J Intell Robot Syst Theory Appl. 2017;86(2):277–89. doi:10.1007/s10846-016-0421-5. [Google Scholar] [CrossRef]

83. Dong X, Zhou Y, Ren Z, Zhong Y. Time-varying formation tracking for second-order multi-agent systems subjected to switching topologies with application to quadrotor formation flying. IEEE Trans Ind Electron. 2016;64(6):5014–24. doi:10.1109/TIE.2016.2593656. [Google Scholar] [CrossRef]

84. Tang Z, Cunha R, Hamel T, Silvestre C. Formation control of a leader-follower structure in three-dimensional space using bearing measurements. Automatica. 2021;128(2):109567. doi:10.1016/j.automatica.2021.109567. [Google Scholar] [CrossRef]

85. Ji H, Yuan Q, Li C, Li X. Bearing-only formation control of multi-agent system without leader’s velocity information. IFAC-PapersOnLine. 2020;53(2):11044–49. doi:10.1016/j.ifacol.2020.12.231. [Google Scholar] [CrossRef]

86. Sun T, Liu H, Yao Y, Li T, Cheng Z. Distributed adaptive formation tracking control under fixed and switching topologies: application on general linear multi-agent systems. Symmetry. 2021;13(6):941. doi:10.3390/sym13060941. [Google Scholar] [CrossRef]

87. Liu Z, Li Y, Wang F, Chen Z. Reduced-order observer-based leader-following formation control for discrete-time linear multi-agent systems. IEEE/CAA J Autom Sin. 2020;8(10):1715–23. doi:10.1109/JAS.2020.1003441. [Google Scholar] [CrossRef]

88. Yang H, Ye D. Time-varying formation tracking control for high-order nonlinear multi-agent systems in fixed-time framework. Appl Math Comput. 2020;377(4):125119. doi:10.1016/j.amc.2020.125119. [Google Scholar] [CrossRef]

89. Wang R. Adaptive output-feedback time-varying formation tracking control for multi-agent systems with switching directed networks. J Franklin Inst. 2020;357(1):551–68. doi:10.1016/j.jfranklin.2019.11.077. [Google Scholar] [CrossRef]

90. Aryankia K, Selmic RR. Neuro-adaptive formation control and target tracking for nonlinear multi-agent systems with time-delay. IEEE Control Syst Lett. 2020;5(3):791–6. doi:10.1109/LCSYS.2020.3006187. [Google Scholar] [CrossRef]

91. Yu J, Dong X, Li Q, Ren Z. Practical time-varying formation tracking for high-order nonlinear multi-agent systems based on the distributed extended state observer. Int J Control. 2019;92(10):2451–62. doi:10.1080/00207179.2018.1441554. [Google Scholar] [CrossRef]

92. Li Y, Wu Y, He S. Network-based leader-following formation control of second-order autonomous unmanned systems. J Franklin Inst. 2020;358(1):757–75. doi:10.1016/j.jfranklin.2020.11.008. [Google Scholar] [CrossRef]

93. Wang J, Han L, Dong X, Li Q, Ren Z. Distributed sliding mode control for time-varying formation tracking of multi-UAV system with a dynamic leader. Aerosp Sci Technol. 2021;111(1):106549. doi:10.1016/j.ast.2021.106549. [Google Scholar] [CrossRef]

94. Hassan MF, Hammuda M. Leader-follower formation control of mobile nonholonomic robots via a new observer-based controller. Int J Syst Sci. 2020;51(7):1243–65. doi:10.1080/00207721.2020.1758233. [Google Scholar] [CrossRef]

95. Hua Y, Dong X, Hu G, Li Q, Ren Z. Distributed time-varying output formation tracking for heterogeneous linear multi-agent systems with a nonautonomous leader of unknown input. IEEE Trans Autom Control. 2019;64(10):4292–9. doi:10.1109/TAC.2019.2893978. [Google Scholar] [CrossRef]

96. Wang B, Ashrafiuon H, Nersesov S. Leader-follower formation stabilization and tracking control for heterogeneous planar underactuated vehicle networks. Syst Control Lett. 2021;156(27):105008. doi:10.1016/j.sysconle.2021.105008. [Google Scholar] [CrossRef]

97. Zuo S, Song Y, Lewis FL, Davoudi A. Adaptive output formation-tracking of heterogeneous multi-agent systems using time-varying L2-gain design. IEEE Control Syst Lett. 2018;2(2):236–41. doi:10.1109/LCSYS.2018.2814071. [Google Scholar] [CrossRef]

98. Pereira PO, Cunha R, Cabecinhas D, Silvestre C, Oliveira P. Leader following trajectory planning: a trailer-like approach. Automatica. 2017;75(5853):77–87. doi:10.1016/j.automatica.2016.09.001. [Google Scholar] [CrossRef]

99. Cao M, Yu C, Anderson BD. Formation control using range-only measurements. Automatica. 2011;47(4):776–81. doi:10.1016/j.automatica.2011.01.067. [Google Scholar] [CrossRef]

100. Yang S, Bai W, Li T, Shi Q, Yang Y, Wu Y, et al. Neural-network-based formation control with collision, obstacle avoidance and connectivity maintenance for a class of second-order nonlinear multi-agent systems. Neurocomputing. 2021;439(1):243–55. doi:10.1016/j.neucom.2020.12.106. [Google Scholar] [CrossRef]

101. Guo J, Li Y, Huang B, Ding L, Gao H, Zhong M. An online optimization escape entrapment strategy for planetary rovers based on Bayesian optimization. J Field Robot. 2024;41(8):2518–29. doi:10.1002/rob.22361. [Google Scholar] [CrossRef]

102. Li Q, Wei J, Gou Q, Niu Z. Distributed adaptive fixed-time formation control for second-order multi-agent systems with collision avoidance. Inf Sci. 2021;564(3):27–44. doi:10.1016/j.ins.2021.02.029. [Google Scholar] [CrossRef]

103. Yu J, Dong X, Li Q, Ren Z. Practical time-varying output formation tracking for high-order multi-agent systems with collision avoidance, obstacle dodging and connectivity maintenance. J Franklin Inst. 2019;356(12):5898–926. doi:10.1016/j.jfranklin.2019.05.014. [Google Scholar] [CrossRef]

104. Zhou R, Ji W, Xu Q, Si W. Collision avoidance and connectivity preservation for time-varying formation of second-order multi-agent systems with a dynamic leader. IEEE Access. 2022;10:31714–22. doi:10.1109/ACCESS.2022.3157300. [Google Scholar] [CrossRef]

105. Shi Q, Li T, Li J, Chen CP, Xiao Y, Shan Q. Adaptive leader-following formation control with collision avoidance for a class of second-order nonlinear multi-agent systems. Neurocomputing. 2019;350(6):282–90. doi:10.1016/j.neucom.2019.03.045. [Google Scholar] [CrossRef]

106. Wu X, Wang S, Xing M. Observer-based leader-following formation control for multi-robot with obstacle avoidance. IEEE Access. 2018;7:14791–98. doi:10.1109/ACCESS.2018.2889504. [Google Scholar] [CrossRef]

107. Hacene N, Mendil B. Behavior-based autonomous navigation and formation control of mobile robots in unknown cluttered dynamic environments with dynamic target tracking. Int J Autom Comput. 2021;18(5):766–86. doi:10.1007/s11633-020-1264-x. [Google Scholar] [CrossRef]

108. Martinez JB, Becerra HM, Gomez-Gutierrez D. Formation tracking control and obstacle avoidance of unicycle-type robots guaranteeing continuous velocities. Sensors. 2021;21(13):4374. doi:10.3390/s21134374. [Google Scholar] [PubMed] [CrossRef]

109. Khatib O. Real-time obstacle avoidance for manipulators and mobile robots. Auton Robot Veh. 1990;2:396–404. doi:10.1109/ROBOT.1985.1087247. [Google Scholar] [CrossRef]

110. Pozna C, Troester F, Precup R, Tar JK, Preitl S. On the design of an obstacle avoiding trajectory: method and simulation. Math Comput Simul. 2009;79(7):2211–26. doi:10.1016/j.matcom.2008.12.015. [Google Scholar] [CrossRef]

111. Mondal A, Behera L, Sahoo SR, Shukla A. A novel multi-agent formation control law with collision avoidance. IEEE/CAA J Autom Sin. 2017;4(3):558–68. doi:10.1109/JAS.2017.7510565. [Google Scholar] [CrossRef]

112. Mondal A, Bhowmick C, Behera L, Jamshidi M. Trajectory tracking by multiple agents in formation with collision avoidance and connectivity assurance. IEEE Syst J. 2017;12(3):2449–59. doi:10.1109/JSYST.2017.2778063. [Google Scholar] [CrossRef]

113. Wen G, Chen CLP, Dou H, Yang H, Liu C. Formation control with obstacle avoidance of second-order multi-agent systems under directed communication topology. Sci China Inf Sci. 2019;62(9):1–14. doi:10.1007/s11432-018-9759-9. [Google Scholar] [CrossRef]

114. Yang S, Li T, Shi Q, Bai W, Wu Y. Artificial potential-based formation control with collision and obstacle avoidance for second-order multi-agent systems. In: 2020 7th International Conference on Information, Cybernetics, and Computational Social Systems (ICCSS); 2020. p. 58–63. doi:10.1109/ICCSS52145.2020.9336836. [Google Scholar] [CrossRef]

115. Hwang J, Lee J, Park C. Collision avoidance control for formation flying of multiple spacecraft using artificial potential field. Adv Space Res. 2022;69(5):2197–209. doi:10.1016/j.asr.2021.12.015. [Google Scholar] [CrossRef]

116. Liu Y, Huang P, Zhang F, Zhao Y. Distributed formation control using artificial potentials and neural network for constrained multiagent systems. IEEE Trans Control Syst Technol. 2018;28(2):697–704. doi:10.1109/TCST.2018.2884226. [Google Scholar] [CrossRef]

117. Li J, Fang Y, Cheng H, Wang Z, Huangfu S. Unmanned aerial vehicle formation obstacle avoidance control based on light transmission model and improved artificial potential field. Trans Inst Meas Control. 2022;44(16):3229–42. doi:10.1177/01423312221100340. [Google Scholar] [CrossRef]

118. Wang Y, Chen X, Ran D, Zhao Y, Chen Y, Bai Y. Spacecraft formation reconfiguration with multi-obstacle avoidance under navigation and control uncertainties using adaptive artificial potential function method. Astrodynamics. 2020;4(1):41–56. doi:10.1007/s42064-019-0049-x. [Google Scholar] [CrossRef]

119. Chen Q, Sun Y, Zhao M, Liu M. A virtual structure formation guidance strategy for multi-parafoil systems. IEEE Access. 2019;7:123592–603. doi:10.1109/ACCESS.2019.2938078. [Google Scholar] [CrossRef]

120. Dong L, Chen Y, Qu X. Formation control strategy for nonholonomic intelligent vehicles based on virtual structure and consensus approach. Procedia Eng. 2016;137(6):415–24. doi:10.1016/j.proeng.2016.01.276. [Google Scholar] [CrossRef]

121. Riah A, Agustinah T. Formation control of multi-robot using virtual structures with a linear algebra approach. J Adv Res Electr Eng. 2020;4(1). doi:10.12962/j25796216.v4.i1.111. [Google Scholar] [CrossRef]

122. Chen X, Huang F, Zhang Y, Chen Z, Liu S, Nie Y, et al. A novel virtual-structure formation control design for mobile robots with obstacle avoidance. Appl Sci. 2020;10(17):5807. doi:10.3390/app10175807. [Google Scholar] [CrossRef]

123. Li Z, Duan Z. Cooperative control of multi-agent systems: a consensus region approach. Boca Raton, FL, USA: CRC Press; 2017. doi:10.1201/b17571. [Google Scholar] [CrossRef]

124. Zhou S, Dong X, Hua Y, Yu J, Ren Z. Predefined formation-containment control of high-order multi-agent systems under communication delays and switching topologies. IET Control Theory Appl. 2021;15(12):1661–72. doi:10.1049/cth2.12150. [Google Scholar] [CrossRef]

125. Wei M, Yang S, Wu W, Sun B. A multi-objective fuzzy optimization model for multi-type aircraft flight scheduling problem. Transport. 2024;39(4):313–22. doi:10.3846/transport.2024.20536. [Google Scholar] [CrossRef]

126. Ferrari-Trecate G, Egerstedt M, Buffa A, Ji M. Laplacian sheep: a hybrid, stop-go policy for leader-based containment control. In: International Workshop on Hybrid Systems: Computation and Control; 2006. p. 212–26. doi:10.1007/11730637-18. [Google Scholar] [CrossRef]

127. Han L, Dong X, Li Q, Ren Z. Formation-containment control for second-order multi-agent systems with time-varying delays. Neurocomputing. 2016;218(3):439–47. doi:10.1016/j.neucom.2016.09.001. [Google Scholar] [CrossRef]

128. Li T, Li Z, Zhang H, Fei S. Formation tracking control of second-order multi-agent systems with time-varying delay. J Dyn Syst Meas Control. 2018;140(11):111015. doi:10.1115/1.4040327. [Google Scholar] [CrossRef]

129. Li X, Zhu Y, Zhao X, Lu J. Bearing-based prescribed time formation tracking for second-order multi-agent systems. IEEE Trans Circuits Syst II Express Briefs. 2022;69(7):3259–63. doi:10.1109/TCSII.2022.3141735. [Google Scholar] [CrossRef]

130. Zhao J, Yu X, Li X, Wang H. Bearing-only formation tracking control of multi-agent systems with local reference frames and constant-velocity leaders. IEEE Control Syst Lett. 2020;5(1):1–6. doi:10.1109/LCSYS.2020.2999972. [Google Scholar] [CrossRef]

131. Liu C, Wu X, Mao B. Formation tracking of second-order multi-agent systems with multiple leaders based on sampled data. IEEE Trans Circuits Syst II Express Briefs. 2020;68(1):331–5. doi:10.1109/TCSII.2020.3001223. [Google Scholar] [CrossRef]

132. Zheng B, Mu X. Formation-containment control of second-order multi-agent systems with only sampled position data. Int J Syst Sci. 2016;47(15):3609–18. doi:10.1080/00207721.2015.1107148. [Google Scholar] [CrossRef]

133. Zheng B, Mu X. Formation-containment control of sampled-data second-order multi-agent systems with sampling delay. Trans Inst Meas Control. 2018;40(16):4369–81. doi:10.1177/0142331217748190. [Google Scholar] [CrossRef]

134. Xia M, Liu C, Liu F. Formation-containment control of second-order multiagent systems via intermittent communication. Complexity. 2018. doi:10.1155/2018/2501427. [Google Scholar] [CrossRef]

135. Dong X, Hua Y, Zhou Y, Ren Z, Zhong Y. Theory and experiment on formation-containment control of multiple multirotor unmanned aerial vehicle systems. IEEE Trans Autom Sci Eng. 2018;16(1):229–40. doi:10.1109/TASE.2018.2792327. [Google Scholar] [CrossRef]

136. Dong X, Shi Z, Lu G, Zhong Y. Formation-containment analysis and design for high-order linear time-invariant swarm systems. Int J Robust Nonlinear Control. 2015;25(17):3439–56. doi:10.1002/rnc.3274. [Google Scholar] [CrossRef]

137. Dong X, Li Q, Ren Z, Zhong Y. Formation-containment control for high-order linear time-invariant multi-agent systems with time delays. J Franklin Inst. 2015;352(9):3564–84. doi:10.1016/j.jfranklin.2015.05.008. [Google Scholar] [CrossRef]

138. Dong X, Hu G. Time-varying formation tracking for linear multi-agent systems with multiple leaders. IEEE Trans Automat Contr. 2017;62(7):3658–64. doi:10.1109/TAC.2017.2673411. [Google Scholar] [CrossRef]

139. Gong X, Cui Y, Shen J, Feng Z, Huang T. Necessary and sufficient conditions of formation-containment control of high-order multi-agent systems with observer-type protocols. IEEE Trans Cybern. 2020;1–15. doi:10.1109/TCYB.2020.3037133. [Google Scholar] [PubMed] [CrossRef]

140. Zou Z, Yang S, Zhao L. Dual-loop control and state prediction analysis of QUAV trajectory tracking based on biological swarm intelligent optimization algorithm. Sci Rep. 2024;14(1):19091. doi:10.1038/s41598-024-69911-5. [Google Scholar] [PubMed] [CrossRef]

141. Zhang J, Su H. Time-varying formation for linear multi-agent systems based on sampled data with multiple leaders. Neurocomputing. 2019;339(11):59–65. doi:10.1016/j.neucom.2019.02.018. [Google Scholar] [CrossRef]

142. Wang R. Distributed time-varying output formation tracking control for general linear multi-agent systems with multiple leaders and relative output-feedback. IEEE Access. 2021;9:59586–96. doi:10.1109/ACCESS.2021.3073633. [Google Scholar] [CrossRef]

143. Dong X, Li Q, Ren Z, Zhong Y. Output formation-containment analysis and design for general linear time-invariant multi-agent systems. J Franklin Inst. 2016;353(2):322–44. doi:10.1016/j.jfranklin.2015.11.004. [Google Scholar] [CrossRef]

144. Yu J, Dong X, Li Q, Zhang R. Practical time-varying formation tracking for second-order nonlinear multiagent systems with multiple leaders using adaptive neural networks. IEEE Trans Neural Netw Learn Syst. 2018;29(12):6015–25. doi:10.1109/TNNLS.2018.2817880. [Google Scholar] [PubMed] [CrossRef]

145. Han T, Chi M, Guan Z, Hu B, Xiao J, Huang Y. Distributed three-dimensional formation containment control of multiple unmanned aerial vehicle systems. Asian J Control. 2017;19(3):1103–13. doi:10.1002/asjc.1445. [Google Scholar] [CrossRef]

146. Yu J, Dong X, Liang Z, Li Q, Ren Z. Practical time-varying formation tracking for high-order nonlinear multiagent systems with multiple leaders based on the distributed disturbance observer. Int J Robust Nonlinear Control. 2018;28(9):3258–72. doi:10.1002/rnc.4082. [Google Scholar] [CrossRef]

147. Yu J, Xiao W, Dong X, Li Q, Ren Z. Practical formation-containment tracking for multiple autonomous surface vessels system. IET Control Theory Appl. 2019;13(17):2894–905. doi:10.1049/iet-cta.2018.6242. [Google Scholar] [CrossRef]

148. Liu ZW, Hou H, Wang YW. Formation-containment control of multiple underactuated surface vessels with sampling communication via hierarchical sliding mode approach. ISA Trans. 2019;124(2–3):458–67. doi:10.1016/j.isatra.2019.12.003. [Google Scholar] [PubMed] [CrossRef]

149. Su H, Zhang J, Zeng Z. Formation-containment control of multi-robot systems under a stochastic sampling mechanism. Sci China Technol Sci. 2020;63(6):1025–34. doi:10.1007/s11431-019-1451-6. [Google Scholar] [CrossRef]

150. Wang Y, Liu X, Xiao J, Lin X. Output formation-containment of coupled heterogeneous linear systems under intermittent communication. J Franklin Inst. 2017;354(1):392–414. doi:10.1016/j.jfranklin.2016.10.011. [Google Scholar] [CrossRef]

151. Liu C, Wu X, Wan X, Lü J. Time-varying output formation tracking of heterogeneous linear multi-agent systems with dynamical controllers. Neurocomputing. 2021;441(1):36–43. doi:10.1016/j.neucom.2021.01.113. [Google Scholar] [CrossRef]

152. Hua Y, Dong X, Wang J, Li Q, Ren Z. Time-varying output formation tracking of heterogeneous linear multi-agent systems with multiple leaders and switching topologies. J Franklin Inst. 2019;356(1):539–60. doi:10.1016/j.jfranklin.2018.11.006. [Google Scholar] [CrossRef]

153. Altafini C. Consensus problems on networks with antagonistic interactions. IEEE Trans Automat Contr. 2012;58(4):935–46. doi:10.1109/TAC.2012.2224251. [Google Scholar] [CrossRef]

154. Wang J, Han L, D X, L Q, Zhang R. Bipartite antagonistic time-varying formation tracking for multi-agent system. In: 2019 Chinese Control Conference (CCC); 2019. p. 6118–23. doi:10.23919/ChiCC.2019.8866328. [Google Scholar] [CrossRef]

155. Hu J, Xiao Z, Zhou Y, Yu J. Formation control over antagonistic networks. In: Proceedings of the 32nd Chinese Control Conference; 2013. p. 6879–84. [Google Scholar]

156. Lu W, Gao H, Dai M. Collective four-group antagonistic formation motion. In: Proceedings of the 33rd Chinese Control Conference; 2014. p. 1293–8. doi:10.1109/ChiCC.2014.6896815. [Google Scholar] [CrossRef]

157. Zong C, Ji Z, Tian L, Zhang Y. Distributed multi-robot formation control based on bipartite consensus with time-varying delays. IEEE Access. 2019;7:144790–98. doi:10.1109/ACCESS.2019.2942642. [Google Scholar] [CrossRef]

158. Li W, Zhang H, Cai Y, Wang Y. Fully distributed event-triggered bipartite formation tracking for multi-agent systems with multiple leaders and matched uncertainties. Inf Sci. 2022;596(2):537–50. doi:10.1016/j.ins.2022.03.033. [Google Scholar] [CrossRef]

159. Lu W, Zong C, Li J, Liu D. Bipartite consensus-based formation control of high-order multi-robot systems with time-varying delays. Trans Inst Meas Control. 2022;44(6):1297–308. doi:10.1177/01423312211049896. [Google Scholar] [CrossRef]

160. Liu Y, Xie W, Zhao Y, Huang W. Leader-following bipartite formation control of multiple nonholonomic robot systems over signed graph. J Phys Conf Ser. 2021;1754(1):012141. doi:10.1088/1742-6596/1754/1/012141. [Google Scholar] [CrossRef]

161. Wang W, Wang L, Huang C. Event-triggered control for guaranteed-cost bipartite formation of multi-agent systems. IEEE Access. 2021;10(8):18338–51. doi:10.1109/ACCESS.2021.3086404. [Google Scholar] [CrossRef]

162. Liang J, Bu X, Cui L, Hou Z. Data-driven bipartite formation for a class of nonlinear MIMO multi-agent systems. IEEE Trans Neural Netw Learn Syst. 2021. [Google Scholar]

163. Cai Y, Zhang H, Wang Y, Gao Z, He Q. Adaptive bipartite fixed-time time-varying output formation-containment tracking of heterogeneous linear multi-agent systems. IEEE Trans Neural Netw Learn Syst. 2021;33(9):4688–98. doi:10.1109/TNNLS.2021.3059763. [Google Scholar] [PubMed] [CrossRef]

164. Zhang J, Zhang H, Ming Z, Mu Y. Adaptive event-triggered time-varying output bipartite formation containment of multi-agent systems under directed graphs. IEEE Trans Neural Netw Learn Syst. 2022. doi:10.1109/JAS.2024.124260. [Google Scholar] [CrossRef]

165. Wang W, Zhang W, Yan C, Fang Y. Distributed adaptive bipartite time-varying formation control for heterogeneous unknown nonlinear multi-agent systems. IEEE Access. 2021;9:52698–707. doi:10.1109/ACCESS.2021.3068966. [Google Scholar] [CrossRef]

166. Li W, Zhang H, Zhou Y, Wang Y. Bipartite formation tracking for multi-agent systems using fully distributed dynamic edge-event-triggered protocol. IEEE/CAA J Autom Sin. 2022;99(5):1–7. doi:10.1109/JAS.2021.1004377. [Google Scholar] [CrossRef]

167. Zhang H, Li W, Zhang J, Wang Y, Sun J. Fully distributed dynamic event-triggered bipartite formation tracking for multiagent systems with multiple nonautonomous leaders. IEEE Trans Neural Netw Learn Syst. 2022;34(10):7453–66. doi:10.1109/tnnls.2022.3143867. [Google Scholar] [PubMed] [CrossRef]

168. Cai Y, Zhang H, Gao Z, Yang L, He Q. Adaptive bipartite event-triggered time-varying output formation tracking of heterogeneous linear multi-agent systems under signed directed graph. IEEE Trans Neural Netw Learn Syst. 2022;33(9):4688–98. doi:10.1109/TNNLS.2021.3059763. [Google Scholar] [PubMed] [CrossRef]

169. Dong X, Li Q, Zhao Q, Ren Z. Time-varying group formation analysis and design for second-order multi-agent systems with directed topologies. Neurocomputing. 2016;205(9):367–74. doi:10.1016/j.neucom.2016.04.030. [Google Scholar] [CrossRef]

170. Dong X, Li Q, Zhao Q, Ren Z. Time-varying group formation analysis and design for general linear multi-agent systems with directed topologies. Int J Robust Nonlinear Control. 2017;27(9):1640–52. doi:10.1002/rnc.3650. [Google Scholar] [CrossRef]

171. Yu J, Wang L. Group consensus in multi-agent systems with switching topologies and communication delays. Syst Control Lett. 2010;59(6):340–8. doi:10.1016/j.sysconle.2010.03.009. [Google Scholar] [CrossRef]

172. Hu J, Bhowmick P, Jang I, Arvin F, Lanzon A. A decentralized cluster formation containment framework for multirobot systems. IEEE Trans Robot. 2021;37(6):1936–55. doi:10.1109/TRO.2021.3071615. [Google Scholar] [CrossRef]

173. Hu J, Chen B, Ghosh BK. Formation-circumnavigation switching control of multiple ODIN systems via finite-time intermittent control strategies. IEEE Trans Control Netw Syst. 2024;11(4):1986–97. doi:10.1109/TCNS.2024.3371597. [Google Scholar] [CrossRef]

174. Han L, Xie Y, Li X, Dong X, Li Q, Ren Z. Time-varying group formation tracking control for second-order multi-agent systems with communication delays and multiple leaders. J Franklin Inst. 2020;357(14):9761–80. doi:10.1016/j.jfranklin.2020.07.048. [Google Scholar] [CrossRef]

175. Wang Q, Hu J, Wu Y, Zhao Y. Output synchronization of wide-area heterogeneous multi-agent systems over intermittent clustered networks. Inf Sci. 2023;619(1):263–75. doi:10.1016/j.ins.2022.11.035. [Google Scholar] [CrossRef]

176. Jin T, Liu ZW, Zhou H. Cluster formation for multi-agent systems under disturbances and unmodeled uncertainties. IET Control Theory Appl. 2017;11(15):2630–5. doi:10.1049/iet-cta.2016.1660. [Google Scholar] [CrossRef]

177. Tian L, Hua Y, Dong X, Lv J, Ren Z. Distributed time-varying group formation tracking for multi-agent systems with switching interaction topologies via adaptive control protocols. IEEE Trans Ind Informat. 2022;18(12):8422–33. doi:10.1109/TII.2022.3149912. [Google Scholar] [CrossRef]

178. Li M, Ma Q, Zhou C, Qin J, Kang Y. Distributed time-varying group formation control for generic linear systems with observer-based protocols. Neurocomputing. 2020;397(4):244–52. doi:10.1016/j.neucom.2020.01.065. [Google Scholar] [CrossRef]

179. Ge X, Han QL, Zhang XM. Achieving cluster formation of multi-agent systems under aperiodic sampling and communication delays. IEEE Trans Ind Electron. 2017;65(4):3417–26. doi:10.1109/TIE.2017.2752148. [Google Scholar] [CrossRef]

180. Ma L, Wang YL, Han QL. H∞ cluster formation control of networked multi-agent systems with stochastic sampling. IEEE Trans Cybern. 2021;51(12):5761–72. doi:10.1109/TCYB.2019.2959201. [Google Scholar] [PubMed] [CrossRef]

181. Zhang S, Li T, Cheng X, Li J, Xue B. Multi-group formation tracking control for second-order nonlinear multi-agent systems using adaptive neural networks. IEEE Access. 2021;9:168207–15. doi:10.1109/ACCESS.2021.3137205. [Google Scholar] [CrossRef]

182. Wang W, Huang C, Cao J, Alsaadi FE. Event-triggered control for sampled-data cluster formation of multi-agent systems. Neurocomputing. 2017;267(3):25–35. doi:10.1016/j.neucom.2017.04.028. [Google Scholar] [CrossRef]

183. Long S, Huang W, Wang J, Liu J, Gu Y, Wang Z. A fixed-time consensus control with prescribed performance for multi-agent systems under full-state constraints. IEEE Trans Autom Sci Eng. 2024;22:1–10. doi:10.1109/TASE.2024.3445135. [Google Scholar] [CrossRef]

184. Yin Y, Wang Z, Zheng L, Su Q, Guo Y. Autonomous UAV navigation with adaptive control based on deep reinforcement learning. Electronics. 2024;13(13):2432. doi:10.3390/electronics13132432. [Google Scholar] [CrossRef]

185. Gao N, Zeng Y, Wang J, Wu D, Zhang C, Song Q, et al. Energy model for UAV communications: experimental validation and model generalization. China Commun. 2021;18(7):253–64. doi:10.23919/JCC.2021.07.020. [Google Scholar] [CrossRef]

186. Zhu W, Cao W, Jiang Z. Distributed event-triggered formation control of multiagent systems via complex-valued Laplacian. IEEE Trans Cybern. 2019;51(4):2178–87. doi:10.1109/TCYB.2019.2908190. [Google Scholar] [PubMed] [CrossRef]

187. Li T, Li Z, Shen S, Fei S. Extended adaptive event-triggered formation tracking control of a class of multi-agent systems with time-varying delay. Neurocomputing. 2018;316(4):386–98. doi:10.1016/j.neucom.2018.08.019. [Google Scholar] [CrossRef]

188. Liu X, Ge SS, Goh CH, Li Y. Event-triggered coordination for formation tracking control in constrained space with limited communication. IEEE Trans Cybern. 2018;49(3):1000–11. doi:10.1109/TCYB.2018.2794139. [Google Scholar] [PubMed] [CrossRef]

189. Yi X, Wei J, Dimarogonas DV, Johansson KH. Formation control for multi-agent systems with connectivity preservation and event-triggered controllers. IFAC-PapersOnLine. 2017;50(1):9367–73. doi:10.1016/j.ifacol.2017.08.1444. [Google Scholar] [CrossRef]

190. Li X, Dong X, Li Q, Ren Z. Event-triggered time-varying formation control for general linear multi-agent systems. J Franklin Inst. 2019;356(17):10179–95. doi:10.1016/j.jfranklin.2018.01.025. [Google Scholar] [CrossRef]

191. Chai X, Liu J, Yu Y, Xi J, Sun C. Practical fixed-time event-triggered time-varying formation tracking control for disturbed multi-agent systems with continuous communication free. Unmanned Syst. 2021;9(1):23–34. doi:10.1142/S2301385021500035. [Google Scholar] [CrossRef]

192. Namerikawa T, Toyota R, Kotani K, Akiyama M. Event-triggered and self-triggered formation control of a multi-agent system. Artif Life Robot. 2020;25(4):513–22. doi:10.1007/s10015-020-00646-y. [Google Scholar] [CrossRef]

193. Deng J, Li K, Wu S, Wen Y. Distributed adaptive time-varying formation tracking control for general linear multi-agent systems based on event-triggered strategy. IEEE Access. 2020;8:13204–17. doi:10.1109/ACCESS.2020.2966042. [Google Scholar] [CrossRef]

194. Cai Y, Zhang H, Wang Y, Zhang J, He Q. Fixed-time time-varying formation tracking for nonlinear multi-agent systems under event-triggered mechanism. Inf Sci. 2021;564(4):45–70. doi:10.1016/j.ins.2021.02.071. [Google Scholar] [CrossRef]

195. Chu X, Peng Z, Wen G, Rahmani A. Distributed formation tracking of multi-robot systems with nonholonomic constraint via event-triggered approach. Neurocomputing. 2018;275(6):121–31. doi:10.1016/j.neucom.2017.05.007. [Google Scholar] [CrossRef]

196. Yang J, Xiao F, Chen T. Event-triggered formation tracking control of nonholonomic mobile robots without velocity measurements. Automatica. 2020;112(10):108671. doi:10.1016/j.automatica.2019.108671. [Google Scholar] [CrossRef]

197. Yan B, Shi P, Lim CC. Robust formation control for nonlinear heterogeneous multiagent systems based on adaptive event-triggered strategy. IEEE Trans Autom Sci Eng. 2021;19(4):2788–800. doi:10.1109/TASE.2021.3103877. [Google Scholar] [CrossRef]

198. Van Tran Q, Trinh MH, Zelazo D, Mukherjee D, Ahn H-S. Finite-time bearing-only formation control via distributed global orientation estimation. IEEE Trans Control Netw Syst. 2019;6(2):702–12. doi:10.1109/TCNS.2018.2873155. [Google Scholar] [CrossRef]

199. Han T, Guan ZH, Liao RQ, Chen J, Chi M, He DX. Distributed finite-time formation tracking control of multi-agent systems via FTSMC approach. IET Control Theory Appl. 2017;11(15):2585–90. doi:10.1049/iet-cta.2016.1619. [Google Scholar] [CrossRef]

200. Qiu Z, Zhao X, Li S, Xie Y, Chen C, Gui W. Finite-time formation of multiple agents based on multiple virtual leaders. Int J Syst Sci. 2018;49(16):3448–58. doi:10.1080/00207721.2018.1542754. [Google Scholar] [CrossRef]

201. Lan Y, Zhao J. Improving track performance by combining Padé-approximation-based preview repetitive control and equivalent-input-disturbance. J Electr Eng Technol. 2024;19(6):3781–94. doi:10.1007/s42835-024-01830-x. [Google Scholar] [CrossRef]

202. Du H, Li S, Lin X. Finite-time formation control of multiagent systems via dynamic output feedback. Int J Robust Nonlinear Control. 2012;23(14):1609–28. doi:10.1002/rnc.2849. [Google Scholar] [CrossRef]

203. Liu Y, Geng Z. Finite-time formation control for linear multi-agent systems: a motion planning approach. Syst Control Lett. 2015;85(1):54–60. doi:10.1016/j.sysconle.2015.08.009. [Google Scholar] [CrossRef]

204. Du H, Yang C, Ruting J. Finite-time formation control of multiple mobile robots. In: IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER); 2016 May. p. 416–21. doi:10.1109/CYBER.2016.7574861. [Google Scholar] [CrossRef]

205. Cheng Y, Jia R, Du H, Wen G, Zhu W. Robust finite-time consensus formation control for multiple nonholonomic wheeled mobile robots via output feedback. Int J Robust Nonlinear Control. 2018;28(6):2082–96. doi:10.1002/rnc.4002. [Google Scholar] [CrossRef]

206. Li Y, Ruohan Y. Distributed finite-time formation of networked nonlinear systems via dynamic gain control. Asian J Control. 2022;24(6):3299–310. doi:10.1002/asjc.2719. [Google Scholar] [CrossRef]

207. Mei F, Wang H, Yao Y, Fu J, Yuan X, Yu W. Robust second-order finite-time formation control of heterogeneous multi-agent systems on directed communication graphs. IET Control Theory Appl. 2020;14(6):816–23. doi:10.1049/iet-cta.2019.0212. [Google Scholar] [CrossRef]

208. Wang G, Wang X, Li S. Signal generator based finite-time formation control for disturbed heterogeneous multi-agent systems. J Franklin Inst. 2022;359(2):1041–61. doi:10.1016/j.jfranklin.2021.11.023. [Google Scholar] [CrossRef]

209. Fei Y, Shi P, Lim CC. Neural-based formation control of uncertain multi-agent systems with actuator saturation. Nonlinear Dyn. 2022;108(4):3693–709. doi:10.1007/s11071-022-07434-2. [Google Scholar] [CrossRef]

210. Yu J, Dong X, Han L, Li Q, Ren Z. Practical time-varying output formation tracking for high-order nonlinear strict-feedback multi-agent systems with input saturation. ISA Trans. 2020;98(2–3):63–74. doi:10.1016/j.isatra.2019.08.019. [Google Scholar] [PubMed] [CrossRef]

211. Shojaei K. Output-feedback formation control of wheeled mobile robots with actuators saturation compensation. Nonlinear Dyn. 2017;89(4):2867–78. doi:10.1007/s11071-017-3631-x. [Google Scholar] [CrossRef]

212. González A, Aranda M, López-Nicolás G, Sagüés C. Robust stability analysis of formation control in local frames under time-varying delays and actuator faults. J Franklin Inst. 2019;356(2):1131–53. doi:10.1016/j.jfranklin.2018.06.020. [Google Scholar] [CrossRef]

213. Chang Y, Wu C, Lin H. Adaptive distributed fault-tolerant formation control for multi-robot systems under partial loss of actuator effectiveness. Int J Control Autom Syst. 2018;16(5):2114–24. doi:10.1007/s12555-016-0587-4. [Google Scholar] [CrossRef]

214. Vazquez Trejo JA, Theilliol D, Adam Medina M, García Beltrán CD, Witczak M. Leader-following formation control for networked multi-agent systems under communication faults/failures. Adv Diagn Process Syst. 2020;45–57. doi:10.1007/978-3-030-58964-6-4. [Google Scholar] [CrossRef]

215. Hua Y, Dong X, Li Q, Ren Z. Fault-tolerant time-varying formation tracking for second-order multi-agent systems with actuator faults and a non-cooperative target. IFAC-PapersOnLine. 2018;51(24):68–73. doi:10.1016/j.ifacol.2018.09.530. [Google Scholar] [CrossRef]

216. Khalili M, Zhang X, Gilson MA, Cao Y. Distributed fault-tolerant formation control of cooperative mobile robots. IFAC-PapersOnLine. 2018;51(24):459–64. doi:10.1016/j.ifacol.2018.09.617. [Google Scholar] [CrossRef]

217. Hentout A, Maoudj A, Ouahal M, Gasmi A. Fault-tolerant multi-agent scheme for leader/follower formation control of homogeneous mobile robot team. Int J Syst Control Commun. 2019;10(2):95–125. doi:10.1504/IJSCC.2019.098977. [Google Scholar] [CrossRef]

218. Wang Z, Wu Y, Li T, Zhang H. Adaptive fault-tolerant time-varying formation tracking for multi-agent systems with multiple leaders. Int J Robust Nonlinear Control. 2019;29(6):1807–22. doi:10.1002/rnc.4459. [Google Scholar] [CrossRef]

219. Ren Y, Zhang K, Jiang B, Cheng W, Yong D. Distributed fault-tolerant time-varying formation control of heterogeneous multi-agent systems. Int J Robust Nonlinear Control. 2022;32(5):2864–82. doi:10.1002/rnc.5870. [Google Scholar] [CrossRef]

220. Gong J, Ma Y, Jiang B, Zehui M. Distributed adaptive fault-tolerant formation control for heterogeneous multi-agent systems under switching directed topologies. J Franklin Inst. 2022;359(8):3366–88. doi:10.1016/j.jfranklin.2022.03.048. [Google Scholar] [CrossRef]

221. Van Vu D, Trinh MH, Nguyen PD, Ahn HS. Distance-based formation control with bounded disturbances. IEEE Control Syst Lett. 2020;5(2):451–6. doi:10.1109/LCSYS.2020.3003418. [Google Scholar] [CrossRef]

222. Yao H, Wu J, Xi J, Wang L. Active disturbance rejection controller based time-varying formation tracking for second-order multi-agent systems with external disturbances. IEEE Access. 2019;7:153317–26. doi:10.1109/ACCESS.2019.2948377. [Google Scholar] [CrossRef]

223. Wang J, Xu Y, Xu Y, Yang D. Time-varying formation for high-order multi-agent systems with external disturbances by event-triggered integral sliding mode control. Appl Math Comput. 2019;359(2):333–43. doi:10.1016/j.amc.2019.04.066. [Google Scholar] [CrossRef]

224. Jiang W, Wang C, Meng Y. Fully distributed time-varying formation tracking control of linear multi-agent systems with input delay and disturbances. Syst Control Lett. 2020;146(6):104814. doi:10.1016/j.sysconle.2020.104814. [Google Scholar] [CrossRef]

225. Hua Y, Dong X, Han L, Li Q, Ren Z. Finite-time time-varying formation tracking for high-order multiagent systems with mismatched disturbances. IEEE Trans Syst Man Cybern Syst. 2018;50(10):3795–803. doi:10.1109/TSMC.2018.2867548. [Google Scholar] [CrossRef]

226. Yang X, Fan X. Robust formation control for uncertain multi-agent systems with an unknown control direction and disturbances. IEEE Access. 2019;7:106439–52. doi:10.1109/ACCESS.2019.2932234. [Google Scholar] [CrossRef]

227. Ran M, Xie L, Li J. Time-varying formation tracking for uncertain second-order nonlinear multi-agent systems. Front Inf Technol Electron Eng. 2019;20(1):76–87. doi:10.1631/FITEE.1800557. [Google Scholar] [CrossRef]

228. Alotaibi ET, Alqefari SS, Koubaa A. LSAR: multi-UAV collaboration for search and rescue missions. IEEE Access. 2019;7:55817–32. doi:10.1109/ACCESS.2019.2912306. [Google Scholar] [CrossRef]

229. Liu Y, Li W, Dong X, Ren Z. Resilient formation tracking for networked swarm systems under malicious data deception attacks. Int J Robust Nonlinear Control. 2024;35(6):2043–52. doi:10.1002/rnc.7777. [Google Scholar] [CrossRef]

230. Bandyopadhyay S, Foust R, Subramanian GP, Chung S, Hadaegh FY. Review of formation flying and constellation missions using nanosatellites. J Spacecr Rockets. 2016;53(3):567–78. doi:10.2514/1.A33291. [Google Scholar] [CrossRef]

231. Yang S, Du Y, Wang W, Chen J, Wu J. A novel navigation approach of low Earth orbit satellites formation based on reduced relative orbital elements. Adv Guid Navig Control. 2022;644:343–54. doi:10.1007/978-981-15-8155-7. [Google Scholar] [CrossRef]

232. Cao X, Guo L. A leader-follower formation control approach for target hunting by multiple autonomous underwater vehicles in three-dimensional underwater environments. Int J Adv Robot Syst. 2019;16(4):1729881419870664. doi:10.1177/1729881419870664. [Google Scholar] [CrossRef]

233. Li Z, You K, Song S. AUV-based source seeking with estimated gradients. J Syst Sci Complex. 2018;31(1):262–75. doi:10.1007/s11424-018-7373-8. [Google Scholar] [CrossRef]

234. Wang T, Huang P, Dong G. Cooperative persistent surveillance on a road network by multi-UGVs with detection ability. IEEE Trans Ind Electron. 2021;69(11):11468–78. doi:10.1109/TIE.2021.3121729. [Google Scholar] [CrossRef]

235. Litimein H, Huang ZY, Hamza A. A survey on techniques in the circular formation of multi-agent systems. Electronics. 2021;10(23):2959. doi:10.3390/electronics10232959. [Google Scholar] [CrossRef]