Multi-View Picture Fuzzy Clustering: A Novel Method for Partitioning Multi-View Relational Data

1  Introduction

In the era of big data, multi-view data has become increasingly significant due to its ability to provide complementary information from different perspectives. This data type is extensively utilized in areas such as data science, pattern recognition, and relational data analysis [1,2], providing a holistic view of complex phenomena. Multi-view data supports the discovery of complex patterns and hidden relationships that are often overlooked when considering a single view [1–3]. However, exploiting multi-view data presents significant challenges, including the need to effectively combine, aggregate, and compare information across views while also addressing the inherent uncertainty that exists in real-world data [4,5].

A variety of methods have been developed to address the challenges associated with multi-view data. Traditional techniques, such as Fuzzy C-Means (FCM) and its variants, have been widely used to uncover latent patterns; however, they encounter limitations in fully exploiting the multi-view nature of the data [6,7]. To overcome these limitations, multi-view clustering methods have been proposed to simultaneously process information from multiple views, thereby reducing uncertainty and improving clustering accuracy [8–11]. One such approach is graph-based multi-view clustering, which has become a key technique in this area [12–14]. In [12], a novel algorithm, robust graph-based multi-view clustering (RG-MVC), is proposed to overcome the non-convexity and local optimum issues in traditional graph-based multi-view clustering (G-MVC). The proposed Graph-based Multi-view Clustering (GMC) technique overcomes the limitations of current multi-view clustering methods by combining the data graph matrices from all views into a unified graph matrix [15]. Subsequently, the unified graph matrix enhances the individual graph matrices of each view and directly produces the final clusters. The proposed bipartite graph-based multi-view clustering (BIGMC) method tackles the challenge of capturing consensus cluster structures by learning similarity graph matrices for various views and merging them into a unified graph matrix [16]. BIGMC constructs bipartite graph matrices for each view and integrates representative anchor points to capture consensus information. It then optimizes the objective function in an alternating fashion, adapting weights for each view and enforcing a low-rank constraint to ensure robust clustering. However, existing graph-based methods still face significant challenges, particularly due to the high computational cost associated with the time-consuming processes of learning similarity matrices, calculating spectral embeddings, and discretizing them.

To mitigate these issues, recent research has shifted focus to anchor graph-based methods [17–19]. These methods select representative anchor instances from multi-view data, which are then used to generate anchor graphs for clustering. For example, Zhang et al. proposed a flexible method for exploring multi-view data by learning multi-group anchor instances and multi-level anchor graphs for each view, along with a fusion mechanism to combine these graphs efficiently [13]. CAMVC, another advanced technique introduced by Zhang et al., is a dynamic Cluster-wise Anchor learning-based MVC model that assumes an initial clustering arrangement for target anchors through a consensus-based cluster indicator matrix. This approach establishes a clear cluster pattern for hidden anchors by learning a variety of centroids, thereby improving both the diversity between clusters and the consistency within clusters, which leads to better subspace representation discrimination [20]. Despite these advances, challenges remain, particularly when applying these methods to data with complex structures and high dependencies, such as in relational data environments [21].

To model uncertainty more effectively, Bui Cong Cuong introduced the concept of Picture Fuzzy Sets (PFS) [22], which is a direct extension of fuzzy sets and Intuitionistic Fuzzy Sets (IFS) [23]. This extension is achieved by integrating advanced mechanisms that represent degrees of membership degrees, neutral degrees, and refusal degrees [22]. In the study [7], the Fuzzy Clustering method on PFS (FC-PFS) clustering method was proposed, demonstrating superior performance compared to the standard fuzzy clustering method, particularly when handling noisy data. This improvement is attributed to the fact that FC-PFS uses PFS, which involve four key attributes: positive membership, neutral membership, negative membership, and refusal membership, each indicating the degree of membership for each data point in relation to the clusters. Although significant progress has been made in handling uncertainty, current methods based on PFS have not yet been optimized for integrating multi-view information, which limits their overall clustering accuracy [24].

Recently, a number of advanced methods for multi-view clustering have been introduced. For example, semi-supervised fuzzy clustering, which uses consensus between views to handle relational data [25], and deep multi-view clustering, such as the SDMVC method [11]. The SDMVC technique adopts a self-supervised discriminative feature extraction framework for deep multi-view clustering, leveraging auto-encoders to autonomously capture embedded representations from individual perspectives. These representations are then integrated into global feature spaces to mitigate the adverse effects caused by ambiguous clustering patterns. This approach has demonstrated effectiveness in enhancing clustering accuracy, particularly by optimizing the exploitation of inter-view dependencies. Zhang et al. [17] introduced the Dual Anchor Graph Fuzzy Clustering (DAG_FC) approach, specifically designed for handling multi-view data. This method applies matrix factorization to refine the data, enhancing latent representations and anchor graphs while using a unified optimization process to construct both common and view-specific anchor graphs, thereby improving accuracy and representational power. Shi et al. [26] proposed the Enhanced Latent Multi-view Subspace Clustering (ELMSC) method, which overcomes the limitations of traditional latent multi-view subspace clustering by constructing an augmented data matrix that integrates both complementary and consistent information. The ELMSC method enhances clustering performance through sparse regularization and an iterative algorithm based on the ADMM. However, these methods still encounter challenges in modeling uncertainty and integrating information from multiple views, particularly when the data is noisy or the views are inconsistent. These limitations highlight the need for more robust and flexible multi-view clustering solutions, especially in the context of relational data with high-dimensional feature spaces and large-scale datasets [27].

To address these challenges, we propose a novel clustering method that integrates picture fuzzy sets with a dual-anchor graph-based fuzzy clustering approach designed explicitly for multi-view data. The main objectives of this study are to: (i) Improve clustering accuracy by extracting highly discriminative latent representations from multi-view data using a dual-anchor graph mechanism; (ii) Effectively handle uncertainty in real-world datasets through the integration of Picture Fuzzy Sets, which represent positive, neutral, negative, and refusal degrees of membership; (iii) Integrate multi-view information in a robust and scalable manner by simultaneously capturing both shared and view-specific patterns through dual-anchor graph construction; (iv) Enhance the stability and interpretability of clustering results by optimizing fuzzy membership learning with low-rank representation and entropy-based regularization techniques.

The primary contributions of this paper are as follows:

(1)   This paper introduces a novel multi-view clustering method based on picture fuzzy set theory and dual-anchor graphs, which effectively leverages dual-anchor graphs by constructing a fuzzy membership structure preservation mechanism and minimizing negative Shannon entropy while also addressing the inherent uncertainty in multi-view data.

(2)   Conducting extensive experimental evaluations to demonstrate the effectiveness of the proposed method across multiple multi-view datasets, thereby enhancing clustering accuracy and robustness.

Unlike existing methods, our proposed method is the first to combine Picture Fuzzy Sets with dual anchor graph learning to simultaneously address uncertainty and structure in multi-view data.

The structure of the paper is as follows: Section 2 outlines the theoretical foundations, Section 3 provides a detailed description of the proposed method, Section 4 presents the experimental results, analysis, and comparative evaluation, and Section 5 concludes the paper by summarizing key findings and suggesting directions for future research.

2  Related Work

2.1 Multi-View Clustering: Challenges and Advances

Multi-view clustering (MVC) is a technique designed to leverage complementary information from multiple views or feature sets of the same data to enhance clustering accuracy and robustness. By integrating diverse sources of information, MVC allows for a more comprehensive understanding of the data structure. Traditional methods, such as co-training [1] and Canonical Correlation Analysis (CCA) [28], laid the foundation for cross-view integration. These techniques mainly focused on linear relationships between views and provided early insights into how to combine information effectively across multiple representations. However, such approaches have limitations in capturing nonlinear dependencies and are highly sensitive to noise and outliers present in the raw data.

To address these shortcomings, more recent advances have shifted toward graph-based representations. In these methods, similarity matrices or anchor graphs are constructed for each view, which are then fused to capture shared cluster structures [12–15]. This approach enhances the ability to model complex data relationships, but it still assumes linear relationships and is vulnerable to noise, which can degrade clustering accuracy. As a result, these methods struggle in environments where the data exhibits high variability or contains significant outliers.

The introduction of deep learning has marked a significant breakthrough in MVC, as it allows for modeling complex, nonlinear relationships between views. Deep learning-based MVC methods, such as Deep Canonical Correlation Analysis (DCCA) [29] and Self-supervised Discriminative Feature Learning for Deep Multi-view Clustering (SDMVC) [11], use deep neural networks to project each view into a latent space. These projections are then aligned or fused for clustering. By learning a shared latent space for all views, deep learning models are better equipped to handle nonlinear dependencies. Additionally, Graph Neural Networks (GNNs) have been applied to MVC to improve graph-based methods. GNNs learn adaptive edge weights and propagate information across view-specific graphs, improving the ability to capture intricate relationships between views and enhancing clustering performance [30]. Despite the advantages offered by deep learning techniques, they require substantial computational resources for training and often rely on large amounts of data. Furthermore, these models are not explicitly designed to handle uncertainty or conflicting information between views, which is a critical challenge when dealing with noisy or partially unreliable data. For instance, many deep models assume that the available data is largely complete and accurate, which is often not the case in real-world applications.

A recent advancement in the field is the Elastic Deep Multi-view Autoencoder with Diversity Embedding (EDMVAE-DE), introduced by Daneshfar et al. [31]. This model combines an elastic deep autoencoder with a diversity constraint and graph regularization to jointly address challenges such as noise sensitivity, feature redundancy, and manifold preservation. Specifically, the elastic loss function, which combines Frobenius and L2,1 norms, helps improve robustness against both Gaussian and Laplacian noise. The model also imposes orthogonality constraints on the latent features across views, encouraging complementary representations. In addition, Laplacian-based graph regularization helps preserve the intrinsic geometric structure of the data. Unlike earlier approaches that decouple representation learning and clustering, EDMVAE-DE integrates both tasks within an end-to-end framework, making it more efficient and effective.

Although deep learning-based approaches show promising results, there is a need for more flexible frameworks that can effectively handle uncertainty and conflicting information in multi-view clustering, particularly with noisy or incomplete data.

2.2 Picture Fuzzy Sets in Multi-View Clustering

(a) Picture Fuzzy Sets in Traditional Fuzzy Clustering

Fuzzy clustering is a fundamental technique in data mining and machine learning, widely used to analyze datasets with ambiguous or overlapping boundaries. The classical Fuzzy C-Means (FCM) algorithm assigns each data point to multiple clusters based on fuzzy membership values derived from the distances between points and cluster centroids. While FCM is computationally efficient and effective for datasets with uncertain boundaries, it is limited in handling noisy data and complex uncertainty structures due to its inability to model hesitation or ambiguity explicitly [7].

To overcome these limitations, more expressive models such as Type-2 Fuzzy Sets (T2FS) [32,33] and Intuitionistic Fuzzy Sets (IFS) [34] have been introduced. T2FS extends classical fuzzy sets by allowing membership degrees to be represented as intervals, thereby introducing the concept of the Footprint of Uncertainty (FOU). Although powerful, T2FS suffers from high computational cost and complex parameter tuning, especially in large-scale scenarios [33]. IFS improves upon FCM by including a degree of hesitation in addition to membership and non-membership values, offering better handling of incomplete or contradictory information. However, IFS still lacks the ability to explicitly express neutrality and is computationally more demanding.

Building on these developments, Picture Fuzzy Sets (PFS), introduced by Cuong [22], further extend IFS by incorporating a neutral membership degree and a refusal degree, thereby providing a richer representation of uncertainty. PFS has been successfully applied in tasks such as weather forecasting [24,35], where multiple levels of uncertainty and conflict exist. However, this increased expressive power comes with a drawback: it has the highest computational cost among fuzzy clustering techniques, making it unfeasible for very large-scale problems [7].

The PFS, introduced by Cuong [22], extends the IFS [23] by adding a parameter called the refusal degree (ξ(x)), alongside the positive membership (μ(x)), neutral degree (η(x)), and negative membership (γ(x)) values. A Picture Fuzzy Set in a non-empty set X satisfies the following constraints:

A={(x,μ(x),η(x),γ(x))|x∈X}μ(x)+η(x)+γ(x)+ξ(x)=1,∀x∈X(1)

where μ(x), η(x) and γ(x) represent the positive membership, neutral degree, and negative membership of the element x in the set X, and ξ(x) is the refusal degree.

The degree of refusal of an element is computed as follows:

ξ(x)=1−(μ(x)+η(x)+γ(x)),∀x∈X(2)

if ξ(x)=0, the PFS becomes an IFS. Similarly, if ξ(x)=η(x)=0, the PFS becomes a classical fuzzy set.

Compared to IFS, which implicitly models hesitation, PFS provides explicit modeling of neutral and refusal states, enabling it to capture complex forms of ambiguity. Neutrosophic Sets (NS) offer even more generality by allowing truth, indeterminacy, and falsity values to vary independently. However, their lack of constraint and difficult parameter control make them less practical in clustering applications. In contrast, PFS offers a balanced trade-off between expressiveness and computational manageability, making it well-suited for tasks involving structured uncertainty and partial conflict.

Advanced fuzzy clustering techniques like IFS and PFS primarily focus on modeling uncertainty in data from a single view. However, as multi-view data becomes increasingly prevalent, multi-view clustering methods address a broader challenge by integrating different perspectives or feature sets from datasets. This shift underscores the need for uncertainty modeling techniques that not only address ambiguity within each view but can also reconcile conflicting or inconsistent information across views—something that PFS is uniquely positioned to address.

(b) Potential of PFS in Multi-View Clustering

While PFS has demonstrated strong performance in modeling uncertainty in single-view clustering tasks, such as weather prediction and medical diagnosis, its integration into multi-view clustering frameworks remains limited. This presents an opportunity to explore how PFS can be effectively leveraged to model inconsistencies and complementary relationships across multiple views, where data from different sources may partially agree, contradict, or contain varying levels of confidence.

Multi-view clustering aims to combine feature sets from different views to construct a more comprehensive clustering structure. Hard multi-view clustering methods [5,9] often fail to capture ambiguity across views. More recent methods, such as non-negative matrix factorization (NMF) and deep multi-view clustering techniques [10,11], project data into unified spaces, but often assume linear relationships or require extensive computational resources. Although effective, these methods often rely on assumptions about the linearity of the data or require large computational resources to train deep models, which limits their scalability. In contrast, fuzzy clustering methods are advantageous when working with multi-view data due to their ability to model the overlap between membership values. Multi-view fuzzy clustering techniques integrate membership values from different views to form a unified clustering structure, thereby improving accuracy and flexibility in clustering complex and heterogeneous data scenarios [25,36,37].

Fuzzy clustering techniques are advantageous in multi-view contexts because they naturally model partial memberships across views. However, existing multi-view fuzzy clustering methods still face several challenges: (1) Incomplete utilization of view-specific and shared features, (2) Graph-based methods often build anchor graphs or similarity matrices directly from the raw data, which may contain noise or poor discrimination, reducing clustering performance, (3) Lack of strong integration mechanisms: Current methods struggle with balancing contributions from different views, especially when some views contain noise or are unreliable.

These limitations highlight the lack of effective mechanisms to model and integrate uncertainty across multiple views. Given PFS’s ability to represent multi-dimensional uncertainty through its four membership degrees, it holds strong potential to improve robustness and accuracy in multi-view clustering, particularly in complex, noisy, and high-dimensional datasets. By incorporating PFS into the multi-view clustering paradigm, we aim to bridge the gap between uncertainty modeling and view integration, offering a new approach that is both theoretically sound and practically applicable in real-world multi-view scenarios.

In summary, compared to Intuitionistic Fuzzy Sets (IFS), which represent uncertainty through degrees of membership and non-membership with an implicit hesitation degree, Picture Fuzzy Sets (PFS) introduce two additional explicit components: the neutral degree and the refusal degree. This enables a more nuanced representation of ambiguous or conflicting information, particularly in scenarios where data points do not clearly belong to or reject a specific cluster. Neutrosophic Sets (NS) further generalize the concept of uncertainty by allowing the degrees of truth, indeterminacy, and falsity to be mutually independent. While theoretically flexible, NS-based models often suffer from lack of interpretability, absence of constraints, and increased complexity in parameter tuning, which limit their practical adoption in clustering-especially in high-dimensional or large-scale multi-view datasets.

In contrast, PFS strikes a practical balance by providing richer uncertainty representation than IFS, while maintaining mathematical constraints (i.e., the sum of all degrees is ≤1), ensuring computational tractability. These characteristics make PFS well-suited for multi-view clustering, where multiple views may introduce inconsistencies, contradictions, or partial agreements in the data. Thus, our method leverages PFS to better model real-world uncertainty and improve robustness in clustering performance across heterogeneous views.

2.3 Multi-View Dual Anchor Graph Learning

(a) Multi-View Anchor Graph Learning

Anchor graph learning is an effective method for modeling the intrinsic structure of data by approximating the original dataset with a small set of representative anchor points and constructing a similarity graph to represent the relationships between data points and the anchor points [17]. Given a multi-view dataset {Xl∈Rdl×N|l=1,2,…,L}, where N denotes the number of data samples, L represents the number of views, and dl corresponds to the feature size of the l-th view, the standard multi-view anchor graph learning is defined as follows:

minZl∑l=1L‖Xl−AlZl‖F2Zl≥0,(Zl)T1=1(3)

where Xl∈Rdl×N is the data matrix for the l-th view. Al∈Rdl×m is the anchor matrix for the l-th view, generated using methods such as K-Means or random sampling. m is the number of anchor points, much smaller than N. Zl∈Rm×N is the anchor graph for the l-th view, representing the relationship between the data points and the anchor points. The constraint (Zl)T1=1 ensures that the columns of Zl sum to one, preserving the membership distribution.

Recent studies have introduced several advancements in anchor graph learning to improve its effectiveness: specifically, Ma et al. (2024) [38] introduced the 3AMVC (Multi-view Clustering with Automatic and Aligned Anchor) method, which employs an adaptive anchor selection strategy and automatic anchor alignment to address the challenges of determining the optimal number of anchors and enhancing the representational capacity of anchors across different views in multi-view clustering. Ji et al. (2020) [39] presented an adaptive partial multi-view clustering method (AAPMC) utilizing anchor graphs, which integrates an adaptive neighbor assignment strategy to enhance the computation of similarity matrices. This approach eliminates the necessity for parameter tuning and offers a more efficient solution for handling large-scale datasets. Yang et al. (2022) [18] introduced the ECMC algorithm, which improves clustering performance by combining anchor graph embedding and NMF, while enhancing robustness through correntropy to reduce noise and outliers. ECMC outperforms existing methods in speed and robustness. Yang et al. (2022) [19] proposed the ERMC-AGR algorithm, which enhances anchor graph quality using a novel regularization technique (ARG), reduces computational complexity with a lightweight approach, and improves robustness through correntropy, leading to better clustering efficiency and robustness. Fu et al. (2024) [40] introduced an anchor graph network for incomplete multi-view clustering (IMVC), employing a generative model to construct bipartite graphs, using graph convolution networks (GCNs) to learn structural embeddings, and incorporating an adaptive learning strategy to improve the robustness of bipartite graph construction. This approach significantly reduces computational complexity, enabling efficient handling of large-scale data while achieving superior performance compared to state-of-the-art methods. However, existing anchor graph learning methods still face several challenges: (1) Sensitivity to raw data: Directly constructing graphs from raw data makes these methods vulnerable to noise and redundant data. (2) Overlooking the distinctive features of each view: Most methods focus on the shared information between views, without fully exploiting the unique features of each individual view. (3) Incomplete use of graph information: Many methods do not fully utilize the information from the anchor graph, leading to incomplete improvements in clustering accuracy and robustness. To tackle these challenges, the multi-view dual anchor graph learning method is proposed as an effective solution.

(b) Multi-View Dual Anchor Graph Learning

Current multi-view anchor graph learning techniques can generally be divided into two main categories: (1) methods that directly learn common anchor instances to construct a unified anchor graph [13,41], and (2) methods that simultaneously learn anchor instances and graphs for each view, followed by fusing the individual graphs into a common representation using post-processing techniques [42,43]. Nevertheless, both approaches have limitations in fully leveraging the rich and complementary information inherent in multi-view data. Specifically, these methods struggle to effectively capture both the common information shared across views and the view-specific details. To overcome these limitations, a dual anchor graph learning method is proposed as a more robust approach to simultaneously extract both common and view-specific information from multi-view data [27,44].

Zhang et al. introduced the multi-view dual anchor graph learning (MV_DAGL) algorithm [17]. The objective function is defined as follows:

minBk,Hk,AC,ZC,ASk,ZSkJ1(Bk,Hk)+J2(Hk,AC,ZC,ASk,ZSk)(4)

where J1(Bk,Hk) is used to purify the original multi-view data by applying matrix factorization. J2(Hk,AC,ZC,ASk,ZSk) is used to extract the dual anchor graphs.

The method employs matrix factorization to refine the raw data, eliminating noise and errors, which allows for the extraction of high-quality latent representations for each view. This refinement boosts the discriminative ability of the anchor graphs, thereby improving the efficiency in modeling the relationships between data points and anchor points. The method simultaneously constructs a common anchor graph to capture shared information across all views, along with separate anchor graphs to preserve view-specific features. A key feature of this approach is the unified optimization process that combines latent representation learning with anchor graph learning. This iterative optimization generates complementary interactions between the two components, ultimately improving the accuracy and representational power of the anchor graphs.

The Dual Anchor Graph Fuzzy Clustering (DAG_FC) algorithm is presented, and its objective function is formulated as follows [17]:

minwk,U,VkwK+1∑iN∑lCul,i‖Fc,i−VlK+1‖22+∑kKwk∑iN∑lCul,i‖Fs,ik−Vlk‖22+β∑lC∑iNSc,i,j‖ul,i−ul,j‖22+β∑lC∑iN∑jNSs,i,jk‖ul,i−ul,j‖22+γ∑kK+1wkln⁡(wk)+δ‖U‖F2s.t.∑lcul,i=1,ul,i,wk≥0,∑vV+1wk=1(5)

where Fc,i represents the i-th instance of the common representation, Fs,ik denotes the i-th instance of the k-th specific representation. The membership matrix is given by U=[ul,i]C×N, which is used to determine clustering partitions. The clustering center matrix of the k-th specific representation is denoted as Vk=[vlk]C×C, where as VK+1 corresponds to the clustering center matrix of the common representation. The view weighting factor wk is utilized to adjust the relative importance of different representations. β,γ,δ are hyperparameters, which can be manually set or determined using a cross-validation strategy.

The anchor graph-based multi-view fuzzy clustering method effectively leverages dual anchor graphs by constructing a fuzzy membership structure preservation mechanism and incorporating negative Shannon entropy to enhance clustering performance.

Although dual-anchor graphs have been successfully used in areas like image classification and community detection in social networks, their integration with advanced uncertainty modeling frameworks like PFS has not been thoroughly explored. This combination holds strong potential for improving robustness in multi-view clustering.

2.4 Enhanced Multi-View Latent Subspace Clustering

The Enhanced Latent Multi-view Subspace Clustering (ELMSC) method [26] is introduced to overcome the limitations of latent multi-view subspace clustering, which may result in incomplete information recovery. Rather than simply concatenating data matrices vertically, ELMSC constructs an augmented data matrix by positioning multi-view data in block-diagonal form to leverage complementary information, while non-block-diagonal elements capture the consistency across views. Furthermore, sparse regularization is employed to avoid redundant computations. An iterative algorithm based on ADMM is proposed to optimize the model, with theoretical analysis confirming its convergence.

The mathematical formulation of the is given as follows:

minP,Ha,Za,B1,B2‖B‖2,1+λ‖Za−diag(Za)‖1s.t.Xa=PHa+B1,Ha=HaZa+B2,B=[B1;B2],PPT=I(6)

here, λ is a positive balance parameter, Xa represents an augmented data matrix, Ha denotes the augmented latent representation matrix, and Za refers to the augmented self-representation matrix. B1 and B2 represent the error matrices, while ‖.‖2,1 and ‖.‖1 denote the l2,1-norm and l1-norm operations, respectively. Alternatively, these error matrices can be combined by stacking B1 and B2 into a unified error matrix for further processing.

Research Gap and Motivation:

Despite considerable progress in multi-view clustering, three major gaps remain:

(1)   Most deep or graph-based methods do not explicitly represent uncertainty, which limits interpretability and robustness when views are noisy or partially inconsistent.

(2)   Existing fuzzy clustering methods lack mechanisms to integrate information across views, often treating each view independently or combining them in ad hoc ways.

(3)   Techniques such as PFS and dual-anchor graphs have not yet been fully leveraged together in a unified framework to address both structural and uncertainty-related challenges in multi-view data.

These gaps highlight the need for a novel approach that can jointly model multi-dimensional uncertainty and exploit both common and specific information across views in a principled manner.

3  Proposed Method

Fuzzy clustering methods, such as FC-PFS [7], have significantly advanced in handling uncertainty and ambiguity. However, their integration with multi-view data remains limited due to challenges such as high computational complexity and the difficulty in effectively handling the diverse nature of multi-view data. Similarly, current multi-view clustering techniques still struggle to effectively balance shared information with view-specific information, as well as handle noisy or unreliable views. To address these challenges, this study proposes a novel method that combines PFS and dual-anchor graph fuzzy clustering with multi-view data. The proposed method is called Multi-view Picture Fuzzy Clustering (MPFC). This model is designed to:

•   Represent nuanced uncertainty using four membership components from PFS,

•   Construct dual-anchor graphs to simultaneously capture shared and view-specific structures,

•   Improve clustering robustness, adaptability, and scalability in complex, real-world multi-view scenarios.

Through this integration, our method bridges the gap between uncertainty modeling and structural learning in multi-view clustering, providing a theoretically grounded and practically effective solution.

3.1 Main Idea

In the MPFC model, we propose a dual-anchor graph learning mechanism to simultaneously capture both shared and view-specific structures in multi-view data. For each view l, a set of representative anchor points is selected using clustering-based sampling or random sampling strategies. Subsequently, a similarity matrix Sl is constructed between data samples and anchors using cosine similarity. These view-specific similarity matrices are jointly optimized through matrix factorization to learn a shared latent representation. This process results in the construction of two types of graphs: (1) a common anchor graph, and (2) view-specific anchor graphs for each individual view. The dual-anchor structure enables the model to effectively extract both consensus information across views and unique characteristics of each view. To integrate with Picture Fuzzy Sets (PFS), the edge weights in the dual-anchor graphs are treated as fuzzy relational values, from which the four membership components of PFS. This approach not only models the fuzzy relations between data points and anchors but also allows for the multi-dimensional representation of uncertainty based on inter-view similarity and consistency. The dual-anchor graph plays a critical role in: Reducing computational complexity by avoiding the construction of full pairwise similarity matrices; Preserving clustering structures of both individual views and global consensus; Supporting robust learning of fuzzy membership degrees, especially in scenarios with noisy, conflicting, or incomplete data.

Through the integration of dual-anchor graphs and PFS, the proposed MPFC model effectively captures data structure while modeling uncertainty comprehensively. This results in improved clustering accuracy, stability, and interpretability for complex, real-world multi-view datasets.

The key steps of the algorithm are outlined as follows:

Step 1: Initialization of membership values. Membership values based on PFS are initialized for each view, including positive membership (μ(x)), neutral degree (η(x)), and refusal degree (ξ(x)). This initialization ensures that all membership values satisfy the PFS constraints: μ(x)+η(x)+ξ(x)<1; μ(x),η(x),ξ(x)∈[0,1]. This step provides a solid initialization, laying the foundation for the optimization process and maintaining consistency across views.

Step 2: Data preprocessing and dual anchor graph construction. In this step, the data preprocessing and the construction of key components are carried out simultaneously to prepare for the clustering process. Specifically, the process is as follows:

Principal Component Analysis (PCA): PCA is applied to each view of the data to reduce its dimensionality while retaining only the most significant principal components. This technique helps eliminate features with low variance or little informational value, thereby reducing computational complexity and enhancing processing efficiency. When PCA is applied, the data features are projected onto the space defined by the principal components, where each principal component is a linear combination of the original attributes. To ensure that essential information is preserved, PCA is conducted in a way that the variance explained by the principal components captures most of the variability in the original data. This allows the model to maintain a majority of the data’s variability while eliminating redundant factors, thus improving processing speed and reducing computational costs.

Dual Anchor Graph Construction: A common anchor graph is constructed from all views, reflecting the relationships between objects across the entire dataset. Simultaneously, a specific anchor graph is built for each view to capture the unique features of each data source. This process helps establish connections between objects within each individual view, as well as across the shared data space. Fig. 1 illustrates an example of the common and specific information in a two-view dataset.

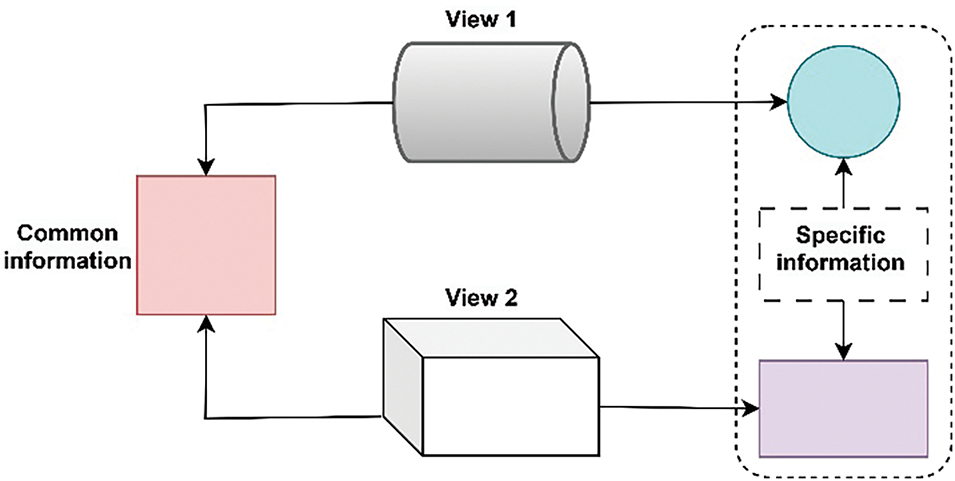
Figure 1: A demonstration of the common and specific information in a two-view dataset

We employ the multi-view dual anchor graph learning (MV_DAGL) [17] algorithm, which produces two outputs: ZC (common anchor graph) and ZS (specific anchor graph). Once the optimal common and specific anchor graphs are learned, we apply Singular Value Decomposition (SVD) [13] to obtain the latent representations RC and RS, where: RC=R0 represents the common features and RS=R1,R2,…,RL represents the specific features. These representations are then used for subsequent clustering.

Similarity Matrix Creation: After constructing the anchor graphs, a similarity matrix is created to measure the similarity between objects, aiding the clustering process. This matrix captures relationships based on proximity in the anchor graphs. To further leverage the information in dual anchor graphs, a membership structure-preserving mechanism is introduced, which maintains cluster integrity by preserving the membership relationships between data points. Unlike traditional methods that calculate the similarity matrix directly from raw data, our approach computes it using the dual anchor graphs, significantly reducing the computational burden. This method improves efficiency without compromising clustering quality, and the resulting matrix aligns better with the multi-view structure. The reduction in computational time enhances scalability and allows for more efficient processing of larger datasets.

The detailed calculation function is as follows:

SS=(ZS)TZS;SC=(ZC)TZC(7)

where SC and SS are the common and specific similarity matrix, respectively [17].

Augmented Matrix Creation and Latent Representations: Alongside constructing the Dual Anchor Graph, an augmented matrix is created to effectively integrate information from various views, facilitating the processing of multi-source data. This matrix aggregates key features from each view, ensuring a more comprehensive data representation. Simultaneously, the ELMSC [26] method is employed to generate latent representations for the objects, reducing the data’s dimensionality while preserving essential relationships. This aids in identifying key clustering patterns, thereby improving both efficiency and accuracy.

Building the Augmented Data Matrix: The augmented data matrix Ya∈Rd×vn is constructed by stacking the data matrices from different views into the diagonal positions of the matrix [26]. Specifically, the views are placed in the diagonal blocks of the matrix to maintain complementary information from each view. The augmented matrix takes the following form:

Ya=[Y(1)Y(1,2)…Y(1,v)Y(2,1)Y(2)…Y(2,v)…………Y(v,1)Y(v,2)…Y(v)](8)

where:

•   Y(p) is the data matrix of the p-th view.

•   Y(p,q) is the correlation matrix between the p-th and q-th views, computed as Y(p,q)=Y(p)S(p,q),p≠q with S(p,q) being the cosine similarity matrix between the two views p and q.

Calculating the Correlation Matrix: The correlation matrices S(p,q) between two views are computed using cosine similarity:

Si,j(p,q)=Y:,i(p).Y:,j(q)2‖Y:,i(p)‖2‖Y:,j(q)‖2+12(9)

where Y:,i(p) and Y:,j(q) represent the feature vectors of the i-th and j-th samples in views p and q, respectively.

Applying Sparse Regularization: Sparse regularization is applied to the non-diagonal blocks of the augmented self-representation matrix Za to eliminate redundant calculations and retain only the essential correlation information between views. This ensures that the correlation information between views is not redundant, improving the efficiency of latent representation learning.

With this process, the augmented matrix can leverage both complementary information from individual views and consistent information across views to construct a better latent representation.

Finally, the augmented self-representation matrix Z^ is calculated using the following equation: Z^=∑iv∑jvZa(i,j). Where Za(i,j) refers to the (i, j)-th block matrix. The resulting values are then used as inputs to the FCM algorithm, which outputs the membership matrix μ¯.

All the results obtained from the three tasks above are used for the subsequent clustering process.

Step 3: Optimization of the objective function, convergence, and finalization of clustering results. In this step, the algorithm minimizes the objective function using the Lagrangian method, ensuring that the PFS constraints are satisfied in each iteration. After completing the iterative optimization process, the algorithm checks for convergence of the objective function, confirming that the updated membership values comply with the PFS constraints. The final result consists of the optimal membership values (μ, η, ξ) for each data point across all views, as well as the cluster centroids, providing a consistent and stable clustering solution across the multiple views.

Fig. 2 illustrates the framework of the proposed multi-view picture fuzzy clustering method.

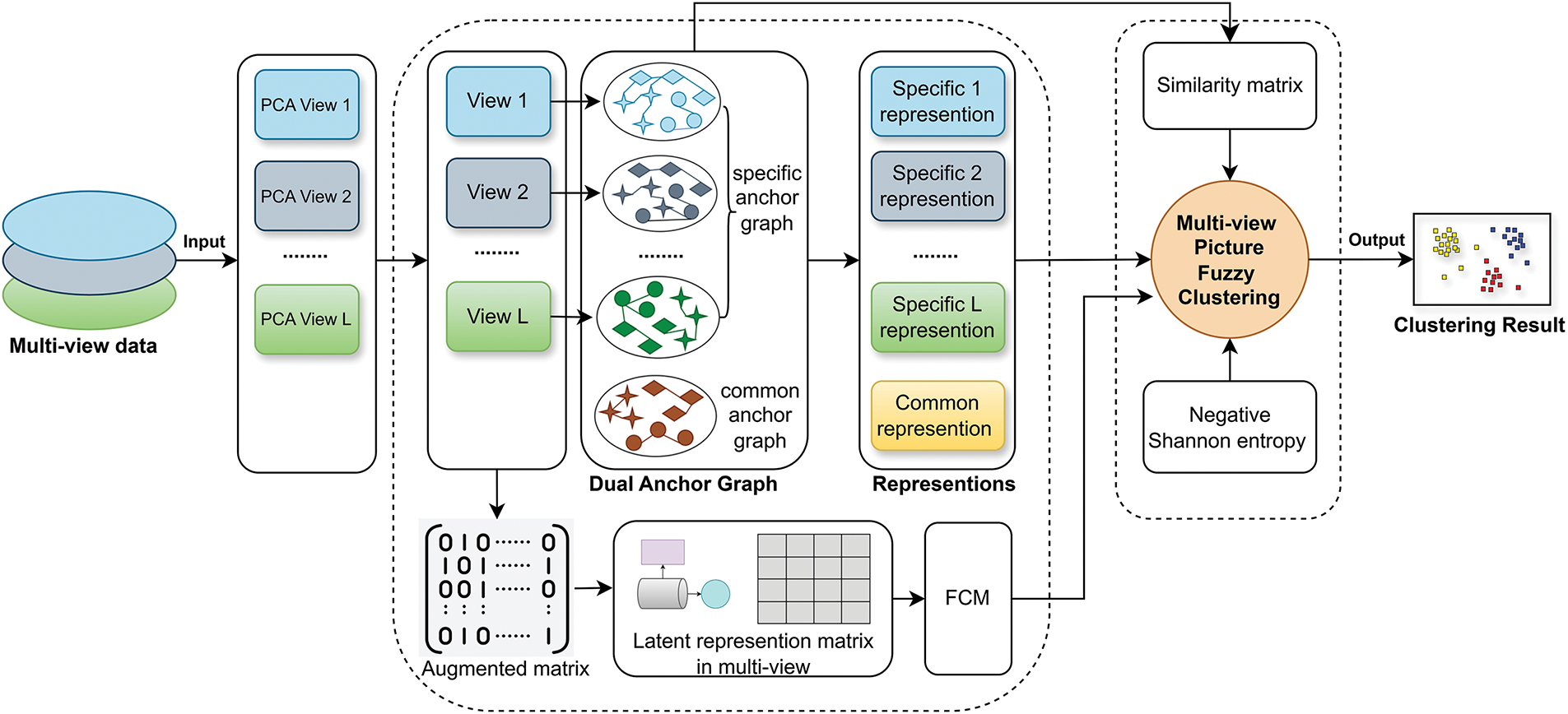
Figure 2: Diagram illustrating the framework of the proposed method

3.2 Algorithm Details

A. Mathematical notation

Let X={x1,x2,x3,…,xN} denote a dataset containing N data samples, where xi represents the i-th sample. In a multi-view dataset, each data sample is linked to features derived from several views. Thus, the multi-view dataset can be represented as X={X1,X2,X3,…,XL}, where Xl∈RN×dl is the data matrix of the l-th view, L is the total number of views, and dl is the dimensionality of the l-th view. To clarify the terminology used, Table 1 provides a summary of the notations throughout this paper. The objective of Multi-view clustering is to effectively combine the information from different views to improve the clustering process. In large-scale multi-view scenarios, where the dataset size N can be considerably large, the challenge lies in robustly integrating the multi-view information while maintaining both efficiency and practicality.

B. The objective function

Based on the idea presented in the previous section, this part will model the proposed method. The objective function of the method is as follows:

F=α∑l=0Lwl∑k=1N∑j=1C((1−ξkj)μkj)2dlkj−β∑k=1N∑j=1Cηkj(ln⁡(ηkj)−ξkj)−σ∑l=0Lwl(ln⁡(wl))+θ∑l=0L∑j=1C∑k=1N∑i=1NSlkiS(μkj−μij)2+ω∑l=0Lwl∑j=1C∑k=1N(μkj−μkj¯)2dlkj+ρ∑k=1N∑j=1Cμkj2→Min(10)

The constraint conditions:

μkj,ξkj,ηkj∈[0,1](11)

μkj+ξkj+ηkj<1(12)

∑j=1C(μkj)=1(13)

∑j=1C(ηkj)=1L(14)

∑j=1C(ξkj)=1L(15)

∑j=1L(wj)=1(16)

the proposed model in Eqs. (10)–(16) is based on the principles of picture fuzzy sets combined with dual anchor graph fuzzy clustering, applied in multi-view scenarios. The objective function F consists of six main components, each designed to address different objectives in the multi-view picture fuzzy clustering problem. The primary goal is to find a balance between the views, minimize discrepancies in membership degrees, and reduce the impact of noise or unreliable factors during the clustering process. The weight coefficients α,β,σ,θ,ρ,ω help adjust the importance of each component in the objective function. wl is the weight for each view.

The following is a detailed explanation of each component:

The first component α∑l=0Lwl∑k=1N∑j=1C((1−ξkj)μkj)2dlkj measures the distribution of data points across clusters, calculating their separation based on the cluster centroids.

The second component β∑k=1N∑j=1Cηkj(ln⁡(ηkj)−ξkj) adjusts the degree of uncertainty of neutral and refusal.

The third component σ∑l=0Lwl(ln⁡(wl)) uses Shannon entropy to adjust the weight distribution between views, aiming to prevent overemphasis on certain views.

The fourth component θ∑l=0L∑j=1C∑k=1N∑i=1NSlkiS(μkj−μij)2 ensures stability and consistency across clusters. SlkiS represents the similarity matrix between data points.

The fifth component ω∑l=0Lwl∑j=1C∑k=1N(μkj−μkj¯)2dlkj measures the difference between the centroids of different views, helping to adjust and ensure compatibility between the views during the clustering process.

The sixth component ρ∑k=1N∑j=1Cμkj2 helps minimize the excessive spread of membership degrees, thereby making the clustering process clearer and more accurate.

C. The optimal solution of the algorithm

The Lagrange method is applied to find the optimal solution for the Eqs. (10)–(16), with specific results as follows: The cluster centroids, membership degrees, neutral degrees, refusal degrees and weights are calculated according to Eqs. (17)–(21), respectively.

Vlj=α∑k=1N((1−ξkj)μkj)2Flk+ω∑k=1N(μkj−μkj¯)2Flkα∑k=1N((1−ξkj)μkj)2+ω∑k=1N(μkj−μkj¯)2(17)

μkj=1Bkj−∑i=1CGkiAkiBkj+GkjAkj(18)

ηkj=eξkjL∑i=1Ceξki(19)

ξkj=1−βηkjEkj+1L−C+β∑i=1C(ηkiEki)∑i=1C(EkjEki)(20)

wl=Kl∑h=0LKh(21)

in which:

{Akj=((α(1−ξkj)2+ω)∑l=0Lwldlkj+θ∑l=0L∑i=1NSlkiS+ρ)Bkj=∑i=1CAkjAkiGkj=θ∑l=0L∑i=1NμijSlkiS+ω∑l=0Lwlμkj¯dlkj {Kl=eα∑k=1N∑j=1C((1−ξkj)μkj)2dlkjS+ω∑j=1C∑k=1N(μkj−μkj¯)2dlkjσdlkj=‖Rk−Vj‖2Ekj=2αμkj2∑l=0Lwldlkj

The Multi-view Picture Fuzzy Clustering (MPFC) algorithm is presented in Algorithm 1.

D. Algorithmic complexity

In this subsection, the complexity of the presented approach is discussed. The proposed method mainly includes two stages: (1) Preprocessing data with dual anchors graph learning [17] and Augmented Matrix Creation and Latent Representations [26]; (2) Updating parameters by optimizing the proposed objective function. The complexity for dual anchors graph learning, in [17], is O (rmN2LT) for updating ZC (common anchor graph), ZS (specific anchor graph), and for creating Latent Representation [26] is O (L3N3). The presented method has a loop with t iteration, for each step V is calculated with O (LCN), μ is O (LC2N2), η is O (C2N), ξ is O (LC2N), w is O (LCN). Then, the total complexity of the second one is O (LC2N2t). Because t has a maximum value in the maxstep, which is less than N. Then, the total complexity of the proposed method is O (LC2N2t) + O (L3N3) ~ O (L3N3).

4  Experimental Results

4.1 Experimental Conditions

The experimental setup was carried out on an ASUS PC with a configuration core i7 7700 with24 GB of RAM, using Python programming language version 3.11. All experiments were conducted in the same environment.

To assess performance, we employ the following criteria: Adjusted Rand Index (ARI), Accuracy score (ACC), Normalized Mutual Information (NMI), and Purity (PUR) [10]. Higher ARI, ACC, NMI, and PUR values reflect better clustering quality, with a higher degree of accuracy and similarity between the model and actual clustering. These evaluation metrics are widely used in clustering tasks due to their ability to quantify different aspects of clustering performance. Each metric is chosen to capture a specific dimension of clustering quality, and their relevance to the multi-view clustering problem is outlined below:

(a)   Adjusted Rand Index (ARI): ARI is a measure of the similarity between two data clusterings, adjusted for chance. It compares the predicted clustering labels with the true labels, accounting for random assignments to avoid overestimating the clustering performance. ARI is computed as:

ARI=RI−E[RI]max(RI)−E[RI](22)

where RI is the Rand Index, and E[RI] is its expected value under random assignments. The ARI ranges from −1 (no agreement) to 1 (perfect agreement), with 0 indicating random clustering. ARI is particularly useful in multi-view clustering because it evaluates the overall consistency between cluster assignments across multiple views while adjusting for random chance. This helps in assessing whether the method effectively utilizes the complementary information provided by multiple views.

(b)   Accuracy (ACC): Accuracy measures the proportion of correct cluster assignments to the true labels, after optimal matching. It is calculated as:

ACC=∑i=1NI(yi=y^i)N(23)

where I is the indicator function, yi is the true label, and y^i is the predicted label. N is the total number of samples. While clustering is typically unsupervised, many multi-view datasets come with ground-truth labels. ACC serves as a practical measure of how closely the clustering results align with the actual class labels, providing an intuitive sense of the clustering quality.

(c)   Normalized Mutual Information (NMI): NMI is a measure of the shared information between the predicted clusters and the ground truth. It quantifies how much knowing one clustering reduces the uncertainty about the other. It is defined as:

NMI(X,Y)=I(X;Y)H(X)H(Y)(24)

where I (X; Y) is the mutual information between the predicted labels X and the true labels Y, and H (X) and H (Y) are the entropies of the respective label distributions. NMI ranges from 0 (no mutual information) to 1 (perfect correlation). NMI is particularly effective for multi-view clustering because it captures the amount of shared information across multiple views. This helps evaluate how well the proposed method integrates the diverse sources of information (views) into a unified clustering structure, while accounting for both shared and view-specific characteristics.

(d)   Purity (PUR): Purity measures the extent to which each cluster contains data points from a single class. It is computed as:

PUR=1N∑k=1Cmaxi|Ck∩Ti|(25)

where Ck is the set of data points in the k-th cluster, and Ti is the set of data points in the i-th true class. C is the total number of clusters, and N is the total number of data points. Purity is an important metric when evaluating the effectiveness of clustering methods, especially in multi-view scenarios, where the goal is to ensure that the resulting clusters are cohesive and contain as few mixed-class data points as possible. It highlights how well the multi-view clustering method consolidates information from each view to form distinct and meaningful clusters.

These metrics were selected because they provide a well-rounded assessment of clustering performance. ARI and NMI focus on the consistency between the predicted and true clustering, which is essential in multi-view clustering where the objective is to integrate multiple views accurately. ACC, while straightforward, offers a clear evaluation of how closely the method aligns with known labels when available. PUR, on the other hand, ensures that the clusters are internally coherent, an important aspect in multi-view clustering where diversity between views could lead to less pure clusters. In comparison with other methods, these metrics have been widely used in the multi-view clustering literature and are recognized for their ability to capture different aspects of clustering quality. Our choice of these four metrics enables a comprehensive evaluation of clustering quality, particularly in the context of integrating information from multiple views, managing uncertainty, and ensuring the robustness of the clustering solution.

Parameter settings: Regularization parameters: α=10, β=0.00001, σ=10, θ=0.1, ω=10, ρ=10, Number of anchors: {C, 2C,…,5C}, where C is the number of clusters, ε=0.001. Where α,β,σ,θ,ω,ρ are hyperparameters, they can be set manually or determined by a cross-validation strategy. Specifically, cross-validation involves splitting the data into multiple folds (commonly k-fold). For each fold, the model is trained on a portion of the data (training set) and tested on the remaining portion (validation set). The performance metrics are computed for each fold, and the hyperparameter values are chosen based on the average performance across all folds. This approach helps ensure that the model is evaluated on all data points, thus improving the generalizability of the model. The cross-validation process can be repeated for different values of the hyperparameters, and the set of hyperparameters that maximizes the model’s performance on the validation set is selected as the optimal configuration. To ensure a fair comparison, the regularization parameters for all methods are meticulously optimized to attain the best performance. This parameter selection strategy may differ from those used in existing approaches, so it is anticipated that our results for these methods may vary from those presented in the corresponding literature.

To evaluate the effectiveness of the proposed method, the research team conducted simulations on different kinds of image and text multi-view datasets [45]. A detailed overview of these datasets is provided in Table 2, along with a brief description below.

•   3Sources: 169 news stories were collected from 3 popular online news sources: BBC, Reuters and The Guardian. Each story belongs to one of 6 topics: business, entertainment, health, politics, sport, and technology. A word histogram of each story is extracted to make three views, namely Reuters view (3068 dimensions), BBC view (3560 dimensions), and Guardian view (3631 dimensions).

•   MSRC-v5: This dataset is a subset of the Microsoft Research in Cambridge. It consists of 210 images of 7 object types. We selected five views: 24-D Color moments feature, 576-D Histogram of oriented gradients feature, 512-D GIST feature, 256-D Local binary patterns feature, and 254-D CENTRIST feature.

•   Wikipedia-test: This dataset is a subset of the Wikipedia dataset. It is collected from 693 text-image pair documents from Wikipedia’s featured articles of 10 categories. Each image is represented as a bag of visual features obtained through the Scale-Invariant Feature Transform (SIFT) method to form one view with 10 dimensions, and text is processed into word histograms to make another view with 128 dimensions.

•   CiteSeer: This dataset contains 3312 scientific publications categorized into one of six academic fields: Agents, IR, DB, AI, HCI, and ML. The first view represents each publication as a binary word vector, where each entry indicates the presence (1) or absence (0) of a word from a dictionary of 3703 unique terms. The second view is a citation network consisting of 4732 links, capturing the relationships between publications.

4.2 Results and Discussion

This section presents the experiments conducted on four multi-view datasets to assess the performance of the proposed method. The results are compared with those from two other methods: DAG_FC [17] and ELMSC [26]. A brief description of these two methods is provided below:

•   DAG_FC: A dual anchor graph learning technique is proposed to capture shared and view-specific information, combining latent representations with anchor graph learning via matrix factorization. A new multi-view fuzzy clustering method is then developed to incorporate these anchor graph representations with a membership structure preservation mechanism to enhance clustering performance further. The multi-view dual anchor graph learning (MV_DAGL) algorithm is a sub-algorithm within DAG_FC designed to learn the optimal common and specific anchor graphs.

•   ELMSC: This innovative latent multi-view subspace clustering approach builds an augmented multi-view data matrix, where diagonal blocks stack data matrices from each view to retain complementary information, and non-diagonal blocks capture inter-view similarities to maintain consistency. This approach enhances the recovery of latent representations. Additionally, sparse regularization is applied to the non-diagonal blocks to reduce redundant computations, and a novel iterative algorithm using ADMM is developed for optimization.

•   MPFC: The proposed Multi-view Picture Fuzzy Clustering (MPFC) method integrates picture fuzzy sets with dual-anchor graph fuzzy clustering to extract common and specific information from multiple views. By employing the MV_DAGL algorithm and the ELMSC method, MPFC generates robust latent representations and optimizes clustering iteratively. The fuzzy clustering process is performed iteratively to refine the results at each step. The optimization minimizes the objective function using the Lagrangian method, ensuring that Picture Fuzzy Sets constraints are satisfied at each iteration.

MPFC algorithms were run 10 times, with the maximum number of iterations set to 100 in each execution. Table 3 presents the experimental results evaluated according to the metrics. The bolded values represent the best results for each dataset.

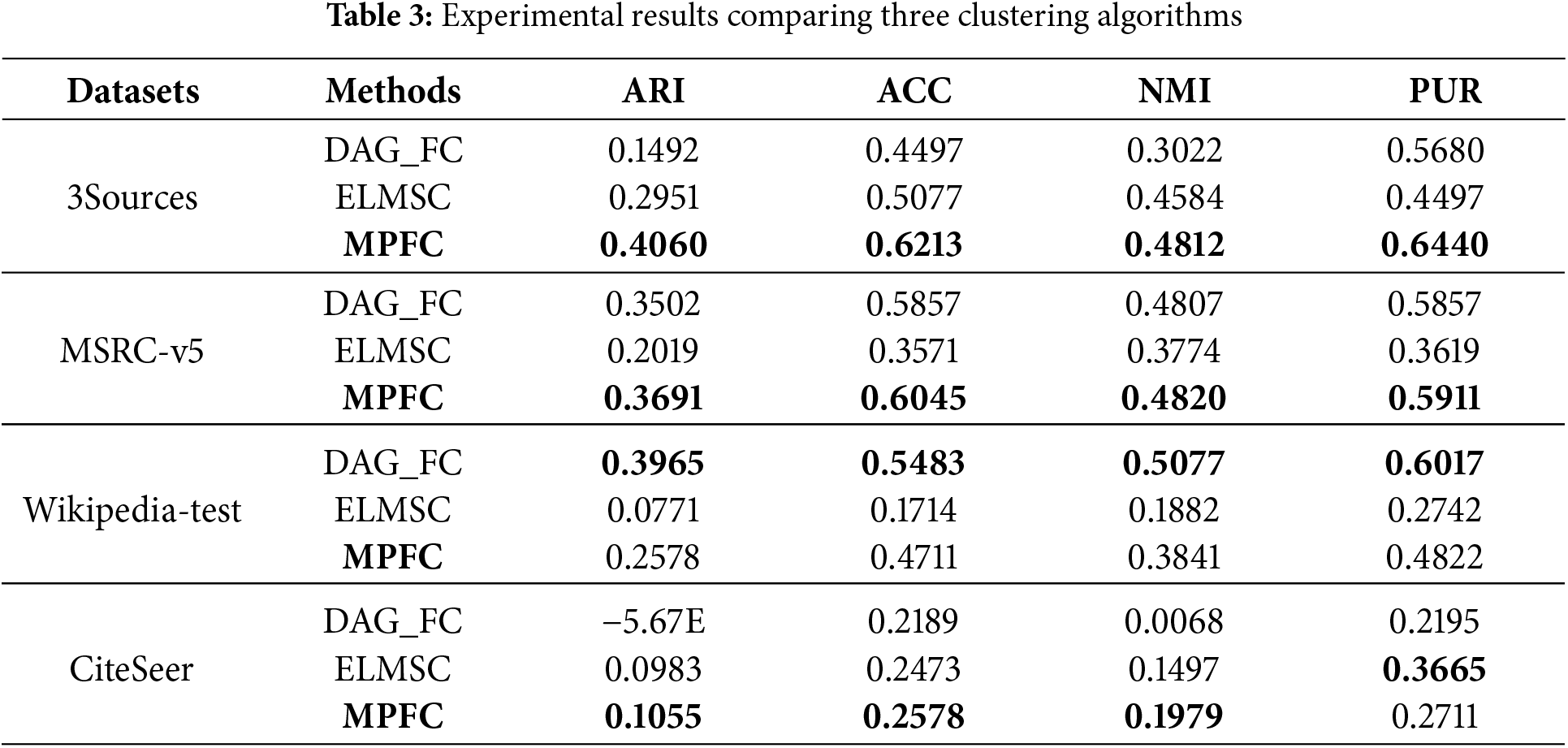
Table 3 presents the experimental results of three clustering algorithms on four datasets: 3Sources, MSRC-v5, Wikipedia-test, and CiteSeer. The experimental results show that the proposed method outperforms the two methods, DAG_FC and ELMSC, across most datasets and evaluation metrics. Specifically, on the 3Sources dataset, the proposed method achieves ARI (0.4060), ACC (0.6213), NMI (0.4812), and PUR (0.6440), outperforming both DAG_FC and ELMSC. This demonstrates that the proposed method can more accurately cluster multi-view data, particularly in environments with complexity and heterogeneity across views. This confirms that our method enhances clustering accuracy and ensures stability and scalability, especially when handling multi-view data with complexity and heterogeneity across views. Similarly, on the MSRC-v5 dataset, the proposed method also shows significant improvement in ARI (0.3691), ACC (0.6045), NMI (0.4820) and PUR (0.5911) compared to DAG_FC and ELMSC, although the difference in NMI is not as pronounced. This indicates that the proposed method optimizes clustering accuracy and improves stability in grouping data points. On the Wikipedia-test dataset, the proposed method outperforms ELMSC in ARI (0.2578 vs. 0.0771), ACC (0.4711 vs. 0.1714), NMI (0.3841 vs. 0.1882), and PUR (0.4822 vs. 0.2742), but still performs worse than DAG_FC on all metrics. This result indicates that while the proposed method improves consistency across views, further optimization is required for classification accuracy on some data clusters. Finally, on the CiteSeer dataset, although all methods produced lower results, the proposed method still achieved promising results, such as ACC (0.2578) and PUR (0.2711), demonstrating its ability to detect similarities among clusters in multi-view data, even in the presence of noise.

The experimental results shown in Fig. 3 illustrate the clustering performance of MPFC compared to DAG_FC and ELMFC across four evaluation metrics: ARI, ACC, NMI, and PUR on various datasets (3Sources, MSRC-v5, Wikipedia-test, and CiteSeer). The bar charts show that MPFC consistently outperforms DAG_FC and ELMFC across most datasets and all evaluation metrics.

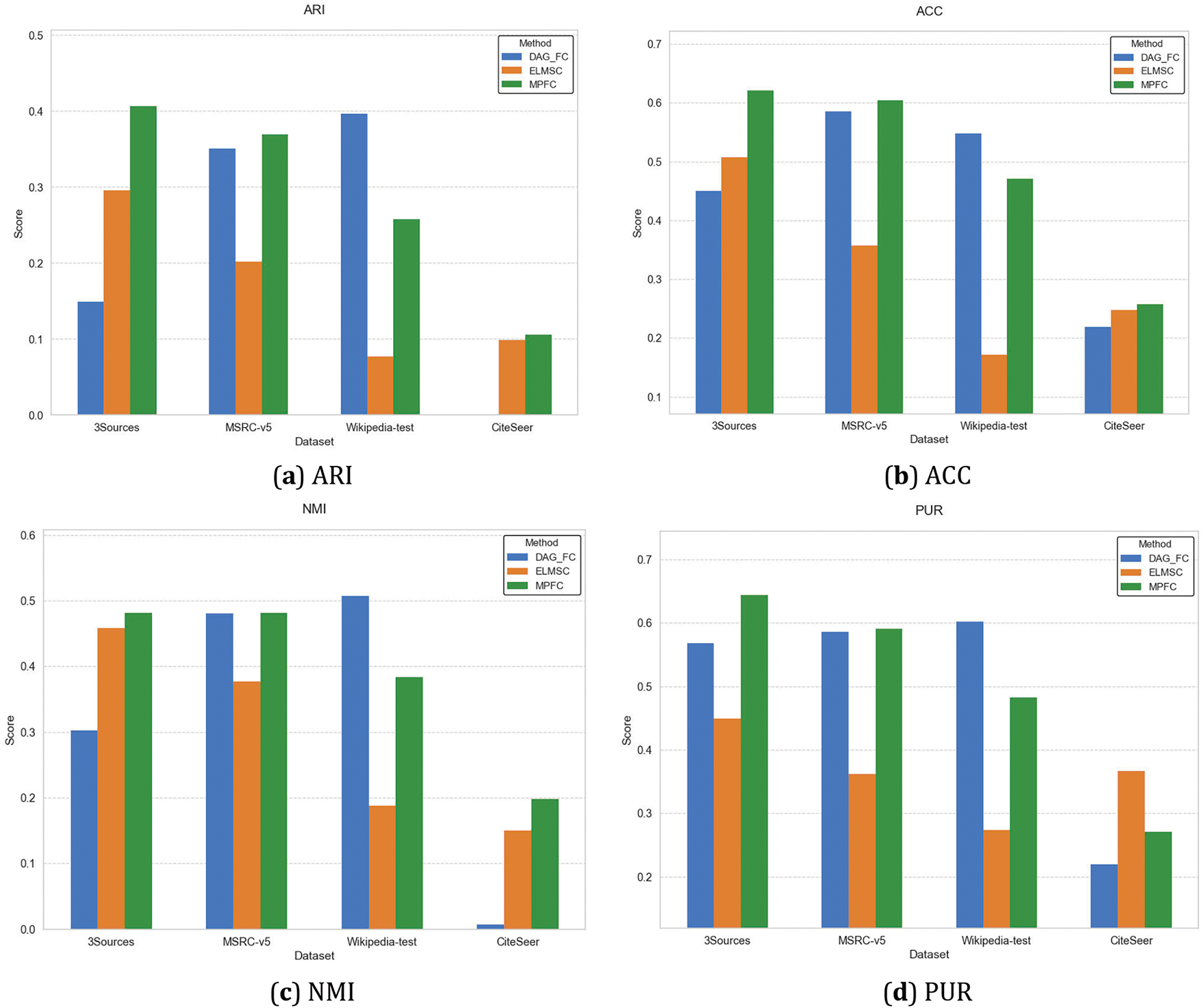
Figure 3: The experimental comparison of three methods on the metrics ARI, ACC, NMI, PUR

Overall, the experimental results demonstrate that the proposed method is effective for clustering multi-view data, especially in preserving consistency across views and enhancing clustering accuracy. However, there remain areas for improvement when dealing with datasets that have high noise levels and significant heterogeneity between views.

5  Conclusion and Future Work

This study introduces a novel method called Multi-view Picture Fuzzy Clustering (MPFC), which integrates picture fuzzy sets with dual-anchor graph fuzzy clustering. The method utilizes the Multi-view Dual Anchor Graph Learning (MV_DAGL) algorithm to extract both common and specific information between views, combining hidden representations and anchor graph learning through matrix factorization. Once the anchor graphs are constructed, a similarity matrix is created to measure the similarity between objects, facilitating the clustering process. An augmented matrix is then generated to integrate information from multiple views, improving the handling of data from different sources. This matrix captures key features across views, resulting in a more comprehensive and robust data representation. To further enhance clustering performance, the Enhanced Latent Multi-view Subspace Clustering (ELMSC) method is employed to generate latent representations for the objects.

The fuzzy clustering algorithm is performed iteratively to refine the clustering results at each step. The optimization process minimizes the objective function using the Lagrangian method, ensuring that Picture Fuzzy Sets constraints are satisfied at each iteration. After completing the iterative optimization, the algorithm verifies the convergence of the objective function, ensuring that the updated membership values comply with the PFS constraints.

The key contributions of the proposed method are as follows:

1.    Integration of matrix factorization with anchor graph learning: This integration helps purify the original data by removing noise and errors, leading to the construction of higher-quality anchor graphs. As a result, the clustering performance is significantly improved, particularly in noisy or complex data environments.

2.    A novel dual-anchor graph extraction mechanism: The proposed method introduces an effective strategy for extracting both common and view-specific anchor graphs, which enables the model to fully exploit complementary and diverse information across multiple views, thereby enhancing the accuracy and adaptability of the clustering process.

3.    Application of Picture Fuzzy Sets theory in fuzzy clustering: By incorporating Picture Fuzzy Sets, the method is able to represent and handle multiple types of uncertainty (positive, neutral, negative, and refusal degrees) inherent in multi-view data. This leads to a more robust clustering framework capable of dealing with ambiguous and inconsistent information.

We performed experiments to assess the effectiveness of the proposed method, utilizing four key metrics ARI, ACC, NMI, and PUR across various datasets. The results show that the proposed method outperforms the DAG_FC and ELMSC methods, particularly on the 3Sources dataset. However, on datasets like Wikipedia-test and CiteSeer, the clustering performance is not as outstanding, particularly in terms of ARI and ACC. This indicates that additional optimization is required to improve accuracy, especially in noisy and complex data settings.

Overall, the experimental findings confirm the viability and efficiency of the proposed method, highlighting its potential for clustering complex datasets. The combination of the Picture Fuzzy Sets theory with multi-view fuzzy clustering using dual-anchor graphs notably enhances the method’s flexibility and adaptability for real-world data. Nevertheless, further research and algorithm optimization are needed to address challenges posed by high data variability and noise. One area for improvement is the computational complexity, which escalates as the number of views increases in the data. This issue becomes more pronounced when the data exhibits high variability or noise, potentially affecting model performance. Therefore, optimizing the algorithm to reduce computational costs in such situations would be beneficial. Additionally, when data is missing from one or more views, the model may face difficulties in maintaining clustering accuracy. This underscores the importance of developing more effective strategies for handling missing data, ensuring reliable results even in such cases. Future research will focus on extending the proposed MPFC method to incorporate advanced learning paradigms and expand its applicability to real-world problems. A primary direction involves the development of semi-supervised multi-view fuzzy clustering, where limited labeled data can be leveraged to enhance clustering accuracy and robustness. Integrating labeled information into the current unsupervised framework is expected to improve the model’s adaptability, particularly in domains where annotated data is scarce but critical. Building upon this foundation, the integration of deep learning techniques, such as autoencoders and graph neural networks (GNNs), will be explored to better capture complex, non-linear relationships across different views. Autoencoders can facilitate effective dimensionality reduction while preserving data structure, whereas GNNs are well-suited to model topological dependencies among structured or graph-based inputs, further enhancing clustering performance. In addition, efforts will be made to equip the model with the capability to handle incomplete or missing data, thereby increasing its robustness and applicability to imperfect and high-noise datasets. The method will also be evaluated in new domains, including pattern recognition and large-scale clustering tasks, to demonstrate its scalability and versatility.

Building upon these methodological extensions, one particularly promising application domain is satellite image segmentation. Satellite imagery presents unique challenges due to its high dimensionality and heterogeneous nature, typically comprising data from multiple sources such as spectral bands, spatial textures, and geographic attributes—each of which can be treated as a distinct view. By leveraging the multi-view learning capability of MPFC, it is possible to integrate this rich and diverse information to improve the accuracy and consistency of land cover classification, including forests, urban areas, and water bodies. These capabilities are especially vital for environmental monitoring, urban planning, and agricultural management. To enable effective deployment in this domain, future work will focus on adapting the algorithm to handle high-dimensional satellite data, exploring efficient integration strategies that balance computational complexity and feature relevance. The method will also be extended to jointly exploit spatial and spectral information, providing a more context-aware and robust segmentation approach. Empirical evaluations on real-world datasets such as Landsat and Sentinel will be conducted to validate the model’s practical utility. Moreover, MPFC’s capacity for temporal multi-view integration will be harnessed for change detection tasks, enabling the identification of subtle transformations in land use and environmental patterns over time.

Collectively, these research directions are expected to significantly enhance the MPFC framework, establishing it as a powerful, scalable, and adaptable tool for complex clustering problems—particularly in high-impact domains such as remote sensing, urban analytics, and environmental data science.

Acknowledgement: The authors are grateful to all the editors and anonymous reviewers for their comments and suggestions.

Funding Statement: This work was funded by the Research Project: THTETN.05/24-25, Vietnam Academy of Science and Technology.

Author Contributions: Study conceptualization: Pham Huy Thong, Hoang Thi Canh, Nguyen Long Giang, Luong Thi Hong Lan; data collection and experiment: Pham Huy Thong, Hoang Thi Canh, Nguyen Tuan Huy; analysis and interpretation of results: Pham Huy Thong, Hoang Thi Canh, Nguyen Long Giang; draft manuscript preparation: Hoang Thi Canh, Luong Thi Hong Lan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets used in this study are openly available at https://github.com/ChuanbinZhang/Multi-view-datasets, accessed on 15 January 2025.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Yang Y, Wang H. Multi-view clustering: a survey. Big Data Min Anal. 2018;1(2):83–107. doi:10.26599/BDMA.2018.9020003. [Google Scholar] [CrossRef]

2. Ding Z, Zhao H, Fu Y. Learning representation for multi-view data analysis. Berlin/Heidelberg, Germany: Springer; 2018. [Google Scholar]

3. Jung MC, Zhao H, Dipnall J, Gabbe B, Du L. Uncertainty estimation for multi-view data: the power of seeing the whole picture. Adv Neural Inf Process Syst. 2022;35:6517–30. [Google Scholar]

4. Xie M, Han Z, Zhang C, Bai Y, Hu Q. Exploring and exploiting uncertainty for incomplete multi-view classification. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2023 Jun 18–22; Vancouver, BC, Canada. [Google Scholar]

5. Bickel S, Scheffer T. Multi-view clustering. In: Proceedings of the IEEE International Conference on Data Mining (ICDM); 2004 Nov 1–4; Brighton, UK. [Google Scholar]

6. Chao G, Sun S, Bi J. A survey on multiview clustering. IEEE Trans Artif Intell. 2021;2(2):146–68. doi:10.1109/TAI.2021.3065894. [Google Scholar] [PubMed] [CrossRef]

7. Thong PH, Son LH. Picture fuzzy clustering: a new computational intelligence method. Soft Comput. 2016;20(9):3549–62. doi:10.1007/s00500-015-1712-7. [Google Scholar] [CrossRef]

8. Xu C, Tao D, Xu C. Multi-view learning with incomplete views. IEEE Trans Image Process. 2015;24(12):5812–25. doi:10.1109/TIP.2015.2490539. [Google Scholar] [PubMed] [CrossRef]

9. Kumar A, Rai P, Daume H. Co-regularized multi-view spectral clustering. In: Proceedings of the 24th Advances in Neural Information Processing Systems (NIPS 2011); 2011 Dec 5–10; Granada, Spain. [Google Scholar]

10. Liu J, Wang C, Gao J, Han J. Multi-view clustering via joint nonnegative matrix factorization. In: Proceedings of the 2013 SIAM International Conference on Data Mining; 2013 May 2–4; Austin, TX, USA. doi:10.1137/1.9781611972832.28. [Google Scholar] [CrossRef]

11. Xu J, Ren Y, Tang H, Yang Z, Pan L, Yang Y, et al. Self-supervised discriminative feature learning for deep multi-view clustering. IEEE Trans Knowl Data Eng. 2022;35(7):7470–82. doi:10.1109/TKDE.2022.3193569. [Google Scholar] [CrossRef]

12. Liang W, Liu X, Zhou S, Liu J, Wang S, Zhu E. Robust graph-based multi-view clustering. In: Proceedings of the Thirty-Sixth AAAI Conference on Artificial Intelligence; 2022 Feb 22–Mar 1; Palo Alto, CA, USA. doi:10.1609/aaai.v36i7.20710. [Google Scholar] [CrossRef]

13. Zhang P, Wang S, Li L, Zhang C, Liu X, Zhu E, et al. Let the data choose: flexible and diverse anchor graph fusion for scalable multi-view clustering. In: Proceedings of the AAAI Conference on Artificial Intelligence; 2023 Feb 7–14; Washington, DC, USA. doi:10.1609/aaai.v37i9.26333. [Google Scholar] [CrossRef]

14. Kang Z, Shi G, Huang S, Chen W, Pu X, Zhou JT, et al. Multi-graph fusion for multi-view spectral clustering. Knowl-Based Syst. 2020;189(4):105102. doi:10.1016/j.knosys.2019.105102. [Google Scholar] [CrossRef]

15. Wang H, Yang Y, Liu B. GMC: graph-based multi-view clustering. IEEE Trans Knowl Data Eng. 2020;32(6):1116–29. doi:10.1109/TKDE.2019.2903810. [Google Scholar] [CrossRef]

16. Li L, He H. Bipartite graph based multi-view clustering. IEEE Trans Knowl Data Eng. 2022;34(7):3111–25. doi:10.1109/TKDE.2020.3021649. [Google Scholar] [CrossRef]

17. Zhang W, Huang X, Li A, Zhang T, Ding W, Deng Z, et al. Dual anchor graph fuzzy clustering for multi-view data. IEEE Trans Fuzzy Syst. 2024;33(2):730–44. doi:10.1109/TFUZZ.2024.3489025. [Google Scholar] [CrossRef]

18. Yang B, Zhang X, Chen B, Nie F, Lin Z, Nan Z. Efficient correntropy-based multi-view clustering with anchor graph embedding. Neural Netw. 2022;146(8):290–302. doi:10.1016/j.neunet.2021.11.027. [Google Scholar] [PubMed] [CrossRef]

19. Yang B, Zhang X, Lin Z, Nie F, Chen B, Wang F. Efficient and robust MultiView clustering with anchor graph regularization. IEEE Trans Circuits Syst Video Technol. 2022;32(9):6200–13. doi:10.1109/TCSVT.2022.3162575. [Google Scholar] [CrossRef]

20. Zhang C, Jia X, Li Z, Chen C, Li H. Learning cluster-wise anchors for multi-view clustering. In: Proceedings of the AAAI Conference on Artificial Intelligence; 2024 Feb 20–27; Vancouver, BC, Canada. doi:10.1609/aaai.v38i15.29609. [Google Scholar] [CrossRef]

21. Fang U, Li M, Li J, Gao L, Jia T, Zhang Y. A comprehensive survey on multi-view clustering. IEEE Trans Knowl Data Eng. 2023;35(12):12350–68. doi:10.1109/TKDE.2023.3270311. [Google Scholar] [CrossRef]

22. Cuong BC. Picture fuzzy sets. J Comput Sci Cybern. 2014;30(4):409. [Google Scholar]

23. Atanassov KT. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986;20(1):87–96. doi:10.1016/S0165-0114(86)80034-3. [Google Scholar] [CrossRef]

24. Thong PH, Son LH. Picture fuzzy clustering for complex data. Eng Appl Artif Intell. 2016;56(1):121–30. doi:10.1016/j.engappai.2016.08.009. [Google Scholar] [CrossRef]

25. Canh HT, Thong PH, Huan PT, Trang VT, Hieu NN, Phuong NT, et al. A novel semi-supervised consensus fuzzy clustering method for multi-view relational data. Int J Electr Comput Eng. 2024;14(6):6883–93. doi:10.11591/ijece.v14i6.pp6883-6893. [Google Scholar] [CrossRef]

26. Shi L, Cao L, Wang J, Chen B. Enhanced latent multi-view subspace clustering. IEEE Trans Circuits Syst Video Technol. 2024;34(12):12480–95. doi:10.1109/TCSVT.2024.3430041. [Google Scholar] [CrossRef]

27. Sharma KK, Seal A. Multi-view spectral clustering for uncertain objects. Inf Sci. 2021;547:723–45. doi:10.1016/j.ins.2020.08.080. [Google Scholar] [CrossRef]

28. Hardoon DR, Szedmak S, Shawe-Taylor J. Canonical correlation analysis: an overview with application to learning methods. Neural Comput. 2004;16(12):2639–64. doi:10.1162/0899766042321814. [Google Scholar] [PubMed] [CrossRef]

29. Andrew G, Arora R, Bilmes J, Livescu K. Deep canonical correlation analysis. Proc Mach Learn Res. 2013;28(3):1247–55. [Google Scholar]

30. Cheng J, Wang Q, Tao Z, Xie D, Gao Q. Multi-view attribute graph convolution networks for clustering. In: Proceedings of the Twenty-Ninth International Conference on International Joint Conferences on Artificial Intelligence; 2021 Jan 7–15; Yokohama, Japan. doi:10.24963/ijcai.2020/411. [Google Scholar] [CrossRef]

31. Daneshfar F, Saifee BS, Soleymanbaigi S, Aeini M. Elastic deep multi-view autoencoder with diversity embedding. Inf Sci. 2025;689:121482. doi:10.1016/j.ins.2024.121482. [Google Scholar] [CrossRef]

32. Mendel JM, John RIB. Type-2 fuzzy sets made simple. IEEE Trans Fuzzy Syst. 2002;10(2):117–27. doi:10.1109/91.995115. [Google Scholar] [CrossRef]

33. Mendel JM. Type-2 fuzzy sets and systems: an overview. IEEE Comput Intell Mag. 2007;2(1):20–9. doi:10.1109/MCI.2007.380672. [Google Scholar] [CrossRef]

34. Xu Z, Chen J, Wu J. Clustering algorithm for intuitionistic fuzzy sets. Inf Sci. 2008;178(19):3775–90. doi:10.1016/j.ins.2008.06.008. [Google Scholar] [CrossRef]

35. Son LH, Thong PH. Some novel hybrid forecast methods based on picture fuzzy clustering for weather nowcasting from satellite image sequences. Appl Intell. 2017;46(1):1–15. doi:10.1007/s10489-016-0811-1. [Google Scholar] [CrossRef]

36. Canh HT, Thong PH, Giang LT, Hung PD. Fake news detection based on multi-view fuzzy clustering algorithm. In: Proceedings of the 14th EAI International Conference, AdHocNets 2023; 2023 Nov 10–11; Hanoi, Vietnam. doi:10.1007/978-3-031-55993-8_12. [Google Scholar] [CrossRef]

37. Wang Y, Chen L. Multi-view fuzzy clustering with minimax optimization for effectively clustering data from multiple sources. Expert Syst Appl. 2017;72(4):457–66. doi:10.1016/j.eswa.2016.10.006. [Google Scholar] [CrossRef]

38. Ma H, Wang S, Yu S, Liu S, Huang JJ, Wu H, et al. Automatic and aligned anchor learning strategy for multi-view clustering. In: Proceedings of the 32nd ACM International Conference on Multimedia; 2024 Oct 28–Nov 1; Melbourne, Australia. doi:10.1145/3664647.3681273. [Google Scholar] [CrossRef]

39. Ji X, Yang L, Yao S. Adaptive anchor-based partial multiview clustering. IEEE Access. 2020;8:175150–9. doi:10.1109/ACCESS.2020.3025881. [Google Scholar] [CrossRef]

40. Fu Y, Li Y, Huang Q, Cui J, Wen J. Anchor graph network for incomplete multiview clustering. IEEE Trans Neural Netw Learn Syst. 2024;36(2):3708–19. doi:10.1109/TNNLS.2024.3349405. [Google Scholar] [PubMed] [CrossRef]

41. Wang S, Liu X, Liu S, Jin J, Tu W, Zhu X, et al. Align then fusion: generalized large-scale multi-view clustering with anchor matching correspondences. Adv Neural Inf Process Syst. 2022;35:5882–95. [Google Scholar]

42. Cai X, Huang D, Zhang GY, Wang CD. Seeking commonness and inconsistencies: a jointly smoothed approach to multi-view subspace clustering. Inf Fusion. 2023;91(2):364–75. doi:10.1016/j.inffus.2022.10.020. [Google Scholar] [CrossRef]

43. Kang Z, Zhou W, Zhao Z, Shao J, Han M, Xu Z. Large-scale multi-view subspace clustering in linear time. In: Proceedings of the AAAI Conference on Artificial Intelligence; 2020 Feb 7–12; New York, NY, USA. doi:10.1609/aaai.v34i04.5867. [Google Scholar] [CrossRef]

44. Zhang W, Deng Z, Zhang T, Choi KS, Wang S. One-step multiview fuzzy clustering with collaborative learning between common and specific hidden space information. IEEE Trans Neural Netw Learn Syst. 2024;35(10):14031–44. doi:10.1109/TNNLS.2023.3274289. [Google Scholar] [PubMed] [CrossRef]

45. Zhang C. Multi-view datasets [Internet]. [cited 2025 Jan 15]. Available from: https://github.com/ChuanbinZhang/Multi-view-datasets. [Google Scholar]