A Fully Homomorphic Encryption Scheme Suitable for Ciphertext Retrieval

1  Introduction

In the current era of informatization and big data. Data has the characteristics of massive information, massive distribution, and strong timeliness. Therefore, data-oriented storage and sharing systems demand enhanced confidentiality, integrity, authenticity, and availability. As a result, cloud storage with cost-effectiveness, robust security, operational efficiency, and scalability gradually supplants traditional local database storage, garnering widespread attention and adoption across various industries.

When it is necessary to ensure data security and user identity privacy during cloud storage operations, data is maintained in a ciphertext state within cloud databases. To retrieve and query data in the ciphertext state, Song et al. [1] pioneered the concept of ciphertext retrieval in 2000, which can reduce privacy leakage risks. Research on ciphertext retrieval bifurcates into two categories: attribute-preserving encryption [2] and Searchable Encryption (SE) [3], with this study focusing on the latter [4]. In 1978, Rivest et al. [5] first proposed the concept of homomorphic encryption, which enables direct arithmetic operations (addition/multiplication) on the ciphertext while maintaining plaintext-equivalent computation results. As a cryptographic technique rooted in mathematical hard problems, homomorphic encryption provides exceptional algorithmic security, rendering Homomorphic Encryption-based Ciphertext Retrieval (HECR) schemes particularly promising for secure data processing.

The fundamental principle of HECR schemes involves performing homomorphic operations between encrypted data and ciphertext search terms, followed by similarity comparisons to ensure retrieval accuracy. HECR technology demonstrates significant practical value across privacy-sensitive domains, including healthcare [6], IoT systems [7], deep learning [8], and cloud services [9]. Our current research concentrates on implementing HECR solutions in cloud storage environments. While effectively addressing third-party storage concerns regarding data security, sharing efficiency, and access control, these implementations significantly enhance both security and accuracy in ciphertext retrieval through its implementation of homomorphic encryption algorithms. Our primary objectives are to reduce algorithmic computational complexity and cloud computing operational costs while resolving key management challenges in cloud storage scenarios. This study is based on the integer-based FHE scheme DGHV proposed by Van Dijk et al. [10] and Coron et al. [11], whose security foundation relies on the Approximate Greatest Common Divisor (Approximate GCD) problem [12]. Compared with other FHE algorithms, DGHV demonstrates superior operational security and computational efficiency with lower complexity. Consequently, it has been extensively adopted in HECR systems for cloud storage environments, exhibiting significant potential for scheme optimization and providing a robust theoretical foundation for cryptographic research.

Building upon research methodologies for enhancing the DGHV algorithm, our proposed fully homomorphic encryption (FHE) scheme integrates data retrieval access control capabilities and implements a triple-key encryption mechanism where distinct cryptographic entities manage separate keys to execute corresponding system functionalities. The designed HECR mechanism extends beyond conventional ciphertext comparison approaches, enabling multi-keyword queries with similarity-ranked results. Simultaneously, the proposed scheme confines key-sharing scopes while maintaining compatibility with application scenarios involving either multi-verifier coexistence or third-party retrieval service providers. Through rigorous theoretical analysis and comprehensive simulation experiments, we demonstrate that the scheme enhances algorithmic security and operational usability, thereby significantly increasing the practical applicability of HECR mechanisms. The principal contributions to our work are outlined as follows:

1.    A fully homomorphic encryption scheme based on a triple-key encryption mechanism is proposed. The keys in the scheme are divided into the encryption key, retrieval key, and retrieval authorization key, which are assigned to different system entities. The solution reduces the scope of key sharing, decentralizes the centralized data control authority, and mitigates cascading impacts caused by single-point failures. Specifically, the separation of the encryption key and the retrieval key addresses the key security issue in the untrusted third-party cloud storage scenario. The verification key can be used independently by retrieval authorization verifiers to implement access control over retrieval requests without compromising the security or operational processes of the other two keys.

2.    An authorization code is introduced into the algorithm, which enables data owners to implement hierarchical control of ciphertext data and configure retrieval authorizations. This enables the retrieval of files of different security levels and retrievers with different retrieve authorizations to influence retrieval results, thereby enhancing the security of HECR to a certain extent.

3.    The DGHV ciphertext retrieval mechanism is improved to support multi-keyword retrieval and similarity-based ranking of results, enhancing the retrieval scheme’s functionality and practicability.

4.    The correctness and security of the scheme are theoretically analyzed in detail, and the security of the algorithm, key, and retrieval is proved. The proposed FHE scheme is formulated and implemented. Comparative evaluations with existing schemes demonstrate its enhanced security, efficiency, and usability.

The rest of this paper is organized as follows. We briefly introduce related work in Section 2 and detail the design of the HECR scheme in Section 3. Section 4 provides a theoretical analysis of the scheme’s correctness and security, and Section 5 presents the simulation implementation and comparative performance analysis. We conclude the paper in Section 6.

2  Related Works

HECR technology has remained a research hotspot since its proposal. In 2010, Van Dijk et al. [10] introduced an integer-based homomorphic encryption algorithm and discussed its corresponding ciphertext retrieval mechanism. In 2019, Wang et al. [13] proposed ECRS, an encrypted ciphertext retrieval scheme for enterprise cloud storage using fully homomorphic encryption. Gong et al. [14] developed a Quantum Homomorphic Encrypted Ciphertext Retrieval (QHECR) scheme in 2020 based on the Grover algorithm. In 2021, He et al. [15] proposed an efficient Ciphertext Retrieval scheme based on Homomorphic encryption for Multiple data owners in a hybrid cloud, incorporating an encrypted balanced binary index tree structure and a large-integer arithmetic-based homomorphic encryption method. Wang et al. [16] designed an efficient and privacy-preserving encrypted data range query scheme under a dual-server architecture in 2022. In 2023, Wang et al. [17] proposed an approximate homomorphic encryption-based ciphertext image content retrieval scheme for mobile cloud computing. Song et al. [18] designed an effective privacy information retrieval model based on hybrid fully homomorphic encryption, significantly improving the computational efficiency of schemes. In 2024, Cheng et al. [19] proposed a secure quantum homomorphic encryption ciphertext retrieval scheme. Current research primarily focuses on addressing key management, computational efficiency, and security challenges in homomorphic encryption systems.

Our work proposes a DGHV improvement scheme targeting cloud storage security. Existing DGHV optimization studies generally aim to enhance security, usability, and efficiency, falling into two categories: key-related improvements and cloud storage security solutions. The former involves technical enhancements in key quantity, key-sharing scope, encryption/decryption efficiency, ciphertext expansion rate, and multi-bit ciphertext processing capabilities. The latter adds algorithmic functionalities to support encrypted cloud database operations across multiple scenarios. Xi et al. [20] proposed an algorithm with reduced public key size and 2-bit plaintext encryption capacity while concealing private keys during retrieval, countering cloud data theft risks. Hong et al. [21] developed the G_DGHV algorithm for direct cloud platform implementation, enhancing retrieval security and user privacy. Kumar et al. [22] introduced a lightweight dual-encryption scheme with efficient tamper detection. These solutions assume trusted cloud providers and unrestricted key-sharing scopes, neglecting potential security vulnerabilities like key exposure during retrieval. Qin et al. [23] pioneered the SDC homomorphic encryption algorithm using dual-key separation (encryption/retrieval keys) to address untrusted third-party cloud storage scenarios. Ping [24] enhanced SDC security through randomized parameters. Li et al. [25] improved SDC to create the HES algorithm with compact public keys and accelerated retrieval.

Existing schemes primarily resolve key-related cloud storage issues but fail to consider: (1) malicious query attacks using valid ciphertext keywords; (2) separated retrieval authorization verifiers and service providers; (3) lack of retrieval access control capabilities. Our work effectively addresses these gaps, providing significant theoretical value for cloud storage security and reliable technical support for cloud computing platforms.

3  The Proposed Scheme

3.1 Homomorphic Encryption Algorithm

Our work proposes six novel cryptographic algorithms: the Key Generation algorithm (Keygen()), Encryption algorithm (Encrypt()), Authorization Upload algorithm (Upload()), Authorization Verification algorithm (Verification()), Return algorithm (Return()), and Decryption algorithm (Decrypt()). This cryptographic framework demonstrates comparable security characteristics to the DGHV scheme. The following provides detailed descriptions of these algorithms.

1.    Keygen(): Randomly generate secure large prime number P with secure parameter λ as the number of digits, obtain the generators g1 and g2 of Zp, and select the secret numbers x1 and x2 so that g1x1 and g2x2 are the idempotent elements of the finite semigroup ⟨Zp,∗⟩. Let the encryption key p1=g1x1, the verification key p2=g2x2, use the generated secure large prime number P as the retrieval key p3 and ensure that p1,p2≪p3. Among them, the function of the encryption key p1 is to protect plaintext data, which the data owner exclusively enjoys. The verification key p2 is provided to the retrieval authorization verifier to run the Verification(). The retrieval key p3 can be shared with the cloud database and runs an improved ciphertext retrieval mechanism.

2.    Encrypt(): Randomly generate large prime numbers q of length α. The encryption process is Formula (1). The algorithm is fully homomorphic encryption and satisfies additive and multiplication homomorphism.

c=m×p1×p2+q×p2×p3(1)

3.    Upload(): Randomly generate smaller prime numbers r of length β. The operation object of this process is the keywords extracted by the data owner from the ciphertext data, in which the retrieval authorization level of the ciphertext data is set, and the data retrieval authorization code s is added to control the retrieval access of the retriever. As shown in Formula (2).

cr=c+r×s(2)

among them, c is the ciphertext encrypted by Encrypt(), r is a random prime number that is used to increase the randomness of the algorithm and protect the privacy of the authorization code, s is the data retrieval authorization code (s≪p2), that is, the retrieval authorization level set by the data owner for ciphertext data.

4.    Verification(): This process is used to verify whether the authorization level of the retriever is greater than the retrieval authorization level of the ciphertext document. It requires the retrieval authorization verifier to request the verification key p2 from the data owner and, simultaneously, find the retrieval authorization level in the retriever’s identity information through other authoritative methods, the user retrieval authorization code s’. As shown in Formula (3).

(crmodp2)mods′{=0Verificationsuccessful≠0Verificationfailed(3)

among them, cr is the ciphertext keyword carrying the data retrieval authorization code s. The algorithm requires the random number r to be a small prime number so that the algorithm r×s is not affected by mod p2. If the result of the Formula (3) is 0, the retriever’s authorizations are higher, and ciphertext retrieval is allowed; if the result is not equal to 0, the retrieval request is rejected, and the information that the retriever’s authorizations do not meet the requirements is returned.

5.    Return(): Before the retrieval authorization verifier sends the ciphertext retrieval keywords to the cloud database, the data retrieval authorization code s specified by the data owner for the ciphertext must be removed. The formula is shown in (4).

c=cr−(cr mod p2)(4)

The result of this step is the retrieval request value c. It separates the retrieval authorization process and the data retrieval process so that their keys are relatively independent. It ensures that the ciphertext retrieval scheme running on the cloud database can correctly retrieve the ciphertext and guarantee the confidentiality of the data retrieval authorization code s.

6.    Decrypt(): As Formula (5) shows, the final decryption obtains plaintexts m.

m=(c×p1−1×p2−1)mod p3(5)

The large-integer authorization code introduced in the aforementioned Upload() algorithm serves to embed data owners’ predefined retrieval authorization levels into ciphertext data. This enables the scheme to verify requesters’ access privileges through the retrieval authorization verification server or database before initiating ciphertext retrieval operations, thereby achieving retrieval service access control. The authorization code configuration is specified as follows:

Set the authorization code identifier as s, generated via s=a×rs, where a is the authorization code seed, and rs is the power exponent that specifies the authorization level. The following is the process in detail.

1.    The authorization code seed a is a cryptographically secure large prime number requiring confidential storage.

2.    Power exponent rs=ei, and different i determines different rs:

(1)   e is the base (fixed positive integer, with smaller values required when the retrieval authorization level increases; post-configuration values remain immutable and confidential).

(2)   i is the exponent representing privilege levels (a positive integer where higher values correspond to lower access privileges).

3.    The authorization code s=a×rs represents differentiated user retrieval authorizations. By integrating this authorization code into the FHE scheme, granular control over users’ retrieval privileges is systematically enforced.

3.2 Ciphertext Retrieval Scheme

The DGHV retrieval scheme exhibits advantageous characteristics, including low computational overhead, operational simplicity, and efficient retrieval performance. However, its implementation necessitates that cloud databases possess the secret key p to execute correct ciphertext retrieval. This single-key sharing mechanism presents inherent security vulnerabilities, rendering it unsuitable for deployment scenarios involving untrusted retrieval service providers. Such architectural constraints may potentially compromise data confidentiality during retrieval operations and diminish the scheme’s practical applicability. Furthermore, while the retrieval mechanism of DGHV functionally equates to ciphertext comparison, the computational efficiency of homomorphic encryption algorithms remains fundamentally inferior to conventional encryption paradigms. Consequently, ciphertext comparison operations under homomorphic encryption inherently incur higher computational costs than standard encrypted data comparisons. Without substantial improvements to the ciphertext retrieval mechanism of DGHV and enhanced functional capabilities, these inherent limitations of homomorphic retrieval mechanisms cannot be effectively mitigated.

This scheme retrieves the complete ciphertext file C, formed by encrypting the plaintext block with an improved algorithm, as shown in Fig. 1.

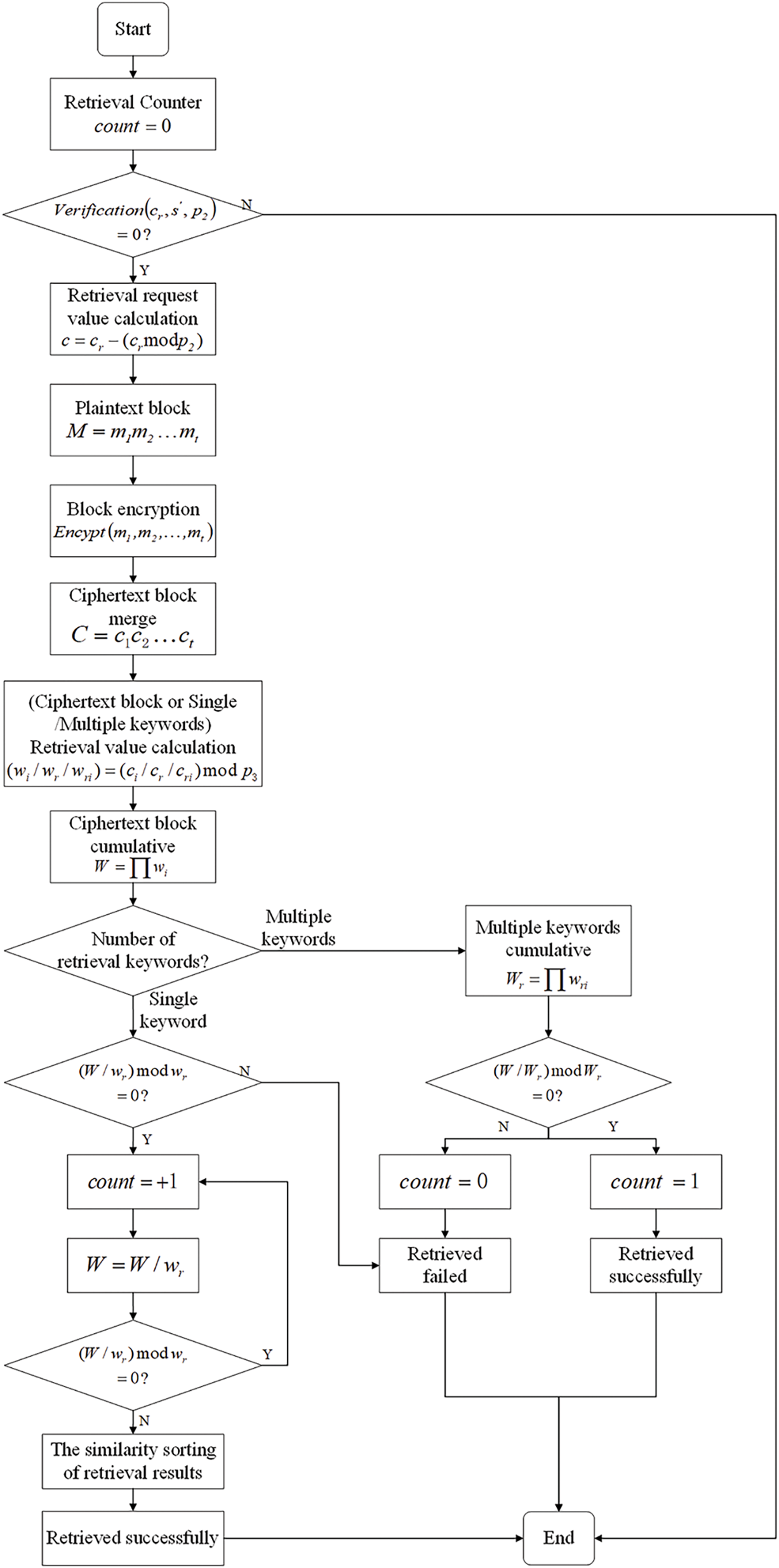
Figure 1: Flow chart of ciphertext retrieval based on homomorphic encryption

1.   Retrieval Preparation

(1)   Before retrieval, the retriever must ensure the retrieval authorization verifier can query the user’s retrieval authorization code through the authoritative channel.

(2)   The retriever provides the retrieval authorization verifier with the ciphertext keyword cr carrying the data retrieval authorization code, and provides personal identity information. It is convenient for the retrieval authorization verifier to verify the authenticity of the retriever’s identity and whether it is higher than the retrieval authorization level set on the ciphertext keyword.

(3)   Firstly, Verification() described in the previous section is called to verify that the retrieval authorization has passed; secondly, the retrieval authorization verifier removes the data retrieval authorization code with the Return() to obtain the retrieval request value; finally, the retrieval authorization verifier sends the retrieval request value to the cloud database for retrieval.

(4)   Before retrieval, the cloud database needs to have the ciphertext file C as the retrieval object:

(1)   Plaintext block: the plaintext is grouped, and the length of the plaintext block is l bit, that is M=m1,m2,⋯,mt, where t=|M|/l;

(2)   Block encryption: The Encrypt() is called to encrypt mi (1≤i≤t);

(3)   Ciphertext block merge: Ciphertext blocks are concatenated to form a complete ciphertext file C=c1c2,⋯,ct.

(5)   The cloud database generates a retrieval counter count and initializes count=0.

2.   Retrieval Process

(1)   Read the ciphertext blocks ci (1≤i≤t) in sequence from the encrypted file C.

(2)   The cloud database uses the retrieval key p3 to calculate the retrieval value of each ciphertext block ci in turn.

wi=ci mod p3=mip1p2,

        then calculate W:

W=∏wi.

(1)   Retrieve single keyword cr

        Cloud database uses the retrieval key p3 to calculate the retrieval value wr=cr mod p3=mrp1p2 of the keyword cr, and calculate (W/wr)mod wr. If the result is 0, the keyword matches the document and count+1; otherwise, it does not match the document, and the retrieval process ends, as shown in the following formula.

w1,w2,⋯,wtwrmod wr=p1tp2tm1,m2,⋯,mtp1p2mrmod p1p2mr{=0count+1≠0Retrieval end 

        Let W=W/wr and recalculate (W/wr)modwr. If the result is still 0, count+1 again and repeat this step; otherwise, the retrieval process ends, and the retrieval counter count is output, as shown in the following formula.

w1,w2,…,wr−1,wr+1,…,wtwr mod wr=p1t−1p2t−1m1,m2,…,mr−1,mr−1,…,mtp1p2mrmod p1p2mr{=0count+1≠0Retrieval end

(2)   Retrieve multiple keywords cri

        Cloud database uses the retrieval key p3 to calculate the retrieval value wri=cri mod p3 (1≤i≤n) of multiple keywords cri, where n is the number of keywords. Calculate the multiple keywords cumulative Wr=∏wri, then calculate (W/Wr) modWr. If the result is 0, multiple keywords match the document, count=1, and output the retrieval counter; otherwise, it is not matched, count=0, and the retrieval process ends, as shown in the following formula.

WWr mod Wr=p1tp2tm1,m2,⋯,mtp1np2nmr1,mr2,⋯,mrn mod Wr{=1Retrieval successful=0Retrieval failed 

3.   Retrieval Result

            The cloud database can use the retrieval value wi as the final retrieval result returned to the retriever, and then the formula of Decrypt() is changed as follows:

m=wi×p1−1×p2−1

       This process can protect the security of the retrieval key p3 and reduce the sharing scope of the key p3. At the same time, the computation of Decrypt() can also be reduced, and the system efficiency can be improved.

When retrieving a single keyword cr, according to the value count of the retrieval counter, the cloud database sorts the matching similarity of the documents containing keywords to reflect the correlation of different files and increase the correctness of the retrieval results. When retrieving multiple keywords cri, the retrieval counter count=1 indicates that the multiple keywords are successfully matched, and the matching documents are output directly. Cloud databases can finally return one or more retrieval results with high matching similarity according to the needs of the actual scenario.

4  Theoretical Analysis

4.1 Correctness Proof

Theorem 1: In the improved algorithm, users holding keys p1, p2, and p3 can restore plaintext m; or when retrieval value wi as the final retrieval result, users only holding keys p1 and p2 can restore the plaintext m.

Proof of Theorem 1: For any plaintext m, we know p1,p2≪p3, so the decryption operation of the ciphertext result c or the retrieval value wi is as follows:

Decrypt(c)=(c×p1−1×p2−1) mod p3#=[(m×p1×p2+q×p2×p3)×p1−1×p2−1] mod p3#=m#

Decrypt(wi)=wi×p1−1×p2−1=(mi×p1×p2)×p1−1×p2−1=mi

It is necessary to ensure that m×p1×p2≪p3, so that the ciphertext m×p1×p2 will not be affected during the decryption process. □

Theorem 2: The improved algorithm is a fully homomorphic encryption algorithm.

Proof of Theorem 2: The plaintexts m1 and m2 are encrypted separately to obtain:

{c1=m1×p1×p2+q1×p2×p3c2=m2×p1×p2+q2×p2×p3

1.   Additive Homomorphism Verification

Ciphertext addition operation Encrypt (m1+m2)=(m1+m2)×p1×p2+(q1+q2)×p2×p3.

Ciphertext decryption operation Decrypt(c1+c2)=((c1+c2)×p1−1×p2−1) mod p3=m1+m2. The decryption result is the same as the addition result of the original plaintext.

2.   Multiplicative Homomorphism Verification

Ciphertext multiplication operation Encrypt(m1×m2)=(m1×p1×p2+q1×p2×p3)×(m2×p1×p2+q2×p2×p3).

Ciphertext decryption operation Decrypt(c1×c2)=((c1×c2)×p1−1×p2−1)modp3= m1×m2, where p1=g1x1 and p2=g2x2. In the decryption process, there will be an operation step of [(m1×m2×g12x1×g22x2)×g1−x1×g2−x2]modp3, which is transformed into (g12x1×g1−x1)modp3 and (g22x2×g2−x2)modp3. Considering that the retrieval key p3 is a large prime number P, and g1x1 and g2x2 are the idempotent elements of the finite semigroup ⟨Zp,∗⟩, then g12x1modp3=g1x1modp3 and g22x2mod p3=g2x2modp3. The result of decrypting c1×c2 is still m1×m2, and the algorithm satisfies the multiplicative homomorphism.

The improved algorithm in this paper satisfies both additive homomorphism and multiplication homomorphism. Since addition and multiplication can realize subtraction and division, it has been theoretically proved that it is a fully homomorphic encryption algorithm. □

4.2 Security Analysis

1. Algorithmic Security Proof

Definition 1 (Advantage Function): In the process of attacking the cryptographic scheme, the absolute value of the difference between the probability of the adversary A winning and 1/2 is recorded as the adversary’s advantage, which is recorded as:

Adv(A)=|Pr[succ]−1/2|

Theorem 3: The improvement of the algorithm in this paper has achieved provable security; that is, the security of the encryption algorithm can be regarded as the solution to the approximate GCD problem. The scheme has semantic security. It has indistinguishability (IND) and non-malleability (NM) under chosen plaintext attack (CPA).

Proof of Theorem 3: In the scheme, after the data sent by the data owner is processed by Encrypt() and Upload(), the final ciphertext form is cr=m×p1×p2+q×p2×p3+r×s.

(1) IND-CPA

Set up the attack model of a challenger and an adversary. The specific attack and defense stages are as follows:

(1)   Initial stage: The challenger has the encryption key p1, verification key p2, retrieval key p3, i.e., Keygen()→(p1,p2,p3).

(2)   Access phase: Under the bounded polynomial degree, the adversary can request the challenger to encrypt any plaintext multiple times.

(3)   Challenge stage: The adversary selects two distinguishable plaintexts m0 and m1 of equal length, sending them to the challenger. The challenger randomly selects 1-bit b(bϵ{0,1}) and uses the random numbers q and r to encrypt plaintext mb, that is, Cb=mb×p1×p2+qb×p2×p3+rb×sb. The ciphertext Cb is sent to the adversary, where b is kept secret.

If b=0, C0=m0×p1×p2+q0×p2×p3+r0×s0

If b=1, C1=m1×p1×p2+q1×p2×p3+r1×s1.

(4)   Guessing stage: After the adversary receives the ciphertext, it operates on the ciphertext Cb, judges whether it is C0 or C1, and guesses the result of the plaintext b′.

When b=b′, the adversary successfully guesses the value of b in polynomial time, then the adversary wins, and the adversary has at least a 1/2 probability of winning. The final winning advantage of the adversary under the CPA of this scheme is Adv(A)=|Pr[b=b′]−1/2|, and its value is infinitely close to 0 in the following several cases: (1) The random prime numbers q and r in each encryption process are not equal, which results in the algorithm being a probability polynomial. (2) The authorization code s with high randomness is composed of a large prime number a and a power exponent ei, which can be introduced into the encryption algorithm to improve the randomness of the algorithm to a certain extent. (3) In the algorithm scheme using the three-key encryption mode, the keys can protect and balance each other, making it difficult for the adversary to obtain a single key. The security of the key is based on the discrete logarithm problem (DLP), and the algorithm’s security is based on the approximate GCD problem, so the scheme’s security is high. Therefore, even if the same data is encrypted, different ciphertexts will be obtained, and the plaintext and ciphertext have a one-to-many mapping relationship. The adversary cannot guess the plaintext and ciphertext relationship and has no advantage under the CPA. The improved scheme has IND or semantical security under CPA. A more detailed proof process is shown in [10].

(2)   NM-CPA

We can encrypt the plaintext m and obtain ciphertext c=m×p1×p2+q×p2×p3+r×s, in which the existence of random numbers q,r, and authorization code s makes it extremely difficult for the adversary to construct another ciphertext c′ whose corresponding plaintext m′ has some connection with the original plaintexts. The proposed algorithm in this paper is NM and can resist CPA.

(3)   Cryptographic hard problem

Definition 2 (Approximate-GCD): For a randomly selected large prime number q of α bits and a small prime number r of β bits, the distribution of multiple sets of ciphertexts c is:

{c1=m1×p1×p2+q1×p2×p3+r1×s1c2=m2×p1×p2+q2×p2×p3+r2×s2⋮ci=mi×p1×p2+qi×p2×p3+ri×si

In the ciphertext distribution, polynomial number samples are sampled, where c1, c2,…,ci can be seen as an approximate multiple of the key p1. The adversary’s process of solving the key p1 is computationally difficult, and this is the solution to the approximate GCD problem.

The parameters q, r, and authorization code s in the algorithm make it computationally difficult for the adversary to infer the key from the ciphertext, which can ensure that the encryption process satisfies the approximate GCD problem. It increases the encryption result’s randomness and reduces the similarity between ciphertexts. The improved scheme based on two cryptographic hard problems can resist CPA and is semantically secure.

2. Key Security

(1)   Three-key encryption mode

The improved algorithm adopts the three-key homomorphic encryption mode of the encryption key p1, the retrieval authorization key p2, and the retrieval key p3. Different keys can be assigned to different identity objects within the system. The keys protect and balance each other and jointly protect the security of the retrieved data. The following are the objects, system functions, and security analysis of different keys:

(1)   The encryption key p1 is unique to the data owner, which keeps the data in the ciphertext state during storage and retrieval and guarantees the security of the data.

(2)   The retrieval authorization verifier owns the retrieval authorization key p2 and is the ability given by the data owner to control access to data retrieval. After the verification is successful, the retrieval authorization verifier needs to run the Return() to generate ciphertext keywords that can be successfully retrieved by the cloud database and do not carry the data retrieval authorization code. The verification key can prevent illegal retrievers with correct ciphertext keywords from maliciously sending a large number of retrieval requests to the cloud database, resulting in low operation efficiency of the cloud database or inability to process other legitimate search requests quickly, and resulting in waste of system resources, low retrieval efficiency, error results. It can prevent illegal retrievers from holding correct ciphertext keywords and retrieve correct ciphertext data from the database. It can separate the ability of access control from the retrieval service provider and provide it to a more authoritative retrieval authorization verifier, improving the security and efficiency of the data sharing system.

(3)   The retrieval key p3 is owned by the retrieval service provider, that is, owned by the cloud database set in the scheme of this paper, which gives the database the normal retrieval ability to the data. This key can solve the trust problems of the retrieval service of the single-key homomorphic algorithm; that is, the third-party retrieval service provider has the correct ciphertext keywords but does not have the correct retrieval key, and the retrieval mechanism still cannot be operated normally. It can reduce the shared scope of the single key and reduce the security threat to the data caused by the third-party retrieval service provider.

From the analysis of the above-mentioned various keys, the retrieval authorization verifier does not have the conditions to retrieve and decrypt the ciphertext, and the retrieval service provider does not have the conditions to verify the authorizations and decrypt the ciphertext. When the algorithm is applied to scenarios where multiple retrieval authorization verifiers coexist or retrieval service providers are not trusted, it can ensure the keys’ security, data confidentiality, and retrieval accuracy.

(2)   High Security of Encryption Key

In the improved algorithm, the data security is protected by the encryption key p1, only taken by the data owner, a power exponent composed of a generator g and a secret number x, which satisfies DLP. The encryption key p1 has high security, and guessing the secret x from p1=gx is also difficult. The keys p2 and p3, random numbers q and r, jointly participate in the homomorphic encryption process to protect plaintext m, improving the security of encryption key p1.

(3)   The Uniqueness of Verification Key

In the improved scheme designed in this paper, the structure of the verification key is the same as that of the encryption key. As a retrieval authorization key p2, it is used in the encryption part m1×p1×p2 in the function Encrypt() and can protect the original data m in the ciphertext state. At the same time, it is flexible that we can choose whether to share it with the retrieval authorization verifier. Moreover, when shared with the retrieval authorization verifier, the encryption key p1 required in the Decrypt() will not be leaked, and the plaintext m is safe. The algorithm adds random numbers q and r, increasing noise interference and improving plaintext security.

(4)   Anti-Brute Force Cracking of Key

The length of the retrieval key p3 in the improved algorithm is set as the security parameter λ, the value of which is a randomly generated secure large prime number P, and the key space size is 2λ. If an adversary wants to crack the key violently, he may need to try 2λ times cracking calculation. It means that when the pre-specified security parameter λ is larger, the probability of the key being cracked violently by an adversary is lower.

3. Retrieval Security

The authorization code is introduced into the improved algorithm, which can give priority to verifying the retrieval authorization of the retriever before implementing the large-scale ciphertext data retrieval process and effectively controlling the retrieval service request of the retriever. If the data owner does not need the retrieval authorization service, the following steps can be completed to remove the retrieval authorization:

(1)   The data owner does not generate the retrieval authorization code s and does not need to send the verification key p2 to the retrieval authorization verifier.

(2)   The data owner does not add the data retrieval authorization code s to the ciphertext keyword; that is, skip the algorithm step of Upload().

(3)   The retriever does not need to send a retrieval authorization request to the retrieval authorization verifier; that is, skip the algorithm step of Verification().

(4)   The retrieval authorization verifier does not execute the Return().

The ciphertext keywords and encrypted files in the retrieval mechanism are in one-to-one or many-to-one correspondence. They are encrypted with the same three kinds of keys, but the encryption process’s random numbers q and r are different. It requires the retrieval service provider to have a retrieval key p3 and perform retrieval value calculation on ciphertext blocks or ciphertext keywords to ensure the correct execution of the subsequent retrieval mechanism. An authorization code can improve the security of the retrieved data and restrict the retrieval behavior of the retriever. Verification key p2 enables the data owner to set the range of persons allowed to retrieve data according to different retrieval authorization verifiers or retrievers. It can achieve multi-level retrieval authorization control of different types of private data and grade the security of ciphertext retrieval. □

5  Performance Analysis

5.1 Comparative Analysis

1. Performance Comparison and Analysis

The application value of the algorithm scheme is analyzed by comparing it with DGHV, and the specific results are shown in Table 1.

It can be seen from Table 1 that the scheme in this paper is consistent with DGHV in terms of security and continuity. When the number of keys increases, the key size increases, but multiple kinds of keys can protect and balance each other. Compared with the DGHV algorithm, this scheme reduces the sharing scope of a single key, can adapt to application scenarios where multiple third-party service providers exist, and improves key security. At the same time, the improved ciphertext retrieval mechanism based on homomorphic encryption becomes complicated due to the participation of multiple keys. The proposed scheme sacrifices a small part of the operational efficiency but greatly improves the functionality and usability of the fully homomorphic encryption scheme. Table 2 compares various homomorphic encryption schemes based on the DGHV improvement.

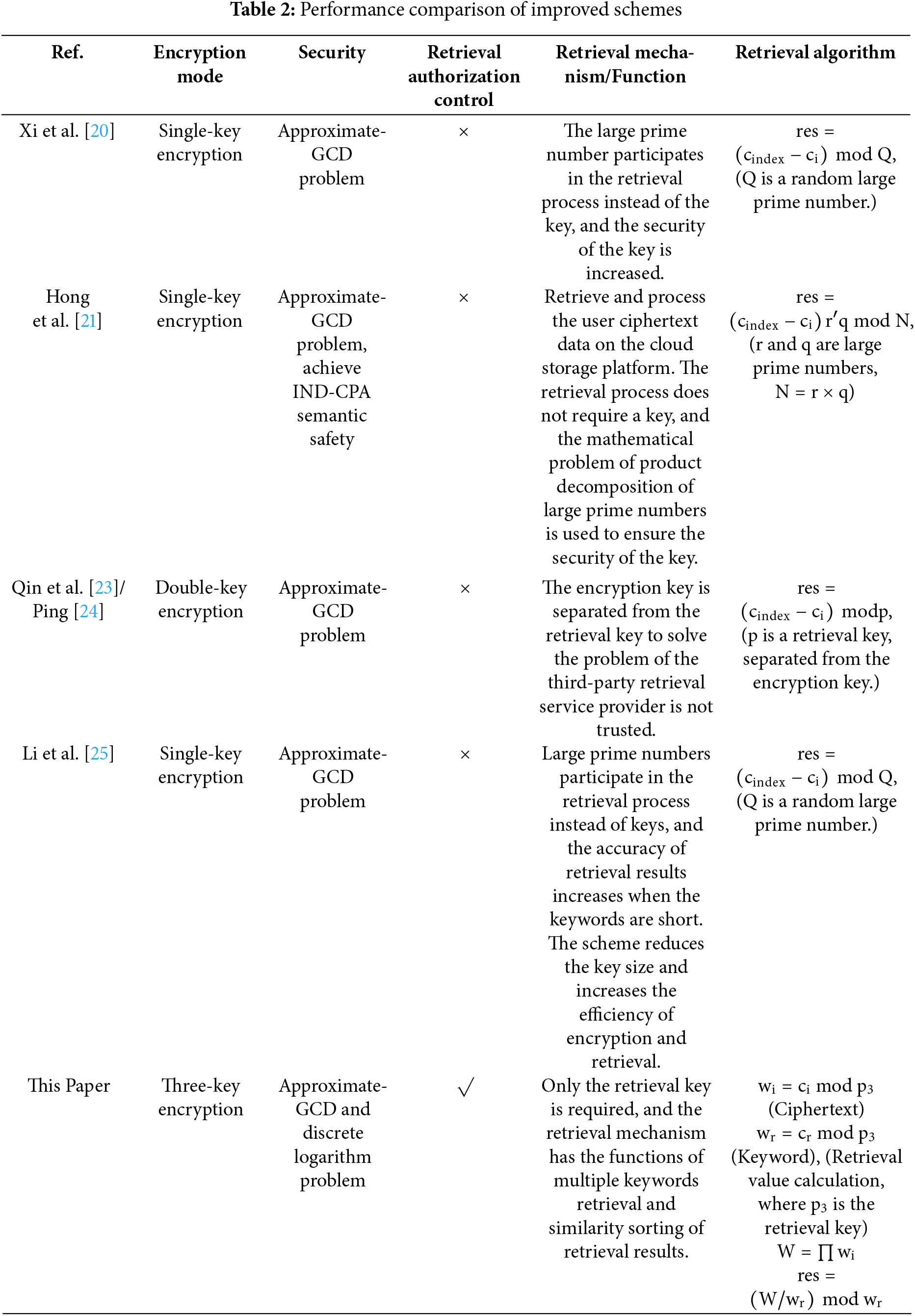
As can be seen from Table 2, the literature [20] and [21] are single-key encryption modes, and random large prime numbers replace the key to participate in the retrieval process, ensuring that the key is not shared with third-party retrieval service providers, and ensuring the encryption key security. The double-key encryption mode adopted in literature [23] and [24] separates the encryption key from the retrieval key and improves the security of the key. Literature [25] proposed an improved scheme with more advantages than the double-key encryption algorithm in the single-key encryption mode. None of the above schemes can control the retrieval authorization, and the retrieval mechanism is based on comparing the ciphertext. The retrieval process cannot highlight the advantages of the homomorphic encryption algorithm. The scheme of this paper introduces the authorization code, which has a low correlation with the user’s identity information, and its relative independence protects the user’s identity privacy to a certain extent. The combination of the authorization code and the homomorphic encryption algorithm will not affect the security of the encryption algorithm, and it has the advantages of simple operation, a small amount of computation, and strong functionality. It is suitable for application scenarios that require access authorization to ciphertext data. From the comparison of the retrieval mechanism/function and retrieval algorithm in Table 2, the retrieval mechanism of the improved scheme also has functions such as multiple keywords retrieval and similarity sorting of retrieval results. It is more functional than other schemes, and the application value of the homomorphic encryption algorithm is greater. The specific advantages are as follows:

(1)   Extracting multiple keywords with different attributes from the original file for retrieval can improve retrieval efficiency and accuracy and broaden the application scenarios of the scheme.

(2)   The similarity sorting of retrieval results can make the retrieval results have a correlation range, meet the multi-value requirements of the retrieval results in different application scenarios, and improve the correctness of the retrieval results.

(3)   In the improved retrieval scheme, the retrieval key p3 is used to calculate the retrieval value of the ciphertext, and then the ciphertext retrieval scheme is run. It can reduce the retrieval cost and improve the retrieval efficiency.

2. Computational Comparison and Analysis

The improved scheme of this paper and several other existing schemes are compared and analyzed from the computation of the algorithm. In Table 3, Tp represents the time to generate random numbers (large prime numbers, integers), Te represents the time of exponentiation, Ta represents the time of addition or subtraction, To represents the time of multiplication or division, and Tm represents the time of modulo operation.

5.2 Simulation Analysis

1. Simulation Environment

Our experiments were conducted on a CentOS 7 Operating System utilizing the GNU Multiple Precision Arithmetic Library (GMP) for large-number computations. The simulation employed C language programming through the VSCode environment, with result visualization performed in MATLAB. The scheme ingests custom-designed plaintext data documents to emulate authentic operational environments, while authorization codes were randomly generated at specified bit lengths, and security parameters were configured according to the DGHV framework. Comprehensive evaluations validated the full workflow, including key generation, document encryption/decryption, access-controlled retrieval, and ciphertext search operations, conclusively demonstrating the scheme’s cryptographic security and functional viability.

2. Analyzing Algorithm Efficiency

The simulation implements multiple improvement schemes listed in Table 3 in the previous subsection. The running time of Keygen(), Encrypt(), and Decrypt() in the test scheme is shown in Fig. 2 for the comparison results.

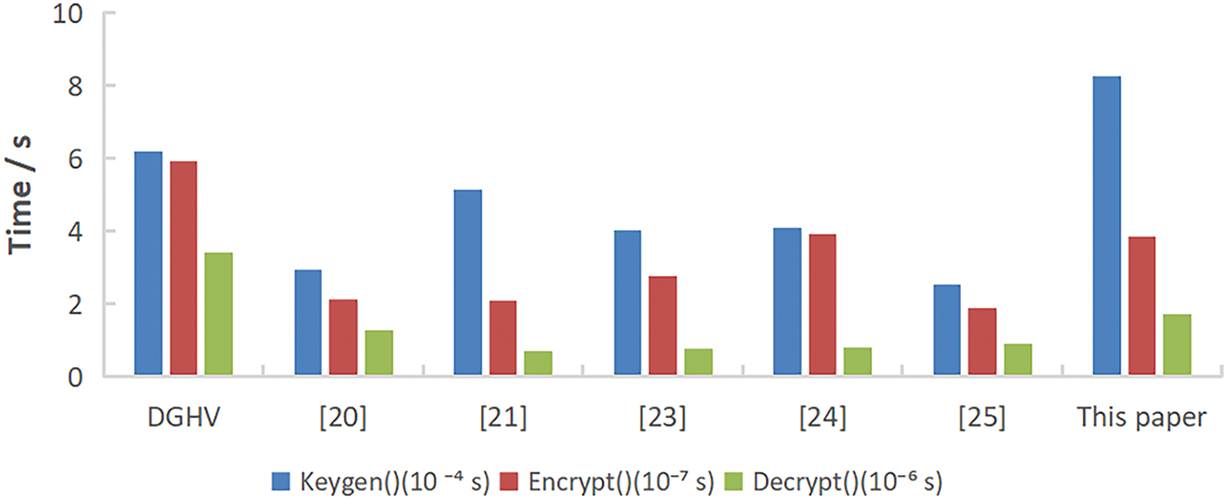
Figure 2: The running time comparison of the improved algorithm [20,21,23–25]

Because the scheme in this paper needs to generate additional retrieval authorization key p2 and retrieval key p3 and increases the generation process of secure large prime number P and idempotent element gx, the running time of Keygen() is relatively high. Although the Encrypt() and Decrypt() algorithms need to call three keys to participate, the running time is still close to the average. This scheme improves the security of the data storage and retrieval process by generating keys with different functionalities at the expense of algorithm efficiency.

To prove that the overall algorithm is more efficient, the bit-by-bit encryption of data documents with different plaintext digits is tested and then compared with the DGHV scheme and the double-key improvement scheme in reference [24]. This process only needs to run the Keygen() once; the key is the same. Table 4 below shows the number of bits of encrypted documents selected during the test. Under the same conditions, the comparison results of the encryption and decryption running times are shown in Fig. 3.

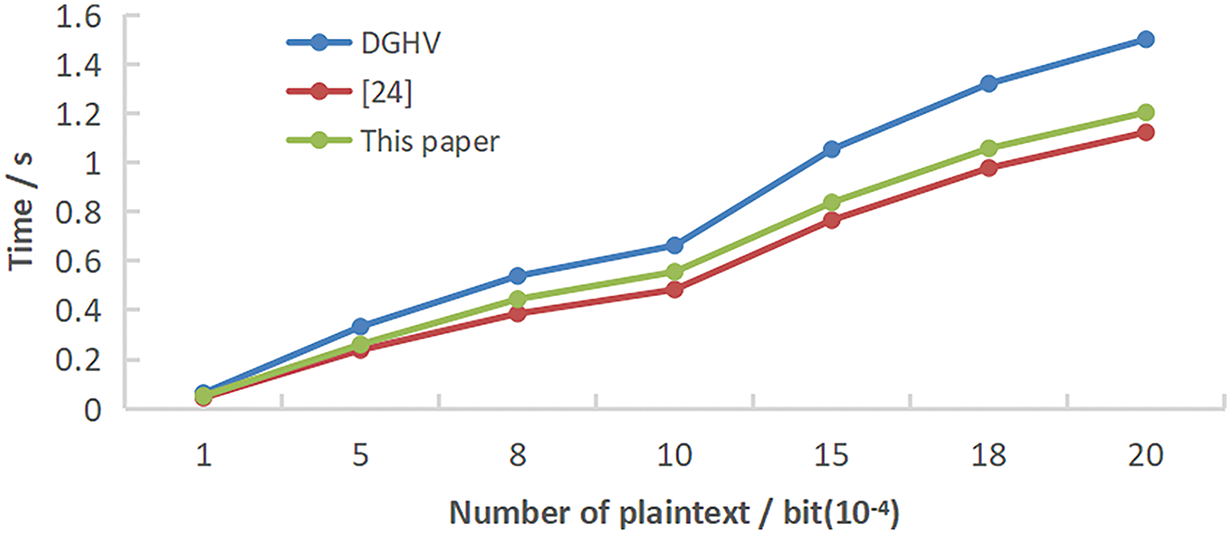
Figure 3: Comparison of the running time of encryption and decryption of different bit documents [24]

As seen from the above figure, the algorithm’s running time is closely related to the number of bits of the encrypted plaintext. The fully homomorphic encryption scheme encrypts and decrypts plaintext of different lengths bit by bit and draws the conclusion on the premise of ensuring the correctness of the operation result: The operation efficiency of the proposed scheme in the three-key encryption mode is higher than that of DGHV, and there is little difference compared with the operation efficiency of the scheme in the double-key encryption mode. The scheme in this paper only sacrifices a small part of the efficiency in exchange for the high security of the algorithm. It added a retrieval authorization key, a separate encryption key, and a retrieval key. The joint participation of multiple keys can significantly improve the security of the fully homomorphic encryption scheme and is suitable for more application scenarios than the double-key and single-key schemes.

3. Analysis, Retrieval Access Control

In the above process of encrypting and decrypting a 1-bit plaintext, Upload(), Verification(), and Return() algorithms are added to simulate the process of verifying the retrieval authorization and test the running time. First, only run the encryption and decryption algorithm on the 1-bit plaintext, then add the retrieval authorization process. Compare the running time test of the before and after solutions. The results are shown in Table 5 below.

The test results show that the verification process of the retrieval authorization code is highly efficient. It does not increase the extra algorithm operating cost but can better protect the retrieved data’s security and verify the retriever’s legal identity.

4. Analysis of the Ciphertext Retrieval Mechanism

Fig. 4 is a time comparison of the ciphertext retrieval mechanism based on homomorphic encryption for each improved scheme for different numbers of data documents. This paper’s scheme takes longer to retrieve data than other schemes. However, the algorithm of the retrieval mechanism is not a simple ciphertext comparison but adds the function of retrieving multiple keywords and sorting the similarity of retrieval results. It improves the retrieval scheme’s security, functionality, and application value, and it is enough to compensate for the lack of efficiency.

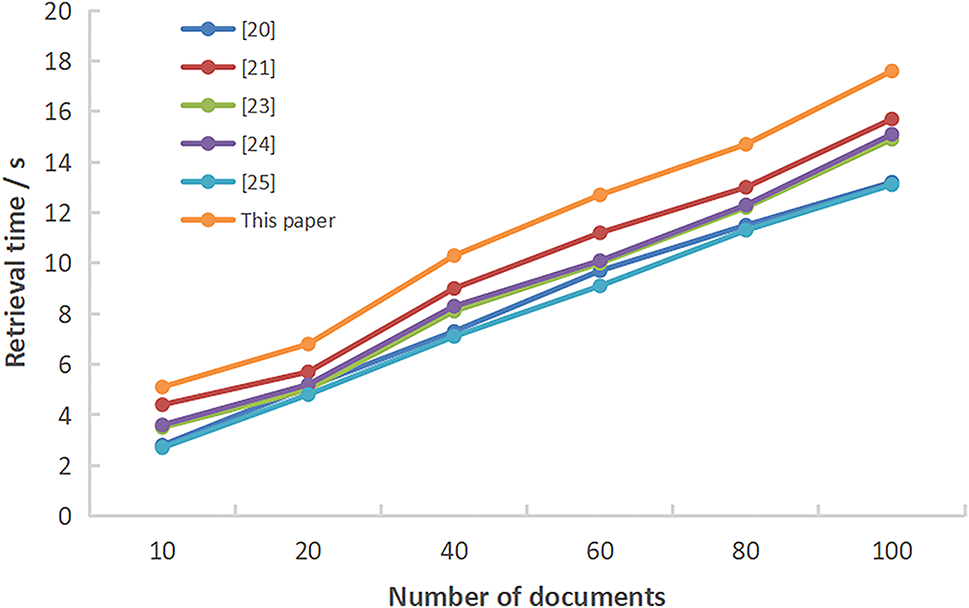
Figure 4: Retrieval time comparison [20–25]

6  Conclusions

This paper proposes an enhanced fully homomorphic encryption scheme for ciphertext retrieval applications, specifically designed as an improved variant of the DGHV algorithm tailored for cloud storage environments. Building upon the original DGHV framework, our solution introduces three critical innovations: verifiable search authorization, a triple-key cryptographic mechanism, and enhanced ciphertext search functionality. The research encompasses four principal components: (1) homomorphic encryption scheme design, (2) ciphertext retrieval protocol development, (3) formal verification of scheme correctness and security properties, and (4) theoretical benchmarking and simulation-based validation of scheme performance. The final theoretical analysis and simulation results demonstrate that, compared with existing improved schemes, the enhanced FHE solution proposed in this paper exhibits measurable advantages. It effectively guarantees both the security of cloud-stored data and the precision of retrieval operations, while simultaneously ensuring the legitimacy of searcher identity authorizations, the cryptographic integrity of data owners’ keys, and the functional versatility of ciphertext retrieval mechanisms. Although cryptographic primitives (key generation, encryption/decryption algorithms) and retrieval operations demonstrate lower throughput than comparative studies, this limitation is counterbalanced by the scheme’s highly efficient authorization verification protocols and its robust key management architecture. Our work addresses evolving requirements in cloud storage applications through novel methodologies that resolve critical security challenges, providing both innovative cryptographic mechanisms and practical implementation frameworks, the cryptographic integrity of data owners’ keys, and the functional versatility of ciphertext retrieval mechanisms.

Acknowledgement: Not applicable.

Funding Statement: This work was supported by the Innovation Program for Quantum Science and technology (2021ZD0301300). This work was supported by the Fundamental Research Funds for the Central Universities (Nos. 3282024046, 3282024052, 3282024058, 3282023017).

Author Contributions: The authors confirm contribution to the paper as follows: write the main manuscript: Ronglei Hu, Chuce He; figures and tables preparation: Sihui Liu, Dong Yao; manuscript translation: Xiuying Li; data collection: Xiaoyi Duan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Song DX, Wagner D, Perrig A. Practical techniques for searches on encrypted data. In: Proceeding 2000 IEEE Symposium on Security and Privacy. S&P 2000; 2000 May 14–17; Berkeley, CA, USA. p. 44–55. doi:10.1109/SECPRI.2000.848445. [Google Scholar] [CrossRef]

2. Kerl M, Bodin U, Schelén O. Privacy-preserving attribute-based access control using homomorphic encryption. Cybersecurity. 2025;8(1):5. doi:10.1186/s42400-024-00323-8. [Google Scholar] [CrossRef]

3. Sharma D. Searchable encryption: a survey. Inf Secur J A Glob Perspect. 2023;32(2):76–119. doi:10.1080/19393555.2022.2033367. [Google Scholar] [CrossRef]

4. Lu S, Zheng J, Cao Z, Wang Y, Gu C. A survey on cryptographic techniques for protecting big data security: present and forthcoming. Sci China Inf Sci. 2022;65(10):201301. doi:10.1007/s11432-021-3393-x. [Google Scholar] [CrossRef]

5. Rivest R, Adleman L, Dertouzos M. On data banks and privacy homomorphisms. Found Secur Comput. 1978;4(11):169–80. [Google Scholar]

6. Xu L, Zhao C, Jiang W, Ye J, Zhao Y, Zhang Z. Secure encryption scheme for medical data based on homomorphic encryption. In: 2023 International Conference on Data Science and Network Security (ICDSNS); 2023 Jul 28–29; Tiptur, India. p. 1–9. doi:10.1109/ICDSNS58469.2023.10245348. [Google Scholar] [CrossRef]

7. Hou Y, Yao W, Li X, Xia Y, Wang M. Lattice-based semantic-aware searchable encryption for Internet of Things. IEEE Internet Things J. 2024;11(17):28370–84. doi:10.1109/JIOT.2024.3400816. [Google Scholar] [CrossRef]

8. Zhang QY, Wen YW, Huang YB, Li FP. Secure speech retrieval method using deep hashing and CKKS fully homomorphic encryption. Multimed Tools Appl. 2024;83(26):67469–500. doi:10.1007/s11042-024-18113-2. [Google Scholar] [CrossRef]

9. Liu J, Lin S. An efficient and more secure searchable encryption algorithm based on fully homomorphic encryption. In: 2023 International Conference on Automation, Control and Electronics Engineering (CACEE); 2023 Oct 20–22; Chongqing, China. p. 83–92. doi:10.1109/CACEE61121.2023.00025. [Google Scholar] [CrossRef]

10. Van Dijk M, Gentry C, Halevi S, Vaikuntanathan V. Fully homomorphic encryption over the integers. In: Advances in Cryptology—EUROCRYPT 2010: 29th Annual International Conference on the Theory and Applications of Cryptographic Techniques; 2010 May 30–Jun 3; French Riviera,France. p. 24–43. doi:10.1007/978-3-642-13190-5_2. [Google Scholar] [CrossRef]

11. Coron JS, Mandal A, Naccache D, Tibouchi M. Fully homomorphic encryption over the integers with shorter public keys. In: Annual Cryptology Conference; 2011 Aug 14–18; Santa Barbara, CA, USA. p. 487–504. doi:10.1007/978-3-642-22792-9_28. [Google Scholar] [CrossRef]

12. Black N. Homomorphic encryption and the approximate GCD problem [Internet]. Clemson, SC, USA: Clemson University; 2014 [cited 2025 Mar 24]. Available from: https://tigerprints.clemson.edu/all_dissertations/1280. [Google Scholar]

13. Wang L, Ge L, Geng B, Wang Q. Encryption cipher text retrieval scheme based on fully homomorphic encryption enterprise cloud storage. J Phys Conf Ser. 2019;1237(4):042005. doi:10.1088/1742-6596/1237/4/042005. [Google Scholar] [CrossRef]

14. Gong C, Du J, Dong Z, Guo Z, Gani A, Zhao L, et al. Grover algorithm-based quantum homomorphic encryption ciphertext retrieval scheme in quantum cloud computing. Quantum Inf Process. 2020;19(3):105. doi:10.1007/s11128-020-2603-0. [Google Scholar] [CrossRef]

15. He H, Chen R, Liu C, Feng K, Zhou X. An efficient ciphertext retrieval scheme based on homomorphic encryption for multiple data owners in hybrid cloud. IEEE Access. 2021;9:168547–57. doi:10.1109/ACCESS.2021.3135050. [Google Scholar] [CrossRef]

16. Wang W, Jin Y, Cao B. An efficient and privacy-preserving range query over encrypted cloud data. In: 2022 19th Annual International Conference on Privacy, Security & Trust (PST); 2022 Aug 22–24; Fredericton, NB, Canada. p. 1–10. doi:10.1109/PST55820.2022.9851989. [Google Scholar] [CrossRef]

17. Wang Y, Chen L, Wu G, Yu K, Lu T. Efficient and secure content-based image retrieval with deep neural networks in the mobile cloud computing. Comput Secur. 2023;128:103163. doi:10.1016/j.cose.2023.103163. [Google Scholar] [CrossRef]

18. Song WT, Zeng G, Zhang WZ, Tang DH. Research on privacy information retrieval model based on hybrid homomorphic encryption. Cybersecurity. 2023;6(1):31. doi:10.1186/s42400-023-00168-7. [Google Scholar] [CrossRef]

19. Cheng ZW, Chen XB, Xu G, Chang Y, Miao LH, Yang YX, et al. A secure quantum homomorphic encryption ciphertext retrieval scheme. Soft Comput. 2025;29(3):1497–509. doi:10.1007/s00500-025-10454-w. [Google Scholar] [CrossRef]

20. Xi X, Cao B. An Improved fully homomorphic encryption scheme under conditions of cloud computing. Comput Technol Dev. 2015;2:144–7. (In Chinese). [Google Scholar]

21. Hong J, Chen J. A ciphertext retrieval algorithm based on full homomorphic encryption. J Langfang Norm Univ (Nat Sci Ed). 2018;4:15–8,30. (In Chinese). [Google Scholar]

22. Kumar V, Buksh B, Sharma I. Double fully homomorphic encryption for tamper detection in incremental documents. In: Satapathy SC, Das S, editors. Proceedings of First International Conference on Information and Communication Technology for Intelligent Systems. Berlin/Heidelberg, Germany: Springer; 2016. Vol. 2, p. 165–71. doi:10.1007/978-3-319-30927-9_17. [Google Scholar] [CrossRef]

23. Qin Z, Han Y, Zhu X. Research on ciphertext full-text retrieval of cloud storage based on improved DGHV algorithm. Netinfo Secur. 2019;19(1):8–15. (In Chinese). [Google Scholar]

24. Ping E. Research on data security scheme of cloud storage platform. Mod Inf Technol. 2019;3(23):156–7, 160. (In Chinese). [Google Scholar]

25. Li L, Yu X. HES: a homomorphic encryption scheme with better public key size. J Hengyang Norm Univ. 2016;3:19–25. (In Chinese). [cited 2025 Jan 1]. Available from: https://www.docin.com/p-1731972759.html. [Google Scholar]