Advancing Code Obfuscation: Novel Opaque Predicate Techniques to Counter Dynamic Symbolic Execution

1  Introduction

With the growing integration of the Internet into everyday life, software has become a key tool for providing essential services across various domains, including scientific research and daily life. However, the widespread distribution and use of terminal software have also incurred significant security risks, such as malware, software cracking, and information leakage, causing damage to both developers and end-users. To counter these threats, researchers have developed various protective methods, including encryption [1] and code obfuscation [2,3]. Encryption, while effective in securing data, has limitations when it comes to software protection, as encrypted programs must eventually be decrypted into executable forms, allowing attackers to intercept and analyze them in untrusted environments. Among the alternatives, code obfuscation has emerged as a promising solution for software protection due to its flexibility, efficiency, and relatively low overhead. Among the various types of obfuscation, control obfuscation, which modifies the control-flow structure of a program, is particularly effective in preventing reverse engineering. Techniques such as control flow flattening and opaque predicates are commonly employed to complicate the program’s control flow. Among these, opaque predicates are attractive due to their ability to increase control flow complexity while having minimal impact on execution performance. However, these control-flow obfuscation techniques are increasingly vulnerable to detection due to advances in Dynamic Symbolic Execution [4–7].

In our work, we address the limitations of existing methods by introducing a new class of opaque predicates specifically designed to resist symbolic execution. Our approach focuses on two key weaknesses of symbolic execution: path explosion and constraint solving. We propose opaque predicates based on single-way functions, such as hash functions and logarithmic computations, which complicate the generation of valid inputs for symbolic execution. Additionally, we introduce path-explosion techniques that generate irrelevant bogus control-flow branches, overwhelming the sources of symbolic execution engines.

We implement our approach in a prototype obfuscation tool based on the Obfuscator-LLVM [8] framework. To evaluate the resilience of our approach, we conducted experiments using two prominent dynamic symbolic execution engines: KLEE [9] and Angr [10]. Our results demonstrate that the proposed opaque predicates exhibit strong resilience against symbolic execution-based attacks while maintaining acceptable performance overhead compared to the default opaque predicates in Obfuscator-LLVM. Furthermore, our scheme integrates seamlessly with existing opaque predicates, enhancing their resilience without sacrificing performance.

This paper makes the following contributions:

•   A framework of strong resilience against symbolic execution: We implemented a prototype obfuscation tool that integrates our proposed opaque predicates into the Obfuscator-LLVM framework. This tool enables developers to apply our resilient opaque predicates in the form of optional parameter configurations during the compilation process, ensuring that their software is well-protected against symbolic execution attacks.

•   Novel Opaque Predicates Using Single-Way Functions: We propose the use of single-way functions, such as hash functions and logarithmic computations, in combination with traditional opaque predicates. These predicates make it difficult for symbolic execution engines to recognize and solve the constraints generated by the obfuscated code. Our experiments demonstrate that these enhanced opaque predicates are highly effective in resisting symbolic execution attacks.

•   Path-Explosion Opaque Predicates: We construct opaque predicates that induce path explosion, a known challenge for symbolic execution. By generating numerous irrelevant bogus control-flow branches, these predicates cause symbolic execution engines to waste time solving irrelevant paths, effectively disabling the analysis.

•   Comprehensive Evaluation of Security and Performance: We evaluate the security of our opaque predicates against two prominent symbolic execution engines, KLEE and Angr, using a diverse set of benchmarks and real-world applications. Our results show that the proposed predicates significantly increase resilience against symbolic execution, while the performance overhead remains negligible compared to the default obfuscation methods used in Obfuscator-LLVM.

2  Literature Review and Motivation

2.1 Code Obfuscation and Opaque Predicates

Code obfuscation is a well-established technique for protecting software from reverse engineering and tampering. Collberg et al. [2] classified code obfuscation into four categories: layout obfuscation, data obfuscation, control obfuscation, and preventive transformation. Control obfuscation, which alters the control-flow structure of a program, plays a crucial role in thwarting reverse engineering attempts. One of the key techniques within control obfuscation is the use of opaque predicates. Opaque predicates [2] are Boolean expressions whose outcome is predetermined by the developer but appear ambiguous to an external observer, especially during static or dynamic analysis. By embedding these complex predicates, developers make it harder for attackers to discern the program’s logic, thus increasing its protection against analysis.

Opaque predicates can be categorized into two types: static and dynamic, shown in Fig. 1. Static opaque predicates have Boolean values that are determined at compile-time and remain constant throughout the program’s execution. An example of a static opaque predicate is a complex mathematical expression that always evaluates to true, such as (x2−x)mod2=0 for any integer x. In contrast, dynamic opaque predicates change their values based on runtime conditions, making them more unpredictable and challenging to analyze. For instance, a dynamic opaque predicate might depend on the system time, such as time mod2=0 which would evaluate to true or false based on whether the system time is an even or odd number.

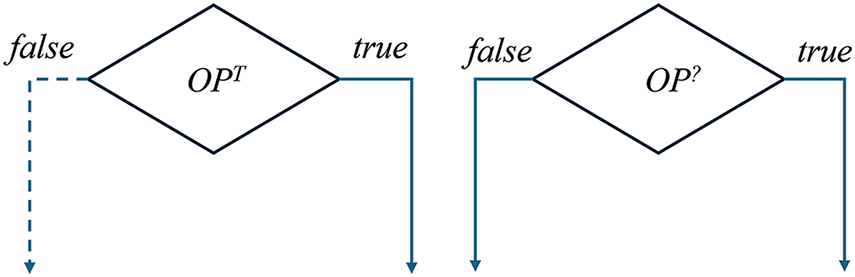
Figure 1: Static and dynamic opaque predicates. OPT means opaque predicates that are always true, OP?means opaque predicates that are uncertain. Solid lines indicate paths that may sometimes be taken, and dashed lines indicate paths that will never be taken

2.2 Symbolic Execution

Symbolic execution, first introduced by King [11], is a program analysis technique that systematically explores program paths by treating inputs as symbolic variables rather than concrete values. This method allows for the analysis of all possible execution paths by representing inputs with symbolic expressions and constructing path conditions—conjunctions of constraints on the symbolic inputs—along each path. As the symbolic executor navigates through the program, it builds these path conditions and relies on constraint solvers to check their satisfiability. If a path condition is unsatisfiable, the corresponding execution path is considered infeasible. Symbolic execution is particularly useful for identifying security vulnerabilities and generating test cases that cover edge cases and rare scenarios that might be missed by traditional testing methods [12].

Dynamic Symbolic Execution [13,14] combines symbolic execution with concrete execution [15–17], enabling more practical and scalable exploration of multiple execution paths within a program. After executing a path with concrete inputs, DSE employs a constraint solver to generate new inputs that can drive the program along unexplored paths. Unlike pure symbolic execution, which attempts to explore all possible paths, DSE focuses on paths encountered during actual runs, making it more efficient.

However, symbolic execution faces several challenges, most notably path explosion [18], where the number of possible execution paths grows exponentially with program complexity. This issue can overwhelm the analysis, especially in larger programs with many branching conditions or loops. Additionally, symbolic execution struggles with complex data structures, external libraries, and interactions with operating systems or networks, which often require sophisticated modeling to simulate their behavior accurately [17].

Another significant limitation of symbolic execution is its reliance on constraint solvers [18], such as STP [19] and Z3 [20]. While constraint solvers play a critical role in reasoning about program paths, they can become a bottleneck, particularly when dealing with large or complex constraints. As the complexity of the symbolic expressions grows, the efficiency of the solver decreases, leading to longer analysis times or even failure to find solutions within reasonable limits. Scalability issues further exacerbate this problem, as handling a large number of constraints can be computationally expensive and time-consuming.

2.3 Code Obfuscation against Dynamic Symbolic Execution

DSE combines dynamic program analysis with symbolic reasoning, enabling the exploration of multiple execution paths based on symbolic values rather than concrete inputs. This makes it an efficient tool for identifying and neutralizing obfuscation techniques [21–23], including opaque predicates. Tools like Angr can easily distinguish opaque predicates by identifying branches that are never satisfied, thereby stripping them from the program. To address this challenge, researchers have proposed several solutions, including hard-to-solve predicates such as Mixed Boolean Arithmetic (MBA) [24] formulas and cryptographic hash functions [25]. However, MBA formulas are often unsuitable for opaque predicates, and cryptographic functions, while secure, tend to introduce significant overhead and are vulnerable to key extraction attacks, possibly through DSE. More recently, path-explosion techniques have been introduced to complicate symbolic execution. For instance, Banescu et al. [18] demonstrate that standard obfuscation tools like Obfuscator-LLVM and Tigress [26] have limited effectiveness against DSE and propose Ranger Divider, a path-explosion obfuscation technique. However, this approach suffers from excessive code duplication. Ollivier et al. [27] developed SPLIT and FOR transforms that limit branch choices to reduce code duplication, but these techniques are only available at the C source code level. Dinu [28] extended these techniques to the Low Level Virtual Machine (LLVM) level, though the project source code is not publicly available. Xu et al. [29] introduced Bi-Opaque Predicates, which employ symbolic memory and parallel programming to complicate symbolic analysis. Hirano and Ohtaki [30] proposes an opaque predicate design based on homomorphic encryption, which significantly enhances resilience against static and symbolic execution analysis by leveraging the mathematical properties of encryption. However, it is burdened by high computational overhead, limited compatibility with modern binary analysis frameworks, and increased deployment complexity, all of which significantly hinder its practical application in real-time or resource-constrained environments. De Pasquale et al. [31] proposes ROPfuscator that leverages Return-Oriented Programming (ROP) to transform code into ROP chains, and then augments the obfuscation by integrating opaque predicates and an instruction hiding mechanism to protect critical gadget addresses, while ROPfuscator effectively disrupts static disassembly and hampers dynamic analysis, its robustness is heavily contingent on the availability of suitable ROP gadgets extracted from the target libraries, and it incurs significant performance and code size overhead.

2.4 Motivation

2.4.1 Adversary Model

In our adversary model, we assume that attackers have access to the binary program obfuscated using our framework but not to the source code. These adversaries are skilled in program analysis and equipped with advanced symbolic execution tools, allowing them to attempt deobfuscation of our protections in conjunction with other analysis techniques. However, they operate with limited resources, including time and computational capacity. Importantly, we do not expect attackers to invest in the development of specialized tools. Our goal is to sufficiently delay the attack process to the extent that the costs—both in terms of time and resources—become prohibitive, dissuading further attempts at deobfuscation.

2.4.2 Motivating Example

To illustrate the effectiveness of our obfuscation protections, we present a simple example program. As depicted in Fig. 2a, the program prompts users to input an integer. If the input is 30, the program outputs a success message; otherwise, it prompts the user to “try again.” The obfuscation utilized in this example is based on the Obfuscator-LLVM project, initiated in June 2010 by the Information Security Group at the University of Applied Sciences and Arts in Western Switzerland. This project aims to enhance software security through various code obfuscation techniques. Specifically, we focus on the bogus control flow transformation, which employs number theory-based opaque predicates.

Figure 2: Example program structure

As shown in Fig. 2b, the original control flow of the example program consists of two subsequent choices represented in LLVM IR. The obfuscated control flow introduced by the bogus control flow transformation complicates the structure significantly, as illustrated in Fig. 3. The opaque predicates, represented by the expression

(x(x−1))mod 2=0||y<10(1)

are highlighted in red boxes.

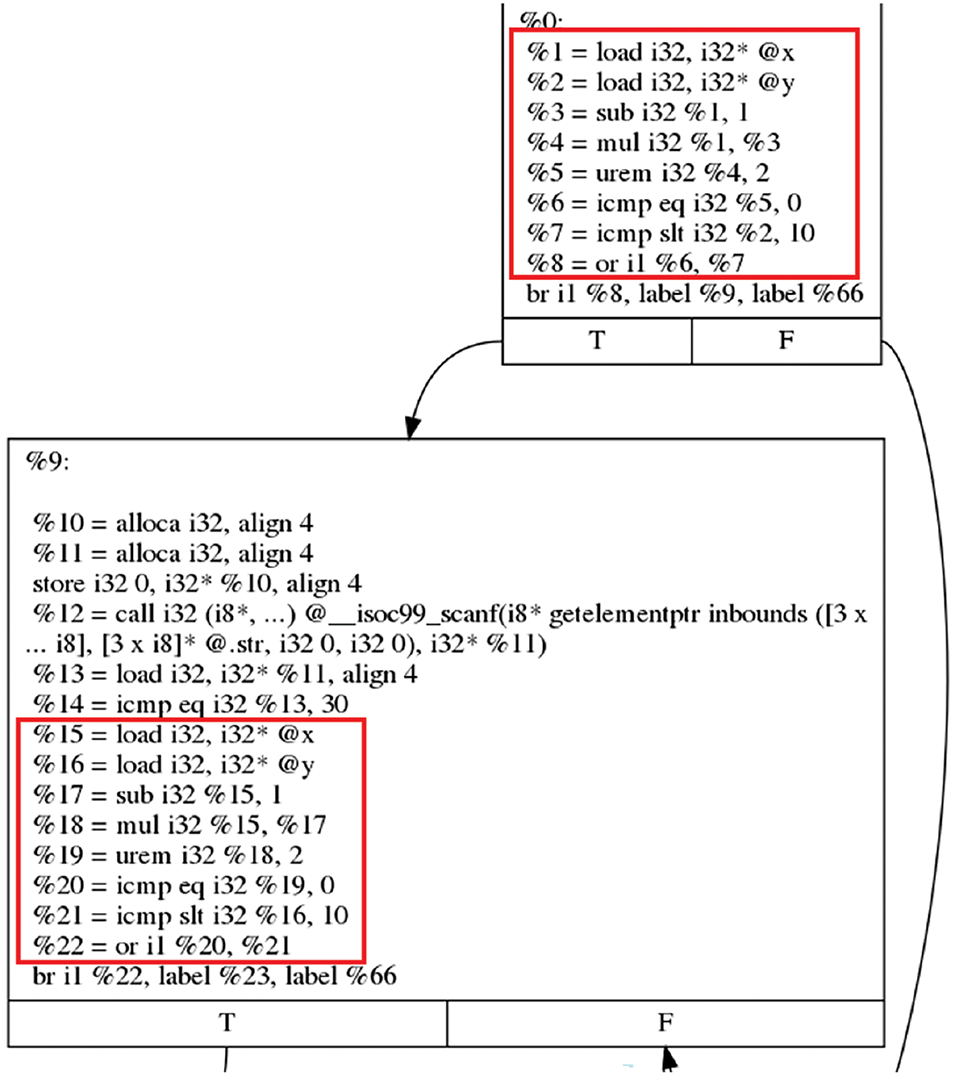
Figure 3: Opaque predicate in LLVM intermediate representation (IR)

When subjected to symbolic execution, as demonstrated in Fig. 4, the symbolic execution engine simulates the execution of the obfuscated program and identifies blocks of code that are never executed. Consequently, these bogus blocks enable the detection of associated opaque predicates. The obfuscation introduced by Obfuscator-LLVM is thus revealed, leading to the elimination of the opaque predicates from the protected program [32]. As shown in Fig. 5, instructions in the unexecuted blocks are replaced with no-operation (nop) instructions, confirming that the opaque predicates have been successfully recognized by the symbolic execution engine. This example underscores the vulnerabilities inherent in current opaque predicate techniques, as evidenced by similar findings in other investigations [33,34].

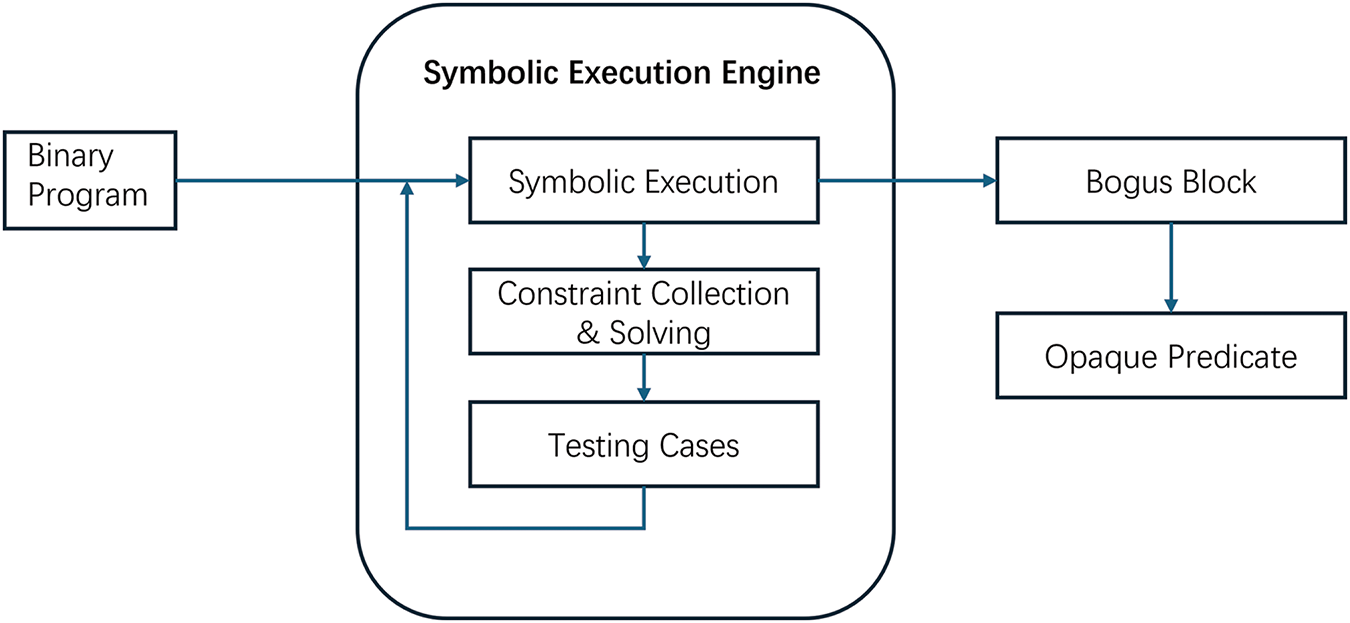
Figure 4: Framework for detecting opaque predicates using symbolic execution techniques

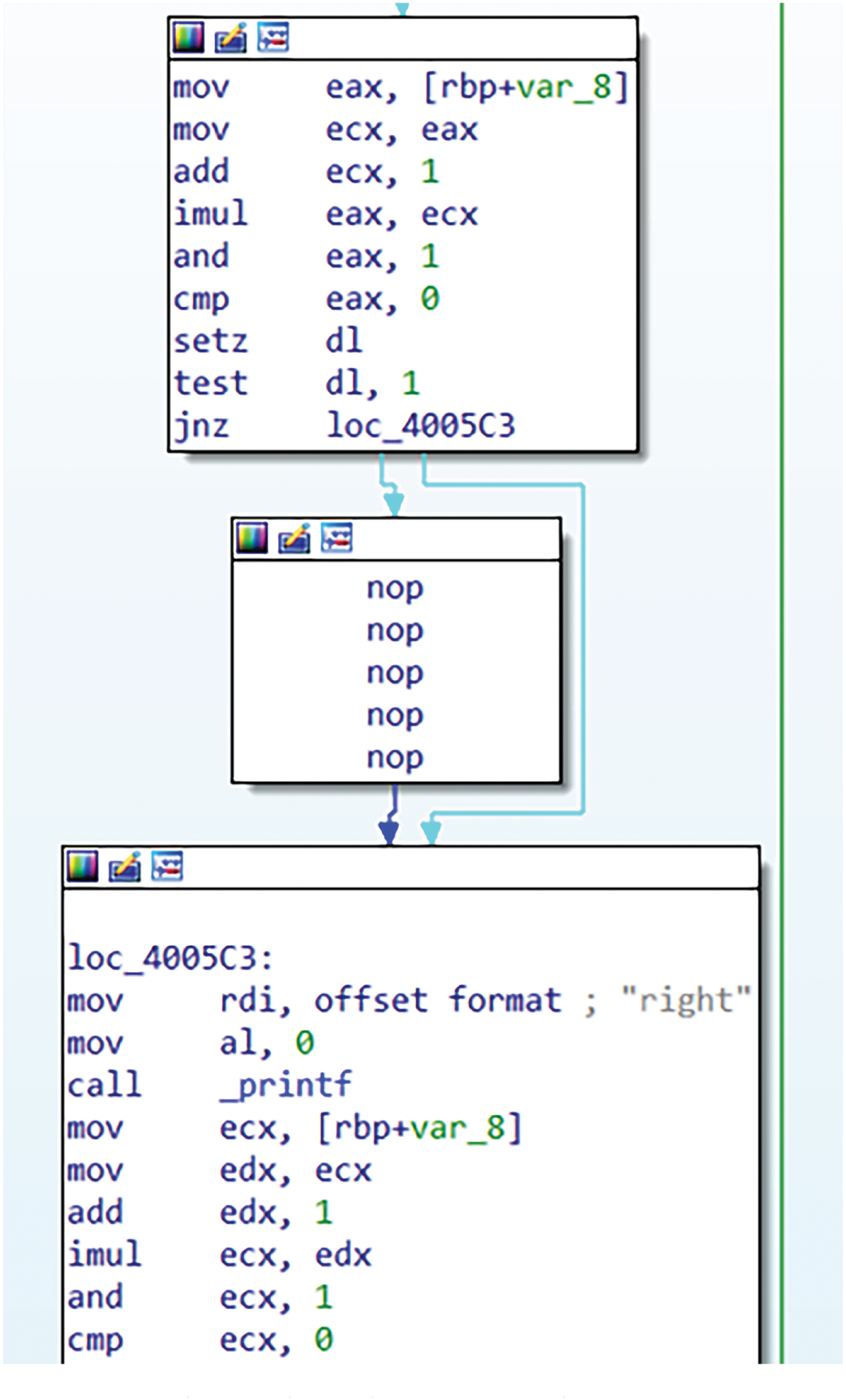
Figure 5: Binary file analyzed by symbolic execution in IDA Pro

3  Approach

We implemented a prototype tool based on Obfuscator-LLVM, leveraging the LLVM infrastructure to focus specifically on control-flow obfuscation for securing program code. As illustrated in Fig. 6, the implementation framework involves several key stages. Initially, the source code is processed through the LLVM Frontend, which transforms it into an Intermediate Representation (IR). This IR serves as a flexible, platform-independent abstraction, enabling various optimizations and transformations before compilation into the final machine code. The LLVM Backend ultimately converts this IR into binary code executable on specific hardware.

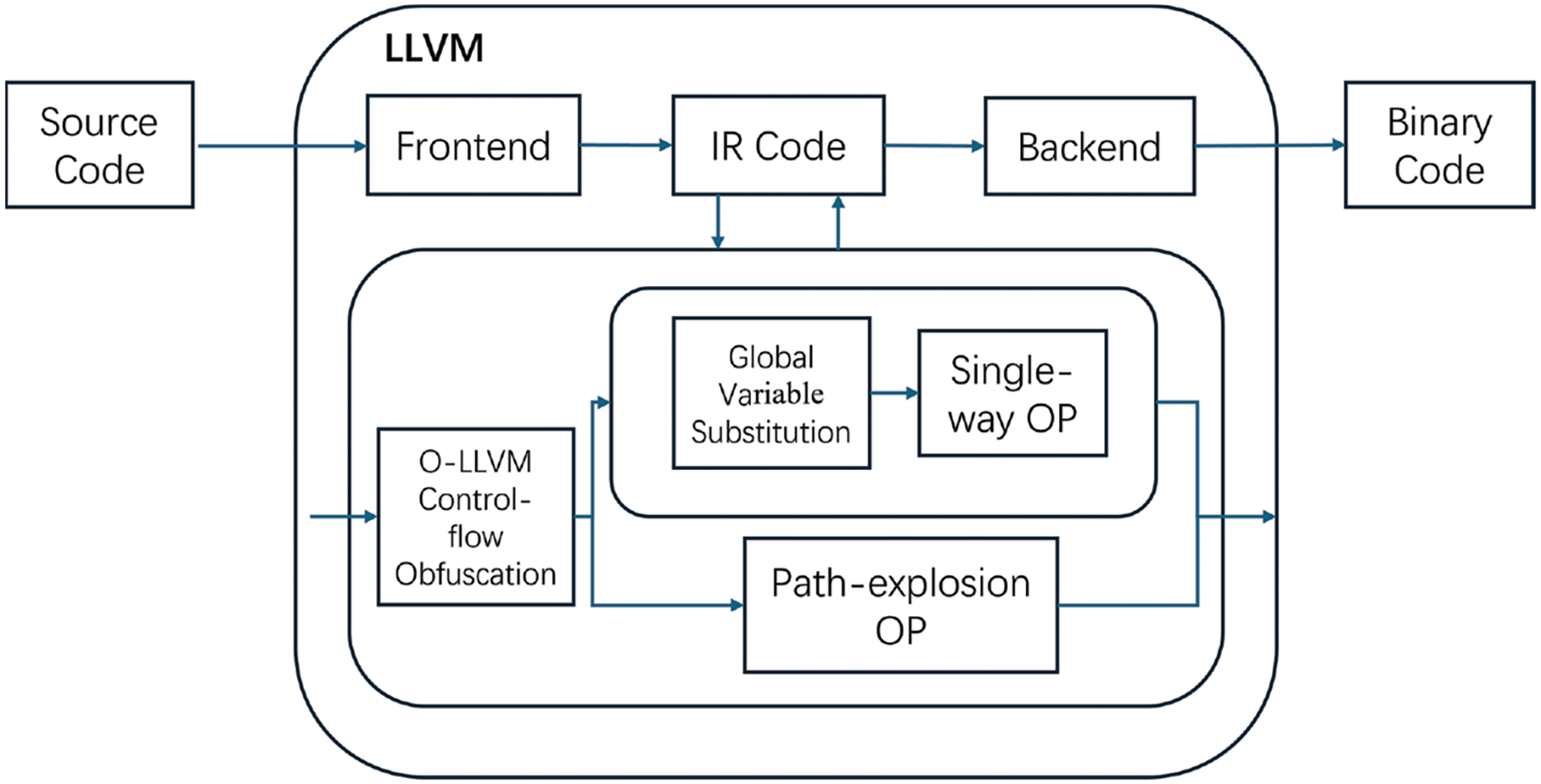
Figure 6: Framework of the prototype implementation, OP indicates opaque predicates

Within this LLVM framework, we integrate our opaque predicates as a dedicated compiler pass, replacing the default predicates generated by Obfuscator-LLVM with more resilient variants. One significant enhancement is the introduction of single-way opaque predicates, which replace global variables with input-related or local variables. This replacement makes it difficult for reverse engineers and symbolic execution tools, as the opaque predicates become strongly correlated with the program inputs, preventing attackers from simply setting global variables to zero and recompiling. Additionally, we use hash functions or logarithmic transformations to obscure the values of the predicates, further complicating their resolution. Alongside this, path-explosion opaque predicates are used as an alternative approach. These predicates introduce numerous bogus branches into the control flow, causing symbolic execution engines to waste resources on irrelevant paths, significantly increasing the complexity of analysis.

3.1 Single-Way Opaque Predicates

As symbolic execution explores the obfuscated program, constraint solvers attempt to get the inputs that satisfy conditions for path traversal. By transforming opaque predicates into forms that are difficult to solve, we aim to render the corresponding bogus blocks that follow the opaque predicates unrecognizable during symbolic execution. The single-way transformation effectively results in an algorithm that is easy to compute in one direction but is infeasible to invert. Specifically, given an input x, computing f(x) is computationally efficient; however, deducing the original input x from y=f(x) is practically infeasible within reasonable time limits.

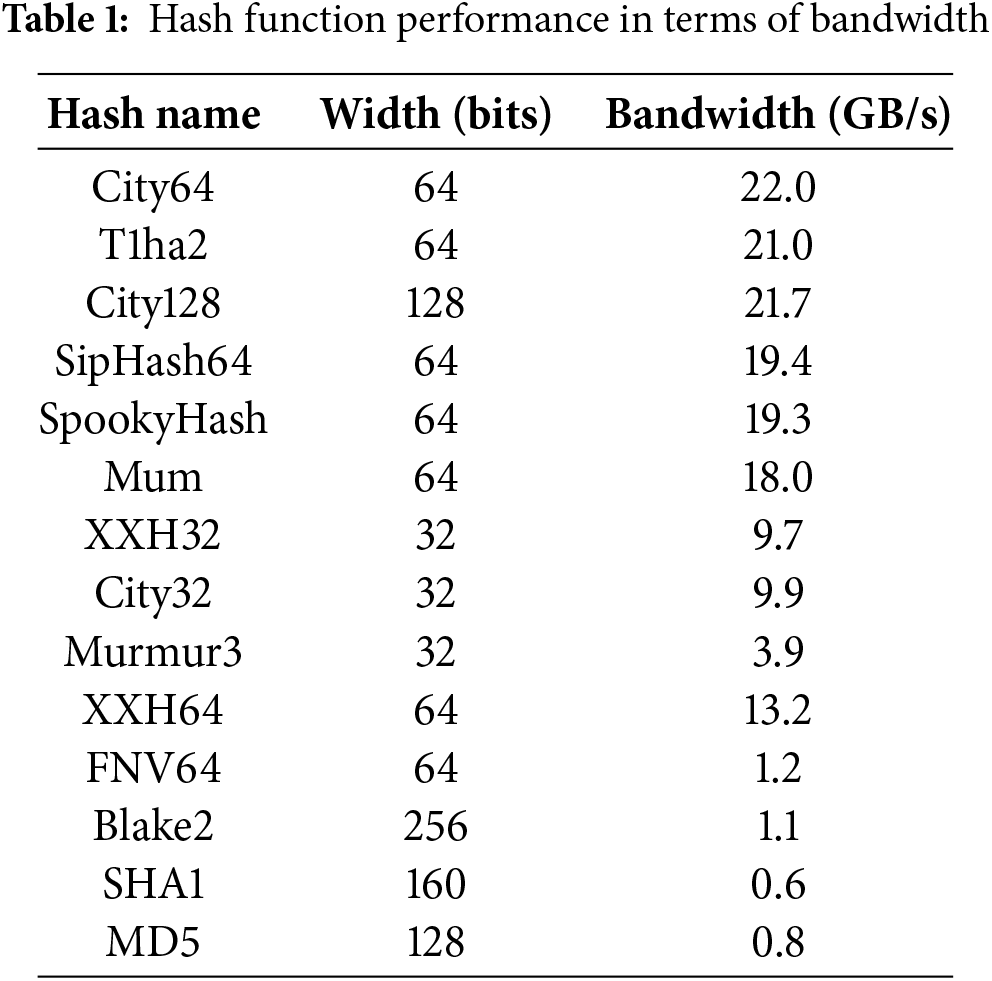
Hash functions, as classical examples of single-way functions, convert inputs into fixed-size byte strings, typically resulting in hash values or codes. The outputs are short, fixed-length values that are unique for each distinct input. To ensure efficient computation, we select CityHash64 [35] as our hashing algorithm. Developed by Google, CityHash is optimized for modern Central Processing Units (CPU) and provides efficient hashing across various platforms and input sizes. It includes multiple variations, such as CityHash64, CityHash128, and CityHash32, accommodating different input lengths and hash space requirements. A comparison of common hash algorithms is presented in Table 1, where we can clearly see the reason for CityHash64 being selected.

As Fig. 7 shows, our approach involves computing the hash values of both the left and right components of the opaque predicate expressions using CityHash. Consequently, the feasible solutions that satisfy our modified predicates cannot be easily determined. For example, given the value of hash(0), it is theoretically impossible to reverse-engineer the original value of zero, thus obscuring the true nature of our opaque predicates from symbolic execution.

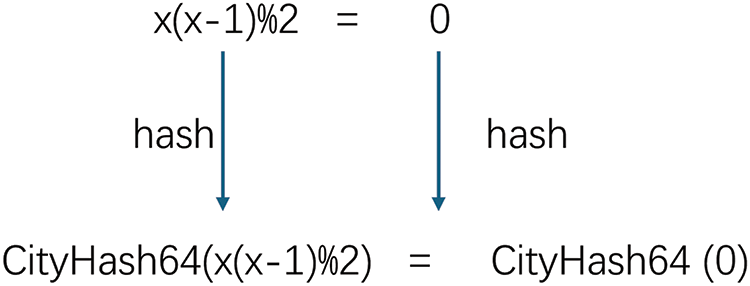
Figure 7: Hash function opaque predicate

However, there are two critical challenges in implementing this approach. First, hash computations introduce additional execution time. As we add multiple opaque predicates to the target program, each execution incurs the overhead of two hash computations. To mitigate this issue, we establish an obfuscation probability limit of 30%–70%, which regulates the number of opaque predicates to reduce computational demands. Additionally, we precompute the hashes of constants (e.g., hash(0)) and incorporate these into the opaque predicates.

Second, the optimal way to compute CityHash is through a dynamically linked library, providing flexibility and reusability. As mentioned, symbolic execution faces challenges when dealing with external libraries. Thus, during testing, we simulate loading the library to execute the code within it, and the results are returned to the symbolic execution state.

If the opaque predicate expressions lack direct comparisons, such as in the case of x2≥0, it becomes irrelevant to compare the relative sizes of two hash values. To address this, we propose an alternative single-way transformation that is more lightweight and suitable for various scenarios.

3.2 Fermat’s Little Theorem Opaque Predicate

Fermat’s Little Theorem, a fundamental concept in number theory discovered by Pierre de Fermat, states that: If p is a prime number and a is an integer not divisible by p, then:

a(p−1)≡1modp(2)

This implies that if you raise a to the power of p−1 and divide by p, the remainder is always 1. It can also be extended to state that for any integer a:

ap≡amodp(3)

Thus, we can replace x with xpmodp, where p is a large prime number. For example, the expression x2≥0 can be transformed into (x2)pmodp≥0. This obfuscation does not alter the program’s semantics and can be computed efficiently using modular exponentiation with a time complexity of O(log⁡p). We utilize an efficient algorithm for fast exponentiation, allowing for quick computation of xpmodp, even when p is large. The pseudocode for this algorithm is illustrated in Algorithm 1. The algorithm shows an efficient method for computing modular exponentiation. It uses the method of successive squaring, reducing the power p by half at each step and multiplying the result when necessary, which significantly reduces the computational complexity. Because this property is transparent to existing symbolic execution tools (e.g., KLEE), it takes O(p) time complexity for the symbolic execution tool to solve this branching condition. So if we choose an appropriate prime p, the symbolic execution will take a fair amount of time to solve. By the way, modular exponentiation causes path explosion with its branch condition and high power computation. Both of them make it infeasible to remove our obfuscation with the help of symbolic execution, thereby enhancing the security of our obfuscation technique.

3.3 Path-Explosion Opaque Predicate

Path explosion occurs when the number of potential execution paths in a program increases exponentially with the number of branching points, such as conditional statements and loops. This exponential growth can render symbolic execution analysis infeasible for larger programs due to constraints related to time and memory. We implement path-explosion opaque predicates through two methods: recursive Fibonacci and the Collatz Conjecture.

3.3.1 Recursive Fibonacci Opaque Predicate

The Fibonacci sequence is defined such that each number is the sum of the two preceding ones, starting typically with 0 and 1. The recursive definition is expressed as follows:

Fn={0,if n=0;1,if n=1;Fn−1+Fn−2,if n>1.(4)

Our Recursive Fibonacci opaque predicate is defined with Fn=Fn−1+Fn−2 that is always true. Upon selecting an appropriate value for n, symbolic execution encounters an explosion of path constraints, leading to excessive time consumption. There are two considerations when using a recursive Fibonacci-based opaque predicate. First, the value of n should be chosen appropriately to ensure the symbolic execution tool fails while not incurring excessive computation time. We conducted experiments with various values for n. Fig. 8 illustrates the impact on symbolic execution time as n varies in our tests, based on the code from Fig. 2. From Fig. 8, it is evident that as n increases, the time required for symbolic execution grows rapidly. When n is set to 20, the execution time exceeds three hours.

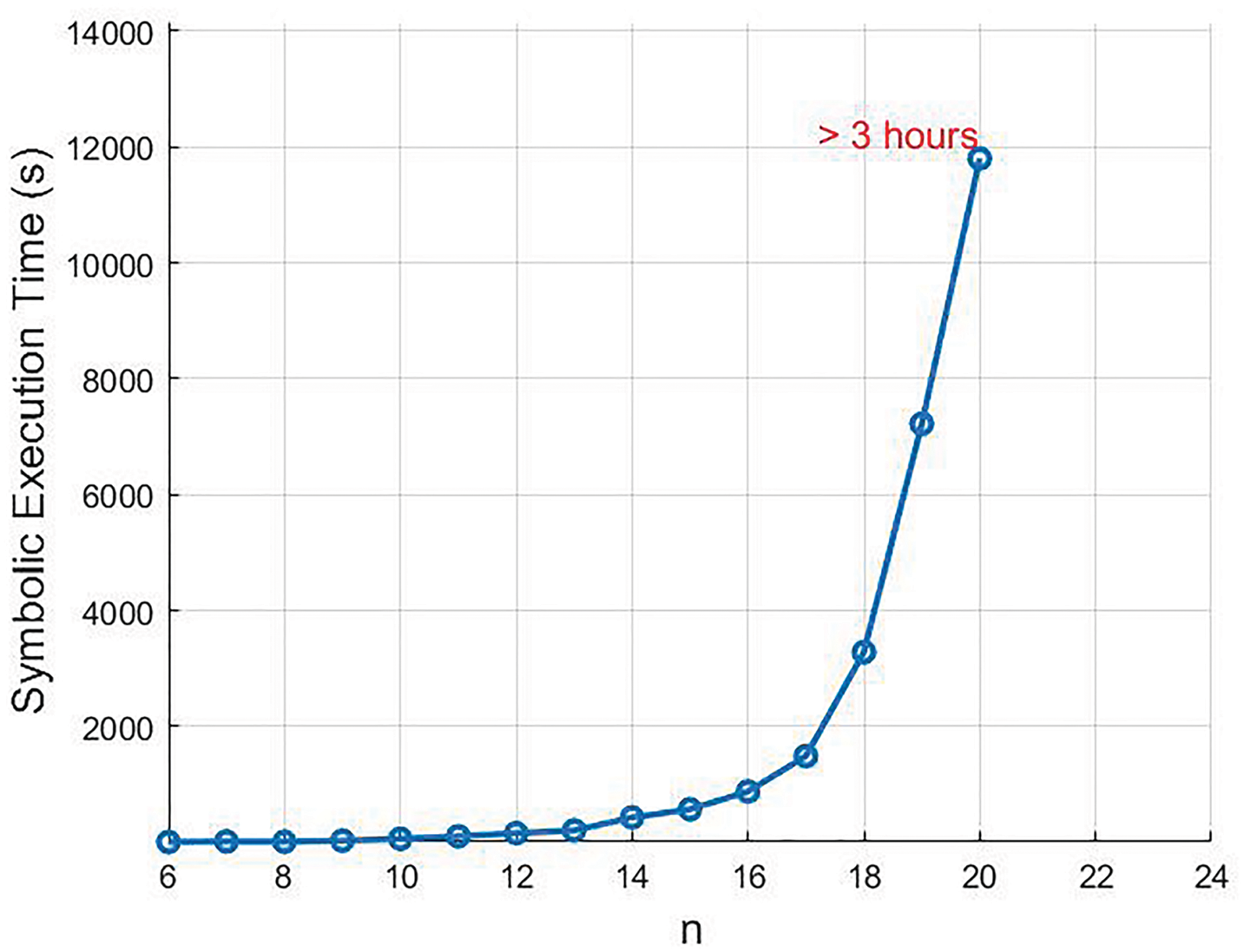
Figure 8: Symbolic execution time of the recursive Fibonacci opaque predicate as n changes

The second issue involves the significant time overhead incurred when calculating the Fibonacci sequence with n set to 20. To improve the efficiency of these calculations, we employ dynamic programming (memorized recursion), which is a top-down dynamic programming approach that stores previously computed Fibonacci numbers in an array to avoid redundant calculations, significantly reducing the time complexity from O(n2) to O(n).

3.3.2 Collatz Conjecture Opaque Predicate

The Collatz Conjecture, also known as the 3n+1 conjecture, defines sequences based on the following rules. Given a positive integer n, define the next term in the sequence T(n) as:

T(n)={n2,if n is even;3n+1,if n is odd.(5)

The conjecture posits that for any initial value n, repeated application of this transformation will eventually yield the value 1. The Collatz Conjecture opaque predicate is structured as shown in Fig. 9. For a given number n, if the transformation T(n) results in a value not less than 1, the true block leads to the next block where T(n)=1 and loops back to the original block when T(n)>1. Otherwise, the subsequent block becomes a bogus block. The multiple loops and conditional judgments induce path constraint explosion, rendering symbolic execution ineffective.

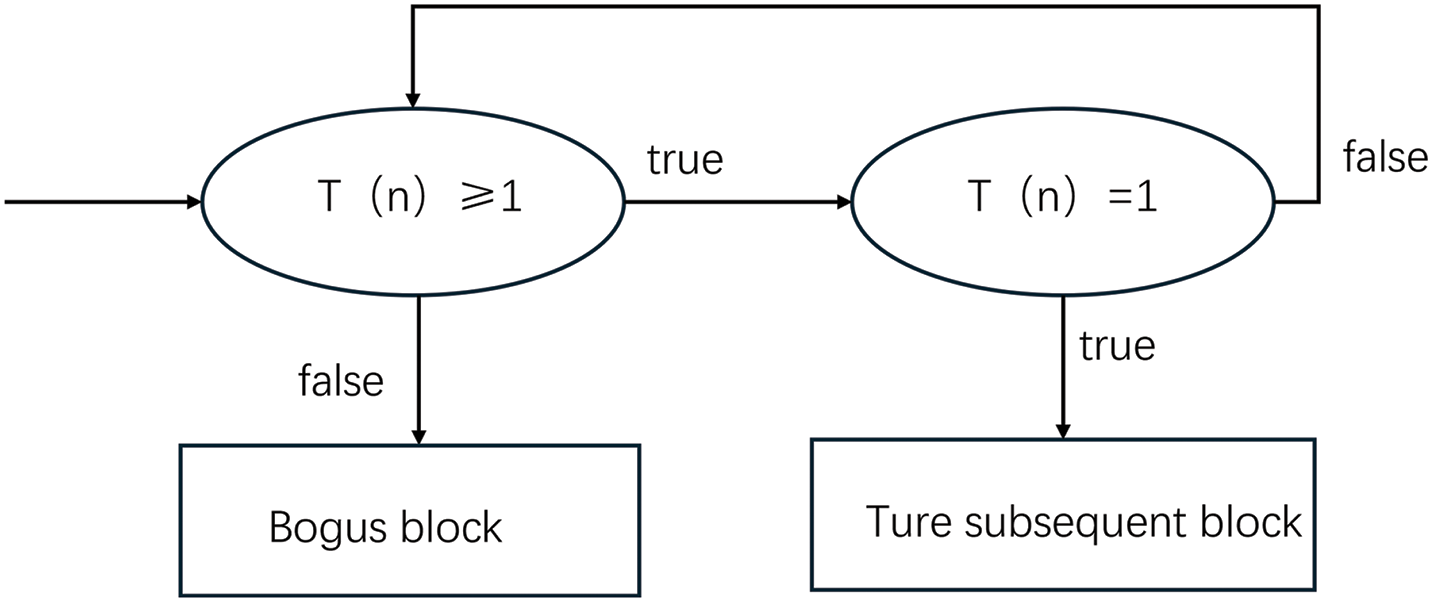
Figure 9: The Collatz Conjecture opaque predicate

4  Experimental Evaluation

4.1 Evaluation Criteria

According to Collberg et al. [2], the evaluation criteria for assessing the quality of software obfuscation include potency, resilience, stealth, and cost. However, not all of these criteria are applicable to our study. We focus specifically on evaluating the resilience and cost of symbolic opaque predicates. Resilience measures the ability of the obfuscation technique to withstand automatic attacks, particularly from adversaries using symbolic execution. In this work, we assume that attackers are skilled in utilizing symbolic execution-based tools to deobfuscate our protections. Cost assesses the overhead introduced by the obfuscation process, encompassing both program size and execution time. We evaluate this overhead by comparing the performance of real programs obfuscated with our symbolic opaque predicates against existing opaque predicates.

We do not evaluate potency, as it primarily pertains to the overall obscurity added to the program, which is a major objective of general obfuscation or control-flow obfuscation, rather than specifically to opaque predicates. Additionally, stealth assesses whether an obfuscation technique appears suspicious to human analysts. A stealthy opaque predicate should not exhibit abnormal instruction patterns or significant statistical differences compared to normal predicates. Currently, no standardized evaluation method exists for stealth. As a result, to comprehensively evaluate our obfuscation approach, we consider a diverse set of metrics encompassing resilience, runtime overhead, code size, memory usage, coverage, correctness, and extensibility. Resilience gauges the obfuscation’s ability to withstand both static and dynamic attacks, especially those involving symbolic execution. Runtime overhead measures the increase in runtime performance costs introduced by the obfuscation, while code size captures the relative growth of the binary compared to the unobfuscated version. Memory usage quantifies the additional resources required during execution. Coverage reflects the proportion of code actually protected by the obfuscation transformations. Correctness ensures that the obfuscated program preserves the original functionality and outputs, and extensibility assesses how readily the technique can be adapted to new architectures, programming languages, or evolving threat models.

4.2 Prototype Implementation

We developed a prototype obfuscation tool based on Obfuscator-LLVM. The source code of a program is initially processed by the LLVM frontend, which transforms the code into an Intermediate Representation. For C programs, the frontend utilized is Clang. The IR serves as the core object processed in LLVM, providing a framework for various program analysis tasks, including optimization and obfuscation.

Obfuscator-LLVM inherently applies several compilation passes to obfuscate programs at the IR level. Finally, the IR is compiled into binary code by the corresponding backend, suitable for specific hardware architectures (e.g., x86-64). Within the LLVM framework, we implement our strengthened opaque predicates as a compiler pass. This pass allows for the substitution of opaque predicates generated by Obfuscator-LLVM with more resilient versions. Users can select which opaque predicates to employ during the obfuscation process.

4.3 Experiment Setup

•   addedHardware and Software Configuration: All experiments were conducted on a desktop computer running Arch Linux (Kernel version 5.4.0), equipped with a 12th Gen Intel® Core™ i5-12500H processor at 2.50 GHz and 16 GB of RAM.

•   Obfuscation Probability: An obfuscation probability of 70% was set, meaning that in each compilation, approximately 70% of eligible candidate locations have the opaque predicates inserted.

4.4 Dataset

In this study, we utilized two distinct test datasets. The first dataset originates from the research paper “Code Obfuscation Against Symbolic Execution Attacks [18]” which includes a diverse range of test functions specifically designed to evaluate resistance against dynamic symbolic execution. This dataset features various control-flow statements, integer arithmetic, and system calls to printf, with code lengths varying from 11 to 24 lines.

The second dataset comprises commonly used cryptographic algorithms to assess the practical effectiveness of our obfuscation methods. This dataset includes hash functions (SHA and MD5) and cryptographic encoding functions (AES and DES), with code sizes ranging from 73 to 400 lines.

4.5 Evaluation Results

4.5.1 Resilience

To evaluate the impact on dynamic symbolic execution, we employed two key metrics. The first metric was the timeout duration imposed on symbolic execution. If the symbolic execution engines could not identify opaque predicates within three hours, we deemed this a successful resistance against symbolic execution. The second metric focused on false negatives (FN), defined as instances where opaque predicates were incorrectly identified as non-opaque by the symbolic execution tool. The results of these tests are summarized in Tables 2 and 3. We use Hash, Fermat, Fib, and Collatz to represent Single-Way, Fermat’s Little Theorem, Recursive Fibonacci, and Recursive Fibonacci Opaque Predicate, respectively.

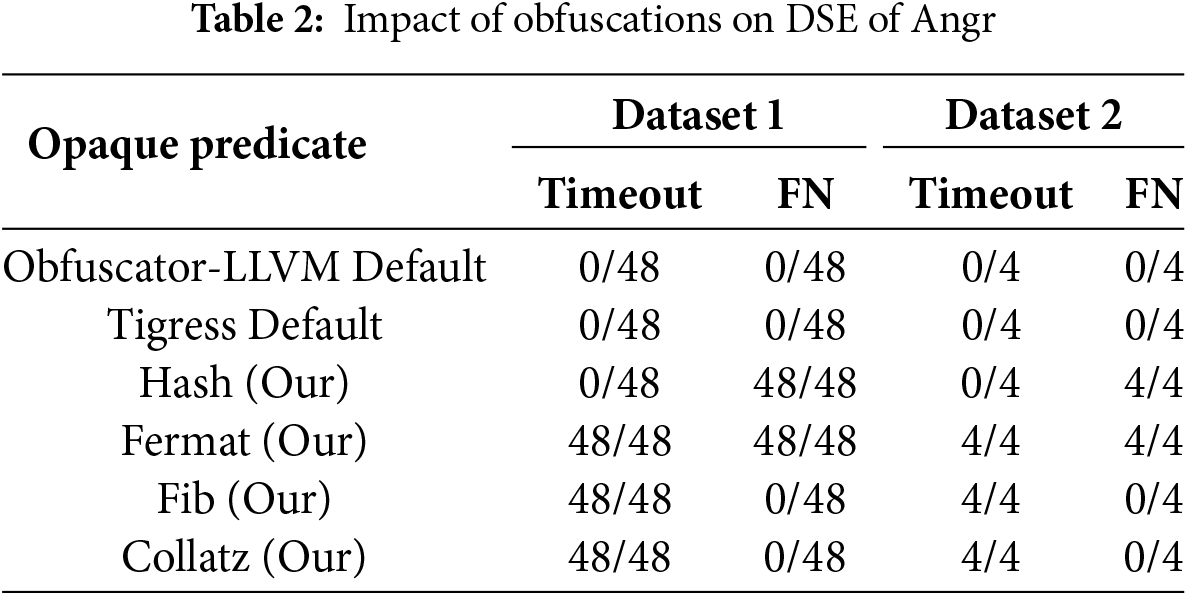
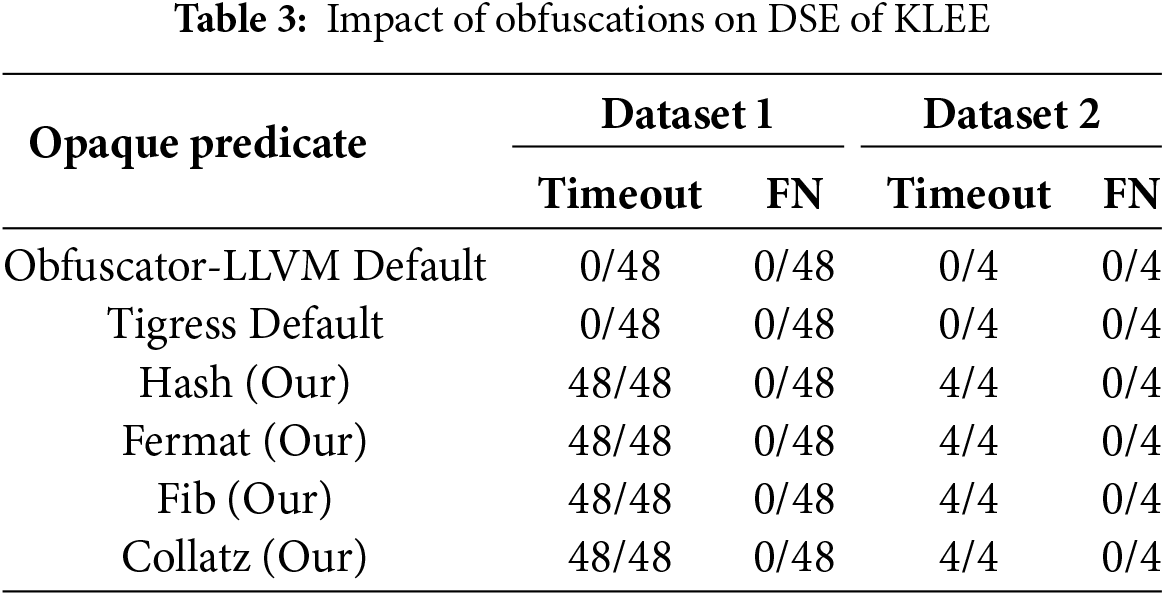
The data in the tables indicate that obfuscation using the four types of opaque predicates consistently resulted in timeout on two datasets, preventing the symbolic execution tools from recognizing these predicates. While using the Angr tool, no timeout occurred during hash obfuscation; however, false blocks were misclassified as normal blocks due to the constraint solver’s inability to resolve the constraints. In the case of Fermat obfuscation, a timeout occurred, and similar misclassifications (FN) were observed. These results demonstrate that all four types of obfuscation exhibit strong resilience against dynamic symbolic execution that Obfuscator-LLVM Default and Tigress Default opaque predicates do not have.

4.5.2 Impact on Runtime Performance

We assessed the cost of our obfuscation methods by measuring the runtime overhead and changes in code size relative to the original code. The formula used to calculate the runtime increase factor is as follows:

Timeratio=Execution Time of Obfuscated CodeExecution Time of Original Code(6)

To evaluate changes in runtime, we employed the Linux profiling tool, perf, focusing exclusively on CPU time while ignoring I/O time. The C source files from the datasets were compiled into native executable format and profiled using the perf program. The profiler results of the obfuscated code were compared to their unobfuscated counterparts to determine the runtime overhead increase factor. The change in code size was straightforward to measure; we utilized the ls command to determine the file sizes in bytes post-obfuscation. The formula used to calculate the code size increase factor is as follows:

CodeSizeratio=Code Size of Obfuscated CodeCode Size of Original Code(7)

Changes in Runtime Overhead

From the Fig. 10, we observe that both Obfuscator-LLVM Default and Tigress Default introduce relatively lower runtime overhead, remaining close to 1.0–1.5× the baseline execution time. Meanwhile, our proposed obfuscation techniques exhibit a higher time overhead, with the Hash and Collatz methods leading to the most significant increases. The runtime overhead for Fermat and Fib remains moderate, positioned between 2.0× and 2.5×. This result highlights a key trade-off in opaque predicate design: while our methods significantly enhance obfuscation strength, they come at the cost of increased execution time. However, the overhead remains within a practical range, demonstrating the feasibility of applying these techniques in real-world scenarios where security is prioritized over minimal performance impact.

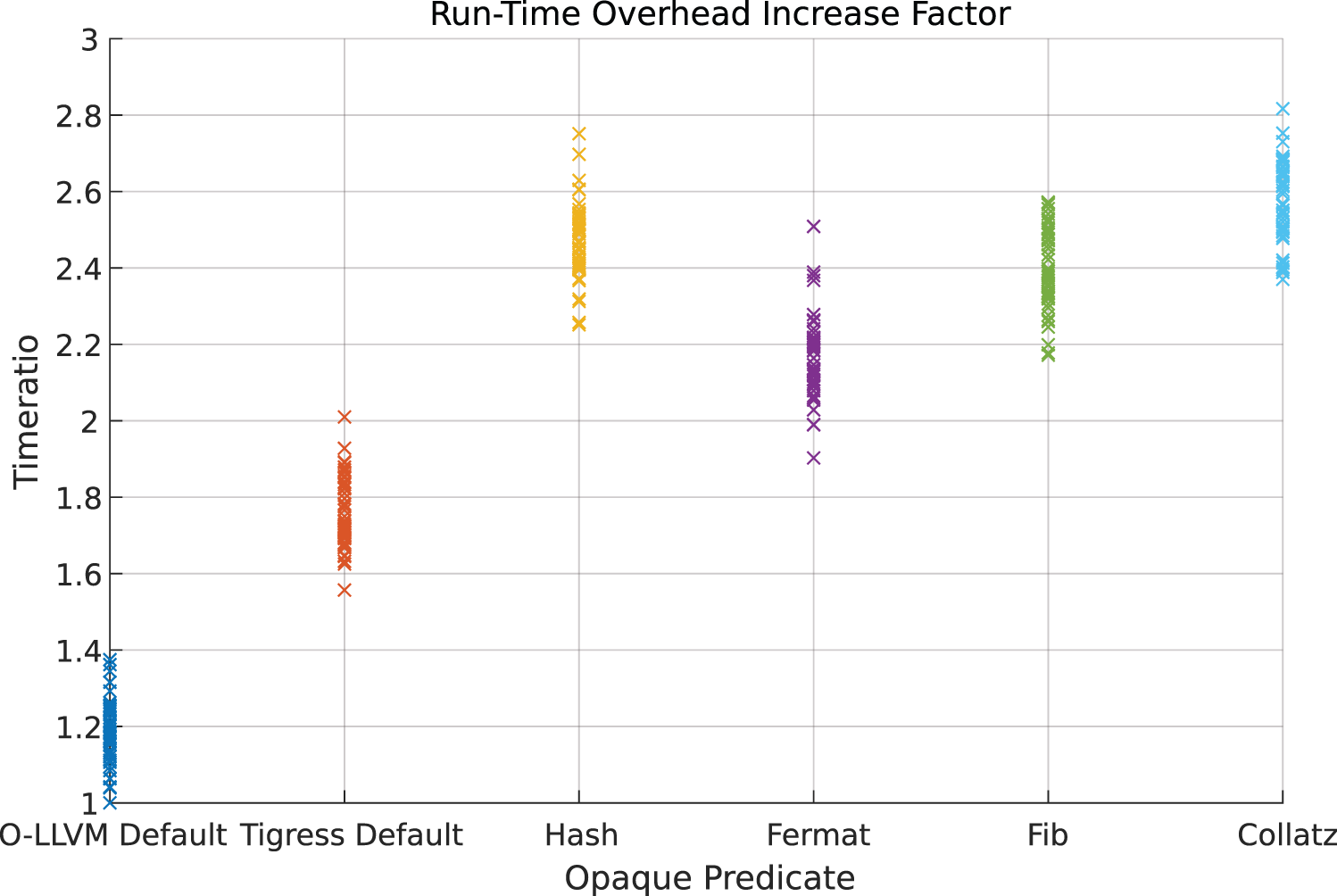
Figure 10: Dataset 1 time overhead increase factor

For several utility programs in Dataset 2 shown in Fig. 11, any program exhibiting a runtime ratio exceeding 100 was labeled as “greater than 100”, indicating an unacceptable delay. We appended a “+” sign to the names of obfuscation methods where algorithmic improvements were made. The results reveal that execution time ratios for our obfuscated programs are generally kept below five times, particularly highlighting the negligible overhead incurred by the improved Fermat and Fibonacci obfuscation methods. This illustrates the effectiveness of our optimized algorithm while also emphasizing that it achieves a reasonably acceptable runtime overhead.

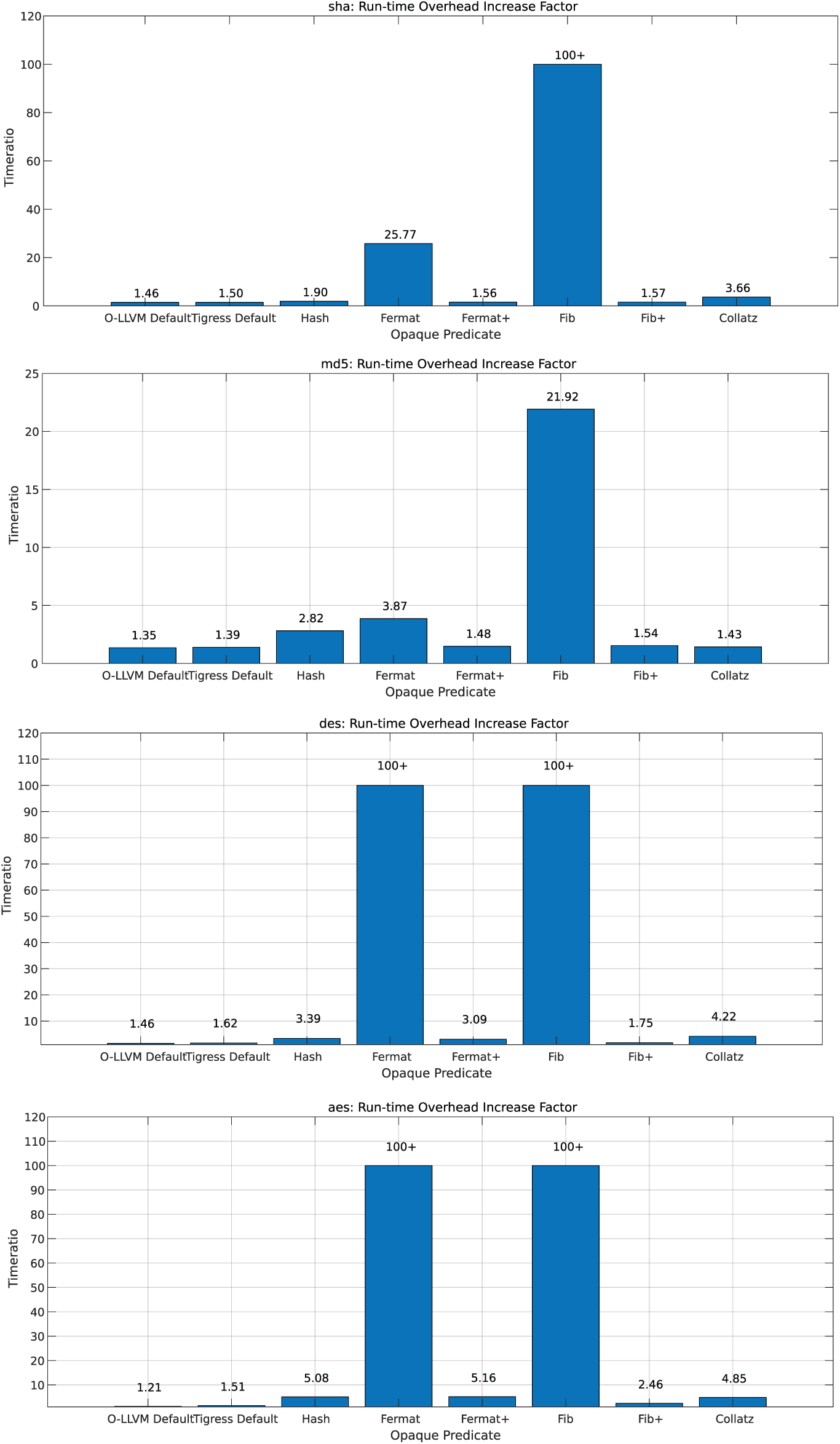
Figure 11: Dataset 2 time overhead increase factor

Changes in Code Size

In Dataset 1, the changes in code size for four obfuscation techniques were minimal, ranging from 1 to 1.01, suggesting that the increase in code size is virtually negligible, as shown in Fig. 12. For Dataset 2, changes in code size are depicted in Fig. 13. The average change in code size ranged from one to two times, with the Collatz obfuscation resulting in a relatively higher increase, varying between 1.6 and 3.2 times. While Collatz obfuscation offers robust resistance to symbolic execution, its high overhead makes it less suitable for resource-sensitive environments. In contrast, optimized techniques like Fermat+ and Fib+ present a more balanced approach, making them ideal for scenarios with limited resources.

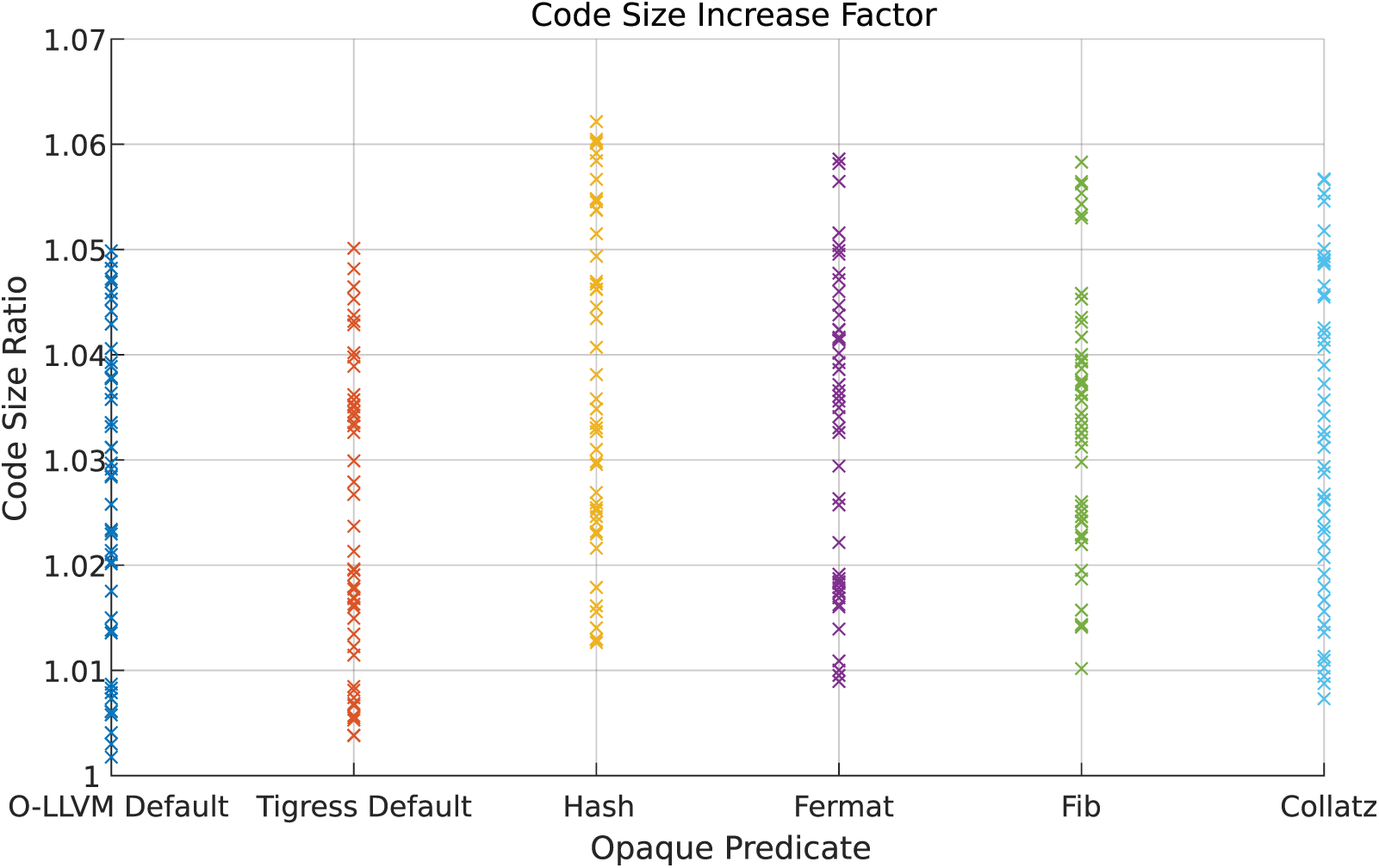
Figure 12: Dataset 1 code size increase factor

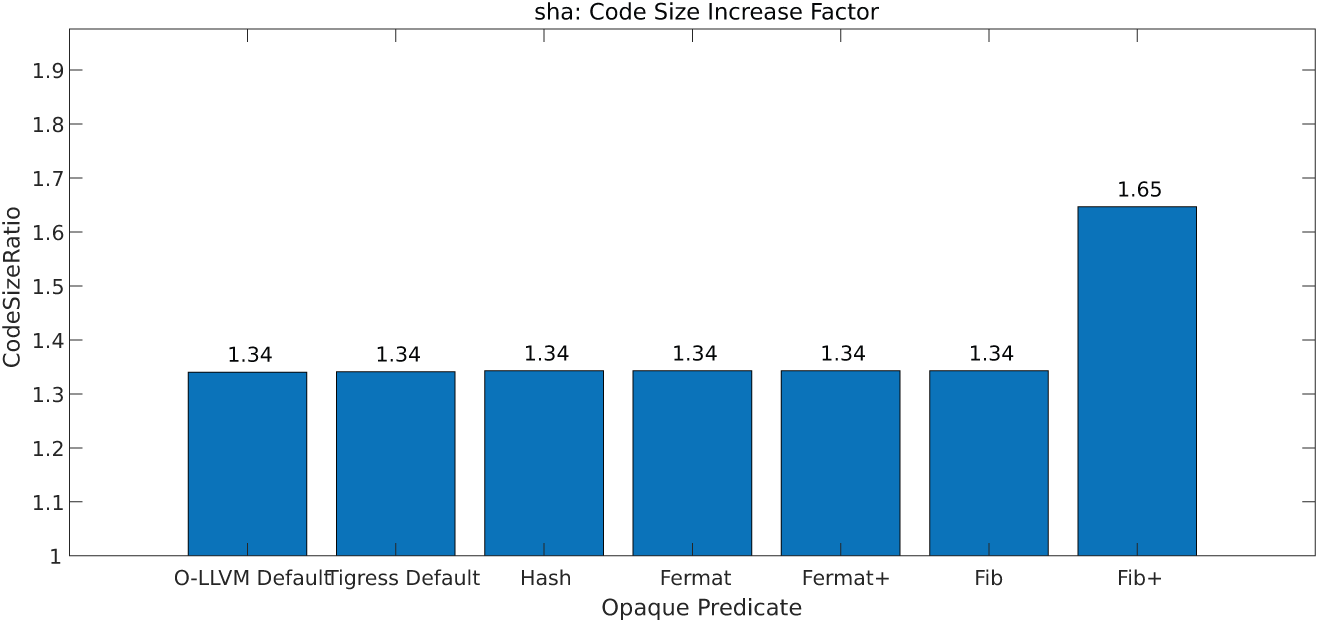
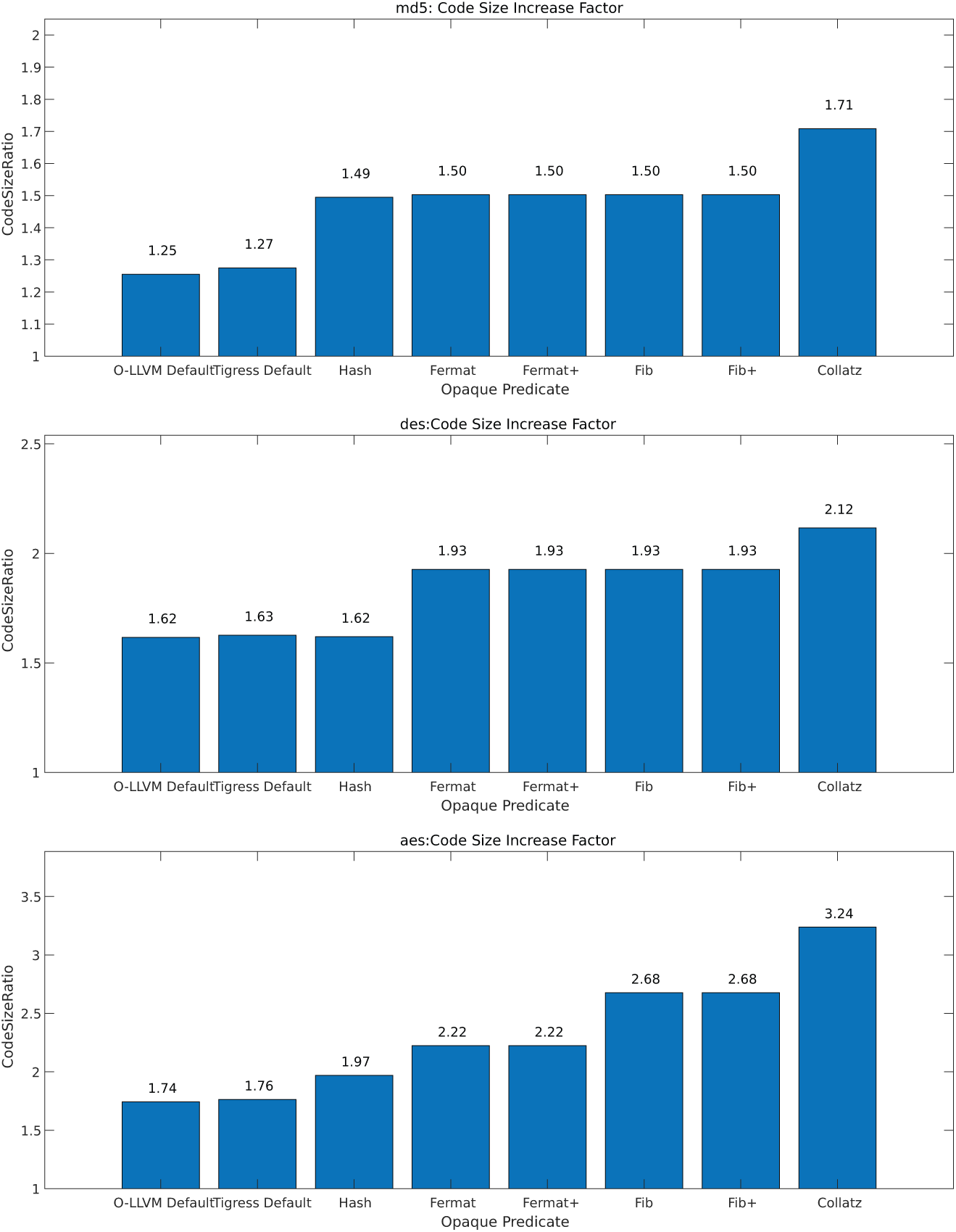
Figure 13: Dataset 2 code size increase factor

4.5.3 Other Metrics

To comprehensively assess the effectiveness of different opaque predicate obfuscation techniques, we define and evaluate four key metrics: memory usage, correctness, coverage, and extensibility. These metrics provide quantitative insights into the trade-offs between security, efficiency, and adaptability. Memory usage refers to the amount of memory consumed by the program during execution after obfuscation. We measure this by running the obfuscated binaries on a standard evaluation environment and recording the peak resident set size during execution. The final value represents the average memory consumption across multiple test runs for each dataset. Correctness measures whether the obfuscated program maintains its original functional behavior. We evaluate correctness by executing a set of predefined test cases and comparing the outputs with the original, unobfuscated program. Coverage quantifies the proportion of the program’s control flow that has been obfuscated. This is computed using static analysis tools that measure the number of obfuscated basic blocks relative to the total number of basic blocks in the program. Extensibility assesses how well the obfuscation technique can be adapted to different software architectures, programming paradigms, and application domains. This is a qualitative measure based on three factors: Platform Independence, Language Agnosticism, Configurability. Each opaque predicate is scored on a scale from 1 (low extensibility) to 10 (high extensibility) based on empirical observations and experimental results.

Table 4 presents a comprehensive comparative evaluation of our proposed obfuscation techniques—Hash, Fermat, Fib, and Collatz—against the default opaque predicate implementations in Obfuscator-LLVM and Tigress. The results underscore the significant advantages of our approach across multiple critical dimensions. First, our methods achieve a coverage rate of 75%–86%, which substantially surpasses the 6% coverage of Obfuscator-LLVM and the 65%–68% coverage of Tigress. This higher coverage indicates that our obfuscation techniques affect a larger portion of the program’s control flow, thereby enhancing its resilience against reverse engineering and symbolic execution attacks. By obscuring a greater number of execution paths, our approach makes it significantly more challenging for attackers to analyze and deobfuscate the protected code. Second, all of our techniques maintain 100% correctness, ensuring that the obfuscation transformations do not introduce any semantic inconsistencies or disrupt normal program execution. This is a crucial advantage as it guarantees that the obfuscated programs continue to function as intended without introducing errors or unintended behaviors. In contrast, some obfuscation techniques may inadvertently alter program semantics, leading to potential vulnerabilities or functional issues. Our methods, however, strike a careful balance between security and correctness, making them highly reliable for practical use. Third, while our approaches introduce a moderate increase in memory consumption—ranging from 10% to 3% compared to Obfuscator-LLVM and Tigress—the additional overhead remains within practical limits. This slight increase in memory usage is a reasonable trade-off for the enhanced security provided by our obfuscation techniques. Given the growing importance of software protection in untrusted environments, the marginal increase in resource consumption is justified by the significant improvement in resilience against reverse engineering and symbolic execution attacks. Finally, our methods achieve extensibility scores of 8–9, outperforming Obfuscator-LLVM (7–8) and Tigress (6–7). This higher extensibility demonstrates that our approach is more adaptable to different software environments and use cases, making it more suitable for real-world deployment. The flexibility of our techniques allows developers to apply them across a wide range of applications without requiring extensive modifications, further enhancing their practicality and appeal.

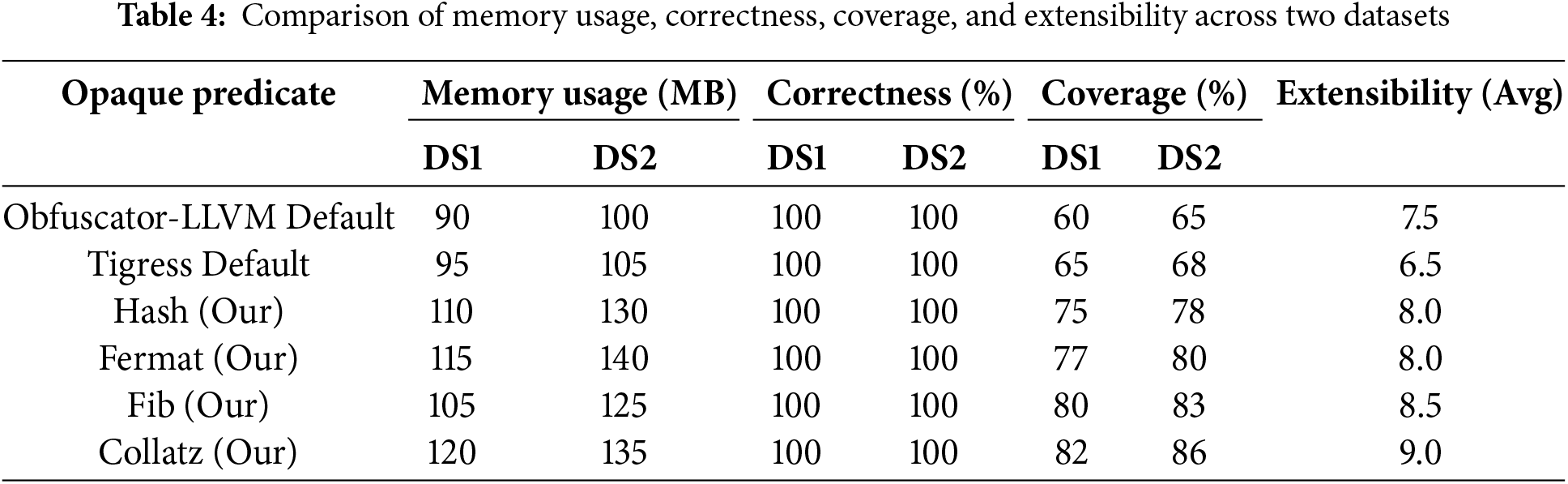
Therefore, our proposed obfuscation techniques not only provide superior coverage and extensibility but also maintain high correctness and introduce only moderate memory overhead. These advantages make our approach a robust and practical solution for enhancing software security in the face of increasingly sophisticated reverse engineering and symbolic execution attacks.

5  Conclusion

In this paper, we have introduced a novel class of anti-Dynamic Symbolic Execution opaque predicates designed to enhance the resilience of code obfuscation techniques against reverse engineering and automated analysis. Addressing the inherent weaknesses of traditional opaque predicates under DSE, our work proposed two key techniques: single-way function opaque predicates and path-explosion opaque predicates. By leveraging hash functions and logarithmic transformations, single-way function opaque predicates effectively hinder constraint solvers from generating feasible inputs, while path-explosion predicates exponentially increase the number of execution paths, significantly burdening symbolic execution engines. To validate the efficacy of our approach, we implemented a prototype obfuscation tool based on Obfuscator-LLVM and conducted comprehensive experimental evaluations using two widely adopted symbolic execution engines, KLEE and Angr. Our results demonstrate that our proposed predicates consistently increase the complexity of symbolic execution, forcing timeouts in numerous cases where traditional obfuscation methods fail. Compared to default opaque predicates in Obfuscator-LLVM and Tigress, our techniques exhibited higher resilience against symbolic execution-based deobfuscation while maintaining acceptable performance overhead. Specifically, our methods achieved higher coverage rates, ensuring a broader scope of protection, while keeping execution overhead within a feasible range, making them suitable for real-world deployment.

Moving forward, our future work will focus on broadening the experimental scope and enhancing the dataset to encompass a wider variety of real-world scenarios. In particular, we plan to evaluate our anti-DSE opaque predicates across more diverse applications and larger datasets, which will help us better understand their strengths and limitations in practical settings. Moreover, integrating our current method with other obfuscation techniques, such as advanced control-flow and data-flow transformations, could provide a multi-layered defense mechanism, thereby increasing the overall robustness against symbolic execution attacks. Finally, addressing the performance overhead associated with our approach is crucial, therefore, we intend to explore optimization strategies and develop an automatic parameter tuning framework, possibly leveraging machine learning techniques, to dynamically balance security and efficiency. These enhancements are expected to not only validate our current approach over a broader range of applications but also lay the groundwork for a more adaptive and comprehensive software protection framework.

Acknowledgement: First and foremost, I would like to express my heartfelt gratitude to my supervisors, Professor Yan Cao and Professor Yan Zhuang, for their invaluable guidance and support throughout my studies and research. Their insightful advice and encouragement in academic exploration, paper writing, and critical thinking have been a constant source of inspiration and motivation for me to improve and grow. I am also deeply grateful to the Zhengzhou University Infrastructure Laboratory for providing essential resources and experimental conditions that laid a solid foundation for the successful completion of my research. Lastly, I would like to extend my thanks to my classmates, friends, and family who have supported and encouraged me during this period. Your unwavering support has been instrumental in enabling me to stay focused on my academic pursuits and persevere through challenges.

Funding Statement: The work was supported by Open Foundation of Key Laboratory of Cyberspace Security, Ministry of Education of China (No. KLCS20240211) and Henan Science and Technology Major Project No. 241110210100.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Yan Cao and Zhizhuang Zhou; methodology, Zhizhuang Zhou; software, Zhizhuang Zhou; validation, Yan Cao, Zhizhuang Zhou and Yan Zhuang; formal analysis, Zhizhuang Zhou; investigation, Zhizhuang Zhou; resources, Zhizhuang Zhou; data curation, Zhizhuang Zhou; writing—original draft preparation, Zhizhuang Zhou; writing—review and editing, Zhizhuang Zhou and Yan Zhuang; visualization, Yan Zhuang; supervision, Yan Cao, Zhizhuang Zhou and Yan Zhuang; project administration, Yan Cao, Zhizhuang Zhou and Yan Zhuang; funding acquisition, Yan Cao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors.

Ethics Approval: This study did not involve human or animal subjects.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Collberg C, Nagra J. Surreptitious software. In: Addison-Wesley software security series. Upper Saddle River, NJ, USA: Addison-Wesley; 2010. p. 713–36. [Google Scholar]

2. Collberg C, Thomborson C, Low D. A taxonomy of obfuscating transformations. Auckland, New Zealand: The University of Auckland; 1997. Technical Report No: 148. [Google Scholar]

3. Rajba P, Mazurczyk W. Data hiding using code obfuscation. In: Proceedings of the 16th International Conference on Availability, Reliability and Security (ARES ’21); 2021 Aug 17–20; Vienna, Austria. p. 75. [Google Scholar]

4. Sen K, Marinov D, Agha G. CUTE: a concolic unit testing engine for C. In: Wermelinger M, Gall HC, editors. Proceedings of the 10th European Software Engineering Conference held jointly with 13th ACM SIGSOFT International Symposium on Foundations of Software Engineering; 2005 Sep 5–9; Lisbon, Portugal. p. 263–72. [Google Scholar]

5. Cadar C, Sen K. Symbolic execution for software testing: three decades later. Commun ACM. 2013;56(2):82–90. doi:10.1145/2408776.2408795. [Google Scholar] [CrossRef]

6. Schwartz EJ, Avgerinos T, Brumley D. All you ever wanted to know about dynamic taint analysis and forward symbolic execution (but might have been afraid to ask). In: 2010 IEEE Symposium on Security and Privacy (SP); 2010 May 16–19; Oakland, CA, USA. p. 317–31. [Google Scholar]

7. Schrittwieser S, Katzenbeisser S, Kinder J, Merzdovnik G, Weippl E. Protecting software through obfuscation: can it keep pace with progress in code analysis? ACM Comput Surv. 2016;49(1):4. [Google Scholar]

8. Junod P, Rinaldini J, Wehrli J, Michielin J. Obfuscator-LLVM: software protection for the masses. In: Proceedings of the 1st International Workshop on Software Protection (SPRO-15); 2015 May 16–24; Florence, Italy. p. 3–9. [Google Scholar]

9. Cadar C, Dunbar D, Engler D. KLEE: unassisted and automatic generation of high-coverage tests for complex systems programs. In: Proceedings of the 8th USENIX Conference on Operating Systems Design and Implementation; 2008 Dec 8–10; San Diego, CA, USA: USENIX Association. p. 209–24. [Google Scholar]

10. Shoshitaishvili Y, Wang R, Salls C, Stephens N, Polino M, Dutcher A, et al. SOK: (State of) the art of war: offensive techniques in binary analysis. In: 2016 IEEE Symposium on Security and Privacy (SP); 2016 May 22–26; San Jose, CA, USA. p. 138–57. [Google Scholar]

11. King JC. Symbolic execution and program testing. Commun ACM. 1976;19(7):385–94. doi:10.1145/360248.360252. [Google Scholar] [CrossRef]

12. Bardin S, David R, Marion JY. Backward-Bounded DSE: targeting infeasibility questions on obfuscated codes. In: 2017 IEEE Symposium on Security and Privacy (SP); 2017 May 22–26; San Jose, CA, USA. p. 633–51. [Google Scholar]

13. Godefroid P, Levin MY, Molnar DA. SAGE: whitebox fuzzing for security testing. Commun ACM. 2012;55(3):40–4. doi:10.1145/2093548.2093564. [Google Scholar] [CrossRef]

14. David R, Bardin S, Feist J, Mounier L, Potet ML, Ta TD, et al. Specification of concretization and symbolization policies in symbolic execution. In: International Symposium on Software Testing and Analysis (ISSTA 2016); 2016 Jul 18–20; Saarbrücken, Germany. p. 36–46. [Google Scholar]

15. Cadar C, Ganesh V, Pawlowski PM, Dill DL, Engler DR. EXE: automatically generating inputs of death. In: Proceedings of the 13th ACM Conference on Computer and Communications Security; 2006 Oct 30–Nov 3; Alexandria, VA, USA. [Google Scholar]

16. Godefroid P, Klarlund N, Sen K. DART: directed automated random testing. In: Proceedings of the 2005 ACM SIGPLAN Conference on Programming Language Design and Implementation; 2005 Jun 12–15; Chicago, IL, USA. p. 213–23. [Google Scholar]

17. Xu H, Zhou Y, Kang Y, Lyu MR. Concolic execution on small-size binaries: challenges and empirical study. In: 2017 47th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN); 2017 Jun 26–29; Denver, CO, USA. p. 181–88. [Google Scholar]

18. Banescu S, Collberg CS, Ganesh V, Newsham Z, Pretschner A. Code obfuscation against symbolic execution attacks. In: The 32nd Annual Conference on Computer Security Applications (ACSAC 2016); 2016 Dec 5–8; Los Angeles, CA, USA. p. 189–200. [Google Scholar]

19. Ganesh V, Dill DL. A decision procedure for bit-vectors and arrays. In: International Conference on Computer Aided Verification; 2007 Jul 3–7; Berlin, Germany. p. 519–31. [Google Scholar]

20. De Moura L, Bjørner N. Z3: an efficient smt solver. In: International Conference on Tools and Algorithms for the Construction and Analysis of Systems; 2008 Mar 29–Apr 6; Budapest, Hungary. p. 337–40. [Google Scholar]

21. Coogan K, Lu G, Debray SK. Deobfuscation of virtualization obfuscated software: a semantics-based approach. In: The 18th Conference on Computer and Communications Security (CCS); 2011 Oct 17–21; Chicago, IL, USA. p. 275–84. [Google Scholar]

22. Salwan J, Bardin S, Potet ML. Symbolic deobfuscation: from virtualized code back to the original. In: 5th Conference on Detection of Intrusions and malware & Vulnerability Assessment (DIMVA); 2018 Jun 28–29; Saclay, France. p. 372–92. [Google Scholar]

23. Yadegari B, Johannesmeyer B, Whitely B, Debray S. A generic approach to automatic deobfuscation of executable code. In: 2015 Symposium on Security and Privacy (SP); 2015 May 17–21; San Jose, CA, USA. p. 674–91. [Google Scholar]

24. Zhou Y, Main A, Gu YX, Johnson H. Information hiding in software with mixed boolean-arithmetic transforms. In: Information Security Applications (WISA 2007); 2007 Aug 27–29; Jeju Island, Republic of Korea. p. 61–75. [Google Scholar]

25. Sharif MI, Lanzi A, Giffin JT, Lee W. Impeding malware analysis using conditional code obfuscation. In: Network and Distributed System Security Symposium (NDSS 2008); 2008 Feb 10–13; San Diego, CA, USA. [Google Scholar]

26. Tigress. The tigress diversifying C Obfuscator [Internet]. [cited 2024 Jan 1]. Available from: https://tigress.wtf/. [Google Scholar]

27. Ollivier M, Bardin S, Bonichon R, Marion JY. How to kill symbolic deobfuscation for free (or: unleashing the potential of path-oriented protections). In: Proceedings of the 35th Annual Computer Security Applications Conference (ACSAC’ 19); 2019 Dec; 2019; New York, NY, USA. p. 177–89. [Google Scholar]

28. Dinu D. ObfuscatorDynamic-LLVM: dynamic symbolic execution attack protections for the masses [dissertation]. Philadelphia, PA, USA: Drexel University; 2023. [Google Scholar]

29. Xu H, Zhou Y, Kang Y, Tu F, Lyu M. Manufacturing resilient Bi-Opaque predicates against symbolic execution. In: 2018 48th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN); 2018 Jun 25–28; Luxembourg. p. 666–77. [Google Scholar]

30. Hirano Y, Ohtaki Y. Constructing opaque predicate using homomorphic encryption. In: Barolli L, Miwa H, Enokido T, editors. Advances in network-based information systems (NBiS 2022). Lecture notes in networks and systems. vol. 526. Cham, Switzerland: Springer; 2022. [Google Scholar]

31. De Pasquale G, Nakanishi F, Ferla D, Cavallaro L. ROPfuscator: robust obfuscation with ROP. In: Proceedings of the 2023 IEEE Security and Privacy Workshops (SPW); 2023 May 22–25; San Francisco, CA, USA. IEEE; 2023. p. 1–10. [Google Scholar]

32. Bluesadi. DeBogus: automated Deobfuscation Tool [Internet]. [cited 2024 Jan 1]. Available from: https://github.com/bluesadi/debogus. [Google Scholar]

33. Myles G, Collberg C. Software watermarking via opaque predicates: implementation, analysis, and attacks. Electron Commer Res. 2006;6(2):155–71. doi:10.1007/s10660-006-6955-z. [Google Scholar] [CrossRef]

34. Borello JM, Mé L. Code obfuscation techniques for metamorphic viruses. J Comput Virol. 2008;4(3):211–20. doi:10.1007/s11416-008-0084-2. [Google Scholar] [CrossRef]

35. Google. CityHash: fast hash functions for strings [Internet]. [cited 2024 Jan 1]. Available from: https://github.com/google/cityhash. [Google Scholar]