URLLC Service in UAV Rate-Splitting Multiple Access: Adapting Deep Learning Techniques for Wireless Network

1  Introduction

As 5G has inspired widespread research efforts, ultra-reliable and low-latency communications (URLLC) will be crucial in driving the future of wireless industrial automation and are designed to support critical applications that require highly reliable communication [1,2]. By the 3rd Generation Partnership Project (3GPP) standard, the implementation of URLLC needs to ensure that data packets are delivered in a few milliseconds with the target reliability of 99.999% or higher [3]. However, this result can be obtained through a combination of advanced network technologies like non-orthogonal multiple access (NOMA). When NOMA is applied, data is decoded sequentially based on its power levels. This approach facilitates improved interference management and ensures that users with high reliability demands receive more consistent and reliable data [4]. Moreover, NOMA-based beamforming can meet the specific needs of URLLC communications by adapting networks to constantly changing conditions and varied application requirements [5,6]. Although NOMA has several benefits for URLLC communications, it comes up against problems of great complexity and unsatisfactory effect when multiple antennas are introduced for transmission [7]. Consequently, Rate-Splitting Multiple Access (RSMA) [8–10] has recently been suggested as an appropriate approach to achieve a more general and robust transmission framework than NOMA Systems [11–13], particularly in environments where users have different expectations when it comes to transmission rates. The main idea is to split user messages into two parts, a common part and a private part. Thus, the common parts and the private parts are encoded separately in a common data stream and private data streams, respectively [9]. Noting that interference generated by other users is partially decoded and treated as noise [14]. During reception, the signals are successively decoded. First, the user subtracts the common data stream and decodes their own private data stream, followed by the decoding of their own private data stream [15]. Applied in this context, RSMA could offer great spectral efficiency and reduce interference between users. RSMA flexibility can better control the problems inherent in NOMA by adapting the undercoats to suit channel conditions and user requirements. In the URLLC, the time and reliability requirements can hardly be met by a single communication link [16]. To overcome this challenge, a new support system architecture should be designed.

Joint optimization of beamforming vectors, rate allocation, and UAV trajectory under URLLC constraints forms a highly non-convex problem that cannot be solved efficiently using conventional optimization techniques [17]. Existing approaches typically address these components separately, leading to suboptimal solutions that fail to meet URLLC’s real-time processing requirements. For instance, the alternating optimization method proposed in [18] requires iterative updates that introduce unacceptable latency (≥2.5 ms) for true URLLC applications. While Deep Reinforcement Learning (DRL) has shown promise for wireless resource allocation [19], current single-agent frameworks lack the capability to simultaneously handle the continuous action space of beamforming/rate allocation and the discrete nature of trajectory planning. The work in [20] demonstrates this limitation, where a 23% performance degradation was observed when applying single-agent DRL to similar problems. There exists a significant gap in incorporating domain-specific knowledge from communication theory into DRL frameworks. Most existing solutions treat the optimization problem as a black box [21], failing to leverage known mathematical structures that could accelerate convergence and improve interpretability. This is particularly problematic for URLLC applications where performance guarantees are essential. To this end, we study the URLLC in multiuser UAV rate splitting multiple access to maximize the average data rate.

1.1 Motivations and Contributions

Motivated by recent advancements and the need for real-time URLLC services in multiuser UAV-aided RSMA networks, this paper leverages state-of-the-art deep learning methodologies to address the inherent complexities and optimization challenges. Our contributions are detailed as follows.

•   First, we investigate a downlink multiuser UAV RSMA MIMO network targeting the maximization of the achievable rate, subject to stringent URLLC quality-of-service (QoS), power budget constraints, rate allocation, and UAV trajectory limitations. The resulting problem formulation leads to a nonconvex optimization challenge that is difficult to solve directly within the latency constraints characteristic of next-generation networks.

•   To effectively address the intractability of jointly optimizing beamforming vectors, rate allocations, and UAV trajectory parameters, we propose a novel distributed deep reinforcement learning (DRL) framework utilizing dual-agent deep deterministic policy gradient (DA-DDPG). This framework introduces a sophisticated neural network architecture for beamforming and rate allocation. Specifically, we integrate inception-like and deep unfolding mechanisms to construct the network layers, allowing multi-scale feature extraction and accelerated convergence.

•   To apply the above mechanisms, we develop a successive pseudo-convex approximation (SPCA) and numerical solutions for rate allocation and the beamforming subproblem. To the best of our knowledge, this work represents the first attempt at incorporating these recent deep learning advances into solving complex optimization problems in wireless communications. Additionally, a fully connected deep neural network (DNN) is employed for the critic network.

•   Regarding UAV trajectory optimization, we utilize a fully connected DNN to build the corresponding actor-critic-based agent, ensuring efficient learning and robust decision-making.

•   We also apply an incremental learning training procedure [1] to improve model accuracy, reduce the complexity of the deep unfolding-based model, and significantly lower the volume of required training sequences.

•   Simulation experiments conducted validate the efficacy of the proposed DA-DDPG framework. Numerical results illustrate that our proposed method consistently outperforms existing state-of-the-art techniques, underscoring its suitability and effectiveness for real-time URLLC-enabled UAV communications.

2  Related Work

Over the past few years, the research community has made significant efforts to investigate the complex and new challenges of URLLC-UAV communication based on the NOMA or the RSMA approaches [22–24]. Notably, the study in [22] proposed a model to deploy UAVs as relays between the base station and remote devices. The aim was to overcome the poor connectivity due to the presence of obstacles. In the proposed model, the authors targeted the maximization of the transmission rate on the backward link while satisfying the requirement of URLLC on the forward link. More recently, the authors in [23] considered the joint optimization problem for UAV-enabled URLLC-based mobile edge computing, which is divided into three subproblems. The first two subproblems optimize the UAV’s horizontal and vertical locations, while the third one optimizes the offloading bandwidths and processing frequencies. Within this framework, they minimized the system’s computation latency under an overall resource constraint.

In [24], a global iterative algorithm based on the alternating direction method of multipliers and random perturbation was proposed to minimize total error probability and jointly optimize blocklength allocation and UAV deployment. These contributions have made significant efforts in the field of URLLC-assisted UAV communication. However, the studies referred to above were carried out in the NOMA scenario, and the RSMA has received relatively little attention in the context of URLLC-assisted UAV networks. NOMA uses successive interference cancellation (SIC), which increases the complexity of processing in UAVs. This additional complexity can result in delays, causing problems in URLLC scenarios where extremely low latency is essential. In the current technical literature, only a few studies have explored RSMA-based URLLC-assisted wireless networks, as evidenced by [25]. In [25], RSMA was introduced to achieve energy-efficient (EE) URLLC in cell-free massive MIMO systems. In particular, the power allocation problem was formulated to enhance the EE.

Huang et al. introduced an artificial intelligence named RSMA-Deep Reinforcement Learning (DRL)-based approach. The authors demonstrated that, compared to the space-division multiple access (SDMA)-DRL protocol, the proposed method can achieve higher energy efficiency. Similarly, to maximize transmission power at every moment under energy harvesting, the authors in [26] presented a DRL method called the soft actor-critic algorithm. In particular, they used the Han–Powell quasi-Newton approach in sequential least squares programming (SLSQP) to optimize the sum-rate for the specified transmission power through DRL. The work in [27] presents a framework that integrates the Reconfigurable Intelligent Surface (RIS) with an intelligent satellite UAV-terrestrial network. The multiple access technique used in the communication architecture was NOMA. The authors formulated a multi-objective optimization problem that optimizes UAV trajectory, RIS phase shift, and transmit beamforming while minimizing UAV energy consumption and maximizing the sum rate. To solve the optimization problem, the multi-objective deep deterministic policy gradient (MO-DDPG) technique was suggested. In simulations, better data rates, energy consumption, and throughput were achieved when compared to systems without integrated RIS or random phase shift systems. The authors in [28] proposed a deep learning (DL)-based RSMA system for RIS-assisted terahertz massive multiple-input multiple-output (MIMO) systems. They presented a low-complexity approximate weighted minimum mean square error (AWMMSE) digital precoding scheme. Then, by combining AWMMSE with deep learning (DL), the deep unfolding [29] active precoding network (DFAPN) scheme was performed at the Base Station (BS), while passive precoding was performed using a transformer-based data-driven RIS reflecting network (RRN) at the RIS. Results showed that channel state information has a better achievable rate for the worst user device when compared to corresponding SDMA-based systems. Authors in [30] introduced the deep deterministic policy gradient (DDPG) approach to maximize the sum rate in downlink UAV-aided RSMA systems, where the trajectory and UAV beamforming matrix are jointly optimized. In this context, the UAV’s uniform rectangular array (URA) beamforming design and mobility functions are considered. Unfortunately, there is currently a lack of research on the combination of URLLC and RSMA in a wireless UAV network. Hence, it is a mathematically challenging task to study the downlink achievable rate in UAV communication based on URLLC-RSMA.

3  System Model and Problem Formulation

In this work, a downlink multiuser UAV RSMA-URLLC system is considered, as depicted in Fig. 1, where the UAV is equipped with M antennas and serving N single-antenna users via short-packet communication (SPC), where the latency is always considered less than 1 ms, which indicates that the channel conditions can be viewed as quasi-static since this latency is shorter than the channel coherence time. The flying period of the UAV is divided into T time slots, with δt denoting the set of users as N={1,2,⋯,N} and the locations of the UAV and the users are respectively given as Ln=(xn,yn)T, n∈N and qn[t]=(xu[t],yu[t],zu[t])T. The UAV movement can be defined as

‖qu(t+1)−qu(t)‖2≤D2,t=1,⋯,T−1qu(0)=q0,t=1,⋯,T−1‖qu(T)−quF‖2≤D2,(1)

where D=δtvmax with vmax represents the maximum velocity of the UAV.

Figure 1: Multiuser RSMA-URLLC UAV network

Since RSMA is employed, the transmitted message from the UAV to the user n is divided into a common message wc and a private message wn. Hence, two data streams are transmitted, and performing the precoding on these data streams, the transmitted signal at the time slot t is given as

x[t]=vc[t]ss[t]+∑n=1Nvn[t]sn[t],(2)

where vc[t]∈CM×1 and vn[t]∈CM×1 are the beamforming vectors with Pc[t]=vcvcH[t] and Pn[t]=vnvnH[t] denote the transmit power of the common and private streams, respectively; sc and sn are the data streams of the common and private messages with EssH=I, and s is the total transmit data stream. The received signal at the user n at the time slot t is given as

yn[t]=hu,nH[t]x[t]+ηn[t],(3)

where hu,n∈CM×1 is the channel vector between the UAV and the user n and ηn∼CN(0,σn2) is the additive white Gaussian noise (AWGN). Based on RSMA protocol, each user first decodes the common message using successive interference cancellation (SIC) and then decodes its own private signal. The signal-to-interference-plus-noise ratio (SINR) of the user n decoding the common message at the time slot t is given as

γn,c[t]=|hu,nH[t]vc[t]|2∑l=1K|hu,nH[t]vl[t]|2+σn2.(4)

Similarly, the SINR of the user n decoding its private message at the time slot t is given as follows:

γn,p[t]=|hu,nH[t]vn[t]|2∑l=1,l≠nK∑n2|hu,nH[t]vl[t]|2.(5)

To formulate the quality-of-service (QoS) constraints of URLLC, we follow the derivation in Eq. (5), where the approximate maximum achievable rate of the user n at the time slot t and for a multi-antenna with quasi-static flat fading channel can be expressed as follows:

ru,n,c(ϵ)[t]=log2⁡(1+γn,c[t])−V(γn,c[t])BQ−1(ϵn,c)ln2,(6)

where V(γn,c[t])=1−(1−γn,c[t])−2 is the channel dispersion, and B is the transmission channel blocklength, Q−1(ϵn,c) is the inverse of the Gaussian Q-function, and ϵn,c[t]=Q(f(γn,c[t],B,ru,n,c[t])) denotes the decoding error probability with f(γn,c[t],B,ru,n,c[t]) defined as follows:

f(γn,c[t],B,ru,n,c[t])=ln2⁡Bv(log2)(1+γn,c[t])−ru,n,c(ϵ)[t].(7)

To guarantee the decoding of the common message by the user n, the constraints ∑n=1NCu,n,c(ϵ)[t]≤minn∈N{ru,n,c(ϵ)[t]} is imposed.

Similarly, the achievable data rate of the user n to decode the private stream is given as

ru,n,c(ϵ)[t]=log2⁡(1+γn,p[t])−V(γn,p[t])BQ−1(ϵn,p)ln2.(8)

The achievable rate of the user n at the time slot t is defined as

Ru,n(ϵ)[t]=Cu,n,c(ϵ)[t]+ru,n,p(ϵ)[t].(9)

Aiming at maximizing the total achievable rate of the system, we formulate our optimization problem as follows:

maxv,C,Q∑n=1NRu,n(ϵ)[t],s.t.C1:∑n=1NCu,n,c(ϵ)[t]≤minn∈N{ru,n,c(ϵ)[t]}C2:|vc[t]|2+∑n=1N|vn[t]|2≤PmaxC3:Cu,n,c(ϵ)[t]≥0,C4:ru,n,c(ϵ)[t]≥0,C5:ϵn,p≤ϵth,ϵn,c≤ϵthC6:Ru,n(ϵ)[t]≥Ru,n(min)C7:vn[t]≥0,vc[t]≥0,(10)

where v=[vc,v1,...,vN]T∈C(N+1)×M and C=[ru,n,c(ϵ),Cu,1,c(ϵ),Cu,2,c(ϵ),⋯,Cu,N,c(ϵ),Cu,1,p(ϵ),Cu,2,p(ϵ),⋯,Cu,N,p(ϵ)]T∈R(2N+1)×1. The constraint C1 ensures the successful decoding of the common stream by all users. The constraint C2 is the power budget. The constraints C5 and C6 are the QoS of URLLC with Ru,nmin representing the minimum rate requirements.

Problem (10) is nonconvex due to the nonconvexity of the objective function and the tight coupling of v,C, and Q. Joint optimization of the beamforming, rate allocation, and UAV trajectory is intractable. Next, instead of directly solving the problem mathematically, we design a DRL framework to jointly optimize the above three parameters.

In the following sections, we provide a novel deep reinforcement framework to handle the problem in (10). The proposed framework combines inception-like mechanisms, deep unfolding, and dual-agent DRL within the context of URLLC and RSMA-assisted UAV networks. It offers a practical and scalable DRL framework tailored specifically for real-time wireless optimization scenarios involving multiple antennas and stringent QoS demands.

4  Deep Unfolding-Based Inception-like Model

The proposed model architecture incorporates an inception-like block, where the inception mechanism is employed to enhance the design of the beamforming and rate allocation actor. The inception mechanism, inspired by convolutional neural networks, allows the model to process different features at multiple scales by applying several operations (e.g., different filter sizes or layers) in parallel. This increases the flexibility and expressiveness of the model, allowing it to better capture the diverse patterns and correlations between beamforming and rate allocation decisions. Additionally, the concept of deep unfolding is integrated into the actor’s design [31,32]. Deep unfolding involves converting iterative optimization algorithms into neural networks by mapping each iteration to a neural network layer. This technique allows the model to mimic traditional optimization algorithms while leveraging the learning capability of deep neural networks. By using deep unfolding, the beamforming and rate allocation actor is able to emulate efficient optimization steps, improving both accuracy and convergence speed.

To build the proposed deep unfolding-based inception-like model, first, we solve the problem using a traditional optimization method, namely, successive pseudo-convex optimization for the beamforming and the interior point for the rate allocation. The beamforming and rate allocation subproblem is given as (we removed [t] for simplicity)

maxv,C∑n=1NRu,n(ϵ),(11)

s.t.∑n=1NCu,n,c(ϵ)≤minn∈N{ru,n,c(ϵ)}(11a)

|vc|2+∑n=1N|vn|2≤Pmax(11b)

Cu,n,c(ϵ)≥0,(11c)

ru,n,c(ϵ)≥0,(11d)

ϵn,p≤ϵth,ϵn,c≤ϵth(11e)

Ru,n(ϵ)≥Ru,n(min)(11f)

vn≥0,vc≥0.(11g)

The problem in (11) can be further decoupled into rate allocation and beamforming. The rate allocation subproblem is given as

maxv,C∑n=1NRu,n(ϵ)s.t.(11a),(11c),(11d),(11e),(11f).(12)

Following the analysis in [2], constraint (11f) can be transformed into Cu,n,c(ϵ)≥Ru,n(min)−ru,n,p(ϵ)∗, assuming that the solution ru,n,p(ϵ)∗ is given. Then, the problem is decoupled into two subproblems as follows:

Cc∗ =argmaxCc∑n=1NCu,n,c(ϵ)(13)

s.t.  Cu,n,c(ϵ)≥Ru,n(min)−ru,n,p(ϵ∗)∀n∈𝒩,(13a)

Cn,p∗   =arg⁡maxCn,p⁡∑n=1Nru,n,p(ε)(14)

s.t.0≤ru,n,p(ε)≤log2(1+γn,p)−V(γn,p)B𝒬−1(εn,p)ln⁡2,∀n∈𝒩,(14a)

where Cc∗,Cn,p∗∈C=[ru,n,c(ε),Cu,1,c(ε),Cu,2,c(ε),...,Cu,N,c(ε),Cu,1,p(ε),...,Cu,N,p(ε)]T∈R(2N+1)×1. The problem in (13) is convex and can be solved by standard optimization methods such as the interior point. For Cc∗, the objective function is linear, and the optimal solution can be expressed as follows:

Cc∗={Cn,cmaxifγn,c=maxl∈N{γl,c}Cn,cminotherwise,(15)

where Cn,cmax=max{ru,n,c(ϵ)−∑l=1,l≠nNCu,n,c(ϵ),0} and Cn,cmin=max{Ru,nmin−ru,n,c(ϵ∗),0}. The structure of the proposed solution in (15) is very helpful in designing deep unfolding layers for our proposed rate allocation network. However, the solution for (14) is numerical. Therefore, we use linear layers to design the corresponding neural network of (14).

The successive pseudo-convex approximation (SPCA) has emerged as a pivotal technique in wireless communications for transforming nonconvex optimization problems into tractable convex forms through iterative approximations [3,33]. This approach is particularly effective for beamforming design, where the core subproblem is formulated as

maxv∑n=1NRu,n(ϵ)(16)

s.t.|vc[t]|2+∑n=1N|vn[t]|2≤Pmax,(16a)

ϵn,p≤ϵth,ϵn,c≤ϵth,(16b)

vn[t]≥0,vc[t]≥0.(16c)

Problem (16) is nonconvex due to the nonconvexity of the objective function and constraint (16b). Using the conventional Software Communications Architecture (SCA), a surrogate function R^u,n(ϵ) is approximated at the points vn(τ) of Ru,n(ϵ) is defined. Assuming that problem (10) has a closed and convex solution set V and an optimal point V(τ), where vn(τ)∈V,R^u,n(ϵ) should satisfy the following technical conditions:

1.    R^u,n(ϵ) is pseudo-concave for any vn(τ)∈V.

2.    R^u,n(ϵ) is continuously differentiable in vn∈V and for any given vn(τ)∈V. Moreover, R^u,n(ϵ) is continuous in vn∈V for vn(τ)∈V.

3.    The gradients of R^u,n(ϵ) is identical to that of Ru,n(ϵ) for vn(τ)∈vn.

4.    The set V is nonempty for τ=1,⋯,

5.    The sequence {𝒱(τ)}τ=1T is convergent for any convergent sequence {v(τ)}τ=1T.

On the highlights of these technical conditions, the surrogate R^u,n(ϵ) function is defined as

R^u,n(ϵ)=R^u,−n(ϵ)(v;v(τ))+(v−v(τ))∑l=1,l≠nN∇vRu,n(ϵ)(vn(τ)).(17)

Using the objective function, problem (16) can be rewritten as

maxv∑n=1NR^u,n(ε)(18)

s.t.(16a),(16c),f(γ−n,c(vc;vc(τ)),B,ru,−n,c(ε))+(vc−vc(τ))∑l=1N∇vcf(γn,c(vn(τ)),B,ru,n,c(ε))≤Q−1(εth),(18a)

f(γ−n,p(vn;vn(τ)),B,ru,−n,p(ε))+(vn−vn(τ))∑l=1,l≠nN∇vnf(γn,p(vn(τ)),B,ru,n,p(ε))≤Q−1(εth),(18b)

where constraints (18a) and (18b) are transformations of constraint (16b). Applying Lagrange relaxation and Karush-Kuhn-Tucker (KKT) conditions, the beamforming can be expressed in the following closed-form expressions:

vn(τ)=(βn,p(τ)+ζn,p(τ))Ψu,n,12(2βn,p(τ)−2)(Tr(hu,nhu,nH))6(2−(Θu,n(ε))2)−Ωu,n(ε)Ψu,n,26Tr(hu,nhu,nH)Ψu,n,32βn,p(τ),(19)

where Θu,n(ϵ)=22ln⁡2e2(erfc−1(ϵ))2, Ωu,n(ϵ)=Q−1(ϵ)ln⁡2(βn,p(τ)−1(βn,p(τ))2) with βn,p(τ) and ζn,p(τ) denote Lagrange multipliers associated with constraint (15). ψu,n,1=∑l=1,l≠nK∑2Tr(hu,lhu,lH), ψu,n,2=∑n=1KTr(hu,nhu,nH)+σn2 and ψu,n,32=∑l=1KTr(hu,lhu,nH)+σn2. The proposed deep unfolding-based solution is designed using the formulas in (15) and (19), and the solution of (13). Fig. 2 illustrates a block structure of the proposed deep-unfolding-based neural network.

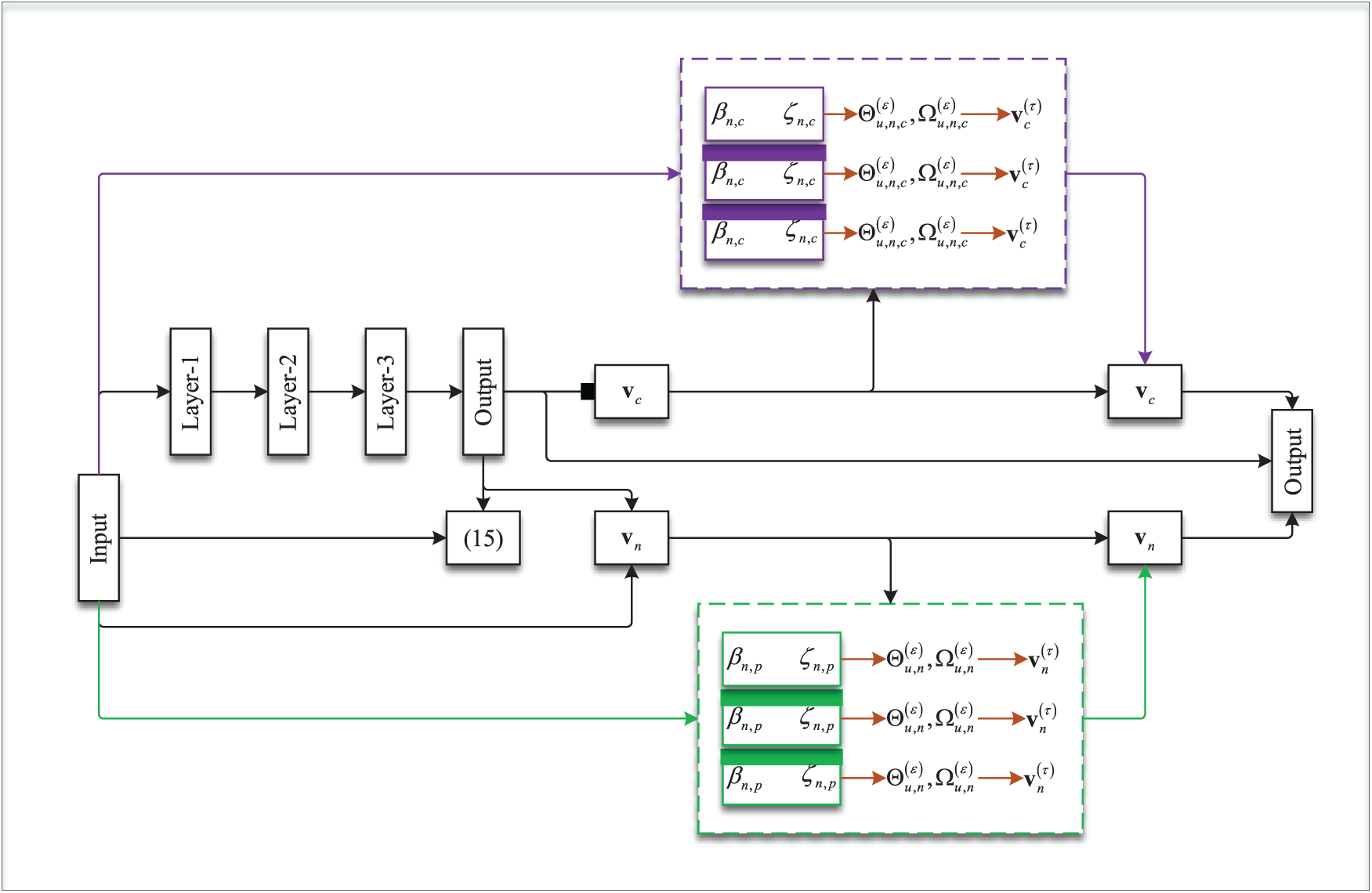
Figure 2: The structural design of a block of the proposed deep-unfolding-based neural network

The deep unfolding-based layer in 2 is built to resemble an inception block by accommodating neurons and layers in a mixed sequential and parallel structure to avoid the vanishing gradient problem. The block in 2 will be used in the actor network in the proposed DA-DDPG framework in Section 4.

5  Proposed Deep Unfolding-Based DDPG Framework

This section presents a novel design of a DRL framework using the dual-agent deep deterministic policy gradient (DA-DDPG) algorithm, and reformulates the problem as a Markov decision process (MDP). DA-DDPG is an extension of the standard DDPG method, which incorporates two agents working in parallel. One agent focuses on optimizing the continuous action space for beamforming and rate allocation, while the other agent handles the UAV trajectory optimization. By using dual agents, the framework can effectively decouple these two tasks, allowing for more specialized learning and faster convergence during training.

5.1 MDP Formulation

The traditional MDP consists of the following six-tuples: ⟨𝒮,𝒜,ℛ,𝒯,υ⟩, which respectively stand for the state space, action space, reward function, transition policies, and discount factor. During the learning process, the state value Qπ(s) function is maximized to find the optimal policy π∗(s,a). The transition policy π(a(t)|s(t)) is mapping the state s(t) and the probability of choosing each possible action. The state-value function Qπ(s) is defined as

Qπ(s)=Eπ[A(t)|s(t)]=Eπ[∑k=1∞v(k)r(t+k+1)|s(t)]∀s∈𝒮,(20)

where Eπ is the expectation of the random variable when the agent follows the transition policy. A(t)=∑k=1∞v(k)r(t+k+1) can be considered the action that maximizes the sum discount reward obtained during the process. The discount parameter v∈[0,1] is used to weight the short-term and long-term rewards.

The state-value function Qπ(s|a) can be written for the policy π(s(t)|a(t)) when the state value is known to obtain the expected reward. Thus, we have

Qπ(s|a)=Eπ[A(t)|s(t),a(t)]=Eπ[∑k=1∞v(k)r(t+k+1)|s(t),a(t)]∀a∈𝒜.(21)

And the Bellman expectation equation can be expressed

Vπ(s)=Eπ[A(t)|s(t)]=Qπ(s|a)=Eπ[A(t)|s(t),a(t)]=Eπ[∑k=1∞v(k)r(t+k+1)|s(t)]=∑a∈𝒜π(a(t)|s(t))(ℛ(s,a)+v∑s′∈𝒮Γ(s,s′,a)Qπ(s′)),(22)

where ℛ(s,a)=Eπ[r(t+1)|s(t),a(t)] represents the reward function, and Γ(s,s′,a)=P[s(t+1)|s(t),a(t)] is the matrix probability of the state transition.

By interacting with the environment through behaviors, the agent in DRL learns the policy and modifies its behavior in response to rewards. The following provides a thorough explanation of the state space, action space, and reward:

1.    State space 𝒮: The state space in our case includes two state subspaces 𝒮1(t) for the case of the beamforming and rate allocation agent, and 𝒮2(t) for the UAV trajectory. 𝒮1(t) and 𝒮2(t) are given as follows:

𝒮1(t)={{hu,n[t]}n=1N,Pmax,a1(t−1),A(t),M},(23)

𝒮2(t)={qu[t],a2(t−1),A(t),{Ln}n=1N},(24)

where a1(t−1) and a2(t−1) denote the actions from the last time slot for the beamforming and rate allocation network and the UAV trajectory network, respectively.

2.    Action space 𝒜: Similar to the case of the state space, the action space includes the actions from both agents. Two action subspaces can be defined as follows:

𝒜1(t)={v[t],C[t]},(25)

𝒜2(t)={qu[t]},(26)

3.    Reward: Following the structure of problem (10), the reward function should be built to maximize the total achievable rate for the given constraints. Therefore, penalties are set to force the satisfaction of the constraints while maximizing the objective function. Hence, the reward can be defined as follows:

ℛ(t)={−ρifsis negative∑n=1NRu,n(ϵ)[t]otherwise.(27)

5.2 Algorithm Description

The DA-DDPG algorithm is a reinforcement learning framework tailored specifically for continuous optimization problems, incorporating two separate agents. The actor network creates actions depending on the current state of each agent’s actor-critic structure, and the critic network assesses these actions to guide policy improvements.

Specifically, each agent consists of two neural networks: a training network and a slowly updated target network. The target networks are periodically updated using parameters from the training networks, significantly contributing to stable and robust training by mitigating potential divergence issues common in reinforcement learning.

The critic network is responsible for estimating the expected cumulative reward (Q-value) associated with performing a specific action given a particular state. During training, the critic network parameters θcritic are adjusted by minimizing the temporal difference loss, which quantifies the discrepancy between the predicted Q-value from the critic training network and the target network’s estimated Q-value. This update is mathematically represented as

L(θcritictrain)=(r(t)+vQ(θcritictarget|s(t+1),a′)−Q(θcritictrain|s(t+1),a′))2,(28)

where r(t) is the immediate reward received after executing action a′ in state s(t), v is the discount factor balancing immediate vs. future rewards, Q(θcritictarget|s(t+1),a′) is the target critic network’s Q-value prediction, and Q(θcritictrain|s(t+1),a′) is the critic training network’s current Q-value estimation. The actor network aims to find the optimal policy that maximizes expected rewards by following the policy gradient derived from the critic network. Its parameters are updated using the critic’s gradients concerning the action, thus directly influencing the actions produced by the actor network to optimize the policy.

θactor(t+1)=θactor(t)−iactor∇aQ(θcritictarget|s(t),a′)∇θactortrainπ(θactortrain|s(t)).(29)

The parameters of the target networks for both the actor and critic are updated through a soft update procedure to slowly track the training networks, helping stabilize the training process.

θtarget←τθtrain+(1−τ)θtarget,(30)

where τ is typically set to a small value such as 0.001. Algorithm 1 illustrates the training procedure for the proposed DA-DDPG.

The overall structure of the proposed DRL framework is given as in Fig. 3a. The network consists of two agents, each agent has actor-critic structure for both training and target networks.

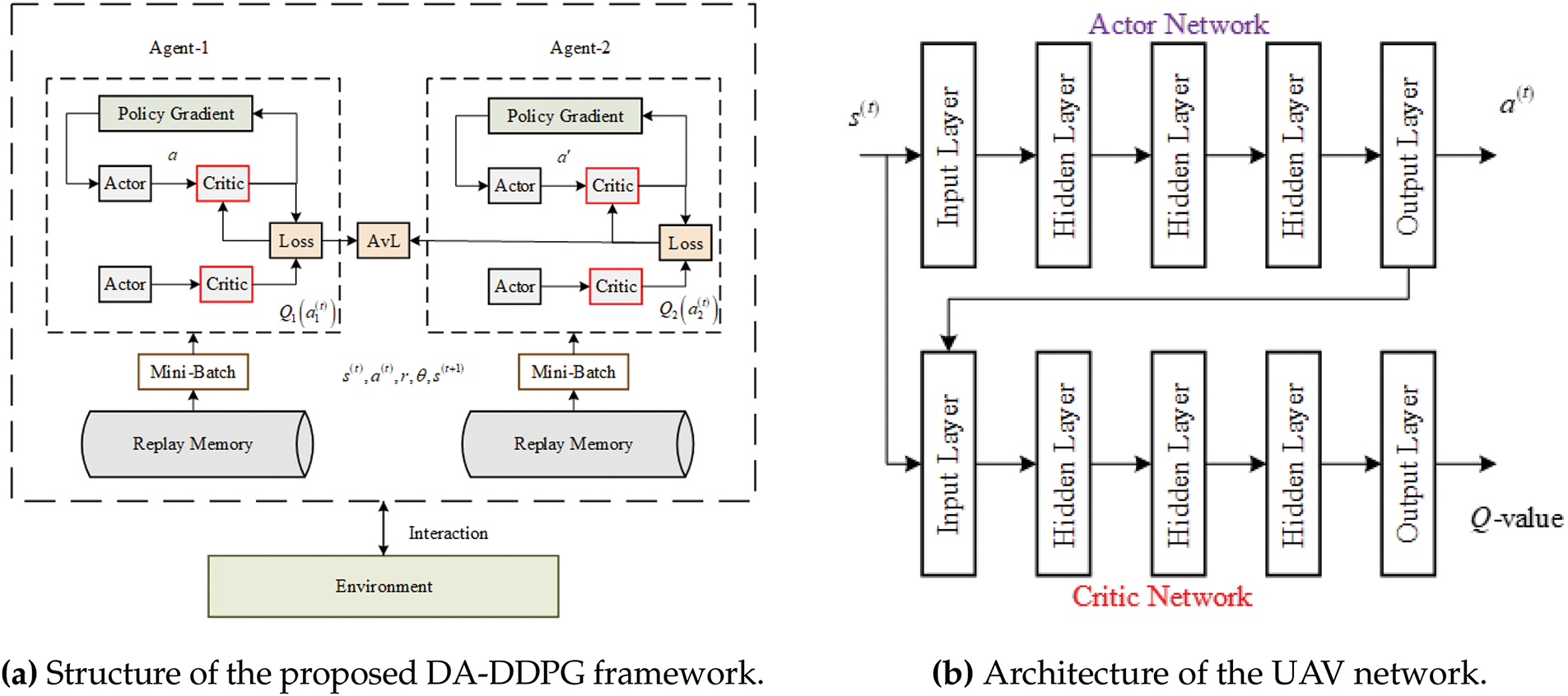
Figure 3: Architectural diagrams of the proposed system: (a) The DA-DDPG framework structure and (b) The UAV network architecture

The beamforming and rate allocation actor is constructed using an inception-like deep unfolding-based model from Section 4, while the critic is built using a fully connected deep neural network (DNN). On the other hand, a fully connected DNN-based actor-critic architecture is used to design the UAV trajectory network. The structure of the UAV trajectory is a DNN, as in Fig. 3b. In this architecture, the actor predicts the optimal UAV trajectory, while the critic evaluates the predicted trajectory by calculating the value function. The actor-critic structure ensures that the UAV trajectory network continuously improves its trajectory decisions based on feedback from the critic, leading to more efficient trajectory optimization over time.

5.3 Inference Steps and Complexity Analysis

During inference, the trained DA-DDPG algorithm executes actions based on learned policies without further training. Initially, given the current state s(t), the beamforming and rate allocation actor network generates optimized beamforming vectors v[t] and rate allocation C[t], processing the state information, which includes channel conditions hu,n[t]n=1N, previous actions, available power Pmax, and antenna configurations M. Concurrently, the UAV trajectory actor receives its state comprising UAV location qu[t], previously taken actions a2(t−1), and user locations Lnn=1N, then computes the next UAV position qu[t+1], adhering to trajectory constraints.

The computational complexity during inference primarily arises from the neural network architectures. For the beamforming and rate allocation agent, employing inception-like and deep unfolding structures, the complexity can be represented as 𝒪(LuNinc2), where Lu denotes the number of unfolding layers and Ninc indicates the number of neurons per inception-like layer. For the UAV trajectory agent, using a fully connected deep neural network, the complexity is 𝒪(LtrajNtraj2), with Ltraj being the number of layers and Ntraj the number of neurons per layer. Consequently, the total inference complexity of DA-DDPG is expressed as

𝒪(LuNinc2+LtrajNtraj2),(31)

making the framework suitable for real-time applications required by URLLC scenarios.

6  Simulation Results

This section presents simulation results to judge the performance of the proposed DA-DDPG framework for the multiuser UAV URLLC network. We consider a network architecture as outlined in Section II, where a total of N users are uniformly and randomly distributed within a circular area with a radius of R=500 m. To support the ground Internet of Things (IoT) units in URLLC applications, the UAV is deployed over the region, with altitudes of 150 m. Unless stated otherwise, other simulation parameters are summarized in Table 1. The simulation parameters for the DA-DDPG framework are illustrated in Table 2. Fig. 4 shows the performance evaluation of the proposed framework through four different metrics. Fig. 4a gives the total achievable rate for different values of Pmax. We fix the minimum rate at Ru,nmin bps/Hz, and the number of users is set as 10. The performance of the proposed DA-DDPG is closer to that of SPCA and surpasses the performance of DRL. The behavior of the proposed DA-DDPG is similar to that of SPCA, and that is because the structure of the proposed neural network is mostly based on the highlights of the SPCA solution. The performance gap between DA-DDPG and SPCA is about 1.86%. The gap is mostly due to the data-driven parts of the proposed agents. In the mean, the performance of DA-DDPG is 10.77% better than that of DRL for M = 2 and 8.09% for M = 4.

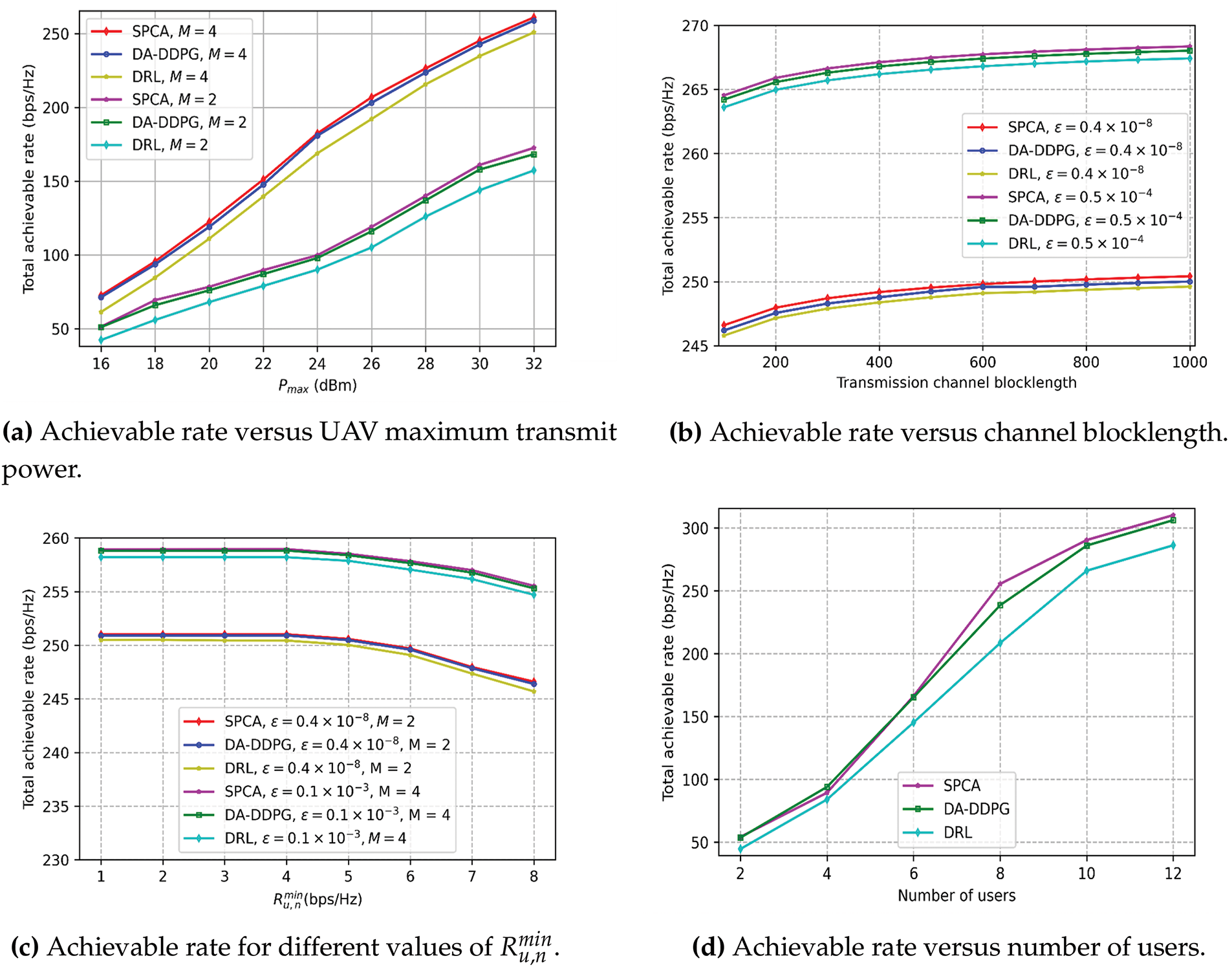
Figure 4: Performance evaluation of the proposed DA-DDPG framework. (a) Achievable rate vs. UAV maximum transmit power, (b) Achievable rate vs. channel blocklength, (c) Achievable rate for different values of Ru,nmin, and (d) Achievable rate vs. number of users

The performance in terms of achievable rate vs. transmission channel blocklength is depicted in Fig. 4b. Different values of the error threshold are set to examine the impact. We set Ru,nmin bps/Hz, and the number of users is set to 6, while the number of antennas is set to M=2 and M=4. As can be observed from the figure, the total achievable rates of all three frameworks increase with the increase of the blocklength. Moreover, it is obvious that DA-DDPG has closer performance to that of SPCA; however, it requires a longer blocklength to achieve similar performance. Similarly, DRL requires a longer blocklength than that in the case of DA-DDPG to achieve similar performance to that of SPCA. The increase of the error threshold leads to better performance, and the performance gap between DA-DDPG and SPCA slightly decreases as such. However, the performance gap between the DRL and the other two frameworks increases, i.e., for the case of error threshold 0.5×10−4.

Fig. 4c shows the total achievable rate for different values of Ru,nmin. Different values of the error threshold and number of antennas are considered. The total achievable rate is decreasing with the increasing of Ru,nmin. The performance gap between SPCA and DA-DDPG is small, while it is relatively larger for the case of DRL. The decrease in the total achievable rate becomes more severe for higher Ru,nmin in the case of DRL. For instance, when Ru,nmin bps/Hz and M=2, the performance gap between DRL and DA-DDPG is 6.92%, and when Ru,nmin bps/Hz, the gap is 7.83%. In general, similar conclusions to those in Fig. 4b can be drawn from Fig. 4c.

The relationship between the total achievable rate and the number of users is depicted in Fig. 4d. The number of antennas is fixed at M=4, the error threshold is ϵth=5×10−3, and Ru,nmin bps/Hz. The performance in terms of achievable rate increases dramatically with the increase of the number of users. Even with the fluctuation in the performance gap between DA-DDPG and SPCA, on average the gap is smaller compared to that between SPCA and DRL or DA-DDPG and DRL. On the other hand, Table 3 clearly shows the superiority of the proposed DA-DDPG over other frameworks in terms of inference speed. The proposed DA-DDPG proves to be a better choice for large-scale communication systems compared with DRL.

7  Conclusion

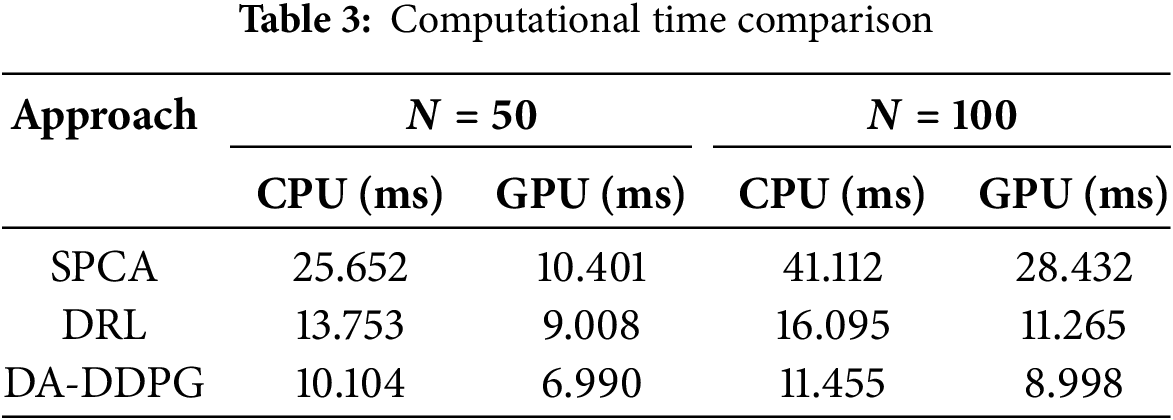
In this work, we proposed a design of a distributed DRL framework with dual-agent deep deterministic policy gradient (DA-DDPG). A novel structure of the beamforming and rate allocation is proposed, where an inception-like mechanism and deep unfolding are employed to build the layers. To apply these two mechanisms, we designed a successive pseudo-convex approximation (SPCA) to handle both beamforming and rate allocation. A fully connected deep neural network is used for the critic network. Successive pseudo-convex approximation (SPCA) lays the ground for applying the above two techniques. The second agent is the UAV trajectory, in which both the actor and critic are based on DNN. Simulation results demonstrated the effectiveness of the proposed framework. Moreover, the proposed model outperforms other well-known methods in the literature. Additionally, developing joint resource allocation frameworks for multiple UAVs and RISs will improve scalability and load balancing, particularly in dense urban areas. Addressing security challenges in UAV-RIS networks will also ensure robust and secure communication in mission-critical applications.

Acknowledgement: The authors extend their appreciation to the Deputyship of Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number RI-44-0291.

Funding Statement: The study was supported by the Deputyship of Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number RI-44-0291.

Author Contributions: The authors confirm their contribution to the paper as follows: Conceptualization, Samia Allaoua Chelloug and Ammar Muthanna; methodology, Dina S. M. Hassan; software, Mohammed Saleh Ali Muthanna; validation, Reem Alkanhel and Samia Allaoua Chelloug; formal analysis, Abuzar B. M. Adam and Dina S. M. Hassan; investigation, Samia Allaoua Chelloug; resources, Ammar Muthanna and Abuzar B. M. Adam; data curation, Mohammed Saleh Ali Muthanna and Abuzar B. M. Adam; writing—original draft preparation, Reem Alkanhel and Abuzar B. M. Adam; writing—review and editing, Samia Allaoua Chelloug; visualization, Dina S. M. Hassan.; supervision, Ammar Muthanna; project administration, Reem Alkanhel; funding acquisition, Samia Allaoua Chelloug. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Chen K, Wang Y, Zhao J, Wang X, Fei Z. URLLC-oriented joint power control and resource allocation in UAV-assisted networks. IEEE Int Things J. 2021;8(12):10103–16. doi:10.1109/jiot.2021.3051322. [Google Scholar] [CrossRef]

2. Zeng C, Wang JB, Xiao M, Ding C, Chen Y, Yu H, et al. Task-oriented semantic communication over rate splitting enabled wireless control systems for URLLC services. IEEE Transact Commun. 2023;72(2):722–39. doi:10.1109/tcomm.2023.3325901. [Google Scholar] [CrossRef]

3. 3GPP. Study on scenarios and requirements for next generation access technologies. 3rd generation partnership project (3GPPTR 38913; 2022 [Internet]. [cited 2025 Apr 26]. Available from: https://www.etsi.org/deliver/etsi_tr/138900_138999/138913/18.00.00_60/tr_138913v180000p.pdf. [Google Scholar]

4. Bing L, Gu Y, Aulin T, Wang J. Design of autoconfigurable random access NOMA for URLLC industrial IoT networking. IEEE Transact Indust Informat. 2023;20(1):190–200. doi:10.1109/tii.2023.3257841. [Google Scholar] [CrossRef]

5. Soleymani M, Santamaria I, Jorswieck E, Clerckx B. Optimization of rate-splitting multiple access in beyond diagonal RIS-assisted URLLC systems. IEEE Transact Wireless Commun. 2023;23(5):5063–78. doi:10.1109/twc.2023.3324190. [Google Scholar] [CrossRef]

6. Ou X, Xie X, Lu H, Yang H. Channel blocklength minimization in MU-MISO nonorthogonal multiple access for URLLC services. IEEE Systems J. 2023;18(1):36–9. doi:10.1109/jsyst.2023.3329721. [Google Scholar] [CrossRef]

7. Sun Y, Ding Z, Dai X. On the performance of downlink NOMA in multi-cell mmWave networks. IEEE Commun Lett. 2018;22(11):2366–9. doi:10.1109/lcomm.2018.2870442. [Google Scholar] [CrossRef]

8. Mao Y, Dizdar O, Clerckx B, Schober R, Popovski P, Poor HV. Rate-splitting multiple access: fundamentals, survey, and future research trends. IEEE Commun Surv Tutor. 2022;24(4):2073–126. doi:10.1109/COMST.2022.3191937. [Google Scholar] [CrossRef]

9. Kong C, Lu H. Cooperative rate-splitting multiple access in heterogeneous networks. IEEE Commun Lett. 2023;27(10):2807–11. doi:10.1109/lcomm.2023.3309818. [Google Scholar] [CrossRef]

10. Lyu X, Aditya S, Kim J, Clerckx B. Rate-splitting multiple access: the first prototype and experimental validation of its superiority over SDMA and NOMA. IEEE Transact Wireless Commun. 2024;23(8):9986–10000. doi:10.1109/twc.2024.3367891. [Google Scholar] [CrossRef]

11. Li X, Li J, Liu Y, Ding Z, Nallanathan A. Residual transceiver hardware impairments on cooperative NOMA networks. IEEE Transact Wireless Commun. 2019;19(1):680–95. doi:10.1109/twc.2019.2947670. [Google Scholar] [CrossRef]

12. Pivoto DGS, de Figueiredo FAP, Cavdar C, Tejerina GRDL, Mendes LL. A comprehensive survey of machine learning applied to resource allocation in wireless communications. IEEE Commun Surv Tutor. 2025;1. doi:10.1109/COMST.2025.3552370. [Google Scholar] [CrossRef]

13. Huang Y, Jiang Y, Zheng FC, Zhu P, Wang D, You X. Energy-efficient optimization in user-centric cell-free massive MIMO systems for URLLC with finite blocklength communications. IEEE Transact Vehic Technol. 2024;73(9):12801–14. doi:10.1109/tvt.2024.3382341. [Google Scholar] [CrossRef]

14. Nguyen DC, Cheng P, Ding M, Lopez-Perez D, Pathirana PN, Li J, et al. Enabling AI in future wireless networks: a data life cycle perspective. IEEE Commun Surv Tutor. 2021;23(1):553–95. doi:10.1109/COMST.2020.3024783. [Google Scholar] [CrossRef]

15. Wang D, Liu Y, Yu H, Hou Y. Three-dimensional trajectory and resource allocation optimization in multi-unmanned aerial vehicle multicast system: a multi-agent reinforcement learning method. Drones. 2023;7(10):641. doi:10.3390/drones7100641. [Google Scholar] [CrossRef]

16. Robaglia BM, Coupechoux M, Tsilimantos D. Deep reinforcement learning for uplink scheduling in NOMA-URLLC networks. IEEE Transact Mach Learn Commun Netw. 2024;2(12):1142–58. doi:10.1109/tmlcn.2024.3437351. [Google Scholar] [CrossRef]

17. Ouamri MA, Barb G, Singh D, Adam AB, Muthanna MSA, Li X. Nonlinear energy-harvesting for D2D networks underlaying UAV with SWIPT using MADQN. IEEE Commun Lett. 2023;27(7):1804–8. doi:10.1109/lcomm.2023.3275989. [Google Scholar] [CrossRef]

18. Alkama D, Azni M, Ouamri MA, Li X. Modeling and performance analysis of vertical heterogeneous networks under 3D blockage effects and multiuser MIMO systems. IEEE Transact Vehic Technol. 2024;37(7):10090–105. doi:10.1109/tvt.2024.3366655. [Google Scholar] [CrossRef]

19. Ranjha A, Kaddoum G. Quasi-optimization of distance and blocklength in URLLC aided multi-hop UAV relay links. IEEE Wireless Commun Lett. 2019;9(3):306–10. doi:10.1109/lwc.2019.2953165. [Google Scholar] [CrossRef]

20. Ranjha A, Javed MA, Piran MJ, Asif M, Hussien M, Zeadally S, et al. Towards facilitating power efficient URLLC systems in UAV networks under jittering. IEEE Transact Consumer Elect. 2023;70(1):3031–41. doi:10.1109/tce.2023.3305550. [Google Scholar] [CrossRef]

21. Liu CF, Wickramasinghe ND, Suraweera HA, Bennis M, Debbah M. URLLC-aware proactive UAV placement in internet of vehicles. IEEE Transact Intell Transport Syst. 2024;25(8):10446–51. doi:10.1109/tits.2024.3352971. [Google Scholar] [CrossRef]

22. Cai Y, Jiang X, Liu M, Zhao N, Chen Y, Wang X. Resource allocation for URLLC-oriented two-way UAV relaying. IEEE Transact Vehic Technol. 2022;71(3):3344–9. doi:10.1109/tvt.2022.3143174. [Google Scholar] [CrossRef]

23. Wu Q, Cui M, Zhang G, Wang F, Wu Q, Chu X. Latency minimization for UAV-enabled URLLC-based mobile edge computing systems. IEEE Transact Wireless Commun. 2023;23(4):3298–311. doi:10.1109/TWC.2023.3307154. [Google Scholar] [CrossRef]

24. Feng R, Li Z, Wang Q, Huang J. An ADMM-based optimization method for URLLC-enabled UAV relay system. IEEE Wirel Commun Lett. 2022;11(6):1123–7. doi:10.1109/lwc.2022.3153142. [Google Scholar] [CrossRef]

25. Huang Y, Jiang Y, Zheng FC, Zhu P, Wang D, You X. Enhancing energy-efficient URLLC in cell-free mMIMO systems with transceiver impairments: an RSMA-DRL based approach. IEEE Wirel Commun Lett. 2024;13(5):1443–7. doi:10.1109/lwc.2024.3373826. [Google Scholar] [CrossRef]

26. Seong J, Toka M, Shin W. Sum-rate maximization of RSMA-based aerial communications with energy harvesting: a reinforcement learning approach. IEEE Wirel Commun Lett. 2023;12(10):1741–5. doi:10.1109/lwc.2023.3290372. [Google Scholar] [CrossRef]

27. Guo K, Wu M, Li X, Song H, Kumar N. Deep reinforcement learning and NOMA-based multi-objective RIS-assisted IS-UAV-TNs: trajectory optimization and beamforming design. IEEE Transact Intell Transport Syst. 2023;24(9):10197–210. doi:10.1109/tits.2023.3267607. [Google Scholar] [CrossRef]

28. Wu M, Gao Z, Huang Y, Xiao Z, Ng DWK, Zhang Z. Deep learning-based rate-splitting multiple access for reconfigurable intelligent surface-aided tera-hertz massive MIMO. IEEE J Selec Areas Commun. 2023;41(5):1431–51. doi:10.1109/jsac.2023.3240781. [Google Scholar] [CrossRef]

29. Khalili A, Monfared EM, Zargari S, Javan MR, Mokari N, Jorswieck EA. Resource management for transmit power minimization in UAV-assisted RIS HetNets supported by dual connectivity. IEEE Transact Wirel Commun. 2021;21(3):1806–22. doi:10.1109/twc.2021.3107306. [Google Scholar] [CrossRef]

30. Hua DT, Do QT, Dao NN, Cho S. On sum-rate maximization in downlink UAV-aided RSMA systems. ICT Express. 2024;10(1):15–21. doi:10.1016/j.icte.2023.03.001. [Google Scholar] [CrossRef]

31. Adam ABM, Elhassan MAM. Enhancing Secrecy in UAV RSMA Networks: Deep Unfolding Meets DeepReinforcement Learning. In: 2023 International Conference on Communications, Computing, Cybersecurity, andInformatics (CCCI). China: Chongqing: 2015. p. 1–5. doi:10.1109/CCCI58712.2023.10290852. [Google Scholar] [CrossRef]

32. Adam ABM, Wan X, Elhassan MAM, Muthanna MSA, Muthanna A, Kumar N, et al. Intelligent and robust UAV-aided multiuser RIS communication technique with jittering UAV and imperfect hardware constraints. IEEE Trans Veh Technol. 2023;72(8):10737–53. doi:10.1109/tvt.2023.3255309. [Google Scholar] [CrossRef]

33. Adam ABM, Wang Z, Wan X, Xu Y, Duo B. Energy-efficient power allocation in downlink multi-cell multi-carrier NOMA: special deep neural network framework. IEEE Transact Cognit Commun Netw. 2022;8(4):1770–83. doi:10.1109/tccn.2022.3198652. [Google Scholar] [CrossRef]