Multi-Phase Modeling for Vulnerability Detection & Patch Management: An Analysis Using Numerical Methods

1  Introduction

Vulnerability identification and patch management have emerged as crucial focus areas for guaranteeing software security in an era of quickly changing cybersecurity threats. Software systems are more vulnerable to security breaches as they get more complex; therefore, protecting data availability, confidentiality, and integrity requires prompt vulnerability identification and efficient patch deployment. However, static frameworks, a lack of adaptive learning methods, and inefficient patch application are only a few of the drawbacks of the vulnerability management solutions that are currently in use. Conventional vulnerability detection algorithms are inadequate against zero-day vulnerabilities and changing attack tactics because they rely on preset criteria and signature-based techniques. Furthermore, the cascade consequences of flawed patches are frequently overlooked by current patch management systems, which could introduce new vulnerabilities rather than the mitigation of existing ones. These models’ inability to incorporate dynamic learning methods further restricts their capacity to adjust to new threats. This work suggests a multi-phase mathematical modelling technique for vulnerability discovery and patch management to address these issues. The framework integrates dynamic learning methods to reduce the risks associated with defective patches and increase patch deployment efficiency. Furthermore, numerical techniques like the Runge-Kutta approximation are employed in complex situations where closed-form solutions are impractical. Software engineering is systematically planning, creating, testing, and managing software systems. It includes a collection of guidelines, procedures, and equipment to guarantee that software is dependable, effective, and satisfies user requirements. Software quality has become crucial as modern life increasingly depends on digital systems, from personal devices to vital infrastructure. Nevertheless, these systems’ complexity and the quickly evolving technological environment provide weaknesses that malicious actors might exploit [1]. To manage these risks, software developers must focus on secure coding practices, conduct thorough testing, and implement security features like encryption, access controls, and regular upgrades. Nevertheless, no system is infallible in the end. To lessen the possibility and impact of exploitation, a proactive approach that includes frequent monitoring, vulnerability assessments, and timely updates is essential. For the fixation of Vulnerabilities, Patches are deployed. Reducing software system vulnerabilities is primarily dependent on patch management [2]. Programming mistakes, bugs, and design defects are frequently the source of software vulnerabilities, which hackers can use to obtain unauthorised access or interfere with normal operations. Finding, obtaining, testing, and implementing patches (software updates) to fix these vulnerabilities before they can be exploited are all components of effective patch management. Patches are released by software developers to address vulnerabilities when they appear. However, systems become vulnerable to assaults if these fixes are not timely. This is particularly true when vulnerabilities are made public because unpatched systems can be the target of attackers.

Patches are remedial measures used to address vulnerabilities in software programs. They are snippets of code created to enhance functionality and secure or fix problems with software applications. One of the most important components of preserving the security and stability of software systems is patch management. It consists of a systematic process for locating, acquiring, testing, and implementing patches—also known as updates—for software systems and apps. Effective patch management is more critical than ever with increasingly complex and interconnected software systems. In addition to reducing the risks associated with vulnerabilities, timely and effective patching guarantees the software’s ongoing dependability and functionality [3].

Patch management ensures these updates are implemented as soon as possible, minimising the exposure window and drastically lowering the chance of an attack. Patch management is essential to keeping software systems stable and secure [4]. It entails the systematic procedure for locating, obtaining, testing, and distributing updates or patches to systems and software applications. Effective patch management is more important than ever as software systems get more intricate and networked. Patching vulnerabilities in a timely and effective manner not only reduces the dangers they offer, but it also maintains the dependability and functionality of software environments. Vulnerabilities in software systems discovered during development are fixed via patches. Several rigorous testing processes involve creating a patch, including unit, integration, system and user acceptance testing [5]. The main aim is to guarantee that the patch resolves the identified issues without adversely affecting other software elements. One of the most critical parts of a patch is its comprehensive documentation, which details the changes made, their rationales, and the expected consequences on the system.

The significance of efficient vulnerability and patch management is highlighted by numerous real-world occurrences. The 2020 SolarWinds supply chain hack (https://www.csoonline.com/article/570537/the-solarwinds-hack-timeline-who-knew-what-and-when.html, accessed on 15 June 2023) was an alarming instance of the vulnerabilities in secure software systems. Hackers accessed the company’s development process and installed Sunburst, a malicious backdoor, into updates for its popular Orion program. This breach remained undiscovered for months, giving hackers access to private networks. It illustrated the catastrophic effects a single hacked vendor could have on global cybersecurity and emphasised the significance of data security.

An additional illustration is a flaw in the MOVEit (https://community.progress.com/s/article/MOVEit-Transfer-Critical-Vulnerability-15June2023, accessed on 15 June 2023) managed file transfer software that was used by cybercriminals to compromise data, impacting almost 100 million people and thousands of organizations. Even though patches were available, the vulnerability was exploited by attackers due to delayed implementation, highlighting the importance of applying patches. The importance of prompt patch distribution and efficient vulnerability management techniques is underscored by these instances. In addition, businesses must adhere to a systematic procedure for efficient vulnerability and patch management to guarantee that vulnerabilities are fixed quickly and successfully; usually, this cycle includes the following phases:

1.    Vulnerability Induced: Vulnerabilities arise during software development due to coding or design flaws.

2.    Discovery: Researchers or attackers identify weaknesses in the system.

3.    Exploit Availability: Attackers create tools to exploit the vulnerability.

4.    Disclosure: The vulnerability is reported to the vendor or made public.

5.    Vendor Patch: The vendor develops and releases a patch to fix the issue.

6.    Patch Installed: Users apply the patch to secure their systems.

The methodical procedure for efficient vulnerability and patch management is shown in Fig. 1. It gives each cycle stage a graphic representation.

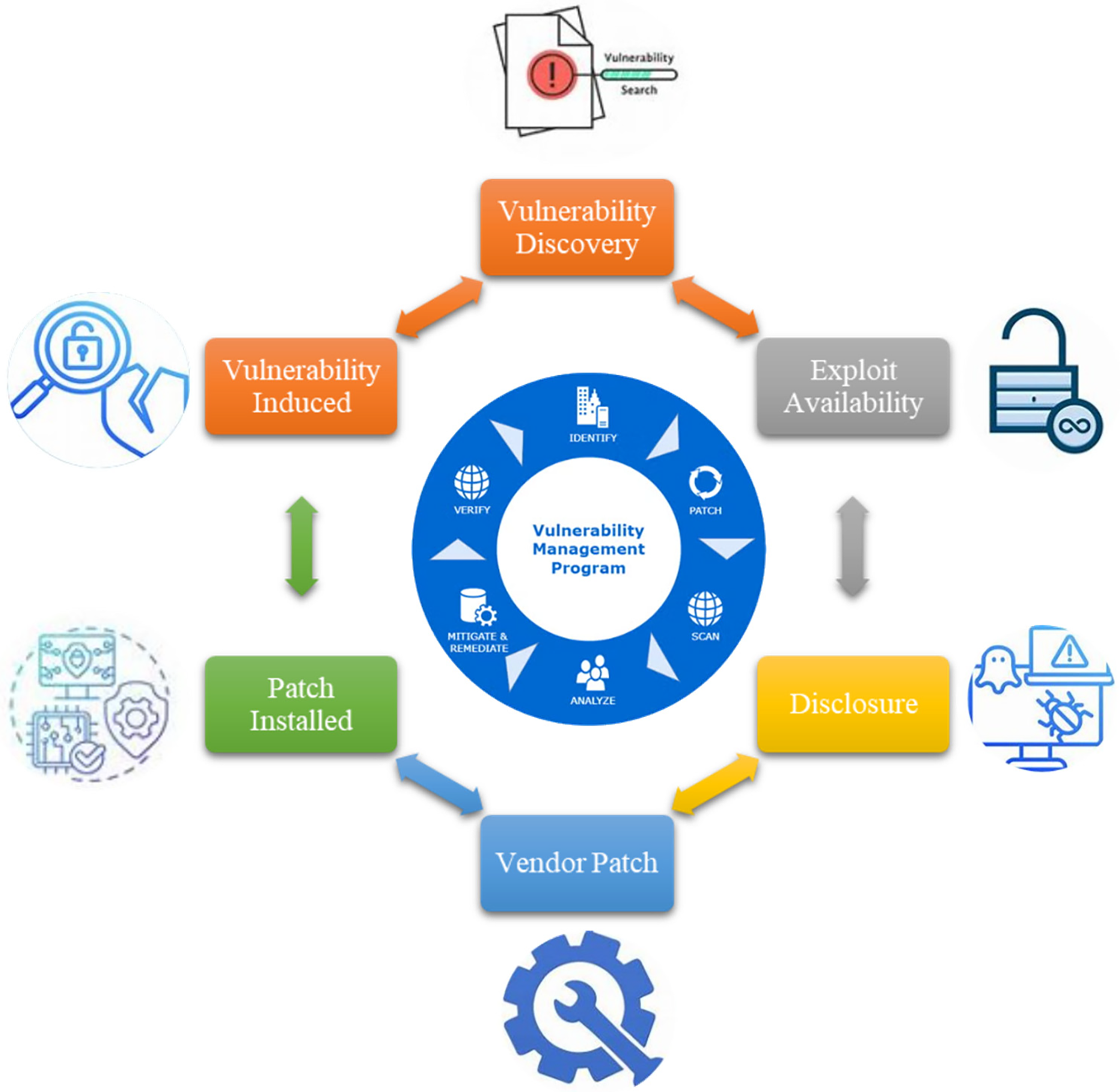
Figure 1: Vulnerability lifecycle and patch management process

An ongoing cycle that is essential to software maintenance and security management is the identification of vulnerabilities and the subsequent implementation of fixes. Every step must be carefully planned and carried out to guarantee that vulnerabilities are fixed quickly and effectively. However, there may be a situation where, after vulnerabilities have been discovered and patches are applied to address them, the patches may, for whatever reason, also be to blame for the increase in the overall number of vulnerabilities found; these patches are known as faulty patches. When using these fixes, there is a significant risk to the software’s dependability and security. Due to the requirement to address serious problems or vulnerabilities, some patches may be hurried into release without adequate testing. A poorly designed patch could introduce new issues, break existing functionality, and introduce new security flaws.

The author of this paper presented a multi-phased methodology for vulnerability identification and patch management. Using a logistic learning function to describe vulnerability fixation, the model integrated the idea of the learning phenomena. In the first stage, the authors modelled the process of detecting vulnerabilities; in the second stage, they incorporated the learning phenomena into the process of fixing vulnerabilities. Through the incorporation of dynamic elements of learning and improvement, this holistic approach seeks to better understand how vulnerabilities are recognized and handled over time. The authors of this paper have covered three scenarios for vulnerability detection and repair; in one of these scenarios, the closed-form solution was not accessible, so the authors approximated the parameter values using the numerical approach, namely the fourth-order Runge-Kutta approach.

There are multiple sections to this work. The proposed modelling framework for this study is discussed in Section 3, the solution methodology is covered in Section 4, and model validation is completed in Section 5. The authors also discuss previous work related to the current study in Section 2, which is a comprehensive literature review. The author talked about the study’s findings in Section 6. Sections 7 and 8 contain the author’s conclusions on this study, and the same part also discusses the study’s limitations and future scope.

2  Literature Review

Vulnerability Discovery Models (VDMs) are mathematical models designed to predict and explain the process for discovering vulnerabilities in software systems. These models are essential for analysing vulnerability detection dynamics and creating effective vulnerability management plans. As per a basic VDM initially introduced by Rescorla [6], the pace of vulnerability discovery grows exponentially before slowing down as the number of undiscovered vulnerabilities decreases. Alhazmi et al. [7] presented a mathematical model for the vulnerability discovery process by considering that an operating system’s vulnerabilities are impacted by its particular usage environment. The learning, linear, and saturation phases of vulnerability detection rates were also covered. To improve the existing vulnerability discovery models Ozment [8] proposed a standard set of definitions relevant to measuring characteristics of vulnerabilities and their discovery process. A method for assessing the quality and predictability of VDM performance was developed by Massacci et al. [9]. Croft et al. [10] provided a systematic literature review for software vulnerability prediction. A neural network model for vulnerability detection was presented by Movahedi et al. [11]. Also, Liu et al. [12] in the year 2012, proposed research on software vulnerability techniques, including static analysis, Fuzzing, and penetration testing. Research on the effect of shared code on vulnerability and patching was conducted in 2015 by Nappa et al. [13]. Vulnerability discovery in multi-version software has been proposed by Kim et al. [14]. In 2016, Sharma et al. [15] researched vulnerability discovery modelling for open-source and closed-source software. In 2017, Bhatt et al. [16] modelled and described software vulnerability. A case study on software vulnerability coordination was given by Ruohonen et al. [17] in the year 2018. Additionally, a comprehensive empirical analysis of security patches was first carried out in 2017 by Li et al. [18]. In recent years, a great deal of effort has been put into modelling the framework for vulnerability discovery modelling. A small amount of work has been done concerning the patch after VDM. In 2022, Costa et al. [19] defined the challenges of prioritizing patching in software systems. Shrivastava et al. [20] introduced a new approach to vulnerability modelling in 2018. They divided vulnerabilities into direct and indirect categories according to how they are fixed by using the time lag phenomenon of vulnerability patching upon identification. In 2019, Almukaynizi et al. [21] introduced a unified method for locating specific software flaws.

The same year, Anand et al. [22] suggested a quantitative approach to guarantee the Safety Integrity Level (SIL) in software systems to identify the best patch release schedule for addressing vulnerabilities following software deployment. Furthermore, the primary focus of patch-related modelling is on the procedures involved in developing, releasing, and putting into practice patches to address vulnerabilities. The goal of these models is to capture the dynamics of patch management, such as the optimal number of patches published [23], the rate at which patches are released, and the effectiveness of the patch deployment procedure. A mathematical model based on the idea of directly, indirectly, and unsuccessfully patched vulnerabilities was proposed by Kansal et al. [24]. In the year 2023, Xu et al. [25] presented a patch presence test approach to identify binary vulnerabilities by extracting key basic blocks of patch and vulnerability as their signatures for patch discovery.

A two-dimensional vulnerability-patch model based on reported vulnerabilities and patch release time was proposed by Shrivastava et al. [26]. A systematic literature review of challenges, approaches, tools and practices of software security patch management proposed by Dissanayake et al. [27] in the year 2022. In 2020, Wang et al. [28] proposed a machine-learning approach to classify security patches into vulnerability types. This approach highlights the value of proactive patch management and the necessity of balancing patch releases with the continuous identification of new vulnerabilities. In 2024, Divya et al. [29] presented a study involving the study of faulty and safe patches. In 2022, Xu et al. [30] discussed the tracking patches for OSS vulnerabilities. Bhatt et al. [31] in the year 2024 discussed the Selection of the Best Software Vulnerability Scanner Using an Intuitionistic Fuzzy set.

In this paper, the authors used a numerical method to approximate the closed-form solution. Numerical approaches are essential when tackling mathematical problems without analytical answers. In 1990, Dahlquist and Bjorck introduced higher-order numerical methods for solving fractional differential equations [32]. In 1996, Dennis et al. [33] studied the numerical methods for unconstrained optimisation and nonlinear equations. In 2014, Rice et al. [34] studied numerical methods in software and analysis. Butcher and Charles, in 2016, studied numerical methods for ordinary differential equations [35]. Butcher and Charles carried out a study in 1996 that constituted a centennial survey of Runge-Kutta procedures. It examines a few of Runge, Heun, Kutta, and Nystrom’s early works. In addition to discussing implicit methods, stability analysis, error estimation techniques, and dense output, it culminates in the idea of Runge-Kutta methods’ order of accuracy [36]. Current models provide useful information on patch management and vulnerability detection, but they often treat both processes independently and ignore the dynamic learning phenomenon that occurs over time. Building on earlier methods, this work proposes a comprehensive multi-phase mathematical model for vulnerability identification and effective patch management.

3  Proposed Modeling Framework

The vulnerability discovery and fixation processes are correlated. This paper proposes a thorough multi-phase mathematical approach for discovering vulnerabilities and efficient patch management. To capture the dynamics of vulnerability discovery and fixation, the model inculcates the learning factor notion, which was first put forth by Xia et al. [37]. In vulnerability detection and maintenance rates, the learning phenomenon is the process through which the effectiveness and efficiency of finding and fixing vulnerabilities improve over time. Experience and expertise help software development and maintenance teams find and address vulnerabilities more quickly and effectively. Additional factors that impact the learning process of vulnerability detection and fixation include resource allocation, feedback loops, and enhanced tools and technology. The authors in this case believe that the process of detecting and fixing vulnerabilities is divided into two phases, with learning functions being applied to the first phase of vulnerability fixation. The model used a logistic learning function to describe vulnerability fixation, incorporating the idea of the learning phenomena to characterize these processes in a new way. Additionally, in situations where an analytical solution is challenging to achieve, the authors have approximated the solution of the suggested framework using numerical techniques. There are two steps in the mathematical modelling process for the suggested model. The author models the total number of vulnerabilities found in the first step. In order to fix the vulnerabilities discovered in the first stage, a number of patches were released in the second step. Also, this study has a particular case in which the authors discuss the concept of faulty patches.

3.1 Assumptions

The modelling methodology proposed in this study depends on the following hypotheses:

•   The vulnerability identification process is time-dependent.

•   Time affects the patch deployment process.

•   In the vulnerability-identifying process the Non-Homogenous Poisson Process (NHPP) is used.

•   The quantity of vulnerabilities discovered influences how many patches are released.

3.2 Notations

This work uses the following Notations:

Ω(t) = cumulative number of vulnerabilities discovered by time t.

P(t)= cumulative number of patches released/deployed by the time t.

N(t) = total number of vulnerabilities present in the software.

b1 = the rate by which the vulnerabilities have been discovered.

b2 = the rate by which the patches are deployed.

α = rate of vulnerability increment.

β = learning function.

3.3 Model Development

The use of mathematical modelling to guide the discovery process is seen in the literature on vulnerability discovery modelling. To tackle this problem, researchers have employed the Non-homogenous Poisson process (NHPP). The vulnerability discovery process provided by Rescorla has made extensive use of Eq. (1), which is shown below.

dΩ(t)dt=b{N−Ω(t)}(1)

Various procedures for vulnerability discovery have been used in the past to develop plenty of mathematical models. The authors of the present work, however, have taken this vulnerability discovery as a step in between in the software patching process, moving one step further.

Furthermore, in contrast to other researchers, this work assumes that the overall number of vulnerabilities varies over time rather than remaining constant.

Consequently, the differential equation that supports this framework can be expressed using Eq. (2):

dΩ(t)dt=b1{N(t)−Ω(t)}(2)

where N(t) is the total number of vulnerabilities present in the software and Ω(t) is the cumulative number of vulnerabilities discovered over time (t) with vulnerability discovery rate (b1). Eq. (2) represents the cumulative number of vulnerabilities discovered by period (t) which gets exploited.

Now, after the discovery of new security holes by the aggressors, Ω(t) security holes exposed to defenders or the patch team are notified of security flaws, which they then eliminate in accordance with the number of vulnerabilities found during a vulnerability fixation procedure. The authors also inculcate the notion of learning function here.

It is represented by Eq. (3).

dP(t)dt=b21+βe−b2t{Ω(t)−P(t)}(3)

here, P(t) is the cumulative number of patches deployed by time (t) and b21+βe−b2t is the rate of providing patches.

This study also incorporates the three mathematical forms of time-dependent vulnerabilities.

Case 1: When during the upgradation the count increases exponentially with rate α i.e., N(t)=Neαt.

Case 2: When the number of security loopholes increases linearly with time (t) and rate α, i.e., N(t)=N(1+αt).

Case 3: When the faulty patch increases the total number of security loopholes in the system, i.e., N(t)=N+αP(t).

Furthermore, this study is a multi-phase modelling for vulnerability discovery and vulnerability fixation. For both the above cases, the authors have taken two rates into consideration: for the first phase, the authors have taken the vulnerability discovery rate as constant, and for vulnerability fixation, the authors have incorporated the learning function, b21+βe−b2t.

For the above three cases, the sets of equalities can be represented by Eqs. (4)–(9):

For Case 1,

dΩ(t)dt=b1{Neαt−Ω(t)}(4)

dP(t)dt=b21+βe−b2t{Ω(t)−P(t)}(5)

For Case 2,

dΩ(t)dt=b1{N(1+αt)−Ω(t)}(6)

dP(t)dt=b21+βe−b2t{Ω(t)−P(t)}(7)

For Case 3, when the faulty patches increase the vulnerability content in the system,

dΩ(t)dt=b1{N+αP(t)−Ω(t)}(8)

dP(t)dt=b21+βe−b2t{Ω(t)−P(t)}(9)

Case 1 and Case 2 can be solved using the traditional methods. Using the initial condition, Ω(t)=0, to solve Eqs. (4)–(7) we have,

For Case 1,

P(t)=Nb1b2(α+b1)(1+βe−b2t)[eαt(α+b2)−e−b1t(b2−b1)−e−b2t(α+b2)+e−b2t(b2−b1)](10)

For Case 2,

P(t)=N1+βe−b2t[1+αt−αb2−αb1−b2(b2−b1)(1−αb1)e−b1t−e−b2t+αb2e−b2t+αb1e−b2t+b2(b2−b1)(1−αb1)e−b2t](11)

When the count grows exponentially during the upgrading or debugging, Eq. (10) shows the total number of patches deployed by time t. When security flaws increase linearly with time t, the cumulative number of patches deployed by time t is represented by Eq. (11). Conventional techniques cannot be used to obtain the closed-form answer for Case 3.

Case 3 also makes it very clear that there will be an increase in the number of software vulnerabilities as a result of this case. This scenario can be called a faulty patch. Patches are necessary, but not all of them are produced equal. Patches may be inaccurate for several reasons, such as inadequate testing, rushed development processes, and ignorance of the underlying vulnerability. These flawed patches may fail to fix the vulnerability, inadvertently introduce new ones, or cause unexpected software behaviour such as crashes or reduced functionality. Faulty patches are updates designed to fix vulnerabilities but cause additional issues or security concerns instead. One common cause is inadequate testing. The Authors used the Runge-Kutta method because it provides high accuracy without requiring excessively small step sizes. It efficiently handles nonlinear differential equations arising in Case 3. It converges faster than Euler’s method, reducing computational overhead.

4  Solution Methodology

Case 3 requires more discussion, as was covered in the section before this one about the solutions for the three cases under consideration. Since the traditional solution approaches provide a closed-form solution, Cases 1 and 2 can be successfully resolved by utilizing them. Case 3, on the other hand, does not have such a clear advantage. Even if there are a series solution for this specific framework, their infinite nature and growing errors as the independent variable’s value increases make them extremely difficult to evaluate numerically. This study uses numerical methods to address this complexity and get over the challenges of generating closed-form answers. The authors have employed the Fourth-Order Runge Kutta Method to approximate the value because it yields the best results out of all the numerical methods, which include Euler’s method, Improved Euler’s method, Modified Euler’s method, the Runge–Kutta method, and Heun’s method. However, Eqs. (8) and (9) are simultaneous equations. Fig. 2 represents the solution methodology for the proposed modelling framework.

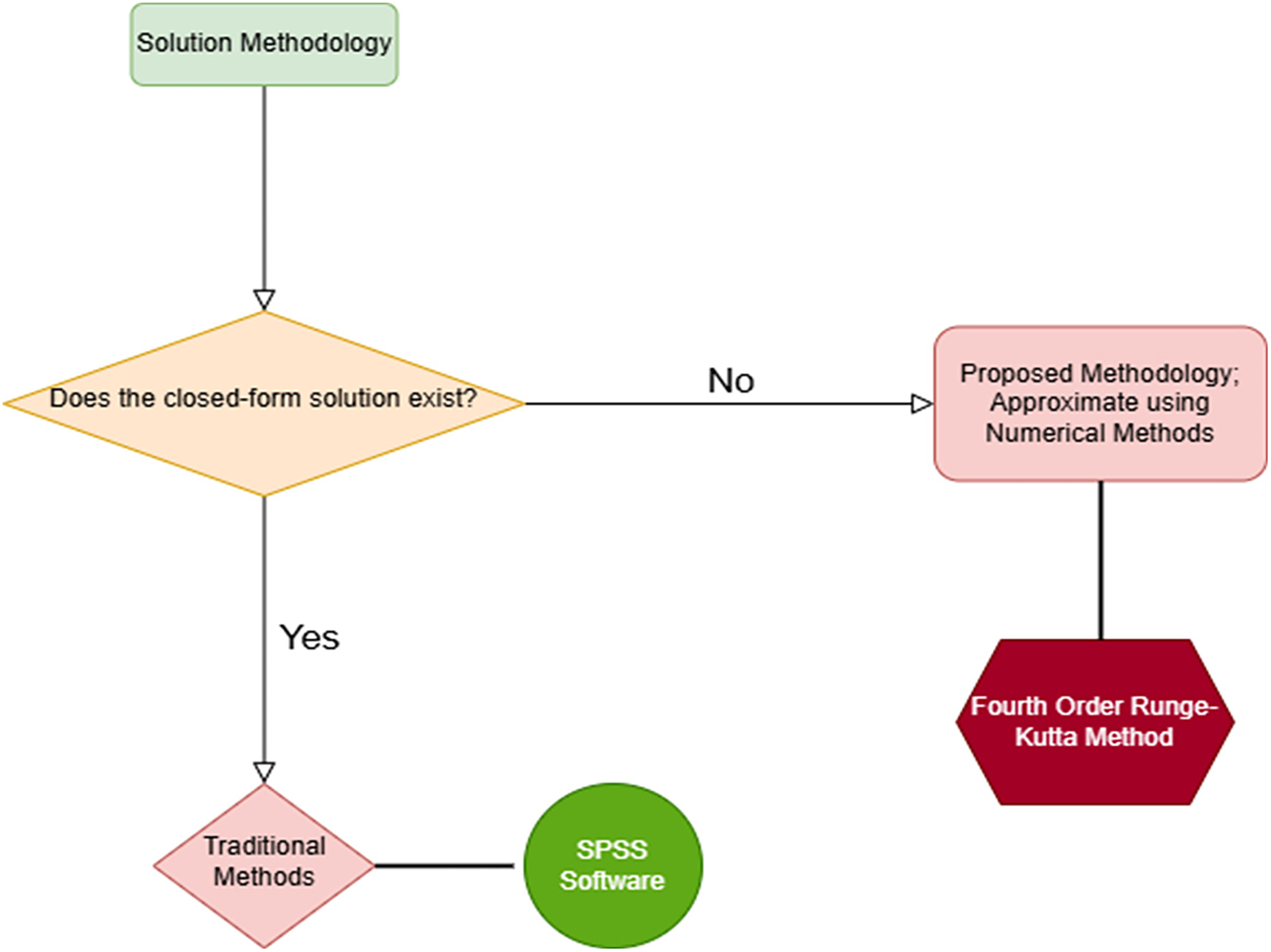
Figure 2: Flowchart of the solution methodology

The Runge-Kutta Method for Simultaneous Equations can be given as:

dΩ(t)dt=f1(t,Ω(t), P(t)); Ω(t=0)=Ω(t0)dP(t)dt=f1(t,Ω(t), P(t)); Ω(t=0)=Ω(t0)(12)

Approximation using RK Method can be given as by Eqs. (13) and (14).

Ω(t0+h)=Ω(t0)+k1+2k2+2k3+k46(13)

P(t0+h)=P(t0)+m1+2m2+2m3+m46(14)

where h is a very small positive value and

k1=hf1(t0,Ω(t0),P(t0))m1=hf2(t0,Ω(t0),P(t0))(15)

here, k1 represents the initial slope for Ω evaluated at the starting point t0 and m1 represents the initial slope for P, which is also evaluated at t0.

k2=hf1(t0+h2,Ω(t0)+k12,P(t0)+m12)m2=hf3(t0+h2,Ω(t0)+k12,P(t0)+m12)(16)

where, k2 represents the slope for Ω evaluated at the midpoint t0+h2, with the predicted values Ω(t0)+k12 and P(t0)+m12.

Also, m2 represents the slope for P under the same conditions as k2.

k3=hf1(t0+h2,Ω(t0)+k22,P(t0)+m22)m3=hf3(t0+h2,Ω(t0)+k22,P(t0)+m22)(17)

here, k3 represents another slope estimation for Ω, again evaluated at t0+h2, but now using the updated slopes k22 and m22.

m3 represents the updated slope for P under the same conditions as k3.

k4=hf1(t0+h2,Ω(t0)+k3,P(t0)+m3)m4=hf3(t0+h2,Ω(t0)+k3,P(t0)+m3)(18)

k4 represents the slope for Ω evaluated at the endpoint t0+h2 using predicted values Ω(t0)+k3 and P(t0)+m3. Also, m4 represents the slope for P under the same conditions as k4. The suggested two-phase modelling approach for vulnerability discovery and efficient patch management is shown to be flexible and adaptive in the three instances mentioned above. Moreover, it offers a thorough foundation for comprehending many facets of software vulnerability management.

5  Model Validation

To validate the suggested modelling approach, a real-world patch dataset for three well-known operating systems—Linux Kernel, Android, and Redhat—was taken from CVE Details. For Case 1 and Case 2, non-linear regression was performed using SPSS. The Runge-Kutta Method of order four has been used in Case 3. The main steps for obtaining the information required to assess the suggested modelling framework and performing a goodness-of-fit study are described in this section. To best match the actual data, the model parameters must be estimated. These repositories provide patch details and advisory reports on vulnerabilities that have been found. Using the IBM SPSS version 26 software, the author established the parameters of the proposed model. Several factors determine whether a vulnerability patch deployment model statistically fits the provided sample data points. The author has taken into account R-squared, variance, biasness, mean square error (MSE), and mean absolute error (MAE). When measures like variance, bias, and MSE are reduced, the model shows a good match for the observed data. However, a closer fit between the expected and actual data points is indicated by a greater R-squared value. Tables 1–3 display the estimated parameter values for each dataset, and it is clear that all three situations produce favourable results.

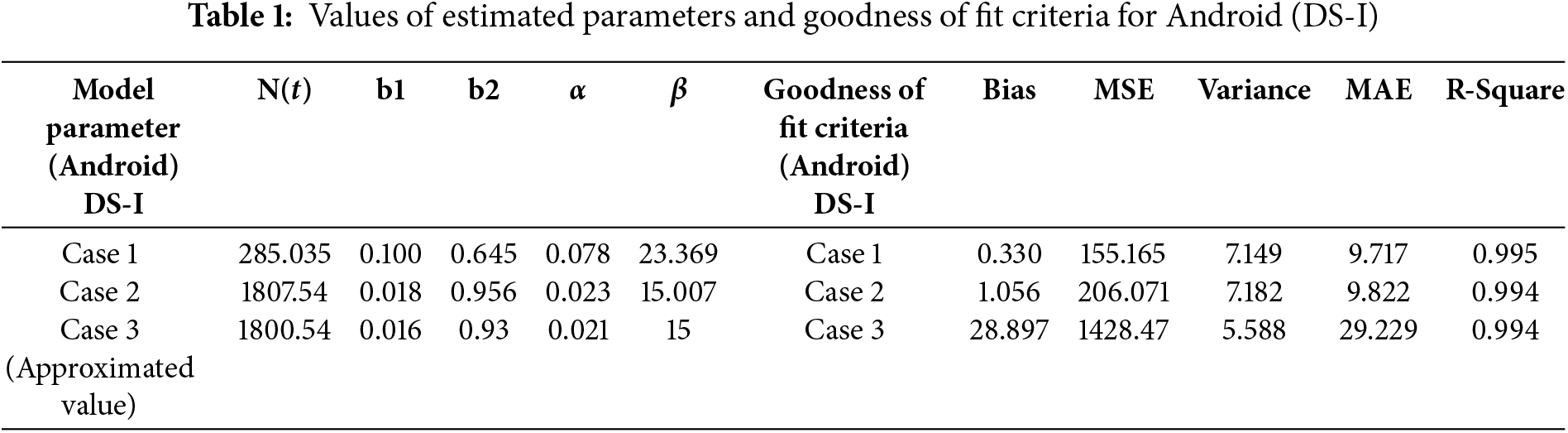
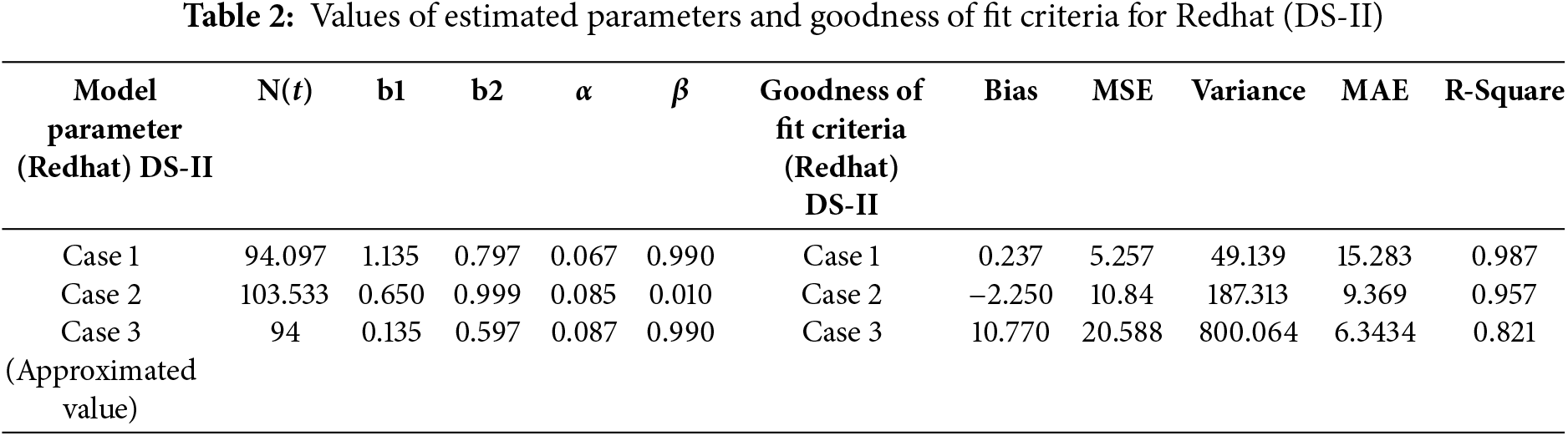
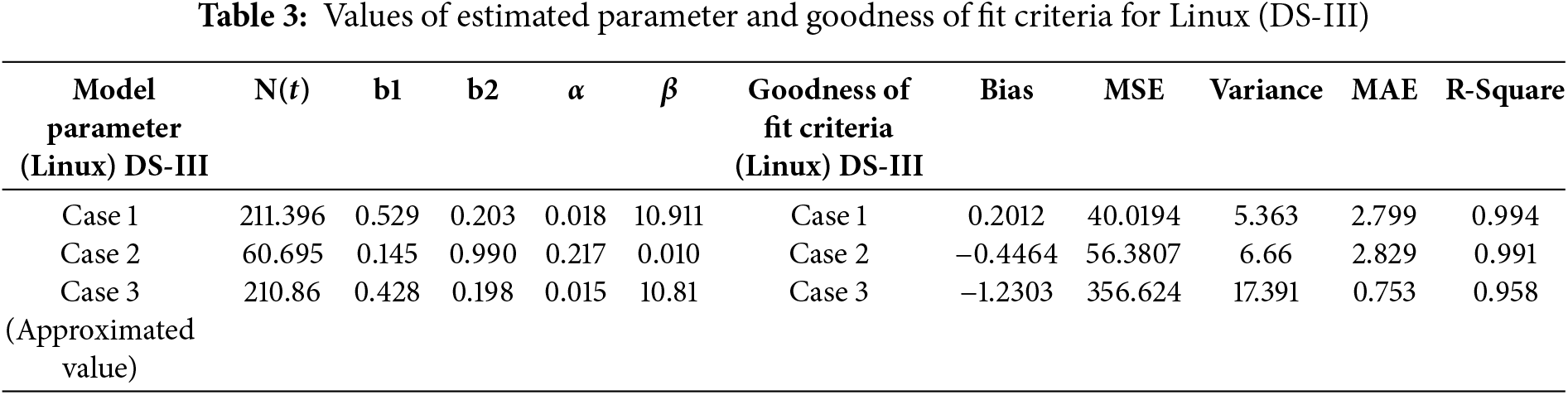
Tables 1–3 represent the comparison criteria for all the three datasets. The proposed modelling framework perfectly fits the observed sample. Further, the R-square shows a close fit, as seen in Fig. 3, for DS-I, DS-II and DS-III, respectively.

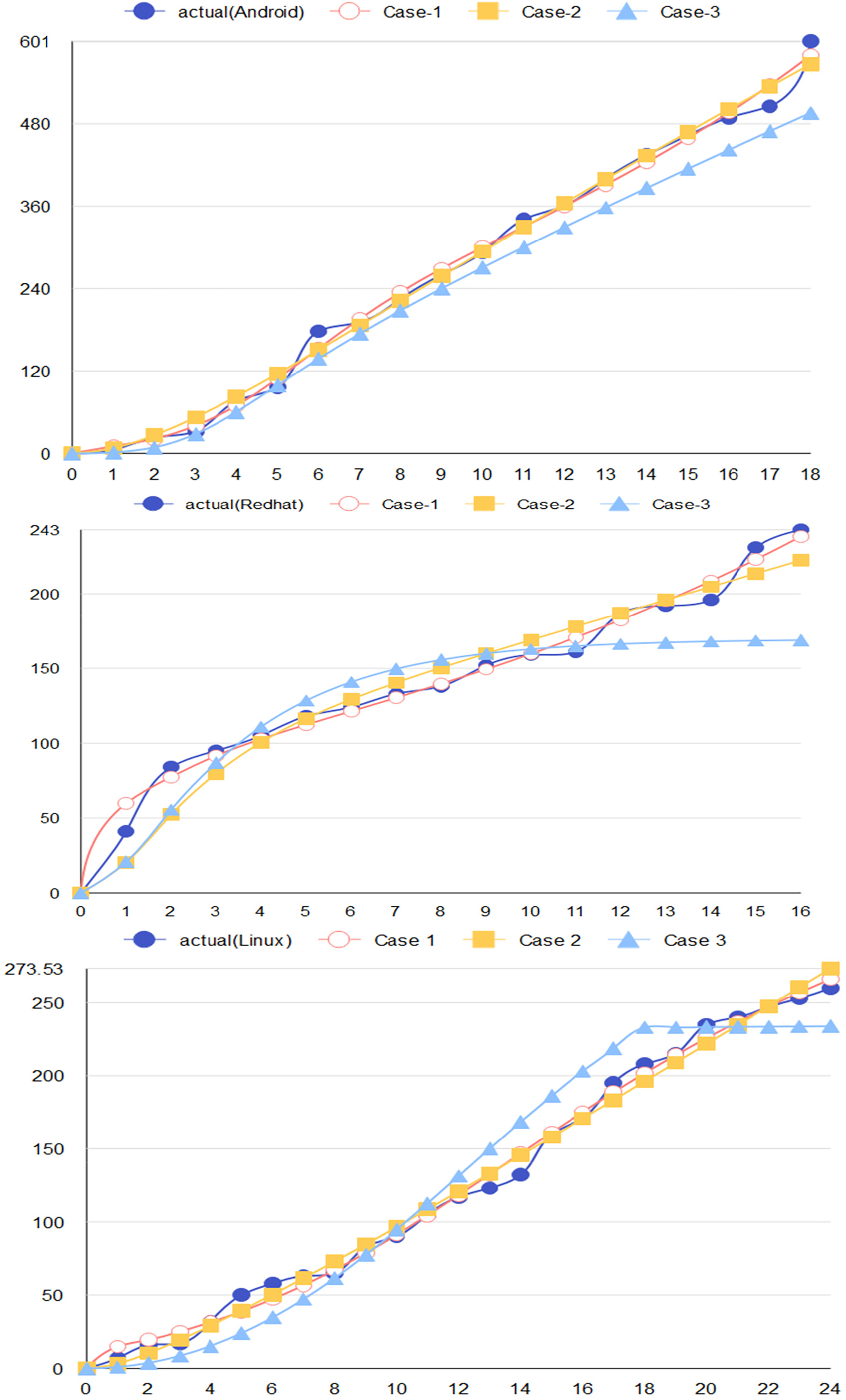
Figure 3: The goodness of fit curve for DS-I, DS-II and DS-III, respectively

The aforementioned graphs show how the model’s predicted values and the actual effective patch data concurred. The graphical analysis for DS-I, DS-II, and DS-III demonstrates how well the proposed multi-phase model fits the observed data and forecasts successful patches over time. The close agreement between actual and expected values in both detailed and cumulative perspectives demonstrates the model’s effectiveness in a variety of software contexts. In addition to the statistical goodness-of-fit criteria, this visual validation validates the model’s usefulness for strengthening software security and vulnerability management tactics.

6  Results and Discussions

The paper outlines a comprehensive multi-stage modelling approach aimed at analysing the processes of vulnerability identification and patch deployment within systems. The study explores two distinct scenarios: Linear Increase in vulnerabilities and Exponential Increase in vulnerabilities. For both scenarios, the authors derive closed-form solutions, providing a clear mathematical framework to understand the dynamics of vulnerability and patch management. Additionally, the paper introduces the concept of faulty patches, which complicates the scenario by considering patches that may not fully resolve vulnerabilities or could introduce new issues. The authors develop a novel mathematical framework to address the unique challenges posed by faulty patches. The authors use the Runge-Kutta approximation method to solve the equations numerically in situations when closed-form solutions are not practical, especially in the case of the broken patch. The outcomes show that the models function remarkably effectively in every situation. The high R-squared values—a statistical indicator of how well the data match the fitted regression line—especially in Table 2, where the R-squared value hits 0.99, provide proof of this. The correctness and dependability of the suggested framework are confirmed by this near-perfect number, which indicates that the model accounts for nearly all of the data variability. Tables 1–3: The performance metrics of the models under various conditions are probably displayed in these tables, with Table 2 particularly emphasizing the model’s high accuracy when considering defective patches. The models’ excellent accuracy and dependability imply that they can be applied successfully in real-world situations to anticipate and handle vulnerabilities and patches, particularly in intricate settings where problematic patches are an issue. The introduction of flawed patches creates new research opportunities, especially in the areas of minimizing the effects of such patches and enhancing patch deployment techniques. The use of advanced mathematical techniques like the Runge-Kutta method further underscores the sophistication of the proposed framework.

7  Limitations and Future Scope

The dynamic nature of patch management procedures can be represented by more complex mathematical modelling techniques, such as stochastic processes and agent-based modelling. Additionally, behavioural research might provide insights into how human factors influence patch management practices, directing the development of more precise models. Automated patching systems that employ machine-learning algorithms may result in more effective and efficient patch deployment operations. Risk-based patch prioritisation models may help improve patch management practices by considering vulnerability severity and organisational risk tolerance. In light of changing cyber threats, future research projects seek to improve cybersecurity posture and patch management procedures.

8  Conclusion

The study’s main goal was to develop a thorough multi-phase model that addresses vulnerabilities and patching procedures while incorporating the idea of learning dynamics. This novel method acknowledges that software systems and the patches that accompany them change over time, making the distinction between safe and faulty patches essential. While faulty patches may unintentionally cause new problems, safe patches guarantee that vulnerabilities are effectively fixed without causing any new ones. Differential equations can be solved with these mathematical methods, especially when closed-form solutions—explicit formulas that explain the system’s behaviour—are unavailable. These techniques allowed the study to produce numerical solutions that faithfully capture the system’s change over time. In addition to addressing the limitations brought about by the absence of closed-form solutions, this procedure showed how Approximation Methods might be used to solve comparable problems in other fields. The paradigm developed in this study provides avenues for more efficient vulnerability analysis and mitigation in dynamic systems. Additionally, Approximation Methods’ versatility guarantees that they may be used in various intricate situations, making them invaluable instruments for solving issues in a range of scientific and engineering fields where precise answers are sometimes elusive.

Acknowledgement: All the individuals included in this section have consented to the acknowledgment.

Funding Statement: The work in this paper has been supported by grants received by the first author and third author from the Institute of Eminence, Delhi University, Delhi, India, as part of the Faculty Research Program via Ref. No. /IoE/2024-25/12/FRP.

Author Contributions: The following contributions to the work are confirmed by the authors: Examine the design and conception: Adarsh Anand, Deepti Aggrawal; Divya, data collection; Divya, analysis and interpretation of findings; Omar H. Alhazmi and Adarsh Anand prepared the draft manuscript. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The information supporting the study’s conclusions is publicly accessible at www.cvedetails.com (accessed on 10 January 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. McGraw G. Software security. IEEE Secur Priv. 2004;2(2):80–3. doi:10.1109/MSECP.2004.1281254. [Google Scholar] [CrossRef]

2. Wu Y, Jiang N, Pham HV, Lutellier T, Davis J, Tan L, et al. How effective are neural networks for fixing security vulnerabilities. In: Proceedings of the 32nd ACM SIGSOFT International Symposium on Software Testing and Analysis; 2023 Jul 18–20; Seattle, WA, USA. [Google Scholar]

3. Zhao S, Zhu J, Peng J. Software vulnerability mining and analysis based on deep learning. Comput Mater Contin. 2024;80(2):3263–87. doi:10.32604/cmc.2024.041949. [Google Scholar] [CrossRef]

4. Anand A, Gupta P, Klochkov Y, Yadavalli VSS. Modeling software fault removal and vulnerability detection and related patch release policy. In: Anand A, Ram M, editors. System reliability management. Boca Raton, FL, USA: CRC Press; 2018. p. 19–34. [Google Scholar]

5. Williams L, McGraw G, Migues S. Engineering security vulnerability prevention, detection, and response. IEEE Softw. 2018;35(5):76–80. doi:10.1109/MS.2018.290110854. [Google Scholar] [CrossRef]

6. Rescorla E. Is finding security holes a good idea? IEEE Secur Priv. 2005;3(1):14–9. doi:10.1109/MSP.2005.17. [Google Scholar] [CrossRef]

7. Alhazmi OH, Malaiya YK. Modeling the vulnerability discovery process. In: Proceedings of the 16th IEEE International Symposium on Software Reliability Engineering; 2005 Nov 8–11; Chicago, IL, USA. [Google Scholar]

8. Ozment A. Improving vulnerability discovery models. In: Proceedings of the QoP’07: Proceedings of the 2007 ACM Workshop on Quality of protection; 2007 Oct 29; Alexandria, VA, USA. [Google Scholar]

9. Massacci F, Nguyen VH. An empirical methodology to evaluate vulnerability discovery models. IEEE Trans Softw Eng. 2014;40(12):1147–62. doi:10.1109/TSE.2014.2354037. [Google Scholar] [CrossRef]

10. Croft R, Xie Y, Babar MA. Data preparation for software vulnerability prediction: a systematic literature review. IEEE Trans Softw Eng. 2022;49(3):1044–63. doi:10.1109/TSE.2022.3171202. [Google Scholar] [CrossRef]

11. Movahedi Y, Cukier M, Gashi I. Vulnerability prediction capability: a comparison between vulnerability discovery models and neural network models. Comput Secur. 2019;87(1):101596. doi:10.1016/j.cose.2019.101596. [Google Scholar] [CrossRef]

12. Liu B, Shi L, Cai Z, Li M. Software vulnerability discovery techniques: a survey. In: Proceedings of the 2012 Fourth International Conference on Multimedia Information Networking and Security; 2012 Nov 2–4; Nanjing, China. [Google Scholar]

13. Nappa A, Johnson R, Bilge L, Caballero J, Dumitras T. The attack of the clones: a study of the impact of shared code on vulnerability patching. In: Proceedings of the 2015 IEEE Symposium on Security and Privacy; 2015 May 17–21; San Jose, CA, USA. [Google Scholar]

14. Kim J, Malaiya YK, Ray I. Vulnerability discovery in multi-version software systems. In: Proceedings of the 10th IEEE High Assurance Systems Engineering Symposium; 2007 Nov 14–16; Plano, TX, USA. [Google Scholar]

15. Sharma R, Sibal R, Shrivastava AK. Vulnerability discovery modeling for open and closed source software. Int J Secur Softw Eng. 2016;7(4):19–38. doi:10.4018/IJSSE. [Google Scholar] [CrossRef]

16. Bhatt N, Anand A, Yadavalli VSS, Kumar V. Modeling and characterizing software vulnerabilities. Int J Math Eng Manag Sci. 2017;2(4):288–99. doi:10.33889/24557749. [Google Scholar] [CrossRef]

17. Ruohonen J, Rauti S, Hyrynsalmi S, Leppänen V. A case study on software vulnerability coordination. Inf Softw Technol. 2018;103(3):239–57. doi:10.1016/j.infsof.2018.06.005. [Google Scholar] [CrossRef]

18. Li F, Paxson V. A large-scale empirical study of security patches. In: Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security; 2017 Oct 30–Nov 3; Dallas, TX, USA. [Google Scholar]

19. Costa TF, Tymburibá M. Challenges on prioritizing software patching. In: Proceedings of the 2022 15th International Conference on Security of Information and Networks (SIN); 2022 Nov 11–13; Sousse, Tunisia. [Google Scholar]

20. Shrivastava AK, Sharma R. Modeling vulnerability discovery and patching with fixing lag. In: Proceedings of the Advanced Informatics for Computing Research: Second International Conference, ICAICR 2018; 2018 Jul 14–15; Shimla, India. [Google Scholar]

21. Almukaynizi M, Nunes E, Dharaiya K, Senguttuvan M, Shakarian J, Shakarian P. Patch before exploited: an approach to identify targeted software vulnerabilities. In: Sikos LF, editor. AI in cybersecurity. Berlin/Heidelberg, Germany: Springer; 2018. p. 81–113. [Google Scholar]

22. Anand A, Agrawal M, Bhatt N, Ram M. Software patch scheduling policy incorporating functional safety standards. In: Ram M, Davim JP, editors. Advances in system reliability engineering. Amsterdam, The Netherlands: Elsevier; 2019. p. 267–79. [Google Scholar]

23. Ding Y, Ray B, Devanbu P, Hellendoorn VJ. Patching as translation: the data and the metaphor. In: Proceedings of the 35th IEEE/ACM International Conference on Automated Software Engineering; 2020 Dec 21–25; Online, Australia. [Google Scholar]

24. Kansal Y, Kumar D, Kapur PK. Vulnerability patch modeling. Int J Reliab Qual Saf Eng. 2016;23(6):1640013. doi:10.1142/S0218539316400131. [Google Scholar] [CrossRef]

25. Xu X, Zheng Q, Yan Z, Fan M, Jia A, Zhou Z, et al. PatchDiscovery: patch presence test for identifying binary vulnerabilities based on key basic blocks. IEEE Trans Softw Eng. 2023;49(12):5279–94. doi:10.1109/TSE.2023.3332732. [Google Scholar] [CrossRef]

26. Shrivastava AK, Kapur PK, Anjum M. Vulnerability discovery and patch modeling: state of the art. In: Ram M, editor. Reliability engineering. Boca Raton, FL, USA: CRC Press; 2019. p. 401–19. [Google Scholar]

27. Dissanayake N, Jayatilaka A, Zahedi M, Babar MA. Software security patch management systematic literature review of challenges, approaches, tools and practices. Inf Softw Technol. 2022;144(1–2):106771. doi:10.1016/j.infsof.2021.106771. [Google Scholar] [CrossRef]

28. Wang X, Wang S, Sun K, Batcheller A, Jajodia S. A machine learning approach to classify security patches into vulnerability types. In: Proceedings of the 2020 IEEE Conference on Communications and Network Security (CNS); 2020 Jun 29–Jul 01; Avignon, France. [Google Scholar]

29. Divya, Anand A, Bhatt N, Johri P. Assessing the impact of software patching on vulnerabilities: a comprehensive framework for faulty and safe patches. Int J Reliab Qual Saf Eng. 2024;32(2):2450031. doi:10.1142/S0218539324500311. [Google Scholar] [CrossRef]

30. Xu C, Chen B, Lu C, Huang K, Peng X, Liu Y. Tracking patches for open source software vulnerabilities. In: Proceedings of the 30th ACM Joint European Software Engineering Conference and Symposium on the Foundations of Software Engineering; 2022 Nov 14–18; Singapore. [Google Scholar]

31. Bhatt N, Kaur J, Anand A, Alhazmi OH. Selecting best software vulnerability scanner using intuitionistic fuzzy set TOPSIS. Comput Mater Contin. 2022;72(2):3613–29. doi:10.32604/cmc.2022.026554. [Google Scholar] [CrossRef]

32. Dahlquist G, Bjorck A. Numerical methods. Mineola, NY, USA: Dover Publications; 2012. 592 p. [Google Scholar]

33. Dennis JEJr, Schnabel RB. Numerical methods for unconstrained optimization and nonlinear equations. Philadelphia, PA, USA: Society for Industrial and Applied Mathematics; 1996. 375 p. [Google Scholar]

34. Rice JR. Numerical methods in software and analysis. Amsterdam, The Netherlands: Elsevier; 2014. 720 p. [Google Scholar]

35. Butcher JC. Numerical methods for ordinary differential equations. 3rd ed. Hoboken, NJ, USA: John Wiley & Sons, Inc.; 2016. 544 p. [Google Scholar]

36. Butcher JC. A history of Runge-Kutta methods. Appl Numer Math. 1996;20(3):247–60. doi:10.1016/0168-9274(95)00108-5. [Google Scholar] [CrossRef]

37. Xia G, Zeephongsekul P, Kumar S. Optimal software release policies for models incorporating learning in testing. Asia-Pac J Oper Res. 1992;9(2):221–34. [Google Scholar]