Enhancing Hierarchical Task Network Planning through Ant Colony Optimization in Refinement Process

1  Introduction

Hierarchical Task Network (HTN) planning is a powerful paradigm in the field of artificial intelligence, designed to tackle complex problem-solving tasks by decomposing them into a hierarchical structure of subtasks. Despite its effectiveness, achieving optimal solutions in HTN planning remains a significant challenge due to the intricate nature of the planning process and the vast search space involved. Traditional search algorithms often struggle to efficiently navigate through this space, resulting in suboptimal solutions and computational inefficiencies [1–3].

Optimization methods, particularly heuristic and metaheuristic algorithms, have played a crucial role in advancing automated planning and artificial intelligence. Heuristic algorithms, such as A* and greedy search, utilize domain-specific knowledge to guide the search process, offering speed and precision in relatively structured problem domains. However, these approaches often fall short when applied to complex, nonlinear, and high-dimensional spaces. In contrast, metaheuristic algorithms, inspired by natural phenomena, have emerged as robust solutions to these challenges [4]. Techniques such as Genetic Algorithms (GAs), Particle Swarm Optimization (PSO), and Ant Colony Optimization (ACO) have demonstrated remarkable success across a range of optimization tasks. These algorithms offer adaptability, decentralized decision-making, and the ability to navigate large and intricate solution spaces, making them particularly suitable for AI-driven applications. Among these, ACO has been widely recognized for its efficiency in solving combinatorial optimization problems, such as scheduling, routing, and planning.

Subsequently, the evolution of these optimization techniques has also seen the rise of hybrid approaches, where metaheuristics are combined with other computational methods to enhance their performance. For instance, ACO’s probabilistic decision-making and pheromone-guided search have been integrated with machine learning models to dynamically adapt heuristics, leading to more context-aware and efficient solutions. Such hybridization not only improves algorithmic performance but also extends its applicability to emerging domains like IoT, big data optimization, and real-time decision-making systems [5–8].

Moreover, recent advancements in metaheuristic optimization have demonstrated significant progress across various application domains. For instance, Xu et al. advanced the application of nature-inspired metaheuristic algorithms in mobile robot path planning by proposing a new algorithm classification and focusing on detailed analyses of specific algorithms, such as the firefly and cuckoo search algorithms, to enhance the path planning capabilities of mobile robots in dynamic and high-dimensional environments [9]. Whereas, Roberts et al. [10] introduced an innovative dual-phased framework that optimizes energy-efficient, cluster-based routing in Wireless Sensor Networks (WSNs) by synergizing two advanced meta-heuristic algorithms that significantly enhance network performance metrics such as energy efficiency, network lifetime, and Packet Delivery Ratio (PDR). Furthermore, Bhattacharjee et al. in [11] proposed and validated two meta-heuristic algorithms, a Genetic Algorithm (GA) and its refined version, demonstrating that the refined GA improves service cost minimization in the Hierarchical Single-Allocation Hub Median Problem (SA-H-MP) on the CAB data set. These innovations underscore the versatility and potential of metaheuristic approaches, highlighting the need for further exploration, as seen in this study’s application of Ant Colony Optimization in enhancing HTN planning.

In this paper, the authors aim to investigate the potential of leveraging ACO to enhance the refinement process in HTN planning. Using the adaptive and decentralized nature of ACO, the authors seek to develop a hybrid approach, termed ACO-HTN, that can effectively guide the search for optimal solutions while mitigating the computational complexities associated with traditional planning algorithms.

In this paper, the authors aim to investigate the potential of incorporating ACO to enhance the refinement process in HTN planning. Using the adaptive, decentralized, and collaborative characteristics of ACO, this paper proposes the development of a novel hybrid framework, referred to as ACO-HTN. This framework integrates the foraging-inspired mechanisms of ACO with the hierarchical decomposition structure of HTN planning to address two key challenges: efficiently navigating the vast and complex search space of HTN planning and mitigating the computational overhead typically associated with traditional planning algorithms. By employing pheromone-based probabilistic decision-making and heuristic guidance, ACO-HTN is designed to iteratively refine task networks, improving both the quality and efficiency of plan generation. This hybrid approach not only enhances solution quality but also demonstrates resilience to the inherent uncertainties and dynamism of real-world planning scenarios, positioning it as a significant advancement in the domain of automated planning optimization. Moreover, the integration of ACO into the refinement process of HTN planning offers several potential advantages. Firstly, ACO’s ability to efficiently explore solution spaces and adaptively refine plans can lead to the discovery of higher-quality solutions. Secondly, its decentralized decision-making mechanism allows for parallel exploration of multiple solution paths, enabling faster convergence towards optimal solutions. Lastly, ACO’s robustness to noisy and uncertain environments makes it well-suited for handling real-world planning scenarios with incomplete information.

Through empirical experimentation and evaluation, our objective is to assess the effectiveness and efficiency of the ACO-HTN approach compared to traditional HTN planning algorithms. By demonstrating the potential of ACO in enhancing HTN planning, this research contributes to advancing state-of-the-art AI planning methodologies and opens up new avenues for the development of more robust and adaptive problem-solving techniques.

2  Related Work

Optimal solutions play a pivotal role across diverse real-world domains, including healthcare, manufacturing, public transportation, and driver assistance systems, significantly influencing stakeholders and enhancing organizational efficiency [12,13]. The increasing demand for comprehensive automation in these areas has underscored the importance of research in automated planning optimization. Despite this, achieving optimal solutions remains a formidable challenge, even in fundamental search scenarios. Although some optimal planners are available, the majority provide satisfactory yet non-optimal solutions. Furthermore, Hierarchical Task Network (HTN) planning, a widely utilized framework in various applications, requires well-structured planners due to its formalism, which directly affects both the search space and the quality of the solutions.

To enhance the overall effectiveness of HTN planners, a number of innovative techniques for HTN planning have been developed in response to these problems. While there exists a multitude of methods to tackle HTN planning problems, the authors will discuss some pertinent ones from the author’s perspective.

Plan space search algorithms represent one such approach, offering significant advantages by maintaining a partial ordering of tasks during exploration. This reduces the number of search nodes compared to algorithms that require a complete task ordering. In classical methods, the search process begins with an empty plan, which is iteratively modified until a solution is achieved [14–16]. These iterative refinements streamline the search process, making plan space search algorithms an essential component of HTN planning.

Conversely, progression search starts with the original job and moves forward, taking into account only tasks that have no predecessors in the ordering relations [17–19]. With this approach, plans are created in advance, giving the planning system all available state data. However, since a single partly ordered collection may produce many entirely ordered sequences, it leads to a less compact representation of the search space. The formalism required for translation into propositional logic is quite different from that of modern HTN planning techniques. In order to achieve a state-based objective similar to classical planning issues, the planner inserts primitive and abstract tasks in place of a starting task or task network. Nevertheless, task networks with repeating tasks cannot be well represented by this translation, which is restricted to recursion-free situations.

In contrast, translating into classical planning simulates a progression search through the state space. A specific section of the state description delineates the task network, with actions modified to be executable solely within the context of the current task network. Furthermore, the newly introduced actions alter this section of the state description in accordance with decomposition methods. To enable the representation of task networks within the state, the size of intermediate networks produced during the search is limited [20].

This paper introduces the ACO-HTN plan selection strategy, which integrates the Ant Colony Optimization (ACO) algorithm into the refinement planning process. This adaptive approach is distinguished by its probabilistic step-by-step construction of solutions. While previous works [21] incorporated the messy genetic algorithm alongside HTN planning, and reference [5] adapted metaheuristic Ant Colony Optimization with classical planning.

The proposed approach represents the plan space as a directed graph, with partial plans as vertices and plan modifications as edges. Ants conduct a forward search, selecting among different plans (vertices) based on three functions. The first function, τ(a), evaluates the desirability of action applicability in the current state. The second function, η(a), computes the heuristic value. The third function updates pheromone levels, increasing them for actions contributing to the current solution plan and decreasing them for unselected plans (vertices). Our strategy is implemented on top of the PANDA planner and empirically evaluated on hierarchical domains, demonstrating superior performance in terms of solved cases compared to other strategies [22,23].

Overall, our research offers insights into the synergistic integration of hierarchical planning and swarm intelligence techniques, paving the way for more robust and adaptive problem-solving methodologies in AI.

Hierarchical Task Network (HTN) planning is a prominent framework utilized in the domain of automated planning [24]. In HTN planning, two core concepts, tasks and methods, serve as the foundation for its operational structure. Complex tasks represent high-level activities, such as transporting goods between locations, while primitive tasks align with individual actions typical of classical planning. Hierarchical domain models employ a multi-layered approach to problem-solving, where complex tasks are decomposed into simpler subtasks using various decomposition methods. This process generates task networks, or partial plans, that outline abstract solutions for the original complex tasks. Hierarchical planning problems begin as task networks, which are gradually refined through iterative decomposition until they consist entirely of primitive tasks. This refinement involves substituting complex tasks with detailed plans derived from the corresponding decomposition methods, effectively transforming the abstract problem into a concrete solution.

On the other hand, in classical planning, pre-processing the planning domain model and/or problem description can reduce planning effort significantly [18]. While the existence of a solution plan in classical planning is a decidable problem, the same cannot be said for Hierarchical Task Network (HTN) planning [20]. The introduction of decomposition methods, though intended to expedite the planning process, unfortunately, contributes to the undecidability of HTN planning. To address this challenge, hierarchical planners often incorporate constraints on decomposition methods, ensuring that the problem of plan existence remains decidable within the framework of the planning system [1].

On the other side, the Ant Colony Optimization Algorithm (ACO) is a probabilistic technique devised for tackling computational problems that can be formulated as the search for optimal paths within graphs. Originally proposed by [5]. This algorithm draws inspiration from the foraging behavior of ants. In the wild, ants venture out from their colony in search of food, initially exploring their surroundings in random directions. Upon discovering food, an ant retraces its steps back to the colony while depositing a trail of chemical substances known as pheromones along its path. Subsequent ants detect these pheromones and, guided by their presence, follow the same route. The strength of the pheromone trail determines the attractiveness of a path, with pheromone concentration naturally diminishing over time due to evaporation. As a result, shorter paths become more favored by ants, as they can more rapidly reinforce the pheromone concentration along them, counteracting evaporation. This collective behavior among ants leads to the emergence of the shortest path from the colony to the food source. The algorithm mimics this natural behavior, aiming to identify optimal paths within a given graph by leveraging the principles observed in ant foraging.

Fig. 1 provides a visual representation of heuristic progression search as a foundational approach for enhancing hierarchical task network (HTN) planning systems. This method leverages progression search to compute heuristics dynamically by integrating real-time tracking of the current state throughout the planning process [25]. The framework incorporates two innovative progression algorithms designed to minimize redundant branching in partially ordered problem spaces. These algorithms ensure both soundness and completeness in the planning process. Additionally, the approach introduces a method for adapting classical planning heuristics to guide HTN planning effectively. This is achieved by temporarily relaxing the HTN planning model into a classical planning framework solely for heuristic computation. The relaxed model is dynamically updated during the search process to generate refined heuristic values, facilitating efficient and adaptive HTN search strategies.

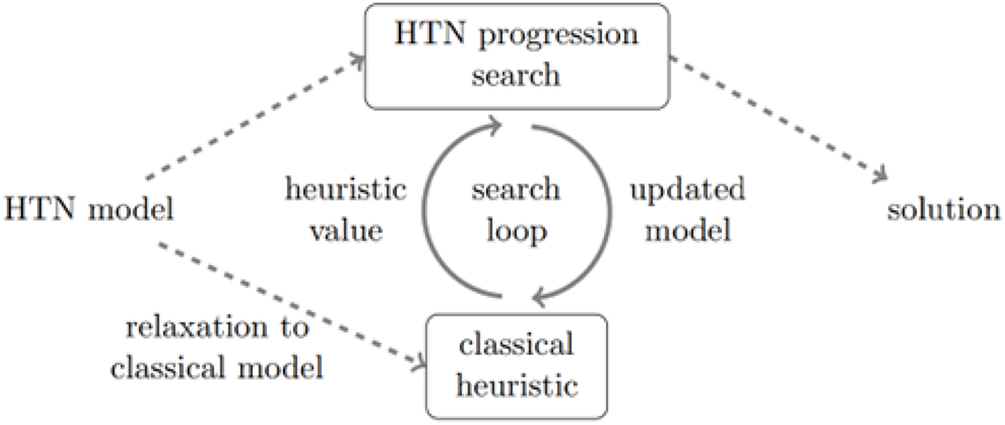
Figure 1: Leveraging progression search for heuristic HTN planning

Furthermore, the outlined strategy demonstrates several advantageous theoretical properties for HTN planning, including safety, goal-oriented behavior, and admissibility, as validated through empirical analysis. Substantial improvements in system performance are achieved by integrating an advanced pre-processing stage and tailoring heuristic search mechanisms to the unique requirements of the HTN framework [26,27]. One significant enhancement involves an admissible heuristic inspired by the Task Decomposition Graph (TDG) [28]. The TDG encapsulates the AND/OR relationships within the task hierarchy, enabling the identification of the minimum-cost set of primitive actions necessary to decompose abstract tasks. This process estimates the refinement cost of an abstract task node by considering the minimal efforts required across its associated method nodes, while the refinement cost for each method node is computed as the cumulative effort of its constituent tasks. Although recomputing the TDG effectively narrows the search space in most scenarios, it can occasionally lead to increased runtime in more complex cases.

After that, the authors in [29,30] improved the performance of hierarchical task network (HTN) planning by using domain-independent heuristic search. An extended HTN formalism called HTN-e is developed to facilitate the adaptation of classical planning heuristics for HTN applications. This effort introduces the modified algorithm OTD-h, which integrates domain-independent heuristics with ordered task decomposition. Using OTD-h and SHOP (Simple Hierarchical Ordered Planner), a novel HTN planning approach, dubbed the SHOP-h planning algorithm, is formulated and implemented in Python, referred to as Pyhop-h. Pyhop-h combines domain-independent state-based heuristics with HTN planning, selecting the optimal decomposition for each task based on applicable HTN methods. This domain-independent technique enhances the performance of SHOP and SHOP2 planners, making them less dependent on the order of appearance of the HTN method and simplifying the composition of the HTN domain description.

A messy genetic algorithm for optimal solution search in HTN planning is introduced by [21]. The author presents a genetic algorithm designed to address the challenge of finding optimal solutions in HTN planning. Using length-variant chromosomes, the algorithm represents potential planning solutions in the form of dynamic decomposition trees with varying number of nodes. Initially, the Genetic algorithm initializes with a randomly selected chromosome, obtained from the Abstract-HTN algorithm, serving as the initial population encoding potential solutions. However, the search for the optimum solution becomes challenging in the absence of sufficient heuristic knowledge to guide the search process effectively. After that, the authors in [31] introduced a generic method to guide the search for the progression of HTN using classical heuristics. The authors proposed leveraging progression-based search due to its concrete state representation. Initially, an enhanced progression algorithm is introduced, which streamlines search space exploration to improve performance. Furthermore, they demonstrate that the inclusion of hierarchical information in non-hierarchical problem segments can be used for the estimation of goal distance using arbitrary state-based classical heuristics. Evaluation conducted on standard HTN models highlights the efficiency of this approach in overcoming challenges associated with classical heuristic integration in HTN planning, outperforming existing HTN planning systems.

The structure of this paper is as follows: Section 3 provides a brief explanation of the hierarchical planning framework. In Section 4, the proposed technique and our search algorithm are explained. Section 5 offers our experimental results and comparison findings as well as comparative and complexity analysis. Finally, in Section 6, the authors discuss potential extensions to our strategy aimed at enhancing the HTN paradigm.

3  The Hierarchical Planning Framework

Our proposed planning approach is integrated within a hybrid framework that combines elements of Partial-Order Causal-Link (POCL) planning and Hierarchical Task Network (HTN) methods [32–34]. POCL planning is primarily utilized to solve classical planning problems. In this approach, plans consist of a set of actions organized in a partial order, where explicit causal links between actions highlight their dependencies. This structure offers users a clear understanding of the causal relationships that underpin the plan, enhancing interpretability and insight into the planning process.

Unlike classical planning, HTN planning delineates tasks into two distinct types: primitive tasks, akin to actions in classical planning, which entail pre- and post-conditions; and complex tasks, denoting intricate activities (termed abstract tasks), such as goods transportation, along with predefined standard solutions (referred to as decomposition methods) for these abstract tasks.

Our framework is constructed utilizing the Action Description Language (ADL) [35], which characterizes tasks via the schema t(τ)=⟨prec(t(τ)),add(t(τ)),del(t(τ))⟩. This schema delineates the pre-conditions and post-conditions of a task through the integration of positive and negative literals related to the task parameters τ=τ1,…,τn. The hybrid planning framework incorporates both primitive and complex tasks that feature pre-conditions and post-conditions, facilitating the encoding of Partial-Order Causal-Link (POCL) planning operations at elevated, more abstract levels. Additionally, multiple instances of the same task may appear in a single partial plan, necessitating the use of unique identifiers for differentiation. Each task instance is represented by the tuple ps(τ)=⟨id,t(τ)⟩, where id∈N (natural number), and this is referred to as a plan step.

In this framework, a partial plan is denoted as P=⟨PS,CS⟩, where PS represents the set of plan steps, and CS=⟨≺,VC,CL⟩ denotes the set of constraints. The CS set comprises three categories of constraints. The symbol ≺ denotes the partial order of the plan steps, whereas VC specifies equations for the co-designation and non-co-designation of parameters between the plan steps in PS and constants (e.g., {v1=v2}). Additionally, the collection of causal links referred to as CL, defines causal relationships among the plan steps PS within the partial plan P. Each causal link is represented as ⟨psi,,psj⟩, indicating that the precondition is fulfilled by the postcondition of plan step psj and acts as a prerequisite for plan step psi. Furthermore, the methods m(τ)=⟨ps(τ),P⟩ establish the connection between an abstract task ps(τ) and its corresponding partial plan P. Each complex task is generally executed through multiple methods.

In order to develop a solution plan P[sol] for a given hybrid planning problem, the hybrid planner refines the initial plan Pinit into a partial plan Psol=⟨PSsol,CSsol⟩, where the constraint set CSsol=⟨≺sol,VCsol,CLsol⟩. This refinement process continues until the solution plan meets the necessary conditions specified by the final constraint set.

As with classical planning, a hybrid planning problem /Pi[hyb]=/left/langleD,P[init],IS,GS/right/rangle consists of a domain model D, an initial state IS, a goal state GS, and an initial partial plan P[init]. D=/left/langleTp,TC,M/right/rangle includes a set of primitive task schemas Tp, a finite set of complex tasks TC, and a set of decomposition methods M.

In a solution plan P[sol]=/left/langlePS[sol],CS[sol]/right/rangle, the plan steps PS[sol] are accompanied by constraints CS[sol]=/left/langle/prec[sol],VC[sol],CL[sol]/right/rangle. The structure and dependencies of the solution plan are defined by these constraints, which include ordering constraints, variable constraints, and causal link constraints.

The proposed solution strategy must adhere to the following conditions:

1.   The solution plan Psol should be a refinement of the initial plan Pinit, and the set of plan steps PSsol must exclusively contain grounded instances of primitive task schemata.

2.   Each precondition associated with any plan step in PSsol must be validated by a corresponding causal link in CLsol.

3.   The ordering constraints defined in ≺sol must not create a cyclic dependency among the plan steps in PSsol.

4.   There should be no threats to any causal links within CLsol. A causal threat is identified when the partial order permits a plan step psk, whose post-condition negates, to be placed between two plan steps psi and psj, where a causal link ⟨psi,,psj⟩ exists.

In the pursuit of generating a solution plan, the planner explores a space of potential refinements. This involves recursively decomposing abstract tasks through the application of their respective decomposition methods. Causal links are managed by either establishing open preconditions for specific plan steps or by incorporating ordering constraints and variable restrictions. This ongoing cycle of refinement, known as plan modification, gradually advances the plan toward a complete solution.

Our proposed planning algorithm, denoted as Algorithm 1, iteratively refines the given planning problem, Πhyb, until a feasible solution plan is discovered. This iterative process involves successive updates to the problem formulation, guided by the algorithm’s underlying heuristics and search strategies.

When addressing a hybrid planning problem Πhyb, our planner systematically navigates the plan space. At the core of this process is the fringe, a structured data repository that maintains an ordered sequence of plans, represented as P1…Pn, arranged for sequential evaluation. The fringe specifically contains all unexplored plans that arise from previously assessed non-solution plans, referred to as intermediate plans. The efficiency of the search strategy dictates which plans are selected as the most promising candidates for finding a solution. For example, a plan Pi is given precedence over another plan Pj if it is expected to lead to a solution more efficiently, where j > i. As a result, once a partial plan P is selected from the fringe using the plan selection module PlanSel, it is immediately removed from the fringe to allow further refinement and progression in the planning process.

The planning algorithm operates in an iterative manner, continuing either until a solution is identified or until there are no remaining plans in the fringe that require refinement (line 1). When a plan is selected by the PlanSel module, it is subsequently removed from the fringe F (line 3). The flaw detection process is then carried out by the FlawSel module, which identifies any existing flaws within the selected plan (line 6). These flaws can either be complex task flaws caused by the presence of an unresolved abstract task or threat flaws, which involve a conflict between a causal link and a threatened plan step. If no flaws are found in the selected plan and all solution criteria are satisfied, the algorithm terminates by returning the current plan as the solution (lines 4 to 5).

The PlanSel function plays a crucial role in structuring the plans stored within the fringe. As part of this process, any plans containing irreconcilable issues, such as contradictory task order constraints, are discarded. The planner continues its search until either a feasible solution is identified, leading to a successful termination, or the fringe is completely depleted, indicating that no valid solution exists.

A single planning flaw f may be addressed through various potential resolutions. For instance, an unresolved precondition might have multiple actions that could serve as producers for the necessary causal link. Each of these potential resolutions, termed modifications m to the current plan P, is calculated and applied, resulting in the creation of a set of successor plans (line 7).

Within the framework, two control strategies are defined: a modification selection strategy and a plan search strategy. The modification selection strategy, denoted by FlawSel(), identifies which branches should be explored first. Similarly, the plan selection strategy denoted as PlanSel(), prioritizes plans for exploration. Multiple strategies can be combined into cascades, offering a diverse range of planning strategies. This flexibility allows our framework to support the creation of various planning approaches.

4  The Proposed Strategy

In our proposed framework, ACO-HTN integrates a plan selection strategy into the refinement plan generation process along with the Ant System Optimization technique. Specifically, ACO is particularly well-suited for the refinement process in HTN planning due to its ability to efficiently explore large and complex solution spaces. Inspired by the foraging behavior of ants, ACO employs probabilistic decision-making based on pheromone trails and heuristic evaluations, enabling it to balance the exploration of new paths with the exploitation of known promising ones. This aligns seamlessly with the needs of HTN planning, where the refinement process involves selecting and applying modifications to partial plans. ACO’s decentralized decision-making allows it to evaluate multiple solution paths in parallel, making it highly adaptive to the hierarchical and dynamic nature of HTN planning. Moreover, its robustness in handling noisy or incomplete information ensures that the search converges toward high-quality solutions while avoiding local optima. These characteristics make ACO an ideal method for enhancing the refinement process in HTN planning, improving both efficiency and solution quality. This section introduces our plan selection strategy [22], aimed at attaining near-optimal plan solutions within the Hierarchical paradigm.

Plan Space Strategy Procedure: The authors will outline the procedure of the proposed strategy ACO-HTN (Algorithm 2). Drawing inspiration from the Ant system procedure, the authors incorporate heuristic information η regarding the problem state being addressed, which encompasses visibility into the problem and considers the number of flaws present in the current task network. A higher value is assigned to η when a low number of flaws are detected, and vice versa. The quantity of pheromone τi deposited into edgei signifies the ants’ inclination to select one of the various refinements in the current plan, with an initial pheromone value of τ0 = 1.

The plan transition rule follows a probabilistic approach that prioritizes the attractiveness of refinements based on pheromone quantity, which increases with the frequency of selection of the same refinement. Additionally, the flaw selection strategy, guided by heuristic information, directs the ants toward the most promising solutions. Following the application of the chosen refinement, the quality of all refinements is assessed to inform the pheromone update calculation at the conclusion of each iteration.

The quality calculation considers the heuristic value (e.g., LCF strategy [22]) of refinements. For instance, edge1 with h_lcf = 3 is preferred over edge2 with h_lcf = 5, as the value returned indicates the number of flaws to be resolved. Additionally, the step at which a refinement was chosen influences its quality; refinements selected in earlier steps are deemed of higher quality. If a refinement successfully contributes to the solution, its quality is incremented by one, increasing its likelihood of selection in subsequent iterations. Parameters δ and σ are used to fine-tune the preference calculation for each expression. Following this step, the local quality value localPlan is locally updated.

Plan Evaluation: To update the quality globally, the authors compare the local quality obtained in the current iteration with the best quality achieved in previous iterations. Finally, in the last step of our algorithm, the pheromone updating rule is used. This rule incorporates the pheromone evaporation rate ρ and the total sum of the quality of the route constructed by each ant.

Pheromone Updating: The algorithm presented illustrates a plan space, as shown in Fig. 2. This figure visualizes the plan space as explored by the ACO-HTN algorithm, represented as a directed graph, where nodes symbolize partial plans, and edges represent possible refinements derived during the search process that lead to a node solution (food) using the Ant System (AS) algorithm. Ants, acting as agents, traverse the graph based on a probabilistic decision-making model influenced by pheromone levels and heuristic values.

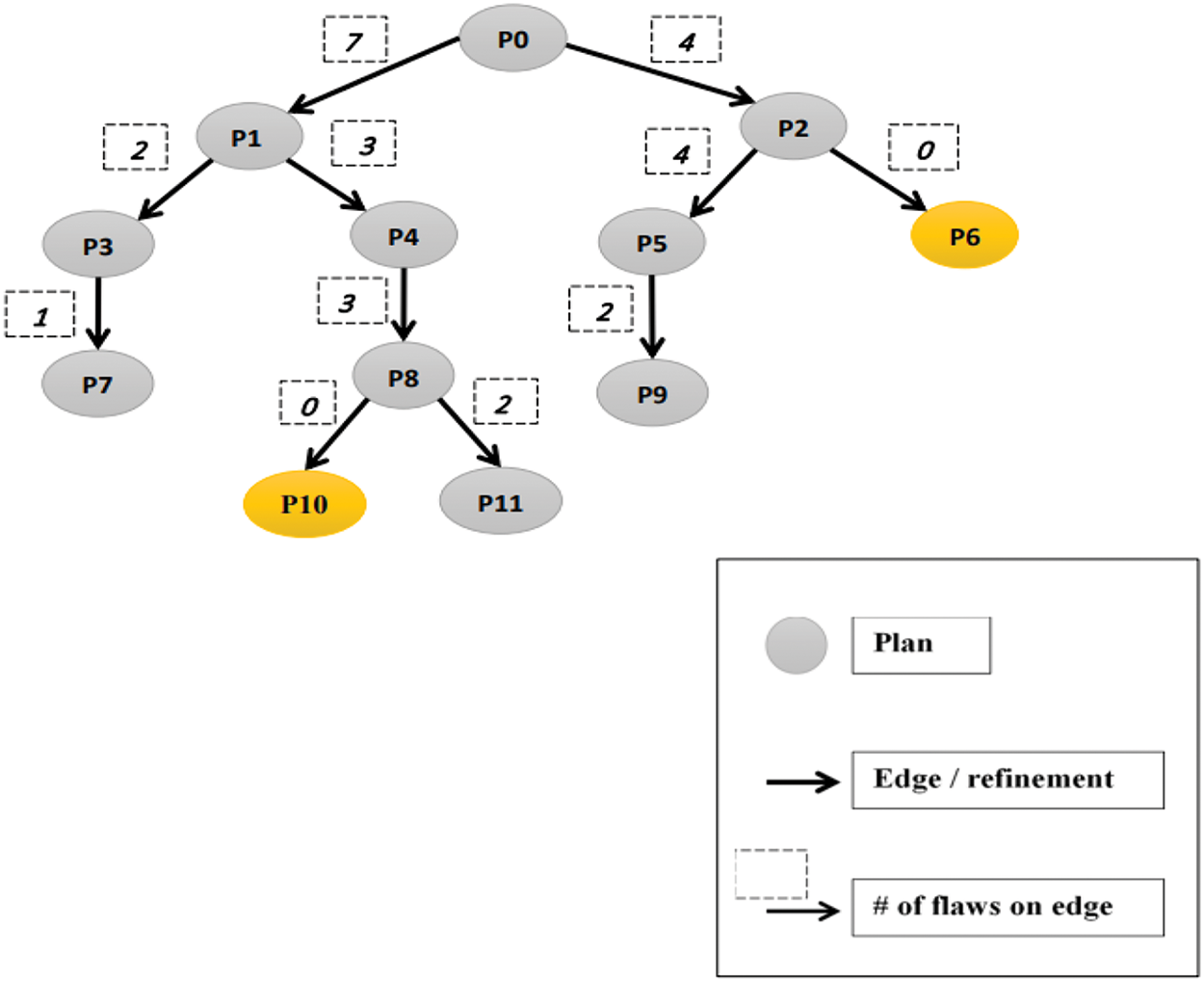
Figure 2: ACO-HTN algorithm plan space illustration

The proposed algorithm begins by initializing the fundamental variables, with the subsequent steps continuing to initialize other variables. The Key variables governing the algorithm’s flow include those set in lines 3 and 4.

•   Max_tries is set to 3, serving as the master loop (for loop starting at line 5) governing the count of search executions.

•   Each search attempt is allotted a maximum time of 1800 s.

•   Probability parameters are tuned as follows: α=1, β=1, and ρ=0.5.

Initialization of Try While Loop: Level 0: Starting at line 4, the algorithm initiates three tries 0≤i < 3. At line 6, timers are activated, and the step count is set to 0. Lines 7 to 9 involve clearing the ants’ memories. Following this, lines 10 to 12 entail distributing ants randomly across plans, beginning from 0 up to the total number of plans at the current level. Ants number one to 4 are assigned to Plan-0. At this stage, the elapsed time to execute the preceding steps is 3 s.

On line 9, a while loop condition is set as follows: while ¬(3≥1800∨0≥2\l). As long as the condition remains true, the loop continues. In Fig. 3, the decision-making process of ants is depicted as they navigate the plan space to select optimal refinements. Each ant (numbered 1 through 4) evaluates potential edges (refinements) based on calculated probabilities influenced by the flaw count and associated heuristic values. The figure illustrates a scenario where all the ants are initially positioned at node P0, which offers two potential refinements (edges):

•   Edge 1 has a flaw count (n_flaws) of 7.

•   Edge 2 has a flaw count (n_flaws) of 4.

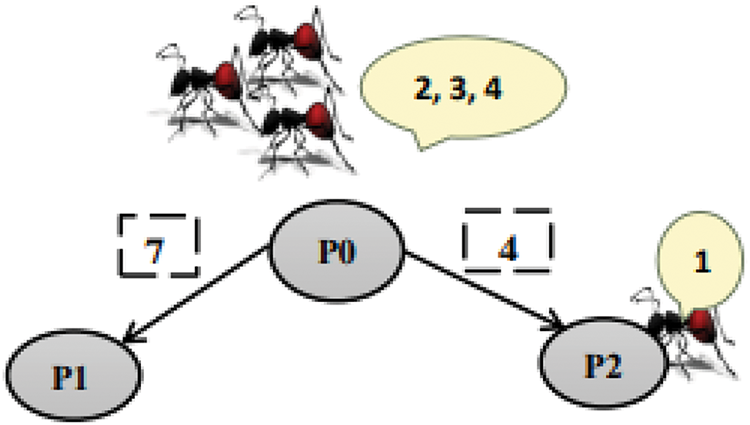
Figure 3: Ant-1 choose edge with higher probability

By computing the probabilities for each edge, the ants probabilistically select the most promising refinement, demonstrating the algorithm’s ability to prioritize edges with lower flaw counts while maintaining diversity in exploration. This visual provides an intuitive understanding of how the ACO-HTN algorithm balances heuristic evaluation and probabilistic decision-making to guide the search process effectively.

The authors will commence in ascending order based on the ant number.

•   ant (1): Line 11: There are 2 refinements (edges) denoted as M. In Line 12: For each refinement in M, the “visibility” value η is determined. Line 13: N_flaws1 = 7 and N_flaws2 = 4, where η1 = 1/7 and ′eta2 = 1/4. Utilizing τ0 = 1, α=1, and β=1. Line 18:

Nominator1=τ01⋅η11=11⋅(17)1

Nominator2=τ11⋅η21=11⋅(14)1

Line 19: Denominator = Nominator1 + Nominator2 = 11/28, and then calculating edge probability (from line 20 to 21) Edgeprob1=171128≈0.36

Edgeprob2=141128≈0.64

Line 22: Edge 2 (P0, P2) with Edge_prob2 = 0.64 will be chosen, leading to P2, as shown in Fig. 3.

Line 23: ant1.tour = [P0, P2] Calculating edge quality, assuming LCF strategy returns 6 and step = 1, δ=1, and σ=1. Since P2 does not satisfy the goal (solution plan), the plan quality is measured using the equation in line 24.

Line 25: Q(newP)=(11+6)1⋅(11)1=0.143

iterPQuality=Q(newP)=0.143

Line 26 to 27: Checking the local plan quality to determine if the iteration plan quality “iterP_Quality” is greater than the local plan quality “localPlan_Quality”. If (iterP_Quality > localPlan_Quality), Then storing the ant tour “ant.tour” and its quality “iterP_Quality” value is executed. If (0.143 > 0), Then: localPlan_Quality = 0.143 and localPlan = P0, P2.

•   ant (2): Line 11: M = 1 refinement (edge) Line 12: For the refinement in M, the “visibility” value will be:

Line 13: N_flaws1=7,η1=17

Line 18: Nominator1=τ01⋅η11=1⋅17

Line 19: Denominator = Nominator1

Line 20 to 21: Edgeprob1=1717=1

Line 22: Edge 1 will be chosen, leading to P1.

Line 23: ant2.tour = [P0, P1]

Ant2 chooses the edge with a higher probability. Assuming LCF strategy returns 7, step = 1, δ=1,andσ=1. Since P1 does not satisfy the goal (solution plan), the plan quality is measured by line 25: Q(newP)=(11+7)1⋅(11)1=0.125

iterP_Quality=Q(newP)=0.125

Line 26 to 27: If (0.125>0.143), which is false.

•   ant (3) and ant (4): Fig. 4 illustrates the distribution of ants at the next level of the plan space after performing the same probabilistic calculations as described for Ants (1) and (2). Ants (3) and (4) follow similar evaluation processes, assessing the potential refinements (edges) based on flaw counts and heuristic probabilities. The figure highlights how these ants transition to new nodes within the plan space, demonstrating the decentralized and adaptive behavior of the ACO-HTN algorithm as it explores various paths in search of optimal solutions.

Ant3.tour = [P0, P2]

Ant4.tour = [P0, P1]

Furthermore, the values of localPlan_Quality and localPlan will remain unchanged. If the condition is met, storing the localPlan_Quality and its corresponding plan “iterP_Quality” value into the best and best plan variables, respectively.

Line 28: If (0.143 > 0), then: best = 0.143 and localPlan = P0, P2.

Line 29: Finally, the process of updating pheromone trails is completed at the end of the while loop, as shown in Fig. 5. This process involves two key sub-steps: pheromone evaporation, which reduces the intensity on all edges to prevent over-concentration on specific paths, and pheromone reinforcement, where ants deposit additional pheromone on edges based on the quality of the solutions they contributed to. This adaptive mechanism ensures a balance between the exploration of new refinements and the exploitation of promising paths, guiding the algorithm toward convergence on optimal solutions.

This process consists of two sub-processes:

•   Reducing the pheromone value on all refinements (edges) using ρ

•   Each ant-j puts pheromone on the traversed refinements (edges) according to the value Δj (ant.tour).

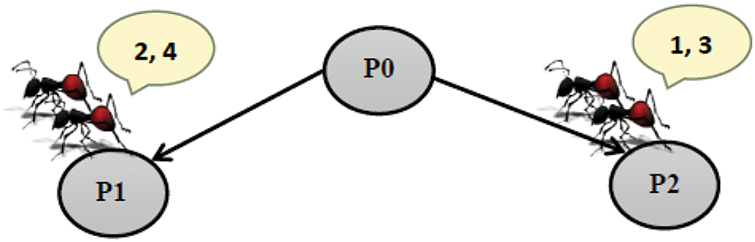
Figure 4: Ants distribution i next level

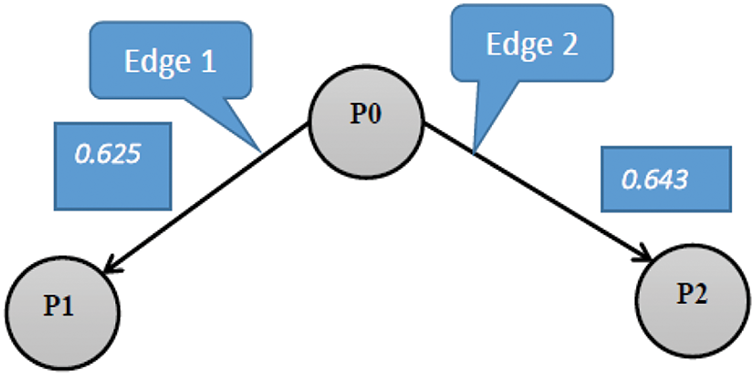
Figure 5: Update pheromone quantity

In the first sub-process, the pheromone quantity of each traversed refinement (edge) decreases by: (1−ρ)⋅τold to become (1−0.5)⋅1=0.5. Next, each ant (j), where j = (1, 2, 3, 4), starts putting pheromone on refinements according to the tour quality Qj(p). For refinement (edge1: P0, P1), the quality in response to ant (2) ∑Q2(p) and ant (4) ∑Q4(p) will be the same, 0.125:

Δ2(P0,P1)=Q2(P0,P1)=0.125

Δ4(P0,P1)=Q4(P0,P1)=0.125

τnew=0.5+0.125=0.625

For refinement (edge2: P0,P2), the quality in response to ant1 ∑Q1(p) and ant3 ∑Q3(p) will be the same, 0.143:Δ1(P0,P1)=Q1(P0,P1)=0.143 Δ3(P0,P2)=Q3(P0,P2)=0.143

τnew=0.5+0.143=0.643

After subsequent phases, the resulting solution plan gained by ant (1) (Fig. 6) has a quality value Δ1(P0,P1,P6)=1.768, which is the optimum plan. This value signifies the highest quality among all evaluated paths, showcasing the algorithm’s effectiveness in converging to an optimal solution through iterative refinement and probabilistic decision-making.

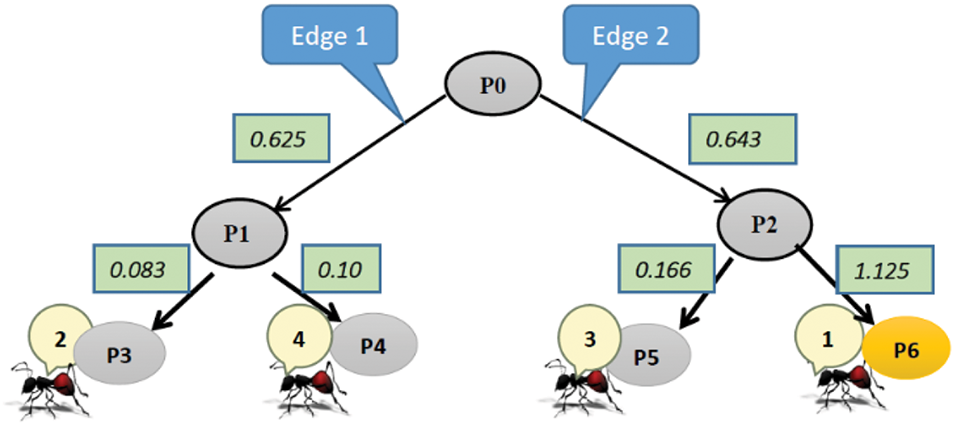
Figure 6: Illustration of ants tour in plan space, and optimum plan gained from ant [1]

Finally, the relationship and synergy between Algorithm 1 and Algorithm 2 in the proposed hybrid framework is as follows. Firstly, Algorithm 1 provides the overarching framework for solving Hierarchical Task Network (HTN) planning problems through iterative refinement, while Algorithm 2 implements the Ant Colony Optimization (ACO) strategy to guide the refinement process within this framework. Specifically, Algorithm 1 selects a partial plan from the fringe and detects flaws, invoking Algorithm 2 to probabilistically choose and apply refinements based on pheromone levels and heuristic evaluations. The feedback loop between the two algorithms ensures that successful refinements are reinforced through pheromone updates in Algorithm 2, dynamically influencing subsequent iterations in Algorithm 1. This integration allows Algorithm 2 to enhance the exploration and exploitation capabilities of Algorithm 1, ensuring that the refinement process prioritizes promising solution paths while avoiding less effective ones. Together, these algorithms create a hybrid strategy in which the structured iterative approach of Algorithm 1 is enriched by the optimization-driven decision-making of Algorithm 2, enabling the system to converge on high-quality solutions efficiently.

5  Implementation and Experiments

In order to assess the practical performance improvements facilitated by our approach, the authors execute our planning framework in various domains of the problem. The experimental trials were conducted on a system equipped with an Intel Core i7 4790 GHz processor and 8 GB of memory. It is worth noting that this system is outfitted with a single processor unit. The implementation was carried out using the Java programming language, and the Eclipse IDE was utilized to develop our proposed framework. The proposed approach is implemented on the PANDApss HTN Plan Space Search, which is a framework that integrates various techniques related to HTN planning. PANDA, developed at the Institute of Artificial Intelligence at Ulm University, serves as the foundation for PANDApss. The source code for the tested version of PANDA, named PANDApss, is available on GitHub under an open-source license.

The authors present the evaluation of the efficiency of our strategy across several domains sourced from the International Planning Competitions (IPC). These domains serve as standard benchmarks for comparing planner performance. Also, a series of systematic computational tests in the satellite and UM-Translog domains are conducted. Although there are other benchmark domains available, we selected these particular ones due to their diverse nature and the suitability of their corresponding problems and plan solutions to conduct insightful evaluations of our proposed strategy through a series of experiments.

5.1 Evaluation Benchmark Suite

Our experiment utilizes four domain models. Two of these models were adapted from the International Planning Competition (IPC) benchmarks [17], which are widely recognized in classical planning, and were modified for use in a hierarchical context. The other two domain models were developed as part of an ongoing research project.

To assess the effectiveness of our proposed hierarchical planning algorithm, we utilized two modified planning domains: the Satellite domain and the WoodWorking domain. As outlined in Table 1, the Satellite domain, initially designed for non-hierarchical planning, was adapted to incorporate three complex tasks, six primitive tasks, and eight decomposition methods. In contrast, the WoodWorking domain, derived from the IPC, focused on processing raw wood into finished components, featuring thirteen primitive tasks, six complex tasks, and fourteen decomposition methods. These domains offered diverse and intricate scenarios, allowing for a comprehensive evaluation of our algorithm’s performance.

To further enrich our experimental evaluation, the authors incorporated two additional hierarchical planning domains, the UM-Translog domain and the SmartPhone domain. The UM-Translog domain, a complex domain encompassing transportation and logistics tasks, provided a deep hierarchical structure for testing our algorithm. Additionally, the authors introduced a novel hierarchical domain, SmartPhone, focusing on everyday smartphone activities like messaging, contact management, and appointment scheduling. As illustrated in Table 1, the SmartPhone domain exhibited a deeply nested decomposition structure, offering a challenging test case for our hierarchical planner.

It is worth highlighting that planning problems within the Satellite domain grow in complexity when modeling specific observational tasks. This is primarily due to the necessity of repeatedly applying a limited set of decomposition methods across different planning scenarios. Our experimental evaluation covered a spectrum of complexities. In the WoodWorking domain, the challenge stemmed from the variety of parts requiring processing. Meanwhile, the SmartPhone domain, which revolves around routine daily activities, introduced difficulties due to the broad scope of tasks involved. The UM-Translog domain, with its hierarchical decomposition structure, introduced additional complexity, as different package types required specific transportation methods. For example, transporting hazardous materials by train involves distinct decomposition methods compared to standard package transportation by truck. By varying locations and the number of packages, our experiments covered a diverse set of qualitatively different problems.

The figures presented in our experimental results depict the runtime performance of different planners on a set of benchmark planning problems. Runtime is measured in seconds, representing the total execution time required to generate a solution. If a planner fails to find a solution within the established time limit of 9000 s, the process is terminated.

The experimental results are analyzed from two perspectives. Firstly, state-of-the-art planners with ACO-HTN are compared. Fig. 7 displays the processing runtime in seconds required to solve six planning problems using four different planners: ACO-HTN (our approach), Pruning, SHOP, and UMCP (Universal Method Composition Planner) planners. As shown in Fig. 7a, ACO-HTN demonstrates the lowest runtime across all problems, consistently outperforming the other planners. The Fig. 7a clearly illustrates that ACO-HTN is the most efficient planner among the four, achieving the shortest runtimes across all tested problems. The Pruning planner performs moderately well but not as efficiently as ACO-HTN, which shows a 66.67% improvement over the Pruning planner. SHOP and UMCP exhibit considerably longer runtimes, indicating lower performance efficiency for the given planning problems. Specifically, ACO-HTN achieves an 83.33% improvement over the SHOP planner, which further increases to 88.89% when compared to the UMCP planner.

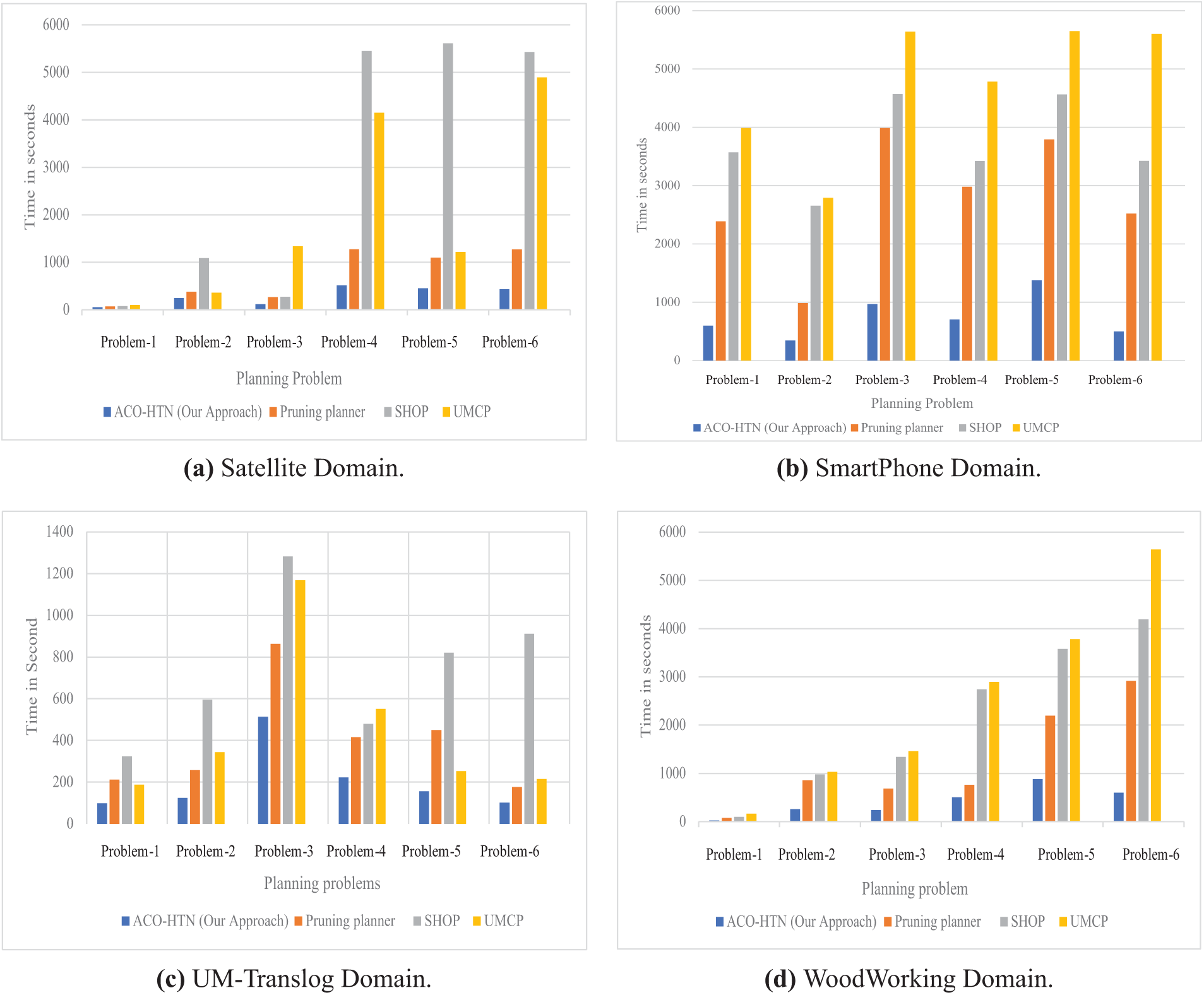
Figure 7: Comparative analysis of planning algorithm performance across diverse domains: runtime evaluation

In the other side, in the UMTranslog domain (Fig. 7c), in all problems, ACO-HTN demonstrates a significant reduction in planning time compared to the other planners. For instance, in Problem-1, ACO-HTN completes in approximately 200 s, while the other planners exceed 800 s. Similarly, in Problem-3, ACO-HTN takes around 400 s, whereas the other methods range between 800 to 1200 s. This consistent reduction across multiple problems highlights the improved efficiency of the ACO-HTN method, showcasing an average performance improvement of over 50% compared to the next best planner in many instances.

Moreover, The SmartPhone and WoodWorking domains, along with the UMtranslog domain, represent examples of deeply hierarchical planning problems (Fig. 7b,d). These domains, characterized by their intricate structures and extensive information content, are particularly well-suited to our proposed approach. Our planner demonstrated superior performance in these domains, consistently outperforming other planners within the specified resource constraints. On average, ACO-HTN exhibited a significant improvement of 50% to 70% in terms of runtime compared to the next best planner across various problems.

Finally, computations were conducted again using the same domains and problems, but with six plan selection strategies and the two modification selection strategies: HotZone (see Fig. 8) and preferEarlyFlow strategy (see Fig. 9).

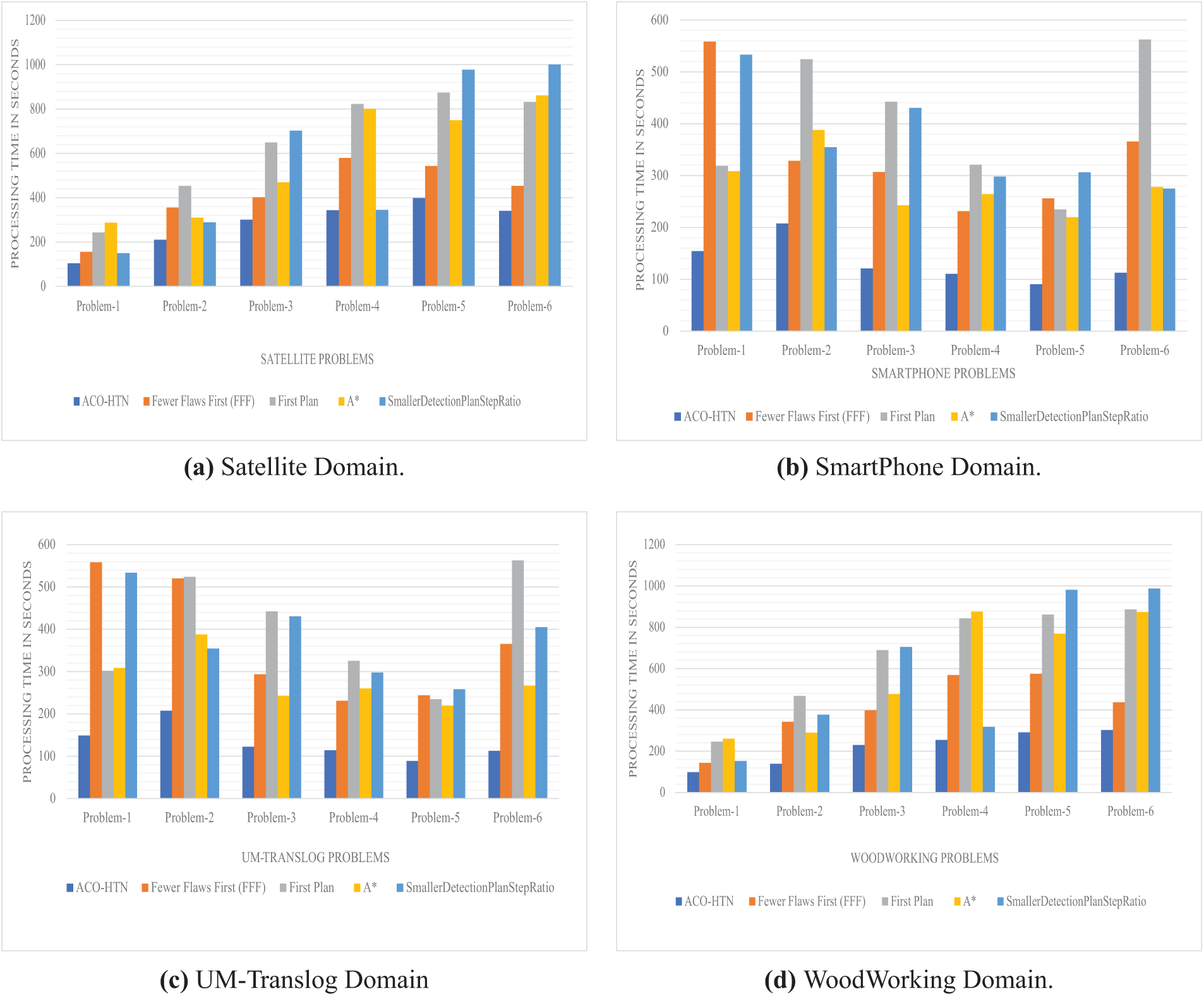
Figure 8: Comparison between different plan selection strategies with fixed modification selection strategy: HOT-Zone

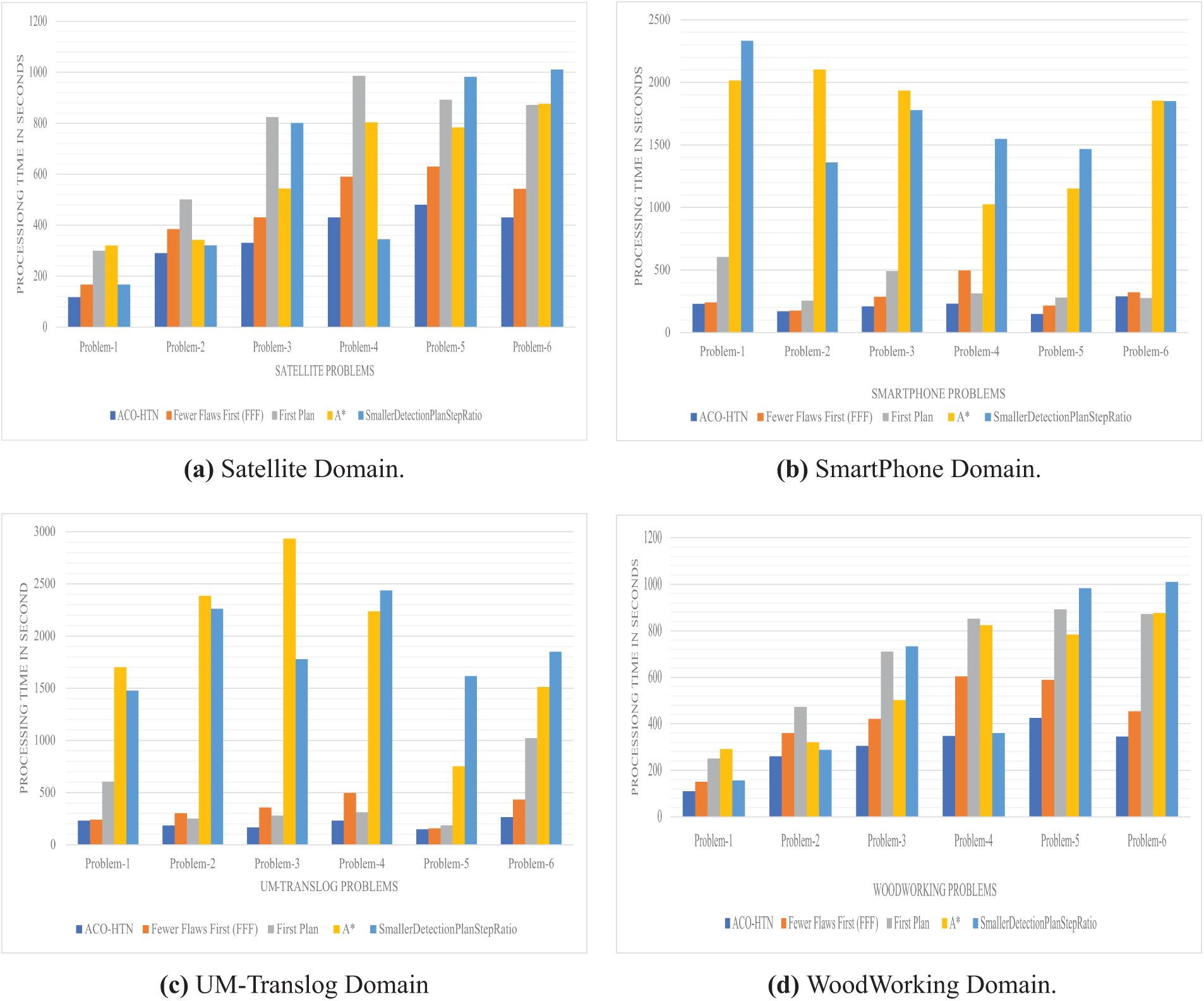
Figure 9: Comparison between different plan selection strategies with Fixed Modification selection strategy: prefer early flow

Additionally, when utilizing the Prefer Early Flaws modification selection strategy, ACO-HTN again outperformed the other strategies, as illustrated in Fig. 9.

The PreferEarlyFlaws and HotZone modification selection strategies both aim to enhance the efficiency and effectiveness of the problem-solving process, but they differ significantly in their approaches and outcomes. PreferEarlyFlaws focuses on identifying and addressing issues as early as possible, preventing minor problems from escalating, and ensuring a stable foundation for subsequent modifications. This early intervention approach leads to consistently lower processing times and improved performance, as demonstrated across various domains such as Smartphones, Translog, and WoodWorking. In contrast, the HotZone strategy prioritizes modifications in critical areas or “hot zones” with the highest potential impact. While this can be effective in targeting significant issues, it often results in longer processing times, especially in complex domains where hot zones are numerous or challenging. Comparative analysis shows that PreferEarlyFlaws outperforms HotZone in terms of processing efficiency, achieving substantial percentage improvements by minimizing the time spent on modifications and enhancing overall solution quality. Finally, the proposed technique suggests a way to prepare tasks for hybrid planning. It gets rid of tasks that don’t matter and changes the problem into a simpler, STRIPS-like format. This makes sure the planning process can always find a solution and works much faster, particularly when dealing with really complicated, layered tasks. Older ways of optimizing HTN planning, like in SHOP2 and UMCP, concentrate on breaking down tasks and managing how they affect each other. However, these methods often have trouble with complexity and large search spaces, especially when there are many tasks that aren’t relevant to the goal. The proposed technique slashes planning time by a whopping 59% when stacked up against pruning-based hybrid planners, and a massive 77% compared to old-school HTN planners. Plus, it ensures decidability by cleverly transforming the problem into a classical planning setup. This makes the proposed technique more efficient and scalable for complex domains, outperforming traditional HTN optimization techniques.

5.2 Comparative Analysis

As shown in the comparison analysis (Table 2), ACO-HTN presents a hopeful way to fine-tune HTN planning in those tricky, layered domains by cashing in on ACO’s strong points. But it might call for some extra tricks (like trimming down possibilities or changing things up) to make sure we can actually get a clear answer and not wear out our computing power too much. Current HTN streamlining methods, such as SHOP2 and UMCP, work great in areas where the number of options isn’t overwhelming, but they hit a wall when faced with deep layers and a bunch of tasks that don’t really matter. The pruning approach really shines because it mixes techniques for cutting out the fat and reworking things to get way better performance and guarantee we can get a solid result. This makes it especially good for domains with deep hierarchies.

5.3 Complexity Analysis

Suppose (m) represents the number of artificial ants used to construct solutions. (n) denotes the number of tasks (both primitive and complex) in the HTN domain. (d) represents the domain model. (k) indicates the maximum depth of the task decomposition tree, which depends on the hierarchical structure of the domain. And the number of iterations (or generations) that the ACO algorithm runs is represented by (t).

Each ant constructs a solution by decomposing tasks recursively until only primitive tasks remain. At each step, the ant selects a decomposition method for a complex task. The selection is based on pheromone trails and heuristic information, which involves evaluating all possible decomposition methods for the current task. The complexity of constructing a single solution (plan) by an ant is O(k⋅d). Since there are m ants constructing solutions in parallel, the total complexity of the construction of a solution in one iteration is: O(m⋅k⋅d).

After constructing a solution, each plan must be evaluated to determine its quality (e.g., cost, feasibility). Evaluating a plan involves checking the preconditions and effects of all primitive tasks in the plan, which depends on the number of primitive tasks (np) in the solution. The complexity of evaluating a single solution is O(np). Since there are m ants, the total complexity for the evaluation of the solution in one iteration is O(m⋅np).

After all ants have constructed and evaluated their solutions, the pheromone trails are updated based on the quality of the solutions. Updating the pheromone trails involves iterating over all the decomposition methods used in the best solutions and updating their pheromone values. So, the complexity of updating the pheromone trails is O(d).

So, the total complexity per iteration is constructed by combining the complexities of solution construction, evaluation, and pheromone update: O(m⋅k⋅d)+O(m⋅np)+O(d). Simplifying, the dominant term is O(m⋅k⋅d), as k⋅d is typically larger than np and d.

Since the algorithm runs for t iterations, the total complexity of ACO-HTN is: O(t⋅m⋅k⋅d). Finally, the overall time complexity of ACO-HTN is: O(t⋅m⋅k⋅d).

The space complexity of ACO-HTN is dominated by the storage of pheromone trails and the solutions constructed by the ants. The space required for the pheromone trails is O(d), and the space required to store solutions constructed by (m) ants is O(m⋅np). Therefore, the total complexity of the space is: O(d+m⋅np).

Finally, the complexity of ACO-HTN depends heavily on the number of decomposition methods (d) and the maximum depth of decomposition (k). In domains with deep hierarchies and many decomposition methods, the algorithm may become computationally expensive. The number of ants (m) and iterations (t) can be tuned to balance exploration and exploitation, but increasing these parameters will increase the runtime. The pruning technique described in the article can reduce d and k by removing irrelevant tasks and methods, significantly improving the efficiency of ACO-HTN.

In future work, careful parameter tuning and the integration of ACO-HTN with pruning and transformation techniques can enhance the algorithm’s scalability and efficiency for hybrid planning problems.

6  Conclusion

The adaptation of the Ant System algorithm to AI planning, particularly in conjunction with efficient approaches like Hierarchical Planning, holds significant promise. In this study, we’ve presented the initial application of the Ant Colony Optimization meta-heuristic to Hierarchical Planning. The preliminary empirical analysis has yielded promising results, indicating the feasibility of this approach for optimizing HTN planning. Given these encouraging findings, the authors aim to enhance and expand upon this work in several directions. Firstly, the authors plan to refine the implementation of the Ant System by replacing it with the Ant Colony Optimization algorithm. Additionally, the authors intend to optimize the tuning parameters to reduce computation time. This optimization may allow for the utilization of a less resource-intensive heuristic function while still achieving sensitive performance improvements. Furthermore, we are considering a shift in the adaptation strategy within the plan generation process, focusing on the “modification selection” strategy. This adjustment aims to explore alternative avenues for optimizing the planning process and improving overall efficiency. Finally, future research on the ACO-HTN approach includes transitioning from the Ant System to the Ant Colony Optimization algorithm for enhanced performance and optimizing parameter tuning to reduce computation time, enabling efficient use of heuristic functions. Moreover, integrating machine learning offers the potential for dynamic adaptability based on real-time data and historical patterns. Additionally, applying the ACO-HTN framework to emerging fields like IoT and big data optimization presents exciting opportunities to address large-scale challenges, such as resource allocation and data processing, showcasing the approach’s versatility and potential.

Acknowledgement: The study at St. Petersburg State University of Telecommunications, Prof. M.A. Bonch-Bruevich was supported by the Ministry of Science and High Education of the Russian Federation by the grant 075-15-2022-1137. This work also was supported by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R323), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contributions to the paper as follows: Conceptualization, Mohamed Elkawkagy and Ibrahim A. Elgendy; methodology, Mohamed Elkawkagy and Heba Elbeh; software, Mohamed Elkawkagy; validation, Mohamed Elkawkagy, Ibrahim A. Elgendy and Reem Ibrahim Alkanhel; formal analysis, Heba Elbeh and Mohamed Elkawkagy; investigation, Ammar Muthanna and Ibrahim A. Elgendy; resources, Reem Ibrahim Alkanhel; writing—original draft preparation, Mohamed Elkawkagy and Ibrahim A. Elgendy; writing—review and editing, Heba Elbeh; supervision, Ammar Muthanna; project administration, Reem Ibrahim Alkanhel; funding acquisition, Ammar Muthanna. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Kutluhan E, Hendler J, Nau D. UMCP: a sound and complete procedure for hierarchical task network planning. In: AIPS Proceedings; 1994. Vol. 61, p. 249–54. [Google Scholar]

2. Nau D, Tsz-Chiu A, Ilghami O, Kuter U, Murdock W, Yaman F. SHOP2: an HTN planning system. J Artif Intell Res. 2003;20:379–404. doi:10.1613/jair.1141. [Google Scholar] [CrossRef]

3. Nau D, Ghallab M, Traverso P. Automated planning: theory and practice. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc. 2004. [Google Scholar]

4. Dokeroglu T, Sevinc E, Kucukyilmaz T, Cosar A. A survey on new generation metaheuristic algorithms. Comput Indust Eng. 2019;137(5):106040. doi:10.1016/j.cie.2019.106040. [Google Scholar] [CrossRef]

5. Dorigo M, Birattari M, Stutzle T. Ant colony optimization. IEEE Comput Intell Mag. 2006;1(4):28–39. doi:10.1109/MCI.2006.329691. [Google Scholar] [CrossRef]

6. Liu C, Wu L, Huang X, Xiao W. Improved dynamic adaptive ant colony optimization algorithm to solve pipe routing design. Knowl Based Syst. 2022;237(3):107846. doi:10.1016/j.knosys.2021.107846. [Google Scholar] [CrossRef]

7. Aashdeep S, Sakshi D, Jyoti V, Gurpreet S, Amanpreet K. Using ant colony optimised algorithms for shortest path exploration by robots. IEEE Int Conf Interdiscip Approach Tech Manag Social Innov (IATMSI). 2024;2:1–4. [Google Scholar]

8. Seeniappan K, Paranthaman V, Raj Kamal MD, Sudhakar A, Muthukannan M. A novel approach of particle swarm and ANT colony optimization for task scheduling in cloud. In: 14th International Conference on Cloud Computing, Data Science & Engineering (Confluence); 2024; Noida, India. p. 272–8. [Google Scholar]

9. Xu Y, Li Q, Xu X, Yang J, Chen Y. Research progress of nature-inspired metaheuristic algorithms in mobile robot path planning. Electronics. 2023;12(15):3263. doi:10.3390/electronics12153263. [Google Scholar] [CrossRef]

10. Roberts MK, Thangavel J, Aldawsari H. An improved dual-phased meta-heuristic optimization-based framework for energy efficient cluster-based routing in wireless sensor networks. Alex Eng J. 2024;101(1):306–17. doi:10.1016/j.aej.2024.05.078. [Google Scholar] [CrossRef]

11. Bhattacharjee AK, Mukhopadhyay A. An improved genetic algorithm with local refinement for solving hierarchical single-allocation hub median facility location problem. Soft Comput. 2023;27(3):1493–509. doi:10.1007/s00500-022-07448-3. [Google Scholar] [CrossRef]

12. Abualigah L, Elaziz MA, Khasawneh AM, Alshinwan M, Ibrahim RA, Al-Qaness MA et al. Meta-heuristic optimization algorithms for solving real-world mechanical engineering design problems: a comprehensive survey, applications, comparative analysis, and results. Neural Comput Appl. 2022;34(6):1–30. doi:10.1007/s00521-021-06747-4. [Google Scholar] [CrossRef]

13. Rajwar K, Deep K, Das S. An exhaustive review of the metaheuristic algorithms for search and optimization: taxonomy, applications, and open challenges. Artif Intell Rev. 2023;56(11):13187–257. doi:10.1007/s10462-023-10470-y. [Google Scholar] [PubMed] [CrossRef]

14. Elkawkagy M, Schattenberg B, Biundo S. Landmarks in hierarchical planning. In: Procedings of the ECAI-2010; 2010; Amsterdam, Netherlands. [Google Scholar]

15. Elkawkagy M, Bercher P, Schattenberg B, Biundo S. Improving hierarchical planning performance by the use of landmarks. In: Procedings of the 26th National Conference on Artificial Intelligence (AAAI 2012); 2012. p. 1763–9. [Google Scholar]

16. Bercher P, Alford R, Höller D. A survey on hierarchical planning-one abstract idea, many concrete realizations. In: Procedings of Twenty-Eighth International Joint Conference on Artificial Intelligence; 2019; Freiburg, Germany. p. 6267–75. [Google Scholar]

17. McDermott D. The 1998 AI planning systems competition. J AI Mag. 2000;21(2):35–55. [Google Scholar]

18. Hoffmann J, Nebel B. The FF planning system: fast plan generation through heuristic search. J Artif Intell Res. 2001;14(1):253–302. doi:10.1613/jair.855. [Google Scholar] [CrossRef]

19. Dvorák F, Toropila D, Barták R. Towards AI planning efficiency: finite-domain state variable reformulation. In: Proceedings of the 4th Workshop on Knowledge Engineering for Planning and Scheduling (KEPS 2013); 2013. [Google Scholar]

20. Elkawkagy M. Improving the Performance of hybrid planning. Int J Artif Intell. 2016;14(2):98–116. [Google Scholar]

21. Luo J, Zhu C, Zhang W. Messy genetic algorithm for the optimum solution search of the HTN planning. In: Foundations of Intelligent Systems: Proceedings of the Sixth International Conference on Intelligent Systems and Knowledge Engineering (ISKE2011); 2011; Shanghai, China. [Google Scholar]

22. Schattenberg B, Bidot J, Biundo S. On the construction and evaluation of flexible plan-refinement strategies. In: Procedings of the 30th German Conference on Artificial Intelligence (KI 2007). Osnabrück, Germany: Springer; 2007. p. 367–81. [Google Scholar]

23. Elkawkagy M, Elbeh H. Improving AI planning using map reduce. Int J Innov Technol Explor Eng. 2020;9(4):615–8. doi:10.35940/ijitee.D1309.029420. [Google Scholar] [CrossRef]

24. Georgievski I, Aiello M. HTN planning: overview, comparison, and beyond. Artif Intell. 2015;222(3):124–56. doi:10.1016/j.artint.2015.02.002. [Google Scholar] [CrossRef]

25. Höller D, Bercher P, Behnke G, Biundo S. HTN planning as heuristic progression search. J Artif Intell Res. 2020;67:835–80. doi:10.1613/jair.1.11282. [Google Scholar] [CrossRef]

26. Penberthy S, Weld D. UCPOP: a sound, complete, partial order planner for ADL. In: Procedings of the Third International Conference on the Principles of Knowledge Representation; 1992; San Francisco, CA, USA. p. 103–14. [Google Scholar]

27. Bechon P, Barbier M, Lesire C, Infantes G, Vidal V. Using hybrid planning for plan reparation. In: 2015 European Conference on Mobile Robots (ECMR); 2015; Lincoln, UK. p. 1–6. [Google Scholar]

28. Bercher P, Behnke G, Holler D, Biundo S. An admissible HTN planning heuristic. In: Proceedings of the 26th International Joint Conference on Artificial Intelligence; 2017. p. 480–8. [Google Scholar]

29. Cheng K, Wu L, Yu X, Yin C, Kang R. Improving hierarchical task network planning performance by the use of domain-independent heuristic search. Knowl-Based Syst. 2018;142(4):117–26. doi:10.1016/j.knosys.2017.11.031. [Google Scholar] [CrossRef]

30. Li M, Liu X, Jiang G, Liu W. A novel hierarchical task network planning approach for multi-objective optimization. Expert Syst Appl. 2024;251(8):124058. doi:10.1016/j.eswa.2024.124058. [Google Scholar] [CrossRef]

31. Höller D, Bercher P, Behnke G, Biundo S. A generic method to guide HTN progression search with classical heuristics. Proc Int Conf Autom Plan Sched. 2018;28:114–22. doi:10.1609/icaps.v28i1.13900. [Google Scholar] [CrossRef]

32. Biundo S, Bercher P, Geier T, Müller F, Schattenberg B. Advanced user assistance based on AI planning. J Cogn Syst Res. 2011;12(3–4):219–36. doi:10.1016/j.cogsys.2010.12.005. [Google Scholar] [CrossRef]

33. Bercher P, Keen S, Biundo S. Hybrid planning heuristics based on task decomposition graphs. In: Procedings of the 7th Annual Symposium on Combinatorial Search (SoCS); 2014; Washington, DC, USA. p. 35–43. [Google Scholar]

34. Bercher P, Höller D, Behnke G, Biundo S. User-centered planning—a discussion on planning in the presence of human users. In: Procedings of the International Symposium on Companion Technology; 2015; Ulm, Germany. [Google Scholar]

35. Pednault E. ADL: exploring the middle ground between STRIPS and the situation calculus. In: Proceedings of the First International Conference on Principles of Knowledge Representation and Reasoning; 1989; San Francisco, CA, USA. p. 324–32. [Google Scholar]