SW-DDFT: Parallel Optimization of the Dynamical Density Functional Theory Algorithm Based on Sunway Bluelight II Supercomputer

1  Introduction

The theoretical framework of this work mainly employs the first-order mean spherical approximation to derive the direct correlation functions between nanoparticles and polymer moieties. By explicitly incorporating lattice orientation in crystalline structures, we construct an orientation-dependent direct correlation function and integrate it into the free energy functional of the system. By combining the Dynamical Density Functional Theory (DDFT) algorithm, we analyze the orientational interactions between structural units in ordered structure and further investigate the crystal structure and crystallization dynamics of nanoparticles and polymer molecules.

The supporting part of this paper mainly leverages the architectural features and computational capabilities of the Sunway Bluelight II supercomputer to port and optimize the DDFT program. The Sunway Bluelight II offers powerful computational performance and larger node storage capacity, enabling the full potential of the DDFT algorithm to be realized.

Main contributions of this paper:

•   This paper proposes three optimization strategies using the Computation Processing Element array (CPEs), including direct parallel optimization, local-memory constrained optimization for CPEs, and multi-core groups collaboration and communication optimization. These optimization strategies fully utilize the hardware resources of the Sunway Bluelight II supercomputer, improving computational efficiency and data transmission performance.

•   For the first time, the DDFT program has been successfully ported and optimized on the Sunway Bluelight II supercomputer, expanding its application ecosystem. Compared to the original program, this optimization achieves a speedup of up to 6.67 times within a single-core group, with six core groups (a total of 384 CPEs), the maximum speedup can reach 28.64 times.

The structure of this paper is as follows: Section 2 introduces Dynamical Density Functional Theory and the Sunway Bluelight II supercomputer; Section 3 analyzes the DDFT program and its algorithms; Section 4 presents three parallel optimization strategies for the program; Section 5 presents experimental results and performance analysis; Section 6 discusses related work; Section 7 concludes the paper.

2  The Dynamical Density Functional Theory and the Sunway Bluelight II Supercomputer

2.1 Dynamical Density Functional Theory

In recent years, DDFT, derived from the Density Functional Theory (DFT), has been increasingly applied to the study of crystallization dynamics mechanisms [1]. Polymer nanocomposites have garnered significant attention in academia due to their exceptional mechanical properties and functional characteristics [2]. With advancements in production technologies, there is a growing demand for improved performance of polymer nanocomposites. Using the DDFT method to study the crystallization behavior of polymer nanocomposite systems has become a key research direction.

However, due to the complexity of crystalline structures and the intensive large-scale Fast Fourier Transform computations involved, solving such problems using supercomputers has become essential. Porting and optimizing the DDFT algorithm on the new generation of the China’s Sunway supercomputer to fully leverage its high-performance computing capabilities, which can maximize the algorithm’s computational efficiency. This not only advances materials research but also aids in the design and development of novel materials.

2.2 Sunway Bluelight II Supercomputer

As a new generation of Sunway supercomputers, the core components of the Sunway Bluelight II, such as processors and network chipsets, are entirely China’s developed. Its core architecture consists of one cabinet and four computing super-nodes. Each super-node is composed of 64 computing blades, with each blade containing two computing node boards. Each computing node board houses a single computing node, meaning each super-node consists of 128 computing nodes. Each computing node includes two SW39000 processors, two Sunway message processing chips, and 192 GB of DDR4 memory. The entire system is comprised of 512 computing nodes and 1024 SW39000 processors, delivering a total peak performance of 3.13 PFLOPS, with each node capable of achieving a computing performance of up to 6.12 TFLOPS.

The SW39000 processor consists of six Core Groups (CGs), each comprising one Management Processing Element (MPE, also known as the master core) and a Computation Processing Element array (CPEs). The CPEs is a 8 × 8 array of Computation Processing Element (CPE, also referred to as the slave core). Each CG is equipped with an independent Memory Controller (MC), which connects to 16 GB of DDR4 memory via Direct Memory Access (DMA) with a bandwidth of 51.2 GB/s. Data transfer between the CPE within the same CPEs is achieved through Remote Memory Access (RMA). Each CPE is equipped with 256 KB of fast Local Data Memory (LDM). The SW39000 processor consists of a total of 390 processing units. A single processor delivers approximately 14 TB/s of floating-point performance and a memory bandwidth of about 307.2 GB/s. The hardware architecture of the SW39000 processor is illustrated in Fig. 1.

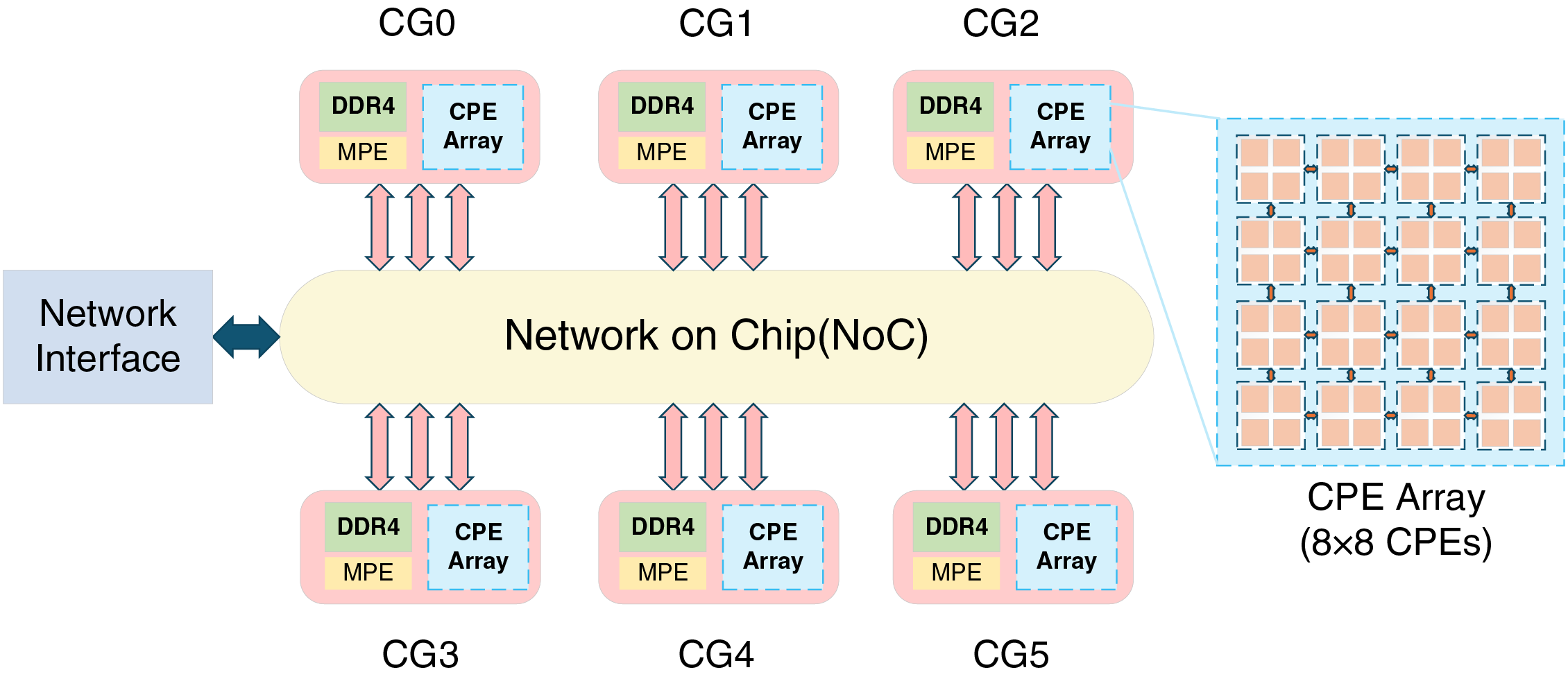
Figure 1: Architecture of SW39000 processor

3  Analysis and Parallelization of Dynamical Density Functional Theory Algorithm

3.1 Analysis of Theoretical Algorithms

DDFT is developed from classical DFT. DFT was initially proposed by Thomas [3] and Fermi [4] based on quantum mechanics to study electron cloud density and electronic ground state properties. In 1976, building on previous research, Ebner and Saam [5] and Yang et al. [6] developed classical Density Functional Theory to describe the structural and energetic characteristics of classical fluid systems.

The core of DFT is to establish the Helmholtz free energy functional F[ρ(r)] of the system, and further get the grand potential Ω[ρ(r)] of the system. Both are functions of the density distribution ρ(r) of the system. By finding the minimum value of the grand potential of the system, the corresponding density distribution can be obtained, enabling the calculation of various thermodynamic properties of the system. In DFT, the expression of the grand potential Ω[ρ(r)] of the system is given as follows:

Ω[ρ(r)]=F[ρ(r)]+∫[Vext(r)−μb]ρ(r)dr(1)

In the DFT framework, F[ρ(r)] represents the Helmholtz free energy of the system, Vext(r) is the external potential energy, and μb is the chemical potential of the main fluid.

By combining classical DFT with the fundamental Smoluchowski dynamical equation, DDFT can be obtained. DDFT can describe the evolution of heterogeneous fluid density distribution over time. Thus, the density distribution and free energy functional of the system are related to the dynamic change of time.

The DDFT model was initially proposed by Evans [7] and Dieterich et al. [8]. It starts from the dynamical equations, performs ensemble averaging on the noise term, and approximates the equilibrium density distribution under a certain external field as the density distribution of the system at a certain time. Based on this theory, the expression of DDFT is as follows:

kBT∂ρ(r,t)∂t=D∇{ρ(r,t)∇δF[ρ(r,t)]δρ(r,t)}(2)

kB is the Boltzmann constant.

T represents the system temperature.

ρ(r,t) is the density distribution at time t.

D is the effective molecular hard-sphere diameter.

δ is the Dirac delta function.

Vext denotes the external potential energy.

r represents the distance in real space.

ρ is the density.

In this equation, t represents time, and F[ρ(r,t)] is a functional of the density distribution ρ(r,t) at time t. This equation is typically solved using Fourier spectral method. For the classical DFT model based on the RY- approximation, its dynamic form can be expressed as:

kBT∂ρ(r,t)∂t=D{∇2ρ(r,t)+∇[ρ(r,t)∇Vext(r,t)]−∇[ρ(r,t)∇∫dr′ρ(r′)c(2)(|r−r′|;ρ)]}(3)

The establishment of DDFT has expanded the scope of research from equilibrium states to nonequilibrium processes, making it particularly significant for analyzing the evolution of density distributions over time in inhomogeneous systems. Löwen employed DDFT to study the nucleation and growth processes of simple crystals in both homogeneous and inhomogeneous systems [9], providing in-depth analyses of crystal face adjustments and structural evolution during polycrystalline crystal growth.

However, up to now, research using DDFT in crystallization processes remains in its infancy and its research objects mainly focus on spherical particles, colloidal particles, and small molecular crystal systems. The research of polymer crystals with complex structures and long chain molecules and their crystallization kinetics is still a blank field. This paper adopts DDFT as the primary research method, further extending the existing theoretical framework to apply it to the study of the microscopic dynamical mechanisms of crystallization behavior in various polymer nanocomposite systems.

3.2 Code Hotspot Analysis

The DDFT program implements a density evolution simulator based on the framework of DDFT, describing the evolution of density distributions over time within a system. Its primary functions include: Calculating the time evolution of density distributions; Analyzing the processes of crystal nucleation, diffusion, and growth; Outputting density and related data for subsequent analysis. This simulator is broadly applicable for studying crystal nucleation and growth in inhomogeneous systems, as well as particle density diffusion and aggregation under the influence of external fields or free energy. The DDFT source code used in this study is a self-developed program. Its core methodology can be found in Reference [1], including the theoretical framework, implementation process.

The main workflow of the program is as follows: First, input external field conditions and construct the computational grid. Next, initialize the density and compute the chemical potential under the hard-sphere approximation. Then, sequentially perform a series of Fourier transform operations. Finally, output results such as the density distribution and mean square displacement after each iteration.

To further improve program performance, we employed the Swprof hotspot analysis tool provided by the Sunway supercomputer, along with manual piling timing method, to conduct a detailed analysis of performance bottlenecks during execution.

According to the analysis results (as shown in Fig. 2), the main performance bottleneck lies in the Crystal Structure Transformation function. This function is called multiple times during each iteration, and its high frequency of calls significantly increases the overall runtime. As a result, our optimization efforts focused on parallelizing this function. Taking into account the characteristics of the DDFT program and the hardware architecture of the Sunway Bluelight II supercomputer, we identified and summarized several key challenges encountered during the parallel optimization process.

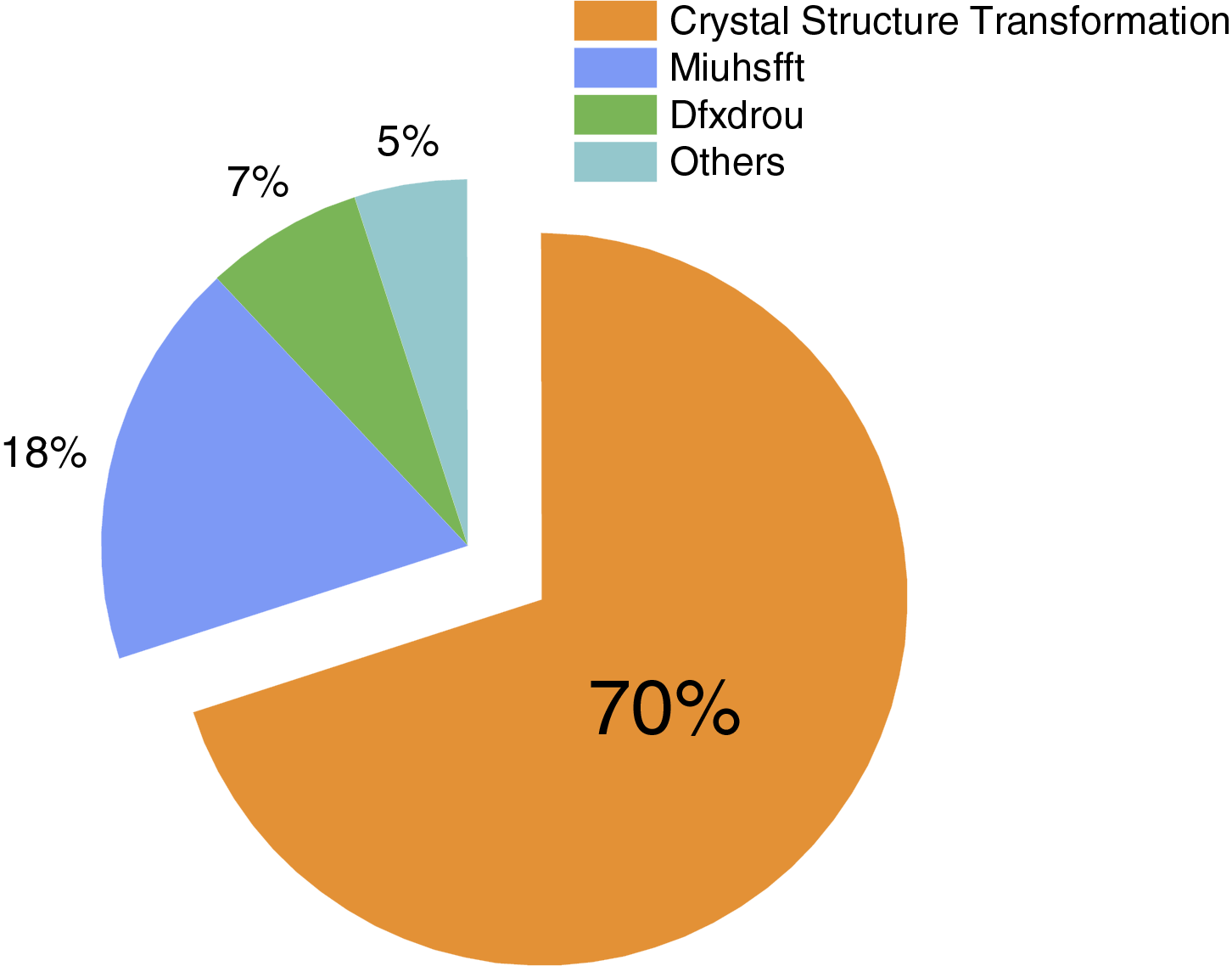
Figure 2: Hotspot analysis chart of DDFT

1.    Loop Dependency Issues: When moving hotspot sections to CPEs for parallel optimization, some loops exhibit data dependency relationships, preventing tasks from being directly assigned to CPEs, which limits the efficiency of parallelization.

2.    LDM Space of CPEs Constrained: Due to the architectural constraints of the Sunway chip, each LDM space is small. When the MPE transfers data to the CPEs, LDM space may be insufficient. In such cases, the CPEs have to fetch required variables by directly accessing main memory, leading to significant time overhead.

3.    Insufficient Computational Resources and Excessive Communication: When the program runs within a single-core group, computational resources may become insufficient. Additionally, excessive communication among CPEs within a single-core group or across core groups can further affects the execution efficiency of the program.

For the above challenges, this paper proposes three acceleration strategies based on the architecture of the Sunway many-core processor, including direct parallel optimization, local-memory constrained optimization for CPEs, and multi-core groups collaboration and communication optimization.

4  Optimization of the Dynamical Density Functional Theory program

This section focuses on three acceleration strategies, including direct parallel optimization, local-memory constrained optimization for CPEs, and multi-core groups collaboration and communication optimization. These methods not only significantly improve the performance of the DDFT algorithm but also provide a certain reference value for parallelization implementations of other similar programs on the Sunway supercomputer.

4.1 Direct Parallel Optimization

Direct parallel optimization is the basic strategy of thread-level parallel optimization. Based on the preliminary hotspot test analysis, approximately 70% of the computation time is concentrated on crystal structure transformation. To improve execution efficiency, first of all, this paper migrates the hotspot section to the CPEs for parallel optimization. Then, other hotspot sections are migrated to the CPEs for optimization.

During data transfer, directly accessing the main memory, while straightforward, is inefficient. Therefore, this paper adopts the following two optimized data transmission methods. The detailed process is illustrated in Fig. 3.

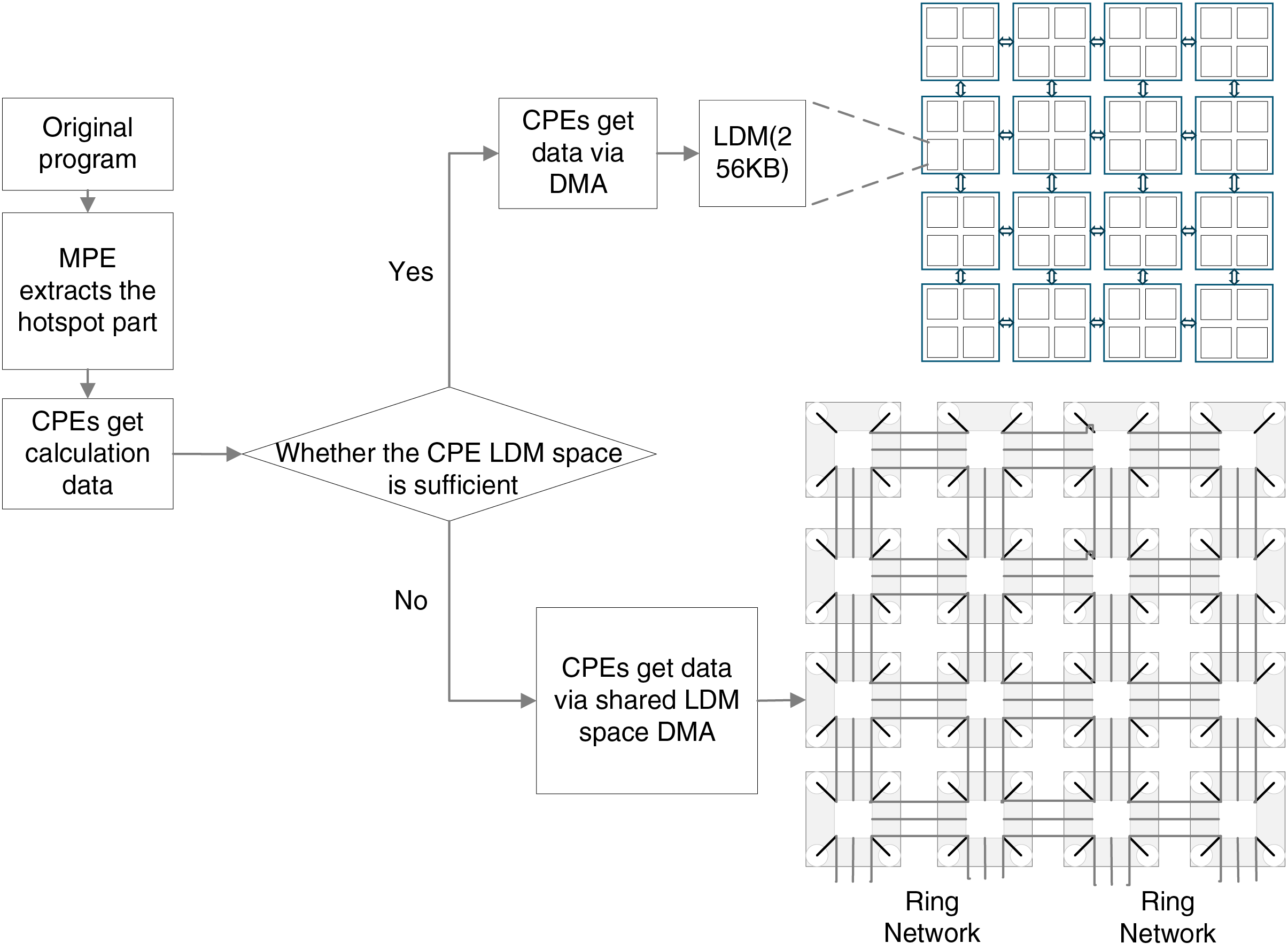
Figure 3: CPEs data acquisition method

1.    CPEs obtain data from MPE through DMA. For computational tasks with small data volumes, the private LDM space of CPEs can accommodate the required data. Therefore, CPEs can load the data into its private LDM space by invoking the DMA transfer function, thereby improving the efficiency of accessing the main memory.

2.    CPEs obtain data from MPE through shared LDM space DMA. For computational tasks involving large data volumes, the LDM space of CPEs may be insufficient to store all the required data. In such cases, a shared LDM space can be utilized. Specifically, each CPE in the array provides a LDM space of the same capacity, which is arranged in a contiguous address space. The CPEs then invoke the shared LDM space DMA transfer function to load the data into the shared contiguous LDM space, thereby improving the efficiency of accessing the main memory.

The specific operation process is as follows: First, for hotspot regions, the MPE initializes the CPEs and loads loops with high iteration counts and no forward or backward dependencies to the CPEs. The computational tasks are then distributed to each CPE, which retrieves data from the MPE using the aforementioned methods to enable fast access and modification of the required data. After the complete of computation, the results are transmitted back to the MPE via DMA or shared LDM space DMA. Subsequently, this process is repeated for other hotspot regions to achieve optimization using the CPEs.

4.2 Local-Memory Constrained Optimization for CPEs

When the hotspot computing section of Crystal Structure Transformation is ported to CPEs for acceleration, the whole task cannot be transferred to CPEs and assigned to each CPE directly due to the dependency of variables in multiple triple loops. An example pseudocode snippet is shown in Algorithm 1. Such dependencies require decentralized migration, increasing program runtime. In addition, loop-dependent data is often bound to stride iterations, which can take up a lot of storage space if stored in arrays. Moreover, the LDM capacity of CPEs is limited and cannot accommodate all the dependent data.

Although the LDM provides a contiguous shared space (where each CPE in the array offers the same LDM capacity with continuous addressing), which alleviates memory constraints to some extent. However, when the data size expands to the point where the array size becomes too large, transferring it directly to the LDM of CPEs not only wastes storage space but also may cause storage overflow.

To solve the above problems, this paper proposes an innovative method, including the following two optimization strategies:

Small-Scale Dependency Data Handling: When the dependency data occupies storage space less than the maximum storage capacity of the shared LDM, the MPE precomputes the dependent portions of the loop and stores the results in an array. The CPEs then fetch the dependency data from MPE via DMA or shared LDM space DMA to complete the computation.

Large-Scale Dependency Data Handling: When the dependency data occupies storage space no less than the maximum storage capacity of the shared LDM, a hash table is constructed in the MPE. The MPE precomputes the dependent portions of the loop and stores the results in the hash table. The CPEs fetch the hash table via DMA or shared LDM space DMA, and extract the required data according to the mapping relationship for calculation.

This method enables the CPEs to efficiently access the necessary dependency data, reducing the frequency of CPEs start-up and shut-down operations, while effectively solving the LDM memory constraints. This significantly improves the program’s execution efficiency. The detailed workflow is illustrated in Fig. 4.

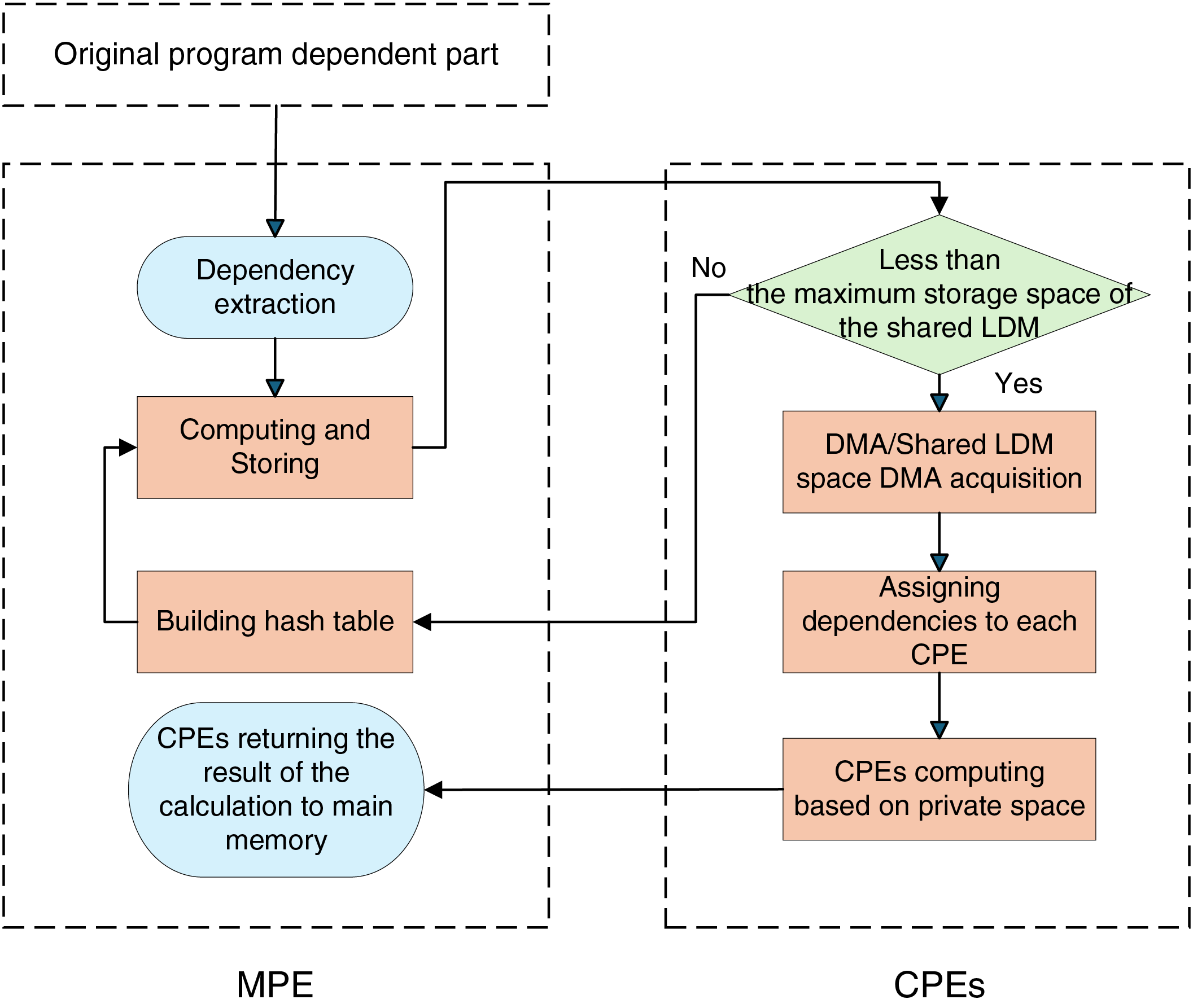
Figure 4: Solution for the flowchart of data acquisition process limited by CPE LDM space

This method proposes an optimization strategy of constructing a hash table for cases where the dependent data exceeds the maximum storage capacity of the shared LDM and the loops are stride iterations. As shown in Fig. 5, the loop to be optimized exhibits significant stride iteration characteristics. If the loop and its corresponding data are directly mapped to an array, it would not only occupy a large amount of storage space, leading to space wastage, but also potentially fail to load due to exceeding the LDM capacity limitation of the CPEs.

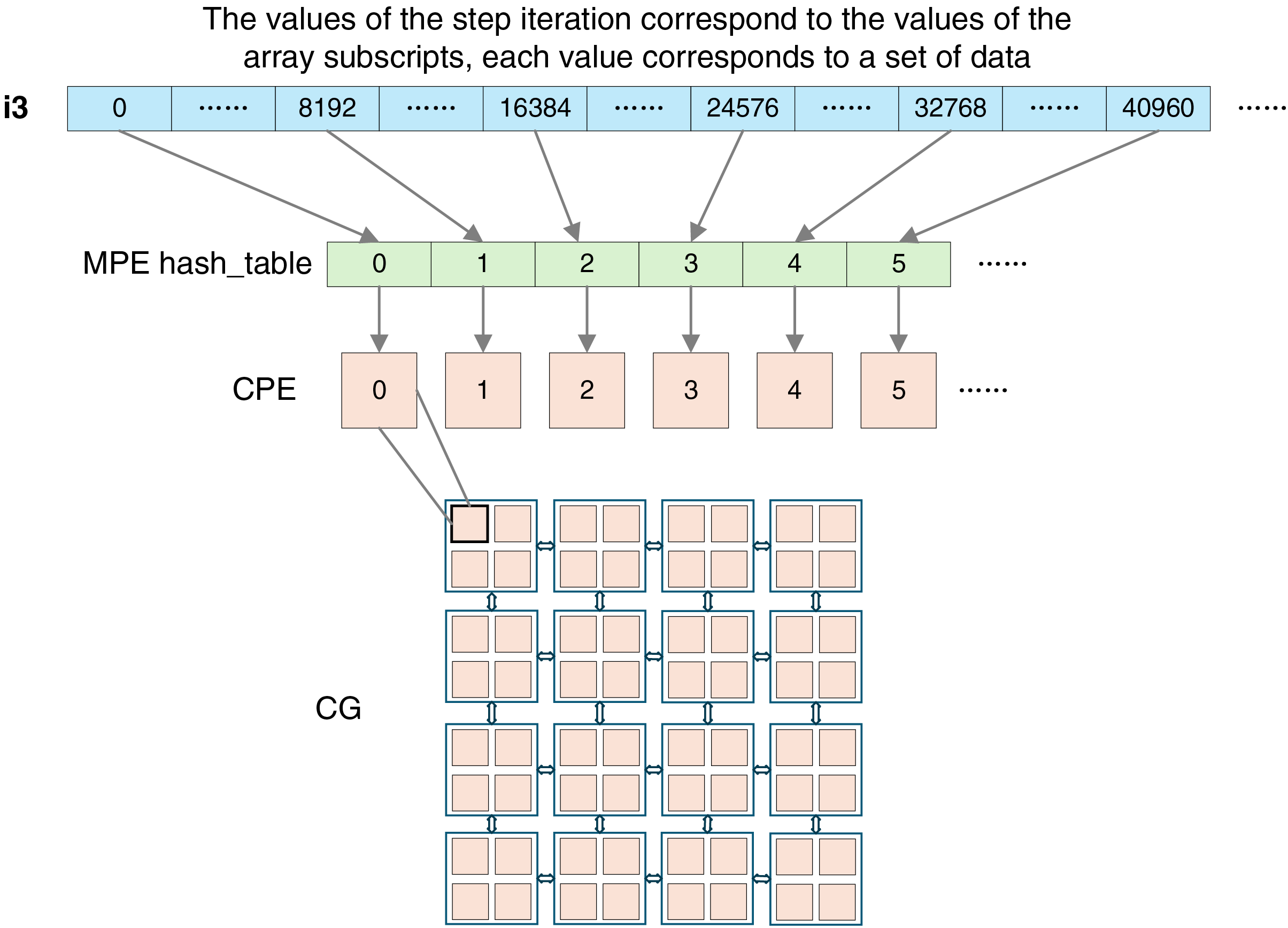
Figure 5: Corresponding diagram of stepwise iteration, hash table and CPEs

Therefore, by constructing a hash table, the stride iteration loop and its corresponding data are mapped into the hash table. By leveraging the efficient indexing and storage mechanism of the hash table, the data required for loop dependencies can be stored in a more compact manner, effectively reducing storage space usage and solving the limitation of the LDM capacity of CPEs. At the same time, CPEs fetch the hash table via DMA or shared LDM space DMA, enabling high-speed data transfer and efficient data utilization, further improving computational efficiency and performance.

4.3 Multi-Core Groups Collaboration and Communication Optimization

When MPI is introduced into this program for process-level optimization, the acceleration effect of multi-process running is not ideal because of the high communication time and the difficulty of decomposing certain hotspots. Therefore, this paper proposes a solution that leverages multi-core groups for collaborative computation. At the same time, data collection and transmission within and between core groups are optimized, reducing the frequency of data transfers between the MPE and CPEs, thereby improving execution efficiency and performance of the program.

When determining the number of core groups, it is generally necessary to analyze the iteration count and computational complexity of the hotspot loops and estimate the required number of core groups. In order to select the number of core groups more accurately, it is also necessary to run the program to test the execution effect of different core group configurations and perform comparative verification. To simplify this process, this paper introduces a machine learning model. By training a model to predict the optimal number of core groups based on features such as loop iterations and computational complexity, the program can automatically select the best configuration scheme. The process is illustrated in Fig. 6.

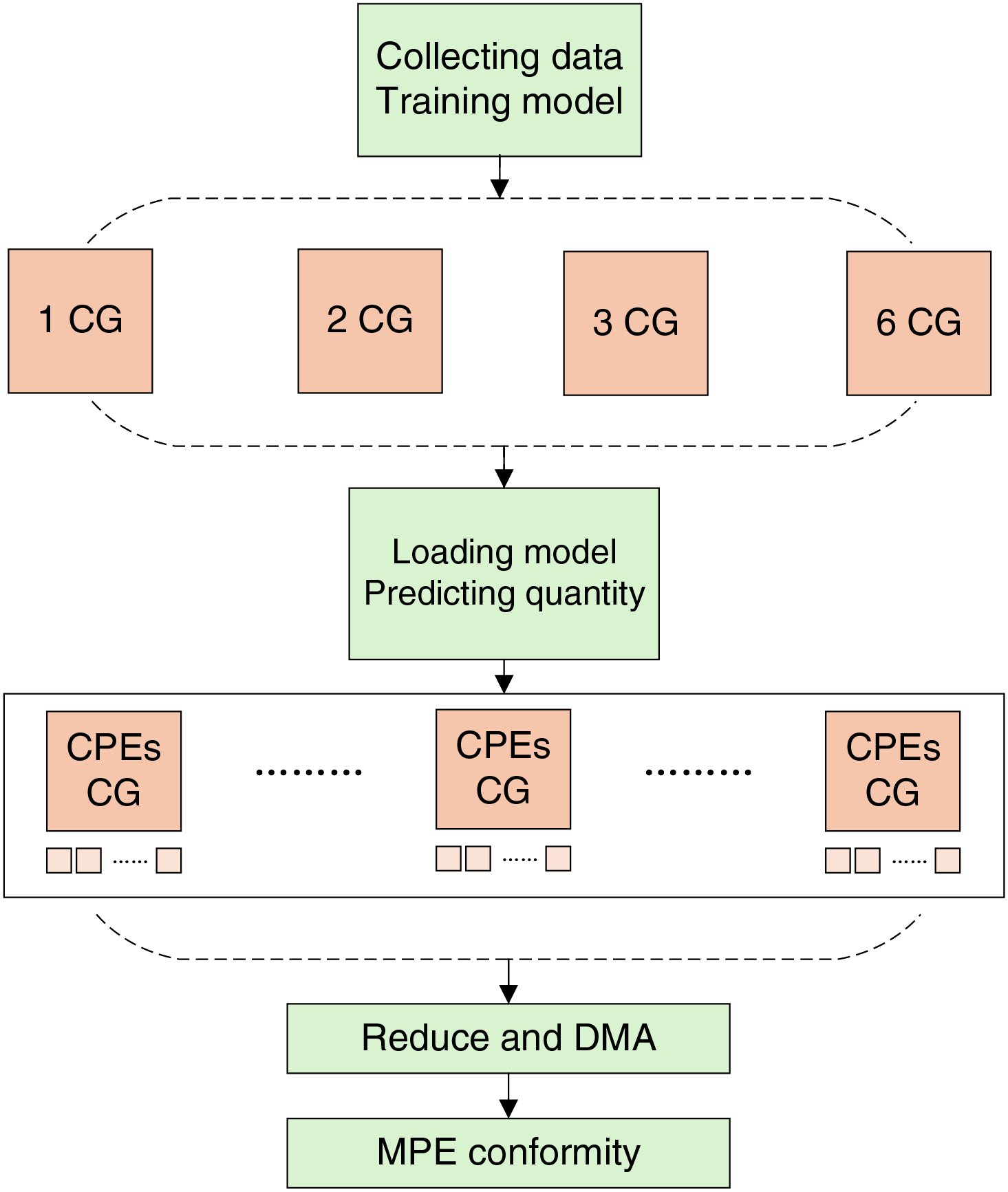
Figure 6: Diagram of machine learning prediction for the number of core groups

In the cooperative optimization of multi-core groups, 2, 3, 4, 5, or 6 core groups can be selected for collaborative computation. Taking the 2 core groups cooperative computation as an example, the thread numbers range from 0 to 127, and the core group numbers range from 0 to 1, each thread corresponds to one core group number. According to the characteristics of the program’s computational hotspots, the calculation tasks are reasonably allocated to each CPE.

Each CPE obtains the required data from the MPE via DMA or direct memory access to the main memory. Each CPE independently completes its assigned computational tasks, and computations of CPEs across different core groups do not interfere with one another. Within each core group, after performing operations such as reduction on the computation results, the final results are then sent back to the MPE. This optimization method effectively utilizes multi-core resources, improving computational parallelism and efficiency. The detailed process is illustrated in Fig. 7.

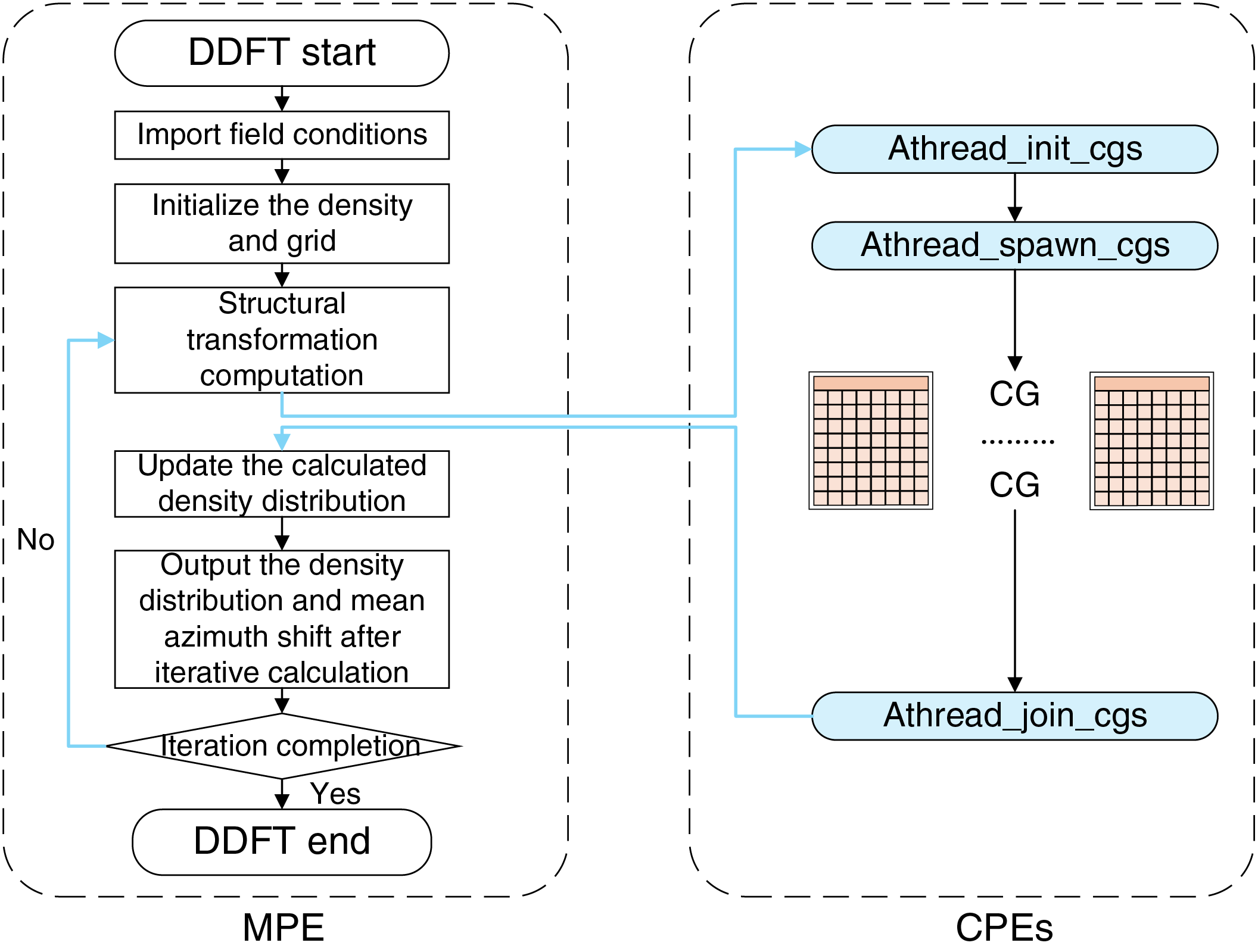
Figure 7: Diagram of multi-core groups collaborative computation

In single-core group and multi-core groups optimizations, tasks often involve critical resources, and multiple CPEs accessing the same memory area may lead to competition issues. To avoid data race errors, it is necessary to allocate independent private LDM spaces for each CPE, allowing them to only operate on and update private variables. After the completion of the task, each CPE needs to aggregate results and send them back to the MPE for final computations. However, this approach introduces additional overhead during aggregation and data transfer in a single-core group or multi-core groups environment. Therefore, the aggregation and transfer processes need to be optimized. The pseudocode for the specific operation is shown in Algorithm 2.

The following are the specific steps of multi-core groups collaborative optimization:

Divide CPE Groups: When executing tasks with multiple CPEs, the CPEs are divided into small groups, with each group consisting of four CPEs, logically numbered as 0, 1, 2, and 3. Contiguous shared space of LDM is allocated to each group. After computation, each CPE stores its results in this shared space.

Third-Level Aggregation: Designate the CPE with logical number 0 in each group as the “Third-Level Aggregation CPE”. This CPE collects computation results of other CPEs directly from the shared LDM space within the group, avoiding resource contention and reducing data transfer overhead.

Second-Level Aggregation: Within each core group, designate the CPE numbered 0 as the “Second-Level Aggregation CPE”. This CPE gathers results from all third-level aggregation CPE within the same core group. The specific operation involves third-level aggregation CPE sending their results to the second-level aggregation CPE via RMA.

First-Level Aggregation: Designate the CPE numbered 0 of core group 0 as the “First-Level Aggregation CPE.” This CPE collects results from all second-level aggregation CPE across different core groups and performs the final aggregation.

Return Results to Main Memory: The first-level aggregation CPE sends the final aggregated results back to main memory via DMA, achieving efficient storage of computational results.

In this process, each small group of CPEs utilizes shared LDM space, effectively avoiding excessive RMA communications and thereby improving intra-group data transfer efficiency. Through the three-level, two-level, and one-level aggregation mechanisms, data is progressively collected from local to global levels, significantly reducing the frequency of direct transmissions to the MPE, Which in turn lowers communication overhead and improves overall computational efficiency.

5  Performance Analysis

5.1 Configuration

Based on the Sunway Bluelight II supercomputer, this paper evaluates the optimization efficiency of the SW-DDFT. Table 1 lists the specific configurations used for the evaluation. To assess the program’s performance under different mesh points, the external field conditions are set to three initial states and defined as three mesh points: small mesh point (16 × 16 × 16), medium mesh point (32 × 32 × 32), and large mesh point (64 × 64 × 64). In the following experiments, the small, medium, and large mesh point scales all follow the default mesh point scale. In the multi-core groups, the mesh point scales have been redefined.

5.2 Performance Testing of Optimization

This section is divided into three parts. First, the program is tested with different numbers of CPEs, and the specific number of CPEs to be used for subsequent optimization is determined. Then, tests the execution times of three optimizing strategies on the Sunway Bluelight II supercomputer. Based on the test results, the speedup of the parallelized program compared to the original implementation is calculated. The original program here refers to the initial implementation of the SW-DDFT program, which performs calculations only on the MPE. By comparing the speedup, the performance improvement of the parallel optimization strategies can be directly reflected. Finally, the changes in hotspots before and after optimization are analyzed.

5.2.1 Analysis of Speedup with Different Number of CPEs

To perform the optimization of CPEs, first, it is necessary to determine the number of CPEs to be used. Since all optimizations are improved on the basis of direct parallel optimization, we use direct parallel optimization as a test method here. Then, runtime and speedup under different numbers of CPEs will be compared and analyzed to determine the most suitable number of CPEs.

Experimental results at different mesh points are shown in Fig. 8. With the increase of the number of CPEs, the running time of the program under the three mesh points is gradually shortened, and the speedup is also continuously improved.

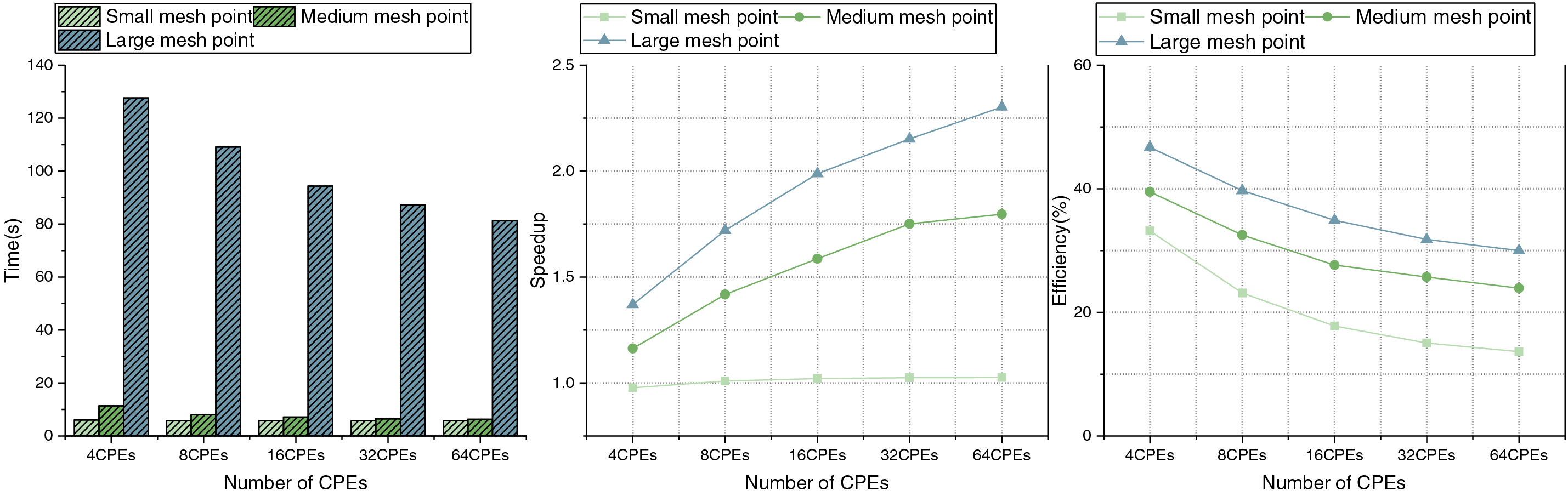
Figure 8: Running time, speedup and efficiency at different mesh points

At the same time, we conduct a weak scalability test, by using the parallel efficiency of 4 CPEs as the baseline, the details are shown in Fig. 9. In the weak scalability test, since different numbers of CPEs require testing mesh points of different scales, we set up the multiple simulation regions with N = 1, 2, 4, 8, 16 and test three different mesh points. During the simulation, the number of mesh points executed for different numbers of CPEs is the product of the mesh point scale and N.

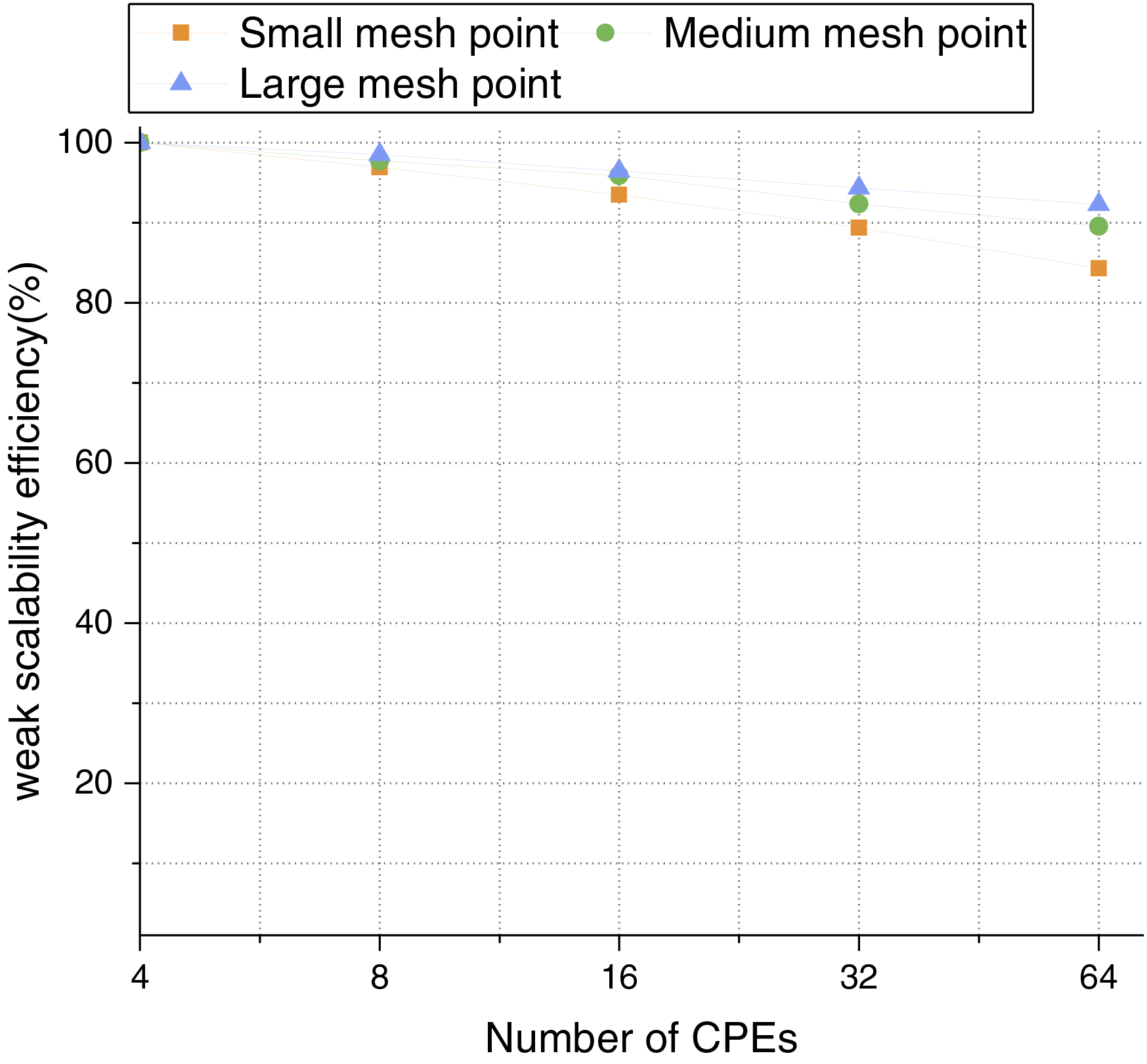
Figure 9: Weak scalability testing at different mesh points

Based on the experimental results, in order to balance the performance and resource utilization efficiency, 64 CPEs are selected to accelerate the three optimization strategies, so as to obtain the best computational efficiency.

5.2.2 Effect Analysis of Three Optimizing Strategies

Based on the analysis in the previous section, we conclude that the highest acceleration efficiency is achieved by using 64 CPEs. Therefore, subsequent optimizations will be based on direct parallel optimization, utilizing 64 CPEs for acceleration.

In the single-core group experiment, the first optimization strategy is direct parallel optimization, defined as Level 1 optimization. The speedup can reach up to 2.23 times at different mesh points. The second optimization strategy is local-memory constrained optimization for CPEs, superimposing the first optimization strategy, defined as Level 2 optimization. Under different mesh points, the speedup can reach up to 3.96 times. The third optimization strategy is multi-core groups collaboration and communication optimization, superimposing the first and second strategies, defined as Level 3 optimization. Under different mesh points, the speedup can reach up to 6.67 times.

The corresponding relationship between each optimization level and the optimization strategy used is shown in Table 2.

At the three mesh points, the running time and speedup corresponding to different optimization strategies are shown in Fig. 10. With the gradual superposition of the optimization strategies, the running time of the program is significantly reduced at all mesh points. In small mesh point cases, due to the small amount of calculation, the improvement of the speedup is relatively insignificant. With the increase of the mesh points, the calculation amount increases, and the speedup increases more significantly.

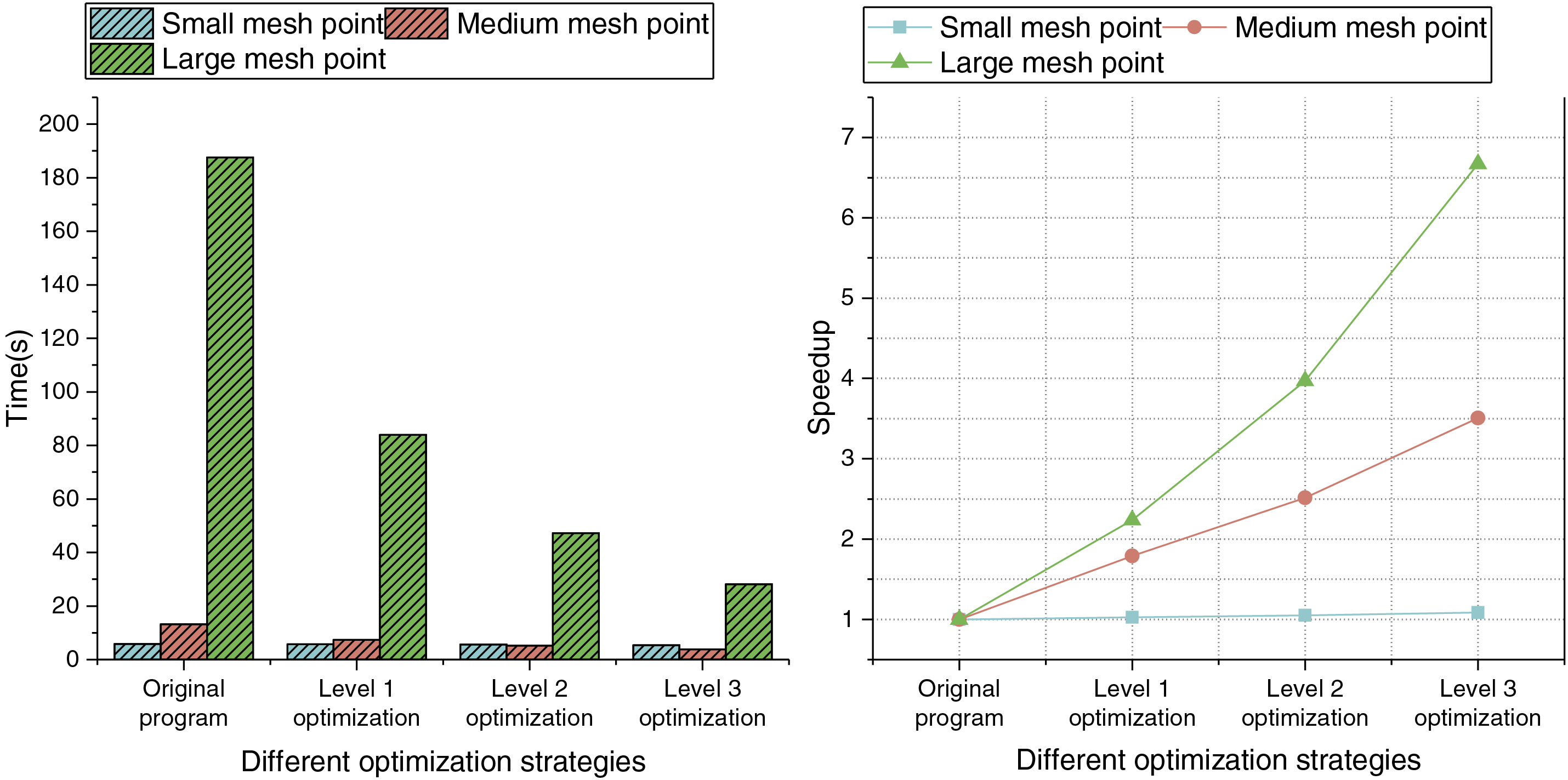
Figure 10: Running time and speedup at different mesh points and 64 CPEs

In the multi-core groups experiment, we conduct tests on core groups of 1, 2, 3, 4, 5, and 6. We designate the three grid sizes of 64 × 64 × 64, 128 × 128 × 128, and 256 × 256 × 256 as small mesh point, medium mesh point, and large mesh point, respectively. The speedup and execution efficiency are evaluated across different core groups and grid sizes. With six core groups (a total of 384 CPEs), the maximum speedup can reach 28.64 times, and parallel efficiency can reach 71%. The details are shown in the Fig. 11.

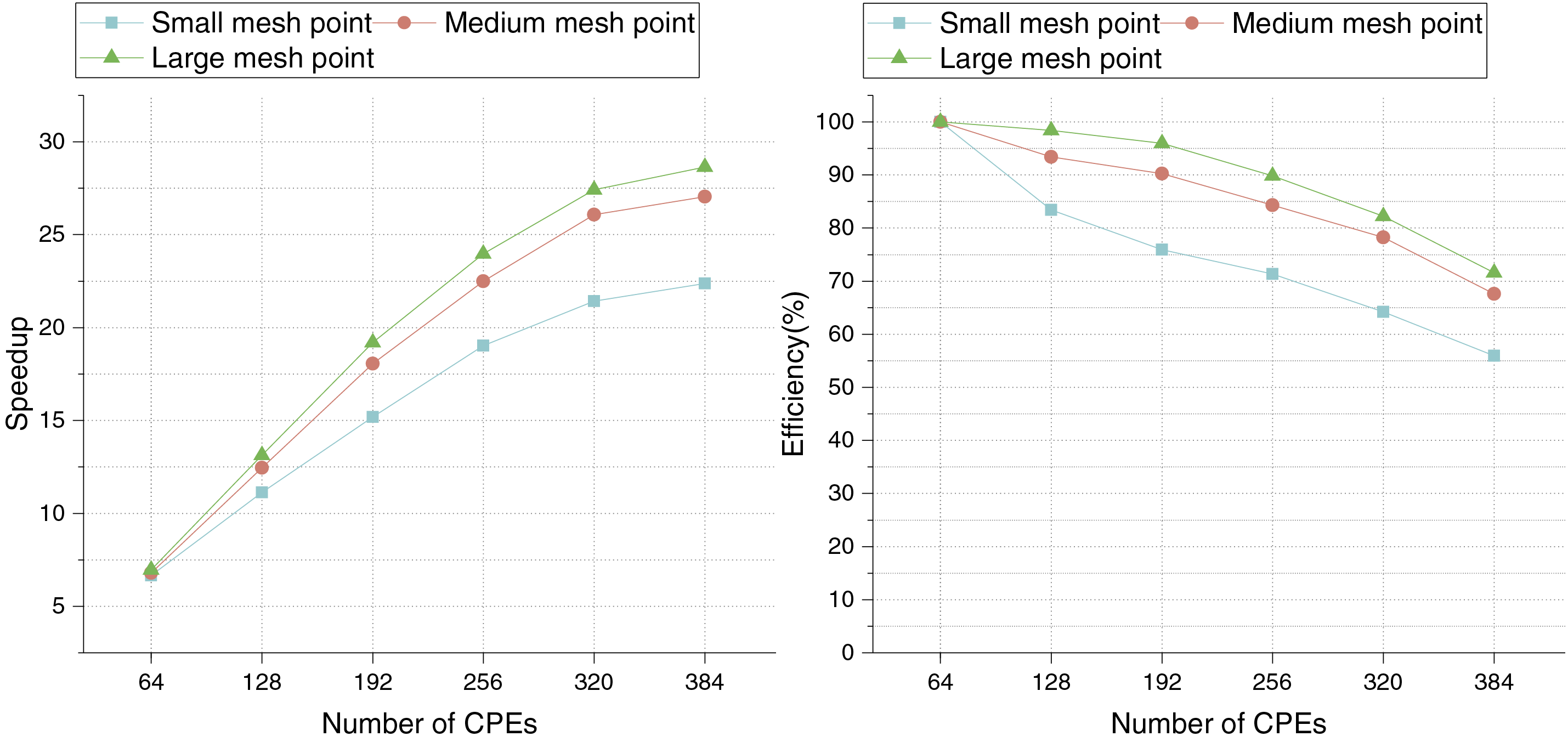
Figure 11: Speedup and execution efficiency in six core groups

From the above experimental results, it can be seen that under different mesh points, the three parallel optimization strategies proposed in this paper can significantly improve the running efficiency of the program. And with the increase of the mesh points, the acceleration effect becomes more obvious.

In the direct parallel optimization solution, CPEs access data from the main memory via DMA or shared LDM space DMA, storing it in private LDM to improve access speed. Tasks are then distributed to the CPEs for execution. In the solution of local-memory constrained optimization for CPEs, the loop dependency issue is resolved, and a hash table is constructed to reduce memory usage, enabling better utilization of the LDM space on CPEs, which significantly improves execution efficiency. In the solution of multi-core groups collaboration and communication optimization, the use of more CPEs and the optimization of intra-core and inter-core group communication further improve overall computational performance and efficiency.

5.2.3 Results of Parallel Optimization

With the optimization of the program, the hotspots of the program changed. We tested the execution time of each part before and after optimization and obtained the change of the proportion of each part as shown in Fig. 12:

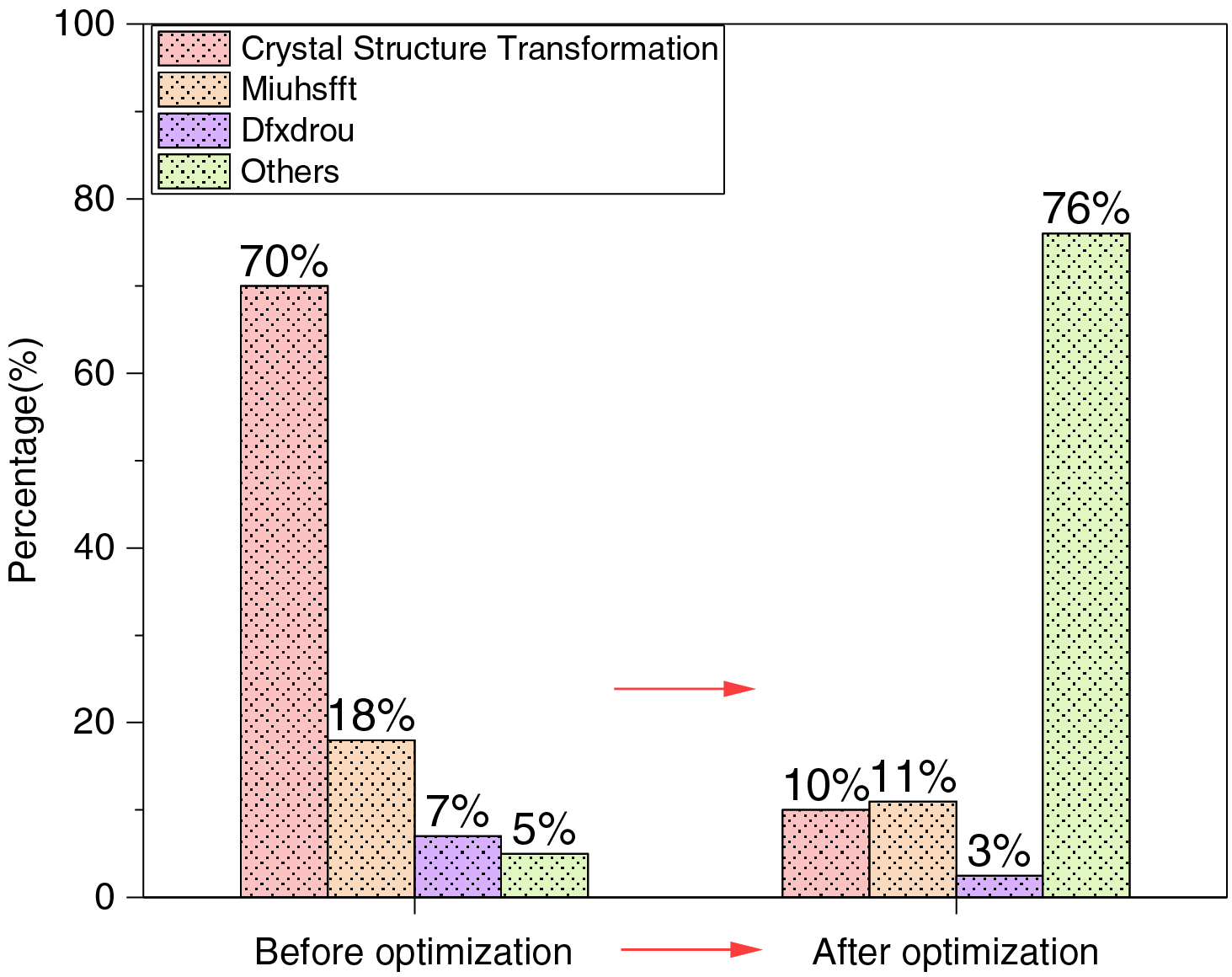
Figure 12: Hotspot function change diagram

The percentages in the figure represent the proportional contribution of different functions to the total program execution time, as measured through profiling. The percentage changes observed indicate that the optimizations applied to the hotspot functions effectively reduce their relative computational weight in the overall workload.

“Others” functions are the scattered functions with low computational complexity. This scattered piece of code mainly iterates over all mesh points and performs a series of calculations for each mesh point. Most of these functions have been optimized. However, some parts with low computational complexity are not optimized, because the efficiency after optimization is not high. We port these parts into the Sunway supercomputer, which requires migrating the computation code to CPEs and then fetching data and allocating computation on the CPEs.

It can be seen from the test results that the acceleration effect of Crystal Structure Transformation function is obvious, Miuhsfft, Dfxdrou also have a certain acceleration effect.

6  Related Work

For supercooled liquid crystallization, Ramakrishnan, Yussouff, Singh, Evans, Oxtoby, et al. and Löwen developed a DFT model to describe the crystal-liquid phase interface. References [10,11] showcase recent advances in DFT-related research, reference [10] uses DFT to calculate the electronic properties of molecules, reference [11] employs DFT to evaluate the activity of three investigated molecules. This model uses a uniform fluid as a reference and performs a perturbation expansion of the functional. In this theoretical model, the crystal phase is considered as a perturbation to the liquid phase. By associating classical DFT with the fundamental Smoluchowski dynamical equation, DDFT is obtained. DDFT can describe the evolution of the inhomogeneous fluid density distribution over time, thereby linking the density distribution, free energy functional, and time within the system.

The DDFT model was proposed by Evans [7] and Dieterich et al. [8], based on the dynamical equation. By ensemble averaging the noise term, it approximates the equilibrium density distribution under a certain external field as the density distribution at a certain time in the system. The establishment of DDFT extends the research from equilibrium states to non-equilibrium processes, making it highly significant for studying the evolution of density distributions over time in inhomogeneous systems. Löwen and others applied DDFT to investigate the nucleation and growth processes of simple crystals in both homogeneous and inhomogeneous systems [9].

Research based on the Sunway series supercomputers has achieved remarkable results in various fields in recent years. Among these, three projects have won the Gordon Bell Prize. Reference [12] successfully ported the full Community Atmosphere Model (CAM) to the “Sunway TaihuLight,” achieving a sustainable double-precision performance of 3.3 PFLOPS using 10,075,000 cores, with the work expanding to over 10 million cores. Reference [13] implemented a highly scalable nonlinear earthquake simulation tool on the “Sunway TaihuLight” supercomputer. Reference [14] realized a tensor-based random quantum simulation circuit on the new generation Sunway supercomputer, completing the simulation sampling work in 304 s.

In addition, the Sunway series supercomputers have made significant contributions in other areas [15–19]. Reference [15] developed brain simulation software SWsnn on the “Sunway TaihuLight”, successfully achieving real-time biological simulation of a 104-neuron fully connected network. Reference [16] extended TVM to the “Sunway TaihuLight.” Using the code generated by swTVM, an average performance improvement of 1.79 times was achieved compared to the most advanced deep learning framework, swCaffe, on the Sunway.

In summary, there are many projects based on the Sunway supercomputers, and there are also many DDFT studies. However, research on the porting and optimization of DDFT on the Sunway Bluelight II supercomputer remains relatively scarce. Therefore, conducting parallel optimization research on DDFT on the Sunway Bluelight II supercomputer is of great significance. The SW-DDFT proposed in this paper not only meets the requirements for numerical simulations on the Sunway supercomputer in terms of speed and accuracy, but also enriches the application ecosystem of the Sunway supercomputer.

7  Conclusion

This paper implements a parallel optimization program called SW-DDFT based on the Sunway Bluelight II supercomputer. For the parallel optimization of SW-DDFT, we propose three acceleration strategies: direct parallel optimization, local-memory constrained optimization for CPEs, and multi-core groups collaboration and communication optimization. Experimental results show that compared to the original DDFT implementation, the SW-DDFT program achieves a speedup of 6.67 times within a single-core group, with six core groups (a total of 384 CPEs), the maximum speedup can reach 28.64 times, and parallel efficiency can reach 71%.

Acknowledgement: I express my sincere gratitude to all individuals who have contributed to this paper. Special thanks to my advisor, Prof. Tao Liu, for his meticulous and patient guidance throughout the entire research process.

Funding Statement: This work is supported by National Key Research and Development Program of China under Grant 2024YFE0210800, National Natural Science Foundation of China under Grant 62495062, and Beijing Natural Science Foundation under Grant L242017.

Author Contributions: Write the main manuscript text and do most of the experiments, Xiaoguang Lv and Tao Liu; Provide software and software compilation, Han Qin; Provide assistance with the use of the Sunway Bluelight II supercomputer, Ying Guo and Jingshan Pan; supervision, Dawei Zhao, Xiaoming Wu and Meihong Yang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data used to support the findings of this study are available from the corresponding author upon request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Hou Y. Dynamic density functional theory study on the kinetics of lattice formation and growth in polymer nanocomposite systems [dissertation]. Beijing, China: Beijing University of Chemical Technology; 2018. doi:10.7666/d.Y3389850. [Google Scholar] [CrossRef]

2. Gao K. Molecular dynamics simulation study on interface design of polymer nanocomposite mazterials [dissertation]. Beijing, China: Beijing University of Chemical Technology; 2022. doi:10.26939/d.cnki.gbhgu.2022.000117. [Google Scholar] [CrossRef]

3. Thomas LH. The calculation of atomic fields. Math Proc Camb Philos Soc. 1927;23(5):542–8. doi:10.1017/S0305004100011683. [Google Scholar] [CrossRef]

4. Fermi E. Eine statistische Methode zur Bestimmung einiger Eigenschaften des Atoms und ihre Anwendung auf die Theorie des periodischen Systems der Elemente. Z Phys. 1928;48(1):73–9. doi:10.1007/BF01351576. [Google Scholar] [CrossRef]

5. Ebner C, Saam WF. New phase-transition phenomena in thin argon films. Phys Rev Lett. 1977;38(25):1486–9. doi:10.1103/PhysRevLett.38.1486. [Google Scholar] [CrossRef]

6. Yang AJM, Fleming PD, Gibbs JH. Molecular theory of surface tension. J Chem Phys. 1976;64(9):3732–47. doi:10.1063/1.432687. [Google Scholar] [CrossRef]

7. Evans R. The nature of the liquid-vapour interface and other topics in the statistical mechanics of non-uniform, classical fluids. Adv Phys. 1979;28(2):143–200. doi:10.1080/00018737900101365. [Google Scholar] [CrossRef]

8. Dieterich W, Frisch HL, Majhofer A. Nonlinear diffusion and density functional theory. Z Phys B Condens Matter. 1990;78(2):317–23. doi:10.1007/BF01307852. [Google Scholar] [CrossRef]

9. Löwen H. Melting, freezing and colloidal suspensions. Phys Rep. 1994;237(5):249–324. doi:10.1016/0370-1573(94)90017-5. [Google Scholar] [CrossRef]

10. Chaithra N, Swarup HA, Chandrasekhar S, Jayanna BK, Kumara K, Mantelingu K, et al. Regioselective benzylation of imidazo [1, 5-a] pyridines and indoles via iodine catalyzed reaction using alcohols—an approach to crystal structure prediction, DFT studies and Hirshfeld surface analysis. J Mol Struct. 2024;1295(1):136591. doi:10.1016/j.molstruc.2023.136591. [Google Scholar] [CrossRef]

11. Al Ati G, Chkirate K, El-Guourrami O, Chakchak H, Tüzün B, Mague JT, et al. Schiff base compounds constructed from pyrazole-acetamide: synthesis, spectroscopic characterization, crystal structure, DFT, molecular docking and antioxidant activity. J Mol Struct. 2024;1295(7):136637. doi:10.1016/j.molstruc.2023.136637. [Google Scholar] [CrossRef]

12. Fu H, Liao J, Ding N, Duan X, Gan L, Liang Y, et al. Redesigning CAM-SE for peta-scale climate modeling performance and ultra-high resolution on Sunway TaihuLight. In: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis; 2017; Denver, CO, USA. p. 1–12. doi:10.1145/3126908.3126909. [Google Scholar] [CrossRef]

13. Fu H, He C, Chen B, Yin Z, Zhang Z, Zhang W, et al. 18.9-Pflops nonlinear earthquake simulation on Sunway TaihuLight: enabling depiction of 18-Hz and 8-meter scenarios. In: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis; 2017; Denver, CO, USA. p. 1–12. doi:10.1145/3126908.3126910. [Google Scholar] [CrossRef]

14. Lin H, Zhu X, Yu B, Tang X, Xue W, Chen W, et al. Shentu: processing multi-trillion edge graphs on millions of cores in seconds. In: SC18: International Conference for High Performance Computing, Networking, Storage and Analysis. Dallas, TX, USA: IEEE; 2018. p. 706–16. doi:10.1109/SC.2018.00059. [Google Scholar] [CrossRef]

15. Li X, Zhu X, Wei Y, Feng S. Application of Sunway TaihuLight accelerated computing in brain neural network simulation. Chin J Comput. 2020;43(6):1025. doi:10.11897/SP.J.1016.2020.01025. [Google Scholar] [CrossRef]

16. Li M, Liu C, Liao J, Zheng X, Yang H, Sun R, et al. Towards optimized tensor code generation for deep learning on Sunway many-core processor. Front Comput Sci. 2024;18(2):182101. doi:10.1007/s11704-022-2440-7. [Google Scholar] [CrossRef]

17. Li F, Liu X, Liu Y, Zhao P, Yang Y, Shang H, et al. SW_Qsim: a minimize-memory quantum simulator with high-performance on a new Sunway supercomputer. In: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis; 2021; St. Louis, MO, USA. p. 1–13. doi:10.1145/3458817.3476161. [Google Scholar] [CrossRef]

18. Hao X, Fang T, Chen J, Gu J, Feng J, An H, et al. Swmpas-a: scaling MPAS-A to 39 million heterogeneous cores on the new generation Sunway supercomputer. IEEE Trans Parallel Distrib Syst. 2022;34(1):141–53. doi:10.1109/TPDS.2022.3215002. [Google Scholar] [CrossRef]

19. Ma Z, He J, Qiu J, Cao H, Wang Y, Sun Z, et al. BaGuaLu: targeting brain scale pretrained models with over 37 million cores. In: Proceedings of the 27th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming; 2022; Seoul, Republic of Korea. p. 192–204. doi:10.1145/3503221.3508417. [Google Scholar] [CrossRef]