TGI-FPR: An Improved Multi-Label Password Guessing Model

1  Introduction

Password-based authentication remains a critical component in cybersecurity [1]. However, password security relies on heuristic methods that often lack strong theoretical support. Historically, research in this field has reached a mature phase, with advanced algorithms that adhere to rigorous probabilistic models. The introduction of Markov models [2] and Probabilistic Context-Free Grammars (PCFG) [3,4] has significantly propelled password-guessing algorithms [5–8]. In response to pressing password security concerns, Huang et al. [9] proposed a user authentication scheme that avoids preset passwords by utilizing instant messaging services, effectively reducing phishing vulnerabilities. These theories and techniques enable more precise password-guessing methods, especially in the context of large-scale personal information breaches, which adds to the increasing importance of research in this field. In recent years, the security research community has shown great concern for these leakage events [10–12]. Emerging trends include the development of targeted password-guessing algorithms that use individuals’ Personally Identifiable Information (PII) to predict possible passwords [13–15].

Das et al. [15] highlighted the risk of password reuse and introduced the concept of a cross-site cracking algorithm. However, this algorithm did not account for common passwords, leading to sub-optimal performance. Li et al. [14] explored the impact of PII on password security and suggested a personalized PCFG model that matches and replaces PII based on length. Although this approach affected the effectiveness of the cracking process, it lacked precision in gathering the PII usage of users. Wang et al. [13] pioneered a password-guessing framework, TarGuss, which integrates a category-specific, PII-aware PCFG and detects password reuse behavior, and this model achieves improved performance compared to previous cracking algorithms. These studies have advanced password security research [16–18] and have influenced updates to the NIST SP800-63-3 standard [19].

In the realm of password guessing, contemporary research predominantly centers on algorithmic development, often neglecting systematic discussions on the efficacy of these algorithms across varying scenarios. Machine learning-based guessing algorithms, such as FLA, constrained by the rate of password generation, are more aptly suited for application as password strength meters (PSMs). Conversely, statistical guessing algorithms like PCFG, while faster in generation, frequently encounter performance bottlenecks under extensive guess counts due to their reliance on training datasets. Moreover, in practical scenarios, attackers might employ diverse tactics for password guessing, making the selection of the most efficient algorithm under fixed computational resources a topic worthy of thorough exploration.

Password guessing has recently emerged as a research hotspot, yielding a plethora of scholarly contributions. In 2022, Li et al. [20] introduced a targeted password guessing model, PG-Pass, which treats directed password guessing as a summarization task. By employing pointer network technology, this model has pioneered new methodologies and perspectives in the field of directed password guessing. In the same year, He et al. [21] unveiled PassTrans, a transformer-based model designed to simulate credential stuffing attacks. This model, tailored around user behaviors of reusing or slightly altering old passwords to create new ones, offers fresh insights into the patterns of password reuse and the security risks inherent in such scenarios. In 2023, Wang et al. [17] developed RFGuess, a framework based on random forests that delineates three typical password guessing scenarios, thus enriching the methodological spectrum of password guessing research. Concurrently, Xu et al. [16] proposed PassBERT, a bi-directional Transformers framework that marks the inaugural application of pre-training to password cracking. By designing a universal password pre-training model and proposing three fine-tuning approaches tailored to different attack scenarios, this framework also introduced a hybrid password strength detector, thereby charting new technical directions and conceptual approaches for password guessing attacks and defense research. In 2024, Su et al. [22] introduced a password guessing model, PagPassGPT, constructed using a generative pre-trained Transformer (GPT), and a password generation algorithm, D&C-GEN. Demonstrating superior performance in both trawling and cross-site guessing scenarios, these developments achieve higher hit rates with lower repetition.

In selecting TarGuess-I as the baseline for our study, we focused on its unique approach of leveraging personally identifiable information (PII) for targeted password guessing. This method is particularly relevant in real-world scenarios where attackers often have access to some user PII, thus providing a practical and significant benchmark for comparison. Despite the emergence of newer models, TarGuess-I’s incorporation of PII remains critical for understanding how such information can enhance the effectiveness of password guessing strategies. Additionally, grammar-based models like TarGuess-I offer advantages in terms of interpretability and resource efficiency. These models allow for clearer insights into the password generation process, crucial in security applications where understanding model decisions is necessary. They also require significantly less computational power and data, making them suitable for environments with resource limitations. While newer neural network approaches are promising due to their ability to capture complex patterns, the foundational attributes of TarGuess-I ensure its continued relevance in comparative studies, providing a baseline that complements the more recent data-driven techniques.

The TarGuess framework was developed to address password guessing issues, with four models (TarGuess-I to IV) created to respond to different attack scenarios by analyzing vulnerable user behaviors. In TarGuess-I, attackers exploit users’ explicit PII, such as names, birthdays, and phone numbers—readily accessible on the internet for password construction [13,23]. Additionally, the other three models cater to attack needs, involving either users’ implicit PII (like gender and profession) or information leaked from other accounts, including ‘sister’ passwords leaked from other user accounts. This study primarily focuses on TarGuess-I, whose practical application and impact have become increasingly significant with the rising occurrences of PII leakage.

Wang et al. noted that the TarGuess-I model excels in password cracking by leveraging users’ PII, and it achieves a success rate of over 20% within 100 attempts [13]. In recent years, improving the performance of password-guessing models has emerged as a key research focus [24]. Through an analysis of user behavior in constructing passwords based on the TarGuess-I model, we found some limitations of the model. Accordingly, we made three improvements to the TarGuess-I model and verified their feasibility through experiments. Based on these enhancements, we propose a novel model, TGI-FPR (where TGI abbreviates TarGuess-I, and the FPR represents three specific labels), which integrates three semantic methods. Performance evaluations show that the TGI-FPR model achieves a 2.65% improvement in success rate compared to the original model, which demonstrates the feasibility of these improvements.

The main contributions of this work are as follows:

Modified Password Guessing Model

By analyzing the vulnerable password-creation behaviors of users in 158,483,166 publicly leaked data records based on TarGuess-I, we identified effective semantic tags previously unverified and unused in TarGuess-I. To address this gap, we utilized the adaptability of the TarGuess-I’s PII tags and defined two new tags: Popular Password Tag P and Frequent Substring Tag F. We further subdivided the original six categories of personal information and set matching priorities for each subcategory to prevent data duplication. This led to a derivative of TarGuess-I, named TGI-FPR.

A New Insight

We propose a novel method for modifying password guessing models: passwords are parsed into frequent substring ‘F-tags’, such as fragments of a user’s name or birthday. These pieces of information do not appear in the user’s PII. This method incorporates incremental information or enhances the model’s recognition of personally generated identifiers (such as name and birthday fragments). This method offers new insights into targeted password guessing.

Extensive Evaluation

To validate the effectiveness of these tags, we conducted experiments using six substantial datasets from actual leaks. The experimental results demonstrate that our single-tag enhanced model outperforms TarGuess-I by 0.72% in the best case and 0.32% on average with the first 100 guesses. Among the ten models tested, our modified model, TGI-FPR, performed the best. With the same PII as TarGuess-I, TGI-FPR effectively cracked passwords with a 21.1% success rate within 100 guesses, exceeding TarGuess-I by 2.65%.

The remaining sections of this paper are organized as follows: Section 2 elaborates on the vulnerable behaviors of users when setting passwords and reviews the current research on targeted password guessing; Section 3 describes the preparatory work, including datasets used and an in-depth analysis of user-vulnerable password creation behaviors; Section 4 introduces our model in detail; Section 5 presents the experimental results and provides a detailed analysis. Section 6 concludes the study and outlines directions for future research.

2  Related Work

TarGuess utilizes PII for targeted guessing based on PCFG. This section discusses vulnerable user behaviors and provides a brief overview of the PCFG-based algorithm and the TarGuess-I model.

2.1 Explanation of User Vulnerable Behaviors

Since the initial exploration of user password security behaviors in 1979, the impact of user-vulnerable behaviors on password traceability has become a focal point in information security research. Current studies on this subject generally fall into two main categories: data-based analysis and user surveys. The former [2,9,11,25,26] examines user behaviors through empirical data, revealing behavioral vulnerabilities, while the latter [15,27–30] delves into security risks in user password settings through survey studies. Overall, user-vulnerable behaviors can be grouped into three primary categories.

Popular Passwords. Extensive research [2,9] indicates that users often opt for simple combinations of words or symbols as passwords. To meet password policy requirements (e.g., including letters and numbers), users often employ simple transformations, such as using “Password1.” We define such commonly used and simple passwords as “popular passwords.” Wang et al. [31] have found that popular passwords follow a Zipf distribution, which demonstrates that a few items dominate.

Password Reuse. Research by Stobert and Biddle [30] reveals users’ challenges in managing numerous accounts and passwords. The complexity of multiple passwords can make them difficult to remember, especially as it is easy to reuse a single login credential across accounts. Research has found that users typically maintain over 20 accounts, making it difficult to set unique passwords for each. Consequently, password reuse has become commonplace, and although seemingly reasonable, it poses security risks by compromising account security. The research emphasizes effective and secure strategies for password reuse to mitigate these potential risks.

Passwords Containing PII. Research by Wang et al. [32] indicates that Chinese users tend to incorporate pinyin names and related numbers (e.g., phone numbers and birthdays) into their passwords, in stark contrast to the password construction habits of English-speaking. Furthermore, the research reveals that native language significantly impacts password construction, with linguistic habits potentially affecting password security considerably. Generally, Chinese users regard personal information (e.g., names, phone numbers, and birthdays) as components of their passwords, increasing the risk to their potential security when protecting personal information. Given that TarGuess-I is suitable for Scenario #1, this study focuses on two types of vulnerable passwords: popular passwords and passwords containing personal information.

2.2 PCFG-Based Password Guessing Algorithm

Weir et al.’s foundational PCFG algorithm [4] has proven tremendous success in batch-guessing scenarios [13]. In this algorithm, the probabilistic context-free grammar (PCFG) is defined as G=(V,Σ,S,R), where:

(1) V is a finite set of non-terminal symbols;

(2) Σ is a finite set of terminal symbols;

(3) S is the set of start symbols, and S∈V;

(4) R is a finite set of rules of the form α→β, where α∈V and β∈V∪Σ.

The core assumption of the algorithm is that the letter, number, and symbol segments in a password are independent. The algorithm defines a set of tags that parse the password into segments of letters (L), numbers (D), and symbols (S). These segments are further subdivided in the set V, excluding the start symbol S, into length-based types of tag sets, e.g., Ln,Dn, and Sn, where n indicates the length of the segment. During the training phase, the algorithm counts the frequency of segments within each tag set and generates a context-free grammar G. In the guessing generation phase, the algorithm derives passwords using grammar G and a statistically obtained segment frequency table. The generation of candidate passwords relies on the product of probabilities of segment frequencies. The final guess of candidate passwords is determined by ranking these probabilities, multiplied by the frequencies of the middle segments of all passwords, as shown in Fig. 1.

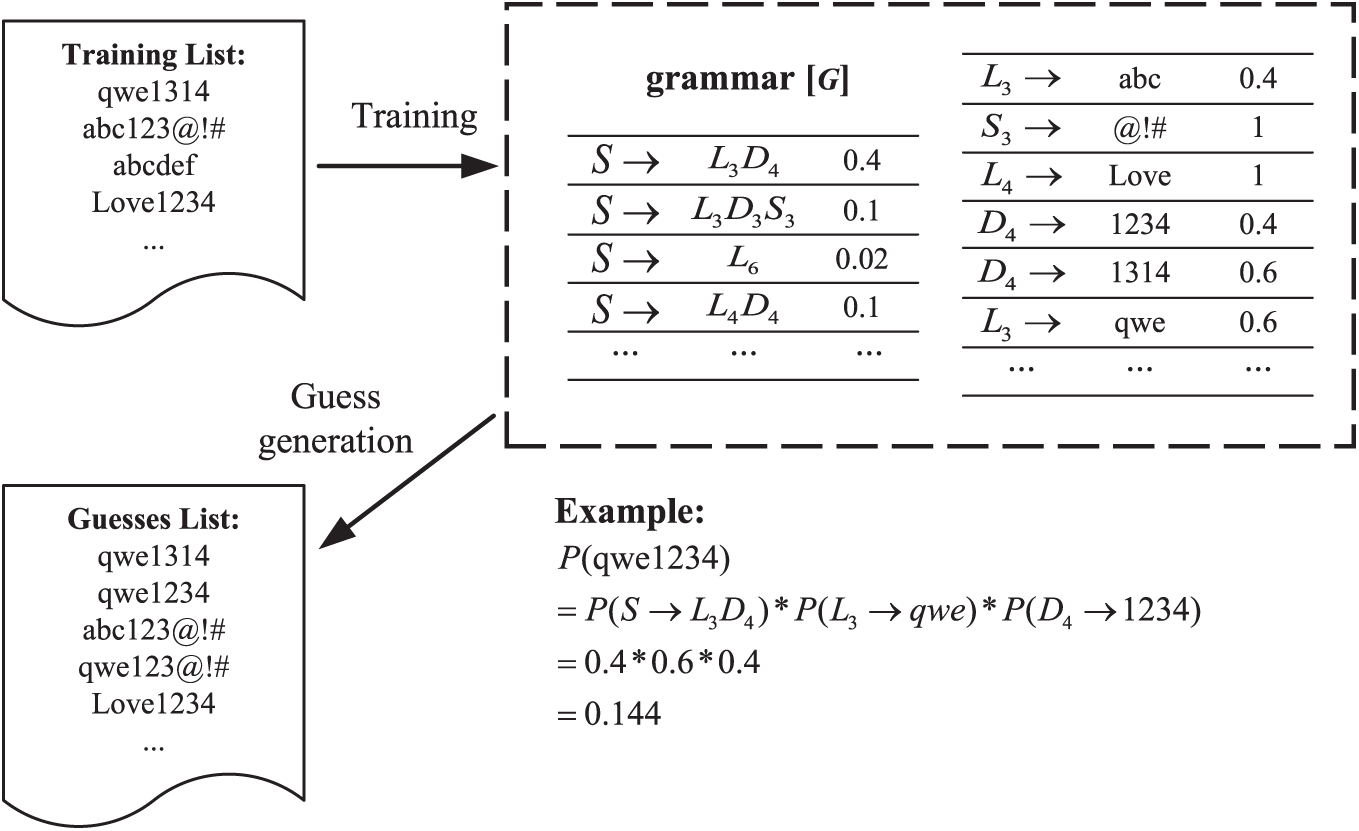
Figure 1: Schematic diagram of the PCFGs model

The algorithm is divided into two phases. In the training phase, the frequency of segments within each tag set is counted to generate a context-free grammar G. In the guessing generation phase, the algorithm utilizes grammar G and the statistically derived segment frequency table to generate candidate passwords. The generation of these candidate passwords depends on the product of the probabilities of segment frequencies. The final guessed candidate passwords are ranked based on the probability obtained by multiplying the frequencies of the middle segments of all passwords.

2.3 TarGuess-I Model

Wang et al. introduced the TarGuess-I model, which constructs a semantically aware PCFG based on type-specific PII tags [13]. This model enhances the basic labels in traditional PCFG, LDS, by adding six new tags: Name (Nn), Username (Un), Birthday (Bn), Telephone Number (Tn), Identity Card (In), and Email Address (En). Each PII tag is assigned a specific index number, n, which represents different generation rules. For example, N1 refers to the full name, while N2 refers to the abbreviated form of the full name (e.g., “Wang Lili” abbreviated as “wll”). For more details, see Fig. 2. This structure allows the model’s grammar GI to demonstrate high adaptability, allowing adjustments through the addition of incremental tags without altering its overall structure.

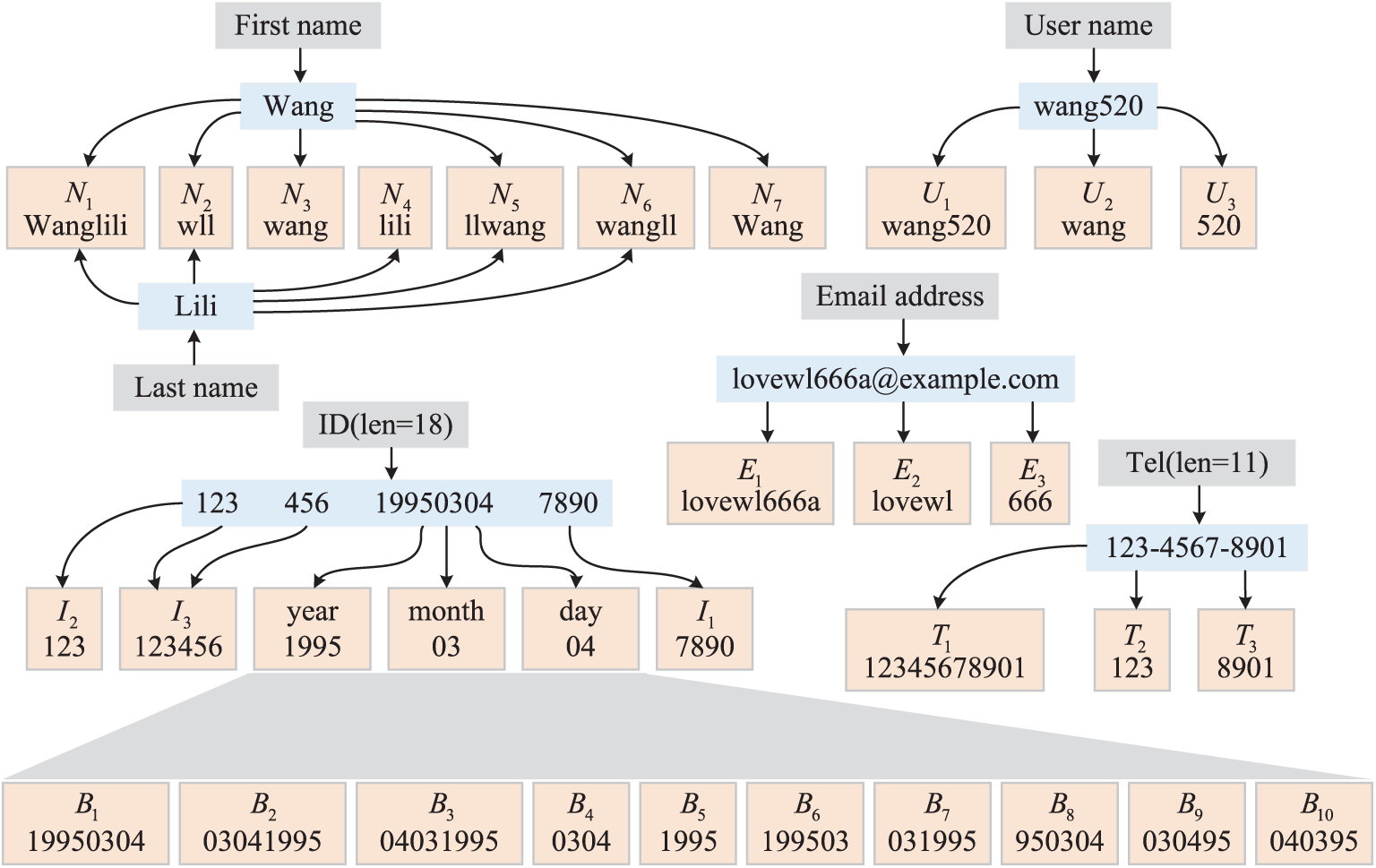
Figure 2: Schematic of PII label generation for TarGuess-I

As shown in Fig. 3, a segment frequency table is created for each user based on their PII data, classifying and tallying the frequency of PII labels. During the training phase, the PII-related components of the credentials are parsed and marked with PII labels. In contrast, the remaining parts are marked with LDS labels, separating sensitive from non-sensitive information. In the guessing phase, an algorithm similar to PCFG is used to generate intermediate candidate password forms based on PII labels, e.g., N1B8 or N1 abcd. After matching the corresponding segments in the user’s PII data, these candidates are added to the final guessing options.

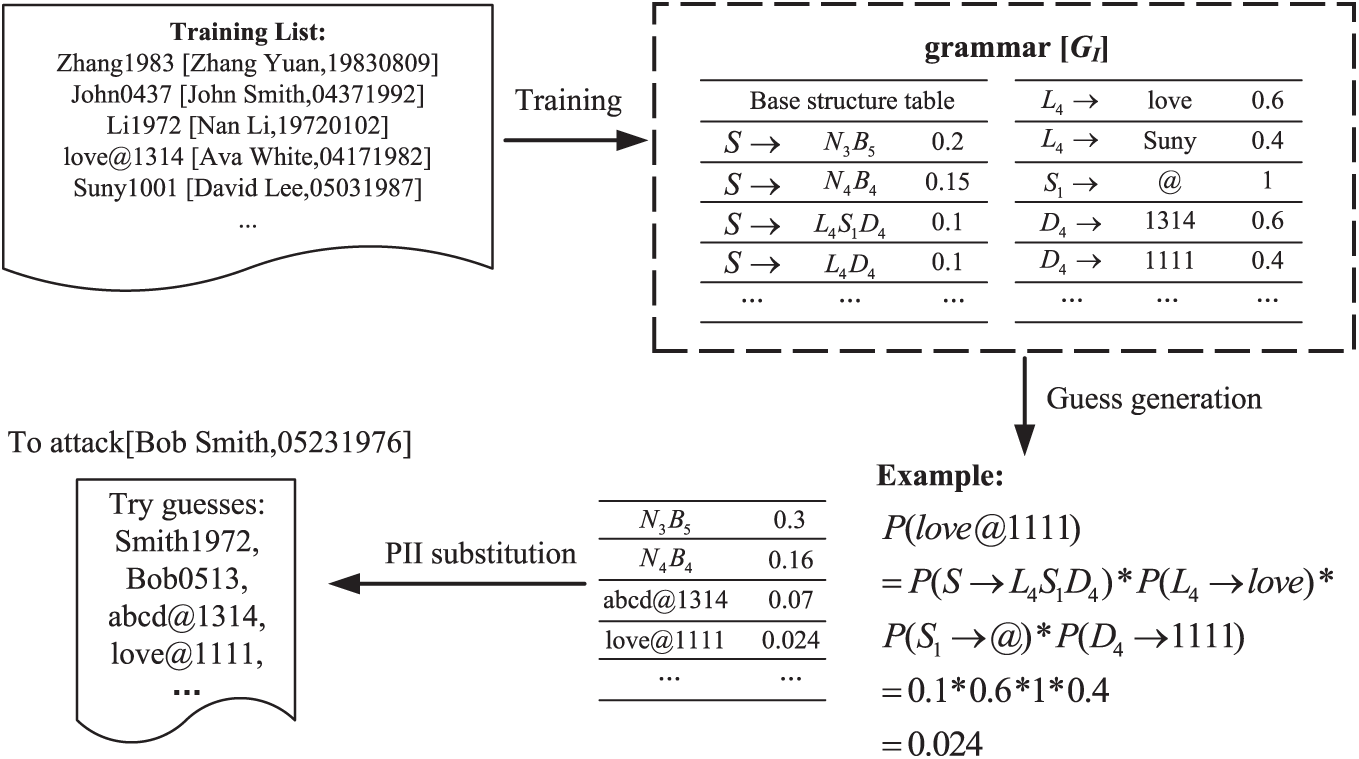
Figure 3: Schematic of TarGuess-I

3  Preliminary Work

In this section, we analyze compromised datasets to reveal vulnerabilities in the password settings of Chinese users and propose optimization strategies for the TarGuess-I model. This approach can also be applied to languages with similar structures, such as Korean and Japanese, where personal name formats share similarities with Chinese, allowing for broader applicability of the model in these linguistic contexts.

3.1 Basic Dataset

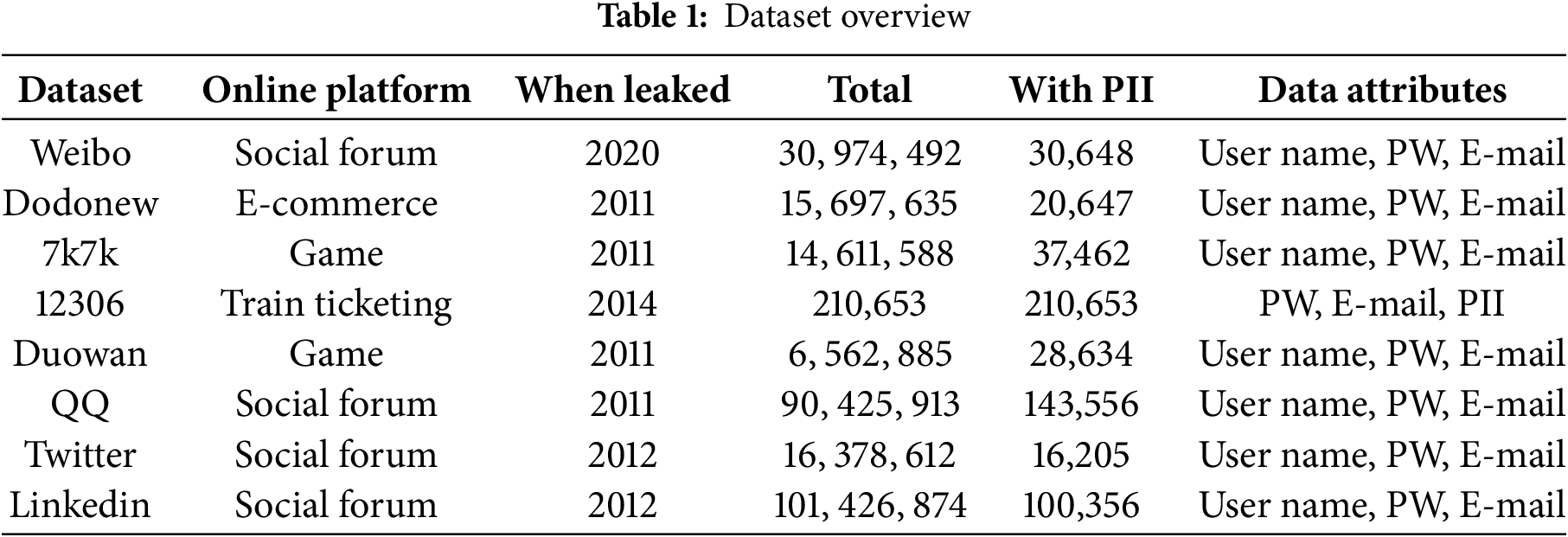
We analyzed 158,483,166 user password data leaked from six websites. These data primarily originate from hacker attacks or insider leaks that have been publicly released online. Due to the lack of datasets containing complete PII, the study specifically selected the unique PII (email addresses) from the 12306 dataset to correlate passwords in other datasets, thereby facilitating tracking of corresponding PII across these collections. Table 1 provides details of the size of the matching datasets that contain PII across various datasets.

3.2 Analysis Based on Frequent Substrings, Popular Passwords, and Heterogeneous Personal Information Data

Users may be inclined to use frequent substrings rather than popular passwords. An analysis of the top ten frequent substrings and popular passwords across six password datasets reveals that the inclusion rate for frequent substrings ranges from 0.91% to 13.34%, slightly higher than that of popular passwords, which range from 0.79% to 10.43%, as shown in Table 2. This finding indicates that users prefer frequent substrings when constructing their passwords. Notably, users often opt for simple numeric sequences like “666666” and “000000,” as well as semantically rich strings, such as, “iloveyou” and “woaini” in their password choices.

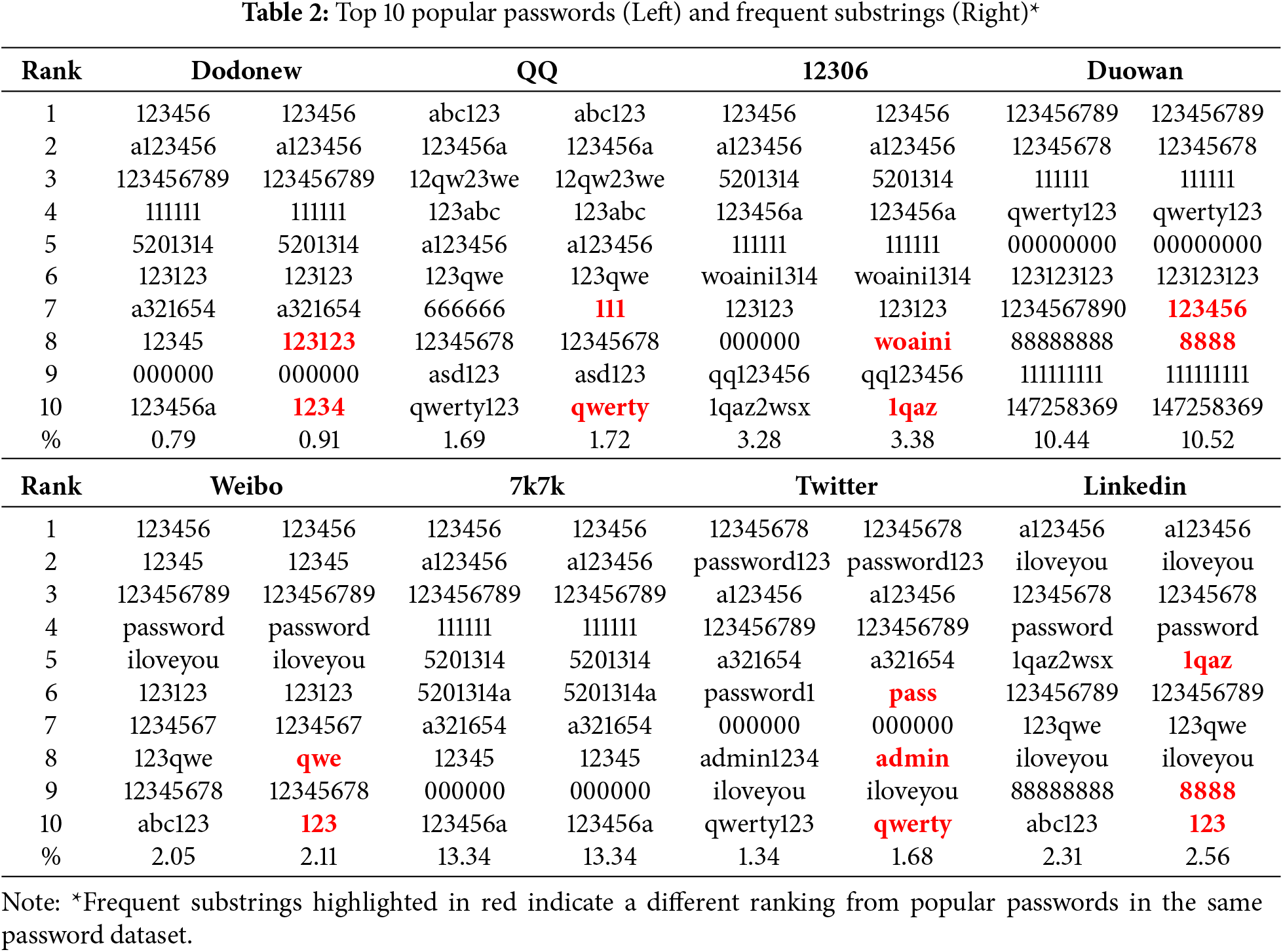
Furthermore, this study extracted the top ten and top hundred frequent substrings and popular passwords, subsequently matching them with the 12306 datasets containing PII labels for email matching. This enables the use of certain PII tags (e.g., names and email addresses) for password tagging and analysis. In Table 3, we display the proportion of passwords that include tags in the left column and those that completely match the tags in the right column. For instance, if the tag value is “123abc,” the left column includes passwords such as “123abcd” and “a123abc,” while the right column includes only “123abc.” Passwords with specific PII tags constitute a significant proportion of up to 13.64%. This indicates that using PII to construct passwords is common and poses security risks.

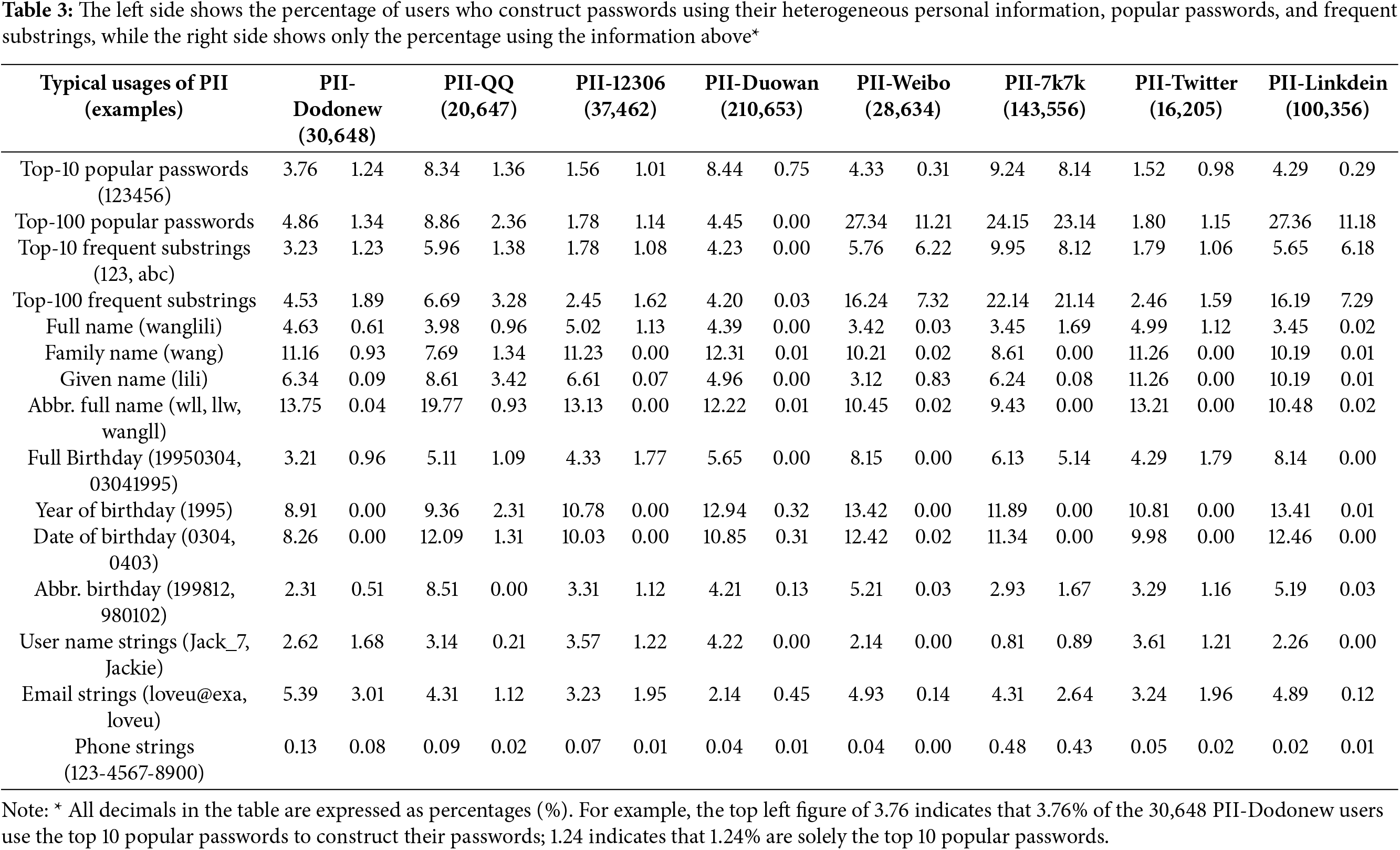
This study delves into the relationship between frequent substrings, popular password labels, and heterogeneous personal information labels in password datasets, revealing four key findings.

(1) Data analysis shows that the ratio of passwords containing the top ten and top hundred frequent substrings is slightly higher than those with the same level of popular passwords. This suggests that frequent substrings more accurately capture password characteristics.

(2) Some passwords are composed of the top ten or top hundred frequent substrings, with a proportion similar to those composed constructed with popular passwords. This indicates that some frequent substrings function effectively as popular passwords.

(3) The results indicate that expanding frequent substring labels from the top ten to the top hundred significantly increases the number of covered passwords, capturing more password characteristics.

(4) By subdividing personal information labels, such as splitting the full name “wanglili” into “wang” and “lili,” and the birth date “19950304” into “1995” and “0304,” we can increase the password coverage and better capture password characteristics.

3.3 Password Structure

This study explores the expression of frequent substring labels and common password labels in password structures. We convert the frequent substrings and popular password labels into GTarGuess−I grammar labels and conduct a comparative analysis of the structural representation of the top hundred popular passwords alongside frequent substrings. In this analysis, specific labels are defined: “Pn” represents a popular password of length n, while “Fni” refers to the frequent substrings ranked i among substrings of length n. The analysis employs the longest prefix matching rule, which prioritizes matching the PII segments in the password and subsequently aligns the remaining segments with frequent substring labels. This method facilitates the acquisition of the structural representation of passwords.

Table 4 displays the top ten password structures and their distributions of Pn, illustrating that these structures often consist of simple components such as Pn,Ln,Dn, etc. These components are usually unrelated to PII labels, highlighting the ubiquity of common yet simple strings in passwords. Besides, with the incorporation of Pn and labels, the password probability model GTarGuess−I can better identify these common and simple strings, thereby enhancing the efficiency of password cracking.

4  Our Model, TGI-FPR

4.1 Framework of the Improved Model

As mentioned earlier, the TarGuss-I fails to fully consider popular passwords and frequent substrings, and it also suffers from issues related to the overly broad categorization of personal information types and extensive duplicate counting. To address these issues, we propose a novel model, TGI-FPR, which modifies the TarGuess-I in three main aspects. The details of TGI-FPR are as follows:

(1) Add the popular password label P1 in grammar GI and employ a list of popular passwords generated from datasets similar to the target site;

(2) Introduce the frequent substring label Fni in grammar GI to identify frequently occurring password segments in the data;

(3) Further subdivide the existing six major categories of personal information labels and establish priorities for each category to avoid duplicate counting.

Fig. 4 outlines the refinement of the TarGuess-I algorithm to develop the TGI-FPR algorithm, with the parts highlighted in red showing the improvements and examples of incrementally parsed passwords. In this section, we will explore the methods for these enhancements.

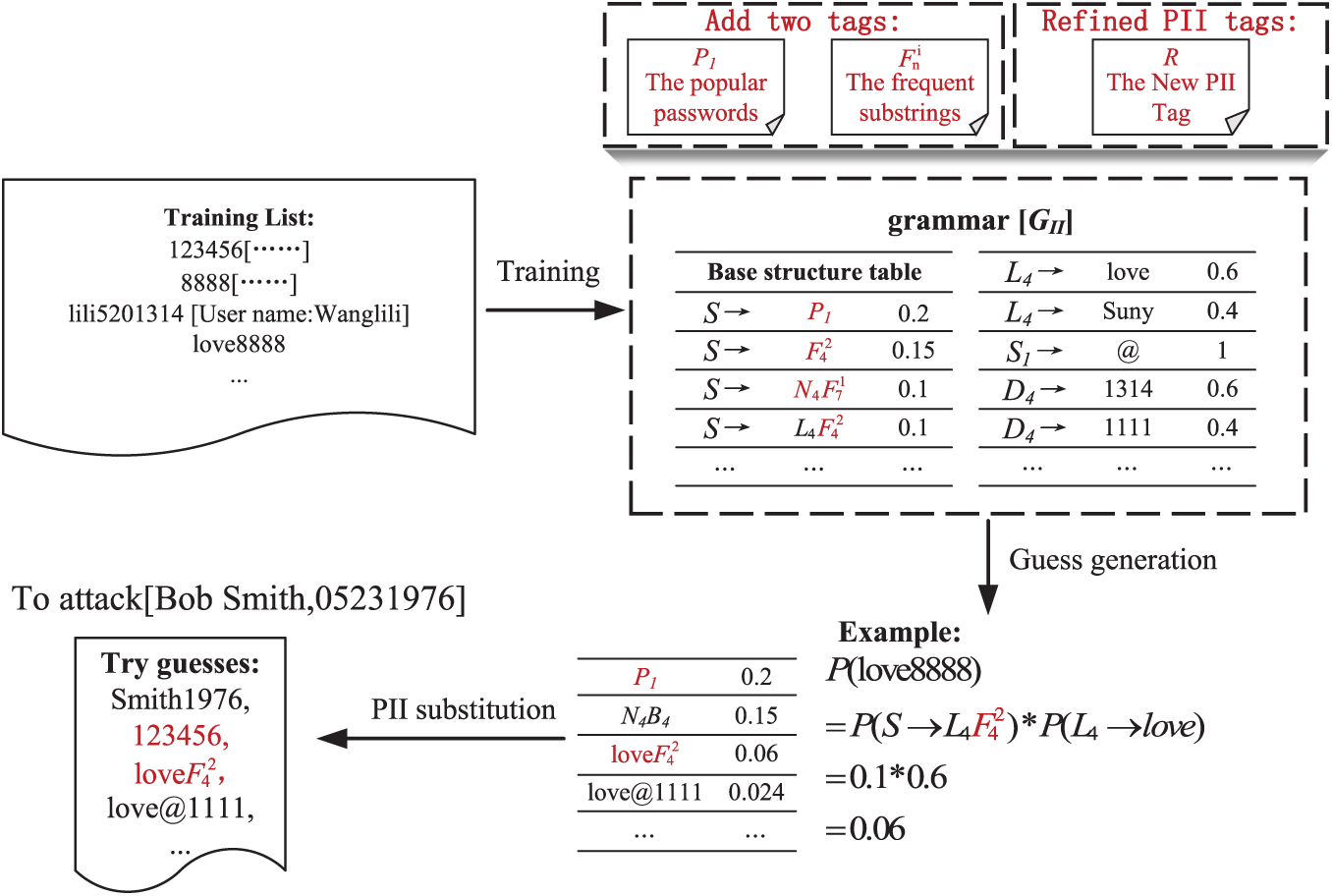
Figure 4: Test cases and the modifications we employed for TGI-FPR The parts marked in red are the semantic tags we added, and the model identified additional password structures after adding these semantic tags

The context-free grammar of our TGI-FPR model G=(V,Σ,S,R) is described as follows:

(1)   S∈V denotes the start symbol;

(2)   V={S;Ln,Dn,Sn;Nn,Bn,Un,En,In,Tn;P1,Fni;e} is a finite set of variables, where:

Letters (Ln), Digits (Dn), and Symbols⁡(Sn) are the basic tags of the PCFG algorithm [4], representing strings of letters, digits, and symbols of length n, respectively;

(b)   Name⁡(Nn), User name (Un), Birthday (Bn), ID number (In), E-mail address (En) and Phone number (Tn) are syntactic tags of TarGuess-I [13], and they indicate various forms of names, birthdays, usernames, email addresses, ID numbers, and phone numbers, differentiated by the number n, respectively; In this work, we have refined the personal information tags from the traditional model into six major categories and further divided them into 36 subcategories;

(c)   Popular Password (P1) is proposed in this paper, with implementation details presented in this subsection; the number 1 in P1 has no special meaning; it merely complies with the grammatical format and does not represent length;

(d)   Frequent Substrings (Fni) is proposed in this paper, referring to a set of substrings of length n, ranked by frequency in descending order and positioned at i;

(e)   ε is the terminal symbol.

Σ is the set of 95 printable ASCII characters;

R is a set of rules in the form α→β, where α∈V and β∈V∪Σ.

4.2 Identification of Popular Passwords

In the grammar GII, we introduce a label to identify popular passwords, which consists of elements based on the top N popular passwords derived from typical website data statistics. The number ‘1’ is arbitrary and is used solely to conform to the grammatical structure. For a detailed analysis of the P1 label, see Fig. 5.

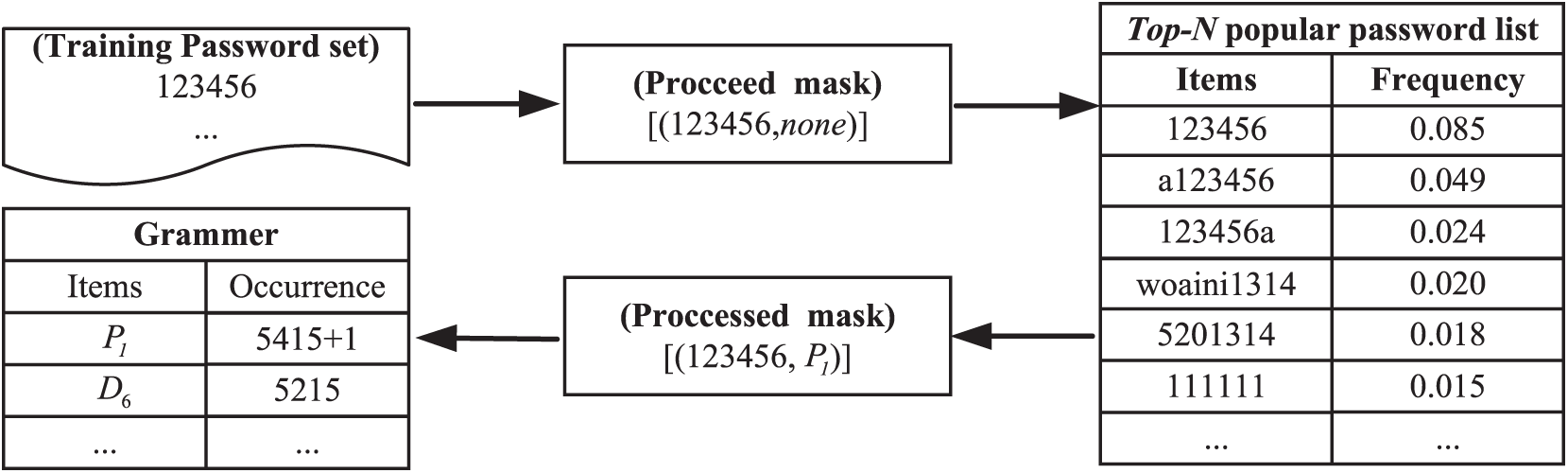
Figure 5: Illustration of P1 label analysis

During training, the system matches passwords in the training data with a popular password list using regular expressions. If a match is found, the frequency of the associated password in the P1 element set increases. The output of this phase is the context-free semantic representation GII of the P1 label, which provides foundational data for the guessing phase. In the guessing phase, the system calculates the probability of the semantic structure of passwords containing the P1 label, followed by the probability of each password within the P1 element set. The system multiplies these two probabilities to obtain the final probability for each password and ranks them accordingly.

Fig. 6 demonstrates the similarity of the top N passwords across two distinct services. The study finds that the similarity exhibits significant fluctuations within the top hundred passwords. When the N value is increased to about 300, similarity reaches a stable peak; however, further increases in the N value result in a gradual decline in similarity. Analysis of the data for the top 300 most popular passwords shows that, with the exception of the comparison between Duowan and 12306, the similarity generally exceeds 60%. Furthermore, it is important to note that the datasets analyzed in this experiment are predominantly focused on Chinese password patterns. The popular passwords identified in the Chinese datasets may not be directly applicable to English-language services, as linguistic and cultural factors significantly influence password choices. The structure and frequency of popular passwords in English are quite distinct from those observed in Chinese datasets, reflecting different user behaviors. Given this, we decided not to include the English datasets in this specific analysis, as the password preferences and trends may differ too greatly to yield meaningful comparisons across the two languages in the context of this experiment. The variation in the share ratio of these passwords reveals the influence of different types of services on the choice of popular passwords. Based on these findings, we set the N value to 300 in cross-site password-guessing scenarios.

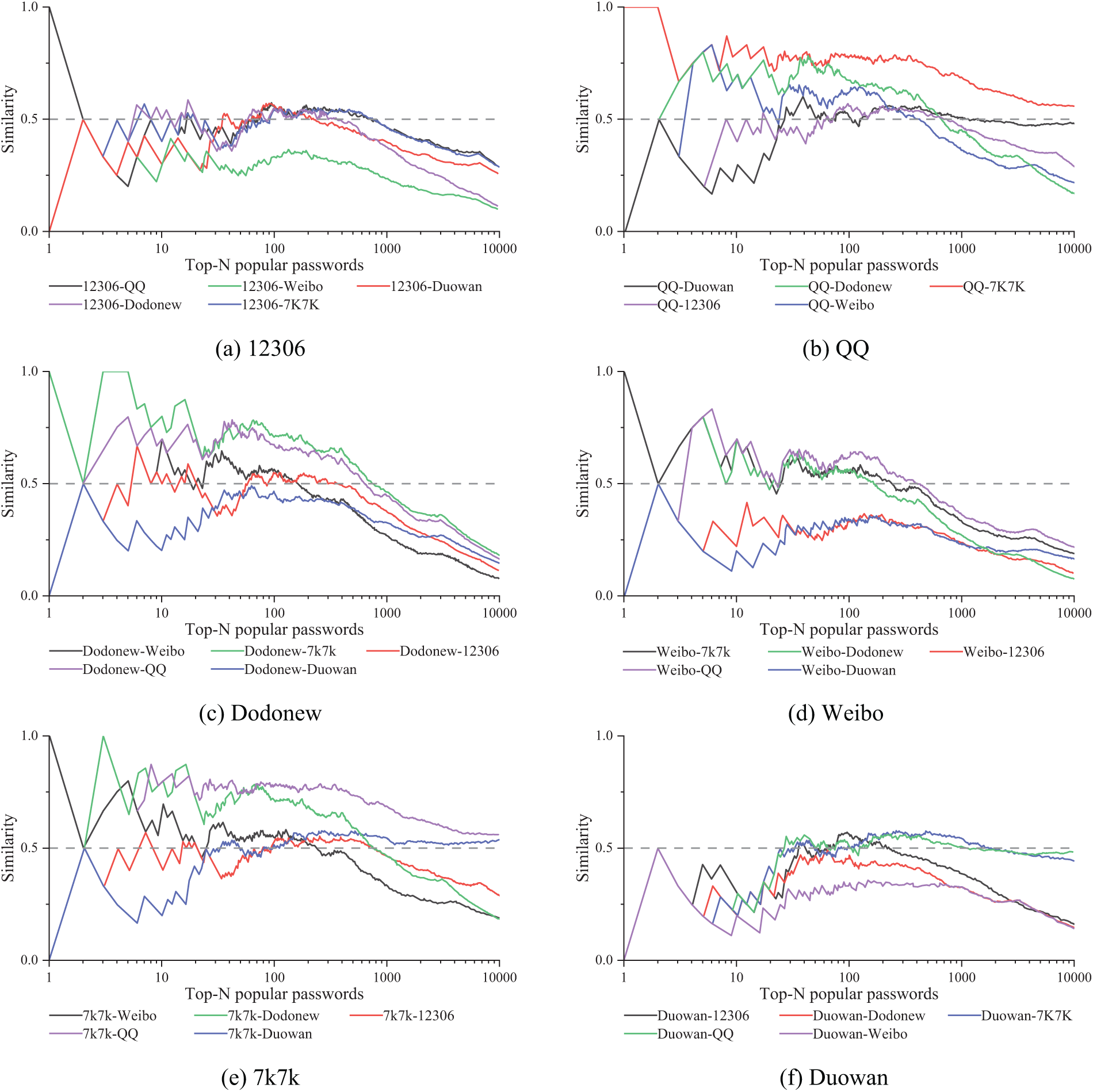
Figure 6: Similarity of the Top-N popular password lists between two datasets. We use difflflib function in Python to calculate the similarity of the Top-N popular passwords between each site

4.3 Recognition of More Detailed Personal Information Structures

In this subsection, we explore the processing methods of the “12306” dataset, focusing on effectively classifying and matching the personal information it contains. Each record in the dataset is separated by “- - - -” into different information items, such as login email, password in plaintext, real name and ID number, username, mobile number, and bound email. Data processing begins by splitting the record strings based on “- - - -,” generating a list of information components. Using string inclusion relationships, we achieve the matching and prioritization of six types of personal information, ensuring that the information categories are non-repetitive. The dataset displays consistency between “login email” and “bound email.” Structured processing adheres to the format requirements defined in Fig. 7, ensuring the accuracy and consistency of the data. To further clarify, I have added Table 1, which provides a detailed explanation of the data structure and formatting.

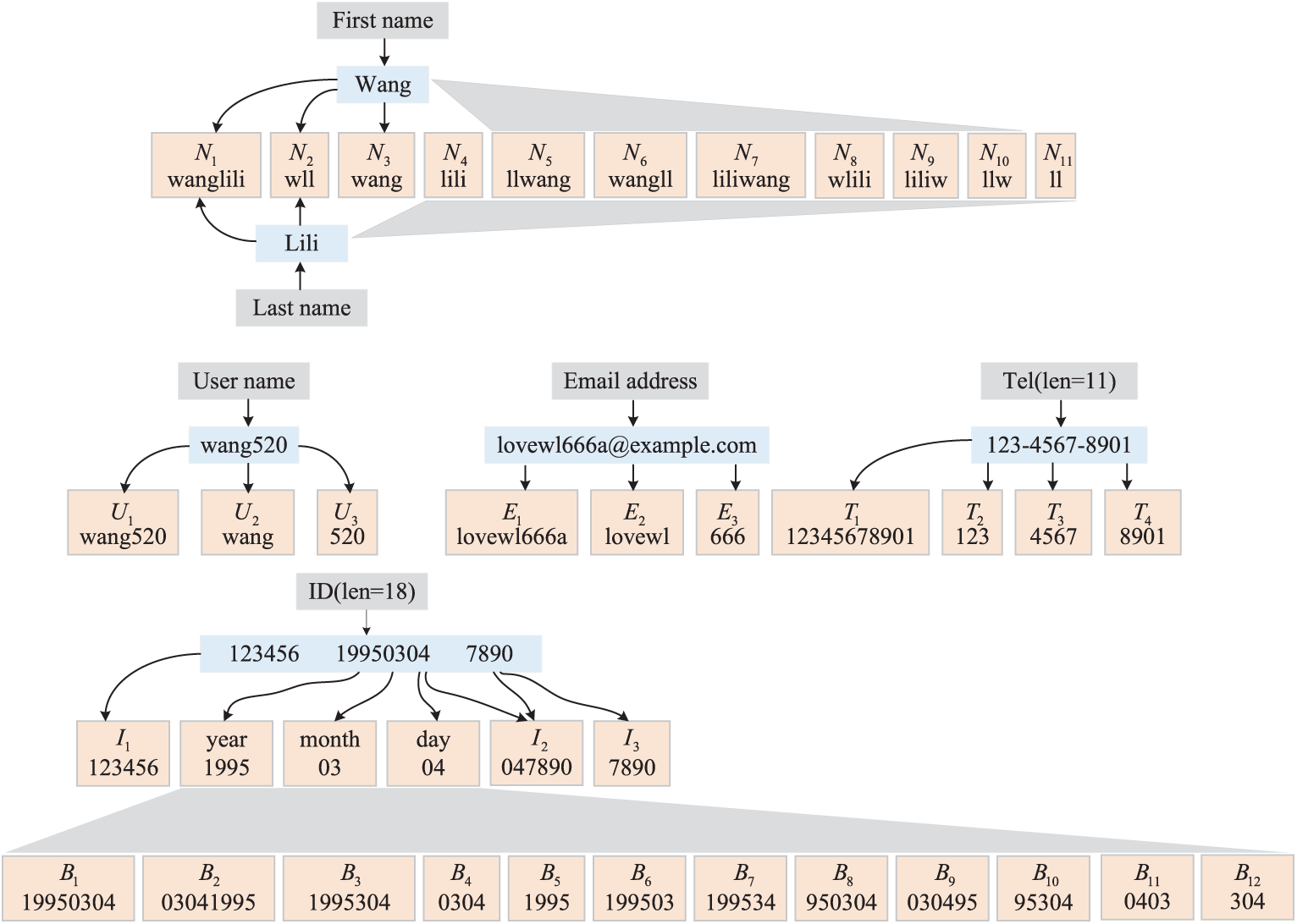
Figure 7: Subdivision of personal information tags

The following sections will introduce the capture matching algorithm for each type of personal information, starting with the name capture matching algorithm, which is designed to handle Chinese names. In Chinese culture, names typically consist of a surname followed by a given name. The algorithm utilizes the PyPinyin library to convert each character of the name into its pinyin (the Romanized phonetic representation of Chinese characters) without tone marks, and then generates various name permutations by reordering the surname and given name, or using initials. These variations are then checked against passwords for potential matches.

(1) Name Structure Capture and Matching

We use the ‘PyPinyin’ library to process name information. The primary goal of this technique is to convert Chinese characters in names into a pinyin form without tones. For data standardization, the preprocessing step removes names that include compound surnames and ethnic minority characteristics.

The aim is to retain only names that are two or three characters long.

Algorithm 1 is used for name recognition and can convert two or three-character passwords. In this algorithm, the lazy_pinyin (string) function takes a string as its input and yields a one-dimensional list as the output result.

In Algorithm 1, the analysis of substructure is conducted on the “Name” field to ensure that all statistical data are independent and non-redundant. This method determines data duplication based on name length, assigning the longest names (e.g., “wangll”) to their corresponding longest digit tags (e.g., “N6”). Shorter tags (e.g., “N3” for “wang” or “N11” for “ll”) do not account for names already represented by longer tags.

The research analyzes a dataset containing over 140,000 passwords and discovers that more than 30,000 passwords incorporate “Name” information. This finding indicates a significant proportion of passwords containing name information within the dataset. Furthermore, integrating name information is crucial for the model’s learning process, as it enhances the model’s ability to process and recognize relevant data.

(2) Capturing and Matching Structures of “Date of Birth,” “ID Number,” and “Mobile Number.”

This section discusses methods for password structure detection through analysis of the birthday information in ID numbers. The seventh to fourteenth digits of the ID number contain the individual’s date of birth, which is extracted and formatted into a “yyyy-mm-dd” string. Based on this information, the study designs 12 logical structures and generates 10 different string formats, as shown in Algorithm 2. These strings are used to detect specific structures within passwords, organized in descending order from the highest to the lowest digit.

In processing data regarding date of birth, strict formatting rules are employed to ensure accuracy and prevent misclassification. Specific formats such as “B8” (950304) are clearly distinguished and are not misclassified as “B1” (19950304) or “B4” (0304). When the month and date data are the same, the system prioritizes recognition based on a predefined order; for example, “0303” is by default recognized as “B4” rather than “B11,” effectively preventing duplicate counting of data. Data indicate that the Chinese typically record dates of birth in the “year-month-day” sequence. Other sequences, such as those where the year or month is placed at the end (e.g., B2, B9, B11), are seldom used and occur with low frequency.

For “ID numbers” and “mobile numbers,” we apply a similar method that treats them as purely numeric strings. We simply match them one by one according to the categories defined in Fig. 7.

(3) Capturing and Matching Structures of “Username” and “Email Address”

For name fields, the algorithm identifies data composed of character strings, such as N1 to N10, and sorts them by string length from longest to shortest. The processing method applies a similar approach to fields such as date of birth, ID number, and mobile number, employing numeric strings and ensuring independence between fields.

However, the processing of username and email address fields is more complex, as these fields contain both characters and numbers and may also include subsets of other data fields (such as names or ID numbers). The algorithm splits letters and numbers using regular expressions and matches them in a predefined order.

4.4 Identification of Frequent Substrings

In this work, we propose a novel method for identifying frequent substrings on a password dataset to effectively filter information from complex data. Initially, the method involves a preliminary dataset analysis of the dataset by recording the occurrence count of each password substring of length n(n≥3). Subsequently, a threshold TI is established to remove low-frequency substrings whose occurrences fall below this threshold, thereby reducing the scale of data analysis. Based on this, the count of each substring is adjusted using the following the formula:

C(ps)new=C(ps)old−∑c∈Σ[C(c+ps)old+C(ps+c)old](1)

The specific operation involves deducting the total counts of all extended substrings associated with ps from the original count C(ps)old to obtain the new count C(ps)new. After this adjustment, a second threshold, T2, is set to filter out substrings that still meet the criteria, and they are identified as frequent substrings. Finally, all frequent substrings of length are stored in the set Fn and sorted in descending order of frequency. Substrings ranked i in the set are denoted as Fni.

All substrings satisfying the specified length and exceeding the threshold T2 are placed in the pending set Fn and sorted in descending order of frequency. Substrings ranked i in the set are denoted as shown in Fig. 8.

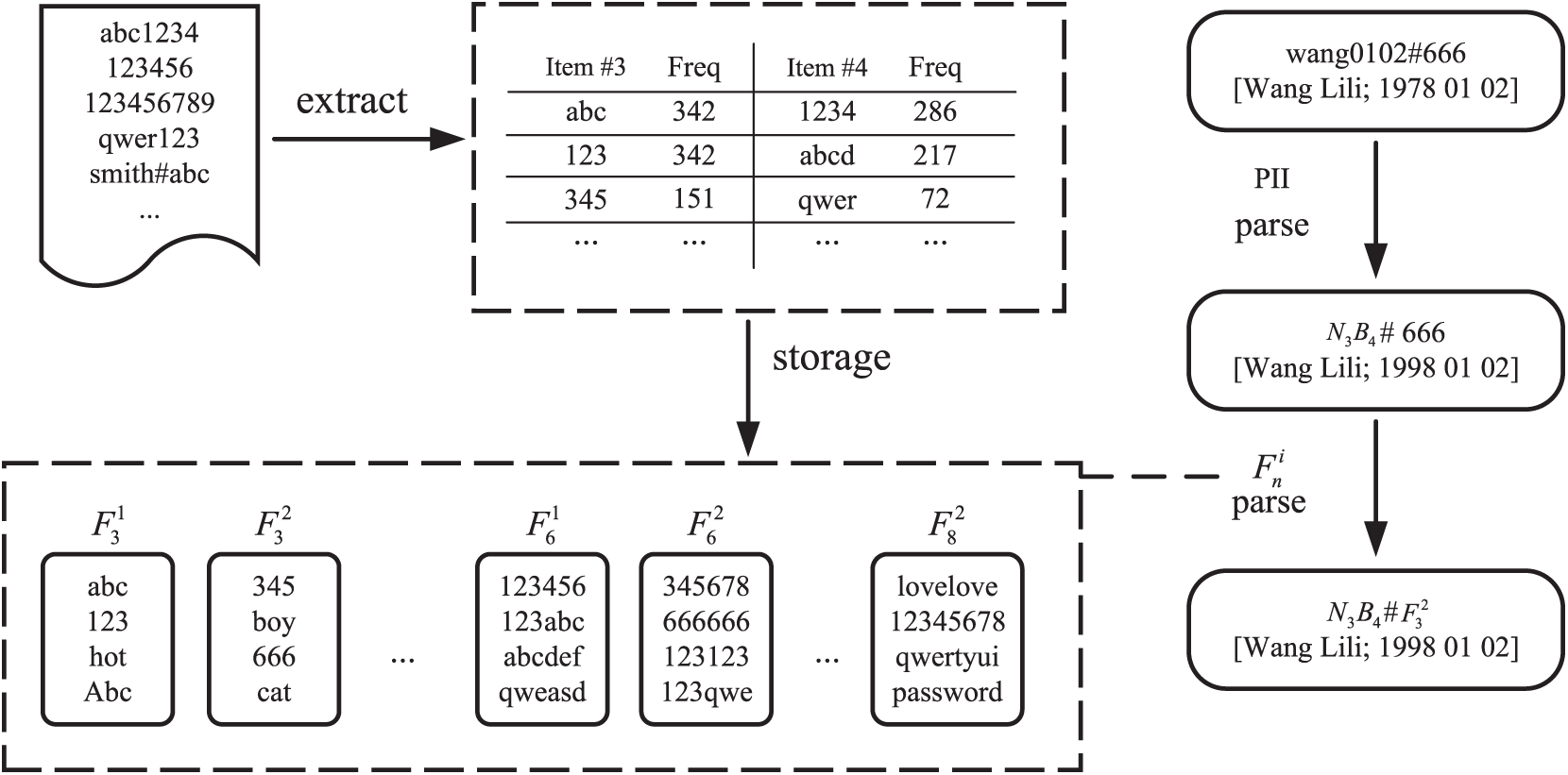
Figure 8: Schematic of the tagging process. Represents the frequent substring ranked i in frequency among substrings of length n

When improving the TarGuess-I model, we introduced labels and considered the impact of frequent substrings. To enhance the training set, we selected the Rockyou and Tianya datasets, which contain many weak passwords and have been extensively used in password research. To optimize model performance, we conducted multiple experiments with different parameter configurations for frequent substrings. The final parameter configuration set the frequent substrings thresholds at T1=400 and T2=30, with frequent substrings lengths ranging from 3 to 8. The frequent substrings dictionary consisted of the top hundred frequent substrings. However, the currently set parameters may not be optimal, and adjustments may be necessary for different datasets. The implementation of the F tag will be further explored in future studies.

5  Experiment

5.1 Experimental Design

In online password guessing with TarGuess-I, resource limitations are primarily reflected in the number of allowed guesses rather than in computational power or bandwidth. This experiment aims to evaluate the success rate of the password-guessing model within a limited number of guesses.

The experimental design follows three core rules:

(1) Ensure separation between the training set and the test set;

(2) Ensure that comparative experiments are based on the same dataset to maintain consistency in experimental conditions;

(3) Use as large a dataset as possible to improve the model’s generalizability.

To this end, we selected the QQ and 12306 datasets, each containing 105 data points, as the training set. This setup ensures that this data was not used for testing in compliance with the aforementioned rules. Given the high heterogeneity of passwords in these datasets, we employed the Monte Carlo method to stochastically produce ten test sets, each with 103 data points, to minimize the impact of heterogeneity on the experimental results.

Table 5 displays the four-dimensional variables of the experimental setup. In the study of the TarGuess-I password guessing model, nine different models were constructed to explore methods for improving password guessing efficiency based on the following three methods, either singly or in combination: (1) Adding popular password tags P; (2) Incorporating frequent substring tags F; (3) Further refining personal information tags. Four models using the improvement tags independently (TGI-F, TGI-R, TGI-P, and TGI-P′) were used to assess the individual effects of each tag. Moreover, two scenarios were defined to enhance the realism of the experiment: the ideal scenario (P tag) and the realistic scenario (P′ tag). In the P tag scenario, it is assumed that the attacker can obtain the top 300 popular passwords from the target website, while in the P′ tag scenario, it is assumed that the attacker only has access to a list of the top 300 passwords from a website similar to the target site. Additionally, we established four combined tag models (TGI-FP, TGI-PR, TGI-FR, TGI-FP′R, and TGI-FPR) to further explore their impact on efficiency. Ten repeated experiments were conducted across 80 different attack scenarios to verify the effectiveness of each model.

Fig. 9 shows the average number of guesses, n, and the cracking success rates for nine models trained on two websites and tested on four websites. As shown, when the models are compared based solely on the number of guesses, the differences in cracking success rates are not pronounced. To facilitate a clearer analysis of the experimental results, we calculated the relative values, Rn, for each model at guess number n relative to the original TGI model, as follows:

Rn=Mean⁡(rnTGi+−rnTGirnTGi)×100%(2)

Figure 9: Average prediction success rates of nine models

In this context, rnTGi+ is the success proportion of the improved model on the ith test set at n guesses, while rnTGi is the success rate of the original TGI under the same conditions.

5.2 Experiment 1: Validating the Effectiveness of Improved Models

In this work, we compare the performance of four single-tag modification models (TGI-F, TGI-R, TGI-P, and TGI-P′) with the baseline model TGI. Analysis of the cracking success rates provided by Fig. 10 and Table 6 shows that, with the exception of the TGI-P′ model—which slightly underperformed TGI on the QQ dataset by an average success rate of 0.05%—the other three single-tag modification models exceeded the baseline model TGI in average success rates within 100 guesses, improving by 0.20% to 0.72% over TGI. These results clearly demonstrate the advantages of the three modification methods in enhancing cracking success rates.

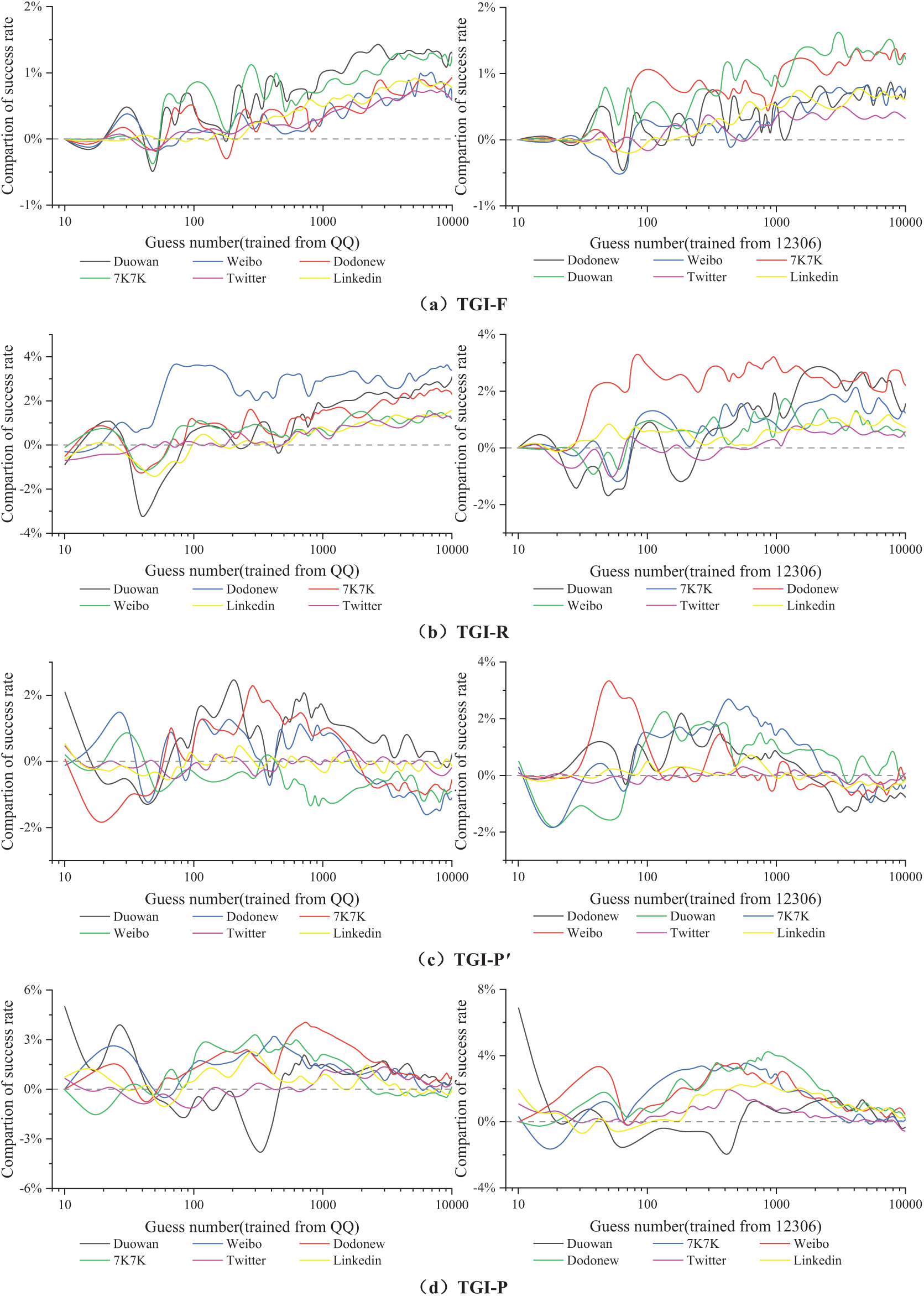
Figure 10: Experimental results of four single-tag modification models. Panels (a) to (d) display the Rn of the four single-tag modification models. The 0% dashed line on the y-axis signifies our TGI cracking success rate as the reference baseline

Fig. 10a,b illustrates the performance of models TGI, TGI-F, and TGI-R from 10 to 104 guesses. The results indicate that within the 10 to 102 guess range, the improved models TGI-F and TGI-R did not outperform TGI and, in some cases, performed even worse. Specifically, when TGI-R was evaluated using the Duowan test dataset with the 12306 and QQ training data, it performed 2.78% worse than TGI at 50 guesses (using 12306 training data) and 3.62% worse at 40 guesses (using QQ training data). This underperformance partly stems from the scarcity of F tags or detailed personal information tags in passwords, which primarily affect lower-ranked candidate passwords. Furthermore, TGI-R’s performance was impacted by the finely divided personal information tags, which failed to capture the vulnerable behaviors of users in password creation, leading to higher-ranked candidate passwords that hindered its early guessing performance. However, as the number of guesses increased, TGI-F and TGI-R showed slight improvement between 102 and 103 guesses and significantly outperformed TGI between 103 and 104 guesses. Notably, at 104 guesses, the TGI-F and TGI-R perform better than TGI with improvements of 1.29% and 3.37% in terms of cracking success rates. The study indicates that TGI-F and TGI-R models excel in trawling scenarios with over 102 guesses, where they significantly enhance the cracking success rates.

However, when using English datasets like Twitter and LinkedIn for testing, the TGI-R model performed poorly. This could be attributed to the cultural differences between Chinese and English-speaking users, which lead to different structures in how personal information is categorized. The training datasets were based on the personal information structure of Chinese users, which may not align well with the way English-speaking users structure their personal information, thus resulting in suboptimal performance when tested on English datasets.

As shown in Fig. 10c and d, models with the P tag outperformed m the TGI model within the range of 102 to 103 guesses. Specifically, the TGI-P′ model achieved maximum increases in cracking success rates of 2.67% and 2.46% using the 12306 and QQ training datasets, respectively, compared to the TGI model. However, the TGI-P model’s highest cracking success rates using 12306 and QQ training data exceeded those of the TGI model by 4.46% and 4.18%, respectively. This difference can be attributed to several key factors. Firstly, the popular password tag P1 ranks highly within the syntax GII, showing its advantage in cracking attempts. Secondly, even though compound popular passwords are present in the top 300 password list, most are ranked in the lower half, which reduces cracking efficiency. Furthermore, this compound form of passwords caused the TGI model to generate many ineffective outputs, further reducing the success rate of cracking.

When comparing the TGI-P′ and TGI models, we found that TGI-P′ had a lower success rate than TGI in 102 attempts. Analysis shows that the P′ tag in the TGI-P′ model, which includes the top 300 popular passwords, does not match the password database of the testing site. This inconsistency led to several ineffective outputs among the first 100 candidate passwords in the TGI-P model. In contrast, the TGI-P model, unaffected by such issues, demonstrated improved performance under identical testing conditions.

In Fig. 10b–d, some curves show significant deviations from the average Rn values, exhibiting an anomaly curve phenomenon. Performance comparisons reveal that the TGI-R model achieves a 2.73% higher guess success rate on the Dodonew test data than the TGI model and an average of 0.89% higher on other datasets. In contrast, the TGI-P model (trained on QQ data) shows a 4.75% lower guess success rate on the Duowan test data and underperforms by 1.73% lower on other test datasets compared to TGI. These differences may stem from the distribution differences among the password datasets. Particularly, the Duowan dataset includes some “uncleaned” password data, such as the frequently used “e10adc3949ba59abbe56e057f20f883e,” which ranks 32nd among the top 300. Insufficient cleaning likely contributed to the reduced success rate of the model on this dataset.

5.3 Experiment 2: Comparison and Evaluation of Improved Models

We evaluated each combined tag modification model to determine the ideal solution. Table 7 lists the average Rn for each modification model compared to TGI. The results show that our three incremental tag modification models, TGI-FPR, improved best (see Fig. 11f).

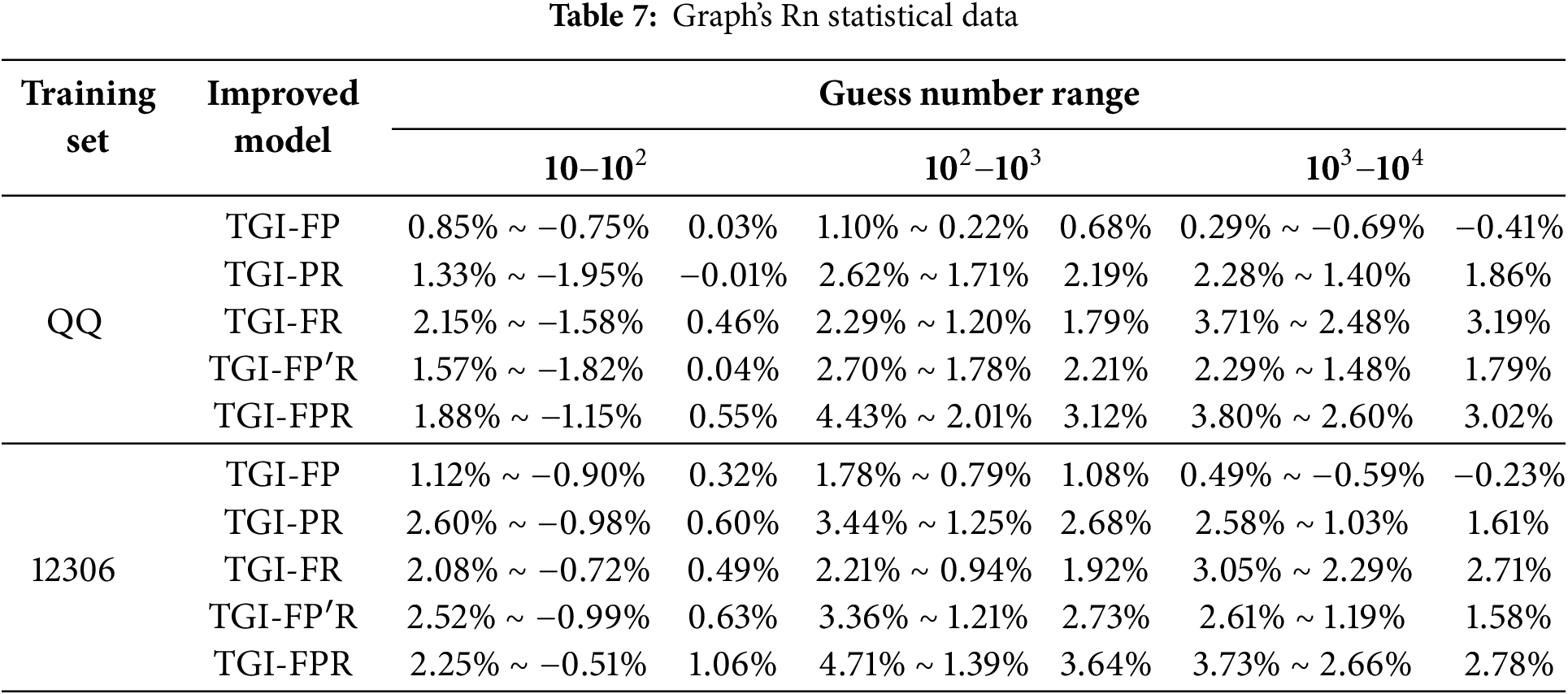
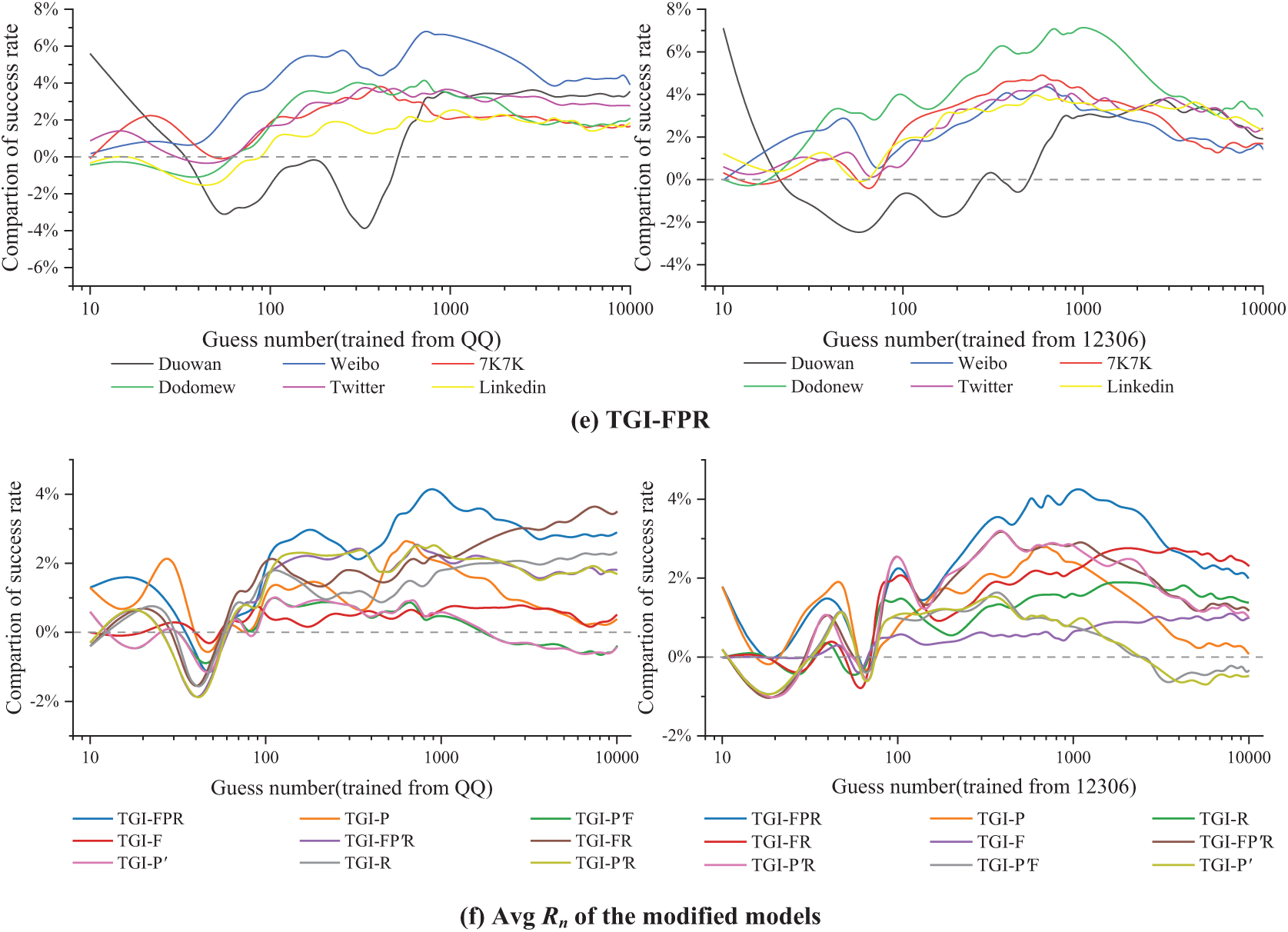
Figure 11: Experimental results for five combined tag modification models, compared across nine modification models. Panels (a–e) display the Rn values of 5 combined tag modification models; (f) compare the Rn values of 10 modification models. The dashed line on the y-axis is positioned at 0%, representing our reference baseline (i.e., the cracking success rate of TGI)

Fig. 11f shows that increasing the number of tags enhances the performance of models such as TGI-F, TGI-R, and TGI-FR. Meanwhile, models like TGI-P′, TGI-P′R, TGI-FP′, and TGI-FP′R also show similar improvements. However, the improvement effect correlation between models combining the P tag and those containing only F or R tags is insignificant. Further analysis indicates that popular passwords (P tag) occupy a larger proportion of the overall password distribution. In contrast, passwords with frequent substrings or more detailed personal information structures (F and R tags) are relatively uncommon. Therefore, adding the P tag has a more significant impact on guessing success rates than the F or R tags.

In this study, we propose the TGI-FPR model, an improvement upon the TarGuess-I model, enabling the model to capture a wider variety of password structures and thus enhance the accuracy of password guessing. Specifically, the TarGuess-I model generates password candidates based on users’ personal information (PII) and the PCFG algorithm. However, it is relatively limited in capturing password structures, particularly by not considering common password construction techniques such as popular passwords and high-frequency substrings. By incorporating the popular password label (P), the model is able to identify commonly used password structures that are prevalent across multiple websites, thereby improving the prediction accuracy for these passwords. The high-frequency substring (F) label further expands the scope of password structures by identifying more granular password patterns, such as “love.” Additionally, the more detailed personal information label (R) captures finer personal information structures (e.g., variations of birthdays), which may not directly appear in the user’s personal information but hold special significance for the user, thereby increasing the likelihood of successful guesses.

Through the introduction of these incremental labels, the TGI-FPR model is capable of identifying and generating a broader range of password structures, which were not captured by the traditional TarGuess-I model. As a result, the model can generate more password candidates that incorporate these incremental labels, significantly enhancing the guess accuracy. As shown in the results of Table 8, TGI-FPR generated nearly 11% more password candidates with incremental labels compared to TG-I, directly leading to an improvement in password guessing accuracy. This improvement is particularly evident when the model encounters passwords with similar structures, where its performance is notably superior.

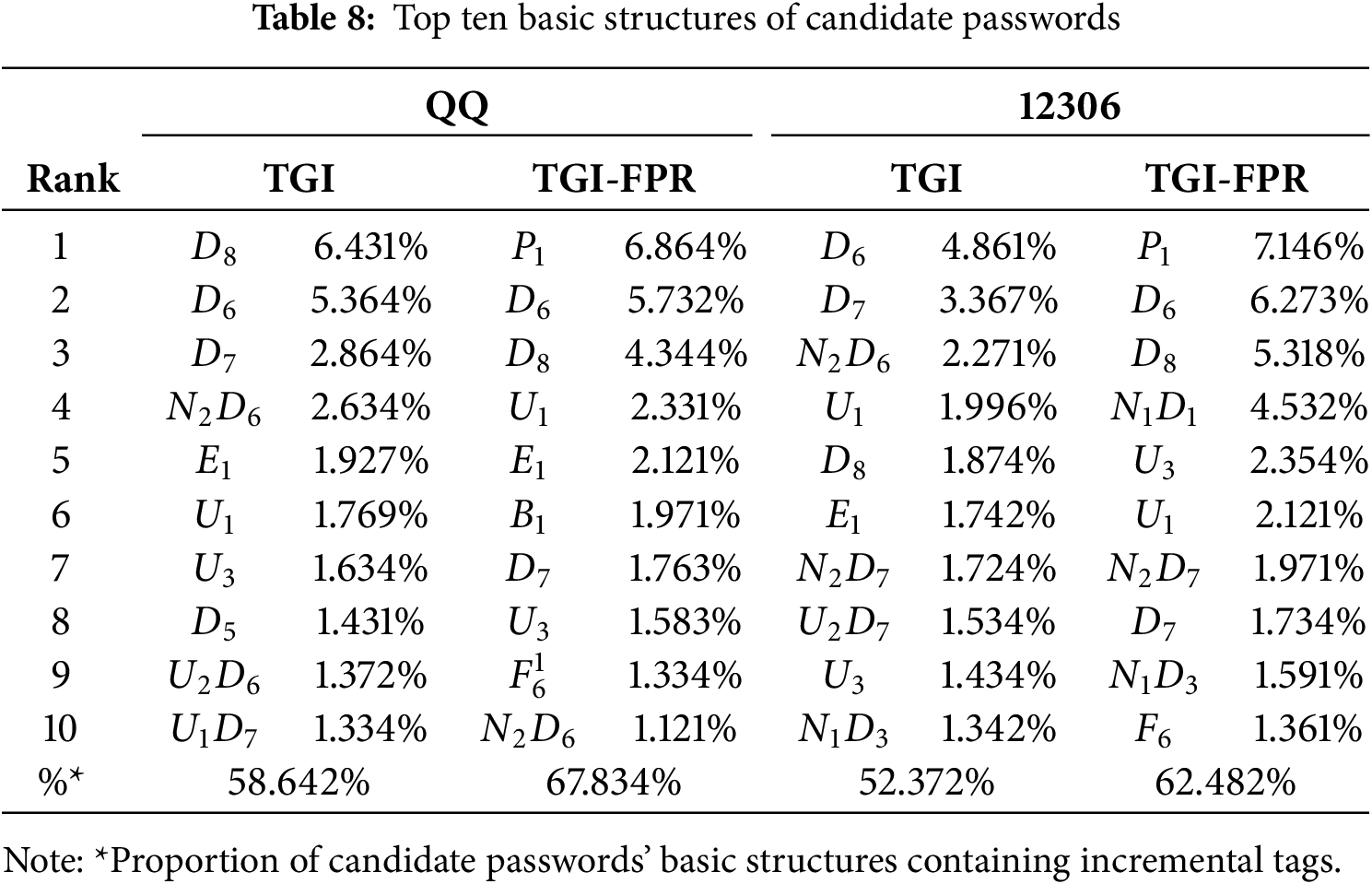
Table 9 evaluates the TGI-FPR’s guessing performance on each test dataset. The experimental results indicate that in most cases, the TGI-FPR outperforms TGI. Specifically, on the QQ training dataset, TGI-FPR achieved success rate improvements from 0.02% to 2.15%, while on the 12306 training dataset, its success rates increased by 0.75% to 2.65%. However, TGI-FPR underperformed on the Duowan dataset, a result discussed in detail previously in the analysis of TGI-P′.

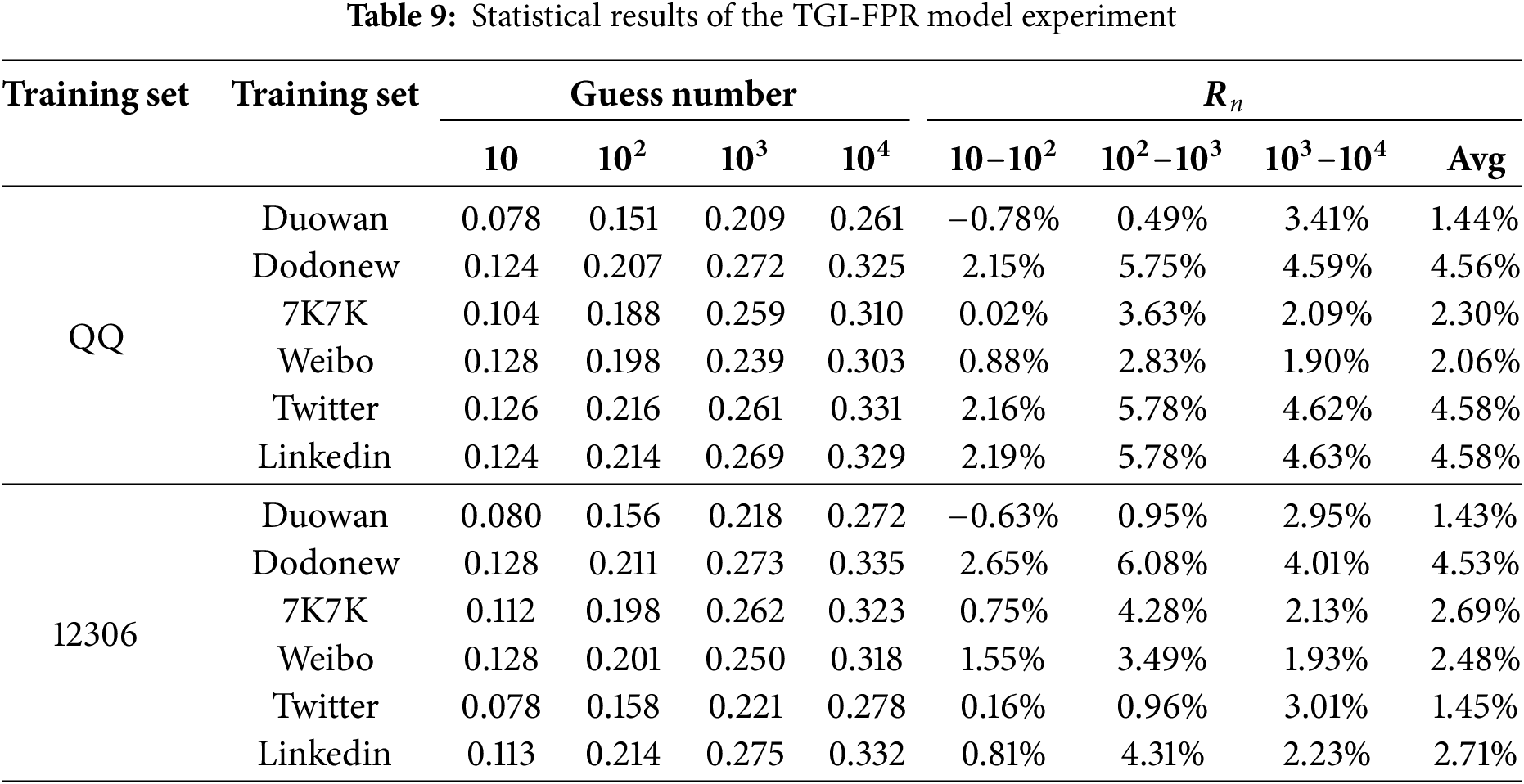
This study validated the effectiveness and feasibility of the proposed improvement methods. The research also found a tendency among users to use popular passwords, frequent substrings, and personal information, which increases the risk of cracked passwords. As attackers acquire more personal information, the risk of targeted password guessing rises significantly. Therefore, multi-factor authentication schemes are necessary for critical applications to enhance overall account security [33–35].

6  Conclusion and Future Work

The TarGuess-I algorithm demonstrates superior password-guessing performance and has attracted significant attention in password security research. We conducted an in-depth analysis of users’ vulnerable password behaviors and targeted password guessing patterns, with three feature parameters missing in the TarGuess-I algorithm. Based on these findings, we developed an improved password-guessing algorithm, TGI-FPR, which effectively recognizes popular passwords, frequent substrings, and more refined PII structures. Extensive experiments show that TGI-FPR achieves a 2.65% higher guessing success rate than TarGuess-I within 100 attempts. This study emphasizes the security risks of targeted password guessing. Our innovative approach to frequent substrings introduces new perspectives for password-guessing strategies, though further optimization of these methods is needed. Future work will continue to explore this direction, including experiments on how the success rate improvement varies across different attack scenarios, such as cracking common passwords, long passwords, and passwords from security-conscious users. Additionally, we plan to extend our work by integrating and comparing our proposed model with recent developments, such as PassGAN, DeepCode, and other state-of-the-art password guessing models that utilize different data-driven approaches. This will help us refine our approach, identify the most effective strategies, and provide more targeted improvements to password-guessing techniques.

Acknowledgement: The authors are very grateful to the anonymous reviewers fortheir valuable advice that improves the completeness of this paper.

Funding Statement: This work was supported by the Joint Funds of National Natural Science Foundation of China (Grant No. U23A20304), the Fund of Laboratory for Advanced Computing and Intelligence Engineering (No. 2023-LYJJ-01-033), the Special Funds of Jiangsu Province Science and Technology Plan (Key R&D Program Industry Outlook and Core Technologies) (No. BE2023005-4), the Science Project of Hainan University (KYQD(ZR)-21075).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Shuai Liu, Wei Ou; data collection: Shuai Liu, Wei Ou; analysis and interpretation of results: Shuai Liu, Wei Ou; draft manuscript preparation: Shuai Liu, Wei Ou; manuscript guidance and revision: Wei Ou, Mengxue Pang, Jianqiang Ma, Qiuling Yue, Wenbao Han. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, S Liu, upon reasonable request. And the probabilistic context-free grammar- (PCFG-) based algorithm code can be found at https://github.com/lakiw/pcfg_cracker, accessed on 28 April 2025.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Zimmermann V, Gerber N. The password is dead, long live the password—A laboratory study on user perceptions of authentication schemes. Int J Hum-Comput Stud. 2020;133:26–44. doi:10.1016/j.ijhcs.2019.08.006. [Google Scholar] [CrossRef]

2. Ma J, Yang W, Luo M, Li N. A study of probabilistic password models. In: 2014 IEEE Symposium on Security and Privacy. Berkeley, CA, USA: IEEE; 2014. p. 689–704. doi:10.1109/SP.2014.50. [Google Scholar] [CrossRef]

3. Hranický R, Zobal L, Ryšavý O, Kolář D, Mikuš D. Distributed PCFG password cracking. In: Computer security—ESORICS 2020. Cham: Springer International Publishing; 2020. p. 701–19. doi:10.1007/978-3-030-58951-6_34. [Google Scholar] [CrossRef]

4. Weir M, Aggarwal S, De Medeiros B, Glodek B. Password cracking using probabilistic context-free grammars. In: 2009 30th IEEE Symposium on Security and Privacy; 2009; Oakland, CA, USA. p. 391–405. doi:10.1109/SP.2009.8. [Google Scholar] [CrossRef]

5. Hitaj B, Gasti P, Ateniese G, Perez-Cruz F. Applied cryptography and network security. Cham: Springer International Publishing; 2019. p. 217–37. [cited 2025 Mar 20]. Available from: https://arxiv.org/abs/1709.00440. [Google Scholar]

6. Tirado E, Turpin B, Beltz C, Roshon P, Judge R, Gagneja K. A new distributed brute-force password cracking technique. In: Future network systems and security. Cham: Springer International Publishing; 2018. p. 117–27. doi:10.1007/978-3-319-94421-0_9. [Google Scholar] [CrossRef]

7. Aggarwal S, Houshmand S, Weir M. New technologies in password cracking techniques. Cyber Secur Power Technol. 2018;93:179–98. doi:10.1007/978-3-319-75307-2_11. [Google Scholar] [CrossRef]

8. Melicher W, Ur B, Segreti SM, Komanduri S, Bauer L, Christin N, et al. Fast, lean, and accurate: modeling password guessability using neural networks. In: 25th USENIX Security Symposium (USENIX Security 16); 2016; Austin, TX, USA. p. 175–91. doi:10.5555/3241094.3241109. [Google Scholar] [CrossRef]

9. Huang CY, Ma SP, Chen KT. Using one-time passwords to prevent password phishing attacks. J Netw Comput Appl. 2011;34(4):1292–301. doi:10.1016/j.jnca.2011.02.004. [Google Scholar] [CrossRef]

10. Veras R, Collins CM, Thorpe J. On semantic patterns of passwords and their security impact. In: Network and Distributed System Security Symposium; 2014; Reston, VA, USA. [cited 2025 Mar 20]. Available from: https://api.semanticscholar.org/CorpusID:6703730. [Google Scholar]

11. Li Z, Han W, Xu W. A large-scale empirical analysis of Chinese web passwords. In: 23rd USENIX Security Symposium (USENIX Security 14); 2014; San Diego, CA, USA. p. 559–74. doi:10.5555/2671225.2671261 [Google Scholar] [CrossRef]

12. Ahvanooey MT, Zhu MX, Li Q, Mazurczyk W, Choo KR, Gupta BB, et al. Modern authentication schemes in smartphones and IoT devices: an empirical survey. IEEE Internet Things J. 2021;9(10):7639–63. doi:10.1109/JIOT.2021.3138073. [Google Scholar] [CrossRef]

13. Wang D, Zhang Z, Wang P, Yan J, Huang X. Targeted online password guessing: an underestimated threat. In: Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security; 2016; Vienna Austria: ACM. p. 1242–54. doi:10.1145/2976749.2978339 [Google Scholar] [CrossRef]

14. Li Y, Wang H, Sun K. A study of personal information in human-chosen passwords and its security implications. In: IEEE INFOCOM 2016—The 35th Annual IEEE International Conference on Computer Communications. San Francisco, CA, USA: IEEE; 2016. p. 1–9. doi:10.1109/INFOCOM.2016.7524583. [Google Scholar] [CrossRef]

15. Das A, Bonneau J, Caesar M, Borisov N, Wang X. The tangled web of password reuse. In: Proceedings 2014 Network and Distributed System Security Symposium; 2014; San Diego, CA, USA: Internet Society. p. 23–6. doi:10.14722/ndss/2014.23357 [Google Scholar] [CrossRef]

16. Xu M, Yu J, Zhang X, Wang C, Zhang S, Wu H, et al. Improving real-world password guessing attacks via bi-directional transformers. In: 32nd USENIX Security Symposium (USENIX Security 23); 2023; Anaheim, CA, USA. p. 1001–18. doi:10.1109/SP.2019.00056. [Google Scholar] [CrossRef]

17. Wang D, Zou Y, Zhang Z, Xiu K. Password guessing using random forest. In: 32nd USENIX Security Symposium (USENIX Security 23); 2023; Anaheim, CA, USA. p. 965–82. [cited 2025 Mar 20]. Available from: https://www.usenix.org/conference/usenixsecurity23/presentation/wang-ding-password-guessing. [Google Scholar]

18. Oesch S, Ruoti S. That was then, this is now: a security evaluation of password generation, storage, and autofill in browser-based password managers. arXiv:1908.03296. 2019. [Google Scholar]

19. Hayata J, Nomura K, Takata Y, Kumagai H, Kamizono M, Kono T, et al. A trust service model adaptable to various assurance levels by linking digital IDs and certificates. In: 8th International Conference on Cryptography, Security and Privacy (CSP); 2024 Apr 20–22; Osaka, Japan: IEEE; 2022. p. 38–45. doi:10.1007/978-3-319-75307-2_11. [Google Scholar] [CrossRef]

20. Li Y, Li Y, Chen X, Shi R, Han J. PG-Pass: targeted online password guessing model based on pointer generator network. In: 2022 IEEE 25th International Conference on Computer Supported Cooperative Work in Design (CSCWD); 2022 May 4–6; Hangzhou, China: IEEE; 2022. p. 507–12. doi:10.1109/cscwd54268.2022.9776149 [Google Scholar] [CrossRef]

21. He X, Cheng H, Xie J, Wang P, Liang K. Passtrans: an improved password reuse model based on transformer. In: ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); 2022 May 23–27; Singapore, Singapore: IEEE; 2022. p. 3044–8. doi:10.1109/ICASSP43922.2022.9746496. [Google Scholar] [CrossRef]

22. Su X, Zhu X, Li Y, Li Y, Chen C, Esteves-Veríssimo P. PagPassGPT: pattern guided password guessing via generative pretrained transformer. In: 2024 54th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN); 2024 Jun 24–27; Brisbane, Australia: IEEE; 2024. p. 429–42. doi:10.1109/DSN58291.2024.00049. [Google Scholar] [CrossRef]

23. Guri M, Shemer E, Shirtz D, Elovici Y. Personal information leakage during password recovery of internet services. In: 2016 European Intelligence and Security Informatics Conference (EISIC); 2016; Uppsala, Sweden: IEEE. p. 136–139. doi:10.1109/EISIC.2016.035. [Google Scholar] [CrossRef]

24. Wang C, Jan STK, Hu H, Bossart D, Wang G. The next domino to fall: empirical analysis of user passwords across online services. In: Proceedings of the Eighth ACM Conference on Data and Application Security and Privacy; 2018; Tempe, Arizona, USA. p. 196–203. doi:10.1145/3176258.3176332. [Google Scholar] [CrossRef]

25. Miao Y, Chen C, Pan L, Han QL, Zhang J, Xiang Y. Machine learning-based cyber attacks targeting on controlled information: a survey. ACM Comput Surv. 2021;54(7):1–36. doi:10.1145/3465171. [Google Scholar] [CrossRef]

26. Wang Q, Wang D, Cheng C, Quantum2FA He D. Efficient quantum-resistant two-factor authentication scheme for mobile devices. IEEE Trans Dependable Secure Comput. 2021;20(1):193–208. doi:10.1109/TDSC.2021.3129512. [Google Scholar] [CrossRef]

27. Shay R, Bauer L, Christin N, Cranor LF, Forget A, Komanduri S, et al. A spoonful of sugar? The impact of guidance and feedback on password-creation behavior. In: Proceedings of the 33rd Annual ACM Conference on Human Factors in Computing Systems; 2015; New York, NY, USA. p. 2903–12. doi:10.1145/2702123.2702586. [Google Scholar] [CrossRef]

28. Ur B, Noma F, Bees J, Segreti SM, Shay R, Bauer L, et al. “I added ‘!’ at the end to make it secure”: observing password creation in the lab. In: Eleventh Symposium on Usable Privacy and Security (SOUPS 2015); 2015; Ottawa, ON, Canada. p. 123–40. doi:10.5555/3235866.3235877. [Google Scholar] [CrossRef]

29. Kelley PG, Komanduri S, Mazurek ML, Shay R, Vidas T, Bauer L, et al. Guess again (and again and againmeasuring password strength by simulating password-cracking algorithms. In: 2012 IEEE Symposium on Security and Privacy. San Francisco, CA, USA: IEEE; 2012. p. 523–37. doi:10.1109/SP.2012.38. [Google Scholar] [CrossRef]

30. Stobert E, Biddle R. The password life cycle. ACM Trans Priv Secur. 2018;21(3):1–32. doi:10.1145/3183341. [Google Scholar] [CrossRef]

31. Wang D, Cheng H, Wang P, Huang X, Jian G. Zipf’s law in passwords. IEEE Trans Inf Forensics Secur. 2017;12(11):2776–91. doi:10.1109/TIFS.2017.2721359. [Google Scholar] [CrossRef]

32. Wang D, Wang P, He D, Tian Y. Birthday, name and bifacial-security: understanding passwords of Chinese web users. In: 28th USENIX Security Symposium (USENIX Security 19); 2019. p. 1537–55. [cited 2025 Mar 20]. Available from: https://www.usenix.org/conference/usenixsecurity19/presentation/wang-ding. [Google Scholar]

33. Wang D, Li W, Wang P. Measuring two-factor authentication schemes for real-time data access in industrial wireless sensor networks. IEEE Trans Ind Inform. 2018;14(9):4081–92. doi:10.1109/TII.2018.2834351. [Google Scholar] [CrossRef]

34. Jiang Q, Zhang N, Ni J, Ma J, Ma X, Choo KK. Unified biometric privacy preserving three-factor authentication and key agreement for cloud-assisted autonomous vehicles. IEEE Trans Veh Technol. 2020;69(9):9390–401. doi:10.1109/TVT.2020.2971254. [Google Scholar] [CrossRef]

35. Wang C, Wang D, Tu Y, Xu G, Wang H. Understanding node capture attacks in user authentication schemes for wireless sensor networks. IEEE Trans Dependable Secure Comput. 2020;19(1):507–23. doi:10.1109/TDSC.2020.2974220. [Google Scholar] [CrossRef]