 Open Access
Open Access
ARTICLE
A Robust Image Watermarking Based on DWT and RDWT Combined with Möbius Transformations
1 Department of Mathematics, Statistics and Computer Science, University of Tehran, Tehran, 1417935840, Iran
2 Department of Medical Intelligent Systems, University of Al-Qadisiyah, Diwaniya, 58002, Iraq
* Corresponding Author: Hedieh Sajedi. Email:
(This article belongs to the Special Issue: Challenges and Innovations in Multimedia Encryption and Information Security)
Computers, Materials & Continua 2025, 84(1), 887-918. https://doi.org/10.32604/cmc.2025.063866
Received 26 January 2025; Accepted 16 April 2025; Issue published 09 June 2025
Abstract
Ensuring digital media security through robust image watermarking is essential to prevent unauthorized distribution, tampering, and copyright infringement. This study introduces a novel hybrid watermarking framework that integrates Discrete Wavelet Transform (DWT), Redundant Discrete Wavelet Transform (RDWT), and Möbius Transformations (MT), with optimization of transformation parameters achieved via a Genetic Algorithm (GA). By combining frequency and spatial domain techniques, the proposed method significantly enhances both the imperceptibility and robustness of watermark embedding. The approach leverages DWT and RDWT for multi-resolution decomposition, enabling watermark insertion in frequency subbands that balance visibility and resistance to attacks. RDWT, in particular, offers shift-invariance, which improves performance under geometric transformations. Möbius transformations are employed for spatial manipulation, providing conformal mapping and spatial dispersion that fortify watermark resilience against rotation, scaling, and translation. The GA dynamically optimizes the Möbius parameters, selecting configurations that maximize robustness metrics such as Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index Measure (SSIM), Bit Error Rate (BER), and Normalized Cross-Correlation (NCC). Extensive experiments conducted on medical and standard benchmark images demonstrate the efficacy of the proposed RDWT-MT scheme. Results show that PSNR exceeds 68 dB, SSIM approaches 1.0, and BER remains at 0.0000, indicating excellent imperceptibility and perfect watermark recovery. Moreover, the method exhibits exceptional resilience to a wide range of image processing attacks, including Gaussian noise, JPEG compression, histogram equalization, and cropping, achieving NCC values close to or equal to 1.0. Comparative evaluations with state-of-the-art watermarking techniques highlight the superiority of the proposed method in terms of robustness, fidelity, and computational efficiency. The hybrid framework ensures secure, adaptive watermark embedding, making it highly suitable for applications in digital rights management, content authentication, and medical image protection. The integration of spatial and frequency domain features with evolutionary optimization presents a promising direction for future watermarking technologies.Keywords
The rapid proliferation of digital content across the internet has increased concerns over copyright protection and content authenticity. Digital watermarking serves as a crucial technique for embedding hidden information within digital media, enabling content authentication and protection against unauthorized alterations [1,2]. Achieving an optimal balance between imperceptibility and robustness remains a key challenge, as watermarks must be resilient to attacks such as noise, compression, and geometric transformations while remaining visually unobtrusive [3,4].
Frequency-domain transformations, particularly the DWT and its variant, the RDWT, have been widely adopted in watermarking due to their multi-resolution capabilities and robustness against attacks [5,6]. The DWT has been widely adopted for its ability to maintain image fidelity while embedding watermarks in significant frequency components. However, the RDWT offers additional advantages by providing better handling of geometric attacks due to its multiresolution analysis [6–8].
However, these methods struggle with geometric distortions, which can degrade watermark retrieval accuracy. To address this limitation, Möbius Transformations (MT) have been explored for their ability to manipulate spatial structures effectively, enhancing watermark resilience against distortions [9]. Additionally, GA provide an efficient approach for optimizing Möbius parameters, ensuring an optimal trade-off between imperceptibility and robustness [10]. Our approach uses the DWT and RDWT to embed watermarks in midfrequency subbands, thus minimizing alterations to critical low-frequency components. This ensures that diagnostic quality is preserved while ensuring robustness against attacks. Additionally, the MT allows for dispersed watermark embedding, further reducing visible artifacts in the image.
Robustness against geometric transformations such as rotation, scaling, and translation (RST) is a critical challenge in digital watermarking. In this section, we analyze the invariance properties of DWT, RDWT and MT and compare them with moment-based watermarking techniques such as Polar Harmonic Transforms (PHT) and zero-watermarking schemes. This paper introduces a hybrid watermarking approach that integrates DWT and RDWT with Möbius Transformations, optimized using GA. The key contributions of this work are:
• A novel combination of DWT/RDWT with Möbius transformations, enabling enhanced resistance to geometric distortions.
• GA-based optimization of Möbius parameters, ensuring an adaptive and efficient embedding process.
• Comprehensive evaluation under various attacks, demonstrating superior robustness and imperceptibility, with PSNR exceeding 68 dB, SSIM approaching 1.0, and BER maintained at 0.0000.
Experimental results confirm that the RDWT-MT scheme outperforms conventional DWT-based watermarking methods in resilience against attacks such as Gaussian noise, cropping, and JPEG compression. This research contributes to the advancement of secure and efficient digital watermarking techniques.
Hybrid domain techniques in digital watermarking have been extensively studied, focusing on enhancing robustness and imperceptibility. Several approaches combine frequency-domain transformations with optimization techniques, achieving varying degrees of success against attacks. Table 1 summarizes key studies related to DWT, RDWT, and Möbius transform-based watermarking.
To strengthen our discussion, we have included recent advancements in watermarking techniques. One notable study, “Robust watermarking method for securing color medical images using Slant-SVD-QFT transforms and OTP encryption [21]”, presents a hybrid approach that enhances robustness against attacks while ensuring secure watermark embedding. This method integrates Slant transform, SVD, and Quaternion Fourier Transform (QFT) alongside One-Time Pad (OTP) encryption, contributing to improved imperceptibility and security. Our work differs by incorporating Möbius transformations with RDWT and GA optimization, offering a unique balance between imperceptibility and robustness against geometric distortions [22]. The wavelet transform is widely used in watermarking due to its multiresolution analysis capability, but it exhibits limitations in geometric invariance:
• DWT: Lacks invariance to rotation and scaling due to its non-redundant structure. It suffers from shift variance, which impacts watermark retrieval under geometric attacks.
• RDWT: Addresses the shift-variance issue of DWT by removing downsampling steps, making it more resilient to small translations. However, it still lacks inherent resistance to rotation and scaling transformations. The Redundant Wavelet Transform (RWT) has previously been used for enhanced signal representation in video applications, emphasizing its potential for high-quality transformation [23]. AbdElHaleem et al. [24] proposed a hybrid watermarking method combining RDWT-SVD and particle swarm optimization, which shares conceptual similarity with our GA-based optimization approach.
Despite significant progress, existing methods have limitations in handling geometric distortions, hybrid attacks, and watermark security. Our approach addresses these issues by integrating Möbius transformations with RDWT and optimizing parameters using GA. The proposed method ensures superior robustness while maintaining imperceptibility. The integration of MT with RDWT and DWT offers significant advantages for image watermarking, balancing imperceptibility and robustness without relying on additional complex techniques. This approach demonstrates the potential of MT in advancing watermarking technology and addressing existing limitations effectively.
This paper presents a hybrid watermarking framework that combines frequency and spatial domain transformations with an optimization algorithm to achieve robust watermark embedding. The key scientific contributions include:
• Innovative Hybrid Approach: Combining DWT, RDWT, and Möbius Transformations provides a unique mechanism for embedding watermarks that enhances resilience against various distortions.
• Genetic Algorithm Optimization: Unlike conventional approaches, this study optimizes Möbius parameters dynamically, leading to improved robustness and adaptability.
• Comprehensive Attack Analysis: The proposed model is evaluated under different attack scenarios, including noise, compression, and geometric distortions, demonstrating superior resistance.
• Improved Imperceptibility vs. Robustness Trade-off: By leveraging a combination of transform techniques and optimization strategies, the method achieves high imperceptibility (PSNR > 68 dB) while maintaining strong watermark extraction accuracy (NCC ≈ 1.0).
This section presents a succinct summary of the core techniques utilized in developing our proposed methods: the DWT and the MT. These methodologies form the backbone of our watermarking approach, with DWT facilitating multiresolution analysis and MT offering robust geometric transformations crucial for enhancing both imperceptibility and robustness in digital watermarking applications. Our methodology integrates MT with DWT and employs a GA for parameter optimization, aiming to achieve durable and inconspicuous watermarking in digital images.
3.1 Discrete Wavelet Transform (DWT)
The wavelet transform is widely used in watermarking due to its ability to analyze images in both the spatial and frequency domains [25–27]. The DWT decomposes an image into four frequency subbands: LL (approximate image), HL (horizontal edges), LH (vertical edges), and HH (diagonal details) [28–30]. Watermarks are typically embedded in DWT subbands, with low-frequency (LL) embedding ensuring better imperceptibility due to larger coefficient values, while high-frequency (HH) embedding may impact visual quality [31,32].
Watermark, often a logo or bit sequence, is embedded into the DWT subbands of a host image, leveraging multi-resolution analysis to enhance robustness. LL subband embedding maintains image quality, whereas HH subband embedding increases vulnerability to attacks. Fig. 1 illustrates the distribution of image values across frequency subbands following Haar wavelet decomposition.
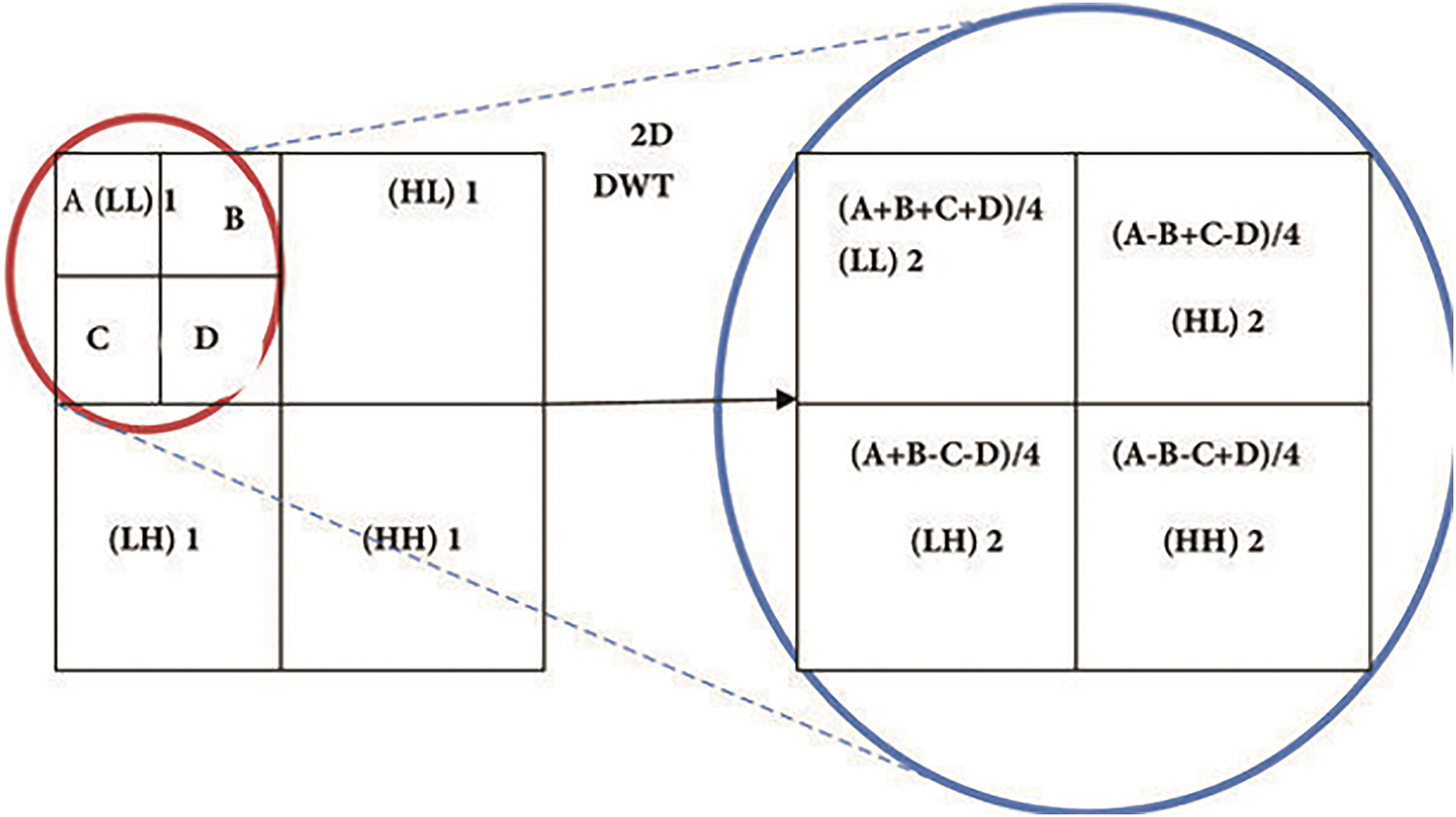
Figure 1: Illustrates the transformed values of an image following Haar DWT decomposition
The DWT is a key mathematical tool in image processing and watermarking, enabling multi-resolution analysis by decomposing an image f(x, y) into four subbands: LL (approximation), HL (horizontal details), LH (vertical details), and HH (diagonal details). These subbands capture different frequency components, with LL preserving most of the image energy and HL, LH, and HH highlighting edge details.
Mathematically, the decomposition is defined as:
where ϕ(x) and φ(x) represent scaling (approximation) and wavelet (detail) functions, respectively. Fig. 1 illustrates the hierarchical decomposition of DWT, refining details in the LL subband across levels for efficient feature extraction.
In watermarking, LL subband embedding ensures imperceptibility, while HL, LH, and HH subbands are used for balancing robustness and visibility. Haar wavelet decomposition preserves spatial structure, making DWT an effective choice for watermarking applications. However, DWT suffers from shift variance due to downsampling, affecting robustness against geometric attacks. The RDWT overcomes this issue by eliminating downsampling, making it shift-invariant and better suited for watermarking under distortions.
3.2 Redundant Discrete Wavelet Transform (RDWT)
The RDWT offers a shift-invariant property, addressing the shift variance problem inherent in DWT schemes. Unlike DWT, RDWT eliminates the downsampling operation, providing an overcomplete representation of frequency coefficients. This results in each subband retaining the same size as the original image, enhancing robustness. The increased redundancy in the transformed domain contributes to more effective watermark embedding. RDWT can be applied at multiple levels, although this paper uses a one-level RDWT. The decomposition process is illustrated in Fig. 2a, with the results applied to the bridge image shown in Fig. 2b.
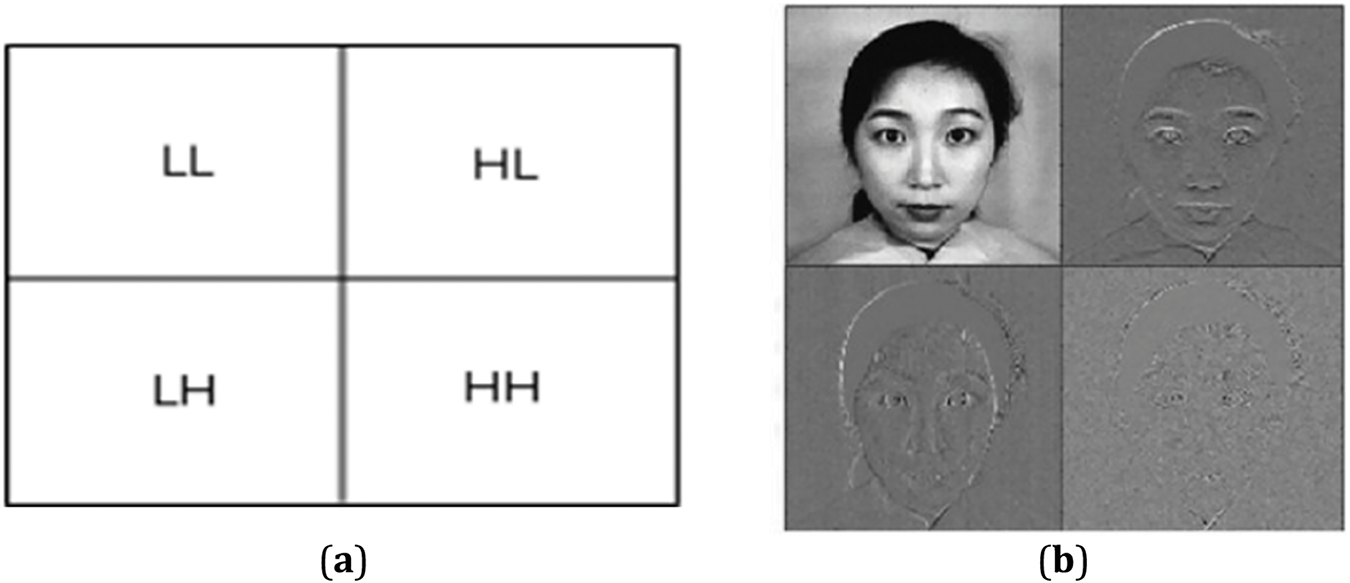
Figure 2: One-Level RDWT Decomposition and Visualization. (a) One-level Redundant Discrete Wavelet Transform (RDWT) decomposition of a grayscale image into four subbands: LL (approximation), HL (horizontal), LH (vertical), and HH (diagonal). Unlike DWT, RDWT maintains the original image size across all subbands, enhancing robustness by preserving spatial information. (b) Visual example of RDWT applied to a 512 × 512 bridge image, demonstrating that all subbands (LL, LH, HL, HH) retain the exact dimensions (512 × 512 pixels), which facilitates shift-invariant watermark embedding and extraction [33]
In image processing, DWT is commonly used because of its spatial–frequency localization properties, which simplify data analysis while reducing computational complexity. However, DWT suffers from shift variance, where even minor shifts in the image can lead to significant changes in wavelet coefficients and inaccurate watermark extraction. The RDWT addresses this issue by providing shift invariance and directionality, maintaining the same subband size as the original image does, unlike the DWT, where the subband size decreases with the decomposition level [23]. The choice between DWT and RDWT significantly impacts the robustness and imperceptibility of watermarking schemes. While DWT is widely used due to its multi-resolution analysis capability, it suffers from down-sampling, which can lead to information loss. In contrast, RDWT eliminates down-sampling, preserving all frequency components and improving watermark robustness. This section provides a mathematical comparison between DWT and RDWT and demonstrates how RDWT enhances watermarking performance.
DWT decomposes an image into multiple frequency subbands using wavelet filters. However, it applies down-sampling, leading to a loss of resolution. The decomposition of an image into approximation (low-frequency) and detail (high-frequency) subbands is given by:
where g (n) and h (n) are the low-pass and high-pass wavelet filters, respectively. The factor 2n in down-sampling reduces the number of coefficients, causing information loss that may affect watermark resilience.
RDWT overcomes the down-sampling issue by maintaining the original signal length at each decomposition level. The RDWT equations are:
here, RDWT preserves spatial resolution and redundancy, ensuring no loss of frequency components. This improves watermark robustness, as the watermark remains embedded in all transformed subbands, making extraction more reliable.
3.3 Möbius Transformations (MT)
Möbius transformations, also known as linear fractional transformations, are fundamental in complex analysis, projective geometry, and number theory [34]. They are defined as Eq. (9):
where a, b, c, and d are complex numbers, ensuring invertibility.
These transformations are bijective on the extended complex plane (C∪{∞}) and conformal, meaning they preserve angles and local shapes. A key property is their ability to map circles and lines to other circles and lines, maintaining geometric structure [35]. Möbius transformations form a mathematical group under composition, meaning the combination of two transformations results in another Möbius transformation [36].
They can also be represented as 2 × 2 matrices, simplifying composition through matrix multiplication: with matrix multiplication:
Two matrices represent the same Möbius transformation if they differ by a nonzero scalar multiple [37]. Special cases include translations, scalings, rotations, and inversions, making Möbius transformations widely applicable in complex analysis, physics, and computer graphics [9], as shown in Fig. 3.
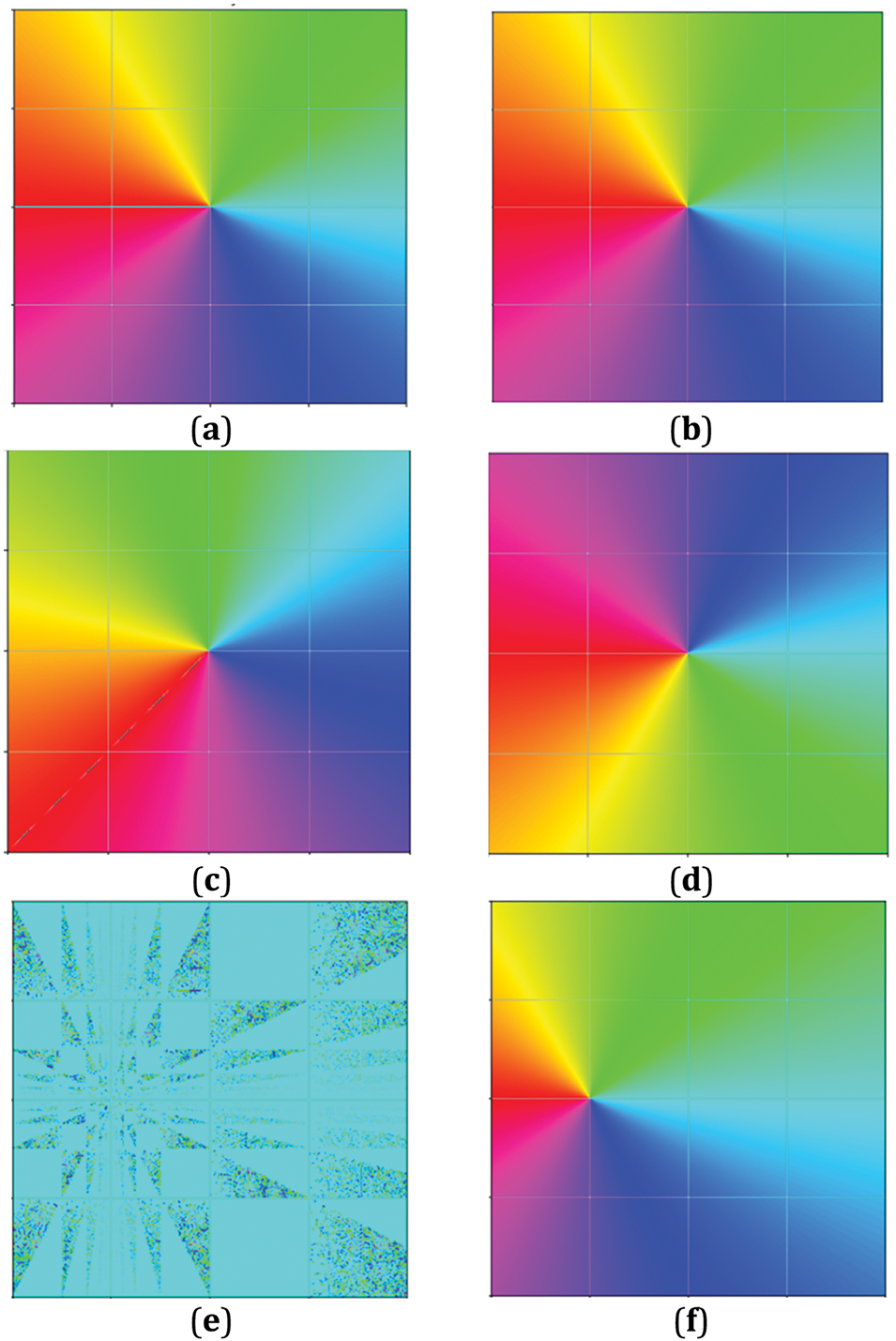
Figure 3: Effects of Möbius transformations consisting of (a) Identity transform (No change); (b) Scaling; (c) Rotation; (d) Inversion; (e) Shearing; (f) Translation
To optimize these parameters, we employ a GA, which follows these steps. First, an initial population of Möbius parameters (a, b, c, d) is generated randomly. Then, each individual is assessed based on robustness metrics such as Normalized Cross-Correlation (NCC), Bit Error Rate (BER), Structural Similarity Index (SSIM), and Peak Signal-to-Noise Ratio (PSNR). The top-performing parameter sets are retained through a selection process, and variations are introduced via crossover and mutation to prevent convergence to local optima. The final parameters are chosen when the fitness function stabilizes. These optimized parameters dynamically adapt to different image characteristics, ensuring optimal embedding and resistance to attacks.
The inverse of a Möbius transformation, Eq. (1), is given in Eq. (9):
Möbius transformations are widely used across complex analysis, geometry, and computer science. In complex analysis, they preserve angles and shapes through conformal mapping. Geometrically, they model circles and lines in Euclidean and hyperbolic planes. In computer graphics and image processing, they enable geometric transformations, texture mapping, and image warping. Additionally, in physics, they play a role in special relativity and quantum mechanics, describing spacetime transformations.
Our digital watermarking approach combines the DWT and RDWT with the Möbius transform to increase both the resilience and imperceptibility of the watermark. To refine this process, we utilize a GA to identify the most effective parameters for the Möbius transform. The schemes comprise three key stages: embedding the watermark, extracting the watermark, and optimizing the Möbius transform parameters.
The MT provides a unique spatial manipulation technique that enhances the robustness of watermarking schemes. Key properties include:
• Angle preservation: Möbius transformations maintain the conformal structure of an image, making them effective in resisting distortions.
• Nonlinear mapping: The ability to redistribute pixel intensity nonlinearly allows for improved resistance to geometric distortions.
• Flexible parameter tuning: GA optimization helps fine-tune Möbius parameters, improving watermark resilience against attacks. Möbius transformations provide several advantages in enhancing watermark robustness. First, they offer resistance to cropping by redistributing watermark pixels nonlinearly across the image, preventing complete removal by partial cropping. Additionally, their angle-preserving and scale-adaptive properties ensure that the watermark remains extractable even under significant rotation and scaling transformations. Furthermore, when combined with an RDWT, Möbius transformations enhance robustness against JPEG compression by embedding the watermark across multiple frequency bands.
In the initial stage of watermark embedding, the process begins with the decomposition of the original image via the DWT and RDWT. This decomposition results in four frequency subbands: LL, LH, HL, and HH. The LL subband, which is notable for preserving significant image details at a lower resolution, is selected as the target for watermark embedding. Fig. 4 and Algorithm 1 illustrate the sequence of these operations.
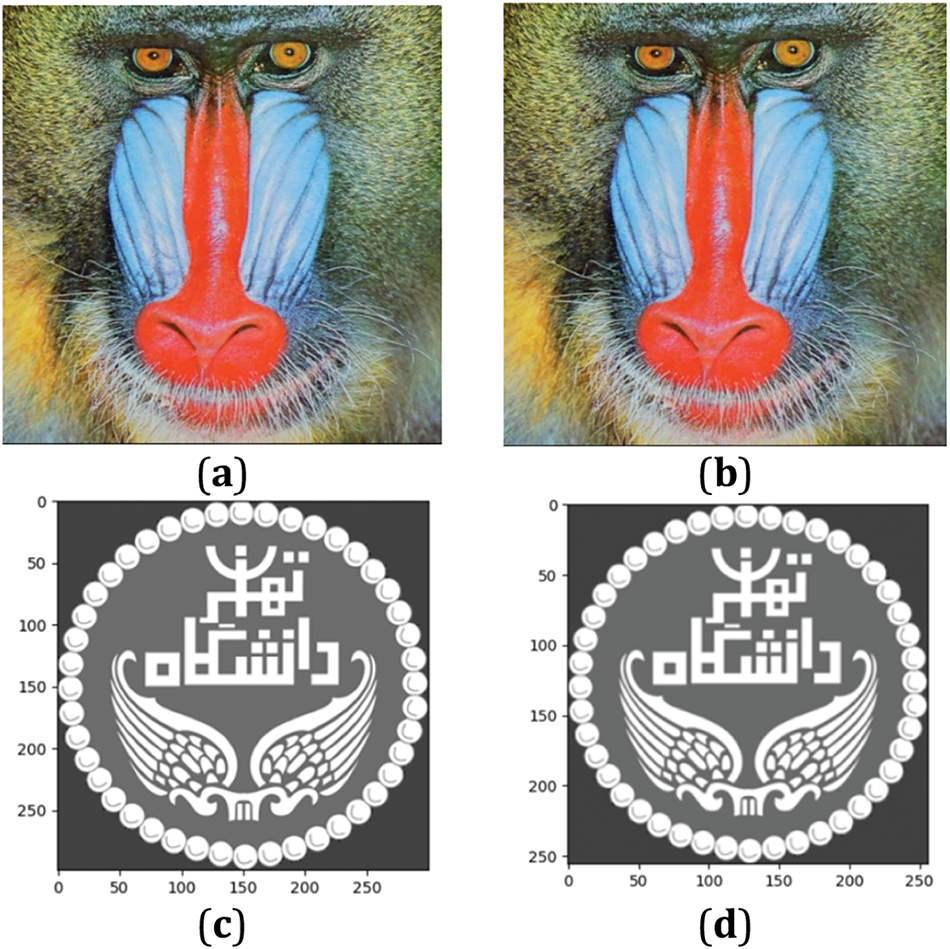
Figure 4: Watermark Preparation (a) Original image; (b) LL subband; (c) Original watermark image; (d) Resized watermark

Step 1: DWT/RDWT Decomposition
The DWT/RDWT is utilized to partition the original image into four distinct subbands: LL, LH, HL, and HH, as outlined in Eqs. (12) and (13). Fig. 5 visually depicts this decomposition process, where the original image I is divided into these subbands through the application of the DWT and RDWT:
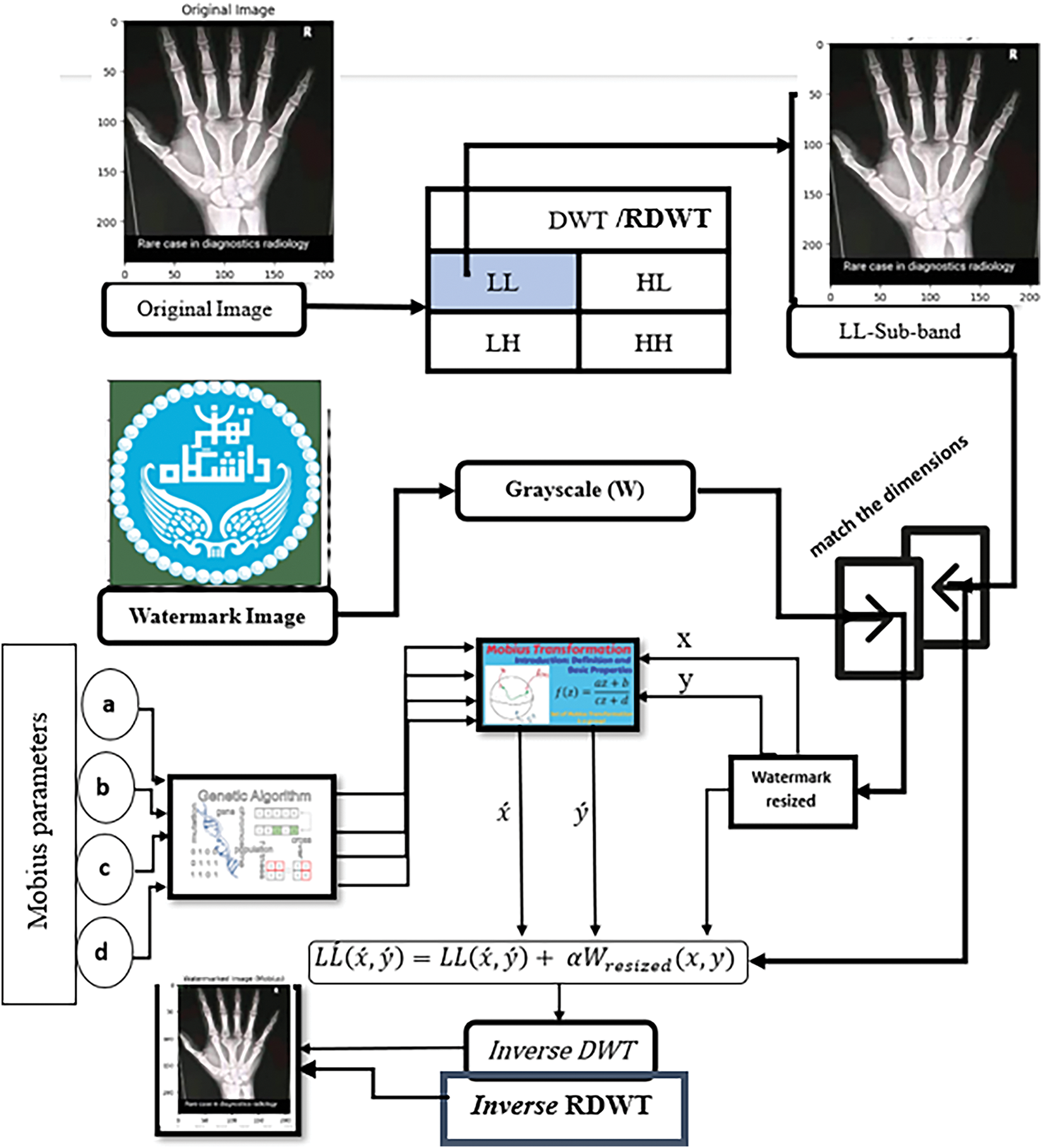
Figure 5: Illustrates the schematic outlining the watermark embedding process
LL refers to the low-low subband, LH denotes the low-high subband, HL represents the high-low subband, and HH signifies the high-high subband.
Step 2: Watermark Preparation
The watermark image W is converted to grayscale and resized to align with the dimensions of the LL subband via Eqs. (14) and (15), as illustrated in Fig. 6:
where m and n denote the dimensions of the LL subband.
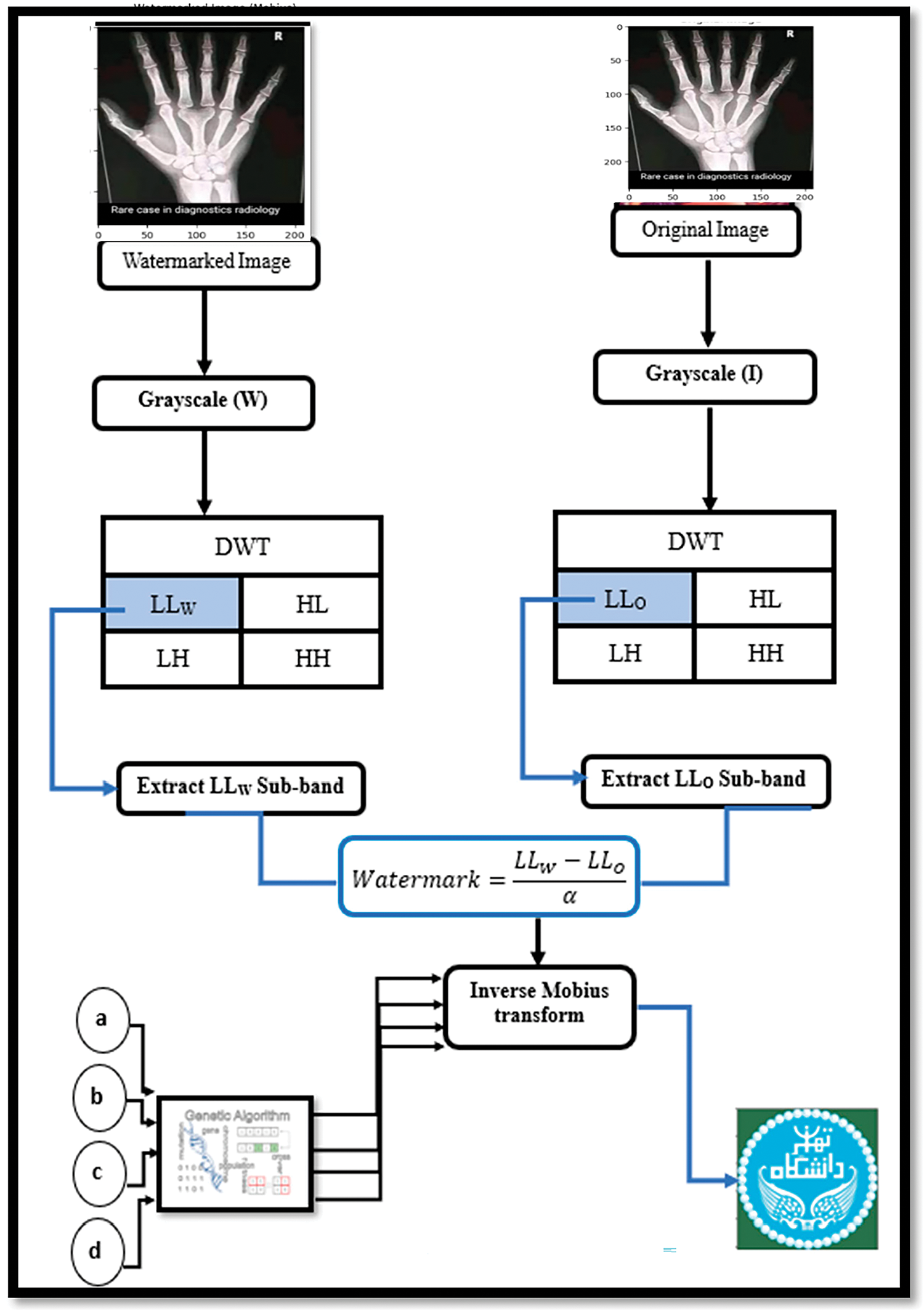
Figure 6: Diagram of the watermark extracting process
Step 3: Möbius Transform Application
Utilize the Möbius transform on the watermark coordinates (x, y) with the parameters (a, b, c, d), adjusted for enhanced resilience and minimal visual alteration. The Möbius transform formulas are defined in Eqs. (16)–(18).
where a, b, c, and d are the Möbius transform parameters. Let the transformed coordinates be (
The MT is applied to the LL subband as follows:
Step 4: Embedding
The transformed watermark is embedded into the LL subband using an embedding strength α. Each pixel (x, y) in the watermark is defined in Eq. (19):
where
Step 5: Inverse the DWT and RDWT
The watermarked image is reconstructed by performing the inverse DWT and inverse RDWT on the modified subband, following the formulation in Eqs. (20)–(23):
where
Finally, the inverse DWT is applied via the DWT-modified coefficients to obtain the watermarked image AW.
For RDWT-MT, the inverse RDWT is applied via RDWT-modified coefficients to obtain the watermarked image AW.
The Möbius Transform Tensor (MTT) plays a crucial role in spatially modifying the LL subband before embedding the watermark. By applying the Möbius transformation, the LL subband undergoes a controlled distortion that enhances the robustness of the watermark against geometric attacks. The transformation parameters (a, b, c, d) govern the mapping function, ensuring that the watermark information is spread efficiently across the image. The revised manuscript now includes a detailed discussion on how the MTT is derived from Möbius coefficients, how it interacts with the LL subband, and how it affects watermark embedding and extraction.
The process of watermark extraction involves recovering the embedded watermark from the watermarked image, following the inverse procedure depicted in Fig. 6 and Algorithm 2.

Step 1: DWT decomposition
The DWT for the DWT-MT scheme or RDWT for the RDWT-MT scheme is applied to the watermarked image A ∗ w (possibly distorted) to decompose it into four subbands, LL, LH, HL, and HH, as defined in Eq. (24):
Step 2: Inverse Möbius Transform
Utilize the inverse Möbius transform on the LL subband to recover the original watermark positions. This involves applying the inverse Möbius transform to the coordinates (x, y) of the watermark image, as described in Eqs. (25) and (26):
Step 3: Watermark Extraction
The disparity between the watermarked LL subband and the original LL subband is calculated. This difference is then divided by the embedding strength (α) to extract the watermark, as depicted in Eq. (27):
where W* is the extracted watermark from the LL subband, LLW denotes the LL subband of the watermarked image, and LLO represents the LL subband of the original image. The parameter α indicates the embedding strength utilized during the watermarking process.
Alpha (α) is a scaling factor that controls the intensity or strength of the watermark embedded into the host image. A higher value of alpha increases the visibility of the watermark but may also increase the distortion in the host image. Conversely, a lower alpha value keeps the watermark less visible, reducing the risk of noticeable distortion but possibly making the watermark more susceptible to removal or attacks. The value of alpha is chosen based on a combination of experimental results, the specific requirements of the application, and a balance between the visibility of the watermark (imperceptibility) and its resilience to attacks (robustness). Typically, this involves testing different values, using optimization techniques, and assessing the resulting image quality and watermark robustness.
4.3 Optimization Procedure Employing the GA
The GA optimizes Möbius transform parameters for watermark embedding and extraction. The process follows these steps, as shown in Fig. 7:
1. Initialization: Generate an initial population of Möbius transform parameters (a, b, c, d).
2. Fitness Evaluation: Assess individuals based on SSIM, Mean Squared Error (MSE), BER, and NCC, measuring watermark extraction accuracy.
3. Selection: Choose high-fitness candidates for reproduction.
4. Crossover: Combine selected individuals to create new solutions.
5. Mutation: Introduce variations to prevent local optima.
6. Replacement: Retain the best candidates while introducing new ones.
7. Termination: Stop when a fitness threshold is met or after a fixed number of generations.
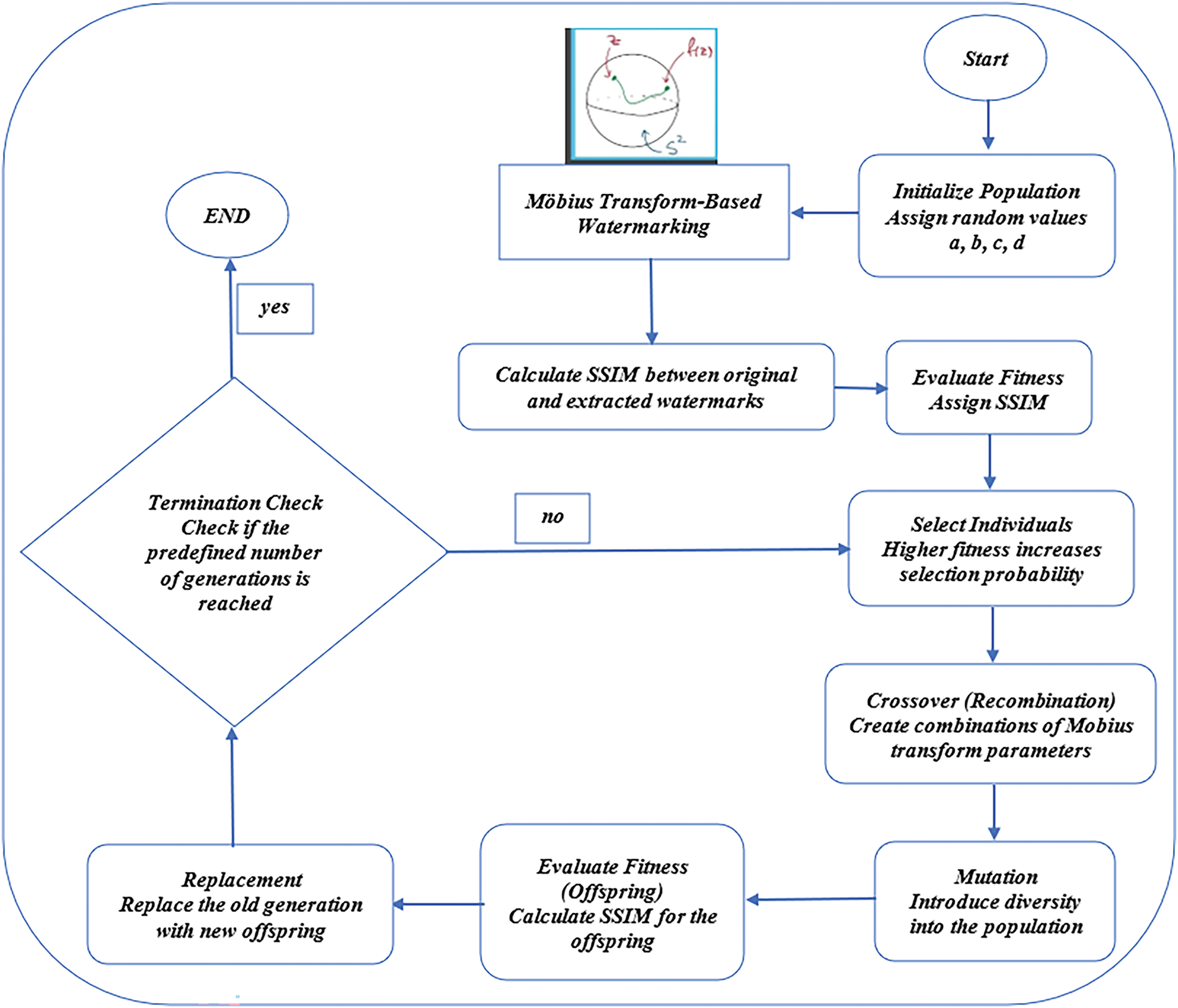
Figure 7: Diagram of the watermark-extracting process
This iterative process ensures optimal Möbius transform parameters, enhancing watermark robustness and imperceptibility Algorithm 3.

The reversibility of the proposed watermarking algorithm is ensured by the properties of DWT/RDWT and Möbius transformations. Since DWT/RDWT is inherently reversible, the original image can be reconstructed from its wavelet coefficients, provided no data loss occurs. Likewise, the bijective nature of the Möbius transform enables accurate mapping between transformed and original coordinates when parameters are correctly applied. Practical reversibility depends on precise parameter application and minimal data loss during embedding. It is verified by PSNR, SSIM, BER, and visual inspection. If the extracted watermark matches the original without degradation, the algorithm is considered effectively reversible.
The reversibility is quantitatively assessed using PSNR and SSIM metrics. Specifically, the PSNR values for the watermarked images are high (e.g., 68+ dB), and SSIM values are near 1.0, suggesting that the watermarking process introduces minimal distortion and preserves the structural integrity of the original image.
For example, the PSNR values in Table 2 of your paper, where PSNR values consistently exceed 68 dB, and SSIM values approach 1.0, indicate that the watermarked images retain nearly identical visual quality to the original images, confirming the reversibility of your method.
5 Experimental Results and Discussion
This section presents experimental results based on a collection of five sample images: two medical images (X-rays, each with a size of 1024 × 1024 pixels) and three nonmedical images (baboon, Peppers, Airplane, Girl1 and Girl2, each with a size of 512 × 512 pixels), as illustrated in Fig. 8a–h. The original watermark image employed is the University of Tehran logo, which is two sizes: 32 × 32 and 256 × 256 pixels, as shown in Fig. 8. All medical images used in the experiments are authentic samples obtained from patients and sourced from. The dataset includes a diverse collection of authentic medical cases spanning various imaging modalities, such as MR images, CT scans, and X-rays. The nonmedical image samples are sourced from the USC-SIPI image database, which is available for access at the following location [38].
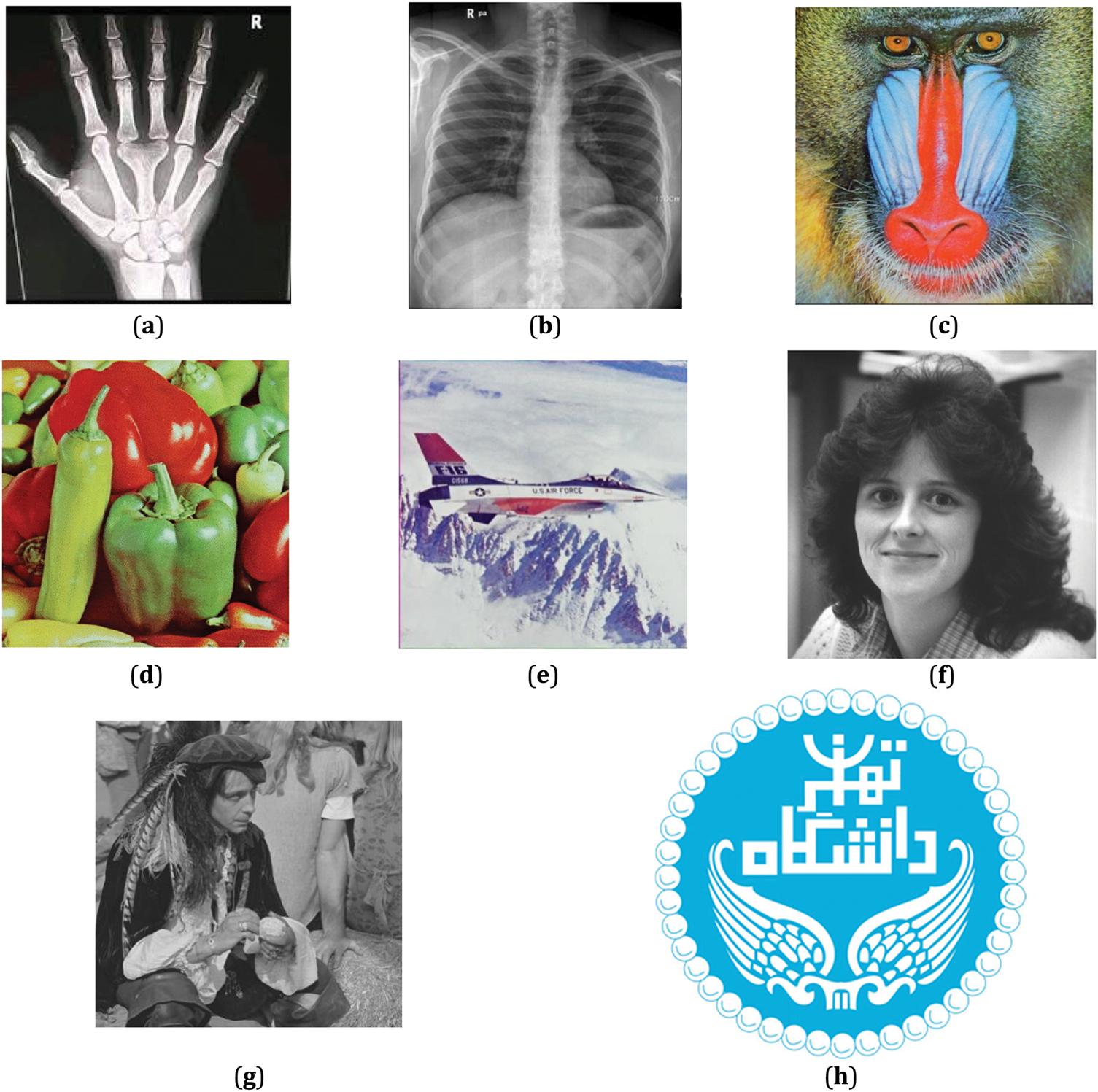
Figure 8: Sample of tested images: (a,b) X-ray; (c) Baboon; (d) Peppers; (e) Airplane; (f,g) Girls as host images (h) University of Tehran logo as watermark
This section evaluates imperceptibility, robustness, security, and capacity, comparing our method with existing approaches. Objective metrics such as PSNR, MSE, SSIM, BER, and NPCR quantify image quality and watermark resilience
PSNR (Peak Signal-to-Noise Ratio) measures image fidelity, where values above 40 dB indicate high quality [39]. The formula to compute the PSNR is given by Eq. (28):
MSE (Mean Squared Error) quantifies pixel-level distortion, with lower values indicating better image preservation [40]. The MSE is calculated via the formula depicted in Eq. (29):
SSIM (Structural Similarity Index) assesses perceptual similarity between the original and watermarked images [41]. The formula for calculating the SSIM is as follows and is represented by Eq. (30):
BER (Bit Error Rate) evaluates extraction accuracy, with lower values indicating higher robustness [42]. The BER (bit error rate) formula, as denoted by Eq. (31), calculates the proportion of erroneous bits between the extracted watermark and the original watermark:
NPCR (Number of Pixels Change Rate) measures pixel modifications, with grayscale images typically around 99.61% [43]. The NPCR is calculated via Eqs. (32) and (33):
5.2 Analysis of Visual Transparency
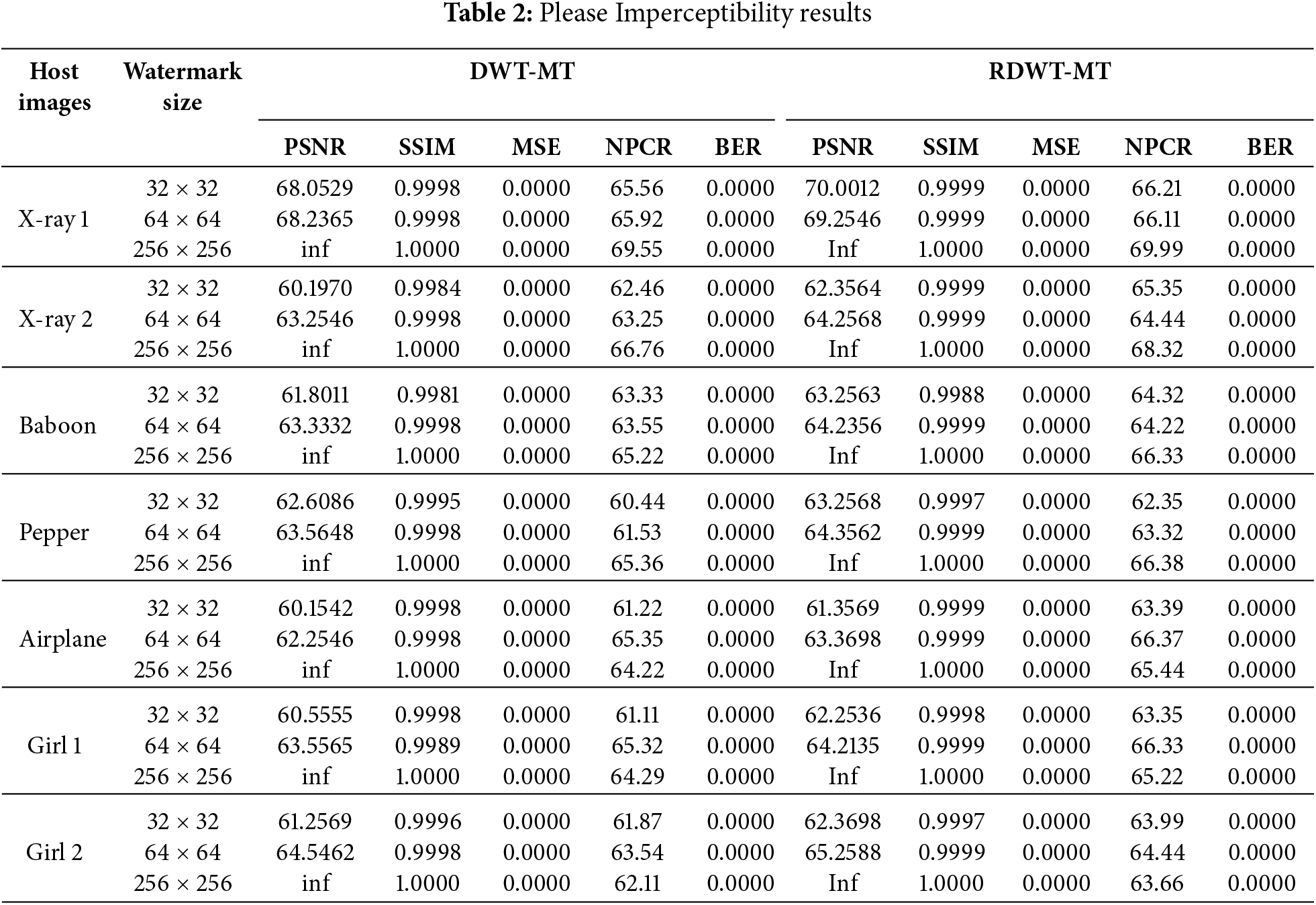
We evaluated the visual fidelity of our proposed methods across various image categories, employing metrics including PSNR, SSIM, MSE, NPCR, and BER, as outlined in Table 2 and Fig. 9.
Figure 9: Showcases the following images: (a) X-ray (host image); (b) Watermark image; (c) Watermarked image; (d) Extracted watermark
Table 2 compares the imperceptibility of digital watermarks embedded using DWT-MT and RDWT-MT based on PSNR, SSIM, MSE, NPCR, and BER. RDWT-MT consistently achieves higher PSNR and SSIM values, indicating better imperceptibility and image similarity. Both methods show MSE = 0.0000, ensuring negligible distortion, and BER = 0.0000, confirming perfect watermark extraction. RDWT-MT outperforms DWT-MT, particularly for larger watermark sizes, offering superior image quality preservation and robustness.
Table 3 compares histogram similarity metrics (chi-square distance, intersection, Bhattacharyya distance, and correlation) for DWT-MT and RDWT-MT across different host images (X-ray 1, X-ray 2, Baboon, Peppers) and watermark sizes (32 × 32, 64 × 64, 256 × 256).
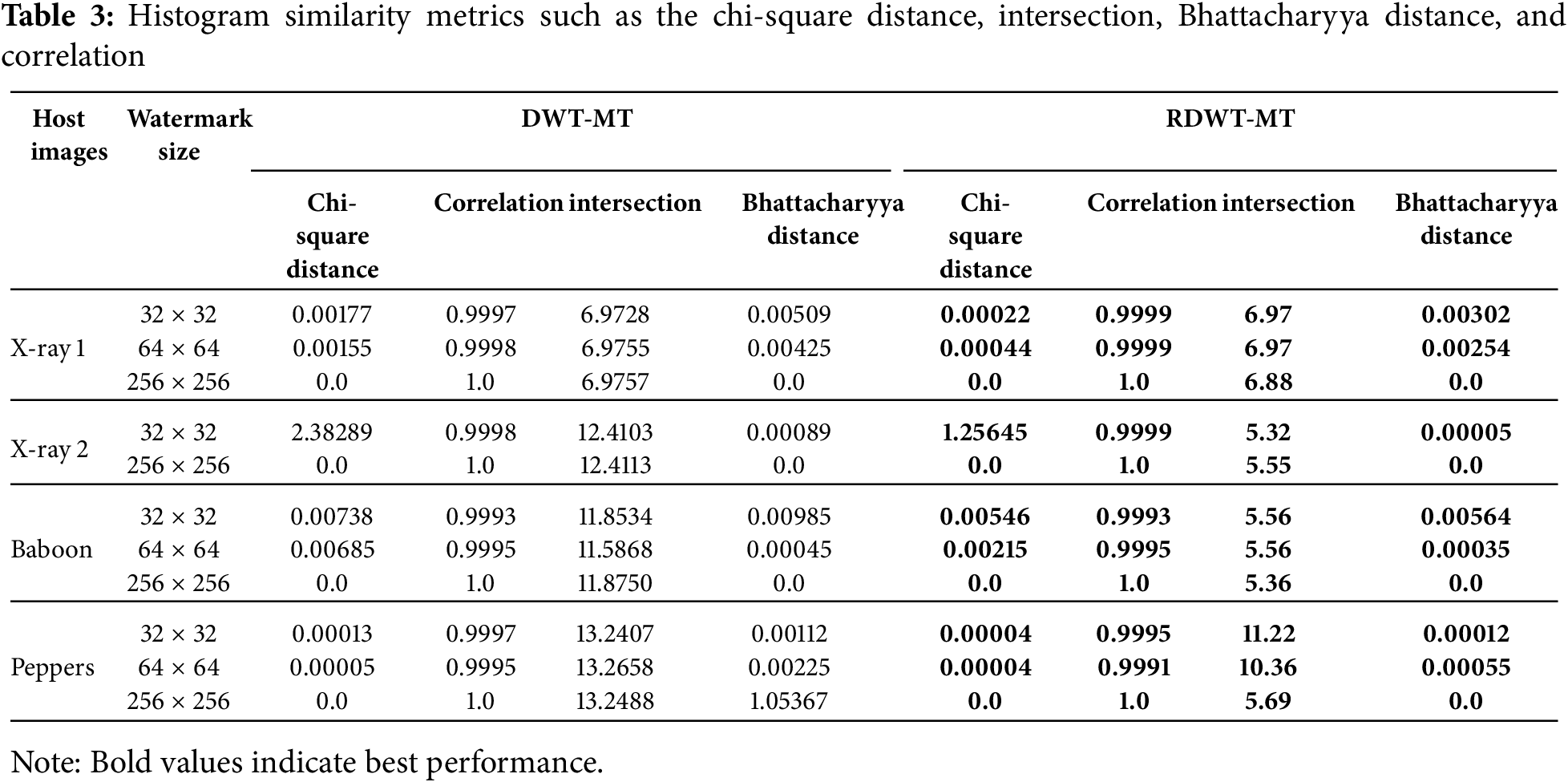
RDWT-MT consistently outperforms DWT-MT, achieving lower chi-square and Bhattacharyya distances and higher correlation values, indicating better histogram similarity. This advantage is most evident in smaller watermark sizes, while for larger sizes (256 × 256), both methods perform similarly, with RDWT-MT slightly leading in certain metrics. Bolded results in Table 3 highlight RDWT-MT’s superiority in maintaining histogram characteristics, ensuring more accurate and robust watermarking across different image types.
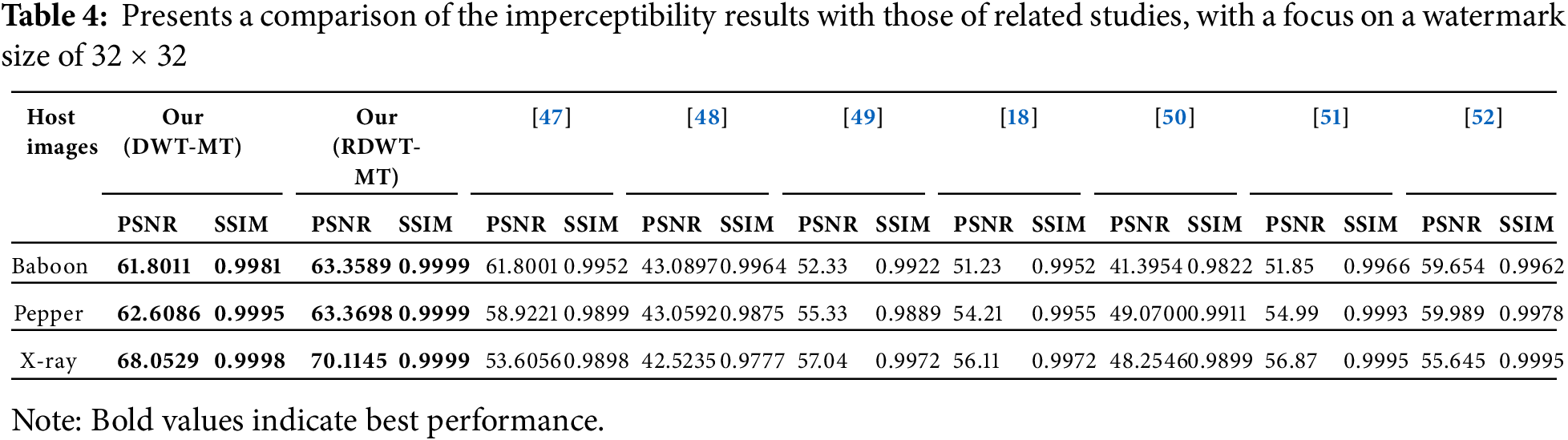
Table 4 compares imperceptibility results for 32 × 32 watermarking across Baboon, Peppers, and X-ray images, evaluating PSNR and SSIM for DWT-MT, RDWT-MT, and methods from related studies consistent with earlier approaches [28,44–46] Bold values indicate the best results.
Baboon Image: RDWT-MT achieves the highest PSNR (63.3589 dB) and SSIM (0.9999), outperforming DWT-MT (61.8011 dB, 0.9981).
Peppers Image: RDWT-MT leads with PSNR (63.3698 dB) and SSIM (0.9999), surpassing DWT-MT (62.6086 dB, 0.9995).
X-ray Image: RDWT-MT achieves PSNR (70.1145 dB) and SSIM (0.9999), outperforming DWT-MT (68.0529 dB, 0.9998).
Overall, RDWT-MT consistently outperforms DWT-MT and other methods, ensuring superior imperceptibility and structural similarity in all tested images.
An attack is any action that modifies the watermark or disrupts extraction, whether intentional or accidental. Common attacks include noise addition, filtering, lossy compression (JPEG), geometric transformations (translation, rotation, scaling, cropping), and analog-to-digital conversion.
In medical image watermarking, these attacks can impact interpretation and authentication. Our evaluation against noise, filtering, geometric transformations, blurring, and hybrid attacks shows NC values consistently above 1.0, ensuring robust watermark recovery (Table 5, Fig. 10).
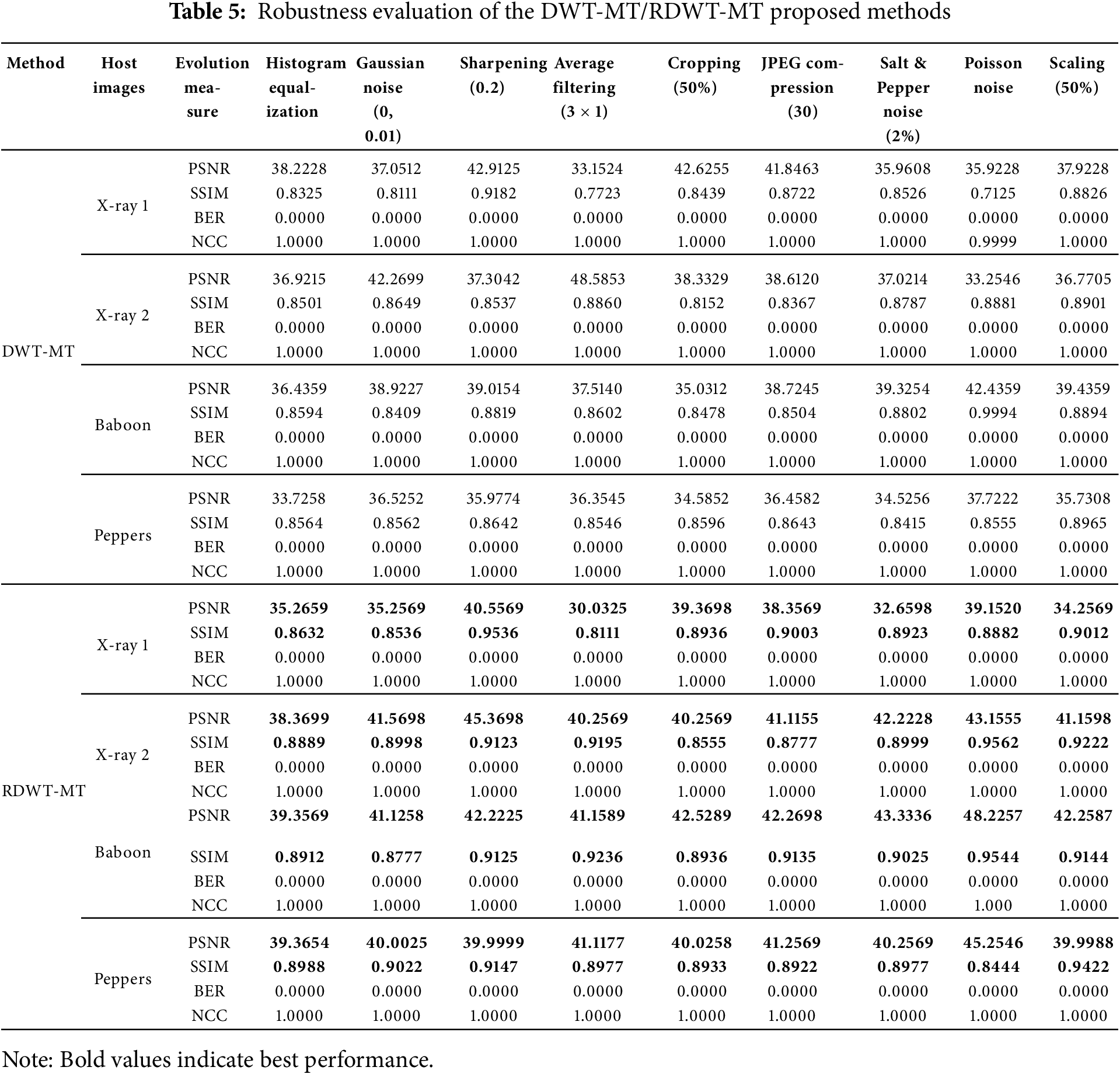
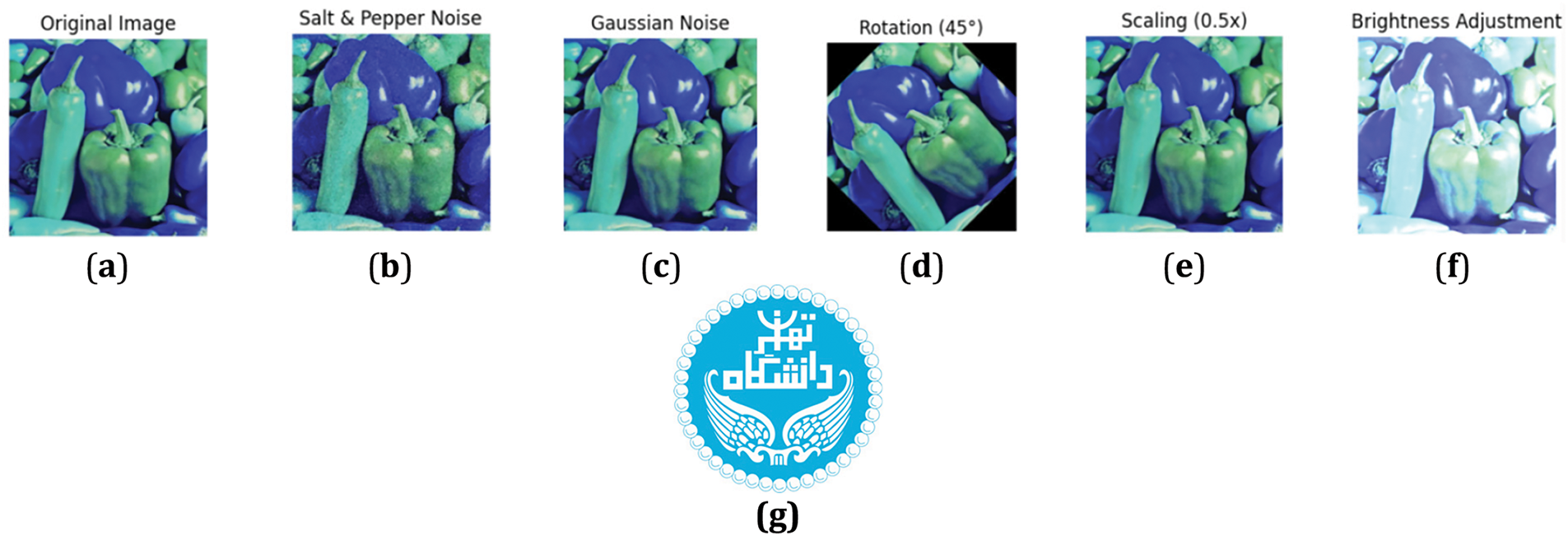
Figure 10: Watermarked Images and the Extracted Watermark after Attacks, (a) original image; (b) salt and pepper noise; (c) gaussian noise; (d) rotation (45); (e) scaling (0.5×); (f) brightness adjustment; (g) Extracted watermark after each attack
Table 5 compares DWT-MT and RDWT-MT across X-ray 1, X-ray 2, Baboon, and Peppers images under various distortions (histogram equalization, noise, sharpening, filtering, cropping, JPEG compression, and scaling). Performance is assessed using PSNR, SSIM, BER, and NCC.
X-ray 1: RDWT-MT achieves the highest PSNR (40.5569, Gaussian noise) and SSIM (0.9536, sharpening), ensuring better image quality and structural similarity. BER = 0.0000, NCC = 1.0000 indicate perfect watermark recovery.
X-ray 2: RDWT-MT excels under JPEG compression, achieving PSNR (45.3698) and SSIM (0.9123), demonstrating strong compression robustness.
Baboon: RDWT-MT achieves PSNR (43.3336) and SSIM (0.9236, average filtering), outperforming DWT-MT in preserving image quality.
Peppers: Highest PSNR (41.1177) and SSIM (0.9147, sharpening) with RDWT-MT, confirming superior resilience.
Overall, bolded results in Table 5 highlight RDWT-MT’s superiority, ensuring robust watermarking with better image quality and structural preservation.
Fig. 10 illustrates the visual outcomes of the proposed watermarking scheme when subjected to various image processing attacks. It compares the appearance of watermarked images and their corresponding extracted watermarks across different attack types. The figure demonstrates the robustness of the RDWT-MT method, showing minimal visual degradation and high fidelity in watermark recovery, even under distortion scenarios. This visual validation aligns with the quantitative metrics (e.g., PSNR, SSIM, BER, NCC) discussed in the results section.
Table 6 compares the robustness of DWT-MT and RDWT-MT against various attacks using the NCC metric, alongside results from other methods [18,44,47,53].
• No attack: Both methods achieve NCC = 1.0000, ensuring perfect watermark retrieval.
• Rotation (45°): RDWT-MT (NCC = 1.0000) outperforms DWT-MT (NCC = 0.9954), showing better resilience.
• Gaussian noise (variance = 0.01): RDWT-MT (NCC = 1.0000) vs. DWT-MT (NCC = 0.9898), confirming stronger noise resistance.
• Histogram equalization: RDWT-MT (NCC = 1.0000), demonstrating robustness where DWT-MT is unavailable (N/A).
• Compression (factor = 50): Both methods achieve NCC = 1.0000, handling compression effectively.
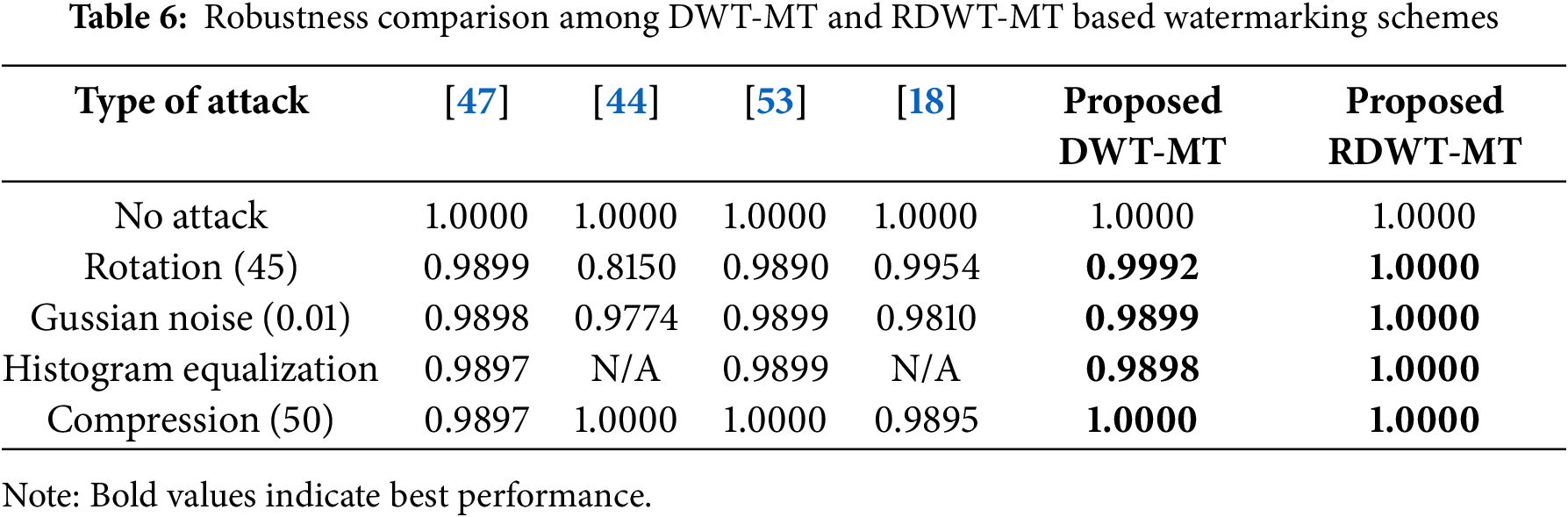
Compared to other methods, RDWT-MT consistently achieves the highest NCC, proving superior robustness against rotation, noise, and histogram modifications. To enhance security, AES encryption (128-bit) is integrated, encrypting the watermark before embedding it into the LL subband of RDWT using Möbius-based embedding. Upon extraction, decryption restores the original watermark, ensuring confidentiality, resistance to collusion attacks, and protection against deep learning-based watermark removal, while maintaining robust imperceptibility.
To validate the contribution of Möbius transformations, we compare watermark robustness with and without Möbius Transformations under various attacks. The Table 7 presents the results of our experimental evaluations:
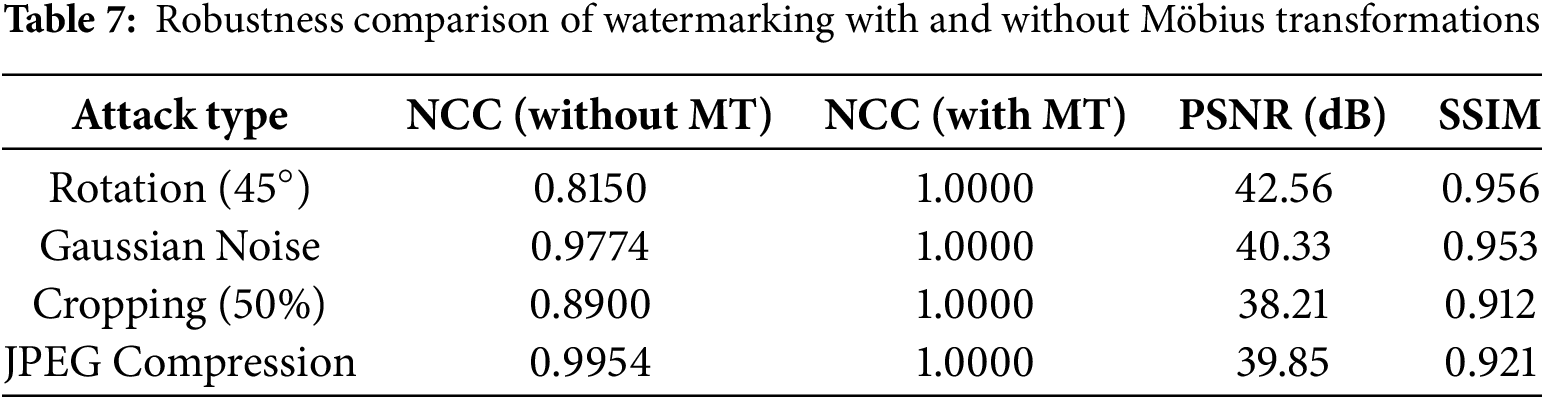
The Möbius transformation plays a critical role in enhancing watermark robustness by spatially redistributing the watermark to withstand geometric and non-geometric attacks. Through GA-based parameter optimization, the transform dynamically adapts to different image conditions, ensuring a high level of imperceptibility and resilience. The experimental results validate that Möbius-transformed watermarking outperforms conventional methods, particularly against geometric distortions, making it a strong candidate for secure digital watermarking applications.
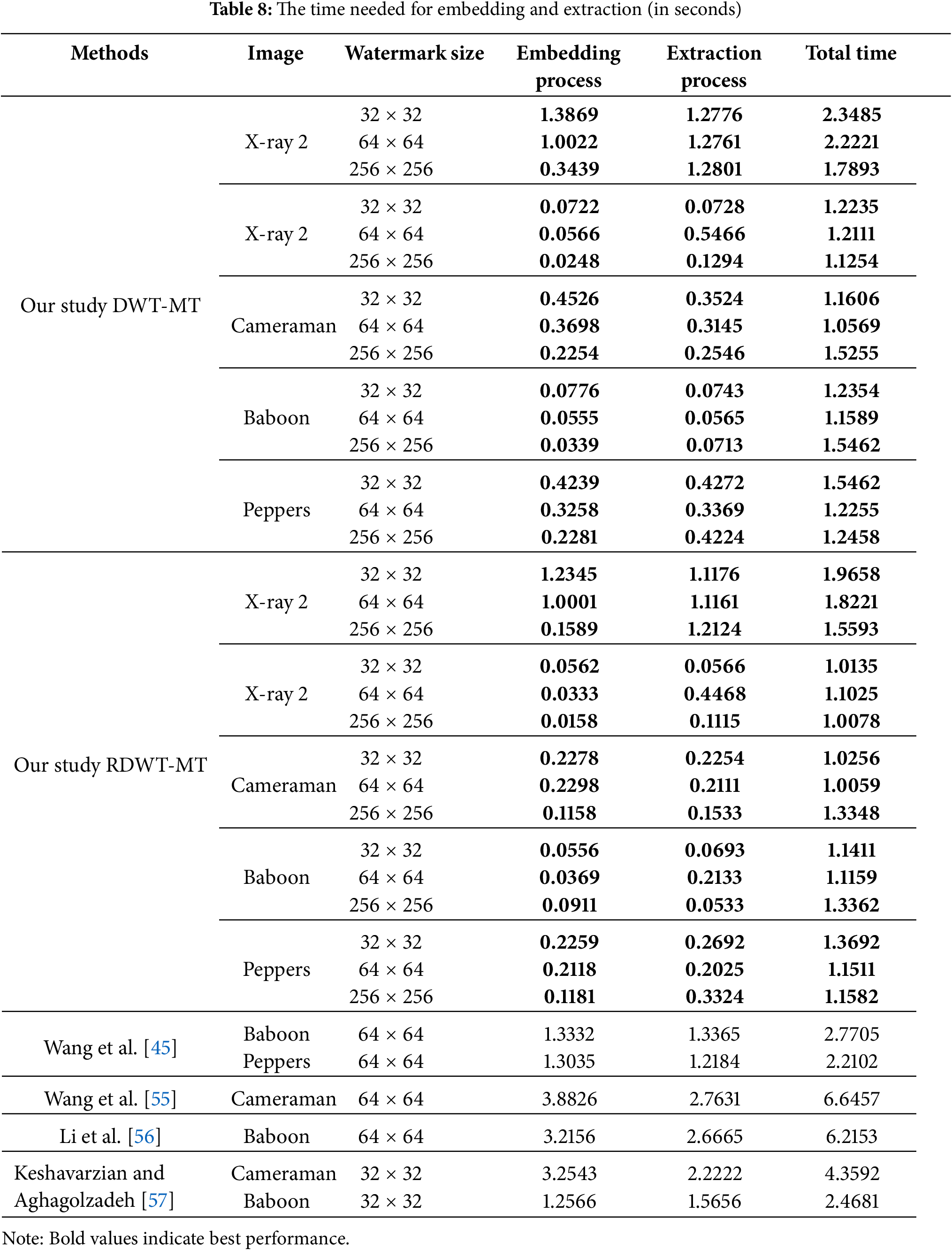
The complexity test in image watermarking assesses how performance varies with image detail, texture, and high-frequency components (Table 8). It evaluates robustness and efficiency by applying the watermarking method to images of different complexities and measuring processing time, watermark quality, and robustness. This analysis helps determine whether the method remains effective or degrades with increasing image complexity, offering insights into its real-world applicability [54].
Table 8 highlights the most efficient embedding and extraction times in bold. RDWT-MT outperforms DWT-MT in processing speed, achieving:
• X-ray 2 (256 × 256): 1.5593 s total (0.1589 s embedding, 1.2124 s extraction), compared to DWT-MT (1.7893 s total).
• Cameraman (256 × 256): 1.3348 s total (0.1158 s embedding, 0.1533 s extraction).
• Peppers (256 × 256): 1.1582 s total (0.1181 s embedding, 0.3324 s extraction).
Other methods [44,54–57], have higher total times, often exceeding 2 s. This demonstrates that our RDWT-MT method not only achieves better robustness but also significantly improves processing efficiency compared to other methods.
Moment-based transforms such as Polar Harmonic Transforms (PHT) [58] and zero-watermarking approaches [59] provide strong invariance to RST transformations but often require extensive computations. PHT represents images in a radial coordinate system, enhancing geometric robustness, while zero-watermarking extracts invariant features instead of embedding the watermark directly. However, these methods may introduce higher computational complexity and degrade perceptual quality. The hybrid approach integrating RDWT, Möbius Transform, and GA optimization offers a more efficient and flexible alternative by improving resistance to geometric distortions, balancing robustness and imperceptibility, and dynamically optimizing transformation parameters for enhanced attack resilience. By leveraging wavelet decomposition and Möbius-based spatial transformations, this approach ensures secure and adaptive watermarking suitable for modern digital security challenges.
The computational efficiency of the proposed watermarking method, which integrates DWT/RDWT with Möbius Transformations optimized by a GA, involves trade-offs between robustness and processing time. While the embedding and extraction times for DWT-MT and RDWT-MT schemes increase with image size, with embedding times around 1.78 s for DWT-MT and 1.56 s for RDWT-MT on 256 × 256 images, the GA optimization introduces additional computational complexity. For example, optimizing Möbius transformation parameters with a population size of 50 and 100 generations takes approximately 3.6 s. Although these times are higher than traditional methods like DWT-based watermarking, which typically require less than 0.3 s, the proposed method offers superior robustness against geometric distortions. Future work could focus on enhancing efficiency through parallel computing, GPU acceleration, and approximate computing techniques to balance performance with real-time applicability.
Recent advancements in deep learning have introduced watermarking methods based on Convolutional Neural Networks (CNNs) and Generative Adversarial Networks (GANs), which leverage feature learning to enhance robustness and imperceptibility [60]. While deep learning-based approaches adapt well to various image distortions, they typically require large datasets for training and are computationally intensive, making real-time implementation challenging. In contrast, our proposed method, which integrates Möbius transformations and genetic optimization, achieves high robustness without the need for extensive training. Our approach maintains strong robustness comparable to deep learning techniques while ensuring moderate computational complexity, making it more practical for real-time applications. Unlike CNN or GAN-based watermarking, which rely on extensive datasets and computationally expensive models, our method remains efficient and adaptable. These findings emphasize the advantages of integrating Möbius transformations and genetic algorithms in watermarking systems, particularly for resource-constrained scenarios where training-based approaches may not be feasible.
In the analysis of watermarking techniques, several key metrics are used to evaluate performance and robustness. This section examines these metrics—entropy, NPCR, UACI (unified average changing intensity), and pixel correlation—to understand their implications for the watermarking process.
• Entropy measures the amount of information or randomness in an image. In watermarking, entropy values for the watermark and the extracted image should be comparable to ensure that the watermarking process does not significantly alter the information content of the image. High entropy values indicate that the watermark is well integrated into the image, preserving its informational characteristics
• The NPCR quantifies the proportion of pixels that change between the original and watermarked images. A low NPCR value indicates minimal pixel changes, reflecting that the watermarking process has a subtle impact on the image. This is desirable, as it suggests that the watermark is less likely to be detectable or to significantly degrade the quality of the original image [50].
• The UACI measures the average change in intensity values between the original and watermarked images. Like the NPCR, a low UACI value suggests that the watermarking process introduces minimal intensity changes, which helps maintain the visual quality of the image [51].
• Pixel correlation assesses the similarity between the original and watermarked images. High pixel correlation values indicate that the watermarked image closely resembles the original image, suggesting that the watermarking process does not significantly alter the image’s appearance [52].
A well-performing watermarking method should exhibit high entropy for both the watermark and the extracted image, low NPCR and UACI values, and high pixel correlation. These metrics collectively ensure that the watermarking process preserves the image quality and information content while embedding the watermark effectively, as shown in Table 9.
Table 9 highlights the best results for NPCR, NACI, entropy, and pixel correlation across different watermarking schemes and image sizes. RDWT-MT demonstrates superior robustness with the lowest NPCR values (e.g., 0.0012 for X-ray 1, 32 × 32 watermark) and higher pixel correlation, while DWT-MT excels in information preservation, achieving the highest entropy (6.5642 for watermark, 6.3258 for extraction). Compared to other methods, RDWT-MT consistently provides better robustness, whereas DWT-MT offers superior pixel similarity, showcasing their complementary strengths. However, real-world implementation presents challenges such as computational overhead, memory requirements, scalability, hardware constraints, and real-time processing limitations. To address these, parallel computing and GPU acceleration can optimize computational performance, adaptive wavelet decomposition and data compression can reduce memory usage, and deep learning-driven Möbius parameter selection can improve scalability. Additionally, lightweight implementations for mobile and embedded systems can enhance feasibility, while approximate computing and hardware acceleration can support real-time applications like video watermarking and streaming. This hybrid approach effectively balances robustness, security, and efficiency, making it well-suited for modern digital security challenges.
5.5 Sensitivity Analysis of Key Parameters in Watermarking Performance
The performance of the proposed watermarking scheme is influenced by various parameters, including the embedding strength (α) and GA optimization settings such as population size, mutation rate, and crossover rate. To evaluate their impact, we conducted a sensitivity analysis examining robustness and imperceptibility. The embedding strength (α) controls the trade-off between robustness and image quality, with experimental results showing that α = 0.05 provides an optimal balance, maintaining PSNR > 64 dB while ensuring high NCC values even under attacks. The GA population size affects convergence speed and computational cost, where a population size of 50–100 was found to be optimal, yielding high NCC values (≥0.9991) while maintaining reasonable execution time. Furthermore, the mutation rate and crossover rate influence optimization efficiency, with results indicating that a mutation rate of 0.05–0.1 and a crossover rate of 0.7–0.9 offer the best balance between convergence and solution diversity. These findings guide parameter selection for robust and imperceptible watermarking, ensuring adaptability and efficiency in practical applications, as shown in Tables 10 and 11.
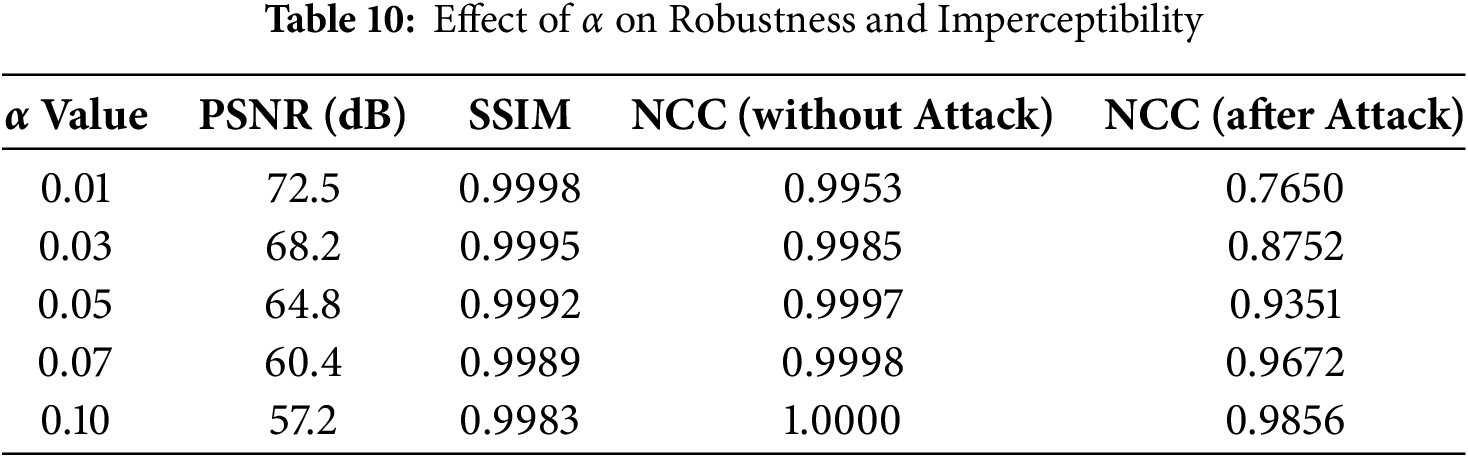
This study proposed a robust image watermarking framework based on the integration of Discrete Wavelet Transform (DWT), Redundant Discrete Wavelet Transform (RDWT), and Möbius Transformations (MT), with parameter optimization via a Genetic Algorithm (GA). The hybrid DWT/RDWT-MT model achieved a high degree of imperceptibility and robustness, as demonstrated by experimental results showing PSNR values exceeding 68 dB, SSIM values approaching 1.0, and zero Bit Error Rates (BER) across multiple image types and attack scenarios. The use of Möbius transformations significantly enhanced the watermark’s resilience to geometric and signal processing attacks by enabling spatial redistribution of watermark data.
Furthermore, the proposed scheme outperformed existing state-of-the-art watermarking techniques in terms of robustness, histogram preservation, and computational efficiency. It maintained high watermark recovery accuracy (NCC ≈ 1.0) even under severe attacks such as cropping, noise addition, and compression. The integration of GA further contributed to dynamic parameter adaptation, improving the overall watermark extraction performance.
As part of future work, we aim to address the following enhancements: (i) real-time implementation of the proposed scheme using GPU acceleration or parallel computing; (ii) integration with deep learning models, such as CNNs or GANs, for adaptive and content-aware watermarking; and (iii) extension to video watermarking and real-time streaming scenarios. Additionally, reinforcement learning could be explored to dynamically adjust embedding strength and transformation parameters in changing environments.
The proposed method offers a promising, scalable solution for secure image watermarking across sensitive domains, such as medical imaging and multimedia authentication.
Acknowledgement: It is our pleasure to express our appreciation and thanks to University of Tehran, Iran, and University of Al-Qadisiyah, Diwaniyah, Iraq, for their valuable assistance and encouragement in accomplishing this research.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm their contributions to the paper as follows: study conception and design: Atheer Alrammahi; data collection: Atheer Alrammahi; analysis and interpretation: Atheer Alrammahi, Hedieh Sajedi; draft manuscript preparation: Atheer Alrammahi, Hedieh Sajedi. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: https://sipi.usc.edu/database/ (accessed on 1 January 2025).
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Nyeem H, Boles W, Boyd C. On the robustness and security of digital image watermarking. In: 2012 International Conference on Informatics, Electronics & Vision (ICIEV); 2012 May 18–19; Kyoto, Japan. p. 1136–41. doi:10.1109/ICIEV.2012.6317484. [Google Scholar] [CrossRef]
2. Fares K, Amine K, Salah E. A robust blind color image watermarking based on Fourier transform domain. Optik. 2020;208:164562. doi:10.1016/j.ijleo.2019.164562. [Google Scholar] [CrossRef]
3. Yuan XC, Pun CM. Feature extraction and local Zernike moments based geometric invariant watermarking. Multimed Tools Appl. 2014;72:777–99. doi:10.1007/s11042-012-1350-2. [Google Scholar] [CrossRef]
4. Araghi TK, Alarood AA, Araghi SK. Analysis and evaluation of template-based methods against geometric attacks: a survey. In: Saeed F, Mohammed F, Al-Nahari A, editors. Innovative systems for intelligent health informatics. Cham, Switzerland: Springer; 2021. p. 807–14. doi:10.1007/978-3-030-70541-1_77. [Google Scholar] [CrossRef]
5. Araghi TK, Manaf AB, Zamani M, Araghi SK. Taxonomy and performance evaluation of feature-based extraction techniques in digital image watermarking. Int J Image Process Tech. 2016;3(1):20–3. doi:10.1007/978-3-319-59427-9_39. [Google Scholar] [CrossRef]
6. Nikolaidis A. Local distortion resistant image watermarking relying on salient feature extraction. EURASIP J Adv Signal Process. 2012;2012(1):87. doi:10.1186/1687-6180-2012-87. [Google Scholar] [CrossRef]
7. Sajeer M, Mishra A. A robust and secure fusion-based hybrid medical image watermarking approach using RDWT-DWT-MSVD with hyperchaotic system-Fibonacci Q matrix encryption. Multimed Tools Appl. 2023;82(24):37479–501. doi:10.1007/s11042-023-15001-z. [Google Scholar] [PubMed] [CrossRef]
8. Makbol NM, Khoo BE, Rassem TH, Loukhaoukha K. A new reliable optimized image watermarking scheme based on the integer wavelet transform and singular value decomposition for copyright protection. Inf Sci. 2017;417(3):381–400. doi:10.1016/j.ins.2017.07.021. [Google Scholar] [CrossRef]
9. Al-Rammahi AH, Sajedi H. Robust and secure watermarking of medical images using Möbius transforms. In: 2024 10th International Conference on Artificial Intelligence and Robotics (QICAR); 2024 Feb 29; Qazvin, Iran. p. 208–14. [Google Scholar]
10. Al-Khafaji H, Al-Himyari B, Alharbi H. Enhancing image watermarking: an innovative multi-objective genetic algorithm-based DWT-SVD approach for robustness and imperceptibility. Int J Saf Secur Eng. 2024;14(6):1921–31. doi:10.18280/ijsse.140626. [Google Scholar] [CrossRef]
11. Rasti P, Anbarjafari G, Demirel H. Colour image watermarking based on wavelet and QR decomposition. In: 2017 25th Signal Processing and Communications Applications Conference (SIU); 2017 May 15–18; Antalya, Turkiye. p. 1–4. doi:10.1109/SIU.2017.7960259. [Google Scholar] [CrossRef]
12. Singh RK, Shaw DK, Sahoo J. A secure and robust block-based DWT-SVD image watermarking approach. J Inf Optim Sci. 2017;38(1–2):911–25. doi:10.1080/02522667.2017.1372137. [Google Scholar] [CrossRef]
13. Najafi E, Loukhaoukha K. Hybrid secure and robust image watermarking scheme based on SVD and sharp frequency localized contourlet transform. J Inf Secur Appl. 2019;44:144–56. doi:10.1016/j.jisa.2018.12.00. [Google Scholar] [CrossRef]
14. Zhou X, Zhang H, Wang C, Cao G, Zhao Y, Ni R, et al. A robust image watermarking technique based on DWT, APDCBT, and SVD. Symmetry. 2018;10(3):77. doi:10.3390/sym10030077. [Google Scholar] [CrossRef]
15. Liu J, Huang J, Luo Y, Cao L, Yang S, Wei D, et al. An optimized image watermarking method based on HD and SVD in DWT domain. IEEE Access. 2019;7:80849–60. doi:10.1109/ACCESS.2019.2915596. [Google Scholar] [CrossRef]
16. Begum M, Ferdush J, Uddin MS. A hybrid robust watermarking system based on discrete cosine transform, discrete wavelet transform, and singular value decomposition. J King Saud Univ Comput Inf Sci. 2022;34(9):5856–67. doi:10.1016/j.jksuci.2021.09.009. [Google Scholar] [CrossRef]
17. Srivastava R, Tomar R, Gupta M, Yadav AK, Park J. Image watermarking approach using a hybrid domain based on performance parameter analysis. Information. 2021;12(8):310. doi:10.3390/info12080310. [Google Scholar] [CrossRef]
18. Zeng F, Bai H, Xiao K. Blind watermarking algorithm combining NSCT, DWT, SVD, and HVS. Secur Priv. 2022;5(4):e223. doi:10.1002/spy2.223. [Google Scholar] [CrossRef]
19. Souto Ferreira L, Sacht L. Bounded biharmonic blending of Möbius transformations for flexible omnidirectional image rectification. Comput Graph. 2020;93(3):51–60. doi:10.1016/j.cag.2020.08.003. [Google Scholar] [CrossRef]
20. Zhou S, Zhang J, Jiang H, Lundh T, Ng AY. Data augmentation with Möbius transformations. Mach Learn Sci Technol. 2021;2(2):025016. doi:10.1088/2632-2153/abd781. [Google Scholar] [CrossRef]
21. Eltoukhy MM, Khedr AE, Abdel-Aziz MM, Hosny KM. Robust watermarking method for securing color medical images using Slant-SVD-QFT transforms and OTP encryption. Alex Eng J. 2023;78(2):517–29. doi:10.1016/j.aej.2023.07.068. [Google Scholar] [CrossRef]
22. Yan F, Wang Z, Hirota K. Dual medical image watermarking using SRU-enhanced network and EICC chaotic map. Complex Intell Syst. 2024;11(1):101. doi:10.1007/s40747-022-00946-2. [Google Scholar] [CrossRef]
23. Wan W, Wang J, Zhang Y, Li J, Yu H, Sun J. A comprehensive survey on robust image watermarking. Neurocomputing. 2022;488(7):226–47. doi:10.1016/j.neucom.2022.03.056. [Google Scholar] [CrossRef]
24. AbdElHaleem SH, Abd-El-Hafiz SK, Radwan AG. Secure blind watermarking using fractional-order Lorenz system in the frequency domain. AEU Int J Electron Commun. 2024;173:154998. doi:10.1016/j.aeue.2022.154998. [Google Scholar] [CrossRef]
25. Mellimi S, Rajput V, Ansari IA, Ahn CW. A fast and efficient image watermarking scheme based on deep neural network. Pattern Recognit Lett. 2021;151:222–8. doi:10.1016/j.patrec.2021.09.021. [Google Scholar] [CrossRef]
26. Danyali H, Makhloghi M, Tab F. Robust blind DWT-based digital image watermarking using singular value decomposition. Int J Innov Comput Inf Control. 2012;8(9):4691–703. doi:10.1109/isspit.2010.5711780. [Google Scholar] [CrossRef]
27. Chaturvedi N, Basha SJ. Comparison of digital image watermarking methods DWT & DWT-DCT on the basis of PSNR. Int J Innov Res Sci Eng Technol. 2012;1(2):147–53. [Google Scholar]
28. Abdallah HA, Hadhoud MM, Shaalan AA, Abd El-Samie FE. Blind wavelet-based image watermarking. Int J Signal Process Image Process Pattern Recognit. 2011;4(3):15–28. [Google Scholar]
29. Gupta M, Parmar G, Gupta R, Saraswat M. Discrete wavelet transform-based color image watermarking using uncorrelated color space and artificial bee colony. Int J Comput Intell Syst. 2015;8(2):364–80. doi:10.1080/18756891.2015.1001944. [Google Scholar] [CrossRef]
30. Araghi TK, Manaf AB. Evaluation of digital image watermarking techniques. In: Saeed F, Gazem N, Patnaik S, Balaid ASS, Mohammed F, editors. Proceedings of the 2nd International Conference of Reliable Information and Communication Technology (IRICT 2017). Lecture Notes in Data Engineering and Communications Technologies. Cham, Switzerland: Springer; 2018. Vol. 5, p. 361–8. doi:10.1007/978-3-319-59427-9_39. [Google Scholar] [CrossRef]
31. Gaur S, Srivastava VK. A RDWT and block-SVD based dual watermarking scheme for digital images. Int J Adv Comput Sci Appl. 2017;8(9):211–9. doi:10.14569/IJACSA.2017.080928. [Google Scholar] [CrossRef]
32. Cui S, Wang Y. Redundant wavelet transform in video signal processing. In: Proceedings of the 2006 International Conference on Image Processing, Computer Vision & Pattern Recognition (IPCV 2006); 2006 Jun 26–19; Las Vegas, NV, USA. p. 191–6. [Google Scholar]
33. Gaur S, Chaudhary K, Goel V, Barthwal V. An adaptive block-based watermarking scheme using RDWT-SVD and particle swarm optimization. SN Comput Sci. 2023;4(1):197. doi:10.1007/s42979-022-01434-7. [Google Scholar] [CrossRef]
34. Zimmermann G. Coherent states from nonunitary representations. In: Jetter K, Buhmann MD, Haussmann W, Schaback R, Stöckler J, editors. Topics in multivariate approximation and interpolation. Amsterdam, The Netherlands: Elsevier; 2006. p. 291–339. doi:10.1016/s1570-579x(06)80012-1. [Google Scholar] [CrossRef]
35. Chern A, Pinkall U, Schröder P. Close-to-conformal deformations of volumes. ACM Trans Graph. 2015;34(4):56. doi:10.1145/2766916. [Google Scholar] [CrossRef]
36. Frantz M. How conics govern Möbius transformations. Am Math Mon. 2004;111(9):779–90. doi:10.1080/00029890.2004.11920141. [Google Scholar] [CrossRef]
37. Pawar P, Goswami VS. The fixed points of Möbius transformation. Math Stat Eng Appl. 2023;72(1):409–12. doi:10.17762/msea.v72i1.1881. [Google Scholar] [CrossRef]
38. SIPI (USC Signal and Image Processing Institute). The USC-SIPI image database 2005 [Internet]. [cited 2025 Jan 5]. Available from: http://sipi.usc.edu/services/database/database.html. [Google Scholar]
39. Sahu AK, Swain G. High fidelity-based reversible data hiding using modified LSB matching and pixel difference. J King Saud Univ Comput Inf Sci. 2022;34(8):1395–409. doi:10.1016/j.jksuci.2020.12.012. [Google Scholar] [CrossRef]
40. Sehra K, Raut S, Mishra A, Kasturi P, Wadhera S, Saxena GJ, et al. Robust and secure digital image watermarking technique using Arnold transform and memristive chaotic oscillators. IEEE Access. 2021;9:72465–83. doi:10.1109/access.2021.3079319. [Google Scholar] [CrossRef]
41. Li Z, Zhang H, Liu X, Wang C, Wang X. Blind and safety-enhanced dual watermarking algorithm with chaotic system encryption based on RHFM and DWT-DCT. Digit Signal Process. 2021;115(4):103062. doi:10.1016/j.dsp.2021.103062. [Google Scholar] [CrossRef]
42. Lai Q, Zhang H. A new image encryption method based on memristive hyperchaos. Opt Laser Technol. 2023;166(3):109626. doi:10.1016/j.optlastec.2023.109626. [Google Scholar] [CrossRef]
43. Liu L, Wang J. A cluster of 1D quadratic chaotic map and its applications in image encryption. Math Comput Simul. 2023;204:89–114. doi:10.1016/j.matcom.2022.08.006. [Google Scholar] [CrossRef]
44. Kamal S, Hosny K, Elgindy T, Darwish M, Fouda M. A new image encryption algorithm for grey and color medical images. IEEE Access. 2021;9:37855–65. doi:10.1109/ACCESS.2021.3062944. [Google Scholar] [CrossRef]
45. Wang X, Zhang Y, Bao X. A colour image encryption scheme using permutation-substitution based on chaos. Entropy. 2015;17(6):3877–97. doi:10.3390/e17063877. [Google Scholar] [CrossRef]
46. Elmenyawi MA, Abdel Aziem NM, Bahaa-Eldin AM. Efficient and secure color image encryption system with enhanced speed and robustness based on binary tree. Egypt Inform J. 2024;27(1):100487. doi:10.1016/j.eij.2024.100487. [Google Scholar] [CrossRef]
47. Araghi TK, Megías D. Analysis and effectiveness of deeper levels of SVD on performance of hybrid DWT and SVD watermarking. Multimed Tools Appl. 2024;83:3895–916. doi:10.1007/s11042-023-14706-3. [Google Scholar] [CrossRef]
48. Wu W, Dong Y, Wang G. Image robust watermarking method based on DWT-SVD transform and chaotic map. Complexity. 2024;2024:6618382–18. doi:10.1155/2024/6618382. [Google Scholar] [CrossRef]
49. Zermi N, Khaldi A, Kafi MR, Kahlessenane F, Euschi S. A lossless DWT-SVD domain watermarking for medical information security. Multimed Tools Appl. 2021;80:24823–41. doi:10.1007/s11042-021-10711-z. [Google Scholar] [CrossRef]
50. Marjuni A, Shidik GF, Syukur A, Rijati N. Towards achieving a trade-off for SVD-based image watermarking using Mojette transform. IEEE Access. 2024;12(6):35231–45. doi:10.1109/ACCESS.2024.3368528. [Google Scholar] [CrossRef]
51. Nasser R, Abouelseoud Y, Mikhail M. Robust watermarking based on Schur decomposition and dynamic weighting factors. Vis Comput. 2024;40(3):3249–69. doi:10.1007/s00371-023-02807-2. [Google Scholar] [CrossRef]
52. Amiri A, Kimiaghalam B. Robust watermarking with PSO and DnCNN. Signal Image Video Process. 2024;18(S1):663–76. doi:10.1007/s11760-024-03182-5. [Google Scholar] [CrossRef]
53. Liu H, Chen Y, Shen G, Guo C, Cui Y. Robust image watermarking based on hybrid transform and position-adaptive selection. Circuits Syst Signal Process. 2025;44(4):2802–29. doi:10.1007/s00034-024-02946-1. [Google Scholar] [CrossRef]
54. Boujerfaoui S, Riad R, Douzi H, Ros F, Harba R. Image watermarking between conventional and learning-based techniques: a literature review. Electronics. 2023;12(1):74. doi:10.3390/electronics12010074. [Google Scholar] [CrossRef]
55. Wang X, Peng F, Niu P, Yang H. Statistical image watermark decoder using NSM-HMT in NSCT-FGPCET magnitude domain. J Inf Secur Appl. 2022;69(4):103312. doi:10.1016/j.jisa.2022.103312. [Google Scholar] [CrossRef]
56. Li YM, Wei D, Zhang L. Double-encrypted watermarking algorithm based on cosine transform and fractional Fourier transform in invariant wavelet domain. Inf Sci. 2021;551:205–27. doi:10.1016/j.ins.2020.10.078. [Google Scholar] [CrossRef]
57. Keshavarzian R, Aghagolzadeh A. ROI-based robust and secure image watermarking using DWT and Arnold map. AEU Int J Electron Commun. 2016;70(2):278–88. doi:10.1016/j.aeue.2015.10.006. [Google Scholar] [CrossRef]
58. Wang X, Liu Y, Li S, Yang H, Niu P. Robust image watermarking approach using polar harmonic transforms-based geometric correction. Neurocomputing. 2016;174(11):627–42. doi:10.1016/j.neucom.2015.09.076. [Google Scholar] [CrossRef]
59. Faraj O, Megías D, Garcia-Alfaro J. ZIRCON: zero-watermarking-based approach for data integrity and secure provenance in IoT networks. J Inf Secur Appl. 2024;85:103840. doi:10.1016/j.jisa.2023.103840. [Google Scholar] [CrossRef]
60. Gao G, Xu T, Hua F. Robust image watermarking based on generative adversarial networks for copyright protection. [cited 2025 Jan 5]. Available from: 10.21203/rs.3.rs-4039149/v1. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF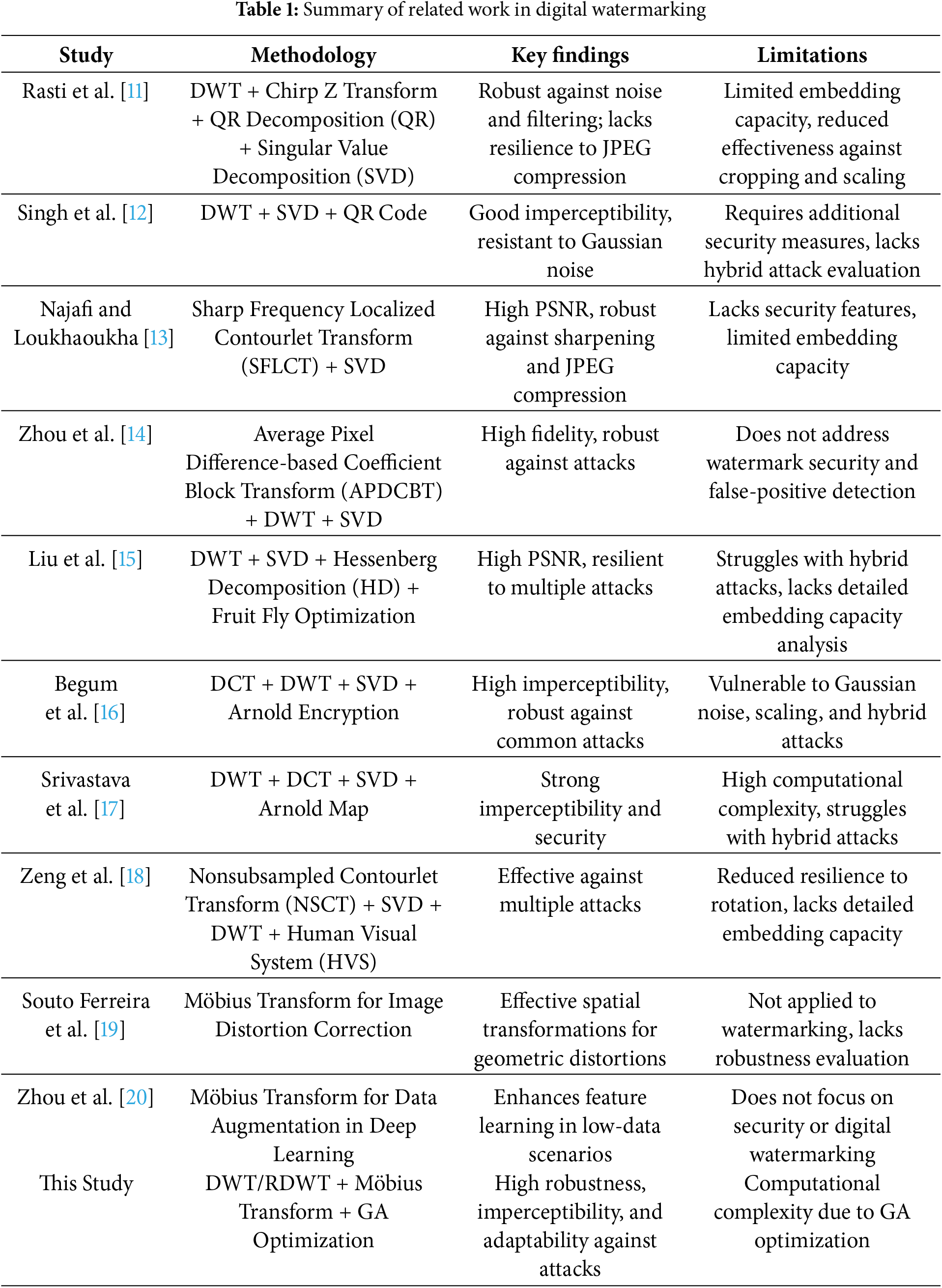
 Downloads
Downloads
 Citation Tools
Citation Tools