Intelligent Scheduling of Virtual Power Plants Based on Deep Reinforcement Learning

1  Introduction

With the continuous growth of global energy demand and the emergency need to address climate change, the power industry is undergoing a profound transformation, and countries around the world are committed to achieving carbon neutrality goals [1]. Renewable energy sources such as wind and solar power are widely used around the world due to their cleanliness and sustainability [2]. However, solar photovoltaic power generation is significantly influenced by regional meteorological and climatic factors, leading to considerable uncertainty in its output power [3]. Wind power generation, on the other hand, exhibits even greater volatility and intermittency due to random changes in weather conditions [4]. This characteristic of energy production, driven by natural conditions, poses significant challenges to the stability of the grid and the real-time supply-demand balance after renewable energy sources are integrated into the grid. Traditional power systems mainly rely on centralized generation models, with relatively fixed scheduling methods that are difficult to adapt to the random fluctuations of renewable energy. Meanwhile, rapid integration of distributed energy sources [5] (such as small-scale wind power, solar power, energy storage, and electric vehicle charging facilities) further exacerbates the complexity of the power system, making grid coordination and management more challenging. In the face of this challenge, there is an emergency need to introduce new scheduling technologies to enhance the power system’s ability to accommodate new energy sources and achieve efficient energy management and resource optimization.

Against this backdrop, the Virtual Power Plant (VPP) [6,7] has emerged as an innovative power management framework. At its core, the VPP integrates various distributed energy and load resources to enhance the flexibility and economic efficiency of the power system. Unlike the traditional single-unit dispatch model, the VPP emphasizes fine-grained management and optimized scheduling of internal generation units based on the distinct characteristics of renewable energy generation, grid dispatch requirements, and user load profiles. The efficient operation of a VPP depends on its intelligent scheduling capabilities, which excel in handling the volatility of renewable energy output and the complexity of diverse and dynamic load demands. By integrating multiple distributed energy resources and responding to load variations, the VPP achieves flexible dispatch and optimized resource allocation that traditional grids find challenging. This not only mitigates the stability challenges posed by the intermittency of renewable energy, but also improves resource utilization efficiency across the power system, providing strong support for achieving carbon neutrality goals.

In a Virtual Power Plant (VPP), generation resources can be categorized into dynamic peaking unit (DPU) and stable baseload unit (SBU). DPU are extremely flexible and capable of responding quickly to renewable energy fluctuations and short-term load changes. They are well-suited for frequent start-ups and shutdowns, providing frequency and voltage support on both the supply and grid sides. Typically composed of gas turbines, fast-start natural gas units, and battery storage systems, DPU can rapidly respond to system load variations. They are particularly effective in offering short-term regulation and dynamic load tracking during periods of high renewable energy volatility, ensuring system balance and stability [8]. In contrast, SBU provide stable, low-cost, long-term power output and are primarily composed of coal-fired units, large-scale natural gas units, and nuclear power units. These units operate at lower frequencies of startup and adjustment, making them suitable for meeting the system’s baseload demand, reducing the costs and efficiency losses associated with frequent adjustments.

However, due to the significant differences in cost and flexibility among various units, achieving efficient coordination between DPU and SBU while maintaining system stability has become a central challenge in the operation of virtual power plants. Particularly in the case of the volatility and uncertainty of renewable energy sources (such as wind and solar power) and the complex and diverse user load demands, the virtual power plant needs to optimize the coordinated scheduling of DPU and SBU, making it much more challenging to meet the electricity demand and response time requirements of power tasks. This issue not only tests the real-time performance and economic efficiency of the virtual power plant’s scheduling method in complex environments, but also requires ensuring system stability and rapid responsiveness. Traditional scheduling strategies have many limitations when addressing such complex power system scenarios, such as insufficient flexibility, limited scalability, and difficulty in adapting to the increasingly growing dynamic scheduling demands. Therefore, developing intelligent and efficient scheduling technologies to reduce operational costs, improve task completion rates, and enhance the system’s adaptability and scheduling flexibility has become an important research direction in modern power systems.

Currently, various intelligent optimization methods have been proposed within the academic community. For example, research [9] proposed an economic-environmental scheduling model that integrates the reliability of generation units into the optimization objective. While this method significantly improves the security of the power system with slightly increased fuel costs and carbon emissions, its capability to handle complex nonlinear constraints is limited, and its applicability to large-scale power systems remains restricted. To address the uncertainty issue in virtual power plant scheduling, research [10] proposed a scheduling optimization method based on Mixed-Integer Linear Programming (MILP). This method reduces computation time through scenario generation and reduction techniques, and improves the stability of the solution. However, in high-dimensional complex scenarios, this method requires significant computational resources and is highly dependent on prior information about the scenarios, limiting its applicability in dynamic and uncertain power market environments. Furthermore, to improve the coordinated scheduling efficiency of distributed energy resources in virtual power plants, research [11] developed a scheduling model based on stochastic optimization, introducing novel energy technologies such as photovoltaic-thermal (PVT) panels to optimize the joint scheduling of electrical and thermal loads. Although this method demonstrates strong performance in improving energy utilization and economic efficiency, its adaptability to high levels of randomness and uncertainty remains relatively limited, thereby restricting its application in real-time scheduling environments. Similarly, research [12] proposed a multi-agent-based scheduling strategy aimed at optimizing the coordinated operation of conventional and renewable energy units. This method enhances scheduling efficiency and solution quality through agent collaboration and distributed optimization, demonstrating greater adaptability than traditional mathematical programming approaches in addressing complex scheduling problems. However, as it relies on information exchange and coordination mechanisms among agents, it may introduce additional computational complexity in large-scale grid scheduling scenarios, affecting computational efficiency and real-time scheduling performance.

In recent years, Deep Reinforcement Learning (DRL)–an advanced approach that combines deep learning with reinforcement learning–has been widely applied to intelligent scheduling and dynamic resource allocation. By leveraging neural networks to approximate optimal policies, DRL can effectively manage high-dimensional decision spaces and adapt to real-time operational changes, making it a highly attractive solution for complex scheduling challenges. For example, research [13] proposed a DRL-based fast-converging scheduling method, DDPG-CPEn, to address the Transient Security-Constrained Optimal Power Flow (TSC-OPF) problem. This method enables dynamic adjustment of generator outputs, voltage levels, and power flow distribution, significantly enhancing system scheduling efficiency and stability. However, due to the high-dimensional state space and the discontinuity of dynamic constraints, it still encounters the sparse reward problem, which slows down training convergence and hinders the optimization of dynamic resource allocation strategies. Meanwhile, DRL methods are being increasingly applied in the field of power system scheduling. Research [14] evaluated the performance and applicability of various DRL algorithms (including DDPG, TD3, SAC, and PPO) in energy system scheduling. Compared with traditional mathematical programming approaches, these algorithms can adaptively optimize energy distribution strategies in response to real-time load variations and the uncertainty of renewable energy output, thereby effectively reducing operational costs and delivering high-quality real-time scheduling solutions. However, under extreme peak load conditions, these methods still struggle to produce feasible solutions, which compromises their reliability in practical applications. In addition to power system scheduling, DRL has also been widely applied to industrial dynamic scheduling problems. Research [15] and [16] proposed a DQN-based optimization method to address Dynamic Parallel Machine Scheduling (DPMS) and Dynamic Job Shop Scheduling Problem (DJSSP), aiming to cope with dynamic factors such as equipment failures and task demand fluctuations. Compared with other DRL methods and heuristic approaches, DQN exhibits greater adaptability in handling discrete action spaces and dynamic scheduling environments, enabling it to more effectively respond to task variations and optimize scheduling decisions. Furthermore, research [17] further explored the application of DQN in smart grid rescheduling, optimizing the mapping relationship between grid state features and scheduling actions. Experimental results on the IEEE 39-bus system demonstrate that DQN shows significant advantages in handling high-dimensional state spaces and non-convex optimization problems, further proving its applicability in the scheduling of complex energy systems.

Given the superiority of Deep Q-Networks (DQN) in handling discrete action spaces and dynamic scheduling environments, and considering the volatility of renewable energy, the uncertainty in generation resource scheduling, and the dynamic variation of load demands, this paper proposes an intelligent scheduling method for Virtual Power Plants (VPPs) based on Deep Reinforcement Learning (DRL), employing DQN for dynamic optimization. The proposed method addresses the discrete scheduling problem involving multiple units in a VPP by incorporating the characteristics of both DPU and SBU, and adaptively learns to select the optimal unit scheduling strategy. It effectively manages the uncertainty arising from renewable energy fluctuations, ensuring the stable operation of the VPP.

The main contributions of this study are summarized as follows:

•   We propose a Deep Reinforcement Learning (DRL)-based intelligent scheduling algorithm for Virtual Power Plants (VPPs), aimed at optimizing the resource allocation problem among different generation units in the VPP. Particularly in the complex environment of renewable energy fluctuations and dynamic load demand changes, this method can intelligently allocate generation unit resources, reducing costs while improving task completion rates and ensuring the system has low response times.

•   We present a detailed design of a deep reinforcement learning (DRL) model for the intelligent scheduling problem of a virtual power plant. Specifically, we formulate the scheduling problem as a Markov decision process (MDP) and consider cost, response time, and task success rate in the design of the core reward function.

•   We use Deep Q-Learning (DQN) to implement the proposed intelligent scheduling method for VPPs, and compare it with other typical scheduling methods (including other DRL methods) under different load curves, renewable energy fluctuations, and system scale expansion conditions. Experimental results show that the proposed method outperforms others in terms of task response time, task success rate, and cost, while demonstrating stronger robustness and adaptability in complex environments such as expanded system scale and renewable energy fluctuations, further proving its scalability and application potential in intelligent scheduling.

The remainder of the paper is organized as follows: Section 2 presents the system framework and problem formulation; Section 3 provides the detailed design and implementation of the DQN-based intelligent scheduling method; Section 4 presents experimental results and performance evaluation; Section 5 concludes the paper and outlines directions for future research.

2  Scheduling Framework and Problem Statement

This section provides a detailed introduction to the proposed intelligent scheduling framework for Virtual Power Plant (VPP) generation units based on deep reinforcement learning, and elaborates on the scheduling optimization problem and its cost minimization objective.

2.1 Virtual Power Plant Generator Scheduling System Framework

The Virtual Power Plant (VPP) can dynamically integrate heterogeneous resources (such as wind energy, solar energy, energy storage devices, etc.) to achieve optimal resource utilization. This study proposes an intelligent scheduling method based on Deep Q-Networks (DQN), which seamlessly integrates diversified task demands with the scheduling characteristics of generation units, demonstrating its potential advantages in the efficient scheduling of VPPs. Fig. 1 illustrates the intelligent scheduling system framework of the VPP proposed in this study. The scheduling scenario consists of a power system, a DQN-based scheduling controller, and the virtual power plant. The power system [18] primarily comprises substations, transmission systems, distribution systems, backup systems, and renewable energy sources such as wind and solar power. As the core component of the framework, the scheduling controller is responsible for real-time decision-making. The virtual power plant includes M dynamic peaking units and N stable baseload units, which operate in different modes to provide generation services for the power system and meet diverse electricity demands.

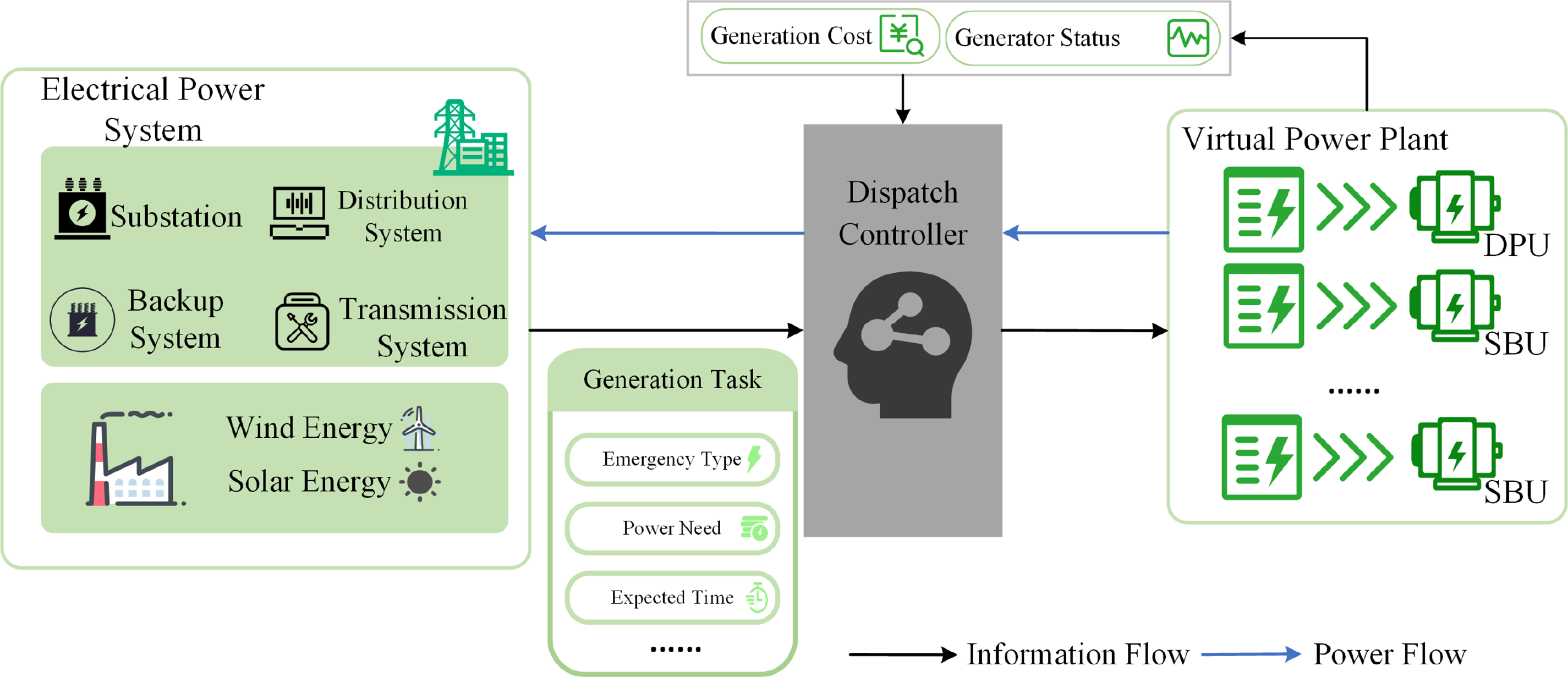
Figure 1: Virtual power plant intelligent scheduling system framework

When a power generation task arrives, the power system submits task information to the scheduling controller, including parameters such as the urgency type, power generation amount, and expected completion time. Based on this information and the current state of each generation unit, the scheduling controller formulates a generation strategy π. According to this strategy, the scheduling controller selects the appropriate generation unit to execute the task and decides whether to start the task immediately based on the unit’s status. At the same time, in order to model this scheduling problem, this study provides mathematical definitions for the generation task and the generation units.

Generation task: A power generation task Ri={Riid,Ritype,Ni,Tiarr,Ei} is defined as the i-th power generation task of the power system. Specifically, Riid is the ID of the i-th power generation task assigned to the scheduling controller; Ritype is the identifier for the i-th power generation task type, used to categorize the power demand into two types: emergency power demand and non-emergency power demand; Ni is the amount of electrical energy required to complete the i-th power generation task. Meanwhile, Tiarr is the arrival time of the i-th power generation task, which is recorded by the scheduling controller; Ei is the expected completion time of the i-th power generation task, and this information is immediately submitted to the scheduling controller upon the arrival of the power generation task.

Generation units: This study primarily considers two types of generation unit modes: dynamic peaking unit (DPU) and stable baseload unit (SBU). For emergency generation tasks, DPU are prioritized to ensure a rapid response to load demand, although this may result in higher operational costs. For non-emergency generation tasks, SBU are prioritized to minimize generation costs and ensure the long-term stability of the power system. By appropriately allocating different types of generation units to meet various generation demands, the load on the power system can be effectively alleviated, while providing diversified generation service options.

For the generation unit set in the Virtual Power Plant, the j-th generation unit can be represented as Uj={Ujid,Ujtype,Pj,Ujloss}, where Ujid is the ID of the j-th generation unit; Ujtype is the type of the j-th generation unit (DPU or SBU); Pj is the generation power of the j-th generation unit; Ujloss is also the energy loss rate per unit time of the j-th generation unit.

2.2 Problem Statement

From the perspective of the Virtual Power Plant, one of the main optimization problems in this study is to minimize the total operational cost ω, which can be expressed as:

(1)ω=min∑i=1nCi(1)

where Ci represents the total cost of the power generation task, which consists of two components: the cost of electricity production and the energy loss cost during the generation process. The main objective of the scheduling controller is to minimize Ci, thereby reducing the total production cost over the entire operation period. The specific formula for Ci is:

(2)Ci=ptNi+UjlossTigen(2)

where Ujloss represents the energy loss of the j-th generation unit; Tigen is the generation time of the i-th power generation task. The energy loss cost corresponding to the power generation unit Uj for the power generation task Ri is expressed as the product of the unit energy loss rate Ujloss and the generation time Tigen. The electricity production cost is determined by the energy demand Ni of the power generation task and the cost per unit of electricity pt, which is related to the type of generation unit and the time period of generation.

During high load demand periods, the frequency of start-ups and shut-downs, as well as the output adjustment frequency of generation units, will increase, leading to higher operational costs for dynamic peaking unit. This will cause a slight increase in the short-term levelized cost of energy (LCOE). However, during periods of lower and more stable load demand, stable baseload units typically provide the basic load, operating more smoothly, and at such times, the LCOE tends to approach its average value or may even decrease.

In generator scheduling, in addition to minimizing costs, another important objective is to reduce the average response time. The average response time directly impacts the operational efficiency of the system and is a key indicator of power generation scheduling performance. The response time Ti of a power generation task is defined as the total duration from the arrival of the i-th task to its completion, which consists of the following two parts:

(3)Ti=Tigen+Tijwait(3)

Here, Tigen represents the generation time of the i-th power generation task; Tijwait represents the time the i-th power generation task waits for execution in the generation unit Uj. The definition of generation time is:

(4)Tigen=NiPj(4)

where Pj represents the generation power of the j-th generation unit. Assume that when the power generation task Ri arrives, there are q waiting tasks in the generation unit Uj’s request queue, and there are n tasks Ri′ allocated to Uj before Ri. Then, the waiting time Tijwait can be calculated as:

(5)Tijwait={∑i=0nTijgen,if q>00,if q=0(5)

where Tijgen represents the generation time of the i-th power generation task in the j-th generation unit. Based on the above definitions, this study introduces another important metric, Eisp, which is the reciprocal of the response time of the power generation task Ri. This reflects the efficiency of the system’s response time and is used to evaluate the effectiveness of the power generation scheduling:

(6)Eisp=1Ti(6)

As mentioned earlier, power generation tasks can be sent to the scheduling controller by the power system at any time. To meet the task requirements, it must be ensured that the power generation tasks are completed within the specified time. Each power generation task Ri has an expected completion time Ei, which is the deadline. If the power generation is completed within the deadline, the power generation task is considered successfully executed; otherwise, the power system cancels the task, leading to a failure response. Based on this, the conditions for the successful execution of the power generation tasks are defined as follows:

(7)success(Ri,Uj)={1,if Ti≤Ei0,otherwise(7)

where Ei represents the maximum acceptable response time for the power generation task Ri. Based on the above formula, it is possible to determine whether the power generation task Ri is successfully completed after being assigned to the generation unit Uj.

3  DRL-Based Power Generation Unit Scheduling Implementation

3.1 Deep Q-Network

For the virtual power plant generation unit scheduling problem, this study proposes a solution based on deep reinforcement learning (DRL), utilizing one specific implementation of DRL–Deep Q-Network (DQN) [19]. DQN [20] was first introduced by Mnih et al., combining convolutional neural networks with traditional Q-learning, which significantly improved the performance of reinforcement learning algorithms in handling problems with continuous state spaces.

In traditional Q-learning, the agent evaluates the effectiveness of performing a certain action in different states using the Q-value function Q(s,a), and relies on a lookup table to store the Q-value for each state-action pair. The Q-value reflects the expected long-term reward that can be obtained by choosing a particular action in a given state. By continuously updating the Q-values in the lookup table, the agent can gradually learn the optimal action strategy for different states. However, this table-based approach is primarily suitable for tasks with small-scale, discrete state spaces. For example, in board games or simple grid worlds, the number of states and actions is limited, making it easy to map each state-action pair to the lookup table and store its Q-value. As the agent learns, the Q-values are progressively updated and eventually converge to the optimal strategy.

But in complex environments, the combination of states and actions may reach millions or even billions, causing the size of the lookup table to grow exponentially. This significantly increases storage and computational costs, making traditional Q-learning inefficient. To address this issue, Deep Q-Networks (DQN) propose an innovative solution: using a deep neural network (DNN) to directly approximate the Q-values instead of storing all state-action pairs. Specifically, DQN approximates the optimal Q-values (Q(s,a,θ)) using the neural network parameters θ, and continuously optimizes θ through gradient descent, allowing the Q-values to gradually converge to the optimal strategy. Compared to traditional methods, DQN can efficiently handle high-dimensional state spaces while achieving dual improvements in computational efficiency and strategy accuracy in dynamic scheduling tasks. Additionally, to ensure that the agent explores the unknown environment while utilizing existing knowledge, DQN employs an ε-greedy strategy.

(8)a={random A,if β<εarg⁡maxa∈AQ(s,a),if β≥ε(8)

In the equation, A is the action set, including all possible actions the agent can choose from; β is a random number generated in the interval [0,1], used to decide whether to explore; ε is the exploration rate. Specifically, the agent selects a random action (exploration) with probability ε at each time step, and with probability 1−ε, it selects the action that maximizes the Q-value (exploitation).

In the high-dimensional environment studied in our research, the Virtual Power Plant (VPP) scheduling system involves multiple variables, including unit operating status, real-time load demand, and the characteristics of various load curves (e.g., residential, commercial, and industrial patterns). Additionally, the scheduling process includes a series of discrete decisions, such as when to start or stop specific types of generation units (e.g., dynamic peaking unit or stable baseload unit) and adjusting task allocation strategies. Therefore, the various state-action combinations in VPP scheduling form a vast state-action space. Traditional reinforcement learning algorithms, such as Q-learning, struggle to address this challenge due to their slow learning rate. DQN offers an effective solution by utilizing deep neural networks to estimate Q-values. Unlike traditional Q-learning, which uses lookup tables, DQN uses DNNs to approximate Q-value computation, significantly improving the ability to handle discrete action space problems. Furthermore, DQN does not rely on explicitly labeled actions or predefined training samples for training. Instead, it learns Q-values from experience data through continuous interaction between the agent and the environment, gradually optimizing the scheduling strategy. This method is particularly effective in dynamic resource allocation problems, allowing it to adjust decisions based on the changing environment and achieve better scheduling results. Currently, this DRL-based approach has proven effective in various applications, particularly in complex systems requiring dynamic and real-time optimization [16]. Therefore, this study adopts the DQN model as the DRL approach to solve the VPP generation unit scheduling problem.

3.2 Markov Decision Process for Power Generation Unit Scheduling

When using DQN to solve complex problems, we can represent the mathematical model of the problem as a Markov Decision Process (MDP) [21], formalized as a five-tuple (S, A, P, R, γ). Here, S represents the set of all possible states perceivable by the environment; A represents the set of all actions available to the agent; P represents the state transition probability, which is the probability of transitioning to the next state given the current state and action; R represents the immediate reward obtained after performing an action in a specific state, and γ is a discount factor between 0 and 1, used to quantify the importance of future rewards relative to immediate rewards. Through the optimization of this process, the agent can learn how to make the best decision based on the current state and target requirements in a complex environment, thereby achieving efficient task scheduling and resource allocation.

In this study, we model the scheduling problem of Virtual Power Plant (VPP) generation units as a Markov Decision Process (MDP). At each time step, the scheduling controller selects an action based on the current state, then transitions to the next state after executing the action, while receiving an immediate reward based on the reward function. The agent continuously interacts with the environment, learning how to select the optimal action in different states to maximize long-term rewards. Through this process, the MDP framework helps optimize the scheduling strategy, ensuring that the power system not only completes the generation tasks on time but also minimizes production costs while meeting system stability requirements. Each component of the MDP will be described in detail below.

3.2.1 State Space

The state space is denoted asS, which consists of vectors st at each time step t. Each state vector st contains key information about the current power generation task and the status of the generator units. Specifically, the state vector st includes not only the type Ritype of the i-th power generation task, the electricity demand Ni of the task, and the expected completion time Ei of power generation task i, but also the allocated generator units Uj, the power cost pt, and the waiting time Tijwait of the i-th power generation task in generator unit Uj. Therefore, the state vector st is defined as:

(9)st=(Ritype,Ni,Ei,Uj,pt,Ti1wait,Ti2wait,…,Tijwait)(9)

This state representation provides the core information required by the scheduling controller for real-time decision-making, supporting the optimization decisions of the scheduling controller. For example, during peak demand periods, the state vector at a certain time step t may be represented as st = (Emergency, 100 KW, 0.4 h, U3, 0.05/kWh, 0, 8, … , 10 min).

3.2.2 Action Space

The action space A represents the set of scheduling actions that the scheduling controller can take at each time step, where each action involves selecting an appropriate generation unit to meet the current power demand. Specifically, each action is denoted by a and is defined as follows:

(10)at=(U1,U2,…,Uj)(10)

In the equation, Uj represents the selected generation unit j. For example, when an emergency power generation task arrives, the scheduling controller may take an action at=U2, which involves selecting a dynamic peaking unit U2 to quickly provide power output, ensuring the balance between power supply and demand.

3.2.3 Reward Function

The reward function r(st,at,st+1) in deep reinforcement learning is used to evaluate the effectiveness of the agent’s actions. It quantifies the immediate reward the agent receives after taking an action in a given state, helping the agent learn to select the optimal action to maximize long-term returns. To achieve the lowest cost and ensure that tasks are completed on time, the reward function designed in this study is as follows:

(11)r=(1+eλ−Ci)Eisp(11)

In the equation, Ci represents the total cost of the power generation task, which includes electricity production cost and energy losses, as shown in Eq. (2); Eisp represents the inverse of the response time of the power generation task, reflecting the efficiency of the system’s response time, as shown in Eq. (6). The reward function takes into account the total cost of the power generation task (including production costs and energy losses) and the task’s response time. The exponential term is used to penalize high-cost tasks, encouraging the selection of low-cost scheduling solutions. The term Eisp, which is inversely proportional to the response time, is used to increase the sensitivity of the scheduling controller to response time, ensuring the quality of scheduling services.

Specifically, the exponential term eλ−Ci introduces a hyperparameter λ, which is used to balance the weight between cost and response time. When λ is higher, the impact of the cost Ci in the exponential term of the formula on the reward increases, making the scheduling controller more inclined to choose low-cost power generation schemes to maximize economic benefits. At the same time, this also encourages the system to prefer more cost-efficient operations in power generation decisions, effectively reducing costs. Conversely, when λ is lower, the impact of generation costs on the reward diminishes, and the scheduling controller will focus more on the response time, prioritizing generation units that can complete tasks more quickly. On the other hand, the term Eisp, which is inversely proportional to the response time, ensures that the scheduling controller completes the power generation task in the shortest time possible, thereby ensuring service quality. When Eisp is smaller, it indicates a longer response time for the task, resulting in a lower reward. Conversely, when the response time is shorter, the scheduling controller is able to complete the task more quickly, and the corresponding reward is higher. Through this dual optimization strategy, the optimization of cost and response time is effectively integrated, ensuring the minimization of costs while maintaining service quality, thereby further enhancing the overall operational efficiency and economic viability of the Virtual Power Plant.

3.3 Model Implementation

The optimization process of the intelligent scheduling framework for the Virtual Power Plant (VPP) proposed in this study consists of three key steps: First, the agent interacts with the environment to collect transition data, including the current state, action taken, reward received, and next state. Then, the collected data are stored in a replay buffer, forming an experience pool for subsequent learning. Finally, the agent randomly samples mini-batches from this pool to optimize and update its neural network parameters. In this section, we provide a detailed description of the scheduling process based on Deep Q-Networks (DQN) and summarize the complete optimization procedure in Algorithm 1.

Interaction Process: At the initial stage of each time step t, the Virtual Power Plant (VPP) receives scheduling requests from different power generation tasks. By analyzing key parameters such as task type, expected completion time, and required power generation, the system determines its initial state. Subsequently, the agent collects the current waiting time and per-unit electricity cost information from each generation unit. After integrating this information, an example state can be observed as {Ritype,Ni,Ei,Uj,pt,Ti1wait,Ti2wait,…,Tijwait}. Subsequently, the agent selects the optimal scheduling strategy based on the policy π generated by the neural network and evaluates it using a specific reward function. By continuously optimizing the decision-making policy, this mechanism enables the agent to gradually improve the scheduling plan, enhancing scheduling efficiency while effectively reducing costs.

Experience Replay: Traditional deep reinforcement learning methods typically operate under the assumption of a static and invariant data distribution. However, in real-world applications, data often exhibits significant temporal correlations. To address this issue and improve the stability of the training process, we introduce the experience replay mechanism. Under this mechanism, the interaction between the agent and the environment is stored as a tuple, which includes the current state st, the chosen action at, the received reward rt, and the subsequent state st+1, and is stored in the experience replay buffer, as shown in Fig. 2. During training, the agent no longer learns solely from immediate samples but instead randomly samples a batch of historical records from the experience replay buffer (i.e., mini-batches) for learning. This random sampling approach effectively reduces the temporal correlation between samples, mitigates noise interference in the training process, and significantly enhances the stability and convergence of the model.

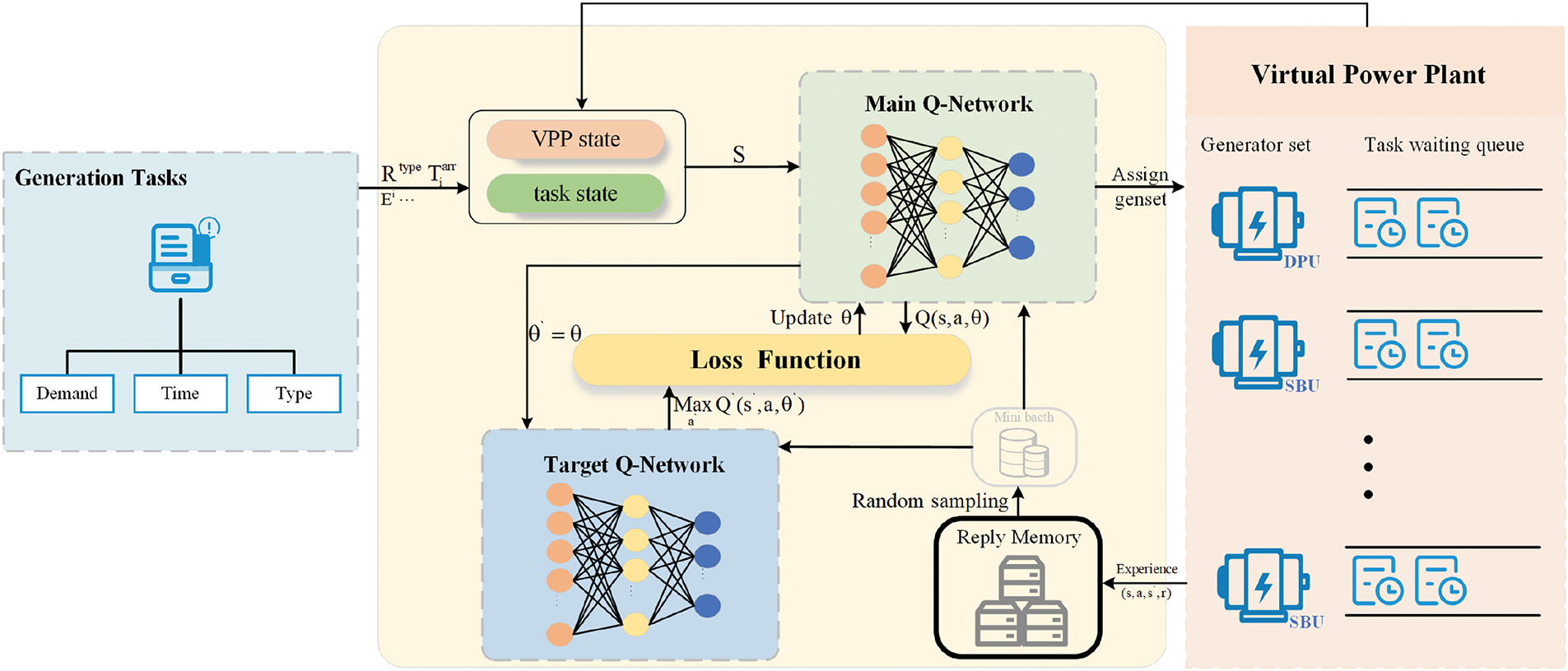
Figure 2: Implementation framework of virtual power plant intelligent scheduling based on DRL

Training Process: At the beginning of training, the system first initializes all parameters and performs deep neural network training based on the input data. To improve training stability and convergence speed, we employ a double-network architecture in the deep Q-network (DQN). The main Q-network is used to calculate Q-values and guide the agent in selecting the optimal action by minimizing the mean squared error between the current estimated value and the target value. Meanwhile, the target network generates stable target Q-values as a training reference to avoid instability caused by overly frequent policy updates. In each iteration, the agent executes scheduling decisions based on the policy of the main Q-network and records the corresponding rewards and state transition information. These data are then stored in the experience replay buffer. During subsequent training, the system randomly samples small batches of data from the buffer, uses the loss function to evaluate the deviation between the predicted Q-values and the target Q-values, and optimizes the parameters of the main Q-network through stochastic gradient descent (SGD) to continuously improve the accuracy of scheduling decisions. To further enhance training stability and reduce parameter update fluctuations, we adopt a delayed update mechanism, periodically copying the parameters of the primary Q-network to the target network. This ensures a smooth transition of target Q-values and prevents instability caused by frequent updates.

To effectively balance the trade-off between exploration and exploitation, we adopt the ε-greedy strategy for action selection. At the early stage of training, the agent selects actions randomly with a high ε value to fully explore the state space of the environment. As training progresses, the ε value gradually decreases, and the agent increasingly relies on the Q-values output by the DQN model to select actions with higher expected rewards, gradually converging toward the optimal strategy. With the accumulation of interaction experience, the training process updates the parameters of the DQN model through the experience replay mechanism, improving learning efficiency and enhancing model stability.

4  Experiment Evaluation

This section provides a detailed evaluation of the proposed DQN-based intelligent scheduling method for Virtual Power Plants (VPPs) in comparison with other scheduling methods. We built a simulation environment using Python 3.9 and conducted experiments on a desktop equipped with an 11th Gen Intel(R) Core(TM) i7-11700 @ 2.50 GHz processor and 16 GB of RAM. The experiment was conducted using the PyTorch framework to train and evaluate the deep reinforcement learning model, with the primary objective of demonstrating the superiority of the proposed method in terms of average response time, task success rate, and cost efficiency.

4.1 Experiment Setup

This experiment simulates a power scheduling system consisting of 10 generation units, including dynamic peaking unit and stable baseload unit, with the goal of optimizing scheduling strategies to meet diverse electricity demands. Stable baseload unit are primarily responsible for providing a steady long-term power supply, meeting the base load demand at a lower cost. In contrast, dynamic peaking unit are used to quickly respond to short-term fluctuations and sudden load changes, offering flexible scheduling support to the system. Power generation tasks are categorized into emergency tasks and regular tasks. emergency tasks are typically handled by dynamic peaking unit to ensure a fast system response, while regular tasks are mainly undertaken by stable baseload units to achieve continuous low-cost power generation. To better reflect real-world scenarios, each generation unit is assigned different energy loss rates and power generation costs, effectively simulating the complexity of actual scheduling operations.

To better reflect real-world power load conditions, this experiment introduces three typical daily load curves: residential, commercial, and industrial. The residential load curve exhibits distinct morning and evening peak characteristics. The morning peak typically occurs between 6:00–9:00 AM, while the evening peak is concentrated between 6:00–10:00 PM. During these two peak periods, electricity demand accounts for approximately 60% of the total daily load, whereas demand during off-peak hours is relatively low and remains stable [22]. The commercial load curve gradually increases in the morning and reaches its peak between 10:00 AM–4:00 PM. This load pattern is characterized by high stability and concentration, requiring the system to maintain a strong response capacity during daytime hours. In contrast, the industrial load curve remains relatively stable throughout the day, operating at high load levels most of the time. This makes it more suitable for stable baseload unit, which provide long-term, steady power support.

Considering that the power generation capacity of renewable energy sources (such as wind and solar power) is significantly influenced by natural factors such as wind speed and solar radiation intensity, their output exhibits volatility and intermittency. This experiment simulates renewable energy output using a segmented modeling approach. The peak output of wind power is mainly concentrated in the early morning hours (2:00–5:00 AM), with power generation randomly distributed in the range of 70 to 100 kWh. The peak output of photovoltaic (PV) power occurs during midday (10:00–2:00 PM), with a generation range of 50 to 70 kWh. During other periods, the output remains relatively low, fluctuating between 0 and 50 kWh. To better reflect real-world conditions, this experiment incorporates the time-varying characteristics of renewable energy output into the demand modeling of power generation tasks. The task demand is dynamically adjusted based on the contribution of renewable energy at the time of arrival. This approach effectively captures the impact of renewable energy fluctuations on virtual power plant scheduling tasks, optimizing the distribution of the generation unit workload.

In the experiment, the expected completion time and energy demand for power generation tasks are designed to follow a truncated normal distribution. Specifically, the energy demand Ni follows a normal distribution 𝒩(200,202), with a mean of 200 kWh and a standard deviation of 20 kWh. Therefore, most energy demands are concentrated between 195 and 205 kWh. To fully reflect the impact of renewable energy fluctuations on power generation tasks, the energy demand Ni is dynamically adjusted after initial generation based on the renewable energy contribution at the task’s arrival time. Additionally, the expected completion time Ei for each power generation task is set to follow a normal distribution 𝒩(0.5,0.12), meaning most values are concentrated between 0.3 hours and 0.7 h. To simulate the arrival times of power generation tasks, the experiment refers to the time distribution characteristics of the residential, commercial, and industrial daily load curves as presented in [23]. The task arrival rate is set for three different scenarios: peak, normal, and off-peak periods. The arrival of tasks in each period is modeled using a Poisson distribution to analyze the performance of the DQN-based scheduling method under different load demand patterns.

Hyperparameter Settings: To ensure the neural network model can learn efficiently, this experiment designs a deep neural network (DNN) with a feedforward structure as the model architecture. Specifically, the DNN consists of two hidden layers, each containing 10 neurons, which can extract complex state features. During the training process, an experience replay mechanism is used, with the replay memory size set to 1000. The mini-batch size is set to 30 to ensure the model learns from a sufficient number of samples during each training iteration. The learning rate is set to 0.01 to prevent drastic fluctuations during parameter updates, ensuring training stability. The parameters of the target network θ′ are synchronized with the evaluation network every 50 iterations.

To further improve model performance, the experiment configures other key hyperparameters: the discount factor γ is set to 0.9, indicating that the model prioritizes maximizing long-term rewards; the learning frequency f is set to 1; the initial exploration rate ε is set to 0.9 and gradually decays at a rate of 0.006 per iteration. This setup encourages thorough exploration of the state space in the early stages of training while shifting the focus toward optimization in later stages.

Evaluation Metrics: During the evaluation process of the experiment, we use average response time, success rate, and average cost as core performance metrics to balance the trade-off between scheduling efficiency and economic benefits. The average response time measures the timeliness of scheduling response, representing the average time required for tasks to be allocated and completed by the scheduling controller. It is calculated as follows:

(12)Tavg=∑i=1NTiN(12)

where N represents the total number of power generation tasks, and Ti is the response time of power generation task i, i.e., the duration from the task’s arrival to its completion.

The success rate quantifies the proportion of tasks completed within the specified time, reflecting the reliability of the scheduling strategy. It is calculated as follows:

(13)Sr=100×(NsuccessN)(13)

where Nsuccess represents the number of successfully completed power generation tasks, which are tasks satisfying Ti≤Ei. Meanwhile, N denotes the total number of power generation tasks.

The average cost represents the average energy cost of power generation tasks, which comprehensively considers operational costs, energy losses, and scheduling overhead during the execution process. It is calculated as follows:

(14)Cavg=∑i=1NCiN(14)

where Ci represents the cost of power generation task i, and N is the total number of power generation tasks. A lower average cost indicates that the scheduling strategy effectively optimizes energy consumption and reduces operational costs, demonstrating superior performance in economic efficiency.

4.2 Experimental Results

This study evaluates various intelligent scheduling strategies for Virtual Power Plant (VPP), including two traditional approaches: Earliest Allocation (EA) and Discrete Particle Swarm Optimization (DPSO). The EA strategy adopts a time-priority approach, assigning power generation tasks to the earliest available generation unit to minimize average response time. DPSO, based on swarm intelligence optimization, utilizes particle swarm search to find the optimal task allocation scheme, aiming to improve scheduling efficiency. Additionally, we explore three deep reinforcement learning-based scheduling methods, including our proposed DQN-based intelligent scheduling method, an improved DDQN-based model, and a PPO-based baseline model. Although these methods employ different neural network architectures, they all enable efficient discrete action decision-making and have been widely applied to similar intelligent scheduling problems [24].

It is important to note that, to prevent the unit differences among various metrics in the reward function from affecting the agent’s learning strategy, this experiment applies normalization to all metrics. Therefore, the “average cost” and “average response time” in the figures are represented as dimensionless abstract values. In the following experimental results, we use the following abbreviations to denote different scheduling strategies: EA (Earliest Allocation), DPSO (Discrete Particle Swarm Optimization), DQN (the proposed scheduling method based on Deep Q-Network), DDQN (Double Deep Q-Network method), and PPO (Proximal Policy Optimization-based scheduling method).

4.2.1 Different Proportions of Emergency Tasks

In this section, we evaluate the impact of the proportion of emergency tasks on five scheduling strategies. To achieve this, we construct a scheduling scenario where the number of power generation tasks arriving at the Virtual Power Plant (VPP) at any given time exceeds the number of available generation units. The proportion of emergency tasks gradually increases from 10% to 90% in increments of 20%. The ratio of dynamic peaking units to stable baseload units (SBU) is fixed at 1:1.

From Figs. 3a, 4a and 5a, it can be observed that as the proportion of emergency tasks increases, the proposed DQN scheduling method consistently outperforms other methods in terms of average response time. Specifically, under the residential daily load curve, when the proportion of emergency tasks is 10%, the average response time of DQN is reduced by 15% and 34% compared to DPSO and PPO, respectively. When the proportion of emergency tasks increases to 90%, DQN still achieves reductions of 13% and 9% compared to DDQN and PPO, respectively. Under the commercial daily load curve, DQN achieves the highest reduction in response time compared to DDQN, reaching 39% (at 10% emergency task proportion), and remains significantly lower than PPO and Earliest Allocation (EA) across all emergency task proportions. Under the industrial daily load curve, DQN demonstrates outstanding adaptability in high emergency task proportion scenarios (90%), with its average response time reduced by 12% and 34% compared to PPO and DDQN, respectively.

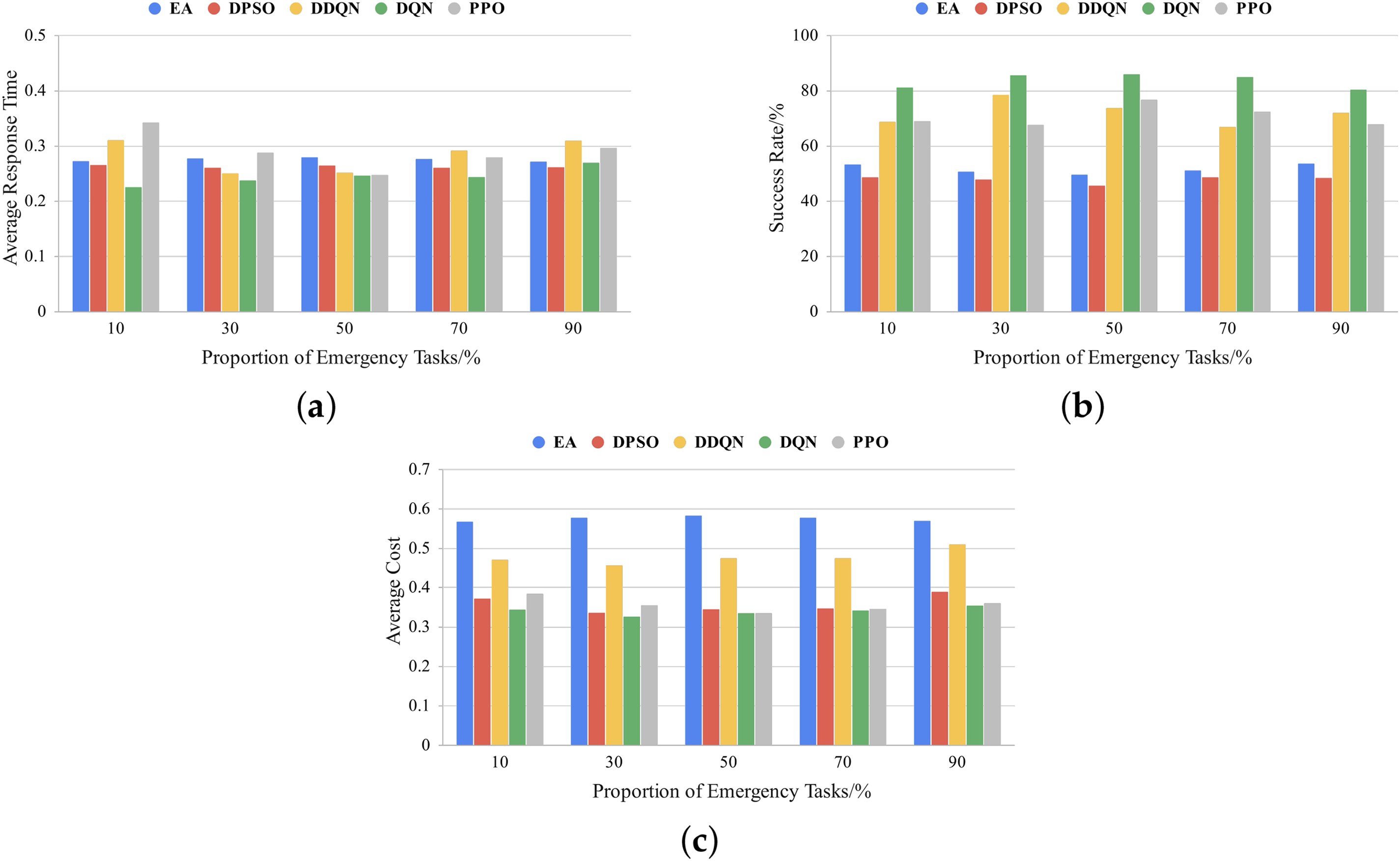
Figure 3: Comparison of different proportions of emergency tasks under the residential daily load curve: (a) average response time; (b) success rate, (c) average cost

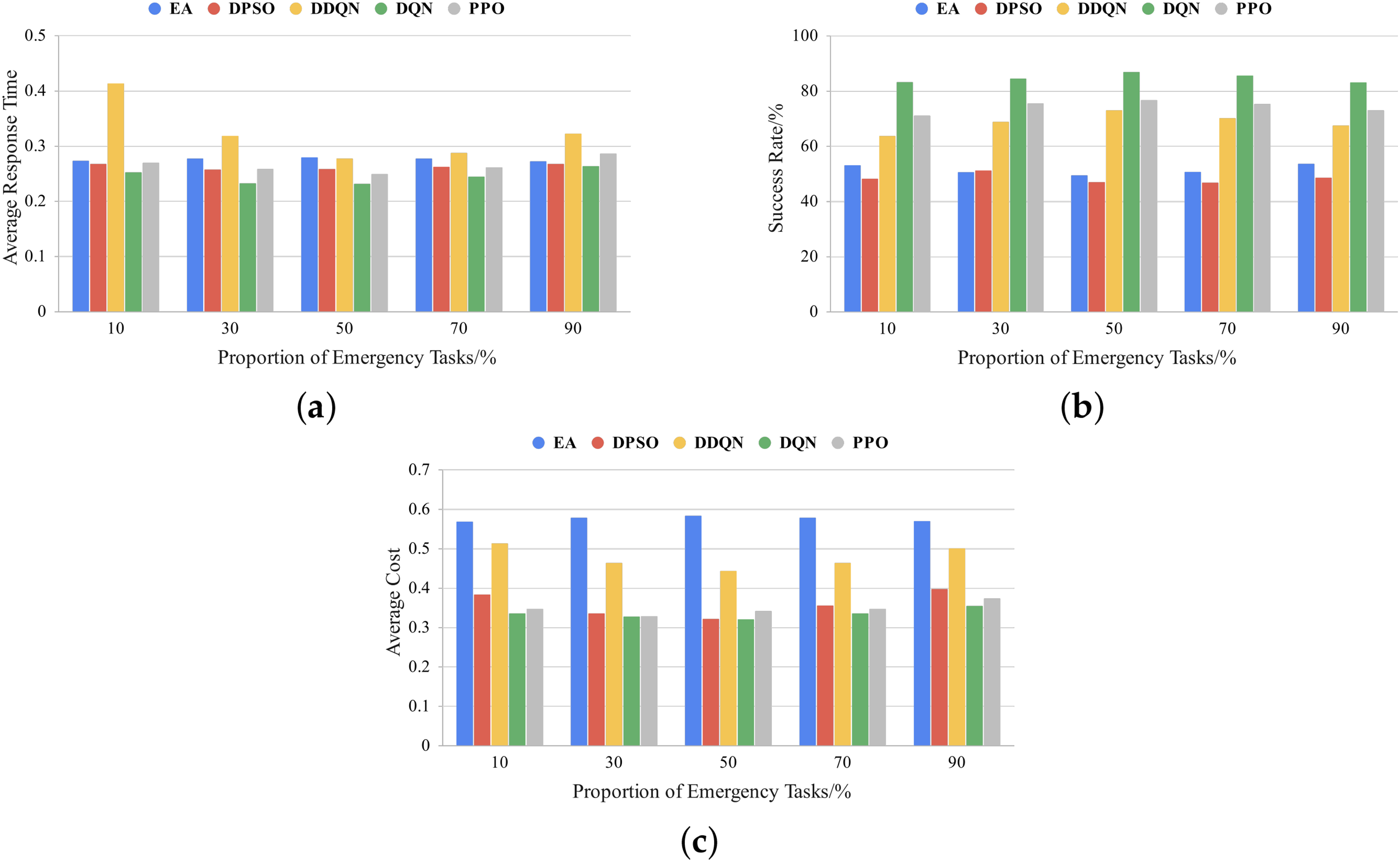
Figure 4: Comparison of different proportions of emergency tasks under the commercial daily load curve: (a) average response time; (b) success rate; (c) average cost

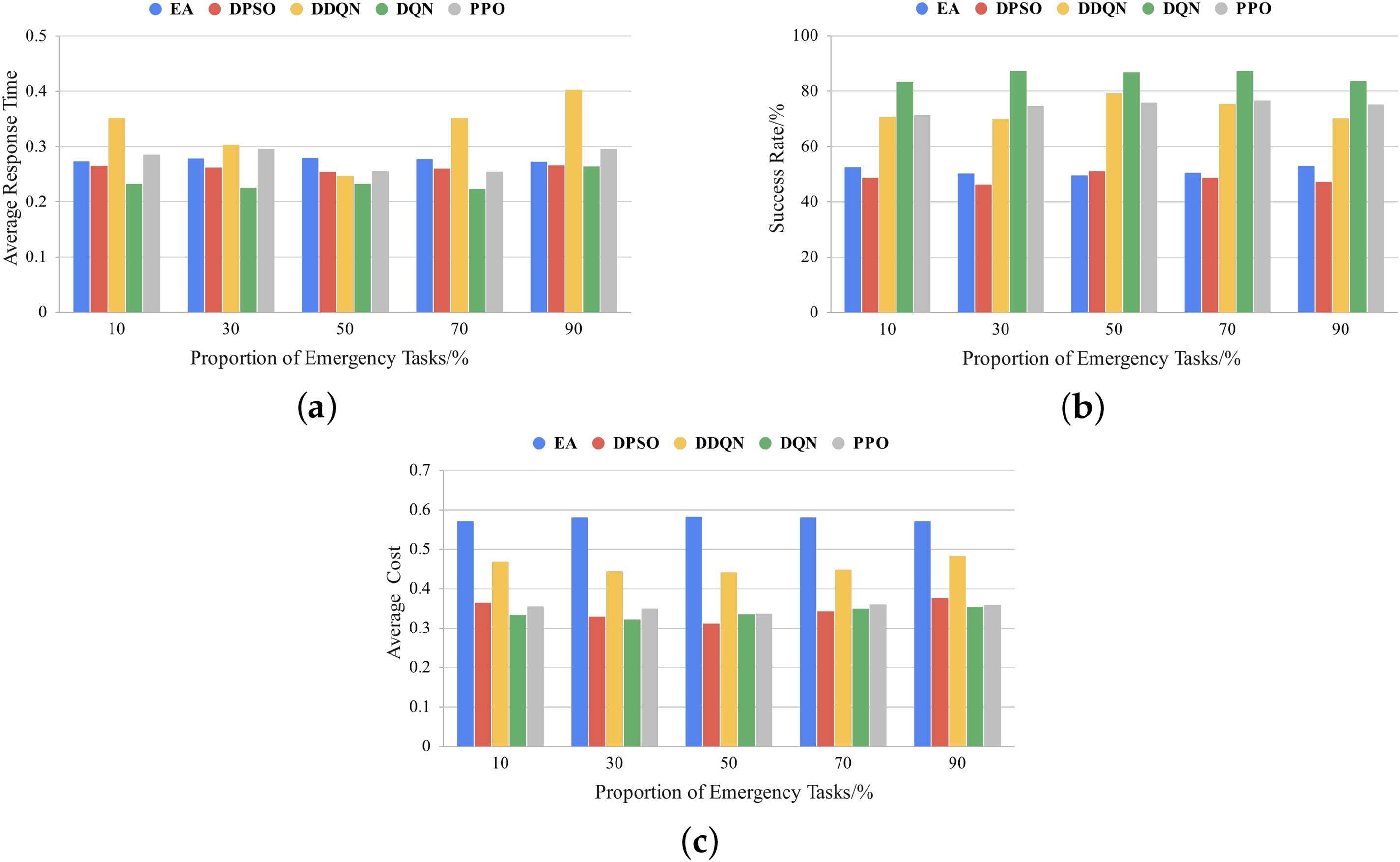
Figure 5: Comparison of different proportions of emergency tasks under the industrial daily load curve: (a) average response time; (b) success rate; (c) average cost

Figs. 3b, 4b and 5b show that regardless of the proportion of emergency tasks, the task success rate of the DQN method remains significantly higher than that of other scheduling methods, consistently exceeding 80%. As the proportion of emergency tasks increases, the DQN method exhibits greater advantages over DDQN, PPO, DPSO, and EA, especially in high emergency task proportion conditions, where it maintains a leading success rate. Specifically, under the industrial daily load curve, when the proportion of emergency tasks reaches 90%, the task success rate of the DQN method is approximately 1.19 times that of DDQN and 1.11 times that of PPO. This indicates that in high-load task environments, the DQN method can more effectively adapt to scheduling demands and ensure reliable task completion.

Meanwhile, as shown in Figs. 3c, 4c and 5c, the DQN method generally outperforms DDQN and EA in cost reduction and, in some cases, achieves a performance close to that of PPO. Under the residential daily load curve, the cost of the DQN method is reduced by approximately 27% and 39% compared to DDQN and EA, respectively, across different emergency task proportions. Notably, when the proportion of emergency tasks reaches 90%, the DQN method achieves significantly lower costs than DDQN and EA, demonstrating excellent cost control capabilities. Under the commercial daily load curve, the DQN method also performs exceptionally well, achieving a cost reduction of 27% and 6% compared to DDQN and PPO, respectively, when the proportion of emergency tasks is 50%. Under the industrial daily load curve, the DQN method consistently demonstrates stable cost optimization capabilities across different emergency task proportions. Even when the proportion of emergency tasks reaches 90%, the cost of the DQN method remains lower than that of DDQN and PPO, further illustrating its adaptability and economic efficiency in high-load environments.

From the above results, it can be concluded that regardless of the proportion of emergency tasks, the DQN method exhibits strong adaptability and stability, effectively reducing response time while maintaining a high task success rate. Additionally, DQN outperforms DDQN and DPSO in cost control and even surpasses PPO in some cases, indicating its ability to improve scheduling performance while maintaining strong economic efficiency. Overall, the DQN-based scheduling method demonstrates high robustness, scheduling flexibility, and economic efficiency across different emergency task proportions, making it well-suited for highly dynamic load scheduling environments.

4.2.2 Different Proportions of Dynamic Peaking Unit

In this section, we evaluate the impact of the dynamic peaking unit (DPU) proportion on scheduling strategies. The proportion of emergency tasks is fixed at 50%, while the DPU proportion is gradually increased from 30% to 70% in increments of 10%. The experimental results, as shown in Figs. 6–8, indicate that the DQN method outperforms other scheduling strategies in terms of response time and success rate under residential, commercial, and industrial daily load curves, especially when the DPU proportion increases to 60%–70%. For example, under the industrial load curve, the average response time of DQN is approximately 12% lower than that of PPO, while its success rate is about 13% higher than that of DDQN. Furthermore, in cost control, as the DPU proportion increases, the costs of DDQN and DPSO rise significantly, whereas DQN maintains a relatively low cost level. Notably, when the DPU proportion reaches 70%, the cost of DQN is approximately 58% lower than that of DDQN and 39% lower than that of DPSO, demonstrating its outstanding economic efficiency.

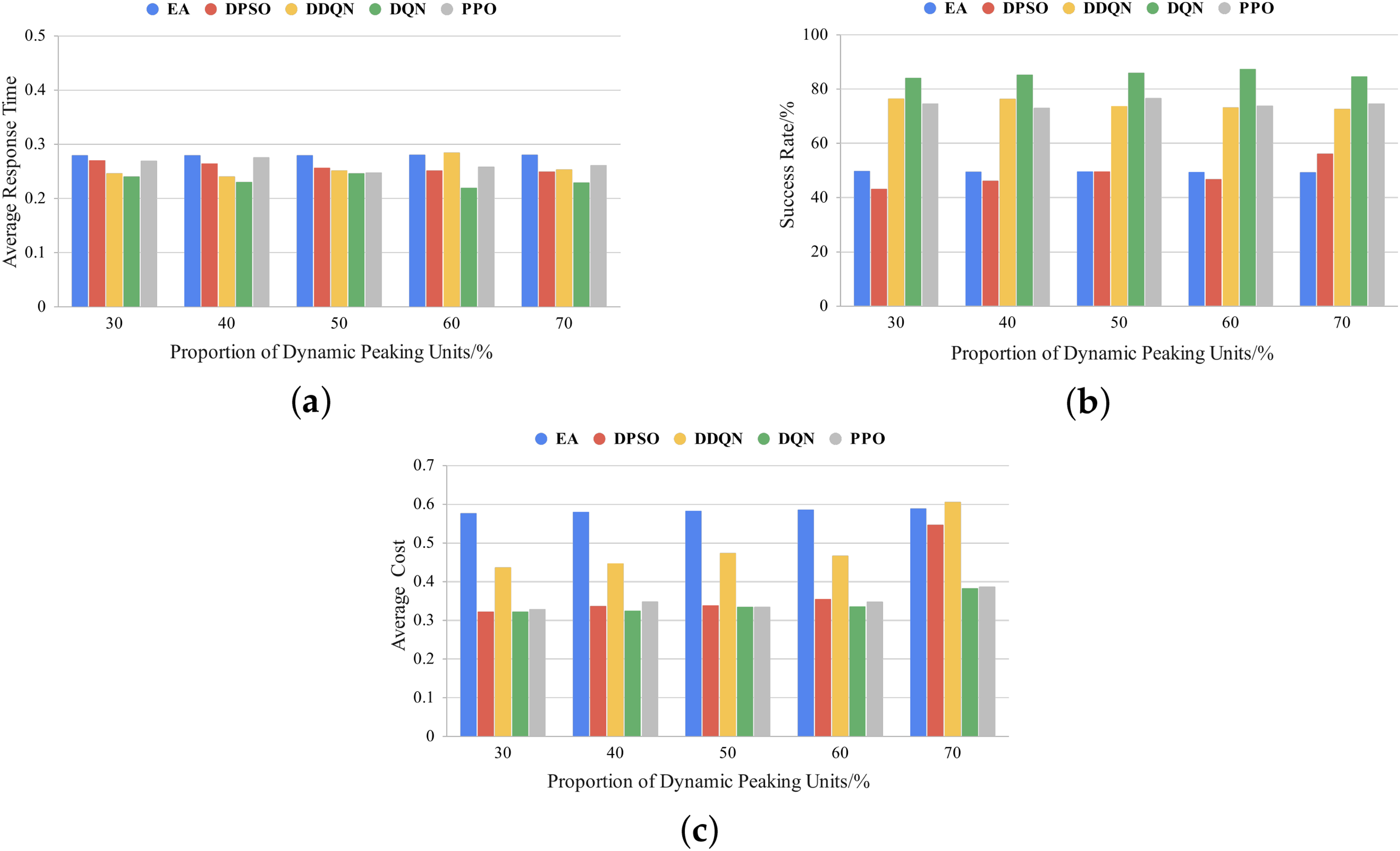
Figure 6: Comparison of different proportions of dynamic peaking units under the residential daily load curve: (a) average response time; (b) success rate; (c) average cost

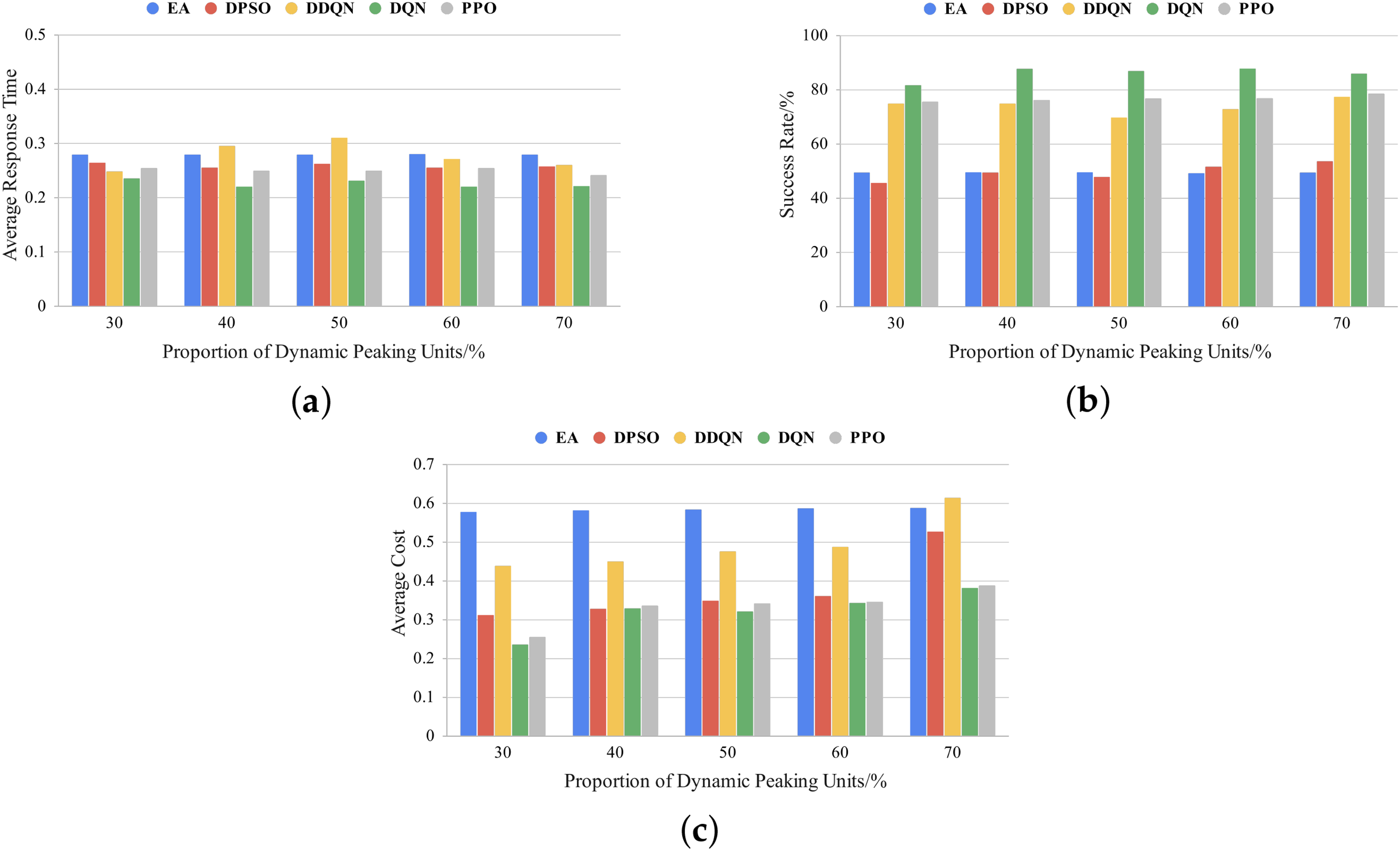
Figure 7: Comparison of different proportions of dynamic peaking units under the commercial daily load curve: (a) average response time; (b) success rate; (c) average cost

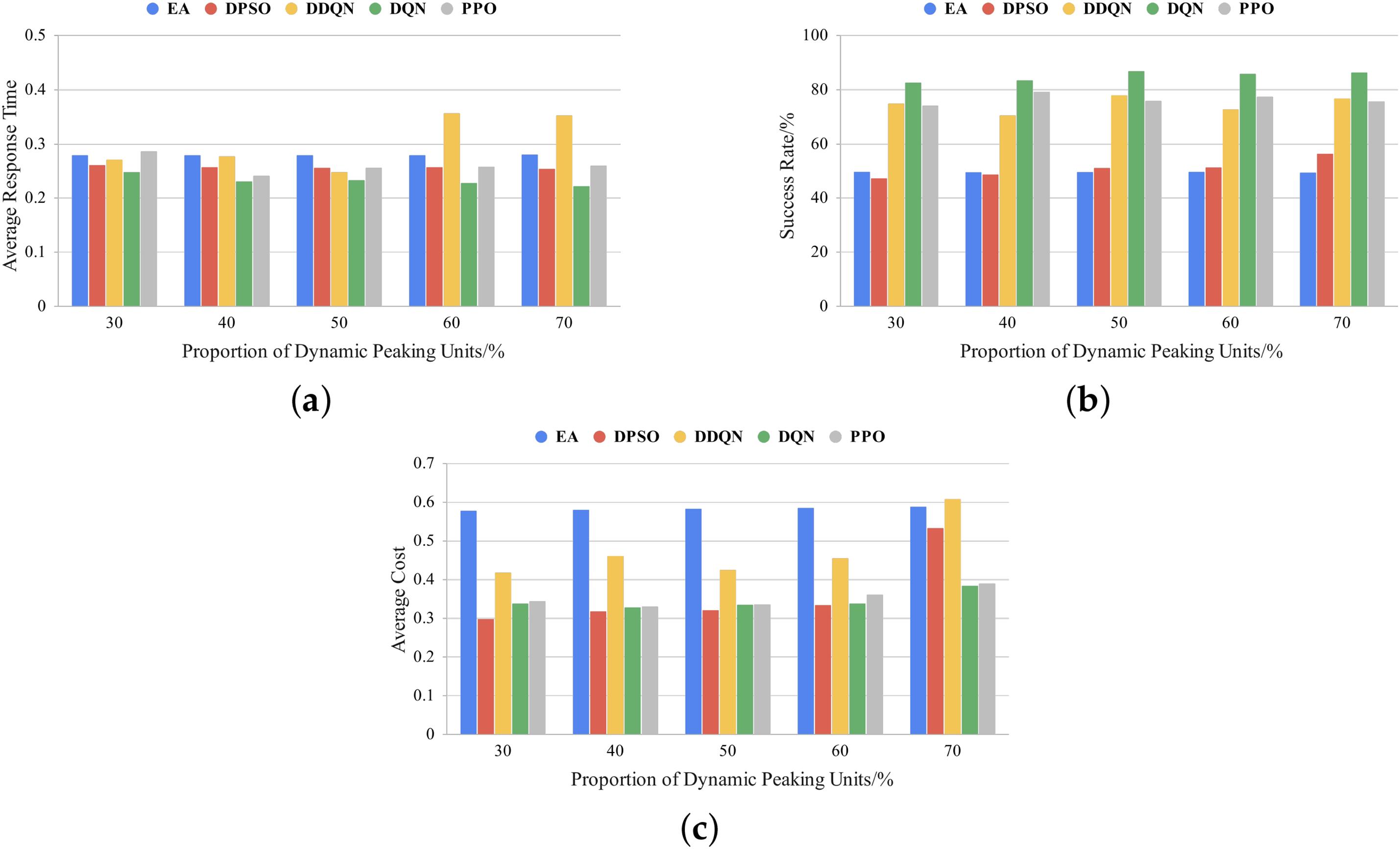
Figure 8: Comparison of different proportions of dynamic peaking units under the industrial daily load curve: (a) average response time; (b) success rate; (c) average cost

4.2.3 Different Virtual Power Plant Scales

In this section, to verify the scalability of the proposed deep reinforcement learning (DQN)-based scheduling method in large-scale virtual power plant systems, we expand the scheduling scenario and evaluate the performance of various scheduling strategies under different system scales (20, 50, and 100 generation units). Additionally, to simulate resource-constrained real-world operating conditions, the experiment sets the task load of the virtual power plant significantly higher than the available generation unit capacity. Furthermore, the ratio of dynamic peaking units to stable baseload units is fixed at 1:1, and the proportion of emergency tasks is maintained at 50%, ensuring a more realistic reflection of the complexity of actual operational environments.

As shown in Fig. 9, as the system scale expands, the advantage of cost optimization weakens to some extent, particularly when the number of generation units increases to 100, where the cost is slightly higher than that of PPO. However, in terms of response time, DQN consistently maintains a low level across all system scales, significantly outperforming other methods. Specifically, in larger system scales, DQN achieves a 23% and 6% reduction in response time compared to DDQN and DPSO, respectively, ensuring stable scheduling efficiency. Regarding task success rate, DQN also performs exceptionally well, maintaining a higher success rate than other methods across all system scales. Although there is a slight decline in the largest system scale, DQN still achieves a 75.8% success rate, demonstrating strong scheduling stability. Overall, the DQN-based scheduling method exhibits strong scheduling capabilities across different system scales. Notably, in large-scale virtual power plant environments, it continues to effectively reduce response time, improve task success rate, and maintain competitive cost control, demonstrating excellent scalability.

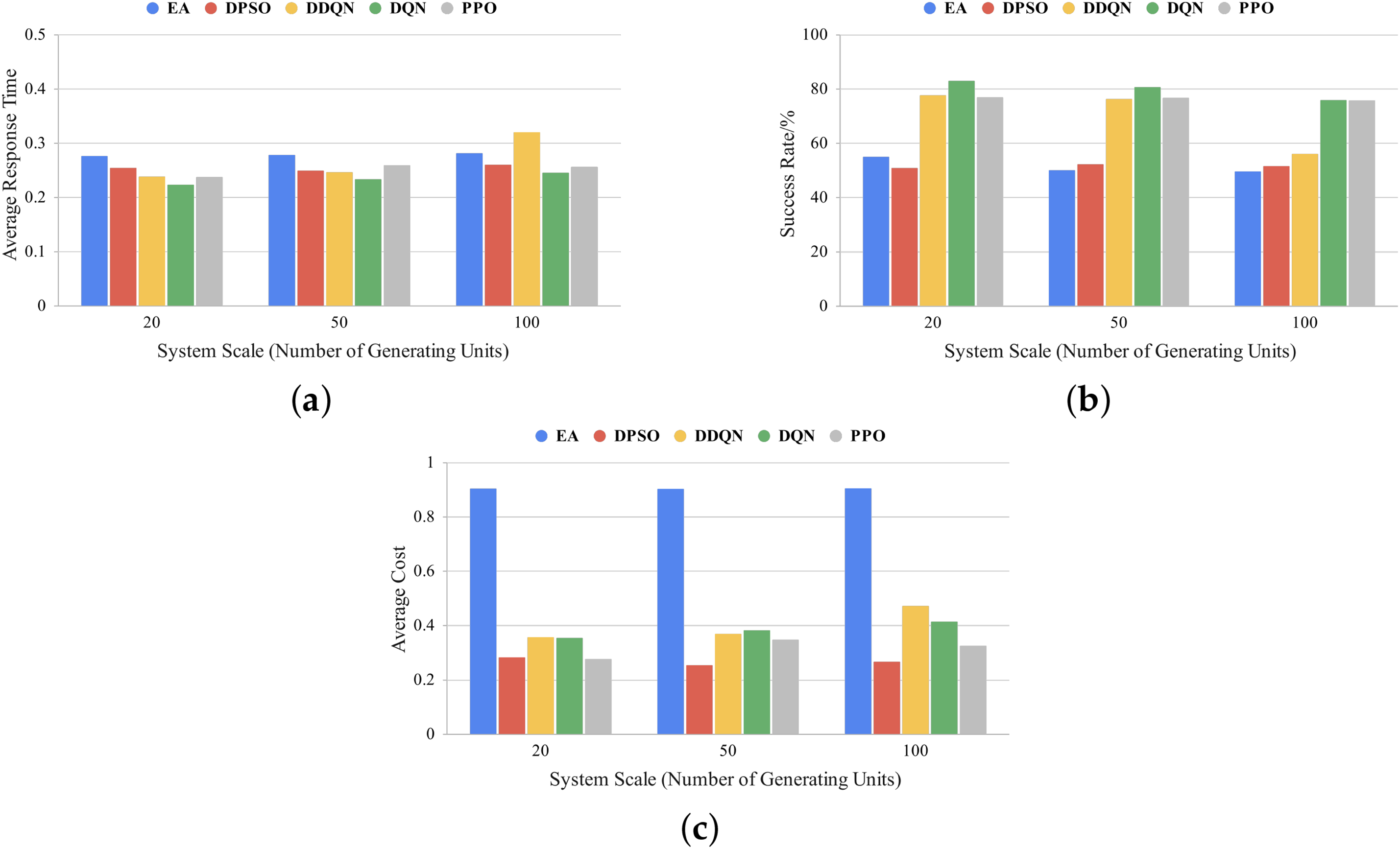
Figure 9: Comparison under different system scales: (a) average response time; (b) success rate; (c) average cost

4.2.4 Evaluation of Scheduling Strategy Robustness under Renewable Energy Fluctuations

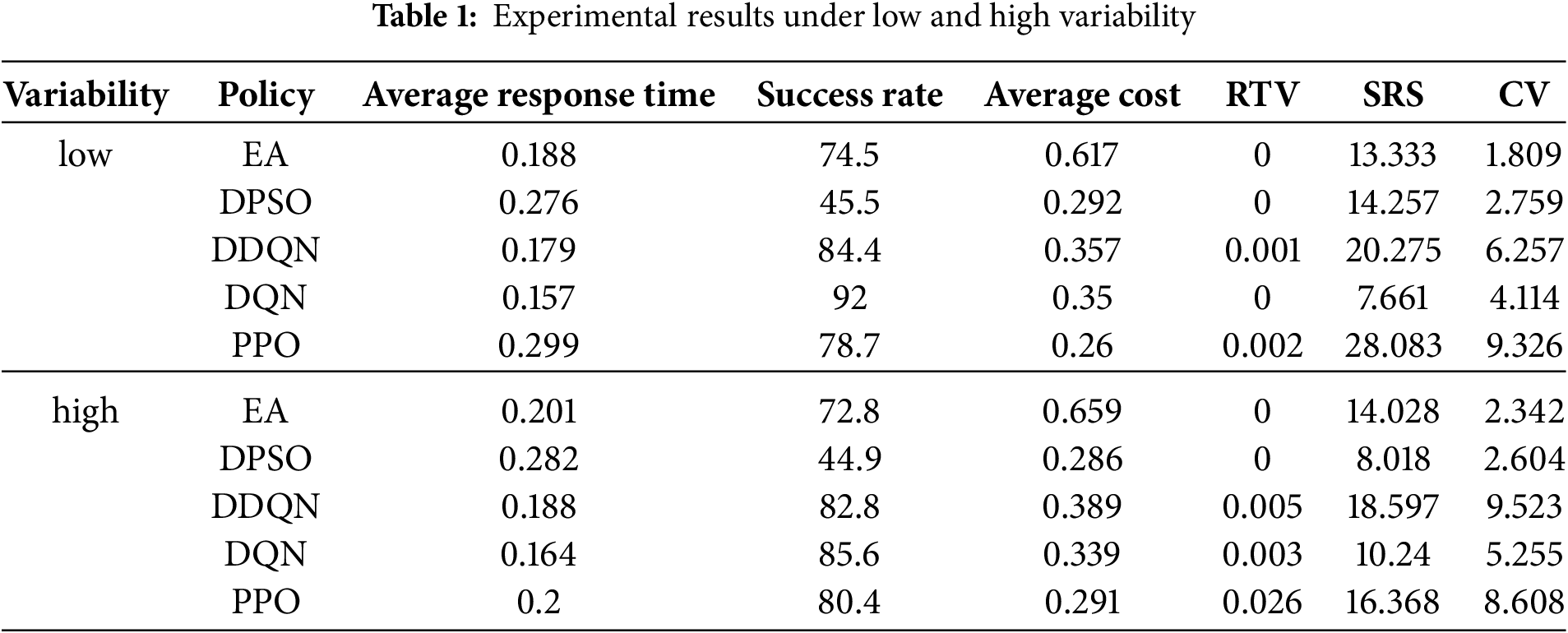
The volatility of renewable energy sources (such as wind and solar power) often affects the scheduling performance of virtual power plants. To evaluate the robustness of different scheduling strategies in uncertain environments, we define two scenarios: low volatility and high volatility. In the low volatility scenario, wind power output is set within the range of 80 to 90 kWh (±5% fluctuation), and solar power output is set within 60 to 65 kWh (±5% fluctuation). The total renewable energy output remains relatively stable, and the scheduling system is minimally affected by renewable energy fluctuations. In the high volatility scenario, wind power output expands to a range of 50 to 120 kWh (±35% fluctuation), and solar power output expands to 30 to 80 kWh (±40% fluctuation). The renewable energy output exhibits significant randomness, which may lead to extended task response times or an increased task failure rate.

Meanwhile, to quantify the robustness of different scheduling strategies under these two scenarios, we introduce three key evaluation metrics: (1) Response Time Variance (RTV)-Measures the fluctuation in task completion time. A smaller variance indicates that the scheduling system is more stable in a renewable energy fluctuation environment. (2) Success Rate Stability (SRS)-Measures the decline in task success rate between the high volatility and low volatility scenarios, assessing the adaptability of scheduling strategies to renewable energy fluctuations. (3) Cost Variability (CV)-Measures the fluctuation in scheduling costs under different environments. A smaller coefficient of variation indicates greater stability in economic efficiency. The calculation formula for response time variance (RTV) is as follows:

(15)RTV=1N∑i=1N(Ti−Tavg)2(15)

where Ti is the response time of power generation task i; Tavg is the average response time of power generation tasks; and N is the total number of power generation tasks. The definition of Success Rate Stability (SRS) is:

(16)SRS=(Smaxr−SminrSmaxr)×100%(16)

where Smaxr and Sminr represent the maximum and minimum values of task success rate, respectively. The calculation method for Cost Variability (CV) is as follows:

(17)CV=(σcostμcost)×100%(17)

where σcost and μcost represent the standard deviation and mean of the cost, respectively.

From the results in Table 1, it can be seen that the DQN scheduling method we adopted demonstrates stronger robustness in dealing with the volatility of renewable energy. Compared to other methods, DQN maintains the lowest response time and the highest success rate in both low and high volatility environments. At the same time, DQN’s response time variance (RTV) and success rate standard deviation (SRS) are much lower than those of other baseline methods, indicating its ability to remain stable even in fluctuating environments. Furthermore, DQN’s cost volatility (CV) is also lower than that of DDQN and PPO, ensuring the stability of scheduling economics. These results prove that DQN can effectively adapt to the volatility of new energy sources, providing a more stable and efficient task scheduling strategy.

The four experiments mentioned above comprehensively assess the advantages of DQN in virtual power plant intelligent scheduling, including average response time, task success rate, cost control, and robustness under different renewable energy volatility environments. These experiments verify the stability of the DQN method in various operating scenarios and show that it can maintain good scheduling performance under different experimental variables. The reason DQN excels across all evaluation metrics is primarily due to its Q-learning-based dynamic optimization mechanism, which allows it to adjust the scheduling strategy according to different load environments and task urgency levels. Specifically, DQN can continuously optimize scheduling decisions through reinforcement learning. Under high emergency task proportions, it prioritizes scheduling dynamic peaking unit (DPU) to ensure quick task execution, while under low emergency task proportions, it tends to use stable baseload unit (SBU) to reduce overall production costs, thereby effectively controlling energy consumption while ensuring task success rates.In addition, DQN employs the Experience Replay mechanism, allowing the agent to learn long-term optimal strategies in complex and dynamic load environments, rather than relying solely on short-term task feedback. As a result, it can still maintain low response times and high task success rates under different load curves. Compared to PPO and other methods, DQN, through value function optimization, can quickly find the optimal strategy, ensuring timely task response. By applying a target network, it avoids instability in strategy updates due to load fluctuations, demonstrating stronger adaptability and stability when facing different virtual power plant scales and renewable energy volatility. In terms of cost control, DQN can make intelligent decisions during task allocation, making the coordination between DPU and SBU more efficient. This avoids the high energy consumption problems caused by traditional methods’ over-reliance on DPU, while also ensuring the economic efficiency of the overall scheduling by maximizing cumulative rewards and reducing additional costs due to frequent start-ups and shut-downs of units. Moreover, when faced with different virtual power plant scales and renewable energy volatility, the DQN method demonstrates greater adaptability and stability, with task success rates always above 75%. Even when the system scale expands to 100 generation units, it still maintains good cost control ability, further proving its excellent scalability and environmental adaptability. In summary, DQN not only outperforms traditional methods and other deep reinforcement learning methods in overall scheduling performance but also provides robust and efficient intelligent scheduling strategies when facing dynamic load changes and renewable energy volatility, offering strong support for the intelligent operation of virtual power plants.

4.2.5 Comparison and Analysis of DQN, PPO, and DDQN Methods

In the above experiments, we compare and evaluate the virtual power plant scheduling strategies optimized using DQN, PPO, and DDQN by varying multiple experimental parameters. Preliminary experimental results indicate that the deep reinforcement learning scheduling method using DQN demonstrates a clear advantage in terms of convergence speed and stability. Next, we will conduct a detailed analysis of this comparative result. To this end, we further compare the differences in loss convergence and reward values among DQN, PPO, and DDQN in an environment where the proportion of urgent tasks is fixed at 50%, and the ratio of dynamic peaking units to stable baseload units is set to 1:1. Additionally, the hyperparameter settings for this experiment are completely consistent with those described in Section 4.1, including the replay memory size (1000), mini-batch size (30), learning rate (0.01), discount factor (0.9), exploration rate (initial value of 0.9), and learning frequency (1).

In the virtual power plant scheduling problem, the scheduling strategy needs to efficiently allocate tasks between dynamic peaking unit (DPU) and stable baseload unit (SBU). Since the action space of this problem is discrete, the Q-network structure of DQN is particularly well-suited for solving such tasks. As shown in Fig. 10a, DQN calculates the loss using Mean Squared Error (MSE), providing stable Q-value estimates and directly outputting the Q-values for each unit to achieve optimized scheduling. In contrast, the PPO method shown in Fig. 10b optimizes through policy loss and value function loss, mainly used to generate continuous action probability distributions or discrete action values. Although the loss calculation methods of the two algorithms differ, their convergence trends are generally similar in the iterative process. However, DQN has a clear advantage in handling this entirely discrete scheduling problem, as it focuses on the selection of discrete actions without dealing with the complexity of continuous action spaces. Additionally, as shown in Fig. 10c, DDQN reduces the bias in Q-value estimation by adopting a double Q-network structure, but its convergence speed is significantly slower than that of DQN. Specifically, during the first 400 training iterations, the loss of DQN decreases more rapidly, indicating that it can converge to a better solution more quickly in the early stages of learning. In contrast, DDQN has a more conservative update mechanism, leading to lower learning efficiency in the initial training phase.

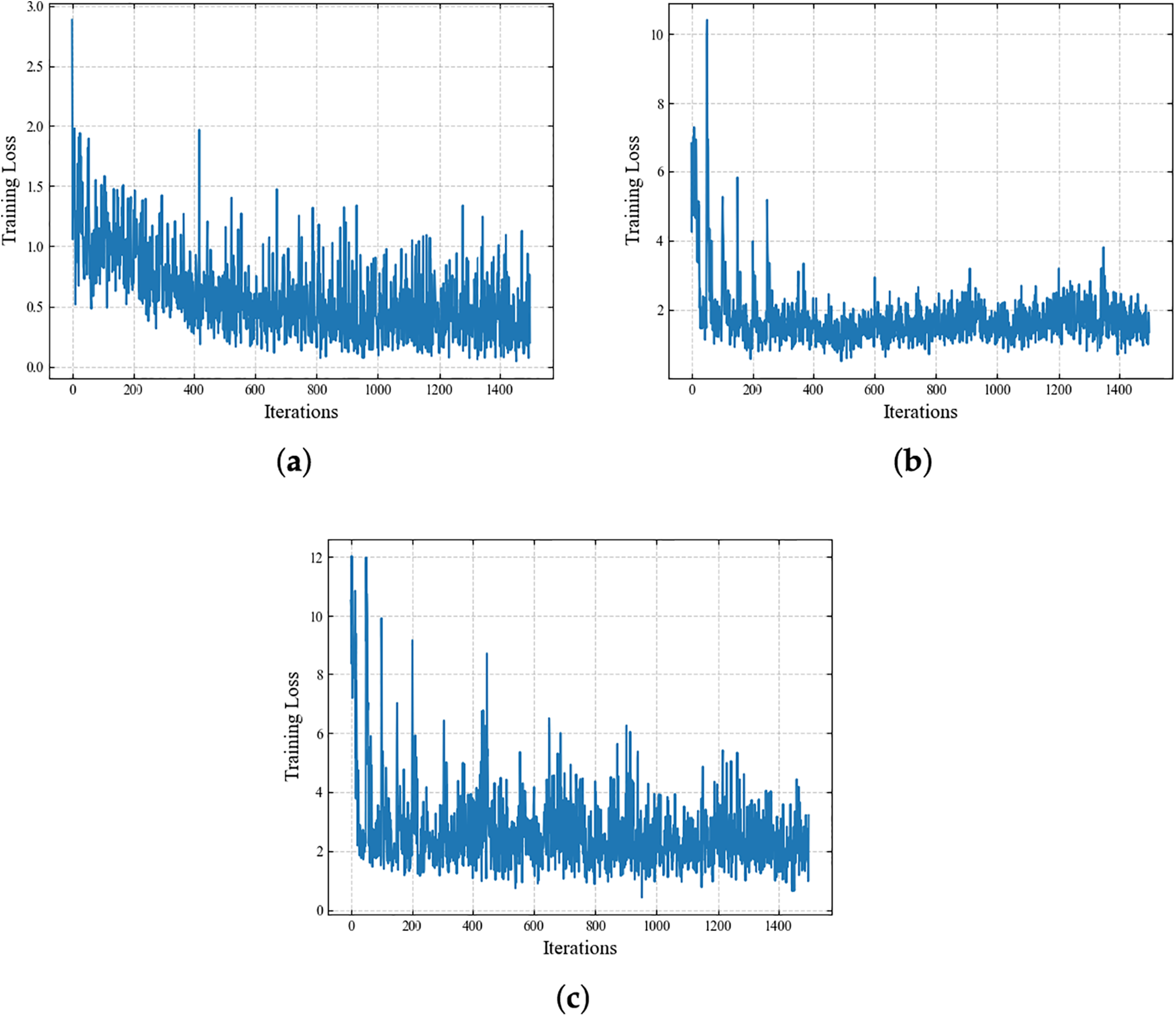
Figure 10: Comparison of loss convergence between DQN, PPO, and DDQN. (a) shows the loss convergence curve of DQN at the 100th training epoch; (b) shows the loss convergence curve of PPO at the 100th training epoch; (c) shows the loss convergence curve of DDQN at the 100th training epoch

In the comparison of transfer learning performance, PPO collects new data for online learning with each policy update, which typically requires complex gradient calculations. DQN, on the other hand, uses the experience replay mechanism to sample from past experiences and implement parallel learning, which generally allows DQN to be more efficient during the training process. In contrast, DDQN introduces a more conservative Q-value update strategy through the double Q-network structure. While it reduces the overestimation of Q-values, it also limits the exploration ability of the policy, making it difficult for the model to quickly find the optimal scheduling solution in the early stages. As shown in Fig. 11, DQN reaches reward convergence after approximately 15 training epochs, while PPO requires about 50 training epochs to stabilize and converge, with significant reward fluctuations during the convergence process. The convergence speed of DDQN is significantly slower than that of DQN. During the first 25 training epochs, its reward value is noticeably lower than that of DQN, showing lower initial learning efficiency, and it only stabilizes and converges after about 35 training epochs. Therefore, in virtual power plant scheduling tasks, DQN shows higher training efficiency and greater stability, especially when handling rapidly changing load demands, allowing it to adapt more quickly and optimize scheduling strategies.

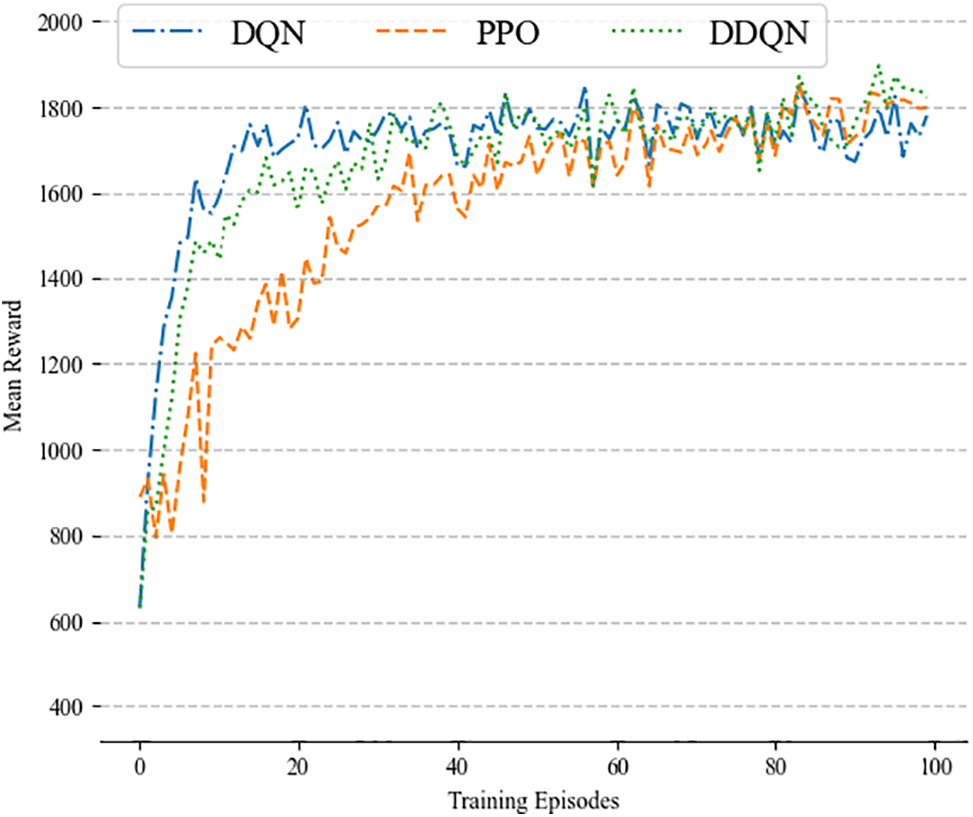
Figure 11: Comparison of mean reward between DQN, PPO, and DDQN

5  Conclusion

This paper proposes a deep reinforcement learning-based intelligent scheduling method for Virtual Power Plants (VPPs) to address the volatility and uncertainty of renewable energy sources such as wind and solar power, as well as the complexity and diversity of user load demands. The method uses Deep Q-Network (DQN) to optimize the coordinated scheduling of dynamic peaking unit (DPU) and stable baseload unit (SBU) to meet the electricity demand and strict response time requirements of power generation tasks. Experimental results show that, compared to traditional scheduling methods (such as Earliest Allocation and Discrete Particle Swarm Optimization) and other deep reinforcement learning algorithms (such as DDQN and PPO), the proposed DQN-based intelligent scheduling method demonstrates significant advantages in task response time, task success rate, and cost control, particularly in high-dynamic load demand and renewable energy fluctuation environments, where it shows stronger robustness.Furthermore, this study further explores the scalability of the DQN-based intelligent scheduling method under different virtual power plant scales. The results indicate that it can stably adapt to large-scale complex scheduling environments, effectively improving the system’s flexibility and economic efficiency. Future work will focus on exploring more efficient deep reinforcement learning models, such as those incorporating attention mechanisms or multi-agent reinforcement learning, to further optimize scheduling strategies and enhance the adaptability and generalization capabilities of virtual power plants.

Acknowledgement: The authors express their sincere gratitude to all individuals who have contributed to this paper. Their dedication and insights have been invaluable in shaping the outcome of this work.

Funding Statement: This work was supported by the National Key Research and Development Program of China, Grant No. 2020YFB0905900.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Wenchao Cui and Hairun Xu; methodology, Shaowei He, Gang Li and Wenchao Cui; software, Shaowei He; validation, Yu Tai, Gang Li and Hairun Xu; formal analysis, Shaowei He; investigation, Shaowei He and Wenchao Cui; resources, Xiang Chen; data curation, Hairun Xu and Shaowei He; writing—original draft preparation, Shaowei He; writing—review and editing, Wenchao Cui. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Chen L, Msigwa G, Yang M, Osman AI, Fawzy S, Rooney DW, et al. Strategies to achieve a carbon neutral society: a review. Environ Chem Lett. 2022;20(6):2277–310. doi:10.1007/s10311-022-01435-8. [Google Scholar] [PubMed] [CrossRef]

2. Fernández-Guillamón A, Muljadi E, Molina-García A. Frequency control studies: a review of power system, conventional and renewable generation unit modeling. Electric Power Syst Res. 2022;211(3):108191. doi:10.1016/j.epsr.2022.108191. [Google Scholar] [CrossRef]

3. Min H, Hong S, Song J, Son B, Noh B, Moon J. SolarFlux predictor: a novel deep learning approach for photovoltaic power forecasting in South Korea. Electronics. 2071 2024;13(11):2071. doi:10.3390/electronics13112071. [Google Scholar] [CrossRef]

4. Notton G, Nivet M-L, Voyant C, Paoli C, Darras C, Motte F, et al. Intermittent and stochastic character of renewable energy sources: consequences, cost of intermittence and benefit of forecasting. Renew Sustain Energy Rev. 2018;87(8):96–105. doi:10.1016/j.rser.2018.02.007. [Google Scholar] [CrossRef]

5. Ufa RA, Malkova YY, Rudnik VE, Andreev MV, Borisov VA. A review on distributed generation impacts on electric power system. Int J Hydrogen Energy. 2022;47(47):20347–61. doi:10.1016/j.ijhydene.2022.04.142. [Google Scholar] [CrossRef]

6. Wang X, Liu Z, Zhang H, Zhao Y, Shi J, Ding H. A review on virtual power plant concept, application and challenges. In: 2019 IEEE innovative smart grid technologies-Asia (ISGT Asia). Chengdu, China; 2019. p. 4328–33. doi:10.1109/ISGT-Asia.2019.8881433. [Google Scholar] [CrossRef]

7. Ghavidel S, Li L, Aghaei J, Yu T, Zhu J. A review on the virtual power plant: components and operation systems. In: IEEE International Conference on Power System Technology (POWERCON); 2016; Wollongong, NSW, Australia. p. 1–6. doi:10.1109/POWERCON.2016.7754037. [Google Scholar] [CrossRef]

8. Bellman R. A Markovian decision process. J Math Mech. 1957;6(5):679–84. [Google Scholar]

9. Gjorgiev B, Kančev D, Čepin M. A new model for optimal generation scheduling of power system considering generation units availability. Int J Electr Power Energy Syst. 2013;47:129–39. doi:10.1016/j.ijepes.2012.11.001. [Google Scholar] [CrossRef]

10. Osório GJ, Lujano-Rojas JM, Matias JCO, Catalão JPS. A fast method for the unit scheduling problem with significant renewable power generation. Energy Convers Manag. 2015;94(7):178–89. doi:10.1016/j.enconman.2015.01.071. [Google Scholar] [CrossRef]

11. Rahimi M, Jahanbani Ardakani F, Jahanbani Ardakani A. Optimal stochastic scheduling of electrical and thermal renewable and non-renewable resources in virtual power plant. Int J Electr Power Energy Syst. 2021;127:106658. doi:10.1016/j.ijepes.2020.106658. [Google Scholar] [CrossRef]

12. Cui W, Zhao J, Bai L. Study on hybrid generator scheduling based on multi-agent. Shaanxi Electr Power. 2014;42(4):74–7. [Google Scholar]

13. Xiao T, Chen Y, Diao H, Huang S, Shen C. On fast-converged deep reinforcement learning for optimal dispatch of large-scale power systems under transient security constraints. arXiv:2304.08320. 2024. [Google Scholar]

14. Shengren H, Salazar EM, Vergara PP, Palensky P. Performance comparison of deep RL algorithms for energy systems optimal scheduling. In: IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe); 2022; Novi Sad, Serbia. p. 1–6. doi:10.1109/ISGT-Europe54678.2022.9960642. [Google Scholar] [CrossRef]

15. Liu C-L, Tseng C-J, Huang T-H, Wang J-W. Dynamic parallel machine scheduling with deep Q-network. IEEE Trans Syst Man Cybern Syst. 2023;53(11):6792–804. doi:10.1109/TSMC.2023.3289322. [Google Scholar] [CrossRef]

16. Workneh AD, Gmira M. Deep Q network method for dynamic job shop scheduling problem. In: Masrour T, El Hassani I, Barka N, editor. Artificial intelligence and industrial applications. A2IA 2023. Lecture notes in networks and systems. Vol. 771. Cham: Springer; 2023. doi:10.1007/978-3-031-43524-9-10. [Google Scholar] [CrossRef]

17. Liu J, Liu Y, Qiu G, Gu Y, Li H, Liu J. Deep-Q-network-based intelligent reschedule for power system operational planning. In: 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC); 2020; Nanjing, China. p. 1–6. doi:10.1007/978-3-031-43524-9-10. [Google Scholar] [CrossRef]

18. Sharifi V, Abdollahi A, Rashidinejad M. Flexibility-based generation maintenance scheduling in presence of uncertain wind power plants forecasted by deep learning considering demand response programs portfolio. Int J Electr Power Energy Syst. 2022;141(2):108225. doi:10.1016/j.ijepes.2022.108225. [Google Scholar] [CrossRef]

19. Zhu Y, Cai M, Schwarz CW, Li J, Xiao S. Intelligent traffic light via policy-based deep reinforcement learning. Int J Intell Transp Syst Res. 2022;20(4):734–44. doi:10.1007/s13177-022-00321-5. [Google Scholar] [CrossRef]

20. Arulkumaran K, Deisenroth MP, Brundage M, Bharath AA. Deep reinforcement learning: a brief survey. IEEE Signal Process Mag. 2017;34(6):26–38. doi:10.1109/MSP.2017.2743240. [Google Scholar] [CrossRef]

21. Schlosser R. Heuristic mean-variance optimization in Markov decision processes using state-dependent risk aversion. IMA J Manag Math. 2022;33(2):181–99. doi:10.1093/imaman/dpab009. [Google Scholar] [CrossRef]

22. Tarish H, Ong HS, Elmenreich W. A review of residential demand response of smart grid. Renew Sustain Energy Rev. 2016;59:166–78. doi:10.1016/j.rser.2016.01.016. [Google Scholar] [CrossRef]

23. Liu J, Wang Y, Xiong C, Lei X, Lu C. Daily load curve based power consumption mode extraction and clustering analysis. Diangong Dianen Xinjishu. 2023;42(5):57–63. [Google Scholar]

24. Ma Y, Cai J, Li S, Liu J, Xing J, Qiao F. Double deep Q-network-based self-adaptive scheduling approach for smart shop floor. Neural Comput Applic. 2023;35(30):22281–96. doi:10.1007/s00521-023-08877-3. [Google Scholar] [CrossRef]