Polynomial Commitment in a Verkle Tree Based on a Non-Positional Polynomial Notation

1  Introduction

Public-key encryption is vulnerable to attacks using quantum computers. Currently, the most well-known and widely used public-key encryption systems are Elliptic Curve Cryptography (ECC) and Rivest-Shamir-Adleman (RSA). The security of ECC is based on the intractability of the elliptic curve discrete logarithm problem, whereas the security of RSA cryptography relies on the intractability of integer factorization of large numbers. Both ECC and RSA are susceptible to attacks utilizing quantum computers [1–3].

Shor’s algorithm is a well-known quantum algorithm capable of efficiently factoring large integers in polynomial time, significantly reducing the security of cryptographic algorithms such as ECC and RSA. Such attacks pose a threat to many applications that rely on public-key cryptography, including Transport Layer Security (TLS), Secure/Multipurpose Internet Mail Extensions (S/MIME), Pretty Good Privacy (PGP), and digital signatures. If Shor’s algorithm is implemented on a quantum computer with a sufficient number of qubits, it can break the elliptic curve digital signature algorithm (ECDSA), which is the primary public-key signature algorithm used for Bitcoin, Ethereum, and many other blockchains [4–7].

One of the most critical aspects of implementing post-quantum cryptography is ensuring compatibility with existing technological systems. This is essential to allow the transition to new cryptographic standards without the need for a complete overhaul of current digital infrastructure. By maintaining such continuity, organizations can smoothly and efficiently upgrade their security frameworks, significantly reducing the risks posed by potential quantum computer-based attacks. Therefore, the integration of new algorithms into current protocols and software becomes a key component of any information protection strategy in the era of quantum technologies [8].

In July 2022, after three rounds of evaluation, the National Institute of Standards and Technology (NIST) announced the first batch of standardized post-quantum cryptographic algorithms. Ultimately, four algorithms were selected: CRYSTALS-KYBER, CRYSTALS-Dilithium, FALCON, and SPHINCS+ [9]. Among them, NIST recommends two primary algorithms: CRYSTALS-KYBER (for key establishment) and CRYSTALS-Dilithium (for digital signatures) for most use cases, while also endorsing FALCON and SPHINCS+ for signature schemes [10]. NIST-standardized algorithms, such as CRYSTALS-KYBER, belong to the field of post-quantum cryptography, but they are designed for entirely different tasks—specifically, encryption and key exchange. In contrast, the proposed method focuses on efficient polynomial commitments in Verkle trees.

Traditional hash-based signature schemes, such as those based on Merkle trees, require strict key management to prevent reuse, as key reuse can lead to security compromises [11,12].

The primary issue with Merkle trees is that in the process of “proving something”, nearly all hashes must be revealed, even if they do not contain relevant information. As the Ethereum blockchain scales, running nodes and verifying data integrity becomes increasingly challenging due to the growing amount of stored information. This has led to the need for a new approach that enables more efficient data verification without requiring the disclosure of all hashes throughout the process. The solution currently being developed is the Verkle tree [13].

In recent years, Verkle trees have emerged as a promising approach to organizing Merkle-like structures in blockchains. Their main advantage lies in significantly reducing proof sizes and accelerating verification processes, which is particularly critical for scalable blockchain systems. Unlike Merkle trees, which require a logarithmic number of hashes for proof generation, Verkle trees utilize polynomial commitments, providing compact proofs of fixed size. The issue of polynomial commitment efficiency remains relevant, as modern approaches such as Kate-Zaverucha-Goldberg-based (KZG-based) or Bulletproofs-based commitments have their limitations despite offering substantial proof size reductions. In particular, KZG commitments require a trusted setup, whereas Bulletproofs, despite not having such requirements, involve relatively high computational complexity. This motivates the search for alternative solutions that can offer a balance between efficiency, security, and computational costs [14,15].

The Verkle tree is a key component of Ethereum’s next upgrade. It serves the same purpose as the Merkle tree but offers a significant advantage with its shorter proof size. If there are 1,000,000 data fragments, a Merkle tree requires a 1 KB proof, whereas a Verkle tree needs only 150 bytes. Verkle trees were first proposed by John Kuszmaul in 2018. While Verkle trees provide substantial benefits, they require advanced cryptographic and mathematical knowledge.

2  Literature Review

In recent years, cryptographic structures that enable compact and efficient data storage and verification have garnered significant attention from researchers. Among them, Verkle trees, polynomial commitments, and vector commitments play a crucial role in modern cryptographic systems, including blockchain and post-quantum protocols. This section focuses on analyzing contemporary research related to Verkle trees, as well as polynomial and vector commitments. Specifically, it examines their cryptographic properties, efficiency, and applicability in the context of blockchain and post-quantum cryptography.

The study [16] explores Verkle trees, a cryptographic data structure designed as an alternative to Merkle trees. The author provides a detailed analysis of their architecture, mathematical properties, the use of vector commitments, and their advantages over traditional Merkle trees. John Kusmaul’s research demonstrates that Verkle trees can significantly reduce storage and proof verification overhead, making them a promising solution for next-generation blockchain systems.

The work [17] proposes an adaptive restructuring of Merkle and Verkle trees to enhance blockchain scalability. It highlights the unique advantages of adaptive restructuring, such as simplicity, security, and increased efficiency, without introducing additional complexity or dependencies. The study suggests modifying the structure of Merkle and Verkle trees in response to data usage patterns, thereby shortening the average verification path length and lowering the computational overhead associated with data validation.

In [18], the authors propose an efficient Bulletproofs protocol for range proofs and other zero-knowledge proof tasks. This protocol is designed for confidential transactions in blockchains like Monero and Bitcoin. Its key advantages include short proof sizes, making it more efficient than existing approaches, the absence of a trusted setup, eliminating the need for a trusted initialization phase, and efficient verification. Bulletproofs is based on the discrete logarithm problem, making them potentially resistant to quantum attacks.

Traditional approaches to spatiotemporal queries in blockchain often require additional external storage or rely on static indexes. In light of this, study [19] introduces a novel adaptive indexing method for spatiotemporal data in blockchain to improve query efficiency and data verification. This method employs encrypted signatures for spatiotemporal indexing and features an adaptive algorithm capable of modifying the tree structure based on query history, optimizing the index for current needs.

Traditional vector commitment schemes require recomputation of all proofs when adding new elements, leading to significant computational overhead. To address this issue, the authors of [20] propose a new scheme of aggregatable subvector commitments based on Newton interpolation. This scheme enables efficient updates of commitments and proofs when adding new elements, eliminating the need for complete recomputation.

The study [21] focuses on the development of a lattice-based commitment scheme aimed at reducing communication overhead in cryptographic protocols. The authors provide a comprehensive security analysis of the proposed scheme, demonstrating its resistance to various attacks, including those potentially feasible with quantum computing. Additionally, experimental results confirm the scheme’s efficiency and practical applicability in real-world scenarios. Overall, this work makes a significant contribution to post-quantum cryptography by offering an efficient and secure solution for low-communication-cost commitments.

Thus, the Verkle tree represents a promising technology that can significantly enhance blockchain system performance and scalability. Polynomial and vector commitments serve as powerful tools that can contribute to improving the efficiency and scalability of cryptographic systems. However, as the literature review suggests, further research is needed, particularly in the areas of security and practical implementation.

3  Materials and Methods

This section presents the theoretical and practical approaches used in the study. It describes the mathematical models, algorithms, and experimental attack methodologies applied for the analysis and verification of the proposed method. Additionally, key research parameters, data used, and evaluation criteria for assessing the efficiency of the proposed method are outlined.

3.1 Verkle Tree

The Verkle tree is a data structure that combines the properties of Merkle trees and polynomial commitments. It is designed to improve blockchain scalability by reducing the size of data inclusion proofs [22]. The Verkle tree is used to represent a large set of elements while providing provable integrity guarantees (Fig. 1).

Figure 1: Verkle Tree Structure

Key Characteristics of the Verkle Tree:

•   More Compact Proofs: The Verkle tree requires significantly less computationally expensive proofs compared to Merkle trees, which is crucial for conserving computational resources and increasing blockchain throughput [23].

•   Flat Structure: Unlike binary Merkle trees, Verkle trees can utilize nodes with a higher branching factor, reducing their height.

•   Fast Membership Proofs: Clients can quickly verify the presence of elements in the tree using short proofs.

3.2 Polynomial Commitments

Polynomial commitments enable the verification of polynomial computations without revealing the polynomial itself or its coefficients.

Key Properties:

•   Polynomial Representation: A polynomial commitment is a compact representation of a polynomial from which proofs of its values at specific points can be derived.

•   Proof Correctness: The party generating the commitment can produce proofs for any given points, while the verifying party can check their correctness without knowing the polynomial itself.

Types of Polynomial Commitments:

•   KZG-based Commitments (Kate, Zaverucha, and Goldberg): Widely used in modern implementations of Verkle trees.

•   Bulletproofs-based Commitments: Do not require trusted setups but have higher computational costs.

3.3 Construction of a Non-Positional Polynomial Notation

The construction of a non-positional polynomial notation based on the Chinese Remainder Theorem (CRT) represents an intriguing approach in cryptography, information encoding, and number theory. The key steps and principles for implementing this system are as follows:

3.3.1 Chinese Remainder Theorem (CRT)

The CRT states that the system of congruences:

{x≡r1modp1x≡r2modp2⋮x≡rkmodpk(1)

has a unique solution x in the ring ZP, where P=p1⋅p2⋅…⋅pk, provided that the moduli pi are pairwise coprime. This allows any number x∈ZP to be represented as a set of residues (r1,r2,…,rk) [24–26].

Eq. (1) represents a system of congruences stating that for any number x in the ring ZP, a unique set of remainders (r1,r2,…,rk) can be determined modulo p1,p2,…,pk, provided that the moduli are pairwise coprime. This follows from the Chinese Remainder Theorem (CRT). In the context of the proposed polynomial commitment scheme, this representation plays a key role in constructing commitments and computing verifiable values.

3.3.2 Non-Positional Representation

Instead of the traditional positional numeral system, where each digit has a specific weight, the non-positional representation based on the CRT operates with residues ri modulo pi.

A number x is represented as: x→(r1,r2,…,rk), where ri=x mod pi. In this system, the order of residues ri does not affect the representation, making it non-positional.

Example:

Suppose we want to represent the number 29 using the moduli (5, 7). In this case:

The remainder of 29 divided by 5: 29 mod 5 = 4

The remainder of 29 divided by 7: 29 mod 7 = 1

Thus, the representation of 29 in the Non-Positional Notation (NPN) with moduli (5, 7) is (4, 1). By applying the Chinese Remainder Theorem (CRT), the original number can be reconstructed, enabling efficient computations within this system.

3.3.3 Polynomial Structure

For a polynomial notation, the moduli pi can be chosen as polynomials over a finite field ZP. For example, the moduli can be: p1(x),p2(x),…,pk(x), where pi(x) are irreducible polynomials. Any polynomial f(x) from the ring Fp[x] can be represented as a set of residues [27,28]:

f(x)→(f(x)mod p1(x),f(x)mod p2(x),…,f(x)mod pk(x)).

3.3.4 Polynomial Reconstruction Algorithm

Using the CRT, the original polynomial f(x) can be reconstructed from the given residues using the formula:

f(x)=∑i=1kri⋅Pi(x)⋅Pi−1(x)modP(x)(2)

here,

•   P(x) is the common modulus, which is the product of all polynomial moduli pi(x).

•   Pi(x) is defined as the quotient of the common modulus divided by a specific modulus pi(x).

•   The polynomial Pi−1(x) is the multiplicative inverse of Pi(x) modulo pi(x), ensuring correct reconstruction.

•   Each remainder ri(x), which corresponds to the remainder of the polynomial f(x) modulo Pi(x), is combined with the respective modular polynomials to reconstruct the original f(x) modulo P(x).

Eq. (2) allows for the reconstruction of the original polynomial f(x) based on its remainders modulo pi(x). In the context of the proposed polynomial commitment scheme, this equation enables efficient recovery of the polynomial from its representation in a non-positional notation. This is crucial for verifying the correctness of commitments and ensuring computational efficiency.

3.4 GCD-Based Attacks and the LLL Algorithm

Greatest common divisor (GCD) attacks are used to compromise public-key cryptographic systems. These attacks allow an adversary to find common factors of different users’ keys or expose private keys if a weak prime number generator is used. In RSA, DSA, or other cryptosystems, insufficient randomness in key generation can lead to vulnerabilities that an attacker can exploit in seconds. The attack concept is as follows: In classical RSA, the public key consists of a modulus N=p⋅q, where p and q are large prime numbers. If two different users accidentally select the same prime number p when generating their keys, it becomes trivial to discover p using the GCD operation. Suppose there are two RSA keys: N1=p⋅q1,N2=p⋅q2. An attacker can compute d=gcd (N1,N2). If d=p, then both keys can be factorized: p=d,q1=N1/p,q2=N2/p.

The LLL (Lenstra–Lenstra–Lovász) Algorithm is a powerful method used in cryptanalysis, including attacks on RSA, factorization, and finding short vectors in lattices. It is an efficient technique for computing a reduced lattice basis, making it more orthogonal and containing shorter vectors. This is crucial because short vectors help solve difficult cryptographic problems, such as identifying weak secret keys.

4  Results and Discussion

4.1 Development of a New Scheme Based on CRT

Verkle trees are an advanced alternative to Merkle trees, designed for efficient data storage and verification in decentralized systems. One of the key components of a Verkle tree is the use of polynomial commitments. This section describes the process of constructing such commitments using the CRT. Fig. 2 illustrates the structure of a Verkle tree, where the commitment and proofs are built based on CRT. An example is provided using a cross-section of a single root and three leaves.

Figure 2: Polynomial commitments based on NPN

The scheme operates as follows: first, a hash code hi is computed for the information mi using the hash function H. The obtained hash code is then combined with a pre-generated key gi using the XOR operation, resulting in the proof πi. The XOR operation with pre-generated keys, as shown in Fig. 2, enhances security and is accompanied by a whitening process. The whitening process plays a crucial role in strengthening cryptographic resistance, as it improves diffusion in the early stages. This, in turn, helps prevent attacks based on known structures, complicates related-key attacks, and increases the entropy of input data. This process is repeated for all proofs πi. Next, using these proofs and predefined irreducible polynomials pi, the commitment C1 is determined using Eq. (2). An important aspect to consider is that all gi and hi must have the same degree: deg⁡(gi)=deg⁡(hi)=n. Additionally, all pi must also have the same degree, given by: deg⁡(pi)=n+1, where i=1,…,k. Consequently, the degree of the polynomial commitment C(x) must be deg⁡(C(x))=k ∗ (n+1).

KeyGen(1n,k). n—security parameter, which represents either the polynomial degree or its length in binary representation. The parameter k∈N determines the number of nodes in the Verkle tree. A cryptographically secure hash function H:{0,1}∗→{0,1}n is used for hashing data.

At this stage, the degree of the polynomial pi(x) is set to n+1 and depends on the requirements of the cryptographic scheme. As a working basis, irreducible polynomials pi(x) of degree n+1 are randomly selected, where i=1,k¯. Then, using a pseudorandom sequence generator G, the required number of keys gi(x) are generated, forming the complete key G(x)=(g1(x),g2(x),…,gk(x)), where each gi(x) has a degree of n.

Compp(m1(x),…,mk(x)). To compute the polynomial commitment C(x) for all messages mi(x), the commitment πi(x) is first calculated for each given message mi, where i=1,k¯. Using the cryptographic hash function H:{0,1}∗→{0,1}n, the hash value is computed as hi(x)=H(mi(x)). Then, the proof πi(x) is determined as πi(x)=hi(x)⊕gi(x), where i=1,k¯.

Now, based on the CRT, the polynomial commitment C(x), can be reconstructed using all πi as its remainders. C(x) can be uniquely restored provided that its degree is smaller than the degree of the product of all pi(x), i.e., deg(C(x))<deg(p1(x)⋅p2(x)⋅…⋅pk(x)). The reconstruction of C(x) consists of the following four steps:

•   Compute the product of the working bases: P(x)=p1(x)⋅p2(x)⋅…⋅pk(x).

•   Compute Pi(x)=P(x)/pi(x),i=1,k¯.

•   Find the inverse polynomial Pi−1(x) such that Pi(x)⋅Pi−1(x)≡1(mod pi(x)), i=1,k¯.

•   Compute C(x) using the formula: C(x)=∑i=1kπi(x)⋅Pi(x)⋅Pi−1(x)modP(x) and declare it as the public key for message verification. C(x)=∑i=1lπi(x)⋅Pi(x)⋅Pi−1(x)modP(x),l≤k.

Open(mi(x),πi(x),i). The algorithm declares that the message mi(x) is committed to πi(x) and that this commitment is indeed included in C(x) without revealing all other values of πi(x).

Ver(C(x),pi(x),gi(x),i). The algorithm verifies that the provided commitment πi(x) is indeed contained in C(x) and, accordingly, that the signed or received message mi(x) has not been modified. To do this, the proof (pi(x),gi(x)) is sent, and the following computations and comparisons are performed: πi(x)=C(x)modpi(x), yi(x)=H(mi(x))⊕gi(x).

If πi(x)=yi(x), then the commitment is valid, and it is concluded that mi is authentic.

Update(C(x),mi(x),mi′(x),gi′(x),i). The algorithm is initiated by the sender who wishes to update the commitment C(x) by replacing the ith message. To perform the update, the commitment is recomputed as follows: C′(x)=∑i=1kπi′(x)⋅Pi′(x)⋅Pi′−1(x)modP(x), while there is no need to recompute P(x).

ProofUpdate(C′(x),mj′(x),πj′(x),j). When one or more nodes in a Verkle tree are modified, the corresponding commitments are recomputed upwards in the tree, altering the root commitment. To update the proof for query j, only the changed paths need to be considered. Instead of recomputing the entire proof from scratch, the algorithm modifies the existing proof by incorporating the difference between the old and new commitment states.

The use of polynomial commitments in tree nodes minimizes proof sizes, making them more efficient for transmission and verification. This significantly accelerates data authentication, which is particularly important in scenarios with limited computational resources.

By leveraging polynomial commitments with the CRT, Verkle trees enable faster data verification. Unlike traditional methods that require sequential hash function computations, this structure employs a compact representation that substantially reduces verification time. This is especially crucial for distributed systems where authentication speed plays a key role.

Vector commitments for Verkle trees based on CRT allow for compact storage and verification of nodes, eliminating the need for discrete logarithm operations. At the same time, the structure remains concise while supporting efficient inclusion and update proofs. Table 1 presents a comparative analysis of various polynomial commitment methods.

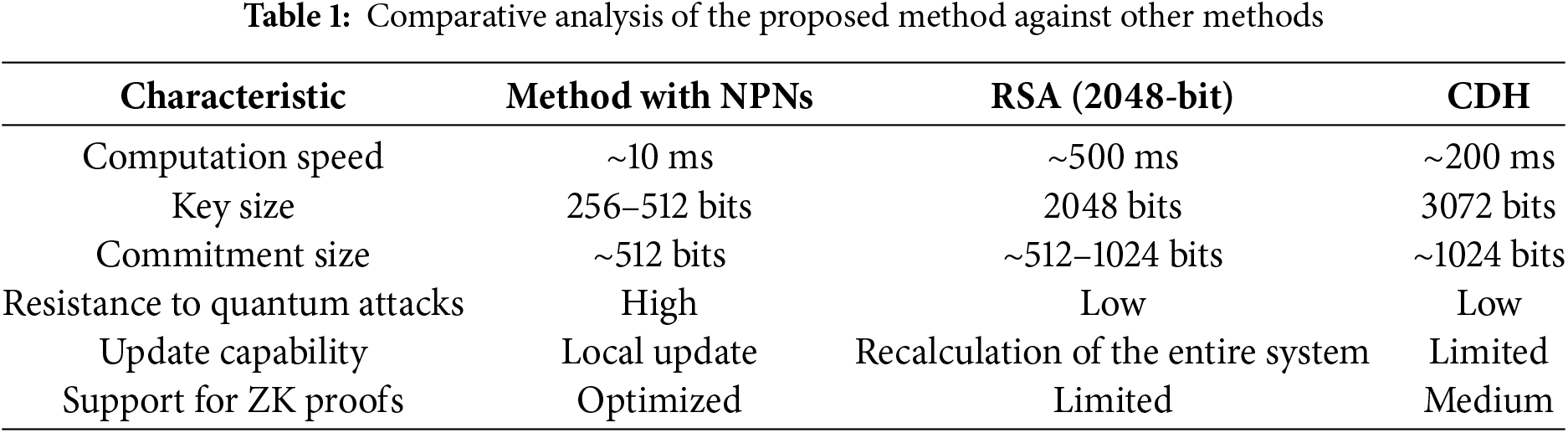
For an objective evaluation of the proposed method, a comparison was conducted with existing schemes, including KZG and Bulletproofs (Table 2). The evaluation criteria included commitment generation time and proof verification time.

As seen from the results, the proposed scheme provides a balance between commitment size and computational speed while demonstrating lower verification costs compared to Bulletproofs and eliminating the need for a trusted setup, which is required by KZG.

Table 3 provides a comparative analysis of the polynomial commitment scheme based on the Chinese Remainder Theorem (CRT) and the classical KZG scheme. We examine the parameters—proof size and computational complexity—at the Commitment and Verify stages, as well as their security properties.

Here, EC mult stands for Elliptic Curve Multiplication, i.e., point multiplication on an elliptic curve. While KZG grows more efficiently with large polynomial degree d, in practice it tends to be slower due to the high computational cost of elliptic curve operations.

4.2 Analysis of Potential Attacks on the Proposed Method Based on NPNs

Problem Statement: Let us consider a system of congruences based on the CRT for polynomials:

C(x)≡r1(x)modp1(x)C(x)≡r2(x)modp2(x)⋮C(x)≡rk(x)modpk(x)

Is it possible to compute the moduli pi(x) given only C(X) and all ri(x) for i=1,k¯?

4.2.1 Greatest Common Divisor (GCD) Attack

One fundamental attack approach is attempting to compute pi(x) through GCD-based attacks. Given C(x) and ri(x), one can construct the difference: di(x)=C(x)−ri(x). Since di(x) must be divisible by pi(x), an adversary can attempt to compute: pi(x)=gcd(d1(x),d2(x),…,dk(x)), where i=1,k¯. To mitigate such attacks, the following precautions must be taken:

•   Selecting moduli pi(x) without common factors, ensuring that: ∀i≠j:gcd(pi(x),pj(x))=1.

•   Making moduli pi(x) random and unrelated to each other.

4.2.2 Approximate Multiples Attack (LLL Lattice Reduction)

If the moduli pi(x) exhibit a specific structure or belong to a certain class of polynomials, an adversary may attempt to recover them using the approximate multiples method. If these moduli have small coefficients or a known form (e.g., many zeroes or fixed bits), a lattice can be constructed based on the residues, and the LLL algorithm can be used to approximate pi(x). The LLL algorithm finds a reduced basis for the lattice, which may help reconstruct the target moduli.

To protect against such attacks, the moduli should be chosen as random dense polynomials, i.e., without fixed bits or known coefficients. If only irreducible polynomials of degree 256 are used as moduli in the CRT, the probability of an attacker recovering them becomes negligible because:

•   Irreducible polynomials cannot be factored into lower-degree polynomials, which eliminates the possibility of a GCD attack.

•   The number of possible irreducible polynomials is large, and they are uniformly distributed, making it difficult to identify patterns or predict their structure.

•   An LLL-based lattice attack becomes ineffective if the coefficients of irreducible polynomials are chosen randomly.

4.2.3 Brute-Force Search for Irreducible Polynomials

If an adversary knows that the moduli are irreducible polynomials of degree 256, they may attempt to enumerate them exhaustively. However, such enumeration has exponential complexity.

Estimation of the Number of Possible Irreducible Polynomials

In the scheme, the proof components consist of two parts, pi(x) and gi(x), which are generated independently. The first part of the proof represents a pseudorandom sequence, while the second part consists of the selected system of polynomial bases p1(x),p2(x),…,pk(x). It is known that the number of operations required to enumerate all possible keys gi(x) of length n bits is 2n. To determine the number of irreducible polynomials of degree n over a finite field Fq, where q is the power of a prime number, the following formula can be used: Nq(n)=1n∑d|nμ(d)qn/d, where Nq(n) is the number of irreducible polynomials of degree n over the field Fq, μ(d) is the Möbius function, and the sum is taken over all divisors d of n.

The Möbius function is defined as follows:

μ(d):={0,if d has a squared factor,(−1)k,if d is the product of k distinct prime numbers,+1,if d=1.

For n=256 and q=2 (field F2): N2(256)=1256∑d|256μ(d)q256/d.

The divisors of 256 are d={1,2,4,8,16,32,64,128,256}, and the values of the Möbius function for these divisors are: μ(1)=1,μ(2)=−1,μ(4)=0,μ(8)=0,μ(16)=0, μ(32)=0,μ(64)=0,μ(128)=0,μ(256)=0.

Since only the terms for d=1 and d=2 are nonzero in the summation:

N2(256)=1256(μ(1)q256/1+μ(2)q256/2)=1256(2256−2128)=2248−2120

As a result, the number of irreducible polynomials of degree 256 over the field F2 is: N2(256)=2248−2120. From this, the total proof space is given by 2256⋅(2248−2120)=2504−2376. This is an extremely large number, making an exhaustive search infeasible, even for quantum computers.

Using Coefficient Information

If the moduli pi(x) have a specific structure (e.g., some coefficients are zero or follow a known pattern), an adversary might attempt to reconstruct them. To mitigate this risk, the algorithm ensures that:

•   The moduli are generated using cryptographically secure random methods.

•   No predictable patterns are used in the coefficients.

Using irreducible polynomials of degree 256 makes it extremely difficult to determine the moduli because:

•   GCD attacks are ineffective, as irreducible polynomials cannot be factored.

•   LLL-based lattice attacks are useless if the coefficients are randomly chosen.

•   The number of possible moduli is enormous, making exhaustive search infeasible.

Verkle trees represent an advanced data structure that significantly outperforms traditional Merkle trees and Patricia Tries in several key aspects. They provide more compact data storage and proof sizes, which is critical for the scalability of blockchains and distributed systems. By leveraging polynomial commitments in tree nodes, Verkle trees minimize proof sizes to the lowest possible level, making them more efficient for transmission and verification. This reduces network load and speeds up data authentication, which is particularly important in resource-constrained environments.

Another major advantage of Verkle trees is their memory efficiency. Unlike classical structures that require storing numerous intermediate hashes, Verkle trees reduce the amount of necessary data, improving overall system performance. This is especially beneficial in environments where data growth is rapid, and efficient storage is essential.

The flexibility of data updates in Verkle trees is another key advantage. Unlike Merkle trees, where modifying a single node requires recomputing an entire hash chain, Verkle trees allow individual elements to be updated with minimal computational overhead. This makes them ideal for dynamic systems where data changes in real time. Table 4 presents the key characteristics of Verkle trees compared to Merkle trees and Patricia Tries. The values presented in Table 4 are theoretical estimates based on the analysis of the characteristics of various data structures.

4.3 Future Works

As shown in Section 4.2, no vulnerabilities have been identified so far as a result of the theoretical analysis. Given the limited scope of our study, which focused primarily on the theoretical foundations of the proposed method, the next stage of our work will involve identifying potential practical vulnerabilities (e.g., side-channel attacks and fault injection attacks) and exploring possible countermeasures. In addition, further efforts will be directed toward optimizing computational processes and investigating the applicability of the scheme to real-world blockchain platforms.

5  Conclusion

The use of the CRT for constructing polynomial commitments in Verkle trees opens new prospects in cryptography and information security. This approach enhances key properties of the scheme, such as computational efficiency, data compactness, and resistance to quantum attacks. A CRT-based system relies on decomposition into multiple pairwise coprime moduli, allowing large polynomials to be represented as a set of remainders corresponding to these moduli. This method facilitates the development of efficient verification and update mechanisms for commitments while optimizing computations by leveraging the properties of the CRT.

In the proposed scheme, we use a combination of the Chinese Remainder Theorem (CRT) and hash functions to construct polynomial commitments. This combination ensures resistance to quantum computer attacks due to:

•   The absence of reliance on complexity assumptions vulnerable to quantum attacks. Unlike schemes based on discrete logarithms or factorization, our scheme does not rely on mathematical problems solvable by Shor’s algorithm.

•   The use of hash functions. Properly chosen cryptographic hash functions are assumed to remain secure even against quantum computer attacks (e.g., against Grover’s algorithm, which only provides a quadratic speedup for preimage searches). This makes our scheme potentially post-quantum secure.

Another crucial feature of polynomial commitments based on CRT is their compactness. Traditional schemes relying on RSA or CDH often involve large commitments and proofs, posing challenges for data storage and transmission. The use of CRT reduces these sizes by representing polynomials as remainders over multiple moduli, thereby decreasing memory requirements and accelerating data transfer operations. This compactness is particularly important in the context of Verkle trees, where numerous polynomial commitments must be structured hierarchically with minimal overhead.

Polynomial commitments constructed using CRT can also exhibit resistance to quantum attacks. Unlike conventional schemes based on hard mathematical problems, such as the discrete logarithm problem, which are vulnerable to quantum algorithms, CRT-based approaches can be adapted to ensure post-quantum security. For instance, combining CRT with lattice-based cryptography or homomorphic hash functions can yield a commitment scheme resistant to quantum computing attacks. This enhances the system’s long-term reliability, especially in light of advancing quantum technologies. Since one of the proposed approaches to constructing quantum-resistant cryptographic primitives involves the use of cryptographically secure hash functions, incorporating hashing of the signed message in the proposed method provides additional protection against quantum attacks, as well as other cryptanalytic algorithms that pose a threat to classical cryptographic systems [29].

An additional advantage of CRT-based commitments is the flexibility and efficiency of updates. In classical schemes, updating a commitment may require extensive data recomputation, increasing computational costs. The CRT allows for partial commitment updates, as changes in one remainder do not necessitate recomputation of the entire system. This is particularly beneficial for dynamic Verkle trees, where nodes may change over time. The ability to update commitments locally without recalculating the entire structure improves system efficiency in practical applications. Furthermore, the mathematical foundation of CRT enables additional optimization of cryptographic operations.

Thus, employing the CRT for constructing polynomial commitments in Verkle trees provides numerous advantages. It accelerates computations through residue representations, reduces the size of commitments and proofs, enhances system updatability, and increases resistance to quantum attacks. These properties make CRT-based approaches a promising direction in cryptographic commitments, with potential applications ranging from blockchain technology to secure distributed computing.

As shown in Section 4.2, no vulnerabilities have been identified so far as a result of various types of theoretical analysis. The study of potential practical attacks remains a subject for future research. Future work will focus on further optimization of computational processes and exploring the possibility of applying the scheme to real blockchain platforms.

Acknowledgement: The authors express their gratitude to the staff of the Information Security Laboratory of the Institute of Information and Computational Technologies for their assistance, as well as to all reviewers for their valuable comments, which have significantly improved the presentation of this paper.

Funding Statement: The research work was funded by the Ministry of Science and Higher Education of Kazakhstan and carried out within the framework of the project AP23488112 “Development and study of a quantum-resistant digital signature scheme based on a Verkle tree” at the Institute of Information and Computational Technologies.

Author Contributions: The authors confirm contribution to the paper as follows: conceptualization: Kunbolat T. Algazy and Kairat S. Sakan; methodology: Kunbolat T. Algazy and Kairat S. Sakan; software: Ardabek Khompysh; validation: Saule E. Nyssanbayeva; formal analysis: Saule E. Nyssanbayeva; investigation: Kunbolat T. Algazy and Kairat S. Sakan; resources: Saule E. Nyssanbayeva; data curation: Kairat S. Sakan and Ardabek Khompysh; writing—original draft preparation: Kunbolat T. Algazy; writing—review and editing: Kairat S. Sakan; visualization: Kairat S. Sakan; supervision: Kunbolat T. Algazy; project administration: Saule E. Nyssanbayeva; funding acquisition: Saule E. Nyssanbayeva. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Thilagam JST. Rsa encryption using VLSI architecture for high speed applications. Int J Adv Signal Image Sci. 2017;3(2):21. doi:10.29284/IJASIS.3.2.2017.21-26. [Google Scholar] [CrossRef]

2. Cotan P, Teşeleanu G. A security analysis of two classes of RSA-like cryptosystems. J Math Crypt. 2024;18(1):20240013. doi:10.1515/jmc-2024-0013. [Google Scholar] [CrossRef]

3. Boneh D. Twenty years of attacks on the RSA cryptosystem. Not AMS. 1999;46(2):203–13. [Google Scholar]

4. Wardhani RW, Putranto DSC, Cho J, Kim H. A highly efficient ECPM quantum circuit for binary elliptic curve cryptanalysis. IEEE Access. 2024;12(2):161569–83. doi:10.1109/ACCESS.2024.3489552. [Google Scholar] [CrossRef]

5. Larasati HT, Kim H. Quantum cryptanalysis landscape of shor’s algorithm for elliptic curve discrete logarithm problem. In: Information Security Applications: 22nd International Conference; 2021 Aug 11–13; Jeju-do, Republic of Korea. doi:10.1007/978-3-030-89432-0_8. [Google Scholar] [CrossRef]

6. Banegas G, Bernstein DJ, Van Hoof I, Lange T. Concrete quantum cryptanalysis of binary elliptic curves. IACR Trans Cryptogr Hardw Embed Syst. 2020;1:451–72. doi:10.46586/tches.v2021.i1.451-472. [Google Scholar] [CrossRef]

7. Putranto DSC, Wardhani RW, Larasati HT, Ji J, Kim H. Depth-optimization of quantum cryptanalysis on binary elliptic curves. IEEE Access. 2023;11:45083–97. doi:10.1109/ACCESS.2023.3273601. [Google Scholar] [CrossRef]

8. Begimbayeva Y, Zhaxalykov T, Ussatova O. Investigation of strength of E91 quantum key distribution protocol. In: 2023 19th International Asian School-Seminar on Optimization Problems of Complex Systems (OPCS); 2023 Aug 14–22; Novosibirsk, Moscow, Russian. doi:10.1109/OPCS59592.2023.10275771. [Google Scholar] [CrossRef]

9. Buchmann J, Dahmen E, Szydlo M. Hash-based digital signature schemes. In: Bernstein DJ, Buchmann J, Dahmen E, editors. Post-quantum cryptography. Berlin/Heidelberg, Germany: Springer; 2009. p. 35–93. doi:10.1007/978-3-540-88702-7_3. [Google Scholar] [CrossRef]

10. Algazy K, Sakan K, Khompysh A, Dyusenbayev D. Development of a new post-quantum digital signature algorithm: syrga-1. Computers. 2024;13(1):26. doi:10.3390/computers13010026. [Google Scholar] [CrossRef]

11. Algazy K, Sakan K, Nyssanbayeva S, Lizunov O. Syrga2: post-quantum hash-based signature scheme. Computation. 2024;12(6):125. doi:10.3390/computation12060125. [Google Scholar] [CrossRef]

12. Lee J, Park Y. HORSIC+: an efficient post-quantum few-time signature scheme. Appl Sci. 2021;11(16):7350. doi:10.3390/app11167350. [Google Scholar] [CrossRef]

13. Kuznetsov O, Frontoni E, Kuznetsova K, Arnesano M. Optimizing merkle proof size through path length analysis: a probabilistic framework for efficient blockchain state verification. Future Internet. 2025;17(2):72. doi:10.3390/fi17020072. [Google Scholar] [CrossRef]

14. Kate A, Zaverucha GM, Goldberg I. Constant-size commitments to polynomials and their applications. [cited 2025 Mar 1]. Available from: https://www.iacr.org/archive/asiacrypt2010/6477178/6477178.pdf. [Google Scholar]

15. Kate A, Zaverucha GM, Goldberg I. Polynomial commitments. [cited 2025 Feb 22]. Available from: https://cacr.uwaterloo.ca/techreports/2010/cacr2010-10.pdf. [Google Scholar]

16. Kuszmaul J. Verkle trees. [cited 2024 May 22]. Available from: https://math.mit.edu/research/highschool/primes/materials/2018/Kuszmaul. [Google Scholar]

17. Kuznetsov O, Kanonik D, Rusnak A, Yezhov A, Domin O, Kuznetsova K. Adaptive Merkle trees for enhanced blockchain scalability. Internet Things. 2024;27(14):101315. doi:10.1016/j.iot.2024.101315. [Google Scholar] [CrossRef]

18. Bünz B, Bootle J, Boneh D, Poelstra A, Wuille P, Maxwell G. Bulletproofs: short proofs for confidential transactions and more. In: 2018 IEEE Symposium on Security and Privacy (SP); 2018 May 20–24; San Francisco, CA, USA. p. 315–34. doi:10.1109/SP.2018.00020. [Google Scholar] [CrossRef]

19. Chen H, Liang D. Adaptive spatio-temporal query strategies in blockchain. ISPRS Intern J Geo-Inf. 2022;11(7):409. doi:10.3390/ijgi11070409. [Google Scholar] [CrossRef]

20. Xu Q, Gao C, Wang Y. Aggregatable subvector commitment with efficient updates. App Sci. 2025;15(2):554. doi:10.3390/app15020554. [Google Scholar] [CrossRef]

21. Miyaji H, Wang Y, Miyaji A. Lattice-based commitment scheme for low communication costs. IEEE Access. 2024;12:111400–10. doi:10.1109/ACCESS.2024.3421995. [Google Scholar] [CrossRef]

22. Zhao X, Zhang G, Long HW, Si YW. Minimizing block incentive volatility through Verkle tree-based dynamic transaction storage. Decis Support Syst. 2024;180(5):114180. doi:10.1016/j.dss.2024.114180. [Google Scholar] [CrossRef]

23. Iavich M, Kuchukhidze T, Bocu R. A post-quantum digital signature using Verkle trees and lattices. Symmetry. 2023;15(12):2165. doi:10.3390/sym15122165. [Google Scholar] [CrossRef]

24. Omondi A. Residue number systems: theory and implementation. London, UK: Imperial College Press; 2016. doi:10.1007/978-3-319-41385-3 [Google Scholar] [CrossRef]

25. Wang Y, Xia Y. Residue number systems: a new paradigm to datapath optimization for low-power and high-performance digital signal processing applications. IEEE Circuits Syst Mag. 2010;10(2):45–56. doi:10.1109/MCAS.2015.2484118. [Google Scholar] [CrossRef]

26. Biyashev RG, Kalimoldayev MN, Nyssanbayeva SE, Kapalova NA, Dyusenbayev DS, Algazy KT. Development and analysis of the encryption algorithm in nonpositional polynomial notations. Euras J Math Comp App. 2018;6(2):19–33. doi:10.32523/2306-6172-2018-6-2-19-33. [Google Scholar] [CrossRef]

27. Kapalova N, Sakan K, Algazy K, Dyusenbayev D. Development and study of an encryption algorithm. Computation. 2022;10(11):198. doi:10.3390/computation10110198. [Google Scholar] [CrossRef]

28. Biyashev RG, Smolarz A, Algazy KT, Khompysh A. Encryption algorithm “QAMAL NPNS” based on a nonpositional polynomial notation. J Math Mech Comp Sci. 2020;105(1):198–207. doi:10.26577/JMMCS.2020.v105.i1.17. [Google Scholar] [CrossRef]

29. Iavich M, Kapalova N. Optimizing post-quantum digital signatures with Verkle trees and quantum seed-based pseudo-random generators. Computers. 2025;14(3):103. doi:10.3390/computers14030103. [Google Scholar] [CrossRef]