Relative-Density-Viewpoint-Based Weighted Kernel Fuzzy Clustering

1  Introduction

Clustering is an unsupervised machine learning algorithm that groups similar data points in a dataset by calculating similarity while ensuring that the data points between clusters are as different as possible [1–3]. The method aims to divide the data set into subsets so that data points within the same subgroup have the greatest similarity while significant differences remain between different subsets. This process reveals the data’s inherent structure and provides powerful support for applications in areas such as image processing, speech recognition, and market analysis [4]. This study addresses a critical gap in clustering research by proposing a novel method that enhances robustness and scalability for complex datasets.

Clustering algorithms can handle large data sets without prior training, so clustering algorithms are widely used in various industries. Early clustering algorithms mainly use complex clustering methods; each data point is strictly assigned to a specific cluster, and each point belongs to only one cluster. The DPC (Density Peak Clustering) algorithm proposed by Rodriguez and Laio [5] is a typical complex clustering method, which can effectively identify the peak density of data sets and thus achieve efficient clustering.

In 1969, Ruspini introduced fuzzy sets into cluster analysis and promoted the development of fuzzy clustering methods. Fuzzy clustering represents the degree of data points belonging to different clusters by membership value, which provides a more flexible way of classification. Among all kinds of fuzzy clustering algorithms, the FCM (Fuzzy C-Means) algorithm [6,7] is the most extensively utilized. By minimizing the objective function, FCM effectively calculates the cluster centre and membership degree of each data point, minimizes the intra-cluster distance, and maximizes the inter-cluster separation degree. However, FCM’s sensitivity to initial clustering centres and vulnerability to noise points remain significant limitations. For this reason, Krishnapuram and Keller proposed the Probabilistic C-Means (PCM) algorithm [8], which alleviates the membership constraint of FCM and enhances the robustness of noise points. Although PCM solves the overlapping problem of cluster centres to a certain extent, it still faces the challenge of initialization sensitivity [9].

At the same time, with the wide application of kernel methods in machine learning, kernel-based clustering methods are also developing. The KFCM (Kernel Fuzzy C-Means) algorithm utilizes kernel functions to map data into high-dimensional spaces [10,11], thus improving clustering performance. For example, it improves important clustering effect evaluation indicators such as classification accuracy (ACC) [11]. However, choosing a suitable kernel function remains a major challenge. To solve this problem, Huang et al. proposed the MKFC (Multi-Kernel Fuzzy Clustering) algorithm [12], which uses the weight of each kernel function to enhance the clustering results. In addition, Yang and Benjamin proposed the FWPCM (Feature-weighted Probability C-Mean algorithm) algorithm [13], which combines probability clustering and subspace clustering and enhances the clustering effect by applying feature weighting.

In recent research on fuzzy clustering, introducing domain knowledge into clustering algorithms has become a very popular method for improving clustering quality. Hussain et al. introduce novel weighted multi-view k-means algorithms using L2 regularization [14], designed specifically for clustering multi-view data. Pedrycz and colleagues developed the Viewpoint-based Fuzzy C-Means (V-FCM) algorithm [15], which uses domain knowledge to guide the clustering process to optimize the results from a specific perspective. However, the selection of viewpoints in V-FCM relies on subjective input, which limits its automation and flexibility. The algorithm still has difficulties in dealing with noisy points. In order to solve these problems, Tang et al. proposed the DVPFCM (Density View-induced Probabilistic Fuzzy C-Means) algorithm [16], which uses density peaks as viewpoints to improve the stability of cluster centre initialization. Despite the progress, DVPFCM still faces challenges in making full use of the intrinsic structure of the data for viewpoint optimization. Subsequently, Tang et al. [17] proposed the Kernel-based Hypersphere Density Initialization (KHDI) algorithm as a certain premise and proposed the density Viewpoint-based Weighted Kernel Fuzzy Clustering (VWKFC) algorithm.

In practice, although the VWKFC algorithm shows good results, we believe that the algorithms based on KHDI and VWKFC still have the potential to be further optimized to achieve better results in various data sets. We note that the information granularity factor in the new algorithm plays an important role in membership adjustment and optimization, but there are still two problems to be solved.

The suitability of information granularity factors for adjusting fuzziness has not been properly evaluated. It is not clear whether the adjustment to ambiguity has been efficiently implemented. Therefore, we try to apply the double fuzzy fusion of information granularity factors and further optimize some steps and algorithms in the initialization process of KHDI in the VWKFC algorithm.

In order to solve these problems, this paper proposes a double fuzzy fusion strategy for information granularity factors and further optimizes the key steps in the initialization process of KHDI and the clustering algorithm under the framework of VWKFC.

Unlike previous studies, this paper proposes a knowledge extraction algorithm based on relative density. The algorithm selects the initial viewpoint by identifying the relatively high-density region in the data, provides an ideal initial clustering centre for the clustering algorithm, and improves the accuracy of the initial clustering process. We introduce the adaptive weight mechanism into the fuzzy clustering framework and build the information granularity weight model. By dynamically adjusting the importance of data points in the clustering process, the algorithm effectively reduces the influence of noise and outliers, thus improving the robustness and accuracy of clustering. In addition, we also designed a dynamic optimization algorithm, which adaptively adjusts the weights according to the changes in data distribution and further improves the flexibility and robustness of the algorithm in different feature spaces and dimensions.

The contributions of this paper are as follows:

Cluster initialization method based on relative density: We propose an innovative knowledge extraction algorithm based on relative density, which takes the relatively high-density region in the data as the clustering initialization viewpoint, and significantly improves the quality of the initial clustering process. This algorithm uses the local density feature of data to locate the potential cluster centre accurately, reduces the error caused by traditional random initialization, and enhances stability and accuracy.

Adaptive information granularity weighting mechanism: We introduce an adaptive information granularity weighting model, which dynamically adjusts the influence of data points according to their importance in the clustering process. The proposed mechanism effectively reduces the influence of noise and outliers, especially when the data is unevenly distributed or contains outliers, thus improving the accuracy and robustness of the clustering results.

Dynamic weight optimization algorithm: A dynamic optimization algorithm is designed to adjust the weight of data points based on the change in data distribution. By combining the local characteristics of the data, the algorithm has strong adaptability and flexibility, which ensures robust clustering performance in different feature Spaces and high-dimensional environments.

A new adaptive weighted clustering algorithm: By integrating the above innovations, we propose the RDVWKFC algorithm to combine the advantages of the above different algorithms and methods. An excellent linkage algorithm mechanism is formed, which provides a comprehensive and effective solution to the complex data clustering problem.

2  Related Work

In this section, we will review the previous works and concisely introduce some algorithms concerning the new algorithm proposed in this paper.

Referring to [18], a maximum entropy regularized weighted fuzzy C-means algorithm (EWFCM) is proposed, which breaks through the limitation that the traditional Euclidean distance as a measure of membership cannot identify and distinguish these attributes unrelated to clustering. The EWFCM algorithm achieves feature selection by providing weights for the features. Increasing the maximum entropy regularization term effectively affects the feature weight distribution. However, the clustering effect of this algorithm depends very much on the initialization of the cluster centre. The appearance of noise points in the data will seriously interfere with the clustering results.

Oskouei et al. [19] proposed an intuitionistic fuzzy c-means-based clustering algorithm for multi-view clustering (VCoFWMVIFCM) to artificially solve the problems of noise sensitivity, outliers’ influence, and different perspectives, features, and sample importance. The algorithm combines membership degree, non-membership degree, and hesitation degree to design intuitive fuzzy C-mean (IFCM) loss terms, which greatly enhances the processing ability of the algorithm for uncertain data. At the same time, by weighting three different levels of features, views, and samples, the low coupling between classes and high aggregation within classes are more significant, and the clustering effect is further enhanced. Moreover, Oskouei et al. also designed a neighbourhood agreement term to enhance the stability and robustness of the local structure of the cluster by punishing the membership difference of domain samples.

Hashemzadeh et al. [20] proposed a New fuzzy C-means clustering method based on feature-weight and cluster-weight learning (FWCW-FCM). The algorithm solves two problems of traditional FCM by simultaneously optimizing feature weight and cluster weight: feature importance difference and initialization sensitivity. The innovation of the algorithm is to independently adjust the feature weight in each cluster with the help of the local feature weight to improve the quality of clustering. The cluster weight was dynamically adjusted to punish the clusters with large intra-cluster distances to reduce the dependence of the algorithm on initialization. This algorithm significantly improves the clustering performance of traditional FCM by jointly optimizing the feature and cluster weights and reducing the initialization sensitivity. Dynamically adjusting the importance of features and clusters is suitable for complex real datasets. This algorithm outperforms the traditional FCM algorithm in terms of feature weighting and resistance to initialization jitter, but its performance is highly dependent on parameter tuning and data type.

Nie et al. [21] proposed a new graph Clustering model called Fast Clustering with Anchor Guidance (FCAG), which significantly solved the high computational cost and difficulty in adjusting hyperparameters. FCAG introduces anchor technology to construct a bipartite graph, which significantly reduces the size of the similarity matrix and makes it suitable for large-scale data sets. By designing a parameterless optimization objective function, the model effectively avoids the complex parameter tuning problem caused by the regularization term in traditional methods and the trivial solutions of “all samples belong to the same class” or “uniform distribution” in the clustering results.

Hu et al. [22] proposed a novel clustering algorithm called self-regulating possibilistic C-means (PCM) with high-density points (SR-PCM-HDP), which combines Density Peak Clustering (DPC) and possibilistic C-means (PCM) to determine the optimal number of clusters. The density-based knowledge extraction method (DBKE) was introduced to estimate the initial number of clusters without a predefined density radius and extract high-density points as knowledge guidance. Through the adaptive mechanism and knowledge guidance, the clustering efficiency and robustness are improved so that it can be effectively applied to complex data scenarios.

In order to better solve the sensitive problem of cluster initialization, Tang et al. [17] proposed the VWKFC algorithm. This algorithm mainly puts forward the concept of information granules, which mainly contains two aspects: for one thing, it gives a feature matrix that assigns different weights to different features of any data. For another, it provides sample weights for each data point in the dataset. Thus, in the process of clustering, the raw data is transformed into weighted information granules. In the research of initialization methods for clustering analysis, traditional density peak detection methods and initialization strategies based on Euclidean distance often face problems with sensitivity to noise and insufficient processing ability of high-dimensional data. Tang et al. proposed a Kernel-based Hypersphere Density Initialization (KHDI) method. VWKFC achieves efficient clustering for complex data through kernel density initialization, weight mechanism, and viewpoint guidance and is obviously ahead of the traditional fuzzy clustering algorithms in noise robustness, high-dimensional processing, and convergence speed. The idea of combining domain knowledge with data-driven methods provides a new optimization paradigm for fuzzy clustering.

3  The Proposed RDKM Method

In previous clustering algorithms, the initialization process of the cluster centres is highly sensitive, and this problem has been significantly improved and solved in the previously proposed KHDI algorithm [17]. The KHDI algorithm uses a Gaussian kernel to calculate the local density and determine whether the data points belong to the same cluster based on a fixed radius. However, choosing this fixed radius may lead to inaccurate density estimates, especially in data sets with uneven distribution or high dimensionality, thus affecting the quality of clustering results.

To improve the KHDI algorithm, in this study, we propose a relative density-based knowledge Extraction method (RDKM) and introduce an adaptive density radius calculation method.

By designing an appropriate function, the DPC algorithm dynamically adjusts the radius to ensure that the average density remains within 2% to 3% of the total number of data points. This adaptive mechanism allows the local density calculation to be optimized according to the actual distribution of the datasets rather than relying on a fixed radius parameter. This innovation significantly improves the robustness of the DPC algorithm in datasets with non-uniform density and avoids the error caused by the fixed radius.

In some cases, it is difficult to directly define an appropriate similarity measure function in the original feature space, especially when the data distribution is complex. In this case, using Euclidean distance often fails to produce desirable clustering results.

We introduce the Gaussian kernel function as an effective tool for constructing a clustering model to try to solve this problem. By normalizing each sample feature, we will constrain the eigenvalues in a standardized range, thus greatly enhancing the stability in the subsequent kernel function calculation. This preprocessing step not only improves the numerical stability of the model but also enhances the adaptability and robustness of the algorithm in high-dimensional space. The data points are mapped from the original feature space to the higher-dimensional space through the kernel function, where the clustering structure becomes clearer and clearer. This method makes good use of its advantages, overcomes the limitations of traditional clustering algorithms in processing high-dimensional data, and provides a new perspective for revealing internal data patterns.

The selection of initial clustering centres is particularly important in the process of fuzzy clustering, which directly affects the convergence of the algorithm and the quality of clustering results. The traditional random initialization method is inefficient and may cause the algorithm to converge to a suboptimal solution. In addition, the density calculation based on Euclidean distance shows limited performance when dealing with high-dimensional or noisy data. In order to solve these problems, this paper proposes an initial clustering centre selection method based on the DPC algorithm and kernel density optimization. Adaptability of the RDKM method to complex data distribution by designing a reasonable density radius and viewpoint selection mechanism.

The local density of a point is defined by the following formula:

ρi=∑j=1Nχ(dij−r),χ(x)={1,if x<00,otherwise(1)

here, dij represents the kernel distance between the representing point xi and point xj, and r is the density radius. The kernel distance is calculated as follows:

dij=∥ϕ(xi)−ϕ(xj)∥2=K(xi,xi)−2K(xi,xj)+K(xj,xj)(2)

The kernel function is a mapping function used to map the data from the original space to the high-dimensional feature space. Gaussian Radial Basis Function (RBF) is used as the kernel function K(x,y).

K(x,y)=exp(−∥x−y∥22σ2)(3)

here, σ is the width parameter of the Gaussian kernel, which controls the sensitivity of the kernel function to distance variations. Through the introduction of the normalization formula, its key role in data preprocessing is revealed. By using the range transformation technique, the effect of diverse variables (features) in the data is productively eliminated. This process maps features of different orders of magnitude to a unified [0, 1] interval, ensuring that the entire set of features has equal importance in the cluster analysis.

xjl=xjl−min(xkl)max(xkl)−min(xkl)(4)

Another advantage of normalization is that the transformed data is restricted to the range [0, 1], which simplifies the choice of parameters.

Using the Radial Basis Function (RBF), the optimal result can be obtained by setting σ=1 for normalized features.

Based on the distance matrix, D=[dij], the density radius r is initialized as follows:

r=[max(dij)+min(dij)]/2(5)

This formula makes the density distribution more stable by smoothing the interference of noise and outliers on the local density calculation, especially for the processing of high-dimensional data.

The selection of the density radius significantly impacts local density estimation and global clustering. A large radius can cause uniform density estimates, reducing the algorithm’s ability to capture local structural features, while a small radius leads to excessive sensitivity to noise, affecting the clustering accuracy and effectiveness. To address this complex issue, we present a method designed to dynamically optimize the density radius:

(1)   Density sorting: All data points are sorted by their density value ρi to form a density sequence.

(2)   Average density calculation: Select all the data points and calculate their average density.

ρ¯=1N∑i=1Nρ(i)(6)

(3)   Density radius optimization: We adjust the density radius r so that the average density meets the following conditions. Character p is the percentage of the total data volume (e.g., p=2% to3% ):

ρ¯=p×N(7)

Therefore, we can consider the local density estimation to be consistent with the overall characteristics of the data distribution. By dynamically adjusting the density radius, the new algorithm can capture the local distribution characteristics of the data adaptively, so as to avoid the limitation of fixed parameters.

According to the results of kernel density calculation, the cluster centres and viewpoints can be further determined:

For each data point, we identified all the points with a density greater than. nd computed the minimum distance between xj and these points, and then we obtained the standard distance δi.

δi=minjdij, where ρj>ρi(8)

For each data point, we define a co-weight parameter τj that integrates the density and pivot distance.

τi=ρi×δi(9)

In the process of selecting the cluster centre, the larger the parameter value τi, the more likely the corresponding data point xj is to be the cluster centre. Specifically, if xj is not a cluster centre, its local density ρj may be relatively high, but its pivot distance δj is small. On the contrary, for noisy points or outliers, their pivot distance is larger, but their local density is usually lower. Therefore, by introducing a selection mechanism that favours larger values, the potential cluster centres can be effectively distinguished while significantly resisting the interference of noise and outliers.

Based on this, we sort the data points τi in descending order and select potential cluster centres from this ranked list. To prevent the selected initial cluster centres from being too close to each other, a reasonable strategy is to ensure that the distance between any two selected cluster centres exceeds the following critical distance dc.

dc=max(dij)aC,(i,j∈1,2,…,N)(10)

The max(dij) represents the maximum distance between any two data points in the dataset, C represents the number of cluster centres, and a is the parameter used to adjust the minimum distance between cluster centres. This constraint not only ensures the reasonable distribution of the initial clustering centres in the feature space but also improves the stability of the clustering algorithm.

Users usually directly provide the selection of “viewpoints” to guide the clustering process. However, a new viewpoint selection strategy is used in this study. Specifically, after obtaining the initial cluster centres, we select the data point τj with the largest computed value (that is, the first data point in descending order) as the “viewpoint xd” selection. The rationale is that this data point has a high local density ρ and a large pivot distance δ, which makes it a true cluster centre.

With the help of the setup of viewpoint xd, we observe the structure of the whole dataset starting from core locations with high density and large critical distance. This method not only avoids the subjective deviation caused by the traditional viewpoint selection but also improves the rationality and scientific validity of the viewpoint, which lays the foundation for the subsequent clustering process.

In the cluster centre, the data point τj that has the largest value is selected as the viewpoint xd, that is,

xd=arg⁡maxjτi(11)

The pseudocode for this algorithm is shown below. We mainly follow the principles of modularity and simplicity when writing this part of the pseudocode. The detailed flow of the RDKM algorithm is given in Table 1.

4  The Proposed RDVWKFC Algorithm

In this paper, a Relative-Density-Viewpoints-based Weighted Kernel Fuzzy Clustering Algorithm with Adaptive Weights (RDVWKFC) is proposed. The objective function is as follows:

J=∑i=1,i≠qC∑j=1Nαj′uijm∑l=1Lωil∥ϕ(xjl)−ϕ(vil)∥2+∑j=1Nαj′uqjm∑l=1Lωql∥ϕ(xjl)−ϕ(xdl)∥2+η∑i=1C∑j=1Nuijlnuij+γ−1∑i=1C∑l=1Lωillnωil+λ∑i=1C∑j=1Nuijlnuij1K(12)

Among them, the constraints on the parameters are as follows:

∑i=1Cuij=1(13)

∑l=1Lωil=1,ωil>0(14)

αj′=1C∑i=1Cuij⋅exp⁡(−∥xj−vi(0)∥)(15)

In Eq. (12), C denotes the number of clusters, and N denotes the number of data points to be processed. L denotes the feature dimension of the data and q denotes the row position of the viewpoint. uij denotes the degree of membership of a data point xj to cluster i, its range is [0, 1]. m is the fuzzy coefficient, and its range is (0, +∞). In general, the optimal range of m is between 1.5 and 2.5. The feature weight ωil can represent the significance of the characteristics of the data to the cluster i. The xdl denotes the feature l of the viewpoint xd obtained by the RDKM algorithm. The αj′ is defined as the sample weight and the vi(0) represents the i-th initial cluster centre obtained by RDKM. The γ parameter is the regularization parameter, and its value is an adjustable parameter. By choosing an appropriate γ, a balance between the first two terms and the third term can be achieved to achieve better clustering performance.

In Eq. (12), αj represents the weight xj of a data point, reflecting its importance. vi(0) refers to the centre of the initial cluster i obtained by the RDKM algorithm. The initial cluster centres obtained by the methods are generally close to the reference cluster centres. Therefore, the initial cluster centre can be used to measure the importance of the data point xj. The closer xj is to the initial clustering centre V(0), the larger the weight φj is, indicating that the data point has a greater impact on the clustering results. In this way, the weights of noise points far away from the initial clustering centre will be minimized, which significantly reduces the influence of noise points on the clustering results.

The significance of the objective function design is as follows:

•   First item: In the case that the cluster centre is not the viewpoint, the sample weight αj′ is combined with the feature weight ωij to form a weighted information granule. Then, the weighted information granule was adjusted and optimized adaptively and dynamically by combining the membership degree, and the adaptive, optimized weighted information granule was obtained.

•   Second item: In the case that the cluster centre is a viewpoint, the importance of the viewpoint is emphasized, and the number of clusters need not be included.

•   Third item: This term enhances the fuzziness of the clustering and prevents the membership from going over degree extremes.

•   Fourth item: Negentropy regularization is applied to optimize the distribution of feature weights, preventing the clustering process from relying on only a few dimensions.

•   Fifth item: By adjusting the weight of KL (Kullback-Leibler) divergence, the distribution of membership entropy can be controlled, and the dispersion of membership can be promoted.

Based on the mathematical concept of weighted information granule, we propose an objective function structure of adaptive optimization weighted information granule, which includes the following three main stages:

•   Feature weight matrix construction: We assign different weights to different features of the data to achieve the effect of reducing the adverse influence of irrelevant features.

•   Sample weight assignment: We assign varying weights to the features of the data to reduce the effect of influence of irrelevant features.

•   Adaptive adjustment of information granules: We dynamically adjust the weighted information granules to optimize their adaptability and improve the clustering performance.

This paper introduces the concept of applying weighted information granularity in fuzzy clustering, which mainly includes two research aspects:

In the clustering process, the weighted information granules are dynamically optimized to obtain better clustering results. We name this structure the weighted information granule for adaptive optimization.

Moreover, we can combine the first and second terms in the objective function to unify the representation of viewpoint and non-viewpoint cluster centres into a single form. Finally, the reduced objective function can be expressed as follows.

JRDVWKFC=∑i=1C∑j=1Nαj′uijm∑l=1Lωil∥ϕ(xjl)−ϕ(gil)∥2+γ−1∑i=1C∑l=1Lωillnωil+η∑i=1C∑j=1Nuijlnuij+λ∑i=1C∑j=1Nuijlnuij1K(16)

among them:

gil={ xdli=qxili≠q(17)

We describe this procedure in detail below.

Firstly, the RDVWKFC algorithm was used to obtain the V(0) and xd. To determine the row position d of the viewpoint xd in the cluster centre matrix V, we need to find the cluster centre xd in the matrix that is closest to the viewpoint vq. Specifically, suppose the row position of the viewpoint in the cluster centre matrix is q and the cluster centre is vq. By calculating the kernel distance, the cluster centre closest to the viewpoint can be found.

dqd=‖φ(xd)−φ(vq)‖2(18)

dqd reflects the shortest distance between the viewpoint and the cluster centre. At this point, the viewpoint replaces the location of the cluster centre.

In the process of algorithm execution, because the value of the viewpoint will shift constantly, its position in the cluster centre matrix will also shift. A key aspect of this process is the calculation of the kernel distance, which ensures that viewpoints can adjust their position according to the density of the data distribution, thus reflecting the data structure more accurately.

On this framework, the proposed RDVWKFC algorithm aims to achieve more accurate and robust clustering analysis by considering the local density and feature weights of the data. The algorithm improves the stability and accuracy of clustering results by dynamically adjusting the density viewpoint.

The mechanism and derivation of the objective function of the new algorithm are described in detail above.

Finally, the running process of the new algorithm is summarized as shown in Table 2.

5  Experiments

To verify the effectiveness of the proposed RDVWKFC algorithm, we conduct a series of experiments to observe the clustering results. In addition, nine other algorithms were selected for comparison, including FCM, KFCM, V-FCM, EWFCM, FRFCM, DVPFCM, VWKFC, FCAG, and SR-PCM-HDP. The experiments were performed on the Windows 10 platform and the programming was done in Matlab 2022b. During the experiments, the algorithm was run on 13 datasets, including 5 synthetic datasets (Data-a, Data-b, Data-c, Data-d, and Data-e) and 8 UCI datasets. The UCI datasets used include Iris, Wisconsin Breast Cancer dataset, Letter recognition (A, B) dataset, SPECT heart dataset, Wine dataset, Landsat, seed and Wifi localization dataset.

To quantitatively evaluate the clustering performance, we used five different evaluation metrics: classification accuracy (ACC), Normalized Mutual Information (NMI) [23], Calinski-Harabasz index [24] (CH), ARI (Adjusted Rand Index) Expansion Index (EARI) [25,26], and Xie-Beni (XB) index [27]. Among them, ACC, NMI, and CH are hard clustering metrics that are applicable to both hard and soft clustering algorithms. EARI and XB indices are soft clustering metrics. EARI and XB index are only suitable for soft clustering algorithms because a membership degree is required for calculation.

5.1 Experiments on Synthetic Datasets

We first conduct an experimental evaluation on five synthetic datasets (Data-a to Data-e) to verify the performance of the proposed algorithm. These datasets are generated by Python’s scikit-learn library and have clear cluster structure characteristics. We focused our analysis on the results of Data-a and b. The datasets used here are all two-attribute datasets, which can be visualized as scatter plots. Among them, Data-a and Data-b, as benchmark sets, both contain 7 clusters and 1000 two-dimensional data points, which are characterized by moderate overlap between clusters and tight internal structure. Data-d, on the other hand, presents a higher complexity, containing 12 clusters and 1500 data points, where the clusters are closely linked and there is some degree of overlap between the classes. Although Data-e has the same number of clusters (7) and Data size (1000 points) as Data-a and Data-b, its spatial distribution pattern is more complex. In contrast, Data-c, as the simplest test set, contains only three clusters and 150 data points, but its remarkable feature is that there is a greater degree of overlap between clusters, which puts forward higher requirements for the robustness of the clustering algorithm. A greater degree of overlap between classes poses a more significant challenge to clustering algorithms.

In Table 3, we present the evaluation metric values obtained after running the proposed algorithm and the comparison algorithm on different artificial datasets. Here, “(+)” means that the evaluation criterion is “bigger is better”, which indicates higher values, while “(−)” means “smaller is better”, which indicates lower values. It can be seen that our proposed new algorithm achieves the best results in all evaluation metrics, among which the ACC, NMI, and EARI values on the datasets are the highest.

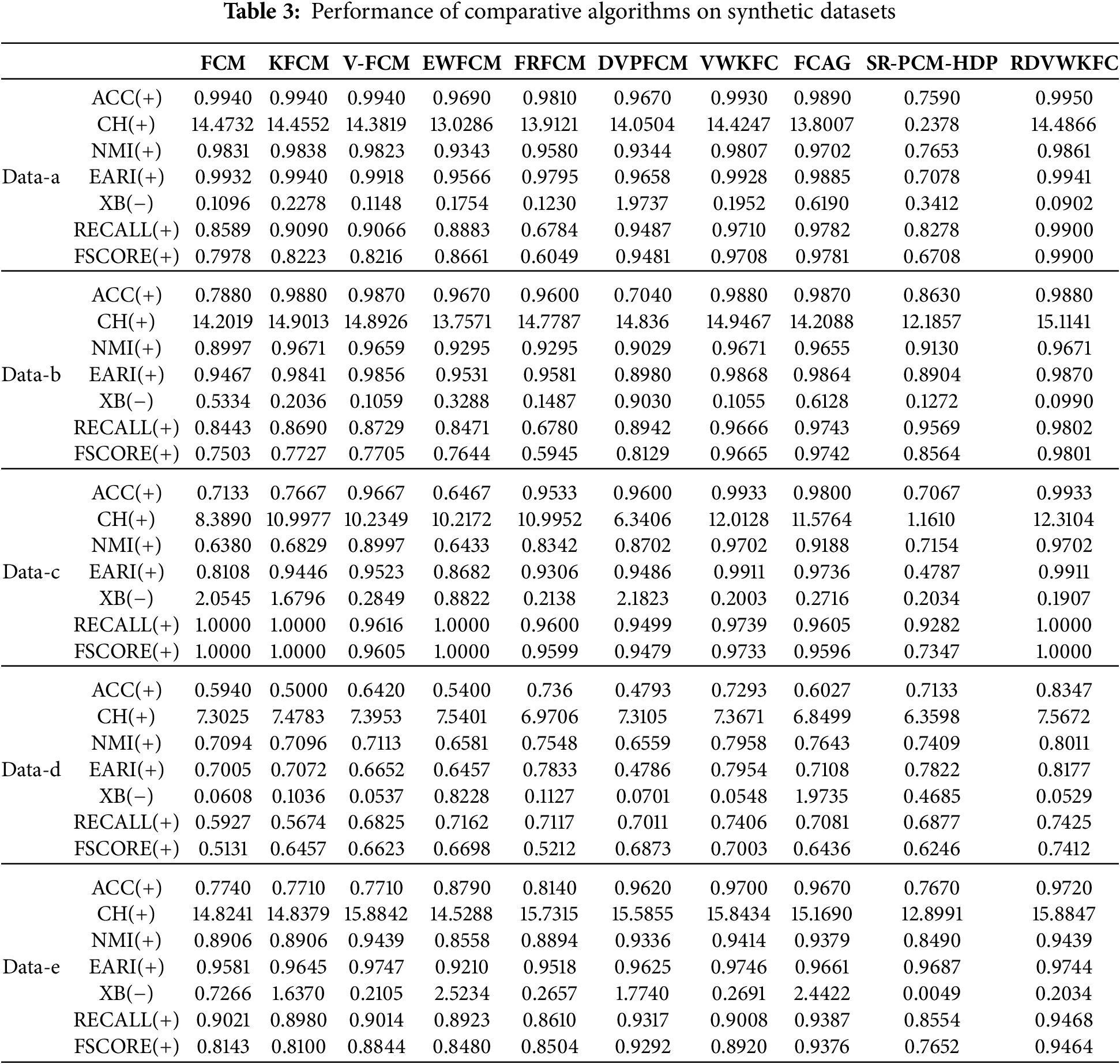
The new algorithm uses the RDKM method to initialize the cluster centres, which avoids the problem of convergence to a local optimum caused by improper initialization of the cluster centres. In the clustering process, feature selection is carried out by feature weights to make the clustering results more accurate. In addition, the introduction of high-density viewpoints reduces the influence of outliers and noise points on the clustering results. As shown in Table 3, the accuracy of the new algorithm on the artificial dataset Data-b is the highest, which is 0.9880, and the CH index value reaches 15.1141. Table 3 shows the results for different synthetic datasets.

5.2 Experiments with UCI Datasets

Subsequently, we conducted experiments using eight UCI datasets. These datasets are as follows: Iris, Wisconsin Breast Cancer, letter recognition (A, B), SPECT heart data, Wine, Statlog (Landsat satellite), Seed, and Wifi localization.

The Iris dataset is one of the most classic datasets in the field of machine learning. It contains 150 data points, and each data point contains four feature attributes: sepal length, sepal width, petal length, and petal width. The Iris dataset can be divided into three classes: Iris-setosa (Iris mountain), Iris-versicolor (Iris changing colors), and Iris-virginica (Iris Virginia). The Wisconsin Breast Cancer dataset is a cancer dataset containing 569 sample data points, which can be divided into two classes: benign and malignant. The Letter Recognition (A, B) dataset is a character recognition dataset. The Spect heart dataset is a heart disease dataset with binary data. Wine is a dataset about wine, containing 178 samples and 13 numerical features. It is divided into three categories, each with a different sample size. The Stalog (Land Satellite) dataset is a Landsat dataset with 36 feature attributes. The Seed dataset is about wheat seeds, contains 70 data samples, and belongs to three different wheat varieties: Kama, Rosa, Canadian. Table 4 gives the details of the UCI datasets we used in the experiments, which include the number of data samples, the number of categories, and the number of features.

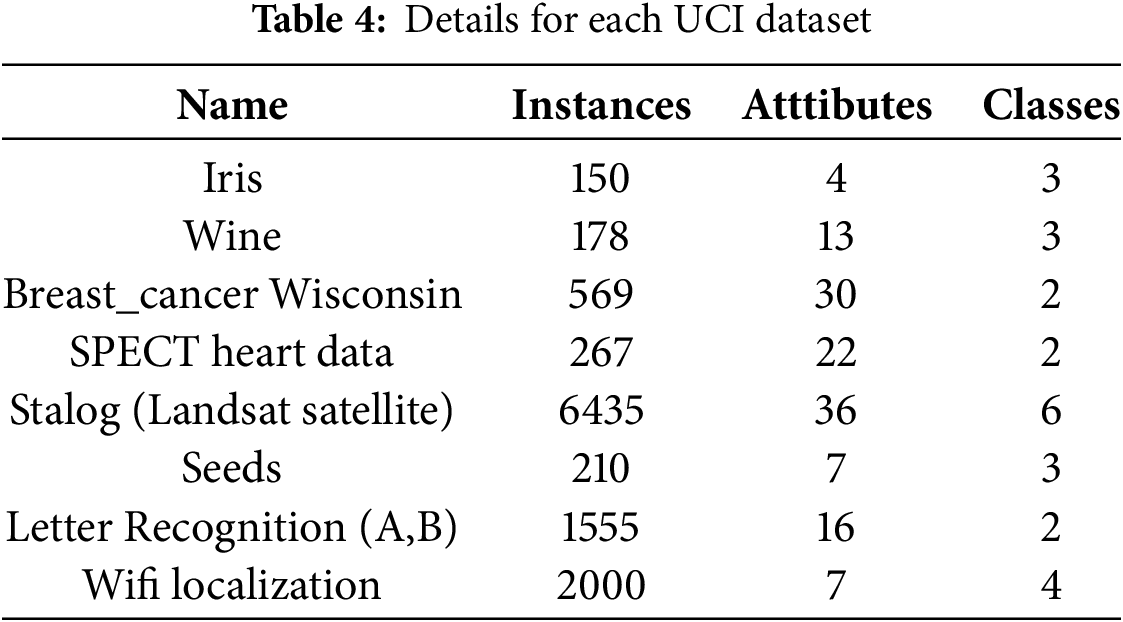
Table 5 presents the evaluation metrics for different clustering algorithms applied to various UCI datasets.

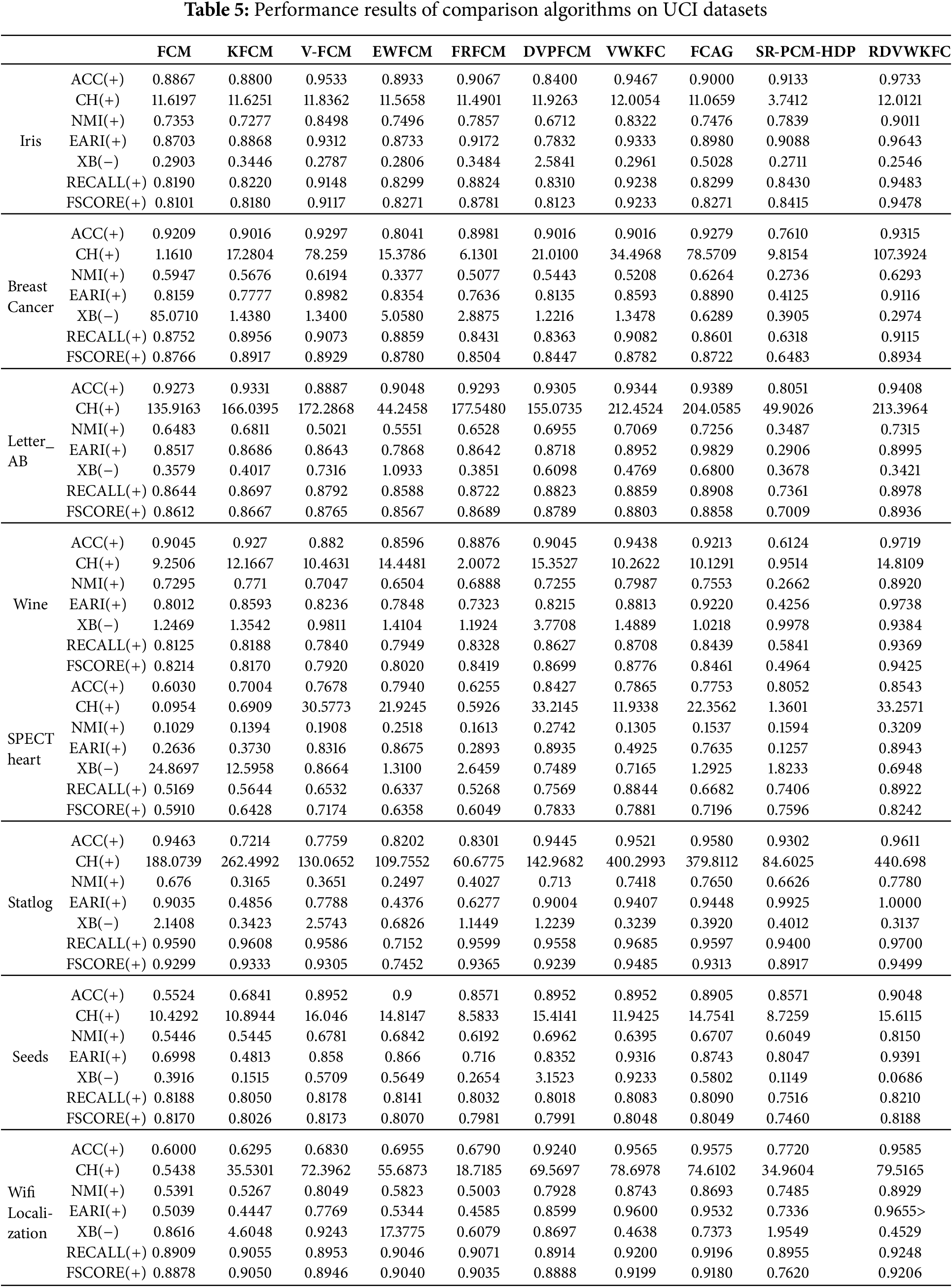
From the data in this tables, it can be seen that the proposed algorithm has high accuracy and is better than previous clustering algorithms in other indicators. For the classic Iris dataset, the accuracy of the new algorithm reaches 0.9733. In the datasets with high feature dimensions, such as Wisconsin Breast Cancer dataset, SPECT heart dataset and Statlog dataset, the accuracy of the new algorithm reaches 0.9315, 0.8543 and 0.9611, respectively. This shows that the new algorithm has certain advantages over the previous algorithms when dealing with data sets with more attribute features.

We summarize the performance metrics of the RDVWKFC algorithm on eight UCI datasets in the Appendix A, the proposed RDVWKFC algorithm can obtain the best results on these eight UCI datasets.

5.3 Experiments on High-Dimensional Datasets

In order to verify the performance of the RDVWKFC algorithm in clustering high-dimensional datasets, we conducted several experiments by randomly selecting three classes from the Mfeat dataset with 649 features. The clustering performance is evaluated using two metrics: ACC and EARI. Table 6 presents each algorithm result in Mfeat dataset. The calculation accuracy of the algorithm on the Mfeat dataset is 0.6150, and the EARI value is 0.9555. The experimental results present that the proposed algorithm on the data set has the best clustering performance.

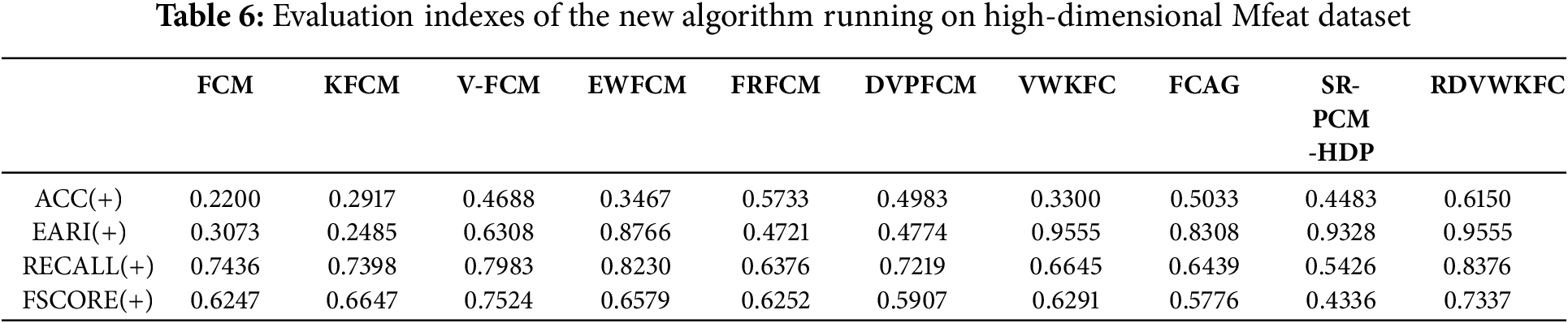
Table 6 presents the evaluation metrics for different clustering algorithms applied to the high-dimensional Mfeat dataset.

Through the above experimental results, we can see that the algorithm shows comprehensive advantages in four indicators. The value of ACC is ahead of the second place FRFCM, indicating that its clustering results have the highest matching degree with the true label, and the value of the EARI index is tied for the first place, which verifies its robustness under a complex clustering structure. RECALL and FSCORE both rank first, which indicates that the algorithm performs best in the balance of coverage and precision.

Different from the traditional feature weighted clustering algorithm in the past, the new algorithm uses RDKM method to initialize the clustering centre and introduces the viewpoint, which avoids the local minimum problem in the objective function, which avoids the local minimum problem in the objective function. In contrast to previous studies, our method assigns weights to feature attributes, so that it can show better results while dealing with complex datasets.

Please refer to the Appendix A for the relevant supplementary experiments and discussions.

6  Conclusion and Outlook

In this paper, we proposed a new adaptive weighted clustering algorithm and the main contributions and work are summarized as follows:

(i)   Faced with the challenges that traditional clustering algorithms often encounter in the initialization phase, the clustering results are highly sensitive to the initial centroid selection and unstable to noise and outliers. We innovatively introduce the Relative Density based Knowledge Extraction Method (RDKM) as the initialization strategy on the original KHDI algorithm. This method determines the initial centroid by identifying relatively high-density regions in the data, which lays a more reasonable foundation for the subsequent clustering process. Compared with the existing methods, RDKM significantly improves the quality of the clustering initialization stage, effectively reduces the risk of clustering results deviation caused by improper selection of initial centroids, and the algorithm has significant advantages in the initial stage.

(ii)   In order to alleviate the negative impact of noise and outliers on clustering accuracy, we propose an adaptive weighting mechanism through the construction of the Information Granularity Weight Model (IGWM). We implement the dynamic adjustment of the weights of data points according to their importance in the clustering process. By giving more weight to the data points with higher importance to make them play a key role in the clustering decision, and giving less weight to the points that may be noise or outliers, it effectively weakens their influence on the clustering results. This method improves the reliability of clustering results and significantly enhances the adaptability of the algorithm to complex data environments.

(iii)   In order to further improve the performance of the algorithm in different data characteristics and dimensions (the function can adapt to low dimensions, but also can adapt to high and ultra-high dimensions), we design an adaptive optimization algorithm (AOA). AOA can adjust the weights in real-time according to the dynamic change of the data distribution and always maintain good adaptability of the algorithm. At the same time, when dealing with high-dimensional or feature-diverging data, AOA shows a high degree of flexibility, which enables the algorithm to run stably in various complex scenarios and effectively overcomes the limitations of traditional algorithms in dealing with such data.

(iv)   Combining the above innovations, we propose a new adaptive weighted clustering algorithm—RDVWKFC. This algorithm integrates the advantages of each algorithm or method to build an excellent collaborative algorithm mechanism and provides a comprehensive and effective solution for dealing with complex data clustering problems.

(v)   Experimental verification results show that the algorithm has achieved a remarkable application effect in the application. In the test of various comparison algorithms, the new algorithm shows superior performance on multiple data sets. For example, ACC, NMI, CH, EARI, and XB are superior to other algorithms on key evaluation indicators. In addition, in terms of algorithm efficiency, the number of iterations required by this algorithm is significantly less than that of the comparison algorithm, indicating that it can quickly converge to stable clustering results and significantly improve computing efficiency. It is worth noting that when the new algorithm is applied to the image segmentation data set for the image clustering task, its clustering effect is superior to the existing methods, which further verifies its effectiveness and superiority in practical applications.

Our study demonstrates that the proposed algorithm significantly improves clustering accuracy and computational efficiency compared to existing methods. Future research will expand the application scope of the new algorithm, especially in fields such as fuzzy inference and fuzzy systems [28]. We also expect that the novel algorithm will exhibit superior performance in these real-world application scenarios, and provide a more effective solution for solving complex data clustering problems.

Acknowledgement: Special thanks to the reviewers of this paper for their valuable feedback and constructive suggestions, which greatly contributed to the refinement of this research.

Funding Statement: This work was supported by the National Natural Science Foundation of China under Grants 62176083, 62176084, 61877016, and 61976078.

Author Contributions: Conceptualization, Yiming Tang and Yuhan Xia; methodology, Xu Li; software, Ye Liu; validation, Xu Li and Wenbo Zhou; formal analysis, Yiming Tang; investigation, Ye Liu; resources, Wenbo Zhou; data curation, Yuhan Xia; writing—original draft preparation, Yuhan Xia and Xu Li; writing—review and editing, Yiming Tang; visualization, Ye Liu; supervision, Yiming Tang; project administration, Xu Li; funding acquisition, Yiming Tang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Appendix A

Appendix A.1 Summary of the Experiments

Fig. A1 presents scatter plots of these five synthetic datasets. These datasets are composed of two-dimensional data. The horizontal and vertical coordinates in Fig. A1 correspond to two dimensions of the data, respectively.

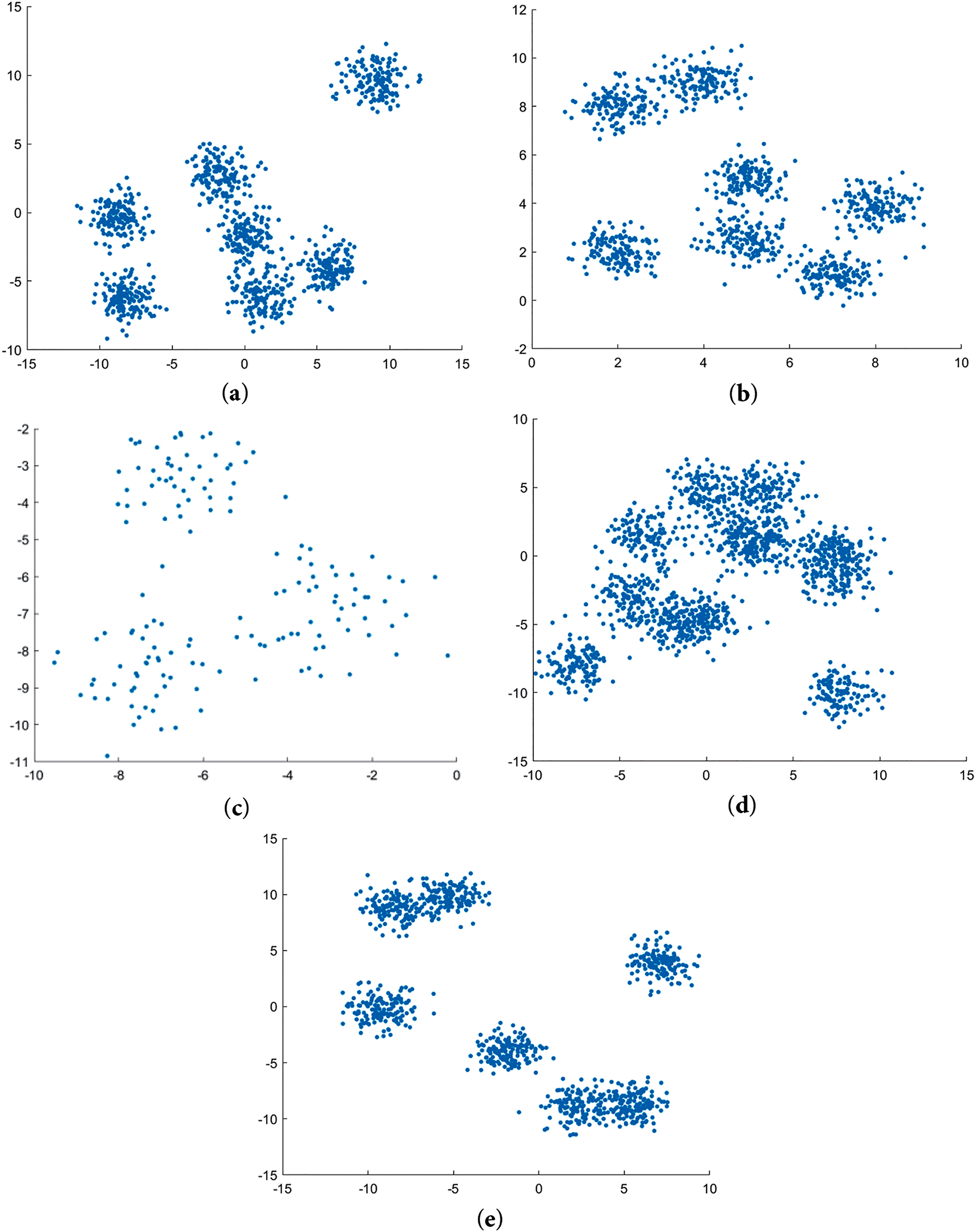
Figure A1: Scatter diagrams of artificial data sets. (a) Data-a dataset. (b) Data-b dataset. (c) Data-c dataset. (d) Data-d dataset. (e) Data-e dataset

The results of the proposed RDVWKFC algorithm on the five synthetic datasets are shown in Fig. A2. The horizontal and vertical coordinates in Fig. A2 also correspond to two dimensions of the data, respectively.

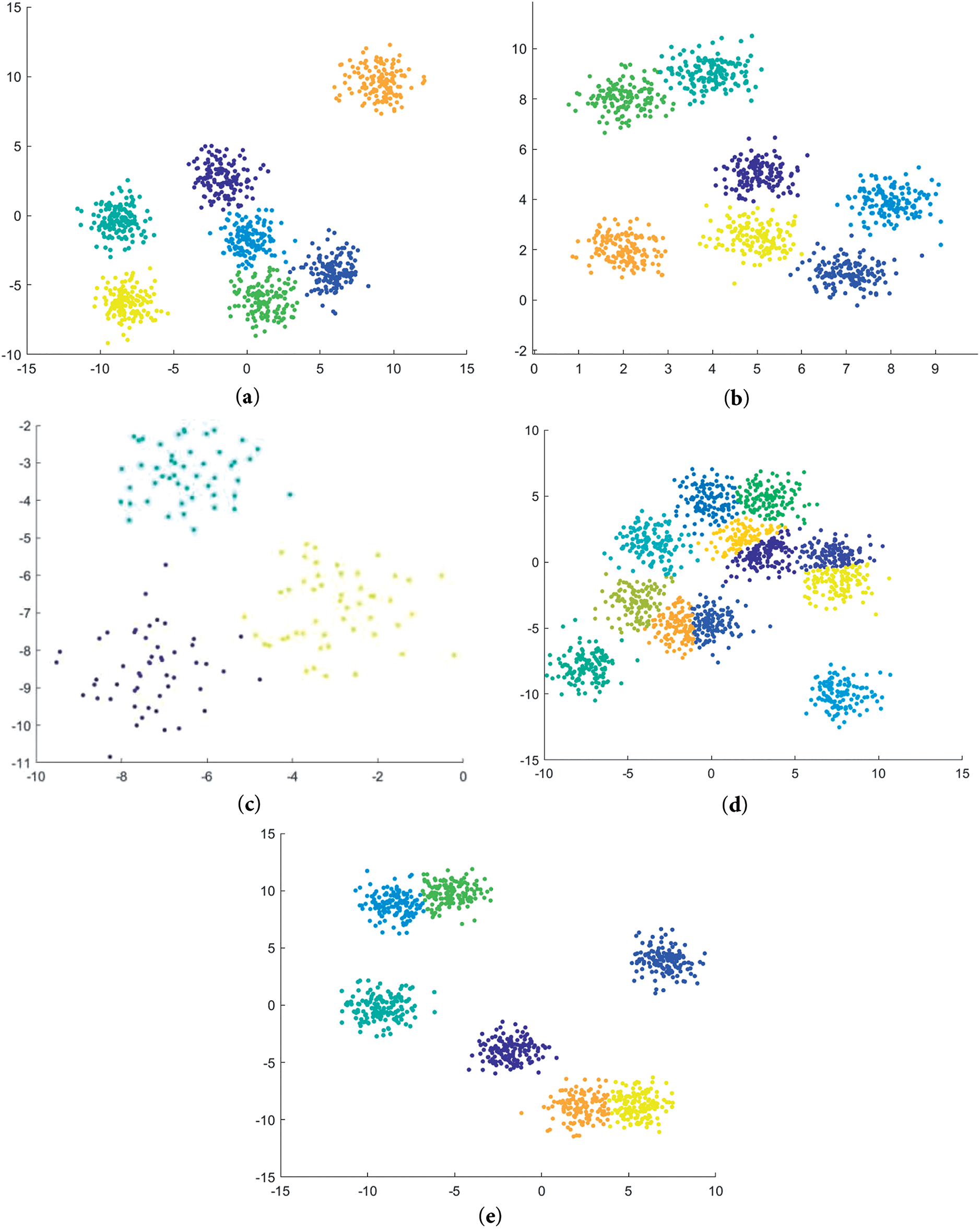
Figure A2: Operation results of the RDVWKFC algorithm on artificial data sets. (a) Data-a dataset. (b) Data-b dataset. (c) Data-c dataset. (d) Data-d dataset. (e) Data-e dataset

As shown in Fig. A3, our proposed new algorithm processes data points from different clusters in different datasets and labels them with easily distinguishable colors and shapes. From the visualized results of the operation, it is not difficult to see that our algorithm shows excellent results on these data sets. The black dots in the rendering represent the location of the cluster centre obtained by the new algorithm. The proposed algorithm can accurately locate the cluster centre, which is particularly obvious in the dataset Data-e. Even though there is significant overlap between the different twelve categories. The algorithm can still accurately identify 12 different clustering centres.

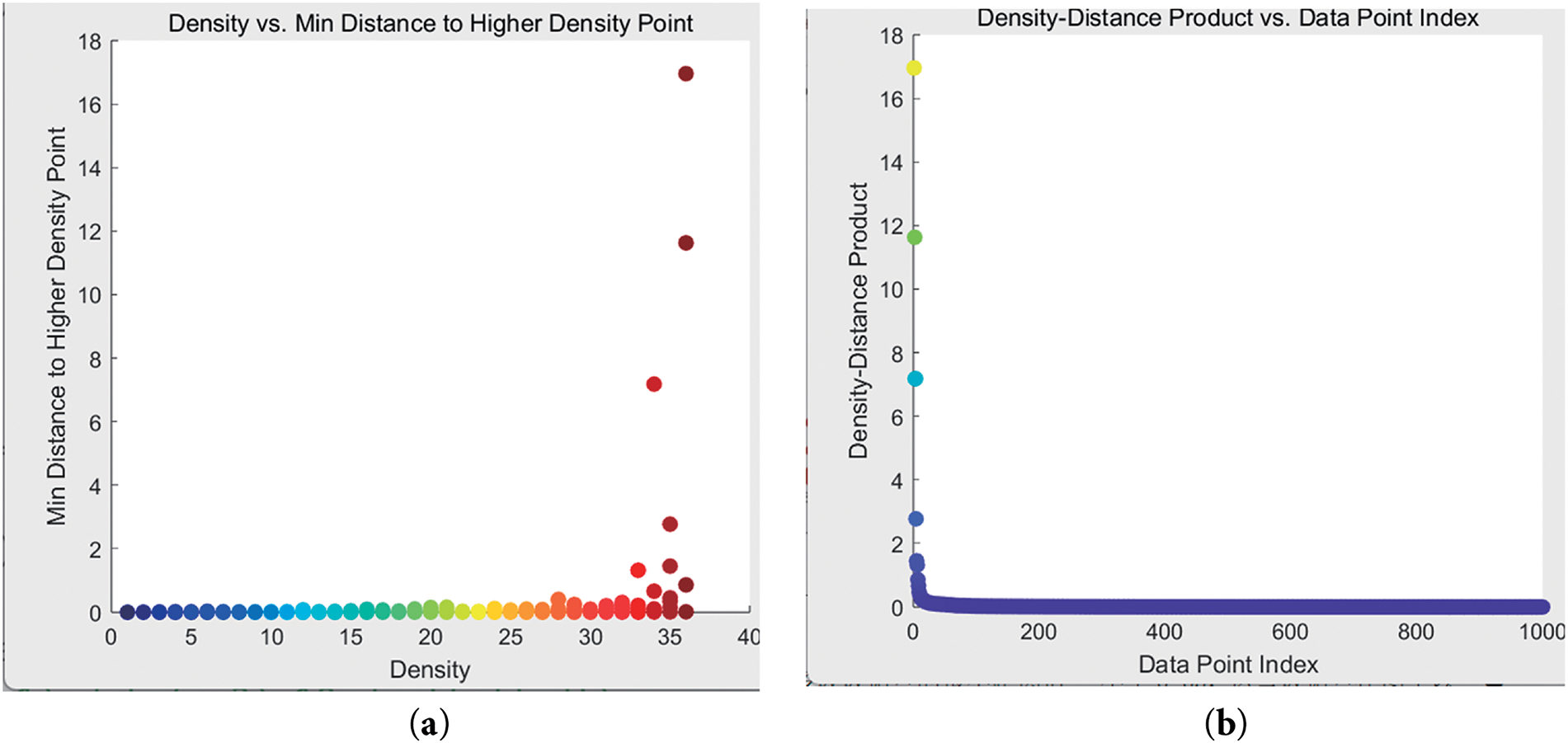
Figure A3: The density-distance (ρ−δ) decision plot on the Data-b dataset. (a) Density vs. min distance to higher density point. (b) Density-distance product vs. data point index

To further validate the effectiveness of the proposed RDKM method, we examine the density-distance (ρ−δ) determination plot and the parameter τ distribution plot after running the RDKM method on the Data-b dataset, as shown in Fig. A3.

Fig. A3a shows the density-distance (ρ−δ) decision diagram after processing the dataset using the RDKM method. It can be seen from the Fig. A3a that the local density of the data points is evenly distributed throughout the range. Most of the data points have a minimum distance value less than 0.05, and these data points are represented by a “●” in the figure. By examining Fig. A3a, it can be noticed that there are seven data points that are significantly different from the others. These points have relatively large minimum distance values and significantly higher local density values compared to the other data points. In the decision diagram, the seven points are marked with different symbols. Accordingly, Fig. A3b shows the parameter distribution plot for the Data-b dataset. It is evident from the figure that the parameter values of seven data points in Fig. A3b are significantly larger than those of most of the data points. Most of the data points have values close to 0. According to the RDKM method, these seven data points correspond to the seven initial cluster centres in the Data-b dataset. From Fig. A3a,b, we can see that the RDKM method successfully distinguishes the potential cluster centres from the regular data points and effectively identifies the initial cluster centres.

Appendix A.2 The Proof of the RDVWKFC Algorithm

We use the Lagrange multiplier method to derive the update iteration formula for the new algorithm.

Firstly, we construct the Lagrangian function L through Eqs. (16) and (17) as follows:

L=JRDVWKFC+∑j=1Nλj⋅(1−∑i=1Cuij)+∑i=1Cβi⋅(1−∑l=1Lωil)(A1)

In order to obtain the minimum value of Eq. (16), the necessary conditions need to be satisfied, and the mathematical constraints are expressed as follows:

∂L∂uij=0,∂L∂gil=0,∂L∂ωil=0,(i=1,2,…,C;j=1,2,…,N;l=1,2,…,L)(A2)

And then, we calculate the result with a partial derivative of 0 with respect to uij, based on Eq. (16), and get the following (i=1,2,…,C;j=1,2,…,N):

∂L∂uij=(αj⋅uijm+m⋅uijm−1⋅αj′)⋅∑l=1Lωil∥ϕ(xil)−ϕ(gil)∥2+η(lnuij+1)+λ(lnuij+1)+λlnK−λj=0(A3)

from (A3):

λj−η(lnuij+1)−λ(lnuij+1)−λlnK=(αj⋅uijm+m⋅uijm−1⋅αj′)⋅∑l=1Lωil∥ϕ(xjl)−ϕ(gil)∥2(A4)

Obviously, when η+λ=0, these two different constraints cancel each other out, preventing the membership from becoming overly concentrated without forcing them to be nearly uniform. This allows membership to more flexibly reflect the clustering structure inherent in the data. The iteration is as follows:

uij=(λj−λlnKαj(mC+1)⋅∑l=1Lωil⋅∥ϕ(xjl)−ϕ(gil)∥2)1m(A5)

Due to the constraints of membership uij, we get the following formula:

∑i=1Cuij=(λj−λlnK)1m⋅∑i=1C(1αj(mC+1)⋅∑l=1Lωil⋅∥ϕ(xjl)−ϕ(gil)∥2)1m=1(A6)

From the above formula, it can be deduced:

(λj−λlnK)1m=1∑s=1C(1αj(mC+1)⋅∑l=1Lωsl⋅∥ϕ(xjl)−ϕ(gsl)∥2)1m(A7)

Then, the Eq. (A7) is substituted into the Eq. (A5), that is, the updated iterative formula of membership is obtained:

uij=1∑s=1C(∑l=1Lωil⋅∥ϕ(xjl)−ϕ(gil)∥2∑l=1Lωsl⋅∥ϕ(xjl)−ϕ(gsl)∥2)1m(A8)

Similarly, calculate the partial derivative of the feature weight and set it to 0 to get the following result (i=1,2,…,C;l=1,2,…,L):

∂L∂ωil=∑j=1Nαj′⋅uijm⋅∥ϕ(xjl)−ϕ(gil)∥2+γ−1⋅(1+lnωil)−βi(A9)

After differentiating, we get the following:

ωil=eβi⋅γ−1⋅e−γ⋅∑j=1Nαj′⋅uijm⋅∥ϕ(xjl)−ϕ(gil)∥2(A10)

Further, we get:

eβiγ−1=1∑l=1Le−γ∑j=1Nαj′⋅uijm⋅∥ϕ(xjl)−ϕ(gil)∥2(A11)

Then we get the updated iterative formula for the feature weights ωil:

ωil=e−γ⋅∑j=1Nαj′⋅uijm⋅∥ϕ(xjl)−ϕ(gil)∥2∑l=1Le−γ∑j=1Nαj′⋅uijmcdot∥ϕ(xjl)−ϕ(gil)∥2(A12)

When we use the Gaussian kernel function to calculate the distance between a data point and the cluster centre, the mathematical expression is as follows:

∥ϕ(xjl)−ϕ(gil)∥2=2−2⋅K(xjl,gil)=2−2⋅e−(xjl−gil)22σ2(A13)

according to the equation:

X=[x11⋯x1L⋮⋱⋮xn1⋯xnL](A14)

When i=q, the cluster centre has the same value as the viewpoint, i.e., gil=xdl. When i≠q, it is not a viewpoint, calculate the partial derivative of the cluster centre gil, and set the resulting equation to 0, get the following formula (i=1,2,…,C;l=1,2,…,L):

∂L∂gil=∑j=1Nαj′⋅uijm⋅ωil⋅(−2)⋅e−(xjl−gil)22σ2⋅(xjl−gil)σ2=0(A15)

Therefore, it is not difficult to obtain:

gil=∑j=1Nαj′⋅uijm⋅ωil⋅e−(xjl−gil)22σ2⋅xjl∑j=1Nαj′⋅uijm⋅ωil⋅e−(xjl−gil)22σ2(A16)

Finally, by combining Formula (17) and formula (A16), the updated iterative formula of cluster centre gil is obtained:

gil={xdl,i=q∑j=1Nαj′⋅uijm⋅ωil⋅e−(xjl−gil)22σ2⋅xjl∑j=1Nαj′⋅uijm⋅ωil⋅e−(xjl−gil)22σ2,i≠q(A17)

Appendix A.3 Time Complexity of the Algorithm

Table A1 shows the time complexity of the proposed algorithm along with the algorithms used for comparison. Let denote the number of iterations and let denote the number of samples in the dataset. The C is the number of clusters, W={wil}i=1,l=1C,L represents the dimension of the data features. Since the new algorithm involves an additional weight matrix to be updated, its time complexity is O(tNl2C).

Updating the membership values includes distance calculation as the main computational cost. The complexity of each distance calculation is O(l2) (due to the complexity of the feature map). Therefore, the total complexity of membership update is O(Nl2C).

For cluster centre updates, the complexity of computing the weighted sum of each cluster i and each feature l is O(Nl), resulting in a total complexity of O(NlC). The complexity of updating the weight parameters for each cluster i and featurel is O(1), so the overall complexity is O(NlC).

Considering that the algorithm needs to iterate, the overall time complexity of retaining the highest order term is O(tNl2C).

Appendix A.4 Iteration Count and Runtime of the Algorithm

We calculated the average number of iterations of each algorithm on different data sets, and the statistical results are shown in Table A2. We rank the average number of iterations of the different algorithms on the same dataset in ascending order and fill in the brackets of the table indicating their rank.

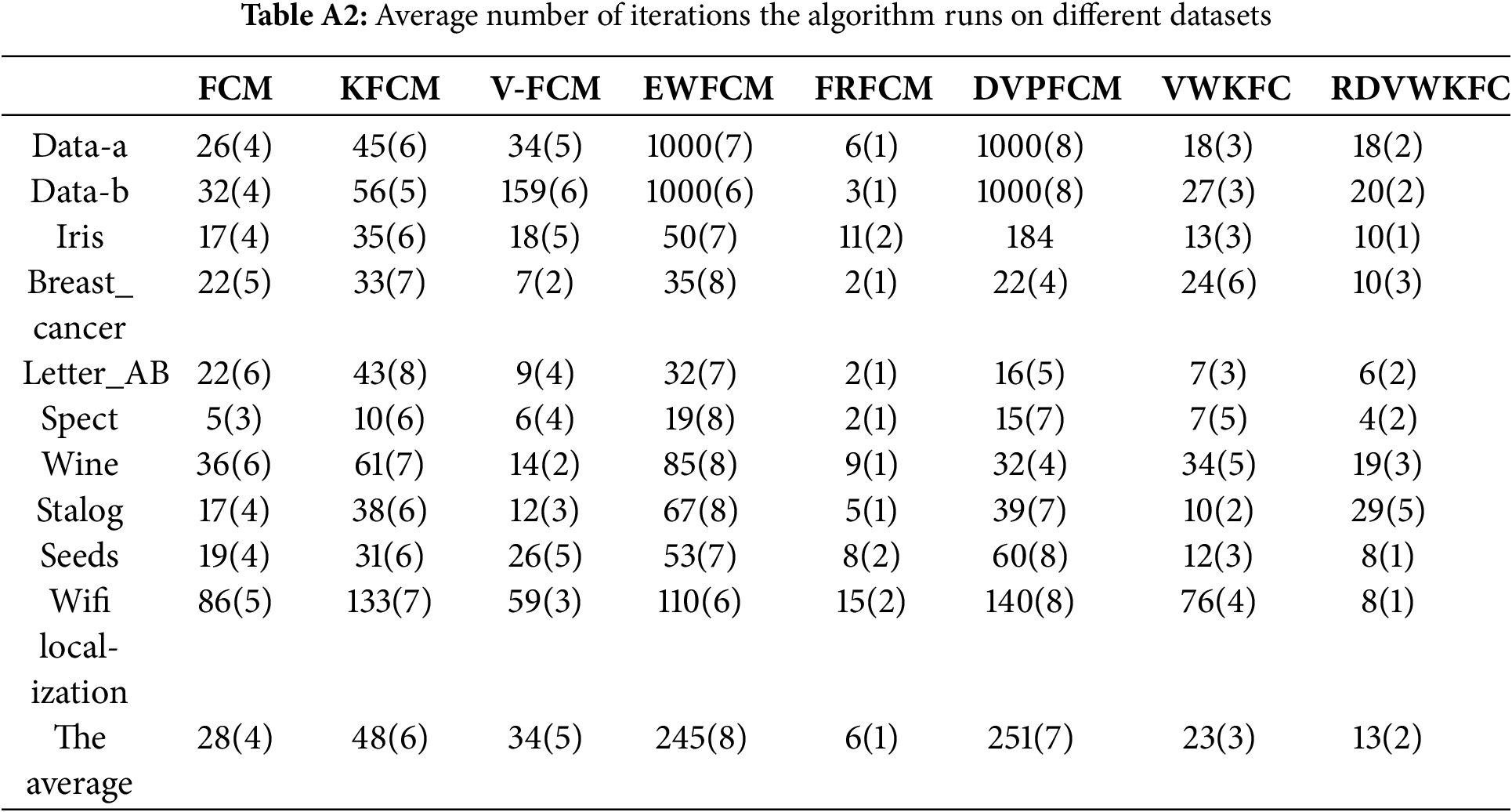
Through the analysis, it is found that the average iteration count of the proposed algorithm is the lowest among all the algorithms on the data sets of Iris, Seeds, heart disease and Wifi localization. On datasets such as Data-a, Data-b, Letter_AB and Spect, its average number of iterations ranks second among all algorithms. However, it is still worth noting that on the Statlog (Landsat) dataset, the average iteration count of the proposed algorithm reaches 29, which is higher than some clustering algorithms such as FCM and V-FCM. This observation indicates that the algorithm may encounter certain limitations when dealing with recognition tasks related to satellite image datasets, which indicates that the algorithm does not show perfect performance on all types of datasets, and also provides research directions and focus for future algorithm optimization and targeted improvement.

However, from the overall experimental results, our proposed algorithm achieves convergence in fewer iterations than the other algorithms. The main reason is that we introduce more effective initial clustering centres as well as the initial viewpoints obtained from the initializing RDKM algorithm to improve the convergence speed of the algorithm. Therefore, the proposed algorithm can quickly reach the steady state in most cases, and reduce the time required for iterative calculation and computing resource overhead, which realizes the superiority of the algorithm in performance.

In Table A3, we calculate the average runtime of each algorithm on different datasets. In doing so, we rank the average running time of each algorithm in ascending order, denoted by the corresponding rank in parentheses.

By observing the experimental data, it is easy to find that the new algorithm needs fewer iterations to reach convergence, but in some cases the running time cost is longer than other algorithms. This can be attributed to the running time overhead caused by the additional computation of the weight matrix in the algorithm. However, given the significant advantages possessed by the proposed algorithm, this additional runtime computational cost is worth the investment. Although the extra computation increases the time cost, we consider the overall performance improvement and clustering result optimization for these advantages, the positive impact is enough to offset the increase in running time. This lays a solid foundation for the algorithm to be used in practice.

Appendix A.5 Discussion

We verify the performance of the algorithm through a series of experiments. Initially, the algorithm was performed on a manual dataset. The experimental results show that the algorithm has good performance in the artificial data set environment. In order to accurately quantify the clustering performance of the algorithm, we calculate 7 key indicators of the algorithm and the comparison algorithm on the artificial datasets. The experimental results strongly show that the proposed algorithm outperforms other algorithms on all seven indexes.

We then experimented with the new algorithm on eight UCI datasets. The experimental data show that the proposed algorithm has superior performance on all evaluation indexes of each UCI dataset compared with other algorithms. The test results show that it can show more outstanding advantages in many aspects, including precision, stability and anti-interference.

The time complexity of each of the other clustering algorithms is given, along with the average number of iterations and running times on different datasets. It is easy to see that in most cases, the average number of iterations of this algorithm is less than that of other comparison algorithms, which shows that the iterative effect of our designed algorithm is efficient and convergent.

Finally, we use the high dimensional state data set to carry out the experiment. The results show that RDVWKFC algorithm has good performance. Compared with other algorithms, this algorithm mainly shows its advantages in the following aspects:

•   Innovative initialization strategy: This method is based on Relative Density Knowledge Extraction (RDKM), which can accurately identify relatively high-density regions and thus determine the initial viewpoint. This method overcomes the sensitivity of traditional clustering algorithms to initialization and reduces the risk of result bias. It significantly improves the initial quality of clustering and provides clear advantages over previous methods.

•   Effective anti-interference mechanism: We introduce the adaptive weight mechanism and construct the Information Granularity Weight Model (IGWM). The model dynamically adjusts the influence of data points according to the importance of data points to reduce the bad interference of noise and outliers on clustering results. It improves the adaptability of the algorithm to a complex data environment and improves the reliability of the clustering results.

•   Outstanding performance: We design an adaptive optimization algorithm (AOA) to significantly improve the performance of different data characteristics and dimensions. The algorithm can dynamically adjust the weights according to the real-time distribution of data and can run stably in a high-dimensional or feature differentiated data environment, which overcomes the limitations of traditional algorithms. By integrating a variety of innovative elements, the proposed algorithm is superior to the comparison algorithms on multiple data sets and related key evaluation indicators, and realizes the goals with fewer iterations, faster convergence speed and higher computational efficiency. The above performance indicators fully prove its effectiveness and superiority in practical applications.

Appendix A.6 Limitations

Our findings confirm that the performance of the algorithm does depend heavily on a few key parameters. These parameters include fuzzy coefficient, regularization parameter and the width of the Gaussian kernel. The process of tuning these parameters can be quite subjective and may not always produce optimal results.

Appendix A.7 Comparison of Different Clustering Algorithms

The comparison in Table A4 ensures a balance between classical foundational work and recent research, effectively strengthening the context of our study.

Appendix A.8 Abbreviation of Various Clustering Algorithms

Table A5 shows the abbreviations of clustering algorithms mentioned in the manuscript.

References

1. Li XL, Zhang H, Wang R, Nie FP. Multi-view clustering: a scalable and parameter-free bipartite graph fusion method. IEEE Trans Pattern Anal Mach Intell. 2022;44(1):330–44. doi:10.1109/tpami.2020.3011148. [Google Scholar] [PubMed] [CrossRef]

2. Hu XH, Tang YM, Pedrycz W, Jiang JC, Jiang YC. Knowledge-driven possibilistic clustering with automatic cluster elimination. Comput Mater Contin. 2024;80(3):4917–45. doi:10.32604/cmc.2024.054775. [Google Scholar] [CrossRef]

3. Zhang J, Fan R, Tao H, Jiang J, Hou C. Constrained clustering with weak label prior. Front Comput Sci. 2024;18(3):183338. doi:10.1007/s11704-023-3355-7. [Google Scholar] [CrossRef]

4. Hussain I, Sinaga KP, Yang MS. Unsupervised multi-view fuzzy C-means clustering algorithm. Electronics. 2023;12(21):4467. doi:10.3390/electronics12214467. [Google Scholar] [CrossRef]

5. Rodriguez A, Laio A. Clustering by fast search and find of density peaks. Science. 2014;344(6191):1492–6. doi:10.1126/science.1242072. [Google Scholar] [PubMed] [CrossRef]

6. Xu K, Pedrycz W, Li Z, Nie W. Constructing a virtual space for enhancing the classification performance of fuzzy clustering. IEEE Trans Fuzzy Syst. 2019;27(9):1779–92. doi:10.1109/tfuzz.2018.2889020. [Google Scholar] [CrossRef]

7. Pedrycz W, Amato A, Lecce VD, Piuri V. Fuzzy clustering with partial supervision in organization and classification of digital images. IEEE Trans Fuzzy Syst. 2008;16(4):1008–26. doi:10.1109/tfuzz.2008.917287. [Google Scholar] [CrossRef]

8. Krishnapuram R, Keller JM. A possibilistic approach to clustering. IEEE Trans Fuzzy Syst. 1993;1(2):98–110. doi:10.1109/91.227387. [Google Scholar] [CrossRef]

9. Pal NR, Pal K, Keller JM, Bezdek JC. A possibilistic fuzzy c-means clustering algorithm. IEEE Trans Fuzzy Syst. 2005;13(4):517–30. doi:10.1109/tfuzz.2004.840099. [Google Scholar] [CrossRef]

10. Hu J, Wu M, Chen L, Zhou K, Zhang P, Pedrycz W. Weighted kernel fuzzy C-means-based broad learning model for time-series prediction of carbon efficiency in iron ore sintering process. IEEE Trans Cybern. 2022;52(6):4751–63. doi:10.1109/tcyb.2020.3035800. [Google Scholar] [PubMed] [CrossRef]

11. Graves D, Pedrycz W. Kernel-based fuzzy clustering and fuzzy clustering: a comparative experimental study. Fuzzy Sets Syst. 2010;161(4):522–43. doi:10.1016/j.fss.2009.10.021. [Google Scholar] [CrossRef]

12. Huang H, Chuang Y, Chen C. Multiple kernel fuzzy clustering. IEEE Trans Fuzzy Syst. 2012;20(1):120–34. doi:10.1109/tfuzz.2011.2170175. [Google Scholar] [CrossRef]

13. Yang MS, Benjamin JBM. Feature-weighted possibilistic C-means clustering with a feature-reduction framework. IEEE Trans Fuzzy Syst. 2021;29(5):1093–106. doi:10.1109/tfuzz.2020.2968879. [Google Scholar] [CrossRef]

14. Hussain I, Nataliani Y, Ali M, Hussain A, Mujlid HM, Almaliki FA, et al. Weighted multi-view K-means clustering with L2 regularization. Symmetry. 2024;16(12):1646. doi:10.3390/sym16121646. [Google Scholar] [CrossRef]

15. Pedrycz W, Loia V, Senatore S. Fuzzy clustering with viewpoints. IEEE Trans Fuzzy Syst. 2010;18(2):274–84. doi:10.1109/tfuzz.2010.2040479. [Google Scholar] [CrossRef]

16. Tang YM, Hu XH, Pedrycz W, Song XC. Possibilistic fuzzy clustering with high-density viewpoint. Neurocomputing. 2019;329(2):407–23. doi:10.1016/j.neucom.2018.11.007. [Google Scholar] [CrossRef]

17. Tang YM, Pan ZF, Pedrycz W, Ren FJ, Song XC. Viewpoint-based kernel fuzzy clustering with weight information granules. IEEE Trans Emerg Top Comput Intell. 2023;7(2):342–56. doi:10.1109/tetci.2022.3201620. [Google Scholar] [CrossRef]

18. Zhou J, Chen L, Chen CLP. Fuzzy clustering with the entropy of attribute weights. Neurocomputing. 2016;19(8):125–34. doi:10.1016/j.neucom.2015.09.127. [Google Scholar] [CrossRef]

19. Oskouei AG, Samadi N, Tanha J, Bouyer A, Arasteh B. Viewpoint-based collaborative feature-weighted multi-view intuitionistic fuzzy clustering using neighborhood information. Neurocomputing. 2025;617(5):128884. doi:10.1016/j.neucom.2024.128884. [Google Scholar] [CrossRef]

20. Hashemzadeh M, Oskouei AG, Farajzadeh N. New fuzzy C-means clustering method based on feature-weight and cluster-weight learning. Appl Soft Comput. 2019;78:324–45. doi:10.1016/j.asoc.2019.02.038. [Google Scholar] [CrossRef]

21. Nie F, Xue J, Yu W, Li X. Fast clustering with anchor guidance. IEEE Trans Pattern Anal Mach Intell. 2024;46(4):1898–912. doi:10.1109/tpami.2023.3318603. [Google Scholar] [PubMed] [CrossRef]

22. Hu XH, Jiang YC, Pedrycz W, Deng ZH, Gao JW, Tang YM. Automated cluster elimination guided by high-density points. IEEE Trans Cybern. 2025;55(4):1717–30. doi:10.1109/tcyb.2025.3537108. [Google Scholar] [PubMed] [CrossRef]

23. Strehl A, Ghosh J. Cluster ensembles—a knowledge reuse frame work for combining multiple partitions. J Mach Learn Res. 2002;3(1):583–617. [Google Scholar]

24. Calinski T, Harabasz J. A dendrite method for cluster analysis. Commun Stat. 1972;3(1):1–27. [Google Scholar]

25. Campello RJGB. A fuzzy extension of the rand index and other related indexes for clustering and classification assessment. Pattern Recognit Lett. 2007;28(7):833–41. doi:10.1016/j.patrec.2006.11.010. [Google Scholar] [CrossRef]

26. Hubert L, Arabie P. Comparing partitions. J Classif. 1985;2(1):193–218. [Google Scholar]

27. Xie XL, Beni G. A validity measure for fuzzy clustering. IEEE Trans Pattern Anal Mach Intell. 1991;13(8):841–7. doi:10.1109/34.85677. [Google Scholar] [CrossRef]

28. Tang YM, Chen JJ, Pedrycz W, Ren FJ, Zhang L. Universal quintuple implicational algorithm: a unified granular computing framework. IEEE Trans Emerg Top Comput Intell. 2024;8(1):1044–56. doi:10.1109/tetci.2023.3327719. [Google Scholar] [CrossRef]