 Open Access
Open Access
ARTICLE
Schweizer-Sklar T-Norm Operators for Picture Fuzzy Hypersoft Sets: Advancing Suistainable Technology in Social Healthy Environments
1 Fujian Provincial Key Laboratory of Big Data Mining and Applications, Fujian University of Technology, Fuzhou, 350118, China
2 Department of Applied Sciences, Advanced Centre of Research & Innovation (ACRI), Chandigarh Engineering College, Chandigarh Group of Colleges Jhanjeri, Mohali, 140307, Punjab, India
3 Department of Electronics and Communications, Chandigarh University, Gharuan, 140413, Punjab, India
4 Department of Mathematics, Jaypee University of Information Technology, Waknaghat, Solan, 173234, Himachal Pradesh, India
5 Allenhouse Institute of Technology, Kanpur, 208008, Uttar Pradesh, India
* Corresponding Author: Himanshu Dhumras. Email:
Computers, Materials & Continua 2025, 84(1), 583-606. https://doi.org/10.32604/cmc.2025.066310
Received 04 April 2025; Accepted 29 April 2025; Issue published 09 June 2025
Abstract
Ensuring a sustainable and eco-friendly environment is essential for promoting a healthy and balanced social life. However, decision-making in such contexts often involves handling vague, imprecise, and uncertain information. To address this challenge, this study presents a novel multi-criteria decision-making (MCDM) approach based on picture fuzzy hypersoft sets (PFHSS), integrating the flexibility of Schweizer-Sklar triangular norm-based aggregation operators. The proposed aggregation mechanisms—weighted average and weighted geometric operators—are formulated using newly defined operational laws under the PFHSS framework and are proven to satisfy essential mathematical properties, such as idempotency, monotonicity, and boundedness. The decision-making model systematically incorporates both benefit and cost-type criteria, enabling more nuanced evaluations in complex social or environmental decision problems. To enhance interpretability and practical relevance, the study conducts a sensitivity analysis on the Schweizer-Sklar parameter (). The results show that varying affects the strictness of aggregation, thereby influencing the ranking stability of alternatives. A comparative analysis with existing fuzzy and hypersoft-based MCDM methods confirms the robustness, expressiveness, and adaptability of the proposed approach. Notably, the use of picture fuzzy sets allows for the inclusion of positive, neutral, and negative memberships, offering a richer representation of expert opinions compared to traditional models. A case study focused on green technology adoption for environmental sustainability illustrates the real-world applicability of the proposed method. The analysis confirms that the approach yields consistent and interpretable results, even under varying degrees of decision uncertainty. Overall, this work contributes an efficient and flexible MCDM tool that can support decision-makers in formulating policies aligned with sustainable and socially responsible outcomes.Keywords
Modeling a decision science problem primarily involves optimizing beneficial outcomes within the constraints of preferences specified by decision-makers, based on the given attribute values. However, effectively processing these preferences is often complex due to the inherent vagueness and uncertainty found in real-world problems. One of the significant areas of application in decision science lies in addressing human-centric environmental and social concerns. There is a growing global need for clean, eco-friendly, and sustainable solutions in production, energy, and transportation to tackle challenges such as climate change, global warming, and resource/waste management.
Three core pillars of green technology adoption aimed at improving social well-being include: promoting digital equity and environmental responsibility through strategic policies, fostering green alliances, and embedding sustainability as a societal value. These efforts contribute to cultivating responsible behaviors, sustainable practices, and lifestyles that enhance human health and well-being.
Fuzzy systems have been widely employed in real-life applications such as solar photovoltaic systems [1] and robotic manipulators [2,3]. Fuzzy decision-making, in particular, plays a vital role in evaluating performance indicators that are typically affected by uncertain data. For instance, Bhatia and Diaz-Elsayed [4] applied fuzzy TOPSIS techniques to support smart manufacturing adoption for small and medium-sized enterprises. Similarly, Aytekin and colleagues [5] evaluated sustainable green strategies in logistics using T-spherical fuzzy methods, and TODIM-based approaches have been implemented for green supplier selection under type-2 neutrosophic environments [6]. Moreover, complex q-rung picture fuzzy frameworks have been applied to power and energy decision-making [7], while interval-valued fermatean neutrosophic super hypersoft sets have been introduced in healthcare assessments [8].
Numerous researchers have developed methodologies rooted in fuzzy set theory and its extensions—such as picture fuzzy sets [9], fuzzy soft sets [10], and fuzzy hypersoft sets [11]. Naeem et al. [12] proposed sigma-algebraic measures for fuzzy neutrosophic soft sets, and later introduced picture fuzzy soft sigma-algebra measures with practical implications [13]. Aggregation operators for picture fuzzy soft sets have also been investigated using weighted average and hybrid models [14].
In certain decision-making scenarios, attributes require further categorization, where conventional soft sets are insufficient. Hypersoft set theory, as introduced by Smarandache [11], becomes essential in such cases. Over time, various hybrid fuzzy-hypersoft models have emerged. Saqlain et al. [15] presented neutrosophic hypersoft extensions of the TOPSIS method. Plithogenic hypersoft sets [16] and intuitionistic fuzzy hypersoft models [17,18] have also been proposed, including Pythagorean fuzzy hypersoft sets with Einstein-based aggregation operators [19] and their application in COVID-19 safety assessment [20].
The generalization of picture fuzzy soft sets by Khan et al. [21], and the development of
Recent advancements include the modified MARCOS method in a 2-tuple linguistic
The Schweizer-Sklar
1.1 Motivation and Research Gap
This study aims to develop a novel decision-making tool tailored for real-life, sub-parameterized complex information scenarios. A core focus is to support green technology adoption within socially healthy frameworks by proposing a new score function that incorporates Schweizer-Sklar
The main motivations include:
• The PFHSS model effectively incorporates an additional refusal/abstain component along with sub-parameterized attributes, offering deeper insight for decision-making problems.
• Schweizer-Sklar-based aggregation operators provide increased flexibility for modeling uncertain data within PFHSS structures.
• The proposed set-theoretic properties for PFHSS aggregation (e.g., weighted average and weighted geometric forms) enable more robust and interpretable aggregation.
• To date, no studies have explored Schweizer-Sklar norm/co-norm based aggregation operators within the PFHSS framework—highlighting a significant research gap addressed in this paper.
1.2 Novelty and Contributions of the Present Study
This paper introduces Schweizer-Sklar-based weighted average and geometric aggregation operators within the PFHSS framework for the first time. These operators provide a flexible and powerful foundation for sustainable decision-making in human-centric applications. The paper presents their set-theoretical properties—such as idempotency, boundedness, homogeneity, and monotonicity—in detail.
The PFHSS-based formulation addresses real-world uncertainty and offers decision-makers the freedom to assign uncertainty components based on expert insights using the adjustable
The rest of the manuscript is organized as follows:
• Section 2 reviews core definitions related to soft/hypersoft sets, PFHSS, score functions, and Schweizer-Sklar operations.
• Section 3 presents the proposed aggregation operators and their theoretical properties.
• Section 4 outlines the algorithmic framework and procedural flowchart for solving MCDM problems.
• Section 5 presents a detailed case study on green technology adoption.
• Section 6 includes graphical analysis based on the
• Section 7 provides comparative insights.
• Section 8 concludes the study and summarizes key contributions.
2 Fundamental Concepts & Definitions
In this section, some basic and fundamental definitions which are necessary to understand the propositions of aggregation operators for
Definition 1: Picture Fuzzy Set (PFS) [9]. “For a universe of discourse V a picture fuzzy set
where
and,
Definition 2: Soft Set (SS) [35]. “For a universal set V and K be a set of parameters. Then the pair (R,K) is known as a soft set over the universe of discourse V, where R is a function from R: K
Definition 3: Hypersoft Set (HSS) [11]. “For a universal set V be the universal set and P(
Definition 4: (Picture Fuzzy Hypersoft Set) [24]. “Consider V be a universe of discourse and PFS(V) be the collection of all picture fuzzy subsets from the universal of discourse V. Let
where
The term
Also, the picture fuzzy hypersoft number can be defined as
Definition 5: [36] “Let
In literature, Schweizer-Sklar [30] has recommended some special types of algebraic operations, i.e., triangular norms for which definitions may be written as follows:
Definition 6: [30] “Let
where,
3 Average/Geometric Aggregation Operators
The concept of an aggregation operator logically combines the related numerous inputs into a single output value, is a crucial tool in the information fusion process and is frequently applied to a wider range of decision science problems. The issues are not exclusive to mathematics; they are also extensively present in the area of physical sciences, socio-economic fields, engineering applications and other related fields. In this section, we develop two kinds of aggregation operators based on Schweizer-Sklar triangular norms for picture fuzzy hypersoft numbers and describe some outcomes based on them.
For proposing the Schweizer-Sklar based picture fuzzy hypersoft weighted averaging operator/geometric operator, it is required to understand some basic operations of
3.1 Schweizer-Sklar Operations on
In this section, we discuss some Schweizer-Sklar (SS) operations and some of its fundamental notions. Suppose that the
•
•
Definition 7: Let
(a)
(b)
(c)
(d)
(e)
3.2 PFHS Schweizer-Sklar Weighted Averaging Aggregation Operators
Definition 8: Suppose
where
Theorem 1: Suppose
And
Proof: Here, we use the technique of mathematical induction to carry out the proof.
By definition (8), we have
Now, by using the above-stated operations (a)–(e), we get
Also, For
Then, from Eq. (1), we have
Hence, Eq. (5) is satisfied for the initial values of
Now for
Thus, the proposition is valid for
Properties of PFHSSSWA Operator
• Idempotency
If
Proof.Let
Hence, the idempotency holds.
• Boundedness
Suppose
Let
Proof.
Let
Similarly,
Then, by definition of order relation,
• Homogeneity
For
Proof. Suppose
Thus,
• Monotonicity Let
Proof. By using definitions it can be easily proved on similar lines.
3.3 PFHS Schweizer-Sklar Weighted Geometric Aggregation Operators
Definition 9: Suppose
where
Theorem 2: Suppose
And
Proof: Here, we use the technique of mathematical induction to carry out the proof.
By definition (9), we have
Now, by using the above-stated operations (a)–(e), we get
Also, For
Then, from Eq. (5), we have
Hence, Eq. (6) is satisfied for the initial values of
Now for
Thus, the proposition is valid for
Properties of PFHSSSWG Operator
• Idempotency
If
Proof. The proof of idempotency is done in the same way as done in the weighted averaging case.
• Boundedness Suppose
Proof. Proof can be done in the same way as done in a weighted averaging case.
• Homogeneity For any positive real number
Proof. The proof of monotonicity is done in the same way as done in weighted averaging case.
• Monotonicity Let
Proof. By using definitions it can be easily proved on similar lines.
4 Decision-Making Methodology Based on Schweizer-Sklar Aggregation Operators inPFHS Environment
This section proposes a novel scheme for solving an MCDM problem based on proposed SSAOs in
Consider
Apply thePFHSSSWA andPFHSSSWG aggregation operators to aggregate the PFHSNs
Phase 1. Construct an expert matrix
Phase 2. In this phase, normalization of the cost-type parameters into benefit-type parameters is done and the normalized aggregated matrices are obtained.
Phase 3. Now, use the normalized
Phase 4. In the next phase, compute the score values of the alternatives by making use of Definition 2.
Phase 5. Select the alternative having the highest score value and prioritize them accordingly.
Also, a detailed diagram based on these methodological phases is shown in Fig. 1.
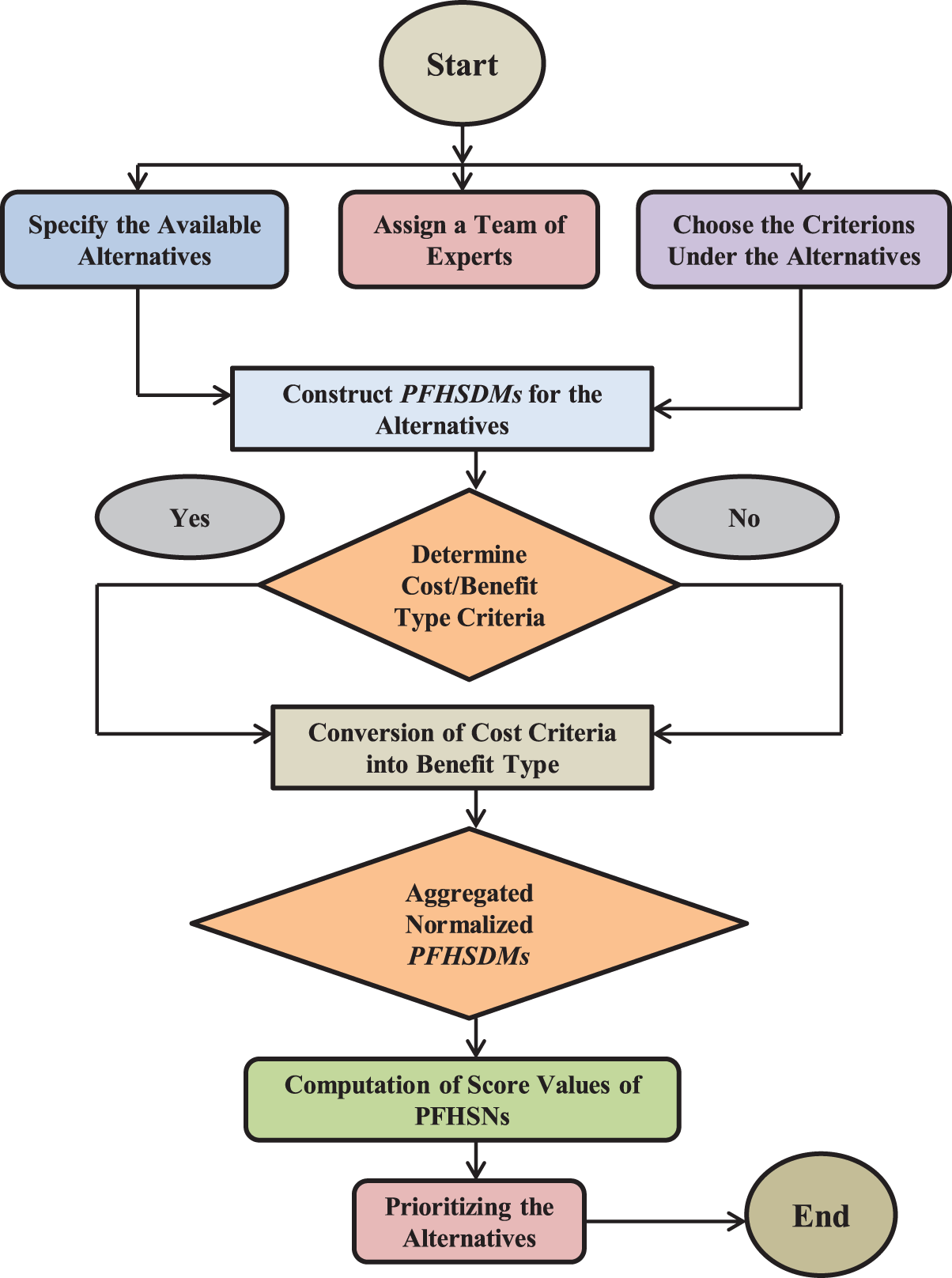
Figure 1: Flow diagram of the proposed methodology
5 Utilization of Proposed Decision-Making Methodology in Green Technology Adoption for Healthy Social Environment
Human living environments are shaped by their surroundings because the behaviour of humanity depends on all environmental elements-such as air, food, goods, locations, and a host of other things—a clean environment (biotic/abiotic) is necessary for a healthy and trouble-free existence. A clean environment is essential to the global advancement of lifestyles. However, the globe is currently dealing with several environmental problems, such as pollution, solid waste, water supplies, global warming, temperature increases, and expanding populations. A sustainable green environment, green production, green energy, and eco-friendly transportation are what the public needs.
All countries on the earth are attempting, via the use of their resources, to address environmental challenges. In recent years, the clean environment has gained international attention. The contrastive features of such important concern are re-iteratively pushing for improvements to the clean, eco-friendly environment. The unfavorable state of the ecosystem has altered traditional wisdom, which could spell doom for a clean environment. While each nation has unique problems with maintaining a clean environment, most of the problems are global.
Suppose that a committee of experts has been formed to examine and decide on the key issues relating to environmental protection. The group of experts looked at many fundamental problems and expressed them in the form of available alternatives. The five possible alternatives that need to be assessed by the experts are; Rise in population
•
•
•
•
Suppose
Now, for the simplification processes the set of all sub-criterions can be redefined as
along with their respective weight vectors are
Evaluation and selection of choices have gotten harder over the past few years because of the fuzziness of the data that is now accessible and the necessity for more accuracy when analyzing qualities. To manage these situations, decision-making mechanisms must be enhanced. This picture fuzzy hypersoft paradigm can take into account a variety of sub-attributes and both perspectives of the three-dimensional information associated with the inclusion of three important uncertainty parameters which are very useful for making decisions. Experts provide their preferences in the form of
5.1 By Utilizing PFHSSSWA Operators
Phase 1. In the first phase, all the picture fuzzy hypersoft expert matrices for the alternatives are listed from Tables 1–5.
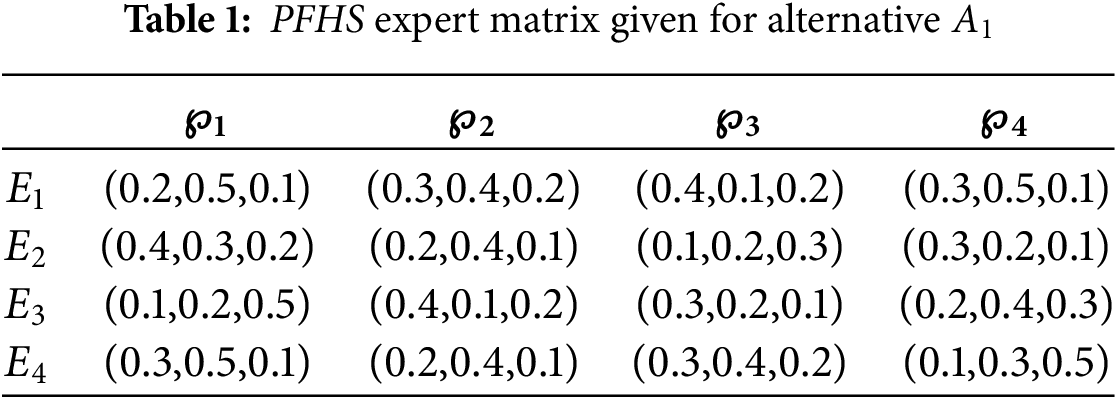
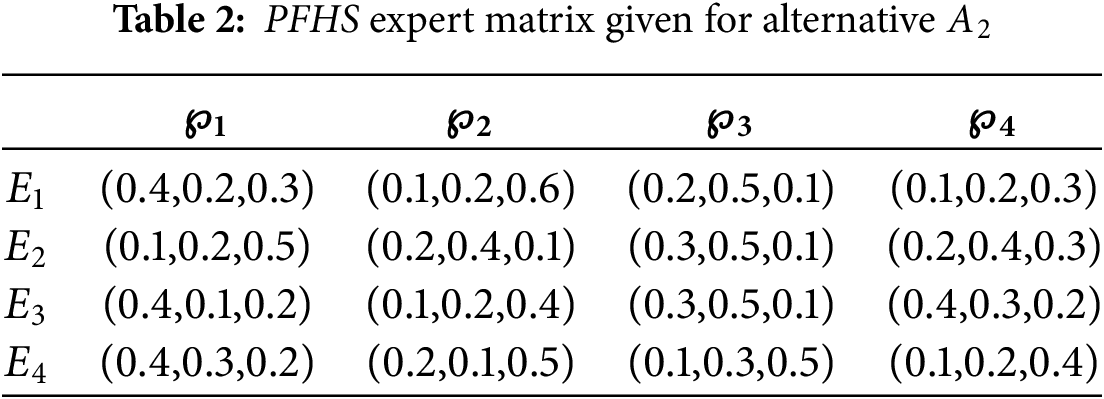
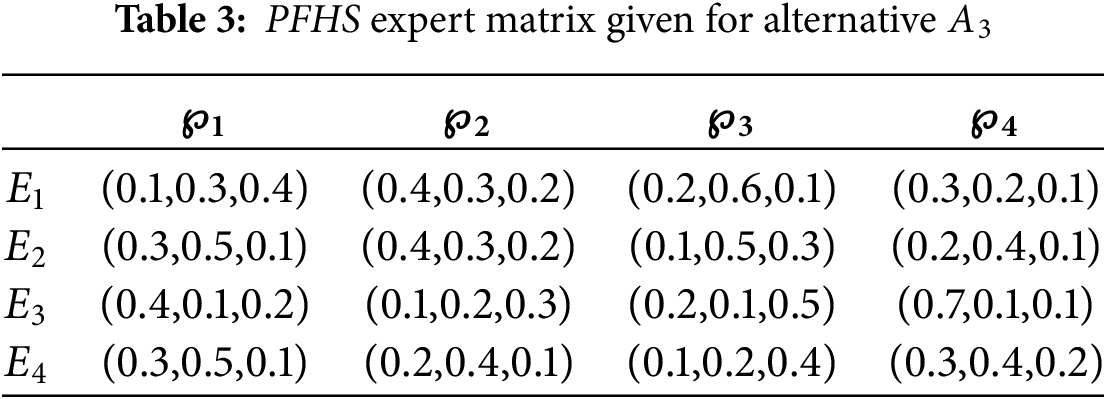
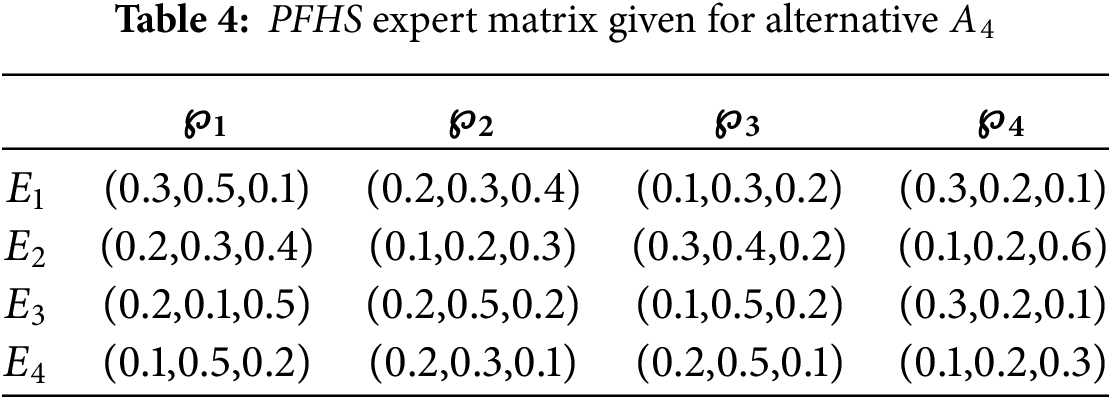
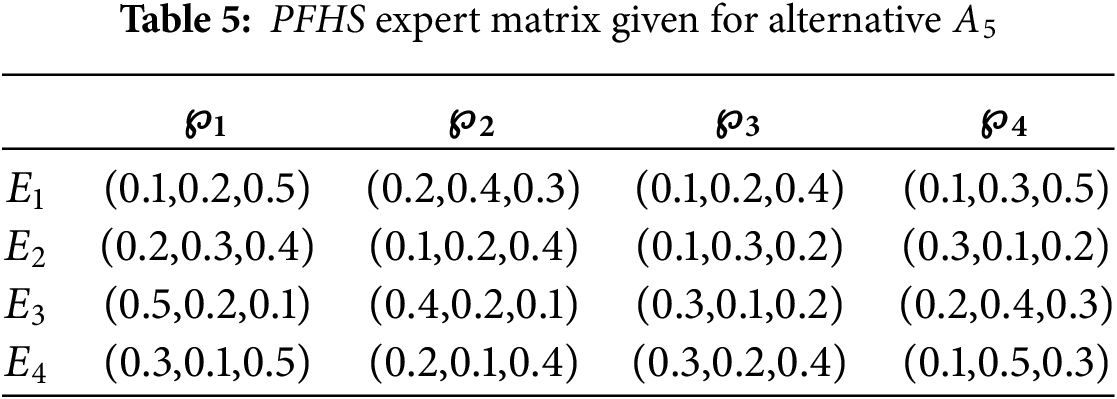
Phase 2. As every criterion is of benefit type, therefore normalization is not necessary.
Phase 3. Now, we applied the proposed picture fuzzy hypersoft SSAOs on the obtained expert matrices and acquired the required information from the experts in terms of
For
Phase 4. Now utilize the score function formula to compute the scores of all the available alternatives.
Phase 5. Based on score values for the alternatives, the prioritization of alternatives can be done as follows:
Further, on similar lines, all the computations can be done for the weighted average aggregation operators.
5.2 By Utilizing PFHSSSWG Operators
Phase 1. This phase is the same as in PFHSSSWA operators.
Phase 2. This phase is also the same as in PFHSSSWA operators.
Phase 3. Now, we applied the proposed picture fuzzy hypersoft SSAOs on the obtained expert matrices and acquired the required information from the experts in terms of
For
Phase 4. Now utilize the score function formula to compute the scores of all the available alternatives.
Phase 5. Based on score values for the alternatives, the prioritization of alternatives can be done as follows:
6 Overview of Schweizer-Sklar Parameter (
To demonstrate the impact of the SS (
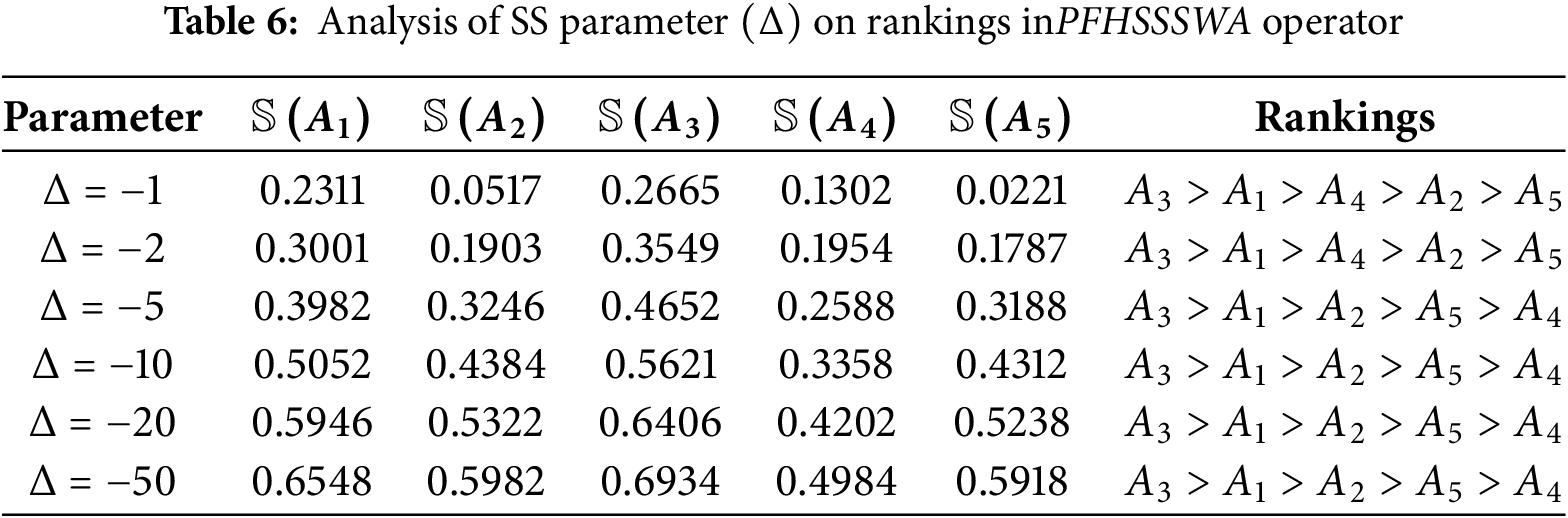
It is clear from Fig. 2 that with the decreasing value of the SS parameter, the score values are increasing based on the PFHSSSWA operator. Numerous prioritization orderings can be used with the same PFHSSSWA operator. For the
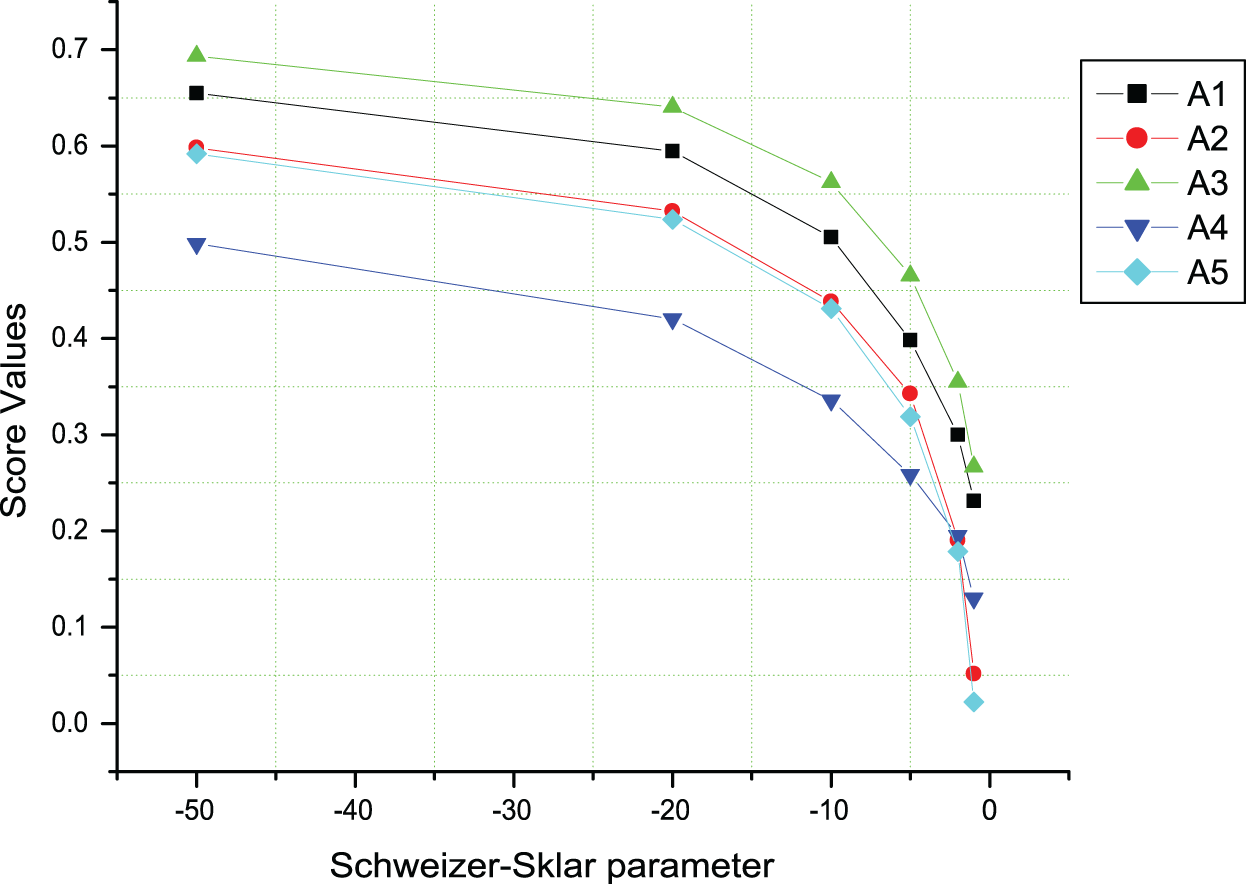
Figure 2: Impact of SS
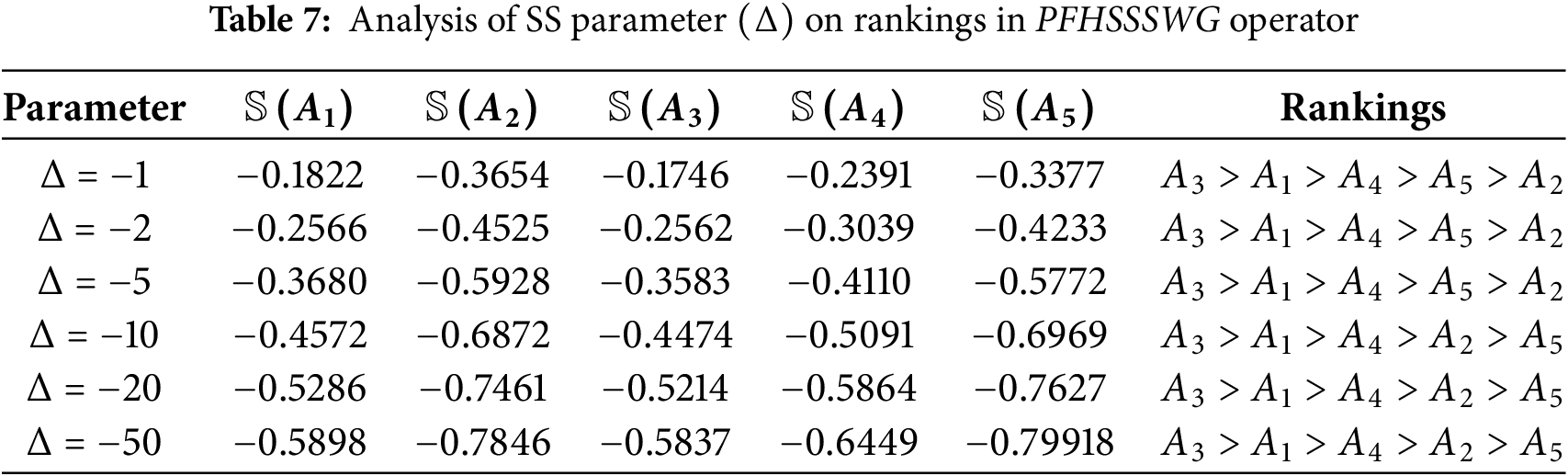
Similarly, from Fig. 3 with the decreasing value of the SS parameter the score values are decreasing based on the PFHSSSWG operator. And different ranking orders can be utilized with the same PFHSSSWG operator. Further, For the

Figure 3: Impact of SS
Now, depending on the perceptions of the experts, a decision-maker may have a positive or negative view. Therefore, choosing a larger value for the SS parameter is advised for decision-makers who have a negative outlook on a viable alternative based on criteria. Also, this suggests that the approach under consideration is supposed to be computationally robust and the process with the obtained results is valid.
7 Comparative Analysis & Advantages
The presented decision-making technique that can be utilized in PFHSSSWA or PFHSSSWG aggregation operators under a picture fuzzy hypersoft environment. The devised technique which is executed is decisive and useful in practical scenarios. Our anticipated methodology outperforms some of the existing methodologies and is capable of handling even more complex decision-making situations. The presented model performs numerous tasks and is more flexible to incorporate the variations while dealing with the process of uncertain problems. In the literature, there are various Schweizer-Sklar aggregation operators under different fuzzy environments and the evaluation system for every methodology is unique. These research deliberations and analyses have led us to the conclusion that the hybrid decision-making technique produces more reliable results than the conventional one.
Also, the criterion and decision maker’s weights for the evaluation of alternatives under these criteria are very important factors for decision-making technique. Further, we compare our methodologies based on these terms with some existing methodologies tabulated in Table 8 and one can say that the proposed decision-making methodologies are equally consistent with some of the existing techniques.
The key distinctions and advantages of our method are as follows:
• Improved Handling of Uncertainty:
– Unlike traditional fuzzy or intuitionistic fuzzy methods, our approach leverages picture fuzzy sets, which incorporate positive, neutral, and negative membership degrees. This allows for a more expressive and realistic modeling of human judgments, especially in complex or ambiguous decision environments.
– Competing methods often fail to explicitly account for neutrality or hesitation, limiting their effectiveness in real-world uncertain scenarios.
• Flexible Aggregation with the Schweizer-Sklar Operator:
– The use of the parameterized Schweizer-Sklar operator provides a tunable mechanism to control the level of compensation among criteria.
– This flexibility allows decision-makers to adapt the model based on their preferences (risk-averse, neutral, or compensatory), whereas most traditional methods apply fixed aggregation rules that cannot be adjusted.
• Computational Efficiency:
– Although our method introduces additional components (e.g., picture fuzzy logic and parameterized aggregation), the computational complexity remains linear with respect to the number of criteria and alternatives, which is comparable to or even better than some iterative or optimization-based MCDM techniques.
– Additionally, the closed-form formulations used in the aggregation and scoring steps make the method scalable for large decision problems.
• Ranking Stability and Robustness:
– Through our sensitivity analysis on the Schweizer-Sklar parameter (
– Some benchmark methods show ranking reversals or inconsistencies under slight model perturbations, suggesting lower robustness.
• Limitations and Scope for Future Work:
– We acknowledge that our method requires parameter tuning (
– Moreover, while picture fuzzy sets enhance uncertainty modeling, they also increase the cognitive load on decision-makers during input elicitation.
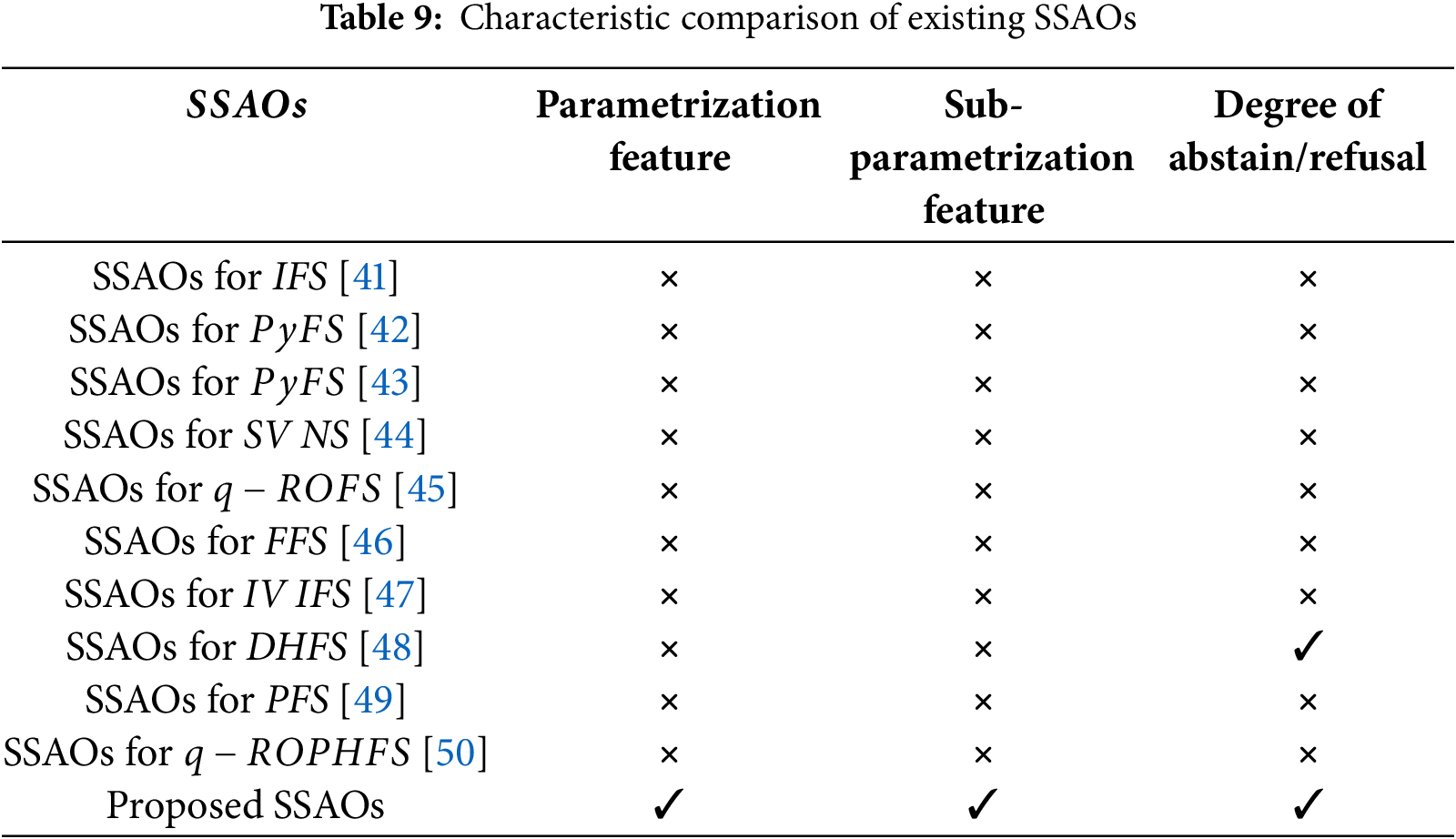
Furthermore, due to various unique circumstances, the tool of parametrization and sub-parametrization is very useful which is not yet covered by the existing Schweizer-Sklar aggregation operators. As a result, the approach we have devised will be substantially stronger, more reliable, and better than the various existing techniques. Table 9 presented the characteristic comparison analysis of the proposed aggregation operators with existing aggregation operators.
Where,
The significant findings and contributions of this study are summarized as follows:
• We proposed novel Schweizer-Sklar-based aggregation operators (both weighted average and geometric average) for picture fuzzy hypersoft information systems. These operators generalize existing ones by incorporating a tunable parameter (
• A structured multi-criteria decision-making (MCDM) algorithm was developed using the proposed operators. Its effectiveness was demonstrated through an illustrative example related to green technology adoption in social environments. Comparative analysis highlighted the advantages of the proposed method over existing approaches.
• The sensitivity of the decision-making results to the Schweizer-Sklar parameter was examined, revealing that the PFHSSSWA operator yields increasing scores with decreasing
This work opens several avenues for further research:
• Extending the proposed framework to more generalized fuzzy environments such as T-spherical fuzzy sets, indetermSoft sets, and indetermHyperSoft sets [51] to handle larger and more complex decision problems.
• Applying the aggregation operators in hybrid or ensemble decision models, particularly in AI-driven applications such as intelligent recommendation systems, stochastic simulations, and ML-integrated decision support systems.
• Developing data-driven consensus models and real-time decision tools that incorporate the tunable behavior of the Schweizer-Sklar parameter for adaptive analysis.
Acknowledgement: The authors acknowledge the National Natural Science Foundation of China for creating a conducive and enabling environment that supports this research.
Funding Statement: This work was supported by the National Natural Science Foundation of China (No. 62172095).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Xingsi Xue, Himanshu Dhumras, Garima Thakur, Rakesh Kumar Bajaj, Varun Shukla; analysis and interpretation of results: Xingsi Xue, Himanshu Dhumras, Garima Thakur, Rakesh Kumar Bajaj; draft manuscript preparation: Xingsi Xue, Himanshu Dhumras, Garima Thakur, Rakesh Kumar Bajaj, Varun Shukla. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: All data used to justify the proposed model are given in the manuscript.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Chauhan U, Chhabra H, Rani A, Kumar B, Singh V. Efficient MPPT controller for solar PV system using GWO-CS optimized fuzzy logic control and conventional incremental conductance technique. Iran J Sci Technol Trans Electr Eng. 2023;47(2):463–72. doi:10.1007/s40998-022-00569-3. [Google Scholar] [CrossRef]
2. Chhabra H, Mohan V, Rani A, Singh V. Robust nonlinear fractional order fuzzy PD plus fuzzy I controller applied to robotic manipulator. Neural Comput Applic. 2020;32:2055–79 doi: 10.1007/s00521-019-04074-3. [Google Scholar] [CrossRef]
3. Chhabra H, Mohan V, Rani A, Singh V. Multi-objective cuckoo search algorithm-based 2-DOF FOPD controller for robotic manipulator. In: Rawat B, Trivedi A, Manhas S, Karwal V, editors. Advances in signal processing and communication. Lecture notes in electrical engineering. Singapore: Springer; 2019. Vol. 526. [Google Scholar]
4. Bhatia P, Diaz-Elsayed N. Facilitating decision-making for the adoption of smart manufacturing technologies by SMEs via fuzzy TOPSIS. Int J Prod Econ. 2023;257(8):108762. doi:10.1016/j.ijpe.2022.108762. [Google Scholar] [CrossRef]
5. Aytekin A, Korucuk S, Bayazit Bedirhanoglu S, Simic V. Selecting the ideal sustainable green strategy for logistics companies using a T-spherical fuzzy-based methodology. Eng Appls of Art Intell. 2024;127(Part B):107347. doi:10.1016/j.engappai.2023.107347. [Google Scholar] [CrossRef]
6. Wang Z, Cai Q, Wei G. Modified TODIM method based on cumulative prospect theory with Type-2 neutrosophic number for green supplier selection. Eng Appls of Art Intell. 2023;126(Part B):106843. doi:10.1016/j.engappai.2023.106843. [Google Scholar] [CrossRef]
7. Petchimuthu S, Mahendiran C, Premala T. Power and energy transformation: multi-criteria decision-making utilizing complex q-rung picture fuzzy generalized power prioritized yager operators. Spect Operat Res. 2025;2(1):219–58. doi:10.1016/j.engappai.2025.110621. [Google Scholar] [CrossRef]
8. Abdalla MEM, Uzair A, Ishtiaq A, Tahir M, Kamran M. Algebraic structures and practical implications of interval-valued fermatean neutrosophic super hypersoft sets in healthcare. Spect Operat Res. 2025;2(1):199–218. doi:10.3390/sym16060766. [Google Scholar] [CrossRef]
9. Cuong BC, Kreinovich V. Picture fuzzy sets-A new concept for computational intelligence problems. In: 2013 Third World Congress on Information and Communication Technologies (WICT 2013). Hanoi, Vietnam; 2013. pp. 1–6. doi:10.1109/WICT.2013.7113099. [Google Scholar] [CrossRef]
10. Maji PK, Biswas R, Roy AR. Fuzzy soft sets. J of Fuzzy Math. 2001;117(2):589–602. doi:10.1016/s0165-0114(98)00235-8. [Google Scholar] [CrossRef]
11. Smarandache F. Extension of soft set to hypersoft set, and then to plithogenic hypersoft set. Neutro Sets Syst. 2018;22:168–70. doi:10.61356/j.hsse.2025.3470. [Google Scholar] [CrossRef]
12. Naeem K, Riaz M, Afzal D. Fuzzy neutrosophic soft σ-algebra and fuzzy neutrosophic soft measure with applications. J Intell Fuzzy Syst. 2020;39(1):277–87. doi:10.3233/jifs-191062. [Google Scholar] [CrossRef]
13. Naeem K, Memis S. Picture fuzzy soft σ -algebra and picture fuzzy soft measure and their applications to multi-criteria decision making. Gran Comput. 2023;8(2):397–410. doi:10.1007/s41066-022-00333-2. [Google Scholar] [CrossRef]
14. Jan N, Mahmood T, Zedam L, Ali Z. Multi-valued picture fuzzy soft sets and their applications in group decision-making problems. Soft Comp. 2020;24(24):18857–79. doi:10.1007/s00500-020-05116-y. [Google Scholar] [CrossRef]
15. Saqlain M, Saeed M, Ahmad MR, Smarandache F. Generalization of TOPSIS for neutrosophic hypersoft set using accuracy function and its application. Neutro Sets Syst. 2019;27(1):131–7. doi:10.61356/j.nswa.2023.41. [Google Scholar] [CrossRef]
16. Martin N, Smarandache F. Introduction to combined plithogenic hypersoft sets. Neutro Sets Syst. 2020;35:503–10. doi:10.61356/j.hsse.2025.3470. [Google Scholar] [CrossRef]
17. Yolcu A, Ozturk TY. Fuzzy hypersoft sets and its application to decision-making. Vol. 20, In: Theory and application of hypersoft set. Pons Publishing House; 2021. p. 50–64. [Google Scholar]
18. Yolcu A, Smarandache F, Ozturk TY. Intuitionistic fuzzy hypersoft sets. Commun Facul Scie Univ Ankara Series A1 Mathem Statist. 2021;70(1):443–55. doi:10.61356/j.hsse.2024.2396. [Google Scholar] [CrossRef]
19. Zulqarnain RM, Siddique I, Ali R, Awrejcewicz J, Karamti H, Grzelczyk D, et al. Einstein ordered weighted aggregation operators for Pythagorean fuzzy hypersoft set with its application to solve MCDM problem. IEEE Access. 2022;10:95294–320. doi:10.1109/access.2022.3203717. [Google Scholar] [CrossRef]
20. Zulqarnain RM, Siddique I, Jarad F, Ali R, Abdeljawad T. Development of TOPSIS technique under pythagorean fuzzy hypersoft environment based on correlation coefficient and its application towards the selection of antivirus mask in COVID-19 pandemic. Complexity. 2021;2021(1):6634991. doi:10.1155/2021/6634991. [Google Scholar] [CrossRef]
21. Khan MJ, Kumam P, Ashraf S, Kumam W. Generalized picture fuzzy soft sets and their application in decision support systems. Symmetry. 2019;11(3):415. doi:10.3390/sym11030415. [Google Scholar] [CrossRef]
22. Khan S, Gulistan M, Wahab HA. Development of the structure of q-rung orthopair fuzzy hypersoft set with basic operations. Pun Univ J Math. 2021;53(12):881–92. doi:10.32604/cmes.2023.026169. [Google Scholar] [CrossRef]
23. Chinnadurai V, Robin V. Picture Fuzzy Hypersoft TOPSIS method based on correlation coefficient. J Hyper. 2021;10(2):86–107. doi:10.22436/jmcs.027.02.05. [Google Scholar] [CrossRef]
24. Dhumras H, Bajaj RK. On various aggregation operators for picture fuzzy hypersoft information in decision making application. J Intell Fuzzy Sys. 2023;44(5):7419–47 doi: 10.3233/jifs-222437. [Google Scholar] [CrossRef]
25. Akram M, Khan A, Luqman A, Senapati T, Pamucar D. An extended MARCOS method for MCGDM under 2-tuple linguistic q-rung picture fuzzy environment. Eng Appls Art Intell. 2023;120(11):105892. doi:10.1016/j.engappai.2023.105892. [Google Scholar] [CrossRef]
26. Sirbiladze G, Kacprzyk J, Midodashvili B, Khachidze M, Midodashvili L, Parshutkin I. Possibilistic simulation based interactive fuzzy MAGDM under discrimination q-rung picture linguistic information. Application in educational programs efficiency evaluation. Eng Appls of Art Intell. 2023;123(Part A):106278. doi:10.1016/j.engappai.2023.106278. [Google Scholar] [CrossRef]
27. Dhumras H, Bajaj RK. On novel hellinger divergence measure of neutrosophic hypersoft sets in symptomatic detection of COVID-19. Neutro Sets Sys. 2023;55:265–84 doi: 10.5281/zenodo.7832749. [Google Scholar] [CrossRef]
28. Dhumras H, Bajaj RK, Shukla V. On utilizing modified TOPSIS with R-norm q-rung picture fuzzy information measure green supplier selection. Int J Inf Tech. 2023;15(5):2819–25. doi:10.1007/s41870-023-01304-9. [Google Scholar] [CrossRef]
29. Dhumras H, Shukla PK, Bajaj RK, Jain DK, Shukla V, Shukla PK. On federated learning-oriented q-rung picture fuzzy TOPSIS/VIKOR decision-making approach in electronic marketing strategic plans. IEEE Trans Cons Elec. 2023;70(1):2557–65. doi:10.1109/TCE.2023.3325434. [Google Scholar] [CrossRef]
30. Schweizer B, Sklar A. Probabilistic metric spaces. clustering of interval data based on city-block distances. Pattern Recogn Lett. 1960;25(3):353–65. doi:10.1016/j.patrec.2003.10.016. [Google Scholar] [CrossRef]
31. Liu P, Wang P. Some q-rung Orthopair fuzzy aggregation operators and their applications to multiple-attribute decision making. Int J of Intell Syst. 2018;33(2):259–80 doi: 10.1002/int.21927. [Google Scholar] [CrossRef]
32. Rong Y, Li Q, Pei Z. A novel Q-rung orthopair fuzzy multi-attribute group decision-making approach based on Schweizer-Sklar operations and improved COPRAS method. In: Proceedings of the 4th International Conference on Computer Science and Application Engineering; IOS Press; 2020. p. 1–6. [Google Scholar]
33. Wang P, Liu P. Some Maclaurin symmetric mean aggregation operators based on Schweizer-Sklar operations for intuitionistic fuzzy numbers and their application to decision making. J Intell Fuzzy Syst. 2019;36(4):3801–24 doi: 10.3233/jifs-18801. [Google Scholar] [CrossRef]
34. Khan Q, Khattak H, AlZubi AA, Alanazi JM, Jan N. Multiple attribute group decision-making based on intuitionistic fuzzy Schweizer-Sklar generalized power aggregation operators. Math Probl Eng. 2022:1–34. doi: 10.1155/2022/4634411. [Google Scholar] [CrossRef]
35. Molodtsov DA. Soft set theory-first results. Comp Math Appls. 1999;37(4–5):19–31. [Google Scholar]
36. Dhumras H, Bajaj RK. Modified EDAS method for MCDM in robotic agrifarming with picture fuzzy soft Dombi aggregation operators. Soft Comput. 2023;27:5077–98. doi:10.1007/s00500-023-07927-1. [Google Scholar] [CrossRef]
37. Haiyun C, Zhixiong H, Yuksel S, Dincer H. Analysis of the innovation strategies for green supply chain management in the energy industry using the QFD-based hybrid interval-valued intuitionistic fuzzy decision approach. Renew & Sus Ener Revs. 2021;143:110844. doi:10.1016/j.rser.2021.110844. [Google Scholar] [CrossRef]
38. Alshammari I, Parimala M, Ozel C, Riaz M. Spherical linear diophantine fuzzy TOPSIS algorithm for green supply chain management system. J Fun Spac. 2022;2022:3136462. doi:10.1155/2022/3136462. [Google Scholar] [CrossRef]
39. Toosi SR, Samani JMV. Prioritizing watersheds using a novel hybrid decision model based on fuzzy DEMATEL, fuzzy ANP and fuzzy VIKOR. Water Resour Manag. 2017;31(9):2853–67. doi: 10.1007/s11269-017-1667-9. [Google Scholar] [CrossRef]
40. Lu J, Zhang S, Wu J, Wei Y. Copras method for multiple attribute group decision making under picture fuzzy environment and their application to green supplier selection. Tech Econ Devel of Econ. 2021;27(2):369–85. doi:10.3846/tede.2021.14211. [Google Scholar] [CrossRef]
41. Garg H, Ali Z, Mahmood T, Ali MR, Alburaikan A. Schweizer-Sklar prioritized aggregation operators for intuitionistic fuzzy information and their application in multi-attribute decision-making. Alex Eng J. 2023;67(3):229–40. doi:10.1016/j.aej.2022.12.049. [Google Scholar] [CrossRef]
42. Biswas A, Deb N. Pythagorean fuzzy Schweizer and Sklar power aggregation operators for solving multi-attribute decision-making problems. Gran Comput. 2021;6(4):991–1007. doi:10.1007/s41066-020-00243-1. [Google Scholar] [CrossRef]
43. Mahmood T, Ali Z. Schweizer-Sklar muirhead mean aggregation operators based on pythagorean fuzzy sets and their application in multi-criteria decision-making. In: Garg H, editor. Pythagorean fuzzy sets. Singapore: Springer; 2021. [Google Scholar]
44. Zhang H, Wang F, Geng Y. Multi-criteria decision-making method based on single-valued neutrosophic Schweizer-Sklar muirhead mean aggregation operators. Symmetry. 2019;11(2):152. doi:10.3390/sym11020152. [Google Scholar] [CrossRef]
45. Gayen S, Sarkar A, Biswas A. Schweizer-Sklar operations based hybrid aggregation operator to dual hesitant q-rung orthopair fuzzy set and its application on MCGDM. Exp Sys. 2023;40(7):13257. doi:10.1111/exsy.13257. [Google Scholar] [CrossRef]
46. Wei D, Meng D, Rong Y, Liu Y, Garg H, Pamucar D. Fermatean fuzzy Schweizer-Sklar operators and BWM-entropy-based combined compromise solution approach: an application to green supplier selection. Entropy. 2022;24(6):776. doi:10.3390/e24060776. [Google Scholar] [PubMed] [CrossRef]
47. Peide L, Peng W. Some interval-valued intuitionistic fuzzy Schweizer-Sklar power aggregation operators and their application to supplier selection. Int J Sys Sci. 2018;49(6):1188–211. doi:10.1080/00207721.2018.1442510. [Google Scholar] [CrossRef]
48. Xu Y, Wang J. A novel multiple attribute decision-making method based on Schweizer-Sklar t-norm and t-conorm with q-rung dual hesitant fuzzy information. Arch Cont Sci. 2022;32(1):175–228. doi:10.24425/acs.2022.140870. [Google Scholar] [CrossRef]
49. Tian C, Peng JJ, Zhang ZQ, Wang JQ, Goh M. An extended picture fuzzy MULTIMOORA method based on Schweizer-Sklar aggregation operators. Soft Comp. 2022;26(7):3435–54. doi:10.1007/s00500-021-06690-5. [Google Scholar] [CrossRef]
50. Chen Z, Shen D, Yu F, Tang X, Zhang Z. Multi-attribute decision-making method based on q-rung orthopair probabilistic hesitant fuzzy Schweizer-Sklar power weighted hamy mean operator. PLoS One. 2023;18(2):0266779. doi:10.1371/journal.pone.0266779. [Google Scholar] [CrossRef]
51. Smarandache F. Introduction to the IndetermSoft set and IndetermHyperSoft set. Neutro Sets Syst. 2022;50:629–50. doi:10.61356/j.nswa.2023.41. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF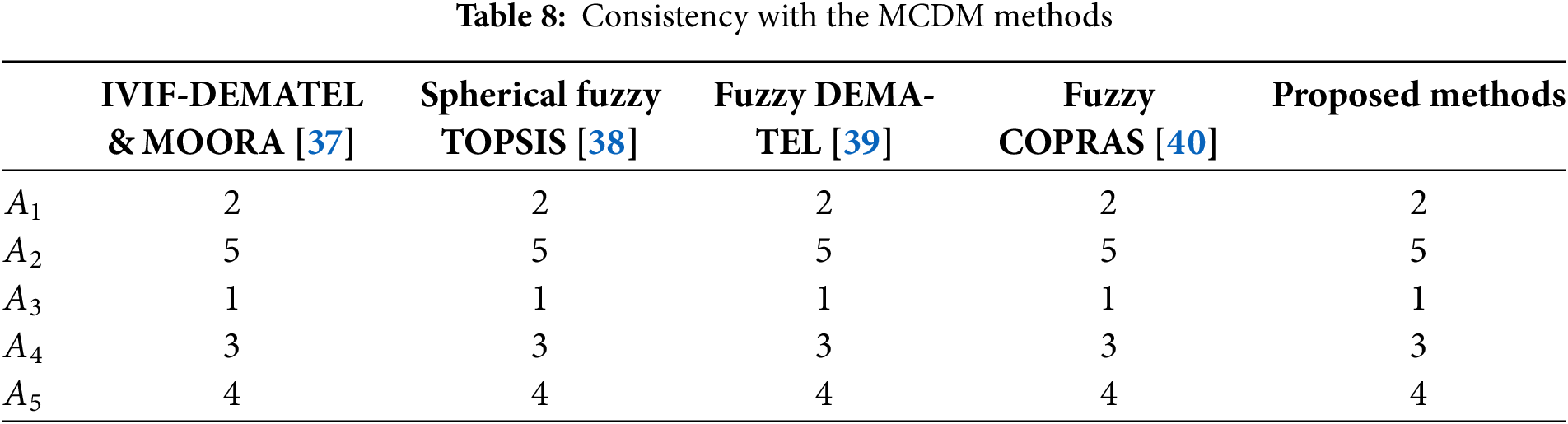
 Downloads
Downloads
 Citation Tools
Citation Tools