Handling Stagnation in Differential Evolution Using Elitism Centroid-Based Operations

1  Introduction

In the engineering domain, mathematical equations describe the behaviour of real systems. However, such an approach requires accurate knowledge of the system. With the system’s increasing complexity, its modelling becomes nonrealistic and inaccurate. To deal with this problem, the artificial neural network (ANN), which can learn and approximate relationships between input and output, was proposed. It has been successfully applied to solve a lot of industrial problems, such as fault diagnosis [1], system control [2], object recognition [3], noise detection [4], image processing [5] and so on. The objective function describing the neural network training problem is multimodal. As a result, gradient-based algorithms easily suffer from a local minimum. Global optimization techniques can be used to remedy this problem. Differential evolution (DE) [6,7], proposed by Storn and Price, is one of the most successful and popular evolutionary algorithms (EAs) for global optimization [8]. In the last two decades, a steady rise has been occurring in the research of DE and its applications to real-world optimization problems [9–11], expert systems [12] and machine learning [13]. Numerous advanced DE variants, such as rank-based DE (RBDE) [14], self-adaptive DE (SaDE) [15], and parameter adaptive DE (JADE) [16], have been proposed, achieving impressively enhanced performance on artificial benchmark functions compared to the classic DE algorithm. However, when DE was applied to train a neural network [17], the performance of most existing variants, such as SaDE and JADE, was unsatisfactory due to stagnation.

The stagnation problem of the DE algorithm was first reported by Lampinen et al. [18] and further discussed by Guo et al. [19]. It refers to the situation where the algorithm fails to improve before finding a global optimal solution. However, unlike premature convergence, stagnation occurred even though the diversity of the population was relatively high. On stagnation, the newly generated individuals are rarely better solutions. To alleviate this problem, many archive-based strategies have been proposed to improve the evolution of stagnant individuals in populations. Historical information in the archive can help the algorithm to make more accurate operations. A successful-parent-selecting (SPS) framework was introduced in [19]. Its main idea was to archive successful update solutions in an external population for parent selection when stagnation occurred. Besides, Zhou et al. [20] presented a DE framework with a guiding archive (GAR) for the same purpose. If a stagnated individual was found, the base solution in the mutation strategy would be replaced by an individual from the guiding archive. The guiding archive stored individuals in several non-overlapping sub-regions of the entire space. Meanwhile, Liang et al. proposed a new Gaussian estimation of distribution algorithm (EDA2) [21], which uses the historical excellent solution archive to assist in estimating the covariance matrix of the Gaussian model. When dealing with the basins of attraction (BoAs), Wang et al. proposed history-guided hill exploration (HGHE-DE) [22], which introduces an archive to store all evaluated solutions. The archived information is used to help separate the search space into hill regions that correspond to the BoAs and calculate the potential of the hill regions. Wang et al. proposed dynamic hybrid niching-based DE (DHNDE) [23] with two archives to store inferior offspring and optimal offspring. The inferior archive limits the exploratory DE runtime to improve diversity, and the optimal archive collects all the excellent solutions to avoid losing them. In the particle swarm optimization (PSO), a PSO variant named scatter learning PSO algorithm (SLPSOA) was proposed by Ren et al. [24], and a scattered pool of high-quality solutions was introduced. Particles select their exemplars in the archive according to a roulette wheel rule to find promising solution regions.

Although the above work has made significant progress in the stagnation problem using historical information in the archive, associations between elite individuals in the parent population are often overlooked in the stagnation problem. This motivates us to propose a framework of elitism centroid-based operations (CMX), where the centroid will be assembled from elite individuals. When stagnation is detected, a centroid-based crossover (CX) rather than the classic binomial crossover is adopted in the DE algorithm. In addition, a novel centroid-based mutation (CM) strategy, “origin-to-centroid”, is also proposed in the framework to improve the convergence efficiency. Empirical results on typical test functions indicate that the proposed CMX method can significantly improve the performance of the classic DE algorithm and its advanced variants. The effectiveness of CMX is further observed in artificial neural network training. DE algorithms improved by CMX achieve the best performance in testing and significantly outperform the original, SPS and GAR methods.

The rest of the paper is organized as follows: Section 2 introduces the basic DE and related work. Section 3 presents the proposed CMX method. Section 4 identifies its superiority through a performance comparison with the original DEs and emerging SPS and GAR frameworks (SPS-DEs and GAR-DEs, respectively) on CEC2014 benchmark functions. Section 5 concludes this paper.

2  Backgrounds

2.1 Classic DE Algorithm

Differential evolution (DE) is a simple yet powerful evolutionary algorithm. Considering a D-dimensional optimization problem, DE maintains a population of candidates, denoted by PG={x→1,G,x→2,G,⋯,x→NP,G}, where NP is the population size, x→i,G=(xi,1,G,xi,2,G,⋯,xi,D,G) is a D-dimensional parameter vector, and G is the generation number. Starting with an initial population P0, three operations are executed at each generation until terminal conditions are fulfilled, as described below.

Mutation: Mutation is conducted on the target vector x→i,G to generate a mutant vector v→i,G. The most frequently used mutation strategies include:

(1) DE/rand/1

v→i,G=x→r1,G+F(x→r2,G−x→r3,G)(1)

(2) DE/best/1

v→i,G=x→best,G+F(x→r1,G−x→r2,G)(2)

(3) DE/current-to-best/1

v→i,G=x→i,G+F(x→best,G−x→i,G)+F(x→r1,G−x→r2,G)(3)

(4) DE/current-to-pbest/1

v→i,G=x→i,G+F(x→pbest,G−x→i,G)+F(x→r1,G−x→r2,G)(4)

where rm∈{1,2,⋯,NP}∖{i} with m=1,2,3 and rm≠rn if m≠n. x→best,G and x→pbest,G are, respectively, the optimal solution and one of the top p × NP fittest solutions at the current generation G, where p is within (0, 1). F is a scaling parameter within (0, 1].

Crossover: Following mutation, crossover is performed between v→i,G and x→i,G to generate a trial individual u→i,G. The widely used binomial crossover is formulated as follows:

ui,j,G={vi,j,Gifrandj(0,1)<CRorj=jrandxi,j,Gotherwise(5)

where randj (0, 1) is a uniformly distributed random number within (0, 1), jrand is a random integer in the range of [1, D], and CR is a crossover factor within [0, 1].

Selection: In selection, the trial vector u→i,G and target vector x→i,G compete, while the fitter one is selected as offspring, i.e.,

x→i,G+1={u→i,Giff(u→i,G)≤f(x→i,G)x→i,Gotherwise(6)

where f(⋅) is the objective function of the problem (Note: Minimization is assumed in Eq. (6)).

2.2 Advanced DE Variants

Many advanced DE variants have been proposed in the past two decades, and their work is summarized in Table S1. The relevant research background is next described in detail in two categories: advanced strategies for mutation/crossover and parameter setting/adaptation.

Concerning advances in mutation/crossover strategies, many modifications have been proposed. The rank-based DE (RBDE) proposed by Sutton et al. [14] imposes pressure by introducing a rank-based differential mutation. Qin et al. [15] proposed the SaDE algorithm, in which four mutation strategies with different characteristics are adaptively used at different searching stages. JADE [16], developed by Zhang and Sanderson, introduces a new “current-to-pbest/1” strategy. In the ensemble of mutation strategies and control parameters with the DE (EPSDE) [25], Mallipeddi et al. improved the performance of DE by ensemble mutation strategies. Composite DE (CoDE) [26], presented by Wang et al., employs three well-studied strategies to sample three candidates and then select the best one. Multi-population ensemble DE (MPEDE) [27], designed by Wu et al., ensembles different mutation strategies into multi-population to effectively adjust the mutation strategies. Wang et al. proposed a novel DE variant based on covariance matrix learning and bimodal distribution parameter setting named CoBiDE [28]. Yu et al. proposed the Global Optimum-based Search in Differential Evolution (DEGoS) [29], which dynamically adjusts the search strategy for stagnant individuals by monitoring unsuccessful global optimum updates and utilizing feedback from the global optimum. Zhang et al. proposed a novel DE based on evolutionary scale adaptation (ESADE) [30] that selects offspring based on the successful evolutionary scale. The Biased Selection Operation in discrete DE (EDE) [31] innovatively reduces individual stagnation probability by permitting inferior trial vectors to enter the subsequent generation population. In objective-dimension feedback method (ODFDE) [32], dimensional information is applied to the adjustment of strategies. Meanwhile, Gao et al. proposed a novel JADE variant with chaotic local search (CLSDE) [33], which integrates a chaotic local search mechanism to enhance the exploration and exploitation of JADE. Meng et al. proposed the Two-stage Differential Evolution (TDE) algorithm [34], which constructs an archive of non-stagnant individuals specifically designed for regenerating stagnant solutions. Furthermore, Zeng et al. introduced a Target Vector Replacement Strategy (TVRS) [35], where stagnant individuals are randomly replaced with non-stagnant individuals to crossover. Besides, Liu et al. proposed the DE algorithm with an attention-based prediction strategy (CDE-AP) [36], significantly enhancing information exchange in mutation operators through an archive that systematically collects non-dominated solutions across all populations. In an adaptive framework (ACoS) [37] proposed by Liu et al., the cumulative superior solutions archive establishes an Eigen coordinate system, which accurately reflects the features of the function landscape.

Concerning parameter settings/adaptation, self-adaptive DE (jDE) [38] encodes F and CR into each solution and has them self-adaptively adjusted. JADE [16] collects the successful parameters F and CR and uses them to produce new parameters using the Cauchy and normal distribution, respectively. Success-history-based adaptive DE (SHADE) [39], proposed by Tanabe et al., enhances the performance of the JADE algorithm by introducing a success history parameters adaptation scheme. CoBiDE [28] introduces a bimodal distribution parameter scheme. Sinusoidal DE (sinDE) [40] introduces a sinusoidal function for setting the F and CR values. The SHADE variant (L-SHADE) [41] improves the performance of SHADE by a linear population size reduction scheme. An L-SHADE variant (L-SHADE_cnEpSin) [42] uses the sinusoidal parameter settings to further enhance L-SHADE. Other techniques, such as Alopex local search (MDEALS) [43] and two-phase-based promising basins identification (TPDE) [44], have also been incorporated into DE to improve performance. DE with ensembling populations (EJADE) algorithm [45] improves JADE with a dual crossover strategy mechanism. DE with domain transform (DTDE) [46], as Zhang et al. proposed, enhances DE’s performance with the domain transform technique. Learning adaptive DE (LDE) [47] combines offline knowledge with online adaptation. Besides, Das et al. introduce the Dynamic DE with Brownian and quantum individuals (DDEBQ) [48], incorporating an Aging mechanism to eliminate individuals. An improved multi-operator DE (IMODE) [49], proposed by Sallam et al., divides populations into sub-populations assigned to distinct operators, their size updated dynamically. A local search (SQP) is used to enhance performance. Tang et al. developed an Individual-Dependent Parameter (IDP) [9] that assigns values to F and CR according to the fitness ranking of each individual. Moreover, two-level parameter adaptation (ADE) [50] was proposed to adjust F and CR based on both the status of the population and individual status. Collective ensemble learning DE (CELDE) [51] combines the advantages of multiple DEs by introducing component decomposition and integration. Recent advancements have seen reinforcement learning techniques effectively integrated into DE frameworks [52,53].

2.3 Stagnation of DE

The stagnation of DE was initially discussed in [18] by investigating the following two phenomena:

(1) The population has not converged to a fixed point, and

(2) DE failed to find any better solutions.

To indicate the diversity of the population PG in generation G, a measure based on the average distance of PG to its centroid, dG has been adopted [19] and defined as

dG=1NP∑i=1NP‖x→i,G−x¯G‖(7)

where x→i,G∈PG, ‖∙‖ is the Euclidean distance and

x¯G=(1/NP)∑i=1NPx→i,G(8)

is the center of PG. If dG could not reach a small enough value, it means that PG converges poorly.

Another measure suggested in [19] helps to reflect DE’s capability to find better solutions. Define qi,G as the number of recent consecutive unsuccessful updates of the i-th candidate in the population PG. We have

qi,G+1={0iff(u→i,G)≤f(x→i,G)qi,G+1otherwisefor i=1,2,⋯,NP(9)

When qi,G≥Q, it implies that DE fails to find better solutions. Here, Q is a pre-defined positive integer called stagnation tolerance. Together with the fact that PG remains diverse, it can be concluded that stagnation occurs in the i-th individual.

3  Proposed Framework

3.1 Motivation

The motivations of the proposed framework lie in the facts that:

(a)   A primary cause of stagnation in the DE algorithm is the limited number of trial vectors that can be generated using the classic binomial crossover operator [18]. In archive-based strategies, historically elite individuals are often employed in the mutation and crossover operations of stagnant solutions. While this approach can enhance the population’s ability to generate promising solutions, reusing historical elites may inadvertently perpetuate stagnation, especially in repetitive evolutionary cycles. To mitigate this risk, it is crucial to prioritize the use of elite individuals from more recent populations, as they better reflect the current evolutionary state of the population.

(b)   For a stagnated solution x→i,G, it is preferable to conduct a crossover between v→i,G and other candidates x→j,G∈PG in the population (or some form of their combinations) rather than between v→i,G and x→i,G. This strategy is based on the understanding that a strong correlation exists between a stagnant solution and the derived mutation vectors. Decreasing this correlation can generate more diverse and potentially beneficial trial vectors. Furthermore, introducing an external candidate solution can offer fresh insights into the fitness landscape, providing valuable new information that may help overcome the current solution’s stagnation.

(c)   In the case of complex multimodal optimization problems, elite individuals are often distributed across multiple local optima during the evolutionary process. As a result, operations that rely on a single elite individual to guide the evolution of stagnant solutions may inadvertently push the population towards multiple sub-optimal regions. To counter this issue, it is essential to consider the positions of various elite individuals within the fitness landscape. This approach allows for a richer pool of information, facilitating a more comprehensive search. Consequently, the trial vectors generated are more likely to survive the selection process, increasing the likelihood of discovering better global optima.

3.2 The CMX Framework

The proposed CMX framework utilizes the stagnation tolerance Q defined in Section 2.3 to detect stagnation. When stagnation occurs in generation G, i.e., qi,G≥Q, a newly designed Centroid-based crossover (CX) replaces the classical binomial crossover. The CX is formulated by:

ui,j,G={vi,j,Gifrandj(0,1)<CRorj=jrandck,j,Gotherwise(10)

where ck,G is the centroid vector defined by:

c→k,G=1k∑i=1kx→i,G(11)

assuming that the population is ranked according to the objective value, i.e., f(x→1,G)≤f(x→2,G)≤⋯≤f(x→NP,G). Therefore, c→k,G is a linear combination of the top k elitism individuals in PG. Furthermore, in order to make the stagnated vectors converge more efficiently, a novel Centroid-based “origin-to-centroid” mutation (CM) strategy is proposed, in which the terminal vector(s) of the difference vector(s) in mutation strategies is replaced by the centroid vector c→k,G. The word “origin” in “origin-to-centroid” indicates the randomly selected or target vector in the original mutation strategy. For instance, the proposed CM strategies for “DE/rand/1” (Eq. (1)) and “DE/current-to-best/1” (Eq. (3)) are given as follows:

v→i,G=x→r1,G+F(c→k,G−x→r2,G)(12)

v→i,G=x→i,G+F(x→best,G−x→i,G)+F(c→k,G−x→r1,G)(13)

Remark: If the terminal vector(s) of difference vector(s) is (are) the best-so-far vector x→best,G or the pbest-so-far vector x→pbest,G as used in the “DE/current-to-pbest/1” [16] mutation strategy in the JADE and SHADE algorithms, there is no need for modification.

To illustrate the effectiveness of CM and CX, we consider a simple example with parameter dimension D = 2 and DE/rand/1. As shown in Fig. 1a, when CX is conducted merely, the original mutation operation, DE/rand/1, may cause the stagnated solution to move away from the centroid c→k,G. Consequently, the possible trial vectors 1 and 2 could still be far from c→k,G even after CX. Fig. 1b illustrates the case for which only CM is adopted. Based on Eq. (11), the mutant vector v→i,G can get close to c→k,G. However, after the classical binomial crossover, the potential trial vectors 1 and 2 are still far from c→k,G. In contrast, by performing CX and CM together, as depicted in Fig. 1c, the generated trial vectors are the closest to the centroid. Due to space limitations, the relation between population diversity dG against generation is included in Fig. S2. As observed, CMX achieves better convergence performance than CM and CX on all the functions, confirming the illustration given.

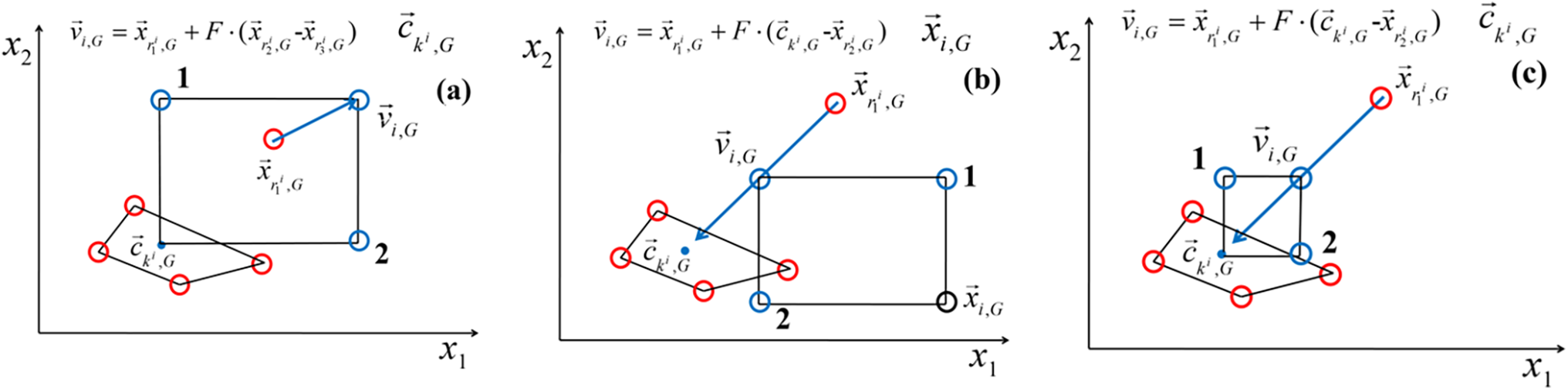
Figure 1: Illustration of centroid based crossover (CX) and centroid based mutation (CM): (a) with CX only; (b) with CM only; (c) with both CX and CM

Algorithm 1 presents the pseudo-code of the proposed CMX framework for DE/rand/1/bin. The green block shows the operation in each generation, while the two yellow blocks show the operations that must be performed depending on whether stagnation has been detected or not.

4  Experimental Result

In this section, experiments are performed on 30 CEC2014 benchmark functions [54] to identify the effectiveness of the proposed CMX method. Following the suggestion in [54], the performance of an algorithm is measured by the best solution E obtained with 104 × D function evaluations, where D is the parameter dimension of the function. E will be taken as zero if smaller than 10–8. For comparison, the “CMX” variants (CMX-DEs) and their competitors (DEs, SPS-DEs [19] and GAR-DEs [20]) are independently run on each function for 51 trials [54]. All the algorithms were implemented using MATLAB language and executed on an Intel Core i7 3.4 GHz PC with 8 GB of RAM in a Windows 10 environment.

For clarity, the significantly better-performed algorithm is highlighted in bold, while the smallest value of E obtained by all compared algorithms is underlined. To compare different algorithms, a 5% significance level Wilcoxon signed-rank test is used to compare each pair of the 51 E values. It should be remarked that the Wilcoxon test considers all 51 results to give conclusive remarks on performance. The symbols “+”, “=”, and “−” indicate that CMX-DEs are significantly better than, the same as and worse than the compared algorithm, respectively. The “+/=/−” in the last rows of the tables gives the comparison summary.

4.1 Effectiveness of the CMX Framework

The CMX framework is integrated with six classic and advanced DE variants: DE/rand/1/bin [6], DE/best/1/bin [6], SaDE [15], RBDE [14], JADE [16], and SHADE [39]. The parameter settings for these algorithms are tabulated in Table S2.

The experimental results on the 30-D (i.e., D = 30) CEC2014 test set are shown in Tables S3 and S4, and the comparison results based on the Wilcoxon signed-rank test are summarized in Table 1. From Tables 1, S3 and S4, it is clear that the CMX framework significantly improves the performance of the original DEs. In 180 cases, CMX-DEs outperform original DEs in 106 cases, perform similarly in 56 cases and only underperform in 18 cases. Specifically, CMX-DE/rand/1/bin wins, ties and loses to DE/rand/1/bin in 26, 1 and 3 functions, respectively. CMX-DE/best/1/bin significantly improves DE/best/1/bin in 19 functions and loses in 1 case (F28). Compared with SaDE, CMX-SaDE is superior in 8 functions and worse in 5 cases. CMX-RBDE exhibits better performance than RBDE in 26 functions. CMX-JADE outperforms JADE in 14 functions but underperforms in 2 (F10 and F14). CMX-SHADE is significantly better than SHADE in 13 functions and worse in 5 (F1, F14, F22, F25 and F28).

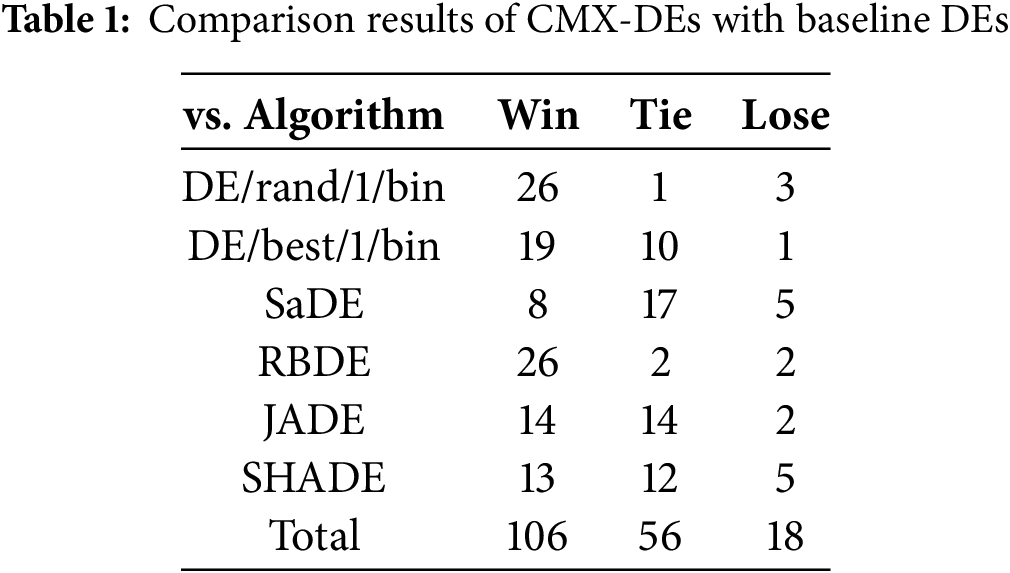
In summary, the CMX framework significantly improves the performance of all six algorithms except SaDE. In SaDE, one of the strategies is the rotationally invariant strategy “DE/current-to-rand/”, in which no crossover is employed. As a result, CX operation is not applied for this case.

To thoroughly evaluate the effectiveness of the CMX framework, we conducted a detailed comparative analysis of CMX-JADE and JADE, focusing on the characteristics of various test functions. As shown in Table S4, CMX-JADE demonstrates a significant performance improvement over JADE across four distinct characteristics of the test functions:

(1)   Unimodal Functions (F1–F3): For functions F1 and F3, CMX-JADE consistently outperforms JADE, while for function F2, both algorithms exhibit comparable performance. Incorporating an elitism centroid within the CMX framework enhances JADE’s convergence capabilities on simpler problems.

(2)   Simple Multimodal Functions (F4–F16): CMX-JADE performs superior on seven functions (F5, F6, F9, F11–F13). This improvement can be attributed to effectively utilizing the elitism centroid within local search regions. In the crossover operations of the CMX framework, the randomly selected x→r1,g element in the “DE/current-to-best/1” strategy has been replaced by the elitism centroid. This modification provides more relevant information that effectively addresses the exploitation needs during the latter stages of the evolutionary process, as opposed to relying solely on random individuals.

(3)   Hybrid Function (F17–F21): CMX-JADE significantly enhances JADE’s performance on functions F18 and F19. In complex problems, the fitness landscape is often characterized by multiple local optima, making it challenging to generate promising solutions using traditional external archives and binomial crossover operations. The elitism centroid leverages multiple elite individuals in the crossover operation, supplying stagnant individuals with information about new candidates outside the current population, thereby improving their exploration capabilities.

(4)   Composition Functions (F23–F30): CMX-JADE outperforms JADE on functions F26 and F28 while demonstrating comparable performance on the remaining functions.

The analysis presented above illustrates that the integration of the CMX framework significantly enhances JADE’s performance, particularly in the context of Simple Multimodal Functions, through effective crossover operations. Furthermore, the CM operations contribute additional potential candidate solutions to the population, thereby improving the algorithm’s overall exploration.

Table 2 shows the comparison results according to multi-problem Wilcoxon’s test. It can be observed that CMX-DE/rand/1/bin, CMX-DE/best/1/bin, CMX-RBDE and CMX-JADE significantly outperform the corresponding baseline DE with a p-value < 0.05. CMX-SHADE also performs better than SHADE but is less significant with a p-value = 0.10.

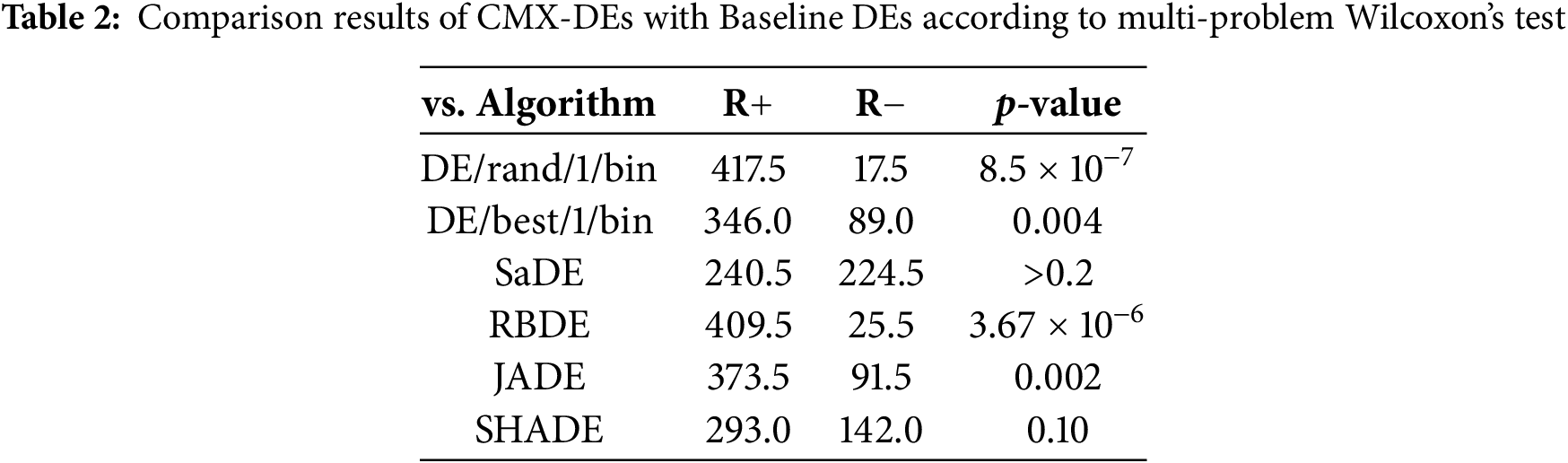
To investigate the stagnation issue, the values of dG and qi,G of each algorithm against generation G are plotted on four representative 30-dimensional functions (unimodal function F3, simple multimodal function F9, hybrid function F19 and composition function F25) over 51 trials, as presented in Figs. 2 and 3.

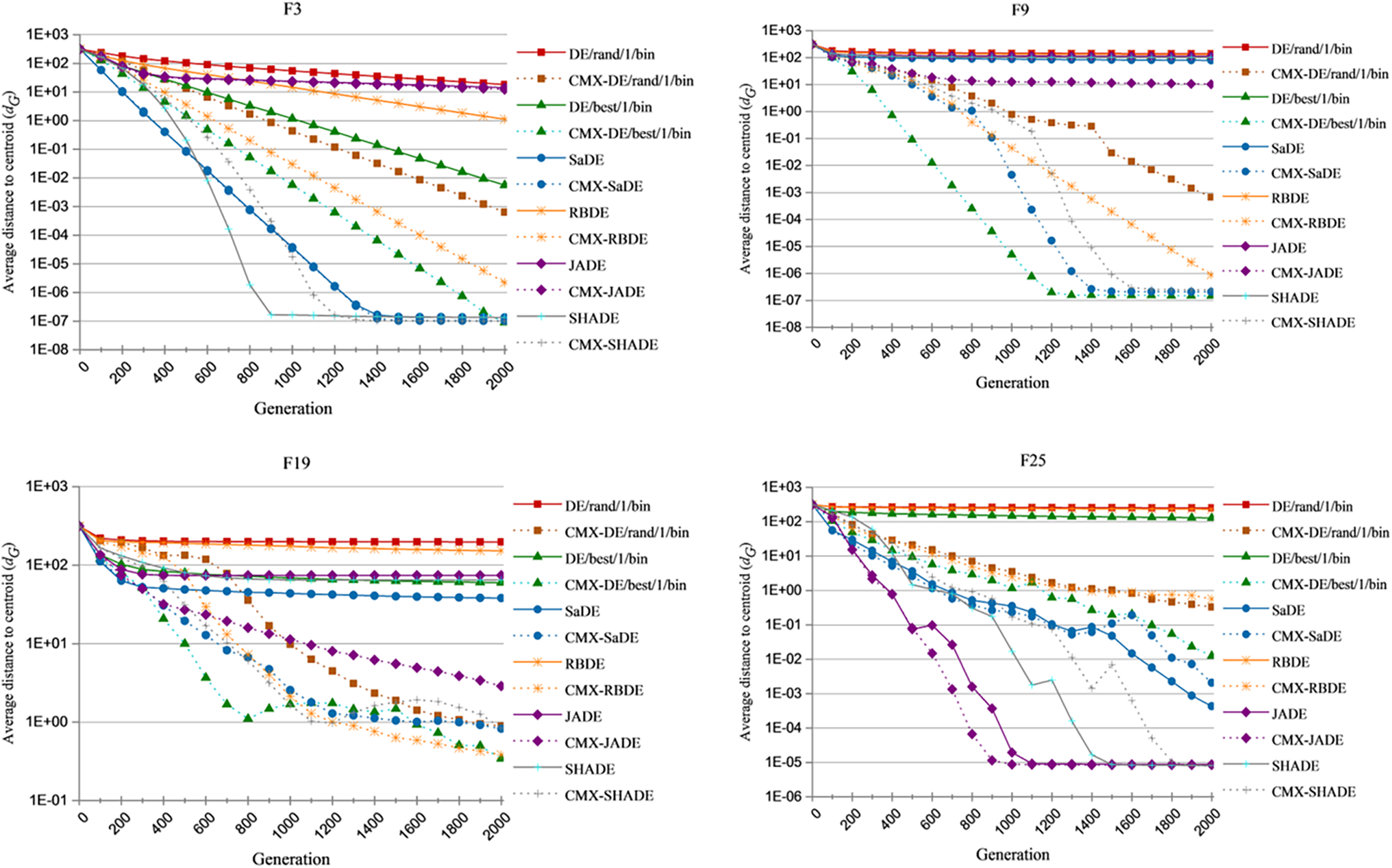
Figure 2: The values of dG achieved by the original DEs and CMX-DEs against generation G on 30-dimensional CEC2014 benchmark functions F3, F9, F19 and F25 over 51 independent runs

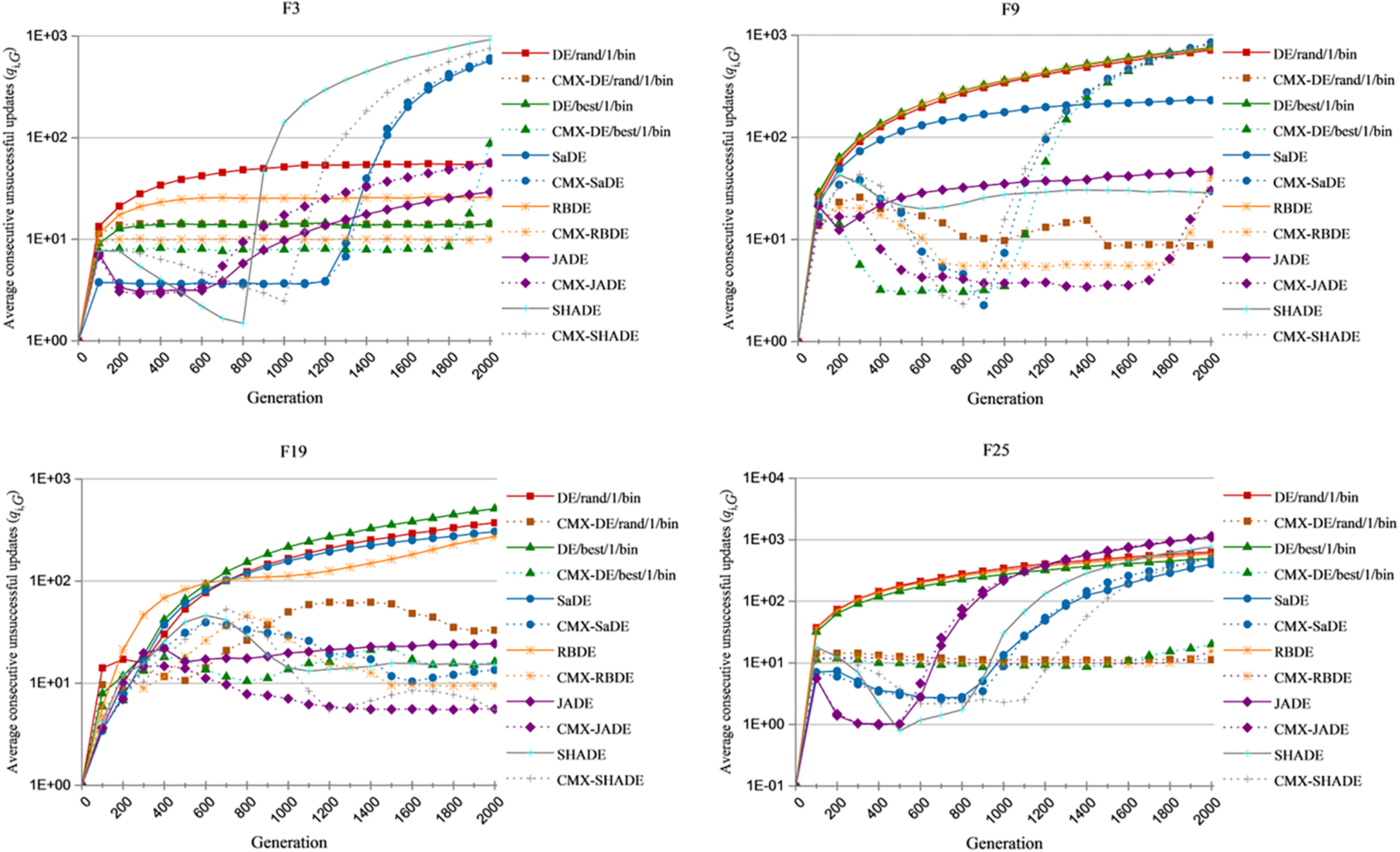
Figure 3: The values of qi,G achieved by the original DEs and CMX-DEs against generation G on 30-dimensional CEC2014 benchmark functions F3, F9, F19 and F25 over 51 independent runs

Fig. 2 shows that dG for most CMX-DEs is much smaller than for the original DEs. For F3, dG for CMX-DE/rand/1/bin, CMX-DE/best/1/bin and CMX-RBDE are much smaller than those for the original DEs. dG has already dropped to small values for SaDE and SHADE, showing no stagnation problem in F3. The CMX framework solves the first F3 stagnation problem, except for JADE. dG remains high for F9 and F19, showing stagnation problems for both. dG values for all CMX-DEs decrease, showing CMX effectiveness. For F25, the dG decrease is significant for most CMX-DEs, except for CMX-SADE, CMX-JADE and CMX-SHADE, which are already at low values. The CMX framework can help the initial DEs converge more efficiently and avoid stagnation.

Fig. 3 shows the variation of the average q values of the CMX-DEs and the original DEs. For F3, the values of qi,G for CMX-DE/rand/1/bin and CMX-RBDE decrease to lower than those of the corresponding DEs. The value of qi,G in CMX-DE/best/1/bin increases with generation, but dG remains small. The population is converging. New individuals are hard to find but not stuck. For F9 and F19, qi,G falls to lower values than the DEs. For F25, qi,G decreases in CMX-DE/rand/1/bin, CMX-DE/best/1/bin and CMX-RBDE. The decrease of qi,G in the CMX-DEs allows the algorithms to search more efficiently and prevents stagnation.

Overall, Figs. 2 and 3, Tables S3 and S4, conclude that the CMX method can deal with stagnation in the original DEs and significantly enhance performance.

4.2 Comparison with the SPS Framework

This subsection compares the CMX framework with the SPS framework presented in [19]. The parameter settings for this subsection are tabulated in Table S2.

The experimental results of CMX-DEs and SPS-DEs on the 30-D CEC2014 functions, presented in Tables S5 and S6 and summarized in Table 3, show that CMX-DEs outperform SPS-DEs in 77 cases, are similar in 69 cases, and inferior in 34 cases out of 180. Specifically, CMX-DE/rand/1/bin excels in 24 functions and underperforms in 6. CMX-DE/best/1/bin outperforms SPS-DE/best/1/bin in 13 functions and lags in 6. CMX-SaDE surpasses SPS-SaDE in 5 functions (F9, F13, F16, F19, F26), but performs worse in 8 (F5, F8, F10, F12, F18, F20, F22, F30). CMX-RBDE is superior in 23 functions and inferior in 4 (F5, F12, F14, F24) compared to SPS-RBDE. CMX-JADE outperforms SPS-JADE in 5 cases (F3, F5, F9, F12, F13) and underperforms in 6 (F6, F10, F11, F15, F22, F28). CMX-SHADE shows superior performance in 7 functions (F5, F9, F17, F18, F19, F21, F23) and inferior performance in 4 (F10, F13, F16, F22) compared to SPS-SHADE. Wilcoxon’s test results in Table 4 indicate that CMX-DE/rand/1/bin and CMX-RBDE significantly outperform their SPS counterparts with other comparable cases.

To evaluate the ability of SPS and CMX frameworks to handle stagnation, the values of dG and qi,G of all the SPS-DEs and CMX-DEs vs. generation G on the four representative functions (F3, F9, F19 and F25) are shown in Figs. S1 and S3, respectively.

Fig. S1 shows that most of the CMX-DEs obtain a much smaller dG value than those of the corresponding SPS-DEs. Moreover, Fig. S3 also shows that CMX-DEs can achieve a smaller qi,G than SPS-DEs in most stagnation cases unless it converges. The smaller dG and qi,G confirm the superiority of CMX over SPS in dealing with stagnation and conclude with the comparison results shown in Tables S4 and S5.

4.3 Comparison with the GAR Framework

This subsection compares the CMX framework with the GAR framework presented in [20]. The related parameters in this subsection are shown in Table S6. It is remarked that the parameters for the GAR method are the same as those suggested in the original literature [20] except DE/best/1/bin. Because the parameter setting of DE/best/1/bin in the original work [20] will cause CMX and GAR to be too convergent. The characteristics of CMX and GAR when solving the stagnation cannot be observed. Thus, a different parameter setting is utilized. Both frameworks are incorporated into the previous six DEs and evaluated for performance comparison.

Tables 5, S8 and S9 summarize the experimental results of CMX-DEs and GAR-DEs on the 30-D test suit. CMX-DEs are more efficient than GAR-DEs. CMX-DEs outperform GAR-DEs in 99 cases, perform similarly in 60 and lose in 21 cases out of 180. Specifically, CMX-DE/rand/1/bin performs better, similar and worse than GAR-DE/rand/1/bin in 18, 5 and 7 functions. CMX-DE/best/1/bin performs better, the same or worse in 28, 2 and 0 functions. CMX-SaDE outperforms GAR-SaDE in 9 cases (F5, F9, F10, F12, F13, F15, F16, F22 and F26) and loses in 5 cases (F6, F8, F14, F23 and F28). CMX-RBDE outperforms GAR-RBDE in 13 functions but underperforms in 2. CMX-JADE performs better than GAR-JADE in 12 functions and worse in 5. CMX-SHADE outperforms GAR-SHADE in 19 functions and performs lower on two (F1 and F25). Table 6 shows that CMX is significantly better in 3 cases (DE/best/1/bin, RBDE and SHADE) with p-value < 0.05.

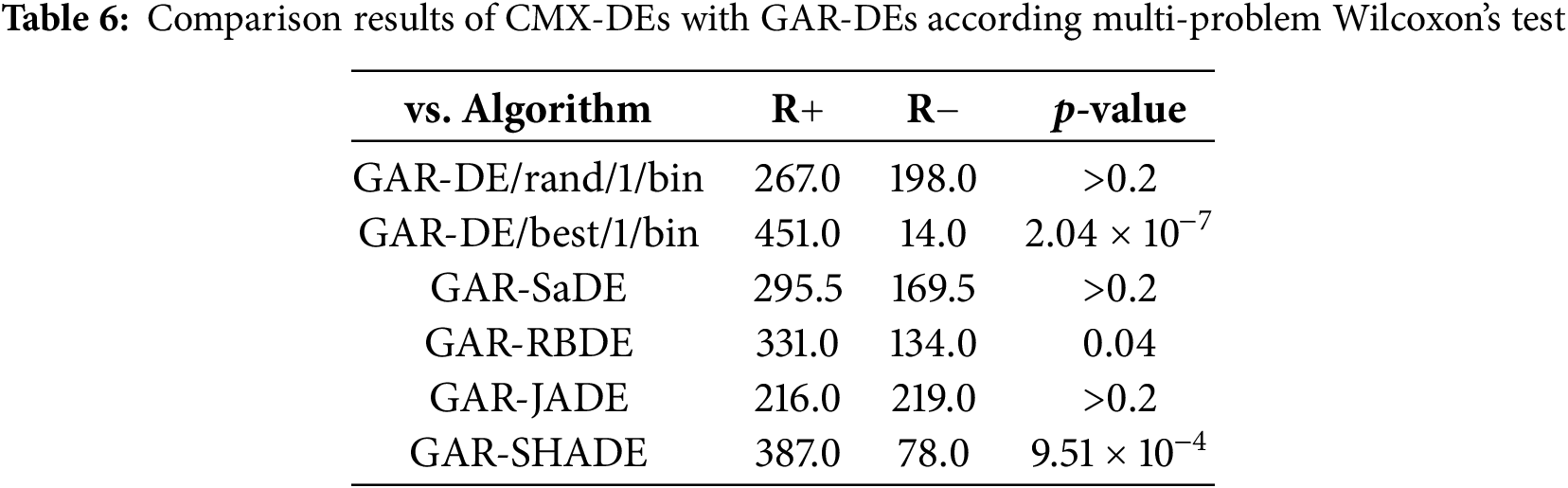
To evaluate the ability of GAR and CMX to solve stagnation, the values of dG and qi,G of all the GAR-DEs and CMX-DEs vs. generation G on the four representative functions (F3, F9, F19 and F25) are shown in Figs. S4 and S5, respectively.

From Fig. S4, it can be observed that most CMX-DEs obtain much smaller dG values than those of the corresponding GAR-DEs. Moreover, Fig. S5 shows that CMX-DEs can achieve smaller qi,G than GAR-DEs in most stagnation cases.

4.4 Comparison with CEC2021 High-Ranking Algorithm

To evaluate the CMX framework, we integrate it with the advanced DE variant (MadDE) algorithm [55], a top performer in CEC 2021 competitions. MadDE uses a multiple adaptation (Mad) strategy and secured second place in non-shifted problem categories. Our analysis compares the CMX-MadDE framework with the baseline MadDE implementation.

Detailed comparative results for 30-D and 50-D problems are presented in Table S14 of the supplementary file. Statistical analysis shows that CMX-MadDE performs best in 12 benchmark functions, equally well in 17, and worst on F17 in 30-D. CMX-MadDE outperforms MadDE in 12 functions, matches its performance in 18, and shows no inferior performance. The following sections explain the improvements of CMX-MadDE through a detailed examination of four problem categories.

(1) Unimodal Functions (F1–F3): CMX-MadDE shows statistically significant improvements over MadDE in F1 and F3 across 30-D and 50-D search spaces.

(2) Simple Multimodal Functions (F4–F16): The CMX-MadDE achieves performance enhancements in F6 and F19 regardless of dimensionality. Notably, in 30-D space, it exhibits superior optimization precision in F9 compared to the baseline algorithm.

(3) Hybrid Function (F17–F21): The statistical results indicate that as the dimensions increase to 50, CMX-MadDE shows a significant improvement in Hybrid Function, except for F19.

(4) Composition Functions (F23–F30): The CMX’s advantage is especially significant in 30-D composition problems, where it outperforms MadDE in 62.5% of cases (5 out of 8 functions). This substantial improvement demonstrates CMX’s effectiveness in navigating complex, multi-component optimization landscapes.

4.5 Overall Performance

The presentation of the results is concluded by summarizing all the functions that have been considered. The empirical cumulative probability distribution function (ECDF) of the normalized solution errors (NSE) measure is employed. Due to page limitations, the definition is provided in the supplemental file. The overall performance of CMX-DEs over the 30-D and 50-D CEC2014 benchmark functions with 51 independent trials is compared with that of its competitor by utilizing the ECDF measure. To this end, the NSEs for all CMX-DEs and their competitors are computed first. The algorithms are then classified as CMX-DE, and comparative DE and their ECDFs are calculated.

Fig. 4 compares CMX-DEs with different DEs, including original DEs, SPS-DEs, and GAR-DEs. These three figures show that the ECDF values of CMX-DEs are almost always higher than those of the original DEs, SPS-DEs, and GAR-DEs, confirming that CMX-DEs exhibit better performance than their competitors.

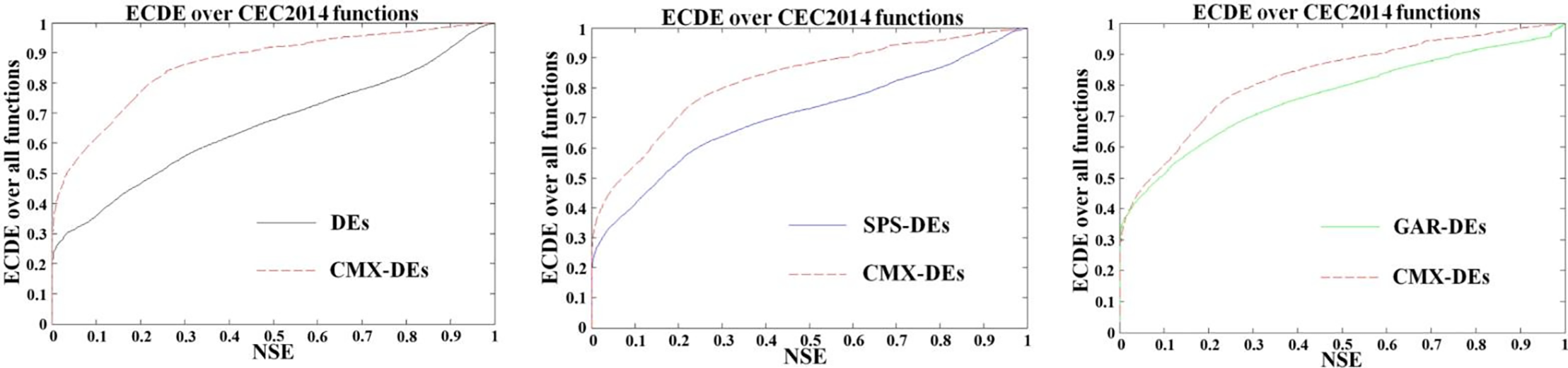
Figure 4: Empirical cumulative probability distribution function (ECDF) of normalized solution errors (NSE) for CMX-DEs and the compared DEs over 30-dimensional and 50-dimensional CEC2014 benchmark sets: (left) vs. original DEs; (middle) vs. SPS-DEs; (right) vs. GAR-DEs

Table S16 compares the time complexity of the considered methods. CMX’s complexity is higher than the origin and SPS but lower than GAR. Due to page limitations, relevant procedures and discussions are presented in the supplemental file.

4.6 Performance Sensitivity to Q

To investigate the performance sensitivity to Q, performances of the previous six CMX algorithms with nine Q values {1, 2, 4, 8, 16, 32, 64, 128, 256} are measured, and the ranking is summarized in Table 7. It can be seen that over-small or over-large Q does not perform well. This is because when Q is too small, CMX is frequently used, which results in a diversity loss, while an over-large Q value indicates that CMX will rarely be performed. Fig. 5 shows the population diversity (dG) against generation on functions F3, F9, F19 and F25 with three Q values: 1, 32 and 256. It is seen that on all the functions, the CMX variant with a smaller Q value has a faster population diversity decrease.

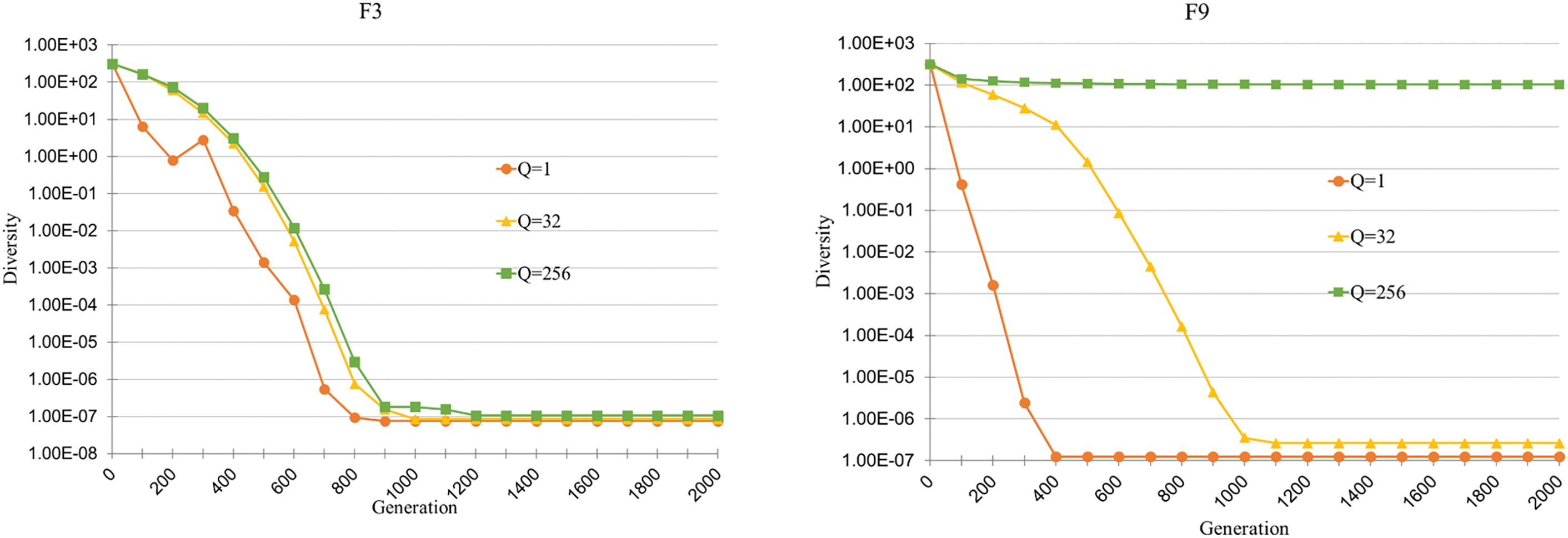
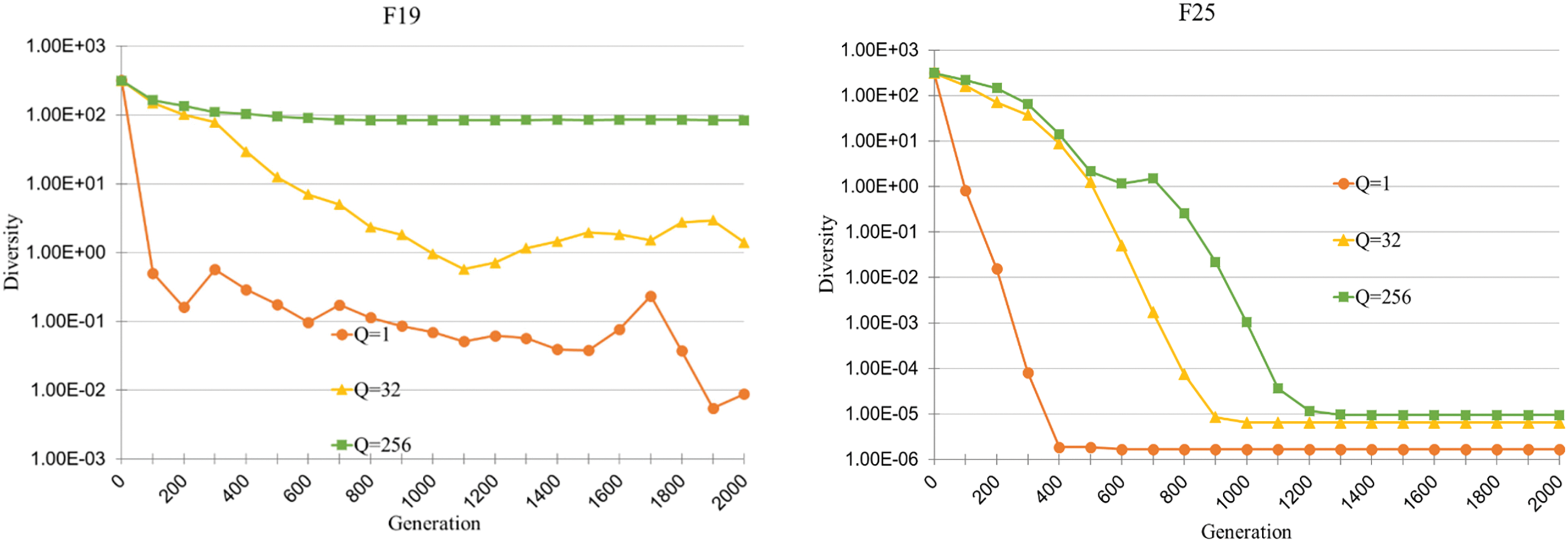
Figure 5: Population diversity against generation of three CMX-SHADE variants with Q = 1, 32, and 256 in the median run

4.7 Comparison of CMX-SHADE with Well-Known DEs

As presented in Tables S5, S6, S8 and S9, the improved CMX-SHADE variant is the best among all the aforementioned algorithms. In addition, we have found that it achieves the optimal performance with Q = 128. In this subsection, CMX-SHADE is further compared with ten well-known DE variants, i.e., jDE [38], SaDE [15], EPSDE [25], JADE [16], CoDE [26], CoBiDE [28], SHADE [39], MPEDE [27], IDE [9] and sinDE [40] on the CEC2013 functions [56]. Parameters for the considered DEs are kept the same as the original literature, and the parameter settings for CMX-SHADE are NP = 100, H = 100, MF = {0.7}, MCR = {0.5}, and Q = 128. The experimental results on the 30- and 50-dimensional CEC2013 functions are shown in Tables S10 and S11, and the comparison results are summarized in Table 8. The number of best (NoB) results obtained by each algorithm out of 28 functions and the overall performance ranking are also presented.

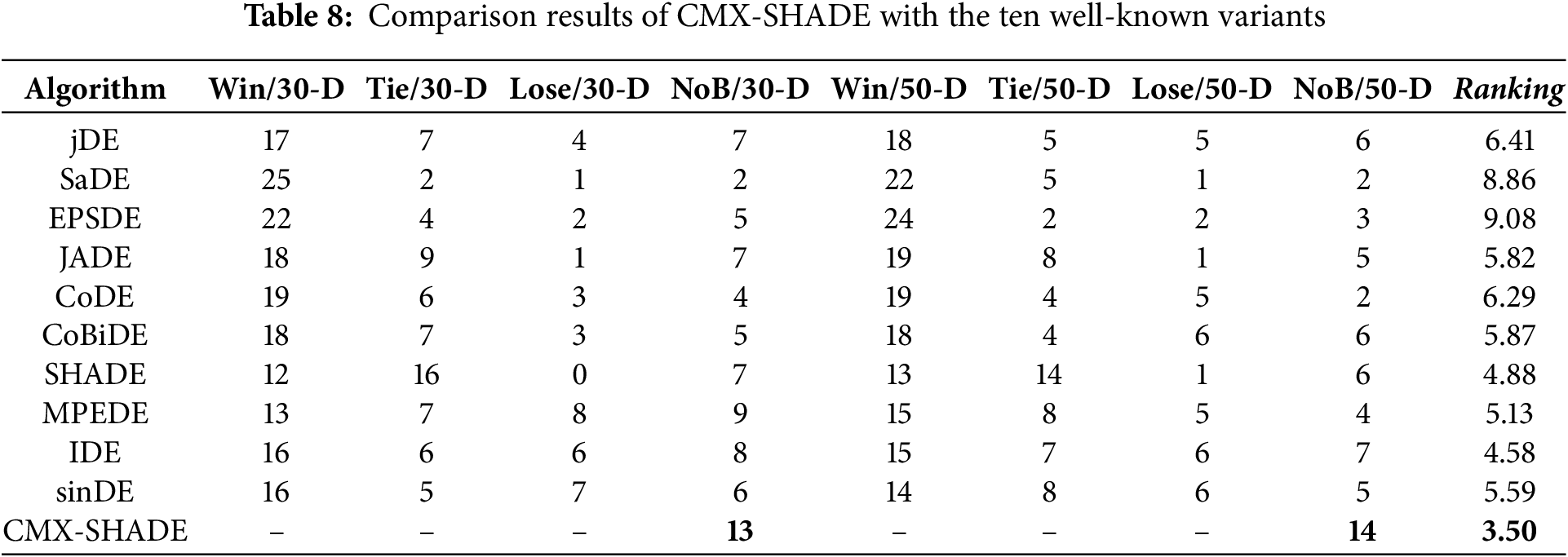
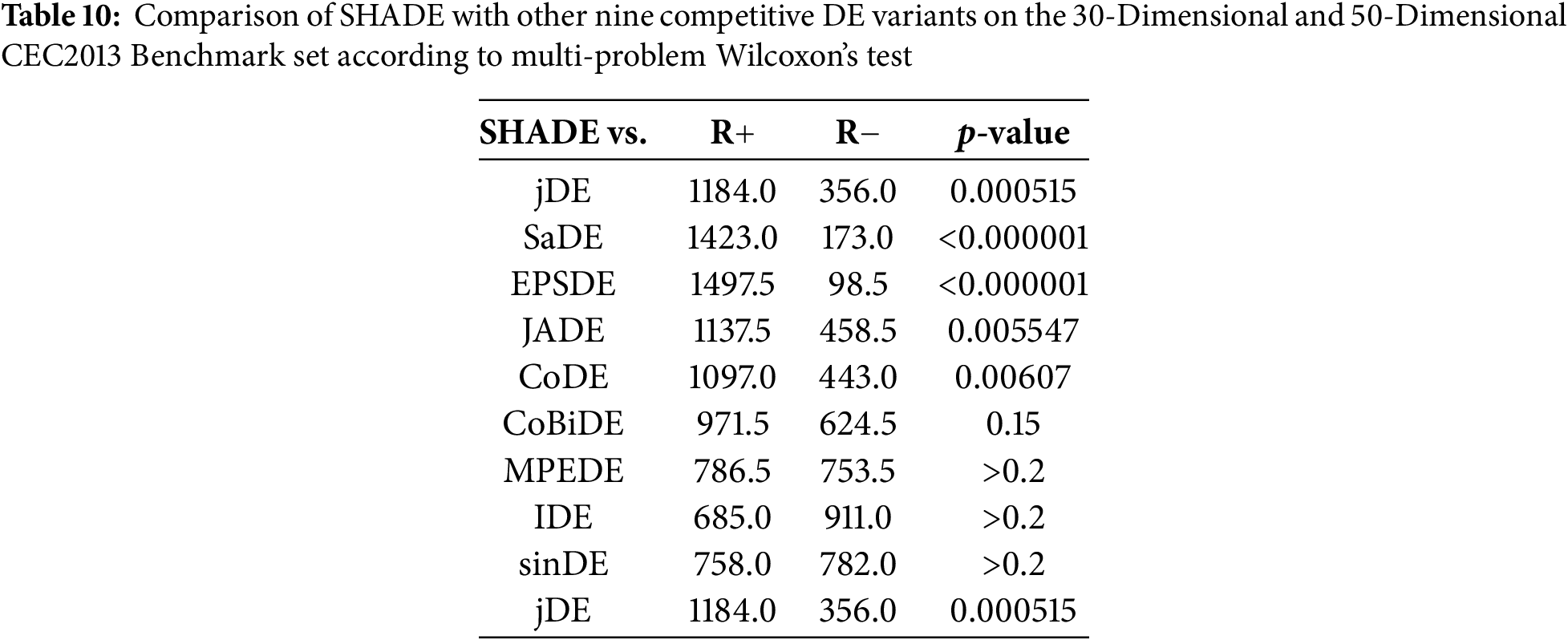
Table 8 shows that CMX-SHADE significantly outperforms the other ten DEs in 30-D and 50-D functions, resulting in a much smaller performance ranking of 3.50. Tables 9 and 10 summarize the multi-problem Wilcoxon’s test of CMX-SHADE and SHADE against other algorithms, respectively. From Table 9, it is seen that CMX-SHADE performs significantly better than all the ten compared algorithms with p-value < 0.05. Unlike Table 10, SHADE is not significantly better in 4 cases (CoBiDE, MPEDE, IDE and sinDE). Thus, it can be concluded that CMX significantly enhances SHADE.

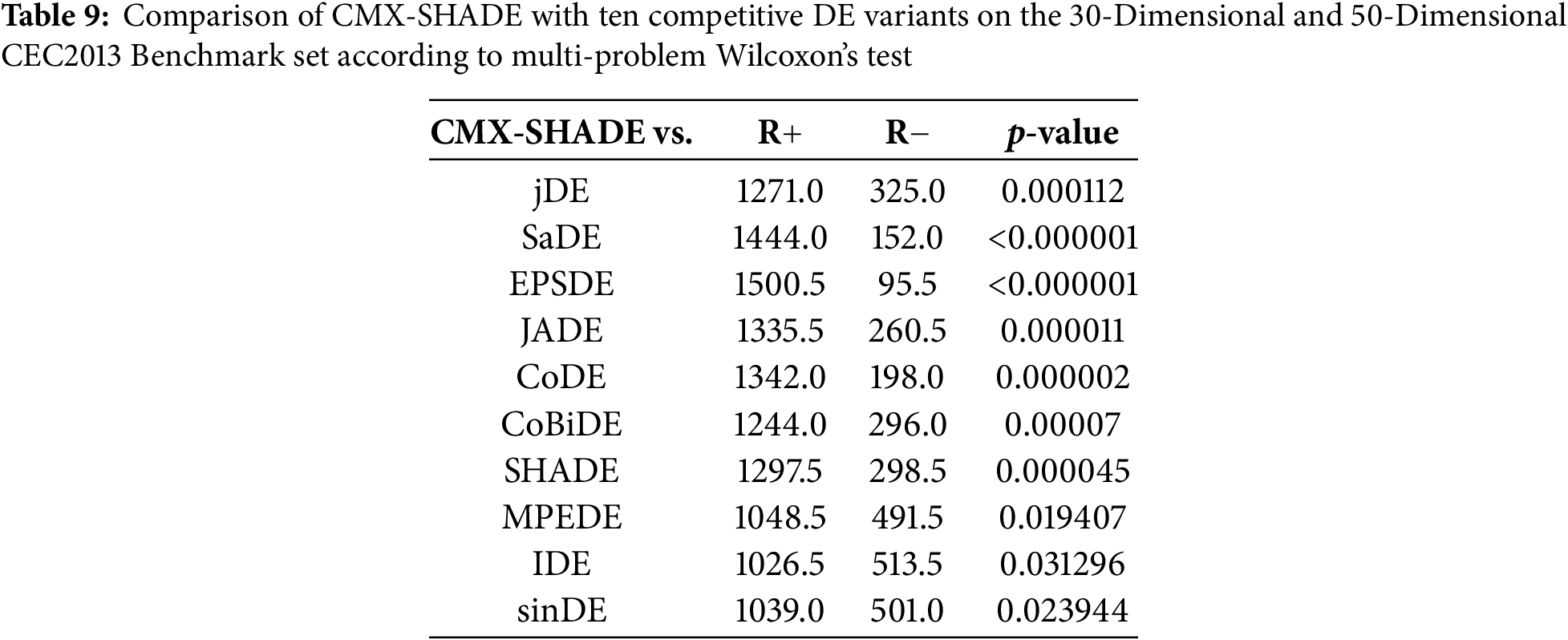
4.8 Incorporation into DEs with Linear Population Size Reduction

To verify CMX’s flexibility, it is further incorporated into two state-of-the-art DEs, namely L-SHADE [41] and L-SHADE_cnEpSin [42], with linear population size reduction. The Q value is set to 64 for optimal performance.

From Tables 11 and S12, CMX-L-SHADE wins in 14 (=8 + 6) and loses in 4 (=3 + 1) cases. CMX-L-SHADE_cnEpSin is significantly better in 15 (=8 + 7) cases and worse in 4 (=2 + 2) cases. This is further confirmed using a multi-problem comparison, as shown in Table 12. The two CMX variants significantly outperform the baselines with p-value < 0.05.

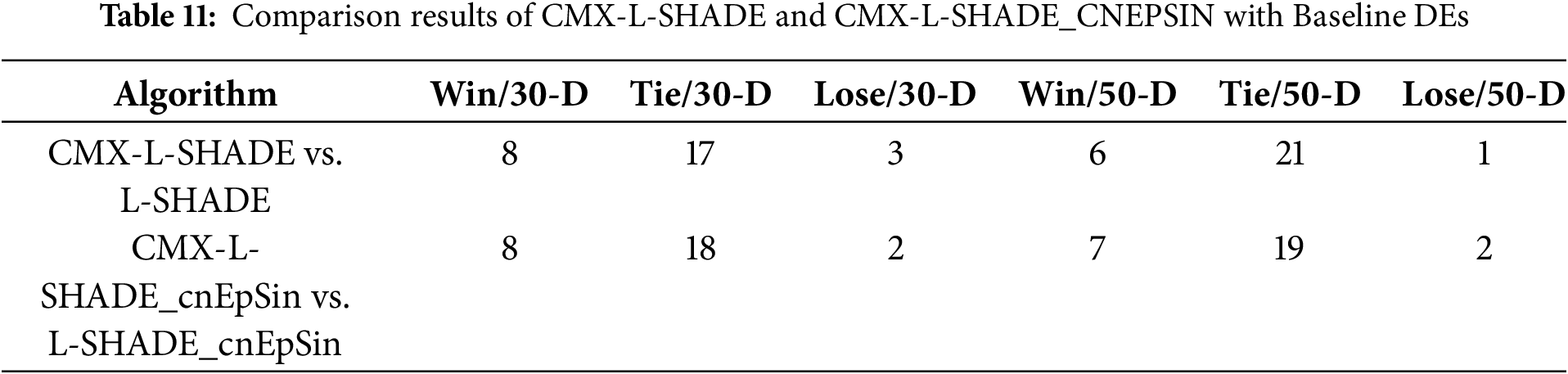
Table S13 compares CMX-L-SHADE_cnEpSin with other competitive evolutionary algorithms (EAs) and swarm-intelligence-based algorithms (SIs), including the continuous non-revisiting genetic algorithm (cNrGA) [57], the dynamic multi-swarm differential learning particle swarm optimizer (DMSDL-PSO) [58] and the restart CMA evolution strategy with increasing population size (IPOP-CMA-ES) [59]. From Table S13, CMX-L-SHADE-cnEpSin outperforms cNrGA, DMSDL-PSO and IPOP-CMA-ES in 52 (=27 + 25), 38 (=20 + 18) and 30 (=13 + 17) cases and underperform in 3 (=1 + 2), 8 (=3 + 5) and 9 (=5 + 4) cases, respectively. From Table S16, according to the multi-problem Wilcoxon’s test, CMX-L-SHADE-cnEpSin is significantly better in all three cases.

5  Conclusion

This paper proposes an elitism centroid-based operations (CMX) framework to deal with the stagnation of classic DE algorithms and advanced DE variants. Once stagnation is detected, the proposed centroid-based mutation and crossover operations help the DE algorithm escape the situation. The proposed CMX method has been incorporated into several classic, well-known and state-of-the-art DE algorithms. Experimental studies on the benchmark functions show the proposed method’s effectiveness and superiority over two recently proposed frameworks. The CMX-SHADE variant, which is improved by the CMX framework, significantly outperforms several well-known DE algorithms. It is also found that CMX has flexibility with DE variants with varying population sizes, namely the L-SHADE and L-SHADE_cnEpSin algorithms. From benchmark results, the CMX-L-SHADE_cnEpSin algorithm demonstrates the best performance.

The effect of parameter Q has also been investigated. Studies show that an overly small or overly large Q setting is inappropriate. Although different algorithms’ optimal settings vary, Q values between 32 and 128 generally perform well. Further investigation into how to adaptively adjust this parameter for different problems or even in different evolution processes of a single problem is an interesting topic.

Future work will refine CMX through enhanced adaptive mechanisms with dynamic parameter tuning and hybrid stagnation metrics using diversity analytics. Validation will extend to other optimization problems, combinatorial optimization, and complex multimodal problems, with theoretical convergence analysis in non-convex environments.

Acknowledgement: Not applicable.

Funding Statement: This research was funded by National Special Project Number for International Cooperation under Grant 2015DFR11050, the Applied Science and Technology Research and Development Special Fund Project of Guangdong Province under Grant 2016B010126004.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, writing—review and editing, funding acquisition, Li Ming Zheng; methodology, software, resources, writing—original draft, Jun Ting Luo. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Supplementary Materials: Supplementary Materials are uploaded separately on submission. https://www.techscience.com/doi/10.32604/cmc.2025.063347/s1.

References

1. Wen L, Gao L, Li X. A new deep transfer learning based on sparse auto-encoder for fault diagnosis. IEEE Trans Syst Man Cybern Syst. 2019;49(1):136–44. doi:10.1109/TSMC.2017.2754287. [Google Scholar] [CrossRef]

2. Yang X, Zheng X. Gradient descent algorithm-based adaptive NN control design for an induction motor. IEEE Trans Syst Man Cybern Syst. 2021;51(2):1027–34. doi:10.1109/TSMC.2019.2894661. [Google Scholar] [CrossRef]

3. Liang M, Hu X. Recurrent convolutional neural network for object recognition. In: Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 2015 Jun 7–12; Boston, MA, USA. p. 3367–75. doi:10.1109/CVPR.2015.7298958. [Google Scholar] [CrossRef]

4. Stallmann CF, Engelbrecht AP. Gramophone noise detection and reconstruction using time delay artificial neural networks. IEEE Trans Syst Man Cybern Syst. 2017;47(6):893–905. doi:10.1109/TSMC.2016.2523927. [Google Scholar] [CrossRef]

5. Jin KH, McCann MT, Froustey E, Unser M. Deep convolutional neural network for inverse problems in imaging. IEEE Trans Image Process. 2017;26(9):4509–22. doi:10.1109/TIP.2017.2713099. [Google Scholar] [PubMed] [CrossRef]

6. Storn R, Price K. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J Global Optim. 1997;11(4):341–59. doi:10.1023/A:1008202821328. [Google Scholar] [CrossRef]

7. Price K, Storn R, Lampinen J. Differential evolution: a practical approach to global optimization. Berlin/Heidelberg, Germany: Springer-Verlag; 2005. [Google Scholar]

8. Das S, Mullick SS, Suganthan PN. Recent advances in differential evolution—an updated survey. Swarm Evol Comput. 2016;27(3):1–30. doi:10.1016/j.swevo.2016.01.004. [Google Scholar] [CrossRef]

9. Tang L, Dong Y, Liu J. Differential evolution with an individual-dependent mechanism. IEEE Trans Evol Comput. 2015;19(4):560–74. doi:10.1109/TEVC.2014.2360890. [Google Scholar] [CrossRef]

10. Gong W, Wang Y, Cai Z, Wang L. Finding multiple roots of nonlinear equation systems via a repulsion-based adaptive differential evolution. IEEE Trans Syst Man Cybern Syst. 2020;50(4):1499–513. doi:10.1109/TSMC.2018.2828018. [Google Scholar] [CrossRef]

11. Wang K, Gao S, Zhou M, Zhan ZH, Cheng J. Fractional order differential evolution. IEEE Trans Evol Comput. 2024. doi:10.1109/TEVC.2024.3382047. [Google Scholar] [CrossRef]

12. Zheng Y, Xu Z, Li Y, Pedrycz W, Yi Z. Biobjective optimization method for large-scale group decision making based on hesitant fuzzy linguistic preference relations with granularity levels. IEEE Trans Fuzzy Syst. 2024;32(8):4759–71. doi:10.1109/TFUZZ.2024.3409720. [Google Scholar] [CrossRef]

13. Hancer E, Xue B, Zhang M. A multimodal multiobjective evolutionary algorithm for filter feature selection in multilabel classification. IEEE Trans Artif Intell. 2024;5(9):4428–42. doi:10.1109/TAI.2024.3380590. [Google Scholar] [CrossRef]

14. Sutton AM, Lunacek M, Whitley LD. Differential evolution and non-separability: using selective pressure to focus search. In: Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation; 2007 Jul 7–11; London, UK. p. 1428–35. doi:10.1145/1276958.1277221. [Google Scholar] [CrossRef]

15. Qin AK, Huang VL, Suganthan PN. Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Trans Evol Comput. 2009;13(2):398–417. doi:10.1109/TEVC.2008.927706. [Google Scholar] [CrossRef]

16. Zhang J, Sanderson AC. JADE: adaptive differential evolution with optional external archive. IEEE Trans Evol Comput. 2009;13(5):945–58. doi:10.1109/TEVC.2009.2014613. [Google Scholar] [CrossRef]

17. Piotrowski AP. Differential evolution algorithms applied to Neural Network training suffer from stagnation. Appl Soft Comput. 2014;21(3):382–406. doi:10.1016/j.asoc.2014.03.039. [Google Scholar] [CrossRef]

18. Lampinen J, Zelinka I. On stagnation of the differential evolution algorithm. In: Proceedings of the 6th International Conference on Soft Computing; 2000 Jun 7–9; Brno, Czech Republic. p. 76–83. [Google Scholar]

19. Guo SM, Yang CC, Hsu PH, Tsai JSH. Improving differential evolution with a successful-parent-selecting framework. IEEE Trans Evol Comput. 2015;19(5):717–30. doi:10.1109/TEVC.2014.2375933. [Google Scholar] [CrossRef]

20. Zhou Y, Wang J, Zhou Y, Qiu Z, Bi Z, Cai Y. Differential evolution with guiding archive for global numerical optimization. Appl Soft Comput. 2016;43(4):424–40. doi:10.1016/j.asoc.2016.02.011. [Google Scholar] [CrossRef]

21. Liang Y, Ren Z, Yao X, Feng Z, Chen A, Guo W. Enhancing Gaussian estimation of distribution algorithm by exploiting evolution direction with archive. IEEE Trans Cybern. 2020;50(1):140–52. doi:10.1109/TCYB.2018.2869567. [Google Scholar] [PubMed] [CrossRef]

22. Wang J, Li C, Zeng S, Yang S. History-guided hill exploration for evolutionary computation. IEEE Trans Evol Comput. 2023;27(6):1962–75. doi:10.1109/TEVC.2023.3250347. [Google Scholar] [CrossRef]

23. Wang K, Gong W, Deng L, Wang L. Multimodal optimization via dynamically hybrid niching differential evolution. Knowl Based Syst. 2022;238(3):107972. doi:10.1016/j.knosys.2021.107972. [Google Scholar] [CrossRef]

24. Ren Z, Zhang A, Wen C, Feng Z. A scatter learning particle swarm optimization algorithm for multimodal problems. IEEE Trans Cybern. 2014;44(7):1127–40. doi:10.1109/TCYB.2013.2279802. [Google Scholar] [PubMed] [CrossRef]

25. Mallipeddi R, Suganthan PN, Pan QK, Tasgetiren MF. Differential evolution algorithm with ensemble of parameters and mutation strategies. Appl Soft Comput. 2011;11(2):1679–96. doi:10.1016/j.asoc.2010.04.024. [Google Scholar] [CrossRef]

26. Wang Y, Cai Z, Zhang Q. Differential evolution with composite trial vector generation strategies and control parameters. IEEE Trans Evol Comput. 2011;15(1):55–66. doi:10.1109/TEVC.2010.2087271. [Google Scholar] [CrossRef]

27. Wu G, Mallipeddi R, Suganthan PN, Wang R, Chen H. Differential evolution with multi-population based ensemble of mutation strategies. Inf Sci. 2016;329:329–45. doi:10.1016/j.ins.2015.09.009. [Google Scholar] [CrossRef]

28. Wang Y, Li HX, Huang T, Li L. Differential evolution based on covariance matrix learning and bimodal distribution parameter setting. Appl Soft Comput. 2014;18(4):232–47. doi:10.1016/j.asoc.2014.01.038. [Google Scholar] [CrossRef]

29. Yu Y, Gao S, Wang Y, Todo Y. Global optimum-based search differential evolution. IEEE/CAA J Autom Sin. 2019;6(2):379–94. doi:10.1109/JAS.2019.1911378. [Google Scholar] [CrossRef]

30. Zhang SX, Hu XR, Zheng SY. Differential evolution with evolutionary scale adaptation. Swarm Evol Comput. 2024;85(1):101481. doi:10.1016/j.swevo.2024.101481. [Google Scholar] [CrossRef]

31. Zhao F, Zhao L, Wang L, Song H. An ensemble discrete differential evolution for the distributed blocking flowshop scheduling with minimizing makespan criterion. Expert Syst Appl. 2020;160:113678. doi:10.1016/j.eswa.2020.113678. [Google Scholar] [CrossRef]

32. Zhang SX, Zheng SY, Zheng LM. Differential evolution with objective and dimension knowledge utilization. Swarm Evol Comput. 2023;80:101322. doi:10.1016/j.swevo.2023.101322. [Google Scholar] [CrossRef]

33. Gao S, Yu Y, Wang Y, Wang J, Cheng J, Zhou M. Chaotic local search-based differential evolution algorithms for optimization. IEEE Trans Syst Man Cybern Syst. 2021;51(6):3954–67. doi:10.1109/TSMC.2019.2956121. [Google Scholar] [CrossRef]

34. Meng Z, Yang C. Two-stage differential evolution with novel parameter control. Inf Sci. 2022;596(6):321–42. doi:10.1016/j.ins.2022.03.043. [Google Scholar] [CrossRef]

35. Zeng Z, Zhang M, Hong Z, Zhang H, Zhu H. Enhancing differential evolution with a target vector replacement strategy. Comput Stand Interfaces. 2022;82:103631. doi:10.1016/j.csi.2022.103631. [Google Scholar] [CrossRef]

36. Liu XF, Zhang J, Wang J. Cooperative differential evolution with an attention-based prediction strategy for dynamic multiobjective optimization. IEEE Trans Syst Man Cybern Syst. 2023;53(12):7441–52. doi:10.1109/TSMC.2023.3298804. [Google Scholar] [CrossRef]

37. Liu ZZ, Wang Y, Yang S, Tang K. An adaptive framework to tune the coordinate systems in nature-inspired optimization algorithms. IEEE Trans Cybern. 2019;49(4):1403–16. doi:10.1109/TCYB.2018.2802912. [Google Scholar] [PubMed] [CrossRef]

38. Brest J, Greiner S, Boskovic B, Mernik M, Zumer V. Self-adapting control parameters in differential evolution: a comparative study on numerical benchmark problems. IEEE Trans Evol Comput. 2006;10(6):646–57. doi:10.1109/TEVC.2006.872133. [Google Scholar] [CrossRef]

39. Tanabe R, Fukunaga A. Success-history based parameter adaptation for differential evolution. In: Proceedings of the 2013 IEEE Congress on Evolutionary Computation; 2013 Jun 20–23; Cancun, Mexico. p. 71–8. doi:10.1109/CEC.2013.6557555. [Google Scholar] [CrossRef]

40. Draa A, Bouzoubia S, Boukhalfa I. A sinusoidal differential evolution algorithm for numerical optimisation. Appl Soft Comput. 2015;27(2):99–126. doi:10.1016/j.asoc.2014.11.003. [Google Scholar] [CrossRef]

41. Tanabe R, Fukunaga AS. Improving the search performance of SHADE using linear population size reduction. In: Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC); 2014 Jul 6–11; Beijing, China. p. 1658–65. doi:10.1109/CEC.2014.6900380. [Google Scholar] [CrossRef]

42. Awad NH, Ali MZ, Suganthan PN. Ensemble sinusoidal differential covariance matrix adaptation with Euclidean neighborhood for solving CEC2017 benchmark problems. In: Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC); 2017 Jun 5–8; Donostia, Spain. p. 372–9. doi:10.1109/CEC.2017.7969336. [Google Scholar] [CrossRef]

43. Leon M, Xiong N, Molina D, Herrera F. A novel memetic framework for enhancing differential evolution algorithms via combination with Alopex local search. Int J Comput Intell Syst. 2019;12(2):795–808. doi:10.2991/ijcis.d.190711.001. [Google Scholar] [CrossRef]

44. Ghosh A, Das S, Das AK. A simple two-phase differential evolution for improved global numerical optimization. Soft Comput. 2020;24(8):6151–67. doi:10.1007/s00500-020-04750-w. [Google Scholar] [CrossRef]

45. Yi W, Chen Y, Pei Z, Lu J. Adaptive differential evolution with ensembling operators for continuous optimization problems. Swarm Evol Comput. 2022;69(4):100994. doi:10.1016/j.swevo.2021.100994. [Google Scholar] [CrossRef]

46. Zhang SX, Wen YN, Liu YH, Zheng LM, Zheng SY. Differential evolution with domain transform. IEEE Trans Evol Comput. 2023;27(5):1440–55. doi:10.1109/TEVC.2022.3220424. [Google Scholar] [CrossRef]

47. Sun J, Liu X, Bäck T, Xu Z. Learning adaptive differential evolution algorithm from optimization experiences by policy gradient. IEEE Trans Evol Comput. 2021;25(4):666–80. doi:10.1109/TEVC.2021.3060811. [Google Scholar] [CrossRef]

48. Das S, Mandal A, Mukherjee R. An adaptive differential evolution algorithm for global optimization in dynamic environments. IEEE Trans Cybern. 2014;44(6):966–78. doi:10.1109/TCYB.2013.2278188. [Google Scholar] [PubMed] [CrossRef]

49. Sallam KM, Elsayed SM, Chakrabortty RK, Ryan MJ. Improved multi-operator differential evolution algorithm for solving unconstrained problems. In: 2020 IEEE Congress on Evolutionary Computation (CEC); 2020 Jul 19–24; Glasgow, UK. p. 1–8. doi:10.1109/cec48606.2020.9185577. [Google Scholar] [CrossRef]

50. Yu WJ, Shen M, Chen WN, Zhan ZH, Gong YJ, Lin Y, et al. Differential evolution with two-level parameter adaptation. IEEE Trans Cybern. 2014;44(7):1080–99. doi:10.1109/TCYB.2013.2279211. [Google Scholar] [CrossRef]

51. Zhang SX, Liu YH, Zheng LM, Zheng SY. Differential evolution with collective ensemble learning. Swarm Evol Comput. 2024;87:101521. doi:10.1016/j.swevo.2024.101521. [Google Scholar] [CrossRef]

52. Huynh TN, Do DTT, Lee J. Q-Learning-based parameter control in differential evolution for structural optimization. Appl Soft Comput. 2021;107(11):107464. doi:10.1016/j.asoc.2021.107464. [Google Scholar] [CrossRef]

53. Tatsis VA, Parsopoulos KE. Reinforcement learning for enhanced online gradient-based parameter adaptation in metaheuristics. Swarm Evol Comput. 2023;83(2):101371. doi:10.1016/j.swevo.2023.101371. [Google Scholar] [CrossRef]

54. Liang JJ, Qu BY, Suganthan PN. Problem definitions and evaluation criteria for the CEC 2014 special session and competition on single objective real-parameter numerical optimization. Singapore: Nanyang Technological University; 2013. Report No.: 201311. [Google Scholar]

55. Biswas S, Saha D, De S, Cobb AD, Das S, Jalaian BA. Improving differential evolution through Bayesian hyperparameter optimization. In: 2021 IEEE Congress on Evolutionary Computation (CEC); 2021 Jun 28–Jul 1; Kraków, Poland. p. 832–40. doi:10.1109/cec45853.2021.9504792. [Google Scholar] [CrossRef]

56. Liang JJ, Qu BY, Suganthan PN, Hernández-Díaz AG. Problem definitions and evaluation criteria for the CEC2013 special session on real-parameter optimization. Singapore: Nanyang Technological University; 2013. Report No.: 201212. [Google Scholar]

57. Lou Y, Yuen SY. Non-revisiting genetic algorithm with adaptive mutation using constant memory. Memet Comput. 2016;8(3):189–210. doi:10.1007/s12293-015-0178-6. [Google Scholar] [CrossRef]

58. Chen Y, Li L, Peng H, Xiao J, Wu Q. Dynamic multi-swarm differential learning particle swarm optimizer. Swarm Evo Comput. 2018;39(1):209–2. doi:10.1016/j.swevo.2017.10.004. [Google Scholar] [CrossRef]

59. Auger A, Hansen N. A restart CMA evolution strategy with increasing population size. In: Proceedings of the 2005 IEEE Congress on Evolutionary Computation; 2005 Sep 2–5; Edinburgh, UK. p. 1769–76. doi:10.1109/CEC.2005.1554902. [Google Scholar] [CrossRef]