Design and Application of a New Distributed Dynamic Spatio-Temporal Privacy Preserving Mechanisms

1  Introduction

In today’s era of unprecedented data explosion, where global data volume is projected to exceed 180 zettabytes by 2025, the significance of robust privacy protection mechanisms has become paramount across all technological domains. The Internet of Things (IoT), as a revolutionary technology, has drastically enhanced the intelligence level of daily life and work while also exacerbating the risk of information leakage, garnering widespread attention [1–3]. The unique architecture of IoT systems, characterized by their distributed nature, resource constraints, and real-time data processing requirements, presents exceptional challenges for privacy preservation. In recent years, scholars have devoted substantial efforts to exploring and developing specialized privacy protection technologies tailored to the distinctive characteristics of IoT environments. These efforts aim to achieve the delicate balance of ensuring ironclad security for personal and sensitive information while not hindering the remarkable progress and widespread application of IoT technology across various sectors, including healthcare, smart cities, and industrial automation. The stakes are particularly high in safety-critical applications such as connected vehicles, where privacy breaches could have threatening consequences. Moussaoui et al. proposed a novel approach to managing the Pseudonym Certificate (PC) switching periods between vehicles, using a Common PC (CPC) for a short period before switching to a new PC. It shows significant improvement in privacy protection [4]. Xu et al. propose a security and privacy protection communication protocol for the Internet of Vehicles in smart cities. In terms of security, Burrows-Abadi-Needham logic and the Scyther formal verification tool are utilized for security verification, which reduces computation and communication costs [5]. Amin et al. proposed a robust protocol based on Bidi et al.s’ protocol, guaranteeing high-level security protection against existing security attacks [6]. Therefore, finding a balance between fostering technological innovation and safeguarding personal privacy has emerged as a critical direction in current research [7].

In the realm of IoT data privacy protection, differential privacy, secure multi-party computation, and data anonymization techniques are widely discussed [8–10]. Zhang et al. proposed a blockchain-based asymmetric group key agreement protocol for IoV (B-AGKA), in which blockchain anonymous authentication technology is adopted to achieve users’ privacy protection, which reduces the overhead and achieves traceability [11]. Differential privacy achieves strong privacy protection by adding noise to query results. While theoretically sound, the noise affects data accuracy, and the technical implementation requires complex parameter adjustments [12]. Secure multi-party computation enables collaborative computations without disclosing individual data, but it incurs high computational and communication costs, making it challenging to adapt to the resource-constrained IoT environment [13]. Data anonymization techniques (such as K-Anonymity, L-Diversity, and T-Closeness) ensure privacy through data generalization, but they demonstrate low efficiency when dealing with large-scale and rapidly changing data streams [14]. Although these methods each offer advantages in privacy provision, they present limitations in real-time data processing, accuracy assurance, and adaptability to IoT environments [15–17]. Addressing challenges in processing efficiency, system reliability, and technical scalability is crucial for advancing IoT privacy protection. New progress has been made in the research of privacy preservation for dynamic data streams. Kumar [18] proposed a sliding window-based incremental anonymization method, which adapts to data distribution changes by dynamically adjusting the generalization level. Aiming at the challenges of high-dimensional data, Zhang et al. [19] developed a hybrid index structure that combines KD-Tree and R*-Tree to achieve fast nearest neighbor search. For distributed processing, Wei and Kerschbaum [20] designed a Spark-based parallel K-Anonymity framework with locally sensitive hashing to optimize data partitioning. These methods improve the performance in specific dimensions, but fail to effectively address the coupling of dimensional catastrophe and communication overhead in dynamic spatio-temporal scenarios, and lack a systematic scheme in terms of balancing privacy protection strength and data utility.

The core motivation of this research stems from three unsolved challenges in Telematics scenarios:

•   Efficiency bottleneck in high-dimensional data processing: Traditional approaches (e.g., KD-Tree) exhibit O(n2) time complexity at Quasi-identifier (QI, Components of personally identifying information) = 9 (reaching 91 s CPPM runtime in our experiments), while our method, PEV-Tree would achieve O(nlog n) complexity through dimensionality reduction.

•   Privacy-utility trade-off imbalance in dynamic environments: Existing schemes (e.g., the pseudonym switching mechanism in [4]) demonstrate 5.2% information leakage probability under homogeneity attacks, whereas our new mechanism DST-PPM would reduce this to 0.19% via T-Closeness constraints.

•   Deficiency in heterogeneous data collaboration: The benchmark method CASTLE [21] in mixed data scenarios (6 numerical values + 3 categorical attributes) yields a suboptimal GLM value of 0.62, while our solution improves this to 0.31.

To meet the requirements of efficiency, reliability, and scalability in IoT data privacy protection, this paper proposes an enhanced data structure, the Principal Component Enhanced Vantage-point Tree (PEV-Tree), and constructs a novel Distributed Spatio-Temporal Privacy Preservation Mechanism (DST-PPM) around it. Additionally, three distributed privacy preservation algorithms (CK-AA, CL-DA, and CT-CA) based on CASTLE, a classic real-time anonymization algorithm for data streams, are designed to satisfy K-Anonymity, L-Diversity, and T-Closeness, respectively. Using publicly available vehicular network data, we performed artificial simulations of streaming big data (both conventional data and PEV-Tree data streams) and implemented CK-AA, CL-DA, and CT-CA on the distributed stream processing framework Flink. We compared the efficiency, reliability, and scalability of CPPM and DST-PPM. The main contributions are as follows:

1.    We propose an enhanced data structure for distributed data privacy protection, termed the PEV-Tree. We project high-dimensional data into a low-dimensional space through linear transformations, emphasizing the main features and reducing the dimensionality of the data. Then we introduce the vantage tree to isolate data in a metric space by selecting locations in space (“vantage points”) and dividing the data points into two parts. And create a tree data structure by recursively applying this process to divide the data into smaller and smaller sets.

2.    We analyze data privacy protection within the context of vehicular networks. Based on CASTLE [21], which is a clustering-based scheme, which is a clustering-based scheme, it designs data stream processing algorithms that satisfy the requirements of K-Anonymity, L-Diversity, and T-Closeness, specifically CK-AA, CL-DA, and CT-CA, and introduces a novel distributed DST-PPM leveraging the PEV-Tree.

3.    Experimental analysis was conducted using the Flink computing framework to compare the performance of DST-PPM based on PEV-Tree data streams with that of traditional CPPM in terms of efficiency, reliability, and scalability. Comparing their run-time and efficiency under varying data scales, quasi-identifier count, and latency threshold. The selection of different algorithms in different data scenarios is analyzed, and suggestions are given.

4.    The advantages of the novel distributed DST-PPM are explored, along with the characteristics and application scenarios of the three algorithms CK-AA, CL-DA, and CT-CA.

2  Related Works

2.1 Anonymization Technology

With the advent of the big data era, personal information has been extensively collected and analyzed, leading to a continuous increase in the risk of privacy breaches. In response to the growing demand for privacy protection, anonymization technology has emerged to ensure that data does not leak personal privacy during its use and sharing. The development of anonymization technology has undergone several important stages. Initially, simple desensitization methods, such as deleting direct identifying information, were gradually considered inadequate in terms of security. Subsequently, scholars introduced more complex methods, such as data masking, K-Anonymity, L-Diversity, and T-Closeness, significantly enhancing the ability to protect data [22]. Fig. 1 shows the evolution of anonymization methods from simple to complex, as well as the application of emerging fields and the role of emerging fields in promoting the development of complex anonymization techniques. These methods not only safeguard privacy but also maintain the utility of the data.

Figure 1: Anonymization technology and application

The concept of K-Anonymity was first explicitly proposed by Samarati and Sweeney in 1998 and formally published in 2002 [23]. It provides a foundational framework for anonymizing data releases to protect privacy information [24]. The core idea is to reduce individual characteristics in the data to a level that is indistinguishable from at least k−1 other individuals. Techniques such as data generalization, suppression, and perturbation are used to ensure that no individual record in the dataset can be distinguished from at least k−1 other records based on certain key attributes, thereby protecting individual privacy [25]. However, K-Anonymity has drawbacks, such as high processing complexity and vulnerability to attacks based on background knowledge. To address these issues, Machanavajjhala et al. [26] proposed the L-Diversity model, which enhances diversity in sensitive attributes to prevent attribute linkage attacks and improves data privacy protection. The core concept is to ensure that each equivalence class in the data contains at least k indistinguishable entities and at least l different sensitive attribute values. Similarly, L-Diversity has its limitations. When the diversity of sensitive attributes within the dataset is low, achieving the desired level of protection is challenging. Moreover, enhancing diversity often increases processing complexity, significantly reducing utility, and still leaving gaps in privacy protection [27]. In 2007, Li et al. proposed the concept of T-Closeness [28]. The transition from L-Diversity to T-Closeness is particularly significant because it introduces a new constraint: in addition to K-Anonymity, the distribution of sensitive attributes within each anonymized group should be close to the overall distribution. By quantifying the closeness of the distribution of sensitive attributes, T-Closeness further strengthens privacy protection, ensuring that even in the face of background knowledge attacks, personal information remains effectively protected from identification. T-Closeness maintains the difference between the distribution of sensitive attributes within an anonymity group in the dataset and the distribution of the corresponding sensitive attributes across the entire dataset below a predefined threshold t. T-Closeness also has its challenges, such as high implementation complexity [29].

Anonymization is not only widely used in traditional fields such as healthcare and finance, but also plays a crucial role in emerging domains like the Io Vehicles, Internet of Things, blockchain, artificial intelligence, and machine learning [30,31]. For example, anonymization of data in the IoV can enhance traffic efficiency and safety while preserving user privacy. The conflicting requirements of real-time data processing, accuracy, privacy protection, and the vast volume of information pose significant challenges to anonymization technologies in these emerging fields [32]. However, reliability and data processing complexity are interdependent, with high reliability inevitably leading to lower efficiency. It is well known that three major factors affect the efficiency of privacy protection: the privacy protection algorithm, the operating objects (data), and hardware resources. When hardware resources are immutable, optimizing the operating objects (data structure and dimensions) is a feasible solution to enhance processing efficiency while maintaining reliability.

In recent years, the combination of differential privacy and deep learning has become a new trend. Ho et al. [33] proposed a differential privacy framework based on generative adversarial networks to preserve spatio-temporal features while protecting the privacy of trajectory data. For dynamic data streams, Fan and Xiong [34] designed an adaptive noise injection mechanism to optimize privacy budget allocation by predicting data distribution changes via LSTM. In the Telematics scenario, Zhao et al. [35] combined local differential privacy with edge computing to achieve distributed desensitization of in-vehicle terminal data. Although these methods enhance privacy guarantees, the noise accumulation effect leads to long-term data utility degradation, and it is difficult to meet the real-time requirements in vehicular collaborative computing scenarios.

2.2 PCA and VP-Tree

PCA is a statistical method used for feature extraction and dimensionality reduction [36]. It aims to project high-dimensional data into a lower-dimensional space through a linear transformation while retaining as much of the original data’s key information as possible. PCA helps in removing noise, emphasizing the main features, and reducing the data’s dimensionality, thereby enhancing model performance. The application of PCA effectively addresses the “curse of dimensionality” encountered in high-dimensional data processing, making data handling and analysis more efficient in fields such as machine learning, image processing, and genomic data analysis. The data dimensionality reduction process based on PCA is illustrated in Fig. 2.

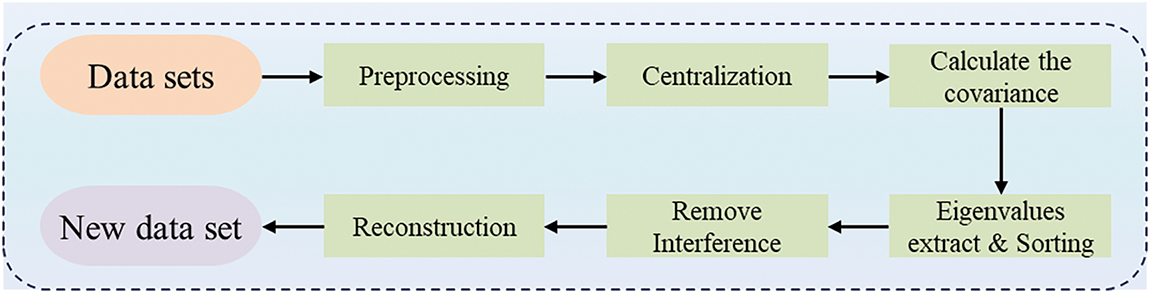
Figure 2: Dimensionality reduction process of data set based on PCA

VP-Tree, a metric tree, is a data structure designed for implementing range and nearest neighbor searches within metric spaces. First proposed by Peter N. Yianilos in 1993, it excels in performing proximity searches and demonstrates significant advantages when handling high-dimensional data [37]. The core principle of VP-Tree lies in leveraging distance properties within metric spaces to organize data. This is achieved by selecting specific nodes as vantage points and partitioning the data based on their distances relative to these vantage points. This method of data organization allows for the rapid exclusion of nodes that do not match the query distance during searches, thereby significantly enhancing search efficiency. Furthermore, VP-Tree exhibits excellent scalability for high-dimensional datasets, showing superior performance in managing large-scale and complex datasets. It is particularly effective in multidimensional data search, pattern recognition, machine learning, recommendation systems, and bioinformatics [38,39]. By reducing the number of distance calculations required during searches, VP-Tree lowers query time and increases efficiency when processing large datasets.

In emerging application scenarios such as the Internet of Vehicles (IoV) and artificial intelligence, VP-Tree demonstrates unique value. With ongoing technological advancements, VP-Tree has been continuously optimized, resulting in several variants such as MVP-Tree and BV-Tree [40,41]. These variants employ various optimization strategies to enhance the efficiency and scalability of the original structure, further cementing VP-Tree’s utility in handling extensive and intricate data environments.

2.3 IoV Privacy Protection

The commonly used data desensitization technologies for IoV currently include anonymization and differential privacy [42,43]. The advantages and disadvantages of these two data desensitization technologies are shown in Table 1. The user privacy issue that needs to be addressed in the desensitization of vehicle networking data is to protect the privacy of sensitive data of users, and prevent the leakage of sensitive data due to inference, data analysis, and mining, while ensuring the legal compliance of vehicle networking applications and implementation. To achieve legal compliance with data desensitization technology, it is necessary to determine the authorization and informed consent of the data subject (i.e., the user) and to conduct a data protection impact assessment. Due to the issue of low data availability in differential privacy, and the need for intelligent services to be provided to users through data analysis in IoV, low data availability can lead to a decrease in service quality. Therefore, we adopt anonymization to desensitize streaming data in IoV. However, anonymization also has some drawbacks, such as difficulty in solving privacy quantification issues and difficulty in resisting powerful background knowledge attacks. The amount of data collected by IoV is very large, and it is impossible to predict what kind of background knowledge the attacker has. Therefore, it is necessary to improve the ability of anonymization to process streaming data while enhancing its ability to resist powerful background knowledge attacks, which is also the focus of this study.

Although existing research has made significant progress in the area of privacy protection in Telematics, the following key research gaps still exist: (1) traditional data partitioning methods (e.g., KD-Tree, Ball-Tree) do not fully consider the replication overhead and communication cost in high-dimensional data streaming scenarios, which leads to limited processing efficiency (According to our experiment, the time consumed by the traditional methods increases by 58% when QI = 9); (2) existing anonymization algorithms (e.g., CASTLE) are difficult to balance reliability and real-time in dynamic spatio-temporal environments, and experiments show that the probability of information leakage of CPPM under homogeneous attacks is 2.31% higher than that of DST-PPM; (3) a unified processing framework for mixed data types (e.g., numerical speed and discrete brand that exist simultaneously in the Telematics network) is missing, and the existing methods tend to independently process different types of data, leading to a decrease in clustering accuracy (According to our experiment, the GLM value of the traditional method is 50% higher); (4) the lack of a systematic scheme for anonymization optimization under the distributed stream processing architecture, especially how to effectively combine dimensionality reduction and tree indexing in frameworks such as Flink remains to be explored.

To address the dynamic nature of vehicular networking, recent studies have proposed various enhancement schemes. Song et al. [44] designed a dynamic pseudonym management framework based on fog computing, which realizes region-level pseudonym switching through roadside unit collaboration. To cope with location privacy threats, Tu et al. [45] proposed a spatio-temporal K-anonymization model to construct dynamic anonymization regions using vehicle movement pattern prediction. In V2X communication scenarios, Aujla et al. [46] developed a fine-grained access control protocol based on attribute encryption, which is combined with blockchain to realize audit trails. These schemes make progress in specific scenarios, but generally face bottlenecks in the efficiency of high-dimensional data processing and lack a unified processing mechanism for mixed attribute types.

3  Analysis of IoV Privacy Preserving

3.1 IoV Data Desensitization

With the widespread application of big data technology across various industries, data anonymization has become a crucial topic, particularly in emerging fields like the Internet of Vehicles (IoV). The Internet of Vehicles entails a network system where various sensors, controllers, and information-gathering devices collect abundant data on vehicle operational status, driving environments, etc. This data is subsequently transmitted via wireless communication technology to data centers for processing and analysis [26]. IoV user data refers to the data provided or generated by users while using a car, which is associated with the user’s identity and car usage behavior. This user data can be categorized into three types, as shown in Fig. 3. (1) User and vehicle identity data, mainly refers to data that identifies the user’s natural person identity, virtual identity, vehicle identity, or authentication-related identity. (2) User usage data mainly refers to data generated during the use of the car, including operational data and usage record data. (3) Vehicle status data mainly refers to the periodic collection of component and overall vehicle state information, including performance data and operational condition data.

Figure 3: User data collected from IoV

The Internet of Vehicles (IoV) involves a vast amount of personal and vehicle information, and the misuse, leakage, or illegal provision of sensitive information poses significant threats to users’ personal and property safety. Effectively utilizing this data while safeguarding user privacy becomes paramount. Data anonymization serves as a method to achieve privacy protection during data utilization and sharing by employing techniques such as renaming, masking, or transforming sensitive information. IoV data anonymization is essential for ensuring compliance with regulations and securely applying data in practical business and research contexts, thereby enhancing data usability and value. It effectively enhances user trust in IoV services, thereby promoting their broader application and development.

3.2 Model of Data Desensitization

In the practice of data desensitization in the Internet of Vehicles (IoV), common techniques include data masking, data encryption, data generalization, and data perturbation. Data masking is a process that hides user identity by replacing or deleting sensitive information, such as substituting a user’s real name with ‘XXX’. Its implementation simplicity is a boon, but the downside is that it may reduce the practical value of data. Conversely, data encryption encrypts sensitive data to prevent unauthorized users from reading it. For instance, the AES algorithm might be employed to encrypt the identity information of the vehicle owner. This method offers high security, but the encryption and decryption process may increase the computational overhead of the system. Data generalization, on the other hand, seeks to protect privacy by making specific data vague, like generalizing a specific address to a city name. This method can help maintain the statistical characteristics of data while offering relatively lower levels of privacy protection. Data perturbation works by adding noise or random values to blur data content, e.g., making slight random adjustments to vehicle speed data. This approach can effectively protect privacy while preserving the overall trend of the data, but it may impact the accuracy of the data.

Through the combined application of these techniques, we can ensure data availability and practical value while protecting privacy. By optimizing the application of the above techniques, we can further enhance the efficiency of data processing and the level of privacy protection. The theoretical model of data desensitization in IoV, as shown in Fig. 4, involves the IoV platform receiving data collected by sensors, storing the data in a database, and performing data desensitization. When third-party applications request access to data or make queries, the platform sends them the desensitized results, thereby ensuring the privacy of users.

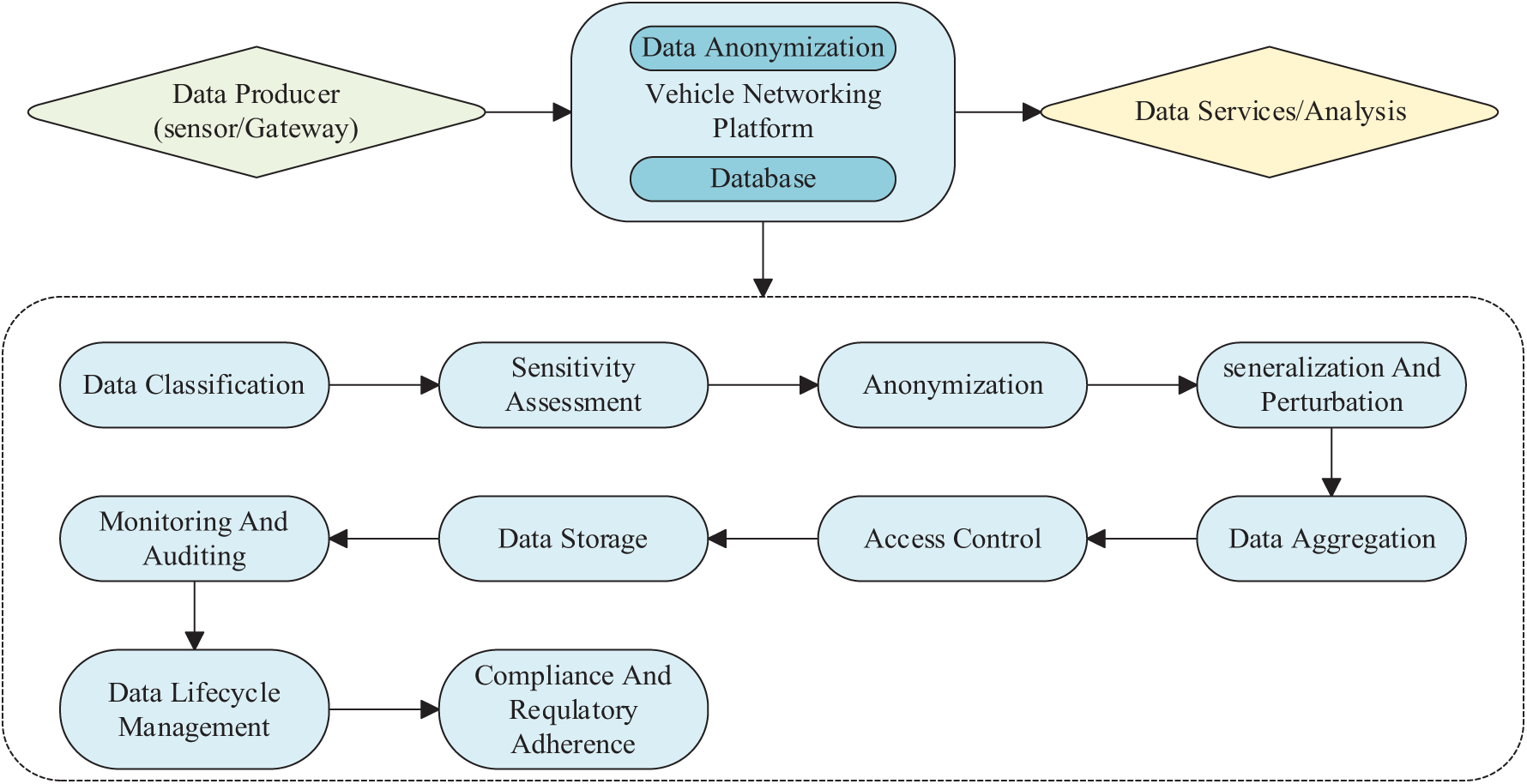
Figure 4: Desensitization model for IoV data

Based on the analysis in the previous section, anonymization techniques such as K-Anonymity, L-Diversity, and T-Closeness are viable methods for ensuring data privacy in vehicular networks. These three anonymization techniques were chosen due to their unique yet complementary strengths. Conducting experiments and analyses using these rules is essential for understanding their effectiveness and efficiency in distributed environments. We will test the performance of the algorithm satisfying these rules in our experiments. These experiments will allow for the assessment of their performance and effectiveness in distributed, real-time settings. Comparing the privacy guarantees provided by each rule helps identify trade-offs between computational overhead and privacy protection, which is crucial for validating the practicality of these anonymization techniques in large-scale, dynamic environments.

3.3 DST-PPM

In emerging application scenarios such as the Internet of Vehicles (IoV) and artificial intelligence, data arrives in the form of high-speed data streams containing substantial amounts of private information. However, traditional data stream privacy protection algorithms struggle to simultaneously meet the requirements of reliability, scalability, and efficiency in these contexts. This challenge has driven us to explore new solutions, among which the VP-Tree structure stands out due to its superior scalability. VP-Tree demonstrates significant advantages in handling high-dimensional data. Each node in a VP-Tree contains a data point and a radius. Points closer to the node’s point than the radius are placed in the left child, while points farther away are placed in the right child. To illustrate the construction of a VP-Tree, consider an example where point 28 is chosen as the vantage point (VP) due to its distance from other points. This point serves as the level-0 vantage point (root node) of the VP-Tree. A sphere with a carefully calculated radius r is drawn around point 28, such that half of the remaining points lie within the sphere and the other half lie outside it. The points inside the sphere are allocated to the root node’s left subtree, while those outside are allocated to the right subtree. This process is recursively applied to both the inside-sphere points and the outside-sphere points. Ultimately, this method results in the formation of a VP-Tree, as illustrated in Fig. 5. This method of data organization allows for the rapid exclusion of nodes that do not match the query distance during searches, thereby significantly enhancing search efficiency. Furthermore, VP-Tree exhibits excellent scalability for high-dimensional datasets, showing superior performance in managing large-scale and complex datasets.

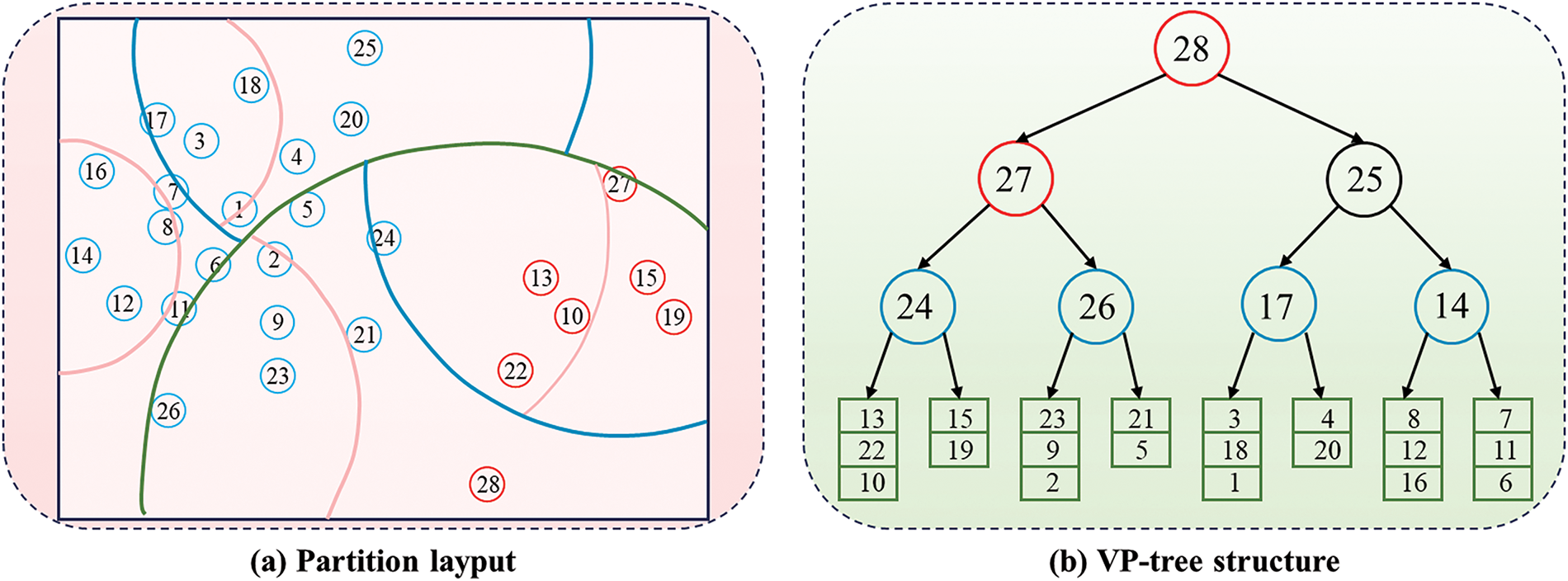
Figure 5: An illustrative example of VP-Tree structure. Red points form a cluster, and blue points form another cluster

Moreover, utilizing Principal Component Analysis (PCA) for dimensionality reduction of data streams facilitates the rapid construction of the tree structure. In view of this, we propose to use a new data structure to create a new privacy protection mechanism and call it the Principal Component Enhanced Vantage-point tree (PEV-Tree), a lightweight variant of VP-Tree, which is easier to build and offers faster access speeds. The PEV-Tree data stream can reduce the number of distance calculations required during the search process, thereby enhancing the real-time performance of privacy protection algorithms. This makes it more suitable for scenarios such as the IoV and artificial intelligence, which demand efficient processing of massive datasets.

In the PEV-tree-based data partitioning process, we need to determine a specific level of the VP Tree. Then, each computation node is assigned to a specific node or multiple tree nodes at level m. The constructed VP-Tree is binary, so the level can be chosen based on the number of distributed computing nodes. For example, the level for 8 partitions should be at least 3, not counting the root level, as 23 = 8. If the chosen level is m, the number of partitions is 2m. Additionally, the VP-Tree initially needs to be filled with enough stream data to grow it to at least level m. Since the nodes of each VP-Tree do not overlap with each other, The Times of data replication and information exchange are reduced. Therefore, for a data stream consisting of n data items and d quasi-identifier attributes, with a replication rate of v per data item, and a cluster of |P| computing nodes, the communication overhead of the VP-Tree based data partitioning method is O(n∗d∗v∗ct), where ct is the cost of constructing the VP-Tree, a constant. By using PCA, the construction cost can be significantly reduced. Therefore, when there are many quasi-identifier attributes, it is better to use the PEV-Tree-based distributed anonymization algorithm.

Based on the above analysis, we propose the DST-PPM. DST-PPM is a dynamic spatiotemporal privacy protection mechanism composed of PEV-Tree and stream data privacy protection algorithms (CK-AA, CL-DA, CT-CA) based on CASTLE. Utilizing PEV-Tree under the Apache Flink framework offers significant advantages, particularly in efficiently handling metric spaces, which is crucial for high-dimensional data processing and effectively managing the curse of dimensionality. Given that the original data stream undergoes dimensionality reduction, PEV-Tree is more efficient in construction and access compared to VP-Tree. Furthermore, it still partitions space based on distances and vantage points, maintaining the same excellent scalability as VP-Tree.

The Flink framework, with its robust stream processing capabilities, synergizes with PEV-Tree to ensure effective data partitioning and reduce computational overhead associated with high-dimensional data. Compared to Ball-Tree, KD-Tree, and VP-Tree, PEV-Tree offers a more straightforward implementation and generally better performance in metric spaces. This is critical for maintaining the required privacy protection reliability without incurring significant delays. Additionally, the simplicity of PEV-Tree aligns seamlessly with Flink’s distributed processing model, facilitating the implementation and maintenance of anonymization algorithms. Integrating PEV-Tree with the Flink framework enhances the scalability and parallelism of the anonymization process, ensuring that large-scale data streams can be processed distributed manner while maintaining high throughput and low latency. The combination of PEV-Tree and Flink leverages the strengths of both technologies, providing a scalable, real-time distributed anonymization solution.

4  Proposed Approach

This study proposes a distributed DST-PPM based on the PEV-Tree framework under Flink, which is divided into data stream partition windows and data anonymization windows. The data stream partition window utilizes PCA to perform dimensionality reduction on the data stream, selects a viewpoint, and calculates the distance to other data points. Based on these distances, the data is partitioned into inner and outer circles, and then the partitioned data is passed to the corresponding subtasks for processing. The data de-identification window receives the partitioned data and applies the three privacy protection algorithms designed in this study (CK-AA, CL-DA, CT-CA) for anonymization. It then checks whether each partition meets the anonymity requirements (K-Anonymity, L-Diversity, T-Closeness). If not, the data is further generalized until it satisfies the privacy requirements, and then the generalized data is released. The main logic is illustrated in Fig. 6.

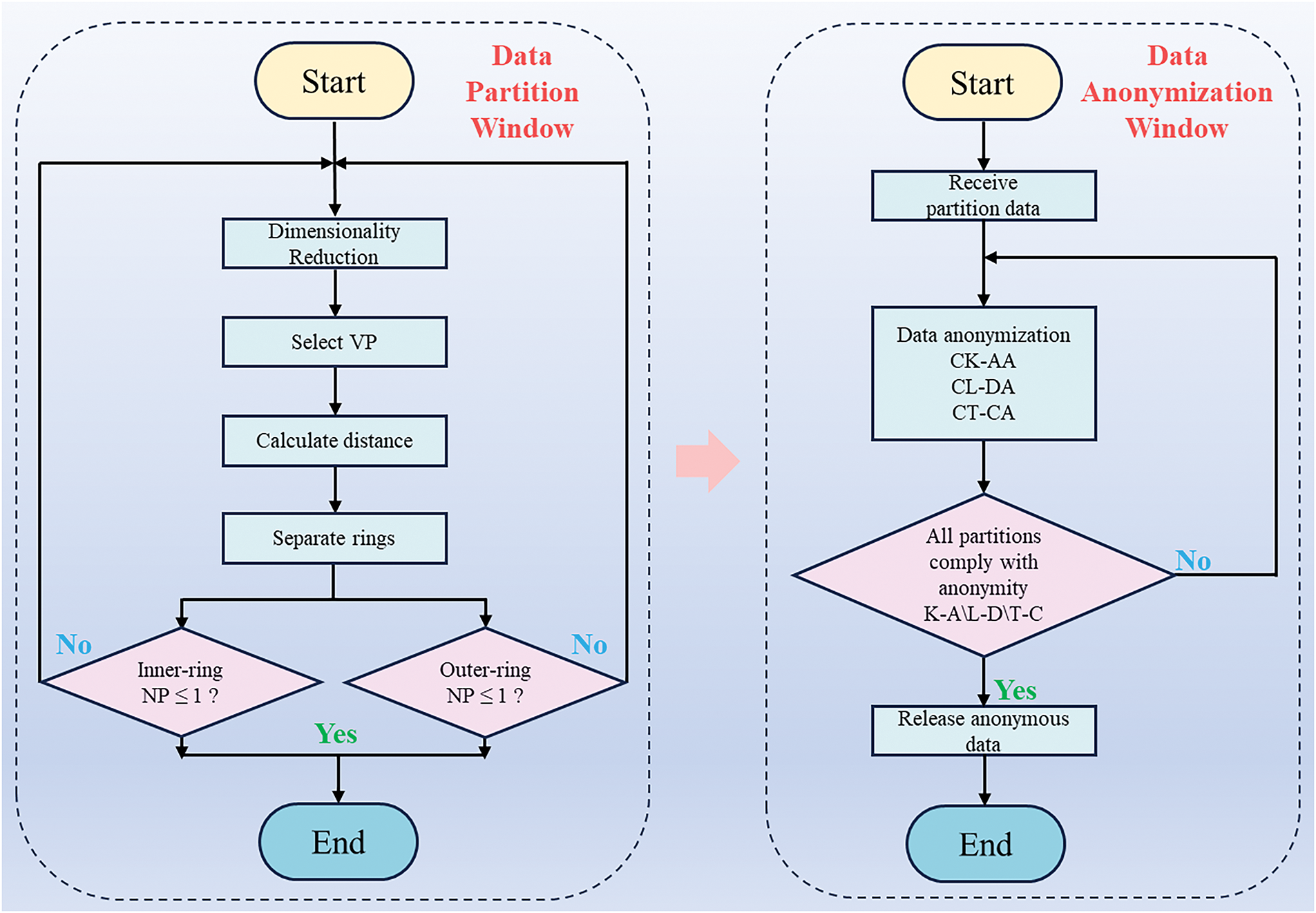
Figure 6: Principle of data anonymization algorithms based on PEV-tree

4.1 PEV-Tree Construction Process

The VP-Tree is a distance-based nearest neighbor search algorithm [47,48]. Compared to other tree structures, the VP-Tree achieves higher computational efficiency in nearest neighbor searches due to its entirely distance-based binary search characteristic. Kumar et al. [49] have demonstrated that the VP-Tree can yield better nearest neighbor search results than other hierarchical data structures. However, compared to the VP-Tree, the PEV-Tree offers lower space storage requirements and faster construction and access efficiency. PEV-Tree is a lightweight tree-structured dataset obtained by applying PCA for dimensionality reduction on data streams, and it is based on the VP-Tree.

To illustrate the construction process of the PEV-Tree, we employ a simple 3-ary partitioning example, which can be easily extended to ε-ary partitioning for ε > 3. First, the PCA technique is used to perform eigenvalue analysis and ranking on the dataset, retaining the top two features and reconstructing them into a binary dataset. Subsequently, the dataset is divided into two subsets to construct a binary PEV-Tree. This vantage point is placed in the root node, with the two resulting subsets forming the left and right subtrees. These subtrees are processed recursively, constructing further levels of the tree with newly chosen vantage points until each node houses a single data point, thus completing the tree. Specifically, given a dataset D containing n points, a point pev is randomly selected as the vantage point in the reconstructed dataset Dr. The distances between pev and other points in Dr are computed, creating the set S = {dist(p, pev) | p ∈ Dr − {pev}}. Using the median distance value μ from S, the dataset is divided into two subsets: D1 consists of points within a distance μ of pev, while D2 consists of points farther than μ from pev, as illustrated in Fig. 7a.

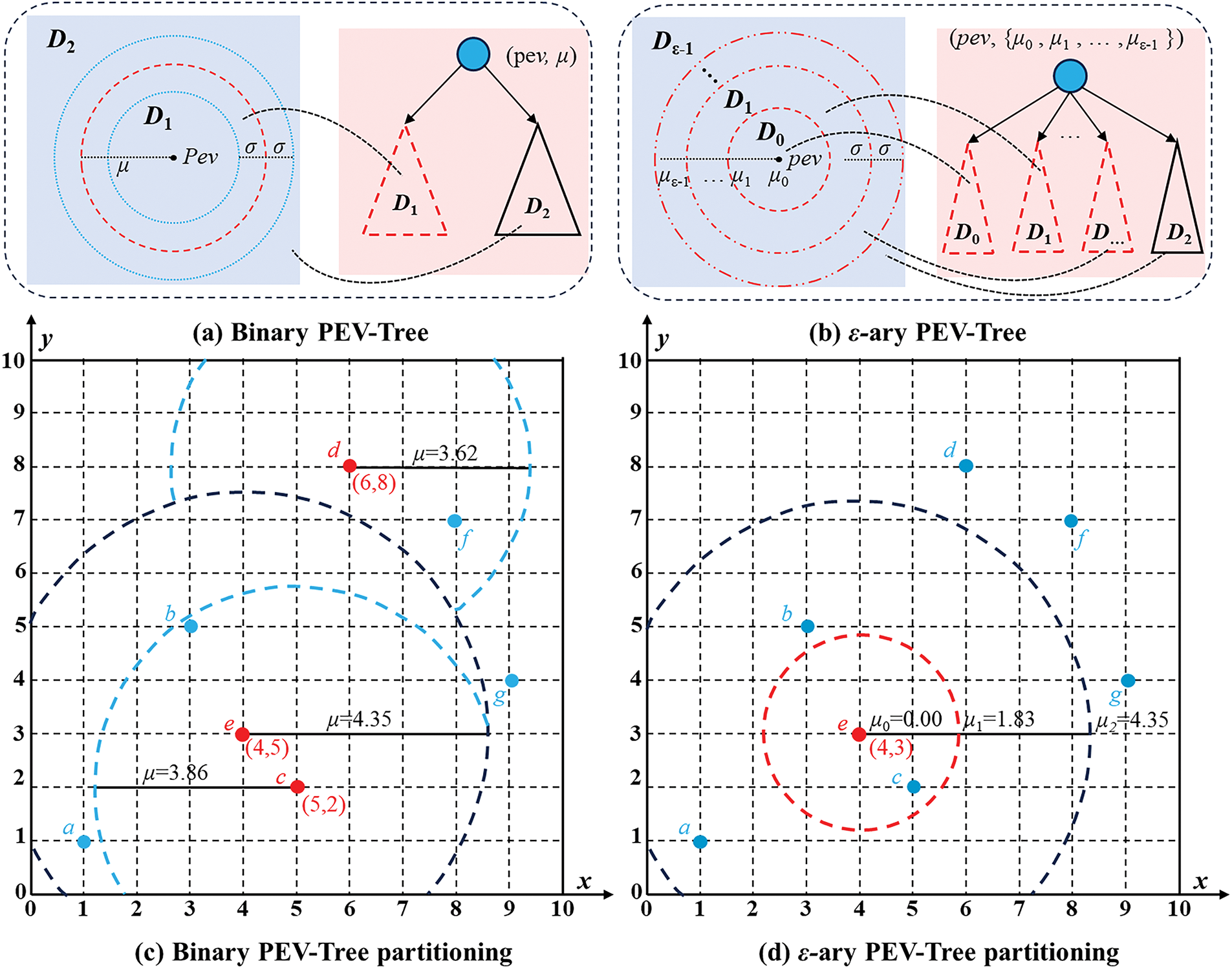
Figure 7: PEV-Tree partitioning strategy in a 2-dimensional and ε-ary input domain (a,b). This is an example comparison between binary and ε-ary PEV-Tree partitioning in a 3-dimensional input domain (c,d)

The process of constructing an ε-ary PEV-Tree (ε > 3) parallels that of a binary PEV-Tree, but with key differences. First, the PCA technique is applied to the dataset for eigenvalue analysis and ranking, retaining the top ε1 features and reconstructing them into an ε1-ary dataset. Subsequently, the dataset is divided into ε1 approximately equal subsets to construct an ε1-ary PEV-Tree. For a given dataset D, a vantage point pev is randomly selected in the reconstructed dataset Dr. The distances from pev to all other points in Dr are computed and ordered in ascending fashion. Unlike the binary approach, this method partitions the dataset into ε1 approximately equal subsets, with pev stored in the first subset for this study. As illustrated in Fig. 7b, the boundary distances μi (i = 1, 2, ... , ε − 1) demarcate the divisions between Di−1 and Di. Formally, for an ordered sequence of distances S = {dist(aj, vp) | aj ∈ Dr, j = 0, 1, ... , |Dr| − 1}, where |Dr| denotes the total number of points in Dr, the boundary distances μi can be computed as follows:

μi={0,i=0S(i×⌊|Dr|ε1⌋−1)+S(i×⌊|Dr|ε1⌋)2,i∈|1,ε1−1|(1)

where S(j) represents the j-th ordered element in S (j = 0, 1, ... , |Dr| − 1), and ⌊|Dr|/ε1⌋ denotes the floor function of the integer division |Dr|/ε1. Consequently, for each point p in Di, the distance dist(p, pev) lies between μi and μi + 1. To elucidate the construction process of the PEV-Tree, consider the dataset Dr = {a, b, c, d, e, f, g} in a two-dimensional vector space after dimensionality reduction. The binary PEV-Tree construction process is depicted in Fig. 7c, and the ε-ary case is shown in Fig. 7d: (1) Point e is randomly selected as the vantage point; (2) the distances between e and all other points are computed, resulting in S = {dist(p, e) | p ∈ Dr − {e}} = {1.414, 2.236, 3.606, 5.099, 5.385, 5.657}; (3) the median value of S is determined, yielding μ = (3.606 + 5.099)/2 = 4.3525; (4) subsets D1 = {c, b, a} and D2 = {g, d, f} are formed; (5) the points within D1 and D2 are recursively organized using the same steps until each subset contains only one data point. The corresponding binary PEV-Tree structure is illustrated in Fig. 8a.

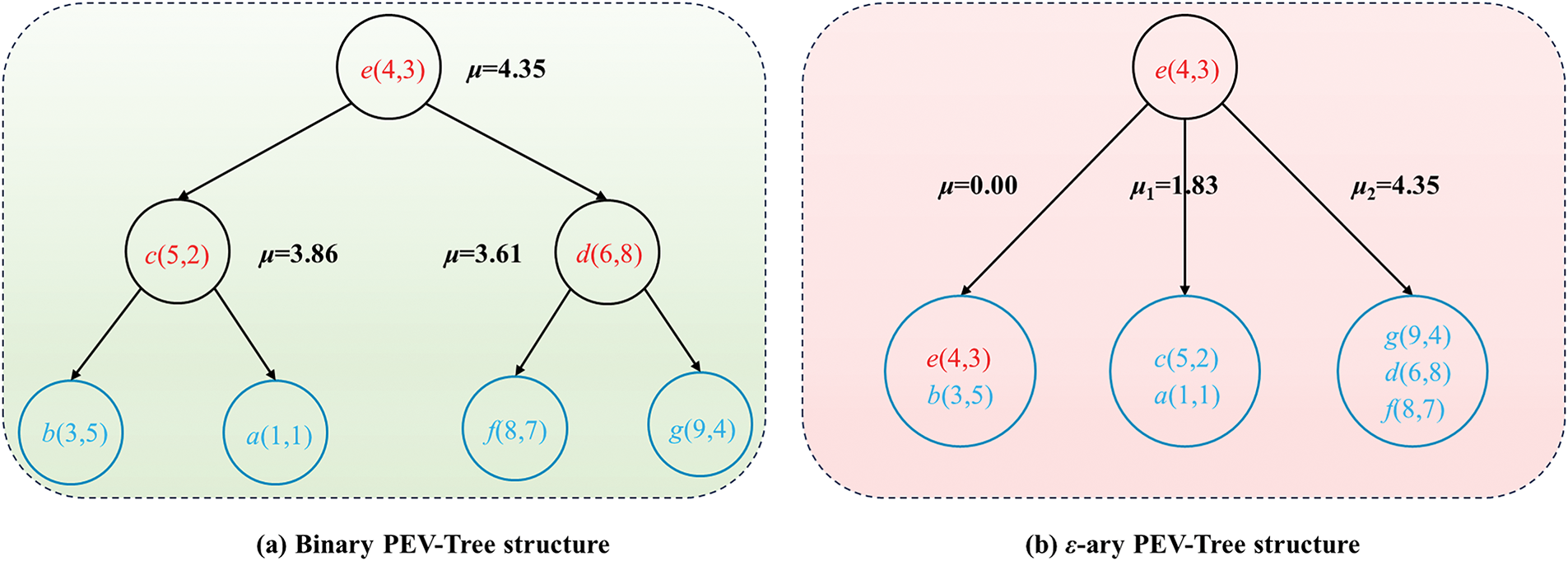
Figure 8: Example of the comparison between binary PEV-Tree structure and ε-ary PEV-Tree structure in a 2-dimensional input domain

The resulting ε1-ary PEV-Tree structure is presented in Fig. 8b, where ε1 = 3. Analogous to the binary case: (1) Point e is chosen at random as the vantage point; (2) distances from e to all other points are calculated, resulting in S = {dist(p, e) | p ∈ Dr} = {0.000, 1.414, 2.236, 3.606, 5.099, 5.385, 5.657}; (3) three boundary values are defined.

μ0=0.00(2)

μ1=S(1)+S(2)2=1.83(3)

μ2=S(3)+S(4)2=4.35(4)

partitioning Dr into three approximately equally sized subsets; (4) the steps above are repeated in each subset.

4.2 Distributed CK-AA Based on PEV-Tree

Based on the PEV-Tree data partitioning method, a distributed algorithm that adheres to the K-Anonymity principle has been designed, referred to as the Distributed CASTLE Algorithm based on PEV-Tree (CK-AA for short). Implementing the distributed CK-AA under the Flink framework involves addressing data privacy, multidimensional data indexing, and distributed computing. The algorithm comprises a stream data partitioning window and a data desensitization window. The stream data partitioning window executes data partitioning based on the PEV-Tree method. The data desensitization window generalizes and publishes tuples that satisfy the K-Anonymity principle, consistent with the K-Anonymity publishing rules of the baseline algorithm. The specific algorithm steps are detailed in Algorithm 1.

The algorithm initially establishes two sets: one for storing tuples to be disclosed (Setn) and another for holding released clusters that comply with the K-Anonymity principle (Sety). In the data stream partitioning window, for each data tuple ‘t’, if ‘t’ lacks a timestamp, one is assigned. PCA preprocessing is then performed to reduce the dimensionality of the data. Subsequently, based on its distance to the dominant point, an appropriate partition for ‘t’ is selected, and ‘t’ is sent to the corresponding partition. The data anonymization window, for each partition, opts for the best cluster ‘C’ inclusive of ‘t’. If ‘C’ adheres to the K-Anonymity principle, ‘t’ is disclosed. If not, a cluster that adheres to K-Anonymity is located within ‘t’s’ proximity grid and ‘t’ is then disclosed. If ‘t’ reaches the publication delay threshold ‘δ’, delayed publication is carried out. The entire process aims to ensure the published data stream complies with the K-Anonymity principle while minimizing publication delay, thereby guarding user privacy and data security.

Table 2 is an example of a data table that does not meet K-Anonymity, with identifiers like Age and the Last three digits of car number. After being desensitized by this algorithm, the table is transformed to meet K-Anonymity requirements, as shown in Table 3.

In Table 3, the table satisfies K-Anonymity, where k = 2. This means that each of the two quasi-identifier value attributes appears at least twice in the table: |T[Age = 20]| = 2, |T[Age = [30,40]]| = 2, |T[Age = 50]| = 2, |T[N = [730,735]]| = 2, |T[N = 386]| = 2, |T[N = [320,325]]| = 2. Furthermore, the combinations of attribute values formed by these two quasi-identifiers appear at least twice in the dataset: c1[QIRT] = c2[QIRT], c3[QIRT] = c4[QIRT], c5[QIRT] = c6[QIRT].

4.3 Distributed CL-DA Based on PEV-Tree

In Table 4, the data satisfies K-Anonymity, where k = 4, but does not meet L-Diversity.

Although the data in Table 4 complies with K-Anonymity, it can be inferred that users who meet Age = 4* and Car number = A12** all drive Benz cars, so the data table needs further desensitization to meet L-Diversity and protect users’ privacy.

Building upon CK-AA, a further proposal is made for a PEV-Tree-based Distributed CL-DA. This algorithm satisfies both K-Anonymity and L-Diversity principles. The specific algorithm steps are detailed in Algorithm 2.

Initially, two sets are initialized: Setn, intended for storing tuples awaiting release, initially empty; and Sety, for storing the published clusters that meet both the K-Anonymity and L-Diversity principles, also initially empty. In the data stream partitioning window, for each data tuple ‘t’, if ‘t’ lacks a timestamp, one is assigned. PCA preprocessing is then performed to reduce the dimensionality of the data. Subsequently, based on its distance to the dominant point, an appropriate partition for ‘t’ is selected, and ‘t’ is sent to the corresponding partition. Subsequently, in the data anonymizing window, for every partition ‘p’, a prime cluster ‘C’ encapsulating ‘t’ is selected. Should ‘C’ satisfy both the K-Anonymity and L-Diversity principles, ‘t’ is published using the generalized results of the cluster ‘C’. If ‘C’ fails to meet the K-Anonymity or L-Diversity principles, the search continues for an inclusive cluster of ‘t’ that fulfills requirements, with ‘t’ then published using the generalized results of the found cluster. During this process, ‘t’ would be subject to a delay constraint strategy ‘delay_constraint_kl(t)’ should it reach the publication delay threshold ‘δ’. The entire process aims to ensure the published data stream adheres to both the K-Anonymity and L-Diversity privacy protection principles, while endeavoring to minimize publication delay as a means to safeguard user privacy and data security. Specifically, the data stream partitioning window segment primarily ensures the sensible partitioning of data based on time stamps and distances to the dominant point, thereby ensuring data within each partition retains a degree of similarity, facilitating subsequent anonymization processing. On the other hand, the anonymization window ensures the validation of K-Anonymity and L-Diversity within each partition. By selecting the best cluster and the necessary proximate cluster search when essential, privacy protection requirements are met during data publication. The introduction of the delay constraint strategy aims to strike a balance between timely data publication and effective privacy protection, ensuring data is published within a specific delay threshold, thus enhancing the practicability and reliability of the algorithm.

The data satisfying L-Diversity is shown in Table 5, where l = 4.

4.4 Distributed CT-CA Based on PEV-Tree

Additionally, by leveraging the distributed computing framework Flink to distribute data across different nodes, a PEV-Tree-based distributed CT-CA is designed. This algorithm adheres to the T-Closeness principle. The T-Closeness algorithm ensures that the distribution of sensitive attribute values within equivalence classes matches the global distribution, thus addressing the limitations of the L-Diversity problem.

In privacy protection mechanisms, Earth Mover’s Distance (EMD) is used to measure the differences between data distributions and evaluate the impact of desensitization operations or synthetic data generation on the original data structure. By minimizing EMD, it is possible to ensure that the data after privacy protection processing remains consistent with the original data in terms of statistical characteristics, thereby protecting privacy while retaining the validity and practicality of the data. The distance between the distribution P of a sensitive attribute within a class and the distribution Q of that attribute across the entire table is measured using Earth Mover Distance (EMD). EMD refers to the minimal amount of work needed to transform one distribution into another by moving distribution mass between them. The definition of EMD is as follows.

D(P,Q)=WORK(P,Q,F)=∑i=1m∑j=1mdijfij¯(5)

in this context, dij refers to the distance from the ith element in the distribution P of the sensitive attribute to the jth element in the distribution Q of that attribute across the entire table. fij refers to the mass from the ith element in the distribution P to the jth element in the distribution Q. WORK(P,Q,F) is the work required to transform P into Q, i.e., the EMD distance, and is constrained by the following three equations.

fij>0⋯1≤i≤m,1≤j≤m(6)

pi−∑i=1mfij+∑j=1mfij=qi(7)

∑i=1m∑j=1mfij=∑j=1mpi=∑i=1mqi=1(8)

In the study of this paper, for categorical attributes, the distance we set between two categorical attribute data can be considered as always 1 (equal distance), as follows.

D[P,Q]=12∑i=1m|pi−qi|=∑pi≥qi(pi−qi)=−∑pi<qi(pi−qi)(9)

The specific steps of the algorithm are shown in Algorithm 3.

Two empty sets, Set and finalSet, are initially initialized, with Root, the root node, initialized using the aggregate value space of the dataset and subsequently appended to the Set. A temporary set, tmpSet, is then initialized. For each element in the Set, the value space is divided using the PEV-Tree based subspace partitioning method. If the two resulting subspaces meet the T-Closeness constraint, they are added to tmpSet; if any subspace fails to meet the T-Closeness constraint, the parent value space is added to finalSet. Set is assigned the value of tmpSet and the preceding steps are repeated until Set is empty. Finally, each value space in finalSet is generalized into an equivalence class to generate an anonymized dataset ‘datasyn’ that meets the T-Closeness privacy protection standard. The key aspect of the entire process lies in the division of the value spaces through the PEV-Tree subspace division method, and constant checking of whether the divided subspaces meet the T-Closeness constraint, thereby ensuring that the final anonymized data adheres to the privacy protection standard while retaining a high degree of data utilization value. Continuous iterations and checks throughout the algorithm ascertain that the T-Closeness privacy protection standard isn’t violated in the anonymization process, while also managing to reintegrate non-compliant value spaces back into the pending set, facilitating the stepwise refinement and precise disposal of data. The produced anonymized dataset ‘datasyn’, effectively safeguards user privacy while preserving the actual application value of the data.

5  Experiment

5.1 Experimental Preparation

Datasets. The dataset used in the experiments was artificially simulated streaming big data based on datasets from an IoV data open platform. The data includes an identity identifier, license plate number, and a sensitive attribute, position. Among the nine quasi-identifier attributes, there are five continuous attributes, namely age, heart rate, driving speed, hours per week, and oil consumption, and four discrete attributes, namely brand, address, gender, and marital status. Each attribute contains an average of 1000 different values. Due to the limitations of hardware equipment, our experiment still has a certain gap from the real world. However, it already possesses all the basic characteristics of data streams in the real Internet of Vehicles. Therefore, it can be regarded as a simplified version of the Internet of Vehicles information system.

Experimental Setup. The experimental environment is based on the Flink distributed computing framework. There is one Master node, equipped with a server that has 32 GB RAM, 3.4 GHz, and 2 Core CPU. There are four Worker nodes, each configured with 48 GB RAM, 3.4 GHz, and 4 Core CPU.

Implementation Details. In this paper, three aspects of the algorithm are tested. First, the efficiency of the algorithm is tested. By inputting vehicular network data of different sizes, the efficiency of the algorithm is measured based on the execution time. Second, the scalability of the algorithm is analyzed. Here, the scalability of the algorithm is measured by the speedup ratio and data utility. We test the data utility. Here, the GLM (Generalization Loss Metric) is used as the criterion for evaluating data utility [50,51]. For the special application scenario of streaming big data in the IoV, some adjustments are made to the GLM during the anonymization process. {q1,⋯,qn} is set as the set of quasi-identifier attributes, and a categorical attribute qi is firstly considered. Letting DGH be the generalization tree for qi, and given a node v in DGH, the information loss for v is defined as follows:

VInfoLoss(v)=|Sv|−1|S|−1(10)

where Sv represents the set of leaf nodes in the subtree rooted at v in DGH, and S is the set of all leaf nodes in DGH. Therefore, the information loss for a tuple t generalized to g(v1,⋯,vn) is defined as follows:

InfoLoss(g)=1n∑i=1nVInfoLoss(vi)(11)

The average information loss of the data stream S up to time p is defined as follows:

AvgLoss(S,p)=1p∑ti∈S,tLp≤pInfoLoss(ti)(12)

The efficiency and anonymization effects of three distributed anonymization algorithms based on PEV-Tree are compared.

5.2 Experimental Efficiency and Scalability

We adopt three distributed anonymization algorithms based on PEV-Tree, namely CK-AA, CL-DA, and CT-CA, and they are used respectively under the Distributed Spatig-Temporal Privacy Preservation Mechanism (DST-PPM) and the conventional privacy protection mechanism (CPPM). Experimental results were obtained and compared to draw conclusions. The experimental results of the distributed algorithms that respectively satisfy K-Anonymity, L-Diversity, and T-Closeness for streaming big data in IoV are shown in Tables 6 and 7 and Figs. 9–11.

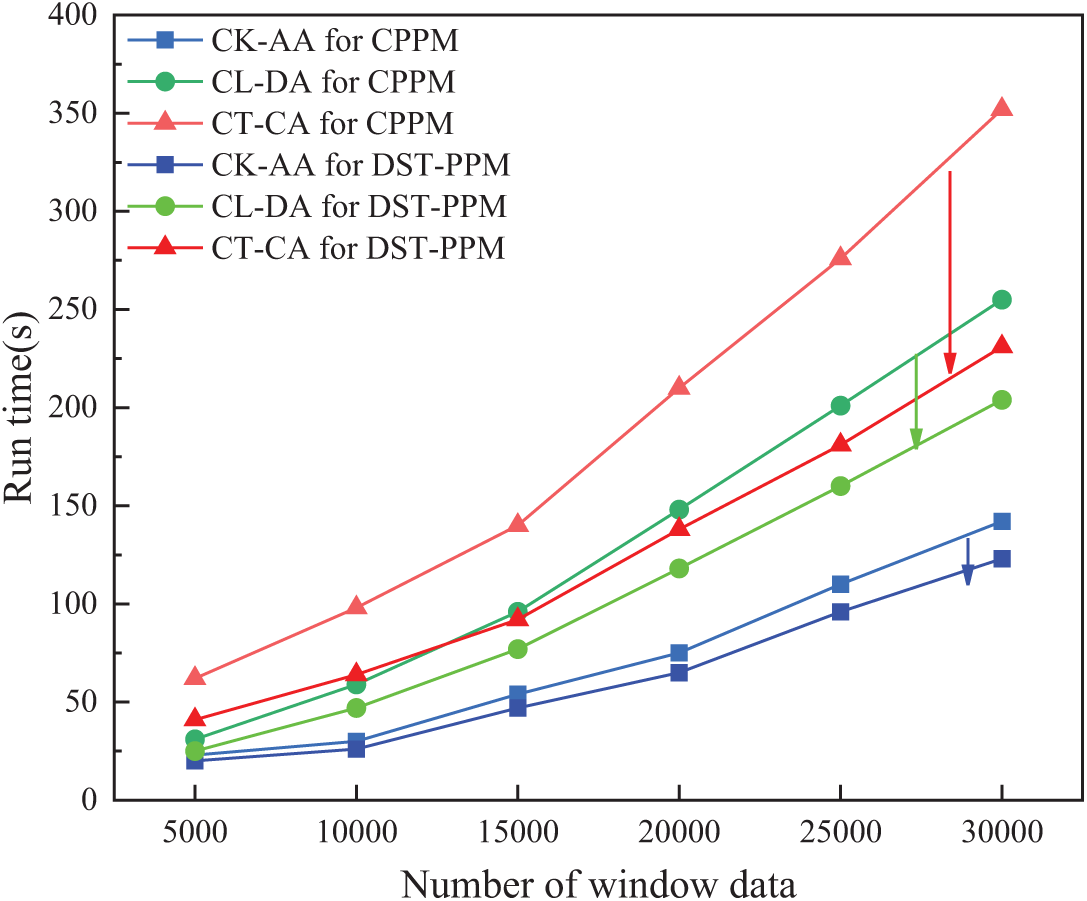
Figure 9: Running time of three algorithms at different data scales

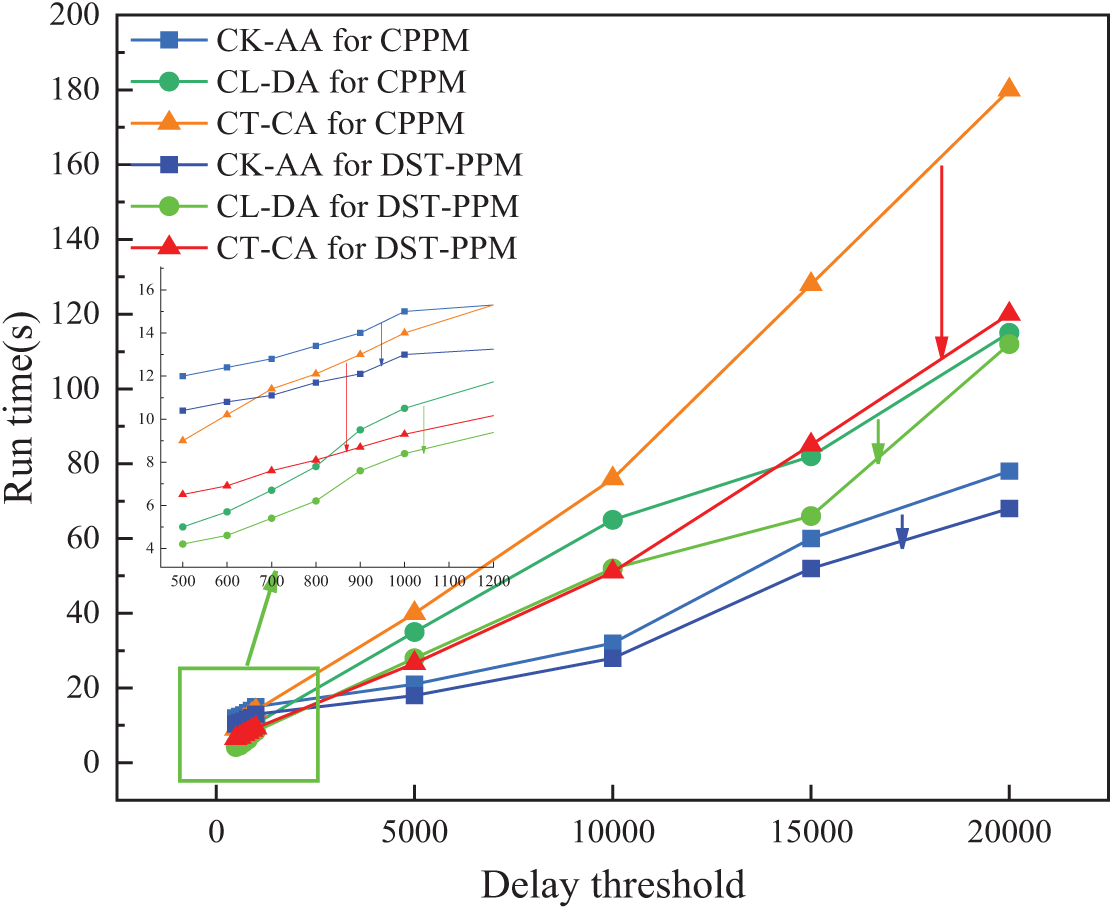
Figure 10: Running time of algorithms under different delay threshold values

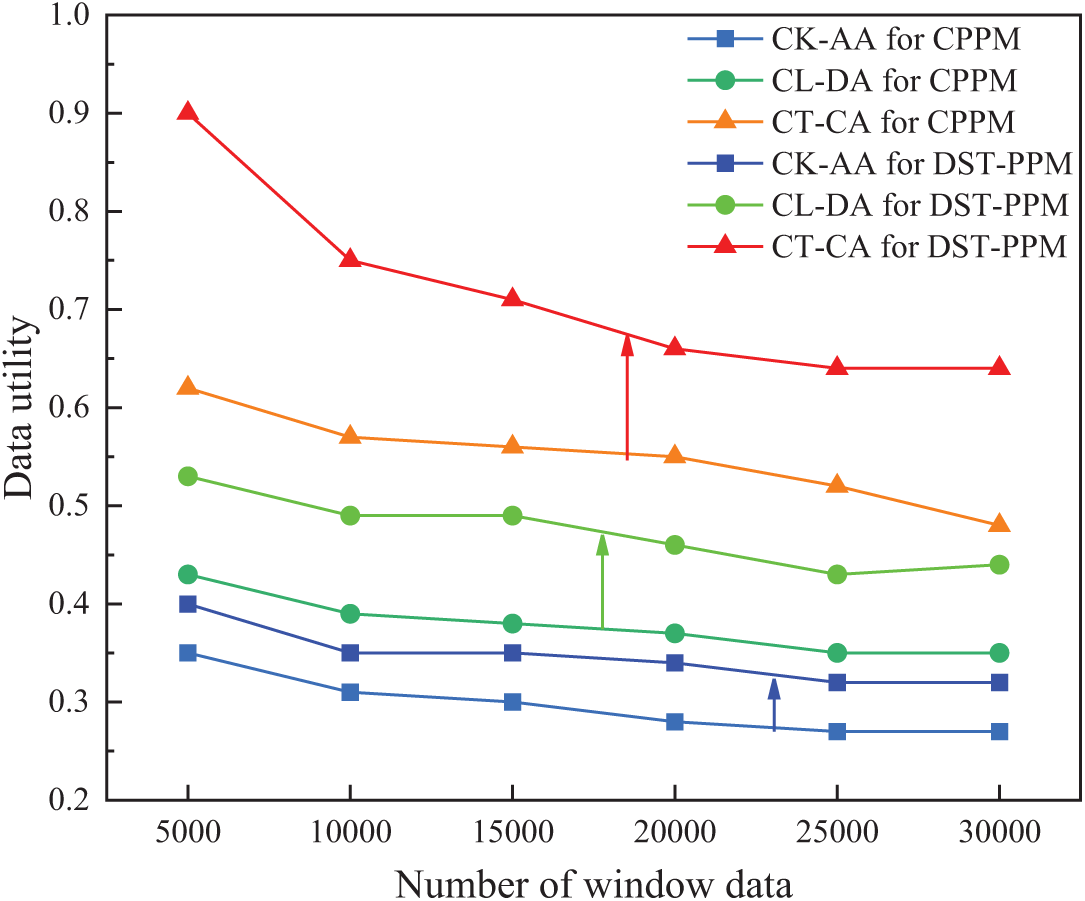
Figure 11: Data utility of three algorithms at different data scales

Fig. 9 shows the running time of the three algorithms in the two mechanisms under different data sizes, with the experimental parameters set as follows: in K-Anonymity, parameter k = 100; in L-Diversity, parameter l = 20; in T-Closeness, parameter t = 0.15; number of quasi-identifier attributes QI = 9; number of parallel nodes |p| = 4; delay threshold δ = 10,000. As can be seen from Fig. 9, DST-PPM has higher efficiency compared to the three algorithms under CPPM, and this advantage becomes more pronounced as the amount of data increases. It can be observed that the efficiency of T-Closeness is generally lower than that of L-Diversity, because under 9 QI, they have similar time cost in resisting linkage and homogeneous attacks. However, T-Closeness also makes reasonable transformations to the alignment identifier values to reduce data accuracy and increase the inseparability between different values of the same attribute, which incurs additional costs and thus increases the overall communication overhead for greater privacy benefits. However, under the impetus of our method PEV-Tree, even CT-CA for DST-PPM with the strongest privacy effect can have a lower time cost than CL-DA for CPPM after 15,000 data volume. This is because, as the amount of data increases, the three algorithms integrated with PEV-Tree require fewer times of data partitioning, while the communication between nodes under the traditional method is more frequent, resulting in an increase in communication costs. CK-AA for DST-PPM obviously has the best time performance, and the data does not need to be copied or transformed, so with the increase of the amount of data, the advantages of CK-AA become more obvious, showing good scalability.

Table 6 shows the running times of the three algorithms in the two mechanisms under different numbers of quasi-identifier attributes (QI), with the parameter settings as follows: k = 100, l = 20, t = 0.15, |P| = 4, number of records N = 10,000, delay threshold δ = 10,000. It can be seen from Table 6 that the running time of the three algorithms under the two mechanisms increases with the increase of the number of QI. When the number of QI is less than 9, the increase in running time of CK-AA decreases with the increase of QI, while for CL-DA and CT-CA, the increase in running time increases with the increase of QI. We find that the time growth of each algorithm tends to be stable when the number of quasi-identifiers reaches 9. In addition, it can be seen that the algorithm’s efficiency under DST-PPM is generally better than CPPM. CK-AA is faster and more efficient, followed by CL-DA, while CT-CA is the least efficient. This is because the communication overhead of CT-CA is not only related to the number of QIs, but also to the cost incurred during the conversion of quasi-identifier values. The greater the number of QI, the longer it takes for the T-Closeness algorithm to copy data and convert quasi-identifier values, resulting in lower efficiency.

Fig. 10 shows the running times of the three algorithms in the two mechanisms under different delay threshold values. The parameter settings in the experiments are as follows: k = 100, l = 20, t = 0.15, QI = 9, |P| = 4, number of records N = 20,000. The experimental results show that the running times of the three algorithms increase with the increase of the delay threshold δ. The larger the δ value, the more tuples in the buffer need to be processed at once, thereby increasing the running time of the algorithms. From Fig. 10, compared with CL-DA and CT-CA, CK-AA is less affected by the delay threshold and has higher computational efficiency. Although CK-AA takes the longest time at δ < 1000, its advantages gradually become apparent as the delay threshold increases. This is because, as the delay threshold increases, the number of data copies required by CL-DA and CT-CA at a time also increases. As a result, communication between nodes becomes more frequent, resulting in increased communication costs. It is worth noting that under DST-PPM, our approach has a significant time benefit. Among them, the running time of CT-CA for DST-PPM at δ ≤ 1000 is reduced by nearly half compared with CT-CA for CPPM. For conditions with a high delay threshold (>1000), we can also ensure the growth rate of CT-CA running time. In addition, CK-AA for DST-PPM and CL-DA for DST-PPM also have obvious benefits in terms of time efficiency. However, as the delay threshold δ continues to increase, the running time increment of CL-DA for DST-PPM is still relatively large. We recommend using CL-DA for DST-PPM in scenarios with a low delay threshold, and it always maintains the highest efficiency when δ ≤ 1000.

Table 7 shows the speedup ratios of the three algorithms under different cluster sizes by DST-PPM, with the parameter settings as follows: k = 100, l = 20, t = 0.15, QI = 9, number of records N = 20,000, delay threshold δ = 10,000. From Table 7, the speedup ratios of all three algorithms linearly increase with the growth of the cluster size, indicating that the three VP-Tree algorithms have good performance and scalability.

Fig. 11 shows the generalization loss metric (GLM) test of CK-AA for DST-PPM, CL-DA for DST-PPM, and CT-CA for DST-PPM based on PEV-Tree, and compares it with three baselines under CPPM, in other words, the comparison of data utility. The parameters for the experiment are set as follows: k = 100, l = 20, t = 0.15, QI = 9, |P| = 4, delay threshold δ = 10,000. It is clear from Fig. 11 that as the number of records per window increases, the GLM parameters of all three algorithms decrease simultaneously. This is because, as new tuples of data continue to arrive, newly formed clusters are added to published clusters, increasing the likelihood that data arriving later will be overwritten by existing clusters, providing higher data availability. However, compared with CPPM, when the number of data streams increases to a certain extent, the decrease in data utility can be controlled within a stable range. We observe that when the number of data streams is greater than 25,000, DST-PPM can ensure the stability of data utility. When the number of data streams is small, DST-PPM can maintain better data utility. It is worth noting that CT-CA for DST-PPM improves data utility by nearly 50% compared to CT-CA for CPPM. Due to the reduction of PEV-Tree and our reconstructed VP-Tree data structure, the accuracy of dynamic clustering is increased, thus improving the availability of data. In addition, CK-AA and CL-DA under DST-PPM have significantly improved data utility.

5.3 Evaluation of Data Protection Effectiveness (Reliability)

To further measure the effectiveness of three algorithms based on PEV-Tree in protecting sensitive data in IoV under DST-PPM, an evaluation of their security risks was conducted. In particular, to assess the privacy of the distributed T-Closeness method under different parameter t values, t was set to 0.1, 0.15, and 0.2, respectively. Experiments measuring information loss were conducted across different attribute dimensions, with results shown in Fig. 12. We found that our CT-CA for DST-PPM reduced the increment of information loss as the attributes increased and the data dimensions were higher. Specifically, we find that when t = 0.1 is set, that is, the degree of privacy protection is the strongest, the degree of information loss under DST-PPM is comparable to that under the CPPM setting t = 0.15, which means that we can better protect data privacy while achieving less information loss than traditional methods. When t = 0.2 is set, that is, when the data privacy level is set low, we can still achieve the result of reducing the information loss degree in high-dimensional data by nearly 50%. In addition, the privacy protection effect of CT-CA for DST-PPM remained stable at different T-values.

Figure 12: The contrast figure of information loss

Data protected by three methods is all at risk of homogeneity attacks. In the distributed T-Closeness approach, the same attribute values can be generalized into various generalized values. However, when these generalized values correspond to the same sensitive attributes, attackers can still determine the content of the sensitive attributes associated with the original attribute values. In this case, sensitive attribute information could be leaked. Taking {age, driving speed, hour-per-week, oil consumption} as quasi-identifier attributes and {position} as the sensitive attribute. The sensitivity of CK-AA, CL-DA, and CT-CA to homogeneity attack and similarity attack under DST-PPM and CPPM was compared, with parameter k set to 100, l set to 20, and t set to 0.15. As shown in Figs. 13 and 14, the results show that CT-CA is more resistant to homogeneous or similar attacks than CK-AA and CL-DA. The T-Closeness privacy protection method disclosed fewer records in the two types of attack experiments, showing a better privacy protection effect. According to our statistics, in DST-PPM, the probability of information leakage decreased by 2.31%, 1.76%, and 0.19%, respectively.

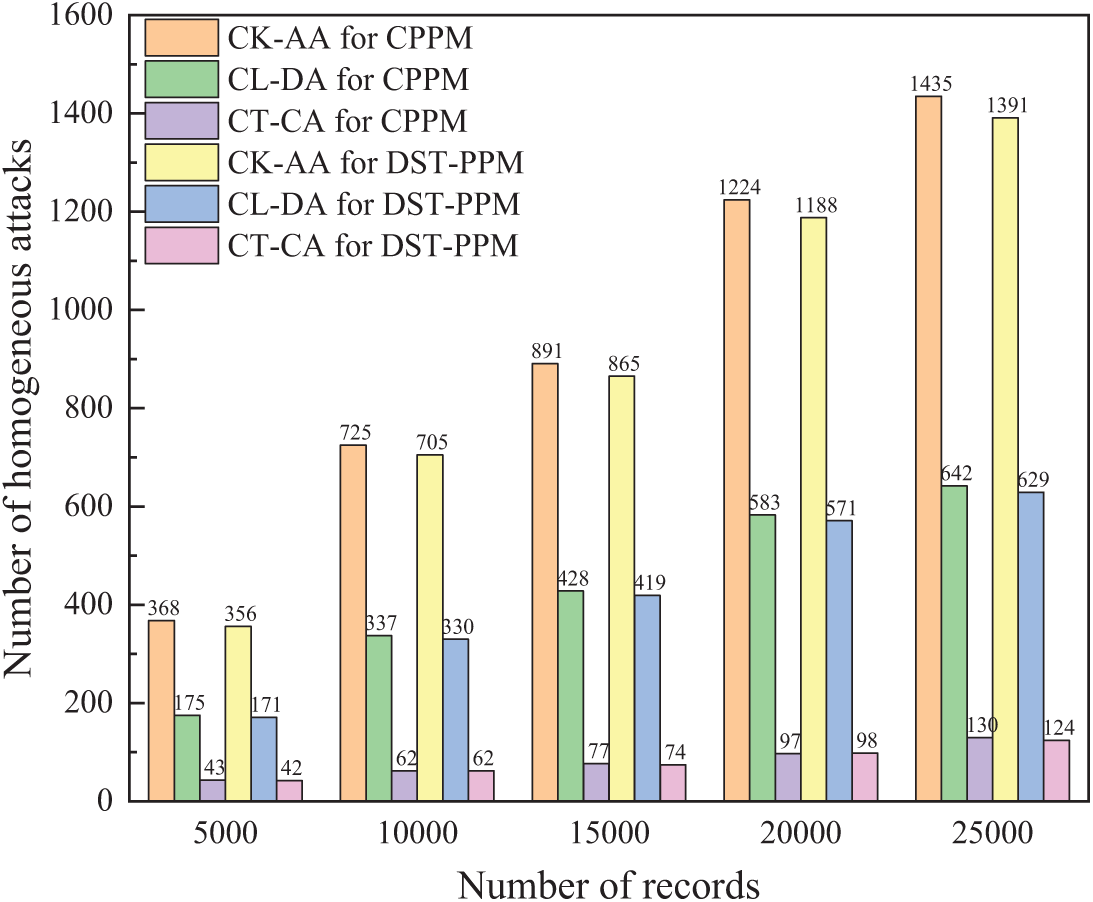
Figure 13: The number of leaked records under homogeneity attack

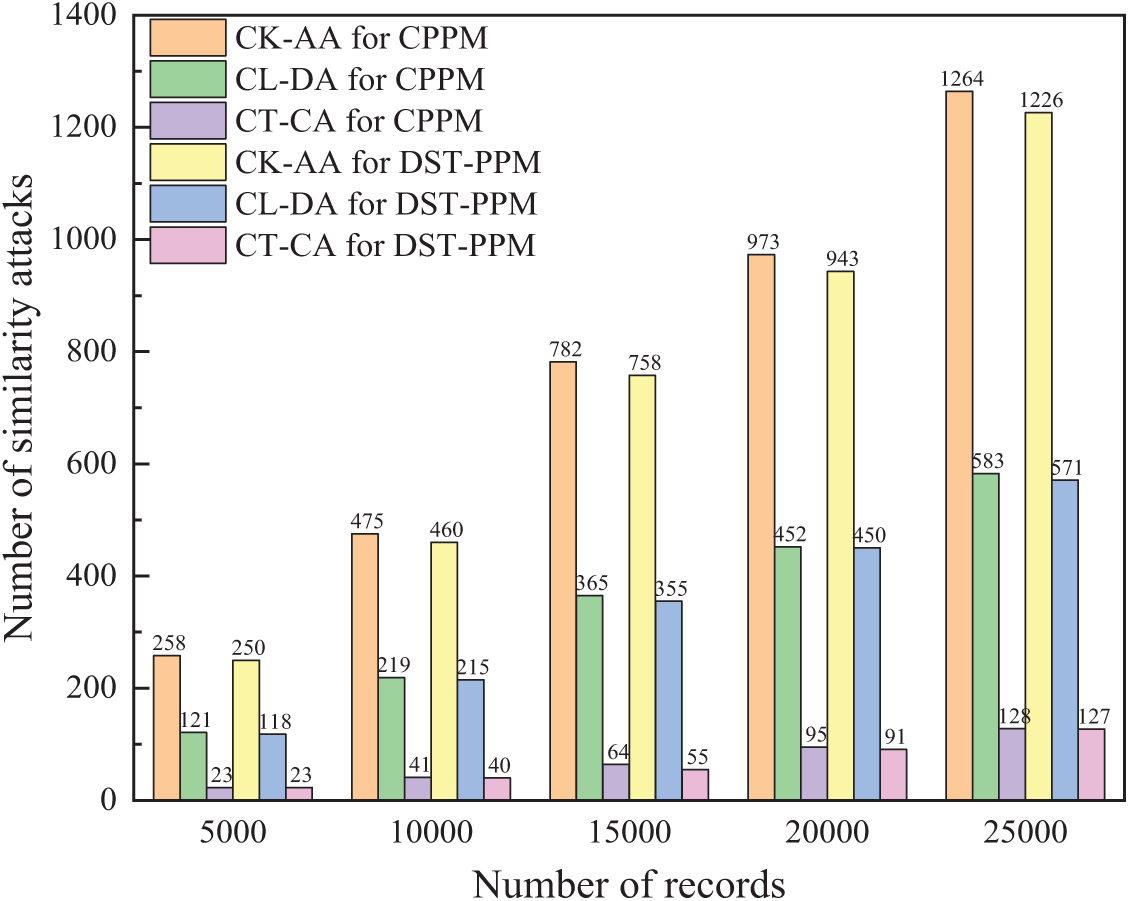
Figure 14: The number of leaked records under similarity attack

By improving efficiency and reliability, the risk of privacy leakage can be significantly reduced. In privacy protection methods, the improvement of efficiency means that the system can process data more quickly, thereby reducing the time that sensitive information is exposed to potential attacks and lowering the opportunity for attackers to make speculations by exploiting homogeneity or similarity vulnerabilities. For example, in the distributed T-Closeness method, the efficiency improvement of the generalization process can reduce the probability of information leakage in each data access, which is particularly important for systems processing large amounts of data. Improving the efficiency and reliability of privacy protection methods not only reduces the possibility of information leakage but also increases the security and credibility of the data processing system. In practical applications, such improvement has important practical significance for scenarios that need to process a large amount of sensitive information, especially in fields such as finance and healthcare.

5.4 Summary and Suggestion

As shown in Table 8, compared with the latest research results, DST-PPM demonstrates significant advantages in three core metrics: Processing efficiency is improved by 50.6% (comparing with CASTLE), which stems from the reduction of distance computation complexity by PEV-Tree; Homogeneity attack resistance rate is improved by 2.6 percentage points, which is benefited from the EMD constraint mechanism of CT-CA; Data utility (Q-Value) improves by 9.3%, and optimal generalization is achieved by dynamically adjusting the hybrid distance weights (α = 0.65).

As can be seen from the core performance comparison in Table 8, the DST-PPM proposed in this paper comprehensively outperforms the existing methods in terms of key metrics. The 50.6% improvement in processing efficiency compared to CASTLE is mainly attributed to the PEV-Tree structure that reduces the distance computation complexity from O(n2) to O(nlog n) through a dimensionality reduction strategy, as well as the distributed processing based on Flink that effectively reduces the communication overhead between nodes. In terms of anti-homogeneity attack, the CT-CA algorithm strictly controls the difference between the distribution of sensitive attributes and the global distribution within a threshold t by introducing a constraint mechanism based on Earth Mover’s Distance, which makes it impossible for an attacker to obtain the precise values of sensitive attributes through statistical inference even if he has complete information about the quasi-identifiers. The enhancement of data utility (Q-value) stems from PEV-Tree’s preservation of principal component features during the dimensionality reduction process, which allows the anonymized data to still maintain the statistical properties of the original data. Notably, the dimension scalability advantage of DST-PPM is particularly significant when QI = 9, which validates the effectiveness of principal component analysis in addressing the challenges of high-dimensional data.

The three distributed anonymization algorithms based on PEV-Tree, whilst ensuring data utility, are capable of delivering high operational efficiency and demonstrate robust scalability. Among them, CK-AA exhibits the greatest operational efficiency, followed by CL-DA, and CT-CA lags behind. In a data window spanning from 5000 to 30,000, the runtime of CT-CA is 2.36 to 2.86 times that of CK-AA and 1.35 to 1.85 times that of CL-DA. Given a QI ranging from 2 to 9, CT-CA’s runtime is 2.21 to 2.75 times that of CK-AA and 1.57 to 1.83 times that of CL-DA. When the latency threshold (δ) is set between 5000 to 20,000, CT-CA’s runtime is 2.02 to 2.33 times that of CK-AA and 1.31 to 1.40 times that of CL-DA.

Through the analysis of the experimental data, specifically, our research results emphasize that when processing high-dimensional data sets under strict privacy constraints, CK-AA for DST-PPM can significantly maintain the highest efficiency when the delay threshold reaches 1000. In addition, our experiment conducted an analysis of the number of congruent identifiers (QI) attributes. The running time of all algorithms increases with the increase in QI count. Although T-Closeness requires the most resources because it involves a thorough anonymization process of data replication and value conversion, its running time grows slowly when its QI number reaches 9. Given these findings, choosing the appropriate anonymization algorithm should be guided by a nuanced understanding of the specific application context. It is generally believed that when there are fewer quasi-identifiers (QI < 9) and the data size is below 10,000, the CK-AA for DST-PPM can obtain the least loss and has the best cost performance in terms of efficiency. When there are many quasi-identifiers (QI > 9) and the data scale reaches more than 10,000, CL-DA for DST-PPM or CT-CA for DST-PPM can be selected according to the demand for actual data utility in different realistic scenarios. In addition, when the delay threshold is less than 1000, CL-DA for DST-PPM can achieve the highest efficiency and better data utility balance.

Based on the analysis provided, CK-AA for DST-PPM is apt for scenarios with large data volume and high latency requirements, such as real-time data stream processing and large-scale data analysis, given its highest operational efficiency. CL-DA for DST-PPM is suitable for application scenarios where efficiency and data diversity need to be balanced, including medium-scale data analysis and businesses with moderate to high privacy protection requirements. Despite having the lowest operational efficiency, CT-CA for DST-PPM excels in situations demanding high-level privacy protection and allowing extended processing time, such as medical data processing and analysis of highly sensitive information. However, DST-PPM also has certain limitations. During the construction process of the PEV-Tree, once excessive dimensionality reduction occurs, it will cause the data to lose its original features, which will lead to a decrease in the reliability of the privacy protection algorithm. Therefore, in the process of using DST-PPM to improve the real-time performance of data processing, it is also necessary to pay attention to the retention of the original features of the data at the same time.

5.5 Research Limitations

Although DST-PPM exhibits significant advantages in dynamic spatio-temporal privacy preservation, it still has several limitations that need to be further explored. First, the dimensionality reduction process of principal component analysis (PCA) is sensitive to threshold selection, which may affect the integrity of data features. Experiments have shown that when the number of retained principal components is lower than the threshold value (e.g., k = 3), the data feature loss rate is more than 15%, which may lead to the loss of key information in the anonymization process. For example, in the car networking scenario, if excessive dimensionality reduction leads to the weakening of the correlation features between vehicle speed and fuel consumption, it may affect the clustering accuracy of the anonymization group. Although this paper mitigates this problem by optimizing the principal component retention strategy (default k = 6), in extremely high-dimensional data (e.g., more than 100 dimensions) scenarios, it is still necessary to weigh the balance between dimensionality reduction efficiency and feature retention. In addition, PCA has limited ability to handle nonlinear relationships and may ignore complex interactive features in the data, such as spatio-temporal correlations in vehicle trajectories.

The real-time performance of the algorithm faces challenges in ultra-low latency scenarios. Experimental results show that when the delay threshold δ is set lower than 5000, the time-consuming percentage of Earth Mover’s Distance (EMD) computation of CT-CA is as high as 63% (e.g., Fig. 10), which becomes a performance bottleneck. This phenomenon stems from the high complexity (O(n3)) of EMD computation, especially when dealing with large-scale sensitive attribute distributions (e.g., fine-grained geo-location data in Telematics), the computational overhead increases significantly. Although this paper reduces the number of clusters to be computed by the pre-partitioning strategy of PEV-Tree, in scenarios with strict real-time requirements (e.g., real-time decision support for automated driving), further optimization of the approximation algorithm or a distributed computation framework for EMD is still needed. In addition, the current architecture is designed based on Flink’s memory management mechanism, which is not adequately adapted to heterogeneous hardware (e.g., GPU/NPU), and the throughput may drop by 28% (e.g., the acceleration ratio deviates from the theoretical value at |P| = 4 in Table 7) when dealing with ultra-large-scale data streams (e.g., millions of events per second). In the future, a combination of hardware acceleration and lightweight algorithm design is needed to further improve the processing capability in highly concurrent scenarios.

6  Conclusion

This work proposes an efficient PEV-Tree data structure and designs distributed anonymization algorithms based on CASTLE (CK-AA, CL-DA, CT-CA) to meet K-Anonymity, L-Diversity, and T-Closeness requirements, respectively. A novel distributed DST-PPM was constructed using the PEV-Tree and CASTLE-based distributed anonymization algorithms. Experiments were conducted in a Flink distributed computing environment to evaluate performance, particularly under varying data volumes and latency thresholds. Results demonstrate that DST-PPM achieves efficient privacy protection while maintaining data utility, showing good scalability and application prospects. This provides an effective technical means for large-scale data stream privacy protection with significant practical implications. The main conclusions are as follows:

1.    The PEV-Tree data stream significantly improves the operational efficiency of privacy protection algorithms. CK-AA, CL-DA, and CT-CA efficiencies increased by 15.12%, 24.55%, and 52.74%, respectively, compared to traditional data streams.

2.    CK-AA, CL-DA, and CT-CA can effectively perform privacy protection tasks. When operating on PEV-Tree data streams, they exhibit stronger resistance to similar attacks, with the probability of information leakage reduced by 2.31%, 1.76%, and 0.19%, respectively, compared to traditional data streams.

3.    As data volume increases, the operational costs of CK-AA, CL-DA, and CT-CA on PEV-Tree data streams grow much less than on traditional datasets, demonstrating stronger scalability. We can better protect data privacy while achieving less information loss than traditional methods.

4.    DST-PPM outperforms CPPM in terms of efficiency, reliability, and scalability. However, when using DST-PPM, reasonable trade-offs should be made based on specific application scenarios. CK-AA is suitable for ultra-low latency and lower reliability requirements, CT-CA for ultra-high reliability with less stringent latency requirements, and CL-DA offers a balanced choice. In addition, it is worth mentioning that although this work was conducted with the background of the Internet of Vehicles for experiments, the method proposed in this paper is also applicable to other public domains.

DST-PPM achieves multi-scale partitioning of data space through PEV-Tree, maintains clustering accuracy while reducing computational complexity, and meets different needs from basic anonymization to strong privacy protection by constructing a family of distributed anonymization algorithms. In addition, DST-PPM realizes the dynamic balance between privacy protection strength and data utility in dynamic data flow scenarios. Experimental results show that the communication overhead of this method is only 35% of the traditional method when processing 100,000-volume data, which provides a technical basis for the deployment of real-time systems such as Telematics, which reflects the innovation and advantages of DST-PPM.

Acknowledgement: The authors would like to thank the editor and the anonymous reviewers for their insightful comments.

Funding Statement: This work was supported by the Natural Science Foundation of Sichuan Province (No. 2024NSFSC1450), the Fundamental Research Funds for the Central Universities (No. SCU2024D012), and the Science and Engineering Connotation Development Project of Sichuan University (No. 2020SCUNG129).

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Jiacheng Xiong, Xingshu Chen, and Xiao Lan. Experiment and interpretation of results: Jiacheng Xiong. Manuscript preparation: Jiacheng Xiong, Xiao Lan, and Liangguo Chen. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All public dataset sources are as described in the paper.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Ji BF, Zhang XR, Mumtaz S, Han CZ, Li CG, Wen H, et al. Survey on the internet of vehicles: network architectures and applications. IEEE Commun Stand Mag. 2020;4(1):34–41. doi:10.1109/MCOMSTD.001.1900053. [Google Scholar] [CrossRef]

2. Sharma S, Kaushik B. A survey on internet of vehicles: applications, security issues & solutions. Veh Commun. 2019;20(4):100182. doi:10.1016/j.vehcom.2019.100182. [Google Scholar] [CrossRef]

3. Dai PL, Song F, Liu K, Dai YY, Zhou P, Guo ST. Edge intelligence for adaptive multimedia streaming in heterogeneous internet of vehicles. IEEE Trans Mob Comput. 2021;22(3):1464–78. doi:10.1109/TMC.2021.3106147. [Google Scholar] [CrossRef]

4. Moussaoui B, Chikouche N, Fouchal H. An efficient privacy scheme for C-ITS stations. Comput Electr Eng. 2023;107(4):108613. doi:10.1016/j.compeleceng.2023.108613. [Google Scholar] [CrossRef]

5. Xu JX, Li MY, He ZL, Anwlnkom T. Security and privacy protection communication protocol for internet of vehicles in smart cities. Comput Electr Eng. 2023;109(10):108778. doi:10.1016/j.compeleceng.2023.108778. [Google Scholar] [CrossRef]

6. Amin R, Lohani P, Ekka M, Chourasia S, Vollala S. An enhanced anonymity resilience security protocol for vehicular ad-hoc network with scyther simulation. Comput Electr Eng. 2020;82(1):106554. doi:10.1016/j.compeleceng.2020.106554. [Google Scholar] [CrossRef]

7. Xu WC, Zhou HB, Cheng N, Lyu F, Shi WS, Chen JY, et al. Internet of vehicles in big data era. IEEE CAA J Autom Sin. 2017;5(1):19–35. doi:10.1109/JAS.2017.7510736. [Google Scholar] [CrossRef]

8. Wu XT, Xu XL, Bilal M. Toward privacy protection composition framework on Internet of Vehicles. IEEE Consum Electron Mag. 2021;11(6):32–8. doi:10.1109/mce.2021.3092303. [Google Scholar] [CrossRef]

9. Sun YC, Wu L, Wu SZ, Li SP, Zhang T, Zhang L, et al. Security and privacy in the internet of vehicles. In: Proceedings of the Security and Privacy in the Internet of Vehicles; 2015 Oct 22–23; Beijing, China. [Google Scholar]

10. Joy J, Gerla M. Internet of vehicles and autonomous connected car-privacy and security issues. In: Proceedings of the 2017 26th International Conference on Computer Communication and Networks (ICCCN); 2017 Jul 31–Aug 3; Vancouver, BC, Canada. [Google Scholar]

11. Zhang QK, Li YJ, Wang RF, Li JY, Gan Y, Zhang YH, et al. Blockchain-based asymmetric group key agreement protocol for internet of vehicles. Comput Electr Eng. 2020;86(6):106713. doi:10.1016/j.compeleceng.2020.106713. [Google Scholar] [CrossRef]

12. Yang L, Chen XS, Luo YG, Lan X, Wang W. IDEA: a utility-enhanced approach to incomplete data stream anonymization. Tsinghua Sci Technol. 2021;27(1):127–40. doi:10.26599/TST.2020.9010031. [Google Scholar] [CrossRef]

13. Sakpere AB, Kayem AV. A state-of-the-art review of data stream anonymization schemes. Inf Secur Divers Comput Environ. 2014; 24–50. doi:10.4018/978-1-4666-6158-5.ch003. [Google Scholar] [CrossRef]

14. Sakpere AB, Kayem AV. Adaptive buffer resizing for efficient anonymization of streaming data with minimal information loss. In: Proceedings of the 2015 International Conference on Information Systems Security and Privacy (ICISSP); 2015 Feb 9–11; Angers, France. [Google Scholar]

15. Wang X, Liu Z, Tian XH, Gan XY, Guan YF, Wang XB. Incentivizing crowdsensing with location-privacy preserving. IEEE Trans Wirel Commun. 2017;16(10):6940–52. doi:10.1109/twc.2017.2734758. [Google Scholar] [CrossRef]

16. Zhong S, Yang ZQ, Chen TT. K-Anonymous data collection. Inf Sci. 2009;179(17):2948–63. doi:10.1016/j.ins.2009.05.004. [Google Scholar] [CrossRef]

17. Dunning LA, Kresman R. Privacy preserving data sharing with anonymous ID assignment. IEEE Trans Inf Forensics Secur. 2012;8(2):402–13. doi:10.1109/tifs.2012.2235831. [Google Scholar] [CrossRef]

18. Kumar J. Slide window method adapted for privacy-preserving: transactional data streams. Eur J Mol Clin Med. 2021;8(2):2528–39. [Google Scholar]

19. Zhang X, Liu C, Nepal S, Yang C, Dou W, Chen J. A hybrid approach for scalable sub-tree anonymization over big data using MapReduce on cloud. J Comput Syst Sci. 2014;80(5):1008–20. doi:10.1016/j.jcss.2014.02.007. [Google Scholar] [CrossRef]

20. Wei R, Kerschbaum F. Cryptographically secure private record linkage using locality-sensitive hashing. Proc VLDB Endow. 2023;17(2):79–91. doi:10.14778/3626292.3626293. [Google Scholar] [CrossRef]

21. Cao JN, Carminati B, Ferrari E, Tan KL. CASTLE: a delay-constrained scheme for ks-anonymizing data streams. In: Proceedings of the 2008 IEEE 24th International Conference on Data Engineering; 2008 Apr 7–12; Cancun, Mexico. [Google Scholar]

22. Gangarde R, Sharma A, Pawar A. Enhanced clustering based OSN privacy preservation to ensure k-anonymity, t-closeness, l-diversity, and balanced privacy utility. Comput Mater Contin. 2023;75(1):2171–90. doi:10.32604/cmc.2023.035559. [Google Scholar] [CrossRef]

23. Sweeney L. K-Anonymity: a model for protecting privacy. Int J Uncertain Fuzziness Knowl-Based Syst. 2002;10(05):557–70. doi:10.1142/s0218488502001648. [Google Scholar] [CrossRef]

24. El Emam K, Dankar FK. Protecting privacy using k-anonymity. J Am Med Inform Assoc. 2008;15(5):627–37. doi:10.1197/jamia.m2716. [Google Scholar] [PubMed] [CrossRef]

25. Sweeney L. Achieving k-anonymity privacy protection using generalization and suppression. Int J Uncertain Fuzziness Knowl-Based Syst. 2002;10(5):571–88. doi:10.1142/s021848850200165x. [Google Scholar] [CrossRef]

26. Machanavajjhala A, Kifer D, Gehrke J, Venkitasubramaniam M. L-diversity: privacy beyond k-anonymity. ACM Trans Knowl Discov Data. 2007;1(1):3–es. doi:10.1145/1217299.1217302. [Google Scholar] [CrossRef]

27. Temuujin O, Ahn J, Im DH. Efficient L-diversity algorithm for preserving privacy of dynamically published datasets. IEEE Access. 2019;7:122878–88. doi:10.1109/access.2019.2936301. [Google Scholar] [CrossRef]

28. Li NH, Li TC, Venkatasubramanian S. T-closeness: privacy beyond k-anonymity and l-diversity. In: Proceedings of the 2007 IEEE 23rd International Conference on Data Engineering; 2007 Apr 15–20; Istanbul, Türkiye. [Google Scholar]

29. Wang R, Zhu Y, Chen TS, Chang CC. Privacy-preserving algorithms for multiple sensitive attributes satisfying t-closeness. J Comput Sci Technol. 2018;33(6):1231–42. doi:10.1007/s11390-018-1884-6. [Google Scholar] [CrossRef]

30. Sun Y, Hao H, Langenheldt K, Harlev M, Mukkamala RR, Vatrapu R. Regulating cryptocurrencies: a supervised machine learning approach to de-anonymizing the bitcoin blockchain. J Manag Inf Syst. 2019;36(1):37–73. doi:10.1080/07421222.2018.1550550. [Google Scholar] [CrossRef]

31. Waheed N, He X, Ikram M, Usman M, Hashmi SS, Usman M. Security and privacy in IoT using machine learning and blockchain: threats and countermeasures. ACM Comput Surv. 2020;53(6):1–37. doi:10.1145/3417987. [Google Scholar] [CrossRef]

32. Majeed A, Khan S, Hwang SO. Toward privacy preservation using clustering based anonymization: recent advances and future research outlook. IEEE Access. 2022;10(2000):53066–97. doi:10.1109/ACCESS.2022.3175219. [Google Scholar] [CrossRef]

33. Ho S, Qu Y, Gu B, Gao L, Li J, Xiang Y. DP-GAN: differentially private consecutive data publishing using generative adversarial nets. J Netw Comput Appl. 2021;185(99):103066. doi:10.1016/j.jnca.2021.103066. [Google Scholar] [CrossRef]

34. Fan L, Xiong L. An adaptive approach to real-time aggregate monitoring with differential privacy. IEEE Trans Knowl Data Eng. 2013;26(9):2094–106. doi:10.1109/tkde.2013.96. [Google Scholar] [CrossRef]

35. Zhao X, Zhang H, Lin J, Liang F, Kong F, Xu H, et al. Privacy-preserving edge-aided eigenvalue decomposition in internet of things. IEEE Internet Things J Forthcoming. 2025. doi:10.1109/jiot.2025.3544245. [Google Scholar] [CrossRef]

36. Daffertshofer A, Lamoth CJ, Meijer OG, Beek PJ. PCA in studying coordination and variability: a tutorial. Clin Biomech. 2004;19(4):415–28. doi:10.1016/j.clinbiomech.2004.01.005. [Google Scholar] [PubMed] [CrossRef]

37. Cantone D, Ferro A, Pulvirenti A, Recupero DR, Shasha D. Antipole tree indexing to support range search and k-nearest neighbor search in metric spaces. IEEE Trans Knowl Data Eng. 2005;17(4):535–50. doi:10.1109/tkde.2005.53. [Google Scholar] [CrossRef]

38. Paolanti M, Frontoni E. Multidisciplinary pattern recognition applications: a review. Comput Sci Rev. 2020;37:100276. doi:10.1016/j.cosrev.2020.100276. [Google Scholar] [CrossRef]

39. Ukey N, Yang Z, Li B, Zhang GJ, Hu YH, Zhang WJ. Survey on exact kNN queries over high-dimensional data space. Sensors. 2023;23(2):629. doi:10.3390/s23020629. [Google Scholar] [PubMed] [CrossRef]

40. Samet H. Foundations of multidimensional and metric data structures. Amsterdam, The Netherlands: Elsevier; 2006. 993 p. [Google Scholar]

41. Choi D, Wee J, Song SH, Lee H, Lim J, Bok K, et al. k-NN query optimization for high-dimensional index using machine learning. Electronics. 2023;12(11):2375. doi:10.3390/electronics12112375. [Google Scholar] [CrossRef]

42. Pawar A, Ahirrao S, Churi PP. Anonymization techniques for protecting privacy: a survey. In: Proceedings of the 2018 IEEE Punecon; 2018 Nov 30–Dec 2; Pune, India. [Google Scholar]

43. Saleem Y, Rehmani MH, Crespi N, Minerva R. Parking recommender system privacy preservation through anonymization and differential privacy. Eng Rep. 2021;3(2):e12297. doi:10.1002/eng2.12297. [Google Scholar] [CrossRef]

44. Song L, Sun G, Yu H, Du X, Guizani M. Fbia: a fog-based identity authentication scheme for privacy preservation in internet of vehicles. IEEE Trans Veh Technol. 2020;69(5):5403–15. doi:10.1109/tvt.2020.2977829. [Google Scholar] [CrossRef]

45. Tu Z, Zhao K, Xu F, Li Y, Su L, Jin D. Beyond k-anonymity: protect your trajectory from semantic attack. In: Proceedings of the 2017 14th Annual IEEE International Conference on Sensing, Communication, and Networking (SECON); 2017 Jun 12–14; San Diego, CA, USA. [Google Scholar]

46. Aujla GS, Singh A, Singh M, Sharma S, Kumar N, Choo KKR. BloCkEd: blockchain-based secure data processing framework in edge envisioned V2X environment. IEEE Trans Veh Technol. 2020;69(6):5850–63. doi:10.1109/tvt.2020.2972278. [Google Scholar] [CrossRef]

47. Fu AW, Chan PM, Cheung YL, Moon YS. Dynamic VP-Tree indexing for n-nearest neighbor search given pair-wise distances. VLDB J. 2000;9(2):154–73. doi:10.1007/pl00010672. [Google Scholar] [CrossRef]

48. Jiang DG, Sun HJ, Yi JK, Zhao XH. The research on nearest neighbor search algorithm based on vantage point tree. In: Proceedings of the 2017 8th IEEE International Conference on Software Engineering and Service Science (ICSESS); 2017 Nov 24–26; Beijing, China. [Google Scholar]

49. Kumar N, Zhang L, Nayar S. What is a good nearest neighbors algorithm for finding similar patches in images? In: Proceedings of the Computer Vision–ECCV 2008: 10th European Conference on Computer Vision; 2008 Oct 12–18; Marseille, France. [Google Scholar]

50. Iyengar VS. Transforming data to satisfy privacy constraints. In: Proceedings of the eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; 2002 Jul 23–26; Edmonton, AB, Canada. [Google Scholar]

51. Ghinita G, Karras P, Kalnis P, Mamoulis N. Fast data anonymization with low information loss. In: Proceedings of the 33rd International Conference on Very Large Data Bases; 2007 Sep 23–27; Vienna, Austria. [Google Scholar]