Cluster Federated Learning with Intra-Cluster Correction

1  Introduction

As information technology rapidly advances, the generation and widespread application of big data have become significant characteristics of modern society [1]. From business analytics to healthcare and public services, data is being used to drive innovation, improve efficiency, and enhance the quality of life. However, recent frequent incidents of personal data breaches have heightened societal concern for data privacy protection [2]. The traditional method of direct data collection and centralized training on servers is limited by data security risks. To address compliance challenges in data use, federated learning has emerged as a novel machine learning paradigm gaining high recognition in both academia and industry. Federated learning allows clients to train models locally and send model parameters to a central server for aggregation [3]. By aggregating model parameters from different clients, federated learning can leverage cross-client data information to train an optimized global model [4].

Data distribution significantly impacts the performance of federated learning algorithms, making client data heterogeneity a critical challenge in implementing federated learning. In many general scenarios, client datasets often exhibit non-independent identically distributed (non-IID) characteristics, which not only significantly degrade the overall performance of the global model but also slow down its convergence [5]. Studies have identified label distribution shift as one of the primary factors leading to non-IID states, where there are substantial differences in label distributions across clients. This inconsistency in label distribution makes it particularly challenging to construct a globally effective generalization capability, directly affecting the fairness and accuracy of the final model [6]. To mitigate the impact of data heterogeneity, researchers have proposed various strategies to alleviate the negative effects caused by data heterogeneity. These methods include employing robust optimization techniques, designing specialized model structures tailored for non-IID data, and developing new communication protocols [7,8]. For example, some researchers recommend dynamic client clustering methods combined with gradient regularization and global label alignment to effectively reduce the impact of distribution differences among clients on global model performance [8]. Others adopt adaptive label alignment techniques that adjust the global model’s alignment strategy based on local data distribution [9,10]. Additionally, researchers use variational Bayesian inference techniques to enhance federated learning performance by building complex probabilistic distribution models [11–13]. However, these methods require abundant local data to approximate posterior distributions, leading to significantly weaker inference effects in clients with scarce data or missing label categories, resulting in suboptimal global model performance. In addition, these approaches attempt to compensate for data heterogeneity by increasing model complexity, but this contradicts the basic goal of adapting to resource constraints on edge devices. On clients with missing labels, local training may overfit to a few labels, and global regularization cannot effectively correct this bias, instead suppressing the model’s generalization capability.

Although there has been extensive research on the issue of data heterogeneity in federated learning, effective model training with severely unbalanced label distribution is still an underexplored area [14]. Extreme imbalances in label distribution have been observed in a variety of real-world applications, including but not limited to medical image analysis, autonomous driving technology, and intelligent educational platforms [15,16]. Taking modern education systems as an example, unequal distribution of educational resources can result in a significant shift in the learning materials available for different subjects on online learning platforms [17]. Popular courses may attract a large number of students, resulting in massive high-quality datasets; however, materials related to niche areas appear to be scarce, posing challenges for the development of effective intelligent tutoring systems [18,19]. Therefore, conducting extensive research into these label imbalance phenomena and developing corresponding solutions is critical for furthering the development of federated learning technologies.

For this purpose, we innovatively propose a Cluster Federated Learning Algorithm with Intra-cluster Correction (CFIC). This method is particularly suited for scenarios where clients predominantly possess only a few or even a single type of label. By extracting label distribution characteristics, clients with similar data distributions are clustered together into the same group. Each cluster then independently aggregates its model to mitigate the impact of non-IID data on federated learning. Specifically, CFIC selects samples from each cluster in every round of sampling, ensuring a more reasonable overall data distribution and preventing certain specific categories from disproportionately dominating the model training process. However, the cluster models obtained by aggregating each cluster might deviate to some extent from the direction of the global optimum, leading to a decline in overall performance. To address this issue, CFIC not only leverages local information but also focuses on maintaining consistency with the global model. During each iteration, CFIC adjusts its parameters based on the information shared by other clusters besides updating the local model based on local data. This ensures that the final cluster model better reflects the true situation of the entire dataset. This process can be viewed as a correction in the direction of the global model. It ensures that even when label distributions are extremely imbalanced, the resulting negative impacts are significantly mitigated, thereby improving the global model’s performance. Based on the above analysis, we summarize the following main contributions.

•   We cluster clients based on their label distribution characteristics and then use a specific sampling strategy within these clusters to ensure dynamic label balance in each round of sampling. This method reduces the decline in model performance caused by the non-IID nature of client data.

•   We incorporate a model correction strategy into cluster federated learning. This strategy enables the cluster models to update towards the direction of the global model’s optimal solution, thereby enhancing the convergence speed and accuracy of the model.

•   We conducted extensive experiments on real-world datasets, demonstrating that our method outperforms baseline algorithms in terms of convergence speed and testing accuracy. Particularly, in scenarios with extreme label imbalance, our approach achieves superior results compared to benchmark methods.

2  Related Works

2.1 Federated Learning

Federated learning has emerged as a pivotal approach to safeguard data privacy while effectively integrating disparate data silos. FedAvg, as a classic federated learning framework, can enhance the performance of edge device models through an algorithm that ensures user privacy [4]. In this algorithm, the central server first selects a subset of clients to participate in the training and distributes the global model to these selected clients. Each client independently trains the model using their local data and the central server aggregates the model updates from the participating clients to form a new global model. However, due to differences in user demographics or usage habits, the local data on clients may exhibit non-IID characteristics. Li et al. further confirmed that traditional FedAvg faces challenges such as slow convergence of the global model and deviation from optimal solutions under non-IID conditions [6].

Many researchers have proposed to mitigate the biases that arise during local training on non-IID data, aiming to alleviate the adverse effects in the federated averaging process and enhance the performance of the global model. For instance, FedProx introduces a regularization term during local training that constrains updates based on the distance between the local model and the global model, thereby reducing overfitting of the local models [20]. MOON normalizes local training by leveraging the similarity between the representations of local and global models, incorporating a contrastive learning approach that maximizes the similarity to improve model generalization [21]. FedLC further calibrates at the logit level to reduce updates for minority classes, thereby enhancing model performance when dealing with imbalanced data [22]. FedNova refines the global aggregation phase by adjusting the contribution weights of each client, making the global model more aligned with the global optimum [23]. These existing methods have addressed label shift issues to some extent, but further research and improvements are necessary to enhance their effectiveness in real-world scenarios.

A comprehensive survey categorizes heterogeneous federated learning into data space, statistical, system, and model heterogeneity, suggesting further research to improve model generalization and performance across diverse clients [24]. Researchers have proposed several strategies to mitigate these issues. For example, HeteroFL addresses computational heterogeneity by enabling the training of heterogeneous local models with varying complexities [25]. Exploiting Model and Data Heterogeneity in FL (MDH-FL) employs knowledge distillation and symmetric loss to tackle both data and model heterogeneity [26]. Recent approaches also explore adaptive data distribution, regularization terms, contrastive learning, and multi-task learning to address heterogeneity issues [27]. These methods aim to optimize algorithms and model structures to cope with heterogeneity, but they do not address the diversity of client data distributions. Consequently, some researchers propose clustered federated learning (CFL) to group clients with similar data distributions, thereby improving model performance and enhancing privacy protection level.

2.2 Clustered Federated Learning

CFL is a model-agnostic distributed multi-task optimization framework that enhances both model performance and privacy protection. In recent years, various CFL frameworks have been proposed, including confidential aggregation techniques for securing individual updates and customized systems tailored for human activity recognition applications [28]. The latest advancements focus on efficiently identifying the distributional similarity between client data subspaces using principal angles, which accelerates cluster formation and provides convergence guarantees for non-convex objectives [29]. Furthermore, some researchers have adopted non-convex pairwise fusion, enabling autonomous estimation of cluster structures without prior knowledge [30]. As specific examples in the CFL domain, ClusterFL presents a multi-task federated learning framework that automatically captures inherent clustering relationships among nodes, thereby improving accuracy and reducing communication overhead, particularly in human activity recognition applications [28]. ACFL introduces a mean-shift clustering algorithm and an auction-based client selection strategy aimed at mitigating data heterogeneity and balancing energy consumption in mobile edge computing systems [31]. By leveraging the geometric properties of the federated learning loss surface, clients are grouped into clusters with jointly trainable data distributions, suitable for general non-convex objectives, while performing multi-task optimization under privacy preservation [32]. IFCA addresses non-IID data through iterative clustering and model updates, partitioning clients with similar data distributions into several clusters where each cluster independently conducts model training and updates followed by global model aggregation [33]. FedAC effectively integrates global knowledge into cluster learning by decoupling neural networks and employing different aggregation methods for each submodule, thus significantly enhancing performance [22]. FeSEM introduces an expectation-maximization algorithm for client clustering, ensuring that clients within each cluster share similar data distributions [34].

The CFL methods described above address the issue of model parameter inconsistency by incorporating clustering steps during local training, reducing the global model performance decline caused by label shift. They excel at increasing model accuracy, convergence rate, and efficiency. However, there are two major issues that most studies have not addressed. The first issue is model consistency; model consistency across different clusters can have an impact on overall performance, especially when data distribution is complex. The second issue is the ability to adapt dynamically. Most existing methods’ adaptive adjustment capacity may be restricted for extremely uneven data distributions. To address data heterogeneity in federated learning distributed training, this study introduces an intra-cluster correction method based on the CFL framework. We use a specific sampling strategy to ensure that labels are dynamically balanced with each round of sampling, allowing the cluster model to update towards the optimal global solution.

3  The Proposed CFIC Algorithm

Traditional federated learning’s global averaging aggregation assumes that client data follows the same underlying distribution. However, in actual non-independent and identically distributed (non-IID) scenarios, client data may belong to multiple significantly different sub-distributions. Directly averaging the parameters of all clients blurs these distribution boundaries. If client data can be divided into multiple clusters, we can identify these clusters and then sample and aggregate the cluster models, which can significantly reduce task conflicts. Additionally, even if clients within the same cluster have similar label distributions, their data may still suffer from feature shifts or noise interference. A mechanism is needed to correct the intra-cluster models, forcing the alignment of different client models in latent space, thereby reducing the impact of feature shifts on the global model.

The overall framework of the algorithm proposed in this paper is shown in Fig. 1. This algorithm is a variation on traditional independent and identically distributed federated learning. Unlike the standard federated learning approach, which simply averages all uploaded data to update the global model, our study uses clustering analysis performed by the central server based on the label features received from each client. The goal of this manipulation is to identify a group of clients who share similar characteristics, thereby better capturing potential pattern differences between populations. Rather than creating a global aggregated model for all nodes, the server examines the label features collected from clients and divides them into multiple clusters. For each identified cluster, the server computes the information contributed by its members and creates a local model that represents the cluster’s characteristics. Finally, the global model update direction is determined by the multiple cluster models obtained during the preceding process.

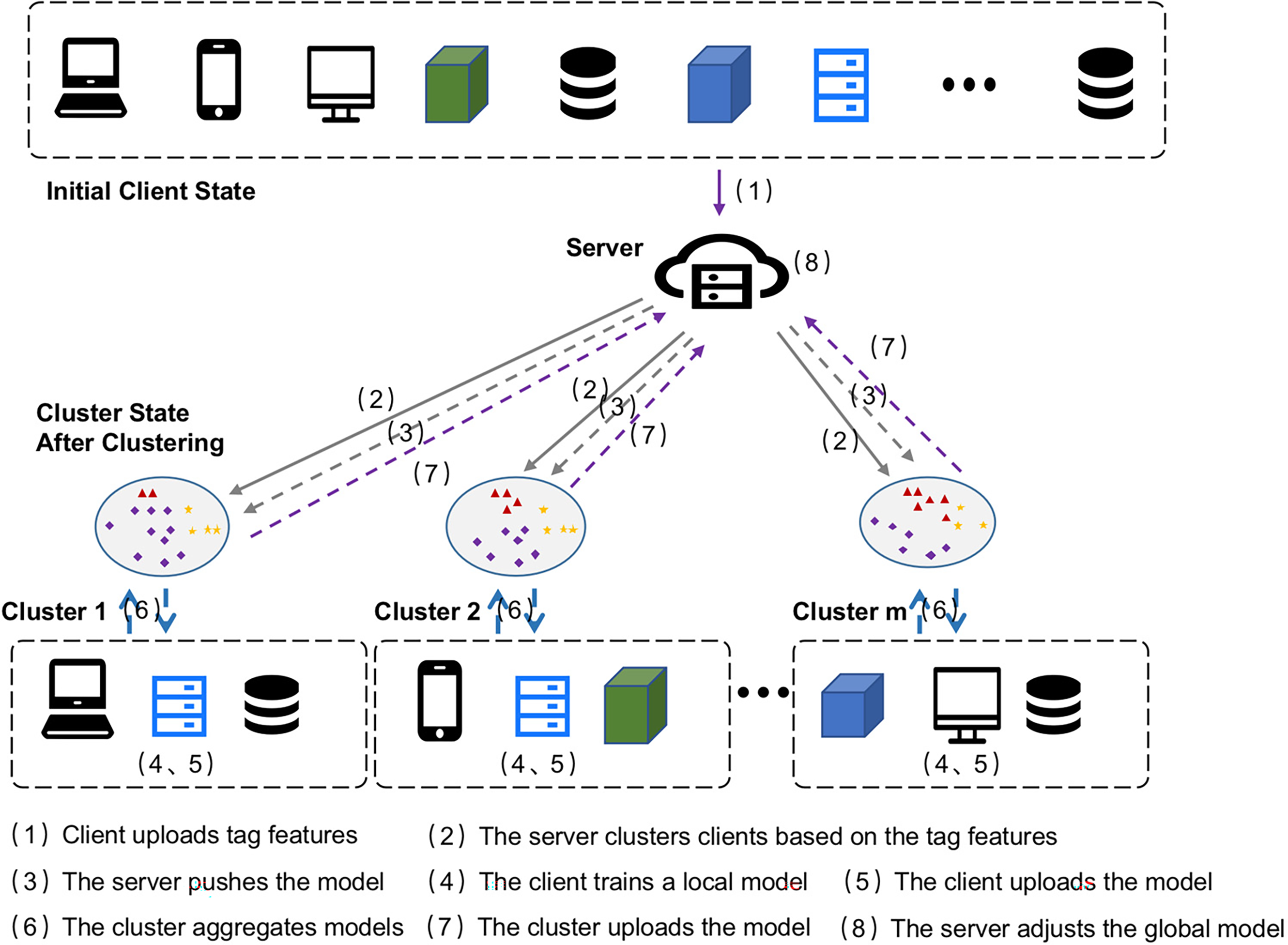
Figure 1: Overall framework

3.1 Problem Formulation

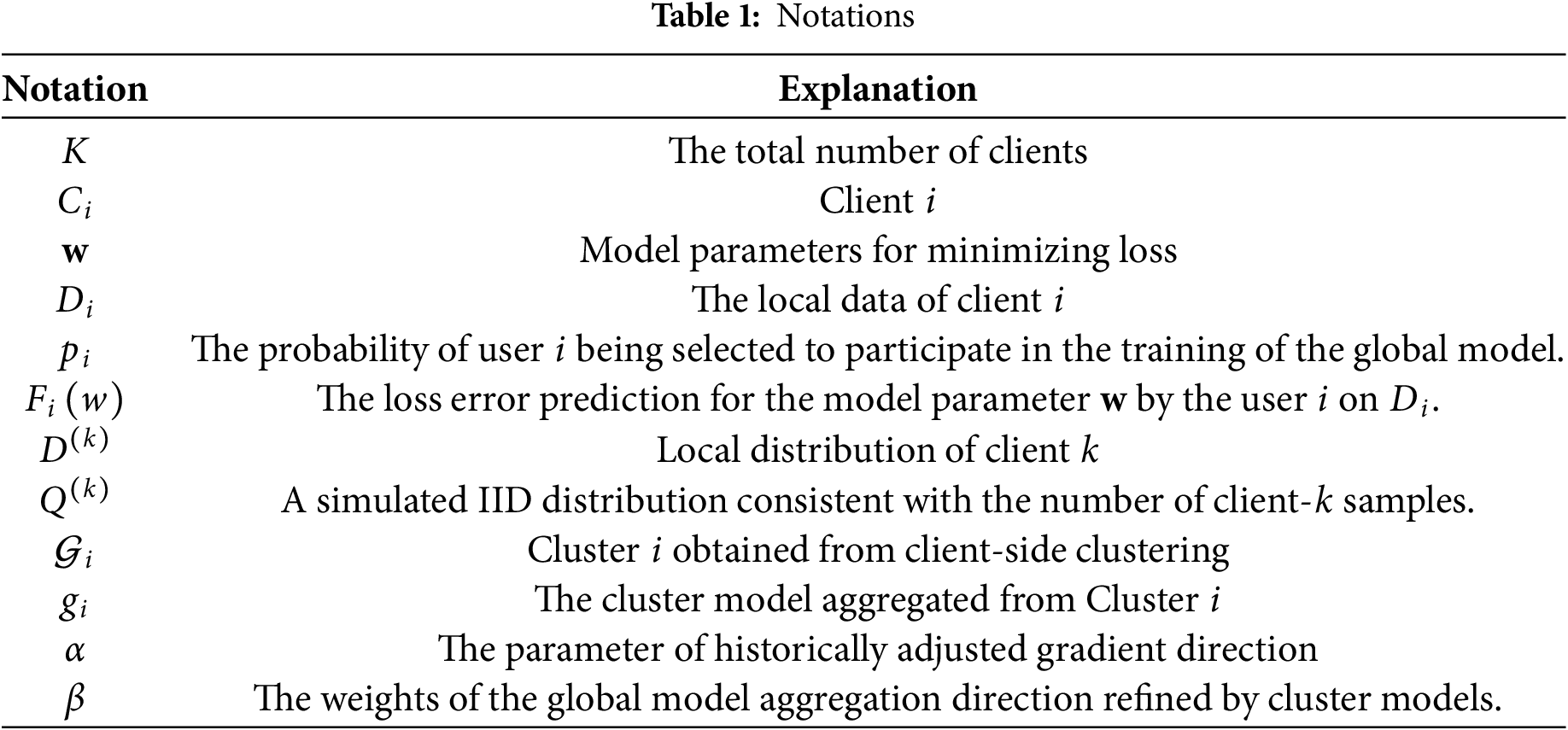
In traditional federated learning algorithms, each iteration typically involves either selecting all clients to participate in the aggregation of the global model or choosing a subset of clients based on a specific sampling strategy. However, when the private datasets on client devices exhibit non-IID characteristics, the performance of the aggregated global model can significantly deteriorate. The purpose of CFIC is to mitigate the issue of client model drift caused by label distribution shifts, thereby obtaining a globally aggregated model with guaranteed performance. The symbols used in this study are shown in Table 1.

In the context of federated learning across devices, consider a system composed of K clients, denoted as {C1,C2,⋯,CK}. All clients are dedicated to integrating their respective data {D1,D2,⋯,DK} in order to obtain a better-performing machine learning model. The central server interacts with these clients to collaboratively find model parameters w that minimize loss through Eq. (1).

minwf(w)=∑i=1KpiFi(w)=Ei[Fi(w)](1)

In this setup, pi represents the probability that participant user i is chosen to contribute to the global model training process, and this probability pi satisfies pi≥0 and ∑i=1Kpi=1. Fi(w) indicates the loss error prediction for model parameters w by the client j on its local dataset (xi,yi), typically calculated using function Fi(w)=ℓ(xi,yi,w), where ℓ(⋅) is a predefined loss function relevant to the specific task. Typically, the FedAvg method is used to minimize model parameters w through unbiased sampling. The probability pi follows a uniform distribution, implying that all users have an equal random chance of being selected to participate in the training.

3.2 Label Distribution Clustering of Clients

Existing research primarily focuses on clustering client-trained local models based on their similarities, which poses a significant challenge for large-scale distributed applications in federated learning. In iterative clustering methods, calculating model similarity is a resource-intensive process that requires substantial computational resources. This is especially true in highly heterogeneous environments where the dataset may contain only a few labels. To address this issue, we can introduce a simulated IID data distribution as a reference. By comparing the local client’s data distribution with this reference distribution, we can obtain the differences between them. We map these distributional differences to a value that represents the deviation of different clients’ data from the ideal distribution. By performing calculations based on these values, we can significantly reduce the required computational scale. Following the work [35], we assume a uniform global class distribution when computing local discrepancies to prevent global label information leakage. Simultaneously, only the maximum categorical label is retained during constructed a feature extraction function Ψ(⋅), thereby mitigating unnecessary local label information exposure, as shown in Eq. (2).

Ψ(D(k))=arg⁡mini(log⁡|Di(k)−Qi(k)|∑jlog⁡|Dj(k)−Qj(k)|)(2)

In this equation, Di(k) represents the actual proportion of samples with label i in the data set ∑i=1CDi(k)=1 of client k, C denotes the total number of labels, and |Di(k)−Qi(k)| indicates the distributional variance of label i within client k. Clients then upload their extracted label distribution features to the server. The server uses these uploaded features to perform client clustering without needing to predefine the number of clusters. The number of clusters is determined by the distribution characteristics of the clients. Client clustering is initiated only during the first round of communication and when new clients join, thereby conserving significant computational resources. This approach involves clients locally mapping feature extraction functions to numerical values. Clients then only upload these mapped values, ensuring that their own label distributions are not exposed. This method provides a level of privacy protection, as the raw data remains on the clients’ local machines and only aggregated, mapped values are shared.

3.3 Global Model with Intra-Cluster Correction

In this step, we mitigate the issue of client model drift caused by extreme label distribution imbalance. In such scenarios, most clients contain only a few or even just one type of label. For clustering groups, the data within each group is more likely to follow an independent and identically distributed distribution. Traditionally, scholars often adopt aggregation functions such as FedAvg, Krum, and Trimmed Mean, which can effectively protect user data privacy [36]. These aggregation functions are used to summarize local model updates from clients into a global model. The choice of aggregation function directly affects the robustness of the model. However, the results of ablation experiments show that using the FedAvg aggregation function decreases model performance. While the Krum and Trimmed Mean aggregation functions have advantages in terms of robustness and simplicity, they require the use of local model gradients from the previous round, making it vulnerable to adversarial samples and limiting their applications in certain dynamically changing scenarios [37]. In this paper, instead of using traditional aggregation functions, we aggregate each cluster into a cluster model, which exhibits higher accuracy for the labels within its respective cluster. However, these cluster models might deviate from the direction of model aggregation in terms of loss-minimizing model parameters w. Therefore, this paper introduces an intra-cluster model correction strategy to update the cluster models towards the direction of the global model’s optimal solution.

To ensure model stability, we have improved the sampling strategy to make the number of samples from each cluster relatively uniform across iterations. Specifically, K clients are clustered into m clusters represented as {𝒢1,𝒢2,𝒢3,⋯,𝒢m}, with a sampling ratio of γ. Within each cluster, each client’s opportunity to participate in training is determined by uniform random sampling, denoted as ∑i∈𝒢pi=1. The sampling number for each cluster is min(⌊Kγm⌋,1), and then additional Kγ−∑i∈𝒢mini(⌊Kγm⌋,1) clients are sampled from the remaining clients to form a final set of clients S(t) as the sampling result for the t-th communication round. If it is the first round of communication, Kγ clients are randomly and uniformly sampled to form client set S(t).

At the beginning of the t-th communication, the server obtains the current global model parameters wt and distributes them to each local client to get local model parameters wkt+1. This paper aggregates m cluster models {g1,g2,g3,⋯,gm} from m clusters. The cluster model update formula is given in Eq. (3).

git+1=∑k∈𝒢inknwkt+1(3)

For the standard gradient descent formula w=w−ηΔw, where η represents the learning rate and Δw is the step size for gradient adjustment at each time step. As it approaches the optimal value, the gradient becomes smaller. Since the learning rate is fixed, the standard gradient descent method converges slowly and may even fall into local optima. This paper introduces momentum h to correct the direction of the global model. Specifically, this is done by comparing the deviation between the cluster model and the direction of the previous round’s global model to correct the direction of the global model aggregation in the current round. We also consider that the cluster model might deviate from the direction of the optimal solution of the global model in some rounds. Therefore, we add the historical correction gradient direction to improve the stability of the model, shown in Eq. (4).

ht+1=(α⋅ht−β⋅∑i=1mningit+1−wt‖git+1−wt‖2)(4)

In this formula, α is the momentum term, representing the influence of historical gradients. The larger α is, the greater the impact of the historical correction gradient direction on the current round. The incorporation of the momentum term offers significant advantages in the high non-IID scenario, which is the focus of this study. On one hand, it accelerates the escape from local minima by leveraging historical accumulation. On the other hand, it mitigates the update oscillations caused by client sampling fluctuations. This design is inspired by the classical convergence theory of distributed optimization, where the core idea is to reduce client gradient variance through exponential smoothing, thereby enhancing convergence efficiency. Therefore, the server can smooth the direction of historical updates to alleviate the impact of heterogeneity among client updates. Finally, we update the global model w by averaging the local models wkt+1 trained by clients in this round and adding the correction from the cluster model, shown in Eq. (5).

wt+1=∑k∈S(t)nknwkt+1−ht+1(5)

Based on the above theoretical analysis, we provide the following pseudocode for the CFIC algorithm as follows (Algorithm 1):

In the provided pseudocode, the algorithm takes the number of clients k, the number of communication rounds t, the sampling ratio γ, the server-side client list 𝒜, gradient information h0, initial model parameters w0, and the learning rate η as input. On the server side, the algorithm initializes w0 with all client values Lk set to empty (Line 1). For the t-th communication round, the algorithm randomly and uniformly samples clients within clusters based on the sampling ratio γ, forming the client set for this round (Line 3). The algorithm then iterates over the client set for this round and updates the client model parameters (Lines 4–5). If a client is not in the central server’s-maintained client table, the algorithm updates the client in the central server’s client table and re-clusters the client to form a new cluster (Lines 6–8). After completing these steps, the algorithm updates the cluster model at Line 9, corrects the gradient at Line 10, and updates the global model parameters at Line 11.

The client-side update process is as follows: The client first obtains the model parameters at Line 13 and then processes the client set in parallel, updating the model parameters (Lines 14–15). If the client is not within the label distribution characteristics, the algorithm uses a label distribution feature extraction function for client clustering (Lines 16–17). Finally, the client returns the model parameters and label distribution characteristics to the server side (Line 18).

3.4 Cold Start Problem of CFIC Algorithm

The cold start problem typically arises when new clients join a federated learning system for the first time. Due to the lack of sufficient historical data to train their local models, these new clients are unable to make meaningful contributions to the global model during the initial phase. This issue not only affects the performance of the new clients’ own models but also potentially slows down the overall performance and stability of the entire system. To address this challenge, we propose the CFIC algorithm, which can meet the needs of new clients joining the federated learning system by mitigating the cold start issue. Specifically, we maintain a client table on the server-side that records all participating clients in the federated learning system. When a new client attempts to join the system, the server detects its absence from the maintained client table 𝒜 and subsequently triggers a re-clustering process. During this re-clustering phase, the new client is incorporated into an appropriate cluster based on certain criteria, thereby facilitating its integration and enabling it to contribute more effectively to the global model.

4  Experiment

4.1 Datasets

We conducted experiments on seven real-world datasets to validate the accuracy and fairness of our algorithm. The purpose of using these real-world datasets is to test the performance of the proposed algorithm in a realistic setting when compared with other algorithms, as well as to evaluate the accuracy of various algorithms on these datasets under heterogenous conditions.

•   MNIST dataset [38]. This dataset consists of images of handwritten digits from 0 to 9. The input for the dataset is 784-dimensional (28 × 28) flattened images, and the output is class labels ranging from 0 to 9.

•   CIFAR10 dataset [39]. This dataset contains 32 × 32-pixel RGB images. There are 60,000 samples in total, with 50,000 samples for training and 10,000 for testing. CIFAR10 includes 10 classes of objects, labeled from 0 to 9.

•   CIFAR100 dataset [40]. This dataset has 100 classes. Each class containing 600 images with 500 for training and 100 for testing. Each image comes with a “fine” label indicating the specific class it belongs to and a “coarse” label indicating the broader category it falls under.

•   EMNIST dataset [41]. This dataset includes both the “by class” and “by merge” datasets, each containing a complete set of 814,255 characters. These datasets differ in the number of categories assigned. Consequently, the distribution of sample letters varies between the two datasets, while the number of samples in the digit class remains consistent across them.

•   SVHN dataset [42]. This dataset is a benchmark for digit classification, consisting of 600,000 32 × 32 RGB cropped images of handwritten digits (from 0 to 9) extracted from house number plates. The cropped images center around the digit of interest but include nearby digits and other distracting elements within the image.

•   FMNIST (Fashion-MNIST) dataset. This dataset is an MNIST replacement featuring 10 fashion categories, each with 6000 28 × 28 grayscale training images and 1000 test images. Its fine-grained details (e.g., shirt vs. coat differences) and built-in non-IID data structure make it a key benchmark for testing federated learning under uneven data splits, especially for simulating real-world data imbalances.

•   FEMNIST is a benchmark dataset in federated learning, extended from EMNIST, containing 62 classes of handwritten characters with both digits and letters. Partitioned by real users via the LEAF framework, it inherently exhibits client-level non-IID characteristics. Each client corresponds to a writer, comprising approximately 800,000 28 × 28 grayscale images across 3400 clients, directly reflecting data heterogeneity in federated scenarios. It enables algorithm validation without artificial synthesis and is widely applied to image classification, aggregation strategy evaluation, and privacy-preserving assessments.

4.2 Baseline Algorithms

We compared our proposed algorithm with the following six federated learning algorithms to test its performance.

1.   FedAvg algorithm. This algorithm is a widely used aggregation method in federated learning. In each round, the server sends the global model parameters to a randomly selected group of clients. Each client trains the model on its local dataset and then sends the local updates back to the server for aggregation. The updated global model is subsequently disseminated to the clients for the next round of training.

2.   FedProx algorithm [20]. This algorithm was designed to address issues related to non-IID data distributions and asymmetric participation among clients. In each round, the server distributes the global model parameters to the clients. Clients train the model on their local datasets and incorporate a regularization term to constrain the extent of local parameter changes, thereby mitigating divergence between clients’ models. The local updates are then aggregated at the server, and the refined global model is redistributed to the clients for subsequent rounds.

3.   FedDyn algorithm [42]. This algorithm introduces an adaptive risk objective for each client. During each communication round, the current global model is sent to selected active devices. Each device optimizes its local empirical loss along with a dynamically updated penalty function based on the difference between the local device model and the received server model. This ensures that the optimal direction of the devices aligns consistently with the static point of the global empirical loss.

4.   FedFa algorithm [43]. This algorithm incorporates a dual momentum gradient optimization scheme to accelerate model convergence. It also proposes a weighting algorithm that combines training accuracy and frequency information to measure the appropriateness of weights. This approach helps mitigate fairness issues in federated learning that may arise due to certain clients’ preferences.

5.   FedMGDA+ algorithm [44]. This algorithm is a multi-objective optimization algorithm aimed at resolving conflicting gradient issues in federated learning. By calculating multiple clients’ gradients in each round and performing multi-objective optimization at the server side, the algorithm balances these gradients, thus reducing inter-client conflicts.

6.   Clustered sampling algorithm [45]. This algorithm enhances the efficiency and effectiveness of federated learning by clustering clients. This ensures that each round of training involves representative clients, thereby improving the generalization capability of the global model. Additionally, by reducing the number of participating clients in each training round, the algorithm can lower communication overhead.

4.3 Setups

The model structure used in this study is as follows: MNIST adopts dual 5 × 5 convolutional layers (32 → 64 channels) and dual fully connected layers (3136 → 512 → 10); CIFAR-10/100 and SVHN are both dual 5 × 5 convolutions (64 channels) combined with three fully connected layers (1600 → 384 → 192 → output), with CIFAR-100 adjusted to 192 → 100 through the final linear layer; EMNIST uses a three convolutional layer (32 → 32 → 64 channels) and a double fully connected layer (576 → 256 → 62), with a unique pooling connection sequence and custom dimension transformation layers. All models use ReLU activation and 2 × 2 max pooling, and non-linear mapping between fully connected layers is achieved through ReLU. The training and testing ratio is 0.9: 0.1.

The experimental setup utilized an Intel(R) Xeon(R) Gold 5218 CPU operating at 2.30 GHz and CentOS Linux release 7.9.2009 (Core) as the operating system. The platform was built using the Python library PyTorch and equipped with three NVIDIA Tesla V100S PCIe 32 GB graphics cards. We assumed a scenario involving 100 devices participating in federated learning with a sampling rate of 0.3. The batch size was set to 64, and the learning rate was uniformly set to 0.01 across all experiments. Additionally, the number of local iterations was fixed at five for each round of communication.

To simulate the class distribution of client data, we employed the Dirichlet distribution to partition the datasets. Sampling was conducted based on corresponding probability values. For the five real-world datasets, different alpha values (0.05, 0.1, 0.3, 0.5) were selected to conduct experiments aimed at evaluating the testing accuracy under various Dir partitions. Due to variations in dataset sizes and partitioning methods, different algorithms required varying numbers of communications to achieve convergence in terms of testing accuracy and training loss across the datasets. Consequently, the number of communications used in the experiments varied accordingly among the five real-world datasets. Fig. 2 illustrates the distribution of classes owned by clients for the CIFAR10 dataset under different alpha values. The distributions of the other datasets are omitted due to space constraints.

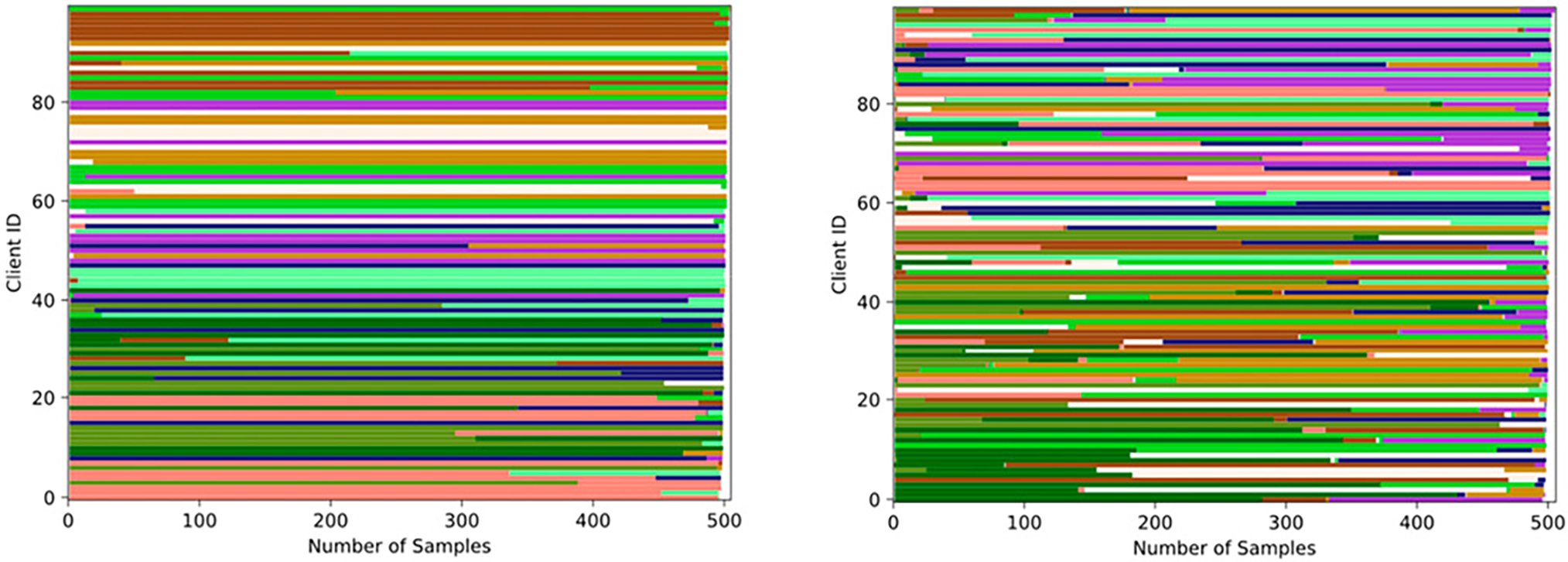
Figure 2: Distribution of client samples under different values. The alpha value of left part is 0.05 and the alpha value of right part is 0.5

4.4 Experimental Results

(1) Testing accuracy

Table 2 illustrates the testing accuracy of various algorithms under different data distribution scenarios. FedAvg exhibits a significant disadvantage in handling highly heterogeneous data, particularly on the CIFAR-100 dataset where its accuracy is only 13.50%, compared to 44.94% on the CIFAR-10 dataset. This demonstrates that FedAvg’s global model generalization ability is insufficient when addressing label imbalance across clients. Conversely, algorithms that incorporate regularization and optimization strategies, such as FedProx and FedDyn, achieve performance improvements. FedProx reduces inter-client model update discrepancies through regularization, while FedDyn mitigates the impact of label shift with dynamic regularization, performing particularly well on large-scale datasets like CIFAR-10 and CIFAR-100.

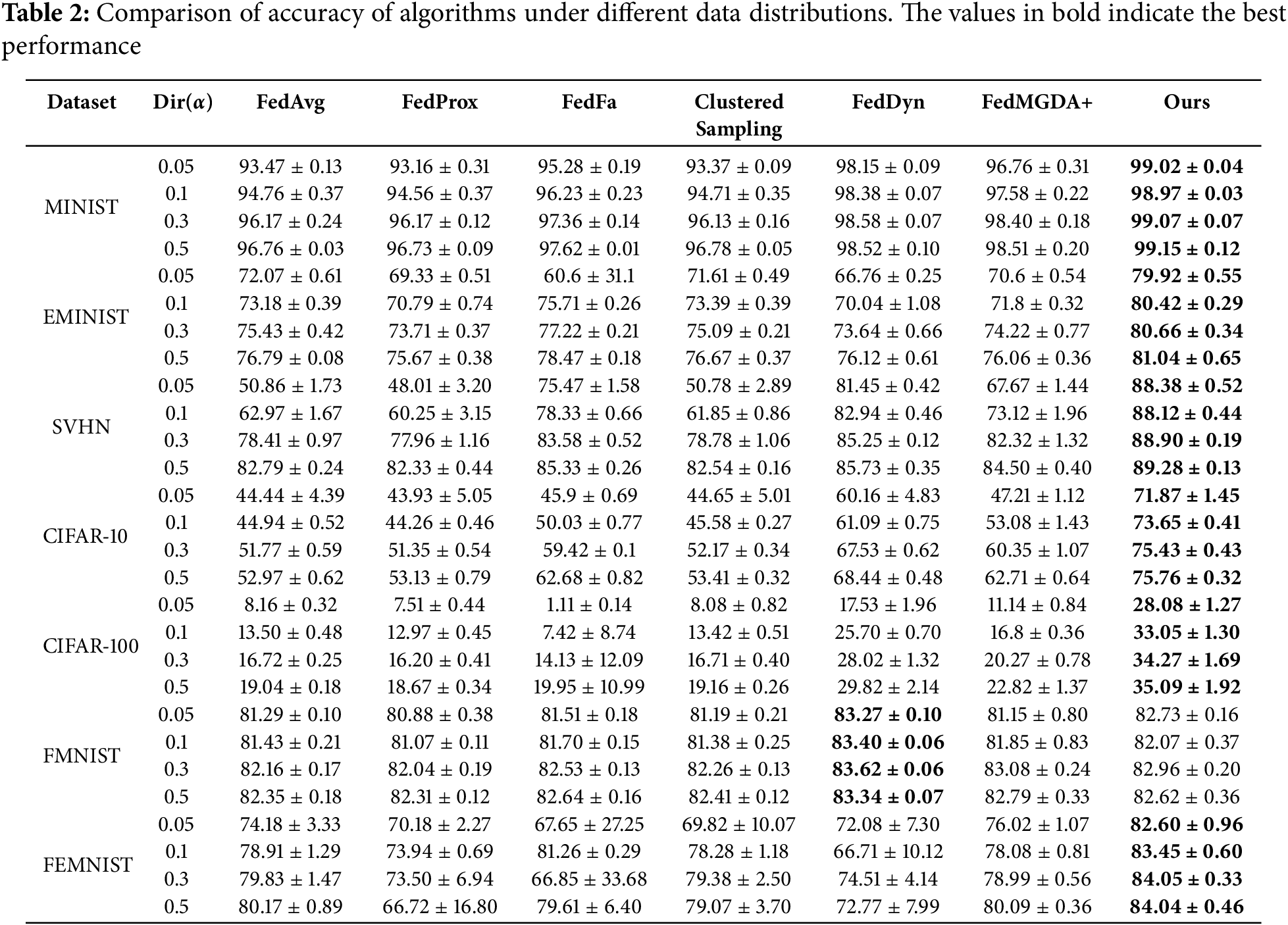
Comparative experiments demonstrate that the proposed CFIC algorithm significantly improves testing accuracy under non-IID conditions through its intra-cluster calibration strategy. While demonstrating suboptimal performance on FMNIST, the proposed algorithm consistently outperformed state-of-the-art methods across all six remaining benchmark datasets. Specifically, CFIC achieved accuracy rates of 73.65%, 33.05%, and 83.45% on CIFAR-10, CIFAR-100, and FEMNIST benchmarks, surpassing all baseline algorithms. Notably, CFIC maintains efficient convergence and superior accuracy even under extreme label imbalance conditions. Although FedFa and FedMGDA+ demonstrate strong generalization capabilities in certain scenarios, their effectiveness diminishes significantly when handling severe data skewness, particularly under small alpha values where substantial performance degradation is observed.

(2) Communication efficiency

To evaluate the communication efficiency of the CFIC algorithm, we measured the number of communication rounds required for each algorithm to reach the target accuracy on various datasets. The accuracy achieved by FedAvg in the last round was used as the benchmark, where “0” indicates that the algorithm failed to reach the target accuracy within a limited number of communication rounds. Fig. 3 illustrates the number of communication rounds needed for different algorithms to achieve this benchmark accuracy across various datasets. By incorporating a unique intra-cluster correction mechanism, the CFIC algorithm optimizes the direction of global model updates, significantly reducing the number of communication rounds. This advantage has been validated across seven different datasets and has significantly lowered the data transmission frequency during federated learning, effectively reducing communication costs and latency. These results demonstrate that CFIC improves both model performance and overall system efficiency in federated learning.

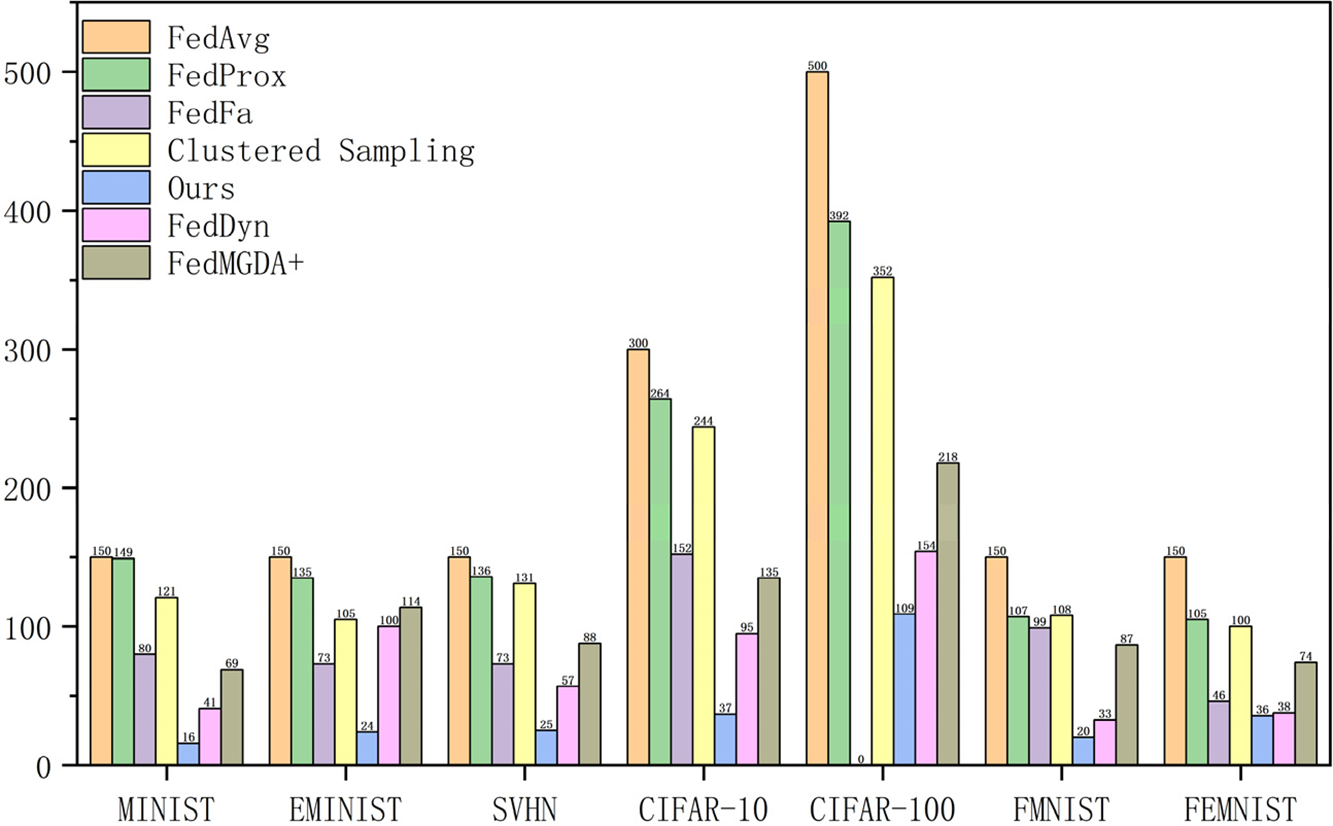
Figure 3: Comparison of communication efficiency

(3) Client experiment

To further validate the effectiveness of the CFIC algorithm in handling data heterogeneity, we conducted a series of experiments on the CIFAR-10 dataset, examining the impact of varying client numbers (20, 500) in a Dir(0.05) heterogeneous environment. The results, shown in Fig. 4, indicate that as the number of clients increases, the CFIC algorithm not only adapts to large-scale federated learning environments but also maintains high accuracy and stability across all scales. Specifically, in an experiment with 20 clients, CFIC achieved an accuracy of approximately 37.19%; with 500 clients, the accuracy reached 52.85%, surpassing other algorithms. These outcomes robustly demonstrate CFIC’s superior performance in non-IID data settings, highlighting its reliability and scalability under different scales and extreme data heterogeneity conditions.

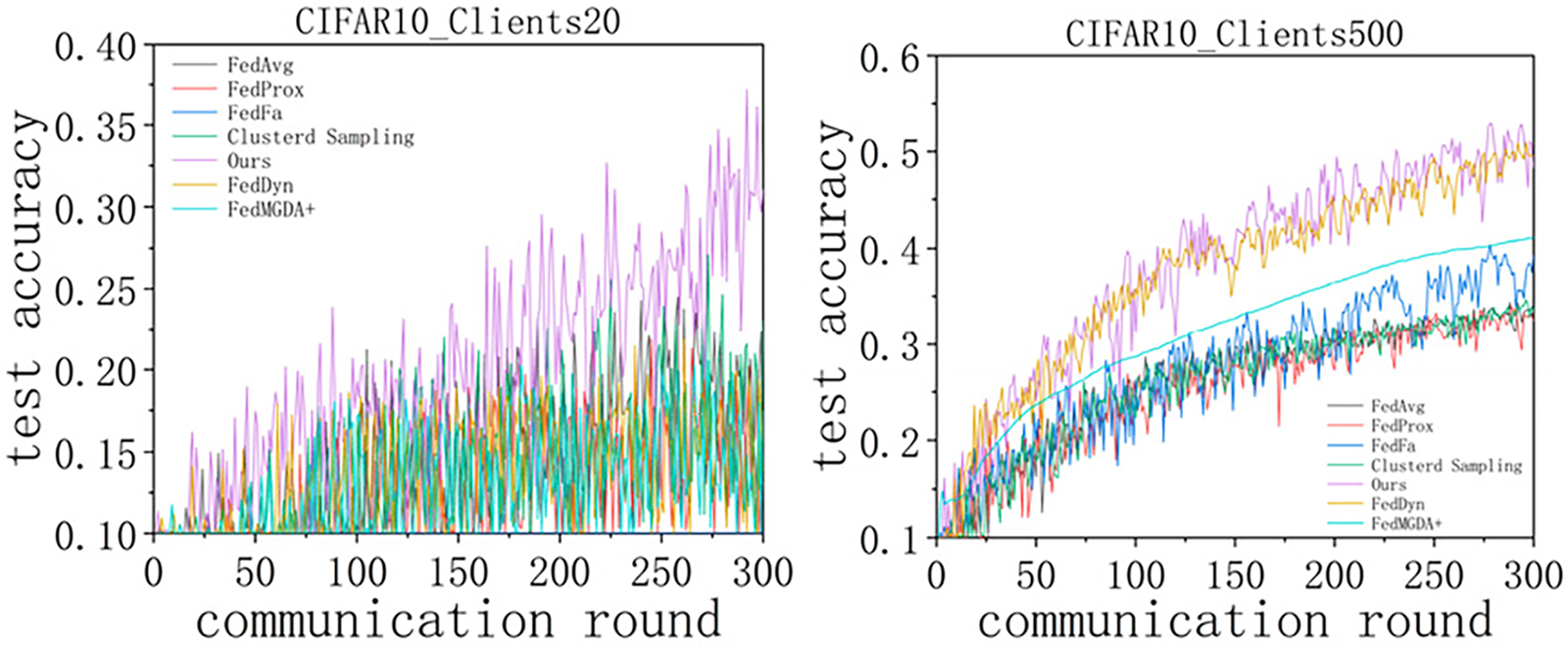
Figure 4: Comparison of accuracy under different clients

(4) Ablation experiment

The CFIC algorithm is divided into two main parts, i.e., inter-cluster sampling and intra-cluster correction. During the inter-cluster sampling phase, it involves sampling members from each clustered group. This effectively reduces the impact caused by non-IID data among clients, thereby optimizing communication efficiency and the consistency of model training. In the model aggregation phase, the global model is adjusted through an intra-cluster correction strategy, enhancing the generalization performance of the global model. This phase critically affects the model’s ability to handle heterogeneous data. To validate the effectiveness of the CFIC, we remove either of the two core components to evaluate their specific impact on model performance. The experimental results, as shown in Fig. 5, indicate that the removal of either component leads to a significant performance drop on both the CIFAR-100 and SVHN datasets.

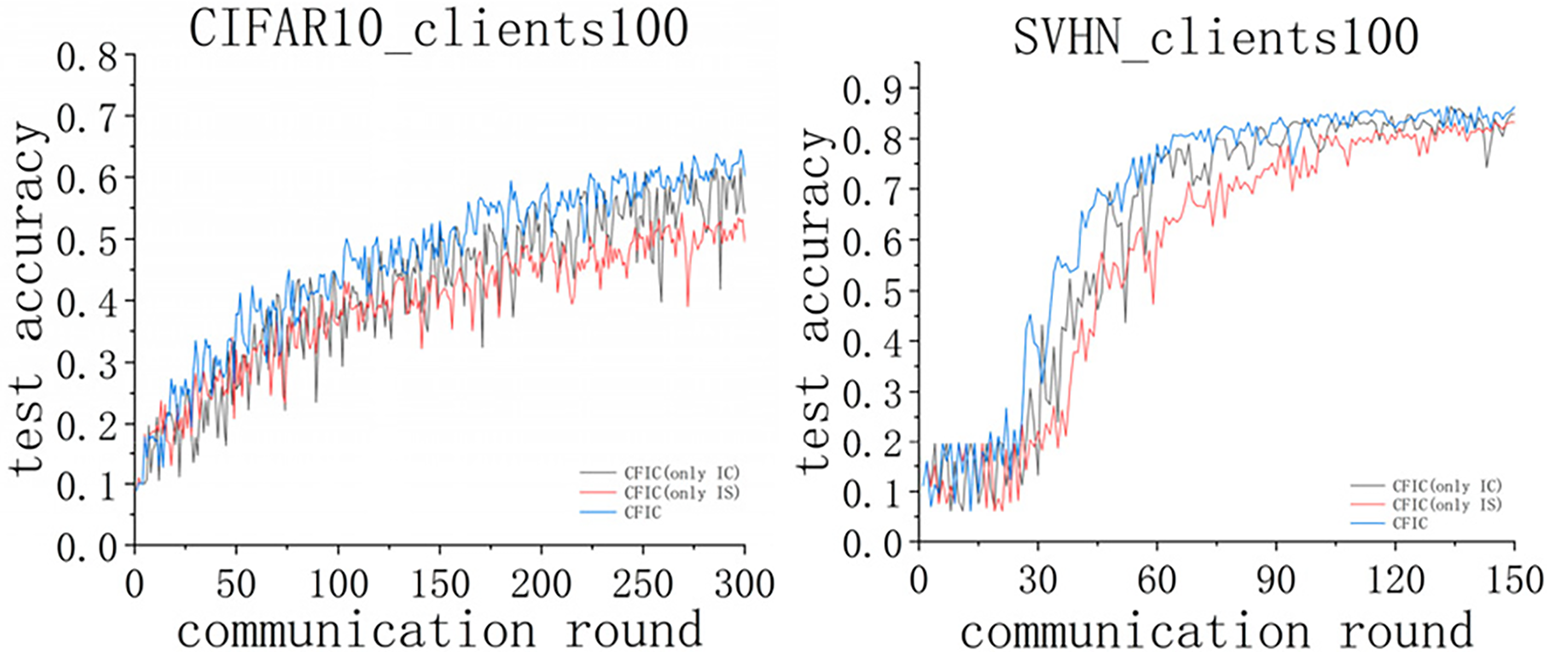
Figure 5: Comparison of accuracy of ablation experiment. IC is the abbreviation for intra-cluster correction, and IS the abbreviation for inter-cluster sampling

5  Conclusion

This paper presents a cluster-based correction federated learning algorithm that enhances the generalization ability of models in non-IID data scenarios through clustering based on label distribution characteristics and global model weight adjustment. To validate the effectiveness of the CFIC algorithm, extensive experiments were conducted. The results demonstrate that the CFIC algorithm has significant advantages in heterogeneous data scenarios and maintains high accuracy even with extreme label shifts, exhibiting minimal impact from data heterogeneity. However, there are certain limitations that must be acknowledged. First, although incorporating momentum helps improve stability during model training, research on optimizing momentum calculation to further enhance algorithm performance is still insufficient. Future work could explore more dynamic and adaptive momentum adjustment strategies. For example, automatic tuning of momentum parameters based on changes in client data distribution or model update gradients could achieve better convergence speed and generalization ability. Second, while this study uses a label distribution characteristic extraction function for client clustering, existing analyses have not thoroughly examined the effectiveness of these feature extraction functions under various types of label distribution skew and their relationship with model performance. Future work should also develop feature representation methods that adapt to multiple label skew patterns and clarify the impact of the feature extraction mechanism on the overall performance of the federated learning system through theoretical analysis and experimental evidence. Last, the scale and complexity of clients in the experimental scenarios do not match real-world applications. For instance, practical implementations often involve tens of thousands or more edge devices, and client computing conditions and communication conditions may be affected by many uncertain tasks. Therefore, future work should be conducted in realistic complex application scenarios to further verify the robustness and scalability of the CFIC algorithm.

Acknowledgement: None.

Funding Statement: This work was supported by National Natural Science Foundation of China under Grant (No. 62277043) and Science and Technology Research Project of Chongqing Education Commission under Grant (No. KJZD-K202300515).

Author Contributions: Yunong Yang: Conceptualization, funding acquisition, methodology, writing—original draft; Long Ma: data curation, formal analysis, investigation, software, writing—original draft, validation; Liang Fan: resources, supervision, validation; Tao Xie: conceptualization, funding acquisition, methodology, writing—review and editing, supervision. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data supporting the results presented in this article are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Sery T, Shlezinger N, Cohen K, Eldar YC. Over-the-air federated learning from heterogeneous data. IEEE Trans Signal Process. 2021;69:3796–811. doi:10.1109/tsp.2021.3090323. [Google Scholar] [CrossRef]

2. Kairouz P, McMahan HB, Avent B, Bellet A, Bennis M, Bhagoji AN, et al. Advances and open problems in federated learning. Found Trends® Mach Learn. 2021;14(1–2):1–210. [Google Scholar]

3. Bonawitz K, Ivanov V, Kreuter B, Marcedone A, McMahan HB, Patel S, et al. Practical secure aggregation for privacy-preserving machine learning. In: Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security; 2017 Oct 30–Nov 3; Dallas, TX, USA. p. 1175–91. doi:10.1145/3133956.3133982. [Google Scholar] [CrossRef]

4. McMahan B, Moore E, Ramage D, Hampson S, Arcas BA. Communication-efficient learning of deep networks from decentralized data. In: Proceedings of the Artificial Intelligence and Statistics; 2017 Apr 20–22; Fort. Lauderdale, FL, USA. p. 1273–82. [Google Scholar]

5. Karimireddy SP, Kale S, Mohri M, Reddi S, Stich S, Suresh AT. SCAFFOLD: stochastic controlled averaging for federated learning. In: Proceedings of the International Conference on Machine Learning; 2020 Jul 13–18. p. 5132–43. [Google Scholar]

6. Li Q, Diao Y, Chen Q, He B. Federated learning on non-IID data silos: an experimental study. In: Proceedings of the 2022 IEEE 38th International Conference on Data Engineering (ICDE); 2020 May 9–12; Piscataway, NJ, USA: 2022. IEEE. p. 965–78. [Google Scholar]

7. Duan M, Liu D, Ji X, Liu R, Liang L, Chen X, et al. FedGroup: efficient clustered federated learning via decomposed data-driven measure. arXiv:2010.06870. 2020. [Google Scholar]

8. Liu Z, Guo J, Yang W, Fan J, Lam KY, Zhao J. Dynamic user clustering for efficient and privacy-preserving federated learning. IEEE Trans Dependable Secur Comput. 2024;1–12. doi:10.1109/tdsc.2024.3355458. [Google Scholar] [CrossRef]

9. Zhou T, Zhang J, Tsang DHK. FedFA: federated learning with feature anchors to align features and classifiers for heterogeneous data. IEEE Trans Mob Comput. 2023;23(6):6731–42. doi:10.1109/tmc.2023.3325366. [Google Scholar] [CrossRef]

10. Sun W, Yan R, Jin R, Zhao R, Chen Z. FedAlign: federated model alignment via data-free knowledge distillation for machine fault diagnosis. IEEE Trans Instrum Meas. 2023;73:1–12. doi:10.1109/tim.2023.3345910. [Google Scholar] [CrossRef]

11. Zhang X, Li Y, Li W, Guo K, Shao Y. Personalized federated learning via variational bayesian inference. In: Proceedings of the International Conference on Machine Learning; 2022 Jul 17–23. p. 26293–310. [Google Scholar]

12. Kotelevskii N, Vono M, Durmus A, Moulines E. Fedpop: a bayesian approach for personalised federated learning. Adv Neural Inf Process Syst. 2022;35:8687–701. [Google Scholar]

13. Zhu J, Ma X, Blaschko MB. Confidence-aware personalized federated learning via variational expectation maximization. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2023 Jun 17–24; Vancouver, BC, Canada. p. 24542–51. [Google Scholar]

14. Li T, Sahu AK, Talwalkar A, Smith V. Federated learning: challenges, methods, and future directions. IEEE Signal Process Mag. 2020;37(3):50–60. doi:10.1109/msp.2020.2975749. [Google Scholar] [CrossRef]

15. Yan Z, Wicaksana J, Wang Z, Yang X, Cheng KT. Variation-aware federated learning with multi-source decentralized medical image data. IEEE J Biomed Health Inform. 2020;25(7):2615–28. doi:10.1109/jbhi.2020.3040015. [Google Scholar] [PubMed] [CrossRef]

16. Zhou X, Liang W, She J, Yan Z, Kevin I, Wang K. Two-layer federated learning with heterogeneous model aggregation for 6G supported internet of vehicles. IEEE Trans Veh Technol. 2021;70(6):5308–17. doi:10.1109/tvt.2021.3077893. [Google Scholar] [CrossRef]

17. Ma X, Zhu J, Lin Z, Chen S, Qin Y. A state-of-the-art survey on solving non-IID data in federated learning. Future Gener Comput Syst. 2022;135(3):244–58. doi:10.1016/j.future.2022.05.003. [Google Scholar] [CrossRef]

18. Zhang T, Liu H, Tao J, Wang Y, Yu M, Chen H, et al. Enhancing dropout prediction in distributed educational data using learning pattern awareness: a federated learning approach. Mathematics. 2023;11(24):4977. doi:10.3390/math11244977. [Google Scholar] [CrossRef]

19. Chu YW, Hosseinalipour S, Tenorio E, Cruz L, Douglas K, Lan AS, et al. Multi-layer personalized federated learning for mitigating biases in student predictive analytics. IEEE Trans Emerg Top Comput. 2024;1–15. doi:10.1109/tetc.2024.3407716. [Google Scholar] [CrossRef]

20. Li T, Sahu AK, Zaheer M, Sanjabi M, Talwalkar A, Smith V. Federated optimization in heterogeneous networks. Proc Mach Learn Syst. 2020;2:429–50. [Google Scholar]

21. Li Q, He B, Song D. Model-contrastive federated learning. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2021 Jun 20–25; Nashville, TN, USA. p. 10713–22. [Google Scholar]

22. Zhang J, Li Z, Li B, Xu J, Wu S, Ding S, et al. Federated learning with label distribution skew via logits calibration. In: Proceedings of the International Conference on Machine Learning; 2022 Jul 17–23. p. 26311–29. [Google Scholar]

23. Wang J, Liu Q, Liang H, Joshi G, Poor HV. Tackling the objective inconsistency problem in heterogeneous federated optimization. Adv Neural Inf Process Syst. 2020;33:7611–23. [Google Scholar]

24. Gao D, Yao X, Yang Q. A survey on heterogeneous federated learning. arXiv:2210.04505. 2022. [Google Scholar]

25. Wang C, Yang Y, Zhou P. Towards efficient scheduling of federated mobile devices under computational and statistical heterogeneity. IEEE Trans Parallel Distrib Syst. 2020;32(2):394–410. doi:10.1109/tpds.2020.3023905. [Google Scholar] [CrossRef]

26. Madni HA, Umer RM, Foresti GL. Federated learning for data and model heterogeneity in medical imaging. In: Proceedings of the International Conference on Image Analysis and Processing; 2023 Sep 11–15; Berlin/Heidelberg, Germany: Springer; 2023. p. 167–78. [Google Scholar]

27. Wang X, Cheng N, Ma L, Sun R, Chai R, Lu N. Digital twin-assisted knowledge distillation framework for heterogeneous federated learning. China Commun. 2023;20(2):61–78. doi:10.23919/jcc.2023.02.005. [Google Scholar] [CrossRef]

28. Ouyang X, Xie Z, Zhou J, Xing G, Huang J. ClusterFL: a clustering-based federated learning system for human activity recognition. ACM Trans Sens Netw. 2022;19(1):1–32. doi:10.1145/3554980. [Google Scholar] [CrossRef]

29. Vahidian S, Morafah M, Wang W, Kungurtsev V, Chen C, Shah M, et al. Efficient distribution similarity identification in clustered federated learning via principal angles between client data subspaces. In: Proceedings of the AAAI Conference on Artificial Intelligence; 2023 Feb 7–14; Washington, DC, USA. p. 10043–52. [Google Scholar]

30. Yu X, Liu Z, Wang W, Sun Y. Clustered federated learning based on nonconvex pairwise fusion. Inf Sci. 2024;678:120956. doi:10.1016/j.ins.2024.120956. [Google Scholar] [CrossRef]

31. Lu R, Zhang W, Wang Y, Li Q, Zhong X, Yang H, et al. Auction-based cluster federated learning in mobile edge computing systems. IEEE Trans Parallel Distrib Syst. 2023;34(4):1145–58. doi:10.1109/tpds.2023.3240767. [Google Scholar] [CrossRef]

32. Sattler F, Müller KR, Samek W. Clustered federated learning: model-agnostic distributed multitask optimization under privacy constraints. IEEE Trans Neural Netw Learn Syst. 2020;32(8):3710–22. doi:10.1109/tnnls.2020.3015958. [Google Scholar] [PubMed] [CrossRef]

33. Ghosh A, Chung J, Yin D, Ramchandran K. An efficient framework for clustered federated learning. IEEE Trans Inf Theory. 2022;68(12):8076–91. doi:10.1109/tit.2022.3192506. [Google Scholar] [CrossRef]

34. Long G, Xie M, Shen T, Zhou T, Wang X, Jiang J. Multi-center federated learning: clients clustering for better personalization. World Wide Web. 2023;26(1):481–500. doi:10.1007/s11280-022-01046-x. [Google Scholar] [CrossRef]

35. Ye R, Xu M, Wang J, Xu C, Chen S, Wang Y. FedDisco: federated learning with discrepancy-aware collaboration. arXiv.2305.19229. 2023. [Google Scholar]

36. Nabavirazavi S, Taheri R, Shojafar M, Sitharama Iyengar S. Impact of aggregation function randomization against model poisoning in federated learning. In: Proceedings of the 22nd IEEE International Conference on Trust, Security and Privacy in Computing and Communications, TrustCom; 2023 Nov 1–3; Exeter, UK. Piscataway, NJ, USA: Institute of Electrical and Electronics Engineers Inc.; 2024. p. 165–72. [Google Scholar]

37. Taheri R, Arabikhan F, Gegov A. Robust aggregation function in federated learning. In: Proceedings of the International Conference on Information and Knowledge Systems; 2023 Jun 22–23; Portsmouth, UK. Cham, Switzerland: Springer Nature; 2023. p. 168–75. [Google Scholar]

38. LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proc IEEE. 1998;86(11):2278–324. doi:10.1109/5.726791. [Google Scholar] [CrossRef]

39. Krizhevsky A, Hinton G. Learning multiple layers of features from tiny images; 2009 [cited 2025 May 18]. Available from: https://www.cs.utoronto.ca/~kriz/learning-features-2009-TR.pdf. [Google Scholar]

40. Cohen G, Afshar S, Tapson J, van Schaik A. EMNIST: anextension of mnist to handwritten letters. arXiv:1702.05373. 2017. [Google Scholar]

41. Netzer Y, Wang T, Coates A, Bissacco A, Wu B, Ng AY. Reading digits in natural images with unsupervised feature learning. In: Proceedings of the NIPS Workshop on Deep Learning and Unsupervised Feature Learning; 2011 Dec 12–17; Granada, Spain. [Google Scholar]

42. Acar DAE, Zhao Y, Navarro RM, Mattina M, Whatmough PN, Saligrama V. Federated learning based on dynamic regularization. arXiv:2111.04263. 2021. [Google Scholar]

43. Huang W, Li T, Wang D, Du S, Zhang J. Fairness and accuracy in federated learning. arXiv:2012.10069. 2020. [Google Scholar]

44. Hu Z, Shaloudegi K, Zhang G, Yu Y. Federated learning meets multi-objective optimization. IEEE Trans Netw Sci Eng. 2022;9(4):2039–51. doi:10.1109/tnse.2022.3169117. [Google Scholar] [CrossRef]

45. Fraboni Y, Vidal R, Kameni L, Lorenzi M. Clustered sampling: low-variance and improved representativity for clients selection in federated learning. In: Proceedings of the International Conference on Machine Learning; 2021 Jul 12–14. p. 3407–16. [Google Scholar]