HEaaN-ID3: Fully Homomorphic Privacy-Preserving ID3-Decision Trees Using CKKS

1  Introduction

Decision trees (DT) are widely used despite their simpler structure compared to advanced machine learning algorithms, such as deep neural networks. This is because of the ease of use of these simpler structures in various domains and their ability to yield explainable models.

Currently, research in privacy-preserving machine learning and information encryption is rapidly advancing. In particular, studies on encryption based on chaotic systems and neural network applications have yielded notable results [1]. Additionally, homomorphic encryption (HE)-based machine learning algorithms have garnered significant attention owing to the growing importance of privacy-preserving machine learning [2–6]. These algorithms allow us to perform any computation on encrypted data that can also be performed on plaintext, thereby enabling us to train an encrypted model using encrypted training data. Thus, these algorithms ensure a secure and privacy-preserving solution for machine learning, because classification can be performed using an encrypted model on an encrypted input without any decay in the process.

In this paper, we propose a fully homomorphic version of Iterative Dichotomiser 3 (ID3) [7] using the Cheon-Kim-Kim-Song (CKKS) method [8], named HEaaN-ID3. HEaaN-ID3 is based on a variant of the original ID3 algorithm [7] and can handle both nominal and ordinal categorical variables. This creates as many child nodes as the number of categories in a categorical variable. Despite the advantages of enabling secure computation in untrusted cloud environments and allowing clients to utilize server computing resources without revealing sensitive information, a privacy-preserving homomorphic ID31 has not been realized to date. The reason is that the large number of child nodes results in high computational overhead in both training and inference. However, existing privacy-preserving binary DTs that use FHE cannot handle the data of nominal categorical variables.

HEaaN-ID3 has the unique characteristic of not utilizing a decryption function during training. Despite the potential of homomorphic encryption in machine learning, recent studies have required decryption during the training process for various reasons. This is owing to the slow and impractical performance of algorithms that use only homomorphic operations, or the lack of methods for performing specific operations without decryption. As a result, decryption has been necessary in the training process [9,10].

While decryption during the training step can reduce the computational cost of privacy-preserving machine learning, it may not be feasible in certain situations. For instance, if the training data consists of data from multiple parties, some participants may not consent to using decryption key for fear of exposure of their data. Furthermore, if there is a large amount of data to be decrypted, the entity with the decryption key may not have sufficient computational power, causing a bottleneck that is not desirable for users of the learned data.

Additionally, HEaaN-ID3 enables a single-cloud service model. We do not have to assume that there are multiple cloud services in separate security domains. Thus, we can realize the execution environment of HEaaN-ID3 at a lower cost than those that require multiple cloud service models [9].

The key challenge in developing HEaaN-ID3, which enables training without decryption, is to achieve an affordable level of speed for training and inference, even with operations supported by FHE, which are known as heavy operations. For this purpose, we employ the CKKS FHE to leverage its beneficial features as much as possible. In addition, we employed the following:

First, in the proposed method, we adopt the modified Gini impurity (MGI) score [11] instead of entropy or the original Gini score for the split rule. The use of the MGI eliminates the need for complex inverse operations, allowing for efficient calculations when performed homomorphically with encrypted inputs. Because the MGI must be calculated at every non-leaf node in the DT, it can significantly reduce the amount of computation required for training. It is quite significant—while MGI performs computations using only addition and multiplication, calculating the traditional Gini impurity requires an additional ApproxInv() operation. The exact computational demands and multiplication depth for ApproxInv() are not disclosed. However, according to previous studies [8,12], it is presumed that these methods involve high-degree polynomials. Therefore, the multiplication depth is roughly proportional to the logarithm of the polynomial’s degree, and the total number of multiplication operations is expected to be on the order of several tens. Our experiments demonstrate that there is no significant difference in terms of inference accuracy when using the MGI score compared with using the entropy as the original ID3 implemented in the scikit learn library.

The second optimization involves making full use of the single instruction multiple data (SIMD) feature of CKKS FHE. Here, the SIMD refers to one of the features of the CKKS homomorphic encryption scheme, in which the structure of a ciphertext is in the form of a vector, enabling vectorized operations between ciphertexts. This is different from traditional SIMD, which requires additional hardware-level costs. During the training and classification of homomorphic decision trees, every node in the tree must be processed, resulting in high computational costs. In the training process, determining the variables for branching based on the MGI score in an encrypted state involves the following steps: (1) calculate the distribution of target categories for all combinations of variables, (2) compute the MGI score for each variable, (3) find the minimum score among them, and (4) identify the minimum score variable. This process can consume a significant amount of computation if there are many combinations of variables and categories to be calculated, because each case must be calculated individually in an encrypted state for each node during training. This amount of computation is unacceptable when the number of nodes in a DT is large.

However, as HEaaN-ID3 can deal with the step (1) efficiently by using SIMD and MGI, training can be performed without decryption. This is in contrast to a recent work [10], where the calculation of step (2) is delegated to a client who has the decryption key, and the output of step (2) is sent to the client, who then decrypts it. Subsequently, the client performs steps (3) and (4) using the decrypted plaintext. The result is then encrypted again and sent back to the server for continued training.

In the inference task, the split conditions in all non-leaf nodes must be evaluated in HEaaN-ID3, unlike plaintext inference, which only evaluates the split functions in a sequence of non-leaf nodes in a path from the root node to a leaf node. This raises the inference complexity from logarithmic to polynomial, in terms of the number of nodes in the tree.

However, in HEaaN-ID3, certain computations required by nodes at the same level can be performed simultaneously by utilizing the SIMD function. The number of slots required for each node is determined by the number of variables involved in training and the number of categories for each variable. When the number of required slots is significantly smaller than the total number of available slots in a ciphertext, multiple nodes’ training can be performed at once. This approach was computationally more efficient than that described in [10].

In addition, we discovered and solved various problems that can occur when realizing homomorphic DT, especially during training. First, there are some cases that are difficult to handle with encrypted data, such as the case where in no training data is mapped to a certain node in the tree. The next problem is that there are multiple cases where in their MGI scores are almost identical. We address these situations while maintaining the efficiency of training and inference as much as possible.

We verified the performance of HEaaN-ID3 with widely used dataset in the UCI repository [13], such as Iris, Wine, and Cancer, which consist of multiple numerical variables, after binning them as well as the data of nominal categorical variables such as soybean and breast cancer. We verified that the same level of accuracy was obtained using HEaaN-ID3 compared to the training and inference algorithms with plaintext version of the data implemented in the Scikit-learn library [14].

The following are primary contributions of this paper.

•   Homomorphic ID3 Decision Training on encrypted state without decryption: This study is the first to perform the entire ID3 decision tree algorithm training in an encrypted state. We propose an optimization method to address high computational costs of Fully Homomorphic Encryption (FHE) during training. Our approach leverages CKKS encryption’s SIMD characteristics and uses a modified Gini impurity score. In the same environment, our proposed method required approximately 7.41% more time to process a single node than the method proposed in [10] for the Iris dataset. However, their study executed most computations in plaintext after decryption. Our research demonstrates the feasibility of conducting the entire training process securely and efficiently in an encrypted state.

•   Efficient inference: We propose a method that enables efficient inference with encrypted inputs and models. The proposed method maximizes efficiency by leveraging the SIMD feature of CKKS to process nodes at the same level simultaneously. In our experiments using the UCI dataset, the most similar method proposed in [10] took 2.3 s to evaluate 31 nodes. In contrast, our approach evaluated 16,105 nodes, the largest number of nodes, in just 657.32 ms.

The remainder of this paper is structured as follows. Section 2 compares existing studies according to the proposed requirements and Section 3 explains the fundamental concepts necessary to understand this research. Section 4 details the system and security models of the proposed method. In Section 5, the training and inference methods of the proposed HEaaN-ID3 are described. Section 6 provides the performance evaluation results of the schemes used and the proposed method in this study. Section 7 offers a security analysis of the proposed method. In Section 8, we discusses whether the established objectives have been successfully achieved and how accuracy is maintained in exceptional situations. Finally, Section 9 presents the conclusion.

2  Related Work

Related works are summarized in Table 1. It checks whether the existing work satisfies the goals specified in Section 4.3. The last column of Table 1 indicates whether the corresponding works deal with an ID3 or other types of DTs.

The research on privacy-preserving decision trees (PPDTs) can be categorized into two primary approaches: those that mainly deal with the inference process [15–19] and those that emphasize the training phase [20–24]. Despite significant advances, these studies face common challenges, such as an increase in communication overhead as the complexity of the tree grows and a rise in the amount of interaction required during both training and inference stages. For a detailed comparison of the existing methodologies, refer to [10].

Recent developments in the field of PPDT have introduced a variety of approaches. In Liu et al.’s PPDT framework [9], the Cloud Service Provider (CSP) and the Evaluation Service Provider (ESP) operated within distinct security domains while utilizing Pailler’s Partial Homomorphic Encryption (PHE). This setup allowed for secure and efficient computations on encrypted data by employing two-party secure computation protocols, enabling resource-intensive PPDT training and evaluation processes. However, one challenge arises in a multi-user multi-key environment where both the CSP and ESP share a master decryption key. This creates a potential vulnerability, as collusion between the two entities could compromise all user data. Without a reliable method to detect malicious collusion, the practical implementation of such a system is hindered.

Reference [25] presented a method that leverages multiple cloud servers, where one server performs decryption. Due to this setup, it is not directly comparable to HEaaN-ID3. Liang et al. proposed an approach to evaluate PPDTs by using efficient cryptographic techniques [26]. While this method achieves excellent classification performance, it lacks a solution for training and overlooks situations where multiple splits are needed during tree evaluation. Zheng et al. put forward a PPDT evaluation scheme using additive secret sharing [27], but their approach required two distinct cloud service providers and does not address training using encrypted data.

Cong et al. recently proposed a highly efficient method for securely evaluating decision trees utilizing GSW-based homomorphic encryption, particularly with TFHE [28]. Their approach introduced PolyComp(), a homomorphic comparison function that efficiently extracts constant terms from RLWE-based ciphertext, as outlined in [29,30]. Additionally, they harnessed the advantages of homomorphic XNOR operations characteristic of GSW-based encryption, which made bit-wise encrypted value comparisons more effective. Building on this, they developed a streamlined homomorphic tree traversal algorithm, facilitating smooth computation between encrypted and plaintext values—highlighting the distinct benefits of GSW-based homomorphic encryption.

Similarly, reference [31] introduced an efficient inference method for privacy-preserving binary decision trees encrypted with TFHE. Their technique integrated algorithms for blind node selection and blind array access. Unfortunately, this approach also does not address the challenge of privacy-preserving training for encrypted data.

The work most relevant to ours is that of [10], which addresses a privacy-preserving binary decision tree. They proposed a method capable of training and evaluating encrypted data using CKKS. Independent of Cheon et al.’s method [12], it proposes an efficient sign function for encrypted input, which returns (an encryption of) 1 for positive numbers and −1 for negative numbers, and suggested an effective training/inference method based on this.

Among alternative FHE models, the hybrid approach was proposed in [10], its training speed is more efficient than that of the proposed method. However, a limitation of this method is that it delegates the calculation of the information gain for each case of data and determines the case with the greatest information gain to an external entity. The external entity receives the ciphertexts containing the information gain for each case from the cloud server performing the training, decrypts them, encrypts the information for the case with the greatest information gain, and delivers it to the cloud server. The external entity should not collude with the cloud server because it has decryption capability. Because this exposes important information related to the model, according to an external entity, the entity should be a trusted party, such as the owner of the data. This can be unsuitable for certain situations in which privacy-preserving decision tree (PPDT) to perform machine learning with data from multiple security tasks. In this case, some data owners may not want to decrypt ciphertexts derived from their data.

There is research proposing privacy decision tree evaluation (PDTE) based on the replicated secret sharing (RSS) scheme from a different perspective [32–35]. These studies proposed methods to enhance security by using multiple cloud servers. They followed an approach where the information of the model and the input values used for evaluation are distributed among three computing servers in an outsourced environment. This approach assumed that there is no possibility of malicious collaboration between the servers. The study in [36] not only conducted the inference process but also carried out the training process. This study also utilized RSS, which necessitates additional assumptions. Since these papers do not meet the conditions outlined in 4.3, it is not appropriate to compare them directly with the method proposed in this paper.

3  Backgrounds

3.1 Notation

The notations used in this study are listed in Table 2. If a vector is entirely composed of either 0→s or 1→s and a ciphertext are operands in an expression, we suppose the vector’s size is M. If the description of the vector does not specify all M slots, we assume the undescribed slots are set to zero.

3.2 Decision Tree

DTs are widely used to construct classifiers for real-world applications. They are categorized as non-parametric methods, which implies that they do not require assumptions regarding the distribution of the underlying data. In addition, a DT has the advantages of high interpretability, because decision rules are extracted during its growth [49]. Depending on the rule induction method, DT algorithms can be classified as greedy or randomDTs. However, in a single DT model, the greedy approach has been more popular than the random approach. Various greedy DT algorithms have been developed for several years and the typical algorithms are Iterative Dichotomiser 3 (ID3) [7], C4.5 [50], C5.0 [51] Classification and Regression Tree (CART) [52], χ2 Automatic Interaction Detection (CHAID) and a Scalable Parallel Classifier for Data Mining (SPRINT) [53].

The ID3 algorithm is primarily used to handle nominal datasets. It generates a decision tree based on maximizing Information Gain, which is a measure of the reduction in entropy that results from splitting a dataset based on a specific attribute. Entropy, in this context, is a measure of uncertainty or disorder within the data, quantifying how mixed the data is. ID3 works by selecting, at each iteration, the attribute that minimizes entropy the most, effectively splitting the data in a way that makes it more homogeneous. This process is repeated to construct an optimal decision tree.

While ID3 is efficient and provides a high level of interpretability, it can struggle with noisy data and is prone to overfitting, where the model becomes too tailored to the training data and performs poorly on unseen data. To address these limitations, successor algorithms like C4.5 were developed, which include mechanisms to handle noise and prevent overfitting.

Regardless of the greedy DT algorithm, DTs are built by the process of top-down rule induction in the “greedy” way. At each iteration, DT algorithms determine a rule that splits the node into child nodes, by maximizing the splitting criterion function. Different DT algorithms employ various splitting criteria.

In this study, we propose a privacy-preserving ID3 using FHE for datasets consisting of nominal categorical attributes. We borrowed several elements from ID3. ID3 determines an attribute that splits the current node into child nodes individually corresponding to each category in the attribute among the unused attributes using the information gain based on entropy as a splitting criterion function, which requires the calculation of log2. According to [54], to efficiently perform entropy operations, an approximated entropy function (ApEn) is proposed. The proposed method involved maximum and comparison operations throughout the process, followed by a natural logarithm operation. As a result, it requires more computationally complex and intensive calculations compared to MGI, which primarily consists of additions and multiplications. Owing to the high computational cost of calculating log2 on an encrypted input, this study utilizes MGI to reduce the computation cost. MGI is a variation of the Gini impurity G(S) for sample set S, defined as follows:

G(S)=∑i∈Cp(i)∑j∈C∖{i}p(j)=1−∑c∈Cp(c)2(1)

Herein, C represents the set of target classes in S and p(⋅) indicates the probability of the specific sample set in S (e.g., p(i) denotes the probability of target class i, which can be defined as the proportion of the class i in S). Additionally, A represents the attribute used for the split. The attribute to maximize the difference between the Gini impurity of the current node and the weighted Gini impurity of the child nodes is selected for the split rule. Because the Gini impurity of the current node is identical for all possible split rules at the current node, the gain based on the Gini impurity depends on the weighted average of the Gini impurities of the child nodes obtained using attributes A, G(S|A), which can be formulated as follows:

G(S|A)=∑t∈Tp(t)G(t)=∑t∈T|St||S|(1−∑c∈C|St,c|2|St|2)=1−1|S|∑t∈T∑c∈C|St,c|2|St|2(2)

where G(t) represents the Gini impurity for the set of samples in child node t, |⋅| denotes the size (cardinality) of a set, T is the set of all child nodes, and St and St,c indicate the samples assigned to node t and those samples within t that belong to class c, respectively. Because |S| is the common factor for all split rules, the best split rule is a rule to maximize ∑t∈T∑c∈C|St,c|2|St|2, which requires the division operation.

Unlike the gain of the Gini impurity, the gain of the MGI uses the squares of p(t) as weights for G(t) as follows [11]:

MG(S|A)=∑t∈Tp(t)2G(t)=∑t∈T|St|2|S|2(1−∑c∈C|St,c|2|St|2)=1|S|2∑t∈T(|St|2−∑c∈C|St,c|2)(3)

Under the MGI framework, the best split is determined by minimizing |St|2−∑c∈C|St,c|2, a form that eliminates the need for division. According to the literature [11], one of the Gini impurities and the MGI are not always superior to the other; thus, considering the computational cost, we decided to use the MGI. By binning a numerical feature into several bins, a continuous feature can be treated as a categorical feature; thus, it is possible to apply the same algorithm to a dataset consisting of categorical features.

In addition, while MGI is effective in reducing bias and improving classification performance, it tends to be more sensitive to data variability in terms of variance. From the bias perspective, MGI leads to more accurate classification results compared to the traditional Gini impurity. According to the study in [11], a decision tree trained based on the MGI criterion achieved an average classification error rate of 29.05%, which is lower than the 30.31% obtained using Gini impurity, demonstrating improved overall classification performance. On the other hand, in terms of variance, MGI tends to generate a larger number of decision rules and exhibits greater standard deviation across datasets. On average, MGI produces 482.29 decision rules, which is significantly more than the 143.43 rules generated by Gini impurity. Additionally, the standard deviation of the classification error rate is the highest at 27.43%, indicating that the model is more responsive to changes in data characteristics. Due to these characteristics, MGI is advantageous for high-precision splitting but should be applied with caution when consistency across datasets is important. In homomorphic encryption environments, applying entropy-based metrics can be computationally expensive and inefficient. MGI, on the other hand, eliminates the need for division operations, making it a more practical choice while still maintaining strong classification performance under such constraints.

3.3 CKKS

CKKS is an FHE method in which multiplication can be performed efficiently on two encrypted complex numbers [8]. Although it only supports approximate arithmetic over encrypted data, numerous privacy-preserving applications have adopted it because of its extremely fast computation speed [55]. In addition, ciphertexts can contain numerous complex numbers. Thus, the CKKS operations function as vector operations. For example, a vector of complex numbers can be encrypted into a ciphertext in CKKS, and the result of the multiplication between two ciphertexts is a ciphertext that contains the vector that has the result of a component-wise multiplication of the underlying two vectors in the input ciphertexts. This can significantly enhance the performance of privacy-preserving machine-learning algorithms that are implemented in addition CKKS operations. Moreover, the CKKS scheme is designed based on the Ring Learning With Errors (RLWE) problem and incorporates randomness during encryption, resulting in different ciphertexts even when encrypting the same plaintext multiple times. Therefore, an attacker cannot infer the original plaintext even if they attempt to encrypt arbitrary plaintexts, which ensures that the scheme satisfies IND-CPA security.

CKKS supports the following algorithms:

∙ KeyGen(1λ) uses security parameter λ as the input and returns pk, sk, and evk.

∙ Encpk(x→) outputs ⟦x⟧ that maintains the vector structure as x→.

∙ Decsk(⟦x⟧) outputs x→ if ⟦x⟧ is a valid encryption from x→, which is a result of Enc or is created through a set of operations with valid ciphertexts with correct pk and evk, and sk is also correct. Else it returns ⊥.

∙ Add(⟦x⟧,⟦y⟧)(Sub(⟦x⟧,⟦y⟧)) produces a new ciphertext c, which is an encryption of x→+y→ (x→−y→). We may denote it as ⟦x⟧⊞⟦y⟧ (⟦x⟧⊟⟦y⟧) to simplify the description.

∙ Add(⟦x⟧,k)(Sub(⟦x⟧,k)) outputs a new ciphertext that is an encryption of (x0+k,⋯,xM−1+k) ((x0−k,⋯,xM−1−k)) for given k∈C. We may describe it as ⟦x⟧⊞k (⟦x⟧⊟k) to simplify the description.

∙ Level(⟦x⟧) returns ⟦x⟧’s level l, the number of further possible multiplications with ciphertext x.

∙ Multevk(⟦x⟧,⟦y⟧) returns an (approximate) encryption of (x0∗y0,⋯,xM−1∗yM−1) whose level is Min(Level(⟦x⟧),Level(⟦y⟧))−1. We denote this as ⟦x⟧⊡⟦y⟧ to simplify the description.

∙ Multevk(⟦x⟧,k) outputs a c′ that is an encryption of (kv0,⋯,kvM−1) where k∈C. The level of c′ is decremented from the level of [[x]] by 1. We describe it as ⟦x⟧⊡k to simplify the notation.

∙ Rotevk(⟦x⟧,i) returns an encryption of (xk,xk+1,⋯,xM−1,x0,⋯,xi,⋯), where i∈[0,M−1]. If i∈[−(M−1),−1], we set i=i+M to make i∈[0,M−1].

∙ Bootevk(⟦x⟧) returns a new ciphertext c′ that has an approximation of ⟦x⟧ if Level(⟦x⟧)≥lminboot, the number of multiplication levels required to perform Boot(). lminboot depends on the bootstrapping algorithm used and security parameter.

∙ Powevk(⟦x⟧,i) considers ⟦x⟧ and i∈N and returns c that is an encryption of {2i∗x0,⋯,...,2i∗xM−1}. It consumes one level as a single Mult() with two ciphertexts.

We assume that the rescaling algorithm in [8] is executed inside the Mult() algorithm, as in [3]. In addition, if bootstrapping is required to perform multiplication, it is assumed to be performed automatically. The corresponding part is omitted for clarity in the description of the algorithm. In addition, we use the RNS-CKKS implementation, which is aided by the GPU, to enhance the performance [55–58].

The following parameters were used for CKKS: the number of slots is 32,768, 9 multiplications are allowed between the bootstrapping operations, the initial number of multiplication depth possible before the first bootstrapping is 21, and lminboot is 3. Upon bootstrapping, we can consume 9 multiplicative depth until the next bootstrapping.

We used a method reported in the literature [12], expressed as ApproxSign(⟦x⟧): it considers a ciphertext ⟦x⟧ and returns an encryption of a vector (a0,⋯,aM−1) where ai = 1 if ⟦x⟧[i]>0; ai = 0 if ⟦x⟧[i]=0, or ai=−1 otherwise (i∈[0,M−1]). We also used the method reported in [3] to create an inverse of an input ciphertext, which is written as ApproxInverse(⟦x⟧): it assumes a ciphertext ⟦x⟧ and returns an encryption of the multiplicative inverse of the values in ⟦x⟧ [3].

4  Models

4.1 System Setting and Protocol Overview

We followed the system setting introduced in the literature [3]. The aim of this setting is to combine data from multiple security domains to produce a better model for inference. In addition, according to [3], owing to the legal regulation in South Korea, the inference result should be investigated by a trusted third party (here in, the Key Manager (KM)) to check whether the inference result has certain information regarding the privacy breach of the original data for training. Therefore, in this setting, KM is involved in the inferences.

The system has three types of participants: users (ui, i∈[1,m]), KM, and cloud server (CS). A user is a participant who owns data for training or transfers input data to request inferences after encryption. The CS receives the system evaluation key from KM and receives the encrypted training data from users to perform training. Consequently, the encrypted training model is stored and managed in its own storage. After training is completed, the CS performs an inference using the encrypted input data from the users. The encrypted inference result is delivered to the user through KM after the investigation is completed. A summary of all the participants and the operating protocols is shown in Fig. 1.

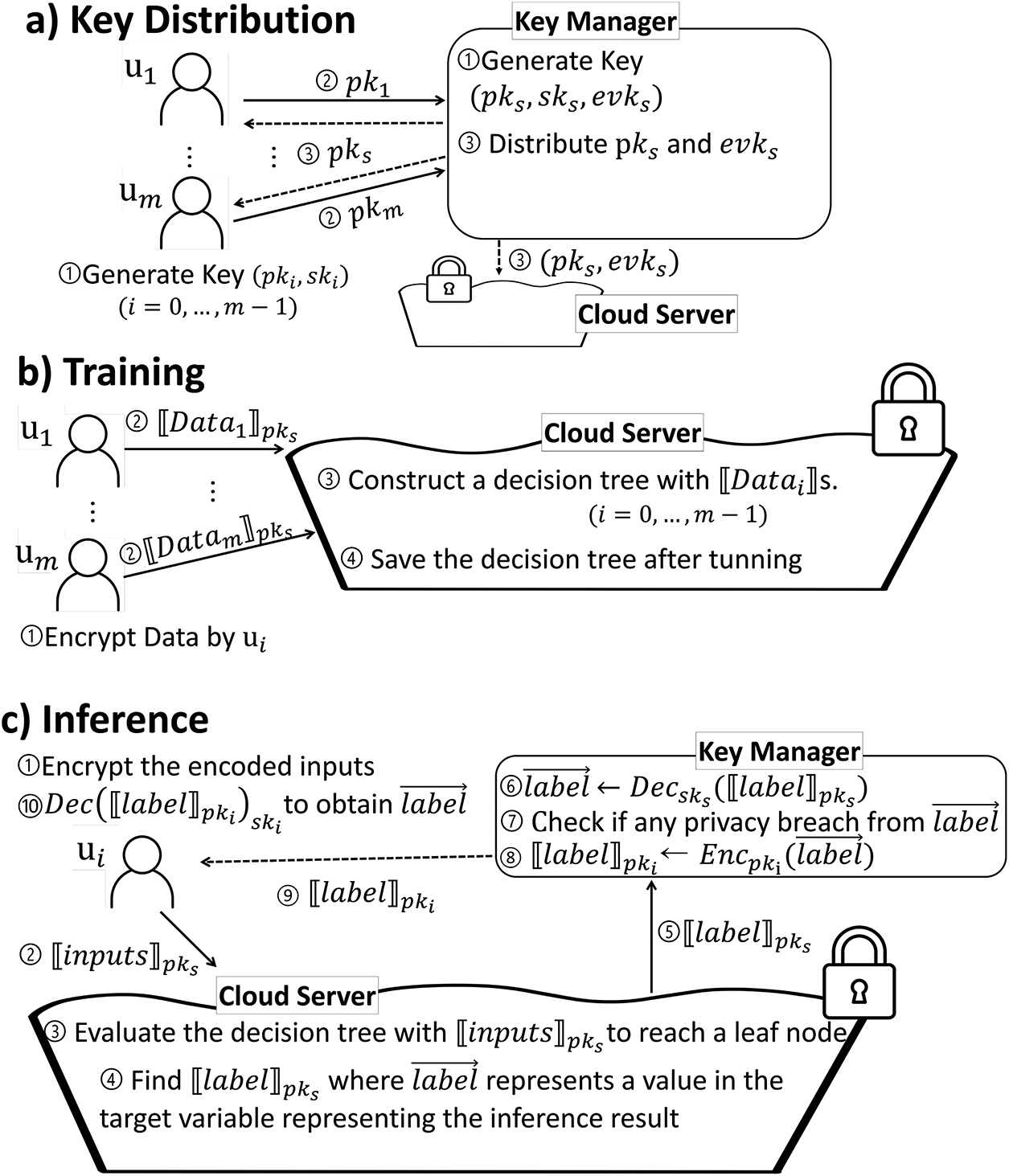
Figure 1: System setting and protocol overview

The goal of this setting is, as described in Fig. 2, for a set of the companies with data of different attributes to combine their data to create a model with high prediction accuracy for the target variable of each company’s interest. Therefore, the owners of the training data and the entities that aim to obtain the inference result with their input are the same set of entities (users in this setting). To separate the training data owners from the entity who want to obtain the inference results, the public keys of the clients should be registered in the KM. In this case, if a client is an individual person, many keys must be registered in KM, and all the inference results for all clients should be processed via KM, which renders KM a bottleneck in the inference process. Therefore, different settings are required such cases.

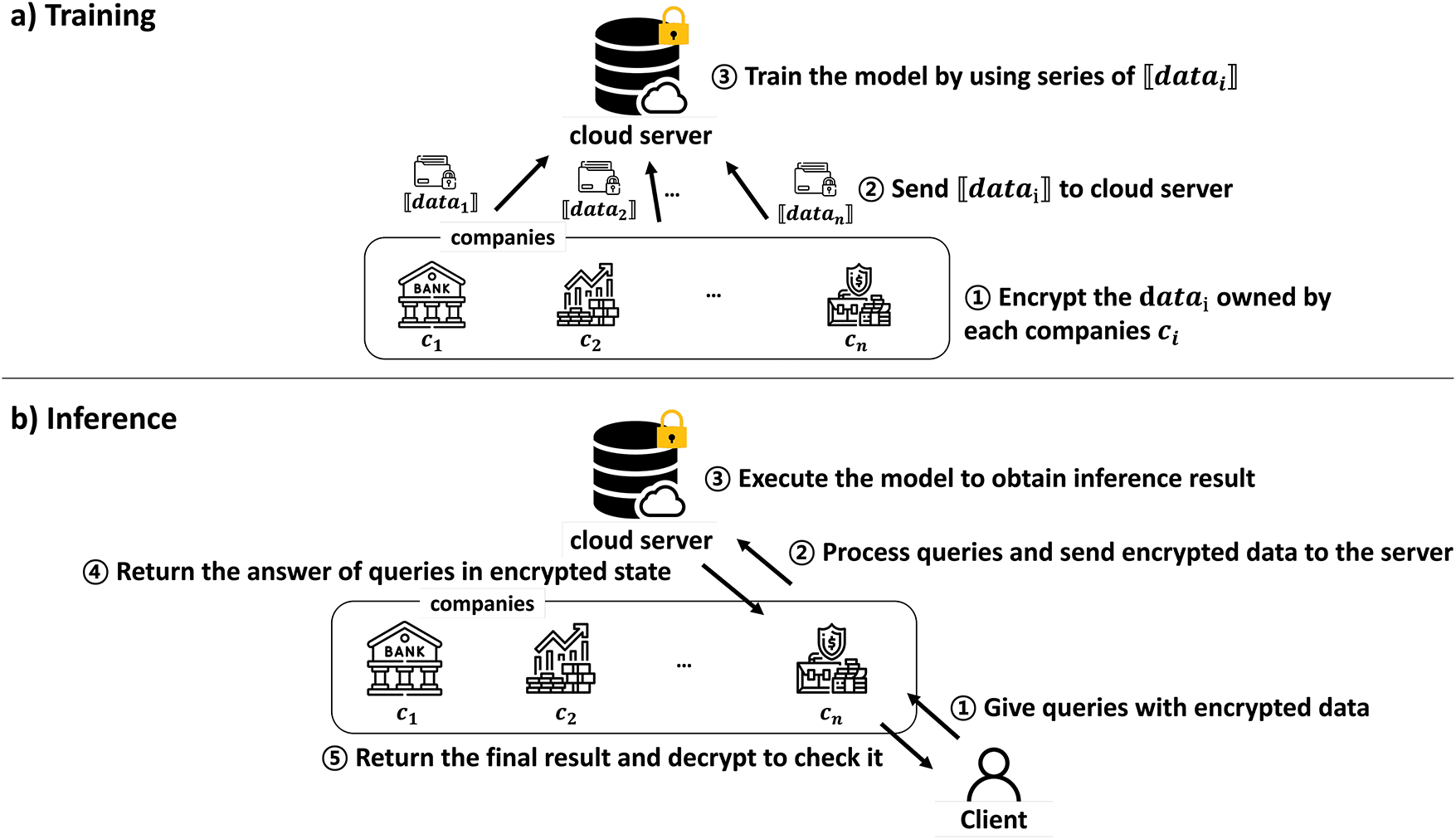
Figure 2: The goal of system setting (a: Training, b: Inference)

4.2 Security Model

Analogous to previous study [59], each participant in the protocol can play the role of an adversary, and their behavior is defined as an honest-but-curious (HBC) model.

The proposed method considers two aspects of privacy: First, the CS should not be able to access the encrypted information sent by the user. Second, the user should not be able to access information regarding the model created by the CS. Assuming KM is a trusted third party, privacy can be defined as follows:

First, the CS is considered an attacker. The information to which the CS has access includes encrypted data and metadata. During the training process, users encrypt and send their training data, and the CS creates a model using this data. In the inference process, a user sends encrypted input information and the CS performs the computation in an encrypted state and delivers the resulting ciphertext to the KM.

Thus, the CS only has access to the ciphertext input and cannot obtain the original information through the ciphertext. Based on this situation and the ciphertext-only attack (CPA) model, the privacy of the CS in the proposed method can be defined.

(CS Privacy in the proposed protocol) We consider that the proposed protocol supports CS-privacy if CS wins the following game with a non-negligible advantage:

1.   The CS generates two sets of messages for training and inference, denote as (m0→,m1→). These are then sent to the user.

2.   The user randomly selects a bit value b (∈{0,1})

3.   The user and the CS run the proposed protocol with mb→. Essentially, mb→ is provided to the CS in an encrypted form.

4.   CS can encrypt any desired message using the system public key.

5.   Finally, the CS outputs a message to guess which message is used in the protocol, denote as b′.

6.   CS wins if b=b′.

Second, we examined the privacy of the model during inference. The key concern is whether the user can extract information about the model from the received output. In our proposed method, except for the KM which is a trusted entity, users receive only the inference result, and no additional information is obtained. This implies that if users can gain information about the model from the inference output of our proposed method, the same outcome is possible in the plaintext version of the model and the inference input scenario. The issue of model information exposure from inference results in conventional machine learning is beyond the scope of this study. Thus, we did not address this aspect further, as explored in research [27].

4.3 Problem Definition

We designed HEaaN-ID3 to maintain the same requirements as proposed in [60].

1.   Training data privacy: The information belonging to one data owner must remain confidential and not be accessible by any other participants.

2.   Model privacy: No participant should have access to any details about the model.

3.   Inference privacy: The CS must not gain access to any details about the inputs submitted by users for classification.

4.   Non-interactive training: After the training data owner submits the data to the CS, the entire training process is handled independently by the CS, without requiring any assistance from other entities.

5.   Single security domain for CS: CSs cooperate with each other because they exist in a single security domain, and it is impossible to use decryption keys.

Please note that requirements (2) and (3) can be demonstrated using the security model described in Section 4.2. The other conditions should be considered individually.

5  HEaaN-ID3

We explain training and inference process of HEaaN-ID3. First, we discuss how the data is encrypted and explain how each node of HEaaN-ID3 is represented in an encrypted state. Then, we describe the key algorithm steps in the training process and how to select the optimal splitting variables using encrypted data. Finally, we provide a detailed discussion of the inference process using the encrypted model resulting from the training process and its optimized handling methods.

5.1 Data Representation

Let X1,⋯,Xd be the independent variables, and Y be the target variable. Each category is represented by a positive integer. Each independent variable Xj has nj categories nj∈N+ and nmax=max(nj), where j∈{1,2,⋯,d}. Let the number of categories in Y be t. We define n:=2⌈log2⁡nmax⌉ and N:=2⌈log2⁡sz⌉.

We suppose that the training data are composed of a set of sz rows, where the i-th row is represented as a tuple of vectors (x→1(i),⋯,x→d(i),y→(i)), where x→j(i) and y→(i) is the one-hot encoding vector of a category value in Xj, Y whose length are n and t, respectively. That is, x→j(i)=(xj,1(i),xj,2(i),⋯,xj,n(i)), where xj,k(i)∈{0,1}. Here, xj,k(i)=1 and the other components are zeroes if the value in Xj in the i-row is k. For every ni<k≤n, xj,k(i)=0.

For efficient calculation, we grouped the values in the same position in the one-hot encoded vectors of each variable. Thus, we organized a set of vectors b→j,k=(xj,k(0),xj,k(1),⋯,xj,k(sz−1)) for all j∈[1,d],k∈[1,n] and b′→q=(yq(0),yq(1),⋯,yq(sz−1)) for all q∈[1,t]. We call this the Bin Mask Vector [3]. For efficient computation, we attach 0→(N−sz) to every bj,k→ and b′→q to make their lengths N. Therefore, every |b→j,k|,|b′→q|=N. This is depicted in Fig. 3.

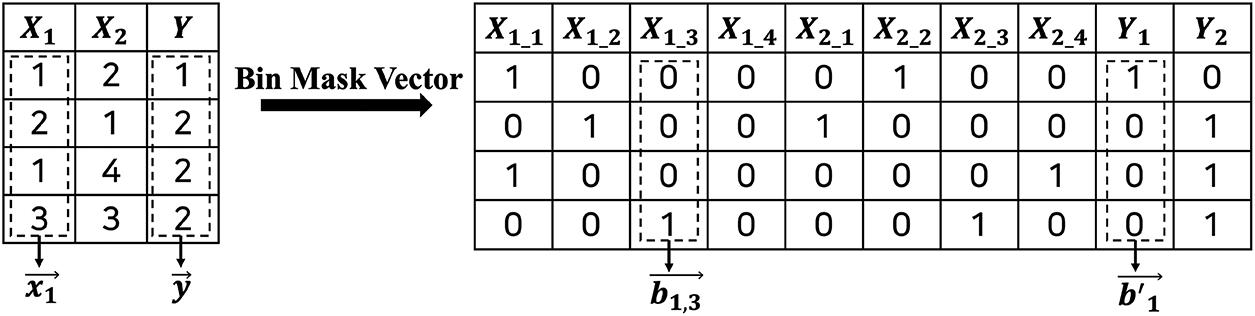
Figure 3: Data representation

We generated encrypted training data by placing all the data for a single variable into the same ciphertext. Therefore, we assume M≥N∗n. We supposed dctxt is the number of the variables of which the training data can be accommodated in the single ciphertext (dctxt=⌊M/(N∗n)⌋). The number of ciphertexts u used to create the training data was calculated as ⌈d/dctxt⌉. Let B→i=bi,1→||⋯||bi,n→. For the encrypted data, we can create a set of ciphertexts Train0,0={ci|i=1,2⋯,u}∪{cyq|q=1,⋯,t}, where ci=⟦B→i||B→u+i||⋯||B→(dctxt−1)u+i||0(M−dctxt∗N∗n)⟧ and cyq=⟦b′→q||⋯||b′→q||0(M−dctxt∗N∗n)⟧.

5.2 (Encrypted) Tree Representation

We consider the Iterative Dichotomiser 3 (ID3) [7] algorithm. As depicted in Fig. 4-(1), non-leaf nodes set the independent variable that splits the node, denoted as Xcv, where cv∈{1,2,⋯,d}. The leaf nodes represent the predicted value of the node as cy, where cy∈{1,2,⋯,t}. In the proposed HEaaN-ID3, both cv and cy are maintained in an encrypted state. Additionally, as shown in Fig. 4-(2), HEaaN-ID3 also stores the predicted value in non-leaf nodes. Since the data is encrypted, it is impossible to know whether valid data exists in the corresponding node. Predicted value made from nodes processed with invalid data cannot produce correct results, so the predicted value must be updated with that of the parent node containing valid data. The ciphertext used to perform this process is denoted as ca, where ca∈{0,1}.

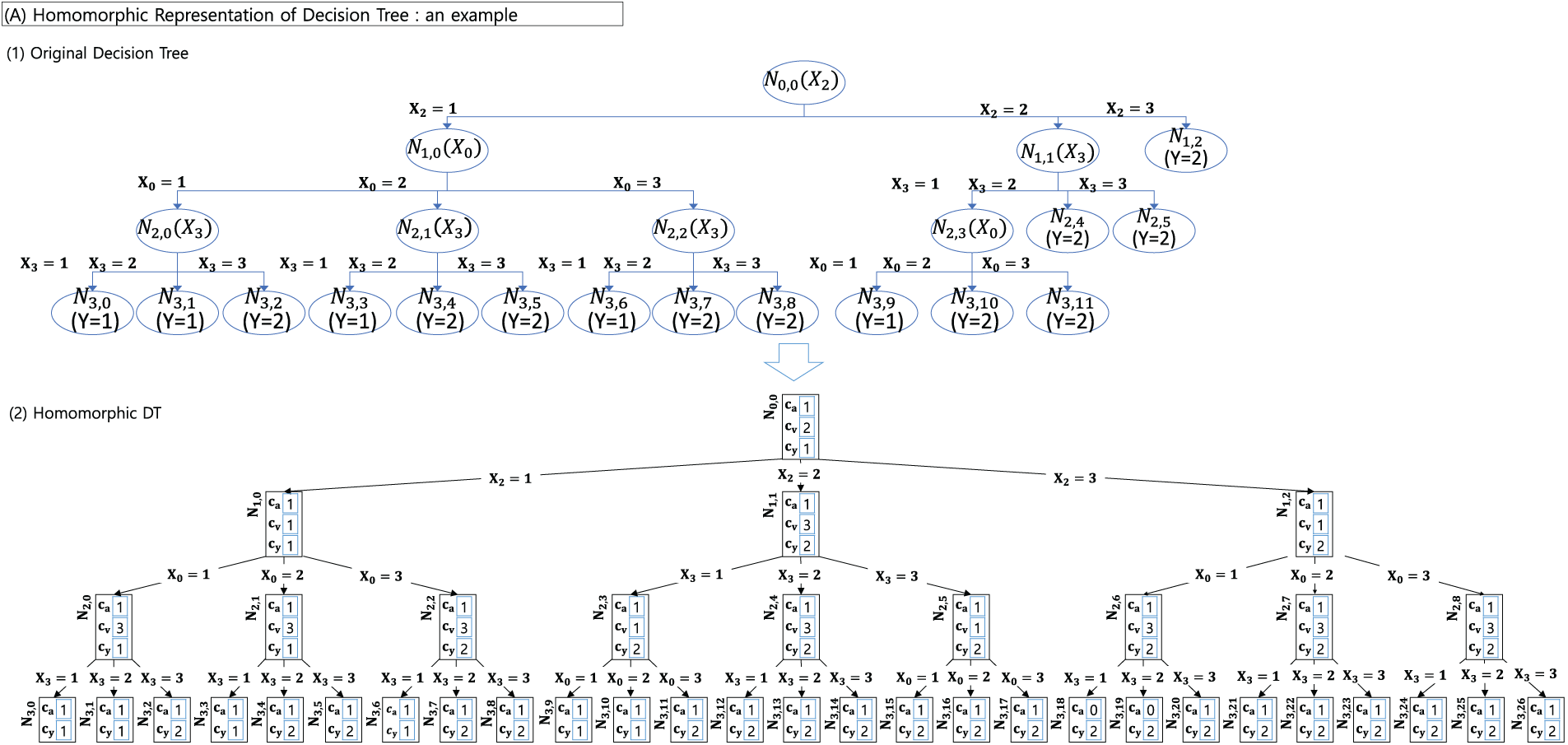
Figure 4: (A)-Tree representation ((1): original decision tree, (2): homomorphic DT)

5.3 Training

To visually present the training process of the tree—including data encryption, MGI computation, and SIMD optimization—a flowchart is illustrated in Fig. 5. When the training process begins, as shown in Fig. 5-(1), the input data is encrypted to initiate the process. At this stage, the SIMD technique is used to pack multiple data into a single ciphertext, in order to improve computational efficiency. The steps from Fig. 5-(2) to Fig. 5-(5) constitute the core of the algorithm, which is executed in the encrypted domain. These steps proceed as follows: (2) measures the most frequent Y label at each node; (3) generates a ciphertext that contains information used to determine whether the data at a node is valid; (4) sets the splitting criteria for the node. Here, MGI is used to enhance computational efficiency; (5) updates the data for the child nodes based on the determined splitting criteria. At the bottom of the tree, i.e., the leaf nodes, there is no need to create further child nodes, so only steps (2) and (3) are performed.

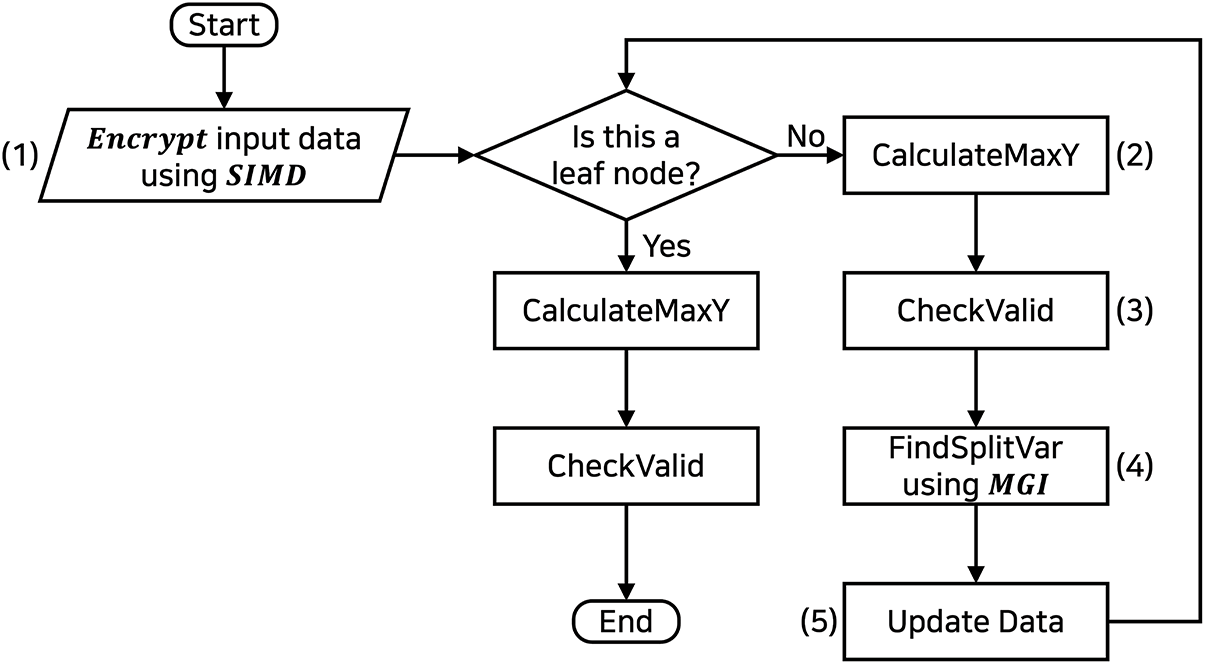
Figure 5: CalculateMaxY

In addition, the training algorithm of HEaaN-ID3 is specified in Algorithm 1. It first performs training N0,0 with the initial training data Train0,0 then repeats for all nodes in the tree up to the depth provided as input. The following provides a detailed description of each algorithm.

The CalculateMaxY() in line #5 of Algorithm 1 finds the most frequent Y label of the target variable at each node. Using the data from Fig. 3, the process of CalculateMaxY() is illustrated in Fig. 6. It calculates the distribution of the target variable values from the data. This process involves log2⁡(N) rotations and addition operations, resulting in the frequency of each category being placed in the first slot of each ciphertext. The total t ciphertexts generated in this manner are sequentially combined to create a ciphertext called cytotal, after which a multiplication operation is performed with a ciphertext that has only the first t slots set to 1. This operation removes unnecessary values from the ciphertext. Next, the cytotal is passed through the FindMaxGroupPos() function in Appendix A.1 of [60] that sets the slot with the largest value to 1 and the others to 0. Finally, t−1 rotations are applied to generate ⟦p⟧, multiplying by a constant corresponding to the number of rotations at each step.

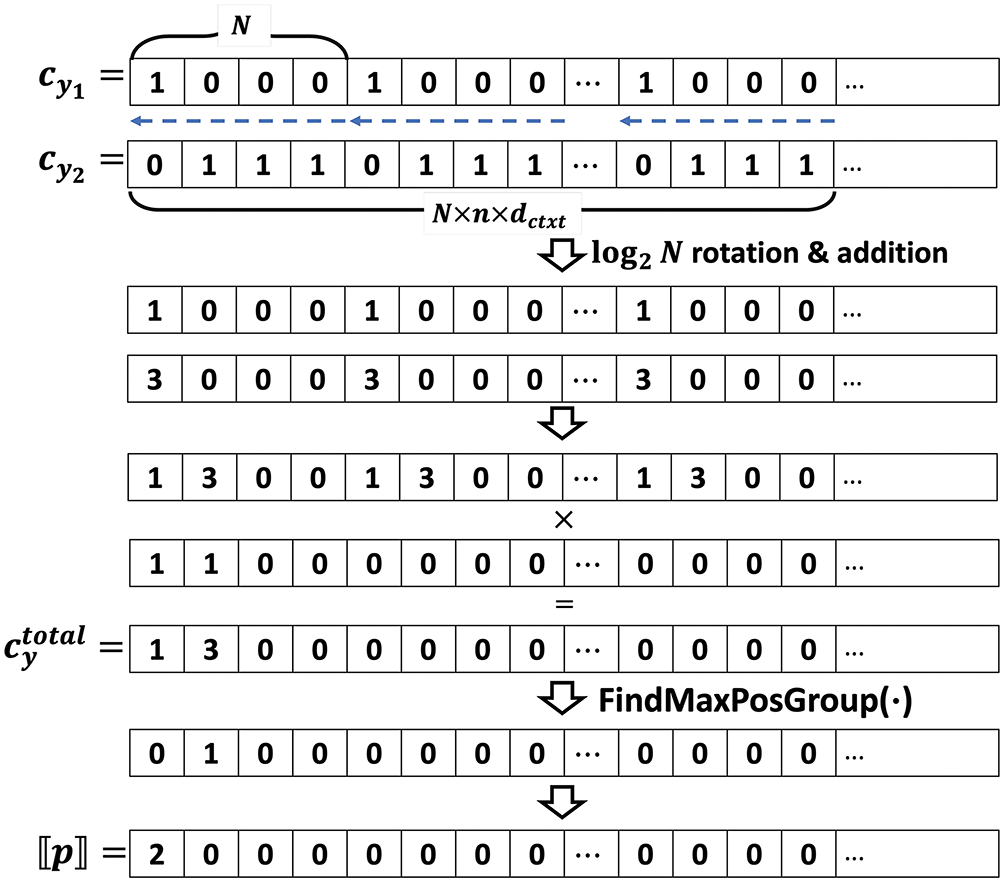
Figure 6: CalculateMaxY

Line #6 of Algorithm 1 is the step where the input data of the corresponding node is checked for validity. Since the data is encrypted, it is not possible to verify whether the node information has been generated from valid values. Consequently, all nodes are generated regardless of the data’s validity, necessitating additional measures to handle nodes created from invalid data. In CalculateMaxY(), instead of combining the ciphertexts representing the distribution of each Y label into a single ciphertext through rotation, a new ciphertext is created by adding all the individual ciphertexts together. Let the ciphertext for this operation be denoted as ⟦w⟧. The reciprocal can be obtained through ApproxInv(⟦w⟧). According to the properties of ApproxInv() mentioned in [3], if ⟦w⟧⋅ApproxInv(⟦w⟧)=0, then Nlv,j.⟦ca⟧ becomes 0, and if it is not 0, Nlv,j.⟦ca⟧ becomes 1. Finally, this result is applied in line #8 of Algorithm 1 to obtain Nlv,j.⟦cy⟧, which represents the predicted value for the corresponding node.

A critical part of the training process is finding the splitting variable Xcv that minimizes the MGI score. This corresponds to line #11 of Algorithm 1. The function FindSplitVar() proceeds in two steps: first, it calculates the frequency of each classified case, and then, it compares the information gain based on the MGI scores for all possible cases. To explain the first step of FindSplitVar(), we begin by creating a ciphertext cgini,j that stores all MGI scores for each variable. Here, j represents the position of a node at the same level. Since the number of independent variables used is d, only the first d slots from the left in the ciphertext cgini,j are used.

The key of the first step is calculating the frequency by determining the distribution of the target variable for each value of the independent variables using the result of cyq⊡ci, where q∈[1,2,⋯,t] and i∈[1,2,⋯,u]. The ciphertexts generated through multiplication are processed using log2⁡(N) rotation and addition operations to ensure that the frequency is stored in the first slot of the N slots, which are divided according to the categories of each variable. Any slots that do not contain valid values are then set to zero.

The second step is to identify the variable with the highest Information Gain (IG) among the independent variables based on the results obtained from the previous process. The IG is computed as the difference between the MGI score of the parent node and the sum of the MGI scores of all children. To determine the independent variable that maximizes IG, it is sufficient to search for the independent variable that minimizes the sum of the MGI scores for the child nodes because the parent is fixed to the current node. Therefore, this step calculates the sum of the MGI scores for each independent variable and stores them in separate slots in the ciphertext.

In the plaintext version, the two steps can be described as follows: First, calculate xi→←bi,1→+⋯+bi,nmax→ and then compute si,q=xi→⋅yq→. Based on this result, calculate Ginii,q=(∑q=1tsi,q)2−∑q=1t(si,q)2 to obtain the final MGI score for the corresponding variable.

Finally, the independent variable that has the smallest MGI score among the d values stored in the ciphertext cgini,j for each node is determined, where j corresponds to the node ID. This involves identifying the position i of the slot that contains the minimum value (i.e., this means Xi maximizes IG) within each cgini,j obtained from the second step. Because locating the slot with the minimum value is computationally expensive in the CKKS sheme, we implement the FindMinGroupPos() function in Appendix A.1 of [60] to reduce the computational cost. This function efficiently reduces the number of operations by consolidating the values of multiple cgini,j ciphertexts into a single ciphertext. Subsequently, it identifies the position of the slot with the minimum value within each group of d slots. Only the slot with the minimum value is assigned a value of 1, whereas the remaining slots are set to 0. This approach is effective because the number of slots in a ciphertext, denoted as M, is often much larger than the number of independent variables, d. Consequently, the number of operations required to determine the minimum value is reduced by a factor of d/M.

The final step of the training process is to update the training data for the child nodes. This corresponds to line #12 of Algorithm 1. To aid understanding, we will explain this in plaintext as depicted in Fig. 7. The child nodes of the currently processing node only use the data corresponding to the classification result of the current node. For example, assume that the variable selected for classification at the current node is X1. To generate the training data for the first child node, we multiply the column where X1=1 by the entire training dataset. Similarly, we multiply each of the nmax columns to generate the data for all child nodes of the corresponding node. In the encrypted state, a single ciphertext is created by copying each column’s data N∗n∗dctxt times and then multiplying it by a total of u+t ciphertexts.

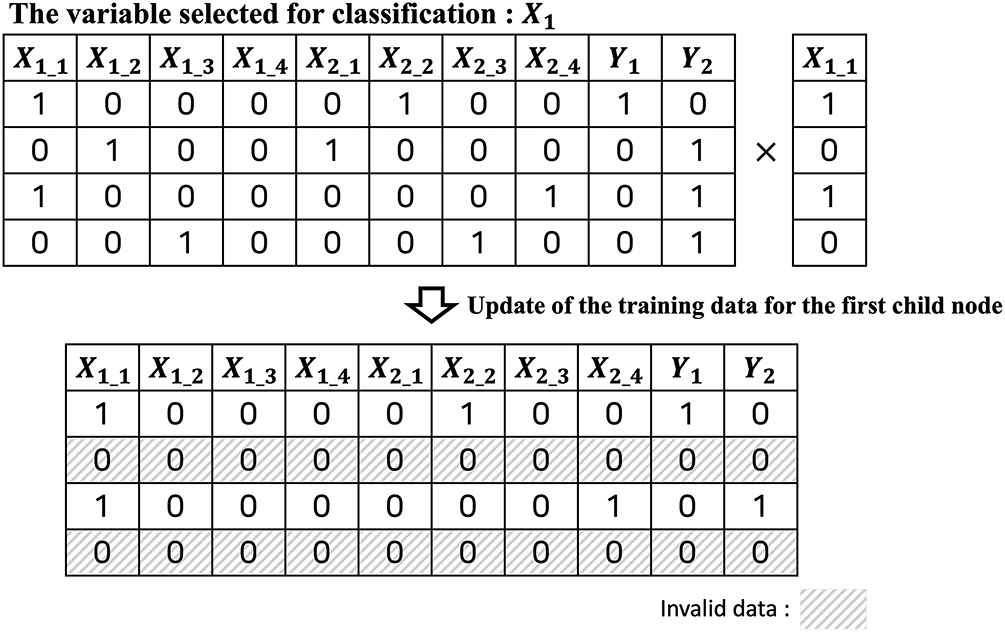
Figure 7: UpdateData-plaintext version

5.4 Inference

We describe a strategy for representing the original model shown in Fig.4-(1) in an encrypted state and for performing inference using the encrypted model. Fig. 4-(2) shows the representation of the plaintext model in Fig. 4-(1) with encrypted values. Fig. 8 illustrates the encrypted model in Fig. 4-(2) using ciphertexts. Observably, ca (cv or cy) values of all nodes at the same level are stored in a single ciphertext, denoted as ca.leveli (cv.leveli or cy.leveli) on different slot positions.

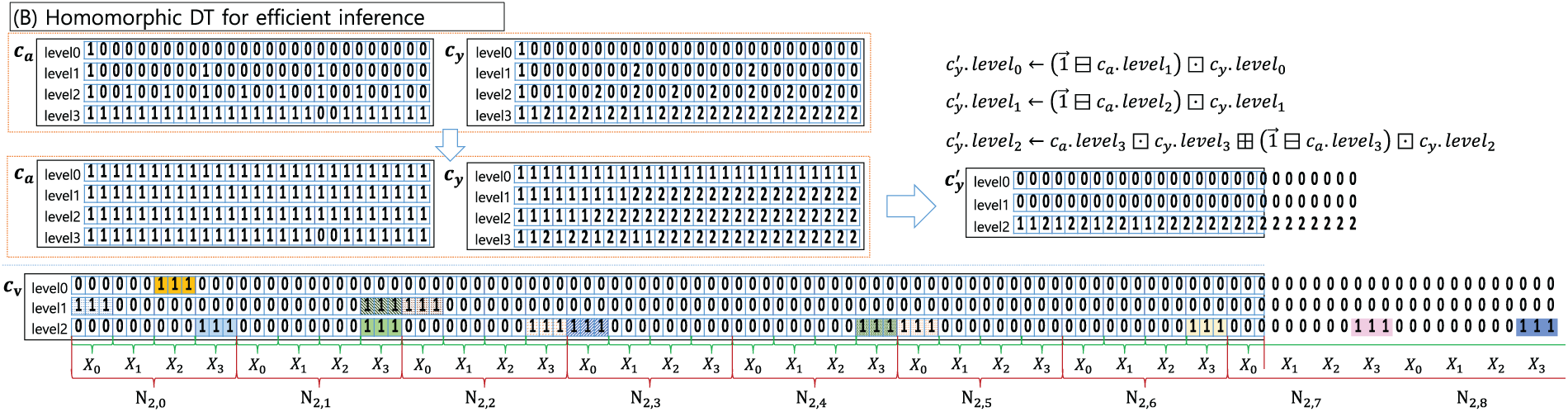
Figure 8: (B)-Tree representation

In Fig. 8, the cv, cy and ca values were pre-processed: as they can be computed independently from the input data for inference, they were pre-computed. The actual inference process was performed using ca from the middle in Fig. 8, cy′ in Fig. 8, and cv at the bottom in Fig. 8.

Fig. 9 illustrates an example of the inference process using a HEaaN-ID3 tree represented in Fig. 8 with an input at the top of Fig. 9. The input comprises four independent variables, each with up to three categories. In the example, the input is (X0, X1, X2, X3) = (2, 1, 1, 1). The owner of this input encrypts it after representing it as a form of Bin Mask Vector [3] (0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0). We duplicated it as much as possible to ensure that the size of the input vector was the same as the number of slots in the ciphertext before encryption. The size of the input vector was nmax∗d, which was duplicated by ⌊M/(nmax∗d)⌋ times. The resultant ciphertext is expressed as follows: cinp in Fig. 9 was sent to the CS.

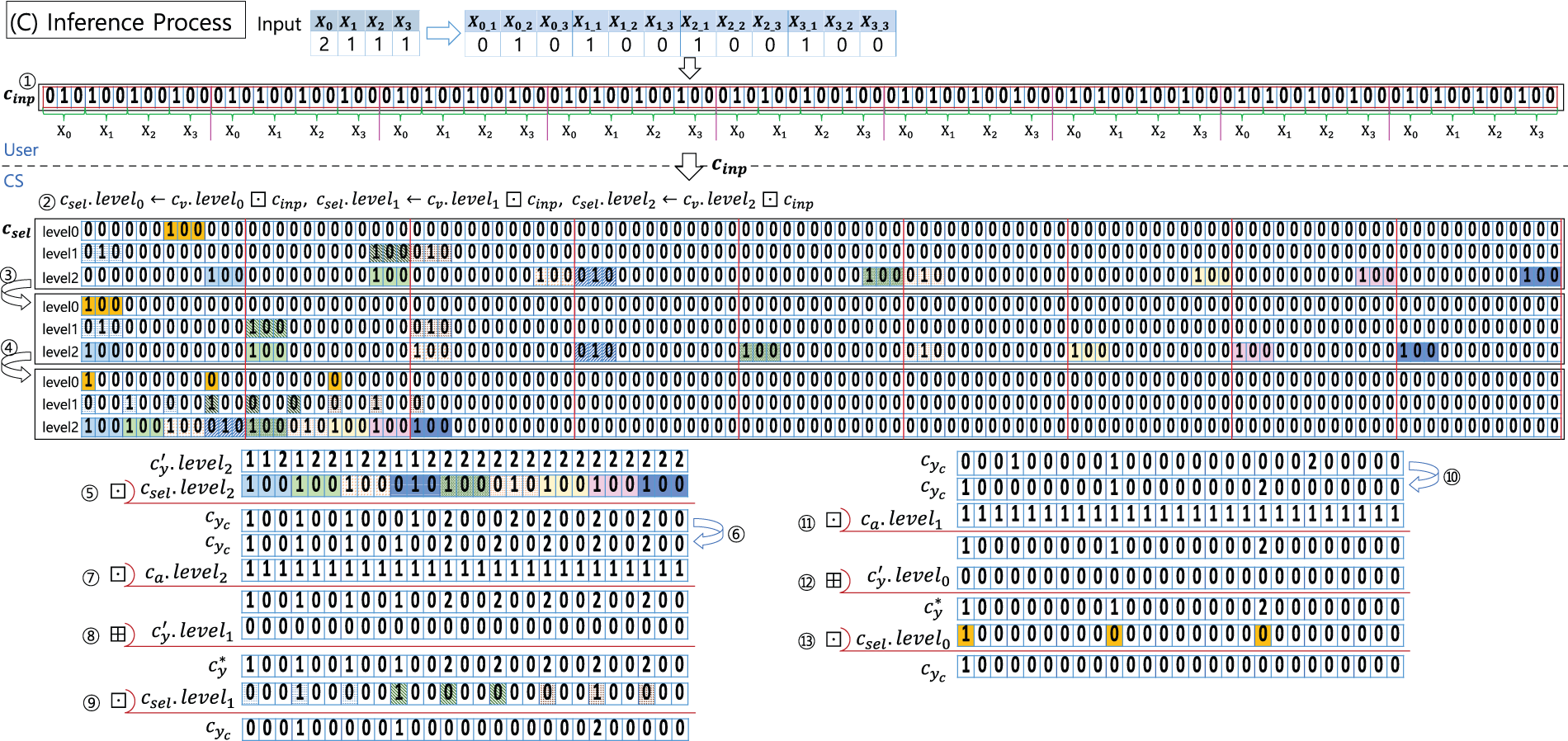
Figure 9: An example of inference process

Once the input ciphertext is received, CS begins the inference process. Unlike in the plaintext version, the inference process proceeds in reverse order, starting from the leaf nodes and moving towards the root. Among all possible outputs in the leaf nodes, one is chosen for each of their parent nodes based on the input values of the variables used for splitting by the parents. After the choice is made, every parent node has a target value which is from one of its children2. We update the tree such that the parent nodes become the leaf nodes. Thus, the depth of the tree is decreased by one. We then repeat the process until only the root node remains in the tree with a target value, which is returned as the final inference result.

In addition, the split conditions on the nodes in the same levels were performed in parallel using a cryptographic SIMD operation. This contributes significantly to the efficient inference of the proposed method.

For convenience, we provide a detailed explanation of the inference process depicted in Fig. 9, under the assumption that M≥nmaxdep for convenience. The process consisted of four main steps, as follows. Step ② involves extracting from cinp the values corresponding to the variables used for split at every non-leaf node in a tree. To achieve this, we perform a multiplication operation between the values of cv.leveli and cinp for each level i in the tree. The resulting values are stored in csel.leveli. Step ③ aligns the extracted results to specific fixed positions to ensure accessibility. This is achieved by applying rotation operations O(log2d) times. In Step ③, we reposition the values in csel to proceed to further processing. In step ④, we make the spacing between neighboring components of the encrypted one-hot encoding vectors obtained in the previous step equal to the number of nmaxdep−level slots, where is the current level. This rendered the inference process more efficient.

Using cy′s created in the training process and csels created in the previous steps, we obtain the inference result through Steps ⑤ to ⑬. This process of multiplying cy and csel at the leaf level. It then processes one level at a time from its parent level, moving upward until it reaches the root level. The calculation of cy′ from cy and ca is performed as follows: ⑦ to ⑧ and ⑪ to ⑫. Finally, after Step ⑬, we obtain the inference result cyc while processing the root level. The final step involves moving the resultant y value into the first slot in cyc. This should be done at Step ⑭.

A detailed description of the tree inference protocol is presented in Fig. 10. In the description, SumGroup() and AdjustMargin() presented as Algorithm 2 and Algorithm 3 correspond to Steps ③, ⑥, ⑩ and ④ in Fig. 9, respectively.

Figure 10: The proposed HEaaN-ID3 inference algorithm

6  Experimental Results

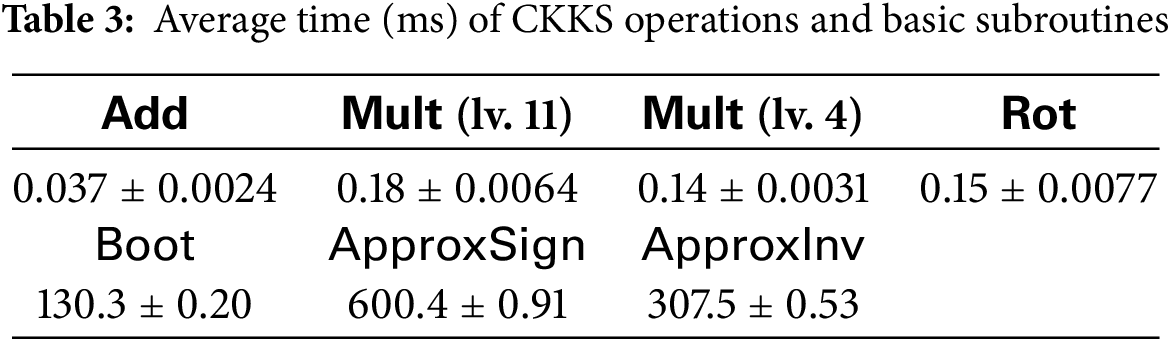
The experimental results of the proposed FHDT on various datasets are presented in this section. The experimental environment was an AMD RYZEN 5950X CPU, NVIDIA Quadro RTX A6000 48 GB GPU, 128 GB RAM. Section 6.1 provides the performance of the basic operations in CKKS. In Section 6.2, we compare the performance of the proposed method with that of [10]. Although the execution environment and the parameters used for CKKS HE were different, we observed that the soft-step function in [10] and the ApproxSign() function in our environment had similar execution times. To the best of our knowledge, the multiplication depth and polynomial degree used are the same in both functions; therefore, we can infer that the performance difference between the two methods can be derived to some extent from the differences in their execution times measured in each environment.

6.1 CKKS

Table 3 lists the performance of the CKKS unit operations and subroutines. Boot() operations required 130.3 ms as we employed a GPU [55]. Approximately 600 ms was required for ApproxSign() used for the proposed training algorithm. The relative error of ApproxInv() was measured as 5.592E−07±6.03E−07%. The relative errors of the other unit operations are less than 1E−05%. We used the GPU version of the HEaaN library for CKKS (https://heaan.it).

6.2 HEaaN-ID3

We evaluated the performance of the proposed HEaaN-ID3 using the data listed in Table 4. They belong to the UCI repository [13], and for binning the numeric variables, the Scott and Sturges binning method was used.

6.2.1 Inference

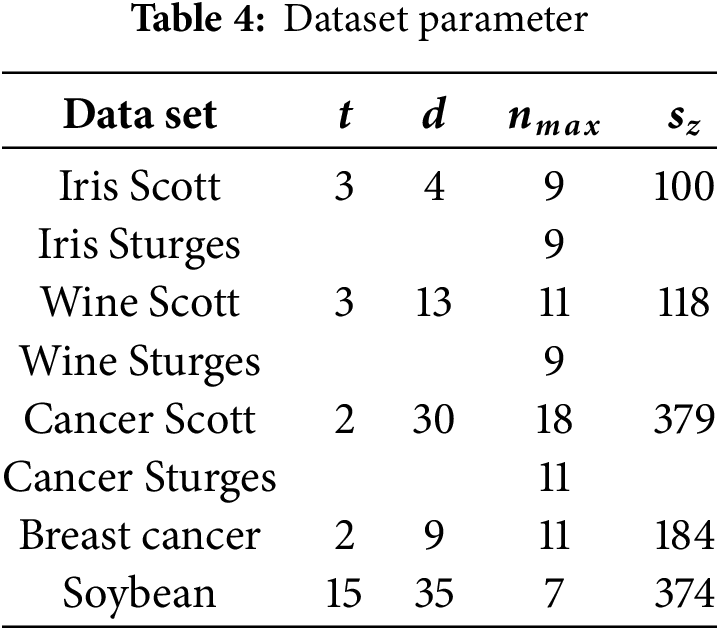
Fig. 11 shows the results for the inference time. Compared to the performance of the method in [10], which requires 2.3 s to process a total of 31 nodes, HEaaN-ID3 requires 657.32 ms even for depth 4 DT trained with the Breast Cancer data, which has 16105 nodes. This indicates that HEaaN-ID3 is superior when considering the number of nodes in the tree. Unfortunately, the inference time increased sharply as the tree depth increased, indicating that the tree depth of the proposed method should be limited. However, in an ID3 DT, owing to the large number of child nodes in the tree, it is possible to achieve a high inference accuracy with a shallow tree depth compared to a binary DT.

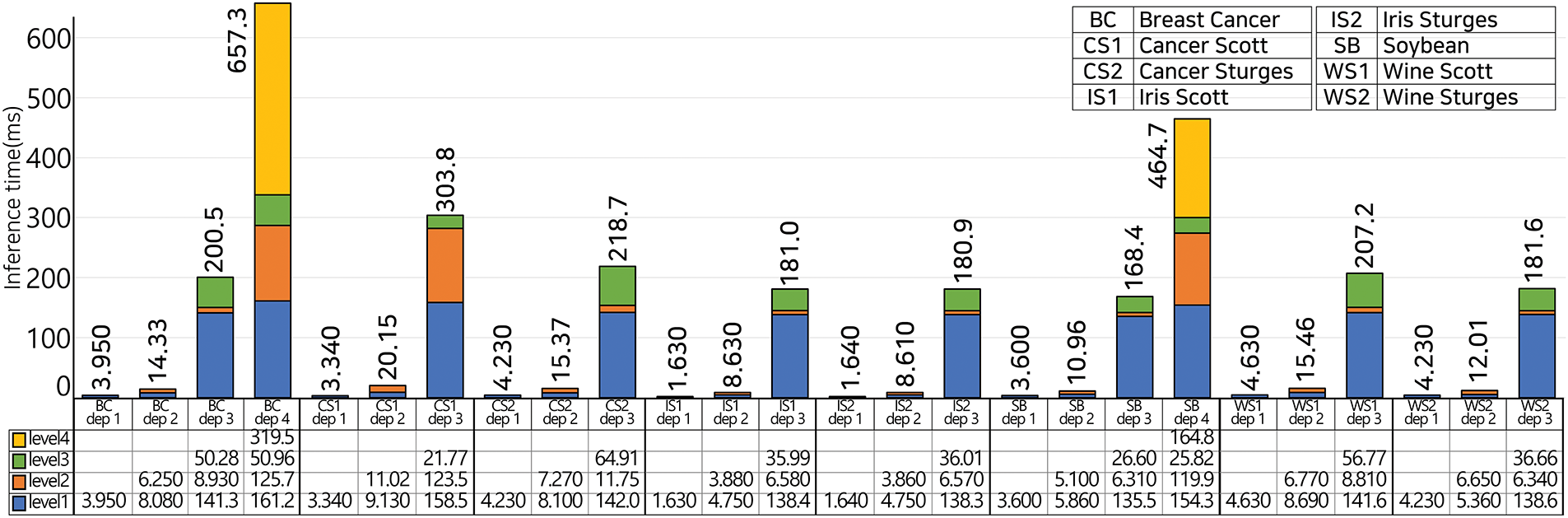
Figure 11: Inference time (The color of the bar indicates the execution time per level of the tree. Because the inference procedure iterates per level, as the depth of the tree increases, the number of iterations also increases. The execution time for each level is described in the table below each bar in the graph)

The inference is performed from the leaf level to the root level. Therefore, if the tree is deep, a bootstrapping operation occurs when processing at the lower level. Thus, the execution time of Level 1 becomes very long if the depth of the tree is three or more. In addition, the number of nodes at the low (close to the leaf) level was extremely large, owing to the characteristics of ID3. Therefore, when the depth of the tree increases, the execution time at a low level increases. As shown in Fig. 11, for the DT of depth 4 trained with the Breast Cancer data, the processing time for the level 4 of 14641 nodes is 319.47 ms, and in the case of the depth 4 DT with Soybean data, 164.79 ms is required to process the level 4 of 2401 nodes.

Regarding inference accuracy, Table 5 shows that the performance of HEaaN-ID3 is comparable to that of the well-known Scikit-Learn [14] library, which is evaluated using plaintext data.

6.2.2 Training

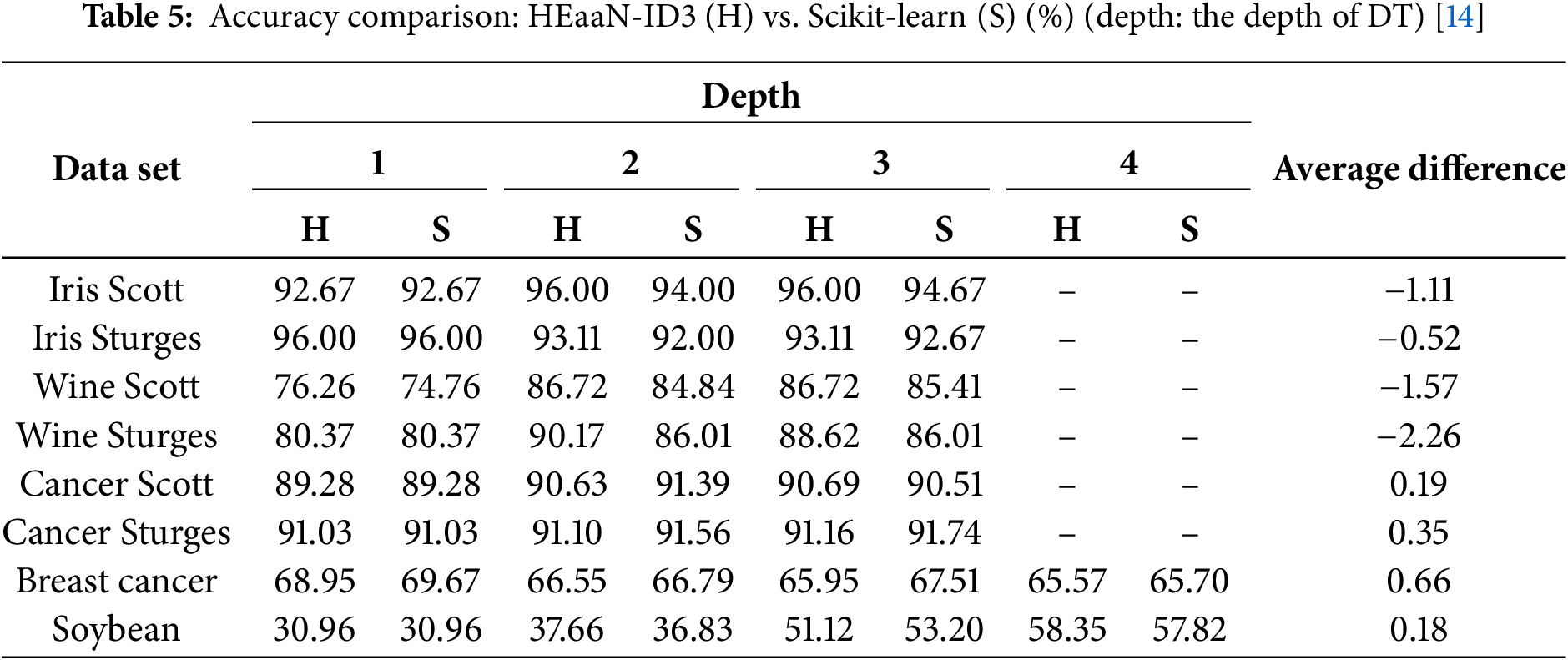
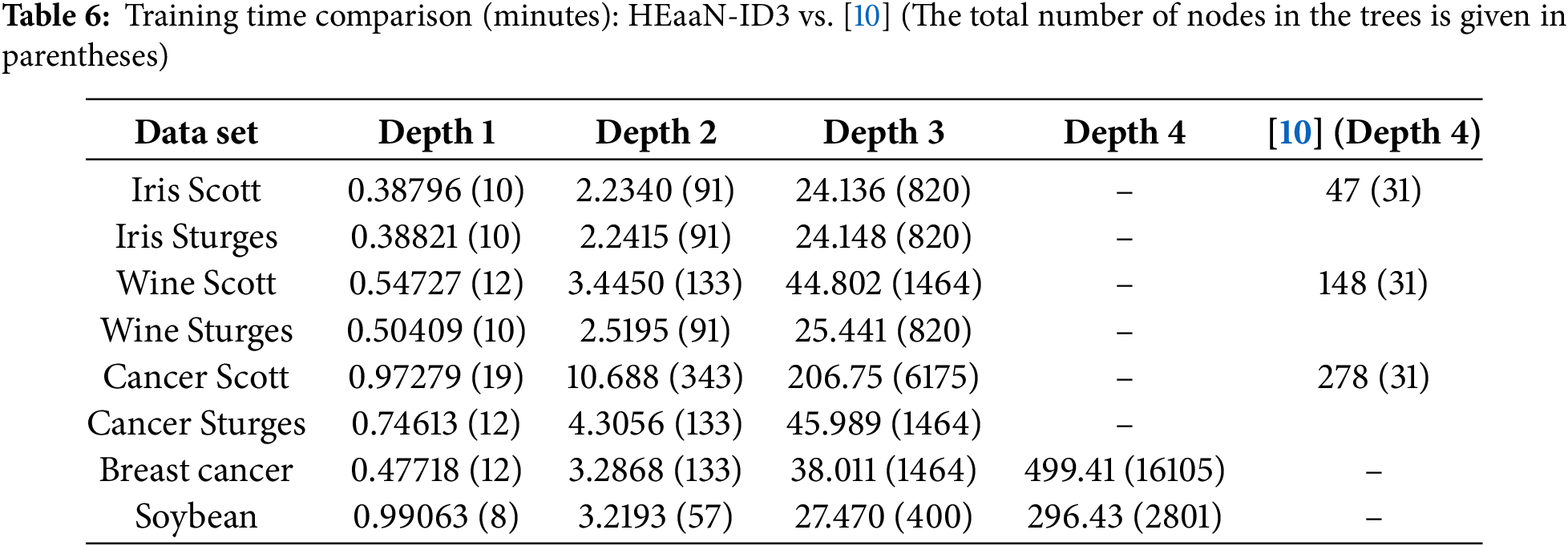
Table 6 compares the training times of the proposed method with those of [10]. For a fair comparison, the estimated time after adjusting the experimental environment from [10] to that of this study is 0.851 min for the Iris dataset with a depth of 4. When comparing the training time per node, HEaaN-ID3 takes 0.029 min, while [10] takes 0.027 min. Although [10] is slightly faster in terms of performance, the proposed method in this study provides safer training as it does not involve decryption during the training process.

7  Security Analysis of the Proposed Method

In this section, we present the security analysis. Under the assumption of the HBC (Honest-But-Curious) model, we assessed whether any participant (either CS or ui) could obtain information from the ciphertexts they received from other participants. We first assume KM to be a trusted third party and it is well-known that the CKKS scheme supports CPA (Chosen Plaintext Attack) security [61].

We begin by considering the case where the CS is an adversary. If the CS can obtain any information from the ciphertexts it receives from the users, it will compromise the CPA security of the underlying CKKS scheme. However, in the proposed protocol, the CS receives only ciphertexts, excluding certain metadata; therefore, it cannot obtain any information from them.

Subsequently, we considered a scenario in which users acted as adversaries and attempted to obtain information from other users’ ciphertexts or from the results of homomorphic computation using CS. Unlike in the CS case, users receive the inference result, which is a decryption result. Therefore, the situation must be assessed differently. Because users receive only the inference result and there are no other users’ ciphertexts, we must verify that the inference result does not reveal any information about the models or data used for inference. Nevertheless, with our method, the amount of information that a user can obtain from inference is the same as if the same protocol is used without encryption. Hence, we can conclude that users cannot obtain any meaningful information from ciphertexts that does not belong to them or cannot be derived from their ciphertexts because even the corresponding plaintext-version of the ID3 DT protocol may reveal the same amount of information as the proposed method. In conclusion, based on the aforementioned argument, we can affirm that our method is secure in the HBC setting and that KM is a trusted third party.

To set up a key distribution, HEaaN-ID3 follows the same settings as [3]. Therefore, please refer to [3] for the security of the key distribution.

8  Discussion

8.1 Checking the Objectives Met by HEaaN-ID3

In Section 5, we determine whether HEaaN-ID3 satisfies the five objectives presented in the Problem Definition. For 1) Data privacy, 2) Model privacy, and 3) Inference privacy: We can confirm these based on the analysis of security in Section 7. Regarding 4), because of the features of HEaaN-ID3, if a user encrypts and delivers the training data to the CS, it can generate a model without the help of other participants; thus, it is satisfied. Finally, for compound 5), HEaaN-ID3 used a single CS that does not have access to the decryption key. Therefore, the condition is satisfied.

8.2 Correctness in Exceptional Situation

HEaaN-ID3 aims to address situations not considered in [10] during the training process. These situations include the following.

•   Scenarios in which the number of training data branches to a specific node is zero.

•   Dealing with multiple variables or pairs of variables and condition that maximize information gain at a specific node.

Although these cases were not discussed in detail in [10], they may still occur. However, reference [10] can handle these situations because all information gain values can be viewed in plaintext form during training. In the proposed method, wherein everything is processed in an encrypted state, these cases must be addressed to prevent any potential impact on the accuracy of the inference results.

When there is no data branching to a specific node: For example, consider a scenario in which training is performed at a node in a DT and there is no training data branching to that node. In this case, all BMV values in TD became zero, leading to a MGI score to become 0. Consequently, all FindMaxGroupPos() values become 1, and the cy value of the corresponding node is set to 0. This sets the ca value of the corresponding node to zero and the training process continues with the child nodes.

If the ca value of a node is zero, all values returned by that node and its descendants are ignored during the inference process. Therefore, the result of the inference process is returned from a node whose ca value is one of the ancestor nodes. The closest ancestor was selected if more than two ancestors were present. In addition, if there is at least one row of training data, the ca value of the root node is always equal to one. This ensures that HEaaN-ID3 returns the correct result, even when there is no data branching in a specific node.

When there are multiple variables that maximize information gain: In this scenario, the result of the function FindMaxGroupPos() has a ciphertext with multiple slots of value 1, representing the number of variables (and branching conditions) that maximize information gain. To address this, the function FindRandomPos() is called to select only one slot with a value of 1 and set the others to zero. The chosen variable (and branching condition) are then used to split the current node, and the training process proceeds normally to the next step.

8.3 Computation Complexity Analysis and Comparision with [10]

The most relevant study to HEaaN-ID3 was by Adiakavia et al. in 2022 [10]. In this subsection, HEaaN-ID3 is compared [10]. The first point to discuss is the differences in the perspective of the system model. In [10], the client has all the data required to learn and classify. During the training process, the client encrypts the training data and sends them to a server. The server learns using the received encrypted data. For critical operations that require heavy computation, the encrypted ciphertext is sent to the client, who then deciphers it, performs critical operations, and encrypts the result before sending it back to the server. In this case, the server and the client must perform h rounds of communication to train a tree with a depth of h. However, the communication volume for each round increases geometrically in proportion to the level of the tree being processed.

HEaaN-ID3, on the other hand, allows multiple users to encrypt their data and send them to the cloud server, where training can take place without further communication. This eliminates the cost and difficulty of communication between the decryption key holder and the cloud server during the training process. Consequently, the proposed method is more advantageous in environments wherein communication with the decryption key holder is expensive or difficult or when the decryption key holder has limited computational resources.

Table 7 presents the execution time for a single node, but since FindMaxGroupPos() and FindMinGroupPos() are executed simultaneously for all nodes at the same level, the execution time per single node can be estimated by dividing by the number of nodes at that level nmaxlv. In addition, since inference is performed by level, only the ”Reconstructing model for efficient inference” step in the training process represents the execution time for a single level. We suppose dctxt is the number of the variables of which the training data can be accommodated in the ciphertext (dctxt=⌊M/(N∗n)⌋). The number of ciphertexts u used to create the training data was calculated as ⌈d/dctxt⌉. Additionally, for a fair comparison, Line 11 of Algorithm 1 should be excluded from the comparison and its execution time is not included in Table 8, since the method in [10] performed the Gini impurity calculation by decrypting the data.

The analysis of the computation complexity in [10] shows that for each non-leaf node, the training algorithm performs a total of 2sz⋅nmax⋅d2⋅t homomorphic multiplications and the same number of additions. In addition, the algorithm invokes the ApproxSign() function 2sz(dnmax+1) times. Since each homomorphic operation is performed separately per sample, feature, and threshold, the total computational load scales quadratically with the number of features d and linearly with the number of samples sz and class count t. Furthermore, the multiplicative depth per node corresponds to the depth of ApproxSign() plus one, which is approximately 5 in practice.

In contrast, the HEaaN-ID3 training algorithm significantly reduces the number of operations by leveraging SIMD operation. As summarized in Table 7, the number of multiplications per node is bounded by 2t+mai+3+2d+u, which results in a total complexity of O(t+d+u). Moreover, the number of ApproxSign() invocations is limited to O(⌈log4(d)⌉) through the use of the FindMaxGroupPos() subroutine. This may result in a slightly greater multiplicative depth compared to [10] as the number of features increases, the total number of high-cost nonlinear operations is substantially lower. Consequently, the proposed HEaaN-ID3 method provides a more efficient and scalable approach to privacy-preserving decision tree training, particularly in high-dimensional or large-sample scenarios.

The analysis of the usage frequency of each homomorphic operation and depth of multiplication in the inference method in [10] is straightforward. For all non-leaf nodes, this method executes the ApproxSign() algorithm twice, multiplication twice and addition once. As a result, the total computation consists of 2dep−2 runs of ApproxSign() and multiplication, and 2dep−1−1 runs of additions. In addition, the multiplication depth consumed by each node is the multiplication depth incurred during the execution of ApproxSign() increased by one, and the width becomes 2lv∗(width of ApproxSign()∗2) if the node is located at level lv of the tree.

The analysis of the HEaaN-ID3 inference algorithm is presented in Table 9. Since the inference process is performed level by level, the computation cost specified in Table 9 corresponds to a single level. To enable efficient inference, the information of the leaf nodes is precomputed during the training phase, so the inference process is carried out only up to the level preceding the depth. As shown in Table 9, the computational cost of the inference process is determined by the value of nmax. The dataset with the largest nmax requires the longest inference time under the same tree depth. In contrast to [10], the number of required invocation for ApproxSign() is 0. This is replaced by an additional multiplication, which is linearly proportional to the depth. Also in terms of depth, ApproxSign() requires a multiplication operation depth of at least 4, so we can see that the proposed method is more favorable.

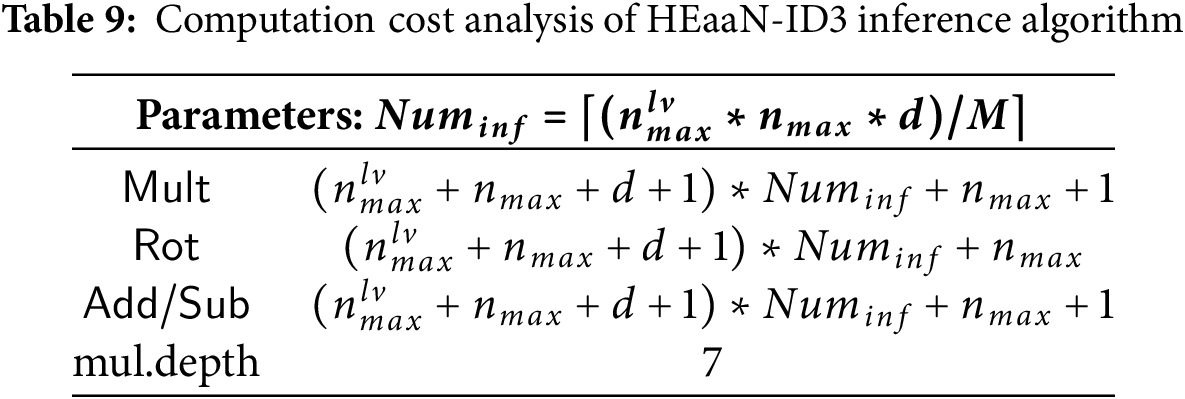
8.4 Scalability of the Proposed Method

As shown in Tables 7 and 9, when the number of features, the variety of categories, and the size of the dataset become very large, the proposed method requires a significant amount of computation. To overcome this, each data owner is encouraged to perform feature selection in advance, which would allow the proposed method to be executed more efficiently. However, pruning is difficult to apply to encrypted trees. Because the data remain encrypted and cannot be checked directly, optimization techniques such as pruning cannot be applied. As a result, the structure of the decision tree generated during training becomes fixed and can grow inefficiently. In particular, due to the characteristics of the HEaaN-ID3 training algorithm, each internal node generates up to nmax child nodes, corresponding to the maximum number of categories of the explanatory variable. Therefore, when the tree depth is dep, the total number of nodes is given by (nmaxdep+1−1)/(nmax−1). As the depth increases, the total number of nodes grows exponentially, which leads to the number of slots required for encrypted computation exceeding what a single ciphertext can handle. Consequently, multiple ciphertexts must be used, resulting in increased computational overhead. This structure negatively impacts the scalability of the system.

However, on the other hand, if the depth of the ID3 decision tree is not large, the proposed method can still enable efficient training and inference. According to [7], the ID3 algorithm typically stops splitting and creates a leaf node when any of the following three conditions are met:

•   There are no remaining attributes available for splitting.

•   All data at the current node belong to the same class.

•   The information gain is zero or below a certain threshold.

Since all of these conditions are determined based on the actual data values, they cannot be directly applied in an encrypted setting. Therefore, estimating the typical depth of an ID3 tree, or the number of nodes generally generated, in advance is valuable for analyzing the scalability of the proposed method.

To this end, we compared the datasets and resulting tree structures (i.e., total number of nodes) used in existing studies on privacy-preserving ID3 decision trees. For example, reference [37] used the UCI Car dataset (car100, car50, car25), which contains 6 attributes and a total of 1728 instances, and generated 407, 248, and 178 nodes, respectively. Although [7] is a study on traditional ID3, it also provides information on the number of nodes generated in the ID3 decision tree. In [7], a chess dataset with 49 attributes and 715 instances resulted in a tree with 150 nodes, and a similar number of nodes was observed for another dataset with 39 attributes and 551 instances. Our proposed method generates a significantly larger number of nodes even at lower depths, as shown in Table 6. This demonstrates that the proposed approach can produce a sufficiently shallower ID3 decision tree without pruning, thereby maintaining practical classification performance without requiring excessive tree depth.

Moreover, HEaaN-ID3 does not need to consider scalability with respect to high-dimensional datasets. As previously discussed, the proposed method is capable of generating a sufficient number of nodes even at shallow tree depths, enabling effective learning without excessive branching or complex tree structures. One of the most common methods for representing categorical data numerically is one-hot encoding, which was also adopted in this study. However, as noted in [62], this approach assigns a separate dimension to each category value, causing the dimensionality of the input vector to grow rapidly as the number of categories increases. This results in increased model complexity, a larger number of training parameters, and a higher risk of overfitting. In particular, high-dimensional input often leads to sparse data representations, which are known to negatively affect both training efficiency and generalization performance. Therefore, the proposed method achieves both practical scalability and efficiency by avoiding unnecessary expansion of tree depth and input dimensionality while still maintaining strong classification performance.

The inference algorithm proposed in this paper has a computational complexity that depends on the depth of the tree, which is closely related to scalability. However, as previously discussed, compared to existing studies, the proposed HEaaN-ID3 was able to achieve sufficient classification performance by generating a large number of nodes even at relatively low depths, without requiring an excessively deep tree. Thanks to this structural characteristic, the number of leaf nodes required during the inference process is also limited. Therefore, the level of complexity presented in this paper is sufficient to ensure practical efficiency in real-world applications.

HEaaN-ID3 does not consider structural scalability in terms of the decision tree itself (i.e., excessive increases in tree depth) for the reasons previously discussed. However, scalability with respect to large-scale datasets must be addressed. In particular, when the number of rows in the training data exceeds the number of slots M that a single ciphertext can hold, it becomes necessary to use multiple ciphertexts to process the data, which leads to increased computational complexity. To handle such cases, this paper presents a generalized training algorithm that accommodates scenarios where the dataset size sz>M, and analyzes the corresponding computational complexity in Table 10. This demonstrates that while HEaaN-ID3 limits structural expansion, it can effectively ensure scalability with respect to data size. Each process represents the complexity computed when training the entire tree, and the training complexity per single node can be obtained by dividing by the total number of nodes, given as TN=(nmaxdep+1−1)/(nmax−1). Additionally, NummaxPos and NumminPos represent the number of ciphertexts required when using FindMaxGroupPos() and FindMinGroupPos() in Appendix A.1 of [60]. To use these two algorithms, each node requires ⌈d/4⌉∗4∗1.5 slots. Since this process is performed per level, the number of ciphertext slots required to process one level is proportional to the number of nodes at that level. Therefore, the values of NummaxPos and NumminPos are given by ⌈(⌈d/4⌉∗4∗1.5∗nmaxlv)/M⌉.

All operations in Lines 5~8 of Algorithm 1 increase linearly with the number of target classes t per node. However, the main factor that significantly increases the computational cost in this part is FindMaxGroupPos(). This algorithm is affected by the number of nodes at the corresponding level, nmaxlv, which causes the computational cost to grow exponentially. Similarly, the process in Line 11 of Algorithm 1 also uses the FindMinGroupPos() algorithm, and its cost increases exponentially due to its dependence on nmaxlv. Additionally, since the processes in Line 11 and Line 12 of Algorithm 1 are not executed at the leaf nodes, they are only applied to the portion of the tree that excludes the leaf nodes. The complexity of the ”Reconstructing model for efficient inference” process is the same as that in Table 7, and thus it has been omitted.

8.5 Security Threat Analysis

In this study, we propose a homomorphic encryption—based framework, HEaaN-ID3, and since all computations are performed on encrypted data, we believe that strong security satisfying the requirements of Section 4.3 can be achieved. However, because the focus of this work is on the implementation of HEaaN-ID3 itself, various existing defense strategies against threats such as malicious actors, model inversion attacks, data poisoning attacks, and side-channel attacks—though they can also be realized under homomorphic encryption—are excluded from the scope of this research. The studies proposing defense strategies for each of these attacks are described below.

First, malicious actors refer to entities that attempt to exploit system vulnerabilities to modify data, leak information, or maliciously manipulate model updates. In a typical environment, these threats can be countered by applying encryption and secure communication protocols (e.g., TLS) during data collection and transmission, as well as by employing input data validation and anomaly detection techniques. Moreover, in federated learning environments, the impact of malicious actors can be minimized using secure aggregation techniques [63] and Byzantine-tolerant gradient descent algorithms [64]. Additionally, if malicious actors perform side-channel attacks, there is a risk that auxiliary information—such as memory access patterns, power consumption, or execution time—generated during encryption computations could be exploited to leak encryption keys or internal states. To defend against this, techniques such as constant-time implementations, randomization of memory access patterns, cache partitioning, and the addition of random noise are employed. In particular, reference [65] demonstrated that these defensive measures can be effectively applied by using cache attacks on AES implementations as an example.

Second, model inversion attacks are techniques in which an attacker leverages the model’s output information (e.g., prediction probabilities, confidence scores, etc.) to reverse-engineer sensitive information from the training data. Previous research has proposed methods to limit the exposure of sensitive information, such as injecting noise into the output [66] and applying softmax post-processing [67].

Finally, data poisoning attacks refer to attacks where maliciously manipulated data is inserted into the training dataset to distort the model’s learning outcomes or induce specific behaviors. There are studies based on Differential Privacy (DP) that mitigate these attacks by adding noise during gradient computation [68] or performing gradient clipping [69] to limit the contribution of each data sample during training.

9  Conclusion

In this study, we proposed HEaaN-ID3, a privacy-preserving ID3 DT using CKKS homomorphic encryption. The ID3 DT enables the training and classification of data consisting of nominal categorical variables, which is differentiated from the existing binary tree-based classification. This requires a comparison operation over input data. However, because the number of child nodes is equal to the number of categories of the variable selected for splitting, to the best of our knowledge, there has been no implementation using only homomorphic encryption owing to the high computational cost. HEaaN-ID3 can generate a model using only encrypted training data without the help of other decryption key-owning entities, and when encrypted input data are received based on this model, classification results can also be obtained without the help of other entities. To demonstrate the practicality of the proposed method, we conducted a performance evaluation after implementing the HEaaN-ID3. The results showed that the training time per node was a few tens of times faster than that in [10], and the required wall-clock time for classification was within a few hundred milliseconds. We also confirmed that the classification performance was similar to that of the plaintext DT implemented in the Scikit-Learn library. The proposed method can be utilized when decryption keys are difficult to use or when the security of the training data is very important; thus, no decryption of the training data or its derivation is mandatory.

Acknowledgement: The authors sincerely appreciate the editors and anonymous reviewers for their valuable comments and suggestions.

Funding Statement: This work was supported by Institute of Information communications Technology Planning Evaluation (IITP) grant funded by the Korea government (MSIT) [No. 2022-0-01047, Development of statistical analysis algorithm and module using homomorphic encryption based on real number operation, 100%].

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization: Younho Lee; methodology: Dain Lee, Hojune Shin, Jihyeon Choi and Younho Lee; software: Dain Lee, Hojune Shin, Jihyeon Choi and Younho Lee; validation: Dain Lee, Hojune Shin, Jihyeon Choi and Younho Lee; writing—original draft preparation: Dain Lee, Hojune Shin, Jihyeon Choi and Younho Lee; writing—review and editing: Dain Lee, Hojune Shin, Jihyeon Choi and Younho Lee; project administration: Younho Lee; funding acquisition: Younho Lee. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

1This refers to a privacy-preserving ID3 DT, where training and inference are performed only with homomorphic operations without using decryption, except for decrypting the inference result.

2The parent may use its own target value if no children is valid.

References

1. Gao S, Iu HHC, Erkan U, Simsek C, Toktas A, Cao Y, et al. A 3D memristive cubic map with dual discrete memristors: design, implementation, and application in image encryption. IEEE Trans Circuits Syst Video Technol. 2025. doi:10.1109/tcsvt.2025.3545868. [Google Scholar] [CrossRef]

2. Lee S, Lee G, Kim JW, Shin J, Lee M-K. HETAL: efficient privacy-preserving transfer learning with homomorphic encryption. In: Proceedings of the International Conference on Machine Learning (ICML); 2023 Jul 23–29; Honolulu, HI, USA. p. 19010–35. [Google Scholar]

3. Lee Y, Seo J, Nam Y, Chae J, Cheon JH. HEaaN-STAT: a privacy-preserving statistical analysis toolkit for large-scale numerical, ordinal, and categorical data. IEEE Trans Dependable Secure Comput. 2023;21(3):1224–1241. doi:10.1109/tdsc.2023.3275649. [Google Scholar] [CrossRef]

4. Gul M. Fully homomorphic encryption with applications to privacy-preserving machine learning; [bachelor’s thesis], Cambridge, MA, USA: Harvard College; 2023. [Google Scholar]

5. Kim D, Guyot C. Optimized privacy-preserving CNN inference with fully homomorphic encryption. IEEE Trans Inf Forensics Secur. 2023;18(11):2175–87. doi:10.1109/tifs.2023.3263631. [Google Scholar] [CrossRef]

6. Yazdinejad A, Dehghantanha A, Karimipour H, Srivastava G, Parizi RM. A robust privacy-preserving federated learning model against model poisoning attacks. IEEE Trans Inf Forensics Secur. 2024;19:6693–6708. doi:10.1109/tifs.2024.3420126. [Google Scholar] [CrossRef]

7. Quinlan JR. Induction of decision trees. Mach Learn. 1986;1(1):81–106. [Google Scholar]

8. Cheon JH, Kim A, Kim M, Song Y. Homomorphic encryption for arithmetic of approximate numbers. In: International Conference on the Theory and Application of Cryptology and Information Security; 2017 Dec 3–7; Hong Kong, China. p. 409–37. [Google Scholar]

9. Liu L, Chen R, Liu X, Su J, Qiao L. Towards practical privacy-preserving decision tree training and evaluation in the cloud. IEEE Trans Inf Forensics Secur. 2020;15:2914–29. doi:10.1109/tifs.2020.2980192. [Google Scholar] [CrossRef]

10. Akavia A, Leibovich M, Resheff YS, Ron R, Shahar M, Vald M. Privacy-preserving decision trees training and prediction. ACM Trans Priv Secur. 2022;25(3):1–30. doi:10.1145/3517197. [Google Scholar] [CrossRef]

11. Bădulescu LA. Experiments for a better Gini index splitting criterion for data mining decision trees algorithms. In: 2020 24th International Conference on System Theory, Control and Computing (ICSTCC); 2020 Oct 8–10; Sinaia, Romania. p. 208–12. [Google Scholar]

12. Cheon JH, Kim D, Kim D. Efficient homomorphic comparison methods with optimal complexity. In: International Conference on the Theory and Application of Cryptology and Information Security; 2020 Dec 7–11; Daejeon, Republic of Korea. [Google Scholar]

13. Markelle Kelly KN Rachel Longjohn. The UCI machine learning repository [Internet]; 2023 [cited 2025 Apr 28]. Available from: https://archive.ics.uci.edu. [Google Scholar]

14. Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, et al. Scikit-learn: machine learning in Python. J Mach Learn Res. 2011;12:2825–30. [Google Scholar]

15. Barni M, Failla P, Kolesnikov V, Lazzeretti R, Sadeghi AR, Schneider T. Secure evaluation of private linear branching programs with medical applications. In: Computer Security—ESORICS 2009: 14th European Symposium on Research in Computer Security; 2009 Sep 21–23; Saint-Malo, France. p. 424–39. [Google Scholar]

16. Bost R, Popa RA, Tu S, Goldwasser S. Machine learning classification over encrypted data. In: NDSS Symposium 2015; 2015 Feb 8–11; San Diego, CA, USA. [Google Scholar]

17. Brickell J, Porter DE, Shmatikov V, Witchel E. Privacy-preserving remote diagnostics. In: Proceedings of the 14th ACM Conference on Computer and Communications Security; 2007 Nov 2–Oct 31; Alexandria VA, USA. p. 498–507. [Google Scholar]

18. De Cock M, Dowsley R, Horst C, Katti R, Nascimento AC, Poon WS, et al. Efficient and private scoring of decision trees, support vector machines and logistic regression models based on pre-computation. IEEE Trans Dependable Secure Comput. 2017;16(2):217–30. doi:10.1109/tdsc.2017.2679189. [Google Scholar] [CrossRef]

19. Joye M, Salehi F. Private yet efficient decision tree evaluation. In: Data and Applications Security and Privacy XXXII: 32nd Annual IFIP WG 11.3 Conference, DBSec 2018; 2018 Jul 16–18; Bergamo, Italy. p. 243–59. [Google Scholar]

20. De Hoogh S, Schoenmakers B, Chen P, op den Akker H. Practical secure decision tree learning in a teletreatment application. In: Financial Cryptography and Data Security: 18th International Conference, FC 2014; Christ Church,Barbados; 2014 Mar 3–7. p. 179–94. [Google Scholar]

21. Du W, Zhan Z. Building decision tree classifier on private data. In: CRPIT ’14: Proceedings of the IEEE International Conference on Privacy, Security and Data Mining; 2002 Dec 1; Maebashi City, Japan. p. 1–8. [Google Scholar]

22. Emekçi F, Sahin OD, Agrawal D, El Abbadi A. Privacy preserving decision tree learning over multiple parties. Data Knowl Eng. 2007;63(2):348–61. [Google Scholar]

23. Agrawal R, Srikant R. Privacy-preserving data mining. In: Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data; 2000 May 15–18; Dallas, TX, USA. p. 439–50. [Google Scholar]

24. Lory P. Enhancing the efficiency in privacy preserving learning of decision trees in partitioned databases. In: Privacy in Statistical Databases: UNESCO Chair in Data Privacy, International Conference, PSD 2012; 2012 Sep 26–28; Palermo, Italy. p. 322–35. [Google Scholar]

25. Li Y, Jiang ZL, Wang X, Yiu SM. Privacy-preserving ID3 data mining over encrypted data in outsourced environments with multiple keys. In: 2017 IEEE International Conference on Computational Science and Engineering (CSE) and IEEE International Conference on Embedded and Ubiquitous Computing (EUC); 2017 Jul 21–24; Guangzhou, China. p. 548–55. [Google Scholar]

26. Liang J, Qin Z, Xue L, Lin X, Shen X. Efficient and privacy-preserving decision tree classification for health monitoring systems. IEEE Internet Things J. 2021;8(16):12528–39. doi:10.1109/jiot.2021.3066307. [Google Scholar] [CrossRef]

27. Zheng Y, Duan H, Wang C, Wang R, Nepal S. Securely and efficiently outsourcing decision tree inference. IEEE Trans Dependable Secure Comput. 2022;19(3):1841–55. doi:10.1109/tdsc.2020.3040012. [Google Scholar] [CrossRef]

28. Cong K, Das D, Park J, Pereira HV. SortingHat: efficient private decision tree evaluation via homomorphic encryption and transciphering. In: Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security; 2022 Nov 7–11; Los Angeles, CA, USA. p. 563–77. [Google Scholar]

29. Kim M, Song Y, Cheon JH. Secure searching of biomarkers through hybrid homomorphic encryption scheme. BMC Med Genomics. 2017;10(2):69–76. doi:10.1186/s12920-017-0280-3. [Google Scholar] [CrossRef]

30. Kim P, Jo E, Lee Y. An efficient search algorithm for large encrypted data by homomorphic encryption. Electron. 2021;10(4):484. doi:10.3390/electronics10040484. [Google Scholar] [CrossRef]

31. Azogagh S, Delfour V, Gambs S, Killijian MO. PROBONITE: private one-branch-only non-interactive decision tree evaluation. In: Proceedings of the 10th Workshop on Encrypted Computing & Applied Homomorphic Cryptography. WAHC’22; 2022 Nov 7; Los Angeles, CA, USA. p. 23–33. doi:10.1145/3560827.3563377. [Google Scholar] [CrossRef]

32. Cheng N, Gupta N, Mitrokotsa A, Morita H, Tozawa K. Constant-round private decision tree evaluation for secret shared data. Proc Priv Enhanc Technol. 2024;2024(1):397–412. [Google Scholar]

33. Bai J, Song X, Zhang X, Wang Q, Cui S, Chang EC, et al. Mostree: malicious secure private decision tree evaluation with sublinear communication. In: Proceedings of the 39th Annual Computer Security Applications Conference; 2023 Dec 4–8; Austin, TX, USA. p. 799–813. [Google Scholar]

34. Ji K, Zhang B, Lu T, Li L, Ren K. UC secure private branching program and decision tree evaluation. IEEE Trans Dependable Secure Comput. 2022;20(4):2836–48. doi:10.1109/tdsc.2022.3202916. [Google Scholar] [CrossRef]

35. Zhang Z, Zhang H, Song X, Lin J, Kong F. Secure outsourcing evaluation for sparse decision trees. IEEE Trans Dependable Secure Comput. 2024;21(6):5228–5241. doi:10.1109/tdsc.2024.3372505. [Google Scholar] [CrossRef]

36. Wang Q, Cui S, Zhou L, Dong Y, Bai J, Koh YS, et al. GTree: GPU-friendly privacy-preserving decision tree training and inference. arXiv:230500645. 2023. [Google Scholar]

37. Vaidya J, Kantarcıoğlu M, Clifton C. Privacy-preserving naive bayes classification. VLDB J. 2008;17(4):879–98. doi:10.1007/s00778-006-0041-y. [Google Scholar] [CrossRef]

38. Wang K, Xu Y, She R, Yu PS. Classification spanning private databases. In: AAAI’06: Proceedings of the 21st National Conference on Artificial Intelligence; 2006 Jul 16–20; Boston, MA, USA. p. 293–8. [Google Scholar]

39. Li Y, Jiang ZL, Wang X, Fang J, Zhang E, Wang X. Securely outsourcing ID3 decision tree in cloud computing. Wirel Commun Mob Comput. 2018;2018:2385150. [Google Scholar]

40. Li Y, Jiang ZL, Wang X, Yiu SM, Zhang P. Outsourcing privacy preserving ID3 decision tree algorithm over encrypted data-sets for two-parties. In: 2017 IEEE Trustcom/BigDataSE/ICESS; 2017 Aug 1–4; Sydney, NSW, Australia. p. 1070–5. doi:10.1109/trustcom/bigdatase/icess.2017.354. [Google Scholar] [CrossRef]

41. Samet S, Miri A. Privacy preserving ID3 using Gini index over horizontally partitioned data. In: 2008 IEEE/ACS International Conference on Computer Systems and Applications; 2008 Mar 31–Apr 4; Doha, Qatar. p. 645–51. [Google Scholar]

42. Xiao MJ, Huang LS, Luo YL, Shen H. Privacy preserving ID3 algorithm over horizontally partitioned data. In: Sixth International Conference on Parallel and Distributed Computing Applications and Technologies (PDCAT’05); 2005 Dec 5–8; Dalian, China. p. 239–43. [Google Scholar]

43. Kiss Á, Naderpour M, Liu J, Asokan N, Schneider T. SoK: modular and efficient private decision tree evaluation. Proc Priv Enh Technol. 2019;2019(2):187–208. doi:10.2478/popets-2019-0026. [Google Scholar] [CrossRef]

44. Tai RK, Ma JP, Zhao Y, Chow SS. Privacy-preserving decision trees evaluation via linear functions. In: Computer Security–ESORICS 2017: 22nd European Symposium on Research in Computer Security; 2017 Sep 11–15; Oslo, Norway. p. 494–512. [Google Scholar]

45. Wu DJ, Feng T, Naehrig M, Lauter K. Privately evaluating decision trees and random forests. Proc Priv Enh Technol. 2016;4(4):335–55. doi:10.1515/popets-2016-0043. [Google Scholar] [CrossRef]

46. Tueno A, Kerschbaum F, Katzenbeisser S. Private evaluation of decision trees using sublinear cost. Proc Priv Enh Technol. 2019;2019(1):266–86. doi:10.2478/popets-2019-0015. [Google Scholar] [CrossRef]

47. Wj Lu, Zhou JJ, Sakuma J. Non-interactive and output expressive private comparison from homomorphic encryption. In: Proceedings of the 2018 on Asia Conference on Computer and Communications Security; 2018 Jun 4; Incheon, Republic of Korea. [Google Scholar]

48. Tueno A, Boev Y, Kerschbaum F. Non-interactive private decision tree evaluation. In: Data and Applications Security and Privacy XXXIV: 34th Annual IFIP WG 11.3 Conference, DBSec 2020; Jun 25–26; Regensburg, Germany. p. 174–94. [Google Scholar]

49. Huysmans J, Dejaeger K, Mues C, Vanthienen J, Baesens B. An empirical evaluation of the comprehensibility of decision table, tree and rule based predictive models. Decis Support Syst. 2011;51(1):141–54. doi:10.1016/j.dss.2010.12.003. [Google Scholar] [CrossRef]

50. Quinlan JR. C4.5: programs for machine learning. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc; 1993. [Google Scholar]

51. Quinlan JR. Improved use of continuous attributes in C4.5. J Artif Intell. 1996;4:77–90. doi:10.1613/jair.279. [Google Scholar] [CrossRef]

52. Breiman L, Friedman JH, Olshen RA, Stone CJ. Classification and regression trees. London, UK: Routledge; 2017. [Google Scholar]

53. Shafer J, Agrawal R, Mehta M. SPRINT: a scalable parallel classifier for data mining. In: VLDB ’96: Proceedings of the 22th International Conference on Very Large Data Bases; 1996 Sep 3–6; Mumbai, India. p. 544–55. [Google Scholar]

54. Delgado-Bonal A, Marshak A. Approximate entropy and sample entropy: a comprehensive tutorial. Entropy. 2019;21(6):541. doi:10.3390/e21060541. [Google Scholar] [PubMed] [CrossRef]

55. Jung W, Kim S, Ahn JH, Cheon JH, Lee Y. Over 100x faster bootstrapping in fully homomorphic encryption through memory-centric optimization with GPUs. IACR Trans Cryptogr Hardw Embed Syst. 2021;2021(4):114–48. doi:10.46586/tches.v2021.i4.114-148. [Google Scholar] [CrossRef]

56. Han K, Ki D. Better bootstrapping for approximate homomorphic encryption. In: Cryptographers’ Track at the RSA Conference; 2020 Feb 24–28; San Francisco, CA, USA. p. 364–90. [Google Scholar]

57. Cheon JH, Han K, Kim A, Kim M, Song Y. A full RNS variant of approximate homomorphic encryption. In: International Conference on Selected Areas in Cryptography; 2018 Aug 15–17; Calgary, AB, Canada. p. 347–68. [Google Scholar]

58. Lee JW, Lee E, Lee Y, Kim YS, No JS. High-precision bootstrapping of RNS-CKKS homomorphic encryption using optimal minimax polynomial approximation and inverse sine function. In: Annual International Conference on the Theory and Applications of Cryptographic Techniques; 2021 Oct 17–21; Zagreb, Croatia. p. 618–47. [Google Scholar]

59. Han B, Shin H, Kim Y, Choi J, Lee Y. HEaaN-NB: non-interactive privacy-preserving Naive Bayes using CKKS for secure outsourced cloud computing. IEEE Access. 2024;12(196):110762–80. doi:10.1109/access.2024.3438161. [Google Scholar] [CrossRef]

60. Shin H, Choi J, Lee D, Kim K, Lee Y. Fully homomorphic training and inference on binary decision tree and random forest. In: Computer Security—ESORICS 2024: 29th European Symposium on Research in Computer Security; 2024 Sep 16–20; Bydgoszcz, Poland. [Google Scholar]

61. Cheon JH, Hong S, Kim D. Remark on the security of ckks scheme in practice. Cryptology EPrint Archive. [cited 2025 May 22]. Available from: https://eprint.iacr.org/2020/1581. [Google Scholar]

62. Micci-Barreca D. A preprocessing scheme for high-cardinality categorical attributes in classification and prediction problems. ACM SIGKDD Explor Newsletter. 2001;3(1):27–32. doi:10.1145/507533.507538. [Google Scholar] [CrossRef]

63. Blanchard P, El Mhamdi EM, Guerraoui R, Stainer J. Machine learning with adversaries: byzantine tolerant gradient descent. Adv Neural Inf Process Syst. 2017;30:119–29. [Google Scholar]

64. Yin D, Chen Y, Kannan R, Bartlett P. Byzantine-robust distributed learning: towards optimal statistical rates. In: International Conference on Machine Learning; 2018 Jul 10–15; Stockholm, Sweden. p. 5650–9. [Google Scholar]

65. Osvik DA, Shamir A, Tromer E. Cache attacks and countermeasures: the case of AES. In: Topics in Cryptology–CT-RSA 2006: The Cryptographers’ Track at the RSA Conference 2006; 2005 Feb 13–17; San Jose, CA, USA. p. 1–20. [Google Scholar]

66. Fredrikson M, Jha S, Ristenpart T. Model inversion attacks that exploit confidence information and basic countermeasures. In: Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security; 2015 Oct 12–16; Denver, CO, USA. p. 1322–33. [Google Scholar]

67. Nasr M, Shokri R, Houmansadr A. Comprehensive privacy analysis of deep learning: passive and active white-box inference attacks against centralized and federated learning. In: 2019 IEEE Symposium on Security and Privacy (SP); 2019 May 19–23; San Francisco, CA, USA. p. 739–53. [Google Scholar]

68. Abadi M, Chu A, Goodfellow I, McMahan HB, Mironov I, Talwar K, et al. Deep learning with differential privacy. In: Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security; 2016 Oct 24–28; Vienna, Austria. p. 308–18. [Google Scholar]

69. Steinhardt J, Koh PWW, Liang PS. Certified defenses for data poisoning attacks. Adv Neural Inf Process Syst. 2017;30:3517–29. [Google Scholar]