An Energy Optimization Algorithm for WRSN Nodes Based on Regional Partitioning and Inter-Layer Routing

1  Introduction

Wireless Sensor Network (WSN) has been widely applied in various fields; however, limited energy supply remains a major bottleneck restricting their long-term operation [1]. Wireless Rechargeable Sensor Network (WRSN) offers an effective solution to the energy constraints of WSN and has become one of the research hotspots [2,3]. WRSN is a WSN in which a wireless charging base station or mobile wireless charging device is identified to replenish the energy of the depleted node in a timely manner through this wireless power transfer technology [4]. Depending on the size of the monitored area, WRSN models can be categorized into large-scale and small/medium-scale networks. Compared to small medium-scale WRSN, large-scale WRSN has a broader scope of application, greater scalability, and offers higher research potential and value [5]. Therefore, the background of this paper is a large-scale WRSN environment. The wireless charging technologies used in WRSN mainly include electromagnetic radiation, inductive coupling, and magnetic resonant coupling. Among these, magnetic resonant coupling is widely employed due to its advantages of high transmission power, high efficiency, and omnidirectional charging capabilities [6]. A typical magnetic resonant coupling-based WRSN generally comprises a base station node, multiple rechargeable sensor nodes, one or more mobile chargers (MC), and a service station node. The sensor nodes and the base station node together form the WRSN, which is responsible for data collection, processing, storage, and transmission, while the service station node and the MC constitute the charging system that replenishes energy for both the MC and the sensor nodes.

In practical applications, due to the limited energy capacity carried by the MC and its restricted charging coverage, ensuring the continuous and efficient operation of the WRSN requires reducing or balancing network node energy consumption. This helps lower the complexity of charging scheduling, improve energy conversion efficiency, and extend the network’s lifespan. Although WRSN shares some similarities with the energy optimization methods used in WSN, the ability of sensor nodes in WRSN to rapidly replenish energy means that balancing sensor node energy consumption is no longer the primary objective. Instead, WRSN energy optimization should focus on minimizing the charging movement path of the MC and balancing node charging time while further reducing sensor node energy consumption. Additionally, large-scale WRSN requires more energy, and the dynamic and heterogeneous nature of sensor node energy consumption rates makes the energy constraint issue even more significant in large-scale WRSN.

Current research on WRSN node energy consumption optimization primarily focuses on maximizing network lifespan, with clustering-based routing algorithm optimization being the predominant approach [7]. Han et al. [8] applied the K-means algorithm to cluster WRSN, balancing energy consumption caused by data transmission. However, the selection of initial anchor node positions significantly affects clustering results, and the method is unsuitable for large-scale WRSN due to its inability to adjust the clustering radius dynamically. Dong et al. [9] proposed an improved clustering algorithm based on K-means, in which the cluster radius calculation formula comprehensively considers three factors: the remaining energy of intra-cluster nodes, the distance to the cluster center, and the number of times a node has been selected as a cluster head. A multi-objective optimization algorithm is used to optimize the weight parameters. Although this clustering method effectively balances node load, it cannot prevent the overcharging of central nodes within a cluster during multi-node charging by a single MC. Han et al. [10] proposed a non-uniform clustering algorithm that selects cluster head nodes based on remaining energy and distance from the base station while determining the clustering radius by considering the number of neighboring nodes and their positions. However, the MC’s charging coverage radius in this method is fixed, which does not align with real-world scenarios. Zhou et al. [11] applied evolutionary game theory to clustering routing algorithms, where each node acts as a game participant and makes decisions based on its remaining energy, the number of neighboring nodes, and other factors, thereby balancing energy consumption among nodes. However, this method imposes high computational demands on each decision-making node, making it impractical for energy-constrained wireless sensor networks. Wang and Jiang [12] proposed an energy consumption optimization algorithm based on dynamic clustering for large-scale WSN. By considering node location and residual energy, the algorithm utilizes dynamic energy data information to identify the optimal cluster head node. However, this approach follows a traditional routing mechanism. Boukerche et al. [13] selected the MC charging radius as the clustering radius while considering node independence, residual energy, and neighbor distances as criteria for cluster head election. This method prevents premature energy depletion of heavily loaded cluster head nodes and effectively balances the number of clusters and inter-cluster communication energy consumption. However, it is only applicable to WRSN with uniformly distributed nodes. Yi et al. [14] proposed a real-time non-uniform clustering charging algorithm that prioritizes charging based on node charging deadlines and distance from the MC. However, this method does not consider multi-hop routing. Sha et al. [15] proposed a multi-hop data forwarding strategy based on candidate cluster heads while dividing the network into multiple annular sector regions of different sizes, each equipped with an MC for node charging. This method alleviates the energy hole problem and balances energy consumption during data transmission. However, it is limited to WRSN scenarios with uniformly deployed nodes. Ijemaru et al. [16] constructed a topology using a novel clustering algorithm designed to balance the number of clusters and inter-cluster communication energy consumption in a large-scale WRSN. However, their method still employs a traditional forwarding routing mechanism, differing from the routing mechanism proposed in this paper. Rajaram et al. [17] developed an enriched energy-optimized LEACH protocol for data transfer, combining efficient clustering with an optimal route selection mechanism to enable energy-efficient routing in WSN. However, this method is specifically designed for WSN environments using the LEACH protocol. Hu et al. [18] proposed a clustering and routing protocol that integrates quantum particle swarm optimization and fuzzy logic to enhance energy efficiency and prolong network lifespan. Their method employs an enhanced quantum particle swarm optimization algorithm for optimal cluster head selection, but is tailored for WSN environments with traditional forwarding routing mechanisms.

From the above analysis, it is evident that in traditional WRSN clustering-based routing algorithms, sensor nodes within a cluster transmit monitored data to the base station via cluster head nodes, which contributes to balancing and reducing node energy consumption. However, since these methods fail to account for the Mobile Charger (MC)’s movement distance during charging, they often result in low energy utilization efficiency [19]. To address these issues, this paper proposes a hierarchical routing mechanism-based WRSN node energy consumption optimization algorithm. This algorithm effectively balances and reduces WRSN node energy consumption, extends network lifespan, and produces a more reasonable WRSN cluster structure. Meanwhile, the algorithm transfers the energy consumption of the outermost nodes to the inner layers, thereby enhancing the energy utilization efficiency of the MC in the WRSN network. The main contributions of this paper are as follows:

•   A hierarchical routing mechanism is proposed. The monitoring area is partitioned using a dynamic cluster radius-based method, with distance serving as the inter-cluster division criterion. Subsequently, the outermost cluster head node dynamically selects relay routing layers for data transmission based on maximum communication distance.

•   An analysis of key parameters is conducted, including routing selection functions, cluster head rotation energy thresholds, and routing layer division structures. These parameters are optimized through simulation experiments.

•   A region-partitioning and hierarchical routing-based energy optimization algorithm is developed. Comparative simulations with traditional forward clustering routing algorithms demonstrate the superiority of the proposed method in network lifespan extension, cluster structure stability, and MC charging efficiency.

The remaining sections of the paper are organized as follows: Section 2 presents the WRSN energy consumption model and analysis; Section 3 details the energy optimization method incorporating region partitioning and inter-layer routing; Section 4 provides simulation results and analysis; Section 5 concludes the study paper.

2  WRSN Energy Consumption Model and Analysis

2.1 WRSN Energy Consumption Model

This paper adopts the first-order wireless communication model, which is widely used in WSN, as the energy consumption model for WRSN nodes [20], as shown in Fig. 1. The primary energy consumption of a node includes communication energy consumption and data processing energy consumption. Communication energy consumption consists of the energy consumed by the transmission circuit when sending data, the power amplifier energy consumption, and the energy consumed by the receiving circuit when receiving data. Meanwhile, data processing energy consumption refers to data fusion energy consumption. Since the transmission and reception circuits have similar structures, the energy consumption of the transmission circuit is approximately equal to that of the reception circuit.

Figure 1: WRSN sensor node energy consumption model

In Fig. 1, ε represents the energy consumption required to transmit 1 bit of data through the power amplifier in the channel model (the value varies depending on the channel model). dij denotes the communication distance between nodes i and j. Etx−elec refers to the energy consumption of the transmission circuit for sending 1 bit of data (with a value of Ee). Etx−amp(dij) represents the energy consumption of the power amplifier during data transmission between node si and node sj (with a value of εdij). Erx−elec denotes the energy consumed by the receiving circuit for receiving k bits of data (with a value of kEe). Eda represents the energy consumption of the cluster head node when fusing 1 bit of data. In terms of node transmission energy consumption, different communication distances correspond to different channel models: the free-space channel model and the multi-path fading channel model. Both models assume a symmetric wireless channel, meaning that the energy consumption for node si to send data to node sj is affected by the transmitted data volume and the transmission distance between si and sj. Similarly, the energy consumption for node si to send the same amount of data to node sj is identical to the energy consumption for node sj to send the same data to node si. The energy consumed by node si when transmitting data to node sj is calculated as shown in Eq. (1).

Etx(dij)=Etx−elec+Etx−amp(dij)={Ee+εfs×dij2,dij≤d0Ee+εamp×dij4,dij>d0.(1)

In Eq. (1), εfs represents the energy consumption for transmitting 1 bit of data through the power amplifier in the free-space channel model. The typical value of εfs is 10pJ/(bit⋅m2). On the other hand, εamp represents the energy consumption for transmitting 1 bit of data through the power amplifier in the multi-path fading channel model. The typical value of εamp is 0.0013pJ/(bit⋅m4). If the communication distance dij between nodes exceeds d0, the multi-path fading channel model is selected. If dij does not exceed d0, the free-space channel model is chosen [21]. d0 represents the boundary distance between the two channel models, and its calculation is shown in Eq. (2).

d0=εfsεamp.(2)

Since the energy consumption of a node receiving data is only related to the amount of received data, the energy consumption of node si when receiving data can be expressed as shown in Eq. (3).

Erx−elec=Ee.(3)

In WRSN, if a node serves as a cluster head node, it will perform data fusion on both the monitoring data transmitted by other ordinary nodes within the cluster and the data it collects itself. Typically, after data fusion, the cluster head node compresses the data by a certain ratio. The data compression formula is shown in Eq. (4), where a represents the data compression ratio during data fusion, and its value range is given in 0<a≤1 [22].

k1=(1a−1)k2.(4)

Assuming that the receiving circuit receives k2 bits of data, this paper considers ultimately aggregating it into 1 bit for data relaying and forwarding, i.e., k1 is 1-bit data. At this point, the energy consumption for data aggregation is k1Eda, which is directly denoted as Eda.

2.2 WRSN Communication and Routing Energy Consumption Analysis

In a small-scale WRSN, a single-hop clustering routing method is generally used for data transmission. That is, after the self-organizing process, all sensor nodes in WRSN form multiple clusters based on the clustering routing protocol. Each cluster selects a cluster head node as the aggregation node to collect data acquired by all nodes within the cluster in the monitoring area. After processing and integrating the intra-cluster information, the cluster head node directly transmits the data to the base station. The energy consumption calculation methods for WRSN nodes using single-hop clustering routing are shown in Eqs. (5)–(8) [22].

E1={EBs−CHDi=Erx−elec×ctrlpackECHDi−CMRj=∑j=1n(Etx−elec+Etx−amp(dij))×ctrlpack,(5)

E2={ECMRj−CHDi=∑t=1T∑j=1n(Erx−elec+Eda)×datapackECHDi−Bs=∑t=1T∑j=1n(Etx−elec+Etx−amp(di−Bs))×datapack,(6)

ECHDi=E1+E2,(7)

e={eCHDi−CMRj=Erx−elec×ctrlpackeCMRj−CHD=(Etx−elec+Etx−amp(dji))×datapack.(8)

In the above expressions, ctrlpack and datapack represents the lengths of the control packets and data packets, respectively. T is the operation cycle of WRSN. The remaining symbols remain consistent with the WRSN sensor node energy consumption model in Fig. 1. In Eq. (7), the energy consumption of the cluster head node i, denoted as ECHDi, mainly consists of two parts: the energy consumption during the clustering phase E1 and the data collection and transmission energy consumption E2. The clustering phase energy consumption E1 includes the energy consumption for receiving control packet data sent by the base station, EBs−CHDi, and the energy consumption for sending control packets from the cluster head node i to the cluster member node j, denoted as ECHDi−CMRj. The data collection and transmission energy consumption E2 consists of the energy consumed in receiving monitoring data sent by cluster member nodes, performing data fusion, and sending the fused monitoring data to the base station. In Eq. (8), the energy consumption of cluster member node j, denoted as e, mainly comprises two parts: the energy for receiving control packets from the cluster head, which allows the node to join the cluster, eCHDi−CMRj, and the energy for sending monitoring data to the cluster head during each period, eCMRj−CHD.

However, in a large-scale WRSN environment, due to the limited communication range of nodes, the cluster head node cannot directly transmit the data collected from cluster members within the current cycle to the base station. Instead, relay nodes are required to collect and forward inter-cluster data. Since the relay function in multi-hop clustering routing is also carried out by cluster head nodes, the energy consumption of ordinary cluster members in multi-hop clustering routing remains the same as in single-hop clustering routing, following the calculation Eq. (8). The energy consumption of cluster head nodes in multi-hop clustering routing is calculated using Eqs. (9)–(11) [22].

E3=∑t=1T(Etx−elec+Etx−amp(dik−ik+1)+Eda)×datapack,(9)

E4=∑t=1T∑k=1mErx−elec×datapack,(10)

EClusterhead={E1+E2+E3,clusterhead≠relaynodeE1+E2+E3+E4,clusterhead=relaynode.(11)

In Eq. (11), the energy consumption of the cluster head node i is divided into two different situations: one where the cluster head does not act as a relay node and the other where it does. The energy consumption of the cluster head consists of six parts, with EBs−CHDi, ECHDi−CMRj, ECMRj−CHDi, and ECHDi−Bs remaining consistent with the energy consumption of cluster head nodes in single-hop clustering routing. The differences lie in the following two energy consumption scenarios: the first scenario involves a cluster head that does not act as a relay node, which must send the data collected from its cluster to a nearby relay cluster head closer to the base station. The energy consumption for this process is denoted as E3. The second scenario involves a cluster head acting as a relay node, which must also receive data sent from different clusters. This energy consumption is denoted as E4.

In large-scale WRSN multi-hop clustering routing, only some nodes located in the peripheral monitoring area of WRSN do not participate in relay routing. A comparison of the energy consumption in both routing methods shows that in multi-hop transmission, relay cluster head nodes closer to the base station experience higher energy consumption due to frequent data reception and forwarding. This leads to premature energy depletion, causing the “energy hole” phenomenon, which disrupts WRSN network connectivity and may result in network failure. To address the energy hole problem, this paper optimizes the cluster structure by integrating node region partitioning with the K-means clustering algorithm. By increasing the number of clusters near the base station, the proposed method effectively balances the relay routing data load, thereby improving network sustainability.

3  Energy Consumption Optimization Method Based on Region Partitioning and Inter-Layer Routing

3.1 Node Area Partitioning Algorithm Based on Dynamic Cluster Radius

The radius of traditional multi-hop clustering routing is fixed and cannot adapt dynamically, making it unsuitable for large-scale WRSN environments, thus requiring improvement. In a large-scale WRSN, if the traditional multi-hop clustering routing is applied, the nodes near the base station will experience rapid energy depletion, regardless of whether this area is designated as a direct transmission zone or a relay zone for data aggregation and transmission to the base station. To address this issue, this paper proposes a node region partitioning method based on dynamic cluster radius. The specific steps are as follows:

Step 1: Considering the minimum deployment distance of nodes, the square monitoring area is defined by four vertices A0, B0, C0 and D0. The maximum cluster radius of WRSN is r. Connecting each vertex to the base station and drawing circles centered at A0,B0,C0,D0 with a radius of r the four circles intersecting the connecting lines at points A1, B1, C1 and D1. The monitoring area A0B0C0D0 is then divided into two parts: a square region A1B1C1D1 and a rectangular region A0B0C0D0−A1B1C1D1. The four arc sections are considered as the maximum cluster structures in the rectangular region.

Step 2: The four vertices of the square region A1B1C1D1 are connected to the base station again, and circles with a radius of ksfir(i=1) are drawn. This results in: a new square region A2B2C2D2 and a new rectangular region A1B1C1D1−A2B2C2D2. Where ksf is the scaling factor, calculated using Eq. (12).

ksf=12(1+cd(r,bs)−dmindmax−dmin).(12)

In Eq. (12), dmax and dmin represent the maximum and minimum distances between WRSN nodes and the base station. d(r,bs) represents the distance from the circular center to the base station, and c is the adjustment factor with a value range of c in [0, 1].

Step 3: Repeat Step 2 for further subdivisions, where the new radius is defined as ksfir(i=2,3,…,n) with n representing the number of partitioning iterations. The process continues until the square region obtained from subdivision is smaller than 2r, at which point the subdivision stops. The circular region closest to the base station is automatically designated as the (n + 1)-th region.

By adopting the above partitioning method, the sub-region farthest from the base station has the largest cluster radius. As the sub-regions get closer to the base station, the cluster radius is adjusted using the scaling factor, gradually reducing the number of nodes within each cluster and the workload of cluster head nodes for data collection. This approach decreases the energy consumption of cluster head nodes for data acquisition and reception, allowing them to allocate more energy for data relay and forwarding tasks. Therefore, this region partitioning method effectively balances energy consumption between clusters near the base station and those farther away, mitigating the “energy hole” problem. Additionally, it determines an appropriate cluster radius for each region, enhancing overall network efficiency. The schematic diagram of the regional division is shown in Fig. 2.

Figure 2: Regional division schematic diagram

3.2 K-Means Clustering Algorithm

The K-means clustering algorithm is used to divide N input data objects into K predefined clusters. The algorithm ensures that data objects within the same cluster have high similarity, while objects in different clusters have low similarity. The similarity criterion is determined by the distance between data objects and the cluster center. The specific steps for applying the K-means algorithm to WRSN node clustering are as follows [23]:

Step 1: Based on the WRSN network scale, predefine the number of clusters K, and randomly select K initial nodes. The coordinates of these nodes are used as the initial cluster center coordinates.

Step 2: Each non-initial node calculates its distance from the K initial cluster centers based on its own location information and joins the closest cluster. Once all non-initial nodes have joined their respective clusters, the first clustering result is generated, forming K initial clusters in WRSN.

Step 3: Each cluster calculates its cluster head position based on the locations of its member nodes.

Step 4: If the coordinates of all cluster heads remain unchanged or the maximum predefined number of iterations is reached, the algorithm outputs the cluster head nodes and cluster member information. Otherwise, steps (2) and (3) are repeated to obtain a more optimal clustering result. The implementation process of the K-means clustering algorithm is shown in Fig. 3.

Figure 3: K-means clustering algorithm

3.3 Inter-Layer Routing Mechanism

After WRSN completes clustering, the nodes enter the data collection and transmission phase. Within each WRSN operational cycle, ordinary nodes in a cluster transmit their collected monitoring data to the cluster head node according to their assigned time sequence. The cluster head node then aggregates and fuses the data before forwarding it to the base station via single-hop or multi-hop transmission, completing one operational cycle of WRSN. In a large-scale WRSN, the most critical aspect of the routing mechanism is the selection of multi-hop relay nodes and the rotation strategy for cluster head nodes after a certain number of operational cycles.

The traditional routing mechanism automatically defines an area within a certain radius from the base station as a single cluster, where all nodes in this region directly transmit data to the base station via single-hop transmission. In other hierarchical regions, except for the outermost layer, cluster head nodes act as relay nodes for data forwarding. A cluster head node at layer n receives data from the cluster head at layer n−1, fuses it with data received from its own cluster members, and then forwards it to the cluster head at layer n+1. This process is repeated until the data is transmitted to the base station. The traditional routing mechanism adds cluster head nodes within the communication range to the candidate cluster head set. The selection of relay nodes considers: 1. Residual energy of candidate cluster head nodes 2. Distance between candidate cluster head nodes 3. Number of cluster members in each candidate cluster. These three factors are normalized, weighted, and summed to obtain the scoring function for selecting cluster heads, as shown in Eq. (13). The candidate node with the highest score is then selected as the relay node, which can be expressed as CHDn+1∗=argmaxj(Scorej), ensuring that the node with the highest residual energy, the shortest distance, and the smallest load is chosen as the relay node.

Score(CHDn,i,CHDn+1,j)=a1REn+1,jREmax+a2dist(CHDn,i,CHDn+1,j)distmax+a3CMRn+1,jCMRmax.(13)

In Eq. (13), REmax, distmax and CMRmax represent the maximum remaining energy of cluster heads in the next hierarchical level, the maximum distance between cluster heads in the communication range, and the number of nodes within the cluster, respectively. a1, a2 and a3 are the weights assigned to these three factors, where |a1|+|a2|+|a3|=1. Since the distance between cluster heads and the number of nodes within a cluster are negatively correlated with the selection of relay nodes, it is set that a2<0 and a3<0.

In the traditional routing mechanism, when the transmission distance is the same or similar, clusters with fewer nodes or isolated cluster nodes often bear a higher relay burden. However, in large-scale WRSN, since forwarding routing at each level requires multiple layers to receive and forward data, the overall circuit transmission and reception energy consumption in the network increases significantly. To address this issue, this paper proposes an improved routing mechanism with the following key methods:

1.    Based on the maximum communication boundary distance d0 in the WRSN energy consumption model and the cluster head routing load, the dynamically partitioned sub-regions are further merged to form m regions, generating m-1 relay routing regions.

2.    Starting from the outermost cluster head nodes, the next relay routing region is selected based on the maximum communication distance, and its corresponding layer is designated as the relay routing layer for data transmission. This process continues until all layers within the relay routing region complete their cluster head selection. Once this is done, the next relay routing region (e.g., from region 1 to region 2) is processed. By designing this inter-layer routing mechanism, the transmission and reception energy consumption of clusters farther from the base station is minimized, while the energy load is shifted toward clusters closer to the base station. This adjustment facilitates efficient and timely energy replenishment by the MC for nodes in need of charging.

After a certain operational period, the cluster head nodes at the inner and outer hierarchical levels tend to deplete their energy quickly due to the relay data forwarding. Although the traditional relay routing selection can somewhat disperse the routing load on cluster head nodes, they still face rapid depletion compared to ordinary nodes. Therefore, a rotation of cluster heads within the cluster is necessary to upgrade nodes with higher remaining energy to become cluster heads, thereby balancing energy consumption among the nodes in the cluster.

After a certain number of operational cycles, the inner and outer cluster head nodes in WRSN experience rapid energy depletion due to relay data forwarding. While the traditional relay node selection method can partially distribute the routing load, cluster head nodes still deplete their energy faster than ordinary cluster members, making them prone to failure. To balance energy consumption, it is necessary to rotate the cluster head role among the remaining nodes, promoting high-energy nodes to cluster heads. This paper introduces a cluster head rotation mechanism based on a remaining energy threshold H: 1. If the current cluster head’s remaining energy falls below the threshold, the node with the highest remaining energy in the cluster is selected as the next cluster head for the upcoming cycle. 2. If all nodes in the cluster fall below the threshold, the next cluster head is chosen sequentially based on the highest remaining energy among cluster members.

Combining the improvements to the traditional routing mechanism with the cluster head rotation strategy, this paper designs a hierarchical routing mechanism with the following specific steps:

Step 1: Integrate the sub-regions to form a set of relay routing intervals {Mi},i=1,…,N, where N is the number of intervals. Each interval Mi can represent R hierarchical sets as {Lki},k=1,…,R, and the clusters within the hierarchy as {clusterji,k},j=1,…,C, where C is the number of clusters.

Step 2: For each cluster clusterji,k within the hierarchy, first select the corresponding relay routing layer Lk′i+1 from the next interval, where k′ corresponds to the current level k in the next interval. Then, in the cluster collection of the relay routing layer {clusterji+1,k′}, select a cluster based on the relay routing selection function described in Eq. (13), and designate the cluster’s cluster head node as the relay node.

Step 3: Repeat step 2 to complete the interval transmission design for data from each cluster’s nodes. During each operational cycle of the WRSN, ordinary nodes within the cluster will transmit data to the cluster head nodes and compute the energy consumption of the nodes based on Eq. (8). Subsequently, the cluster head nodes will forward the data to the corresponding level cluster head nodes based on the interval transmission design and compute their energy consumption using Eq. (11).

Step 4: Set the remaining energy threshold H for the cluster heads and retrieve the energy consumption of the cluster head nodes from step 3. If any cluster head node’s energy consumption is below this threshold, the node with the highest remaining energy in that cluster will be selected as the cluster head for the next cycle. If all nodes in the current cycle are below the threshold H, the next cluster head will be selected sequentially based on the remaining energy of the nodes.

3.4 WRSN Energy Consumption Optimization Algorithm

By integrating the dynamic cluster radius-based node region partitioning algorithm, the K-means clustering algorithm, and the hierarchical routing mechanism, this paper proposes a WRSN energy consumption optimization algorithm. The node region partitioning algorithm and K-means clustering algorithm are used to generate the WRSN network cluster structure, while the hierarchical routing mechanism enables inter-cluster data transmission through relay routing region division and multi-hop inter-layer transmission. The detailed implementation steps of the algorithm are as follows:

Step 1: Use the dynamic cluster radius-based region partitioning method to divide the WRSN monitoring area into hierarchical sub-regions, determining the clustering radius for each sub-region.

Step 2: Based on the clustering radius and nodes obtained from Step 1, apply the K-means clustering algorithm to cluster the nodes within each sub-region. This process determines the number of clusters, cluster head nodes, and cluster members in each region, thereby designing the intra-cluster data transmission strategy.

Step 3: Apply the relay routing region partitioning method to merge the sub-regions obtained in Step 1, forming relay routing regions. First, cluster head nodes from the previous region select the next hierarchical region as the relay routing layer based on the region partitioning method. Then, in the relay routing layer, relay nodes are selected using the relay routing selection function, completing the inter-region data transmission design. During data transmission, cluster head rotation is performed based on the remaining energy threshold, ensuring load balancing and efficient inter-layer data transmission.

Step 4: In each WRSN operational cycle, based on the intra-cluster transmission plan (Step 2) and the inter-region transmission plan (Step 3): Ordinary nodes within a cluster transmit their collected monitoring data to the cluster head according to their assigned time sequence. The cluster head node aggregates and fuses the data before forwarding it to the relay nodes using multi-hop transmission. Data is progressively forwarded layer by layer until it reaches the base station, completing one operational cycle of WRSN. The algorithm implementation flowchart is shown in Fig. 4.

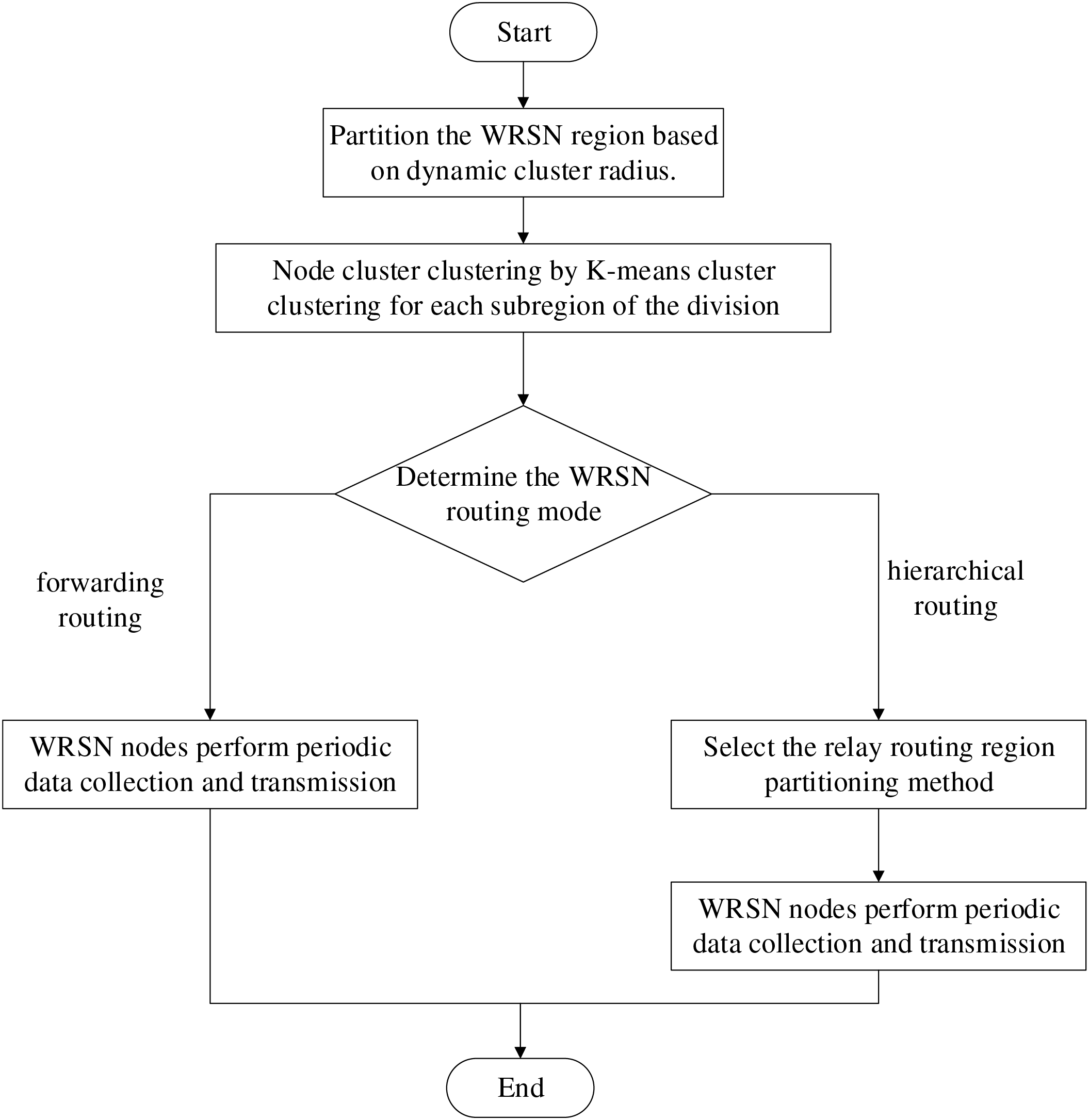
Figure 4: Algorithm implementation flowchart

4  Simulation Results and Analysis

4.1 Experimental Environment and Parameter Settings

The WRSN network model discussed in this paper is constructed using Python 3.8 on the PyCharm 2021 platform. The hardware environment for the experiment consists of an Intel(R) Core (TM) i5-11600KF processor running at 3.90 GHz with 16 GB of RAM, and the operating system is Windows 11 Professional. The experimental simulation parameters are set based on reference [24], as shown in Table 1.

4.2 Analysis of the Impact of Different Network Parameters on the Performance of Different Relay Routing Mechanisms

4.2.1 Analysis of Relay Routing Selection Function Parameters

Considering the impact of the relay routing selection function parameters as described in Eq. (13), this paper tests three different sets of parameter weights for three different factors. The selected parameter groups are as follows: Set 1: a1=0.3, a2=−0.5, a3=−0.2; Set 2: a1=0.5, a2=−0.3, a3=−0.2; Set 3: a1=0.2, a2=−0.5, a3=−0.3. These three parameter groups are used to conduct comparative experiments on metrics such as the number of dead nodes, overall energy consumption, and network coverage in a WRSN environment with 500 nodes. A total of 50 experiments are performed for the analysis of the routing selection function parameters, and the average values from these 50 experiments are considered. Table 2 shows the number of rounds the WRSN network operates until the first node dies, as well as when 30% and 50% of the nodes are dead, for the designed inter-layer routing mechanism and the traditional forward routing mechanism under each set of parameters.

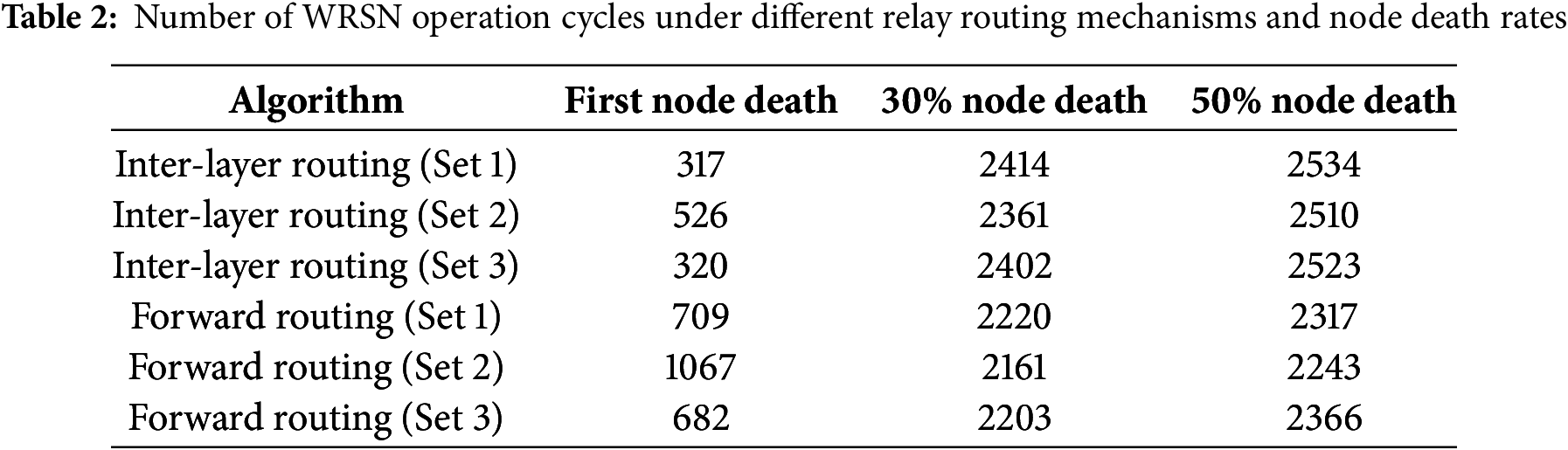
From Table 2, parameter group 2 significantly extends the number of rounds until the first node dies for both the forward routing and inter-layer routing mechanisms. However, the differences in the number of rounds until 30% and 50% of the nodes are dead among the three parameter groups are relatively small. Specifically, the inter-layer routing (Set 1) compared to inter-layer routing (Set 2) and inter-layer routing (Set 3) extends the rounds until the first node dies by 39.7% and 39.2%, respectively. Similarly, for the forward routing mechanism (Set 2), the rounds until the first node dies are extended by 33.6% and 36.1% compared to parameter groups 1 and 3, respectively. Thus, increasing the weight of the remaining energy factor of the cluster head in the three influencing factors can help avoid selecting cluster heads with low remaining energy as relay nodes, balance the energy consumption among relay nodes, and ultimately extend the lifetime of the WRSN.

To further validate the optimization of WRSN network performance and energy consumption with Set 1, the trends in the number of dead nodes, overall energy consumption, and network coverage under the three parameter groups for the two routing mechanisms are compared, as illustrated in Figs. 5–7, respectively. The method for calculating the network coverage is given in Eq. (14).

cWRSN=∑i=1narea(Mi)L×W×nodenumberitotalnodenumberi,(14)

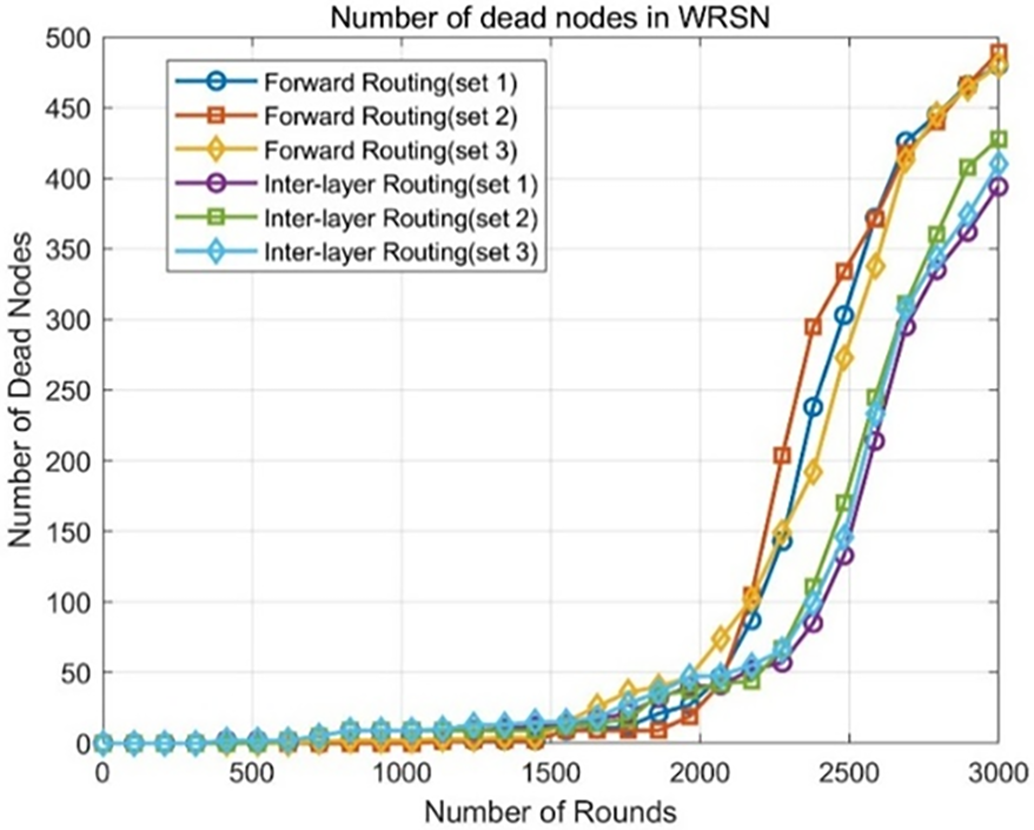
Figure 5: Trend of node death in WRSN under two routing mechanisms with different parameters

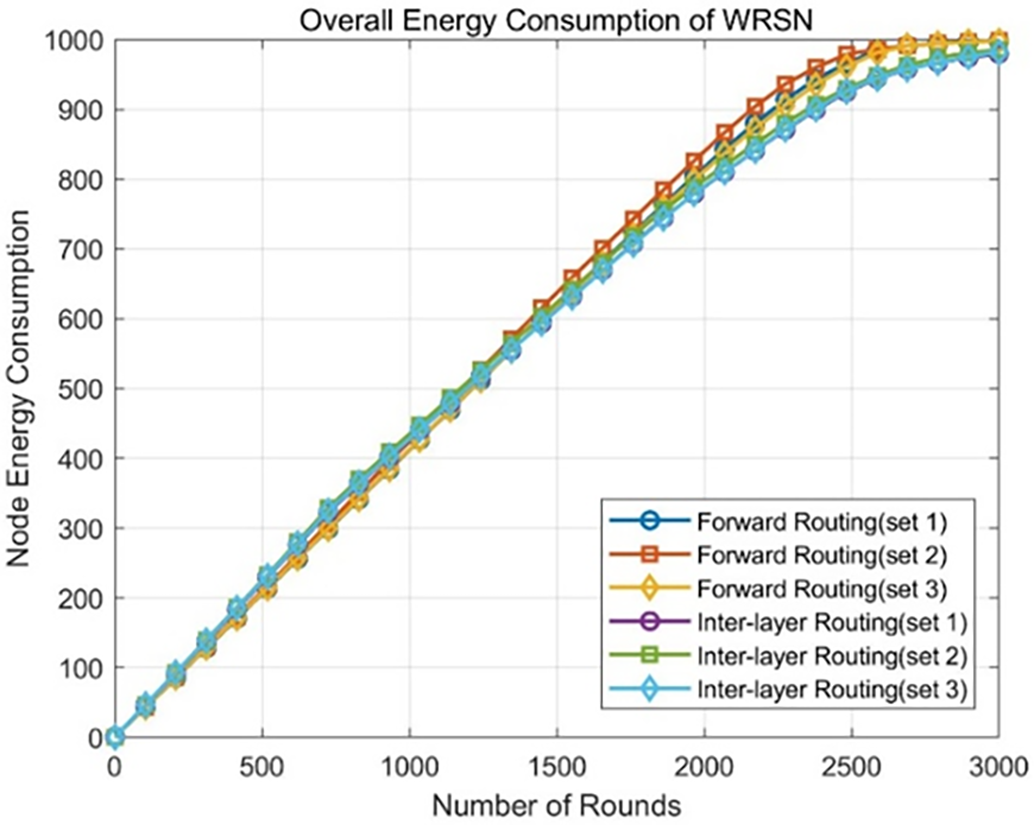
Figure 6: Trend of overall energy consumption in WRSN under two routing mechanisms with different parameters

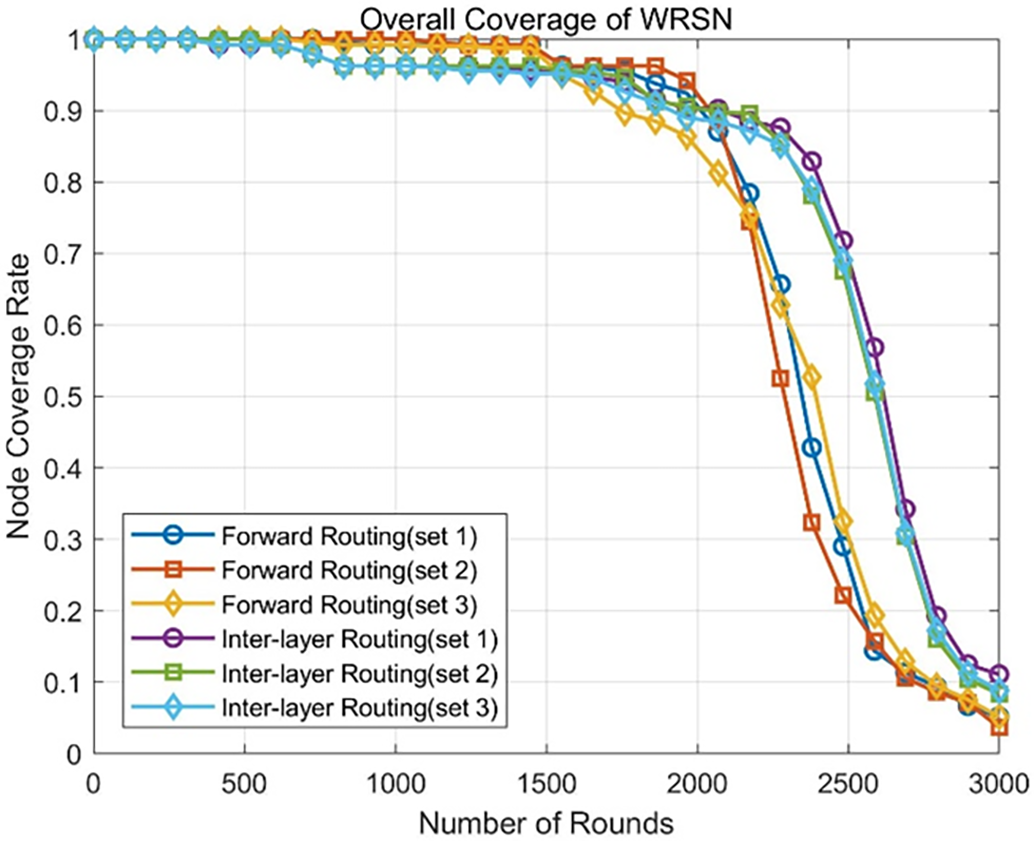
Figure 7: Trend of network coverage in WRSN under two routing mechanisms with different parameters

where area(Mi) represents the coverage area of level i, nodenumberi is the number of surviving nodes at that level, totalnodenumberi is the total number of nodes, and n is the total number of levels.

In Fig. 5, it is observed that for the inter-layer routing mechanism, the influence of the three parameter groups on the total number of dead nodes in the WRSN at round 3000 is relatively small. For the forward routing mechanism, the curve indicating the change in dead nodes shows that in the first 2000 rounds of operation, the number of dead nodes in forward routing (Set 2) is relatively similar to the other two parameter groups. However, in the following 1000 rounds, the number of dead nodes in forward routing (Set 2) increases compared to the other two parameter groups. Combining the observations from Figs. 6 and 7, the overall energy consumption of the WRSN under the three parameter groups is essentially the same, and the trends in coverage are quite similar. Since Set 2 effectively enhances the survival time of all nodes in the WRSN network, it is selected as the relay routing parameters for both the inter-layer routing mechanism and the forward routing mechanism.

4.2.2 Analysis of the Cluster Head Rotation Remaining Energy Threshold Parameter

Considering the impact of the cluster head rotation remaining energy threshold on the routing mechanism, three threshold values are selected for comparative experiments. In the WRSN network with 500 nodes, where the initial energy of each node is 2 J, the initial energies of 80%, 60%, and 40% are taken as the cluster head rotation remaining energy thresholds, denoted as H=0.8, H=0.6 and H=0.4. Comparative experiments are conducted to analyze the number of dead nodes, overall energy consumption, network coverage, and other indicators. A total of 50 experiments are performed for threshold parameter analysis, and the average values from these 50 experiments are considered. The number of rounds the WRSN network operates until the first node dies, as well as when 30% and 50% of the nodes are dead, under different cluster head rotation thresholds for the two routing mechanisms are shown in Table 3. The trends in the number of dead nodes, overall energy consumption, and network coverage are illustrated in Figs. 8–10, respectively.

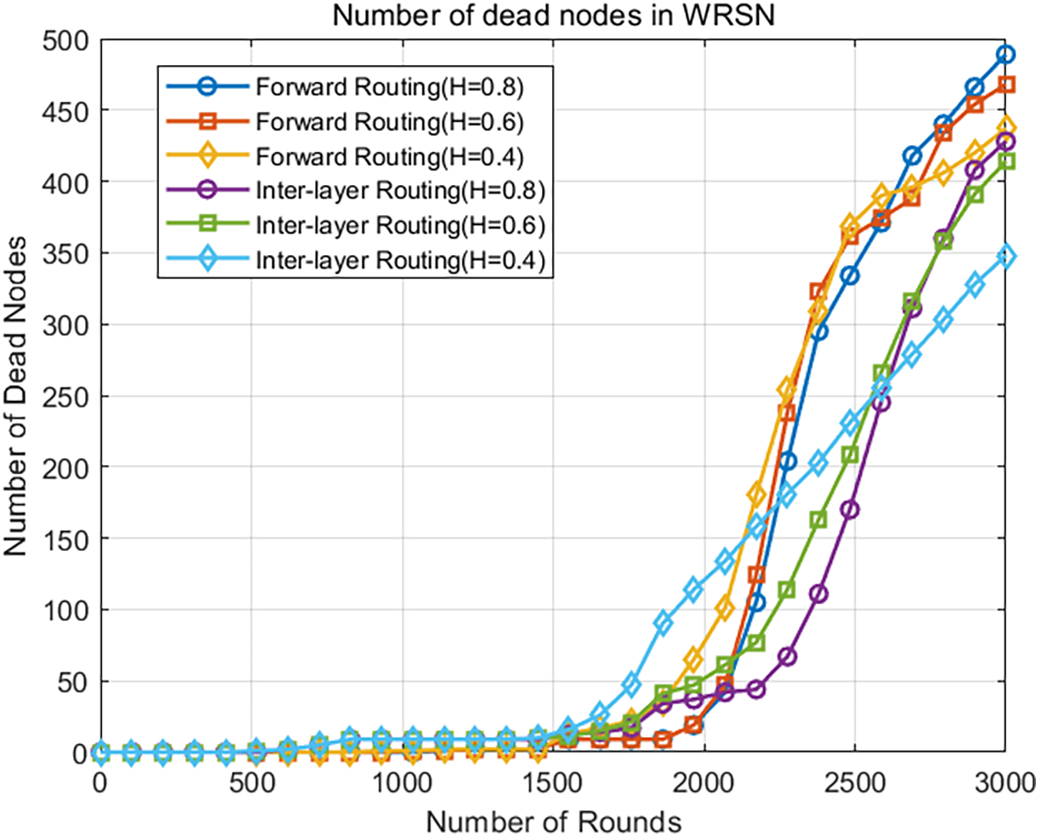
Figure 8: Trend of dead nodes in WRSN with different thresholds under two routing mechanisms

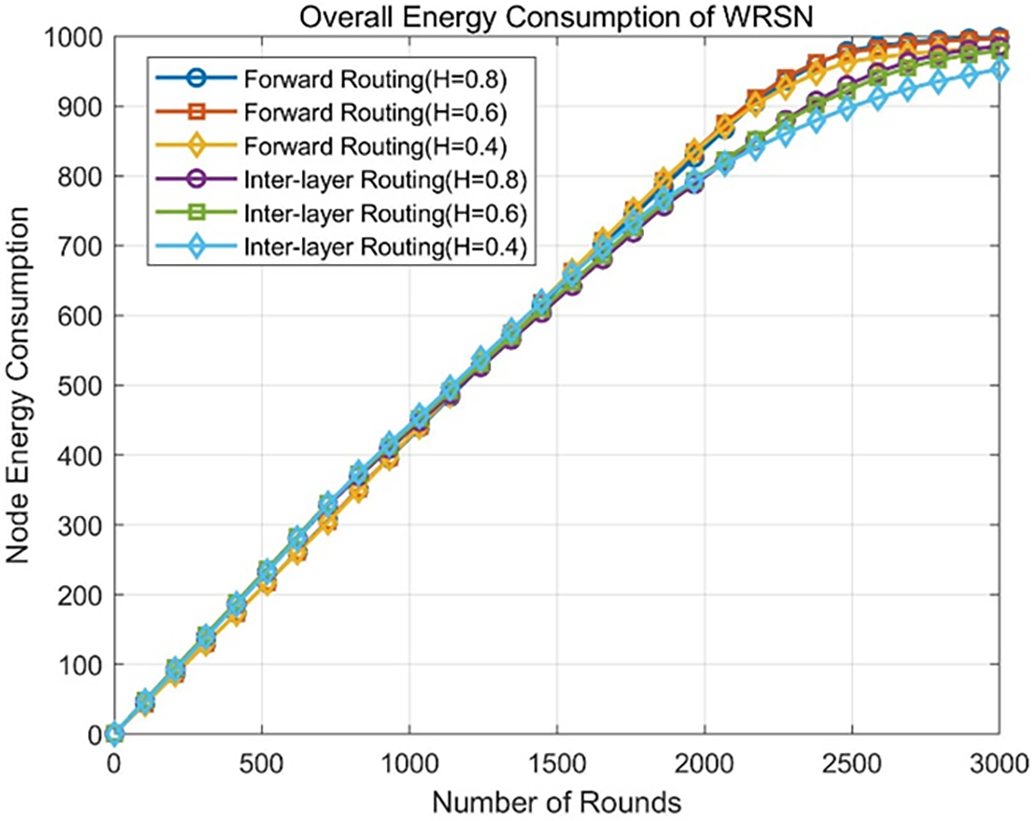
Figure 9: Trend of overall energy consumption in WRSN with different thresholds under two routing mechanisms

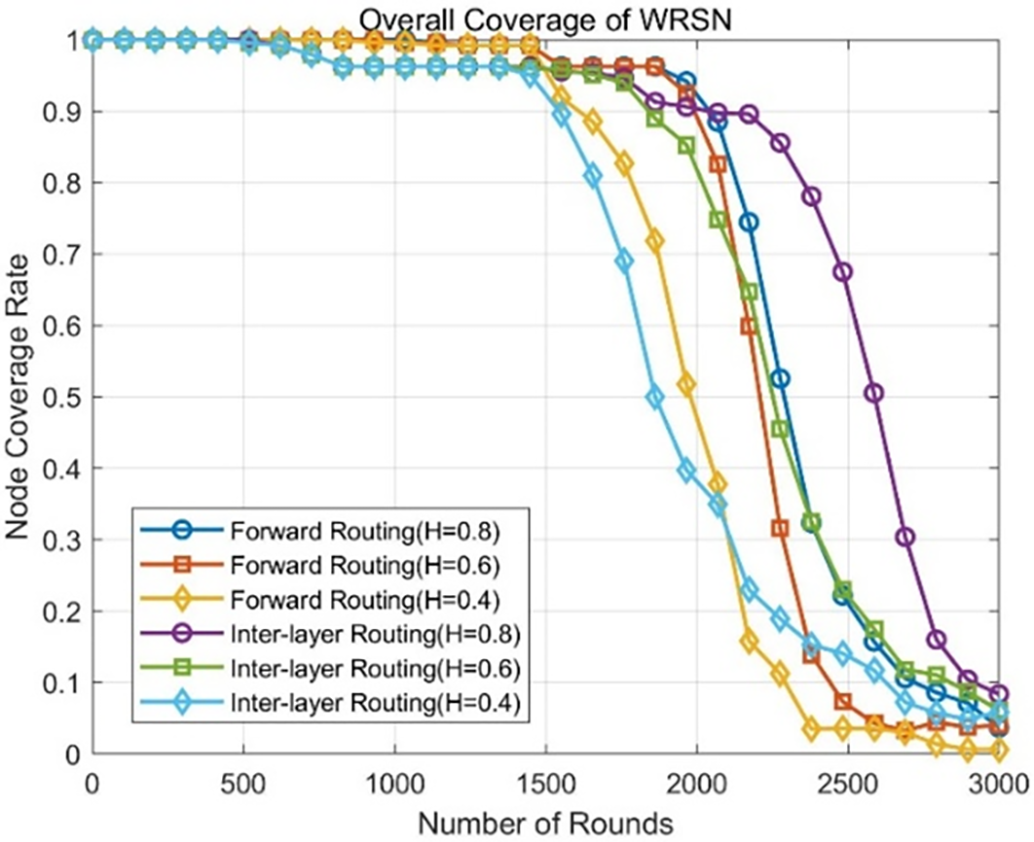
Figure 10: Trend of network coverage in WRSN with different thresholds under two routing mechanisms

From Table 3, when the cluster head rotation threshold is set to 0.8, the number of rounds until the first node dies for both the forward routing mechanism and the inter-layer routing mechanism increases by 12.1%, 20.5% and 7.6%, 20.5%, respectively, compared to the other two cluster head rotation thresholds. Additionally, the number of rounds until 30% and 50% of the nodes are dead also increases for both routing mechanisms when the threshold is set to 0.8 compared to the other thresholds.

Figs. 8 and 9 indicate that the three different thresholds have a minimal impact on the overall energy consumption of the WRSN under both the forward routing and inter-layer routing mechanisms. For the inter-layer routing mechanism, when H=0.8, the number of dead nodes from rounds 1500 to 2500 is significantly reduced compared to H=0.4 and is approximately the same as that for H=0.6. Furthermore, as shown in Fig. 10, when H=0.8, both routing mechanisms exhibit a significant improvement in WRSN network coverage.

Selecting an optimal remaining energy threshold for cluster head rotation can better balance the energy consumption among intra-cluster nodes, reducing the number of surviving nodes in the network due to premature deaths of cluster heads caused by excessive energy consumption, which in turn enhances network coverage, monitoring area, and data collection quality. Based on the above experimental results, this paper selects H=0.8 as the remaining energy threshold for cluster head rotation in both the forward routing mechanism and the inter-layer routing mechanism.

4.2.3 Analysis of Relay Routing Inter-Layer Structure Selection Method

This paper compares three relay routing structures for the inter-layer routing mechanism: typical two-hop routing (4-4 routing interval), three-hop routing (3-3-2 routing interval), and four-hop routing (2-2-2-2 routing interval). As before, 50 experiments are conducted to analyze the relay routing inter-layer structure, and the average values from these 50 experiments are taken for analysis. The trends in the number of dead nodes, overall energy consumption, and network coverage for the three relay routing inter-layer structures in the inter-layer routing mechanism are shown in Figs. 11–13.

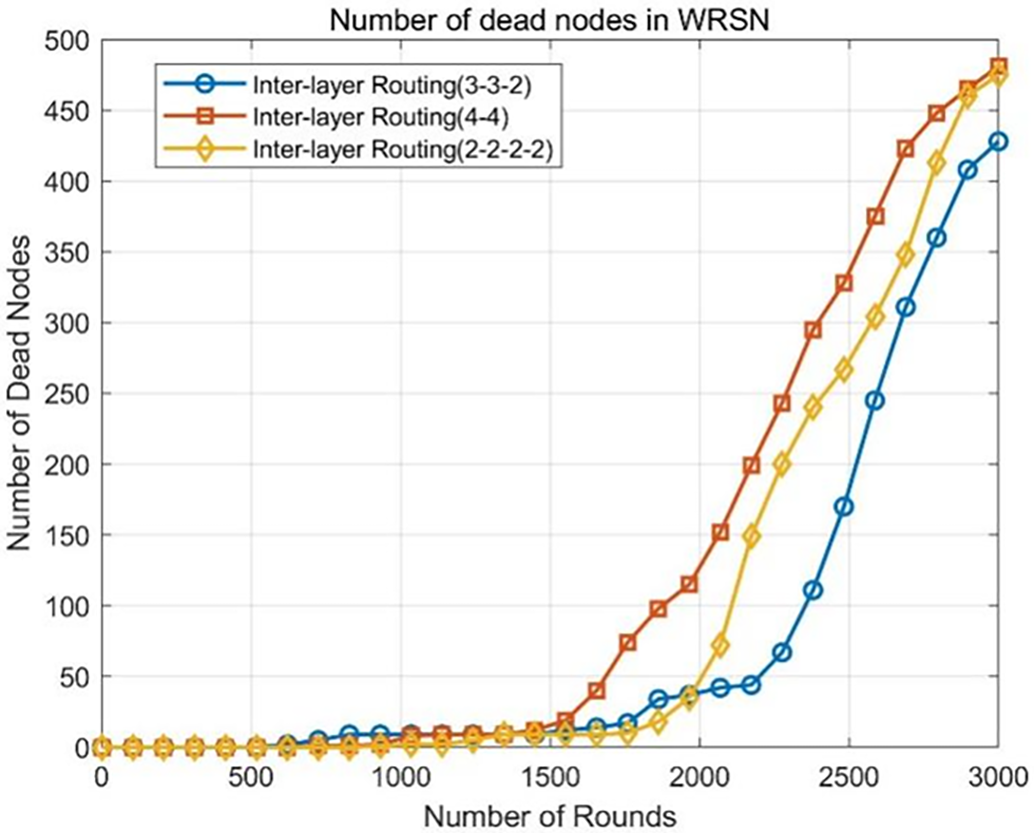
Figure 11: Trend of node death in WRSN with three different inter-layer relay routing structures

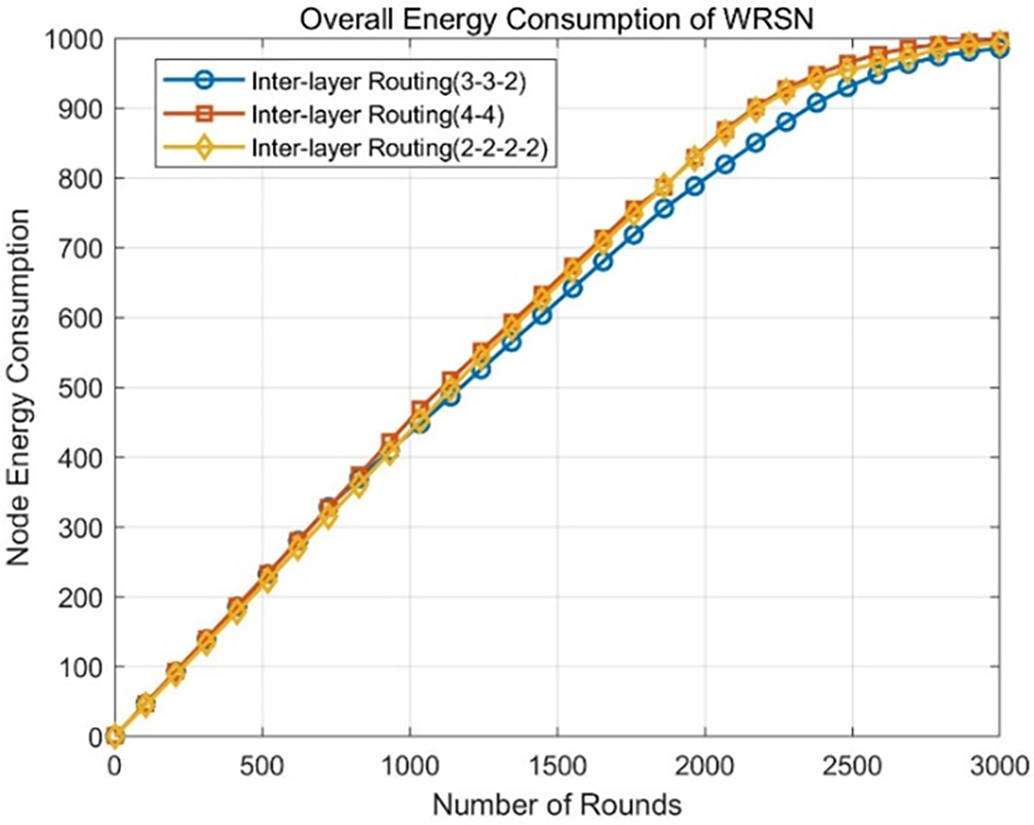
Figure 12: Trend of overall energy consumption in WRSN with three different inter-layer relay routing structures

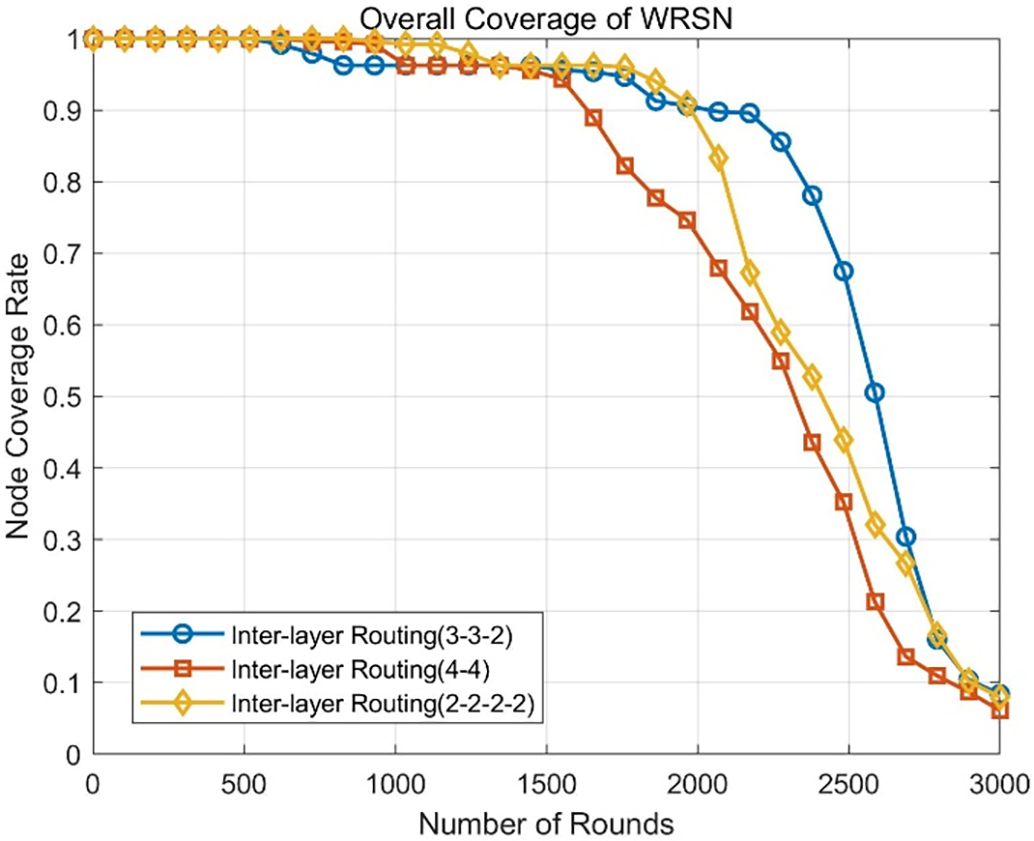
Figure 13: Trend of network coverage in WRSN with three different inter-layer relay routing structures

From Fig. 11, it can be observed that the number of dead nodes in the WRSN using the three-hop relay routing structure (3-3-2) remains lower than those using the two-hop (4-4) and four-hop (2-2-2-2) structures after 1500 rounds. By the 3000th round, the number of dead nodes for the (3-3-2) structure is 428, compared to 465 for the (2-2-2-2) structure and 475 for the (4-4) structure, representing a decrease of 8% and 9.9%, respectively. Additionally, Figs. 11 and 12 demonstrate that the (3-3-2) relay routing structure reduces overall energy consumption in the WRSN and significantly enhances network coverage. This is primarily since during the mid-operation phase of the WRSN, the last four layers of the (4-4) relay routing structure as relay cluster head nodes directly forward data from the first four layers to the base station. The longer data transmission distance leads to higher loads on the relay cluster heads in the last four layers, resulting in faster node deaths.

Although the (2-2-2-2) structure reduces the data transmission distance for individual inter-cluster relay routes, multiple relay hops increase the energy consumption for receiving and forwarding data by the relay cluster head nodes. Therefore, this paper selects the (3-3-2) relay routing structure as the inter-layer relay routing mechanism structure.

4.3 Performance Analysis of Energy Consumption Algorithm

To verify the effectiveness of the energy consumption optimization algorithm proposed in this paper, a comparative analysis is conducted between the inter-layer routing mechanism WRSN energy optimization algorithm (referred to as the proposed algorithm), the traditional forwarding clustering routing mechanism WRSN energy optimization algorithm (referred to as the traditional algorithm), the K-CLP algorithm [25], and the K-CHRA algorithm [26]. Tables 4 and 5 show the comparison of the number of dead nodes and cluster structures of the four algorithms under the same node deployment conditions for different network scales.

From Table 4, it can be observed that as the scale of the WRSN network increases, the node death rounds for the traditional algorithm, K-CLP, and K-CHRA algorithms tend to occur earlier. Notably, with a scale of 400 nodes, the first node death occurs significantly earlier, mainly due to the randomness in node distribution. At the scale of 500 nodes, the proposed algorithm extends the node death rounds for 30% and 50% of the nodes by 39.4% and 47.1% compared to K-CLP, and 19.3% and 8.3% compared to K-CHRA. Furthermore, compared to the traditional algorithm, the proposed algorithm reduces the number of dead nodes in the mid-term WRSN, extending the network’s lifespan. This is because the proposed algorithm employs inter-layer routing transmission, which, although it causes earlier deaths of relay nodes closer to the base station, avoids excessive relay transmissions among cluster head nodes and reduces the energy consumption of cluster head nodes across various layers.

Table 5 indicates that as the WRSN network scale increases, the number of clusters generated by all four algorithms increases. Due to the use of the same clustering method, the number of clusters generated by the traditional and proposed algorithms is the same but fewer than those produced by the K-CLP and K-CHRA algorithms, thus avoiding the occurrence of clusters with too few nodes. It can also be observed that for the same node scale, both the traditional and proposed algorithms exhibit fewer isolated cluster nodes. In a 500-node network, the clustering rate of the traditional algorithm/proposed algorithm is the highest at 92.8%, indicating its superior performance in maintaining node connectivity compared to K-CLP (77.4%) and K-CHRA (82.6%). A lower number of isolated cluster nodes indicates a more uniform distribution of cluster nodes generated by the clustering algorithm, reducing the need for charging individual cluster nodes, thereby enhancing charging efficiency and energy utilization.

Under the condition of deploying the same 500 nodes, a comparative analysis of the number of dead nodes, overall energy consumption, and charging mobility paths for the four algorithms is presented in Figs. 14–16.

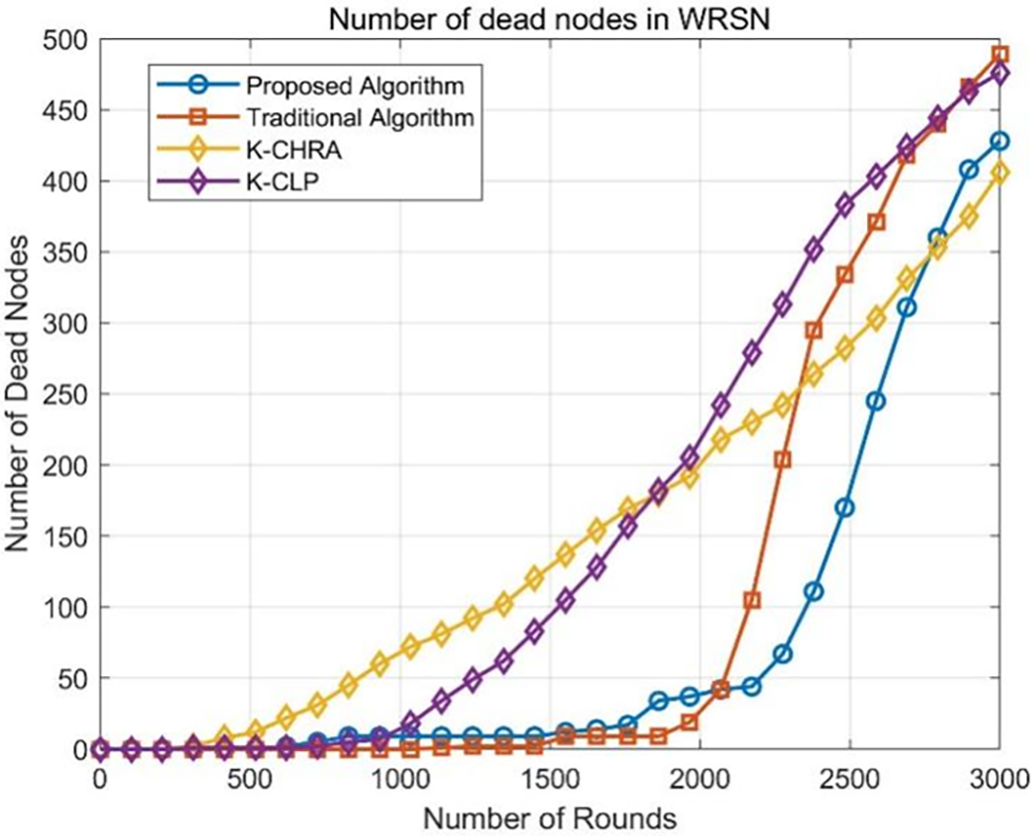
Figure 14: Trend of node deaths for four algorithms in a 500-node WRSN

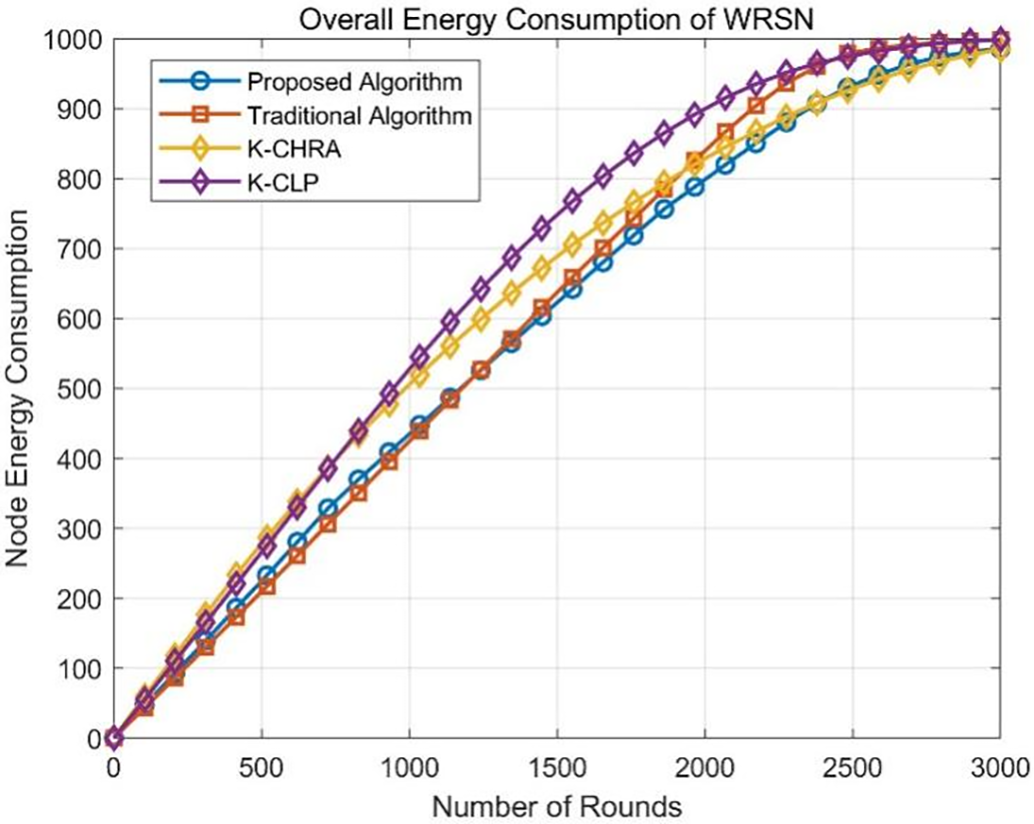
Figure 15: Structures trend of overall energy consumption for four algorithms in a 500-node WRSN

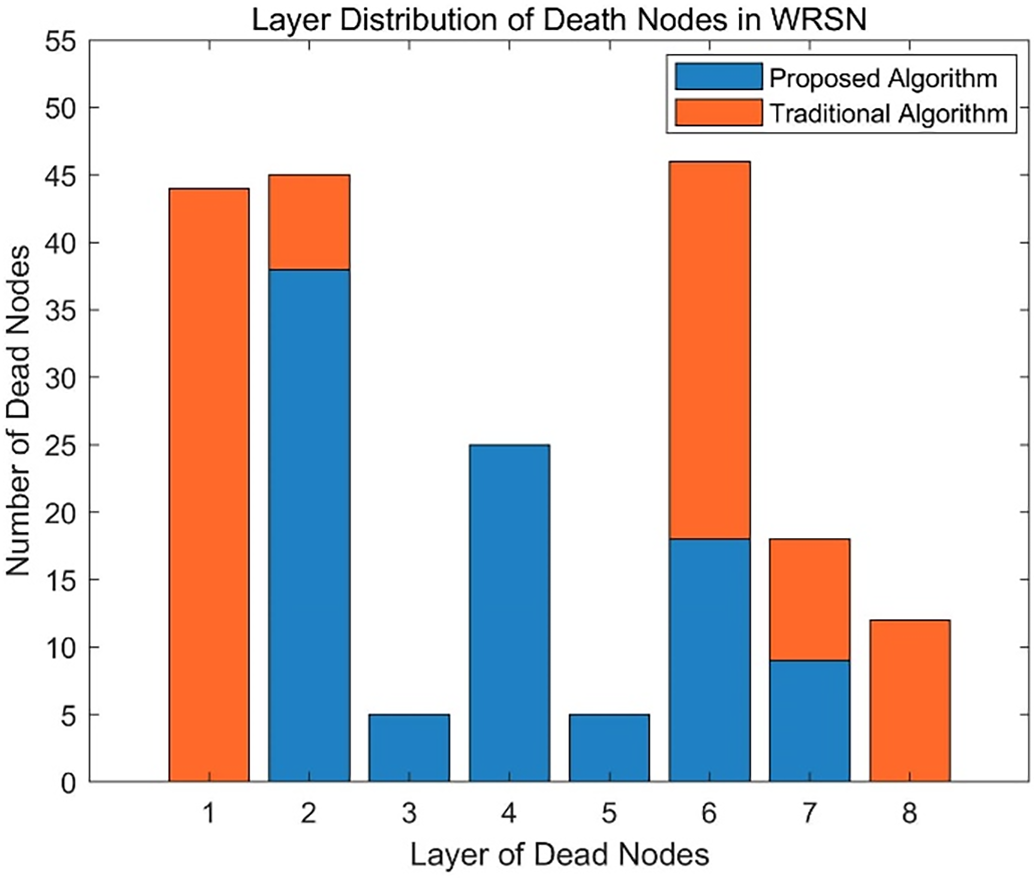
Figure 16: Distribution of the first 100 death node’s layers for the proposed algorithm and traditional algorithm

From Fig. 14, it is evident that the proposed algorithm results in a significantly lower number of dead nodes during the first 2500 rounds compared to the traditional algorithm, K-CLP, and K-CHRA algorithms. Additionally, both the proposed and traditional algorithms exhibit periods during the WRSN network’s operation where the number of dead nodes remains unchanged, whereas the K-CHRA and K-CLP algorithms show a continuous slow increase in the number of dead nodes.

Table 6 shows the energy consumption performance of different algorithms at rounds 1, 1000, 2000, and 3000 in Fig. 15. Combining this with Table 6 and Fig. 15, it can be concluded that the proposed algorithm effectively balances the energy consumption of various cluster nodes and inter-cluster relay head nodes during the early to mid-stage of network operation, thereby extending the network’s lifespan. During the middle and late stages of network operation, the overall energy consumption of the proposed algorithm is lower than that of the K-CLP and traditional algorithms, and is comparable to the K-CHRA algorithm.

The distribution of the first 100 dead nodes for the proposed and traditional algorithms across layers is illustrated in Fig. 16. From the figure, it is observed that the dead nodes of the proposed algorithm are primarily concentrated in the three layers closest to the base station and the outermost layer, while the dead nodes of the traditional algorithm are distributed across all layers. Therefore, when the MC conducts charging planning, the charging mobility path of the proposed algorithm is expected to be shorter than that of the traditional algorithm.

5  Conclusions

This paper proposes a WRSN node energy consumption optimization algorithm for large-scale WRSN environments. The algorithm incorporates a dynamic cluster radius-based region partitioning method to establish a hierarchical division of the WRSN monitoring area, with adaptive radius determination for individual sub-regions. Then, a K-means-based clustering algorithm is designed to optimize the generated cluster structure. Finally, by leveraging the hierarchical structure from region partitioning, an inter-layer routing mechanism is proposed to enable energy-efficient data relay transmission for WRSN cluster head nodes. The proposed algorithm’s efficacy is rigorously assessed through systematic parameter optimization and benchmark comparisons, demonstrating superior performance in energy conservation and operational sustainability. Experimental results demonstrate that the proposed algorithm achieves significant reductions in network-wide energy consumption, extends operational lifespan, and enhances both charging efficiency and energy utilization rates within WRSNs.

The simulation environment of the proposed algorithm is relatively ideal, and further research is needed for the complex WRSN environment with obstacles. In addition, on the basis of the research in this paper, how to further study the WRSN energy consumption optimization algorithm matching the WRSN charging planning scheme is a topic to be further studied.

Acknowledgement: The authors would like to express their gratitude for the valuable feedback and suggestions provided by all the anonymous reviewers and the editorial team.

Funding Statement: This research was funded by National Natural Science Foundation of China (No. 61741303), Guangxi Natural Science Foundation (No. 2017GXNSFAA198161), the Foundation Project of Guangxi Key Laboratory of Spatial Information and Mapping (No. 21-238-21-16).

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Cui Zhang, Lieping Zhang; draft manuscript preparation: Cui Zhang, Zhihao Li; methodology: Lieping Zhang; writing—reviewing & editing: Huaquan Gan; software: Hongyuan Chen, Zhihao Li. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Lieping Zhang, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Abbreviations

References

1. Shakeri M, Sadeghi-Niaraki A, Choi SM, Riazul Islam SM. Performance analysis of IoT-based health and environment WSN deployment. Sensors. 2020;20(20):5923. doi:10.3390/s20205923. [Google Scholar] [PubMed] [CrossRef]

2. Wang Y, Feng Y, Liu M, Liu N. Dynamic spatio-temporal charging scheduling for WRSN based on deep reinforcement learning. J Softw. 2024;35(3):1485–501. doi:10.13328/j.cnki.jos.006814. [Google Scholar] [CrossRef]

3. Zhang Z, Pang H, Georgiadis A, Cecati C. Wireless power transfer—an overview. IEEE Trans Ind Electron. 2019;66(2):1044–58. doi:10.1109/TIE.2018.2835378. [Google Scholar] [CrossRef]

4. Padmanaban Y, Muthukumarasamy M. Scalable grid-based data gathering algorithm for environmental monitoring wireless sensor networks. IEEE Access. 2020;8:79357–67. doi:10.1109/ACCESS.2020.2990999. [Google Scholar] [CrossRef]

5. Zhang H, Jin H, Wang F. Exploration and research on energy saving in wireless sensor networks. Comput Eng Sci. 2021;2(43):295–303. doi:10.3969/j.issn.1007-130X.2021.02.014. [Google Scholar] [CrossRef]

6. Chen T, Chen J, Gao X, Chen T. Mobile charging strategy for wireless rechargeable sensor networks. Sensors. 2020;35:359. doi:10.3390/s22010359. [Google Scholar] [PubMed] [CrossRef]

7. Hu C, Wang Y, Wang H. Research progress on charging planning in wireless rechargeable sensor networks. J Softw. 2016;27(1):72–95. doi:10.13328/j.cnki.jos.004883. [Google Scholar] [CrossRef]

8. Han G, Yang X, Liu L, Chan S, Zhang W. A coverage-aware hierarchical charging algorithm in wireless rechargeable sensor networks. IEEE Netw. 2018;33(4):201–7. doi:10.1109/MNET.2018.1800197. [Google Scholar] [CrossRef]

9. Dong Y, Wang Y, Li S, Cui M, Wu H. Demand-based charging strategy for wireless rechargeable sensor networks. ETRI J. 2019;41(3):326–36. doi:10.4218/etrij.2018-0126. [Google Scholar] [CrossRef]

10. Han G, Guan H, Wu J, Chan S, Zhang W. An uneven cluster-based mobile charging algorithm for wireless rechargeable sensor networks. IEEE Syst J. 2018;13(4):3747–58. doi:10.1109/JSYST.2018.2879084. [Google Scholar] [CrossRef]

11. Zhou Y, Tao Y, Li Z, Yang L. Energy-efficient clustering routing algorithm based on evolutionary game theory for wireless sensor networks. Chin J Sens Actuators. 2020;33(3):436–42. doi:10.3969/j.issn.1004-1699.2020.03.019. [Google Scholar] [CrossRef]

12. Wang J, Jiang P. Large-scale WSN energy consumption optimization algorithm based on dynamic clustering. Control Eng China. 2020;12(S1):48–55. doi:10.14107/j.cnki.kzgc.161282. [Google Scholar] [CrossRef]

13. Boukerche A, Wu Q, Sun P. A novel joint optimization method based on mobile data collection for wireless rechargeable sensor networks. IEEE Trans Green Commun Netw. 2021;5(3):1610–22. doi:10.1109/TGCN.2021.3080918. [Google Scholar] [CrossRef]

14. Yi L, Xie Z, Chen K. A real-time charging algorithm based on nonuniform clustering. Chin J Sens Actuators. 2021;34(2):175–82. doi:10.3969/j.issn.1004-1699.2021.02.006. [Google Scholar] [CrossRef]

15. Sha C, Liu Q, Song S, Wang R. A type of annulus-based energy balanced data collection method in wireless rechargeable sensor networks. Sensors. 2018;18(9):3150. doi:10.3390/s18093150. [Google Scholar] [PubMed] [CrossRef]

16. Ijemaru G, Ang L, Seng K. Optimizing energy consumption and provisioning for wireless charging and data collection in large-scale WRSNs with mobile elements. IEEE Internet Things J. 2023;10(20):17585–602. doi:10.1109/JIOT.2023.3277667. [Google Scholar] [CrossRef]

17. Rajaram V, Pandimurugan V, Rajasoundaran S, Rodrigues P, Kumar SS, Selvi M, et al. Enriched energy optimized LEACH protocol for efficient data transmission in wireless sensor network. Wirel Netw. 2024;31(1):825–40. doi:10.1007/s11276-024-03802-5. [Google Scholar] [CrossRef]

18. Hu H, Fan X, Wang C. Energy efficient clustering and routing protocol based on quantum particle swarm optimization and fuzzy logic for wireless sensor networks. Sci Rep. 2024;14:18595. doi:10.1038/s41598-024-69360-0. [Google Scholar] [PubMed] [CrossRef]

19. Zhao X, Zhong W, Navaei YD. A novel energy-aware routing in wireless sensor network using clustering based on combination of multi-objective genetic and cuckoo search algorithm. Wirel Commun Mob Comput. 2022;2022:14. doi:10.1155/2022/6939868. [Google Scholar] [CrossRef]

20. Dong Y, Bao G, Liu Y, Wei M, Huo Y, Lou Z, et al. Instant on-demand charging strategy with multiple chargers in wireless rechargeable sensor networks. Ad Hoc Netw. 2022;136:102964. doi:10.11999/JEIT170927. [Google Scholar] [CrossRef]

21. Guo H, Wu R, Qi B, Xu C. Deep-q-networks-based adaptive dual-mode energy-efficient routing in rechargeable wireless sensor networks. IEEE Sens J. 2022;22(10):9956–66. doi:10.1109/JSEN.2022.3163368. [Google Scholar] [CrossRef]

22. Wang Z. Research on energy management strategy of wireless sensor network nodes. Chongqing, China: Chongqing University; 2017. [Google Scholar]

23. Jia H, Fan X, Lv Y. KACO: energy efficient routing protocol based on clustering algorithm. J Northwest Univ (Nat Sci Ed). 2017;47(5):681–6. doi:10.16152/j.cnki.xdxbzr.2017-10-010. [Google Scholar] [CrossRef]

24. Miao J, Zhao Y, Zui Y, Chen C, Ding H. Multi-hop routing algorithm with genetic and K-mean clustering in WSN. Mod Electron Tech. 2021;44(17):42–8. doi:10.16652/j.issn.1004-373x.2021.17.009. [Google Scholar] [CrossRef]

25. Dong Y, Cui M, Wu H, Wang Y. Charging scheduling for sub-cluster rechargeable wireless sensor networks based on energy prediction. J Jilin Univ (Eng Technol Ed). 2018;48(4):1265–73. doi:10.16652/j.issn.1004-373x.2021.17.009. [Google Scholar] [CrossRef]

26. Wei Z, Liu F, Ding X, Feng L, Lyu Z, Shi L. K-CHRA: a clustering hierarchical routing algorithm for wireless rechargeable sensor networks. IEEE Access. 2019;7:81859–74. doi:10.1109/ACCESS.2018.2885789. [Google Scholar] [CrossRef]