Med-ReLU: A Parameter-Free Hybrid Activation Function for Deep Artificial Neural Network Used in Medical Image Segmentation

1  Introduction

Medical image segmentation is widely recognized as an essential component in contemporary healthcare practices. This critical process enables the identification and delineation of Regions of Interest (ROIs) within various medical imaging modalities, which include, but are not limited to, Magnetic Resonance Imaging (MRI), Computed Tomography (CT), and X-ray imaging technologies. The ability to perform precise segmentation is of paramount importance as it plays a vital role in several aspects of patient care, including diagnosis, strategic treatment planning, and ongoing monitoring of disease progression. Take, for instance, the field of oncology; accurate and reliable tumor segmentation derived from medical images significantly improves the precision involved in planning radiation therapy, leading to better outcomes for patients undergoing cancer treatment. Moreover, in the realm of orthopedics, effectively segmenting knee cartilage from MRI scans serves to facilitate the early identification and diagnosis of osteoarthritis, which can lead to timely intervention and better management of the condition. Despite the advancements in this area, medical image segmentation continues to face considerable challenges, stemming from the inherent complexity of anatomical structures, the variances found in different imaging techniques, and various issues related to noise and artifacts that can compromise image quality. These challenges highlight the need for ongoing research and development in refining segmentation techniques to further enhance their accuracy and reliability in clinical settings.

Medical Image segmentation is a process that involves the extraction of the ROIs from background medical images such as MR, X-ray, and CT. With the advance of current medical imaging technology, medical image dataset size becomes huge and rich in terms of information content. Medical image segmentation plays an increasingly crucial role in producing accurate segmented objects during the computer-aided diagnostic process. In general, computer-aided segmentation models can be categorized as automatic and semi-automatic segmentation. Existing medical image segmentation techniques have been carried out for brain [1], lung [2], knee [3], and cell segmentation tasks.

Machine learning (ML) is becoming increasingly popular in the field of medical image segmentation. Traditional machine learning involves feature extraction and label classification via supervised or unsupervised learning approaches. The good performance of the classical approach is restricted by relevant small size datasets. In recent years, Deep Learning [4,5] has demonstrated good accuracy in large-scale image datasets, since then, a number of novel models have been introduced. Among these models, the convolutional neural network (CNN) is one state-of-the-art technique used in medical image segmentation. Its architecture is designed to consist of a set of convolution layers, activation function, and pooling, which translate the input vector using a linear convolutional transformation followed by a nonlinear mapping to preserve points, lines, and planes. The final step in the process involves leveraging fully connected layers to extract details of high-level abstractions.

U-net is a benchmark CNN-based architecture. As the model goes deeper, richer feature representation learning is propelled by forward and backward propagation. The activation function will determine if a neuron needs be activated based on the weighted sum and bias. Learning is then attained by adjusting the weights so the predicted output is as close as possible to the corresponding targeted values and subsequently reduces the loss function. When the structure goes deeper, the residual error gets smaller with the depth of the network in the back-propagation algorithm, making it so minimised that the underlying network fails to attain the desired outcomes [6]. This scenario is referred to as the vanishing gradient problem.

It is crucial to recognize that the development of effective activation functions remains a continuous research area in the field of DL. Looking back, two of the earliest continuous nonlinear activation functions were the Sigmoid function and the Hyperbolic Tangent (Tanh) function [7]. The Sigmoid function exhibits a steep gradient within the range of 2≤x≤−2, which is conducive to producing clear outputs. However, it is worth noting that historically, it was commonly used in shallow neural networks. One limitation of the Sigmoid function is its susceptibility to the vanishing gradient problem, primarily because output changes at both extremes are minimal. Consequently, this limitation has hindered its effectiveness in enabling models to learn effectively and has raised concerns related to non-zero centrality.

The tanh function is a smooth AF function centered at zero, ranging from –1 to 1. This function matches negative inputs to negative outputs, and vice versa, to improve training performance. It is symmetric about the origin, with outputs on average closer to zero, which aids backpropagation. Unfortunately, the Tanh function also struggles to overcome the vanishing gradient issues similar to those of the Sigmoid function. In existing literature, several novel functions have been introduced to replace traditional activation functions. These include Sigmoid [8], Rectified Linear Unit (ReLU) [9], Leaky ReLU (LReLU) [10], Parametric ReLU (PReLU) [11], Exponential Linear Unit (ELU) [12], Scaled ELU (SELU) [13], Gaussian Error Linear Unit (GELU) [14], SWISH [15] and MISH [16].

Currently, ReLU is the most popular traditional activation function in deep learning applications. It is easy to implement using gradient descent techniques. ReLU derivatives are constant, ensuring computation speed. However, ReLU is infamous for dying neurons problem when its input is negative and subsequent output is always zero [17]. By modifying the negative part of ReLU, the resulting function becomes robust to weight updates during the entire backpropagation process. However, the main challenge is tuning the parameters in the modified part.

Existing AFs are predominantly optimized for natural image classification (e.g., CIFAR, MNIST), leaving a gap in medical segmentation tasks. Medical images demand AFs that: (1) preserve gradients across deep networks to capture fine anatomical details, (2) handle noise and intensity variations through bounded responses, and (3) avoid parameter-dependent designs to ensure generalizability. The proposed Med-ReLU (ReLU+Softsign) activation function addresses these needs by combining the simplicity and sparsity of ReLU with the smooth, bounded properties of Softsign. Unlike ReLU, which suffers from dead neurons, ReLU+Softsign allows for smooth transitions in the negative domain, preventing gradient saturation and enhancing gradient flow. This hybrid design ensures robust performance in segmenting complex anatomical structures, such as tumors or cartilage, while maintaining computational efficiency.

Previously, Nandi et al. [18] have examined the combination of different basic AFs consisting of the linear function, ReLU and Tanh on a classification task using the Fashion-MNIST, CIFAR-10, and ILSVRG-2012 datasets. The study has found that combining activation functions usually outperforms their corresponding basic AFs. Some researchers have proposed hybrid activation function architectures. Hasan et al. have combined ReLU with the Tanh activation function [19]. The proposed structure leverages the Tanh function to introduce the information discarded by ReLU units. Meanwhile, Yu et al. have modified the formulation of ReLU by incorporating the memristive window function. The resultant activation function preserves the characteristics of ReLU and SWISH [20].

Comparing Med-ReLU to other activation functions in Table 1 reveals distinct advantages tailored for deep learning models. Functions like Sigmoid and ELU (under certain conditions) are prone to the vanishing gradient problem, hindering effective training in deep networks necessary for capturing intricate medical image details. ReLU and LReLU, while addressing vanishing gradients, suffer from limitations related to negative inputs; ReLU can lead to ‘dying neurons’ due to zero output for negative inputs, and while LReLU allows for negative activations, neither are bound activation functions. SWISH and MISH, while overcoming vanishing gradients and allowing negative activations, are not monotonic, potentially complicating optimization and convergence, and like ReLU, LReLU, and ELU, are not bound activation functions for negative inputs. ReLU-Tanh and RMAF, though also mitigating vanishing gradients and allowing negative activations, are similarly not bound for positive inputs, and while monotonic, share the unboundedness characteristic for positive inputs with many others. In contrast, Med-ReLU uniquely balances these aspects. It avoids vanishing gradients, allows for negative activations mitigating ‘dying neurons’, and crucially, is a bound activation function for negative inputs offering potential stability. Furthermore, its monotonic nature simplifies optimization, and its C1 continuity provides a beneficial smoothness without the extreme smoothness of C∞ functions, potentially offering a robust and balanced gradient behavior well-suited to the noisy and complex nature of medical images, making it a compelling alternative compared to these groups of activation functions.

Attributed to its influential role, numerous descriptive [21,22] and quantitative [23,24] performance analyses on activation functions have been conducted. It is noteworthy that these studies have concentrated mainly on classification tasks by using the MNIST, CIFAR-10, and CIFAR-100 datasets. In this paper, a hybrid activation function named Med-ReLU dedicated to medical image segmentation tasks is proposed. The main highlights of this paper are summarized below:

1.    A novel, parameter-free AF (Med-ReLU) that combines the strengths of ReLU and Softsign. This hybrid function mitigates the vanishing gradient problem and dead neuron issue by providing smooth, bounded activations in the negative domain while retaining ReLU’s efficiency in the positive domain.

2.    ReLU+Softsign’s smooth transitions and bounded outputs make it particularly effective in handling noise and intensity variations common in medical images. Its monotonicity ensures consistent weight updates, critical for segmenting complex structures.

3.    Unlike prior AF studies focused on classification, Med-ReLU is evaluated on large-scale cell and knee MRI datasets, demonstrating superior segmentation accuracy for anatomically complex ROIs.

The remaining paper is organized with Section 3 explaining the materials and methods while in Section 4 results and discussions are presented before Section 5 concludes the paper.

2  Literature Review

Recent advancements in deep learning have profoundly influenced the evolution of various activation functions, each presenting its unique strengths and limitations that are worth exploring. For instance, the Rectified Linear Unit (ReLU) has emerged as the de facto standard activation function primarily due to its notable simplicity and computational efficiency, which are particularly beneficial in deep learning models and increasingly popular for both practitioners and researchers. However, it is not without its drawbacks, as it suffers from the ‘dying ReLU’ problem, a scenario in which neurons can become inactive and unresponsive during the training process, thereby significantly limiting the model’s learning capacity and overall performance. To tackle this pressing issue, alternatives such as Leaky ReLU and Parametric ReLU (PReLU) were introduced, aiming to provide a solution, but they often require manual and painstaking tuning of their parameters, which can be cumbersome and time-consuming for practitioners and researchers alike. More recently, innovative activation functions such as SWISH and MISH have demonstrated promising performance in various classification tasks within deep learning frameworks, showing potential benefits that were previously unrecognized. Yet, their efficacy in medical image segmentation—a critical area that requires high accuracy and detail in performance—remains largely understudied and less explored, leaving a pertinent question mark in the field. Despite the considerable advancements made in the domain of activation functions, there exists a significant gap, as there is a notable lack of activation functions specifically tailored for the diverse needs of medical image segmentation. This particular task often involves handling complex and irregular anatomical structures, which require carefully designed activation functions to enhance performance, reliability, and accuracy in segmentation tasks, proving that further research and development is essential in this regard.

To gain a deeper understanding of the limitations that are inherent in the existing activation functions, Table 1 presents a comprehensive summary of the most commonly utilized activation functions, elucidating their respective strengths as well as their weaknesses. While each activation function possesses its own set of advantages, they frequently encounter challenges such as vanishing gradients, which can impede learning, dying neurons that stop functioning effectively, or the necessity for manual parameter tuning, which can be cumbersome and time-consuming. These limitations become especially problematic in the field of medical image segmentation, where the intricacies of complex anatomical structures and the presence of noisy data demand robust and efficient activation functions capable of delivering reliable performance. As the challenges in this area continue to evolve, finding solutions to these activation function limitations is crucial for advancing the accuracy and reliability of medical imaging techniques.

3  Materials and Methods

3.1 Image Datasets

Two large-scale medical image datasets have been used. The first dataset comprises 2D microscopic images of cells taken from the Kaggle Data Science Bowl Challenge. The dataset consists of a large number of segmented nuclei images of diverse cell types acquired under a variety of conditions, magnifications, and imaging modalities (brightfield vs. fluorescence). The second dataset consists of a normal 3D MR image of the knee acquired from the Osteoarthritis Initiative (OAI). These images are obtained by using a 3.0 Tesla (T) MRI scanner (Siemens Magnetom Trio, Erlangen, Germany) with a quadrature transmit-receive knee coil (USA Instruments, Aurora, OH) using the dual echo steady state (DESS) sequence with water excitation (WE). All knee image datasets used in this experiment are chosen randomly. The DESS knee images have a section thickness of 0.7 mm and an in-plane resolution of 0.365 × 0.365 mm2 (field of view = 140 × 140 mm, flip angle = 25o, TR/TE = 16.3/4.7 ms, matrix size = 384 × 384, bandwidth = 185 Hz/pixel). Notably, the knee image masks were manually segmented as part of this study, but cell image masks used for segmentation were readily available within the Kaggle dataset. To further illustrate the nature of these datasets, we have included sample images from both datasets in Figs. 1 and 2.

Figure 1: Sample microscopic cell image and it’s segmentation mask from the Kaggle Data Science Bowl Challenge Dataset

Figure 2: Sample stack of 2D knee MR images from the Osteoarthritis Initiative (OAI) Dataset with Manually Annotated or Segmented Masks

3.2 Overview of Model Implementation

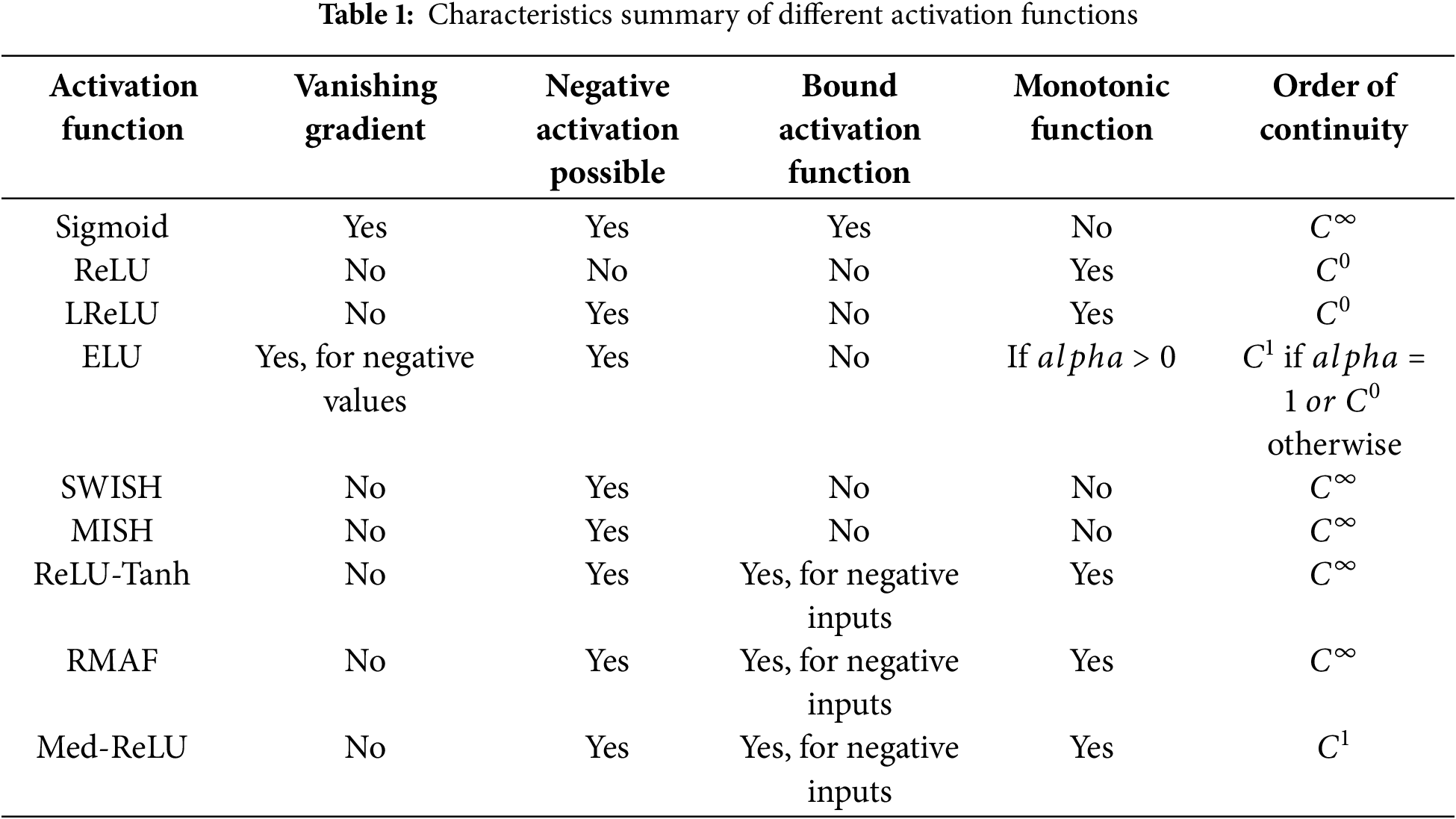
Knee segmentation plays an essential role in searching for pertinent imaging-based biomarkers as signs of normal or abnormal conditions. In clinical applications, the segmented knee model is used to measure the progression pattern of cartilage deterioration and achieve early detection of osteoarthritis (OA). Meanwhile, cell segmentation helps in identifying indicative cellular phenotypically observable features that can reflect the cells’ physiological state. The information provides insights into the oncology research. The Med-ReLU activation function is calculated along with seven basic activation functions, including Sigmoid, ReLU, Leaky ReLU (LReLU), Exponential Linear Unit (ELU), SWISH, and MISH, as well as two multi-activation functions, ReLU-tanh and RMAF. These activation functions are systematically substituted one by one into the state-of-the-art U-Net model, and the model’s performance is evaluated for each change. The knee segmentation was reconstructed into a 3D result using deep learning segmentation as shown in Fig. 3.

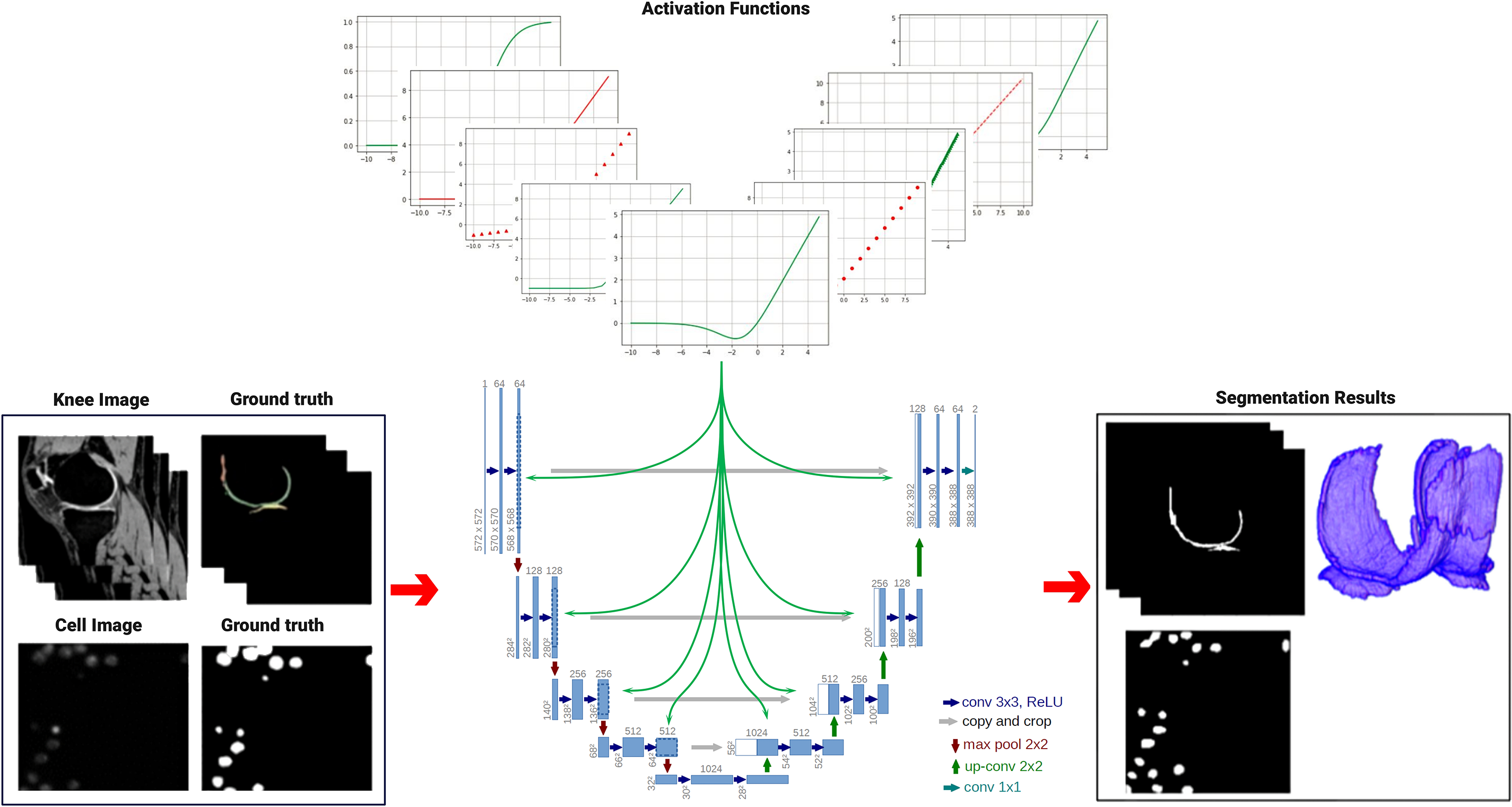
Figure 3: Implementation of U-net model with different activation functions to perform medical image segmentation-Resolution has been improved

3.3 U-Net Model

Because 3D U-Net is extremely computationally heavy, we have implemented the U-Net model with 23 layers for knee and cell segmentation. The U-Net architecture consists of a contraction path and an expansion path. The contraction path consists of multiple convolution layers, each followed by an activation function and a two-step max pooling layer. The expansion path then splits the feature channels in half using upsampling factors and assigns feature distributions and spatial information to the high-resolution layers. A total of 650 cell images and 5120 knee images were used to independently train the U-Net model. While training the knee and cell image datasets, we used traditional zooming by flipping and rotating to generate 5120 knee images. This zooming helps expand the dataset, improving the robustness of the U-Net model.

The U-Net architecture includes ten convolutional layers, each of which uses a 3 × 3 kernel during the downsampling process. This kernel multiplies the feature channels and reduces spatial information. The bottleneck layer that connects the contract path and the expansion path together helps transfer feature maps from the contract path to the expansion path to allow for accurate object localization and improved gradient flow during model training. In the upsampling process, each input from the bottleneck layer is upsampled with a 2 × 2 stride of 2, followed by two 3 × 3 convolution layers. The final 1 × 1 convolution layer matches the 64-component feature vector to the number of target classes. Fig. 4 illustrates the U-Net network architecture.

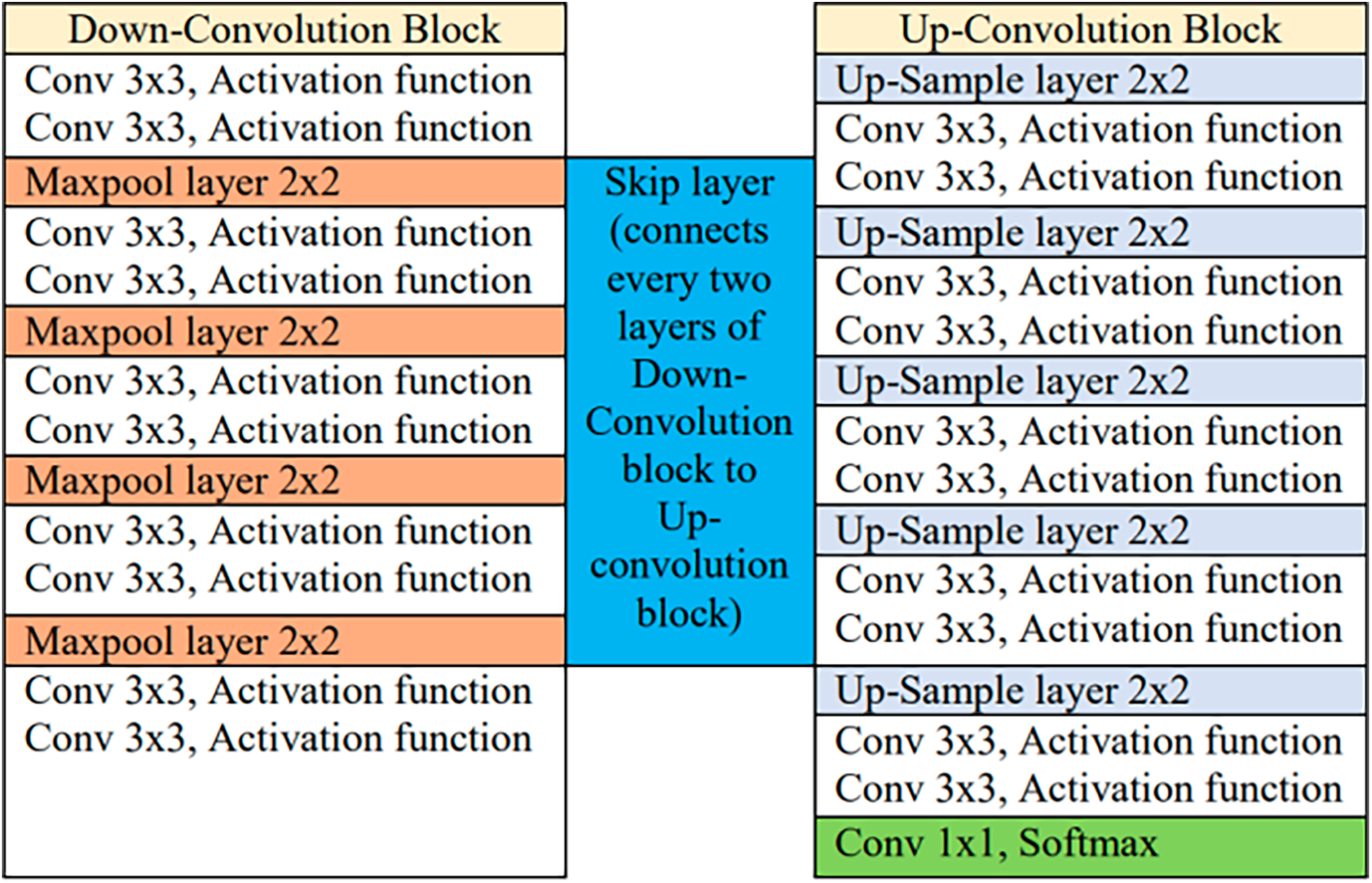
Figure 4: Architecture table of U-net model

3.4 Activation Function

An artificial neural network is propelled by the forward and backward propagation processes. Given that x={x1,x2,…,xn} are inputs to a neuron unit of weights w={w1,w2,…,wn} and bias, b, the output is denoted by y, and a neuron unit within the greater artificial neural networks is as illustrated in Fig. 5.

Figure 5: A forward propagation occurs within a neuron unit. At input layer, all data is fed into the neuron unit. At hidden layer, the total input to each neuron is computed as a sum of weights and bias, ∑wixi+b. Then, an activation function f(⋅) is applied to get the output y

From a number of N prediction data points, the mean squared error E is computed from the value difference between the predicted network output yp and their corresponding targeted values tp as shown in Eq. (1).

E=1N∑N(tp−yp)2(1)

Learning is attained via adjusting the weights so that yp is as near as possible to the corresponding desirable values, tp. Thus, Back-Propagation refers to the gradient-based optimization methods to calculate the mean squared error and adjust the weights wl, whereas l∈{1,…,L} subsequently was used in order to reduce the loss function. A deep network is harder being trained due to gradient instability issues.

In CNN model, an input xi,j is characterized by dimension H × W and a kernel km,n is characterized by dimension k1×k2⋅wm,nl is the weight matrix connecting neurons of layer l with neurons of layer l−1. The activation function exists in between the convolution and pooling layer where we define the output vector is defined as oi,jl=f(xi,jl). Computation of convolved input vector at layer l is as illustrated in Eq. (2).

xi,jl=∑m∑nwm,nloi+m,j+nl−1+bl(2)

Gradients δi,j have been generated during back-propagation. The gradients at layer l are as expressed in Eq. (3).

δi,jl=∂E∂xi,jl(3)

The Chain rule has been utilized to calculate the gradients layer-by-layer. Ultimately, the gradient error propagated from L to L−1 can be presented as a recursively nested expression given in Eq. (4).

δQ∈i,jL−qδQ∈i,jL=∑QL−q+1∑QL−q+2⋯∑QL∏p=1qwQL−pQL−p+1oL−p(xQL−pL−p)(4)

3.4.1 Sigmoid

The sigmoid is an S-shaped bounded monotonic function. It is also known as the logistic function. Regardless of the type of input given to this function, the output will always be either 0 or 1. The sigmoid is expressed as given in Eq. (5).

f(x)=11+e−x(5)

Intuitively, Sigmoid is a more generalized Sigmoidal activation function which is used for multi-class classification tasks.

3.4.2 Rectified Linear Unit (ReLU)

ReLU’s structure resembles a linear function in the range from zero to infinity, which helps to preserve the properties of linear models, making them easy to optimize with gradient-descent methods. ReLU is a threshold-based activation function and does not involve any exponential. Its derivative is always 1 for positive input values, thus contributing to faster computation compared to other activation functions. The ReLU is expressed as given in Eq. (6).

f(x)=max(0,x)={x,ifx≥00,ifx<0(6)

ReLU outputs are identical to inputs in the positive range. Negative inputs are corrected by resetting them to zero. Because the function does not have asymptotic upper and lower bounds, it may introduce errors from later layers when updating weights between them. Therefore, ReLU does not report the vanishing gradient problem. However, a major limitation of ReLU is the neuronal death problem, which means that an inactive unit always produces a zero gradient, preventing weight updates during gradient-based optimization [17]. Neurons remain in a permanent inactive state by ultimately not responding to changes in the input.

3.4.3 Leaky ReLU (LReLU)

LReLU was introduced as a generalized version of ReLU to address the issue of dying neurons caused by hard zero activations. It retains the same structure as ReLU but incorporates a “leaky” rectifier for negative input values, where a constant α is applied to allow a small, nonzero gradient. This modification ensures continuous weight updates throughout the propagation process. The mathematical formulation of LReLU is provided in Eq. (7).

f(x)=max(0,x)={x,ifx≥0αx,ifx<0(7)

The authors in [25] have reported that the value of constant α has been set at 0.01. Based on this modification, LReLU allows a small, non-zero gradient when the unit is saturated for going into an inactive state. Therefore, it contributes to a more robust gradient optimization. The operation implies a compromise to zero sparsity in order to compute the non-zero gradient. LReLU does not fix the exploding gradient problem, and the value of α still needs to be determined manually via carefully yet tedious training.

3.4.4 Exponential Linear Unit (ELU)

ELU was introduced to enhance the learning speed of deep neural networks. The parameter α is used to control the saturation value for negative inputs. Consequently, the vanishing gradient problem is mitigated, as its derivative remains 1, preventing contraction and ensuring a stable learning process. Additionally, an exponential function is applied to negative input values. The ELU function is defined in Eq. (8).

f(x)={x,ifx≥0α(ex−1),ifx<0(8)

The output average of ELU is pushed closer to zero, facilitating faster convergence. Additionally, units with nonzero mean activation values introduce a bias to the subsequent layer. If these units do not counterbalance each other, the learning process leads to a shift in bias for the following layers. Since ELU produces negative values, it mitigates bias shift by driving the mean activation toward zero during training. This shift enhances learning by aligning the normal gradient more closely with the natural gradient. However, the exploding gradient problem remains a concern when using ELU.

3.4.5 SWISH

SWISH is a smooth activation function that nonlinearly interpolates between the linear function and the ReLU function. The degree of interpolation is controlled by introducing a trainable parameter, βx, into the function, leading to a generalized variant known as E-SWISH [26]. The function is unbounded in the positive direction while remaining bounded for negative inputs. SWISH functions are both smooth and non-monotonic, where smoothness enhances optimization outcomes, and non-monotonicity preserves small negative inputs, thereby improving expressivity and gradient flow. The mathematical expressions for SWISH and E-SWISH are provided in Eqs. (9) and (10), respectively, where x serves as the input to the Sigmoid activation function, and z, defined as βxx, is the input to the Swish activation function in Eq. (10).

f(x)=x⋅σ(x), whereσ(x)=Sigmoid⁡(x)=x1+e−x(9)

f(x)=βx⋅σ(βx),whereσ(z)=βx1+e−β∗x(10)

The experiment has shown that SWISH has consistently outperformed ReLU on deeper neural networks. The function is able to leverage the vanishing gradient issue as reported by the Sigmoid function. However, the better performance comes at the expense of greater computational cost when it is compared to ReLU.

3.4.6 MISH

MISH is a smooth and non-monotonic activation function inspired by SWISH. It is bounded below to encourage stronger regularization and unbounded above within the range [≈−0.31,∞] to avert saturation that has dragged down the training speed due to near zero gradient. Based on the outcome of first derivative, the function of MISH is closely related to SWISH. The MISH is expressed as given in Eq. (11).

f(x)=x⋅tanh⁡(softplus⁡(x))=x⋅tanh⁡(In⁡(1+e−x))(11)

Similar to SWISH, the MISH inherits the self-gate property where the non-modulated input is multiplied with the output of the input’s non-linear function. MISH keeps a small amount of negative value input in order to ensure a greater information flow and expressivity. The latter has shown better robustness in optimizing the results of the deep neural network compared to SWISH and ReLU. However, the improved accuracy is a trade-off between higher computational cost and MISH that is validated on the classification task by using CIFAR datasets only.

3.4.7 ReLU-Tanh

Li et al. [27] integrated both the ReLU and Tanh activation functions in their work, where the Tanh function mitigates the limitations of ReLU, particularly in the negative domain. The ReLU and Tanh functions are controlled by the parameters α and β, respectively. The ReLU-Tanh formulation is given in Eq. (12).

f(x)=α∗ReLU⁡(Y)+β∗Tanh⁡(Y)(12)

Both constants can be either fixed or trainable. Consequently, the performance of ReLU-Tanh heavily depends on the appropriate selection of these constants. The Tanh function produces a negative output when the ReLU function outputs zero, which helps mitigate the vanishing gradient problem in ReLU by incorporating information that would otherwise be ignored.

3.4.8 ReLU-Memristor-like-Activation Function (RMAF)

RMAF [28] uses a memristive window function technique to find a scalar activation function. A pair of threshold hyperparameters of p and j have been introduced to scale the flatness of the region, which aims to improve the accuracy of the deep neural network. At the same time, the constant α has also been included as a trainable parameter. The RMAF is expressed as in Eq. (13).

f(x)=αx⋅[j(1(0.25⋅(1+e−x)+0.75)p)](13)

For instance, RMAF is unbounded above and bounded below. Its unbounded nature is crucial for preventing saturation when training slows due to near-zero gradients. Meanwhile, the lower bound enhances regularization effects. Despite these advantageous properties, RMAF is constrained by the choice of learnable parameters and the threshold of hyperparameters.

3.4.9 The Proposed Function: Med-ReLU

ReLU has been serving as the base for most of the newer activation functions because of its intuitiveness at x≥0. However, it is hard to be saturated at x<0, making its activation neuron fragile and vulnerable to irreversible neuronal death. By summarizing from existing literature, we have decided that the proposed activation function that is suitable for medical image segmentation should possess: 1) a parameter-free setting to ease implementation by users, 2) a light architecture to encourage reproducibility in future deep learning models, and 3) robust weight updates at both the positive and negative parts of the activation functions to preserve effective feature learning during the training process. A hybrid activation function known as Med-ReLU has been proposed. The hybrid activation function combines characteristics from different activation functions to create a new one with improved properties, as in our case, ReLU and Softsign. The plots of commonly used activation functions and Med-ReLU are as shown in Fig. 6.

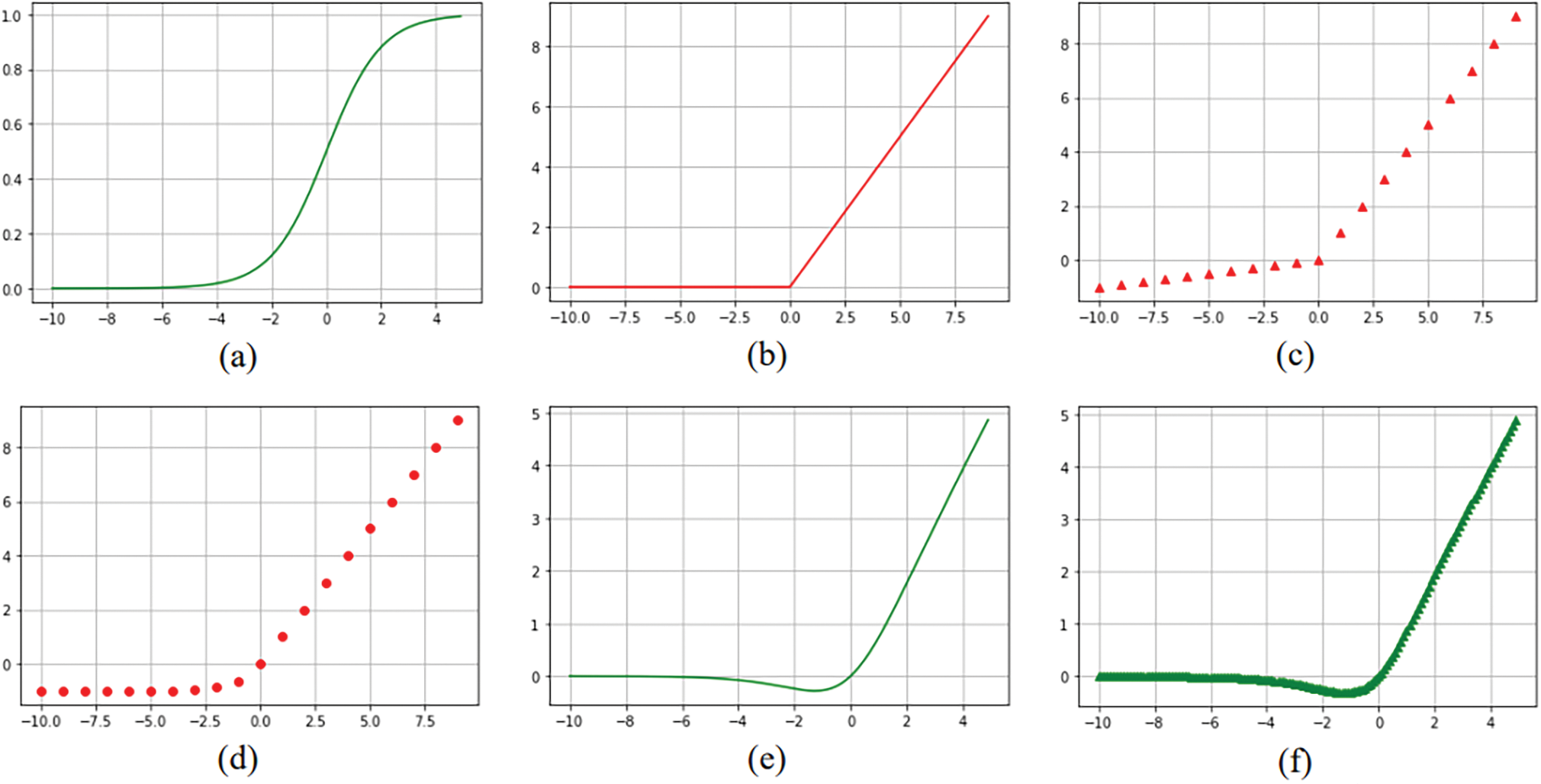
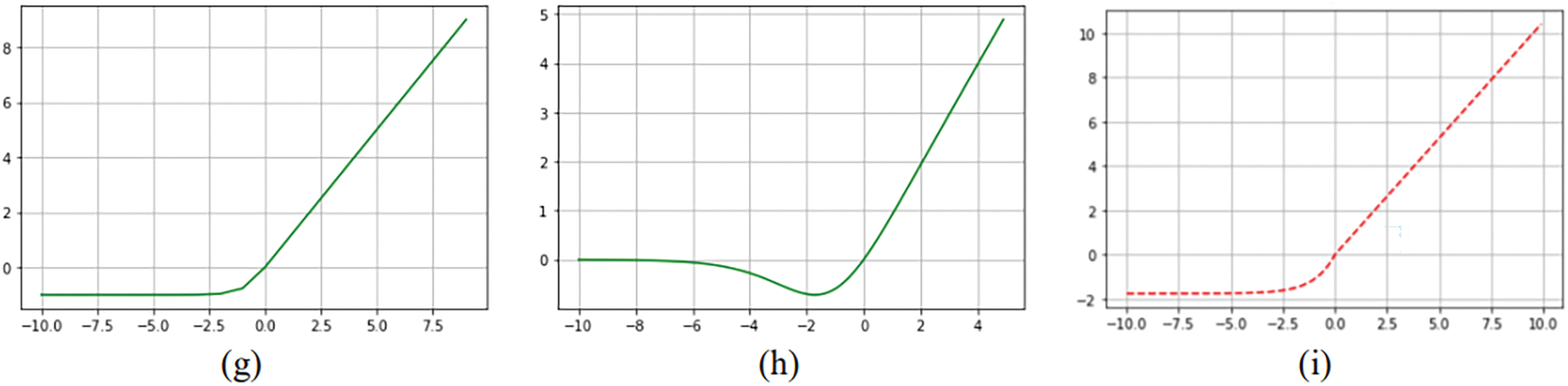
Figure 6: Piecewise activation functions. (a) Sigmoid (b) ReLU (c) LReLU (d) ELU (e) SWISH (f) MISH (g) ReLU-Tanh, (h) RMAF and (i) Med-ReLU

Traditional activation functions such as Tanh and ELU grow exponentially, and their derivatives or gradients are complex which lead to late convergence in the training process of deep learning models. The term “late convergence” suggests that it takes more time or iterations for the model to start making meaningful improvements in its performance, particularly when compared to other scenarios where the model converges quickly. Med-ReLU is developed based on the complementary roles of ReLU and Softsign function. We have retained the nearly linear property of ReLU at x > 0 in order to maintain the light computation and architecture. To ensure effective learning and smooth convergence, we have identified Softsign to compensate the negative part. Softsign has solid theoretical foundation. The function belongs to the quadratic activation functions family, which has proven to be invariant to the translation of a subject across a background of zeros. The principle they draw on is that of spatial correlation and can be written as linear functions of the spatial autocorrelation of an image.

Softsign grows polynomially and has smoother asymptote lines to demonstrate greater degree of non-linearization. The non-linearity nature presented by quadratic function is highly regarded in neural network research to preserve pertinent features. Med-ReLU inherits non-linearity, hence it can delineate complicated object boundary easily. Moreover, Med-ReLU can generate an activation when calculating gradient in negative part, so the dead neuron problem during the training can be averted. Formulation of Med-ReLU and its derivative are given in Eqs. (14) and (15), respectively.

f(x)={x1+|x|x≤0xx>0(14)

f′(x)={11+|x|2x≤01x>0(15)

While various activation functions offer unique benefits, Med-ReLU distinguishes itself through its hybrid design, which allows it to excel in the critical aspects of image processing tasks like medical image segmentation. For instance, the unbounded nature of ReLU in positive values supports quick propagation, allowing Med-ReLU to preserve this advantage, with little added computational burden. Unlike ReLU and LReLU, which suffer from the potential for neuron death, Med-ReLU’s Softsign component addresses this limitation by providing non-zero gradients for all inputs. Similarly, while ELU introduces negative activations, Med-ReLU’s Softsign approach offers bounded values, unlike other unbounded functions, which results in improved feature extraction by providing a controlled level of non-linearity. This combination offers a significant advantage for medical image segmentation.

Furthermore, Med-ReLU’s C1 continuity offers a smoother gradient flow compared to the C0 nature of ReLU and LReLU. This can lead to faster and more stable convergence during model training. While activation functions like SWISH, MISH, ReLU-Tanh and RMAF have demonstrated higher performance in a wide range of tasks, Med-ReLU presents a superior balance of properties, which is suitable for specific demands of complex task like medical image segmentation. Med-ReLU aims to maintain simplicity in implementation, high reproducibility, and robust weight updates in order to preserve effective feature learning in medical image segmentation. Therefore, Med-ReLU aims to combine the computational efficiency of ReLU and the non-linearity of Softsign, making it a strong candidate for achieving good performance. By incorporating the characteristics from different functions into a new activation function, it is possible to create a new function with improved performance in general, and especially medical image segmentation.

4  Results & Discussion

4.1 Experimental Settings

Each knee image dataset has a size of 384 × 384 × 160. Whole cartilage has been segmented from knee images. A total of 32 training datasets, 32 augmented datasets, and 2 validation datasets have been involved. The knee segmentation produces an array of binary segmentation output, which has been reconstructed into 3D. In the cell image dataset, each image has a size of 128 × 128. In total, 650 images have been used for training and 10 for validation. The output is a binary segmentation to extract the whole cell from the background image.

The model has been trained from scratch on an NVIDIA GeForce RTX 3070 GPU, using the Tensorflow and PyTorch libraries as the back-end. We employed the ADAM optimizer for training and applied batch normalization to stabilize the process. To initialize the model, we followed best practices tailored to the specific activation functions:

•   For activation functions such as ReLU, Leaky ReLU, ELU, SWISH, and MISH, which are part of the Med-ReLU family, we utilized the He initialization method, commonly recommended for ReLU-based activations.

•   For traditional sigmoid and tanh activations, we adopted the Glorot (Xavier) [29] initialization method, which aligns with their characteristics.

The model has used a learning rate of 0.01 with a batch size of 8 during training with cell images and was trained for 25 epochs. Subsequently, when training with knee images, the learning rate remained at 0.01, the batch size was set to 2, and the training duration extended to 50 epochs. We computed an activation function using a pixel-wise Sigmoid over the final feature map, combined with a cross-entropy loss function. Please note that for each activation function, we conducted a systematic search for suitable initialization methods and hyperparameters tailored to our specific tasks. The training times varied depending on the dataset and activation function, with cell image training taking approximately 1–2 h and knee image training lasting for around 7–8 h.

Segmentation accuracies produced by U-net with different activation functions have been assessed by using Dice Similarity Coefficient (DSC), a benchmark evaluation metric in medical image segmentation. DSC is defined as the degree of similarity between the segmented object, X, and ground truth,Y, as shown in Eq. (16). We also applied Intersection over Union (IoU) and Volumetric Overlap Error (VOE). IoU is alternatively known as the Jaccard index. In Eq. (17), the metric measures the number of pixels shared by X and Y divided by the total number of pixels present across both masks.

DSC=2|X∩Y||X|+|Y|(16)

IoU=|X∩Y||X∪Y|(17)

Meanwhile, VOE is the corresponding error measure expressed in Eq. (18):

VOE=1−|X∩Y||X∪Y|(18)

4.2 Model Training and Validation Performance

During model training, the accuracy has been measured by using DSC. The training and validation performance of U-net by using cell images are as shown in Fig. 7. Parameters α and β of ReLU-Tanh function are set at 1 and 0, while the parametric values of α, as well as hyperparameteric values of p and j of RMAF have been set at 0.1, 1, and 1, respectively. Based on Fig. 7a, Sigmoid has been converged too swiftly to a suboptimal solution while ELU, MISH and SWISH are training slowly due to the small progress weights updates. ReLU has demonstrated sudden divergence in the middle of training. Among the activation functions, only the Med-ReLU has demonstrated good and stable learning performance throughout model training. Then, the over-fitting endured by U-net is assessed during training. By referring to Fig. 7b,d, Med-ReLU has presented consistent training and validation curves wherein it converges at around DSC of 0.95. The small gap between both curves suggest the proposed function does not suffer from over-fitting. Comparatively, one can observe a slight over-fitting endured by Sigmoid and chaotic validation accuracy performance exhibited by LReLU.

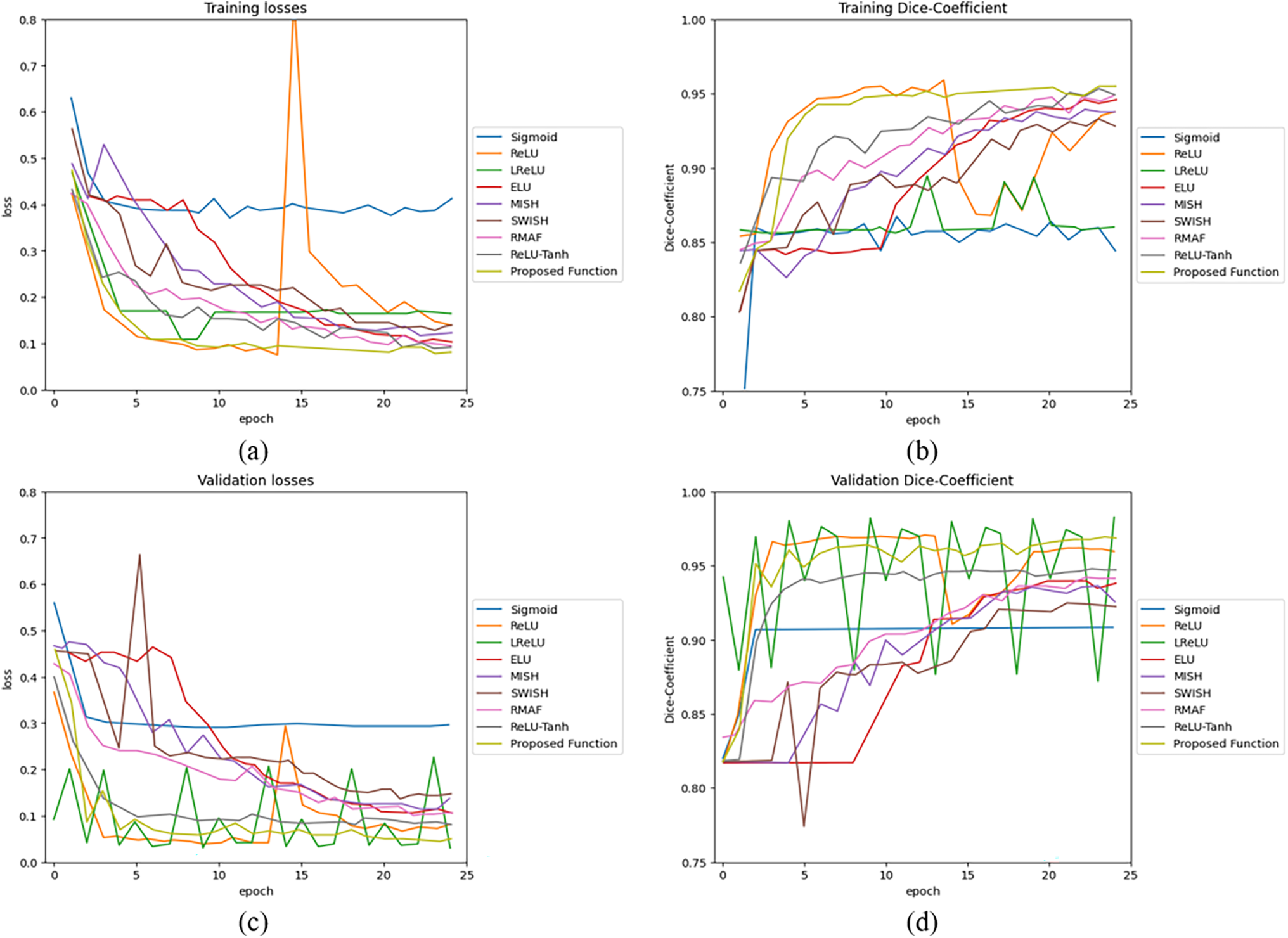
Figure 7: U-net model performance by using 2D cell image: (a) training losses, (b) training accuracy, (c) validation losses, and (d) validation accuracy

The training and validation performance of U-net by using knee images is shown in Fig. 8. Parameters α and β of the ReLU-Tanh function have been set at 1 and 0, respectively, while the parameter α as well as hyperparameters p and j of RMAF have been set at 0.1, 1.5, and 1, respectively. Overall, these plots are showing more wiggles than Fig. 7 due to the small batch size values. By referring to Fig. 8a, Med-ReLU has exhibited a good learning curve and converged smoothly. Sigmoid has demonstrated chaotic learning performance. Besides, its training does not converge. ReLU demonstrates a relatively low learning pace or speed compared to other activation functions. The training and validation accuracy plots for model overfitting are also compared. By referring to Fig. 8b,d, Med-ReLU does not report an overfitting problem given that the gap between both curves is small. The sigmoid is seen to experience volatile training accuracy performance.

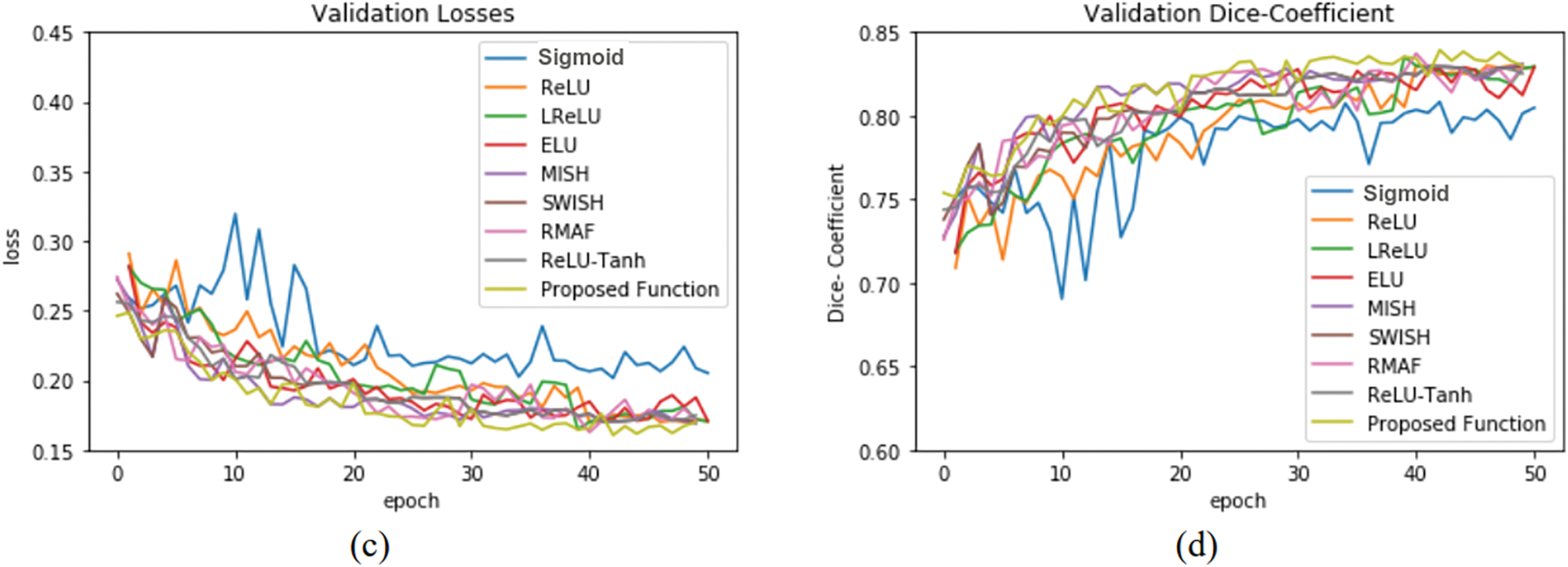
Figure 8: U-net model performance by using 3D knee image: (a) training losses, (b) training accuracy, (c) validation losses, and (d) validation accuracy

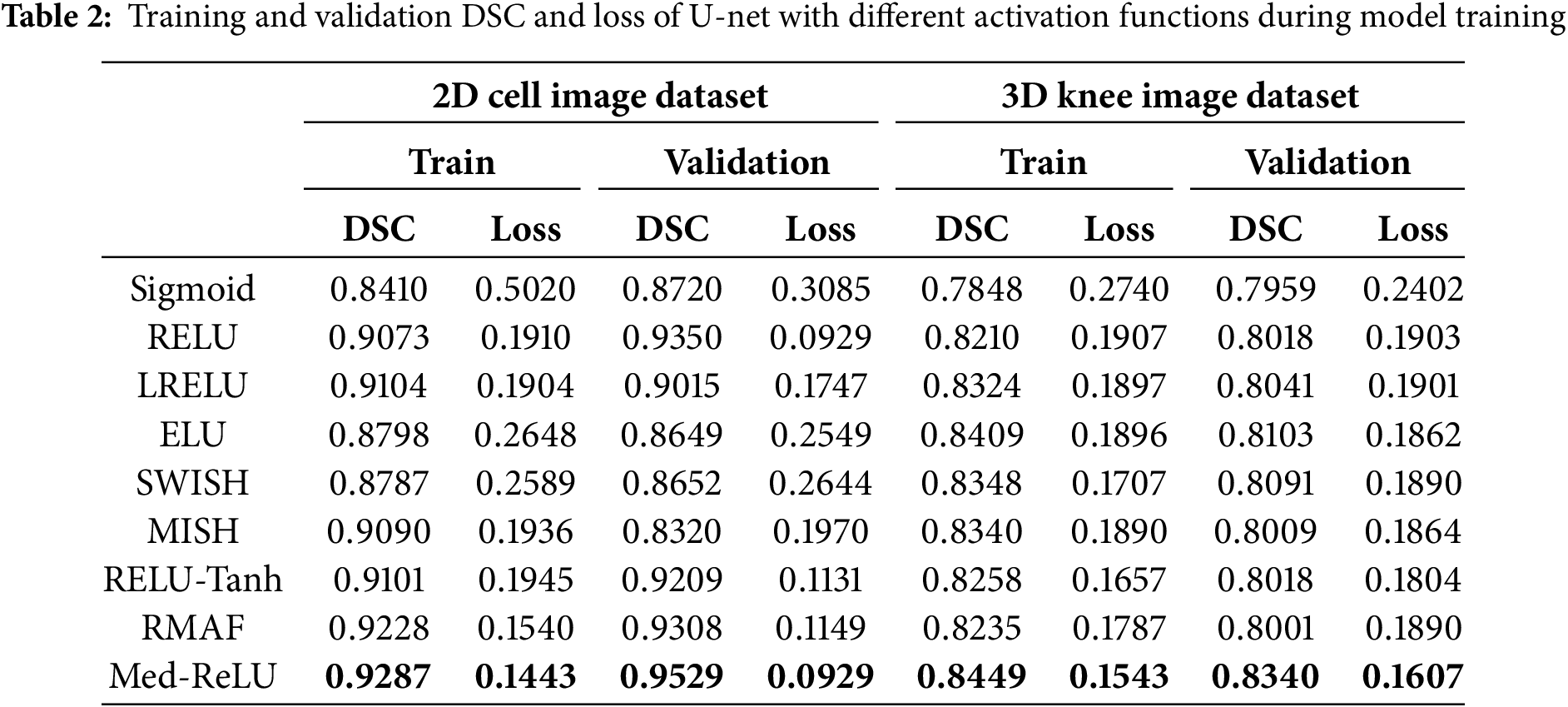
Performances of U-net model training and validation with different activation functions are as summarized in Table 2. The U-net with Med-ReLU outperforms other activation functions. It has demonstrated the best training accuracy and losses of 0.9287 and 0.1443 in cell images and losses of 0.8449 and 0.1543 in knee images. Sigmoid has exhibited the worst training accuracy and loss of 0.8410 and 0.5020 in cell images and 0.7848 and 0.2740 in knee images. The training characteristics as shown in Figs. 7 and 8, and hence it is concluded that the Sigmoid is unsuitable to be deployed in the deep learning segmentation model. Meanwhile, the training and validation results for other activation functions are mixed. For example, RMAF performs well in cell images (Training DSC: 0.9228, Validation DSC: 0.9308) but performs mediocrely in knee images (Training DSC: 0.8235, Validation DSC: 0.8001). A similar observation is made in the case of ReLU-Tanh. As such, the inconsistency of training performance is influenced by the selection of parameters required by both activation functions.

4.3 Segmentation Results

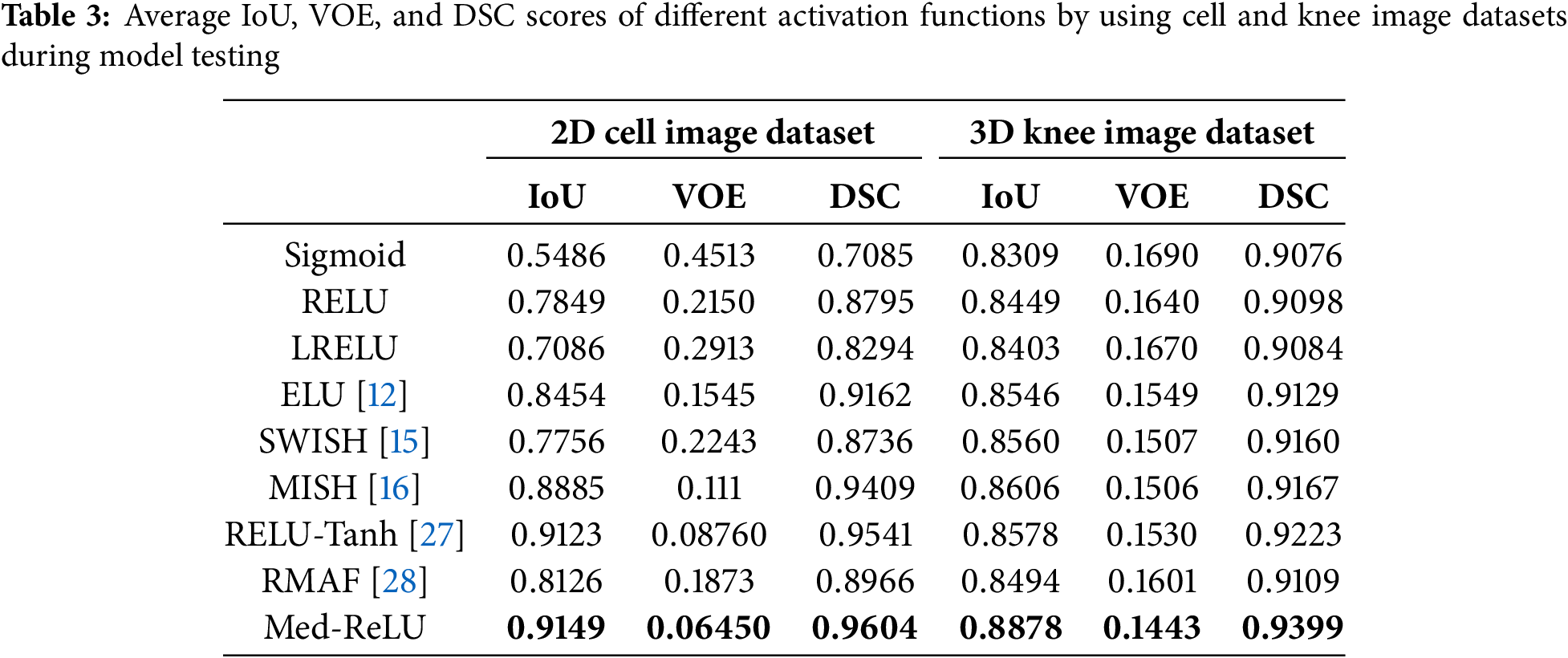
Accurate medical image segmentation is fundamental to subsequent computer-aided diagnostic processes. In this experiment, 320 knee images and 10 cell images are used to test the segmentation performance of the U-net with different activation functions. The segmentation results by using IoU, VOE and DSC are listed in Table 3. The U-net with Med-ReLU outperformed other activation functions consisting of IoU of 0.9149, VOE of 0.06450 and DSC of 0.9604 in cell images and IoU of 0.8878, VOE of 0.1443 and DSC of 0.9399 in knee images. Sigmoid has the worst segmentation results with IoU of 0.5486, VOE of 0.4513 and DSC of 0.7085 in cell images and IoU of 0.8309, VOE of 0.1690 and DSC of 0.9076. The bad segmentation results are inherited by chaotic training performance experienced by the function. Meanwhile, other activation functions have demonstrated mixed accuracies values in different image dataset.

The segmentation results of cell and knee images are illustrated in Fig. 9 and compared with respective ground truth. In cell segmentation, extraction of intact cell shape and the correct number of cells is important. U-net with Sigmoid has produced not very promising under-segmented cell shapes, which cannot be utilized for clinical applications. Meanwhile, U-net with ReLU and LReLU have generated delicate over-segmented cells, where it is observed that some cells are interconnected. Lastly, U-net with Med-ReLU has been able to produce desirable cell segmentation results. Segmentation of the knee, on the other hand, is a more daunting task because of the irregular and changing anatomical geometries across slices. Knee cartilage is divided into femoral, tibial and patellar cartilage. The knee image background is characterized by numerous musculoskeletal tissues such as bones, ligaments, fatty tissues and muscles. The complex landscape as exhibited by the knee image can easily mislead the segmentation model of ineffective learning. Good knee segmentation should preserve accurate cartilage shape (without the issues of under-segmentation or over-segmentation) and clear boundary delineation between different types of cartilages.

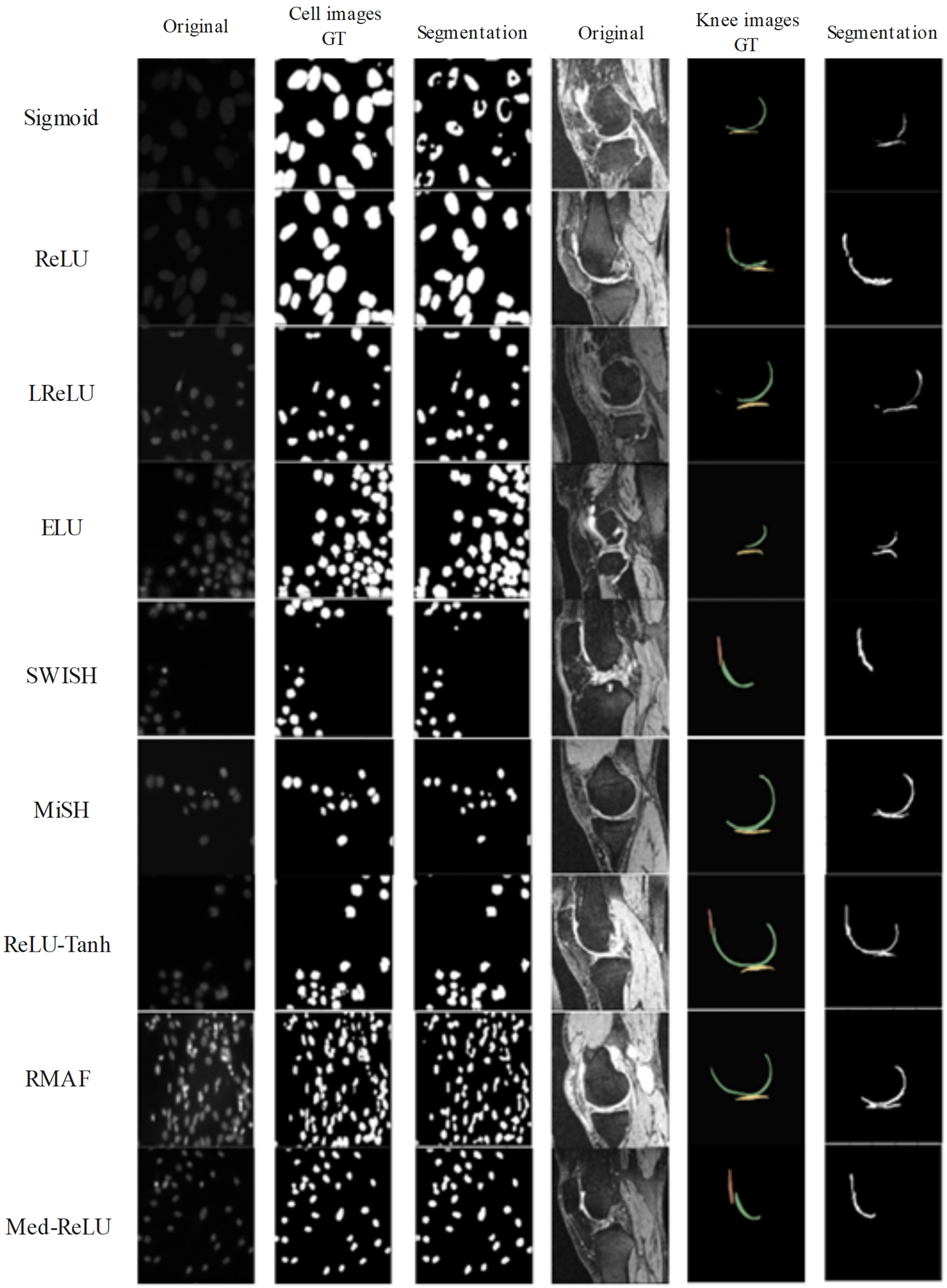
Figure 9: Segmentation results generated by U-net by using different activation functions

Based on Fig. 9, the U-net with Sigmoid has produced the worst segmentation results. The segmented femoral cartilage has been severely deformed, and the anterior section has been missing when compared to the ground truth. ReLU has encountered over-segmentation in tibial cartilage, and LReLU has encountered under-segmentation in middle femoral cartilages. Meanwhile, ReLU-Tanh has produced satisfactory results but has reported minor over-segmentation in patella cartilage. MISH has experienced slight under-segmentation in the anterior femoral cartilage. Only Med-ReLU can produce desirable knee segmentation results.

Fig. 10 shows the 3D knee segmentation results from an anterior view. Knee cartilage produced by Sigmoid has a jaggy and sharply uneven boundary and under-segmentation at the anterior and posterior lateral femoral cartilage. Similar undesirable results have been observed by the knee segmentation model with RMAF. The anterior lateral femoral cartilage has experienced serious under-segmentation while the posterior medial femoral cartilage has shown uneven surface delineation. Results produced by segmentation model with ReLU have produced under-segmented anterior lateral cartilage and undefined anterior medial cartilage boundary with medial tibial cartilage. As a result, the whole cartilage model is deformed. Segmentation results by the model with Med-ReLU have produced a cartilage model with a smooth boundary surface and correct anatomical shape. The boundary delineation between femoral and tibial is also clear.

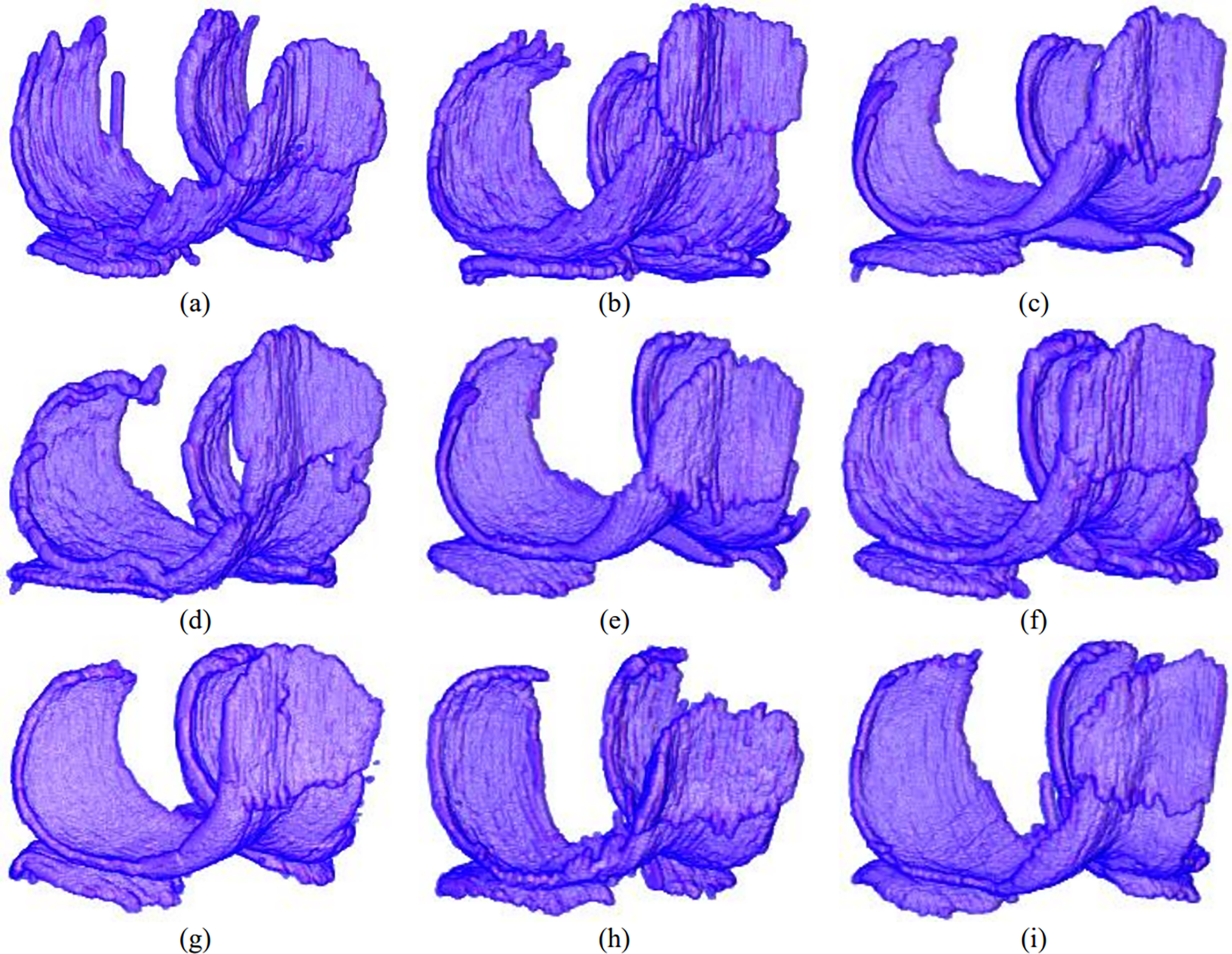
Figure 10: 3D results of cartilage segmentation generated by U-net by using (a) Sigmoid (b) ReLU (c) LReLU (d) ELU (e) SWISH (f) MISH (g) ReLU-Tanh, (h) RMAF and (i) Med-ReLU

Upon visually analyzing the results for cell images and knee cartilage segmentation, certain inconsistencies in Med-ReLU’s performance were observed. While Med-ReLU effectively addresses negative input issues, challenges persisted, particularly in knee cartilage segmentation. One notable issue was the slight over-segmentation of cartilage regions, potentially due to the model’s sensitivity to intensity variations in image modality scans. This over-segmentation can introduce false positives, compromising segmentation precision. Therefore, carefully considering such factors in activation functions and loss functions is a crucial step. These inconsistencies indicate that while Med-ReLU enhances activation handling, further refinements are necessary to improve segmentation accuracy in complex anatomical structures. In future work, we will address these challenges by optimizing parameter tuning and exploring adaptive modifications to enhance overall performance.

5  Conclusions

This study introduces Med-ReLU, a novel activation function tailored for medical image segmentation. Med-ReLU is a parameter-free hybrid function that leverages the linear properties of ReLU for positive inputs and the polynomial convergence of Softsign for negative inputs. This design ensures stable gradient flow, robust training performance, and improved segmentation accuracy. Experimental results demonstrated that Med-ReLU outperforms conventional activation functions, including popular functions like ReLU, ELU, and LReLU, particularly in 2D cell and 3D knee image segmentation. Its effectiveness was validated using standard evaluation metrics such as Intersection over Union (IoU), Volume Overlap Error (VOE), and Dice Similarity Coefficient (DSC), confirming its potential for medical imaging applications. Despite its advantages, Med-ReLU’s generalizability across different network architectures and imaging modalities remains an open challenge. While it mitigates vanishing gradients and dead neuron issues without requiring parameter tuning, its applicability in classification-based medical imaging and large-scale 3D segmentation tasks needs further exploration. Future research could focus on evaluating Med-ReLU across diverse imaging modalities, integrating it with advanced deep learning architectures like Vision Transformers and Graph Neural Networks, and exploring its role in generative models for medical image synthesis. These efforts could further establish Med-ReLU as a robust and versatile activation function for deep learning-based medical image analysis.

Acknowledgement: The researchers would like to thank the Deanship of Graduate Studies and Scientific Research at Qassim University for financial support (QU-APC-2025).

Funding Statement: The researchers would like to thank the Deanship of Graduate Studies and Scientific Research at Qassim University for financial support (QU-APC-2025).

Author Contributions: Conceptualization, Mohammed Aloraini, Muhammad Islam; methodology, Mohammed Aloraini, Nawaf Waqas, Muhammad Islam; software, Mohammed Aloraini, Nawaf Waqas, Muhammad Islam; validation, Muhammad Islam, Sheroz Khan, Nawaf Waqas; formal analysis, Muhammad Yahya, Nawaf Waqas, Muhammad Islam, Mohammed Aloraini, Sheroz Khan; investigation, Muhammad Yahya, Nawaf Waqas, Muhammad Islam, Mohammed Aloraini; resources, Nawaf Waqas, Muhammad Islam; data curation, Muhammad Yahya, Nawaf Waqas, Sheroz Khan; writing—original draft preparation, Shabana Habib, Sheroz Khan; writing—review and editing, Muhammad Islam, Muhammad Yahya, Sheroz Khan; visualization, Shabana Habib, Muhammad Islam, Sheroz Khan; supervision, Shabana Habib, Sheroz Khan; project administration, Shabana Habib, Mohammed Aloraini, Muhammad Islam, Sheroz Khan; funding acquisition, Mohammed Aloraini, Muhammad Islam. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets used in this study are publicly available. The 2D microscopic cell images were obtained from the Kaggle Data Science Bowl 2018 competition, accessible at https://www.kaggle.com/c/data-science-bowl-2018 (accessed on 16 April 2025). The 3D knee MRI images were acquired from the Osteoarthritis Initiative (OAI) database, which is freely available at https://nda.nih.gov/oai (accessed on 16 April 2025). The cell image masks were included within the Kaggle dataset, whereas the knee image masks were manually segmented as part of this research.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Li L, Wei M, Liu BO, Atchaneeyasakul K, Zhou F, Pan Z. Deep learning for hemorrhagic lesion detection and segmentation on brain CT images. IEEE J Biomed Health Inform. 2020;25(5):1646–59. [Google Scholar]

2. Zhi L, Jiang W, Zhang S, Zhou T. Deep neural network pulmonary nodule segmentation methods for CT images: literature review and experimental comparisons. Comput Biol Med. 2023;164(9):107321. doi:10.1016/j.compbiomed.2023.107321. [Google Scholar] [PubMed] [CrossRef]

3. Ridhma, Kaur M, Sofat S, Chouhan D. Review of automated segmentation approaches for knee images. IET Image Process. 2021;15(2):302–24. [Google Scholar]

4. Tsuneki M. Deep learning models in medical image analysis. J Oral Biosci. 2022;64(3):312–20. doi:10.1016/j.job.2022.03.003. [Google Scholar] [PubMed] [CrossRef]

5. Razzak MI, Naz S, Zaib A. Deep learning for medical image processing: overview, challenges and the future. In: Dey N, Ashour A, Borra S, editors. Lecture notes in computational vision and biomechanics. Vol. 26. Cham, Switzerland: Springer; 2017. p. 323–50. [Google Scholar]

6. Liu X, Zhou J, Qian H. Comparison and evaluation of activation functions in term of gradient instability in deep neural networks. In: Proceedings of the 2019 Chinese Control and Decision Conference (CCDC). Nanchang, China: IEEE; 2019. p. 3966–71. [Google Scholar]

7. Konwer S, Sojan M, Kenz PA, Santhosh SK, Joseph T, Bindiya TS. Hardware realization of sigmoid and hyperbolic tangent activation functions. In: Proceedings of the 2022 IEEE International Conference on Industry 4.0, Artificial Intelligence, and Communications Technology (IAICT). Bali, Indonesia: IEEE; 2022 Jul. p. 84–9. [Google Scholar]

8. Sun K, Yu J, Zhang L, Dong Z. A convolutional neural network model based on improved softplus activation function. In: International Conference on Applications and Techniques in Cyber Intelligence (ATCI 2019Applications and Techniques in Cyber Intelligence 7. Huainan, China: Springer International Publishing; 2020. p. 1326–35. [Google Scholar]

9. Bai Y. RELU-function and derived function review. In: SHS Web of Conferences. Dali, China: EDP Sciences. Vol. 144. [Google Scholar]

10. Mastromichalakis S. ALReLU: a different approach on Leaky ReLU activation function to improve Neural Networks Performance. arXiv:2012.07564. 2020. [Google Scholar]

11. Crnjanski J, Krstić M, Totović A, Pleros N, Gvozdić D. Adaptive sigmoid-like and PReLU activation functions for all-optical perceptron. Opt Lett. 2021;46(9):2003–6. [Google Scholar] [PubMed]

12. Devi T, Deepa N. A novel intervention method for aspect-based emotion using Exponential Linear Unit (ELU) activation function in a Deep Neural Network. In: Proceedings of the 2021 5th International Conference on Intelligent Computing and Control Systems (ICICCS). Madurai, India: IEEE; 2021 May. p. 1671–5. [Google Scholar]

13. Too EC, Yujian L, Gadosey PK, Njuki S, Essaf F. Performance analysis of nonlinear activation function in convolution neural network for image classification. Int J Comput Sci Eng. 2020;21(4):522–35. [Google Scholar]

14. Lee M. Mathematical analysis and performance evaluation of the gelu activation function in deep learning. J Math. 2023;2023(1):4229924. doi:10.1155/2023/4229924. [Google Scholar] [CrossRef]

15. Sunkari S, Sangam A, Suchetha M, Raman R, Rajalakshmi R, Tamilselvi S. A refined ResNet18 architecture with Swish activation function for Diabetic Retinopathy classification. Biomed Sig Process Control. 2024;88:105630. [Google Scholar]

16. Mondal A, Shrivastava VK. A novel Parametric Flatten-p Mish activation function based deep CNN model for brain tumor classification. Comput Biol Med. 2022;150(5):106183. doi:10.1016/j.compbiomed.2022.106183. [Google Scholar] [PubMed] [CrossRef]

17. Arnekvist I, Carvalho JF, Kragic D, Stork JA. The effect of target normalization and momentum on dying. arXiv:2005.06195. 2020. [Google Scholar]

18. Nandi A, Jana ND, Das S. Improving the performance of neural networks with an ensemble of activation functions. In: 2020 International Joint Conference on Neural Networks (IJCNN). Glasgow, UK: IEEE; 2020 Jul. p. 1–7. [Google Scholar]

19. Hasan MM, Hossain MA, Srizon AY, Sayeed A. TaLU: a hybrid activation function combining Tanh and rectified linear unit to enhance neural networks. arXiv:2305.04402. 2023. [Google Scholar]

20. Xu Z, Tang B, Zhang X, Leong JF, Pan J, Hooda S, et al. Reconfigurable nonlinear photonic activation function for photonic neural network based on non-volatile opto-resistive RAM switch. Light Sci Appl. 2022;11(1):288. doi:10.1038/s41377-022-00976-5. [Google Scholar] [PubMed] [CrossRef]

21. Jagtap AD, Karniadakis GE. How important are activation functions in regression and classification? A survey, performance comparison, and future directions. J Mach Learn Model Comput. 2023;4(1):21–75. [Google Scholar]

22. Dubey SR, Singh SK, Chaudhuri BB. Activation functions in deep learning: a comprehensive survey and benchmark. Neurocomputing. 2022;503:92–108. [Google Scholar]

23. Szandała T. Review and comparison of commonly used activation functions for deep neural networks. Bio-Inspired Neurocomput. 2021;903:203–24. doi:10.1007/978-981-15-5495-7_11. [Google Scholar] [CrossRef]

24. Nieradzik L, Scheuermann G, Saur D, Gillmann C. Effect of the output activation function on the probabilities and errors in medical image segmentation. arXiv:2109.00903. 2021. [Google Scholar]

25. Castaneda G, Morris P, Khoshgoftaar TM. Evaluating the number of trainable parameters on deep Maxout and LReLU networks for visual recognition. In: 2020 19th IEEE International Conference on Machine Learning and Applications (ICMLA). Miami, FL, USA: IEEE; 2020 Dec. p. 415–21. [Google Scholar]

26. KOÇAK Y, ŞİRAY GÜ. Performance evaluation of swish-based activation functions for multi-layer networks. Artif Intell Studies. 2022;5(1):1–13. [Google Scholar]

27. Li X, Hu Z, Huang X. Combine relu with tanh. In: 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC). Chongqing, China: IEEE; 2020. p. 51–5. [Google Scholar]

28. Yu Y, Adu K, Tashi N, Anokye P, Wang X, Ayidzoe MA. RMAF: ReLU-memristor-like activation function for deep learning. IEEE Access. 2020;8:72727–72741. doi:10.1109/access.2020.2987829. [Google Scholar] [CrossRef]

29. Evangelista LGC, Giusti R. Short-term effects of weight initialization functions in Deep NeuroEvolution. In: The Leading European Event on Bio-Inspired Computation; 2021 Apr 7–9; Online. [cited 2025 May 10]. http://www.evostar.org/2021/. [Google Scholar]