QHF-CS: Quantum-Enhanced Heart Failure Prediction Using Quantum CNN with Optimized Feature Qubit Selection with Cuckoo Search in Skewed Clinical Data

1  Introduction

Myocardial infarctions, also known as heart attacks, stand as the main reason for global mortality statistics because these conditions result in 32% of total cardiovascular disease-related deaths while causing 17.9 million annual fatalities [1]. Age, together with diabetes and hypertension, smoking history, cholesterol levels and family disease background remain insufficient despite modern improvements in heart attack risk hypotheses [2]. The predictive factors yield practical knowledge but fail to grasp the full complexity of cardiovascular diseases during the post-COVID-19 period because systemic inflammation coupled with calcium dysregulation and advanced cardiac-specific biomarkers now exist [3]. The need arises for progressive forecasting models to combine newly discovered biomarkers with imaging-based risk signs and behavioural metrics to enhance risk evaluation methods.

The variety of clinical data makes heart failure prediction harder. Due to the complexity of medical data, advanced cardiac biomarkers cannot be analyzed by conventional models. Clinical biases impair prediction. Stress, depression, and inactivity increase cardiovascular risk, but traditional heart models ignore them. Researchers are refining many patient prediction models at low cost. Due to rising heart failure cases and complex cardiovascular data, modern predictive knowledge is needed to speed diagnosis and surgery.

While effective for many structured tasks, traditional machine learning approaches, often struggle in biomedical domains where datasets are high-dimensional, imbalanced, and statistically skewed. Clinical scenarios such as heart failure prediction especially highlight these limitations, where subtle, non-linear interactions between biomarkers (e.g., ejection fraction, serum sodium, creatinine levels) are critical to diagnosis. Quantum Machine Learning (QML) offers an emerging alternative by leveraging the principles of quantum mechanics—specifically superposition, entanglement, and quantum parallelism—to enhance data representation and modelling. QML encodes classical features into high-dimensional quantum states through quantum feature maps and variational circuits, allowing the model to capture richer interdependencies with fewer parameters and greater generalization potential. This work explores the application of QML within this context, focusing on its capacity to improve clinical prediction where classical techniques may fall short.

At the core of Quantum Machine Learning (QML) are the quantum principles of superposition and entanglement, which offer powerful advantages in analyzing complex biomedical data. Superposition enables qubits to exist in linear combinations of |0⟩ and |1⟩, allowing quantum models to evaluate multiple feature configurations simultaneously—an essential capability for high-dimensional tasks such as gene expression profiling or imaging biomarker analysis in genomics and radiology [4]. Entanglement further enhances this by introducing non-classical correlations between qubits, enabling QML models to effectively capture non-linear dependencies between clinical variables such as ejection fraction, serum sodium, and creatinine levels, which are critical in tasks like heart failure prediction [5]. Quantum feature maps such as ZZFeatureMap, RealAmplitudes, and EfficientSU2 operationalize these capabilities by transforming scalar biomedical inputs into entangled quantum states in high-dimensional Hilbert spaces. The capabilities of QML allow the model to learn complex, combinatorial relationships that classical models often struggle to capture, particularly under data sparsity, heterogeneity, and imbalance [5].

In medical applications characterized by heterogeneous data—spanning continuous biomarkers to categorical indicators—quantum feature maps provide diverse and adaptable encoding strategies that enhance model expressiveness and interpretability. The PauliFeatureMap enables higher-order interaction modelling through tensor products of Pauli operators, making it particularly effective for capturing comorbidities or complex biomarker interplay in conditions like sepsis or cardiovascular disease [6]. AngleEmbedding translates continuous clinical features such as ejection fraction or serum creatinine into qubit rotations, supporting resource-constrained deployment on near-term quantum hardware for tasks like ICU mortality or heart failure prediction [7]. IQPEmbedding introduces a highly expressive and classically hard-to-simulate feature space for kernel-based quantum models, suitable for detecting subtle gene expression patterns and rare disease signatures in small datasets [5]. Meanwhile, the HardwareEfficientAnsatz facilitates depth-efficient variational encoding, making it ideal for real-time diagnostics and quantum-enhanced mobile health applications [8]. These encoding techniques extend QML’s utility across diverse healthcare domains, including oncology, cardiology, and genomics, establishing a foundation for scalable, robust, and interpretable quantum medical AI.

In healthcare applications, particularly those involving small, imbalanced, and high-dimensional clinical datasets, Quantum Machine Learning (QML) offers significant advantages through its ability to encode complex, non-linear feature interactions using quantum principles such as superposition and entanglement. Quantum classifiers like Quantum Support Vector Machines (QSVMs) and Quantum Convolutional Neural Networks (QCNNs) leverage variational parameter tuning and quantum kernels to model intricate class boundaries, making them well-suited for challenging diagnostic tasks such as early-stage heart failure prediction and tumour classification [6,9]. Feature maps like EfficientSU2, which utilize layered RY and RZ rotations with entangling gates, provide enhanced expressiveness for representing multi-biomarker dependencies in domains such as genomics and radiology [7]. Studies have shown that QML models trained on these quantum embeddings outperform classical counterparts in classification accuracy and generalize better in data-scarce conditions, positioning them as a promising solution in personalized and precision medicine [10]. Furthermore, QCNNs, by emulating the convolution-pooling mechanisms of classical CNNs, achieve improved efficiency and accuracy with fewer parameters—making QML increasingly viable within current NISQ-era hardware constraints [10].

QML’s quantum entanglement and superposition principles speed up high-dimensional complex medical data processing [11]. Using quantum speedup, QSVM [12], Quantum K-Nearest-Neighbor (QkNN) [13], and Quantum Decision Tree (QDT) [14] form quantum classifiers for complex data distributions. Because noisy intermediate-scale quantum (NISQ) hardware devices are still under development, developers proceed. In large-scale medical real-time cardiovascular disease risk assessment, quantum-enhanced models outperform classical methods despite their limitations.

Recent advances in ensemble learning, such as HeartEnsembleNet [15], have shown strong performance in cardiovascular risk prediction by combining gradient boosting, random forest, and deep neural networks into a robust hybrid framework [15]. While effective, such models face limitations, including feature redundancy and high computational cost in high-dimensional, skewed clinical datasets. In contrast, the proposed QHF-CS model adopts a quantum-classical hybrid approach, utilizing quantum-enhanced feature encoding, Cuckoo Search-based qubit optimization, and Quantum Convolutional Neural Networks (QCNNs) to capture complex patterns via entanglement and quantum parallelism. QHF-CS thus complements classical ensemble models by offering a more scalable and expressive solution for clinical data modelling.

Quantum Convolutional Neural Networks (QCNNs) overcome traditional machine learning limitations for heart failure prediction [16], especially in the context of cardiovascular medical data, which presents challenges in processing time and feature identification. Quantum superposition and entanglement enable QCNNs to identify complex non-linear patterns, enhance feature extraction, and speed up computations. In skewed clinical datasets, Cuckoo Search Optimization (CSO) [17], along with Artificial Bee Colony (ABC) and Particle Swarm Optimization (PSO) [17], aids in feature selection. Among these, CSO consistently identifies the most optimal biomarkers for quantum circuit construction, such as creatinine phosphokinase, platelets, ejection fraction, and serum sodium. These biomarkers are encoded as feature qubits for the QHF-CS model, enhancing prediction accuracy. Furthermore, advanced quantum circuit feature maps like ZZFeatureMap, RealAmplitudes, and EfficientSU2 significantly improve data processing efficiency in the QHF-CS framework. This study introduces QHF-CS: Quantum-Enhanced Heart Failure Prediction using Quantum CNN with Optimized Feature Qubit Selection via Cuckoo Search in Skewed Clinical Data, a novel quantum-driven approach. Traditional machine learning models face difficulties with high-dimensional, skewed datasets, making advanced optimization methods crucial. CSO, ABC, and PSO facilitate robust feature selection and dimensionality reduction by selecting only the most relevant clinical biomarkers and encoding them into qubits for efficient quantum processing.

After skewness analysis and normalization, CSO-based feature selection optimizes the predictive variable subset for quantum feature extraction in the heart failure dataset. From classical data, quantum circuit feature maps ZZFeatureMap, RealAmplitudes, and EfficientSU2 encode selected features into qubits [18,19]. Quantum convolutional and pooling transformations in the QCNN capture complex, non-linear cardiovascular data patterns with quantum processing’s computational advantages. IBM Qiskit quantum simulations train the QHF-CS model with quantum-enhanced features in 4-qubit configurations. Hyperparameter tuning and advanced quantum speedup optimize model performance. With 94.0% accuracy, precision, recall, and F1-score, the EfficientSU2 feature map QCNN model performed best. Selecting the best quantum feature map is crucial because EfficientSU2 consistently outperforms others in predictive accuracy.

The outcomes of the proposed study model revolved around several key aspects:

•   Investigating the impact of skewness correction and normalization techniques on highly skewed datasets to ensure robust model performance and data integrity.

•   Apply meta-heuristic-based feature selection methods to select feature qubits for efficient quantum circuit construction.

•   Applying the QCNN model to assess the heart failure prediction in the presence of skew data and feature selection.

The article includes the following sections: Section 2 presents a literature review, Section 3 outlines the proposed methodology, Section 4 demonstrates experimental results and model evaluation, and Section 5 introduces concluding remarks and projected research directions.

2  Related Works

Research on ML and DL heart failure prediction methods has improved accuracy and reliability worldwide for decades. SVMs, DTs, and RFs performed moderately but struggled with high-dimensional datasets and medical imaging data’s non-linear complexity [20]. Classical models worked well but required extensive feature engineering and didn’t fully exploit imaging modalities’ rich information. Researchers worldwide use machine learning, deep learning, and quantum computing to predict and diagnose advanced cardiovascular disease. Quantum Machine Learning has transformed ML and DL by eliminating their limitations. Quantum Machine Learning efficiently manages large, complex datasets using superposition and entanglement. Quantum mechanics gives QML an edge over ML and DL. Scientific research on hybrid quantum models grows. The researchers designed HQMLP with OQSVM to diagnose ischemic heart disease 94% accurately [21]. In tests, Quantum K-means had 96.40% medical diagnosis accuracy [22]. These advances demonstrate how hybrid quantum algorithms enhance predictive healthcare.

Combining quantum computing principles like entanglement and superposition with classical classification methods improves prediction accuracy. In high-dimensional data, quantum algorithms and classical preprocessing handle interdependencies and imbalance better. In early medical intervention systems, quantum computing in diagnostics allows quantum technology [23]. Binary classifiers inspired by quantum computing improve machine learning classification [24]. Superposition enables quantum mechanics-inspired computation with high-dimensional data and non-linear interactions. The technique improves medical diagnostic binary classification for healthy and at-risk cardiovascular profiles but doesn’t predict heart attacks. Comparing classical and quantum machine learning methods [25] shows quantum computing’s considerable dataset benefits. Studies show quantum SVMs and QNs converge faster and scale better. Healthcare researchers and practitioners need scalable and robust heart attack prediction methods for high-dimensional, heterogeneous clinical and biomarker data. Quantum algorithms cluster massive datasets using pattern recognition and grouping [26]. Quantum-enhanced clustering predicts heart attacks by grouping patients with similar risk histories and biomarkers. Results suggest quantum clustering may solve personalized medicine’s computational issues. A quantum K-Nearest-Neighbor (QkNN) algorithm classifies images using quantum states to describe features and compare similarities [19]. QkNN outperforms classical algorithms in speed and accuracy. Quantum coronary angiogram classification may improve heart attack prediction [27].

A QDT classifier introduced in [28] to use classical decision trees in quantum computing. Quantum features simplify QDT computing and decision-making. Multi-class classification of cardiovascular illness stages and risk levels improves heart attack prediction [28]. COVID-19 classification uses quantum machine learning with conditional adversarial neural networks [29]. According to this model, quantum computing enables efficient processing of biomedical data by leveraging quantum decision trees. The proposed quantum machine learning framework integrates imaging data, clinical biomarkers, and patient medical records to support accurate diagnosis of COVID-19 and cardiac arrest [30]. Combining quantum and classical methods, QCNNs outperform classical methods in accuracy and computation. ML and DL limits use quantum speedup from superposition and entanglement [12]. According to global experiments, quantum-classical computation systems can handle complex medical data and rebuild predictive healthcare. Complex medical diagnostics are efficient and scalable with the combined system. QkNN, a Hamming distance-based quantum feature space similarity algorithm, is introduced in this study. QkNN outperforms traditional kNN methods in classification, making it a promising tool for heart attack risk classification using clinical and biomarker datasets [13].

Troponin, C-reactive protein, and lipoprotein(a) tests are studied worldwide to improve prediction models. CAC scores and other calcium-based factors improve cardiac risk prediction [31]. Cardiovascular disease kills most globally. Early CVD detection reduces heart attacks and speeds recovery. CVD angiography is costly and risky. Current CVD diagnostic methods’ slow convergence speeds require many iterations to find the best option. So, detection rates drop. QPSO-SVM predicts heart disease susceptibility using QPSO and SVM. Preprocessing began with nominal scaling and numericization. We use QPSO to optimize the SVM fitness equation after finding suitable features. Final QPSO-SVM parameter tuning uses a self-adaptive threshold. Exploiting solution search space and searched territories helps the model avoid local minima. The authors compare the QPSO-SVM model to leading models using Cleveland heart disease data. QPSO-SVM predicted cardiac disease 96.31% better than other methods in Cleveland heart data. QPSO-SVM has high F1 score determination (0.95%), sensitivity (96.13%), specificity (93.56%), and precision (94.23%) [32].

Auto-optimized Aquila and feature selection predicted CVD. This method generated 96.69% accurate hybrid QNN-LSTM models [33]. Classification and prediction are SVM and ML strengths. SVM is mainly used in diagnosis, imaging, and flaw detection. Divide instances by class labels with the ideal hyperplane to improve SVM learning. SVM The hyperparameters affect efficiency and accuracy. MBPSO, GSVMA, GWO [34], CS-PSO-SVM [35], and ant colony optimization use SVM [36] due to their strong parameter dependence. Hybrids outperform traditional ML models. The latest study [37] optimized SVM classification with GOA and SVM. We tested hybrid GOA-SVM on 18 datasets. Compare Ga, PSO, GWO, CS, FF, bat, and multi-verse optimizer experiments. GOA-SVM has many developers, but local optima persist. MBPSO detects septic shock [38]. PSO algorithms performed worse than MBPSO. For cardiac diagnosis, use hybrid PSO-SVM [39]. PSO automatically reduced feature count to improve SVM classifier accuracy.

Globally, 17.8 million die from heart failure [40]. Traditional machine-learning heart disease prediction models struggle with complex, high-dimensional data, class imbalance, interpretability, and short dataset performance. Not all hybrid models support quantum machine learning. For simplicity and generalizability, this hybrid dual-channel network approximates continuous functions with KANs for univariate learnable activation functions. The 4-qubit, 1-layer KACQ-DCNN outperforms 37 benchmark models with 92.03% accuracy, 92.00% macro-average precision, recall, and F1. KACQ-DCNN outperformed nine top models in two-tailed paired t-tests, achieving a 94.77% ROC-AUC with αadjusted = 0.0056. LIME and SHAP explainability methods enhance model transparency and confidence, while ablation investigations reveal quantum-classical interactions. In another study [41], discusses a hybrid EEG signal classification model combining autoregressive features with an inherently quantum recurrent neural network to enhance predictive accuracy. Table 1 summarizes research on quantum learning and feature selection for heart attack prediction.

The survey found that classical machine learning and deep learning models struggle with high-dimensional, skewed clinical datasets, inspiring Qubit Selection with Cuckoo Search. QML, hybrid quantum-classical models, and feature selection improve cardiovascular disease prediction. QHF-CS uses Cuckoo Search Optimization (CSO) to select creatinine phosphokinase, platelets, serum sodium, and ejection fraction for optimal qubit encoding in a QCNN based on studies that integrate biomarkers, neurological markers, and metabolic factors for heart failure prediction. Quantum speedup optimization and quantum feature maps (ZZFeatureMap, RealAmplitudes, EfficientSU2) address skewed data distribution, feature redundancy, and computational complexity to improve classification.

3  Proposed Methodology

The proposed research introduces a novel approach to enhancing heart failure prediction accuracy using a pre-processed, well-defined dataset. The process divides the data into training and test portions for evaluation to improve model robustness. A skew analysis forms the starting point to manage data imbalances in clinical datasets to produce accurate and dependable predictive outcomes. This procedure introduces an innovative architectural design integrating Quantum Convolutional Neural Networks (QCNN) with ZZFeatureMap, RealAmplitudes, and EfficientSU2 advanced quantum circuit feature maps. The QHF-CS model employs Cuckoo Search Optimization (CSO) to optimally select feature qubits and convert clinical data into quantum states. ABC and PSO are comparison methods, but CSO provides the most reliable and accurate feature subset for quantum circuit construction. A Quantum-Enhanced Heart Failure Prediction using the Quantum CNN model (QHF-CS) applies these methods for dealing with complicated health indicators and skewed data distribution patterns. The model implements quantum mechanics principles and advanced clustering methods through which operators perform hyperparameter tuning with quantum algorithms. Researchers use test data to evaluate the model’s predictive capabilities for heart failure outcomes. The heart failure prediction method demonstrates superior performance, as shown by past studies and a comprehensive evaluation process, including measuring accuracy, precision, recall, and F1-score and advanced quantum computing metrics. The proposed method is illustrated in Fig. 1, followed by Algorithm 1, which presents generalized code for the QHF-CS model and shows its actual implementation.

Figure 1: Proposed methodology

QHF-CS represents the new approach that applies QCNN for reliable predictions by combining quantum feature extraction with CSO-based optimization. QHF-CS uses quantum layers and dropout elements to improve accuracy and retain precision through quantum computation technology combined with optimization approaches. After finishing multiple complicated training stages, the model achieves outstanding accuracy levels during training and testing. The medical diagnostics field now has a promising asset through QHF-CS because of its advanced performance capabilities for heart failure prediction.

A. Comprehensive Data Preprocessing for Quantum Readiness in Heart Attack Prediction

The preprocessing stage of the depicted QML workflow for heart attack risk prediction includes multiple sophisticated processing procedures for ensuring data reliability and quantum computation readiness of the dataset.

Data Cleaning and Normalization

Stable parameter training and reduction of data scale variation-related biases require quantum algorithms to use normalized input features. The normalization process transforms all features into a standard range by maintaining their original distributions and fits them for quantum algorithm usage using the Eq. (1).

x¯ij=xij−min(xi)max(xi)−min(xi)(1)

A normalization element exists to establish a consistent range from zero to one for all features to guarantee operational stability in quantum circuit procedures.

Handling Missing Values

The analysis of missing data points is performed to resolve incomplete data points. Mean or median imputation gets applied whenever the missing rate is below 5%. The k-nearest neighbors (k-NN) approach becomes necessary for handling higher degrees of data incompleteness. The implemented strategies lead to full dataset completion because this completeness becomes essential for correct quantum state encoding from features. The imputation techniques are validated through cross-validation to ensure minimal degradation in model accuracy.

B. Skew Analysis

The comprehension of feature skewness has significant importance in the preparation of data for machine learning, since several models make the assumption of a normal distribution of inputs. Highly skewed features may require transformation—such as logarithmic or square root functions—to approximate a normal distribution and improve the effectiveness of statistical and machine learning models [42]. A real-valued random variable’s skewness is a statistical measure that measures how asymmetrical its probability distribution is with regard to its mean. The skewness value may be anything from zero to negative infinity or even something completely unknown. As seen in Eq. (2), the skewness of a random variable X may be expressed analytically.

skewness=E[(X−μσ)3]=∑i=1nx(xi−x′)3(n−1).σ3(2)

This context uses the following symbols: E for expectation, X for random variable, μ for mean, sigma for standard deviation, xi for each value of X, x for sample mean, and n for number of observations in the sample.

•   The presence of a skewness value of zero suggests that the distribution exhibits symmetry.

•   A positive skewness signifies that the distribution exhibits a rightward skew, accompanied by a lengthy tail in the positive direction.

•   Conversely, a negative skewness shows a leftward skew, accompanied by a lengthy tail in the negative direction.

C. Optimal Feature Selection

The Artificial Bee Colony (ABC)

The Artificial Bee Colony (ABC) algorithm, inspired by the foraging behavior of honeybees, serves as a powerful meta-heuristic for feature selection in heart failure prediction. It begins with a randomly initialized population of food sources, where each source represents a feature subset. The optimization process unfolds in three key phases:

•   Employed Bee Phase: Bees explore neighboring solutions by modifying a feature subset using the Eq. (3):

Vij=Xij+ϕij⋅(Xij−Xkj)(3)

•   Onlooker Bee Phase: Based on fitness, onlooker bees choose food sources using the Eq. (4):

Pi=fiti∑1nfitn(4)

•   Scout Bee Phase: When no improvements occur, scout bees introduce diversity by exploring new random solutions.

The ABC algorithm iteratively refines feature subsets by memorizing the best-performing combinations, thereby enhancing model performance and mitigating the challenge of extracting relevant features from high-dimensional clinical datasets.

Particle Swarm Optimization (PSO)

Particle Swarm Optimization (PSO) is a population-based algorithm that simulates the social behavior of birds to discover optimal solutions. In the context of heart failure prediction, PSO optimizes feature subsets by updating each particle’s velocity and position are evaluated using the Eqs. (1) and (6):

•  Velocity Update:

vi,d(t+1)=w.vi,d(t)+c1.r1.(pbesti,d−xi,d(t)+c2.r2.(gbestd−xi,d(t)(5)

•  Position Update:

xi,d(t+1)=xi,d(t)+vi,d(t+1)(6)

here, w is the inertia weight balancing exploration and exploitation Cognitive parameters c1 and social parameters c2 are positive constants; Random numbers r1 and r2 are in the interval [0, 1] are random factors.

PSO evolves the swarm by learning from both individual and collective experiences, effectively identifying feature combinations that improve classification accuracy. Its simplicity and derivative-free nature make it particularly suitable for complex, noisy medical datasets where feature relevance is difficult to determine manually.

Cuckoo Search Optimization (CSO)

Cuckoo Search Optimization (CSO) is used to identify the most relevant clinical biomarkers in the heart failure prediction dataset, reducing dimensionality and improving the Quantum Convolutional Neural Network (QCNN) model. CSO operates as a meta-heuristic method that implements fitness functions to improve solutions while taking inspiration from brood parasitism among cuckoo birds. The heart failure patient classification process optimizes Creatinine phosphokinase, platelets, serum sodium and ejection fraction into quantum circuit qubits for more efficient encoding.

X consists of all extracted features x1 x2 to xn which were obtained from a heart failure database with n features. The method seeks to identify an ideal feature subset Xsub ⊆ X which achieves highest accuracy rates and avoids repetitive characteristics. The CSO algorithm searches the best feature subset through an iterative process of improving potential solutions.

(1) Cuckoo Representation

Each cuckoo in CSO functions as a potential solution which represents a subset of features while being initialized with binary vector Ci = [ci1, ci2, …, cin] containing values of cij ∈ {0, 1} that specify if the j-th feature is selected (1) or not (0) in the i-th cuckoo. CSO selects four essential features which prove to be powerful indicators for heart failure classification: creatinine phosphokinase, platelets, serum sodium and ejection fraction.

(2) Fitness Function

A fitness function determines the classification accuracy score that results from using selected features to build a QCNN model. The fitness function f(Ci) of cuckoo Ci calculates using the Eq. (7):

f(Ci)=AccQCNN(Ci)−λ.|Ci|n(7)

where:

•   AccQCNN(Ci) represents the accuracy of the QCNN trained on the selected feature subset Ci.

•   |Ci| is the number of selected features in cuckoo Ci.

•   λ is a regularization parameter to penalize large feature sets, ensuring that the subset is both compact and informative.

By refining the feature subset, CSO ensures that only the most relevant biomarkers—creatinine phosphokinase, platelets, serum sodium, and ejection fraction—are selected, optimizing heart failure prediction accuracy while reducing computational overhead.

(3) Cuckoo Search Feature Selection Process

CSO uses Levy flight-based random walks to explore the feature space. The location update for each cuckoo is formulated using the Eq. (8):

Ci(t+1)=Ci(t)+α.Levy(β)(8)

where:

•   Ci(t) is the feature subset of cuckoo i at iteration t.

•   α is the step size scaling factor.

•   Levy(β) is a Levy flight distribution controlling the randomness of the search.

•   Evaluation of fitness leads to retention of the best subset gbest which enables detection of optimal solutions.

During the search process the discovery probability pa governs the replacement of existing solutions by newly generated feature subsets. An improved feature subset maintained by the cuckoo’s evaluation against f(gbest) preserves the necessary balance between exploration and exploitation search factors.

(4) Feature Selection and Quantum Mapping

The process of CSO completes multiple iterations to find the most useful subset of features that produces the best results in QCNN classification accuracy. Cuckoo solutions evolve during each iteration through subset adjustments that lead them toward identifying gbest as the most important clinical biomarkers for heart failure prediction. The final set of selected features using the Eq. (9):

S={i|gbest,i>0.5}(9)

The map of features uses gbest,i to show its binary selection state. The CSO process selects the most critical attributes from the list which includes creatinine phosphokinase, platelets, serum sodium, and ejection fraction to populate qubits and delivers better accuracy and faster processing.

D. Feature Attribute Matrix Construction

The QML process uses features chosen by Cuckoo Search Optimization to generate a Feature Attribute Matrix that gets distributed onto quantum circuit qubits. Quantum processing receives its relevant clinical biomarkers from CSO verification and includes creatinine phosphokinase, platelets, serum sodium, and ejection fraction, etc.

The Feature Attribute Matrix is represented using the Eq. (10):

Fi=wi1X1+wi2X2+…+WinXn(10)

The framework contains three components that include the i-th feature attribute Fi and the j-th selected feature Xj with respective weight assignment w{ij} for heart failure classification.

The quantum circuit converts feature elements into quantum states that define the quantum system’s operational structure. Each qubit in optimized clinical biomarkers computes quantum information efficiently using Hilbert space. Quantum representation makes heart failure dataset patterns easier to recognize and correlations easier to extract, improving QCNN-based heart failure classification accuracy.

E. Quantum Circuit Construction for Feature Qubits

Quantum parallelism requires encoding selected features into a quantum state using ZZFeatureMap, RealAmplitudes, and EfficientSU2. We build the feature qubit quantum circuit using quantum feature mapping, convolution, pooling, and parameterized ansatz layers. For classification tasks like heart failure detection, the circuit processes classical data. Like a convolutional neural network, multiple layers extract features, apply transformations, and reduce dimensionality.

The optimal set of CS features corresponds to the circuit’s initialization with n qubits. The classical data is encoded into quantum states in the first layer, a quantum feature map. The feature map is characterized using Eq. (11):

UFM(x)=∏i=1nexp⁡(i.xiZiZi+1)(11)

Takes the selected features xi (obtained from CS) and maps them into quantum states using entangling operations based on the Pauli-Z gate. This transforms the classical features into a quantum representation, enabling the circuit to process high-dimensional input efficiently.

Next, a quantum convolution layer is applied to capture local dependencies between the qubits. This layer performs parameterized single-qubit rotations and introduces entanglement between adjacent qubits. Mathematically, the convolution layer is described using the Eq. (12):

UConv(θ)=∏i=1nRX(θi)RY(θi+n)RZ(θi+2n).CZ(i,i+1)(12)

where θi are trainable parameters, and the convolutional operations extract spatial correlations between the qubits, analogous to classical convolutional filters that detect patterns within the data.

Following the convolution, aquantum pooling layer reduces the qubit count by applying entanglement and pooling operations to neighboring qubits. The pooling process down-samples the quantum data, similar to classical pooling layers, helping to prevent overfitting and reduce the computational complexity. The pooling layer can be expressed using the Eq. (13):

Upool(ϕ)=∏i=i,3,5..nCX(i,i+1).RX(ϕi)RY(ϕi+1)(13)

where ϕi are trainable parameters for the pooling operations, ensuring that important feature information is retained while irrelevant data is discarded.

Uansatz(λ), a parameterized ansatz layer, introduces trainable parameters for model optimization during learning. Using multiple layers of RY rotation gates and entangling operations, the RealAmplitudes ansatz improves the circuit’s classification power as given in Eq. (14):

Uansatz(λ)=RY(λi).CZ(i,i+1)(14)

The overall quantum circuit can be expressed as shown in Eq. (15):

UQCNN(x,θ,ϕ,λ)=Uansatz(λ).Upool(ϕ).UConv(θ).UFM(x)(15)

The circuit structure improves heart failure data classification of malignant vs. benign cases and CS-optimized feature qubit processing speed through quantum operations. Pooling and ansatz layers ensure an efficient and robust classification pipeline, while quantum convolutional layers extract complex feature correlations.

3.1 QHF-CS Model Construction

Fig. 2 illustrates the QHF-CS model architecture, starting with CSO feature qubits that pass through quantum convolutional and pooling layers. The data is then flattened and processed through dense neural network layers, culminating in the final output, effectively integrating quantum and classical computing techniques for enhanced prediction accuracy.

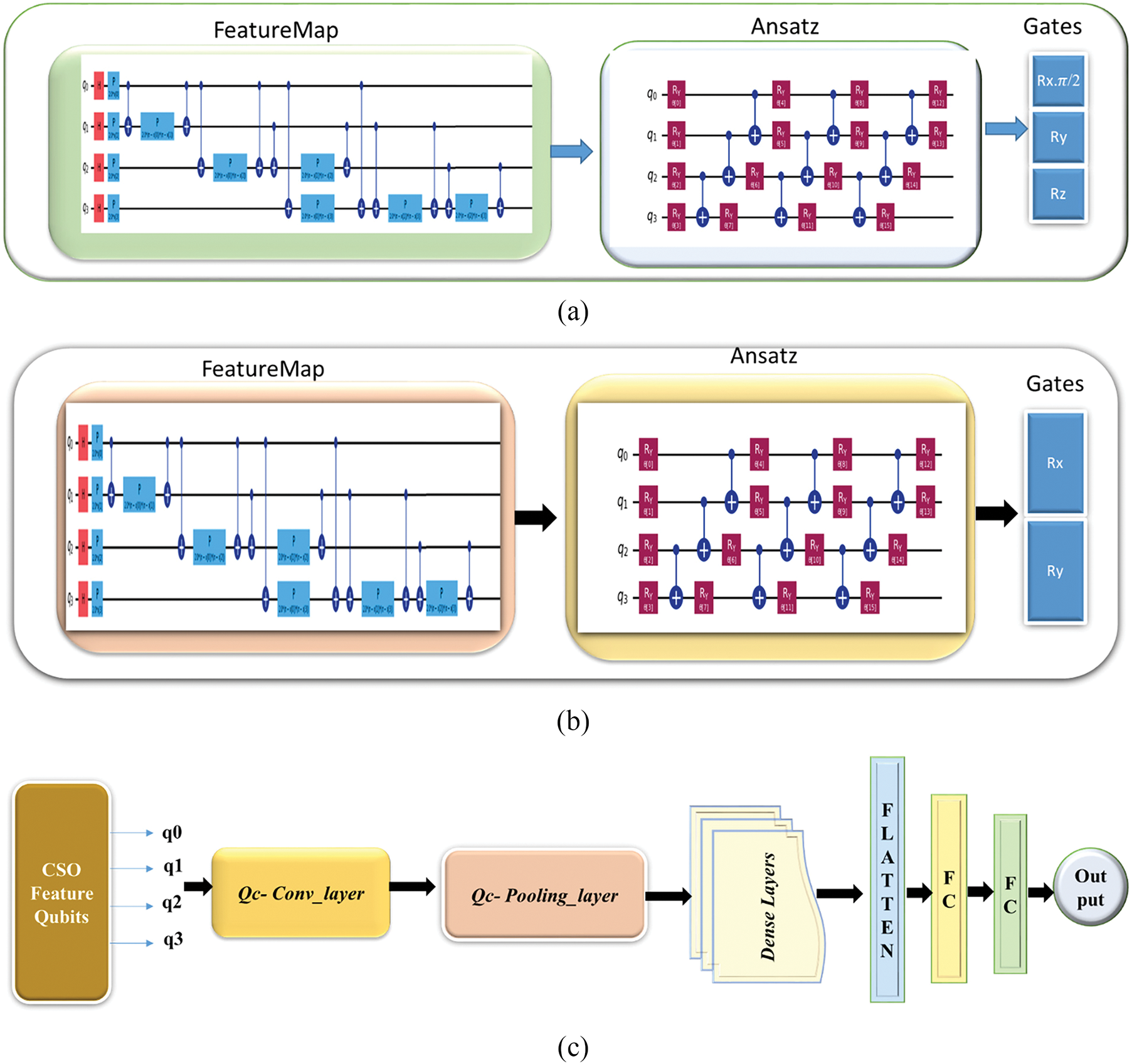
Figure 2: (a): QC-Convolution layer, (b): QC-Pooling layer, (c): QHF-CS model architecture

The QHF-CS model for heart failure prediction is constructed by combining a quantum ansatz with a quantum feature map. The feature map encodes conventional input features, and the ansatz learns the best parameters for data classification. To improve the model’s performance, the whole design uses quantum speedup methods and quantum processing to capture complicated data correlations. The suggested QHF-CS for heart failure prediction is provided by Algorithm 1, which also contains the pseudo-code.

A. Interpretability of Quantum Feature Maps and State Transformations

In the QHF-CS model, quantum feature maps serve as the initial embedding mechanism for transforming classical clinical features—selected using Cuckoo Search Optimization (e.g., creatinine phosphokinase, platelets, serum sodium, ejection fraction)—into quantum states. Each quantum feature map projects these features into a high-dimensional Hilbert space ℋ, enabling the quantum circuit to exploit non-classical correlations for better representation and prediction. The transformed quantum states evolve through parameterized layers and entangling operations that mimic convolution and pooling, forming the core of quantum convolutional neural networks (QCNNs). Below, we describe each feature map’s mathematical encoding and interpretability in the context of clinical decision-making.

(1) ZZFeatureMap—Phase Encoding with Pairwise Correlations

The ZZFeatureMap encodes classical data via entangled Pauli-Z rotations, which introduces phase shifts based on pairwise interactions of feature components using the Eq. (16):

UZZ(x)=∏i<jexp⁡(iθijZiZj)(16)

For normalized feature vector = [x1,x2,x3,x4], the encoding uses controlled phase interactions using the Eq. (17):

UZZ(x)=∏i<jeiπxixjZiZj(17)

This transformation results in a quantum state using the Eq. (18):

|ψZZ⟩=UZZ(x)H⨂n|0⟩⨂n(18)

where H⨂n applies Hadamard gates to initialize superposition across qubits. The entanglement structure introduced by ZiZj terms reflects interactions between biomarkers, e.g., how creatinine phosphokinase interacts with serum sodium in disease manifestation. These correlations alter the interference patterns measured at the end of the circuit and are crucial for understanding biomarker interdependence in heart failure risk.

(2) RealAmplitudes—Rotation-Based Single-Qubit Encodings

The RealAmplitudes ansatz encodes classical clinical features into quantum states by applying single-qubit Y-axis rotations (RY gates) followed by a chain of CNOT gates to entangle adjacent qubits. The unitary transformation applied across all n qubits can be expressed using the Eq. (19):

URA(θ)=∏i=1nRY(θi).CX(i,i+1)(19)

Each θi is a scaled clinical feature (using the Eq. (20)), such that:

θi=α.xi(20)

where xi could represent features like ejection fraction, serum creatinine, or platelet count, and α is a normalization or scaling factor. Each qubit undergoes a rotation via the RY gate defined using the Eq. (21):

RY(θi)=exp(−iθi2Y)=cos(θi2)|0⟩+sin(θi2)|1⟩=[cos⁡(θi/2)sin(θi/2)−sin(θi/2)cos⁡(θi/2)](21)

This results in a quantum superposition of the basis states |0⟩ and |1⟩, where the amplitude of the |1⟩ state reflects the importance or activation strength of the corresponding clinical feature. The CX gates (CNOTs) introduce entanglement between adjacent qubits, enabling the circuit to capture correlations across encoded features.

This structure can be repeated in layers to improve the expressivity of the circuit using the Eq. (22):

URA(L)=(RY.CX)L(22)

In this study, if the ejection fraction (a key predictor of heart failure) is low—indicating impaired heart pumping efficiency—the associated angle θi becomes small. This increases the sine component in the rotation, thereby increasing the probability amplitude of measuring |1⟩ on that qubit. This means that the model associates a lower ejection fraction with a higher risk of heart failure. The CNOT gates that follow entangle adjacent qubits, enabling the circuit to learn local dependencies between features, such as how serum sodium and creatinine levels interact in contributing to cardiac dysfunction.

Thus, the RealAmplitudes ansatz maps scalar clinical features into quantum states and builds meaningful inter-feature relationships that enhance the model’s ability to classify borderline or ambiguous heart failure cases. The RY rotations project each feature into a qubit’s state on the Bloch sphere, while CNOT gates enable the model to capture inter-feature dependencies. This encoding allows the quantum model to represent non-linear decision boundaries and classify complex clinical patterns, even in small or imbalanced datasets.

(3) EfficientSU2—Generalized Parameterized Rotations and Entanglement

The EfficientSU2 ansatz is a highly expressive parameterized quantum circuit architecture combining single-qubit rotational and entangling gates to model complex, high-dimensional data distributions. In this design, each qubit undergoes a sequence of RY and RZ rotations controlled by trainable parameters, followed by a Controlled-X (CX) entanglement layer. The complete transformation is applied in multiple layers (depth L), enhancing the circuit’s learning capacity for i-th qubit and l-th layer, as shown in using Eq. (23):

UESU2(θ,ϕ)=∏l=1L[∏i=1nRY(θi,l).RZ(ϕi,l)].CX Layer(23)

Each qubit’s state is rotated along two axes using the Eq. (24):

Rz(ϕ).RY(θ)|0⟩=e−iϕ2cos(θ2)|0⟩+eiϕ2sin(θ2)|1⟩=[cos⁡(θ/2)e−iϕ2sin(θ/2)eiϕ2−sin(θ/2)e−iϕ2cos⁡(θ/2)eiϕ2](24)

This rotational structure enables the ansatz to represent amplitude and phase information, increasing the circuit’s expressive power. The CX layer introduces entanglement between qubits, allowing the circuit to capture global correlations across clinical features.

In heart failure prediction, classical clinical features such as ejection fraction, serum creatinine, and platelet count are scaled and used to initialize or train the parameters θ and ϕ. While individual features might only weakly correlate with heart failure outcomes, EfficientSU2 captures complex, higher-order interactions—such as the combined influence of low sodium and high creatinine.

(4) Training the QCNN Model

The training process for the QHF-CS model requires a dataset for heart failure prediction fitting and the implementation of components selected from CS as input data. The conventional data X gets transformed into quantum states through the use of the feature map. The optimization process employs COBYLA (Constrained Optimization BY Linear Approximations) as its classical parameter optimization method. COBYLA represents an optimization tool without gradient dependencies, which shows good results when processing non-smooth function objectives in quantum systems.

The cost function to be minimized is the cross-entropy loss L(θ), defined using the Eq. (25):

L(θ)=−1m∑i=1m[yilog⁡(y^i(θ))+(1−yi)log⁡(1−y^i(θ))](25)

B. Quantum Speedup Optimization

Implementation of quantum speedup relies on effective qubit-based classical feature encoding mixed with parallel computation within QHF-CS models. The selected features are processed as quantum states in the feature maps through parallel quantum operations that leverage quantum speedup methods. As qubit numbers increase, QHF-CS benefits from its parallel processing mechanics, which leads to reduced computational difficulty and improved model functioning. The QHF-CS allows better heart failure prediction with high accuracy and efficient computation using qubit encoding and quantum gate operations.

3.2 Proposed Model Algorithm

QHF-CS Model for Heart Failure Prediction uses Cuckoo Search optimization and quantum computing according to Algorithm 1. QHF-CS Model commences its process by creating a quantum circuit containing feature maps and variational ansatz that converts patient data into quantum states. The procedure involves data normalization, and skewness analysis of clinical values and gene expression results to create appropriate input for quantum computational platforms. The essential process targets establishing a quantum convolutional neural network (QCNN) which utilizes selected features for heart failure predictions under COBYLA optimization. Standard diagnostic metrics employed during test dataset evaluation show how the model performs efficiently for advanced healthcare needs.

4  Results and Analysis

Quantum Machine Learning (QML) is explored by building and implementing a QCNN using IBM Pennylane [43]. This framework is famous for its powerful tools for developing quantum algorithms, including quantum machine learning. We apply our QHF-CS model to the prediction of the heart failure dataset to analyze skewness and determine the significance of selecting features in the Cooke search algorithms using quantum computational principles to improve diagnostic accuracy. Table 2 shows the experimental setup.

A. Dataset Description

The heart failure prediction dataset includes 299 medical records from April to December 2015 [44]. This 40–95-year-old study sample consists of 195 men and 105 women. The patients had NYHA class III or IV left ventricular systolic dysfunction. Data includes a 13-variable clinical, bodily, and lifestyle combination. Anaemia, high blood pressure, diabetes, sex, smoking status, CPK, ejection fraction, serum creatinine, and serum sodium are among the 13 variables analyzed. The dataset investigates heart failure outcomes. Over an average 130-day follow-up, a binary target variable represents patient survival as death. Unbalanced data shows 203 survivors and 96 deaths. A thorough TA analysis is crucial for improving heart failure patient outcomes.

Another dataset, the heart disease dataset [45], combines five widely used sources—Cleveland, Hungarian, Switzerland, Long Beach, VA, and Statlog—into a unified dataset with 11 standard features. It comprises 1190 instances, making it the largest for research. The primary goal is to predict the presence of heart disease, represented as a binary classification problem. Many studies use this dataset to benchmark machine learning models in the medical domain. The dataset undergoes further preprocessing with one-hot encoding, increasing the feature count to 18.

B. Evaluation Metrics

This section presents relevant assessment measures used to evaluate the models in this research endeavour. Given that our study involves a classification job, we used many performance indicators, including accuracy, recall, precision, false positive rate (FPR), f1 score, and AUC-ROC curve using the Eqs. (26)–(29). According to the concept of one vs. all, machine learning classification jobs often include four scenarios:

•   The term “True Positive” (TP) refers to the accurate classification of positive samples.

•   The term “False Negative” (FN) refers to the misclassification of positive samples.

•   The term “False Positive” (FP) refers to the misclassification of negative samples.

•   A true negative (TN) refers to samples that have been appropriately classified as negative.

Accuracy

Models involving classification receive their assessment through accuracy measurements. The predictive model demonstrates its performance level through its accuracy percentage [46]. The following presents the precision calculation formula:

Accuracy=TotalNumberofCorrectPredictionsTotalPredictions(26)

Precision

The precision value defines the number of actual positive outcomes correctly identified from all predicted positive outcomes [46]. The formula of precision is

Precision=TPTP+FP(27)

Recall

Recall indicates a fraction of actual positives predicted correctly [46].

Recall=TPTP+FN(28)

F1-Score

The F1-Score reveals the equilibrium between recall accuracy and precision level [46]. The mathematical expression for calculating F1-Score appears thus:

F1−Score=2∗(Precision∗Recall)Precision+Recall(29)

AUC-ROC

The performance evaluation of each model depends on the receiver operating characteristic (ROC) curve area under the curve (AUC) calculation and F-score measurements. The Area Under the Curve (AUC) represents a complete performance assessment method for all possible categorization thresholds [46]. The AUC ratio ranges from 0 to 1. When the value approaches 1, the model exhibits a robust categorization capability.

C. Evaluation of Skew Data Calculation

Values in the dataset deviate from a normal distribution due to imbalance or Skewness. To quantify and understand this deviation, each attribute’s Skewness is calculated using Eq. (1). Skewness statistically measures distribution asymmetry around the mean. A positive or negative skewness indicates a long right or left tail, while a perfectly symmetrical distribution has zero Skewness. Table 3 shows how each attribute’s distribution leans toward higher or lower values, indicating which attributes may need more data preprocessing to meet statistical modelling requirements or improve machine learning algorithm performance. Analytical methods reveal data biases, inform data standards, and model training decisions.

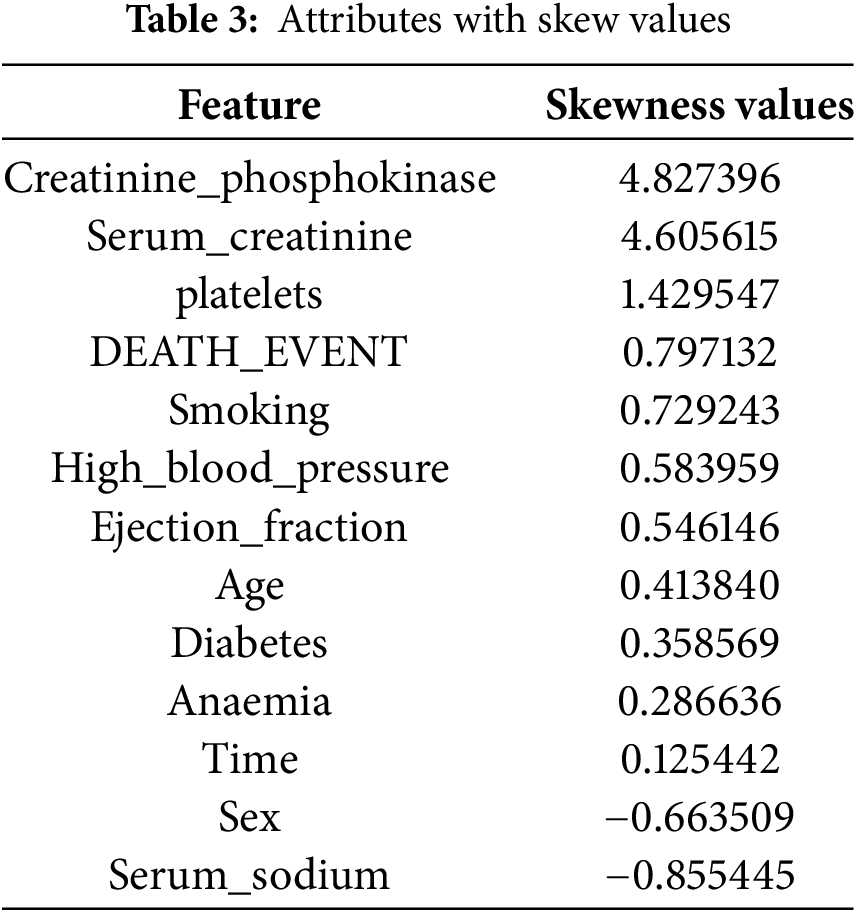
For attribute skewness before normalization, see Table 3—probability distribution skewness around a variable’s mean. Table 3 displays attributes like ‘creatinine_phosphokinase’ and ‘serum_creatinine’ with high positive skewness values of 4.827396 and 4.605615, respectively, indicating a right-skewed distribution with a long tail toward higher values. The data contains lower values with occasional high outliers. Negative skewness values (−0.855445 and −0.663509) indicate left-skewed distributions for serum_sodium and sex, indicating higher values with fewer outliers. Skewness significantly impacts performance in statistical analyses and machine learning models that assume input data is usually distributed. Positive and negative skewness indicate lower and higher distribution values, respectively. Variables like `time` with low skewness values indicate symmetric distributions. Data attribute skewness must be identified and quantified during data preprocessing to determine if data transformation is needed to improve model analytical or predictive performance.

D. Normalization of Skew Data Attributes

After data distribution standardization with Z-score normalization, Table 4 shows dataset attribute skewness. This process normalizes data distribution by setting the attribute mean to 0 and the standard deviation to 1. After normalization, attributes like ‘DEATH_EVENT’, ‘smoking’, and ‘high_blood_pressure’ continue to have positive skewness values (0.797132, 0.729243, and 0.583959), indicating a right-skewed distribution with a longer tail towards higher However, attributes like ‘serum_sodium’ and sex have negative skewness values (−0.855445 and −0.663509), suggesting a left-skewness with a longer tail toward lower values. After normalization, creatinine_phosphokinase, serum_creatinine, and ejection_fraction are near zero, indicating symmetry. Normalization is required in data analysis and modelling because many statistical methods and machine learning algorithms assume input data is usually distributed. Normalizing skewness helps understand data structure and improves predictions and analyses, representing highly skewed attributes before and after normalization. Fig. 3 shows the highly skewed attributes before and after normalization.

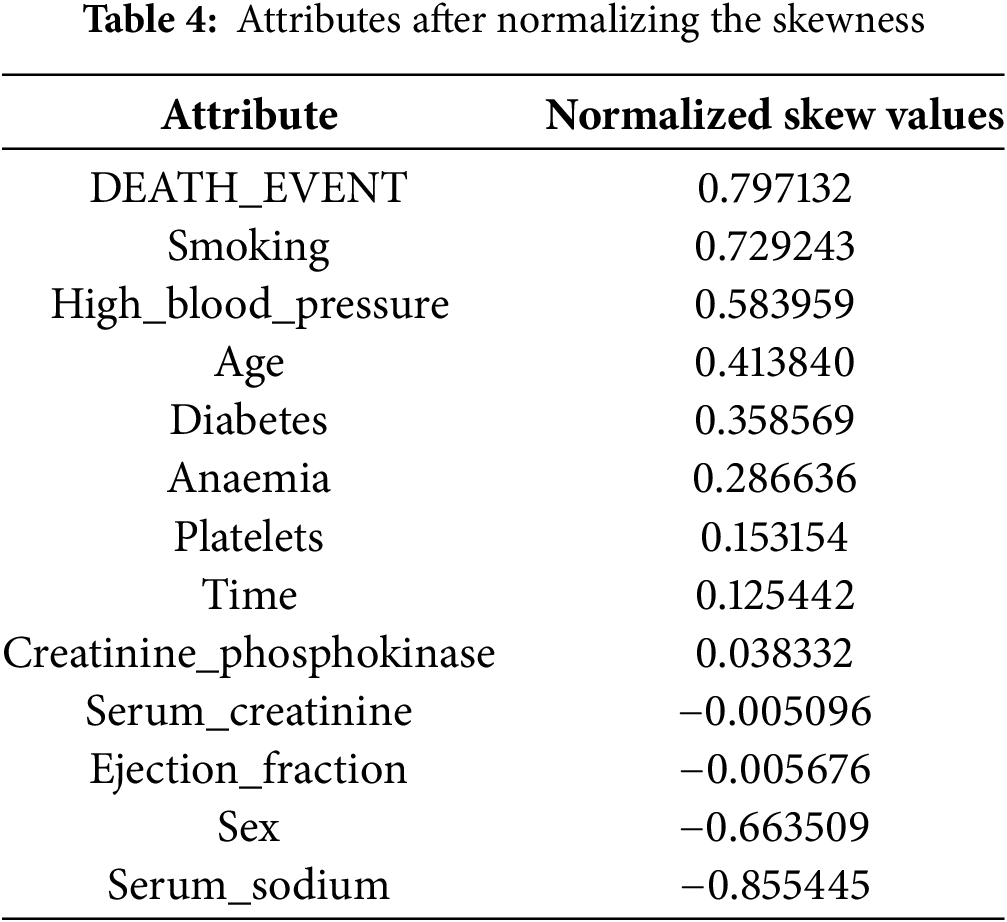
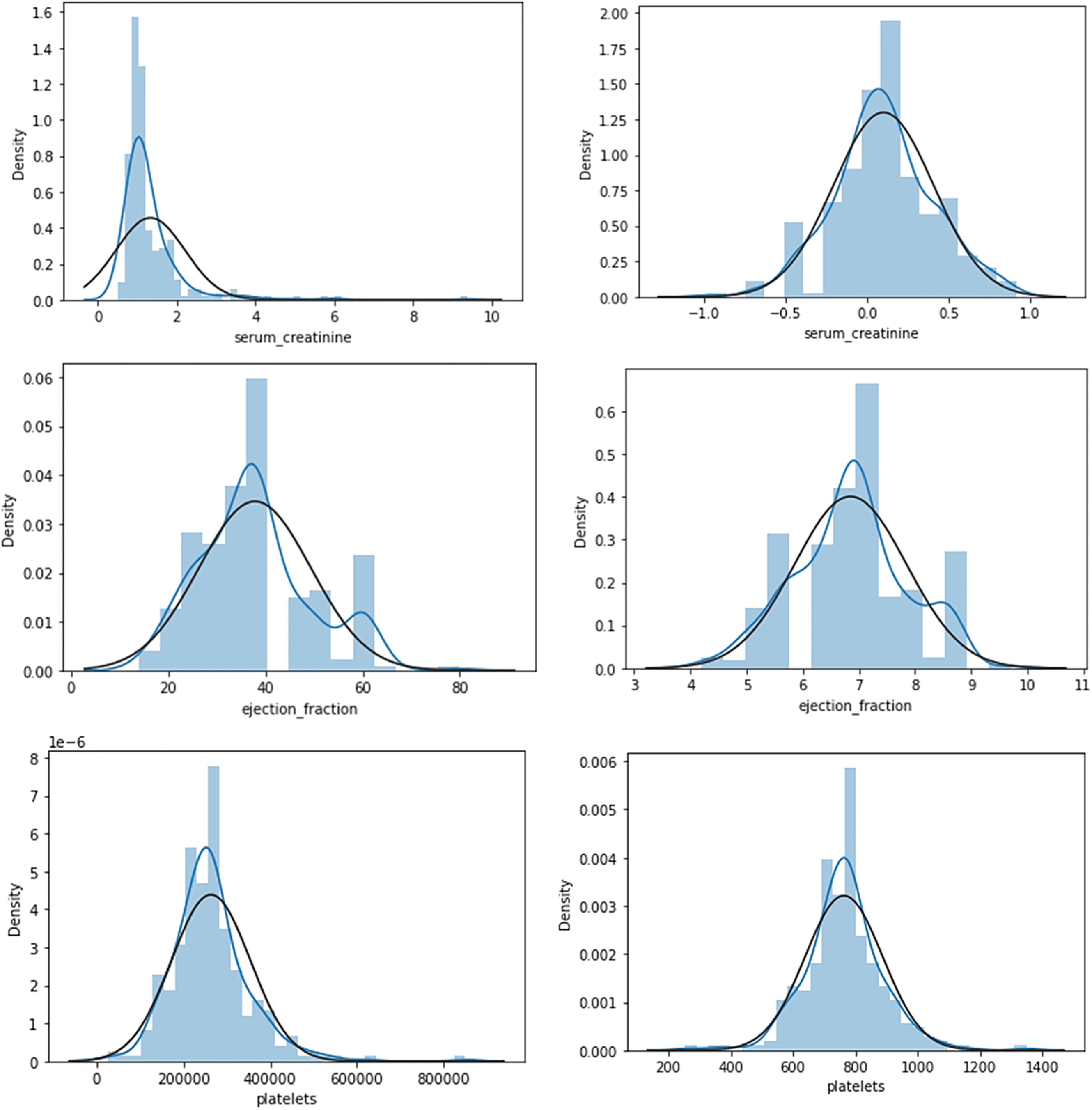
Figure 3: Visualization of highly skewed attributes before and after normalization

E. Feature Selection Impact on Model Performance

Table 5 highlights the performance of different meta-heuristic optimization techniques for top-4 feature selection in the context of quantum circuit training. Among the methods evaluated—Cuckoo Search (CS), Artificial Bee Colony (ABC), and Particle Swarm Optimization (POS)—Cuckoo Search demonstrates the most optimal outcome, achieving the lowest fitness value of 0.1285, which indicates superior feature subset selection, with the chosen feature qubits being creatinine phosphokinase, platelets, serum sodium, and ejection fraction, all selected based on minimal skewness and high relevance. The Cuckoo Search (CS) meta-heuristic algorithm created a population of 10, iterating 100 times to assess the impact of population dynamics on the election results. Since meta-heuristic approaches are stochastic, the algorithm was executed 10 times to ensure the reliability and stability of the selected feature qubits. These features are well-suited for constructing and training an efficient and accurate quantum circuit model, emphasizing Cuckoo Search as the most effective technique in this optimization scenario.

F. Quantum Circuit Using ZZFeatureMap

Fig. 4 shows QHF-CS using ZZFeatureMap on four Cuckoo Search-generated feature qubits. Installing the Pauli-X (Hadamard) gate over four qubits (q0, q1, q2, q3) creates a superposition state. The controlled-Z gates create quantum entanglement that investigates non-linear relationships between creatinine phosphokinase, platelets, ejection fraction, and serum sodium. Heart failure is predicted by ejection fraction, creatinine phosphokinase, serum sodium, and platelets—phase shift gates (P) use feature values to manipulate phase to improve model data distinction strategically. Repeated entanglement and phase operations enhance learning, leading to more accurate heart failure risk assessment simulations. Quantum parallelism improved by ZZFeatureMap improves predictive analytics for detailed heart failure clinical patterns.

Figure 4: QCNN quantum circuit using ZZFeatureMap

G. Quantum Circuit Using RealAmplitudes

The quantum circuit in Fig. 5 includes four Cuckoo Search-selected qubits (q0, q1, q2, q3) for heart failure prediction optimization by the RealAmplitudes feature map algorithm. The RY(θ) rotation gates apply to each qubit in the circuit sequentially. Gates θ0-15 rotate the Bloch sphere’s y-axis by θ when processing real-valued data into qubit quantum states. After rotation gates that encode complex clinical feature correlations, Controlled-NOT (CNOT) gates entangle qubits. RY gates modulate the quantum state at every entanglement stage, giving the circuit many exploration opportunities to match heart failure patterns. The configuration lets quantum machine learning models use qubit superposition and entanglement to compute. The setup improves model detection accuracy for dataset nuances crucial for early heart failure detection while demonstrating quantum mechanics’ medical diagnostic capabilities.

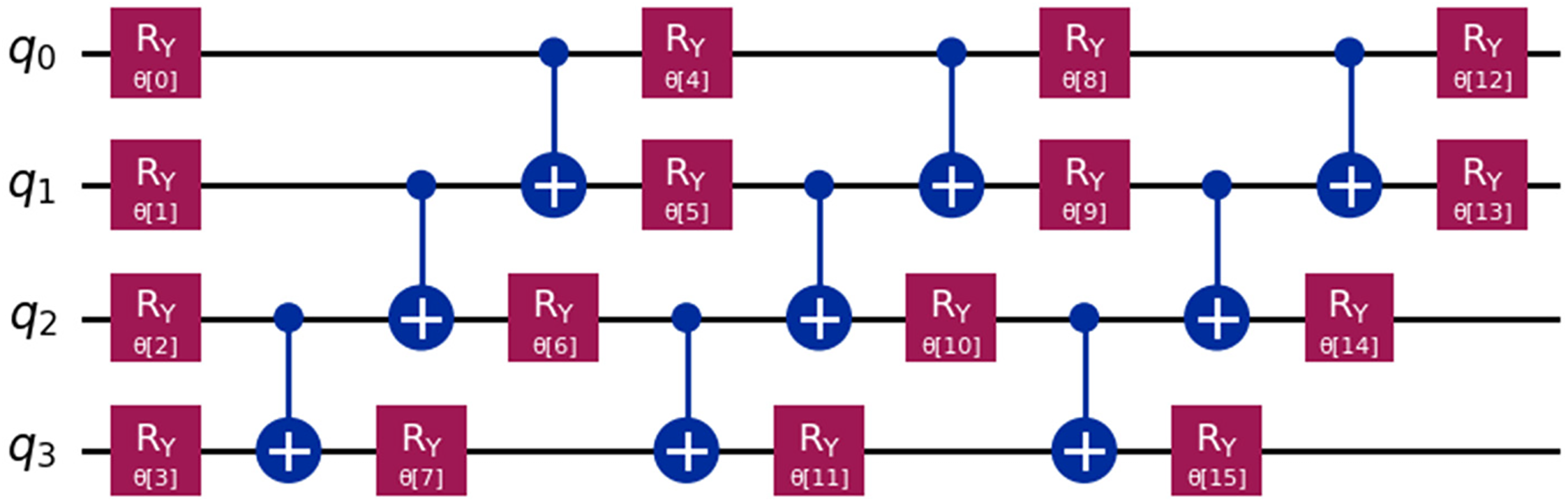
Figure 5: Quantum circuit using RealAmplitudes

H. Quantum Circuit Using RealAmplitudes

The heart failure prediction quantum circuit uses the EfficientSU2 feature map on four qubits (q0, q1, q2, q3) selected by Cuckoo Search (Fig. 6). All qubits receive RY and RZ broad parametric gates from the circuit. Bloch sphere rotation gates rotate axes y and z at angles (θ0 to θ31) associated with their gate subscripts. Rotational gates are needed to build complex quantum data representations for real and imaginary data. At intervals, CNOT gates entangle qubits between rotational gates. Entanglement is required to track creatinine phosphokinase, platelets, serum sodium, and ejection fraction interactions. The model can better explore and represent the high-dimensional heart failure dataset space with active Ry and Rz gate variations before and after every CNOT gate. This arrangement allows the EfficientSU2 feature map to perform quantum mechanical non-linear data transformations for heart failure medical outcome prediction. The circuit structure’s quantum parallelism and entanglement features improve the model’s diagnostic capability and precision for medical quantum computing applications.

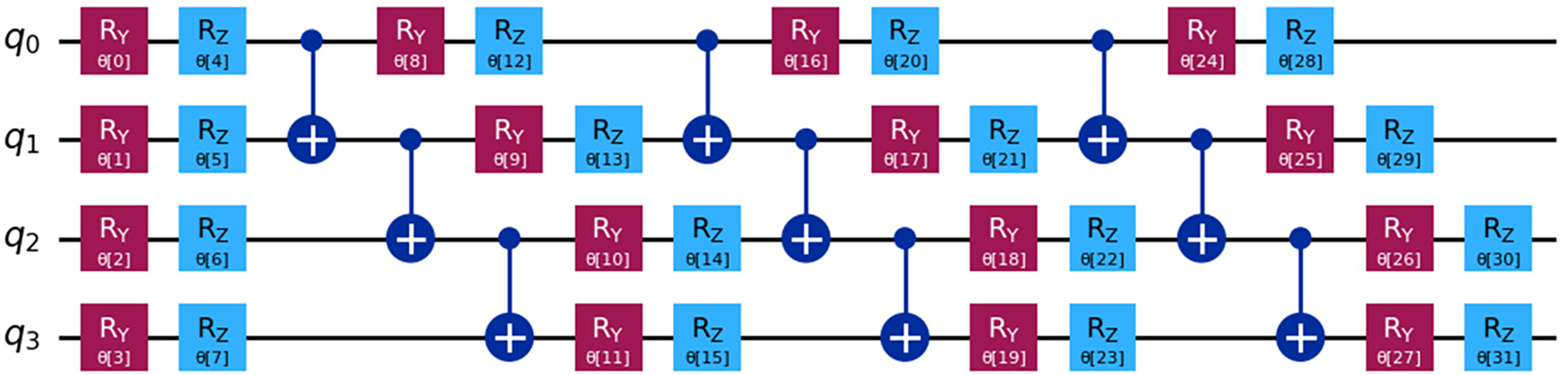
Figure 6: Quantum circuit using EfficientSU2

I. Performance of QHF-CS on Heart Failure Dataset

Fig. 7 illustrates the QHF-CS objective function value changes during each iteration of the Cuckoo Search feature selection process. This behaviour shows optimization. When finding the best feature set to predict heart failure, the function’s subjective value rapidly decreases in the first phase and stabilizes before the tenth iteration. The curve stabilizes and flattens after a sharp initial decrease, indicating a gradual objective function value reduction with minor fluctuations from the 20th iteration onward. Cuckoo searches fine-tuning parameters within a narrow range to find a near-optimal solution. Around iterations 80 to 100, the plateau at the graph’s end shows diminishing returns from additional iterations. The results demonstrate the cuckoo search’s efficiency in finding an optimal solution that improves predictive accuracy without overfitting, balancing exploration and exploitation in the search space.

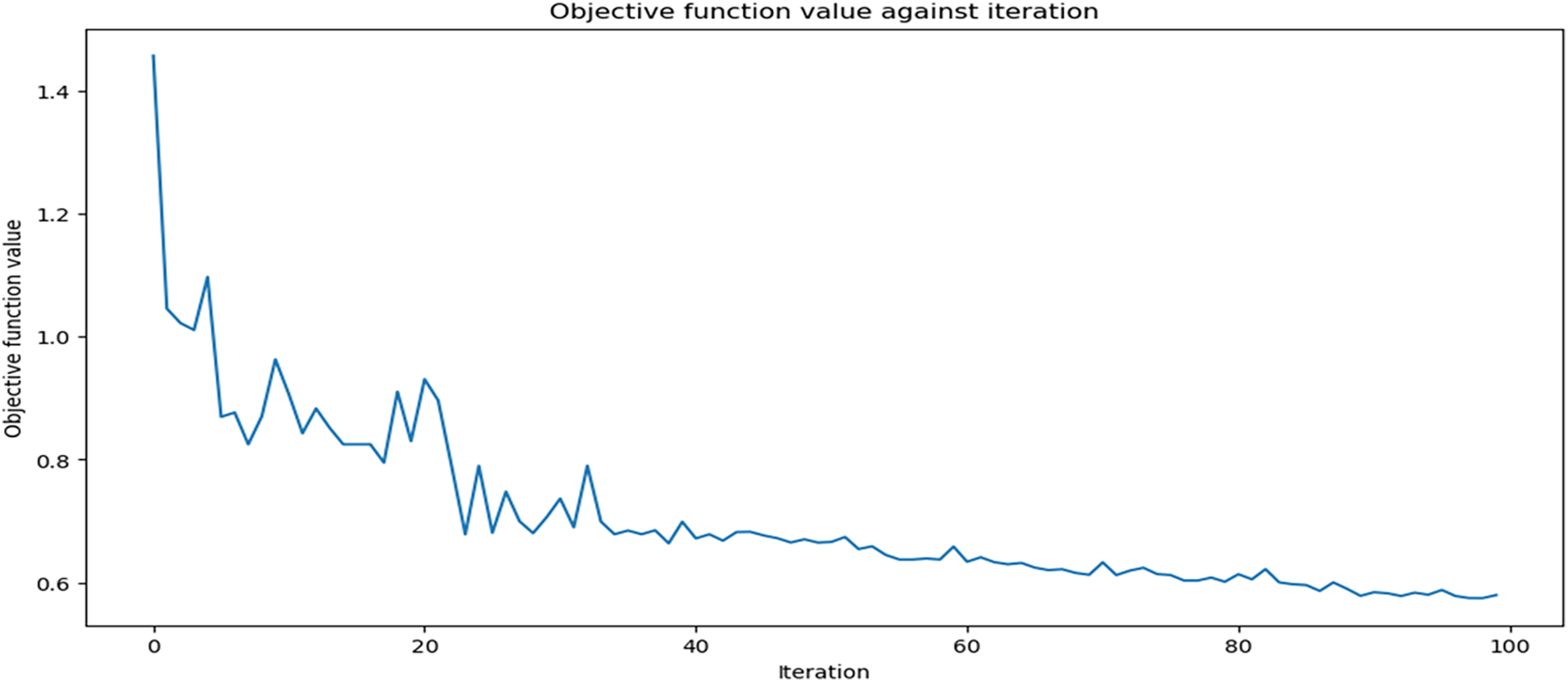
Figure 7: QHF-CS objective function values for 100 iterations

J. Evaluating QHF-CS Model in Heart Failure Classification Performance

Fig. 8 presents the accuracy and loss performance of the QHF-CS model applied to heart failure prediction over 40 epochs, utilizing four feature qubits selected via the Cuckoo Search algorithm. In Fig. 8, both training and validation accuracy exhibit an upward trend, especially noticeable in the initial epochs, where there is a sharp rise in accuracy, signalling rapid learning and effective adaptation to the heart failure dataset. After the initial surge, the accuracy curves plateau, indicating that the model has largely stabilized and is making incremental improvements, which suggests a good generalization on unseen data as the validation accuracy closely tracks the training accuracy without significant divergence.

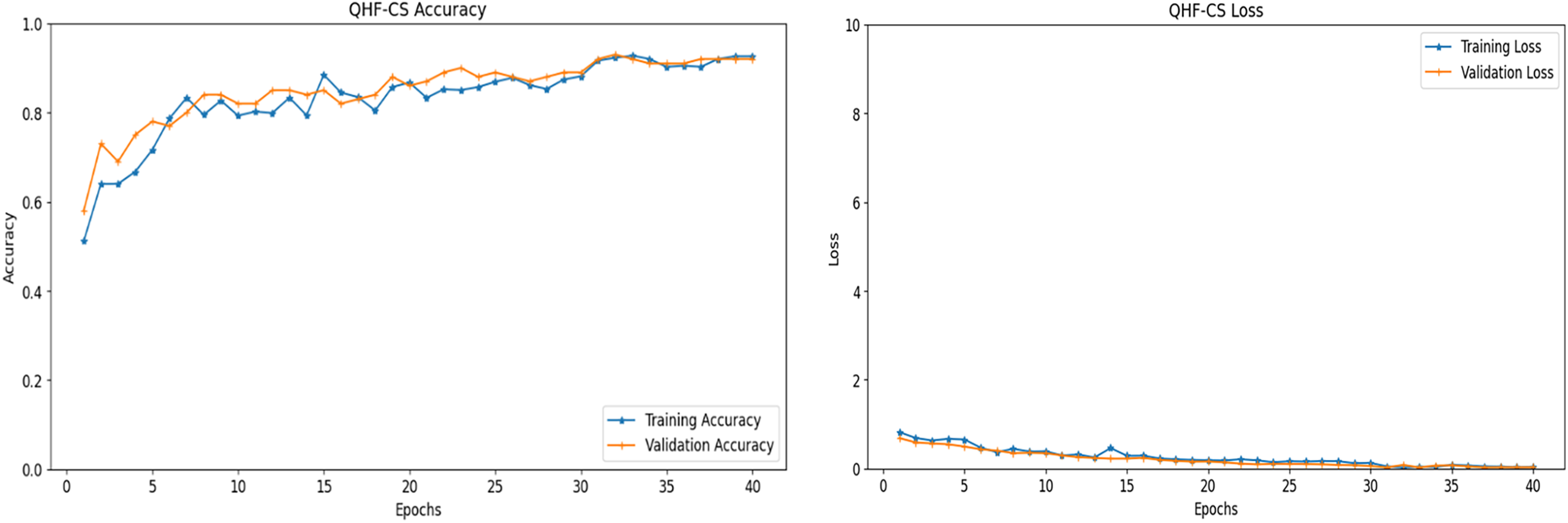
Figure 8: Accuracy and loss performance of QHF-CS on heart failure prediction for 4 qubits

In contrast, in Fig. 8, the training and validation loss decreased sharply in the early epochs and then levelled off. For reliable heart failure prediction, the model must minimize the error between predicted outcomes and actual labels, which this decrease in loss shows. Nearly identical training and validation loss lines across epochs suggest the model is not overfitting, performing consistently on both sets. These performance metrics show that the QHF-CS model’s cuckoo search feature selection efficiently optimizes parameter settings, resulting in robust, generalizable predictions across epochs. After the initial phase, accuracy and loss converge due to a balanced learning process that optimizes quantum circuit parameters to capture complex patterns in heart failure data.

Two quantum feature maps—RealAmplitudes and EfficientSU2—on a four-qubit heart failure prediction dataset in Table 6 compare the QHF-CS model’s performance metrics. High precision, recall, F1-score, and accuracy of 0.92 indicate that RealAmplitudes correctly detect vital patterns for heart failure prediction. EfficientSU2 feature map improves precision and recall to 0.94 and F1-score and accuracy to 0.95 and 0.94. The EfficientSU2 feature map leveraged entanglement and superposition to enhance the representation of complex data structures. EfficientSU2 creates predictive models to strengthen heart failure indicator assessments and reliability, making it a better feature map than RealAmplitudes for quantum circuit design. On a four-qubit dataset, RealAmplitudes and EfficientSU2 show QHF-CS heart failure prediction performance (Fig. 9). EfficientSU2 has higher precision, recall, and F1-score than other feature maps, indicating its potential to detect complex patterns for quantum circuit representation in optimization.

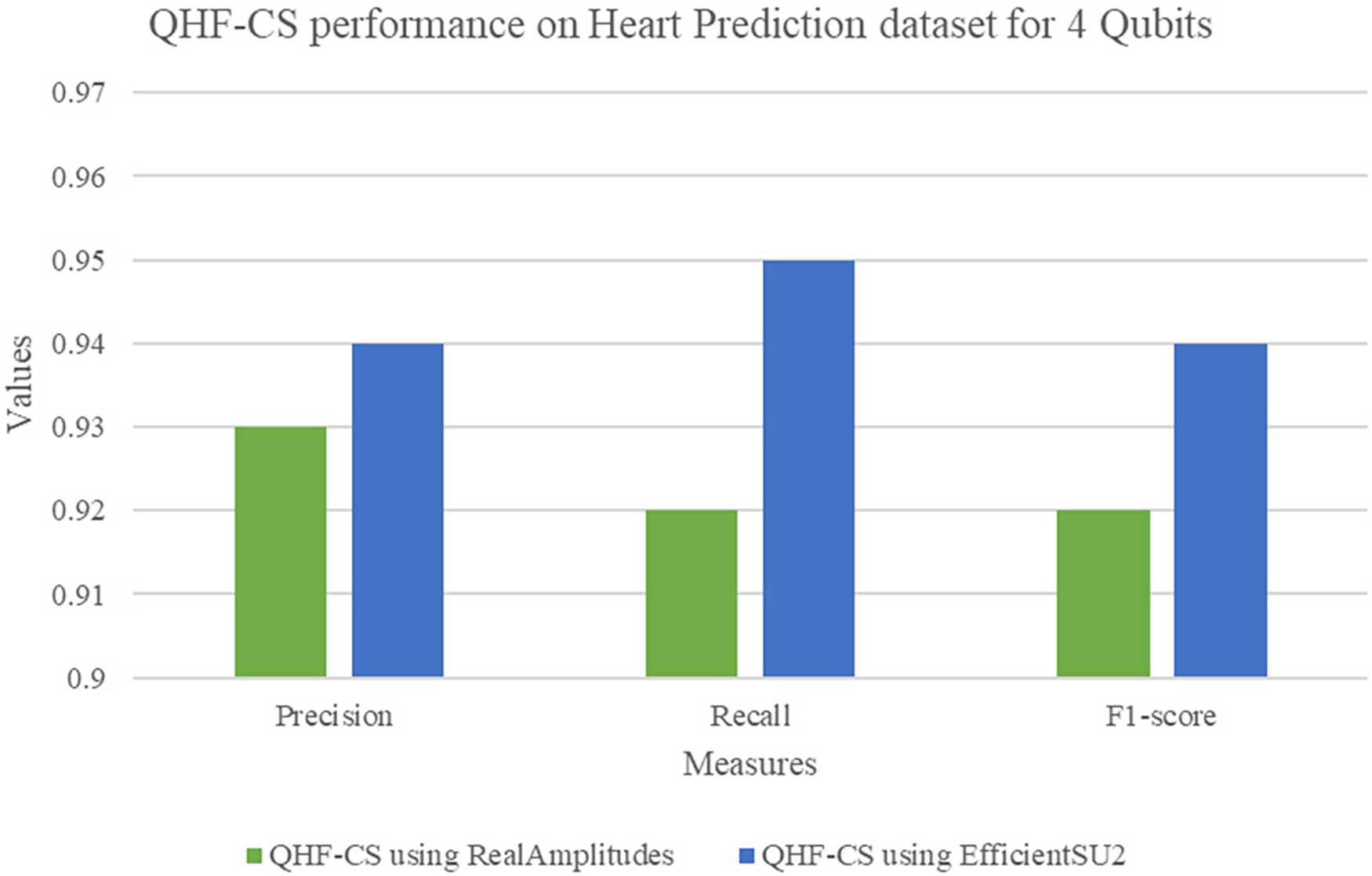
Figure 9: QHF-CS performance measures on heart prediction dataset for 4 qubits

K. QHF-CS ROC analysis

The QHF-CS model’s ROC curve predicts heart failure using four qubits, as shown in Fig. 10. It is sensitive to false favourable rates at different classification thresholds. Because the ROC curve rises steeply, model sensitivity and predictive power appear in the top-left corner. The 0.94 Area Under the Curve shows that the model can distinguish heart failure patients from healthy controls. Because such models verify many true positives while eliminating false positives, AUC values near 1.0 indicate optimal classification results. The dashed diagonal line shows that the QHF-CS model outperforms chance-level prediction (AUC = 0.5). Cuckoo Search and optimal quantum circuit parameterization improve classification results, as demonstrated by the high AUC score. This study shows that the QHF-CS model can predict complex, high-dimensional heart failure, supporting its clinical decision-making potential.

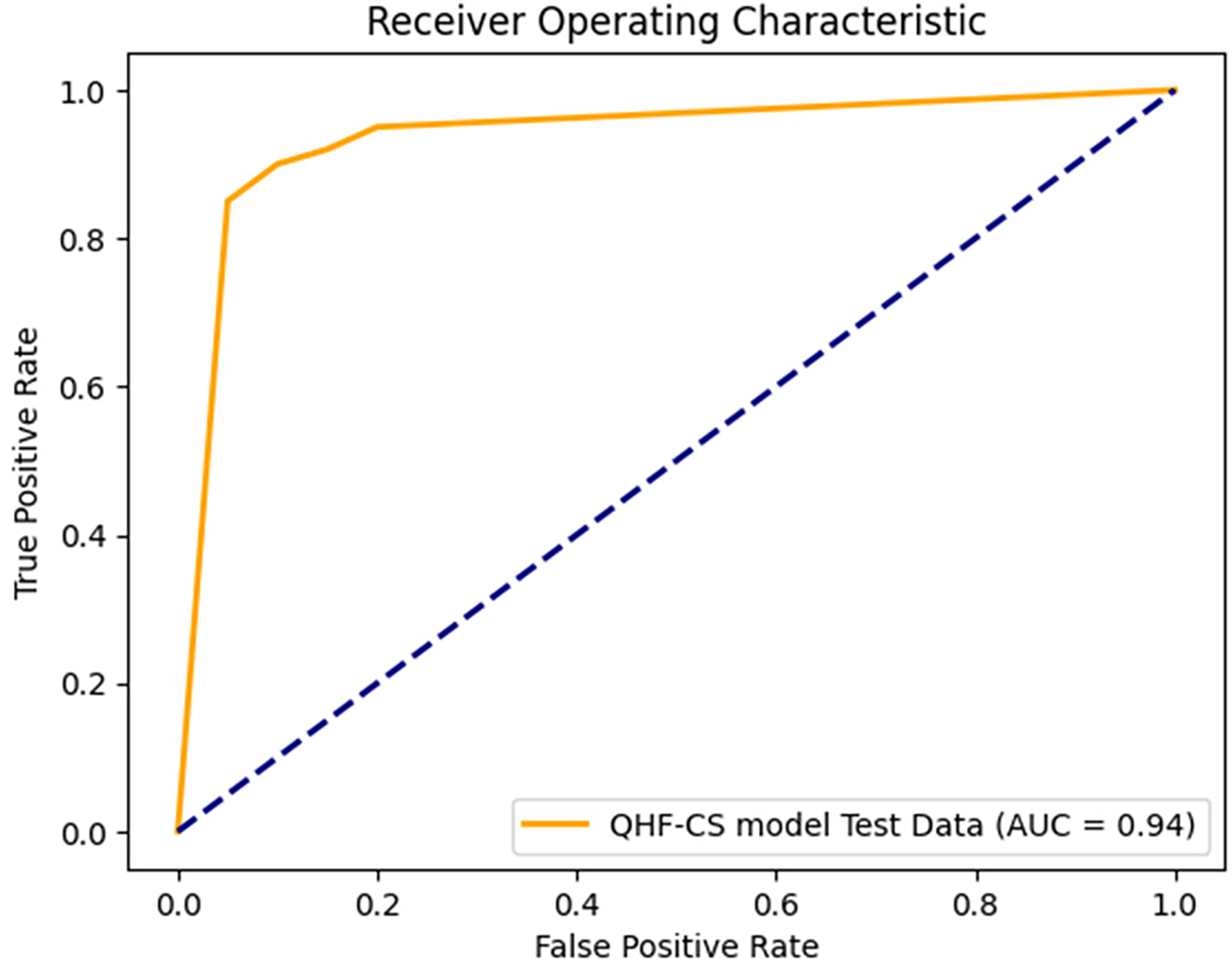
Figure 10: ROC analysis of QHF-CS on heart failure prediction for 4 qubits

L. QHF-CS Performance on Heart Disease Dataset

Table 7 presents the results of the top-4 feature selection using three heuristic optimization techniques—Cuckoo Search, Artificial Bee Colony (ABC), and Particle Swarm Optimization (PSO)—to enhance the generalizability of the proposed QHF-CS model on a secondary heart disease prediction dataset. Cuckoo Search achieved the lowest fitness value of 0.3251, identifying the most optimal and least skewed feature qubits: ST_Slope, ChestPainType, ExerciseAngina, and Sex. ABC and PSO also yielded competitive feature subsets, selecting combinations such as ST_slope_1, Oldpeak, and chest pain type_3. The consistent appearance of features like ExerciseAngina and Sex across all methods highlights their predictive significance. This cross-validated feature selection ensures that the QHF-CS model maintains high performance and robustness across diverse datasets, reinforcing its reliability in real-world clinical applications.

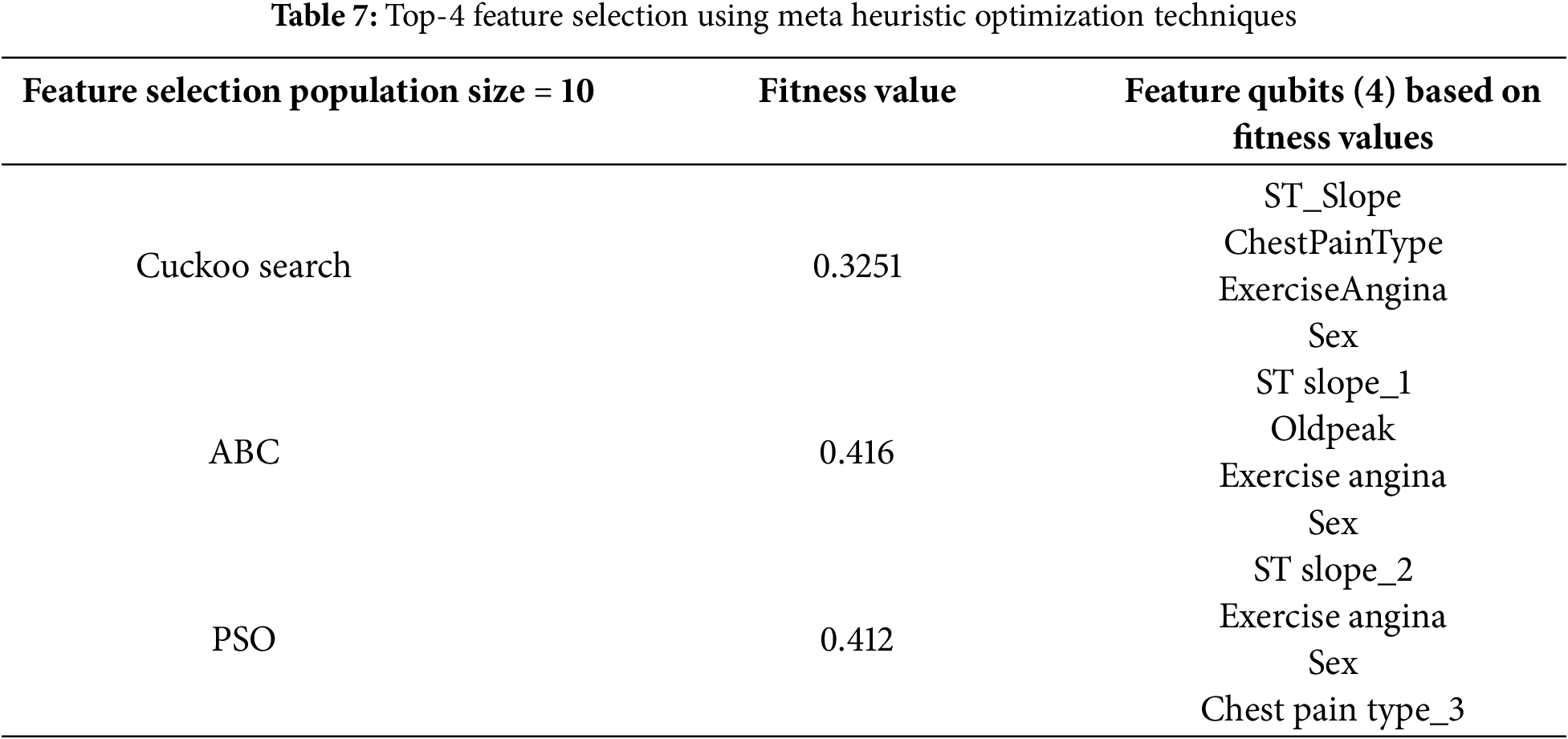
Fig. 11 illustrates the change in objective function value over 100 iterations of the Cuckoo Search algorithm applied to the Heart Disease dataset for feature selection. The objective function value drops sharply in the early iterations (up to around iteration 15), indicating that the algorithm rapidly identifies promising feature subsets. After this initial phase, the curve stabilises with minor fluctuations, reflecting a transition into a fine-tuning stage where the algorithm balances exploration and exploitation to refine the feature set. From iteration 80 onwards, the function plateaus, suggesting that further iterations yield diminishing improvements. This convergence behaviour demonstrates the efficiency of the Cuckoo Search in finding a near-optimal subset of features that enhances predictive performance while avoiding overfitting.

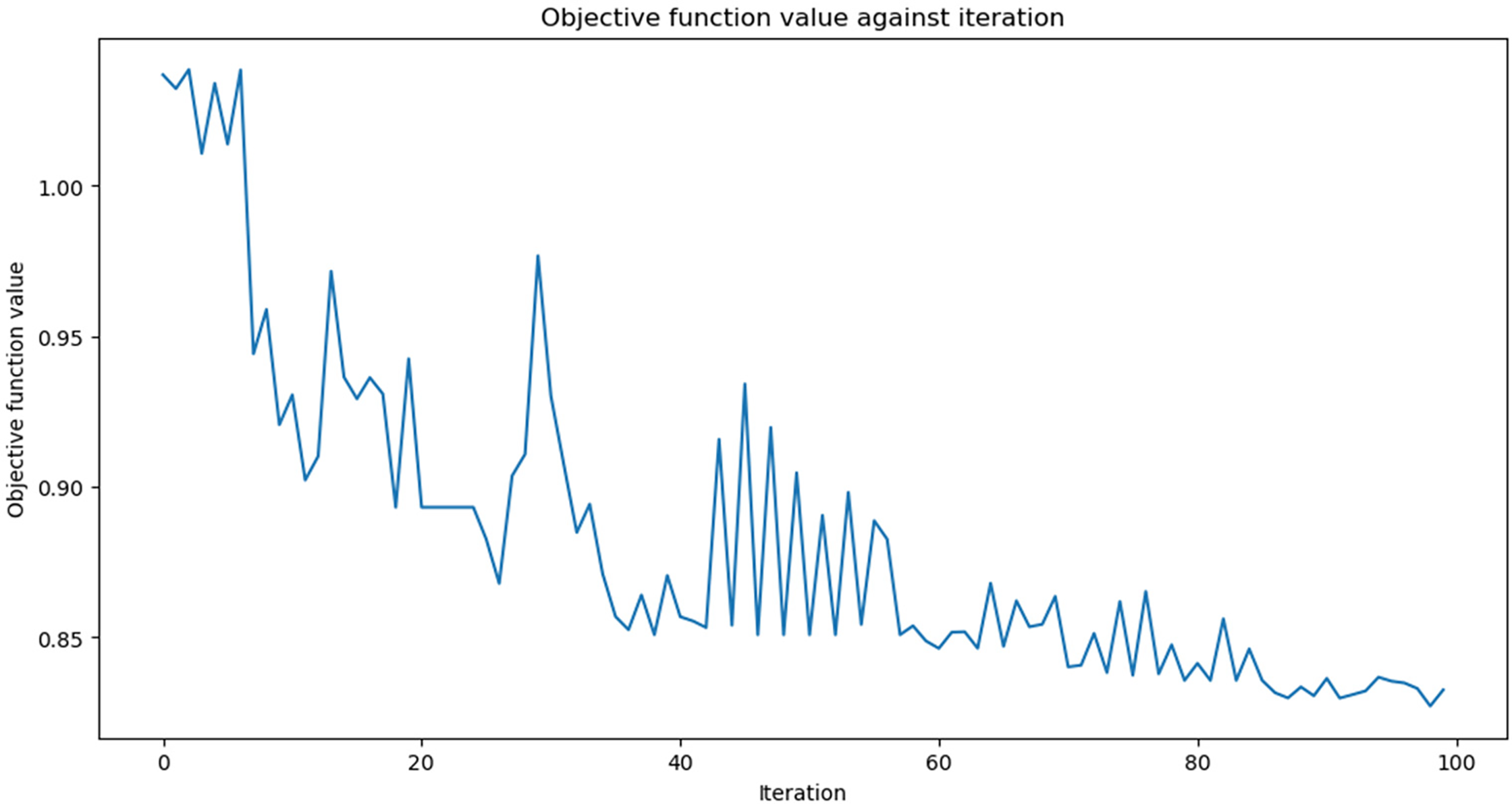
Figure 11: QHF-CS objective function values for 100 iterations on heart disease dataset

(1) Evaluating QHF-CS Model in Heart Disease Dataset

Fig. 12 shows the training and validation accuracy and loss performance of the QHF-CS model applied to heart disease prediction on the dataset using four feature qubits selected through the Cuckoo Search algorithm. Over 50 epochs, the training and validation accuracy curves demonstrate a strong upward trend, especially within the first 15 epochs, indicating rapid model learning and effective feature extraction. As training progresses, the accuracy curves plateau and converge near the maximum value. This suggests the model achieves stable and high performance without significant overfitting, as evidenced by the close alignment of training and validation accuracy. Correspondingly, the loss curves in the right panel depict a steady decline, with both training and validation loss decreasing consistently and converging toward minimal values, further affirming the model’s ability to generalize well to unseen data.

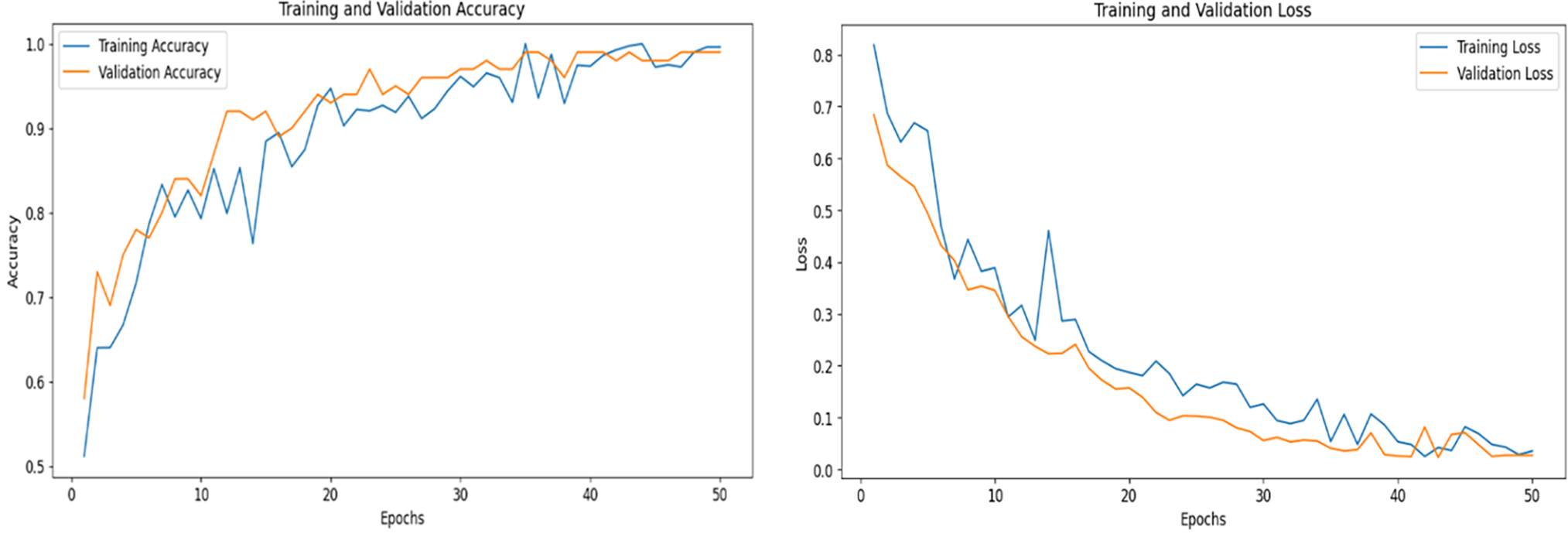
Figure 12: Accuracy and loss performance of QHF-CS on heart disease for 4 qubits

Table 8 presents the performance of the QHF-CS model on the Heart Disease dataset using two different quantum feature maps—RealAmplitudes and EfficientSU2—with four qubits. The results highlight that while both feature maps demonstrate strong predictive capabilities, the EfficientSU2 map slightly outperforms RealAmplitudes across all evaluation metrics. Specifically, EfficientSU2 achieves the highest accuracy of 92.5%, along with superior precision (0.920), recall (0.925), and F1-score (0.915), indicating a better overall balance between sensitivity and specificity. In contrast, RealAmplitudes shows a commendable but slightly lower performance, with an accuracy of 91.04% and an F1-score of 0.9023. These results suggest that the EfficientSU2 map provides a more expressive quantum circuit structure for encoding and extracting relevant heart disease features, improving classification effectiveness in the QHF-CS framework.

M. Comparison with Existing Studies

Table 9 compares the QHF-CS model to QML heart failure prediction methods. With 94% accuracy, the QHF-CS model outperforms QKNN [46] (88%), QML-VQC [47] (86.3%), QSVC [48] (92.09%), and QPSO-SVM [32] (92.31%). QHF-CS also outperforms hybrid quantum-classical models like QRFC (89%), QGNBC (85%), HQRF (91.64%), and HQMLP (92%). Cuckoo Search and the EfficientSU2 feature map help QHF-CS outperform KACQ-DCNN [40] (92.03%). Optimization of qubit encoding and quantum-enhanced learning use quantum entanglement and superposition to extract meaningful patterns from complex high-dimensional data, improving performance. Using quantum machine learning, the QHF-CS model predicts heart failure better than traditional and hybrid quantum-classical models. Fig. 13 shows that the QHF-CS model outperforms all other evaluation models with 94% accuracy. Cuckoo search optimization and quantum machine learning improve heart failure diagnosis, as shown in the graph.

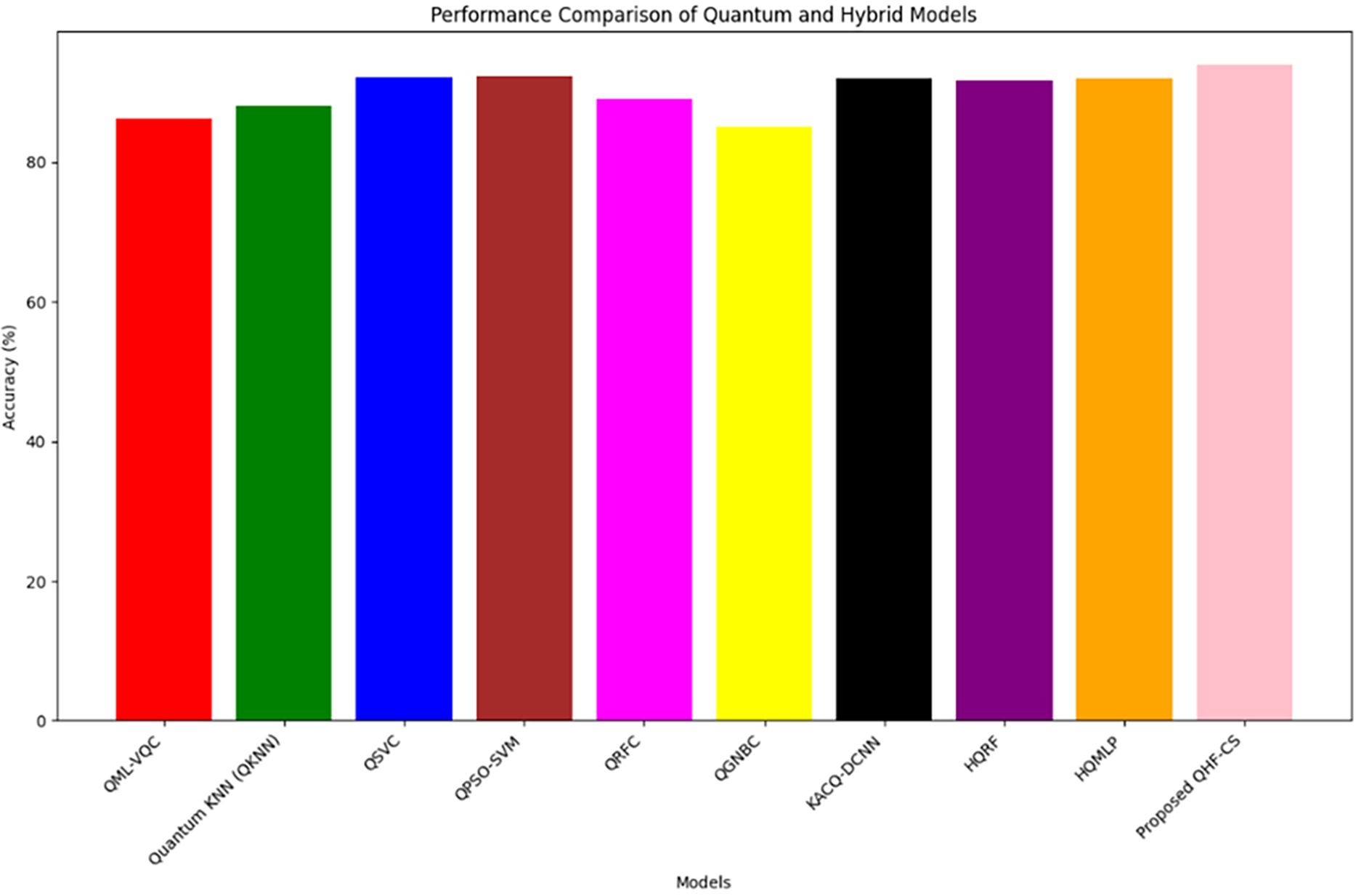
Figure 13: QHF-CS performance comparison with existing studies

Discussion

The QHF-CS model demonstrates superior performance in heart failure prediction by combining Quantum Convolutional Neural Networks (QCNNs) with meta-heuristic feature selection, achieving 94% accuracy on the heart failure dataset and 92.5% on the Heart Disease dataset using the EfficientSU2 feature map. The dataset, comprising 303 patient records with 13 clinical attributes, is widely recognized for its balanced structure and diagnostic relevance. To identify optimal feature qubits, multiple optimization techniques—including Ant Colony Optimization (ACO), Artificial Bee Colony (ABC), Particle Swarm Optimization (PSO), and Cuckoo Search Optimization (CSO)—were applied. Among these, CSO proved most effective, consistently selecting the most prevalent and clinically meaningful features—creatinine phosphokinase, platelets, serum sodium, and ejection fraction—based on a fitness function that maximizes predictive performance. Quantum feature maps like EfficientSU2 excel in capturing non-linear relationships and high-order correlations among patient attributes through quantum entanglement and superposition. This capability allows the model to extract richer representations of cardiovascular risk than traditional QML models such as Quantum KNN (QKNN) [46] (88%), QML-VQC [47] (86.3%), and QSVC [48] (92.09%). The QHF-CS model also shows strong generalization across datasets, handling skewed distributions (e.g., serum creatinine, creatinine phosphokinase) through pre-selection skewness correction and normalization. This improves training stability and enhances quantum circuit efficiency by avoiding noisy or redundant inputs. Furthermore, QHF-CS effectively handles skewed clinical data distributions using skewness correction and normalization during feature selection, reducing noise and overfitting while enhancing quantum circuit efficiency and model generalization across patient populations.

In this study, we do not claim exponential computational speedup typically associated with quantum algorithms like Shor’s or Grover’s. Instead, our justification for using QML lies in its representational advantage, particularly under skewed and sparse clinical data constraints. Quantum feature maps such as RealAmplitudes and EfficientSU2 enable encoding complex, non-linear relationships in a high-dimensional Hilbert space using relatively few parameters, offering improved generalization and reduced reliance on manual feature engineering. Compared to classical models, which often overfit or require extensive tuning in small datasets, QHF-CS consistently outperformed baselines, including Random Forest, QSVC, and QPSO-SVM regarding F1-score and recall (see Table 9). Cuckoo Search-based feature selection also ensures that only clinically relevant biomarkers are encoded, minimizing resource overhead and reinforcing the model’s clinical interpretability. Recent research further supports that quantum-induced kernel spaces, especially those derived from expressive feature maps like EfficientSU2, are intractable for classical models to replicate under certain assumptions. While formal quantum advantage in healthcare remains a frontier, our work positions QHF-CS as a robust and practically grounded step toward quantum-enhanced clinical decision support.

A. Theoretical Implications

This study confirms that optimized qubit selection in QCNNs facilitates accurate quantum machine learning for clinical diagnosis. When applied to high-dimensional datasets such as heart disease and heart failure records, QHF-CS leverages quantum parallelism to process intricate inter-feature correlations. The EfficientSU2 feature map was especially effective in both datasets, preserving predictive information while minimizing redundancies. The results affirm that meta-heuristic approaches, notably Cuckoo Search, are valuable in quantum feature optimization. This hybrid strategy—melding classical CS with quantum architectures—marks a significant step toward scalable and interpretable QML models. Future applications could extend this framework to domains like cancer detection and neurodegenerative disease prediction, where feature imbalance and redundancy are critical challenges.

B. Practical Implications

The exceptional performance of QHF-CS supports its deployment in real-world clinical settings. The Heart Disease dataset achieved 92.5% accuracy, 0.920 precision, 0.925 recall, and 0.915 F1-score using the EfficientSU2 map, compared to 91.04% accuracy with RealAmplitudes. The model demonstrated 94% classification accuracy for the heart failure dataset and an AUC-ROC score of 0.94 (Fig. 8), outperforming all existing QML approaches. This enhanced predictive power can aid early risk stratification of cardiovascular patients, enabling timely interventions and personalized treatment planning. By leveraging serum biomarkers, demographic data, and physiological parameters, QHF-CS delivers context-aware predictions beyond traditional models. The study also underscores the importance of quantum feature map selection, demonstrating that careful encoding choices like EfficientSU2 can substantially influence model performance. These insights pave the way for the next generation of QML-based healthcare tools, offering researchers a roadmap to optimize quantum diagnostic models for broader clinical impact.

C. Emerging Quantum Enhancements and Future Research Directions

As the QHF-CS model progresses from simulation to real-world deployment, emerging quantum techniques offer promising pathways to overcome hardware limitations, improve accuracy, and ensure clinical applicability. The following advancements outline future research directions that align with the evolving capabilities of quantum computing and the growing demands of precision healthcare:

•   Variational Error Mitigation and Circuit Optimization

Addressing hardware-induced noise is critical to scale QHF-CS on Noisy Intermediate-Scale Quantum (NISQ) devices. Techniques such as Zero Noise Extrapolation (ZNE) and Probabilistic Error Cancellation (PEC) enable reliable quantum computations by correcting gate-level errors without fault tolerance. Embedding these into QCNN training—especially when using complex ansatz like EfficientSU2—enhances the fidelity of quantum operations, paving the way for deeper and more accurate models. These methods are essential for transitioning from ideal simulations to robust, real-device execution.

•   Hybrid Quantum-Classical Training Frameworks

Classical optimizers like COBYLA, though effective, may not fully exploit the geometric properties of quantum landscapes. Future iterations of QHF-CS can benefit from quantum-aware optimizers such as Quantum Natural Gradient and Layerwise Learning Rate Scheduling. These techniques better align with the structure of quantum circuits, improving convergence rates and reducing training time. Such hybrid approaches increase generalizability across clinical datasets and ensure more stable training dynamics in noisy environments.

•   Quantum Federated Learning (QFL)

With increasing emphasis on data privacy in healthcare, Quantum Federated Learning (QFL) offers a groundbreaking solution. QFL allows the QHF-CS model to be trained collaboratively across multiple hospitals without transferring patient data. Leveraging quantum communication and distributed learning, QFL maintains strict privacy while enabling richer, more diverse training. The framework is well-suited for large-scale deployment in real-world clinical settings, offering strong privacy-preserving capabilities.

•   Quantum Autoencoders for Dimensionality Reduction

High-dimensional clinical data can overwhelm limited-qubit quantum systems. Quantum Autoencoders (QAE) provide an elegant solution by compressing the feature space before encoding it into qubits. This reduces circuit width and resource demands while retaining essential information. Integrating QAE into QHF-CS optimizes qubit usage and improves model efficiency, especially when working with complex datasets beyond the reach of classical preprocessing or CSO-based methods.

•   Quantum Neural Architecture Search (Q-NAS)

Manually selecting quantum circuit architectures can be suboptimal and time-consuming. Q-NAS automates this process, searching for optimal combinations of ansatz and feature maps tailored to the dataset. Applying Q-NAS to QHF-CS can lead to highly customized and performant architectures adaptable across varying clinical contexts. This adaptability maximizes the model’s predictive capabilities as quantum datasets and use cases expand.

These emerging directions demonstrate how quantum machine learning models like QHF-CS can evolve beyond current capabilities. By integrating cutting-edge techniques in noise mitigation, optimization, privacy, compression, and architecture search, future research can bridge the gap between theoretical quantum advantages and real-world clinical impact—making quantum-enhanced diagnostics a tangible reality.

5  Conclusions

The QHF-CS model, integrating Quantum Convolutional Neural Networks (QCNNs) with meta-heuristic optimization techniques, demonstrates robust performance in heart failure prediction by selecting the most relevant clinical biomarkers for qubit encoding. In this study, multiple optimization algorithms—including Ant Colony Optimization (ACO), Particle Swarm Optimization (PSO), and Cuckoo Search Optimization (CSO)—were explored for feature qubit selection. Among them, CSO proved most effective, as it identifies the most prevalent and clinically significant features based on a fitness function that maximizes classification accuracy while minimizing redundancy. The selected features—creatinine phosphokinase, platelets, serum sodium, and ejection fraction—enable efficient and compact quantum circuit design. Using high-dimensional quantum feature maps like EfficientSU2, the model achieves superior performance with 94% accuracy, 94% precision, 95% recall, and 94% F1-score on the heart failure dataset, and 92.5% accuracy, 92% precision, 92.5% recall, and 91.5% F1-score on the Heart Disease dataset. Unlike traditional models, QHF-CS effectively addresses data skewness and redundancy, enhancing generalization across patient profiles. Its high AUC-ROC and quantum speedup capabilities enable real-time prediction when integrated with clinical systems such as electronic health records (EHRs), making it a scalable and practical solution for personalized cardiovascular care. Future enhancements through quantum LSTM and QGAN frameworks may improve its adaptability and clinical utility.

Acknowledgement: This work was carried out as part of a Post-Doctoral Research (Remote) at the Singapore Institute of Technology (SIT), Singapore. The author sincerely thanks to Dr. Tan Kuan Tak and Dr. Pravin Ramdas Kshirsagar for his continuous support and valuable suggestions, which greatly improved this work. The authors also acknowledge thanks to the Singapore Institute of Technology (SIT), Singapore for doing this Post-Doctoral Research (Remote).

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Prasanna Kottapalle, Tan Kuan Tak; Data collection: Pravin Ramdas Kshirsagar, Gopichand Ginnela, Vijaya Krishna Akula; Analysis and interpretation of results: Prasanna Kottapalle, Tan Kuan Tak, Pravin Ramdas Kshirsagar; Draft manuscript preparation: Prasanna Kottapalle, Gopichand Ginnela, Vijaya Krishna Akula; Supervision: Tan Kuan Tak, Pravin Ramdas Kshirsagar. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Upon reasonable request, the datasets generated and/or analyzed during the present project may be provided by the corresponding author.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. World Health Organization. Cardiovascular diseases (CVDs) 2023 [Online]. [cited 2024 Dec 10]. Available from: https://www.who.int/news-room/fact-sheets/detail/cardiovascular-diseases-(CVDs). [Google Scholar]

2. Yusuf S, Joseph P, Rangarajan S, Islam S, Mente A, Hystad P, et al. Modifiable risk factors, cardiovascular disease, and mortality in 155 722 individuals from 21 high-income, middle-income, and low-income countries (PUREa prospective cohort study. Lancet. 2020;395(10226):795–808. doi:10.1016/S0140-6736(19)32008-2. [Google Scholar] [PubMed] [CrossRef]

3. Krumholz HM, Geraldes F, Wilson C, Horton R. The lancet-JACC collaboration: advancing cardiovascular health. Lancet. 2024;404(10455):833–4. doi:10.1016/j.jacc.2024.08.032. [Google Scholar] [PubMed] [CrossRef]

4. Biamonte J, Wittek P, Pancotti N, Rebentrost P, Wiebe N, Lloyd S. Quantum machine learning. Nature. 2017;549(7671):195–202. doi:10.1038/nature23474. [Google Scholar] [PubMed] [CrossRef]

5. Havlíček V, Córcoles AD, Temme K, Harrow AW, Kandala A, Chow JM, et al. Supervised learning with quantum-enhanced feature spaces. Nature. 2019;567(7747):209–12. doi:10.1038/s41586-019-0980-2. [Google Scholar] [PubMed] [CrossRef]

6. Schuld M, Bocharov A, Svore KM, Wiebe N. Circuit-centric quantum classifiers. Phys Rev A. 2020;101(3):032308. doi:10.1103/physreva.101.032308. [Google Scholar] [CrossRef]

7. Benedetti M, Lloyd E, Sack S, Fiorentini M. Parameterized quantum circuits as machine learning models. Quantum Sci Technol. 2019;4(4):043001. doi:10.1088/2058-9565/ab4eb5. [Google Scholar] [CrossRef]

8. Stokes J, Izaac J, Killoran N, Carleo G. Quantum natural gradient. Quantum. 2020;4:269. doi:10.22331/q-2020-05-25-269. [Google Scholar] [CrossRef]

9. Hur T, Kim L, Park DK. Quantum convolutional neural network for classical data classification. Quantum Mach Intell. 2022;4(1):3. doi:10.1007/s42484-021-00061-x. [Google Scholar] [CrossRef]

10. Khan MU, Ahmad Kamran M, Khan WR, Ibrahim MM, Ali MU, Lee SW. Error mitigation in the NISQ era: applying measurement error mitigation techniques to enhance quantum circuit performance. Mathematics. 2024;12(14):2235. doi:10.3390/math12142235. [Google Scholar] [CrossRef]

11. Heidari H, Hellstern G. Early heart disease prediction using hybrid quantum classification. arXiv:2208.08882. 2022. [Google Scholar]

12. Abohashima Z, Elhosen M, Houssein EH, Mohamed WM. Classification with quantum machine learning: a survey. arXiv:2006.12270. 2020. [Google Scholar]

13. Li J, Lin S, Yu K, Guo G. Quantum K-nearest neighbor classification algorithm based on Hamming distance. Quantum Inf Process. 2021;21(1):18. doi:10.1007/s11128-021-03361-0. [Google Scholar] [CrossRef]

14. Lu S, Braunstein SL. Quantum decision tree classifier. Quantum Inf Process. 2014;13(3):757–70. doi:10.1007/s11128-013-0687-5. [Google Scholar] [CrossRef]

15. Zaidi SAJ, Ghafoor A, Kim J, Abbas Z, Lee SW. HeartEnsembleNet: an innovative hybrid ensemble learning approach for cardiovascular risk prediction. Healthcare. 2025;13(5):507. doi:10.3390/healthcare13050507. [Google Scholar] [PubMed] [CrossRef]

16. Saxena A, Saxena S. Pancreatic cancer data classification with quantum machine learning. J Quantum Comput. 2023;5(1):1–13. doi:10.32604/jqc.2023.044555. [Google Scholar] [CrossRef]

17. Civicioglu P, Besdok E. A conceptual comparison of the Cuckoo-search, particle swarm optimization, differential evolution and artificial bee colony algorithms. Artif Intell Rev. 2013;39(4):315–46. doi:10.1007/s10462-011-9276-0. [Google Scholar] [CrossRef]

18. ZZFeatureMap. [cited 2024 Aug 10]. Available from: https://qiskit.org/documentation/stubs/qiskit.circuit.library.ZZFeatureMap.html. [Google Scholar]

19. RealAmplitudes. [cited 2024 Aug 10]. Available from: https://docs.quantum.ibm.com/api/qiskit/0.24/qiskit.circuit.library.RealAmplitudes. [Google Scholar]

20. Biksham DV, Srujana V, Meghana I, Harshath B, Tarun G. Heart disease prediction using machine learning. YMER Digit. 2022;21(4):489–94. doi:10.37896/ymer21.04/48. [Google Scholar] [CrossRef]

21. Maheshwari D, Sierra-Sosa D, Garcia-Zapirain B. Variational quantum classifier for binary classification: real vs synthetic dataset. IEEE Access. 2021;10(5):3705–15. doi:10.1109/ACCESS.2021.3139323. [Google Scholar] [CrossRef]

22. Kavitha SS, Kaulgud N. Quantum K-means clustering method for detecting heart disease using quantum circuit approach. Soft Comput. 2023;27(18):13255–68. doi:10.1007/s00500-022-07200-x. [Google Scholar] [PubMed] [CrossRef]

23. Babu SV, Ramya P, Gracewell J. Revolutionizing heart disease prediction with quantum-enhanced machine learning. Sci Rep. 2024;14(1):7453. doi:10.1038/s41598-024-55991-w. [Google Scholar] [PubMed] [CrossRef]

24. Tiwari P, Melucci M. Towards a quantum-inspired binary classifier. IEEE Access. 2019;7:42354–72. doi:10.1109/access.2019.2904624. [Google Scholar] [CrossRef]

25. Khan TM, Robles-Kelly A. Machine learning: quantum vs. classical. IEEE Access. 2020;8:219275–94. doi:10.1109/ACCESS.2020.3041719. [Google Scholar] [CrossRef]

26. Amin J, Sharif M, Gul N, Kadry S, Chakraborty C. Quantum machine learning architecture for COVID-19 classification based on synthetic data generation using conditional adversarial neural network. Cognit Comput. 2022;14(5):1677–88. doi:10.1007/s12559-021-09926-6. [Google Scholar] [PubMed] [CrossRef]

27. Wereszczyński K, Michalczuk A, Josiński H, Polański A. Quantum computing for clustering big datasets. In: 2018 Applications of Electromagnetics in Modern Techniques and Medicine (PTZE); 2018 Sep 9–12; Racławice, Poland; p. 276–80. doi:10.1109/PTZE.2018.8503109. [Google Scholar] [CrossRef]

28. Dang Y, Jiang N, Hu H, Ji Z, Zhang W. Image classification based on quantum K-nearest-neighbor algorithm. Quantum Inf Process. 2018;17(9):239. doi:10.1007/s11128-018-2004-9. [Google Scholar] [CrossRef]

29. Tychola KA, Kalampokas T, Papakostas GA. Quantum machine learning—an overview. Electronics. 2023;12(11):2379. doi:10.3390/electronics12112379. [Google Scholar] [CrossRef]

30. Li Z, Terashi K. Quantum decision trees with information entropy. aiXiv:2502.11412. 2025. [Google Scholar]

31. Shrivastava A, Haase T, Zeller T, Schulte C. Biomarkers for heart failure prognosis: proteins, genetic scores and non-coding RNAs. Front Cardiovasc Med. 2020;7:601364. doi:10.3389/fcvm.2020.601364. [Google Scholar] [PubMed] [CrossRef]

32. Elsedimy EI, AboHashish SMM, Algarni F. New cardiovascular disease prediction approach using support vector machine and quantum-behaved particle swarm optimization. Multimed Tools Appl. 2024;83(8):23901–28. doi:10.1007/s11042-023-16194-z. [Google Scholar] [CrossRef]

33. Darolia A, Chhillar RS, Alhussein M, Dalal S, Aurangzeb K, Lilhore UK. Enhanced cardiovascular disease prediction through self-improved Aquila optimized feature selection in quantum neural network & LSTM model. Front Med. 2024;11:1414637. doi:10.3389/fmed.2024.1414637. [Google Scholar] [PubMed] [CrossRef]

34. Eswaramoorthy S, Sivakumaran N, Sekaran S. Grey wolf optimization based parameter selection for support vector machines. COMPEL Int J Comput Math Electr Electron Eng. 2016;35(5):1513–23. doi:10.1108/compel-09-2015-0337. [Google Scholar] [CrossRef]

35. Lu WJ, Ma L, Chen H. Particle swarm optimisation-support vector machine optimised by association rules for detecting factors inducing heart diseases. J Intell Syst. 2017;26(3):573–83. doi:10.1515/jisys-2016-0014. [Google Scholar] [CrossRef]

36. Khourdifi Y, Bahaj M. Heart disease prediction and classification using machine learning algorithms optimized by particle swarm optimization and ant colony optimization. Int J Intell Eng Syst. 2019;12(1):242–52. doi:10.22266/ijies2019.0228.24. [Google Scholar] [CrossRef]

37. Alirezapour H, Mansouri N, Mohammad Hasani Zade B. A comprehensive survey on feature selection with grasshopper optimization algorithm. Neural Process Lett. 2024;56(1):28. doi:10.1007/s11063-024-11514-2. [Google Scholar] [CrossRef]

38. Vieira SM, Mendonça LF, Farinha GJ, Sousa JMC. Modified binary PSO for feature selection using SVM applied to mortality prediction of septic patients. Appl Soft Comput. 2013;13(8):3494–504. doi:10.1016/j.asoc.2013.03.021. [Google Scholar] [CrossRef]

39. Saputra D, Dharmawan WS, Irmayani W. Performance comparison of the SVM and SVM-PSO algorithms for heart disease prediction. Int J Adv Data Inf Syst. 2022;3(2):74–86. doi:10.25008/ijadis.v3i2.1243. [Google Scholar] [CrossRef]

40. Jahin MA, Masud MA, Mridha MF, Aung Z, Dey N. KACQ-DCNN: uncertainty-aware interpretable kolmogorov-arnold classical-quantum dual-channel neural network for heart disease detection. arXiv:2410.07446. 2024. [Google Scholar]

41. Taha SMR, Taha ZK. EEG signals classification based on autoregressive and inherently quantum recurrent neural network. Int J Comput Appl Technol. 2018;58(4):340. doi:10.1504/ijcat.2018.095942. [Google Scholar] [CrossRef]

42. Johnson RA, Wichern DW. Applied multivariate statistical analysis. 6th ed. Hoboken, NJ, USA: Prentice Hall; 2007. [Google Scholar]

43. Bergholm V, Izaac J, Schuld M, Gogolin C, Ahmed S, Ajith V, et al. PennyLane: automatic differentiation of hybrid quantum-classical computations. arXiv:1811.04968. 2018. [Google Scholar]

44. Chicco D. Heart failure clinical records dataset. Irvine, CA, USA: UCI Machine Learning Repository; 2020 [cited 2024 Aug 10]. Available from: https://archive.ics.uci.edu/ml/datasets/Heart+failure+clinical+records. [Google Scholar]

45. Siddhartha M. Heart disease dataset (comprehensive). Piscataway, NJ, USA: IEEE DataPort; 2020 [cited 2025 Apr 25]. Available from: https://ieee-dataport.org/open-access/heart-disease-dataset-comprehensive. [Google Scholar]

46. Kumar Y, Koul A, Sisodia PS, Shafi J, Verma K, Gheisari M, et al. Heart failure detection using quantum-enhanced machine learning and traditional machine learning techniques for Internet of artificially intelligent medical things. Wirel Commun Mob Comput. 2021;2021(1):1616725. doi:10.1155/2021/1616725. [Google Scholar] [CrossRef]

47. Gupta H, Varshney H, Sharma TK, Pachauri N, Verma OP. Comparative performance analysis of quantum machine learning with deep learning for diabetes prediction. Complex Intell Syst. 2022;8(4):3073–87. doi:10.1007/s40747-021-00398-7. [Google Scholar] [CrossRef]

48. Rebentrost P, Mohseni M, Lloyd S. Quantum support vector machine for big data classification. Phys Rev Lett. 2014;113(13):130503. doi:10.1103/PhysRevLett.113.130503. [Google Scholar] [PubMed] [CrossRef]