Improved PPO-Based Task Offloading Strategies for Smart Grids

1  Introduction

The large-scale integration of renewable energy sources and the digital transformation of power grids are imposing new stresses on traditional centralized infrastructures, including increased latency, congestion, and energy consumption [1–5]. Modern information and communication technologies (ICT) enable smart grids to offer real-time monitoring and fine-grained dispatching; however, the high-frequency data streams generated by distributed energy resources (DERs) and massive Internet-of-Things (IoT) devices quickly overwhelm cloud-centric computing [6,7].

Edge computing mitigates these bottlenecks by processing data in close proximity to its source, thereby sharply reducing round-trip latency and easing the load on core networks [8–11]. Yet static or heuristic task-offloading schemes are ill-suited to the smart-grid context, where load fluctuations, link-quality variations, and privacy constraints are the norm. Deep reinforcement learning (DRL), with its ability to learn optimal policies through interaction, has therefore become a popular choice for dynamic offloading [12–15]. Early methods—such as Deep Q-Networks (DQN) and their derivatives—lower mean latency but suffer from slow convergence and limited scalability in highly coupled, multi-variable settings.

To address these challenges, we cast task offloading in smart grids as a Markov Decision Process (MDP) and introduce a DRL-based framework that couples a convolutional neural network (CNN) for feature extraction with an enhanced Proximal Policy Optimization (PPO) algorithm. The proposed approach delivers adaptive, energy-aware scheduling, significantly reducing task latency and energy use in dynamic grid environments while improving overall system performance.

Major contributions:

•   MDP-based modeling across a three-tier architecture. We formulate task characteristics, system dynamics, and energy expenditure for end devices, edge nodes, and cloud servers under a unified MDP, enabling efficient task offloading.

•   CNN-enhanced PPO. By integrating a lightweight CNN encoder with an improved PPO scheme, we accelerate training and bolster adaptability to non-stationary conditions.

•   Comprehensive simulations. Extensive experiments under dynamic, multi-task scenarios demonstrate substantial gains in latency, energy savings, and resource utilization.

The remainder of this paper is organized as follows: Section 2 surveys related research; Section 3 details the system model; Section 4 reviews foundational concepts in deep reinforcement learning; Section 5 presents the MDP formulation; Section 6 describes the DRL-based offloading and scheduling strategy; Section 7 evaluates performance via simulations; and Section 8 concludes the paper.

2  Related Work

Early studies relied on linear/non-linear and mixed-integer programming to solve offloading and resource-allocation problems [16]. While these methods can approximate globally optimal offline solutions, their computational complexity grows exponentially with network size, and they assume static links and loads, limiting real-time applicability.

To reduce complexity, subsequent work adopted greedy, threshold-based, or genetic heuristics [17,18]. More recently, DRL has gained prominence for its model-free, online adaptability. For instance, the Task Prediction and Multi-Objective Optimization Algorithm (TPMOA) minimizes user wait and rendering delay in wireless virtual-reality offloading [19]. Hybrid-PPO, a customized PPO variant with parameterized discrete–continuous action spaces, improves offloading efficiency [20]. Combining a Slime-Mould Algorithm (SMA) with an optimized Harris Hawks Optimizer (HHO), HS-HHO clusters tasks for edge–cloud collaboration, reducing energy consumption alongside delay [21].

In power-IoT (PIoT) scenarios [22,23], offloading must honor the stringent real-time and reliability requirements of power-system operations. Prior art includes quota-matching offloading in wireless sensor networks [24], joint optimization of service caching [25], and Q-learning-driven hydro–power co-scheduling [26]; these methods typically introduce grid-specific priorities or stochastic models to capture pulse-load characteristics. PPO, favored for its stability and implementation ease, has been applied in multi-agent form to cooperative offloading and resource allocation in small-cell MEC [27], vehicular networks [28], and fog–edge hybrids [29], consistently improving delay and energy efficiency with good distributed scalability.

Most existing studies assume stable link bandwidth and homogeneous computing capacity, overlooking the peak-load spikes and link disturbances that frequently occur in smart grids. In addition, when faced with high-dimensional, coupled state variables—such as link rate, task size, and residual central processing unit (CPU) cycles—current models rarely employ lightweight feature extractors, resulting in significant inference delays. To address these shortcomings, we design a Convolutional Neural Network–Proximal Policy Optimization (CNN–PPO) framework: the CNN first distils salient features from the high-dimensional state space, and the resulting embeddings are fed into a shared-parameter actor–critic network that estimates both the policy and the value function. This architecture enables real-time inference while substantially improving training stability and scalability.

3  System Model and Related Mathematical Formulation

3.1 System Architecture

The smart grid integrates distributed energy resources, smart meters, electric vehicles, and other intelligent devices via advanced wireless networks and edge-computing infrastructure, forming a highly interactive, computation-intensive cyber-physical system. In this context, computing resources must not only satisfy the terminal devices’ stringent real-time requirements but also preserve overall grid stability.

Fig. 1 presents a three-tier edge-computing architecture for smart grids comprising: (i) the terminal layer, populated by local processing units (LPUs); (ii) the edge layer, implemented via mobile-edge computing (MEC) nodes; and (iii) the cloud layer, represented by a distribution cloud center (CC). The cloud layer undertakes centralized processing and global coordination. The terminal layer encompasses heterogeneous electrical equipment, while the edge layer supplies intermediate computation and storage through edge nodes and micro-data servers. Each edge node aggregates sampled data from differential-protection terminals together with operational metrics from the distribution network, thereby enabling automated load monitoring, anomaly detection, power-quality assessment, and consumption analytics. The processed insights are then translated into control commands that regulate field devices in real time.

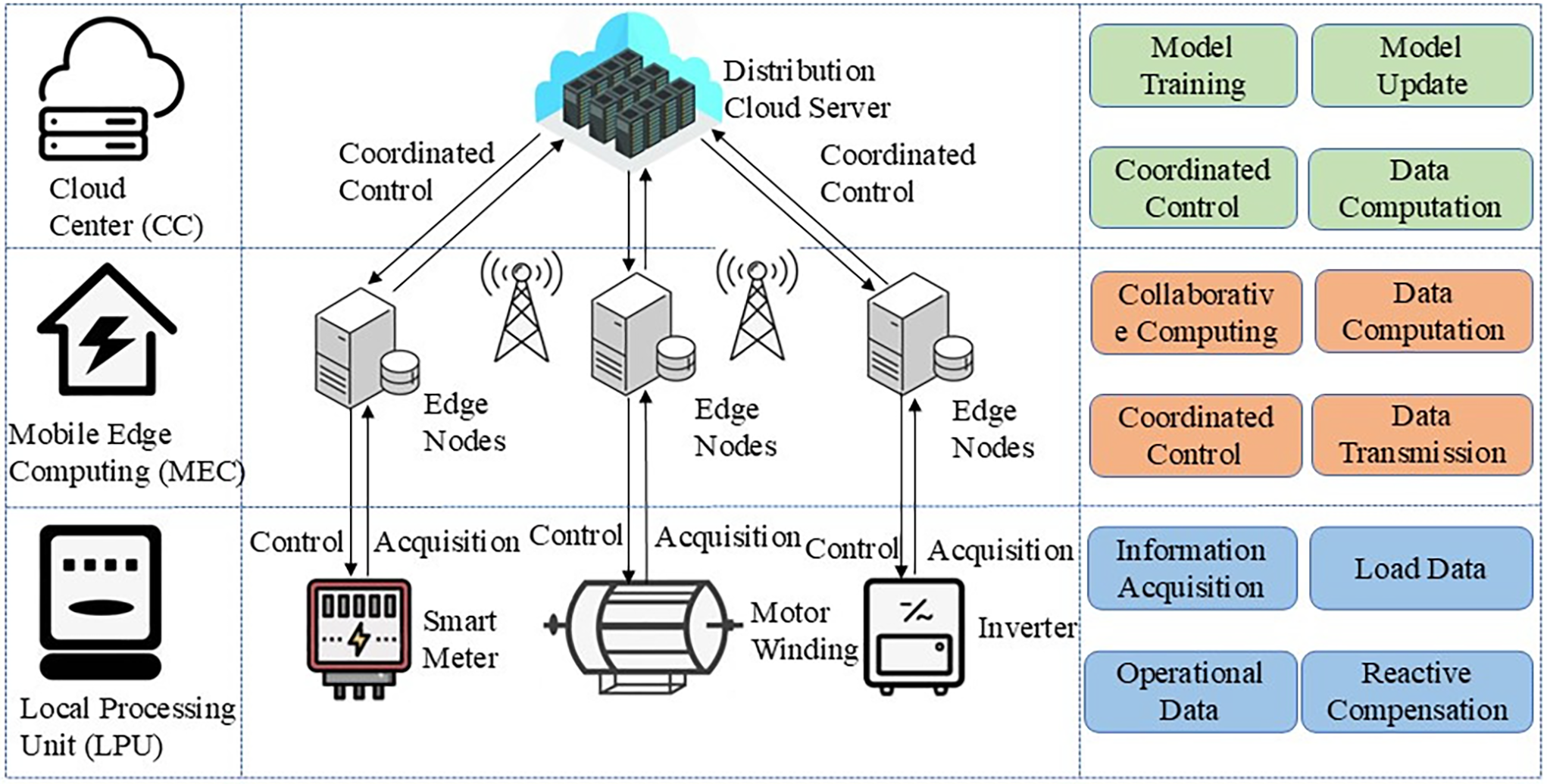
Figure 1: Hierarchical task offloading and execution framework

3.2 Task Queue Model

In a smart-grid environment, every intelligent terminal generates a stream of application-driven tasks—ranging from periodic data acquisition and anomaly detection to device-state monitoring, load forecasting, and advanced analytics. We model the aggregate arrival process as a Poisson process with intensity λ, which denotes the expected number of task arrivals within a given time interval. Each individual task Ji is described by the tuple:

Ji=(tig,di,ki)(1)

where tig is the task generation time, representing the moment a task is triggered or determined by the data sampling period. di is the size of the input data for the task, typically measured in bits. The size of the task is determined by the data volume to be processed, such as power consumption data collected by smart meters or real-time information obtained from sensors. ki is the task’s computation-to-data ratio (CVR), expressed in CPU cycles per bit. This parameter quantifies the computational complexity of the task. For instance, complex forecasting algorithms might have a higher CVR compared to simple state monitoring tasks.

Tasks are serviced under a finite–buffer, first-come–first-served (FCFS) discipline. When the buffer is full, additional arrivals are dropped, producing overflow events. Representing the queue as a fixed-size matrix—each row corresponding to a single task—facilitates efficient, dynamic updates as tasks are admitted or completed, thereby providing a tractable abstraction for subsequent scheduling and off-loading analysis.

3.3 Communication Model

In smart grids and edge-computing scenarios, the communication module is pivotal. Wireless channels, influenced by fading, interference, and device mobility, evolve dynamically. To capture these fluctuations, we employ a sinusoidal time-varying channel model that reflects the periodic changes in transmission rate commonly caused by traffic congestion or multipath propagation. Time is discretised into fixed-length slots; the channel state is assumed to remain constant within each slot but may differ from one slot to the next, thereby affecting both the achievable data rate and task-offloading decisions.

Let R(t) denote the instantaneous communication rate between smart terminal devices and the edge/cloud server. To reproduce the temporal dynamics outlined above, we model R(t) at an arbitrary time t as:

R(t)=Ravg+ΔR⋅sin⁡(2πtT)(2)

where R(t) represents the transmission rate at time t, Ravg is the average transmission rate, ΔR is the amplitude of the rate fluctuation, representing the maximum deviation from the average rate, T is the period, indicating the duration of one cycle of fluctuation.

In this model, periodic fluctuations in transmission rates are suitable for two types of communication scenarios. For edge-to-edge communication, the transmission rate R1(t) (the data rate between devices and edge servers) with periodic variations can be expressed as:

R1(t)=R1,max+R1,min2+R1,max−R1,min2⋅sin⁡(2πtT)(3)

where R1,max and R1,min denote the maximum and minimum edge transmission rates, respectively.

For cloud communication, the transmission rate R2(t) (the data rate between devices and the cloud server) includes a phase offset of 180 degrees, ensuring asynchronous dynamics with edge communication rates. T2 represents the phase offset or time shift of the cloud communication system. This can be represented as:

R2(t)=R2,max+R2,min2+R2,max−R2,min2⋅sin⁡(2π(t+T2)T)(4)

where R2,max and R2,min denote the maximum and minimum cloud transmission rates, and T2 represents the phase offset introduced to simulate asynchronous fluctuations across different communication links.

We employ a sinusoidal model to capture the periodic fluctuations of wireless channels in smart-grid and edge-computing environments. Although this streamlined formulation omits complex phenomena such as multipath fading and sudden blockages, it nevertheless reflects the dominant variability observed in substation-level deployments with largely stationary nodes. Its low computational overhead makes the model well-suited to analysing task-offloading and resource-optimisation strategies. Future work could extend this framework by integrating more sophisticated channel models tailored to highly dynamic scenarios.

3.4 Computational Model

In smart grids, computational tasks can be executed either locally on terminal devices via their on-board Local Processing Units (LPUs) or off-loaded to edge servers over wireless links. To characterise the resulting computation time and energy expenditure, we develop analytical models for local, edge, and cloud execution. These models quantify resource consumption and performance trade-offs among the three modes, thereby providing theoretical guidance for optimising task-offloading decisions.

(1) Local Execution Model. Under the local execution mode, tasks are processed by the LPU on terminal devices. LPUs typically have limited computational power but can efficiently handle latency-sensitive tasks. For a task Ji offloaded at time tia, the local execution time is given as:

til=⌈dikifl⌉(5)

where fl is the CPU frequency of the LPU, measured in cycles per second, which determines the task execution efficiency. diki represents computational demand of the task, expressed in CPU cycles.

The energy consumption of local computation depends on the power consumption model of the LPU. Generally, power pl has a nonlinear relationship with CPU frequency, expressed as:

pl=ε⋅(fl)v(6)

where ε and v are constants specific to the device. Thus, the total energy consumption for local execution is:

eil=pl⋅til(7)

(2) Edge Execution Model. In the edge execution mode, task data is first transmitted via wireless networks to an edge server and then processed at the server. For a task Ji offloaded at time tia, the total delay consists of two parts: data transmission delay and computation delay. It can be expressed as:

tie(tia)=ttx1(di,tia)+tiexe,e(8)

where ttx1(di,tia) represents data transmission delay, depending on the data size and current wireless channel state. tiexe,e: computation delay at the edge server, given as:

tiexe=⌈dikifs⌉(9)

where fs is the CPU frequency of the edge server. From an energy perspective, edge execution energy consumption primarily occurs during data transmission. The energy consumption model is:

eic(tia)=ptx1⋅ttx1(di,tia)(10)

where ptx1 is the power consumption rate for transmission, depending on the communication module and transmission distance.

(3) Cloud Execution Model. In the cloud execution mode, tasks are offloaded to cloud servers for execution. Cloud servers have the highest computational power but incur higher transmission delays and energy costs due to the distance. The execution time for a task Ji offloaded to the cloud at time tia includes both data transmission time and computation time:

tic(tia)=ttx2(di,tia)+tiexe,c(11)

where ttx2(di,tia) represents data transmission time from the terminal device to the cloud server. tiexe,c represents computation time on the cloud server, expressed as:

tiexe,c=⌈dikifc⌉(12)

where fc is the CPU frequency of the cloud server.

(4) Cloud Energy Consumption. Cloud energy consumption includes the energy used for data transmission and the energy consumed by receiving results. Since cloud servers are not energy-constrained, the energy consumption of smart devices is primarily concentrated in the communication stage:

eic=ptx2⋅ttx2(di,tia)(13)

where ptx2 is the transmission power rate, determined by the communication module and transmission distance.

3.5 Objectives

In smart-grid environments, geographically distributed devices continually generate computational workloads—including energy forecasting, real-time monitoring, and data analytics. Minimising latency and energy consumption therefore depends on selecting both an appropriate execution venue and an optimal execution schedule for each task. To address this challenge, we propose an optimisation framework that jointly allocates computational and communication resources while orchestrating task execution, thereby enhancing overall system performance.

For each task Ji, the system must first decide whether the task should be processed locally, offloaded to an edge server, or sent to a cloud server. We use a binary indicator ai to represent this choice: When ai=0, the task Ji is executed locally on the device’s LPU. This option is suitable for latency-sensitive tasks with relatively low computational demands, which can be processed quickly on device, thereby avoiding communication delays. When ai=1, the task Ji is offloaded to an edge server for execution. Edge servers can significantly reduce task execution latency while avoiding the higher transmission latencies associated with cloud computing. When ai=2, the task Ji is further offloaded to a cloud server for execution. Cloud servers are ideal for handling large-scale computationally intensive tasks but incur greater latency and energy consumption due to long-distance communication.

The total delay experienced by a task Ji is defined as the time elapsed from the task generation moment tig to the task completion time tiexe (measured in time units). Therefore, the delay can be expressed as a function of the scheduling decision ai and the task’s start time tia, given by:

li(ai,tia)=tia+T−tig(14)

where tia is the time at which task execution begins, tiexe(ai,tia) is the time required to execute the task at the chosen location, which can be further defined as:

tiexe(ai,tia)=(1−aie−aic)⋅til+aie⋅tie+aic⋅tic(15)

Similarly, combining the system scheduling model, the energy consumption for task execution can be expressed as a function of the scheduling decision and execution time:

ei(ai,tia)=(1−aie−aic)⋅eil+aie⋅eie+aic⋅eic(16)

where α is the weight coefficient for task delay costs, representing the importance of minimizing delays. β is the weight coefficient for energy consumption costs, indicating the priority of reducing energy usage. The system’s optimization objective is to minimize the total cost of the scheduling strategy, defined as the sum of task delays and energy consumption. The comprehensive cost function is:

ci(ai,tia)=αli(ai,tia)+βei(ai,tia)(17)

To optimize the execution efficiency of intelligent tasks in the smart grid, the system’s objective is to minimize the average cost of all tasks generated within a specified time period T. The average cost is defined as:

minlima,tna→∞1n∑i=1nci(ai,tia)(18)

Our model minimizes the average cost per task to optimize long-term system performance despite challenges from random task arrivals and unpredictable wireless conditions. In dynamic smart grid scenarios, where task arrival rates, data volumes, and resource availability vary, static methods fail. We propose a Deep Reinforcement Learning (DRL) approach to achieve optimal task offloading and scheduling through adaptive, continuous learning.

4  Background of Deep Reinforcement Learning (DRL)

Deep Reinforcement Learning (DRL) is an enhancement of traditional reinforcement learning (RL) that introduces deep neural networks (DNNs) to approximate state representations and functions. The core concept of RL is to enable an intelligent agent to interact with its environment and learn an optimal strategy through continuous exploration. In reinforcement learning, at each time step n, the agent observes the environment state sn and selects an action an from the action space A. The action is chosen based on a policy π(an∣sn), which defines the probability of executing action an in state sn. Upon executing the action, the environment transitions to a new state sn+1 and returns a reward signal rn, determined by the transition probability P(sn+1|sn,an) and the reward function R(sn,an,sn+1). This process continues iteratively, starting from an initial state sm, and the cumulative reward expectation Gm is expressed as:

Gm=∑l=0∞γlrm+l(19)

where γ∈(0,1] is the discount factor, used to balance immediate and future rewards. By maximizing the expected value of Gm, the agent can learn an optimal strategy to achieve the highest long-term reward.

In the mathematical framework of RL, the problem is typically defined as a Markov Decision Process (MDP):

M=(S,A,P,R,γ)(20)

where S represents state space, representing all possible environmental states. A represents action space, representing all possible agent actions. P represents state transition probability, describing the likelihood of transitioning from one state s to another s′ after executing action a. R represents reward function, quantifying the immediate reward for performing an action in a specific state. γ: discount factor, controlling the importance of future rewards. The goal of RL is to use policy π to maximize the cumulative reward expectation, defined as:

vπ(s)=Eπ[Gm∣Sm=s](21)

where vπ, referred to as the state value function, represents the cumulative reward expectation for a specific state under policy π. For a specific state-action pair, the action-value function is defined as:

qπ(s,a)=Eπ[Gm∣Sm=s,am=a](22)

The goal of DRL is to find an optimal policy π∗ that maximizes the expected cumulative reward from any state:

vπ∗(s)=maxaqπ∗(s,a),s∈S(23)

In practical applications, DRL uses deep neural networks (DNNs) to approximate policies and value functions. Leveraging the feature representation capabilities of DNNs, DRL can adapt to large-scale state spaces. Currently, DRL methods are categorized into two major approaches: value-based methods and policy-based methods.

Value-Based Methods. In value-based methods, DNNs are employed to approximate the value function, commonly referred to as the Q-network (Deep Q-Network, DQN) and its variations. The core idea is to minimize the loss between the DNN-predicted value and the true target value, formally expressed as:

LV(θ)=En[(vπ∗(sn)−v(sn;θ))2](24)

where sn is the state at time step n, vπ∗(sn) is the value function parameterized by θ, representing the network’s training weights.

Policy-Based Methods. Policy-based methods directly use DNNs to approximate the parameterized policy, known as the policy network. Typical policy-based algorithms include REINFORCE and Actor-Critic, which exhibit higher sample efficiency and learning capabilities. A common policy gradient update equation is:

∇LPG(θ)=En[∇θlog⁡π(an∣sn;θ)A^n](25)

where π(an∣sn;θ) represents the probability of selecting action an in state sn, θ is the network weights, A^n represents advantage function, used to balance the relative quality of action an.

Proximal Policy Optimization (PPO). To enhance exploration while avoiding local optima, the Generalized Advantage Estimation (GAE) method is introduced to balance bias and variance:

A^nGAE(γ,ϕ)=∑l=0∞(γϕ)lηn+lv(26)

where ηn+lv is the temporal difference (TD) error at step n, ϕ adjusts the balance between bias and variance. Additionally, the PPO algorithm introduces a clipped objective function to limit policy updates, ensuring stability and improving model robustness:

LCLIP(θ)=En[min(rn(θ)A^n,clip(rn(θ),1−ϵ,1+ϵ)A^n)](27)

where rn(θ)=π(an∣sn;θ)π(an∣sn;θold), ϵ controls the range of policy updates.

Based on the above framework, this paper employs the PPO-based DRL method to design the task offloading strategy in smart grids. The clipped objective ensures stable policy updates while enhancing the model’s adaptability, enabling the system to make efficient scheduling decisions in dynamic communication environments and achieve resource optimization.

5  MDP Formulation

We address the task-offloading problem with deep reinforcement learning (DRL). By casting dynamic task allocation as a Markov decision process (MDP), we leverage DRL to learn an offloading policy that maximizes efficiency.

5.1 State Space

At each time step during smart grid task offloading and scheduling, the system orchestrator monitors the current system state and determines offloading decisions. To accurately represent tasks, computational resources, and communication link dynamics, we define the state space as a collection of relevant variables, formally expressed as:

S={s∣s=(Q,slpul,stq1,stq2,smec,scc,R1,R2)}(28)

where the state space S includes multiple key variables describing task execution states at the local, edge server, and cloud server levels, as well as data transmission conditions and network states. These components are detailed as follows:

(1) We define the task queue Q as an M×3 matrix, where each row Q[t][j] represents a task’s generation time, data size, and computational demand. These attributes facilitate evaluating queue latency, prioritizing time-sensitive tasks, determining offloading bandwidth to edge or cloud servers, and estimating the CPU cycles required for execution.

(2) Local Processing Unit State slpu: The Local Processing Unit (LPU) is responsible for handling computational tasks at the terminal device level. The state slpu represents the remaining CPU cycles available for processing tasks. At time t, if the orchestrator schedules a task to be executed locally, slpu is updated based on the computational demand of the task di⋅ki, where di is the task’s data size and ki is the computational intensity. As time progresses, the available computational resources gradually decrease, expressed as:

slpu[t]=max{slpul[t−1]−fl,0}(29)

where fl is the fixed computational capacity of the LPU in CPU cycles.

(3) Edge Server Transmission Queue State stq1: This state describes the remaining data to be transmitted from terminal devices to the edge server via the wireless network. At time t, if a task is offloaded to the edge server, stq1[t] is initialized with the task’s data size di. The transmission process depends on the channel’s transmission rate R1(t), and the state is updated as:

stq1[t]=max{stq1[t−1]−r1(t−1),0}(30)

when stq1[t] = 0, the task has been successfully transmitted to the edge server.

(4) Cloud Transmission Queue State stq2: This state represents the remaining data to be transmitted from terminal devices to the cloud server. If a task is offloaded to the cloud, stq2[t] is initialized with the task’s data size di. The state is updated dynamically based on the cloud transmission rate R2(t):

stq2[t]=max{stq2[t−1]−r2(t−1),0}(31)

(5) Edge Server State smec: The edge server is an extension of local processing that allows tasks to be offloaded for execution. smec represents the remaining CPU cycles at the edge server. At time t, if a task is offloaded, smec[t] is updated as:

smec[t]=max{smec[t−1]−fs,0}(32)

where fs is the computational capacity of the edge server.

(6) Cloud Server State scc: The cloud center provides extensive computational power for large-scale tasks. scc represents the remaining computational resources in the cloud. When a task is processed, the state is updated as:

scc[t]=max{scc[t−1]−fcc,0}(33)

where fcc is the computational capacity of the cloud server.

(7) Transmission Rates R: Transmission rates R1(t) and R2(t) represent the data rates between terminal devices, edge servers, and cloud servers. These rates depend on the current channel conditions and device locations, directly influencing the dynamics of stq1 and stq2.

5.2 Action Space

Within the devised MDP framework, the action space comprises three principal task-scheduling options: Local Processing (LP), Edge Processing (EP), and Cloud Processing (CP). These alternatives are selected to optimize task offloading in smart-grid environments by striking an effective balance between execution latency and energy consumption. A detailed description of each action type follows.

1) Local Processing (LP): The Local Processing action refers to assigning tasks from the queue to the Local Processing Unit (LPU) for execution. The complete set of actions can be expressed as:

LE={LE1,LE2,…,LEQ}(34)

where LEi∈{1,2,…,Q} denotes the selection of the i-th task in the task queue for processing by the LPU. This action is valid only under the following conditions: The LPU is currently in an idle state. The i-th task exists in the task queue.

When LEi is selected, the i-th task is removed from the queue, and the LPU state is updated dynamically based on the task’s attributes. The task is then executed according to the time slices defined.

2) Edge Processing (EP): The Edge Processing action refers to offloading tasks from the queue to the Edge Server for execution. This set of actions is defined as:

EP={EP1,EP2,…,EPQ}(35)

where EPi denotes the selection of the i-th task in the task queue for offloading to the edge server. This action is valid only under the following conditions: The Data Transmission Unit 1 (DTU1) is idle. The i-th task exists in the task queue.

When EPi is selected, the i-th task is removed from the queue, and DTU1 initiates the transmission of task data to the edge server. Upon successful data transmission, the edge server begins processing the task, and DTU1 returns to an idle state.

3) Cloud Processing (CP): The Cloud Processing action refers to offloading tasks from the queue to the Cloud Server for execution. This set of actions is defined as:

CP={CP1,CP2,…,CPQ}(36)

where CPi denotes the selection of the i-th task in the task queue for offloading to the cloud server. This action is valid only under the following conditions: The Data Transmission Unit 2 (DTU2) is idle. The i-th task exists in the task queue.

When CPi is selected, the i-th task is removed from the queue, and DTU2 initiates the transmission of task data to the cloud server. Upon successful data reception, the cloud server processes the task with its higher computational capacity, returning the results to the local device, and DTU2 returns to an idle state.

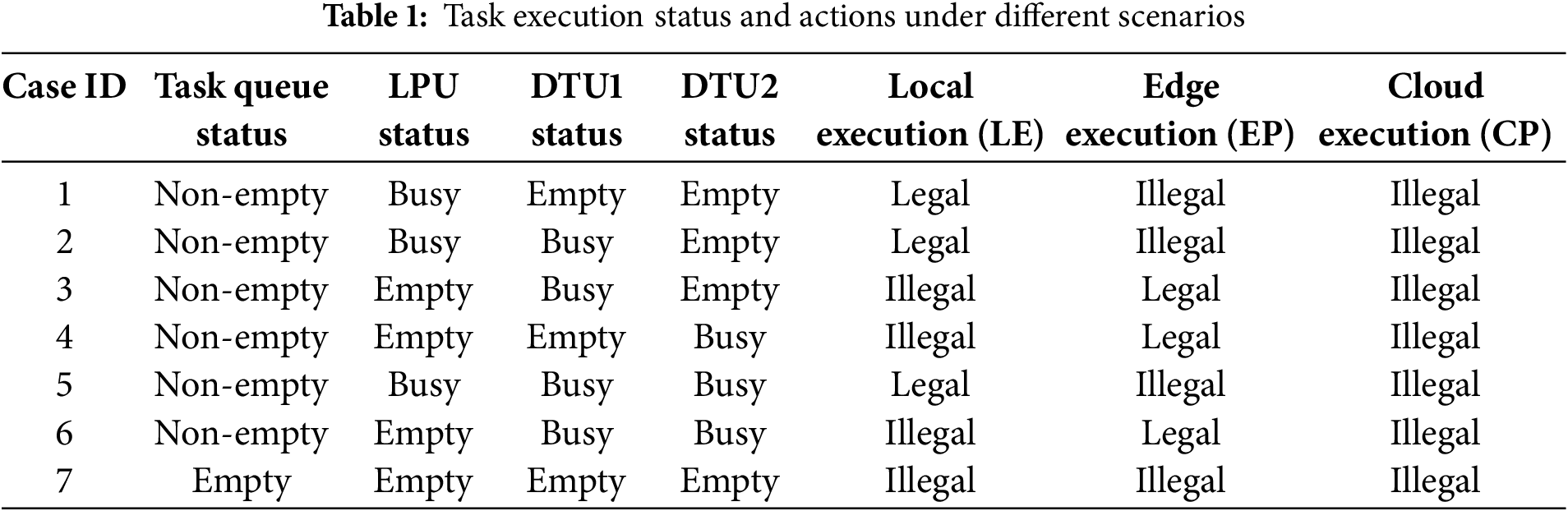
4) We introduce a dynamic action selection mechanism that evaluates the system’s state—task queue, LPU, and DTUs—at each time step. This mechanism adaptively chooses valid actions (Local Execution, Edge Processing, Cloud Processing) based on real-time conditions to optimize resource utilization and minimize delays. For instance, if the task queue is non-empty and the LPU is idle, local execution reduces communication latency. If tasks demand more resources, offloading to edge or cloud servers becomes available when DTUs are idle (Table 1). This dynamic scheduling mechanism ensures effective resource allocation and improved system performance.

5.3 Reward Function

In a three-layer smart grid framework (terminal devices, edge servers, and cloud servers), the reward function optimizes task offloading by balancing delay and energy consumption.

Delay and Energy Consumption Calculation: The orchestrator schedules task offloading decisions at discrete time intervals. Assume that at time tn, an action;an is selected, transitioning the system state from Sn∈S to Sn+1. For all tasks at time t, the total delay and energy consumption are quantified based on the task’s execution or transmission conditions. At time t, the total delay Δts(t) for all tasks can be expressed as:

Δts(t)=q[t]+1{slpu[t]>0}+1{sdtu1[t]>0}+1{smec[t]>0}+1{sdtu2[t]>0}+1{scc[t]>0}(37)

where q[t] is the number of tasks in the task queue. 1{⋅} is an indicator function evaluating whether specific states slpusdtu1 are active. The total delay from state sn to sn+1 is then aggregated as:

Δt(sn,an,sn+1)=∑t=tnatn+1a−1Δts(t)(38)

At time t, the total energy consumption Δes(t) is related to local computation and data transmission. It is given by:

Δes(t)=pl⋅1{slpu[t]>0}+ptx1⋅1{sdtu1[t]>0}+ptx2⋅1{sdtu2[t]>0}(39)

Thus, the total energy consumption during the transition is:

Δe(sn,an,sn+1)=∑t=tnatn+1a−1Δes(t)(40)

Therefore, the overall cost is:

cost(sn,an,sn+1)=αΔt(sn,an,sn+1)+βΔe(sn,an,sn+1)(41)

where α and β are weighting factors balancing delay and energy consumption.

To optimize task offloading strategies, the reward function is defined as the negative of the total cost:

R(sn,an,sn+1)=−ks⋅cost(sn,an,sn+1)(42)

where k is a scaling constant to adjust the range of reward values.

Cumulative Reward Function. In the smart grid task offloading problem, the cumulative reward function evaluates the long-term performance of a scheduling strategy. Starting from an initial state sm∈S, the system interacts with the environment iteratively, selecting actions an∈A. This forms a Markov Decision Process (MDP), and the cumulative reward function is:

Gm=∑n=0∞γnR(sm+n,am+n,sm+n+1),sm∈S(43)

where Gm is the total reward obtained starting from state;sm. γ∈[0,1] is the discount factor balancing immediate and future rewards.

By maximizing Gm, the task offloading strategy can be optimized to minimize delays and energy consumption while maintaining system efficiency. For γ = 1, the cumulative reward represents the sum of all delays and energy costs. Thus, finding the optimal strategy π∗ aligns with minimizing the original objective function. However, due to the vast state space, we plan to utilize Deep Reinforcement Learning (DRL) for training.

6  DRL-Based Task Offloading and Scheduling

This section presents a novel deep neural network (DNN) architecture trained with Proximal Policy Optimization (PPO). The DNN is tailored to extract complex patterns from high-dimensional data, while PPO updates the policy parameters in a way that carefully balances exploration and exploitation, thereby ensuring stable convergence. Comprehensive experiments show that the proposed method yields significant performance improvements over prevailing approaches.

6.1 Network Architecture

As illustrated in Fig. 2, the proposed DRL framework is designed to simultaneously approximate the task offloading policy and estimate the value function. To achieve this, we develop a parameter-sharing deep neural network (DNN) that approximates two objectives: the task offloading policy π(αn∣sn;θ), which selects the optimal offloading action, and the value function v(sn;ω), which evaluates the advantage function to optimize the policy.

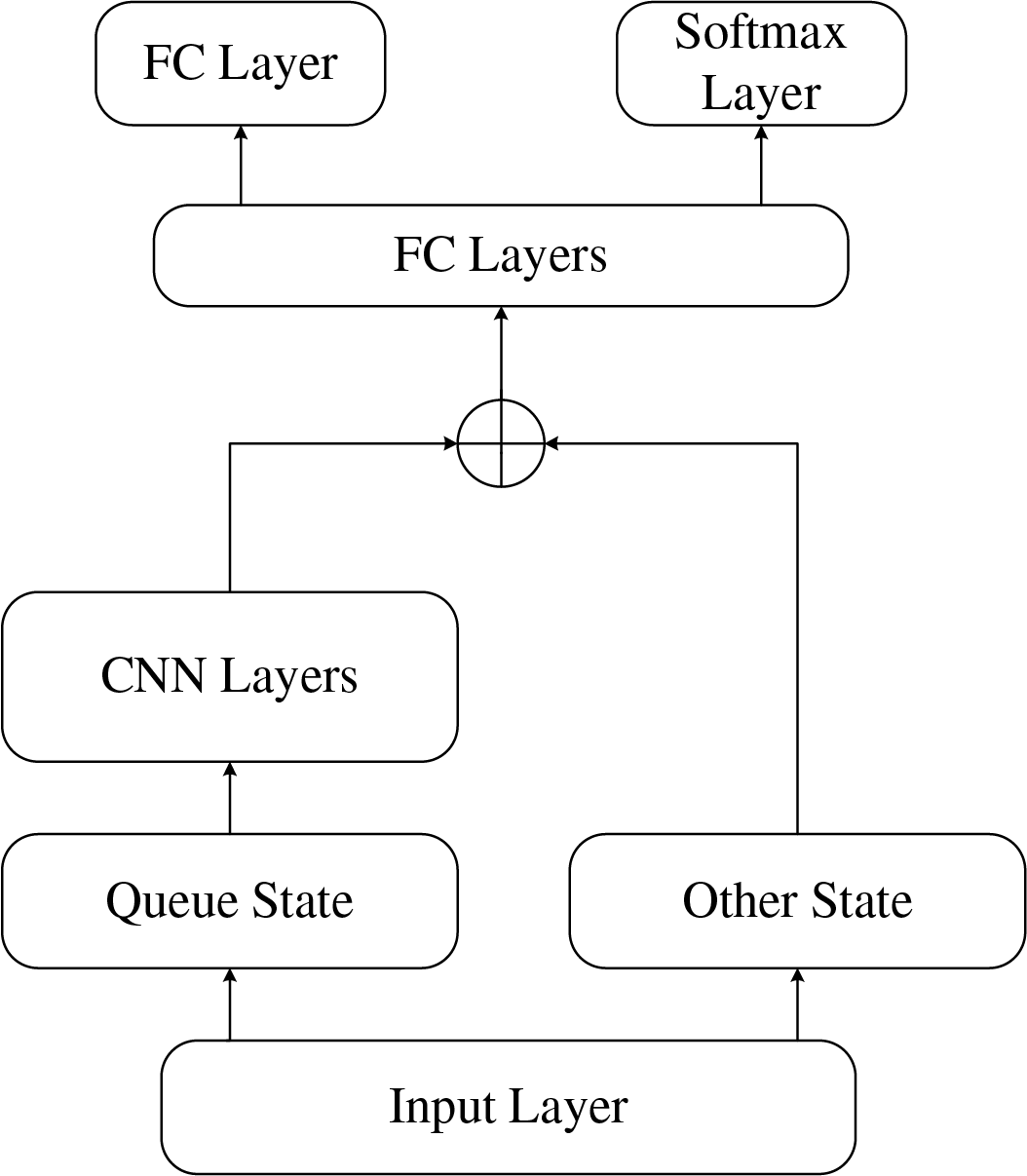
Figure 2: Neural network architecture

Due to the overwhelming size of the input state, processing becomes challenging; moreover, since the data stored in task queue Q are structured, we employed a Convolutional Neural Network (CNN) for feature extraction. Subsequent studies have demonstrated that this architecture significantly enhances training performance compared to using solely fully connected layers.

6.2 Training Algorithm

We use a shared-parameter DNN where the objective function combines errors from both the policy and value networks. To enhance sample efficiency and stabilize policy updates, we employ Generalized Advantage Estimation (GAE).

The policy network is optimized using the PPO Clipped Objective, while the value network minimizes the state-value error. The overall optimization objective is expressed as:

LPPO(θ)=En[LnCLIP(θ)−cLnV(θ)](44)

where c is a loss coefficient used to balance the loss between the policy and value networks.

As shown in Algorithm 1, the training process alternates between sampling and optimization phases. During the sampling phase, the old policy πold is used to generate N trajectories, with each trajectory containing multiple time-step data points: n. At each time step n, based on the current environment state sn, an action is selected, and the corresponding reward and the next state are recorded.

To improve training efficiency, the Generalized Advantage Estimate A^nGAE(γ,λ) is precomputed for each trajectory and stored in two sets: T (Trajectories) and A (Advantages).

During the optimization phase, the collected trajectory data are used to update the policy network. The parameters θ are optimized over multiple epochs using stochastic gradient ascent. The objective is to maximize the PPO loss function LPPO(θ). In each epoch, the Adam optimizer is used to update the policy parameters. After optimization is completed, the updated parameters replace the old policy πold, and the data sets T and A are cleared to prepare for the next iteration.

During sampling, the exploration policy may choose invalid actions—for example, executing tasks locally when the LPU is saturated. To prevent errors, a validity constraint mechanism is implemented: invalid actions are ignored, the current state is maintained, and a valid action is reselected, ensuring that optimization proceeds correctly.

7  Performance Evaluation

This section provides a comprehensive evaluation of the proposed PPO-based Offloading Strategy Method (PPO-OSM) through extensive simulation experiments. The algorithm and its neural architecture are implemented in TensorFlow. Key simulation settings and training hyper-parameters are summarized in Tables 2 and 3 [30], respectively.

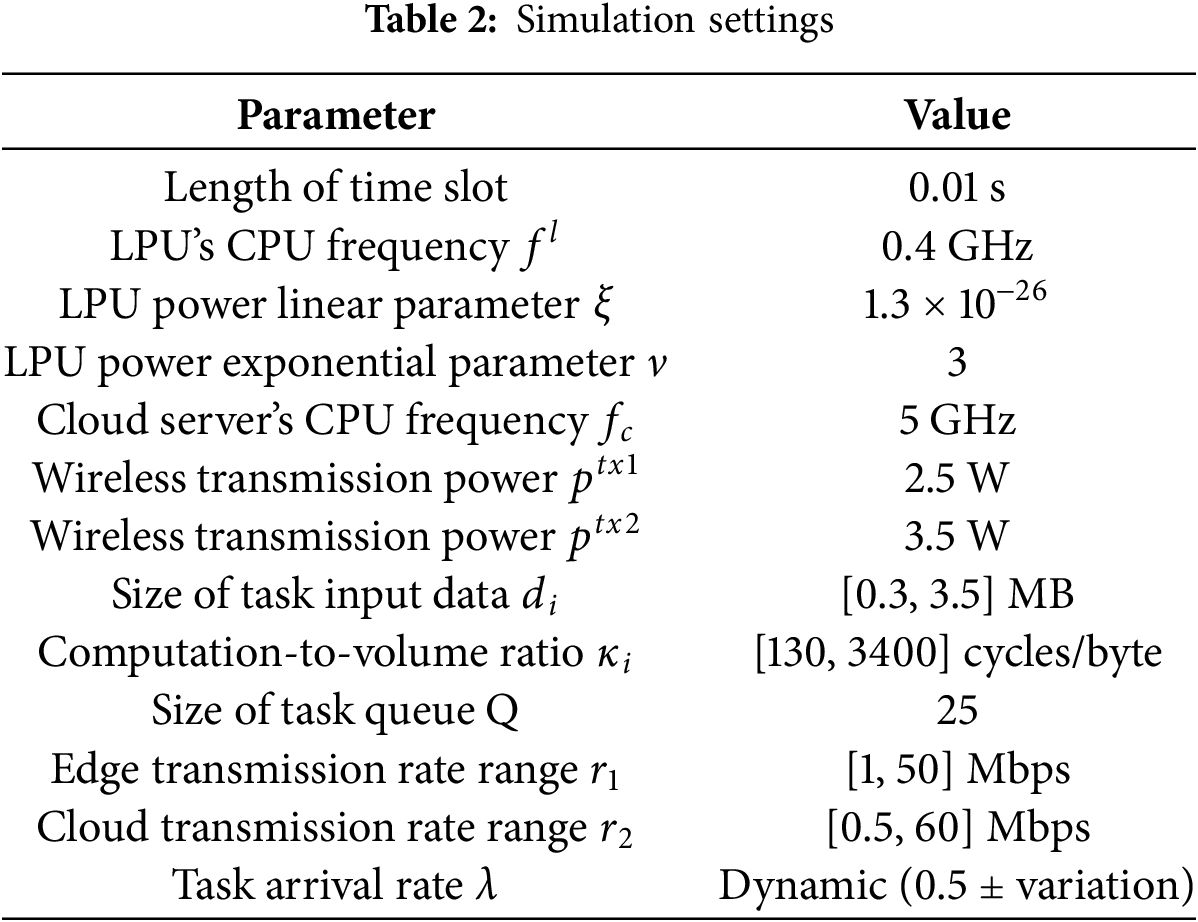
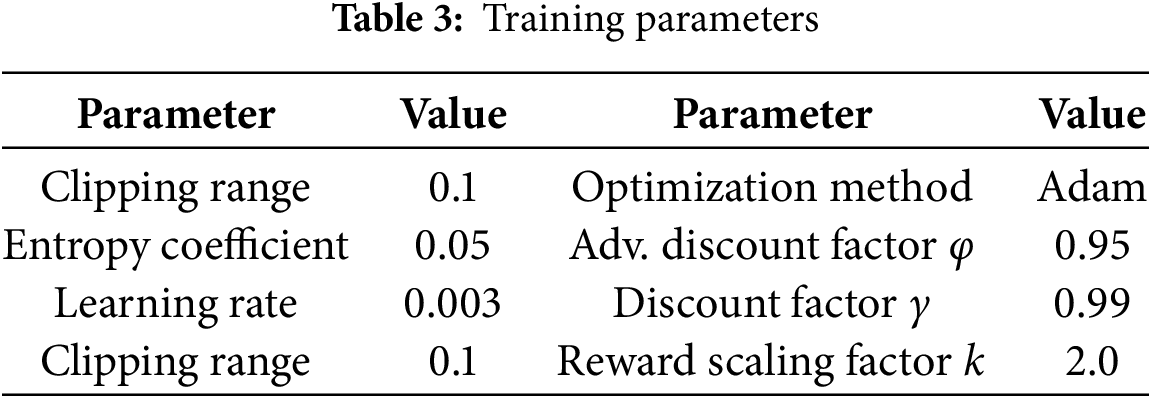
We set the time step duration to 0.01 s, during which the system updates task scheduling and status at each interval. Parameters for the Local Processing Unit (LPU) are configured based on. Thus, the local computational power consumption pl is determined as pl=ξ(fl)ν). The power consumption for edge and cloud transmission is set as ptx1 = 2.5 W, ptx2 = 3.5 W, respectively. Each task’s data size di and computational complexity κi are sampled from uniform distributions defined in Table 2.

In smart grid environments, transmission rates change dynamically over time due to variations in node distance and other factors. We use a sinusoidal model to represent these periodic rate fluctuations. Specifically, R1 simulates communication between users and nearby edge nodes, while R2 models communication between terminal devices and the cloud. Although R2 generally provides higher bandwidth, its variability can be more pronounced, reflecting trade-offs between edge and cloud offloading.

Our simulation integrates system parameters—such as LPU configurations, edge servers (MEC), and cloud computing (CC) resources—to form a cohesive environment. As task complexity increases, DRL-based scheduling strategies like PPOOSM adapt to changing conditions, learn optimal offloading decisions, and enhance overall task scheduling performance.

7.1 Convergence Performance

To assess the efficacy of the proposed PPO-based Offloading Strategy Method (PPO-OSM), we conducted experiments under the conditions illustrated in Fig. 3. PPO-OSM was benchmarked against a baseline PPO implementation that uses only fully connected (FC) layers; both algorithms were trained with identical hyper-parameters, and their learning curves were logged. As shown in Fig. 3, PPO-OSM consistently achieves higher cumulative rewards and converges more rapidly than the baseline.

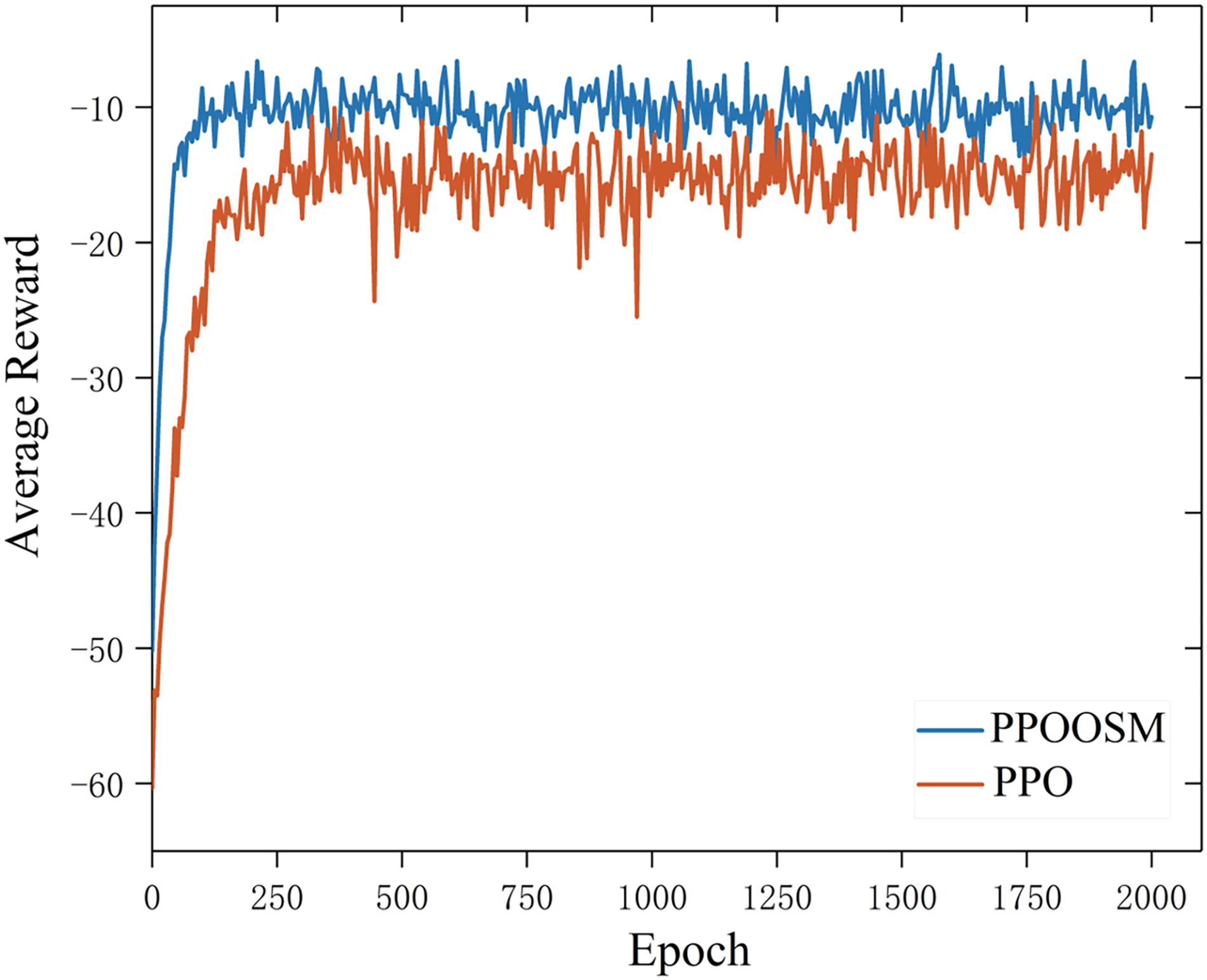
Figure 3: Comparison of average reward over training epochs for PPO and PPO-OSM

Our experiments show that PPOOSM significantly accelerates training, with cumulative rewards stabilizing after about 100 epochs. In contrast, the FC-based PPO algorithm exhibits erratic performance and slower convergence—its cumulative rewards even drop around 500 epochs. Additionally, PPOOSM enhances both task offloading and strategy optimization, effectively balancing task delay and energy consumption. Overall, these results demonstrate that PPOOSM is more efficient, stable, and robust for optimizing task offloading in dynamic environments than the conventional FC-based PPO.

7.2 Analysis of Performance under Different Biases

We assessed the proposed PPO-based offloading strategy (PPOOSM) under a range of latency–energy preference settings and benchmarked it against five representative baselines:

•   All-Local Execution (AL): every task is processed entirely on the device’s local CPU.

•   All-Edge Offloading (AE): all tasks are offloaded to an edge server, regardless of wireless-channel conditions. All-Cloud Offloading (AC): all tasks are transmitted straight to the cloud, ignoring backhaul and fronthaul constraints.

•   PPO: the standard Proximal Policy Optimization algorithm directly applied to the offloading decision problem, with no additional multi-objective shaping.

•   Genetic Algorithm (GA): a heuristic implemented with the DEAP library that evolves offloading decisions through selection, crossover, and mutation.

As illustrated in Figs. 4 and 5—which decompose the overall cost into latency and energy components—the six evaluated strategies display markedly different behaviours as the latency-weighting factor α increases (β is fixed at 1). All-Local execution (AL), in which every task is processed on the resource-constrained device, consistently yields the highest delay and energy consumption. All-Edge (AE) and All-Cloud (AC) offloading shorten latency slightly relative to AL, yet they remain energy-intensive and cannot adapt to wireless-channel fluctuations, causing their performance to cluster in the upper regions of both plots. The heuristic Genetic Algorithm (GA) reduces delay appreciably—especially when α ≤ 0.3—but achieves only moderate energy savings. PPO further lowers energy consumption through policy-gradient updates, although its average delay is still marginally higher than that of GA. By contrast, PPOOSM adapts its offloading policy online and therefore attains the lowest energy usage across all settings; moreover, once α ≈ 0.3, it also achieves the smallest delay among all schemes. These results demonstrate that PPOOSM offers the most favourable latency—energy trade-off in realistic smart-grid scenarios.

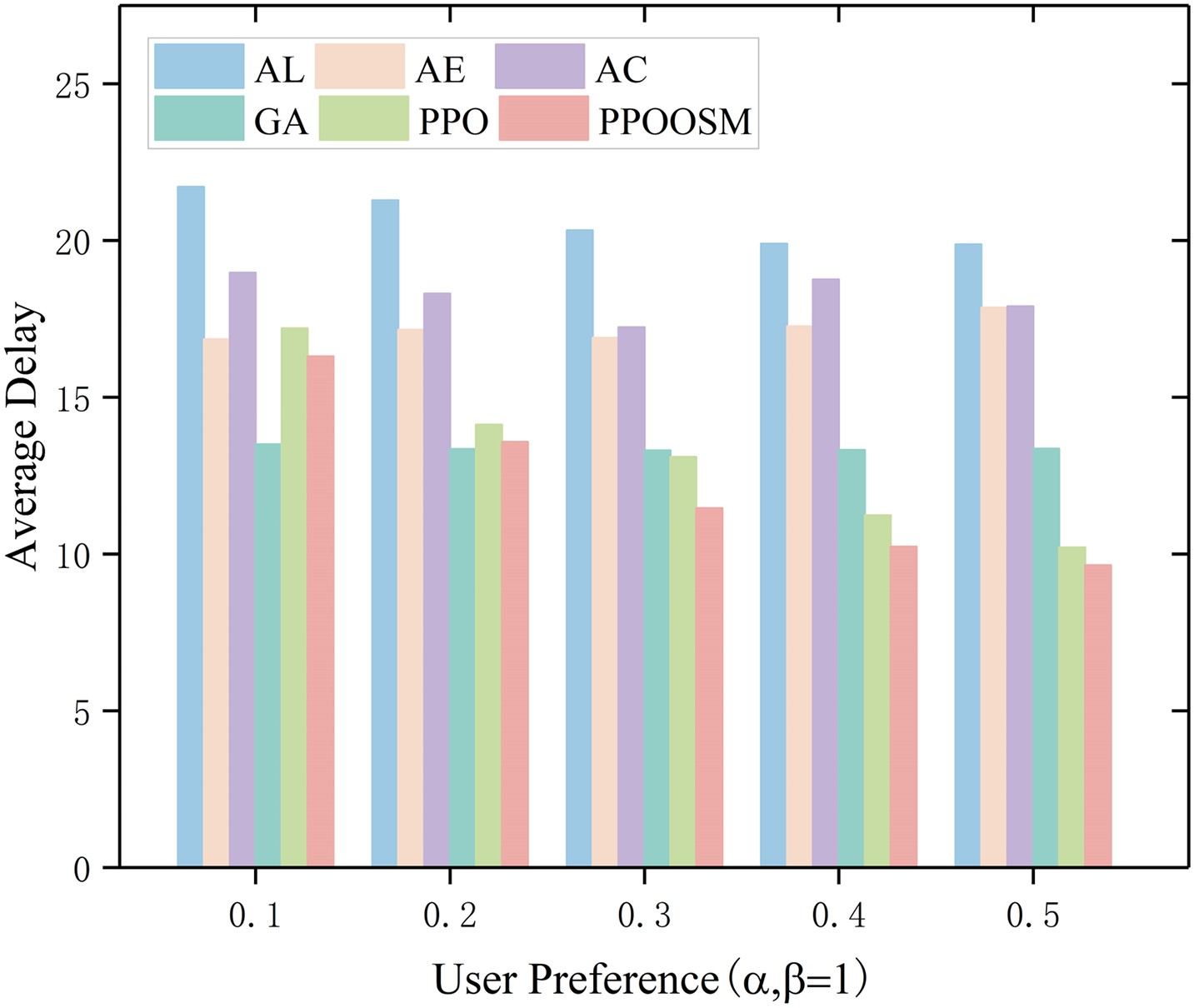
Figure 4: Comparison of average delay

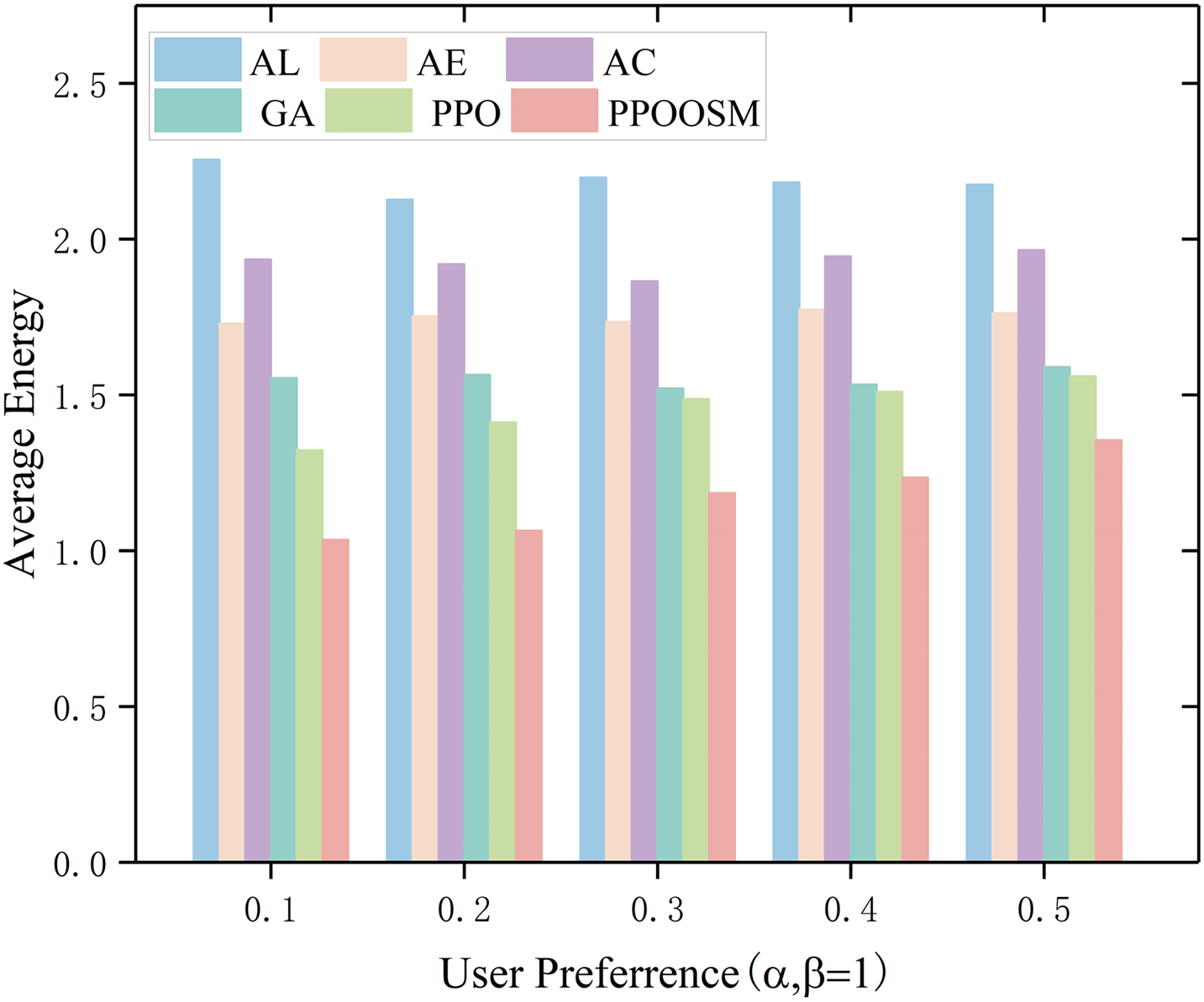
Figure 5: Comparison of average energy

Fig. 6 reveals that the static schemes—AL, AE, and AC—incur the highest overall cost because they lack the flexibility required to cope with a dynamic environment. In contrast, PPOOSM, GA, and PPO strike a more favorable balance between computation and transmission expenses. Notably, by embedding a convolutional neural network (CNN) within its policy network, PPOOSM not only reduces the average cost most substantially but also delivers superior stability and adaptability compared with GA and PPO.

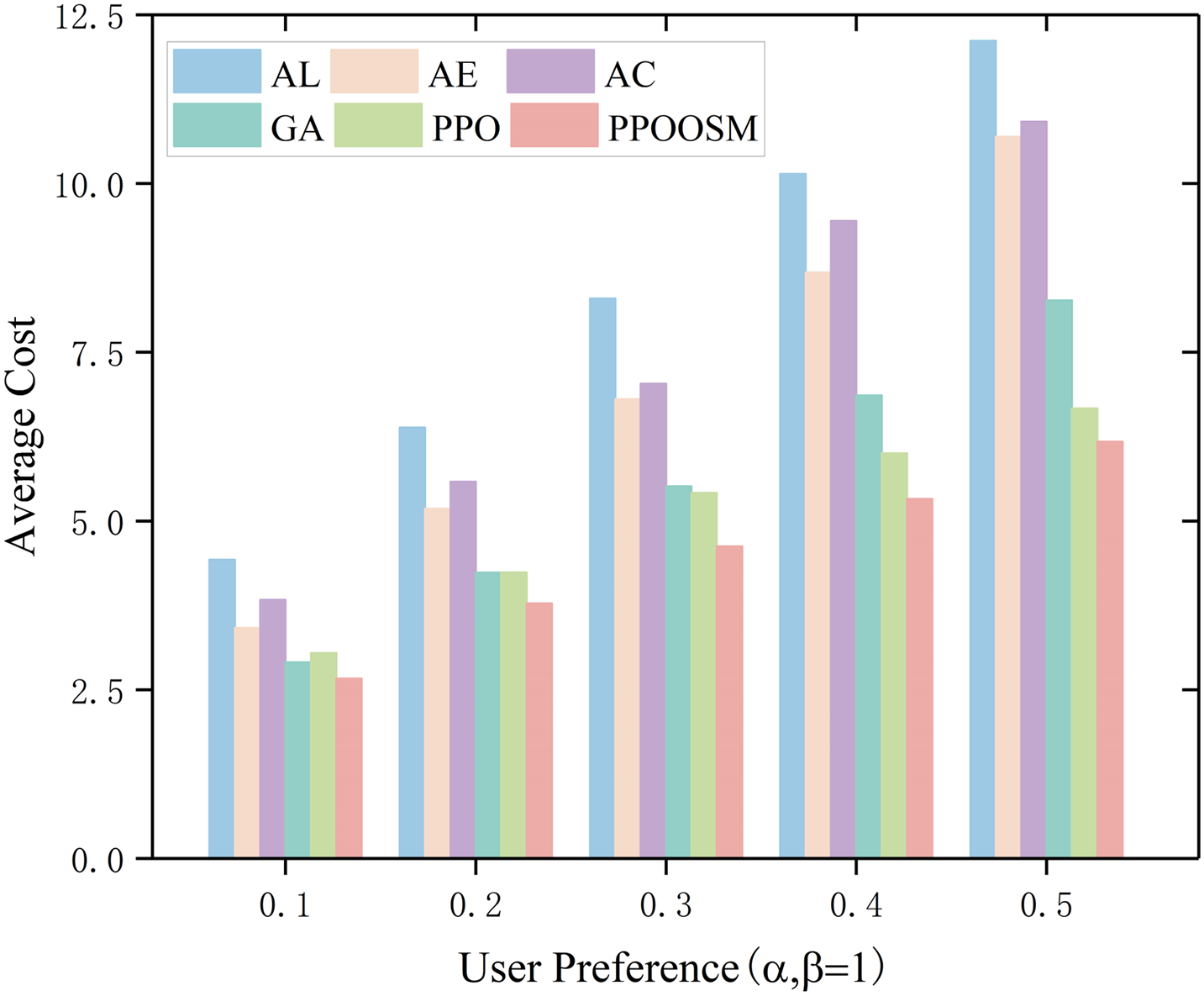
Figure 6: Comparison of average cost

7.3 Performance Analysis in Dynamic Queue Scenarios

In the Dynamic Queue Scenario (DQS), we evaluated the performance of different task offloading strategies as the task load incrementally increased. The analysis particularly focused on variations in average delay, energy consumption, and overall cost. In the experiments, we set the parameters α = 0.4, β = 1, simulating each algorithm under varying load factors ranging from 0.1 (low load) to 1.0 (high load). Through the analysis of experimental data, we could clearly observe the performance advantages of each strategy under different load levels.

As the workload intensity λ increases (Figs. 7 and 8), all schemes experience higher latency, but the growth rates diverge: AL climbs most steeply, while AC and AE deteriorate once network congestion sets in. PPO keeps delay low with an almost linear trend, and PPOOSM flattens the curve even further, achieving the smallest latency across the entire range. Energy consumption follows the same ordering: the static policies (AL, AE, AC) remain high and nearly flat, PPO cuts energy appreciably, and PPOOSM delivers the lowest and most stable profile. Overall, PPOOSM offers the best latency–energy trade-off, with PPO serving as a strong adaptive baseline that consistently outperforms all fixed strategies.

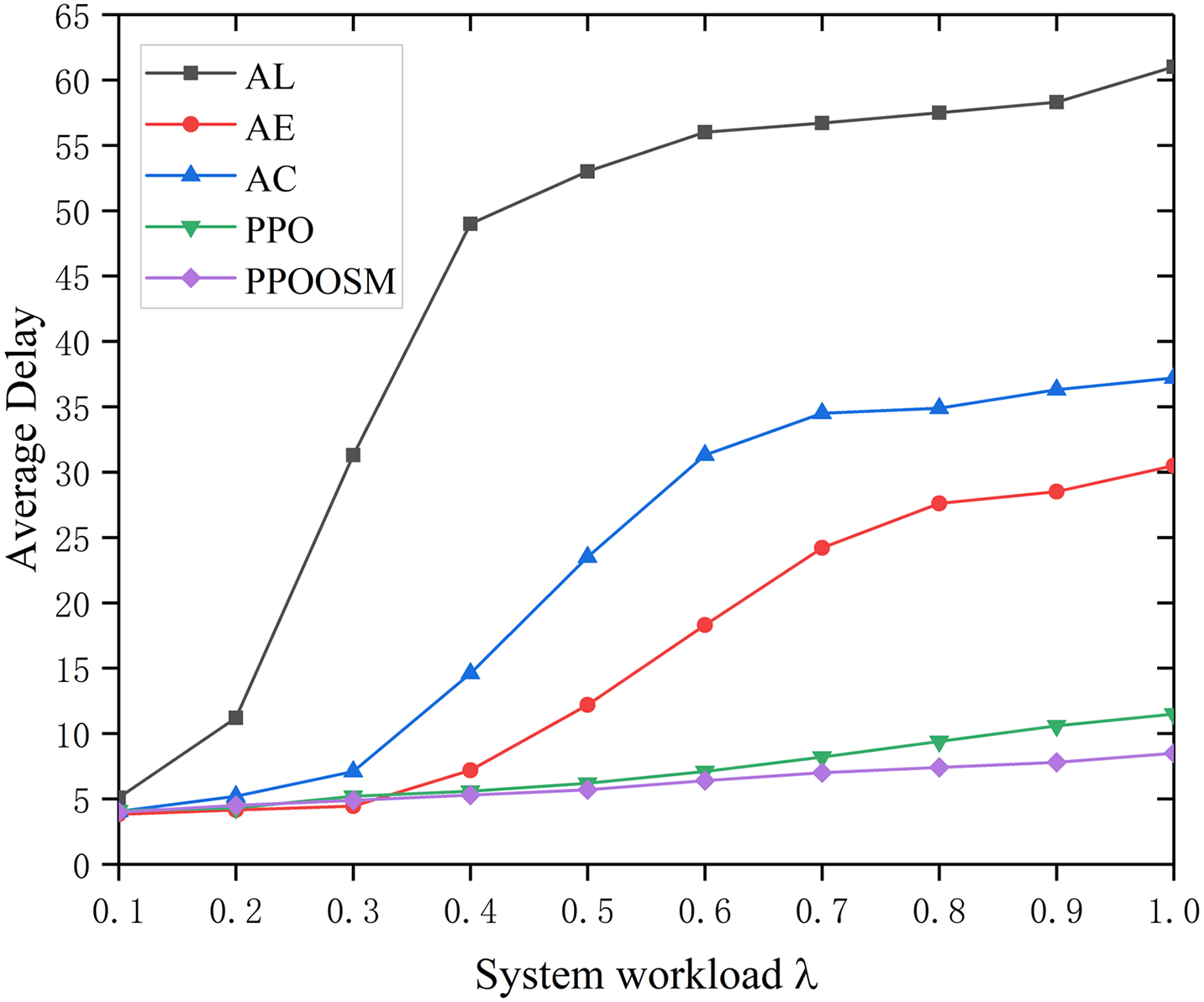
Figure 7: Average delay under different workloads

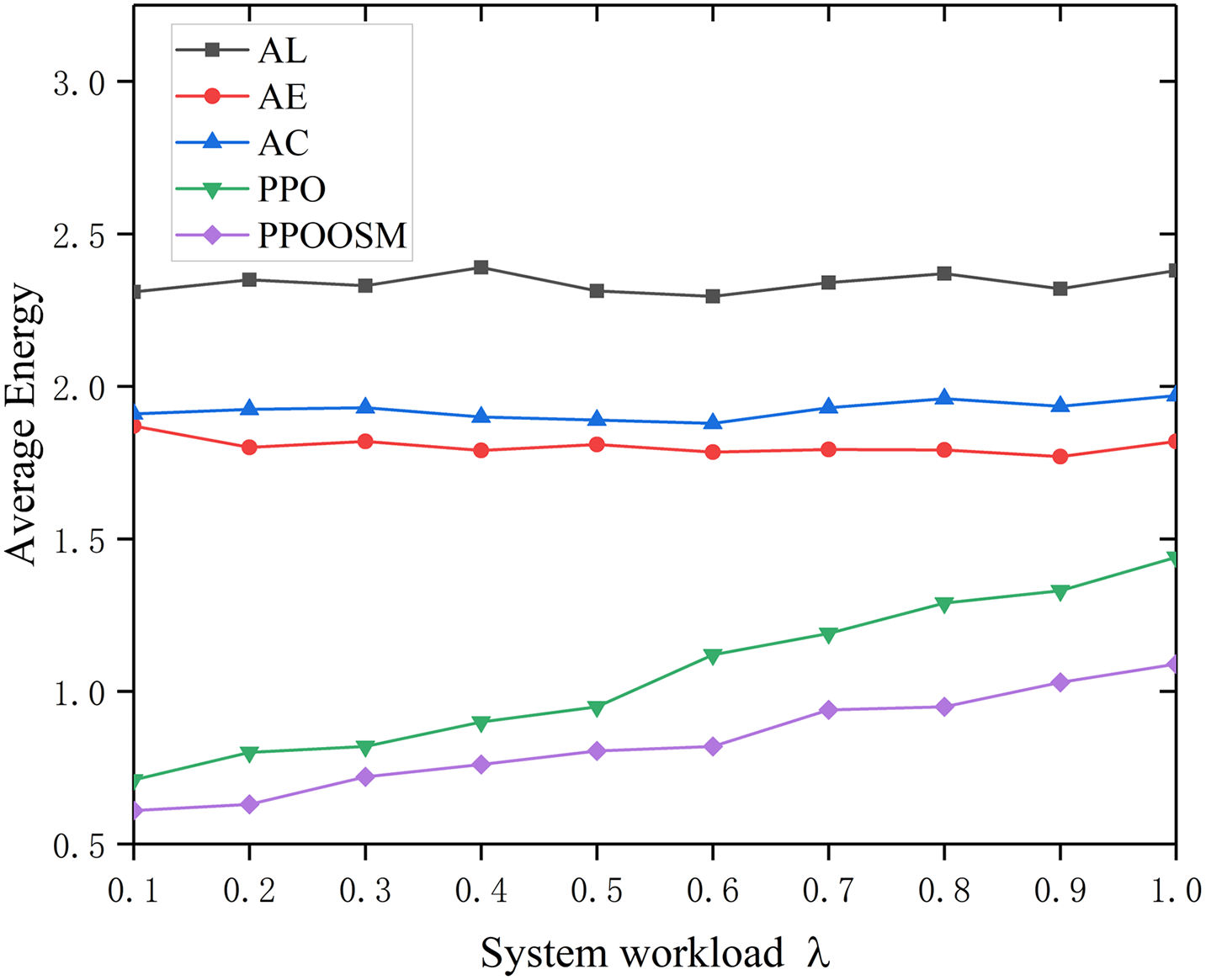
Figure 8: Average energy under different workloads

Fig. 9 charts the composite cost—latency plus energy—against workload intensity λ for five schemes. The three static policies (AL, AE, AC) exhibit the highest and steepest cost growth because they cannot adapt to changing conditions. Vanilla PPO reduces the curve substantially by continuously refining its off-loading policy, yet PPOOSM remains dominant, yielding the lowest cost across the entire workload range. Equipped with a CNN-enhanced state encoder and an α–β-weighted objective, PPOOSM dynamically reallocates tasks in real time, achieving superior multi-objective optimisation in non-stationary edge environments.

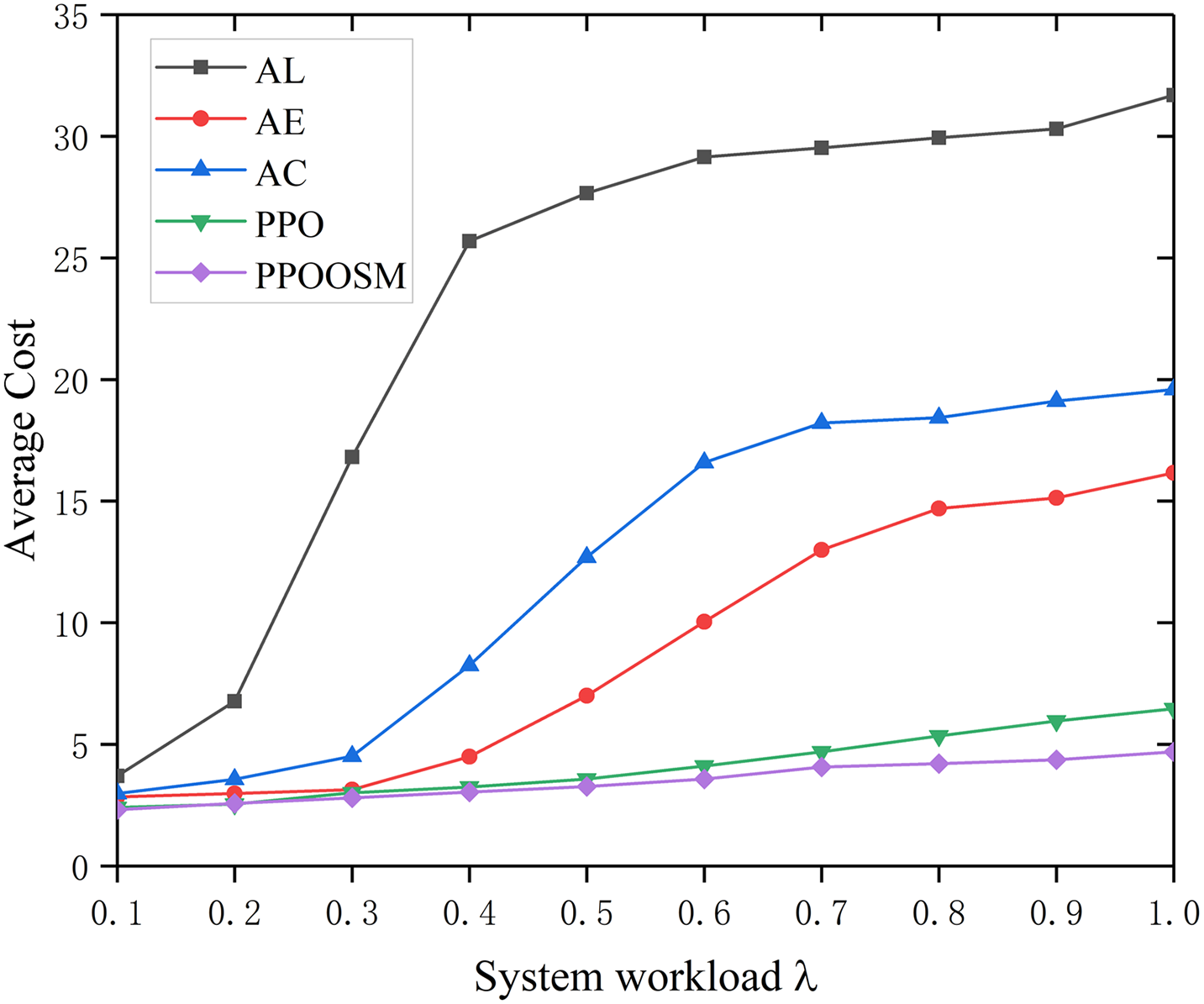
Figure 9: Average cost under different workloads

8  Conclusion

This paper presents a Proximal-Policy-Optimisation-based Offloading Strategy Model (PPOOSM) that allocates computational resources efficiently for task-offloading in smart-grid environments. By formulating the off-loading problem as a Markov decision process (MDP), the framework integrates deep reinforcement learning through a shared convolutional neural network and a clipped objective function, markedly improving training stability. Extensive simulations demonstrate that, under dynamic off-loading conditions, PPOOSM reduces both latency and energy consumption, outperforming conventional baseline algorithms and heuristic methods. Relative to static allocation strategies, it achieves a more favourable latency–energy trade-off and exhibits superior adaptability and robustness, particularly at high load. These findings confirm the viability of deep reinforcement learning for task-offloading decisions and provide an efficient, flexible solution for real-time scheduling in smart grids, underscoring its significant potential for practical engineering deployment and broad adoption.

Acknowledgement: We would sincerely want to thank the peoples who are supported to do this work and reviewing committee for their estimable feedbacks.

Funding Statement: This work was supported by the National Natural Science Foundation of China (Grant No. 62103349) and the Henan Province Science and Technology Research Project (Grant No. 232102210104).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Ya Zhou, Qian Wang; data collection: Qian Wang; analysis and interpretation of results: Qian Wang; draft manuscript preparation: Qian Wang, Ya Zhou. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets generated or analyzed during the current study are not publicly available due to privacy and confidentiality concerns, but are available from the corresponding author on reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Acarali D, Chugh S, Rao KR, Rajarajan M. IoT deployment and management in the smart grid. In: Ranjan R, Mitra K, Jayaraman PP, Zomaya AY, editors. Managing Internet of Things applications across edge and cloud data centres. London, UK: The Institution of Engineering and Technology; 2024. p. 255–75. doi:10.1049/PBPC027E_ch11. [Google Scholar] [CrossRef]

2. Al-Bossly A. Metaheuristic optimization with deep learning enabled smart grid stability prediction. Comput Mater Contin. 2023;75(3):6395–408. doi:10.32604/cmc.2023.028433. [Google Scholar] [CrossRef]

3. Ahmed RA, Abdelraouf M, Elsaid SA, ElAffendi M, Abd El-Latif AA, Shaalan AA, et al. Internet of Things-based robust green smart grid. Comput. 2024;13(7):169. doi:10.3390/computers13070169. [Google Scholar] [CrossRef]

4. Aminifar F. Evolution in computing paradigms for Internet of Things-enabled smart grid applications. In: Proceedings of the 2024 5th CPSSI International Symposium on Cyber-Physical Systems (Applications and Theory) (CPSAT); 2024 Oct 16–17; Tehran, Iran. doi:10.1109/CPSAT64082.2024.10745414. [Google Scholar] [CrossRef]

5. Arcas GI, Cioara T, Anghel I, Lazea D, Hangan A. Edge offloading in smart grid. arXiv:2402.01664. 2024. [Google Scholar]

6. Li K, Meng J, Luo G, Hou L, Cheng H, Liu M, et al. Fusion-communication MEC offloading strategy for smart grid. Dianli Xinxi Yu Tongxin Jishu. 2024;22(6):10–7. (In Chinese). doi:10.16543/j.2095-641X.electric.power.ict.2024.06.02. [Google Scholar] [CrossRef]

7. Liu M, Tu Q, Wang Y, Meng S, Zhao X. Research status of mobile cloud computing offloading technology and its application in the power grid. Dianli Xinxi Yu Tongxin Jishu. 2021;19(1):49–56. (In Chinese). doi:10.16543/j.2095-641X.electric.power.ict.2021.01.007. [Google Scholar] [CrossRef]

8. Zhang N, Li WJ, Liu Z, Li Z, Liu YM, Nahar N. A new task scheduling scheme based on genetic algorithm for edge computing. Comput Mater Contin. 2022;71(1):843–54. doi:10.32604/cmc.2022.017504. [Google Scholar] [CrossRef]

9. Han X, Dai J, Wang Y. Research on edge computing-oriented resource-aware access and intelligent gateway technology for power transmission, transformation and distribution. In: Proceedings of the 2023 International Conference on Applied Intelligence and Sustainable Computing (ICAISC); 2023 Jun 16–17; Dharwad, India. p. 1–6. doi:10.1109/ICAISC58445.2023.10199983. [Google Scholar] [CrossRef]

10. Wei H, Guan Y, Zhao Q, Zhang T, Liu J, Zhang H. A novel distributed computing resource operation mechanism for edge computing. In: Proceedings of the 2023 9th International Conference on Computer and Communications (ICCC); 2023 Dec 8–11; Chengdu, China. p. 2593–8. doi:10.1109/ICCC59590.2023.10507521. [Google Scholar] [CrossRef]

11. Dong S, Tang J, Abbas K, Hou R, Kamruzzaman J, Rutkowski L, et al. Task offloading strategies for mobile edge computing: a survey. Comput Netw. 2024;254(6):110791. doi:10.1016/j.comnet.2024.110791. [Google Scholar] [CrossRef]

12. Park S, Kwon D, Kim J, Lee YK, Cho S. Adaptive real-time offloading decision-making for mobile edges: deep reinforcement learning framework and simulation results. Appl Sci. 2020;10(5):1663. doi:10.3390/app10051663. [Google Scholar] [CrossRef]

13. Peng P, Lin W, Wu W, Zhang H, Peng S, Wu Q, et al. A survey on computation offloading in edge systems: from the perspective of deep reinforcement learning approaches. Comput Sci Rev. 2024;53(5):100656. doi:10.1016/j.cosrev.2024.100656. [Google Scholar] [CrossRef]

14. Zhu C, Xia L, Qin C. Research progress and prospects of deep reinforcement learning in the field of mobile edge computing. In: Ning Z, Xiong Z, editors. Proceedings of the Fifth International Conference on Computer Communication and Network Security (CCNS 2024); 2024 May 3–5; Guangzhou, China. p. 1322813. doi:10.1117/12.3038174. [Google Scholar] [CrossRef]

15. Gao Z, Wu G, Shen Y, Zhang H, Shen S, Cao Q. DRL-based optimization of privacy protection and computation performance in MEC computation offloading. In: IEEE INFOCOM 2022—IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS); 2022 May 2–5; Online. p. 1–6. doi:10.1109/INFOCOMWKSHPS54753.2022.9797993. [Google Scholar] [CrossRef]

16. Alfa AS, Maharaj BT, Lall S, Pal S. Resource allocation techniques in underlay cognitive radio networks based on mixed-integer programming: a survey. J Commun Netw. 2016;18(5):744–61. doi:10.1109/JCN.2016.000104. [Google Scholar] [CrossRef]

17. Wei F, Chen S, Zou W. A greedy algorithm for task offloading in mobile edge computing system. China Commun. 2018;15(11):149–57. doi:10.1109/CC.2018.8543056. [Google Scholar] [CrossRef]

18. Umair M, Saeed Z, Saeed F, Ishtiaq H, Zubair M, Hameed HA. Energy theft detection in smart grids with genetic algorithm-based feature selection. Comput Mater Contin. 2023;74(3):5431–46. doi:10.32604/cmc.2023.033884. [Google Scholar] [CrossRef]

19. Wang J, Xia H, Xu L, Zhang R, Jia K. DRL-based latency-energy offloading optimization strategy in wireless VR networks with edge computing. Comput Netw. 2025;258:111034. doi:10.1016/j.comnet.2025.111034. [Google Scholar] [CrossRef]

20. Wang T, Deng Y, Yang Z, Wang Y, Cai H. Parameterized deep reinforcement learning with hybrid action space for edge task offloading. IEEE Internet Things J. 2024;11(6):10754–10767. doi:10.1109/JIOT.2023.3327121. [Google Scholar] [CrossRef]

21. Li H, Liu L, Duan X, Li H, Zheng P, Tang L. Energy-efficient offloading based on hybrid bio-inspired algorithm for edge-cloud integrated computation. Sustain Comput Inform Syst. 2024;42(11):100972. doi:10.1016/j.suscom.2024.100972. [Google Scholar] [CrossRef]

22. Wang W, Yang L, Long T, Zhang X, Zhang M. Mobile edge computing task offloading method for the power Internet of Things. In: Proceedings of the 2024 IEEE 7th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC); 2024 Sep 20–22; Chongqing, China. p. 118–22. doi:10.1109/ITNEC60942.2024.10733102. [Google Scholar] [CrossRef]

23. Cui J, Li Y, Yang H, Wei Y, Liu W, Ji C, et al. Quota matching-based task offloading for WSN in smart grid. In: Proceedings of the 2022 7th International Conference on Electronic Technology and Information Science (ICETIS 2022); 2022 Jan 21–23; Harbin, China. p. 1–4. [Google Scholar]

24. Hu J, Li Y, Zhao G, Xu B, Ni Y, Zhao H. Deep reinforcement learning for task offloading in edge computing assisted power IoT. IEEE Access. 2021;9:93892–901. doi:10.1109/ACCESS.2021.3092381. [Google Scholar] [CrossRef]

25. Zhou H, Zhang Z, Li D, Su Z. Joint optimization of computing offloading and service caching in edge computing-based smart grid. IEEE Trans Cloud Comput. 2023;11(2):1122–32. doi:10.1109/TCC.2022.3163750. [Google Scholar] [CrossRef]

26. Nimkar S, Khanapurkar MM. Design of a Q-learning based smart grid and smart water scheduling model based on heterogeneous task specific offloading process. In: Proceedings of the 2022 International Conference on Smart Generation Computing, Communication and Networking (SMART GENCON); 2022 Dec 23–25; Bangalore, India. p. 1–9. doi:10.1109/SMARTGENCON56628.2022.10084189. [Google Scholar] [CrossRef]

27. Li H, Xiong K, Lu Y, Chen W, Fan P, Letaief KB. Collaborative task offloading and resource allocation in small-cell MEC: a multi-agent PPO-based scheme. IEEE Trans Mob Comput. 2025;24(3):2346–59. doi:10.1109/TMC.2024.3496536. [Google Scholar] [CrossRef]

28. Mustafa E, Shuja J, Rehman F, Namoun A, Bilal M, Iqbal A. Computation offloading in vehicular communications using PPO-based deep reinforcement learning. J Supercomput. 2025;81(4):547. doi:10.1007/s11227-025-07009-z. [Google Scholar] [CrossRef]

29. Goudarzi M, Palaniswami M, Buyya R. A distributed deep reinforcement learning technique for application placement in edge and fog computing environments. IEEE Trans Mob Comput. 2023;22(5):2491–505. doi:10.1109/TMC.2021.3123165. [Google Scholar] [CrossRef]

30. Dinh TQ, Tang J, La QD, Quek TQS. Offloading in mobile edge computing: task allocation and computational frequency scaling. IEEE Trans Commun. 2017;65(8):3571–84. doi:10.1109/TCOMM.2017.2699660. [Google Scholar] [CrossRef]