VPAFL: Verifiable Privacy-Preserving Aggregation for Federated Learning Based on Single Server

1  Introduction

1.1 Motivation

With the widespread adoption of cloud computing technologies [1], the migration of large amounts of user data to the cloud has become an irreversible trend. To address the risks of privacy breaches, encrypting data for storage has become essential. However, this measure introduces new challenges, particularly in performing operations such as metadata embedding and identity authentication while ensuring data confidentiality.

To address these challenges, the technique of reversible data hiding in the encrypted domain (RDHED) [2–4] has emerged as a promising solution. This technology enables the reversible embedding of data, such as identity markers and integrity labels, within encrypted data [5,6]. Upon decryption, both the original data and the embedded data can be completely recovered, providing an innovative approach to managing encrypted data. Despite significant advancements in traditional RDHED methods, most existing schemes rely on stream cipher encryption mechanisms, which do not support ciphertext operations [2,4–6]. This limitation makes them unsuitable for emerging privacy-preserving computing scenarios, such as federated learning (FL) [7].

In recent years, homomorphic encryption (HE)-based RDHED schemes have gained attention as a potential solution [8–10]. However, these approaches face two major technical challenges. First, their applicability is often limited because most existing research focuses on image data processing, while FL predominantly involves model parameters. Second, compatibility issues arise: existing methods do not adequately address the destructive effects of homomorphic processing on embedded data [11]. For instance, when encrypted data undergo homomorphic processing, such as ciphertext aggregation, embedded data may suffer irreversible distortion, resulting in extraction failures [12–14]. Furthermore, FL usually involves multiple participants, yet enabling each user to independently perform data embedding and extraction independently in decentralized scenarios remains a great challenge.

In a typical FL architecture, users upload their local models to the server, which aggregates the received local models to generate the global model and distributes it back to users. However, this collaborative training mechanism raises concerns about privacy leakage. In particular, a semi-honest server can infer user privacy by analyzing local or global gradients [15–17], while a malicious server could manipulate the aggregation results, thereby compromising the usability of the global model [18]. Existing privacy protection solutions, such as HE [19,20], differential privacy [21,22], and secure multiparty computation [23], can mitigate some privacy risks. However, they fail to address a critical issue: verifying the correctness of model aggregation.

To address these challenges, several verifiable federated learning (VFL) schemes have been successively proposed [18,24–27]. These solutions primarily utilize linear homomorphic hash (LHH) [18,24–26] or dual-aggregation techniques [27] to achieve verifiability. However, they exhibit limitations: the former incurs computational overhead that scales with the model dimension, while the latter suffers from the inflation of communication costs and requires auxiliary protocols for full verifiability [28,29].

1.2 Our Contributions

This study addresses existing challenges by focusing on two core issues: (1) designing a RDHED scheme compatible with homomorphic processing, and (2) integrating this RDHED scheme with cryptographic tools to develop an efficient verifiable privacy-preserving aggregation protocol under a single-server architecture.

To achieve these goals, we propose a joint embedding-extraction mechanism (JEEM). Using the additive homomorphic property of the Paillier encryption algorithm [19], JEEM enables multiple users to collaboratively embed and extract secret messages without altering the original plaintext. Building on JEEM, we further integrate LHH [30] and digital signatures to design a verifiable privacy-preserving aggregation protocol based on a single server (VPAFL).

The contributions of this study can be summarized as follows:

1) RDHED Scheme for Joint Secret Message Embedding and Extraction: This study resolves the compatibility limitations of existing RDHED schemes with homomorphic processing. Each user independently exploits ciphertext redundancy during encryption to embed secret messages. After the server aggregates the ciphertexts, homomorphic properties enable the fusion of all user-embedded messages within the ciphertext space, yielding a joint embedded message. Users can then extract this joint embedded message after decrypting the aggregation result.

2) Efficient Verifiable Aggregation Protocol: Compared to existing LHH-based VFL schemes, VPAFL enhances efficiency by integrating the proposed RDHED scheme. Specifically, VPAFL utilizes the secret message embedded by the users in each communication round as input for the hash value computation. This design decouples hash generation computational overhead from the model dimension, thereby significantly reducing the computational overhead of users for verification. Furthermore, VPAFL maintains minimal communication overhead of users for verification (below 0.2 KB) and achieves verification of aggregation results within only two interaction rounds under a single-server framework, significantly enhancing practical deployability.

1.3 Organization

The rest of this article is organized as follows: Section 2 reviews related works, while Section 3 introduces preliminary concepts. Section 4 provides an overview of the system and the threat Section 5 presents the proposed RDHED scheme and details the VPAFL protocol. Sections 6 and 7 offer theoretical analyses and experimental results, respectively. Finally, Section 8 concludes this study.

2  Related Works

In this section, we provide a brief review of the work related to RDHED schemes in the homomorphic encrypted domain and VFL.

2.1 RDHED Schemes in the Homomorphic Encrypted Domain

With the widespread application of HE in privacy computing, HE-based RDHED methods have emerged as a research hotspot [12]. These schemes are categorized into two types based on their impact on plaintext: plaintext modification schemes (Type I) and lossless data hiding schemes (Type II). Specifically, Type I methods involve embedding operations that result in changes to plaintext [9,10,13,14]. For example, a typical method modifies the ciphertext value c to produce a decrypted plaintext of the form 2m+b, where m is the original plaintext, and b∈{0,1} denotes the embedded 1 bit message. During data extraction, the embedded bit b is extracted by computing (2m+b)mod2, while m is recovered by integer division ⌊(2m+b)/2⌋. However, a critical limitation of Type I schemes is that they are not well suited for directly processing ciphertexts containing embedded messages. As a result, employing Type I methods may limit the processing of ciphertexts.

In contrast, Type II schemes aim to achieve lossless data hiding in ciphertexts (LDH-CT) without altering plaintexts or increasing ciphertext size [8,11,12]. For example, Zheng et al. [12] proposed a LDH-CT scheme based on numerical interval mapping: the data hider modifies the ciphertext to fall into specific subintervals corresponding to embedded bits. Using the homomorphic and probabilistic properties of cryptosystems to ensure invariance of plaintext. Wu et al. [11] proposed a RDHED scheme using random number substitution (RS). In this scheme, binary secret messages are first converted into decimal numbers that then replace the random numbers used during the encryption process to embed the data. However, this method constrains the bit length of embedded messages, as exceeding predefined limits disrupts both encryption and decryption processes.

Despite advances in existing research, two critical challenges hinder the application of RDHED schemes to FL: First, existing RDHED schemes primarily target image data carriers, whereas FL predominantly processes model parameters. Second, existing schemes do not adequately address compatibility with homomorphic processing [12–14]. In particular, when encrypted data containing embedded information undergoes homomorphic computations, such as ciphertext aggregation, the embedded data may suffer irreversible distortion, thereby leading to extraction failure.

2.2 Verifiable Federated Learning

In FL, the trustworthiness of the servers cannot be absolutely guaranteed as malicious servers can return incorrect aggregation results [18,24,25]. Models derived from such compromised servers inevitably underperform in prediction or classification tasks, necessitating VFL schemes to mitigate these risks.

Existing VFL research follows mainly two technical paths: LHH-based schemes [18,24–26] and dual-aggregation frameworks [27]. Xu et al. [18] proposed the first VFL framework, integrating a double-masking protocol [23] for privacy protection with LHH and pseudorandom techniques to achieve verifiable aggregation. However, this scheme suffers from two critical drawbacks: First, communication overheads scale with the model dimension. Second, computationally intensive bilinear pairing operations. To optimize communication efficiency, Guo et al. [24] proposed VeriFL, which decouples communication overhead for verification from model dimensions via LHH combined with equivocal commitments. Recent advances include VPFLI [25] and PriVeriFL [26], where VPFLI [25] designs a novel aggregation protocol to minimize performance degradation caused by heterogeneous client data quality, while PriVeriFL [26] employs a blockwise encryption strategy to alleviate computational bottlenecks of HE, reducing resource demands without compromising security.

However, LHH-based VFL schemes remain plagued by high computational overhead, as the complexity of hash value calculation increases with model dimensions [26]. To enable lightweight verification, Hahn et al. proposed VERSA [27], a dual-aggregation verification framework that eliminates the need for trusted setups and uses a lightweight pseudorandom generator (PRG) to enable efficient verification of the aggregation result. However, recent studies have identified vulnerabilities that compromise its verifiability [28,29].

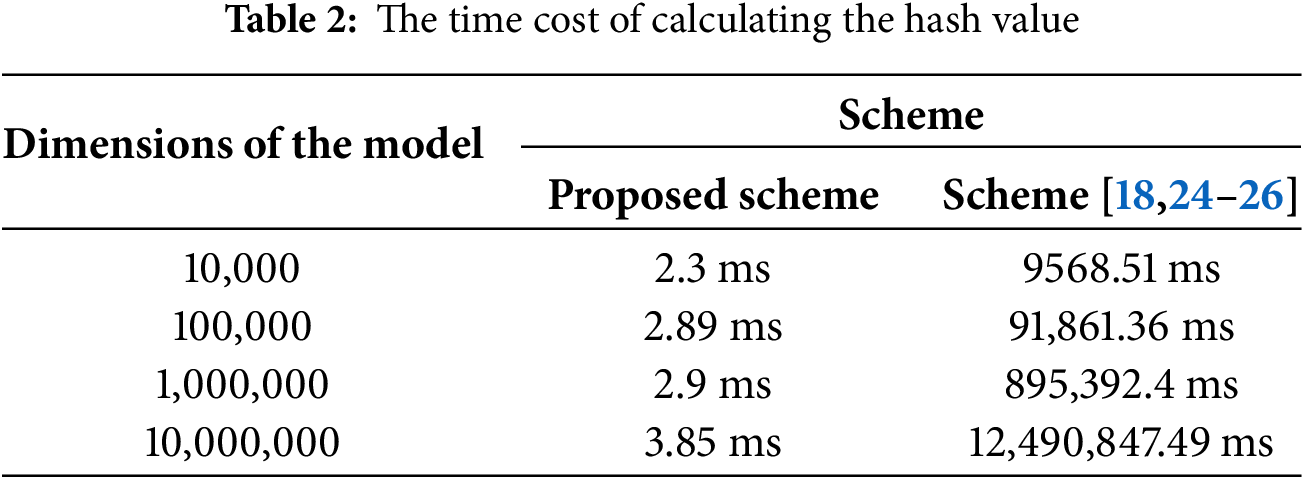
In summary, neither LHH-based VFL nor dual-aggregate verification-based schemes achieve high efficiency. As shown in Table 2 (detailed in Section 7.4.1), the LHH-based approach incurs significant computational overhead during verification as the model dimension grows, requiring approximately 12,490 s to compute the LHH values for models with dimensions reaching 10,000,000. In contrast, dual-aggregate verification-based schemes face substantial communication overhead: Users must submit both local model updates and validation codes derived from these parameters, which doubles their communication expenditure. Furthermore, as the model dimensionality increases, the communication overhead introduced by validation becomes impractical for real-world applications. Crucially, given the resource constraints of end-user devices, the designed VFL framework should maintain lightweight communication and computational overheads for verification to facilitate practical deployment.

3  Preliminaries

In this section, we provide the foundational concepts necessary to understand our VPAFL scheme.

3.1 Federated Learning

Deep learning has attracted significant attention for its remarkable achievements in various fields, though high-performance deep neural networks (DNNs) typically rely on extensive datasets. However, the data used to train DNNs often contain sensitive information. For example, location-based services [31] could expose personal whereabouts, while goods purchase records can be exploited for targeted advertising. More critically, the leakage of health information or facial data poses serious privacy risks. To address these challenges, FL has emerged as a promising solution [7]. Since its inception, FL has been widely adopted in various applications such as the Internet of Things (IoT), smart healthcare [32], and smart cities [33]. FL is a distributed machine learning paradigm that collaboratively trains a global model by coordinating multiple participants without compromising data privacy. In this architecture, the server does not directly access user data; instead, it iteratively aggregates parameters to optimize the global model. Let U denote the set of participating users, where |U|=n represents the total number of users, and each user ui∈U has a private dataset Di. The FL training process proceeds iteratively through the following stages per communication round:

a) Global Model Distribution: The server broadcasts the current global model Mk to all users, where k denotes the current communication round.

b) Local Model Training: Each user ui initializes their local model with Mk and trains on Di using the stochastic gradient descent (SGD) algorithm [34].

c) Model Aggregation: The server aggregates the received local models via the Federated Averaging (FedAvg) algorithm [7] to generate the updated global model Mk+1.

Formally, during the k-th communication round, each user ui updates its local model parameters using the SGD algorithm [34]:

wik=wik−1−lr∇ℒ(wik−1;Di),(1)

where lr denotes the local learning rate, wik denotes the parameters of the local model for user ui during the k-th communication round, and ℒ(⋅) denotes the loss function. Subsequently, the server aggregates the received local models using the FedAvg algorithm [7] as follows:

wk=∑ui∈U|Di||∑ui∈UDi|wik.(2)

3.2 Linear Homomorphic Hash

LHH [30] is a one-way and collision-resistant homomorphic hash function that can calculate the hash of a composite data block based on the hash of a single data block. The LHH scheme is formally defined by three algorithms LHH = (LHH.Gen, LHH.Hash, LHH.Eval):

a) LHH.Gen(κ,v): Given the security parameters κ and a d-dimensional vector v={vi,…,vd}, this algorithm outputs public parameters pp={G,q,{g1,…,gd}}, where G is a cyclic group of prime order q, g is a generator of G, and g1,…,gd are distinct elements in G.

b) LHH.Hash(pp,v): For a d-dimensional vector v, this algorithm computes its LHH value of v: hv←∏i=1dgivi∈G.

c) LHH.Eval(pp,h1,…,hl,α1,…,αl): Given l hash values h1,…,hl and l coefficients α1,…,αl∈Zq, this algorithm outputs the linear combination of the l hash values: h←∏i=1lhlαl.

4  Overview of the System and the Threat Model

4.1 System Model

As illustrated in Fig. 1, the system model of the VPAFL protocol comprises three entities, consistent with previous works [18,24]: The trusted authority (TA), the server, and the users.

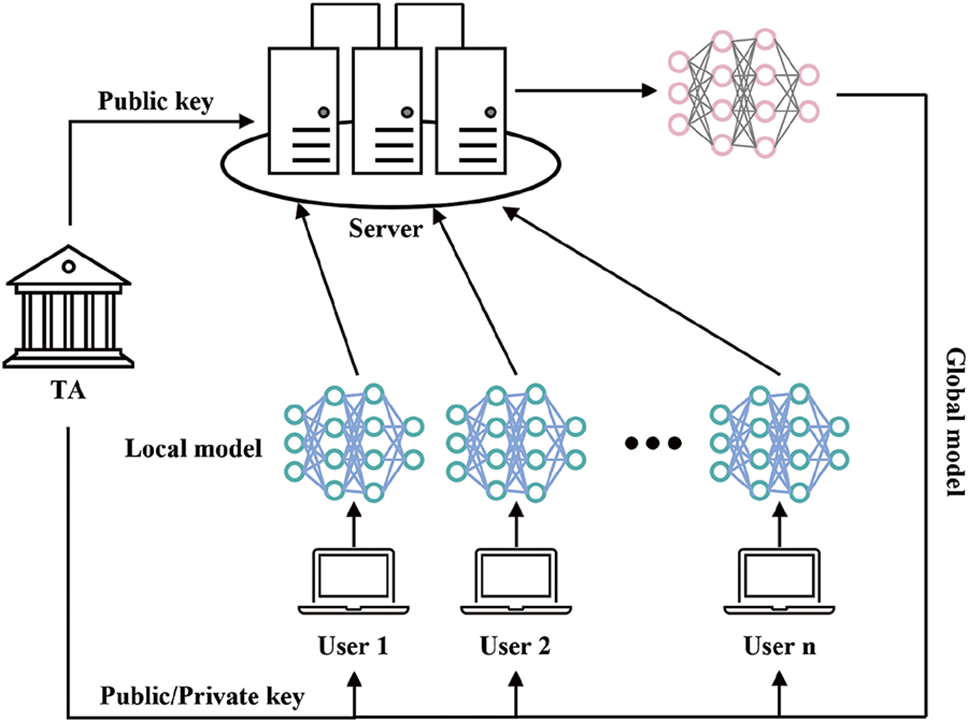
Figure 1: System model of VPAFL

•   TA: The TA initializes the system by generating cryptographic parameters (public/private keys) and distributing the initial global model to all participants. It is considered trustworthy and remains offline after initialization.

•   Server: The server aggregates encrypted local models received from users, updates the global model, and broadcasts the aggregated result to the user for verification.

•   Users: In each communication round (except for the first), users download the latest global model from the server as their local mode. During the first communication round, the TA initializes the global model. Each user trains the local model on their private dataset, encrypts the local model parameters with their private key, and uploads the ciphertext to the server. Upon receiving the aggregated result, users verify its correctness. Training continues only if verification succeeds; otherwise, training is aborted.

4.2 Threat Model

Our threat model is defined as follows:

•   Semi-honest users: Users follow the FL protocol faithfully, but may attempt to infer sensitive information from the data of honest users. Additionally, a subset of users may collude with the server to manipulate the aggregation results.

•   Server: The server may attempt to infer user privacy or forge verifiable aggregation results. In particular, the server can collude with up to t−1 users, where t denotes the threshold parameter in Shamir’s Secret Sharing (SS) protocol [35].

•   Out-of-Scope attacks: In FL systems, not all participants are trustworthy, as malicious users can launch poisoning attacks [36] aimed at manipulating local models to compromise the performance of the global model. However, this paper does not consider poisoning attacks, as our primary objective focuses on ensuring the correctness of the aggregation results while maintaining user privacy protection.

5  Proposed Scheme

In this section, we first propose a RDHED scheme designed for compatibility with homomorphic processing. In particular, we design a JEEM by utilizing the additive homomorphic properties of the Paillier cryptosystem [19]. Subsequently, we further construct the VPAFL protocol by integrating the proposed RDHED scheme with the LHH [30] and digital signature algorithms.

5.1 Joint Embedding-Extraction Mechanism

Extending the drop-tolerant secure aggregation algorithm (DTSA) proposed by Zhao et al. [20], we propose a novel secure aggregation-data hiding (SADH) hybrid algorithm that is compatible with homomorphic processing. The core innovation of SADH lies in its JEEM, which enables users to collaboratively embed secret messages in ciphertext and extract them after aggregation. For simplicity, we assume that no user dropout occurs during training. The scheme operates as follows:

•   SADH.Gen(κ,t,U): This algorithm initializes cryptographic parameters. The inputs include the security parameter κ, the threshold t for the SS protocol [35] and the user set U with |U|=n. First, generate the public key PP={n,g,h,N} shared among all users, along with the private key {SK,SKi} assigned to each user ui, and the public parameter N2 for the server. In particular, two large prime numbers p,q are selected such that |p|=|q|=κ. Then, compute N=p×q and λ=lcm(p−1,q−1), where lcm(a,b) denotes the least common multiple of a and b. Next, choose a random integer g∈ZN2∗ that satisfies gcd(L(gλmodN2),N)=1, where L(x)=x−1/N. Subsequently, compute e=gσmodN2, where σ is a large prime satisfying |σ|≤κ. Finally, construct the polynomial f(x) as follows:

f(x)=a1⋅x+a2⋅x2+…+at−1xt−1modp,(3)

where the private key is denoted as SK={λ,σ} and SKi=sq⋅f(i)modN2, the coefficients a1,…,at−1∈Zp and s∈ZN are randomly chosen.

•   SADH.Ence(SKi,wi,di): This encryption-embedding hybrid algorithm processes the plaintext wi and messages di as input, encrypts wi using SKi and outputs the ciphertext [[wi]]:

[[wi]]=gwi⋅edi⋅SKi(n−1)!∏j∈U,j≠ijj−imodN2.(4)

The core mechanism lies in embedding secret messages through redundant ciphertext values without changing the plaintext, as demonstrated in Section 6.1. The key parameters are defined as follows:

–     The embedded message di=ri×dmi serves two purposes: (1) to carry a secret message and (2) to allow collaborative generation of joint embedded messages. Where mi={b0,…,bl} denotes a binary sequence of length l, and dmi denotes its decimal value.

–     The random number ri∈ZN is used to ensure the confidentiality of the message and |ri×dmi|<κ/2.

–     The user set U contains n users (|U|=n).

SADH.Agg({[[wi]]}ui∈U): The server aggregates the received ciphertexts as follows:

[[w]]=∏ui∈U[[wi]]modN2.=∏ui∈Ugwi⋅edi⋅SKi(n−1)!∏j∈U,j≠ijj−imodN2=e∑ui∈Udi⋅(∏ui∈Ugwi⋅SKi(n−1)!∏j∈U,j≠ijj−i)modN2,(5)

where ∑ui∈Uodi denotes the joint embedded message d, formed by fusing the user-embedded secret messages within the ciphertext domain.

SADH.Dece(SK,[[w]]): After receiving the aggregated ciphertext [[w]], the user decrypts it with the private key SK and extracts the joint embedded message d through the following steps:

w=∑ui∈Uowi=L([[w]]λmodN2)L(gλmodN2)modNmodσ=(∑ui∈Uowi+σ⋅∑ui∈Uodi)modσ=∑ui∈Uowi.(6)

Define w′=(∑ui∈Uowi+σ⋅∑ui∈Uodi)modN. Because ∑ui∈Uowi and σ are known parameters, the user can derive ∑ui∈Uodi, which corresponds to the joint embedded message d.

5.2 Verifiable Privacy-Preserving Aggregation for Federated Learning

In the proposed protocol, users first utilize SADH to encrypt their local models and embed secret messages, subsequently uploading both the hash and the signature to the server. Following this, the server aggregates the received ciphertexts and returns the aggregation results along with the collected hashes and signatures to the users. Finally, after receiving these, each user decrypts the aggregation result to obtain the global model, extracts the joint embedded message, and performs verification to confirm the correctness of the aggregation result. The specific details of VPAFL (Algorithm 1) is illustrated in protocol in particular, the proposed protocol requires two rounds of interaction, with the specific processes for processes for each round described below:

In Round 0, TA initializes the system, distributes the public parameters PP, pp, the global model M, and {spki}i∈{1,2, … ,n}, assigns private keys sski to each user, and transmits the public parameter N2 to the servers.

In Round 1, each user ui∈U1 encrypts their local model wik−1 while embedding a secret message di, obtaining the ciphertext [[wik−1]]←SADH.Ence(SKi,wik−1,di), where k denotes the current communication round. To optimize efficiency, for models with multiple parameters, the user embeds di solely during the encryption of the first parameter, and subsequent parameters replace the embedded message with a random number ri∈ZN. As demonstrated in Section 6.3, embedding the message in even one parameter suffices to verify the aggregation results. Subsequently, the user ui∈U1 computes the LHH value hi of the embedded message di and generates a digital signature sighi for hi. These values will later be used to verify the aggregated result. Finally, the user ui∈U1 sends {[[wik−1]],hi,sighi} to the server. Upon receiving the ciphertexts, the server aggregates them and returns {[[wk−1]],{hj,sighj}uj∈U1,j≠i} to each user ui∈U1.

In Round 2, each user ui∈U1 first checks the validity of the received digital signature {sighj}uj∈U1,j≠i to ensure the integrity of the associated hash values {hj}uj∈U1,j≠i. If valid, the user decrypts the aggregation result to obtain the global model and the joint embedded message (wk−1,d)←SADH.Dece(SK,[[wk−1]]). Next, the user verifies the aggregation result by checking whether LHH.Hash(pp,d)=?LHH.Eval(pp,h1,…,hc,1,…,1), where c=|U1| denotes the total number of participating users. If equality holds, the verification succeeds and the user accepts the aggregation result as valid.

6  Theoretical and Comparative Analysis

6.1 Correctness

We define correctness as the ability to ensure that the user gets the correct aggregation result to update the local model when all entities involved in the FL honestly perform the predetermined operations in the protocol.

Theorem 1. The user can obtain the correct aggregation result if at least t users participate in FL and the server performs the aggregation operation honestly, where t is the threshold of the SS protocol [35].

Proof of Theorem 1: Assume k=1. From Eq. (4), the user ui applies the encryption-embedding hybrid algorithm SADH.Ence(SKi,wi,di) to encrypt the local model wi and embed the message di as follows:

[[wi]]=gwi⋅edi⋅SKi(n−1)!∏j∈U1,j≠ijj−imodN2.(7)

Then, as shown in Protocol 1, the ciphertext received by server aggregation in Round 1 is as follows:

[[w]]=∏ui∈U1[[wi]]modN2=∏ui∈U1gwi⋅edi⋅SKi(n−1)!γimodN2=g∑ui∈U1wi⋅e∑ui∈U1di⋅sq(n−1)!⋅∑ui∈U1f(i)γimodN2,(8)

where γi=∏j∈U1,j≠ijj−i, and SKi=sq⋅f(i)modN2. Based on SS protocol [35] and Lagrange interpolation formula, we can define a polynomial as follows:

F(x)=∑ui∈U1f(i)∏j∈∈U1,j≠ij−xj−imodp(9)

From Eq. (3), F(0)=0. When |U1|≥t, there is ∑ui∈U1f(i)γi=a⋅p, where a∈Zp, thus Eq. (8) can be modified as follows:

[[w]]=g∑ui∈U1wi⋅e∑ui∈U1di⋅sa(n−1)!⋅NmodN2=g∑ui∈U1wi⋅gσ⋅∑ui∈U1di⋅sa(n−1)!⋅NmodN2,(10)

where e=gσmodN2. Finally. users decrypt [[w]] as:

w=∑ui∈U1wi=L([[w]]λmodN2)L(gλmodN2)modNmodσ=(∑ui∈U1wi+σ⋅∑ui∈U1di)modσ=∑ui∈U1wi.(11)

This concludes the proof. ◻

6.2 Privacy-Preserving

This section begins by analyzing the security of SADH and subsequently evaluates the security of VPAFL under two adversarial scenarios: (1) a malicious server operating independently and (2) a malicious server colluding with up to t−1 users.

Theorem 2. If DTSA is indistinguishability under chosen-plaintext attack (IND-CPA) security, then the SADH is IND-CPA security.

Proof of Theorem 2: As mentioned earlier, according to Eq. (4), the user replaces the random number used in the encryption process with the product of a decimal number and the random number ri∈ZN. This substitution does not compromise security, as the decimal multiplier does not alter the underlying randomness of ri. Therefore, the modifications introduced by SADH to DTSA [20] do not weaken the security of the scheme. Furthermore, DTSA [20] is IND-CPA security, then the security of SADH is guaranteed.

Theorem 3. (Security Against Malicious Server) In the absence of collusion between the malicious server and semi-honest users, the privacy of all honest users is preserved.

Proof of Theorem 3: To formally prove privacy guarantees, we employ a standard hybrid argument [37], proved as follows: Under the (SADH, LHH)-hybrid model, assuming that the security parameter of VPAFL is κ, the threshold of SS protocol is t, and the total number of users is n. For simplicity, we define Server as S,V=S∩U1, where U1={u1,…,uc},c≤n and U1∈U. The joint view of all entities inV can be denoted as a random variable REALVU,t,κ. There is also a probabilistic polynomial-time (PPT) simulator SIMVU,t,κ. In order to prove the security of VPAFL, it is necessary to prove that the outputs of SIMVU,t,κ and REALVU,t,κ are indistinguishable, which is formally expressed as follows:

REALVU,t,κ≡SIMVU,t,κ.(12)

hyb0 First, we create a series of random variables, which are indistinguishable from the joint real view of V in REALVU,t,κ in the actual implementation of the VPAFL.

hyb1 In this hybrid, we change the behavior of the user ui through the simulator, and replace the real local model wi with the random vector vi. Then, the user ui is invoked to encrypt the random vector vi and embed the message di. Note that in Section 5, di is defined as the product of two components: (1) a decimal number converted from a binary sequence, and (2) a random number ri∈ZN. However, in the simulation phase, the simulator replaces di with an random value ra∈ZN. The encryption process is adjusted as follows:

[[vi]]=←SADH.Ence(SKi,vi,ra),(13)

where SKi denotes the secret key of user ui. The simulator then invokes the user ui to calculate the hash value of ra: hi←LHH.Hash(pp,ra), and generates the digital signature of hi: sighi←DS.Sign(hi,sski). Finally, the user ui sends {[[vi]],hi,sighi} to the server. Reviewing the proof of Theorem 2, SADH guarantees that [[vi]] is computationally indistinguishable from [[wi]]. In particular, it has been proved that the output of LHH is random and indistinguishable under different inputs. Thus, VPAFL guarantees the same distribution between hyb1 and hyb0.

hyb2 In this hybrid, the server aggregates the received ciphertext and returns the aggregation result, the received LHH value and the digital signature to each user:

[[v]]←SADH.Agg({[[vi]]ui∈U1}).(14)

Similarly, the security of SADH algorithm ensures the same distribution between hyb2 and hyb1.

As mentioned above, based on the security of the SADH and LHH algorithms, we prove that the view in the PPT simulator SIMVU,t,κ is indistinguishable from the real view of V in the REALVU,t,κ, i.e., that the REALVU,t,κ≡SIMVU,t,κ. ◻

Theorem 4. (Security against Colluding Malicious Server and Users) Even if a malicious server colludes with up to t−1 users, the privacy of all honest users is preserved.

Proof of Theorem 4: According to Eq. (7), the user ui encrypted local model wi as follows:

[[wi]]=gwi⋅edi⋅SKi(n−1)!∏j∈U1,j≠ijj−imodN2=gwi⋅edi⋅sq⋅f(i)⋅γi(n−1)!,(15)

where U1={u1,…,uc}, where t(t≤c≤n) denote the threshold of the SS protocol [35], and γi=∏j∈U1,j≠ijj−i. According to the SS protocol [35], if the malicious server colludes with ≥t users, Eq. (15) can be modified as follows:

[[wi]]=gwi⋅edi⋅sa⋅N⋅(n−1)!,(16)

where a∈Zp. At this point, the encrypted local model [[wi]] can be decrypted using the private key SK, otherwise it cannot be decrypted. ◻

According to Theorem 3 and Theorem 4, we further demonstrate the resistance of VPAFL to inference attacks under two threat scenarios: (1) attacks initiated solely by the server and (2) collusion between the server and malicious users.

Regarding the global model, since all users transmit encrypted model parameters, the server exclusively operates on ciphertexts during aggregation. This prevents the server from directly analyzing sensitive information. Even if the server colludes with a user to obtain the private key SK, the inherent lack of auxiliary training data ensures that meaningful inference remains infeasible.

For local updates, in the VPAFL protocol, users employ SADH to encrypt local model updates. Under the first threat model (only malicious server), Theorem 3 guarantees that the server cannot decrypt the encrypted parameters of any user without access to the corresponding private key SKi. Under the second threat model (server-user collusion), Theorem 4 ensures confidentiality even if up to t−1 users conspire with the server: the colluding parties cannot decrypt the local updates of honest users. Since adversaries cannot analyze relevant sensitive information from ciphertext, VPAFL satisfies security requirements against inference attacks in both scenarios.

6.3 Verifiability

Theorem 5. We define verifiability as the ability of each client to independently verify the correctness of the aggregation results under the threat model defined in Section 4.2.

Proof of Theorem 5: According to the operation of the malicious server on the aggregation results, we consider two scenarios to prove the effectiveness of the verification.

Scenario 1 (Partial Model Aggregation): Let the total number of users be n, and let t denote the threshold of the SS protocol [35]. Assume the server aggregates the models received from c (t≤c<n) users. According to Eqs. (7) and (8), the results obtained by the server aggregation as follows:

[[w]]=g∑i=1cwi⋅e∑i=1cdi⋅sq(n−1)!⋅∑i=1cf(i)γimodN2.(17)

According to Eq. (10), the user decrypts the ciphertext using private key SK to to obtain the global model w and extracts the joint embedded message ∑i=1cdi. Subsequently, the user will check if the following equation is true.

LHH.Hash(pp,∑i=1cdi)=?LHH.Eval(pp,h1,…,hn,1,…,1).(18)

Based on the definitions in Section 3.2, we have:

LHH.Eval(pp,h1,…,hn,1,…,1)=∏i=1nhi=g1∑i=1ndi≠g1∑i=1cdi.(19)

Obviously Eq. (18) does not hold and therefore the aggregation result fails to pass validation.

Scenario 2 (Collusion Attack): The server colludes with c (c<t) users to forge aggregated results that pass verification, where t denote the threshold of the SS protocol [35]. Assume the total number of users is n (c<t<n). To forge an aggregation result that passes the validation, the server must craft a result of the following form:

[[w]]=gΔw⋅e∑i=1ndi⋅sq(n−1)!⋅∑i=1nf(i)γi.(20)

Let Δw denote the modified aggregation results. To forge a verified aggregation result, the server must ensure the joint embedded message ∑i=1ndi can be extracted from [[w]]. However, since the server colludes with only c(c<t) users, it cannot access the secret messages {dj}j∉Uc of non-colluding users and must instead guess their values. Suppose the server attempts this forgery by manipulating the aggregation result as follows:

[[w]]=gΔw⋅e∑i=1cdi+∑i=c+1nΔdi⋅sq(n−1)!⋅∑i=1nf(i)γi,(21)

where ∑i=c+1nΔdi denotes the guess of the server of the secret messages embedded by non-colluding users. As defined in Section 5, the user extracts the joint embedded message ∑i=1cdi+∑i=c+1nΔdi from the ciphertext [[w]]. To verify the correctness of the aggregation results, the user checks if the following equation is true:

LHH.Hash(pp,∑i=1cdi+∑i=c+1nΔdi)=?LHH.Eval(pp,h1,…,hn,1,…,1),(22)

where LHH.Eval(pp,h1,…,hn,1,…,1)=∏i=1nhi=g1∑i=1ndi≠g1∑i=1cdi+∑i=c+1nΔdi, therefore the forged aggregation result cannot pass the verification. ◻

6.4 Comparison

We compare VPAFL with existing LHH-based VFL schemes, including VerifyNet [18], VeriFL [24], VPFLI [25], and PriVeriFL [26], as shown in Table 1. VerifyNet [18] and VeriFL [24] are based on the double-masking protocol [23], which effectively protects the local gradients of users but fails to protect the privacy of aggregation results. Moreover, these schemes require multiple rounds of interaction between users and the server, increasing communication overhead. In particular, they do not address the risk that corrupted clients colluding with a malicious server are forged to bypass verification. To mitigate collusion attacks during verification, VPFLI [25], PriVeriFL [26], and our proposed VPAFL employ LHH combined with digital signatures, ensuring collusion-resistant verification.

Regarding aggregation privacy, VPFLI [25] introduces a blinding factor to mask the aggregation results, while VPAFL and PriVeriFL [26] delegate decryption authority to users. This approach prevents the server from directly decrypting the aggregation results, thus enhancing privacy protection. However, it is important to note that neither VPFLI [25], PriVeriFL [26], nor VPAFL can fully preserve aggregation results in privacy under collusion attacks. Since FL inherently involves collaborative training of a unified global model, the server only needs to collude with a single user to obtain the global model.

In terms of verification complexity, we assume that the computational complexity of each call to LHH is O(d), where d represents the model dimension. In VerifyNet [18] and VeriFL [24], users perform LHH twice per verification: once to generate the hash value and once to verify the result. Thus, the verification complexity is O(2d) per communication round. To optimize this, VeriFL [24] employs an amortized verification mechanism. Specifically, users sample a set of random coefficients to compute the linear combination of hash aggregations across multiple communication rounds (for example, after tr rounds). They then verified whether the combined hash matches the hash of the linear combination (using the same coefficients) applied to the aggregation results of those rounds. Consequently, VeriFL [24] reduces the verification complexity to O(d+d/tr). In contrast, VPAFL further optimizes the process by integrating the proposed RDHED with LHH (see Section 7.4.1 for details), thus reducing the verification complexity to O(1). Moreover, VPAFL requires only two interaction rounds, establishing it as a more efficient protocol compared to existing solutions.

7  Experimental Results

In this section, similar to previous studies [18,25], we evaluate the performance of VPAFL in terms of fidelity, computational overhead, and communication overhead.

7.1 Experimental Settings

This subsection describes the experimental settings for VPAFL.

Model Architectures and Datasets: We employ two deep neural network architectures: AlexNet [38] for the CIFAR-100 [39] classification task and FedCNN for the MNIST [40] and CIFAR-10 [39] classification task.

Federated Learning Settings: Based on the open-source personalized FL framework (https://github.com/TsingZ0/PFLlib, accessed on 7 May 2025) [41], we simulate a horizontal FL environment where users employ the SGD algorithm [34] for local model updates during each communication round, with the server using the FedAvg algorithm [7] for model aggregation.

All experiments were conducted on an Ubuntu 22.04 workstation equipped with an Intel Xeon Platinum 8352V 2.10 GHz CPU, 60 GB RAM, and a single NVIDIA 4090 GPU. Our implementation uses Python 3.9 with stable libraries. The LHH is implemented using NIST P-256 curves. FedCNN is a convolutional neural network with the following architecture: Conv(x,32,5×5)→ReLU→MaxPool(2,2)→Conv(32,64,5×5)→ReLU→MaxPool(2,2)→FC(1024,512)→ReLU→FC(512,10), where x denotes the dimension of the input, Conv denotes the convolutional layer, ReLU denotes the type of activation function, MaxPool denotes the pooling layer, and FC denotes the fully connected layer.

7.2 Evaluation Metrics

Fidelity: We measure fidelity using the accuracy of the model on the classification task, denoted by Acc.

Computational and Communication Overhead: Similarly to previous studies [18,24], we measure computational and communication overhead to evaluate the efficiency of the VPAFL.

Baseline: Regarding the selection of the baseline for overhead comparison, we adopt VPFLI [25] because it also uses the DTSA algorithm [20] as the privacy-preserving strategy. In particular, VPFLI [25] introduces a weight aggregation protocol to mitigate the degradation of model performance caused by heterogeneous user data quality. To ensure comparability, we exclusively retain the core modules relevant to VFL during baseline reproduction.

7.3 Fidelity

To validate that the proposed scheme maintains aggregation accuracy without compromising privacy guarantees, we evaluate its performance on three datasets: MNIST [40], CIFAR-10, and CIFAR-100 [39], adopting identical training configurations (e.g., learning rate, batch size) for direct comparison with the FedAvg algorithm [7]. As shown in Fig. 2, the proposed VPAFL protocol achieves an aggregation effectiveness comparable to that of FedAvg [7], with a stable convergence behavior observed across all datasets. This consistency originates from the mathematically lossless encryption and decryption of the plaintext model parameters, thereby preserving data integrity throughout the FL process.

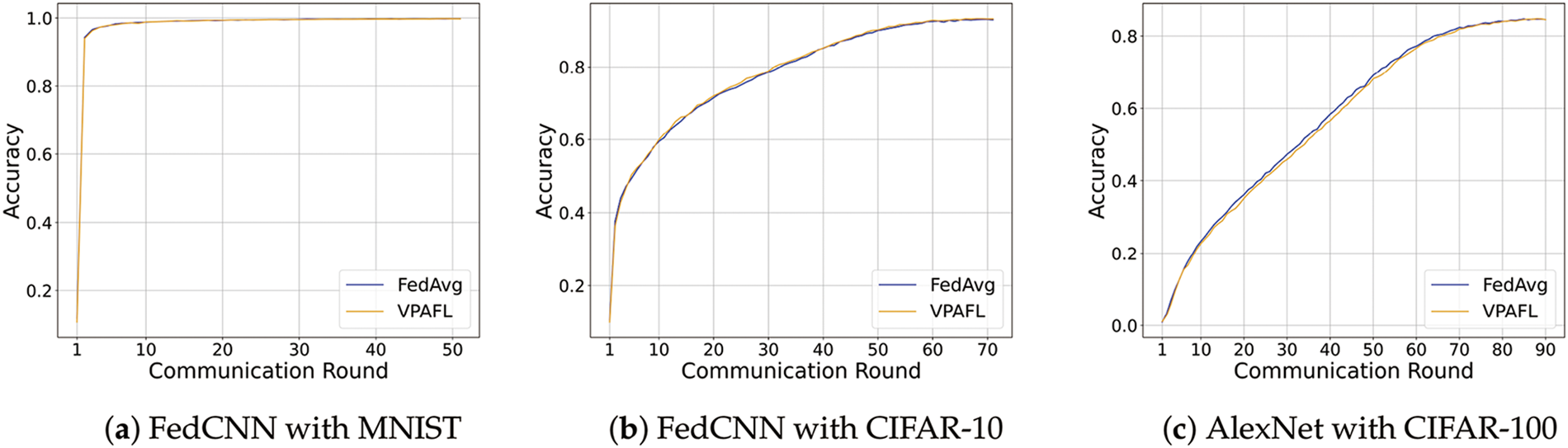
Figure 2: The task accuracy (Acc) on MNIST, CIFAR-10 and CIFAR-100

7.4 Computational and Communication Overhead

To systematically analyze system efficiency, we define n as the number of participating users, κ=512 as the security parameter and d as the model dimension. To isolate variable impacts, we evaluate computational and communication overhead under two scenarios: (1) Different number of users (n from 100 to 1000) with fixed model dimension d=5000. (2) Different model dimension (d from 1000 to 10,000) with fixed number of users n=500.

7.4.1 Computational Overhead

The computational overhead of the user in VPAFL is primarily determined from modular arithmetic operations in ZN and ZN2. Let Tm1 and Tm2 denote the time costs of single modular multiplications in ZN and ZN2, respectively, and Te for modular exponentiation in ZN2. Based on Eqs. (4) and (6), the encryption overhead per user is theoretically d⋅(3Te+2Tm2), while decryption requires d⋅(Tm1+Te). Thus, the total computational overhead per user becomes d⋅(Tm1+2Tm2+4Te).

Fig. 3 illustrates the computational overhead of a single user per communication round. The computational overhead exhibits a positive correlation with both the number of participating users n and the model dimension d. This growth comes from increasing computational demands in both the model encryption and the decryption phases. Mathematically, as the user count n grows, the exponent of the SK term in Eq. (4) increases, resulting in more computationally intensive operations. The higher model dimension d not only expands the set of encryption parameters, but also prolongs the decryption time. In particular, the VPAFL protocol shows superior operational efficiency compared to VPFLI [25], achieving an average reduction in computational overhead of 10 s.

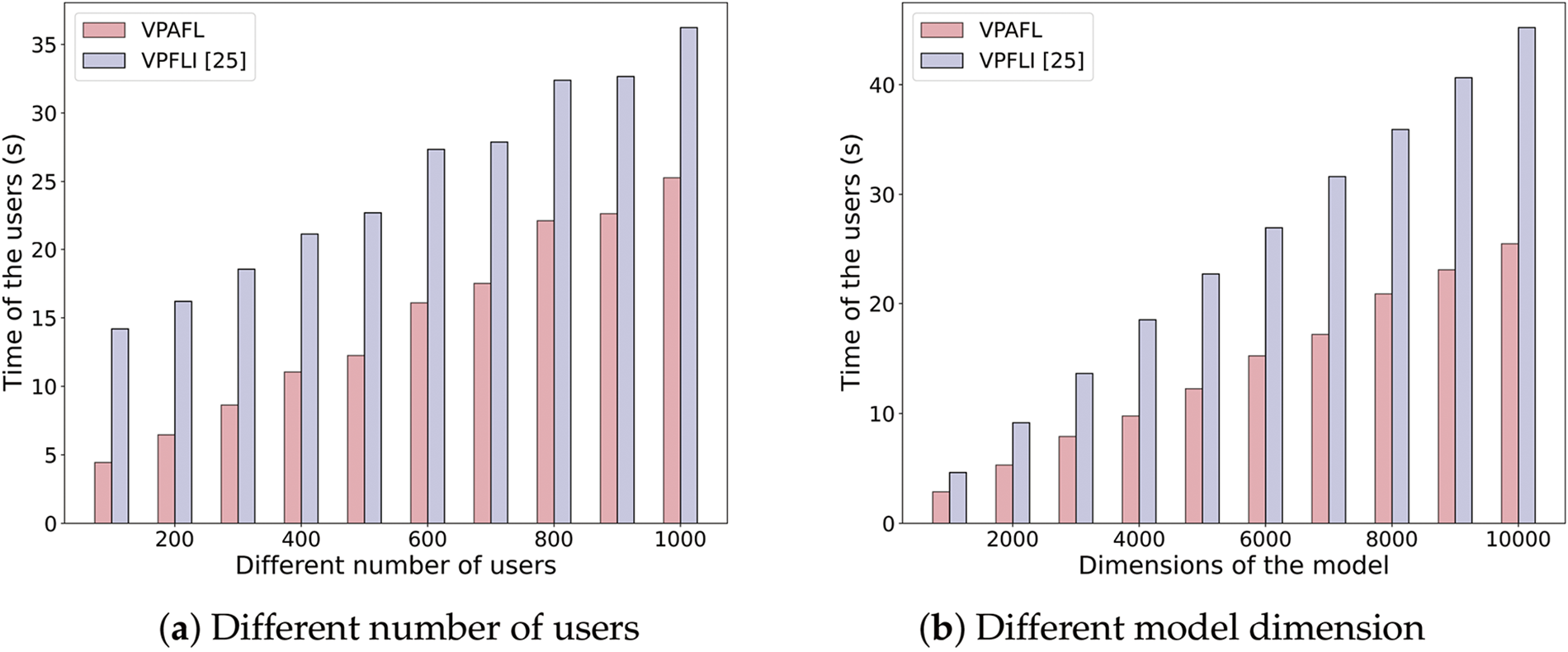
Figure 3: Computational overheads of the users [25]

To further evaluate the efficiency of the verification process, Fig. 4 quantifies the computational overhead for a single user to verify aggregated results. The experimental results show that verification overhead increases with the number of users n, due to the increasing computational demands required to validate a growing number of signatures. Specifically, the verification overhead reaches a maximum of 152.73 ms at n=1000. In contrast, variations in model dimension d exhibit negligible influence on verification overhead, with the results stabilizing at approximately 80 ms in all tested configurations. In particular, VPAFL achieves substantially lower verification overhead than VPFLI [25], reducing the average computational costs by approximately 8 s under identical conditions.

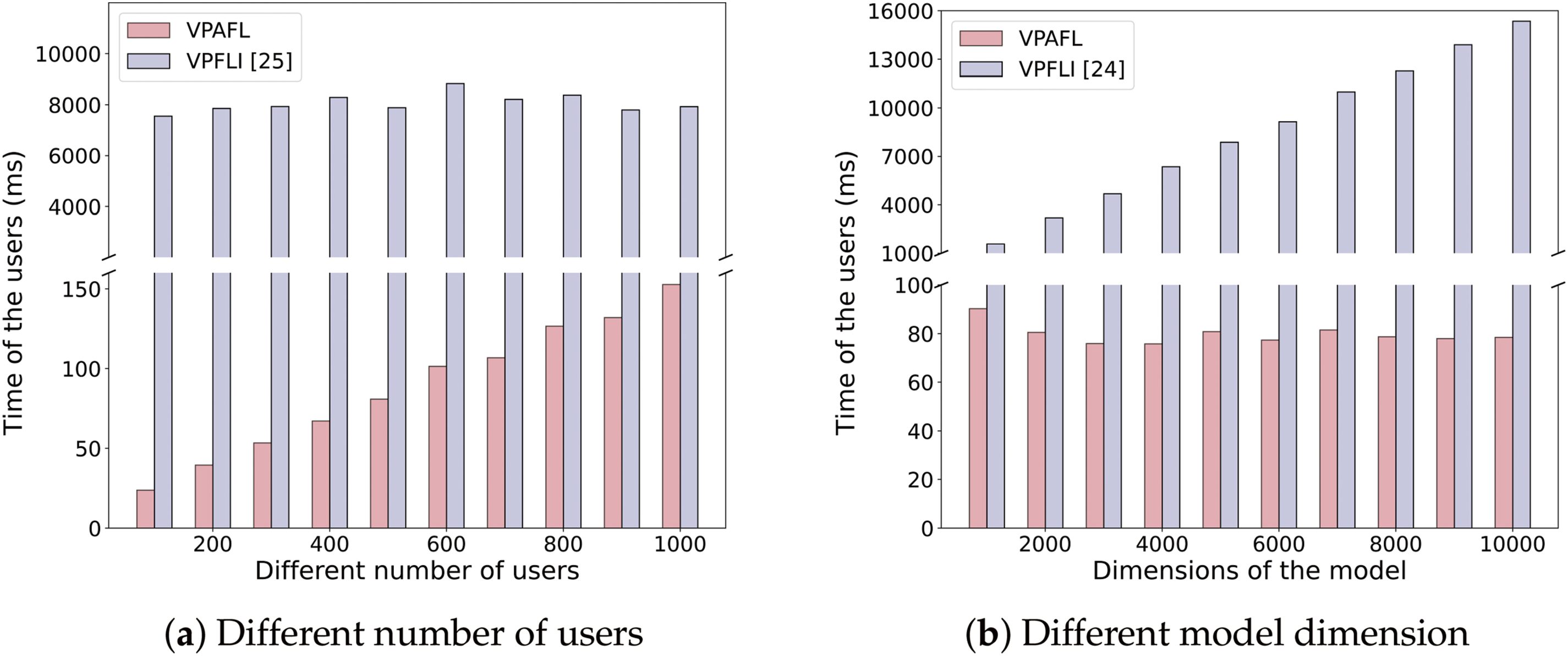
Figure 4: Computational overheads of the users for verification [24,25]

In addition, we further investigate the performance of VPAFL in large-scale user scenarios. To evaluate scalability, we measure the computational overhead per user during validation under a fixed model dimension d=1000 while varying the number of participating users from 1000 to 5000 in increments of 1000 and compared it with VPFLI [25] and PriVeriFL [26].

As illustrated in Fig. 5, the results demonstrate that the computational overhead of the users for verification in all three schemes increases with the number of participating users. This growth pattern originates mainly from the cost of LHH.Eval, whose computational complexity scales with the number of participating users. While the verification process requires checking more digital signatures as user numbers expand, this component contributes minimal overhead, approximately 0.3 ms even at 5000 users. Note that although VPFLI [25] and PriVeriFL [26] employ distinct cryptographic algorithms, they share the same verification mechanism. Therefore, the computational overheads of the users for verification remain identical in both schemes.

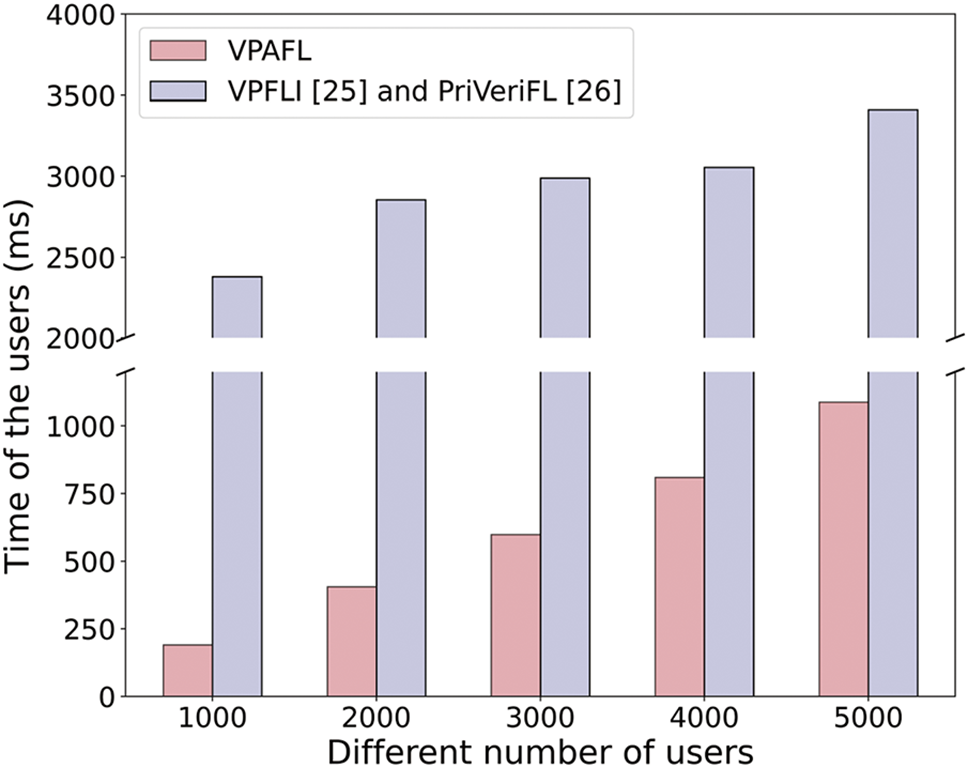
Figure 5: Computational overheads of the users for verification with large user scenarios [25,26]

In particular, VPAFL maintains significantly lower overhead than both VPFLI [25] and PriVeriFL [26]. This advantage arises from differences in LHH implementation, and we elucidate the precise reasons for this disparity in the following analysis.

The performance superiority of VPAFL originates from a fundamental distinction in hash computation mechanisms between the two schemes. Although VPFLI [25] employs LHH to decouple communication overhead from model dimension d, its hash calculation operates directly on the model parameters themselves, resulting in computational demands proportional to d. In contrast, VPAFL integrates RDHED with LHH, restricting the hash computation to the lightweight secret messages embedded by users during each communication round. This strategic change in computational input—from high-dimensional model parameters to compact secret messages—decouples hash-related costs from d, addressing a critical efficiency bottleneck in existing LHH-based VFL schemes [18,24–26]. The benefits of this innovation are significantly amplified in high-dimensional model scenarios, as evidenced by the quantitative comparisons in Table 2. For model sizes of 10,000, 100,000, 1,000,000 and parameters, the hash computation time of VPAFL remains consistently below 4 ms, while the LHH-based VFL [18,24–26] requires up to 12,490 s when d= 10,000,000, a disparity that strikingly validates the efficiency gains enabled by RDHED integration.

In summary, the computational overhead of the users for verification in VPAFL is lightweight, making it more conducive to practical deployment, particularly in scenarios involving large-scale models or numerous participating users.

In VPAFL, the server is responsible for aggregating the encrypted local models received and its computational overhead is d⋅(n−1)⋅Tm2. Fig. 6 clearly shows that the calculation overhead of the server increases when the number n of users and the model dimension d increase. Among them, the computational overhead of the server in VPAFL is slightly lower than that of the server in VPFLI, because the server in VPAFL only involves aggregating local models and does not decrypt the ciphertext.

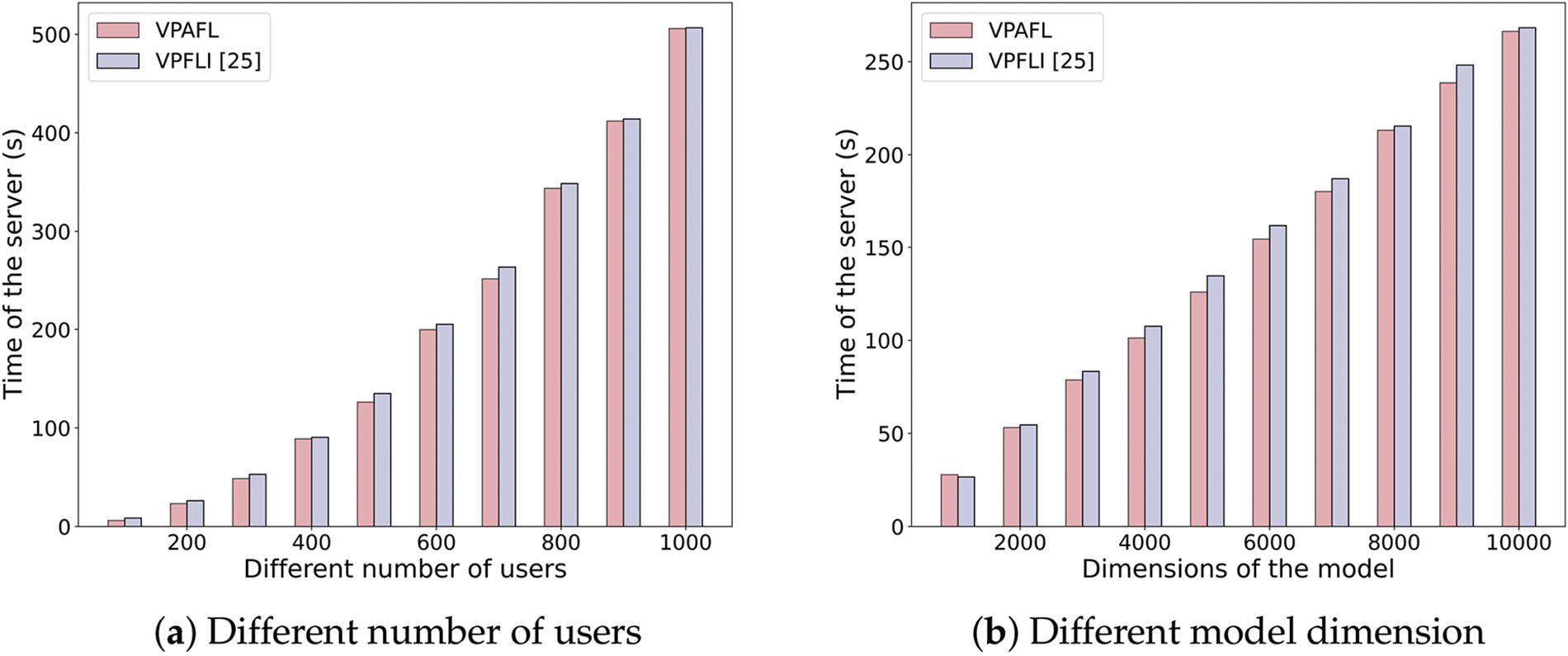
Figure 6: Computational overheads of the server [25]

7.4.2 Communication Overhead

In the experiment, we measure the communication overhead by the size of the uploaded information. As shown in Fig. 7, the communication overhead of the users is not related to the number of users, but related to the model dimension d. With increasing model dimension d, the size of the ciphertext generated by users becomes larger, leading to greater communication overhead. For the server, as shown in Fig. 8, its communication overhead is positively correlated with the number of users n and the model dimension d. The larger the number of users n, the more messages need to be transmitted, and the larger the model dimension d, the larger the ciphertext size generated by server aggregation.

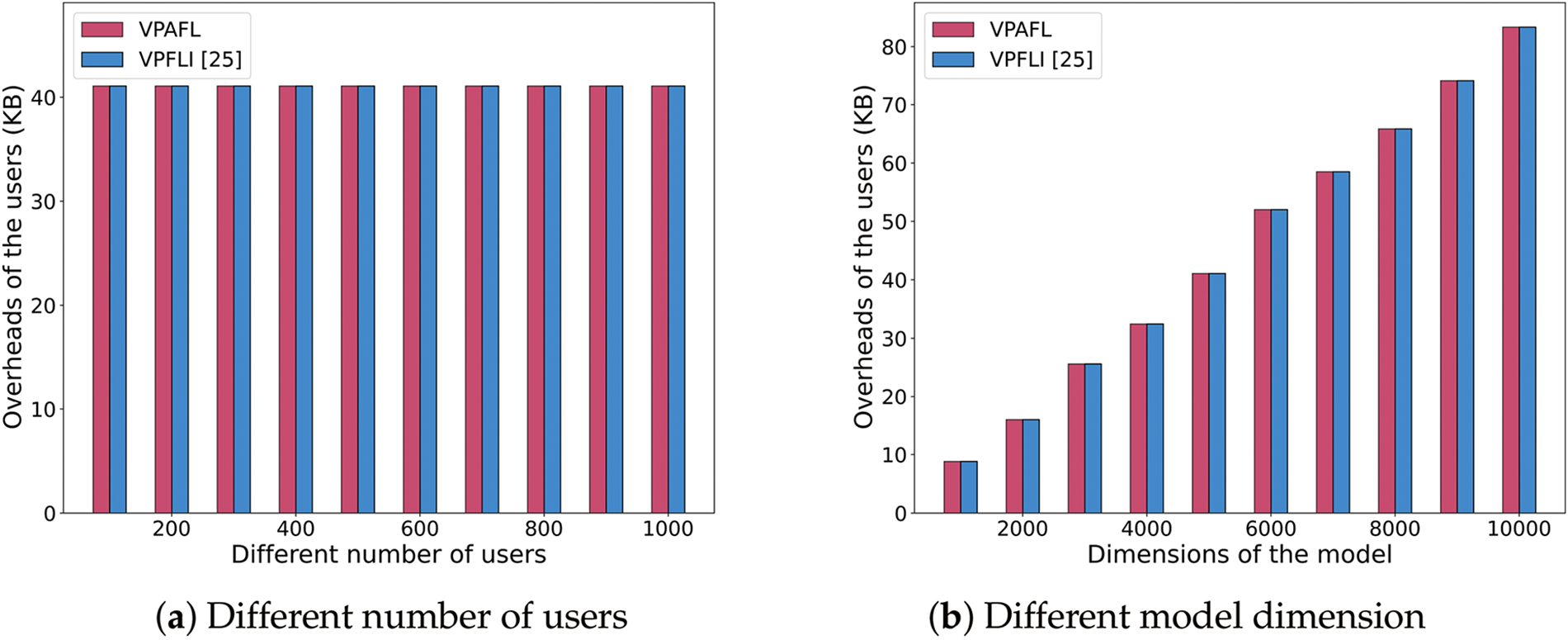
Figure 7: Communication overheads of the users [25]

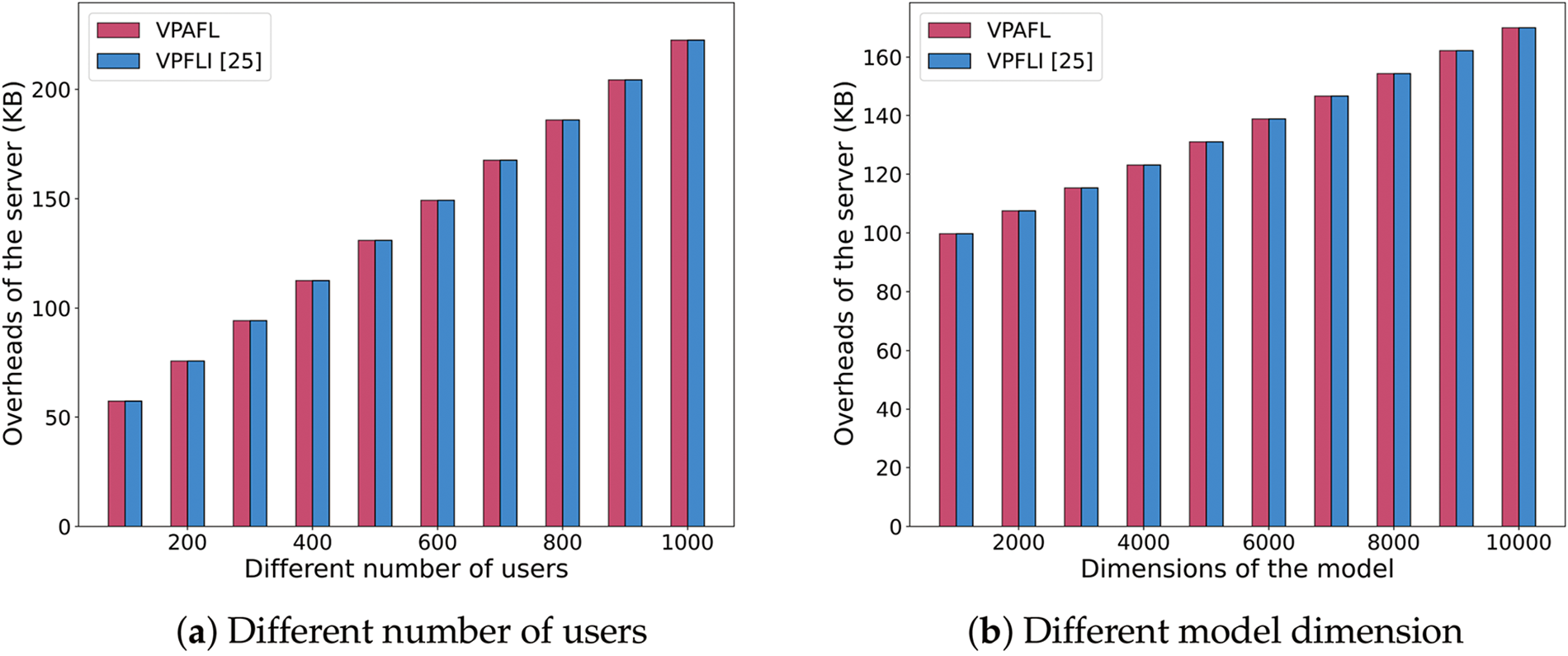
Figure 8: Communication overheads of the server [25]

Finally, we evaluate the communication overhead associated with the verification. Since our implementation reproduces only the verifiable module of VPFLI [25] while maintaining consistency with the proposed scheme in other components, both schemes exhibit identical communication overhead under identical experimental configurations. For the user, LHH and digital signature algorithms transform variable length messages into fixed size outputs, thus decoupling verification-related communication overhead from both the number of users n and the model dimension d. Conversely, the verification-related communication overhead of the server is determined by the cost of broadcasting the received hash values and signatures to all users, causing the communication costs of the server to scale linearly with the number of users n.

Fig. 9 shows the communication overhead for individual users and servers under fixed model dimensions d = 5000 and varying numbers of participating users n. The results show that the communication overhead for verification per user remains below 0.2 KB regardless of n, while the server overhead increases linearly with n due to the increasing volume of hash values and signatures broadcast. Importantly, since user devices typically face stringent computational and storage resource constraints compared to servers, the low verification-related communication overhead for users (0.2 KB) in VPAFL enhances its practicality for real-world deployment.

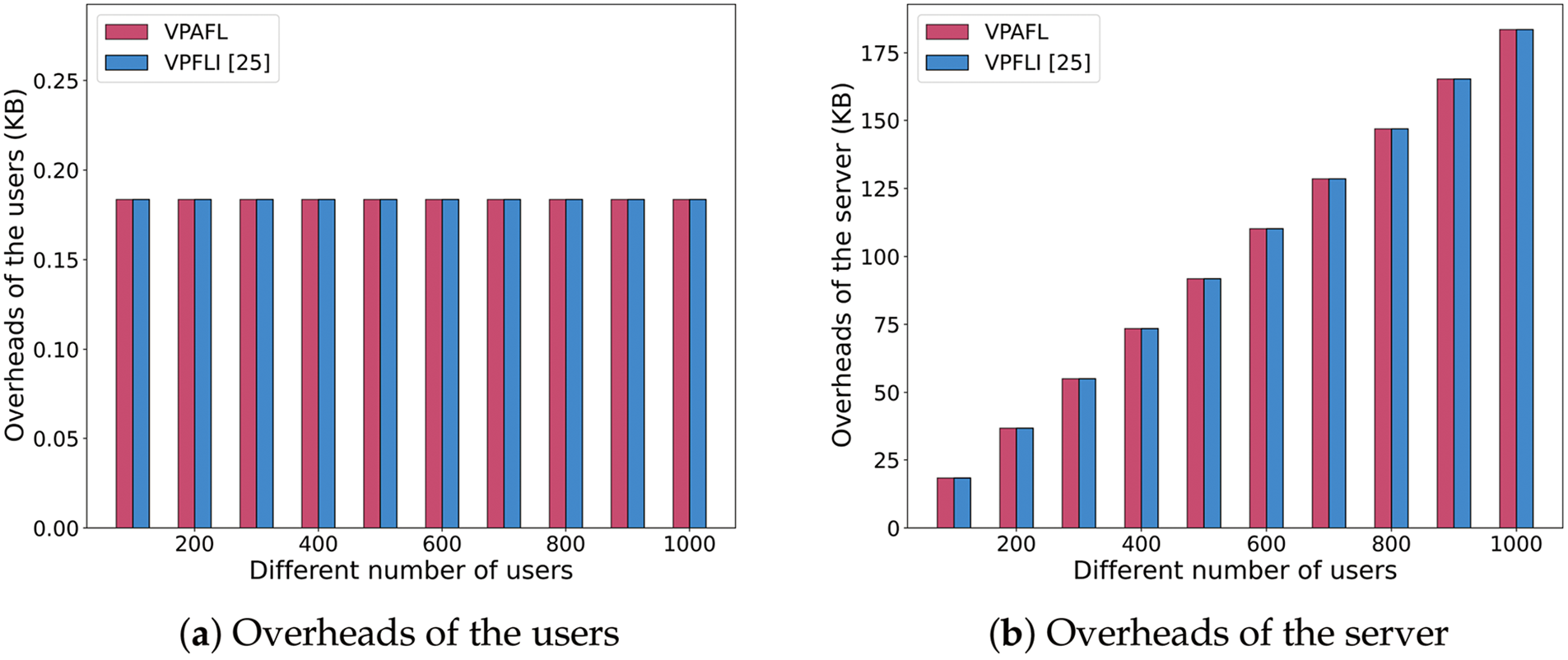
Figure 9: Communication overheads for verification when d = 5000 with different number of users [25]

8  Conclusion

In this paper, we propose a reversible data hiding in encrypted domains (RDHED) scheme that designs a joint message embedding and extraction mechanism. Building on this RDHED scheme, we further design VPAFL, a verifiable privacy-preserving aggregation protocol for single-server architectures, by combining linear homomorphic hash and digital signature algorithms. Unlike prior verifiable federated learning schemes based on linear homomorphic hash, VPAFL computes hash values using secret messages embedded by users during each communication round, thereby decoupling the computational overhead of hash generation from the model dimension. Theoretical analysis demonstrates the security and feasibility of VPAFL, while the experiment results confirm that the computational and communication overheads of the users for verification are lightweight.

Acknowledgement: The authors appreciate the valuable comments from the reviewers and editors.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China under Grants 62102450, 62272478 and the Independent Research Project of a Certain Unit under Grant ZZKY20243127.

Author Contributions: Conceptualization: Peizheng Lai, Minqing Zhang; Experimental operation and data proofreading: Peizheng Lai, Yixin Tang, Ya Yue; Analysis and interpretation of results: Peizheng Lai, Minqing Zhang, Fuqiang Di; Draft manuscript preparation: Peizheng Lai, Ya Yue; Figure design and drawing: Peizheng Lai, Yixin Tang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets used to support the findings of this study are publicly available on Internet as follows: MNIST: http://yann.lecun.com/exdb/mnist/ (accessed on 24 March 2025); CIFAR-10 and CIFAR-100: https://www.cs.toronto.edu/kriz/cifar.html (accessed on 24 March 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Tari Z, Yi X, Premarathne US, Bertok P, Khalil I. Security and privacy in cloud computing: vision, trends, and challenges. IEEE Cloud Computing. 2015;2(2):30–8. doi:10.1109/MCC.2015.45. [Google Scholar] [CrossRef]

2. Cao X, Du L, Wei X, Meng D, Guo X. High capacity reversible data hiding in encrypted images by patch-level sparse representation. IEEE Trans Cybern. 2015;46(5):1132–43. doi:10.1109/TCYB.2015.2423678. [Google Scholar] [PubMed] [CrossRef]

3. Shi YQ, Li X, Zhang X, Wu HT, Ma B. Reversible data hiding: advances in the past two decades. IEEE Access. 2016;4:3210–37. doi:10.1109/access.2016.2573308. [Google Scholar] [CrossRef]

4. Qian Z, Zhou H, Zhang X, Zhang W. Separable reversible data hiding in encrypted JPEG bitstreams. IEEE Trans Depend Secure Comput. 2016;15(6):1055–67. doi:10.1109/tdsc.2016.2634161. [Google Scholar] [CrossRef]

5. Zheng S, Li D, Hu D, Ye D, Wang L, Wang J. Lossless data hiding algorithm for encrypted images with high capacity. Multimed Tools Appl. 2016;75(21):13765–78. doi:10.1007/s11042-015-2920-y. [Google Scholar] [CrossRef]

6. Puteaux P, Puech W. An efficient MSB prediction-based method for high-capacity reversible data hiding in encrypted images. IEEE Trans Inf Forensics Security. 2018;13(7):1670–81. doi:10.1109/TIFS.2018.2799381. [Google Scholar] [CrossRef]

7. McMahan B, Moore E, Ramage D, Hampson S, Arcas BA. Communication-efficient learning of deep networks from decentralized data. In: Artificial intelligence and statistics; 2017; New York, NY, USA: PMLR. p. 1273–82 [Google Scholar]

8. Wu HT, Cheung YM, Tian Z, Liu D, Luo X, Hu J. Lossless data hiding in NTRU cryptosystem by polynomial encoding and modulation. IEEE Trans Inf Forensics Security. 2024;19(11):3719–32. doi:10.1109/TIFS.2024.3362592. [Google Scholar] [CrossRef]

9. Anushiadevi R, Amirtharajan R. Design and development of reversible data hiding-homomorphic encryption & rhombus pattern prediction approach. Multimedia Tools Appl. 2023;82(30):46269–92. doi:10.1007/s11042-023-15455-1. [Google Scholar] [CrossRef]

10. Zhou N, Zhang M, Wang H, Ke Y, Di F. Separable reversible data hiding scheme in homomorphic encrypted domain based on NTRU. IEEE Access. 2020;8:81412–24. doi:10.1109/ACCESS.2020.2990903. [Google Scholar] [CrossRef]

11. Wu HT, Cheung YM, Zhuang Z, Xu L, Hu J. Lossless data hiding in encrypted images compatible with homomorphic processing. IEEE Trans Cybern. 2022;53(6):3688–701. doi:10.1109/TCYB.2022.3163245. [Google Scholar] [PubMed] [CrossRef]

12. Zheng S, Wang Y, Hu D. Lossless data hiding based on homomorphic cryptosystem. IEEE Trans Depend Secure Comput. 2019;18(2):692–705. doi:10.1109/TDSC.2019.2913422. [Google Scholar] [CrossRef]

13. Xiang S, Luo X. Reversible data hiding in homomorphic encrypted domain by mirroring ciphertext group. IEEE Trans Circuits Syst Video Technol. 2018;28(11):3099–110. doi:10.1109/TCSVT.2017.2742023. [Google Scholar] [CrossRef]

14. Ke Y, Zhang MQ, Liu J, Su TT, Yang XY. Fully homomorphic encryption encapsulated difference expansion for reversible data hiding in encrypted domain. IEEE Trans Circuits Syst Video Technol. 2020;30(8):2353–65. doi:10.1109/TCSVT.2019.2963393. [Google Scholar] [CrossRef]

15. Hitaj B, Ateniese G, Perez-Cruz F. Deep models under the GAN: information leakage from collaborative deep learning. In: Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security; 2017; New York, NY, USA. p. 603–18. [Google Scholar]

16. Zhu L, Liu Z, Han S. Deep leakage from gradients. Adv Neural Inf Process Syst. 2019;32:14747–56. [Google Scholar]

17. Ma C, Li J, Ding M, Yang HH, Shu F, Quek TQ, et al. On safeguarding privacy and security in the framework of federated learning. IEEE Network. 2020;34(4):242–8. doi:10.1109/MNET.001.1900506. [Google Scholar] [CrossRef]

18. Xu G, Li H, Liu S, Yang K, Lin X. VerifyNet: secure and verifiable federated learning. IEEE Trans Inf Forensics Security. 2019;15:911–26. doi:10.1109/TIFS.2019.2929409. [Google Scholar] [CrossRef]

19. Paillier P. Public-key cryptosystems based on composite degree residuosity classes. In: International Conference on the Theory and Applications of Cryptographic Techniques; 1999; Berlin/Heidelberg: Springer. p. 223–38. [Google Scholar]

20. Zhao J, Zhu H, Wang F, Lu R, Li H, Tu J, et al. CORK: a privacy-preserving and lossless federated learning scheme for deep neural network. Inform Sciences. 2022;603(3):190–209. doi:10.1016/j.ins.2022.04.052. [Google Scholar] [CrossRef]

21. Wei K, Li J, Ding M, Ma C, Yang HH, Farokhi F, et al. Federated learning with differential privacy: algorithms and performance analysis. IEEE Trans Inf Forensics Security. 2020;15:3454–69. doi:10.1109/TIFS.2020.2988575. [Google Scholar] [CrossRef]

22. Wei K, Li J, Ma C, Ding M, Chen W, Wu J, et al. Personalized federated learning with differential privacy and convergence guarantee. IEEE Trans Inf Forensics Security. 2023;18:4488–503. doi:10.1109/TIFS.2023.3293417. [Google Scholar] [CrossRef]

23. Bonawitz K, Ivanov V, Kreuter B, Marcedone A, McMahan HB, Patel S, et al. Practical secure aggregation for privacy-preserving machine learning. In: Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security; 2017; New York, NY, USA. p. 1175–91. [Google Scholar]

24. Guo X, Liu Z, Li J, Gao J, Hou B, Dong C, et al. VeriFL: communication-efficient and fast verifiable aggregation for federated learning. IEEE Trans Inf Forensics Security. 2020;16:1736–51. doi:10.1109/TIFS.2020.3043139. [Google Scholar] [CrossRef]

25. Ren Y, Li Y, Feng G, Zhang X. VPFLI: verifiable privacy-preserving federated learning with irregular users based on single server. IEEE Trans Services Computing. 2024;18(2):1124–36. doi:10.1109/TSC.2024.3520867. [Google Scholar] [CrossRef]

26. Wang L, Polato M, Brighente A, Conti M, Zhang L, Xu L. PriVeriFL: privacy-preserving and aggregation-verifiable federated learning. IEEE Trans Services Computing. 2024;18(2):998–1011. doi:10.1109/TSC.2024.3451183. [Google Scholar] [CrossRef]

27. Hahn C, Kim H, Kim M, Hur J. VERSA: verifiable secure aggregation for cross-device federated learning. IEEE Trans Depend Secure Comput. 2021;20(1):36–52. doi:10.1109/TSC.2024.3451183. [Google Scholar] [CrossRef]

28. Xu Y, Zhang H, Zhao S, Zhang X, Li W, Gao F, et al. Comments on “VERSA: verifiable secure aggregation for cross-device federated learning”. IEEE Trans Depend Secure Comput. 2024;21(4):4297–8. doi:10.1109/TDSC.2023.3272338. [Google Scholar] [CrossRef]

29. Luo F, Wang H, Yan X. Comments on “VERSA: verifiable secure aggregation for cross-device federated learning”. IEEE Trans Depend Secure Comput. 2024;21(1):499–500. doi:10.1109/TDSC.2023.3253082. [Google Scholar] [CrossRef]

30. Bellare M, Goldreich O, Goldwasser S. Incremental cryptography: the case of hashing and signing. In: Advances in Cryptology-CRYPTO’94: 14th Annual International Cryptology Conference; 1994 Aug 21–25; Santa Barbara, CA, USA: Springer. p. 21–5. [Google Scholar]

31. Huang H, Huang T, Wang W, Zhao L, Wang H, Wu H. Federated learning and convex hull enhancement for privacy preserving WiFi-based device-free localization. IEEE Trans Consum Electron. 2024;70(1):2577–85. doi:10.1109/TCE.2023.3342834. [Google Scholar] [CrossRef]

32. Tian Y, Wang S, Xiong J, Bi R, Zhou Z, Bhuiyan MZA. Robust and privacy-preserving decentralized deep federated learning training: focusing on digital healthcare applications. IEEE/ACM Trans Comput Bi. 2024;21(4):890–901. doi:10.1109/TCBB.2023.3243932. [Google Scholar] [PubMed] [CrossRef]

33. Wehbi O, Arisdakessian S, Guizani M, Wahab OA, Mourad A, Otrok H, et al. Enhancing mutual trustworthiness in federated learning for data-rich smart cities. IEEE Internet Things J. 2025;12(3):3105–17. doi:10.1109/JIOT.2024.3476950. [Google Scholar] [CrossRef]

34. Bottou L. Large-scale machine learning with stochastic gradient descent. In: Proceedings of COMPSTAT’2010: 19th International Conference on Computational Statistics; 2010 Aug 22–27; Paris, France: Springer. p. 177–86. [Google Scholar]

35. Shamir A. How to share a secret. Commun ACM. 1979;22(11):612–3. doi:10.1145/359168.359176. [Google Scholar] [CrossRef]

36. Jagielski M, Oprea A, Biggio B, Liu C, Nita-Rotaru C, Li B. Manipulating machine learning: poisoning attacks and countermeasures for regression learning. In: 2018 IEEE Symposium on Security and Privacy (SP); 2018; San Francisco, CA, USA. p. 19–35. [Google Scholar]

37. Gentry C, Groth J, Ishai Y, Peikert C, Sahai A, Smith A. Using fully homomorphic hybrid encryption to minimize non-interative zero-knowledge proofs. J Cryptol. 2015;28(4):820–43. doi:10.1007/s00145-014-9184-y. [Google Scholar] [CrossRef]

38. Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Adv Neural Inf Process Syst. 2012;25:1097–105. [Google Scholar]

39. Krizhevsky A, Hinton G. Learning multiple layers of features from tiny images. Handb Systemic Autoimmune Dis. 2009;1(4):1–60. [Google Scholar]

40. LeCun Y. The MNIST database of handwritten digits; 1998. [cited 2025 May 7]. Available from: http://yann.lecun.com/exdb/mnist/. [Google Scholar]

41. Zhang J, Liu Y, Hua Y, Wang H, Song T, Xue Z, et al. PFLlib: personalized federated learning algorithm library. arXiv:231204992. 2023. [Google Scholar]