Multi-Level Subpopulation-Based Particle Swarm Optimization Algorithm for Hybrid Flow Shop Scheduling Problem with Limited Buffers

1  Introduction

Given the rapid advancement in the intelligent manufacturing field, production scheduling, as a crucial technology of intelligent manufacturing, plays a pivotal role in the modern manufacturing industry [1,2]. Being the most prevalent scheduling problem in manufacturing systems, the flow shop scheduling problem (FSSP) has been applied in many scenarios [3,4]. As an expansion of the conventional FSSP, the hybrid flow shop scheduling problem (HFSP) considers machine flexibility, thereby possessing a stronger industrial background and higher practical application value [5,6]. At present, the HFSP has been widely applied in the chemical industry, transportation, manufacturing, medical care, and other industries [7,8].

However, the traditional FSSP still faces practical limitations due to its reliance on an infinite buffer size between consecutive stages [9]. Generally, once a job completes processing at a particular stage, it proceeds directly to the next stage if a machine is available. Otherwise, the job enters a buffer zone to wait for an available machine. However, in actual production scenarios, due to constraints such as space and cost, the size of the buffer is often limited [10]. For example, space and storage facilities are finite, especially in the battery and steel production industry [11]. Therefore, studying the flow shop scheduling problem with limited buffers (LBFSSP) holds crucial practical significance [12]. In the case of limited buffers, after the job is processed, the job cannot directly enter the buffer even if no machine is available in the next stage. In detail, if all buffers are occupied, the job can only remain on the present machine, causing congestion. Only when there is an available machine in the subsequent stage, allowing the job stored in the buffer to enter the next stage according to the first-in first-out principle, can the buffer be released. Thus, the job can leave the current machine and enter the released buffer. At this moment, the released machine can be used to process other jobs, and the congestion phenomenon is terminated [13]. Although the blocking phenomenon may occur in LBFSSP, it’s different from the blocking flow shop scheduling problem (BFSSP). The BFSSP has no buffer, while the FSSP has unlimited buffers. However, the quantity of buffers ranges from 1 to N (the number of jobs) in LBFSSP. Therefore, the LBFSSP lies between the BFSSP and the FSSP.

Compared to the FSSP, the hybrid flow shop scheduling problem with limited buffers (LBHFSP) is more widely used in realistic production, so studying the LBHFSP is more meaningful and practical [14]. HFSP, being a classical NP (Non-deterministic Polynomial)-hard problem [15], is hard to solve, while the LBHFSP not only considers machine flexibility but also the buffer size, making it even more difficult to solve [16]. Thus, this paper studies the LBHFSP and proposes a multi-level subpopulation-based particle swarm optimization algorithm (MLPSO), aiming to optimize the goal of total completion time. The primary contributions of this article are summarized below.

(1)   According to the constraint characteristics of this problem, a specific circular decoding strategy is designed in this paper. This method considers the impact of the limited buffers on the process of subsequent operation, which helps to decide the time when the blocked job gets into the buffer and calculates the blocking time.

(2)   Considering the influence of the limited buffers, an initialization strategy based on blocking time is proposed. This strategy helps to produce promising initial solutions through the selection mechanism based on blocking time and makespan, thereby improving the quality and diversity of the population.

(3)   To deal with the shortcomings of the PSO, a multi-level subpopulation collaborative search strategy is designed. This strategy can achieve multi-directional search and information exchange, thereby preventing getting into a local optimum.

(4)   Given the characteristics of the scheduling process of the LBHFSP, a local search strategy based on the first blocked job is developed. This strategy can avoid unnecessary operations and achieve precise search, thereby greatly improving the search efficiency.

The structure of this article is as follows: Section 2 is the review of the literature. Section 3 describes the problem in detail and presents the mathematical model. Section 4 is the detailed framework of the MLPSO algorithm. Section 5 is a comparative experiment. Finally, Section 6 provides a summary of the content and looks forward to promising research subjects.

2  Literature Review

So far, there has been a large amount of literature on the hybrid flow shop scheduling problem owing to its broad range of applications. In addition, many researchers have made an extension on HFSP and proposed effective algorithms to deal with this sophisticated problem. For instance, Guan et al. [17] designed a new crossover operator and developed a modified genetic algorithm incorporating multiple crossover operators to solve the HFSP in collaborative manufacturing. Considering the link between the solution space represented by different solutions, Kuang et al. [18] developed a novel algorithm with a two-stage cross-neighborhood search process for HFSP. Zhang et al. [19] designed a metaheuristic approach including the meta-training and the Q-learning process to deal with the HFSP with learning ability and forgetting factors. There are still kinds of literature on the HFSP and its expansion [20–24].

Traditional FSSP is under the assumption that the buffer capacity is unlimited. However, with the continuous development of production mode, the flow shop scheduling problem with limited buffers (LBFSSP) arises. Therefore, research on the LBFSSP has been continuously emerging. For instance, Moslehi et al. [25] applied the hybridization algorithm combining the simulated annealing algorithm (SA) and the variable neighborhood search method (VNS) to settle the permutation flow shop scheduling problem with limited buffers (LBPFSP). Zhao et al. [26] made improvements to the PSO algorithm by introducing the linearly declining perturbation factor to address this problem better. Zhang et al. [27] developed an efficient discrete artificial bee colony algorithm (DABC) to deal with the FSSP with intermediate buffers. Additionally, Abdollahpour et al. [28] adopted an approach integrating the artificial immune system algorithm with the iterated greedy method to optimize the makespan in this problem. Deng et al. [29] introduced several effective strategies into the DABC algorithm for LBPFSP to minimize the objective of the total flow time. The hybrid shuffled frog leaping [30] was also applied to LBFSSP. Le et al. [31] combined the improved NEH (Nawaz-Enscore-Ham) heuristic with the iterated local search method to solve the two-machine LBPFSP with invariable processing time at a certain machine. Moreover, Lu et al. [32] were the first to investigate the multi-objective distributed LBPFSP and develop an effective collaborative optimization algorithm based on the Pareto to optimize the objective of total energy consumption (TEC) and makespan. In summary, there is much research on LBFSSP.

The PSO algorithm is a population-based optimization algorithm, which is derived from the observation of bird social behavior. In comparison to other algorithms, the PSO algorithm’s framework is more straightforward, and its process is easier to implement. Moreover, it achieves the optimization process through an information-sharing mechanism, which accelerates the algorithm’s convergence. Therefore, the PSO algorithm is widely applied to scheduling problems. For instance, Ding et al. [33] studied the flexible job shop scheduling problem (FJSP) and proposed an improved particle swarm optimization algorithm (IPSO), in which a new chain encoding and effective decoding scheme were proposed to shorten the makespan effectively. To solve the multi-objective FJSP, Zhang et al. [34] proposed an improved hybrid particle swarm optimization algorithm with a new method for updating particles. Hayat et al. [35] proposed the modified PSO algorithm (MPSO) for the permutation flow shop scheduling problem (PFSP). The MPSO is hybridized with VNS and SA. The effectiveness of the MPSO is proven through the experimental results. Leguizamon et al. [36] designed a PSO-based algorithm oriented by decision for the scheduling problems in the flow shop production field. Kaya et al. [37] presented an improved local search method (LS) and applied it to the chaotic hybrid firefly and PSO algorithm to tackle FSSP in production systems. A parallel hybrid PSO-GA (Genetic Algorithm) algorithm that can shorten run time remarkably was proposed for HFSP with transportation [38]. Additionally, Zhang et al. [39] studied the distributed FSSP and specifically designed a bi-objective PSO algorithm to optimize the total processing time and makespan of this problem simultaneously. Later, Zhang et al. [40] also developed a multi-objective PSO algorithm relying on the Q-Learning mechanism to tackle the distributed FFSP with the criteria of makespan and TEC. Additionally, for the FFSP with limited buffers, several academic studies have also used the PSO algorithm. Liu et al. [41] were the first to apply the PSO algorithm with some adaptive search strategies (HPSO) to the LBFSSP due to its excellent performance in continuous optimization problems. Zhao et al. [26] developed a modified PSO algorithm (LDPSO) incorporating a linearly decreasing disturbance term in the velocity to regulate the capability between exploration and exploitation. However, both the encoding methods of the HPSO and LDPSO reduce the initial population’s diversity greatly, which is not beneficial for obtaining the best solution. Therefore, the LDPSO algorithm is required for further improvements to enhance performance. For LBHFSP, Li et al. [42] explored an algorithm that is a mixture of the artificial bee colony algorithm with the tabu search method (TS), and the neighborhood search strategy and LS method based on TS were conceived in it. Besides, Zhang et al. [43] adopted the discrete whale swarm algorithm to address the LBHFSP, in which a hybrid initialization approach and a deduplication mechanism were designed to enrich the initial population’s diversity. Zheng et al. [44] proposed the hybrid metaheuristic algorithm called GVNSA to solve the LBHFSP with step-deteriorating jobs. Additionally, Rooeinfar et al. [45] studied the LBHFSP with preventive maintenance and presented a novel method called HSIM-META, which includes the computer simulation model and GA, PSO, and SA. Zohali et al. [46] introduced batch processing machines into the LBHFSP and designed the discrete fruit fly algorithm to reduce total cost as much as possible. Moreover, Janeš et al. [47] proposed a modified steady-state genetic algorithm to deal with this complex problem. Zheng et al. [48] studied the reentrant LBHFSP with sequence-dependent setup times and proposed a cooperative adaptive genetic algorithm to minimize the makespan. The genetic operations based on the collaborative mechanism are designed to enhance the search capability. Chang et al. [49] proposed a discrete particle swarm optimization algorithm with multi-population reduction for the LBHFSP, in which the elite retention strategy is designed to improve the algorithm’s performance. Although they are efficient in solving LBHFSP and its extension, none of them considered the influence of limited buffers on the processing state of the job. This paper digs into the blocking phenomenon caused by limited buffers and aims to optimize the objective by reducing the occurrence of blocking. Consequently, a multi-level subpopulation-based particle swarm optimization algorithm is put forward for LBHFSP in this article.

3  Problem Description and Mathematical Model

3.1 Problem Description

The hybrid flow shop scheduling problem with limited buffers (LBHFSP) is defined as follows: there are N jobs and S stages. Each stage i(i=1,2,3,…,S) is equipped with Mi parallel machines, with Mi>1 at least one stage. Each job is processed with the same processing path. The buffer capacity between adjacent stages is limited, and the buffer size between stage i and i+1 is Bi. The processing situation of each job is affected by the buffer size between consecutive stages. In detail, when the job is processed in stage i, the following processing scenarios may occur: (1) The job immediately enters the next stage for processing when a machine in stage i+1 is available; (2) In the case of no available machine in stage i+1, the job will go into the buffer for waiting when a buffer between adjacent stages is available; (3) In the case of no available buffer between consecutive stages, the job is not allowed to leave the current machineuntil the buffer or the machine in the next stage is available. The purpose of the LBHFSP is to obtain an optimal schedule that minimizes the maximum completion time of all jobs. The LBHFSP is depicted in Fig. 1.

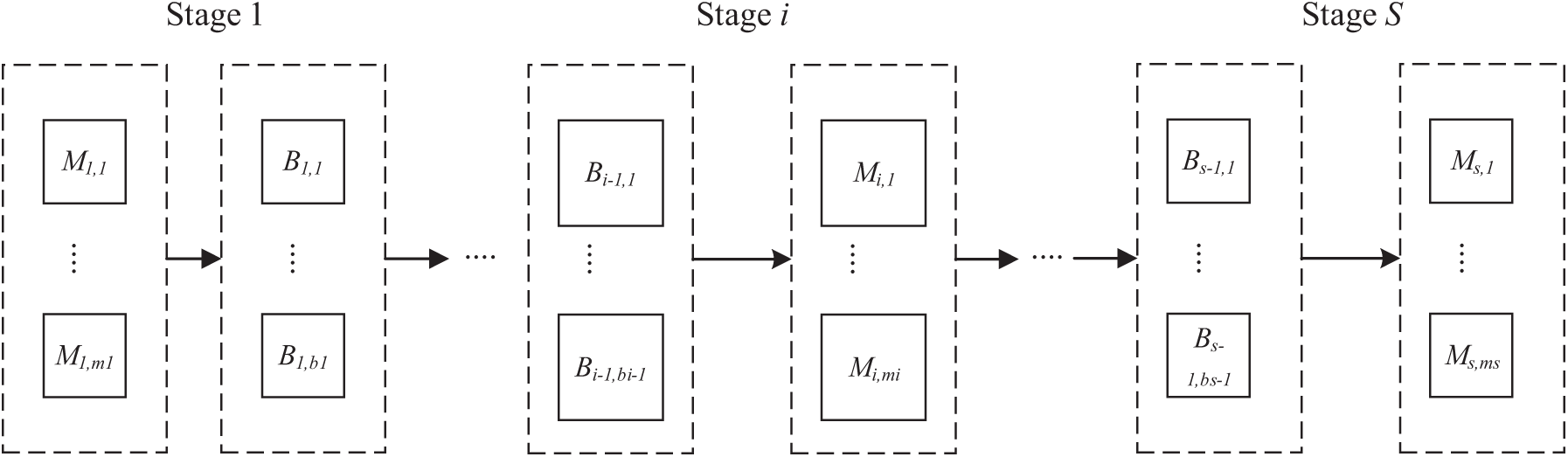
Figure 1: The processing flowchart of the LBHFSP

In addition, the assumptions are as follows:

1.    Each job can only be processed by one machine at a time;

2.    One machine can process at most one job at a time;

3.    All jobs are independent and ready for processing at time 0;

4.    The time for transportation and setup between adjacent stages is negligible;

5.    No preemption and machine breakdown are permitted.

To better illustrate the LBHFSP, we give an example of the problem. This instance discusses the LBHFSP with 10 jobs and 3 stages. Furthermore, each stage contains 3 machines. In this example, the buffer size is set to 2. The time required to process each job in each stage is listed in Table 1. Given a solution π={1,2,3,4,5,6,7,8,9,10}, Fig. 2 shows the Gantt chart pictured by solution π in the case where the buffer size is limited. “B1, B2, B3, and B4”, respectively, represent the buffer between stages, that is, the gray area in the figure; “M1 and M2” indicate the machine in each stage. Due to the limited size of the buffer, jobs might be blocked on the current machines, where “Blocking time” represents the duration during which the job is blocked on the machine, resulting in a final makespan of 29. Meanwhile, under infinite buffers, the makespan corresponding to the solution π is 28. By comparison, the maximum completion time is extended as a result of the limited buffer. However, in terms of practical applications, the limited buffer is more in line with realistic production scenarios, so this article aims to reduce the maximum completion time under limited buffers.

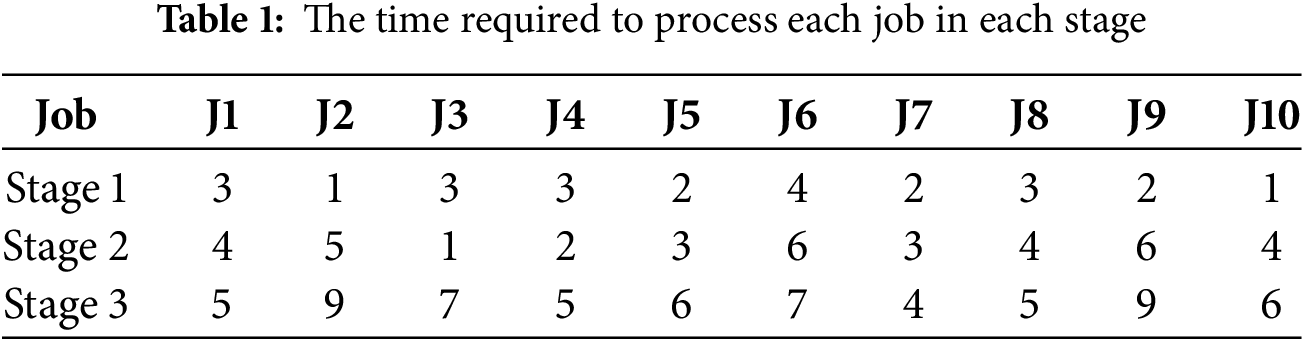
Figure 2: Gantt chart of one solution with limited buffers

3.2 Mathematical Model

The related notations of the LBHFSP are presented in the following:

(1) Indices

j,j′: index of jobs, j=1,2,…,N,j′=1,2,…,N.

i: index of stages, i=1,2,…,S.

k: index of machines, k=1,2,…,M.

b: index of buffers, b=1,2,…,B.

r: index of the position on the machine or buffer, r=1,2,…,N.

(2) Sets

J: set of jobs, J={1,2,…,N}.

B: set of buffers, B={B1,B2,…,Bs−1}.

M: set of machines, M={M1,M2,…,Ms}.

(3) Parameters

N: total number of jobs.

S: total number of stages.

Bi: the number of buffers between stage i and i+1.

pi,j: the processing time of job j in stage i.

Si,j: starting time of job j in stage i.

Ci,j: completion time of job j in stage i.

Bi,j: start waiting time of job j in the buffer between stage i and i+1.

Ei,j: end waiting time of job j in the buffer between stage i and i+1.

BTi,j: the blocking time of job j in stage i.

FAMi: the earliest available time of the machine in stage i.

FABi: the earliest available time of buffer between stage i and i+1.

LA: an infinite positive integer.

(4) Decision variables

wj,i,k,r: a binary number, set 1 if job j is blocked on the k-th machine in the r-th position in stage i; otherwise, set 0.

xj,i,k,r: a binary variable, set 1 if job j is processed on the k-th machine in the r-th position in stage i; otherwise, set 0.

yj,j′,i,k: a binary variable, set 1 if job j is processed on the k-th machine before job j′ in stage i; otherwise, set 0.

uj,i,k,r: a binary variable, set 1 if job j is stored in the k-th buffer in the r-th position between stage i and i+1; otherwise, set 0.

yj,j′,i,k: a binary variable, set 1 if job j is stored in the k-th buffer before job j′ between stage i and i+1; otherwise, set 0.

In summary, LBHFSP aims to minimize the makespan. Below is the mathematical model of the LBHFSP.

Objective function:

OF=minCmax(1)

subject to:

∑k=1Mixj,i,k,r=1,j∈{1,2,…,N},i∈{1,2,…,S}(2)

Si,j≥0,i∈{1,2,…,S},j∈{1,2,…,N}(3)

Ci,j=Si,j+pi,j,i∈{1,2,…,S},j∈{1,2,…,N}(4)

yj,j′,i,k+yj′,j,i,k≥xj,i,k,r+xj′,j,k,r−1,j∈{1,2,…,N},j≠j′(5)

yj,j′,i,k+yj′,j,i,k≤1,j∈{1,2,…,N}j≠j′(6)

Si+1,j≥Ci,j,i∈{1,2,…,S},j∈{1,2,…,N}(7)

Si,j′≥Si+1,j−LA×(3−wj,i,k,r−xj′,i,k,r−yj,j′,i,k),j∈{1,2,…,N},j≠j′,(8)

BTi,j′=wj,i,k,r×(Ei,j−Ci,j′)×yj,j′,i,k,j≠j′,j∈{1,2,…,N}(9)

Si,j′=Ci,j+BTi,j′,j≠j′,j∈{1,2,…,N}(10)

∑k=1Miuj,i,k,r=1,j∈{1,2,…,N},i∈{1,2,…,S−1}(11)

Bi,j>0,i∈{1,2,…,S−1},j∈{1,2,…,N}(12)

Ei,j′=Ci+1,j,j∈{1,2,…,N},i∈{1,2,…,S−1}(13)

zj,j′,i,k+zj′,j,i,k≥uj,i,k,r+uj′,i,k,r−1,j∈{1,2,…,N},i∈{1,2,…,S−1},j≠j′(14)

zj,j′,i,k+zj′,j,i,k≤1,j∈{1,2,…,N},i∈{1,2,…,S−1},j≠j′(15)

Eq. (1) is the objective function of the LBHFSP problem. Eq. (2) indicates that each job can only be processed on one machine at any stage. Eq. (3) ensures that the starting time of each job is not less than 0 in all stages. Eq. (4) gives the method of calculating the completion time of each job. Eqs. (5) and (6) ensure that each machine can only process one job at a time. Eq. (7) ensures that the job can be processed only after the previous stage of processing is completed. Eq. (8) shows that the machine can process subsequent jobs only when the blocking phenomenon on the machine is released. Eq. (9) reveals the relationship between the blocking time of the processing job and the end waiting time of the previous job in the buffer. Eq. (10) indicates that the starting time of the subsequent job is the sum of the completion time and the blocking time of the previous job. Eq. (11) guarantees each job can only be stored in one buffer and cannot be transferred. Eq. (12) indicates that the start waiting time of the job entering the buffer is greater than 0. Eq. (13) shows that the end waiting time in the buffer is equal to the previous job’s completion time in the next stage. Eqs. (14) and (15) ensure that each buffer can only store one job at a time.

4  The Proposed Algorithm for LBHFSP

4.1 The Framework of MLPSO

For LBHFSP, this paper proposes the algorithm MLPSO. Firstly, an initialization strategy is developed under the features of the LBHFSP to enhance the initial population’s quality. Secondly, a multi-level subpopulation collaborative search is developed to protect the MLPSO from being caught in the local optimum. Finally, to promote the search performance of the MLPSO, a local search strategy is proposed depending on the properties of the scheduling process of the LBHFSP. The framework of MLPSO is shown in Algorithm 1. MLPSO is a hybrid framework that combines the discrete PSO with a novel local search method. The basic update method of particles in the discrete PSO can be obtained in this reference [50].

The primary components of MLPSO consist of encoding and decoding, population initialization, collaborative search, and local search. The following subsections describe these components in detail.

4.2 Encoding

To address LBHFSP, this article adopts an encoding method based on the job sequence, where a set of integers represents one solution, with each integer corresponding to a specific job. Taking Fig. 2 as an example, the solution is represented as π={1,2,3,4,5,6,7,8,9,10} which means that the job is processed according to this job sequence during the first stage. In other stages, the processing order is determined by the processing state of the previous operation, buffer size, and the available machines together. The details are given in the following section.

4.3 Decoding

Since the size of the buffer is limited by the realistic production scenario, the decoding method of LBHFSP is different from the classical HFSP, which needs to consider the influence of the limited buffer on the subsequent processing operation. Therefore, a specific circular decoding method is designed according to the properties of LBHFSP. Under this decoding method, the job is selected sequentially according to the initial solution. Once the job is selected, the job is arranged sequentially to each stage until this job is completed, and then the next job is selected circularly. This procedure iterates until all jobs are processed. The circular decoding process is given below:

Step 1: According to the solution π={J1,J2,J3,…,Jj,…,JN}, select the job Jj circularly. At first, j=1. If j≤N, turn to Step 2; otherwise turn to Step 3.

Step 2: Originally, i=1. For each job Jj at each stage i, execute the subsequent steps:

Step 2.1: Select the earliest available machine. The job Jj is directly allocated to the available machine. The starting time Si,Jj and completion time Ci,Jj are recorded. If i=S, it indicates that the job is in the final stage and has completed processing. Therefore, j++ and return to Step 1. If i<S, perform the Step 2.2.

Step 2.2: After the job is finished in the current stage, it is necessary to determine whether the job will proceed directly to the next stage for processing, wait in the buffer, or wait on the current machine. This is achieved by the following steps:

(1)   If Ci,Jj≥FAMi+1, it denotes that there is an available machine and the job proceeds directly to the next stage for processing. Then, let i++ and turn to Step 2.1.

(2)   If FAMi+1>Ci,Jj≥FABi, it means that there is no available machine but an available buffer. Thus, the job gets into the buffer area to wait until the machine is available. The job is sent to the next stage to process. At this point, set i++ and turn to Step 2.1.

(3)   If Ci,Jj<FABi, it indicates that there is neither an available machine nor an available buffer. As a result, the job is supposed to keep on the current machine until the buffer becomes available. Then, BTi,Jj=FABi−Ci,Jj,Ci,Jj=FABi, turn to Step 2.2.

Step 3: All jobs have been finished. And the makespan=maxJj∈J{Cs,Jj}.

4.4 Population Initialization

For LBHFSP, due to the limited buffer, jobs may be blocked on machines, resulting in a longer completion time. Considering the influence of blocking time on completion time, the initialization strategy based on blocking time is designed in this article to enhance the initial population’s quality. This initialization strategy aims to add solutions with a smaller blocking time to the initial population, making it more likely to find better solutions with a smaller completion time. The detail is given below.

As we all know, NEH is one of the famous heuristic methods that has been demonstrated to perform well in solving scheduling problems [51]. In the case of a small buffer size, prioritizing jobs with longer total processing times is more likely to result in a longer blocking time. Given this, we sort jobs in ascending order according to their total processing completion times, giving higher priority to jobs with shorter completion times. Therefore, this article employs the NEH heuristic rule to generate two solutions for the initial population. Other solutions are generated using the following strategy based on the characteristics of the problem. Firstly, randomly generate individuals and adopt the decoding strategy to obtain the makespan and blocking time of an individual. Subsequently, these individuals are ranked in ascending order depending on makespan and blocking time, respectively. Then, the top 50% of individuals from each sorting result are added to the population, while the last individual from both sorting results is recorded. Finally, replace the last two individuals with the two solutions generated by NEH. Consequently, the initial population is obtained. Algorithm 2 gives the pseudocode of the initialization strategy.

4.5 Collaborative Search Strategy

To cope with the poor global search capability of the PSO because of its single population, the multi-level subpopulation collaborative search strategy is proposed. Subpopulations at varying levels can evolve along distinct directions through collaborative search, allowing them to explore and exploit in different directions. This strategy can effectively avoid being trapped in local optimum and enhance the global search ability of the MLPSO. In detail, this strategy includes three parts: population division, particle update, and information exchange between subpopulations.

Firstly, the population is segmented into d subpopulations at the same level according to the makespan. This helps to reduce the differences among subpopulations, making sure that each subpopulation has the same search ability initially. The number of subpopulations d is determined through parameter calibration experiments. Parameter calibration makes the population division more accurate.

Next, to better tackle the scheduling problem, each particle’s update method needs to be discretized. The updating process can be equivalent to the mutation operation, crossover with its historical optimal particle, and crossover with the historical optimal particle of the population, respectively. Both crossover and mutation operations are performed with a certain probability. Among them, MR represents a mutation probability, PCR and GCR represent crossover probability with its own historical best particle and the group’s historical best particle. PCR and GCR are also called learning factors and represent the probabilities of learning from themselves and the group. However, in the beginning, the historical best position of the particle is identical to its current position. If the particle does not perform mutation operation, then crossover with its own historical best position is invalid. To avoid invalid crossover operation, a moving-based crossover operator (MBX) is specifically designed. Even if the two individuals to be crossed are the same, crossover results different from their parents can be obtained by MBX. Fig. 3 displays the process of the moving-based crossover operator. In addition, when two crossover individuals differ, the partial matching crossover (PMX) is adopted. The mutation operation adopts the exchange operation, which randomly selects two points and exchanges the job at these two points.

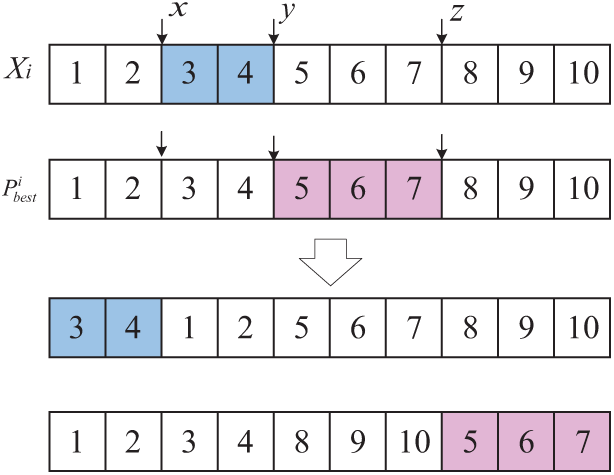
Figure 3: MBX crossover operator

Finally, the multi-level subpopulation collaborative search is achieved through information exchange. The information exchange between populations is achieved through particle migration. The migration method is as follows: the worst particle in an excellent subpopulation replaces the worst particle in an inferior population, and the best particle in an inferior population replaces the worst particle in an excellent population. The substitution of superior particles for the inferior particles of another population can not only guide the evolution of the population in a good direction but also retain the excellent solution structure. The substitution between the inferior particles is beneficial to enrich the population’s diversity and boost the optimization capability. After each collaborative search, the subpopulations will evolve towards the level of excellent, common, and inferior. The pseudocode of the collaborative search strategy is expressed in Algorithm 3.

4.6 Local Search Strategy

As we know, limited buffers usually lead to the blocking phenomenon during the process of manufacturing. Therefore, given the characteristics of the scheduling process of the LBHFSP, a local search strategy based on the first blocked job is designed. The local search strategy is aimed at reducing the occurrence of blocking by performing insertion operations on the blocked jobs, thereby shortening the processing completion time. This method can reduce unnecessary operations to improve search efficiency.

The key to this strategy is to find the first blocked job, determine the local search area accordingly, and then perform the local search process within the specific area. The detailed process of local search can be explained in conjunction with Fig. 4, where the blue square represents the blocked job. From Fig. 4, we can know that the blocked jobs are J7,J8, and J10. The first blocked job is J7, which means the solution structure before J7 is not blocked. This part is denoted as the optimal substructure s1, so the local search process is executed in the s2 region. First, randomly pick a job within the s2 region, then insert it into all reasonable positions in s2, and find the position that minimizes the makespan. Finally, the job is inserted into the specific position to form the solution s′. If the new solution outperforms the original solution, it takes the place of the original one. The pseudocode of the local search strategy is illustrated in Algorithm 4.

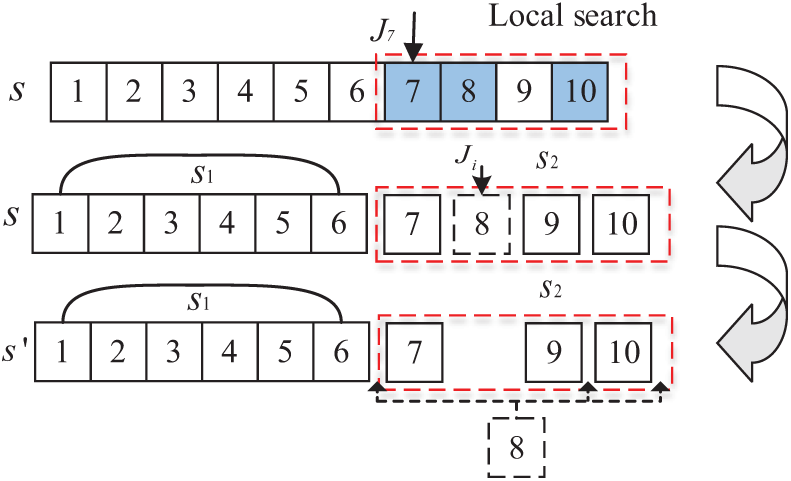
Figure 4: The process of local search based on the first blocked job

4.7 Complexity of the MLPSO

In this part, a comprehensive analysis of the algorithm’s time complexity is made. In the initialization stage, initial solutions are produced at random. Then the quality of each solution is assessed through the decoding process, which consists of 2×PS×N operations, where PS represents the population size and N denotes the number of jobs. In the collaborative search stage, the population is separated into d subpopulations, and the subpopulations are updated to achieve collaborative search through migration, which includes PS×N×S+d∗N∗PSd+N∗d operations. In the local search phase, locate the first blocked position pos according to each blocked job from the current solution. Then the insertion operation is performed in the local search area, which involves only one insertion operation. d and S are constants that are much smaller than N, and the value of PS is close to N. Therefore, the MLPSO algorithm’s time complexity is O(N2).

5  Experimental Comparison and Analysis

5.1 Experimental Instances

At this part, 90 instances are generated randomly, with the number of stages S∈{4,5,6,7,8}, the number of jobs N∈{40,60,80,100,120,160}, the size of buffers between consecutive stages B∈{1,2,4}. The time required for processing is randomly produced from the discrete distribution ranging from 1 to 99. However, each job’s processing time at each stage remains consistent once the number of jobs and stages is the same, regardless of the buffer size between adjacent processing stages. Moreover, the number of machines for processing varies for different instances, but the quantity of machines at each stage is identical for the same instance.

All comparative algorithms are realized by using IntelliJ IDEA2022 on the same PC. To ensure the fairness and accuracy of the comparison experiment results, each algorithm is independently executed 20 times for each data. The criterion for termination is determined by the CPU (Central Processing Unit) running time. The largest operation time is established to LOT=N∗S∗ω, where ω, a constant, is up to a specific instance. For different cases, the constant ω∈{20,30,40}. In this paper, the average relative percentage deviation (ARPD) is applied to evaluate the results. The ARPD is expressed as follows:

ARPD=1R∑i=1RCi−CbestCbest×100%(16)

In Eq. (16), R signifies the total iteration times carried out by each algorithm on each instance, Ci denotes the makespan of the solution received by a specific algorithm in the i-th iteration for a specific instance, and Cbest represents the makespan of the best solution found for a certain instance.

5.2 Parameter Calibration

Parameter configuration significantly influences the algorithm’s overall performance. Therefore, the MLPSO algorithm’s ideal parameter configuration is up to the Taguchi method of design-of-experiment (DOE). MLPSO includes five key parameters: (1) Population size PS∈{60,90,120,150}. (2) Mutation rate MR∈{0.2,0.4,0.6,0.8}. (3) Crossover rate with Pbest PCR∈{0.2,0.4,0.6,0.8}. (4) Crossover rate with Gbest GCR∈{0.2,0.4,0.6,0.8}. (5) The number of subpopulations d∈{2,3,4,5}. To obtain a more representative parameter configuration, we specially perform the DOE test on medium-sized instances and the ARPD is adopted as the evaluation indicator. In this context, the ARPD serves as the response variable (RV). Table 2 presents each parameter’s RV value and significance ranking, utilizing the Delta metric to capture the maximum deviation in average RV values at diverse levels. The importance of the corresponding parameter increases with the Delta value. Additionally, Fig. 5 displays the main effect plot for five parameters of MLPSO.

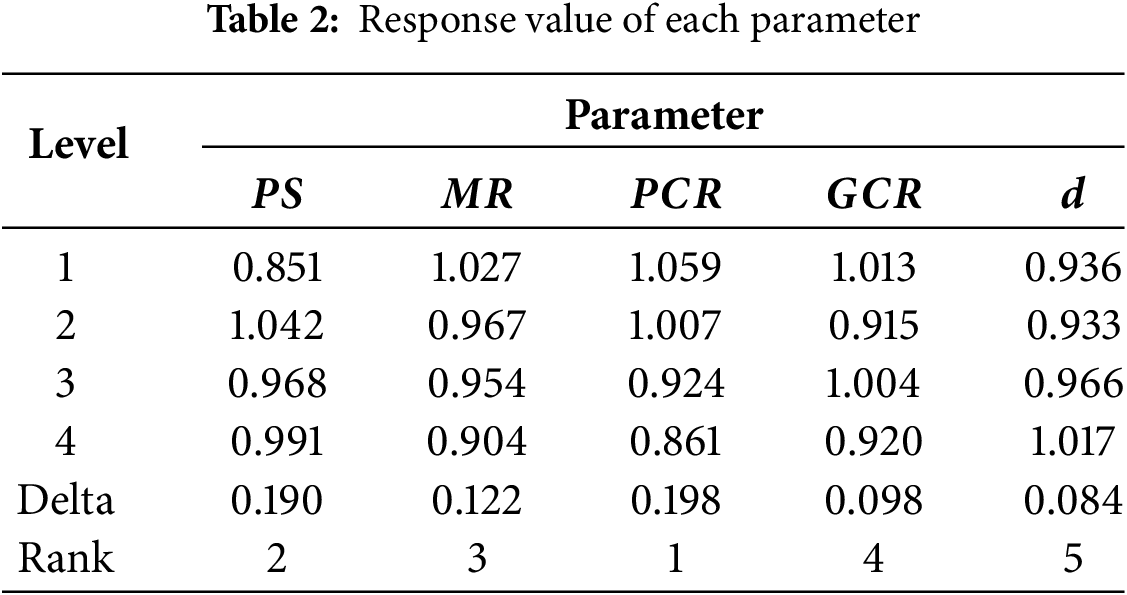
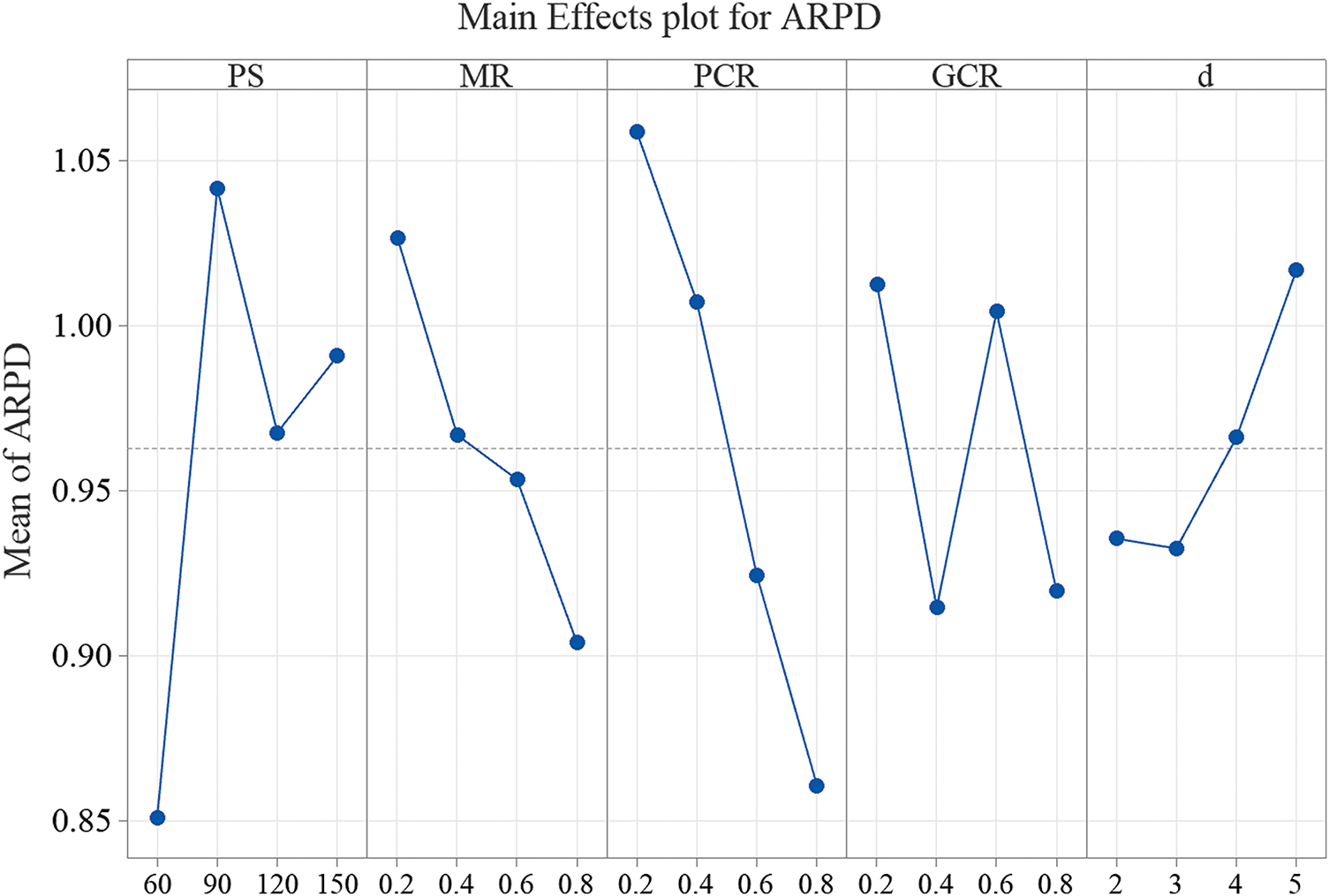
Figure 5: The main effect plot of the five parameters

The data in Table 2 indicates the parameter PCR is ranked first, with the population size PS following in second place. Meanwhile, the parameters MR and GCR rank third and fourth, respectively, and the last parameter is the number of subpopulations d. From Fig. 5, it is apparent that the PCR curve has the steepest slope compared to all other parameters, indicating that the crossover rate with Pbest has a significant impact on MLPSO. Based on the main effect plot, we make a comprehensive analysis and conclude that the best configuration of parameters is PS = 60, MR = 0.8, PCR = 0.8,GCR = 0.4, and d = 3.

5.3 Effectiveness of Initialization Strategy

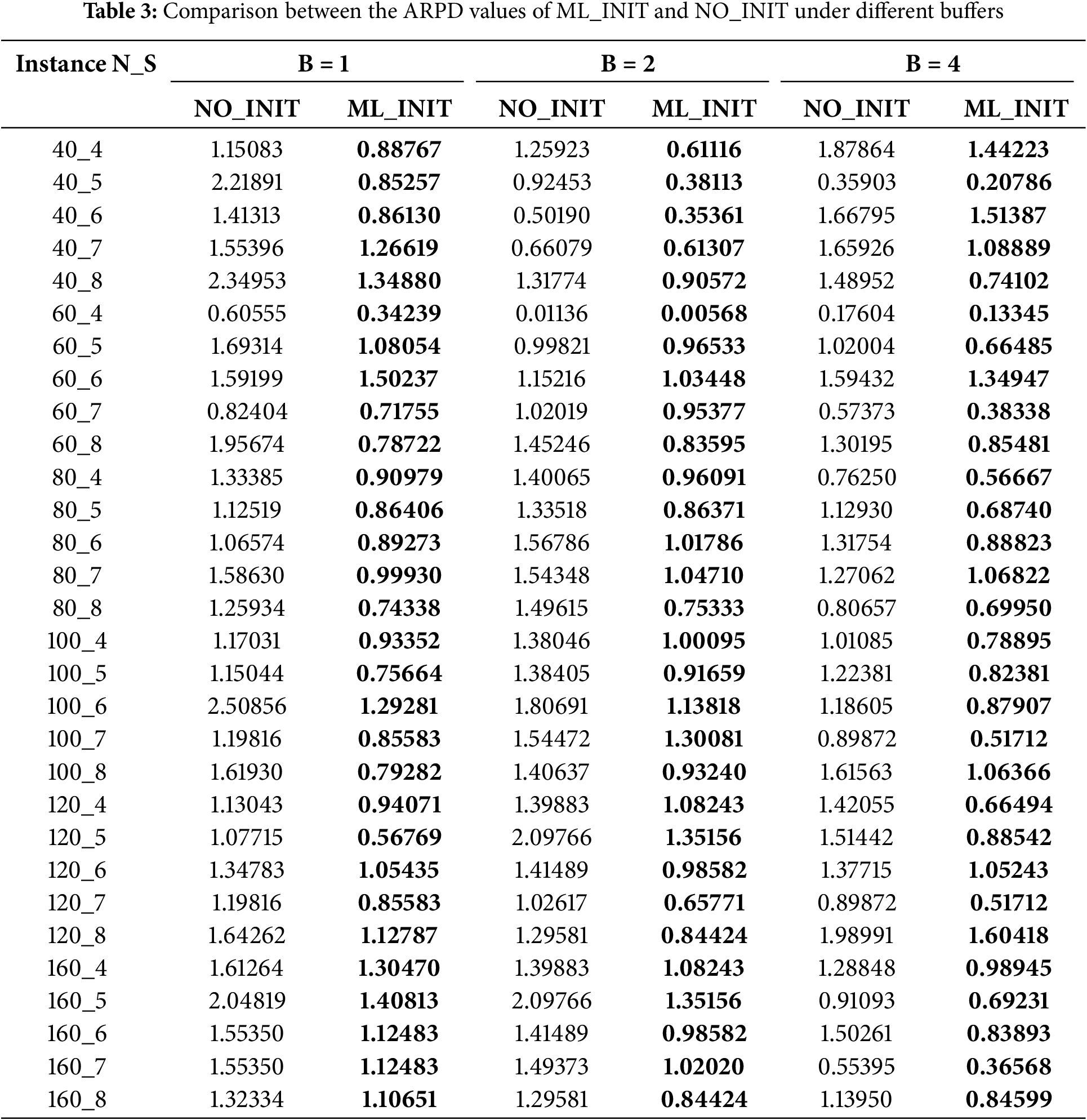
The performance of the proposed initialization method is evaluated comprehensively in this section. The experimental results are acquired by different initialization methods on 30 instances under different buffers. Table 3 shows the ARPD values derived from 20 independent runs for two distinct initialization strategies on each instance. The bold entries in Table 3 is explained in this sentence. The NO_INIT stands for the initialization method that two individuals are generated by NEH and others are generated randomly. Meanwhile, the proposed initialization strategy is denoted as the ML_INIT. Notably, for all different jobs, stages, and buffers, the ARPD values generated by the ML_INIT are consistently smaller compared to the NO_INIT. To verify the significant difference in the initialization strategy, a Kruskal-Wallis test is undertaken using the experimental data, with a p-value of 0.00395, adequately indicating that the strategy is significantly effective at the 0.05 level. This initialization strategy fully considers the impact of blocking time due to limited buffers, making it more possible to search for a potential solution from the solution with a smaller blocking time. Consequently, this initialization strategy can enhance both the initial population’s quality and diversity, which helps to find promising solutions.

5.4 Effectiveness of Collaborative Search Strategy

In this part, the effectiveness of the collaborative searchstrategy will be verified by performing experiments. The NO_CS, which represents the search strategy within the single population, is compared with the proposed ML_CS with the multi-level subpopulation collaborative search strategy. The NO_CS and the ML_CS algorithms are performed on 30 instances under different buffers to obtain the ARPD value. After analyzing the results, we conclude that the ML_CS exhibits superior performance than the NO_CS for all instances within the same running time. According to the ARPD, a violin plot is pictured as shown in Fig. 6. From Fig. 6, we realize that the ML_CS obtains a smaller mean value than the NO_CS. The violin plot of ML_CS is wider than NO_CS, indicating a relatively concentrated distribution of results, that is, the results of ML_CS are more stable and reliable. Moreover, the Kruskal-Wallis test is implemented utilizing the experimental result, yielding a p-value far smaller than 0.05, indicating the remarkable difference in the result distribution of the ML_CS and the NO_CS algorithms at the level of 0.05. The multi-level subpopulation collaborative search strategy enables subpopulations at different levels to search in different directions, which can improve the search diversity capability and prevent being trapped in the local optimum. As a result, the collaborative search strategy contributes to finding more excellent solutions.

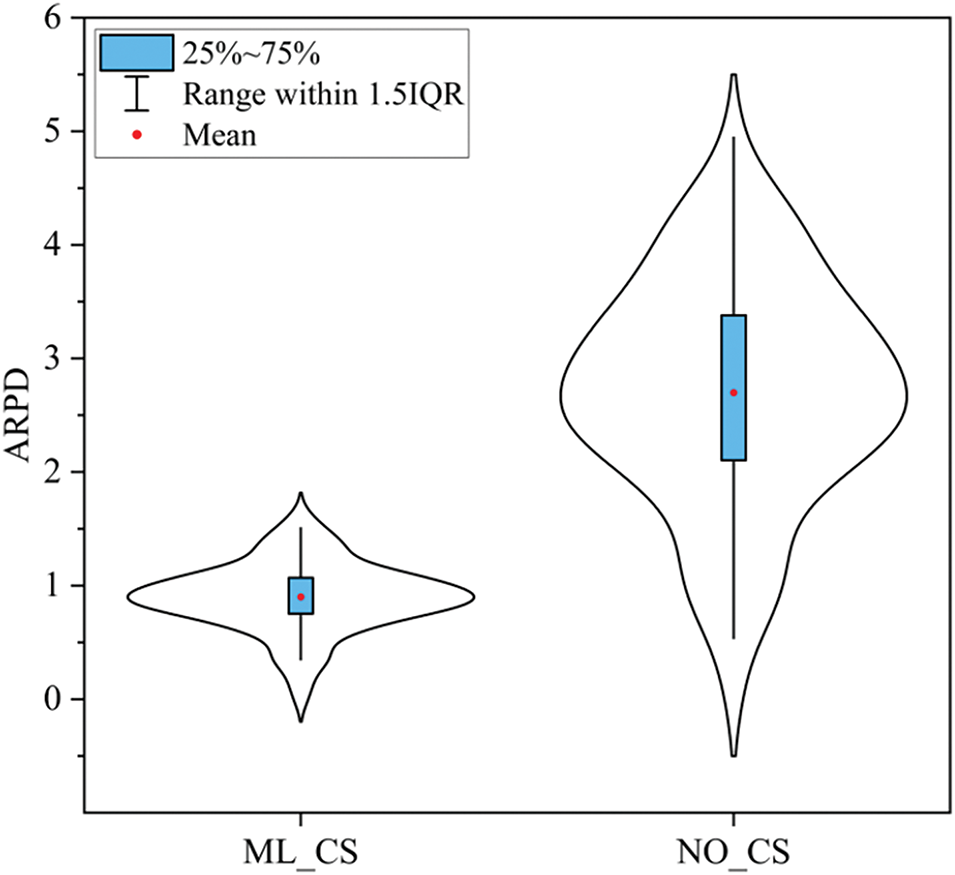
Figure 6: Violin plot of NO_CS and ML_CS

5.5 Effectiveness of Local Search Strategy

In this section, we conduct experiments to verify the efficacy of the proposed local search strategy. The NO_LS, which excludes the local search strategy based on the first blocked job, is compared with the proposed ML_LS including the local search strategy. We experiment under different buffers to obtain the ARPD value. According to the ARPD of different instances, the violin plot with a box is pictured as shown in Fig. 7. From Fig. 7, ML_LS obtains a smaller mean value compared to NO_LS. In addition, all other values obtained by ML_LS are also smaller than those of NO_LS. Moreover, a detailed analysis of the experimental findings is conducted by the Kruskal-Wallis test, and the p-value is far smaller than 0.05, implying that the NO_LS and the ML_LS algorithms’ result distribution differs remarkably at the 0.05 level. In the proposed local search method, the operation that inserts the first blocked job into the specific area is beneficial to explore a better solution further. The local search strategy can avoid unnecessary insertion operations and reduce the occurrence of blocking. Therefore, the proposed local search strategy based on the first blocked job is effective.

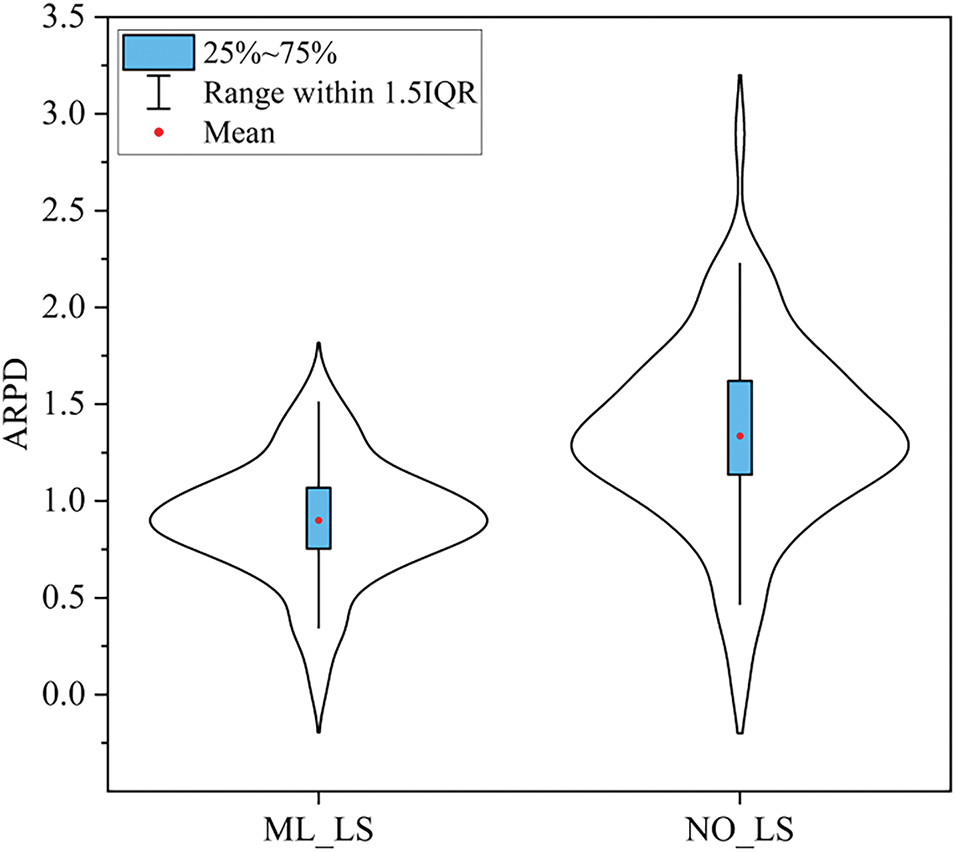
Figure 7: Violin plot of NO_LS and ML_LS

5.6 Comparison of MLPSO with Other Algorithms

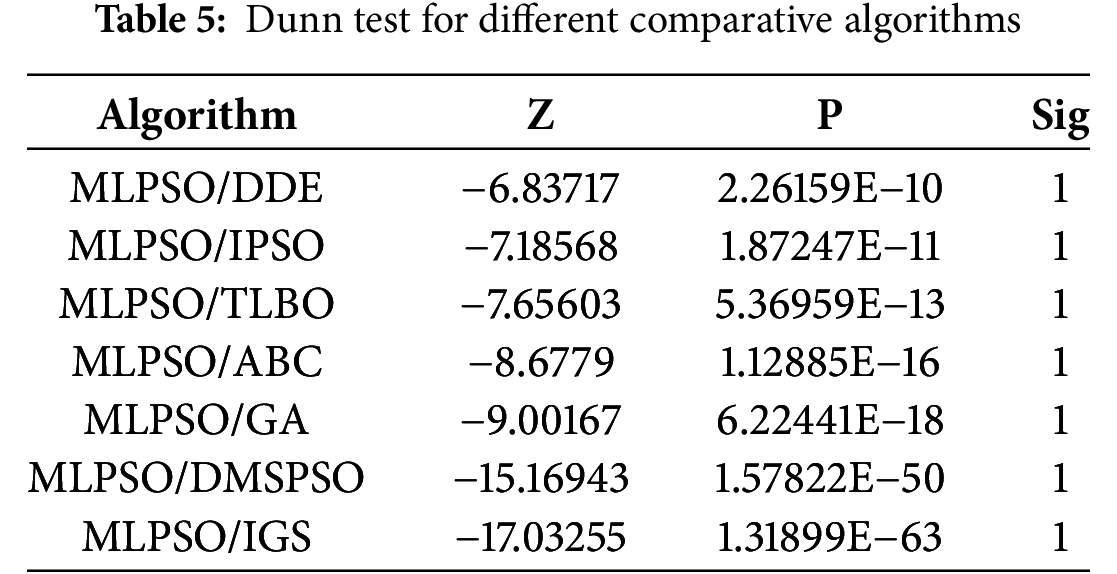
To fully validate the proposed algorithm’s effectiveness, the MLPSO algorithm is compared with seven excellent algorithms. Among these are two improved algorithms upon the PSO algorithm, namely IPSO [52] and DMSPSO [53], respectively. Besides, four swarm intelligent optimization algorithms also serve as comparison algorithms, namely DDE [54], ABC [42], TLBO [55], and GA [17]. In addition, there is also an intelligent optimization algorithm namely IGS [56]. Research demonstrates that these seven algorithms have good performance in addressing LBFSSP. Therefore, the MLPSO algorithm is compared with these seven algorithms by performing experiments in this section to prove its efficacy. The experimental results show its superiority in addressing the LBHFSP problem. Notably, the parameter configuration of comparison algorithms remains consistent with the original. To guarantee the fairness of the experiment, the termination criteria are identical for all algorithms, and each instance is run 20 times to ensure the solution’s stability and reliability.

Table 4 displays the ARPD values calculated by each algorithm in 90 instances. The bold entries in Table 4 is explained in this sentence. Table 4 reveals that the MLPSO algorithm can achieve the minimum ARPD in all 90 instances. To further analyze the experimental results and evaluate each algorithm’s performance, the interval plot is pictured in Fig. 8 using the data from Table 4. In Fig. 8, the lowest mean ARPD is generated by the MLPSO, while there is little difference between the mean ARPD of IPSO, DDE, TLBO, ABC, and DMSPSO. Additionally, the interval line of the MLPSO doesn’t have any overlap with those of other algorithms. This means that the solutions obtained by MLPSO are far better than those obtained by other algorithms. Next, the Dunn test is applied to analyze the experimental data, with the analysis result displayed in Table 5. In Table 5, when the mean difference is significantly present at the 0.05 level, the value of Sig is 1. Otherwise, the value of Sig is 0. The experimental validation indicates a remarkable distinction between the MLPSO and several comparison algorithms at the 0.05 level, which suggests that the MLPSO algorithm has advantages in addressing LBHFSP. On the whole, the MLPSO has greater suitability for solving LBHFSP.

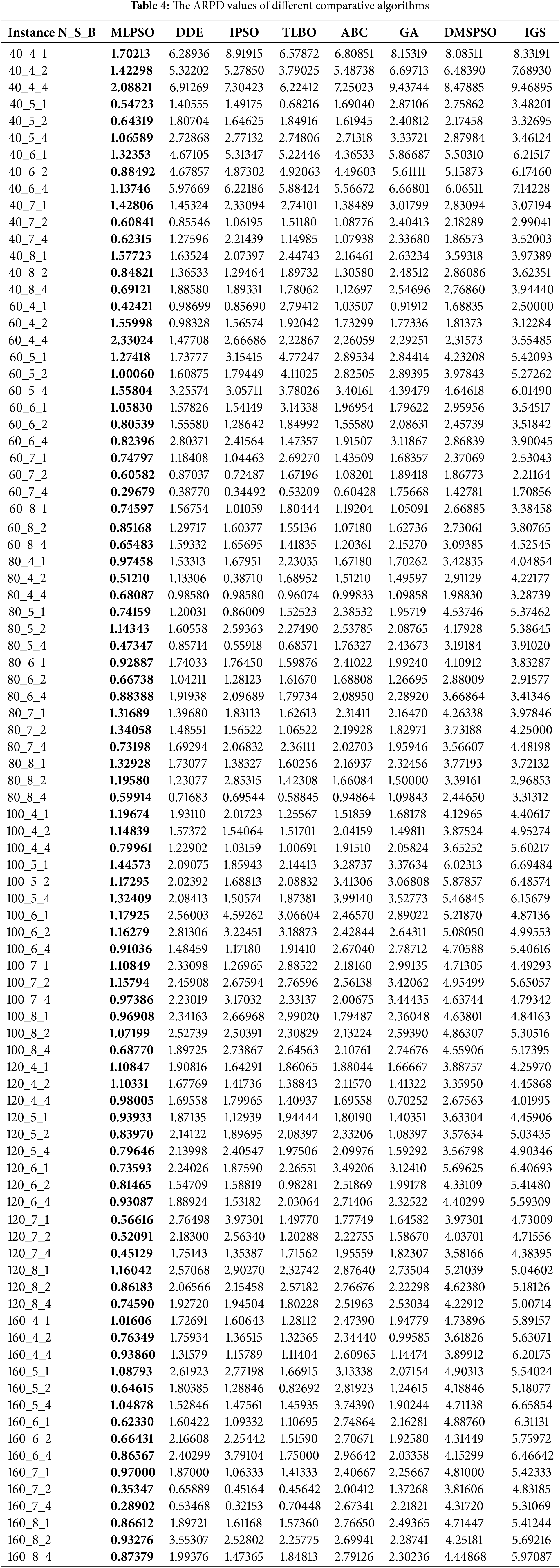
Figure 8: Interval plot of compared algorithms

To further explore the effectiveness of the MLPSO algorithm, its performance is visually displayed through interaction charts. Fig. 9a provides a visual representation of the relationship between the algorithm performance and the number of jobs when the buffer size between consecutive stages is 1, while Fig. 9b displays the relationship when B is 4. According to Fig. 9a, it can be observed that with a single buffer, the ARPD acquired by the proposed MLPSO initially presents a decreasing trend with the number of jobs increasing. Subsequently, it increases gradually, reaching its peak when N is 100. Finally, the ARPD decreases as the number of jobs grows continuously. In addition, the ARPD obtained by DDE, DMSPSO, IGS, and GA algorithm also declines as the number of jobs rises, ranging from 40 to 60 and 100 to 160. Based on Fig. 9b, as the buffer size is 4, the ARPD of the MLPSO algorithm gradually declines as the number of jobs increases from 40 to 80, reaching its minimum value when N is 80. As the number of jobs climbs from 80 to 100, the ARPD of the MLPSO algorithm grows; however, it decreases again as the number of jobs is beyond 100. The changes in other algorithms are generally similar to the trend observed in MLPSO.

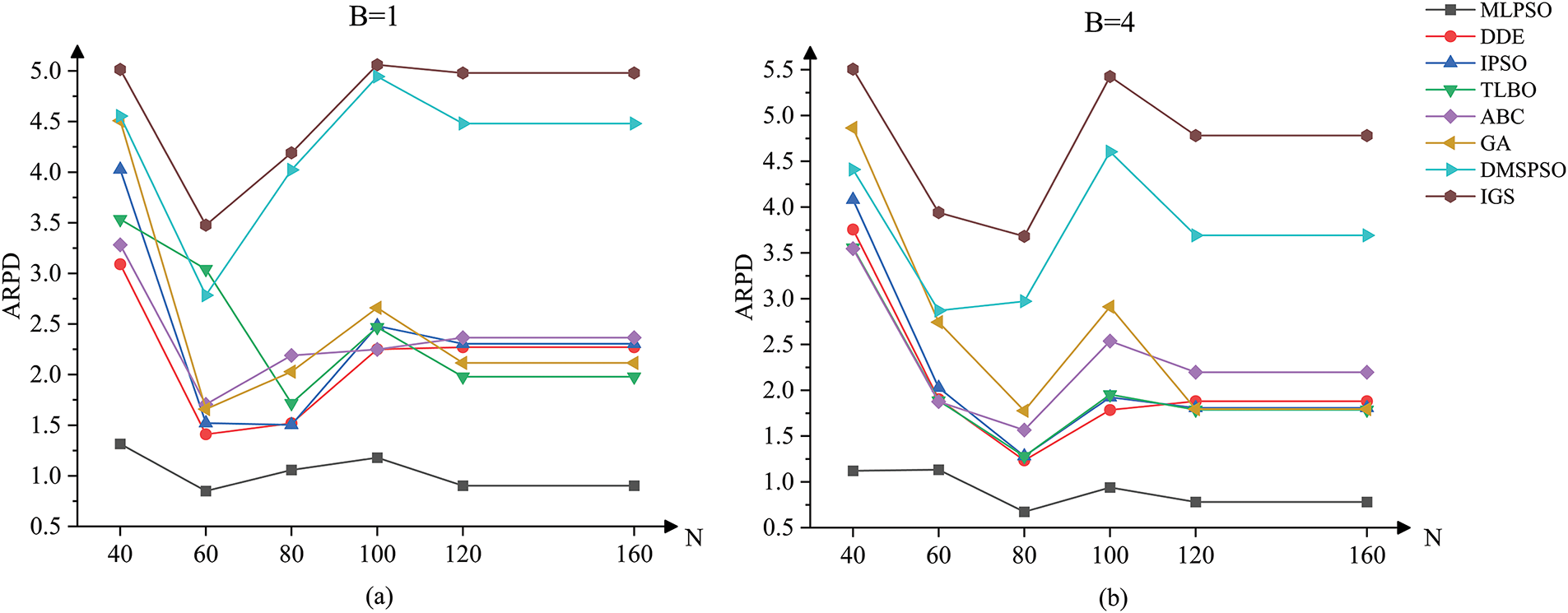
Figure 9: (a) Interaction diagram between algorithm and the number of jobs when B=1; (b) Interaction diagram between algorithm and the number of jobs when B=4

In Fig. 10, the interaction chart is pictured to visually illustrate the connection between the algorithm performance and the number of stages. As depicted in Fig. 10a, when N is 60, the ARPD of the MLPSO algorithm decreases accompanied by the increase in the number of stages before stage 7, while the ARPD of other algorithms increases first and then decreases. After stage 7, the ARPD of all algorithms increases with the number of stages. However, in contrast to other algorithms, the ARPD generated by the MLPSO algorithm changes mildly as a whole, which indicates that the number of stages exerts less impact on the MLPSO algorithm’s performance. That is, the MLPSO algorithm has better stability than other algorithms. As can be seen from Fig. 10b, except for MLPSO, the overall performance of other algorithms declines along with the growth in the number of processing stages, revealing the stability of the MLPSO algorithm is better.

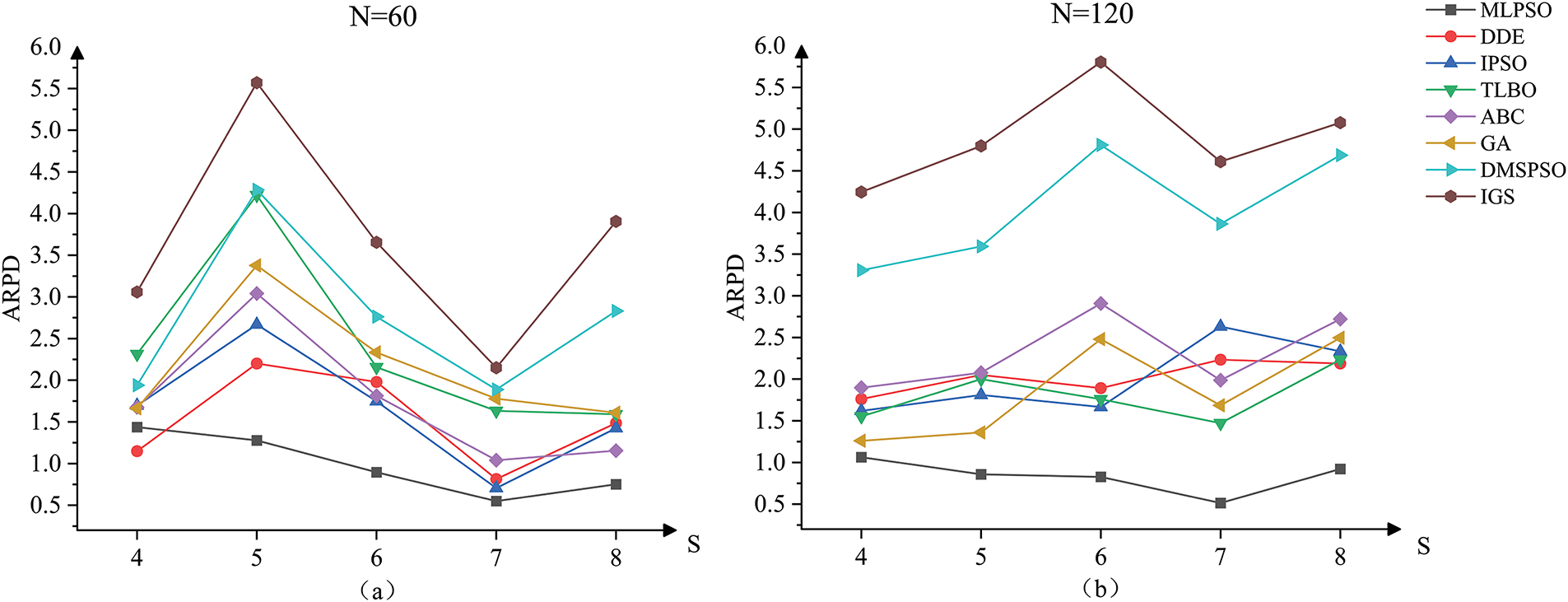
Figure 10: (a) Interaction diagram between algorithm and the number of stages when N=60; (b) Interaction diagram between algorithm and the number of stages when N=120

After a comprehensive analysis of all experimental statistics, we conclude that MLPSO is a useful algorithm with high efficiency in solving the LBHFSP aiming at optimizing makespan. The MLPSO algorithm’s strengths are mainly demonstrated as follows: (1) The initialization strategy based on blocking time contributes to generating potential solutions; (2) The multi-level subpopulation collaborative search strategy avoids being caught in local optimum and enhances the ability to look for the global optimal solution; (3) The local search strategy based on the first blocked job avoids blind search and improves search efficiency.

6  Conclusion and Future Work

This paper investigates LBHFSP with the objective of makespan and develops an effective MLPSO algorithm for LBHFSP. A decoding strategy is given considering the characteristics of the scheduling process under the condition of limited buffers. During the initialization phase, an initialization strategy based on blocking time is developed under the characteristics of the problem, which can not only enhance the initial population’s diversity but also improve its quality. Furthermore, a multi-level subpopulation collaborative search is developed to prevent getting stuck in a local optimum and promote the global exploration ability. During the period of the local search, a local search strategy based on the first blocked job is designed to enhance the exploitation capability. Several experiments are performed to validate the efficacy of these developed strategies on the MLPSO. Additionally, seven famous optimization algorithms are applied to assess the MLPSO algorithm’s performance on instances. Ultimately, the comparative results show that MLPSO finds better results in almost all instances, revealing that MLPSO is more suitable for the LBHFSP.

The research direction in the future will be pursued in two aspects:

(1)   Under the background of economic globalization, the distributed production model is increasingly becoming a dominant trend with the constant expansion of enterprises’ production demands. Therefore, in the future, we will study the distributed hybrid flow shop scheduling problem with limited buffers.

(2)   In real production scenarios, cost is also a factor that enterprises must consider. Therefore, in the future, the number of buffers can be linked to cost while optimizing resource costs and makespan to maximize benefits.

Acknowledgement: The author would like to express gratitude to the supervisor for guidance and support throughout this research. His expertise and academic rigor have profoundly influenced me. The author is also deeply grateful to family and friends for their unconditional understanding and emotional support during this research.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China under Grant No. 52175490.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Yuan Zou and Chao Lu; software, Yuan Zou; validation, Yuan Zou; formal analysis, Yuan Zou; investigation, Yuan Zou; resources, Yuan Zou and Chao Lu; data curation, Yuan Zou; writing—original draft preparation, Yuan Zou; writing—review and editing, Yuan Zou; visualization, Yuan Zou; supervision, Chao Lu, Lvjiang Yin and Xiaoyu Wen; project administration, Yuan Zou and Chao Lu; funding acquisition, Chao Lu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Jauhar SK, Priyadarshini S, Pratap S, Paul SK. A literature review on applications of Industry 4.0 in project management. Oper Manag Res. 2023;16(4):1858–85. doi:10.1007/s12063-023-00403-x. [Google Scholar] [CrossRef]

2. Zhou J, Gao L, Lu C, Yao X. Transfer learning assisted batch optimization of jobs arriving dynamically in manufacturing cloud. J Manuf Syst. 2022;65(5):44–58. doi:10.1016/j.jmsy.2022.08.003. [Google Scholar] [CrossRef]

3. Márquez CRH, Ribeiro CC. Shop scheduling in manufacturing environments: a review. Int Trans Operational Res. 2022;29(6):3237–93. doi:10.1111/itor.13108. [Google Scholar] [CrossRef]

4. Ostermeier FF, Deuse J. A review and classification of scheduling objectives in unpaced flow shops for discrete manufacturing. J Sched. 2024;27(1):29–49. doi:10.1007/s10951-023-00795-5. [Google Scholar] [CrossRef]

5. Utama DM, Primayesti MD, Umamy SZ, Kholifa BMN, Yasa AD. A systematic literature review on energy-efficient hybrid flow shop scheduling. Cogent Eng. 2023;10(1):2206074. doi:10.1080/23311916.2023.2206074. [Google Scholar] [CrossRef]

6. Neufeld JS, Schulz S, Buscher U. A systematic review of multi-objective hybrid flow shop scheduling. Eur J Oper Res. 2023;309(1):1–23. doi:10.1016/j.ejor.2022.08.009. [Google Scholar] [CrossRef]

7. Xue HT, Meng LL, Duan P, Zhang B, Zou WQ, Sang H. Modeling and optimization of the hybrid flow shop scheduling problem with sequence-dependent setup times. Int J Ind Engi-Neering Comput. 2024;15(2):473–90. doi:10.5267/j.ijiec.2024.1.001. [Google Scholar] [CrossRef]

8. Geetha M, Chandra Guru Sekar R, Marichelvam MK, Tosun Ö. A sequential hybrid optimization algorithm (SHOA) to solve the hybrid flow shop scheduling problems to minimize carbon footprint. Processes. 2024;12(1):143. doi:10.3390/pr12010143. [Google Scholar] [CrossRef]

9. Saiem M, Arbaoui T, Hnaien F. Solving the flow-shop scheduling problem using grover’s algorithm. In: Proceedings of the Companion Conference on Genetic and Evolutionary Computation; 2023 Jul 15–19; Lisbon, Portugal. p. 2250–3. doi:10.1145/3583133.3596378. [Google Scholar] [CrossRef]

10. Duan B, Jiang Y. Application research of IICA algorithm in a limited-buffer scheduling problem. Int J E Collab. 2022;18(3):1–18. doi:10.4018/ijec.307131. [Google Scholar] [CrossRef]

11. Tighazoui A, Sauvey C, Sauer N. Heuristics for flow shop rescheduling with mixed blocking constraints. Trans Oper Res. 2024;32(2):169–201. doi:10.1007/s11750-023-00662-8. [Google Scholar] [CrossRef]

12. Ackermann H, Schwehm L, Weiss C. Scheduling a two stage proportionate flexible flow shop with dedicated machines and no buffers. In: Trautmann N, Gnägi M, editors. Operations research proceedings 2021. Berlin/Heidelberg, Germany: Springer; 2022. p. 353–8. doi:10.1007/978-3-031-08623-6_52. [Google Scholar] [CrossRef]

13. Liu F, Li G, Lu C, Yin L, Zhou J. A tri-individual iterated greedy algorithm for the distributed hybrid flow shop with blocking. Expert Syst Appl. 2024;237:121667. doi:10.1016/j.eswa.2023.121667. [Google Scholar] [CrossRef]

14. Han Z, Han C, Lin S, Dong X, Shi H. Flexible flow shop scheduling method with public buffer. Processes. 2019;7(10):681. doi:10.3390/pr7100681. [Google Scholar] [CrossRef]

15. Isik EE, Yildiz ST, Akpunar ÖS. Constraint programming models for the hybrid flow shop scheduling problem and its extensions. Soft Comput. 2023;27(24):18623–50. doi:10.1007/s00500-023-09086-9. [Google Scholar] [CrossRef]

16. Lin CC, Liu WY, Chen YH. Considering stockers in reentrant hybrid flow shop scheduling with limited buffer capacity. Comput Ind Eng. 2020;139(1):106154. doi:10.1016/j.cie.2019.106154. [Google Scholar] [CrossRef]

17. Guan Y, Chen Y, Gan Z, Zou Z, Ding W, Zhang H, et al. Hybrid flow-shop scheduling in collaborative manufacturing with a multi-crossover-operator genetic algorithm. J Ind Inf Integr. 2023;36:100514. doi:10.1016/j.jii.2023.100514. [Google Scholar] [CrossRef]

18. Kuang Y, Wu X, Chen Z, Li W. A two-stage cross-neighborhood search algorithm bridging different solution representation spaces for solving the hybrid flow shop scheduling problem. Swarm Evol Comput. 2024;84:101455. doi:10.1016/j.swevo.2023.101455. [Google Scholar] [CrossRef]

19. Zhang Z, Shao Z, Shao W, Chen J, Pi D. MRLM: a meta-reinforcement learning-based metaheuristic for hybrid flow-shop scheduling problem with learning and forgetting effects. Swarm Evol Comput. 2024;85(1):101479. doi:10.1016/j.swevo.2024.101479. [Google Scholar] [CrossRef]

20. Wang X, Ren T, Bai D, Chu F, Lu X, Weng Z, et al. Hybrid flow shop scheduling with learning effects and release dates to minimize the makespan. IEEE Trans Syst Man Cybern Syst. 2024;54(1):365–78. doi:10.1109/TSMC.2023.3305089. [Google Scholar] [CrossRef]

21. Yu Y, Pan QK, Pang X, Tang X. An attribution feature-based memetic algorithm for hybrid flowshop scheduling problem with operation skipping. IEEE Trans Autom Sci Eng. 2024;22(11):99–114. doi:10.1109/TASE.2023.3346446. [Google Scholar] [CrossRef]

22. Qin HX, Han YY. A collaborative iterative greedy algorithm for the scheduling of distributed heterogeneous hybrid flow shop with blocking constraints. Expert Syst Appl. 2022;201:117256. doi:10.1016/j.eswa.2022.117256. [Google Scholar] [CrossRef]

23. Qin H, Han Y, Wang Y, Liu Y, Li J, Pan Q. Intelligent optimization under blocking constraints: a novel iterated greedy algorithm for the hybrid flow shop group scheduling problem. Knowl Based Syst. 2022;258:109962. doi:10.1016/j.knosys.2022.109962. [Google Scholar] [CrossRef]

24. Wang Y, Han Y, Li H, Li J, Gao K, Liu Y. Theoretical analysis and implementation of mandatory operations-based accelerated search in graph space for hybrid flow shop scheduling. Expert Syst Appl. 2024;257(1):125026. doi:10.1016/j.eswa.2024.125026. [Google Scholar] [CrossRef]

25. Moslehi G, Khorasanian D. A hybrid variable neighborhood search algorithm for solving the limited-buffer permutation flow shop scheduling problem with the makespan criterion. Comput Oper Res. 2014;52(3):260–8. doi:10.1016/j.cor.2013.09.014. [Google Scholar] [CrossRef]

26. Zhao F, Tang J, Wang J, Jonrinaldi J. An improved particle swarm optimisation with a linearly decreasing disturbance term for flow shop scheduling with limited buffers. Int J Comput Integr Manuf. 2014;27(5):488–99. doi:10.1080/0951192x.2013.814165. [Google Scholar] [CrossRef]

27. Zhang SJ, Gu XS. An effective discrete artificial bee colony algorithm for flow shop scheduling problem with intermediate buffers. J Cent South Univ. 2015;22(9):3471–84. doi:10.1007/s11771-015-2887-x. [Google Scholar] [CrossRef]

28. Abdollahpour S, Rezaeian J. Minimizing makespan for flow shop scheduling problem with intermediate buffers by using hybrid approach of artificial immune system. Appl Soft Comput. 2015;28(4):44–56. doi:10.1016/j.asoc.2014.11.022. [Google Scholar] [CrossRef]

29. Deng G, Yang H, Zhang S. An enhanced discrete artificial bee colony algorithm to minimize the total flow time in permutation flow shop scheduling with limited buffers. Math Probl Eng. 2016;2016:7373617. doi:10.1155/2016/7373617. [Google Scholar] [CrossRef]

30. Liang X, Wang P, Huang M. Flow shop scheduling problem with limited buffer based on hybrid shuffled frog leaping algorithm. In: 2019 IEEE 7th International Conference on Computer Science and Network Technology (ICCSNT); 2019 Oct 19–20; Dalian, China. p. 87–93. doi:10.1109/iccsnt47585.2019.8962427. [Google Scholar] [CrossRef]

31. Le HT, Geser P, Middendorf M. Iterated local search and other algorithms for buffered two-machine permutation flow shops with constant processing times on one machine. Evol Comput. 2021;29(3):415–39. doi:10.1162/evco_a_00287. [Google Scholar] [PubMed] [CrossRef]

32. Lu C, Huang Y, Meng L, Gao L, Zhang B, Zhou J. A Pareto-based collaborative multi-objective optimization algorithm for energy-efficient scheduling of distributed permutation flow-shop with limited buffers. Robot Comput Integr Manuf. 2022;74(4):102277. doi:10.1016/j.rcim.2021.102277. [Google Scholar] [CrossRef]

33. Ding H, Gu X. Improved particle swarm optimization algorithm based novel encoding and decoding schemes for flexible job shop scheduling problem. Comput Oper Res. 2020;121(3):104951. doi:10.1016/j.cor.2020.104951. [Google Scholar] [CrossRef]

34. Zhang Y, Zhu H, Tang D. An improved hybrid particle swarm optimization for multi-objective flexible job-shop scheduling problem. Kybernetes. 2019;49(12):2873–92. doi:10.1108/k-06-2019-0430. [Google Scholar] [CrossRef]

35. Hayat I, Tariq A, Shahzad W, Masud M, Ahmed S, Ali MU, et al. Hybridization of particle swarm optimization with variable neighborhood search and simulated annealing for improved handling of the permutation flow-shop scheduling problem. Systems. 2023;11(5):221. doi:10.3390/systems11050221. [Google Scholar] [CrossRef]

36. Leguizamon LE, Leguizamon LA, Leguizamon CE. Scheduling of flow shop production systems with particle swarm optimization. Tecciencia. 2021;16(31):1–13. doi:10.18180/tecciencia.2021.30.1. [Google Scholar] [CrossRef]

37. Kaya S, Gümüşçü A, Aydilek İB, Karaçizmeli İH, Tenekeci ME. Solution for flow shop scheduling problems using chaotic hybrid firefly and particle swarm optimization algorithm with improved local search. Soft Comput. 2021;25(10):7143–54. doi:10.1007/s00500-021-05673-w. [Google Scholar] [CrossRef]

38. Amirteimoori A, Mahdavi I, Solimanpur M, Ali SS, Tirkolaee EB. A parallel hybrid PSO-GA algorithm for the flexible flow-shop scheduling with transportation. Comput Ind Eng. 2022;173(9):108672. doi:10.1016/j.cie.2022.108672. [Google Scholar] [CrossRef]

39. Zhang W, Li C, Gen M, Yang W, Zhang Z, Zhang G. Multiobjective particle swarm optimization with direction search and differential evolution for distributed flow-shop scheduling problem. Math Biosci Eng. 2022;19(9):8833–65. doi:10.3934/mbe.2022410. [Google Scholar] [PubMed] [CrossRef]

40. Zhang W, Geng H, Li C, Gen M, Zhang G, Deng M. Q-learning-based multi-objective particle swarm optimization with local search within factories for energy-efficient distributed flow-shop scheduling problem. J Intell Manuf. 2025;36(1):185–208. doi:10.1007/s10845-023-02227-9. [Google Scholar] [CrossRef]

41. Liu B, Wang L, Jin YH. An effective hybrid PSO-based algorithm for flow shop scheduling with limited buffers. Comput Oper Res. 2008;35(9):2791–806. doi:10.1016/j.cor.2006.12.013. [Google Scholar] [CrossRef]

42. Li JQ, Pan QK. Solving the large-scale hybrid flow shop scheduling problem with limited buffers by a hybrid artificial bee colony algorithm. Inf Sci. 2015;316(1):487–502. doi:10.1016/j.ins.2014.10.009. [Google Scholar] [CrossRef]

43. Zhang C, Tan J, Peng K, Gao L, Shen W, Lian K. A discrete whale swarm algorithm for hybrid flow-shop scheduling problem with limited buffers. Robot Comput Integr Manuf. 2021;68(8):102081. doi:10.1016/j.rcim.2020.102081. [Google Scholar] [CrossRef]

44. Zheng QQ, Zhang Y, Tian HW, He LJ. An effective hybrid meta-heuristic for flexible flow shop scheduling with limited buffers and step-deteriorating jobs. Eng Appl Artif Intell. 2021;106:104503. doi:10.1016/j.engappai.2021.104503. [Google Scholar] [CrossRef]

45. Rooeinfar R, Raissi S, Ghezavati VR. Stochastic flexible flow shop scheduling problem with limited buffers and fixed interval preventive maintenance: a hybrid approach of simulation and metaheuristic algorithms. Simulation. 2019;95(6):509–28. doi:10.1177/0037549718809542. [Google Scholar] [CrossRef]

46. Zohali H, Naderi B, Mohammadi M. The economic lot scheduling problem in limited-buffer flexible flow shops: mathematical models and a discrete fruit fly algorithm. Appl Soft Comput. 2019;80(1):904–19. doi:10.1016/j.asoc.2019.03.054. [Google Scholar] [CrossRef]

47. Janeš G, Ištoković D, Jurković Z, Perinić M. Application of modified steady-state genetic algorithm for batch sizing and scheduling problem with limited buffers. Appl Sci. 2022;12(22):11512. doi:10.3390/app122211512. [Google Scholar] [CrossRef]

48. Zheng Q, Zhang Y, Tian H, He L. A cooperative adaptive genetic algorithm for reentrant hybrid flow shop scheduling with sequence-dependent setup time and limited buffers. Complex Intell Syst. 2024;10(1):781–809. doi:10.1007/s40747-023-01147-8. [Google Scholar] [CrossRef]

49. Chang D, Shi H, Liu C, Meng F. Scheduling optimization of flexible flow shop with buffer capacity limitation based on an improved discrete particle swarm optimization algorithm. Eng Optim. 2025;57(2):571–97. doi:10.1080/0305215X.2024.2328191. [Google Scholar] [CrossRef]

50. Fan YA, Liang CK. Hybrid discrete particle swarm optimization algorithm with genetic operators for target coverage problem in directional wireless sensor networks. Appl Sci. 2022;12(17):8503. doi:10.3390/app12178503. [Google Scholar] [CrossRef]

51. Sharma M, Sharma M, Sharma S. An improved NEH heuristic to minimize makespan for flow shop scheduling problems. Decis Sci Lett. 2021;10(3):311–22. doi:10.5267/j.dsl.2021.2.006. [Google Scholar] [CrossRef]

52. Marichelvam MK, Geetha M, Tosun Ö. An improved particle swarm optimization algorithm to solve hybrid flowshop scheduling problems with the effect of human factors—a case study. Comput Oper Res. 2020;114(3):104812. doi:10.1016/j.cor.2019.104812. [Google Scholar] [CrossRef]

53. Liang JJ, Pan QK, Chen T, Wang L. Solving the blocking flow shop scheduling problem by a dynamic multi-swarm particle swarm optimizer. Int J Adv Manuf Technol. 2011;55(5):755–62. doi:10.1007/s00170-010-3111-7. [Google Scholar] [CrossRef]

54. Zhang G, Xing K. Differential evolution metaheuristics for distributed limited-buffer flowshop scheduling with makespan criterion. Comput Oper Res. 2019;108:33–43. doi:10.1016/j.cor.2019.04.002. [Google Scholar] [CrossRef]

55. Li J, Guo X, Zhang Q. Multi-strategy discrete teaching-learning-based optimization algorithm to solve No-wait flow-shop-scheduling problem. Symmetry. 2023;15(7):1430. doi:10.3390/sym15071430. [Google Scholar] [CrossRef]

56. Qin HX, Han YY, Zhang B, Meng LL, Liu YP, Pan QK, et al. An improved iterated greedy algorithm for the energy-efficient blocking hybrid flow shop scheduling problem. Swarm Evol Comput. 2022;69(3):100992. doi:10.1016/j.swevo.2021.100992. [Google Scholar] [CrossRef]