A Metamodeling Approach to Enforcing the No-Cloning Theorem in Quantum Software Engineering

1  Introduction

Quantum computing introduces a new approach to computation by using quantum mechanical phenomena to perform calculations that are difficult for classical computers. It relies on superposition, where quantum bits (qubits) can exist in multiple states simultaneously, and entanglement, which connects the states of multiple qubits such that no single qubit’s state can be determined independently. These characteristics enable quantum computers to process information in parallel, enhancing the speed of certain computations. However, quantum mechanics also brings specific limitations, notably the no-cloning theorem [1], which prevents the exact duplication of an arbitrary unknown quantum state. This principle is essential to quantum information theory and affects quantum cryptography, error correction, and communication protocols.

While quantum software development is advancing, there remains a gap in software engineering methods for modeling and representing quantum mechanical principles like the no-cloning theorem. Metamodeling techniques, particularly those based on UML, have been effective in outlining domain concepts and relationships in emerging areas. These frameworks offer detailed abstractions and formal specifications that can adapt to include quantum mechanical principles. When extended, these methods provide a foundation for designing, analyzing, and validating quantum software systems, helping to bridge the gap between quantum mechanics and software engineering methodologies.

Several quantum software modeling approaches have been proposed (e.g., [2–6]). These include graph-based modeling of unitary circuits, offering circuit-level abstractions for quantum computation using model-driven engineering [2]; a UML profile for designing hybrid classical-quantum systems through stereotypes and multiple diagram types [3]; the Talavera Manifesto, which outlines principles and commitments for establishing quantum software engineering as a discipline [4]; a lifecycle model for developing hybrid quantum applications that integrate quantum and classical components via workflow technology [5]; and a quantum software testing framework that addresses post-implementation quality assurance challenges [6]. However, there remains a clear gap in the availability of rigorous theoretical frameworks for the formal design and verification of quantum-specific constraints, particularly the no-cloning theorem. Such a framework is crucial for supporting traditional software engineers, who are experienced in classical software development but often lack expertise in quantum software principles.

This paper presents a metamodeling approach using UML-style notation to describe the no-cloning theorem in quantum mechanics, demonstrating how traditional software engineering techniques can effectively represent and analyze quantum principles. The metamodel defines key quantum concepts related to the no-cloning theorem and their relationships, incorporating formal invariants to reinforce quantum mechanical constraints. Two edge cases—conditional copying with CNOT gates and quantum teleportation—are examined through instance models to assess the metamodel’s effectiveness in analyzing quantum principles. While these cases may seem to violate the no-cloning theorem, the analysis confirms their compliance with its constraints. This metamodeling approach provides a structured framework that integrates quantum mechanics with software engineering, helping traditional software engineers better engage with quantum computing and apply established software engineering methodologies to quantum software development.

The remainder of this paper is structured as follows: Section 2 provides an overview of related work. Section 4 discusses the no-cloning theorem and introduces the metamodel for the theorem. Section 5 describes two edge cases of cloning, captured by instance models of the metamodel and their implementations. Section 8 concludes the paper and outlines future research directions.

2  Related Work

Recent research in quantum software engineering has focused on applying modeling techniques to quantum computing systems. Alonso et al. [2] developed a unified metamodel for quantum circuits using model-driven engineering, showing how systematic modeling can standardize quantum software development. Following this, Sánchez and Alonso [7] investigated modularity in quantum programming, addressing challenges related to non-clonability and probabilistic operations. Bibbo et al. [8] conducted a comprehensive review of software engineering resources in quantum computing, emphasizing the importance of modeling across the software lifecycle.

The theoretical foundation for quantum software engineering has been developed through several studies. Ahmad et al. [9] discussed the integration of quantum mechanics principles with software engineering practices, particularly focusing on quantum software architectures and their importance in development and validation. Ali et al. [10] analyzed the need for new methodologies that can handle quantum characteristics such as superposition and entanglement. Pérez-Castillo and Piattini [3] proposed a UML profiling mechanism that extends standard UML to support the design of hybrid classical-quantum systems by modeling quantum components, classical-quantum interactions, and system architectures. Piattini et al. [4] present Talavera Manifesto which emphasizes the foundational vision for quantum software engineering (QSE) as a discipline, proposing broad principles and commitments for systematically building, testing, maintaining, and managing quantum software at an industrial scale. Their work advocates for adapting classical software engineering processes to quantum contexts and highlights the importance of governance, quality assurance, reuse, and security. In contrast, the our work provides a much more concrete and technical contribution by introducing a formal metamodel with OCL constraints that captures fundamental quantum mechanical laws, specifically the no-cloning theorem, aiming to prevent conceptual errors at the design phase. Thus, while the Talavera Manifesto lays out a high-level roadmap for the future of QSE as a discipline, our work operationalizes part of that vision by formally modeling quantum-specific constraints that can be directly applied in early-stage quantum software modeling.

Implementation aspects of quantum software systems have been explored through various methods. Sabzevari et al. [11] introduced quantum computing as a service to broaden access to quantum computing resources. Gallardo et al. [12] developed Quirk+, a tool that enhances quantum circuit development capabilities. The work by Weder et al. [5] presents a comprehensive lifecycle framework for developing hybrid quantum applications that integrate quantum and classical components. They focus on orchestrating these components through workflow technology and present three interwoven lifecycles: the quantum workflow lifecycle, the classical software lifecycle, and the quantum circuit lifecycle. Their approach emphasizes practical implementation considerations such as deployment, observability, and DevOps practices. In contrast, our work advances the conceptual formalization of quantum mechanical principles, specifically the no-cloning theorem, by introducing a UML-based metamodel with OCL constraints. While both works bridge quantum computing and software engineering, Weder et al. emphasize operational processes, covering the entire application lifecycle, whereas our work concentrates on formalizing specific quantum mechanical principles, enforcing fundamental quantum constraints at the modeling phase to demonstrate how traditional software modeling techniques can be adapted to quantum software development.

Testing and validation in quantum systems present unique challenges. Garcia de la Barrera et al. [13] analyzed existing strategies in quantum software testing, focusing on the inadequacies of classical testing methods for quantum systems. Ali [6] presents an introductory overview of quantum software testing (QST), focusing on the challenges of testing quantum programs due to the unique characteristics of quantum computing (e.g., superposition, entanglement). The work outlines three main topics: quantum computing fundamentals, QST challenges compared to classical software testing, and current QST techniques along with their limitations. Ali specifically highlights specialized testing approaches such as input/output coverage criteria, metamorphic testing, and noise-aware testing for quantum programs. In contrast, our work addresses pre-implementation correctness by formally modeling quantum mechanical constraints—specifically the no-cloning theorem—through a UML-based metamodel with OCL constraints. Rather than testing quantum software after it is built, our work aims to embed quantum correctness directly into the design phase, preventing conceptual errors at the modeling level. Thus, whereas Ali emphasizes improving the quality assurance process for quantum software, our work emphasizes design-time correctness enforcement rooted in fundamental quantum principles.

Process management in quantum software development has been explored in various studies. Khan et al. [14] examined the integration of agile practices into quantum software development, using interviews with practitioners from multiple countries. Separately, Thompson et al. [15] investigated the use of machine learning with quantum computing, suggesting non-algorithmic approaches to programming that are suited for Noisy Intermediate-Scale Quantum (NISQ) devices.

This diverse body of research highlights the advancing maturity of quantum software engineering. This work builds on these foundations by focusing on the formal representation of the no-cloning theorem through metamodeling, aiming to connect traditional software engineering practices with the development of quantum software systems.

3  Comparing with Existing Quantum Computing Modeling Approaches

In this section, we compare the metamodeling approach with quantum circuit diagrams [1], and other quantum software modeling approaches [2,3].

3.1 Comparing with Quantum Circuit Diagrams

Quantum circuit diagrams are the de facto standard for representing quantum algorithms and operations, offering a visual syntax that is intuitive for physicists and quantum developers.

Table 1 presents the differences between the metamodeling approach and quantum circuit diagrams. The metamodeling approach operates at a higher level of abstraction, focusing on the conceptual relationships between quantum constructs such as states, gates, and operations. This abstraction enables software engineers to represent complex theoretical principles, like the no-cloning theorem, in a structured manner. In contrast, quantum circuit diagrams provide a lower-level, implementation-focused view that captures the sequential application of quantum gates on qubits. While effective for illustrating algorithms, they do not represent the underlying theoretical constraints (e.g., no-cloning theorem, unitarity of quantum operations) explicitly.

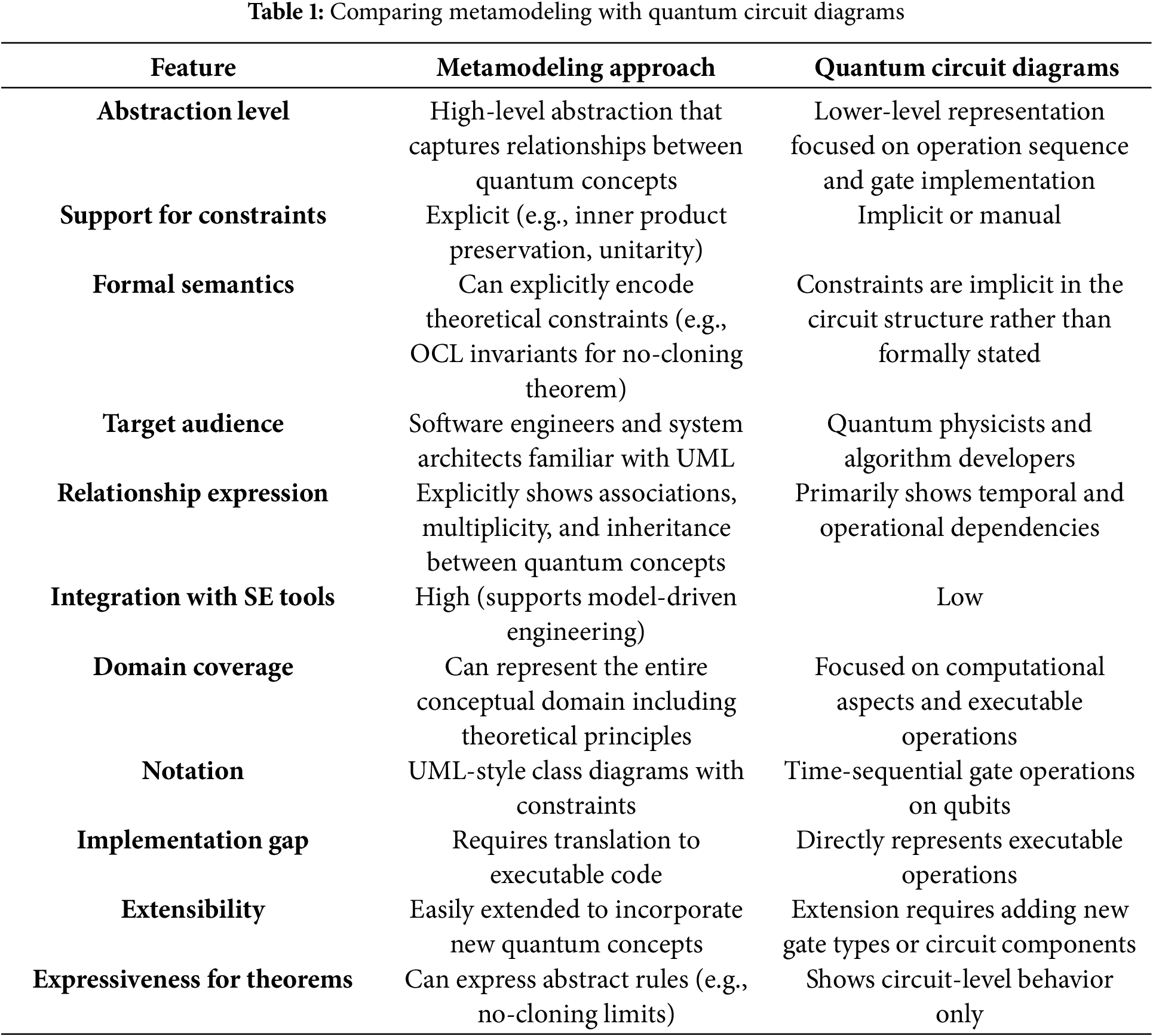
A key strength of the metamodeling approach is its support for explicitly specifying constraints, such as inner product preservation and unitarity, through Object Constraint Language (OCL) invariants. These formal semantics enable rigorous validation against quantum mechanical rules. Circuit diagrams, however, rely on implicit correctness, with constraint adherence being verified through simulation or domain expertise rather than formal specification.

The intended audiences for these approaches also differ. Metamodeling is primarily suited for software engineers, particularly those working within model-driven engineering environments, whereas quantum circuit diagrams are tailored for physicists and quantum algorithm developers. In terms of expressiveness, metamodels make use of associations, multiplicity, and inheritance to define complex relationships between quantum entities. Circuit diagrams, on the other hand, emphasize operational dependencies and time-ordered execution. Furthermore, the metamodeling approach integrates well with software engineering modeling tools, while circuit diagrams often exist in isolation from such tools.

In terms of domain coverage, metamodels can capture both operational procedures and foundational principles, providing a comprehensive view of quantum systems. Circuit diagrams are generally limited to computational aspects and do not encode theoretical abstractions. The notations also reflect this distinction: metamodels use UML-style diagrams with formal constraints, whereas circuit diagrams depict time-sequential gate operations.

A limitation of metamodeling is the implementation gap—it requires translation from model to executable code. In contrast, circuit diagrams represent executable operations directly and can be compiled to run on quantum hardware. However, the extensibility of metamodels is a notable advantage; they can be adapted to include new quantum concepts through standard modeling techniques, while extending circuit diagrams requires the introduction of new gate symbols or custom logic.

Together, the metamodeling approach and quantum circuit diagrams serve complementary roles in quantum software engineering. Metamodels offer a rigorous theoretical framework for design and verification, particularly suited for traditional software engineers working with formal models. In contrast, quantum circuit diagrams provide practical, implementation-oriented representations tailored to the needs of quantum physicists and algorithm developers.

3.2 Comparing with Other Quantum Software Modeling Approaches

We compare the proposed approach with two existing quantum software modeling approaches: the work of Alonso et al. [2] and that of Pérez-Castillo and Piattini [3]. Table 2 presents a detailed comparison.

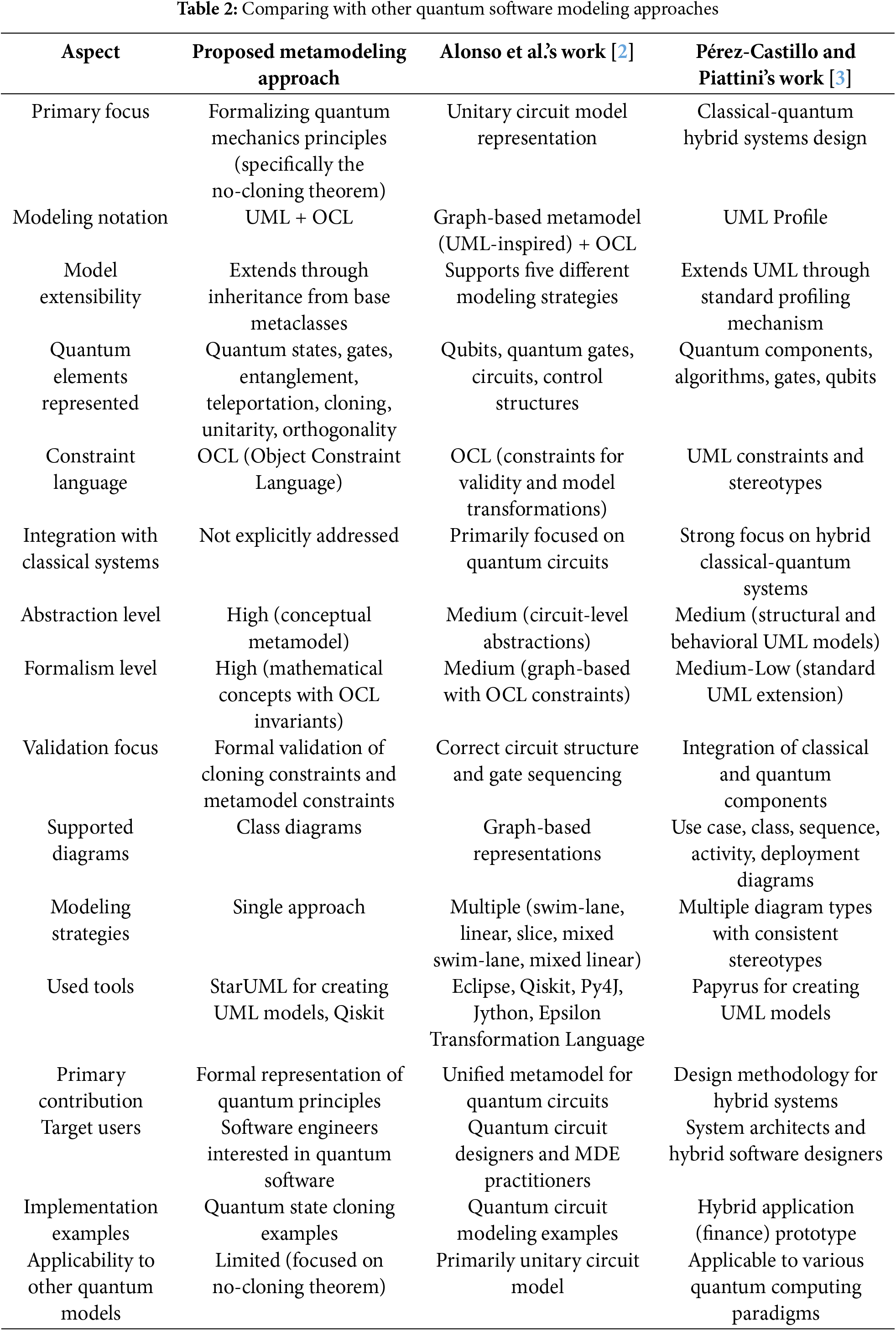
A notable strength of the proposed approach is its high level of abstraction, employing OCL for formal constraint validation. This enables the explicit formalization of quantum rules such as entanglement and teleportation. It offers a more rigorous formalism than the medium-level circuit abstractions (e.g., quantum gates as graph nodes) in Alonso et al.’s method or the medium-low structural focus (e.g., quantum concepts as UML stereotypes) in Pérez-Castillo and Piattini’s profile.

From a tooling perspective, all approaches leverage UML-based tools (e.g., StarUML, Papyrus, Eclipse), but their target users differ: the proposed approach is aimed at software engineers interested in quantum software design, while Alonso et al.’s and Pérez-Castillo and Piattini’s frameworks are intended for quantum circuit developers and hybrid system architects, respectively.

In terms of modeling strategy, the proposed metamodel employs a single, inheritance-based class structure, in contrast to Alonso et al.’s multi-strategy graph-based representation (e.g., swim-lane and slice-based graphs) and Pérez-Castillo and Piattini’s multi-diagram UML profiling (e.g., class, sequence, and deployment diagrams). However, its scope is narrower, being tailored to the no-cloning theorem, whereas the other two frameworks offer broader applicability to unitary models or hybrid paradigms.

Validation strategies also differ: the proposed approach focuses on formal validation of cloning constraints, Alonso emphasizes correct circuit structure, and Pérez-Castillo prioritizes classical-quantum component integration.

In summary, the novelty of this work lies in developing a formal metamodel that goes beyond representing quantum concepts to explicitly encode the mathematical constraints of quantum mechanics—specifically the no-cloning theorem—using verifiable OCL invariants. This enables early-stage validation of quantum software models within established software engineering practices, effectively bridging foundational quantum principles with model-driven software engineering methodologies in a formal and verifiable manner.

4  Metamodeling “No-Cloning Theorem”

In this section, we discuss the no-cloning theorem and introduce a metamodel that represents it. Theorem 1 [1] details the no-cloning theorem.

Theorem 1 (No-Cloning Theorem): The no-cloning theorem states that creating an exact copy of an arbitrary unknown quantum state is impossible. This theorem is crucial as it sets fundamental limits on quantum computing and information processing, in contrast to classical mechanics where state duplication is feasible.

Consider a quantum machine designed to clone quantum states, which includes two slots: slot A (data slot) and slot B (target slot). Slot A contains an unknown pure quantum state |ψ⟩, and slot B starts in a standard pure state |s⟩. The initial combined state of the system can be represented by Eq. (1):

|ψ⟩⊗|s⟩.(1)

where ⊗ denotes the tensor product of the states in slots A and B.

Suppose there is a unitary operation U purported to clone quantum states. Specifically, U is applied to the combined system with the state defined by Eq. (1). The intended outcome of this operation is to duplicate the state |ψ⟩, as shown in Eq. (2):

U(|ψ⟩⊗|s⟩)=|ψ⟩⊗|ψ⟩.(2)

Assuming the cloning process works for states |ψ⟩ and |ϕ⟩, the effects of the unitary operation can be examined by considering inner products, as shown in Eq. (3):

U(|ψ⟩⊗|s⟩)=|ψ⟩⊗|ψ⟩,U(|ϕ⟩⊗|s⟩)=|ϕ⟩⊗|ϕ⟩(3)

For any two states |ψ⟩ and |ϕ⟩, a unitary operation U must comply with Eq. (4):

⟨ψ|ϕ⟩=⟨Uψ|Uϕ⟩(4)

This stipulates that the inner product between the states before applying U must equal the inner product between the states after applying U.

In the hypothetical cloning scenario, before applying the unitary operation U, the states |ψ⟩ and |s⟩ (the standard state) are combined using tensor products, as are |ϕ⟩ and |s⟩. The objective of U is to replicate |ψ⟩and |ϕ⟩. If successful, after applying U, the states would transform into |ψ⟩⊗|ψ⟩ and |ϕ⟩⊗|ϕ⟩, respectively. This transformation is represented in Eq. (5):

⟨U(ψ⊗s)|U(ϕ⊗s)⟩=⟨ψ⊗ψ|ϕ⊗ϕ⟩(5)

Given the unitarity of U, the following equation holds:

⟨U(ψ⊗s)|U(ϕ⊗s)⟩=⟨ψ⊗s|ϕ⊗s⟩(6)

If we assume cloning is feasible, then Eq. (5) is simplified by Eq. (6) to:

⟨ψ⊗s|ϕ⊗s⟩=⟨ψ⊗ψ|ϕ⊗ϕ⟩(7)

Unitary operations must preserve the inner products of states, meaning if U could theoretically clone both |ψ⟩ and |ϕ⟩, their post-cloning inner products must reflect their original inner products. The inner product between tensor product states ⟨ψ⊗s|ϕ⊗s⟩ can be decomposed into the product of the inner products of their components due to the separable nature of tensor products in Hilbert spaces, as shown in Eq. (8).

⟨ψ|ϕ⟩⟨s|s⟩(8)

where ⟨ψ|ϕ⟩is the overlap between |ψ⟩ and |ϕ⟩, and ⟨s|s⟩ is the self-inner product of |s⟩. Assuming |s⟩is normalized, ⟨s|s⟩=1, leading to Eq. (9).

⟨ψ⊗s|ϕ⊗s⟩=⟨ψ|ϕ⟩(9)

This result shows that the similarity or overlap between the tensor product states |ψ⊗s⟩ and |ϕ⊗s⟩ is determined solely by the overlap between |ψ⟩ and |ϕ⟩, with the normalized state |s⟩ having no impact on the comparison.

After applying U, Eq. (10) is established since the tensor product of inner products is the product of the inner products.

⟨ψ⊗ψ|ϕ⊗ϕ⟩=⟨ψ|ϕ⟩⟨ψ|ϕ⟩=⟨ψ|ϕ⟩2(10)

Then, Eq. (9) simplifies to Eq. (11).

⟨ψ|ϕ⟩=⟨ψ|ϕ⟩2(11)

This equation holds true only if ⟨ψ|ϕ⟩=0 or ⟨ψ|ϕ⟩=1, indicating that |ψ⟩ and |ϕ⟩ must be either the same state or orthogonal states. This result demonstrates that a unitary cloner can effectively operate for two states only if those states are either identical or orthogonal. For orthogonal states, the inner product is zero, which means there is no overlap between the states and they are perfectly distinguishable with a probability of 1 upon measurement. This ensures a 100% probability of correctly identifying the state as either |ψ⟩ or |ϕ⟩ without confusion. Orthogonality before applying a unitary operation implies they must remain orthogonal afterward.

However, for general quantum states that are neither orthogonal nor identical, no such unitary cloner U can exist, as no unitary operation can satisfy this equation for all possible pairs of states, thereby negating the possibility of a universal cloner. When states are non-orthogonal, they have a non-zero probability amplitude overlap, indicating they cannot be perfectly distinguished by any measurement. Non-orthogonal states, due to their inherent overlap, cannot be perfectly cloned as this would necessitate altering the inner product, which is invariant under unitary evolution. This fundamental limitation applies to both pure and mixed states.

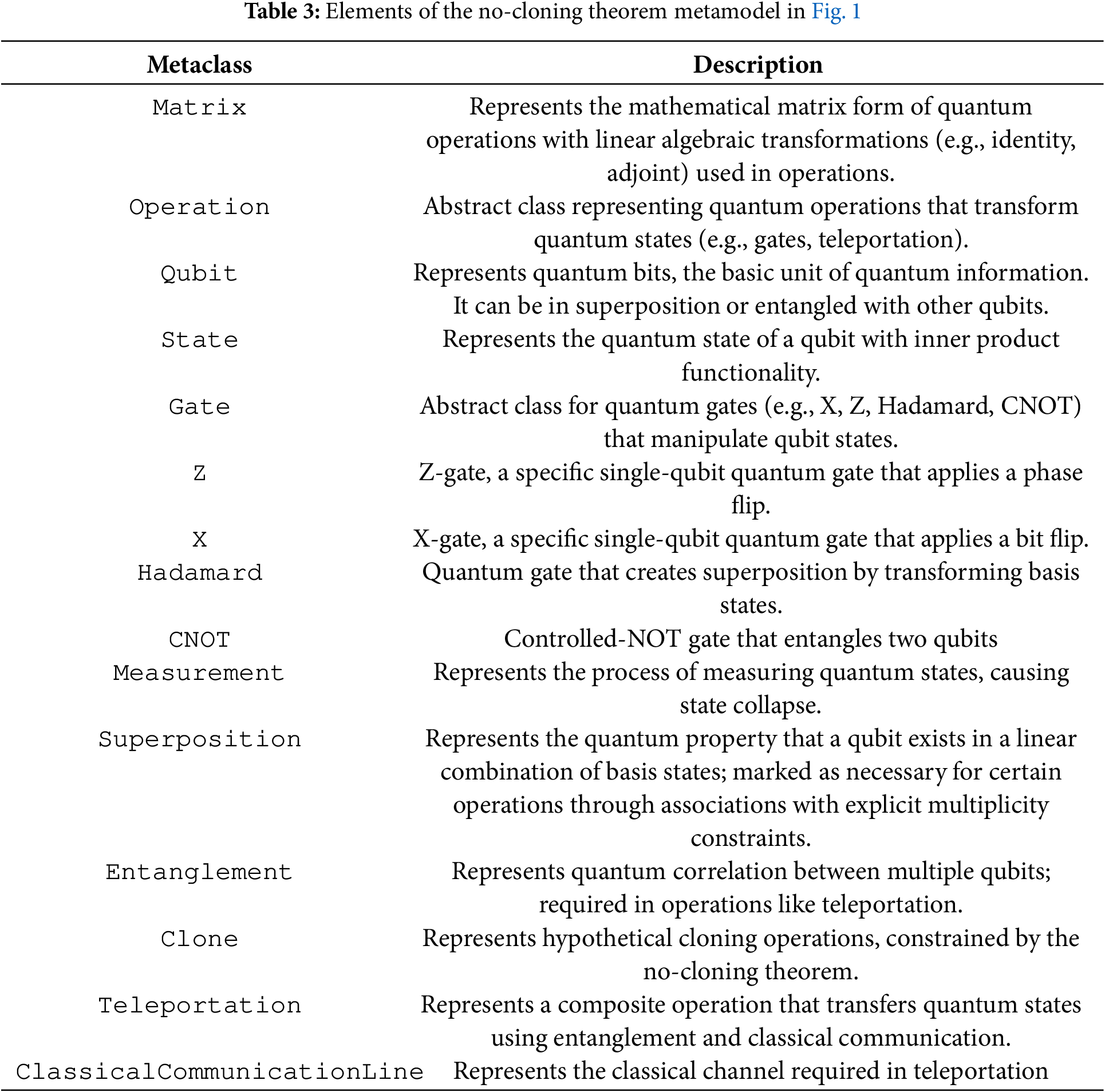
Fig. 1 illustrates a metamodel for the no-cloning theorem in quantum mechanics using UML-style notation to outline quantum concepts, their relationships, and multiplicity constraints. The model was developed using StarUML1, a UML modeling tool. The Clone metaclass represents hypothetical cloning operations, adhering to the no-cloning principle as specified in Invariant (14), which allows only identical or orthogonal states to be cloned. The Matrix metaclass depicts the matrix representation of quantum operations, with Invariant (13) ensuring that these operations are unitary by requiring that the product of a matrix and its conjugate transpose yields the identity matrix. The model includes quantum gates such as the Hadamard, CNOT, X, and Z gates, and the Teleportation metaclass, which represents an operation that uses entanglement and classical communication to transfer a quantum state from a source qubit to a target qubit without direct cloning. These teleportation interactions are linked through associations to Qubit, Entanglement, and ClassicalCommunicationLine, capturing the structural dependencies necessary for modeling the protocol. Orthogonality between states is represented through a self-association on the State metaclass, indicating that two states involved in a cloning operation must satisfy the orthogonality condition when not identical. Table 3 provides descriptions of the individual metaclasses represented in the metamodel.

Figure 1: Metamodel for no-cloning theorem

We employ the Object Constraint Language (OCL) [16], a companion language to UML, to specify the principles of the no-cloning theorem on relevant metaclasses. Invariant (12) maintains that the inner product of orthogonal states must be zero, emphasizing the uniqueness and independence of orthogonal quantum states in cloning operations.

Context:CloneInv:InnerProductPreservationself.Qubit→(forAll q1,q2∣if q1.State.orthogonal→includes(q2.State)thenq1.State.innerProduct(q2.State)=0elsetrue)(12)

Invariant (13) ensures the unitarity of matrices within the system, a fundamental property in quantum mechanics that governs state evolution. Notably, unitarity is a sufficient condition for general inner product preservation across quantum operations. In contrast, Invariant (12), defined specifically in the context of cloning, explicitly enforces that inner products between orthogonal states must be preserved in hypothetical cloning operations, reflecting a core constraint of the no-cloning theorem.

Context:MatrixInv:Unitarity(self.multiply(self.adjoint())=Matrix::identity()andself.adjoint().multiply(self))=Matrix::identity()))(13)

Invariant (14) enforces the no-cloning theorem by ensuring that no universal cloning operation can replicate all quantum states. It specifies that for any cloning operation, if two qubits have distinct states, they must remain distinct unless they are orthogonal. If orthogonal, the operation may result in the states becoming identical, reflecting the ability to clone states only when their orthogonal relationship is predefined, and prior knowledge of the states is available.

Context:CloneInv:CloneInvariantself.qubit→forAll(q1, q2|let s1:State= q1.State,s2:State =q2.State inif s1≠s2then (not self.applyTensor(s1, s2) = s1.tensor(s1) andnot self.applyTensor(s1, s2) = s2.tensor(s2)) or(s1.orthogonal→includes (s2) impliesself.applyTensor(s1, s2) = s1.tensor(s1) orself.applyTensor(s1, s2) = s2.tensor(s2))elsetrue(14)

Invariant (15) ensures that any Entanglement associated with a Teleportation operation involves only those Qubit instances that participate in the Teleportation. This constraint enforces consistency between the qubits engaged in the teleportation protocol and those entangled as part of its implementation.

Context:TeleportationInv:TeleportationEntanglementself.Entanglement.Qubit→forAll(q∣self.Qubit→includes(q))(15)

In teleportation, the receiving (target) qubit is adjusted to replicate the original state through classical communication. Invariant (16) ensures that the target qubit of a teleportation operation is included among the qubits associated with its corresponding classical communication line.

Context:TeleportationInv:TeleportationCommunicationself.ClassicalCommunicationLine.Qubit→includes(self.target)(16)

Invariant (17) ensures that the original quantum state is destroyed during the Bell-state measurement phase of teleportation. It prohibits the coexistence of the original and teleported quantum states, thereby preventing any implicit or residual duplication of state information.

Context:TeleportationInv:TeleportationDestructionself.source.Measurement→notEmpty() impliesself.source.State.oclIsUndefined()(17)

While the proposed metamodel provides a structural foundation for representing key quantum computing concepts, it is important to acknowledge its limitations in directly modeling dynamic phenomena such as quantum state evolution. Quantum state evolution, governed by continuous unitary transformations and probabilistic measurement collapses, involves temporal and process-oriented behaviors that static structural metamodels, such as those based on UML, are not inherently designed to capture. However, relevant constraints associated with quantum state evolution (e.g., unitarity, inner product preservation) can be formally expressed through OCL, as demonstrated. Similarly, while the no-cloning impossibility is captured in the proposed metamodel through a dedicated Clone metaclass and associated OCL invariants, the enforcement of no-cloning across dynamic sequences of operations exceeds the expressiveness of static class diagrams.

The no-cloning theorem forms a fundamental basis for quantum computing and is explicitly integrated into the design of the proposed metamodel; therefore, it does not adversely affect model interoperability. Any models developed based on the metamodel remain inherently interoperable by design. In current quantum computing practice, modularity is typically defined at the level of operations and algorithms, both of which are explicitly represented within the metamodel, thereby ensuring strong modularity support. We anticipate that the metamodel will continue to evolve and expand to encompass a broader range of quantum computing aspects, enhancing its flexibility and applicability for developing diverse quantum software systems.

The no-cloning theorem is a fundamental law of quantum mechanics and does not directly impact model qualities such as reusability. Model qualities are typically determined at the instance-level (design-level) of the metamodel by applying software engineering principles such as coupling, cohesion, and separation of concerns, as established in traditional software engineering. The applicability of these traditional principles to quantum software systems remains an open area for further investigation. Once reusability is intentionally designed at the model-level, it is inherently reflected in the construction of programming components at the implementation-level.

In quantum communication systems (e.g., quantum teleportation, entanglement swapping [1]), which transmit information between two or more parties using quantum phenomena such as superposition and entanglement, the constraints imposed by the no-cloning theorem can be used to reason about the impossibility of duplicating qubit states during information transfer. The metamodel helps structurally represent these systems while formally enforcing no-cloning constraints through OCL invariants, thereby enabling systematic validation of quantum communication protocols to ensure they adhere to fundamental quantum mechanical principles.

The metamodel can be extended to support approximate or probabilistic cloning techniques (e.g., universal quantum cloning machines (UQCM) [17]), which allow the creation of imperfect copies of quantum states by relaxing the strict limitations of the no-cloning theorem at the cost of reduced fidelity. This can be achieved by extending the Clone metaclass into a hierarchy representing different types of cloning: perfect cloning (strictly prohibited by the no-cloning theorem for arbitrary unknown states), approximate cloning (allowing imperfect copies with reduced fidelity), and probabilistic cloning (allowing perfect copies but only with a certain probability). Depending on how these extended elements are incorporated into the model, the fidelity of quantum simulations may vary, with approximate cloning introducing fidelity degradation and probabilistic cloning introducing conditional success rates. Such extensions would enhance the metamodel’s practical applicability to real-world quantum systems where noise and imperfections exist.

5  Presenting Cloning-Like Operations as Instance Models of Metamodel

This section examines two edge cases – conditional copying using CNOT gates and quantum teleportation – through instance models to evaluate the metamodel’s effectiveness in analyzing quantum principles. All instance models were created using StarUML. These two scenarios were selected based on the following criteria: (1) both are canonical operations in quantum computing that are commonly misinterpreted as potential violations of the no-cloning theorem, and (2) each exercises distinct aspects of the metamodel and its associated OCL invariants. The CNOT case specifically tests constraints related to orthogonality and conditional behavior (e.g., Invariants (12) and (14)), while the teleportation case engages constraints involving state destruction, entanglement, and classical communication consistency (e.g., Invariants (15)–(17)). Together, these cases probe the boundary conditions of cloning behavior and validate the internal consistency of the metamodel’s formal constraints.

5.1 Conditional Cloning Using CNOT Gate

Unitary operations preserve inner products, allowing only orthogonal states known prior to cloning to be perfectly cloned without violating the no-cloning theorem. Orthogonality is essential for maintaining consistency with quantum laws, particularly in preserving probability amplitudes and ensuring state distinguishability. A specific example is the CNOT gate, which acts as a cloning operation under certain conditions.

Applying a CNOT gate to two qubits where the control qubit is |1⟩ and the target qubit is |0⟩, orthogonal to |1⟩, results in the target flipping to |1⟩, simulating conditional copying of the control bit. While CNOT(|1⟩⊗|0⟩) = |1⟩⊗|1⟩ might suggest cloning, the non-replication in scenarios where the control is |0⟩ and the target is |1⟩, CNOT(|0⟩⊗|1⟩) results in |1⟩⊗|0⟩, demonstrates the conditional and non-universal nature of this operation, aligning with the no-cloning theorem. Moreover, when the control qubit is initialized in a superposition α|0⟩+β|1⟩ and the target qubit is initialized in |0⟩, the CNOT gate produces an entangled state (α|0⟩+β|1⟩)⊗|0⟩=α|0⟩|0⟩+β|1⟩|0⟩ rather than two independent copies. Thus, the CNOT gate operation preserves the no-cloning theorem by preventing universal replication of arbitrary quantum states. Accordingly, the metamodel distinguishes the CNOT gate from the Clone metaclass to capture these nuances.

Fig. 2 presents an instance model of the metamodel illustrating this conditional simulation of cloning, highlighting that CNOT’s copying is situationally dependent and not a form of true cloning. The instance model for conditional cloning using the CNOT gate concretely demonstrates how a control-target configuration enables replication of basis states. In this model, qubit q1 is initialized to the orthogonal basis state |1⟩—a critical condition for the operation’s validity within the no-cloning theorem—while q2 is initialized to |0⟩. The CNOT gate, with q1 as control and q2 as target, conditionally flips the target qubit based on the control qubit’s state. As a result, when the control qubit is in |1⟩, the target qubit transitions from |0⟩ to |1⟩, effectively mirroring the control state. This structural arrangement demonstrates how the CNOT operation facilitates controlled state transfer when specific preconditions are met, namely, when predetermined orthogonal states are involved. This validates that conditional cloning of orthogonal basis states can be achieved exactly. The model effectively captures that the CNOT gate does not perform universal cloning (which would violate quantum principles) but instead carries out a conditional copying operation that depends entirely on the initial states of the qubits being known in advance. This implies that if the control qubit is initialized in the |0⟩ state or in a superposition state, perfect cloning would not occur, consistent with the no-cloning theorem. Thus, the instance model provides concrete evidence of how conditional operations achieve exact cloning for basis states while respecting the fundamental quantum mechanical constraints imposed by the no-cloning theorem for general states.

Figure 2: Conditional cloning of states using the CNOT gate

The instance of the metamodel that demonstrates conditional cloning using the CNOT gate is detailed in Listing 1. The program initializes two qubits, [0] and [1], in state |0⟩ (line 8). An X gate is applied to qubit [0] to transition it to |1⟩ (line 13), making it orthogonal to qubit [1]. A cx (CNOT) gate then correlates qubit [0] (control) with qubit [1] (target) (line 16), flipping qubit [1] to |1⟩ if qubit [0] is |1⟩, thereby simulating cloning in this controlled setup. The qubits are measured (line 19), and the circuit is run 1000 times using Aer’s qasm simulator (lines 22–27) to gather the outcomes (lines 30–31).

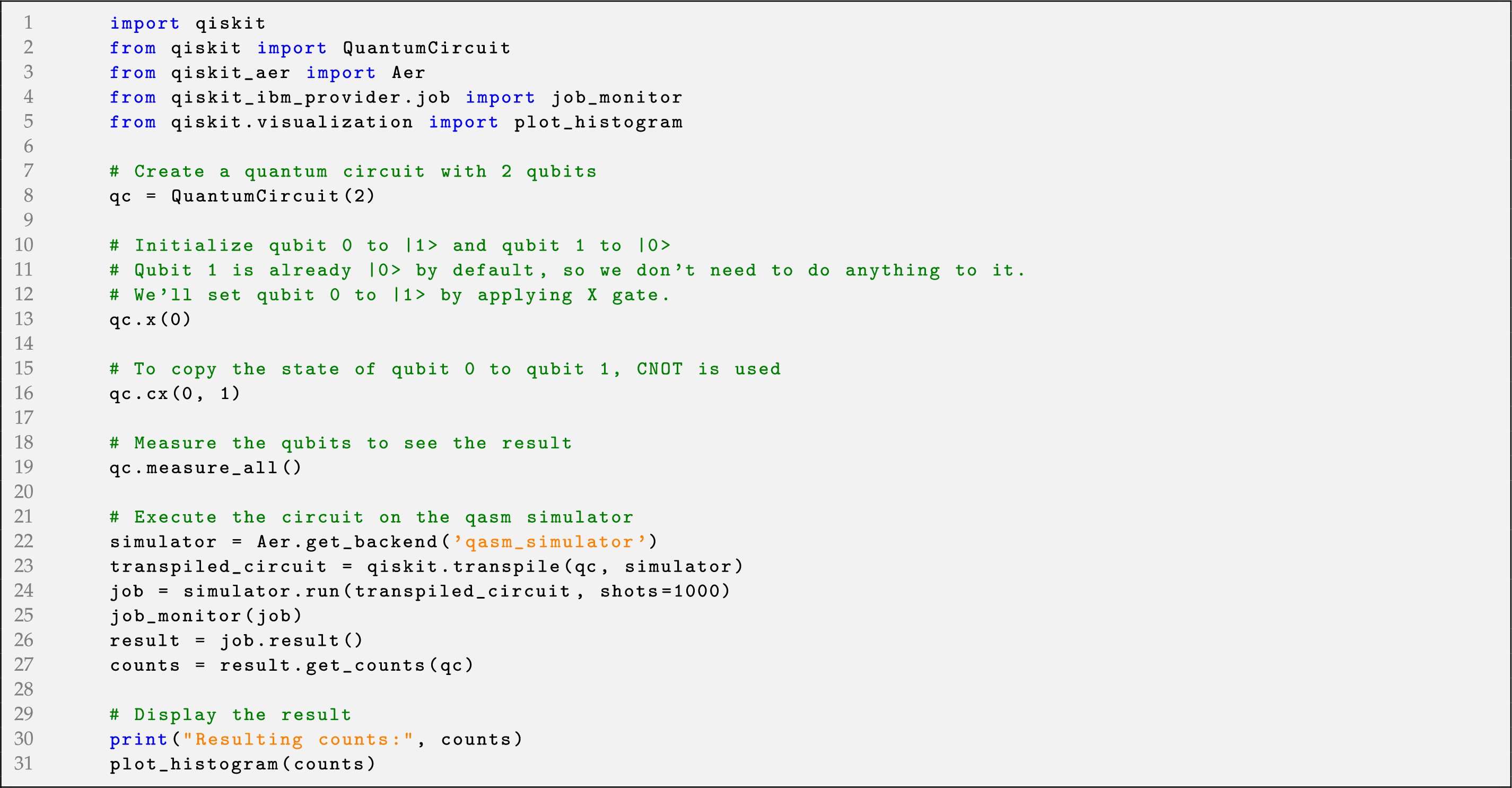
Listing 1: Simulating cloning of orthogonal states using the CNOT gate

The program leads to the measurement outcome ‘11’ with a consistent count of 1000. This indicates that both qubits were measured in state |1⟩ in all trials, demonstrating conditional cloning under known configurations, consistent with the no-cloning theorem.

5.2 State Transfer via Teleportation

Quantum teleportation presents another nuanced case with respect to the no-cloning theorem. It involves transferring a quantum state from one particle to another without physically moving the particles themselves. The process utilizes entanglement between particles to transmit an arbitrary quantum state across different locations, a Bell-state measurement to identify the necessary correction operations, and classical communication to adjust the receiving qubit’s state to reproduce the original state. Although teleportation might appear similar to cloning, it adheres to the no-cloning theorem by preventing duplication: the original quantum state is destroyed during the measurement process, ensuring that only a single copy of the state exists at any time.

Fig. 3 displays a metamodel instance illustrating teleportation. The diagram outlines the interactions among three qubits (q1, q2, and q3) involving superposition, entanglement, and measurements to replicate the state of q1 in q3. Each qubit’s operation is sequentially marked (e.g., 1, 2, 3, etc.) to show the order and dependencies within the teleportation protocol. Initially, q1 is set to the superposition state |+⟩ using a Hadamard gate, while q2, also brought to superposition by a Hadamard gate, is entangled with q3, initially in |0⟩, using another Hadamard and a CNOT gate. This setup prepares the quantum states for subsequent entanglement and teleportation, depicted through connections that illustrate the correlation between the qubits. A Bell-state measurement on q1 and q2 then collapses the system into one of the four Bell states, each representing a maximally entangled state. Below are descriptions of the four Bell states:

•   Outcome ‘00’: |Φ+⟩=12(|00⟩+|11⟩) This outcome indicates no flips or phase changes are necessary. When the measurement results in ‘00’, it suggests that qubits q1 and q2 were measured in a state maintaining their original correlation, without any phase or bit flips. Thus, qubit q3 will not require any corrections to match the original state of q1.

•   Outcome ‘01’: |Φ−⟩=12(|00⟩−|11⟩) The negative sign indicates a phase difference. Specifically, the ‘01’ outcome tells us that qubits q1 and q2 were measured in states that lead to a phase flip relative to their original superposition states. The Z gate is a phase flip gate, which introduces a phase shift of π (or changes the sign of the amplitude) in the |1⟩ component of a qubit’s state. When we measure ‘01’, it means the phase information has been altered, and to correct it back to the original state, we need to apply the Z gate (relative phase of π).

•   Outcome ‘10’: |Ψ+⟩=12(|01⟩+|10⟩). This outcome signifies a bit flip has occurred. The ‘10’ measurement indicates that qubits q1 and q2 had their bits flipped relative to their entangled partners, necessitating a bit flip (X gate) correction on qubit q3 to align with the original state of q1. The X gate inverts the state from |0⟩ to |1⟩ or vice versa.

•   Outcome ‘11’: |Ψ−⟩=12(|01⟩−|10⟩) This outcome implies both a bit and phase flip. The ‘11’ result indicates that qubits q1 and q2 were measured in a state that not only swapped their original bits but also introduced a phase shift. To correct this, a combination of the X and Z gates must be applied to qubit q3. The X gate will address the bit flip, and the Z gate will correct the phase inversion.

Figure 3: Teleportation cloning

This instance model demonstrates the rigorous enforcement of the constraints of the no-cloning theorem and teleportation specified in the metamodel. The entanglement of qubits enforces Invariant (15), ensuring consistency between the entangled qubits. The structural representation of ClassicalCommunicationLine directly aligns with Invariant (16), which requires classical communication for proper state reconstruction. The measurement performed on qubit q1 enforces Invariant (17), ensuring the destruction of the original quantum information. More importantly, the destruction of the original state guarantees adherence to the no-cloning theorem by preventing the duplication of quantum states.

Note that the instance model incorporates stepwise labels to represent the order and dependencies of operations, enabling a limited form of sequential behavior modeling. While this auxiliary feature is specific to the instance level and cannot be captured directly at the metamodel level, it supports simulation-oriented reasoning within the model and highlights the potential for future integration with model execution tools, such as Papyrus Moka2, an fUML (the Foundational UML subset3) execution engine.

The teleportation process is implemented in the instance model outlined in Listing 2. The program sets up a circuit qc with three qubits and three classical bits (lines 11). Qubit [0] is placed in superposition |+⟩=12(|0⟩+|1⟩) using a Hadamard gate (line 14). Qubit [1], also in superposition, is prepared alongside qubit [2] for entanglement via a CNOT gate, where qubit [1] acts as control and qubit [2] as target (lines 17–18). A subsequent CNOT gate entangles qubits [1] and [2] (line 21). A Hadamard gate on qubit [0] prepares it for a Bell-state measurement with qubit [1] (line 22), converting its basis to align with the Bell states for measurement (line 23). Depending on the measurement outcome, corrections are applied to qubit [2]: no correction for ‘00’, an X gate for ‘10’, a Z gate for ‘01’, and both gates for ‘11’ (lines 27–32). These operations utilize the c_if method, which implements classical communication by conditionally applying quantum operations based on classical register values. This models the classical communication channel required in quantum teleportation protocols, where measurement results must be transmitted via classical means to complete the quantum state transfer process. This adjusts qubit [2]’s state to match the originally altered state of qubit [0]. Qubit [2] is measured last (line 35). This setup uses classical values to guide quantum corrections, simulating quantum teleportation by transferring the original state to the target. It does not constitute cloning since the original state of qubit [0] is destroyed during Bell state measurement, adhering to the no-cloning theorem.

Listing 2: Simulating state transfer via teleportation

Fig. 4 shows the output of the teleportation program. The histogram represents counts for eight possible measurement outcomes across three qubits, formatted as “qubit [2] qubit [1] qubit [0]” (000, 001, 010, etc.), with each outcome occurring roughly 108 to 135 times over 1024 shots. This uniform distribution (about 120–130 counts per outcome) reflects the initial equal superposition state, equal probability of Bell-state measurement outcomes, and preservation of the state by corrective operations. Variations in counts, such as 108 vs 135, arise from the probabilistic nature of quantum measurements and are typical of quantum shot noise in experiments. The consistent distribution across outcomes confirms the teleportation protocol’s effectiveness, as deviations significantly outside expected ranges would indicate operational failures.

Figure 4: Histogram of teleportation simulating state transfer

6  Discussion

In this section, we discuss the implicit validation embedded in the approach itself, as well as the practical application of the proposed approach in real-world quantum software engineering contexts.

6.1 Validation

The two concrete instance models—conditional cloning via CNOT and quantum teleportation—serve as empirical validation, demonstrating the practical application of the metamodel in capturing specific scenarios governed by the no-cloning constraint. These examples are grounded in well-established quantum operations and validate the correctness and utility of the metamodel. Their implementation in Qiskit, along with measurable outcomes, provides empirical evidence that software derived from the metamodel conforms to the quantum mechanical principles it is designed to represent.

A more comprehensive validation strategy may involve developing a suite of test cases that explore the boundary conditions of the no-cloning theorem, thereby demonstrating the metamodel’s ability to prevent invalid model instantiations—such as attempts to clone non-orthogonal, unknown quantum states or to construct teleportation operations that preserve the original state. In addition, user studies with quantum software developers could be conducted to assess the metamodel’s practical utility and correctness in real-world quantum software design contexts.

6.2 Practical Applications of the Proposed Metamodel in Quantum Software Engineering

By formalizing foundational quantum principles—such as the no-cloning theorem and teleportation constraints—as enforceable OCL invariants, the framework enables early detection of conceptual modeling errors before code implementation. This early-stage validation helps prevent violations of core quantum mechanics that could otherwise lead to failures or inefficiencies in later development phases, supporting reliable design and reduce development time. For example, during quantum circuit modeling, the metamodel ensures the unitary nature of operations, preserving quantum information. In the case of potential cloning operations, the model enforces relevant constraints (e.g., orthogonal states must have zero inner product), thereby ensuring compliance with the no-cloning theorem.

The instance models presented in Figs. 2 and 3 were manually constructed with careful adherence to the structural and semantic constraints defined in the metamodel, including associations, multiplicity rules, and OCL invariants. Their correctness reflects intentional conformance to the metamodel’s design principles. Currently, the metamodel has not been fully implemented or integrated into a modeling tool that actively enforces these constraints. The integration of the metamodel and OCL constraints with existing software engineering tools enables automated enforcement of quantum principles throughout the development lifecycle. UML tools such as Eclipse MetaModelAgent4 support domain-specific modeling and OCL constraint checking, making the approach directly applicable within established environments. These tools can automatically validate instance models against defined constraints and provide immediate feedback when quantum principles are violated. For instance, during the modeling of quantum error correction codes, OCL constraints can validate that error syndrome measurements [1] do not inadvertently violate the no-cloning theorem while detecting errors through qubit correlations.

Additionally, many UML-based tools (e.g., StarUML) support code generation from models defined over standard UML metamodels. In a similar manner, the proposed metamodel can act as a bridge between quantum design models and implementation code via a translation framework that maps metamodel elements to constructs in quantum programming languages such as Qiskit5 and Cirq6. This enables bidirectional transformations between design and implementation. The implementations in Listings 1 and 2 illustrate how metamodel elements correspond to Qiskit constructs—for example, translating a Qubit element into a qubit initialization, or converting a Teleportation instance into a full Qiskit script with entangled state preparation, Bell measurements, and conditional operations. This integration supports model-driven development of quantum applications, facilitating both forward engineering (from models to code) and reverse engineering (from code to conceptual models), thereby enhancing maintainability and scalability of quantum software systems.

6.3 Extensibility

A major benefit of the approach is the extensibility of the metamodel to accommodate other concepts. In this section, we demonstrate the extensibility of the metamodel by extending the metamodel in Fig. 1 for projective measurement, which is a specific type of quantum measurement that projects the state vector of a qubit onto orthogonal subspaces of a Hilbert space. Fig. 5 shows the extension.

Figure 5: Metamodel defining projective measurement

The extension shown in the figure models projective measurement as a specialization of the Measurement metaclass (stereotyped as «core») from the base metamodel in Fig. 1. Projective measurement operates through orthogonal projectors, represented by the Projector metaclass. Each projector acts on a quantum State, producing a transition from a pre to a post state, along with a corresponding measurement Outcome. The Outcome is recorded as a real eigenvalue (via the value attribute) and corresponds to an eigenspace in the HilbertSpace of the observable. The multiplicity of 1..* on the State class indicate that the eigenspace (defined by a given eigenvalue) contains one or more valid quantum states that the system may collapse into upon measurement. The observable itself is captured by the HermitianObservable metaclass, which generalizes concrete Pauli operators such as X, Y, and Z, each defined over a 2-dimensional Hilbert space. A HermitianObservable includes multiple projectors via spectral decomposition, as indicated by the multiplicity * on the association with Projector. Upon measurement, the qubit’s state collapses to a normalized post-measurement state aligned with the eigenspace corresponding to the observed eigenvalue. This collapse behavior reflects the physical semantics of projective measurement, governed by the projective postulate, formally defined as follows:

•   Upon measurement, the system collapses to an eigenvalue in the eigenspace corresponding to the observed eigenvalue. This behavior is formally defined by the invariant (18) in OCL.

Context:ProjectiveMeasurementInv:Collapseself.HermitianObservable.Projector→forAll(p |p.pre = self.HermitianObservable.Qubit.Stateandp.Outcome.correspondence.HilbertSpace = self.Hermitian.HilbertSpace)(18)

•   The probability of obtaining outcome i is ⟨ψ|Pi|ψ⟩, where Pi is the projector associated with eigenvalue λi. This rule is formally specified by invariant (19) in OCL.

Context: ProjectiveMeasurementInv:Probabilityself.HermitianObservable.Projector→forAll(p |p.Outcome.value=self.HermitianObservable.Qubit.State.innerProduct(p.apply(p.pre)))(19)

•   The post-measurement state is Pi|ψ⟩‖Pi|ψ⟩‖, provided Pi|ψ⟩≠0. This normalization rule is formally specified by invariant (20) in OCL.

Context: ProjectiveMeasurementInv:Normalizationself.HermitianObservable.Projector→forAll(p |p.apply(p.pre).norm() \lt > 0 impliesp.post = p.apply(p.pre).normalize())(20)

where the norm() function returns the norm (or length) of the projected state Pi|ψ⟩, given by ⟨ψ|Pi|ψ⟩. The normalize() function then returns the corresponding post-measurement state as a unit vector in the same direction as Pi|ψ⟩, defined as Pi|ψ⟩‖Pi|ψ⟩‖, assuming Pi|ψ⟩≠0.

These postulates are fundamental axioms of quantum mechanics and must be satisfied by any correct implementation of projective measurement. In practical quantum computing platforms, such as the qasm_simulator in Qiskit, these behaviors are implemented natively within the simulation backend.

We acknowledge that modeling other quantum mechanical principles—such as the Heisenberg uncertainty principle [1]—may pose certain challenges, particularly those that involve operator algebra (e.g., non-commutative observables) and probabilistic semantics (e.g., continuous-valued inequalities). Unlike the no-cloning theorem or projective measurement, the Heisenberg uncertainty principle requires expressing commutation relations and real-valued uncertainty bounds, which are more complex to represent using standard UML/OCL constructs. Capturing such principles may necessitate the introduction of richer mathematical abstractions, such as operator algebras, commutation relations, or even probabilistic logic layers.

7  Threats to Validity

This section discusses potential threats to the validity of the proposed metamodeling approach, organized according to common validity dimensions: internal validity, external validity, construct validity, and conclusion validity.

Internal Validity. Internal validity is concerned with the correctness of the metamodel, which relies on the formal representation of quantum mechanical principles using OCL constraints. Any misinterpretation or incomplete formalization of these principles could lead to inaccurate modeling. We mitigated this threat by grounding the constraints in established quantum mechanical formulations [1]. The translation from mathematical notation to OCL introduces another potential source of error. Different interpretations of quantum mechanical equations could result in varying constraint definitions. To address this concern, we provided detailed explanations of the mapping between quantum mathematical formulations and corresponding OCL expressions.

External Validity. External validity pertains to the generalizability of the metamodel beyond the specific cases analyzed. Although the presented edge cases are representative and grounded in canonical quantum behavior, the applicability of the metamodel to other quantum phenomena—such as mixed states, approximate cloning, entanglement distillation, or quantum error correction—has not yet been explored. To address this limitation, we demonstrate the extensibility of the metamodel through the incorporation of projective measurement, as discussed in Section 6. Additionally, the validation focused on relatively simple quantum systems with few qubits. While the metamodel and its associated OCL invariants are not directly impacted by system scale—since the metamodel abstracts quantum concepts independently of the number of qubits—scalability concerns arise primarily at the instance level. As the system grows, an increasing number of metaclass instances (e.g., Qubit, State, Measurement) must be created and managed. This expansion may introduce computational overhead, particularly in evaluating OCL constraints over large collections of instances. Additionally, state explosion may become a practical concern at the instance-level. As quantum systems evolve—particularly those involving entangled or superposed states—the complexity of instance models increases, making it more difficult to maintain, validate, and reason about their correctness without dedicated tool support.

Construct Validity. Construct validity concerns whether the metamodel accurately represents the theoretical concepts it is intended to capture—in this case, the principles underlying the no-cloning theorem. While the metamodel is grounded in quantum mechanical formalism and includes formal constraints (e.g., unitarity, inner product preservation) via OCL invariants, it may still omit subtle physical nuances (e.g., imperfect gates, noise) not easily formalized in UML-based notation. Additionally, the mapping of inherently mathematical quantum operations to software modeling constructs may lead to oversimplification or loss of semantic nuance.

8  Conclusion

This paper employs metamodeling techniques to analyze the no-cloning theorem in quantum mechanics through a UML-style metamodel. This metamodel incorporates essential quantum concepts and relationships relevant to the no-cloning theorem, emphasizing the inability to replicate arbitrary unknown quantum states. It validates its utility with instance models that explore edge cases like conditional copying with CNOT gates and quantum teleportation, ensuring they adhere to the theorem’s constraints in line with conventional software engineering practices. This research provides the quantum software engineering community with a structured framework for integrating quantum mechanics into software design, promoting advancements in quantum software development. There is also a potential learning curve for software engineers who may lack quantum mechanics background. This interdisciplinary knowledge gap could limit the approach’s adoption. However, by leveraging UML—a widely practiced and standardized graphical modeling language in software engineering—as the foundation of the approach, the barrier to entry is significantly reduced. UML provides a familiar and intuitive framework for software engineers, allowing them to engage with quantum concepts without requiring deep mathematical expertise. By embedding quantum principles within this modeling paradigm, the approach translates complex mathematical formalisms into structured visual representations and declarative rules. These abstractions serve as conceptual scaffolding, helping learners incrementally develop intuition for quantum behavior without being overwhelmed by the underlying formalism.

Future work will focus on broadening the scope of the metamodel beyond the no-cloning theorem. Specifically, we plan to explore its applicability to other areas of quantum computing such as mixed states, approximate cloning, entanglement distillation, and quantum error correction. These topics introduce additional complexity, including probabilistic behaviors, partial fidelity constraints, and hybrid quantum-classical interactions. Extending the metamodel to represent such phenomena will require incorporating new modeling constructs, constraints, and validation mechanisms, and will serve to assess the scalability, flexibility, and robustness of the approach across a wider range of quantum scenarios. The practical utility of the metamodel for quantum software developers depends on integration with existing quantum development tools and workflows. Currently, most quantum programming relies on circuit-based representations rather than UML-style models. Further work is needed to bridge the gap between the metamodeling approach and practical quantum software development environments. By doing so, we aim to further integrate metamodeling with the evolving needs of quantum software engineering.

Acknowledgement: The author expresses gratitude to all editors and anonymous reviewers for their insightful comments and suggestions, which have significantly enhanced the quality of this manuscript.

Funding Statement: The author received no specific funding for this study.

Availability of Data and Materials: The data and materials supporting the findings of this study are openly available at https://github.com/hanbyul1/No-Cloning-Theorem (accessed on 25 May 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The author declares no conflicts of interest to report regarding the present study.

1https://staruml.io (accessed on 25 May 2025).

2https://marketplace.eclipse.org/content/papyrus-moka (accessed on 25 May 2025).

3https://www.omg.org/spec/FUML/1.4/About-FUML (accessed on 25 May 2025).

4https://www.metamodelagent.com (accessed on 25 May 2025).

5https://www.ibm.com/quantum/qiskit (accessed on 25 May 2025).

6https://quantumai.google/cirq (accessed on 25 May 2025).

References

1. Nielsen MA, Chuang IL. Quantum computation and quantum information. 10th ed. Cambridge, UK: Cambridge University Press; 2010. [Google Scholar]

2. Alonso D, Sánchez P, Álvarez B. A graph-based approach for modelling quantum circuits. Appl Sci. 2023;13(21):11794. doi:10.3390/app132111794. [Google Scholar] [CrossRef]

3. Pérez-Castillo R, Piattini M. Design of classical-quantum systems with UML. Computing. 2022;104(11):2375–403. doi:10.1007/s00607-022-01091-4. [Google Scholar] [CrossRef]

4. Piattini M, Peterssen G, Pérez-Castillo R, Hevia JL, Serrano MA, Hernández G, et al. The Talavera Manifesto for quantum software engineering and programming. In: 1st QANSWER 2020; 2020 Feb 11-12; Talavera de la Reina, Spain. p. 1–5. doi:10.1145/3402127.3402131. [Google Scholar] [CrossRef]

5. Weder B, Barzen J, Leymann F, Vietz D. Quantum software development lifecycle. In: Quantum software engineering. 1st ed. Cham, Switzerland: Springer; 2022. p. 61–83. doi:10.1007/978-3-031-05324-5_4. [Google Scholar] [CrossRef]

6. Ali S. Quantum software testing 101. In: Proceedings of the 2024 IEEE/ACM 46th International Conference on Software Engineering: Companion Proceedings; 2024 Apr 14–20; Lisbon, Portugal. p. 426–7. [Google Scholar]

7. Sánchez P, Alonso D. On the definition of quantum programming modules. Appl Sci. 2021;11(13):5843. doi:10.3390/app11135843. [Google Scholar] [CrossRef]

8. Bibbo LM, Fernandez A, Suarez JM, Pastor O. Modelling quantum software: an annotated bibliography. Memoria Investigaciones En Ingeniería. 2024;27(27):285–301. doi:10.36561/ing.27.19. [Google Scholar] [CrossRef]

9. Ahmad A, Khan AA, Waseem M, Fahmideh M, Mikkonen T. Towards process centered architecting for quantum software systems. In: 2022 IEEE International Conference on Quantum Software (QSW); 2022 Jul 10–16; Barcelona, Spain. p. 26–31. [Google Scholar]

10. Ali S, Yue T, Abreu R. When software engineering meets quantum computing. Commun ACM. 2022;65(4):84–8. [Google Scholar]

11. Sabzevari MT, Esposito M, Taibi D, Khan AA. QCSHQD: quantum computing as a service for hybrid classical-quantum software development: a vision. In: QSE-NE 2024-Proceedings of the 1st ACM International Workshop on Quantum Software Engineering: The Next Evolution; 2024 Jul 16; Porto de Galinhas, Brazil. p. 7–10. [Google Scholar]

12. Gallardo JZ, Moguel E, Canal C, Garcia-Alonso J. Quirk+: a tool for quantum software development based on quirk. In: 2024 IEEE International Conference on Software Analysis, Evolution and Reengineering-Companion (SANER-C); 2024 Mar 12; Rovaniemi, Finland. p. 151–8. [Google Scholar]

13. García de la Barrera A, García-Rodríguez de Guzmán I, Polo M, Piattini M. Quantum software testing: state of the art. J Softw Evol Process. 2023;35(4):e2419. doi:10.1002/smr.2419. [Google Scholar] [CrossRef]

14. Khan AA, Akbar MA, Ahmad A, Fahmideh M, Shameem M, Lahtinen V et al. Agile practices for quantum software development: practitioners’ perspectives. In: 2023 IEEE International Conference on Quantum Software (QSW); 2023 Jul 2–8; Chicago, IL, USA. p. 9–20. [Google Scholar]

15. Thompson N, Steck J, Behrman E. A non-algorithmic approach to “programming” quantum computers via machine learning. In: 2020 IEEE International Conference on Quantum Computing and Engineering (QCE); 2020 Oct 12–16; Denver, CO, USA. p. 63–71. [Google Scholar]

16. Group OM. Object constraint language (OCL) version 2.4; 2014 [Internet]. [cited 2025 Jan 27]. Available from: http://www.omg.org/spec/OCL/2.4. [Google Scholar]

17. Buzek V, Hillery M. Quantum copying: beyond the no-cloning theorem. arXiv:quant-ph/9607018. 1996. [Google Scholar]