Efficient One-Way Time Synchronization for VANET with MLE-Based Multi-Stage Update

1  Introduction

Time synchronization is an indispensable requirement in Vehicular Ad hoc Networks (VANETs) to ensure reliable and low-latency communication. As networking performance demands continue to increase, maintaining precise synchronization has become a fundamental necessity for guaranteeing key metrics such as low-latency data transmission and high reliability [1,2]. Despite the effectiveness of two-way synchronization techniques in achieving high precision in VANETs with wireless local area networks (WLANs) and wireless sensor networks (WSNs), these methods heavily rely on frequent packet exchanges and persistent, stable connectivity with higher-stratum time sources [1,3]. Therefore, in environments where power constraints limit packet transmission, such as IoT networks, or VANETs where wireless connectivity fluctuates unpredictably due to physical obstructions like tunnels, urban canyons, or indoor environments, packet delivery can be severely restricted [4,5]. Maintaining accurate synchronization presents significant challenges (the position estimation transmission of vehicles is validated through simulation, as detailed in Section 4). To maintain stable time synchronization, a persistent connection with a higher-stratum source, typically an access point (AP), is required. However, in vehicular networks where maintaining continuous connectivity with a specific AP is challenging, this limitation introduces potential synchronization instabilities. Additionally, in VANETs, mission-critical control data, state information, odometry, position data, and sensor data from cameras and other sources must be transmitted and received in a timely manner [6]. As a result, synchronization should not impose additional bandwidth overhead. Similarly, in IoT networks, which primarily consist of low-power devices, two-way synchronization may be impractical due to energy constraints [7]. Under these conditions, one-way synchronization can be considered as a practical and resource-efficient solution that mitigates these constraints [8]. Unlike two-way synchronization, which requires bidirectional communication with access points (APs) or dedicated time servers, one-way synchronization operates passively, allowing nodes to receive timing information without inducing additional network overhead. This makes it particularly suitable for resource-limited IoT deployments and dynamic vehicular networks where sustained infrastructure connectivity cannot be guaranteed.

The latest one-way synchronization methods leverage Maximum Likelihood Estimation (MLE)-based clock skew estimation using the Cramér-Rao Lower Bound (CRLB) to achieve highly precise synchronization, outperforming traditional approaches [9]. This method optimally estimates clock skew in a controlled environment where key variables such as device clock precision, network channel characteristics, and AP clock stability remain consistent. The primary advantage of this approach is that it can achieve highly accurate synchronization using only a few broadcast packets, significantly reducing network load and synchronization overhead. In MLE-based one-way synchronization, timestamps are extracted from received beacon frames, and an estimation model is applied to minimize the impact of transmission delays and jitter. The Gaussian delay model is typically employed to model variable delays, ensuring robustness against network fluctuations. The effectiveness of this method has been widely recognized, particularly in environments where precise synchronization is necessary but bidirectional communication is costly or impractical.

Given these challenges, one-way synchronization is often adopted as a practical alternative; however, it also has inherent limitations. While MLE-based estimation provides gradual and stable clock updates, achieving an accurate clock skew estimation requires multiple synchronization cycles. This issue becomes even more pronounced in the presence of unstable clock sources affected by power constraints, channel conditions, and mobility, further delaying the synchronization process. In particular, when the clock source is unreliable due to fluctuations in power availability, network congestion, or frequent handovers between APs, synchronization becomes less responsive and more prone to errors. To address these challenges, we propose an aggressive clock update strategy during the initial synchronization stage. This approach is inspired by network time protocol (NTP)’s polling interval, where frequent updates occur in the early stages to achieve rapid convergence before transitioning to longer intervals for stability [10]. By introducing an additional synchronization stage before MLE-based estimation, we aim to improve synchronization efficiency in dynamic environments. We analyze the causes of beacon frame reception instability from unreliable clock sources and introduce a multi-stage synchronization approach. Specifically, we propose a multi-stage WLAN-based synchronization scheme that integrates a hard update-based smooth landing mechanism with adaptive sampling and filtering techniques. This method is designed to optimize synchronization performance in highly dynamic wireless environments. Our proposed scheme consists of an initial hard update for clock correction, followed by gradual adjustments using MLE-based filtering. (1) We analyze the problem of heterogeneous beacon frame reception in one-way time synchronization during the initial access stage under intermittent connectivity. (2) The system first applies an initial hard update by directly setting the system clock to the minimum offset value observed from received beacon frames, rather than conservatively updating clock differences through skew or drift estimation. This ensures a rapid initial correction, reducing the time required for synchronization convergence. (3) Once the initial correction is applied, WMC seamlessly carries forward the samples collected during the initial stage into the MLE-based estimation, which then gradually refines clock skew to maintain stability while Gaussian modeling of delay minimizes synchronization errors over time. Additionally, the synchronization rate is dynamically adjusted based on network conditions, ensuring robustness in environments with intermittent connectivity. By implementing this multi-stage approach, synchronization performance is significantly improved, particularly in vehicular networks, where maintaining stable AP access is challenging. Our method enhances both short-term and long-term synchronization accuracy while also minimizing computational and network overhead.

The rest of this paper is organized as follows. In Section 2, we review typical studies of clock synchronization and those specifically for vehicular networks. Section 3 describes the architecture of the proposed clock synchronization method and presents a problem with sample freshness. In Section 4, we evaluate the performance of the proposed system. Finally, the conclusion is given in Section 5.

2  Related Work

This section describes time synchronization methods and the related work on message-based exchanges in wireless networks. Additionally, it discusses previous works on one-way time synchronization and their limitations associated with the proposed study.

Message-based time synchronization in wireless networks is primarily achieved through either one-way or two-way message exchanges [11,12]. This approaches are commonly adopted in hierarchical classifications, divided by stratum (a hierarchically lower stratum serves as the reference clock), where synchronization occurs between servers and clients at different levels. As illustrated in Fig. 1, a server (s) sends a timing message at the i-th instance, and the client (c) receives it. The relationship between the transmission time titx,s and the reception time tirx,c allows the client to estimate the server’s original transmission time, denoted as titx,c. The superscripts tx and rx denote transmission and reception times, respectively. The discrepancy between titx,c and tirx,c, denoted as δi, is predominantly influenced by the end-to-end delay between the server and the client. This delay due to frequency difference is a dominant factor and is redefined as clock skew.

Figure 1: One-way time synchronization process

Meanwhile, the server and client inherently maintain independent clocks, differing in resolution and performance. This discrepancy leads to the phenomenon known as clock drift. Clock drift arises due to frequency differences between the client and server clocks (Cc(t)=(1+ϵ)Cs(t)), which represents the ideal server clock value, Cc(t) denotes the actual client clock value, and ϵ is the drift rate of the client clock. The drift rate ϵ quantifies the rate at which the client clock deviates from the server clock over time. Typically, clock drift occurs in the range of several parts per million (ppm) per second. Over extended periods, synchronization errors accumulate if left uncorrected. Therefore, without compensation for clock drift in message-based synchronization, the client clock increasingly deviates from the server clock. To mitigate this, synchronization in WLANs is performed through the transmission of timing messages via packets.

There are several motivations for applying one-way synchronization in real-world systems. Huan et al. [7] target low-power IoT networks with a looped sample-mean (LSM) broadcast scheme but do not evaluate convergence behavior. Shim et al. [13] apply a lightweight NTP-based method for UAV networks, yet likewise omit any analysis of synchronization convergence time. Shi et al. [8] proposed a one-way synchronization technique based on broadcast messages from edge nodes connected to wired infrastructures (e.g., base stations or APs). Wang et al. [14] later introduced the Best Linear Unbiased Estimator (BLUE) as a lightweight alternative to MLE, but noted that its initial convergence speed is slower than that of MLE. Nonetheless, neither work provides a concrete strategy for optimizing convergence speed until the clock is stably adjusted. Maximum Likelihood Estimation (MLE) is a well-established technique whose convergence behavior can be indirectly inferred from the number of iterations required [15]. Guchhait and Karthik. [16] model the network delay as a Gaussian random variable and derive the corresponding Cramér–Rao lower bound (CRLB) to quantify the minimum estimation error; they demonstrate this bound in simulation by varying the number of message iterations. Wang et al. [9] present a hybrid one-way scheme that includes reverse-direction messaging—allowing convergence to be assessed via synchronization accuracy over iterations—but this approach still does not yield a direct measure of absolute convergence time. By contrast, consensus-based time synchronization protocols have begun to address convergence speed explicitly. Shi et al. [17] propose an iterative message exchange method that accelerates convergence in wireless sensor networks, and Wang et al. [18] most recently present a two-way packet exchange scheme that improves convergence speed under high-delay conditions. However, comparable strategies for rapid convergence in one-way MLE-based synchronization remain unexplored. The related works mentioned above are summarized in Table 1.

3  WMC: Proposed Time Synchronization Model

This section presents the design methodology of WMC, a multi-stage one-way time synchronization approach that enables fast convergence in the initial stage and long-term stability in the stable stage under dynamic wireless environments. In Sections 3.2 and 3.3, we describe the stage–specific methodologies for the initial and stabilization phases, respectively, each tailored to its objectives and connected through a cohesive, seamlessly integrated process. We first discuss how beacon sequence omissions and stochastic reception delays across nodes introduce heterogeneity in the initial stage, leading to instability in early offset estimation. To address this, we describe a hard update-based sampling and filtering method that quickly stabilizes offset samples by rejecting outliers and applying median-based filtering. In the subsequent stabilization stage, we introduce a procedure to estimate clock offset and skew using maximum likelihood estimation (MLE), and then perform adaptive clock compensation. The section concludes by explaining how a smooth transition from the initial stage to the MLE-based stable stage ensures both synchronization precision and robustness against transient network fluctuations.

3.1 Heterogeneity in Beacon Reception Timing

In wireless environments, beacon frames are periodically broadcast from the access point (AP) to multiple receiving nodes for one-way synchronization. However, due to the inherent nature of wireless propagation, several challenges arise in how these beacons are received across different nodes. Despite being transmitted simultaneously from the same AP, nodes may receive different beacon sequence numbers or, in many cases, even when the same sequence number is received, they experience heterogeneous delays caused by varying channel conditions, interference, or hardware-specific reception timing. This phenomenon is illustrated in Fig. 2, where the perceived beacon timing at each node differs from the reference due to stochastic transmission delay and reception offset. Such heterogeneity in beacon reception leads to inconsistencies in estimating the timing offset (DOFFSET) between each node’s local clock (TLOCAL) and the AP’s reference time (TAP). Without effective handling, these inconsistencies degrade synchronization performance and result in unstable system clock updates. Therefore, a robust preprocessing strategy is required to manage this temporal uncertainty prior to applying high-precision estimation techniques such as Maximum Likelihood Estimation (MLE).

Figure 2: Heterogeneity in beacon frame arrival

This heterogeneity affects synchronization accuracy in two critical ways. First, when different nodes receive different beacon sequence numbers, each node references a different AP timestamp TAP,i, resulting in offset values computed as DOFFSET,i=TLOCAL,i−TAP,i that correspond to different reference points in time. Since each transmission from the AP may involve different transmission-side delays, these offsets do not align to a common clock model. Especially during the initial synchronization phase, before any statistical filtering is applied, this misalignment leads to increased uncertainty and wider offset variance across nodes, hindering early convergence of synchronization. Second, even when nodes receive the same beacon sequence number, the local reception timestamp TLOCAL,i can still vary significantly due to diverse wireless channel conditions, hardware interrupt latencies, and kernel-level processing delays. In such cases, the computed offset can be more accurately expressed as DOFFSET,i=(TLOCAL,i+δi)−TAP,i, where δi represents a stochastic delay term caused by reception-side variability. This δi is typically modeled as a zero-mean Gaussian random variable, introducing unpredictable noise into the offset measurement even under identical beacon conditions. The combination of these two issues—sequence misalignment and stochastic delay variation—leads to large offset dispersion during the early synchronization stage. This makes the system vulnerable to unreliable or unstable clock updates. To address this, a mechanism capable of absorbing such uncertainty and refining offset samples is essential prior to applying precise synchronization techniques.

3.2 Hard Update-Based Sampling and Filtering Algorithm

The process of sampling and filtering this temporal data is implemented as shown in Algorithm 1. First, TLOCAL,i is obtained from the local time of the Linux kernel, while TAP,i is extracted from the received BF. By computing the difference between these timestamps as DOFFSET,i, the kernel system time deviation from the AP, which serves as a reference clock, is estimated. A sample is added to DOFFSET,i only if it is valid, ensuring that outlier samples do not introduce significant errors in the synchronization process. To maintain efficiency, a moving average characteristic is incorporated by replacing the oldest sample when a new one is added. Unlike a fixed sampling period, this algorithm dynamically determines the period length by calculating the period length every time a sample is added. Once DOFFSET,i accumulates period_size samples, a filtering process is applied to derive a robust time correction value. The filtering approach consists of two key steps (outlier sampling and median estimation). Outlier rejection is performed based on statistical thresholds to eliminate abnormal values. In particular, the greatest obstacle to synchronizing multiple clients is the common low—quality frames (i.e., heterogeneous receptions). Moreover, clients do not exchange information to confirm whether they have received the same sequence or to compare and evaluate each other’s sequence data. Because the client cannot assess frame quality immediately upon initial reception, we proactively discard any sample whose DOFFSET,i deviates from the running median by more than λ⋅σD, thereby suppressing abrupt fluctuations caused by stochastic delays and mitigating heterogeneous arrival effects. For median estimation, rather than performing a full sort operation, we employ Quickselect, an efficient selection algorithm that finds the median with lower computational overhead. This ensures that the filtering step remains stable under varying network conditions. By selecting the median from DOFFSET,i, the algorithm ensures that the time offset correction, denoted as DMIN, remains robust against extreme deviations. The system clock is then updated based on DMIN through update_clock, and the process is repeated continuously. This approach accelerates the synchronization process by directly applying the offset-based DMIN to the system clock rather than indirectly updating through skew or drift estimation.

To quantitatively evaluate the effectiveness of the proposed time synchronization method in reducing the time difference between two nodes, we compared it to a pure hard update approach. The analysis consists of three steps: first, we define the time model of the beacon frame transmitted from the AP; second, we construct a mathematical model of direct BF-based time updating, which serves as a baseline approach; and third, we analyze how the proposed method improves synchronization stability and precision. We define a random variable for the i-th beacon frame reception time from the AP as Xi. The node’s reception outcome is represented as a binary random variable Wi, where reception failure and success are defined as P(W=0)=p and P(W=1)=q, respectively. The received time is modeled as:

Υi=Xi−ti.(1)

The most recent valid received time at the node, incorporating reception success probability, is defined as:

Υi∗=Φ(Υ1,W1,Υ2,W2,⋯,Υi,Wi).(2)

For a given sequence of received time values, the expected latest valid time error is derived as:

E[Υi∗]=p(E[Υi]+qE[Υi−1]+q2E[Υi−2]+⋯+qi−1E[Υ1])=pE[Υ](1+q+q2+⋯+qi−1)≈p1−qi1−qE[Υ]=E[Υ].(3)

The inter-node time difference is then given by:

Z=Xnode1−Xnode2=Υnode1−Υnode2.(4)

To compare the variance reduction effect of the proposed method, we analyze the median-based filtering process. The median estimation follows:

u¯={Υm′,if n is odd,n=2m+112(Υj′+Υm+1′),if n is even,n=2m,(5)

where Υm′ is target time to synchronize, and leads to:

E[Υm′]=12E[(Υm′+Υm+1′)]=12(E[Υm′]+E[Υm+1′])=E[Υm′].(6)

Given that the received time errors Υi and Υi′ are assumed to follow a normal distribution, the variance σ′ of the median-based filtering system is approximated as:

σ2 ′=18mf(u¯)2=πσ24m≈π32σ2.(7)

As a result, the proposed system reduces time error variance to about fracπ32 of the baseline hard update with m=16 sample size. Retaining the offset sample set {DOFFSET,i}, the median-based correction Dmin (or u¯), and the filtering window m defined, we now incorporate these same filtered samples into our MLE approach for stable stage (Section 3.3). The adoption of Quickselect enhances filtering efficiency by significantly reducing computational complexity. Instead of sorting the entire dataset, Quickselect finds the median in expected O(N) time, allowing fast convergence to a stable offset estimation. This approach ensures that unstable samples are quickly discarded while still achieving a precise clock. Although this method does not achieve the ultra-low error margins of MLE-based methods (e.g., 10 µs error range), it provides a practical balance between fast synchronization and stability, typically achieving a 30 µs error margin while maintaining real-time adaptability.

3.3 MLE-Based Estimation and Adaptive Clock Correction

To enhance synchronization accuracy in one-way communication environments, we apply Maximum Likelihood Estimation (MLE) to estimate both the clock offset and clock skew. In dynamic wireless networks, the observed timing offset between the access point (AP) and receiving node is influenced not only by the true clock difference but also by stochastic transmission delays, which vary due to channel conditions and system load.

Building on the median-filtered samples Dmin and sample indices i from Section 3.2, we refine the offset representation by modeling the network delay di as a Gaussian variable, ensuring a seamless transition to the MLE-based estimation stage. Let TAP,i denote the timestamp embedded in the i-th beacon frame from the AP, and TLOCAL,i the corresponding reception timestamp at the node. The observed offset is expressed as:

DOFFSET,i=TLOCAL,i−TAP,i.(8)

This offset includes both the actual clock offset θ and a variable network-induced delay di, modeled as a Gaussian random variable:

DOFFSET,i=θ+di,di∼𝒩(µd,σd2).(9)

Given a collection of such samples, we estimate the optimal offset θ^MLE by maximizing the likelihood function, which leads to the closed-form estimator:

θ^MLE=1N∑i=1NDOFFSET,i.(10)

To further track the clock skew ϕ, we employ a time-differential method based on successive offset changes:

ϕ^=1N−1∑i=1N−1DOFFSET,i+1−DOFFSET,iTAP,i+1−TAP,i.(11)

Unlike static averaging, this method allows for continuous adaptation, making it suitable for environments with fluctuating delay and mobility. The estimated θ^MLE and ϕ^ are then used to correct the local system clock with high precision. In practice, the MLE-estimated offset θ^MLE is applied in a single step or gradually as a slew correction with the estimated skew ϕ^ to adjust the system clock.

Once a rapid convergence is achieved through the initial hard update mechanism described earlier, the synchronization process transitions into this MLE-based estimation stage. In this stage, adaptive sampling and lightweight filtering are applied to mitigate transient delay fluctuations, and clock correction is performed gradually to ensure smooth tracking of the reference time. This approach contributes to overall stability and robustness of the synchronization system under real-world wireless dynamics.

4  Performance Evaluation

In this section, we compare the synchronization performance of WMC with two approaches; one based on a one-way synchronization method using an MLE-based hard update, and the other based on a two-way synchronization method implemented by Chrony. We employ a WLAN network interface card (NIC) attached to an access point (AP), serving as a low-quality clock source. Two single-board computers (SBCs), suitable for deployment on unmanned aerial vehicles (UAVs), are equipped with identical NICs and act as client nodes. The client devices are two Odroid XU4 boards running Ubuntu 18.04 with Linux kernel 4.14. The network driver is based on the RTL8812AU chipset. All synchronization schemes (WMC, MLE, and Chrony) are identically deployed on both devices. To evaluate timing accuracy, we measure the output pulses generated by the pps_gen_gpio driver and emitted through general purpose input/output (GPIO) pins, using a Tektronix TBS1102B-EDU digital oscilloscope, which provides a sample rate of 2 GS/s via two channels. The oscilloscope captures the pulses from the two clients after synchronization is applied. We analyze the offset data during the synchronization process and verify the timing error by comparing the output clock pulses between the two clients as observed on the oscilloscope.

Any packet transmission-based scheme inherently incurs overhead. Data rates must be considered for practical VANET deployment. Therefore, we present each estimated data rate in its formulated expression along with practical parameter ranges. The data rate of Chrony (RChrony) can be expressed as follows:

RChrony=2⋅LntpTpolling,(12)

where 2⋅Lntp is the packet size for two-way NTP exchanges and Tpolling is the polling interval. Similarly, the data rate of WMC (RWMC) also can be written as follows:

RWMC=α⋅LbeaconTbeacon,(13)

where Lbeacon is the size of beacon frame for one-way synchronization, Tbeacon is beacon interval,and α∈[0,1] is reception ratio. According to these parameters, the practical data rate is summarized in Table 2, and the estimated data rate (at α=0.5) is negligibly small.

4.1 Clock Offset Analysis in the Synchronization Process

The clock offset refers to the time difference between two devices for the same nominal second, expressed as Cc−Cs. However, in synchronization processes such as NTP, PTP, or Chrony, it is the client that corrects the skew and drift. Thus, the offset can be more precisely defined as the difference between the reception time at the client tirx,c and the transmission time at the server titx,s. Based on the timing messages received by the client, offset samples are collected and used as parameters to operate the schemes proposed in Section 3. Accordingly, the variation of the offset becomes one of the most critical values in the synchronization process. We compare the offset pattern of WMC, a one-way synchronization method, with Chrony, a state-of-the-art two-way synchronization technique, as shown in Fig. 3. We define the first 10 minutes after the execution of the synchronization driver as the initial stage, during which we log the offset values of both WMC and Chrony. Since each raw offset sample is discarded by filters or diluted into mean or variance, the tendency of offset is more informative than the raw values themselves. Thus, we apply logistic regression based on a sigmoid function to the offset pattern, as shown in Fig. 3. The y-axis represents the normalized offset from the regression fit. The WMC scheme shows a normalized mean offset of 357.41 µs, whereas Chrony yields a higher initial mean offset of 1558.92 µs. A noteworthy observation is that the offset level reverses significantly between 400 to 500 s after the synchronization process begins. While WMC consistently maintains a lower offset level, Chrony initially exhibits unstable offset values but surpasses WMC in accuracy after 500 s. This behavior indicates that traditional two-way synchronization methods, like Chrony, adopt a conservative correction strategy that is effective not only for direct links but also via large scale network or backbone network. The use of adaptive polling intervals further reflects the design philosophy of NTP-based synchronization. Therefore, in scenarios with direct WLAN AP connections, WMC demonstrates superior performance over the initial stage.

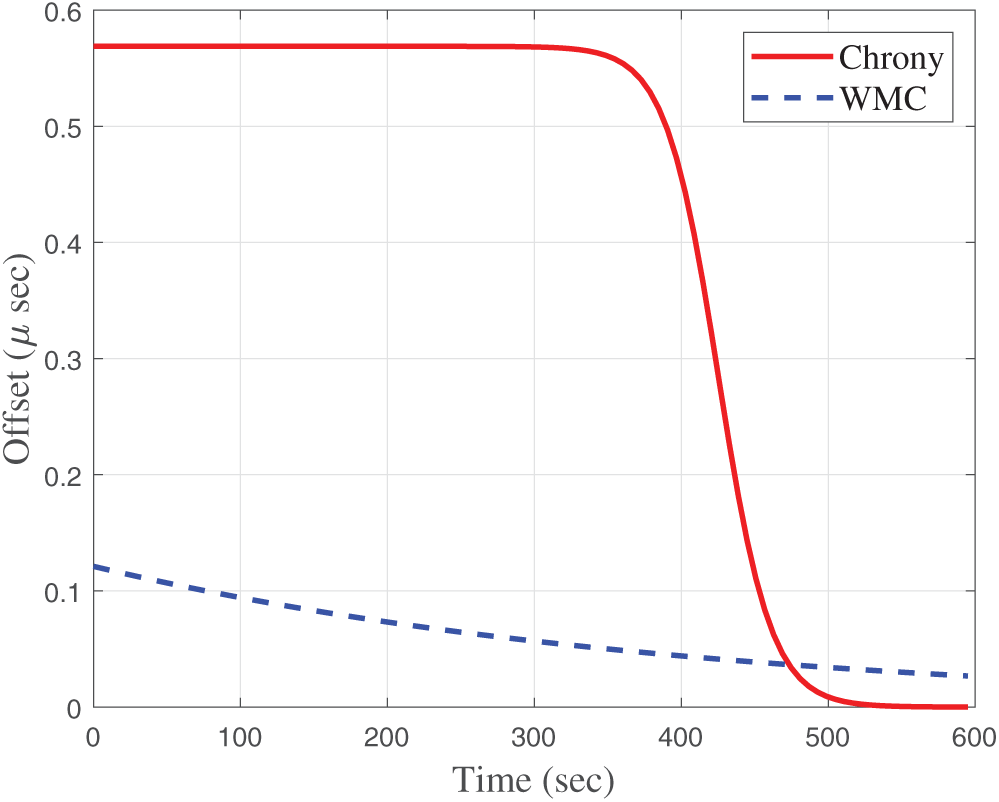
Figure 3: Logistic regression of clock offset during the initial stage

4.2 Clock Synchronization Error Analysis

This subsection analyzes how accurately the two clients were synchronized to the server. For a fair comparison, the proposed WMC scheme is evaluated alongside a one-way synchronization method based on MLE with hard updates and a two-way synchronization method implemented by Chrony. The difference between the clocks of the two clients, Cc1 and Cc2, is defined as the synchronization error and is measured using an oscilloscope. The actual timing precision of the client clocks during the initial phase, corresponding to the offset trend analyzed in Fig. 3, is shown in Fig. 4. Similarly, the error observed among the stable stage is presented in Fig. 5. The synchronization error between the two clients during the initial stage is presented in Fig. 4. Due to the non-dynamic scale limitation of the oscilloscope, the maximum error values were capped at 1000 µs for MLE and 2000 µs for Chrony. As shown in Fig. 4a, Chrony exhibits significantly higher error values in the early part of the initial stage, with a maximum windowed average of 15,190.00 µs and a mean error of 2610.90 µs. In contrast, WMC maintains a much lower error level, with a mean of 47.00 µs and a maximum average of 65.64 µs. MLE also outperforms Chrony, with a mean error of 341.75 µs and a maximum average of 924.83 µs. The corresponding cumulative distribution functions (CDF) in Fig. 4b confirm that WMC achieves the most stable and consistent synchronization, followed by MLE. Chrony’s error distribution is heavily skewed toward higher values, indicating less reliable synchronization during the initial stage. After 400 s, all three methods converge to a similar level of synchronization performance. During the entire experimental period, the clock error results are shown in Fig. 5. The two methods maintain low error levels with reduced fluctuations. For the final 300 s, Chrony achieves a mean error of 46.07 µs and a maximum windowed average of 86.73 µs, while WMC shows the best performance with a mean error of 34.49 µs and a lower maximum average of 48.17 µs. Specifically, compared to Chrony’s stabilization performance (690 s to reach 90% of the steady-state offset), WMC reaches the same 90% level in only 35 s, i.e., 5.1% of the baseline time. These results suggest that switching to an WMC mechanism is also more effective than Chrony in the stable stage.

Figure 4: Clock error during the initial stage

Figure 5: Clock error between two clients

Therefore, the results in Figs. 4 and 5 demonstrate that, in vehicular networks where WLAN-based synchronization is often transient and unstable, a hard update-based multi-stage approach is effective in achieving rapid convergence toward operational synchronization accuracy.

4.3 Vehicle-Based Time Offset Effects on Localization

This subsection presents a simulation-based evaluation examining how time synchronization accuracy influences position estimation performance in vehicular communication systems. The experiment was conducted using the simulation of urban mobility (SUMO) simulator on an urban canyon map with dense building structures, as shown in Fig. 6a. Six and sixty vehicles were deployed on a closed-loop road approximately 1 km in length. The vehicles were allowed to accelerate up to 33.3 m/s, and the loop path was repeated to maintain continuous motion, resulting in a consistent trajectory illustrated in Fig. 6b. Within a general cooperative localization scenario [19,20], local position estimation is modeled as a Gaussian distribution such that P(|X|>0.1 m)<0.01. Each vehicle’s position was recorded using ground truth (GT) data, which were not available to the vehicle themselves, and distributed localization was modeled by assuming that the position of a reference vehicle (vehicle A) was shared with other vehicles as an input parameter for global estimation. In this context, we analyze the impact of time synchronization at the infrastructure level on the performance of vehicular localization systems. Two different clock offset correction methods were applied: Chrony and WMC (vehicles B and C). Localization accuracy was evaluated by computing the Fréchet distance between the GT trajectory and the offset-corrected trajectories. As shown in Fig. 7, Chrony resulted in a maximum error of 0.5870 m, with a mean of 0.0697 m and a standard deviation of 0.0854 m. In contrast, WMC significantly improved the accuracy, achieving a maximum error of only 0.1516 m, a mean of 0.0429 m, and a standard deviation of 0.0235 m. To illustrate the performance differences under various synchronization stages, two sample time windows were analyzed. In the early stage, shown in Fig. 8a, the position error in Chrony exceeded 0.4 m, while WMC reduced this to less than 10% of that error. During the stable stage (Fig. 8b), however, the difference between the two methods became less dominant, suggesting that the benefit of WMC is most significant during initial synchronization periods. These results collectively confirm that time synchronization plays a critical role in high-precision distributed localization, particularly in the early phases of cooperative motion. Meanwhile, the case with 60 nodes is shown in Fig. 8c and 8d. Chrony experienced a maximum localization error of 1.5483 m due to the increased packet exchanges, whereas that of WMC remained low at 0.1282 m.

Figure 6: Simulation environment (SUMO)

Figure 7: Fréchet distance between ground truth and offset trajectories

Figure 8: Positional estimation under different synchronization stages (6/60 vehicles)

5  Conclusion

To provision emergency time synchronization in vehicular networks where primary clock sources may become unavailable, we proposed WMC, a one-way time synchronization method based on WLAN broadcasts. For the design of WMC, we analyzed the timing uncertainty caused by the departure of beacon frames from the server and their arrival at each individual client, dividing the process into an initial stage and a stable stage. In the initial stage, we proposed an approach that reflects the effects of beacon sequence omissions and reception delay variation. For the stable stage, we applied a hard update mechanism based on Maximum Likelihood Estimation (MLE), one of the most widely used techniques in time synchronization. Experimental results show that WMC reduces convergence time more effectively than Chrony and MLE-based hard updates under initial conditions. Furthermore, the transition to MLE in the stable stage achieves a synchronization accuracy of 34.49 µs, demonstrating a 33.6% improvement over Chrony’s 46.07 µs. The results of the synchronization methods were applied to the localization application in the SUMO simulation, where synchronization was shared from a reference vehicle. Compared to Chrony, the proposed method achieved an average improvement of 38.5% and up to 74.2% at peak.

As future work, we plan to investigate how WMC can complement widely used synchronization protocols such as Chrony and the Precision Time Protocol (PTP) in a hybrid or cooperative synchronization framework.

Acknowledgement: We would like to extend our sincere appreciation to the editor and reviewers for their valuable feedback and constructive comments, which greatly improved the quality of this paper.

Funding Statement: This work was supported by Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korea government (MOTIE) (No. 20224B10300090) and also supported by the MSIT (Ministry of Science and ICT), Republic of Korea, under the ITRC (Information Technology Research Center) support program (IITP-2025-RS-2021-II211835) supervised by the IITP (Institute of Information & Communications Technology Planning & Evaluation).

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Hyeontae Joo and Hwangnam Kim; methodology, Hyeontae Joo and Hwangnam Kim; software, Hyeontae Joo and Kiseok Kim; validation, Hyeontae Joo, Kiseok Kim and Hwangnam Kim; formal analysis, Hyeontae Joo and Sangmin Lee; investigation, Hyeontae Joo and Kiseok Kim; resources, Hyeontae Joo; data curation, Hyeontae Joo and Sangmin Lee; writing—original draft preparation, Hyeontae Joo, Sangmin Lee, kiseok Kim and Hwangnam Kim; writing—review and editing, Hyeontae Joo and Hwangnam Kim; visualization, Hyeontae Joo; supervision, Hwangnam Kim; project administration, Hwangnam Kim; funding acquisition, Hwangnam Kim. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data sharing not applicable.

Ethics Approval: This study did not involve human participants or animal subjects. Ethical approval is not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Romanov AM, Gringoli F, Sikora A. A precise synchronization method for future wireless TSN networks. IEEE Trans Ind Inform. 2020;17(5):3682–92. doi:10.1109/tii.2020.3017016. [Google Scholar] [CrossRef]

2. Seijo O, Lopez-Fernandez JA, Val I. w-SHARP: implementation of a high-performance wireless time-sensitive network for low latency and ultra-low cycle time industrial applications. IEEE Trans Ind Inform. 2020;17(5):3651–62. doi:10.1109/tii.2020.3007323. [Google Scholar] [CrossRef]

3. Mahmood A, Ashraf MI, Gidlund M, Torsner J, Sachs J. Time synchronization in 5G wireless edge: requirements and solutions for critical-MTC. IEEE Commun Magaz. 2019;57(12):45–51. doi:10.1109/mcom.001.1900379. [Google Scholar] [CrossRef]

4. Guo X, Liu K, Meng Z, Li X, Yang J. Pseudolite-based lane-level vehicle positioning in highway tunnel. IEEE Trans Intell Transp Syst. 2023;25(2):1612–24. doi:10.1109/tits.2023.3314520. [Google Scholar] [CrossRef]

5. Bozorgzadeh E, Barati H, Barati A. 3DEOR: an opportunity routing protocol using evidence theory appropriate for 3D urban environments in VANETs. IET Commun. 2020;14(22):4022–8. doi:10.1049/iet-com.2020.0473. [Google Scholar] [CrossRef]

6. Azhdari MS, Barati A, Barati H. A cluster-based routing method with authentication capability in Vehicular Ad hoc Networks (VANETs). J Parallel Distrib Comput. 2022;169(12):1–23. doi:10.1016/j.jpdc.2022.06.009. [Google Scholar] [CrossRef]

7. Huan X, Chen W, Wang T, Hu H, Zheng Y. A one-way time synchronization scheme for practical energy-efficient lora network based on reverse asymmetric framework. IEEE Trans Commun. 2023;71(11):6468–81. doi:10.1109/tcomm.2023.3305515. [Google Scholar] [CrossRef]

8. Shi F, Li H, Yang SX, Tuo X, Lin M. Novel maximum likelihood estimation of clock skew in one-way broadcast time synchronization. IEEE Trans Ind Electron. 2019;67(11):9948–57. doi:10.1109/tie.2019.2955427. [Google Scholar] [CrossRef]

9. Wang H, Gong P, Yu F, Li M. Clock offset and skew estimation using hybrid one-way message dissemination and two-way timestamp free synchronization in wireless sensor networks. IEEE Commun Lett. 2020;24(12):2893–7. doi:10.1109/lcomm.2020.3019521. [Google Scholar] [CrossRef]

10. Durairajan R, Mani SK, Sommers J, Barford P. Time’s forgotten: using NTP to understand internet latency. In: Proceedings of the 14th ACM Workshop on Hot Topics in Networks (HotNets-XIV). New York, NY, USA: Association for Computing Machinery; 2015. p. 1–7. doi:10.1145/2834050.2834108. [Google Scholar] [CrossRef]

11. Shin M, Park M, Oh D, Kim B, Lee J. Clock synchronization for one-way delay measurement: a survey. In: Kim Th, Adeli H, Robles RJ, Balitanas M, editors. Advanced communication and networking. ACN 2011. Communications in computer and information science. Vol. 199. Berlin/Heidelberg: Springer; 2011. p. 1–10. doi:10.1007/978-3-642-23312-8_1. [Google Scholar] [CrossRef]

12. Lévesque M, Tipper D. A survey of clock synchronization over packet-switched networks. IEEE Commun Surveys Tutorials. 2016;18(4):2926–47. [Google Scholar]

13. Shim H, Joo H, Kim K, Park S, Kim H. Provisioning high-precision clock synchronization between UAVs for low latency networks. IEEE Access. 2024;12:190025–38. doi:10.1109/access.2024.3516856. [Google Scholar] [CrossRef]

14. Wang H, Lu R, Peng Z, Li M. Clock synchronization with partial timestamp information for wireless sensor networks. Signal Process. 2023;209(3):109036. doi:10.1016/j.sigpro.2023.109036. [Google Scholar] [CrossRef]

15. Leng M, Wu YC. Low-complexity maximum-likelihood estimator for clock synchronization of wireless sensor nodes under exponential delays. IEEE Trans Signal Process. 2011;59(10):4860–70. doi:10.1109/tsp.2011.2160857. [Google Scholar] [CrossRef]

16. Guchhait A, Karthik RM. Joint minimum variance unbiased and maximum likelihood estimation of clock offset and skew in one-way packet transmission. In: 2015 IEEE 81st Vehicular Technology Conference (VTC Spring). Glasgow, UK: IEEE; 2015. p. 1–6. doi:10.1109/VTCSpring.2015.7145899. [Google Scholar] [CrossRef]

17. Shi F, Tuo X, Ran L, Ren Z, Yang SX. Fast convergence time synchronization in wireless sensor networks based on average consensus. IEEE Trans Ind Inform. 2019;16(2):1120–9. doi:10.1109/tii.2019.2936518. [Google Scholar] [CrossRef]

18. Wang H, Zou Y, Liu X, Meng Z. A rapid time synchronization scheme using virtual links and maximum consensus for wireless sensor networks. IEEE Internet Things J. 2024;12(3):3318–29. doi:10.1109/jiot.2024.3480331. [Google Scholar] [CrossRef]

19. Yang P, Duan D, Chen C, Cheng X, Yang L. Multi-sensor multi-vehicle (MSMV) localization and mobility tracking for autonomous driving. IEEE Trans Veh Technol. 2020;69(12):14355–64. doi:10.1109/tvt.2020.3031900. [Google Scholar] [CrossRef]

20. Min H, Li Y, Wu X, Wang W, Chen L, Zhao X. A measurement scheduling method for multi-vehicle cooperative localization considering state correlation. Veh Commun. 2023;44(8):100682. doi:10.1016/j.vehcom.2023.100682. [Google Scholar] [CrossRef]