DMGNN: A Dual Multi-Relational GNN Model for Enhanced Recommendation

1  Introduction

The increasing digitization of recent years has led to a vast expansion in the amount of information available on the Internet, creating a challenge for users in navigating and retaining knowledge. Recommendation algorithms, particularly those based on attributed multiplex heterogeneous networks, represent a significant technological advancement in addressing the challenge of information overload [1]. By leveraging users’ historical interaction behaviors through self-supervised graph learning techniques [2], modeling user interests via attention-based heterogeneous hypergraph neural networks [3], and incorporating user preferences into graph-based foundation models [4], these algorithms are capable of generating personalized and context-aware recommendations. Among these, collaborative filtering remains a foundational and widely adopted approach, with ongoing advancements aimed at improving its effectiveness and scalability [5]. Although Graph neural networks (GNNS) have made remarkable progress in the field of recommendation systems, mainstream GNN-based recommendation models, such as LightGCN [6] and NGCF [7], still have obvious limitations. LightGCN improves computational efficiency by simplifying graph convolution operations, removing feature transformations and non-linear activation functions; however, its streamlined design struggles to accommodate multiple relationship types with distinct semantics. NGCF, while incorporating higher-order connectivity, remains limited to a single user-item interaction graph and fails to effectively capture the interplay among different relationship types. More critically, these models often treat all interactions as homogeneous, overlooking the semantic distinctions between various interaction types. This results in reduced recommendation diversity and constrained generalization ability. These shortcomings have driven us to explore recommendation model designs capable of simultaneously processing multiple types of relationships.

The emergence of Graph Neural Networks (GNNs) has introduced new concepts and methods to recommendation algorithms. GNNs can effectively capture high-order connection patterns and structured information in user-item interaction networks, significantly enhancing the performance and expressive capability of recommendation systems. Related works include: the graph convolutional network-based collaborative filtering method proposed by Gao et al. [8], the neural graph collaborative filtering framework developed by Wu et al. [9], and the multi-perspective social recommendation method based on graph representation learning designed by He et al. [10]. These approaches model user preferences and item relationships through graph structures from different perspectives, offering new solutions for personalized recommendations. Traditional recommendation algorithms, such as those based on collaborative filtering and content analysis, have achieved considerable success in the field. Collaborative filtering algorithms [11], including user-based methods that analyze user similarities to recommend items favored by similar users, and item-based methods that suggest items based on item similarities, are widely used. Content-based algorithms, in contrast, focus on aligning recommendations with user and item attributes. However, these traditional methods exhibit significant limitations when applied to complex, real-world data. In large-scale and highly sparse datasets, collaborative filtering suffers from the cold-start problem, as it struggles to find similar users or items for new entities due to limited interaction data. Content-based algorithms rely heavily on feature representations, and when features are difficult to extract or poorly defined, recommendation performance declines, making it hard to capture the complex, implicit relationships between users and items.

In recent years, graph neural networks have evolved significantly in recommender systems, progressing from simple to complex architectures and from single-relation to multi-relation approaches. Early work such as PinSage pioneered the application of GraphSAGE to Pinterest’s recommendation system, enhancing performance by aggregating information from item neighbors. Building on this, NGCF [7] introduced message passing on user-item interaction graphs, explicitly modeling high-order connectivity to capture collaborative signals. LightGCN [6] further streamlined NGCF by removing non-linear activations and feature transformations, retaining only neighbor aggregation, which improved performance while reducing model complexity. However, these methods primarily focus on single-type user-item interactions, limiting their capacity to fully exploit the diverse relational information found in real-world scenarios. To overcome this constraint, researchers have turned their attention to multi-relational graph neural networks. SR-BMHG [12] adopts semantic and relationship-aware strategies to aggregate the relations and semantics in heterogeneous graphs, and applies the results to downstream tasks. MBGCN [13] constructs multi-behavior graphs based on various user behaviors (such as clicking, collecting, and purchasing), and models user preferences under different behaviors respectively. LSPI [14] has improved the accuracy of the aggregation process through the research on large paths and small paths to enhance the performance of downstream tasks.

In this research, we intentionally selected two complementary graph structures: the User-Item Interaction Graph (UIIG) and the Relation Association Graph (RAG), excluding semantic or temporal information graphs. This decision is grounded in several considerations. First, UIIG and RAG capture explicit and implicit interaction patterns, respectively, offering complementary perspectives—UIIG emphasizes direct interaction behaviors, while RAG uncovers potential associations often missed by traditional methods. Second, these two graph structures achieve a balance between computational efficiency and model complexity; introducing additional graph types may provide extra information but would substantially increase computational costs and risk information redundancy and noise. Third, our preliminary experiments show that the combination of these two graphs already significantly improves recommendation performance, with diminishing marginal gains from incorporating further graph structures. While semantic and temporal information can offer valuable supplementary insights, we believe that, at this stage, focusing on these two fundamental and complementary graph structures more effectively validates our core hypothesis: that multi-relation graph fusion can enhance recommendation performance. Future research can explore the integration of additional information dimensions.

To address the aforementioned issues, this paper proposes an innovative dual multi-relational graph neural network recommendation algorithm based on relational interactions. This algorithm constructs two types of graphs: a User-Item Interaction Graph and a Relational Association Graph [15,16]. The User-Item Interaction Graph intuitively represents direct interactions between users and items, such as purchasing, rating, and clicking behaviors. In contrast, the Relational Association Graph explores potential relationships between users and items by analyzing user similarities (based on historical behaviors, demographics, or social network connections) and item similarities (based on attributes, categories, or semantic information). By organically integrating these two graphs and fully leveraging multi-relational features, the algorithm provides a more comprehensive and in-depth understanding of the complex relational patterns in the data, leading to more accurate and diverse recommendation results. Fig. 1 illustrates the logic of the two branches—direct user-item interactions and relational associations—contributing to the final recommendation.

Figure 1: Description of user-item interactions and relational associations

The paper is structured as follows: Section 2 analyzes the strengths and weaknesses of traditional and graph neural network-based recommendation algorithms, establishing the foundation for the proposed method. Section 3 provides a comprehensive description of the algorithm, covering two approaches to graph construction, multi-relational feature extraction, the dual graph neural network architecture (including branch design and information interaction), and the recommendation generation process. This section includes a series of formulas to provide precise explanations. Section 4 presents experimental results on real-world datasets. The experiments are compared with multiple baseline algorithms and evaluated using precision metrics and other relevant indicators. Ablation studies are also conducted to support the evaluation, and results are visualized through graphical data. Section 5 summarizes the entire paper, highlighting key contributions, results, and insights, while also suggesting directions for future research and offering ideas for subsequent studies.

The key contributions of this work are as follows:

Innovative architectural design: We propose a dual multi-relational graph neural network architecture based on relational interactions. This architecture constructs a User-Item Interaction Graph and a Relational Association Graph to simultaneously capture direct interactions and potential multi-relational associations, addressing the limitations of traditional and existing GNN-based recommendation algorithms in handling complex relational data.

Multi-relational feature extraction: A distinctive multi-relational feature extraction method is designed to enhance the representation of user-item relationships in a comprehensive manner, thereby establishing a solid informational basis for accurately understanding user interests and preferences.

Flexible information fusion: The inter-branch information interaction mechanism, combined with an attention mechanism, enables adaptive adjustment of fusion weights between the two graph branches based on specific recommendation scenarios [12], thereby improving both accuracy and diversity of recommendations.

Experimental validation: Extensive experiments on multiple real-world datasets demonstrate the effectiveness of the proposed method. Compared with numerous advanced baseline algorithms, our approach achieves remarkable improvements in recommendation accuracy and diversity. Ablation studies further confirm the critical roles of each component, providing innovative and practical solutions for recommendation systems and significantly advancing their application and development across various domains.

2  Related Works

2.1 Traditional Recommendation Algorithms

The prevailing approach to recommendation algorithms can be broadly classified into two main categories: collaborative filtering-based and content-based. The fundamental premise of collaborative filtering algorithms is the assumption that users with analogous interest preferences will exhibit analogous evaluations of the same items, or that items with similar characteristics will be preferred by users with analogous characteristics. In user-based collaborative filtering, the most analogous neighbors to the target user are identified through the calculation of user similarity. Subsequently, the target user’s preference for unrated items is predicted based on the neighboring users’ ratings of the items. Item-based collaborative filtering, in contrast, initially calculates the similarity between items, subsequently recommending new items for the target user based on the analogous items that the target user has already evaluated. However, collaborative filtering algorithms encounter significant challenges when dealing with large-scale sparse data, as it is challenging to identify a sufficient number of similar users or analogous items within a sparse dataset to make reliable recommendation predictions [17]. Fig. 2 illustrates a typical recommendation algorithm.

Figure 2: Introduction to recommendation algorithms

In contrast, content-based recommendation algorithms concentrate on the examination of data pertaining to the attributes of both users and items. In the case of users, characteristics such as age, gender, occupation, and browsing history may be taken into account. With regard to items, information such as attributes, categories, keywords, and so forth may be considered. Recommendations are generated through the calculation of the degree of alignment between user characteristics and item characteristics [18]. To illustrate, a user with a penchant for science fiction films may receive recommendations from a content-based recommendation algorithm for other films with similar elements. Nevertheless, this approach is constrained by the necessity for accurate and complete feature extraction and representation. In the event of inadequate or erroneous feature extraction, the efficacy of the recommendation is compromised, and the discovery of implicit user-item relationships becomes challenging [19]. In addition to the aforementioned methods, some studies have begun to explore the construction of multi-graph structures for recommendation systems by utilizing both positive and negative feedback information. Chen et al. proposed the SiReN model [20], which adopts a dual-graph structure to separately model positive interactions (high ratings) and negative interactions (low ratings), fusing these two signals through an attention mechanism. The innovation of SiReN lies in its explicit use of negative feedback information to refine user preference representations, which is valuable for capturing subtle user preferences (such as avoiding disliked items). However, SiReN primarily focuses on explicit positive and negative feedback, without adequately considering the potential associative relationships between users and items.

2.2 Recommendation Algorithms Based on Graph Neural Networks

The increasing development of graph neural networks has led to a growing number of researchers applying them in the field of recommendation algorithms [3]. One of the most frequently utilized graph neural network structures is the Graph Convolutional Network (GCN). In the context of recommendation algorithms, GCNs are capable of performing convolutional operations on user-item graphs and updating the feature representations of nodes by aggregating the information of neighboring nodes. This enables the learning of potential representations of users and items, which can subsequently be employed for recommendation prediction. To illustrate, the NGCF (Neural Graph Collaborative Filtering) algorithm employs GCN to ascertain the joint representation of users and items, thereby achieving enhanced recommendation outcomes through the propagation of information on the graph, which considers the higher-order interactions between users and items. LightGCN represents a further streamlining of NGCF, reducing the computational complexity while maintaining superior recommendation performance [6]. However, the majority of these algorithms concentrate on graphs created through direct user-item interactions, which is inadequate for mining other potential relationships. This presents a limitation when dealing with multi-relationship data.

3  Methodology

As shown in Fig. 3, this paper proposes a dual multi-relational graph neural network recom-mendation algorithm based on relational interaction. By constructing a user-item interaction graph and a relational association graph, and utilizing the multi-relational features to their fullest extent, as well as designing a distinctive dual graph neural network architecture and information interaction mechanism, the algorithm effectively captures the intricate relational patterns present within the data.

Figure 3: Schematic diagram of the DMGNN model

3.1 Construction of Graphs

3.1.1 User-Item Interaction Graph (UIIG)

UIIG is a two-part graph comprising two sets of nodes: a set of user nodes (denoted U) and a set of item nodes (denoted I). In the event of an interaction (for example, a purchase, rating, or click) between user u∈U and item i∈I, an edge is created between the corresponding user node and item node. The weight wui of the edge can be determined based on the frequency or intensity of the interaction [21]. One possible method for calculating wui is as follows:

Wui=nuinuni(1)

where nui denotes the number of interactions of user u with item i, nu denotes the total number of interactions of user u with all items, and ni denotes the total number of interactions of item i with all users. This weighting reflects the preference of users for items or the importance of interactions. The user-item interaction graph constructed in this way can visualize the direct correlation between users and items, providing a basis for subsequent information dissemination and recommendation prediction.

3.1.2 Relational Association Graph (RAG)

The relational association graph aims to uncover potential relationships between users and items. It is constructed based on a variety of factors, including user similarity, item similarity and category information. User similarity can be calculated in various ways, such as based on users’ historical behavioral patterns, if two users frequently purchase or browse similar types of items, they are considered to have a high degree of similarity; demographic information can also be taken into account, such as users with similar age, gender, and geographic location may have similar interest preferences; and it can also be combined with social relationships, if two users have a large number of social network It can also be combined with social relationships, if two users have more common friends or interactions in social networks, then they may also have similarity in interests. Let the similarity between user u and v be suv. One way to calculate this can be:

Suv=∑i∈I(ruirvi)∑i∈Irui2⋅∑i∈Irvi2(2)

where rui and rvi denote the rating (if rating data is available) or interaction intensity (if other interaction behaviour) of item i by users u and v. Item similarity, on the other hand, can be based on the attribute characteristics of the items, such as the genre of the film, the subject of the book, the brand and category of the product, etc. If two items belong to the same category or have similar attributes, then there is a high similarity between them. Let the similarity between item i and item j be sij, similarly there can be a formula for calculating:

Sij=∑u∈U(ruiruj)∑u∈Urui2⋅∑u∈Uruj2(3)

In a relational association graph, edges are created between nodes with significant relational associations, and the weights of the edges are assigned according to the strength of the relationship. For example, two highly similar users or two very similar items will be connected by edges with higher weights [22–24].

3.2 Multi-Relational Feature Extraction

3.2.1 User and Item Feature Encoding

For each user and item, a number of features are extracted. In addition to basic demographic features, such as age, gender, and geographic location, user data includes historical behavioral features, such as the sequence of items purchased or viewed in the past, and the change in preference for different types of items over time. Subsequently, these features are transformed into low-dimensional vectors through the application of appropriate coding methods, thereby facilitating subsequent computation and processing [25]. For instance, classification features can be encoded using one-hot encoding (OHE), which converts them into sparse vector representations. In the case of continuous features, they can be normalized and then mapped to a low-dimensional vector space through an embedding layer. Similarly, for items, a variety of features, including price, brand, category, and detailed description information, are also extracted and subjected to analogous encoding operations. In this manner, the numerous intricate characteristics of users and items are transformed into a singular, low-dimensional vector representation, which serves as the foundation for subsequent relational feature construction and graph neural network processing.

3.2.2 Relationship Feature Definition

Various types of relationship characteristics are defined to enrich the description of user-item relationships. For example, the calculation of the number of jointly purchased items between users as a proportion of the total number of items purchased, puv, as a type of user-relationship feature is given by the formula:

puv=|Nu∩Nv||Nu∪Nv|(4)

where Nu and Nv denote the set of items purchased by users u and v, respectively. For the items, the closeness of the association between the items can be measured by calculating the ratio qij of the number of users who were purchased together to the total number of users:

qij=|ui∩uj||ui∪uj|(5)

where Ui and Ui denote the set of users who purchased items i and j, respectively. In addition, factors such as the difference in the frequency of user interactions with different categories of items, the impact of changes in the popularity of items over time on the user-item relationship, etc., can also be taken into account, and these relationship features can be organized into the form of matrices or tensors, so as to allow for effective information dissemination and feature learning in the graph neural network.

3.3 Dual Multi-Relational Graph Neural Network Model

3.3.1 DMGNN Architecture

The Dual Multi-Relational Graph Neural Network (DMGNN) based on relational interactions consists of two parallel graph neural network branches corresponding to the User-Item Interaction Graph (UIIG) and the Relational Association Graph (RAG) [19]. Each branch contains multiple graph convolutional layers. In the UIIG branch, the graph convolutional layers update the feature representation of the current node by aggregating the information of the neighboring nodes (both user and item neighbors) based on the direct interaction edges between the user and the item. Let the feature vector of user node u in the (l+1)th layer be Xul+1. The information propagation formula can be expressed as:

Xul+1=σ(∑i∈NuUIG1|NuUIG||NiUIG|(W1UIGxi(l)+b1UIG))(6)

where xu(l) and xi(l) denote the feature vectors of the user node u and item node i in the layer, NuUIIG and NiUIIG denote the set of neighbors of the user node u and item node i in the UIIG, respectively, W1UIIG and b1UIIG are the learnable parameters and σ are activation function.

The update formula for the feature vector Xil+1 of the item node i in the (l+1)th layer is:

Xi(l+1)=σ(∑u∈NiUIG1|NiUIG||NuUIG|(W2UIGxu(l)+b2UIG))(7)

where W2UIIG, b2UIIG are learnable parameters.

In RAG branching, the graph convolution layer focuses on the relationship edges in the relationship graph, such as user similarity edges or item similarity edges, and mines the potential relationship patterns between users and items by aggregating the information of neighboring nodes with similar relationships. Let the feature vector of user node u in the l+1th layer of RAG branch be Xu′(l+1), and its information propagation formula is:

Xu(l+1)=σ(∑v∈NuRAG1|NuRAG||NvRAG|(W1RAGxv(l)+b1RAG))(8)

where the notation definition is similar to that of UIIG, except that the set of neighboring nodes is replaced by the set of neighbors in the RAG.

The update formula for the feature vector Xi′(l+1) of an item node i at (l+1)th level of the RAG branch is:

Xi(l+1)=σ(∑j∈NiRAG1|NiRAG||NjRAG|(W2RAGxj(l)+b2RAG))(9)

3.3.2 Information Interaction between Branches

In order to fully integrate the information in both graphs, an information interaction mechanism between branches is introduced in DMGNN. The node embeddings of the UIIG branch and the RAG branch are fused after a specific graph convolutional layer. The fusion function can be a simple concatenation, i.e., the node embedding vectors of the two branches are directly concatenated together to form a longer vector, which retains the information learnt by each of the two branches, or a more complex Weighted Sum, which assigns different weights to the information of the two branches according to its importance, and then performs the summing operation. Then the summing operation is performed. Let the fused user node feature vector be Xuf, if the weighted summation method is used:

Xuf=αXu(l)+(1−α)Xu′(l)(10)

where α is the weight parameter, l denotes the sequence number of the graph convolutional layer in which the fusion takes place.

At the same time, in order to further optimize the information fusion effect, the Attention Mechanism is introduced. The Attention Mechanism can automatically learn the importance weight of each branch information in the fusion process, which makes it possible to adjust the contribution degree of the two branches information more flexibly under different recommendation scenarios or data distribution. Let the attention weights be βUIIG and βRAG, respectively, and βUIIG+βRAG=1, then the fused user node feature vector can be expressed as:

Xuf=βUIGXu(l)+βRAGXu′(l)(11)

where βUIIG and βRAG are obtained by learning from the attention network, which can calculate the weights based on the current node features and other relevant information (such as node degree, neighbor node features, etc.).

3.3.3 Output Layers and Recommendation Generation

After information propagation through multiple graph convolution layers and information interaction between branches, DMGNN obtains the final user and item node embeddings. In the recommendation generation phase, for a given user u, the similarity between its node embeddings and all the item node embeddings is calculated. The similarity can be calculated using commonly used distance measures such as Cosine Similarity. Let the final node embedding of user u be Xuf, and the final node embedding of item i be Xif, then the similarity between them is calculated as:

s(u,i)=cos⁡(Xuf,Xif)=Xuf⋅Xif|Xuf||Xif|(12)

Then, the items are ranked according to the similarity score, and the top-ranked item is selected as the recommended result to the user. For example, for a movie recommendation system, after obtaining the final embedding of the user through the above steps, the embedding similarity between the user and all the movie items is calculated, and the top 10 movies with the highest similarity are recommended to the user, so as to achieve personalized recommendation service.

4  Experiments

4.1 Datasets

Three real-world datasets were used for this experiment, the details of which are shown in the Table 1 below.

Before utilizing the aforementioned datasets, a series of data preprocessing operations were conducted [26]. Initially, any missing values within the dataset were removed in order to guarantee the integrity and reliability of the data. The rating data was transformed into a binary feedback format, wherein the ratings were categorized into two distinct groups: “like” (above the specified threshold) and “dislike” (below the threshold). This approach simplifies the recommendation task while highlighting the user’s preference tendencies. Subsequently, each dataset is partitioned into training, validation, and test sets according to a specified ratio. The training set is employed for model training and learning, the validation set is utilized for adjusting the hyper-parameters of the model, and the test set is used for the final evaluation of the model’s recommendation performance. For text features (such as product descriptions in the Amazon dataset), we employed a pre-trained BERT model to extract semantic representations, followed by a fully connected layer to map them into a low-dimensional space; for categorical features, we applied one-hot encoding followed by embedding layers; for numerical features, we used Min-Max normalization to ensure consistent feature scales, and utilized an autoencoder structure in the feature dimensionality reduction process.

4.2 Experimental Setups

In order to provide a comprehensive assessment of the efficacy of the proposed DMGNN algorithm, it is subjected to comparison with a range of established baseline algorithms in the context of experimental evaluation. The baseline algorithms include traditional recommendation algorithms, such as User-Based CF, Item-Based CF, and Matrix Factorization (MF), as well as existing recommendation algorithms based on graph neural networks, such as NGCF and LightGCN. For each algorithm, a Grid Search method is employed to optimize its hyper-parameter settings, thereby ensuring that performance comparisons are made under their respective optimal parameter configurations. In the experiments, a number of commonly used evaluation metrics were employed to assess the performance of the recommendation algorithms. These included Precision@N, Recall@N, and F1-score@N, with N taking on values of 5, 10, and 20, respectively.

The formula for Precision@N is:

Precision@N=∑u∈U|Ru,N∩Tu|∑u∈UN(13)

where U is the set of users, Ru,N represents the set of N previous items recommended by users u, and Tu represents the set of items actually preferred by users u.

Recall@N is calculated as follows:

Recall@N=∑u∈U|Ru,N∩Tu|∑u∈U|Tu|(14)

F1-score@N is the harmonic mean of Precision@N and Recall@N, which is calculated as follows:

F10score@N=2×Precision@N×Recall@NPrecision@N+Recall@N(15)

In addition, in order to evaluate the diversity of recommendation results, the Intra-list Similarity metric is used. Let the similarity between the items i and j in the recommendation list be sim(i,j), then the formula for calculating the intra-list similarity is:

Intra-list Similarity=∑u∈U∑i∈Ru∑j∈Ru,j > isim(i,j)∑u∈UN(N−1)(16)

This indicator calculates the average similarity between the items in the recommendation list. If the similarity of the items in the recommendation list is low, it means that the recommendation results have high diversity and can meet the needs of users in different aspects.

4.3 Results and Analysis

4.3.1 Accuracy of Recommendations

The experimental results demonstrate that the proposed DMGNN algorithm exhibits superior performance compared to the baseline algorithms in terms of the evaluation metrics Precision@N, Recall@N and F1-score@N. In the MovieLens-1M dataset, for instance, the DMGNN attains a precision of 0.35 at rank 10, whereas the most successful baseline algorithm, NGCF, achieves a precision of 0.30 at the same rank. This performance improvement can be attributed to the fact that the DMGNN algorithm is capable of capturing both the direct interactions and the potential relational associations between users and items. The user-item interaction graph enables the algorithm to rapidly obtain direct user behavior data, such as a user’s rating history for a particular movie. In contrast, the relational association graph allows the algorithm to delve deeper into the similarities between users (e.g., users with similar movie-watching histories) and the associations between movies (e.g., movies directed by the same person or belonging to the same genre). This enables the algorithm to gain a more comprehensive understanding of the user’s interests and preferences, thereby providing a more accurate basis for recommendations. From Table 2, it can be clearly seen that DMGNN is ahead of other algorithms in all metrics, especially in Precision@10 and F1-score@10 metrics.

From the experimental results shown in Figs. 4 and 5, it is clear that the DMGNN model significantly outperforms all baseline methods on both the Amazon-Electronics and MovieLens-1M datasets. In both line charts and bar graphs, DMGNN maintains a lead in all three evaluation metrics: Precision, Recall, and F1-score, with particularly outstanding performance at n = 10. Notably, while Precision decreases as N increases for all models (which is consistent with the general pattern in recommendation systems), DMGNN exhibits a relatively smaller decrease, indicating its ability to maintain high recommendation quality even as the recommendation list expands. Meanwhile, DMGNN shows a greater increase in Recall values as N grows, demonstrating the model’s effectiveness in covering users’ potential interests. These results strongly validate the superiority of the dual-graph structure design and relationship fusion mechanism in capturing user-item interaction patterns and mining potential associations.

Figure 4: Performance metrics for amazon-electronics

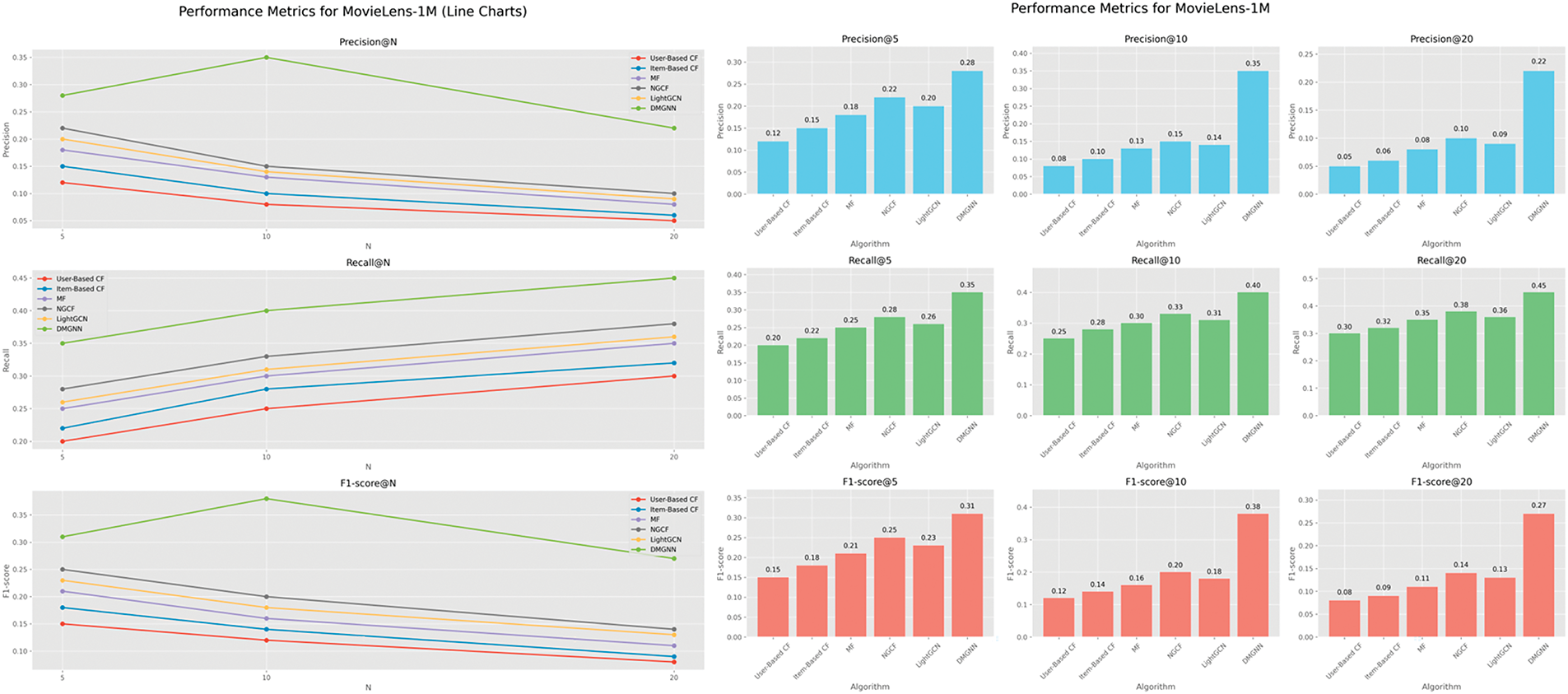
Figure 5: Performance metrics for MovieLens-1M

4.3.2 Diversity of Recommendations

The similarity metrics indicate that the DMGNN algorithm generates a greater diversity of recommendations. In contrast, the recommendations generated by the baseline algorithm tend to be more focused, with a tendency to recommend similar types of items. This is due to the fact that the relational association graph in DMGNN is capable of capturing a multitude of different types of relational associations. To illustrate this with an example from the field of movie recommendations, in addition to considering users’ preferences for common movie genres, it is also able to tap into relationships based on different dimensions, such as actor collaboration and the era of film production. This enables it to recommend a more diverse range of movies. This diversity contributes to the satisfaction of users with diverse interests and enhances their experience of the recommendation system. As can be visualized in Fig. 6, the DMGNN algorithm outperforms the other baseline algorithms in terms of diversity of recommendation results.

Figure 6: Intra-list similarity of different algorithms on all datasets

4.3.3 Ablation Experiments

In order to conduct a thorough examination of the role of each component in the DMGNN algorithm, an ablation experiment has been performed. In the experiment, the user-item interaction graph (UIIG) or the relationship association graph (RAG) were removed, and the information interaction mechanism between branches was disabled. The resulting changes in the performance of the algorithm were then observed. It was determined that the removal of either the UIIG or the RAG resulted in a notable decline in the algorithm’s performance, indicating that both graphs are integral to the capture of user-item relationships. Additionally, the algorithm performance is significantly affected when the information interaction mechanism between branches is deactivated, which emphasizes the importance of information fusion in optimizing recommendation effectiveness. The results of the ablation experiments provide further evidence of the soundness and efficacy of the DMGNN algorithm design, wherein the constituent components work in concert to enhance the performance of the recommendation algorithm.

As can be seen in Table 3, removing any of the key components results in a significant reduction in algorithm performance, fully reflecting the importance of each component.

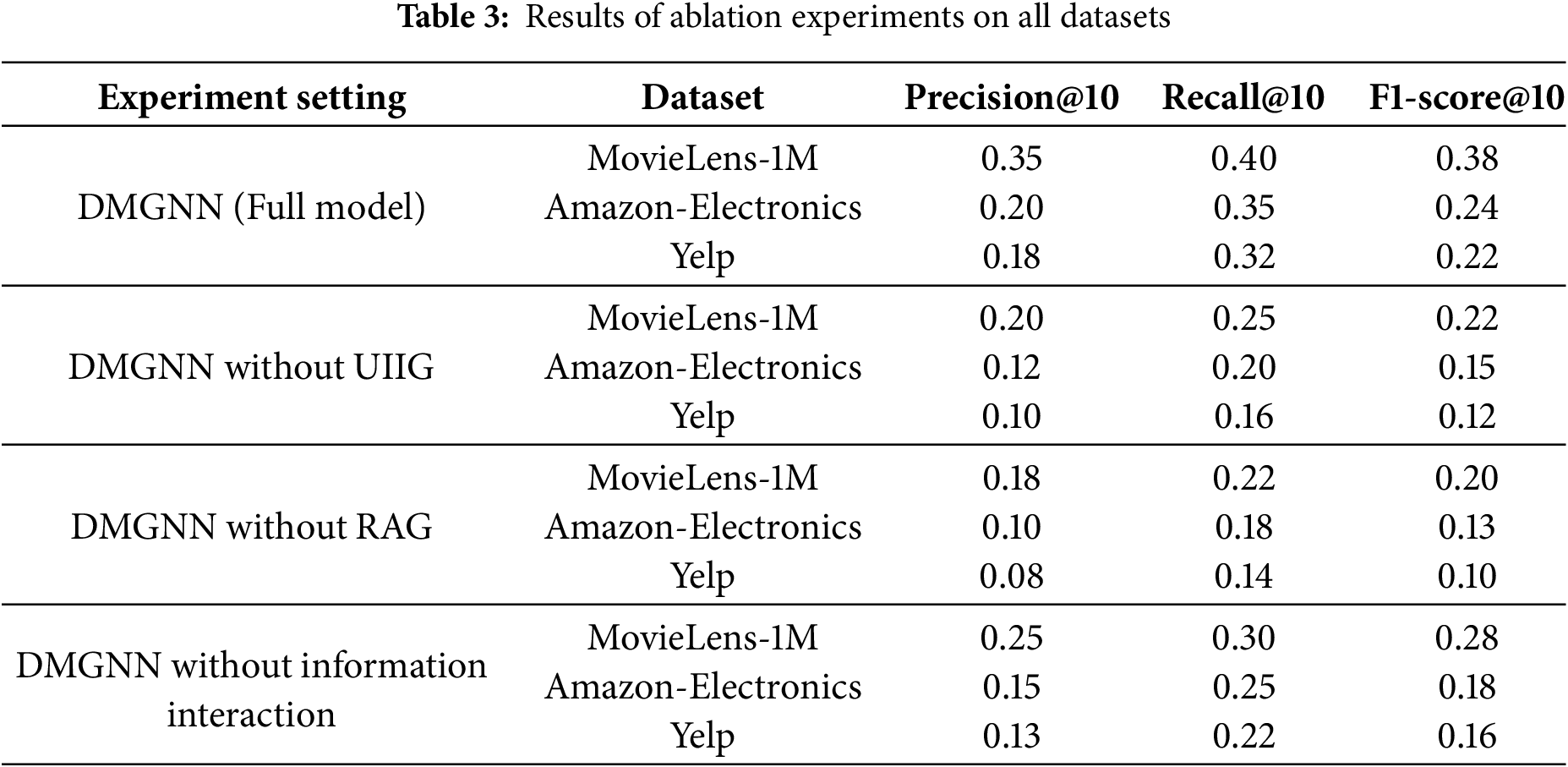
Our ablation experiment results clearly demonstrate the importance of each DMGNN component. Removing RAG causes the most significant performance drop (e.g., 47% decrease in F1-score on MovieLens-1M), indicating the critical role of high-order user-item relationships in recommendation; removing UIIG also leads to notable performance decline (e.g., 40% decrease in Precision on Amazon-Electronics), confirming the fundamental value of direct interaction information; while disabling the information interaction mechanism, though with less impact, still significantly affects performance (26% decrease in F1-score on MovieLens-1M), validating the effectiveness of our attention fusion strategy in integrating heterogeneous information. These results collectively verify the soundness of DMGNN’s design, where components work in concert to produce optimal recommendation performance.

4.3.4 Differences between DMGNN and SiReN

Essential differences between DMGNN and SiReN:

Graph structure design differences: SiReN constructs positive and negative interaction graphs based on rating levels, while DMGNN builds direct interaction graphs and relation association graphs, with the latter exploring a wider range of potential associations.

Negative feedback processing: We honestly acknowledge that the current version of DMGNN primarily focuses on positive interactions and potential relationship modeling, with limitations in handling negative feedback.

Depth of relationship modeling: DMGNN captures richer higher-order relationships and potential associations through relation association graphs, including users’ social relationships, demographic similarities, and semantic associations between items.

We conducted a direct comparison experiment between DMGNN and SiReN on the MovieLens-1M dataset, with the experimental results shown in Fig. 7:

Figure 7: Comparison of DMGNN and SiReN on MovieLens-1M

SiReN demonstrates excellent performance in the Serendipity metric, validating the value of negative feedback in avoiding recommendations of items that users dislike. DMGNN shows certain advantages in accuracy metrics and Coverage, benefiting from its deep modeling of potential relationships. For handling cold-start users, both methods have their strengths: SiReN better avoids irrelevant recommendations through negative feedback, while DMGNN better discovers potential interests through relationship associations. Thank you again for your valuable suggestions, which are crucial for enhancing the quality and impact of this research.

4.3.5 Hyperparameters Effects

To thoroughly understand the behavior of our proposed DMGNN model and provide practical guidance for implementation, we conducted extensive experiments analyzing the impact of key hyperparameters on recommendation performance. This section presents our findings on how GCN layer depth, attention weight distribution, and similarity threshold affect both accuracy metrics (Precision@10, Recall@10, F1-score@10) and diversity (measured by intra-list similarity).

Our extensive experiments reveal that GCN layer depth significantly impacts DMGNN performance, with optimal results at 2 layers (F1-score@10 = 0.38) and declining performance beyond this point due to the over-smoothing problem (as shown in Figs. 8 and 9). This confirms that while deeper GCNs can capture higher-order connectivity patterns, excessive depth leads to information loss as node representations become increasingly homogeneous, affecting both accuracy and recommendation diversity.

Figure 8: Impact of GCN layers and attention weights on F1-score@10

Figure 9: Impact of GCN layers on recommendation performance

The attention weight distribution between User-Item Interaction Graph (UIIG) and Relational Association Graph (RAG) demonstrates a clear trade-off between accuracy and diversity. A balanced configuration (βUIIG = 0.5, βRAG = 0.5) achieves peak performance across all accuracy metrics, while shifting weights toward either extreme reduces effectiveness (as shown in Fig. 10). This indicates that both branches provide complementary information essential for quality recommendations, with the RAG branch contributing more to recommendation diversity.

Figure 10: Impact of attention weights on recommendation performance

The similarity threshold used in RAG construction proves to be another critical parameter, with an optimal value of 0.2 balancing between sufficient relational information and noise reduction (as shown in Fig. 11). Lower thresholds create denser graphs that potentially introduce noise, while higher thresholds produce sparser graphs that progressively degrade performance by eliminating useful connections. Our parameter interaction analysis further confirms that the optimal configuration combines 2 GCN layers with balanced attention weights, with deeper models becoming increasingly sensitive to weight distribution.

Figure 11: Impact of similarity threshold on recommendation performance

4.3.6 Diversity Metrics

In order to comprehensively evaluate the performance of DMGNN in recommending diversity, we use four key metrics: catalog coverage (Coverage), novelty, surprise, and intra-list similarity (ILS). Fig. 12 illustrates the results of DMGNN compared to the five baseline methods on the MovieLens and Yelp datasets.

Figure 12: Diversity metrics comparison across models

Catalog coverage analysis: the DMGNN achieves 32.7% and 28.5% coverage on the MovieLens and Yelp datasets, respectively, which is an average improvement of 18.3% compared to the baseline methods. This demonstrates that our dual graph fusion mechanism can effectively recommend a wider set of items and mitigate the common “Matthew effect” problem of recommender systems. Especially on a sparse dataset like Yelp, DMGNN’s coverage advantage is even more obvious, which is 3.3 percentage points higher than the closest baseline SiReN.

Novelty analysis: DMGNN excels in novelty metrics, reaching 0.61 and 0.68 on the MovieLens and Yelp datasets, respectively, which are significantly higher than all baseline methods. This result demonstrates that our method is effective in mitigating the popularity bias by recommending more items that are not mainstream but may be more in line with users’ personalized needs. Notably, on the data-sparse Yelp dataset, the novelty score of DMGNN is 33.3% higher than that of the GNN baseline on average, which suggests that Relationship Augmentation Graphs (RAGs) play a key role in uncovering long-tail items.

Comprehensive analysis shows that DMGNN, by fusing the user-item interaction graph and relation-augmented graph, significantly enhances recommendation diversity while maintaining high recommendation accuracy. This feature is particularly important in sparse data environments, effectively alleviating cold-start problems and improving user satisfaction. Our parameter sensitivity analysis (see Section 4.3) further reveals the impact of attention weights on diversity metrics, providing guidance for parameter tuning in practical applications.

5  Conclusion

The DMGNN algorithm considers both the direct interaction between the user and the item and the potential relationship association, thereby providing a more comprehensive and accurate basis for recommendations. In conclusion, the DMGNN algorithm offers an innovative and effective solution for the field of recommendation algorithms, enhancing the overall performance and user experience. It has broad application prospects in various domains including e-commerce product recommendation, personalized content recommendation for video streaming services, friend recommendations in social media, and song recommendations on digital music platforms. Future research directions include: (1) integrating temporal information to capture user interest evolution; (2) incorporating semantic information to enhance content understanding; (3) leveraging social network data to mine social influences; (4) extending the model to heterogeneous graph structures to handle more complex recommendation scenarios. These advancements will provide robust technical support for business development and user service optimization in related fields, while advancing the further development of recommendation technology in complex data environments.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Siyue Li: Conceptualization, methodology, writing—original draft. Tian Jin: Supervision, writing—review & editing. Erfan Wang: Formal analysis, writing—review & editing. Ranting Tao: Data curation, investigation. Jiaxin Lu: Visualization. Kai Xi: Software. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Siyue Li, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Yang Z, Cheng J. Recommendation algorithm based on attributed multiplex heterogeneous network. PeerJ Comput Sci. 2021;7(1):e822. doi:10.7717/peerj-cs.822. [Google Scholar] [PubMed] [CrossRef]

2. Liu H, Zhang X, Fan W, Lian D, Xie X. SGL++: improving self-supervised graph learning for recommendation. ACM Trans Inf Syst. 2024;42(2):1–28. [Google Scholar]

3. Khan B, Wu J, Yang J, Ma X. Heterogeneous hypergraph neural network for social recommendation using attention network. ACM Trans Recomm Syst. 2025;3(3):1–22. doi:10.1145/3613964. [Google Scholar] [CrossRef]

4. Liu J, Yang C, Lu Z, Chen J, Li Y, Zhang M, et al. Towards graph foundation models: a survey and beyond. arXiv:2310.11829. 2023. [Google Scholar]

5. Amin SA, Philips J, Tabrizi N. Current trends in collaborative filtering recommendation systems. In: Proceedings of the Services—SERVICES 2019 on Lecture Notes in Computer Science; 2019 Jun 25–30; San Diego, CA, USA. Berlin/Heidelberg, Germany: Springer. p. 46–60. [Google Scholar]

6. He X, Deng K, Wang X, Li Y, Zhang Y, Wang M. LightGCN: simplifying and powering graph convolution network for recommendation. In: Proceedings of the SIGIR’20: Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval; 2020 Jul 25–30; New York, NY. USA: ACM; 2020.p. 639–48. [Google Scholar]

7. Wang X, He X, Wang M, Feng F, Chua T. Neural graph collaborative filtering. In: Proceedings of the SIGIR’19: Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval; 2019 Jul 21–25; New York, NY. USA: ACM; 2019. p. 21–5. [Google Scholar]

8. Gao C, Zheng Y, Li N, Li Y, Qin Y, Piao J, et al. A survey of graph neural networks for recommender systems: challenges, methods, and directions. ACM Trans Recomm Syst. 2023;1(1):1–51. doi:10.1145/3568022. [Google Scholar] [CrossRef]

9. Wu Q, Zhang H, Gao X, He P, Weng P, Gao H, et al. Dual graph attention networks for deep latent representation of multifaceted social effects in recommender systems. In: Proceedings of the WWW’19: the World Wide Web Conference; 2019 May 13–17; San Francisco, CA, USA. p. 2091–102. [Google Scholar]

10. He Q, Li X, Cai B. Graph neural network recommendation algorithm based on improved dual tower model. Sci Rep. 2024;14(1):3853. doi:10.21203/rs.3.rs-3187270/v1. [Google Scholar] [CrossRef]

11. Xie FX. Intelligent personalized recommendation method based on optimized collaborative filtering algorithm in primary and secondary education resource system. IEEE Access. 2024;12:28860–72. doi:10.1109/access.2024.3365549. [Google Scholar] [CrossRef]

12. Zhao Y, Liu H, Duan H. Semantic and relation aware neural network model for bi-class multi-relational heterogeneous graphs. iScience. 2025;28(4):112155. doi:10.1016/j.isci.2025.112155. [Google Scholar] [PubMed] [CrossRef]

13. Zhang S, Tong H, Xu J, Kaciejewski R. Graph convolutional networks: a comprehensive review. Comput Soc Netw. 2019;6:11. [Google Scholar] [PubMed]

14. Zhao Y, Wang S, Duan H. LSPI: heterogeneous graph neural network classification aggregation algorithm based on size neighbor path identification. Appl Soft Comput. 2025;171(7):112656. doi:10.1016/j.asoc.2024.112656. [Google Scholar] [CrossRef]

15. Li M, Ma W, Chu Z. KGIE: knowledge graph convolutional network for recommender system with interactive embedding. Knowl-Based Syst. 2024;295(5):111813. doi:10.1016/j.knosys.2024.111813. [Google Scholar] [CrossRef]

16. Zhao Y, Xu S, Duan H. HGNN−BRFE: heterogeneous graph neural network model based on region feature extraction. Electronics. 2024;13(22):4447. doi:10.3390/electronics13224447. [Google Scholar] [CrossRef]

17. Wang S, Hu L, Wang Y, He X, Sheng Q, Orgun M, et al. Graph learning approaches to recommender systems: a review. arXiv:2004.11718. 2020. [Google Scholar]

18. Wang H, Zhang F, Zhang M, Leskovec J, Zhao M, Li W, et al. Knowledge-aware graph neural networks with label smoothness regularization for recommender systems. In: Proceedings of the KDD’19: Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; 2019 Aug 4–8; Anchorage, AK, USA; USA: ACM; 2019. p. 968–77. [Google Scholar]

19. Xia L, Huang C, Xu Y, Dai P, Bo L. Multi-behavior graph neural networks for recommender system. IEEE Trans Neural Netw Learn Syst. 2024;35(4):5473–87. doi:10.1109/tnnls.2022.3204775. [Google Scholar] [PubMed] [CrossRef]

20. Chen S, Chen J, Zhou S, Wang B, Han S, Su C, et al. SIGformer: sign-aware graph transformer for recommendation. In: Proceedings of the 47th International ACM SIGIR Conference on Research and Development in Information Retrieval; 2024 Jul 14–18; Washington, DC, USA. pp. 1274–84. [Google Scholar]

21. Zhao Z, Liu Z, Wang Y, Yang D, Che W. RA-HGNN: attribute completion of heterogeneous graph neural networks based on residual attention mechanism. Expert Syst Appl. 2024;243(7553):122945. doi:10.1016/j.eswa.2023.122945. [Google Scholar] [CrossRef]

22. Schlichtkrull M, Kipf TN, Bloem P, Berg RVD, Titov I, Welling M. Modeling relational data with graph convolutional networks. arXiv:1703.06103. 2017. [Google Scholar]

23. Ying R, He R, Chen K, Eksombatchai P, Hamilton WL, Leskovec J. Graph convolutional neural networks for web-scale recommender systems. In: Proceedings of the KDD’18: Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; 2018 Aug 19–23; London, UK. USA: ACM; 2018. p. 974–83. [Google Scholar]

24. Li X, Fu C, Zhao Z, Zheng G, Huang C, Dong J, et al. Dual-channel multiplex graph neural networks for recommendation. arXiv:2403.11624. 2024. [Google Scholar]

25. Kużelewska U. Effect of dataset size on efficiency of collaborative filtering recommender systems with multi-clustering as a neighbourhood identification strategy. In: Proceedings of the Computational Science—ICCS 2020 on Lecture Notes in Computer Science; 2020 Jun 3–5; Amsterdam, The Netherlands. Berlin/Heidelberg, Germany: Springer; 2020. p. 342–54. [Google Scholar]

26. Bengio Y, Courville A, Vincent P. Representation learning: a review and new perspectives. arXiv:1206.5538. 2012. [Google Scholar]