NTSSA: A Novel Multi-Strategy Enhanced Sparrow Search Algorithm with Northern Goshawk Optimization and Adaptive t-Distribution for Global Optimization

1  Introduction

As optimization problems become increasingly complex, many of them no longer have known polynomial-time algorithms to solve them. Therefore, metaheuristic algorithms are often employed to approximate solutions. Metaheuristic algorithms are optimization methods that perform global search by simulating natural phenomena or biological processes. Metaheuristics often find near-optimal solutions more quickly than exact algorithms. The efficacy of these methodologies has been demonstrated through their successful application in the resolution of complex optimization problems, which are typically challenging to address with precision using conventional methods. These algorithms are not contingent upon particulars of the problem, thereby ensuring their broad applicability. They are capable of adapting to a range of optimization problems. Metaheuristics typically provide approximate solutions, particularly for large-scale and complex solution spaces, and feature adjustable search mechanisms that can be optimized according to the characteristics of the problem.

Metaheuristic algorithms are typically categorized into four major types: those based on evolutionary principles, swarm intelligence, human behavior, and phenomena from physics, chemistry, or biology. Among them, evolution-based algorithms are inspired by natural evolutionary processes, particularly the concept of “survival of the fittest” derived from Darwinian theory. These algorithms aim to optimize solutions through iterative procedures that mimic natural selection, reproduction, and mutation. The primary objective of this study is the identification of a global optimum within the solution space. Due to their robustness in handling complex, nonlinear, and non-differentiable high-dimensional problems, evolution-based methods are highly effective at escaping local optima. Notable representatives of this class include Genetic Algorithms (GA) [1] and Differential Evolution (DE) [2]. Nevertheless, a common drawback of these techniques is their relatively slow convergence, largely because they do not utilize gradient information.

However, despite the commendable performance of these algorithms in their respective fields, they still have their limitations, as per the “No Free Lunch” (NFL) theorem [3]. These limitations encompass challenges such as suboptimal convergence accuracy, inadequate global search capability, and the pervasive issue of encountering local optima. In accordance with the NFL theorem, the expected performance of any optimization algorithm is equivalent for all possible problems, signifying that no single algorithm can perfectly solve all problems. Based on this principle, researchers are continually improving existing algorithms and introducing new and enhanced versions to address both current and future optimization challenges.

This paper presents an improved version of the SSA algorithm, NTSSA: A Novel Multi-Strategy Enhanced Sparrow Search Algorithm with Northern Goshawk Optimization and Adaptive t-Distribution for Global Optimization, to enhance local exploitation ability and randomness. The performance of the proposed algorithm is evaluated on the CEC2005 benchmark function set. The contributions of this study are a new, superior-performing algorithm and new insights and approaches for future research. The following is a brief overview of the main contributions of this paper:

(1)   The Northern Goshawk Optimization (NGO) algorithm has been integrated. In the Sparrow Search Algorithm (SSA), the initial phase of each iteration often sees a single scout rapidly converging on the global optimum, exhibiting strong exploitation ability. However, this approach neglects exploration of nearby search space, leading to a lack of global exploration and a tendency to become trapped in local optima. The update strategy of the Northern Goshawk, in which prey selection is random in the search space, is incorporated to enhance the SSA algorithm’s exploration capability.

(2)   The objective is to enhance the convergence speed of the algorithm. An adaptive t-distribution mutation strategy is introduced during the follower phase of the Sparrow Search Algorithm. This does not alter the original update mechanism of the SSA, ensuring that the algorithm maintains good global exploration ability in the early iterations and effective local exploitation ability in the later iterations, thereby accelerating convergence.

(3)   In order to enrich the initial population with a greater variety of characteristics, Bernoulli chaotic mapping and sinusoidal chaotic mapping are integrated into the initialization process. The goal is to improve the algorithm’s ability to find the best solution for different functions.

(4)   An innovative elitism strategy is introduced in the population update mechanism. By selectively retaining the best individuals in each generation based on fitness, this strategy effectively solves the problem of losing high-quality solutions during the iteration process, which is common in traditional SSA.

The structure of this paper is as follows. Sections 2 and 3 offer concise overviews of the SSA and NGO algorithms, along with an analysis of their respective strengths and weaknesses. Section 4 explores the concepts of adaptive t-distribution and chaotic mapping. In Section 5, the elitism strategy is introduced. Section 6 elaborates on the core principles and implementation details of the NTSSA algorithm. Section 7 thoroughly examines the experimental results. Lastly, Section 9 summarizes the study and outlines possible directions for future research.

2  Related Work

Swarm intelligence algorithms optimize by simulating group intelligence to find global solutions. These algorithms model groups as biological populations, where individuals collaborate to achieve tasks impossible for any one individual. The Grey Wolf Optimizer (GWO) [4] is a swarm intelligence-based algorithm that mimics grey wolf packs’ hunting behavior. GWO updates positions to approach the target, achieving global optimization. However, these algorithms face challenges, such as local optima, slow convergence, high sensitivity to initial solutions, and premature convergence. These limitations affect their performance in complex optimization problems.

The development of human behavior-based algorithms is predominantly driven by various human behaviors, including teaching, social interaction, learning, emotional responses, and management. Common algorithms in this category include Internal Search Algorithm (ISA) [5] and Social Group Optimization (SGO) [6], among others. While these algorithms can offer strong global search capabilities, they may be limited in terms of how quickly they can converge and how accurately they can find the solution. This is particularly true when dealing with large-scale complex problems, where issues such as local optima and slow convergence rates can arise.

Physics and chemistry-based algorithms optimize solutions by simulating fundamental principles of physical and chemical processes, such as thermodynamic processes, molecular motion, and chemical reactions. These algorithms are inspired by phenomena in physics and chemistry. For example, the Simulated Annealing (SA) algorithm mimics the changes in molecular states during physical annealing, optimizing the search process by gradually lowering the temperature to avoid local optima [7]. Such algorithms are characterized by their ability to perform extensive global searches, rendering them well-suited for addressing large-scale, complex optimization problems. However, in high-dimensional and multimodal optimization tasks, they may suffer from premature convergence, which can impact their performance. As a result, in practical applications, these algorithms are often combined with other methods or modified to improve their efficiency and accuracy.

Swarm intelligence-based algorithms, due to their global search capabilities, exhibit strong adaptability, parallelism, and flexibility, making them highly effective at addressing complex, non-linear optimization problems while providing efficient and stable solutions. These features offer significant advantages and considerable development potential. Machine learning (ML) has achieved a wide range of applications in image recognition, natural language processing, and predictive modeling, and has demonstrated excellent performance relying on powerful data-driven modeling capabilities. However, ML methods often rely on large-scale, high-quality training data and assume that the problems have learnable mapping relationships, and are suitable for problems with clear structure, microscopic objective functions, and sufficient samples. When dealing with NP-hard problems such as combinatorial optimization and path planning, traditional ML methods may face modeling difficulties, weak generalization ability, and the risk of falling into local optimal solutions. Compared to machine learning algorithms, including traditional machine learning and deep learning algorithms, evolutionary algorithms (EAs) are more applicable to nonlinear, nonconvex, and high-dimensional optimization problems and have better robustness. They can help solve noise [8] and local optimal solution [9] issues. EAs usually do not need gradient information, can perform efficient global search in highly complex or unstructured search spaces [10–12]. In some application scenes, researchers would like to use EAs rather than machine learning algorithms to avoid unknown black-box procedures [13]. Therefore, this paper adopts EAs as the main solution method, aiming to make full use of their advantages in terms of search capability and flexibility to overcome the limitations faced by traditional MLs in such tasks, so as to solve the optimization objectives and constraints proposed in the study more effectively. In 1995, Kennedy and colleagues introduced the Particle Swarm Optimization (PSO) algorithm [14]. Around the same period, Dorigo et al. developed the Ant Colony Optimization (ACO) algorithm [15], which emulates the foraging patterns of ants to determine the shortest path. ACO proved effective in solving the traveling salesman problem and attracted significant academic interest. Building upon this foundation, Passino proposed the Bacterial Foraging Algorithm (BF) in 2002 [16], followed by Karaboga’s introduction of the Artificial Bee Colony (ABC) algorithm in 2005 [17]. In 2006, Basturk et al. presented the Monkey Search (MS) algorithm [18], and in 2008, Yang developed the Firefly Algorithm (FFA) [19]. A year later, Yang and colleagues introduced the Cuckoo Search (CS) algorithm [20], and in 2010, Yang also proposed the Bat Algorithm (BA) [21], which leverages echolocation behavior to perform global optimization. This sparked a surge of interest in enhancing swarm intelligence-based techniques. Subsequently, in 2011, Teodorovic et al. proposed the Bee Colony Optimization (BCO) algorithm [22], and Yang et al. introduced the Wolf Search (WS) algorithm [23]. In 2012, Gandomi and collaborators developed the Sea Urchin Algorithm (KH) [24]. The year 2014 saw the release of two notable algorithms by Mirjalili: the Ant Lion Optimizer (ALO) [25] and the Grey Wolf Optimizer (GWO). In 2015, Mirjalili also proposed the Whale Optimization Algorithm (WOA) [26]. The following year, Askarzadeh introduced the Crow Search Algorithm (CSA) [27], while Saremi et al. presented the Grasshopper Optimization Algorithm (GOA) [28]. In 2017, Singh and coauthors proposed the Squirrel Search Algorithm (SSA) [29]. Arora et al. introduced the Butterfly Optimization Algorithm (BOA) in 2018 [30], and Mirjalili followed in 2019 with the Harris Hawk Optimization (HHO) algorithm [31]. More recently, in 2022, Kuyu et al. proposed the GOZDE algorithm [32], and in 2024, Zhong et al. proposed the Starfish Optimization Algorithm (SFOA) [33].

Xue et al.’s Sparrow Search Algorithm (SSA) is a metaheuristic algorithm inspired by the foraging behavior of sparrows. Sparrows are divided into two types: discoverers and joiners. Discoverers search for food and provide foraging area information, while joiners use this information to locate food. In the natural environment, sparrows engage in mutual monitoring, and joiners, to increase their predation rates, often compete for food resources with higher foraging peers. All individuals remain alert to their surroundings while foraging to guard against potential predators. Compared to other algorithms, SSA has the advantages of fast convergence and high precision in solving many optimization problems. However, it also has drawbacks, such as low population diversity, poor global search capability, and premature convergence into local optima. The main reasons for these issues are: the sparrow population initialization process is simply a random placement of initial positions, and as iterations progress, population diversity rapidly decreases; the sparrow position update mechanism does not effectively balance global search and local exploitation, leading to premature convergence; and there is insufficient exploration of the optimal sparrow position, which results in the algorithm becoming trapped in local optima.

To address the aforementioned issues, there are currently two main approaches: directly improving the SSA itself and integrating other intelligent optimization algorithms to enhance the SSA.

There are many methods for directly improving the SSA, with some representative ones being the Adaptive Mutation Sparrow Search Optimization Algorithm (AMSSA) proposed by Tang et al. (2021) [34], which aims to enhance the balance between the global and local search capabilities of SSA. This algorithm initializes the population using a chaotic mapping sequence, which increases the randomness of the initial population, thereby enhancing the global search ability. The introduction of the Cauchy mutation and Tent chaotic disturbance further improves the local search capability, helping the algorithm escape from local extrema. Additionally, AMSSA optimizes the collaborative work between global and local searches by adaptively adjusting the number of explorers and followers, effectively improving the optimization accuracy and convergence speed. Another approach is the Improved Sparrow Search Algorithm (ISSA) proposed by Mao et al. (2022), which integrates Cauchy mutation and reverse learning [35]. This algorithm addresses the issue of population diversity reduction and premature convergence to local optima in the later stages of SSA iterations. It combines chaotic initialization with optimization of individual positions based on the previous generation’s global best solution, improving global search ability. The introduction of Cauchy mutation and reverse learning strategies enhances the algorithm’s ability to escape from local extrema and achieves a better balance between global and local search. Compared to AMSSA, ISSA further optimizes search efficiency and accuracy by adaptively adjusting weight strategies. Finally, Huang (2022) proposed a Sparrow Search Algorithm that integrates the t-distribution and Tent chaotic mapping [36]. Unlike the previous two studies, this research focuses on using the t-distribution to mutate individual positions to enhance the algorithm’s ability to escape local optima, while using Tent chaotic mapping to generate the initial population, thus improving global search diversity and accelerating convergence speed. Huang also applied the improved algorithm to optimize SVM classifiers and BP neural networks to solve malware and malicious domain name classification problems, demonstrating the algorithm’s effectiveness and practicality in real-world applications.

The integration of other optimization algorithms compensates for the deficiencies of SSA by combining the strengths of different methods. For instance, Tang et al. integrated the Sine Cosine Algorithm (SCA) [37]; Gao et al. incorporated the Golden Sine Algorithm [38]; Xu and Jiang separately combined SSA with the Bird Swarm Algorithm (BSA) [39,40]; Zhang et al. integrated the Butterfly Optimization Algorithm (BOA) [41]; Gao et al. applied the Particle Swarm Optimization (PSO) algorithm [42]; Liu and Mo combined SSA with the Firefly Algorithm (FA) [43]; and Yang et al. incorporated the Slime Mold Algorithm (SMA) [44]. Notably, due to its strong performance, this hybrid approach exhibits promising prospects for further development. Finally, Kathiroli integrated SSA with the Differential Evolution Algorithm (DEA) [45].

3  The Sparrow Search Algorithm (SSA)

The Sparrow Search Algorithm (SSA) is a recently developed swarm intelligence optimization method that draws inspiration from avian foraging strategies and behaviors, particularly the evasive maneuvers exhibited by sparrows when confronted with predators [46]. The model simulates the biological characteristics of sparrow populations in their foraging and anti-predation activities. This algorithm was first proposed by Xue in 2020 and is designed to solve global optimization problems, characterized by high solution accuracy and efficiency.

3.1 Algorithm Principle

In the Sparrow Search Algorithm (SSA), the sparrow population is divided into two categories: explorers and joiners. Explorers are responsible for locating new food sources (i.e., discovering new solutions in the search space) and are typically the fittest individuals in the population. They guide the entire population toward potential high-quality solutions. Joiners, on the other hand, follow the explorers and search for food by imitating their behavior.

(1)   Explorers: Representing 10%–20% of the total population, explorers actively search new regions of the solution space. They possess higher exploration capabilities and a broader search range.

(2)   Joiners: Comprising 80%–90% of the total population, joiners locate food sources by mimicking the behavior of explorers. Their exploration ability is relatively lower, and their search range is more limited.

In a natural setting, individuals within a population monitor each other. To increase their foraging success, joiners in a sparrow population often compete for food resources with companions with higher intake rates. While foraging, all individuals remain vigilant to their surroundings to guard against potential predators. Based on these observations, the following rules can be established:

(1)   Within the entire population, discoverers have higher energy reserves and are responsible for searching food-rich areas, providing foraging regions, and directions for all joiners. In the algorithm, sparrows with higher fitness values possess greater energy reserves.

(2)   In the event of predator detection by a sparrow, the sparrow will immediately signal an alarm. In the event that the alarm value exceeds a predetermined safety threshold, the discoverers will guide the joiners to an alternate safe area for foraging.

(3)   the identity of a sparrow in the algorithm is determined based on its ability to identify superior food sources. Despite the potential for fluctuations in the composition of individual roles, the ratio of discoverers and joiners within the population remains constant.

(4)   Sparrows with higher energy reserves act as discoverers. To acquire more energy, joiners with lower reserves may relocate to other areas for foraging.

(5)   During foraging, joiners always follow discoverers with higher energy reserves. To improve their foraging success, individuals monitor the discoverers and compete for food resources.

(6)   When predators pose a significant threat, sparrows at the periphery of the group quickly move to safer regions to secure a better position, whereas those in the center move randomly.

3.2 Algorithm Steps

In this subsection, we will introduce the procedures of the algorithm. Details are presented in each subsection.

3.2.1 Initialization

The first step is to establish the parameters: the size of the sparrow population, the range of the search space, and the maximum number of iterations. The initial sparrow population is randomly generated, and the fitness of each individual is computed. There are N sparrows in the population, with each sparrow’s position in the solution space represented as xi = (xi1, xi2,…, xid), where d is the problem’s dimension, and ub and lb represent the upper and lower bounds of the search space, respectively.

X=lb+rand×(ub−lb)(1)

3.2.2 Population Division

The avian population is divided into two distinct categories: discoverers and followers. This classification is predicated on the birds’ relative fitness values. The discoverers constitute a segment of the populace, while the remaining individuals are adherents.

3.2.3 Updating the Discoverers

Discoverers update their positions by referencing their current location, the number of iterations, and random factors. The update formula takes into account the sparrow’s foraging behavior and exploration capability. Assuming that discoverers make up 20% of the population, after ranking the population based on fitness values, the top 20% of individuals are designated as discoverers. In other words, in the implementation, updating the positions of the top 20% of individuals corresponds to updating the discoverers’ positions. Based on Rules (1) and (2), the position update of the discoverers during each iteration is described as follows:

Xi,jt+1={Xi,jt⋅e(−iα⋅itermax),ifR2<STXi,jt+Q⋅L,ifR2≥ST(2)

In this equation, Xi,jt represents the standpoint of the i-th sparrow in the j-th dimension at the t-th iteration. α∈(0,1] is a random number, and itermax denotes the maximum number of iterations. Q is a random number following a normal distribution, and L is a 1×d matrix of ones. R2 (∈[0, 1]) and ST(∈[0.5,1]) represent the warning value and the safety threshold, respectively.

When the warning value R2 is less than the safety threshold ST, it indicates that the environment is safe, and thus the discoverer’s search range is large. When the warning value R2 is greater than (or equal to) the safety threshold ST, it indicates the presence of a certain number of predators, and the sparrows need to move to a safer area, performing a random walk based on a normal distribution.

3.2.4 Updating the Followers

For the followers, they need to execute rules (4) and (5). The followers update their positions based on the discoverer’s location and their state. Some followers may fly to other areas to search for food due to hunger, thereby increasing the diversity of the population. The follower’s position update considers both the distance to the global best position Xbest and random factors. Assuming that the followers constitute 80% of the population, the bottom 80% of individuals, after sorting the population according to their fitness values, are considered followers. That is, in the code implementation, only the positions of the bottom 80% of individuals need to be updated, which corresponds to updating the positions of the followers. When the follower belongs to the better half of the population, the first subformula is used to update its position. If the follower belongs to the poorer half, it is as if the sparrow is very hungry and needs to randomly fly to another location. The position update of the followers is described as follows:

Xi,jt+1={Q⋅e(Xworst−Xi,jti2),ifi>n2XPt+1+|Xi,jt−XPt+1|⋅A+⋅L,otherwise(3)

where XP is the position of the current best solution occupied by the discoverer, and Xworst represents the current worst global position. A is a 1×d matrix, where all elements are randomly assigned values of 1 or −1, and A+ = AT(A·AT)−1.

3.2.5 Updating the Position of Sparrows Aware of Danger

The simulation experiment assumes 10% to 20% of sparrows are aware of danger. Their positions are randomly generated. The expression is represented as follows:

Xi.jt+1={Xbestt+β⋅|Xi,jt−Xbestt|,iffi>fgXi,jt+K⋅(|Xi,jt−Xworstt|(fi−fg)+ε),iffi=fg(4)

where Xbest is the current global best position. β, as the step size control parameter, is a random number that follows a normal distribution with a mean of 0 and a variance of 1. K∈[−1,1] is a random number, and fi is the fitness value of the current sparrow individual. fg and fw represent the current global best and worst fitness values, respectively. ε is a very small constant to avoid division by zero.

For simplicity, when fi > fg, it indicates that the sparrow is located in the periphery of the population and is highly vulnerable to predator attacks. Xbest, representing the position of the sparrow, is the best and safest position in the population. If fi = fg, the sparrow in the middle of the population has realized the danger and needs to move closer to others to minimize risk. K represents direction and step size.

3.2.6 Fitness Evaluation and Identity Conversion

Subsequently, the intrinsic value of each individual is recalculated. Conversely, the alterations in fitness values permit the conversion of identities between discoverers and followers.

3.2.7 Iteration and Termination

It is imperative to reiterate the aforementioned steps until the desired number of iterations is attained or alternative stopping rules are fulfilled. The objective of this study is to determine the global optimal solution or the position of the optimal individual.

4  Northern Goshawk Optimization (NGO)

In this section, the objective of the paper is to present the methodology proposed by the researchers. The paper first talk about the origin of the algorithm, presenting an overview. Subsequently, mathematical reasoning is provided to support the methodology. Meanwhile, the procedures are presented.

4.1 Origin of the Algorithm

The Northern Goshawk Optimization (NGO) algorithm, proposed in 2022 by Mohammad Dehghani and colleagues, simulates the hunting behavior of the Northern Goshawk [47]. The Northern Goshawk is a medium-to-large raptor species in the Accipitridae family. Its scientific name was first described by Linnaeus in 1758 in his work Systema Naturae. The Northern Goshawk preys on a variety of animals, including both small and large birds, as well as small mammals such as mice, rabbits, and squirrels, and even larger animals like foxes and raccoons. It is the only member of the genus Accipiter that is distributed across both the Eurasian continent and North America. Males are slightly smaller than females, with males measuring 46–61 cm in length, having a wingspan of 89–105 cm, and weighing approximately 780 g. In contrast, females are 58–69 cm long, weigh 1220 g, and have an estimated wingspan of 108–127 cm. The hunting strategy of the Northern Goshawk involves two stages: the first stage consists of moving at high speed toward the prey after recognizing it; the second stage involves chasing and capturing the prey.

4.2 Mathematical Model of the Algorithm

The Northern Goshawk Optimization (NGO) algorithm has two stages: prey recognition and attack (exploration phase), and pursuit and escape (exploitation phase).

4.2.1 Initialization

In the Northern Goshawk Optimization algorithm, the population of Northern Goshawks can be represented by the following population matrix:

X=[X1⋮Xi⋮XN]N×m=[x1,1…x1,j…x1,m⋮⋱⋮⋮xi,1…xi,j…xi,m⋮…⋱⋮xN,1…xN,j…xN,m]N×m(5)

In this equation, X denotes the population matrix of Northern Goshawks, while Xi represents the position vector of the i-th individual. The component Xi,j refers to the j-th dimension of the position of the i-th Northern Goshawk. Here, N indicates the total number of individuals in the population, and m specifies the dimensionality of the optimization problem. Within the Northern Goshawk Optimization algorithm, the objective function is employed to evaluate each individual, producing objective function values for the entire population. These values can be collectively expressed as an objective function value vector:

F=[F1⋮Fi⋮FN]N×1=[F(X1)⋮F(Xi)⋮F(XN)]N×1(6)

In the aforementioned equation, F denotes the objective function vector of the Northern Goshawk population, while Fi signifies the objective function value of the i-th Northern Goshawk.

4.2.2 Exploration Phase

The Northern Goshawk’s hunting strategy involves selecting prey randomly and quickly attacking it. This phase’s random search space enhances the NGO algorithm’s exploration capability. The goal is to identify the optimal region through a global search. In this phase, the behavior of prey selection and attack by the Northern Goshawk is described by the following equation:

PI=Xk,i=1,2,…,i−1,i+1,…N(7)

xi,jnew,P1={xi,j+r(pi,j−Ixi,j),Fpi<Fxi,j+r(xi,j−pi,j),Fpi≥F(8)

Xi={Xinew,P1,Finew,P1<FXi,Finew,P1≥F(9)

In the above formula, Pi represents the position of the i-th Northern Goshawk’s prey; FPi denotes the objective function value at the position of the i-th Northern Goshawk’s prey; k is a random integer within the range of [1, N]; Xinew,P1 is the new position of the i-th Northern Goshawk; Xi.jnew,P1 represents the new position of the i-th Northern Goshawk in the j-th dimension; Finew,P1 is the objective function value of the i-th Northern Goshawk after the update in Phase 1; r is a random number within the range of [0, 1]; and I is a random integer that takes values 1 or 2.

4.2.3 Exploitation Phase

After the Northern Goshawk attacks its prey, the prey attempts to escape. Therefore, in the final stage of chasing the prey, the Northern Goshawk must continue its pursuit. Due to the high speed of the Northern Goshawk, it is capable of chasing and eventually capturing prey in almost any scenario. The simulation of this behavior enhances the algorithm’s ability to conduct local searches within the search space. It is assumed that this hunting activity is close to an attack position with a radius of R. In the second phase, this behavior is described by the following formula:

xi,jnew,P2=xi,j+R(2r−1)xi,j(10)

R=0.02(1−tT)(11)

Xi={Xinew,P2,Finew,P2<FiXi,Finew,P2≥Fi(12)

In the formula, t represents the current iteration number, and T denotes the maximum number of iterations. Xinew,P2 is the new position of the i-th Northern Goshawk, while xinew,P1 refers to the new position of the i-th Northern Goshawk in the j-th dimension. xi,jP1 represents the updated position of the i-th Northern Goshawk in the j-th dimension after the second phase. Finew,P2 indicates the objective function value of the i-th Northern Goshawk after the update in the second phase.

5  Adaptive t-Distribution and Chaotic Mapping

In this subsection, we will introduce the Adaptive t-Distribution and Chaotic Mapping, Details are presented in each subsection.

5.1 Adaptive t-Distribution

The t-distribution, also known as Student’s t-distribution, has a probability density function with a degree of freedom parameter m, which is given by:

p(x)=Γ(m+12)mπΓ(m2)(1+x22)−m+12(13)

In this case, Γ(m+12)=∫0+∞xm+12−1e−xdx refers to the second-type Euler integral. As m→∞, the t-distribution converges to the Gaussian distribution, and as m→1, the t-distribution becomes a Cauchy distribution. It is easy to understand that the Gaussian distribution and the normal distribution are two boundary special cases of the t-distribution. The visualization diagram of the three distributions is shown below in Fig. 1:

Figure 1: Three types of distributions. (a) Gaussian distribution (m→∞); (b) Cauchy distribution (m→1); (c) A distribution when m is 2; (d) A distribution when m is 10 (equivalent to (c), both are intermediate values)

In the follower phase of the Sparrow Algorithm, t-distribution perturbation mutation is applied with a certain probability. This not only does not alter the original update principle of the Sparrow Algorithm but also enables the algorithm to possess strong global exploration capabilities in the early stages of iteration while maintaining good local exploration ability in the later stages. As a result, this accelerates the convergence speed of the Sparrow Algorithm.

5.2 Chaos Mapping

Experiments show that using chaos mapping to generate random numbers improves the fitness function values. Replacing the uniform distribution random number generator with chaos mapping gets better outcomes, especially when there are many local solutions in the search space, as it’s easier to find the global optimum. This study uses Bernoulli and Sinusoidal chaos mapping to enhance the sparrow population diversity. The Sinusoidal mapping’s solutions are more evenly distributed, making it suitable for fast convergence on unimodal functions. The Bernoulli mapping’s solutions are more random, helping avoid local optima in high-dimensional complex problems. The Bernoulli mapping’s randomness effectively expands the search space and increases solution diversity, thereby enhancing the algorithm’s global search capabilities. This allows the Sparrow Search Algorithm to better perform global exploration when dealing with multimodal functions or complex optimization problems and avoid premature convergence. Combining these two types of chaos mapping allows for more flexible adjustment of the balance between exploration and exploitation, leading to better performance across various types of optimization problems.

5.2.1 Bernoulli Chaotic Mapping Formula

xk+1={xk1−β,if0≤xk<1−βxk−(1−β)β,if1−β≤xk<1(14)

where β ∈ (0, 1) is the control parameter, usually β = 0.4.

5.2.2 Sinusoidal Chaotic Mapping Formula

xk+1=(xk)2⋅asin⁡(πxk)(15)

where a = 2.3, x(0) = 0.7.

6  Elitism Strategy

The Elitism Strategy, proposed by De Jong in the domain of Genetic Algorithms (GAs) [48], is a mechanism designed to preserve high-quality individuals within a gene pool. The core principle of this strategy involves directly retaining a subset of the fittest individuals (referred to as “elites”) in each generation. These elite individuals are copied unchanged into the next generation, bypassing crossover and mutation operations. Meanwhile, the remaining individuals undergo the standard selection, crossover, and mutation processes to form the rest of the new population.

Strategy Principle

Let the population at generation t be denoted as P(t)={x1(t),x2(t),…,xN(t)}, where each individual xi(t) has a fitness value given by f(xi(t)). The elite set E(t) is formed by selecting the top kk individuals with the highest fitness values from P(t):

E(t)={x∈P(t)|f(x)≥f(xj(t)),∀xj(t)∉E(t)}(16)

where |E(t)| = k ≤ αN, with α representing the elitism ratio. At this stage, the next-generation population P(t + 1) consists of two components: the directly retained elite individuals E(t) and new individuals generated through the optimization algorithm. The formulation is given by:

P(t+1)=E(t)∪(GeneticOperations(P(t)∖E(t)))(17)

where GeneticOperations represents the new individuals generated through the optimization algorithm, which typically includes selection, crossover, and mutation operations. Subsequent to the execution of these operations, the population individuals are arranged in descending order based on their fitness values. Finally, if the algorithm consistently retains the historically best solution xbest(t), then:

xbest(t+1)=argmax{f(x)|x∈P(x+1)∪{xbest(t)}}(18)

This ensures that the algorithm does not lose the best solution found thus far, thereby preventing the loss of high-quality solutions during the iterative process and maintaining the overall quality of the population.

7  NTSSA Algorithm

This paper is based on the Sparrow Search Algorithm (SSA), integrating the Northern Goshawk Optimization (NGO) and adaptive t-distribution mutation, resulting in the NTSSA algorithm. The algorithm’s exploration strategy is based on the NGO, enhancing global search capabilities, while the introduction of adaptive t-distribution mutation strikes a balance between exploratory and exploitative practices. Additionally, Bernoulli and Sinusoidal chaotic mappings are used to generate the initial population.

7.1 Mathematical Model of the Algorithm

7.1.1 Chaotic Mapping Initialization

NTSSA utilizes the Bernoulli chaotic mapping or the Sinusoidal chaotic mapping to generate the initial population. If the objective function is unimodal, the Sinusoidal chaotic mapping is used. If the objective function is multimodal, the Bernoulli chaotic mapping is used. The formulas are as follows:

xi,j(0)={lbj+b(i,j)⋅(ubj−lbj),iff(x)isunimodallbj+s(i,j)⋅(ubj−lbj),iff(x)isotherwise(19)

where xi,j(0) represents the initial position of the i-th individual in the j-th dimension; b(i,j) represents the chaotic number generated by the Sinusoidal chaotic mapping, with a value range of [0, 1]; s(i,j) represents the chaotic number generated by the Bernoulli chaotic mapping, with a value range of [0, 1]; lbj and ubj represent the lower and upper bounds of the j-th dimension, respectively.

7.1.2 Integration of the NGO Exploration Strategy

To enhance the search adequacy of the discoverer model in the solution space and improve the solution performance in optimization problems, the position update formula for the discoverer with R2 < ST is replaced with the exploration stage position update formula of the Northern Goshawk Optimization (NGO). This approach effectively improves the exploration capability of the SSA. The updated formula is as follows:

Xi,jt+1={Xi,jt+r1⋅(P−I⋅Xi,jt),ifR2<STXi,jt+Q⋅L,ifR2≥ST(20)

In the formula, P represents the guiding position selected from the better individuals (if the current individual has a poor fitness, then P = xbest; otherwise, a better individual is randomly selected); I∈{1,2} is a random integer used to control the direction; r1∈[0, 1] represents a random number uniformly distributed.

7.1.3 Adaptive t-Distribution Mutation

In the joiner phase of the Sparrow Search Algorithm, a t-distribution perturbation mutation is applied with a certain probability. This mutation does not alter the original update principle of the SSA, thereby enabling the algorithm to maintain optimal global exploration capability in the early stages of iteration while exhibiting strong local exploitation ability in the later stages. This phenomenon has been shown to accelerate the convergence speed of the SSA. The formula is as follows:

xi(t+1)=xbest(t)+trnd(v)⋅xbest(t)(21)

In this context, trnd(v) denotes a random number derived from a t-distribution with v degrees of freedom. The probability density function according to the t-distribution is as follows:

f(x;v)=Γ(v+12)vπΓ(v2)(1+x2v)−v+12(22)

The degrees of freedom v are adaptively adjusted as follows:

v=e4(tM)2(23)

In the above equation, because of its growth rate first slow and then fast, in line with the requirements of the previously mentioned “first broad and then refined”; coefficient 4 is used to adjust the growth rate, so that when t = M, the formula is close to the Gaussian distribution, in practice, when v > 30, the t-distribution and the Gaussian distribution is almost overlap, as shown in Fig. 2 below:

Figure 2: Dynamic t-distribution vs. theoretical limits

When t→0 (early iterations), v→1, the t distribution is close to the Cauchy distribution with heavy-tailed property, which is favorable for global exploration (avoiding falling into a local optimum).

When t→M (late iterations), v→e4, the t-distribution is close to a Gaussian distribution with concentrated peaks, which facilitates local exploitation (fine tuning).

7.1.4 Elite Retention Strategy

In this paper, an innovative elite retention strategy is integrated into the population update mechanism. By selectively retaining the most adaptive individuals from each generation, this approach effectively addresses the problem of losing high-quality solutions during the iterations of the traditional SSA algorithm. Specifically, after each iteration, the system automatically selects the top 10% of the elite individuals based on fitness and directly retains their genotypes in the next generation.

The adaptive retention ratio is adjusted according to the following formula, ensuring that the retention ratio fluctuates dynamically between 5% and 15%, balancing development efficiency and the maintenance of diversity.

Pe=0.1×(1+sin(πtM))(24)

The sinusoidal function has a smooth periodicity, which is suitable for the dynamic adjustment of the strategy. The period of 2M is chosen to ensure that half of the cycle is completed within the total number of iterations M, that is, from the initial to the end of the gradual increase and then slight fluctuations. The base value of 0.1 ensures that a minimum of 5% of the elite is retained to prevent the loss of high-quality solutions, and the amplitude of 0.1 restricts the proportion of the elite from fluctuating dynamically from 5% to 15% to avoid a sudden drop in the diversity of the population [49].

Design of Elite Perturbation Operator:

xe′=xe+N(0,σt)(25)

where: σt=0.01⋅‖ub−lb‖t is used to introduce controllable noise while preserving the elite genes. This strategy enhances the algorithm’s performance through the following mechanism:

Convergence Acceleration Mechanism: In single-modal function optimization, the optimal position information carried by elite individuals forms an implicit gradient direction guide, ensuring that the population maintains stable evolution along a clear fastest descent path.

Dynamic Balance Mechanism: The core anchor points formed by elite individuals, together with the exploratory individuals generated by chaotic perturbations and t-distribution mutations, create a “development-exploration” synergy.

Restart Protection Mechanism: When the algorithm becomes trapped in a local optimum, the elite library provides high-quality initial solutions for population restart.

7.1.5 Random Perturbation

Random perturbation can enhance diversity and prevent the algorithm from getting stuck in local optima. In this paper, 20 individuals are randomly selected for perturbation, as shown in the following formula:

xj(t+1)={xbest(t)+randn⋅|xj(t)−xbest(t)|,iff(xj(t))>fminxj(t)+(2⋅rand−1)⋅|xj(t)−xworst(t)|f(xj(t))−fmax+ϵ,otherwise(26)

7.2 Theoretical Analysis

Although NTSSA is a stochastic metaheuristic, we provide a theoretical justification for its convergence properties. Let P(t)={x1(t),…,xpop(t)} be the population at iteration t, and let the best-so-far solution be:

xt∗=argminx∈P(t)f(x)(27)

where f(x) is the objective function. Due to elitist preservation in NTSSA, the best fitness value is monotonically non-increasing:

f(xt+1∗)≤f(xt∗),∀t(28)

Assuming f(x) is bounded below (i.e., ∃ finf > ∞), the sequence {f(xt∗)} converges:

limt→∞f(xt∗)=f∗(29)

Moreover, the incorporation of adaptive mutation and chaotic initialization ensures that P(t) maintains sufficient diversity, which, under mild ergodicity assumptions, allows the algorithm to approximate global optima asymptotically in probability.

Therefore, NTSSA converges in the probabilistic weak sense, which is consistent with theoretical results established for other metaheuristic frameworks such as PSO and DE. NTSSA Pseudocode is shown in Algorithm 1.

8  Algorithm Performance Testing

This study compares NTSSA with four standard algorithms (SSA, GWO, NGO, and HHO) and two enhanced variants of the sparrow algorithm (ISSA and CSSOA). The comparison uses 23 benchmark functions (F1–F23) from the CEC2005 test suite. These include unimodal (F1–F7), multimodal (F8–F13), and fixed-dimensional multimodal (F14–F23) functions with a dimensionality of 30. All experiments are performed in the same computational environment (MATLAB 2017b on Microsoft Windows 11) to ensure consistency and fairness. Uniform parameters are applied across all algorithms, with a population size of 50, a maximum of 500 iterations, and 50 independent runs for each algorithm.

To verify NTSSA’s superiority, it is compared with six other algorithms using performance metrics, including mean values and standard deviations, to assess the effectiveness of the algorithms. Statistical analysis is performed by examining the results of multiple runs. However, due to the randomness of the Moving Average method (MAs), non-parametric tests are used to ensure the robustness and reliability of the algorithms.

8.1 CEC2005 Test Functions

Single-modal functions have a single global optimum. Their purpose is to evaluate an algorithm’s exploitation capability. Multi-modal functions have multiple optima, with one being the global optimum and the others being local optima. These functions assess an algorithm’s exploration capability. Finally, multi-modal functions have low dimensions and fewer local optima, allowing for balanced evaluation of the algorithm’s exploration ability during local and global search processes. Table 1 and Fig. 3 present the basic parameters of the CEC2005 test functions and their three-dimensional visualization effects.

Figure 3: 3D depictions of the CEC2005 test functions

8.2 Algorithm Performance Comparison and Analysis

This study evaluated and compared seven algorithms, including NTSSA, using 23 benchmark functions from the CEC2005 test suite. Each function was independently run 50 times per algorithm. The best (optimal) value, worst value, mean, and standard deviation were computed for every set of runs to provide a performance overview. The experimental results are summarized in Table 2 below:

The NTSSA algorithm shows significant advantages in stability and global convergence accuracy. In the single-peak benchmark function, multiple independent runs of NTSSA converge to the theoretical optimum with standard deviation indicating its robustness to zero fluctuation. In multi-peak and complex functions, the worst value of NTSSA significantly out-performs the comparative algorithms, verifying the effectiveness of its improvement strategy. NTSSA achieves the optimal or sub-optimal mean in 19 out of 23 tested functions, ranking first in the overall rankings.

Taking the best result out of 50 times, the following Table 3 was obtained:

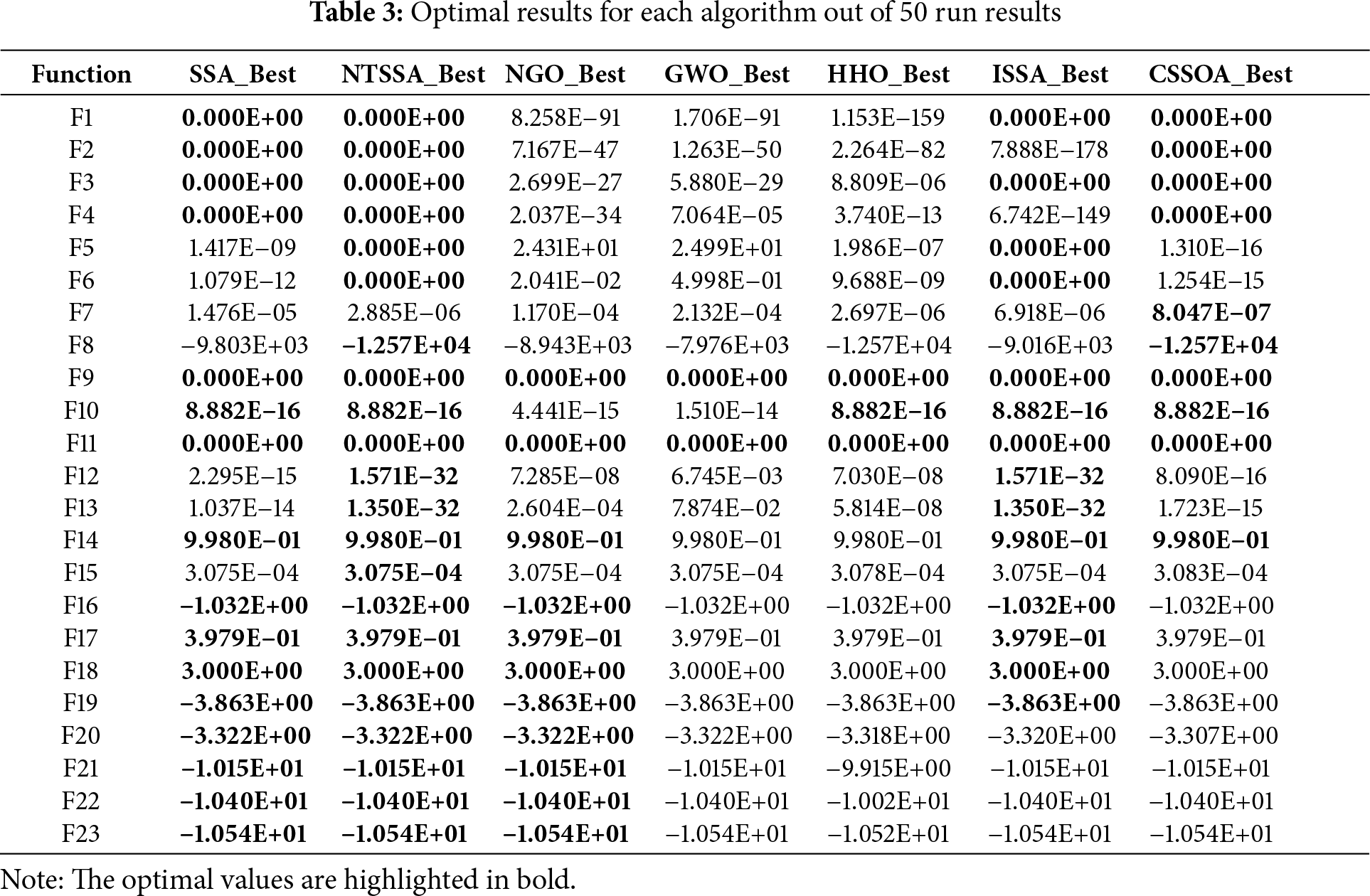
From Table 3 above, it can be seen that the proposed NTSSA algorithm exhibits outstanding performance across various function categories in the CEC2005 benchmark. For unimodal functions (F1–F7), NTSSA achieves the theoretical optimal value (0.000E+00) in F1–F6, significantly outperforming traditional algorithms such as NGO and GWO (e.g., F5: NTSSA = 0 vs. NGO = 24.31). In F7, although NTSSA slightly lags behind CSSOA (8.047E−07), it still reaches 2.885E−06, demonstrating high precision and strong local exploitation capabilities.

For multimodal functions (F8-F13), NTSSA shows excellent global search capabilities: in F8, it reaches −1.257E+04 (on par with HHO and CSSOA), and in F12 (1.571E−32) and F13 (1.350E−32), it approaches zero, surpassing its competitors by several orders of magnitude (e.g., F12: NGO = 7.285E−08, GWO = 6.745E−03). This highlights its effectiveness in escaping local optima. For fixed-dimensional multimodal functions (F14-F23), NTSSA maintains stability, performing comparably to other algorithms in F14-F19, and excelling in F21-F23 (e.g., F21 = −1.015E+01 vs. HHO = −9.915E+00).

F7 and F20 show minor limitations, suggesting parameter sensitivity improvement. F7 (high-dimensional single peak) has slightly inferior convergence accuracy of NTSSA over CSSOA. This is due to the adaptive t-distribution approximating the Gaussian distribution too soon in the late iteration, which restricts ability to capture subtle gradients in high-dimensional space. CSSOA’s golden sinusoidal mechanism approaches the optimal solution more efficiently through symmetric interval contraction. To solve this, the growth rate of the degrees of freedom can be reduced by decreasing the growth rate of the degrees of freedom (e.g., by decreasing the coefficients to 2) to retard the Gaussianization process. In F20 (fixed dimension multi-peaks), NTSSA over-preserves the historical optimal solution, leading to decreased population diversity. CSSOA better maintains solution space exploration. The elite proportion can be made more stable in the medium term by adjusting the phase of the sinusoidal function in the elite retention strategy.

However, NTSSA still balances the dynamics of exploration and exploitation well, and the dynamic balance of exploration-exploitation under the multi-strategy collaborative optimization framework still has a significant advantage, especially in the high-dimensional complex solution space and multi-peak optimization problems.

8.3 Comparison of Algorithm Convergence Curves

The convergence curves of the benchmark test functions illustrate the convergence speed of the algorithms, the accuracy of the solutions, and the ability to escape local optima. As illustrated in Fig. 4, the convergence trajectories for all 23 benchmark functions are depicted, with d set at 30. The vertical axis shows the fitness value, and the horizontal axis indicates the value of iterations.

Figure 4: Convergence curves for 23 benchmark functions

The NTSSA algorithm generally demonstrates faster convergence and smoother performance across different benchmark functions, as shown by the convergence curves. A lower fitness value on the vertical axis reflects higher optimization accuracy, while the earlier emergence of a turning point on the curve indicates a quicker convergence toward the optimal solution.

8.4 Wilcoxon Rank-Sum Test

The results obtained from 50 independent runs alone cannot fully demonstrate the superiority of NTSSA, and statistical verification is required. Therefore, in this study, we will perform additional statistical analyses. When p < 5%, the null hypothesis (H0) is rejected, indicating a significant difference between the two algorithms. When p > 5%, the null hypothesis is accepted, indicating that the two algorithms are not significantly different. Conversely, when p < 5%, the null hypothesis is rejected, suggesting a significant difference between the two algorithms and implying that their optimization capabilities are comparable.

Table 4 below presents the significance levels (p = 5%) for NTSSA and several other algorithms under different test functions, with each algorithm run 50 times:

A p-value less than 0.05 indicates a significant difference between the two algorithms. When the p-value exceeds 0.05, it is deduced that there is no statistically significant discrepancy between the two groups. As illustrated in the above table, NTSSA exhibits a substantial superiority in the majority of the comparisons, particularly in relation to NGO, GWO, HHO, and CSSOA. However, a comparative analysis reveals that NTSSA exhibits comparable performance to SSA and ISSA in specific features.

To further verify the performance differences between NTSSA and other algorithms, if a significant difference is found between the algorithms, the median of NTSSA will be compared with those of the other algorithms. If the median of NTSSA is smaller than that of another algorithm, it indicates that NTSSA performs worse; if the median of NTSSA is greater than or equal to that of the other algorithm, it indicates that NTSSA performs better. This analysis is visualized in the following heatmap (Fig. 5), where 0 indicates equal performance, −1 indicates NTSSA performs better, and 1 indicates NTSSA performs worse.

Figure 5: Performance comparison of NTSSA with other algorithms

From the heatmap, it can be observed that NTSSA outperforms or is at least equal to other algorithms in the majority of test functions. Only in a few cases, such as in the F7 and F8 test functions, does NTSSA perform slightly worse than improved algorithms like CSSOA and ISSA. However, in the case of multimodal functions, NTSSA consistently maintains its leading position.

8.5 Component Effectiveness Analysis

In order to verify the effectiveness of multi-strategy synergy in NTSSA, this section analyzes the contribution of each core component in combination with the experimental results, and selects representative algorithms and corresponding functions to obtain the following Table 5:

From the above table, we can draw the following conclusions:

(1)   The effect of NGO exploration strategy: comparing the performance of NTSSA and ISSA (unconverged NGO) in F8 (multi-peak function), the average adaptation of NTSSA (−1.14E+04) is significantly better than that of ISSA (−5.06E+03), which suggests that NGO’s stochastic prey selection mechanism expands the search radius through NGO algorithms and avoids falling into a local optimum.

(2)   The role of adaptive t-distribution: in F5 (high-dimensional single-peak), the convergence accuracy of NTSSA (2.53E−07) is improved by two orders of magnitude compared to the original SSA (1.93E−05). This is attributed to the design of the degree-of-freedom parameter, which allows the algorithm to approximate the Gaussian distribution in the later iterations and strengthen the local development.

(3)   The necessity of dual-chaos initialization: comparing the performance of CSSOA (without dual-chaos mapping) in F12, the accuracy of NTSSA (2.42E−18 vs. 6.62E−09) is improved by nine orders of magnitude. The randomness of Bernoulli mapping synergistically enhances the initial population diversity with the uniformity of Sinusoidal mapping.

(4)   Balance of elite retention strategies: the Wilcoxon test showed that NTSSA significantly outperformed HHO and GWO in most functions. dynamic elite proportions maintained the balance of population quality and diversity through periodic fluctuations.

9  Conclusion and Future Directions

In this paper, an enhanced Sparrow Search Algorithm (NTSSA) is proposed by integrating the Northern Goshawk Optimization (NGO) algorithm and adaptive t-distribution. A total of 23 test functions from the CEC2005 benchmark were selected for the simulation study. A Wilcoxon rank-sum test was then employed to assess the performance of the algorithm. The following conclusions can be drawn:

(1)   Improved Optimization Capability: NTSSA has shown significant improvement in finding optimal solutions and escaping local minima. The initial positions of sparrows are crucial for global search, and by incorporating adaptive t-distribution and chaotic mapping, the population is enriched, balancing the global and local exploration capabilities of the algorithm. The NGO algorithm integrates to enhance the algorithm’s ability to find optimal solutions, and the elite retention strategy strengthens this capability. The simulation results also validate the effectiveness of the proposed method.

(2)   Superior Performance Compared to Other Algorithms: The 23 test functions show that NTSSA outperforms traditional algorithms such as HHO and GWO, as well as improved algorithms like ISSA and CSSOA, in terms of convergence accuracy, solution speed, and the balance between local and global optima. NTSSA exhibits outstanding optimization capability, and the W-test results confirm this conclusion.

(3)   Future Work: Future research can focus on further improving the optimization mechanism and algorithm structure of the Sparrow Search Algorithm, or exploring other advanced optimization algorithms to propose more powerful intelligent algorithms. Additionally, extending NTSSA to dynamic optimization and multi-objective engineering applications could broaden the scope of its applications.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Hui Lv; methodology, Hui Lv; software, Hui Lv; validation, Hui Lv; formal analysis, Hui Lv; investigation, Hui Lv; resources, Hui Lv; data curation, Hui Lv; writing—original draft preparation, Hui Lv; writing—review and editing, Hui Lv, Yuer Yang, and Yifeng Lin; visualization, Hui Lv; supervision, Yifeng Lin; project administration, Hui Lv and Yuer Yang; funding acquisition, Hui Lv. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors. The data that support the findings of this study are available from the first author, Hui Lv, upon reasonable request. Please also consider referring to https://github.com/BatchClayderman/NTSSA (accessed on 15 June 2025) for data used in this paper.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Holland JH. Adaptation in natural and artificial systems. Cambridge, MA, USA: MIT Press; 1992. [Google Scholar]

2. Storn R, Price K. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J Glob Optim. 1997;11:341–59. doi:10.1023/A:1008202821328. [Google Scholar] [CrossRef]

3. Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE Trans Evol Comput. 1997;1(1):67–82. doi:10.1109/4235.585893. [Google Scholar] [CrossRef]

4. Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Adv Eng Softw. 2014;69:46–61. doi:10.1016/j.advengsoft.2013.12.007. [Google Scholar] [CrossRef]

5. Gandomi AH. Interior search algorithm (ISAa novel approach for global optimization. ISA Trans. 2014;53(4):1168–83. doi:10.1016/j.isatra.2014.03.018. [Google Scholar] [PubMed] [CrossRef]

6. Satapathy S, Naik A. Social group optimization (SGOa new population evolutionary optimization technique. Complex Intell Syst. 2016;2(3):173–203. doi:10.1007/s40747-016-0022-8. [Google Scholar] [CrossRef]

7. Kirkpatrick S, Gelatt CDJr, Vecchi MP. Optimization by simulated annealing. Science. 1983;220(4598):671–80. doi:10.1126/science.220.4598.671. [Google Scholar] [PubMed] [CrossRef]

8. Zhao W, Yang Y, Lu Z. Interval short-term traffic flow prediction method based on CEEMDAN-SE noise reduction and LSTM optimized by GWO. Wirel Commun Mob Comput. 2022;2022(1):5257353. doi:10.1155/2022/5257353. [Google Scholar] [CrossRef]

9. Lin Y, Yang Y, Zhang Y. Improved differential evolution with dynamic mutation parameters. Soft Comput. 2023;27(23):17923–41. doi:10.1007/s00500-023-09080-1. [Google Scholar] [CrossRef]

10. Zhou M, Cui M, Xu D, Zhu S, Zhao Z, Abusorrah A. Evolutionary optimization methods for high-dimensional expensive problems: a survey. IEEE/CAA J Autom Sin. 2024;11(5):1092–105. doi:10.1109/jas.2024.124320. [Google Scholar] [CrossRef]

11. Callaway R, McGregor S. Evolutionary algorithms for complex optimization problems in engineering. Int J Adv Comput Theory Eng. 2024;13(1):1–9. [Google Scholar]

12. Li Y, Li W, Li S, Zhao Y. A performance indicator-based evolutionary algorithm for expensive high-dimensional multi-/many-objective optimization. Inf Sci. 2024;678(1):121045. doi:10.1016/j.ins.2024.121045. [Google Scholar] [CrossRef]

13. Chan KHR, Yu Y, You C, Qi H, Wright J, Ma Y. ReduNet: a white-box deep network from the principle of maximizing rate reduction. J Mach Learn Res. 2022;23(114):1–103. [Google Scholar]

14. Kennedy J, Eberhart R. Particle swarm optimization. In: Proceedings of the ICNN’95—International Conference on Neural Networks; 1995 Nov 27-Dec 1; Perth, WA, Australia. Piscataway, NJ, USA: IEEE; 2002. p. 1942–8. doi:10.1109/ICNN.1995.488968. [Google Scholar] [CrossRef]

15. Dorigo M, Maniezzo V, Colorni A. Ant system: optimization by a colony of cooperating agents. IEEE Trans Syst Man Cybern Part B Cybern. 1996;26(1):29–41. doi:10.1109/3477.484436. [Google Scholar] [PubMed] [CrossRef]

16. Passino KM. Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Syst Mag. 2002;22(3):52–67. doi:10.1109/MCS.2002.1004010. [Google Scholar] [CrossRef]

17. Karaboga D, Basturk B. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm. J Glob Optim. 2007;39(3):459–71. doi:10.1007/s10898-007-9149-x. [Google Scholar] [CrossRef]

18. Basturk B, Karaboga D, Akay B. A comprehensive study on artificial bee colony algorithm and its applications. Int J Innov Comput Inf Control. 2006;2(4):897–914. doi:10.11121/ijocta.01.2017.00342. [Google Scholar] [CrossRef]

19. Yang XS. Nature-inspired metaheuristic algorithms. Liverpool, UK: Luniver Press; 2010. [Google Scholar]

20. Yang XS, Deb S. Cuckoo search via lévy flights. In: Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC); 2009 Dec 9–11; Coimbatore, India. Piscataway, NJ, USA: IEEE; 2009. p. 210–4. doi:10.1109/NABIC.2009.5393690. [Google Scholar] [CrossRef]

21. Yang XS. A new metaheuristic bat-inspired algorithm. In: Nature inspired cooperative strategies for optimization (NICSO 2010). Berlin/Heidelberg, Germany: Springer; 2010. p. 65–74. doi:10.1007/978-3-642-12538-6_6. [Google Scholar] [CrossRef]

22. Teodorovic D, Lucic P, Markovic G, Orco MD. Bee colony optimization: principles and applications. In: Proceedings of the 2006 8th Seminar on Neural Network Applications in Electrical Engineering; 2006 Sep 25–27; Belgrade, Serbia. Piscataway, NJ, USA: IEEE; 2006. p. 151–6. doi:10.1109/NEUREL.2006.341200. [Google Scholar] [CrossRef]

23. Tang R, Fong S, Yang XS, Deb S. Wolf search algorithm with ephemeral memory. In: Proceedings of the Seventh International Conference on Digital Information Management (ICDIM 2012); 2012 Aug 22-24; Macao, China. Piscataway, NJ, USA: IEEE; 2012. p. 165–72. doi:10.1109/ICDIM.2012.6360147. [Google Scholar] [CrossRef]

24. Gandomi AH, Alavi AH. Krill herd: a new bio-inspired optimization algorithm. Commun Nonlinear Sci Numer Simul. 2012;17(12):4831–45. doi:10.1016/j.cnsns.2012.05.010. [Google Scholar] [CrossRef]

25. Mirjalili S. The ant lion optimizer. Adv Eng Softw. 2015;83:80–98. doi:10.1016/j.advengsoft.2015.01.010. [Google Scholar] [CrossRef]

26. Mirjalili S.Lewis A. The whale optimization algorithm. Adv Eng Softw. 2016;95(12):51–67. doi:10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]

27. Askarzadeh A. A novel metaheuristic method for solving constrained engineering optimization problems: crow search algorithm. Comput Struct. 2016;169(2):1–12. doi:10.1016/j.compstruc.2016.03.001. [Google Scholar] [CrossRef]

28. Saremi S, Mirjalili S, Lewis A. Grasshopper optimisation algorithm: theory and application. Adv Eng Softw. 2017;105:30–47. doi:10.1016/j.advengsoft.2017.01.004. [Google Scholar] [CrossRef]

29. Jain M, Singh V, Rani A. A novel nature-inspired algorithm for optimization: squirrel search algorithm. Swarm Evol Comput. 2019;44(4):148–75. doi:10.1016/j.swevo.2018.02.013. [Google Scholar] [CrossRef]

30. Arora S, Singh S. Butterfly optimization algorithm: a novel approach for global optimization. Soft Comput. 2019;23(3):715–34. doi:10.1007/s00500-018-3102-4. [Google Scholar] [CrossRef]

31. Heidari AA, Mirjalili S, Faris H, Aljarah I, Mafarja M, Chen H. Harris Hawks optimization: algorithm and applications. Future Gener Comput Syst. 2019;97:849–72. doi:10.1016/j.future.2019.02.028. [Google Scholar] [CrossRef]

32. Kuyu YÇ, Vatansever F. GOZDE: a novel metaheuristic algorithm for global optimization. Future Gener Comput Syst. 2022;136(13):128–52. doi:10.1016/j.future.2022.05.022. [Google Scholar] [CrossRef]

33. Zhong C, Li G, Meng Z, Li H, Yildiz AR, Mirjalili S. Starfish optimization algorithm (SFOAa bio-inspired metaheuristic algorithm for global optimization compared with 100 optimizers. Neural Comput Appl. 2025;37(5):3641–83. doi:10.1007/s00521-024-10694-1. [Google Scholar] [CrossRef]

34. Tang YQ, Li CH, Song YF. Adaptive variational sparrow search optimisation algorithm. J Beijing Univ Aeronaut Astronaut. 2023;49(3):681–92. doi:10.13700/j.bh.1001-5965.2021.0282. [Google Scholar] [CrossRef]

35. Mao Q, Zhang Q. An improved sparrow algorithm incorporating Cauchy variation and reverse learning. Comput Sci Explor. 2021;15(6):1155–64. doi:10.3778/j.issn.1673-9418.2010032. [Google Scholar] [CrossRef]

36. Huang J. Research on sparrow search algorithm incorporating t-distribution and tent chaos mapping [master’s thesis]. Lanzhou, China: Lanzhou University; 2021. doi:10.27204/d.cnki.glzhu.2021.001329. [Google Scholar] [CrossRef]

37. Tang AD, Han TT, Xu DW, Xie L. UAV trajectory planning method based on chaotic sparrow search algorithm. Comput Applicat. 2021;41(7):2128–36. [Google Scholar]

38. Gao CF, Chen JQ, Shi MH. A multi-strategy sparrow search algorithm incorporating golden sine and curve adaptive. Comput Appl Res. 2022;39(02):491–9. [Google Scholar]

39. Xu L, Zhang ZY, Chen X, Zhao SW, Wang LY, Wang T. Optimisation of BP neural network based on improved sparrow search algorithm for offset prediction in aerodynamic optical imaging. Optoelectron-Laser. 2021;32(6):653–8. [Google Scholar]

40. Jiang NL. Research on short-term power load forecasting based on improved sparrow search algorithm opti-mising long and short-term memory network [master’s thesis]. Nanchang, China: Nanchang University; 2021. [Google Scholar]

41. Zhang WK, Liu S, Ren CH. Mixed strategy improved sparrow search algorithm. Comput Eng Appl. 2021;57(24):74–82. (In Chinese). [Google Scholar]

42. Gao B, Zheng A, Qin J, Zou QJ, Wang Z. Network intrusion detection algorithm based on sparrow search algorithm and improved particle swarm optimisation algorithm. Comput Appl. 2022;42(4):1201–6. [Google Scholar]

43. Liu R, Mo YB. An improved sparrow search algorithm. Comput Technol Dev. 2022;32(3):21–6. [Google Scholar]

44. Yang Z, Long EW, Ji MM, Gu JC. Chaotic sparrow search algorithm incorporating spiral slime mold algorithm with applications. Comput Eng Appl. 2023;59(14):124–33. [Google Scholar]

45. Kathiroli P, Selvadurai K. Energy efficient cluster head selection using improved Sparrow Search Algorithm in Wireless Sensor Networks. J King Saud Univ Comput Inf Sci. 2022;34(10):8564–75. doi:10.1016/j.jksuci.2021.08.031. [Google Scholar] [CrossRef]

46. Xue J, Shen B. A novel swarm intelligence optimization approach: sparrow search algorithm. Syst Sci Control Eng. 2020;8(1):22–34. doi:10.1080/21642583.2019.1708830. [Google Scholar] [CrossRef]

47. Dehghani M, Hubálovský Š, Trojovský P. Northern goshawk optimization: a new swarm-based algorithm for solving optimization problems. IEEE Access. 2021;9:162059–80. doi:10.1109/access.2021.3133286. [Google Scholar] [CrossRef]

48. De Jong KA. An analysis of the behavior of a class of genetic adaptive systems. Ann Arbor, MI, USA: University of Michigan; 1975. [Google Scholar]

49. Mirjalili S. Evolutionary algorithms and neural networks: theory and applications. Berlin/Heidelberg, Germany: Springer; 2019. doi:10.1007/978-3-319-93025-1. [Google Scholar] [CrossRef]