 Open Access
Open Access
ARTICLE
Computational Assessment of Energy Supply Sustainability Using Picture Fuzzy Choquet Integral Decision Support System
1 Department of Mathematics, Riphah International University (Lahore Campus), Lahore, 54000, Pakistan
2 Department of Mathematics, Saveetha School of Engineering, Saveetha Institute of Medical and Technical Sciences, Saveetha University, Chennai, 602105, Tamil Nadu, India
3 Széchenyi István University, Győr, H-9026, Hungary
4 Faculty of Transport and Traffic Engineering, University of Belgrade, Vojvode Stepe 305, Belgrade, 11010, Serbia
5 Department of Computer Science and Engineering, College of Informatics, Korea University, Seoul, 02841, Republic of Korea
6 Yuan Ze University, College of Engineering, Department of Industrial Engineering and Management, Taoyuan City, 320315, Taiwan
* Corresponding Author: Dragan Pamucar. Email:
(This article belongs to the Special Issue: Fuzzy Logic: Next-Generation Algorithms and Applications)
Computers, Materials & Continua 2025, 85(1), 1311-1337. https://doi.org/10.32604/cmc.2025.066569
Received 11 April 2025; Accepted 03 June 2025; Issue published 29 August 2025
Abstract
For any country, the availability of electricity is crucial to the development of the national economy and society. As a result, decision-makers and policy-makers can improve the sustainability and security of the energy supply by implementing a variety of actions by using the evaluation of these factors as an early warning system. This research aims to provide a multi-criterion decision-making (MCDM) method for assessing the sustainability and security of the electrical supply. The weights of criteria, which indicate their relative relevance in the assessment of the sustainability and security of the energy supply, the MCDM method allow users to express their opinions. To overcome the impact of uncertainty and vagueness of expert opinion, we explore the notion of picture fuzzy theory, which is a more efficient and dominant mathematical model. Recently, the theory of Aczel-Alsina operations has attained a lot of attraction and has an extensive capability to acquire smooth approximated results during the aggregation process. However, Choquet integral operators are more flexible and are used to express correlation among different attributes. This article diagnoses an innovative theory of picture fuzzy set to derive robust mathematical methodologies of picture fuzzy Choquet Integral Aczel-Alsina aggregation operators. To prove the intensity and validity of invented approaches, some dominant properties and special cases are also discussed. An intelligent decision algorithm for the MCDM problem is designed to resolve complicated real-life applications under multiple conflicting criteria. Additionally, we discussed a numerical example to investigate a suitable electric transformer under consideration of different beneficial key criteria. A comparative study is established to capture the superiority and effectiveness of pioneered mathematical approaches with existing methodologies.Keywords
One of the most important energy carriers, electricity, is crucial for maintaining economic growth [1]. However, manufacturing electricity has become extremely reliant on fossil fuels, resulting in several serious issues, including air pollution, significant greenhouse gas emissions, imported energy, and inadequate energy security [2,3]. To improve the security of power, numerous nations implemented a variety of policies. For example, China established the renewable energy development plan with the aim of reducing harmful emissions, reducing reliance on energy imports, and improving air and water quality [4]. In order to reduce its reliance on fossil fuels for electricity generation, improve environmental performance, and potentially increase the security of the electricity supply, Brazil has implemented or planned a number of biofuel projects. These include the production of electricity from sugarcane bagasse [5], hybrid concentrated solar power (CSP)–biomass plants [6], and the production of rice husk electricity [7]. The goal of each study was to improve the reliability of the electrical supply. The basis for recommending practical policies and initiatives to improve a nation’s electrical supply sustainability and security (ESSS) is the examination of ESSS and its evolving trend [8]. Nonetheless, the quantity of research works that concentrate on creating the techniques for ESSS state analysis is constrained. The creation of the ESSS evaluation framework is, therefore, a necessary and crucial step. Multiple dimensions are typically taken into account when evaluating ESSS. Power system reliability analysis and power market analysis were linked by Kjølle and Gjerde [9] to create an integrated framework for the security of energy supply analysis. Numerous studies have also taken into account more than three variables for the analysis and evaluation of ESSS.
Especially in the field of energy planning, multi-criteria decision-making techniques have proven to be a very helpful instrument for resolving conflicts between disparate criteria. Nevertheless, social and environmental factors frequently conflict with technical and financial factors in the design of rural electrification plans. To choose the best option for remote rural locations’ electrical supply while taking into account social, economic, environmental, and technical factors, we suggest advanced multi-attribute decision-making (MADM) technique. The MADM problem has been applied to various complex issues. We assess different decision-making problems in daily life and important goods, and we can learn how to make the best decisions. We saw several research scholars working on the decision-making problems under different mathematical models [10–12].
To handle unpredictable situations of crisp theory, an innovative theory of fuzzy set (FS) was developed by Zadeh [13] with a certain membership degree (MD) of an object. The concept of intuitionistic fuzzy sets (IFSs) was introduced by Atanassov [14], who modified a version of fuzzy theory. The IFS contains two different aspects of an object, like membership degree (MD) and non-membership degree (NMD). The sum of MD and NMD lies in a close interval
Yager [20,21] explored the aggregation operators (AOs) made use of in view of humans under the consideration of picture fuzzy informing by different researchers from different states. Cuong et al. [22] explored the idea of picture triangular norm (t-corm) and picture triangular co-norms (t-conorms) and discussed the properties of PFS. Hussain et al. [23] discussed the significance of vendor management enterprises by exploring the characteristics of the Hamy mean model with advanced picture fuzzy theory. Wang et al. [24] suggested a possible plan for the Choquet integral and proposed operator. Hussain et al. [25] classified diverse construction materials, taking into account Hamy mean models and Aczel-Alsina operators in the decision-making process. Sahoo et al. [26] resolved energy energy-related real-life problem using multi-criteria and mathematical aggregation operators. Petchimuthu et al. [27] constructed decision-making models to investigate a suitable optimal option using unknown weights of criteria.
Ali et al. [28] described some methods by using the basic operation of the Aczel-Alsina aggressions operator and the system of PFSs. Mahmood et al. [29,30] explored the PFAAWG operator bases on the Azcel Alsina operation to find effective and reliable proposed aggression operators. Choquet integral is a useful technique for computing rank. Hussain et al. [31] discussed mathematical results of Aczel Alsina Heronian mean operators. Ahmmad et al. [32] initiated a list of Aczel-Alsina averaging operators to resolve a real-life application related to medical diagnosis with decision analysis process. Hussain et al. [33] elaborated on Dombi Bonferroni mean operators for choosing reliable recycling machines to reduce the impact of waste materials.
In order to construct the intuitionistic fuzzy aggregation operators previously stated, the criteria are expected to be independent. It should be noted that correlated criteria, as opposed to independent ones, are used in most MCDM problems. In these cases, the evaluations cannot be aggregated using weighted aggregation operators, and the criterion’s relevance levels are described as fuzzy measures as opposed to weights. Fuzzy measures can effectively capture the correlative relationships between criterion sets, including independent, redundant, and complementary ones. Since the total of all fuzzy measures of a criterion set may be greater than one, fuzzy measures are really extensions of weights because the fuzzy measure of the complete set is only one. Thus, the fuzzy measures have greater versatility. Demirel et al. [34] employed Choquet integral mathematical models to investigate a suitable location for a warehouse under different key criteria. Tan and Chen [35] generalized the concepts of Choquet integral operators to acquire an authentic results from decision analysis process under different criteria. Furthermore, a family of Sugeno-Weber aggregation operators also utilized to investigate unknown degree of weights to assess a suitable security techniques [36]. The intuitionistic fuzzy Choquet averaging and geometric operators based on Einstein were created by Yu [37]. Yu and Xu [38] presented the intuitionistic fuzzy interaction aggregation operators based on the Choquet integral and created a two-sided matching decision-making model based on aggregation operators.
Menger [39] introduced the theoretical concepts of triangular norms with prominent characteristics. Algebraic t-norm and t-conorm are flexible and efficient generalizations of triangular norms. A diverse generalization and extension of triangular norms developed by different scholars, such as Dombi aggregation operators [40], Frank t-norm and t-conorm [41], and Hamacher aggregation operators [42]. Numerous mathematicians employed these aggregation models to acquire smooth aggregated results during the decision analysis process. Aczél and Alsina [43] deduced a family of robust aggregation models by exploring the characteristics of triangular norms. Babu and Ahmed [44] characterized various properties to derive effective mathematical strategies for designing and developing to resolve different applications such as diagnostics, article intelligence, forecasting and pattern recognition. Farahbod and Eftekhari [45] compared various classifications of t-norms and t-conorms to evaluate the best aggregation model. After the evaluation and aggregation process, they concluded that Aczel-Alsina is the best one and Dombi aggregation is the second one. Hussain et al. [46] deliberated a list of Aczel-Alsina aggregation models to handle awkward and incomplete information of human opinion. Senapati et al. [47] proposed Aczel-Alsina aggregation models, taking into account an intuitionistic fuzzy context. Senapati et al. [48] derived innovative mathematical strategies by incorporating the theory of an interval values intuitionistic fuzzy theory. Mu et al. [49] investigated a family of efficient and effective models of Maclaurin symmetric operators with a decision support system. Hussain et al. [50] derived new methodologies of Aczel-Alsina operators to evaluate an electric motor car taking into account the complex spherical fuzzy circumstances. De et al. [51] developed a decision support system with a doubt-fuzzy environment.
Several mathematical approaches and terminologies were established to aggregate expert’s opinions or judgments. Most of them failed to integrate multiple conflicting criteria without any external weights. To investigate the weight of criteria or attributes, Choquet integral operators are authentic mathematical approaches under the system of picture fuzzy environment and Aczel-Alsina triangular norms. We examined that no one worked on this robust mathematical framework under the consideration of a picture fuzzy situation and Choquet integral operators.
The PFS has extended the capabilities of traditional FSs and IFSs by introducing a third dimension: neutrality. In many decision-making scenarios, it’s common to encounter not only positive (supportive) and negative (opposing) opinions but also neutral stances where no clear judgment is made. Traditional fuzzy sets and even intuitionistic fuzzy sets, which include membership and non-membership degrees, fall short in accurately capturing this neutral perspective. For instance, voter express their opinion about any candidate in a specific way, vote to favor (MD), against (NMD), neutral (AD) and refuse to vote (RD). The FSs and IFSs unable to handle such a scenario, which has more than three components of human opinion. However, the PFS is a more abundant and flexible fuzzy framework that contains four aspects of human opinion. Furthermore, the PFSs address the limitation by incorporating a degree of neutrality alongside the traditional membership and non-membership degrees. This three-dimensional approach allows for a more nuanced representation of complex scenarios where neutrality plays a significant role, enabling better modelling and decision-making in situations with uncertain, hesitant, or indeterminate responses.
The Choquet integral operators are used to overcome the limitations of traditional aggregation methods, particularly in contexts where criteria are interdependent. Traditional aggregation operators, like weighted averages, typically assume that criteria are independent, which often oversimplifies the decision-making process. In reality, criteria frequently interact with one another, with some being complementary (synergistic) or substitutive (antagonistic). The Choquet integral was designed to handle such interactions effectively using a fuzzy measure that captures the relationship between criteria. This allows for a more accurate and nuanced aggregation of information, particularly in multi-criteria decision-making situations where the interplay between factors significantly influences the outcome. By accounting for these interactions, the Choquet integral provides a more sophisticated tool for decision-makers, leading to better-informed and more reliable decisions. The primary features of this presentation are given by:
(a) To explore the picture fuzzy theory for handling awkward and unpredictable situations of human opinion. The PFS uniquely captures extensive information, enabling smoother approximations during decision analysis.
(b) Choquet integral operators are more efficient and effective, used to aggregate approximated information with fuzzy measures of criteria and the decision analysis process.
(c) We derive a list of new aggregation operators by incorporating the picture fuzzy theory and Choquet integral operators, namely PFCIAAA and PFCIAAG operators with prominent properties and special cases.
(d) To resolve complicated, genuine real-life dilemmas, an algorithm of the MADM problem is utilized by incorporating derived mathematical methodologies.
(e) To validate the robustness and compatibility of the diagnosed mathematical methodologies, we gave a numerical example to evaluate a suitable electric transformer for electricity supply.
In order to maintain research work, divide the remaining parts as follows: Section 2 briefly discusses fundamental concepts and basic preliminaries of triangular norms, Aczel-Alsina operations, and PFS with dominant rules. Section 3 illustrates a family of averaging Choquet integral operators. Moreover, we also derive mathematical methodologies of geometric Choquet integral operators in the light of picture fuzzy information. The robust technique of the MCDM problem is applied to resolve genuine real-life applications with derived mathematical methodologies in Section 5. An experimental case study is also adopted to reveal the feasibility of the invented approaches. Section 6 conducted an extensive comparative study to mitigate the flexibility of pioneered approaches with previously developed approaches. Section 7 enclosed some remarkable remarks related to the developed research work. Additionally, we also portrayed the main aspects of this article in Fig. 1.

Figure 1: The primary features of the article
This section presents basic and necessary notions of triangular norms, Aczel-Alsina operations, and PFSs with dominant rules.
Definition 1 [52]: A mapping
(a)
(b)
(c)
(d)
For all
Example 1: The following expressions are examples of Definition 1:
(a)
(b)
(c)
(d)
For any
Definition 2 [52]: A mapping
(a)
(b)
(c)
(d)
For any
Example 2: The following expressions are examples of Definition 2:
(a)
(b)
(c)
(d)
For any
Definition 3 [43]: The theory of the Aczel-Alsina t-nom
and
for each
Definition 4 [14]: An IFS
Additionally, a hesitancy degree of
Definition 5 [53]: A PFS
Additionally, the RD of
Definition 6 [33]: Consider any three PFVs
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Definition 7 [54]: Let
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Definition 8 [33]: Let
and
Consider two PFVs
(a) If
(b) If
Example 1: Let
Definition 9 [35]: A mapping
(a)
(b) If
We see above investigation process for finding fuzzy measures is quite complex. Therefore, Sugeno proposed a
where
Definition 10 [35]: Let
here, the permutation on
Definition 11 [54]: Let
(a)
(b)
(c)
(d)
Remark: The above-discussed operations failed, if
Theorem 1 [54]: Let
(a)
(b)
(c)
(d)
(e)
(f)
3 Picture Fuzzy Choquet Integral Aczel-Alsina Averaging Operators
This section developed a family of robust mathematical approaches of Choquet integral operators and Aczel-Alsina operations such as PFCIAAA and PFCIAAOA operators.
Definition 12: For any PFVs
Theorem 2: For any PFVs
Proof: To prove the aforementioned expression, follow the induction method by taking the value of
By using the above Definition 12, we have:
Hence, this is true for
i. Now, suppose that this is true for
Now, for
□
Theorem 3: For any
Proof: Since
□
Theorem 4: Let
Proof: Let
and
So,
□
Theorem 5: Let
Proof: Let
Hence, it is proved that
Definition 13: For any PFVs
where
Theorem 6: For any PFVs
Theorem 7: If all
Theorem 8: Let
Theorem 9: Let
4 Picture Fuzzy Choquet Integral Aczel-Alsina Geometric Aggregation Operators
In order to achieve more flexible and effective mathematical methodologies, we derived a series of new approaches in the presence of picture fuzzy theory, such as PFCIAAG and PFCIAAOG operators.
Definition 14: Let
Theorem 10: For any PFVs
Theorem 11: If all
Theorem 12: For any PFVs
Theorem 13: Let
Definition 15: For any PFVs
Theorem 14: For any PFVs
where
Theorem 15: If all
Theorem 16: Let
Theorem 17: Let
5 Multi-Criteria Decision-Making Problem Based on Picture Fuzzy Framework
To resolve the MADM problem, assume a family of alternative
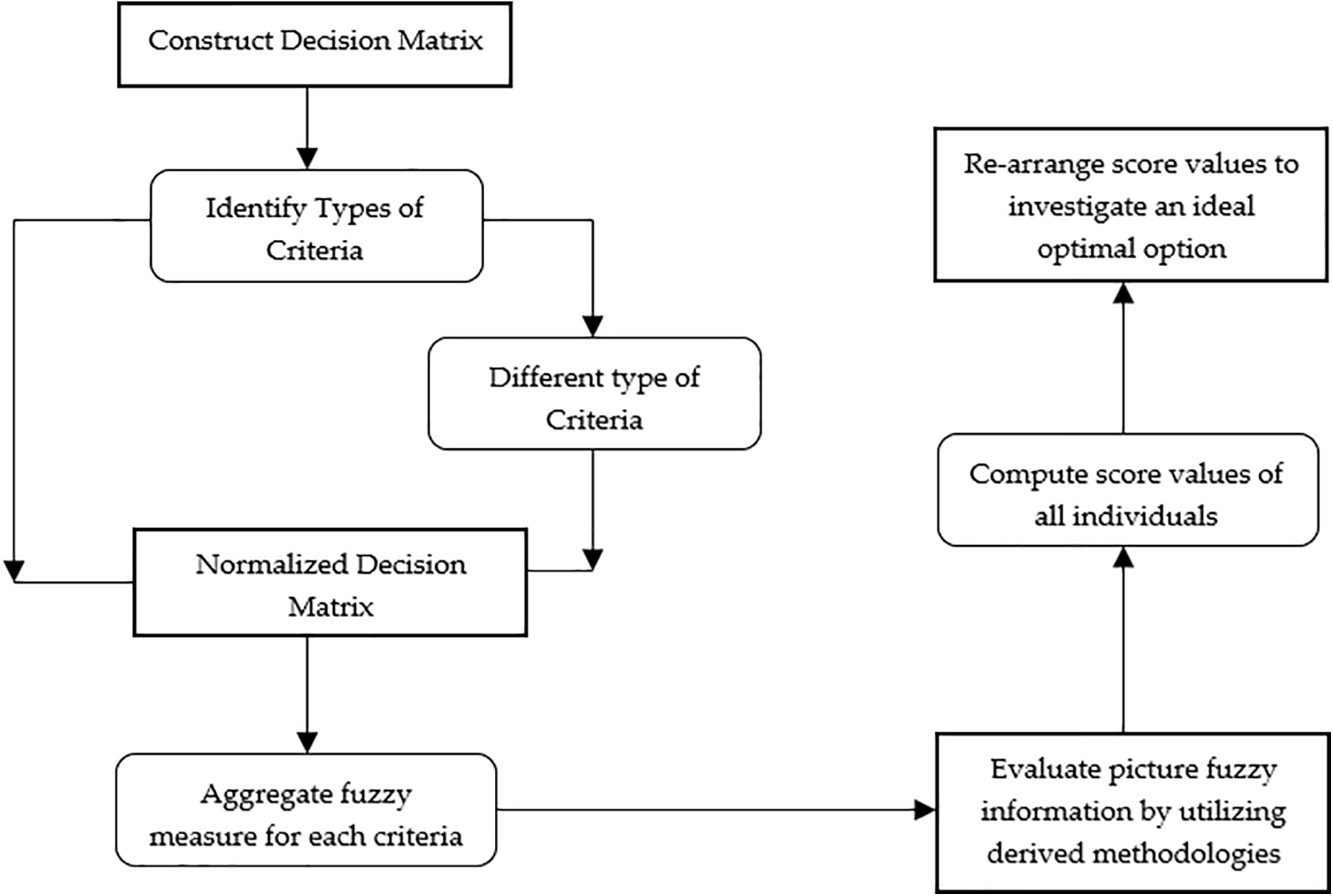
Figure 2: Flowcharts of the MADM problem
Step 1: Construct a decision matrix of picture fuzzy information in the form of alternatives and attributes:
Step 2: To consider the same type of attributes or criteria, the following expression is used to normalize the standard decision matrix into a normalized decision matrix:
If all discussed attributes are the same type, then no need to normalize the process.
Step 2: Compute score and accuracy values to rank the practical evaluation of different preferences by using Definition 8. So, a practical evaluation of
Step 3: It is clear that the investigation of fuzzy measures is quite complex. However, we can compute fuzzy measures by using different expressions or formulas derived by several mathematicians, like linear methods [55], quadratic methods [56,57] and genetic algorithms [58], and many methods are available in the literature [35,59].
Step 4: Aggregate organized picture fuzzy information by utilizing the following expressions:
and
Step 5: Investigate the score or accuracy values of all alternatives according to their need by using the following expressions:
and
Step 6: To analyze a reliable option, we investigate the ranking of alternatives based on computed scores or accuracy values.
The importance of a reliable electric supply cannot be overstated, as electricity powers nearly every aspect of modern life. It serves as the backbone of industries, homes, healthcare, education, and communication systems. In industries, electricity drives machinery, automation, and production processes, enabling large-scale manufacturing and economic growth. It powers computers, servers, and communication networks, ensuring businesses remain operational and connected to the global economy. Without electricity, modern economies would grind to a halt, with productivity and innovation severely limited. Electricity is also vital for critical infrastructure, such as water and transportation systems. It powers pumps for clean water distribution and sewage systems, ensuring public health and sanitation. Electric transportation, from trains to electric vehicles, is becoming increasingly important as societies aim for sustainability and reduced carbon emissions. A stable electricity supply is key to meeting the growing energy demands of our increasingly digital and connected world, supporting both everyday activities and long-term progress.
Electric transformers are essential components in the transmission and distribution of electrical power. They play a critical role in adjusting the voltage levels, allowing electricity generated at power plants to be efficiently transported over long distances. By stepping up the voltage for long-distance transmission, transformers reduce energy losses due to resistance in the wires. When the electricity reaches its destination, another transformer steps down the voltage to a safer, usable level for homes, businesses, and industries. Without transformers, the efficient and widespread distribution of electricity would be nearly impossible, as high-voltage transmission is crucial to minimizing energy loss. In this case study, we assess different types of electric transformers for improving the supply of electricity to spinning textile factories. To achieve this goal, there are five different alternatives are expressed as follows:
Step-up and step-down transformers
Single-phase and three-phase transformers
Distribution and power transformers
Oil-cooled and dry-type transformers
Core type and shell type transformers
Above above-discussed transformers are evaluated under the following four expressed criteria or attributes. The expert assigns fuzzy measures to each criterion or attribute, which are independent to express correlation among the expressed attributes. Some appropriate characteristics of electric transformers also demonstrated in Fig. 3.
Figure 3: Characteristics of electric transformers
Efficient Power Transmission
Flexibility in Power Distribution
Grid Stability and Reliability
Durability and Low Maintenance
By considering an algorithm of the MADM problem and discovering mathematical methodologies, we evaluated a dominant electric transformer under the following steps of the aggregating procedure.
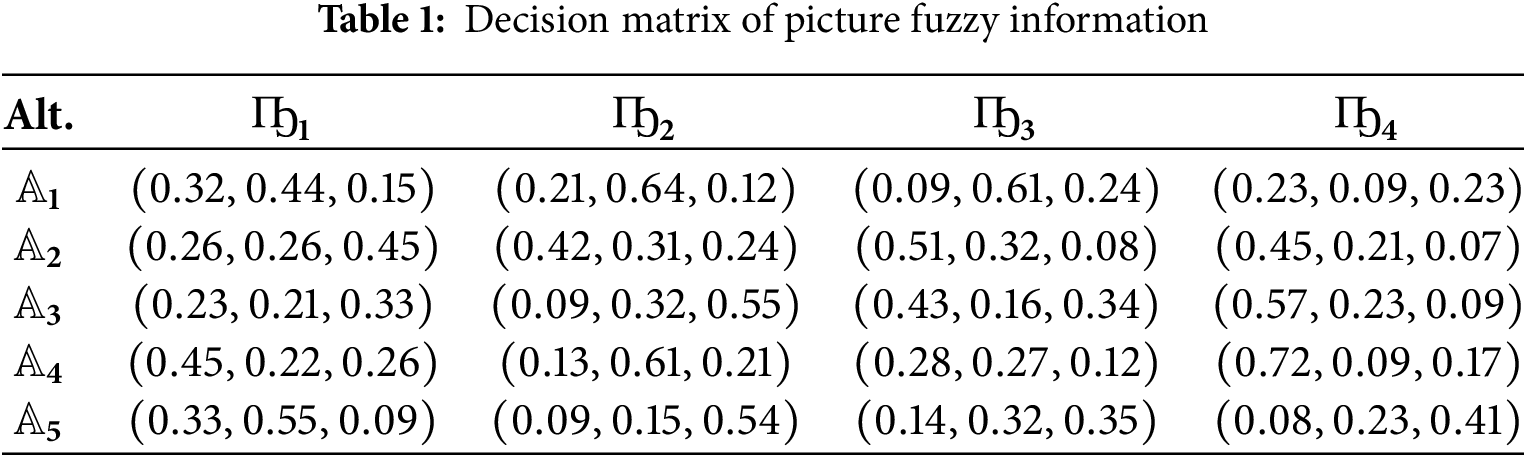
Step 1. Owning a decision matrix of picture fuzzy information in the form of diverse criteria that are associated with each alternative or individual. Table 1 maintains the picture fuzzy information about different types of transformers. The above-discussed experimental case study has only one type of criterion, such as beneficial types. So, there is no need to action on step 2. We can proceed with the evaluation process with the given information in Table 1.
Step 2. The normalization process is meaningless because all discussed criteria are beneficial and same type.
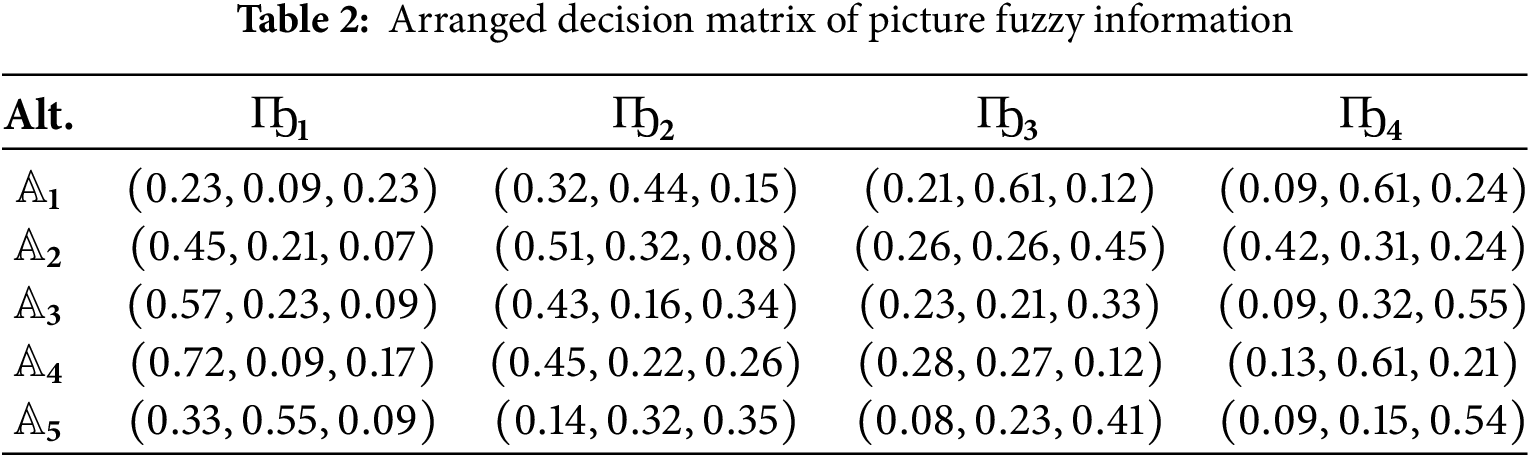
Step 3. By using the score function, re-ordering the attribute information associated with each alternative or individual. So, Table 2 maintained a new ordering of attributes corresponding to each alternative.
Step 4. We see that the investigation process of fuzzy measures is quite complex. In order to avoid these complexities, we have adopted fuzzy measures of criteria and criterion sets from [35].
Step 5. We utilized our proposed aggression operators of PFCIAAA and PFCIAAG operators to aggregate the given information of each attribute corresponding to each alternative that is shown in Table 2. However, Table 3 illustrates aggregated outcomes by the derived methodologies.
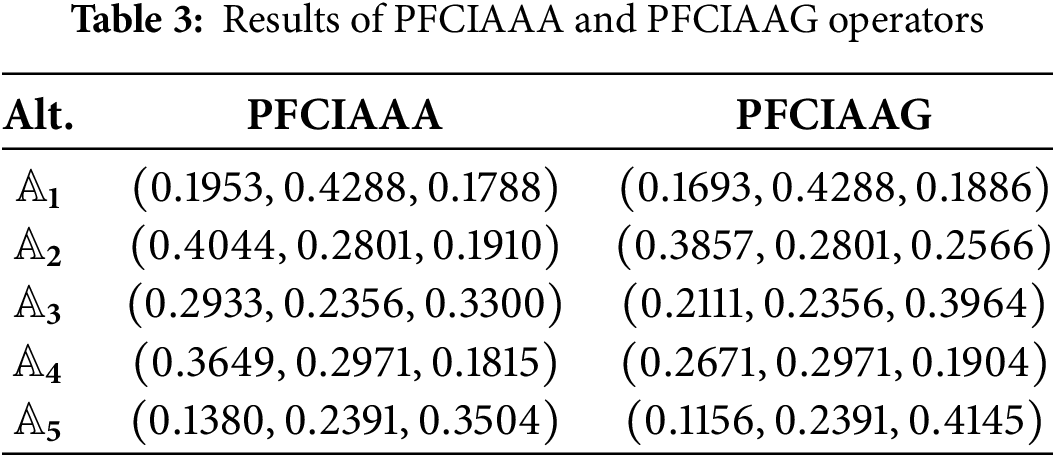
Step 6. Table 4 illustrates computed score values associated with each alternative using Definition 5. To analyze the optimal option for the electric transformer, rank the computed score values of all individuals or alternatives. Fore a better understanding of the aggregated information, we conceive a graphical representation of a bar chart of Fig. 4. This technique plays a significant role in the MADM problem and makes it easier for the readers.

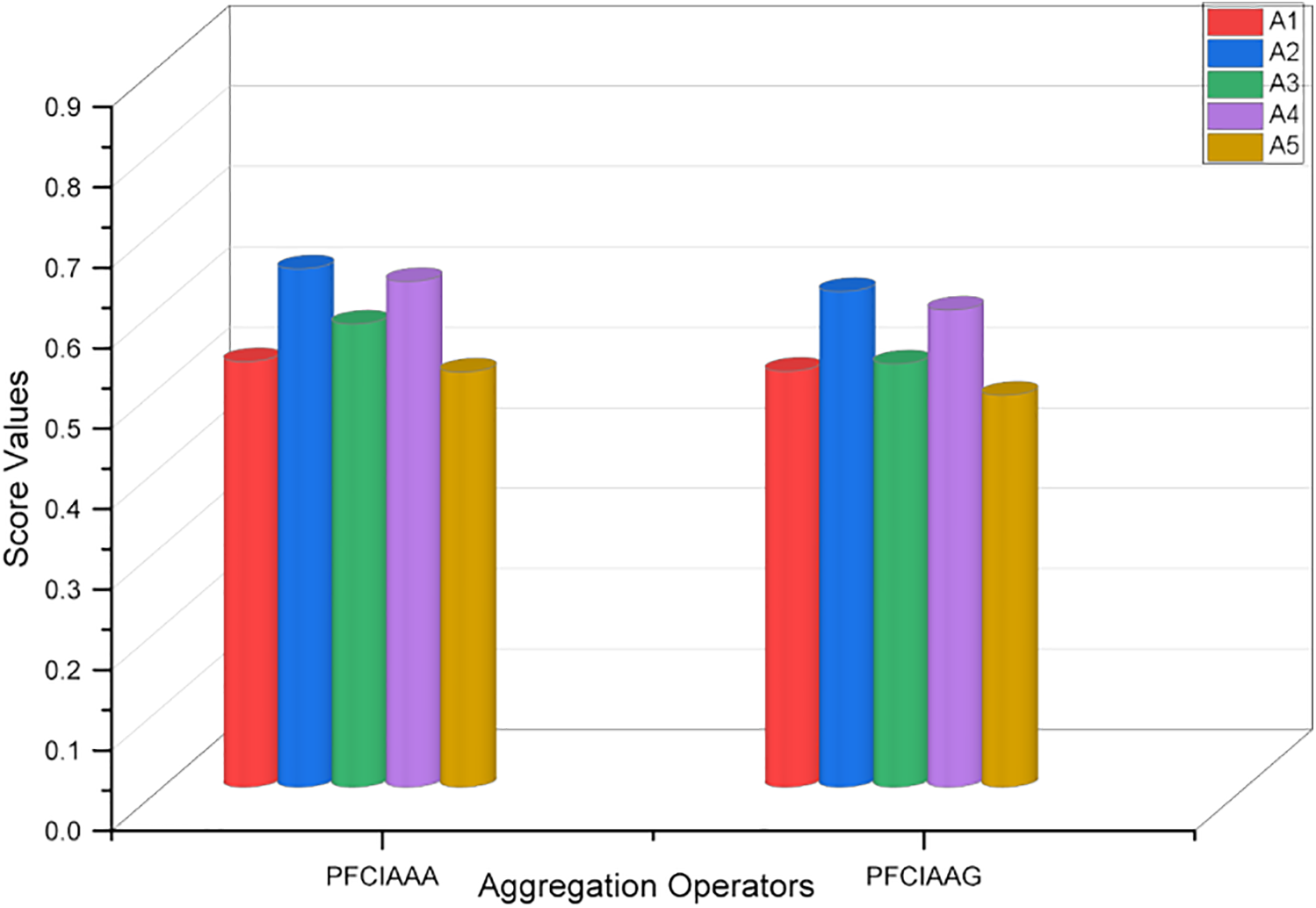
Figure 4: Obtained score values by the PFCIAAA and PFCIAAG operators
In order to maintain the reliability and consistency of derived mathematical approaches in the MADM problem. The decision maker faces diverse challenges during the decision analysis process due to redundant and incomplete information on human opinion. To investigate an ideal and efficient aggregated result, the parametric value of Aczel-Alsina operators can be changed in step 4 of an algorithm for the MADM problem.
By setting different parametric values from
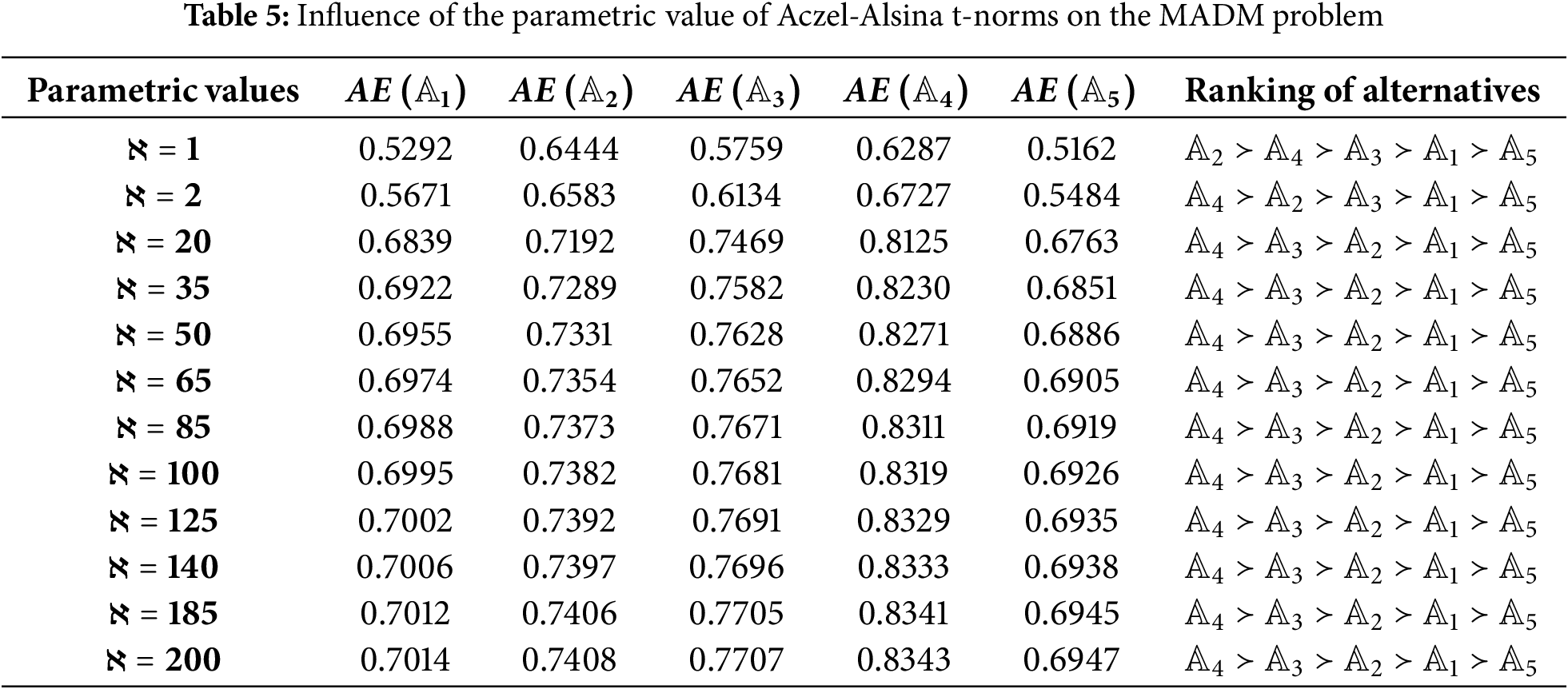
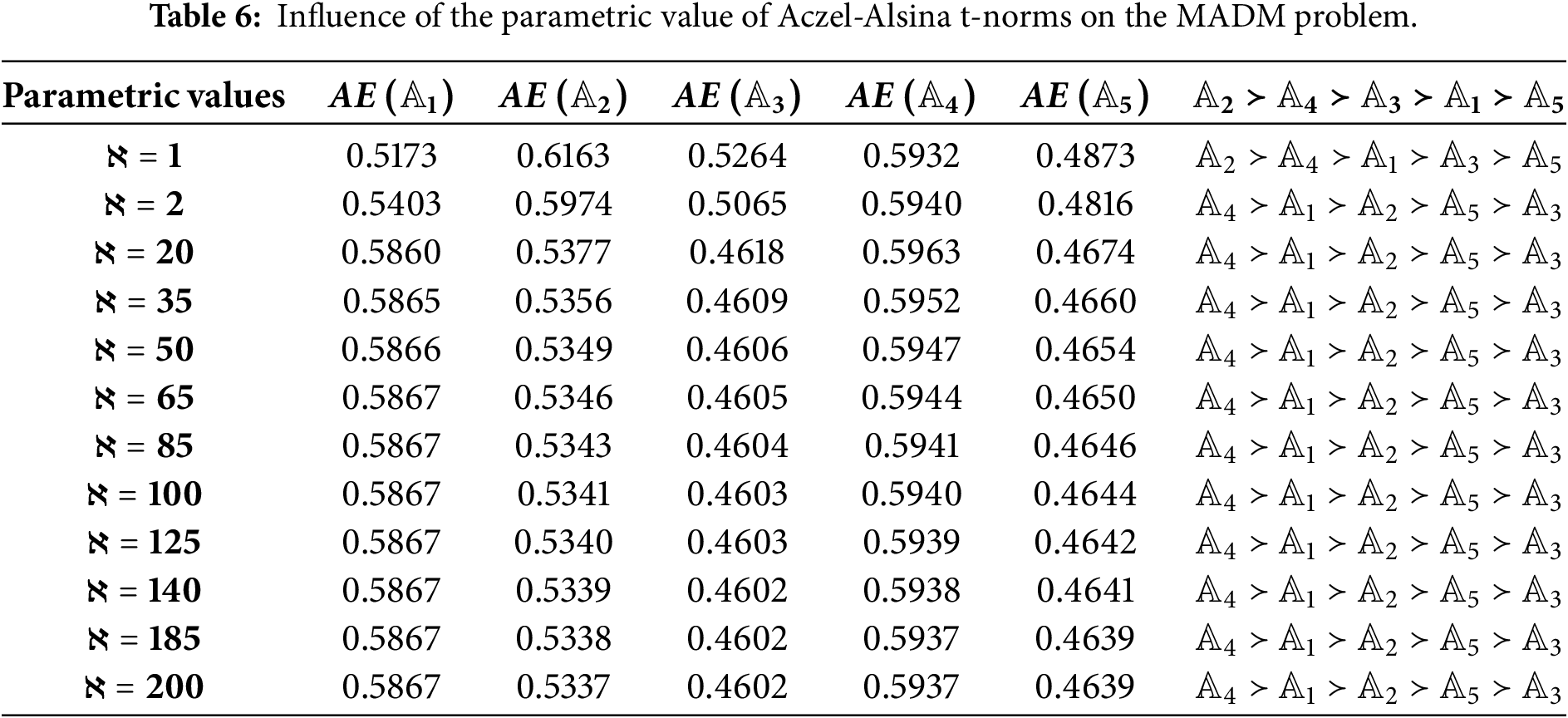
Similarly, the above procedure was repeated for the PFCIAAG operator and the aggregated results are mentioned in Table 6. Ranking of alternatives
In this section, a comprehensive comparison technique is conducted to illustrate the advantages and effectiveness of pioneered mathematical methodologies with previously diagnosed aggregation operators by numerous research scholars. To serve this purpose, we employed different mathematical approaches to the given information in Table 1, which were invented by different scientists namely Wang et al. [24], Senapati [54], Garg [60], Seikh and Mandal [61], Jana et al. [62], Wei [63], Naeem et al. [64]. A brief discussion about these aggregation operators is also presented as picture fuzzy Aczel-Alsina weighted average and picture fuzzy Aczel-Alsina weighted geometric operators by Senapati [54] and Naeem et al. [64], picture fuzzy weighted average and picture fuzzy weighted geometric by Garg [60] and Wang et al. [24], respectively. Seikh and Mandal [61] deliberated the theory of Frank aggregation operators by incorporating picture fuzzy environments. Jana et al. [62] utilized the properties of Dombi aggregation operators to develop new weighted averaging and weighted geometric operators. An innovative approach of Hamacher aggregation operators with picture fuzzy information was developed by Wei [63]. Tables 7 and 8 considered the aggregated results by the existing mathematical approaches in the literature.
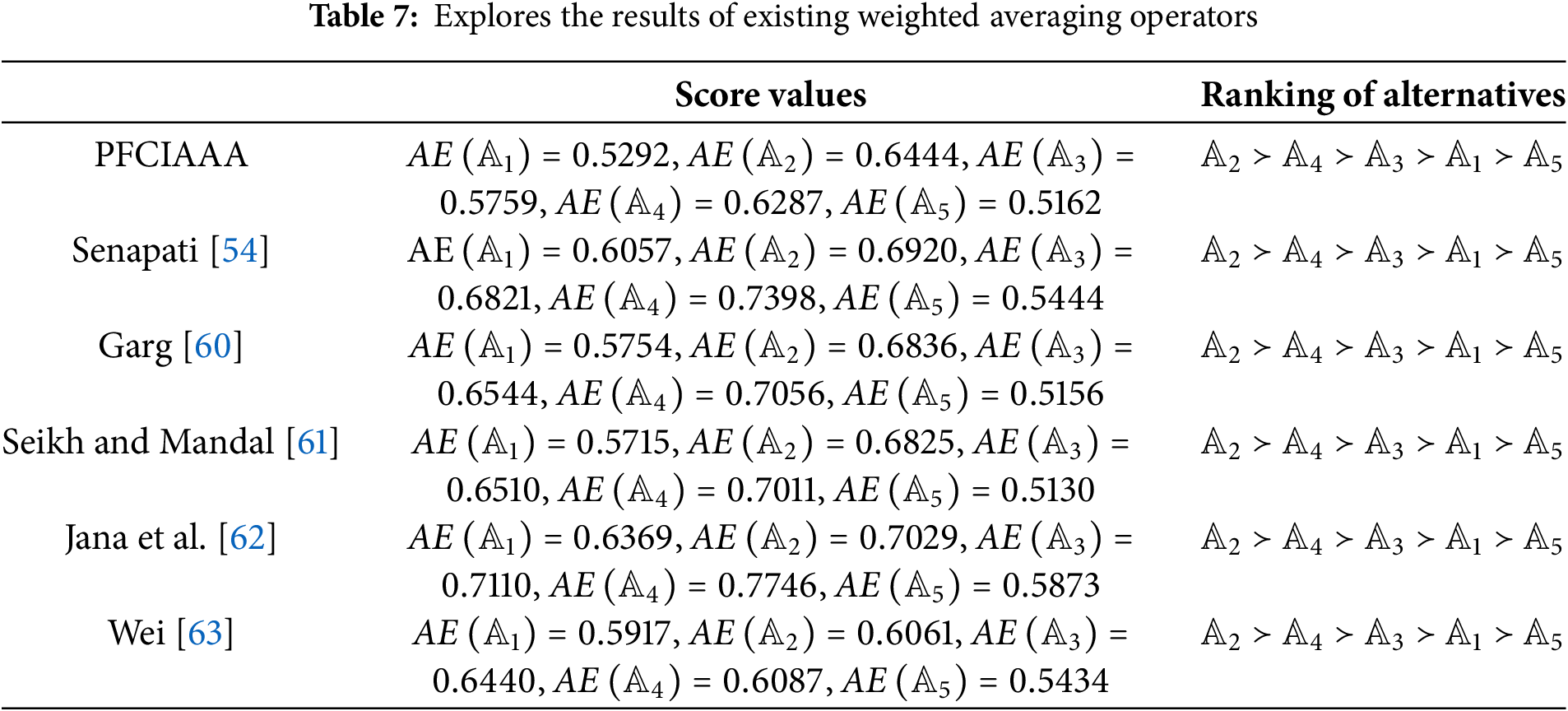
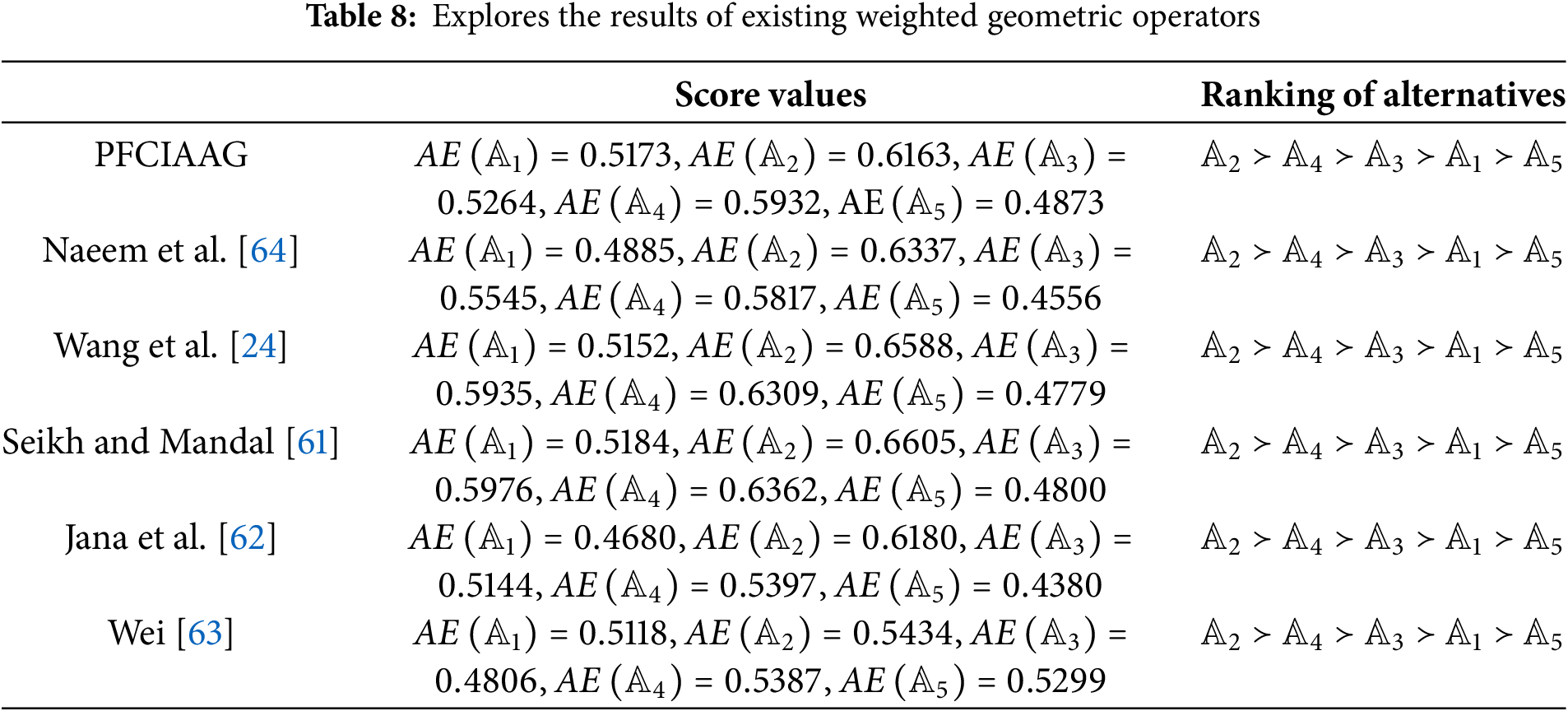
In decision analysis, combining the advantages of the Choquet integral and Aczel-Alsina operators provides a powerful approach for handling complex, uncertain, and interrelated criteria. The Choquet integral excels in managing interactions among criteria, including synergies and redundancies between factors, which is crucial when criteria are not independent. On the other hand, Aczel-Alsina operators bring flexibility by providing parametric control over the aggregation process, making them adept at handling fuzzy or imprecise information. Together, these methods enhance the decision-making process by offering both nuanced handling of criterion interactions and robust aggregation of uncertain data, making them highly effective for multi-criteria decision-making scenarios where precision and flexibility are needed. The consistency in ranking alternatives shows the supremacy and effectiveness of diagnosed theories with existing mathematical approaches. Figs. 5 and 6 illustrate the aggregated outcomes by the existing weighted averaging and weighted geometric operators that exist in the literature.
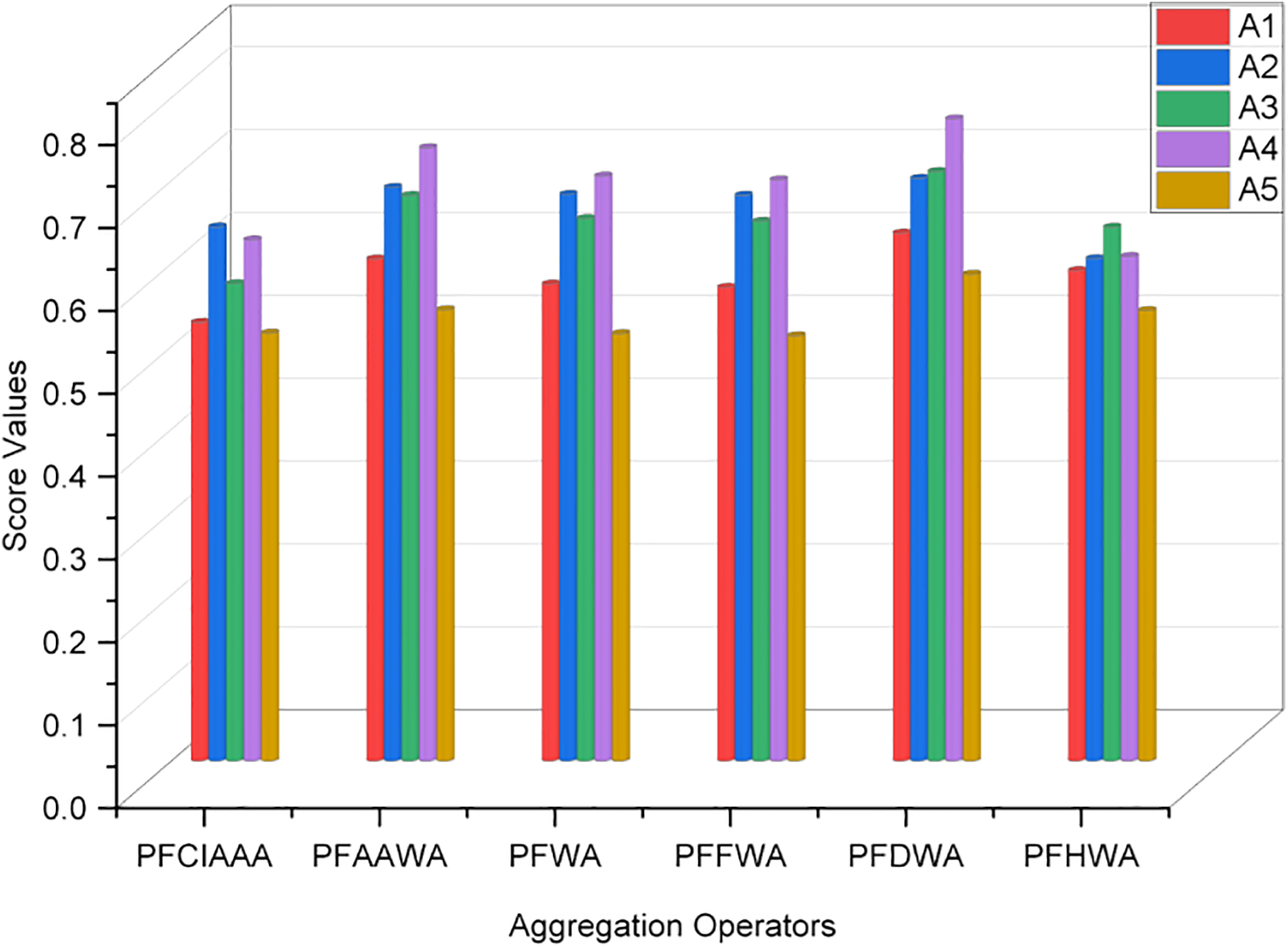
Figure 5: Displayed aggregated outcomes by the existing weighted averaging
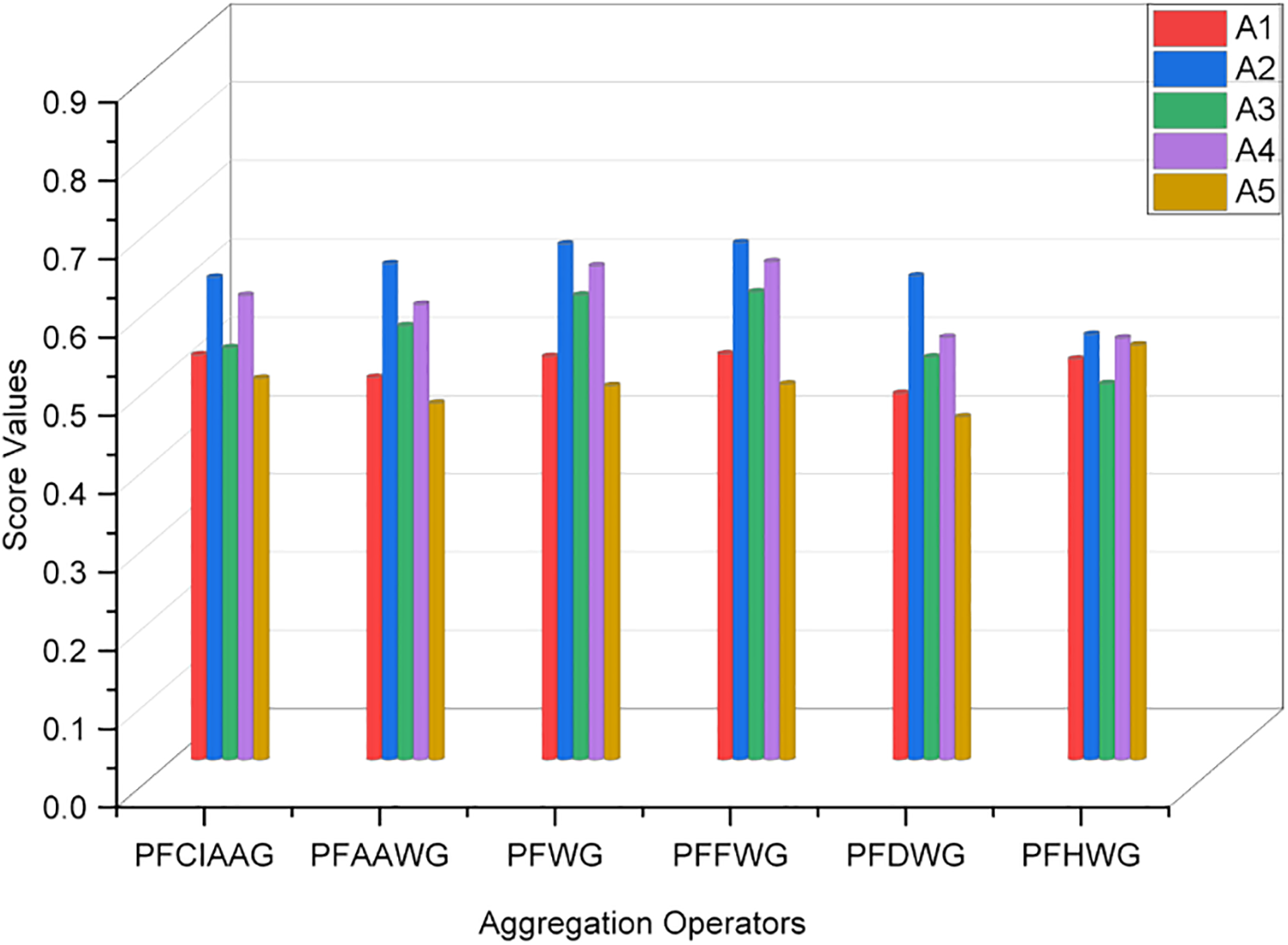
Figure 6: Displayed aggregated outcomes by the existing weighted geometric
This research study contributes to the expanding body of knowledge on aggregation operators by analyzing issues in which the valuations fall within the picture fuzzy environment. The capacity of PFS theory to accurately represent fuzzy information in the context of membership, abstinence, and non-membership functions makes it a classic and important fuzzy theory among those now in existence. Fuzzy measures in fuzzy information systems provide a good description of the correlative links between criterion sets, and the Choquet integral can handle these interactions even further. We have introduced aggregation operators, called the PFCIAAA and PFCIAAG operators, which are inspired by the Choquet integral. We have expanded the definitions of the PFCIAAA and PFCIAAG operators by merging the weights of the various points. Various characteristics of derived approaches, including monotonicity, boundedness, and idempotency, have been demonstrated. An algorithm of the MADM has been presented by considering invented mathematical approaches of the PFCIAAA and PFCIAAG operators. Furthermore, an illustrative numerical example is applied to demonstrate a suitable optimal option based on suggested aggregation operators. Finally, by examining the acquired decision-making outcomes, we have contrasted the suggested approaches with several other aggregation operators that exist in the literature. While different results from the ranking of alternatives show the benefits of the suggested technique, the same findings from the best alternative show that the suggested method is feasible. A comprehensive comparative study shows the flexibility and advantages of derived mathematical approaches by comparing the results of pioneered approaches with suggested aggregation operators that exist in the literature.
In the future, derived mathematical methodologies can be modified to accumulate various complicated frameworks such as interval-valued picture fuzzy domain, triangular picture fuzzy context, and spherical and t-spherical fuzzy theory. We can also apply to resolve various crucial challenges by using advanced decision-making techniques. Some robust optimization techniques may also be discussed to resolve real-life applications using EDAS [65], TOPSIS [66], VIKOR [67], and MARCOS [68] methods.
Acknowledgement: The authors would also like to thank the respected editors and reviewers for their support.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Abrar Hussain, Kifayat Ullah, Hafiz Aftab Anwar; data collection: Abrar Hussain, Hafiz Aftab Anwar, Dragan Pamucar; analysis and interpretation of results: Kifayat Ullah, Dragan Pamucar, Vladimir Simic; draft manuscript preparation: Abrar Hussain, Hafiz Aftab Anwar, Vladimir Simic. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data will be available on reasonable request to the corresponding author.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
List of Symbols
| Symbol | Meaning |
| Membership degree | |
| Abstinence degree | |
| Non-membership degree | |
| Element of non-empty set | |
| Score function | |
| Accuracy function | |
| t-norm | |
| t-conorm | |
| Non-empty set | |
| Attribute | |
| Alternative | |
| Fuzzy measure |
References
1. Cowan WN, Chang T, Inglesi-Lotz R, Gupta R. The nexus of electricity consumption, economic growth and CO2 emissions in the BRICS countries. Energy Policy. 2014;66(2):359–68. doi:10.1016/j.enpol.2013.10.081; [Google Scholar] [CrossRef]
2. Bridges A, Felder FA, McKelvey K, Niyogi I. Uncertainty in energy planning: estimating the health impacts of air pollution from fossil fuel electricity generation. Energy Res Soc Sci. 2015;6(6):74–7. doi:10.1016/j.erss.2014.12.002; [Google Scholar] [CrossRef]
3. Gracceva F, Zeniewski P. A systemic approach to assessing energy security in a low-carbon EU energy system. Appl Energy. 2014;123:335–48. doi:10.1016/j.apenergy.2013.12.018; [Google Scholar] [CrossRef]
4. Qi T, Zhang X, Karplus VJ. The energy and CO2 emissions impact of renewable energy development in China. Energy Policy. 2014;68:60–9. doi:10.1016/j.enpol.2013.12.035; [Google Scholar] [CrossRef]
5. Kabeyi MJB, Olanrewaju OA. Bagasse electricity potential of conventional sugarcane factories. J Energy. 2023;2023(1):5749122. doi:10.1155/2023/5749122; [Google Scholar] [CrossRef]
6. Soria R, Portugal-Pereira J, Szklo A, Milani R, Schaeffer R. Hybrid concentrated solar power (CSP)–biomass plants in a semiarid region: a strategy for CSP deployment in Brazil. Energy Policy. 2015;86(4):57–72. doi:10.1016/j.enpol.2015.06.028; [Google Scholar] [CrossRef]
7. Mayer FD, Salbego PRS, de Almeida TC, Hoffmann R. Quantification and use of rice husk in decentralized electricity generation in Rio Grande do Sul State. Brazil Clean Technol Environ Policy. 2015;17(4):993–1003. doi:10.1007/s10098-014-0850-4; [Google Scholar] [CrossRef]
8. Portugal-Pereira J, Esteban M. Implications of paradigm shift in Japan’s electricity security of supply: a multi-dimensional indicator assessment. Appl Energy. 2014;123(36):424–34. doi:10.1016/j.apenergy.2014.01.024; [Google Scholar] [CrossRef]
9. Kjølle GH, Gjerde O. Integrated approach for security of electricity supply analysis. Int J Syst Assur Eng Manag. 2010;1(2):163–9. doi:10.1007/s13198-010-0014-9; [Google Scholar] [CrossRef]
10. Ali Khan MS, Abdullah S, Ali A. Multiattribute group decision-making based on Pythagorean fuzzy Einstein prioritized aggregation operators. Int J Intell Syst. 2019;34(5):1001–33. doi:10.1002/int.22084; [Google Scholar] [CrossRef]
11. Akram M, Martino A. Multi-attribute group decision making based on T-spherical fuzzy soft rough average aggregation operators. Granul Comput. 2023;8(1):171–207. doi:10.1007/s41066-022-00319-0; [Google Scholar] [CrossRef]
12. Li Z, Gao H, Wei G. Methods for multiple attribute group decision making based on intuitionistic fuzzy dombi hamy mean operators. Symmetry. 2018;10(11):574. doi:10.3390/sym10110574; [Google Scholar] [CrossRef]
13. Zadeh LA. Fuzzy sets. Inf Control. 1965;8(3):338–53; [Google Scholar]
14. Atanassov KT. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986;20(1):87–96. doi:10.1016/s0165-0114(86)80034-3; [Google Scholar] [CrossRef]
15. Yager R, Basson D. Decision making with fuzzy sets. Decis Sci. 1975;6(3):590–600. doi:10.1111/j.1540-5915.1975.tb01046.x; [Google Scholar] [CrossRef]
16. Yager R. Pythagorean fuzzy subsets. In: Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS); 2013 Jun 24–28; Edmonton, AB, Canada. [Google Scholar]
17. Yager RR, Abbasov AM. Pythagorean membership grades, complex numbers, and decision making. Int J Intell Syst. 2013;28(5):436–52. doi:10.1002/int.21584; [Google Scholar] [CrossRef]
18. Peng X, Yang Y. Some results for pythagorean fuzzy sets. Int J Intell Syst. 2015;30(11):1133–60. doi:10.1002/int.21738; [Google Scholar] [CrossRef]
19. Cường BC. Picture fuzzy sets. J Comput Sci Cybern. 2014;30(4):409; [Google Scholar]
20. Yager RR. On ordered weighted averaging aggregation operators in multicriteria decisionmaking. IEEE Trans Syst Man Cybern. 1988;18(1):183–90. doi:10.1109/21.87068; [Google Scholar] [CrossRef]
21. Garg H. Generalized Pythagorean fuzzy geometric aggregation operators using Einstein t-norm and t-conorm for multicriteria decision-making process. Int J Intell Syst. 2017;32(6):597–630. doi:10.1002/int.21860; [Google Scholar] [CrossRef]
22. Cuong BC, Kreinovitch V, Ngan RT. A classification of representable t-norm operators for picture fuzzy sets. In: Proceedings of the 2016 Eighth International Conference on Knowledge and Systems Engineering (KSE); 2016 Oct 6–8; Hanoi, Vietnam. [Google Scholar]
23. Hussain A, Ullah K, Pamucar D, Vranješ Đ. A multi-attribute decision-making approach for the analysis of vendor management using novel complex picture fuzzy hamy mean operators. Electronics. 2022;11(23):3841. doi:10.3390/electronics11233841; [Google Scholar] [CrossRef]
24. Wang C, Zhou X, Tu H, Tao S. Some geometric aggregation operators based on picture fuzzy sets and their application in multiple attribute decision making. Ital J Pure Appl Math. 2017;37:477–92. doi:10.21203/rs.3.rs-418738/v1; [Google Scholar] [CrossRef]
25. Hussain A, Wang H, Ullah K, Pamucar D. Novel intuitionistic fuzzy Aczel Alsina Hamy mean operators and their applications in the assessment of construction material. Complex Intell Syst. 2024;10(1):1061–86. doi:10.1007/s40747-023-01116-1; [Google Scholar] [CrossRef]
26. Sahoo SK, Pamucar D, Goswami SS. A review of multi-criteria decision-making applications to solve energy management problems from 2010-2025: current state and future research. Spectr Decis Mak Appl. 2025;2(1):219–41; [Google Scholar]
27. Petchimuthu S, Mahendiran C, Premala T. Power and energy transformation: multi-criteria decision-making utilizing complex q-rung picture fuzzy generalized power prioritized yager operators. Spectr Oper Res. 2025;2(1):219–58; [Google Scholar]
28. Ali Z, Mahmood T, Yang MS. Aczel-Alsina power aggregation operators for complex picture fuzzy (CPF) sets with application in CPF multi-attribute decision making. Symmetry. 2023;15(3):651. doi:10.3390/sym15030651; [Google Scholar] [CrossRef]
29. Mahmood T, Waqas HM, Ali Z, Ullah K, Pamucar D. Frank aggregation operators and analytic hierarchy process based on interval-valued picture fuzzy sets and their applications. Int J Intell Syst. 2021;36(12):7925–62. doi:10.1002/int.22614; [Google Scholar] [CrossRef]
30. Ahmed D, Dai B. Picture fuzzy rough set and rough picture fuzzy set on two different universes and their applications. J Math. 2020;2020(4):e8823580. doi:10.1155/2020/8823580; [Google Scholar] [CrossRef]
31. Hussain A, Ullah K, Garg H, Mahmood T. A novel multi-attribute decision-making approach based on T-spherical fuzzy Aczel Alsina Heronian mean operators. Granul Comput. 2024;9(1):21. doi:10.1007/s41066-023-00442-6; [Google Scholar] [CrossRef]
32. Ahmmad J, Mahmood T, Mehmood N, Urawong K, Chinram R. Intuitionistic fuzzy rough Aczel-Alsina average aggregation operators and their applications in medical diagnoses. Symmetry. 2022;14(12):2537. doi:10.3390/sym14122537; [Google Scholar] [CrossRef]
33. Hussain A, Zhu X, Ullah K, Tehreem, Pamucar D, Rashid M et al. Recycling of waste materials based on decision support system using picture fuzzy Dombi Bonferroni means. Soft Comput. 2024;28(4):2771–97. doi:10.1007/s00500-023-09328-w; [Google Scholar] [CrossRef]
34. Demirel T, Demirel NÇ, Kahraman C. Multi-criteria warehouse location selection using Choquet integral. Expert Syst Appl. 2010;37(5):3943–52. doi:10.1016/j.eswa.2009.11.022; [Google Scholar] [CrossRef]
35. Tan C, Chen X. Intuitionistic fuzzy Choquet integral operator for multi-criteria decision making. Expert Syst Appl. 2010;37(1):149–57. doi:10.1016/j.eswa.2009.05.005; [Google Scholar] [CrossRef]
36. Hussain A, Ullah K, Pamucar D, Simic V. Intuitionistic fuzzy Sugeno-Weber decision framework for sustainable digital security assessment. Eng Appl Artif Intell. 2024;137(1):109085. doi:10.1016/j.engappai.2024.109085; [Google Scholar] [CrossRef]
37. Yu D. Intuitionistic fuzzy Choquet aggregation operator based on Einstein operation laws. Sci Iran. 2013;20(6):2109–22; [Google Scholar]
38. Yu D, Xu Z. Intuitionistic fuzzy two-sided matching model and its application to personnel-position matching problems. J Oper Res Soc. 2020;71(2):312–21. doi:10.1080/01605682.2018.1546662; [Google Scholar] [CrossRef]
39. Menger K. Statistical metrics. Proc Natl Acad Sci U S A. 1942;28(12):535; [Google Scholar]
40. Dombi J. A general class of fuzzy operators, the DeMorgan class of fuzzy operators and fuzziness measures induced by fuzzy operators. Fuzzy Sets Syst. 1982;8(2):149–63. doi:10.1016/0165-0114(82)90005-7; [Google Scholar] [CrossRef]
41. Alsina C, Schweizer B, Frank MJ. Associative functions: triangular norms and copulas. Singapore: World Scientific; 2006. 237 p. [Google Scholar]
42. Sarkoci P. Domination in the families of Frank and Hamacher t-norms. Kybernetika. 2005;41(3):349–60; [Google Scholar]
43. Aczél J, Alsina C. Characterizations of some classes of quasilinear functions with applications to triangular norms and to synthesizing judgements. Aequationes Math. 1982;25(1):313–5. doi:10.1007/bf02189626; [Google Scholar] [CrossRef]
44. Babu MS, Ahmed S. Function as the generator of parametric T-norms. Am J Appl Math. 2017;5(4):114–8; [Google Scholar]
45. Farahbod F, Eftekhari M. Comparison of different T-norm operators in classification problems. Int J Fuzzy Log Syst. 2012;2(3):33–9; [Google Scholar]
46. Hussain A, Ullah K, Alshahrani MN, Yang MS, Pamucar D. Novel Aczel-Alsina operators for pythagorean fuzzy sets with application in multi-attribute decision making. Symmetry. 2022;14(5):940. doi:10.3390/sym14050940; [Google Scholar] [CrossRef]
47. Senapati T, Chen G, Yager RR. Aczel-Alsina aggregation operators and their application to intuitionistic fuzzy multiple attribute decision making. Int J Intell Syst. 2022;37(2):1529–51. doi:10.1002/int.22684; [Google Scholar] [CrossRef]
48. Senapati T, Chen G, Mesiar R, Yager RR. Novel Aczel-Alsina operations-based interval-valued intuitionistic fuzzy aggregation operators and their applications in multiple attribute decision-making process. Int J Intell Syst. 2022;37(8):5059–81. doi:10.1002/int.22751; [Google Scholar] [CrossRef]
49. Mu Z, Zeng S, Wang P. Novel approach to multi-attribute group decision-making based on interval-valued Pythagorean fuzzy power Maclaurin symmetric mean operator. Comput Ind Eng. 2021;155(1):107049. doi:10.1016/j.cie.2020.107049; [Google Scholar] [CrossRef]
50. Hussain A, Ullah K, Senapati T, Moslem S. Complex spherical fuzzy Aczel Alsina aggregation operators and their application in assessment of electric cars. Heliyon. 2023;9(7):e18100. doi:10.1016/j.heliyon.2023.e18100; [Google Scholar] [CrossRef]
51. De SK, Roy B, Bhattacharya K. Solving an EPQ model with doubt fuzzy set: a robust intelligent decision-making approach. Knowl-Based Syst. 2022;235(2):107666. doi:10.1016/j.knosys.2021.107666; [Google Scholar] [CrossRef]
52. Klement EP, Mesiar R, Pap E. Triangular norms. Berlin/Heidelberg, Germany: Springer; 2000. 406 p. doi:10.1007/978-94-015-9540-7. [Google Scholar] [CrossRef]
53. Cuong B. Picture fuzzy sets-first results. In: Seminar. Vol. 1, Neuro-Fuzzy Syst Appl; 2013. [Google Scholar]
54. Senapati T. Approaches to multi-attribute decision-making based on picture fuzzy Aczel-Alsina average aggregation operators. Comput Appl Math. 2022;41(1):1–19. doi:10.1007/s40314-021-01742-w; [Google Scholar] [CrossRef]
55. Marichal JL, Roubens M. Dependence between criteria and multiple criteria decision aid. In: Proceedings of the 2nd Int Workshop on Preferences and Decision (TRENTO’98); 1998 Jul 1–3; Trento, Italy. [Google Scholar]
56. Grabisch M. The representation of importance and interaction of features by fuzzy measures. Pattern Recognit Lett. 1996;17(6):567–75. doi:10.1016/0167-8655(96)00020-7; [Google Scholar] [CrossRef]
57. Grabisch M, Nicolas JM. Classification by fuzzy integral: performance and tests. Fuzzy Sets Syst. 1994;65(2–3):255–71. doi:10.1016/0165-0114(94)90023-x; [Google Scholar] [CrossRef]
58. Wang W, Wang Z, Klir GJ. Genetic algorithms for determining fuzzy measures from data. J Intell Fuzzy Syst. 1998;6(2):171–83 doi:10.3233/ifs-1998-002; [Google Scholar] [CrossRef]
59. Grabisch M. Fuzzy integral in multicriteria decision making. Fuzzy Sets Syst. 1995;69(3):279–98 doi: 10.1016/0165-0114(94)00174-6; [Google Scholar] [CrossRef]
60. Garg H. Some picture fuzzy aggregation operators and their applications to multicriteria decision-making. Arab J Sci Eng. 2017;42(12):5275–90 doi:10.1007/s13369-017-2625-9; [Google Scholar] [CrossRef]
61. Seikh MR, Mandal U. Some picture fuzzy aggregation operators based on frank t-norm and t-conorm: application to MADM process. Informatica. 2021;45(3):447–61. doi:10.31449/inf.v45i3.3025; [Google Scholar] [CrossRef]
62. Jana C, Senapati T, Pal M, Yager RR. Picture fuzzy Dombi aggregation operators: application to MADM process. Appl Soft Comput. 2019;74:99–109 doi:10.1016/j.asoc.2018.10.021; [Google Scholar] [CrossRef]
63. Wei G. Picture fuzzy Hamacher aggregation operators and their application to multiple attribute decision making. Fundam Informaticae. 2018;157(3):271–320. doi:10.3233/fi-2018-1628; [Google Scholar] [CrossRef]
64. Naeem M, Khan Y, Ashraf S, Weera W, Batool B. A novel picture fuzzy Aczel-Alsina geometric aggregation information: application to determining the factors affecting mango crops. AIMS Math. 2022;7(7):12264–88. doi:10.3934/math.2022681; [Google Scholar] [CrossRef]
65. Garg H, Waqas M, Ali Z, Emam W. EDAS method for circular pythagorean fuzzy with improved Dombi power aggregation operators and their application in policy analysis and decision support systems. Alex Eng J. 2024;106(1):172–93. doi:10.1016/j.aej.2024.06.062; [Google Scholar] [CrossRef]
66. Mahmood T, Rehman UU, Shahab S, Ali Z, Anjum M. Decision-making by using TOPSIS techniques in the framework of bipolar complex intuitionistic fuzzy N-soft sets. IEEE Access. 2023;11:105677–97. doi:10.1109/access.2023.3316879; [Google Scholar] [CrossRef]
67. Shahzadi S, Chohan M, Zafar F. Ranking failure modes with pythagorean fuzzy rough VIKOR approach. Granul Comput. 2024;9(3):70. doi:10.1007/s41066-024-00492-4; [Google Scholar] [CrossRef]
68. Akram M, Khan A, Luqman A, Senapati T, Pamucar D. An extended MARCOS method for MCGDM under 2-tuple linguistic q-rung picture fuzzy environment. Eng Appl Artif Intell. 2023;120(11):105892. doi:10.1016/j.engappai.2023.105892; [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools