DSGNN: Dual-Shield Defense for Robust Graph Neural Networks

1  Introduction

Graph Neural Networks (GNNs) have demonstrated outstanding effectiveness in modeling non-Euclidean data structures and have been widely adopted across various domains, including social network analysis, multimedia recommendation, anomaly detection, and molecular property prediction [1]. This success is largely attributed to the message-passing mechanism, which has become a cornerstone in GNN architectures [2], wherein each node iteratively refines its representation by aggregating information from its neighbors. Through this process, GNNs effectively capture both structural and semantic information, enabling key tasks such as node classification, graph clustering, and link prediction.

Meanwhile, the rapid advancement of large-scale pre-trained models, particularly Large Language Models (LLMs), has significantly expanded the scale and complexity of AI systems, driving an increasing demand for enhanced structural reasoning, knowledge retrieval, and memory management capabilities. In response to these evolving needs, Graph Neural Networks (GNNs) are being increasingly integrated into LLM frameworks and broader AI architectures [3], highlighting their critical role in supporting scalable and robust intelligent systems. Beyond language models, the growing deployment of intelligent systems in complex and dynamic environments—such as anomaly detection [4], real-time intrusion detection in dynamic graph environments [5], visual security probing through adversarial attacks [6], dynamic recommender systems, decentralized financial networks (DeFi), and autonomous driving perception graphs—further underscores the importance of robust graph representation learning. These trends collectively emphasize the pivotal role of GNNs in enabling dynamic reasoning and resilient modeling across diverse real-world applications.

Although GNNs have achieved impressive results on benchmark datasets, these evaluations often assume clean input features and ideal graph structures. However, in real-world scenarios, graph data frequently contains inherent noise, such as irrelevant or misleading edges, and is subject to external disturbances such as adversarial perturbations designed to degrade model performance [7]. In addition to traditional attacks, recent studies have shown that even federated graph learning settings are vulnerable to property inference attacks, exposing sensitive structural information without direct access to the raw graph data [8]. Even slight modifications to node attributes or graph connectivity can substantially impact GNN performance, although these changes often difficult to detect. Nevertheless, existing defense strategies often suffer from two major limitations. First, they are typically designed to handle either structural perturbations or feature perturbations, but not both. This siloed approach limits their effectiveness in real-world scenarios where attackers often employ joint or compound strategies that disrupt both the graph topology and node features concurrently. Second, these methods usually lack adaptive mechanisms capable of dynamically assessing the nature and intensity of the perturbations during inference. As a result, their robustness deteriorates significantly when confronted with sophisticated attacks that exhibit non-uniform or evolving patterns. The absence of an integrated, context-aware defense mechanism thus remains a critical gap in current adversarial robustness research for graph neural networks. These constraints motivate the development of a unified framework capable of decoupling and robustly integrating multi-view perturbations.

To address these challenges, this work proposes DSGNN, a Dual-Channel Shielded Graph Neural Network. DSGNN incorporates two parallel propagation channels, with one dedicated to structural noise and the other to feature perturbations. As illustrated in Fig. 1, the input graph is initially processed through independent structure and feature defense modules. Traditional methods [9,10], depicted in the upper part of the figure, treat each perturbation type separately. Although effective in certain scenarios, single-channel approaches often struggle when structural and feature perturbations coexist, missing critical cross-modal interactions.

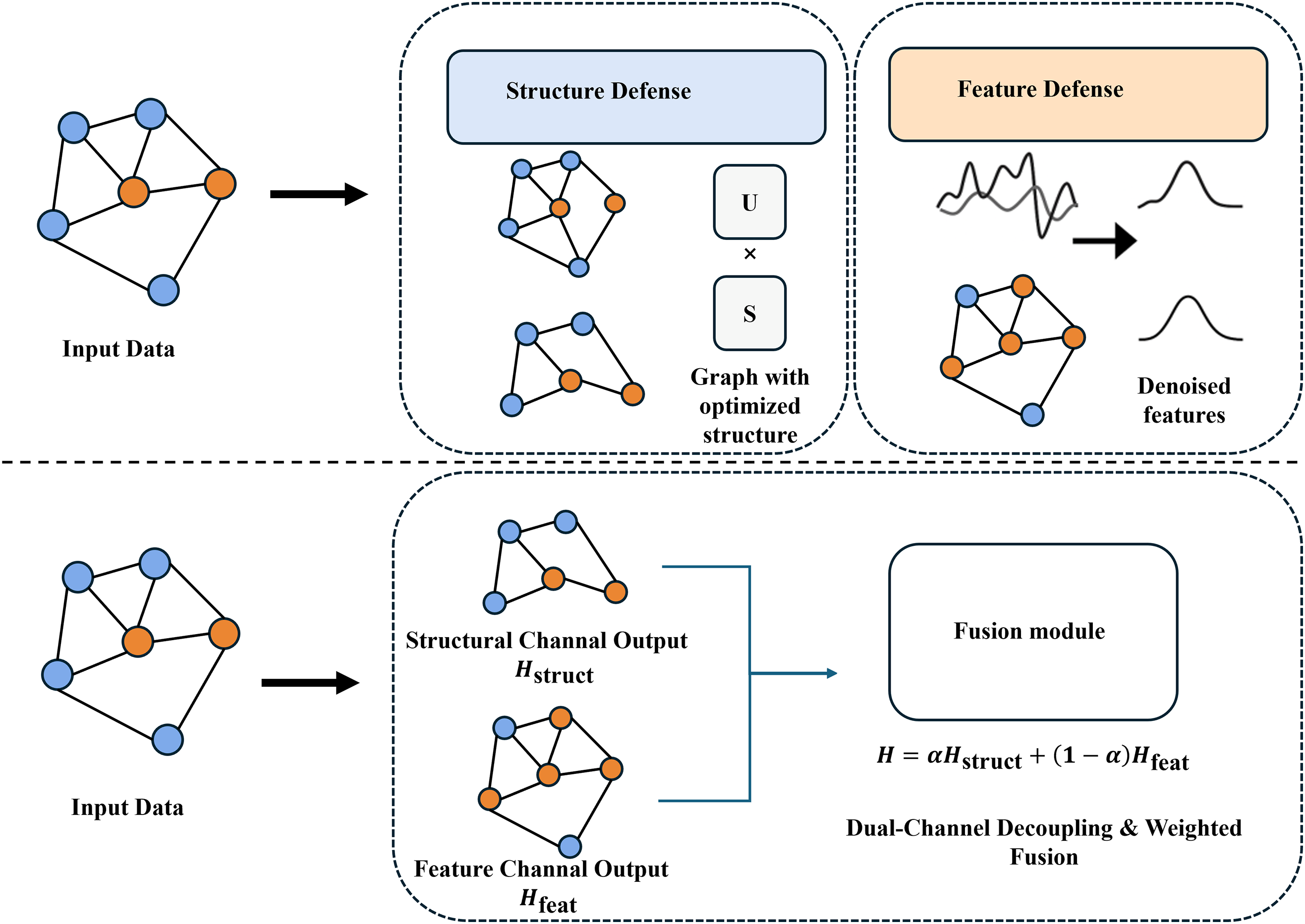
Figure 1: Comparison between the DSGNN model and traditional defense methods. The upper section illustrates traditional defenses, where the input graph is processed through either a structure defense module or a feature defense module, with each module handling a specific perturbation type independently. The lower section shows the proposed DSGNN approach, where the input graph passes through both structural and feature channels simultaneously, followed by a weighted fusion to generate robust node representations. Here, U and S denote the left singular vectors and the singular values obtained from the singular value decomposition (SVD) of the adjacency matrix, respectively

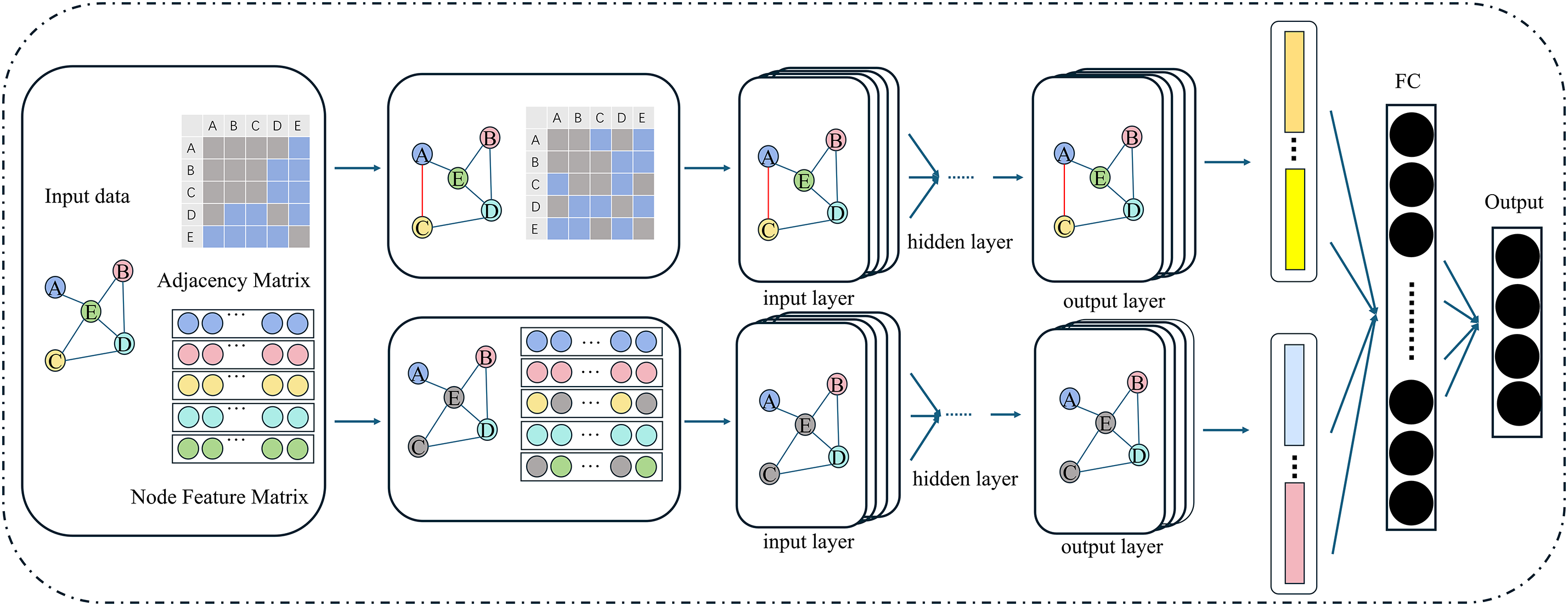
Figure 2: Overview of the DSGNN model. The input graph is processed in parallel through two separate channels focusing on structural and feature perturbations, respectively. Their outputs are then fused to produce a robust node representation. A dynamic fusion layer adaptively weighs the contributions of the two channels based on the reliability of structural and feature information

The resulting representations are propagated through the dual channels and subsequently fused at the final stage (lower part of the figure). This dual-channel decoupling and weighted fusion mechanism enables unified robustness learning, thereby enhancing resilience against complex adversarial attacks.

Extensive experiments on Cora, CiteSeer and Industry datasets validate the effectiveness of the proposed model. DSGNN consistently outperforms existing defense methods under various attack settings, including DICE, PGD, and Metattack, while maintaining competitive performance on noise-free data. These findings underscore the importance of multi-view perturbation modeling in developing robust and generalizable GNN architectures.

Main Contributions

•   DSGNN Architecture: A novel model that explicitly decouples the propagation paths of structural and feature perturbations, thereby enhancing adaptability to compound adversarial attacks.

•   Theoretical Robustness Bound: A theoretical upper bound on robustness risk under joint perturbations is derived, demonstrating that DSGNN provides tighter guarantees compared to conventional defenses.

•   Comprehensive Evaluation: Extensive empirical results across multiple datasets validate the superior robustness of DSGNN against diverse adversarial threats, while maintaining minimal performance degradation on clean inputs.

2  Related Work

GNNs have demonstrated strong capabilities across a variety of graph-based learning tasks. However, in practical applications, even slight perturbations in node features or graph structures can lead to significant performance degradation, particularly in security-sensitive scenarios. To address this issue, numerous defense strategies have been proposed, which can be broadly categorized as follows:

1.   Graph structure preprocessing methods. These approaches statically modify the graph before training to improve model robustness. For instance, GCN-Jaccard [11] removes low-quality edges based on feature similarity, while GCN-SVD [9] suppresses high-frequency noise via low-rank approximation of the adjacency matrix. These methods are computationally efficient and suitable for static graphs but struggle to defend against test-time attacks and lack adaptability to dynamic graphs.

2.   Adversarial training methods. Methods such as GraphAT [12] generate adversarial samples during training and jointly optimize node features and graph structures to enhance resistance against attacks. Although effective under strong adversarial conditions, they often incur high training costs and suffer from poor scalability on large graphs.

3.   Architecture enhancement methods. RobustGCN [13], GNNGuard [10], and related approaches improve robustness by modifying the message-passing mechanism—modeling neighbor importance, adjusting attention weights, or by reassigning edge weights—to mitigate the impact of structural perturbations. While these methods are effective against structural attacks, they often neglect feature perturbations, leading to limited adaptability under joint structural-feature attacks. Recent extensions, such as GCORN [14] and β-GNN [15], attempt to address this gap from different perspectives. GCORN enhances theoretical robustness under feature noise through orthonormal weight constraints, while β-GNN dynamically fuses the outputs of a GNN and an MLP to resist structural perturbations and provide interpretable attack indicators. However, these designs either increase training complexity or target only one type of perturbation.

4.   Noise injection mechanisms. Recent lightweight approaches introduce random noise into model weights or activations to improve robustness. NoisyGNN [16] injects Gaussian noise into hidden layers to enhance resistance against adversarial attacks.

5.   Feature and structure regularization methods. Approaches such as Pro-GNN [17] and RGCN [18] incorporate smoothness constraints on features and structures to improve tolerance to local anomalies. However, these methods often assume smoothness or homophily within the graph, making them unstable on sparse or non-stationary graphs.

Despite their individual strengths, the methods described above share two common limitations:

1.   Most focus exclusively on either structural or feature perturbations, failing to address the realistic scenarios where both types co-occur [19];

2.   They lack the capability to model the interactions between different perturbation sources, rendering them vulnerable to compound adversarial attacks, as summarized in Table 1.

3  Problem Definition

The core notations used throughout this paper are summarized in Table 2.

Given an undirected graph G=(V,E), the adjacency matrix A∈Rn×n and the node feature matrix X∈Rn×d serve as the basic input to a graph neural network. A typical message-passing layer can be formulated as:

H(l+1)=σ(A^H(l)W(l)),(1)

where A^ denotes the normalized adjacency matrix, H(l) is the node representation at layer l, W(l) is the trainable weight matrix, and σ(⋅) is a non-linear activation function.

In real-world deployments, the feature matrix X often contains noise (e.g., sensor measurement errors) or adversarial manipulations (e.g., forged user profiles), while the adjacency matrix A may include spurious edges (e.g., fake links in social networks) or missing critical connections (e.g., due to limitations in biological network observations).

Feature Perturbation Set. The permissible feature perturbation set is defined as:

ℬX={X~|‖X~−X‖F≤ϵX},(2)

where ‖⋅‖F denotes the Frobenius norm, measuring the magnitude of deviations between the original and perturbed feature matrices. This constraint assumes that measurement errors typically follow a Gaussian distribution, and their total magnitude can be bounded by ϵX.

Structure Perturbation Set. Similarly, the permissible structure perturbation set is defined as:

ℬA={A~|‖A~−A‖0≤ϵA},(3)

where ‖⋅‖0 counts the number of modified edges. This formulation captures practical attack cost constraints, as excessive edge modifications (exceeding ϵA) are more likely to trigger detection mechanisms in real-world systems.

Robustness Objective. Given the above perturbation models, the robustness of a GNN can be formulated as the following min-max optimization problem:

minfE(A,X)[max(A~,X~)∈ℬA×ℬXℒ(f(A~,X~),Υ)],(4)

where ℒ(⋅,⋅) denotes the classification loss function, and the inner maximization seeks the worst-case perturbations within the defined budgets.

Challenges of Coupled Perturbations. It is important to emphasize that structural perturbations alter the global topology and disrupt message-passing paths, while feature perturbations directly distort the semantic representations of nodes. The coupling between these two perturbation types can lead to compounded degradation, exceeding the impact of either perturbation individually. This highlights why existing defense strategies that treat structure and feature perturbations independently are often insufficient.

Definition of Joint Perturbations. In this paper, we define joint adversarial perturbations as attack scenarios where both the graph structure and node features are perturbed in the same instance. Importantly, these perturbations are applied simultaneously but independently, meaning that the modifications to the adjacency matrix and the feature matrix are not assumed to be statistically or functionally dependent. This formulation captures realistic attack settings where both topological and semantic information may be corrupted, either by coordinated or uncoordinated attackers, and serves as a general framework that covers compound perturbation types.

4  Methodology

4.1 Model Overview

The DSGNN model is proposed to enhance the robustness of GNNs against simultaneous feature and structural perturbations. DSGNN decouples the propagation paths of the two perturbation types by constructing independent information channels. Each channel learns robust node representations, and the outputs are subsequently combined through a dynamic fusion layer.

DSGNN is designed to be broadly applicable across different GNN architectures. In the experimental evaluation, the model is instantiated based on Graph Convolutional Networks (GCNs) to validate its effectiveness.

Unlike regularization-based or adversarial training methods, DSGNN model mitigates structural and feature perturbations through architectural separation. Controlled noise is introduced into the learning process to better simulate real-world distribution shifts and improve model robustness.

4.2 Dual-Channel Processing Pipeline

Input graph G=(V,E), where A∈Rn×n denotes the adjacency matrix and X∈Rn×d denotes the node features. To model perturbations, two permissible sets are defined: ℬA for structural perturbations and ℬX for feature perturbations.

The proposed DSGNN model introduces two parallel GNN channels, each responsible for independently processing structural and feature noise.

•   Structural channel: Processes clean features with perturbed structure, i.e., Hstruct=GNN(X,A~).

•   Feature channel: Processes perturbed features with clean structure, i.e., Hfeat=GNN(X~,A).

To ensure consistency and comparability, both the structural and feature channels in DSGNN are implemented using standard two-layer Graph Convolutional Networks (GCNs), each with a hidden size of 256. This architecture mirrors the configuration adopted in NoisyGNN [16], enabling fair benchmarking and reproducibility in experimental comparisons.

Each channel is specifically trained to address a distinct type of perturbation:

•   The structural channel: processes the input pair (A~,X), allowing the model to learn robustness against structural perturbations while preserving clean node features.

•   The feature channel: processes (A,X~), focusing on mitigating feature noise while maintaining the original graph topology.

During training, separate perturbations are sampled for both A and X in each epoch. The two GCN channels are optimized jointly based on their respective perturbed inputs. This decoupled learning mechanism enables each channel to specialize in its assigned perturbation type. The outputs of the two channels are then integrated via an adaptive attention-based fusion layer, which dynamically weighs each representation according to its reliability under perturbation. The overall model architecture is illustrated in Fig. 2. This architecture enhances robustness by allowing the model to prioritize more trustworthy modalities in complex attack scenarios.

4.3 Training and Testing Procedure

During training, perturbed graphs A~∈ℬA and X~∈ℬX are sampled at each epoch. Forward propagation is performed through both channels, and the outputs, along with the fusion weights, are optimized jointly.

•   Training: At each epoch, perturbations (A~,X~) are sampled, and the channels are optimized jointly with the fusion mechanism.

•   Testing: The dual-channel format is retained, where the model processes both A~ and X~ and then outputs the fused representation.

4.4 Representation Fusion

The outputs of the two channels are fused as:

H=α⋅Hstruct+(1−α)⋅Hfeat,α∈[0,1],(5)

where α can be a fixed scalar, a learnable parameter, or derived from an attention mechanism. Alternatively, concatenation followed by a multi-layer perceptron (MLP) can be used for nonlinear fusion.

4.5 Loss Function

The fused representation H is passed into a classifier and optimized using the cross-entropy loss:

ℒ=CrossEntropy(softmax(H),Υ).(6)

Backpropagation jointly updates the two channels and the fusion weights. Additional terms, such as adversarial loss or edge regularization, can be incorporated to further enhance robustness.

4.6 Algorithm Description

Algorithm 1 summarizes the DSGNN training procedure. In each epoch, independent perturbations are sampled for the structure and features, and the corresponding representations are obtained through parallel GNN channels. The fusion mechanism combines the outputs into a unified representation, which is optimized against ground-truth labels using cross-entropy loss. Model parameters, including the fusion weights if applicable, are updated through backpropagation to enhance robustness against both types of perturbation.

4.7 Robustness Bound Analysis

Let the fused outputs under clean and perturbed inputs be:

H=αHstruct+(1−α)Hfeat,H~=αHstruct(A~)+(1−α)Hfeat(X~).(7)

The perturbation risk is defined as the output difference:

ℛϵDS[f]=E(A~,X~)∈ℬA×ℬX[dΥ(f(H),f(H~))].(8)

Applying convexity yields the following inequality:

dΥ(f(H),f(H~))≤αdΥ(f(Hstruct),f(Hstruct(A~)))+(1−α)dΥ(f(Hfeat),f(Hfeat(X~))).(9)

Assuming Lipschitz continuity of each submodel, there exist constants C1,C2>0 such that:

dΥ(f(Hstruct),f(Hstruct(A~)))≤C1ϵA2,dΥ(f(Hfeat),f(Hfeat(X~)))≤C2ϵX2.(10)

Thus, the robustness risk is bounded by:

ℛϵDS[f]≤αC1ϵA2+(1−α)C2ϵX2.(11)

4.8 Comparison with Single-Channel Baseline

For a standard GNN baseline that jointly consumes both perturbed inputs:

Hsingle=GNN(X~,A~),(12)

the robustness risk can be bounded as:

ℛϵSingle[f]≤C⋅(ϵA+ϵX)2.(13)

When C1,C2≤C and the perturbations are not highly correlated, the perturbation risks satisfy ℛϵDS[f]<ℛϵSingle[f], demonstrating the tighter robustness guarantee and stronger defense capability of DSGNN.

Moreover, the decoupled architecture of DSGNN offers enhanced resilience against coordinated attacks, contributing to better generalization and stability under diverse perturbation scenarios.

4.9 Computational Complexity Analysis

DSGNN is designed to enhance perturbation robustness while maintaining computational efficiency. The architecture consists of two parallel standard two-layer GCNs and a lightweight attention-based fusion module. For a graph with N nodes, input feature dimension F, and edge set size |E|, the per-layer complexity of a GCN is 𝒪(NF2+|E|F). Therefore, the dual-channel backbone of DSGNN leads to an overall complexity of 𝒪(2L(NF2+|E|F)), where L denotes the number of GCN layers. The fusion module, operating only on two output vectors per node, adds an additional cost of 𝒪(NH), which is negligible in comparison.

Table 3 summarizes the total time complexity of DSGNN and other baseline models, taking into account both architectural components and preprocessing overhead.

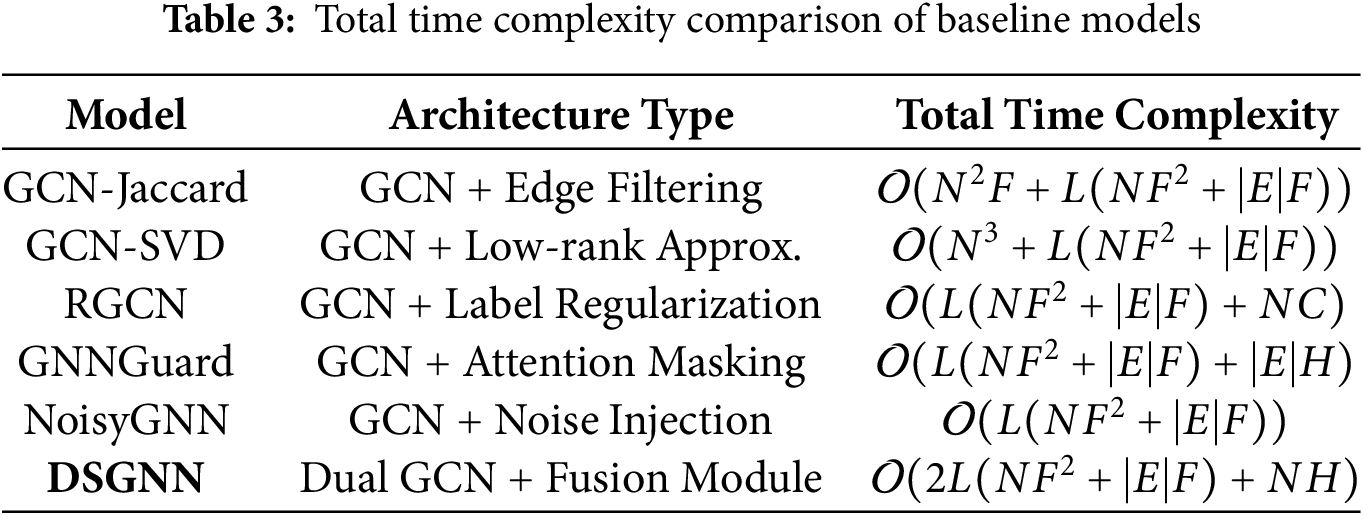
As shown in the comparison, although DSGNN introduces a dual-channel architecture that increases the computational workload relative to a standard GCN, the overall time complexity only grows linearly and remains within a practical range. More importantly, DSGNN does not rely on computationally expensive preprocessing procedures such as node similarity computation or matrix decomposition, which significantly reduces implementation cost and deployment complexity. As a result, DSGNN achieves improved model performance while preserving computational efficiency and structural scalability, making it well-suited for real-world applications.

Notation: N = number of nodes, F = input feature dimension, H = hidden dimension, |E| = number of edges, C = number of classes, L = number of GCN layers.

5  Experimental Parameter Settings

In all experiments, DSGNNs were instantiated based on a standard two-layer Graph Convolutional Network (GCN) architecture. Table 4 summarizes the key architectural and training parameters used throughout the evaluations.

The selected parameter settings follow those commonly adopted in existing works, particularly aligning with the configuration used in NoisyGNN. This ensures consistency with prior research and enables fair and reproducible performance comparisons. Specifically, we adopt the same core settings as NoisyGNN, including a hidden size of 256, two GCN layers, 200 training epochs, and a learning rate of 5e−4.

6  Experimental Evaluation

To assess the robustness of the proposed DSGNN against structural perturbations, extensive experiments were conducted on representative benchmark datasets, covering both citation networks and a real-world industrial semantic graph. The evaluation focused on three key aspects: the model’s stability under adversarial perturbations, its generalization ability to complex industrial data, and the theoretical certifiability of its robustness.

6.1 Datasets

The evaluation was conducted on the following datasets:

•   Cora: A citation network with 2708 nodes and 7 classes, characterized by relatively dense connections.

•   CiteSeer: A citation network with 3327 nodes and 6 classes, exhibiting a sparser graph structure than that of Cora.

•   Industry: A semantic classification graph containing 5312 textual samples, categorized into four types: industrial equipment, process techniques, production materials, and others. The label distribution in this dataset is highly imbalanced.

Compared to standard benchmarks, the Industry dataset exhibits several real-world characteristics:

•   Weak and sparse connectivity: Many nodes are loosely connected or isolated;

•   Semantic heterogeneity: Significant textual variation within and across classes;

•   High noise: Edges may reflect irrelevant or incomplete semantic relationships.

These conditions pose major challenges for ensuring GNN robustness in practical scenarios [20].

6.2 Attack Settings and Baselines

Structural perturbations are simulated using three representative attack strategies:

•   Metattack [21]: A meta-optimization-based white-box structural attack;

•   PGD [22]: A proximal gradient descent method for adversarial edge modification;

•   DICE [21]: A random edge addition and deletion strategy that does not require gradient information.

Perturbation budgets were set to 0%, 5%, and 10%. All methods were trained under consistent settings to ensure fair comparisons.

Baselines included widely adopted robust GNN approaches: GCN-Jaccard, GCN-SVD, RGCN, GNNGuard, and NoisyGNN. The DSGNN extends a standard GCN by injecting feature and structure perturbations into separate, complementary channels.

Following established practices, three perturbation levels were considered to evaluate model robustness: (1) no attack (0%), (2) moderate perturbation (5%), and (3) severe perturbation (10%). These perturbations were applied to the graph structure using Metattack, PGD, and DICE, respectively, and the results are reported in Table 5.

6.3 Robustness Analysis Classification

Model performance was evaluated under varying levels of structural perturbation, focusing on accuracy trends, fluctuation stability, and adaptability to industrial graph conditions.

6.3.1 Noise-Free Graph (0% Perturbation)

On noise-free graphs, DSGNN achieved comparable accuracy to baseline methods, indicating that the dual-channel design does not compromise predictive capacity. DSGNN attained 86.4% accuracy on the Industry dataset, demonstrating effective representation learning even under noisy and imbalanced structures.

6.3.2 Metattack and PGD

Metattack and PGD are optimization-based attacks that strategically disrupt graph connectivity. Many baselines experience severe accuracy degradation. In contrast, DSGNN showed slower performance decline and retained higher residual accuracy.

Under 10% PGD perturbation on Cora, DSGNN achieved the highest accuracy among all compared methods. On the Industry dataset, it maintained 81.6% accuracy under the same perturbation level, demonstrating its robustness in complex real-world graphs. The decoupled dual-channel architecture helps stabilize representation learning even when structural or feature information is partially corrupted.

6.3.3 DICE Attack

DICE introduces random structural noise without gradient-based targeting, reflecting real-world issues such as annotation errors or distribution shifts.

At 10% DICE perturbation, DSGNN achieved the highest accuracy on both CiteSeer (71.3%) and Industry (80.9%), with low variance across runs. Its performance on Cora was relatively lower.

This difference likely arises from Cora’s intrinsic structure: strong local clusters and tightly interconnected nodes within classes. Random edge removals fragment clusters, confusing decision boundaries. Furthermore, Cora’s feature homogeneity amplifies vulnerability to collective perturbations.

In contrast, DSGNN remains robust on the Industry dataset, where sparse connections, noisy edges, and diverse features challenge most models. The dual-channel design enables stable representation learning even when parts of the information are degraded.

6.3.4 Average Accuracy Comparison by Dataset

To further assess the overall robustness of different defense strategies, the average classification accuracy across all attack scenarios for each dataset was computed. The results are summarized in Table 6.

As observed in Table 6, DSGNN consistently achieves the highest average accuracy across all datasets:

•   On Cora, DSGNN outperforms all baselines, slightly surpassing GNNGuard and NoisyGNN.

•   On CiteSeer, DSGNN demonstrates superior robustness under adversarial settings, yielding a 71.94% average accuracy.

•   On the Industry dataset, characterized by weak structural connectivity and semantic noise, DSGNN achieves 81.66%, indicating its practical applicability.

These results show that the dual-channel architecture of DSGNN enhances model robustness across both benchmark and real-world graph datasets.

6.4 Certified Robustness Evaluation

To evaluate the certified robustness of DSGNN against structural perturbations, sparse randomized smoothing [23] was employed. This technique certifies whether a model’s prediction remains stable when a bounded number of graph edges were modified. Certified accuracy was evaluated for DSGNN and the baseline GCN under perturbation radii r∈{0, 1, 2, …, 10}.

In this evaluation, two types of perturbations are considered: feature perturbations and structure perturbations. Certified robustness is established only under structure perturbations, following the standard sparse randomized smoothing protocol. Feature perturbation results are reported as complementary analysis to provide a more comprehensive view of the model’s robustness.

The perturbation radius r denotes the cumulative perturbation steps, where each step introduces approximately 1% of feature noise injection or 1% of cumulative structural modifications. Feature perturbations are applied by randomly modifying node features with a probability proportional to r%, while structure perturbations are performed by progressively adding or removing edges.

As shown in Fig. 3, the DSGNN consistently outperforms the GCN in certified accuracy across all three datasets. In Cora and Industry, the DSGNN demonstrates a significant robustness improvement over GCNs, especially under larger perturbation radii where the gap becomes increasingly noticeable. These results highlight the effectiveness of the dual-channel design in handling complex and noisy graph environments, such as the Industry dataset.

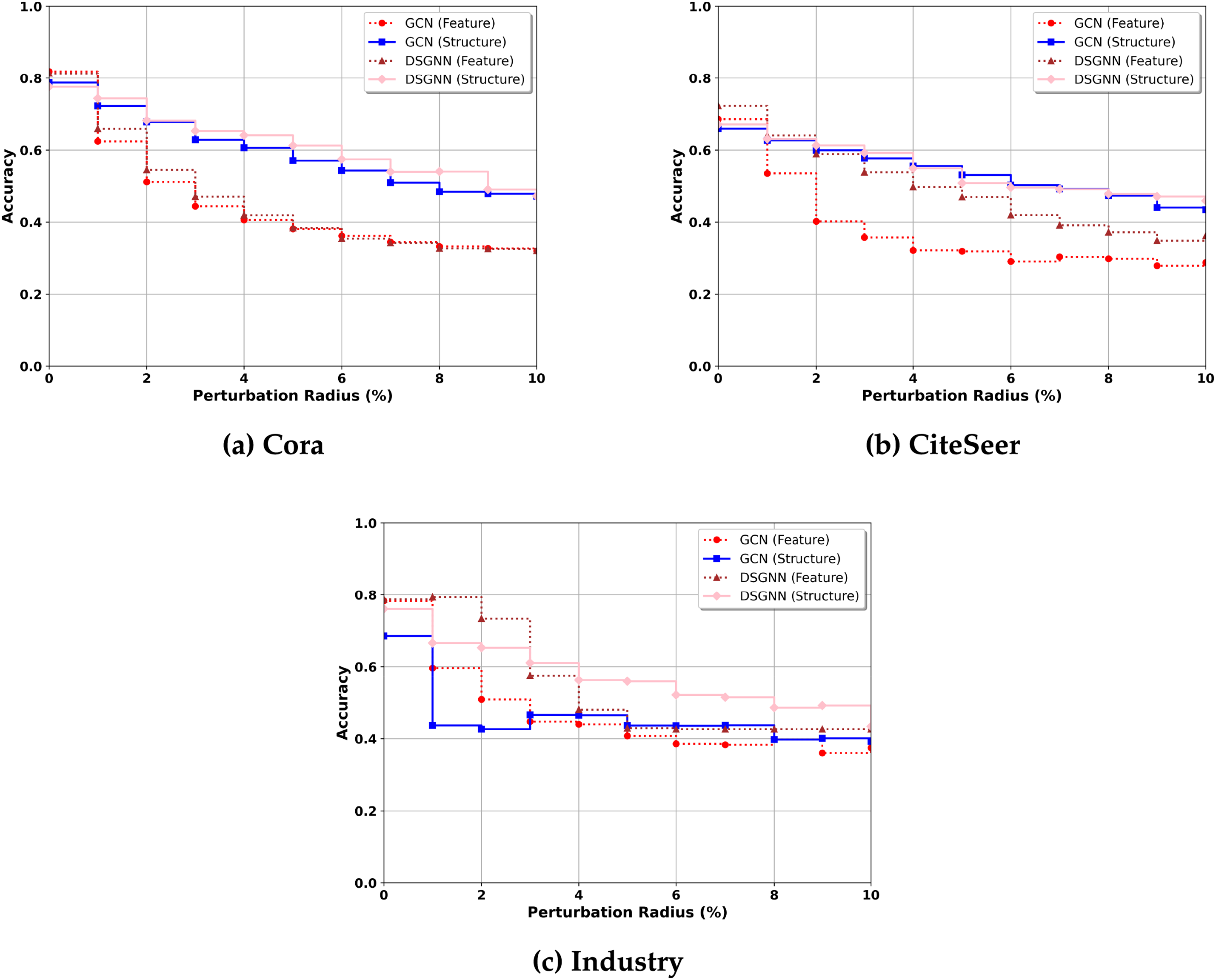
Figure 3: Certified accuracy of DSGNNs and GCNs under varying perturbation radii r. Structure perturbations are certified using sparse randomized smoothing, while feature perturbation results were presented for complementary analysis. Each step corresponds to approximately 1% of feature noise injection or 1% of cumulative structural modifications

In contrast, on the CiteSeer dataset, the advantage of DSGNNs over GCNs is relatively smaller. This could be attributed to the inherently sparse and simpler structure of CiteSeer graphs, where structural perturbations have a smaller impact, and so the benefits of dual-channel processing are correspondingly reduced.

Overall, these results demonstrate that DSGNN enhances the model’s certified robustness under structural perturbations and also exhibits improved stability under feature perturbations.

6.5 Ablation Study on Perturbation Settings

To further examine the contributions of individual components in DSGNN, we performed ablation experiments under three controlled perturbation settings:

•   Structure-only: Only the graph structure was perturbed (A~,X), while the node features remained unchanged.

•   Feature-only: Only the node features were perturbed (A,X~), with the graph structure preserved.

•   Joint-fixed: Both structure and features were perturbed (A~,X~), but the fusion weights were fixed to 0.5 for each channel rather than adaptively learned.

As shown in Table 7, DSGNN achieved competitive performance even in single-modality perturbation scenarios (structure-only and feature-only), which validated the independent robustness of each channel. Furthermore, the dual-channel variant with fixed fusion weights outperformed both single-channel baselines under joint perturbations, which indicated the benefit of integrating both modalities. Most importantly, the full version of DSGNN, which employed a learnable dynamic fusion mechanism, consistently achieved the highest accuracy across all datasets and attack settings. This demonstrated the essential role of adaptive fusion in handling heterogeneous and complex perturbation patterns.

6.6 Summary

Across both accuracy and certification evaluations, DSGNN consistently outperforms existing defenses on benchmark and real-world graphs. Its dual-channel structure improves stability, reduces performance degradation, and adapts well to weakly structured, semantically noisy industrial scenarios.

7  Conclusion and Future Work

DSGNN is proposed as a defense model that decouples structural and feature perturbations through a dual-channel architecture. By isolating the propagation paths of different noise types and dynamically integrating their outputs, DSGNN significantly improves robustness against a wide range of adversarial attacks.

Experimental evaluations show that DSGNN consistently outperforms baseline defense methods across multiple benchmark datasets, maintaining superior stability under both targeted and random perturbations. These results underscore the effectiveness of explicitly modeling perturbation decoupling at the architectural level.

Future work includes extending DSGNN to other graph neural network architectures, such as GAT and GraphSAGE. Additionally, the development of adaptive fusion mechanisms, where the importance weights between channels are dynamically adjusted based on the characteristics of observed perturbations, represents a promising direction.

Acknowledgement: The authors are grateful to the anonymous reviewers and the editor for their insightful comments and suggestions that substantially enhanced the clarity and rigor of this work.

Funding Statement: This research was funded by the Key Research and Development Program of Zhejiang Province No. 2023C01141, and the Science and Technology Innovation Community Project of the Yangtze River Delta No. 23002410100. This work was supported by the Open Research Fund of the State Key Laboratory of Blockchain and Data Security, Zhejiang University.

Author Contributions: Xiaohan Chen: Software implementation, Experimental evaluation, Writing—original draft preparation; Yuanfang Chen: Conceptualization, Methodology design, Project administration, Supervision, Writing—review and editing, Funding acquisition; Gyu Myoung Lee, Noel Crespi, Pierluigi Siano: Methodological guidance, Technical support, Manuscript review, Constructive suggestions. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: This work utilizes the publicly available datasets Cora, CiteSeer, and Industry for model training and evaluation. These datasets are freely accessible through established academic repositories.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Wang H, Fu T, Du Y, Gao W, Huang K, Liu Z, et al. Scientific discovery in the age of artificial intelligence. Nature. 2023;620(7972):47–60. doi:10.1038/s41586-023-06221-2. [Google Scholar] [PubMed] [CrossRef]

2. Jin M, Koh HY, Wen Q, Zambon D, Alippi C, Webb GI, et al. A survey on graph neural networks for time series: fforecasting, classification, imputation, and anomaly detection. IEEE Trans Pattern Anal Mach Intell. 2024;46(12):10466–85. doi:10.1109/TPAMI.2024.3443141. [Google Scholar] [PubMed] [CrossRef]

3. Chen Z, Mao H, Li H, Jin W, Wen H, Wei X, et al. Exploring the potential of large language models (llms) in learning on graphs. ACM SIGKDD Explor Newsletter. 2024;25(2):42–61. doi:10.1145/3655103.3655110. [Google Scholar] [CrossRef]

4. Fang X, Chen Y, Bhuiyan ZA, He X, Bian G, Crespi N, et al. Mixer-transformer: adaptive anomaly detection with multivariate time series. J Netw Comput Appl. 2025;241(1):104216. doi:10.1016/j.jnca.2025.104216. [Google Scholar] [CrossRef]

5. Liu J, Guo M. DIGNN-A: real-time network intrusion detection with integrated neural networks based on dynamic graph. Comput Mater Continua. 2025;82(1):817–42. doi:10.32604/cmc.2024.057660. [Google Scholar] [CrossRef]

6. Chen Y, Fang X, Ma S, Li W. TrackSecurity: an attention-guided physical patch model for perturbing visual trackers in autonomous driving. TechRxiv. Forthcoming 2025. doi:10.36227/techrxiv.175021860.09534391/v1. [Google Scholar] [CrossRef]

7. Chen Y, Yang H, Zhang Y, KAILI M, Liu T, Han B, et al. Understanding and improving graph injection attack by promoting unnoticeability. In: International Conference on Learning Representations; 2022. [cited 2025 Jul 13]. Available from: https://openreview.net/forum?id=wkMG8cdvh7-. [Google Scholar]

8. Liu J, Chen B, Xue B, Guo M, Xu Y. PIAFGNN: property inference attacks against federated graph neural networks. Comput Mater Continua. 2025;82(2):1857–77. doi:10.32604/cmc.2024.057814. [Google Scholar] [CrossRef]

9. Entezari N, Al-Sayouri SA, Darvishzadeh A, Papalexakis EE. All you need is low (rank) defending against adversarial attacks on graphs. In: Proceedings of the 13th International Conference on Web Search and Data Mining. Houston, TX, USA; 2020. p. 169–77. doi:10.1145/3336191.3371789. [Google Scholar] [CrossRef]

10. Zhang X, Zitnik M. GNNGuard: defending graph neural networks against adversarial attacks. In: Proceedings of the 34th Conference on Neural Information Processing Systems (NeurIPS). Vancouver, Canada: NeurIPS; 2020. [Google Scholar]

11. Wu H, Wang C, Tyshetskiy Y, Docherty A, Lu K, Zhu L. Adversarial examples for graph data: deep insights into attack and defense. In: Proceedings of the 28th International Joint Conference on Artificial Intelligence (IJCAI 2019). Macau, China: IJCAI Organization; 2019. p. 4816–23. doi:10.24963/ijcai.2019/669. [Google Scholar] [CrossRef]

12. Feng F, He X, Tang J, Chua TS. Graph adversarial training: dynamically regularizing based on graph structure. IEEE Trans Knowl Data Eng. 2019;33(6):2493–504. doi:10.1109/TKDE.2019.2957786. [Google Scholar] [CrossRef]

13. Zhu D, Zhang Z, Cui P, Zhu W. Robust graph convolutional networks against adversarial attacks. In: Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. Anchorage, AK, USA; 2019. p. 1399–407. doi:10.1145/3292500.3330851. [Google Scholar] [CrossRef]

14. Abbahaddou Y, Ennadir S, Lutzeyer JF, Vazirgiannis M, Boström H. Bounding the expected robustness of graph neural networks subject to node feature attacks. In: The Twelfth International Conference on Learning Representations. Vienna, Austria; 2024 [Google Scholar]

15. Aslan HI, Wiesner P, Xiong P, Kao O. β-GNN: a robust ensemble approach against graph structure perturbation. In: Proceedings of the 5th Workshop on Machine Learning and Systems (EuroMLSys’25). Rotterdam, The Netherlands: ACM; 2025. p. 168–75. doi:10.1145/3721146.3721949. [Google Scholar] [CrossRef]

16. Ennadir S, Abbahaddou Y, Lutzeyer JF, Vazirgiannis M, Boström H. A simple and yet fairly effective defense for graph neural networks. In: Proceedings of the Thirty-Eighth AAAI Conference on Artificial Intelligence and Thirty-Sixth Conference on Innovative Applications of Artificial Intelligence and Fourteenth Symposium on Educational Advances in Artificial Intelligence; 2024 Feb 20–27; Vancouver, Canada. Washington, DC, USA: AAAI Press. p. 21063–71. doi:10.1609/aaai.v38i19.30098. [Google Scholar] [CrossRef]

17. Jin W, Ma Y, Liu X, Tang X, Wang S, Tang J. Graph structure learning for robust graph neural networks. In: Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York, NY, USA: Association for Computing Machinery; 2020. p. 66–74. doi:10.1145/3394486.3403049. [Google Scholar] [CrossRef]

18. Schlichtkrull M, Kipf TN, Bloem P, Van Den Berg R, Titov I, Welling M. Modeling relational data with graph convolutional networks. In: The Semantic Web: 15th International Conference, ESWC 2018; 2018 Jun 3–7; Heraklion, Crete, Greece: Springer. p. 593–607. doi:10.1007/978-3-319-93417-4_38. [Google Scholar] [CrossRef]

19. Dai H, Li H, Tian T, Huang X, Wang L, Zhu J, et al. Adversarial attack on graph structured data. In: Dy J, Krause A, editors. Proceedings of the 35th International Conference on Machine Learning; 2018. Vol. 80, p. 1115–24. [Google Scholar]

20. Lu H, Wang L, Ma X, Cheng J, Zhou M. A survey of graph neural networks and their industrial applications. Neurocomputing. 2025;614(1):128761. doi:10.1016/j.neucom.2024.128761. [Google Scholar] [CrossRef]

21. Zügner D, Günnemann S. Adversarial attacks on graph neural networks via meta learning. In: ICLR Workshop on Safe Machine Learning (SafeML). New Orleans, LA, USA: OpenReview; 2019. [cited 2025 Jul 13]. Available from: https://openreview.net/forum?id=Bylnx209YX. [Google Scholar]

22. Xu K, Chen H, Liu S, Chen PY, Weng TW, Hong M, et al. Topology attack and defense for graph neural networks: an optimization perspective. In: Proceedings of the 28th International Joint Conference on Artificial Intelligence (IJCAI-19). Macau, China: IJCAI Organization; 2019. p. 3961–7. doi:10.24963/ijcai.2019/550. [Google Scholar] [CrossRef]

23. Jin H, Shi Z, Peruri VJSA, Zhang X. Certified robustness of graph convolution networks for graph classification under topological attacks. Adv Neural Inf Process Syst. 2020;33:8463–74. [Google Scholar]