Narwhal Optimizer: A Nature-Inspired Optimization Algorithm for Solving Complex Optimization Problems

1  Introduction

Making anything as efficient or effective as possible is referred to as optimization. Optimization is the process of selecting, given limitations, the optimal option (in terms of cost, performance, or other metrics) from a range of viable options [1–3]. In computer science, optimization is a broad and significant term that touches on a variety of domains, including machine learning, operations research, software engineering, and algorithm design. Its objective is to enhance the efficiency of time, space, and other resources by improving the performance of algorithms, applications, and systems.

Numerous metaheuristic optimization methods have been created in the past ten years. The most popular ones are Genetic Algorithm (GA) [4], Ant Colony Optimization (ACO) [5], and Particle Swarm Optimization (PSO) [6]. Metaheuristics have a lot to give. The first is that all these techniques are quite basic, and the idea is based on physical events, evolutionary theories, or animal behaviors. Their adaptability is the second benefit. There are numerous real-world uses for metaheuristics [7,8].

In Computer science, metaheuristic algorithms can be divided into different categories depending on whether the approach is nature-inspired or not. Additionally, they can be classified according to the type of objective function, including static or dynamic objective, multi-objective, mono-objective, and multi-objective [9,10]. Four categories comprise nature-inspired algorithms: Evolutionary-based algorithms, Swarm Intelligence-based algorithms, Physics-based (PB) algorithms, and Human-based algorithms.

Algorithms that are evolutionary in nature are founded on the ideas of natural evolution. The processes of genetic variation, reproduction, and natural selection serve as their inspiration. GA [4] and Differential Evolution (DE) [11] are two instances of algorithms that are based on evolution.

Algorithms based on swarm intelligence are motivated by the collective actions of social organisms found in the natural world. For instance, to accomplish a goal, a collection of agents interacts with both them and their surroundings, for example, Ant Colony Optimization (ACO) [5], and PSO [6].

Algorithms that are based on human behavior are known as human-based algorithms. It is particularly grounded in human intelligence, intuition, and judgment.

The two most popular algorithms are the Interactive Genetic Algorithm and Crowdsourcing for Optimization. PB algorithms, or physics-based algorithms, these algorithms belong to a class of optimization techniques that draw inspiration from physics-related concepts and phenomena. For example: the Gravitational Search Algorithm [12].

In this research, a novel metaheuristic algorithm, named Narwhal Optimization Algorithm (NWOA), is introduced for solving complex optimization problems. The design of NWOA draws inspiration from the unique behaviors of narwhals, particularly their social hunting strategies and sonar-based communication.

Information about prey locations is being exchanged by narwhals to increase their hunting efficiency. Mimicking this behavior, NWOA simulates underwater sonar communication among agents to facilitate social interaction and navigation in the search space. This approach enables the algorithm to simulate the way narwhals cooperatively hunt. Moreover, through social learning and communication, narwhals use a combination of local and global exploration. The system modifies the sonar signal’s mobility and strength to strike a balance between local and global searches. While the traditional optimizers depend on crossover and mutation to explore the solution space.

Since the narwhals’ sonar enables them to first investigate a large area before converging on the optimum solutions as social interactions direct the movement, the convergence speed is frequently slow. However, if exploration takes precedence, the convergence could be slower than with other techniques. While traditional optimizers, such as GA, the Convergence speed is moderate and depends heavily on the crossover/mutation rate and population size.

NO algorithm is proposed by [13] that mimics the narwhal tusk behavior and social hunting, employing the standard distance-based exploration method without taking sound wave dynamics into account. On the other hand, the proposed algorithm focused on echolocation, tusk functionality, social hunting, and sonar communication. By simulating sonar communication, sound wave propagation, prey energy decay, and group decision-making among narwhals, it further improves realism.

Two main contributions are made in this study. First, it introduces a new optimizer algorithm with a biologically grounded specially incorporates sonar-based communication and prey energy modeling—these features are not considered in the NO algorithm [13]. Second, it formulates a dynamic mechanism for balancing exploration and exploitation through adaptive echolocation patterns and energy-aware decision-making, which enhances both convergence reliability and solution quality.

The rest of this paper is organized as follows. Section 2 presents the literature review of metaheuristic optimizers. Section 3 introduces the mathematical model of NWOA. Section 4 includes tests of benchmark functions and engineering issues for NWOA. Finally, Section 5 summarizes the conclusions.

2  Literature Review

For many years, one of the biggest challenges facing researchers studying optimization issues has been creating efficient methods for locating the best answers. Gradient-based approaches, which employ mathematical derivation to ascertain the lowest or maximum values within a given scenario, have traditionally been the main tactic. However, metaheuristic optimization algorithms have progressively replaced these traditional approaches in recent decades. Metaheuristic algorithms explore a randomly generated search space to approximate the optimal solution instead of exact optimization techniques. We shall explore the most common types of these algorithms in the upcoming subsections.

2.1 Nature-Inspired Algorithms

Nature-inspired algorithms (NIA) are modeled to simulate social creatures, natural processes, or physical laws. NIAs consistently yield dependable and flexible results in various applications. Nature-inspired algorithms will grow as new natural phenomena continue to inspire creative algorithms, improving the effectiveness of problem-solving strategies across multiple fields. The traversal of huge search spaces is balanced between exploration (global search) and exploitation (local refining) to find near-optimal solutions. Because of their versatility, nature-inspired algorithms can be applied to many areas, ranging from data science to artificial intelligence, from engineering design to combinatorial optimization.

Rashedi et al. created the Gravitational Search Algorithm (GSA) in 2009 to model Newton’s law of gravity. Stronger solutions have more weight in GSA because candidate solutions function as masses that pull one another in. GSA is frequently used in feature selection and power system optimization because of its gravitational pull mechanism, which enables it to effectively traverse complex search spaces [12]. Kirkpatrick et al. created the Simulated Annealing (SA) algorithm in 1983, drawing inspiration from mechanical annealing. Machine learning and combinatorial optimization help locate near-global solutions by temporarily accepting poorer solutions with a decreasing probability [14].

In 2010, Yang presented the Firefly Algorithm (FA) [15], one of the most well-known nature-inspired algorithms. FA is modeled after the bioluminescent activity of fireflies, which use light flashes to attract mates and communicate. Brighter fireflies (for better solutions) draw other fireflies, directing the search toward the best areas. FA is helpful in scheduling, image processing, and machine learning problems because it successfully balances exploration and exploitation. The Bat Algorithm (BA) [16], which was also created by Yang, is a roughly related method that imitates bat echolocation. In order to locate their prey and navigate the environment, bats produce ultrasonic pulses that can vary in loudness and frequency to focus their search. Due to the aforementioned flexibility, BA has found many applications for optimizing nonlinear and multimodal functions and is hence popularly chosen for feature selection and numerical optimization.

Some nature-inspired algorithms also simulate processes such as those in chemistry. Lam and Li (2010) developed the Chemical Reaction Optimization (CRO) [17] method, modeling molecular interactions and optimizing solutions through different reaction processes such as synthesis, combination, and breakdown. CRO has been effectively employed for resource allocation, network configuration, and task scheduling.

The introduction of the Flower Pollination Algorithm (FPA) [18] by Yang in 2012 emanated from bio-inspired algorithms simulating the pollination behavior of flowering plants. Self-pollination symbolizes local exploitation, while cross-pollination stands for global search due to its provision of genetic variations. FPA would address both forms of engineering designs and optimization problems regarding wireless sensor networks because of this dual mechanism. The Moth-Flame Optimization (MFO) [19] method developed by Seyedali Mirjalili follows moths’ nocturnal behavior transverse orientation by which they migrate. A natural inclination toward a minimum spiral trajectory due to maximization of angle with the light does not permit moths to spiral trajectory tap into an artificial source. This has been mathematically modeled in MFO to fine-tune search paths using MFO. The applicability of this optimization method can be in domains like robotics, cybersecurity, and feature selection.

Nature-inspired algorithms mimic biological or physical events. Water Wave Optimization (WWO) [20] was designed by Zheng et al. (2015) to imitate water wave motion, reflecting, and breaking from obstacles. The main reason WWO is very efficient in scheduling and structural engineering problems is that these mechanisms force solutions away from suboptimal zones toward optimal areas within the search space. The Lotus Effect Algorithm (LEA) [21] is an algorithm that is based on the way lotus leaves cleanse themselves by repelling minute microscopical features of dirt and water from their surface. According to Shehab et al. (2023), LEA would be employed in bioinformatics and materials sciences optimization due to the fact that it uses this technique to reject unfit solutions. Similar prey and predator models have been examined. The Genghis Khan Shark Optimization (GKS) [22] algorithm seeks to mimic the cooperative techniques of sharks in locating and catching prey. Since its inception by Hu et al. in 2023, GKS has been used successfully in logistics optimization and control systems by modeling these movements.

2.2 Swarm-Based Algorithms

Due to the collective behavior manifestations of social animals, swarm-based algorithms are the most preferred architecture for the solution of hard optimization problems. The cooperation or competition in these algorithms mimics swarming species for the successful exploration and exploitation of search zones. Particle Swarm Optimization (PSO) remains one of the most often utilized particle-based approaches. According to Kennedy and Eberhart (1995) [6], PSO simulates the social interaction of particles moving across the search area, repositioning themselves in response to individual and group experiences. Ant Colony Optimization (ACO) [5], one of the eminent swarm algorithms, mimics ant foraging behavior. In solving problems such as routing in networks and the traveling salesman problem, ants deposit pheromones to lead other ants to better paths.

The Gazelle Optimization Algorithm (GOA) [23] optimizes solutions through group decision-making in dynamic contexts, taking inspiration from gazelles’ quick and coordinated movement in herds. Later, the Cuckoo Search (CS) algorithm [24] was developed, simulating the parasitic behavior of cuckoo birds. It leverages this tendency to replace poor solutions and explore new search areas for optimal solutions.

Mirjalili et al. state that the Salp Swarm Algorithm (SSA) [25] simulates swarming’s cooperative nature by prioritizing adaptability and exploration for efficient optimization. The various strategies for social collaboration and local search make the Spider Monkey Optimization (SMO) [26] method efficient by imitating the foraging behavior of spider monkeys in dense forests.

This algorithm, the Dragonfly Algorithm [27], combines local and global search techniques to hastily identify the best solutions, thereby emulating the hunting behavior of dragonflies. The Whale Optimization Algorithm (WOA) [28] imitates the bubble-net hunting technique of humpback whales. This approach may effectively handle high-dimensional problems by exploiting solutions while balancing the exploration of the search space. Likewise, the Artificial Hummingbird Algorithm (AHA) [29] employs hummingbirds’ rapid and nimble movements to steer the search for optimal solutions in real-time. The Dwarf Mongoose Optimization (DMO) [30] model was based on the collaborative behavior of dwarf mongooses, who join together to find food and defend their community. In other words, the algorithm effectively locates global optima by replicating this cooperative and competitive behavior. The narwhal optimization (NO) algorithm is introduced by [13]. NO algorithm inspired by the hunting behavior of narwhals. Three main phases (signal emission, signal propagation, and position updating) are designed to enhance the exploration and exploitation of NO algorithm within the search space. The algorithm was tested on 13 benchmark functions and compared with PSO and GWO algorithms. The findings illustrated strong convergence performance, superior global search ability, and better avoidance of local optima.

The Squirrel Search Algorithm (SSA) [31] is based on squirrel foraging patterns and makes use of their ability to forage over long distances. This algorithm’s emphasis on achieving a balance between exploration and exploitation leads to improved optimization outcomes. The Horse Herd Algorithm (HOA) [32] provides great efficiency in complex optimization scenarios by imitating the behavior of herding horses, where individuals within the herd collaborate to seek and exploit resources. The Sea Lion Optimization (SLnO) algorithm [33] was inspired by the foraging and hunting behaviors for sea lions. The objective is to solve complex optimization problems through the cooperation, exploration, and hunting of food of sea lions in dynamic marine environments. SLnO achieves an effective mix of exploration and exploitation through the utilization of adaptive movement patterns for searching for the optimal solution. Owing to its simplicity and effectiveness, SLnO has been used with success in various optimization problems within engineering, machine learning, and other scientific fields. The Red Deer Algorithm (RDA) [34] was inspired by red deer social behavior and seasonal movement patterns. As with previous swarm-based approaches, it achieves a balance between local exploitation while discovering optimum solutions and migratory exploration.

By replicating the electrical discharges of electric eels to discover and capture prey, the Electric Eel Foraging Optimization (EEFO) [35] approach increases search skills to identify the best responses. The Orca Optimization Algorithm (OOA) [36] is based on orcas’ social hunting behavior. Orcas mimic this strategy for determining the best responses in challenging regions by working in groups to track and capture their prey. The Manta Ray Foraging Optimization (MRFO) [37] algorithm is based on manta rays’ foraging habits, which involve swarming to discover food sources. This strategy maximizes solution searches in high-dimensional areas by simulating the group behavior of the manta ray. The Beluga Whale Optimization (BWO) algorithm [38] models the beluga whales’ hunting behaviors and social behavior. Cooperative hunting balances exploration with exploitation, and group dynamics are exploited to improve the quality of the solutions.

2.3 Physics-Based Algorithms

Physics-based optimization algorithms refer to optimization approaches that are based on physical principles and phenomena, and by using ideas from actual physical systems, such optimization problems are resolved using many physical concepts that facilitate efficient exploration of this search space. The Mine Blast Algorithm (MBA) [39] is modeled on the force of explosives used in mining. Once “blasted” from an attached point, the movement of the particles across the search space starts to reflect the spread of shockwaves generated under explosions so that it promotes coverage of remote areas and minimizes the chances of early convergence. This same example references the Charged System Search (CSS) algorithm [40], which is inspired by the effect of charged particles in an energy space with respect to one another. Because in this system, the particles modify their positions in response to the forces applied by other particles, one may search space such that it would avoid local minima and would converge towards the global optimum.

The Optics Inspired Optimization (OIO) algorithm [41] is based on the refraction and reflection of light in optics. The light air passages through different media are explored as a metaphor for the reflection and refraction through various paths in the search space while seeking solutions. In mathematics, the sine and cosine functions, characterized by the property of undulations, give birth to the Sine Cosine Algorithm (SCA) [42]. The fluctuations of the algorithm are employed to balance the exploration and exploitation of the search so as to drive the search toward global optima while preventing it from being attractively lured into local optima.

The Young’s Double Slit Experiment (YDSE) algorithm [43] is motivated by the dual behavior of light-particle behavior demonstrated so well by the famous double-slit experiment. This algorithm represents a simulation of the interference of the light waves, where individuals “interfere” amongst themselves to explore the search space in convergence toward the best solutions. The physical phenomenon of gas solubility in liquids is captured by the Henry Gas Solubility Optimization (HGSO) algorithm [44]. Henry’s law determines how gases get partitioned among liquids. The same concept is then used in modeling the behaviors of the solutions in a search space; individuals are actually “solvated” by the optimization process. The Prism Refraction Search (PRS) method [45] is used to simulate the refraction of light through a prism. With the help of PRS agents, all the angles will take place in the search space while searching for an effective solution, as light bends when moved through a prism. In contrast, Candle Flame Optimization (CFO) is introduced by [46], which inspired the behavior of candle flames in nature. It models the dynamic movement and flickering of a flame in response to heat and airflow, among other environmental forces. In CFO, candidate solutions are taken as flame particles, and their motion is guided by mathematical rules that simulate flame oscillation and attraction toward the best solutions and random moves for exploration. The algorithm is intended for global optimization, balancing exploration and exploitation by mimicking how flames spread to reach stable and optimal positions. CFO has proven effectiveness in solving complex, nonlinear, and high-dimensional problems seen in a lot of engineering and scientific applications.

2.4 Human-Based Algorithms

Human-based algorithms are optimization methods by their very nature that have taken inspiration from social interactions, interpersonal relationships, and human behavior. The algorithms are very capable of using competition, cooperation, and learning as their human-analog problem-solving mechanisms to walk around and exploit a search space. Similarly to human decision-making processes or human memory, it makes adroit and strategic choices of search directions and avoids slippage or return to the solution space that has already been investigated by exercising the privilege of using “tabu” or forbidden moves [47].

Its conceptual ground was one of the earliest to be used for the method called Harmony Search (HS) [48], which derives its name from the process by which musicians improvise on an instrument to achieve harmonious ensemble playing. In optimization, this process is borrowed in the sense that the algorithm harmoniously searches for an optimal solution among the candidates by iteratively tuning the decision variables. The imperialist competitive algorithm (ICA) [3] is the rationale behind imperialist competition among countries for dominance. In the competition-oriented approach, the strongest nations dominate the search processes, mimicking the hunt for solutions.

Inspired by the activities occurring in classrooms, the Teaching Learning-Based Optimization (TLBO) algorithm [49] arises. Students derive knowledge from teachers and modify their knowledge base with this information. Similarly, TLBO optimizes the search for the world’s best answer by learning from better solutions.

Firework Algorithm (FA) [50] is yet another popular human-based method inspired by the visuals and blasts of fireworks. It imitates the mechanism of searching for the best possible solutions in the sense of expanding the search space to promote diversity and convergence through a series of explosive movements and sparks. The Human Group Formation (HGF) algorithm [8] simulates creating social groups among human societies. The algorithm promotes collaboration and communication in an individual. This collaborative behavior with the group helps the HGF algorithm explore solutions better.

The Football Game Inspired Algorithm (FGIA) [51] is based on the metaphor of a football game and founded upon the spirit of competitiveness that sports create. In order to achieve high-quality solutions, it imitates players, working both on offense and defense, and changing tactics while they play the game. The Searching Group Algorithm (SGA) [9] is grounded on the collective behavior of human groups whereby members cooperate and share information to find a certain solution. It also combines the stages of exploring known regions and exploring the search space in order to enhance optimization efficiency. The Brainstorm Optimization (BSO) [52] imitates the brainstorming technique through which individuals cooperate in generating ideas and finding solutions; this algorithm has the capability of exploring problem-solving alternatives through the idea-formation process and can evaluate the solutions within it. These human-based algorithms leverage a wide range of human behavioral aspects, from cooperation, learning, and competition to memory, among other mechanisms, for carrying out solution processes of complex optimization problems in diverse fields.

The Perfumer Optimization Algorithm (POA) is a novel human-inspired metaheuristic introduced by [53], which emulates the iterative process of perfume formulation to handle complex optimization issues. POA, inspired by the meticulous approach of perfumers, the Perfumer Optimization algorithm simulates the balance between exploration and exploitation, similar to how perfumers experiment with different fragrance combinations to achieve a harmonious scent. Moreover, candidate solutions represent different “aromatic combinations,” which are iteratively optimized through processes similar to blending and adjusting the scents of perfumes. The algorithm emphasizes the importance of diversity (exploration) and optimization (exploitation) in the search space, ensuring a comprehensive search for optimal solutions. This two-stage approach enables the POA algorithm to effectively handle complex, multi-modal optimization environments.

2.5 Evolutionary Algorithms

Evolutionary algorithms (EAs) are an effective, well-known category of optimization methods that simulate natural evolutionary processes, such as selection, mutation, and reproduction. EA methodologies are inspired by natural selection to enhance the candidate solutions at each iteration continuously. Genetic Algorithm (GA) [4], among the basic EAs, was also known to have been founded in 1975 by Holland. It mimics natural evolution, basically utilizing operators such as selection, crossover, and mutation. The real concept involves developing solutions that are populated through several cycles, then referred to as generations, generating offspring for the fit individual population of prospective solutions toward the succeeding generation, thus producing the fittest ones. GA has been popularly applied in numerous engineering sectors, such as machine learning and optimization. It relies on the actual processes of nature to select and operate on humans by crossover and mutation. It proceeds along cycles within the population up until reaching what has been attained over generations, offspring to the next population of potential solutions, the fittest of which is produced for the generation. GAs have been successfully applied in a variety of engineering fields such as machine learning and optimization [7].

Evolutionary programming (EP) [54] is a method that is similar to GA, but in contrast to GA. In EP, provided by Fogel in 1966, the emphasis is placed on the diversity of solutions rather than on recombination. Whereas in the GA, both crossover and mutation were applied, the emphasis was placed on mutation in the EP. EP consists exclusively of the mutation of candidate solutions, with the best individuals in the current generation being chosen for reproduction in the next. Different from the standard genetic algorithms, GP represents individuals as computer functions or programs, a concept first introduced in 1992 by Koza. GP mutates these programs to solve problems like automated design, machine learning, and symbolic regression. GP provides a more flexible optimization technique by evolving functions instead of prescribing static solutions, especially in difficult optimization problems [55].

Another level of complexity is added to evolutionary techniques by the Differential Evolution (DE) algorithm [11] proposed by Storn and Price in 1997. Essentially, DE emphasizes how individuals differ from one another. A new solution is generated by adding the weighted difference of two randomly selected solutions to a third. This encourages global exploration and fosters diversity. Due to its efficacy in continuous optimization problems, DE has been utilized extensively in numerous optimization applications.

The Cooperation Search Algorithm (CSA) [56] developed by Feng et al. (2021) takes a divergence from the other evolutionary models. It refers to a host of group problem-solving behaviors and indicates the idea of agents cooperating with each other to explore the search space for potential optimal solutions. Each agent contributes its own view, and the algorithm produces high-quality solutions from agents working together. The Local Search-based Genetic Algorithm (LSGA) [57] is a step ahead of the conventional GA, whereby local-search methods for solution refinement are incorporated. The LSGA utilizes local optimization, attempting to reach the optimal solution within enhanced convergence speed and overall performance, while GA is concerned with the global search space.

The Dual-Stage Robust (DREA) [58] is a well-known evolutionary technique for solving uncertain optimization problems. By balancing the dual-phase principle of searching for solutions in the first phase and enhancing these solutions to attain reliability and stability in the second phase, DREA works even more competitively in dynamic and uncertain contexts. COVIDOA, the Coronavirus Optimization Algorithm [59], was created following worldwide happenings to conform to the propagation and mutation processes of the coronavirus. As an added advantage, this bio-inspired algorithm will be able to solve very complex optimization problems through the influence of infection and mutation dynamics.

The No Free Lunch (NFL) theorem states that no optimization algorithm can perform better than all others in every scenario. This basic idea emphasizes creating customized algorithms that take advantage of features unique to a given challenge to attain better results. Motivated by this revelation, this study proposes an innovative optimization technique named Narwhal Optimizer Algorithm (NWOA) that is anticipated to enhance the quality of solutions and convergence efficiency for the specific category of problems. Typical features of the NWOA:

1.   Sonar-Based Communication for Information Sharing:

Narwhal uses sounds to relay information concerning the prey’s locality, thereby increasing the chances of successful hunting. In a similar manner, NWOA employs a sonar-based strategy to improve the ability for local search by allowing individuals (simulated narwhals) to communicate location information back and forth. This prevents premature convergence and encourages global exploration.

2.   Adaptive Local and Global Exploration:

Narwhals are engaged in global exploration (searching for food in larger areas), while it involves local searching (concentration on known prey locations). Unlike conventional methods, which are fixed in crossover and mutation, NWOA alters the power and mobility of the sonar signal, and thus the overall algorithm improves local refining and broad exploration. The functionality of local-global exploration becomes adaptive in narwhals, such as global exploration, which is searching for food within larger areas, and then local searching, such as concentration on known prey locations. These are very unlike established techniques that entirely rest on cross and static mutation, but NWOA modifies the mobility and power of a sonar signal, improving local refining while enabling the algorithm to broaden exploration really quickly.

3.   Convergence Behavior and Exploration Strategy:

The narwhal first explores a large area using sonar and then converges on social interaction toward an optimal location. In like manner, the NWOA initiates broad exploration and gradually concentrates on promising regions, sometimes at the expense of speed of convergence in comparison to GA. This guarantees more comprehensive search and minimizes the chances of getting trapped in local optima. GA thus has a moderate convergence rate but is heavily dependent on population size and crossover/mutation rates. With varying modes of navigation by sonar, adaptive search mechanisms, and social learning strategies, a concept arises known as NWOA, which can be classified into different classes of optimization, inspired by biology. The implementation and comparative performance of NWOA against existing optimization techniques are exhaustively analyzed in the subsequent sections.

3  Narwhal Optimization Algorithm (NWOA)

This section first discusses the proposed method. The mathematical model is then introduced.

3.1 Inspiration

The narwhal has a long, twisting tusk protruding out of its head, giving it the appearance of a whale-and-unicorn combination. Narwhals are a sociable species that live in pods of up to 20 individuals; however, most usually in pods of 3–8 individuals that are often sex separated [60]. Smaller groups merge with other groups to produce vast herds during the migratory season. The average body length of a narwhal is 4.7 m for males and 4 m for females. The pectoral fins are 30–40 cm long, with tail flukes measuring 1–1.2 m wide. Narwhals weigh an average of 900 kg for females and 1600 kg for males; fat accounts for around one-third of each animal’s weight [61].

The male narwhal has a left tooth that will develop into a long, straight tusk, earning it the moniker “unicorn of the sea,” as displayed in Fig. 1. Narwhals’ upper jaw contains two teeth. The tusks are around one-third to one-half the length of the body. Tusks up to three meters long and weighing ten kilograms have been discovered. Rarely, the other tooth will develop into a tusk, and both will spiral counterclockwise as they develop. In addition, females with tusks have occasionally been observed as well. The remainder of the tusk is typically encrusted in algae, despite the bottom end of the tusk seeming clean and polished [61].

Figure 1: Narwhal tusk [3]

The narwhal’s tooth is found to have hydrodynamic sensing capabilities. The narwhal tusk’s internal nerve and its outer surface are connected by ten million little nerve fibers. The tusk, which appears solid and unyielding, is more like a membrane with an extremely sensitive surface that can detect changes in water pressure, temperature, and particle gradients. These whales can sense particle gradients in water to identify their salinity, which might help them survive in their Arctic ice homeland. Moreover, it allows whales to recognize water traces that diverge from the fish that make up their diet. There is no comparison in nature, and there is beyond a doubt no tooth form, functional adaptation, or expression more discrete [61,62].

Narwhals can transmit their echolocating noises in all directions, much like other whales do, which helps them receive information from a considerable distance. The narwhal is the most adept at focusing its clicks on all echolocating creatures, including dolphins and bats. According to the study, narwhals may broaden their sonar beam to cover more area when tracking prey [61,63,64].

Particularly, narwhals utilize echolocation to find food, such as fish, squid, and shrimp. To find their prey, they make a succession of clicking noises, which increase louder as they draw near. Clicking becomes so rapid as the narwhals focus on their prey that it resembles a buzz [61,63,64]. More precisely, a sound must first be made by the narwhal. When the sound waves strike an object, they travel until they reach the object and then return to the narwhal as echoes. Depending on the sound’s frequency, the narwhal either hears these echoes in its lower jaw or right within its skull. Depending on what they need echolocation for, each species has a varied range of frequencies; low-frequency sounds go farther, but high-frequency sounds are best for close quarters. The narwhals may learn a variety of things, including where their food is, from the echoes [61,63,64]. Prey may become confused and helpless because of some noises, making them easier to hunt. Rarely heard, the whistles also trumpet and create noises comparable to a squeaky door [60].

For the first time, researchers captured narwhals hunting for fish on camera. Narwhals beat and stun fish with their tusks before devouring them, according to the video [62].

It is important to note that tusks are a unique feature that is exclusively seen in narwhals. The hunting behavior is mathematically represented in this work in order to achieve optimization.

3.2 Mathematical Model and Optimization Algorithm

This part introduces the mathematical model of searching and tracking prey using echolocation technology, chasing and pestering the prey until it stops moving, then attacking it. The NWOA is then presented.

3.2.1 Initialization of Agents

The Initial position of each agent within the search space is chosen randomly within the upper and lower bounds of the problem using the following equation:

Ni0=lb+(ub−lb)∗U(0,1), where i={1,2,3,…,N}(1)

where Ni0 represents the initial position of ith search agent, lb indicates the lower bound of the search space, ub is the upper bound of the search space, and U(0,1) is a uniform random number.

The best solution will be obtained by using the problem’s objective function. However, the best solution (N∗) is initialized as:

N∗=arg⁡minf(Ni0)(2)

where f(N) represents the objective function.

3.2.2 Searching and Tracking Phase (Exploration Phase)

As mentioned before, a narwhal may produce sounds in the form of clicks, which become louder as they get closer to their prey. The frequency of these clicks is higher than that of communication noises and varies between species. The narwhal initially produces a sound. When the sound wave strikes an item, a portion of its energy is reflected to the narwhal. The narwhal makes another click as soon as an echo is detected. The varied intensity of the signal received on the two sides of the narwhal’s tusk helps him determine the direction; the time delay between click and echo enables the narwhal to calculate the distance from the object being measured. Narwhals can track and locate objects by continually releasing clicks and receiving echoes in this manner. However, narwhals rely on echolocation click rates to define the prey’s location. Fig. 2 displays the echolocation technique that was employed by the narwhal to detect its prey.

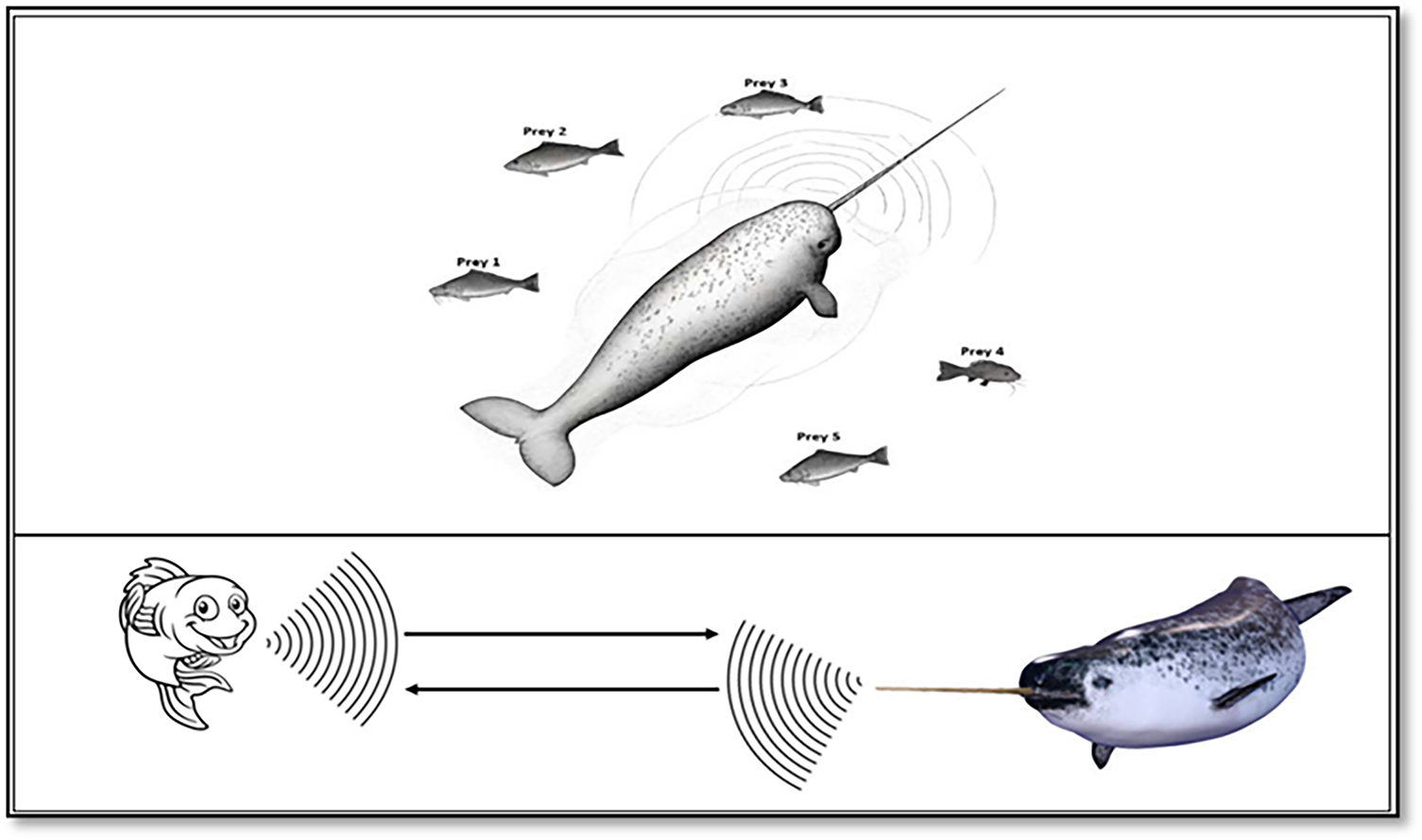
Figure 2: A Narwhal catching its prey using the echolocation click rate technique

Initially, the narwhal searches the whole search zone for the prey. As a narwhal approaches the object, it narrows its search and raises its clicks gradually to focus on the location.

The approach mimics the echolocation of the narwhal by restricting exploration according to the distance (hi) from the target. In other words, the proposed algorithm searches throughout the search space to complete a global search; thus it should explore uncharted areas. This mission is completed by randomly investigating several regions in the search space. The equations below illustrate this behavior:

h(Nit,N∗)=1−Nit∗N∗‖Nit‖∗‖N∗‖(3)

where h(Nit,N∗) is a measure of resemblance between the agent’s present location Nit and the optimal solution position N∗. More precisely, it represents the distance between the narwhal and prey and is modeled as cosine similarity.

The sound wave strength is determined using a sine function that decays over time.

Wave strength(Nit,t)=A⋅|sin⁡(k⋅ hi−ω⋅ t)|⋅e−δt(4)

where A represents the amplitude of the wave and equals 1, k is the wave number (k=2∗π), ω is the angular frequency (ω =2∗π), and δ equals 0.01, which represents the decay constant that causes the wave’s power to reduce e time. They depend on the environment properties hi and t represents the position along the propagation of the wave and the time of propagation.

In case the energy of prey is greater than one, and there is a chance for escape (Escaping chance), the narwhal starts looking for new prey and updates its position. This behavior is mathematically modeled as follows:

Nit+1=Nit+Aexploration∗(N∗−Nit)+WaveStrength(Nit,t)∗U(0,1)(5)

Aexploration=2∗a∗r1−a(6)

r1=rand()(7)

where a denotes the exploration decay factor, with a range [0, 1], U (0, 1) is a random number, r1 indicates a random number and Aexploration represents a coefficient that determines the exploration intensity which controls the search agents’ movement.

3.2.3 Searching and Tracking Phase (Exploration Phase)

When the prey’s energy is high in the early phases, the predator has the ability to investigate a larger variety of choices in pursuit of various solutions. This larger search technique increases the predator’s chances of finding the best hunting areas or more efficient ways to catch prey. Thus, High prey energy levels have an important effect on impacting the predator’s exploratory behavior. When r1<ExplorationRatio, that means the agent moves away from the best position to explore the search space. In other words, it is in the exploration phase.

As the prey’s energy depletes over time, the predator becomes more focused on exploiting the solutions it has already identified. As available energy declines, the predator emphasizes efficiency by employing previously established hunting techniques or areas that have proved effective. This transition from broad exploration to targeted exploitation is motivated by the need to preserve energy. In this case, the narwhal starts hitting and stunning the prey using its tusk until the prey stops moving, as shown in Fig. 3. However, in case the prey has no energy, the narwhal devours the prey by using its mouth, not by using its tusk. More precisely, this means r1>ExplorationRatio. This phase is called the exploitation phase. Fig. 4 illustrates the exploration and exploitation phases.

Figure 3: Narwhal stuns the prey by using its tusk

Figure 4: Attacking prey vs. searching for prey

The following equation is used to calculate the energy of prey in the current iteration.

EnergyPrey(t+1)=EnergyPrey(t)∗e(−λ∗t)(8)

where EnergyPrey(t) indicates the prey’s energy of the previous iteration and λ represents the decay rates a metric that determines how rapidly energy decays, which is set to 0.001. Moreover, the initial energy of the prey equals one. By using this formula, we ensure that the energy will decrease exponentially.

To ensure that energy does not go below zero, use the following equation:

EnergyPrey(t)=Max(EnergyPrey(t),0)(9)

In case the prey has at current iteration (t) energy (E) which is less than one, which means the prey could not move and was ready to be eaten by the narwhal. Thus, the narwhal adjusts its position depending on the prey’s position. However, if the prey’s energy is greater than one, the narwhal starts hitting its prey using its tusk till the prey cannot move and escape (Hunting chance). This behavior is modeled using the following equations:

Nit+1=Nit−Aexploitation∗(N∗−Nit)+Cexploitation∗suctionForce(Nit,N∗)∗WaveStrength(Nit,t)∗U(0,1)(10)

Aexploitation, Cexplotation and SuctionForce(Nit,N∗) are calculated as follows:

r2=rand()(11)

Aexploitation=a∗r1−a(12)

Cexplotation=2∗r2(13)

SuctionStrength(Nit,t)=Energyprey(t)1+‖N∗−Nit‖(14)

SuctionForce(Nit,N∗)=SuctionStrength∗PreyEnergy(15)

where Aexploitation is the exploitation coefficient, which determines how far the agent goes toward the best position, a is the exploration decay factor, r1 and r2 are random numbers, ‖N∗−Nit‖ indicates the distance between best solution and the search agent, and SuctionForce(Nit,N∗) represents a force that pulls the agent into the optimum solution.

3.2.4 Dynamic Exploration-Exploitation Transition

To transition from exploration to exploitation is controlled as follows:

a(t)=2−(2tMaxiteration)(16)

where a (t) is an exploration factor that begins at two and declines linearly over time, and t indicates the maximum number of iterations. The algorithm dynamically adjusts the balance using:

Explorationratio{0.7,if(f(N∗)−f(Nt−1))<0.01(Slowimprovement)0.3,ifPreyEnergy<0.3 (Lowenergy,shifttoexploitation)0.7,Otherwise(17)

Eq. (17) illustrates how the exploration ratio is dynamically adjusted and relies on two factors: fitness improvement and the prey’s energy level. The main idea is to maintain a balance between exploration and exploitation.

The improvement in fitness (fitness_improvement=f(N∗)−f(Nt−1)) is tracked to determine whether the algorithm should focus on exploration or exploitation.

Exploration Ratio: The ratio varies dynamically depending on fitness development and prey energy:

If the fitness increase is tiny, exploration is preferred (Explorationratio=0.7). More precisely, if the improvement in the objective function is minimal this indicates stagnation in progress, and thus the algorithm increases the exploration ratio to 0.7 to search for better regions.

If Prey Energy is less than 0.3, the algorithm moves to exploitation (ExplorationRatio=0.3), which means in case the prey’s energy falls below 0.3, it reflects a high chance of capture, so the algorithm shifts toward exploitation by reducing the exploration ratio to 0.3. Assuming the prey is close to being caught and fine-tuning is more beneficial.

Otherwise, exploration is preferred, with a ratio of 0.7. In other words, in all other situations, exploration is preferred with a default ratio of 0.7.

The algorithm combines exploration and exploitation tactics inspired by the behavior of a predator-prey system, controlled by the decay of Prey Energy and the propagation of sound waves. The algorithm’s dynamic balance of exploration and exploitation enables it to efficiently search the space for optimal solutions. The sound wave component represents a novel technique for altering the agent’s motions, enhancing search variety. The Algorithm 1 shows the pseudocode of the NWOA.

4  Experiment Results

A comparative study was carried out on the results obtained with the new algorithm and the other optimization algorithms for popular test problems. The algorithm’s effectiveness is tested using the benchmark functions from the CEC 2017 test suite [65], which is a well-established standard for assessing metaheuristic algorithms.

NWOA’s performance was assessed in this research using the CEC 2017 benchmark suite, which contains 30 standard test functions divided into four sets: unimodal (C17-F1-C17-F3), multimodal (C17-F4-C17-F10), hybrid (C17-F11-C17-F20), and composition (C17-F21-C17-F30). For a thorough evaluation, the NWOA was benchmarked against six other optimization algorithms, encompassing both population-based and nature-inspired methods: WOA, GWO, CFO, POA, PSO, and GA [66–70].

All simulations were carried out on the different test functions from the CEC 2017 suite, using standard performance indicators such as the mean, best, and worst values, standard deviation, and median. To ensure the robustness and statistical significance of the results, the Wilcoxon Rank Sum test [71] was applied for pairwise comparisons between algorithms.

Simulation results are given in Table 1, along with the performance of each algorithm for various test functions. The table encloses the array of parameters for each algorithm, including mean, best, worst, standard deviation, and median. Additionally, the algorithms were ranked based on average performance across all functions. Overall, NWOA was able to outperform most of the benchmark functions better than all others.

For simple functions such as C17-F1 to C17-F3, NWOA provided the best results. Even in more difficult hybrid functions (C17-F11 to C17-F20) and composition functions (C17-F21 to C17-F30), NWOA was able to maintain its position at the top for the sake of higher precision and solid stability.

The experimental outcomes showed that the NWOA performs better than the comparison algorithms across most of the test functions. In unimodal functions, NWOA demonstrated fast convergence and excellent local search, because of its energy-based prey modeling mechanism as well as its adaptive sonar communication technique. In multimodal and hybrid functions, NWOA was highly robust and diversity-preserving because of its oscillatory wave exploration method that efficiently explores and avoids local optima.

Composition functions with their complexities and deceptive landscapes proved NWOA’s ability to balance between exploration and exploitation. The mechanism entails a gradual transition from exploration to exploitation based on prey energy decay, prevents early convergence, and enables comprehensive search.

Boxplots are shown in Fig. 5 for several representative benchmark functions. NWOA’s boxplots have lower medians and are noticeably narrower, which means that their performance is more stable and reliable across runs. NWOA showed convergence behavior, and less variance compared to PSO and POA.

Figure 5: Boxplot diagrams obtained from NWOA and competing algorithms on CEC 2017 test suite

The nonparametric Wilcoxon signed-rank test was applied at a 5% significance level to verify the statistical significance of NWOA’s superiority. The validity of the improvements was confirmed by NWOA’s significant outperformance of all comparison algorithms, in most situations (p-values < 0.05). As shown in the results, NOWA achieved the highest overall rank across the benchmark suite, as further validated by the Friedman rank test.

The superior performance of NWOA is based on its biologically inspired design, especially its sonar signal modeling, which is employed to adapt its exploration and exploitation. In contrast to conventional optimizers that depend on static operators, such as crossover and mutation in GA. Both global search diversity and local refining precision are improved by employing echolocation and social interaction techniques.

Furthermore, the two-phase architecture, designed based on natural hunting behavior—where sonar clicks intensify as prey approaches—enables a natural and efficient transition from global exploration to local exploitation. This is particularly evident in high-dimensional, multimodal problems, where the NWOA system achieves faster convergence without compromising solution quality.

5  Conclusion

A new swarm-based optimization is introduced in this work, which is called the Narwhal Optimization Algorithm (NWOA). The design and operational mechanisms of NWOA are modeled after the unique foraging behavior of these marine mammals, which exhibit some of the most complex and intelligent search patterns when preying under sea ice: they use social cooperation and echolocation, which are now presumed to be assisted by their long spiral tusks. The optimization process of NWOA mimics these natural behaviors while traversing complex search spaces with the goal of striking a balance between exploration (global search) and exploitation (local search). To assess the efficacy of the NWOA algorithm, a comprehensive set of thirty well-known benchmark functions from the CEC 2017 test suite was employed. The functions evaluate the algorithm in terms of its exploring, exploiting, and converging behaviors across a variety of fields, unimodal as well as multimodal ones. NWOA was then compared regarding performance with four of the most commonly used metaheuristic algorithms, namely, the Perfumer Optimization Algorithm (POA), the Candle Flame Optimization (CFO) Algorithm, the Grey Wolf Optimizer (GWO), the Whale Optimization Algorithm (WOA), the Particle Swarm Optimization (PSO) Algorithm, and the Genetic Algorithm (GA). The experimental results showed that NWOA effectively maintains a balance between exploration and exploitation during the search process. In addition, its performance was compared with six well-known metaheuristic algorithms in the majority of benchmark functions, where NWOA demonstrated superior optimization capabilities by achieving better outcomes in most benchmark functions.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Raja Masadeh, Abdullah Zaqebah and Ahmad Sharieh; methodology, Omar Almomani, Raja Masadeh and Abdullah Zaqebah; software, Raja Masadeh, Abdullah Zaqebah and Omar Almomani; validation, Shayma Masadeh, Kholoud Alshqurat and Ahmad Sharieh; formal analysis, Raja Masadeh, Abdullah Zaqebah and Omar Almomani; investigation, Raja Masadeh, Nesreen Alsharman and Shayma Masadeh; resources, Abdullah Zaqebah, Raja Masadeh and Nesreen Alsharman; data curation, Shayma Masadeh, Kholoud Alshqurat and Raja Masadeh; writing—original draft preparation, Raja Masadeh, Nesreen Alsharman and Ahmad Sharieh; writing—review and editing, Raja Masadeh, Abdullah Zaqebah and Omar Almomani; visualization, Nesreen Alsharman and Raja Masadeh; supervision, Raja Masadeh, Omar Almomani and Abdullah Zaqebah; project administration, Raja Masadeh and Ahmad Sharieh; funding acquisition, Shayma Masadeh, Kholoud Alshqurat and Nesreen Alsharman. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Masadeh R, AlSaaidah B, Masadeh E, Al-Hadidi MR, Almomani O. Elastic hop count trickle timer algorithm in Internet of Things. Sustainability. 2022;14(19):12417. doi:10.3390/su141912417. [Google Scholar] [CrossRef]

2. Masadeh R, Sharieh A, Jamal S, Haj M, Alsaaidah B. Best path in mountain environment based on parallel hill climbing algorithm. Int J Adv Comput Sci Appl. 2020;11(9):107–16. doi:10.14569/ijacsa.2020.0110913. [Google Scholar] [CrossRef]

3. Atashpaz-Gargari E, Lucas C. Imperialist competitive algorithm: an algorithm for optimization inspired by imperialistic competition. In: 2007 IEEE Congress on Evolutionary Computation; 2007 Sep 25–28; Singapore. doi:10.1109/CEC.2007.4425083. [Google Scholar] [CrossRef]

4. Holland JH. Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence. Cambridge, MA, USA: MIT Press; 1992. doi:10.7551/mitpress/1090.001.0001. [Google Scholar] [CrossRef]

5. Dorigo M, Gambardella LM. Ant colony system: a cooperative learning approach to the traveling salesman problem. IEEE Trans Evol Comput. 1997;1(1):53–66. doi:10.1109/4235.585892. [Google Scholar] [CrossRef]

6. Kennedy J, Eberhart R. Particle swarm optimization. In: Proceedings of the ICNN’95—International Conference on Neural Networks; 1995 Nov 27–Dec 1; Perth, Australia. doi:10.1109/ICNN.1995.488968. [Google Scholar] [CrossRef]

7. Mitchell M. An introduction to genetic algorithms. Cambridge, MA, USA: MIT Press; 1998. [Google Scholar]

8. Hosseini H, Al Khaled A, Sabaei M. Human group formation in evolutionary multi-objective optimization algorithms. Inf Sci. 2012;190(4):59–79. doi:10.1016/j.ins.2011.12.006. [Google Scholar] [CrossRef]

9. Jafari H, Tavakkoli-Moghaddam R, Ghoushchi SJ. Searching group algorithm: a new metaheuristic for continuous optimization problems. Appl Math Model. 2017;45(1416):372–94. doi:10.1016/j.apm.2017.01.005. [Google Scholar] [CrossRef]

10. Jin Y, Olhofer M, Sendhoff B. Dynamic evolutionary optimization: a survey of the state of the art. Swarm Evol Comput. 2019;46(4):87–104. doi:10.1016/j.swevo.2019.02.004. [Google Scholar] [CrossRef]

11. Storn R, Price K. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J Glob Optim. 1997;11(4):341–59. doi:10.1023/A:1008202821328. [Google Scholar] [CrossRef]

12. Rashedi E, Nezamabadi-pour H, Saryazdi S. GSA: a gravitational search algorithm. Inf Sci. 2009;179(13):2232–48. doi:10.1016/j.ins.2009.03.004. [Google Scholar] [CrossRef]

13. Medjahed S, Boukhatem F. Narwhal optimizer: a novel nature-inspired metaheuristic algorithm. Int Arab J Inf Technol. 2024;21(3):418–26. doi:10.34028/iajit/21/3/6. [Google Scholar] [CrossRef]

14. Kirkpatrick S, Gelatt CD Jr, Vecchi MP. Optimization by simulated annealing. Science. 1983;220(4598):671–80. doi:10.1126/science.220.4598.671. [Google Scholar] [PubMed] [CrossRef]

15. Yang XS. Nature-inspired metaheuristic algorithms. Bristol, UK: Luniver Press; 2010. [Google Scholar]

16. Yang XS. A new metaheuristic bat-inspired algorithm. In: González JR, Pelta DA, Cruz C, Terrazas G, Krasnogor N, editors. Nature inspired cooperative strategies for optimization (NICSO 2010). Berlin/Heidelberg, Germany: Springer; 2010. p. 65–74. doi:10.1007/978-3-642-12538-6_6. [Google Scholar] [CrossRef]

17. Lam AYS, Li VOK. Chemical-reaction-inspired metaheuristic for optimization. IEEE Trans Evol Computat. 2010;14(3):381–99. doi:10.1109/tevc.2009.2033580. [Google Scholar] [CrossRef]

18. Yang XS. Flower pollination algorithm for global optimization. In: Patitz MJ, Stannett M, editors. Unconventional computation and natural computation. Berlin/Heidelberg, Germany: Springer; 2012. p. 240–9. doi:10.1007/978-3-642-32894-7_27. [Google Scholar] [CrossRef]

19. Mirjalili S. Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm. Knowl Based Syst. 2015;89:228–49. doi:10.1016/j.knosys.2015.07.006. [Google Scholar] [CrossRef]

20. Zheng YJ. Water wave optimization: a new nature-inspired metaheuristic. Comput Oper Res. 2015;55(5187):1–11. doi:10.1016/j.cor.2014.10.008. [Google Scholar] [CrossRef]

21. Dalirinia E, Jalali M, Yaghoobi M, Tabatabaee H. Lotus effect optimization algorithm (LEAa lotus nature-inspired algorithm for engineering design optimization. J Supercomput. 2024;80(1):761–99. doi:10.1007/s11227-023-05513-8. [Google Scholar] [CrossRef]

22. Hu G, Guo Y, Wei G, Abualigah L. Genghis Khan shark optimizer: a novel nature-inspired algorithm for engineering optimization. Adv Eng Inform. 2023;58(8):102210. doi:10.1016/j.aei.2023.102210. [Google Scholar] [CrossRef]

23. Agushaka JO, Ezugwu AE, Abualigah L. Gazelle optimization algorithm: a novel nature-inspired metaheuristic optimizer. Neural Comput Appl. 2023;35(5):4099–131. doi:10.1007/s00521-022-07854-6. [Google Scholar] [CrossRef]

24. Yang XS, Deb S. Cuckoo search via lévy flights. In: 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC); 2009 Dec 9–11; Coimbatore, India. p. 210–4. doi:10.1109/NABIC.2009.5393690. [Google Scholar] [CrossRef]

25. Mirjalili S, Gandomi AH, Mirjalili SZ, Saremi S, Faris H, Mirjalili SM. Salp swarm algorithm: a bio-inspired optimizer for engineering design problems. Adv Eng Softw. 2017;114:163–91. doi:10.1016/j.advengsoft.2017.07.002. [Google Scholar] [CrossRef]

26. Bansal JC, Sharma H, Jadon SS, Clerc M. Spider monkey optimization algorithm for numerical optimization. Memet Comput. 2014;6(1):31–47. doi:10.1007/s12293-013-0128-0. [Google Scholar] [CrossRef]

27. Mirjalili S. Dragonfly algorithm: a new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput Appl. 2016;27(4):1053–73. doi:10.1007/s00521-015-1920-1. [Google Scholar] [CrossRef]

28. Mirjalili S, Lewis A. The whale optimization algorithm. Adv Eng Softw. 2016;95(12):51–67. doi:10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]

29. Zhao W, Wang L, Mirjalili S. Artificial hummingbird algorithm: a new bio-inspired optimizer with its engineering applications. Comput Meth Appl Mech Eng. 2022;388(1):114194. doi:10.1016/j.cma.2021.114194. [Google Scholar] [CrossRef]

30. Agushaka JO, Ezugwu AE, Abualigah L. Dwarf mongoose optimization algorithm. Comput Meth Appl Mech Eng. 2022;391(10):114570. doi:10.1016/j.cma.2022.114570. [Google Scholar] [CrossRef]

31. Jain M, Singh V, Rani A. A novel nature-inspired algorithm for optimization: squirrel search algorithm. Swarm Evol Comput. 2019;44(4):148–75. doi:10.1016/j.swevo.2018.02.013. [Google Scholar] [CrossRef]

32. MiarNaeimi F, Azizyan G, Rashki M. Horse herd optimization algorithm: a nature-inspired algorithm for high-dimensional optimization problems. Knowl Based Syst. 2021;213(2):106711. doi:10.1016/j.knosys.2020.106711. [Google Scholar] [CrossRef]

33. Masadeh R, Basel A, Sharieh A. Sea lion optimization algorithm. Int J Adv Comput Sci Appl. 2019;10(5):388–95. doi:10.14569/ijacsa.2019.0100548. [Google Scholar] [CrossRef]

34. Wang GG, Deb S, Zhao X. Red deer algorithm: a new bio-inspired algorithm for global optimization. Swarm Evol Comput. 2019;50:100489. doi:10.1016/j.swevo.2019.100489. [Google Scholar] [CrossRef]

35. Zhao W, Wang L, Zhang Z, Fan H, Zhang J, Mirjalili S, et al. Electric eel foraging optimization: a new bio-inspired optimizer for engineering applications. Expert Syst Appl. 2024;238(1):122200. doi:10.1016/j.eswa.2023.122200. [Google Scholar] [CrossRef]

36. Golilarz NA, Gao H, Addeh A, Pirasteh S. ORCA optimization algorithm: a new meta-heuristic tool for complex optimization problems. In: 2020 17th International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP); 2020 Dec 18–20; Chengdu, China. doi:10.1109/iccwamtip51612.2020.9317473. [Google Scholar] [CrossRef]

37. Zhao W, Zhang Z, Wang L. Manta ray foraging optimization: an effective bio-inspired optimizer for engineering applications. Eng Appl Artif Intell. 2020;87(5):103300. doi:10.1016/j.engappai.2019.103300. [Google Scholar] [CrossRef]

38. Zhong C, Li G, Meng Z. Beluga whale optimization: a novel nature-inspired metaheuristic algorithm. Knowl Based Syst. 2022;251(1):109215. doi:10.1016/j.knosys.2022.109215. [Google Scholar] [CrossRef]

39. Sadollah A, Bahreininejad A, Eskandar H, Hamdi M. Mine blast algorithm: a new population based algorithm for solving constrained engineering optimization problems. Appl Soft Comput. 2013;13(5):2592–612. doi:10.1016/j.asoc.2012.11.026. [Google Scholar] [CrossRef]

40. Kaveh A, Talatahari S. A novel heuristic optimization method: charged system search. Acta Mech. 2010;213(3):267–89. doi:10.1007/s00707-009-0270-4. [Google Scholar] [CrossRef]

41. Husseinzadeh Kashan A. A new metaheuristic for optimization: optics inspired optimization (OIO). Comput Oper Res. 2015;55:99–125. doi:10.1016/j.cor.2014.10.011. [Google Scholar] [CrossRef]

42. Mirjalili S. SCA: a sine cosine algorithm for solving optimization problems. Knowl Based Syst. 2016;96(63):120–33. doi:10.1016/j.knosys.2015.12.022. [Google Scholar] [CrossRef]

43. Abdel-Basset M, El-Shahat D, Jameel M, Abouhawwash M. Young’s double-slit experiment optimizer: a novel metaheuristic optimization algorithm for global and constraint optimization problems. Comput Meth Appl Mech Eng. 2023;403(9):115652. doi:10.1016/j.cma.2022.115652. [Google Scholar] [CrossRef]

44. Hashim FA, Houssein EH, Mabrouk MS, Al-Atabany W, Mirjalili S. Henry gas solubility optimization: a novel physics-based algorithm. Future Gener Comput Syst. 2019;101(4):646–67. doi:10.1016/j.future.2019.07.015. [Google Scholar] [CrossRef]

45. Kundu R, Chattopadhyay S, Nag S, Navarro MA, Oliva D. Prism refraction search: a novel physics-based metaheuristic algorithm. J Supercomput. 2024;80(8):10746–95. doi:10.1007/s11227-023-05790-3. [Google Scholar] [CrossRef]

46. Hamadneh T, Batiha B, Gharib GM, Montazeri Z, Dehghani M, Aribowo W, et al. Candle flame optimization: a physics-based metaheuristic for global optimization. Int J Intell Eng Syst. 2025;18(4):826–37. doi:10.22266/ijies2025.0531.53. [Google Scholar] [CrossRef]

47. Glover F. Tabu search: part I. ORSA J Comput. 1989;1(3):190–206. doi:10.1287/ijoc.1.3.190. [Google Scholar] [CrossRef]

48. Geem ZW, Kim JH, Loganathan GV. A new heuristic optimization algorithm: harmony search. Simulation. 2001;76(2):60–8. doi:10.1177/003754970107600201. [Google Scholar] [CrossRef]

49. Rao RV, Savsani VJ, Vakharia DP. Teaching-learning-based optimization: a novel method for constrained mechanical design optimization problems. Comput Aided Des. 2011;43(3):303–15. doi:10.1016/j.cad.2010.12.015. [Google Scholar] [CrossRef]

50. Tan Y, Zhu Y. Fireworks algorithm for optimization. In: Advances in Swarm Intelligence: First International Conference ICSI 2010; 2010 Jun 12–15; Beijing, China. doi:10.1007/978-3-642-13495-1_44. [Google Scholar] [CrossRef]

51. Jafari H, Tavakkoli-Moghaddam R, Ghoushchi SJ. A football game inspired optimization algorithm for continuous optimization problems. Appl Soft Comput. 2014;17:61–80. doi:10.1109/CSIEC.2016.7482120. [Google Scholar] [CrossRef]

52. Pereira AG, Ramos JP, de Oliveira JA. Brainstorm optimization algorithm for real-world engineering optimization problems. Appl Soft Comput. 2017;58(2):570–90. doi:10.1007/978-3-642-21515-5_36. [Google Scholar] [CrossRef]

53. Hamadneh T, Batiha B, Gharib GM, Montazeri Z, Dehghani M, Aribowo W, et al. Perfumer optimization algorithm: a novel human-inspired metaheuristic for solving optimization tasks. Int J Intell Eng Syst. 2025;18(4):1–11. doi:10.22266/ijies2025.0531.41. [Google Scholar] [CrossRef]

54. Fogel LJ, Owens AJ, Walsh MJ. Artificial intelligence through simulated evolution. New York, NY, USA: John Wiley & Sons, Inc.; 1966. doi:10.4236/ojapps.2019.910062. [Google Scholar] [CrossRef]

55. Koza JR. Genetic programming: on the programming of computers by means of natural selection. Cambridge, MA, USA: MIT Press; 1992. [Google Scholar]

56. Feng ZK, Niu WJ, Liu S. Cooperation search algorithm: a novel metaheuristic evolutionary intelligence algorithm for numerical optimization and engineering optimization problems. Appl Soft Comput. 2021;98:106734. doi:10.1016/j.asoc.2020.106734. [Google Scholar] [CrossRef]

57. Li X, Wang Y, He Q. A local search-based genetic algorithm for multi-objective optimization. Expert Syst Appl. 2017;79(1):338–48. doi:10.1007/s44196-021-00012-1. [Google Scholar] [CrossRef]

58. Du W, Fang W, Liang C, Tang Y, Jin Y. A novel dual-stage evolutionary algorithm for finding robust solutions. IEEE Trans Emerg Top Comput Intell. 2024;8(5):3589–602. doi:10.1109/TETCI.2024.3369710. [Google Scholar] [CrossRef]

59. Sultana N, Ahmed S, Hassan MR. Coronavirus Optimization Algorithm (COVIDOAa bio-inspired metaheuristic optimization approach. Artif Intell Rev. 2020;55(1):451–80. doi:10.1007/s00521-022-07639-x. [Google Scholar] [PubMed] [CrossRef]

60. Lambert K. How narwhals work [Internet]. [cited 2025 Mar 10]. Available from: https://animals.howstuffworks.com/mammals/narwhal.htm. [Google Scholar]

61. Narwhals, Monodon monoceros (Video) [Internet]. [cited 2025 Mar 10]. Available from: https://www.marinebio.org/species/narwhals/monodon-monoceros/. [Google Scholar]

62. How narwhals use their tusks (Video) [Internet]. [cited 2025 Mar 10]. Available from: https://www.worldwildlife.org/videos/how-narwhals-use-their-tusks. [Google Scholar]

63. Description of Narwhal [Internet]. [cited 2025 Mar 10]. Available from: https://a-dinosaur-a-day.com/post/135006696625/monodon-monoceros-narwhal. [Google Scholar]

64. Narwhals stun fish with their tusk [Internet]. [cited 2025 Mar 10]. Available from: https://rangerrick.org/rr_videos/narwhal-stun-fish-tusk-eat/. [Google Scholar]

65. Awad NH, Ali MZ, Liang JJ, Qu BY, Suganthan PN. Problem definitions and evaluation criteria for the CEC 2017 special session and competition on single objective bound constrained real-parameter numerical optimization. Singapore: Nanyang Technological University; 2016. [Google Scholar]

66. Abualhaj MM, Nabil Alkhatib S, Adel Abu-Shareha A, Alsaaidah AM, Anbar M. Enhancing spam detection using Harris Hawks optimization algorithm. TELKOMNIKA Telecommun Comput Electron Control. 2025;23(2):447. doi:10.12928/telkomnika.v23i2.26615. [Google Scholar] [CrossRef]

67. Abualhaj MM. Spam feature selection using firefly metaheuristic algorithm. J Appl Data Sci. 2024;5(4):1692–700. doi:10.47738/jads.v5i4.336. [Google Scholar] [CrossRef]

68. Almomani O. A feature selection model for network intrusion detection system based on PSO, GWO, FFA and GA algorithms. Symmetry. 2020;12(6):1046. doi:10.3390/sym12061046. [Google Scholar] [CrossRef]

69. Almomani O. A hybrid model using bio-inspired metaheuristic algorithms for network intrusion detection system. Comput Mater Continua. 2021;68(1):409–29. doi:10.32604/cmc.2021.016113. [Google Scholar] [CrossRef]

70. Almomani O, Alsaaidah A, Abu-Shareha AA, Alzaqebah A, Amin Almaiah M, Shambour Q. Enhance URL defacement attack detection using particle swarm optimization and machine learning. J Comput Cogn Eng Forthcoming. 2025. doi:10.47852/bonviewjcce52024668. [Google Scholar] [CrossRef]

71. Wilcoxon F. Individual comparisons by ranking methods. In: Kotz S, Johnson NL, editors. Breakthroughs in statistics. New York, NY, USA: Springer; 1992. p. 196–202. doi:10.1007/978-1-4612-4380-9_16. [Google Scholar] [CrossRef]