An Online Optimization of Prediction-Enhanced Digital Twin Migration over Edge Computing with Adaptive Information Updating

1  Introduction

The digital twin (DT) is a promising paradigm for creating a virtual representation of a physical entity. By enabling simulation and behavior analysis in the digital space, a DT functions as a virtual sandbox to facilitate fine-grained monitoring and intelligent decision-making for complex tasks originating from its physical counterpart [1]. For instance, in the domain of autonomous driving, DTs support realistic testing by virtualizing vehicle behavior and complex road environments, thereby enabling safe and efficient validation of driving tasks via edge communication technologies [2]. In other applications, DTs and multi-agent systems are leveraged to model and coordinate warehouse robots for cargo handling tasks in a smart cyber-physical environment [3]. Similarly, Lv et al. [4] studied a DT-assisted framework for medical delivery tasks using an unmanned aerial vehicle (UAV). Consequently, owing to its capability to address complex real-world challenges, the DT is recognized as a key enabling technology for applications such as Industry 4.0, the metaverse, and smart cities, garnering significant research attention [5].

A DT-enabled task processing framework typically involves numerous DTs and their associated PTs. In this context, PTs represent real-world entities such as humans, vehicles, or devices, with DTs functioning as their virtual counterparts [6]. Ensuring energy-efficient, low-latency task execution for a PT necessitates the meticulous construction and management of its corresponding DT. These requirements motivate the use of edge computing [7], where DTs are deployed on ESs at the network periphery to execute tasks for their PTs. While recent studies have explored related topics, such as industrial DTs and service deployment on ESs, implementing mobile DT-assisted task execution presents unique challenges. First, unlike stationary entities in industrial plants, the high mobility of PTs results in unstable PT-DT connectivity. Second, in contrast to a limited number of shared service applications, a large number of exclusive DTs must concurrently execute complex tasks for their associated PTs. This intensive computation relies on the limited resources of the host ESs [8], leading to potentially high task response latency and energy consumption. Therefore, to maintain seamless PT-DT connectivity while ensuring low-latency, energy-efficient task execution, the dynamic migration of DTs among ESs becomes essential [9].

However, addressing the aforementioned issues is challenging due to several underlying reasons:

1)   Since the transmission of PT status information for mobility prediction is energy-intensive, these updates should occur at a lower frequency. In contrast, the constant movement and task generation of PTs demand that DT migration and resource allocation be optimized more frequently. This suggests that the overall optimization must be handled asynchronously across different timescales.

2)   The frequency of uploading PT status data governs a trade-off between task response latency and energy consumption. Shorter upload intervals can reduce task latency but concurrently increase energy usage, whereas longer intervals have the opposite effect. This implies that the upload frequency must be determined adaptively based on feedback regarding system performance.

3)   The high mobility of PTs, coupled with the need for frequent DT migrations, means that conventional reactive strategies can lead to severe task response latency and even service interruptions. Therefore, it is necessary to proactively migrate DTs by employing a predictive mobility model [10].

To tackle these challenges, we introduce a novel two-timescale online optimization scheme for a DT-assisted task execution system in an edge computing environment. Specifically, we consider a scenario where each PT has an exclusive DT deployed on an ES to execute its complex tasks. To account for PT mobility, the corresponding DTs are proactively migrated among ESs. These migration decisions are based on the PTs’ future trajectories, which are forecast by a predictive model hosted in a cloud center. To support this model, PTs must upload their status information (e.g., moving speed, direction) as predictive inputs. Our primary objective is to minimize the long-term average task response latency of all DTs, subject to a stringent energy consumption constraint and inherent system uncertainties such as unpredictable PT mobility. To this end, we formulate the problem as a two-timescale online optimization problem. This problem involves dynamically optimizing two sets of decisions. The first set, decided at the larger timescale, is the status information uploading frequency for each PT. The second set, decided at the smaller timescale, includes the DT migration strategy and the allocation of computational and communication resources at the ES. To solve this problem, we develop a novel two-timescale mobility-aware online optimization approach based on extended Lyapunov optimization theory. This approach first decomposes the long-term problem into a sequence of subproblems corresponding to the different timescales. An online learning method is then incorporated to adaptively determine the status information update frequency. Subsequently, for each subproblem within the smaller timescale, we first employ a GRU-based scheme to predict the PT’s trajectory. Based on this prediction, an AM-based algorithm is proposed to optimize the small-timescale decisions.

The key contributions of this paper are summarized as follows:

•   We address the problem of proactive DT migration at the network edge for executing complex PT tasks. To this end, we formulate a two-timescale mobility-aware online optimization problem that jointly optimizes three key decisions, including the adaptive status update frequency of PTs, the proactive DT migration decision, and the allocation of computational and communication resources on the ESs.

•   We propose a novel solution framework, termed TMO, which first decomposes the long-term problem into a sequence of subproblems. To solve these subproblems across their different timescales, the TMO framework integrates two main components. An online learning method is employed to address the large-timescale problem, while an AM algorithm, augmented by a GRU-based prediction scheme, is utilized for the small-timescale problems.

•   We conduct both theoretical analysis and extensive simulations to validate the performance of our proposed approach. The results demonstrate that the TMO scheme significantly outperforms existing benchmark methods in reducing both task response latency and overall system energy consumption.

The following section provides a review of related work. The system model and the corresponding problem formulation are detailed in Section 3. Section 4 presents our proposed two-timescale mobility-aware online optimization approach and its theoretical analysis. Section 5 discusses the simulation results, and Section 6 concludes the paper.

2  Related Work

As an accurate digital representation of physical entities, the deployment of DTs enables real-time interaction and shows significant potential for supporting emerging 6G applications. For example, Wang et al. [11] propose a DT-based method for attack detection in the internet of things by fusing spatio-temporal features to enhance identification accuracy within dynamic network environments. Similarly, Zhao et al. [12] designed a DT-based application system to improve the accuracy and efficiency of network management. Jyeniskhan et al. [13] proposed a framework for DT systems in additive manufacturing that incorporates machine learning techniques. However, these studies did not fully consider the impact of a dynamic network environment or varying user status on the quality of the PT-DT interaction.

Edge computing is a crucial technology for delivering latency-sensitive services in wireless networks by offloading computation and storage tasks to the network edge. Recently, research efforts have increasingly focused on DT management within edge environments. For instance, Wen et al. [14] proposed an improved artificial potential field method for edge computing environments to achieve cooperative control and DT monitoring of multi-AUG. Lu et al. [15] proposed a DT-assisted wireless edge network framework designed to facilitate low-latency computation and seamless connectivity. In another study, Zhang et al. [16] proposed a framework for DT systems within wireless-powered communication networks, examining adaptive placement and transfer schemes for the DTs. However, these studies typically assume that DTs are either stationary or designed for a single, specific purpose. This assumption makes their approaches inadequate for supporting mobile PTs that have diverse service demands. Beyond DT-specific management, another stream of relevant research focuses on general service migration at the edge. For instance, He et al. [17] presented an efficient planning and scheduling framework for edge service migration that handles live migrations while ensuring low latency for mobile users. Mustafa et al. [18] proposed a hybrid SQ-DDTO algorithm within a three-layer vehicular edge computing framework to optimize task offloading and resource allocation. The same authors [19] also proposed a PPO-based task offloading algorithm for vehicular edge computing. Their approach addresses task dependencies and dynamic network conditions, aiming to enhance policy stability while minimizing delays and the task drop ratio. Nevertheless, these general migration studies assume a limited set of service entity (SE) types, where a single SE can serve multiple users. This contrasts with the inherent exclusivity of a DT, which is dedicated to handling tasks for only its specific PT.

Lyapunov-based optimization is a widely utilized tool for online optimization problems characterized by system uncertainties, as it can guarantee long-term performance stability without requiring future information [20–22]. However, most existing works in this area focus on decisions made within a single timescale. More recently, some studies have employed a two-timescale Lyapunov method [7,23], where the original problem is decomposed and decisions are subsequently made across different timescales. In a different approach, Huang et al. [24] combined the multi-armed bandit (MAB) method with Lyapunov optimization to schedule queueing systems without prior knowledge of instantaneous network conditions. Nevertheless, these schemes cannot be directly applied to our problem. This is primarily due to two factors. First, our model incorporates a flexible duration for the large timescale. Second, it features a complex coupling of decision variables within both the objective function and the problem constraints.

In contrast to previous works, this paper proposes a novel mobility-aware, two-timescale online optimization approach for edge computing environments. This approach is designed to jointly optimize three coupled decisions, i.e., the uploading frequency of PT status information, the DT migration decision, and the allocation of computational and communication resources.

3  System Model and Problem Formulation

To begin with, an overview on the DT-assisted task execution system is provided. After that, the DT proactive migration together with PT task execution are described more specifically.

3.1 System Overview

As presented in Fig. 1, we present a DT-assisted task execution system built on edge computing. The system comprises a set of I PTs, denoted as ℐ, and M geographically distributed ESs, represented by ℳ. A cloud center functions as the central controller and employs a GRU-based model to enable proactive migration of DTs. PTs generate a stream of complex tasks and require exclusive DTs deployed at the edge for task execution. Due to the complex mobility patterns of PTs, the associated DT should be proactively migrated from one ES to another, based on the mobility prediction model constructed on the cloud center, and each PT should switch its access to the ES that its associated DT newly migrated to. It is worth noting that each ES can support multiple DTs for different PTs, with communication and computation resources shared among all these DTs. Once the DT migration is completed, the PTs can offload their tasks to the associated DTs for execution.

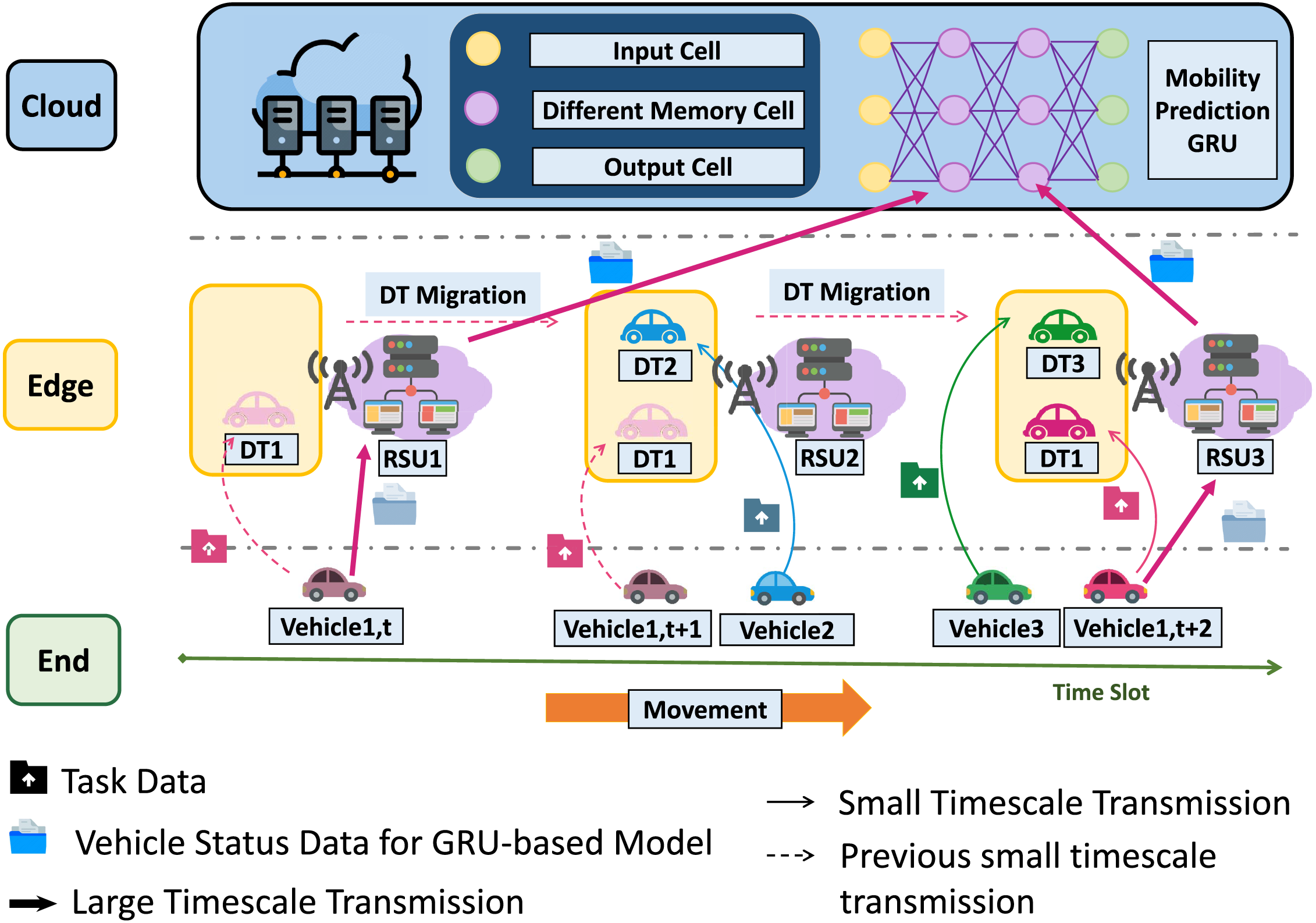
Figure 1: An illustration of DT-assisted task execution system

In practice, due to the frequent mobility and task dynamics of PTs, DT migration and the corresponding resource allocation need to be performed more often than the energy-intensive status information uploading. Therefore, as shown in Fig. 2, in the proposed online optimization problem, we consider that the status update frequency of each PT is determined on a large timescale, while DT migration and the associated communication and computation resource allocation on each ES are handled on a small timescale. To be specific, we first segment the timeline into T∈N+ fine-grained time slots and denote t∈𝒯 as the index of each time slot. The interval between two consecutive status information updates (also defined as large-grained time frame) may contain a varying number of time-slots. Let 𝒦 be the total number of time frames, and the first time slot of time frame k is denoted as t(k).

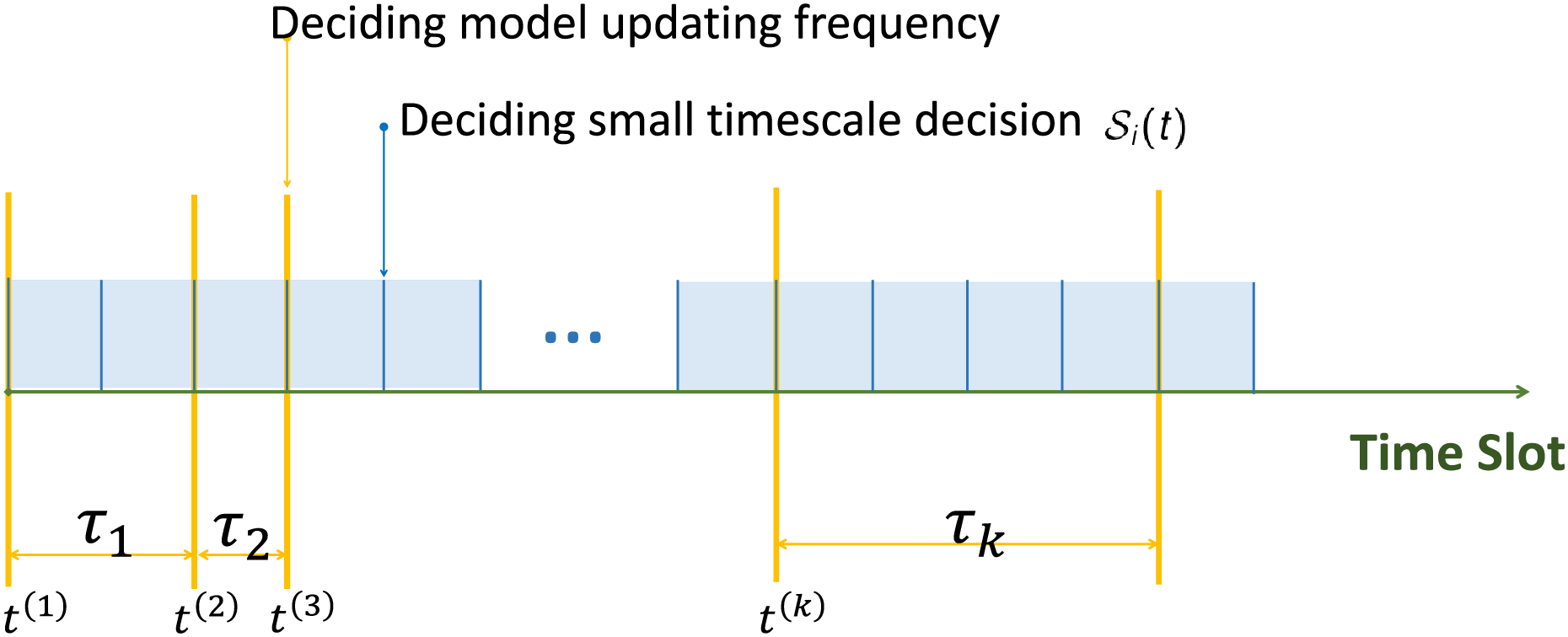
Figure 2: Design of the online two-timescale approach

In general, we aim to optimize the task response latency under the stringent energy consumption constraint by addressing: i) How to adjust the real-time PT status updating of the mobility prediction model. ii) Within every time slot, which ES should be the migration target of each DT and how to allocate the communication and computation resource among the deployed DTs. The detailed system model is described as follows, and Table 1 lists the important notations employed in this paper.

3.2 DT Proactive Migration

To achieve seamless DT-assisted task execution for PTs, each DT should be timely migrated to the new ES in each time slot t∈𝒯. Let ai,m(t)∈{0,1} be the migration decision of DT i in time slot t∈𝒯 indicating whether the corresponding DT of PT i∈ℐ is deployed on ES m∈ℳ. Note that each PT i∈ℐ has one unique DT which can only be deployed on one ES m∈ℳ simultaneously, and ESs are connected through wired links [15]. The energy consumption associated with wired transmission latency between edge servers (ESs) is strongly influenced by the physical distance between them, which can be defined as

Ei,mmig(t)=ϕDid(πi(t−1),m),(1)

where ϕ indicates the per-unit energy cost for data transmission per unit distance, Di is the model size of DT i∈ℐ, and πi(t)=arg⁡maxmai,m(t) is the ES which PT i∈ℐ is accessed to in time slot t∈𝒯.

To achieve proactive DT migration, it is required to obtain the movement trajectories of mobile PTs in the future. Therefore, we construct a GRU-based model at the cloud center for mobility prediction, which is described in detail in Section 4. To make predictions of PTs’ mobile trajectories, the GRU-based model needs to receive status information transmitted from PTs to ES and subsequently uploaded to the cloud. We denote (xi(t),yi(t)) as the location of PT i∈ℐ in time slot t, (xm,ym) as the fixed location of ES m∈ℳ. In accordance with Shannon’s theorem, the data uploading rate between PT i∈ℐ and ES m∈ℳ is given by

ri,m(t)=ui(t)Wmlog⁡(1+(di,m(t))−θpi|hi,m(t)|2N0ui(t)Wm),(2)

in which ui(t) is the allocation of bandwidth resource for PT i∈ℐ in time slot t∈T, di,m(t)=(xi(t)−xm)2+(yi(t)−ym)2 is the distance from PT i∈ℐ to ES m∈ℳ, hi,m(t) captures the Rayleigh fading effect between PT i∈ℐ and ES m∈ℳ in time slot t∈T. Note that the bandwidth allocation ui(t) represents the portion of spectrum resource assigned to each PT, which reflects the multi-user spectrum contention at the ES. Let Ji(t) be the mobility state information data size of PT i∈ℐ in time slot t∈𝒯, the latency and energy consumption of uploading the status information from PT i∈ℐ to ES m∈ℳ in time slot t∈𝒯 can thus be denoted as Ti,mupl(t)=Ji(t)ri,m(t) and Ei,mupl(t)=Ji(t)ri,m(t)pi, where pi is the transmission power of PT i∈ℐ. Correspondingly, the energy consumption of uploading the status information from ES m∈ℳ to the cloud center in time slot t∈𝒯 can be calculated as Em,cupl(t)=Ji(t)rmpm, where pm and rm respectively represents for unit transmission power and the uplink transmission rate via a fiber link channel from ES m to the cloud center. Noting that fiber link is a wired connection with stable communication environment and abundant bandwidth resource, rm and pm are therefore considered as constants [25]. Therefore, the total energy consumption of status information uploading by PT i∈ℐ can be derived as

Ei,cupl(t(k))=∑m∈ℳ(Ei,mupl(t(k))+Em,cupl(t(k))).(3)

3.3 DT-Assisted Task Execution

During each time slot t∈T, each PT can offload tasks to the ES where its corresponding DT is proactively migrated to. The latency and energy consumption for uploading a task from PT i∈ℐ to its DT in each time slot t∈T are respectively expressed as

Ti,mtra(t)=λi(t)ri,m(t),(4)

Ei,mtra(t)=Ti,mtra(t)pi.(5)

Let λi(t) denote the amount of task data produced by PT i∈ℐ during time slot t∈𝒯. The latency experienced by PT i when executing its task with the assistance of its DT on ES m∈ℳ at time t is given by

Ti,mexe(t)=λi(t)Cmfi(t)Fm,(6)

where Cm denotes CPU cycles’ number of ES m∈ℳ to execute one data unit, Fm represents the CPU processing speed (in cycles per second) of ES m∈ℳ, and fi(t) is the allocation of computation resource for PT i∈ℐ in time slot t∈T. In addition, the energy consumption is calculated as

Ei,mexe(t)=ρm(Fm)2λi(t)Cm,(7)

where ρm represents the capacitance of ES m∈ℳ.

3.4 Problem Formulation

The small-timescale and large-timescale energy consumption is derived as

Ests(t)=∑i∈ℐ∑m∈ℳai,m(t)(Ei,mexe(t)+Ei,mmig(t)+Ei,mtra(t)),(8)

Elts(t(k))=∑i∈ℐEi,cupl(t(k)).(9)

To assess the fundamental performance of the DT-assisted task execution system deployed over edge computing, we adopt the long-term average service response latency across all time slots as the evaluation metric, which is computed as

Tresp(t)=∑i∈ℐ∑m∈ℳai,m(t)(Ti,mtra(t)+Ti,mexe(t)+Ti,mupl(t(k))).(10)

We construct a two-timescale online optimization problem that jointly determines i) the adaptive status information updating frequency τk in time frame k, ii) DT migration decision ai,m(t), iii) ES communication resource allocation decision ui(t), and iv) ES computation resource allocation decision fi(t) in time slot t. The problem is expressed as

[𝒫1]: minτk,𝒮i(t)∑t∈𝒯Tresp(t)s.t., ∑m∈ℳai,m(t)=1,∀i∈ℐ,∀t∈𝒯,(11a)

∑i∈ℐui(t)ai,m(t)≤1,∀m∈ℳ,∀t∈𝒯,(11b)

∑i∈ℐfi(t)ai,m(t)≤1,∀m∈ℳ,∀t∈𝒯,(11c)

τk∈[1,τmax],∀k,(11d)

∑t∈𝒯Ests(t)+∑k∈𝒦Elts(t(k))≤C,(11e)

where 𝒮i(t)={ai,m(t),ui(t),fi(t)} is the small-timescale decisions determined in each time slot; constraint (11a) ensures that each PT is associated with only one ES per time slot; constraints (11b) and (11c) guarantees that the total allocated computation and communication resource do not exceed the capacity of any ES in any time slot t; constraint (11d) restricts the maximum time slot number of any time frame; (11e) is the long-term system overall energy consumption constraint.

Obviously, solving 𝒫1 directly is very challenging because: i) The decisions involve continuous and discrete variables, and are all integrated in the constraints and objective function, meaning that 𝒫1 is a non-convex optimization problem involving mixed-integer variables, which is NP-hard. ii) The constant mobility of PTs and the changing network dynamics make it extremely hard to acquire the system statics in advance. This implies that the problem must be addressed in an online manner. iii) τk is not a simple dicision, because its determination should be learned from previous response latency and system energy feedback, necessitating a learning algorithm compatible with the online optimization approach.

4  A Two-Timescale Online Optimization Algorithm

In this section, we proposed a novel two-timescale mobility-aware optimization approach, namely TMO, to jointly optimize the uploading frequency of PT status information, DT migration decision and corresponding resource allocation on ESs over edge computing. Specifically, in particular, we begin by breaking down the long-term optimization task into multiple short-term subproblems using an enhanced Lyapunov-based strategy. Next, we apply an online learning algorithm to adaptively adjust the status information updating frequency based on historical feedback in large-timescal. After that, we design a GRU-based prediction network to predict the location of PT and develop an AM-based method to solve for the remaining small-timescale decisions.

4.1 Problem Decomposition

We begin by defining the energy deficit queue Q(t), which reflects the deviation of total system energy consumption from the long-term average budget C/T. The evolution of this queue over time can be represented as follows:

Q(t+1)=max[Q(t)+Ests(t)+Elts(t)|t=t(k)−CT,0].(12)

Traditional Lyapunov optimization requires fixed constraints to ensure a bounded performance gap. However, since the PT status information updating only occurs when each time frame starts, e.g., at t∈t(k), the total energy consumption will have an abrupt change. To guarantee the stability of Q(t), we distribute the status information uploading energy consumption over a large time frame evenly across all the time slots within it. Thus, for any time slot t in τk, the evolution of Q(t) can be modified as

Q(t+1)=max[Q(t)+Ests(t)+Elts(t(k))τk−CT,0].(13)

Subsequently, the Lyapunov function is defined as L(Θ(t))=12Q(t)2, which is regarded as the quantitative indicator of queue congestion. To maintain queue stability, this function should be driven toward its minimum value. As discussed in [26], let E[⋅] be the expectation operator, and the conditional Lyapunov drift is given by Δ(Θ(t))=E[L(Θ(t+1))−L(Θ(t))|Θ(t)]. The term Δ(Θ(τ)) represents the variation in Lyapunov function across successive time slots. Minimizing this drift effectively curbs queue growth, ensuring compliance with the energy consumption constraint.

Correspondingly, we defined Δ(Θ(t))+VE[Tresp(t)|Θ(t)] as the Lyapunov drift-plus-penalty expression, in which V>0 is a tuning parameter that can be tuned to make a trade-off between optimality and queue stability. A larger V indicates a greater emphasis on meeting the energy consumption constraint, whereas a smaller V suggests a willingness to relax this constraint to some extent to reduce the task response latency.

Theorem 1. Let V>0, and at any given time slot t∈τk, the drift-plus-penalty is bounded under all feasible decisions, i.e.,

Δ(Θ(t))+VE[Tresp(t)|Θ(t)]≤G+E[Q(t)(Ests(t)+Elts(t(k))τk−CT)|Θ(t)]+VE[Tresp(t)|Θ(t)],(14)

where G=12[Ests(max)+Elts(max)τk−CT]2.

Proof. Please see Appendix A. ◻

Theorem 1 demonstrates the upper bound of the drift-plus-penalty in each time slot t∈τk. Then, by aggregating both sides of (14) over all time slots within time frame k, we obtain

∑t∈τkΔ(Θ(t))+V∑t∈τkE[Tresp(t)|Θ(t)]≤Gτk+∑t∈τkE[Q(t)(Ests(t)+Elts(t(k))τk−CT)|Θ(t)]+V∑t∈τkE[Tresp(t)|Θ(t)].(15)

Therefore, 𝒫1 can be decomposed into a series of subproblems, where the right side of (15) is opportunistically minimized in each time frame k∈𝒦 as

[𝒫2]: min𝒮i(t)V∑t∈τkE[Tresp(t)|Θ(t)]+∑t∈τkE[Q(t)(Ests(t)+Elts(t(k))τk|Θ(t)].s.t.(11a),(11b),(11c).(16)

Note that although problem 𝒫2 concentrates on the optimization within one time frame, it still contains variables in two timescales, making it challenging to solve directly. However, it can be observed that decision Si(t) can be solved on top of the determination of adaptive status information uploading frequency. Thus, we divide the problem 𝒫2 into two subproblems (i.e., large-timescale and small-timescale subproblems), and solve them sequentially.

4.2 Solution for Large-Timescale Decision

Due to the fact that the future network dynamics including channel conditions, DT migration together with resource allocation decisions in each time slot have not been revealed when we need to determine τk when each large time frame starts, we develop an online learning approach to adaptively decide τk based on the revealed response latency and system energy from the previous time frames. Specifically, we first construct a multi-armed bandit (MAB) problem to decide the τk at the beginning of each time frame k by defining a selectable arm set {1,2,⋯,τmax} for each arm τk and set the objective function of [𝒫2] as the loss of pulling each arm, i.e.,

[𝒫3]: minτk∈{1,2,⋅⋅⋅,τmax}V∑t∈τkTresp(t)+∑t∈τkQ(t)(Ests(t)+Elts(t(k))τk.(17)

Next, to solve the MAB problem [𝒫3], we apply the upper confidence bound (UCB) method to decide the optimal τk based on historical energy consumption and task response latency. To be specific, the loss of choosing τk is given by

l(τ)=V∑t∈τTresp(t)+∑t∈τQ(t)(Ests(t)+Elts(t(k))τ).(18)

Then, let l¯(τ) be the average revealed loss of previous time frames, and for each feasible arm in set {1,2,⋯,τmax}, we can calculate the UCB of each arm as

−l¯(τ)+2logK/Tτ.(19)

Considering both the average reward and an exploration term that grow with time, the optimal τ of each largr time frame is calculated as

τ=argmax{−l¯(τ)+2logK/Tτ},τ∈[1,τmax].(20)

4.3 Solution for Small-Timescale Decisions

4.3.1 GRU-Based Mobility Prediction Network

After the status information uploading frequency is determined, in each time slot, to optimize small-timescale decisions, the location of mobile PTs to support proactive DT migration is required. Different from traditional time series prediction with input available in each time step, since the PTs only upload their status information at the beginning of each time frame, we need to predict their locations in each time slot regardless of whether PTs’ status information is uploaded. To this end, we extend the conventional GRU model into an input-autoregressive PT mobility prediction model, and its state update equations are designed as:

rt=σ(Wirxt+bir+Whrht−1+bhr),zt=σ(Wizxt+biz+Whzht−1+bhz),nt=tanh⁡(Winxt+bin+rt(Whnht−1+bhn)),ht=(1−zt)nt+ztht−1,yt=Woht+bo,xt+1=yt.

In this model, W and b represent the trainable parameters. In time slot t, zt, rt, nt are respectively the update, reset and new gates. ht is the hidden state at time slot t, while xt and yt correspond to the input and output variables. The function σ(⋅) refers tp the sigmoid activation. The state update process is shown in Fig. 3.

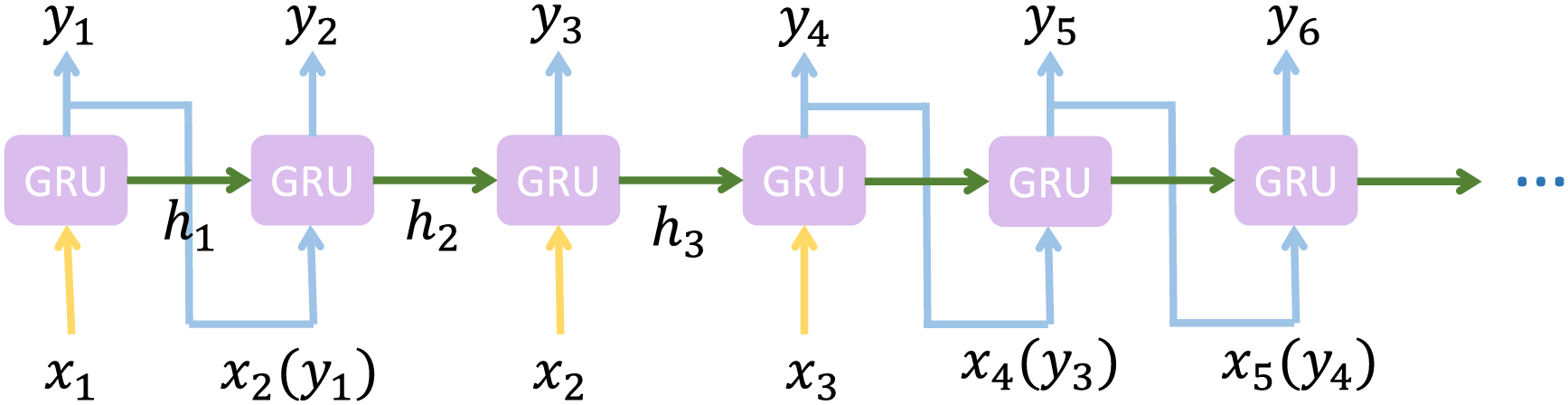
Figure 3: Workflow of the auto-regressive GRU-based model

To train the above-designed GRU-based model for PT mobility prediction, we increase the auto-regressive inference capability during the training phase to address the issue of unavailable ground truth data at each time step. Specifically, we replace the real input data with the model’s previous output based on a probability Pr, which starts from 0 and gradually increases with the number of epochs. Finally, Pr reaches its maximum value of 0.8 after 500 epochs.

At the beginning of each epoch, batches of trajectory samples are fetched from the dataset. For each time step, a random number r∈[0,1] is drawn. if r≥Pr, the real input is used; otherwise, the model’s last output serves as input to the next step. This process is repeated over all sequences and batches in each epoch to enhance the model’s robustness and generalization to various trajectory patterns. The optimization of model parameters is performed using the Adam optimizer with a learning rate of 0.05 and mean squared error (MSE) as the loss function. The GRU network consists of two hidden layers with 30 units each and a dropout rate of 0.2. Training is conducted for 500 epochs with a batch size of 256. To prevent overfitting and improve convergence, a learning rate scheduler reduces the learning rate by half if the validation loss does not improve for three consecutive epochs. The detailed pseudocode is provided in Algorithm 1.

4.3.2 Algorithm for Small-Timescale Decisions

Given τk and the predicted positions of PTs in each time slot of the kth time frame, we further determine the small-timescale decisions 𝒮i(t)={ai,m(t),ui(t),fi(t)} by minimizing the term VE[Tresp(t)|Θ(t)]+E[Q(t)Ests(t)|Θ(t)] in (14), which is formulated as

[𝒫4]: min𝒮i(t)VTresp(t)+Q(t)(Ests(t)+Elts(t(k))τk)s.t.(11a),(11b),(11c).(21)

The subproblem 𝒫4 is a a nonlinear mixed-integer programming problem with coupled decision variables. To solve the problem, we deploy an AM-based method, which divides 𝒫4 into two subproblems and alternately optimize one set of variables with the others fixed until the objective of 𝒫4 converges.

DT Migration Decision: Fix ui(t) and fi(t) and solve for ai,m(t):

[𝒫4−1]: minai,m(t)VTresp(t)+Q(t)(Ests(t)+Elts(t(k))τk)s.t.(11a),(11b),(11c).

Communication and Computation Resource Allocation: Fix ai,m(t) and solve for ui(t) and fi(t):

[𝒫4−2]: minui(t),fi(t)VTresp(t)+Q(t)(Ests(t)+Elts(t(k))τk)s.t.(11b),(11c).

Following the decomposition of 𝒫3, the resulting subproblem 𝒫4-1 becomes a linear integer program that can be efficiently handled using standard optimization solvers. For subproblem 𝒫4−2, since ui(t) and fi(t) are not coupled in both object function and constraint, it can be further divided into two independent subproblems, where ui(t) and fi(t) are computed separately:

[𝒫4−2−1]: minui(t)V∑i∈ℐ∑m∈ℳai,m(t)Ti,mtra+Q∑i∈ℐ∑m∈ℳai,m(t)(Ei,mtra(t)+Ei,mupl(t(k))τk)s.t.(11b).[𝒫4−2−2]: minfi(t)V∑i∈ℐ∑m∈ℳai,m(t)Ti,mexes.t.(11c).

Theorem 2. Problem 𝒫4−2−1 and 𝒫4−2−2 are both convex.

Proof. Details can be found in Appendix B. ◻

Building on Theorem 2, we can slove problems 𝒫4−2−1 and 𝒫4−2−2 efficiently by utilizing standard optimization solvers such as Gurobi. It is important to note that the small-timescale problem is addressed through an iterative process, which concludes when further improvements to the objective of problem 𝒫4−2 are no longer possible.

4.4 Analyses of Proposed TMO Scheme

In our proposed two-timescale mobility-aware optimization framework (TMO), we begin by utilizing an extended Lyapunov technique to divide the problem in the long term into a sequence of short-term subproblems. We then incorporate an online learning algorithm to dynamically adjust the update frequency for status information in the large timescale, guided by historical feedback. Subsequently, a GRU-based prediction model is employed to predict the location of each PT, and an alternating minimization (AM) strategy is used to determine the remaining decisions in the small timescale. The overall structure of TMO is illustrated in Fig. 4.

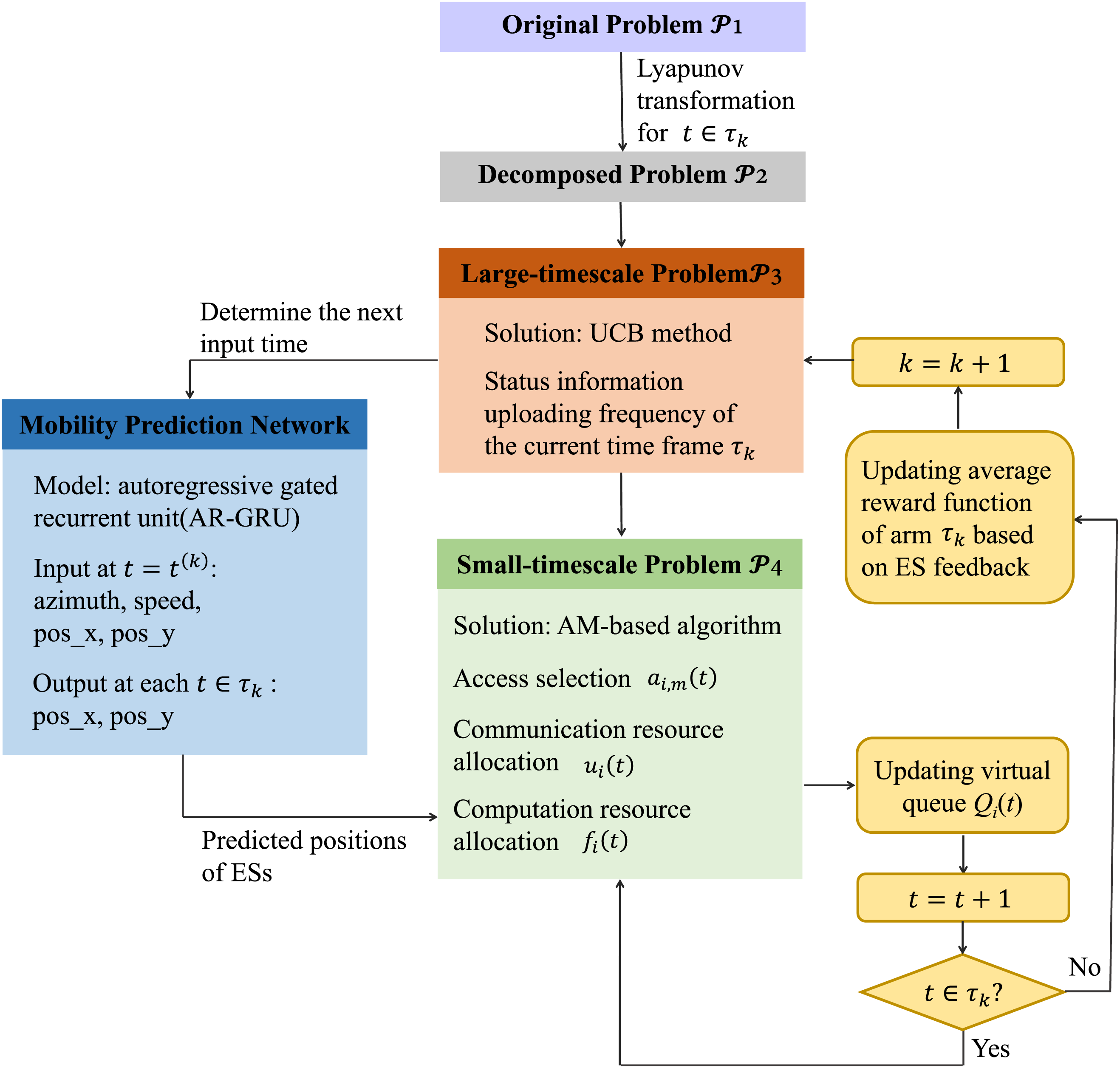
Figure 4: Flowchart of the proposed TMO approach

Theorem 3. Our proposed TMO approach can achieve convergence after finite iterations.

Proof. Since the alternation process is only applied in solving small-timescale problem [𝒫4], we prove the convergence of the AM based method by deriving the partial derivatives of the objective function of subproblem 𝒫4 as

∇a(𝒫4−1)=V∑i∈ℐ∑m∈ℳ(Ti,mtra(t)+Ti,mexe(t)+Ti,mupl(t(k)))+Q(t)∑i∈ℐ∑m∈ℳ(Ei,mtra(t)+Ei,mexe(t)+Ei,mmig(t)+(Ei,mupl(t(k))+Em,cupl(t(k)))),(22)

∇u(𝒫4−2−1)=−V∑i∈ℐ∑m∈ℳai,m(t)λiui2(t)ri,m(t)−Q∑i∈ℐ∑m∈ℳai,m(t)piλiui2(t)ri,m(t),(23)

∇f(𝒫4−2−2)=−V∑i∈ℐ∑m∈ℳai,m(t)λi(t)Cmfi2(t)Fm.(24)

It is evident that the gradient in (22) is constant, while (23) and (24) exhibit bounded first-order derivatives under the constraints of the original problem. This implies that all relevant components are L-Lipschitz continuous. Accordingly, the proposed method converges within finite iterations. ◻

Theorem 4. The proposed TMO scheme’s computational complexity is expressed as O(SmaxK+TNmax((kI+M+2)I3)). I denotes the PT number, M the ES number, K the arms’ number in the UCB algorithm, Nmax the maximum iteration count in the AM-based algorithm,T the number of time slots, and Smax the maximum number of time frames.

Proof. The computationa complexity of the TMO approach mainly determined by the contributions of both UCB method in large timescale and the AM-based algorithm in small timescale. For a standard UCB method, the computational complexity of selecting a arm is O(1), and of updating the expected reward is O(K). Besides, the computational complexity for solving small-timescale decisions can be calculated as O((kI+M+2)I3), by leveraging the interior point scheme [27] in Gurobi solver, where k reflects the efficiency of the branch-and-bound method’s pruning. ◻

In summary, the TMO algorithm has a computational complexity of O(SmaxK+TNmax((kI+M+2)I3)).

Theorem 5. Given Lyapunov control parameter V and UCB arms number K, the performance gap between the TMO approach and the theoretical optimum to problem 𝒫1 is

1T∑t∈𝒯E[∑i∈ℐ∑m∈ℳai,m(t)(Ti,mtra(t)+Ti,mexe(t))]−𝒳≤GV+ΛVT(25)

where 𝒳 represents the optimal solution in theoretical, Λ is the performance gap of UCB algorithm, which can be expressed as O(Klog⁡K).

Proof. The upper-bound of the performance gap (e.g., regret) between our TMO approach and the optimum can be decomposed into two gaps, respectively. The first gap is bounded by UCB algorithm under feedbacks of choosing τk as the arm. The second gap is bounded by the extended Lyapunov optimization theory with periodically changed constraints due to modified τk in each time frame.

To analyze the gap bounded by Lyapunov optimization theory, inequality (14) can be intuitively expanded and rewritten as

△(Θ(t))+VE[Tresp(t)|Θ(t)]≤G+E[Q(t)(Ests(t)+Elts(t(k))τk−CT)|Θ(t)]+VE[Tresp(t)|Θ(t)]≤G+V⋅𝒳+Λ(26)

Then, by aggregating (26) over T time slots, we obtain

(G+V⋅𝒳+Λ)⋅T≥∑t∈𝒯(Δ(Θ(t))+VE[Tresp(t)|Θ(t)])=E[L(Θ(T))−L(Θ(0))]+VE[Tresp(t)|Θ(t)]=E[L(Θ(T))]−E[L(Θ(0))]+VE[Tresp(t)|Θ(t)](27)

By rearranging inequality (27), i.e., subtracting E[L(Θ(0))] from both sides and then dividing by T, we derive inequality (25).

We then analyze the optimal gap Λ brought by UCB algorithm. According to [27], it is equal to 42Kτmaxlog⁡K+∑k=1τmax(△k+π2△k3), where Δk=defμ∗−μk. Note that μk is the reward expectation for arm k and μ∗ is any maximal element in the set {μ1,…,μK}, thus △k is constant and it can be defined as O(Klog⁡K). ◻

5  Simulation Results

In this section, we conducted extensive simulations to verify the advantages of our proposed TMO scheme for optimizing the PT state information uploading frequency and the DT migration decision together with allocation of computation and communication resource over edge computing. All simulations are conducted based on the real-world traffic scenario dataset, and the results are averaged more than 1000 independent runs with varying parameter setting.

5.1 Simulation Settings

Consider a DT-assisted task execution system in a 15 km × 18 km region with I = 40 PTs and M = 10 ESs. The moving trajectories and state information used for mobility prediction are extracted from the “Real-World Bologna” dataset [28]. Which is derived from a real scenario in the city of Bologna and provided in the form of a SUMO simulation package. This dataset involves more than 8000 mobile entities operating in a realistic urban environment. In our experiments, a simulation of over 5000 s was conducted, during which the output file was generated at 1-second intervals to record the spatio-temporal states (object type, position coordinates, travel angle, speed, road gradient, street identifier, and relative distance from the entrance of the current street) of all entities. Table 2 lists the key parameters and their values, most of which are also are consistent with those commonly adopted in prior works [7,29]. Additionally, to assess the performance of the proposed TMO approach, we benchmark it against the following schemes. It is worth noting that, due to the original objectives of these benchmarks differ from ours, to ensure a fair comparison, we have adjusted these benchmark schemes. Specifically, we modified their settings and optimization objectives to align with our proposed framework.

•   SO [30]: Single-timescale optimization. This approach optimizes service migration and task routing to balance the online system performance and service migration cost, yet executed synchronously in a single timescale

•   FTO [31]: Fixed two-timescale optimization. This method optimizes service migration, as well as computing and communication resource allocation asynchronously in different timescales. However, the length of each time frame is fixed.

5.2 Performance Evaluation

Fig. 5 illustrates the stability of our TMO approach by showcasing the energy consumption queue backlog Q(t), which is under the influence of the Lyapunov decomposition for different values of V. The figure reveals that the queue backlog decreases and stabilizes quickly over time. This is because TMO prioritizes minimizing total energy consumption to optimize the objective function of problem 𝒫3, which effectively reduces the queue backlog and achieves a balance between task response latency and energy consumption. Additionally, it is shown in the figure that the average energy consumption increases with V. The reason is that the introduction of the Lyapunov parameter V, which controls the trade-off between minimizing DT task response latency and enforcing energy consumption constraints; a larger V places greater emphasis on reducing response latency.

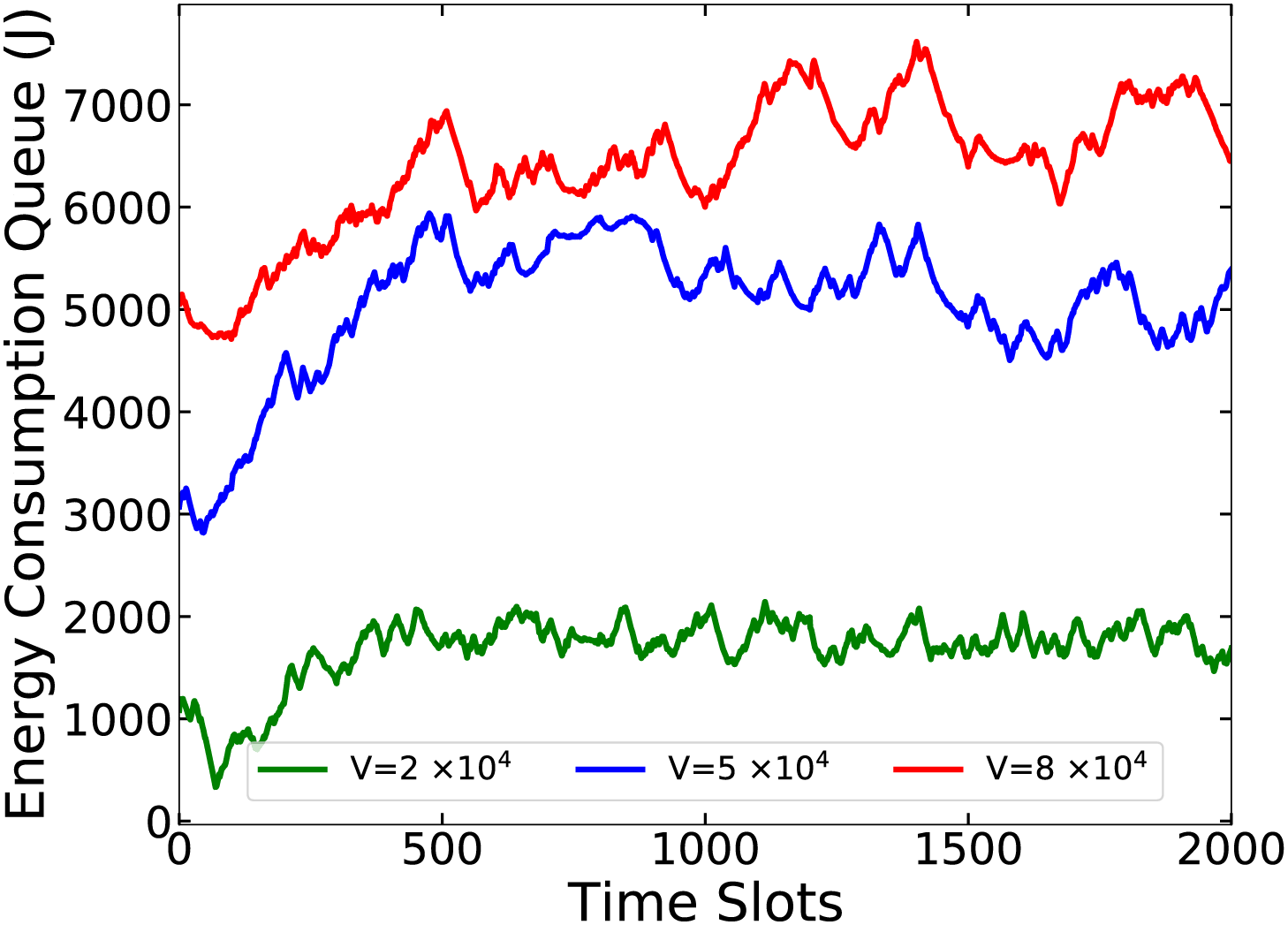
Figure 5: Queue backlogs w.r.t. V

Fig. 6 shows the impact of V’s value on average task reponse latency (i.e., ∑t∈𝒯∑i∈ℐ∑m∈ℳ ai,m(t)(Ti,mtra(t)+Ti,mexe(t))+Ti,mupl(t(k))/TI) and average energy consumption (i.e., ∑t∈𝒯∑i∈ℐ[Ei,cupl ∑m∈ℳai,m(t)(Ei,mexe(t)+Ei,mmig(t)+Ei,mtra(t))]/TI). It can be seen that with V increasing from from 102 to 106, the average energy consumption rises while the task response latency shrinks. The reason is that TMO lays more emphasis on the task response latency than the energy consumption with a larger V.

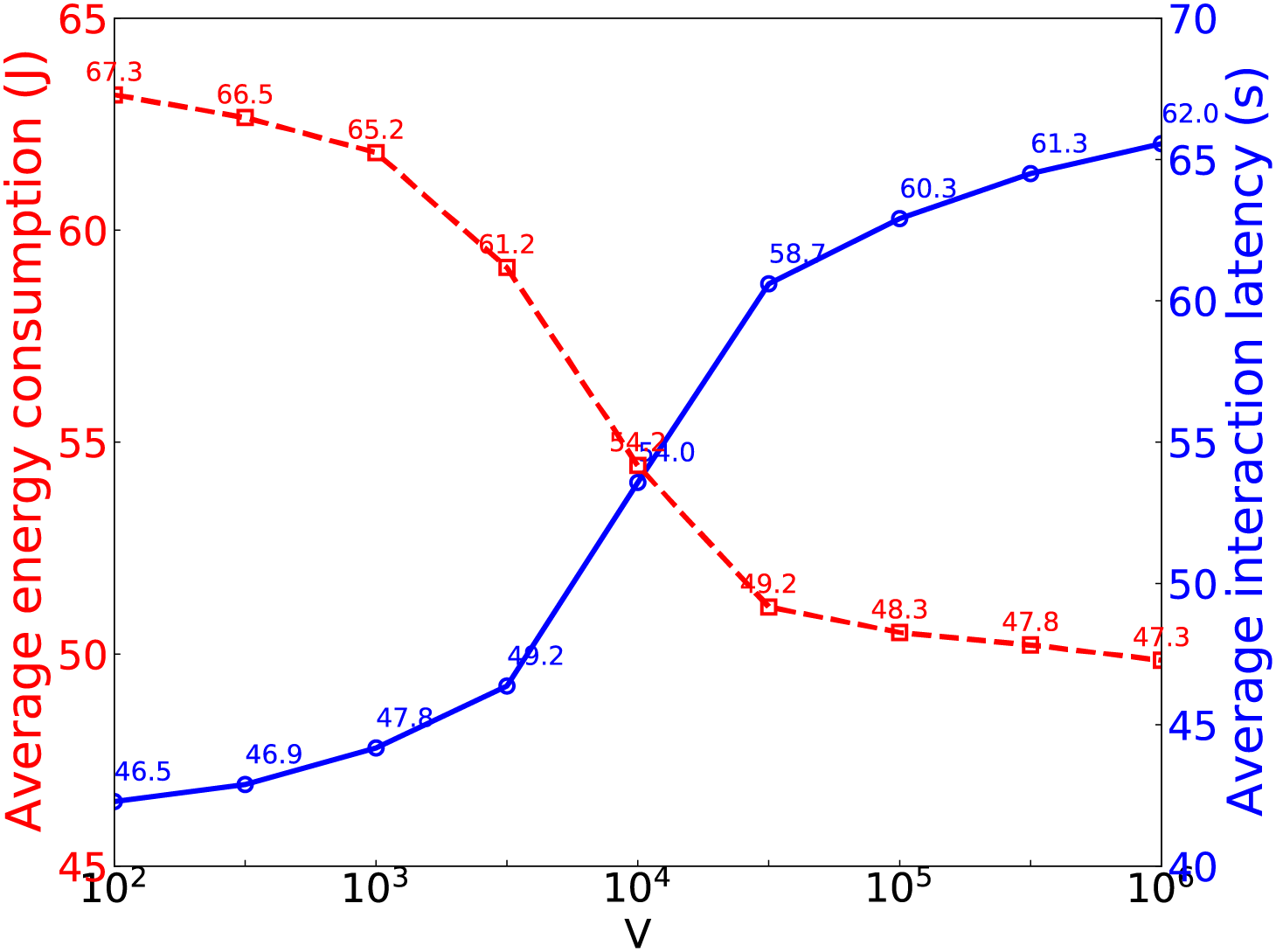
Figure 6: The impact of V on average task response latency and energy consumption

Fig. 7 illustrates the exploration process of τk of our proposed TMO approach. Initially, τk exhibits significant fluctuations, reflecting the exploration phase where the algorithm actively tests various values of τk to gather sufficient information about their performance. This exploration is guided by the Upper Confidence Bound (UCB) principle, which balances the trade-off between exploring less-tested values and exploiting values with lower empirical losses. As the algorithm progresses, the confidence intervals around the estimated losses for different τk values shrink, leading to a gradual stabilization of τk. This stabilization indicates that the algorithm has identified the value of τk that minimizes the long-term average loss, transitioning from exploration to exploitation.

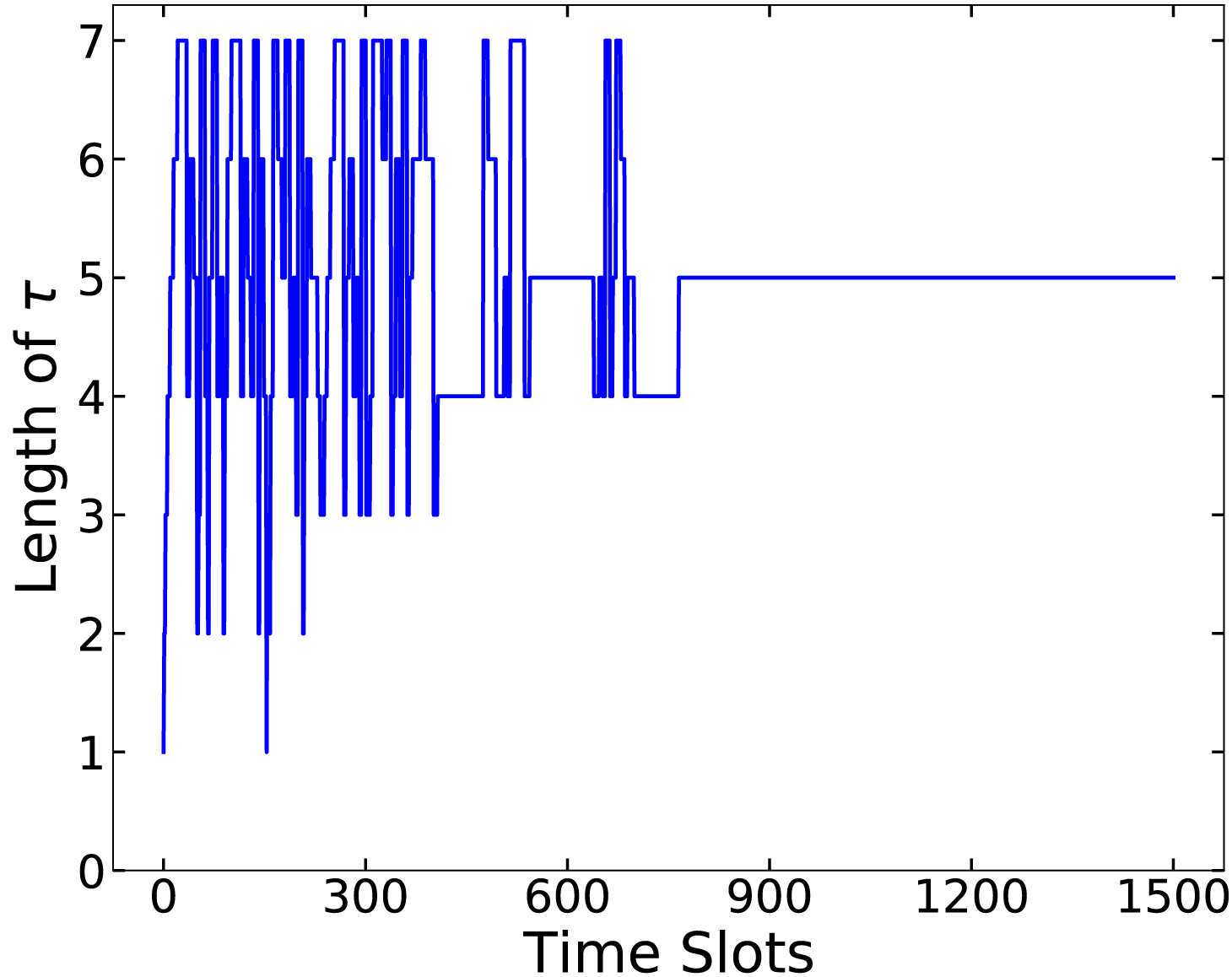
Figure 7: Decisions of τk in TMO

Fig. 8 examines the impact of PT numbers on the average response latency and energy consumption for SO, FTO, and the proposed TMO approach. Both figures demonstrate an exponential increase in response latency and energy consumption for all approaches as I grows, because larger I means more task requests and competition for edge resources. We can tell from the pictures that SO has the worst performance, while FTO and TMO have better performance of both task response latency and average energy consumption than SO because of the less frequent data uploading. Besides, TMO has the best performance on account of more flexible and adjustable data uploading frequency, which can reduce the cost of data transmission mostly.

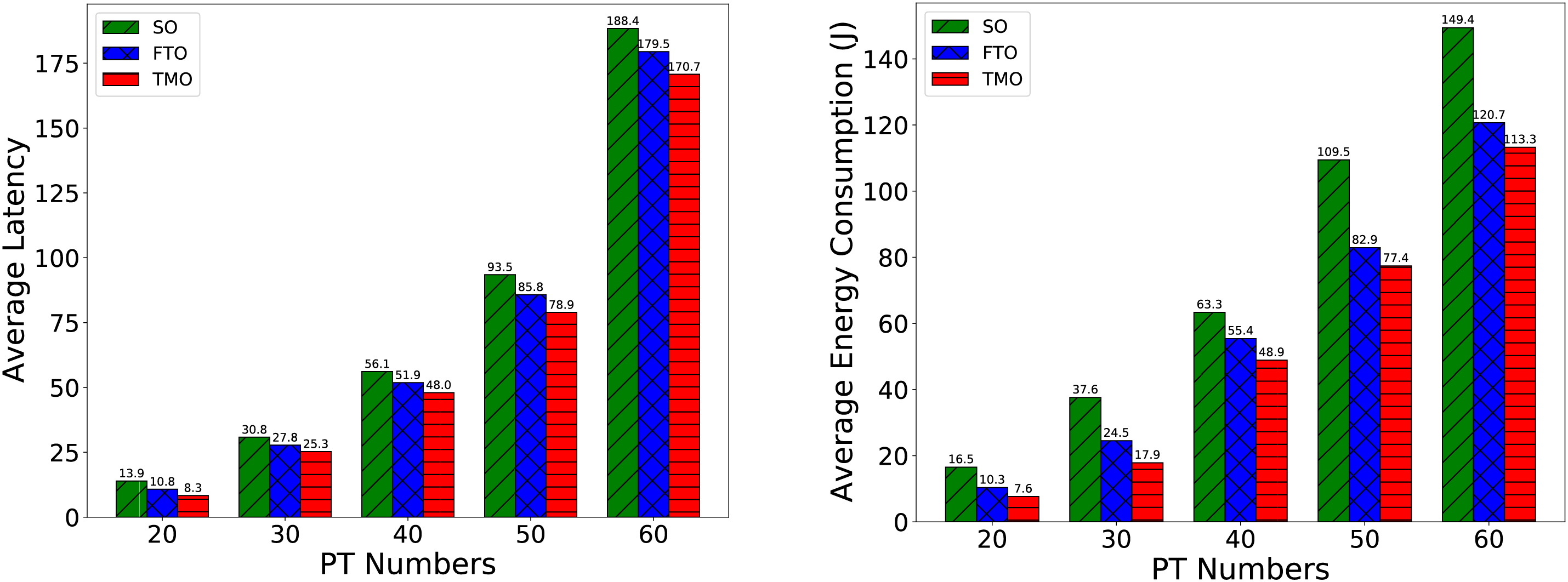
Figure 8: Comparison on average task response latency and energy consumption with varying PT numbers

6  Conclusion

In our work, we explore proactive DT migration over edge computing. Specifically, aiming to minimize the average task response latency of PTs under system uncertainties (e.g., PT mobility), we construct a two-timescale online optimization problem to jointly optimize the PT status information updating frequency, DT migration, and the allocation of communication and computation resources. We introduce a novel solution approach, termed TMO, which first break down the long-term online optimization problem into a sequence of instant subproblems. Additionally, we develop an online learning approach and an AM-based algorithm supported by a GRU-based mobility prediction model, to solve the two subproblems at different timescales. Both theoretical analysis and extensive simulations demonstrate that TMO outperforms existing approaches in minimizing task response latency and reducing total system energy consumption.

Acknowledgement: Not applicable.

Funding Statement: This research was funded by the State Key Laboratory of Massive Personalized Customization System and Technology, grant No. H&C-MPC-2023-04-01.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Lucheng Chen and Xingzhi Feng; methodology, Xinyu Yu and You Shi; validation, Xinyu Yu, Xiaoping Lu and Yuye Yang; formal analysis, Xinyu Yu and Lucheng Chen; investigation, Lucheng Chen and Xiaoping Lu; writing—original draft preparation, Xinyu Yu; writing—review and editing, Xinyu Yu and Yuye Yang; supervision, Xiaoping Lu and You Shi; project administration, Xingzhi Feng and You Shi. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Nomenclature

Appendix A

Squaring both expressions in Eq. (13) describing the energy queue yields

Q2(t+1)=[Q(t)+Ests(t)+Elts(t)−CT]+2≤Q2(t)+(Ests(t)+Elts(t)−CT)2+2Q(t)(Ests(t)+Elts(t)−CT).

By subtracting Q2(t) from both sides, dividing by 2, we have

12(Q2(t+1)−Q2(t))≤12(Ests(t)+Elts(t)−CT)2+Q(t)(Ests(t)+Elts(t)−CT).(A1)

Lastly, by adding V⋅Tresp(t) to both sides of (A1) and taking the expectation of both sides of Θ(t), inequality (14) can be derived.

Appendix B

For subproblem 𝒫4−2−1, we denote γ={γ(t),∀i∈ℐ,∀t∈𝒯} as the corresponding Lagrangian multiplier. The lagrangian function can be calculated as

ℒ1(u,γ)=V∑i∈ℐ∑m∈ℳai,m(t)Ti,mtra+Q∑i∈ℐ∑m∈ℳai,m(t)(Ei,mtra(t)+Ei,mupl(t(k))τk)+∑i∈ℐγi(t)(ai,m(t)ui(t)−1).(A2)

Since 1ri,m(t) in (A2) decreases monotonically, it is convex when ui(t)∈(0,1], thus subproblem 𝒫4−2−1 is convex.

For subproblem 𝒫4−2−2, we denote η={η(t),∀i∈ℐ,∀t∈𝒯} as the corresponding Lagrangian multiplier. The Lagrangian function can be calculated as

ℒ2(f,η)=V∑i∈ℐ∑m∈ℳai,m(t)Ti,mexe+∑i∈ℐηi(t)(ai,m(t)fi(t)−1).(A3)

Taking the first-order and second-order derivatives yields

∂ℒ2∂fi(t)=−V∑i∈ℐ∑m∈ℳai,m(t)λi(t)Cmfi2(t)Fm+∑i∈ℐηi(t)ai,m(t),(A4)

∂2ℒ2∂(fi(t))2=2∑i∈ℐ∑m∈ℳai,m(t)λi(t)Cmfi3(t)Fm.(A5)

Obviously, when fi(t)∈(0,1], ∂2ℒ2∂(fi(t))2≥0, thus subproblem 𝒫4−2−2 is also convex.

References

1. Lin X, Kundu L, Dick C, Obiodu E, Mostak T, Flaxman M. 6G digital twin networks: from theory to practice. IEEE Commun Mag. 2023;61(11):72–8. doi:10.1109/mcom.001.2200830. [Google Scholar] [CrossRef]

2. Niaz A, Shoukat MU, Jia Y, Khan S, Niaz F, Raza MU. Autonomous driving test method based on digital twin: a survey. In: 2021 International Conference on Computing, Electronic and Electrical Engineering (ICE Cube); 2021 Oct 26–27; Quetta, Pakistan: IEEE; 2021. p. 1–7. [Google Scholar]

3. Marah H, Challenger M. Madtwin: a framework for multi-agent digital twin development: smart warehouse case study. Ann Math Artif Intell. 2024;92(4):975–1005. doi:10.1007/s10472-023-09872-z. [Google Scholar] [CrossRef]

4. Lv Z, Chen D, Feng H, Zhu H, Lv H. Digital twins in unmanned aerial vehicles for rapid medical resource delivery in epidemics. IEEE Trans Intell Transp Syst. 2022;23(12):25106–14. doi:10.1109/tits.2021.3113787. [Google Scholar] [PubMed] [CrossRef]

5. Khan LU, Saad W, Niyato D, Han Z, Hong CS. Digital-twin-enabled 6G: vision, architectural trends, and future directions. IEEE Commun Mag. 2022 Jan;60(1):74–80. doi:10.1109/mcom.001.21143. [Google Scholar] [CrossRef]

6. Chen R, Yi C, Zhou F, Kang J, Wu Y, Niyato D. Federated digital twin construction via distributed sensing: a game-theoretic online optimization with overlapping coalitions. arXiv:2503.16823. 2025. [Google Scholar]

7. Yang Y, Shi Y, Yi C, Cai J, Kang J, Niyato D, et al. Dynamic human digital twin deployment at the edge for task execution: a two-timescale accuracy-aware online optimization. IEEE Trans Mob Comput. 2024;23(12):12262–79. doi:10.1109/tmc.2024.3406607. [Google Scholar] [CrossRef]

8. Chen J, Yi C, Okegbile SD, Cai J, Shen X. Networking architecture and key supporting technologies for human digital twin in personalized healthcare: a comprehensive survey. IEEE Commun Sur Tutor. 2024;26(1):706–46. doi:10.1109/comst.2023.3308717. [Google Scholar] [CrossRef]

9. Okegbile SD, Cai J, Wu J, Chen J, Yi C. A prediction-enhanced physical-to-virtual twin connectivity framework for human digital twin. IEEE Trans Cogn Commun Netw. 2024;PP(99):1–1. doi:10.1109/tccn.2024.3519331. [Google Scholar] [CrossRef]

10. Wang C, Peng J, Cai L, Peng H, Liu W, Gu X, et al. AI-enabled spatial-temporal mobility awareness service migration for connected vehicles. IEEE Trans Mob Comput. 2024;23(4):3274–90. doi:10.1109/tmc.2023.3271655. [Google Scholar] [CrossRef]

11. Wang H, Di X, Wang Y, Ren B, Gao G, Deng J. An intelligent digital twin method based on spatio-temporal feature fusion for iot attack behavior identification. IEEE J Sel Areas Commun. 2023;41(11):3561–72. doi:10.1109/jsac.2023.3310091. [Google Scholar] [CrossRef]

12. Zhao J, Xiong X, Chen Y. Design and application of a network planning system based on digital twin network. IEEE J Radio Freq Identif. 2022;6:900–4. doi:10.1109/jrfid.2022.3210750. [Google Scholar] [CrossRef]

13. Jyeniskhan N, Keutayeva A, Kazbek G, Ali MH, Shehab E. Integrating machine learning model and digital twin system for additive manufacturing. IEEE Access. 2023;11:71113–26. doi:10.1109/access.2023.3294486. [Google Scholar] [CrossRef]

14. Wen J, Yang J, Li Y, He J, Li Z, Song H. Behavior-based formation control digital twin for multi-AUG in edge computing. IEEE Trans Netw Sci Eng. 2023;10(5):2791–801. doi:10.1109/tnse.2022.3198818. [Google Scholar] [CrossRef]

15. Lu Y, Maharjan S, Zhang Y. Adaptive edge association for wireless digital twin networks in 6G. IEEE Internet Things J. 2021;8(22):16219–30. doi:10.1109/jiot.2021.3098508. [Google Scholar] [CrossRef]

16. Zhang Y, Zhang H, Lu Y, Sun W, Wei L, Zhang Y, et al. Adaptive digital twin placement and transfer in wireless computing power network. IEEE Internet Things J. 2024;11(6):10924–36. doi:10.1109/jiot.2023.3328380. [Google Scholar] [CrossRef]

17. He T, Toosi AN, Buyya R. Efficient large-scale multiple migration planning and scheduling in SDN-enabled edge computing. IEEE Trans Mob Comput. 2024;23(6):6667–80. doi:10.1109/tmc.2023.3326610. [Google Scholar] [CrossRef]

18. Mustafa E, Shuja J, Rehman F, Namoun A, Bilal M, Bilal K. Deep reinforcement learning and SQP-driven task offloading decisions in vehicular edge computing networks. Comput Netw. 2025;262:111180. doi:10.1016/j.comnet.2025.111180. [Google Scholar] [CrossRef]

19. Mustafa E, Shuja J, Rehman F, Namoun A, Bilal M, Iqbal A. Computation offloading in vehicular communications using PPO-based deep reinforcement learning. J Supercomput. 2025;81(4):1–24. doi:10.1007/s11227-025-07009-z. [Google Scholar] [CrossRef]

20. Shi Y, Yi C, Chen B, Yang C, Zhu K, Cai J. Joint online optimization of data sampling rate and preprocessing mode for edge–cloud collaboration-enabled industrial IoT. IEEE Internet Things J. 2022;9(17):16402–17. doi:10.1109/jiot.2022.3150386. [Google Scholar] [CrossRef]

21. Jia Y, Zhang C, Huang Y, Zhang W. Lyapunov optimization based mobile edge computing for internet of vehicles systems. IEEE Trans Commun. 2022;70(11):7418–33. doi:10.1109/tcomm.2022.3206885. [Google Scholar] [CrossRef]

22. Lin X, Wu J, Li J, Yang W, Guizani M. Stochastic digital-twin service demand with edge response: an incentive-based congestion control approach. IEEE Trans Mob Comput. 2023;22(4):2402–16. doi:10.1109/tmc.2021.3122013. [Google Scholar] [CrossRef]

23. He Y, Ren Y, Zhou Z, Mumtaz S, Al-Rubaye S, Tsourdos A, et al. Two-timescale resource allocation for automated networks in IIoT. IEEE Trans Wirel Commun. 2022;21(10):7881–96. doi:10.1109/twc.2022.3162722. [Google Scholar] [CrossRef]

24. Huang J, Golubchik L, Huang L. When lyapunov drift based queue scheduling meets adversarial bandit learning. IEEE/ACM Trans Netw. 2024;32(4):3034–44. doi:10.1109/tnet.2024.3374755. [Google Scholar] [CrossRef]

25. Mohammadi M, Suraweera HA, Tellambura C. Uplink/Downlink rate analysis and impact of power allocation for full-duplex cloud-RANs. IEEE Trans Wirel Commun. 2018;17(9):5774–88. doi:10.1109/twc.2018.2849698. [Google Scholar] [CrossRef]

26. Georgiadis L, Neely MJ, Tassiulas L. Resource allocation and cross-layer control in wireless networks. Found Trends® Netw. 2006;1(1):1–144. doi:10.1561/1300000001. [Google Scholar] [CrossRef]

27. Auer P, Cesa-Bianchi N, Fischer P. Finite-time analysis of the multiarmed bandit problem. Machine Learning. 2002;47(2):235–56. [Google Scholar]

28. Bieker-Walz L, Krajzewicz D, Morra A, Michelacci C, Cartolano F. Traffic simulation for all: a real world traffic scenario from the city of bologna. In: Modeling mobility with open data. Cham: Springer; 2015. p. 47–60. doi:10.1007/978-3-319-15024-6_4. [Google Scholar] [CrossRef]

29. Ouyang T, Zhou Z, Chen X. Follow me at the edge: mobility-aware dynamic service placement for mobile edge computing. IEEE J Sel Areas Commun. 2018;36(10):2333–45. doi:10.1109/iwqos.2018.8624174. [Google Scholar] [CrossRef]

30. Chen X, Bi Y, Chen X, Zhao H, Cheng N, Li F, et al. Dynamic service migration and request routing for microservice in multicell mobile-edge computing. IEEE Internet Things J. 2022;9(15):13126–43. doi:10.1109/jiot.2022.3140183. [Google Scholar] [CrossRef]

31. Shi Y, Yi C, Wang R, Wu Q, Chen B, Cai J. Service migration or task rerouting: a two-timescale online resource optimization for MEC. IEEE Trans Wireless Commun. 2024;23(2):1503–19. doi:10.1109/twc.2023.3290005. [Google Scholar] [CrossRef]