Modified Watermarking Scheme Using Informed Embedding and Fuzzy c-Means–Based Informed Coding

1  Introduction

The rapid expansion of the Internet and other public communication networks has significantly increased interest in data hiding, a key component of multimedia technology [1]. Watermarking codes embed data into host signals (e.g., images, audio, video, text) with two primary goals: imperceptibility, ensuring minimal degradation, and robustness, maintaining integrity against distortions. This study focuses on digital watermarking, with an emphasis on analyzing the aforementioned trade-offs—robustness, imperceptibility, payload, and complexity—as well as the development of practical algorithms. In recent years, deep learning–based image watermarking approaches have attracted increasing attention for their potential to enable adaptive embedding strategies. However, many existing methods fall short of fully leveraging deep learning’s capacity to learn and automate both embedding and extraction processes [2–4]. Moreover, existing methods often struggle to simultaneously achieve key requirements such as robustness and blind detection. The issue of copyright protection for medical images has garnered considerable attention, positioning digital watermarking as a prominent research focus. Unlike traditional approaches that embed a single watermark directly into a cover image, leveraging deep neural networks to embed multiple watermarks provides enhanced capabilities for image authentication and ownership verification—features particularly valuable in healthcare applications [5–8]. In [9], a novel Residual Chaotic System (RCS) was proposed to generate more complex, unpredictable, and ergodic chaotic sequences, thereby enhancing security. Chaotic systems are widely employed to generate highly random and unpredictable sequences, which serve as the foundation for data encoding, information hiding, and authentication [10]. To improve the imperceptibility and security of the watermark, chaotic sequences are used to encrypt and perturb the watermark information. During the embedding phase, a chaotic map is employed to further encrypt and scramble the watermark, thereby enhancing its robustness and unpredictability [11,12].

The objective of informed coding is to select the most suitable message codeword from a set of candidates that best represents the watermark while introducing minimal perceptual distortion to the host signal. Within this framework, binning schemes are employed to achieve information-theoretic capacity [13]. Theoretical bounds and practical watermarking schemes have been developed based on Costa’s seminal result. Costa demonstrated that random dirty paper codes can be constructed using appropriate random coding techniques; however, his approach did not adequately address issues of practical efficiency.

Implementing such watermarking algorithms is particularly challenging due to the exhaustive search required to identify random dirty paper codes. To enhance practical applicability, structured codes are preferred in watermarking systems, as they allow for the efficient construction of watermarked signals. Miller et al. [14] introduced a dirty-paper trellis framework in which multiple candidate codewords may correspond to the same message. They proposed a suboptimal trellis-based embedding algorithm that starts with the host signal and iteratively refines the watermarked signal, guiding it toward the interior of the Voronoi region associated with the target message codeword. Although the trellis-based approach in [14] achieves a favorable trade-off between imperceptibility and robustness in watermarked images, it remains computationally intensive and difficult to implement in practice.

Miller et al. [14] and Wang et al. [15,16] proposed a robust informed embedding algorithm that utilizes codewords derived from convolutional codes, linear codes, and random codes. In these approaches, each arc in the trellis is labeled with a block codeword corresponding to each trellis section. The embedding algorithm iteratively constructs a watermarked signal by moving it toward the interior of the Voronoi region associated with the message codeword. In the present study, we extend the methods proposed by Miller [14] and Wang [15,16] by modifying their trellis structures. Instead of using randomly generated reference vectors or random codewords as arc labels [14–16], our algorithm employs codewords from linear block codes generated via the fuzzy c-means (FCM) algorithm. FCM, a widely adopted fuzzy clustering method, was originally introduced in [17]. Block codes generated using FCM improve the imperceptibility of watermarked images across various embedding scenarios. Due to its flexibility and robustness in handling uncertainty, FCM has been successfully applied in numerous domains [18–20]. In our approach, the arc labels of block codes are refined by clustering codewords using the FCM algorithm. Refining a linear code while maintaining its linearity can potentially increase its minimum distance, thereby enhancing robustness. FCM exhibits rich structural properties and has been extensively explored in mathematical and theoretical studies. A key feature of emerging clustering methods [20] is the ability for a data sample to belong to multiple clusters, rather than being limited to a single one. To further improve time complexity, Ref. [21] introduced a method for reducing large datasets into smaller, weighted representations. The extended FCM (E-FCM) algorithm, proposed in [22], enhances the clustering process by merging highly similar clusters during each iteration until convergence of the objective function is achieved. In our watermarking system, we apply an informed embedding algorithm to modify the host signal, achieving a balance between the original host and the encoded watermark signal. This algorithm features a parallel arc structure, which connects the current state to the next in each trellis section. By leveraging the characteristics of linear block codes and applying them to trellis partitioning, the system simplifies the process of tuning imperceptibility and robustness. Building on this foundation, we propose an informed embedding algorithm that employs linear block codes based on the FCM algorithm, such as simplex codes and Walsh–Hadamard codes. The embedding process proceeds iteratively, section by section. The algorithm’s parallel structure not only reduces computational complexity but also achieves satisfactory error rate performance, contributing to an improved trellis design. In the informed coding stage, the system selects the message codeword that causes minimal perceptual distortion to the host signal from a parallel set of candidate codewords, thereby defining the watermarked path. Unlike the accumulative nature of the Viterbi algorithm, our method uses the extraction vector solely to identify the closest message codeword within the parallel arc structure. This approach substantially reduces the computational complexity of the encoding process compared to that in [14–16]. The integration of informed embedding and coding in our proposed method further enhances the performance of the informed watermarking system. Our approach is designed to maintain a balance between imperceptibility and robustness, optimizing the trade-off between these two critical aspects in watermarked images [14,23,24]. Moreover, the proposed algorithms are easier to implement and less computationally intensive than other informed watermarking methods. We evaluated the performance of our algorithm in comparison with those presented in [14,15]. First, we assessed embedding distortion by simulating its effect on watermarked image quality. Second, we evaluated robustness against common signal distortions, including Gaussian noise, low-pass filtering, and JPEG compression. Finally, we summarized the complexity comparison in tabular form. We have also summarized the main contributions of this paper as follows: (1) This study employs the FCM technique to select good codewords as labels in the trellis structure, unlike reference [14], which uses random codes as labels. (2) The algorithm proposed in this study can effectively achieve a trade-off between robustness and time complexity. In contrast, the method in Reference [14] has higher time complexity as well as greater computational complexity than our approach. (3) Compared with Reference [15,16], this paper integrates two embedding coding methods, informed embedding and informed coding, for information embedding.

The remainder of this paper is organized as follows: Section 2 reviews the trellis-based informed watermarking system proposed in [14] and introduces our proposed watermarking framework. Section 3 details the core contributions of this study, including the modified informed embedding and coding algorithms. Section 4 presents the experimental results along with a constructive discussion. Finally, conclusions are provided in Section 5.

2  System Description

This paper proposes a trellis-based informed watermarking system with controllable parameters. The proposed system enhances the approach introduced in [14,15] by modifying the arc labels within the trellis structure. Fig. 1 illustrates the fundamental block diagram of the proposed watermarking system, which consists of three primary components: the informed watermarking module, the channel attack process, and the message detection unit.

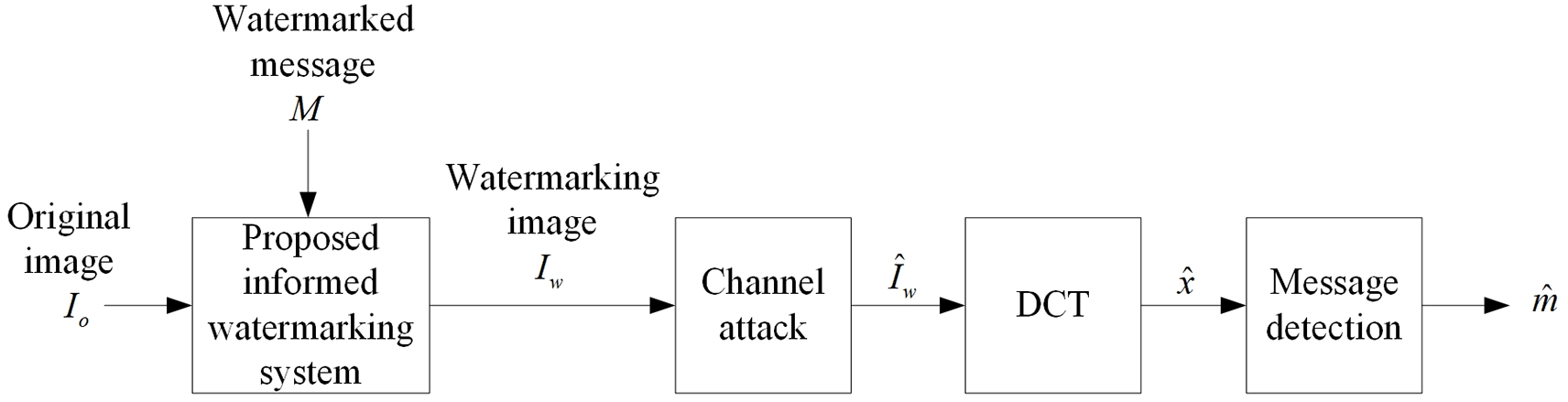
Figure 1: Watermarking system model

In the first component, detailed in Fig. 2, the watermarked message M is divided into smaller sections, referred to as mk, with each mk subsequently mapped onto a coset, Wk, of a linear block code based on the FCM algorithm. The next step involves searching through Wk to identify the codeword signal, wk, closest to the host signal, vk. After the wk is obtained, the informed embedding algorithm is applied to generate an optimally modified watermarked signal, xk, aligned with the vk. In the informed embedding block, four inputs contribute to the embedding process: the extracted vectors from the host sequence v={v1,v2…,vL}, the message codeword w={w1,w2…,wL} generated by the FCM algorithm, and the controllable factors α and β. Each vk and wk is vector of length n, with 1≤k≤L. The parameters α and β play a crucial role in determining the watermarked image’s imperceptibility and robustness. The proposed informed embedding is performed for each section of the trellis. The extracted vector vk (vk={vk.1,…vk,n}) comprises every n coefficients from the sequence v. This variable vk is known at the transmitter, and the system output is denoted by xk=f(wk(mk),uk,α,β), where α is the robust factor and β is the step factor for the message codeword wk(mk) and the extracted vector vk, respectively. The embedding is employed with the aim of satisfying two conflicting criteria: xk should be perceptually indistinguishable from vk and should simultaneously be close enough to wk(mk) to enhance robustness. Finally, Watson’s estimation block in Fig. 2 is a function of v and x. The estimation function, denoted as Was (v,x), is frequently utilized in this context.

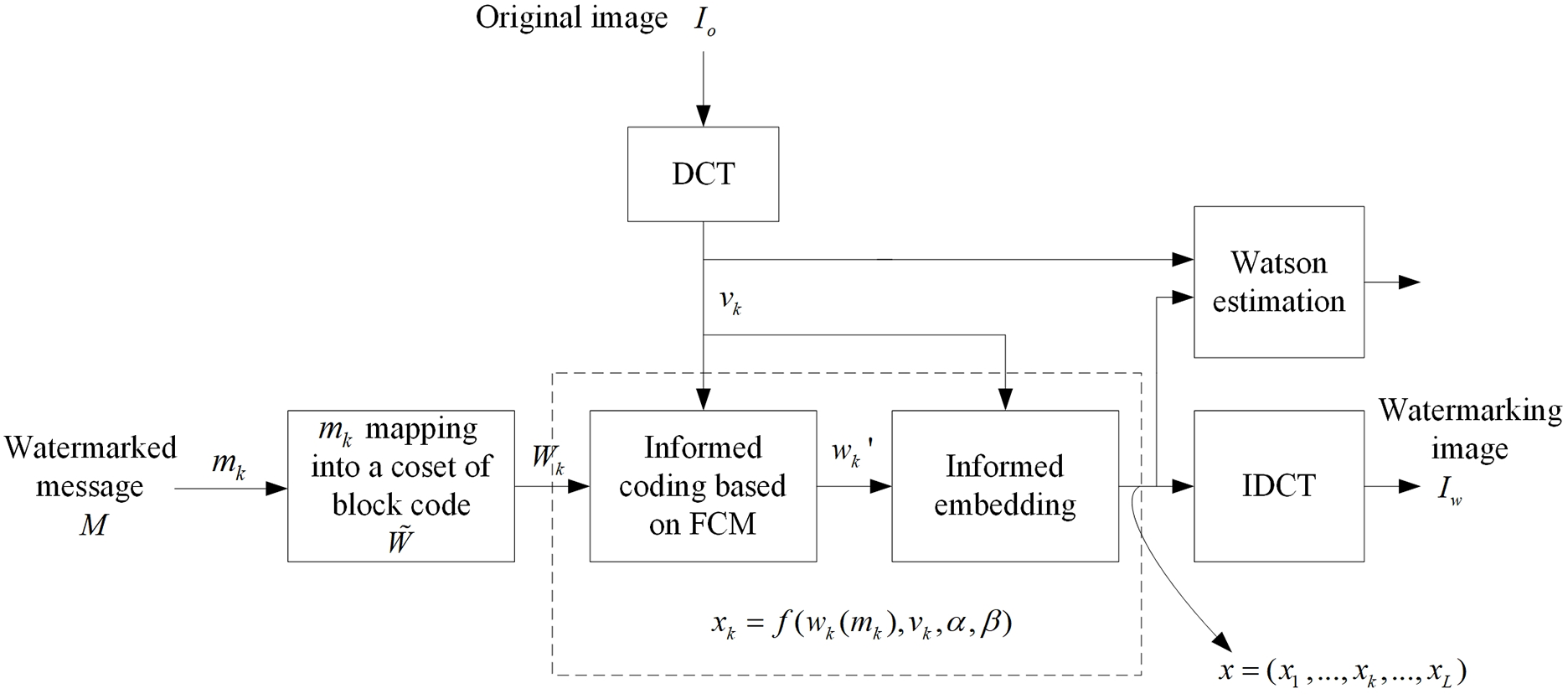
Figure 2: Proposed informed watermarking system

The output of the embedder, which transforms the watermarked sequence x into Iw, is subsequently subjected to various attack channels, such as filtering, scaling, JPEG compression, and Gaussian noise, as illustrated in Fig. 1. In the extraction process, also illustrated in Fig. 1, the noisy I^w is transformed into the frequency domain, from which the watermarked sequence x^ is extracted. The decoder then produces the watermark estimate m^=g(x^), where x^ represents the extracted vector after discrete cosine transform over attack channels, as illustrated in Fig. 1. In the block of informed coding based on FCM, multiple codewords of the linear block code represent the same message mk. The selection of a particular codeword is contingent on the host signal vk. In the informed embedding process, each codeword wk is modified to align with the host signal vk. As indicated in Fig. 1, the current model includes a message detection block, which employs the Viterbi algorithm [25], to find the path most strongly correlated with the detected sequence, x^={x^1,…,x^L}. Typically, the prior probability is assumed to be uniform or undefined, leading to the maximum a posteriori equation:

argmaxS∈TP(S|x)=argmaxS∈Tp(x|S)

where S={s0,s1,…,sL} represents a state sequence in an L-section trellis T. The Viterbi algorithm is then applied as a blind detection algorithm to identify the optimal decoding path.

As demonstrated in [14,15], the watermark is embedded in the frequency domain of the host signal rather than directly on the host image. First, various host images are simulated. Each host signal, Io, with N=512×512 is partitioned into 4096 blocks, each measuring 8×8. The blocks are then converted to the frequency domain using the discrete cosine transform. As demonstrated in [14], the initial 12 low-frequency AC coefficients from each block are extracted and concatenated into the extracted vector v. Each bit of the L-bit watermark, with L=(4096×12)/n, is embedded using every n-th coefficient of v. This process generates the watermarked image x. In the final step, each element of x is reinserted into its corresponding position among the DCT coefficients, and all DCT blocks are converted as the spatial domain, resulting in Iw, as depicted in Fig. 2.

3  Proposed Informed Watermarking Scheme Based on Fuzzy c-Means Algorithm

The efficiency of embedding in informed watermarking is influenced by factors such as the design of the trellis structure, the labeled codeword in the arcs, the informed watermarking algorithm, and the codeword length. On the basis of the design of the trellis structure and the informed watermarking algorithm, Miller et al. [14] and Wang et al. [15,16] proposed a suboptimal algorithm for generating a watermarked image. In their study, an iterative algorithm for informed watermarking was proposed. In informed embedding, the watermarked image is designed to fall within the decoding region of the message codeword and to incur minimal perceptual distortion from the host signal. Identifying the optimal watermarked image is generally challenging. However, several approaches have been developed for identifying suboptimal watermarked images, including the trellis-based informed embedding described in [14–16]. In this approach, it is assumed that every path through the trellis corresponds to a watermark message codeword. Using a Viterbi decoder, the trellis-based informed embedding in [14–16] is used to identify a suitable watermarked image. The watermarked signal is iteratively updated in the geometric interpretation of the suboptimal embedding algorithm, as illustrated in Fig. 3. In this process, the Viterbi decoder is used in the first iteration to identify the codeword vector, c1∈Wk, having the maximum correlation with the current watermarked signal, x0=v.

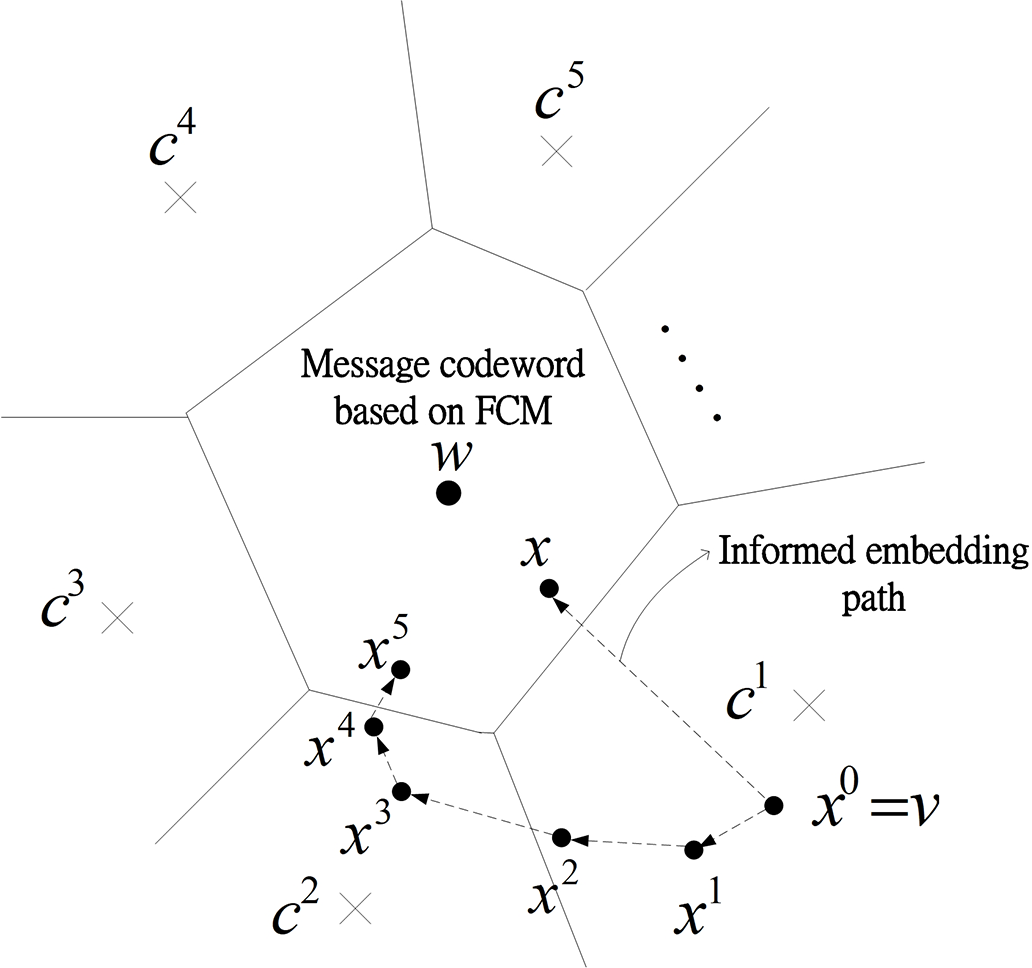
Figure 3: Trellis-based informed embedding [14,15]

Using vectors c1 and x0, we obtain new watermarked signals, x1 to x4, with each iteration moving it nearer to the decoding region of the message codeword w. Embedding proceeds until the final watermarked image falls inside the Voronoi region of w. The final watermarked image, x5, may result in a solution that differs from the optimal one, x, as displayed in Fig. 3. Due to the need for multiple iterations of Viterbi decoding, the embedding process becomes time-consuming before reaching the final watermarked image. Although Miller’s study proposes a watermarking scheme to simplify the optimization problem, the complexity of the proposed algorithm remains high. In the subsequent subsection, we consider an informed embedding algorithm with lower complexity, which leverages the design of labeled codewords in arcs. Finally, acronyms and specific notations frequently encountered throughout this paper are summarized below.

3.1 Informed Embedding Using an Iterative Algorithm with Controllable Parameters

This subsection introduces an iterative informed embedding (IE) algorithm that incorporates tunable parameters to balance computational complexity and embedding effectiveness. Unlike Miller’s approach, which utilizes randomized arc labels in the trellis, our method employs structured codewords derived from linear block codes to enhance efficiency and consistency during encoding. Among these codes, simplex codes with parameters S(2m−1,m,2m−1) are favored for their superior symbol efficiency compared to Hadamard codes H(2m,m,2m−1), which offer equivalent minimum distance but at the cost of increased code length. For instance, a (7, 3, 4) simplex configuration can transmit more information per codeword than its (8, 4, 4) Hadamard counterpart, making it more suitable for applications requiring higher bandwidth efficiency.

To enhance robustness in the watermarking process, our approach incorporates linear block codewords as arc identifiers within the trellis-based embedding framework. The underlying trellis is constructed using a convolutional encoder defined by parameters (nout,kout,v′), where v′ denotes the memory depth. This results in a state space consisting of 2v′ nodes per trellis stage. Each transition between states (i.e., arc) is associated with a codeword selected from a linear block code Γ(n,v′+kout,d), where d is the code’s minimum Hamming distance. Accordingly, each trellis section comprises 2kout+v′ arcs, fully covering the space of codeword labels.

The design allows for flexibility in adjusting performance characteristics: increasing v′ improves robustness by expanding the state space and thus refining decoding resolution, though at the cost of increased computational complexity. In contrast, raising kout boosts embedding throughput by allowing more bits to be represented per trellis section. Notably, when the overall code length n=v′+kout is held constant, one can fine-tune the trade-off between robustness and embedding capacity by adjusting v′ and kout accordingly. The trellis thus partitions the n-dimensional Euclidean space into 2kout+v′ decoding regions, each uniquely associated with a representative codeword. In our implementation, each arc in the k-th section is labeled with the pair (mk,wk), denoting the embedded message and its corresponding codeword, respectively. For illustrative purposes (see Fig. 4), we employ an (nout=2,kout=1,v′=2) convolutional code in conjunction with codewords from a (7, 3, 4) simplex block code to define arc labels.

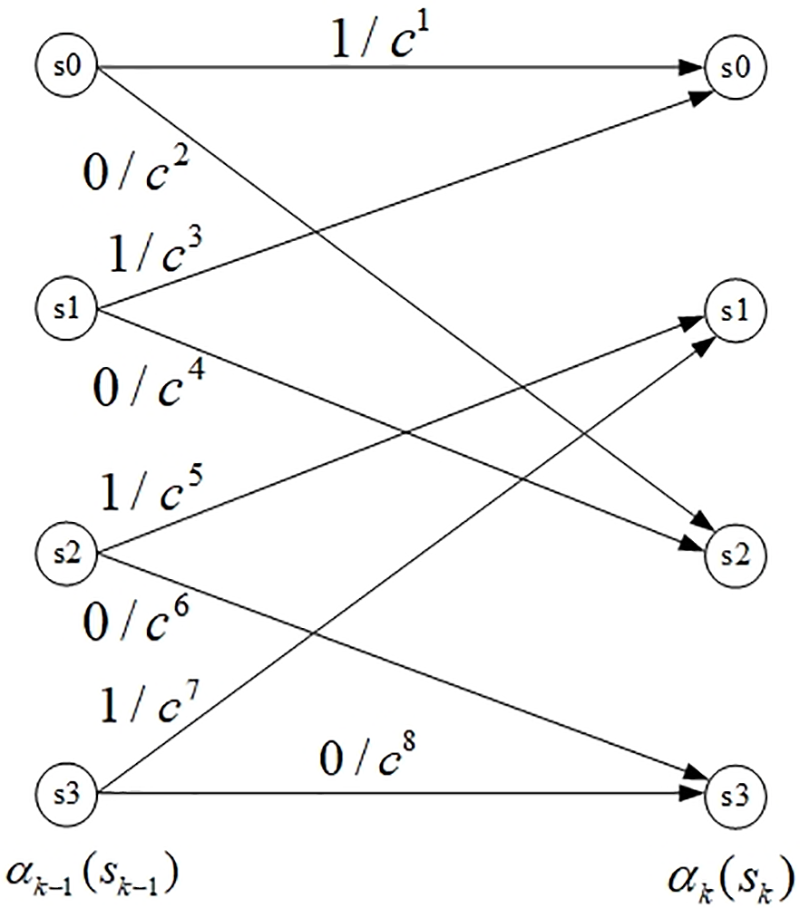
Figure 4: Trellis with eight arcs labeled by a (7, 3, 4) simplex code [15,16]

The proposed informed embedding algorithm is based on trellis partitioning, where at each trellis section k, the extracted vector vk with n components is treated as a point in an n-dimensional real space. The space is partitioned into 2m regions by an (n,m) linear block code, Γ, in each trellis section. In this context, we employ a simplex code as the linear block code as shown in Fig. 4. The simplex code is selected to ensure strong robustness and efficient partitioning of the space. The set Γ={c1,c2,…,c2m} represents 2m disjoint regions, each corresponding to a representative codeword in the informed embedding process. The set of representative codewords, denoted by wk, corresponds to the modified extracted vector xk, which is derived from the original vector vk. To determine the codeword wk, a codeword is selected from the codeword set Γ such that its distance to the modified vector xk is minimized, as mathematically formulated below:

wk=argmincj∈Γd(xk,cj)

where d(⋅) is the Euclidean distance function. The codeword wk is a simplex codeword corresponding to the encoded message in the kth trellis section. On the basis of the description provided, we now consider the following proposed informed embedding algorithms.

(1) Memoryless informed embedding, type-1: Define w=(w1,…,wL) as a valid trellis path derived from the watermark m=(m1,…,mL) and the vector v=(v1,…,vL) is extracted from the host signal. Each wk is a selected n-length codeword within Γ. The embedder constructs the watermarked sequence x=(x1,x2,…,xL) by employing a trellis-based function on each section, defined as xi=f(wi,vi,α,β) for 1≤i≤L, with step factor β in the interval [0,1] and robustness factor α greater than or equal to 1. Fig. 5 depicts the geometric interpretation of the embedding algorithm in the kth section, showing the iterative update of the watermarked image toward wk’s decoding region. In the kth section of the trellis, we iteratively modify the extracted vector uk to form the watermarked image xk. The proposed informed embedding aims to find an xk that minimizes degradation from vk while being closer to αwk than to any other candidate αc, c∈Γ; that is,

αd(wk,xk)≤αd(c,xk),c∈Γand c≠wk(1)

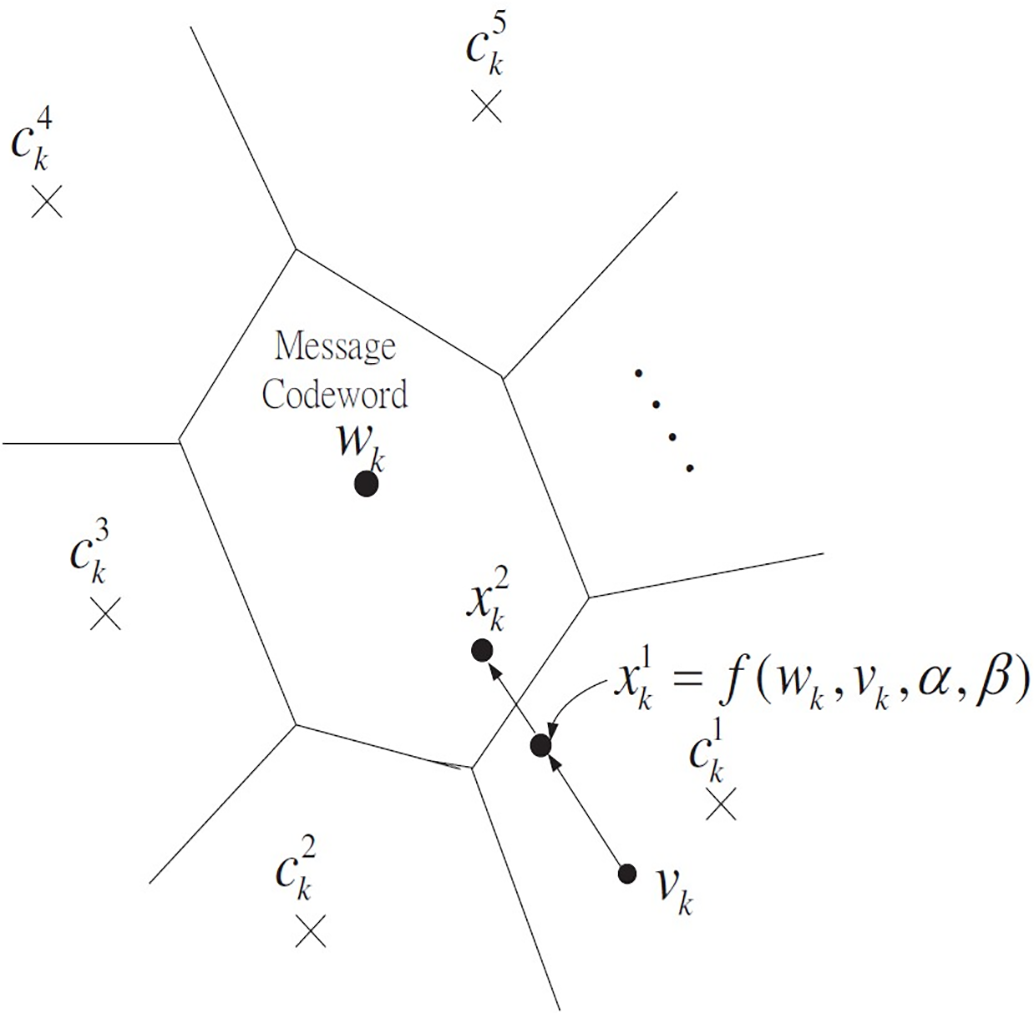
Figure 5: Geometrical view of the informed embedding at trellis section k

The detailed procedure for identifying such an xk is illustrated in the following. Consider hk as the sign vector between vk and wk. For each element of vk and wk, we consider the following:

hk,i=sgn(vk,i⋅wk,i),1≤i≤n(2)

where sgn(⋅) is a sign function and sgn(a)=1 if a≥0 and sgn(a)=−1if a<0.

We construct the ith component of xk as follows: if hk,i=1, then xk,i = vk,i, and if hk,i = −1, then

xk,i={vk,i−β⋅d(αωk,vk),if vk,i≥0vk,i+β⋅d(αωk,vk),if vk,i<0(3)

Essentially, we shift vk toward wk by a distance of βd(αωk,vk) at positions where vk and wk have opposite signs. If the current xk satisfies condition (1), we proceed to the (k+1)-th section; otherwise, we replace vk with the current xk and repeat the procedures described in steps (2) and (3). This informed embedding causes perceptual degradation of the host signal depending on the chosen values of α and β, allowing us to adjust these parameters to find an optimal balance between imperceptibility and robustness in the watermarked images. Summary of the proposed informed embedding algorithm:

1.   Let k=1 and initialize xk=vk, setting a robustness factor α≥1 and a step factor βε[0, 1].

2.   If the current xk meets the criterion (1), proceed to step 4; otherwise substitute vk with xk.

3.   Update the kth watermarked image xk using (2) and (3); after, return to step 2.

4.   If k=L, the process terminates; otherwise, let k=k+1 and xk=vk, and return to step 2.

Illustrated in Fig. 6 is the type-1 informed embedding approach employing a (7, 3, 4) simplex code with parameters α=10 and β=0.1. Positions M={1,2,3,4,7} exhibit complementary signs, implying that the corresponding host components vk, where k∈M, should be adjusted. The initial xk =vk lies within the decoding region of c4, indicating that the type-1 algorithm successfully achieves its objective. In the initial iteration, the updated xk remains in region c1. The decoding region is ultimately shifted to the desired region c6=w during the second iteration. A robustness distance of 23.9 indicates that the modified signal xk is closer to codeword w than to any alternative codeword. For improved robustness, the type-1 algorithm may be repeatedly executed to bring xk closer to the target codeword w.

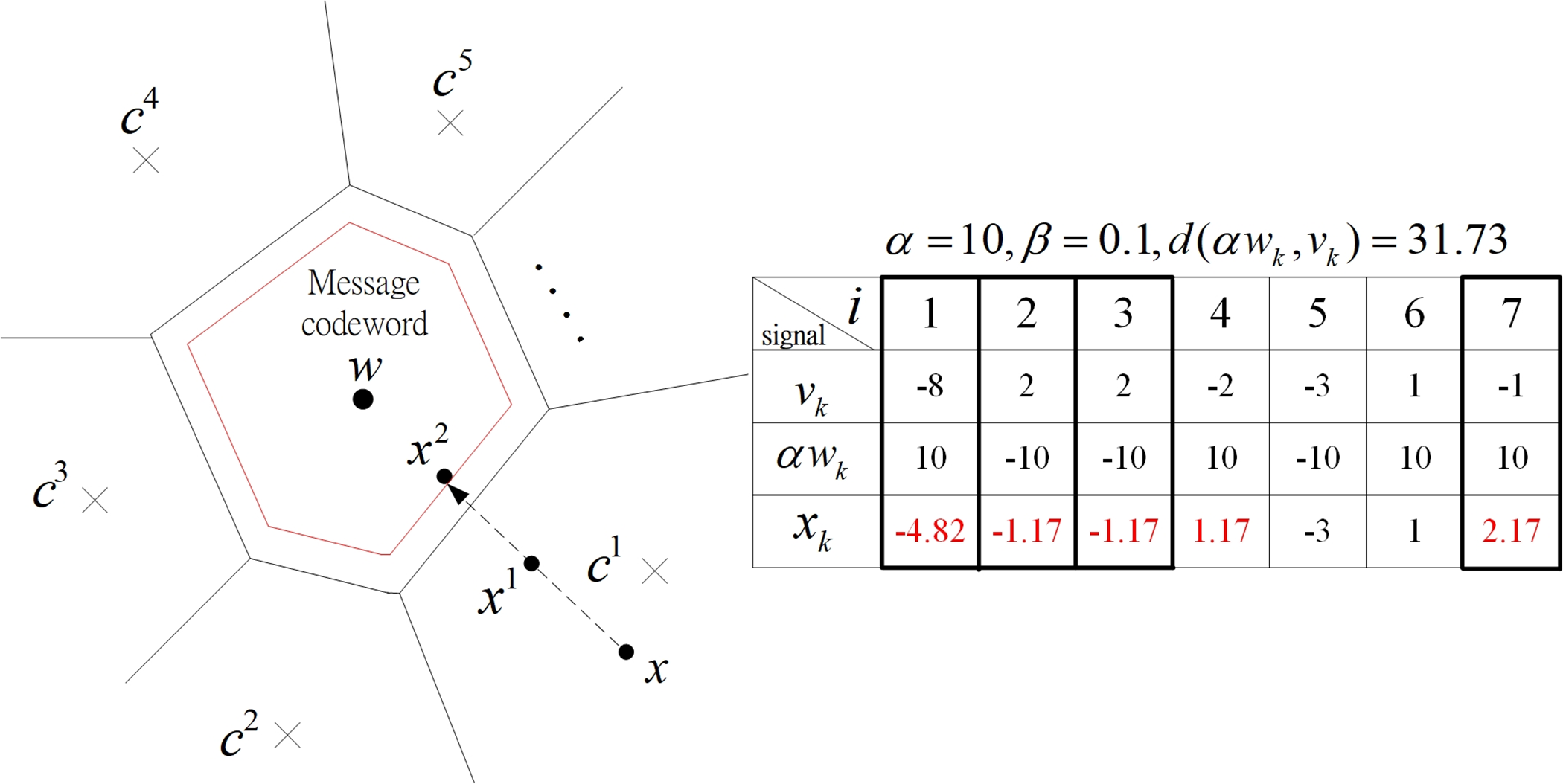
Figure 6: Type-1 informed embedding using a (7, 3, 4) simplex code with α=10 and β=0.1

Because the embedding algorithm operates independently in each section, the type-1 algorithm exhibits high robustness. Although it performs well in terms of robustness, the type-1 algorithm requires an increasing number of iterations. To mitigate the complexity caused by these iterative procedures, a memory-augmented version of the type-1 algorithm is proposed.

(2) Memory-based informed embedding, type-2: The reduced complexity of the algorithm in Section 3.1 arises from its section-wise update of xk in the trellis, which prevents the accumulation of distortion between the message codeword and the watermarked image in the first (k−1) segments. An informed embedding method is proposed in which the Viterbi algorithm is used to accumulate perceptual distortion, thereby enhancing the robustness of the watermarked image with respect to the message codeword. The accumulated metric Jc aggregates state transition metrics across trellis sections. The process begins by assigning x=v and initializing the state metric such that δ0(s0=0)=0and δ0(s0≠0)=∞. During the kth iteration of the trellis, the arc label c(sk−1,sk)∈Γ is computed as the sum of the arc metric Jc(sk−1,sk) and the previously accumulated state metric δk−1(sk−1):

Jc(sk−1,sk)=δk−1(sk−1)+(αc(sk−1,sk))Txk(4)

where cTx is an inner product. In contrast to the previous algorithm’s use of criterion (1) for the kth component of the current watermarked sequence, the proposed approach adopts the accumulation metric presented in Eq. (4). The update of xk in the kth section continues until the accumulated metric for the message codeword wk is less than that for any other codeword in Γ:

Jwk(sk−1,sk)<Jc(sk−1,sk),c∈Γandc≠wk(5)

Eq. (5) indicates that xk has been embedded into the target region, and its position is the closest to the host sequence. The watermarked image obtained from criterion (5) can reside at the boundary of the decoding region corresponding to the message codeword. To enhance robustness, the following is defined:

Rk=minc∈Γ,c≠wk{Jc(sk−1,sk)}−Jwk(sk−1,sk)(6)

Rk is defined by the metric of the code sequence in the trellis structure that is closest to the code sequence wk. It is accumulated from each segment of the code sequence within the trellis. A smaller value of Rk results in greater robustness, but the corresponding sequence will exhibit higher distortion. The optimal embedding region lies along the boundary between wk and vk in the diagram. Here, we choose a constant threshold R; let Rk=kRL. We employ the same procedure as that in Section 3.1, particularly Eqs. (2) and (3), until the current xk is updated to satisfy either criterion (5) or (6). After determining the final xk for the kth section, each state metric in the kth section is updated as follows:

δk(sk)=max∀sk−1{δk−1(sk−1)+(αc(sk−1,sk))Txk}(7)

where the maximum is taken over those sk−1 connected to sk. A smaller distance metric corresponds to a larger inner product value. To minimize the distance metric δk(sk) in (7), an inner product function is used as a substitute for the distance computation. The use of the inner product function reduces computational complexity.

The algorithm proposed in this section embeds information using the procedure outlined previously. It achieves a low level of distortion through hard decoding at the receiver. The reduced embedding complexity compared with that of those discussed in the previous section. This informed embedding algorithm, which accumulates distortion, is summarized as follows:

1.    Let k=1 and initialize xk=vk with selection of a robust factor α≥1 and step factor β ε [0,1].

2.    If the current xk meets the criteria (5) and (6), proceed to step 4; otherwise, substitute vk with xk.

3.    Update the kth watermarked image xk using (2) and (3), and return to step 2.

4.    If k=L, terminate the process; otherwise, let k=k+1 and xk=vk, update the state metric δk(sk) by (7), and return to step 2.

Finally, the proposed type-1 and type-2 algorithms are illustrated as block diagrams in Fig. 7.

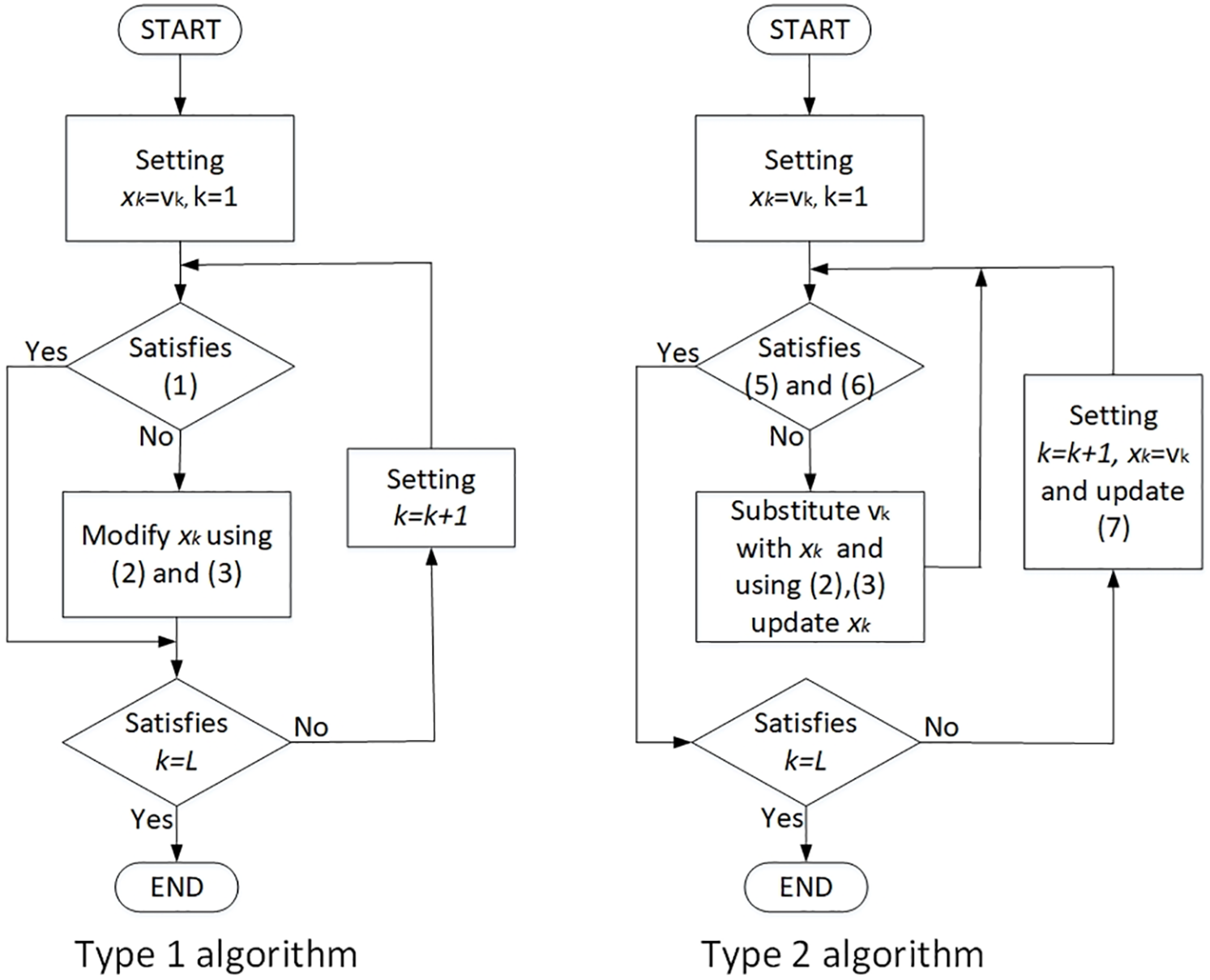
Figure 7: Block diagrams of the proposed type-1 and type-2 algorithms

3.2 Informed Coding with Codewords Based on FCM Algorithm for Parallel Branch Trellis Structure

To improve the distance property, in informed coding (IC), the FCM algorithm is used to construct a codeword space with a large minimum distance. This approach, known as expurgating informed coding based on the FCM algorithm, is used to select codewords for the arc labels in the trellis structure from a subset of all codewords of a block code. It generates new center codewords with a large minimum distance by using the FCM algorithm. The modified informed coding scheme proposed in this study is described as follows: Assume that each block codeword, cx, belongs to every cluster, cy, with a corresponding fuzzy membership. The standard objective function of FCM for grouping 2k′ data points into K clusters is given in the following form:

Jcost=∑j=1K∑i=12k′ui,jb|cix−cjy|2,(8)

where cix∈Rd is the ith sample and 2k′ is the total number of data points; K is a predefined number of clusters; cjy from the candidate codeword set Wk is the cluster centroid or prototype of the jth group; and uij represents the fuzzy membership of the ith sample belonging to jth cluster, which is enforced to satisfy u∈[0,1], ∑j=1Kuij=1. Additionally, the parameter b is a weighting exponent that indicates the level of fuzziness. By setting the first derivatives of Jcost with respect to cjy(j=1,…,K) and uij(j=1,…,n,j=1,…,K) to zero, two updated equations for Jcost can be obtained. These equations are used to find a local optimum of Jcost through an iterative strategy.

cjy=∑i=1nuijbcix∑i=1nuijb(9)

uij=(1/|cix−cjy|2)1/(b−1)∑j=1K(1/|cix−cjy|2)1/(b−1)(10)

The FCM algorithm for linear block codes can provide the codeword space with a large minimum distance. The basic concept underlying watermarking is hiding information into the host signal in such a way that the perceptual imperceptibility of the host signal is minimally affected. Perceptual imperceptibility efficiency can be achieved using informed coding in addition to informed embedding. Informed coding is a structured design of the trellis. We divide the informed coding technique into parallel and scatter structures for trellis architecture. The parallel structure uses a configuration in which the current state connects to the next identical state through multiple arcs, allowing for the selection of various codewords. By contrast, the scatter structure is designed such that the current state connects to a different state and the arcs do not have a parallel configuration. The informed coding with a scatter structure requires the use of the Viterbi algorithm to embed messages. For the informed coding with a parallel structure, the message is embedded without performing the Viterbi algorithm; instead, the closest codeword in the parallel arcs is identified. Thus, the computational complexity when a parallel structure is used is lower than that when a scatter structure is used in the design of informed coding.

Fig. 8 illustrates the concept of the informed coding system. The purpose of the informed coding system is to select a codeword close to the host vk from the candidate codeword set Wk generated by the FCM algorithm. The selected message codeword is referred to as the host signal, wk; wk is adjusted by an embedding strength scale α. Finally, αwk is added to vk to generate the watermarked signal.

wk′=vk+αFCM(Wk)=vk+αwk(11)

where FCM(⋅) is a clustering function. Before discussing informed coding, this study addresses the concept of “blind” coding. “Blind” here implies that the host vk does not play any role in the encoding of the message m. This means that any arbitrary message sequence from a source, M, is mapped to a single codeword path in the trellis. Fig. 9 depicts a trellis structure for blind coding.

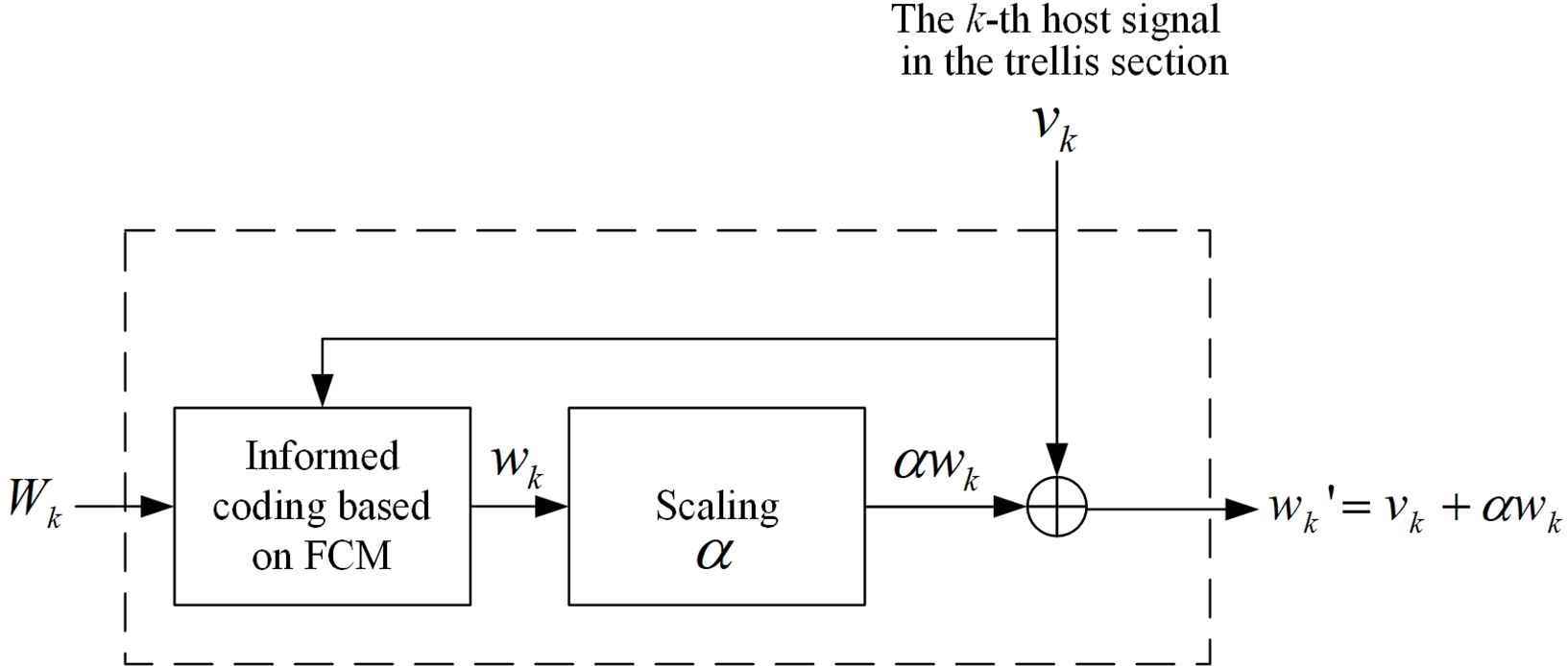
Figure 8: Informed coding system

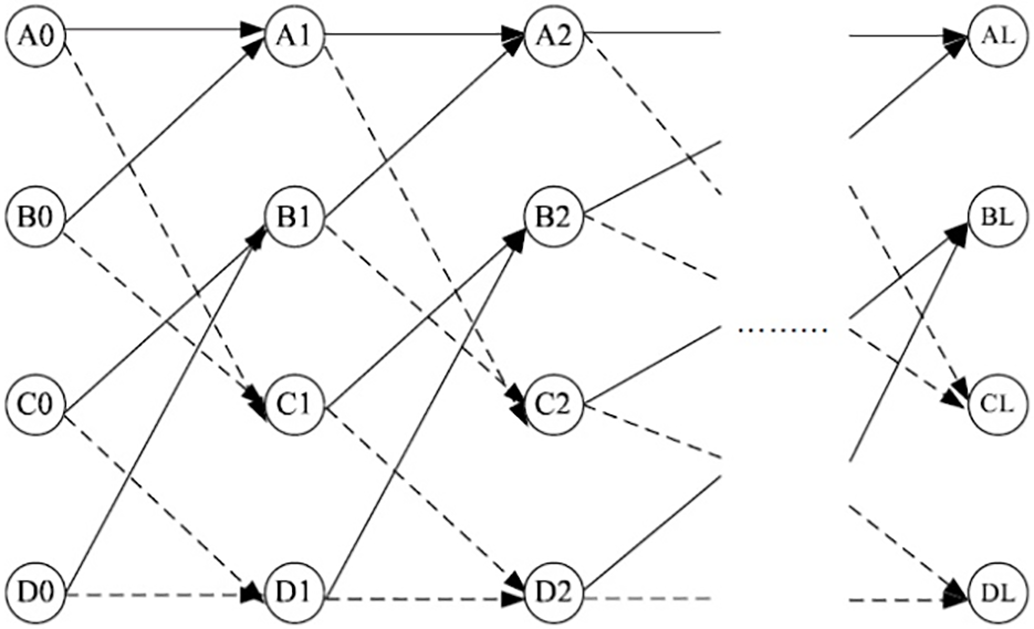
Figure 9: Blind coding: Four-state, eight-arc trellis

As indicated in Fig. 9, each current state node is connected to next state node by two arcs; for example, A0 connects to A1 and C1. A “section” of the trellis comprises current state nodes and their subsequent state node. Transitions from current to next state nodes are represented by arcs. The dotted arc corresponds to the message bit“1”, whereas the solid arc corresponds to message bit“0”. Thus, any arbitrary sequence of L message bits corresponds to a single path through the trellis, forming an embedded sequence of L×N codewords.

The key distinction between blind coding and informed coding lies in the selection of candidate codewords on the basis of perceptual distance. In Fig. 10, the informed coding trellis structure includes four arcs for each state node. The informed coding process can be divided into two steps. First, one of the candidate paths through the trellis is selected. For example, if the message bit is “1”, the dotted arcs in the trellis are disregarded. Subsequently, the Viterbi algorithm [25] is employed to determine the codeword path based on host imperceptibility.

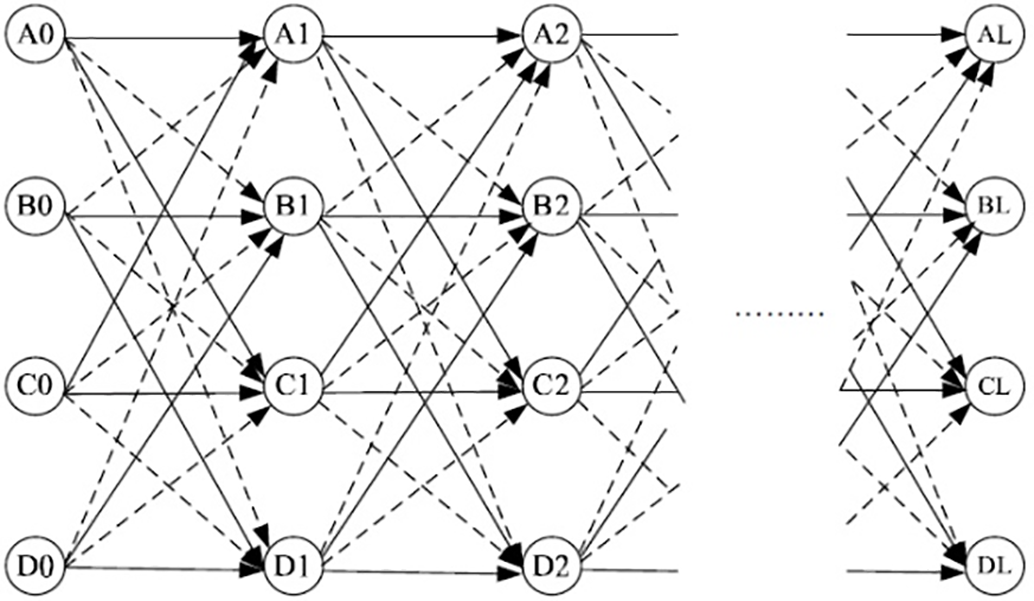
Figure 10: Informed coding: Four-state, sixteen-arc trellis

In modifying the trellis structure depicted in Fig. 10, we introduce a parallel arc configuration, as illustrated in Fig. 11. In this modified trellis, the connection of each state node is similar to that in blind coding but with two arcs (codewords) based on the FCM algorithm leading from one state node to the same state node in the next stage. Essentially, this trellis is similar to the one used in blind coding but includes twice as many arcs. During encoding, the informed coding with a parallel structure selects the candidate arcs that are closest to the host signal according to the encoded message mk, which eliminates the need for the Viterbi algorithm. Thus, the computational complexity of the parallel structure is lower than that of the scatter structure. At the receiver, the detector employs the Viterbi algorithm to identify the hidden message corresponding to each arc in this path.

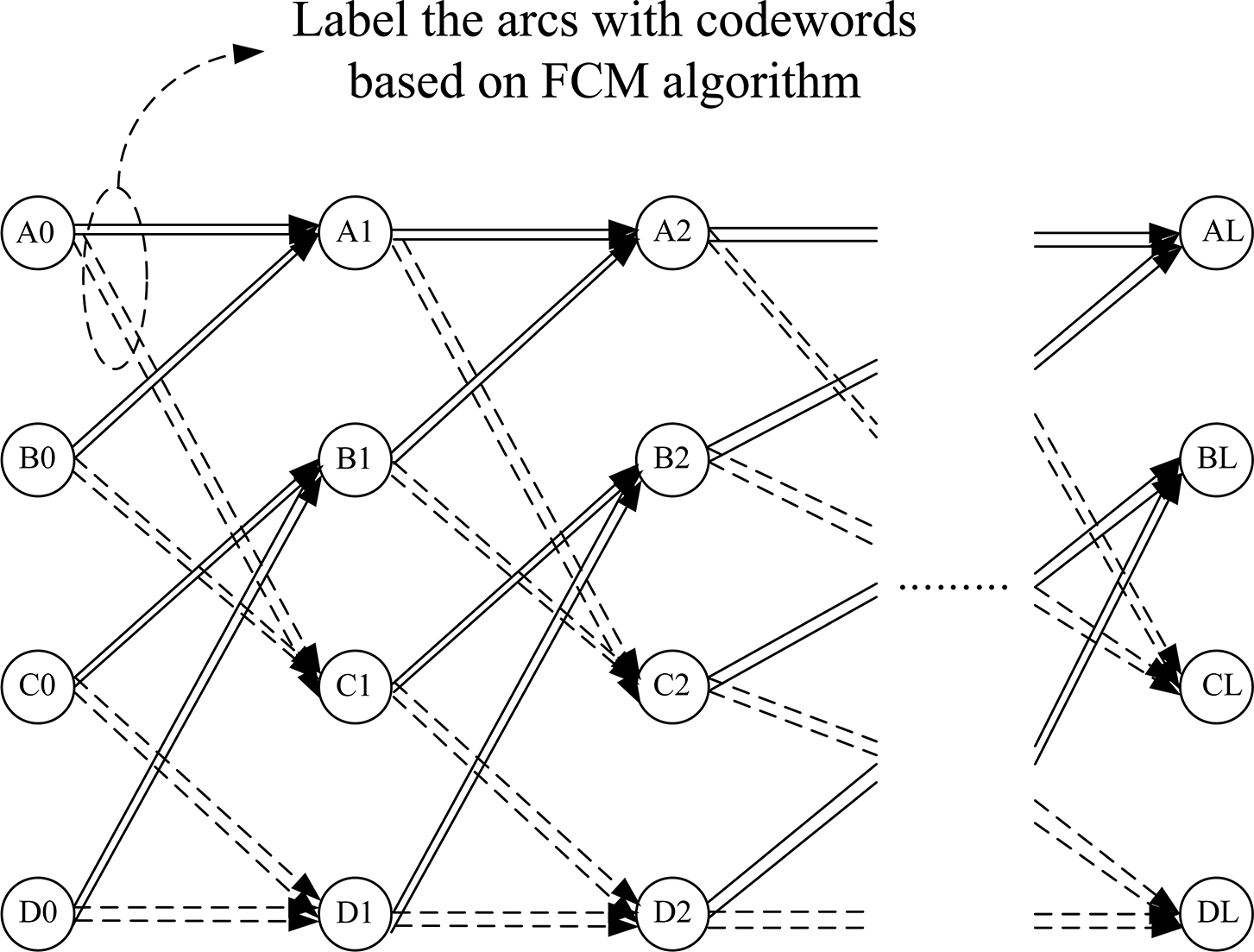
Figure 11: Modified informed coding: Four-state, sixteen-arc trellis

3.3 Combining Informed Embedding with Informed Coding

Regarding robustness, the proposed informed watermarking system primarily benefits from the informed embedding (IE) approach. The type-1 IE is implemented as a section-based, memoryless method that enhances robustness by making the watermarked signal as close as possible to the message codeword while maintaining acceptable imperceptibility. However, achieving the optimal watermarked signal remains challenging. Therefore, we adopt a section-based strategy to generate a robust watermarked signal, which is more practical than optimizing over the entire trellis. The type-1 embedding algorithm adjusts robustness section by section by aligning the watermarked signal with the target message codeword. Although this method achieves high robustness, it incurs considerable iterative complexity and may compromise imperceptibility. To address these issues, we propose the type-2 embedding algorithm, which generates a watermarked signal that better balances robustness and complexity. To further enhance robustness, this approach employs linear block codes instead of random codewords or Miller’s arc labels. The objective of the informed watermarking system is to identify an efficient algorithm that achieves both optimal robustness (i.e., low error rate) and low complexity. Informed coding (IC) selects a target message codeword close to the host signal before applying the embedding algorithm. As discussed in the preceding section, the modified IC scheme with a parallel structure further reduces the encoding complexity. The proposed informed embedding combines a section-based algorithm to improve robustness with reduced computational complexity. The integration of the proposed IE and IC constitutes the informed-coding-embedding (ICE) algorithm.

4  Experiments and Results

As done in [14,15], four standard grayscale images (‘House’, ‘Baboon’, ‘Jet’, and ‘Scene’, each of 512×512 pixels) in BMP format are divided into 4096 blocks, each measuring 8×8; then, each block transformed into the frequency domain using the DCT. The first 12 low-frequency AC coefficients from each block, as displayed in [14], are extracted and concatenated as host signals. In both the Simplex and Hadamard code cases, where n=31 and n=32, respectively, coefficients are used for embedding each bit of a 1536-bit watermark. Here, the trellis is constructed using a (2, 1) convolutional code. The labels of the trellis arcs, each of the length n, include FCM-based Simplex codes, FCM-based Hadamard codes, and random codes. The Watson distance between the original and watermarked images serves as the imperceptibility measure. Experiments are conducted with three objectives: First, to validate the influence of the controllable parameters α and β on the Watson distance and message error rate for the type-1 and type-2 informed embedding algorithms. Second, to test the robustness against a variety of channels, such as additive white Gaussian noise (AWGN), scaling, filtering, and compression, for the proposed ICE algorithms. Third, to determine the computational complexity for the proposed ICE algorithm and the algorithm in [14]. Additionally, the bit error rate and message error rate are used to measure robustness. Finally, the watermarked image quality is defined as follows:

PSNR=10log10⁡2552MSE

where MSE represents the mean square error between the original JPEG image and the decoded image over a slow-fading channel with AWGN. MSE is calculated using

MSE=1N∑i=1512∑j=1512(I0(i,j)−Ir(i,j))2

where Ir represents the watermarked images. In addition, this work also employs the LPIPS (Learned Perceptual Image Patch Similarity) metric for image quality evaluation. The LPIPS is defined as follows:

LPIPS(Io,Ir)=∑lwl(fl(I0)−fl(Ir))2

where fl(I) denotes the feature vector extracted from the l-th layer of the neural network, followed by channel-wise normalization and the difference at each layer is multiplied by a learned weight wl.

(1) Imperceptibility experiments

Parameters α and R: The imperceptibility of the watermarked images was evaluated by varying α without considering an attack channel. The relationship between the peak signal-to-noise ratio (PSNR) and α is shown in Fig. 12, which indicates that PSNR declines as α increases. Notably, the proposed algorithm requires more iterations at higher α values. Image quality improvements of approximately 2–3 dB were observed with the type-2 algorithm compared to the type-1 algorithm when α was varied. Increasing α in both type-1 and type-2 algorithms enhances robustness but reduces PSNR. Fig. 12 also compares the embedded image quality as a function of the robustness parameter R for the two algorithms. As illustrated, the type-2 algorithm exhibits reduced image quality with increasing R, whereas the bit error rate improves as R increases. In contrast, in the type-1 algorithm, increasing R does not result in noticeable degradation in image quality.

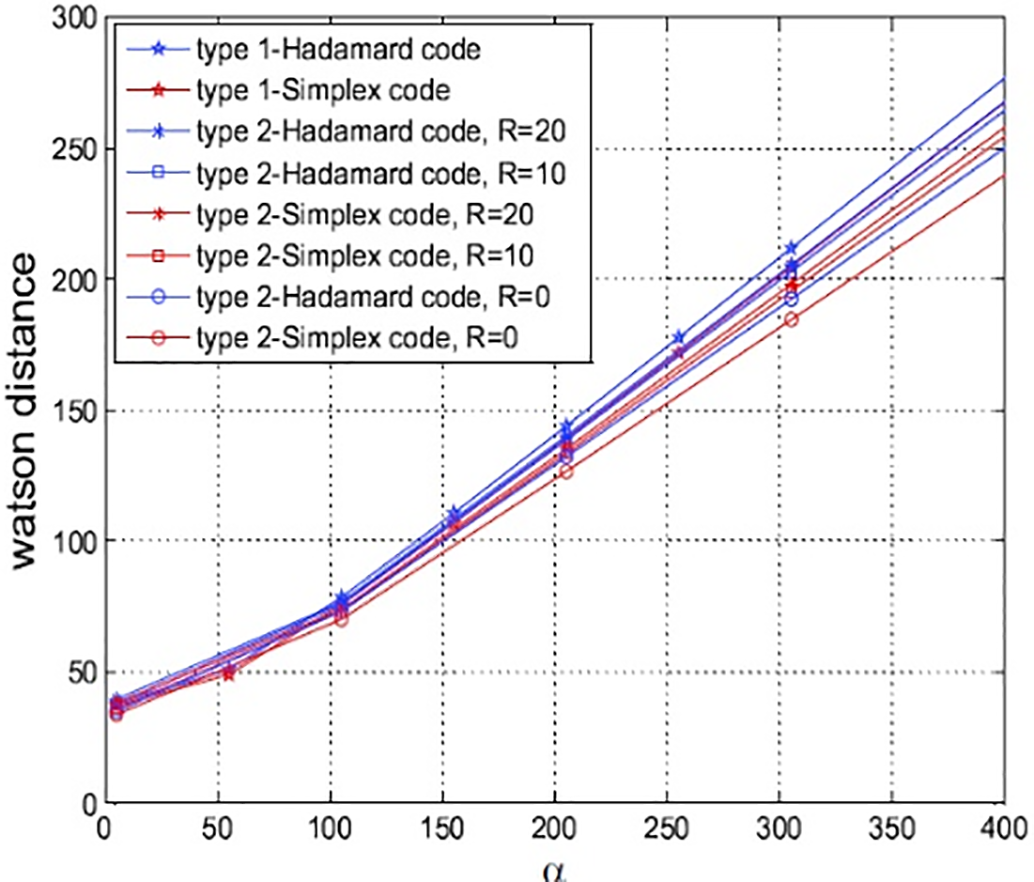
Figure 12: Imperceptibility experiments with variant α and robustness parameter R

The imperceptibility of the watermarked images was evaluated by varying α without considering an attack channel. As shown in Table 1, the PSNR is presented as a function of α and decreases as α increases. The proposed type-1 and type-2 algorithms were also simulated by varying α and β under a Hadamard code. The dependence of image quality on the iteration step factor β is shown in Table 2.

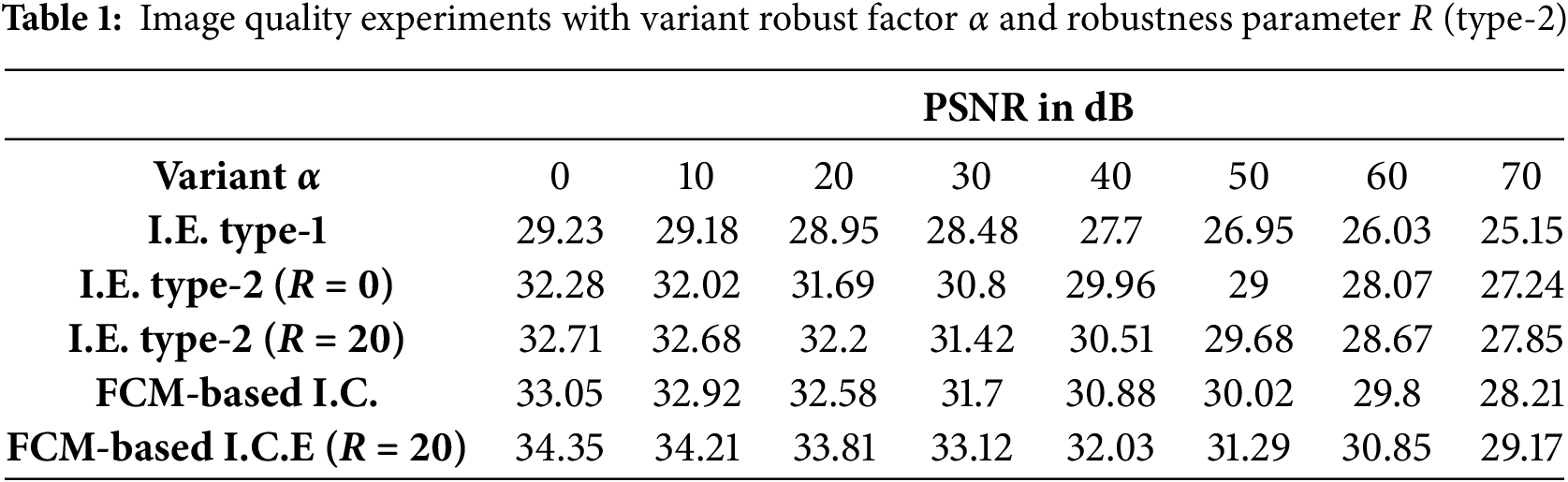
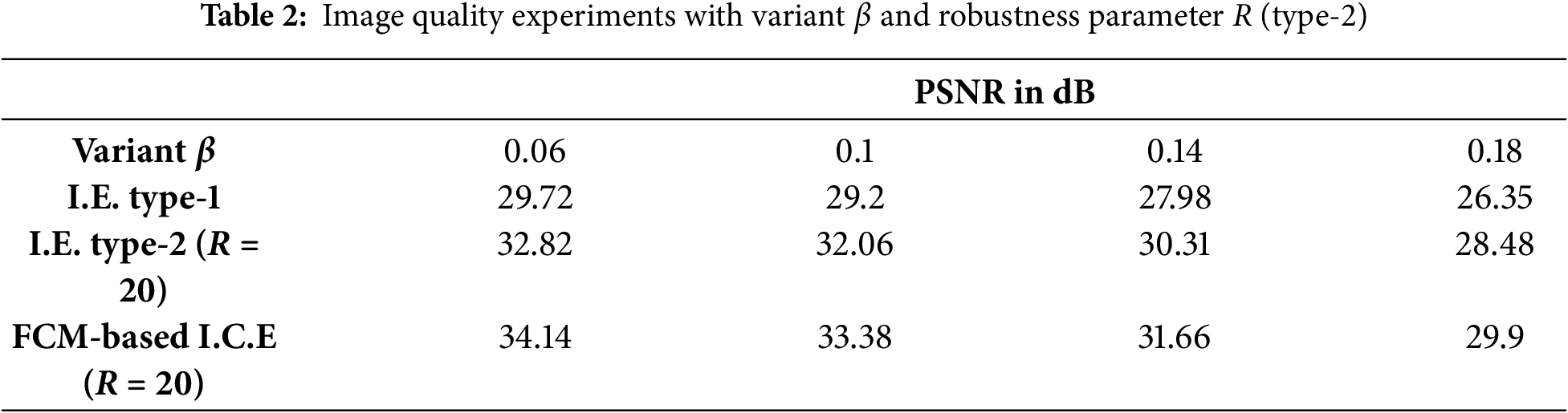
Furthermore, the data presented in Tables 1 and 2 are illustrated using the bar charts shown below.

Fig. 13 illustrates the relationship between PSNR and the parameter α. As α increases, image quality (in terms of PSNR) decreases, indicating a trade-off with improved robustness. In comparison with other algorithms, the FCM-based I.C.E. algorithm consistently achieves superior image quality. Furthermore, Fig. 14 presents the impact of increasing the parameter β on the PSNR performance of the proposed algorithms.

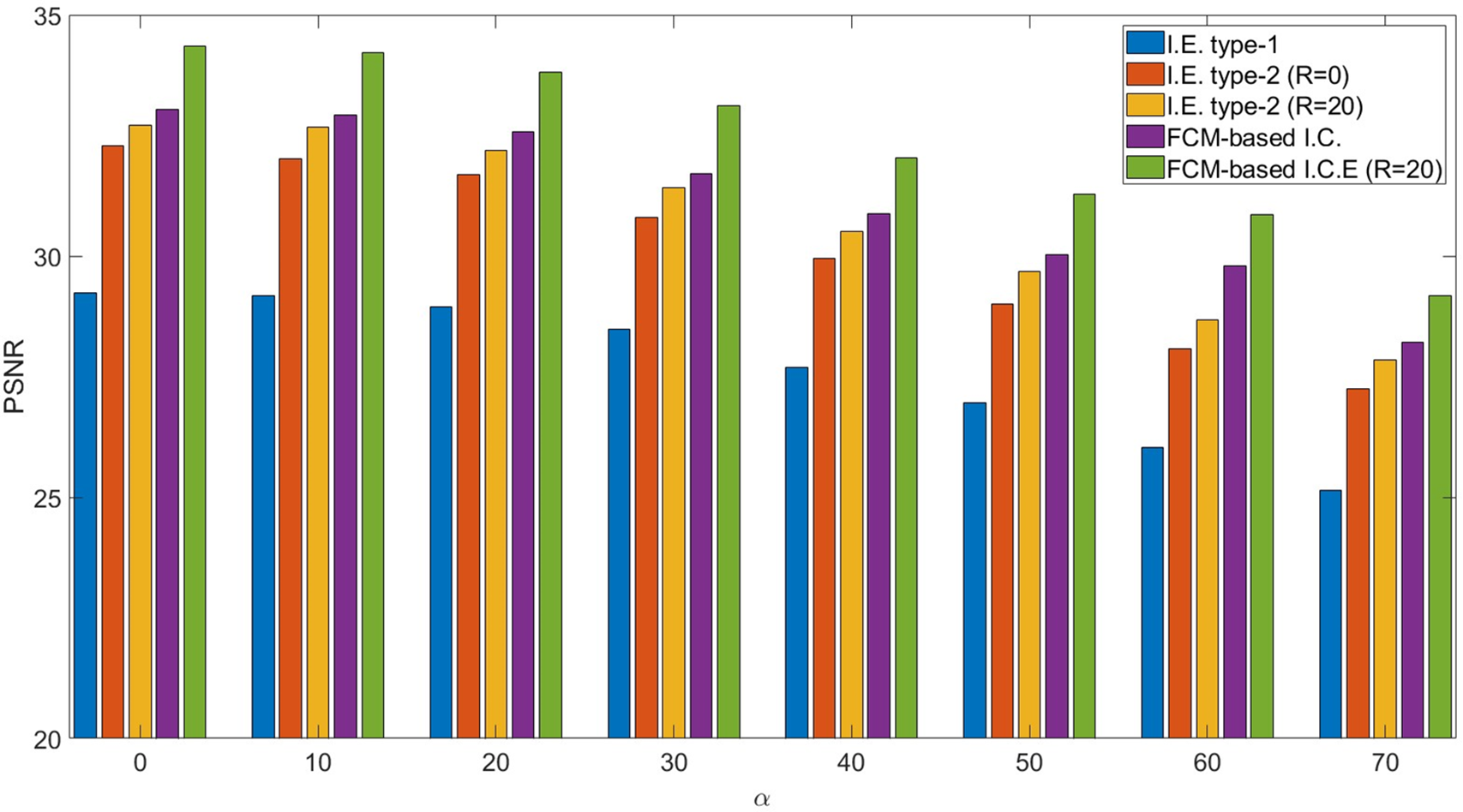
Figure 13: PSNR experiments with variant α

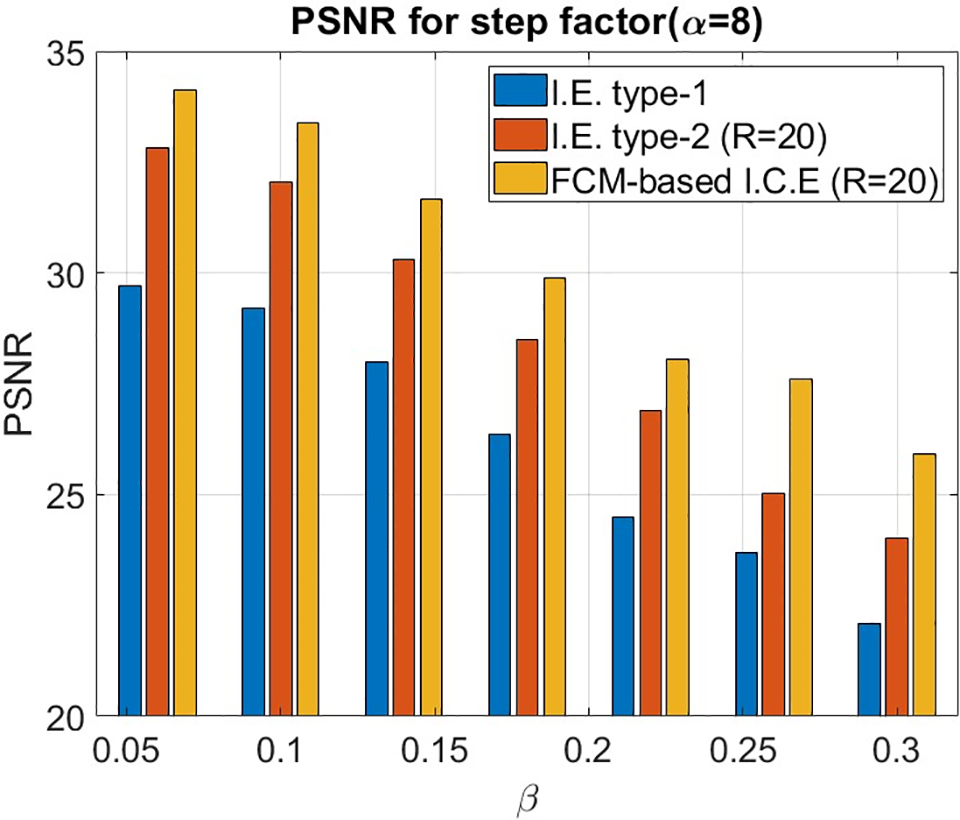
Figure 14: PSNR experiments with variant β

Fig. 14 illustrates that as the step factor β increases, the PSNR of all algorithms decreases. This decline occurs because a larger β reduces the number of iterations, allowing the algorithms to converge more rapidly, but at the expense of increased sensitivity to error. Fig. 15 presents the image differences corresponding to various values of α, demonstrating that achieving greater robustness inevitably leads to a compromise in image quality.

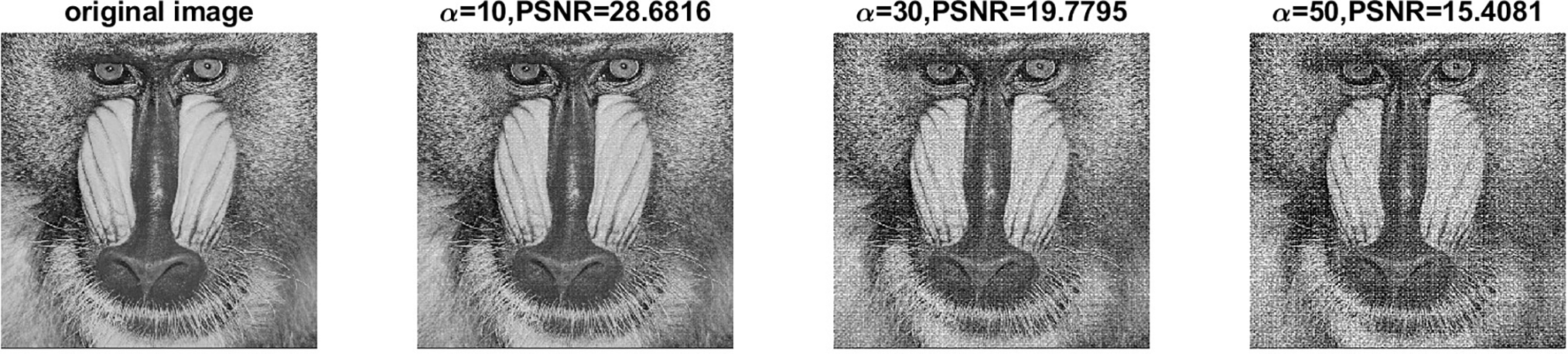
Figure 15: Images at different α values

Fig. 16 illustrates the changes in image quality resulting from variations in the β parameter within the type-2 algorithm. The figure indicates that smaller β values yield better image quality, and that the influence of β on PSNR is less pronounced compared to that of α.

Figure 16: Images at different β values

Performance of proposed informed coding: As indicated in Fig. 17, as α increases, the bit error rate (BER) decreases. When the PSNR is kept equal to 34 dB, the modified informed coding achieves better BER performance. At α = 12 (PSNR = 34 dB), the modified informed coding closely approaches 10−5, whereas the informed coding equals 5×10−4, and the blind coding equals 10−2.

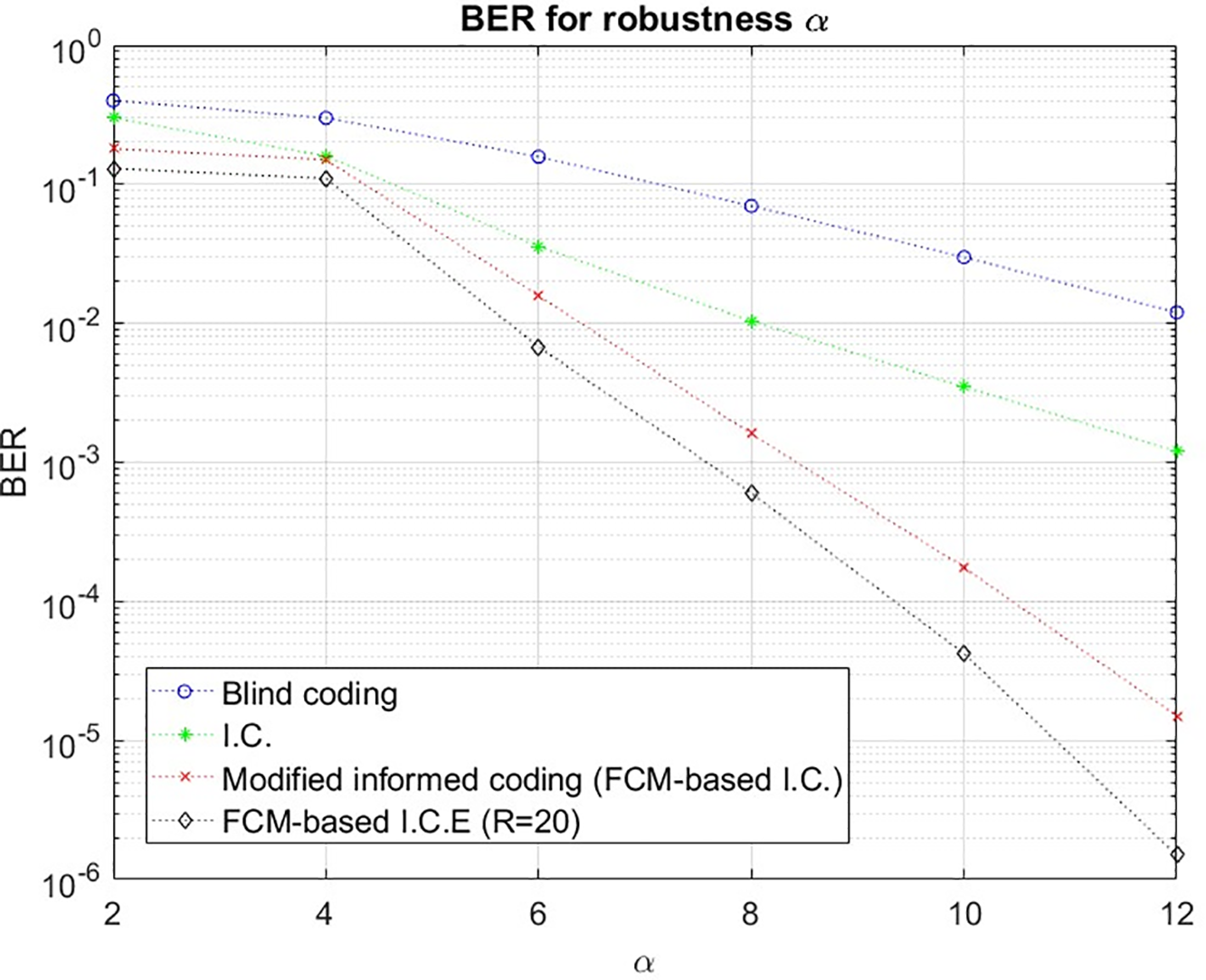
Figure 17: BER for robustness α

The figure illustrates the BER performance of different algorithms as the parameter α varies. Among all algorithms, the FCM-based I.C.E. demonstrates the best BER across a range of α values, albeit with relatively high computational complexity. Finally, with α fixed at 8, Fig. 18 presents the variance and PSNR of the FCM-based I.C.E. algorithm under various AWGN noise conditions

Figure 18: Images under various noise power levels

(1) Attack channel experiments

(a)   AWGN

Considering out of additive white Gaussian noise (AWGN) channel is expressed by y=x+N(0,σw2). The experiment was conducted repeatedly for different variances of σw2, and the BER was computed. Performance under different noise conditions, with variances between 50 and 300, is depicted in Fig. 19 for the proposed algorithm. With a PSNR of approximately 30 dB in each case, the figure shows that the bit error rate (BER) of the proposed algorithm—especially for R≥0—is lower than that of Miller’s algorithm when σw2>200 under AWGN noise. Based on the experimental results, the proposed type-2 informed embedding algorithm with memory demonstrates improved BER performance as the controllable parameter R increases. Among all evaluated cases, the informed embedding without memory results in the highest BER. Nonetheless, it provides a significant advantage in time complexity over the type-1 algorithm and the approach in [14]. Fig. 20 displays the watermarked image under AWGN attack.

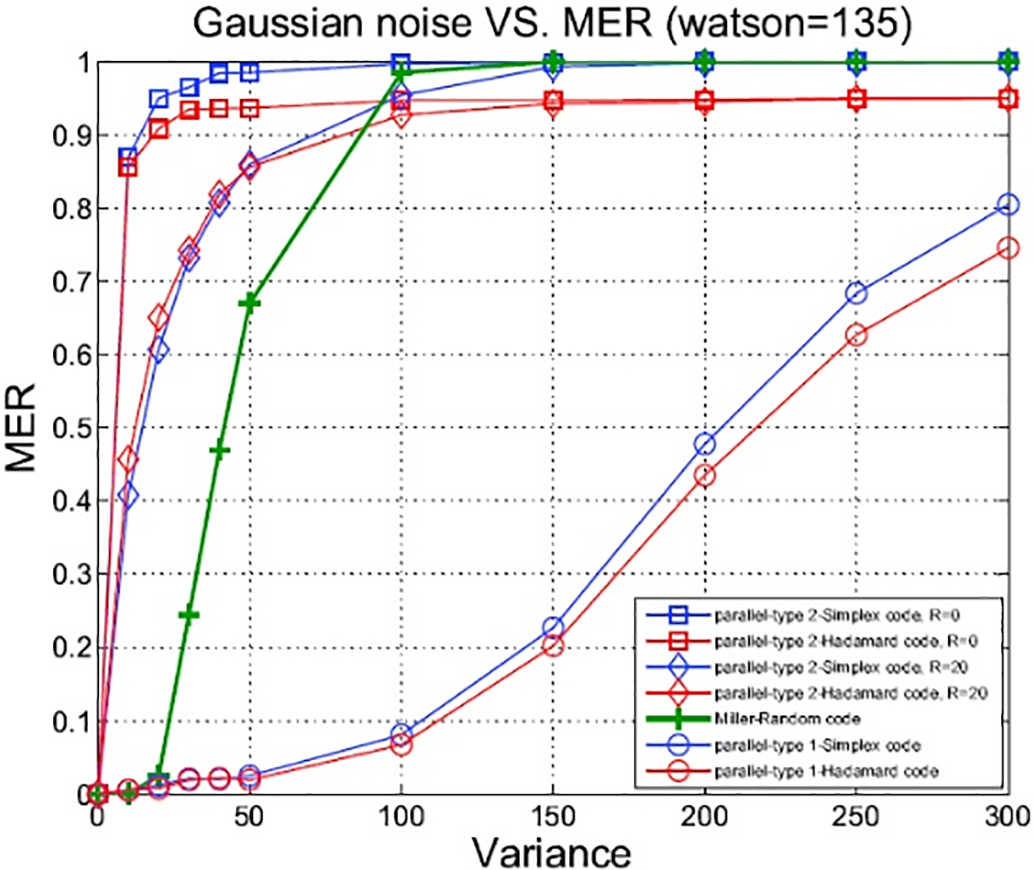
Figure 19: Watermark robustness against AWGN

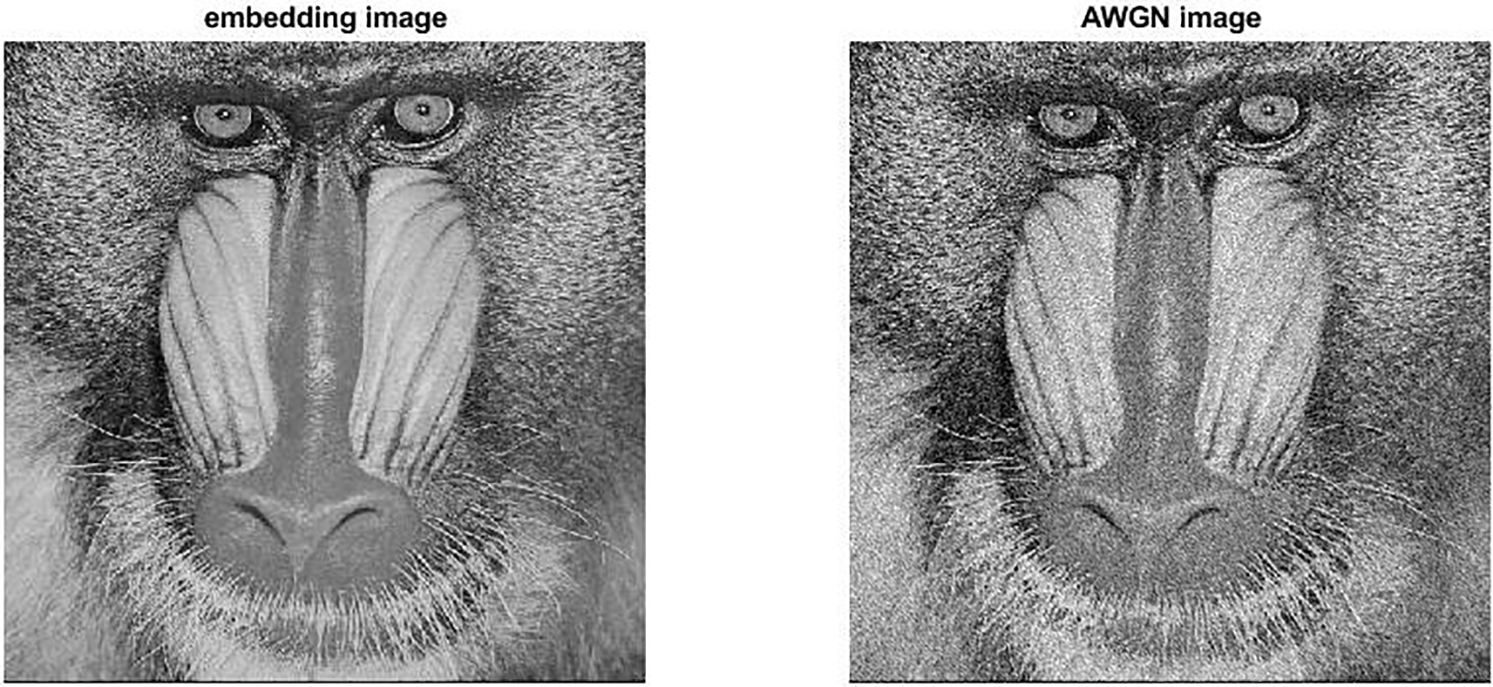
Figure 20: Watermarked image with AWGN and variance = 400

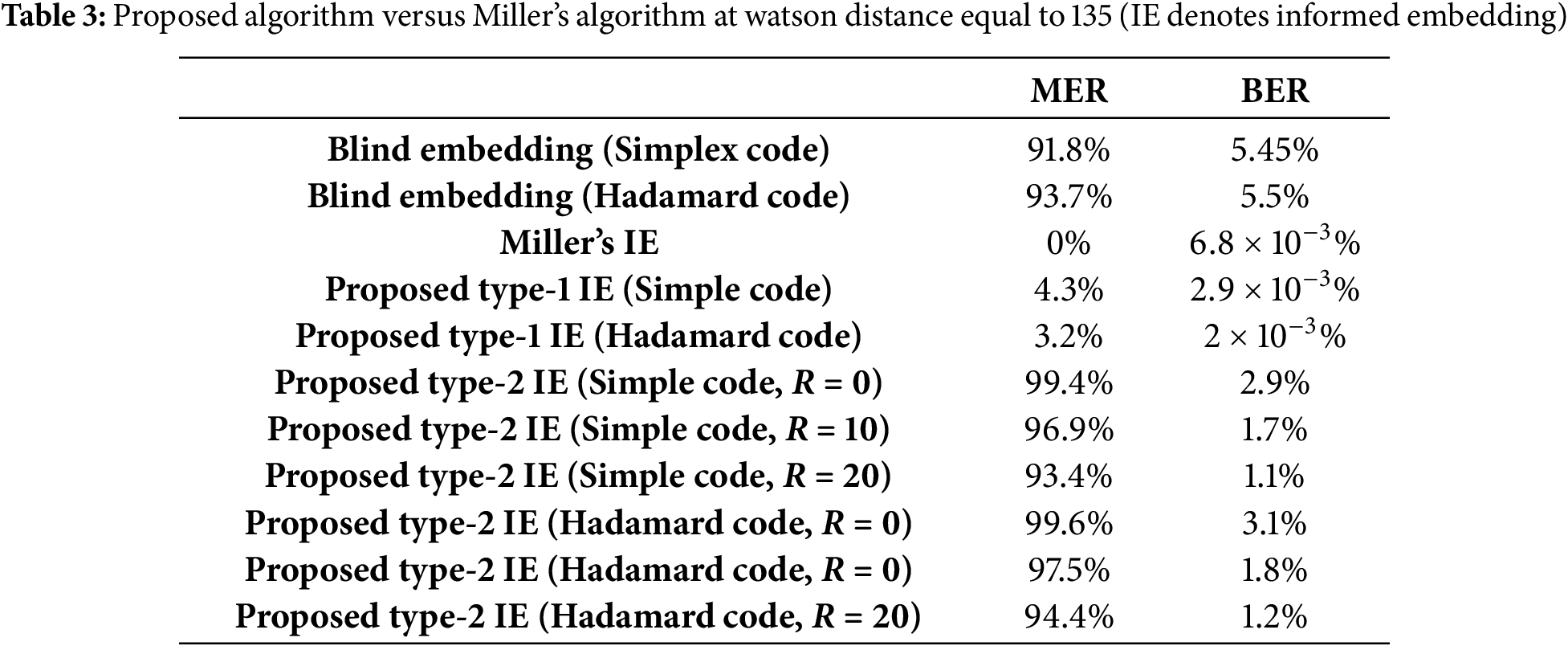
Furthermore, simulation results of the proposed algorithm over the AWGN channel have been carried out. The robustness results of informed embedding for multiple algorithms, subjected to Gaussian noise, are reported in Table 3. For fixed image quality with a Watson distance of 135, the error rate of the type-1 algorithm is comparable to that of Miller’s in terms of robustness. Although the error rate of the type-2 informed embedding algorithm is higher than that of the type-1 and Miller’s algorithm, the complexity of the type-2 algorithm is substantially lower than that of the others.

Regarding robustness, particularly in the context of Gaussian noise addition, we discuss the error ratio performance for different trellis structures, including the scatter and parallel configurations, as illustrated in Table 4. The data presented in Table 4 indicates that the informed coding using the codewords of linear block codes as arc labels achieves a superior error rate to that achieved using random codes as arc labels in Miller’s approach.

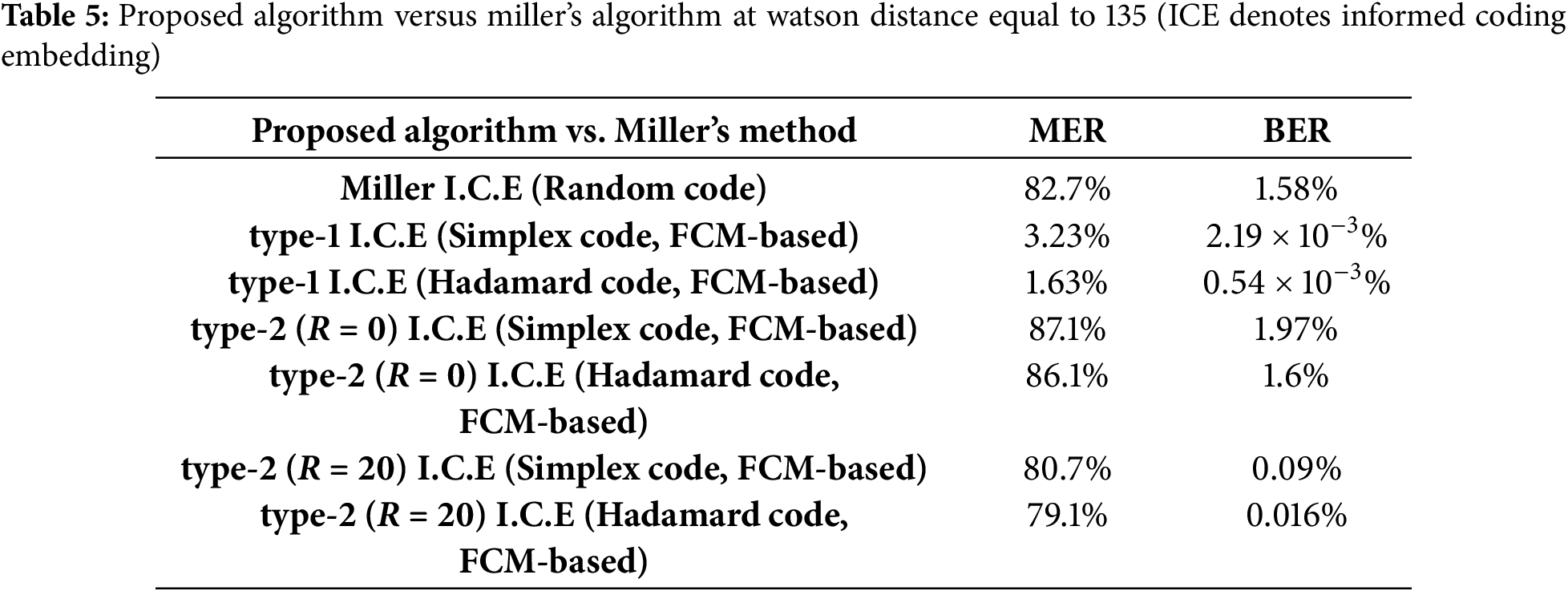
Experimental results are presented in Tables 5 and 6 to facilitate comparison of the robustness and computational complexity among various algorithms. The results in Table 5 demonstrate that the type-1 ICE algorithm exhibits superior robustness compared to other algorithms, owing to the trellis structure design and the use of codewords as arc labels. Furthermore, the proposed algorithm achieves significantly lower overall computational complexity.

(b)   Scaling

Image scaling, a notable form of distortion, involves scaling in amplitude and is herein represented as follows:

Iw′=sf×I0

where I0 is the test image and sf is a scaling parameter. The applied scaling effectively represents common image processing attacks, such as those altering brightness or contrast. This study conducted two experiments—one decreased image intensities from 1 to 0.1, and the other increased them from 1 to 2. The results of the type-1, type-2, and [14] algorithms are illustrated in Fig. 21. The figure shows the variation in BER with increasing scaling factor sf, ranging from 0 to 2. The type-1 and [14] algorithms maintained acceptable performance across the scaling factor range of 1 to 2 in our experiments. Fig. 22 displays the watermarked image affected by scaling at the PSNR = 25.15 dB.

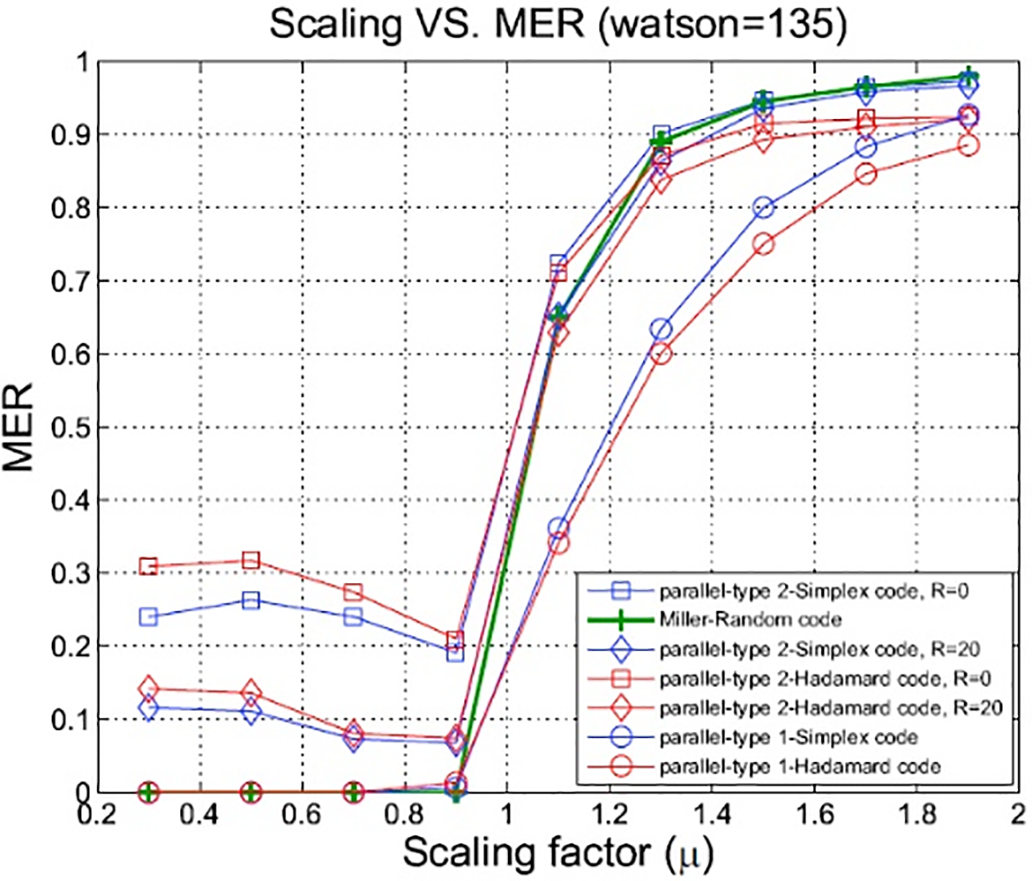
Figure 21: Robustness to the scaling factor sf

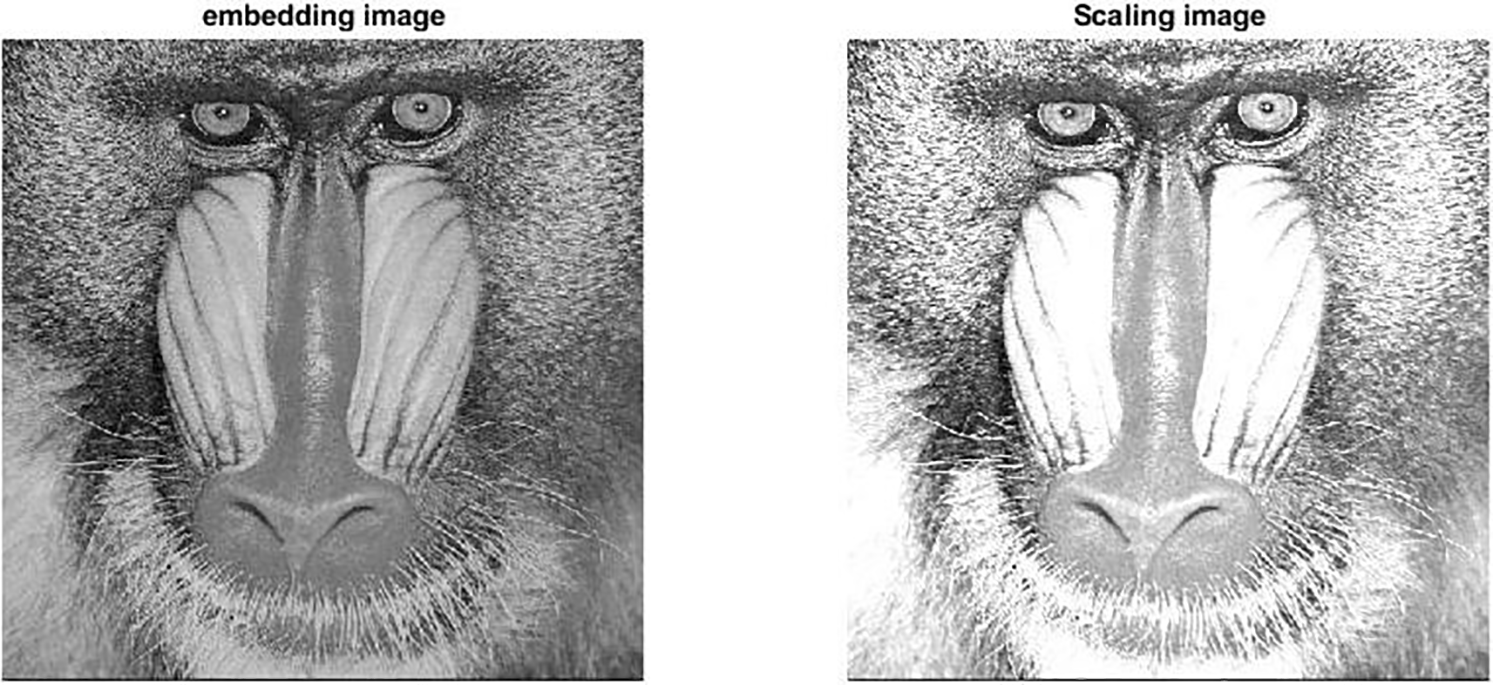
Figure 22: Watermarked image with sf = 1.5

(c)   Low pass filter

Image processing frequently utilizes low-pass filters, such as the running average or Gaussian filter. The Gaussian filter was chosen for use in our simulations in this study. Under the low-pass filter attack, Fig. 23 presents the BER results of four algorithms, including the algorithm optimized by parameters t=3 and 7. Although the Ref. [14] algorithm provides better BER performance, it also has higher complexity than the type-1 and type-2 algorithms do. Conversely, the algorithm has the lowest complexity and provides better performance than the Ref. [14] algorithm does. Fig. 24 displays the watermarked image processed through a Gaussian filter.

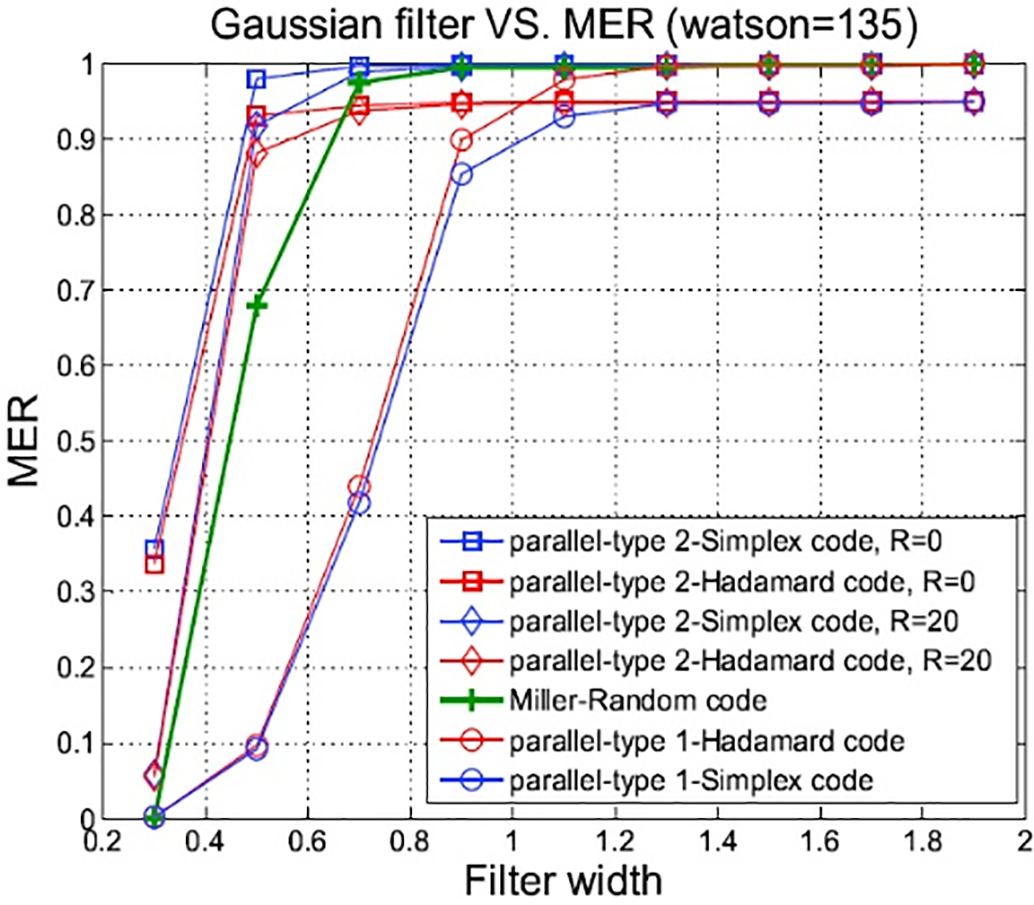
Figure 23: Robustness against low-pass filtering attacks

Figure 24: Watermarked image subjected to [7,7] Gaussian filter αf=1.5

(d)   JPEG

Lossy compression is a widely used technique, making watermark robustness against such compression highly desirable. Hence, we performed experiments to assess the impact of JPEG compression. The bit error rates were analyzed under varying degrees of JPEG compression. These levels specify DCT coefficient quantization values through multiplication by a quantization matrix:

μ×(1611101624405161121214192658605514131624405769561417222951878062182237566810910377243555648110411392496478871031211201017292959811210010399)

where μ is a global quantization level. The quantization level depends on the quality factor (QF), set by the user within the range of 0 to 100, and is defined as follows:

μ={50QF,  if QF<502−0.02∗QF,if QF≥50

The comparison of BERs was conducted over JPEG compression quality factors (QF) ranging between 20 and 80. The BER comparison between the proposed algorithm and the method in [14] is presented in Fig. 25. Using the informed embedding with memory algorithm, the BER quickly drops as QF rises, especially when QF is less than 25. These findings highlight the outstanding robustness of the informed embedding with memory algorithm against watermark degradation when JPEG compression quality is low. The watermarked image subjected to JPEG compression at QF = 20 is illustrated in Fig. 26.

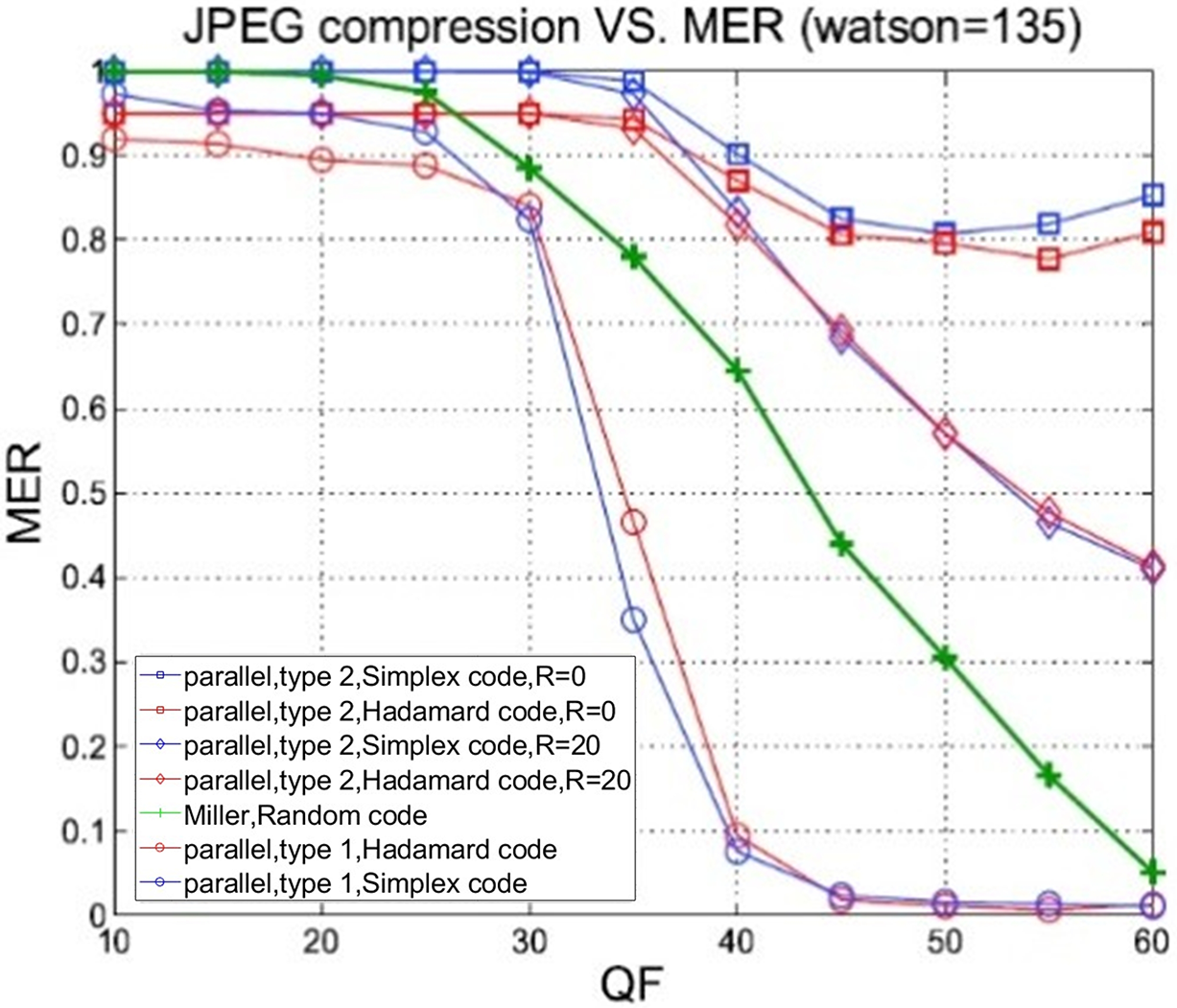
Figure 25: Robustness to JPEG compression at different QF levels

Figure 26: Watermarked image with QF = 20

(e)   Image quality (PSNR) under different attack channels

Finally, the proposed optimal method was employed to evaluate image quality under attack channels. The type 2 algorithm based on Hadamard code is used to simulate under various attack channels. Fig. 27 summarizes the image quality degradation caused by four different channels—AWGN, scaling, low-pass filtering (LPF), and JPEG—under varying attack strengths.

Figure 27: The image quality of watermarked image under different attack channels

(2) Computational complexity

In this section, we compare the algorithmic complexity of the approach outlined in [14] with that of the approach proposed in this study. The proposed ICE watermarking system performs informed coding followed by informed embedding. The complexity of the ICE system primarily arises from the informed coding and embedding algorithms. In the case of informed coding, the computational complexity involves identifying the codeword closest to the object message among parallel candidate arcs on a section-by-section basis. This process contrasts with the approach used in [14] because the accumulation operation in the Viterbi algorithm, which is a key component affecting their complexity, is not required in our informed coding scheme.

In addition to employing informed coding, the proposed informed embedding algorithm is section-based and does not require iterative processing of the overall codeword, as is the case in the algorithm of [14]. Informed coding with a parallel structure exhibits lower computational complexity than informed coding with a scatter structure. Here, we briefly compare the informed embedding algorithms. Complexity assessment for both the proposed method and that of [14] counts each arc in each trellis section as a unit. This metric represents the total computations performed per arc following the completion of embedding. The add-compare-select (ACS) operations performed in each trellis section of memory-based or accumulated Viterbi algorithms result in higher computational complexity than those of memoryless embedding structures. In this study, the operational counts for the proposed algorithm and that of [14] are tabulated and compared. Additionally, three complexity parameters relevant to the trellis structure are defined as follows: Ca: the total number of arcs in a section; Cs: the number of ACS operations required to achieve the specified robustness parameter R, as proposed in Section 3.1 (type-2), and defined as:

Cs=Ca+CACS

where CACS represents the number of adders and comparers in a section; and Ct: the average total number of operations in each section, defined as:

Ct=Cs+Cavg×L

where Cavg is the average number of iterative operations in a section and L is the number of sections. Finally, the total memories required in a trellis are defined as:

Mt=Ns×(L+1)

where Ns is the number of states in a trellis section. In our experiments, 250 life photos of size 512×512 were used. The average results of 100 operations are presented in the following. The experiments were used to compare the result of four types of informed embedding algorithms, namely, type-1, type-2 (R = 5), type-2 (R = 10), and type-2 (R = 20), under the same conditions, with the trellis state number = 16, L = 1536, and Ca = 32 in each arc. The image quality was fixed, with a Watson distance of 135 and a given step factor β = 0.01. To achieve constant Watson image imperceptibility, the parameter α for type-1 (Simplex code), type-2 (Simplex code), type-1 (Hadamard code), and type-2 (Hadamard code) is 181.48, 186.65, 174.45, and 178.85, respectively. Regarding operational complexity, the type-1 algorithm in 3.1 requires finding the minimal distance d(αck,xk) to determine if the arc operation is closer to the selected codeword αwk in section k, requiring 32 comparer operations. The type-2 algorithm involves accumulation through ACS operations, with 16 adder operations and comparer operations required in a section because the number of current and next states is 16. These results that are obtained are compared with those of [14] and tabulated in Table 6.

The computational cost of the four algorithms and [14] is presented in Table 6, with the results revealing the processing requirements of each arc and the ACS operations. The total operational complexity, Ct, of these algorithms is ranked in the following order:

Miller’s method > type-1 > type-2 (R = 20) > type-2 (R = 10) > type-2 (R = 5)

This ranking indicates that despite the proposed algorithms exhibiting lower complexity, they maintain the same level of robustness as the other algorithms. The simulation results reveal that the type-1 algorithm demonstrates high robustness against certain attacks and has low operation complexity.

To more clearly illustrate the advantages and differences of the proposed algorithm, an overall comparison is necessary. Finally, we compared with [14] and tabulated as Table 7. The simulation environment is based on a Gaussian channel with a variance of 25. We evaluated image quality using three metrics: PSNR, and LPIPS, and assessed robustness and complexity through MER and computational complexity Ct estimation. As shown in Table 7, under a Gaussian channel with fixed noise, the proposed algorithm achieves better error rates and image quality compared to [14]. In the experiments, we used PSNR and LPIPS as image quality evaluation metrics. The results show that, under an AWGN channel with fixed noise power, both metrics exhibit a consistent variation trend, indicating that the proposed method indeed provides better image quality. In addition, the proposed method also offers lower computational time complexity. Compared to [15,16], the method proposed in this paper uses FCM to generate linear block codes. These codes exhibit good distance properties and offer better decoding efficiency. However, in terms of time complexity, Refs. [15,16] may achieve better performance than the proposed method.

5  Conclusion

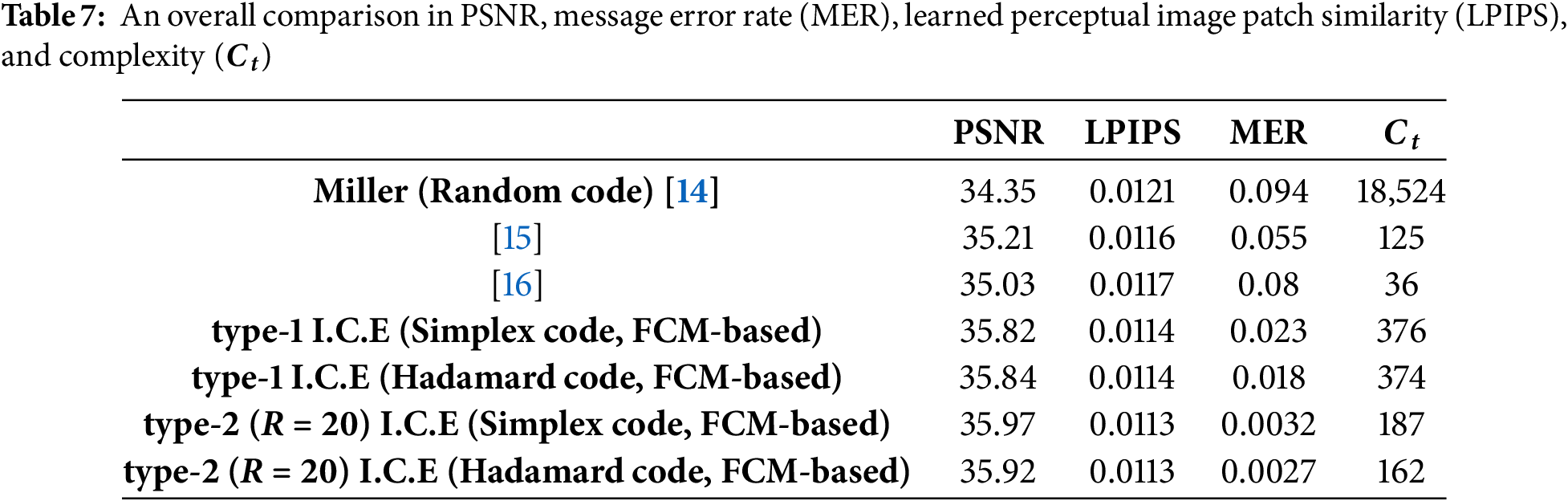
In this paper, we presented three informed embedding algorithms for watermarking systems. These algorithms employ codewords derived from the FCM algorithm applied to linear block codes for labeling arcs in the trellis. They then adjust the imperceptibility and robustness of watermarked images using controllable parameters. The proposed informed coding and embedding algorithms exhibit three key properties: (1) control through parameters; (2) employment of parallel arcs in informed coding; and (3) execution of an iterative algorithm, segment by segment. The trellis is constructed to resist channel attacks while maintaining a predetermined level of imperceptibility. These methods reduce the operational complexity of achieving high-quality watermarked images and provide better BER performance compared with Miller’s informed embedding. Furthermore, the generated watermarked images were subjected to a variety of attacks, and the experimental results demonstrate their performance in terms of the BER and message error rate. Moreover, this study utilizes the FCM algorithm to generate codewords serving as arc labels in each trellis structure. For future research, replacing the FCM algorithm with deep learning–based approaches may be considered, as these methods are expected to provide enhanced encoding performance. This study primarily focuses on embedding binary data into grayscale images. Although other image formats are not explicitly discussed, the proposed algorithm can be extended to any carrier format that represents image content as a data sequence. For instance, a color image can be separated into three channels (R, G, and B), and the proposed method can be applied to embed data into each channel individually. Moreover, the proposed algorithms are mainly designed to withstand non-geometric attacks such as Gaussian noise, compression, and filtering, and they demonstrate strong robustness in these scenarios. However, this study does not comprehensively address geometric channel attacks, which is a limitation of the current work. Future research should therefore prioritize the extension of the algorithm to enhance its robustness against geometric distortions. Especially, we will extend this work by investigating techniques such as synchronization templates, feature points/regions, transform-domain methods, geometric-invariant wavelets/moments, and blind synchronization.

Acknowledgement: Not applicable.

Funding Statement: This research was funded by the National Science and Technology Council, Taiwan, under grant number NSTC 114-2221-E-167-005-MY3, and NSTC 113-2221-E-167-006-.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Jyun-Jie Wang, Yin-Chen Lin, Chi-Chun Chen; data collection: Jyun-Jie Wang, Yin-Chen Lin; analysis and interpretation of results: Jyun-Jie Wang, Chi-Chun Chen; draft manuscript preparation: Jyun-Jie Wang, Chi-Chun Chen. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author on reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Symbols and Specific Notation

References

1. Moulin P, Koetter R. Data-hiding codes. Proc IEEE. 2005;93(12):2083–126. doi:10.1109/JPROC.2005.859599. [Google Scholar] [CrossRef]

2. Tian C, Zheng M, Li B, Zhang Y, Zhang S, Zhang D. Perceptive self-supervised learning network for noisy image watermark removal. IEEE Trans Circuits Syst Video Technol. 2024;34(8):7069–79. doi:10.1109/TCSVT.2024.3349678. [Google Scholar] [CrossRef]

3. Wen S, Zhang Q, Hu T, Li J. Robust audio watermarking against manipulation attacks based on deep learning. IEEE Signal Process Lett. 2024;32:126–30. doi:10.1109/LSP.2024.3501285. [Google Scholar] [CrossRef]

4. Zhong X, Huang PC, Mastorakis S, Shih FY. An automated and robust image watermarking scheme based on deep neural networks. IEEE Trans Multimed. 2020;23:1951–61. doi:10.1109/TMM.2020.3006415. [Google Scholar] [CrossRef]

5. Amrit P, Baranwal N, Singh KN, Singh AK. ConvNet-HIDE: deep-learning-based dual watermarking for health-care images. IEEE Multimed. 2024;31(3):78–87. doi:10.1109/MMUL.2024.3423370. [Google Scholar] [CrossRef]

6. Han B, Jhaveri RH, Wang H, Qiao D, Du J. Application of robust zero-watermarking scheme based on federated learning for securing the healthcare data. IEEE J Biomed Health Inform. 2023;27(2):804–13. doi:10.1109/jbhi.2021.3123936. [Google Scholar] [PubMed] [CrossRef]

7. Anand A, Singh AK. Health record security through multiple watermarking on fused medical images. IEEE Trans Comput Soc Syst. 2022;9(6):1594–603. doi:10.1109/TCSS.2021.3126628. [Google Scholar] [CrossRef]

8. Chen L, Bai W, Yao Z. A secure and privacy-preserving watermark based medical image sharing method. Chin J Electron. 2020;29(5):819–25. doi:10.1049/cje.2020.07.003. [Google Scholar] [CrossRef]

9. Tong G, Liang Z, Xiao F, Xiong N. A residual chaotic system for image security and digital video watermarking. IEEE Access. 2021;9:121154–66. doi:10.1109/access.2021.3108196. [Google Scholar] [CrossRef]

10. Bordel B, Alcarria R, Robles T, Iglesias MS. Data authentication and anonymization in IoT scenarios and future 5G networks using chaotic digital watermarking. IEEE Access. 2021;9:22378–98. doi:10.1109/access.2021.3055771. [Google Scholar] [CrossRef]

11. Wang ZX, Sha KY, Gao XL. Digital watermarking technology based on LDPC code and chaotic sequence. IEEE Access. 2022;10(2):38785–92. doi:10.1109/access.2022.3166475. [Google Scholar] [CrossRef]

12. Singh HK, Singh AK. Using deep learning to embed dual marks with encryption through 3-D chaotic map. IEEE Trans Consum Electron. 2024;70(1):3056–63. doi:10.1109/TCE.2023.3286487. [Google Scholar] [CrossRef]

13. Wainwright MJ. Sparse graph codes for side information and binning. IEEE Signal Process Mag. 2007;24(5):47–57. doi:10.1109/MSP.2007.904816. [Google Scholar] [CrossRef]

14. Miller ML, Doërr GJ, Cox IJ. Applying informed coding and embedding to design a robust high-capacity watermark. IEEE Trans Image Process. 2004;13(6):792–807. doi:10.1109/tip.2003.821551. [Google Scholar] [PubMed] [CrossRef]

15. Wang JJ, Chen H, Lin CY. A robust informed embedding with low complexity of digital watermarking. Int J Innov Comput Inf Control. 2012;8(10A):6849–68. [Google Scholar]

16. Wang JJ, Chen H, Liang H. A trellis-based informed embedding with linear codes for digital watermarking. In: 2011 IEEE 15th International Symposium on Consumer Electronics (ISCE); 2011 Jun 14–17; Singapore. doi:10.1109/ISCE.2011.5973782. [Google Scholar] [CrossRef]

17. Bezdek JC, Hathaway RJ, Sabin MJ, Tucker WT. Convergence theory for fuzzy c-means: counterexamples and repairs. IEEE Trans Syst Man Cybern. 1987;17(5):873–7. doi:10.1109/TSMC.1987.6499296. [Google Scholar] [CrossRef]

18. Bezdek JC. Pattern recognition with fuzzy objective function algorithms. Berlin/Heidelberg, Germany: Springer; 2013, 10.1007/978-1-4757-0450-1. [Google Scholar] [CrossRef]

19. Jain AK. Data clustering: 50 years beyond K-means. Pattern Recognit Lett. 2010;31(8):651–66. doi:10.1016/j.patrec.2009.09.011. [Google Scholar] [CrossRef]

20. Döring C, Lesot MJ, Kruse R. Data analysis with fuzzy clustering methods. Comput Stat Data Anal. 2006;51(1):192–214. doi:10.1016/j.csda.2006.04.030. [Google Scholar] [CrossRef]

21. Hathaway RJ, Hu Y. Density-weighted fuzzy c-means clustering. IEEE Trans Fuzzy Syst. 2009;17(1):243–52. doi:10.1109/TFUZZ.2008.2009458. [Google Scholar] [CrossRef]

22. Kaymak U, Setnes M. Fuzzy clustering with volume prototypes and adaptive cluster merging. IEEE Trans Fuzzy Syst. 2002;10(6):705–12. doi:10.1109/TFUZZ.2002.805901. [Google Scholar] [CrossRef]

23. Desset C, Macq B, Vandendorpe L. Block error-correcting codes for systems with a very high BER: theoretical analysis and application to the protection of watermarks. Signal Process Image Commun. 2002;17(5):409–21. doi:10.1016/S0923-5965(02)00010-3. [Google Scholar] [CrossRef]

24. Lin L, Doerr G, Cox IJ, Miller ML. An efficient algorithm for informed embedding of dirty-paper trellis codes for watermarking. In: IEEE International Conference on Image Processing 2005; 2005 Sep 14; Genova, Italy. doi:10.1109/ICIP.2005.1529846. [Google Scholar] [CrossRef]

25. Forney GD. The viterbi algorithm. Proc IEEE. 1973;61(3):268–78. doi:10.1109/PROC.1973.9030. [Google Scholar] [CrossRef]