 Open Access
Open Access
ARTICLE
Credit Card Fraud Detection Method Based on RF-WGAN-TCN
1 School of Software, East China University of Technology, Nanchang, 330013, China
2 School of Information Engineering, East China University of Technology, Nanchang, 330013, China
* Corresponding Author: Hongzhen Xu. Email:
Computers, Materials & Continua 2025, 85(3), 5159-5181. https://doi.org/10.32604/cmc.2025.067241
Received 28 April 2025; Accepted 15 August 2025; Issue published 23 October 2025
Abstract
Credit card fraud is one of the primary sources of operational risk in banks, and accurate prediction of fraudulent credit card transactions is essential to minimize banks’ economic losses. Two key issues are faced in credit card fraud detection research, i.e., data category imbalance and data drift. However, the oversampling algorithm used in current research suffers from excessive noise, and the Long Short-Term Memory Network (LSTM) based temporal model suffers from gradient dispersion, which can lead to loss of model performance. To address the above problems, a credit card fraud detection method based on Random Forest-Wasserstein Generative Adversarial Network-Temporal Convolutional Network (RF-WGAN-TCN) is proposed. First, the credit card data is preprocessed, the feature importance scores are calculated by Random Forest (RF), the features with lower importance are eliminated, and then the remaining features are standardized. Second, the Wasserstein Distance Improvement Generative Adversarial Network (GAN) is introduced to construct the Wasserstein Generative Adversarial Network (WGAN), the preprocessed data is input into the WGAN, and under the mutual game training of generator and discriminator, the fraud samples that meet the target distribution are obtained. Finally, the temporal convolutional network (TCN) is utilized to extract the long-time dependencies, and the classification results are output through the Softmax layer. Experimental results on the European cardholder dataset show that the method proposed in the paper achieves 91.96%, 98.22%, and 81.95% in F1-Score, Area Under Curve (AUC), and Area Under the Precision-Recall Curve (AUPRC) metrics, respectively, and has higher prediction accuracy and classification performance compared with existing mainstream methods.Keywords
The popularisation of Internet technology has led to significant improvements in people’s living standards, resulting in profound changes in consumption patterns and attitudes. The emergence of new solutions, such as e-commerce and mobile payment, has led to a steady increase in online shopping and the ubiquity of credit card transactions [1]. Given the availability of convenient payment methods and a wide range of consumption choices, individuals are susceptible to falling into consumption traps, while simultaneously attracting the attention of fraudsters [2]. Credit cards, as a convenient payment tool, offer great convenience, but they also pose potential risks. Some users overdraw their credit cards and overestimate their ability to repay their credit card loans on time in pursuit of momentary pleasure and material desires. This irrational consumer behaviour not only puts financial pressure on oneself but also increases the risk of bank lending [3].
Fraud detection is typically accomplished by analyzing transaction history data to identify patterns and build predictive models that estimate the likelihood of fraudulent behavior in future transactions. The field of credit card fraud detection faces three principal challenges. The foremost challenge involves feature redundancy, where certain features in transaction data prove irrelevant or duplicative, negatively impacting model training efficiency and effectiveness. Equally critical is the challenge of severe class imbalance, as demonstrated by the China Banking Association’s Blue Book of China Bank Card Industry Development (2021 Edition), which reports a national fraud rate of just 0.0075% [4], highlighting the extreme scarcity of fraudulent transactions compared to legitimate ones. This scarcity of fraudulent samples necessitates careful modeling approaches to accurately capture data distributions and generate representative samples, often requiring oversampling techniques. Additionally, the field must contend with temporal data drift, where evolving spending patterns—such as increased impulsive consumption during holidays—can alter data distributions and impair model performance [5]. Ultimately, the core research challenge lies in simultaneously extracting meaningful temporal patterns from vast transaction datasets while ensuring any synthetically generated fraud samples remain consistent with the original data distribution.
In this paper, we propose a novel credit card fraud detection method based on Random Forest-Wasserstein Generative Adversarial Network-Temporal Convolutional Network (RF-WGAN-TCN). First, the credit card transaction data undergoes preprocessing, where feature importance scores are computed using Random Forest (RF). Features with lower importance are subsequently eliminated, and the remaining features are standardized. Next, we introduce an improved Generative Adversarial Network (GAN) optimized with Wasserstein Distance, constructing a Wasserstein Generative Adversarial Network (WGAN). The preprocessed data is fed into the WGAN, and through adversarial training between the generator and discriminator, synthetic fraud samples conforming to the target distribution are generated. Finally, a Temporal Convolutional Network (TCN) is employed to capture long-term temporal dependencies, with classification results produced via the Softmax layer.
The main contributions of the paper are in the following areas:
• A method for screening credit card features based on random forest is proposed. This method solves the issue of redundancy in credit card features, simplifies the model, and speeds up training and detection.
• A method for oversampling fraud samples based on WGAN is proposed to address the issue of imbalanced data categories. The method can generate high-quality fraud samples, which improves the accuracy of model detection.
• A method for extracting temporal features based on TCN is proposed. The method addresses the issue of data drift and enables better capture of potential temporal patterns in credit card data.
The remainder of the paper is structured as follows: Section 2 presents the related work. Section 3 presents an extended description of the methodology proposed in this paper. Section 4 is the experimental validation part of the paper. Section 5 concludes the paper.
For the category imbalance problem, data drift problem, and the conceptually related challenge of concept drift, researchers have proposed many solution approaches. In this paper, we systematically review the current research progress in unbalanced classification methods and temporal feature extraction methods, while also examining concept drift detection techniques as an associated research domain.
2.1 Imbalance Classification Methodology
In fraud detection, unbalanced data classification is a major challenge. When one class in a dataset has much less data than another, the dataset is said to be unbalanced [6]. Most classification models have high recognition rates for the majority class and low recognition rates for the minority class, resulting in poor model performance in diagnosing minority class samples. Over-sampling techniques [7] and under-sampling techniques [8] are mainly used to deal with the problem of unbalanced data classes. For example, Rtayli and Enneya [9], Ileberi et al. [10] used synthetic fraudulent samples generated by interpolation using the SMOTE oversampling algorithm, which effectively expands the distribution of minority class samples in the feature space. Ying and Zhang [11] used the K-meansSMOTE algorithm to generate fraudulent samples only in the safe region, which avoids the problem that the SMOTE algorithm can be easily overfitted; such a strategy not only significantly improves the generalisation ability of the model, but also ensures that the generated synthetic samples are closer to the distribution of the real data, Alamri and Ykhlef [12] used utilizes Tomek links for undersampling to eliminate noisy and overlapping instances while employing BIRCH clustering with Borderline-SMOTE to achieve a more balanced distribution of legitimate and fraudulent transactions. Esenogho et al. [13] combined the SMOTE oversampling technique and the ENN undersampling technique to perform hybrid sampling of credit card data, using the domain cleaning rule in the ENN algorithm to remove duplicate and similar samples from a large number of fraudulent samples, and then using the SMOTE algorithm to oversample the fraudulent samples, which significantly improves the overall distribution of the credit card data, making it more balanced. Mqadi et al. [14] proposed a two-step hybrid data point method to solve the data category imbalance problem by using the correlation coefficient for feature screening and the NearMiss algorithm to undersample the dataset, which can significantly improve the performance of the machine learning model. Wang et al. [15] proposed an innovative monitoring mechanism for the category imbalance problem, which can monitor the data through each round of intermediate data during training to infer the occurrence of class imbalance, and designed a new loss function to eliminate the effect of class credit card fraud samples. Almarshad et al. [16] introduced Generative Adversarial Networks to the problem of credit card mismatch classification, where artificial fraudulent samples that are increasingly close to the real samples can be generated by adversarial training between the discriminator and the generator in the GAN.
In existing research, the SMOTE oversampling method is widely used, but it has the problems of fuzzy boundaries and too much noise. To solve this problem, some scholars have proposed the K-meansSMOTE algorithm, i.e., to cluster the fraud samples before oversampling. However, this algorithm mainly expands the fraud samples by interpolation, and the new data are mostly variants of the existing data, without actually introducing new information. In comparison, the data generated by GAN is diverse and can learn the data distribution and generate new samples, providing more diverse data for fraud detection. However, the GAN training process is less stable, which can affect the quality of fraud sample generation. On the other hand, undersampling methods may omit important information or even erroneously delete representative samples, causing serious problems for fraud detection. Therefore, when choosing an unbalanced classification method, it is important to ensure that the problem of data imbalance is addressed while retaining key information.
2.2 Timing Feature Extraction Method
When dealing with the problem of data drift, researchers often choose to use deep learning based time series models. These models have the ability to capture complex patterns and dynamic changes in time series data, and can flexibly adapt to changes in data distribution [17]. In the field of credit card fraud detection, deep learning based time series models have been widely adopted and applied. For example, Kolli and Tatavarthi [18] and others used RNN to implement the fraud detection process and proposed the HarrisWater algorithm to optimise the training process of classification, which is able to detect fraudulent activities more efficiently. Gao et al. [19] used an LSTM model to mine the hidden temporal features of credit card data, which revealed the possible patterns in fraudulent behaviour, and then used a gradient boosting decision tree to construct a classifier to complete the fraud identification and classification tasks, thus achieving high accuracy fraud detection. Benchaji et al. [20] proposed an LSTM model incorporating the attention mechanism, by incorporating the attention layer into the LSTM model, it can achieve the selective attention to the features, thus improving the fraud detection efficiency of the model for financial institutions. provide timely and reliable fraud alerts. Forough and Momtazi [21] aggregated multiple LSTM models into a unified network model based on the voting mechanism in integrated learning, where each LSTM model has equal voting rights and they vote based on their respective classification results, and in this way synthesised each LSTM model to obtain a more comprehensive and accurate fraud detection classification. Forough and Momtazi [22] also proposed another credit card fraud detection model by constructing the model with LSTM and CRF models as the initial and final detection layers, respectively. The combination of LSTM and CRF further enriches the characteristics of the model by exploiting the prediction dependency information between transactions. Liu et al. [23] propose a sequence-based large model based on a Decoder-Only Transformer, utilizing a TimeAttention mechanism to effectively model cross-sequence dependencies in multivariate sequence data. Through large-scale pre-training with 260 billion time points, we achieve leading zero-shot prediction capabilities. Dai et al. [24] propose a lightweight multi-scale linear Transformer that improves prediction efficiency by mining global variable correlations and modeling long-term temporal dependencies. Experiments on eight real-world datasets validate its computational efficiency and accuracy advantages in high-dimensional temporal data.
Temporal modelling has received a lot of attention recently, and significant progress has been made in temporal feature extraction. However, there are still some problems. Traditional RNN models are limited by their hidden state size, which makes it difficult to retain early information effectively and, therefore, perform poorly on long sequence data. In contrast, LSTM models are able to selectively retain and update information through their unique gating mechanism, preserving valuable information over a long period of time. However, LSTM faces the challenges of vanishing gradients and slow convergence, which somewhat limit its effectiveness in certain tasks. While Transformer-based approaches demonstrate superior performance in capturing long-range dependencies through self-attention mechanisms, they typically require substantial computational resources for training and may struggle with real-time processing of high-frequency transaction data due to their quadratic complexity. Therefore, further in-depth research and exploration of more effective temporal feature extraction methods are needed to address these issues.
2.3 Concept Drift Handling Method
Concept drift in credit card fraud detection has attracted growing research attention. Although our approach does not explicitly handle concept drift, the dynamic characteristics of credit card fraud establish drift detection as an essential research direction in this domain. For instance, Yu et al. [25] proposed a meta-learning framework that replaces traditional hypothesis testing while improving both the responsiveness and accuracy of drift detection. In subsequent work, the same research group developed an online learning algorithm for identifying drift in multi-stream environments [26]. Meanwhile, Lu et al. [27] employed prediction uncertainty instead of error rates for early-stage drift detection—an approach particularly suitable for fraud detection systems with delayed feedback. Most recently, Wan et al. [28] introduced a contrastive learning method for label-free drift discrimination in high-dimensional data streams.
While the aforementioned approaches primarily address model maintenance in dynamic environments through concept drift detection, our work focuses specifically on resolving class imbalance and sequential pattern recognition using WGAN and TCN architectures. Future research could investigate the integration of explicit drift detection mechanisms (e.g., adaptive windowing or uncertainty monitoring) with our proposed framework to enhance its robustness in evolving data distributions.
In this section, we present the architectural framework of the RF-WGAN-TCN model, with comprehensive descriptions of its three core components: the preprocessing module, oversampled module, and predictive module.
3.1 RF-WGAN-TCN Credit Card Fraud Detection Model
The problem of credit card fraud detection is, firstly, how to learn the original distribution from the high-dimensional data with complex distribution and generate fraud samples to balance the data. The second is to identify the potential time change patterns from the historical transaction data to improve the classification accuracy of the detection model as much as possible. To address the above problems, this paper proposes a credit card fraud detection method based on RF-WGAN-TCN, and the overall framework is shown in Fig. 1:
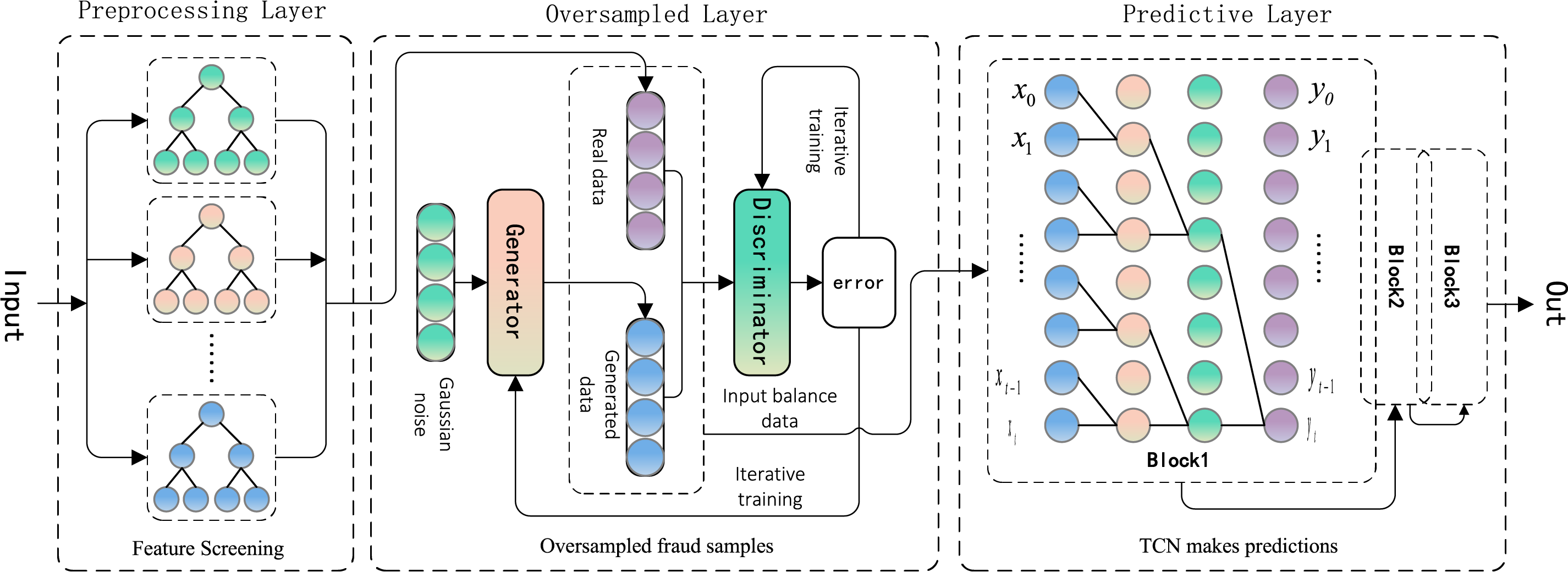
Figure 1: RF-WGAN-TCN credit card fraud detection model
The construction of this model consists of the following steps:
Step 1. Feature Screening. The random forest algorithm is used for feature selection on the credit card dataset, removing features with low importance.
Step 2. WGAN oversampling of fraudulent samples. The preprocessed data is input to the WGAN. Through adversarial training between the generator and discriminator, the generator learns the original data distribution, generating high-quality fraudulent samples to obtain a balanced dataset.
Step 3. TCN extraction of temporal features. The model uses causal convolution layers to capture time series dependencies, with residual connections and normalization techniques to improve feature propagation and stability. The outputs from three residual modules are combined and processed through a softmax function to determine fraud probabilities.
The standardization of the data can be enough to eliminate the quantitative relationship between the features, so that the features are comparable with each other. In this paper, the Z-Score algorithm is used to standardize the credit card data, assuming that the dataset has a total of I features, the standardization formula for the
where:
By eliminating invalid or redundant features, the selection of relevant features from all the features useful for training can improve the classification performance of the model. Based on integrated learning, Breiman [29] proposed Random Forest (RF) based on decision trees, which integrates the prediction results by constructing multiple decision trees for voting. In this paper, the Random Forest algorithm is used as a feature screening method for a given credit card data set. The bootstrap resampling algorithm extracts subsets from it, and decision tree modelling is performed for each subset separately. The training samples used in Random Forest contain 28 credit card desensitization features V1, V2......, and V28, and their feature importance scores are computed in the following steps:
Step 1. For the the
where: K is the number of transaction categories and
Step 2. Calculate the change in Gini index of the th credit card desensitization feature
where:
Step 3. Calculate the total Gini index change for the
Step 4. Calculate the total Gini index change for the
Step 5. Normalize the
where:
Step 6. Eliminate features with feature importance scores less than 0.02.
3.3.1 Wasserstein Distance Improvement GAN
Generative Adversarial Network (GAN) [30] is an unsupervised neural network that contains two adversarial training networks. Among them, the role of the generator is to learn the latent distribution in natural samples to synthesise samples that are difficult for the discriminator to distinguish; the role of the discriminator is to distinguish whether the samples generated by the generator are real samples or not, as far as possible to maximise the accuracy of its judgement. When the generator converges to the optimum in the GAN, the goal of the generator becomes minimising the JS scatter between the generated data and the exact data distribution. However, if there is no overlapping distribution between the generated data and the actual data, the JS scatter will always be a constant and can no longer reflect the distance between the two distributions. For the generator, the gradient of the objective function with respect to the parameters is zero, which leads to training instability in the GAN.
Aiming at the problem of poor training stability of traditional GAN, this paper uses the Wasserstein distance [31] instead of the JS dispersion in traditional GAN to measure the distance between artificial fraud samples and real samples. The advantage is that even if there is no overlap or minimal overlap between the two distributions, the Wasserstein distance can still reflect the degree of proximity between the two distributions. The smaller the value, the more similar the two distributions are, which can effectively reduce the instability of the training process. The Wasserstein distance is defined as follows:
where:
3.3.2 Oversampling of Fraudulent Samples
Assume that the credit card dataset is
Step 1. Initialize the generator and discriminator of WGAN. Both are set as neural networks with three fully connected layers, the network weights are updated using the RMSprop optimizer, the output dimension of the generator is set to the total number of credit card features, and the output dimension of the discriminator is set to one.
Step 2. Generate random noise conforming to Gaussian distribution
Step 3. Input the original sample X and the generated sample
where:
Step 4. The updated discriminator re-discriminates the generated samples
After obtaining the error of G, the network weights of G are updated according to the back-propagation gradient descent algorithm.
Step 5. Repeat the execution of steps 2 to 4, in the generator and the discriminator constantly game training, the discriminator eventually can no longer distinguish the source of the fraudulent samples, at this time to reach the Nash equilibrium [32]. Combine Eqs. (8) and (9) to establish the objective function of WGAN network as follows:
Step 6. Generate random noise in the amount of the difference between
The Temporal Convolutional Network (TCN) was proposed by Lea et al. [33] in 2018, which is mainly applied to solve temporal sequencing problems. The TCN consists of several stacked residual modules, each of which contains two expansion causal convolutions and a constant mapping. Among them, the dilated causal convolution grants the existence of interval convolution operations when processing the input data, which can realize the expansion of the receptive field without changing the size of the convolution kernel and the number of layers of the network, and solves the problem of overly complex training of the traditional causal convolution when expanding the receptive field. The residual module can realise the information transfer between layers, effectively avoiding the information loss problem when the input data is propagated in too many network layers.
Unlike cyclic structures such as RNN, LSTM and GRU, TCN does not rely on time-step propagation to process sequences, but uses convolutional layers to capture patterns in the time dimension. As a result, the gradient propagation of TCN is related to the depth of the network rather than the temporal direction, effectively avoiding the gradient dispersion problem caused by cyclic connections such as RNN. This makes TCNs more efficient in dealing with long sequences and less likely to suffer performance degradation. The TCN constructed in this paper contains three residual modules, each consisting of a dilated causal convolutional layer, a weight norm layer, a ReLU activation function layer, a dropout layer and a constant mapping. The existing category-balanced credit card dataset
Step 1. Initialize the dilation causal convolutional layer. An expansion causal convolutional layer contains one input layer, two hidden layers and one output layer, the convolutional kernel size is set to 2, and the expansion coefficients of each layer are set to 1, 2 and 4, respectively, and the structure of the expansion causal convolutional network constructed in this paper is shown in Fig. 2:

Figure 2: Dilated causal convolutions
Step 2. For the credit card data
Step 3. From step 2, we can get the output
where: X′ is the credit card balanced dataset, K is the size of the convolution kernel,
Step 4. Add WeightNorm layer to normalize the weight vectors of the network to prevent gradient explosion; add ReLU activation function layer to introduce nonlinear factors to improve the expression performance of the model by increasing the sparsity of the model; and add Dropout layer to discard neurons according to a certain probability to prevent overfitting.
Step 5. Repeat the execution of steps 1 to 4 to pass the data across layers by 1 additional
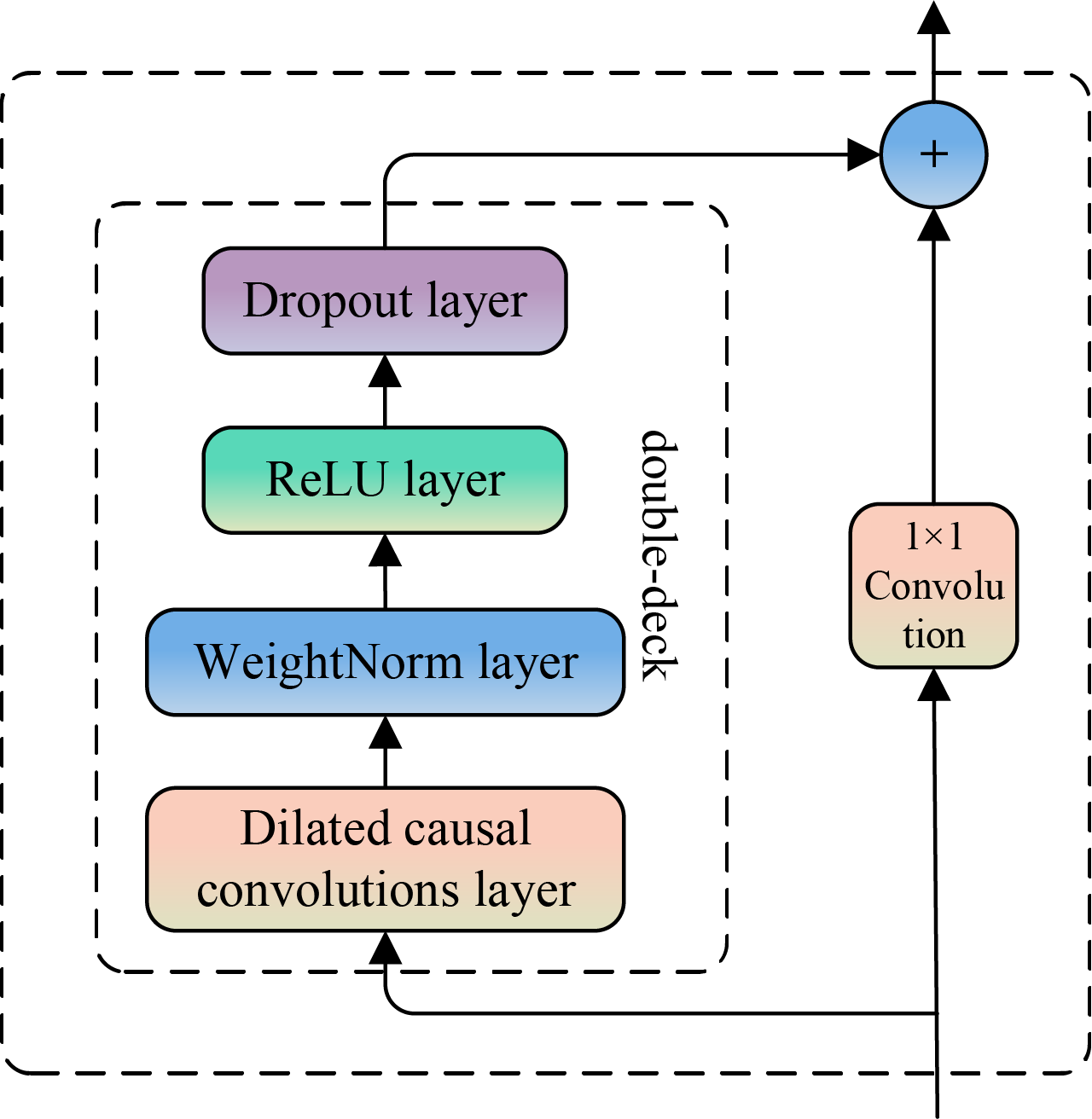
Figure 3: Residual block for TCN
The residual module fuses the input X′ weighted to the output
where:
Step 6. Stack the output of the 3 residual modules and present this result as a probability, i.e., the probability that the sample will be determined to be a fraudulent sample, using a layer of Softmax normalization functions.
This section first presents the publicly available dataset and evaluation metrics and parameter selection used in this paper, followed by experiments to validate the effectiveness of the proposed methodology. The main objective of the experiments in this paper is to answer the following questions:
• Whether Random Forest-based feature screening can effectively improve the classification performance of the model, and how its feature screening threshold is determined.
• Whether the TCN classifier constructed in this paper is better than other temporal models for detecting.
• Whether WGAN-based oversampling methods are better than other oversampling methods, and whether WGAN is more stable than GAN.
Next, the experimental setup of this paper is described and then the results are analysed to answer the above questions.
The dataset used in this paper is derived from a publicly available dataset on the Kaggle platform, collected by the machine learning groups at Worldline and ULB during an extensive data mining exercise related to fraud detection. The dataset contains credit card transaction records from European cardholders over two days in September 2013, with 284,807 transaction records [34]. Of these, only 492 transactions were fraudulent, representing a fraud rate of 0.172%. The specific dataset description is shown in Table 1.

The dataset has a total of 31 feature variables with no missing values. Features V1, V2,
4.2.1 Experimental Environment
The experiments in this paper were conducted using a Windows 10 system, an AMD Ryzen 7 5800H CPU, 16.0 GB of RAM, and an NVIDIA GeForce RTX 3060 graphics card. The Sklearn toolkit and Keras toolkit implementations of the Python programming language were used to build the model.
Evaluation metrics are designed to measure the performance and prediction accuracy of a model, and are used to evaluate the prediction error of a model by calculating the difference between the predicted result and the actual value, thus assessing its predictive capability. The use of evaluation metrics can provide a comprehensive understanding of the strengths and weaknesses of the model, and then optimise the model parameters and improve the prediction accuracy. This paper evaluates the model based on the following metrics.
Accuracy: The proportion of true results (both true positives and true negatives) among the total number of cases examined.
where: TP = True Positives, TN = True Negatives, FP = False Positives, FN = False Negatives.
Precision: The proportion of true positive results among the total number of positive predictions.
Recall: The proportion oftrue positive results among the total number of actual positives.
F1-score: The harmonic mean of precision and recall, providing a balance between the two.
AUC: A Area Under the Receiver Operating Characteristic Curve (AUC ROC) performance metric for binary classification models. The ROC curve plots the True Positive Rate (TPR) against the False Positive Rate (FPR) at various threshold settings. True Positive Rate (TPR), also known as sensitivity or recall:
False Positive Rate (FPR):
The AUC (Area Under the Curve) measures the entire two-dimensional area under the ROC curve, providing an aggregate performance measure across all classification thresholds. The AUC ranges from 0 to 1, with 1 representing a perfect model and 0.5 representing a model with no discrimination ability.
where: d(FPR) is a mathematical notation indicating that the AUC is the area under the curve created by plotting TPR against FPR as FPR changes incrementally from 0 to 1.
AUPRC: The PR curve is constructed by varying the decision threshold and plotting Precision against Recall. The area under the Precision-Recall curve (AUC-PR) can be mathematically expressed as:
When investigating the generalisation ability of a model, the performance of the classifier can be evaluated using the ROC curve and the PR curve. The ROC curve plots the samples as positive examples one by one in the order of the predicted results, using the true rate as the vertical axis and the false positive rate as the horizontal axis. The PR curve, on the other hand, is plotted using the precision rate as the vertical axis and the precision rate as the horizontal axis. Although the ROC curve is more widely used in the evaluation of binary classification problems, the ROC curve cannot effectively reflect the effect on the model when the sample categories are unbalanced and may give a more optimistic result, while the PR curve is more sensitive to extremely unbalanced data sets. Therefore, in this paper, both the ROC curve and the PR curve are used to visualise the classification performance of the model. In addition, the ROC curve includes an important indicator AUC, the value of which is the area under the ROC curve; if the PR curve is closer to the top left or the area under the curve is larger, it indicates that the model’s classification performance is better. Similarly, the PR curve includes an important metric, AUPRC, the value of which is the area under the PR curve, and if the PR curve is closer to the upper right or the area under the curve is larger, it indicates better model classification performance. In the case of extremely unbalanced datasets, the AUPRC metric can provide more accurate evaluation results than the AUC metric [35].
The first 70% of the historical transaction data is selected as a training set for the model to learn to detect fraud. The last 30% of the historical transaction data is selected as a test set to test the classification ability of the model to understand the performance of the model on unknown data.
The selection and tuning of hyperparameters is one of the important aspects of deep learning, and hyperparameters can directly affect the training effect and the performance of the model. The selection and tuning of hyperparameters often need to be optimised according to the specifics of the problem and experience, such as the learning rate, the number of neurons, the number of batches, and so on. In order to explore the effectiveness of the hyperparameters used in the method of this paper, experiments are conducted under different hyperparameter settings on WGAN and TCN, respectively, and the three evaluation indices, namely F1 value, AUC, and AUPRC, are compared, and the results are shown in Tables 2 and 3.
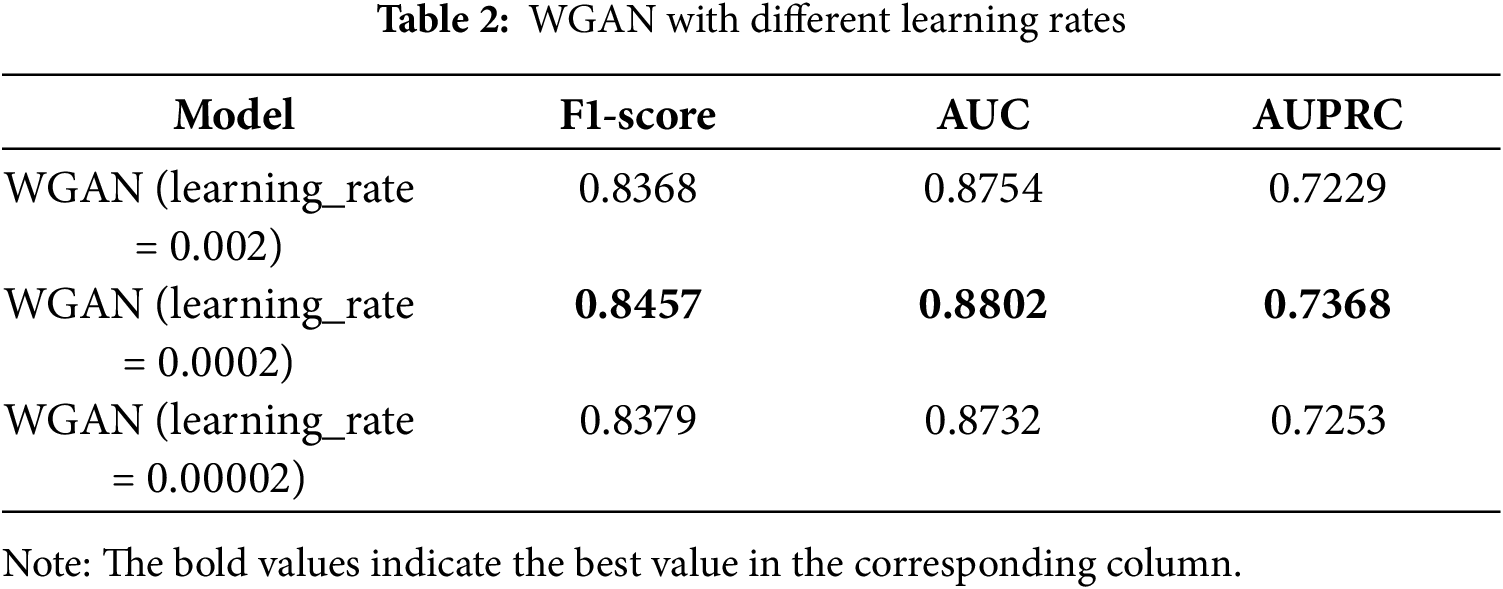
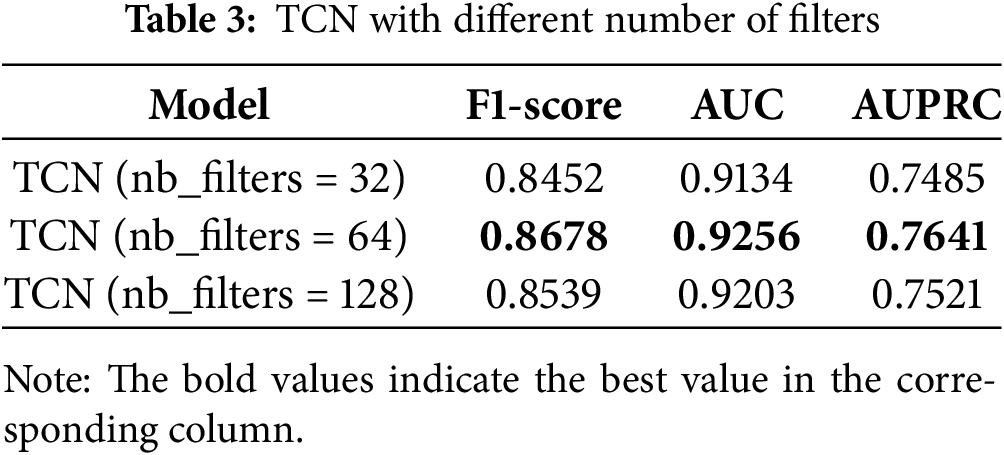
The model shown in Table 2 is WGAN, which first performs an oversampling operation on the fraudulent samples and then directly predicts the results using the fully connected layer at the end of WGAN. It can be seen that the model performs optimally when the learning rate of WGAN is 0.0002. Table 3 shows the detection accuracy of TCN under different numbers of filters, and all the metrics of TCN reach the highest when the number of filters is 64. Therefore, in the following experiments, this paper sets the learning rate of WGAN to 0.0002 and the number of filters in the convolutional layer of TCN to 64. In addition, Table 4 also shows other specific parameters of this paper’s method.
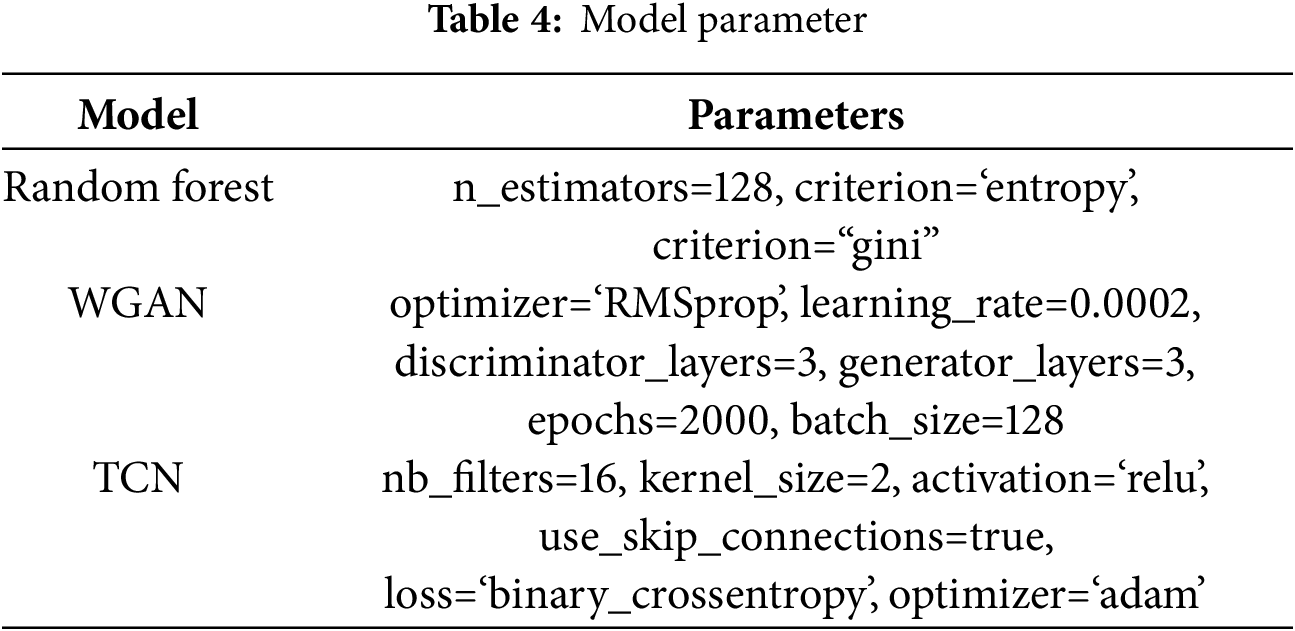
In the data preprocessing stage, the importance scores of credit card desensitized features calculated by the random forest algorithm are shown in Fig. 4. In order to eliminate redundant features and retain important features as much as possible, it is necessary to determine a suitable feature screening threshold. The experiment compares the impact of different feature screening thresholds on the model’s classification performance, and the results are shown in Table 5. The values in the model parentheses indicate the feature screening thresholds.

Figure 4: Feature importance scores calculated by random forest
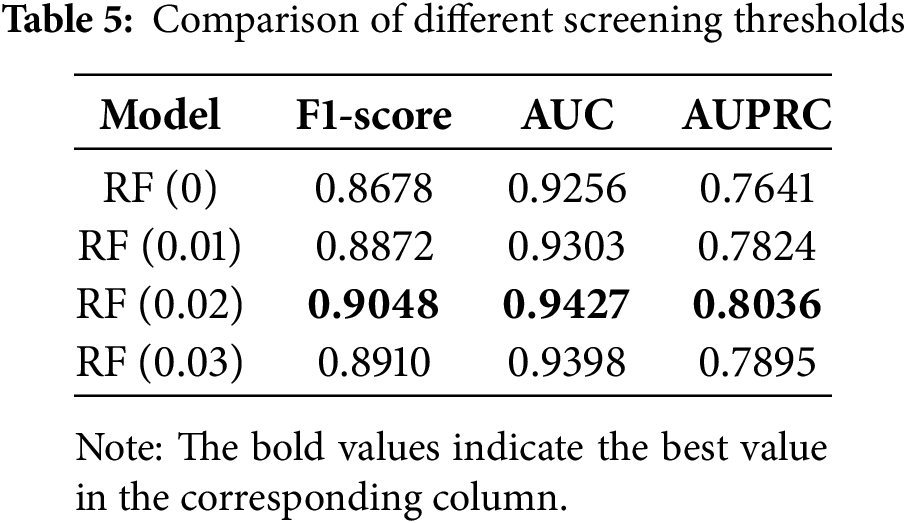
Based on the experimental results, it is observed that the model’s classification performance is the worst without feature screening, indicating that the presence of redundant features in the dataset affects the model’s detection effectiveness. By eliminating features with importance scores lower than 0.02, the evaluation metrics reach their peak and the model’s classification performance is optimised. This verifies the feasibility of the feature screening method based on random forest and determines the optimal feature screening threshold as 0.02.
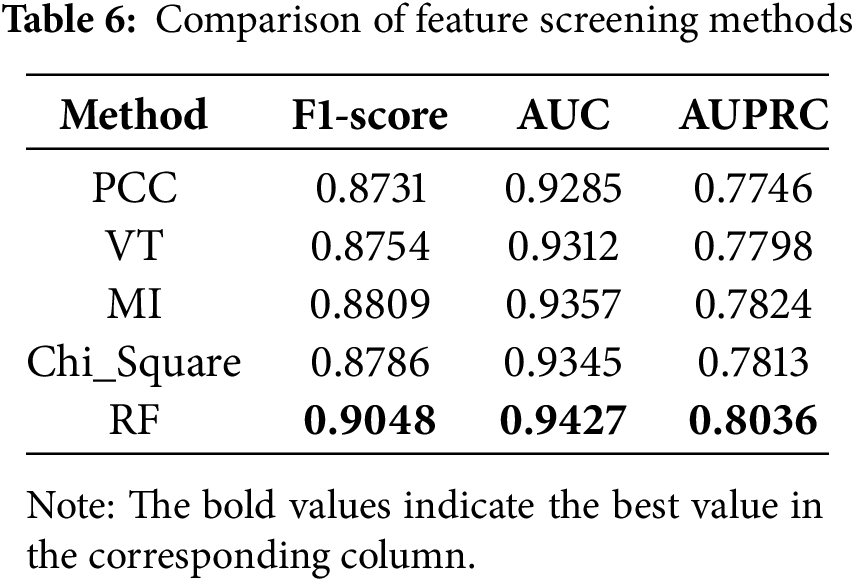
To further validate the effectiveness of the credit card feature screening method based on random forests, this paper compares it with other feature screening methods such as Pearson correlation coefficient (PCC), variance threshold (VT), mutual information (MI) and chi-square validation. Table 6 shows that these traditional feature screening methods are much less effective than Random Forest in improving the model. This is because traditional feature screening methods are usually used to evaluate the linear relationship between features and the target variables. However, in credit card transaction data, the relationship between features and target variables is non-linear. Random Forest is able to capture these non-linear relationships automatically because it does not assume any particular form of relationship between features and target variables.
4.5 Comparison of Timing Models
In order to verify the effectiveness of TCN in extracting time series information from credit card data, this paper compares several neural network models such as BP Neural Network (BPNN), Long-Short-Term Memory Network (LSTM) and Gated Recurrent Unit (GRU) and their variants after filtering and normalising the features with a threshold of 0.02. All of the above models include a dropout layer with a loss rate of 0.1 to prevent overfitting, use the BinaryCrossentropy function as the loss function, and employ the Adam optimiser to update the network weights. To improve the robustness and accuracy of the evaluation results, ten experiments are conducted independently under each parameter condition, and the final results are presented as the mean of the ten experiments. The four evaluation indices, accuracy, F1 value, AUC and AUPRC, are mainly compared, and the specific evaluation results are shown in Table 7.
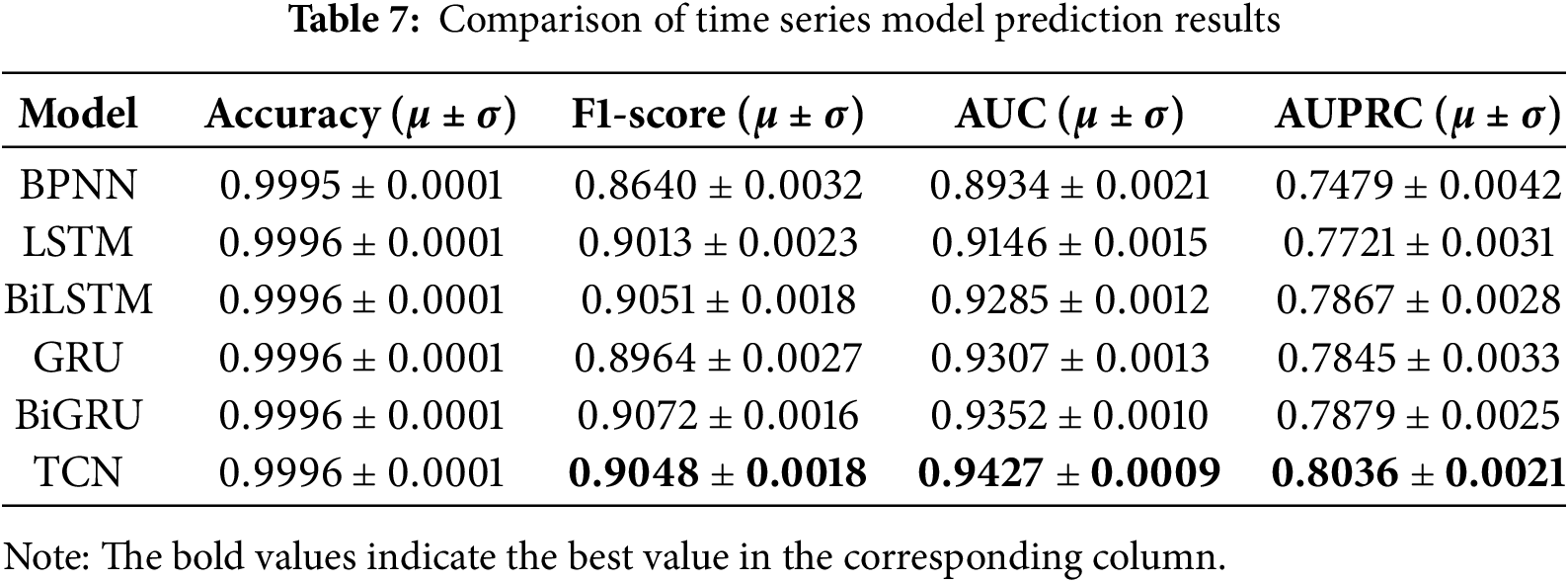
The accuracy rates of the above models are all above 99.9%, probably because the models learn the distribution of a large number of majority class samples in the training set and accurately predict a large number of majority class samples in the test set. However, for the credit card fraud detection problem, the detection of fraudulent transactions is more valuable than the detection of regular transactions, so this paper pays more attention to the classification evaluation indices than to the accuracy rate. From the experimental results, it can be seen that BPNN, as a more basic neural network model, cannot extract temporal information and has the lowest evaluation indexes. LSTM and GRU, as standard temporal models, have a unique structure that can make the network have memory, and together with their bi-directional structure variants, BiLSTM and BiGRU show better classification performance than BPNN. However, the overall performance is not as good as TCN. Except for the F1 score index, which is slightly inferior to BiGRU, TCN achieves the highest AUC index and APRUC index, indicating that its overall classification performance is optimal. Therefore, TCN is used as the classifier for credit card fraud detection in this paper.
4.6 Comparison of Oversampling Methods
The dataset used in this paper has a very uneven distribution of classes, which would lead to poor generalisation of the model if the data were trained directly, and is prone to overfitting most classes of samples. Although the accuracy rate is high, the model needs to learn how to distinguish fraudulent samples. To solve the above problems, it is necessary to perform an oversampling operation on the original data. In this paper, we take RF-TCN as the base model and compare the performance difference after oversampling fraudulent samples using the SMOTE algorithm, ADASYN algorithm, K-MeansSMOTE algorithm, and WGAN algorithm. Among them, the K nearest neighbour value of the SMOTE algorithm and ADASYN algorithm is set to 5, the number of clusters of the K-MeansSMOTE algorithm is set to 30, and the optimiser learning rate and neuron loss rate of the dropout layer of the WGAN algorithm are set to 0.0002 and 0.1, respectively. The number of fraudulent transaction samples after oversampling is equal to the number of standard transaction samples. The model prediction results based on the oversampling method are shown in Figs. 5 and 6.

Figure 5: ROC curve of the model based on the oversampling method

Figure 6: PR curve of the model based on the oversampling method
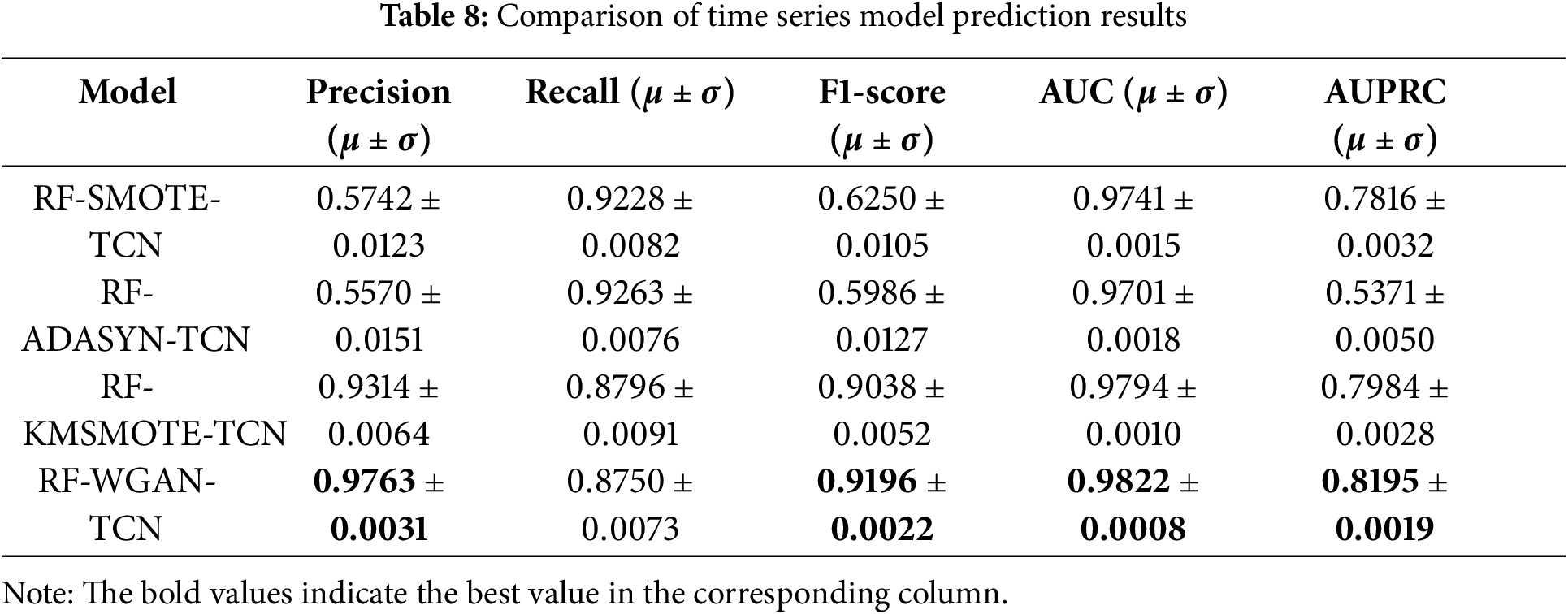
As shown in the image above, the ROC curve and PR curve based on the WGAN oversampling algorithm are basically at the top of the other curves, and the area under their surfaces may be the largest, indicating that their classification performance may be optimal. In order to explore the superiority of the WGAN oversampling algorithm in detail, this paper gives the specific classification evaluation results, which are mainly compared by the five evaluation indices of precision rate, recall rate, F1 value, AUC and AUPRC. As shown in Table 8, the oversampled models based on the SMOTE and ADASYN algorithms show poor results in both precision and F1 value metrics, indicating that they generate too much noise in the oversampling process and the models learn unnecessary data distributions. The model based on the oversampling of the K-MeansSMOTE algorithm has an advantage due to its characteristic of clustering and then oversampling, which has a significant improvement in the overall performance compared to the previous two, but is still slightly inferior to the model based on the oversampling of the WGAN algorithm, i.e., the RF-WGAN-TCN model proposed in this paper. Except for the recall index, which is slightly lower than that of the model based on the ADASYN oversampling algorithm, all the other classification evaluation indices of the RF-WGAN-TCN model are the highest.
Combined with the model confusion matrix based on the oversampling methods in Fig. 7, it can also be seen that the models based on the oversampling of the SMOTE and ADASYN algorithms predict many standard samples as fraudulent samples. In contrast, the number of misclassifications based on the WGAN oversampling algorithm is the lowest. Overall, the RF-WGAN-TCN model has the best integrated classification performance, and the WGAN oversampling algorithm can generate fraud samples that match the original distribution, effectively solving the problems caused by the imbalance of credit card categories.

Figure 7: Confusion matrix after oversampling
Wasserstein distance is theoretically a more stable alternative to JS scatter, which can effectively improve the GAN training process. In order to verify the feasibility of using Wasserstein distance instead of the original JS scatter in GAN to improve the training effect, this paper designs experiments to compare the loss curves of the discriminator and generator of WGAN and the traditional GAN, respectively, which are shown in Figs. 8 and 9, respectively.
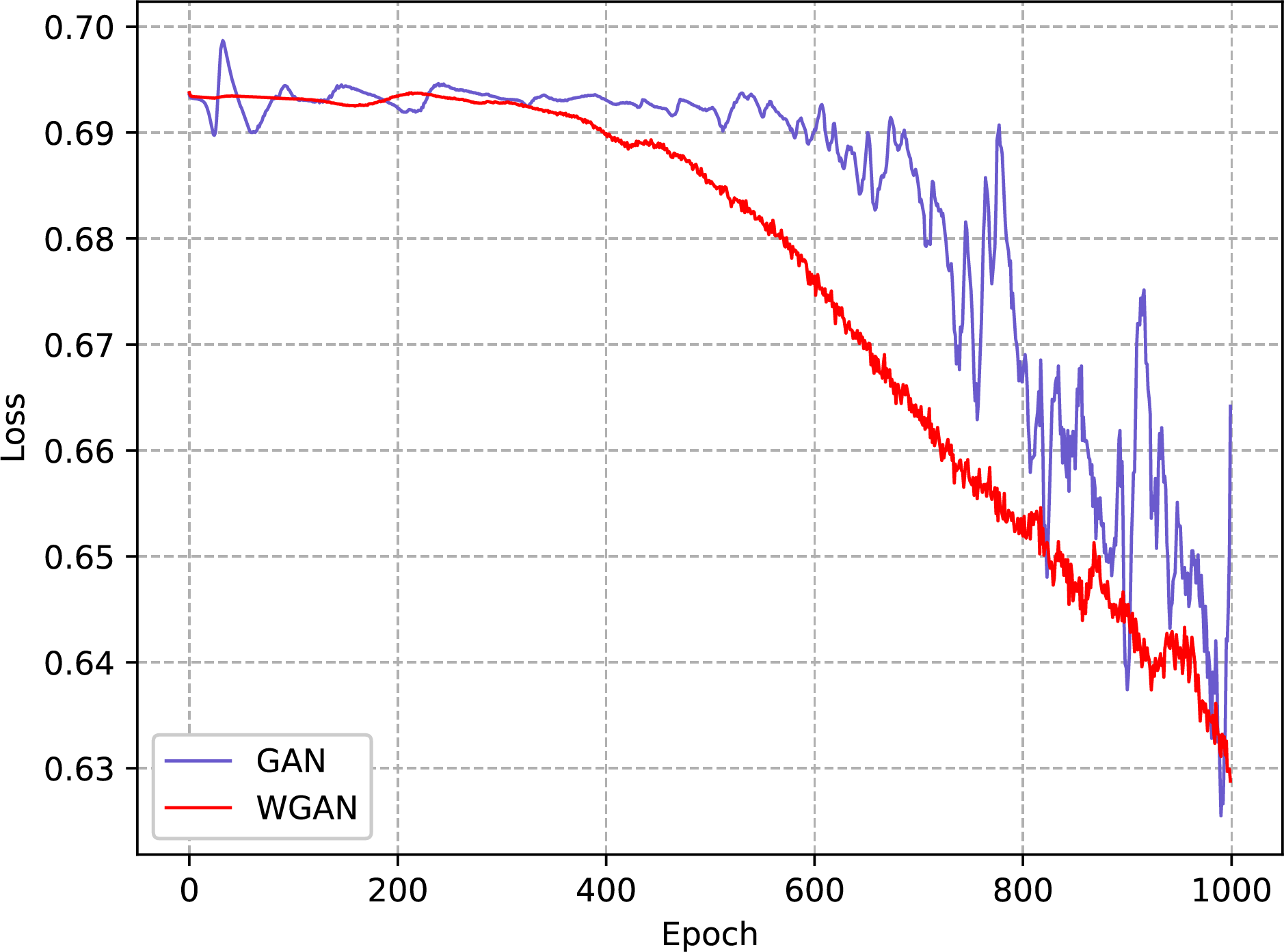
Figure 8: Discriminator loss

Figure 9: Generator loss
Compared to the traditional GAN, the loss curve of the WGAN shows a smaller oscillation amplitude and a more stable convergence, regardless of whether it is the loss curve of the discriminator or the loss curve of the generator. This advantage is mainly due to the fact that WGAN solves the problem of disappearing or exploding gradient that may occur during GAN training by introducing Wasserstein distance as the loss function, thus making the training process more stable and reducing the risk of model collapse. Therefore, WGAN can learn the original distribution of data more stably and efficiently compared to GAN, thus providing high-quality fraud samples for credit card fraud detection tasks. In addition, the loss function of the discriminator does not converge because the quality of the samples generated by the generator is continuously improved in the process of continuous iteration, resulting in the discriminator being unable to accurately identify whether the samples are real or not, and the final assessment accuracy will converge to 50% infinitely.
4.8 Comparison with Existing Work
To further validate the effectiveness of this paper’s methodology, this paper is compared with recent research, as shown in Table 9. The models mentioned in the table are all experimented on the European cardholder dataset, the same dataset used in this paper. The comparison with the existing work shows that the evaluation results of the RF-WGAN-TCN credit card fraud detection model proposed in this paper are all higher than the other models. Therefore, the method in this paper is better than the existing research work and has better classification performance and applicability.
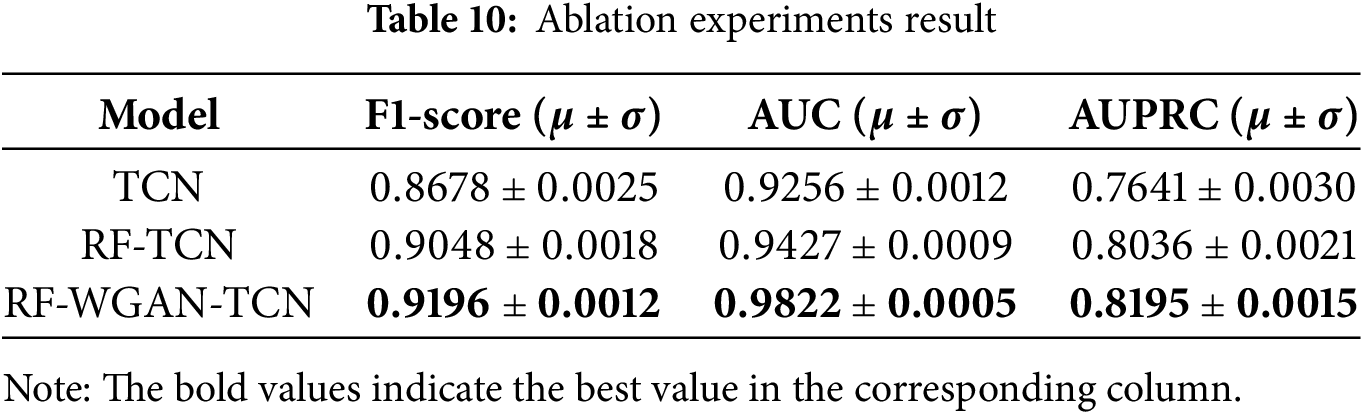
We conducted ablation experiments to interpret our method. The results are presented in Table 10. From the results of ablation experiments, the RF-TCN model has a better detection effect than the single TCN model. The performance of the RF-WGAN-TCN model has a significant improvement over the TCN model and the RF-TCN model, which indicates that both the RF-based feature screening method and the WGAN-based oversampling method have a positive influence on the classification of the model.
This paper investigates how to solve the problems of category imbalance and data drift in credit card fraud detection tasks. To this end, this paper proposes a credit card fraud detection method based on RF-WGAN-TCN, which consists of three modules: a preprocessing layer, an oversampling layer and a prediction layer. In the preprocessing layer, feature importance scores are calculated and filtered based on the scores by dividing the nodes of the random forest. In the oversampling layer, the Wasserstein distance improvement GAN is introduced to increase the stability of the adversarial training and thus generate high quality fraud samples. In the prediction layer, the temporal information in the credit card data is learned using the dilated causal convolution of TCN, and finally the classification results are output through the Softmax layer. The experimental results on the European cardholder dataset show that the RF-WGAN-TCN model has high classification accuracy, and the proposed method in this paper performs better in terms of comprehensive performance compared to previous methods, indicating that the RF-WGAN-TCN model can be competent in the task of credit card fraud detection.
Although the method proposed in this paper has shown significant results in credit card fraud detection, there is still further research direction and space. In future research, this paper will focus on the following points:
• A key challenge in credit card fraud detection is to identify anomalous patterns in a complex network of transactions. In this network, transactions and users are nodes in a graph structure, and intrinsic relationships between transactions, such as temporal continuity, amount similarity, and multiple transactions from the same merchant, can be represented as edges connecting these nodes. Graph Convolutional Network (GCN) is a powerful graph learning technique that excels at handling such graph-structured data and is able to capture the complex relationships and interdependencies between nodes. Therefore, the introduction of GCN for credit card fraud detection has great promise and potential.
• Existing credit card fraud detection methods rely heavily on publicly available data sets and network models to identify fraud patterns through in-depth analysis of data characteristics. However, as fraud tactics continue to evolve and become more sophisticated, these methods often struggle to be effective in the face of new types of fraud, as they are difficult to adapt to unknown or emerging fraud patterns. To address this challenge, future research will consider the introduction of reinforcement learning techniques. Reinforcement learning enables models to optimise their decision-making strategies by continuously learning and adapting as they interact with their environment. In the area of credit card fraud detection, this means that the model can adapt to changes in fraud patterns in real time, and more accurately identify and prevent new types of fraud by continuously adjusting its strategy.
Acknowledgement: Not applicable.
Funding Statement: This work was supported by the National Natural Science Foundation of China under Grant No. 62466001, the Talent Plan Project of Fuzhou City of Jiangxi Province of China under the Grant No. 2021ED008, the Opening Project of Jiangxi Key Laboratory of Cybersecurity Intelligent Perception under the Grant No. JKLCIP202202, and the Priority Unveiled Marshalling Project of Fuzhou City of Jiangxi Province of China under the Grant No. 2023JBB026.
Author Contributions: Ao Zhang: Investigation, Methodology, Software, Validation, Visualization, Writing—original draft, Writing—review & editing. Hongzhen Xu: Conceptualization, Methodology, Project administration, Software, Validation, Writing—review & editing. Ruxin Liu: Formatting, Polish, Validation. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The dataset used in the study is publicly available and can be accessed through the URL: https://www.kaggle.com/datasets/mlg-ulb/creditcardfraud (accessed on 14 August 2025).
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Al Balawi S, Aljohani N. Credit-card fraud detection system using neural networks. Int Arab J Inf Technol. 2023;20(2):234–41. doi:10.34028/iajit/20/2/10. [Google Scholar] [CrossRef]
2. Van Belle R, Baesens B, De Weerdt J. CATCHM: a novel network-based credit card fraud detection method using node representation learning. Decis Support Syst. 2023;164(3):113866. doi:10.1016/j.dss.2022.113866. [Google Scholar] [CrossRef]
3. Wang D, Chen B, Chen J. Credit card fraud detection strategies with consumer incentives. Omega. 2019;88(1):179–95. doi:10.1016/j.omega.2018.07.001. [Google Scholar] [CrossRef]
4. Makki S, Assaghir Z, Taher Y, Haque R, Hacid MS, Zeineddine H. An experimental study with imbalanced classification approaches for credit card fraud detection. IEEE Access. 2019;7:93010–22. doi:10.1109/ACCESS.2019.2927266. [Google Scholar] [CrossRef]
5. Becker A, Becker J. Dataset shift assessment measures in monitoring predictive models. Procedia Comput Sci. 2021;192:3391–402. doi:10.1016/j.procs.2021.09.112. [Google Scholar] [CrossRef]
6. Krawczyk B. Learning from imbalanced data: open challenges and future directions. Prog Artifi Intell. 2016;5(4):221–32. doi:10.1007/s13748-016-0094-0. [Google Scholar] [CrossRef]
7. Chawla NV, Bowyer KW, Hall LO, Kegelmeyer WP. SMOTE: synthetic minority over-sampling technique. J Artifi Intell Res. 2002;16:321–57. doi:10.1613/jair.953. [Google Scholar] [CrossRef]
8. Yen S, Lee Y. Under-sampling approaches for improving prediction of the minority class in an imbalanced dataset. Lecture Notes Control Inf Sci. 2006;344:731–740. doi:10.1007/978-3-540-37256-1_89. [Google Scholar] [CrossRef]
9. Rtayli N, Enneya N. Enhanced credit card fraud detection based on SVM-recursive feature elimination and hyper-parameters optimization. J Inf Secur Appl. 2020;55(3):102596. doi:10.1016/j.jisa.2020.102596. [Google Scholar] [CrossRef]
10. Ileberi E, Sun Y, Wang Z. Performance evaluation of machine learning methods for credit card fraud detection using SMOTE and AdaBoost. IEEE Access. 2021;9:165286–94. doi:10.1109/ACCESS.2021.3134330. [Google Scholar] [CrossRef]
11. Chen Y, Zhang R. Research on credit card default prediction based on k-means SMOTE and BP neural network. Complexity. 2021;2021(1):6618841. doi:10.1155/2021/6618841. [Google Scholar] [CrossRef]
12. Alamri M, Ykhlef M. Hybrid undersampling and oversampling for handling imbalanced credit card data. IEEE Access. 2024;12(1):14050–60. doi:10.1109/ACCESS.2024.3357091. [Google Scholar] [CrossRef]
13. Esenogho E, Mienye ID, Swart TG, Aruleba K, Obaido G. A neural network ensemble with feature engineering for improved credit card fraud detection. IEEE Access. 2022;10:16400–7. doi:10.1109/ACCESS.2022.3148298. [Google Scholar] [CrossRef]
14. Mqadi NM, Naicker N, Adeliyi T. Solving misclassification of the credit card imbalance problem using near miss. Math Probl Eng. 2021;2021(1):7194728. doi:10.1155/2021/7194728. [Google Scholar] [CrossRef]
15. Wang L, Xu S, Wang X, Zhu Q. Addressing class imbalance in federated learning. In: Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 35; 2021 Feb 2–9; Virtual. p. 10165–73. doi:10.1609/aaai.v35i11.17219. [Google Scholar] [CrossRef]
16. Almarshad FA, Gashgari GA, Alzahrani AI. Generative adversarial networks-based novel approach for fraud detection for the european cardholders 2013 dataset. IEEE Access. 2023;11:107348–68. doi:10.1109/ACCESS.2023.3320072. [Google Scholar] [CrossRef]
17. He K, Yang Q, Ji L, Pan J, Zou Y. Financial time series forecasting with the deep learning ensemble model. Mathematics. 2023;11(4):1054. doi:10.3390/math11041054. [Google Scholar] [CrossRef]
18. Kolli CS, Tatavarthi UD. Fraud detection in bank transaction with wrapper model and Harris water optimization-based deep recurrent neural network. Kybernetes. 2021;50(6):1731–50. doi:10.1108/K-04-2020-0239. [Google Scholar] [CrossRef]
19. Gao J, Sun W, Sui X. Research on default prediction for credit card users based on XGBoost-LSTM model. Discrete Dyn Nat Soc. 2021;2021(1):5080472. doi:10.1155/2021/5080472. [Google Scholar] [CrossRef]
20. Benchaji I, Douzi S, El Ouahidi B, Jaafari J. Enhanced credit card fraud detection based on attention mechanism and LSTM deep model. J Big Data. 2021;8(1):1–21. doi:10.1186/s40537-021-00541-8. [Google Scholar] [CrossRef]
21. Forough J, Momtazi S. Ensemble of deep sequential models for credit card fraud detection. Appl Soft Comput. 2021;99:106883. doi:10.1016/j.asoc.2020.106883. [Google Scholar] [CrossRef]
22. Forough J, Momtazi S. Sequential credit card fraud detection: a joint deep neural network and probabilistic graphical model approach. Expert Syst. 2022;39(1):e12795. doi:10.1111/exsy.12795. [Google Scholar] [CrossRef]
23. Liu Y, Qin G, Huang X, Wang J, Long M. Timer-XL: long-context transformers for unified time series forecasting. arXiv:2410.04803. 2024. doi:10.48550/arXiv.2410.04803. [Google Scholar] [CrossRef]
24. Dai R, Wang Z, Jie J, Wang W, Ye Q. VTformer: a novel multiscale linear transformer forecaster with variate-temporal dependency for multivariate time series. Compl Intell Syst. 2025 Jun;11(6):1–9. doi:10.1007/s40747-025-01866-0. [Google Scholar] [CrossRef]
25. Yu H, Zhang Q, Liu T, Lu J, Wen Y, Zhang G. Meta-ADD: a meta-learning based pre-trained model for concept drift active detection. Inf Sci. 2022 Aug 1;608(10):996–1009. doi:10.1016/j.ins.2022.07.022. [Google Scholar] [CrossRef]
26. Yu H, Liu W, Lu J, Wen Y, Luo X, Zhang G. Detecting group concept drift from multiple data streams. Pattern Recognit. 2023 Feb 1;134(1):109113. doi:10.1016/j.patcog.2022.109113. [Google Scholar] [CrossRef]
27. Lu P, Lu J, Liu A, Zhang G. Early concept drift detection via prediction uncertainty. In: Proceedings of the 39th AAAI Conference on Artificial Intelligence. Vol. 39; 2025 Feb 22–26; Sydney, NSW, Australia. p. 19124–32. doi:10.1609/aaai.v39i18.34105. [Google Scholar] [CrossRef]
28. Wan K, Liang Y, Yoon S. Online drift detection with maximum concept discrepancy. In: Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining; 2024 Aug 25–29; Barcelona, Spain. p. 2924–35. doi:10.1145/3637528.3672016. [Google Scholar] [CrossRef]
29. Breiman L. Random forests. Mach Learn. 2001;45(1):5–32. doi:10.1023/A:1010933404324. [Google Scholar] [CrossRef]
30. Goodfellow IJ, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, et al. Generative adversarial nets. In: Advances in Neural Information Processing Systems 27 (NIPS 2014); 2014 Dec 8–13; Montreal, QC, Canada. p. 2672–80. doi:10.1145/3422622. [Google Scholar] [CrossRef]
31. Arjovsky M, Chintala S, Bottou L. Wasserstein generative adversarial networks. In: Precup D, Teh YW, editors. Proceedings of the 34th International Conference on Machine Learning; 2017 Aug 6–11; Sydney, Australia. 2017. p. 214–23. [Google Scholar]
32. Nash JF. Equilibrium points in n-person games. Proc Natl Acad Sci U S A. 1950;36(1):48–9.doi:10.1073/pnas.36.1.48. [Google Scholar] [PubMed] [CrossRef]
33. Lea C, Vidal R, Reiter A, Hager GD. Temporal convolutional networks: a unified approach to action segmentation. In: Hua G, Jégou H, editors. Computer Vision—ECCV 2016 Workshops. Lecture Notes in Computer Science, Vol. 9914; 2016 Oct 8–10 and 15–16; Amsterdam, The Netherlands. Cham, Switzerland: Springer International Publishing; 2016. p. 47–54. doi:10.1007/978-3-319-49409-8_7. [Google Scholar] [CrossRef]
34. Dal Pozzolo A, Caelen O, Johnson RA, Bontempi G. Calibrating probability with undersampling for unbalanced classification. In: 2015 IEEE Symposium Series on Computational Intelligence (SSCI); 2015 Dec 7–10; Cape Town, South Africa. Piscataway, NJ, USA: IEEE; 2015. p. 159–66. doi:10.1109/ssci.2015.33. [Google Scholar] [CrossRef]
35. Hancock JT, Khoshgoftaar TM, Johnson JM. Evaluating classifier performance with highly imbalanced big data. J Big Data. 2023;10(1):42. doi:10.1186/s40537-023-00724-5. [Google Scholar] [CrossRef]
36. Lin TH, Jiang JR. Credit card fraud detection with autoencoder and probabilistic random forest. Mathematics. 2021;9(21):2683. doi:10.3390/math9212683. [Google Scholar] [CrossRef]
37. Alharbi A, Alshammari M, Okon OD, Alabrah A, Rauf HT, Alyami H, et al. A novel text2IMG mechanism of credit card fraud detection: a deep learning approach. Electronics. 2022;11(5):756. doi:10.3390/electronics11050756. [Google Scholar] [CrossRef]
38. Du H, Lv L, Guo A, Wang H. AutoEncoder and LightGBM for credit card fraud detection problems. Symmetry. 2023;15(4):870. doi:10.3390/sym15040870. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF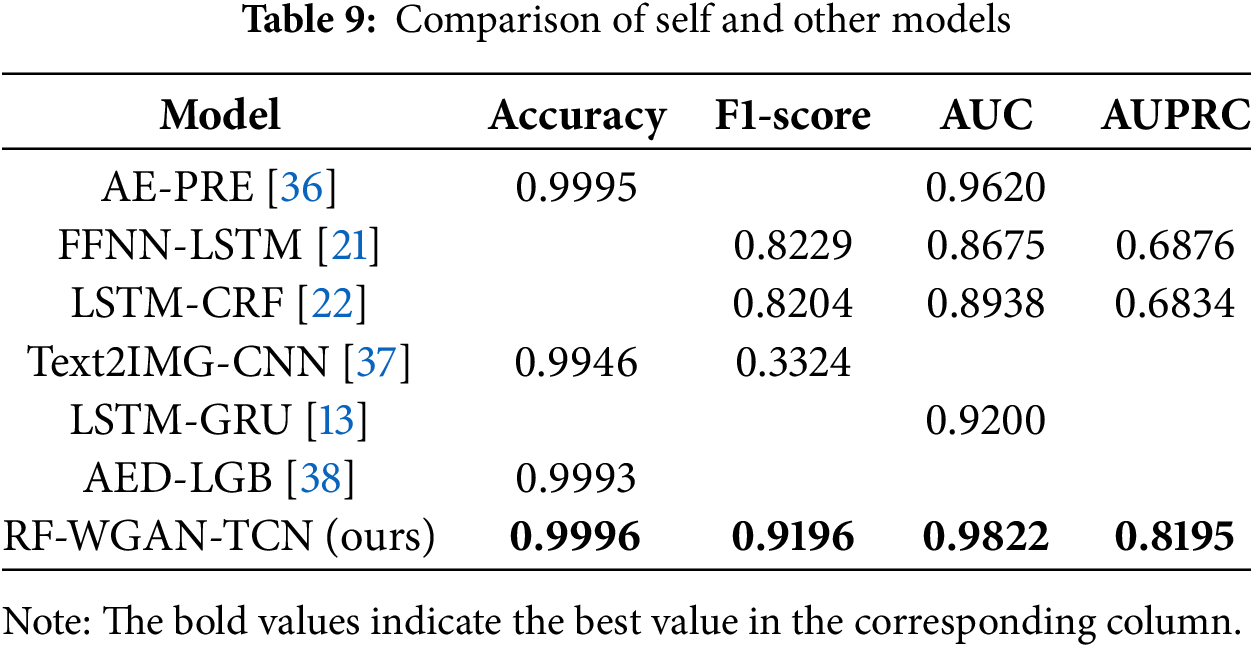
 Downloads
Downloads
 Citation Tools
Citation Tools