An Efficient CSP-PDW Approach for ECG Signal Compression and Reconstruction for IoT-Based Healthcare

1  Introduction

Smart healthcare services are one of the most important aspects of biomedical research, serving humanity. For the last few decades, information and communication technology has played a vital role in the healthcare sector. External or implantable tiny sensors for remote health monitoring have evolved in tandem with the rapid growth of the embedded system and semiconductor industries. Remote healthcare is a technological platform that enables the recording and analysis of vital body parameters, regardless of the patient’s location. This may change the way rural diagnostics and treatment are done. The conventional approach to sampling a signal reliably follows Shannon’s theorem, which states that ‘the sampling rate must be at least twice the maximum frequency present in the signal.’ Breakthrough research [1,2] has been conducted in the field of Compression sensing (CS), and it posed a challenge to the conventional sampling method, stating that ‘sampling frequency can be equal to the maximum frequency component in the signal’. This methodology compresses data while capturing it, ensuring the originality of the data remains intact upon reception. The CS concept is based on two fundamental principles: sparsity and incoherence. Compression algorithms [3] can be classified as lossy and lossless. CS uses the point that most physical signals can be represented as sparse when their sparse basis (Ψ) is computed properly.

A typical ECG signal is semi-periodic, and the variance throughout the signal is non-uniform [4]. The standard deviation of ECG suggests that 70%–80% of the region has low information, 15%–20% has high information, and the rest has medium information. This semi-sparse nature of the ECG signal makes it an ideal choice for CS algorithms. Incoherence means that the signal should be incoherent among its measurements and have a sparsifying basis. It should spread across the measurement basis. CS undergoes two steps—compression and recovery. CS represents the signals on a linear functional or orthonormal basis. Initially, a framework for CS using the basis pursuit theorem and non-adaptive measurements was discussed, along with the methods to find out the essential parameters for Compressive Sensing [5,6]. The Least Mutual coherence between the measurement and the compressed matrix is one of the vital requirements for a successful reconstruction [7]. The absolute diagonal elements of the identical matrix were considered to reduce the coherence. The main limitation of this framework was its mathematical complexity, as implementing complex mathematical equations overloads the system’s main processor, thereby decreasing processing speed, due to the increased time required for memory read/write cycles. Biomedical signals are very dynamic, as each change has a significant contribution to feature extraction. Hence, processing speed and accurate reconstruction are the key factors in biomedical signal processing [8]. General dictionaries, as well as specific dictionaries, can be built using normal and pathological cardiac patterns and can be used for CS [9]. The method ensures the processing of fewer bits of information, reducing memory and power requirements [10]. An ECG signal can be accurately represented as a sparse combination of a few significant bands. Measurement matrix and sensing matrix construction are important parts of CS. The size of the measurement matrix and its lesser coherence with the sensing matrix are key requirements of CS [3]. Authors in [11,12] explained the size of the measurement matrix based on the Robust Uncertainty principle and suggested using an optimized measurement matrix to improve reconstruction efficiency. ECG compression on an embedded Shimmer wireless mote discusses the importance of the Restricted Isometry Property [13] and the Basic Pursuit algorithm in constructing the sensing matrix for successful compression and reconstruction. Another hurdle to processing the ECG signal is its localized behavior. Block Sparse Bayesian Learning frameworks were utilized to enhance patient mobility and mitigate the location dependency of ECG signals [14]. Furthermore, the wavelet transform was suggested to enhance the reconstruction efficiency. It enhances the application of CS on the ECG signal by decomposing the signal into sub-bands, thereby preserving spatial resolution, frequency, and directional characteristics [13,15–17].

Huang et al. [18] utilized down-sampling techniques to reduce and compress the ECG data signals. For this purpose, they have employed the China Physiological Signal Challenge 2018 dataset and root mean square error metrics to evaluate the obtained compression result. Singhai et al. [19] presented nature-inspired algorithms with the discrete wavelet transform (DWT) for the compression of ECG signal data. They utilized DWT to decompose the signals and optimization techniques to select specific and suitable threshold values. They have also calculated various parameters, including PRD, QS, SNR, and CR, to validate the performance of their algorithm. Yildirim et al. [20] presented a 27-layer deep learning structure comprising encoder and decoder sections for compressing large ECG datasets. They utilized 4800 ECG segments from 48 patients to validate the compression result. They obtained a 32.25 compression rate and a 2.73% average percent root mean square difference (PRD) value using the model. The hybrid lossy/lossless compression system Chang and Sobelman [21] suggest has high signal quality and CR properties. After decompression, deep neural networks are used to assess performance. Fathi et al. [22] presented an algorithm for compressing ECG signals from the MIT-BIH arrhythmias database and the ECG-ID database. In their algorithm, they used discrete Krawtchouk moments and Ant Lion Optimizer as feature extractors and feature selectors. They obtained the following average values of quality score (QS), Peak signal-to-noise ratio (PSNR), CR, signal-to-noise ratio (SNR), and PRD: 23.92, 49.04, 15.56, 44.52, and 0.69, respectively. Shi et al. [23] proposed an ECG signal compression method utilizing residual error compensation based on a binary convolutional autoencoder. In this work, they utilized the MIT-BIH dataset to validate their methodology, obtaining a compression ratio of 117.33 and a PRD of 7.76%. Kuldeep and Zhang [24] introduced a lightweight ECG signal compression technique for transmitting signals from the MIT-BIH dataset. In this work, the authors have utilized two pruning methods, sign and binary pruning, which require less computation. The Gaussian elimination method was employed for the reconstruction of ECG signals, and its performance was validated using the metrics QS, PRD, and CR. Pal et al. [25] presented a method for compressing ECG signals using the hybrid coronavirus herd immunity optimizer and tunable-Q wavelet transform (TQWT). To validate their algorithm, they utilized the MIT-BIH dataset and multiple evaluation metrics, CR, SNR, PRD, QS, and correlation coefficient. A Very-Large-Scale Integration architecture for an ECG compression engine is introduced [26]. The processor’s efficiency was confirmed on MIT BIH databases. The authors [27] introduced a compression algorithm that combines an adaptive TQWT with a modified dead-zone quantizer. A new Sparse Grey Wolf Optimization algorithm is presented to optimize TQWT parameters. In [28], a 2-D ECG compression technique whereby DCT and TQWT were combined with both row-wise and column-wise operations employed to grow sparsity in the transform domain. The TQWT and quantizer parameters were tuned using the COOT bird optimization algorithm.

Prior studies on ECG compression have focused on either compressed sensing (CS) or wavelet-based methods, which have limited clinical applicability due to limitations in achieving high compression rates and efficient, high-fidelity reconstruction. The CS-PDW framework combines compressive sensing (CS) with a Primal-Dual wavelet-based reconstruction method that utilizes wavelet-domain sparsity to achieve high compression and high-fidelity reconstruction in a wide range of challenging compression ratios. In contrast to the works above, where parameters are set empirically, the proposed work enables the analytically determination of correct CS and wavelet settings, promising better fidelity and lower computational cost. Aimed at IoT healthcare, CSP-PDW has a low time complexity and achieves excellent performance in preserving diagnostic features. The combination of these features—compression efficiency, robustness, and real-time readiness—makes the proposed scheme a feasible solution for IoT-enabled e-healthcare applications.

CS brought a revolution in the way signals are handled and analyzed worldwide. It enhances the ability of a device to utilize allocated bandwidth effectively, while also improving the battery life of implantable devices and making them more portable. This paper presents a mathematically hardware-realizable and straightforward CS algorithm for ECG signals with moderate compression efficiency. The offered CSP-PDW techniques can also be applied to other biomedical signals. This paper has two segments. The first one is compression, and the second one is the reconstruction and wavelet processing procedure. In the compression procedure, the Fast Fourier Transform (FFT) is applied to generate the sparse representation of the ECG signal. A random Gaussian matrix is used to generate the measurement matrix. Iterative algorithms and optimization algorithms are used to reconstruct the original ECG signal. Additionally, wavelet-based processing is performed to improve the overall reconstruction efficiency.

The paper is organized as follows: Section 2 describes some preliminary state-of-the-art concepts used in this work. Section 3 illustrates the proposed scheme. Section 4 defines the simulation result and performance analysis. Finally, the conclusion is discussed in the last section.

2  Materials and Methods

This section explains the methods used to design the algorithm for efficiently compressing ECG signals. The algorithm consists of two segments: the first compresses the signal, and the second reconstructs without losing information. For this reason, compression sensing (CS), restricted isometry property, and DWT were utilized, along with selected optimization techniques. These methods are briefed in the preceding subsections.

2.1 Compression Sensing

CS relies on two major principles: sparsity and incoherence [5,29]. A sparse signal is a special type of signal that comprises a small amount of information compared to its total length. Consider a vector (X∈RN), which can be expanded in any form of orthonormal basis (Ψ=[ψ1,ψ2,ψ3,…,ψN]). Mathematically, sparsity can be stated as given in Eq. (1).

X(t)=∑i=1Nciψi(t), where c=[c1,c2,…,cN]T∈RN, and |c|0≪N(1)

where X is the coefficient sequence of the original ECG signal c. Generally, CS utilizes the measurement matrix (Φ∈RM×N)(with (M≪N)), and the measurements (Y∈RM) can be expressed as given by Eq. (2).

Y=ΦX+η(2)

where η is the noise and substitute the values of X from Eq. (1) in Eqs. (2) and (3) is obtained:

Y=Φ∑i=1Nciψi(t)+η(3)

Considering sparsity X, Eq. (4) gives the reformulated equation of the problem to find the sparsest solution.

minc|c|1subject to |Y−ΦΨc|2≤ ϵ(4)

where |⋅|1 signifies the l1-norm advocating sparsity, |⋅|2 is the l2-norm, and ϵ reasons for noise tolerance.

Consider a signal X(t) with s non-zero entries, resulting it s-sparse. The error signal can be estimated by Eq. (5).

|Xs−X|l2=|cs−c|l2(5)

If c is compressible and sparse, the approximation will be accurate and the error |Xs−X|l2 will be minimum. Incoherence states that the sensing matrix (Φ) should be having a dense representation in (Ψ) unlike input signal. For successful recovery of the compressed signal, mutual coherence between the measurement matrix Φ and the sensing matrix (Ψ) should be minimal. Coherence (µ) between Ψ and Φ is defined by Eq. (6).

µ(Ψ,Φ)=max1≤i≤Nmax1≤j≤M|⟨ϕj,ψi⟩|(6)

here the columns of (Φ) and (ψi) are represented by (ϕj) of the basis vectors of (Ψ). The coherence (µ(Ψ,Φ)) is also confined by Eq. (7).

µ(Ψ,Φ)≥1M(7)

The limit of the coherence is given by:

1M≤µ(Ψ,Φ)≤N−MM(N−1)(8)

Random numbers adhere to the least mutual coherence. Independent Identically Distributed (i.i.d.) entries of a random Gaussian matrix are used in this paper to construct the measurement matrix. As the signal is represented as sparse, it contains many zero entries, but the actual locations of the non-zero points are unknown. Fixed basis Gaussian random numbers were used in this paper to randomly choose the rows and columns with non-zero entries to generate a sensing matrix. A PDF of i.i.d. entries of a random Gaussian matrix can be written mathematically as

P.D.F.(x;µ,σ)=12πσ2exp⁡(−(x−µ)22σ2)(9)

where, µ= mean; σ = Standard deviation; σ2 = Variance. The CS principle s states that data should be compressed while being measured. Therefore, a measurement matrix with a size smaller than the original signal has to be obtained. The size of the measurement matrix k should be greater than the number of non-zero elements (m) present in the signal; then we have m << k << N [16]. The size of the measurement matrix was estimated using Robust Uncertainty Principle (1), suppose f∈Rn, that the coefficient sequence x of f in the basis Ψ is s-sparse, then size of q, m can be defined as:

m>c1⋅µ2(Ψ,Φ)⋅s⋅log⁡N(10)

where, ‘c1’ is a constant (>0) and ‘s’ is the sparsity of the signal of interest.

2.2 Restricted Isometry Property

The Restricted Isometry Property (RIP) provides sufficient conditions to approximate large matrices for the implementation of the CS concept. The existence of inimitability of the solution can be guaranteed if the sensing matrix (A) follows RIP in order of s as:

(1−δs)|c|l22≤|Ac|l22≤(1+δs)|c|l22(11)

where, δs = isometry constant of sensing matrix (A). The smallest obtained values of δs is called as the Restricted Isometry Constant. To satisfy RIP, all subsets of s column taken from A matrix should be orthogonal. The RIP condition can be related to the mutual coherence (µ(A)) of the sensing matrix (A). For a matrix to satisfy RIP of order (s), the mutual coherence should satisfy:

µ(A)≤1−δss(12)

Given the RIP condition, the relationship between (δs) and mutual coherence can be extended as follows:

δs≤s⋅µ(A)1−s⋅µ(A)(13)

For the matrix (A) to satisfy RIP, it is necessary that all subsets of (s) columns from (A) are nearly orthogonal, and can be mathematically represented by Eq. (14).

|AiTAj|≤µ(A) for i≠j(14)

where (Ai) and (Aj) are different columns from the sensing matrix (A).

2.3 Optimization Techniques

2.3.1 l1 Minimization

In compressed sensing, the l1 minimization plays an important role in recovering the sparse signal. The lp norm, particularly the l1 norm, represents the number of non-zero elements present in the matrix. This is used in CS recovery to solve an ill-imposed problem and obtain the most relevant solution set. Formally, the lp norm of a vector X is defined by Eq. (15).

|x|p=(∑i|xi|p)1/p for p∈R,p=0,1,2,…(15)

In this paper, a convex problem is relaxed by using l1 minimization instead of l0 minimization technique. As l0 minimization lacks mathematical representation and is an NP-hard problem that is very complicated to solve.

2.3.2 Primal-Dual

Compressed sensing often deals with underdetermined systems, where the number of unknowns, n, exceeds the number of measurements, m. In this case, infinite (maximum) solutions exist due to the problem’s underdetermined nature. To obtain the sparsest solution, the problem can be reformulated as a dual problem and solved using the primal-dual approach.

The primal problem seeks to maximize the objective function X0:

Maximize X0Subject to XN×10=yK×1∗AN×KT(16)

here, (XN×10) is the primal variable, (yK×1) is the measurement vector, and (AN×K) is the sensing matrix.

The Dual problem involves minimizing the objective function X.

Minimize X Subject to yk×1=Ak×N∗XN×1(17)

here, (XN×1) is the dual variable, and the constraints ensure that the measurements match the linear transformation of (X).

2.3.3 Backtrack Line Search

The Backline search approach is used to find the step size αj by utilizing continuous iteration till it meets the Armijo–Goldstein condition, which is expressed as

f(X)−f(X+αjp)>=αjt(18)

where, α0>0 is initial step size and p is the search direction (unit vector).

t=−cm,with c∈(0,1) and m defines the slope of α along with p.

The prime dual approach, combined with a backtrack line search algorithm, is utilized for compressed sensing to solve underdetermined systems and ensure convergence to sparse solutions, as outlined in Algorithm 1.

2.4 Discrete Wavelet Transformation

The Wavelet transform provides a multiresolution analysis of the signal, making it useful for enhancing signal reconstruction. The Continuous Wavelet Transform (CWT) provides a redundant representation of the signal, which may not be necessary for full signal reconstruction. The CWT of a function f(t) is defined by Eq. (19).

Wf(a,b)=∫−∞∞f(t)ψ∗(t−ba) dt(19)

where, ψ∗(t) represents the complex conjugate of the wavelet function ψ(t), a and b are scale and translation parameters, respectively. DWT provides a non-redundant representation of the signal for the region of support by discretizing the scale and translation parameters. The DWT of signal f(t) can be mathematically expressed by Eq. (20).

f(t)=∑k=−∞∞∑l=−∞∞d(k,l)2−k2Ψ(2−k∗(t−l))(20)

where, Dilation factor: 2−k2, Translation factor: 2k∗l, wavelet coefficient: d(k,l), scaled and translated wavelet function: Ψ(2−k∗(t−l)). The wavelet coefficient d(k,l) can be computed as:

d(k,l)=W(f(t),2k,l)=∫−∞∞f(t)Ψk,l∗(t) dt(21)

The f(t) remains still in time domain, and discretization happens in a and b. This sampling process is called as dyadic sampling because consecutive values of the discrete scale and sampling interval differ by a factor of 2.

aj=2j,bk=k⋅2j

where j and k are integers representing the dyadic scale and translation levels, respectively. This results in {(aj,bk)|aj=2j,bk=k⋅2j}.

3  Proposed Methodology

This section describes the details of the methods used for ECG signal compression and reconstruction using hybrid compressed sensing and primal-dual wavelet (CSP-PDW) techniques. Fig. 1 shows the block diagram of the proposed methodology. In the first step, data were collected from two sources: the PTB-DB and MIT-BIH databases, both of which are benchmarked and open-access datasets containing various types of ECG signals, available on the PhysioNet website. In the second step, the collected datasets were denoised using the DWT. In the third step, baseline wander was removed using the polynomial fitting technique. ECG signal compression is performed after signal preprocessing, utilizing modified compressed sensing algorithms for the compression process. In the next step, greedy iterative optimization algorithms were applied to reconstruct the compressed ECG signal. Wavelet transform techniques were employed to enhance further the quality and originality of the reconstructed ECG signal. Finally, postprocessing was conducted using various metrics to validate the suggested methodology. Each step is described in detail in the preceding subsections.

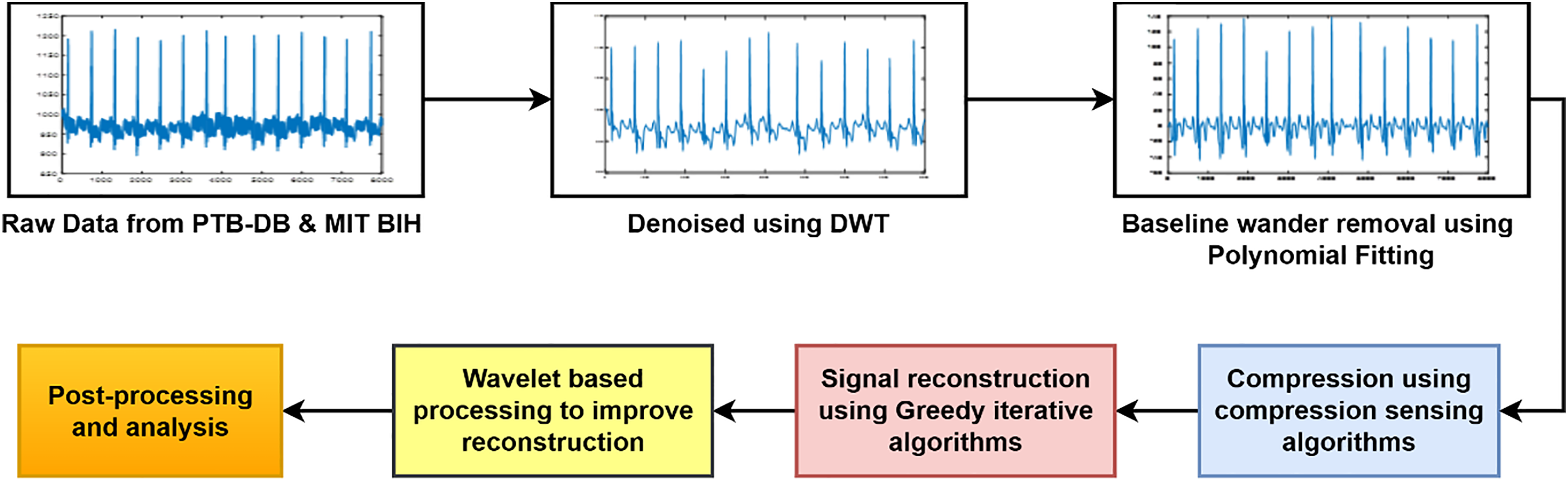
Figure 1: Block diagram of the process

3.1 ECG Data Collection and Preprocessing

ECG signal data are acquired from the PhysioNet database, which serves as a benchmark and open-access directory for ECG datasets. The two ECG datasets, the PTB Diagnostic ECG Database (PTB-DB) and the MIT-BIH arrhythmias database (MIT-BIH), are considered to maintain the generalizability of the methodology. The PTB-BD dataset contains records of 549 patients, consisting of 290 subjects, and includes 15-lead ECG signals. In comparison, the MIT-BIH database contains 48 records, each consisting of 30 min with 2-channel recordings. The dataset is digitized at 360 Hz per channel with an amplitude range of up to 10 mV. As the two datasets differ entirely in both content and length, they were segmented into 2-s recordings. The acquired data is contaminated with several sources of noise. Since the wavelet is a very powerful and efficient tool for noise removal, a wavelet-based denoising algorithm is utilized to denoise the acquired ECG data. The best part of the WT is that it preserves important features while denoising, resulting in no loss of integrity to the original signal. The DWT of 10 levels of decomposition is used to obtain the approximation and detail coefficients of the pre-processed ECG signals, as given by Eq. (22).

{A,D1,D2,…,D10}=DWT(ECG Signal)(22)

where A represents the approximation coefficients and D represents the detail coefficients. The noise level was estimated from the detail coefficients at the highest level using the median absolute deviation (MAD) estimator, as given in Eq. (23).

σ=median(|D10|)0.6745(23)

After that, soft thresholding was applied at each level of the detail coefficients, as given in Eq. (24).

λ=σ2log⁡(N)(24)

Di,thresholded=SoftThreshold(Di,λ) for i=1,2,…,10

Ultimately, the signals are reconstructed by applying the inverse DWT to the threshold coefficients, thereby obtaining the denoised ECG signal, as shown in Eq. (25).

ECGDenoised =Inverse DWT(A,D1,thresholded,D2,thresholded,…,D10,thresholded)(25)

The denoised ECG signals exhibited baseline wander, which was corrected using the polynomial fitting technique. A polynomial of degree 5 was fitted to the denoised ECG signals obtained in Eq. (25) to capture the baseline wander, as shown in Eq. (26).

P(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5(26)

where ai are the polynomial P(t) coefficients and t represents time. To correct the baseline wander, the fitted polynomial curve is subtracted from the denoised ECG signal (ECGDenoised), as given by Eq. (27).

ECGCorrected=ECGDenoised −P(t)(27)

The obtained ECG signal (ECGCorrected) is free from baseline wander, and these signals are further processed in Algorithm 2.

3.2 Proposed ECG Signal Compression Technique

The proposed compression algorithm leverages the features of CS and sparse representation principles to obtain high compression rates while maintaining signal integrity with accurate reconstruction. The stepwise visual representation of the enhanced ECG compression algorithm is presented in Fig. 2. After choosing the ECG signal length and creating a 1D array, the FFT is used to calculate orthonormal bases. The RIP technique uses optimal size selection to build a random Gaussian matrix. The compressed matrix is created by multiplying the sensing matrix by the orthonormal bases. The compressed signal is calculated once the correctness of the sensing matrix is verified. The measurement matrix is recalculated otherwise. Lastly, the signal is reconstructed by pseudo-inverting the orthonormal basis.

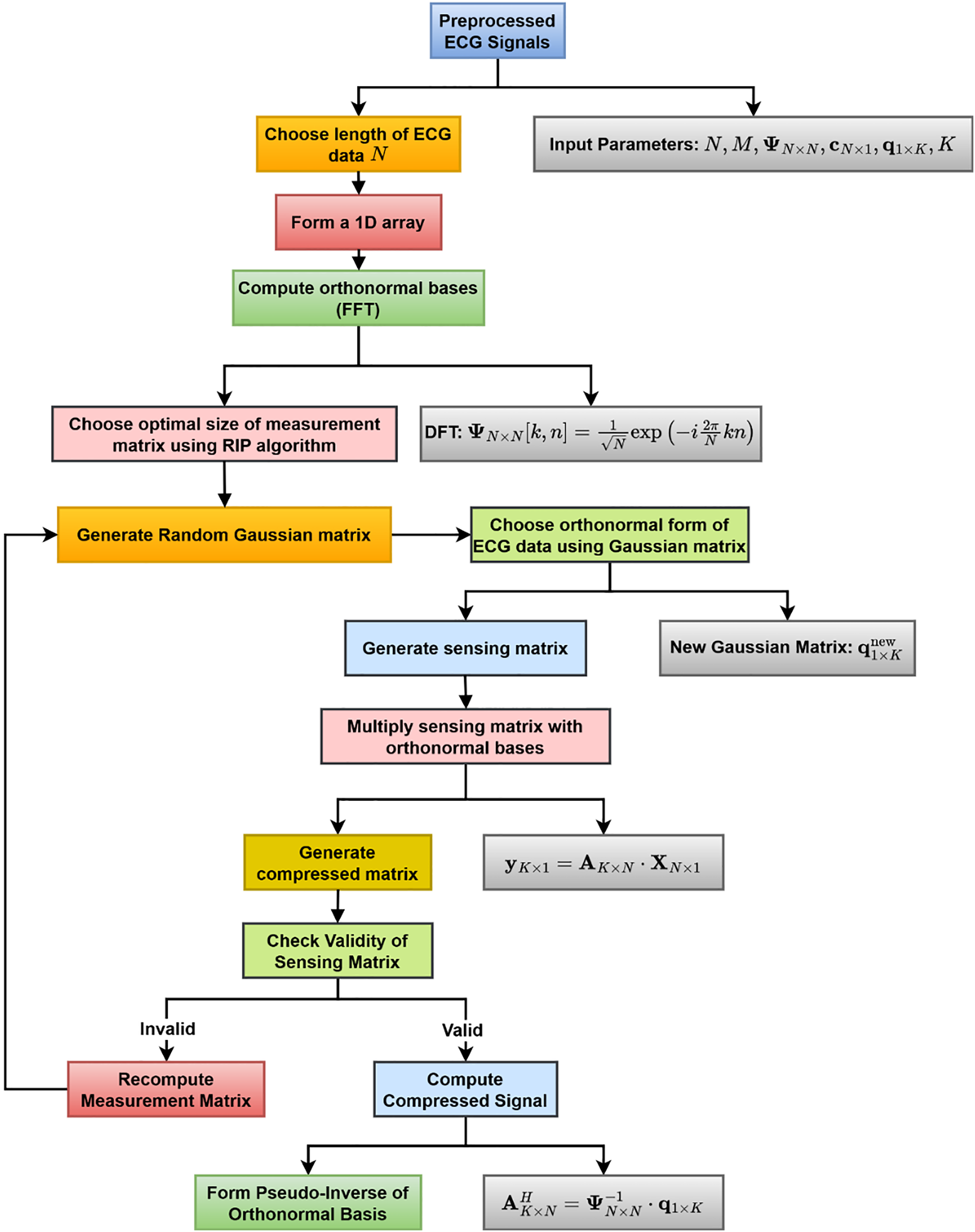
Figure 2: Block diagram of the proposed ECG signal compression technique

In this work, a length (N) of 2000 samples of the ECG signal was chosen for compression. ECG signal is semi-sparse in nature, so FFT is computed to convert the data into its sparse form by computing sparsifying basis matrix (ΨN×N) in the first step (Eq. (28)).

ΨN×N[k,n]=1Nexp⁡(−i2πNkn)(28)

This computation provides a minimal number of non-zero coefficients in the Fourier domain of the ECG signal with a high degree of accuracy. In the next step, the sparse representation of the pre-processed ECG signal (cN×1) by multiplying with the sparsifying basis matrix (ΨN×N), as given in Eq. (29).

XN×1=ΨN×N⋅cN×1(29)

In the following step, the measurement matrix is generated, where the (α) represents the initial step size and (β) denotes the iterative computation. Next, the sensing matrix (AK×N) is calculated utilizing the random Gaussian matrix or measurement matrix (q1×K), ensuring that the number of measurements (K) should be less than the size of the measurement matrix (M), as given in Eq. (30).

AK×N=q1×K⋅ΨN×N−1(30)

The sensing matrix was subsequently validated, and upon validation, the compressed ECG signal (yK×1) was computed by multiplying it with the sparse representation of the ECG signal, as given in Eq. (31).

yK×1=AK×N⋅XN×1(31)

If the validation of the sensing matrix is unsuccessful, the measurement matrix is recomputed, a new sensing matrix is formed, and a new compressed ECG signal is calculated.

q1×KNew and AK×N=q1×KNew⋅ΨN×N−1(32)

yK×1New=AK×N⋅XN×1

Finally, the pseudo-inverse of the orthonormal basis matrix is computed to ensure the accurate reconstruction of the original ECG signal, as represented in Eq. (33).

AK×NH=ΨN×N−1(q1×K)(33)

This approach effectively compresses the ECG signal while preserving the essential features necessary for accurate and reliable reconstruction. The algorithm’s robustness in handling the sparse representation of the ECG signal in the Fourier domain, along with its efficient measurement matrix generation and computation, makes it a highly effective solution for compressing ECG signals. The complete steps of the ECG compression method are presented in Algorithm 2.

3.3 Proposed ECG Signal Reconstruction Technique

Fig. 3 presents the flowchart of the proposed sparse representation and primal-dual wavelet-based ECG reconstruction technique. Optimization techniques, namely Primal-Dual and basis pursuit, were used to recover the coefficients of the original signal for reconstruction. One of the major limitations of the algorithms is that they are only applicable to convex problems. A standardization algorithm was applied to reduce signal variance. Once the master solution set is obtained, greedy iterative algorithms (Backtracking line search) were used to get the optimum solution set. To improve reconstruction efficiency, wavelet-based processing was applied to the reconstructed signal.

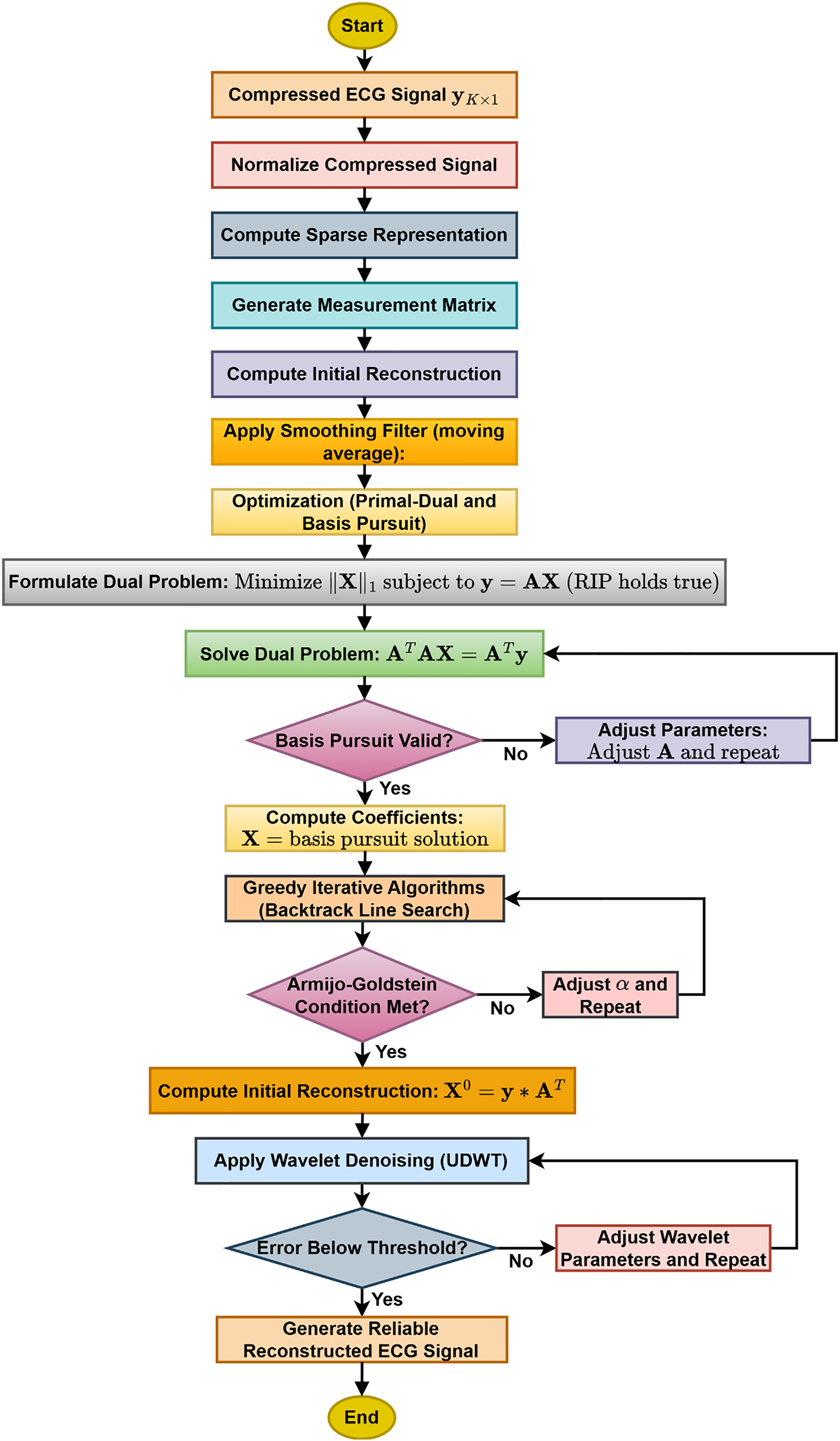
Figure 3: Flowchart of the proposed sparse representation and primal-dual wavelet-based ECG reconstruction technique

The signal X0 is reconstructed by multiplying the compressed signal (y) (where (y∈RM)) with the sensing matrix (A) (where (A∈RN×M)), as described in Eq. (34).

XNX 1o=yKX 1∗ANXKT(34)

The signal X0 should lie in an M-dimensional subspace of RN but cannot be used immediately due to noise in the data; therefore, the signal needs to be smoothened. The duality principle of optimization is employed to achieve the desired results. The given primal problem is transformed into a dual problem using the duality property and then solved to obtain the master solution set. The objective function is (Min|X|L1)subject to (y=AX) when the RIP holds. Once the master solution set is obtained, iterative algorithms, such as the Backtracking Line Search method, are used to find the optimal solution set. This algorithm adheres to the conditions specified in Eq. (35).

f((X)−f(X+αjp))>αjt(35)

A large initial estimate of α is used and iteratively reduced. The reduction process continues until a sufficiently small value is found, resulting in a decrease in the objective function. Since (XN×1=ΨN×N∗cN×1) (Eq. (12)), The ECG input signal (cN×1) needs to be estimated. By applying (ΨN×N−1) to both sides of Eq. (12), the following result is obtained:

XN×1∗ΨN×N−1=(ΨN×N∗ΨN×N−1)∗cN×1(36)

XN×1∗ΨN×N−1=cN×1

Eq. (16) simplifies to Eq. (17), providing the estimated ECG input signal (cN×1). In the next step, wavelet denoising is applied to enhance further the reconstructed ECG signal (cN×1). The undecimated discrete wavelet (UDWT) denoising technique is used to improve reconstruction efficiency. This technique offers shift invariance, anti-aliasing, and noise reduction properties. The Maximum Overlap Discrete Wavelet Transform (MODWT), an orthogonal wavelet, was employed in the developed algorithm, incorporating universal soft thresholding and a level-dependent noise estimation (‘mln’) for 10 levels of wavelet decomposition. Among the orthogonal wavelets tested, the Coiflet 1 wavelet provided the highest accuracy. This wavelet has (2n) moments equal to zero and a scaling function with (2n−1) moments equal to zero, resulting in fewer coefficients and thus more efficient reconstruction. The complete steps of the proposed ECG signal reconstruction technique are detailed in Algorithm 3.

4  Simulation Result and Performance Analysis

In this section, the experimental results and performance of the proposed compression and reconstruction algorithm are discussed. The algorithm that was developed was tested on the PhysioNet database (PTB-DB and MIT-BIH arrhythmia). For the PTB-DB database, the sampling frequency is 1000 Hz with a 16-bit resolution over a ±16 mV range. For the MIT-BIH arrhythmia database, the sampling frequency is 360 Hz with 11-bit resolution over a 10 mV range. Five standard performance metrics were used to quantify the efficiency of the compression and decompression algorithms. Compression ratio (CR) (Eq. (18)) to estimate the amount of compression and the remaining four parameters, namely Mean square Error (MSE) (Eq. (19)), PRD (Eq. (20)), Correlation Coefficient (CoC) (Eq. (21)), and Signal to noise ratio (SNR) (Eq. (22)), reflect on the efficiency of the decompression algorithm to preserve the clinical relevance of ECG data.

CR=(Size of original signal −Size of compressed signal)Size of original signal ×100(37)

MSE=1N∑(x(i)−x′(i))2(38)

PRD=MSE∑i=1N(x[i])2×100(39)

Correlation Coefficient (CoC) =(∑(xi∗xi′)⁢∗N)−(∑xi−∑xi′)((N∗∑xi2)−∑xi2)X⁢((N∗∑xi′2)−∑x⁢i′2))(40)

SNR=20log⁡(0.01×PRD)(41)

where, N = Length of the signal, (i) = Input Reference signal, x′(i) = reconstructed signal output. The correlation between the PRD and the clinical relevance of the reconstructed signal was suggested by Zigei et al. [30]. Table 1 presents the percentage of PRD corresponding to different classes of signal reconstruction quality, categorized by diagnostic relevance.

4.1 Simulation Result for Compression and Reconstruction Algorithm

Fig. 4 illustrates the test results of the developed ECG signal compression and reconstruction algorithm using a healthy record (s-0464) from the PTB-DB database. Fig. 5 illustrates the performance analysis of the proposed reconstruction algorithm at various compression ratios using the same record. Fig. 6 shows some deviations in the isoelectric part of the ECG signal, as Fourier-based denoising techniques suffer from this error, although peaks remain unaltered.

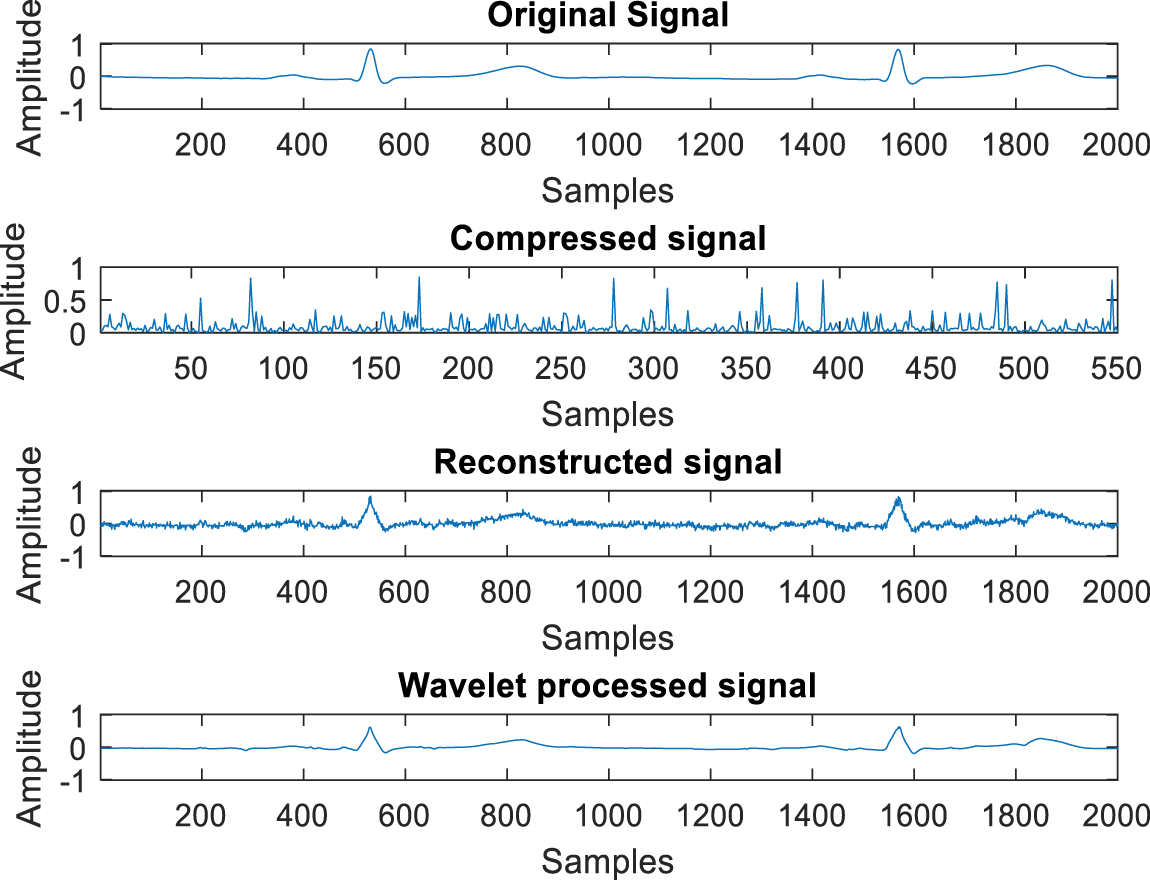
Figure 4: The test result of compression and reconstruction with rec. s_0464

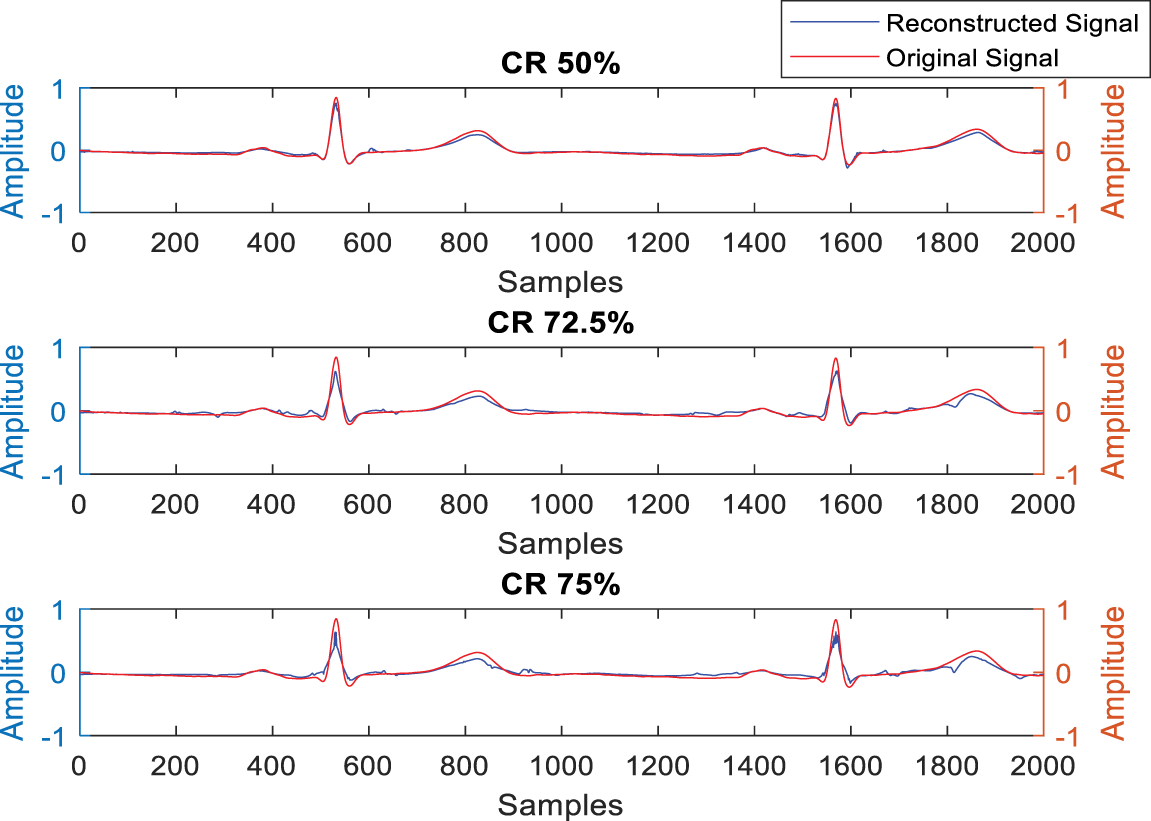
Figure 5: Test result for different compression ratios with rec. s_0464

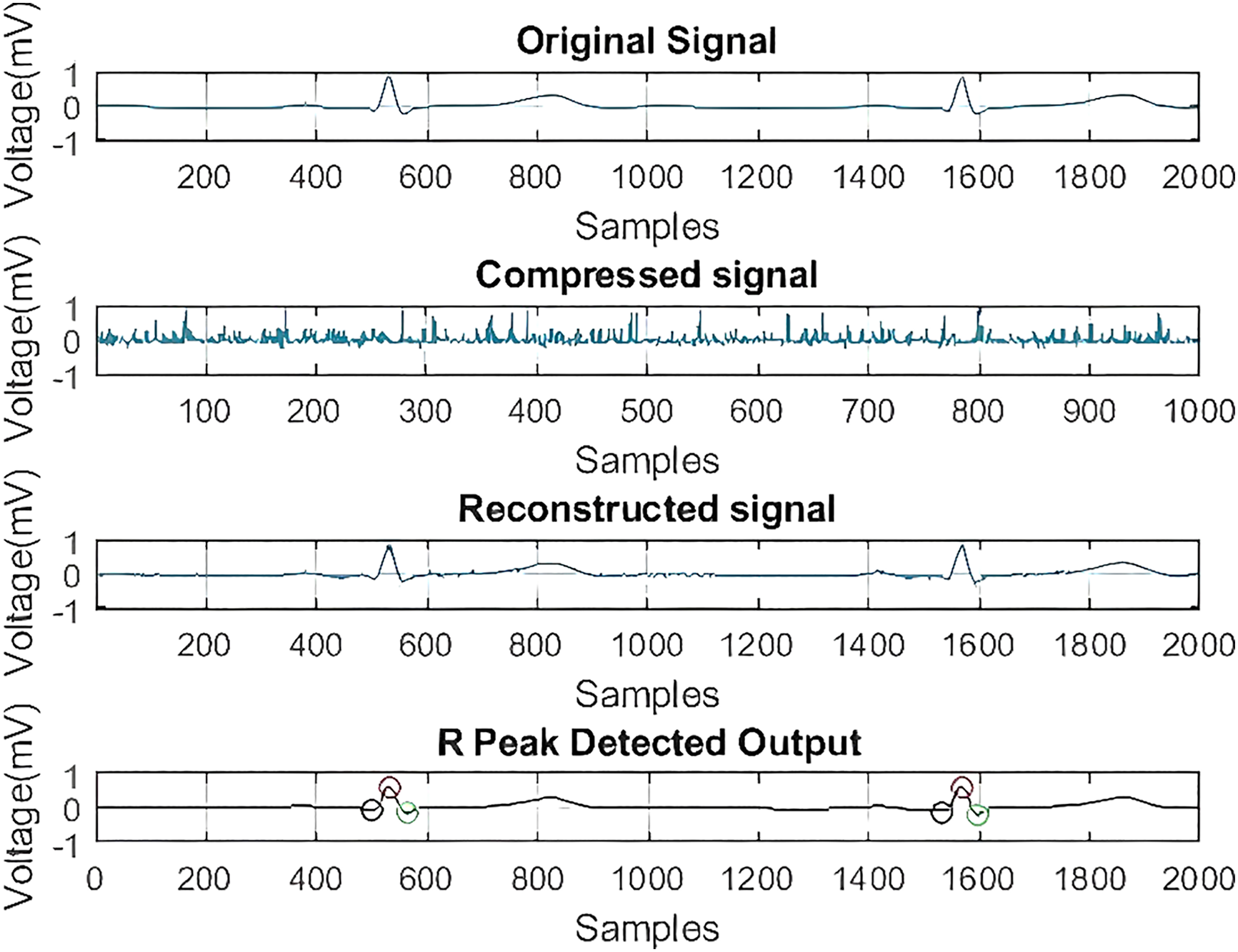
Figure 6: Test result for QRS complex detection after reconstruction with rec. s_0464

4.2 Performance Metrics Calculation

Table 2 indicates the performance analysis of different wavelets. Column I lists the different wavelets used in this comparative study, while columns II, III, IV, V, and VI present five assessment parameters. According to the results obtained in Table 2, the Level-10 Coif-1-based wavelet filtering method showed the most satisfactory reconstruction of the ECG data.

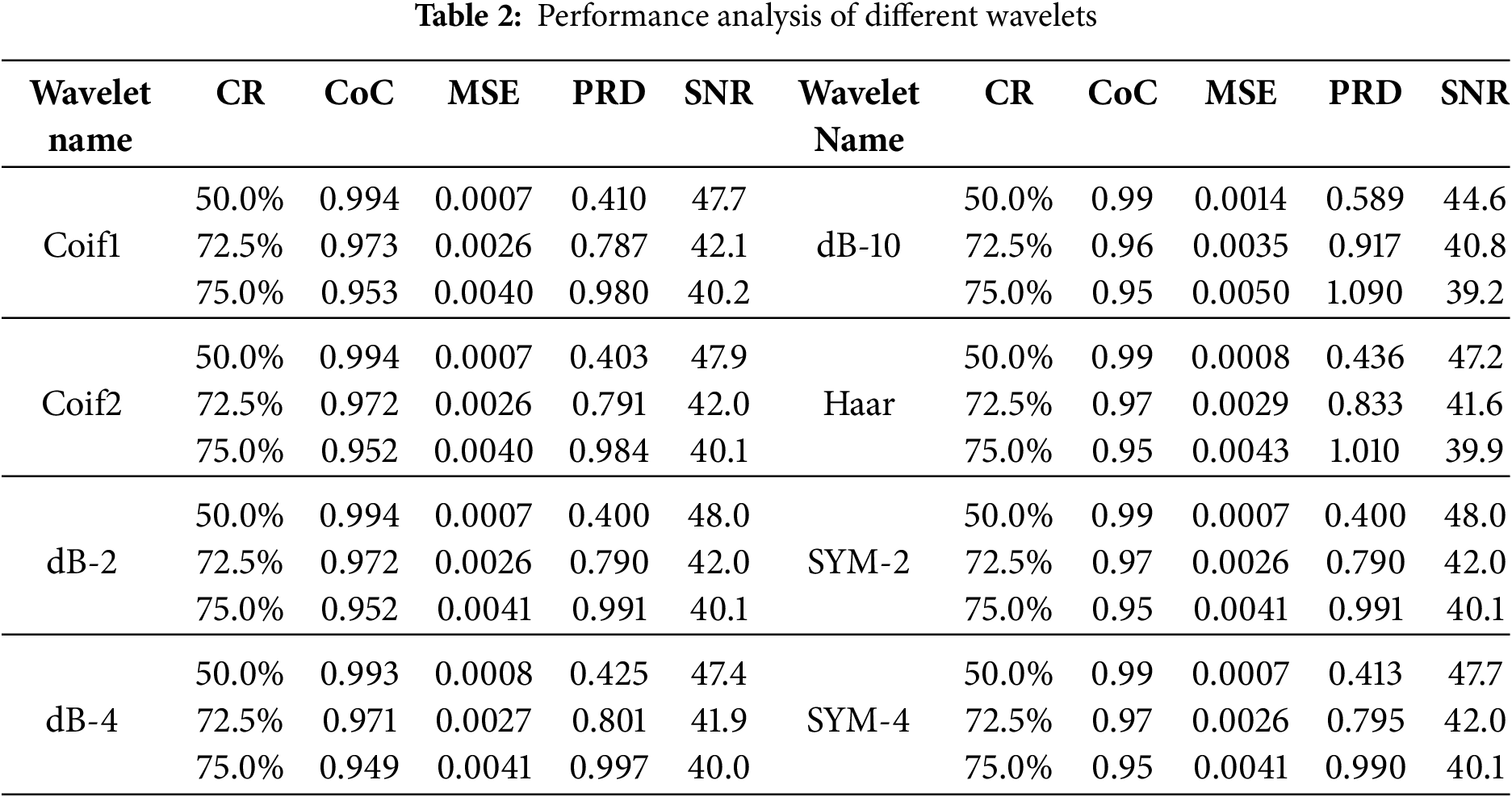
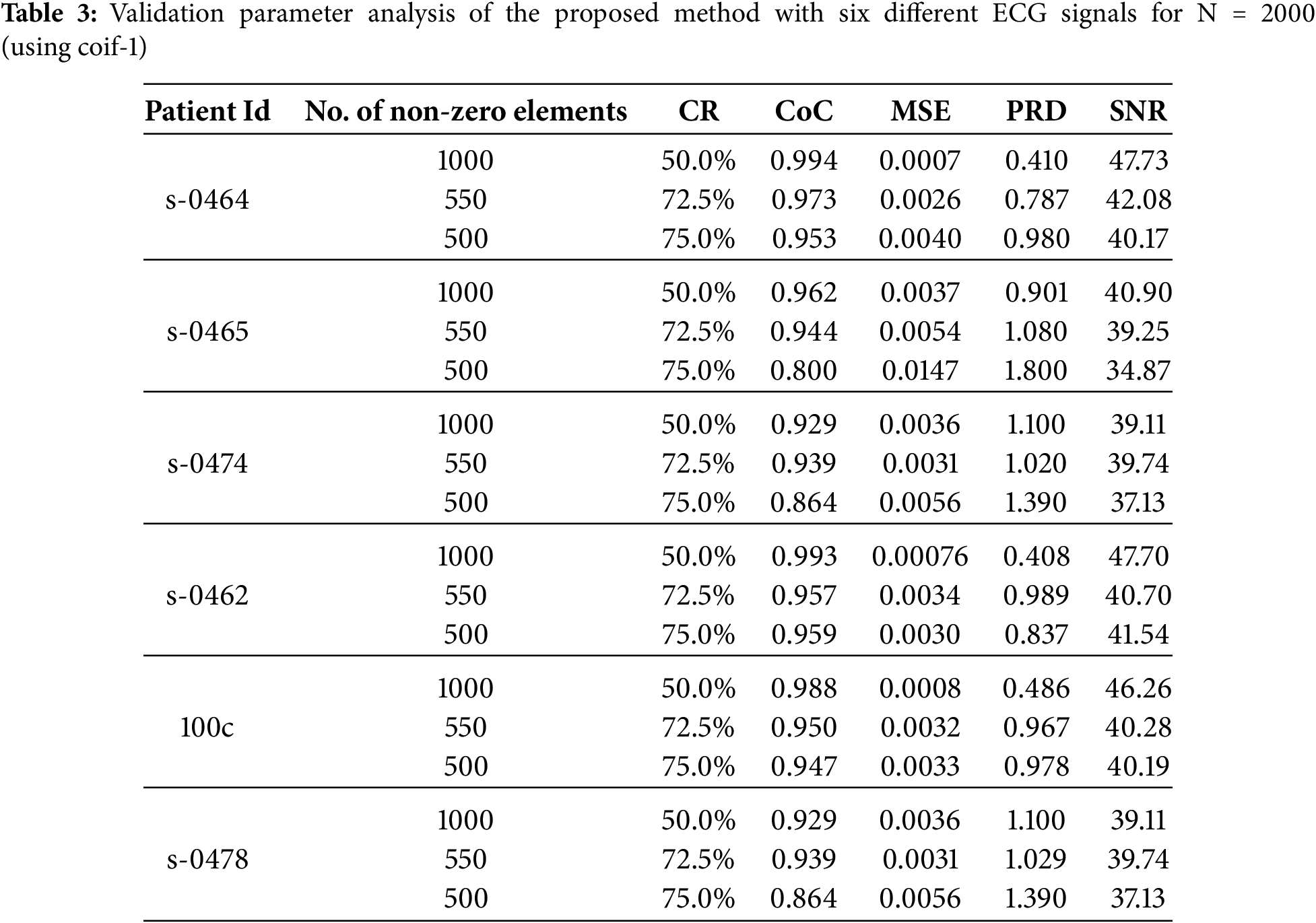
Table 3 presents the estimated assessment parameters for six different ECG signals. Different validation parameters were calculated to justify reliable reconstruction with different compression ratios. Column II indicates compression ratios, while the remaining columns display standard performance metrics used to evaluate the quality of reconstruction. Table 3 indicates a satisfactory reconstruction as per the criteria listed in Table 1.

It is observed from Fig. 7 that with an increase in compression ratio, MSE and PRD increase, so to retain the clinical usability of the reconstructed data, the compression ratio should be adjusted accordingly. Fig. 8 shows that increasing the number of non-zero elements in the sensing matrix improves CoC. PRD values in Fig. 9 indicate the comparative analysis of all validation parameters before and after applying wavelet-based filtering. All validation parameters suggested satisfactory results for all tested samples.

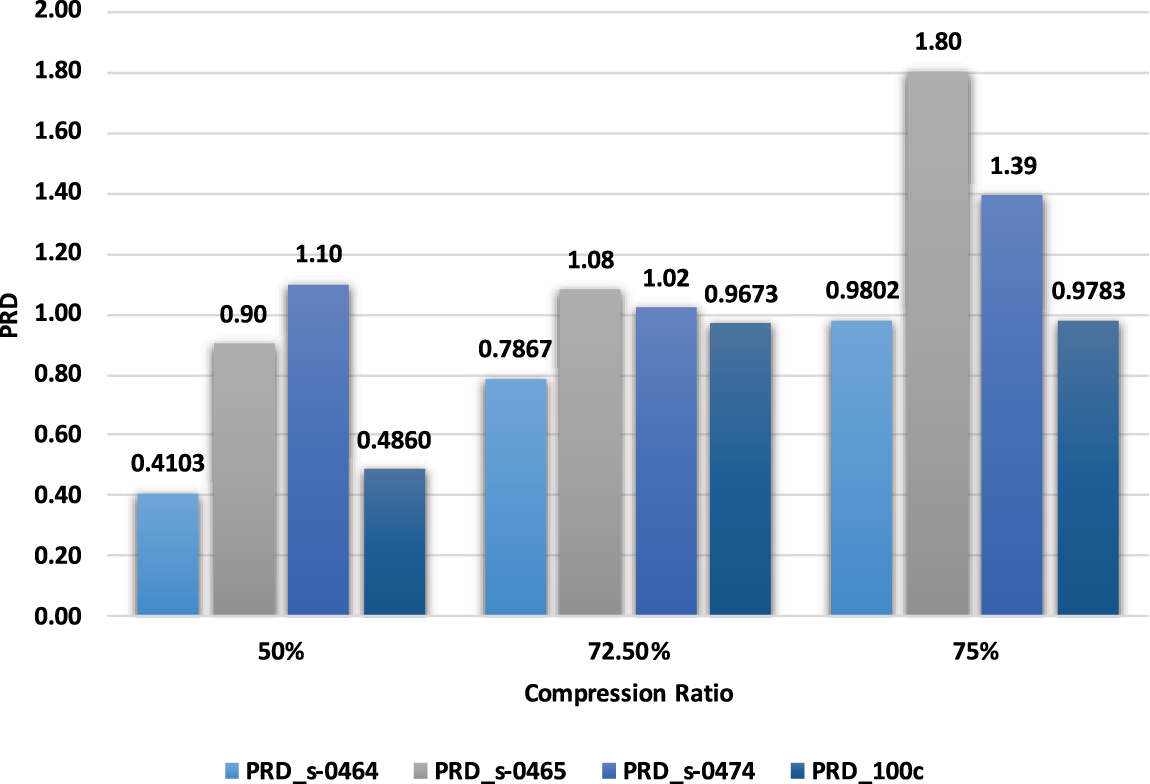
Figure 7: Comparison of PRD with Compression ratio

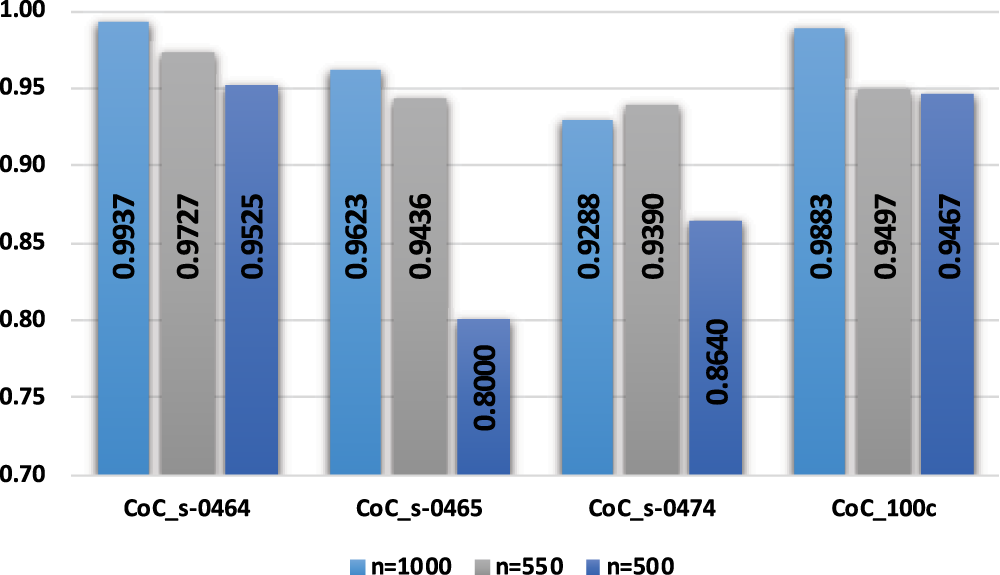
Figure 8: Comparison of CoC with non-zero elements

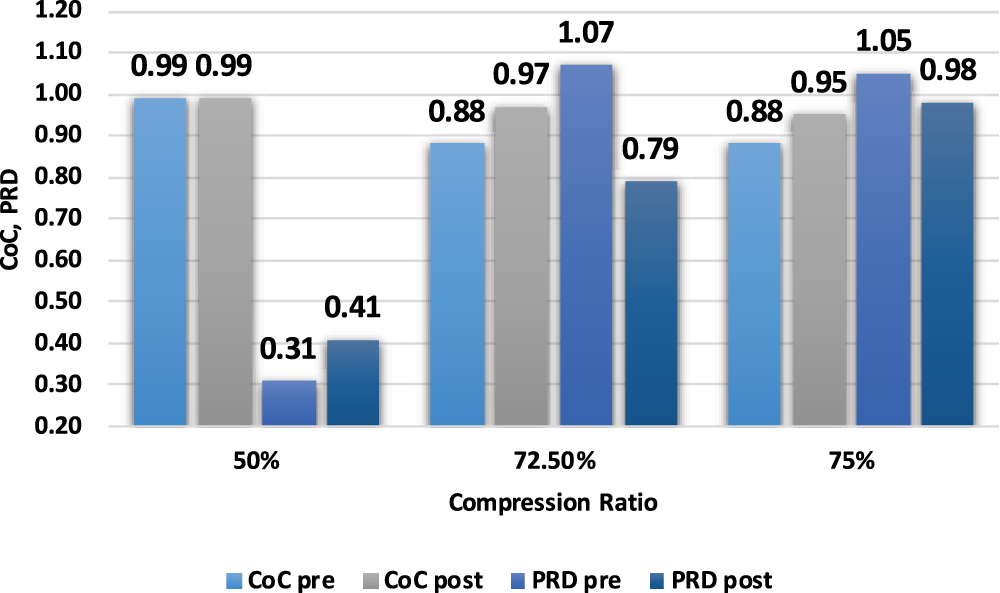
Figure 9: Pre-analysis and post-analysis of validation parameters

The CSP-PDW framework has been designed to meet the needs of real-time ECG analysis in IoT-based e-healthcare, where low latency and energy efficiency are of paramount importance. Through the merger of compressed sensing with wavelet-domain processing, it reduces the number of samples as well as the reconstruction dimension, allowing for diagnostic insights with millisecond precision and without a high burden of postprocessing. We have O(MN) (Gaussian projection) complexity for compression (M ≪ N), O(N) complexity for wavelet transforms, and O(kMN) complexity for Primal-Dual reconstruction, where k is a small number of iterations due to rapid convergence. The approach runs in below 50 ms per 1 s ECG segment (on a mid-range CPU). It achieves a good trade-off between compression efficiency, reconstruction accuracy, and speed, making it practical for embedded medical devices and wireless ECG monitors with scarce computing resources.

4.3 Limitations and Future Directions

Apart from several significant findings, our proposed CSP-PDW method also has some limitations. At extremely high compression ratios, fine morphological details, especially the ECG signals with complex morphological variations or arrhythmias, may be partially lost. The reconstruction quality of the ECG signal is sensitive to the selection of parameters, such as the sparsifying basis, measurement matrix size, and number of iterations. However, the use of a fixed mother wavelet may not be optimal for all patient records or pathological conditions. Although the proposed method is computationally efficient for standard IoT hardware, ultra-low power devices with minimal resources may require further optimization. The evaluation and validation of the proposed method were limited to standard ECG databases, and broader validation on diverse real-world datasets under varying noise conditions remains necessary.

In future work, the CSP-PDW algorithm will also be enhanced for robust processing of multi-class ECG signals across various morphologies and pathological conditions, with automatic parameter tuning and adaptive selection of mother wavelets. We will also extend our approach to utilize hardware-level optimizations for ultra-low-power IoT devices and validate it using larger, realistic datasets with real-world noise and motion artifacts, ensuring future reproducibility for continuous, real-time clinical monitoring.

5  Conclusion

This paper has presented a hybrid CSP-PDW technique for ECG signal compression and reconstruction of original ECG signals. The simplicity of the suggested algorithm makes it suitable for hardware-level implementation. The number of bits during measurement and transmission has been reduced by the suggested algorithm, which in turn has reduced the overall energy consumption. The algorithm presented has been less complex and has thus provided an opportunity to design standalone embedded systems using low-cost embedded boards for various applications. The average value of the correlation coefficient and the validation parameters suggests that the retention of clinical relevance is maintained after reconstruction. Obtained values for PRD, SNR, MSE, and CoC at a maximum compression ratio of 75% were 1.23, 38.05, 0.006, and 0.89, respectively. Fast data acquisition has addressed bandwidth and power issues in rural India, making it suitable for smart healthcare applications.

Acknowledgement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R749), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R749), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Author Contributions: Methodology, Hari Mohan Rai, Chandra Mukherjee, Joon Yoo, Hanaa A. Abdallah, Saurabh Agarwal, Wooguil Pak; Conceptualization, Hari Mohan Rai, Chandra Mukherjee, Joon Yoo, Hanaa A. Abdallah, Saurabh Agarwal, Wooguil Pak; Visualization, Hari Mohan Rai, Chandra Mukherjee, Joon Yoo, Hanaa A. Abdallah, Saurabh Agarwal, Wooguil Pak; Writing—original draft preparation, Hari Mohan Rai, Chandra Mukherjee, Joon Yoo, Hanaa A. Abdallah, Saurabh Agarwal, Wooguil Pak; Writing—review and editing, Hari Mohan Rai, Chandra Mukherjee, Joon Yoo, Hanaa A. Abdallah, Saurabh Agarwal, Wooguil Pak. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The dataset used in this work is publicly available and may be freely downloaded from the given link: MIT-BIH dataset: https://www.physionet.org/content/mitdb/1.0.0/; PTB-DB dataset: https://www.physionet.org/content/ptbdb/1.0.0/ (accessed on 09 September 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Donoho DL. Compressed sensing. IEEE Trans Inf Theory. 2006;52(4):1289–306. doi:10.1109/TIT.2006.871582. [Google Scholar] [CrossRef]

2. Candes EJ, Wakin MB. An introduction to compressive sampling. IEEE Signal Process Mag. 2008;25(2):21–30. doi:10.1109/MSP.2007.914731. [Google Scholar] [CrossRef]

3. Lal B, Gravina R, Spagnolo F, Corsonello P. Compressed sensing approach for physiological signals: a review. IEEE Sens J. 2023;23(6):5513–34. doi:10.1109/jsen.2023.3243390. [Google Scholar] [CrossRef]

4. Gupta V, Chaturvedi Y, Saxena NK, Sharma AK, Salim, Gupta V. ECG signal analysis using emerging tools in current scenario of health informatics. In: 2021 11th International Conference on Cloud Computing, Data Science & Engineering (Confluence); 2021 Jan 28–29; Noida, India. doi:10.1109/confluence51648.2021.9377119. [Google Scholar] [CrossRef]

5. Hassan AMA, Mohsen S, Abo-Zahhad MM. ECG signals compression using dynamic compressive sensing technique toward IoT applications. Multimed Tools Appl. 2023;83(12):35709–26. doi:10.1007/s11042-023-17099-7. [Google Scholar] [CrossRef]

6. Hui C, Zhang S, Cui W, Liu S, Jiang F, Zhao D. Rate-adaptive neural network for image compressive sensing. IEEE Trans Multimed. 2023;26:2515–30. doi:10.1109/TMM.2023.3301213. [Google Scholar] [CrossRef]

7. Mavaddati S. Classification of ECG arrhythmia using wavelet packet transform analysis and sparse learning method. Iran J Sci Technol Trans Electr Eng. 2023;47(4):1583–93. doi:10.1007/s40998-023-00620-x. [Google Scholar] [CrossRef]

8. Alqudah AM, Moussavi Z. A review of deep learning for biomedical signals: current applications, advancements, future prospects, interpretation, and challenges. Comput Mater Contin. 2025;83(3):3753–841. doi:10.32604/cmc.2025.063643. [Google Scholar] [CrossRef]

9. Fira M, Costin HN, Goraş L. A study on dictionary selection in compressive sensing for ECG signals compression and classification. Biosensors. 2022;12(3):146. doi:10.3390/bios12030146. [Google Scholar] [PubMed] [CrossRef]

10. Ansari-Ram F, Hosseini-Khayat S. ECG signal compression using compressed sensing with nonuniform binary matrices. In: The 16th CSI International Symposium on Artificial Intelligence and Signal Processing (AISP 2012); 2012 May 2–3; Shiraz, Iran. doi:10.1109/AISP.2012.6313763. [Google Scholar] [CrossRef]

11. Kot A, Nawrocka A. Measurement uncertainty for biological signals. In: Proceedings of the 2025 26th International Carpathian Control Conference (ICCC); 2025 May 19–21; Starý Smokovec, High Tatras, Slovakia. doi:10.1109/ICCC65605.2025.11022854. [Google Scholar] [CrossRef]

12. Patel S, Vaish A. An efficient optimization of measurement matrix for compressive sensing. J Vis Commun Image Represent. 2023;95(4):103904. doi:10.1016/j.jvcir.2023.103904. [Google Scholar] [CrossRef]

13. Singhai P, Ateek A, Kumar A, Ahmad Ansari I, Bhalerao S. ECG signal compression based on wavelet parameterization and thresholding using PSO. In: 2020 International Conference on Communication and Signal Processing (ICCSP); 2020 Jul 28–30; Chennai, India. doi:10.1109/iccsp48568.2020.9182407. [Google Scholar] [CrossRef]

14. Zhang Z, Jung TP, Makeig S, Rao BD. Compressed sensing for energy-efficient wireless telemonitoring of noninvasive fetal ECG via block sparse Bayesian learning. IEEE Trans Biomed Eng. 2013;60(2):300–9. doi:10.1109/TBME.2012.2226175. [Google Scholar] [PubMed] [CrossRef]

15. Lu Z, Kim DY, Pearlman WA. Wavelet compression of ECG signals by the set partitioning in hierarchical trees algorithm. IEEE Trans Biomed Eng. 2000;47(7):849–56. doi:10.1109/10.846678. [Google Scholar] [PubMed] [CrossRef]

16. Rajoub BA. An efficient coding algorithm for the compression of ECG signals using the wavelet transform. IEEE Trans Biomed Eng. 2002;49(4):355–62. doi:10.1109/10.991163. [Google Scholar] [PubMed] [CrossRef]

17. Ali Hassan AM, Mohsen S. Compression of electrocardiogram signals using compressive sensing technique based on curvelet transform toward medical applications. Multimed Tools Appl. 2025;84(12):11203–19. doi:10.1007/s11042-024-19328-z. [Google Scholar] [CrossRef]

18. Huang R, Xue X, Xiao R, Bu F. A novel method for ECG signal compression and reconstruction: down-sampling operation and signal-referenced network. Electronics. 2023;12(8):1760. doi:10.3390/electronics12081760. [Google Scholar] [CrossRef]

19. Singhai P, Kumar A, Ateek A, Ahmad Ansari I, Singh GK, Lee HN. ECG signal compression based on optimization of wavelet parameters and threshold levels using evolutionary techniques. Circuits Syst Signal Process. 2023;42(6):3509–37. doi:10.1007/s00034-022-02280-4. [Google Scholar] [CrossRef]

20. Yildirim O, Tan RS, Acharya UR. An efficient compression of ECG signals using deep convolutional autoencoders. Cogn Syst Res. 2018;52:198–211. doi:10.1016/j.cogsys.2018.07.004. [Google Scholar] [CrossRef]

21. Chang Y, Sobelman GE. Lightweight lossy/lossless ECG compression for medical IoT systems. IEEE Internet Things J. 2024;11(7):12450–8. doi:10.1109/JIOT.2023.3336995. [Google Scholar] [CrossRef]

22. Fathi IS, Makhlouf MAA, Osman E, Ali Ahmed M. An energy-efficient compression algorithm of ECG signals in remote healthcare monitoring systems. IEEE Access. 2022;10(1):39129–44. doi:10.1109/ACCESS.2022.3166476. [Google Scholar] [CrossRef]

23. Shi J, Wang F, Qin M, Chen A, Liu W, He J, et al. New ECG compression method for portable ECG monitoring system merged with binary convolutional auto-encoder and residual error compensation. Biosensors. 2022;12(7):524. doi:10.3390/bios12070524. [Google Scholar] [PubMed] [CrossRef]

24. Kuldeep G, Zhang Q. Lightweight electrocardiogram signal compression. Biomed Signal Process Control. 2023;85(9):105012. doi:10.1016/j.bspc.2023.105012. [Google Scholar] [CrossRef]

25. Pal HS, Kumar A, Vishwakarma A, Singh GK, Lee HN. An effective ECG signal compression algorithm with self controlled reconstruction quality. Comput Methods Biomech Biomed Engin. 2024;27(7):849–59. doi:10.1080/10255842.2023.2206933. [Google Scholar] [PubMed] [CrossRef]

26. Ez-ziymy S, Hatim A, Hammia S. Real-time hardware architecture of an ECG compression algorithm for IoT health care systems and its VLSI implementation. Multimed Tools Appl. 2024;83(10):30937–61. doi:10.1007/s11042-023-16631-z. [Google Scholar] [CrossRef]

27. Pal HS, Kumar A, Vishwakarma A, Lee HN. Electrocardiogram signal compression using adaptive tunable-Q wavelet transform and modified dead-zone quantizer. ISA Trans. 2023;142:335–46. doi:10.1016/j.isatra.2023.07.033. [Google Scholar] [PubMed] [CrossRef]

28. Pal HS, Kumar A, Vishwakarma A, Singh GK. Optimized tunable-Q wavelet transform-based 2-D ECG compression technique using DCT. IEEE Trans Instrum Meas. 2023;72:1–13. doi:10.1109/TIM.2023.3279885. [Google Scholar] [CrossRef]

29. Polania LF, Carrillo RE, Blanco-Velasco M, Barner KE. Compressed sensing based method for ECG compression. In: 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); 2011 May 22–27; Prague, Czech Republic. doi:10.1109/ICASSP.2011.5946515. [Google Scholar] [CrossRef]

30. Zigel Y, Cohen A, Katz A. The weighted diagnostic distortion (WDD) measure for ECG signal compression. IEEE Trans Biomed Eng. 2000;47(11):1422–30. doi:10.1109/TBME.2000.880093. [Google Scholar] [PubMed] [CrossRef]