An Integrated Approach to Condition-Based Maintenance Decision-Making of Planetary Gearboxes: Combining Temporal Convolutional Network Auto Encoders with Wiener Process

1  Introduction

1.1 Background

In aerospace, energy development, and industrial manufacturing sectors, planetary gearboxes have emerged as critical drive components in wind turbines, aircraft control systems, machine tools, and industrial robots due to their unique structural advantages and performance characteristics. They are indispensable in applications such as wind turbines [1] and helicopter main rotors [2]. While Industry 4.0 has significantly improved productivity, it has also heightened equipment failure risks [3]. As core components of mechanical transmission systems, planetary gearboxes often operate under heavy loads and high-speed conditions, rendering their key parts susceptible to gear wear, tooth surface fatigue pitting, tooth breakage, and bearing wear [4]. Such failures not only compromise transmission performance but may also lead to severe economic and safety consequences. Thus, designing scientifically sound and efficient maintenance strategies is imperative to reduce operational costs while enhancing system reliability and safety. The current maintenance of planetary gearboxes primarily relies on manufacturer-prescribed fixed intervals. This conventional maintenance approach exhibits significant drawbacks: on one hand, it may lead to “over-maintenance”, while on the other hand, it could result in “under-maintenance”, representing one of the key industry pain points. Traditional maintenance strategies based on age or fixed thresholds have been progressively supplanted by CBM decision-making. The widespread adoption of monitoring devices further highlights its broad application prospects in the operation and maintenance of offshore wind turbines [5,6] and gearboxes [7,8]. The CBM employs sensor data acquired through comprehensive condition monitoring systems to establish data-driven reliability models. This proactive strategy enables maintenance personnel to perform continuous health assessments and implement timely, evidence-based maintenance decisions when operational conditions dictate intervention.

With the rapid advancement of information technology and big data analytics, condition monitoring data in modern systems demonstrates increasingly prominent characteristics including high diversity, rapid generation velocity, and massive volume [9]. Traditional machine learning approaches face significant limitations when processing such large-scale datasets, as they excessively rely on signal processing techniques and domain expertise for manual feature extraction. In contrast, deep learning methodologies eliminate the need for manual feature engineering by supporting automated natural feature processing, enabling direct learning of complex feature representations from raw data [10,11]. Following an end-to-end training paradigm from data input to health indicator output, the deep learning effectively circumvents human-induced biases [12]. Current CBM methods typically use statistical models or fault pattern recognition to assess equipment health and predict failures. Unlike traditional approaches relying on manual feature extraction, our TCNAE method automatically learns deep temporal degradation features directly from vibration signals.

The advent of deep learning technology has provided robust technical support for advancing CBM decision-making. Current studies leverage deep neural networks to analyze operational data [13–16], extracting features from large-scale sensor measurements to build predictive models. This enables precise equipment degradation forecasting and optimized maintenance strategies [17]. To achieve the practical implementation of deep learning-based CBM technology for planetary gearboxes, this study innovatively establishes the complete lifecycle degradation dataset for planetary gearboxes and develops an end-to-end intelligent maintenance framework that integrates temporal convolutional network autoencoders (TCNAE) with nonlinear Wiener processes, achieving closed-loop optimization from condition monitoring to maintenance decision-making.

1.2 Related Work

Benefiting from rapid advancements in sensing and condition monitoring technologies, the CBM has gradually attracted significant research attention. The CBM refers to an approach that evaluates current equipment health status by detecting and analyzing condition indicators (such as temperature, pressure, metal content in lubricants, etc.) closely related to equipment health, thereby enabling optimal maintenance decision-making. This approach fundamentally overcomes the limitations of relying solely on expert experience to determine maintenance timing. By effectively monitoring relevant parameters during the degradation process, it becomes possible to infer system reliability information without actual failure occurrence [18–21]. Given the stochastic nature of failures, Markov Chains (MC) are frequently employed for effective fault modeling. Naga Srinivasa Rao and Achutha Naikan [22] proposed a Semi-Markov Decision Process (SMDP) to optimize dynamic threshold strategies. Cheng [23] leveraged reinforcement learning to develop a framework for CBM strategy optimization based on ship fatigue damage mechanisms, which has been successfully applied in practice. Kang et al. [24] addressed maintenance uncertainties and weather impacts by introducing a condition-based maintenance policy for offshore wind turbines, optimizing schedules through maintenance bundling and timing to reduce operational expenditures. Zhao et al. [25] demonstrated a conditional opportunistic maintenance strategy for multi-component systems in wind turbines, utilizing Weibull proportional hazard models to characterize individual degradation processes. However, most current CBM research still relies on strong assumptions (e.g., fixed Weibull distribution, linear degradation, etc.). This assumption-driven approach often demonstrates poor adaptability to nonlinear/abrupt degradation patterns (such as stepwise wear in gearboxes), posing significant challenges for practical engineering implementation. Beyond this, research on CBM for gearboxes remains in its nascent stages, with limited studies available in this area.

Accurate health state evaluation constitutes the fundamental premise for implementing effective CBM strategies. Health Indicator (HI) curves, typically exhibiting monotonic trends, enable equipment health assessment through threshold-based evaluation methods [26]. Shen et al. [27] proposed an approach utilizing Adaptive Order Bispectral Slices (AOBS) and Fault Characteristic Energy Ratio (FCER) to investigate vibration signal characteristics. Huang and Chang [28] developed a wireless measurement system to identify vibration signal models featuring Amplitude Modulation (AM) and Frequency Modulation (FM) induced by gear damage. Al-Bedhany et al. [29] and Huang et al. [30] respectively investigated premature failure of wind turbine gearbox bearings, along with the impact of lubricant selection on gearbox efficiency and energy production. Within the context of CBM for gearboxes, current research exhibits a notable gap in literature integrating fault diagnosis with maintenance decision-making, failing to establish a closed-loop system from data-driven analysis to maintenance strategies.

Accurate degradation modeling represents a pivotal element in CBM systems. The Wiener process has demonstrated superior capability in characterizing degradation patterns of various mechanical components (e.g., rolling bearings, lasers, and gyroscopes) during practical maintenance operations, establishing itself as a predominant model for degradation trend analysis [31]. Li et al. [32] developed a two-phase degradation model accounting for bearing performance deterioration characteristics, employing an autoregressive model coupled with nonlinear Wiener processes to delineate performance degradation in each phase, while utilizing extended Kalman filtering to disregard state increment dynamics during state updates. Sun et al. [33] proposed a comprehensive framework for multi-performance, multi-phase Wiener process modeling and reliability analysis, incorporating a biphasic nonlinear Wiener degradation model with Schwarz Information Criterion (SIC) for change-point identification. The Wiener process is defined by its memoryless property, Markovian nature, and Brownian motion, where stochasticity is key. These traits enable broad applications in modeling stochastic degradation. Due to its intuitive physical interpretation and computational efficiency, the Wiener process effectively describes degradation in critical mechanical components (e.g., rolling bearings, lasers, and gyroscopes).

In recent years, deep learning techniques have achieved remarkable progress in the field of the CBM, emerging as a core methodology for prognostic and health management [34]. The inherent uncertainty and stochastic nature of equipment failures have led to widespread adoption of deep learning models for condition assessment and decision-making. These models demonstrate superior capability in processing high-dimensional, nonlinear, and non-stationary sensor data, thereby delivering precise predictive outcomes. Huang et al. [35] proposed a fault diagnosis method based on cloud computing, wavelet transform, and CADRN deep residual networks. By utilizing the channel attention mechanism (CAM), this approach addresses the issues of information redundancy in training samples and the difficulty of conventional networks in extracting subtle fault features. Comparative experiments demonstrated that incorporating the channel attention module into deep residual networks can effectively improve fault diagnosis accuracy. Under different load or rotational speed conditions, the Collaborative Adversarial Domain Adaptation network (CADA) can reduce domain shift through adversarial training, thereby enhancing the generalization ability of degradation feature extraction. To address the limitation that unsupervised domain adaptation (UDA) models struggle to dynamically adjust according to changes in target tasks, Wang et al. [36] proposed a Dynamic Collaborative Adversarial Domain Adaptation Network (DCADAN) for unsupervised fault diagnosis of rotating machinery. The advantage of the Multiscale Lifting Wavelet Contrastive Network (MLWCN) in multi-resolution analysis of vibration signals lies in its ability to capture both high-frequency fault components and low-frequency degradation trends simultaneously. Addressing the issues of insufficient interpretability of deep models and inadequate capability in mining features from small samples, Dong et al. [37] proposed an interpretable multi-scale lifting wavelet contrastive network for fault diagnosis of planetary gearboxes. The Meta-Learning Network with Sensitivity Penalty (MLSP) discusses its robustness with a small amount of labeled data, especially the improved sensitivity to early weak faults in planetary gearboxes. Mu et al. [38] developed an Enhanced Meta-Learning Network with Sensitivity Penalty (EMLN-SP) for the diagnosis of rare faults under severe domain bias. Nevertheless, the opaque “black-box” nature of deep learning models frequently impedes interpretability in maintenance decision-making, revealing significant gaps in integrating these models with condition information for maintenance strategy formulation.

Current research still exhibits several limitations, which can be categorized into three key issues: First, existing studies generally lack systematic full-lifecycle experimental data support, predominantly relying on fragmented operational data or simplified accelerated aging tests under idealized conditions, which fail to accurately reflect the true degradation patterns in actual complex operating scenarios. Second, there exists a severe disconnection in the workflow from data acquisition to maintenance decision-making, where independent development of each stage leads to substantial information loss, resulting in a significant performance gap between laboratory models and real-world engineering applications. Third, purely data-driven methods suffer from insufficient interpretability, while traditional reliability theories oversimplify actual degradation processes, making current models unable to simultaneously meet the dual requirements of prediction accuracy and engineering applicability.

1.3 Overview

To address these challenges, this study proposes a novel deep learning-based CBM framework for planetary gearboxes. A comprehensive lifecycle degradation experiment was conducted to collect raw vibration signals, which were processed using the TCNAE to extract deep temporal degradation features. Kernel principal component analysis (KPCA) was employed to fuse and normalize these features, enhancing the degradation process characterization. A nonlinear Wiener process model was implemented to characterize the degradation trajectory, with parameters optimized through maximum likelihood estimation. The maintenance strategy was optimized to minimize costs per unit time, determining both the optimal maintenance timing and preventive maintenance thresholds. The principal innovations of this research can be summarized as follows:

(1)   Lifecycle experimentation and high-quality dataset construction. This study pioneers systematic full lifecycle degradation experiments for planetary gearboxes, acquiring comprehensive time-series vibration data that fills a critical gap in high-quality degradation datasets for this field. The dataset is conducive to discovering the degradation law of the gearbox, providing an essential foundation for data-driven degradation modeling research.

(2)   End-to-end intelligent maintenance technology chain. We innovatively establish a complete technical workflow encompassing “condition monitoring-feature extraction-degradation modeling-decision optimization”. The framework employs TCNAE for automated feature extraction, integrates KPCA for feature fusion, and utilizes nonlinear Wiener processes for degradation modeling, ultimately forming a closed-loop intelligent maintenance decision system.

(3)   Innovative integration of deep learning and traditional reliability theory. This work represents the first successful combination of deep learning’s automated feature extraction capabilities with Wiener process-based reliability theory. This hybrid approach overcomes the limitations of manual feature dependency in conventional methods while preserving model interpretability, achieving both enhanced prediction accuracy and engineering practicality.

The remainder of this paper is organized as follows: Section 2 introduces the TCNAE-based method for extracting degradation features from planetary gearboxes. Section 2.1 details the parameter estimation procedures. Section 3 develops the nonlinear Wiener process-based CBM decision model and details the parameter estimation procedures. Section 4 describes the full life-cycle degradation experiment and data processing workflow. Section 5 presents the application results integrating the methodologies from Sections 3, 4. Section 6 concludes the study.

2  Equipment Degradation Feature Extraction

2.1 Procedure

Current research on equipment degradation trend extraction reveals that mechanical systems typically exhibit a biphasic life cycle, as illustrated in Fig. 1. The initial phase represents normal operation, followed by a degradation phase. The transition point, termed First Predicting Time (FPT), is identified when the signal trend crosses a predetermined threshold, marking the onset of accelerated degradation. This critical juncture serves as the optimal timing for initiating CBM decision-making. Fig. 2 presents the systematic implementation workflow for equipment degradation trend extraction methodology.

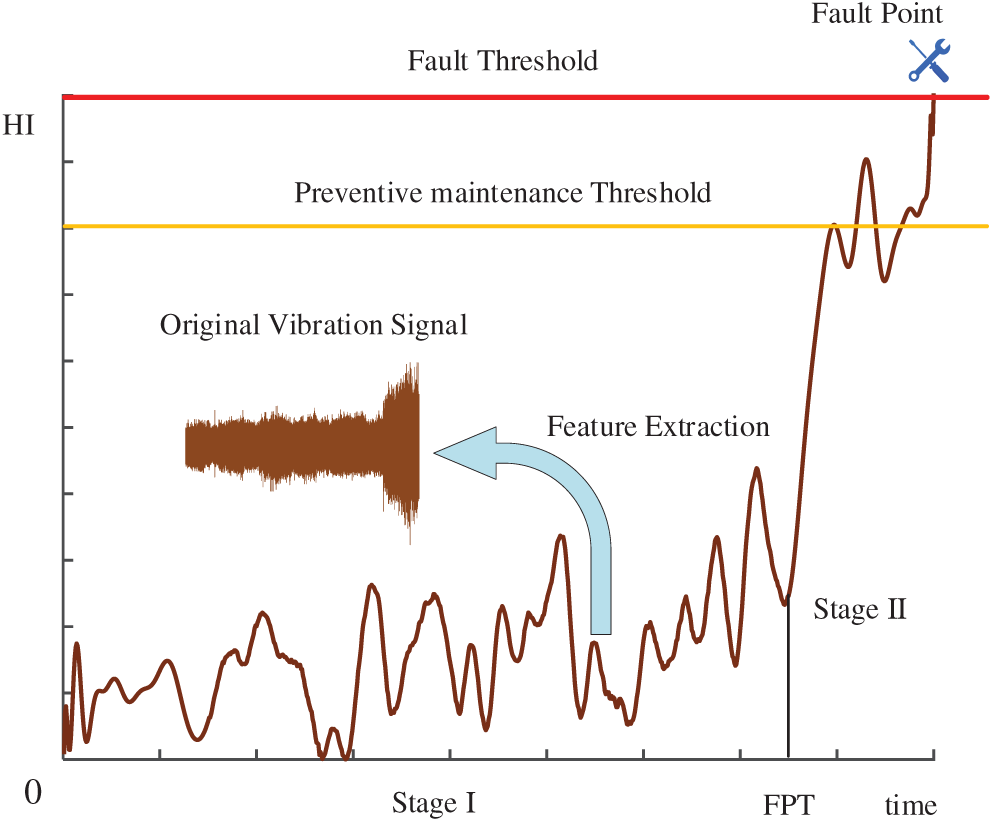
Figure 1: Equipment degradation trend extraction process

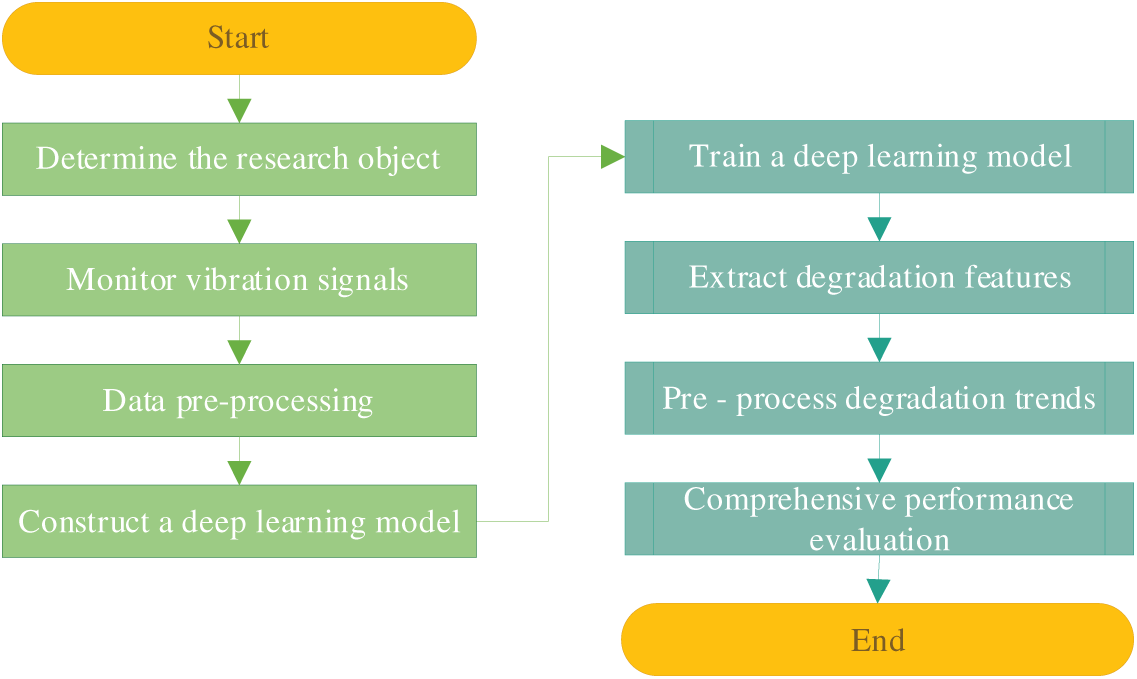
Figure 2: Implementation flowchart of equipment degradation trend extraction method

The proposed methodology enables precise monitoring of equipment health status, facilitating the detection of subtle operational variations by maintenance personnel. This enhanced monitoring capability supports more accurate maintenance intervention decisions. Furthermore, the extracted degradation trends allow for predictive assessment of equipment health progression, thereby providing critical data support for CBM decision-making processes.

2.2 Method

This study employs the computationally efficient Fast Fourier Transform (FFT) algorithm to perform spectral transformation of raw vibration signals. The transformed data is input into TCNAE network. The vibration signals of mechanical systems are typical time-series data, containing rich temporal features and local temporal dependencies. The TCNAE structure can automatically capture these local temporal features through convolutional layers. while its autoencoder structure enables effective feature dimensionality reduction and reconstruction, extracting more representative and robust degradation features. Compared with traditional feature extraction methods or some recurrent neural networks (such as LSTM and GRU), TCNAE does not suffer from gradient vanishing or explosion problems when dealing with long sequence data, and achieves higher computational efficiency. It can better meet the needs of degradation feature extraction for complex mechanical systems like planetary gearboxes, providing a high-quality feature basis for subsequent degradation modeling and maintenance decision making.

The TCN was first proposed by Lea et al. in 2016 [39] and has since gained widespread application in time series analysis. The causal convolution, a unidirectional architecture, determines the current output based solely on present and past inputs. Given an input time series X=(x1,x2,…,xT), X∈Rn and filter F=(f1,f2,…,fK), the causal convolution operation at position xT can be expressed as:

Y(T)=(X∗f)(T)=∑i=0k−1F(i)⋅xT−i(1)

In Eq. (1), k denotes the filter size, representing the number of time steps involved in each convolution operation. The term T − i encodes historical information by considering past temporal directions.

Fig. 3 illustrates the sampling patterns of dilated convolution vs. standard convolution. As shown in Fig. 4, the architecture of dilated convolution employs a base dilation rate d = 1 at the bottom layer, indicating direct sampling of each input element. When d > 1, the hierarchical structure ensures that even shallow networks can cover extensive input ranges. From Fig. 4, given an input time series X=(x1,x2,…,xT), X∈Rn and filter F=(f1,f2,…,fK), the dilated convolution operation at position xT is formulated as:

Y(T)=(X∗df)(T)=∑i=0k−1F(i)⋅xT−dgi(2)

where d represents the dilation rate, k is the filter size, and T − dgi maintains temporal causality by exclusively encoding past-oriented information.

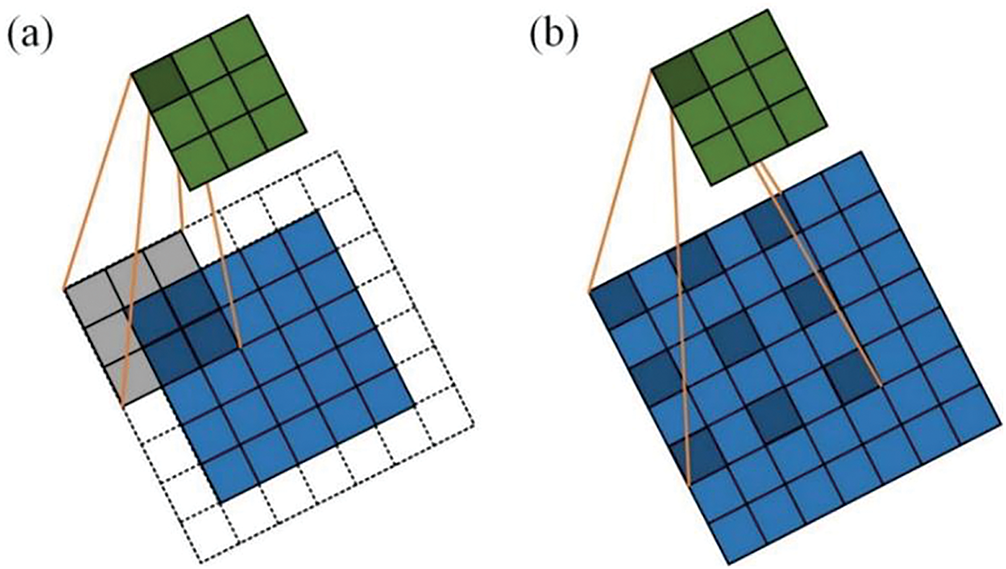
Figure 3: Convolution diagrams: (a) standard convolution (3 × 3 kernel) (b) dilated convolution (3 × 3 kernel, dilation rate of 2)

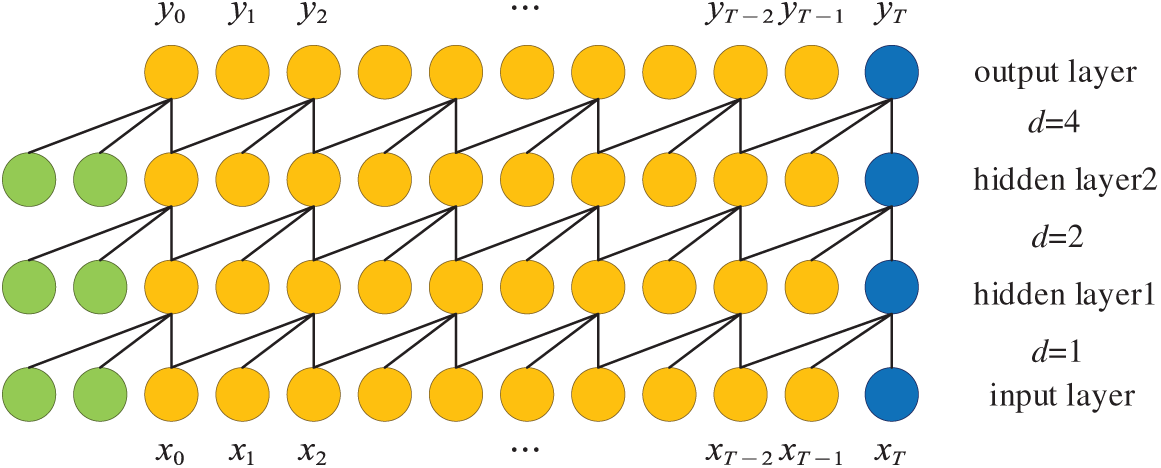
Figure 4: Architecture of dilated convolution

TCN incorporates universal residual modules, whose architecture is depicted in Fig. 5. The residual module replaces simple inter layer connections in conventional networks, enhancing model stability during deep layer propagation while improving generalization capability. The residual module’s operation can be formalized as:

Output=Activation(x+f(x))(3)

where Activation denotes the activation function and f represents the transformation performed within the residual module. The residual module allows the network to learn identity mappings more effectively, mitigating issues such as gradient vanishing and degradation in deep networks.

Figure 5: Residual module

The AE architecture comprises two symmetric components: an encoder that compresses high-dimensional inputs into low-dimensional latent features, and a decoder that reconstructs the original input from these features. In this study, our designed AE processes vibration signals transformed via FFT and progressively compresses the features through multiple layers of dilated causal convolution. This yields compressed bottleneck-layer features containing essential degradation-related information. The decoder then expands these features via a fully connected layer, restores temporal structure using a RepeatVector layer, and fine-tunes temporal correlations with a lightweight single-layer TCN. Finally, a multilayer perceptron (MLP) efficiently reconstructs the input signal, balancing computational cost and processing efficiency.

The TCNAE network’s final residual block employs multiple neurons to preserve feature diversity and discriminative power, enabling multidimensional temporal feature extraction. Experimental validation confirms that a single-neuron configuration performs poorly, as unidimensional features cannot effectively capture complex degradation patterns. Since predictive maintenance models require a single degradation trajectory, this study utilizes KPCA [40,41] to fuse multidimensional outputs into a one-dimensional representation, and the polynomial kernel function is adopted to address nonlinearity:

Φ(x,y)=(ε⋅x⋅y+η)υ(4)

where ε = 1 and η = 1. The parameter ν is determined through distance matrix computation: (1) replacing zero values with infinity, (2) identifying the global minimum distance, (3) computing the average minimum distance, and (4) scaling the average by a factor of 5. The distance matrix itself is obtained by calculating pairwise Euclidean distances between sample points.

The unique temporal features after KPCA processing undergo normalization per Eq. (5):

xi=x−xminxmax−xmin(5)

where xmax and xmin represent the maximum and minimum values of the temporal feature, respectively.

2.3 Evaluation Criteria

This study employs monotonicity, correlation, and robustness as evaluation criteria to quantitatively assess the performance of the extracted degradation trend [42]. First, the degradation trend is decomposed into a smooth trend and random error using polynomial fitting:

H(tn)=HT(tn)+HR(tn)(6)

where H(tn) represents the degradation trend value at time tn, HT(tn) denotes the smoothed trend, and HR(tn) is the random error.

Monotonicity evaluates whether the degradation trend exhibits a consistent increasing or decreasing pattern. It is calculated as:

Mon(HI)=|dHT(tn)>0m−1−dHT(tn)<0m−1|(7)

where Mon(HI) is the monotonicity index and m is the length of the degradation trend vector. A higher Mon value indicates a stronger monotonic trend.

The linear correlation between the degradation trend and time is measured using:

Cor(HI,T)=|∑n=1N(H(tn)−H¯)(tn−T¯)|∑n=1N(H(tn)−H¯)2∑n=1N(tn−T¯)2(8)

In Eq. (8), Cor(HI) represents the correlation between the degradation trend and time, where H¯=1N∑n=1NH(tn), T¯=1N∑n=1Ntn. A higher Cor value indicates a stronger linear relationship.

Robustness evaluates the tolerance of the Health Indicator (HI) to outliers, computed as:

Rob(HI)=1N∑n=1Nexp⁡(−|HR(tn)H(tn)|)(9)

where Rob(HI) is the robustness index. A higher Rob value indicates better resistance to noise and outliers.

To holistically evaluate degradation trend performance, a Comprehensive Indicator (CI) integrating all three metrics is defined:

CI=0.4∗Mon+0.3∗Cor+0.3∗Rob(10)

By combining these three metrics, the degradation trend can be comprehensively assessed. A well-performing trend accurately reflects the equipment’s health state, facilitating precise degradation analysis and CBM decision-making.

3  CBM Decision-Making Model Based on Nonlinear Wiener

While the proposed TCNAE feature extraction method provides high-precision characterization of equipment degradation, effective CBM decisions require translating these deep temporal features into quantifiable degradation models. Therefore, Section 3 establishes a degradation trajectory model based on the nonlinear Wiener process.

The Wiener process, characterized by linear drift and stochastic fluctuations, is inherently suitable for modeling degradation processes that combine deterministic trends with random noise. Its non-monotonic nature accommodates temporary “recovery” in degradation measurements, making it particularly applicable to multi-phase degradation scenarios. Mechanical system degradation typically exhibits complex nonlinear behavior due to mechanisms like wear, lubrication failure, and fatigue crack propagation. The nonlinear Wiener process captures these characteristics through nonlinear functions describing degradation rate changes, accurately reflecting actual degradation trajectories. Additionally, this process effectively models stochastic influences from environmental fluctuations, load variations, and material defects by combining nonlinear functions with random disturbances, providing a comprehensive simulation of degradation uncertainties.

As industrial equipment grows increasingly complex, the linear Wiener process proves inadequate for characterizing performance evolution. This study adopts a nonlinear Wiener process with adaptive time-scale transformation to better capture dynamic degradation characteristics and failure mechanisms. Through maximum likelihood estimation, we develop an analytical nonlinear degradation model that accurately reflects real-world trends, enabling precise CBM decision-making.

Let G(t) denote the degradation amount at time t. The degradation process based on Wiener process can be mathematically expressed as:

G(t)=λt+σB(t)(11)

where λ represents the drift coefficient, σ denotes the diffusion coefficient, B(t) is a standard Brownian motion characterizing the stochastic nature of the degradation process, satisfying B(t)~N(0, t).

Given the current degradation level Xk at time tk, the degradation state at the next monitoring instant tk+1 can be expressed as:

G(tk+1)=G(tk)+λ(tk+1−tk)+σB(tk+1−tk)(12)

To account for nonlinear characteristics, we incorporate a time-scale transformation function into Eq. (12), yielding the modified model:

G(tk+1)=G(tk)+λ~Υ(tk;ς)+σ~B(tk)(13)

where Υ(t;ς) is a nonlinear function of time t, ς represents unknown time-dependent parameters in the nonlinear function.

At the (k + 1)-th monitoring point, the evolution of the degradation process follows:

G(tk+1)=gk+λ~k(Υ(tk+1;ς)−Υ(tk;ς))+σ~kB(Υ(tk+1;ς)−Υ(tk;ς))(14)

When the drift and diffusion coefficients are assumed to follow non-normal distributions, we adopt the parameter estimation method from reference [43]. Suppose there are N sample degradation trajectories, and the inspection time points for each sample are denoted as tn,1, tn,2, …, tn,mn. Here, mn represents the number of degradation values available for the n-th sample trajectory, when n = 1, 2, …, N. Therefore, the degradation amount of the n-th sample trajectory at time tn,j is given by:

Xn(tn,j)=λ~⋅γ(tn,j)+σB(tn,j)(15)

In Eq. (15), γ(tn,j) represents the nonlinear function of time t and j=1,2,…,mn. Let Vn=(Vn,1,Vn,2,…,Vn,mn)′, then Vn,j=γ(tn,j), while also Xn=(xn(tn,1),xn(tn,2),…,xn(tn,mn))′. Here, Xn represents the vector of degradation values for the n-th sample trajectory, and (⋅)′ denotes the vector transpose.

To derive the maximum likelihood estimates for parameters λ~ and σ~, it is essential to formulate the joint probability density function of λ~ and σ~. According to the theory of multivariate normal distribution, Xn obeys a multivariate normal distribution with mean μ~n and variance Σn, where:

μ~n=λ~Vn,Σn=σ~2Ωn(16)

Ωn=[tn,1tn,1⋯tn,1tn,1tn,2⋯tn,2⋮⋮⋱⋮tn,1tn,2⋯tn,mn](17)

Assuming the measurement values from different degradation trajectories are mutually independent, the joint probability density function for the parameter set Θ=(λ~,σ~2)T can be expressed as:

𝒫(Θ|Xn)=12πmn|Σn|−12exp⁡(−12(Xn−λ~Vn)′Σn−1(Xn−λ~Vn))(18)

Taking the natural logarithm of both sides of Eq. (18), we obtain the log-likelihood function:

In𝒫(Θ|Xn)=−12(In(2π)+In|Σn|+(Xn−λ~Vn)′Σn−1(Xn−λ~Vn))(19)

By taking partial derivatives with respect to λ~ and σ~2, respectively, we derive:

∂In𝒫(Θ|Xn)∂λ~=Vn′Σn′Xn−λ~Vn′Σn′Xn(20)

∂In𝒫(Θ|Xn)∂σ~2=−N2σ~2+12σ~4(Xn−λ~Vn)′Ω−1(Xn−λ~Vn)(21)

Setting Eq. (20) to zero, the maximum likelihood estimate of the drift coefficient λ~ is obtained as:

λ~=Vn′Σn−1XnVn′Σn−1Vn=Vn′Ω−1XnVn′Ω−1Vn(22)

Similarly, setting Eq. (21) to zero, the maximum likelihood estimate of the diffusion coefficient σ~2 is obtained as:

σ~2=1N((Xn−λ~Vn)′Ω−1(Xn−λ~Vn))(23)

In Eqs. (20) and (21), Vn′ represents the transpose of the matrix Vn, and Σn−1 denotes the inverse of the vector matrix Σn.

Based on the equipment degradation trend curves presented in Section 2, we establish four distinct degradation modeling phases as follows:

When tk ≤ t1, the degradation process is modeled by:

G(t)=a1e−a2t[1+a3sin⁡(a4t)]+∫0tσ1(s)dB(s)(24)

where s denotes the dummy variable for integration, representing the integration variable when differentiating Brownian motion over the time domain, a1, a2, a3, a4 > 0. The drift and diffusion terms are respectively:

μ1(t)=μ~−a1a2e−a2t(1+a3sin⁡(a4t))+a1a3a4e−a2tcos⁡(a4t)(25)

σ1(t)=σ~+α1sin⁡(ω1t)(26)

When t1 < tk ≤ t2, the degradation process is modeled by:

G(t)=p1+p2arctan⁡(t−t1p3)+p4sin⁡(p5t)+∫t1tσ2(s)dB(s)(27)

where coefficients p1, p2, p3, p4, p5 > 0. The corresponding drift and diffusion terms are:

μ2(t)=μ~+p2p3[1+(t−t1p3)2]+p4p5cos⁡(p5t)(28)

σ2(t)=σ~+α2cos⁡(ω2t)(29)

When t2 < tk ≤ t3, the degradation process is modeled by:

G(t)=q1eq2(t−t2)+q3sin⁡(q4t)+∫t2tσ3(s)dB(s)(30)

where coefficients q1, q2, q3, q4 > 0. The drift and diffusion terms are:

μ3(t)=μ~+q1q2eq2(t−t2)+q3q4cos⁡(q4t)(31)

σ3(t)=σ~+α3sin⁡(ω3t)(32)

When t3 < tk ≤ t4, the degradation process is modeled by:

G(t)=r1(1−e−r2(t−t3))+r3sin⁡(r4t)+∫t3tσ4(s)dB(s)(33)

where coefficients r1, r2, r3, r4 > 0. The drift and diffusion terms are:

μ4(t)=μ~+r1r2e−r2(t−t3)+r3r4cos⁡(r4t)(34)

σ4(t)=σ~+α4e−(t−t3)cos⁡(ω4t)(35)

The developed Wiener process with nonlinear structure effectively captures actual degradation trends, yielding precise degradation trajectories.

This study investigates the degradation performance of planetary gearbox systems, employing variable-period inspection as an indicator for equipment performance degradation [44–46]. Let G(t) denote the system’s degradation amount at time t, with the following assumptions:

(1)   The initial degradation amount is 0, with a continuous and monotonic degradation trend;

(2)   Inspections do not alter the system’s degradation state, and inspection duration is negligible;

(3)   The degradation rate accelerates with both operational duration and preventive maintenance frequency;

(4)   After preventive maintenance, the system’s health state returns to its initial condition.

Under these assumptions, we classify system states based on inspection interval ϑ and preventive maintenance threshold Thpm.

(1)   If G(ti)<Thpm: The system operates normally, incurring only inspection cost Cin;

(2)   If Thpm ≤ X(ti) < Thcm: The degradation exceeds preventive maintenance threshold but remains below failure threshold, requiring preventive maintenance with combined costs (Cin + Cpm);

(3)   If G(ti)>Thcm: The degradation surpasses failure threshold, necessitating corrective maintenance with total costs (Cin + Ccm + Cpuni), where Cpuni represents the time-dependent penalty cost.

From an economic perspective, we establish the maintenance cost rate CR over the system’s total life cycle τ by minimizing the objective function:

minE(CR)=minE(C(t))E(τ)(36)

The total maintenance cost C(t) of the planetary gearbox system can be mathematically expressed as:

C(t)=∑i=1NinCin(ti)+∑j=1NpmCpm(tj)+∑k=1Ncm(Ccm(tk)+CpuniΔtk)(37)

where Cin, Cpm, Ccm denote inspection, preventive maintenance, and corrective maintenance cumulative counts respectively, Δtk represents the downtime duration for the k-th corrective maintenance.

Considering the actual situation that the preventive maintenance threshold decreases with the increase of maintenance times in maintenance activities, a threshold decay function is established as follows:

ϱn=ϱ0⋅e−ρn11+ζn(38)

In Eq. (38), n represents the number of maintenance times, ϱ0 represents the initial preventive maintenance threshold, ρ represents the decay coefficient, and ζ denotes the nonlinear factor.

The objective function derived from Eqs. (36) and (37) is formulated as:

(ϑ∗,Thpm∗)=arg⁡minE(CR(ϑ,Thpm))s.t.{ϑ>0Thcm>Thpm>0(39)

As indicated in Eq. (39), the Condition-Based Maintenance decision model employs simulation methods to analyze and solve for the optimal decision variables.

4  Case Study

To validate the practical utility of the theoretical model, Section 4 presents a full life-cycle experiment on planetary gearboxes, where vibration signals are collected to implement and verify the TCNAE feature extraction and Wiener modeling methods proposed earlier, thereby providing data support for subsequent maintenance decision optimization.

4.1 Experimental Setup

A 900-h full-life degradation experiment was conducted, and the main components of the experimental platform are as follows: the main motor is a three-speed electromagnetic speed-regulating motor (model YCT180-4A) with a rated power of 4 kW; the speed-torque sensor (model JN338) is used to collect the speed and torque signals of the input shaft of the planetary gearbox; the magnetic powder brake (model FZJ-5) provides load to the planetary gearbox, and the SC-1D (3A) load controller adjusts the load value of the magnetic powder brake by controlling the current [47], as shown in Fig. 6.

Figure 6: Experimental platform of planetary gearbox (1—main motor, 2—speed and torque sensor, 3—planetary gearbox, 4—magnetic powder brake, 5—base, 6—coupling)

The test employed an NGW11 single-stage planetary gearbox, with its internal structure schematic shown in Fig. 7 and detailed component parameters provided in Table 1. During operation, the gearbox achieved a transmission ratio of 12.5. Four vibration acceleration sensors were strategically mounted on the gearbox housing at locations depicted in Fig. 8, enabling comprehensive vibration signal acquisition from multiple orientations to effectively monitor degradation progression.

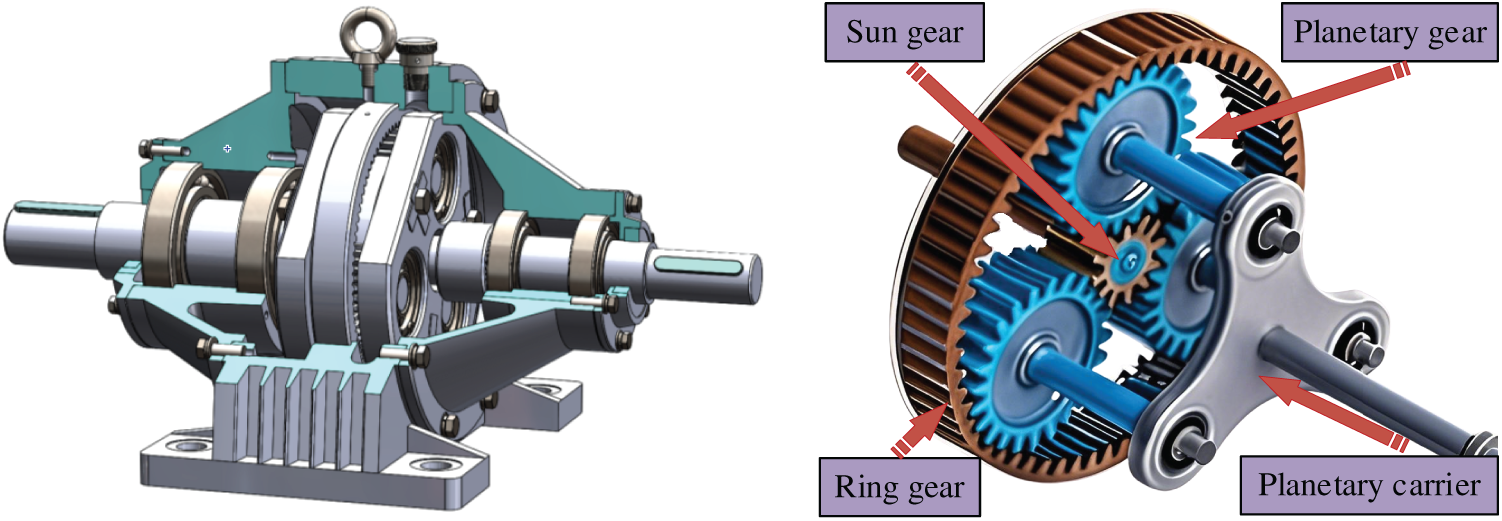
Figure 7: Internal structure diagram of the planetary gearbox

Figure 8: Sensor distribution locations

The main operating parameters of the experiment are as follows: (1) Input shaft speed: 1000 revolutions per minute (rpm). (2) Load current applied to the magnetic powder brake: 1 ampere (A), equivalent to a load of approximately 340 Newton-meters (N·m) on the planetary gearbox. (3) Vibration signal sampling frequency: 20 kHz, with a single sampling duration of 1 s and a sampling interval of 5 min. (4) The ambient temperature in the laboratory is controlled at 20 ± 1°C, and the relative humidity is maintained at 55 ± 5%.

This study selects the sample data collected by Sensor 2 for feature analysis. The planetary gearbox dataset obtained from the PHM laboratory consists of 900 CSV files with a total storage capacity of approximately 2.09 GB. Each file is sequentially named from data-T155412Z to data-T161513Z in chronological order, precisely recording continuous monitoring data throughout the experimental process to ensure the integrity of signal details. Every CSV file contains vibration acceleration data organized in a single column with 240,000 rows, capturing the vertical vibration signals of the planetary gearbox with a precision of five decimal places.

An electromagnetic brake provided a stable load during the experiment, with a load controller precisely adjusting the current to regulate braking torque. The magnetic powder brake operates via electromagnetic effects: when the controller supplies a 1A DC current, the magnetic powder forms chains, coupling the inner and outer rotors to produce a braking torque proportional to the current. To minimize instability effects, vibration signals were collected only during steady-state operation, excluding transient data from motor start-up and shutdown phases.

Following the complete life-cycle testing, the planetary gearbox exhibited multiple failure modes across its primary components, including inner and outer race wear, cracking damage, and varying degrees of tooth surface wear on major gears, as shown in Fig. 9. From Fig. 9, it can be observed that there are obvious signs of fatigue pitting and wear on the tooth surface of the sun gear. A small number of tooth surfaces on the planet gears exhibit wear and local fractures. The tooth surface wear of the ring gear is relatively uniform, but fracture traces were found in some areas. These damage patterns match typical planetary gearbox degradation under prolonged high-load operation, confirming the experimental data’s reliability.

Figure 9: Schematic diagram of wear components in planetary gearbox

4.2 Data Processing

4.2.1 TCNAE Model Training

After multiple pre-training sessions with the TCNAE model and referencing existing literature methods, the optimal hyperparameters are determined as follows: the encoding part consists of a stacked architecture with 3 residual blocks and 2 fully connected layers, where the number of neurons in the 3 residual blocks is 256, 128, and 64, respectively. Based on the time resolution of vibration signals and the requirement for receptive fields, the kernel sizes are set to 7, 5, and 3, which can capture long-period vibrations (such as meshing frequencies), obtain medium-frequency features, and extract transient features (such as impact signals), respectively, with reference to the practical applications of TCN in mechanical signal processing as described in [39].

To cover multi-scale temporal features, the dilation rates are set to 1, 2, and 4, respectively. Since the vibration signals of gearboxes contain high-frequency bearing fault components and low-frequency gear wear components, the design of exponentially increasing dilation rates can cover different time scales. To address the issue that vibration signals involve positive and negative oscillations, and the negative information is prone to loss with the traditional ReLU, we have selected the Leaky ReLU activation function, which adapts to the bidirectional oscillation characteristics of vibration signals by retaining the information on the negative semi-axis and alleviates the problem of gradient vanishing.

The two convolutional layers within each residual block undergo kernel initialization, and layer normalization is used for normalization processing. The decoder part is composed of a residual block with 64 neurons (dilation rate = 1) and an MLP network. Feature integrity is maintained through skip connections. An Adam optimizer with an initial learning rate of 0.001 and an MSE loss function are adopted to form the baseline for the regression task. The batch size is set to 128 to balance GPU memory usage and training efficiency, while the number of training epochs is set to 100 to ensure loss convergence. To avoid overfitting, Dropout is set to 0.25, and shortcut connections are included. The training status of the TCNAE model is shown in Fig. 10, which indicates that the MSE curve gradually declines and tends to stabilize as the epoch increases, with the final loss value remaining at 0.0163.

Figure 10: Training status of the TCNAE network model

For high-dimensional time-series data like the 16,383-dimensional vibration signals in our gearbox dataset, TCNAE demonstrates superior suitability for industrial feature extraction tasks owing to its low parameter requirements, high parallelism, and efficient memory utilization. However, LSTM/GRU struggle to handle high dimensional data due to memory limitations and sequence calculation characteristics.

4.2.2 Degradation Trend Extraction

The TCNAE model autonomously extracted 64 deep temporal features characterizing planetary gearbox degradation. Among these, 53 features exhibited values below zero, resulting in 11 valid deep temporal features. These valid features were smoothed using Savitzky-Golay filtering (window length = 301, polynomial order = 30) to reduce noise, as shown in Fig. 11.

Figure 11: Effective deep temporal features extracted by the TCNAE network model

The KPCA method described in 2.2 fused effective deep time-series features, with a polynomial function. After normalization, the fused deep time-series features are used as the final degradation trend of the planetary gearbox throughout its entire life cycle, as presented in Fig. 12.

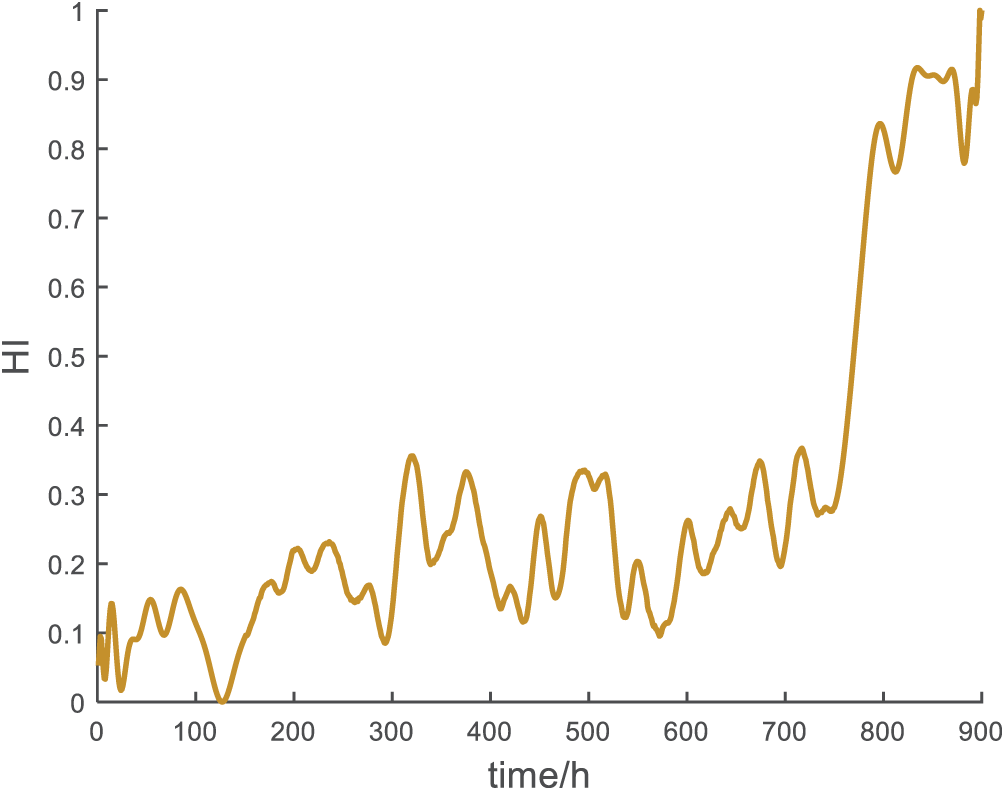
Figure 12: Fused deep temporal features

4.2.3 Comparison of Degradation Trends

As a traditional approach for degradation trend construction, statistical parameter-based methods analyze time-domain features from vibration signals [48]. In planetary gearbox degradation, signal amplitude and probability distribution variations directly affect these parameters, which effectively characterize vibration features. These statistical parameters can intuitively characterize the features of vibration signals. Table 2 lists six key time-domain features among statistical parameters, with their extracted trends displayed in Fig. 13. Here, xi is the sampled time signal, i is the sample index, and N is the number of samples.

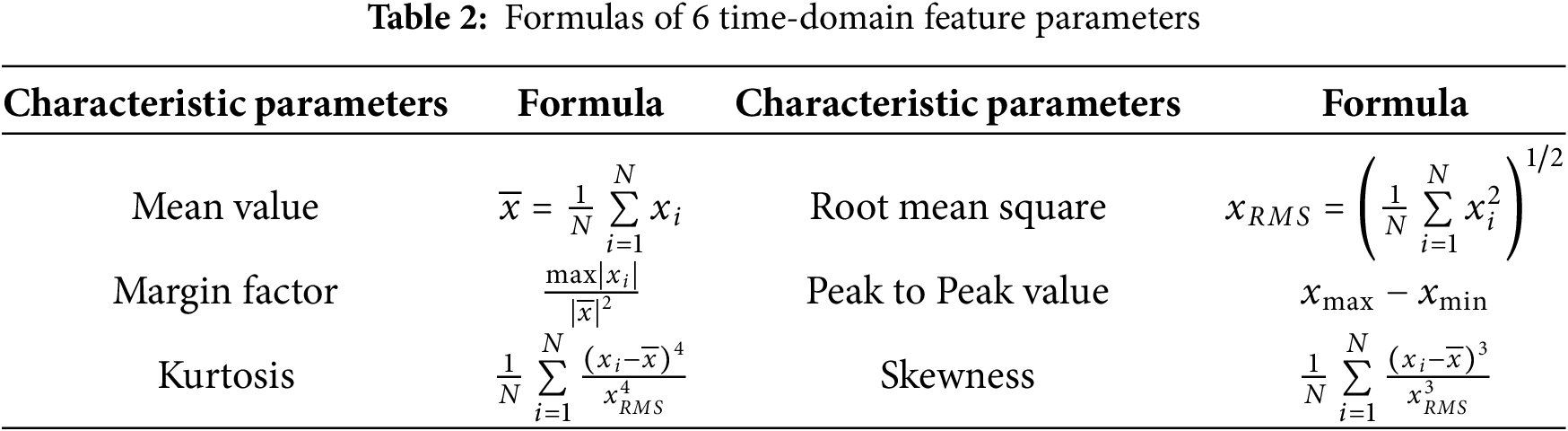
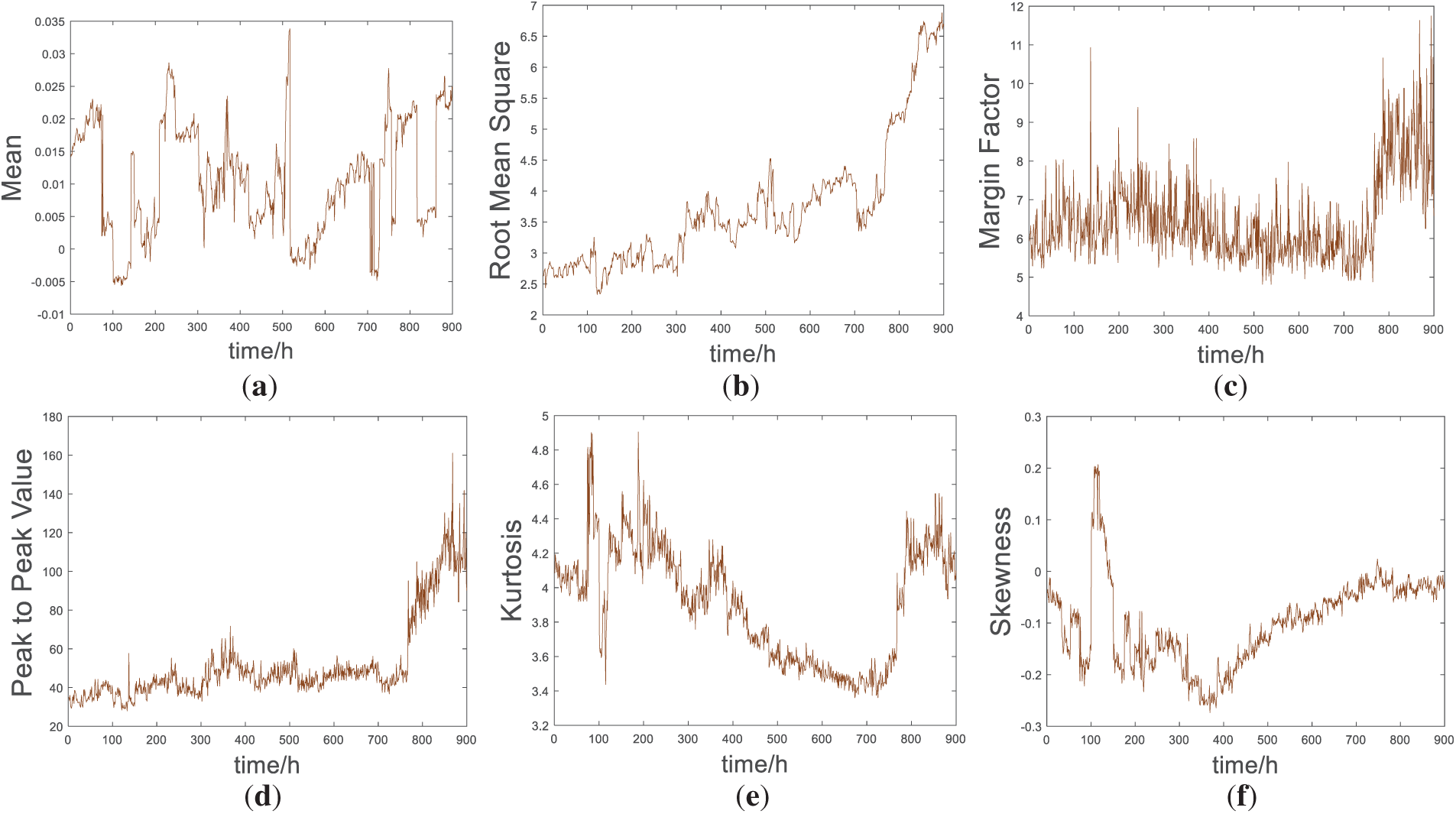
Figure 13: Time-domain characteristics of vibration signals over the full life cycle of the planetary gearbox

5  Results

Based on processed experimental metrics, this section systematically evaluates the feature extraction performance of TCNAE, parameter estimation accuracy, and the superiority of dynamic threshold strategies, offering comprehensive assessment of the framework’s engineering value.

5.1 Data Analysis

According to the experimental protocol outlined in Section 4, the acceleration values of the vibration signals in the vertical direction of the power input shaft are presented in Fig. 14. As shown in Fig. 14, the planetary gearbox exhibited stable operation with minor fluctuations, followed by progressive degradation. A sharp signal change at 750 h indicated component failure, culminating in severe vibration and audible noise at 900 h that marked complete gearbox failure.

Figure 14: Full life cycle vibration signals of the planetary gearbox-sensor 2

Comparative analysis of Fig. 15 and Table 3 clearly demonstrates TCNAE’s superior performance over LSTM and GRU in three key aspects. First, it exhibits stronger feature representation capability, with normalized feature values significantly higher than LSTM/GRU across most sample intervals, indicating more effective capture of vibration signal patterns and higher compression efficiency for high-dimensional FFT signals in its hidden states. Second, it shows better temporal stability, with notably smaller curve fluctuations compared to the pronounced oscillations observed in LSTM/GRU. The fixed receptive field in TCN stabilizes long range feature extraction, making it more suitable for stable industrial monitoring. Third, it demonstrates higher fault sensitivity, displaying significant feature value increases in tail sample intervals through multi-scale convolutional kernels that amplify fault-band energy, whereas LSTM/GRU shows weak responses.

Figure 15: Comparison of time-series features trained by three models

Using the comprehensive evaluation criteria for degradation trend performance proposed in Section 2.3, the CI values (also known as health factors) of the degradation trends derived from six time-domain features and the TCNAE method were calculated, as shown in Table 4.

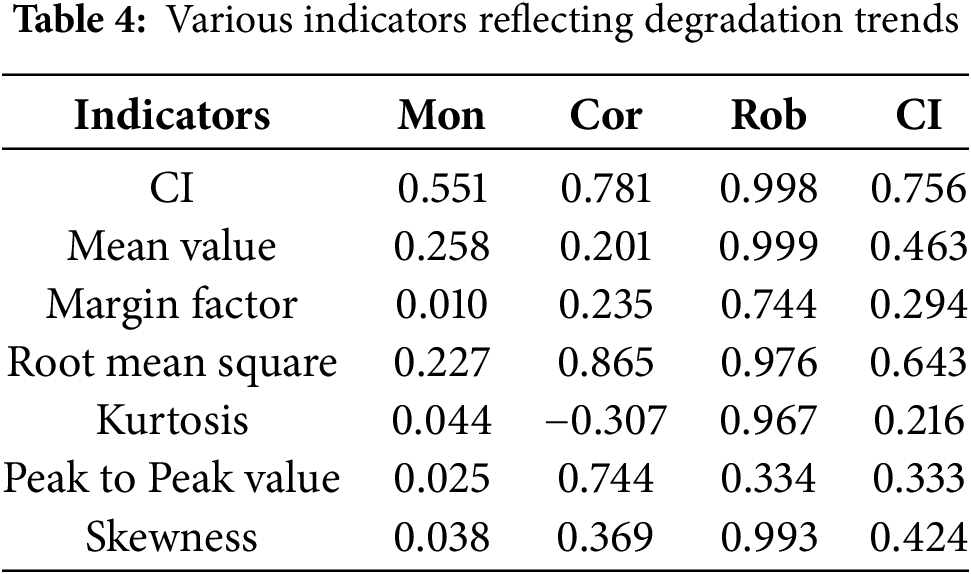
As indicated in Table 4, most time-domain features exhibit severe fluctuations, while the degradation trend extracted by the TCNAE method yields the highest CI value, demonstrating the best characterization effect for the degradation trend of the planetary gearbox.

Based on the parameter estimation method described in Section 3, data fitting was performed on the deep time-series features extracted by TCNAE. Through operations such as nonlinear least squares, matrix computation, and vector manipulation, the estimated value of the drift coefficient λ~ was determined to be 4.5 × 10−3, and the estimated value of the diffusion coefficient squared σ~2 was 1.4256 × 10−4. The estimation process is illustrated in Fig. 16.

Figure 16: Parameter estimation process

5.2 Decision-Making of CBM

The planetary gearboxes degradation progresses through two distinct phases: an initial stable operation phase where degradation remains below the preventive maintenance threshold, followed by an accelerated degradation phase where deterioration exceeds this threshold and may reach failure levels. Based on fused degradation features, we identified four characteristic stages, with degradation paths shown in Fig. 17 and parameters listed in Table 5.

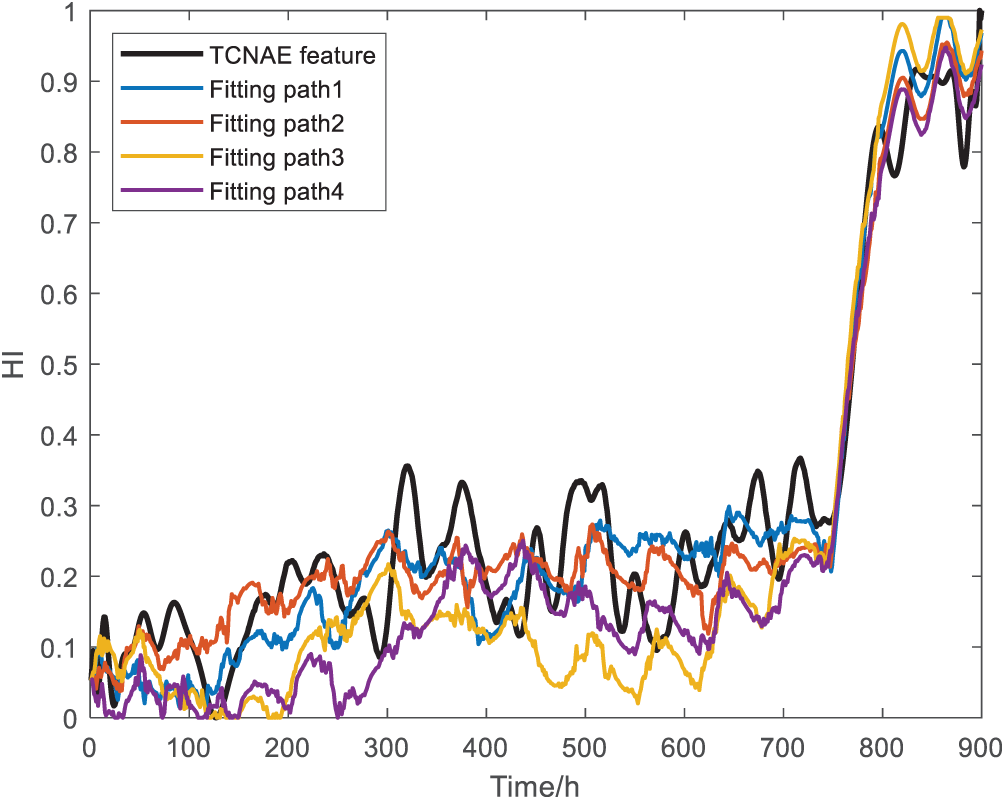
Figure 17: Degradation path fitted by nonlinear Wiener process

Using cost parameters Cin = 100, Cpm = 3500, Ccm = 4800, and Cpuni = 50, Monte Carlo simulation yielded the following results: Under static thresholds, the minimum objective function CR value was 60.9736 with optimal decision variables of 155 and 0.907. With a threshold decay rate of 0.2, the minimum CR value reduced to 55.5556, with optimal decision variables of 151 and 0.752. The corresponding 3D surface plots and contour maps at estimated values are presented in Figs. 18 and 19, respectively.

Figure 18: 3D Surface Plot (a) and Contour Plot (b) of CR under static threshold

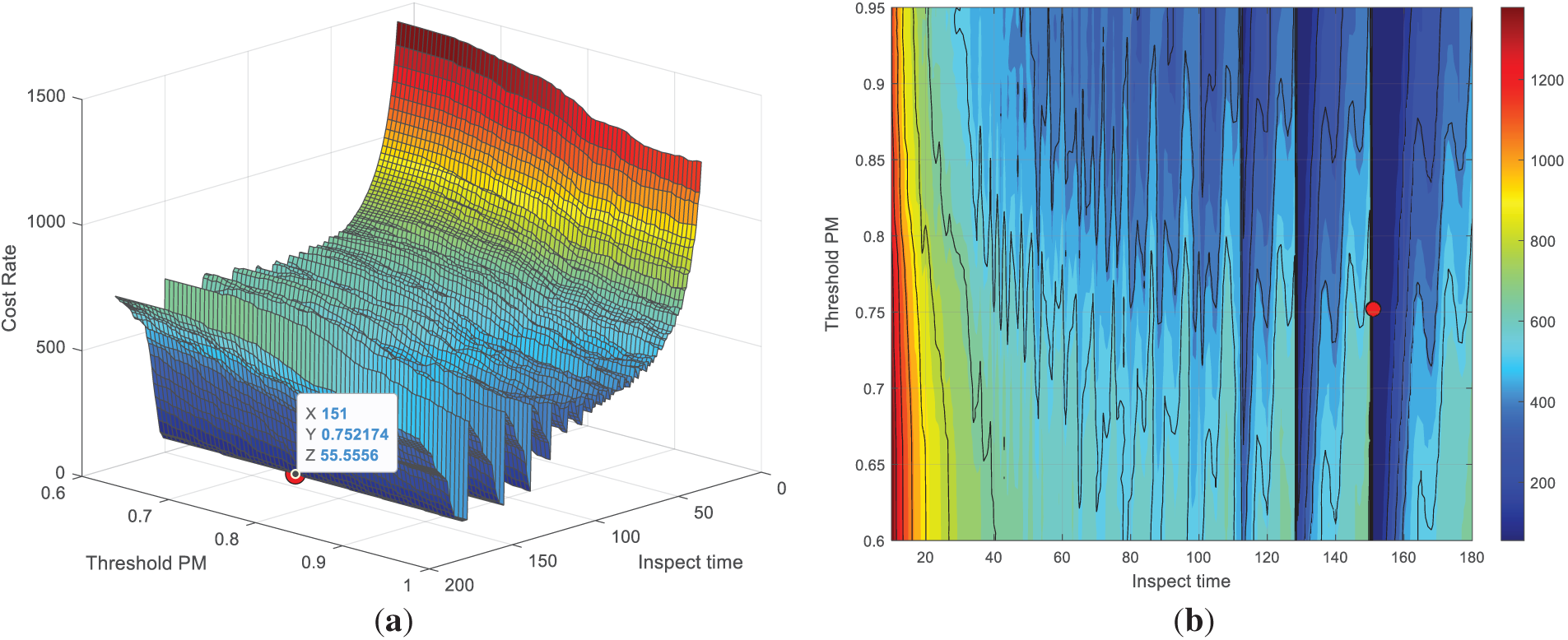
Figure 19: 3D Surface Plot (a) and Contour Plot (b) of CR when the threshold decay rate is 0.2

A comparison of Figs. 18 and 19 reveals the impact of inspection intervals on cost rates. Short intervals yield high costs due to excessive expenses from frequent inspections, leading to “over-maintenance”. While extending intervals initially reduces costs, excessively long intervals risk undetected degradation, causing “under-maintenance” and increasing failure risk and repair costs. Fig. 18a exhibits a smooth surface, suitable for idealized scenario. In contrast, after introducing threshold decay, Fig. 19a displays a rugged surface, accurately reflecting real-world performance degradation from aging and environmental factors. This model simulates a closed loop interaction between dynamic maintenance decisions and cost fluctuations, showing lower final cost rates with dynamic thresholds compared to fixed ones notably. In practical operations, equipment performance and degradation thresholds are not static but naturally deteriorate over time. Fig. 19 more accurately depicts the real-world relationship among “maintenance strategy, dynamic thresholds, and cost control”.

Based on the above research findings, to ensure the effectiveness and reliability of the degradation model for planetary gearboxes of the same type, the following conditions for model applicability can be summarized: First, the model is applicable to gearboxes with the same or similar design characteristics (such as gear size, module, and number of teeth) and material properties (such as material type, hard-ness, and toughness). These characteristics and properties directly affect the degradation mechanisms and rates. Second, the model is applicable to gearboxes operating under similar working conditions, including load levels, speed ranges, operating temperatures, and lubrication conditions. Significantly different working conditions may lead to substantial differences in degradation behavior. Third, the model is applicable to gearboxes operating under similar environmental conditions, such as humidity, temperature, and vibration environments. These factors may influence gearboxes’ degradation rates and patterns.

6  Conclusion

This study proposes a deep learning-based CBM decision framework, establishing a complete closed loop system integrating data-driven analysis with maintenance decision support. Compared with conventional time-based maintenance approaches, the proposed strategy demonstrates superior performance in reducing maintenance costs and preventing unexpected failures. Experimental results validate the effectiveness and practicality of the proposed method, demonstrating its significance in improving maintenance timing and strategies for planetary gearboxes, enhancing system reliability and safety. Future research will explore the potential application of this method to other complex equipment systems, incorporating additional maintenance resources and environmental factors for enhanced CBM decisions. Furthermore, exploring degradation trend extraction under transfer learning frameworks and jointly optimizing maintenance scheduling with spare parts procurement presents a promising direction.

Acknowledgement: The authors sincerely appreciate the Planetary Gearbox experimental equipment and materials provided by the PHM Laboratory at the Shijiazhuang Campus of Army Engineering University of PLA. The laboratory’s advanced testing platform and professional technical support were instrumental in data acquisition and analysis, for which we are deeply grateful.

Funding Statement: This research was funded by scientific research projects under Grant JY2024B011.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Bo Zhu, Zhonghua Cheng; methodology, Xianbiao Zhan; software, Enzhi Dong; validation, Kexin Jiang; formal analysis, Bo Zhu; investigation, Enzhi Dong; resources, Xianbiao Zhan, Rongcai Wang; data curation, Xianbiao Zhan; writing—original draft preparation, Bo Zhu; writing—review and editing, Enzhi Dong, Kexin Jiang, Rongcai Wang, Zhonghua Cheng; visualization, Kexin Jiang; supervision, Zhonghua Cheng; project administration, Zhonghua Cheng. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors. The data that support the findings of this study are available from the corresponding author, Zhonghua Cheng, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Li D, Zhao Y, Zhao Y. A dynamic-model-based fault diagnosis method for a wind turbine planetary gearbox using a deep learning network. Prot Control Mod Power Syst. 2022;7:22. doi:10.1186/s41601-022-00244-z. [Google Scholar] [CrossRef]

2. Zhang L, Hu N. Fault diagnosis of sun gear based on continuous vibration separation and minimum entropy deconvolution. Measurement. 2019;141:332–44. doi:10.1016/j.measurement.2019.04.049. [Google Scholar] [CrossRef]

3. Mourtzis D. Special issue “towards digitalized manufacturing 4.0. Int J Comput Integr Manuf. 2023;36(12):1735–8. doi:10.1080/0951192x.2023.2290394. [Google Scholar] [CrossRef]

4. Tong S, Li J, Cong F, Fu Z, Tong Z. Vibration separation methodology compensated by time-varying transfer function for fault diagnosis of non-hunting tooth planetary gearbox. Sensors. 2022;22(2):557. doi:10.3390/s22020557. [Google Scholar] [PubMed] [CrossRef]

5. Dao CD, Kazemtabrizi B, Crabtree CJ, Tavner PJ. Integrated condition-based maintenance modelling and optimisation for offshore wind turbines. Wind Energy. 2021;24(11):1180–98. doi:10.1002/we.2625. [Google Scholar] [CrossRef]

6. Luo J, Luo X, Ma X, Zan Y, Bai X. An integrated condition-based opportunistic maintenance framework for offshore wind farms. Reliab Eng Syst Saf. 2025;256:110701. doi:10.1016/j.ress.2024.110701. [Google Scholar] [CrossRef]

7. Li S, Zhao M, Ou S, Chen D, Wei Y. A periodic anomaly detection framework based on matrix profile for condition monitoring of planetary gearboxes. Measurement. 2023;218:113243. doi:10.1016/j.measurement.2023.113243. [Google Scholar] [CrossRef]

8. Zhang M, Xie R, Kang T, Chen J, Wang Y, Feng X, et al. A novel co-modulation and hybrid resolution strategy (CHRS) for fault diagnosis of planetary gearboxes. Mech Syst Signal Process. 2025;230:112573. doi:10.1016/j.ymssp.2025.112573. [Google Scholar] [CrossRef]

9. Wei J, Dong G, Chen Z. Remaining useful life prediction and state of health diagnosis for lithium-ion batteries using particle filter and support vector regression. IEEE Trans Ind Electron. 2018;65(7):5634–43. doi:10.1109/TIE.2017.2782224. [Google Scholar] [CrossRef]

10. Chen Z, Cao S, Mao Z. Remaining useful life estimation of aircraft engines using a modified similarity and supporting vector machine (SVM) approach. Energies. 2018;11(1):28. doi:10.3390/en11010028. [Google Scholar] [CrossRef]

11. Pei H, Hu C, Si X, Zhang J. Remaining useful life prediction methods for equipment based on machine learning: a review. J Mech Eng. 2019;55(8):1–13. doi:10.3901/JME.2019.08.001. [Google Scholar] [CrossRef]

12. Zhang W, Yang D, Wang H. Data-driven methods for predictive maintenance of industrial equipment: a survey. IEEE Syst J. 2019;13(3):2213–27. doi:10.1109/JSYST.2019.2905565. [Google Scholar] [CrossRef]

13. Avci O, Abdeljaber O, Kiranyaz S, Hussein M, Gabbouj M, Inman DJ. A review of vibration-based damage detection in civil structures: from traditional methods to machine learning and deep learning applications. Mech Syst Signal Process. 2021;147:107077. doi:10.1016/j.ymssp.2020.107077. [Google Scholar] [CrossRef]

14. Zhao D, Wang T, Chu F. Deep convolutional neural network based planet bearing fault classification. Comput Ind. 2019;107:59–66. doi:10.1016/j.compind.2019.02.001. [Google Scholar] [CrossRef]

15. Zhao M, Kang M, Tang B, Pecht M. Deep residual networks with dynamically weighted wavelet coefficients for fault diagnosis of planetary gearboxes. IEEE Trans Ind Electron. 2018;65(5):4290–300. doi:10.1109/TIE.2017.2762639. [Google Scholar] [CrossRef]

16. Wang Z, Wang J, Wang Y. An intelligent diagnosis scheme based on generative adversarial learning deep neural networks and its application to planetary gearbox fault pattern recognition. Neurocomputing. 2018;310:213–22. doi:10.1016/j.neucom.2018.05.024. [Google Scholar] [CrossRef]

17. Ali A, Abdelhadi A. Condition-based monitoring and maintenance: state of the art review. Appl Sci. 2022;12(2):688. doi:10.3390/app12020688. [Google Scholar] [CrossRef]

18. Alaswad S, Xiang Y. A review on condition-based maintenance optimization models for stochastically deteriorating system. Reliab Eng Syst Saf. 2017;157:54–63. doi:10.1016/j.ress.2016.08.009. [Google Scholar] [CrossRef]

19. Michalak A, Wodecki J, Drozda M, Wyłomańska A, Zimroz R. Model of the vibration signal of the vibrating sieving screen suspension for condition monitoring purposes. Sensors. 2020;21(1):213. doi:10.3390/s21010213. [Google Scholar] [PubMed] [CrossRef]

20. Chen M, Wang H, Cheng J, Zhao L, Yang H, Liu Q, et al. Progress in detection and suppression techniques for processing-induced subsurface defects of fused silica optical elements. J Mech Eng. 2021;57(20):1–19. doi:10.3901/JME.2021.20.001. [Google Scholar] [CrossRef]

21. Liu Z. Smart sensors for structural health monitoring and nondestructive evaluation. Sensors. 2024;24(2):603. doi:10.3390/s24020603. [Google Scholar] [PubMed] [CrossRef]

22. Naga Srinivasa Rao P, Achutha Naikan VN. An algorithm for simultaneous optimization of parameters of condition-based preventive maintenance. Struct Health Monit. 2009;8(1):83–94. doi:10.1177/1475921708094793. [Google Scholar] [CrossRef]

23. Cheng J. Research on full life cycle maintenance strategy of fatigue damage structure based on reinforcement learning [master’s thesis]. Wuhan, China: Huazhong University of Science and Technology; 2021. doi:10.27157/d.cnki.ghzku.2021.003061. [Google Scholar] [CrossRef]

24. Kang J, Wang Z, Guedes Soares C. Condition-based maintenance for offshore wind turbines based on support vector machine. Energies. 2020;13(14):3518. doi:10.3390/en13143518. [Google Scholar] [CrossRef]

25. Zhao H, Xu F, Liang B, Zhang J, Song P. A condition-based opportunistic maintenance strategy for multi-component system. Struct Health Monit. 2019;18(1):270–83. doi:10.1177/1475921717751871. [Google Scholar] [CrossRef]

26. Zhan X, Liu Z, Yan H, Wu Z, Guo C, Jia X. A novel method of health indicator construction and remaining useful life prediction based on deep learning. Eksploat I Niezawodn. 2023;25(4):171374. doi:10.17531/ein/171374. [Google Scholar] [CrossRef]

27. Shen Z, Shi Z, Zhen D, Zhang H, Gu F. Fault diagnosis of planetary gearbox based on adaptive order bispectrum slice and fault characteristics energy ratio analysis. Sensors. 2020;20(8):2433. doi:10.3390/s20082433. [Google Scholar] [PubMed] [CrossRef]

28. Huang LT, Chang JY. Vibration characterization and fault diagnosis of a planetary gearbox with a wireless embedded sensor. Appl Sci. 2023;13(2):729. doi:10.3390/app13020729. [Google Scholar] [CrossRef]

29. Al-Bedhany JH, Mankhi TA, Legutko S. A surface study of failed planetary wind turbine gearbox Bearings to investigate the causes of the Bearing premature failure issue. Heliyon. 2024;10(4):e25860. doi:10.1016/j.heliyon.2024.e25860. [Google Scholar] [PubMed] [CrossRef]

30. Huang X, Li Y, Chai Y. Intelligent fault diagnosis method of wind turbines planetary gearboxes based on a multi-scale dense fusion network. Front Energy Res. 2021;9:747622. doi:10.3389/fenrg.2021.747622. [Google Scholar] [CrossRef]

31. Wen Y, Wu J, Das D, Tseng TL. Degradation modeling and RUL prediction using Wiener process subject to multiple change points and unit heterogeneity. Reliab Eng Syst Saf. 2018;176:113–24. doi:10.1016/j.ress.2018.04.005. [Google Scholar] [CrossRef]

32. Li J, Fan J, Wang Z, Zhang Z, Pang X, Qiu M. Enhanced RUL predictions of rolling bearings using a nonlinear Wiener model with an extended incremental Kalman filter. Meas Sci Technol. 2025;36(1):016196. doi:10.1088/1361-6501/ad9bd3. [Google Scholar] [CrossRef]

33. Sun L, Liang Y, Yan Z. Remaining useful life (RUL) prediction based on the bivariant two-phase nonlinear Wiener degradation process. Entropy. 2025;27(4):349. doi:10.3390/e27040349. [Google Scholar] [PubMed] [CrossRef]

34. Huang Q. Research on health state assessment and remaining useful life prediction method of rolling bearing [master’s thesis]. Suzhou, China: Soochow University; 2022. doi:10.27351/d.cnki.gszhu.2022.002373. [Google Scholar] [CrossRef]

35. Huang X, Qi G, Mazur N, Chai Y. Deep residual networks-based intelligent fault diagnosis method of planetary gearboxes in cloud environments. Simul Model Pract Theory. 2022;116:102469. doi:10.1016/j.simpat.2021.102469. [Google Scholar] [CrossRef]

36. Wang X, Jiang H, Mu M, Dong Y. A dynamic collaborative adversarial domain adaptation network for unsupervised rotating machinery fault diagnosis. Reliab Eng Syst Saf. 2025;255:110662. doi:10.1016/j.ress.2024.110662. [Google Scholar] [CrossRef]

37. Dong Y, Jiang H, Wang X, Mu M, Jiang W. An interpretable multiscale lifting wavelet contrast network for planetary gearbox fault diagnosis with small samples. Reliab Eng Syst Saf. 2024;251:110404. doi:10.1016/j.ress.2024.110404. [Google Scholar] [CrossRef]

38. Mu M, Jiang H, Jiang W, Dong Y, Wu Z. An enhanced meta-learning network with sensitivity penalty for cross-domain few-shot fault diagnosis. Meas Sci Technol. 2024;35(9):095106. doi:10.1088/1361-6501/ad5039. [Google Scholar] [CrossRef]

39. Lea C, Vidal R, Reiter A, Hager GD. Temporal convolutional networks: a unified approach to action segmentation. arXiv:1608.08242. 2016. doi:10.48550/arXiv.1608.08242. [Google Scholar] [CrossRef]

40. Filho JBOS, Diniz PSR. A sparse fixed-point online KPCA extraction algorithm. IEEE Trans Signal Process. 2024;72:4604–17. doi:10.1109/TSP.2024.3446512. [Google Scholar] [CrossRef]

41. Hofmann T, Schölkopf B, Smola AJ. Kernel methods in machine learning. Ann Statist. 2008;36(3):1171–220. doi:10.1214/009053607000000677. [Google Scholar] [CrossRef]

42. Liu S, Gao L, Du J, Liu C. Optimal feature selection and life prediction of rolling bearing based on adaptive order. Ship Sci Technol. 2019;41(11):71–6. doi:10.3404/j.issn.1672-7649.2019.11.014. [Google Scholar] [CrossRef]

43. Si XS, Wang W, Hu CH, Zhou DH, Pecht MG. Remaining useful life estimation based on a nonlinear diffusion degradation process. IEEE Trans Reliab. 2012;61(1):50–67. doi:10.1109/TR.2011.2182221. [Google Scholar] [CrossRef]

44. He R, Tian Z, Wang Y, Zuo M, Guo Z. Condition-based maintenance optimization for multi-component systems considering prognostic information and degraded working efficiency. Reliab Eng Syst Saf. 2023;234:109167. doi:10.1016/j.ress.2023.109167. [Google Scholar] [CrossRef]

45. Yao Y. Research on reliability modeling and condition-based maintenance strategy for two-stage degradation system [master’s thesis]. Tianjin, China: Tianjin University; 2020. doi:10.27356/d.cnki.gtjdu.2020.001899. [Google Scholar] [CrossRef]

46. Oh SY, Joung C, Lee S, Shim YB, Lee D, Cho GE, et al. Condition-based maintenance of wind turbine structures: a state-of-the-art review. Renew Sustain Energy Rev. 2024;204:114799. doi:10.1016/j.rser.2024.114799. [Google Scholar] [CrossRef]

47. Dong E, Zhang Y, Zhan X, Bai Y, Cheng Z. A novel dynamic predictive maintenance framework for gearboxes utilizing nonlinear Wiener process. Meas Sci Technol. 2024;35(12):126210. doi:10.1088/1361-6501/ad762e. [Google Scholar] [CrossRef]

48. Tang H, Tang Y, Su Y, Feng W, Wang B, Chen P, et al. Feature extraction of multi-sensors for early bearing fault diagnosis using deep learning based on minimum unscented Kalman filter. Eng Appl Artif Intell. 2024;127:107138. doi:10.1016/j.engappai.2023.107138. [Google Scholar] [CrossRef]