HUANNet: A High-Resolution Unified Attention Network for Accurate Counting

1  Introduction

Dense target counting, i.e., estimating the number of individual objects within an image or video frame, has broad applications in various fields, such as public safety, traffic monitoring, wildlife conservation, and industrial automation. In particular, the ability to accurately estimate the number of individuals in dense scenes has proven invaluable for applications like crowd management, where real-time insights on crowd dynamics are essential for safety and resource allocation [1,2]. The task of dense counting extends beyond crowds, encompassing diverse contexts such as vehicle counting in parking lots [3,4], product counting in retail settings [5], agricultural counting [6], and object counting in medical imaging [7].

Despite its importance, dense target counting poses several unique challenges. In real-world scenarios, target objects often appear in a wide range of densities, from sparse distributions to highly crowded environments, where objects are heavily occluded or tightly clustered. In high-density scenes, the visual characteristics of targets become less distinct, making it difficult for models to differentiate between individual instances. Additionally, variations in scale, cluttered backgrounds, and significant occlusions further complicate accurate counting.

Most existing approaches to dense target counting, particularly in crowd counting, treat the problem as a density map regression task [8–12]. In these methods, models are trained to generate density maps from point annotations, where the sum of pixel values in the predicted density map approximates the total count. Convolutional Neural Networks (CNNs) have been widely adopted for this purpose, achieving significant success in generating density maps that correlate well with object distributions [13–15]. However, CNN-based regression methods often struggle in highly congested scenarios, where over-smoothing of the predicted density maps leads to a loss of fine-grained detail, particularly when individual targets are small and tightly packed. Moreover, background clutter and complex scene variations further degrade the accuracy of these methods in challenging real-world conditions. This is mainly attributed to the limited discriminative power of features extracted from crowded regions, making it difficult to localize small targets and distinguish between foreground and background.

To overcome the limitations of density-based approaches, several point-based methods have been proposed. These approaches, such as P2PNet [16], attempts to address some of these limitations by directly regressing possible head coordinates through end-to-end training using ground truth point annotations. However, even with point-based methods, the extracted features in congested areas lack sufficient discriminative power, resulting in similar challenges in identifying small targets and separating foreground from background.

In recent years, attention mechanisms have emerged as powerful tools for enhancing feature representation in computer vision tasks. By adaptively focusing on the most informative components of the input, attention mechanisms help mitigate the limitations of conventional CNN-based approaches in complex environments. Channel Attention [17] models the interdependencies among feature channels, enabling the network to emphasize task-relevant features while suppressing redundant information. Spatial Attention [18], in contrast, operates on the spatial dimension of feature maps, learning the importance distribution across different regions to guide the model toward more discriminative cues. Building upon these ideas, hybrid modules such as the Convolutional Block Attention Module (CBAM) [19] combine channel and spatial attention in a sequential manner, achieving joint modeling that enhances both global semantics and local detail. Such mechanisms are particularly well-suited for dense target counting, where the ability to highlight small but critical patterns amidst cluttered backgrounds is essential.

Motivated by these observations, we propose HUANNet (High-Resolution Unified Attention Network), a novel framework designed to improve counting accuracy for small and densely distributed targets in complex environments. HUANNet leverages a high-resolution representation learning framework that combines multi-resolution attention mechanisms with advanced feature fusion strategies to capture both fine-grained local features and global semantics. This approach is tailored to effectively address the difficulties of small target detection and occlusion, while also improving overall counting accuracy in diverse dense target scenarios. Our contributions include:

1) We introduce a High-Resolution Attention Module (HRAM) that dynamically allocates computational resources across multiple resolution branches, ensuring that important resolution scales are prioritized for better feature extraction, especially for small targets in crowded scenes.

2) We design a Unified Multi-Scale Attention Module (UMAM) that integrates spatial, channel, and convolutional kernel attention across multiple levels of the network, enhancing the model’s ability to capture both local and global contextual information for more robust feature representation.

3) We propose a Grid-Assisted Point Matching Module (GPMM), which stabilizes the matching process between predicted and ground-truth points using a grid-based mechanism, improving the accuracy and reliability of point-to-point matching in high-density settings.

Our method is evaluated on both crowd counting and dense object counting benchmarks, demonstrating its competitive performance on the ShanghaiTech Part A/B datasets, while achieving state-of-the-art results on the CARPK and XRAY-IECCD datasets. These results confirm the effectiveness and generalization capabilities of HUANNet in diverse dense target counting scenarios.

The remainder of this paper is organized as follows. In Section 2, we review the related works on dense target counting and attention-based methods. Section 3 details the proposed HUANNet framework, including the HRAM, UMAM, and GPMM modules. Section 4 presents our experimental setup and results on multiple datasets. Finally, Section 5 concludes the paper with a summary of our contributions and future work.

2  Related Work

2.1 Detection-Based Methods

Detection-based methods treat dense target counting as an object detection task, aiming to localize each entity using frameworks like Faster R-CNN [20] and YOLO [21]. To handle small targets and dense scenes, various improvements have been proposed. For instance, RetinaNet [22] employs focal loss to address class imbalance, while GANet [23] introduces a guided attention network leveraging feature pyramids. Although these methods provide high localization accuracy, they often struggle in heavily occluded or crowded scenarios due to the complexity of detecting every individual.

2.2 Density-Based Methods

Density-based methods estimate the spatial density of targets by generating density maps from point annotations convolved with Gaussian kernels [24,25]. Representative models include MCNN [16], MSCNN [26], CSRNet [10], SaCNN [27], SANet [28], PANet [29], Fusion Count [30], and CAN [31]. These models typically enhance robustness to scale variations through multi-column, multi-scale, or context-aware architectures.

Recent methods such as GauNet [32] replace standard convolutions with Gaussian kernels to improve spatial estimation, while STEERER [33] dynamically selects scales to refine density maps. VLCounter [34] employs learnable affine transformations, while SAFECount [4] enhances estimation by comparing regions to a support image for better alignment. CCTrans [35] utilizes a pyramid vision transformer backbone to capture the global crowd information, and TAM-Transformer [36] employs a pure transformer to extract globally-informed features from overlapping image patches. CounTR [3] uses transformer-based attention to capture patch-level relations. CrowdTrans [1] introduces a transformer-based framework that jointly learns a density map estimator and label generator via dual-task supervision, effectively addressing scale variation and improving generalization in crowd counting.

Additionally, TransCrowd [37] reconstructs the weakly supervised crowd counting problem from the perspective of Transformer-based sequences to counting, effectively extracting semantic crowd features through Transformer’s self attention mechanism.

Despite effectively modeling distribution patterns, density maps often lack precise individual localization and may suffer from artifacts introduced by Gaussian kernels. Especially in crowded scenes, smaller kernels can introduce false peaks, leading to false positives or omissions. As shown in [38], such methods struggle to achieve both spatial fidelity and accurate regression, particularly when supervision is limited to point annotations [39–41].

2.3 Point-Based Methods

Point-based methods offer a more direct approach to dense target counting by representing individuals as points and estimating the total count based on point annotations. Compared to detection- and density-based methods, such methods typically regress individual coordinates directly, simplifying the localization process while enabling true end-to-end trainability. This results in more precise location information and improved robustness and computational efficiency. Point-based approaches are particularly well-suited for real-time crowd monitoring in places like train stations and squares, where they can provide useful insights into crowd tendency. Notable methods in this category include P2PNet [16], FGENet [5], and CLTR [42]. P2PNet utilizes an end-to-end framework to directly predict head locations by regressing point coordinates. It leverages a permutation loss to match predicted points with ground truth annotations, aiming to minimize the discrepancies in localization. FGENet introduces a feature-guided matching strategy that refines the point estimation process by improving feature extraction, while CLTR adopts a transformer-based model to learn point relations, enhancing global context understanding through attention mechanisms.

A key advantage of point-based methods is their ability to provide fine-grained localization of individuals, particularly in crowded scenarios. These methods offer a more accurate representation of individual counts, especially in dense environments, where traditional density map-based approaches may fail to distinguish between closely packed individuals. Additionally, they offer a more computationally efficient alternative to detection-based methods, as they do not require exhaustive bounding box regression.

However, point-based methods also face significant challenges. One major issue is the instability in the matching process between predicted and ground-truth points during training. At each epoch, the predicted point sets can vary significantly, and the dynamic relationship between predicted points and ground truth introduces uncertainty into the matching process. This lack of consistency can hinder learning, often leading to either underestimation or overestimation of target counts in certain regions. Furthermore, these methods can struggle in highly congested scenes where individual targets are heavily occluded, making it difficult to precisely estimate points.

To address these challenges, our proposed HUANNet adopts a point-based framework. In HUANNet, we leverage a high-resolution representation learning framework, integrating multi-resolution attention mechanisms with advanced feature fusion strategies to capture both fine-grained local features and global semantic information. Additionally, to resolve the instability inherent in point-based counting methods, we introduce the Grid-Assisted Point Matching Module (GPMM), which transforms the matching process into a more stable grid-based mechanism. This significantly enhances the accuracy and stability of our model, particularly in crowded scenes.

3  Proposed Model

In this section, we introduce our dense target counting framework, the High-Resolution Unified Attention Network (HUANNet), illustrated in Fig. 1. The architecture comprises three core components: the High-Resolution Attention Module (HRAM), the Unified Multi-Scale Attention Module (UMAM), and the Grid-Assisted Point Matching Module (GPMM).

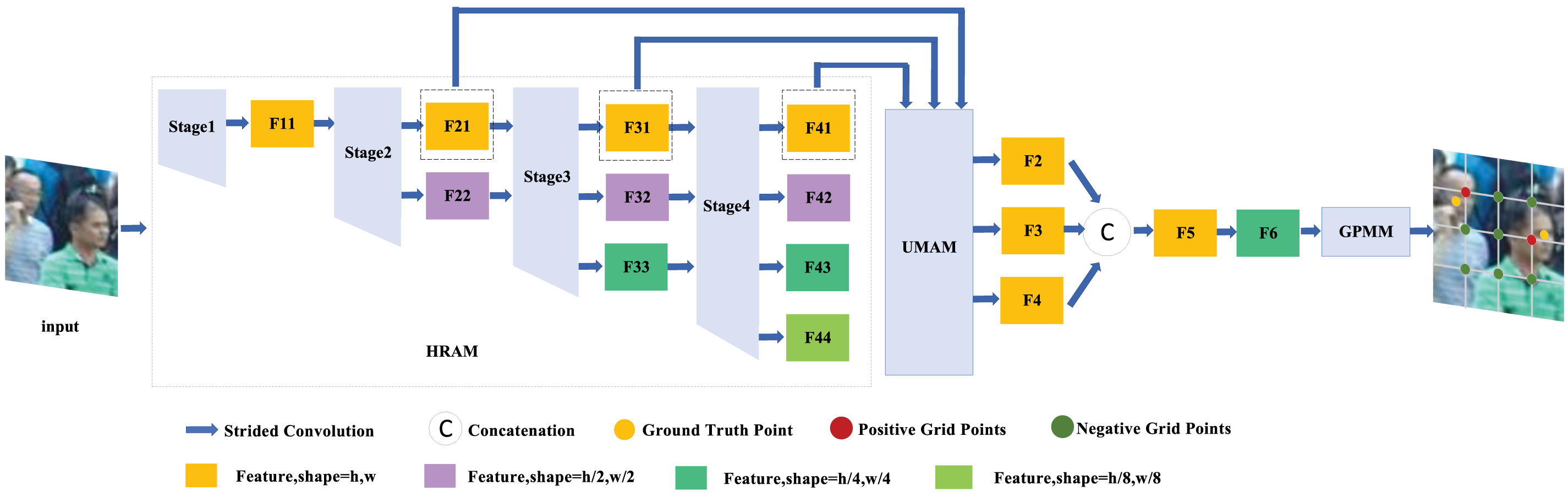
Figure 1: Overall structure of HUANNet. The complete HUANNet architecture consists of HRAM for high-resolution feature extraction, UMAM for multi-scale attention integration, and GPMM for grid based point matching

The HRAM preserves multi-resolution parallelism while enhancing cross-scale feature fusion. By dynamically adjusting weights between high- and low-resolution branches, it retains critical details—especially from high-resolution paths—essential for capturing fine-grained features. This module strikes a balance between local detail preservation and semantic richness, making it particularly suitable for dense predictions.

The UMAM introduces spatial and channel attention, as well as dynamic convolution (ODConv), at various network depths. By combining these mechanisms across multiple scales, UMAM enables the model to focus on informative regions and abstract representations. This fusion of attention and convolution improves the network’s ability to distinguish foreground from background, even in complex scenes.

The GPMM mitigates instability in point-to-point matching through a grid-based strategy. It partitions the image into evenly spaced grid points, which serve as anchors for matching predictions with ground truth. Each grid point is assigned a confidence score, and the matching is formulated as an assignment problem solved via the Hungarian algorithm. This approach enhances both accuracy and robustness, especially in dense, crowded environments.

Together, these modules form a cohesive architecture capable of tackling dense target counting in challenging scenarios with small targets and complex backgrounds. The following sections provide a detailed explanation of each module.

3.1 High-Resolution Attention Module (HRAM)

High-resolution feature representation is essential for accurate predictions in dense target counting tasks. While low-resolution features provide strong semantic information, they often lack the local precision required for pixel-level accuracy. Conversely, high-resolution features retain fine-grained details but may lack the semantic faithfulness necessary for robust predictions. The key challenge lies in effectively balancing these two types of information.

As shown in Fig. 2, an HRAM is constructed to address this challenge. Specifically, we further optimize multi-resolution feature fusion at the end of each stage of the HRNet [43] framework. Unlike the standard HRNet, which assigns equal weights to all branches, HRAM dynamically adjusts the weight distribution between high- and low-resolution branches. Taking stage 3 in HRAM with three different resolution branches as an example, for feature maps of different resolutions, denoted as fi (i=1,2,3), the module performs convolutional transformations to align each branch’s feature maps to the target branch resolution fik (i=1,2,3; k=1,2,3), where i denotes the indices of different resolutions, and k represents different columns within the same resolution. Nearest-neighbor upsampling is used for upsampling operations, while downsampling is achieved via 3×3 stride convolutions. The feature maps of different branches in the same stage are then concatenated, and two 1×1 convolution layers are applied to compute the weights for each branch. These branch weights are assigned to each branch feature map, and the features are fused into a new target branch feature map. The attention-based feature computation is computed as:

fci=Concat(fik)(k=1,2,3;i=1,2,3)(1)

fouti=∑k=13(Sigmoid(Conv1(ReLU(Conv2(fci))))∗fik)(i=1,2,3)(2)

where fci represents the feature map concatenated after adjusting the size and channel of each branch, and fouti represents the fused final target branch feature map at the i-th resolution.

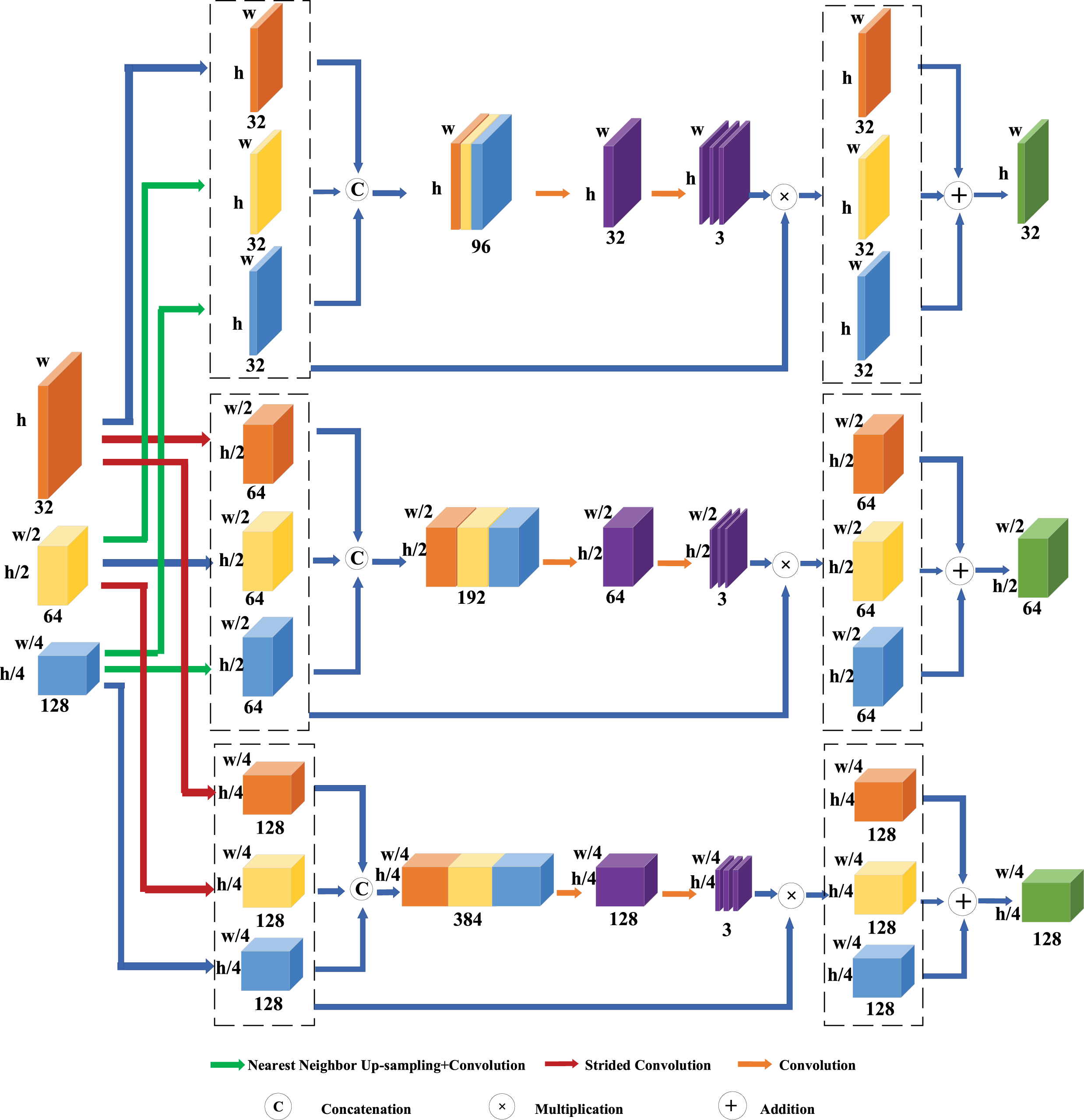
Figure 2: The high-resolution attention module learns reasonable weights when fusing branch feature maps of different resolutions, preserves crucial detail information in dense counting tasks, and reduces the influence of noise

This dynamic adjustment ensures that the appropriate branch receives more attention, which is crucial for capturing fine details in densely crowded scenes. By connecting feature maps of different branches and applying convolutional layers to learn the optimal weights for each branch, the HRAM enables effective multi-resolution fusion. This allows the model to combine local details with global semantic information, ensuring accurate predictions even in highly crowded areas.

3.2 Unified Multi-Scale Attention Module (UMAM)

As shown in Fig. 3, the UMAM is designed to enhance feature extraction by applying attention mechanisms at multiple network depths. It consists of three main components:

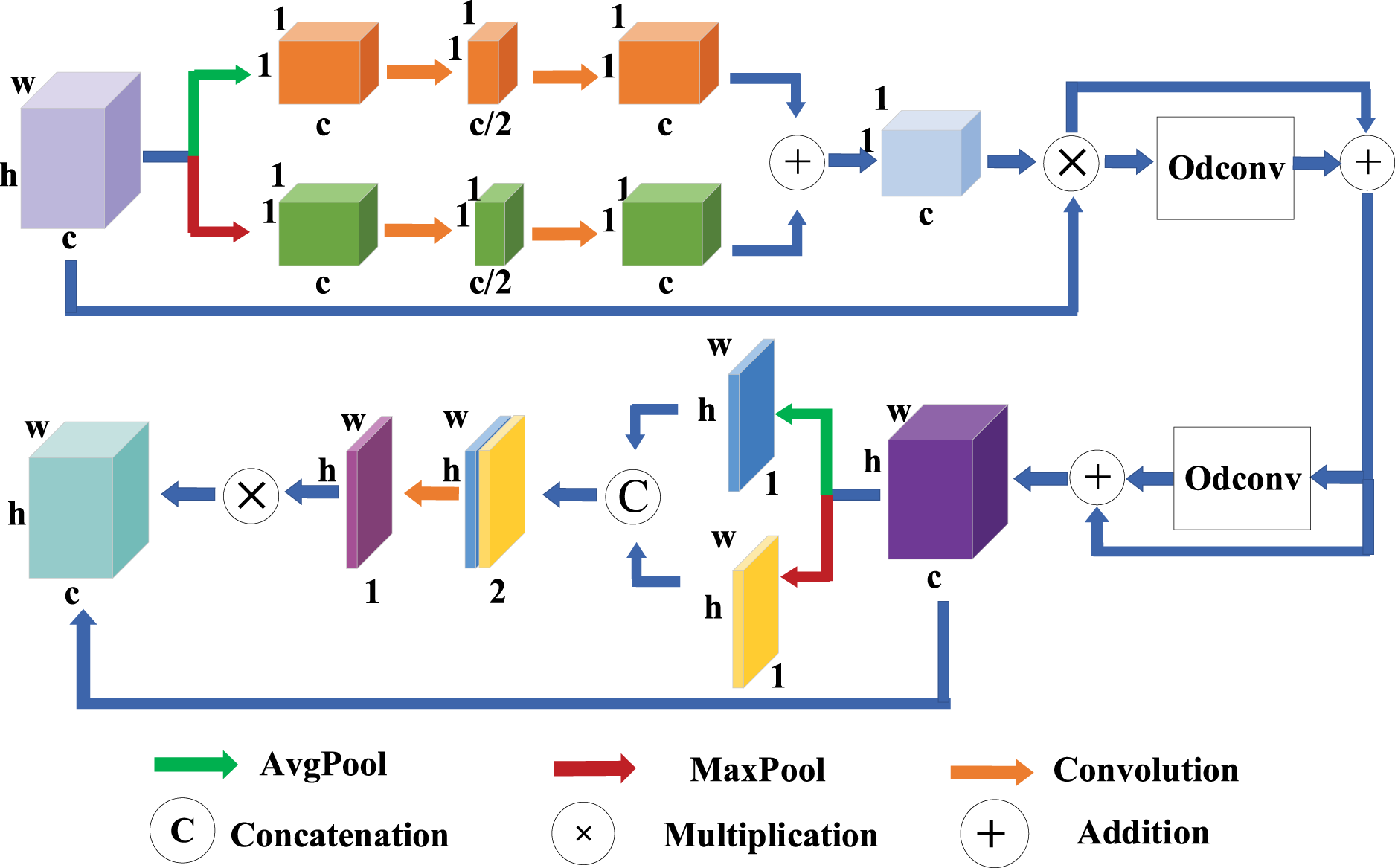
Figure 3: UMAM further improves performance by deeply integrating attention mechanisms into multiple network depths, enabling the model to capture complex relationships between spatial and channel information

Channel Attention: This sub-module assigns attention weights to each channel, allowing the network to focus on the most informative features. The feature maps are processed through a combination of asymmetric pooling and convolution operations, which generate channel-wise attention maps. This process can be expressed as:

Fcm=Conv2(ReLU(Conv1(MaxPool(F))))(3)

Fca=Conv2(ReLU(Conv1(AvgPool(F))))(4)

Fc=Sigmoid(Fcm+Fca)(5)

where F represents the feature map input to the UMAM module, Fcm and Fca represent the two channel attention maps obtained after asymmetric pooling and 1×1 convolutional layers, and Fc represents the normalized channel attention weights.

Omni-Dimensional Dynamic Convolution (ODConv): UMAM integrates the dynamic convolution mechanism, ODConv [44], to enhance the adaptability of convolutional operations. ODConv dynamically adjusts convolutional filters by learning attention weights across four dimensions: the spatial, input channel, output channel, and kernel dimensions. Unlike traditional convolutions with static kernels, ODConv introduces dynamic convolution through multi-dimensional attention mechanisms—including spatial, channel, kernel, and group dimensions. This allows the convolutional kernels to be adaptively modulated based on the input features, enabling more flexible and fine-grained feature extraction across varying densities and complex spatial distributions. Therefore, ODConv can significantly enhance the feature extraction capability of convolution. In UMAM, ODConv is combined with a residual structure, enabling the network to dynamically adjust convolution kernel weights across multiple dimensions based on the specific characteristics of the input data. By applying attention mechanisms to all four dimensions of the convolution kernel, the module provides finer feature processing capabilities, improving the network’s adaptability and sensitivity to input variations.

Spatial Attention: This sub-module complements the channel and convolutional kernel attention mechanisms by applying spatial attention. It highlights important spatial regions within the feature maps, allowing the network to focus on regions of interest in the image, such as densely crowded areas. By assigning higher weights to these regions, the network reduces the influence of irrelevant background features. The process can be expressed as:

Fs=Sigmoid(Conv(Concat(AvgPool(Fo);MaxPool(Fo))))(6)

where Fo represents the feature map obtained after ODConv, and Fs represents the obtained spatial attention weight.

Together, these components allow UMAM to capture rich multi-scale feature representations, improving the model’s ability to distinguish between foreground and background, even in complex and dense scenes. This attention-driven approach ensures that the network focuses on the most critical features for dense target counting tasks.

3.3 Grid-Assisted Point Matching Module (GPMM)

Point-based dense target counting methods often face challenges in the matching process, as the predicted points Y^ and ground truth points Y can vary significantly during different training epochs, leading to instability in predictions. Inspired by P2PNet, we propose the Grid-Assisted Point Matching Module (GPMM) to stabilize the point-matching process by introducing a grid-based strategy, as shown in Fig. 4.

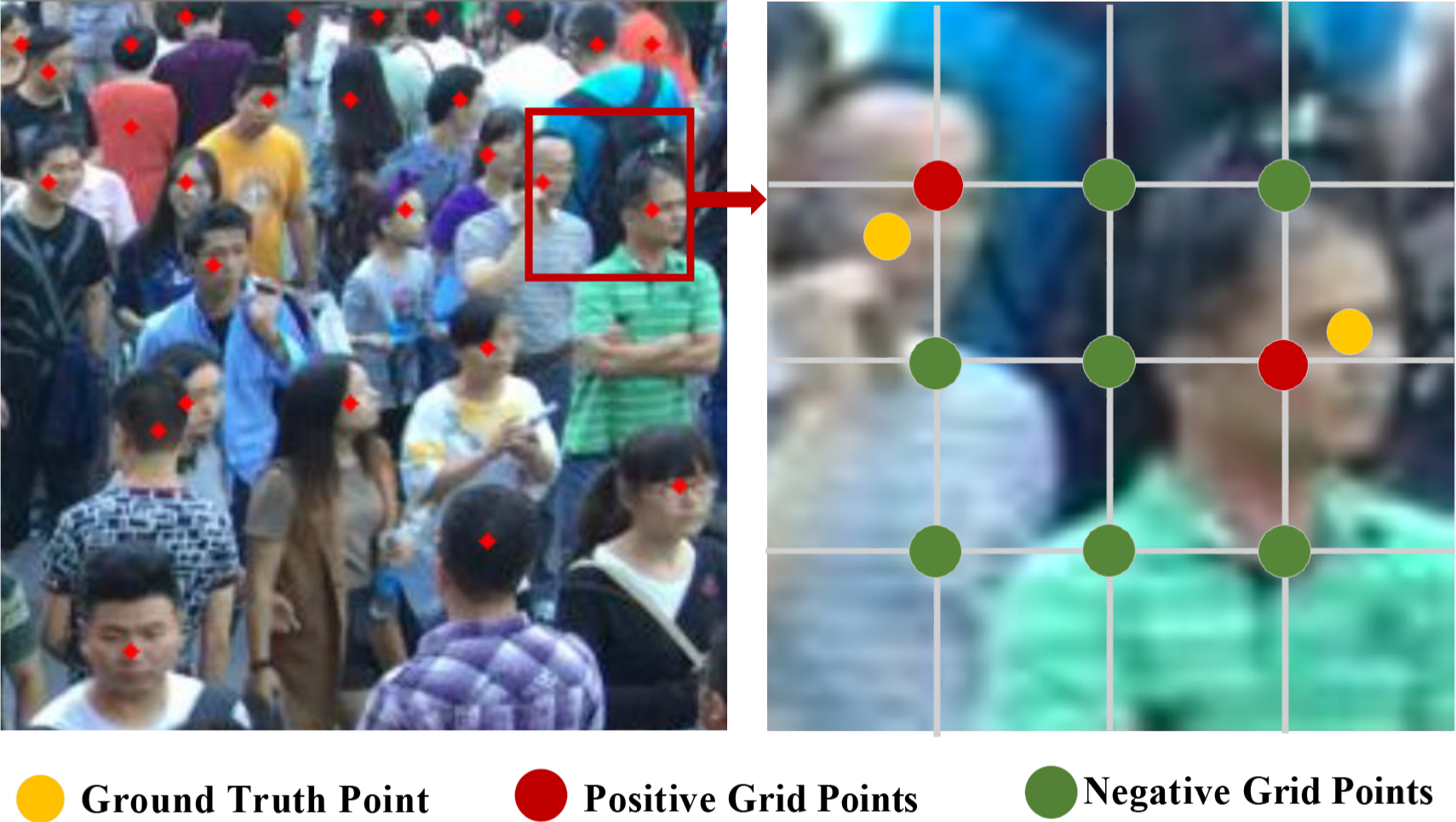
Figure 4: GPMM improves the stability of the point-matching process by leveraging a grid-based matching strategy, ensuring that predictions are more reliable in dense environments

Unlike P2PNet, which regresses the position of individuals by predicting point proposals from an image, GPMM introduces a grid-based approach to improve the stability and accuracy of point matching. Specifically, P2PNet lacks an effective learning strategy to guide the network to consistently select the most suitable point proposals across different epochs. In GPMM, the input image is divided into uniformly spaced grid blocks with a fixed interval d=8 pixels. For each grid point, a confidence score is generated through two convolutional layers followed by a Softmax normalization, ensuring that the grid points are scored based on the likelihood of the true head being located at the current position. The matching strategy transforms the crowd target counting task into an assignment problem, where the cost matrix D is constructed based on the confidence scores C of grid points and their distance from the ground truth points. This problem is solved using the Hungarian algorithm, which guarantees stability and accuracy in the point matching process. The cost matrix D can be represented as follows:

D(T,G)=(τ‖yj−gk‖2−c^k)j∈N,k∈M(7)

where T represents the set of ground truth points, G denotes the grid points, N and M are the number of ground truth and grid points, respectively, c^k represents the confidence scores of the k-th grid point, yj is the location of the j-th ground truth point, gk is the position of the k-th grid point, and ‖yj−gk‖2 is the distance between the j-th ground truth point and the k-th grid point. The factor τ balances the influence of confidence scores and spatial distances in the cost matrix.

Using the obtained cost matrix D, we use the Hungarian algorithm to design an optimal point matching strategy Ω to match the truth point T with the grid point G. This process can be expressed as:

ξ=Ω(T,G,D)(8)

After completing the matching process ξ, grid points can be represented by g^ξ(i). The optimal point matching set g^p={g^ξ(i)|i∈{1,...,N}}, obtained using the point matching strategy Ω, represents the optimal correspondence between N grid points and N ground truth points. g^p is considered to have played a positive role in the matching process. The unmatched grid points among the M total grid points are represented as g^n={g^ξ(i)|i∈{N+1,...,M}} which are considered to have a negative effect.

By binding predicted points to grid locations, GPMM ensures that the point matching process remains stable across different training epochs. This leads to more consistent and reliable counting results, especially in dense and occluded scenarios. The grid-based approach could mitigate the uncertainty inherent in point-to-point matching and provides a more robust solution for dense crowd counting tasks compared to previous methods like P2PNet. Through the synergistic effect of HRAM, UMAM, and GPMM, HUANNet has outstanding feature extraction capabilities. We use heatmaps to visually express HUANNet’s feature extraction capabilities and compare them with P2PNet, demonstrating the advantages of HUANNet in capturing fine-grained local features and grasping global semantic information, as shown in Fig. 5.

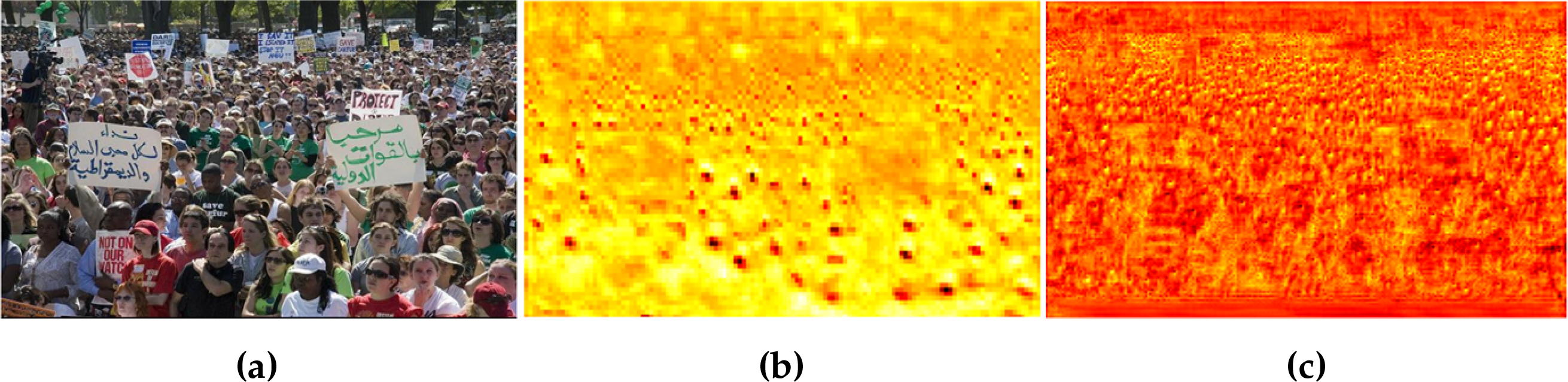
Figure 5: Comparison of feature extraction capabilities. (a) original image, (b) heatmap visualization of P2PNet, and (c) heatmap visualization of of HUANNet. The results demonstrate the enhanced feature extraction ability of our proposed model

3.4 Loss Function

The loss function is defined as:

ℒcls=−1M{∑i=1Nlogc^ξ(i)+λ∑j=N+1Mlog(1−c^ξ(j))}(9)

where c^ξ(i) represents the confidence score of g^p, c^ξ(j) represents the confidence score of g^n. The cross-entropy loss is used for supervision by distinguishing between positive and negative samples, and a weight parameter λ is used to adjust the impact of negative samples on the overall loss.

4  Experiments

To evaluate the performance of HUANNet, we conducted extensive experiments on three different dense target counting datasets, each varying in object density and scene complexity. These datasets were chosen to cover a wide range of real-world scenarios, providing a comprehensive assessment of HUANNet’s robustness and adaptability. Furthermore, we compared our method with several state-of-the-art approaches to validate its competitive performance across different tasks. In addition to the comparative evaluations, we performed ablation studies to systematically analyze the effectiveness of each component within our proposed network.

4.1 Training Details

We trained HUANNet using the Adam optimizer with an initial learning rate of 1e–4. Data augmentation techniques such as random flipping, random scaling (with a scale factor between 0.7 and 1.3), and random cropping to 256×256 pixels were applied to enhance the model’s robustness. For the construction of the cost matrix in the GPMM, the key parameter was set as τ=0.01. The weight factor λ in the loss function was set to 0.5, and the distance between grid points in GPMM was fixed at 8 pixels. We experimented with different grid point spacings (d=4,8,16) on the ShanghaiTech Part A dataset, and found that d=8 yielded the best performance. The results of these experiments are presented in Table 1, and the software and hardware settings used during training are listed in Table 2.

To evaluate the computational complexity and efficiency of HUANNet, we report both the parameter size and inference speed across multiple benchmark datasets. HUANNet contains 40.4 M parameters with a computational cost of 41.29 GFLOPs. For inference efficiency, experiments were conducted on an NVIDIA RTX 3090 GPU. The model achieves an average inference speed of 0.1760 s/frame on the XRAY-IECCD dataset, 0.0725 s/frame on the ShanghaiTech Part A dataset, 0.0542 s/frame on the ShanghaiTech Part B dataset, and 0.0568 s/frame on the CARPK dataset. These results indicate that HUANNet maintains sub-second inference across diverse scenarios, demonstrating its practical feasibility and efficiency for real-world dense target counting tasks.

4.2 Evaluation Metrics

To evaluate the performance of crowd counting, we employed two conventional metrics: Mean Absolute Error (MAE) and Mean Squared Error (MSE). These metrics are defined as follows:

MAE=1N∑i=1N|y^i−yi|(10)

MSE=1N∑i=1N(y^i−yi)2(11)

where yi represents the ground truth count for the i-th image, and y^i represents the predicted count for that image. Lower MAE and MSE values indicate better performance. MAE treats all errors equally, making it robust to outliers and providing a reliable indication of the overall counting accuracy. A lower MAE indicates that, on average, the predicted counts are closer to the ground truth. By squaring the errors, MSE assigns larger penalties to samples with significant prediction deviations. This makes MSE particularly useful for assessing a model’s ability to avoid substantial counting errors. Lower MSE values indicate fewer severe mispredictions, which is important in high-density or challenging scenes. Reporting both MAE and MSE provides a comprehensive evaluation of the model, reflecting its overall accuracy (via MAE) and its robustness to large errors (via MSE).

To reduce randomness in the training process and improve the statistical significance of the results, we take the average of five consecutive training runs as the final MAE and MSE indicators. This helps ensure that performance differences reflect the actual design of the models rather than random variation. Taking HUANNet’s experiment on the ShanghaiTech Part A dataset as an example, we report the mean MAE of 51.78 with a standard deviation of 0.75 and a 95% confidence interval of [51.15, 52.41], indicating stable performance. To further illustrate this, we provide a box plot in Fig. 6a, showing the distribution of MAE values across five runs, with a minimum of 50.8, Q1 of 51.5, median of 51.8, Q3 of 52.0, and a maximum of 52.8. The interquartile range (IQR) is 0.5, indicating low variability. A corresponding statistical summary is shown in Fig. 6b. These results demonstrate the robustness of our method and support the reliability of the observed performance improvements.

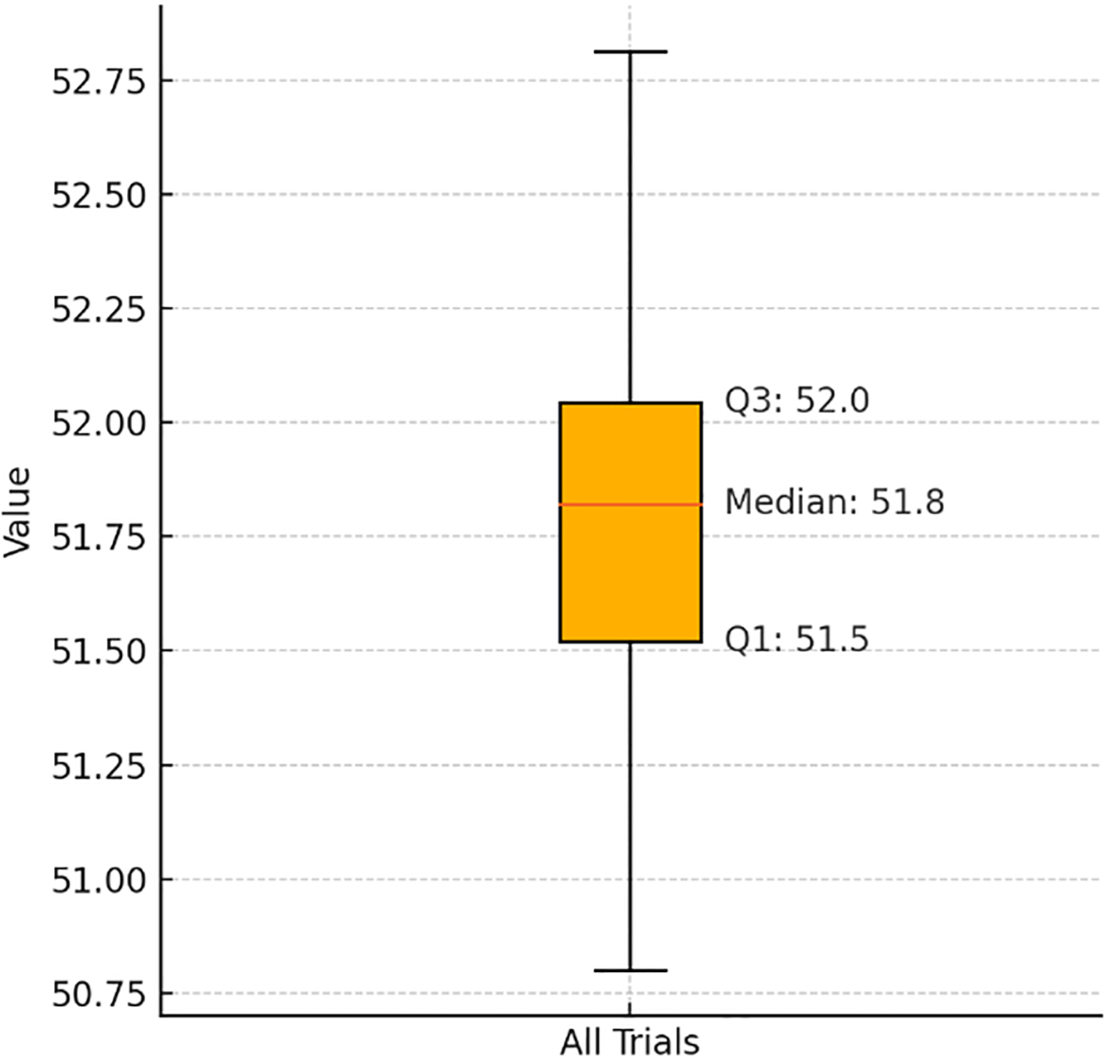
Figure 6: Stability analysis of HUANNet on the ShanghaiTech Part A dataset. (a) Box plot of MAE over five independent runs. (b) Corresponding statistical table, including MAE values, mean ± SD, and 95% confidence interval

4.3 Datasets

We conducted experiments on the following datasets to evaluate the effectiveness of HUANNet:

ShanghaiTech Part A [45]: This dataset contains 482 images with a total of 244,167 annotations, where the number of annotated individuals in each image ranges from 33 to 3139. The dataset is divided into 300 training images and 182 test images. The image resolutions in Part A vary considerably, ranging from 589×868 to 868×1311 pixels, with head sizes in the annotations spanning from approximately 59×73 pixels for nearby individuals to about 12×13 pixels for distant ones. Part A is characterized by high crowd density and significant variations in individual size, and frequent occlusions between targets, making it a highly challenging benchmark for crowd counting models.

ShanghaiTech Part B [45]: Part B consists of 400 training images and 316 test images, with individual counts per image ranging from 9 to 578. The ShanghaiTech Part B dataset has an average resolution of 768×1024 pixels, with head sizes in the annotations generally distributed between 35×42 pixels (for nearer heads) and 19×20 pixels (for farther heads). Unlike Part A, Part B has relatively lower crowd density and less cluttered backgrounds.

CARPK [46]: This dataset features approximately 90,000 cars, captured from drones across four different parking lots, resulting in a total of 1448 images. This dataset presents a unique challenge due to the varying backgrounds and significant lighting variations across scenes. The dataset uses a cross-validation approach, where three parking lot scenes are used for training, and the remaining one for testing, with the results averaged over four-fold cross-validation.

XRAY-IECCD [47]: This dataset contains 1460 X-ray images of electronic components, each with a resolution of 2048×2048. Among them, 1146 images were used for training and 314 for testing, with a total of 2,915,126 annotated points. The number of annotated objects per image ranges from 26 to 9416. The smallest objects measure around 5×5 pixels, representing just 0.0006% of the total image size. This dataset is highly challenging due to the tiny object sizes, dense layouts, and variations in object shape and size.

4.4 Experimental Results

The experimental results of HUANNet on the ShanghaiTech Part A and Part B datasets are presented in Table 3. Compared with state-of-the-art methods, HUANNet achieves competitive results, demonstrating its robustness in handling varying crowd densities and complex backgrounds. Fig. 7 shows the prediction results on the ShanghaiTech Part A dataset, highlighting the excellent performance of our network in densely populated scenarios. Fig. 8 shows the prediction results on the ShanghaiTech Part B dataset, demonstrating that our network is capable of addressing scale variation challenges.

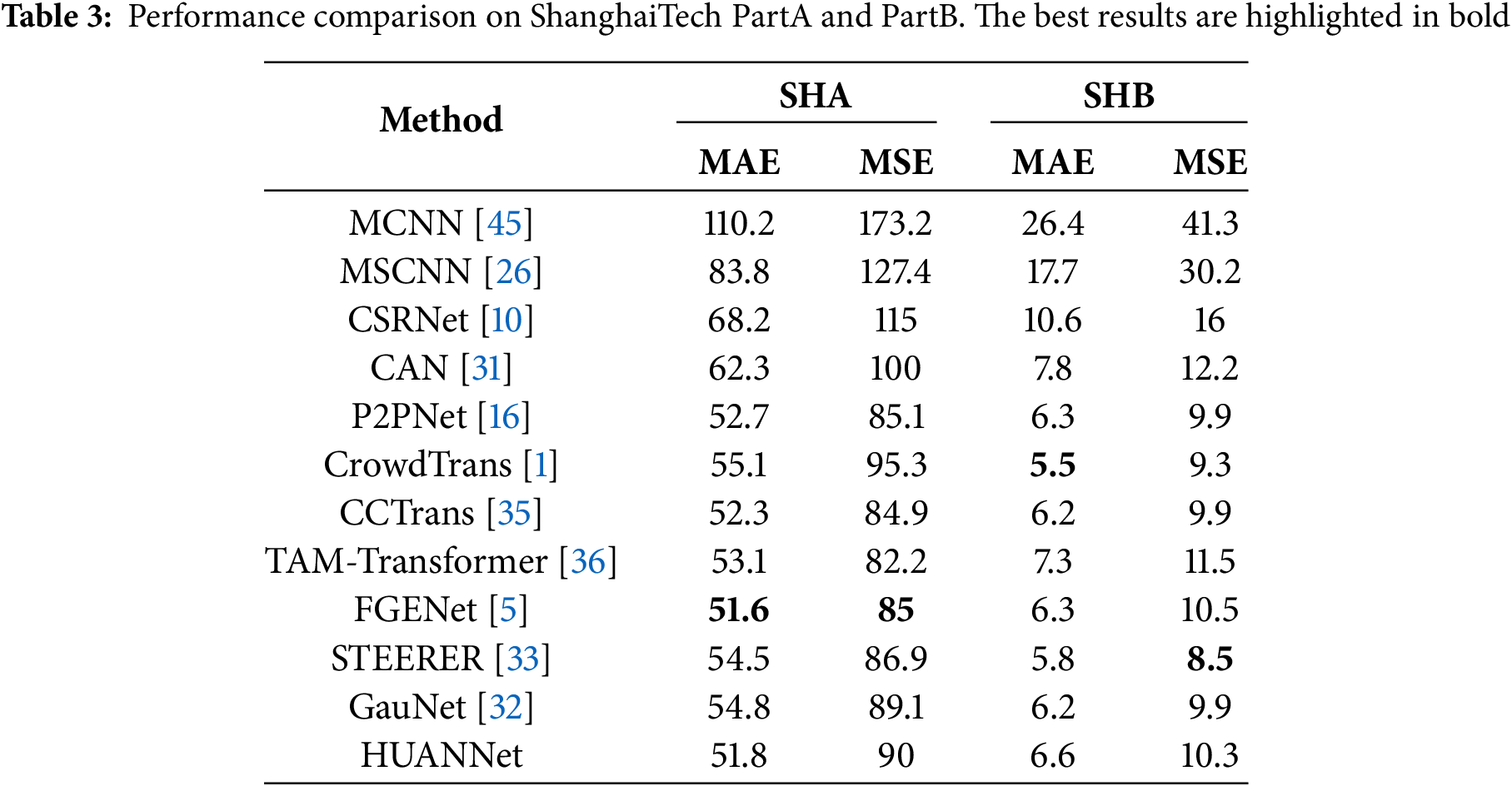
Figure 7: Predicted results on the ShanghaiTech Part A dataset

Figure 8: Predicted results on the ShanghaiTech Part B dataset

Tables 4 and 5 report the experimental results of HUANNet on the CARPK dataset. Compared with other methods, HUANNet achieves state-of-the-art performance across four different scenes, demonstrating its adaptability to challenging backgrounds and varying lighting conditions. Fig. 9 shows the prediction results of the four scenarios in the CARPK dataset. Our model achieves state-of-the-art performance in both excessively bright and dark scenarios, indicating that our model can still achieve excellent performance even in difficult counting tasks involving loss of detailed information and unclear foreground-background separation.

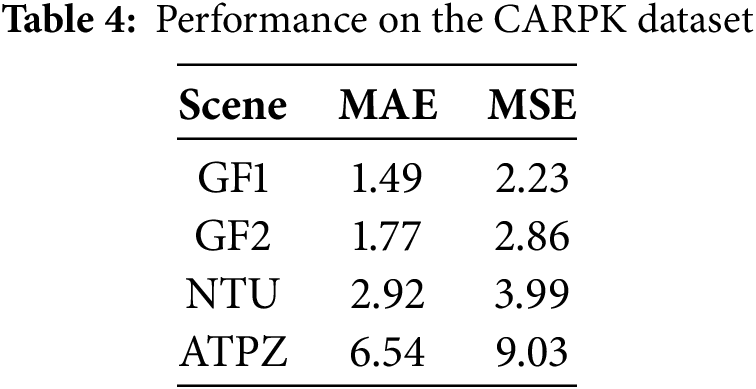
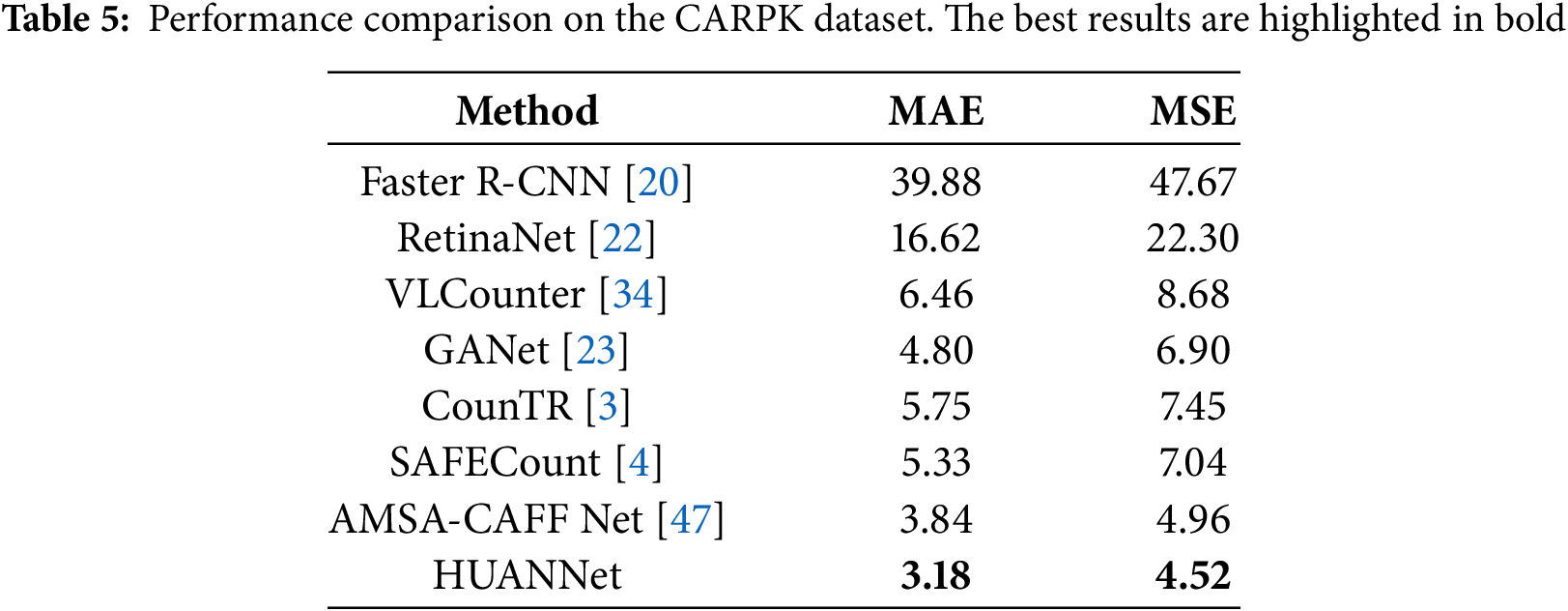
Figure 9: Prediction results in four different scenarios on the CARPK dataset

Finally, we evaluated HUANNet on the XRAY-IECCD dataset, which contains densely packed small objects. Table 6 shows that HUANNet achieves state-of-the-art performance, demonstrating its ability to handle highly dense and small objects. Fig. 10 presents the predicted results on the XRAY-IECCD dataset. Faced with diverse and dense small objects in the XRAY-IECCD dataset, HUANNet has achieved a significant lead in comparison with other methods due to its high-quality feature extraction ability and robust matching strategy.

Figure 10: Prediction results on the XRAY-IECCD dataset

Experiments across these three datasets highlight the superior performance of the proposed method. HUANNet demonstrates robust feature extraction capabilities, enabling it to effectively handle scenarios involving background variations and densely arranged targets, thereby maintaining a stable and accurate counting process. However, as illustrated in Fig. 11, performance degrades in cases of severe occlusion. When multiple targets overlap heavily, critical visual cues are lost, which substantially hinders the extraction of discriminative features. This often results in missed detections or inaccurate density estimations, ultimately reducing overall counting accuracy. Such cases underscore the intrinsic difficulty of crowd counting under extreme occlusion and highlight an important direction for future research.

Figure 11: Prediction performance and detailed visualization under severe occlusion conditions

4.5 Ablation Studies

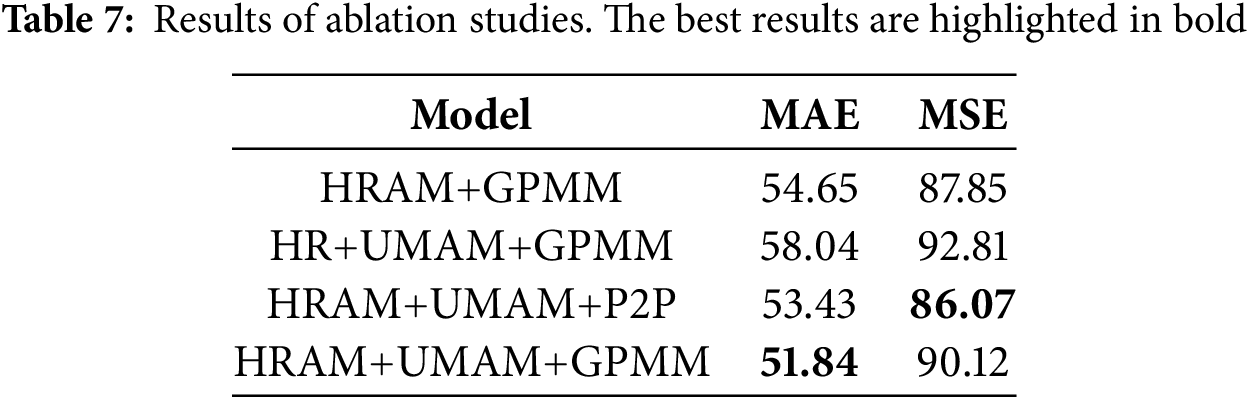
To assess the impact of each component in HUANNet, we conducted ablation studies on the ShanghaiTech Part A dataset. These experiments evaluate the contributions of the HRAM, UMAM, and GPMM modules by removing or modifying certain components of the network.

a. HRAM+GPMM: Complete model without the UMAM mechanism.

b. HR+UMAM+GPMM: Replace HRAM with a standard HRNet in the feature extraction stage.

c. HRAM+UMAM+P2P: Replace GPMM with point regression-based methods in P2PNet.

d. HRAM+UMAM+GPMM: Complete network structure.

The results of the ablation experiments are shown in Table 7. It is evident that the three modules of HRAM, UMAM, and GPMM work together to improve counting accuracy, and these three modules each play a positive role in enhancing the performance.

To evaluate the individual contributions of each sub-module (channel attention, ODConv, and spatial attention) within the UMAM, we further conducted ablation experiments on the ShanghaiTech Part A dataset by combining different sub-modules. The experimental results are presented in Table 8. The data in the table demonstrate that among the three sub-modules of UMAM, the channel attention sub-module makes a greater independent contribution. Under the synergistic effect of the channel attention, ODConv, and spatial attention sub-modules, the model exhibits superior counting accuracy, indicating that all three sub-modules play necessary and positive roles.

5  Conclusions

In this paper, we propose HUANNet, a novel model for dense target counting in complex scenes. The network integrates three key components: the High-Resolution Attention Module (HRAM), the Unified Multi-Scale Attention Module (UMAM), and the Grid-Assisted Point Matching Module (GPMM). By optimizing multi-resolution feature fusion and embedding attention mechanisms at various depths, our model captures fine-grained spatial and channel-wise relationships. Moreover, the grid-based point matching strategy effectively stabilizes the prediction process in dense scenarios. Extensive experiments on challenging datasets, including ShanghaiTech Part A/B, CARPK, and XRAY-IECCD, demonstrate that HUANNet achieves competitive or state-of-the-art performance, confirming its robustness and generalizability. Research involving complex and dense environments shows significant potential across numerous practical applications. In agriculture, precise counting and analysis of densely distributed crops enable accurate control of pesticide and fertilizer application rates, which play a crucial role in determining final yields. In the medical field, particularly in cell counting, accurate counts can inform drug development processes, especially since cells are often densely packed and microscopic. In industrial settings, precise workpiece counting significantly enhances production efficiency. This work may be extended to other visual tasks that require accurate and stable counting and localization in complex, dense environments, providing effective technical support to address a broader range of practical challenges.

Acknowledgement: Not applicable.

Funding Statement: This research was funded by the National Natural Science Foundation of China (62273213, 62472262, 62572287), Natural Science Foundation of Shandong Province (ZR2024MF144), Natural Science Foundation of Shandong Province for Innovation and Development Joint Funds (ZR2022LZH001), and Taishan Scholarship Construction Engineering.

Author Contributions: Conceptualization, Zhiguo Zhang; methodology, Haixia Wang; software, Huan Zhang; validation, Xiuling Wang; investigation, Xiuling Wang; resources, Haixia Wang; data curation, Huan Zhang; writing—original draft preparation, Huan Zhang; writing—review and editing, Zhiguo Zhang; visualization, Xule Xin; supervision, Zhiguo Zhang; project administration, Haixia Wang; funding acquisition, Haixia Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Zhiguo Zhang, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Guo W, Yang S, Ren Y, Huang Y. CrowdTrans: learning top-down visual perception for crowd counting by transformer. Neurocomputing. 2024;587:127650. doi:10.1016/j.neucom.2024.127650. [Google Scholar] [CrossRef]

2. Cheng J, Feng C, Xiao Y, Cao Z. Late better than early: a decision-level information fusion approach for RGB-thermal crowd counting with illumination awareness. Neurocomputing. 2024;594:127888. doi:10.1016/j.neucom.2024.127888. [Google Scholar] [CrossRef]

3. Liu C, Zhong Y, Zisserman A, Xie W. CounTR: transformer-based generalised visual counting. arXiv:2208.13721. 2022. [Google Scholar]

4. You Z, Yang K, Luo W, Lu X, Cui L, Le X. Few-shot object counting with similarity-aware feature enhancement. In: Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision; 2023 Jan 2–7; Waikoloa, HI, USA. p. 6315–24. [Google Scholar]

5. Ma HY, Zhang L, Wei XY. FGENet: fine-grained extraction network for congested crowd counting. In: MultiMedia Modeling: 30th International Conference, MMM 2024, Proceedings III; 2024 Jan 29–Feb 2; Amsterdam, The Netherlands. Berlin, Heidelberg: Springer-Verlag; 2024. p. 43–56. [Google Scholar]

6. Luu TH, Phuc PNK, Ngo QH, Nguyen TT, Nguyen HC. Design a computer vision approach to localize, detect and count rice seedlings captured by a UAV-mounted camera. Comput Mater Contin. 2025;83(3):5643–56. doi:10.32604/cmc.2025.064007. [Google Scholar] [CrossRef]

7. Eaton-Rosen Z, Varsavsky T, Ourselin S, Cardoso MJ. As easy as 1, 2.. 4? Uncertainty in counting tasks for medical imaging. In: Medical Image Computing and Computer Assisted Intervention–MICCAI 2019: 22nd International Conference; 2019 Oct 13–17; Shenzhen, China. p. 356–64. [Google Scholar]

8. Babu Sam D, Surya S, Venkatesh Babu R. Switching convolutional neural network for crowd counting. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2017 Jul 21–26; Honolulu, HI, USA. p. 5744–52. [Google Scholar]

9. Lempitsky V, Zisserman A. Learning to count objects in images. In: Proceedings of the 24th International Conference on Neural Information Processing Systems-Volume 1. NIPS' 10. Red Hook, NY, USA: Curran Associates Inc.; 2010. p. 1324–32. [Google Scholar]

10. Li Y, Zhang X, Chen D. CSRNet: dilated convolutional neural networks for understanding the highly congested scenes. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2018 Jun 18–23; Salt Lake City, UT, USA. p. 1091–100. [Google Scholar]

11. Zhang C, Li H, Wang X, Yang X. Cross-scene crowd counting via deep convolutional neural networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2015 Jun 7–12; Boston, MA, USA. p. 833–41. [Google Scholar]

12. Al-Ghanem WK, Qazi EUH, Faheem MH, Quadri SSA. Deep learning based efficient crowd counting system. Comput Mater Continua. 2024;79(3):4001–20. [Google Scholar]

13. Wang B, Liu H, Samaras D, Nguyen MH. Distribution matching for crowd counting. Adv Neural Inform Process Syst. 2020;33:1595–607. [Google Scholar]

14. Bai S, He Z, Qiao Y, Hu H, Wu W, Yan J. Adaptive dilated network with self-correction supervision for counting. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2020 Jun 13–19; Seattle, WA, USA. p. 4594–603. [Google Scholar]

15. Song Q, Wang C, Wang Y, Tai Y, Wang C, Li J, et al. To choose or to fuse? Scale selection for crowd counting. Proc AAAI Conf Artif Intell. 2021;35:2576–83. doi:10.1609/aaai.v35i3.16360. [Google Scholar] [CrossRef]

16. Song Q, Wang C, Jiang Z, Wang Y, Tai Y, Wang C, et al. Rethinking counting and localization in crowds: a purely point-based framework. In: Proceedings of the IEEE/CVF International Conference on Computer Vision; 2021 Oct 10–17; Montreal, QC, Canada. p. 3365–74. [Google Scholar]

17. Wang X, Girshick R, Gupta A, He K. Non-local neural networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2018 Jun 18–23; Salt Lake City, UT, USA. p. 7794–803. [Google Scholar]

18. Hu J, Shen L, Sun G. Squeeze-and-excitation networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2018 Jun 18–23; Salt Lake City, UT, USA. p. 7132–41. [Google Scholar]

19. Woo S, Park J, Lee JY, Kweon IS. Cbam: convolutional block attention module. In: Proceedings of the European Conference on Computer Vision (ECCV); 2018 Sep 8–14; Munich, Germany. p. 3–19. [Google Scholar]

20. Ren S, He K, Girshick R, Sun J. Faster R-CNN: towards real-time object detection with region proposal networks. IEEE Trans Pattern Anal Mach Intell. 2016;39(6):1137–49. doi:10.1109/tpami.2016.2577031. [Google Scholar] [PubMed] [CrossRef]

21. Ge Z. Yolox: exceeding yolo series in 2021. arXiv: 2107.08430. 2021. [Google Scholar]

22. Lin T-Y, Goyal P, Girshick R, He K, Dollár P. Focal loss for dense object detection. In: Proceedings of the IEEE International Conference on Computer Vision (ICCV). Venice, Italy: IEEE; 2017. p. 2980–8. [Google Scholar]

23. Cai YQ, Du D, Zhang L, Wen L, Wang W, Wu Y, et al. Guided attention network for object detection and counting on drones. In: Proceedings of the 28th ACM International Conference on Multimedia; 2020 Oct 12–16; Seattle, WA, USA. p. 709–17. [Google Scholar]

24. Idrees H, Tayyab M, Athrey K, Zhang D, Al-Maadeed S, Rajpoot N, et al. Composition loss for counting, density map estimation and localization in dense crowds. In: Proceedings of the European Conference on Computer Vision (ECCV); 2018 Sep 8–14; Munich, Germany. p. 532–46. [Google Scholar]

25. Gao J, Han T, Wang Q, Yuan Y. Domain-adaptive crowd counting via inter-domain features segregation and gaussian-prior reconstruction. arXiv:1912.03677. 2019. [Google Scholar]

26. Zeng L, Xu X, Cai B, Qiu S, Zhang T. Multi-scale convolutional neural networks for crowd counting. In: 2017 IEEE International Conference on Image Processing (ICIP); 2017 Sep 17; Beijing, China. p. 465–9. [Google Scholar]

27. Zhang L, Shi M, Chen Q. Crowd counting via scale-adaptive convolutional neural network. In: 2018 IEEE Winter Conference on Applications of Computer Vision (WACV); 2018 Mar 12–15; Lake Tahoe, NV, USA. p. 1113–21. [Google Scholar]

28. Cao X, Wang Z, Zhao Y, Su F. Scale aggregation network for accurate and efficient crowd counting. In: Proceedings of the European Conference on Computer Vision (ECCV); 2018 Sep 8–14; Munich, Germany. p. 734–50. [Google Scholar]

29. Cheng J, Li Q, Chen J, Gao M. Efficient vehicular counting via privacy-aware aggregation network. Meas Sci Technol. 2025;36(2):026213. doi:10.1088/1361-6501/ada6f1. [Google Scholar] [CrossRef]

30. Ma Y, Sanchez V, Guha T. FusionCount: efficient crowd counting via multiscale feature fusion. In: 2022 IEEE International Conference on Image Processing (ICIP); 2022 Oct 16–19; Bordeaux, France. p. 3256–60. [Google Scholar]

31. Liu W, Salzmann M, Fua P. Context-aware crowd counting. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2019 Jun 15–20; Long Beach, CA, USA. p. 5099–108. [Google Scholar]

32. Cheng ZQ, Dai Q, Li H, Song J, Wu X, Hauptmann AG. Rethinking spatial invariance of convolutional networks for object counting. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2022 Jun 18–24; New Orleans, LA, USA. p. 19638–48. [Google Scholar]

33. Han T, Bai L, Liu L, Ouyang W. Steerer: resolving scale variations for counting and localization via selective inheritance learning. In: Proceedings of the IEEE/CVF International Conference on Computer Vision; 2023 Oct 1–6; Paris, France. p. 21848–59. [Google Scholar]

34. Kang S, Moon W, Kim E, Heo JP. VlCounter: text-aware visual representation for zero-shot object counting. Proc AAAI Conf Artif Intell. 2024;38:2714–22. doi:10.1609/aaai.v38i3.28050. [Google Scholar] [CrossRef]

35. Tian Y, Chu X, Wang H. CCTrans: simplifying and improving crowd counting with transformer. arXiv: 2109.14483. 2021. [Google Scholar]

36. Sun G, Liu Y, Probst T, Paudel DP, Popovic N, Van Gool L. Rethinking global context in crowd counting. Mach Intell Res. 2024;21(4):640–51. doi:10.1007/s11633-023-1475-z. [Google Scholar] [CrossRef]

37. Liang D, Chen X, Xu W, Zhou Y, Bai X. TransCrowd: weakly-supervised crowd counting with transformers. Sci China Inf Sci. 2022;65(6):160104. doi:10.1007/s11432-021-3445-y. [Google Scholar] [CrossRef]

38. Xu C, Liang D, Xu Y, Bai S, Zhan W, Bai X, et al. AutoScale: learning to scale for crowd counting. Int J Comput Vis. 2022;130(2):405–34. doi:10.1007/s11263-021-01542-z. [Google Scholar] [CrossRef]

39. Jiang M, Lin J, Wang ZJ. A smartly simple way for joint crowd counting and localization. Neurocomputing. 2021;459:35–43. doi:10.1016/j.neucom.2021.06.055. [Google Scholar] [CrossRef]

40. Liang D, Xu W, Zhu Y, Zhou Y. Focal inverse distance transform maps for crowd localization. IEEE Trans Multimed. 2022;25:6040–52. doi:10.1109/tmm.2022.3203870. [Google Scholar] [CrossRef]

41. Liu C, Weng X, Mu Y. Recurrent attentive zooming for joint crowd counting and precise localization. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2019 Jun 15–20; Long Beach, CA, USA. p. 1217–26. [Google Scholar]

42. Liang D, Xu W, Bai X. An end-to-end transformer model for crowd localization. In: European Conference on Computer Vision. Cham, Switzerland: Springer; 2022. p. 38–54. [Google Scholar]

43. Wang J, Sun K, Cheng T, Jiang B, Deng C, Zhao Y, et al. Deep high-resolution representation learning for visual recognition. IEEE Trans Pattern Anal Mach Intell. 2020;43(10):3349–64. doi:10.1109/tpami.2020.2983686. [Google Scholar] [PubMed] [CrossRef]

44. Li C, Zhou A, Yao A. Omni-dimensional dynamic convolution. arXiv: 2209.07947. 2022. [Google Scholar]

45. Zhang Y, Zhou D, Chen S, Gao S, Ma Y. Single-image crowd counting via multi-column convolutional neural network. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2016 Jun 27–30; Las Vegas, NV, USA. p. 589–97. [Google Scholar]

46. Hsieh MR, Lin YL, Hsu WH. Drone-based object counting by spatially regularized regional proposal network. In: Proceedings of the IEEE International Conference on Computer Vision; 2017 Oct 22–29; Venice, Italy. p. 4145–53. [Google Scholar]

47. Zhang Z, Zhang L, Zhang H, Guo Y, Wang H, Lu X. AMSA-CAFF Net: counting and high-quality density map estimation from X-ray images of electronic components. Expert Syst Appl. 2024;237:121602. doi:10.1016/j.eswa.2023.121602. [Google Scholar] [CrossRef]