Enhanced Capacity Reversible Data Hiding Based on Pixel Value Ordering in Triple Stego Images

1  Introduction

Data hiding is a field of information security. Data hiding is a technique of embedding secret information into a digital product to protect the information or the integrity of the product. Reversible data hiding is a major form of Data hiding. Besides extracting the message, it also restores the cover image. There are many approaches used in RDH, such as difference expansion (DE), histogram shifting (HS), difference error expansion, pixel values ordering, embedding on encrypted images, etc.

This paper presents an RDH method based on the PVO technique. The first RDH-based PVO is proposed by Li et al. [1]. After that, this approach has attracted considerable attention from researchers [2–8]. According to [1], the original image is first divided into discrete blocks. Within each block, the pixel values are sorted in ascending order. Subsequently, the algorithm calculates two types of errors: the difference between the largest and the second-largest pixel values (the maximum error) and the difference between the smallest and the second-smallest pixel values (the minimum error). If the maximum error equals 1, it will embed a bit (a similar process is performed at the smallest side when the smallest error is equal to −1). So, the order of a pixel sequence remains unchanged to serve the information recovery process. Scheme [2] improves [1] by using blocks with the maximum error equal to zero to improve embedding capacity. Ou et al. [3] proposed PVO-k, an improved version of the original PVO method. In this approach, a bit is embedded into k largest pixels if the error between the largest and the second-largest pixel values is zero. Zhang et al. [7] exploit bit-plane segmentation and PVO to embed in rough image regions. Wahed and Nyeem [8] employ a recursive embedding scheme that alternates between horizontal and vertical pixel correlations, enabling dynamic adaptation to different capacity demands.

The technique of reversible data hiding using dual images has recently gained increased attention and development due to its remarkable advantage in embedding capacity [5,9–13]. The dual-image technique was first introduced by Chang et al. [9], based on the Exploiting Modification Direction (EMD) method. In their approach, a 5×5 matrix is used, and the secret data is converted into a sequence represented in base-5 form. Subsequently, each pair of base-5 digits is embedded to generate two stego images. Chang et al. [10] improved upon the work in [9] by employing a 9×9 matrix to enhance embedding capacity. Lu et al. [14] introduced a center folding strategy, in which half of 2k is subtracted, where k is the number of secret bits grouped for embedding at each step. Lu et al. [11] transformed each group of k bits into a decimal number. Similar to the approach in [14], they applied the center folding strategy to reduce the magnitude of each secret decimal value. The resulting folded secret numbers were then embedded based on the frequency of their occurrences.

Subsequently, Niu and Shen [5] proposed an embedding method based on the prediction errors between the second-largest and the largest pixel values, as well as between the second-smallest and the smallest. For each of these error values, they designed embedding rules that allow 1 to 3 bits to be embedded per largest (or smallest) pixel, resulting in two stego images carrying the hidden information. Sao et al. [12] improved image quality by selecting the most frequently occurring 5-bit secret element to embed into pixel pairs with a difference of zero. The hidden data is first divided into 5-bit elements, which are then sorted in descending order of frequency. Higher-frequency elements are associated with lower variation in pixel values, thsereby significantly enhancing the quality of the stego images while also improving embedding capacity. Nguyen and Dao [13] also proposed a dual-image PVO-based method. The authors utilized two variables, the indices of the secret bits and a location map. Based on these two variables, they embedded one bit into each pair of pixels. The method proposed by Weng et al. [15] exemplifies the application of PVO in this context, highlighting that PVO continues to attract significant research interest, even in emerging application domains.

RDH using three stego images offers several advantages. The most notable is its large embedding capacity. With three shadow images, the embedding capacity can reach up to one million bits while maintaining high stego image quality. Another advantage lies in its applicability to multi-party scenarios. For instance, if a message is intended to be disclosed only when all three recipients are present, the message can be embedded using RDH based on three stego images. Each individual receives one stego image, and the secret message can only be extracted when all three images are combined. This property makes the method particularly suitable for applications requiring objectivity and mutual consent. RDH based on three stego images is an emerging research direction, with notable contributions such as [16,17]. In [16], the authors divide the algorithm into three phases. In the first phase, each 3-bit element of the secret message is embedded into individual pixels of the cover image, resulting in three initial stego images. In the second phase, additional secret bits are embedded into these initial stego images using a prediction error-based PVO technique, producing three intermediate stego images. Finally, in the third phase, more secret bits are embedded by modifying prediction errors in the intermediate stego images to obtain the final stego images. Although this method achieves a high embedding capacity, it suffers from relatively low stego image quality and high computational complexity. Chen and Chang [17] also proposed a three-phase embedding scheme. In the first phase, the secret bits are converted into base-5 numbers and embedded into pairs of pixels. In the second phase, additional secret bits are transformed into base-6 numbers and embedded into the stego pixels generated from the first phase. In the final phase, more base-5 secret numbers are embedded into the stego pixels obtained from the previous phase. This method achieves both high embedding capacity and good stego image quality.

Building upon the advantages of reversible data hiding based on three stego images, this paper proposes a novel RDH scheme that also utilizes three stego images. The proposed method is based on the PVO technique, where the cover image is divided into blocks. For each block, 4 to 7 secret bits are embedded into the largest pixel (as well as the smallest pixel), with a maximum modification of 2 units. Additionally, the second-largest and second-smallest pixels may be altered by at most 1 unit. In total, each block is capable of embedding 8 to 14 bits. Experimental results and analysis demonstrate that the proposed method achieves high embedding capacity while maintaining low computational complexity.

The remainder of this paper is organized as follows: Section 2 presents the related works. Section 3 describes the proposed method in detail. Section 4 provides experimental results and analysis. Finally, the conclusion is given in the Section 5.

2  Related Works

2.1 Pvo Method

Li et al. [1] is regarded as the first work to introduce the PVO method. In this approach, the original image is divided into non-overlapping blocks. The pixel values within each block are sorted in ascending order. For a block containing n pixels (x1,x2,…,xn), the sorted sequence is denoted as (xγ(1),xγ(2),…,xγ(n)), where γ:{1,…,n}→{1,…,n} is a one-to-one mapping that satisfies xγ(1)≤xγ(2)≤…≤xγ(n)). Next, the largest and smallest prediction errors, denoted dmax and dmin, are computed using the following formulas:

dmax=xγ(n)−xγ(n−1);dmin=xγ(1)−xγ(2)(1)

Then, a secret data b is embedded in dmax,dmin as follows:

dmax′={dmax, if dmax=0dmax+b, if dmax=1dmax+1, if dmax>1

dmin′={dmin,if dmin=0dmin−b,if dmin=−1dmin−1,if dmin<−1

Finally, the sequence of stego pixels (xγ(1)′, xγ(2)′,…, xγ(n)′) is determined as follows: xγ(n)′=xγ(n−1)+dmax′; xγ(1)′=xγ(2)+dmin′.

An important characteristic of PVO-based methods is that the order of pixel values remains unchanged after embedding. This characteristic ensures the correctness of both data extraction and original image recovery. Since then, many methods have adopted this idea, opening a new research direction in the field of data hiding. The method proposed by Li et al. [1] achieves high stego image quality because each pixel used for embedding is modified by at most 1 unit; however, its embedding capacity remains limited, as each block can carry at most 2 bits.

2.2 Dual-Image PVO Method

This method, proposed by Niu and Shen [5], is based on the PVO method for stego dual images, hereinafter referred to as the NS method. Same as the PVO method, NS method also divides the original image into blocks, and after that, with each block, sorts pixel values in the block in ascending order (xγ(1)′,xγ(2)′,…,xγ(n)′). Determining dmax,dmin as the Formula (1). Dual-stego images are constructed by embedding data into the blocks according to the rules described in Table 1.

As shown in Table 1, each block can embed up to 3 bits on each side, with a maximum pixel modification of 2 units. However, this maximum embedding case occurs with a probability of only 0.5. On average, the expected number of embedded bits per side is 0.5∗1+0.5∗3=2 bits. Therefore, each block can embed an average total of 4 bits. This indicates that, although modifying up to 2 units per pixel is possible, the overall embedding capacity per block remains limited. In contrast, the proposed method allows up to 14 bits to be embedded per block, with improved image quality achieved by selecting the optimal transformation for the embedded bit sequence.

2.3 Triple-Image PVO Method

The method proposed by Sao et al. [6], which is an improvement of the NS method, will hereinafter be referred to as the SLL method. In this approach, the original image is divided into blocks, and the pixel values within each block are sorted in ascending order. Four secret bits are embedded into the maximum pixel, and another four bits are embedded into the minimum pixel. The recovery of the original block and the extraction of the embedded secret bits are then performed based on the correlation among the three stego maximum pixels (and similarly, the three stego minimum pixels).

This method fully utilizes all possible dmax and dmin values by embedding data into the largest and smallest pixels in each block, provided that no overflow occurs. However, the potential of the second-largest and second-smallest pixels remains underutilized, limiting further improvements in embedding capacity. Moreover, each pixel is modified by at most two units, and the quality of the stego images is not satisfactory. The proposed method addresses these limitations by leveraging the second-largest and second-smallest pixels for embedding data. By carefully selecting appropriate pixels and applying an optimized embedding strategy, the proposed approach significantly increases embedding capacity while maintaining improved image quality

3  Proposed Method

In the NS method, pixel values are modified by at most one unit, which helps maintain high image quality. However, each image block can embed at most 6 bits, with an average of 4 bits, resulting in an embedding ratio of only 2 bits per block, a relatively low rate. In contrast, SLL method embeds data into the largest and smallest pixels of each block, achieving up to 8 bits per block with an embedding ratio of approximately 2.7 bits per block. Both methods employ the PVO technique but utilize only the largest and smallest value pixels, leaving the second-largest and second-smallest value pixels unused.

The proposed method improves upon both NS and SLL methods by additionally exploiting the second-largest and second-smallest pixels in each block. As a result, it can embed up to 14 bits per block, with an average embedding ratio of 4.7 bits per block, at least equal to that of the SLL method. To ensure accurate data extraction and image reconstruction, two thresholds is employed, along with an optimal threshold selection strategy to further enhance embedding capacity.

Since pixel values can be altered by up to 2 units during embedding, this may potentially degrade image quality. The proposed method incorporates a transformation selection mechanism inspired by the technique in [12]. Specifically, it uses a rank table to determine embedding parameters, allowing frequently occurring 4-bit groups to be embedded with minimal pixel modification.

Moreover, the proposed method adopts a two-phase embedding process as shown in the Fig. 1. In the first phase, data is embedded into the largest and smallest pixels of each block. In the second phase, additional data is embedded into the second-largest and second-smallest pixels, thereby maximizing the embedding potential of each block.

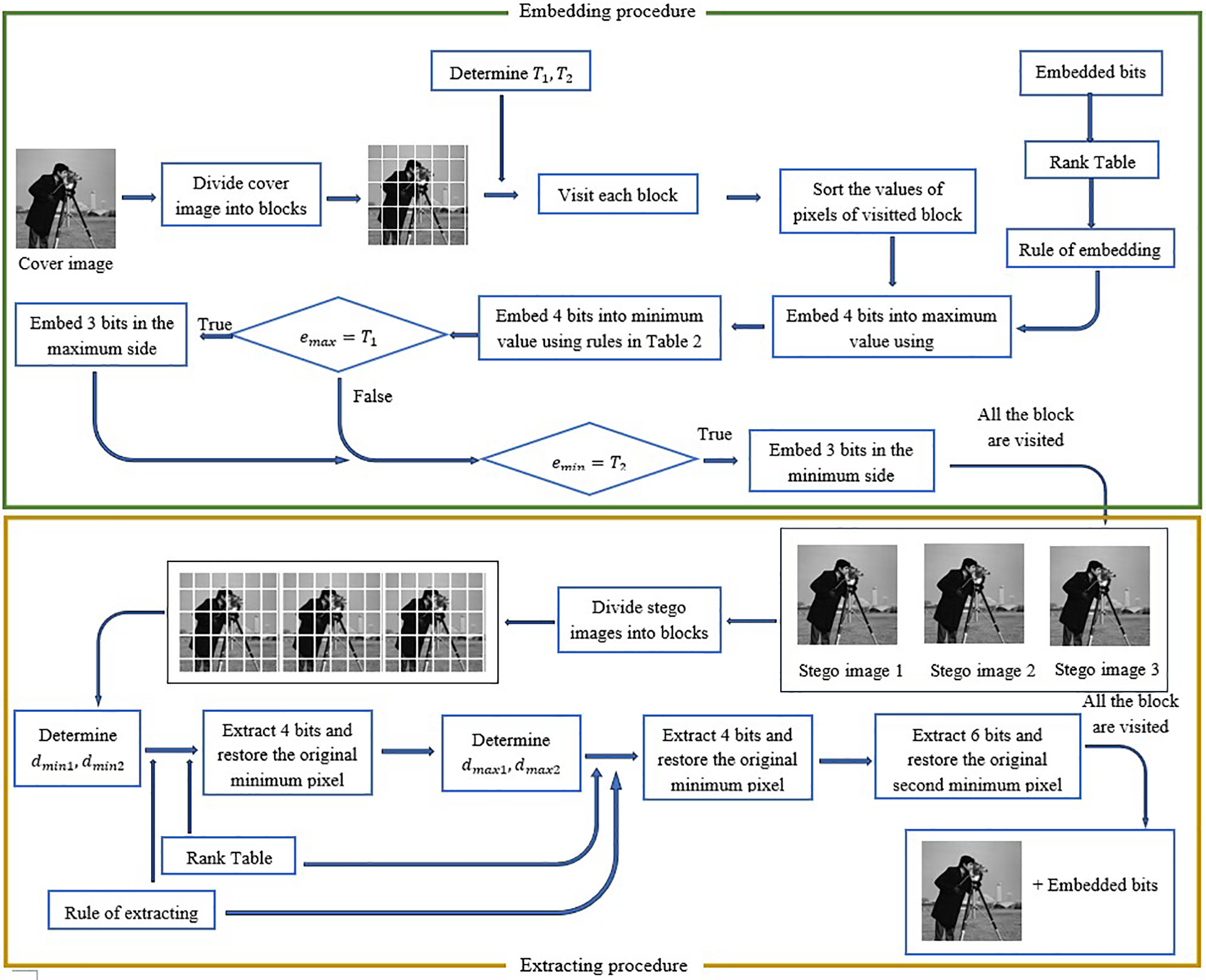
Figure 1: Schema of embedding and extracting procedures

3.1 Rule Table

The secret message is divided into a sequence X of 4-bit elements, and a histogram of X is constructed. The 4-bit element with the highest frequency is assigned rank 1, continuing similarly until all 16 possible 4-bit groups are ranked. Let α1,α2,α3 be variables that determine how the 4-bit elements are embedded into the cover image. To embed a 4-bit element into the largest pixel, α1,α2,α3 are selected based on the frequency rank of the 4-bit element.

Table 2 shows the correspondence between each rank and the parameters α1,α2,α3. Thus, to determine α1,α2,α3, it is sufficient to identify the rank of the 4-bit element to be embedded. A similar process is applied on the minimum side.

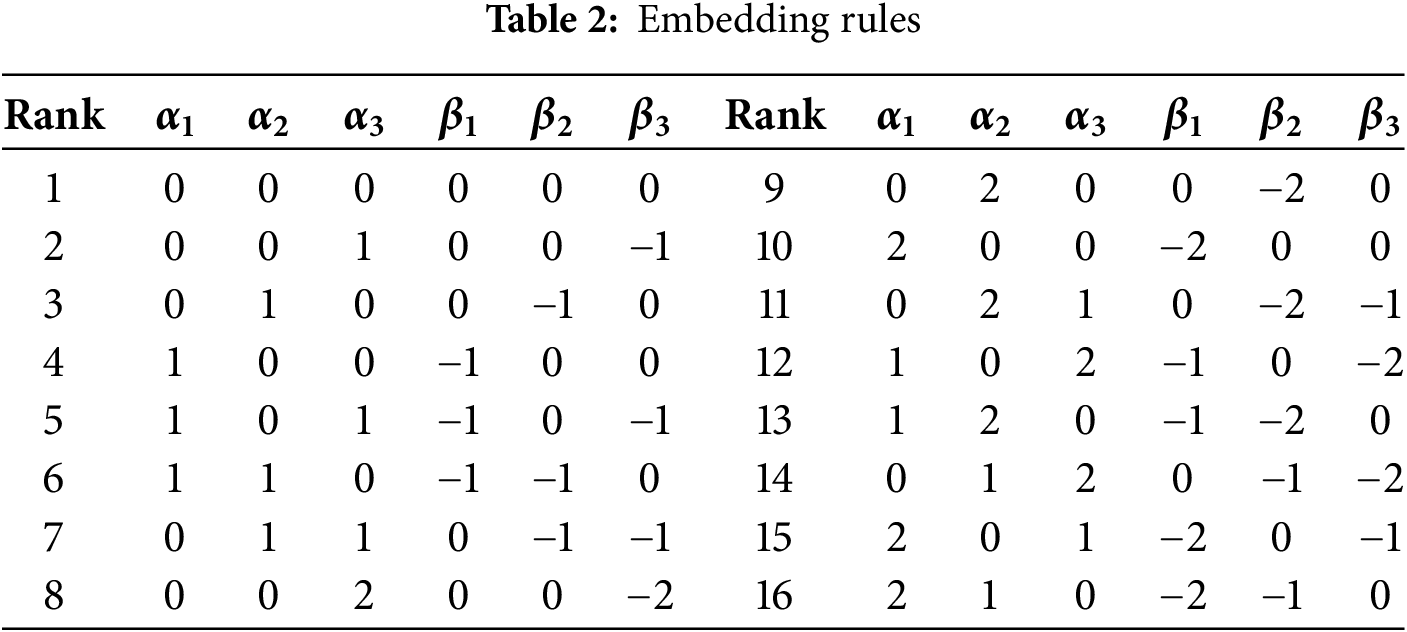
In the extraction procedure, the rank of the 4-bit element embedded into the cover image is determined based on the Extracting Rule Table. Table 3 defines the rank of 4-bit elements and the corresponding α1 values for secret bits embedded on the maximum side. Similarly, Table 4 specifies the rank and β1 values for the minimum side.

3.2 Embedding Algorithm in a Block

3.2.1 Embedding Algorithm in a Block in First Phase

This section presents the algorithm for embedding a bit array B (8 bits) into a block X={x1,x2,…,xn} to produce three stego blocks.

The embedding algorithm for a block is outlined below:

Embedding in the maximum side

Step 1: Sort the pixel values in the block X={x1,x2,…,xn} in ascending order to obtain Xγ={xγ(1),xγ(2),…,xγ(n)}, where γ:{1,…,n}→{1,…,n} is a one-to-one mapping and xγ(1)≤xγ(2)≤…≤xγ(n)).

Step 2: Embedding the array of secret bits B={b1,b2,…,bk}:

Take 4 bits from the array B then refer to Section 3.1 to obtain α1,α2,α3. These 4 bits are embedded in the maximum pixel as: x1γ(n)=xγ(n)+α1; x2γ(n)=xγ(n)+α2; x3γ(n)=xγ(n)+α3. Where x1γ(n),x2γ(n),x3γ(n),xγ(n) are the three stego pixels and the original pixel, respectively, α1,α2,α3 are calculated using Table 2.

After embedding on the maximum side, we proceed to embed on the minimum side as follows:

Embedding in the minimum side

Embed the array of secret bits.

Let B={b1,b2,…,bk} be the array of secret bits. A group of 4 bits from B is used and matched against the frequency table to obtain its rank (refer to Section 3.1). Based on this rank, the corresponding values β1,β2,β3 are determined. These values are then used to embed the 4-bit group into the minimum pixel as: x1γ(1)=xγ(1)+β1; x2γ(1)=xγ(1)+β2; x3γ(1)=xγ(1)+β3. Here, x1γ(1),x2γ(1) represent the three stego pixels, and xγ(1) is the original pixel at the minimum side. The values β1,β2,β3 are determined using Table 2.

3.2.2 Embedding Algorithm in a Block in Second Phase

This section presents the algorithm for embedding 6 bits from B into the second maximum and second minimum pixel, derived from the original block and three embedding parameters obtained during the first phase. Two thresholds, T1 and T2, are used to control embedding reliability.

The detailed embedding algorithm for a single block is outlined below:

Embedding in the maximum side

Using the three parameters α1,α2,α3, along with the threshold T1 and the original pixel xγ(n−1), three secret bits are embedded into the second-largest pixel. Step 1: Calculate the prediction error of the maximum pixel: The maximum pixel is predicted using the second maximum pixel. The prediction error emax is calculated as: emax=xγ(n)−xγ(n−1)

Step 2: If any of the values α1, α2, α3 are non-zero (α1+α2+α3≠0) and emax=T1, we proceed to embed 3 bits ba1,ba2,ba3 into the second-largest pixel.

x1γ(n−1)=xγ(n−1)+ba1;x2γ(n−1)=xγ(n−1)+ba2;x3γ(n−1)=xγ(n−1)+ba3

Otherwise (α1+α2+α3=0 || emax≠T1), the stego pixels remain unchanged.

x1γ(n−1)=xγ(n−1);x2γ(n−1)=xγ(n−1);x3γ(n−1)=xγ(n−1)

where α1,α2,α3 are obtained from first phase and emax=xγ(n)−xγ(n−1) is calculated from the original image. xiγ(n−1), for i=1,2,3 represent the second-largest pixels in the three stego blocks resulting from the first phase.

Embedding in the minimum side

Similar to the maximum side, using emin=xγ(1)−xγ(2), along with the three parameters β1, β2, β3, the threshold T2 and the second-smallest pixel xγ(2). Three secret bits are embedded into the second-smallest pixel as follows: Step 1: Calculate the prediction error of the minimum pixel The minimum pixel is predicted using the second minimum pixel. The prediction error emin is calculated as: emin=xγ(1)−xγ(2). Step 2: If any of the values β1, β2, β3 are non-zero and emin is equal T2, we proceed to embed 3 bits bi1,bi2,bi3 into the second-smallest pixel as follows: x1γ(2)=xγ(2)−bi1; x2γ(2)=xγ(2)−bi2; x3γ(2)=xγ(2)−bi3. Here, xiγ(2), for i=1,2,3 represent the second-smallest pixels in the three stego blocks obtained from the first embedding phase. xγ(2) is the corresponding original pixel. The values β1,β2,β3 are determined during the first phase. If the condition is not met, the stego pixels remain unchanged.

3.3 Extracting Algorithm in a Block

3.3.1 Extracting Algorithm in a Block in First Phase

Given three stego blocks X1, X2, and X3, along with two thresholds T1 and T2, and the rank table, the objective is to recover the original block X and extract the secret message B.

Step 1: Sorting Sort the pixel values in each of the three stego blocks X1, X2, and X3 in ascending order.

Step 2: Extracting secret bits and restoring the original pixel on the minimum side

Calculate the differences among the three stego blocks as follows: dmin1=x2γ(1)−x1γ(1); dmin2=x3γ(1)−x2γ(1);

Step 3: Based on the values of dmin1 and dmin2, refer to Table 4 to determine the value of β1 and the corresponding rank of the 4-bit element. Using this rank and the rank table, retrieve the 4 secret bits. Then, restore the original minimum pixel using the following formula:  xγ(1)=x1γ(1)−β1; where xγ(1) is the original minimum pixel, and x1γ(1) is the stego minimum pixel of the first block.

Step 4: Extract the secret bits and restore the original pixel on the maximum side:

Compute the differences among the three stego blocks as follows: dmax1=x2γ(n)−x1γ(n); dmax2=x3γ(n)−x2γ(n);

Step 5: Extract the secret bits and restore the original maximum pixel.

Based on the values of dmax1 and dmax2, and by referencing the mapping defined in Table 3, the rank of the corresponding 4-bit element is determined. Using this rank and the rank table, the associated 4 secret bits are extracted from the maximum pixel. Subsequently, the original maximum pixel is restored as follows: xγ(n)=x1γ(n)−α1; where xγ(n),x1γ(n) are the original pixel and the stego pixel of the first block, respectively, α1 is referenced from the Table 2.

3.3.2 Extracting Algorithm in a Block in Second Phase

The extraction process uses thresholds T1 and T2, the minimum and maximum values xγ(1) and xγ(n) from Section 3.3.1, along with the values associated with the second-smallest and second-largest pixels, namely x1γ(2),x2γ(2),x3γ(2) and x1γ(n−1),x2γ(n−1),x3γ(n−1), obtained from three stego blocks. We will extract three secret bits and restore the original second pixel.

Step 1: Extract the secret bits and restore the original second minimum pixel.

First, estimate the supposed original second minimum pixel and compute the corresponding three prediction errors for the three stego blocks, as outlined below:

xγ(2)′=xγ(1)−T2;β1min=x1γ(2)−xγ(2)′;β2min=x2γ(2)−xγ(2)′;β3min=x3γ(2)−xγ(2)′.

If any of the three values β1min, β2min, or β3min is less than or equal to T2, we proceed to extract the corresponding bits from the second minimum pixel and restore its original value as follows:

xγ(2)=xγ(1)−T2;bi1=xγ(2)−x1γ(2);bi2=xγ(2)−x2γ(2);bi3=xγ(2)−x3γ(2).

Otherwise, no bit is extracted, and the second minimum pixel is restored as xγ(2)=x1γ(2).

Step 2: Extracting the secret bits and restoring the original second maximum pixel:

First, compute the expected second maximum pixel and calculate the three corresponding errors from the three stego blocks as follows:

xγ(n−1)′=x1γ(n)−T1;α1max=x1γ(n−1)−xγ(n−1)′;α2max=x2γ(n−1)−xγ(n−1)′;α3max=x3γ(n−1)−xγ(n−1)′.

If any of the three values α1max, α2max, or α3max is greater than or equal to T1, we proceed to extract the secret bits from the second maximum pixel as follows:

xγ(n−1)=xγ(n)−T1;ba1=x1γ(n−1)−xγ(n−1);ba2=x2γ(n−1)−xγ(n−1);ba3=x3γ(n−1)−xγ(n−1).

Otherwise, no bits are extracted, and the second maximum pixel is restored as xγ(n−1)=x1γ(n−1).

The remaining pixels in the block are identical to those in the original block.

3.4 Procedure of Embedding in an Image

3.4.1 Threshold T1, T2

To determine the optimal thresholds T1,T2 for maximizing embedding capacity, we aim to maximize the number of blocks where the difference between the maximum pixel and the second maximum pixel (similarly, between the minimum pixel and the second minimum pixel) meets the threshold conditions.

First, we calculate all the prediction errors emax for every block. The threshold T1 is then chosen as the value that appears most frequently in the set Emax={emax|emax>0}. In other words, T1 corresponds to the error value that occurs most often across all blocks. If the cover image is divided into blocks containing more than three pixels, the threshold T2 can be defined based on frequency, similar to T1, by selecting the most frequent value in the set Emin={emin|emin<0}.

T1=max{e(x) | h(emax) is max; emax∈Emax};T2=max{e(x) | h(emin) is max; emin∈Emin};

Here, h(x) denotes the frequency of the value x in the array E. In cases where the blocks contain fewer than three pixels, selecting an optimal value for T2 becomes challenging.

3.4.2 Embedding Procedure

Given an original image I and an array of secret bits B, the goal is to embed B into I to produce three stego images.

Step 1: Divide the original image into non-overlapping blocks of size m×n.

Step 2: Determine or calculate the thresholds T1 and T2 as described in Section 3.4.1.

Step 3: Determine the extra information: To support the extraction process, additional information must be embedded:

32 bits to store the thresholds T1 and T2, 64 bits for the rank table (with 16 entries, each represented by 4 bits), 32 bits to record the indices of the last blocks used in the first and second embedding phases (16 bits for each). In total, the extra information requires 32+64+32=128 bits.

Take the last 32 least significant bits (LSBs) from the first stego image, the last 64 LSBs from the second stego image, and the last 32 LSBs from the third stego image. Prepend these 128 bits to the beginning of the secret bitstream B to obtain the extended bitstream B′.

Step 4: Embed the secret bit array B′ into the image blocks using the algorithm described in Section 3.2.1. Mark the last block that is used for embedding during the first phase.

Step 5: Continue embedding the remaining bits of B′ into the blocks using the algorithm in Section 3.2.2. Mark the last block used in the second phase.

Step 6: Embed the thresholds T1 and T2 into the last 32 LSBs of the first stego image. Embed the rank table into the last 64 LSBs of the second stego image. Embed the index of the last block used for embedding into the last 32 LSBs of the third stego image. All embeddings are performed using the LSB (Least Significant Bit) method.

3.4.3 Extracting Procedure

Given the three stego images S1,S2,S3, the extraction process retrieves the embedded secret bit array B and reconstructs the original image I using the following algorithm:

Step 1: Extract Extra Information:

Extract the last 32 LSBs from S1 to obtain thresholds T1, T2. Extract the last 64 LSBs from S2 to retrieve the rank table. Extract the last 32 LSBs from S3 to determine the order of the last embedded blocks for both embedding phases.

Step 2: Divide the stego images into blocks of size m×n, consistent with the block division used in the embedding procedure.

Step 3: The extraction and restoration process follows a two-phase order: first, the secret bits are extracted and the original image is restored from all blocks using the algorithm defined for the first extraction phase; then, the process continues with the remaining blocks according to the second phase extraction algorithm.

Begin by traversing each block in the three stego images to extract the first 128 bits and restore the original block using the algorithm described in Section 3.3. After extraction, reinsert these 128 bits into the last 32 LSBs of the first stego image, the last 64 LSBs of the second stego image, and the last 32 LSBs of the third stego image using the LSB embedding method.

Step 4: Continue scanning each block in the three stego images to extract the remaining bits of the secret message B and restore the original image using the algorithm described in Section 3.3.

Finally, the complete secret bitstream B is recovered, and the original image is successfully reconstructed.

To analyze the computational complexity of the proposed algorithm, we examine each processing step: The image is divided into non-overlapping blocks of size k×l. For an image of size M×N, this results in approximately Mk×Nl blocks, yielding a complexity of O(M×Nk×l) for operations that involve scanning all blocks. Within each block, sorting is required to determine pixel order. Sorting k×l elements has a complexity of O(k×l×log⁡(k×l)). Since this sorting is applied to each block, the overall sorting complexity across the image is: O(k×l×log⁡(k×l))=O(M×N×log⁡(k×l)). The main computations during both embedding phases (into the largest/smallest and second-largest/second-smallest pixels) also follow the same complexity bound, as each block undergoes sorting and a constant number of arithmetic and conditional operations. Therefore, the total computational complexity of the algorithm is O(M×Nk×l×k×l×log⁡(k×l))=O(M×N×log⁡(k×l)). However, since k and l are small constants in practice, the logarithmic factor becomes negligible. As such, the overall complexity can be approximated as linear in the number of pixels, i.e., O(M×N).

4  Experimental Results

We perform experiments on 15 standard grayscale images of size 512×512, as illustrated in Fig. 2 to compare three recent multi-stego image methods: Niu et al. [5], which employs two stego images, and two methods that use three stego images, namely Chen and Chang [17] and Sao et al. [6].

Figure 2: Experimental images and the data image are embedded in the experimental images

We employ two key metrics to evaluate the efficiency of each method: embedding capacity, measured by the total number of embedded bits and the bits per pixel (bpp), and peak signal-to-noise ratio (PSNR), measured in decibels (dB). The PSNR metric assesses image quality by quantifying the distortion between the cover image and the stego images. A higher PSNR indicates better image quality. The embedding capacity can be calculated using the following ratio: r=Cn×M×N where r is the capacity ratio, C is the maximum number of bits that can be embedded in the image, M×N is the size of the original image, n is the number of stego images (in this paper, n=3). A higher value of r indicates a greater embedding capacity.

When the image is divided into blocks of size 2×1 or 1×2, data is embedded only in the first phase, specifically into the maximum and minimum pixels of each block. For blocks of size 1×3 or 3×1, data can be embedded into the maximum and minimum pixels (first phase), and additionally into either the second maximum or second minimum pixel (second phase). The choice between the second maximum or second minimum for embedding in the second phase depends on the relative magnitudes of thresholds T1 and T2, the side with the larger threshold is selected. When the image is divided into blocks of size 4 pixels or more, both embedding phases are fully applied. That is, data is embedded into the maximum and minimum pixels (first phase), as well as into both the second maximum and second minimum pixels (second phase), where applicable.

In the proposed method, data embedding is carried out in two phases. In the first phase, each image block can embed 4 bits into the maximum pixel and 4 bits into the minimum pixel. In the second phase, if specific conditions are satisfied, an additional 6 bits may be embedded (3 bits into the second-largest pixel and 3 bits into the second-smallest pixel).

Therefore, the theoretical embedding capacity (EC) and embedding rate (ER) for an original image of size M×N can be calculated as follows:

The number of non-overlapping blocks is f=⌊M×Nm×n⌋, where m×n is the size of each block.

The embedding capacity in the first phase is 8×f.

The number of cases in the second phase that satisfy the embedding condition is defined as s=max{h(emax) | emax∈Emax} + min{h(emin) | emin∈Emin}, where h(e) is the histogram count of the prediction error values.

Thus, the total embedding capacity is: EC=8×f+3×s;ER=EC3×M×N.

Table 5 compares the embedding capacity, in terms of the total number of bits and bits per pixel (bpp), for different methods. The comparison is conducted by dividing the cover image into blocks of size 2×2. Method [5] achieves a capacity of 0.43 bpp, embedding an average of 225,299 bits into 2 stego images. Ref. [6] reaches a higher capacity of 0.67 bpp, embedding 523,512 bits across 3 stego images. The proposed method attains the highest capacity of 0.89 bpp, corresponding to 698,375 embedded bits.

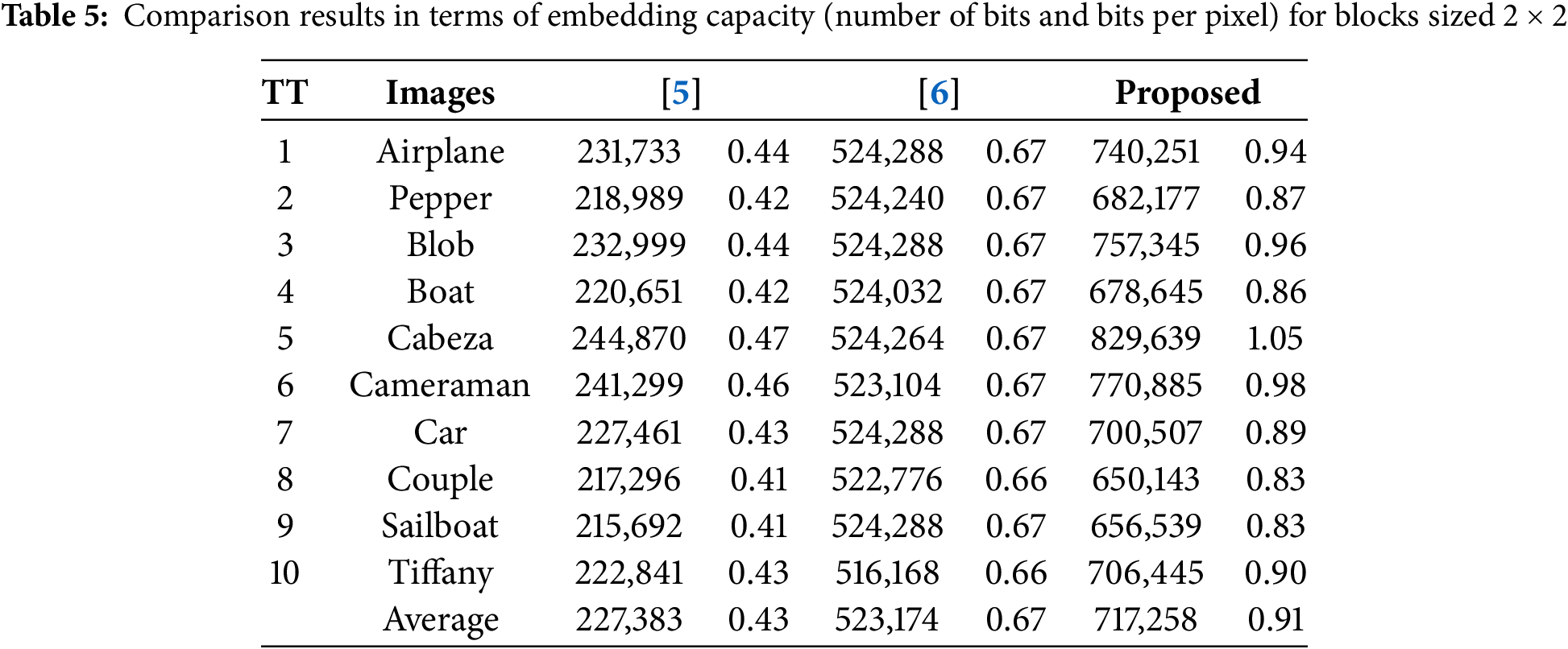
In [5], capacity is estimated based on probability and may slightly exceed the actual capacity when using a random bit array. Each block in [5] can embed from 1 up to 3 bits across two stego images. In contrast, [6] consistently embeds up to 8 bits per block across three stego images. Our proposed method improves on this by embedding from 8 to 14 bits per block, providing a higher overall capacity.

Table 6 presents a comparison of embedding capacities when the cover image is divided into blocks of size 1×2. In [17], each pair of pixels can embed a maximum of 9 bits. In contrast, both the method [6] and the proposed method embed 8 bits per pixel pair. However, due to differences in how embedding opportunities are utilized, Ref. [6] and the proposed method achieve higher effective capacities than [17].

On average, the embedding capacity of [5] is 1.12 bits per pixel (bpp), the Ref. [17] achieves 1.23 bpp, while both the Ref. [6] and the proposed methods reach 1.33 bpp. Notably, although the capacity of the proposed method is on par with [6], the proposed method offers superior stego image quality. Moreover, the proposed method outperforms [17] by a significant margin an increase of 78,116 bits, highlighting the effectiveness of the proposed embedding strategy.

We conducted a comparison using the UCID database, which contains 1338 images. Fig. 3 illustrates the embedding capacity of three methods [5,6], and the proposed method—when the original images are divided into blocks of size 2×2. As shown in the figure, the proposed method achieves the highest embedding capacity among the three. In the case of 1×2 block division, shown in Fig. 4, we compare the proposed method with [6,17]. The proposed method demonstrates a higher capacity than [17] and performs similarly to [6] in terms of capacity. However, the image quality of the stego images generated by the proposed method is superior to both.

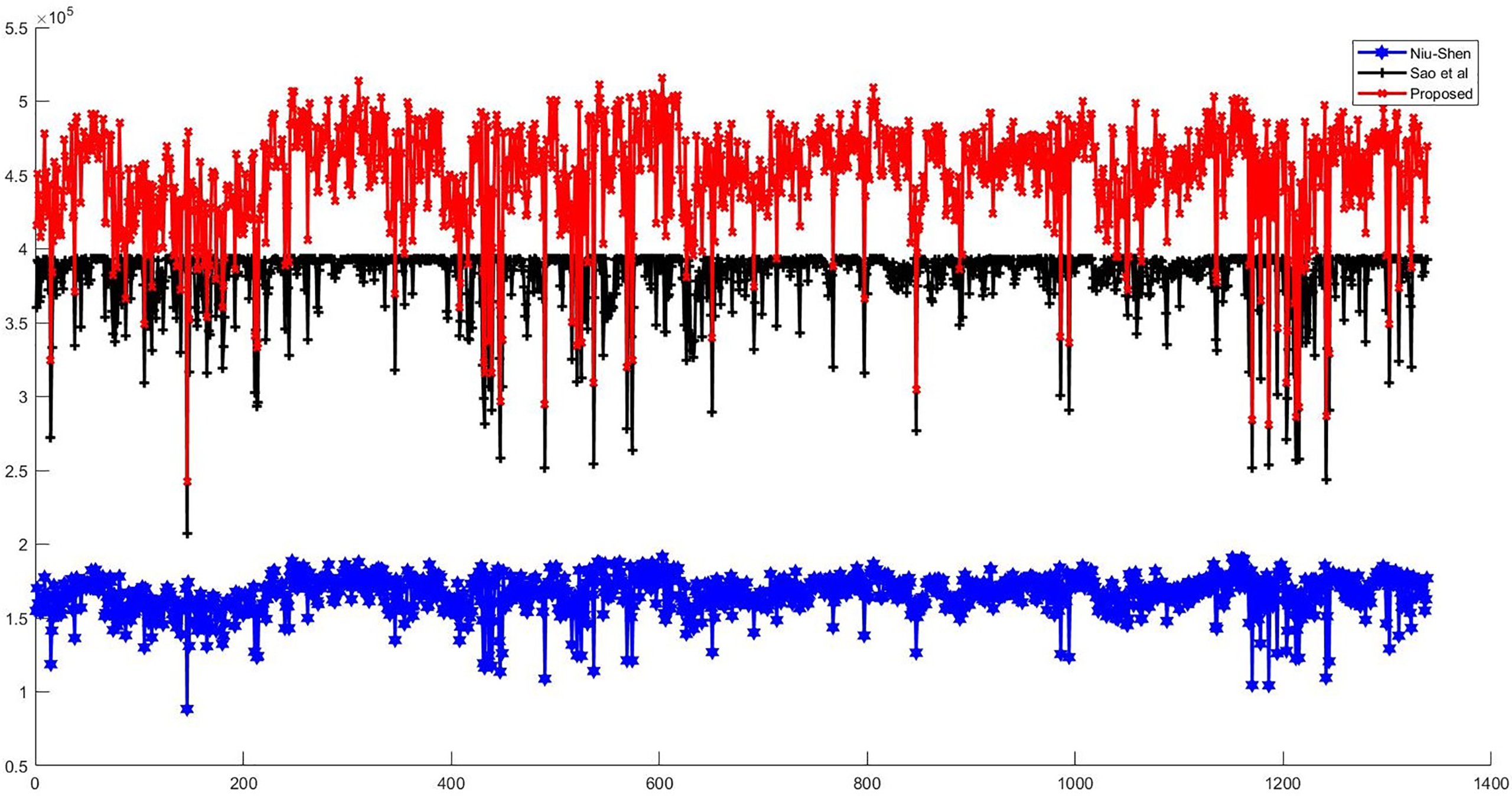
Figure 3: Comparison of embedding capacity with dividing the cover image into a block 2×2 on the UCID database [5,6]

Figure 4: Comparison of embedding capacity with dividing the cover image into blocks 2×1 on the UCID database [5,6]

In terms of PSNR comparison, we evaluate the performance using 15 data images of varying sizes, includes Barbara sized 100×100, Tiffany sized 112×112 Airplane sized 122×122, Number sized 132×132, Pepper sized 141×141 Tank sized 150×150 France sized 158×158 Car sized 166×166 Cameraman sized 173×173 Boat sized 180×180 Sailboat sized 187×187 Couple sized 194×194 Cabeza sized 200×200 Blob sized 206×206 Baboon sized 212×212. These images are embedded into 9 standard experimental grayscale images, shown in Fig. 2.

Fig. 5 presents a chart displaying the average PSNR values across the 8 experimental images when embedding the 15 data images. This chart illustrates that the proposed method consistently achieves the highest average PSNR, indicating superior stego image quality. In this figure, we also observe that when the embedded data is the image Number (sized 132×132), and the rank table is applied to select optimal parameters during embedding, the proposed method produces stego images with superior quality compared to the other methods. This improvement is due to the rank table’s ability to select the best parameters for the 4-bit groups with the highest frequency, thereby minimizing distortion. This improved quality is primarily due to the group of 4-bit patterns that appear most frequently during embedding, which result in the smallest differences between the original and stego pixels. As a result, distortion is minimized. Table 7 further supports this finding, showing that the proposed method offers the best overall image quality among all compared methods.

Figure 5: Comparisons of the proposed method with existing works in PSNR under different payloads [5,6,17]

5  Conclusion

In this paper, we propose a novel reversible data hiding method based on PVO that generates three stego images. The proposed approach is capable of embedding up to 14 bits per block by utilizing both the maximum and second maximum, as well as the minimum and second minimum pixel values within each block. To enhance the quality of the stego images, the method incorporates bit correlation analysis and image transformation techniques. Experimental results on standard test images and a dataset of 1338 images from the UCID database demonstrate that the proposed method achieves high embedding capacity while maintaining excellent visual quality in the stego images.

Acknowledgement: The authors extend their appreciation to the University of Transport and Communications (UTC).

Funding Statement: This research is funded by University of Transport and Communications (UTC) under grant number T2025-CN-004.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Kim Sao Nguyen; analysis and interpretation of results: Kim Sao Nguyen, Ngoc Dung Bui; draft manuscript preparation: Kim Sao Nguyen, Ngoc Dung Bui. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Li X, Li J, Li B, Yang B. High-fidelity reversible data hiding scheme based on pixel-value-ordering and prediction-error expansion. Signal Process. 2013;93(1):198–205. doi:10.1016/j.sigpro.2012.07.025. [Google Scholar] [CrossRef]

2. Peng F, Li X, Yang B. Improved PVO-based reversible data hiding. Digit Signal Process. 2014;25(2):255–65. doi:10.1016/j.dsp.2013.11.002. [Google Scholar] [CrossRef]

3. Ou B, Li X, Zhao Y, Ni R. Reversible data hiding using invariant pixel-value-ordering and prediction-error expansion. Signal Process Image Commun. 2014;29(7):760–72. doi:10.1016/j.image.2014.05.003. [Google Scholar] [CrossRef]

4. Pan Z, Gao E. Reversible data hiding based on novel embedding structure PVO and adaptive block-merging strategy. Multimed Tools Appl. 2019;78(18):26047–71. doi:10.1007/s11042-019-7692-3. [Google Scholar] [CrossRef]

5. Niu Y, Shen S. A novel pixel value ordering reversible data hiding based on dual-image. Multimed Tools Appl. 2022;81(10):13751–71. doi:10.1007/s11042-022-12149-y. [Google Scholar] [CrossRef]

6. Sao NK, Luyen CT, Linh MV. An efficient pixel value ordering data hiding method based on three stego images. TNU J Sci Technol. 2022;227(16):233–40. doi: 10.34238/tnu-jst.6869. [Google Scholar] [CrossRef]

7. Zhang Z, Wang W, Zhao Z, Wang E. PVO-based reversible data hiding using bit plane segmentation and pixel expansion. J Inf Secur Appl. 2023;79:103649 doi: 10.1016/j.jisa.2023.103649. [Google Scholar] [CrossRef]

8. Wahed MA, Nyeem H. High-capacity reversible data hiding with iterative dual pixel value ordering. Alexandria Eng J. 2025;121:580–91 doi: 10.1016/j.aej.2025.02.088. [Google Scholar] [CrossRef]

9. Chang CC, Kieu TD, Chou YC. Reversible data hiding scheme using two steganographic images. In: TENCON 2007-2007 IEEE Region 10 Conference; 2007 Oct 30–Nov 2; Taipei, Taiwan. p. 1–4. doi:10.1109/tencon.2007.4483783. [Google Scholar] [CrossRef]

10. Chang CC, Lu TC, Horng G, Huang YH, Hsu YM. A high payload data embedding scheme using dual stego-images with reversibility. In: 2013 9th International Conference on Information, Communications & Signal Processing; 2013 Dec 10–13; Tainan, Taiwan. p. 1–5. [Google Scholar]

11. Lu TC, Chi LP, Wu CH, Chang HP. Reversible data hiding in dual stego-images using frequency-based encoding strategy. Multimed Tools Appl. 2017;76:23903–29. doi:10.1007/s11042-016-4135-2. [Google Scholar] [CrossRef]

12. Sao NK, Thanh TX, Hong MT. Reversible data hiding based on dual images adapts to the secret message. J Inf Hiding Multim Signal Process. 2023;14(1):20–30. [Google Scholar]

13. Nguyen TD, Dao TT. A novel PVO-based RDH scheme utilizes an interleaved data embedding technique using dual-pixels. J Inf Secur Appl. 2025;89(1):103939. doi:10.1016/j.jisa.2024.103939. [Google Scholar] [CrossRef]

14. Lu TC, Wu JH, Huang CC. Dual-image-based reversible data hiding method using center folding strategy. Signal Process. 2015;115(4):195–213. doi:10.1016/j.sigpro.2015.03.017. [Google Scholar] [CrossRef]

15. Weng CY, Lin TW, Weng HY, Huang CT. Enhanced reversible data hiding in encrypted images via median preserving pixel value ordering and block-wise difference preservation. Signal Image Video Process. 2025;19(6):1–13. doi:10.1007/s11760-025-04054-2. [Google Scholar] [CrossRef]

16. Xie XZ, Chang CC, Lin CC. A hybrid reversible data hiding for multiple images with high embedding capacity. IEEE Access. 2019;8:37–52. doi:10.1109/access.2019.2961764. [Google Scholar] [CrossRef]

17. Chen S, Chang CC. Reversible data hiding based on three shadow images using rhombus magic matrix. J Vis Commun Image Represent. 2021;76(3):103064. doi:10.1016/j.jvcir.2021.103064. [Google Scholar] [CrossRef]