Interactive Dynamic Graph Convolution with Temporal Attention for Traffic Flow Forecasting

1  Introduction

The rapid expansion of urban transportation places escalating pressure on road systems, resulting in intermittent congestion [1,2]. Consequently, researchers have focused on developing intelligent transportation systems (ITS) [3–5]. Precise traffic prediction forms a vital basis for ITS, offering benefits such as enhanced transportation efficiency, alleviated congestion, reduced accidents, minimized energy consumption, and mitigation of environmental pollution [6]. Traffic spatiotemporal data represents a time series recorded at fixed intervals by sensors deployed on road nodes, providing an intuitive reflection of the traffic network’s actual situation [7,8]. Urban road traffic conditions are influenced by numerous external factors, resulting in increased uncertainty in the temporal dimension of traffic flow [9]. Resolving this issue is essential for precise traffic prediction. Consequently, effective time series analysis techniques are commonly applied to predict traffic flow.

In general, traffic flow forecasting methods can be broadly classified into three categories: statistics, machine learning, and deep learning. The statistical approach aims to comprehend the temporal characteristics of traffic flow based on the theoretical foundations of statistical analysis. Statistical models include the historical average model, the autoregressive moving average model, and the vector autoregressive model [10,11]. For instance, Hamed et al. [12] analyzed traffic flow on individual roads and developed an Auto Regressive Integrated Moving Average (ARIMA) model suitable for traffic flow forecasting. Given the challenges faced by statistical forecasting models in handling nonlinear traffic flow data, machine learning models have gained prominence in recent decades. Approaches such as k-nearest neighbor models and Support Vector Regression (SVR) models have emerged. For instance, Mathew and Ali Rawther [13] incorporated data correlation between traffic flows into the classification process using optimized k-nearest neighbor classifiers and sinusoidal k-nearest neighbor classifiers. Wu et al. [14] employed SVR for travel time prediction, offering stronger generalization capabilities and ensuring global optimization. However, machine learning models heavily rely on prior knowledge, making it difficult to determine initial parameters for optimal forecasting accuracy. To overcome these limitations, Huang et al. [15] proposed a network architecture that combines a deep belief network with a regression model, achieving higher accuracy in traffic forecasting. Moreover, Recurrent Neural Network (RNN) and its variants, such as Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU), have been widely utilized in time series prediction tasks leveraging their memory capabilities.

While these deep learning methods have enhanced the capability to capture dynamic spatiotemporal features in traffic flow, they exhibit limited interactive learning ability within the spatiotemporal module. This limitation hampers the traffic flow forecasting model’s perception of time series periodicity, trend changes, and the ability to adequately capture dynamic spatiotemporal features. Consequently, these methods still inadequately capture traffic flow’s latent spatial features.

Addressing these challenges, we propose Attention-based spatiotemporal Interactive Dynamic Graph Convolutional Network (AIDGCN), modeling dynamic spatiotemporal patterns in traffic data. First, we propose a Dynamic Graph Convolutional Network (DGCN) that utilizes prior knowledge to construct dynamic graphs, capturing latent spatial features in traffic flow. These graphs are then embedded into an Interactive Learning framework, forming the Interactive Dynamic Graph Convolutional Network (IDGCN). The IDGCN analyzes traffic flow periodicity, divides sequences into intervals, and facilitates the capture of deep dynamic spatiotemporal features through interactive learning among these segmented sub-sequences. Moreover, adaptive and dynamic neighbor matrices are proposed to model temporal node relationship evolution. Additionally, a Temporal Trend-Aware Multi-Head Self-Attention module captures local context and integrates nonlinear traffic flow temporal features. AIDGCN overcomes existing limitations through accounting for traffic flow periodicity and dynamics, fully leveraging dynamic spatiotemporal features, and demonstrating accurate forecasting potential.

Our primary contributions are:

1.    We propose AIDGCN, the first framework to combine IDGCN with time trend-aware attention. IDGCN’s interleaved interval partitioning mechanism enables bidirectional feature sharing between temporally symmetric sub-sequences.

2.    We introduce a dynamic graph generator that collaborates with an adaptive adjacency matrix and a learnable adjacency matrix. This fusion mechanism is enhanced through Gumbel-softmax reparameterization, addressing the rigid issues of predefined graphs and the instability of purely adaptive methods, enabling robust modeling of spatiotemporal heterogeneity.

3.    We design a temporal multi-head trend-aware self-attention mechanism that integrates 1D convolutions into the attention scoring process. This directly addresses the limitation of standard attention mechanisms in failing to capture local flow trends in continuous data.

The paper is organized as follows: Section 2 presents the related works of traffic flow forecasting, graph convolution network, and attention mechanism. Section 3 elaborates the AIDGCN framework and methodology. Section 4 discusses the results and analysis of the comparative experiment. Section 5 summarizes research findings.

2  Related Works

2.1 Traffic Flow Forecasting

Traffic flow forecasting, a core element of transportation systems, garners substantial research focus. In recent years, it has garnered significant attention as a crucial problem in the development of traffic information systems. Researchers have investigated diverse methodologies, from classical mathematical models to modern data-driven techniques, for developing precise traffic prediction systems. Conventional traffic analysis relies on statistical-mathematical approaches for historical data processing. These models assume that the future forecast data possesses similar attributes to the historical data, thus enabling effective traffic flow forecasting [16].

Progress in computational power and artificial intelligence has revived academic interest in traffic flow forecasting. Non-stationary or complex time series challenge conventional models like ARIMA [17], VAR [18], SVR [19], and FNN [20], resulting in subpar performance. Deep Recurrent Neural Networks, particularly LSTM [21] and GRU [22], demonstrate stronger temporal correlation capture than traditional models. These networks excel at memorizing information from extensive sequential data and learning intricate patterns. However, simple RNNs fail to capture spatial aspects of traffic data, creating a fundamental constraint. To overcome this, CNNs capture spatial variations in Euclidean space but remain constrained by standard grid data formats [23]. Recent studies increasingly employ GCNs to model road networks’ non-Euclidean relationships [24].

2.2 Graph Convolution Network

Graph Convolutional Networks have gained prominence as a research field, extending traditional convolution to graph-structured data. Two distinct graph convolution methodologies exist. The first type focuses on generalizing the spatial neighborhood through convolutional filtering, with node neighborhood selection being a key aspect. Notably, Veličković et al. [25] introduced graph-based attention to allocate distinct weights to neighboring nodes. The second type involves extending convolution to the spectral domain of graphs by searching for the appropriate Fourier bases.

The initial work by Bruna et al. [26] established the foundational graph convolution framework using graph Laplacian operators. Later, Defferrard et al. [27] obtained initial results using Chebyshev polynomial approximation for graph eigenvalue decomposition, eliminating Laplacian eigenvector computation. Zhao et al. [28] introduced T-GCN, combining graph convolutions with traffic forecasting. Though Yu et al. [29] proposed a gated GCN for traffic prediction, though it insufficiently modeled dynamic spatiotemporal patterns. Chen et al. [30] proposed MRA-BGCN, an innovative deep learning framework with cutting-edge traffic forecasting performance.

2.3 Attention Mechanism

Attention mechanisms are prevalent in NLP applications, traffic forecasting, and speech recognition due to its effective dependency modeling. Its core function is to identify and extract task-critical information from extensive datasets.

Liang et al. [31] designed a multilayer attention mechanism for modeling dynamic spatiotemporal correlations in geo-sensors. Nevertheless, training separate models per time series incurred excessive computational costs. In a different approach, Guo et al. [32] developed a graph CNN incorporating attention, yielding initial traffic forecasting outcomes.

Diverging from prior methods, this work explicitly models the traffic network’s graph structure and dynamic spatiotemporal data patterns. A novel Temporal Multi-Head Trend-Aware Self-Attention mechanism is developed, effectively capturing the dynamic dependencies within the network structure for improved feature representation. Prior works utilized GCNs for spatial modeling. However, IDGCN advances these by integrating interleaved sampling to split sequences into symmetric intervals, enabling feature sharing and dynamically fusing adaptive adjacency matrices and learnable adjacency matrices. Simultaneously, the Temporal Multi-Head Trend-Aware Self-Attention uniquely incorporates convolutional operations to capture localized temporal trends, addressing a gap in traditional attention for continuous data, and IDGCN introduces a graph generator with Gumbel reparameterization to simulate dynamic correlations.

3  Methodology

3.1 Problem Definition

As a core time series prediction problem, traffic flow forecasting receives widespread study [33]. The traffic network is modeled as a weighted directed graph G=(V,E,A). The equation specifies |V|=N as the traffic network’s sensor nodes, and E as the set of edges that describe the connection strength among nodes within V. The spatial adjacency matrix A∈RN×N encodes the graph G, with each entry Aij indicating either the similarity in node features or the Euclidean distance between road sensors vi and vj. Aij is set to 1 if both vi,vj∈V and (vi,vj)∈E are satisfied, otherwise, Aij is set to 0. The traffic network G is associated with a graph signal XG(t)∈RN×C at time step t, where each element of XG(t)∈RN×C corresponds to traffic attributes (e.g., speed, flow) recorded by individual sensors. Specifically, the historical speed observations of N nodes over T time steps are denoted as P =[XG(t−T+1),XG(t−T+2),⋯,XG(t)]∈RC×N×T. The traffic speeds of all nodes for the next T′ time steps are to be predicted, denoted as Q=[XG(t+1),XG(t+2),⋯,XG(t+T′)]∈RN×C×T′.

Based on this representation, the traffic prediction task is formulated as:

Q=ℓ(P;G)(1)

where ℓ is the function to be learned. This research focuses on traffic speed prediction, an effective indicator of both density and volume.

3.2 Framework of AIDGCN

This work proposes AIDGCN, a new framework that captures traffic flow’s dynamic spatiotemporal relationships simultaneously. Fig. 1 shows the AIDGCN framework, and it primarily comprises two key components: IDGCN and a Temporal Multi-Head Trend-Aware Self-Attention mechanism.

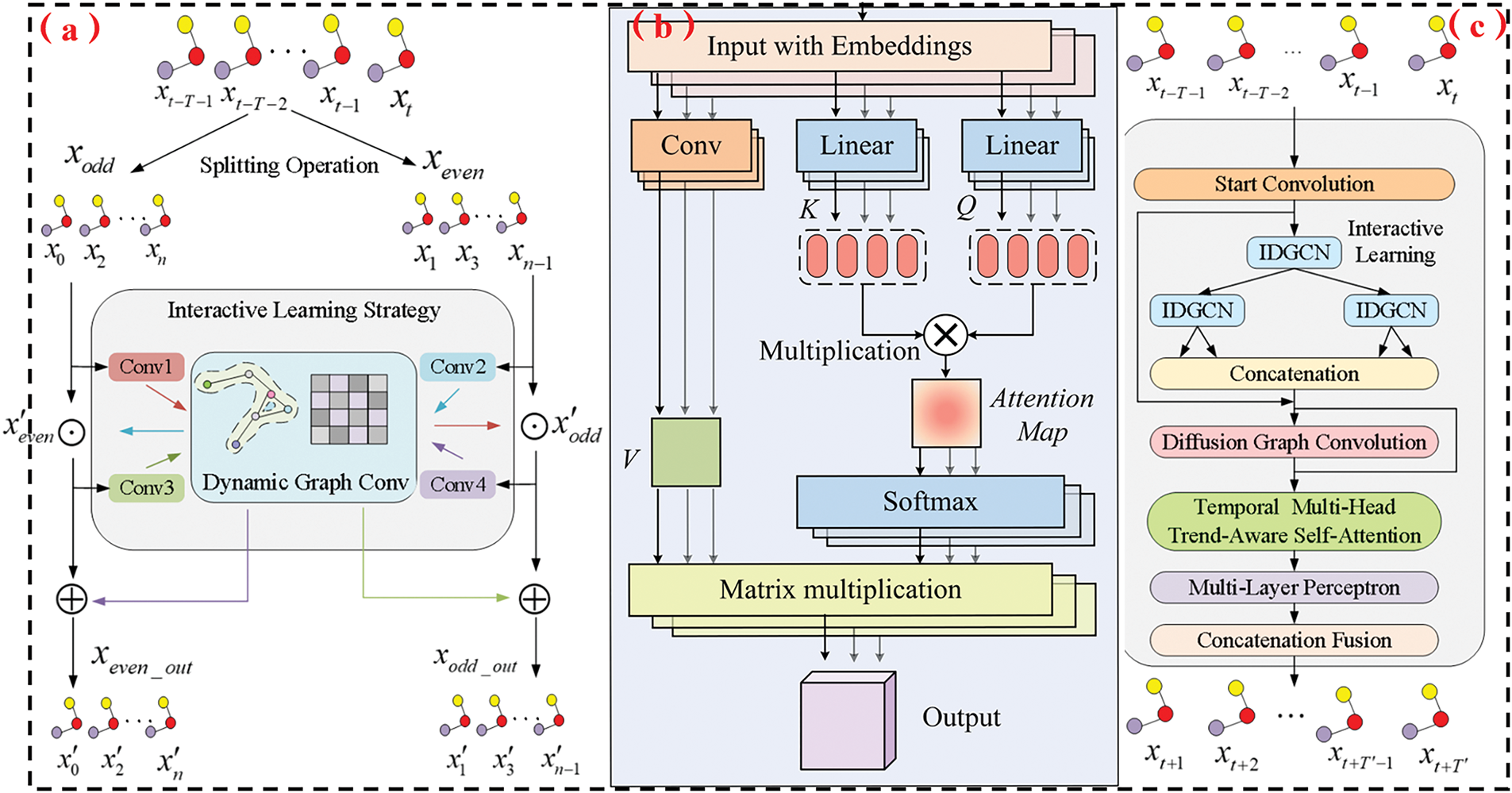
Figure 1: The overall framework of AIDGCN (a) Structure of IDGCN (b) Structure of DGCN (c) AIDGCN Architecture

Firstly, the Start Convolution layer transforms raw data into high-dimensional spatial features, extracting deeper dependencies. Next, the IDGCN is applied on top of the DGCN using an interactive learning strategy. IDGCN recursively generates two equal-sized subsequences through interleaved sampling, which are then interactively learned and share their respective features. This interactive learning structure embeds the DGCN to capture dynamic spatial features while considering temporal dependencies. After extracting spatiotemporal features with IDGCN, the subsequences are organized in time-indexed order using the serial fusion module. Diffusion Graph Convolution processes these subsequences to extract traffic flow’s global spatiotemporal dynamics. The resulting features then pass through Temporal Multi-Head Trend-Aware Self-Attention and an MLP for sequence prediction.

3.2.1 Interactive Learning

To enable interactive learning, this paper employs a combination of CNN and GCN. GCN is particularly suitable for processing non-Euclidean data, allowing for more effective learning of spatiotemporal dependencies in traffic flow. Compared to CNN and TCN-based methods, GCN is better equipped to model spatiotemporal dynamics. Given traffic flow’s periodic, trending nature, the interleaved subsequence preserves most original sequence information. Therefore, we adopt interleaved sampling in this study to perform multi-resolution analysis and expand the sensory field.

The Interactive Learning Framework incorporates three IDGCNs, where the IDGCN module serves as the central element, as depicted in Fig. 1c [34]. This module enables two subsequences to interactively acquire dynamic spatiotemporal features. Prior to feature extraction, convolutional preprocessing expands each subsequence’s receptive field. Shared DGCN parameters between subsequences further improve complementary pattern learning.

This paper defines the initial input of IDGCN as X∈RC×N×T, with 1D convolution operations denoted as Conv1, Conv2, Conv3, and Conv4. Through interleaving sampling, X splits into two subsequences, Xodd∈RC×N×T/2 and Xeven∈RC×N×T/2, which are then outputted as Xodd′∈RC×N×T/2 and Xeven′∈RC×N×T/2 after the first interactive learning phase. Subsequent iterations yield the final outputs Xodd_out∈RC×N×T/2 and Xeven_out∈RC×N×T/2. The detailed steps of interactive dynamic graph convolution are outlined below:

Xeven,Xodd=Split(X)(2)

Xodd′=tanh(DGCN(Conv1(Xeven)))⊙Xodd(3)

Xeven′=tanh(DGCN(Conv2(Xodd)))⊙Xeven(4)

Xodd_out=Xodd′+tanh(DGCN(Conv3(Xeven′)))(5)

Xeven_out=Xeven′+tanh(DGCN(Conv4(Xodd′)))(6)

where ⊙ represents the Hadamard product, tanh is the activation function, and DGCN refers to the dynamic graph convolution operation in IDGCN.

3.2.2 Dynamic Graph Convolution Network

The proposed DGCN architecture integrates two key components: a diffusion graph convolution network and a graph generation module [35]. The DGCN employs diffusion graph convolution combined with dynamic graph generation to effectively capture deep spatial dynamics, thereby enhancing the ability of AIDGCN to capture spatial variations. The DGCN processes both H∈RC×N×T and A∈RN×N through its Diffusion Graph Convolutional Network. This is followed by the Graph Generator and MLP layer, which generate a discrete matrix containing spatiotemporal information, denoted as A′∈RN×N. A′ is represented as:

A′=SoftMax(MLP(GCN(H,A)))(7)

where GCN combines Diffusion Convolution with Graph Generator operations, and MLP represents the Multilayer Perceptron. The training utilizes Gumbel reparameterization for feasible sampling.

Alearn=GumbelSoftmax(A′)=SoftMax((log⁡(A′)−log⁡(−log⁡(g)))/τ)(8)

where g∼Gumbel(0,1) is a random variable, τ denotes SoftMax temperature and fixed at 0.5, and Alearn represents a dynamic adjacency matrix generated by the Graph Generator to capture node dependencies. Furthermore, Aapt∈RN×N constructs an adaptive adjacency matrix, denoted as follows:

Aapt=SoftMax(Relu(E1E2T))(9)

where E1∈RN×c, E2T∈RN×c denote trainable parameters, and Aapt is a predefined connection matrix A∈RN×N.

The hidden dynamic spatiotemporal correlations in traffic roads are captured by combining Alearn and Aapt using a dynamic fusion module. The generated dynamic connection matrix Adyn∈RN×N is then fed into a Diffusion Graph Convolutional Network. The fusion process is:

Adyn=αAapt+(1−α)Alearn(10)

where α represents the learnable adaptive parameter factor.

The Diffusion Graph Convolution is employed in various components, including the graph generator network, fusion graph convolution, and concatenation fusion modules. In these cases, the input to the Diffusion Graph Convolution is uniformly defined as Xin∈RC×N×T. The Diffusion Graph Convolution in graph generator networks is defined as follows:

GCN(Xin,Aapt)=∑k=0KAaptkXinW(11)

where k denotes the diffusion step size, K represents the maximum diffusion steps, and W corresponds to the parameter matrix.

For the fusion graph convolution module with input adjacency matrix Adyn, the diffusion graph convolution is computed as:

GCN(Xin,Adyn)=∑k=0KAdynkXinW(12)

AIDGCN reassembles dynamic spatiotemporal features from the Interactive Learning Mechanism of the Concatenation module, following a time index order. These features are subsequently processed by the Diffusion Graph Convolution to identify and rectify the entire temporal features. Unlike previous approaches, our method employs both a predefined initial adjacency matrix A∈RN×N and a dynamic connection matrix Adyn∈RN×N generated through adaptive learning. The initial connection matrix A is represented by a directed graph, with Pf=A/rowsum(A) and Pb=AT/rowsum(AT) denoting the progressive and regressive transition matrices, respectively. The diffusion graph convolution operation within the concatenation fusion module is formally expressed as:

GCN(Xin,A,Adyn)=∑k=0K(AfkXinW1+AbkXinW2+AdynkXinW3)(13)

The DGCN module captures latent spatial dependencies between traffic network nodes to extract high-order structural features, while simultaneously modeling dynamic data correlations through traffic flow simulations. By incorporating DGCN into an interactive learning paradigm, the framework leverages these adaptive spatial representations to improve temporal dependency learning across traffic sequences during training.

3.2.3 Temporal Multi-Head Trend-Aware Self-Attention

Self-attention operates as an attention mechanism utilizing the same sequence to generate queries, keys, and values. In practice, the widely used multi-head self-attention mechanism enables simultaneous attention to information from multiple subspaces (Fig. 1b). The multi-head attention mechanism performs these key operations:

Attention(Q,K,V)=softmax(QKTdmodel)V(14)

where Q, K, and V denote the query, key, and value, respectively.

In multi-head self-attention, the query, keys, and values are initially projected into separate subspaces. The attention functions are then executed in parallel. The resulting outputs are concatenated and further projected to obtain the final output, represented as follows:

SelfAttention(Q,K,V)=⊕(head1,…,headh)WO(15)

headj=Attention(QWjQ,KWjK,VWjV)(16)

The variable h denotes the quantity of attention heads, WjQ, WjK, and WjV are the projection matrices used on Q, K, and V, respectively. As the terminal projection matrix, WO enables multi-head self-attention to flexibly model intricate traffic data relationships, resulting in precise long-term predictions.

Originally developed for discrete markers, the conventional multi-head self-attention mechanism fails to effectively represent local trend patterns in continuous datasets. Direct application to traffic signal sequence transformation could lead to compatibility problems. To overcome this limitation and incorporate local contextual patterns in numerical forecasting, we introduce Temporal Trend-Aware Multi-Head Self-Attention, a novel Convolutional Self-Attention variant. By incorporating context-aware convolutional layers, the model learns latent local traffic patterns. The Temporal Trend-Aware Multi-Head Attention is formally defined as:

Trendheadj=Attention(Q∗ΦjQ,K∗ΦjK,VWjV)(17)

where ∗ represents the convolution operation, while ΦjQ and ΦjK represent the parameters of the convolution kernel.

In the l-th layer, applying the Temporal Trend-Aware Multi-Head Self-Attention Mechanism to the input χ(l−1) yields an intermediate sequence representation denoted as Z (l−1)=(zt−Th+1(l−1),zt−Th+2(l−1),…,zt(l−1))∈RN ∗ dmodel ∗ Th across all nodes.

3.2.4 Other Components

As a widely-used loss function, Huber Loss [36] integrates the linear components from both Mean Square Error (MSE) and Absolute Error. When predictions approximate the actual values, it demonstrates characteristics similar to Squared Loss, while exhibiting Absolute Loss behavior for significant deviations. Such characteristics significantly reduce outlier influence while maintaining training stability. Therefore, this study employs Huber Loss for optimization.

ξ=1N×Q∑i=1Q∑j=1NR(x^i,j,xi,j)R(x^,x)={12(x^−x)2,|x^−x|≤δδ|x^−x|−12δ2,|x^−x|>δ(18)

where δ serves as the hyperparameter that balances the Squared Error, x^ and x denote the predicted and true values, respectively.

4  Experiment

4.1 Datasets

Our evaluation employs the widely-used METR-LA and PEMS-BAY transportation datasets to measure the AIDGCN predictive capabilities [37–40]. Additional details regarding the experimental datasets can be found in Table 1.

Prior to model input, data underwent min-max normalization (0–1 scaling). Applied normalization equation:

Z inorm=zi−μϑ(19)

where zi denotes the i-th raw data point, with μ and ϑ indicating the dataset’s mean standard deviation, while Z inorm signifies the normalized value.

4.2 Parameter Settings

All models were developed in PyTorch using PyCharm. Using 60 min of past observations (P = 12) to forecast subsequent 60 min (Q = 12), we partitioned the data into 60% training, 20% validation, and 20% test based on actual needs. Traffic flow prediction is performed for 15, 30, and 60 min. For comprehensive performance evaluation, this study employs multiple metrics to quantify the discrepancy between predicted and actual traffic flow speeds:

MAE=1F∑i=1F|∂^i−∂i|(20)

MAPE=1F∑i=1F|∂^i−∂i∂^i|×100%(21)

RMSE=1F∑i=1F(∂^i−∂i)2(22)

where F represents the sample size, with ∂^i and ∂i representing the i-th sample’s ground truth and prediction. The AIDGCN model demonstrates superior forecasting capability when MAE, RMSE, and MAPE values are minimized.

4.3 Baselines

The AIDGCN model is evaluated against 15 baseline models: basic methods like HA [10], VAR [11], SVR [41], and ARIMA [10]; neural networks FNN [42] and FC-LSTM [43]; and advanced spatiotemporal graph networks including DCRNN [40], STGCN [29], ASTGCN [32], STSGCN [44], T-GCN [28], Graph WaveNet [45], MRA-BGCN [30], DGRCN [46], and D2STGNN [47], which capture dependencies using techniques like diffusion convolution, Chebyshev polynomials, attention mechanisms, synchronous modeling, GCN-GRU fusion, dilated convolutions, dual graphs, adaptive adjacency, and decoupled spatiotemporal modeling.

4.4 Experimental Results

4.4.1 Performance Comparison

AIDGCN was compared with 15 baseline models for 15, 30, and 60-min traffic flow forecasting. In most scenarios, AIDGCN outperformed all baseline methods across all datasets.

Table 2 demonstrates the proposed model’s superior forecasting accuracy compared to baselines on METR-LA. For instance, in 15- and 60-min forecasting, AIDGCN outperforms MRA-BGCN by 0.75% and 0.39% in terms of MAE and by 1.32% and 0.14% in terms of RMSE, respectively. Specifically, in the 60-min forecast, AIDGCN reduced MAE by 8.3% compared to DGRCN and reduced RMSE by 6.1% compared to D2STGNN. Predictions for other time intervals also exhibited notable improvements compared to the best baseline results.

In the case of PEMS-BAY, AIDGCN achieves the best forecasting performance. Compared to MRA-BGCN, it achieves 6.28% lower MAE, 4.93% lower RMSE and 7.17% lower MAPE for 60-min long-term forecasting. Our approach achieves cutting-edge results compared to existing methods.

Table 3 evaluates computational efficiency of spatiotemporal models on METR-LA/PEMS-BAY datasets. Among models with advanced capabilities, AIDGCN outperforms MRA-BGCN in both size and speed. While Graph WaveNet is faster than similarly-sized DCRNN, AIDGCN’s inference approaches DCRNN’s despite greater complexity. AIDGCN thus offers a superior accuracy-efficiency trade-off for demanding tasks, delivering high representational power with manageable latency compared to peers like MRA-BGCN.

4.4.2 Ablation Experiment

To evaluate the performance contributions of its modules, seven variants of the AIDGCN model were developed and compared in Fig. 2. These variants systematically remove or modify key components: w/o GCN eliminates the diffusion GCN; w/o DGCN replaces the DGCN with a standard diffusion GCN using the predefined adjacency matrix; w/o Conv removes the 1D convolution from the interactive learning framework; w/o Interaction substitutes the interactive learning component with a sequentially connected temporal convolutional network (TCN); w/o Apt Adj removes the adaptive adjacency matrix from the DGCN module; w/o Learned Adj eliminates the graph generator while retaining the adaptive matrix and replaces the fusion GCN with diffusion GCN; and w/o TMHTAAtt removes the Temporal Multi-Head Trend-Aware Self-Attention component.

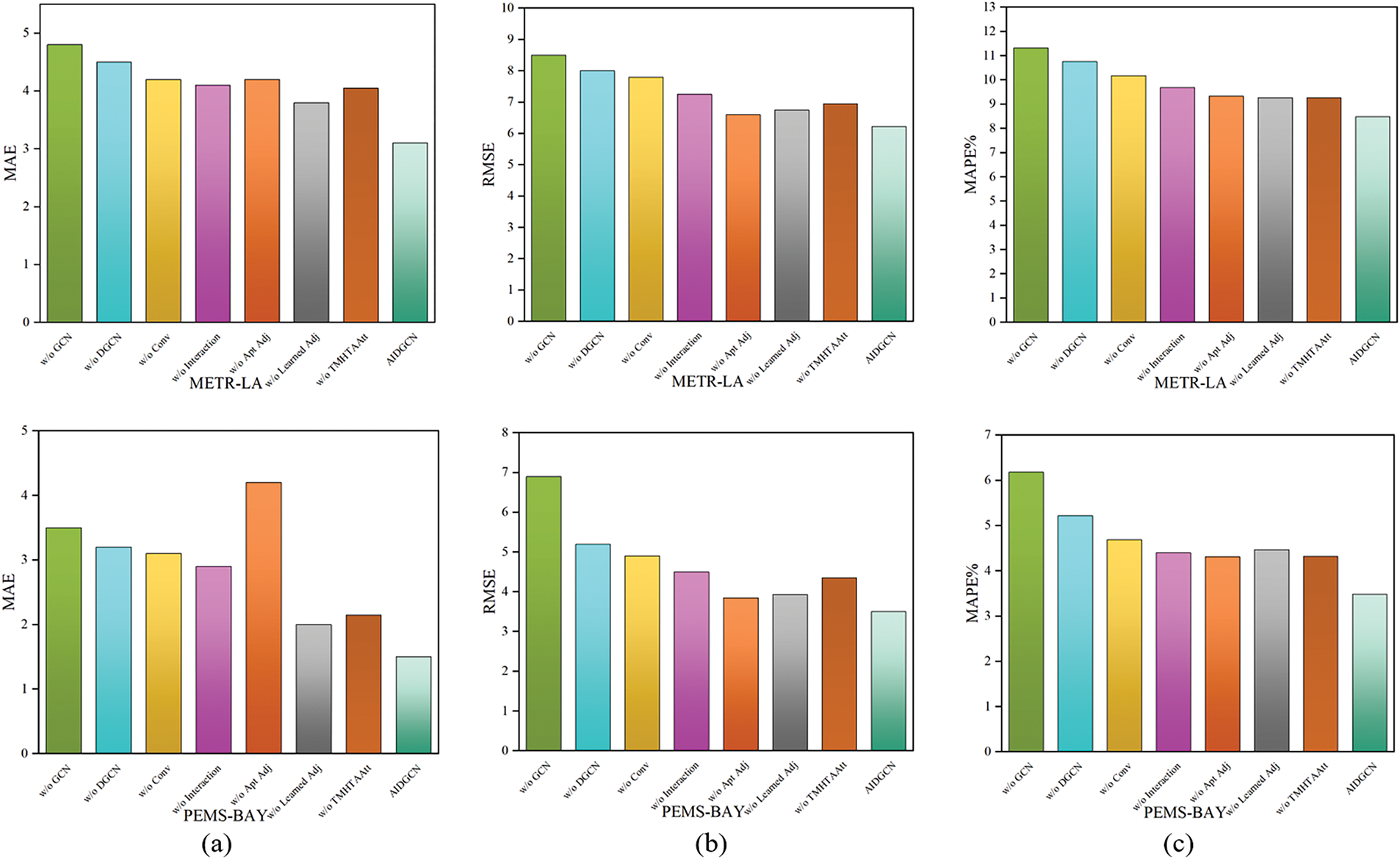
Figure 2: Metrics comparison on the two datasets. (a) MAE; (b) RMSE; (c) MAPE

Ablation studies reveal the dynamic graph structure learning mechanism as AIDGCN’s most critical component, particularly for spatial adaptation, where removing the adaptive adjacency matrix caused a 180% MAE surge in PEMS-BAY. The spatiotemporal interaction module substantially impacts performance (93.3% MAE increase when removed in PEMS-BAY), while the 1D convolution is vital for temporal features (19.9% MAPE rise in METR-LA). Temporal attention shows dataset-specific efficacy but universal value in pattern capture (24.1% MAPE improvement in PEMS-BAY). Cross-dataset analysis highlights PEMS-BAY’s 5× greater sensitivity to graph structures vs. METR-LA’s emphasis on temporal modeling. By impact, adaptive adjacency and interaction structures rank highest, accounting for over 50% of gains, with optimization priorities favoring adaptive graph learning and scenario-specific customization of temporal components.

4.4.3 Visual Analysis

Fig. 3 demonstrates AIDGCN’s superior forecasting performance against baseline models (FNN, FC-LSTM, Graph WaveNet, STGCN) across all prediction steps on PEMS-BAY.

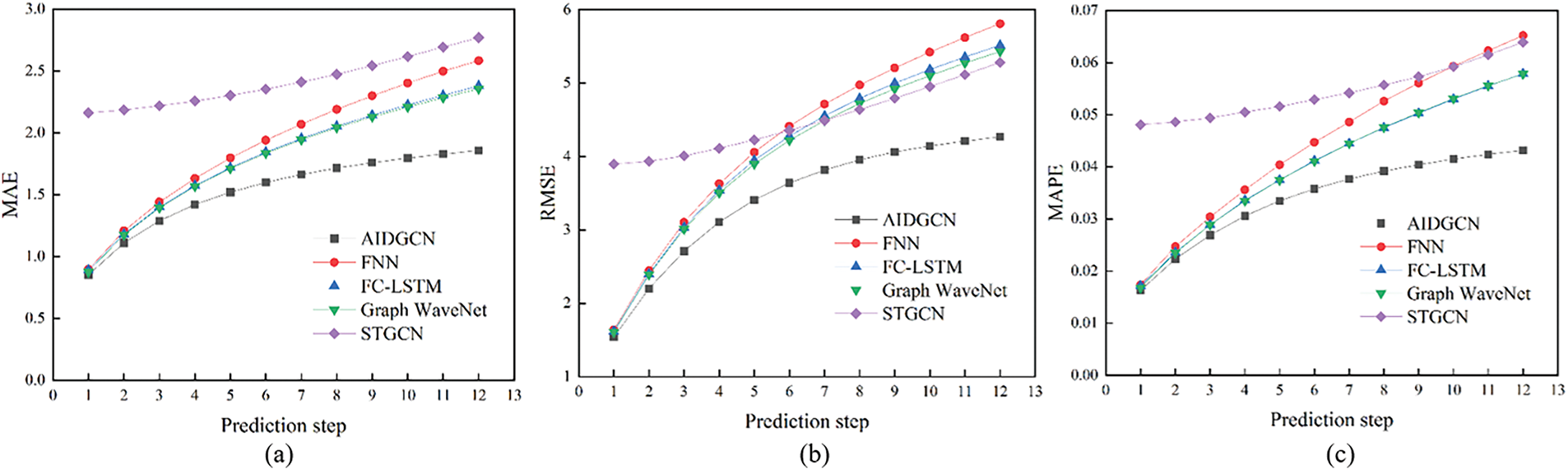
Figure 3: Metrics of different models on PEMS-BAY dataset. (a) MAE; (b) RMSE; (c) MAPE

The significantly slower growth rate of MAE, RMSE, and MAPE for AIDGCN stems directly from its core innovations. The adaptive graph convolution dynamically captures evolving spatial dependencies, preventing error propagation from outdated connections. Simultaneously, the temporal attention mechanism focuses on crucial historical states, effectively mitigating error accumulation over long horizons—a key limitation of baseline models. This synergy results in the observed superior stability beyond 15 min.

The widening performance gap for longer steps underscores AIDGCN’s strength in modeling non-linear, time-evolving traffic patterns. Unlike baselines with static graphs, its adaptive module continuously refines spatial relationships based on real-time data, enabling more accurate capture of complex dynamics like congestion propagation. AIDGCN’s robust long-term accuracy is vital for proactive ITS applications, where reliable forecasts >15 min are essential for effective decision-making.

5  Conclusion

This paper introduced AIDGCN, a novel deep learning model designed to overcome key limitations in traffic forecasting, including static spatial modeling, insufficient capture of complex spatiotemporal dependencies, and degraded long-term prediction accuracy. AIDGCN demonstrably achieves state-of-the-art performance, significantly outperforming existing baselines.

(1) AIDGCN combines a dynamic graph structure and a Temporal Multi-Head Trend-Aware Self-Attention mechanism for learning evolving traffic patterns comprehensively. The dynamic graph structure simulates associations among nodes, uncovering hidden spatial correlations. The interactive learning framework of IDGCN incorporates a DGCN module to simultaneously model periodic patterns, temporal trends, and spatiotemporal relationships.

(2) The Temporal Multi-Head Trend-Aware Self-Attention mechanism leverages dynamic temporal features to improve forecasting accuracy, addressing the insensitivity of traditional attention mechanisms to local trends in continuous data.

(3) On the challenge ng PEMS-BAY dataset for 60-min predictions, AIDGCN reduces MAE, RMSE, and MAPE by 6.28%, 4.93%, and 7.17% respectively compared to the best-performing baseline (MRA-BGCN). Ablation studies further confirm the indispensable contribution of each proposed module to this performance gain. The model’s robust performance across varying prediction horizons highlights its effectiveness for both short and long-term forecasting tasks.

Future research should focus on:

1. Integration of External Factors: Investigating specific mechanisms to incorporate fine-grained weather, events, and holidays.

2. Scalability and Efficiency Optimization: Exploring techniques like model compression and distributed computing for large-scale, real-time deployment.

3. Enhanced Dynamic Graph Learning: Developing more sophisticated and interpretable methods for graph construction.

4. Generalization to Diverse Scenarios: Evaluating and enhancing robustness across varied networks, data conditions, and disruptive events using adaptation techniques.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Zitong Zhao; methodology, Zixuan Zhang; software, Zhenxing Niu; validation, Zitong Zhao; formal analysis, Zixuan Zhang; investigation, Zhenxing Niu; resources, Zitong Zhao; data curation, Zitong Zhao; writing—original draft preparation, Zhenxing Niu; writing—review and editing, Zixuan Zhang; visualization, Zitong Zhao; supervision, Zhenxing Niu; project administration, Zitong Zhao; funding acquisition, Zhenxing Niu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the Corresponding Author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Zhang K, Chu Z, Xing J, Zhang H, Cheng Q. Urban traffic flow congestion prediction based on a data-driven model. Mathematics. 2023;11(19):4075. doi:10.3390/math11194075. [Google Scholar] [CrossRef]

2. Kohan M, Ale JM. Discovering traffic congestion through traffic flow patterns generated by moving object trajectories. Comput Environ Urban Syst. 2020;80(6):101426. doi:10.1016/j.compenvurbsys.2019.101426. [Google Scholar] [CrossRef]

3. Zhang J, Wang FY, Wang K, Lin WH, Xu X, Chen C. Data-driven intelligent transportation systems: a survey. IEEE Trans Intell Transp Syst. 2011;12(4):1624–39. doi:10.1109/TITS.2011.2158001. [Google Scholar] [CrossRef]

4. Zhang X, Liu J, Zhang X, Lu Y. Self-supervised graph feature enhancement and scale attention for mechanical signal node-level representation and diagnosis. Adv Eng Inform. 2025;65:103197. doi:10.1016/j.aei.2025.103197. [Google Scholar] [CrossRef]

5. Zhang X, Liu J, Zhang X, Lu Y. Multiscale channel attention-driven graph dynamic fusion learning method for robust fault diagnosis. IEEE Trans Ind Inform. 2024;20(9):11002–13. doi:10.1109/TII.2024.3397401. [Google Scholar] [CrossRef]

6. Long W, Xiao Z, Wang D, Jiang H, Chen J, Li Y, et al. Unified spatial-temporal neighbor attention network for dynamic traffic prediction. IEEE Trans Veh Technol. 2023;72(2):1515–29. doi:10.1109/TVT.2022.3209242. [Google Scholar] [CrossRef]

7. Wang T, Chen J, Lu J, Liu K, Zhu A, Snoussi H, et al. Synchronous spatiotemporal graph transformer: a new framework for traffic data prediction. IEEE Trans Neural Netw Learn Syst. 2023;34(12):10589–99. doi:10.1109/TNNLS.2022.3169488. [Google Scholar] [PubMed] [CrossRef]

8. Zhang X, Zhang X, Liu J, Wu B, Hu Y. Graph features dynamic fusion learning driven by multi-head attention for large rotating machinery fault diagnosis with multi-sensor data. Eng Appl Artif Intell. 2023;125(6):106601. doi:10.1016/j.engappai.2023.106601. [Google Scholar] [CrossRef]

9. Samaan SS, Korial AE, Sarra RR, Humaidi AJ. Multilingual web traffic forecasting for network management using artificial intelligence techniques. Results Eng. 2025;26(1):105262. doi:10.1016/j.rineng.2025.105262. [Google Scholar] [CrossRef]

10. Williams BM, Hoel LA. Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: theoretical basis and empirical results. J Transp Eng. 2003;129(6):664–72. doi:10.1061/(asce)0733-947x(2003)129:6(664). [Google Scholar] [CrossRef]

11. Wang L, Ding S. Vector autoregression and envelope model. Stat. 2018;7(1):e203. doi:10.1002/sta4.203. [Google Scholar] [CrossRef]

12. Hamed MM, Al-Masaeid HR, Said ZMB. Short-term prediction of traffic volume in urban arterials. J Transp Eng. 1995;121(3):249–54. doi:10.1061/(asce)0733-947x(1995)121:3(249). [Google Scholar] [CrossRef]

13. Mathew A, Ali Rawther F. Hadoop based short—term traffic flow prediction on D2 its using correlation model and KNN HSsine. In: 2017 IEEE International Conference on Power, Control, Signals and Instrumentation Engineering (ICPCSI); 2017 Sep 21–22; Chennai, India. Piscataway, NJ, USA: IEEE; 2017. p. 1123–9. doi:10.1109/ICPCSI.2017.8391885. [Google Scholar] [CrossRef]

14. Wu CH, Wei CC, Su DC, Chang MH, Ho JM. Travel time prediction with support vector regression. In: Proceedings of the 2003 IEEE International Conference on Intelligent Transportation Systems; 2003 Oct 12–15; Shanghai, China. Piscataway, NJ, USA: IEEE; 2003. p. 1438–42. doi:10.1109/ITSC.2003.1252721. [Google Scholar] [CrossRef]

15. Huang W, Song G, Hong H, Xie K. Deep architecture for traffic flow prediction: deep belief networks with multitask learning. IEEE Trans Intell Transp Syst. 2014;15(5):2191–201. doi:10.1109/TITS.2014.2311123. [Google Scholar] [CrossRef]

16. Abdelhafid Z, Harrou F, Sun Y. An efficient statistical-based approach for road traffic congestion monitoring. In: 2017 5th International Conference on Electrical Engineering—Boumerdes (ICEE-B); 2017 Oct 29–31; Boumerdes, Algeria. Piscataway, NJ, USA: IEEE; 2017. p. 1–5. doi:10.1109/ICEE-B.2017.8192228. [Google Scholar] [CrossRef]

17. Yao R, Zhang W, Zhang L. Hybrid methods for short-term traffic flow prediction based on ARIMA-GARCH model and wavelet neural network. J Transp Eng Part A Syst. 2020;146(8):04020086. doi:10.1061/jtepbs.0000388. [Google Scholar] [CrossRef]

18. Song X, Guo Y, Li N, Zhang L. Online traffic flow prediction for edge computing-enhanced autonomous and connected vehicles. IEEE Trans Veh Technol. 2021;70(3):2101–11. doi:10.1109/TVT.2021.3057109. [Google Scholar] [CrossRef]

19. Hu W, Yan L, Liu K, Wang H. A short-term traffic flow forecasting method based on the hybrid PSO-SVR. Neural Process Lett. 2016;43(1):155–72. doi:10.1007/s11063-015-9409-6. [Google Scholar] [CrossRef]

20. Yang H, Du L, Zhang G, Ma T. A traffic flow dependency and dynamics based deep learning aided approach for network-wide traffic speed propagation prediction. Transp Res Part B Methodol. 2023;167(2):99–117. doi:10.1016/j.trb.2022.11.009. [Google Scholar] [CrossRef]

21. Zhang Z, Yang H, Yang X. A transfer learning-based LSTM for traffic flow prediction with missing data. J Transp Eng Part A Syst. 2023;149(10):04023095. doi:10.1061/jtepbs.teeng-7638. [Google Scholar] [CrossRef]

22. Yi X, Zhou H, Zhong S. Real-time adaptive traffic flow prediction based on a GE-GRU-KNN model. Promet-Traffic Transport. 2025;37(3):754–72. doi:10.7307/ptt.v37i3.775. [Google Scholar] [CrossRef]

23. Yao H, Wu F, Ke J, Tang X, Jia Y, Lu S, et al. Deep multi-view spatial-temporal network for taxi demand prediction. Proc AAAI Conf Artif Intell. 2018;32(1):2388–95. doi:10.1609/aaai.v32i1.11836. [Google Scholar] [CrossRef]

24. Lv Z, Xu J, Zheng K, Yin H, Zhao P, Zhou X. LC-RNN: a deep learning model for traffic speed prediction. In: Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence; 2018 Jul 13–19; Stockholm, Sweden. p. 3470–6. doi:10.24963/ijcai.2018/482. [Google Scholar] [CrossRef]

25. Veličković P, Cucurull G, Casanova A, Romero A, Lio P, Bengio Y. Graph attention networks. arXiv:1710.10903. 2017. doi:10.48550/arXiv.1710.10903. [Google Scholar] [CrossRef]

26. Bruna J, Zaremba W, Szlam A, LeCun Y. Spectral networks and locally connected networks on graphs. arXiv:1312.6203. 2013. doi:10.48550/arxiv.1312.6203. [Google Scholar] [CrossRef]

27. Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering. In: Lee DD, Sugiyama M, Luxburg UV, Guyon I, Garnett R, editors. Advances in neural information processing systems 29 (NIPS 2016). Vol. 29. La Jolla, CA, USA: Neural Information Processing Systems (NIPS); 2016. [Google Scholar]

28. Zhao L, Song Y, Zhang C, Liu Y, Wang P, Lin T, et al. T-GCN: a temporal graph convolutional network for traffic prediction. IEEE Trans Intell Transp Syst. 2020;21(9):3848–58. doi:10.1109/TITS.2019.2935152. [Google Scholar] [CrossRef]

29. Yu B, Yin H, Zhu Z. Spatio-temporal graph convolutional networks: a deep learning framework for traffic forecasting. In: Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence; 2018 Jul 13–19; Stockholm, Sweden. San Jose, CA, USA: International Joint Conferences on Artificial Intelligence Organization; 2018. p. 3634–40. doi:10.24963/ijcai.2018/505. [Google Scholar] [CrossRef]

30. Chen W, Chen L, Xie Y, Cao W, Gao Y, Feng X. Multi-range attentive bicomponent graph convolutional network for traffic forecasting. In: Proceedings of the AAAI Conference on Artificial Intelligence; 2020 Feb 7–12; New York, NY, USA. p. 3529–36. [Google Scholar]

31. Liang Y, Ke S, Zhang J, Yi X, Zheng Y. GeoMAN: multi-level attention networks for geo-sensory time series prediction. In: Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence; 2018 Jul 13–19; Stockholm, Sweden. San Jose, CA, USA: International Joint Conferences on Artificial Intelligence Organization; 2018. p. 3428–34. doi:10.24963/ijcai.2018/476. [Google Scholar] [CrossRef]

32. Guo S, Lin Y, Feng N, Song C, Wan H. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. Proc AAAI Conf Artif Intell. 2019;33(1):922–9. doi:10.1609/aaai.v33i01.3301922. [Google Scholar] [CrossRef]

33. Yao Y, Chen L, Wang X, Wu X. Traffic flow forecasting based on augmented multi-component recurrent graph attention network. Transp Lett. 2025;2025:1–9. doi:10.1080/19427867.2025.2450577. [Google Scholar] [CrossRef]

34. Chen L, Chen L, Wang H, Zhang H. Traffic flow prediction based on interactive dynamic spatio-temporal graph convolution with a probabilistic sparse attention mechanism. Transp Res Rec J Transp Res Board. 2024;2678(9):837–53. doi:10.1177/03611981241230545. [Google Scholar] [CrossRef]

35. Zhang H, Zhu S, Zhang X, Gong L. Research on traffic flow forecasting based on interactive dynamic meta-graph learning. Proc Inst Mech Eng Part D J Automob Eng. 2024;33(1):09544070241292392. doi:10.1177/09544070241292392. [Google Scholar] [CrossRef]

36. Xie J, Liu S, Chen J, Jia J. Huber loss based distributed robust learning algorithm for random vector functional-link network. Artif Intell Rev. 2023;56(8):8197–218. doi:10.1007/s10462-022-10362-7. [Google Scholar] [CrossRef]

37. Wang T, Ni S, Qin T, Cao D. TransGAT: a dynamic graph attention residual networks for traffic flow forecasting. Sustain Comput Inform Syst. 2022;36(3):100779. doi:10.1016/j.suscom.2022.100779. [Google Scholar] [CrossRef]

38. Chen H, Wang H, Chen Z. Traffic flow prediction based on dynamic time slot graph convolution. Transp Res Rec J Transp Res Board. 2025;2679(5):785–99. doi:10.1177/03611981241308868. [Google Scholar] [CrossRef]

39. Ounoughi C, Ben Yahia S. Sequence to sequence hybrid Bi-LSTM model for traffic speed prediction. Expert Syst Appl. 2024;236:121325. doi:10.1016/j.eswa.2023.121325. [Google Scholar] [CrossRef]

40. Li Y, Yu R, Shahabi C, Liu Y. Diffusion convolutional recurrent neural network: data-driven traffic forecasting. arXiv:1707.01926. 2017. doi:10.48550/arXiv.1707.01926. [Google Scholar] [CrossRef]

41. Wu Y, Tan H. Short-term traffic flow forecasting with spatial-temporal correlation in a hybrid deep learning framework. arXiv:1612.01022. 2016. doi:10.48550/arXiv.1612.01022. [Google Scholar] [CrossRef]

42. Li HX, Lee ES. Interpolation functions of feedforward neural networks. Comput Math Appl. 2003;46(12):1861–74. doi:10.1016/s0898-1221(03)90242-2. [Google Scholar] [CrossRef]

43. Hu Z, Zhou J, Huang K, Zhang E. A data-driven approach for traffic crash prediction: a case study in Ningbo, China. Int J Intell Transp Syst Res. 2022;20(2):508–18. doi:10.1007/s13177-022-00307-3. [Google Scholar] [CrossRef]

44. Song C, Lin Y, Guo S, Wan H. Spatial-temporal synchronous graph convolutional networks: a new framework for spatial-temporal network data forecasting. In: Proceedings of the AAAI Conference on Artificial Intelligence; 2020 Feb 7–12; New York, NY, USA. [Google Scholar]

45. Wu Z, Pan S, Long G, Jiang J, Zhang C. Graph WaveNet for deep spatial-temporal graph modeling. arXiv:1906.00121. 2019. doi:10.48550/arXiv.1906.00121. [Google Scholar] [CrossRef]

46. Li F, Feng J, Yan H, Jin G, Yang F, Sun F, et al. Dynamic graph convolutional recurrent network for traffic prediction: benchmark and solution. ACM Trans Knowl Discov Data. 2023;17(1):1–21. doi:10.1145/3532611. [Google Scholar] [CrossRef]

47. Shao Z, Zhang Z, Wei W, Wang F, Xu Y, Cao X, et al. Decoupled dynamic spatial-temporal graph neural network for traffic forecasting. Proc VLDB Endow. 2022;15(11):2733–46. doi:10.14778/3551793.3551827. [Google Scholar] [CrossRef]