A Parallelized Grey Wolf Optimizer-Based Fuzzy C-Means for Fast and Accurate MRI Segmentation on GPU

1  Introduction

Image segmentation is a fundamental step in image analysis and computer vision, aiming to partition an image into meaningful regions for further processing. The goal of segmentation is to simplify an image by grouping pixels with similar characteristics, such as intensity, texture, or color, into distinct regions. This process plays a crucial role in various applications, including medical imaging, object detection, and pattern recognition.

Magnetic Resonance Imaging (MRI) is widely used in medical diagnosis, providing high-resolution images of soft tissues. However, analyzing MRI images remains challenging due to factors such as noise, intensity inhomogeneity, and overlapping tissue structures [1].

Clustering-based segmentation techniques are commonly employed to group pixels based on similarity measures. Among these, the Fuzzy C-Means (FCM) algorithm is a globally used approach in MRI segmentation for its ability to handle the inherent uncertainty of medical images [2]. Despite its advantages, FCM has notable limitations, including sensitivity to initial cluster centers, slow convergence, and susceptibility to local optima, which can lead to suboptimal segmentation results [3]. Moreover, the traditional FCM objective is based on minimizing the sum of squared errors (SSE), which measures intra-cluster compactness but remains highly sensitive to MRI artifacts such as noise and intensity inhomogeneity. In this context, fuzzy entropy offers an alternative criterion that explicitly quantifies and reduces uncertainty in memberships. By encouraging more decisive memberships, entropy minimization improves distinguishing tissues with overlapping intensity distributions and ensures clearer anatomical boundaries.

To overcome these challenges, several optimization algorithms have been integrated with FCM to enhance its performance, including Particle Swarm Optimization (PSO) [4], Firefly Optimization Algorithm (FOA) [5], Tuna Swarm Optimization (TSO) [6], Biogeography-Based Optimization (BBO) [7], and Elephant Herding Optimization (EHO) [8]. These metaheuristic algorithms, inspired by natural phenomena, provide powerful global search capabilities and can optimize FCM’s objective function more effectively. By incorporating metaheuristics in FCM, researchers have improved clustering accuracy, reduced noise sensitivity, and enhanced robustness in medical image segmentation.

Among these approaches, Grey Wolf Optimization (GWO), inspired by the hunting behavior of grey wolves [9], has demonstrated strong global search capabilities [10–12], making it particularly suitable for optimizing cluster centers in FCM [13]. By leveraging GWO, the segmentation process becomes more robust, reducing sensitivity to initialization and improving segmentation accuracy. However, the iterative nature of GWO still leads to high computational costs, especially when applied to large-scale MRI.

To address this limitation, we propose an optimized parallelization strategy for GWO-FCM (P-GWO-FCM) using GPU acceleration. The primary objectives of this approach are to enhance the efficiency of FCM and minimize computational time. First, GWO is utilized to select the best initial cluster centers. Then, by exploiting the parallel processing power of GPUs, the computational efficiency of GWO and FCM is significantly improved, enabling faster convergence and real-time segmentation of high-resolution MRI images.

Furthermore, unlike existing hybrid methods that optimize FCM sequentially, our approach parallelizes both GWO and FCM, ensuring efficient workload distribution across GPU cores. The parallelized GWO accelerates the selection of optimal cluster centroids, while the parallelized FCM efficiently updates both the centroids and the membership matrix. By executing these processes concurrently, our method significantly reduces execution time while maintaining high segmentation accuracy. This dual-parallelization strategy makes P-GWO-FCM highly suitable for real-time medical image analysis, particularly for large-scale MRI datasets.

Additionally, the proposed method integrates a Fuzzy Entropy Clustering function within GWO as the fitness function. Unlike traditional objective functions, fuzzy entropy enhances segmentation by effectively handling image uncertainty and preserving structural details. This is particularly beneficial for MRI images, where pixel intensities often exhibit ambiguity. By minimizing fuzzy entropy, the algorithm ensures optimal clustering with well-defined and compact clusters, leading to more accurate segmentation results.

The effectiveness of P-GWO-FCM is evaluated against traditional FCM and the sequential hybrid GWO-FCM method using segmentation quality metrics such as the Jaccard Index, PCI, PEI, and DPI. Experimental results demonstrate that P-GWO-FCM outperforms existing methods in segmentation accuracy while significantly reducing computation time, making it a promising approach for real-time medical image analysis.

The paper is organized as follows: Section 2 reviews related work on parallel approaches used in medical image segmentation. Section 3 describes the proposed methodology. Section 4 presents the experimental results and evaluation metrics. Finally, Section 5 concludes the paper and suggests directions for future research.

2  Related Works

The increasing demand for efficient and accurate MRI segmentation has led to significant advancements in deep learning, clustering, and metaheuristic-based approaches. However, traditional methods often suffer from high computational costs and slow convergence, thereby restricting their applicability in real-time medical imaging. To address these challenges, researchers have explored parallelization techniques to enhance the efficiency of segmentation algorithms. This section reviews existing parallel approaches in deep learning-based segmentation, clustering-based methods, and metaheuristic optimization strategies, highlighting their strengths and limitations.

2.1 Parallel Deep Learning-Based MRI Segmentation

In [14], a hybrid serial and parallel CNN-transformer (SPCT) network was introduced for 3D medical image segmentation. This approach combined convolutional neural networks (CNNs) and transformers. It included a cross-window self-attention transformer (CWST) module for global context learning and a multi-scale local enhancement (MLE) module for feature fusion. Extensive experiments on prostate, atrium, and pancreas MRI/CT datasets demonstrate that SPCT outperforms six state-of-the-art segmentation models in terms of Dice Similarity Coefficient (DSC), Intersection over Union (IoU), and boundary accuracy while maintaining lower computational complexity. The results confirm that SPCT is a promising approach for accurate and efficient 3D medical image segmentation. However, its parallel strategy was limited to enhancing feature learning rather than optimizing clustering or segmentation processes in parallel.

A deep-learning-based MRI reconstruction and segmentation framework was introduced in [15]. This approach utilized a calibrationless parallel image domain deep-learning model to improve image quality while enhancing segmentation robustness against distortions. By integrating deep structured low-rank (Deep-SLR) reconstruction with a segmentation network, the method minimizes aliasing and blurring artifacts, enhancing both segmentation precision and computational efficiency. Experimental results on brain MRI datasets demonstrate superior performance over existing parallel MRI and segmentation methods, particularly in few-shot learning settings.

Another significant deep-learning contribution is BEAP-Net (Bidirectional Efficient Attention Parallel Network) [16] was used to improve 3D medical image segmentation through semi-supervised learning. The model incorporates Supreme Channel Attention (SCA) and Parallel Spatial Attention (PSA) to extract spatial and channel-specific features. Evaluations on LA and Pancreas medical datasets demonstrate that BEAP-Net outperforms eight state-of-the-art methods, achieving higher segmentation accuracy while maintaining computational efficiency. While BEAP-Net achieved state-of-the-art performance on public datasets, its reliance on semi-supervised learning limits its applicability in real-time clinical settings where fully annotated data is available.

Similarly, Multi-Parallel Blocks UNet (MPB-UNet) [17] was introduced for automated brain tumor segmentation. The model enhances the standard UNet design by integrating multiple parallel processing blocks inspired by human visual perception. It integrates Atrous Spatial Pyramid Pooling (ASPP) to capture multi-scale contextual information, improving segmentation accuracy. The proposed architecture was evaluated using the Low-Grade Glioma Segmentation Dataset. The MPB-UNet achieved superior performance with 99.86% accuracy, significantly outperforming existing state-of-the-art methods.

2.2 Parallel Clustering-Based MRI Segmentation

Clustering techniques play a crucial role in image segmentation. Among them K-Means and Fuzzy C-Means (FCM) are widely used due to their ability to segment complex images. However, these methods suffer from high computational costs due to slow convergence and sensitivity to initialization [3]. To accelerate the process, researchers have developed parallelization strategies that significantly reduce execution time while maintaining segmentation accuracy.

Parallel FCM clustering was explored in [18] using GPU acceleration via CUDA for brain tumor segmentation. The method utilized FLAIR MRI images and implemented parallel processing for cluster initialization, membership matrix computation, and spatial function calculation. While the GPU-based approach improved segmentation speed, it did not incorporate any optimization strategy to refine cluster centroids, thus hindering its ability to escape local optima.

A comparative study in [19] examined two parallel implementations of Bias-Corrected FCM (BCFCM) and Spatial FCM (SFCM), focusing on robustness and efficiency in MRI image segmentation. The study evaluates performance improvements in terms of processing speed and segmentation quality. By leveraging GPU architectures, these implementations achieved significant improvements in execution time while maintaining segmentation accuracy. The study highlighted the advantages of parallel processing in optimizing FCM for medical image analysis.

Extending FCM to 3D medical image segmentation introduces additional computational challenges. In [20], a hybrid parallel implementation was proposed to optimize segmentation accuracy while significantly reducing execution time. Experimental validation on real and simulated medical datasets demonstrated up to 5× speedup compared to sequential methods, making it a promising approach for large-scale medical imaging applications.

A novel knowledge-based FCM method, FCM-GENIUS, was introduced in [21] for rapid brain tissue segmentation from MRI scans. The method integrates region of interest (ROI) selection, knowledge-based initialization, and knowledge-based optimization. These enhancements improve centroid selection and reduce computational complexity. Additionally, a CUDA-enabled GPU parallelization further accelerates processing. Experimental results on IBSR datasets show that FCM-GENIUS reduces segmentation time by up to seven times while maintaining accuracy comparable to existing methods.

2.3 Parallel Metaheuristic Optimization for Image Segmentation

To overcome clustering limitations, researchers have turned to metaheuristic optimization techniques such as Genetic Algorithms (GA), Multi-Verse Optimizer (MVO), and Differential Evolution (DE) for improving segmentation accuracy and computational efficiency. By leveraging parallel computing, these approaches accelerate convergence and enhance segmentation quality for high-resolution images.

A parallel compact Differential Evolution (pcDE) algorithm was proposed in [22] for optimization, with applications in image segmentation. The proposed approach enhances the Compact Differential Evolution (cDE) algorithm by dividing the population into multiple groups and implementing two communication strategies: Optimal Elite Strategy (OE) and Mean Elite Strategy (ME). These strategies improve solution stability and convergence speed while maintaining computational efficiency. Experimental results on benchmark test functions demonstrate the superior performance of pcDE over standard cDE. Additionally, its application to image segmentation shows improved accuracy compared to existing methods, highlighting its potential for real-world optimization problems. While effective in improving segmentation accuracy and processing speed, pcDE required significant computational resources for parallel execution.

The paper in [23] presents a parallel genetic-based Fuzzy C-Means (GA-FCM) clustering algorithm for brain MRI segmentation, implemented on multiple embedded GPUs. The proposed method partitions the genetic population into subpopulations, leveraging parallel execution on GPUs to accelerate clustering while maintaining segmentation accuracy. A hybrid approach combining Message Passing Interface (MPI) and CUDA ensures efficient computation across multiple devices. Experimental results demonstrate that the proposed algorithm achieves up to 12× speedup compared to CPU-based FCM implementations, making it a promising solution for large-scale medical image segmentation.

The authors in [24] proposed a Big Data Architecture-based Biomedical Image Classification (BDA-BMIC) system to enhance medical image classification using parallel metaheuristic optimization. The system integrates Genetic Algorithms (GA) and Gradient Approximation (GA) for efficient feature selection and classification, leveraging parallel computing with Apache Spark and Hadoop Distributed File System (HDFS) for large-scale data processing. Additionally, parallelized Support Vector Machines (SVM) and Convolutional Neural Networks (CNN) are employed to accelerate classification. Experimental results demonstrate that the BDA-BMIC system significantly improves accuracy and computational efficiency, making it suitable for real-time biomedical image analysis.

In [25], a hybrid optimization approach is proposed for 2D and 3D medical image segmentation by integrating the Coronavirus Optimization Algorithm (COVIDOA) with Harris Hawks Optimization (HHOA). This hybridization enhances convergence efficiency and balances exploration and exploitation. Otsu’s method and Kapur’s entropy are employed as fitness functions to determine optimal threshold values. The proposed algorithm is evaluated on five IEEE CEC 2019 benchmark functions and tested on medical images from MRI, CT, and X-ray modalities. Comparative analysis against seven metaheuristic algorithms, using metrics such as PSNR, SSIM, and NCC, demonstrates its superior performance. Additionally, the Wilcoxon rank-sum test confirms its statistical significance for medical image segmentation.

2.4 Contributions of Our Approach

While previous research has explored deep learning, clustering, and metaheuristic approaches for MRI segmentation, few studies have addressed the dual-parallelization of both optimization and clustering processes. To overcome this limitation, we propose P-GWO-FCM, a method that introduces two key advancements to enhance segmentation efficiency and accuracy.

First, we implement Parallelized Grey Wolf Optimization (GWO) to optimize cluster centroids. Unlike existing GWO-FCM methods that operate sequentially, our approach executes GWO-based centroid optimization in parallel, leveraging GPU acceleration to achieve faster convergence. This significantly reduces computation time while maintaining the effectiveness of the optimization process.

Second, we introduce Parallelized FCM Membership Update, enabling efficient computation of both cluster centroids and membership matrices in parallel. By distributing these computations across multiple processing units, we further enhance segmentation efficiency, addressing the computational bottlenecks of traditional FCM methods.

To improve segmentation robustness, we integrate fuzzy entropy clustering as a fitness function within the GWO framework. This integration enhances the method’s ability to handle noisy MRI images while preserving high segmentation accuracy.

Compared to prior approaches, P-GWO-FCM achieves superior segmentation performance while significantly reducing computational overhead. Unlike most existing methods, which either accelerate clustering or optimize initialization separately, our approach jointly parallelizes both the optimization and clustering processes. This dual strategy not only reduces computational overhead but also addresses the robustness limitations observed in prior GPU-based FCM implementations that lacked global search. Moreover, unlike deep learning approaches that often require large annotated datasets, our method remains effective on limited data, making it more practical for clinical applications. The combined benefits of dual-parallelization, GPU acceleration, and fuzzy entropy-based optimization make this approach highly suitable for real-time MRI image analysis.

3  Methodology

In this study, we propose a Parallelized Grey Wolf Optimization-based Fuzzy C-Means (P-GWO-FCM) clustering algorithm for MRI segmentation. The approach integrates Grey Wolf Optimization (GWO) to optimize the selection of cluster centers in FCM, thereby reducing sensitivity to initialization and improving segmentation accuracy. To further enhance performance, we employ Fuzzy Entropy Clustering as the fitness function, which better quantifies uncertainty in MRI images, ensuring well-separated and compact clusters while improving noise robustness. However, the iterative nature of GWO and FCM introduces significant computational overhead, particularly for high-resolution medical images. To mitigate this, we leverage GPU-based parallelization, where the GWO update position, the fitness function evaluation and FCM Membership Update are executed in parallel, significantly accelerating convergence.

3.1 Grey Wolf Optimization

The GWO algorithm is a nature-inspired metaheuristic optimization technique that mimics the leadership hierarchy and hunting behavior of grey wolves [9]. GWO models the social structure of a wolf pack, where the most dominant wolves are alpha (α) as a leadership of the pack, then beta (β) wolve, and delta (δ) in the third level, those wolves guide the movement of the remaining wolves omega (ω), allowing the pack to explore and exploit the search space efficiently. The algorithm consists of three key steps: encircling the prey, hunting, and searching for prey (exploration and exploitation). Wolves encircle the prey by adjusting their positions relative to the best solutions, mathematically controlled by coefficient vectors A and C. During hunting, the pack follows the guidance of the top three solutions (α, β, δ), refining their positions using weighted averages. The searching phase dynamically balances exploration and exploitation by adjusting the control parameter a, ensuring global search at the beginning and fine-tuning toward optimal solutions later. Due to its simplicity, adaptability, and strong optimization capability, GWO was used in the present study. Below, the mathematical model of GWO was described.

The encircling step in GWO algorithm is a crucial part of the optimization process. It simulates the behavior of grey wolves as they encircle prey, helping to update the positions of wolves in the search space towards better solutions. Eqs. (1) and (2) represent the mathematical model of encircling step:

X→(t+1)=X→P(t)+A→⋅D→(1)

D→=|C→⋅X→P(t)−X→(t)|(2)

where t indicates the current iteration, A and C are coefficient vectors, XP is the position vector of the prey, and X indicates the position vector of a grey wolf. The vectors A and C are calculated as follows:

A→=2a→⋅r1→−a→(3)

C→=2⋅r2→(4)

where r1 and r2 are random vectors in range [0, 1], a is vector which linearly decreased from 2 to 0 over the course of iterations.

The hunting process is usually guided by alpha, beta, and delta agents. These three wolves are considered as the best solution in the pack and they have better knowledge about the potential location of the prey. Mathematically, the hunting process is formulated as follows [9]:

Dα→=|C1→⋅X→α−X→|,Dβ→=|C2→⋅X→β−X→|,Dδ→=|C3→⋅X→δ−X→|(5)

X1→=Xα→−A1⋅(Dα→),X2→=Xβ→−A2⋅(Dβ→),X3→=Xδ→−A3⋅(Dδ→)(6)

X→(t+1)=X1→+X2→+X3→3(7)

The GWO approach begins with a random population of wolves and the searching process directed by α, β, and δ wolves. When A > 1 they diverge from each other to find the best prey. If A < 1 they diverge from each other and forces the wolves to attack towards the prey.

3.2 Fuzzy Entropy Clustering

Fuzzy Entropy Clustering (FEC) is a clustering method that integrates entropy measures into fuzzy clustering algorithms to improve their ability to handle uncertainty and overlapping clusters [26,27]. FEC extends traditional fuzzy clustering by incorporating entropy to quantify the uncertainty in cluster membership. The entropy function evaluates the fuzziness of the membership matrix, determining how well a pixel belongs to a specific cluster. The objective is to minimize fuzzy entropy during clustering to achieve clearer separation between different segments. The process involves iteratively calculating membership degrees based on distances to cluster centers, minimizing entropy to reduce uncertainty, and updating cluster centers until convergence. By integrating entropy minimization, the method ensures well-defined clusters while handling uncertainty in data. Eq. (8) represents Fuzzy entropy formula.

E=−∑i=1N∑j=1Cuijlog⁡(uij)(8)

where N represents the number of pixels, C the number of clusters and uij is the membership value of pixel i to cluster j.

Unlike the traditional SSE-based FCM objective, which is sensitive to noise and intensity in homogeneity, the fuzzy entropy criterion reduces membership uncertainty. This is crucial in MRI segmentation, where tissue intensities overlap. By encouraging decisive memberships (uij close to 0 or 1), entropy minimization yields clearer tissue boundaries and better separation of gray matter, white matter, cerebrospinal fluid, and tumor regions, enhancing the robustness and accuracy of the hybrid GWO-FCM model.

3.3 FCM-GWO Optimizer Algorithm

We propose a hybrid approach that integrates GWO with fuzzy entropy (FE) as an objective function to enhance the FCM algorithm for image segmentation. By leveraging GWO’s global optimization capabilities, the method refines cluster centers while fuzzy entropy improves the handling of uncertainty in segmentation. Within this framework, GWO iteratively updates solutions through encircling, hunting, and attacking mechanisms, ensuring a balanced exploration-exploitation process. These adaptive adjustments enhance the precision of FCM, leading to more accurate and robust segmentation results. Fig. 1 illustrates the proposed hybrid approach.

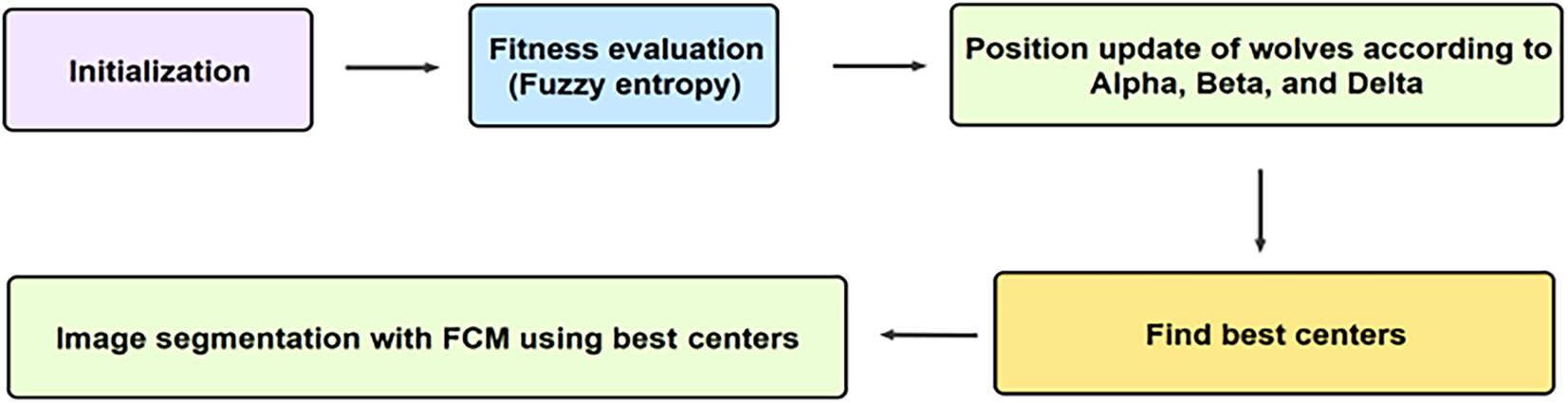
Figure 1: Diagram of hybrid GWO-FCM-FE

The process begins with wolf initialization, where a population of wolves is randomly generated, each representing a potential solution (a set of centroids for the clusters). Next, the fitness computation step evaluates each wolf by applying fuzzy entropy clustering to the image. The fuzzy entropy function is calculated for the cluster memberships, with the objective of minimizing entropy. Subsequently, position updating is performed using the GWO algorithm, where the wolves’ positions are adjusted based on the alpha, beta, and delta wolves, following GWO update rules. This step aims to refine the centroids by exploring the solution space and converging toward optimal cluster centers. The fitness computation and position updating steps are iteratively repeated to further refine the cluster centers and minimize fuzzy entropy, thereby enhancing segmentation accuracy. Finally, in the image segmentation phase, the optimized centroids obtained through GWO are used to assign pixels to their respective clusters based on their membership degrees. The algorithm terminates when either the maximum number of iterations is reached or when successive iterations show negligible improvement in fitness. The final optimized cluster centers are then applied within the FCM algorithm to generate a segmented image, distinguishing different regions based on intensity. The detailed pseudocode of proposed approach is represented in Algorithm 1.

3.4 Parallel Methodology on GPU

In the proposed approach, Parallel Grey Wolf Optimization (PGWO) and Parallel Fuzzy C-Means (PFCM) operate sequentially to efficiently optimize cluster centroids for MRI image segmentation (Fig. 2). In the first stage, PGWO is employed to search for optimal cluster centroids using Fuzzy Entropy as the fitness function. The wolf positions, fitness evaluations, and update mechanisms are parallelized using GPU device, enabling simultaneous processing of multiple candidate solutions. Once the best centroids are determined, PFCM is executed with GPU acceleration, where key computations, including membership matrix updates and cluster center calculations, are efficiently parallelized. Each pixel’s membership values are computed concurrently, while cluster center updates leverage parallel reduction techniques, significantly reducing computational complexity. This parallel strategy enhances the convergence speed of FCM, ensuring that the segmentation process remains both accurate and efficient. The execution of PGWO followed by PFCM ensures that GWO’s global search capability effectively initializes the clustering process, while the local refinement of FCM enhances segmentation accuracy. This hybrid strategy achieves a balance between exploration and exploitation, leading to more robust and computationally efficient segmentation compared to standalone clustering methods.

Figure 2: The process of proposed parallel strategy

The Fig. 3 represents a diagram of the proposed approach including PGWO and PFCM, Firstly, the PGWO with FE for image segmentation follows a structured sequence of steps to optimize cluster centroids efficiently. Then, the PFCM algorithm is applied for refined segmentation process.

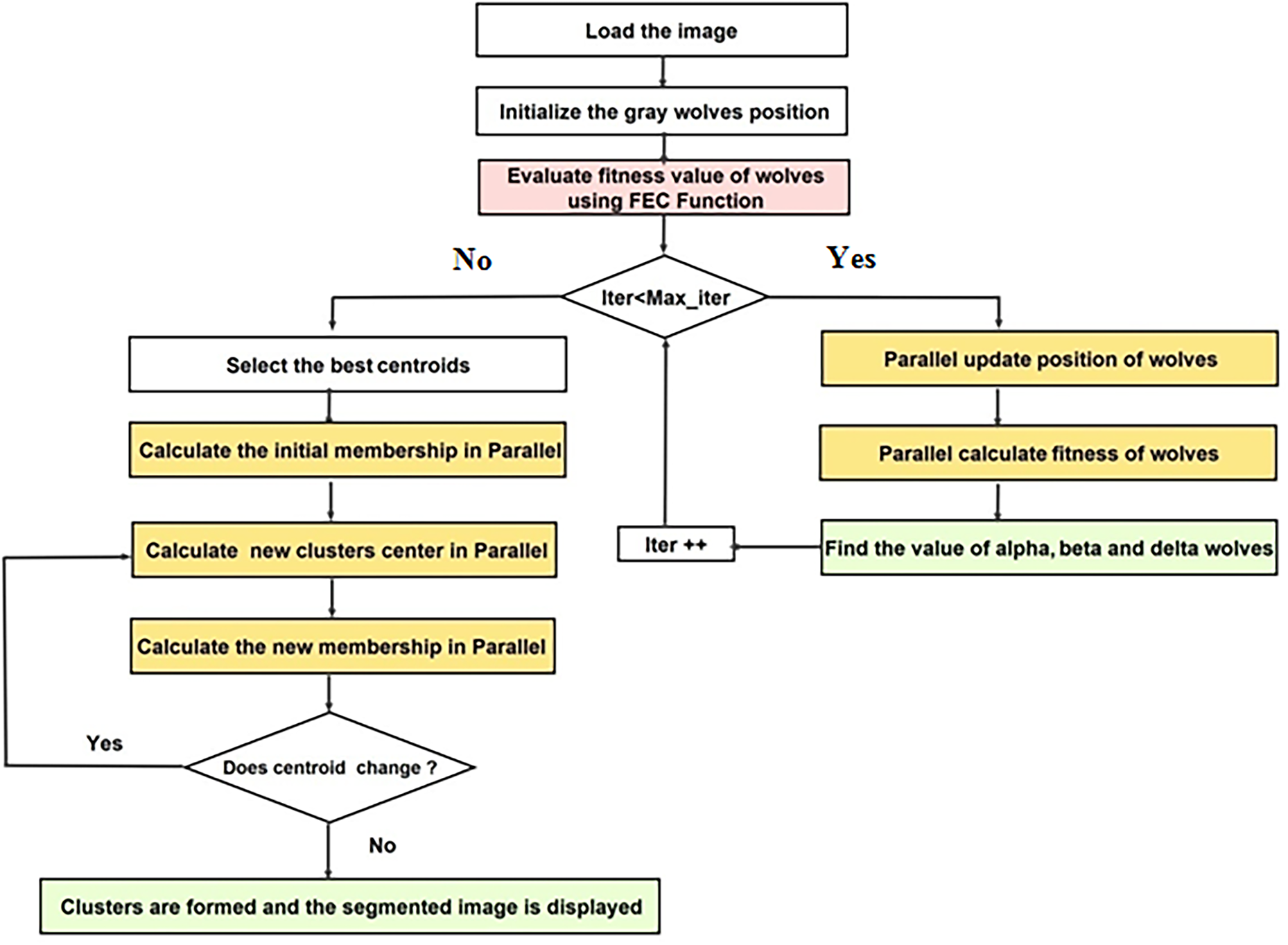
Figure 3: Diagram of the proposed P-GWO-FCM

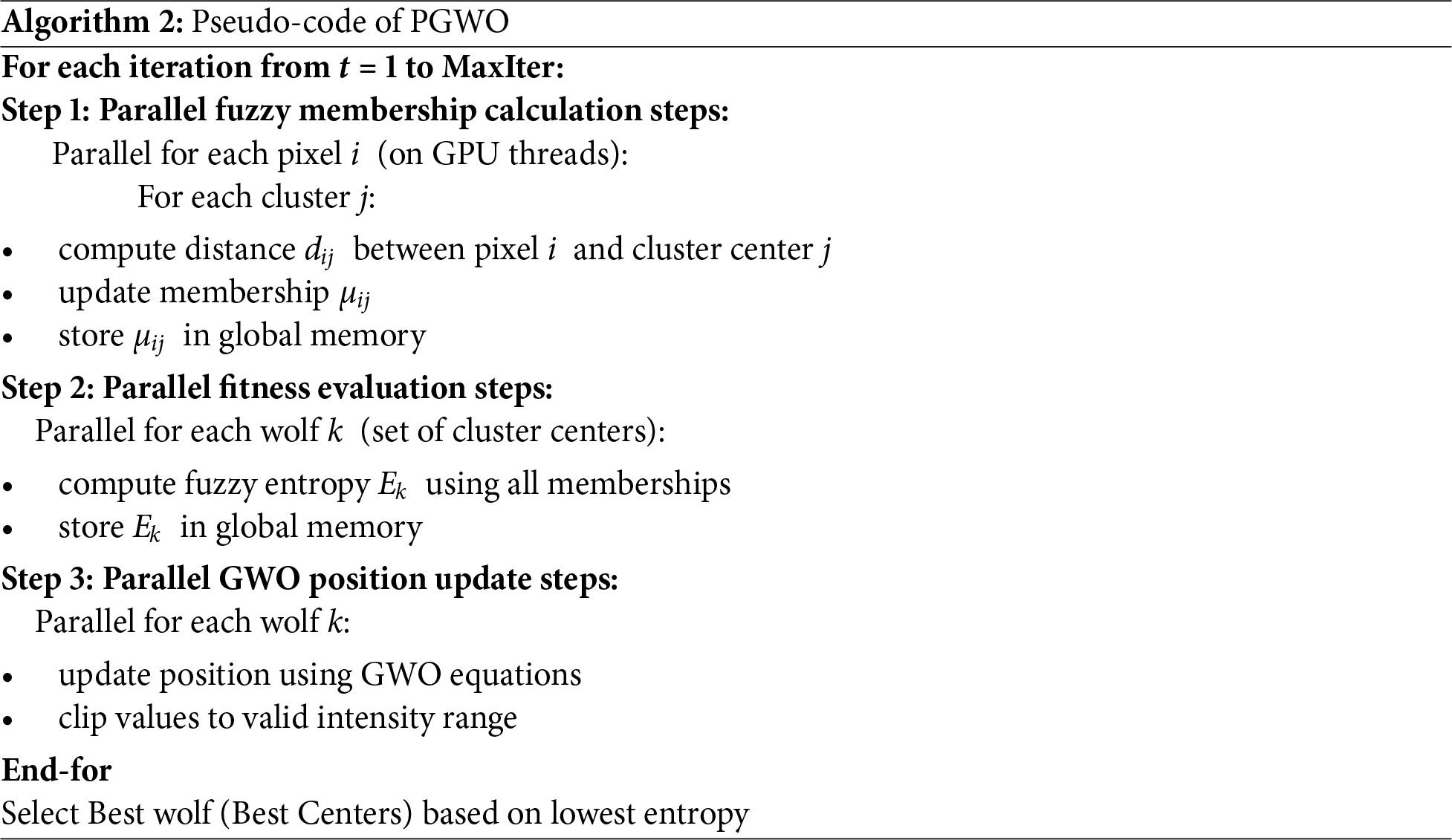
The detailed implementation of the PGWO and PFCM is provided in the Algorithms 2 and 3, respectively. In the proposed approach, two levels of parallelism are exploited on the GPU: population-level parallelism, where all wolves (candidate centroid sets) are evaluated concurrently, and pixel-level parallelism, where membership updates and distance computations are performed simultaneously for all pixels. Fitness and centroid updates are implemented as parallel reduction operations, which ensure efficient workload distribution across GPU cores.

4  Experimental Results

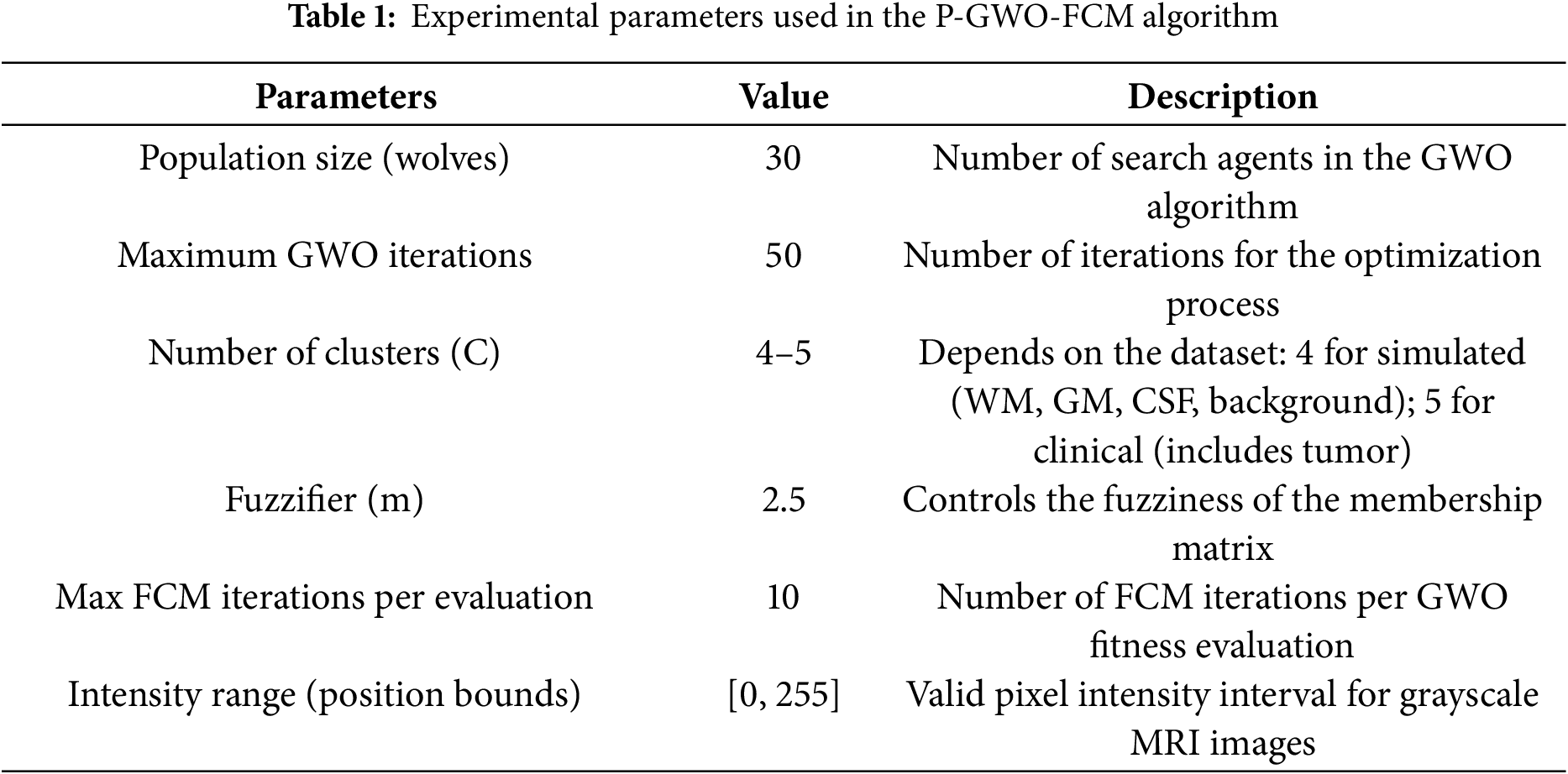
The experimentation is conducted using both a simulated brain dataset [28] and a clinical MRI dataset from Kaggle (https://www.kaggle.com/navoneel/brain-mri-images-for-brain-tumor-detection, accessed on 16 October 2025) to evaluate the effectiveness of the proposed P-GWO-FCM method. Table 1 presents the parameter settings used in our experiments, where fuzzy entropy clustering (FEC) was adopted as the fitness function. These parameters were selected based on prior studies and empirical tuning to balance convergence speed and segmentation quality. In particular, the swarm size, maximum number of iterations, fuzzifier value, and number of clusters were adjusted to ensure consistent performance. The number of clusters (C) was set according to the dataset characteristics: it was fixed at 4 for the simulated dataset to segment white matter, gray matter, cerebrospinal fluid, and background; and increased to 5 for the clinical dataset to account for tumor regions in addition to the main tissue types. The segmentation quality was assessed using the Jaccard similarity (JS), Davies-Bouldin Index (DBI), Partition Coefficient Index (PCI), Partition Entropy Index (PEI), and Dice coefficient (DICE). The performance of the proposed method was compared against traditional FCM, sequential-GWO-FCM, and state-of-the-art methods such as FCM-GENIUS [21] and Deep-JCR (Deep Joint Calibrationless Reconstruction) [15] methods. The mathematical formula of each measure is described below:

Jaccard similarity (JS): The JS measures the similarity between two sets, commonly used for evaluating segmentation accuracy:

JS=|A∩B||A∪B|(9)

where A is the ground truth and B is the segmented region.

Partition Coefficient Index (PCI): PCI evaluates the compactness of clusters in fuzzy clustering, defined as:

PCI=1N∑i=1N∑j=1Cuij2(10)

where uij is the membership value of pixel i in cluster j, and N is the total number of pixels.

Davies-Bouldin Index (DBI): DBI assesses cluster compactness and separation, given by:

DBI=1C∑i=1Cmaxi≠jsi+sjdij(11)

where si is the dispersion of cluster i, and dij is the distance between cluster centroids.

Partition Entropy Index (PEI): PEI measures the fuzziness of cluster memberships:

PEI=−1N∑i=1N∑j=1Cuijlog⁡uij(12)

where uij is the membership value of pixel i in cluster j.

Dice coefficient measure: is a statistic measure used for comparing the similarity between two samples and ranges between 0 and 1:

Dice=2|A∩B||A|+|B|(13)

where A and B are the segmented and gold standard image.

All experiments were conducted on a workstation equipped with an NVIDIA Tesla T4 GPU (16 GB memory) and an Intel Core i7-11700 CPU (2.5 GHz, 8 cores), and 32 GB RAM, running on Ubuntu 20.04 LTS. The proposed P-GWO-FCM algorithm was implemented in PyTorch with CUDA 12.6, leveraging PyTorch’s built-in CUDA kernels rather than direct CUDA C/C++ coding or PyCUDA. All tensor operations, including distance computation, membership updates, and Grey Wolf Optimizer (GWO) position updates, were fully vectorized in PyTorch and executed on the GPU.

Consequently, grid and block dimensions were not manually specified, as PyTorch automatically determines the optimal kernel launch configuration for tensor operations. This high-level design was intentional, since it benefits from PyTorch’s highly optimized CUDA backend, which adapts kernel configurations to the underlying GPU architecture. By abstracting these details, PyTorch ensures efficient utilization of thousands of CUDA cores, scalability to large datasets, and easier reproducibility.

In practice, the algorithm achieves two levels of parallelism: (i) across the wolf population and (ii) within each wolf’s fitness evaluation. Vectorized PyTorch operations, such as reductions for fuzzy entropy, SSE, and centroid updates, are internally mapped to optimized CUDA kernels with coalesced memory access. This design enables efficient large-scale execution across millions of pixels and ensures scalability to high-resolution MRI data.

4.1 Evaluation on Simulated Brain Dataset

The proposed P-GWO-FCM approach is evaluated on a simulated brain dataset [28] to assess its segmentation accuracy in differentiating White Matter (WM), Gray Matter (GM), and Cerebrospinal Fluid (CSF). The Jaccard Index is computed for each tissue type to measure the overlap between the segmented regions and the ground truth. The P-GWO-FCM method was first evaluated on a T1-weighted brain MR image with a resolution of 217 × 181 pixels, incorporating 20% grayscale non-uniformity to simulate real-world imaging challenges. The main goal of this experiment was to achieve precise segmentation and identification of key brain regions such as WM, GM, and CSF. These tissue types play a crucial role in radiological analysis and the diagnosis of neurological disorders.

Fig. 4 visually illustrates the segmentation results, enabling a direct comparison between the FCM algorithm and the two proposed approaches: sequential GWO-FCM and P-GWO-FCM. For reference, the original brain image is depicted in Fig. 4a, while its corresponding ground truth for WM, GM, and CSF is shown in Fig. 4b. The segmentation results obtained using the FCM, sequential GWO-FCM, and P-GWO-FCM methods are presented in Figs. 4c–e, respectively.

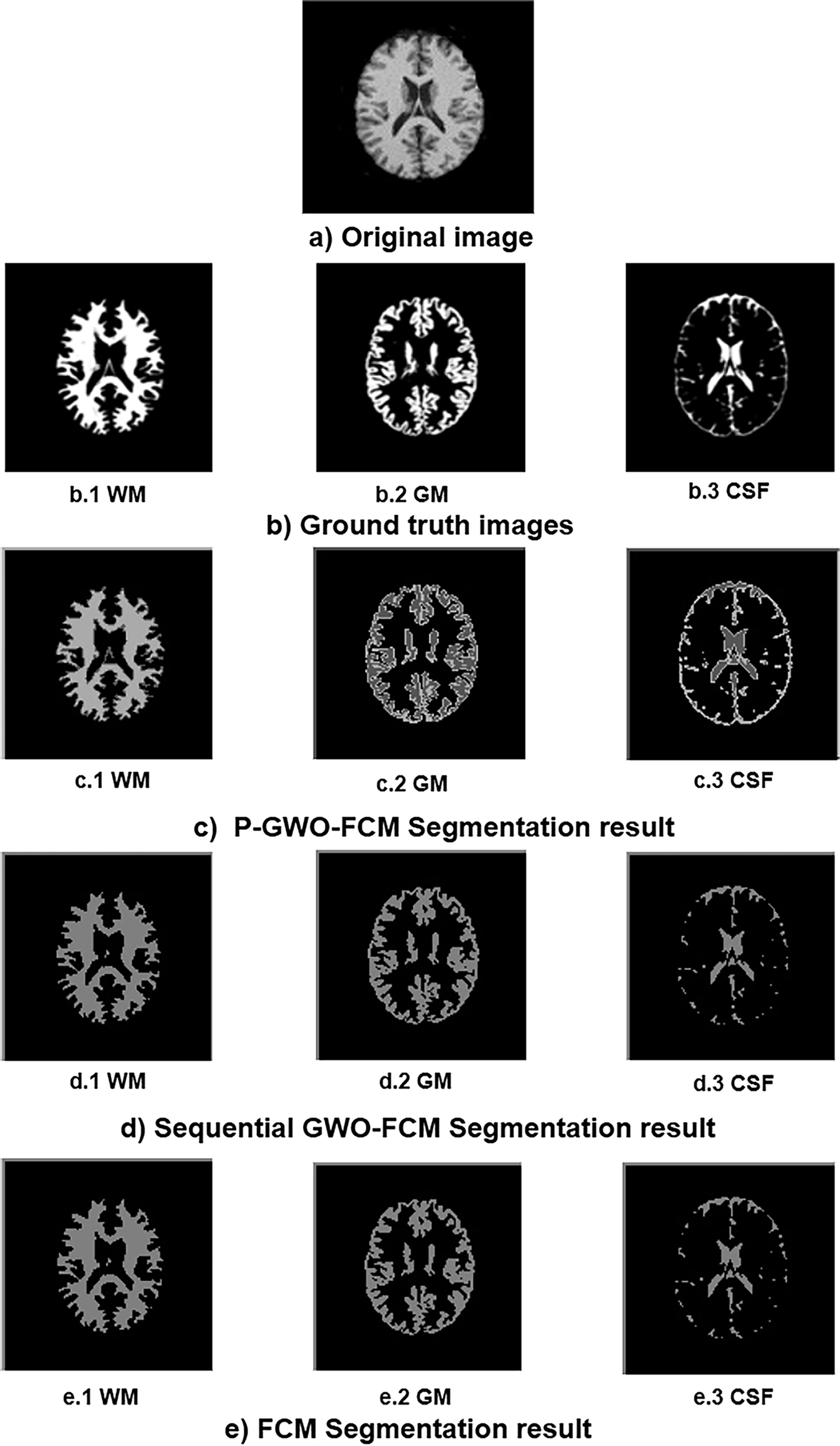
Figure 4: Segmentation results of WM, GM, CSF using FCM, sequential-GWO-FCM, and P-GWO-FCM

This figure demonstrates the effectiveness of P-GWO-FCM in preserving regional homogeneity, ensuring consistent and uniform segmentation. In addition, the algorithm preserves the most intricate details of the original MRI image, essential for maintaining the integrity of anatomical structures. This capability is particularly useful in medical imaging, where subtle differences between tissue types can be of crucial diagnostic importance.

In this experimentation, JS value was used calculated for each method including FCM, Sequential-GWO-FCM, and Parallel-GWO-FCM.

Table 2 provides a comprehensive comparison of the segmentation performance across three methods: FCM, Sequential GWO-FCM, and the proposed Parallel GWO-FCM. The evaluation is based on the Jaccard Similarity (JS) metric, which quantifies the overlap between the segmented regions and the ground truth for the three main brain tissues: WM, GM, and CSF. Higher JS values reflect better segmentation accuracy. The results demonstrate that the proposed method achieves the highest average JS score, outperforming the other two methods.

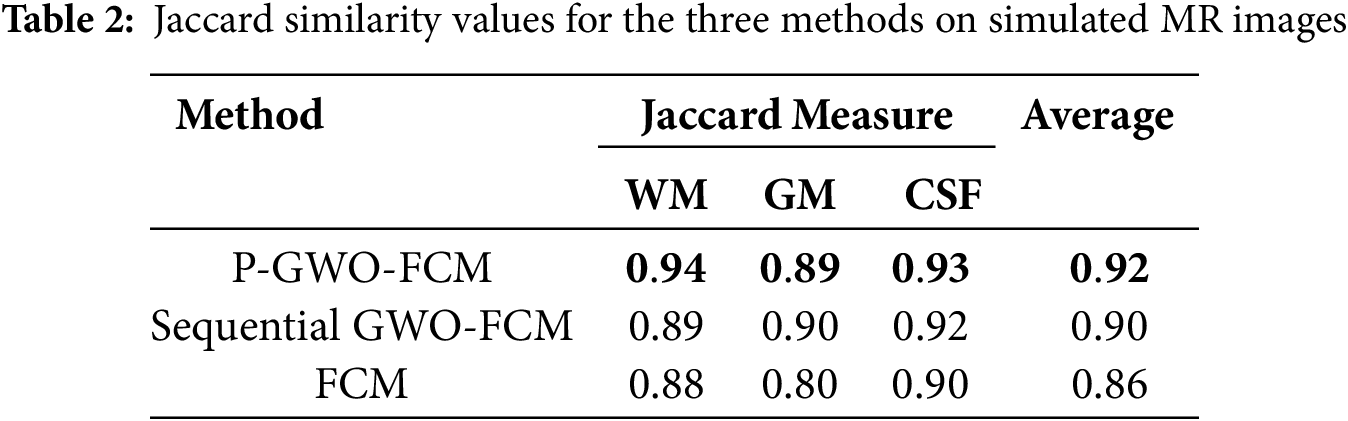
The P-GWO-FCM outperforms other methods, achieving the best JS values across all tissue types: 0.94 for WM, 0.89 for GM, and 0.93 for CSF. These results culminate in an average JS score of 0.92, which surpasses the scores of the other algorithms. This superior performance underscores the advantages of integrating the GWO with FE to enhance the FCM algorithm for Brain MRI segmentation. The GWO algorithm’s global optimization capabilities effectively tackle the challenges of parameter initialization and local minima, leading to more accurate and consistent segmentation of brain tissues. Additionally, integrating fuzzy entropy enhances robustness by better handling uncertainty and preserving subtle structural variations in MRI data. Furthermore, the parallel implementation significantly accelerates computation while maintaining segmentation quality, making the approach more efficient for large-scale medical imaging applications as confirmed by subsequent experiments.

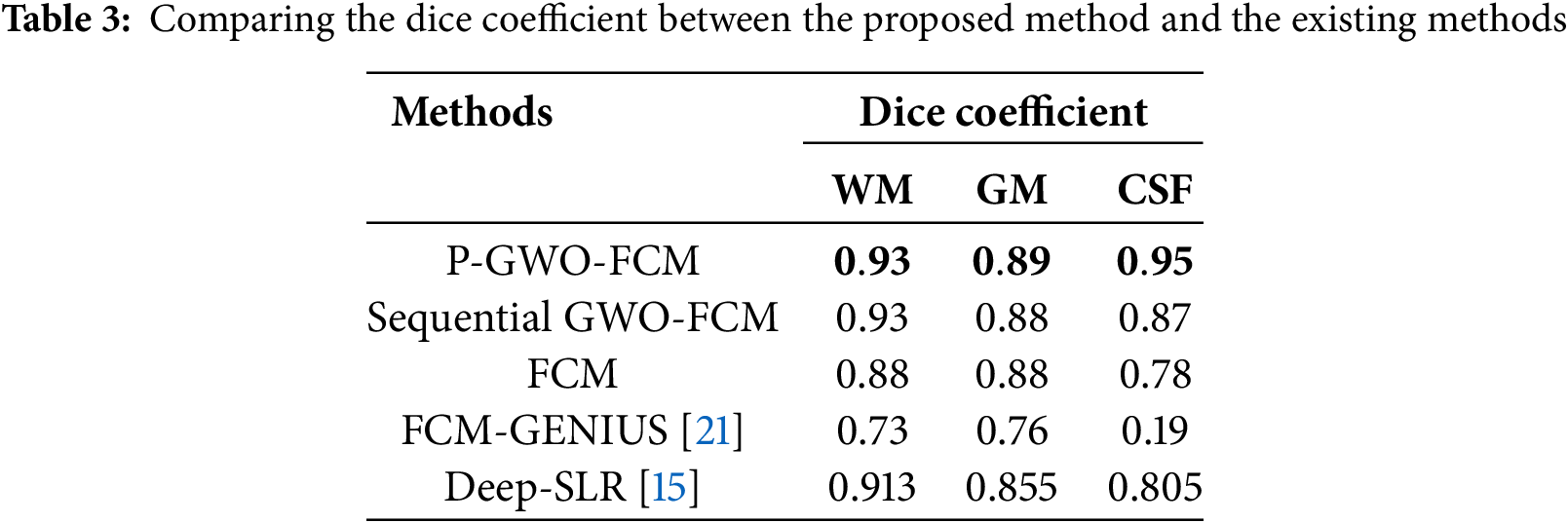
On the other hand, we compared our P-GWO-FCM method with existing approaches such as FCM-GENIUS [18] and Deep-JCR (Deep Joint Calibrationless Reconstruction) [12], both of which use the Dice similarity coefficient as an evaluation metric. The results, presented in Table 3, show that P-GWO-FCM outperforms the other methods, achieving the highest Dice scores across all tissue types: 0.93 for WM, 0.89 for GM, and 0.95 for CSF. This highlights the effectiveness of our approach in enhancing segmentation accuracy while maintaining computational efficiency.

4.2 Evaluation on Clinical MRI Dataset

To further assess the algorithm’s performance, experiments were conducted on a clinical MRI dataset from Kaggle, which includes a variety of tumor patterns with different intensity distributions. The segmentation performance of the P-GWO-FCM method was compared to that of FCM and sequential GWO-FCM. The effectiveness of these three methods was evaluated using the DBI, PEI and PCI metrics, with the results presented in Table 4. Fig. 5 showcases a selection of MRI images from the clinical dataset used in the experiments, displaying 10 images of varying sizes to demonstrate the robustness of the proposed approach. These images were segmented using all three algorithms. Fig. 6 illustrates the segmentation results obtained for these 10 brain MRI images using the P-GWO-FCM method.

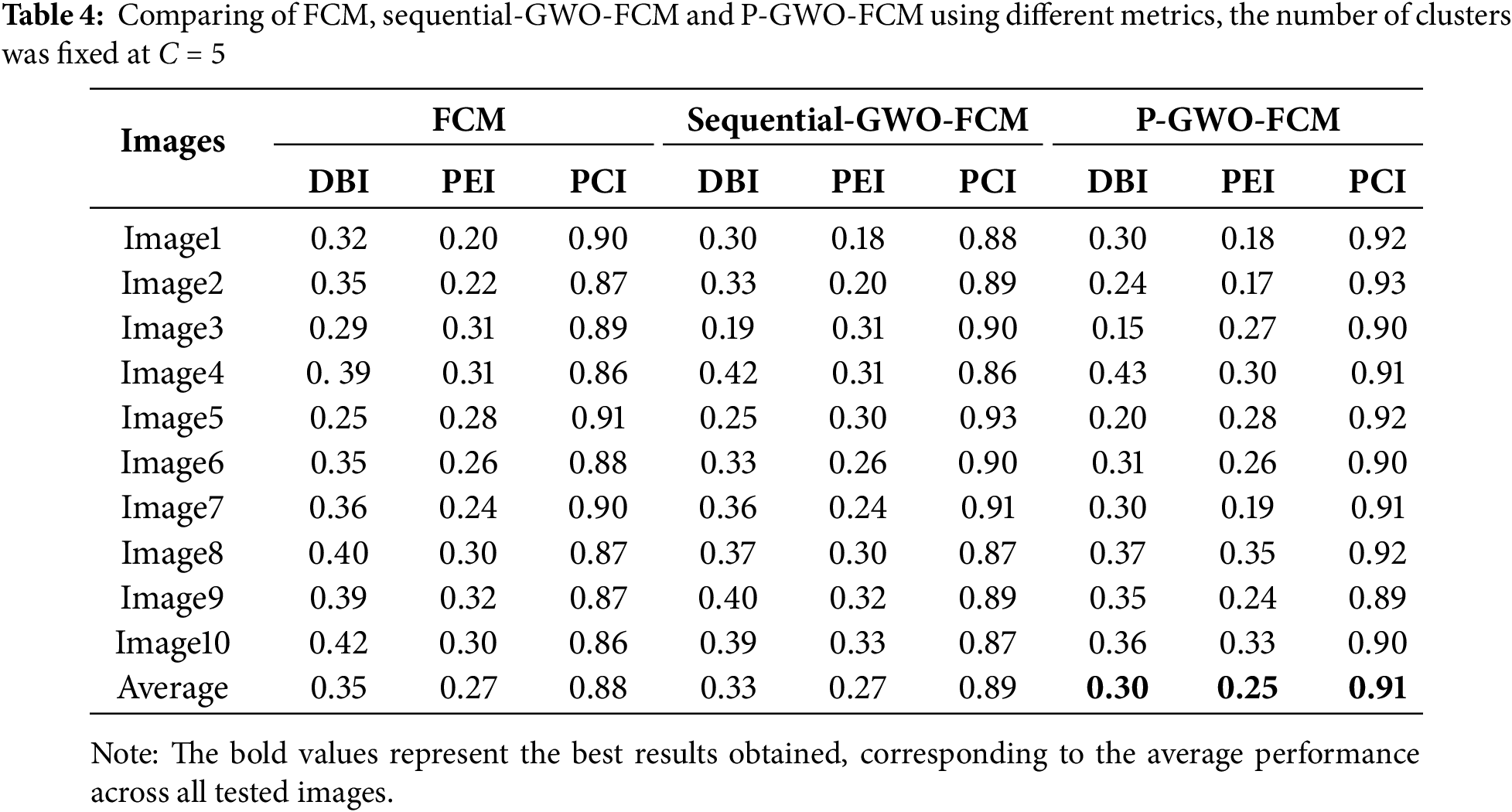
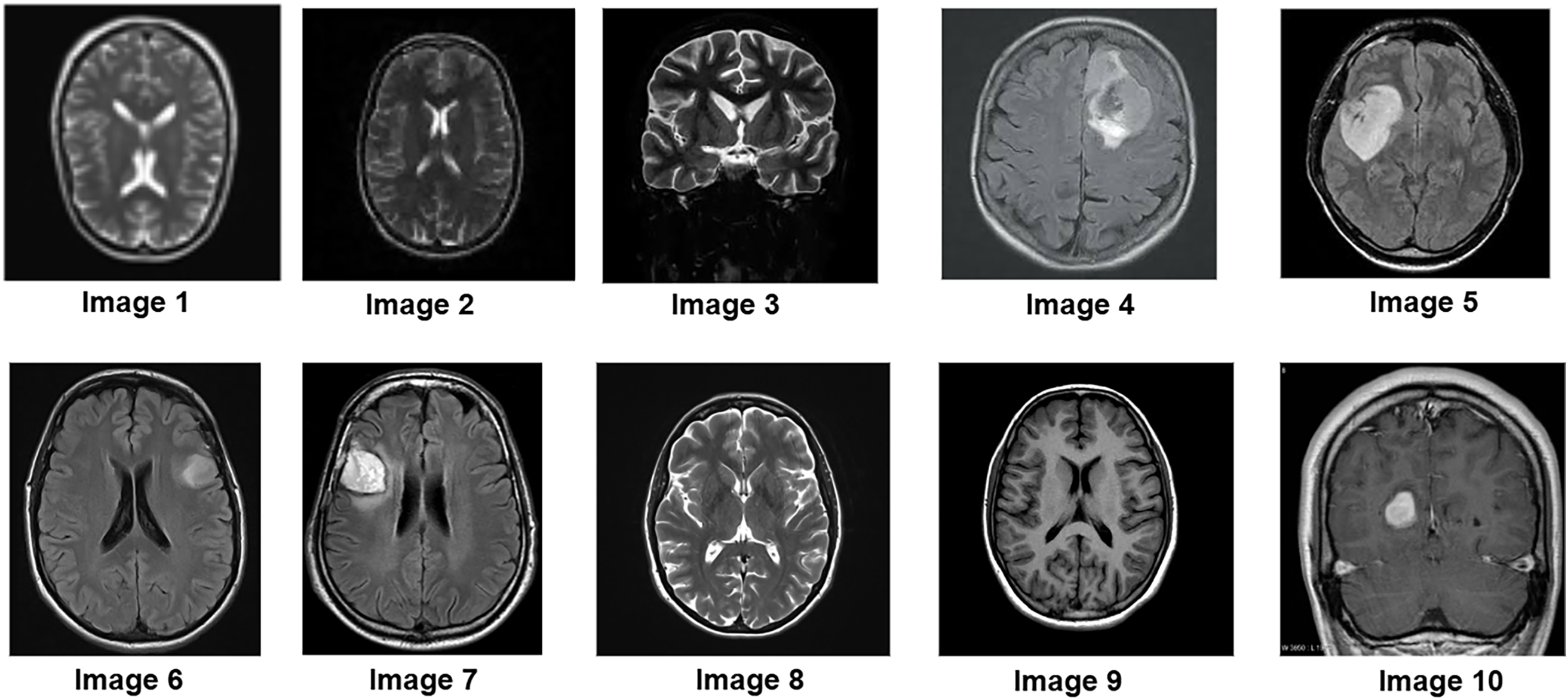
Figure 5: Samples of brain MR images from clinical dataset

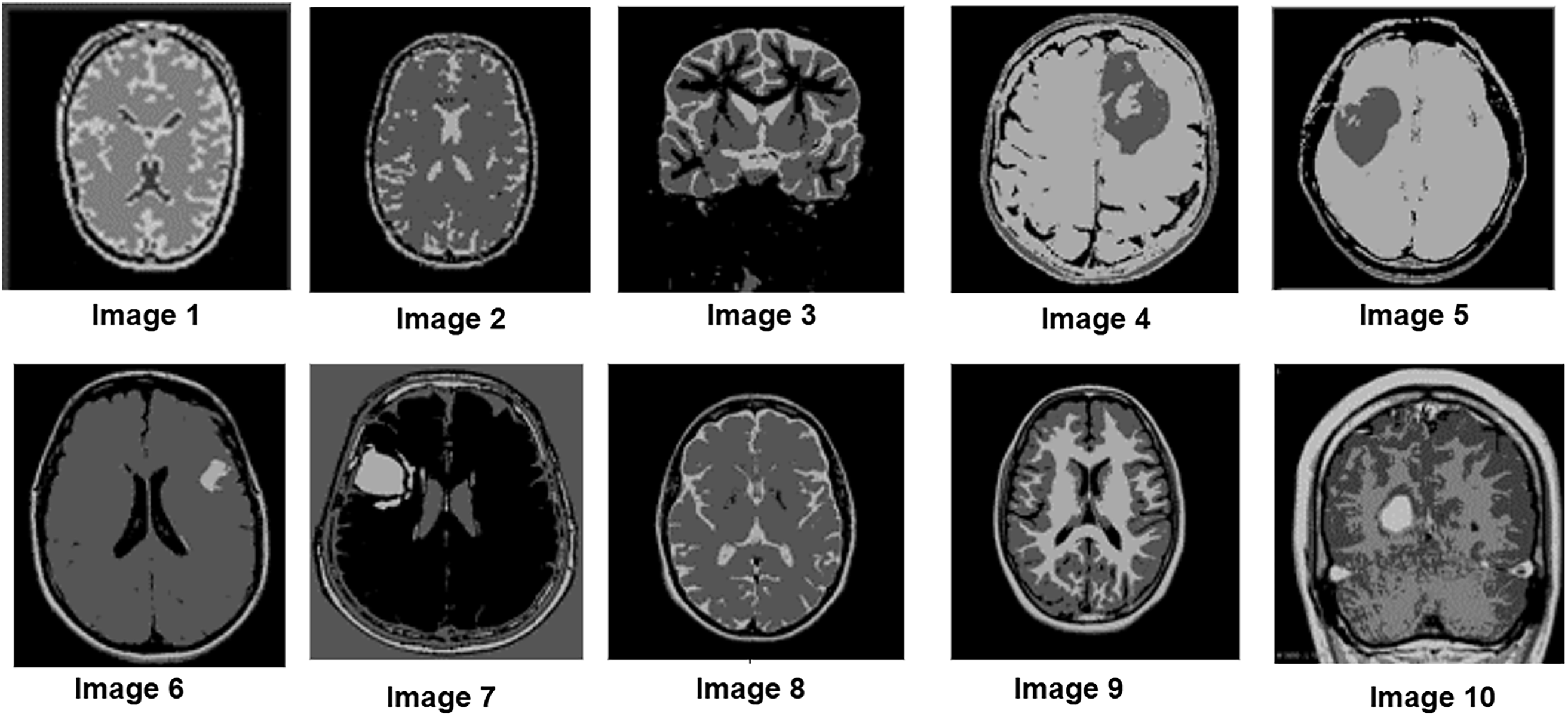
Figure 6: Segmentation results on 10 clinical MRI images from the Kaggle dataset using the proposed P-GWO-FCM. The algorithm partitions the image into C = 5 clusters (background, GM, WM, CSF, tumor)

In this context, the number of clusters was set to C = 5 to simultaneously capture background, GM, WM, CSF, and tumor. While tumor annotations are available in the dataset and used for metric evaluation, the healthy tissue clusters provide additional anatomical context around the tumor.

A visual analysis of the segmented images reveals that the P-GWO-FCM method excels in clarity, detail preservation, and precise delineation of tissue boundaries.

The results in Table 4 provide a comprehensive comparison of P-GWO-FCM, traditional FCM, and Sequential-GWO-FCM, demonstrating that P-GWO-FCM consistently outperforms the other methods across various evaluation metrics. These metrics assess clustering quality, particularly in terms of cluster compactness, separation, and the clarity and reliability of cluster assignments. Regarding the DBI, which evaluates clustering quality by measuring compactness and separation, P-GWO-FCM achieved an average DBI value of 0.30, significantly lower than those of FCM and sequential-GWO-FCM. This result indicates better cluster definition and separation, improving segmentation quality. The PEI, which quantifies uncertainty in membership assignments, further supports the robustness of our approach, as P-GWO-FCM attained an exceptionally low average PEI value of 0.25. This low PEI value reflects the minimal overlap between clusters, demonstrating the algorithm’s ability to assign data points with higher confidence and precision. Additionally, the PCI measures clustering fuzziness and further demonstrates the superiority of P-GWO-FCM. The algorithm achieved an impressive average PCI value of 0.91, indicating clearer partitioning with reduced fuzziness. This high PCI value, consistent across all test images, confirms that cluster memberships are predominantly close to 0 or 1, leading to more definitive segmentation. These quantitative results are consistent with the qualitative analysis shown in Fig. 6, where the lower DBI and PEI values obtained by P-GWO-FCM clearly correspond to more coherent and visually accurate segmentations compared to FCM and sequential GWO-FCM. It is also worth noting that the integration of Fuzzy Entropy into the fitness function enhances robustness against noise and uncertainty. Compared to the standard FCM objective, the FE-based formulation reduces DBI and PEI values, indicating more compact and reliable clusters, which further contributes to the superior performance of the proposed framework.

On the other hand, to assess whether the observed improvements were statistically significant, we performed a Wilcoxon signed-rank test across the ten clinical MRI images. The results in Table 5 confirm that the proposed P-GWO-FCM achieves statistically significant improvements over both FCM and sequential GWO-FCM in terms of PCI and DBI (p < 0.05). For the PEI metric, although P-GWO-FCM obtained lower values on average, the differences were not statistically significant (p > 0.05). These findings demonstrate that the improvements achieved by our method are robust and not due to random variation.

Table 6 compares sequential GWO-FCM with P-GWO-FCM in terms of execution time. Results show that the parallel approach, powered by GPU acceleration, achieves consistently low runtimes and scales efficiently with image size, unlike the sequential version whose runtime increases sharply. For example, on clinical MRI image 10 (dimension 911 ∗ 938), the sequential GWO-FCM required approximately 250 s, whereas P-GWO-FCM completed the segmentation in only 0.89 s, corresponding to a speedup of nearly 280× without compromising segmentation quality (see Tables 4 and 5). Fig. 7 shows execution time vs. image size, highlighting the linear growth in the sequential version and the near-constant runtime of the parallel version, which confirms the scalability of P-GWO-FCM.

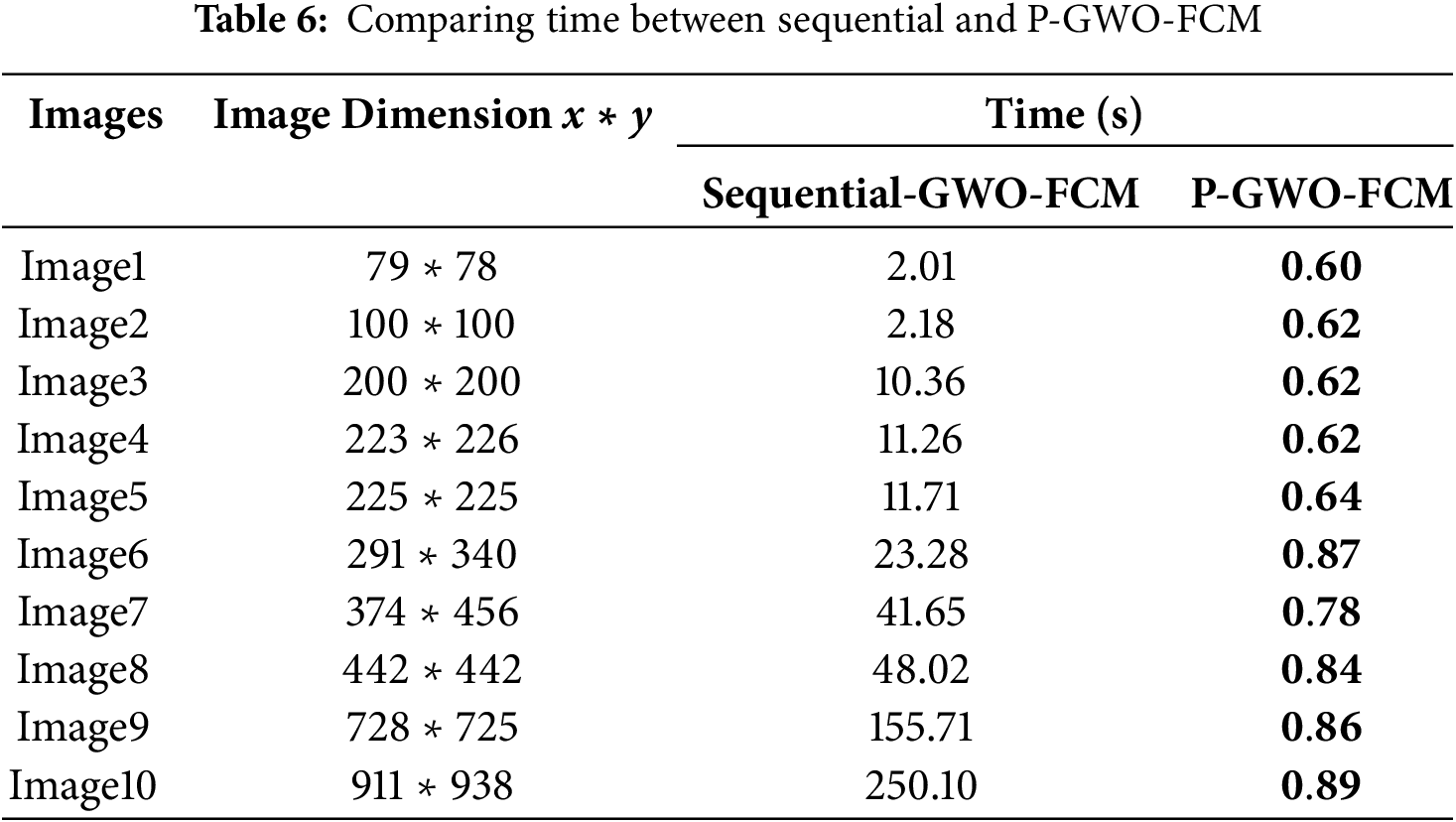
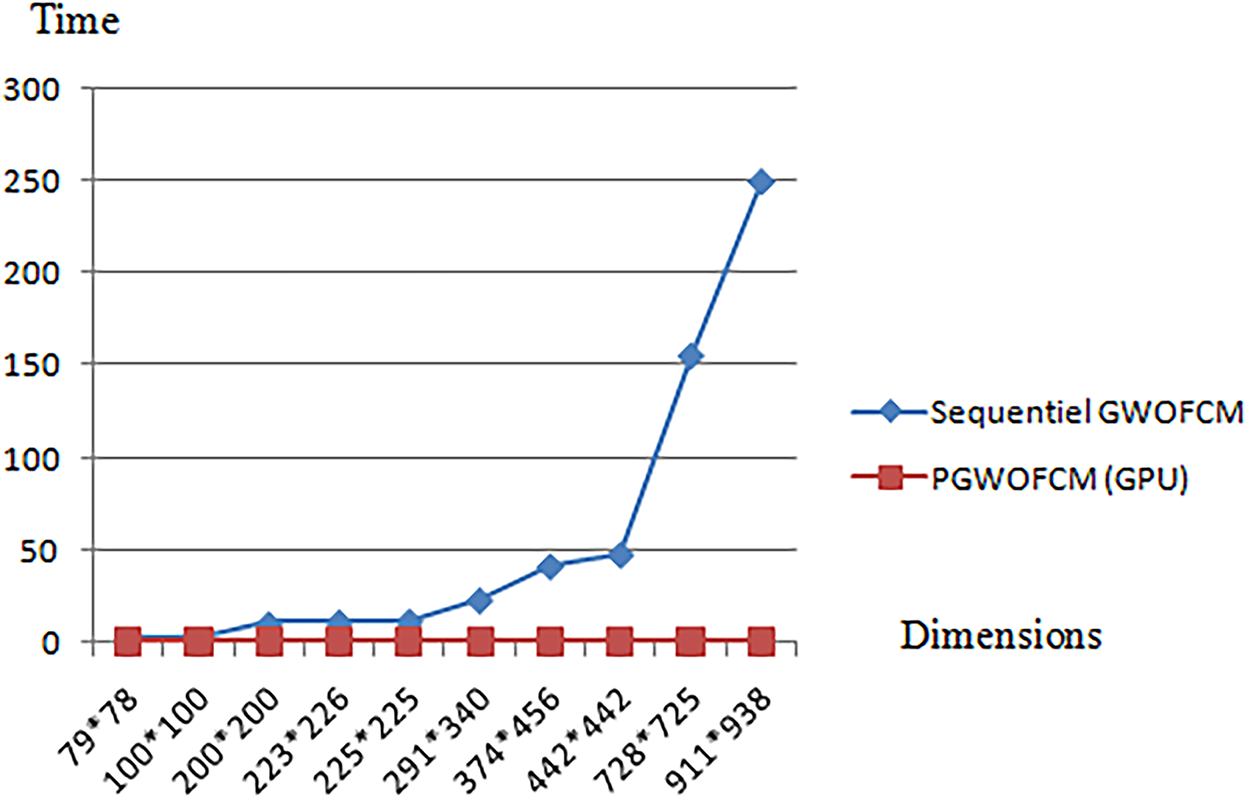
Figure 7: Execution time vs. image size for sequential and parallel GWO-FCM

In addition to the empirical evaluation, the time complexity of the sequential and parallel algorithms can also be analyzed theoretically. For the sequential GWO-FCM, the complexity is O(W, T, N, C, I) where N is number of pixels, C the number of clusters, I the number of FCM iterations, W the population size, and T the number of GWO iterations. In contrast, the proposed parallel P-GWO-FCM distributes the evaluation of wolves and the update steps of FCM across GPU threads, which reduces the effective complexity to approximately O(W·T·N·C·I/P), with P the number of parallel processors. This theoretical analysis is consistent with the empirical results of Table 6, where the parallel version achieves a speedup of nearly 280× compared to the sequential method.

5  Conclusion

In this study, we proposed the P-GWO-FCM approach, a parallelized Grey Wolf Optimization-based Fuzzy C-Means clustering algorithm designed to improve MRI image segmentation. This method has proven to enhance segmentation accuracy by integrating Grey Wolf Optimization (GWO) with fuzzy entropy clustering. Additionally, GPU-based parallelization was leveraged to optimize both the GWO and FCM processes. This parallel implementation effectively addresses key limitations of traditional FCM, including sensitivity to initialization, susceptibility to local optima, and high computational cost. The experimental results on both simulated and clinical brain MRI datasets demonstrate that P-GWO-FCM achieves superior segmentation accuracy. Moreover, the parallel execution significantly reduces computation time, making real-time medical image analysis more feasible. Comparative evaluations highlight the effectiveness of the dual-parallelization strategy, which accelerates both the optimization and clustering processes. The integration of fuzzy entropy enhances the robustness of segmentation by preserving anatomical structures. The proposed approach outperforms existing methods in both segmentation quality and efficiency, making it a promising solution for large-scale MRI analysis.

Although this study focused on 2D MRI slices, the parallel P-GWO-FCM framework is scalable to high-resolution 3D volumes. Remaining challenges include GPU memory limits and data transfer overhead, which could be mitigated by patch-based or mixed-precision strategies. Another limitation is the absence of comparisons with deep learning baselines (e.g., U-Net). Future work will therefore explore lightweight U-Net models and hybrid integration with metaheuristics, aiming to improve efficiency, accuracy, and adaptability for large-scale 3D medical images.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Mohammed Debakla: Study conception and design. Ali Mezaghrani: Conceptualization, methodology, software, programming, interpretation of results. Khalifa Djemal and Imane Zouaneb: Visualization, draft manuscript preparation, formal analysis, supervision, validation, software. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are openly available in [BrainWeb: simulated brain dataset] at [https://brainweb.bic.mni.mcgill.ca/brainweb/]. [Kaggle] at [https://www.kaggle.com/datasets/navoneel/brain-mri-images-for-brain-tumor-detection] (accessed on 16 October 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Poongodan R, Narayan DL, Gadakatte Lokeshwarappa D, Praveena HD, Kang D. Switchable normalization based faster RCNN for MRI brain tumor segmentation. Comput Mater Contin. 2025;84(3):5751–72. doi:10.32604/cmc.2025.066314. [Google Scholar] [CrossRef]

2. Debakla M, Salem M, Bouiadjra RB, Rebbah M. CMA-ES based fuzzy clustering approach for MRI images segmentation. Int J Comput Appl. 2023;45(1):1–7. doi:10.1080/1206212X.2019.1662984. [Google Scholar] [CrossRef]

3. Pei HX, Zheng ZR, Wang C, Li CN, Shao YH. D-FCM: density based fuzzy c-means clustering algorithm with application in medical image segmentation. Procedia Comput Sci. 2017;122:407–14. doi:10.1016/j.procs.2017.11.387. [Google Scholar] [CrossRef]

4. Mohapatra SK, Sahu P, Almotiri J, Alroobaea R, Rubaiee S, Bin Mahfouz A, et al. Segmentation and classification of encephalon tumor by applying improved fast and robust FCM algorithm with PSO-based ELM technique. Comput Intell Neurosci. 2022;2022:2664901. doi:10.1155/2022/2664901. [Google Scholar] [PubMed] [CrossRef]

5. Thomas E, Kumar SN. Fuzzy C-means clustering coupled with firefly optimization algorithm for the segmentation of neurodisorder magnetic resonance images. Procedia Comput Sci. 2024;235:1577–89. doi:10.1016/j.procs.2024.04.149. [Google Scholar] [CrossRef]

6. Sun C, Shao Q, Zhou Z, Zhang J. An enhanced FCM clustering method based on multi-strategy tuna swarm optimization. Mathematics. 2024;12(3):453. doi:10.3390/math12030453. [Google Scholar] [CrossRef]

7. Zhang M, Jiang W, Zhou X, Xue Y, Chen S. A hybrid biogeography-based optimization and fuzzy C-means algorithm for image segmentation. Soft Comput. 2019;23(6):2033–46. doi:10.1007/s00500-017-2916-9. [Google Scholar] [CrossRef]

8. Kollem S, Prasad CR, Ajayan JSS, Leo Joseph LMI, Krishna P. Segmentation of brain MRI images using multi-kernel FCM EHO method. Curr Med Imaging. 2024;20(1). doi:10.2174/1573405620666230822114029. [Google Scholar] [PubMed] [CrossRef]

9. Shoeibi M, Nevisi MMS, Salehi R, Martín D, Halimi Z, Baniasadi S. Enhancing hyperspectral image classification with reinforcement learning and advanced multi-objective binary grey wolf optimization. Comput Mater Contin. 2024;79(3):3469–93. doi:10.32604/cmc.2024.049847. [Google Scholar] [CrossRef]

10. Dagal I, Demirci A, Harrison A, Mbasso WF, Tercan SM, Akın B, et al. Prioritized multi-step decision-making gray wolf optimization algorithm for engineering applications. Eng Rep. 2025;7(5):e70154. doi:10.1002/eng2.70154. [Google Scholar] [CrossRef]

11. Qiu Y, Yang X, Chen S. An improved gray wolf optimization algorithm solving to functional optimization and engineering design problems. Sci Rep. 2024;14:14190. doi:10.1038/s41598-024-64526-2. [Google Scholar] [PubMed] [CrossRef]

12. Yu M, Xu J, Liang W, Qiu Y, Bao S, Tang L. Improved multi-strategy adaptive grey wolf optimization for practical engineering applications and high-dimensional problem solving. Artif Intell Rev. 2024;57:277. doi:10.1007/s10462-024-10821-3. [Google Scholar] [CrossRef]

13. Mohammdian-Khoshnoud M, Soltanian AR, Dehghan A, Farhadian M. Optimization of fuzzy c-means (FCM) clustering in cytology image segmentation using the gray wolf algorithm. BMC Mol Cell Biol. 2022;23(1):9. doi:10.21203/rs.3.rs-808322/v1. [Google Scholar] [CrossRef]

14. Yu B, Zhou Q, Yuan L, Liang H, Shcherbakov P, Zhang X. 3D medical image segmentation using the serial-parallel convolutional neural network and transformer based on cross-window self-attention. CAAI Trans Intell Technol. 2025;10(2):337–48. doi:10.1049/cit2.12411. [Google Scholar] [CrossRef]

15. Pramanik A, Wu X, Jacob M. Joint calibrationless reconstruction and segmentation of parallel MRI. In: European Conference on Computer Vision. Cham, Switzerland: Springer Nature; 2022. p. 437–53. doi:10.1007/978-3-031-25066-8_24. [Google Scholar] [CrossRef]

16. Wang D, Xv T, Liu J, Li J, Yang L, Guo J. Bidirectional efficient attention parallel network for segmentation of 3D medical imaging. Electronics. 2024;13(15):3086. doi:10.3390/electronics13153086. [Google Scholar] [CrossRef]

17. Chahbar F, Merati M, Mahmoudi S. MPB-UNet: multi-parallel blocks UNet for MRI automated brain tumor segmentation. Electronics. 2024;14(1):40. doi:10.3390/electronics14010040. [Google Scholar] [CrossRef]

18. Saxena S, Shama S. Brain tumor segmentation by texture feature extraction with the parallel implementation of fuzzy C-means using CUDA on GPU. In: 2018 Fifth IEEE International Conference on Parallel, Distributed and Grid Computing (PDGC); 2018 Dec 20–22; Solan, India. p. 580–585. [Google Scholar]

19. Ali NA, Cherradi B, El Abbassi A, Bouattane O, Youssfi M. Parallel implementation and performance evaluation of some supervised clustering algorithms for MRI image segmentation. In: Proceedings of the 4th International Conference on Big Data and Internet of Things (BDIoT’19); 2019 Oct 23–24; Rabat, Morocco. p. 1–7. doi:10.1145/3372938.3373007. [Google Scholar] [CrossRef]

20. AlZuÕbi S, Shehab M, Al-Ayyoub M, Jararweh Y, Gupta B. Parallel implementation for 3D medical volume fuzzy segmentation. Pattern Recognit Lett. 2020;130:312–8. doi:10.1016/j.patrec.2018.07.026. [Google Scholar] [CrossRef]

21. Valsalan P, Sriramakrishnan P, Sridhar S, Latha GCP, Priya A, Ramkumar S, et al. Knowledge-based fuzzy c-means method for rapid brain tissue segmentation of magnetic resonance imaging scans with CUDA-enabled GPU machine. J Am Intell Humaniz Comput. 2020;11:1–14. doi:10.1007/s12652-020-02132-6. [Google Scholar] [CrossRef]

22. Sui X, Chu SC, Pan JS, Luo H. Parallel compact differential evolution for optimization applied to image segmentation. Appl Sci. 2020;10(6):2195. doi:10.3390/app10062195. [Google Scholar] [CrossRef]

23. Hung CL, Wu YH. Parallel genetic-based algorithm on multiple embedded graphic processing units for brain magnetic resonance imaging segmentation. Comput Electr Eng. 2016;61:373–83. doi:10.1016/j.compeleceng.2016.09.028. [Google Scholar] [CrossRef]

24. Almutairi L, Abugabah A, Alhumyani H, Mohamed AA. Intelligent biomedical image classification in a big data architecture using metaheuristic optimization and gradient approximation. Wirel Netw. 2024;30(8):7087–7108. doi:10.1007/s11276-023-03573-5. [Google Scholar] [CrossRef]

25. Hosny KM, Khalid AM, Hamza HM, Mirjalili S. Multilevel segmentation of 2D and volumetric medical images using hybrid Coronavirus Optimization Algorithm. Comput Biol Med. 2022;150:106003. doi:10.1016/j.compbiomed.2022.106003. [Google Scholar] [PubMed] [CrossRef]

26. Fu HJ, Wu XH, Mao HP, Wu B. Fuzzy entropy clustering using a possibilistic approach. Procedia Eng. 2011;15:1993–7. doi:10.1016/j.proeng.2011.08.372. [Google Scholar] [CrossRef]

27. Li RP, Mukaidono M. A maximum-entropy approach to fuzzy clustering. In: Proceedings of the Fourth IEEE International Conference on Fuzzy Systems; 1995 Mar 20–24; Yokohama, Japan. Vol. 4, p. 2227–32. [Google Scholar]

28. Cocosco CA, Kollokian V, Kwan RKS, Evans AC. BrainWeb: online interface to a 3D MRI simulated brain database. Neuroimage. 1997;5(4):425. [Google Scholar]