Structure-Based Virtual Sample Generation Using Average-Linkage Clustering for Small Dataset Problems

1  Introduction

Recent advances in machine learning and artificial intelligence have enabled powerful data-driven models in many domains. However, these models typically rely on large, representative datasets. In many practical scenarios, only a small number of samples are available due to high data collection costs, privacy regulations, or the rarity of the underlying phenomenon. Such small datasets often lead to overfitting, poor generalization, and unstable model behavior.

Virtual sample generation (VSG) has emerged as a promising strategy to mitigate small-data limitations by synthetically augmenting the training set. Early work by Cho and Cha [1] introduced the idea of generating virtual samples in population networks, and Niyogi et al. [2] showed that prior knowledge–driven virtual examples can improve object recognition accuracy. Chen et al. [3] proposed a particle swarm optimization–based VSG (PSOVSG) to enhance forecasting models trained on small datasets. More recently, He et al. [4] developed t-SNE-VSG for data-driven soft sensors, demonstrating substantial accuracy gains in data-scarce industrial settings. Several other variants and applications of VSG have also been reported in the literature [5,6]. Together, these studies confirm that well-designed virtual samples can effectively reinforce learning in small-data regimes. In related small-data applications, clustering-based approaches have also been shown to play an important role in learning from limited samples.

In this work, we focus on two common small-data conditions. The first is the genuinely low-sample setting, where the available dataset is too small to capture sufficient variability, as in rare-disease studies with only a handful of cases. The second is the high-dimensional, small-sample scenario, where the number of attributes is large relative to the number of instances. In both cases, the core difficulty lies in the limited information content of the original data set. Recent studies on decision support systems have emphasized that, in the presence of data scarcity, transparent and interpretable modeling is essential for reliable decision-making. To address these challenges, we propose an average-linkage virtual sample generation method (ALVSG) that explicitly exploits the underlying data structure before generating virtual samples.

Cluster analysis provides a natural tool for uncovering latent structure in data by grouping similar instances [7]. Li et al. [8], for example, used DBSCAN to reveal structure and improve prediction on small datasets. Inspired by such structure-aware approaches, ALVSG employs hierarchical clustering with average linkage (UPGMA) to construct a dendrogram of the original data. From the merging process, we derive an average-based representation that reflects how frequently each data point participates in cluster formation. This representation is then used as a sampling prior to generate virtual samples within data-driven attribute bounds. The virtual samples are finally combined with the original data to form an enriched training set that can be used with arbitrary predictive models.

We evaluate the proposed ALVSG method on two real small datasets. The first concerns medical records for predicting the success of radiotherapy treatment for bladder cancer cells, while the second involves multi-layer ceramic capacitors (MLCCs) commonly used in electronic devices. We benchmark ALVSG against baseline models using support vector regression (SVR), a deep learning model (DL), and XGBoost, and assess performance using mean absolute error (MAE), mean square error (MSE), root mean square error (RMSE), and paired statistical t-tests. The results provide a comprehensive view of when and how ALVSG improves prediction accuracy in small-data settings.

The rest of this paper is organized as follows. Section 2 reviews related work on small datasets, virtual sample generation, and forecasting models. Section 3 presents the proposed ALVSG methodology. Section 4 reports the experimental setup and results on the two case-study datasets. Section 5 concludes the paper and outlines directions for future work.

Contributions

This paper makes the following contributions: (i) we propose ALVSG, a structure-informed virtual sample generator that derives average-based weights from agglomerative average-linkage (UPGMA) clustering and uses them as an interpretable sampling prior; (ii) we bound the generator using data-driven ±3σ limits per attribute and adopt uniform sampling within these bounds to mitigate mean overemphasis under small-n uncertainty; (iii) we conduct a model-agnostic plug-in evaluation on two real small datasets (radiotherapy and MLCC) across SVR, DL, and XGBoost with paired resampling t-tests; and (iv) we report consistent error reductions and analyze when ALVSG helps most, offering practical guidance for deploying VSG techniques in small-data regimes.

2  Related Works

This section reviews prior work related to small-dataset learning, virtual sample generation (VSG), and the forecasting models used to evaluate the proposed ALVSG method.

2.1 Small Datasets

Small datasets pose fundamental challenges for machine learning models, including high variance, overfitting, and unreliable generalization [9]. Recent surveys have examined this “small-data dilemma” from different disciplinary perspectives. For example, Xu et al. [10] summarized how data scarcity limits model performance in materials science and grouped existing remedies into three levels: data-source level (e.g., database construction, high-throughput computation), algorithm level (e.g., imbalanced learning, specialized small-data models), and learning-strategy level (e.g., active learning, transfer learning). These reviews highlight that small-data issues are widespread and require both data-centric and model-centric solutions. In addition to methodological studies, practical machine learning workflows have also been developed to accommodate small and heterogeneous datasets; for instance, Zhang and Deng introduced a data-driven machine learning interface for materials science that explicitly targets limited-sample settings and supports model development under data scarcity [11].

In practice, small datasets arise in many engineering and scientific problems, such as rare-disease analysis, optimization of real-world engineering systems [12]. When the number of instances is limited relative to the dimensionality, it becomes difficult to extract stable patterns and to build robust predictive models. Various approaches have been explored to mitigate these issues, including dimensionality reduction (e.g., linear discriminant analysis, LDA [13]) and structure-aware data partitioning for classification under class imbalance [14]. Complementary to these methods, virtual sample generation has emerged as an effective strategy to augment small datasets, and it is the main focus of this work.

2.2 Virtual Sample Generation

Virtual sample generation (VSG) aims to enrich small datasets with synthetic samples that are consistent with the underlying data distribution. Early work, Niyogi et al. [2] introduced the basic idea of generating virtual examples to improve network training and object recognition. These pioneering studies established VSG as a viable tool for strengthening learning under data scarcity.

Subsequent research has proposed more sophisticated VSG mechanisms tailored to specific domains. Li et al. [8] used a mega-trend diffusion membership function that applies DBSCAN clustering and fuzzy membership functions to construct new attributes for small datasets. Chen et al. [3] developed PSOVSG, which employs particle swarm optimization to generate virtual samples that improve forecasting performance on small data. Zhu et al. He et al. [4] introduced t-SNE-VSG, which interpolates manifold features obtained from t-SNE and estimates virtual outputs via random forests to enhance soft-sensor performance in process industries. More recent work has further advanced VSG toward adaptive and statistically constrained frameworks. Zhu et al. [15] presented a co-training-based VSG (CTVSG) that employs two k-nearest neighbor regressors to iteratively generate and validate virtual samples in sparse regions of the feature space. Cui et al. [16] integrated generative adversarial networks with active learning, conditioning the generator on risk levels and screening synthesized samples using maximum mean discrepancy (MMD) and expert validation. Chen et al. [17] proposed APS-VSG, which defines acceptable areas via a compact range of interaction and uses joint probability distribution sampling to reduce randomness and improve the validity of generated samples. Other related works and broader surveys on data augmentation across modalities further underscore the growing interest in VSG-based approaches [5,6,18]. In addition, data augmentation is another virtual sample which can be further enhanced by incorporating structural constraints and adversarial perturbations into the learning process [19].

Compared with these methods, the proposed ALVSG adopts a simpler, purely structure-informed strategy. Instead of relying on complex surrogate models or deep generative networks, ALVSG uses agglomerative average-linkage (UPGMA) hierarchical clustering to construct a dendrogram of the original data. From the merging process, we derive an average-based representation that quantifies how frequently each instance contributes to cluster formation. This representation serves as an interpretable sampling prior for generating virtual samples within data-driven attribute bounds. As a result, ALVSG provides a lightweight, model-agnostic, and interpretable VSG mechanism that is particularly suitable for small tabular datasets.

2.3 Forecasting Models

To evaluate the effectiveness of ALVSG, we consider representative forecasting models that are commonly adopted in practical prediction tasks under limited data conditions. Motivated by such practical settings, we consider three representative forecasting models for tabular regression: support vector regression (SVR), a feed-forward deep learning (DL) regressor, and XGBoost. These models span margin-based learning, neural networks, and tree-based ensembles, and they are widely used in practice due to their strong performance on small to medium-sized structured datasets. Their behavior on original vs. ALVSG-augmented data provides a comprehensive benchmark for our method.

2.3.1 Support Vector Regression (SVR)

Support vector machines (SVMs) were originally proposed for classification based on the principle of structural risk minimization, aiming to find a maximum-margin separating hyperplane in a transformed feature space. Support vector regression (SVR) extends this idea to regression by introducing an ε-insensitive loss: deviations smaller than ε are ignored, while larger deviations are penalized [20]. Given training pairs {(xi,yi)}i=1n, SVR seeks a function

f(x)=w⊤ϕ(x)+b

that is as flat as possible while keeping prediction errors within an ε-tube for most samples:

minw,b,ξi,ξi∗12‖w‖2+C∑i=1n(ξi+ξi∗)s.t.{yi−f(xi)≤ε+ξi,f(xi)−yi≤ε+ξi∗,ξi,ξi∗≥0.

Here ϕ(⋅) denotes the feature mapping induced by a kernel function; we use the radial basis function (RBF) kernel in our experiments. Only samples outside the ε-tube become support vectors and contribute to the final model, which helps control model complexity under small-data conditions.

2.3.2 Deep Learning Regressor

Deep learning models based on feed-forward neural networks can approximate complex nonlinear relationships by stacking multiple layers of linear transformations and nonlinear activation functions. In this study, we employ a fully connected multilayer perceptron (MLP) as a generic deep learning regressor. The network consists of an input layer, several hidden layers with rectified linear unit (ReLU) activations, and a single output neuron for regression. Model parameters are learned by minimizing a mean-squared-error loss using gradient-based optimization with backpropagation. Although deep networks are often associated with large datasets, carefully regularized shallow architectures can still serve as competitive baselines in small-data scenarios.

2.3.3 XGBoost Regressor

XGBoost is a gradient boosting framework that builds an ensemble of regression trees in a stage-wise manner, optimizing a regularized objective that balances data fit and model complexity. At each iteration, a new tree is added to correct the residual errors of the current ensemble, and explicit regularization terms on leaf weights and tree structure help prevent overfitting. XGBoost has demonstrated strong performance on a wide range of structured-data tasks and is particularly effective when the number of samples is limited but informative features are available. In our experiments, we use XGBoost as a representative tree-based ensemble to assess how ALVSG-augmented data affect boosted decision-tree models.

3  Methodology: Average-Linkage Virtual Sample Generation (ALVSG)

This section describes the proposed average-linkage virtual sample generation (ALVSG) method. Given a small regression dataset 𝒟={(xi,yi)}i=1n, where xi∈Rd and yi∈R, ALVSG aims to generate a set of virtual samples that reflect the underlying structure of 𝒟 and can be used to augment the training set. The method consists of three main components: (1) structure extraction via average-linkage hierarchical clustering, (2) construction of an average-based representation that encodes instance importance, and (3) bounded uniform sampling to generate virtual samples within data-driven limits.

3.1 Average-Linkage Clustering and Notation

To exploit the latent structure of the small dataset, we first apply agglomerative hierarchical clustering with average linkage (UPGMA) using the Euclidean distance. Each instance xi is initially treated as a singleton cluster, and at each iteration the two clusters with the smallest average pairwise distance are merged. This process yields a dendrogram that records the sequence of merges until all instances are grouped into a single cluster.

Let ℒ={L1,L2,…,LP} denote the set of merge events (linkages) in the dendrogram, where each Lp corresponds to the set of instances present in the clusters being merged at step p. For each instance i, we define its link count

ci=|{p:xi∈Lp}|,

that is, the number of linkages in which instance i participates. Intuitively, instances that appear more often in the merging process are more central to the clustering structure. We normalise these counts to obtain instance weights

wi=ci∑j=1ncj,i=1,…,n,

which serve as a structure-informed importance measure for each data point.

3.2 Average-Based Representation

Instead of working directly with the original dataset, ALVSG constructs an average-based representation that emphasizes structurally important instances. Conceptually, this can be viewed as forming a “virtual” dataset in which each instance (xi,yi) is replicated proportionally to its weight wi. Equivalently, we can treat {wi} as sample weights and compute weighted statistics over 𝒟.

For each attribute k=1,…,d and the target y, we compute the weighted mean

μk=∑i=1nwixik,μy=∑i=1nwiyi,

and the corresponding weighted standard deviations

σk2=∑i=1nwi(xik−μk)2,σy2=∑i=1nwi(yi−μy)2.

These statistics summarise the average-based dataset implied by the hierarchical clustering structure without explicitly materialising replicated samples. They will be used to define the sampling region for virtual samples in the next step.

3.3 Virtual Sample Generation

The goal of virtual sample generation is to sample new points that (1) respect the empirical scale of each attribute and (2) preserve the structure-informed variability captured by the weights {wi}. To this end, we adopt a bounded uniform sampling strategy.

For each attribute k and the target y, we first define data-driven bounds using the empirical rule:

ℓk=μk−3σk,uk=μk+3σk,

ℓy=μy−3σy,uy=μy+3σy.

Under mild distributional assumptions, approximately 99.7% of the mass lies within ±3σ around the mean. Following the rationale in [21], we use these ±3σ intervals as conservative yet data-driven bounds that reduce the risk of generating implausible outliers. In practice, we additionally clip (ℓk,uk) to the observed min–max range of attribute k to avoid extrapolation far beyond the original data.

Given the hyper-rectangle

ℛ=∏k=1d[ℓk,uk],

we generate Nvs virtual inputs {x~j}j=1Nvs by sampling each dimension independently from a univariate uniform distribution:

x~jk∼𝒰(ℓk,uk),k=1,…,d.

In this study, we set Nvs=100 for both case studies. Uniform sampling is chosen instead of Gaussian sampling because reliable estimation of higher-order moments (skewness, kurtosis) is difficult in small datasets, and Gaussian-based sampling tends to overemphasize the mean region. Uniform sampling within ℛ yields broader coverage of the plausible space implied by the average-based representation, trading a small bias for reduced variance and estimator fragility in extreme small-n regimes.

For the output variable, two options are commonly used in VSG frameworks: (1) assigning virtual outputs via a surrogate model, or (2) sampling directly from a bounded distribution. In this work, we follow the latter and independently sample

y~j∼𝒰(ℓy,uy),j=1,…,Nvs.

The resulting virtual samples {(x~j,y~j)} are then combined with the original dataset 𝒟 to form an augmented training set

𝒟′=𝒟∪{(x~j,y~j)}j=1Nvs.

3.4 Algorithm Summary

Algorithm 1 summarises the overall ALVSG procedure.

In the experiments (Section 4), we compare forecasting models trained on the original dataset 𝒟 and on the ALVSG-augmented dataset 𝒟′ using SVR, a deep learning regressor, and XGBoost. Performance is evaluated via MAE, MSE, and RMSE, and paired resampling t-tests are used to assess the statistical significance of the observed improvements.

4  Experiments

We empirically evaluate the proposed ALVSG method on two real small datasets. The first case concerns radiotherapy response in bladder cancer cell lines, where the goal is to predict resistance to Cobalt-60 treatment from protein expression profiles. The second case involves multilayer ceramic capacitors (MLCC), where the task is to predict the K-value of ceramic powder based on process and material descriptors. In both cases, we compare baseline models (SVR, deep learning, XGBoost) with their ALVSG-augmented counterparts across a range of small training sizes.

4.1 Experimental Setup and Parameter Settings

Table 1 summarizes the hyperparameters used in this study. For SVR we set C=1.0 with an RBF kernel and γ=0.5. The feed-forward deep learning (DL) regressor uses a learning rate of 0.1, ReLU activation, the adam optimizer, 5000 training iterations, and momentum 0.1. XGBoost employs a learning rate of 0.1, maximum depth of 3, and 100 estimators. Hierarchical clustering for ALVSG uses an agglomerative scheme with average-linkage and Euclidean distance.

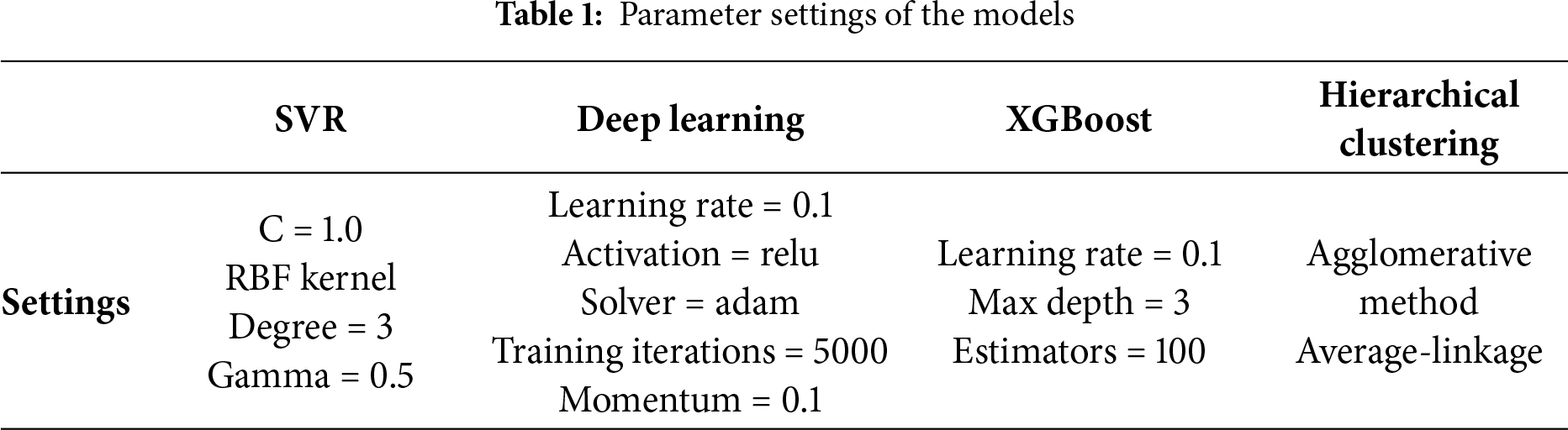
All features are standardized (zero mean, unit variance) using statistics computed on the training split only. To emulate small-dataset regimes, we consider training sizes s∈{5,10,15,20,25} on both datasets (36 and 44 total instances, respectively). For each size s and each dataset, we perform R=20 resamples: we draw s training points without replacement and evaluate on the remaining hold-out instances. Virtual samples are generated only from the training split (100 VS per resample) and appended to the training data; the test set is never augmented. Random seeds are shared between the baseline and +VS conditions to enable paired comparisons. We restricted training sizes to {5,10,15,20,25} to cover the small-sample regime without exhausting the hold-out pool and to avoid highly unstable estimates that arise when the remaining test set becomes too small.

Unless otherwise specified, all statistical comparisons between baseline and ALVSG-augmented models (SVR, DL, XGBoost) use a two-tailed pairedt-test over R=20 resamples at α=0.05. We use the conventional markers *p < 0.05, **p < 0.01, and ***p < 0.001.

4.2 Case 1: Radiotherapy Treatment of Bladder Cancer

Radiotherapy is a common non-surgical treatment for bladder cancer that uses high-energy radiation to destroy tumor cells. In the dataset considered here, nine immortal bladder cancer cell lines were subjected to Cobalt-60 treatment at doses of 5, 10, 20, and 30 Gy. Each observation consists of the expression levels of thirteen proteins related to radiotherapy resistance (MDR, Topo II, EGFR, Neu, c-ErbB-3, c-ErbB-4, cyclin A, cyclin D1, Cdc2, Bcl2, Rb, P16, Bax) plus two additional inputs, for a total of fifteen inputs and one continuous output representing resistance to radiotherapy. The dataset contains 36 valid instances; further details can be found in Chao et al. [22]. Complete per-resample results are omitted here for brevity but are available from the corresponding author upon request.

Results

Tables 2–4 report MAE, MSE, and RMSE for SVR, DL, and XGBoost with and without ALVSG across training sizes. For all three metrics, error decreases as the training size s increases, and in every configuration the ALVSG-augmented variants (SVR+VS, DL+VS, XGBoost+VS) outperform their baselines. Paired t-tests indicate that these improvements are statistically significant for all models and training sizes. Across metrics, XGBoost+VS achieves the lowest errors at larger s, while SVR+VS and DL+VS also exhibit consistent gains, demonstrating that ALVSG provides robust benefits across diverse model classes in this medical small-data setting.

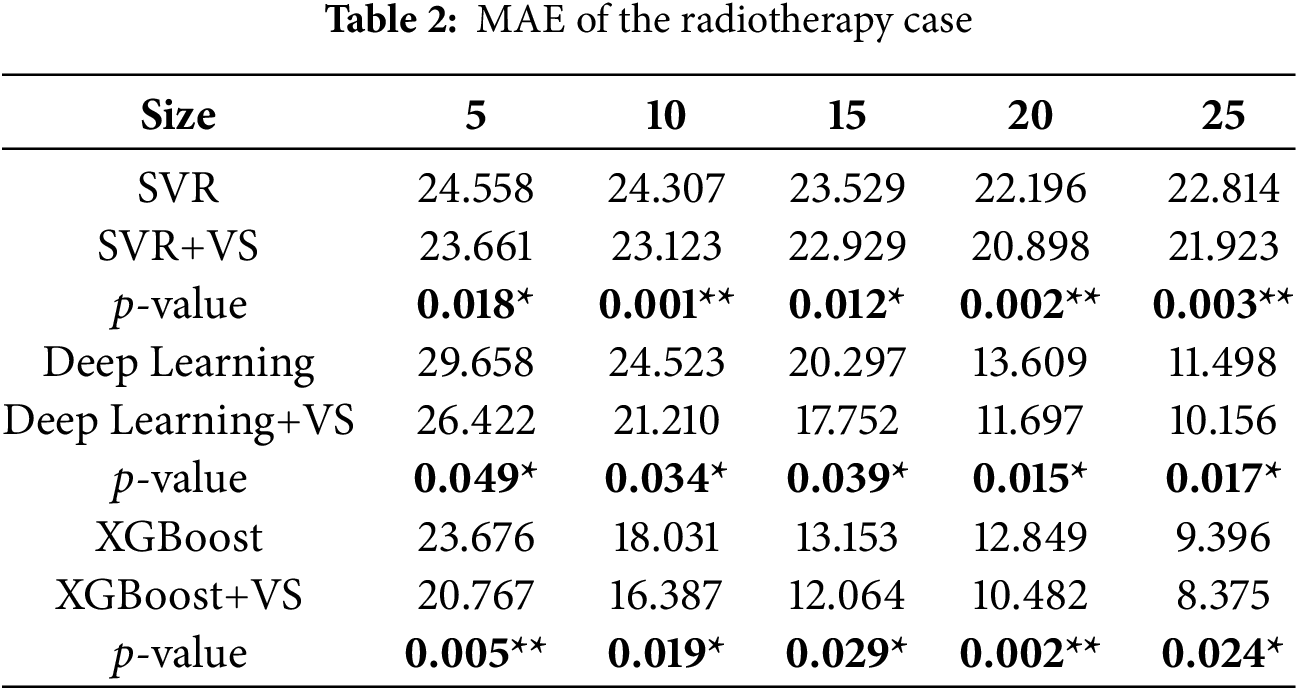
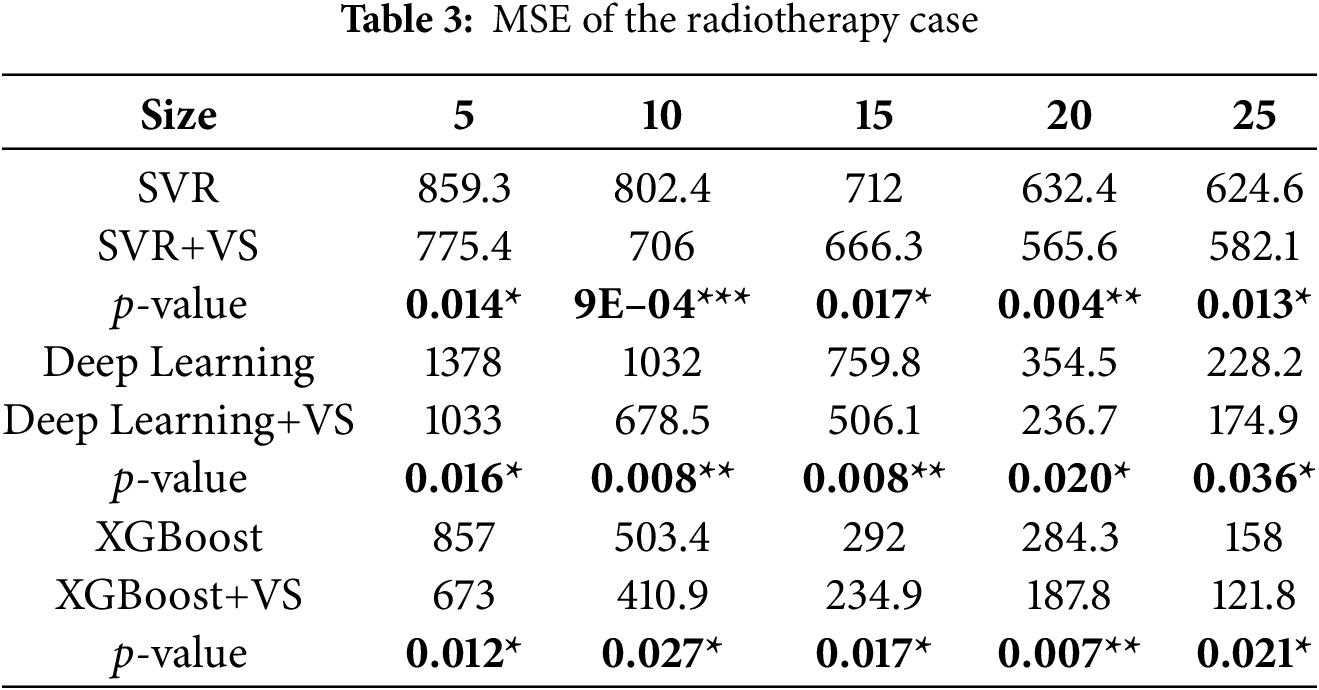
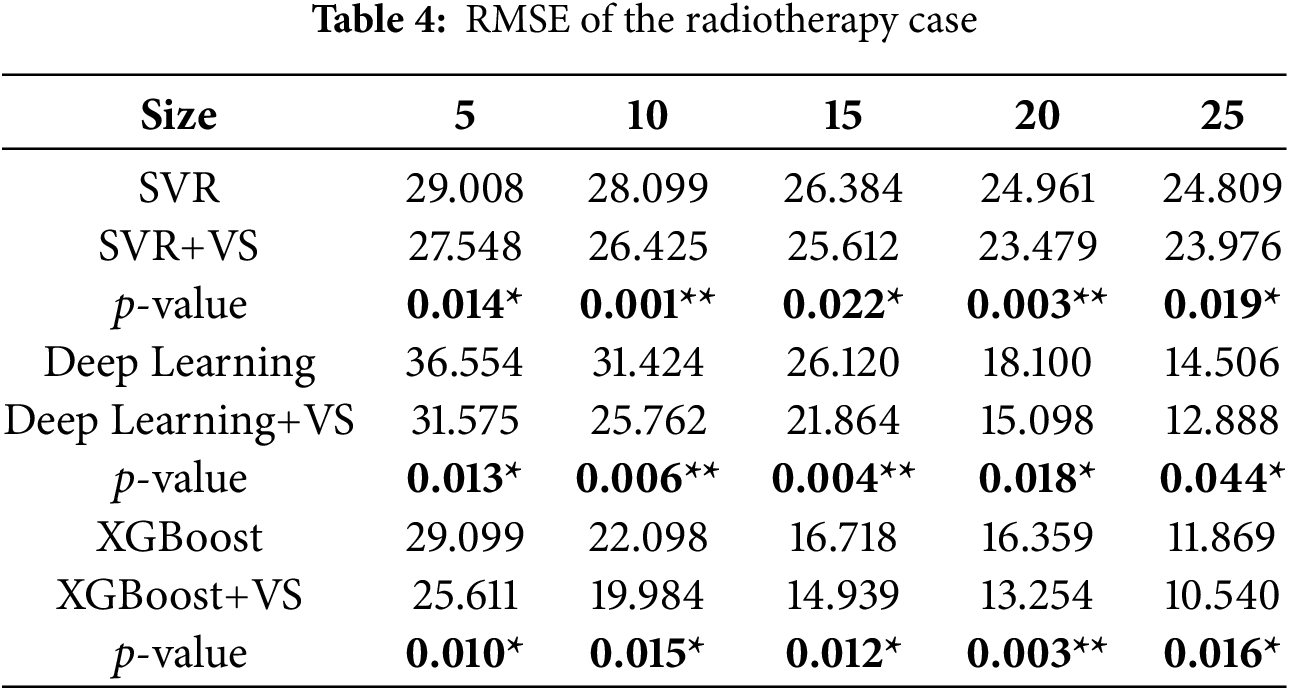
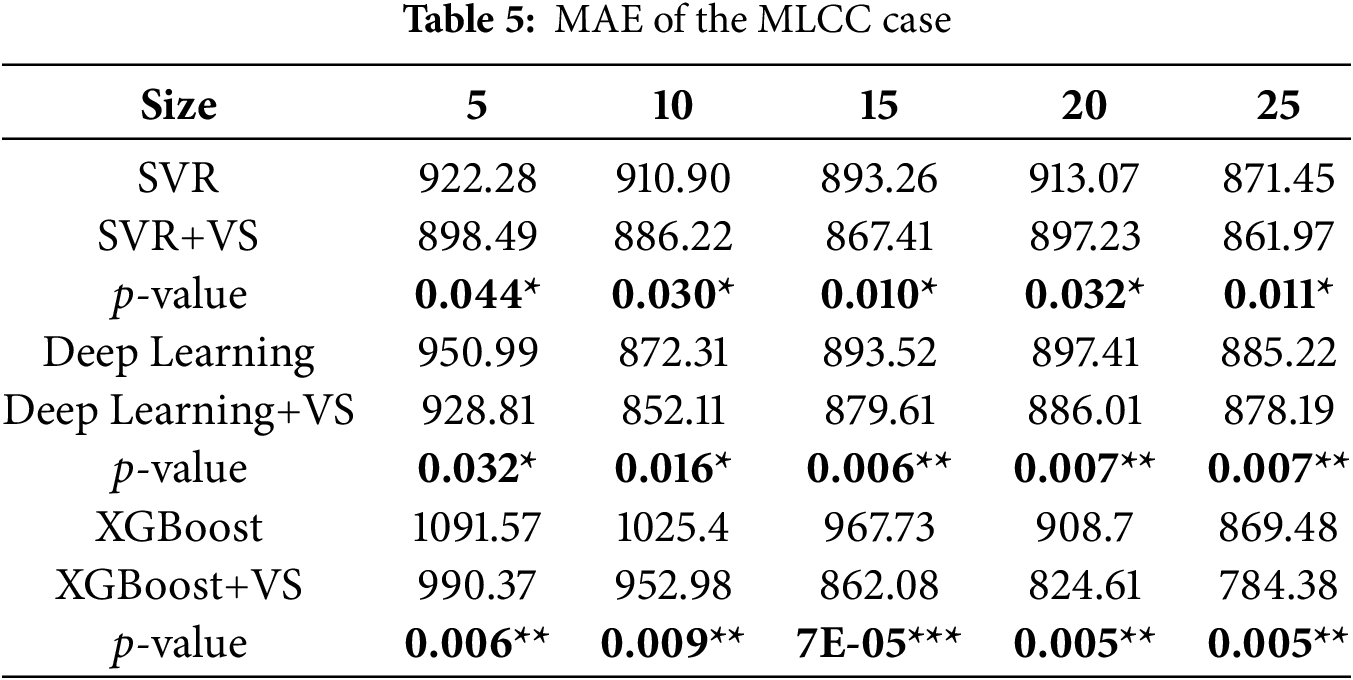
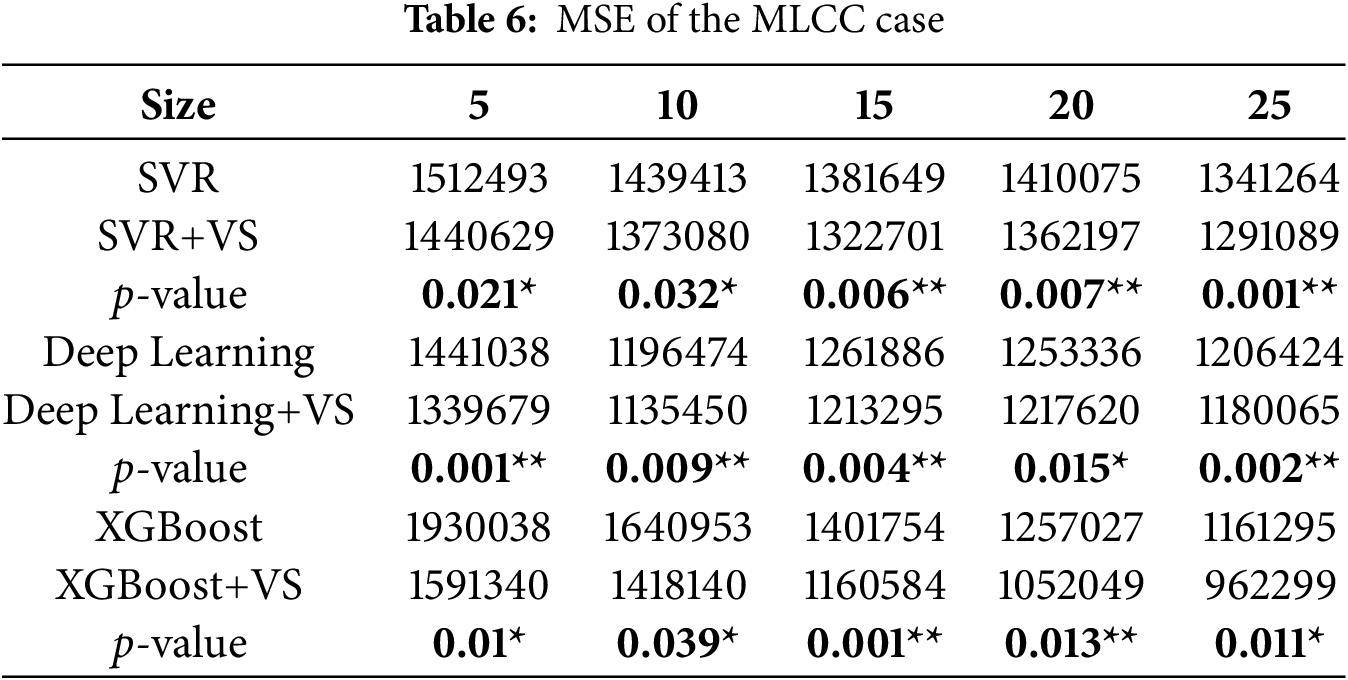
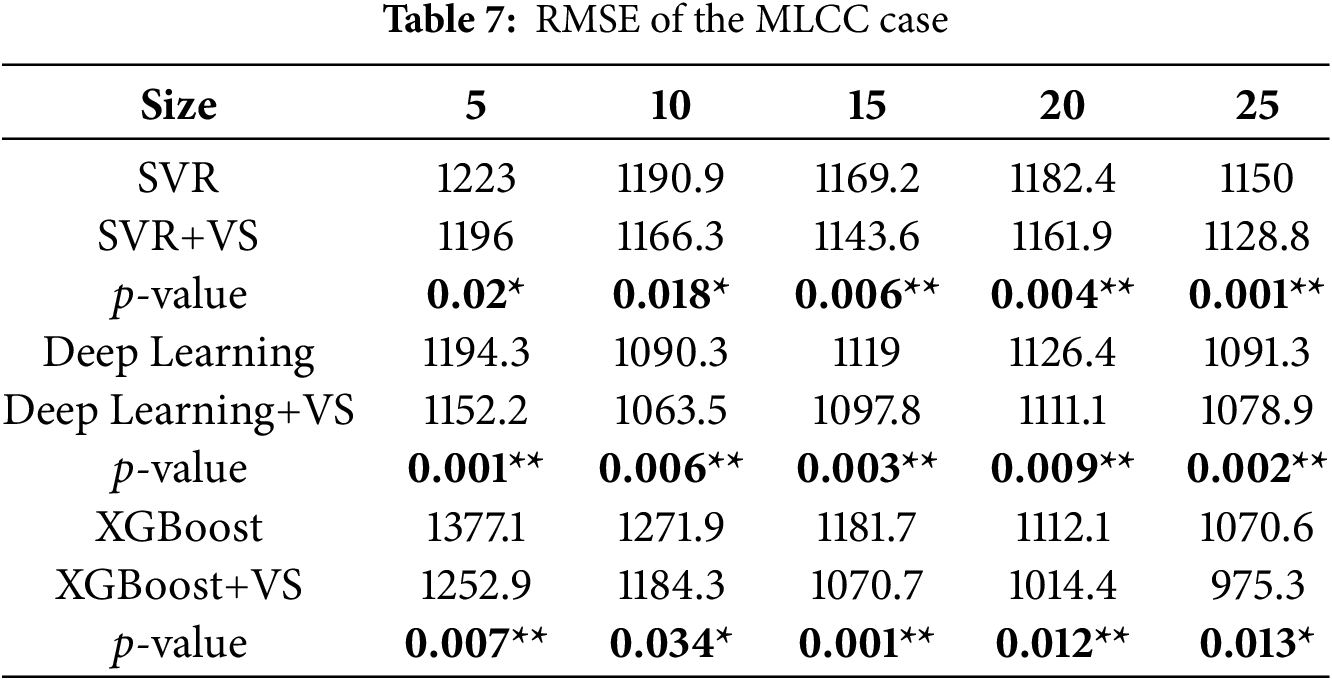
4.3 Case 2: Multilayer Ceramic Capacitors (MLCC)

Multilayer ceramic capacitors (MLCC) are widely used in electronic devices due to their high efficiency and compact form factor. Ceramic powder, a key material in MLCCs, accounts for about 40% of the overall production cost, and its batch-to-batch variability can substantially affect the dielectric constant (K-value) and downstream yield. Manufacturers typically perform pilot runs for each new powder batch to measure the K-value, which increases lead time and cost. In this case study, the goal is to predict the K-value of AD143 ceramic powder from twelve input variables, including surface area (SA), particle size distribution (PSD-90, PSD-50, PSD-10), moisture (Mois), sintering temperature (Sinter Temp), potassium content (K), dissipation factor (DF), and several temperature-coefficient–related descriptors (TC-min, TC-max, TC-peak, D-50). The dataset contains 44 pilot runs. Recent work has shown that ensemble models such as XGBoost are effective for MLCC reliability and degradation modeling [23], providing additional motivation for including XGBoost as a benchmark in this study. Per-resample results are omitted here for brevity; detailed metrics for all resamples can be obtained from the authors upon request.

Results

Tables 5–7 summarize MAE, MSE, and RMSE for the MLCC case. As in the radiotherapy case, ALVSG consistently improves all three models across all training sizes. For SVR, DL, and XGBoost, the +VS variants yield lower errors than their baselines, and the corresponding p-values confirm that these differences are statistically significant at every size. While the absolute errors are larger than in the radiotherapy task due to the different output scales, the relative gains from ALVSG remain substantial, particularly for XGBoost, which shows the largest reductions in MAE, MSE, and RMSE as s increases. These results indicate that ALVSG provides stable benefits even in an industrial setting with measurement noise and batch variability.

4.4 Baselines and Alternatives (Discussion)

Virtual sample generation can be realized via multiple paradigms. Manifold/interpolation-based t-SNE-VSG [4] leverages low-dimensional embeddings; GAN/active-learning hybrids [16] and statistically constrained APS-VSG [17] emphasize generative fidelity and validity; and co-training VSG [15] iteratively accepts samples passing consistency checks. Compared with these, ALVSG is (i) structure-aware yet lightweight, relying only on average-linkage dendrograms; (ii) hyperparameter-lean (no adversarial training or heavy surrogates); and (iii) transparent, since link counts translate directly into sampling weights. On the two real small datasets, ALVSG consistently improves three diverse predictors under paired resampling. A full ablation against the above generative families would be valuable but data-hungry; we therefore leave a calibrated, multi-dataset head-to-head as future work and position ALVSG as a strong, interpretable baseline for very small tabular n, where heavier generators are brittle or hard to tune.

5  Conclusions

This paper proposed average-linkage virtual sample generation (ALVSG), a structure-aware yet lightweight approach for small tabular regression datasets. ALVSG first applies agglomerative hierarchical clustering with average linkage and turns dendrogram link counts into instance weights, yielding an average-based representation that emphasizes structurally central points. It then defines conservative, data-driven ±3σ bounds per attribute and target and samples uniformly within these bounds to generate virtual samples, which are appended to the original training set in a model-agnostic manner.

The method was evaluated on two real small-data cases: radiotherapy response in bladder cancer and K-value prediction for multilayer ceramic capacitors (MLCC). Across both datasets, three forecasting models (SVR, deep learning, XGBoost), and five training sizes (s∈{5,10,15,20,25}), ALVSG consistently reduced MAE, MSE, and RMSE relative to training on the original data alone. Paired t-tests over resampled splits confirmed that these improvements are statistically significant in all configurations, indicating that simple structure-informed augmentation can provide robust gains in very small-n regimes without heavy generative modeling.

Overall, ALVSG shows that exploiting hierarchical clustering structure to construct a weighted representation, combined with bounded uniform sampling, is an effective and practical way to improve predictive performance when data are scarce. Future work will extend the evaluation to additional domains and compare ALVSG head-to-head with more complex virtual-sample generators under carefully controlled small-data benchmarks.

Practical Implications and Limitations

In practice, ALVSG is most useful when (i) the number of samples is very small (n<50), (ii) features are tabular with moderate local structure, and (iii) complex generators such as GANs are difficult to tune or validate. It is plug-in and model-agnostic, requiring only feature scaling, a distance metric, and a choice of Nvs.

Limitations include: (a) the method does not explicitly model the full data density; (b) uniform sampling within ±3σ may under-represent valid extreme tails when strong prior knowledge is available; and (c) performance can be sensitive to feature scaling and the chosen linkage/distance in the clustering step. In domains with reliable priors, ALVSG could be combined with prior-constrained bounds or non-uniform sampling schemes; designing such hybrids and testing them across broader small-data benchmarks is a promising direction for future research.

Acknowledgement: This research was supported by the National Science and Technology Council (NSTC), Taiwan.

Funding Statement: This work received funding support from the National Science and Technology Council (NSTC), Taiwan, under Grant No. 114-2410-H-011-026-MY3.

Author Contributions: Chih-Chieh Chang, Khairul Izyan Bin Anuar and Yu-Hwa Liu contributed to the writing of the main sections, including the introduction, literature review, methodology, experiments, and conclusion. Chih-Chieh Chang and Khairul Izyan Bin Anuar organized the related work and implemented the experimental setup. Chih-Chieh Chang and Yu-Hwa Liu revised the manuscript and discussed the experimental results. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: No datasets were generated or analyzed during the current study.

Ethics Approval: This paper does not contain any studies with human participants or animals performed by any of the authors.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Cho S, Cha K. Evolution of neural network training set through addition of virtual samples. In: Proceedings of IEEE International Conference on Evolutionary Computation; 1996 May 20–22; Nagoya, Japan. p. 685–8. [Google Scholar]

2. Niyogi P, Girosi F, Poggio T. Incorporating prior information in machine learning by creating virtual examples. Proc IEEE. 1998;86(11):2196–209. doi:10.1109/5.726787. [Google Scholar] [CrossRef]

3. Chen ZS, Zhu B, He YL, Yu LA. A PSO based virtual sample generation method for small sample sets: applications to regression datasets. Eng Appl Artif Intell. 2017;59:236–43. doi:10.1016/j.engappai.2016.12.024. [Google Scholar] [CrossRef]

4. He YL, Hua Q, Zhu QX, Lu S. Enhanced virtual sample generation based on manifold features: applications to developing soft sensor using small data. ISA Trans. 2022;126(4):398–406. doi:10.1016/j.isatra.2021.07.033. [Google Scholar] [PubMed] [CrossRef]

5. Wedyan M, Crippa A, Al-Jumaily A. A novel virtual sample generation method to overcome the small sample size problem in computer aided medical diagnosing. Algorithms. 2019;12(8):160. doi:10.3390/a12080160. [Google Scholar] [CrossRef]

6. Zhu QX, Hou KR, Chen ZS, Gao ZS, Xu Y, He YL. Novel virtual sample generation using conditional GAN for developing soft sensor with small data. Eng Appl Artif Intell. 2021;106(2):104497. doi:10.1016/j.engappai.2021.104497. [Google Scholar] [CrossRef]

7. Jain AK. Data clustering: 50 years beyond K-means. Pattern Recognit Lett. 2010;31(8):651–66. doi:10.1016/j.patrec.2009.09.011. [Google Scholar] [CrossRef]

8. Li DC, Chang CC, Liu CW. Using structure-based data transformation method to improve prediction accuracies for small data sets. Decis Support Syst. 2012;52(3):748–56. doi:10.1016/j.dss.2011.11.021. [Google Scholar] [CrossRef]

9. Lu J, Gong P, Ye J, Zhang J, Zhang C. A Survey on Machine Learning from Few Samples. Pattern Recognit. 2023;139(2):109480. doi:10.1016/j.patcog.2023.109480. [Google Scholar] [CrossRef]

10. Xu P, Ji X, Li M, Lu W. Small data machine learning in materials science. npj Comp Mater. 2023;9(42):42. doi:10.1038/s41524-023-01000-z. [Google Scholar] [CrossRef]

11. Zhang L, Deng H. NJmat 2.0: user instructions of data-driven machine learning interface for materials science. Comput Mater Contin. 2025;83(1):1–11. doi:10.32604/cmc.2025.062666. [Google Scholar] [CrossRef]

12. Fan C, Hou B, Zheng J, Xiao L, Yi L. A surrogate-assisted particle swarm optimization using ensemble learning for expensive problems with small sample datasets. Appl Soft Comput. 2020;91:106242. doi:10.1016/j.asoc.2020.106242. [Google Scholar] [CrossRef]

13. Sharma A, Paliwal KK. Linear discriminant analysis for the small sample size problem: an overview. Int J Mach Learn Cybern. 2015;6(3):443–54. doi:10.1007/s13042-013-0226-9. [Google Scholar] [CrossRef]

14. Doan QH, Mai SH, Do QT, Thai DK. A cluster-based data splitting method for small sample and class imbalance problems in impact damage classification. Appl Soft Comput. 2022;120:108628. doi:10.1016/j.asoc.2022.108628. [Google Scholar] [CrossRef]

15. Zhu QX, Zhang HT, Tian Y, Zhang N, Xu Y, He YL. Co-training based virtual sample generation for solving the small sample size problem in process industry. ISA Trans. 2023;134:290–301. doi:10.1016/j.isatra.2022.08.021. [Google Scholar] [PubMed] [CrossRef]

16. Cui C, Tang J, Xia H, Wang D, Yu G. Virtual Sample Generation Method Based on GAN for Process Data with Its Application. In: Proceedings of the 2022 34th Chinese Control and Decision Conference (CCDC); 2022 Aug 12–17; Hefei, China. p. 242–7. [Google Scholar]

17. Chen Z, Lv Z, Di R, Wang P, Li X, Sun X, et al. A novel virtual sample generation method to improve the quality of data and the accuracy of data-driven models. Neurocomputing. 2023;548(01):126380. doi:10.1016/j.neucom.2023.126380. [Google Scholar] [CrossRef]

18. Wang Z, Wang P, Liu K, Wang P, Fu Y, Lu CT, et al. A comprehensive survey on data augmentation. IEEE Trans Knowl Data Eng. 2026;38(1):47–66. doi:10.1109/tkde.2025.3622600. [Google Scholar] [CrossRef]

19. Dong Y, Luo M, Li J, Liu Z, Zheng Q. Semi-supervised graph contrastive learning with virtual adversarial augmentation. IEEE Trans Knowl Data Eng. 2024;36(8):4232–44. doi:10.1109/tkde.2024.3366396. [Google Scholar] [CrossRef]

20. Drucker H, Wu D, Vapnik VN. Support vector machines for spam categorization. IEEE Trans Neural Netw. 1999;10(5):1048–54. doi:10.1109/72.788645. [Google Scholar] [PubMed] [CrossRef]

21. Yang J, Yu X, Xie ZQ, Zhang JP. A novel virtual sample generation method based on Gaussian distribution. Knowl-Based Syst. 2011;24(6):740–8. doi:10.1016/j.knosys.2010.12.010. [Google Scholar] [CrossRef]

22. Chao GY, Tsai TI, Lu TJ, Hsu HC, Bao BY, Wu WY, et al. A new approach to prediction of radiotherapy of bladder cancer cells in small dataset analysis. Expert Syst Appl. 2011;38(7):7963–9. doi:10.1016/j.eswa.2010.12.035. [Google Scholar] [CrossRef]

23. Yousefian P, Sepehrinezhad A, van Duin ACT, Randall CA. Improved prediction for failure time of multilayer ceramic capacitors (MLCCsa physics-based machine learning approach. APL Mach Learn. 2023;1(3):036107. doi:10.1063/5.0221988. [Google Scholar] [CrossRef]