 Open Access
Open Access
ARTICLE
A Distributed Anonymous Reputation System for V2X Communication
1 Faculty of Electrical Engineering, Universiti Teknologi Malaysia, Johor Bahru, 81310, Malaysia
2 Graduate School of Advanced Science and Engineering, Hiroshima University, Higashi-Hiroshima, 739-8527, Japan
* Corresponding Author: Toru Nakanishi. Email:
# These authors contributed equally to this work
(This article belongs to the Special Issue: Advances in IoT Security: Challenges, Solutions, and Future Applications)
Computers, Materials & Continua 2026, 87(1), 41 https://doi.org/10.32604/cmc.2025.073774
Received 25 September 2025; Accepted 19 December 2025; Issue published 10 February 2026
Abstract
V2X communication enables vehicles to share real-time traffic and road-condition data, but binding messages to persistent identifiers enables location tracking. Furthermore, since forged reports from malicious vehicles can distort trust decisions and threaten road safety, privacy-preserving trust management is essential. Lu et al. previously presented BARS, an anonymous reputation mechanism founded on blockchain technology to establish a privacy-preserving trust architecture for V2X communication. In this system, reputation certificates without a vehicle identifier ensure anonymity, while two authorities jointly manage certificate issuance and reputation updates. However, the centralized certificate updates introduce scalability limitations, and the authorities can trace vehicle behavioral information, which threatens privacy guarantees. Several subsequent systems derived from BARS still rely on centralized certificate management and are subject to authority-side privacy leakage. As a result, a key challenge in this line of research remains unresolved: how to decentralize the certificate-update process while preserving privacy against the authorities in privacy-preserving V2X trust management. In this paper, we propose a distributed anonymous reputation system for V2X communication, based on an anonymous reputation system for crowdsensing. In our proposed system for V2X communication, the server is distributed to a certificate authority (CA) and roadside units (RSUs). Each vehicle shows the reputation level to the nearest RSU at the beginning of each time interval, and registers a short-time public key. In the interval, the messages from the vehicle are authenticated under the public key and are scored. At the end of the interval, the nearest RSU updates the certificate anonymously. Our solution decentralizes the certificate-update process by assigning each update to the nearest RSU. A zero-knowledge-proof-based show protocol removes the need for any central authority to handle vehicle certificates and thus prevents the authorities from tracing vehicle activities. Compared with BARS, where centralized authorities must update the reputation certificates of many vehicles and may incur communication and processing delays, our system performs each update locally at the nearest RSU once per interval. The required interaction consists only of a few kilobytes of communication and a zero-knowledge proof that is almost fully precomputed on the vehicle side, while the RSU-side processing is estimated to take about 40 ms based on timing measurements of the underlying cryptographic operations. This distributed update model avoids the centralized bottleneck of BARS and simultaneously removes the privacy risk arising from authority collusion.Keywords
The privacy of one’s location is a major concern, especially for drivers. However, real-time local information, such as traffic and road conditions, is essential for efficient urban management. Therefore, it is critical to collect and share such local information while respecting privacy. Consider a scenario in which vehicles collect local information and exchange it via V2X communication, such as V2V and V2I. To deter message tampering and impersonation, messages from each vehicle should be authenticated. Nevertheless, since location can often be inferred from both the reported content and authentication metadata, linking authenticated messages to persistent vehicle identities can violate privacy.
V2X communication faces significant challenges due to its open and decentralized nature. When malicious vehicles disseminate falsified data, they undermine both the reliability of information exchange and the safety of ordinary drivers. Consequently, trust evaluation and management in V2X communication has attracted significant attention in recent years.
Vehicle ad-hoc network (VANET) reputation systems have been studied in the literature, but most approaches do not consider the privacy aspect of vehicles (e.g., [1–3]). These studies mainly focus on frameworks for evaluating vehicle behavior and message forwarding to detect misbehavior. In contrast, in the context of crowdsensing, a privacy-aware reputation system called ARTSense was proposed in [4]. In crowdsensing, numerous mobile users voluntarily collect sensing data, such as location and environmental information, which are submitted to and analyzed by a centralized server. Therefore, user privacy must be taken into account. To achieve the anonymity of users, ARTSense separates the data reporting process from the reputation updating process. No user identity information is revealed in individual sensing reports. Furthermore, the server cannot link multiple reports to the same participant due to the use of blind IDs. However, this work is not designed for V2X communication, which is characterized by high mobility and a dynamic network topology.
In 2016, Jaimes et al. [5] proposed a centralized anonymous reputation system (ARS) for V2X communication, including VANETs, in which vehicles interact with roadside units (RSUs) to submit feedback to a centralized reputation server (RepS) and to retrieve their current reputation levels under pseudonyms. The server updates the reputation level of each vehicle by associating anonymous identities with real identities. ARS introduced the notion of security states, which can help identify region-specific risks and support the evaluation of neighboring vehicles’ reputation scores. The reputation level of a vehicle is the result of the aggregation of the reputation levels by the characteristics of generation and forwarding of messages. However, the centralized server causes the bottleneck in scalability, single point of failure, and privacy risk that the server can reveal the location history of vehicle.
In 2018, Lu et al. [6] proposed a blockchain-based anonymous reputation system (BARS) to establish a privacy-preserving trust model for V2X communication. In this system, a certificate authority (CA) issues certificates to vehicles and manages revocation. All activities of CA are recorded on the blockchain for transparency. The certificate includes no vehicle ID and is thus anonymous. On the other hand, a law enforcement authority (LEA) is responsible for managing the correspondence between public keys and real identities. In case of disputes, the LEA can trace a vehicle from a public key used for authentication. Furthermore, BARS incorporates a reputation system in which the LEA monitors and evaluates each vehicle’s behavior, and updates its reputation score. The reputation is certified by the certificate, and updated by the CA with the assistance of the LEA. The reputation system is anonymous due to the hidden vehicle’s ID. However, the two authorities CA and LEA cooperatively update the certificate of each vehicle. Thus, when lots of vehicles communicate messages, the centralized update process can become a bottleneck, i.e., BARS also have a scalability disadvantage. In addition, if the two authorities collude, they may reveal the location history of a vehicle.
In this paper, toward a distributed privacy-preserving trust management in V2X communication, we propose an anonymous reputation system for V2X communication, which is derived from an anonymous reputation system for crowdsensing [7]. In the system for crowdsensing, the server updates the reputation certificate of each user s.t. the user’s ID and even the reputation value are hidden. Using a zero-knowledge proof (ZKP), the user can prove the reputation level (an integer range that contains the reputation value). In our proposed system for V2X communication, the server is distributed across CA and RSUs (roadside units). Each vehicle shows the reputation level to the nearest RSU at the beginning of each time interval, similarly to the underlying system [7], and registers a short-time public key. In the interval, the messages from the vehicle are authenticated under the public key and are scored. At the end of the interval, the nearest RSU updates the certificate anonymously.
To situate our contributions within existing approaches, Table 1 summarizes the difference in the architecture, anonymity, and costs across ARS, BARS, and our proposed system. This distributed update in our system avoids the centralized certificate-update process in BARS [6], where two central authorities must update the certificates of many vehicles, potentially causing communication and processing delays. In our system, each update is performed locally at the nearest RSU once per interval, requiring only a few kilobytes of communication and a zero-knowledge proof that is almost fully precomputed on the vehicle side, with the RSU-side processing estimated to take about 40 ms based on timing measurements of the underlying cryptographic operations. This distributed mechanism removes the centralized bottleneck of BARS and mitigates the privacy risk arising from possible authority collusion. Per-message authentication during the interval uses the same pseudonym-certificate mechanism as in existing RSU-assisted V2X systems, and ZKPs are required only once per interval; detailed efficiency considerations are discussed in Section 6. From these efficiency considerations, we consider that the practicality of the proposed system is demonstrated without requiring mobility-level simulations. Network-level performance evaluations under specific traffic and mobility models (e.g., NS-3 or SUMO) are important as complementary research directions that depend on application scenarios. We therefore leave such system-level evaluations as future work.

In our system, a malicious vehicle cannot be traced by authorities such as the LEA. However, the vehicle can be scored low in the anonymous reputation system, and the messages can be flagged as untrustworthy. The secret key of each RSU is unique, and thus a compromised RSU must also be revoked. The revocation is done using a complete subtree (CS) method [8] to compute revocation information for RSUs. In this paper, we do not address blockchain-based transparency, and the detailed reputation evaluation algorithm for scoring is also beyond the scope of our study. While both components are essential for constructing a complete and practical V2X trust management system, they are conceptually separable from the fundamental challenge we focus on in this research line. Since our main contribution is the distributed certificate-update mechanism with zero-knowledge-proof-based privacy protection, the practical evaluation presented in Section 6 concentrates on this fully specified component. The integration of more sophisticated reputation evaluation algorithms and scalable blockchain-based transparency mechanisms, which may require additional cryptographic and system-level design considerations, is left as future work.
1.3 Difference from the Conference Version [9]
A preliminary version of this paper was presented in ICCE 2024 [9], where security requirements are informally defined, and only the proof sketches for the security requirements are shown. In this paper, we formally show game-based security definitions, and prove the security based on the definitions. Furthermore, we extend the original system [9] by adding a revocation function for malicious RSUs, and we newly provide a detailed efficiency evaluation of the system.
The recent works related to BARS and our proposed system are as follows.
In [10], Ahmed et al. propose a privacy-enhancing V2X trust management system that combines pseudo-identity–based anonymous authentication with blockchain-based revocation, similar to BARS. Compared with BARS, it integrates a more sophisticated context-aware trust (reputation) computation and improves verification efficiency through signature aggregation. However, the scheme relies on a fully trusted TA (Trusted Authority) that centrally generates and manages each vehicle’s pseudo-identities and secret keys, and thus TA can compromise user’s privacy by de-anonymization, as in BARS.
In [11], Feng et al. propose a blockchain-based privacy-preserving authentication system for V2X environments. The system adopts a structure similar to BARS by introducing two ID management entities and realizing vehicle anonymity through pseudonym-based public-key certificates. In addition, the system employs an asynchronous accumulator that is a hash-tree-based mechanism, to accelerate revocation verification. However, this approach focuses solely on authentication and revocation, and thus does not incorporate a reputation-based trust management mechanism. Moreover, if the two management entities collude, the linkage of pseudonyms becomes possible, which results in the leakage of vehicle behavioral information.
In [12], Feng et al. proposed a privacy-preserving authentication scheme for V2X communication. In the system, a certification authority issues certificates for pseudonymous identities and enables anonymous authentication, while leveraging polynomial commitments to achieve constant-cost revocation checking. However, the system also focuses solely on authentication and revocation, and does not provide a reputation-based trust management. Moreover, the certificate update process is centrally managed, allowing the authority to link successive certificates, and thus the privacy of vehicles is compromised.
In [13], Hou et al. introduce a double-layer blockchain architecture, consisting of an event chain and a reputation chain, and propose a sophisticated reputation-based trust management system for V2X communication, which resists against on–off attacks and collusive attacks. However, the system does not address privacy protection. It assumes a fully trusted TA that issues public-key certificates, and thus the TA can easily deanonymize any vehicle even when pseudonyms are used. Moreover, since both reputation information and event reports are persistently stored on the blockchain, linkability among observations and historical behavior may still weaken privacy, even under pseudonym-based identifiers.
In [14], Fernandes et al. propose a V2X trust management system based on a consortium blockchain that employs a PoA (Proof of Authority) consensus mechanism, where RSUs collaboratively update reputation scores to improve efficiency. However, the system relies entirely on a centralized CA for certificate issuance and management, and it does not support certificate updates. As a result, it cannot also prevent deanonymization by the CA, and the reputation values tied to static IDs allow vehicle behavior to be tracked through linkable evaluation records.
We adopt the following bilinear groups:
1.
2.
• for all
•
For the security of the proposed system, we use the
Definition 1 (
is negligible, where
We employ the scheme in [15] where a message and the signature can be proven by the zero-knowledge proofs.
Here are the descriptions of the algorithm.
• BB-Setup: Select bilinear group parameters
• BB-KeyGen: Compute
• BB-Sign: On input of a message
• BB-Verify: On inputs of a message
In [15], the security is proved under the
We also use an extension of BB signature, BBS+ signature, which is informally introduced in [16], to sign a vector of numerous messages. The concrete structure is displayed in [17,18].
• BBS+-Setup: Select bilinear group parameters
• BBS+-KeyGen: Compute
• BBS+-Sign: On input of a vector
• BBS+-Verify: For the signature
The security is proved in [18] under the
2.5 Signature-Based Proofs of Knowledges (
For Non-Interactive Zero-Knowledge Protocol (NIZK) proofs on representations, we adopt signature-based proofs of knowledge (SPKs), which are converted from zero-knowledge proofs of knowledge (PoKs) or Sigma protocols [19]. Concretely, we utilize the SPK to prove a representation of
2.6 Complete Subtree (CS) Method
We adopt Complete Subtree (CS) method [8] to achieve efficient user revocation in group signatures [20–22]. First, a group manager (GM) generates a binary tree with the number of leaves equal to the total number of users, N. Each node is assigned a node ID, and each user is assigned to a leaf node. An example is shown in Fig. 1, where each user is assigned to nodes
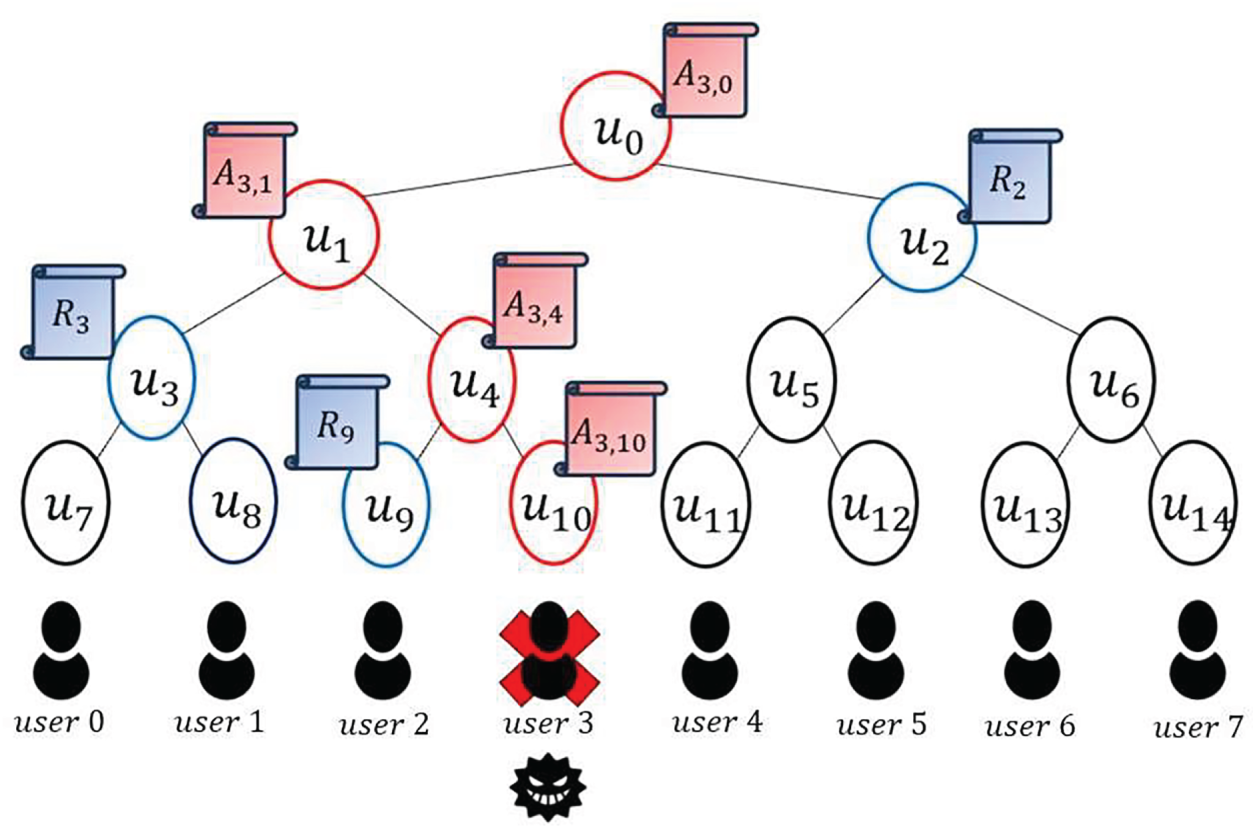
Figure 1: Example of CS method
The proposed anonymous reputation system consists of the following algorithm and protocols. The participants of this system are the certificate authority (CA), the roadside units (RSUs), and vehicles. In this system, messages sent from each anonymous vehicle are linkable via a pseudonym (i.e., short-time public key) during each time interval, and messages across intervals are unlinkable. At the first message in the interval, the vehicle shows the vehicle’s reputation level to the nearest RSU, and the pseudonym at the interval is registered. The vehicle must ensure that the nearest RSU is not being revoked during this authentication. Each message is rated by the nearest RSU, and the scores at each interval are accumulated by RSUs. At the final message in the interval, the reputation of the vehicle is updated by the nearest RSU.
The anonymity of this system ensures that an adversary cannot obtain information about each vehicle other than the evaluation level and linkability (determining whether any two authenticated vehicles are the same) at each interval. This requirement means that the adversary cannot know the ID of the RSU with which each vehicle last communicated in the previous interval. Therefore, while hiding the public key of the last RSU that it communicated with, the vehicle performs a zero-knowledge proof of the certificate of the evaluation value by the RSU.
• Setup: CA takes a security parameter
• Register: This is an interactive protocol between a vehicle and the CA. The common input is
• RevokeRSU: This algorithm allows the CA to revoke an RSU. Given the ID of a revoked RSU, it outputs a revocation list
• Show: This protocol is called in the first communication at each time interval. This is an interactive protocol between a vehicle and the nearest RSU, where the vehicle shows that its reputation value is included in an integer range that is called reputation level. The vehicle also checks that the RSU is not being revoked. The common input are
• Authentication: This is an interactive protocol between a vehicle and the nearest RSU. The common input is
Each message M is rated by the nearest RSU based on some evaluation method (e.g., ARTSense [4]) that uses the reputation level together with other information. A negative rating is possible by using a negative integer. For the rated score
• Update: This protocol is called in the final communication at each time interval, where the total score
As in [7], we consider the following requirements:
• Reputation Unforgeability: Any vehicle cannot prove inappropriate reputation level, i.e., for the correct reputation
• Anonymity: Any adversary cannot obtain any information on each vehicle except the reputation level and the linkability (i.e., whether the vehicles of any two authentications are the same or not ) in each interval from the protocols. This means that the adversary cannot determine whether the vehicles of any two authentications are the same or not across intervals. Furthermore, this requirement means that the adversary cannot know the ID of the nearest RSU that executes the Update protocol.
We adjust the security requirements in the underlying system [7] to our above-mentioned model in the V2X communication, as follows. In the underlying system, each authentication is rated, and the score is added to the reputation of the user, but in the proposed system, scores in each interval are summed and added to the the reputation of the vehicle. Thus, in the underlying system, all authentications are unlinkable w.r.t. the sameness of the user, but in the proposed system, the authentications during each interval are linkable (the authentications across intervals are unlinkable).
Furthermore, we require the following security properties in authentications and RSU revocation.
• Misauthentication resistance: In each Authentication protocol, any vehicle which does not succeed Show protocol in the current interval cannot be accepted.
• RSU revocablity: An RSU can be revoked, and then any vehicle with a reputation certificate issued from a revoked RSU does not succeed Show protocol.
We formally define the security requirements, as follows.
3.2.1 Reputation Unforgeability
In the definition of reputation unforgeability, we utilize the following oracles.
•
•
•
•
•
Then, consider the following reputation unforgeability game, where
Run
Return 1 if
the final
but
Return 0;
Definition 2(Reputation Unforgeability): An anonymous reputation system is reputation unforgeable, if for any PPT adversary
3.2.2 Misauthentication Resistance
In the definition of misauthentication resistance, we utilize the oracles in the reputation unforgeability.
Then, consider the following misauthentication resistance game, where
Run
Return 1 if
the final
but the vehicle
interval.
Return 0;
Definition 3(Misauthentication Resistance): An anonymous reputation system is misauthentication resistant, if for any PPT adversary
In the definition of RSU revocability, we utilize the oracles in the reputation unforgeability.
Then, consider the following revocability game, where
Run
Return 1 if
the final
but for the vehicle
Return 0;
Definition 4(RSU Revocability): An anonymous reputation system is RSU revocable, if for any PPT adversary
In the definition of anonymity, we utilize the following oracles.
•
•
•
•
•
•
Then, consider the following anonymity game, where
Return 1 if
Return 0;
Definition 5(Anonymity): An anonymous reputation system is anonymous, if for any PPT adversary
In BARS [6], two central authorities update a certificate for a short-time public key and the reputation to issue the vehicle, where the authorities have to evaluate each vehicle and update the reputation and the certificate. As a result, the update process is centralized and not scalable.
In our system, distributed RSUs in the V2X system manage the scores of each vehicle in each interval, and the nearest RSU updates a certificate for the new reputation using the RSU’s secret key.
As the base system, we adopt the anonymous reputation system [7] for crowdsensing. In the system, a server and users participate. The server issues a certificate for the reputation to each user, where the certificate is a BBS+ signature on the user’s secret, a certificate tag for checking one-time use of the certificate, and the reputation. Since the concrete value of the reputation can reveal the relevance to other authentications, the reputation level (an integer range where the reputation value is included) is shown in the Show protocol for authentication. In addition, while the reputation value is hidden using commitments, the certificate is updated by the server s.t. the certified reputation is reflected by the score for the authentication using the evaluation method of ARTSense [4].
We extend the system of [7] to construct the anonymous reputation system for V2X communication, as follows. In our system, a CA, RSUs, and vehicles participate. The central CA generates the CA’s key pair, and each RSU’s individual key pairs, and also generates the certificate of the RSU’s public key as a BBS+ signature which can be proved by an SPKs. The BBS+ signature is also used for RSU revocation, as mentioned later. At first, a vehicle is issued as an initial certificate which is similar to the original certificate in [7], i.e., a BBS+ signature on the user’s secret, a certificate tag, and the (initial) reputation. The original Show protocol is separated to Show protocol and Update protocol in our system. In Show called in the first time of each time interval, a vehicle proves the knowledge of the reputation certificate similarly to [7] to show the reputation level. In Update called in the final time of each time interval, instead of the central CA, the nearest RSU updates the reputation certificate reflected by the total score of the vehicle in the interval, where the BBS+ signature of the certificate is generated using the RSU’s secret key.
The point in this construction is that, in Show, the vehicle needs to hide the ID of the RSU updating the certificate, since the RSU’s ID allows one to link Show and Update by the same RSU. This is why we use an SPK where the RSU’s public key of BBS+ signatures is hidden but the correctness is ensured by proving the knowledge of the certificate of the public key.
In addition, we introduce the authentication protocol for each vehicle accepted by Show protocol to send a message to the nearest RSU. In Show protocol, for a short time public key in an ordinary digital signature scheme, the public key certificate is issued from the RSU. In each message authentication, the sent message is signed w.r.t. the public key. Thus, authentications during one interval can be linked. However, authentications across the interval are unlinkable.
Furthermore, we adopt a CS-based revocation method for RSUs. A CS tree is constructed, where each leaf corresponds to an RSU. The certificate of an RSU’s key consists of BBS+ signatures on the RSU’s secret key and on each node ID
4.2 Proposed Algorithm and Protocols
Fig. 2 illustrates the overall protocol flow among the vehicle, the nearest RSU, and the CA. The system public parameters are published to all participants. In Setup, the CA distributes secret keys to RSUs. In Register, the CA provides each vehicle with a vehicle secret key and an initial reputation certificate. The latest RSU revocation list is distributed in RevokeRSU. At the beginning of each interval, the vehicle executes the Show protocol with the nearest RSU to prove its reputation level and register a fresh short-term public key as its pseudonym key. During the interval, messages are authenticated using pseudonym-based signatures, and the RSU locally updates the scores. At the end of the interval, the vehicle anonymously obtains an updated reputation certificate from the nearest RSU through the Update protocol.
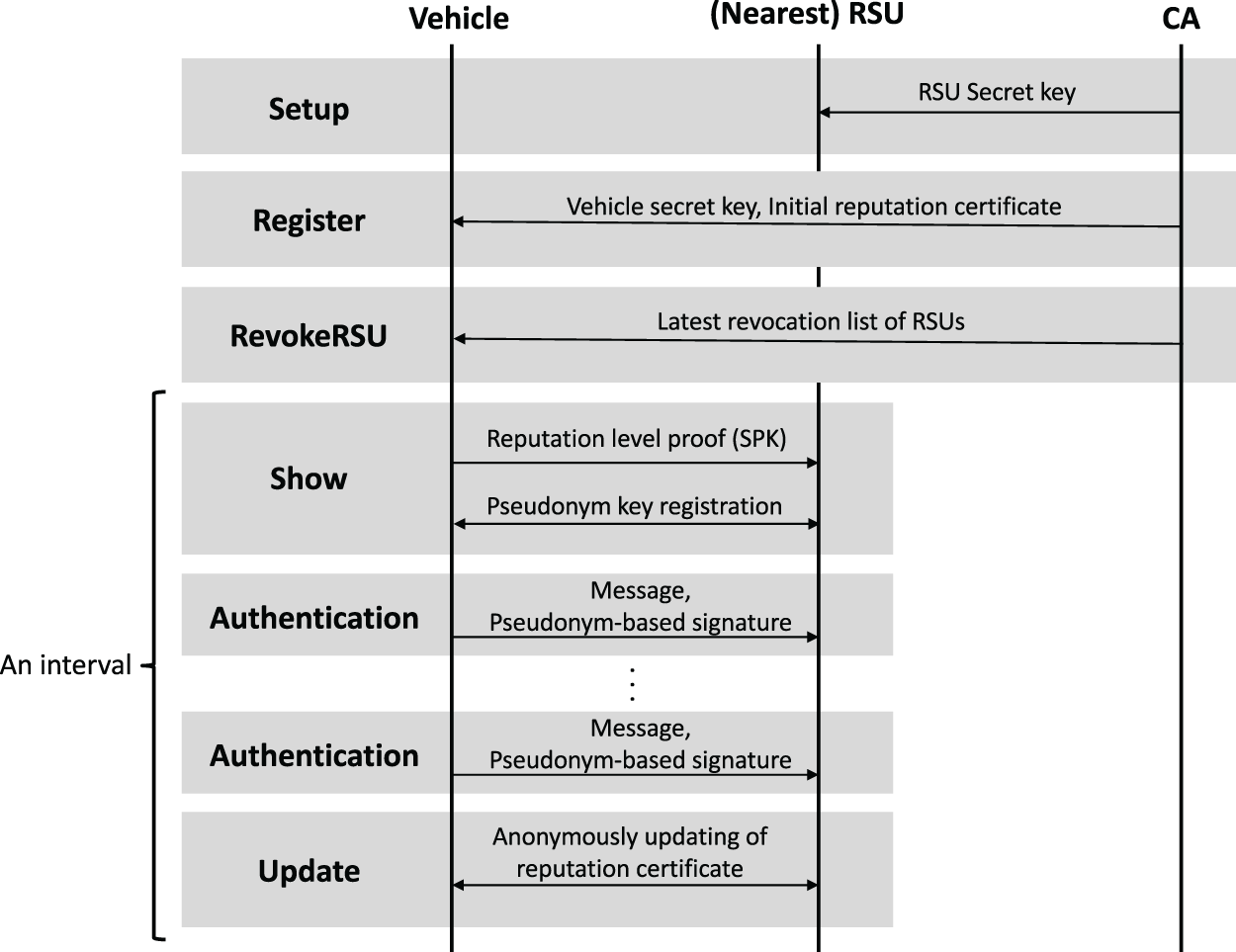
Figure 2: Protocol flow: Setup, Register, RevokeRSU, Show, per-message Authentication in an interval, and Update
The proposed algorithm and protocols are as follows.
Setup: In this algorithm, the CA generates key pairs of BB signatures and BBS+ signatures. Then, the CA computes the BB signature on every value in the integer range of reputation level
1. Select bilinear groups
2. For all
3. The CA assigns RSU
Then, send
4. For pseudonym certificates of each RSU
5. Initialize set
the CA’s secret key
Register: This is an interactive protocol between a vehicle V and the CA. The CA issues an initial reputation certificate
1. [V]: Select secret
2. [CA]: Set the initial reputation as
3. [V]: Set
RevokeRSU: This algorithm enables the CA to revoke an RSU. For the current tree, the cover nodes obtained using the CS method are denoted as
The revocation list is output as
Show: This is an interactive protocol between a vehicle V and the nearest RSU, where the vehicle shows RSU its reputation level
1. [V]: From
The Eq. (1) implies the verification of the (variant of) BB signature
2. [RSU]: To check the freshness of the proved certificate, check if
3. [V]: Generate a short-time key pair in the ordinary digital signature scheme, where the public key is
4. [RSU]: As the certificate on
5. [V]: Verify the signature
Authentication: This is an interactive protocol between a vehicle V and the nearest RSU. The common input is
1. [V]: For message M, using the secret key
2. [RSU]: Using
Update: This is an interactive protocol between a vehicle and the nearest RSU
1. [RSU]: Compute
2. [V]: Compute
For the security of our system, we show the following lemma.
Lemma 1: The SPK in Show proves the knowledge of
Proof: The equation for
Setting
Setting
As mentioned in [7],
Here, we prove the security of the proposed system.
Theorem 1: The proposed scheme is reputation unforgeable, under the security of BB signatures, BBS+ signatures, commitments, and digital signatures in the random oracle model.
Proof: Assume an adversary
• Case 1: In a Show protocol, an extracted BBS+ signature
• Case 2: In a Show protocol, an extracted (variant of) BB signature
• Case 3: In a Register or Show protocol, the extracted committed values compromise the binding property of commitments.
• Case 4: In an Authentication protocol, a digital signature
When all of Cases 1–4 do not happen, any corrupted vehicle cannot prove the incorrect level
Therefore, one of Case 1–4 happens with some non-negligible probability. Case 1 (resp., 2–4) can be reduced to an adversary
•
•
•
•
Theorem 2: The proposed scheme is misauthentication resistant, under the security of digital signatures.
Proof: Assume an adversary
Theorem 3: The proposed scheme is RSU revocable, under the security of BBS+ signatures in the random oracle model.
Proof: Assume an adversary
Theorem 4: The proposed scheme is anonymous in the random oracle model.
Proof: In the random oracle model, SPKs can be simulated. Let Game 0 be the original anonymity game. Consider Game 1 where the followings are modified from Game 0: In the Show protocols for
Then, consider the responses to
On the other hand, due to the zero-knowledge-ness of the SPK and the perfect hiding of the commitments, both games are indistinguishable. Therefore, in Game 0, the probability that
In this section, we discuss the efficiency of our system, compared to BARS [6]. In BARS, two authorities (CA and LEA) cooperatively update the reputation of each vehicle and issue the updated certificate to the vehicle. Thus, the centralized issuing process involving two authorities is a bottleneck. In our system, the issuing process is distributed, which is executed between a vehicle and the nearest RSU, and thus the bottleneck is resolved.
On the other hand, although BARS adopts an ordinary digital signature scheme for the public key and the certificate, our system utilizes the pairing-based computations in Show protocol, whose costs are heavier than the ordinary public key cryptosystems such as RSA and ECC. In Table 2, we present the computational costs of a vehicle and an RSU in the Show protocol, measured as the number of pairings and exponentiations on
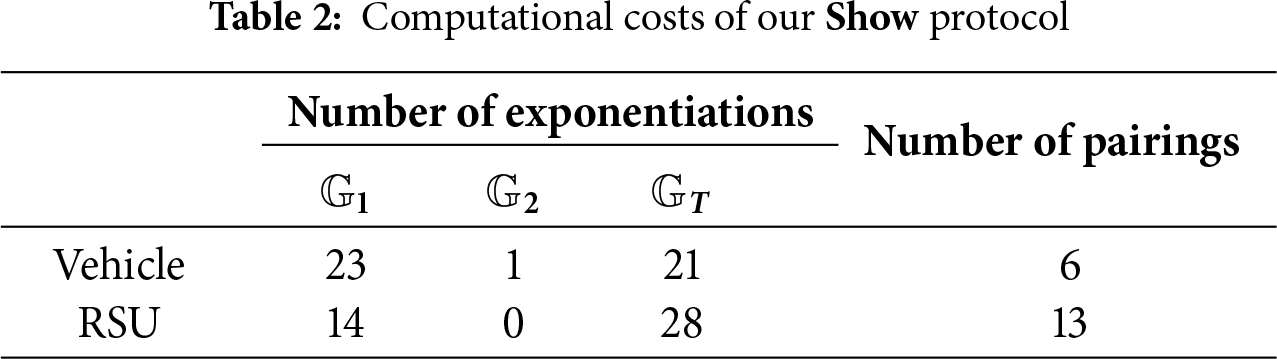
As for the data size submitted by a vehicle in Show protocol, the data contains 8
We emphasize that Show protocol is required only at the beginning of each interval. The interval length can be configured to practical values (e.g., several hours or a day), and the interval boundaries of vehicles can be offset so that Show protocols do not concentrate on a single RSU. During the interval, per-message authentication is performed using the same pseudonym-certificate mechanism as in existing RSU-assisted V2X systems such as BARS, and therefore the communication pattern and verification cost at RSUs remain unchanged from prior work. The SPK-related load is limited to a single proof of approximately 1.5 KB, most of whose computation can be performed offline by the vehicle; The verification cost at the RSU is estimated to be about 40 ms, based on timing measurements of the underlying cryptographic operations. Because the SPK is executed only once per interval and the per-message operations are identical to existing systems, we consider that the proposed system does not impose additional constraints on RSU coverage or handoff latency in high-mobility V2X environments, and that its scalability with respect to the number of RSUs and vehicles is unlikely to become a major concern.
In this paper, a distributed anonymous reputation system for V2X communication is proposed. The proposed system distributes the task to update the vehicles’ reputation certificates to RSUs, in which the nearest RSU updates the certificate anonymously at the end of each interval. This approach resolves the bottleneck in the certificate update process and improves the scalability.
Our future works include the implementation of the proposed system, network-level performance evaluations under specific traffic and mobility models (e.g., NS-3 or SUMO), realizing the transparency based on blockchain, and a detailed reputation evaluation algorithm.
Acknowledgement: Not applicable.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Shahidatul Sadiah and Toru Nakanishi; methodology, Shahidatul Sadiah and Toru Nakanishi; validation, Shahidatul Sadiah and Toru Nakanishi; formal analysis, Shahidatul Sadiah and Toru Nakanishi; investigation, Shahidatul Sadiah and Toru Nakanishi; writing—original draft preparation, Shahidatul Sadiah; writing—review and editing, Shahidatul Sadiah and Toru Nakanishi; supervision, Toru Nakanishi. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Not applicable.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Li Q, Malip A, Martin KM, Ng S, Zhang J. A reputation-based announcement scheme for VANETs. IEEE Trans Veh Technol. 2012;61(9):4095–108. [Google Scholar]
2. Yang N. A similarity based trust and reputation management framework for VANETs. Int J Future Gener Commun Netw. 2013;6(2):25–34. [Google Scholar]
3. Jesudoss A, Raja SK, Sulaiman A. Stimulating truth-telling and cooperation among nodes in VANETs through payment and punishment scheme. Ad Hoc Netw. 2015;24:250–63. [Google Scholar]
4. Wang XO, Cheng W, Mohapatra P, Abdelzaher T. ARTSense: anonymous reputation and trust in participatory sensing. In: Proceedings of IEEE INFOCOM 2013; 2013 Apr 14–19; Turin, Italy. p. 2517–25. [Google Scholar]
5. Jaimes LMS, Ullah K, Moreira ES. ARS: anonymous reputation system for vehicular ad hoc networks. In: Proceedings of the 8th IEEE Latin-American Conference on Communications (LATINCOM); 2016 Nov 15–17; Medellin, Colombia. p. 1–6. [Google Scholar]
6. Lu Z, Liu W, Wang Q, Qu G, Liu Z. A privacy-preserving trust model based on blockchain for VANETs. IEEE Access. 2018;6:45655–64. [Google Scholar]
7. Sadiah S, Nakanishi T. An efficient anonymous reputation system for crowd sensing. In: Seventh International Symposium on Computing and Networking Workshops (CANDAR 2019 WorkshopsWICS 2019; 2019 Nov 26–29; Nagasaki, Japan. p. 374–80. [Google Scholar]
8. Naor D, Naor M, Lotspiech J. Revocation and tracing schemes for stateless receivers. In: Advances in cryptology-CRYPTO 2001. LNCS 2139. Berlin/Heidelberg, Germany: Springer-Verlag; 2001. p. 41–62. [Google Scholar]
9. Sadiah S, Nakanishi T. A distributed anonymous reputation system for V2X communication. In: Proceedings of the IEEE International Conference on Consumer Electronics (ICCE); 2024 Jan 6–8; Las Vegas, NV, USA. p. 1–6. [Google Scholar]
10. Ahmed W, Wu D, Mukathe D. Blockchain-assisted privacy-preserving and context-aware trust management framework for secure communications in VANETs. Sensors. 2023;23(12):5766. [Google Scholar] [PubMed]
11. Feng X, Shi Q, Xie Q, Liu L. An efficient privacy-preserving authentication model based on blockchain for VANETs. J Syst Archit. 2021;117:102158. [Google Scholar]
12. Feng X, Cui K, Wang L, Liu Z, Ma J. PBAG: a privacy-preserving blockchain-based authentication protocol with global-updated commitment in IoVs. IEEE Trans Intell Transp Syst. 2024;25(10):13524–13545. [Google Scholar]
13. Hou B, Xin Y, Zhu H, Yang Y, Yang J. VANET secure reputation evaluation & management model based on double layer blockchain. Appl Sci. 2023;13(9):5733. [Google Scholar]
14. Fernandes CP, Montez C, Adriano DD, Boukerche A, Wangham MS. A blockchain-based reputation system for trusted VANET nodes Ad Hoc Networks. 2023;140:103071. [Google Scholar]
15. Boneh D, Boyen X. Short signatures without random oracles. In: Advances in cryptology-EUROCRYPT 2004. LNCS 3072. Berlin, Heidelberg: Springer-Verlag; 2004. p. 56–73. [Google Scholar]
16. Boneh D, Boyen X, Shacham H. Short group signatures. In: Advances in cryptology-CRYPTO 2004. LNCS 3152. Berlin/Heidelberg, Germany: Springer-Verlag; 2004. p. 41–55. [Google Scholar]
17. Au MH, Susilo W, Mu Y. Constant-size dynamic k-TAA. In: Security and cryptography for networks (SCN 2006). LNCS 4116. Berlin/Heidelberg, Germany: Springer-Verlag; 2006. p. 111–25. [Google Scholar]
18. Camenisch J, Drijvers M, Lehmann A. Anonymous attestation using the strong diffie-Hellman assumption revisited. In: Trust and trustworthy computing (TRUST 2016). Cham, Switzerland: Springer; 2016. p. 1–20. [Google Scholar]
19. Damgård I. On
20. Libert B, Peters T, Yung M. Group signatures with almost-for-free revocation. In: Advances in cryptology-CRYPTO 2012. LNCS 7417. Berlin/Heidelberg, Germany: Springer-Verlag; 2012. p. 571–89. [Google Scholar]
21. Ohara K, Emura K, Hanaoka G, Ishida A, Ohta K, Sakai Y. Shortening the Libert-Peters–Yung revocable group signature scheme by using the random oracle methodology. IEICE Trans Fundam. 2019;102-A(9):1101–17. [Google Scholar]
22. Emura K, Hayashi T. A revocable group signature scheme with scalability from simple assumptions. IEICE Trans Fundam. 2020;103-A(1):125–40. [Google Scholar]
23. Sadiah S, Nakanishi T. An efficient anonymous reputation system for crowdsensing. J Inf Process. 2022;30:694–705. [Google Scholar]
Cite This Article
 Copyright © 2026 The Author(s). Published by Tech Science Press.
Copyright © 2026 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools