A Unified Feature Selection Framework Combining Mutual Information and Regression Optimization for Multi-Label Learning

1  Introduction

Multi-label learning has attracted significant attention in recent years due to its ability to handle scenarios where each instance may be associated with multiple semantic labels simultaneously. It has been successfully applied across a wide range of domains and applications, including image classification [1], text classification [2], emotion recognition [3], fault diagnosis [4], and privacy protection [5]. These diverse applications demonstrate the growing importance of multi-label learning in addressing real-world problems where data exhibit complex and overlapping label structures.

In the fields of machine learning and pattern recognition, it is often necessary to handle high-dimensional data. Such data may contain redundant or irrelevant information that can interfere with learning. Moreover, high-dimensional datasets typically require excessive processing time and a large amount of memory consumption, making them challenging to work with [6]. These issues can degrade the performance of learning algorithms and hinder practical applications. In particular, when the data involves multiple labels per instance-commonly referred to as multi-label data-the complexity of learning grows substantially. In contrast to single-label scenarios, where each sample is associated with a single target, multi-label learning must consider multiple, potentially interdependent targets simultaneously. This increased dimensionality, coupled with inter-label dependency, leads to a combinatorial explosion in both the space and the associated computational complexity [7]. To address these challenges, many studies have introduced feature selection techniques in multi-label settings. Multi-label feature selection algorithms aim to identify and retain the most relevant features while removing unnecessary ones, based on certain evaluation criteria. The resulting feature subset can improve the accuracy of machine learning models, reduce training time, and enhance the interpretability of the data. Moreover, it helps mitigate risks such as the curse of dimensionality and overfitting [8].

Conventional feature selection approaches based on criteria that evaluate features independently of any specific learning model can be broadly categorized into two main streams: information-theoretic filter methods and regression-based embedded methods. The first stream, exemplified by methods such as mRMR [9], evaluates the redundancy between features and relevance to the target using mutual information to tackle the computational intractability of exhaustive subset search. These approaches can effectively capture nonlinear dependencies and pairwise relationships. However, they typically rely on greedy selection strategies, which may fail to consider global feature interactions and often lead to suboptimal solutions. The second stream formulates feature selection as a regression optimization problem, typically minimizing an objective of the form ||XW − ϒ || where X and ϒ are input data and label set, W represents importance of each feature [10]. This framework allows feature selection to be incorporated into a global optimization procedure, thereby enhancing computational efficiency. However, such approaches inherently rely on the assumption of linear dependencies between features and labels, which constrains their capacity to model more complex relationships.

In this paper, we propose a unified feature selection framework that integrates information-theoretic redundancy measures into a regression-based formulation. By unifying these two complementary approaches, the proposed framework mitigates their respective limitations while leveraging their individual strengths. Specifically, we encode the mutual information relationships between features, and between features and labels into a matrix representation, which is then incorporated into the regression objective. This enables the model to retain the nonlinear dependency awareness of mutual information-based methods while benefiting from the efficient optimization capability of regression-based approaches.

The main contributions of this work are as follows:

•   Novel Objective Function: To overcome the limitations of traditional approaches in multi-label feature selection, we introduce a new objective function that merges efficient regression-based approach and mutual information-based criteria. The proposed function is designed to be simple yet capable of capturing essential information for effective feature selection. Its formulation is described in detail in Sections 3.1 and 3.2.

•   Efficient Optimization Algorithm: We develop an efficient algorithm based on gradient descent to optimize the proposed objective function. This algorithm emphasizes fast convergence and reduced computational complexity compared to existing methods. The optimization algorithm is presented in Section 3.3, the complexity analysis is provided in Section 3.4, and the convergence behavior of the algorithm is illustrated in Section 4.3.

•   Improved Classification Performance: Through experiments on seven multi-label datasets, we confirm that the proposed method achieves superior classification performance compared to conventional feature selection techniques. Comprehensive comparison experiments and statistical analyses are reported in Section 4.2, accompanied by extensive figures and tables.

The remainder of this paper is organized as follows. Section 2 reviews background knowledge on multi-label classification and feature selection methods. Section 3 provides a detailed description of the proposed methodology, including the integration of mutual information and regression objectives. Section 4 presents experimental results using seven benchmark multi-label datasets and compares the performance of the proposed approach with existing methods. Finally, Section 5 concludes the study and discusses potential future research directions.

2  Related Works

Feature selection has been widely investigated in single-label learning scenarios, where each instance is associated with only one target. In contrast, multi-label learning, which involves multiple potentially interdependent targets, introduces additional challenges due to increased dimensionality and complex label dependencies. Approaches to handling multi-label data can be broadly classified into two categories: those that transform the problem into a single-label format, and those that directly operate on the multi-label structure [11]. Converting multi-label data into single-label format allows for the direct application of traditional single-label feature selection techniques. However, this transformation often leads to information loss. One common method for this transformation is the Label Powerset (LP) approach, which treats all possible label combinations and treats each as a distinct class label [12]. While straightforward, LP suffers from severe class imbalance, as the number of resulting classes can grow exponentially with the number of labels. To address this, the Pruned Problem Transformation (PPT) method was introduced, which discards infrequent label combinations to mitigate imbalance [13]. However, this pruning also results in the loss of valuable label relationship information.

In contrast, two main feature selection approaches have been proposed to avoid the need for label transformation. The first approach is information-theoretic feature filter. The pairwise multi-label utility (PMU) method is one such approach, which evaluates label correlations using mutual information without transformating labels [14]. However, PMU is easy to finding only locally optimal solutions, since its greedy selection approach inherently constrains the search process and prevents the discovery of globally optimal feature subsets. Lee and Kim conducted a theoretical analysis of feature selection based on interaction information, demonstrating that lower-degree interaction information terms notably influence mutual information under an incremental selection scheme [15]. They further derived the upper and lower bounds of these terms to explain why score functions that consider lower-degree interactions can produce more effective feature subsets. The max-dependency and min-redundancy (MDMR) criterion has been proposed for multi-label feature selection, where a candidate feature is considered beneficial if it exhibits strong relevance to all class labels while remaining non-redundant with respect to other selected features across all labels [16]. However, MDMR is also easy to finding local optimal solution. The quadratic programming feature selection (QPFS) method reformulates mutual information-based evaluation as a numerical optimization problem to escape local optima [7]. However, QPFS requires the computation of a large number of mutual information terms, which can be computationally intensive. Zhang et al. proposed an approach that allows a feature to account for multiple labels by calculating mutual information across pairs of labels [17].

In another research direction, regression-based embedded methods integrate feature selection into the model training process itself. For example, decision tree classifiers naturally perform feature selection during their construction [18]. In multi-label scenarios, several embedded feature selection methods based on regression analysis have been proposed. Fan et al. utilizes ridge regression to construct a selection matrix and employs the l2,1-norm to develop a multi-label feature selection framework [19]. Li et al. introduces a flexible approach that allows feature selection between the l1-norm and l2-norm criteria [20]. Fan et al. incorporates spectral graph theory to capture label correlations while simultaneously addressing feature redundancy [21]. Li et al. designed a matrix that accounts for higher-order label correlations and proposed a multi-label feature selection method that handles feature redundancy using an l2,1-norm regularization term [22]. Hu et al. proposed a method that encodes the mutual information between features and labels into a weight matrix and constructs an objective function accordingly to perform multi-label feature selection [23]. Dai et al. proposed a method that leverages fuzzy mutual information to emphasize strongly related labels and applies conditional mutual information to guide the selection of relevant features [24]. Faraji et al. proposed a method that considers both label correlations and label imbalance by designing an objective function that identifies shared patterns between the feature and label matrices [25]. He et al. designed to capture the variation in inter-label relationships by incorporating sample-wise correlations into the label space and applying the information to a sparse linear regression model [26]. Yang et al. proposed a novel embedded method that simultaneously considers inter-label correlations and label-specific features [27]. Their method constrains the correlation search space, learns distinctive features for each label, and incorporates a robust exploration strategy to reduce the impact of noise and outliers.

Another category is the wrapper approach, which identifies an optimal feature subset through iterative evaluation guided by a learning algorithm. Wrapper methods utilize classification performance as a direct evaluation metric to select the optimal feature subset. Optimization techniques such as boosting and genetic algorithms have been employed to improve selection quality [28]. The genetic algorithm for feature selection can be used for various applications [29,30]. Despite their effectiveness, wrapper methods are computationally expensive due to repeated classifier evaluations. However, wrapper methods are beyond the scope of this work and are therefore not considered here.

Recent studies have explored logic mining as an interpretable approach to feature selection and rule extraction, primarily implemented through Discrete Hopfield Neural Networks (DHNNs). A hybrid DHNN framework with Random 2-Satisfiability rules was introduced [31], where hybrid differential evolution and swarm mutation operators were incorporated to enhance the optimization of synaptic weights and diversify neuron states during retrieval, leading to improved transparency in decision-making. Similarly, Romli et al. proposed an optimized logic mining model using higher-order Random 3-Satisfiability representations in DHNNs, designed to prevent overfitting and flexibly induce logical structures that capture the behavioral characteristics of real-world datasets [32]. Beyond logic-mining-oriented formulations, recent work has also advanced the theoretical foundations of discrete Hopfield architectures. In particular, a simplified two-neuron discrete DHNN model was introduced, where bifurcation analysis, hyperchaotic attractor characterization, and field-programmable gate array(FPGA)-based hardware implementation demonstrated that even minimal DHNN structures can exhibit rich dynamical behaviors and robust randomness properties [33]. These findings highlight the broader modeling flexibility and dynamic expressiveness of DHNNs, complementing logic-mining-based approaches by reinforcing the underlying stability and dynamical mechanisms upon which interpretable feature-selection frameworks can be built.

3  Proposed Method

3.1 Preliminary

Feature selection methods can be broadly categorized into two major streams: mutual information (MI)-based filter approaches and regression-based approaches.

The first stream is represented by classical methods such as mRMR (minimum redundancy maximum relevance) [9], which aim to maximize the relevance between features and labels while minimizing redundancy among selected features. These approaches rely on information-theoretic criteria, particularly mutual information, to measure pairwise dependencies between variables. They are straightforward and model-agnostic, and they can capture nonlinear relationships that linear methods may overlook. Given the full feature set F and the subset of features S that have already been selected, the next feature fj is chosen by maximizing the trade-off between its relevance to the target and its redundancy with the selected features, as follows:

arg⁡maxfj∈F−SMI(fj,y)−1|S|∑fi∈SMI(fi,fj)(1)

where MI(⋅,⋅) denotes the mutual information. However, they typically employ greedy search strategies, selecting features sequentially based on local criteria. As a result, they may fail to consider global interactions among features and often lead to suboptimal feature subsets.

The second stream is exemplified by regression-based methods such as efficient and robust feature selection via joint l2,1-norms minimization [10], which formulate feature selection as an optimization problem. The objective function follows:

minW||XW−Y||2,1+γ||W||2,1.(2)

where X is data matrix, ϒ is label matrix. These approaches aim to minimize reconstruction error, while imposing structural regularization to induce sparsity across features. Such methods benefit from global optimization and can naturally incorporate feature-label dependencies into a unified objective. However, because they fundamentally rely on a linear regression model, they are often limited in capturing complex or nonlinear relationships that are essential in many real-world datasets.

3.2 Objective Function

Given a dataset X∈Rn×d consisting of n patterns and d features, along with a multi-label set ϒ consisting of c labels, the basic objective function of a regression-based feature selection method can be formulated as:

minW||XW−Y||F2s.t. W≥0(3)

where W is a weight matrix that is subject to a non-negativity constraint. The non-negativity constraint ensures that feature selection is represented by positive values, while unselected features are represented by zeros. The larger the absolute value in W, the more reliable the corresponding feature is considered. After solving this optimization problem, features corresponding to rows with larger norms in W are selected.

The objective function is designed to find features that minimize the difference between the data projected by W and the multi-label targets. To construct this objective function, the Frobenius norm is used. The function is convex with respect to W, allowing the optimization problem to be solved efficiently. The top k features are selected based on the magnitude of each row in the optimized W.

Although Eq. (3) offers an efficient convex formulation, its modeling capacity is limited because it only captures linear relationships between features and labels. In multi-label learning, however, three important aspects are often overlooked in such regression-based approaches:

1.   Feature redundancy: selecting highly correlated features reduces the generalization power [9].

2.   Label dependencies: multi-label data often contains significant inter-label correlations that should be preserved [34].

3.   Non-linear dependencies: labels may exhibit complex, non-linear relationships with features.

To address these limitations, we incorporate mutual information into the objective function. Mutual information captures the degree of statistical dependency between random variables and can reflect both linear and non-linear relationships [9,19,24,27,35]. The mutual information between two arbitrary random variables A and B is defined as follows:

MI(A,B)=∑a∈A∑b∈Bp(a,b)log⁡[p(a,b)p(a)p(b)](4)

where P(a,b) represents the joint probability distribution function of A and B, while p(a) and p(b) represent their marginal probability distribution functions. In the case of continuous random variables, this summation is replaced by an integral:

MI(A,B)=∫A∫Blog⁡[p(a,b)p(a)p(b)]da db.(5)

When the i-th feature vector and the j-th label vector are denoted by xi and yj, respectively, the relevance and redundancy using mutual information can be expressed as MI(xi,yj) and MI(xi,xj), respectively. In a multi-label environment, the relationships between labels are additionally considered as [15].

By calculating these associations, three matrices Q∈Rd×d, R∈Rc×c and S∈Rd×c can be constructed, where each element in these matrices is defined as follows:

Qij=MI(xi,xj)(feature redundancy)Rij=MI(yi,yj)(label dependency)Sij=MI(xi,yj)(feature-label relevance)(6)

where Qij refers to the (i,j)-th element of Q. The elements of these matrices represent the associations between features and labels. When the data is binarized for calculating mutual information, the mutual information is always greater than or equal to 0, and less than or equal to 1 when using a base-2 logarithm. Therefore, every elements in the matrices Q, R and S lies in within the range [0, 1]. The matrix Q represents feature redundancy, which should be minimized in order to eliminate redundant or highly correlated features. The matrix R captures the relationships between labels; since features associated with strongly correlated labels are desirable, the negative of this term is included in the objective to encourage their selection under a minimization framework. Similarly, S quantifies the relevance between features and individual labels. By incorporating mutual information into the regression formulation, the model is able to capture not only simple linear relationships but also complex non-linear dependencies. To promote the selection of highly relevant features, the negative of S is also incorporated into the objective function.

By combining these values with the regression Eq. (3), an objective function can be designed as follows:

minW||XW−Υ||F2+αTr(WTQW)−βTr(RWTW)−γTr(STW)s.t. W≥0(7)

where α,β, and γ are weights for redundancy, label correlation, and relevance, respectively, and are all positive. The hyperparameters α,β,γ control the influence of each regularization term. In Tr(WTQW), the i-th value represents the sum of the redundancies of the i-th feature with other features. Similarly, Rw(i)Tw(i) represents the sum of the associations between the i-th feature and the labels, and STw(i) represents the sum of the relevance of the i-th feature across all labels. The interpretation of each term is as follows:

•   Regression loss (||XW−Y||F2): encourages accurate label reconstruction via a linear regression model.

•   Redundancy penalty (Tr(WTQW)): discourages selecting mutually redundant features.

•   Label dependency penalty (Tr(RWTW)): promotes selecting features that explain correlated labels.

•   Relevance reward (Tr(STW)): favors features with stronger associations to multiple labels.

Optimizing the proposed objective function thus corresponds to selecting features that not only minimize redundancy and maximize relevance and label association, but also contribute to accurately reconstructing the label space through a linear regression model. In this formulation, the regression-based loss captures the predictive structure in a supervised setting, while the mutual information-based terms guide the selection toward features that exhibit strong statistical dependency with the labels and minimal overlap with other features. This hybrid design enables the model to balance predictive accuracy with information-theoretic feature quality. In the next subsection, we present an efficient optimization framework to solve the proposed objective function under the non-negativity constraint.

3.3 Optimization

The convexity of the proposed objective function is primarily determined by the terms Tr(WTQW) and Tr(RWTW). When the matrices Q and −R are positive definite, the objective function is convex, which facilitates efficient optimization. However, since Q and −R are not guaranteed to be positive definite, we enforce convexity by adding the absolute value of the minimum eigenvalue of each matrix to its diagonal elements. This modification ensures that both Q and −R become positive definite. Importantly, because Q and R originally have zero diagonal entries, adding a uniform scalar to the diagonal does not change the mutual-information structure that drives feature relevance. This correction preserves the feature selection behavior while ensuring positive definiteness for convex optimization.

To ensure the positive definiteness of the matrices Q and R, we adjust each matrix by adding the absolute value of its minimum eigenvalue to its diagonal entries. This yields modified matrices Q^ and R^, which are guaranteed to be positive definite. The transformation is defined as follows:

Q^=Q+(|λmin(Q)|+ε)⋅Id, R^=R−(|λmax(R)|+ε)⋅Ic(8)

where λmin(Q) and λmax(R) denote the smallest and largest eigenvalues of Q and R, respectively, Id, Ic are identity matrices of appropriate dimensions matching Q and R, and ε is a small positive value to guarantee strict positive definiteness. This adjustment preserves the relative structure of the feature space while ensuring the convexity of the objective function. The optimization objective can be formulated as follows:

minW||XW−Y||F2+αTr(WTQ^W)−βTr(R^WTW)−γTr(STW)s.t. W≥0(9)

To solve the modified convex objective function with a non-negativity constraint, we employ the projected gradient descent (PGD) algorithm. This algorithm performs optimization based on the gradient with respect to W, and any negative entries in W are projected to zero to enforce the non-negativity constraint. The gradient of the objective function with respect to W is given by:

∇W=2XT(XW−Y)+2αQ^W−2βWR^−γS.(10)

Algorithm 1 presents the complete procedure of the proposed method. In Algorithm 1, the step size η is provided as a user-defined input. In practice, a theoretically sound upper bound can be derived from the Lipschitz constant of the gradient. For the proposed objective, the gradient is given by ∇f(W)=2X⊤(XW−Y)+2αQW−2βWR+γS, and the Lipschitz constant can be estimated as L=2‖X⊤X‖2+2α‖Q‖2+2β‖R‖2. Thus, a stable choice is η=1/L, which guarantees monotonic descent and convergence under the projection constraint. Since the linear term γTr(S⊤W) does not affect L, this bound remains valid even for large γ. In addition, a backtracking line search with Armijo condition is used to further ensure stability in early iterations.

3.4 Computational Complexity Analysis

The overall computational complexity of the proposed algorithm consists of three main components: (1) the computation of the mutual information-based matrices Q, R, and S; (2) the eigenvalue correction required to ensure positive definiteness of Q and R; and (3) the iterative optimization procedure via projected gradient descent (PGD).

Q∈Rd×d encodes the pairwise mutual information between features, requiring O(d2) time. R∈Rc×c encodes the mutual information between labels, requiring O(c2) time. S∈Rd×c encodes the mutual information between features and labels, requiring O(dc) time. Thus, the total cost for constructing these matrices is O(d2+c2+dc).

To ensure the convexity of the objective function, we modify Q and R by adding the absolute value of their minimum eigenvalue to their diagonals: Computing the minimum eigenvalue of a symmetric matrix (e.g., via power iteration or Lanczos methods) typically requires O(d2) for Q and O(c2) for R, assuming low-rank approximations or a small number of iterations. Therefore, this step adds O(d2+c2) to the complexity.

In each iteration of PGD, the gradient with respect to W∈Rd×c is computed. The complexity of computing each term is as follows: XT(XW): O(ndc), Q^W: O(d2c), WR^: O(dc2). The term γS is constant once computed: O(dc). Thus, the per-iteration cost of gradient computation is: O(ndc+dc+dc2). Assuming the algorithm converges in T iterations (typically a small constant or logarithmic in practice), the total optimization cost is O(ndc+d2c+dc2).

Combining all components, the overall computational complexity is O(ndc+d2c+dc2+d2+c2). The proposed algorithm is thus computationally efficient for moderate values of d and c, and scalable to larger datasets when T is reasonably small.

The proposed method involves three hyperparameters, α, β, and γ, which control the contributions of smoothness, redundancy penalization, and label-alignment terms, respectively. In practice, these parameters are tuned over a coarse logarithmic grid, which keeps the computational cost manageable due to the convexity of the objective and the low per-iteration complexity of the solver.

4  Experimental Results

4.1 Experimental Settings

This section presents the experimental results to evaluate the effectiveness of the proposed method in improving classification performance. We compared classification performance using the Multi-label k-Nearest Neighbors (MLkNN) classifier [36], the Linear Support Vector Machine (LinSVM) classifier [17,20,23], and the Multi-Label Decision Tree (MLDT) classifier [18]. In MLkNN, the value of k was set to 5. MLkNN has been widely used in previous studies to benchmark the performance of multi-label feature selection methods [7,8,19]. The regularization parameter C of the LinSVM classifier was determined through validation during the training phase. For each experiment, the training and test data were randomly split in an 8:2 ratio, and the process was repeated 10 times to compute the average performance.

Seven datasets were used in the experiments. The cal500 dataset is a multi-label music annotation dataset consisting of 500 Western popular songs, each annotated with multiple tags describing acoustic, emotional, and semantic content [37]. The corel5k dataset is an image annotation dataset comprising 5000 images, each associated with one or more textual labels from a controlled vocabulary of 260 words. The emotions dataset contains 593 music tracks with 72 audio features, each labeled with one or more of six primary emotional categories [38]. The enron dataset is a text corpus derived from company emails [13]. The genbase dataset is a biological dataset for protein function classification, where each instance represents a protein and each label corresponds to a specific function. The medical dataset consists of 978 clinical free-text reports, each labeled with up to 45 disease codes [39]. The slashdot dataset is a relational graph dataset representing a social network of users from the technology news site Slashdot. It includes directional friend/foe relationships among users, making it suitable for multi-label classification and link prediction tasks in networked data [40]. Detailed characteristics of each dataset are summarized in Table 1.

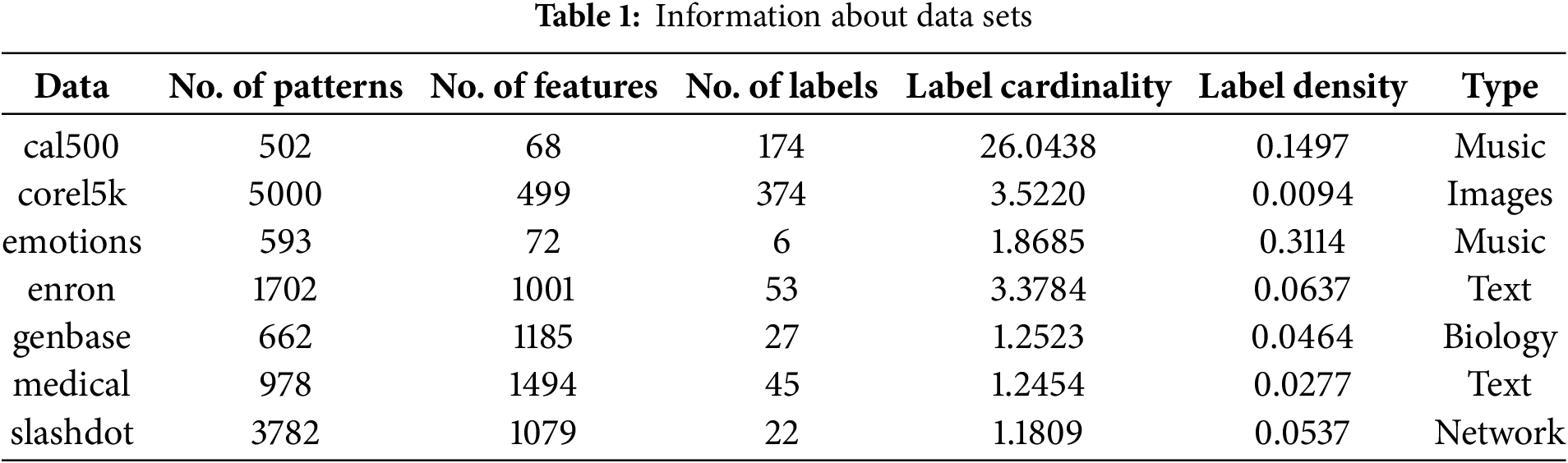
For evaluation, we used three metrics: Hamming Loss (hloss), Ranking Loss (rloss), and Multi-label Accuracy (mlacc) [8]. Lower values of Hamming Loss and Ranking Loss indicate better classification performance, while higher values of Multi-label Accuracy reflect better performance. The number of selected features was determined based on a proportion n of the total number n of feature patterns in each dataset by referring to the methodology in [41]. To uniquely distinguish each sample in a dataset, at least log2⁡n independent binary features are theoretically required, where n denotes the number of samples. For example, only three features are sufficient to perfectly differentiate eight samples. However, this number is often too strict in real-world datasets, since features are typically not fully independent. Therefore, we adopt n as a practical heuristic for the number of selected features, which provides a reasonably small yet representative subset size.

To compare against the proposed method, we selected five existing approaches: AMI [42], MDMR [16], FIMF [8], QPFS [7], and MFSJMI [17]. AMI selects features based on the first-order mutual information between features and labels. MDMR introduces a new feature evaluation function that considers mutual information between features and labels as well as among features. FIMF limits the number of labels considered during evaluation to enable fast mutual information-based feature selection. QPFS reformulates the mutual information problem into a quadratic programming framework to balance feature relevance and redundancy. MFSJMI selects features by considering label distribution and evaluating the relevance using joint mutual information. For all compared methods, including the proposed one, the hyperparameters α, β, and γ were varied over the range 10−3,10−2,…,103. The best-performing result from this grid search was reported. To enable reliable mutual information estimation, continuous features are discretized using the Label-Attribute Interdependence Maximization (LAIM) method [43], which is specifically designed for multi-label learning.

4.2 Comparison Results

Tables 2–4 summarize the classification performance of different multi-label feature selection methods evaluated with the MLkNN classifier. The best result for each dataset and metric is highlighted in bold. Table 2 presents the Hamming loss results. The proposed method achieves the lowest loss on six out of seven datasets, clearly outperforming the existing approaches. In particular, substantial improvements are observed on the emotions, enron, and medical datasets, demonstrating that the proposed formulation effectively reduces label-wise prediction errors. Although FIMF performs slightly better on corel5k, the proposed method achieves the overall best average performance across datasets. Table 3 reports the Ranking loss results. The proposed approach again shows strong superiority, achieving the lowest ranking loss on six datasets. These results indicate that the selected features enable the classifier to preserve the relative ranking of relevant and irrelevant labels more effectively than competing methods. Notably, while AMI achieves the best result on corel5k, the proposed method shows consistent improvements in more complex datasets where label dependencies are pronounced. Table 4 presents the Multi-label accuracy results. The proposed method outperforms all baselines on six datasets, achieving particularly large gains on corel5k, enron, and medical. This confirms that the proposed approach can identify highly discriminative and non-redundant features that generalize well across diverse label spaces. Although QPFS slightly exceeds the proposed method on slashdot, the overall performance trend demonstrates the robustness and adaptability of the proposed method across different data characteristics.

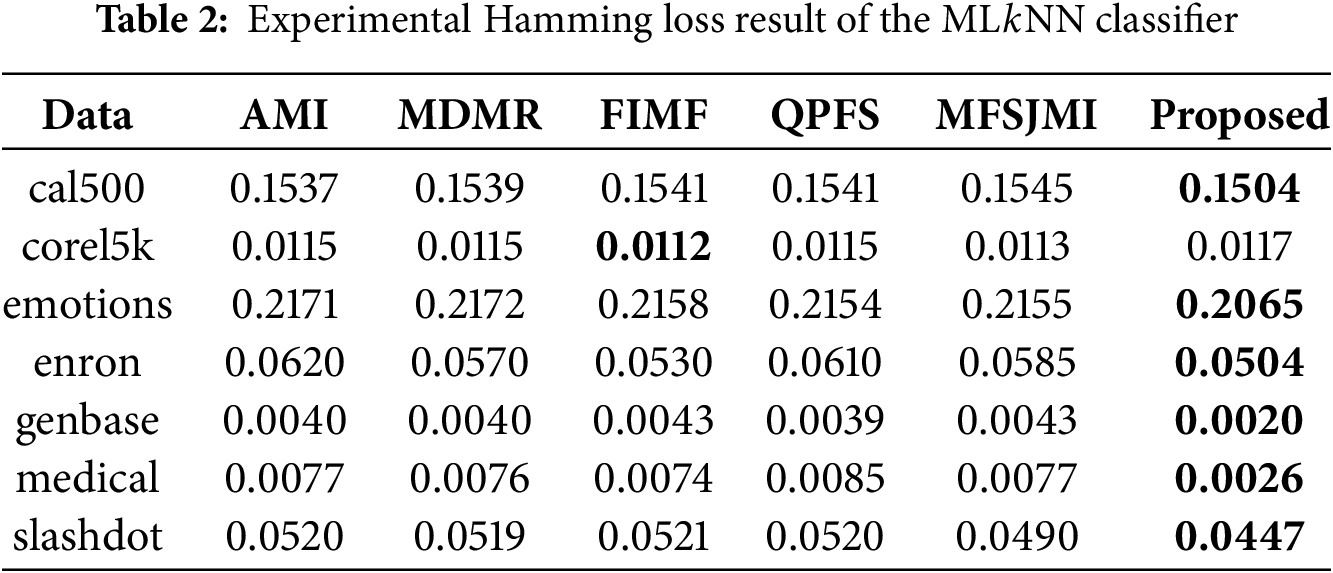
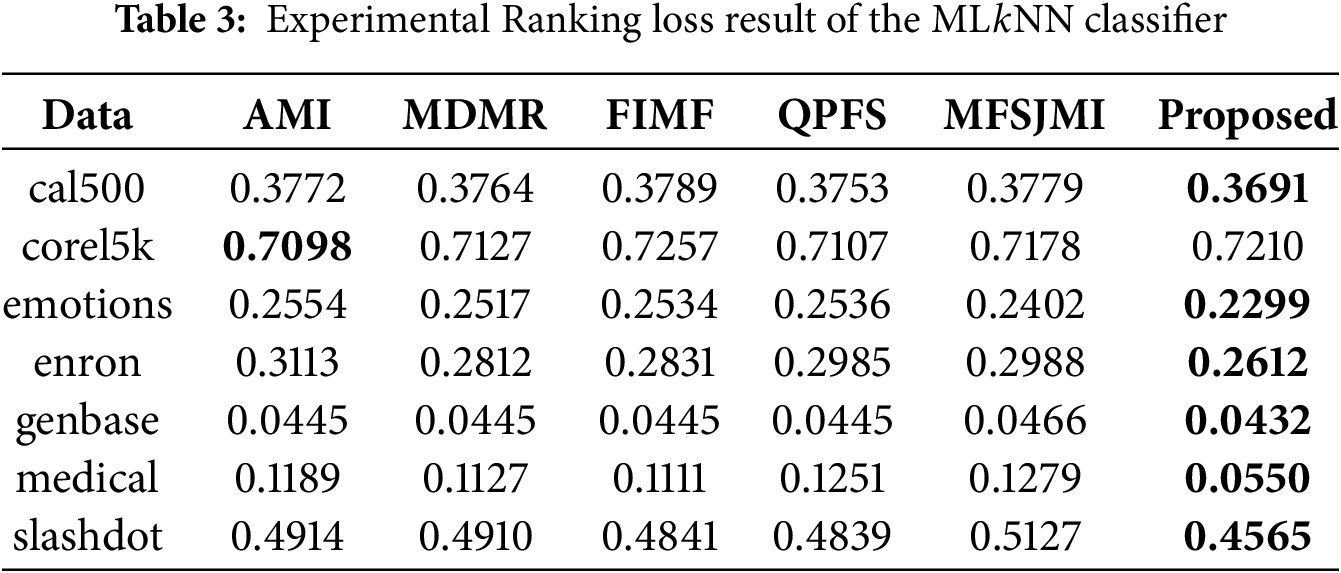
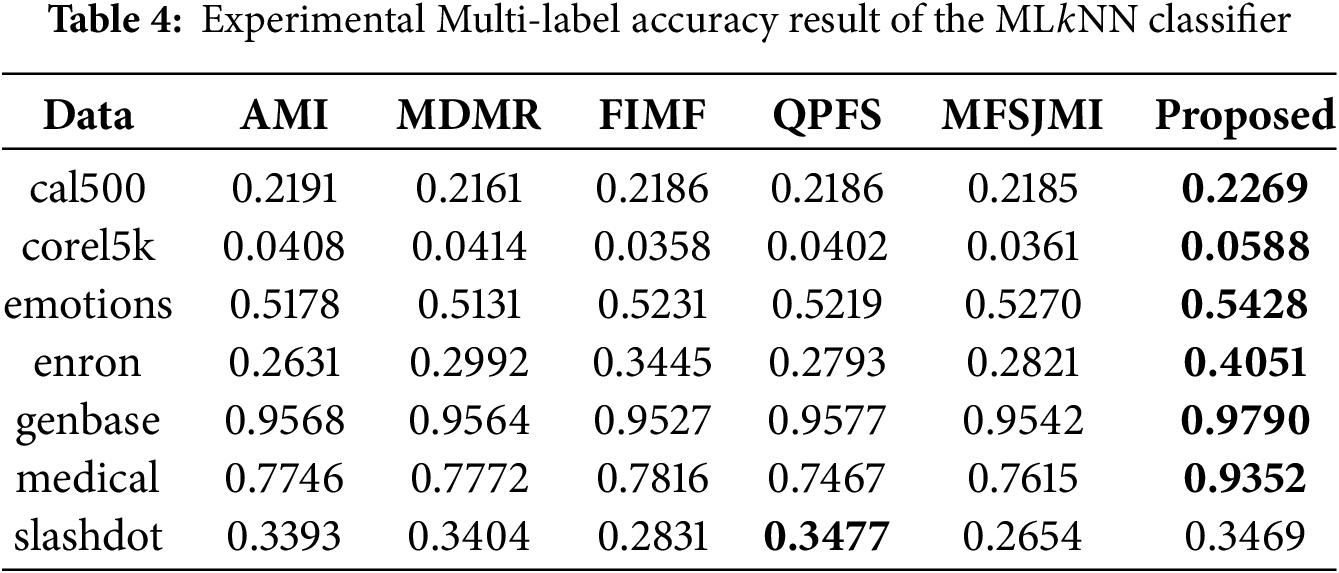
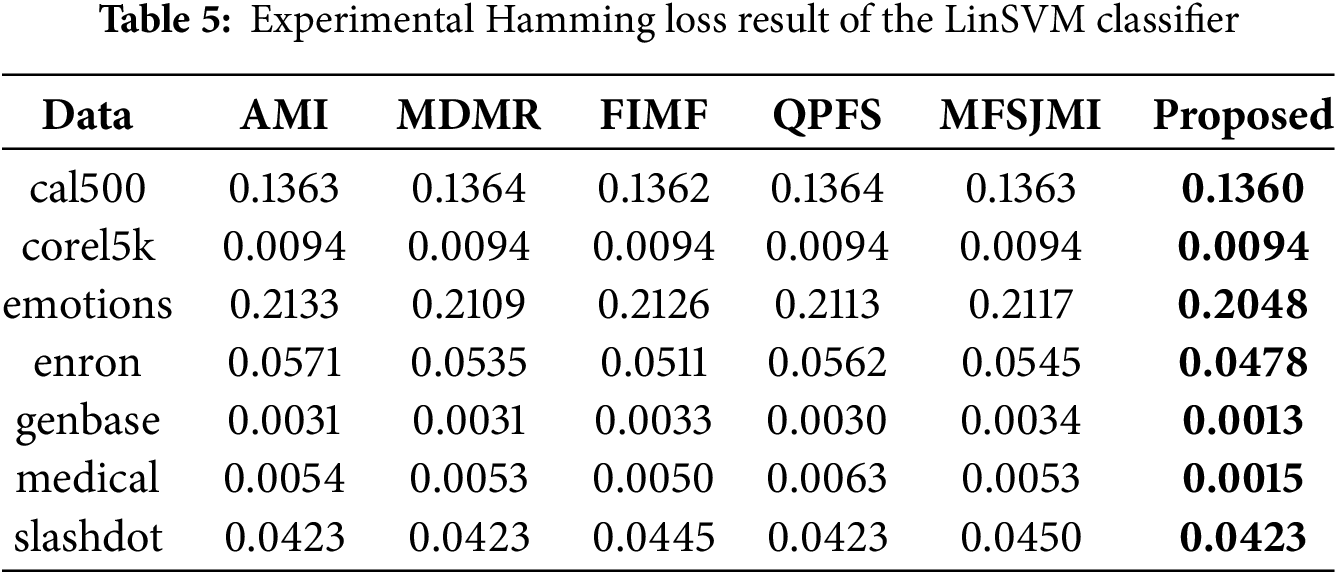
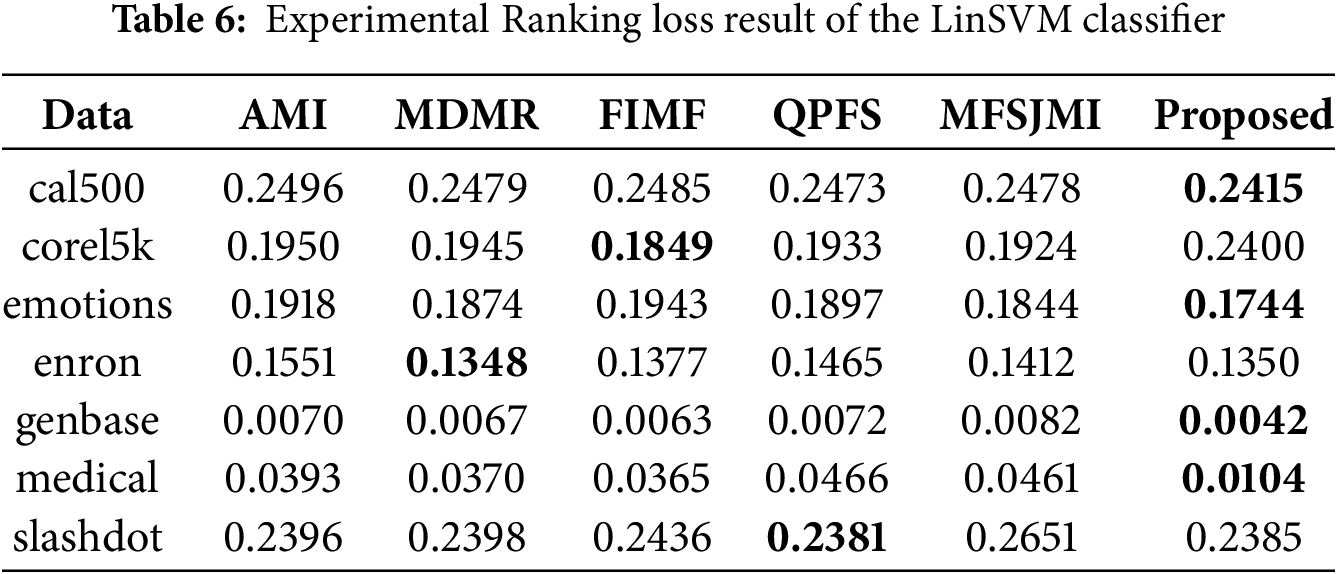
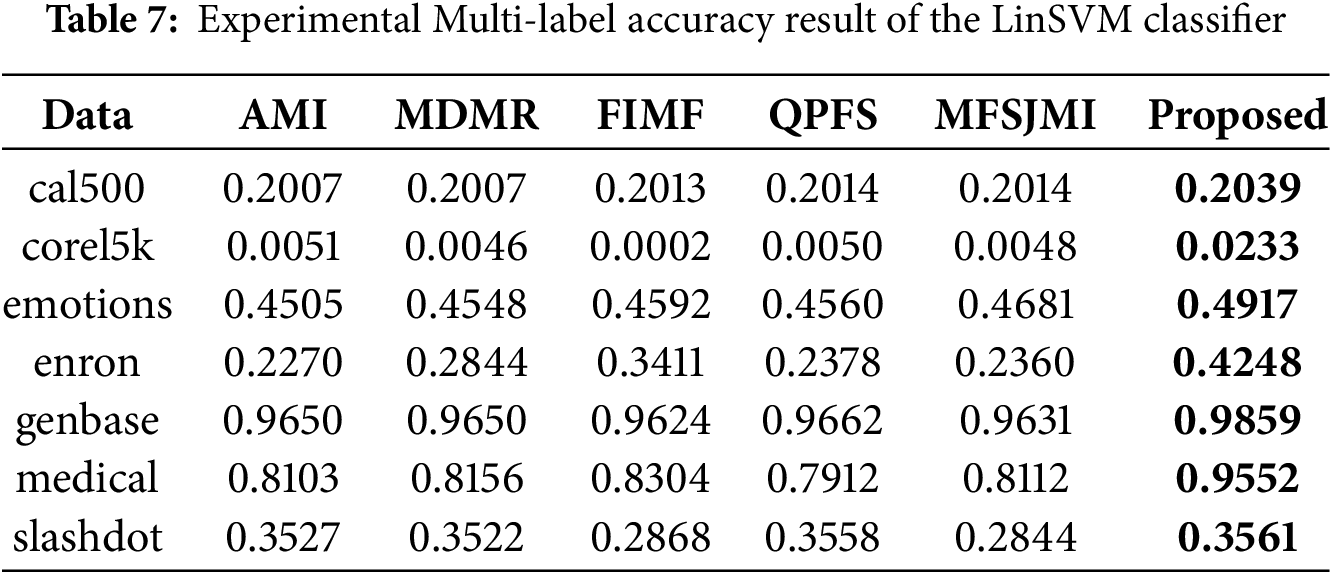
Tables 5–7 present the classification results obtained using the LinSVM classifier. Table 5 summarizes the Hamming loss results. The proposed method achieves the lowest loss on all datasets. These results show that the selected features effectively reduce instance-level prediction errors even when evaluated with a linear classifier. Table 6 presents the Ranking loss results. The proposed method achieves the best results on four datasets-cal500, emotions, genbase, and medical-showing its ability to preserve the label ranking order with minimal degradation. While FIMF slightly outperforms others on corel5k and MDMR performs best on enron, the proposed approach remains highly competitive across datasets. The performance gain on emotions and medical demonstrates that the proposed feature selection method can effectively model label dependencies even under a linear decision boundary. Table 7 reports the Multi-label accuracy results. The proposed method achieves the highest accuracy on six datasets, with particularly large gains on corel5k, enron, and medical. This demonstrates the strong discriminative capability of the selected features and their ability to generalize across datasets with varying label sparsity. FIMF predicted all-zero label vectors in 9 out of 10 runs on Corel5k, leading to nearly zero multi-label accuracy.

Tables 8–10 summarize the experimental results obtained using the MLDT classifier. Table 8 reports the Hamming loss results. The proposed method achieves the lowest loss on all seven datasets, showing remarkable consistency and robustness. In particular, the performance improvements on emotions, enron, genbase, and medical are significant, indicating that the proposed feature selection strategy effectively reduces label-wise prediction errors even for complex label spaces. Table 9 presents the Ranking loss results. The proposed approach achieves the best performance on five datasets while remaining highly competitive on the others. These results suggest that the proposed method allows the MLDT classifier to better preserve the relative ranking between relevant and irrelevant labels. Notably, the performance gain on corel5k and medical is substantial, confirming that the proposed MI-guided optimization enhances feature selection for both high-dimensional and label-dependent data. Table 10 shows the Multi-label accuracy results. The proposed method achieves the highest accuracy on all seven datasets, highlighting its superiority in overall predictive capability. The large gains on emotions, enron, and medical datasets illustrate that the proposed formulation captures label correlations more effectively than existing feature selection methods.

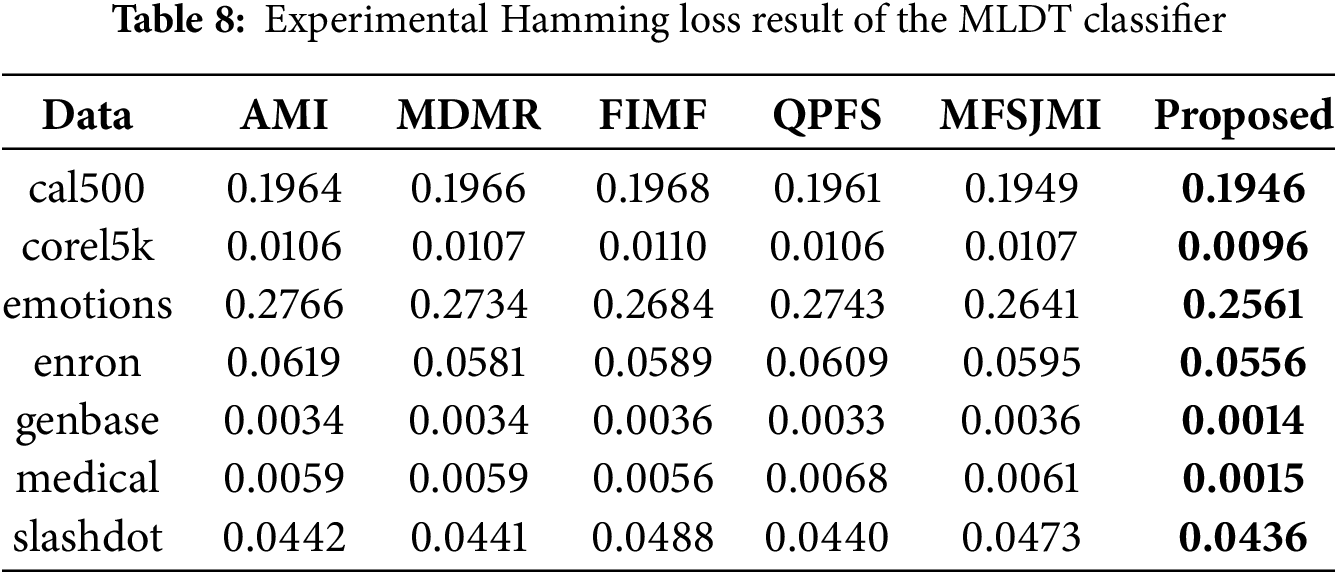
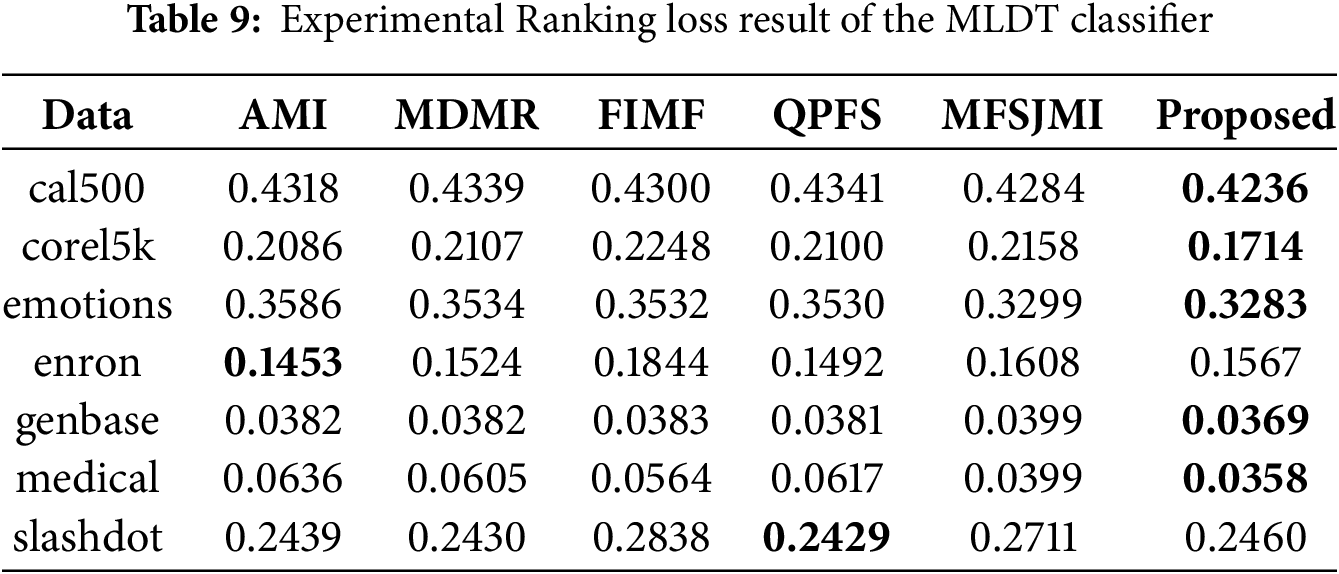
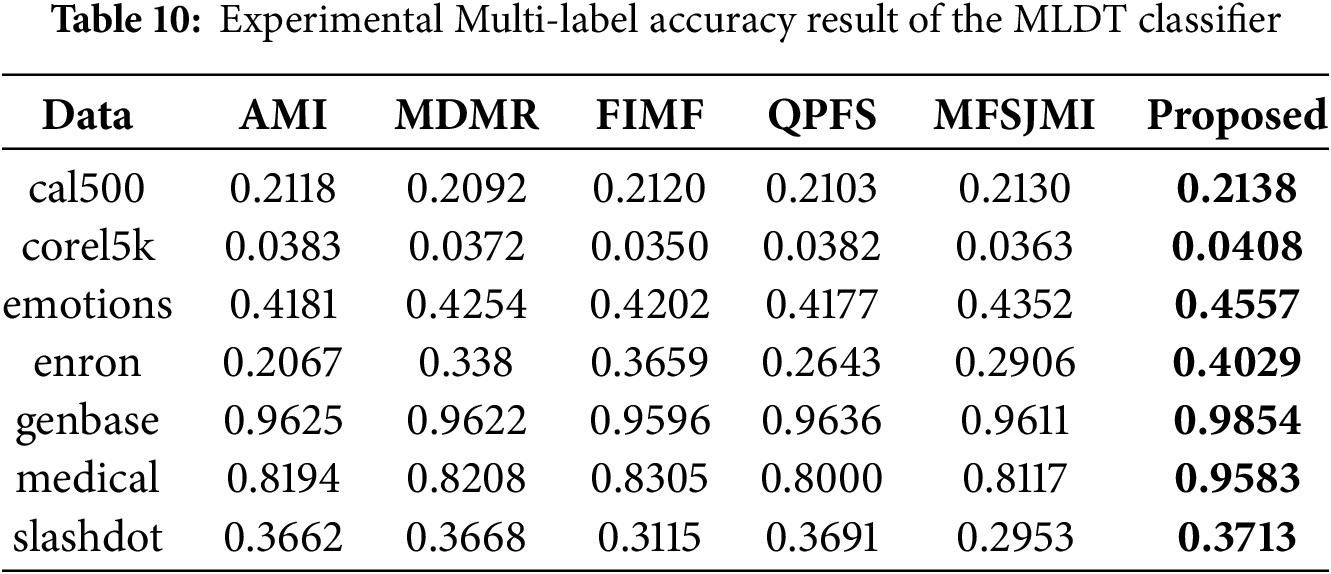
Fig. 1 illustrates the MLkNN performance variation of the proposed and comparative feature selection methods on the emotions dataset, where the number of selected features was gradually increased from 3 to 30. Three evaluation metrics-Hamming loss, Ranking loss, and Multi-label accuracy-were employed to analyze the behavior of each method under different feature subset sizes. As shown in the figures, all methods generally improve as the number of selected features increases, but the rate and stability of improvement differ substantially. For the Hamming loss, the proposed method consistently achieves the lowest values across all feature subset sizes, indicating robust generalization and effective elimination of redundant or noisy features. While MFSJMI and QPFS also exhibit a decreasing trend, their performance fluctuates more notably, suggesting less stability in feature selection. In terms of Ranking loss, the proposed method again demonstrates superior performance, maintaining lower loss values over the entire range of feature counts. This consistent improvement shows that the proposed formulation preserves the relative order between relevant and irrelevant labels more effectively than other methods, particularly when the feature space is limited. Finally, for Multi-label accuracy, the proposed method achieves the highest accuracy throughout the experiment, with a steady upward trend as the number of features increases. Even with a small number of features (e.g., fewer than 10), the proposed method already outperforms all baselines, highlighting its ability to identify highly informative and label-discriminative features early in the selection process.

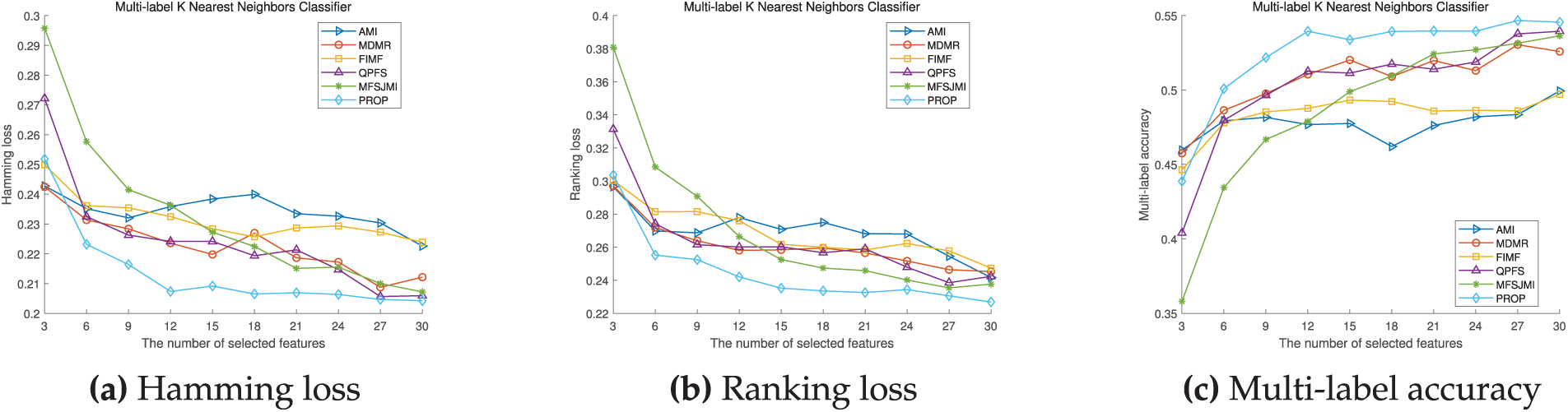
Figure 1: MLkNN performance variation of the number of selected features on (a) Hamming loss, (b) Ranking loss, and (c) Multi-label accuracy for the emotions dataset

To assess whether the observed MLDT performance differences among the compared feature selection methods are statistically significant across the seven datasets, we performed the Friedman–Nemenyi non-parametric statistical test at a significance level of α=0.05. The Friedman test yielded p-values of 0.0069, 0.0897, and 0.0094 for Hamming loss, Ranking loss, and Multi-label accuracy, respectively. These results indicate that, while Ranking loss exhibits only marginal significance, the differences in Hamming loss and Multi-label accuracy are statistically significant, suggesting that the compared methods yield meaningfully distinct performance under these measures. Fig. 2 presents the corresponding Critical Distance (CD) diagrams obtained from the Nemenyi post-hoc analysis. The diagrams visualize the average ranks of the six methods and the critical distance at which the rank differences become statistically significant [44]. As shown in the figure, the proposed method consistently achieves the best rank for all three evaluation metrics, demonstrating robust and stable performance. Complementary to these visual results, Table 11 reports the complete average-rank matrix for each method and metric. The proposed method attains the lowest average ranks (1.00, 1.86, and 1.0 for Hamming loss, Ranking loss, and Accuracy, respectively), confirming that its improvements are systematic rather than dataset-specific. Overall, these findings validate the statistical reliability of the proposed feature selection approach.

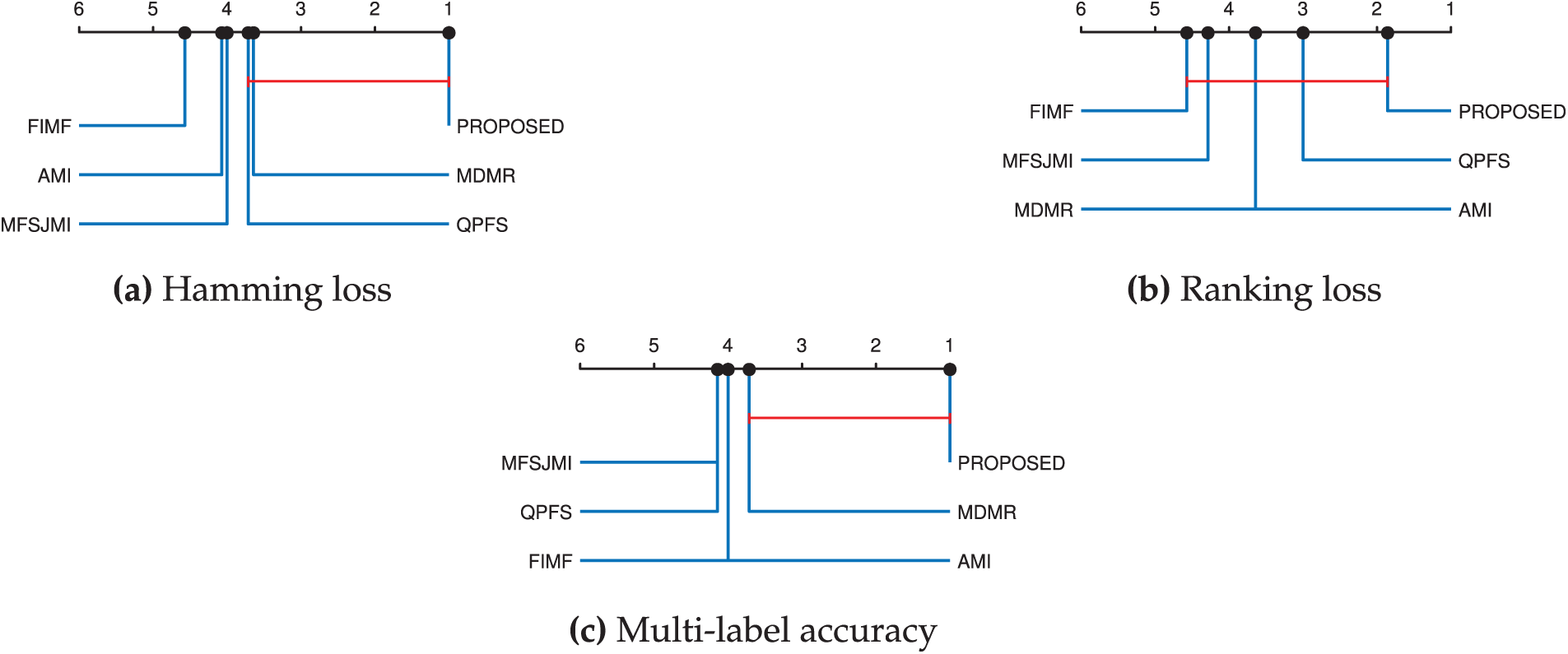
Figure 2: Critical Distance diagrams for six compared methods across seven datasets based on (a) Hamming loss, (b) Ranking loss, and (c) Multi-label accuracy. The diagrams are obtained from the Friedman–Nemenyi statistical test with α=0.05. The Friedman test yielded p-values of 0.0069, 0.0897, and 0.0094 for each metric, respectively

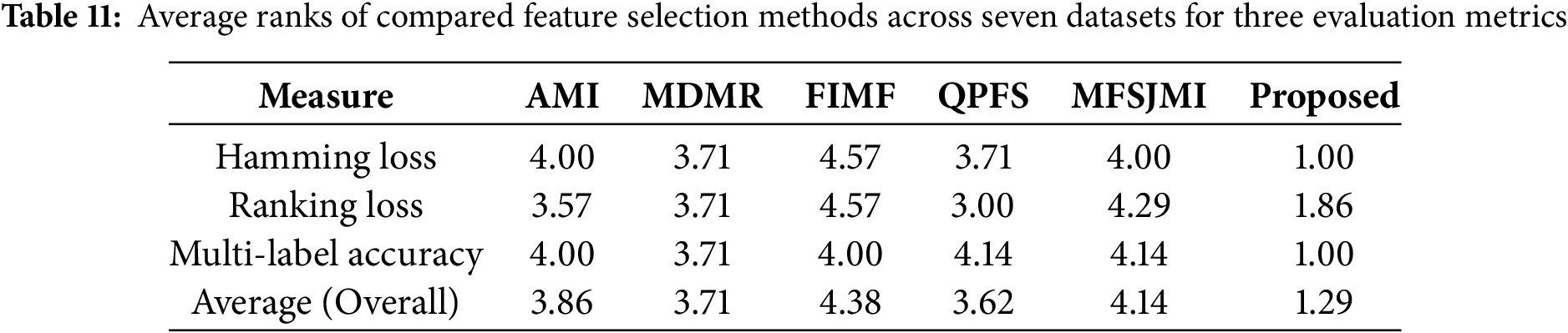
The computational efficiency of each feature selection method was evaluated in terms of total execution time, as summarized in Table 12. All experiments were conducted using MATLAB R2021b on a desktop equipped with an Intel Core i7-11700 CPU (2.5 GHz) and 32 GB of RAM. The maximum number of iterations for the proposed method was set to 100. The proposed method demonstrates competitive or superior computational efficiency compared to most baselines. In particular, it consistently outperforms AMI, MDMR, and MFSJMI, which incur substantial computational overhead due to repeated mutual information estimation or graph construction processes. While the proposed approach is slightly slower than FIMF-whose operations are relatively lightweight-it achieves significantly faster convergence than other information-theoretic methods such as QPFS and MFSJMI, especially on large-scale datasets like enron, genbase, and medical. These results indicate that the proposed optimization framework maintains high scalability without sacrificing selection quality, balancing effectiveness and computational cost efficiently across diverse multi-label datasets.

4.3 Analysis of the Proposed Method

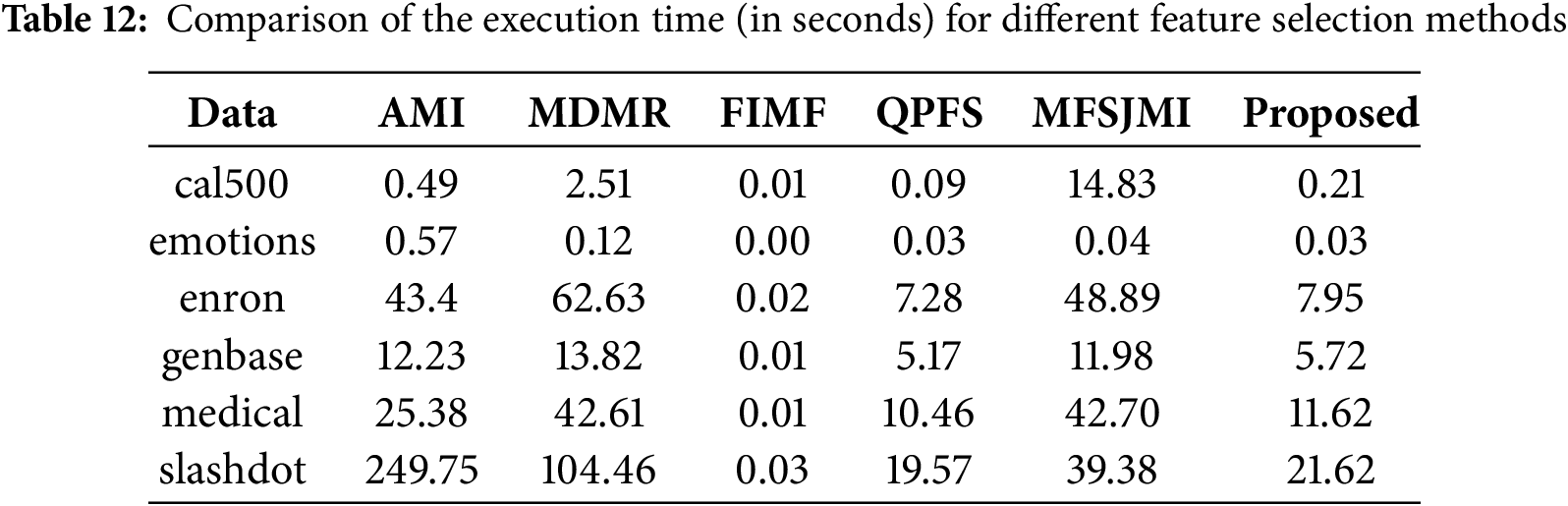
Figs. 3–5 illustrate the sensitivity of the proposed method to its three hyperparameters, α, β, and γ, across the cal500, emotions, and enron datasets, using multi-label accuracy with the MLkNN classifier as the evaluation metric. Each figure contains two subplots: (a) fixes α=0.1 and varies β and γ; (b) fixes β=0.1 and varies α and γ. All surfaces are presented in 3D to visualize the joint effect of the remaining two parameters on classification performance. Overall, the results demonstrate that the proposed method is highly robust to variations in hyperparameters, as long as their values are not excessively large or small. This indicates that the method does not require fine-grained hyperparameter tuning to achieve strong performance. In the Fig. 3, the accuracy remains consistently stable across all combinations of α, β, and γ, suggesting that the method is largely insensitive to hyperparameter changes on this dataset. In the Fig. 4, similar to cal500, the classification accuracy is stable across all hyperparameter settings, confirming the method’s consistent behavior regardless of parameter choice. In the Fig. 5, a minor performance decrease is observed when α=103, while the remaining parameter settings yield stable and strong results. This suggests that overly large values of α—which weights the Q term—may introduce redundancy in this dataset. Empirically, we find that effective values typically lie in the ranges α,β∈[10−3,101] and γ∈[10−2,102]. We therefore recommend performing grid search in a modest neighborhood around these intervals. For larger-scale problems or time-sensitive applications, alternative search strategies such as random search or Bayesian optimization may be employed to further reduce tuning overhead. These guidelines ensure a balance between computational cost and performance while maintaining robustness across datasets.

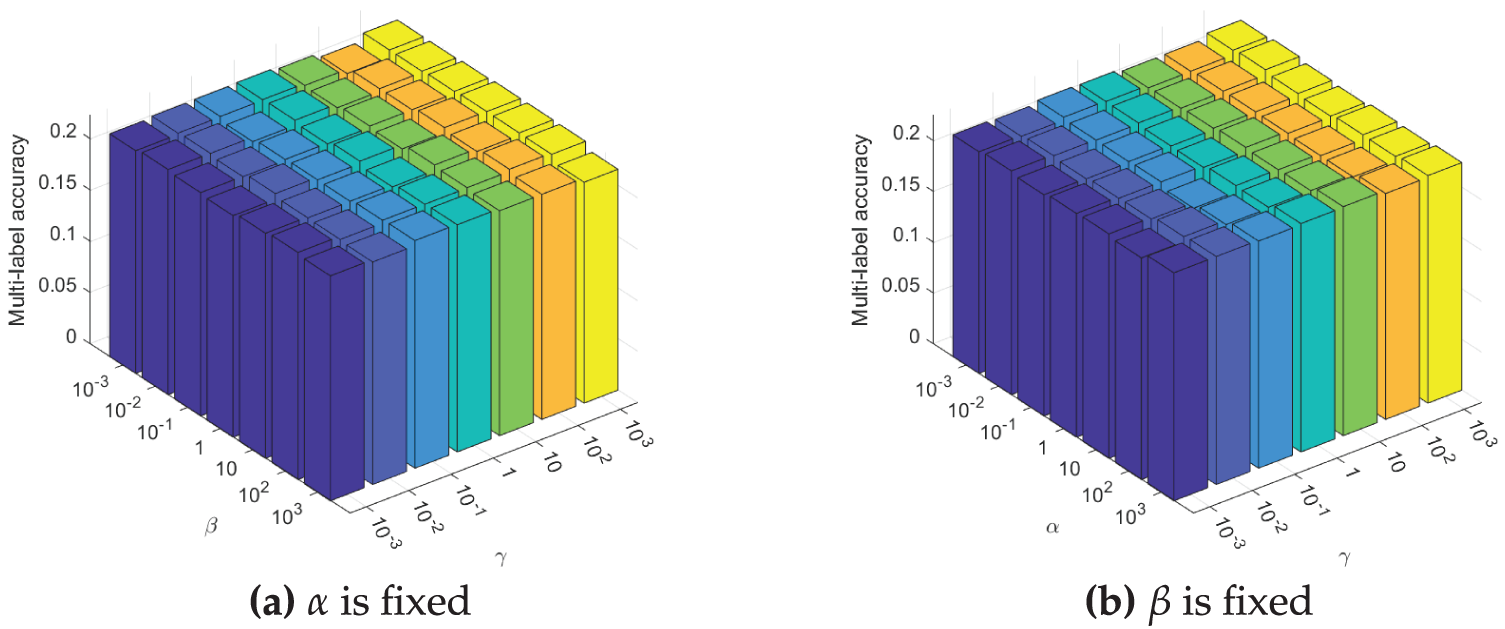
Figure 3: Comparison Multi-label accuracy of MLkNN classification based on parameters change in the cal500 data set

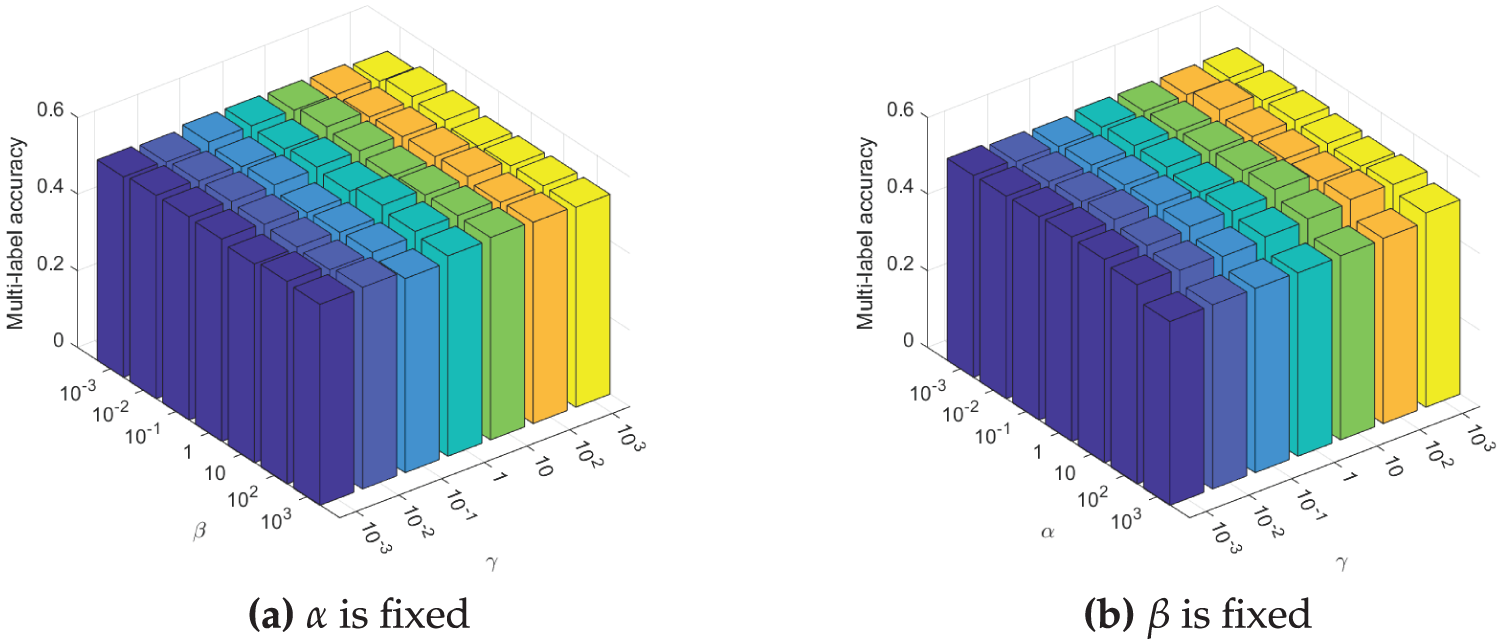
Figure 4: Comparison Multi-label accuracy of MLkNN classification based on parameters change in the emotions data set

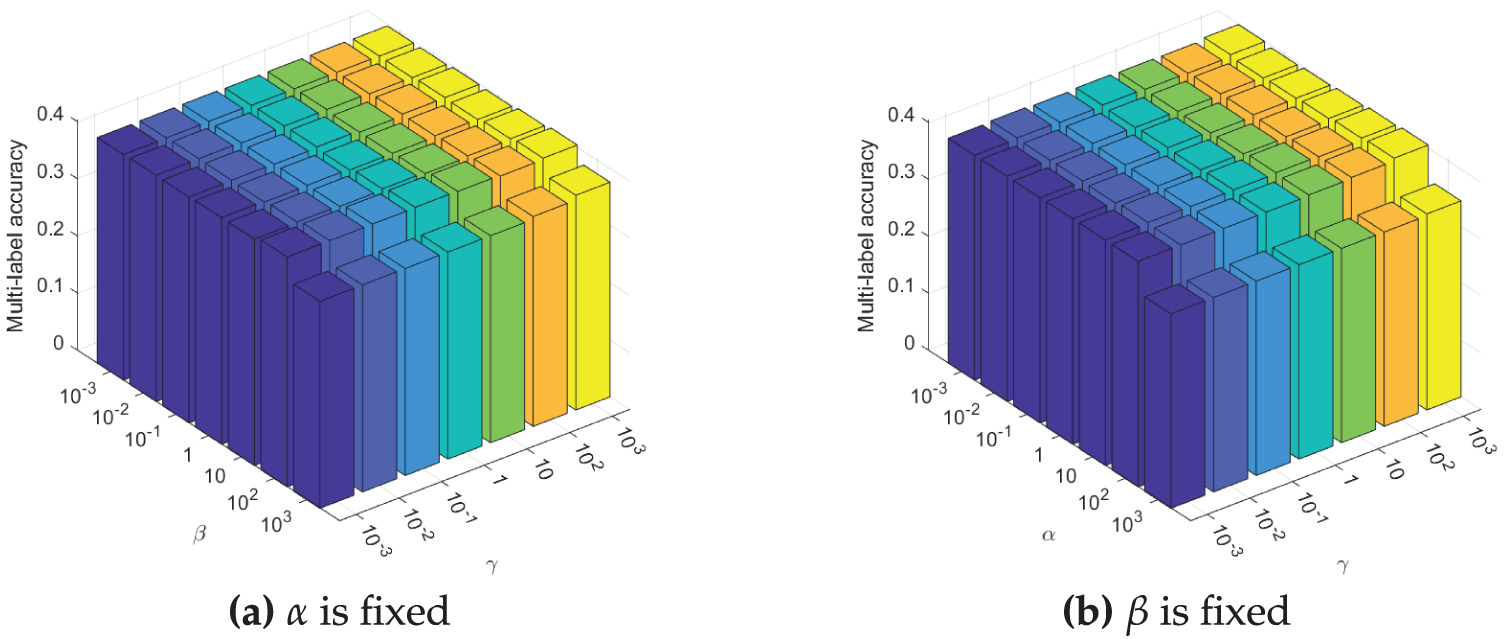
Figure 5: Comparison Multi-label accuracy of MLkNN classification based on parameters change in the enron data set

Fig. 6 displays the convergence behavior of the proposed method for all used datasets. The horizontal axis represents the number of iterations of the proposed algorithm, and the vertical axis shows the value of the objective function. The objective function value drops sharply within the first three iterations and appears to converge before the tenth iteration. This indicates that the proposed algorithm operates efficiently.

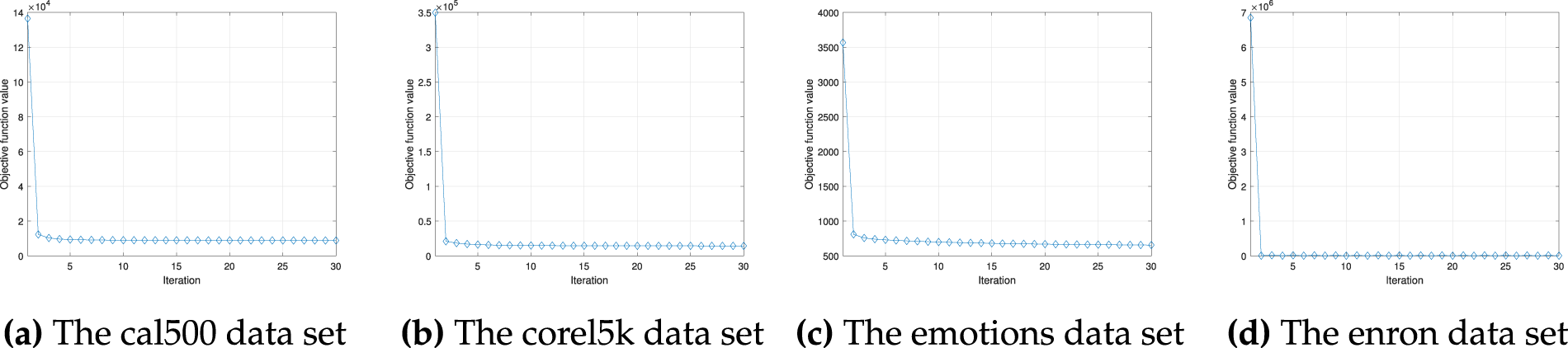
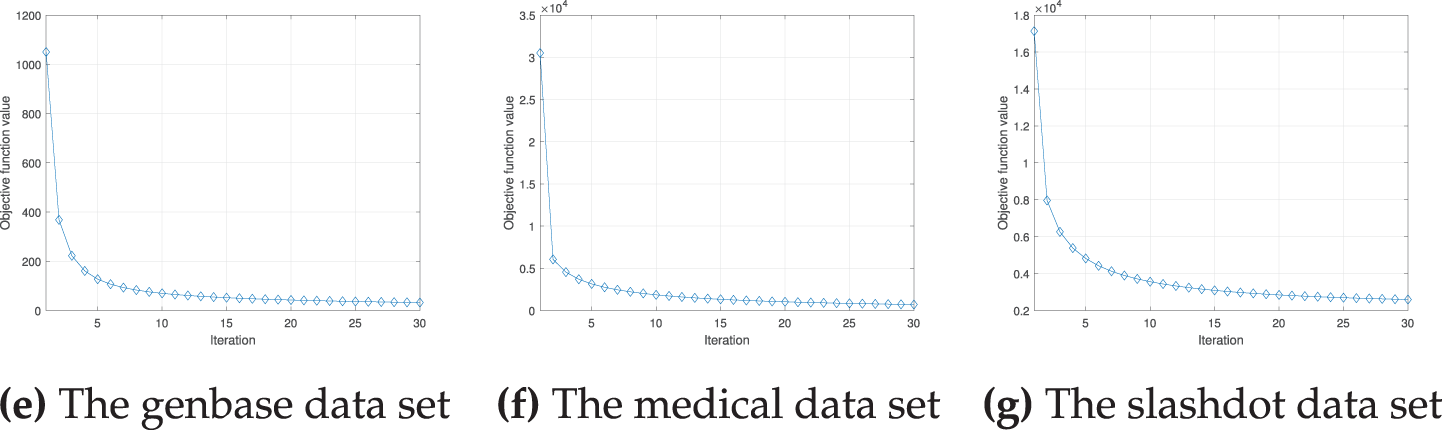
Figure 6: Convergence rate of the proposed method

5  Conclusions

In this study, we proposed a novel regression-based objective function for multi-label feature selection that explicitly incorporates mutual information between features and labels. By integrating a mutual information-aware structure into a convex regression formulation, the proposed method enables efficient optimization via projected gradient descent while preserving important statistical dependencies in the data. Empirical evaluations across multiple benchmark datasets and classifiers demonstrate that our approach consistently achieves superior or competitive performance compared to existing methods, confirming its effectiveness and robustness in various multi-label learning scenarios.

Despite its strong performance, the proposed method has several limitations. First, computing mutual information for all feature—feature and label—label pairs can be computationally expensive, especially for high-dimensional datasets. Exploring approximation techniques or sparse estimation strategies may significantly reduce this overhead. Second, the method involves several hyperparameters whose tuning can impact performance and requires careful consideration. Future work will focus on developing adaptive or data-driven hyperparameter selection mechanisms to further enhance usability and generalization.

Acknowledgement: None.

Funding Statement: This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (RS-2020-NR049579).

Availability of Data and Materials: Details of the dataset used in this study are provided in the main text. The dataset is accessible at https://mulan.sourceforge.net/datasets-mlc.html (accessed on 20 July 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Wang J, Zhang Y, Wang T, Tang H, Li B. Establishing two-dimensional dependencies for multi-label image classification. Appl Sci. 2025;15(5):2845. doi:10.3390/app15052845. [Google Scholar] [CrossRef]

2. Hu W, Fan Q, Yan H, Xu X, Huang S, Zhang K. A survey of multi-label text classification under few-shot scenarios. Appl Sci. 2025;15(16):8872. doi:10.3390/app15168872. [Google Scholar] [CrossRef]

3. Feng Y, Wei R. Method of multi-label visual emotion recognition fusing fore-background features. Appl Sci. 2024;14(18):8564. doi:10.21203/rs.3.rs-4752870/v1. [Google Scholar] [CrossRef]

4. Han Q, Zhang W, Ma C, He J, Gao W. Robust multilabel feature selection with label enhancement for fault diagnosis. IEEE Transact Syst Man, Cybernet: Syst. 2025;55(11):7841–50. doi:10.1109/tsmc.2025.3598796. [Google Scholar] [CrossRef]

5. Huang F, Yang N, Chen H, Bao W, Yuan D. Distributed online multi-label learning with privacy protection in internet of things. Appl Sci. 2023;13(4):2713. doi:10.3390/app13042713. [Google Scholar] [CrossRef]

6. Elhamifar E, Vidal R. Sparse subspace clustering: algorithm, theory, and applications. IEEE Transact Pattern Anal Mach Intelle. 2013;35(11):2765–81. doi:10.1109/tpami.2013.57. [Google Scholar] [PubMed] [CrossRef]

7. Lim H, Lee J, Kim DW. Optimization approach for feature selection in multi-label classification. Pattern Recognition Letters. 2017;89:25–30. doi:10.1016/j.patrec.2017.02.004. [Google Scholar] [CrossRef]

8. Lee J, Kim DW. Fast multi-label feature selection based on information-theoretic feature ranking. Pattern Recognit. 2015;48:2761–71. doi:10.1016/j.patcog.2015.04.009. [Google Scholar] [CrossRef]

9. Peng H, Long F, Ding C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Transact Pattern Anal Mach Intell. 2005;27:1226–38. doi:10.1109/tpami.2005.159. [Google Scholar] [PubMed] [CrossRef]

10. Nie F, Huang H, Cai X, Ding C. Efficient and robust feature selection via joint l2,1-norms minimization. In: Advances in neural information processing systems 23 (NIPS 2010). Red Hook, NY, USA: Curran Associates, Inc.; 2010. [Google Scholar]

11. Pereira RB, Plastino A, Zadrozny B, Merschmann LH. Categorizing feature selection methods for multi-label classification. Artificial Intell Rev. 2018;49(1):57–78. doi:10.1007/s10462-016-9516-4. [Google Scholar] [CrossRef]

12. Tsoumakas G, Vlahavas I. Random k-labelsets: an ensemble method for multilabel classification. In: Machine learning: ECML 2007 (ECML 2007). Berlin/Heidelberg, Germany: Springer; 2007. p. 406–17 doi: 10.1007/978-3-540-74958-5_38. [Google Scholar] [CrossRef]

13. Read J. A pruned problem transformation method for multi-label classification. In: Proceedings of the New Zealand Computer Science Research Student Conference; 2008 Apr 14–18; Christchurch, New Zealand. p. 143–50. [Google Scholar]

14. Lee J, Kim DW. Feature selection for multi-label classification using multivariate mutual information. Pattern Recognit Letters. 2013;34:349–57. doi:10.1016/j.patrec.2012.10.005. [Google Scholar] [CrossRef]

15. Lee J, Kim DW. Mutual information-based multi-label feature selection using interaction information. Expert Syst Applicat. 2015;42:2013–25. doi:10.1016/j.eswa.2014.09.063. [Google Scholar] [CrossRef]

16. Lin Y, Hu Q, Liu J, Duan J. Multi-label feature selection based on max-dependency and min-redundancy. Neurocomputing. 2015;168:92–103. doi:10.1016/j.neucom.2015.06.010. [Google Scholar] [CrossRef]

17. Zhang P, Liu G, Song J. MFSJMI: multi-label feature selection considering join mutual information and interaction weight. Pattern Recognit. 2023;138:109378. doi:10.1016/j.patcog.2023.109378. [Google Scholar] [CrossRef]

18. Clare A, King RD. Knowledge discovery in multi-label phenotype data. In: Principles of data mining and knowledge discovery (PKDD 2001). Berlin/Heidelberg, Germany: Springer; 2001. p. 42–53 doi: 10.1007/3-540-44794-6_4. [Google Scholar] [CrossRef]

19. Fan Y, Chen B, Huang W, Liu J, Weng W, Lan W. Multi-label feature selection based on label correlations and feature redundancy. Knowl Based Syst. 2022;241:108256. doi:10.1016/j.knosys.2022.108256. [Google Scholar] [CrossRef]

20. Li Y, Hu L, Gao W. Multi-label feature selection via robust flexible sparse regularization. Pattern Recognit. 2023;134:109074. doi:10.1016/j.patcog.2022.109074. [Google Scholar] [CrossRef]

21. Fan Y, Liu J, Tang J, Liu P, Lin Y, Du Y. Learning correlation information for multi-label feature selection. Pattern Recognit. 2024;145:109899. doi:10.1016/j.patcog.2023.109899. [Google Scholar] [CrossRef]

22. Li Y, Hu L, Gao W. Label correlations variation for robust multi-label feature selection. Informat Sci. 2022;609:1075–97. doi:10.1016/j.ins.2022.07.154. [Google Scholar] [CrossRef]

23. Hu L, Gao L, Li Y, Zhang P, Gao W. Feature-specific mutual information variation for multi-label feature selection. Informat Sci. 2022;593:449–71. doi:10.1016/j.ins.2022.02.024. [Google Scholar] [CrossRef]

24. Dai J, Huang W, Zhang C, Liu J. Multi-label feature selection by strongly relevant label gain and label mutual aid. Pattern Recognit. 2024;145:109945. doi:10.1016/j.patcog.2023.109945. [Google Scholar] [CrossRef]

25. Faraji M, Seyedi SA, Tab FA, Mahmoodi R. Multi-label feature selection with global and local label correlation. Expert Syst Appl. 2024;246:123198. doi:10.1016/j.eswa.2024.123198. [Google Scholar] [CrossRef]

26. He Z, Lin Y, Wang C, Guo L, Ding W. Multi-label feature selection based on correlation label enhancement. Inf Sci. 2023;647:119526. doi:10.1016/j.ins.2023.119526. [Google Scholar] [CrossRef]

27. Yang Y, Chen H, Mi Y, Luo C, Horng SJ, Li T. Multi-label feature selection based on stable label relevance and label-specific features. Inf Sci. 2023;648:119525. doi:10.1016/j.ins.2023.119525. [Google Scholar] [CrossRef]

28. Zhang ML, Peña JM, Robles V. Feature selection for multi-label naive Bayes classification. Informat Sci. 2009;179:3218–29. doi:10.1016/j.ins.2009.06.010. [Google Scholar] [CrossRef]

29. Cho DH, Moon SH, Kim YH. Genetic feature selection applied to KOSPI and cryptocurrency price prediction. Mathematics. 2021;9(20):2574. doi:10.3390/math9202574. [Google Scholar] [CrossRef]

30. Das H, Prajapati S, Gourisaria MK, Pattanayak RM, Alameen A, Kolhar M. Feature selection using golden jackal optimization for software fault prediction. Mathematics. 2023;11(11):2438. doi:10.3390/math11112438. [Google Scholar] [CrossRef]

31. Guo Y, Kasihmuddin MSM, Zamri NE, Li J, Romli NA, Mansor MA, et al. Logic mining method via hybrid discrete hopfield neural network. Comput Indust Eng. 2025;206:111200. doi:10.1016/j.cie.2025.111200. [Google Scholar] [CrossRef]

32. Romli NA, Zulkepli NFS, Kasihmuddin MSM, Karim SA, Jamaludin SZM, Rusdi N, et al. An optimized logic mining method for data processing through higher-order satisfiability representation in discrete hopfield neural network. Appl Soft Comput. 2025;184(B):113759. doi:10.1016/j.asoc.2025.113759. [Google Scholar] [CrossRef]

33. Bao B, Tang H, Bao H, Hua Z, Xu Q, Chen M. Simplified discrete two-neuron hopfield neural network and FPGA implementation. IEEE Trans Ind Electron. 2025;72(4):4105–15. doi:10.1109/tie.2024.3451052. [Google Scholar] [CrossRef]

34. Huang S, Hu W, Lu B, Fan Q, Xu X, Zhou X, et al. Application of label correlation in multi-label classification: a survey. Appl Sci. 2024;14(19):9034. doi:10.3390/app14199034. [Google Scholar] [CrossRef]

35. Klonecki T, Teisseyre P, Lee J. Cost-constrained feature selection in multilabel classification using an information-theoretic approach. Pattern Recognition. 2023;141(1):1–18. doi:10.1016/j.patcog.2023.109605. [Google Scholar] [CrossRef]

36. Zhang ML, Zhou ZH. ML-KNN: a lazy learning approach to multi-label learning. Pattern Recognit. 2007;40:2038–48. doi:10.1016/j.patcog.2006.12.019. [Google Scholar] [CrossRef]

37. Turnbull D, Barrington L, Torres D, Lanckriet G. Semantic annotation and retrieval of music and sound effects. IEEE Transact Audio, Speech, Lang Process. 2008;16(2):467–76. doi:10.1109/tasl.2007.913750. [Google Scholar] [CrossRef]

38. Trohidis K, Tsoumakas G, Kalliris G, Vlahavas IP. Multilabel classification of music into emotions. In: International Conference on Music Information Retrieval. Philadelphia, PA, USA: ISMIRSociety; 2008. p. 325–30. [Google Scholar]

39. Pestian J, Brew C, Matykiewicz P, Hovermale DJ, Johnson N, Cohen KB, et al. A shared task involving multi-label classification of clinical free text. In: BioNLP ′07:Proceedings of the Workshop on BioNLP 2007: Biological, Translational, and Clinical Language Processing. Stroudsburg, PA, USA: ACL; 2007. p. 97–104. [Google Scholar]

40. Leskovec J, Huttenlocher D, Kleinberg J. Signed networks in social media. In: CHI ′10:Proceedings of the SIGCHI Conference on Human Factors in Computing Systems. New York, NY, USA: ACM; 2010. p. 1361–70. [Google Scholar]

41. Lee J, Kim DW. SCLS: multi-label feature selection based on scalable criterion for large label set. Pattern Recognit. 2017;66:342–52. doi:10.1016/j.patcog.2017.01.014. [Google Scholar] [CrossRef]

42. Lee J, Lim H, Kim DW. Approximating mutual information for multi-label feature selection. Elect Letters. 2012;48(15):929–30. doi:10.1049/el.2012.1600. [Google Scholar] [CrossRef]

43. Cano A, Luna JM, Gibaja EL, Ventura S. LAIM discretization for multi-label data. Informat Sci. 2016;330:370–84. doi:10.1016/j.ins.2015.10.032. [Google Scholar] [CrossRef]

44. Demšar J. Statistical comparisons of classifiers over multiple data sets. J Mach Learn Res. 2006;7:1–30. [Google Scholar]