Multilevel Military Image Encryption Based on Tri-Independent Keying Approach

1  Introduction

In recent military communication technologies, the transfer of sensitive visual information has become a critical component that requires robust security tools for defense operations. Safeguarding military images, which include drone surveillance footage, satellite maps, reconnaissance photos, or any battlefield situational-awareness images, from unauthorized access provides a secure channel of communication for mission-based visual imagery data [1,2]. The protection of this imagery data is not only a matter of confidentiality but also a necessary step for achieving mission success and operational security. As military images often comprise confidential contents such as mission plans, troop positions, and equipment details, tampering or interception with this visual data during transmission can cause many risks such as mission failures, national security threats, and intelligence leaks [3,4].

To overcome these risks, military image encryption is essential for ensuring the confidentiality and integrity of visual data transmission across tactical networks. The encryption technologies protect classified visual information by converting meaningful visual information into an unintelligible format [1–4]. This makes the original image unreadable and useless to adversaries while maintaining the integrity of the communication system, where only authorized recipients with the deception key have the ability to reconstruct the original image. As a result, the task of military image encryption requires the use of a robust and secure cryptographic approach that has unique features for ensuring a high level of security. In order to produce reliable encryption results, there are several challenges that need to be addressed when designing a reliable encryption method for military images. These challenges can include encryption key length and management, high data redundancy, statistical cryptanalysis, differential attacks, high-resolution data volume (e.g., satellite images), and computational time and cost.

Many cryptographic algorithms have been presented for securing image transmission in various applications [5–7]. An effective image encryption framework in [8] was proposed by employing cellular automata neighborhood and a novel two-dimensional hyperchaotic map for enhancing the security level of the image encryption process. Shahbaz Khan et al. [9] proposed a quantum image encryption algorithm that used four distinct confusion-diffusion modules, attaining successful performance against occlusion attacks. A gate-efficient quantum image encryption method is presented in [10] by using pre-encryption quantum compression and chaos-based qubit encryption, which resulted in a strong resistance against differential attacks. However, a few methods have been introduced in the literature for image encryption-based military applications. Alexan et al. [3] proposed a reconnaissance imagery encryption method that employed a Genetic Algorithm (GA) utilizing a Mersenne Twister key and DNA coding for securing the communication over unmanned aerial vehicle-assisted relaying networks. The proposed method in [3] offered a solution that overcame the need for reliable and efficient transfer of reconnaissance images over wireless ad-hoc networks, which are of great importance in war zones. In [4], Nithya and Dhanasekaran presented a hybrid chaotic approach based on the distinctive features of quadratic, Gingerreadman, and Baker’s maps to encrypt images in a visual sensor network for a smart military surveillance system. The proposed encryption method [4] processed only the dominant sub-band from input RGB images to develop a reliable and fast real-time encryption for situational awareness in danger-prone zones. Rajendiran [11] introduced a chaotic image encryption algorithm based on Baker’s map for designing reliable military surveillance systems. The chaotic [11] algorithm improved the security and efficiency of visual information collected by the sensor nodes, which are installed in the various spots of the remotely operated devices and vision sensor networks. It aimed to reduce the computation time in the network of visual sensors while providing robust encryption results. Bazeer Ahamed and Krishnamoorthy [12] presented a sensible image encryption for military applications using the Advanced Encryption Standard (AES) to provide a secure transmission of sensitive visual information against intercepted attacks. In [13], a lightweight image encryption algorithm was proposed using Peter De Jong’s chaotic system for military images. A secure military communication system is presented in [14] using image steganography and block-rotary encryption for the safe military transfer of visual data. The block-rotary encryption scheme [14] aimed to rotate the blocks of original image data by a private key array obtained from a key image. The rotation step was performed for each block, where it was shifted by the number of locations given by the corresponding pixel value in the key array. The existing methods have achieved great results for military image encryption. However, the following aspects need to be addressed to provide reliable encryption results. These aspects include high correlations resulting from large-scale structures, strong spatial relationships between adjacent pixels in the regions of similar intensity values, key length and management, computational complexity, and the use of a statistical encryption key.

Therefore, this paper addresses these challenges by introducing a new Tri-independent keying approach that achieves robust multilevel encryption for military imagery. The proposed approach involves pixel-level scrambling, bit-level manipulation, and block-level shuffling operations. Each operation is controlled with a secret key that is independently generated by hashing an input password to a 256-bit length. The contributions of this paper are summarized as follows:

•   This paper introduces a new military imagery cryptography framework based on a Tri-independent keying approach, which has prominent features of determinism, dynamism, unpredictability, and randomness, thereby offering a high degree of security in defence communication.

•   A piecewise pixel-level scrambling process is proposed to break the direct relationships between adjacent pixels, which avoids visual analysis attacks inside local image regions.

•   A dynamic masking scheme is introduced to provide distinct keys for ensuring that the encryption of two similar regions at the bit-level stage produces two different encrypted results.

•   A chaotic block-level shuffling system is presented to address the global correlations between regions with large-scale patterns.

•   Tri-deterministic keys are independently generated based on a hashing algorithm to increase the computational efficiency and reliability of the encryption process.

•   The proposed method has strong resistance against various image cryptographic attacks.

The rest of this paper is organized as follows. Section 2 explains in detail the proposed encryption and decryption methods, which include the piecewise scramble function, dynamic masking scheme, and chaotic index-map system. In Section 3, experimental results on military images are provided along with a comprehensive security performance analysis. Finally, the conclusion is given in Section 4.

2  Methodology

In this section, we present a Tri-independent keying method for secure multilevel encryption of military images. The proposed method is block-level cryptography, consisting of three independent stages for increasing the security and robustness of the encryption process. Fig. 1 shows the overall description of the proposed image encryption method. As a pre-processing step, the input image is divided into a number of non-overlapping blocks with a size of 8×8 bytes. A zero padding process may be used when the dimension of the input image is not perfectly aligned with the block size. Further, the Secure Hash Algorithm 256-bit (SHA-256) is first employed for generating secure Tri-keys for multilevel security stages, which are a piecewise flipping function, a dynamic masking scheme, and a chaotic index map system.

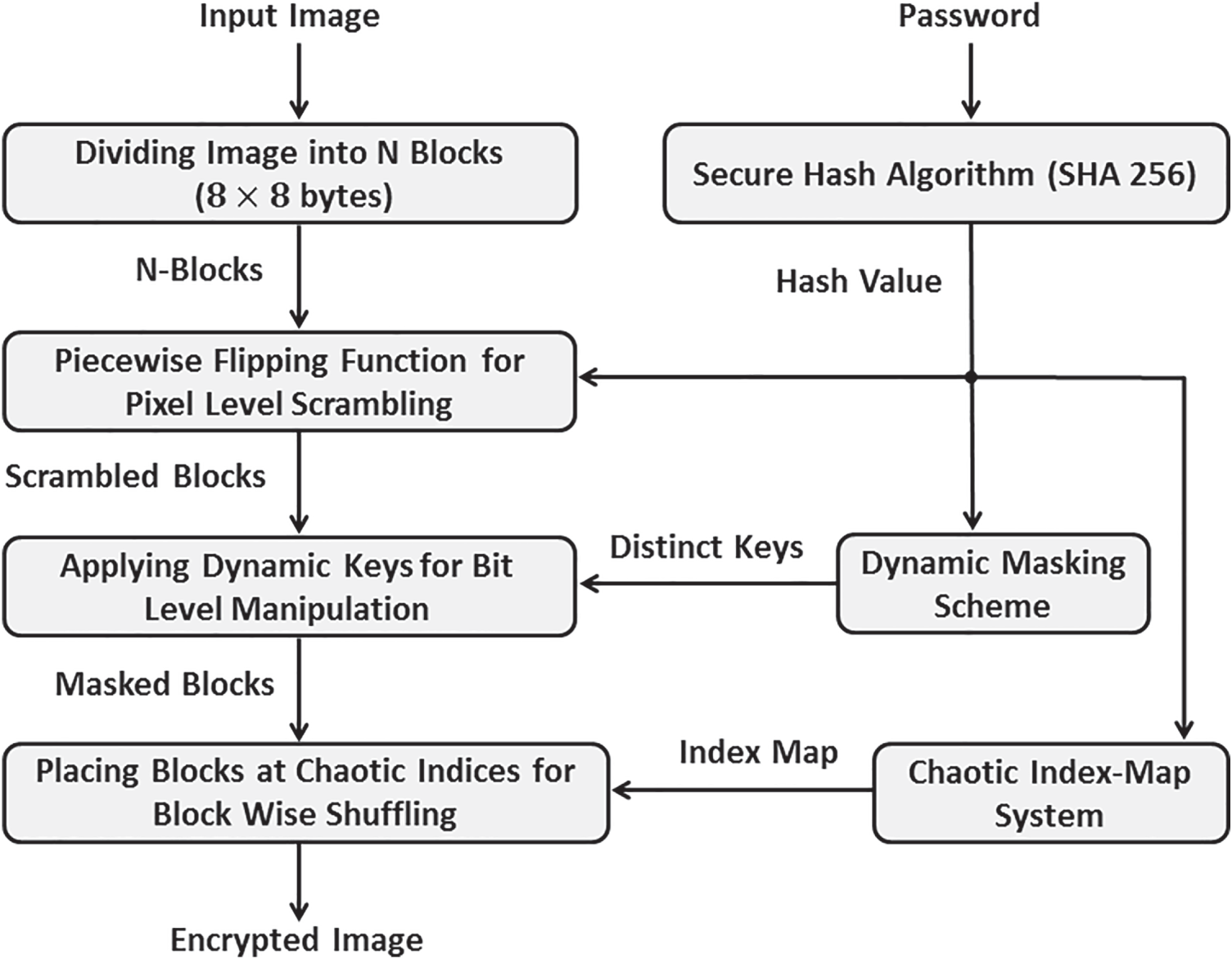
Figure 1: The block diagram of the proposed encryption method

2.1 Secure Hash Algorithm 256-Bit

The Secure Hash Algorithm 256-bit (SHA-256) [15–17] was mainly used as a cryptographic hash method for verifying data integrity, but not for reversible encryption. It can accept an input message up to (264−1 bits) and generates a fixed-size hash value of 256 bits (32 bytes), which is represented as a hexadecimal number of 64 digits. The SHA-256 processes the input data in two main stages: preparation and processing, as shown in Fig. 2. First, the preparation step ensures that the size of the original input (lm-bit) is a multiple of 512, allowing the division of the input into a set of blocks with a predefined size (512 bits). This is done by padding the original input with pt-bit, then appending the length of the original input in bits. The padding process starts with adding a single ‘1’ bit to the end of the input, followed by the required number of ‘0’ bits, forming a padded input with a length that is 64 bits less than a multiple of 512. Then, the length of the original input is appended to the end of the padded input as a 64-bit big-endian integer. As a result, the final input (L=lm+pt+64) can be divided into K (L/512) equally sized blocks with 512-bit length.

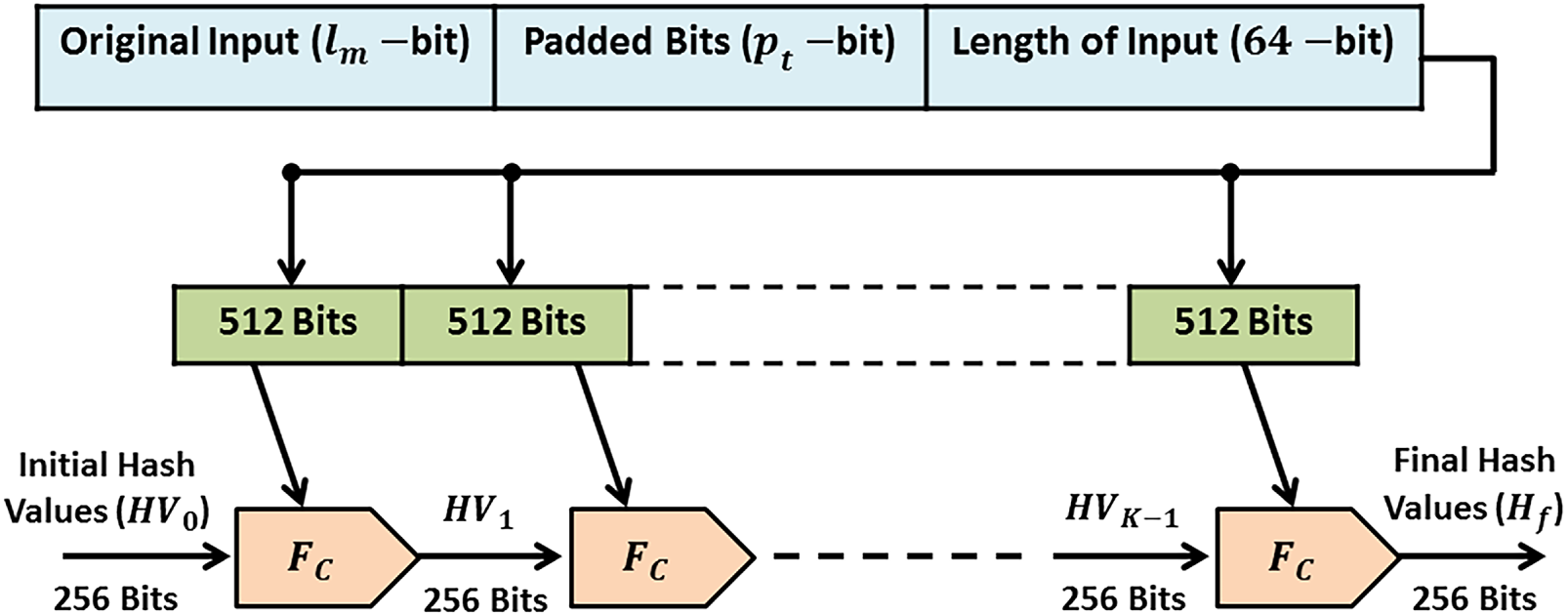
Figure 2: Hash value generation from input password using the SHA-256 algorithm

In the second stage, each 512-bit block is processed in 64 rounds by using a compression function (Fc), as illustrated in Fig. 2. Before processing, a set of initial hash values (HV0) is employed in the first round of processing to start the hash computation, generating intermediate hash values (HVK). These initial values (HV0) are pre-defined eight 32-bit constants (256-bit length) in the SHA-256 specification. At each round, the compression function performs bitwise operations, modular additions, conditional functions, and bit shifts on the input block and intermediate hash values. These operations mix up the bits of the input blocks and intermediate hash values to ensure that a minor modification in the input will produce a significant change in the output. After processing all blocks, the hash value of the last block (Hf) is considered the final hash of the original input. In our work, the SHA-256 is adapted for hashing the input password and generating strong keys, which are further utilized in designing a multilevel secure approach for image encryption.

2.2 Piecewise Pixel-Level Scramble Function

A piecewise function is introduced for achieving a pixel-level scramble inside each block of the input image, where the positions of individual pixels are locally rearranged to new locations. This process is a fundamental step for accomplishing the confusion concept, which aims to make the relationship between the input image and the scrambled image as obscure as possible. In particular, the pixel-level scrambling performs the confusion by breaking the spatial correlation between the adjacent pixels without changing the pixel intensities, making the input image securely unrecognizable against visual analysis attacks. The proposed piecewise function involves a dual scramble process controlled by an adaptive scramble key (Knp) to perform either up-down or left-right pixel flipping. The proposed scrambling function (Sn) is defined as:

Sn(i,j)={Bn(i,w−j+1)Knp=0Bn(h−i+1,j)Knp=1(1)

where Bn denotes an equal-size block with finite extent of h×w (8×8) while n∈[1,N] refers to the number of blocks resulting from the division of the input image. The coordinate (i,j) represents the position of a pixel inside the block, and are expressed as i∈[1,h] andj∈[1,w]. The adaptive key (Knp) is expressed as:

Knp=mod(Df(mod (n−1,32)+1)+n,2)(2)

Df=[d1,d2,…d32](3)

where mod represents the modulus after the division operation and Df is a vector including 8-bit unsigned integers that are derived from the hexadecimal hash values (Hf). As shown in Fig. 3, for left-right flipping, the column pixels are mirrored horizontally, while the row pixels are reflected vertically for up-down flipping.

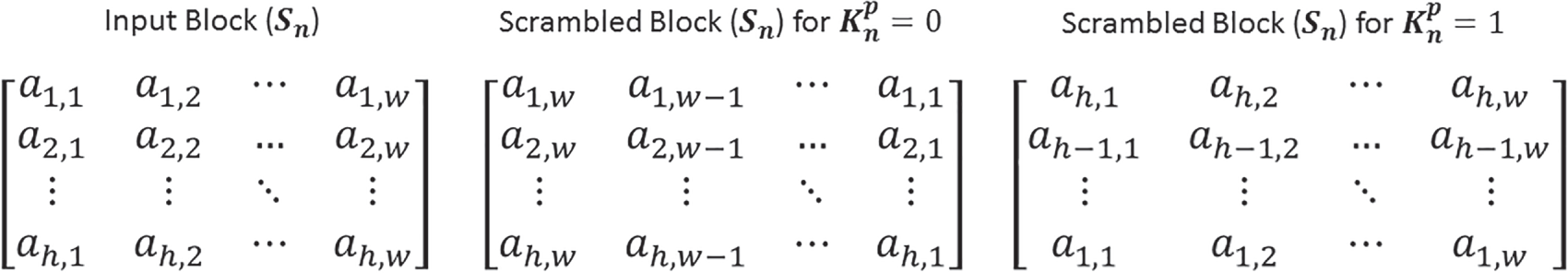
Figure 3: The process of the proposed piecewise function for performing the dual scrambling operation

2.3 Dynamic Masking Scheme

In the context of image data, the use of a statistical key can lead to serious security issues. For example, when the same key is repeatedly used over all images, identical image regions will result in the same encrypted output, revealing some structural clues. This weakness allows attackers to analyze the statistical properties of the encrypted image and infer information about the image or encryption key. To address this problem, we introduce a dynamic masking scheme to provide distinct encoding keys that change for each scrambled block. These keys (Knm) are independently generated and have the same block size (512 bits), as follows:

Knm(i,j)=pn((i−1)∗8+j)(4)

pn=mod(bn+n+(1:64),256)(5)

bn=Df(mod(n−1,32)+1)(6)

Then, each scrambled block is individually masked with a unique dynamic key using the bitwise XOR operation for bit-level manipulation. Fig. 4 shows the overall description of the proposed masking scheme. The masked blocks (Cn) are obtained as:

Cn(i,j)=Knm(i,j)⊕Sn(i,j)(7)

where ⊕ denotes the bitwise XOR operation. The masking process is performed on a bit-by-bit basis to target the finest possible granularity in scrambled blocks. The binary representation of each pixel in the scramble blocks is XORed with those from the corresponding byte in the dynamic keys, making the scrambled blocks visually random and noisy.

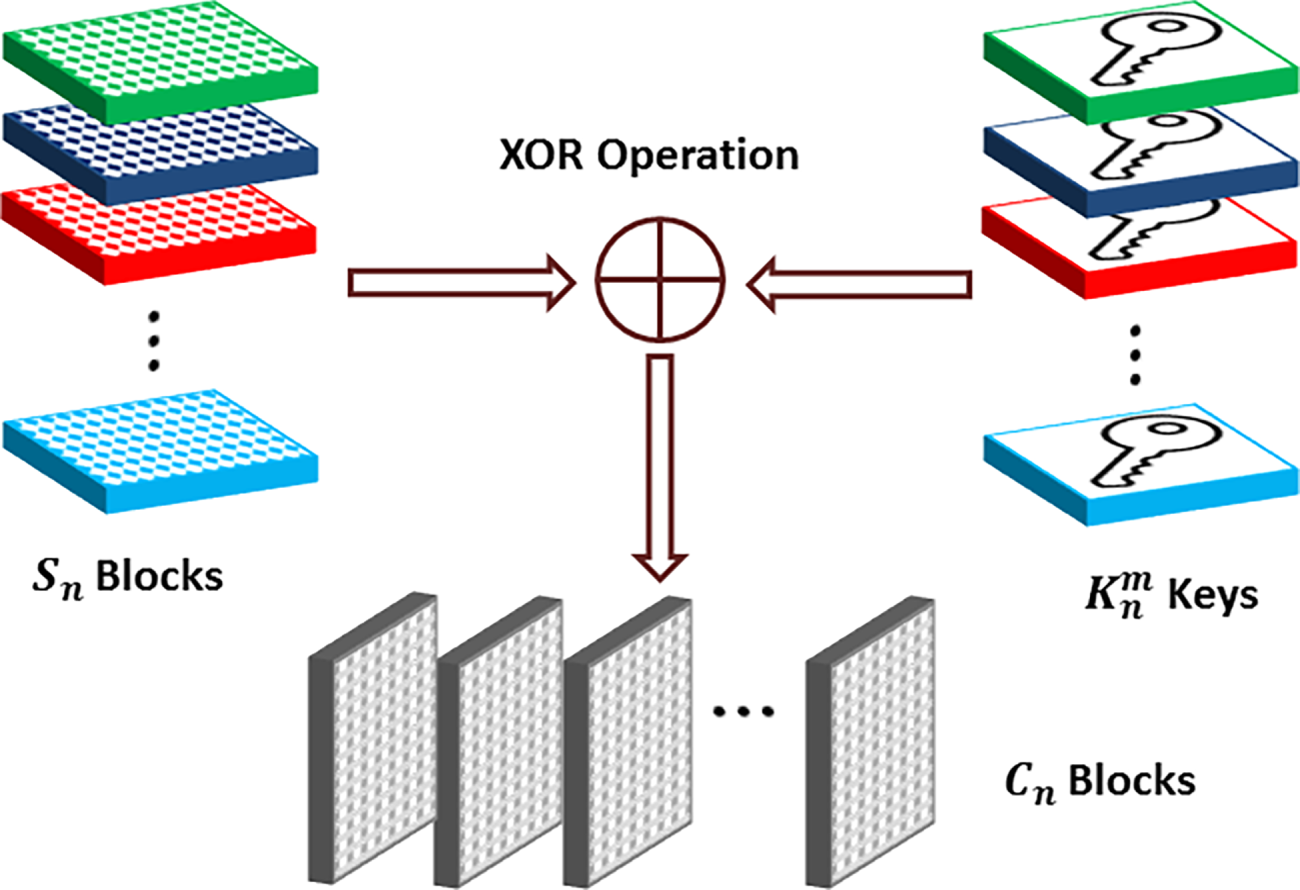
Figure 4: The description of the proposed dynamic masking scheme for bit-level manipulation

2.4 Chaotic Block-Wise Shuffling System

After performing pixel-level scrambling and bit-level masking steps, some global correlation or residual patterns might survive, particularly in the regions where large-scale structures are present. This weakness can be utilized to partially recover some parts of image areas by inspecting pixel frequency patterns and border transitions. To handle this problem, rearranging image regions can obscure large-scale features and increase the security and randomness of the encrypted image, making it difficult for attackers to infer object boundaries or shapes. Hence, a chaotic index-map system is presented to conduct block-wise shuffling for breaking any residual correlation or global image features. More specifically, the shuffling process reallocates the masked blocks randomly across the image domain according to a chaotic logistic map based on a seeding key. The logistic map [18] is a nonlinear function that produces a pseudo-random sequence (yn), as follows:

yn+1=r∗yn∗(1−yn)(8)

where the parameter (r) is set to (3.57,4] for attaining a chaotic behavior, while yn is a random value between 0 and 1. Due to the fact [18] that a small change in the initial value (y0) can create a drastically different sequence of numbers, we propose to implement the value of y0 as a seeding key (Kf), which is given as:

Kf=y0=(∑t=18dt∗256t−1)/264(9)

where dt is a sub-vector taken from the Df vector defined in Eq. (3). The logistic map function is iterated for a number of blocks (N times) to produce the chaotic sequence (yn). Then, the produced sequence is sorted in descending order to obtain a chaotic index map x(n) as:

x(n)=argsort(yn,descending)(10)

where x(n)∈[x(1),x(N)]. This index map is applied to determine the new positions for shuffling the masked blocks in a chaotic order across the image domain, forming the final encrypted blocks (Fn) of image as:

Fn(i,j)=Cx(n)(i,j)(11)

2.5 Decryption Process

The goal of the decryption process is to fully restore the original image from its encrypted equivalent. As the proposed encryption method is symmetric, the decryption process is the exact opposite of the encryption process. First, the input password is shared at receiver to be hashed for generating the Tri-independent secret keys, which are the scrambling key (Eq. (2)), dynamic masking key (Eq. (4)), and seeding key (Eq. (9)). Also, if the dimension of the encrypted image is not perfectly aligned with the block size, the zero padding is applied to fit the encrypted image into uniform square blocks. This step ensures that the image has a consistent block structure, which facilitates subsequent operations. Then, the divided blocks are rearranged using a chaotic logistic map based on the seeding key. By which, the blocked are inversely shuffled back to their original spatial placements as given in Eqs. (8)–(11). After that, since the XOR operation is reversible, it is applied on the shuffled blocks to mask them back with the dynamic keys, which are defined in Eqs. (4)–(7). Finally, the masked blocks are reversely flipped by the scrambling key to retrieve the original image contents.

3  Results and Security Analysis

In this section, the experimental findings of the proposed military image encryption method are presented and investigated. In particular, the proposed method is assessed on a dataset of relevant images taken from the standard image processing library [19], which is a publicly available volume offered by the Signal and Image Processing Institute (SIPI) in the University of Southern California (USC). The military dataset (12 images) includes tanks, airplanes, airports, trucks, and armoured personnel carriers, as given in Fig. 5. These images have a gray-scale format with various resolutions of 512 × 512 pixels (9 images), 1024 × 1024 pixels (2 images), and 256 × 256 pixels (1 image). Further, the performance of the proposed encryption method is assessed on a number of security metrics, including histogram analysis, entropy, peak signal-to-noise ratio, and number of pixel change rate.

Figure 5: The military images used for the performance evaluation of the proposed encryption method

3.1 Histogram Analysis

Histogram analysis (HA) is a fundamental metric employed for evaluating the robustness of the encryption method against statistical attacks. The histogram of the encrypted image has to show a completely different distribution from that exhibited by the original image [20]. Original images usually produce a histogram that is non-uniformly distributed and has predictable pixel values, while an effectively encrypted image attains a histogram with a uniform distribution. This uniformity is a crucial security feature to verify the ability of the encryption process in obscuring any information about input image characteristics. Fig. 6 reveals the histogram analysis of the original, encrypted, and decrypted images using the proposed method applied to various military images. For each tested image in Fig. 6a–d, the first row shows the input, the encrypted, and the decrypted images, whereas the second row presents their histogram distributions, respectively.

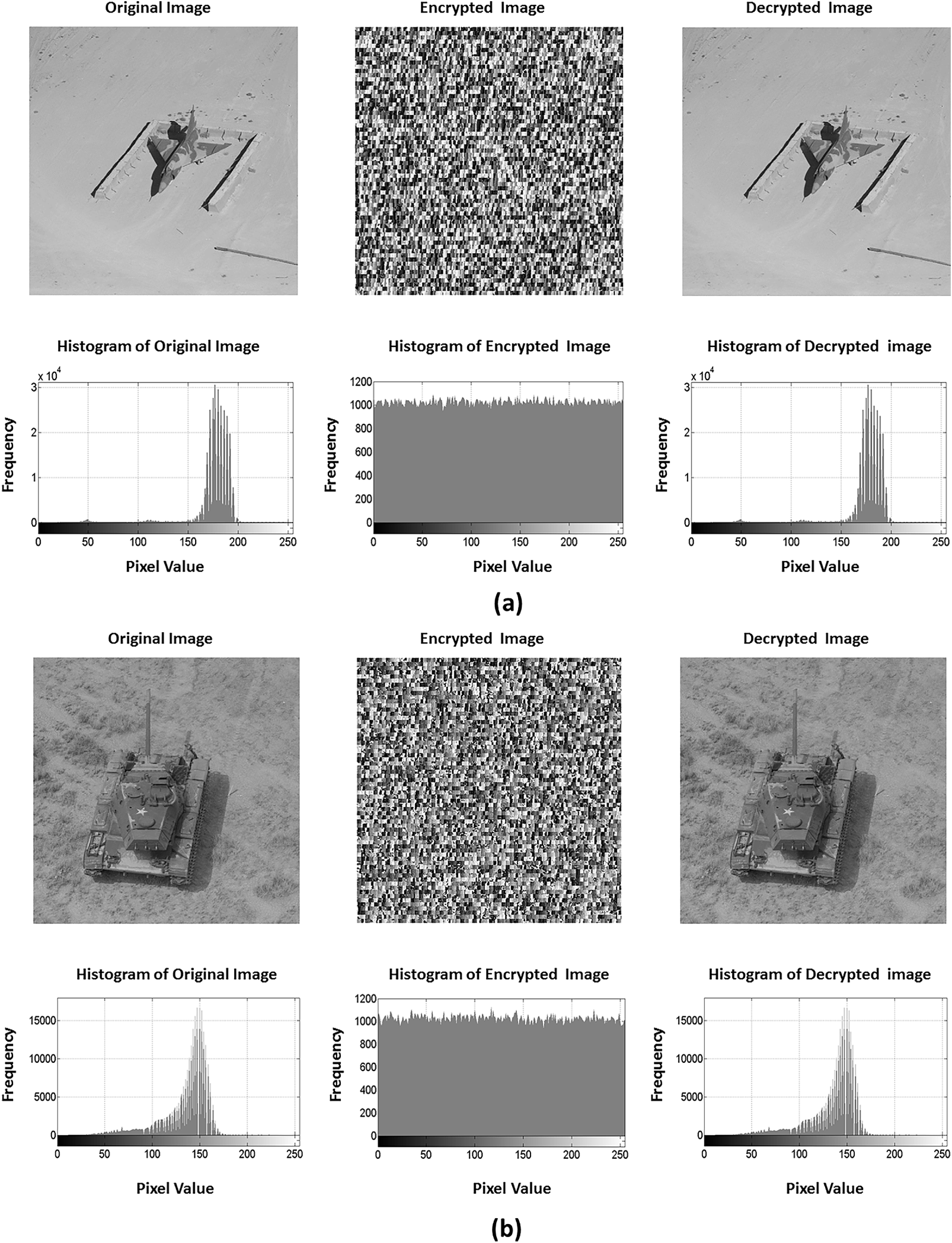
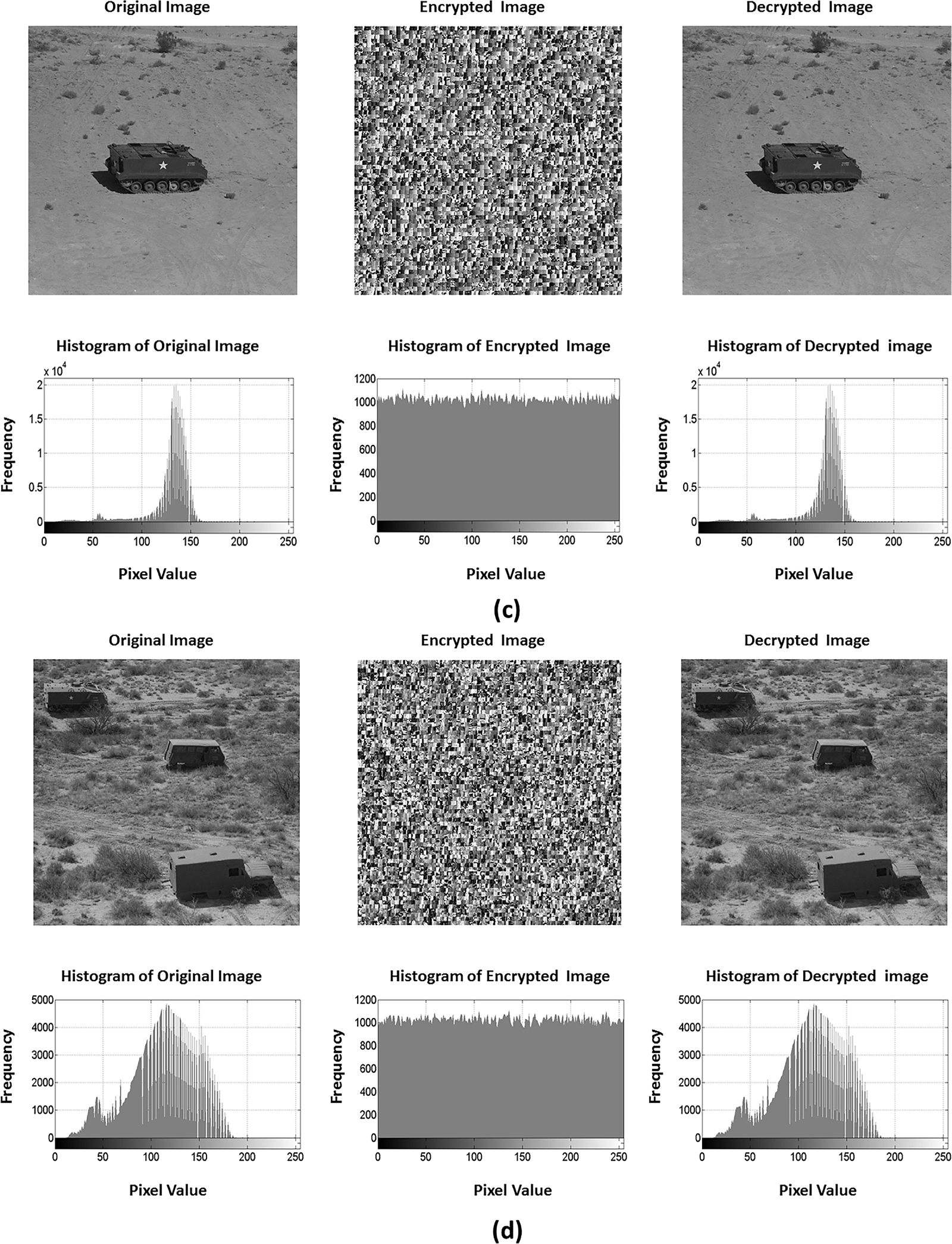
Figure 6: Illustrations from (a–d) are the histogram analysis on example images using the proposed method. For each Figure in (a–d), the first row shows the original image along with encryption and decryption results, respectively, while the second row displays their corresponding histogram distributions

As shown in Fig. 6, the pixel intensity distribution for each tested input image has a distinct and non-uniform histogram. However, it can be noticed that the histograms of the encrypted images exhibit a nearly uniform and flat distribution across all intensity values, withholding any visual peaks or valleys that correspond to original image features. This ensures that the proposed encryption method successfully obfuscates the statistical properties of original images, thereby indicating a high resistance to statistical attacks. Further, it can be seen from Fig. 6 that the decrypted images and their histograms are visually and statistically identical to the original image, which confirms the integrity of our decryption process and perfect recovery of the input image.

3.2 Entropy Analysis

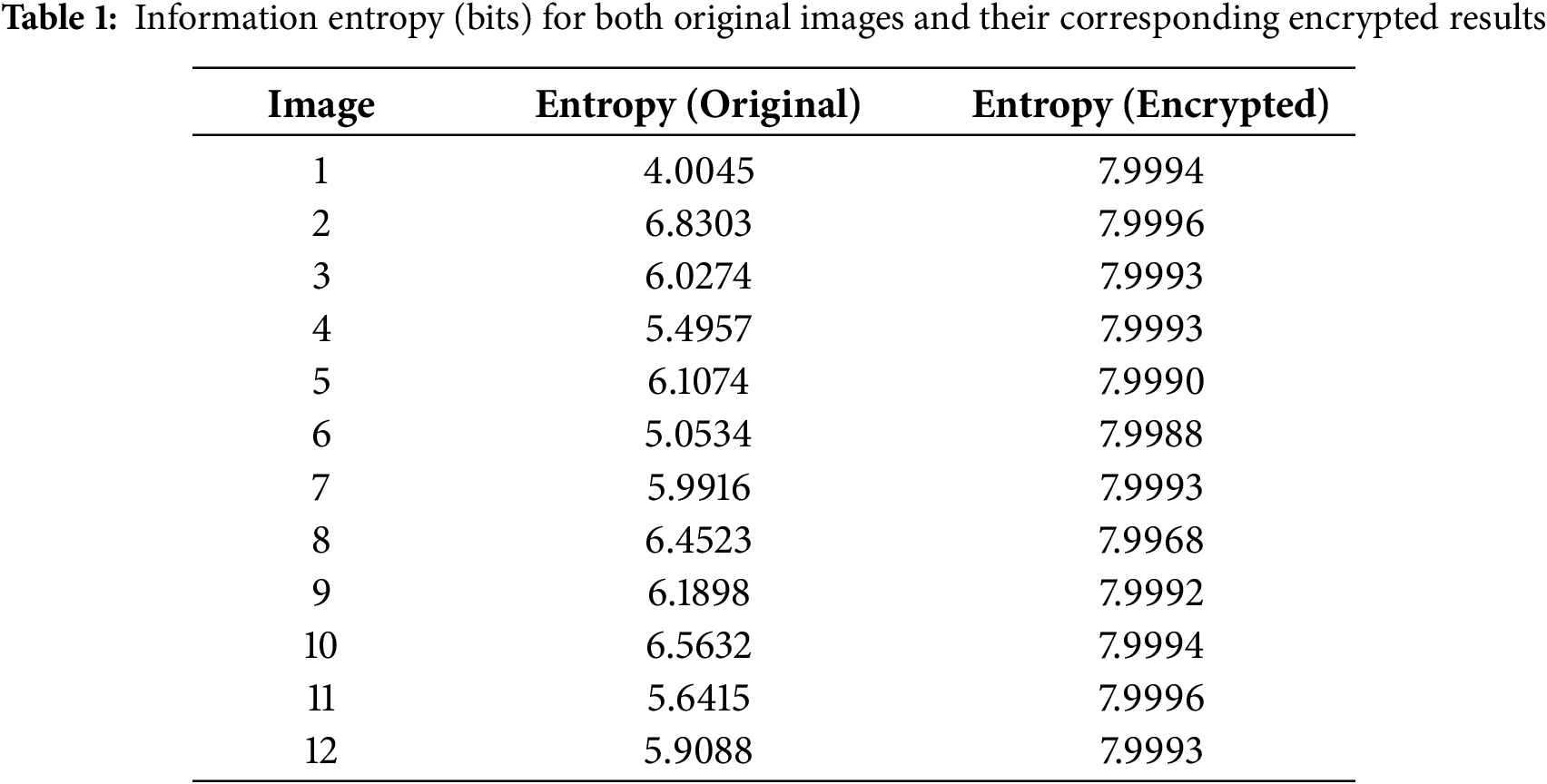
To inspect the level of uncertainty or randomness in the distribution of pixel values, it is essential to measure the information entropy, which computes the average amount of information per pixel [21,22].

An 8-bit grey-scale image has a maximum entropy of 8 bits, which corresponds to a perfectly uniform distribution of pixel intensities. The information entropy is expressed as follows:

Entropy=−∑ij=0255P(xij)log2⁡P(xij)(12)

where P(xij) denotes the probability of a pixel intensity having the value xij from 0 to 255. The entropy for an encrypted image should be close to the ideal value (8 bits for an 8-bit grey-scale image), where a higher entropy measurement means stronger resistance to statistical attacks. Table 1 reports the information entropy measurements for the original military images, illustrated in Fig. 5, along with the encryption results of the proposed method. The proposed approach achieves a greater level of randomness for all tested images by attaining higher entropies close to the perfect value (8 bits). This indicates that the proposed method has a successful performance in eliminating the correlation and visual structures from the original image, thereby avoiding the possibility of information leakage and statistical prediction.

3.3 Number of Pixel Change Rate (NPCR) Analysis

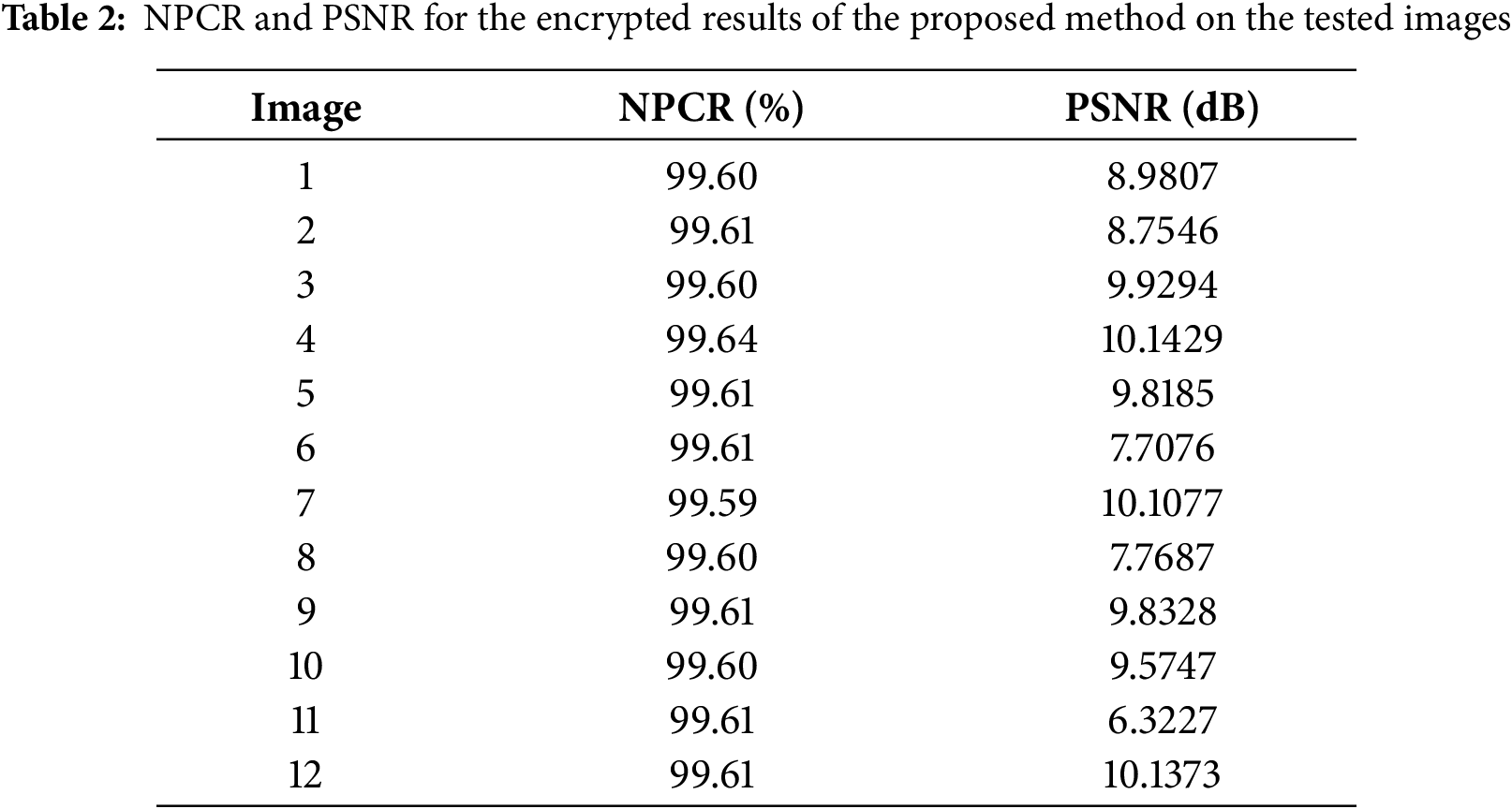
In a differential cryptanalysis, attackers inspect how tiny changes in an input image affect the corresponding encrypted image to exploit the relationship between two images, finding features and eventually recovering the secret key. A strong encryption method should be highly sensitive to small changes in the input image for producing a completely different encrypted image, making differential attacks practically impossible. To assess the robustness of the proposed method against differential attacks, the number of pixel change rate (NPCR) analysis [23] is employed to quantify the percentage of pixels that have changed between two images. The NPCR is computed by comparing two encrypted images (E1 and E2) obtained from two original images that differ by a single pixel, and is defined as:

NPCR=∑ii=1H∑jj=1WD(ii,jj)H×W×100(13)

D(ii,jj)={0ifE1(ii,jj)=E2(ii,jj)1ifE1(ii,jj)≠E2(ii,jj)(14)

where H and W represent the height and width of the image, respectively. In practice, an NPCR value of above 99.5% is generally considered an optimal encryption result for a gray-scale image. From Table 2, the reported results show that the NPCR scores of the proposed encryption approach exceed 99.5% across all tested images. This indicates that the pixel change in the original images causes a significant modification in the encrypted images, confirming the encouraging performance of the proposed approach in resisting the differential attacks.

3.4 Peak Signal-to-Noise Ratio (PSNR) Analysis

The PSNR metric is measured to validate the visual quality of the encryption results by the proposed method. A PSNR of 0 value means that the encrypted image is perfectly equivalent to random noise, but a higher PSNR value is obtained when the encrypted image is closer to the original image [24]. Thus, the PSNR value for encrypted images should be as low as possible since it is intentionally a distorted version of the original image. The PSNR metric is expressed as:

PSNR=10log10⁡MAXp2MSE(15)

where MSE denotes the mean square error value between the original and encrypted images, while MAXp represents the maximum gray scale intensity that a pixel can have (255 for 8-bit grey-scale images). In Table 2, the proposed method attains low PSNR results in the range of (6.3227 to 10.1429 dB). Such results confirm the ability of the proposed encryption method to reveal no information about the original image and making pixel data difficult to analyze statistically and visually by attackers.

3.5 Key Space Analysis

The proposed cryptographic method is based on a vast key space of 256 bits in length, which is essentially required for creating a military-grade security system. Such a key space provides a huge number of possible key combinations (2256 attempts), making the search space practically infeasible for attackers to retrieve the correct key and decrypt the original image. For example, a brute-force attack [24] would have to make 2256 possible attempts to crack the key with 256 bits in length. Even with powerful computing resources, this key length would computationally take an impractical amount of time to try all possible combinations of a 256-bit key.

3.6 Robustness Analysis

In actual communication, encrypted images might be prone to disturbances such as noise interference and data loss when transferred over a network. A reliable cryptographic algorithm needs to have a certain resistance capability to retrieve the majority of the original image contents when the encrypted image is affected by these network disturbances. To verify the robustness of the proposed method against noise, we added Salt-and-Pepper noise at various densities into an encrypted image. Fig. 7—first row illustrates the encrypted image with Salt-and-Pepper noise at a density level of (0.01, 0.05, and 0.1), respectively, while the corresponding decrypted images by the proposed method are shown in Fig. 7—second row, respectively. It is encouraging to see from the results in Fig. 7 that the original image information can still be distinguished in the decrypted images, confirming the ability of the proposed method in resisting noise attacks. Further, the robustness of the proposed cryptographic method is tested against data loss attacks, which are referred to as occlusion attacks. In occlusion attacks, an adversary has the ability to crop a portion of the encrypted image to hinder the decryption process or to make the decrypted image worthless. As shown in Fig. 8, first row, multiple portions on an encrypted image are blocked with different severities of data occlusions (6.25% cropping, 12.5% cropping, and 25% cropping). Then, the encrypted images with data occlusions are decrypted by the proposed approach, as displayed in Fig. 8, second row. It can be observed from Fig. 8 that the main details of the original image content can still be recognized in the decrypted images. This demonstrates the promising performance of the proposed method in withstanding the occlusion attacks at various cropping sizes.

Figure 7: Robustness test of the proposed cryptographic approach against noise interferences. First row: an encrypted image is affected by the Salt-and-Pepper noise at various levels of 0.01, 0.01 and 0.1, respectively. Second row: the corresponding decrypted images by the proposed approach

Figure 8: Visual analysis of the proposed method against occlusion attacks. First row: an encrypted image is blocked with various cropping sizes (6.25%, 12.5%, and 25%), respectively. Second row: the corresponding decrypted images by the proposed approach

3.7 Computational Efficiency

The computation time of an image encryption method is considered an important aspect in real-time applications. The proposed cryptography method is run on a PC with Intel® Core™ i7, 2.3 GHz CPU, and 16 GB RAM using MATLAB 2020a software. The proposed approach is a symmetric cryptography, in which the encryption and decryption processes perform similar mathematical operations. As a result, the execution time for both processes of the proposed approach is generally the same when applied on the same computation system specifications. In particular, the proposed cryptography method takes, on average, a computation time of 0.1099, 0.1422, and 0.2401 s for encrypting/decrypting military images with the resolution of 256 × 256 pixels, 512 × 512 pixels, and 1024 × 1024 pixels, respectively. Further, the processing time can be significantly decreased by implementing the proposed cryptographic approach in C/C++ programming. Hence, the proposed method can be suitable for real-time applications.

4  Conclusion

This paper proposes a new Tri-independent keying method for the reliable encryption of military images. The proposed method includes multi-level security stages of confusion and diffusion concepts based on block-level operations. The encryption process starts by dividing the input image into small blocks (8×8 bytes). Then, the SHA-256 algorithm is applied to hash the input password and derive Tri-deterministic keys: adaptive flipping, dynamic masking, and chaotic seeding keys. The multilevel security stages of the proposed method consist of a piecewise scrambling function, a dynamic masking scheme, and a chaotic shuffling system. The piecewise function is performed as a fundamental step in achieving pixel-level scrambling that locally rearranges the positions of individual pixels within image blocks to new locations. This step contributes to breaking the local connections between the neighboring pixels without altering the pixel values. As a result, this makes the encrypted image unrecognizable against visual analysis attacks while producing a higher entropy value and uniform histogram distribution. Also, the dynamic masking scheme is introduced for generating distinct keys to conduct bit-level manipulation on the divided image regions using the bitwise XOR operation. More importantly, the use of dynamic masking keys is required to overcome the problem of using a static key, which can provide the same encryption results on similar image regions. This causes the leaking of some information about image structures, which can be utilized by attackers to analyze image contents. Thus, the proposed method employs the dynamic masking keys that change over image regions, providing completely different encryption results for any identical regions. This is evident by attaining higher NPCR scores and lower PSNR values. Further, the proposed chaotic index-map system is performed for block-level shuffling that addresses the weakness of persisting some residual patterns, which result from the presence of regions with large-scale structures. This problem can be exploited in cryptanalysis through examining pixel frequency patterns and inferring shape boundaries, thereby retrieving some parts of the image areas. Therefore, the proposed shuffling process aims to obscure any residential regions or global correlation by reallocating image regions randomly across the image domain, making the encrypted results very challenging for attackers to recover the border transitions of objects.

Extensive experimental results and security analyses show the effectiveness and robustness of the proposed method for the encryption of military imagery. By testing the proposed approach on a diverse dataset of military images taken from the SIPI volume, the evaluation results validate the capability of the proposed cryptographic method in providing an excellent performance over various image sizes and contents. The proposed method attains high entropy values, a uniform histogram, great NPCR scores, and low PSNR, along with a large key space, while demonstrating promising performance against noise and occlusion disturbances. Such evaluation results indicate that the encrypted images by the proposed method have strong resistance to statistical, differential, and brute-force attacks, a greater level of randomness in pixel distribution, and minimal information leakage. Thus, the proposed encryption approach can be used in defense communication channels as a reliable tool for safeguarding sensitive military images from cryptographic attacks and unauthorized access. Future research will extend the proposed approach for the encryption of remote sensing images that include terrain patterns (roads, rivers, etc.), which require a comprehensive visual analysis for differential attacks. Another future work will explore various chaotic maps and integrate them with the proposed method to generate pseudorandom numbers with a better even distribution.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization: Shereen S. Jumaa and Mohsin H. Challoob; methodology: Shereen S. Jumaa and Mohsin H. Challoob; software: Shereen S. Jumaa; validation: Shereen S. Jumaa, Mohsin H. Challoob, and Amjad J. Humaidi; formal analysis: Shereen S. Jumaa, Mohsin H. Challoob, and Amjad J. Humaidi; investigation: Amjad J. Humaidi; resources: Mohsin H. Challoob; data curation: Shereen S. Jumaa; writing—original draft preparation: Shereen S. Jumaa and Mohsin H. Challoob; writing—review and editing: Amjad J. Humaidi; visualization: Shereen S. Jumaa and Mohsin H. Challoob; supervision: Amjad J. Humaidi; project administration: Amjad J. Humaidi. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The military images used in this paper are taken from the publicly available dataset offered by the Signal and Image Processing Institute (SIPI) at the University of Southern California (USC). The dataset can be accessed via the link: http://sipi.usc.edu/database/ (accessed on 05 September 2025).

Ethics Approval: This research does not involve human participants, animals, or sensitive data requiring formal ethical approval.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Kaur M, Singh S, Kaur M. Computational image encryption techniques: a comprehensive review. Math Probl Eng. 2021;2021:5012496. doi:10.1155/2021/5012496. [Google Scholar] [CrossRef]

2. Mahalakshmi K, Nagarajan S. Comprehensive review and analysis of image encryption techniques. IEEE Access. 2025;13:109783–813. doi:10.1109/ACCESS.2025.3578158. [Google Scholar] [CrossRef]

3. Alexan W, Aly L, Korayem Y, Gabr M, El-Damak D, Fathy A, et al. Secure communication of military reconnaissance images over UAV-assisted relay networks. IEEE Access. 2024;12:78589–610. doi:10.1109/access.2024.3407838. [Google Scholar] [CrossRef]

4. Nithya R, Dhanasekaran D. Novel dominant color subband image encryption in visual sensor network for smart military surveillance system. Traitement Du Signal. 2022;39(3):951–60. doi:10.18280/ts.390322. [Google Scholar] [CrossRef]

5. Ye G, Liu S, Xiao X, Hunag X. Image hiding algorithm based on local binary pattern and compressive sensing. Math Comput Simul. 2025;237:316–34. doi:10.1016/j.matcom.2025.05.005. [Google Scholar] [CrossRef]

6. Hu LL, Chen MX, Wang MM, Zhou NR. A multi-image encryption scheme based on block compressive sensing and nonlinear bifurcation diffusion. Chaos Solitons Fractals. 2024;188:115521. doi:10.1016/j.chaos.2024.115521. [Google Scholar] [CrossRef]

7. Zou JZ, Chen MX, Gong LH. Invisible and robust watermarking model based on hierarchical residual fusion multi-scale convolution. Neurocomputing. 2025;614:128834. doi:10.1016/j.neucom.2024.128834. [Google Scholar] [CrossRef]

8. Lai Q, Liu Y. A family of image encryption schemes based on hyperchaotic system and cellular automata neighborhood. Sci China Technol Sci. 2025;68(3):1320401. doi:10.1007/s11431-024-2678-7. [Google Scholar] [CrossRef]

9. Shahbaz Khan M, Ahmad J, Al-Dubai A, Pitropakis N, Ghaleb B, Ullah A, et al. Chaotic quantum encryption to secure image data in post quantum consumer technology. IEEE Trans Consumer Electron. 2024;70(4):7087–101. doi:10.1109/tce.2024.3415411. [Google Scholar] [CrossRef]

10. Khan MS, Al-Dubai A, Ahmad J, Pitropakis N, Boulila W, Ghaleb B. Quantum image encryption with reduced gate complexity for gate-efficient encryption pipelines in IoT networks. In: Proceedings of the 2025 IEEE International Conference on Communications Workshops (ICC Workshops); 2025 Jun 8–12. Montreal, QC, Canada. p. 1444–9. doi:10.1109/ICCWorkshops67674.2025.11162326. [Google Scholar] [CrossRef]

11. Rajendiran NP. Baker’s map based chaotic image encryption in military surveillance systems. In: Proceedings of the International Conference on Internet of Everything and Quantum Information Processing. Cham, Switzerland: Springer Nature; 2024. p. 107–15. doi:10.1007/978-3-031-61929-8_16. [Google Scholar] [CrossRef]

12. Bazeer Ahamed B, Krishnamoorthy M. Sensible image encryption for military applications based on advanced encryption standard algorithm (AES) [Internet]. 2023 [cited 2025 Sep 5]. Available from: https://www.researchsquare.com/article/rs-3561133/v1. [Google Scholar]

13. Albahadily HK, Altaay AAJ, Jabbar IA. Encryption of military maps ImagesUsing peter de jong chaotic maps and lightwaght encryption. In: Proceedings of the 2022 Fifth College of Science International Conference of Recent Trends in Information Technology (CSCTIT); 2022 Nov 15–16; Baghdad, Iraq. p. 137–42. doi:10.1109/csctit56299.2022.10145728. [Google Scholar] [CrossRef]

14. Malavika V, Vinish A, Shaji B, Jose DJ. Advanced system for secure military communication using image steganography and block-rotary encryption. Int J Multidiscip Res. 2025;7(2):39928. doi:10.36948/ijfmr.2025.v07i02.39928. [Google Scholar] [CrossRef]

15. FIPS 180-2. Federal information processing standards publication 180-2. Gaithersburg, MD, USA: Department of Commerce National Institute of Standards and Technology; 2002. [Google Scholar]

16. Guesmi R, Farah MAB, Kachouri A, Samet M. A novel chaos-based image encryption using DNA sequence operation and Secure Hash Algorithm SHA-2. Nonlinear Dyn. 2016;83(3):1123–36. doi:10.1007/s11071-015-2392-7. [Google Scholar] [CrossRef]

17. Suman RR, Mondal B, Mandal T. A secure encryption scheme using a Composite Logistic Sine Map (CLSM) and SHA-256. Multimed Tools Appl. 2022;81(19):27089–110. doi:10.1007/s11042-021-11460-4. [Google Scholar] [CrossRef]

18. Roy A, Mahanta DR, Mahanta LB. A semi-synchronous federated learning framework with chaos-based encryption for enhanced security in medical image sharing. Results Eng. 2025;25:103886. doi:10.1016/j.rineng.2024.103886. [Google Scholar] [CrossRef]

19. Signal and Image Processing Institute. The USC-SIPI Image Database [Databases]. 2025 [cited 2025 Sep 5]. Available from: http://sipi.usc.edu/database/. [Google Scholar]

20. Helen Vijitha P, Asnath Victy Phamila Y. A novel image encryption and decryption scheme integrating two-way chaotic maps, iterative cellular automata, and online tessellation automata. Results Eng. 2025;27:105673. doi:10.1016/j.rineng.2025.105673. [Google Scholar] [CrossRef]

21. Jirjees SW, Alkalid FF, Shareef WF. Image encryption using dynamic image as a key based on multilayers of chaotic permutation. Symmetry. 2023;15(2):409. doi:10.3390/sym15020409. [Google Scholar] [CrossRef]

22. Jirjees S, Yousif N, Hashim A. Colour image privacy based on cascaded design of symmetric block cipher. J Eng Sci Technol. 2022;17(3):2135–56. [Google Scholar]

23. Sivakumar T, Li P. A secure image encryption method using scan pattern and random key stream derived from laser chaos. Opt Laser Technol. 2019;111:196–204. doi:10.1016/j.optlastec.2018.09.048. [Google Scholar] [CrossRef]

24. Himthani V, Dhaka VS, Kaur M, Singh D, Lee HN. Systematic survey on visually meaningful image encryption techniques. IEEE Access. 2022;10:98360–73. doi:10.1109/ACCESS.2022.3203173. [Google Scholar] [CrossRef]