Coupled CUBIC Congestion Control for MPTCP in Broadband Networks

1  Introduction

Transmission control protocol (TCP) [1] is a reliable transport protocol supporting error control and congestion control. Congestion control plays a role of adjusting the transmission rate according to the network condition observed at the sender using a sliding window based mechanism through the end-to-end connected path. TCP has improved continuously its congestion control performance considering such factors as network bandwidth, end-to-end delay, packet loss rate, wired or wireless networks [1–5], and etc. Since the initial TCP was designed considering only single-path sessions, the overall resources cannot be fully utilized, even if there exist several paths between source and destination. In today’s network, multipath TCP (MPTCP) [6] was standardized as a transport protocol to efficiently use existing multiple-path resources in one session. MPTCP can enable various communication terminals such as smartphones, tablets, and laptops to connect to various networks such as Ethernet, 3G, Wi-Fi, 4G, 5G, and so on simultaneously, to utilize total resources through multiple paths rather than only single path. Using multiple paths avoids bottlenecks, supports reliability, and allows more efficient use of resources than a single TCP can provide.

Most of congestion control researches for MPTCP [7,8] have mainly focused on heterogeneous paths with different delays. However, in network paths having asymmetrical bandwidth including both high bandwidth and low bandwidth links, MPTCP performance deteriorates severely because high bandwidth link cannot be fully used. The basic coupled congestion control method such as linked-increases algorithm (LIA) [9] and opportunistic LIA (OLIA) [10], which are basic congestion control methods of MPTCP, have a disadvantage in that they do not respond appropriately to heterogeneous networks. They do not fully utilize resources of the high speed paths when applied to multiple paths having a large bandwidth-delay product (BDP) paths. To improve this, MPTCP’s congestion control should be enhanced to utilize a high-speed network resources efficiently, but research on proper MPTCP congestion control is still insufficient on this topic.

In this paper, we propose a new MPTCP congestion control algorithm for improving the resource utilization when the MPTCP is adopted in multipath networks including high-speed long-distance paths. Among single-path TCP congestion controls, the TCP CUBIC [5] was designed to be applied to high-bandwidth and large delay networks, and has been used as the basic congestion control mechanism in Linux. The MPTCP congestion control, LIA, can utilize multi-path resources and maintain fairness between paths even when competing with general TCP at the bottleneck through linked congestion window control. By combining the advantages of TCP CUBIC and MPTCP LIA congestion control, we propose a new “Coupled CUBIC congestion control” for MPTCP that improves MPTCP performance in multipath networks including a high BDP path, besides maintaining MPTCP fairness by adopting tightly coupling action with subflow congestion window sizes. The Coupled CUBIC algorithm adopts a modified TCP CUBIC for a large BDP path in a linked increase manner like LIA for maintaining fairness with an ordinary TCP traversing the same bottleneck path. For the appropriate coupling and increasing between congestion windows in a small BDP path and a large BDP path, we normalize each window size to be compared under the same network situation, for example, in small BDP network circumstance. We calculate the normalization factor by comparing the average congestion window sizes of the Reno and the CUBIC congestion control, as explained in Section 3.1. The proposed congestion control algorithm is designed for two main purposes. The one is to enhance the MPTCP transmission performance in high BDP path, and the other is to satisfy the MPTCP fairness goals even for the high BDP path.

To verify the performance excellence of the proposed algorithm, we implemented the Coupled CUBIC into a Linux kernel by modifying the legacy MPTCP LIA congestion control source code. We constructed heterogeneous network testbeds with large and small BDP paths, and compared the performances of the legacy LIA and the Coupled CUBIC by experiments. Experimental results show that the proposed Coupled CUBIC utilizes almost over 80% of the bandwidth resource in the high BDP path, while the LIA utilizes only less than 20% of the bandwidth for the same path. It was confirmed that the resource utilization and traffic transmission performance have been greatly improved by using the proposed Coupled CUBIC compared to the legacy MPTCP congestion control.

This paper is organized as follows. Section 2 presents the related works about MPTCP congestion control and CUBIC. Section 3 provides detailed explanations about our suggested Coupled CUBIC congestion control algorithm. Experimental testbed environments and performance results are described in Section 4, and finally Section 5 concludes this paper.

2  Related Works

In this Section, the MPTCP connection method and operation principle are explained first, and then the MPTCP congestion control implemented in the actual Linux kernel is introduced. Next, TCP CUBIC [5] whose performance has been verified in high-speed, long-distance network is described. Finally, after explaining the limitations of the current MPTCP congestion control, we suggest a method for combining TCP CUBIC with MPTCP congestion control.

2.1 MPTCP and its Congestion Control

The MPTCP is a transport protocol to use multiple path connections in one session using multiple interfaces to increase resource efficiency, avoid congested paths, and utilize empty paths [6]. As shown in Fig. 1, congestion control is performed by adding an MPTCP layer on top of one or more TCP subflows that have subdivided the transport layer, and it has excellent compatibility with general TCP.

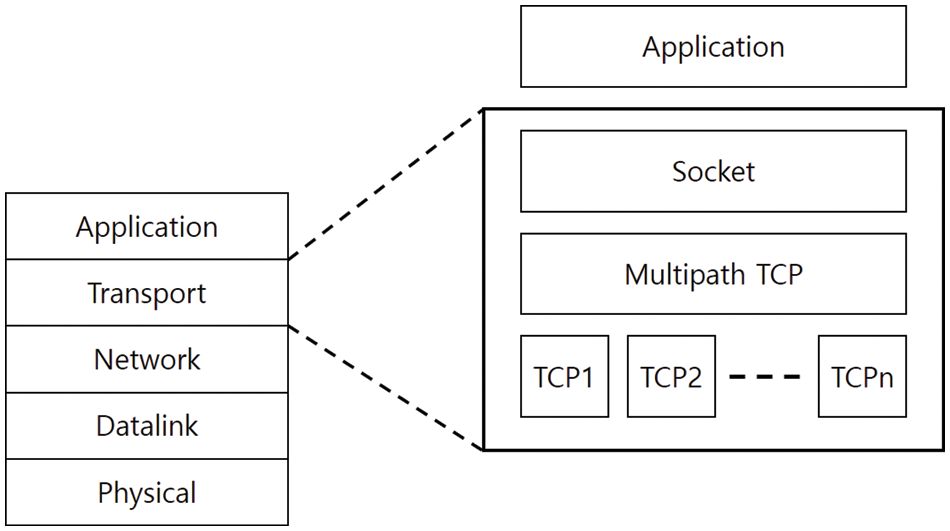
Figure 1: Structure of MPTCP layer

In MPTCP, when 3-way handshaking is performed for connection, the transmitter applies the MP-CAPABLE option and transmits a SYN message to the receiver including a sender’s random unique key. If the receiving end supports the MPTCP function, the MP-CAPABLE option is applied and the receiving end’s unique key is included in the SYN + ACK message. When the unique key is confirmed, a response message is sent to establish the first subflow connection. Another additional subflow is linked using the MP-JOIN option to verify the unique key. These connected subflows allow traffic to be transmitted simultaneously using multiple paths. In addition, it can be used as a backup path when traffic transmission through one path fails.

If a general TCP congestion control is applied to each subflow of MPTCP, fairness with existing TCP may be violated. For example, when competing with an ordinary TCP on a bottleneck link, multiple subflows would take up a lot of the bandwidth portion of that link. In general, MPTCP congestion control should be designed with three main considerations in mind [9]. First, multipath flows should perform not less than single-path flows do on the best available paths. Second, a multipath flow should not have more bandwidth among the resources it shares than a single path flow utilizes. Third, a multipath flow should distribute the traffic of congested links to different paths as much as possible. As MPTCP was recognized as the next-generation TCP protocol by the IETF, various congestion control studies were conducted including various window-based and rate-based algorithms. Representative examples include LIA, OLIA, and wVegas [11], and all three congestion controls are implemented and distributed in recent MPTCP Linux kernels.

The LIA was designed based on the goals of MPTCP congestion control design described above. As shown in Eq. (1), the congestion window is increased by calculating the increase factor α of each subflow. The wr is the size of congestion window, and the rttr is the round trip time (RTT) of the r-th subflow, respectively. The wr is updated as in Eq. (2). Whenever an ACK is received, the smaller value between the sum of all congestion window sizes divided by increase factor α and the inverse of the corresponding congestion window, is used for the update of wr . This linked increase operation keeps the MPTCP fairness goals that prevent the aggressive total increase of all subflow congestion window [9].

α=∑r⁡wr×Maxrwrrttr2(∑rwrrttr)2 (1)

wr=wr+min(α∑r⁡wr,1wr) (2)

When a packet loss occurs in each subflow, the congestion window size is halved, the same as that of normal TCP. Since the LIA tries to balance the congestion windows of multiple subflows, it maintains fairness even when sharing network link with ordinary TCPs at bottleneck. However, in an MPTCP environment having a large BDP path, performance degradation occurs because bandwidth resources are not used properly. In a large BDP path, it is necessary to increase the congestion window rapidly to transmit a lot of data. The LIA shows similar behaviors to TCP Reno even in the path with large BDP. Since the congestion window increases slowly each time an ACK is received and decreases significantly when packet loss occurs, the resource of the path cannot be used properly.

OLIA improved the flappy phenomenon of LIA to make network resources more stable. wVegas is an algorithm that performs MPTCP congestion control based on delay time. Similar to calculating the Diff value in TCP Vegas [12], the congestion window is increased if the buffered packets in the queue is less than the threshold. Otherwise, it reduces the congestion window by half. However, neither algorithm has a proper prescription for high BDP networks.

2.2 TCP CUBIC Congestion Control

TCP CUBIC is used as default congestion control in Linux OS [5]. TCP CUBIC was suggested to simplify the computational complexity and complement the weaknesses of TCP BIC [13], a congestion control method using binary search algorithm. TCP CUBIC is not severely affected by the RTT when calculating its congestion window. Therefore, when several sessions compete for bandwidth using TCP CUBIC, the congestion window size appears the same. In addition, since it is not affected by RTT, resource utilization efficiency is higher than that of general TCP in a long-distance high-speed network. The following Eqs. (3) to (5) show how to calculate the congestion window size in TCP CUBIC [5].

W(t)=C(t−K)3+Wm (3)

K=βWmC3 (4)

W(t)=(1−β)Wm+3β2−βtT (5)

Here, W(t) represents the congestion window size at time t, and the t means the elapsed real time (not related to RTT) from when the packet loss occurred. It can be seen that the congestion window is calculated using a cubic function in Eq. (3). Wm represents the congestion window just before a packet loss is occurred. After a packet loss event, congestion window decreases to (1−β)Wm , and it becomes recovered to Wm when time t is equal to K. When t is smaller than K, it increases in a concave shape, and when t is larger than K, it increases in a convex shape. In (3), the increase factor C is set to 0.4 in Linux kernel. K is calculated by the increase factor C, the decrease factor β , and the congestion window size Wm when the last packet loss occurs, in Eq. (4). β is defined as a constant value of 0.7. Eq. (5) is the congestion window when TCP operates the congestion control using an addictive increase multiplicative decrease (AIMD) method like TCP Reno. Since CUBIC window increases according to real time t, irrespective of RTT, as in Eq. (3), for a small value of RTT, CUBIC window size can be less than Reno window size because of fast ACK clocking increase of Reno window in case of small RTT. TCP CUBIC calculates the current congestion window size using Eqs. (3) and (5) and selects a larger value between the two. This is an operation to provide fairness with TCP Reno when TCP CUBIC is operated in a small BDP network. That is, in a network with a small BDP, Eq. (5) can have a larger value than Eq. (3), so TCP CUBIC does not have much difference from TCP Reno. Conversely, when Eq. (3) has a larger value in a large BDP path, the congestion window increases quickly to enhance the bandwidth utilization efficiency.

2.3 MPTCP Congestion Control with Large BDP Paths

In spite of various studies on improvement of MPTCP congestion control, a large performance degradation phenomenon occurs when the characteristics of the paths used in MPTCP congestion control are different from each other [14,15]. Although there is a great need for MPTCP that can utilize various paths, studies on congestion control including a path with a high-speed, long-distance environment are insufficient. If the basic LIA is used, the resource of the high-speed path cannot be used properly because it is affected by the low-speed paths.

The most well-known MPTCP protocols adopting CUBIC in a dynamic environment including high BDP networks are [16–18]. Le et al. [16] proposed MPCubic algorithm that try to achieve MPTCP fairness goals and high throughput. Although they could utilize all the paths simultaneously, their implementation considered only CUBIC in their congestion window coupling. So, in order to adopt another kind high BDP congestion controls into MPTCP, another complex linking calculation for each algorithm is needed. However, our coupling method is rather simple and clear to adapt to another congestion control because our mechanism only needs normalization of increase factor α for coupling of two or more congestion control mechanisms.

Kato et al. [17] suggested a CUBIC-like congestion control algorithm for MPTCP called mpCUBIC. Their algorithm achieved better performance for high BDP networks. However, their algorithm can be applied only two subflows at a time, so it cannot utilize all available paths simultaneously. Moreover, they did not explain clearly whether their algorithm satisfies the MPTCP fairness goals.

Recently, Mahmud et al. [18] proposed a bottleneck-aware multipath CUBIC congestion control for MPTCP called BA-MPTCP. Although they claim to achieve better performance in a non-shared bottleneck high BDP path and fair bandwidth sharing in a shared bottleneck high BDP path, their algorithm heavily depends on the performance of a shared bottleneck detection algorithm. If some of detection filters cannot be used and there happens an error in distinguishing shared bottleneck detection algorithm, their algorithm may violate the MPTCP fairness goals and restrict the performance of another single-path flow. Also, although they tried to enhance the performance of the shared bottleneck detection by adopting three detection filters instead one, their mechanism cannot guarantee the perfect detection of a shared bottleneck.

Therefore, in this paper, we propose a new congestion control that is operated as TCP CUBIC on a large BDP path to fully utilize the link bandwidth, and is operated as the existing LIA congestion control on a small BDP path. In this method, in order to maintain the fairness that MPTCP must provide, different congestion control methods are combined with each other in a linked increase manner and operated to have a tightly-coupled correlation, so as to maintain the fairness of MPTCP like LIA. Through performance evaluation, it was shown that this control method effectively utilizes path resources while maintaining fairness even when it includes a high BDP path. Our algorithm does not need a detection algorithm of shared bottleneck and provides efficient traffic shift from more congested paths to less congested paths and satisfies the MPTCP fairness design goals.

3  Design of the Coupled CUBIC Congestion Control

In this section, we introduce the design of the Coupled CUBIC congestion control that aims to improve link utilization when MPTCP is used in a broadband network with long latency and large bandwidth. Basically, after detecting the wide bandwidth, it operates a TCP CUBIC control which includes an algorithm that properly calculates the increase factor α of the LIA so that the congestion window increases in a linked increase manner.

3.1 Coupled CUBIC Congestion Control

An ordinary MPTCP congestion control manipulates its congestion window by an AIMD technique similar to TCP Reno when an ACK is received. In a general wired network, the congestion window cannot reach the maximum link capacity because of the occurrence of at least 10−6 packet error rates, so that the bandwidth of the broadband link cannot be used sufficiently. Therefore, MPTCP LIA-like congestion control slows down the congestion window increase rate in a network with large BDP. Therefore, in designing MPTCP congestion control, multipath networks having a large BDP path must be considered.

Basically, the proposed Coupled CUBIC operates using TCP CUBIC congestion control in subflows with a large BDP path. In a subflow with a small BDP, it operates like LIA by adjusting the congestion window using the AIMD technique by referring to the MPTCP increase factor α , which is used to control the linked increase of congestion window of multiple subflows. In this case, if the congestion window of the subflow with a large BDP is used as it is, the α value is distorted abnormally from the value in the original LIA. Here, we designed an algorithm that converts the congestion window of a large BDP subflow into a virtual LIA window value and then calculates the α of the LIA.

Tab. 1 represents the average congestion windows of TCP Reno and TCP CUBIC according to packet loss rates when RTT is 100 ms [5]. As the packet loss probability decreases, it can be seen that the sizes of the average congestion window between the two become significantly different.

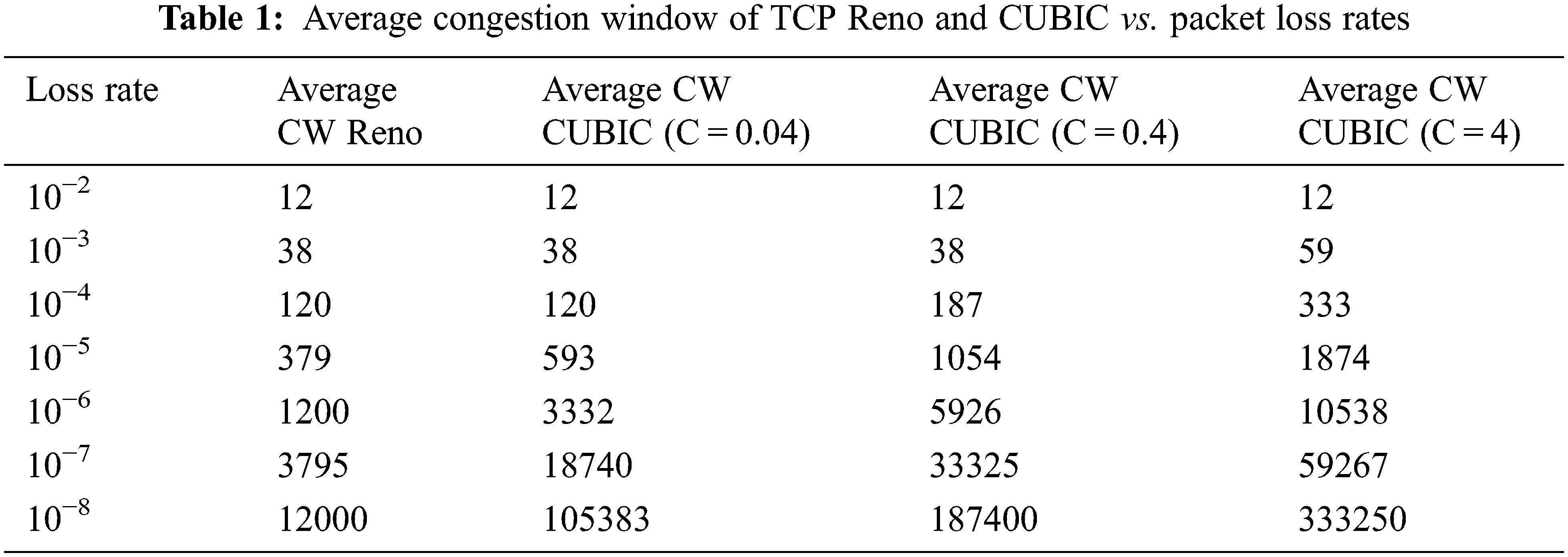
Eq. (6) below represents the average congestion window size of TCP CUBIC according to the packet loss rate p [5], called “response function of the CUBIC”. Eq. (6) can be obtained by the usual approximation analysis technique that the average TCP throughput Ravg can be calculated by “ Ravg=N/τ ”, where N represents the number of packets transmitted in one cycle between two packet losses and τ means a cycle time, actually τ=K in the TCP CUBIC case. Then, the average window size W is equal to W=Ravg⋅T=N/τ⋅T . After some typical calculation and taking logarithms on both sides of the W equation, we can get Eq. (6). The lower row in Eq. (6) shows the average congestion window of TCP Reno according to p. In this equation, the loss rate p¯ , which is the reference point for switching the two equations of the CUBIC congestion window, is determined by Eq. (7). Since constant values of C = 0.4 and β = 0.7 are used in Eq. (7), the  p¯ value is determined by the T factor, which is the RTT. When the current packet loss rate is greater than the calculated p¯ , the upper expression in Eq. (6) is used as the congestion window formula, and when the current packet loss rate is smaller than p¯ , the lower expression is used for the congestion window formula.

log⁡w={0.25logC(4−β)4β+0.75log⁡T−0.75log⁡pifp<p¯0.09−0.5log⁡pifp≥p¯ (6)

log⁡p¯=logC(4−β)4β+3log⁡T−0.36 (7)

Fig. 2 shows the response function of congestion window of TCP CUBIC and Reno according to the packet loss rate. When the RTT is 100 ms, if the packet loss rate is less than about 0.0002, it can be seen that the window size is calculated by switching to the upper expression representing the congestion window of the large BDP.

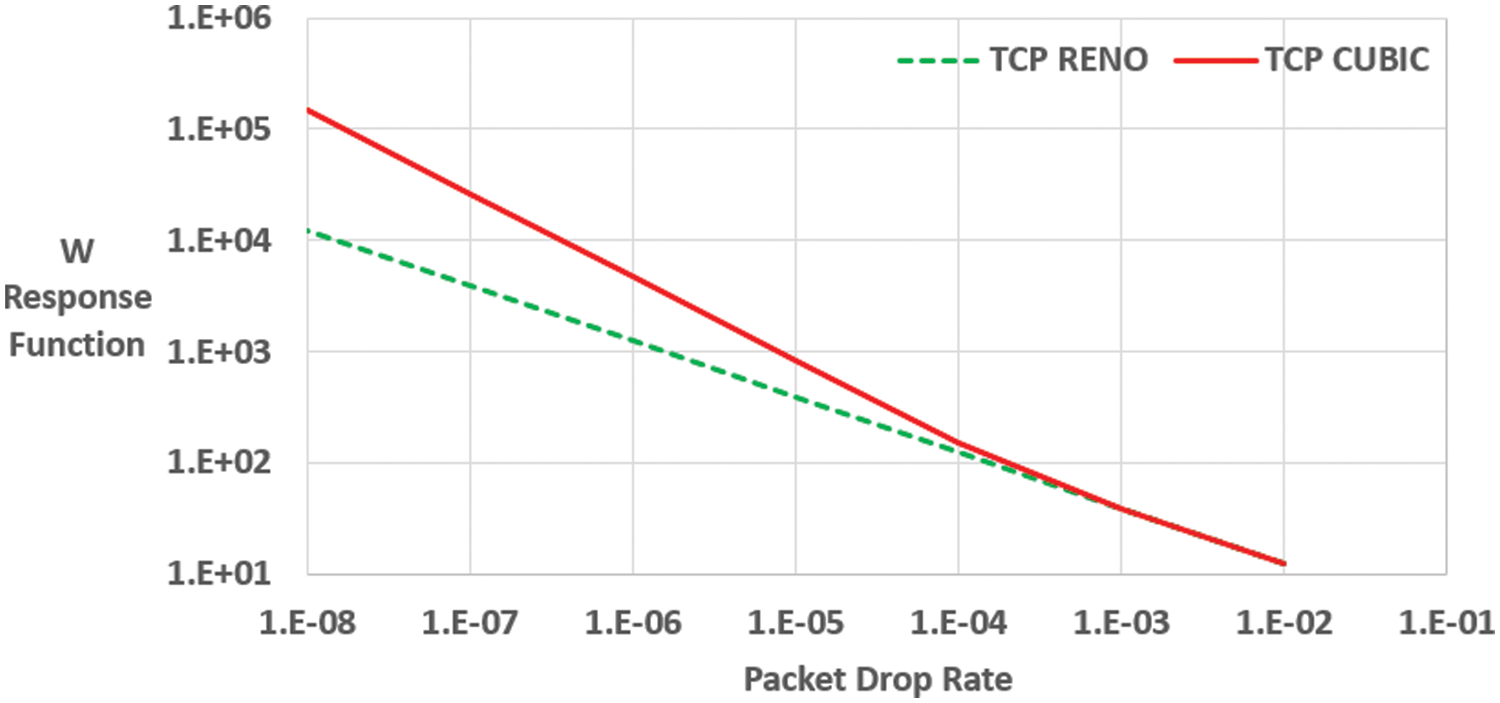
Figure 2: Response function of congestion window according to packet loss rate

The Coupled CUBIC calculates the congestion window considering the fairness of each path in the same way as LIA did for a small BDP path. However, considering the fairness with the existing single path TCP CUBIC flow, it operates as a congestion control of the coupled virtual TCP CUBIC presented in this paper, in a large BDP path. A path operating a virtual TCP CUBIC has the advantage of almost fully utilizing network resources by performing a high BDP congestion control action, under the coupling of the LIA congestion window. However, if the congestion window value of TCP CUBIC is used directly to calculate the LIA increase factor α , the congestion window increase rate becomes too slow in a small BDP path. Therefore, it goes against the design goal of MPTCP to utilize resources of all available paths to the maximum. So, we need to calculate a normalized virtual congestion window value as if the LIA works for the path operating TCP CUBIC, and use it to calculate the increase factor α of another path.

The Coupled CUBIC algorithm operates as follows. When increasing the congestion window in a small BDP path, Eq. (2) is used like LIA, adopting the window increase factor α of Eq. (1). If the congestion control operation of the low BDP path looks as if the MPTCP LIA is operating in the high BDP path by applying a normalized virtual congestion window of TCP CUBIC, the change rate of the congestion window for the low BDP path is not quite different from the existing LIA. It will be able to maintain fairness with other single path TCPs at the bottleneck. How to normalize the CUBIC congestion window to the virtual congestion window of LIA can be explained as follows using the response functions in Tab. 1 and Fig. 2. The response function of TCP Reno’s average congestion window (WRENO) is the same as the lower row in Eq. (6). We can convert it into Eq. (8) by detaching logarithms from the equation, which is the well-known “square root formula” of TCP Reno. The response function of TCP CUBIC’s average congestion window of (WCUBIC) is the same as the upper row in Eq. (6), and we can transform it into Eq. (9) by detaching logarithms, where we use C = 0.4 and β  = 0.7. Therefore, in a network environment with the same packet loss rate, the virtual RENO window size ‘Virtual WRENO’ can be expressed as a ratio of the two congestion windows shown in Eqs. (8) and (9). This becomes Eq. (10).

WRENO=32p (8)

WCUBIC=1.054×RTT34÷p34 (9)

VirtualWRENO=CurrentWCUBIC×WRENOWCUBIC (10)

Fig. 3 shows a flow chart of Coupled CUBIC that calculates the increase factor α of LIA using the virtual TCP Reno congestion window obtained by normalizing the congestion window of TCP CUBIC. An MPTCP session is established using multipath, and the characteristics of each subflow is identified. If the path BDP is large, it chooses the Coupled CUBIC as congestion control. Conversely, if the path BDP is small, it operates LIA congestion controls. The congestion window of the large BDP path is transformed into a virtual TCP Reno congestion window by Eq. (10). The α1 in Fig. 3 is calculated using the virtual TCP Reno congestion window, other congestion window of the remaining paths, and the RTTs as shown in Eq. (1). After that, the virtual congestion window is multiplied by α1 , and we finally obtain the corresponding congestion window if the LIA algorithm would be applied. The reason for multiplying by α1 is explained in the next subsection after describing the Linux code. The increase factor α2 is calculated using Eq. (1) with the finally obtained virtual congestion window, other congestion windows of the remaining paths, and the RTTs. In the Fig. 3, the part that refers to the congestion window of the other party is indicated by a dotted arrow. The α2 is used when LIA congestion control works on the remaining small BDP paths. The values of α1 and α2 are calculated iteratively for convergence to correct values, as the algorithm goes on.

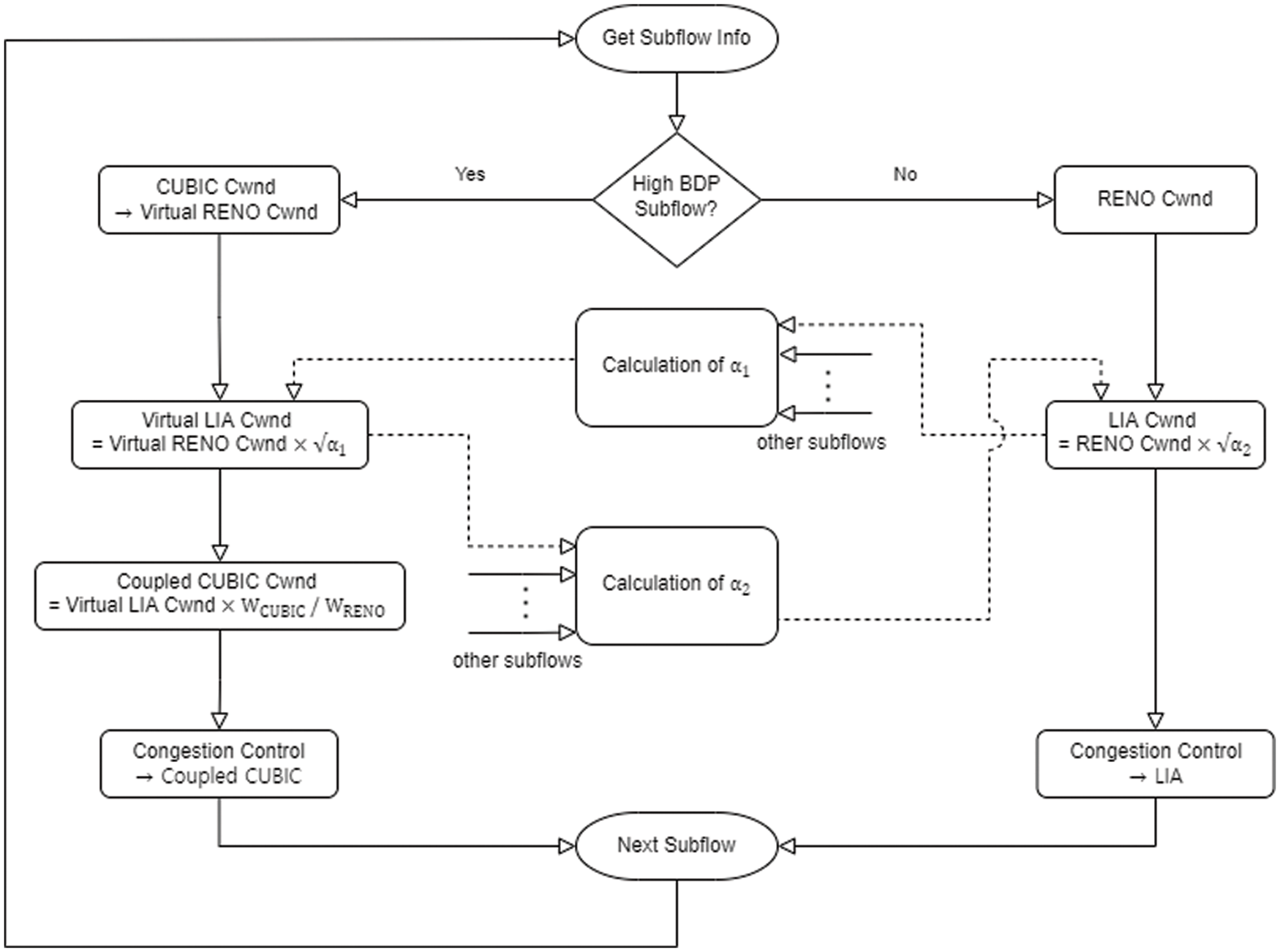
Figure 3: Flowchart of Coupled CUBIC congestion control

In the large BDP path, α1 is used to calculate the Coupled CUBIC congestion window (WcoupledCUBIC) as shown in Eq. (11). Then WcoupledCUBIC is applied to control the amount of data transmitted to the large BDP path. In the path with a small BDP, the broadband path is recognized as one of LIA subflows to maintain fairness. Therefore, when the Coupled CUBIC is used, there is no decrease in the congestion window increase rate in the normal path, and resources are shared in the same way as the basic LIA in terms of fairness.

WcoupledCUBIC=VirtualWRENO×α1×WCUBICWRENO (11)

3.2 Implementation of the Coupled CUBIC Congestion Control

For performance evaluation of the proposed algorithm, the Coupled CUBIC was implemented based on the basic LIA source code in the Linux kernel MPTCP version. The parameters required for the Coupled CUBIC algorithm have been added to the LIA source code. The increase and decrease algorithms of TCP CUBIC were also added to the LIA source code. As described in the previous section, the Coupled CUBIC operates on a large BDP path and stores the virtual congestion window and delay time in some predefined global variables. If the BDP is recognized small, the increase factor is calculated. The calculation parameters are congestion window and delay time received from the remaining subflows and virtual congestion window and delay time stored in the global variables for large BDP paths.

Tab. 2 shows the average congestion window values and their ratio of TCP Reno and LIA. It can be seen that the ratio of average congestion window differs by the square root of α . This can be derived by using the congestion window calculation method of the AIMD in consideration of the window increase method shown in Eq. (2). Therefore, in Fig. 3, the virtual LIA congestion window is finally obtained by multiplying the virtual TCP Reno congestion window by α .

To change the congestion window of TCP CUBIC into a virtual TCP Reno congestion window, we used Eqs. (8)–(10) to create conversion tables applied corresponding to the RTT values in the kernel. Finally, a virtual LIA congestion window should be created by multiplying by α . In the LIA of Linux kernel, to reduce the complexity of computation and to remove manipulation of floating point numbers, the calculation was performed using the normalized α value divided by the αs (scaled α ) as shown in Tab. 2.

4  Performance Evaluation of Coupled CUBIC

In this section, we evaluated the MPTCP throughput and fairness of the proposed Coupled CUBIC algorithm by experiments in a small testbed.

4.1 Experimental Environment

In order to compare the performance of the proposed Coupled CUBIC and the MPTCP LIA, the experimental environment is configured as shown in Fig. 4.

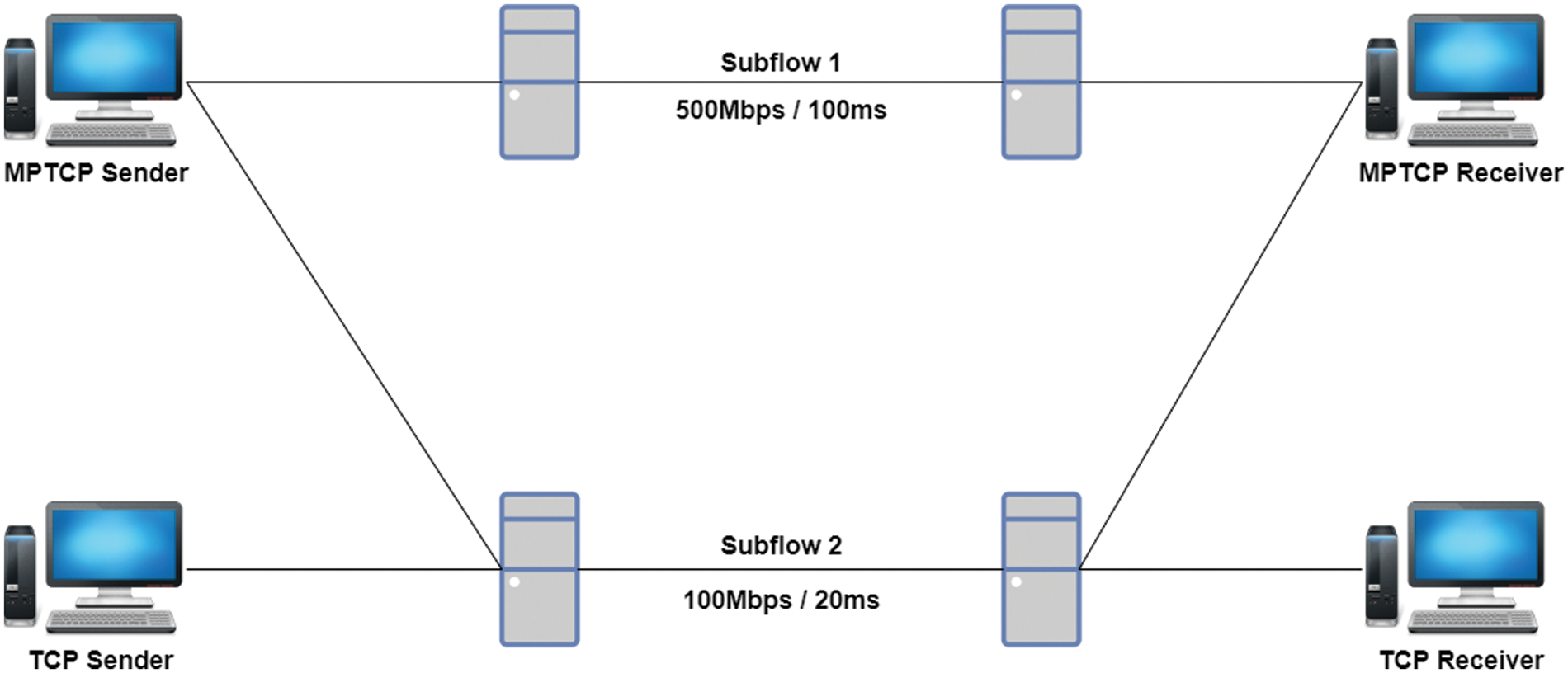
Figure 4: Testbed network for experiments

A total of 8 PCs were used for the testbed shown in Fig. 4. We installed Linux OS Ubuntu 18.04 LTS on all PCs. At the MPTCP senders and receivers, the basic LIA source code in the kernel provided by the MPTCP group was modified to be mixed with the Coupled CUBIC code. To configure the broadband network, the buffer size and receiver window settings were changed appropriately. The buffer size of all intermediate points of subflows 1 and 2 through which data is transmitted was set to about 100% of the corresponding BDP, and the size of the receiver window was set large enough not to limit the congestion control performance. The bandwidth of each NIC was set to 1 Gbps. Intermediate link of subflow 1 was configured to have bandwidth of 500 Mbps and delay time of 100 ms using the QoS settings of Dummynet [19] in the intermediate node. The physical bandwidth of subflow 2 is set to 100 Mbps and the delay time is set to 20 ms to configure a small BDP path. By setting static routing in each node, the MPTCP transceiver goes through the paths of subflows 1 and 2, respectively. The single-path TCP flow was made to go through the same path of subflow 2. As for the packet loss rate, 10−6, which is a loss rate of the general wired network, was set in the subflow 1 and 2 bottleneck links. The experimental parameters of test scenarios are summarized as shown in Tab. 3.

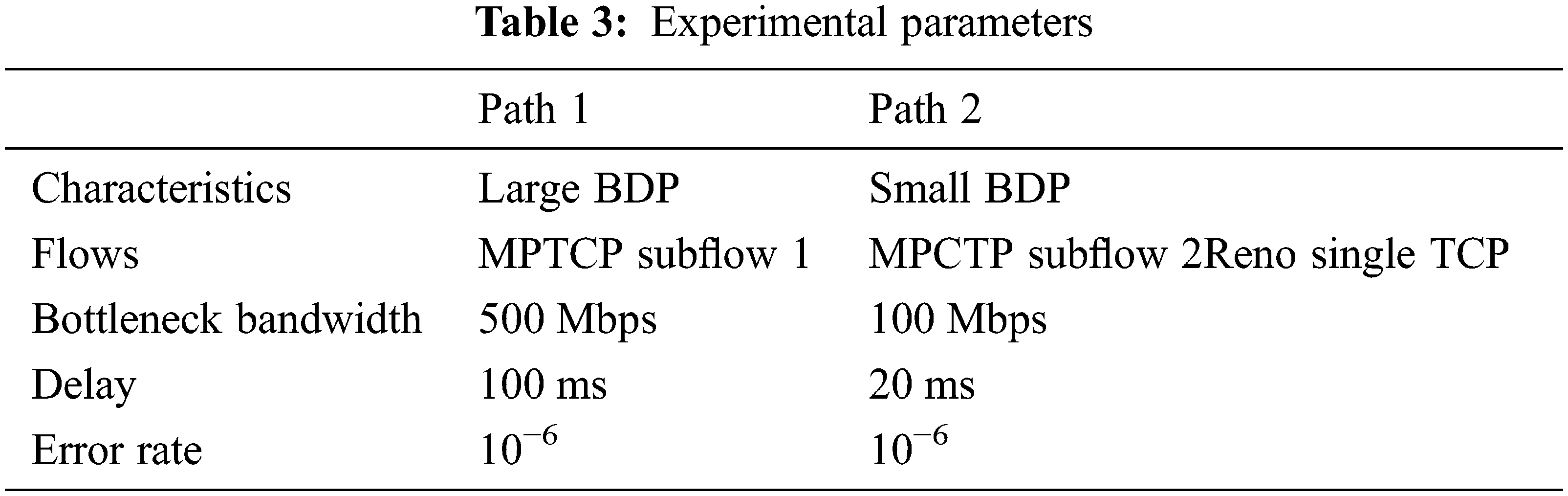
TCP traffic was generated using the Iperf tool [20], and the maximum segment size was set to 1460 bytes. For packet analysis, the Wireshark tool [21] was used to measure the total transmission time and average transmission rate. We use Linux GNUPLOT tool to represent measurement results. To measure the value of the virtual congestion window, a specific variable was defined in the source code, and the value of that variable is read in the tcp_probe function and displayed as a graph.

4.2 Experiment Results

Figs. 5 and 6 show experiment results of the MPTCP session maintained for a long time. By configuring the testbed in Fig. 4, the MPTCP sender transmits traffic through subflows 1 and 2 for 1000 s. The singe-path TCP sender transmits traffic through the same path of subflow 2 to compare fairness performance.

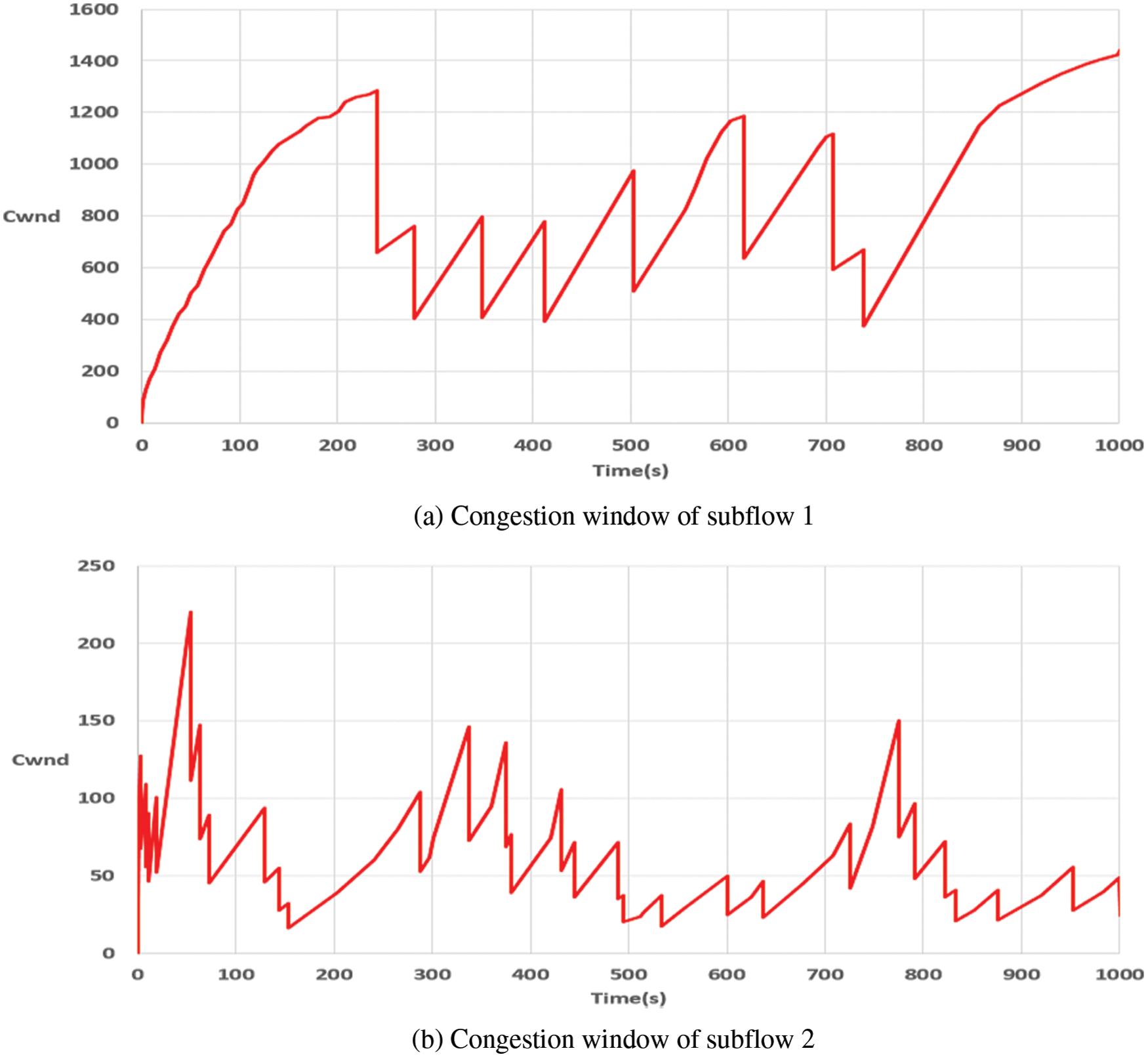
Figure 5: Congestion window change in the LIA

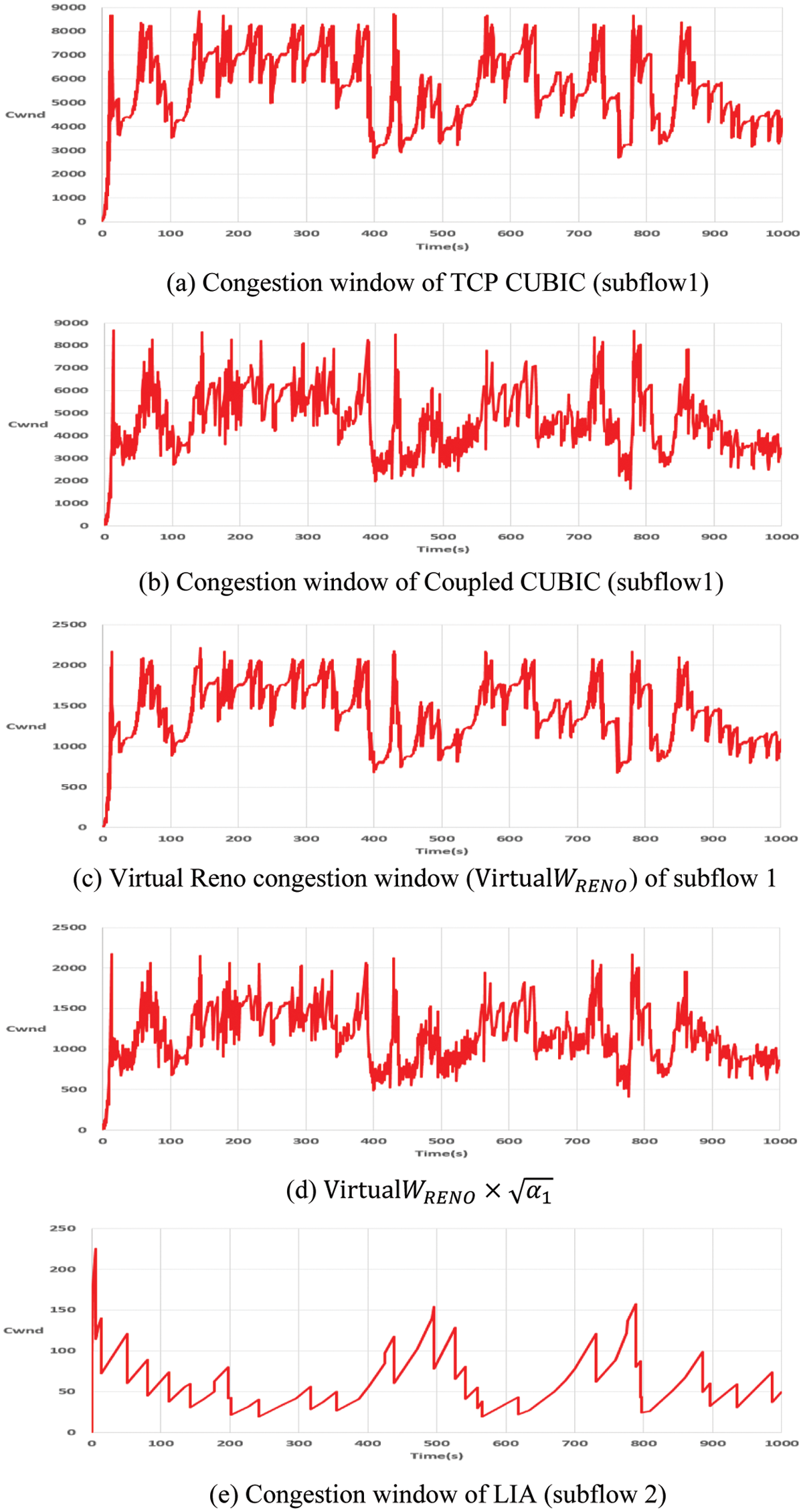
Figure 6: Congestion window change in the Coupled CUBIC

Fig. 5 shows the results when the LIA is adopted for MPTCP congestion control. Subflow 1 is a path with a large BDP, and the maximum congestion window capacity including the buffer size would have been 8332. In the graph of subflow 1 in Fig. 5a, the LIA congestion window increases for 240 s to about 1290. A packet loss occurs around 240 s, reducing the congestion window by half. The congestion window is varied by repeating the increase and decrease, but the maximum capacity cannot be reached. In even a large BDP path, only less than 15% of the link resource is utilized and the remaining resource is wasted. Average congestion windows are shown in Tab. 4.

The Fig. 6a is the congestion window graph of subflow 1 operating the TCP CUBIC ( WCUBIC) in the large BDP path shown in Eq. (9). The Fig. 6b shows congestion window graph of the Coupled CUBIC ( WcoupledCUBIC ) of subflow 1 shown in Eq. (11). The Fig. 6c shows the virtual Reno congestion window ( VirtualWRENO ) of subflow 1 converted using Eq. (10). The Fig. 6d shows the virtual LIA congestion window calculated by multiplying VirtualWRENO and α1 . The virtual congestion window affects the calculation of increase factor of subflow 2. The last figure, Fig. 6e, shows the LIA congestion window of subflow 2 transmitted through the small BDP path.

Comparing the results of Figs. 5 and 6, we can see clearly the difference in the operational performance of the basic LIA and the Coupled CUBIC proposed in this paper. First, if we compare the transmission amount of subflow 1, that of the Coupled CUBIC is much larger than that of the LIA method, as expected. Comparing the congestion window variation of subflow 2 through the small BDP path in Figs. 5 and 6, it shows a similar pattern except for the first 100 s. It shows that calculation of the increase factor α using the normalized virtual congestion window is similar to calculating the linked congestion window in LIA. The difference appears in the first 100 s interval because the LIA congestion control increases slowly and the Coupled CUBIC increases rapidly up to the link maximum congestion window. When a TCP connection operates for a long time, there is little difference in congestion window or transmission performance of subflow 2. Average congestion windows are given in Tab. 5.

Fig. 7 is a graph showing the average transmission performance of the experimental results shown in Figs. 5 and 6. We used the Wireshark tool to capture packets for each path and the entire path to obtain average transmission performance. The CCUBIC( α1 ) is the performance result by using VirtualWRENO directly in the flowchart in Fig. 3 in calculating the increase rate of the congestion window of subflow 2. The CCUBIC( α2 ) is the performance result by including both α1 and α2 in the flowchart. Fig. 7 shows subflows 1, 2 and the total transmission rates when operating with LIA, CCUBIC( α1 ), and CCUBIC( α2 ) to evaluate the performance of two MPTCP congestion controls. The overall average transmission speed of LIA congestion control for 1000 s is about 115 Mbps. The average transmission speed of subflow 1 is about 95 Mbps, and that of subflow 2 is about 20 Mbps. Since subflow 1 does not interfere with other traffic, if enough time passes, it should use close to the maximum transmission rate of 500 Mbps. However, due to frequent packet loss and slow congestion window increase, the transmission speed of the path is limited to about 95 Mbps. It means that only about 1/5 of the path resources are used. The first bar graph in Fig. 7 shows the transmission performance when TCP CUBIC operates alone along the high BDP path for performance comparison. Although it shows higher transmission performance than MPTCP operating with LIA, it can be seen that it is slightly lower than the overall transmission performance of MPTCP operating with Coupled CUBIC. When CCUBIC( α1 ) is applied, the average transmission speed of subflow 1 is about 397 Mbps, subflow 2 is about 25 Mbps, and the total is about 422 Mbps. When CCUBIC( α2 ) is applied, the average transmission speed of subflow 1 is 402 Mbps, subflow 2 is 21 Mbps, and the total is about 423 Mbps. Subflow 1 of Coupled CUBIC uses more than 400 Mbps, which is about 80% of the total path bandwidth, by controlling the congestion window in the TCP CUBIC manner in the high BDP path. This corresponds to using 4 times more resources than when using LIA. Through all these results, if a simple LIA is used, the resource utilization efficiency is significantly lowered. However, if the Coupled CUBIC proposed in this paper is used, it can be seen that the resource utilization efficiency of the high BDP path is greatly improved. The total aggregated throughput is compared in Tab. 6.

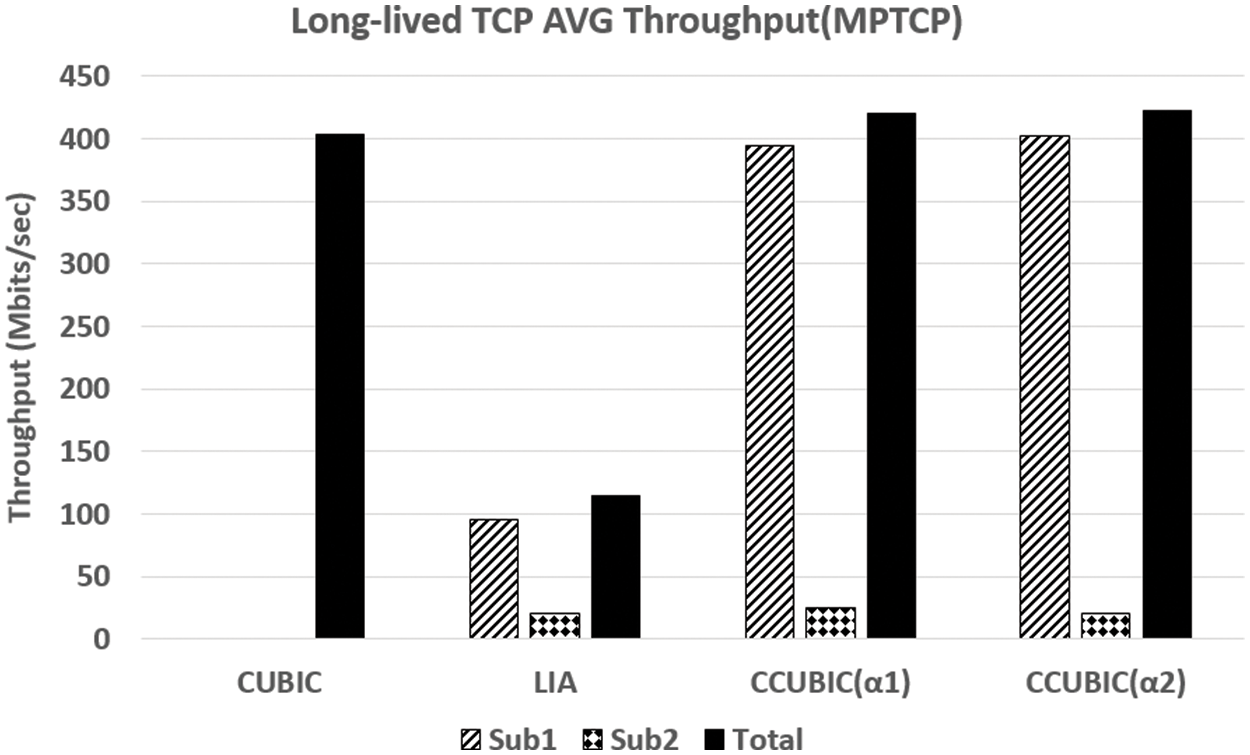
Figure 7: Average throughput comparison between LIA and Coupled CUBIC

Next, we describe the congestion control of a small BDP path operated by MPTCP LIA. The design purpose of Coupled CUBIC is to make the MPTCP congestion control operate like TCP CUBIC congestion control in a large BDP path, and make it operate like LIA for a small BDP path. Therefore, in the path operating the LIA, it is assumed that the path in which TCP CUBIC is operating looks like operating the LIA. The normalized virtual congestion window value should be received and applied to the calculation of the increase rate of other subflows. If the congestion window converted to TCP Reno is simply used as it is, distortion different from the original LIA will occur, as shown in CCUBIC( α1 ). VirtualWRENO calculated in Eq. (10) is the congestion window value when TCP Reno is assumed to operate independently, and it is a value that differs by 1/α1 from when LIA is applied. Like CCUBIC( α2 ), it is necessary to calculate α2 again using the value obtained by multiplying VirtualWRENO by α1 , and apply α2 to other increase rate calculations iteratively. Comparing the average transmission rates of subflow 2, it can be seen that LIA and CCUBIC( α2 ) are similar at 20 and 21 Mbps. However, in CCUBIC( α1 ), the virtual congestion window of subflow 1 ( VirtualWRENO) is measured to be larger than that of LIA, so the increase rate of subflow 2 becomes small and the average transmission rate is 17 Mbps, which is about 3 Mbps smaller.

Through the experimental results, it is confirmed that the transmission performance is greatly enhanced when the Coupled CUBIC is used in the path with large BDP. When MPTCP connection is made, the Coupled CUBIC fully utilizes resources in large BDP paths. In addition, by applying the virtual congestion window transformation formula, it was confirmed that the path with a small BDP operates similarly to the original LIA and complies with the performance criterion of the MPTCP.

5  Conclusion and Future Works

In this paper, a new MPTCP congestion control algorithm named “Coupled CUBIC congestion control” was designed and performance evaluation was shown to improve the transmission performance of MPTCP in a multipath network having a large BDP path. In high-speed long-distance networks, the existing MPTCP congestion control degrades traffic transmission performance due to packet loss and slow congestion window increase. The proposed Coupled CUBIC congestion control operates like TCP CUBIC in a large BDP path and utilizes the path resources efficiently. In the ordinary path with a small BDP, it is designed to control congestion in the same way as the original LIA, so that the fairness of the transmission performance in MPTCP itself is maintained. For the appropriate coupling of congestion window satisfying the MPTCP fairness goals, we first normalize the CUBIC window into Reno window and then use it to the calculation of increase factor α . For the high BDP path, the TCP CUBIC window is also modified adopting the increase factor α to maintain fairness with a single-path TCP CUBIC flow sharing the same bottleneck bandwidth. We constructed asymmetric heterogeneous network testbeds mixed with large and small BDP paths and compared the performances of LIA and Coupled CUBIC by experiments using Linux kernel implementation code. Experimental results show that the proposed Coupled CUBIC effectively utilizes almost over 80% of the bandwidth resource in the high BDP path, while the LIA uses only less than 20% of the bandwidth for the same path. It was confirmed that the resource utilization and traffic transmission performance have been greatly improved by using the proposed Coupled CUBIC in high-speed multipath networks, as well as maintaining MPTCP fairness goals with competing single-path TCP CUBIC flows.

In the future, we will configure various network environments and check the performance of the Coupled CUBIC. In addition to TCP CUBIC, we plan to design MPTCP congestion control algorithms using other types of high-speed congestion control for large BDP paths. QUIC protocol [22], which has been standardized by the IETF recently, is a transport layer protocol with various advantages, and research is underway to graft the multipath function to it [23]. We plan to study how to apply the Coupled CUBIC method proposed in this paper as congestion control of the multipath QUIC protocol.

Acknowledgement: We would like to express our great appreciation to the Chungnam National University and Agency for Defense Development for providing the necessary lab environments for this research.

Funding Statement: This result was supported by “Regional Innovation Strategy (RIS)” through the National Research Foundation of Korea (NRF) funded by Ministry of Education (MOE)(2021RIS-004).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  V. Jacobsen and M. J. Karels, “Congestion avoidance and control,” ACM CCR, vol. 18, no. 4, pp. 314–329, 1995. [Google Scholar]

 2.  T. Henderson, S. Floyd, A. Gurtov and Y. Nishida, “The NewReno modification to TCP’s fast recovery algorithm,” RFC 6582, Internet Engineering Task Force, 2012. [Google Scholar]

 3.  L. A. Greico and S. Mascolo, “End-to-end bandwidth estimation for congestion control in packet networks,” in Proc. QoS-IP, Milano, Italy, pp. 645–658, 2003. [Google Scholar]

 4.  C. P. Fu and S. C. Liew, “TCP veno: TCP enhancement for transmission over wireless access networks,” IEEE Journal on Selected Areas in Communications, vol. 21, no. 2, pp. 216–228, 2003. [Google Scholar]

 5.  I. Rhee, L. Xu, S. Ha, A. Zimmermann, L. Eggert et al., “CUBIC for fast long-distance networks,” RFC 8312, Internet Engineering Task Force, 2018. [Google Scholar]

 6.  A. Ford, C. Raiciu, M. Handley and O. Bonaventur, “TCP extensions for multipath operation with multiple addresses,” RFC 6824, Internet Engineering Task Force, 2013. [Google Scholar]

 7.  N. Kuhn, E. Lochin, A. Mifdaoui, G. Sarwar, O. Mehani et al., “DAPs: Intelligent delay-aware packet scheduling for multipath transport,” in Proc. IEEE ICC, Sydney, Australia, pp. 1222–1227, 2014. [Google Scholar]

 8.  H. Shi, Y. Cui, X. Wang, Y. Hu, M. Dai et al., “STMS: Improving MPTCP throughput under heterogeneous networks,” in Proc. USENIX ATC, Boston, MA, USA, pp. 719–730, 2018. [Google Scholar]

 9.  C. Raiciu and M. H. D. Wischik, “Coupled congestion control for multipath transport protocols,” RFC 6356, Internet Engineering Task Force, 2011. [Google Scholar]

10. R. Khalili, N. Gast and M. Popovic, “Opportunistic linked-increases congestion control algorithm for MPTCP,” IETF, 2014. [Online] Available: https://datatracker.ietf.org/doc/html/draft-khalili-mptcp-congestion-control-00. [Google Scholar]

11. Y. Cao, M. Xu and X. Fu, “Delay-based congestion control for multipath TCP,” in Proc. IEEE ICNP, Austin, TX, USA, pp. 1–10, 2012. [Google Scholar]

12. L. S. Brakmo and L. L. Peterson, “TCP vegas: End to end congestion avoidance on a global internet,” IEEE Journal on Selected Areas in Communications, vol. 13, no. 8, pp. 1465–1480, 1995. [Google Scholar]

13. L. Xu, K. Harfoush and I. Rhee, “Binary increase congestion control (BIC) for fast long-distance networks,” in Proc. IEEE INFOCOM, Hong Kong, China, pp. 2514–2524, 2004. [Google Scholar]

14. S. Ferlin, T. Dreibholz and O. Alay, “Multi-path transport over heterogeneous wireless networks: Does it really pay off?,” in Proc. IEEE GLOBECOM, Miami, FL, USA, pp. 1–6, 2010. [Google Scholar]

15. S. H. Baidya and R. Prakash, “Improving the heterogeneous paths using slow path adaptation,” in Proc. IEEE ICC, Sydney, Australia, pp. 3222–3227, 2014. [Google Scholar]

16. T. A. Le, R. Haw, C. S. Hong and S. Lee, “A multipath cubic TCP congestion control with multipath fast recovery over high bandwidth-delay product networks,” IEICE Trans. Communications, vol. E95.B, no. 7, pp. 2232–2244, 2012. [Google Scholar]

17. T. Kato, S. Haruyama, R. Yamamoto and S. Ohzahata, “mpCUBIC: A CUBIC-like congestion control algorithm for multipath TCP,” in Proc. World Conf. on Information Systems and Technologies, Budva, Montenegro, pp. 306–317, 2020. [Google Scholar]

18. I. Mahmud, T. Lubna, G. H. Kim and Y. Z. Cho, “BA-MPCUBIC: Bottleneck-aware multipath CUBIC for multipath-TCP,” Sensors, vol. 21, no. 18, pp. 1–21, 2021. [Google Scholar]

19. Dummynet, http://info.iet.unipi.it/∼luigi/dummynet/, 2021 [Google Scholar]

20. Iperf, https://iperf.fr/, 2021. [Google Scholar]

21. Wireshark, https://www.wireshark.org/, 2021. [Google Scholar]

22. J. Iyengar and M. Thomson, “QUIC: A UDP-based multiplexed and secure transport,” RFC 9000, Internet Engineering Task Force, 2021. [Google Scholar]

23. T. Viernickel, A. Froemmgen, A. Rizk, B. Koldehofe and R. Steinmetz, “Multipath QUIC: A deployable multipath transport protocol,” in Proc. IEEE ICC, Kansas City, MO, USA, pp. 1–7, 2018. [Google Scholar]