Determination of AVR System PID Controller Parameters Using Improved Variants of Reptile Search Algorithm and a Novel Objective Function

1  Introduction

1.1 Research Background

Automatic voltage regulator (AVR) system is a closed loop system that keeps the terminal voltage of a synchronous generator at its desired value under different disturbances such as changing load conditions and turbine output (generator input) fluctuations. If the terminal voltage of generators cannot be sustained to a constant level, power system stability, as well as power quality, will be degraded. However, AVR by itself may not deal with these problems due to its oscillating transient response, larger overshoot, and steady-state errors if a properly designed controller does not accompany it.

1.2 Literature Survey

Several types of controllers have been used so far to maintain the terminal voltage of generators in a stable and robust way. Proportional, integral, derivative (PID) [1–16], fuzzy logic PID (FLCPID) [17,18], gray PID (GPID) [19], sigmoid PID (SPID) [20], PID and acceleration (PIDA) [16], PID plus second order derivative (PIDD2) [9–11,21], two degree of freedom PI (2DOF-PI) [22] and 2DOF fractional PI (2DOF-FOPI) [23], fractional order PID (FOPID) [9–11,24–30], and filtered versions of above-mentioned controllers such as filtered PID (PIDF) [9–11,31], fractional filter FOPID (FOPIDFF) [32], and FOPID plus derivative with filter (FOPID-DN) [33], sliding mode controller (SMC) with PID type sliding surface function (PID-SSF) [34], and PID type SMC with state feedback [35], as well as model predictive controllers (MPC) [36–39] are some to name. Among these controller types, the PID controller is the most used controller due to its simplicity and ease of use, which is also the preferred controller in this study. However, no matter what type of controller has been chosen, if not properly designed, even the most effective and robust one will perform poorly in terms of stability metrics and fast response.

For successful dynamic and steady state performance, metaheuristic optimization methods that have been proposed for tuning controller parameters within the last decade are Lévy flight-based reptile search with Nelder-Mead (L-RSANM) [1], whale optimization algorithm (WOA) [23] and improved WOA (IWOA) [2,21], genetic algorithm (GA) [3,18], equilibrium optimizer (EO) algorithm [4,33], slime mould algorithm (SMA) [5] and improved SMA [26], particle swarm optimization (PSO) [22] and hybrid PSO with bacteria foraging (BF-PSO) [6], tree seed algorithm (TSA) [7], cuckoo search (CS) algorithm [8], fitness distance balance-based Lévy flight distribution (FDB-LFD) algorithm [9], archimedes optimization algorithm (AOA) [10], hybrid simulated annealing with manta ray foraging optimization algorithm (SA-MRFO) [11], sine cosine algorithm (SCA) [12,32] and nonlinear SCA (NSCA) [20], improved kidney-inspired algorithm (IKA) [13], symbiotic organism search (SOS) algorithm [31] and hybrid SOS with SA (hSOSSA) [14], stochastic fractal search (SFS) algorithm [15], harmony search algorithm (HSA) [16], local unimodal sampling (LUS) [16], teaching learning-based optimization (TLBO) [16,17], imperialist competitive algorithm (ICA) [19], chaotic black widow algorithm (ChBWA) [24], gradient-based optimization (GBO) algorithm [25], jaya algorithm (JA) [27], henry gas solubility optimization (HGSO) algorithm [28], and chaotic yellow saddle goatfish algorithm (C-YSGA) [29].

1.3 Contributions of This Study

From the literature review above it is obvious that newly developed optimization techniques for different controllers have been reported to improve AVR system performance. Since there is no definite algorithm to find the best solution for the AVR system, studying a new metaheuristic optimization algorithm to find the optimal parameters of a chosen controller in an AVR system is an observable problem, which is the main motivation of this paper. Therefore, this study proposes two variants of the recently proposed reptile search algorithm (RSA), opposition learning-based RSA (ORSA) and hybrid ORSA with pattern search algorithm (ORSAPS) to optimally determine the parameters of a PID controller. The RSA algorithm is a recent metaheuristic optimizer mimicking the behavior of crocodiles on two principal activities that both of them are performed in two main strategies: (i) encircling with high walking or belly walking; (ii) hunting with coordination or cooperation [40]. Although the standard RSA algorithm tries to achieve a balance between exploration and exploitation by splitting the total iteration into the aforementioned four stages, it may still fail in population diversity and trap into local optima [41]. Therefore, the proposed methods aim to solve these main weaknesses of the original algorithm to find better solutions. Another motivation of this study is to compare the successful performance of the proposed design approaches with studies presented within the last decade that are proposed for the same controller type and have found the best results so far. Hence, the contribution of this study can be summarized as follows:

•   Two novel variants of the RSA algorithm, namely the opposition learning-based RSA (ORSA) and the hybrid ORSA with pattern search (ORSAPS) are proposed for the first time. To the best of the author’s knowledge, there is a Lévy flight-based RSA with Nelder-Mead (L-RSANM) hybridization that is proposed before in the literature, which uses a different mechanism (Lévy flight) for global search enhancement and a different algorithm (NM) for local search enhancement.

•   In addition, a novel objective function (J=ITAE+mZLG) was proposed that is created by summing the integral of time multiplied absolute error (ITAE) with the slightly modified version of Zwe-Lee Gaing’s time domain objective function (ZLG) [42]. A slight modification of ZLG consists of multiplying its first term (sum of overshoot and steady-state error) with a weighting factor, which is called α, to add more degree of freedom to adjust the effects of each term of ZLG separately, and so that the newly proposed objective function. Note that, when α is equal to one the proposed objective function becomes the sum of ITAE with the original ZLG which is previously proposed by [24].

•   The proposed variants of RSA, the ORSA, and ORSAPS, are both used to determine the PID controller parameters of an AVR system for the first time.

•   The performances of the proposed controller design approaches are compared with the best-performing approaches in the literature for the same PID controller, using L-RSANM [1], SMA [5], CS [8], and hSOSSA [14] algorithms.

•   With the results of conducted analyses such as transient response, frequency response, robustness, disturbance rejection, and trajectory tracking, the superiority of the proposed algorithms, especially the ORSAPS, has been proven.

The rest of the paper is organized as follows. Section 2 describes the RSA algorithm. Section 3 proposes two new variants of RSA, namely ORSA, and ORSAPS. Section 4 presents the AVR system and Section 5 describes the implementation of PID controllers for the AVR system based on the proposed approaches. Section 6 presents simulation results and comparisons in detail. Section 7 concludes the paper.

2  Reptile Search Algorithm (RSA)

The RSA algorithm is a recently proposed metaheuristic optimizer that is inspired by the hunting behavior of crocodiles and mathematically models this behavior to perform its optimization process [40]. As in all metaheuristic optimization algorithms, it starts with the initialization stage by generating an N×D matrix randomly where, N and D are the number of candidate solutions and the dimension of the problem, respectively. Then, the exploration stage kicks in by high walking (for iter≤T/4) and belly walking (iter>T/4) to mimic the encircling behavior of crocodiles to find the next position as in Eq. (1).

xij(iter+1)={Bestj(iter)−hij(iter)×σ−Sij(iter)×rnd,iter≤T/4Bestj(iter)×xr1j(iter)×PR(iter)×rnd,iter>T/4}(1)

Here, iter is the current iteration and T is the maximum number of iterations. Bestj(iter) denotes the jth position of the currently found best solution, σ is the sensitivity parameter that is responsible for the exploration accuracy, r1 is random integer within [1,N], and xr1j is a random position within the current population for the ith solution. hij(iter)=Bestj(iter)×PDij is the hunting operator for jth position of ith solution, where PDij is the percentage difference between the jth position of the current solution and the best-found solution as in Eq. (2), Sij is the shrinking operator as in Eq. (3), and PR(iter) is the probability ratio as in Eq. (4).

PDij=a+xij−M(xi)Bestj(iter)×(UBj−LBj)+ε(2)

Sij=Bestj(iter)−xr2jBestj(iter)+ε(3)

PR(iter)=2×r3×(1−1T)(4)

Here, a is a parameter controlling the exploration accuracy through iterations by considering the difference between candidate solutions, ε is a small value, M(xi) is the average of positions of ith solution, r2 is a random integer number within [1,N], xr2j is a random position within the current population for the ith solution, and r3 is a random integer number within [−1,1]. Like the exploration stage, RSA also has two hunting behavior to mimic for its exploitation stage, namely the hunting coordination (for T/2<iter≤3T/4) and the hunting cooperation (for 3T/4<iter≤T) as in Eq. (5).

xij(iter+1)={Bestj(iter)×Pij(iter)×rnd,T/2<iter≤3T/4Bestj(iter)−hij(iter)×ε−Sij×rnd,3T/4<iter≤T}(5)

In all equations above, rnd is a random number within [0,1]. Note that, all RSA parameters that are used in this paper are the same as in [40]. The flowchart of the RSA algorithm is given in Fig. 1.

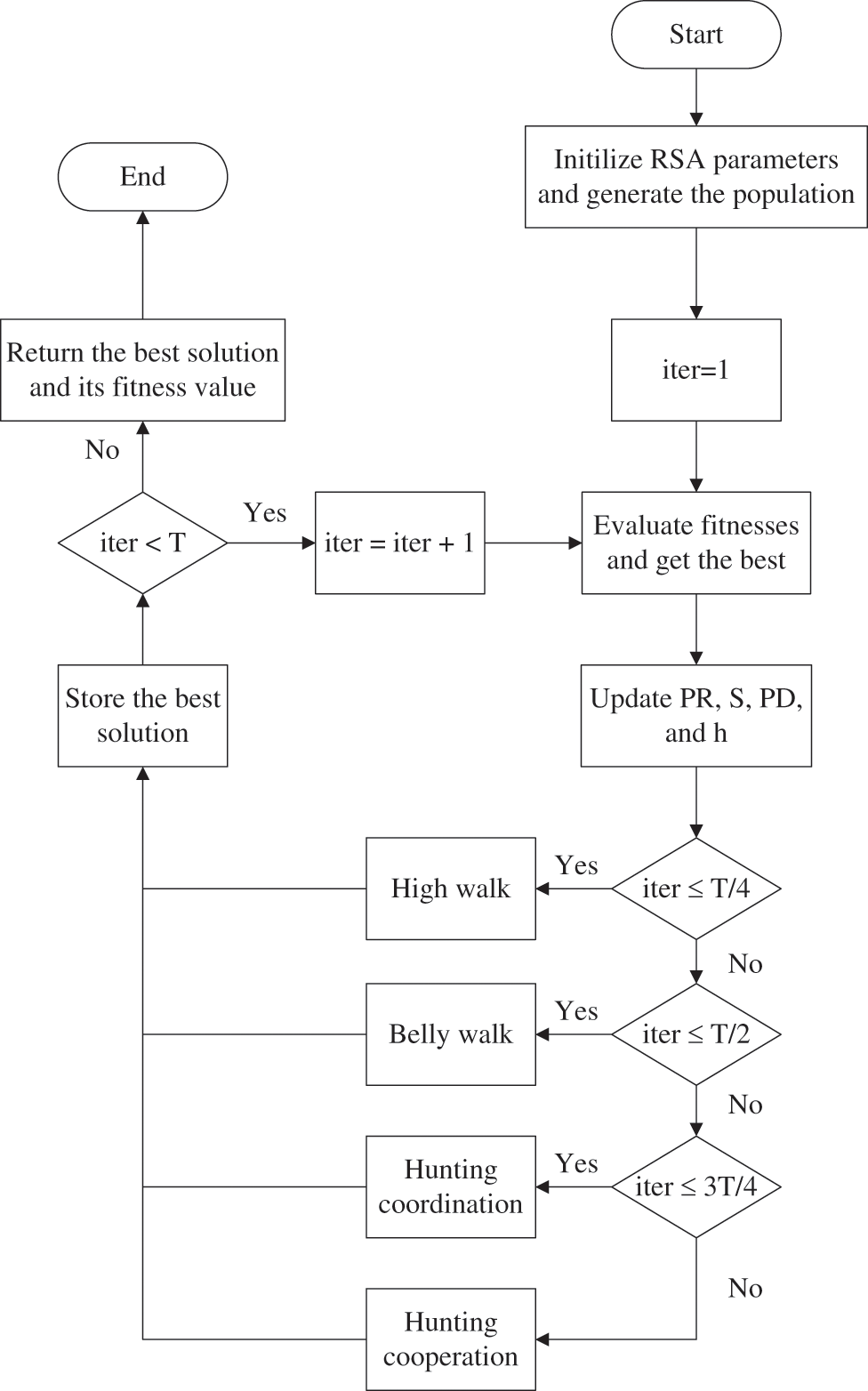
Figure 1: Flowchart of RSA algorithm

3  Improved Variants of RSA Algorithm—The ORSA and ORSAPS

Exploration (diversification) and exploitation (intensification) are two important stages of any swarm-based metaheuristic algorithm. The balance between these two stages is a trade-off problem and determines the effectiveness of the algorithm. In [43], it is shown that the desired capabilities of exploration and exploitation are problem specific and the trade-off balance between them does not necessarily mean a ratio of 50%:50%. For instance, a search mechanism that is avoiding too much exploration or having considerably scarce exploitation may obtain better results [43]. Besides, a poor-performing algorithm in one optimization problem may outperform other algorithms in another one. Hence, when the reasons behind the better or poor performance of an algorithm are understood then one can revise the algorithm’s searching strategies according to the desired needs. For that matter, measuring exploration and exploitation quantitatively becomes essential.

This section presents the two proposed improved variants of RSA aiming to solve the main weaknesses of the original algorithm such as low population diversity, unbalanced exploitation and exploration, and the tendency to fall into local optima [44]. The first one is the opposition learning-based RSA, which improves the population diversity so that the global search abilities of the original RSA algorithm and is given the name of ORSA and the second one is a further improvement of the newly proposed ORSA through hybridization with the pattern search (PS) algorithm, which improves the local search abilities of the algorithm and so that the solution accuracy of the algorithm and is given the name of ORSAPS. Both improvements integrated into the ORSAPS algorithm will also balance the exploitation and exploration stages of the algorithm to find better solutions without stagnating into local optima. The searching ratio of each stage during the course of iterations will be measured quantitatively by dimension-wise diversity measurement as suggested in [43] in a later subsection to show the effectiveness of the proposed algorithms.

3.1 Opposition-Based Learning RSA (ORSA)

The opposition-based learning (OBL) is a machine learning strategy to use for improving the performance of metaheuristic algorithms [45]. This mechanism has been successfully applied to various problems with modified variants such as logarithmic spiral opposition-based learning [46], adaptive opposition-based learning [47], and random opposition-based learning [48]. This paper uses the original OBL strategy [45] as follows:

Xopp=UB+LB−X(6)

Here, X is a real number within the values of [LB,UB] that represents the position of a solution and so Xopp is also a real number representing the opposite position of the current solution. Both positions of X and Xopp are considered together and the best solutions are selected from their combination. Fig. 2 illustrates the flowchart of the proposed ORSA algorithm. As illustrated, at first the basic steps of the RSA algorithm are run and then the objective function values of the current and the opposite populations are calculated and the best N number of solutions are selected as the next population.

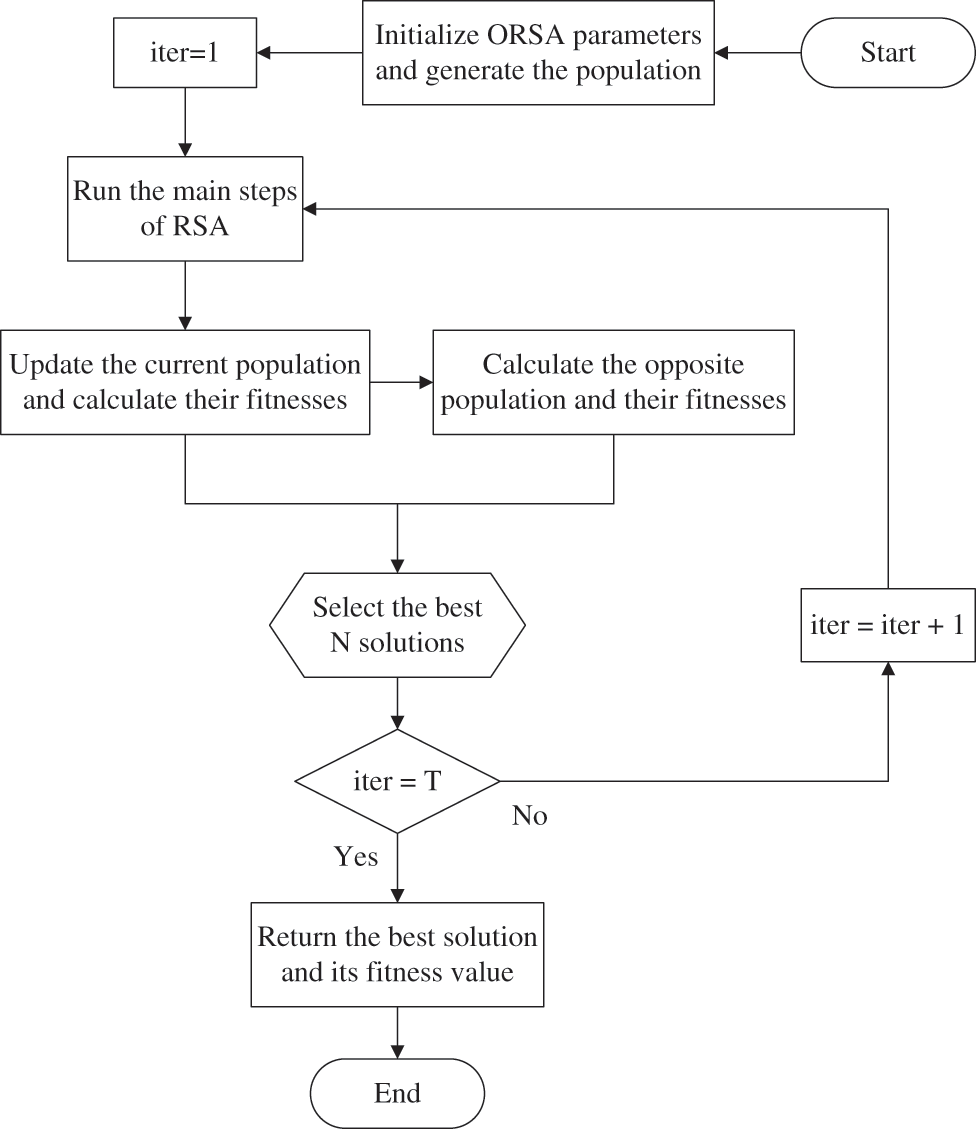
Figure 2: Flowchart of the proposed ORSA algorithm

3.2 Multidirectional Search (MDS) Type Pattern Search (PS) Algorithm

Pattern search (PS) methods identify the pattern of successful search points from the recent past and use this information to predict potentially successful search points in the future, and they are a type of direct search method, which is a category of algorithms that also includes the Simplex algorithm [49]. In this context, the multidirectional search (MDS) is a pattern search algorithm developed by [50] to solve unconstrained minimization problems that can find the optimal solution to a problem by retaining the best previous vertex and performing concurrent line searches in multiple directions to gather exploratory data. In Fig. 3, the flowchart of the MDS-type PS algorithm is given. Here, after choosing the initial simplex S0 along with expansion and contraction factors µ and θ, for each iteration, a search is performed from the current best vertex v0k in each of the n directions determined by the edges connected to v0k. The purpose of the search is to find a new vertex with a function value that is lower than the function value at v0k and replace v0k with the new vertex. To do so, the algorithm uses three steps. The reflection step is always performed to see if the best new vertex has been found. If so, it performs the expansion step otherwise, it performs the contraction step. In the contraction step, the algorithm runs until f(cik)<f(v0k) is satisfied, then replaces the current vertex with cik whose function is lower than the previous. In the expansion step, the algorithm calculates f(eik) and compares it with f(cik) and then according to the outcome, it replaces vik with either expansion eik or reflection rik. The reflection, expansion, and contraction factors, ρ, µ, and θ, determine the lengths of the steps relative to the original edges of the simplex. In this implementation, ρ, µ, and θ are set to 1, 2, and 0.5, respectively. Also, the initial step size needed for the first simplex generation and the tolerance value needed for algorithm termination are set to 0.05 and 10−5, respectively. PS algorithm terminates when the iteration counter is equal to the maximum number of iterations, which is 50 in this case, or when the difference between the worst and best solutions, which is called the distance, is less than the tolerance value.

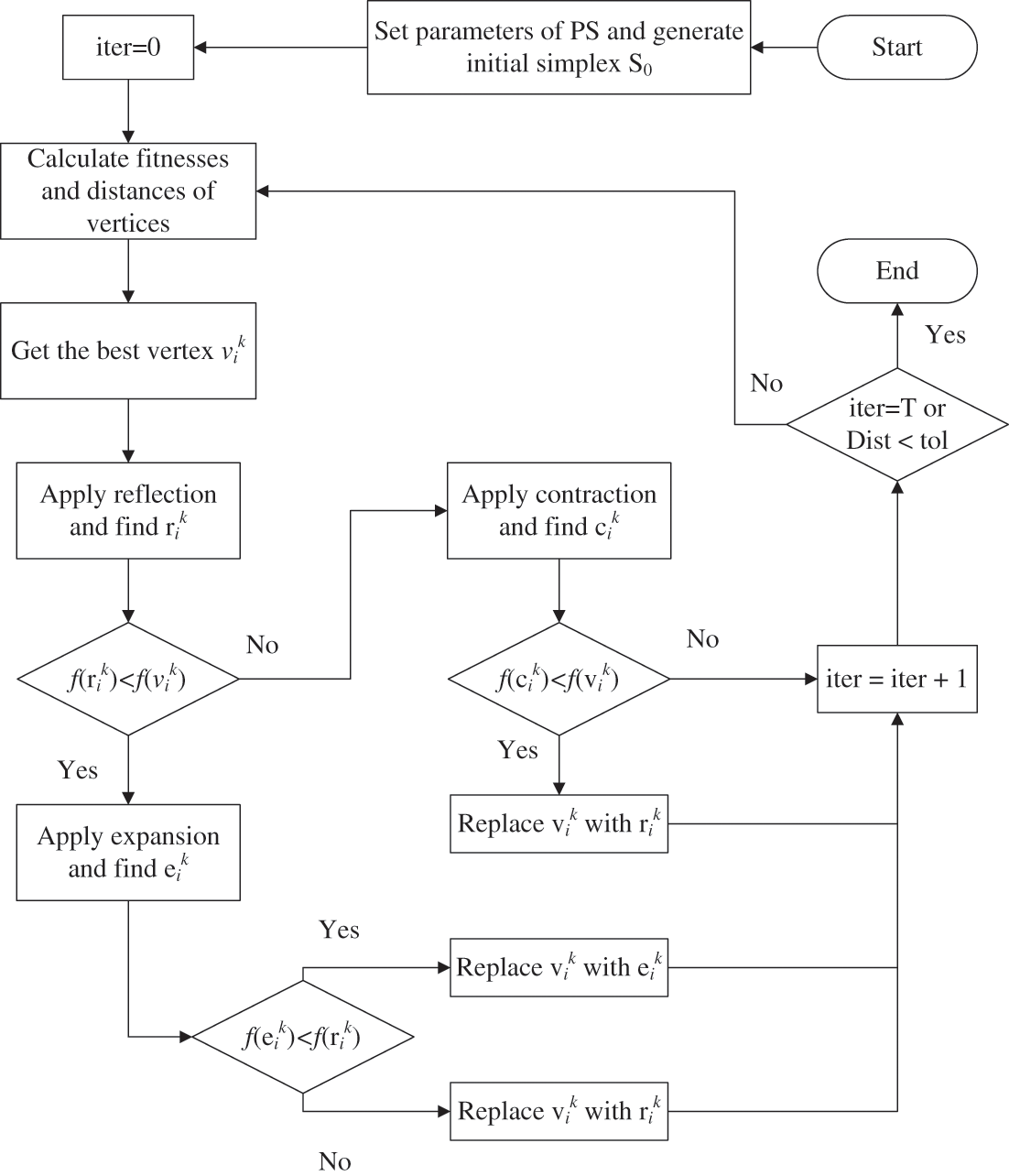
Figure 3: Flowchart of MDS-type PS algorithm

3.3 Hybrid ORSA with Pattern Search Algorithm (ORSAPS)

The proposed ORSAPS algorithm is created by hybridization of opposition learning-based RSA with MDS-type PS, aiming to have better global and local search capabilities. It starts the optimization process with ORSA and then applies PS at every ten iterations. This allows the utilization of good global search ability of the ORSA algorithm together with good local search ability of the PS algorithm. Fig. 4 illustrates the flowchart of the proposed ORSAPS algorithm in detail.

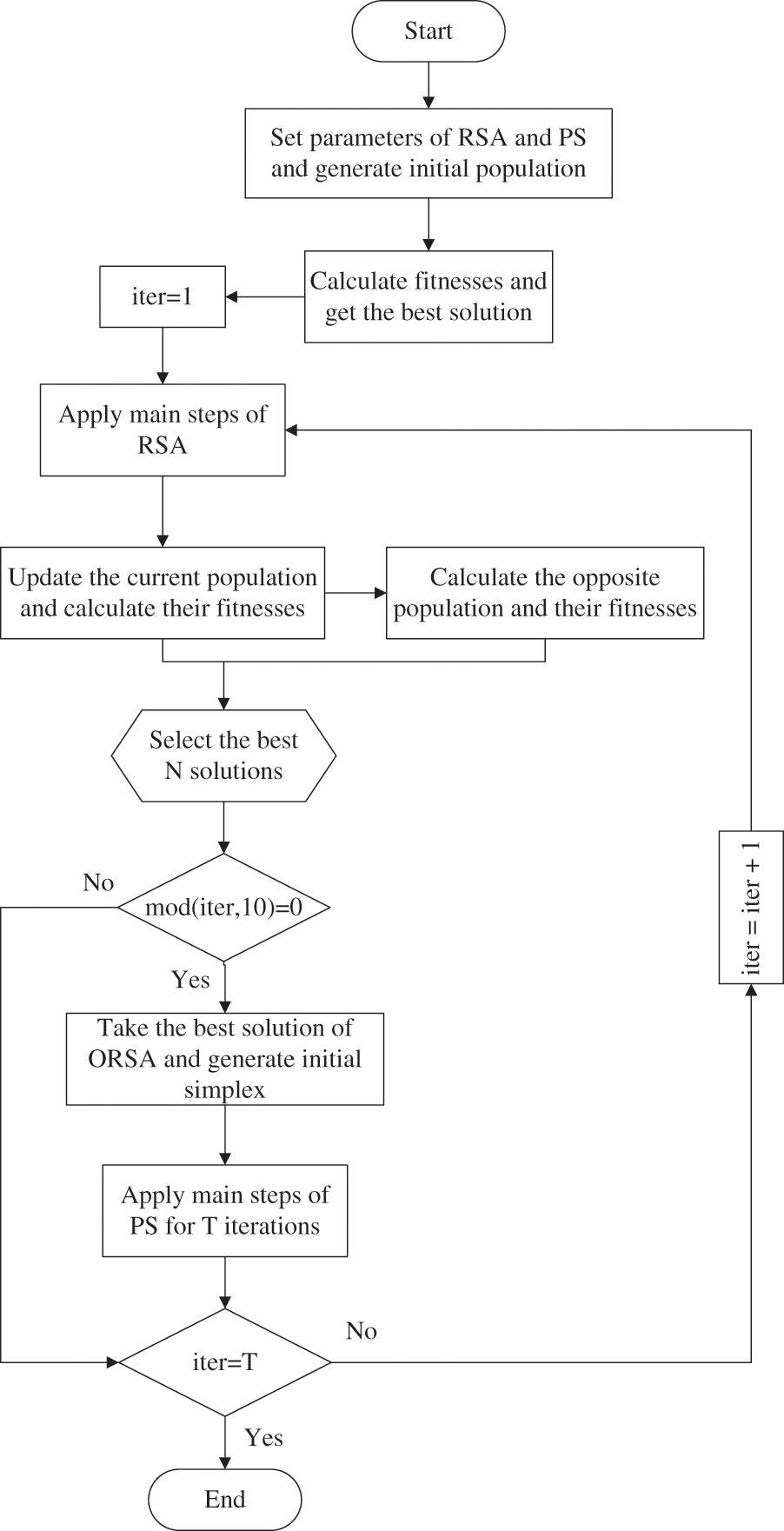
Figure 4: Flowchart of the proposed ORSAPS algorithm

4  Uncontrolled AVR System

Fig. 5 illustrates the general structure of an AVR system whose function is to keep the terminal voltage magnitude of a generator at a specified level [51]. The transfer functions of all main AVR components are shown in Fig. 6.

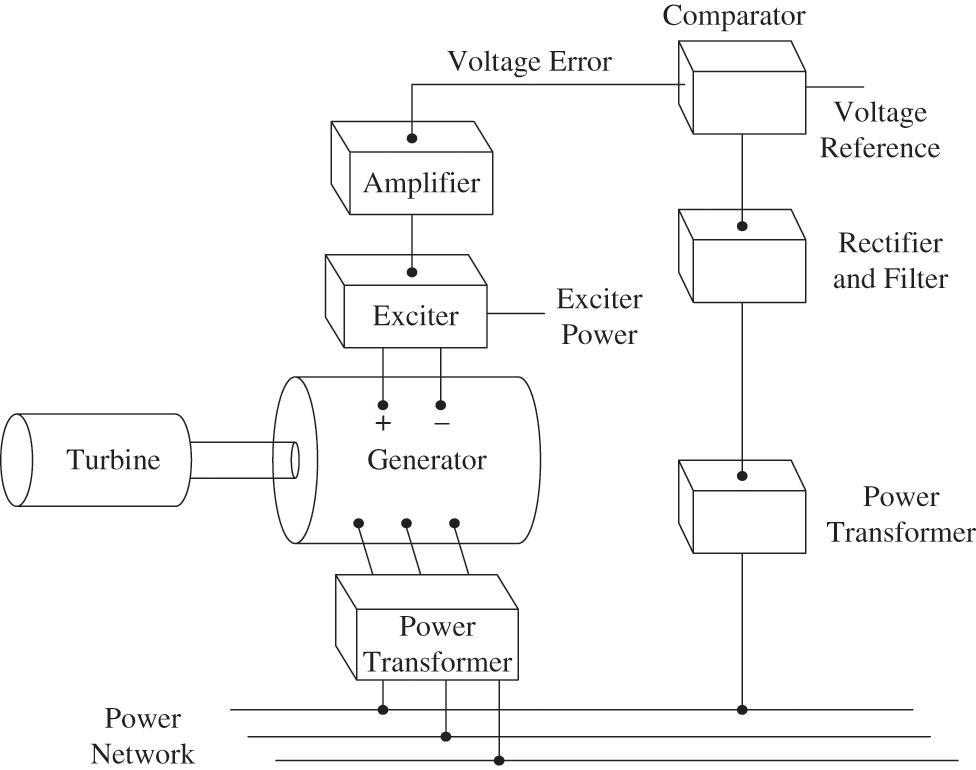
Figure 5: AVR system

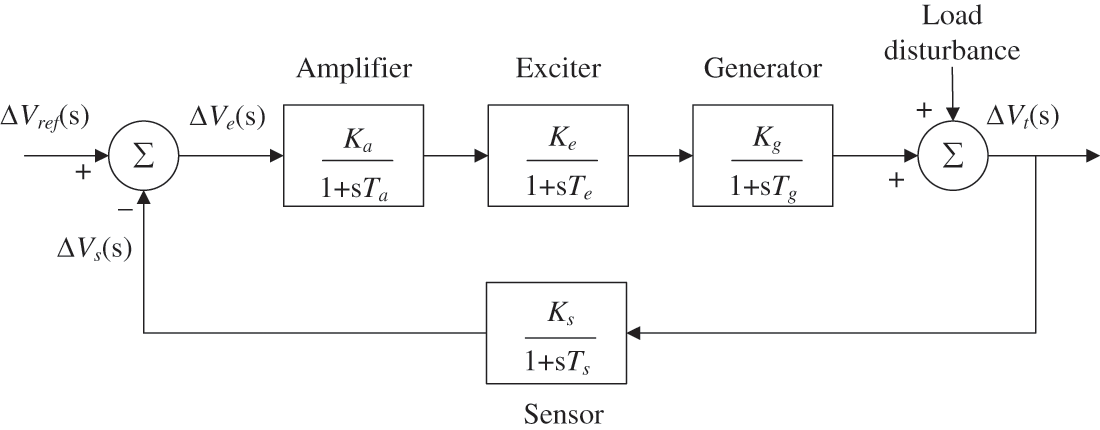
Figure 6: Transfer function model of uncontrolled AVR system

Here, Ka, Ke, Kg, Ks, Ta, Te, Tg, Ts, are gains and time constants of amplifier, exciter, generator, and sensor, respectively, while ΔVref(s), ΔVs(s), ΔVe(s) and ΔVt(s) are reference input voltage, sensor output voltage, error voltage, and generator terminal voltage, respectively. The transfer function of an uncontrolled AVR system is given as

ΔVt(s)ΔVref(s)=KaKeKg(1+sTs)(1+sTa)(1+sTe)(1+sTg)(1+sTs)+KaKeKgKs(7)

In Table 1, parameter ranges and values of all AVR system components are given. Using these values for the uncontrolled AVR system, despite being stable, the step voltage response is highly oscillatory as shown in Fig. 7. This illustration indicates that the dynamic response of the AVR system needs to be improved and the steady state error must be canceled by using a controller.

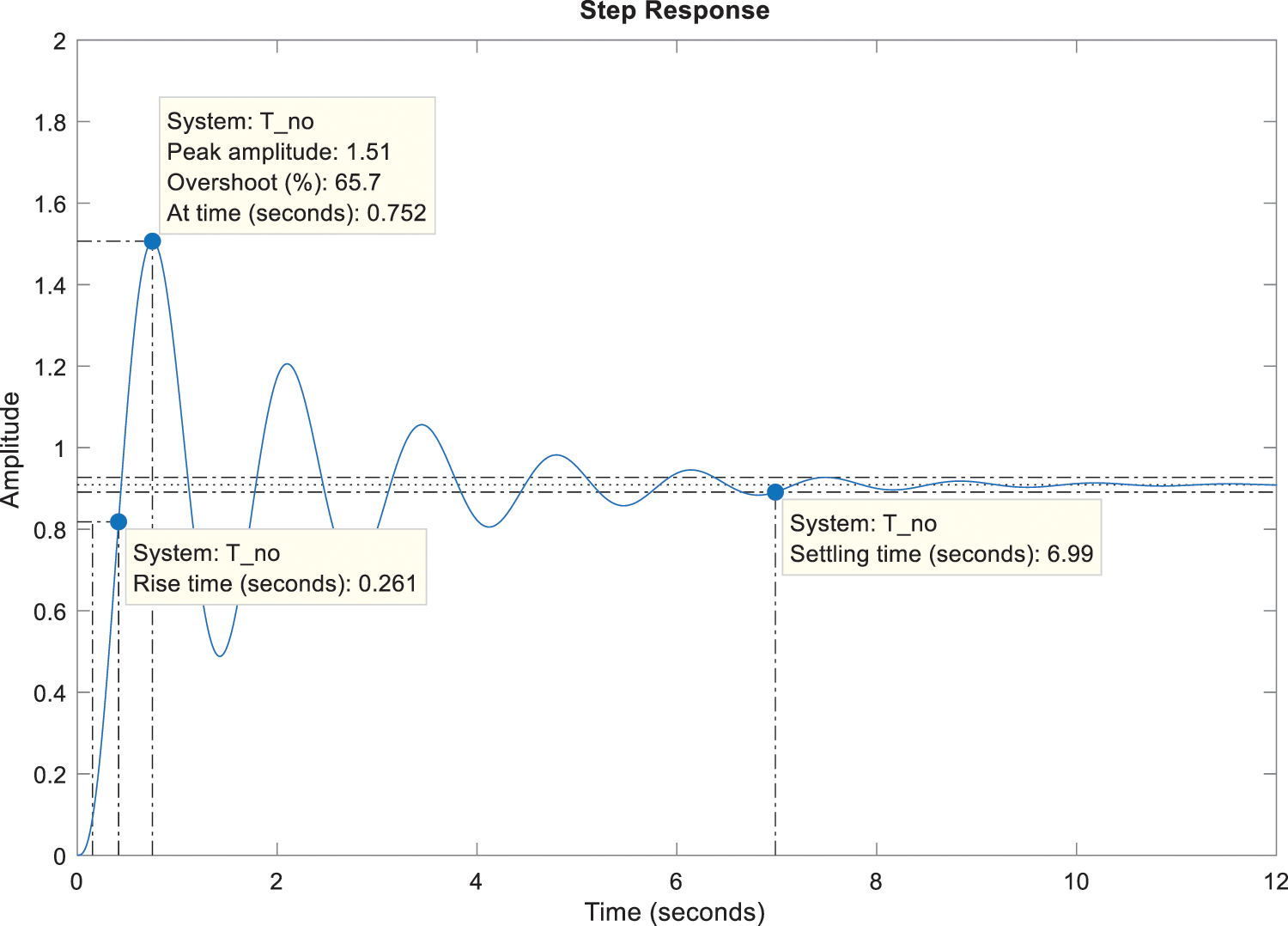
Figure 7: Step response of uncontrolled AVR system

5  PID Control of the AVR System with the Proposed Algorithms of ORSA and ORSAPS

The controller used in this paper is a PID, which is commonly used in AVR system control. The transfer function of the PID controller and the closed loop transfer function of the AVR system are as follows:

Kp+Kis+Kds(8)

T(s)=(s2Kd+sKp+Ki)(KaKeKg)(1+sTs)s(1+sTa)(1+sTe)(1+sTg)(1+sTs)+(KaKeKgKs)(s2Kd+sKp+Ki)(9)

where Kp, Ki, and Kd are proportional, integral, and derivative gains of the controller, respectively. The range of all PID controller parameters are the same and is given as 0.2≤Kp,Ki,Kd≤2.

In the literature, there are different performance indices available to analyze and design controllers. The most popular and basic ones are the integral of absolute error (IAE), integral of time multiplied absolute error (ITAE), integral of squared error (ISE), integral of time multiplied squared error (ITSE), and time domain performance index of Zwe-Lee Gaing (ZLG) [42]. In this paper, a novel objective function, which is created by the sum of ITAE with modified ZLG, is proposed since it effectively improves the dynamic response performance of the AVR system and augments flexibility of adjusting the associated objective function terms according to the design needs. The proposed objective function is given as follows:

J(Kp,Ki,Kd)=ITAE+mZLG=∫0Tsimte(t)d(t)⏞ITAE+α∗(1−e−β)(Mp+Ess)+e−β(ts−tr)⏞mZLG(10)

where Ess, Mp, ts, and tr represent steady-state error, overshoot, settling time, and rise time, respectively. α and β are weighting factors within the ranges of [1, 10] and [0.5, 1.5], respectively. For a fair comparison with the studies from the literature [1,5,8,14] β is chosen as 1. Finally, Tsim is the simulation time that is set to 5 s. Please note that the addition of α weight factor allows one to solely change the effect of the (Mp+Ess) term such that if it is increased the algorithm will more likely find solutions with less overshoot and steady-state error step responses. For PID controller design this may mean slower system responses but increased phase and gain margins which will be shown in the following subsections. The detailed implementation of ORSA, ORSAPS, and the original RSA algorithms applied to optimize PID controller parameters for improvement of the AVR performance is shown in Fig. 8. Either of the proposed algorithms of ORSA and ORSAPS as well as the original RSA algorithm will be used to reduce the objective function by updating the PID controller parameters at each iteration. Optimal or near-optimal parameters are the ones that are obtained when the stopping criterion is met. The step-by-step procedure of ORSA and ORSAPS along with the original RSA in tuning the PID controller of the AVR system is given as follows.

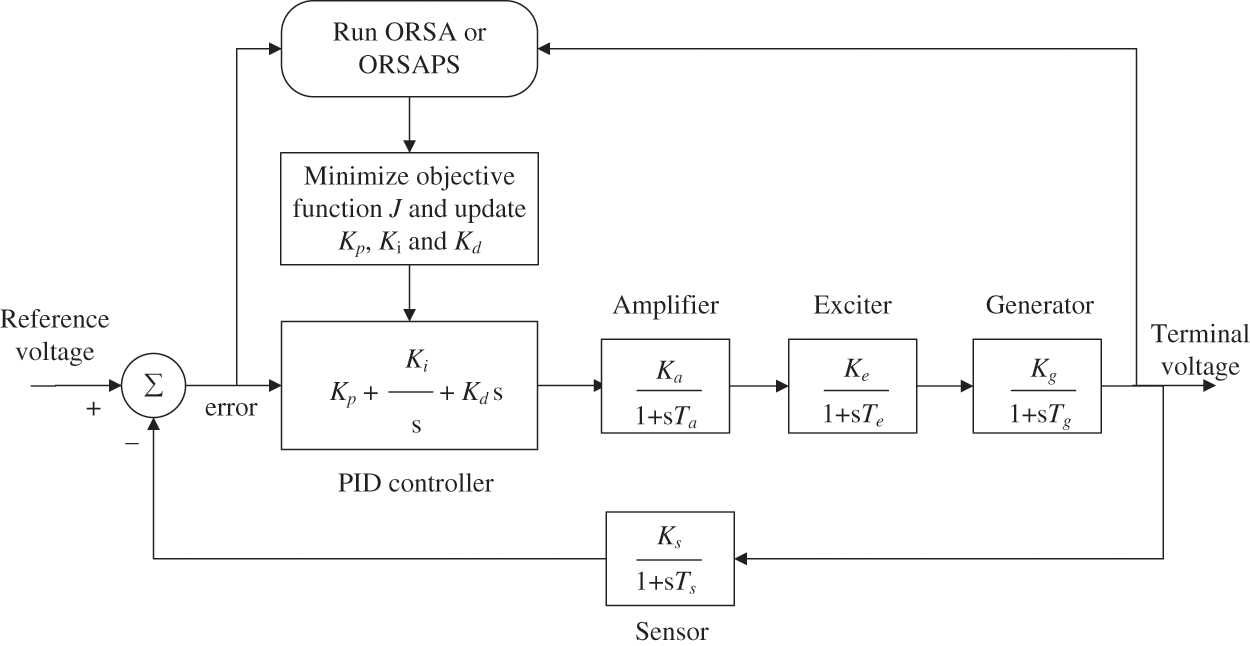
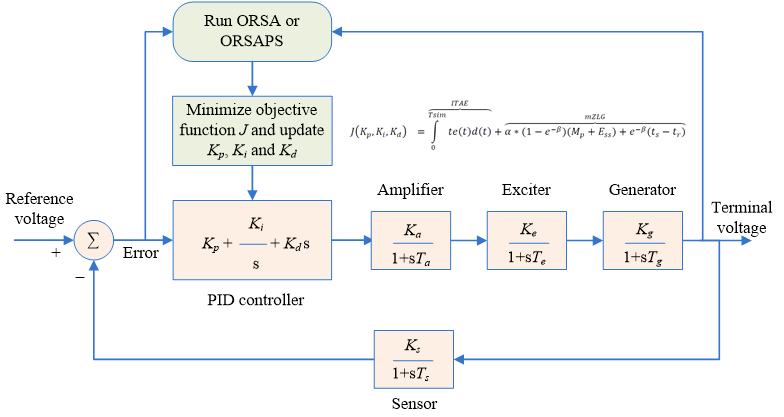
Figure 8: Implementation of the proposed algorithms of ORSA and ORSAPS and the original RSA to AVR system

Step 1: Specify the number of search agents, maximum iteration number, upper and lower bounds of the PID controller parameters.

Step 2: State the coefficients of α and β. For slower system responses with increased phase and gain margins choose a larger α value and for faster (high bandwidth) system responses with acceptable phase and gain margins choose a smaller α value.

Step 3: Randomly initialize the position of all search agents and find the best initial solution.

Step 4: Update the parameters of the algorithm.

Step 5: Run the main steps of the algorithm for each search agent, calculate their objective function values, and find the best (minimum) one.

Step 6: If the iteration count reaches the highest value, move to the next step, otherwise, return to Step 4.

Step 7: Report the best solution that produces the lowest objective function value as the best parameter set of the PID controller.

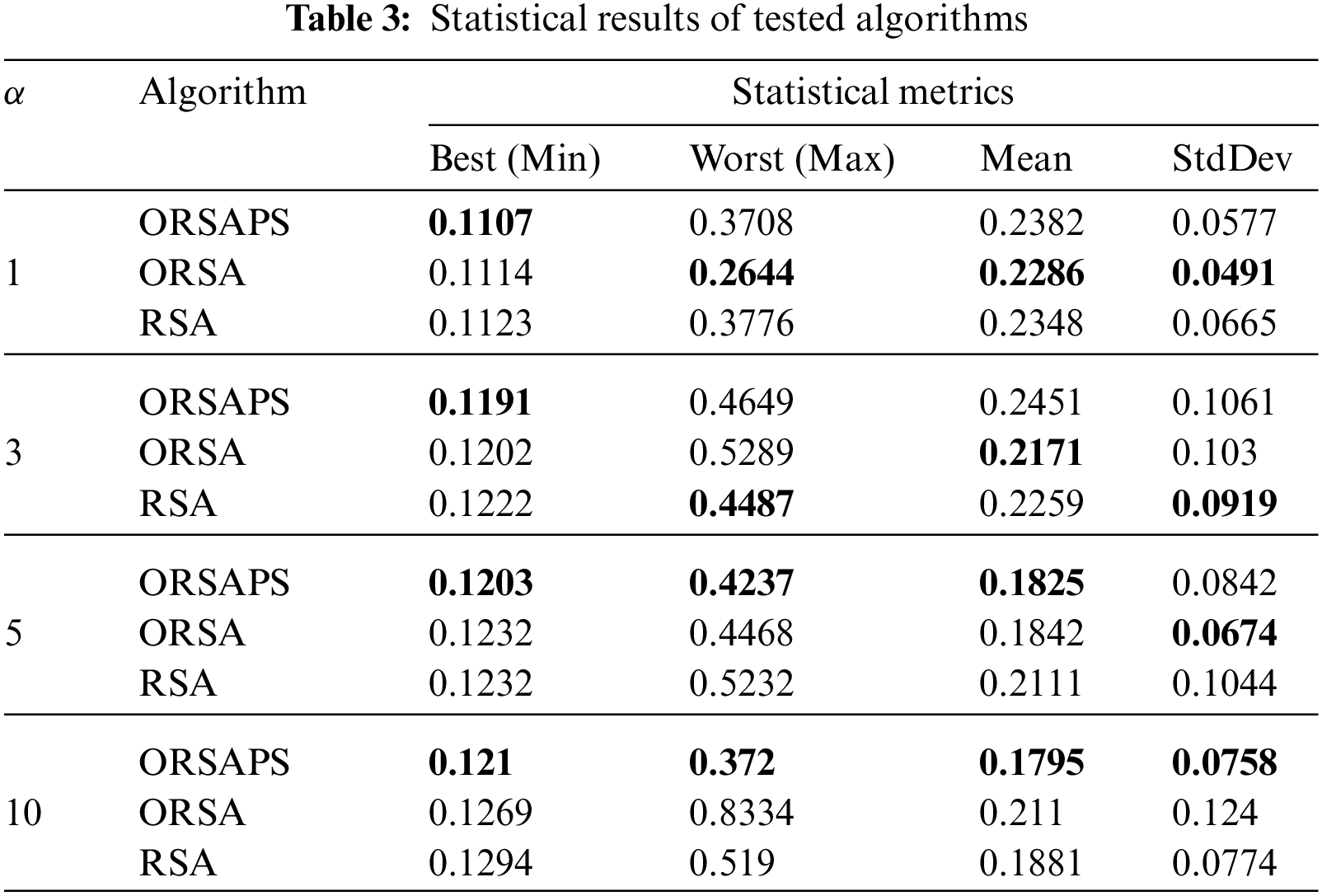
The population size and the total number of iterations are chosen as 30 and 50, respectively. All three algorithms are run 30 times. After the optimization process, the optimized PID controller parameters obtained by using ORSA, ORSAPS, and the original RSA algorithms are given in Table 2. The convergence curves of these three algorithms are illustrated in Fig. 9 while the statistical results are tabulated in Table 3. As seen from Fig. 9 and Table 3, the proposed ORSA and ORSAPS algorithms have provided lower objective function values than the original RSA algorithm.

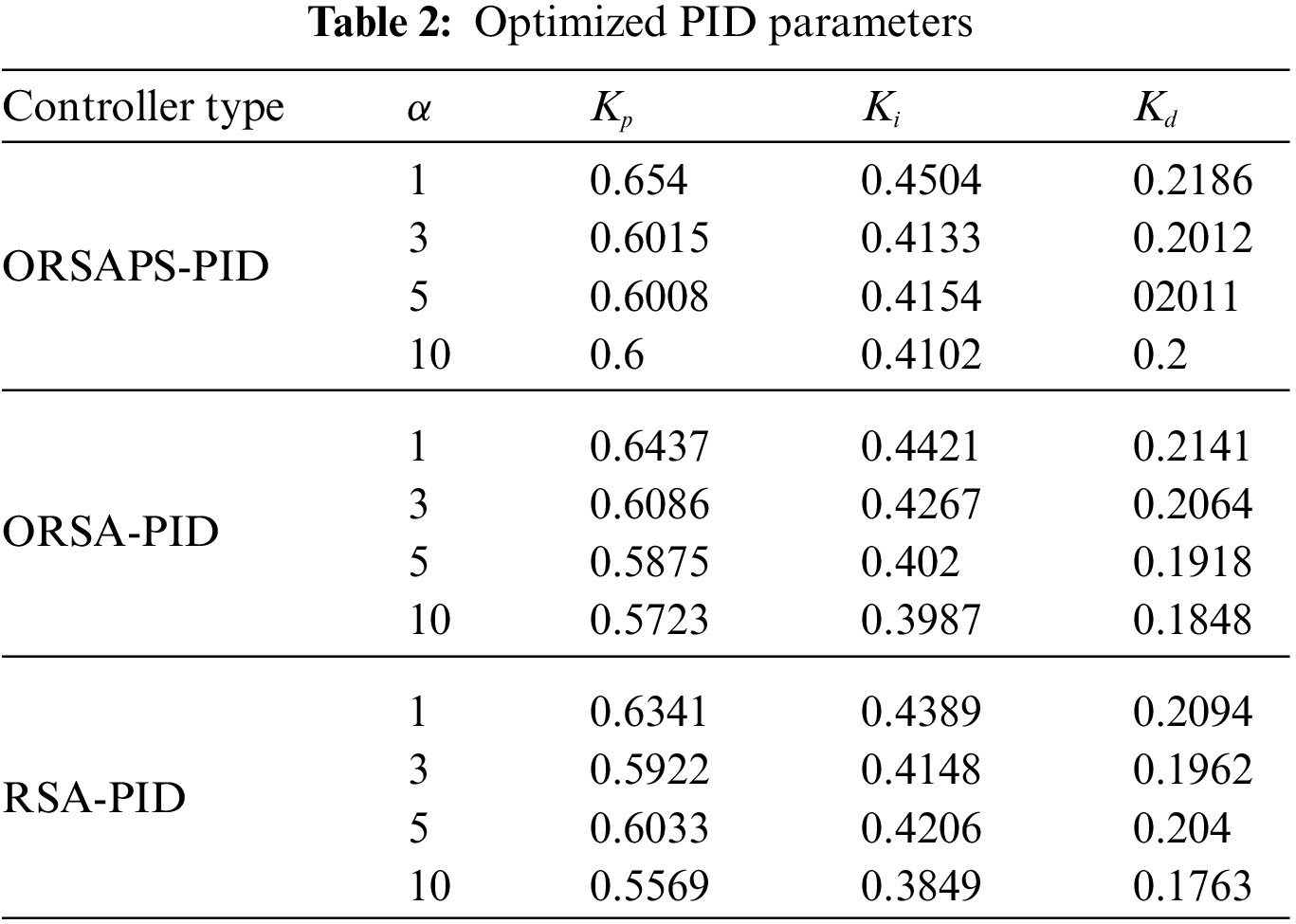
Figure 9: Convergence curves of RSA, ORSA, and ORSAPS algorithms for α = 1

As mentioned before, to understand the searching behavior of the proposed algorithms, the exploration and exploitation stages of the proposed algorithms along with the original RSA algorithm are calculated according to the dimension-wise diversity measurement proposed in [43] as shown in Figs. 10 and 11. As seen from the figures, despite splitting its search mechanism into four stages, the original RSA algorithm seems highly exploitative for the PID controller design problem of the AVR system. ORSA algorithm with OBL mechanism improves population diversity so the exploration capability of the original RSA to some extent whereas ORSAPS with both OBL mechanism and PS algorithm makes it capable in both exploration and exploitation stages and finds better results. It is evident that, for this optimization problem at hand, the trade-off balance between these two stages does not mean having a searching percentage ratio of 50%:50%, as well, which suggests that the PID controller design problem for the AVR system requires a more exploitative search mechanism than explorative one.

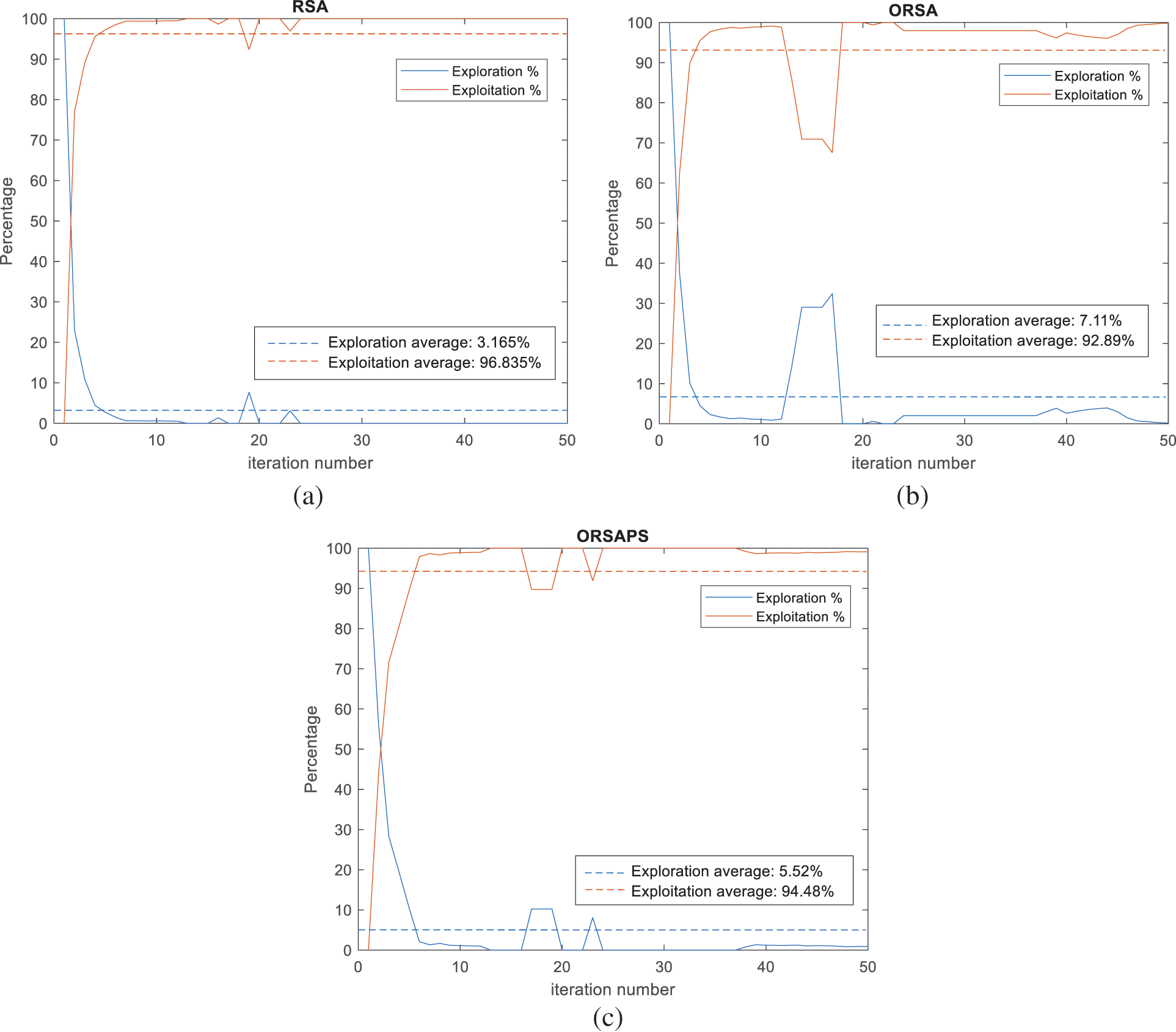
Figure 10: Exploration and exploitation percentages of algorithms at each iteration for α = 1 (a) RSA (b) ORSA, and (c) ORSAPS

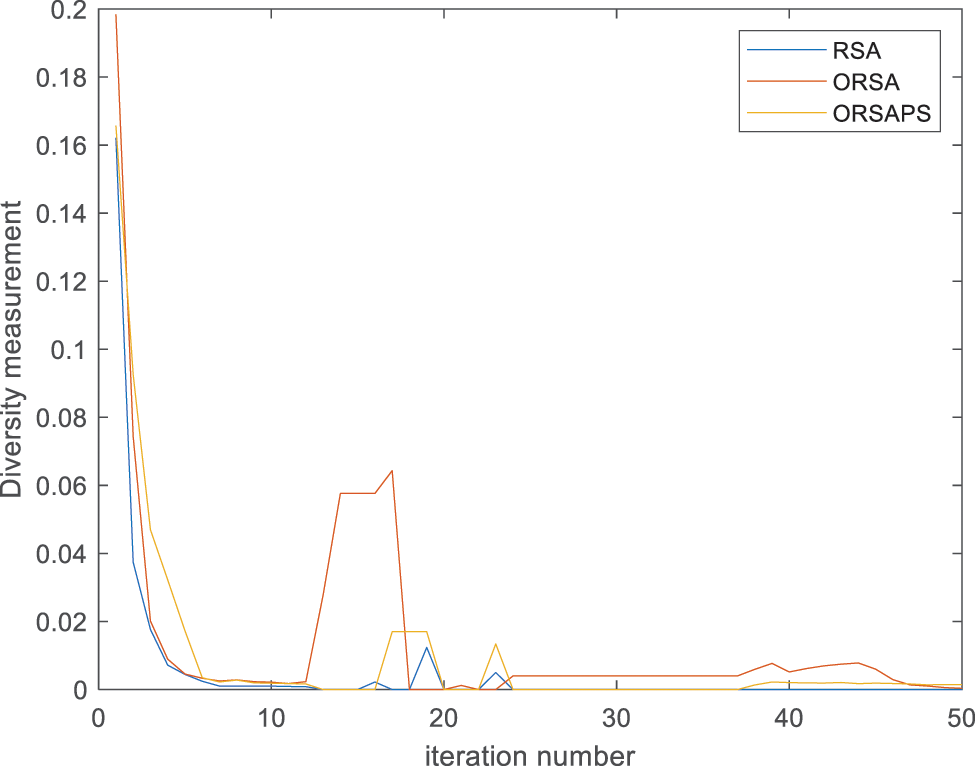
Figure 11: Swarm diversity of algorithms (RSA, ORSA, and ORSAPS) at each iteration for α = 1

Using the obtained parameters given in Table 2, only for α equals 1, the transfer functions of the AVR system with its PID controller tuned by the proposed algorithms of ORSA and ORSAPS, along with the original RSA algorithm are given in the following equations:

TRSA(s)=0.02094s3+2.15741s2+6.38489s+4.3890.0004s5+0.0454s4+0.555s3+3.604s2+7.341s+4.389(11)

TORSA(s)=0.02141s3+2.20537s2+6.48121s+4.4210.0004s5+0.0454s4+0.555s3+3.651s2+7.437s+4.421(12)

TORSAPS(s)=0.02186s3+2.2514s2+6.58504s+4.5040.0004s5+0.0454s4+0.555s3+3.696s2+7.54s+4.504(13)

The comparative simulation results obtained for step responses of the AVR system with different controllers for two different alpha values are shown in Fig. 12. As seen from these responses, increasing the α weight factor has resulted in step responses with less overshoots as mentioned before. This has also slowed down the system, however, in return, it has improved the phase and gain margins of the system, which will be shown in the next subsections.

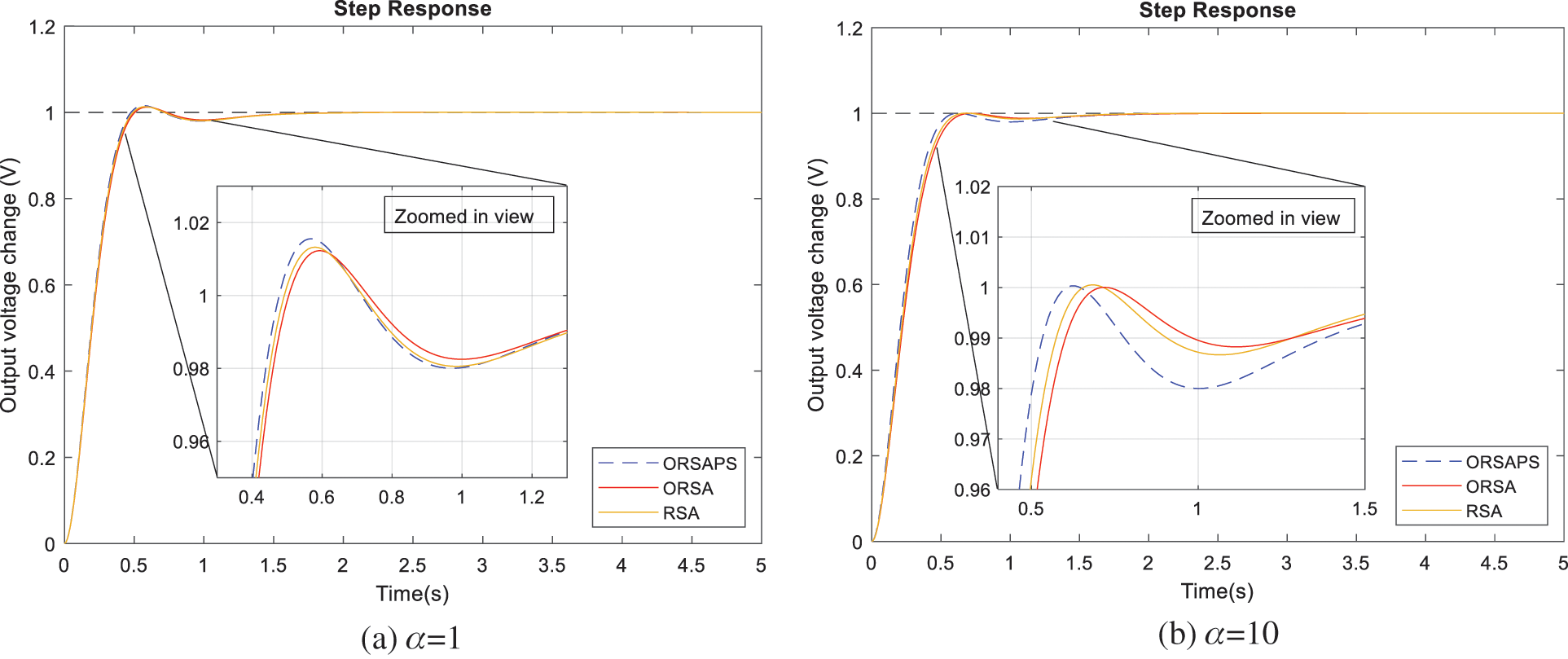
Figure 12: Step responses of RSA-, ORSA- and ORSAPS-based AVR system for α = 1 and α = 10

6  Comparative Simulation Results and Discussion

6.1 Transient Response Analysis

In order to demonstrate the capabilities of the proposed ORSA and ORSAPS algorithms in PID controller design for the AVR system, a comparative step response for different algorithms that are reported with the best performance in the literature are illustrated in Fig. 13. The chosen best-performing algorithms from the literature for the same PID controller design are Lévy flight-based reptile search with Nelder-Mead (L-RSANM) [1], slime mould algorithm (SMA) [5], cuckoo search (CS) algorithm [8], and hybrid symbiotic organism search (SOS) with simulated annealing (SA) algorithm (hSOSSA) [14]. Comparative numerical results are also provided in Table 4. Note that the steady-state values of all algorithms are found to be the same as zero and therefore not tabulated in the table. As can be seen from the results presented in Fig. 13 and Table 4, the proposed ORSAPS-based controller achieves the lowest rise time and settling time along with the lowest objective function value and an acceptable overshoot value, proving its excellent transient response performance for AVR system control. As said before, if the designer needs to reduce the overshoot value, then the α weight factor needs to be increased. The latter case is also experimented, and results are tabulated in Table 4. From these results, it is obvious that the system response slows down when the algorithm tries to find solutions with less overshoot. So that the designer may adjust the objective function according to his/her needs as suggested.

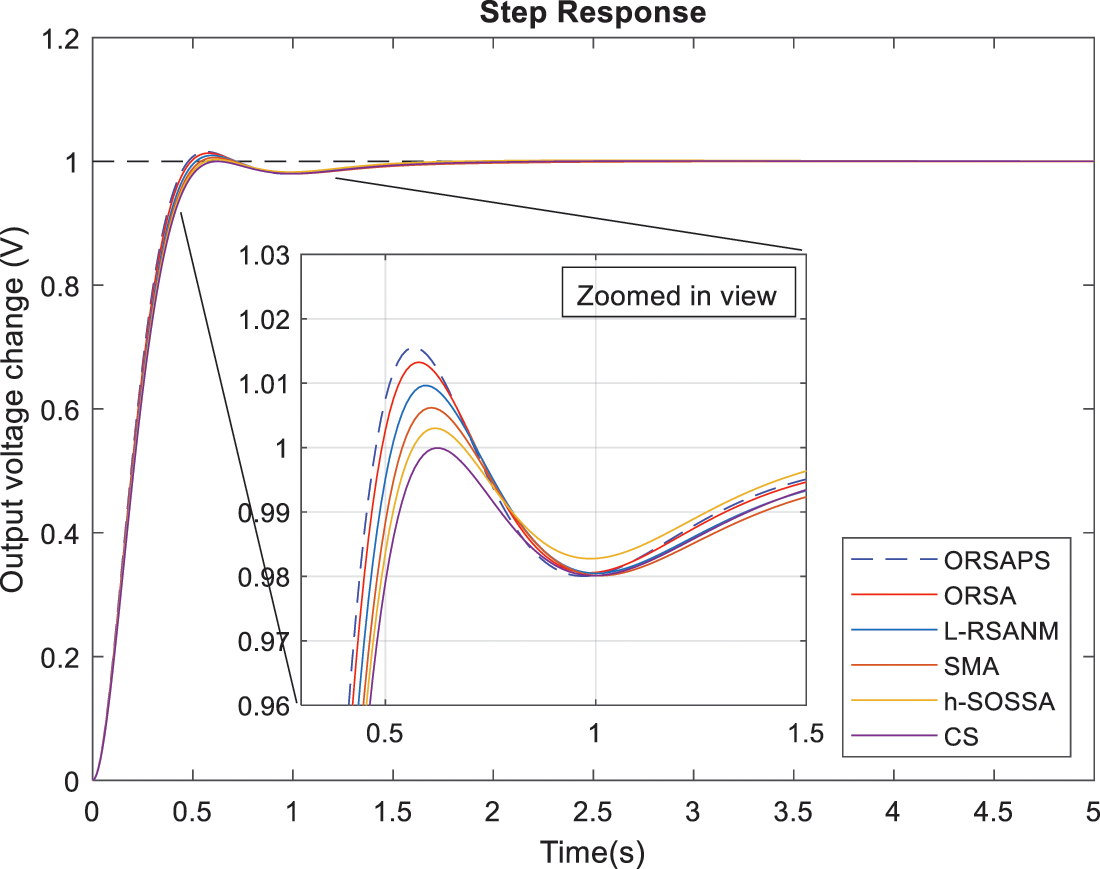
Figure 13: Step responses of AVR system with best-performing algorithms in the literature

6.2 Frequency Response Analysis

Observing phase and gain margins along with bandwidth with Bode analysis enables one to analyze the stability of a system in the frequency domain. Fig. 14 illustrates the open- and closed-loop Bode plots of the proposed ORSA- and ORSAPS-based PID controllers while comparative numerical results are given in Table 5. As seen from the table, when a faster system response is needed (for α=1) with the least rise and settling times, the ORSAPS-based PID control design has the highest bandwidth, but with the lowest phase and gain margins. Quantitatively, the proposed ORSAPS-PID system is 2.08% faster (has more bandwidth) than the ORSA-PID system and 5.1% faster than the L-RSANM-PID system, which is the fastest among the other compared algorithms from the literature. If the system design does not need to be fast or higher phase and gain margins are required (for α=10), then ORSA-based PID control design has the maximum phase and gain margins with less bandwidth compared to ORSAPS, L-RSANM, SMA, CS, and hSOSSA. Quantitatively, the proposed ORSA-PID system has 0.53% more phase margin and 2.18% more gain margin than the proposed ORSAPS-PID system and has 0.71% more phase margin and 2.25% more gain margin than the CS-PID system, which is the best among the other compared algorithms from the literature in terms of phase and gain margins. Please note that, since a phase margin over 65 is usually considered a robust design in linear control theory, then the fastest ORSAPS- and ORSA-based PID controller designs (α=1) can be considered as the best designs compared to others, which further proves the effectiveness of the proposed algorithms.

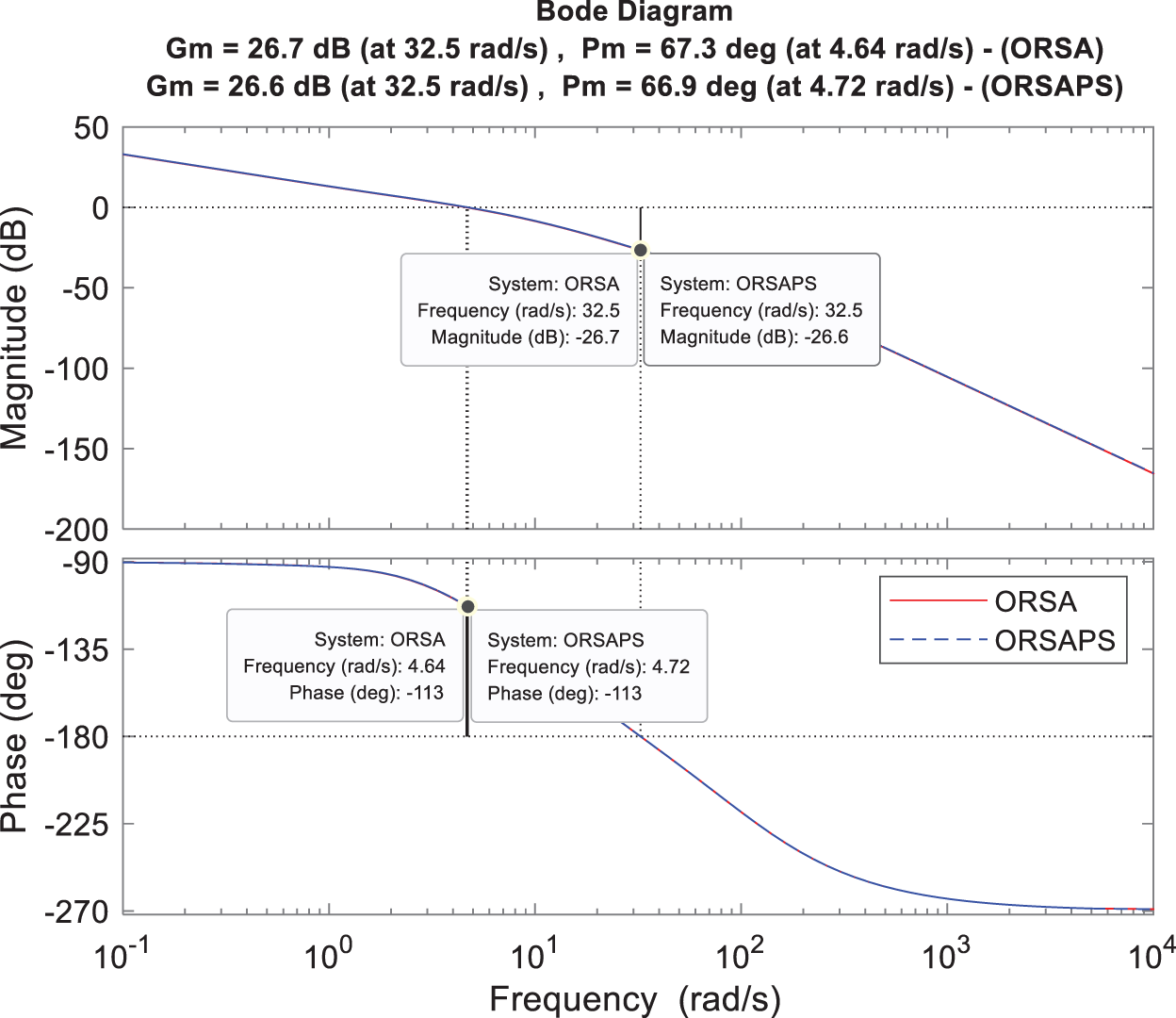
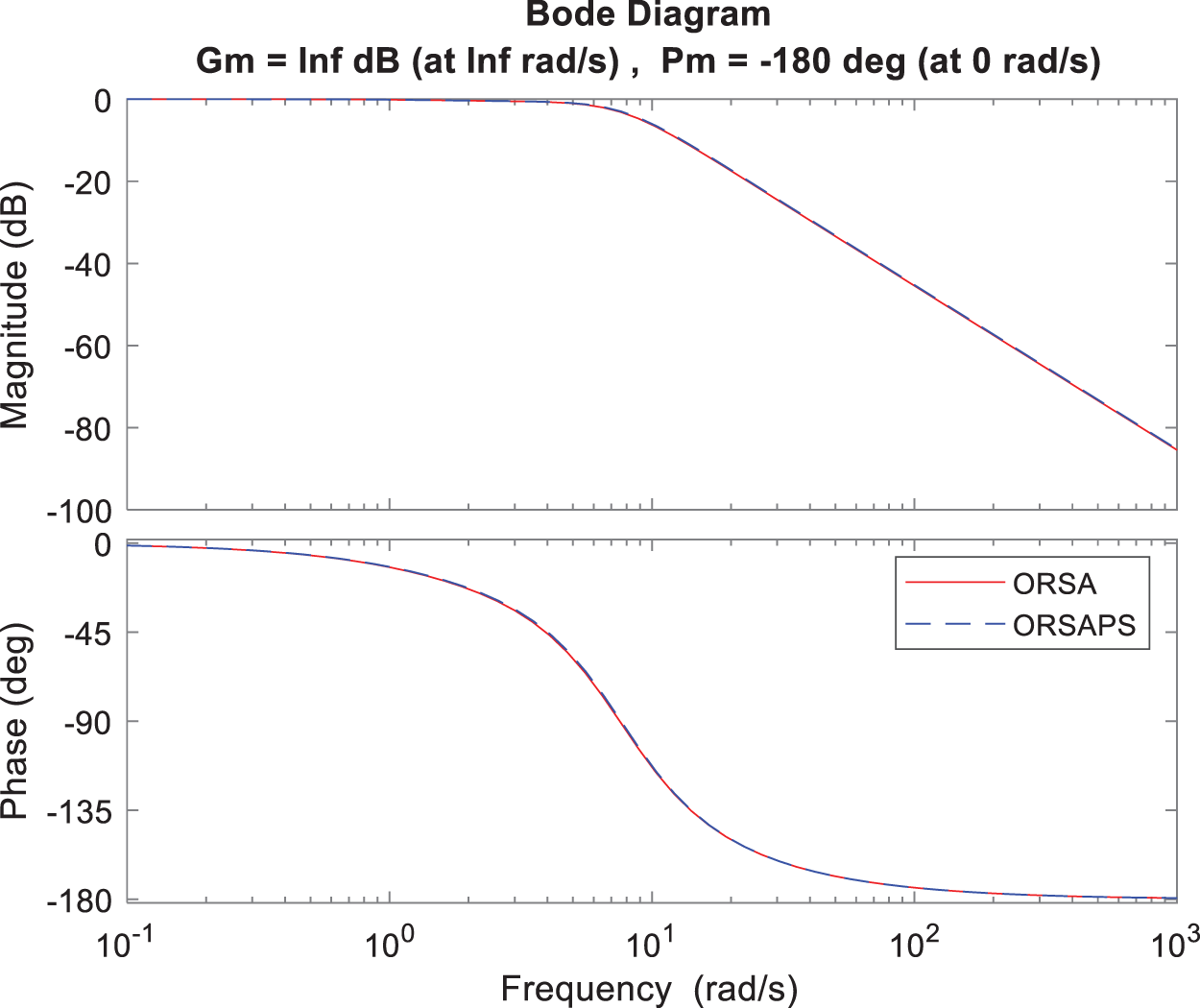
Figure 14: Bode plot of open- and closed-loop AVR system with ORSA-PID and ORSAPS-PID controllers for α=1

6.3 Robustness Analysis

To illustrate the robustness of the proposed method, time constants of AVR components have been changed separately in the range of ±50% with a step size of 25%, and the step response performance of the AVR system under these changes is examined through illustrations given in Figs. 15–18. The comparative numerical results are also given in Table 6. From these figures and the table, it can be seen that ORSAPS-based controller design has less change in terminal voltage with better performance compared to ORSA-based design in terms of maximum overshoot, settling time, and rise time when a change in a system parameter occurs. These results validate the robustness of the proposed ORSA-PID and ORSAPS-PID controllers for the AVR system, meaning that they can cope with the changes in system parameters without affecting the system’s closed-loop stability.

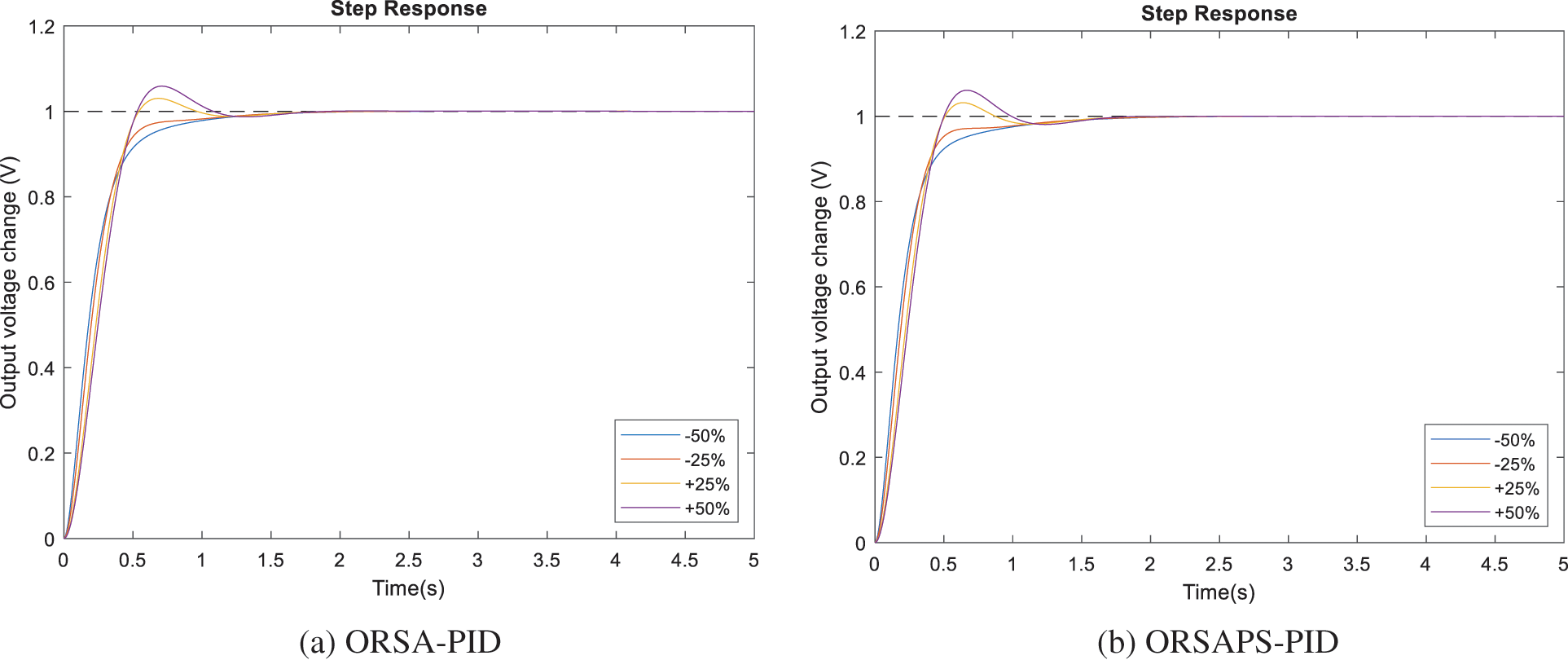
Figure 15: Step responses of AVR system with ORSA-PID and ORSAPS-PID controller for variation in Ta

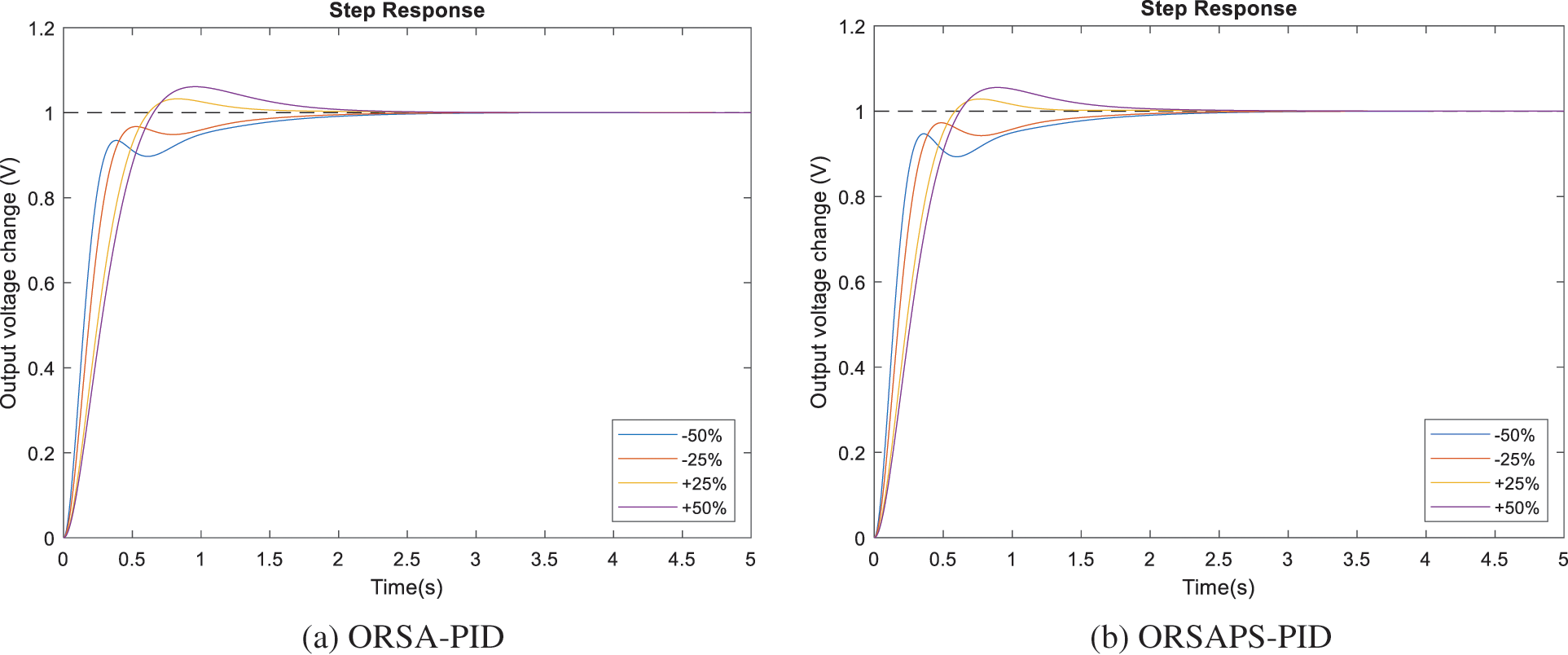
Figure 16: Step responses of AVR system with ORSA-PID and ORSAPS-PID controller for variation in Te

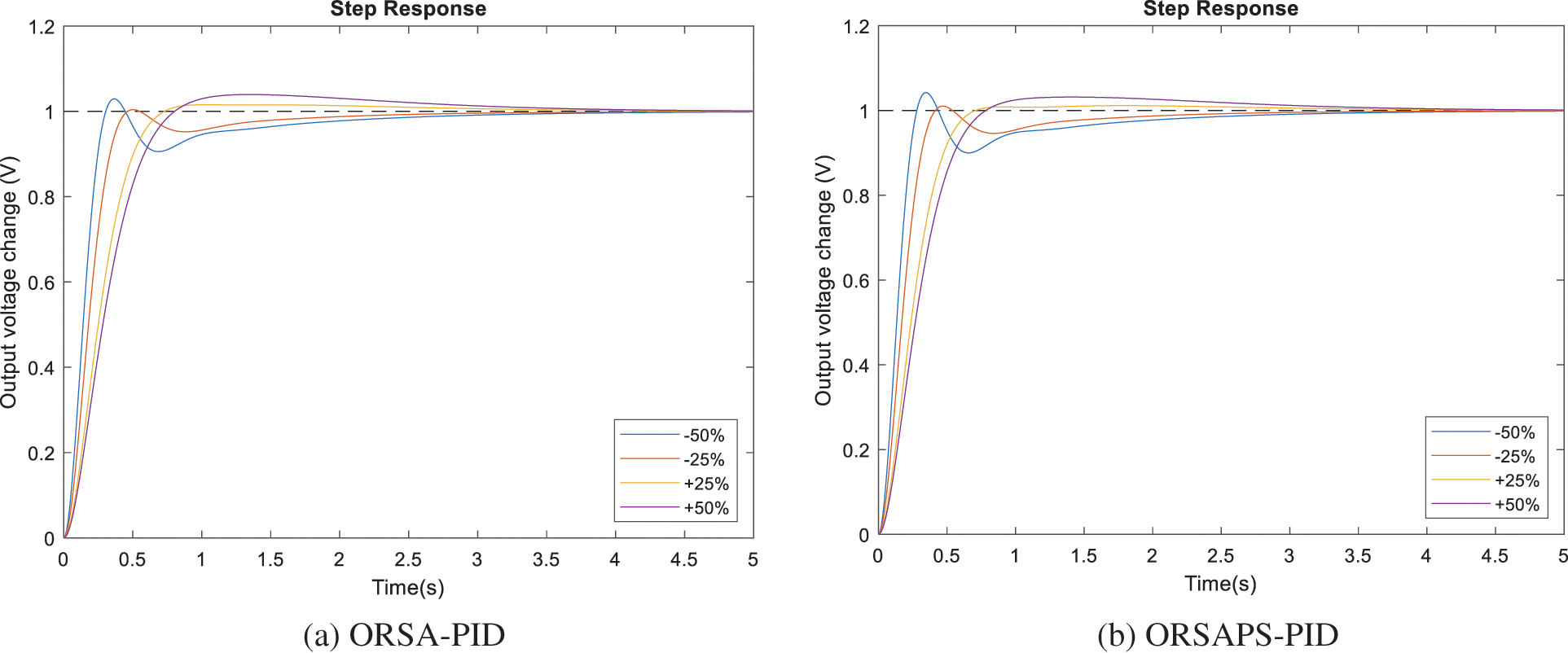
Figure 17: Step responses of AVR system with ORSA-PID and ORSAPS-PID controller for variation in Tg

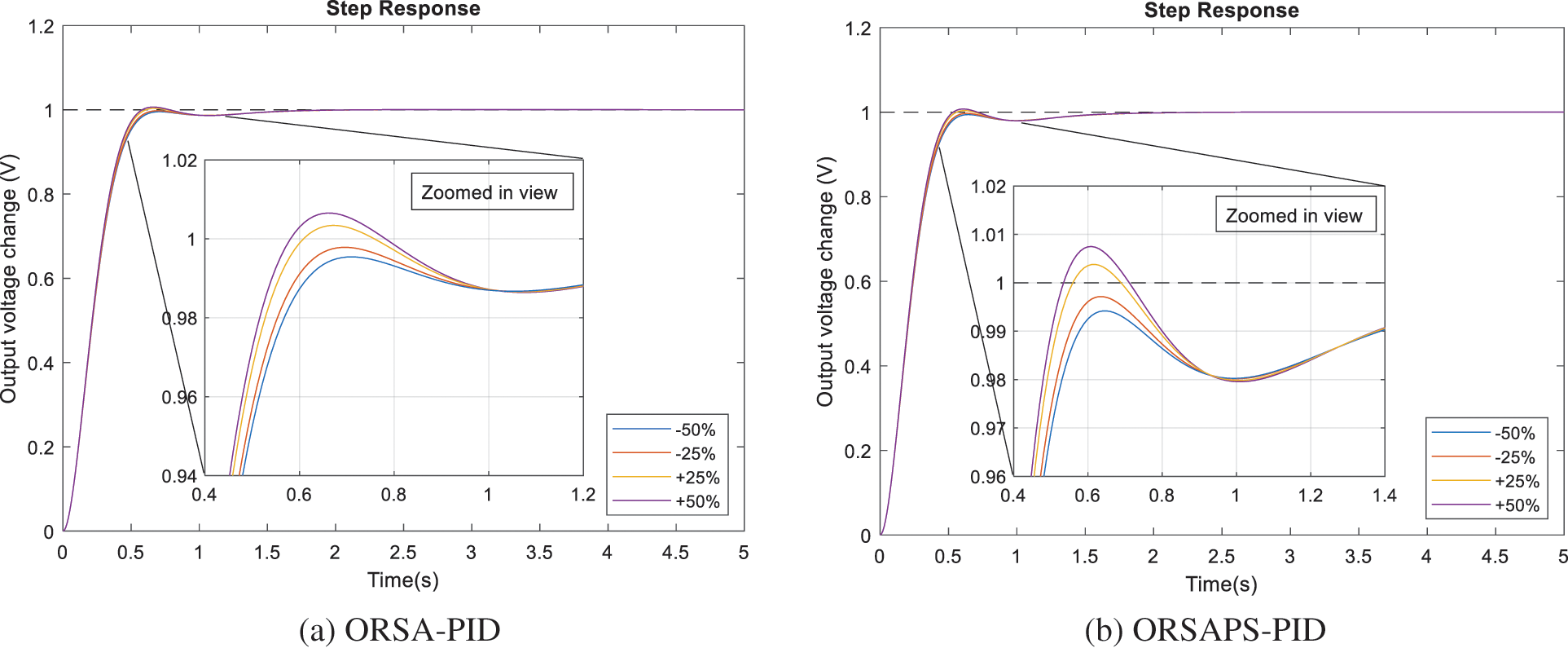
Figure 18: Step responses of AVR system with ORSA-PID and ORSAPS-PID controller for variation in Ts

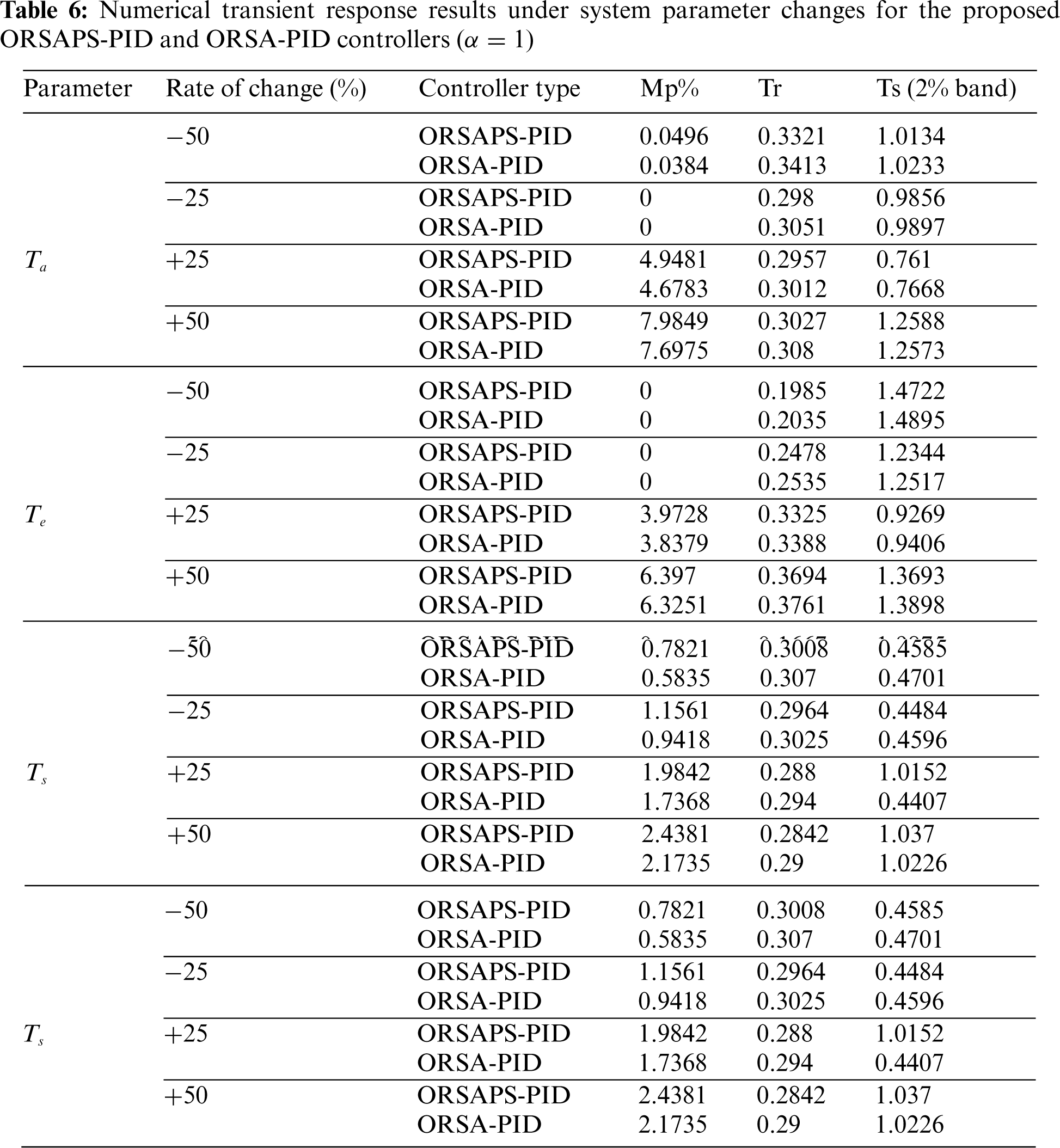
6.4 Disturbance Rejection Analysis

The analysis of the ability of the proposed PID controllers (ORSA-PID and ORSAPS-PID) to deal with the introduced load disturbance is provided in this subsection. To illustrate the application of the load disturbance, the block diagram given in Fig. 6 is considered. A load disturbance causing a 25% increase in terminal voltage is assumed at the instant of t=2s. The comparative step responses are illustrated in Fig. 19. From this figure, it can be seen that the proposed ORSA-PID and ORSAPS-PID controllers are both responding quickly under a load disturbance.

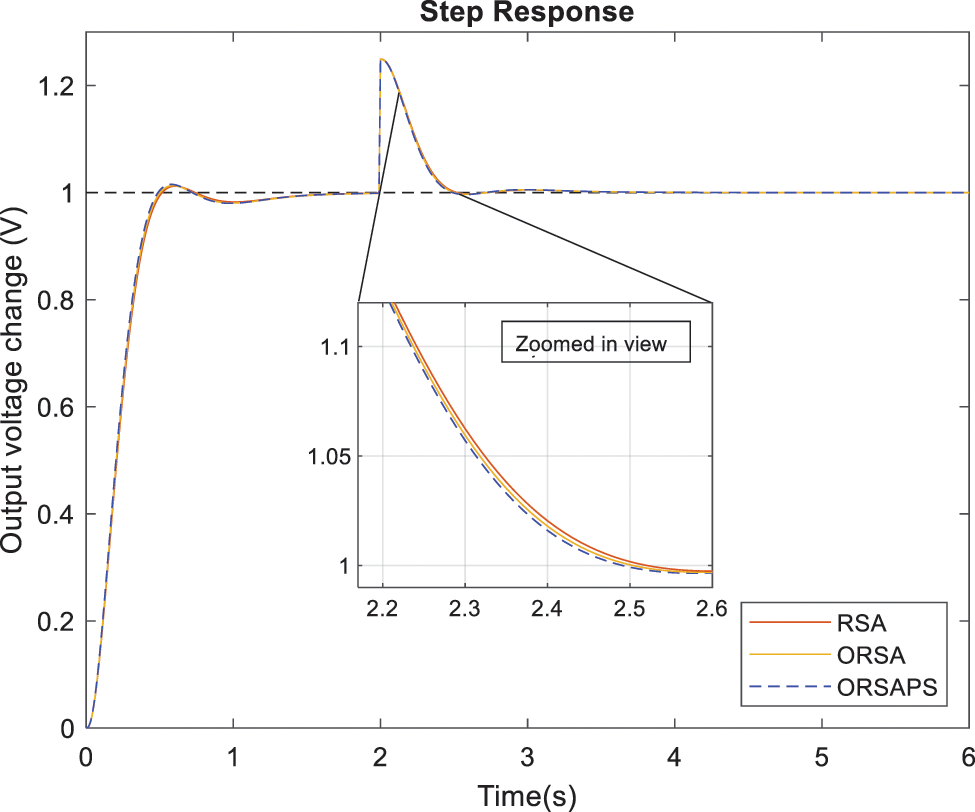
Figure 19: Disturbance rejection performances of AVR system with RSA-PID, ORSA-PID, and ORSAPS-PID controllers

6.5 Trajectory Tracking Analysis

This subsection intends to illustrate the trajectory tracking performance of the proposed controllers when reference voltage change occurs. Fig. 20 illustrates the step responses under such reference voltage changes. As can be seen from this figure, the trajectory tracking performance of the proposed controllers under reference voltage changes are very good in terms of rise and settling times.

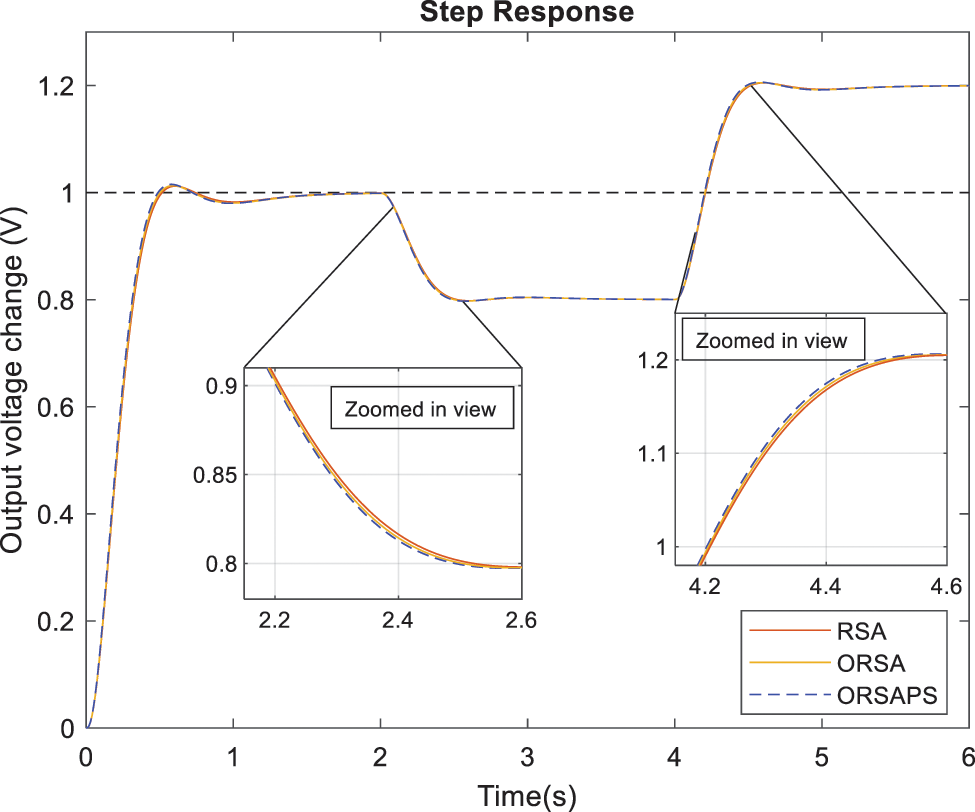
Figure 20: Trajectory tracking performances of AVR system with RSA-PID, ORSA-PID, and ORSAPS-PID controllers

7  Conclusion

This study presented two improved variants of the recently proposed RSA algorithm, ORSA, and ORSAPS, to design effective PID controllers for an AVR system. Furthermore, a novel objective function with augmented flexibility has been proposed. The performances of the proposed algorithms with the proposed objective function are validated through transient response, frequency response, and robustness analysis and compared with the four best-performing algorithms from the literature. The comparative evaluations confirmed the promising capabilities of the proposed algorithms of ORSA and ORSAPS for AVR system PID controller design. For future works, either controlling other systems such as buck converter and magnetic levitation with PID controller or controlling the same AVR system with different controllers such as filtered PID (PIDF) and fractional order PID (FOPID) can be realized with the proposed algorithms and the objective function.

Funding Statement: The author received no specific funding for this study.

Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.

References

1. Ekinci, S., Izci, D., Abu Zitar, R., Alsoud, A. R., Abualigah, L. (2022). Development of Lévy flight-based reptile search algorithm with local search ability for power systems engineering design problems. Neural Computing, and Applications, 34(22), 20263–20283. https://doi.org/10.1007/s00521-022-07575-w [Google Scholar] [CrossRef]

2. Habib, S., Abbas, G., Jumani, T. A., Bhutto, A. A., Mirsaeidi, S. et al. (2022). Improved whale optimization algorithm for transient response, robustness, and stability enhancement of an automatic voltage regulator system. Energies, 15(14), 5037. https://doi.org/10.3390/en15145037 [Google Scholar] [CrossRef]

3. Elsisi, M. (2019). Optimal design of non-fragile PID controller. Asian Journal of Control, 23(2), 729–738. https://doi.org/10.1002/asjc.2248 [Google Scholar] [CrossRef]

4. Micev, M., Ćalasan, M., Oliva, D. (2021). Design and robustness analysis of an automatic voltage regulator system controller by using equilibrium optimizer algorithm. Computers & Electrical Engineering, 89, 106930. https://doi.org/10.1016/j.compeleceng.2020.106930 [Google Scholar] [CrossRef]

5. Izci, D., Ekinci, S. (2021). Comparative performance analysis of slime mould algorithm for efficient design of proportional–integral–derivative controller. Electrica, 21(1), 151–159. https://doi.org/10.5152/electrica.2021.20077 [Google Scholar] [CrossRef]

6. Kiran, H. U., Tiwari, S. K. (2021). Hybrid BF-PSO algorithm for automatic voltage regulator system. International Conference on Innovative Computing and Communications. Advances in Intelligent Systems and Computing, vol. 1166. Singapore: Springer. [Google Scholar]

7. Kose, E. (2020). Optimal control of AVR system with tree seed algorithm-based PID controller. IEEE Access, 8, 89457–89467. https://doi.org/10.1109/ACCESS.2020.2993628 [Google Scholar] [CrossRef]

8. Sikander, A., Thakur, P. (2020). A new control design strategy for automatic voltage regulator in power system. ISA Transactions, 100(2B), 235–243. https://doi.org/10.1016/j.isatra.2019.11.031 [Google Scholar] [PubMed] [CrossRef]

9. Bakir, H., Guvenc, U., Kahraman, H. T., Duman, S. (2022). Improved Lévy flight distribution algorithm with a FDB-based guiding mechanism for AVR system optimal design. Computers & Industrial Engineering, 168(4), 108032. https://doi.org/10.1016/j.cie.2022.108032 [Google Scholar] [CrossRef]

10. Agwa, A., Elsayed, S., Ahmed, M. (2022). Design of optimal controllers for automatic voltage regulation using archimedes optimizer. Intelligent Automation & Soft Computing, 31(2), 799–815. https://doi.org/10.32604/iasc.2022.019887 [Google Scholar] [CrossRef]

11. Micev, M., Ćalasan, M., Ali, Z. M., Hasanien, H. M., Abdel Aleem, S. H. E. (2021). Optimal design of automatic voltage regulation controller using hybrid simulated annealing—Manta ray foraging optimization algorithm. Ain Shams Engineering Journal, 12(1), 641–657. https://doi.org/10.1016/j.asej.2020.07.010 [Google Scholar] [CrossRef]

12. Hekimoğlu, B. (2019). Sine-cosine algorithm-based optimization for automatic voltage regulator system. Transactions of the Institute of Measurement and Control, 41(6), 1761–1771. https://doi.org/10.1177/0142331218811453 [Google Scholar] [CrossRef]

13. Ekinci, S., Hekimoğlu, B. (2019). Improved kidney-inspired algorithm approach for tuning of PID controller in AVR system. IEEE Access, 7, 39935–39947. https://doi.org/10.1109/ACCESS.2019.2906980 [Google Scholar] [CrossRef]

14. Çelik, E., Öztürk, N. (2018). A hybrid symbiotic organisms search and simulated annealing technique applied to efficient design of PID controller for automatic voltage regulator. Soft Computing, 22(23), 8011–8024. https://doi.org/10.1007/s00500-018-3432-2 [Google Scholar] [CrossRef]

15. Çelik, E. (2018). Incorporation of stochastic fractal search algorithm into efficient design of PID controller for an automatic voltage regulator system. Neural Computing and Applications, 30(6), 1991–2002. https://doi.org/10.1007/s00521-017-3335-7 [Google Scholar] [CrossRef]

16. Mosaad, A. M., Attia, M. A., Abdelaziz, Y. Z. (2018). Comparative performance analysis of AVR controllers using modern optimization techniques. Electric Power Components and Systems, 46(19–20), 2117–2130. https://doi.org/10.1080/15325008.2018.1532471 [Google Scholar] [CrossRef]

17. Chatterjee, S., Mukherjee, V. (2016). PID controller for automatic voltage regulator using teaching learning-based optimization technique. Electric Power and Energy Systems, 77(4), 418–429. https://doi.org/10.1016/j.ijepes.2015.11.010 [Google Scholar] [CrossRef]

18. Dogruer, T., Can, M. S. (2022). Design and robustness analysis of fuzzy PID controller for automatic voltage regulator system using genetic algorithm. Transactions of the Institute of Measurement and Control, 44(9), 1862–1873. https://doi.org/10.1177/01423312211066758 [Google Scholar] [CrossRef]

19. Tang, Y., Zhao, L., Han, Z., Bi, X., Guan, X. (2016). Optimal gray PID controller design for automatic voltage regulator system via imperialist competitive algorithm. Machine Learning and Cybernetics, 7(2), 229–240. https://doi.org/10.1007/s13042-015-0431-9 [Google Scholar] [CrossRef]

20. Suid, M. H., Ahmad, M. A. (2021). Optimal tuning of sigmoid PID controller using nonlinear sine cosine algorithm for the automatic voltage regulator system. ISA Transactions, 128, 265–286. [Google Scholar] [PubMed]

21. Mokeddem, D., Mirjalili, S. (2020). Improved whale optimization algorithm applied to design PID plus second order derivative controller for automatic voltage regulator system. Journal of the Chinese Institute of Engineers, 43(6), 541–552. https://doi.org/10.1080/02533839.2020.1771205 [Google Scholar] [CrossRef]

22. Gozde, H. (2020). Robust 2DOF state-feedback PI-controller based on meta-heuristic optimization for automatic voltage regulation system. ISA Transactions, 98, 26–36. https://doi.org/10.1016/j.isatra.2019.08.056 [Google Scholar] [PubMed] [CrossRef]

23. Padiachy, V., Mehta, U., Azid, S., Prasad, S., Kumar, R. (2022). Two degree of freedom fractional PI scheme for automatic voltage regulation. Engineering Science and Technology, an International Journal, 30(4), 101046. https://doi.org/10.1016/j.jestch.2021.08.003 [Google Scholar] [CrossRef]

24. Munagala, V. K., Jatoth, R. K. (2022). Improved fractional PIλDμ controller for AVR system using Chaotic Black Widow algorithm. Computers & Electrical Engineering, 97(1), 107600. https://doi.org/10.1016/j.compeleceng.2021.107600 [Google Scholar] [CrossRef]

25. Altbawi, S. M. A., Bin Mokhtar, A. S., Jumani, T. A., Khan, I., Hamadneh, N. N. et al. (2021). Optimal design of fractional order PID controller based automatic voltage regulator system using gradient-based optimization algorithm. Journal of King Saud University–Engineering Sciences, 17(2), 171. https://doi.org/10.1016/j.jksues.2021.07.009 [Google Scholar] [CrossRef]

26. Izci, D., Ekinci, S., Zeynelgil, H. L., Hedley, J. (2021). Fractional order PID design based on novel improved slime mould algorithm. Electric Power Components and Systems, 49(9–10), 901–918. https://doi.org/10.1080/15325008.2022.2049650 [Google Scholar] [CrossRef]

27. Jumani, T. A., Mustafa, M. W., Hussain, Z., Md. Rasid, M., Saeed, M. S. et al. (2020). Jaya optimization algorithm for transient response and stability enhancement of a fractional-order PID based automatic voltage regulator system. Alexandria Engineering Journal, 59(4), 2429–2440. https://doi.org/10.1016/j.aej.2020.03.005 [Google Scholar] [CrossRef]

28. Ekinci, S., Izci, D., Hekimoğlu, B. (2020). Henry gas solubility optimization algorithm based FOPID controller design for automatic voltage regulator. 2020 International Conference on Electrical, Communication, and Computer Engineering (ICECCE), pp. 1–6. Istanbul, Turkey. [Google Scholar]

29. Micev, M., Ćalasan, M., Oliva, D. (2020). Fractional order PID controller design for an AVR system using chaotic yellow saddle goatfish algorithm. Mathematics, 8(7), 1182. https://doi.org/10.3390/math8071182 [Google Scholar] [CrossRef]

30. Mok, R. H., Ahmad, M. A. (2022). Fast and optimal tuning of fractional order PID controller for AVR system based on memorizable-smoothed functional algorithm. Engineering Science and Technology, an International Journal, 35(9), 101264. https://doi.org/10.1016/j.jestch.2022.101264 [Google Scholar] [CrossRef]

31. Ozgenc, B., Ayas, M. S., Altas, I. H. (2022). Performance improvement of an AVR system by symbiotic organism search algorithm-based PID-F controller. Neural Computing and Applications, 34(10), 7899–7908. https://doi.org/10.1007/s00521-022-06892-4 [Google Scholar] [CrossRef]

32. Ayas, M. S., Sahin, E. (2021). FOPID controller with fractional filter for an automatic voltage regulator. Computers & Electrical Engineering, 90(1), 106895. https://doi.org/10.1016/j.compeleceng.2020.106895 [Google Scholar] [CrossRef]

33. Paliwal, N., Srivastava, L., Pandit, M. (2021). Equilibrium optimizer tuned novel FOPID-DN controller for automatic voltage regulator system. International Transactions on Electrical Energy Systems, 31(8), e12930. https://doi.org/10.1002/2050-7038.12930 [Google Scholar] [CrossRef]

34. Furat, M., Cücü, G. G. (2022). Design, implementation, and optimization of sliding mode controller for automatic voltage regulator system. IEEE Access, 10, 55650–55674. https://doi.org/10.1109/ACCESS.2022.3177621 [Google Scholar] [CrossRef]

35. Sharma, V., Naresh, R., Kumar, V. (2021). Automatic voltage regulator system with state-feedback and PID based sliding mode control design. International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), pp. 1–6. Bhilai, India. [Google Scholar]

36. Elsisi, M., Tran, M. Q., Hasanien, H. M., Turky, R. A., Albalawi, F. et al. (2021). Robust model predictive control paradigm for automatic voltage regulators against uncertainty based on optimization algorithms. Mathematics, 9(22), 2885. https://doi.org/10.3390/math9222885 [Google Scholar] [CrossRef]

37. Mazibuko, N., Akindeji, K. T., Sharma, G. (2022). Modeling and performance analysis of an automatic voltage regulator (AVR) using model predictive controller (MPC). IEEE PES/IAS PowerAfrica, pp. 1–5. Kigali, Rwanda. [Google Scholar]

38. Deghboudj, I., Ladaci, S. (2021). Automatic voltage regulator performance enhancement using a fractional order model predictive controller. Bulletin of Electrical Engineering and Informatics, 10(4), 2424–2432. https://doi.org/10.11591/eei.v10i5.2435 [Google Scholar] [CrossRef]

39. Kumar, V., Sharma, V., Kumar, V. (2022). Performance evaluation of HHO optimized model predictive controller for AVR system and its comparison with conventional controllers. In: Tomar, A., Malik, H., Kumar, P., Iqbal, A. (Eds.Machine learning, advances in computing, renewable energy and communication. Lecture notes in electrical engineering, vol. 768. Singapore: Springer. [Google Scholar]

40. Abualigah, L., Elaziz, M. A., Sumari, P., Geem, Z. W., Gandomi, A. H. (2022). Reptile search algorithm (RSAA nature-inspired meta-heuristic optimizer. Expert Systems with Applications, 191, 116158. https://doi.org/10.1016/j.eswa.2021.116158. [Google Scholar] [CrossRef]

41. Al-Shourbaji, I., Helian, N., Sun, Y., Alshathri, S., Abd Elaziz, M. (2022). Boosting ant colony optimization with reptile search algorithm for churn prediction. Mathematics, 10(7), 1031. https://doi.org/10.3390/math10071031 [Google Scholar] [CrossRef]

42. Gaing, Z. L. (2004). A particle swarm optimization approach for optimum design of PID controller in AVR system. IEEE Transactions on Energy Conversion, 19(2), 384–391. https://doi.org/10.1109/TEC.2003.821821 [Google Scholar] [CrossRef]

43. Hussain, K., Salleh, M. N. M., Cheng, S., Shi, C. (2018). On the exploration and exploitation in popular swarm-based metaheuristic algorithms. Neural Computing and Applications, 31(11), 7665–7683. https://doi.org/10.1007/s00521-018-3592-0 [Google Scholar] [CrossRef]

44. Yuan, Q., Zhang, Y., Dai, X., Zhang, S. (2022). A modified reptile search algorithm for numerical optimization problems. Computational Intelligence and Neuroscience, 2022, 1–20. https://doi.org/10.1155/2022/9752003 [Google Scholar] [PubMed] [CrossRef]

45. Tizhoosh, H. R. (2005). Opposition-based learning: A new scheme for machine intelligence. International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), pp. 695–701. Vienna, Austria. [Google Scholar]

46. Izci, D., Ekinci, S., Eker, E., Kayri, M. (2022). Augmented hunger games search algorithm using logarithmic spiral opposition-based learning for function optimization and controller design. Journal of King Saud University–Engineering Sciences, 157, 6311. https://doi.org/10.1016/j.jksues.2022.03.001 [Google Scholar] [CrossRef]

47. Nasser, A. B., Zamli, K. Z., Hujainah, F., Ghanem, W. A. H. M., Saad, A. M. H. Y. et al. (2021). An adaptive opposition-based learning selection: The case for Jaya Algorithm. IEEE Access, 9, 55581–55594. https://doi.org/10.1109/ACCESS.2021.3055367 [Google Scholar] [CrossRef]

48. Long, W., Jiao, J., Liang, X., Cai, S., Xu, M. (2019). A random opposition-based learning grey wolf optimizer. IEEE Access, 7, 113810–113825. https://doi.org/10.1109/ACCESS.2019.2934994 [Google Scholar] [CrossRef]

49. Torczon, V. (1997). On the convergence of pattern search algorithms. SIAM Journal on Optimization, 7(1), 1–25. https://doi.org/10.1137/S1052623493250780 [Google Scholar] [CrossRef]

50. Torczon, V. (1989). Multi-directional search: A direct search algorithm for parallel machines (Ph.D. Thesis). Rice University, Houston, Texas, USA. [Google Scholar]

51. Saadat, H. (1999). Power system analysis. New York, NY, USA: McGraw-Hill. [Google Scholar]